8. Резонанс при изменяющейся частоте; обзор литературы

Вопрос о поведении резонансной системы под воздей ствием внешней силы с изменяющейся частотой оказался интересным для различных отраслей техники. Вопрос этот ставили и разрешали инженеры самых различных специальностей. А так как в наше время нелегко в совершенстве знать литературу даже только по своей прямой специальности, то не удивительно, что авторы - механики не знали

зачастую о работах на ту же тему электриков, и обратно. В результате литература по рассматриваемому вопросу представляет собой довольно любопытную картину, которую мы здесь вкратце и рассмотрим.

Предварительно заметим, что резонанс при изменяющейся частоте вынуждающей силы представляет интерес по меньшей мере с трех точек зрения: 1) с точки зрения анализа последовательным методом посредством вспомогательной частоты, — это и заставляет нас заниматься этим вопросом так подробно в рамках данной книги; 2) с точки зрения явлений, возникающих при пуске и остановке машин с вращающимися частями при наличии критической скорости вращения (т. е. скорости, при которой возникают резонансные колебания изгиба вала с насаженными на него динамически - неуравновешенными массами); при этом предполагается, что рабочая скорость выше критической и для достижения рабочей скорости нужно пройти критическую; очевидно, что при этом возможны аварии, и детальное понимание явления и умение оценить количественные соотношения и выбрать безопасные режимы пуска крайне важны; 3) с точки зрения пуска и остановки электрических машин переменного тока. Оказывается, что физико - математическая формулировка задачи совершенно одинакова во всех этих с инженерной точки зрения совершенно различных случаях.

Одной из ранних работ является статья Залингера [1], поставившего совершенно естественный вопрос о допустимой скорости анализа методом вспомогательной частоты. Однако Залингер основывал свои рассуждения и выводы на анализе физически неосуществимой системы. Поэтому его результаты практической ценности не имеют, и мы на них останавливаться не будем.

Другая ранняя работа Пешля [2] ставит вопрос с позиций механики. Однако и эта работа не представляет для нас интереса, так как автор ограничивается исследованием системы без затухания.

Краткое изложение постановки задачи и результатов, полученных в этой работе, можно найти у Лойцянского и Лурье 13]. В 1932 г. появилась заслуживающая серьезного внимания работа Льюиса [4]. Интересуясь явлениями при прохождении через критическую скорость, автор совершенно

правильно ставит и решает задачу. Для получения решения он прибегает к контурному интегрированию в комплексной плоскости. Придя к решению в нетабулированных функциях, он вычисляет их при помощи степенных и асимптотических рядов и строит ряд графиков для различных значений параметров.

В 1947 г. Кац [5] опубликовал в высшей степени обстоятельную работу, вызванную нуждами конструирования быстроходных дизелей (публикация работы задержалась по условиям военного времени, она поступила в редакцию в 1943 г.). В этой работе Кац, отправляясь с тех же исходных позиций, что и Льюис, применяет несколько иные пути интегрирования; получив сходные результаты, он идет значительно дальше. Во-первых, он уделяет в своей статье большое внимание технике вычислений, что сильно повышает ее практическую ценность. Во-вторых, он рассматривает также более общий случай, когда не только частота, но и амплитуда вынуждающей силы изменяется со временем. В-третьих, обрабатывая численные данные, он выводит эмпирические формулы, позволяющие просто определить основные параметры динамической резонансной кривой — смещение максимума и его высоту.

В 1948 г. появляется одновременно несколько работ. Прежде всего следует назвать статью Быковой [6]. В этой также очень обстоятельной работе, написанной с радиотехническим подходом к проблеме, решение получается операционным методом. Затем приводятся ряды для вычисления выражающих решение функций для больших и малых значений аргумента, а также приближенный метод вычисления для значений аргумента порядка единицы. Быкова также идет дальше своих предшественников: она решает задачу не только для простой резонансной системы (с одной степенью свободы), но и для двух связанных контуров. Она намечает также пути решения задачи для более сложных систем. Кроме того, работа ценна еще и тем, что в ней помещены результаты обширной экспериментальной работы. К сожалению, достоинства этой интересной работы в значительной степени умаляются исключительно небрежной редакционной обработкой; работа пестрит бесчисленными опечатками, обозначения путаные и т. п. Следует отметить, что

предшествующие работы механиков Быковой, повидимому, не были известны.

В том же 1948 г. опубликованы работы американца Хока [7] и англичан Барбера и Арсела [8]. Хок решает задачу операционным методом и вычисляет нетабулированные функции при помощи рядов. В приведенные им формулы асимптотических рядов вкралась ошибка, которая впоследствии была исправлена [9]. Кроме обычных динамических резонансных кривых, подкрепленных экспериментальными кривыми, снятыми с кварцевого резонатора, автор приводит еще графики вещественных и мнимых частей вычисленных им функций. Следует отметить, что Хок рассматривает и обратную задачу: поведение медленно перестраивающегося резонатора под воздействием напряжения постоянной частоты; автор приходит к заключению, что картина явления получается вполне аналогичная.

В работе Хока приведен также график эффективной ширины динамической резонансной кривой.

Работа Барбера и Арсела возникла в непосредственной связи с проблемами анализа. Задача решается двумя методами, близкими методу Ван-дер-Поля. Результаты, конечно, получаются те же. Однако в работе есть оригинальные черты. Во-первых, интересна графическая интерпретация результата в форме кривых, вырождающихся в спираль Корню для случая нулевого затухания. Во-вторых, сделана попытка определения оптимальных соотношений (на мой взгляд, совершенно неудачная). Кроме того, рассмотрена обратная задача, т. е. задача о вынужденных колебаниях системы с изменяющейся резонансной частотой. Интересно, что Барбер и Арсел не знали о работе Льюиса, а Хок узнал о ее существовании только после выполнения своего исследования. Друг о друге англичане и американец тоже не знали, равно как и о работе Каца.

Несколько особняком стоит опубликованная в 1949 г. работа Казовского [10]. Автор интересуется процессами в электрических машинах. Поэтому речь идет о явлениях в нерезонансной цепи. В частности, в статье в качестве примера рассматривается торможение асинхронной машины нагрузкой.

По поводу работ [6], [7] и [8] нужно сделать одно замечание. Дело в том, что во всех трех работах отмечается,

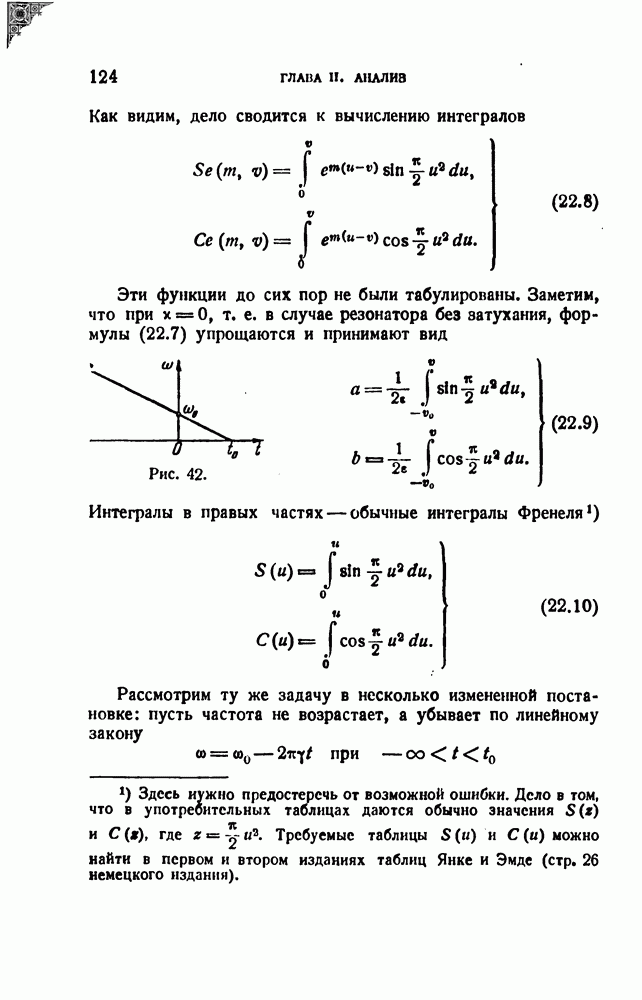
что выражение для огибающей зависит от одного параметра в наших обозначениях этот параметр есть , а следовательно, могут быть построены универсальные динамические характеристики. Здесь получилось недоразумение. Как видно из формул (22.7), выражение для огибающей в случае линейно возрастающей от нуля частоты зависит не только от параметра, но и от нижнего предела интегрирования который зависит только от скорости изменения частоты. Быкова [6] правильно пишет интегралы, но не замечает этого обстоятельства; без всяких оснований берет нижний предел равным — (эту ошибку Хока отмечает и Казовский). Что же касается Барбера и Арсела [8], то и они берут бесконечный нижний предел, но они рассматривают убывающую частоту, так что их результат совершенно верен.

Итак, построение универсального семейства возможно, но только для убывающей частоты, когда нижний предел интегрирования есть постоянная величина.

ЛИТЕРАТУРА К РАЗДЕЛУ 8

(см. скан)