| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДОБАВЛЕНИЯ
1. Подробности вычисления
Для читателя, который пожелал бы проверить выкладки § 11 или проделать аналогичные, ниже приведены некоторые детали этих выкладок.
а. Прямоугольный импульс.  это очевидно. Далее,
это очевидно. Далее,

Здесь и ниже встречаются интегралы вида

которые вычисляются по частям, пока не закончатся на слагаемом  или
или  . В результате мы получаем для
. В результате мы получаем для  уравнение
уравнение

решение которого, легко получаемое методом ложных корней, есть

б. Треугольный импульс. Для треугольного импульса из условия

получаем уравнение

решая которое, находим

Спектр треугольного импульса есть

Составляя выражение

и выполняя интегрирование, получим уравнение

решение которого есть

в. Косинусоидальный импульс. Для определения  имеем соотношение
имеем соотношение

что приводит к уравнению

Отсюда находим

Спектр косинусоидального импульса есть

и выражение для определения  принимает вид
принимает вид

Входящий сюда интеграл вычисляется путем разложения подинтегрального выражения на простые дроби. В результате интегрирования получаем уравнение

где

Здесь возникает затруднение:  несомненно, отрицательно, и мы не можем подставлять его в качестве аргумента ни под знак
несомненно, отрицательно, и мы не можем подставлять его в качестве аргумента ни под знак  ни под знак
ни под знак  Это затруднение, однако, очень легко преодолеть. Рассмотрим функцию
Это затруднение, однако, очень легко преодолеть. Рассмотрим функцию

Вспоминая известное разложение  в степенной ряд, получим
в степенной ряд, получим

где Е — эйлерова постоянная. Таким образом, оказывается,  четная функция, и следовательно, мы имеем право при выполнении вычислений подставлять под знаки
четная функция, и следовательно, мы имеем право при выполнении вычислений подставлять под знаки  вместо отрицательных аргументов положительные. Принимая, кроме того, во внимание, что
вместо отрицательных аргументов положительные. Принимая, кроме того, во внимание, что  есть функция нечетная, и проделывая все вычисления, находим
есть функция нечетная, и проделывая все вычисления, находим

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
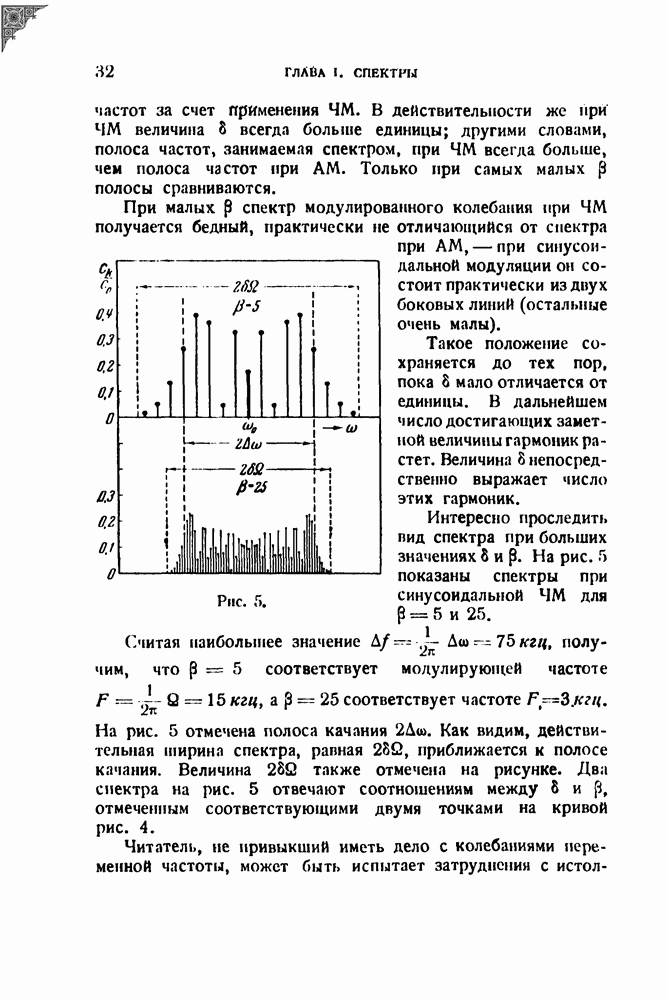
- § 6. Спектры при модуляции
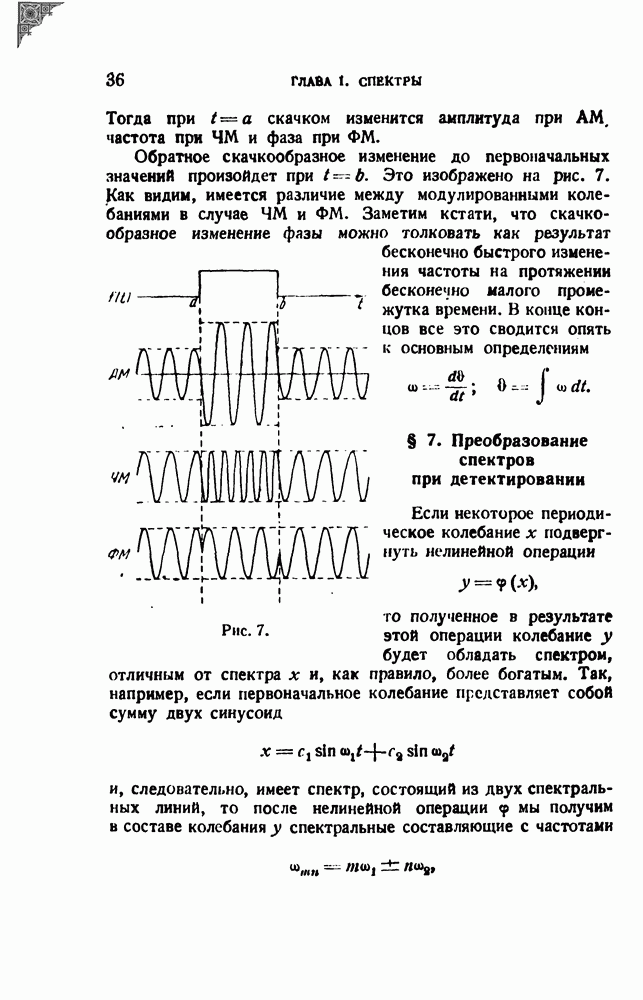
- § 7. Преобразование спектров при детектировании
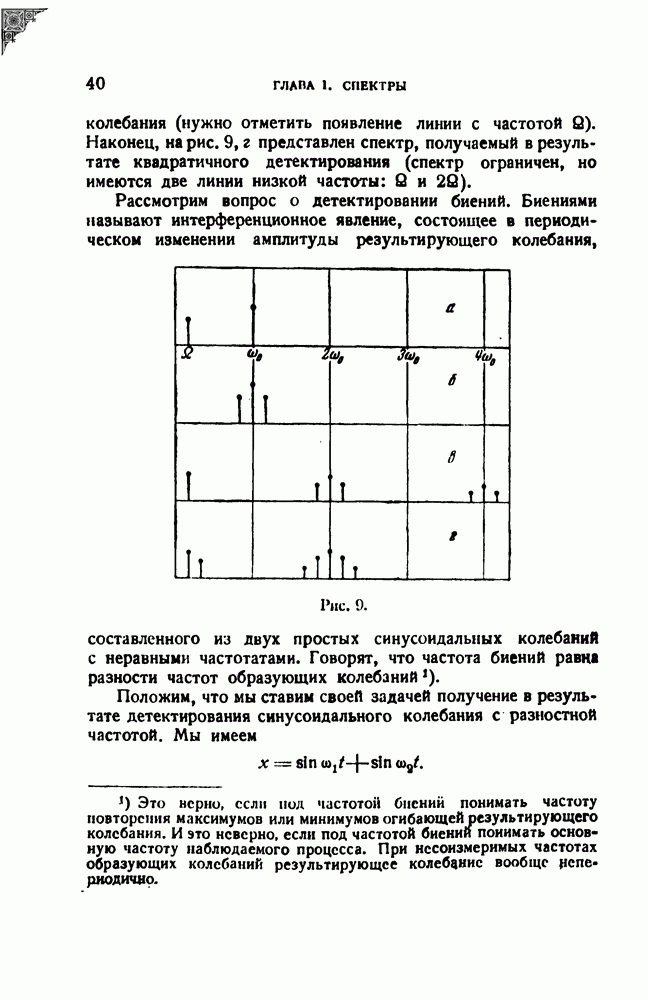
- § 8. Спектр суммы периодических функций
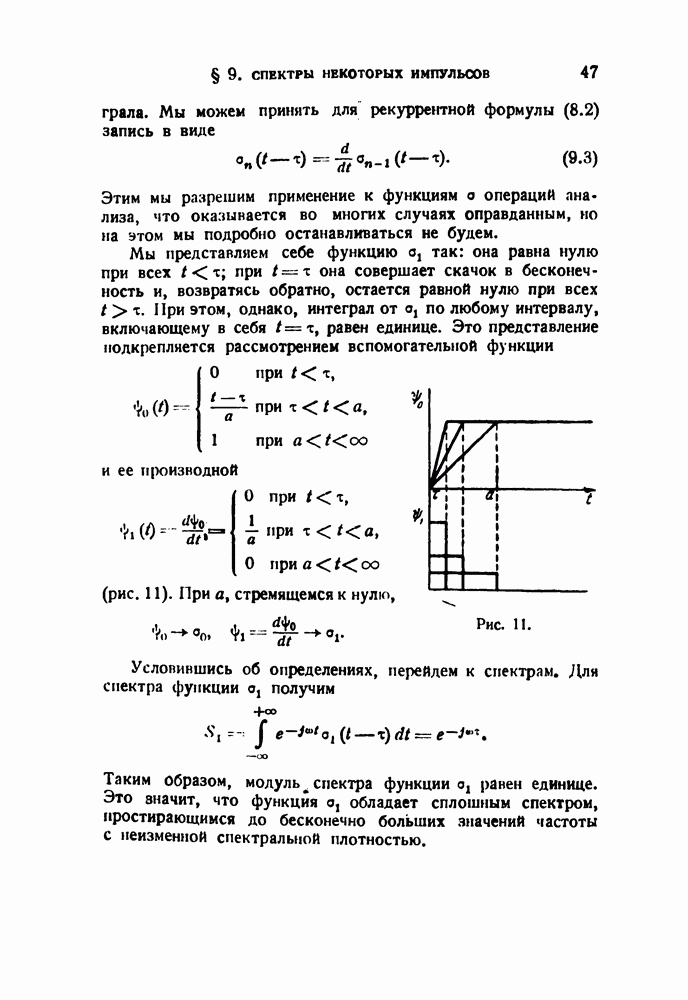
- § 9. Спектры некоторых импульсов
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА