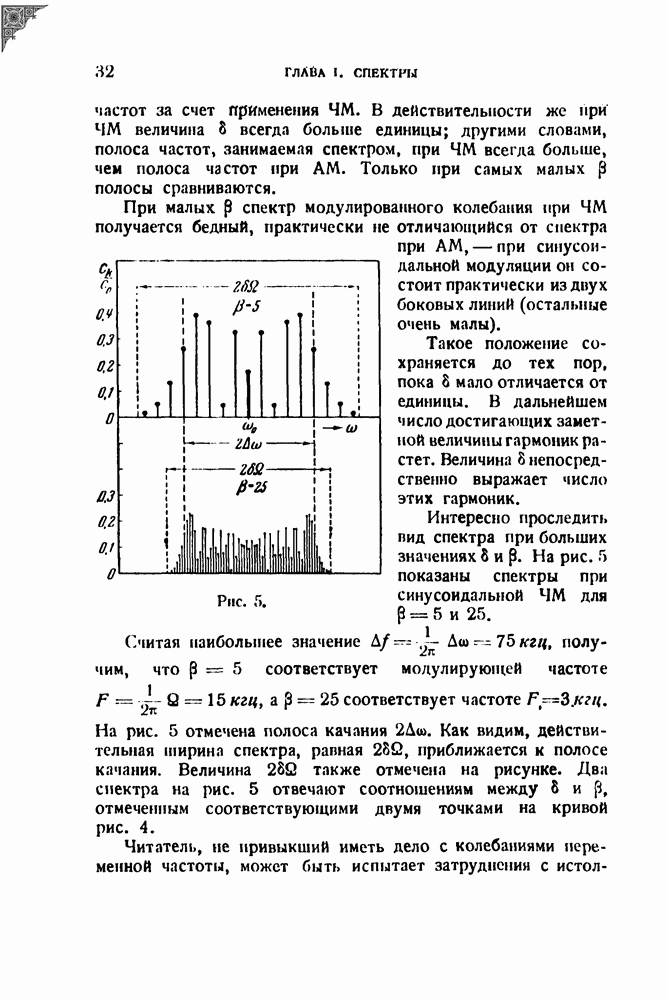
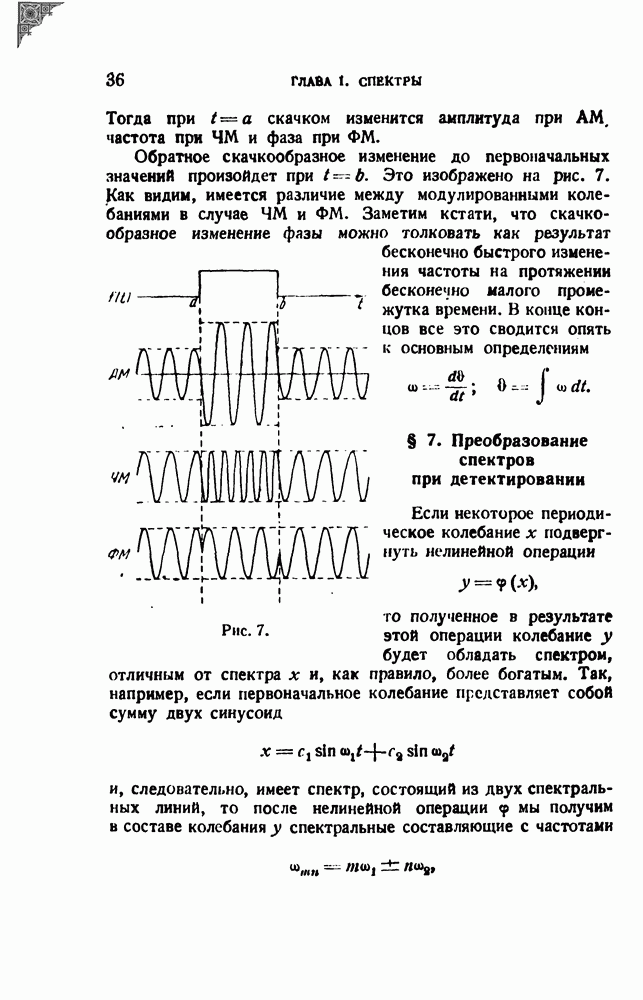
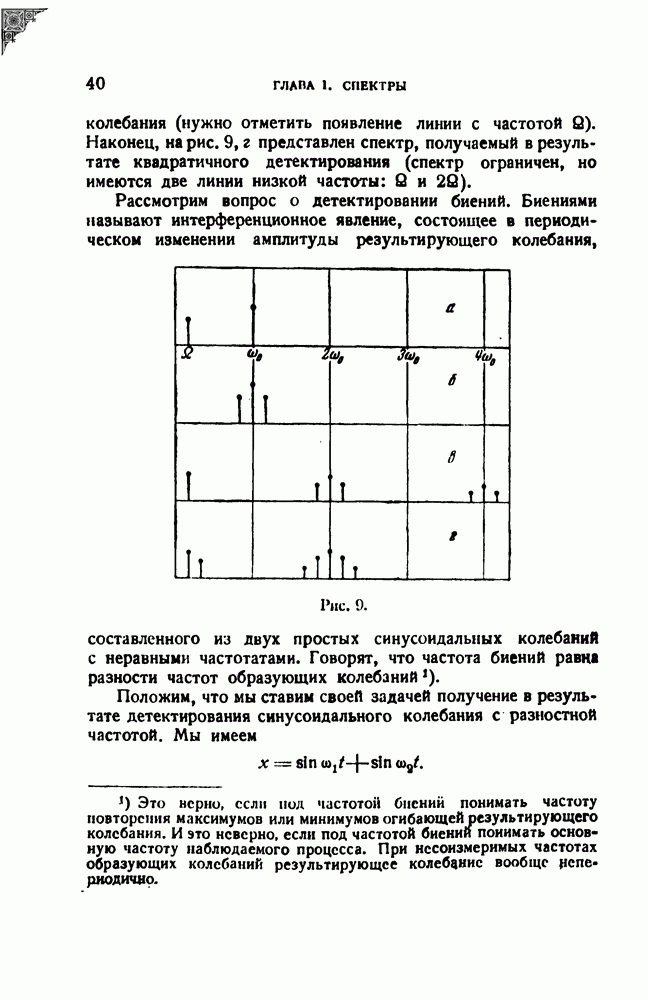
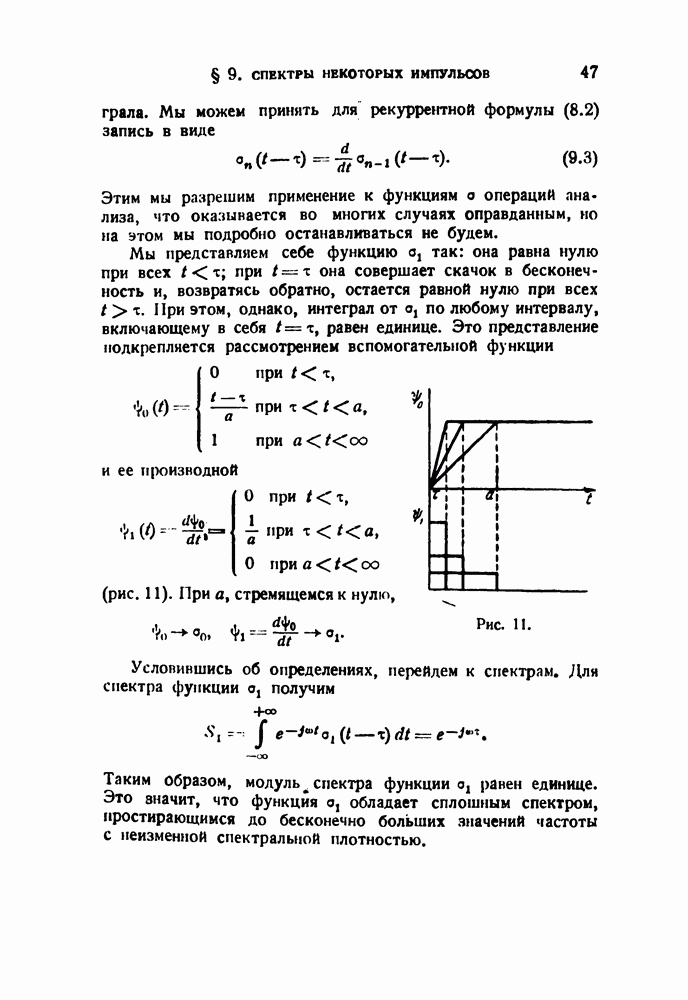
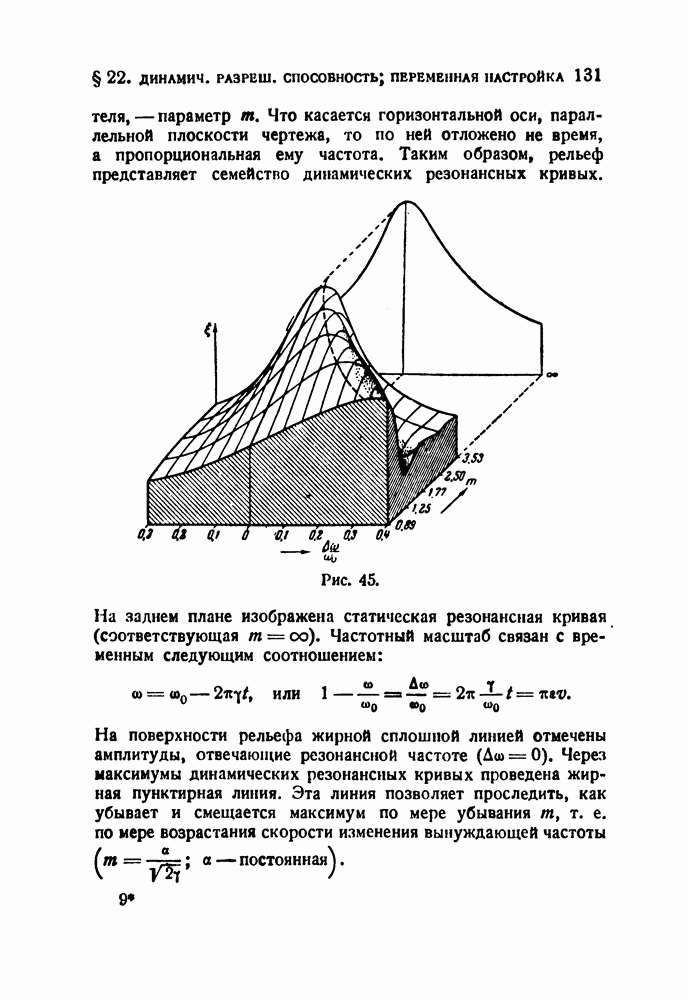
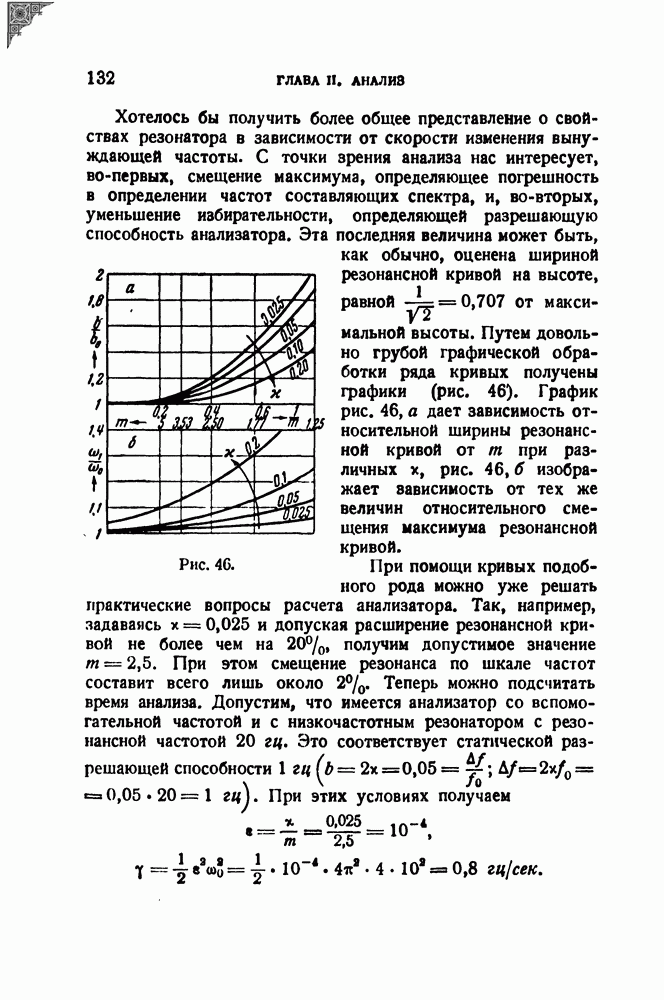
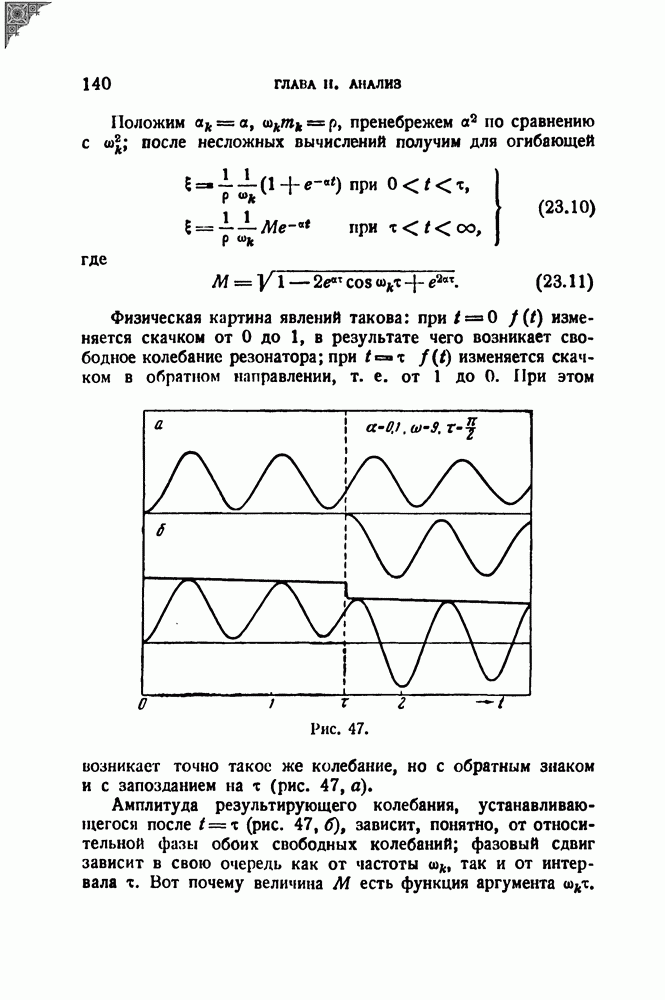
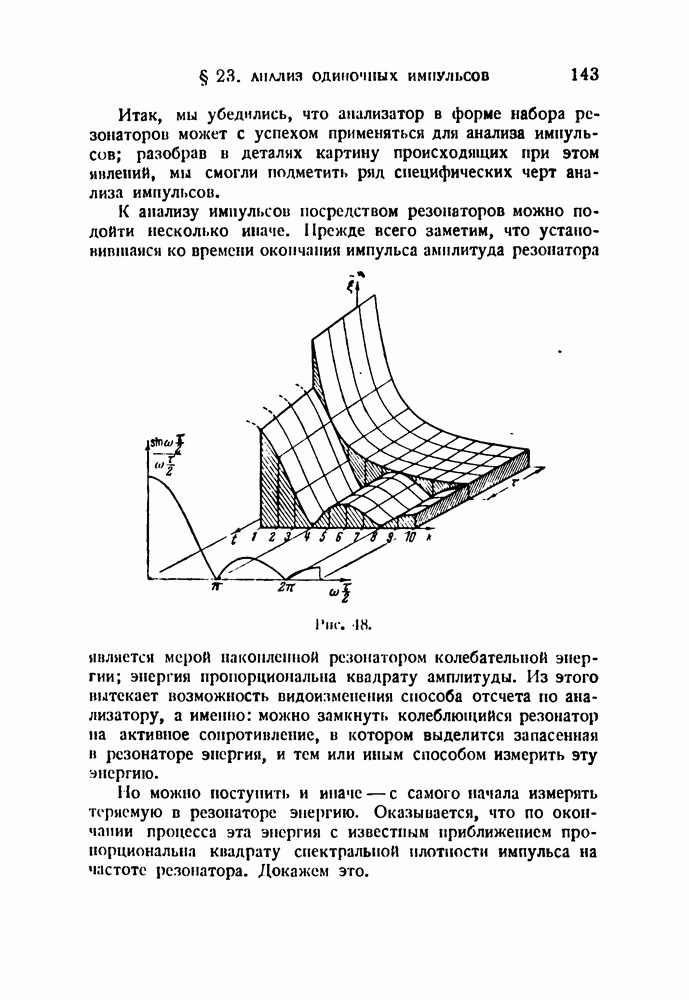
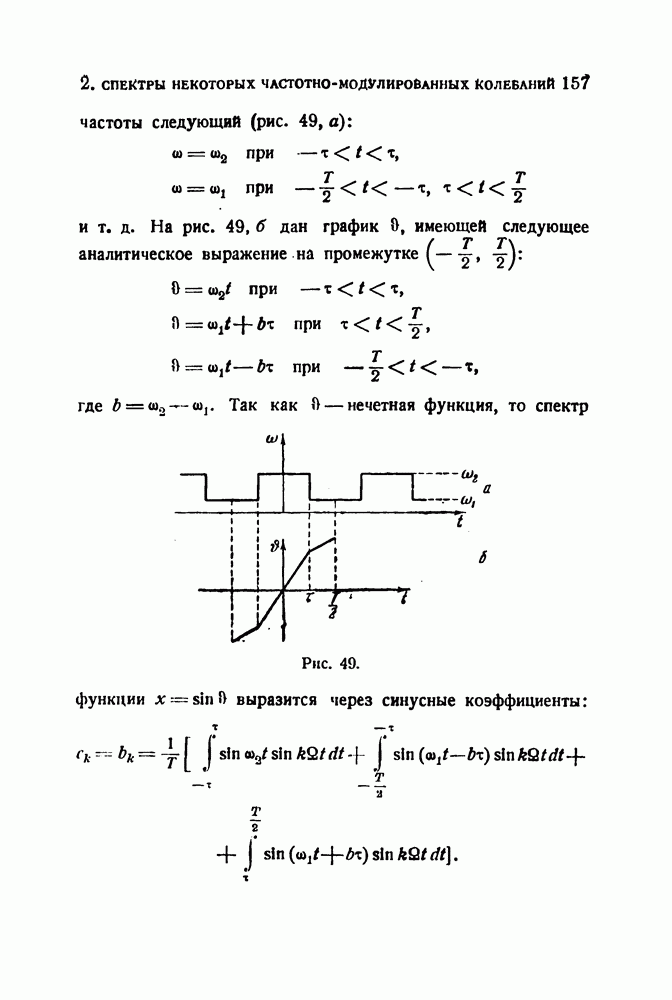
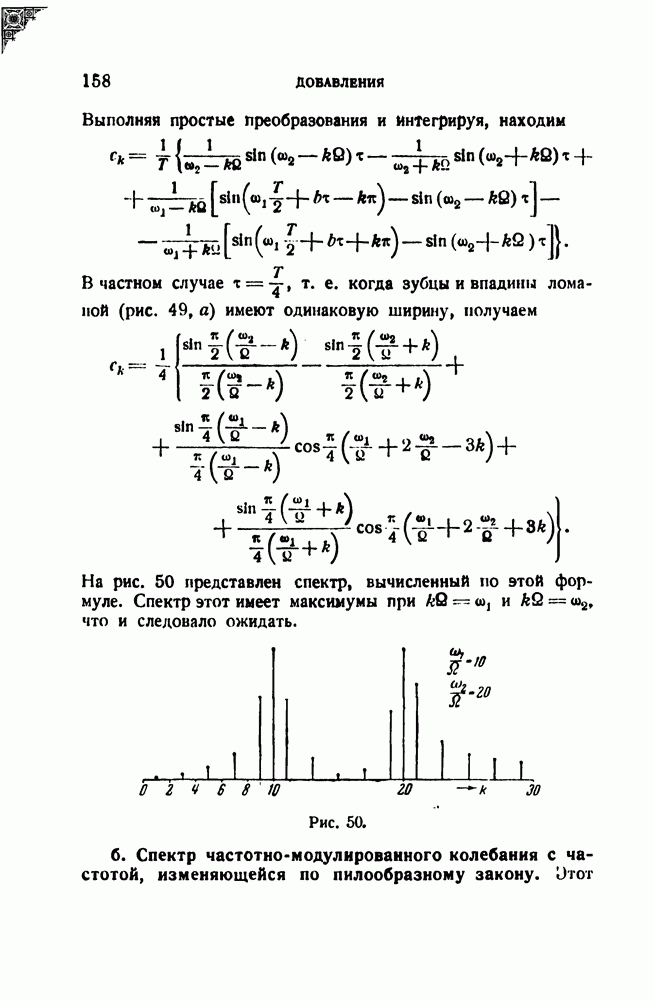
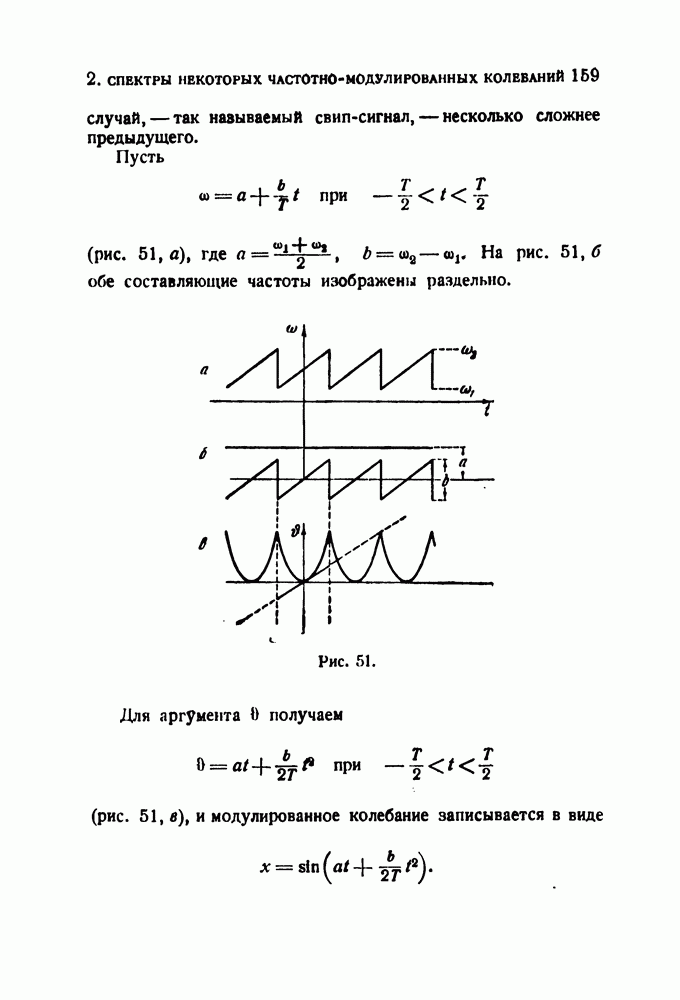
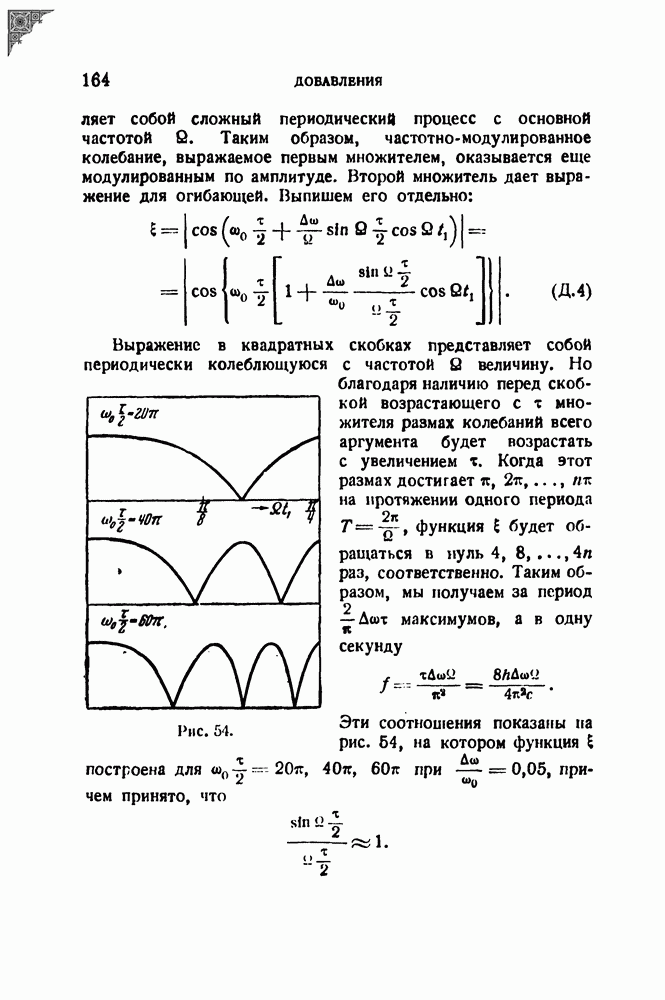
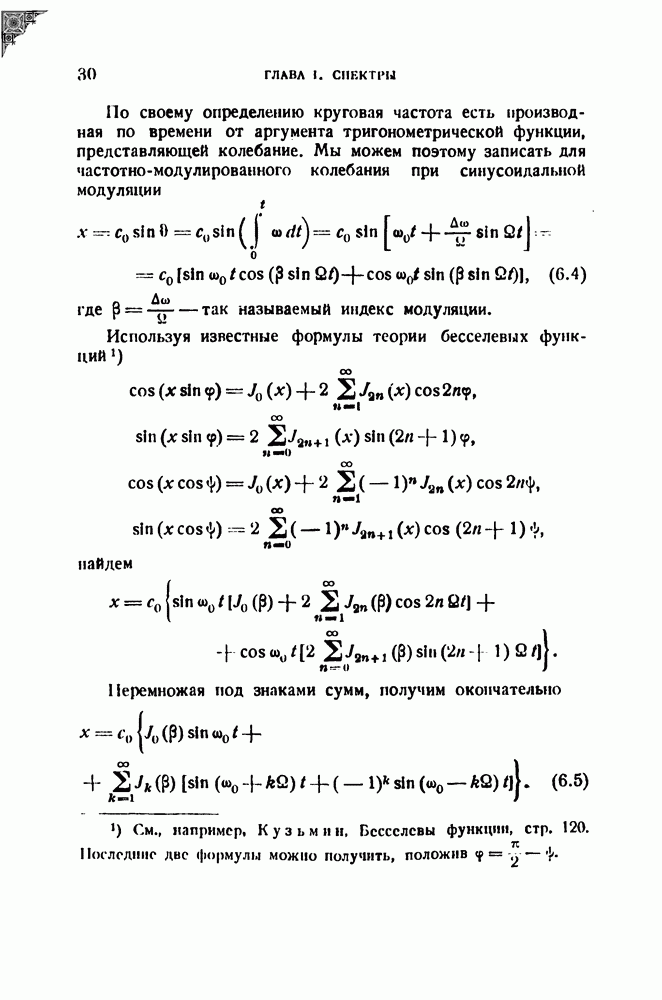| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Связь между спектрами одиночного и повторяющегося импульсов
Очень часто импульсы определенной формы периодически повторяются. Установим связь между спектрами одиночного импульса и периодической последовательности таких же импульсов. Наперед ясно одно: спектр одиночного импульса есть спектр сплошной, так как импульс есть непериодическая функция. Если же импульс какой угодно формы периодически повторять, то мы получим периодическую функцию, обладающую дискретным гармоническим спектром.
Пусть спектр одиночного импульса есть

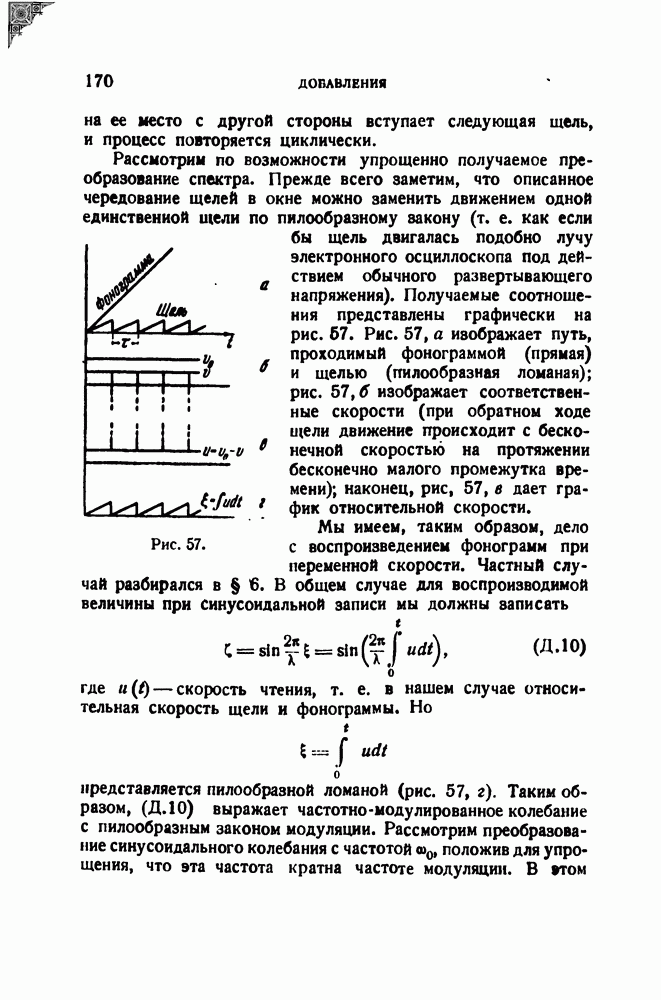
Если такой импульс повторять через промежутки времени Т, то получится периодическая функция с периодом Т (рис. 19). Спектр этой функции может быть получен по формуле

Сопоставляя (10.1) и (10.2), мы видим, что значения непрерывной функции  совпадают со значениями
совпадают со значениями  (с точностью до постоянного множителя
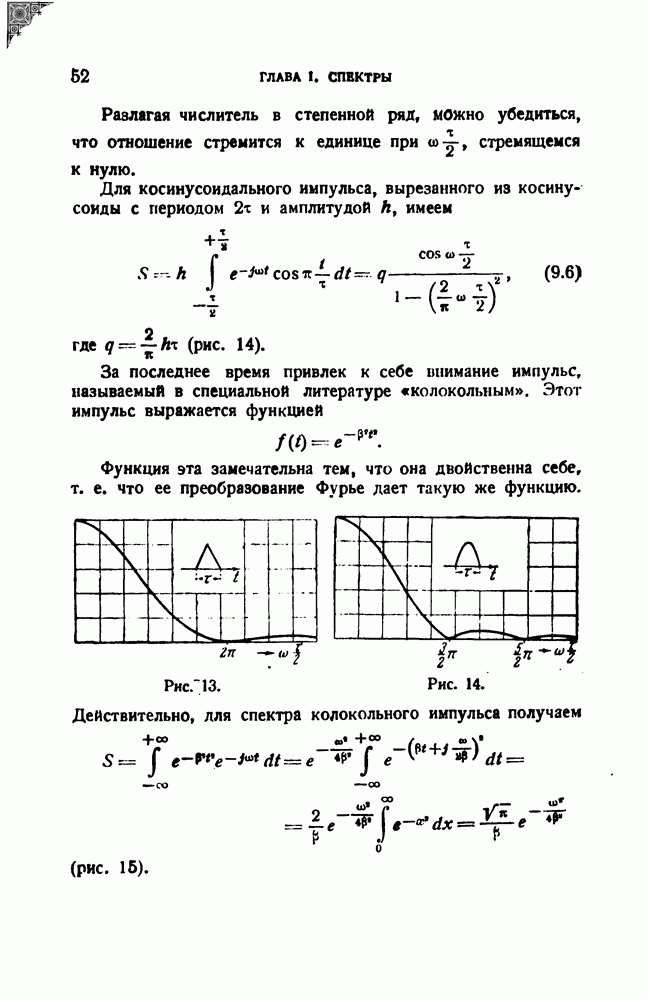
(с точностью до постоянного множителя  ) при определенных значениях аргумента, а именно при
) при определенных значениях аргумента, а именно при

 де
де  — круговая частота повторения.
— круговая частота повторения.
Таким образом, совокупность точек  определяющих дискретный спектр периодической последовательности импульсов, лежит на кривой 50, определяющей спектр одиночного импульса.
определяющих дискретный спектр периодической последовательности импульсов, лежит на кривой 50, определяющей спектр одиночного импульса.
Можно еще сказать, что линейчатый спектр периодической последовательности импульсов вписывается в кривую сплошного спектра одиночного импульса.

Рис. 19.
На этом примере лёгко проследить предельный Переход от ряда к интегралу Фурье: если период повторения возрастает, т. с. если импульсы повторяются все реже и реже, то точки, изображающие линейчатый спектр, оставаясь на кривой  располагаются на пей все теснее, пока не образуют непрерывную последовательность, т. е. кривую, совпадающую с
располагаются на пей все теснее, пока не образуют непрерывную последовательность, т. е. кривую, совпадающую с 
Если последовательность повторяющихся импульсов непериодична, то в общем виде связь между спектром такой
последовательности и спектром одиночного импульса установить нельзя. Существует, однако, один замечательный частный случай, для которого эта связь может быть установлена, и оказывается исключительно простой. Речь идет о случае, когда импульсы повторяются беспорядочно. Этот случай рассмотрен Н. Н. Андреевым [2].
Пусть попрежнему спектр одиночного импульса есть

Предположим, что имеется последовательность импульсов

Спектр каждого такого импульса на основании теоремы (5.5) может быть записан в виде

так что спектр всей последовательности, т. е. функции  имеет вид
имеет вид

Перейдем к модулю спектра. Имеем

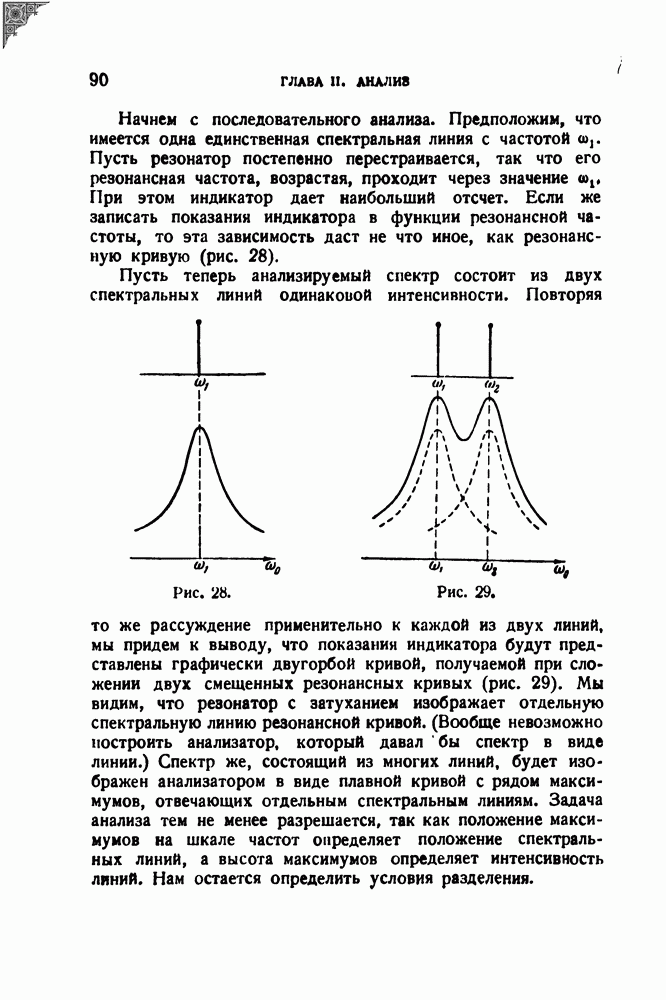
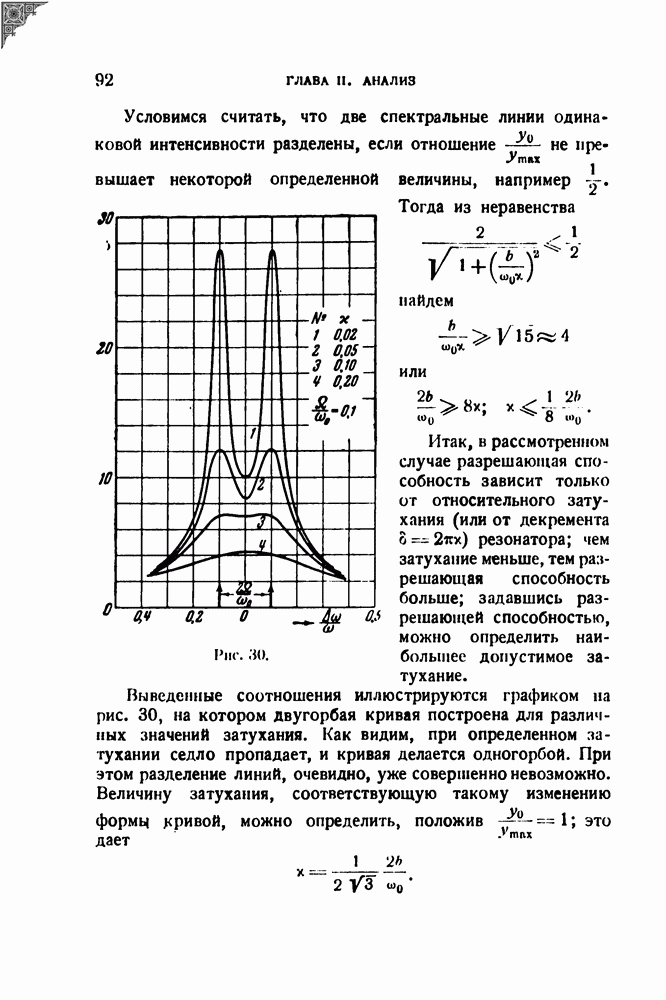
Рассмотрим отдельно второй множитель в правой части. Его квадрат равен

Но в силу нашего предположения о распределении промежутков разность  может принимать любые значения, а следовательно, и
может принимать любые значения, а следовательно, и  может принимать все
может принимать все
значения между —1 и +1, причем каждое из этих значений равновероятно. Следовательно, сумма в (10.4) флюктуирует около нуля, и в среднем

т. е. спектр беспорядочной последовательности одинаковых импульсов совпадает в среднем (до постоянного множителя) со спектром одиночного импульса.
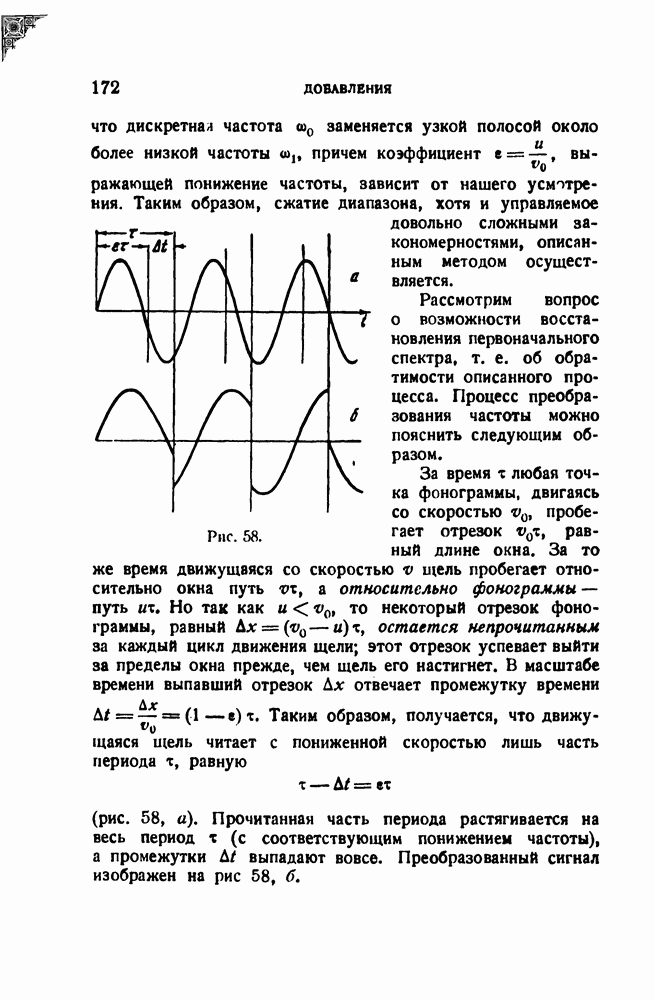
Следует остановиться на множителе  Раньше мы получили, что множитель при спектре пропорционален площади импульса. Если это так, то в рассмотренном случае мы должны были бы ожидать множитель
Раньше мы получили, что множитель при спектре пропорционален площади импульса. Если это так, то в рассмотренном случае мы должны были бы ожидать множитель  , но не
, но не  Однако дело заключается в том, что благодаря беспорядочному следованию импульсов их спектральные компоненты некогерентны. А при наложении некогерентных колебаний суммируются, как известно, не амплитуды, а энергии, т. е. квадратичные функции амплитуд.
Однако дело заключается в том, что благодаря беспорядочному следованию импульсов их спектральные компоненты некогерентны. А при наложении некогерентных колебаний суммируются, как известно, не амплитуды, а энергии, т. е. квадратичные функции амплитуд.
Вот почему множитель  фигурирует в выражении (10.4) для квадрата модули суммы колебательных множителей
фигурирует в выражении (10.4) для квадрата модули суммы колебательных множителей  -Когда же мы возвращаемся от энергии к амплитудам, то выражаем спектр амплитуд как корень квадратный из спектра энергий. Этим же определяется невозможность выполнения вычисления в комплексной форме (без привлечения сопряженных величин).
-Когда же мы возвращаемся от энергии к амплитудам, то выражаем спектр амплитуд как корень квадратный из спектра энергий. Этим же определяется невозможность выполнения вычисления в комплексной форме (без привлечения сопряженных величин).
Соотношение (10.5) проливает свет на физическую природу колебаний, получивших за последнее время название «белого шума». Под белым шумом (термин указывает на спектральную аналогию с белым светом) понимается длительное колебание, обладающее равномерной спектральной плотностью вплоть до достаточно высоких частот. Теперь нам становится ясным, что способ получения белого шума состоит в беспорядочном повторении достаточно коротких импульсов (смысл выражений «достаточно высокая частота» и «достаточно короткий импульс» был выяснен в предыдущем параграфе). В природе такого тина явления существуют в виде всякого рода флюктуаций. Условие беспорядочности выполняется в силу самой природы флюктуационных явлений. Что касается протяженности спектра, зависящей от кратковременности отдельных возмущений, то следует лишь выбрать
явление с подходящими масштабами. Как мы знаем, для гене рирования белого шума в практике используются тепловые флюктуации высокоомных сопротивлений, флюктуации эмиссии электронных ламп, флюктуации ионного тока в газовых лампах и тому подобные явления.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
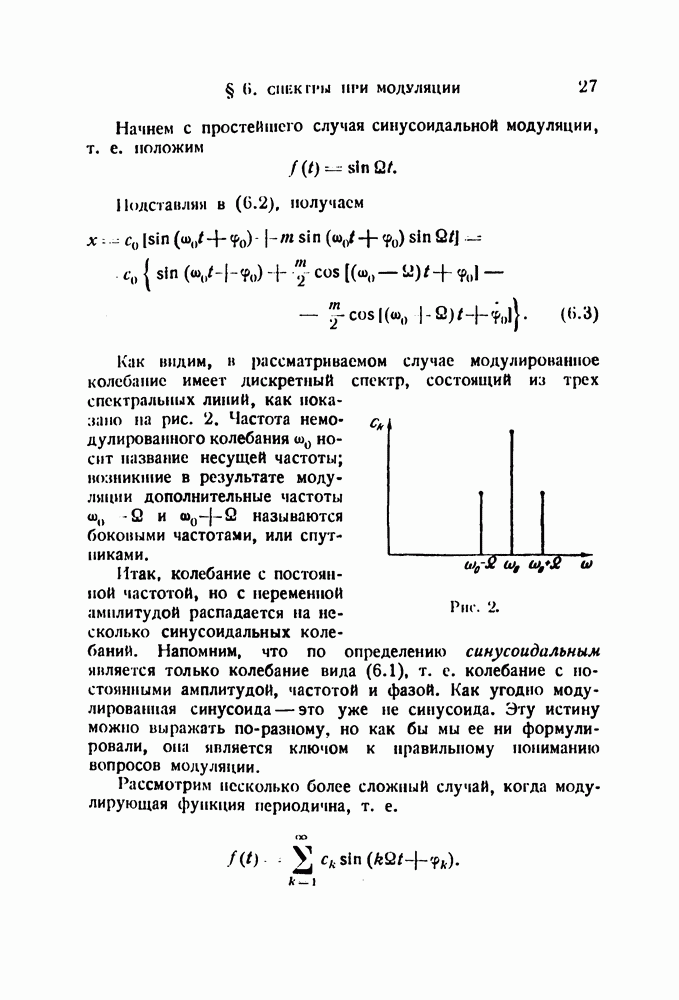
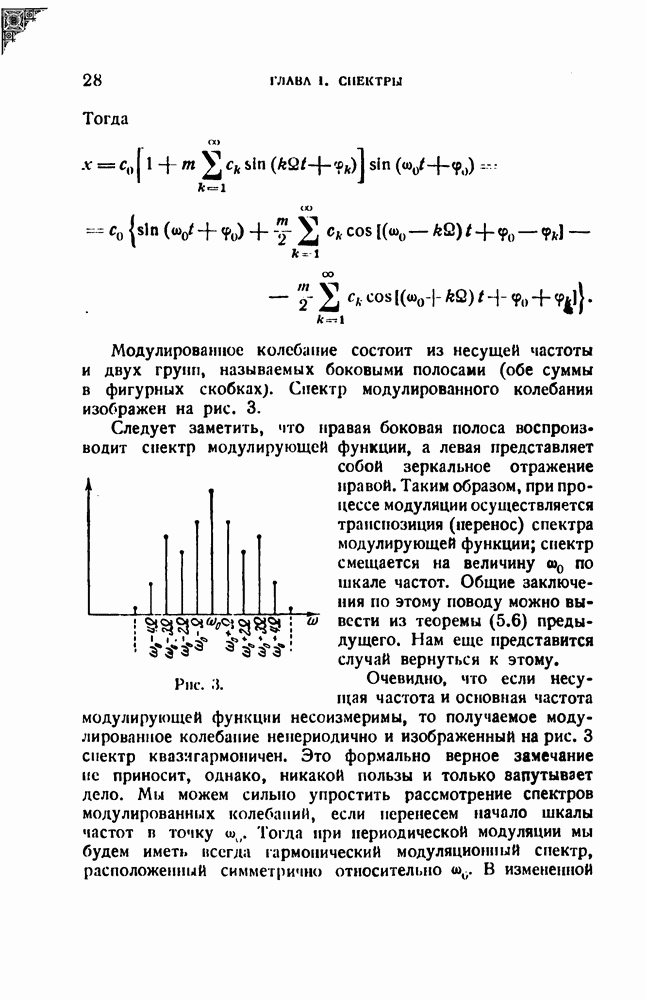
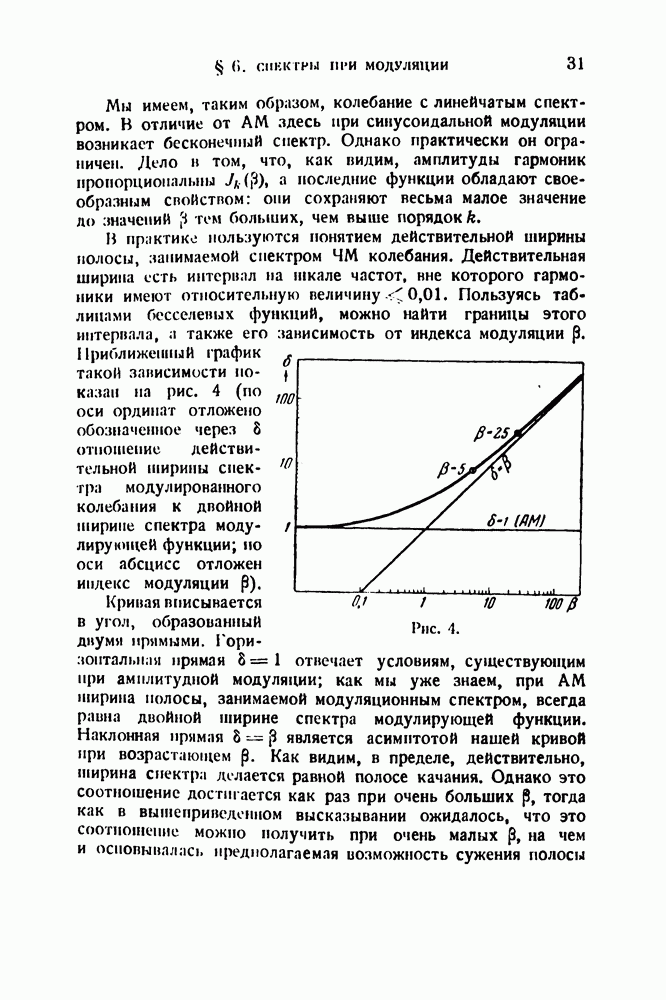
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
- § 9. Спектры некоторых импульсов
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
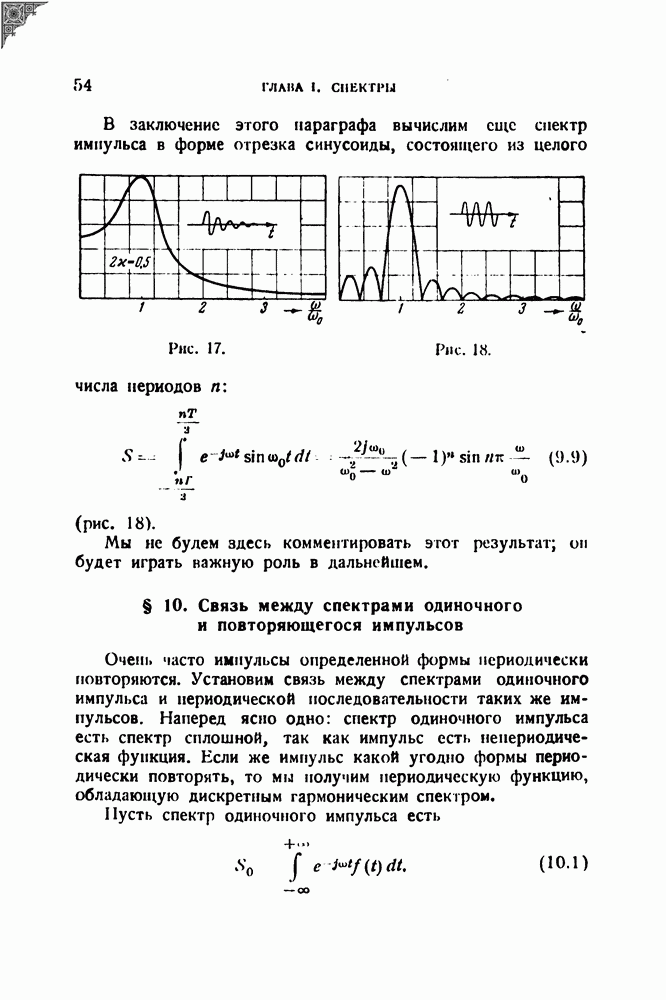
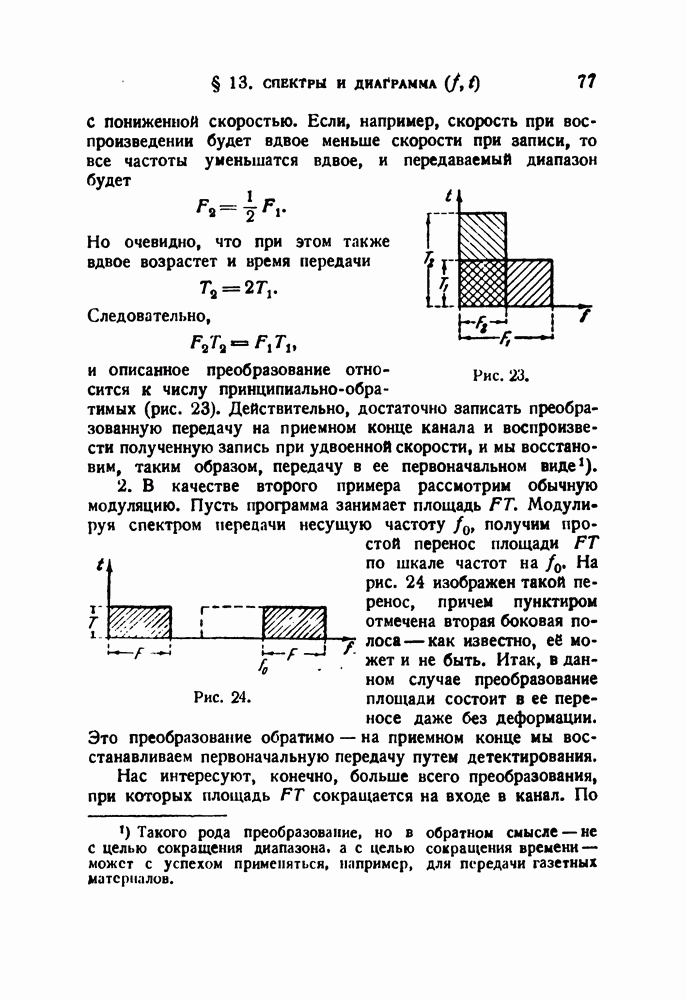
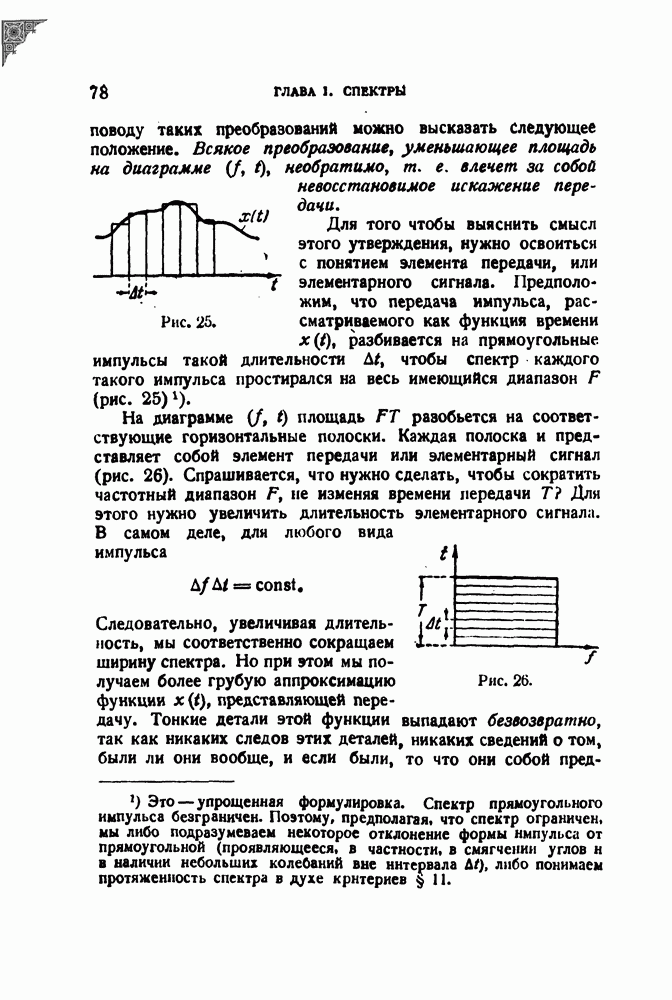
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА