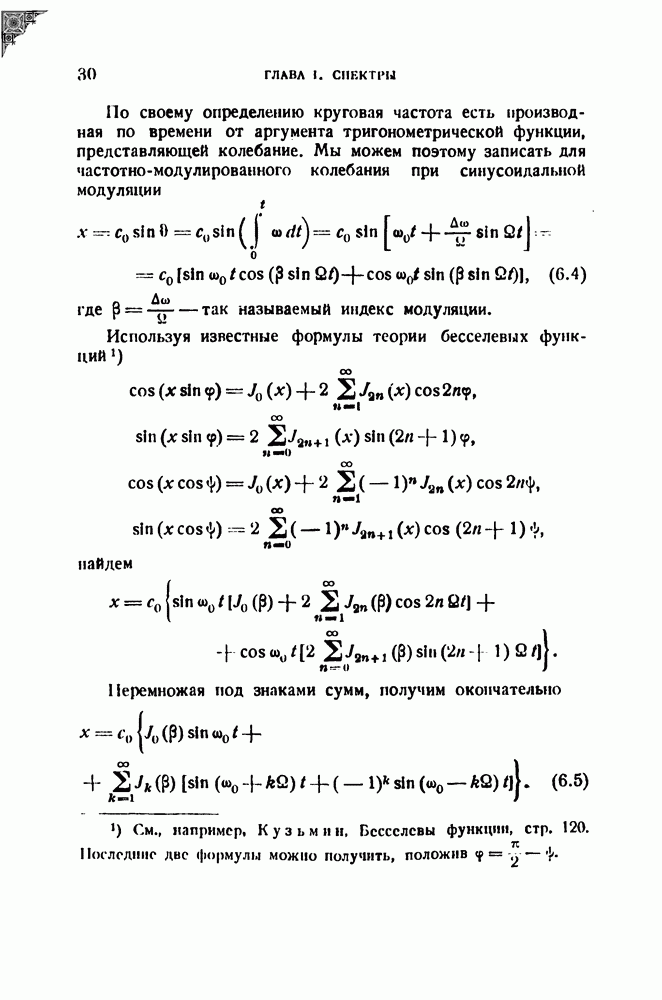| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
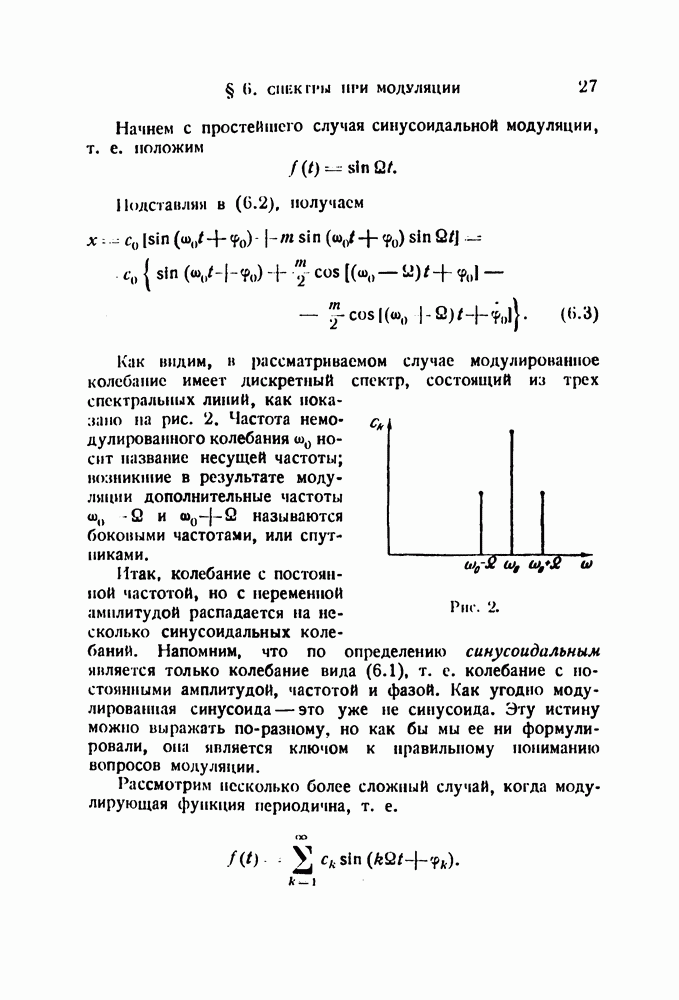
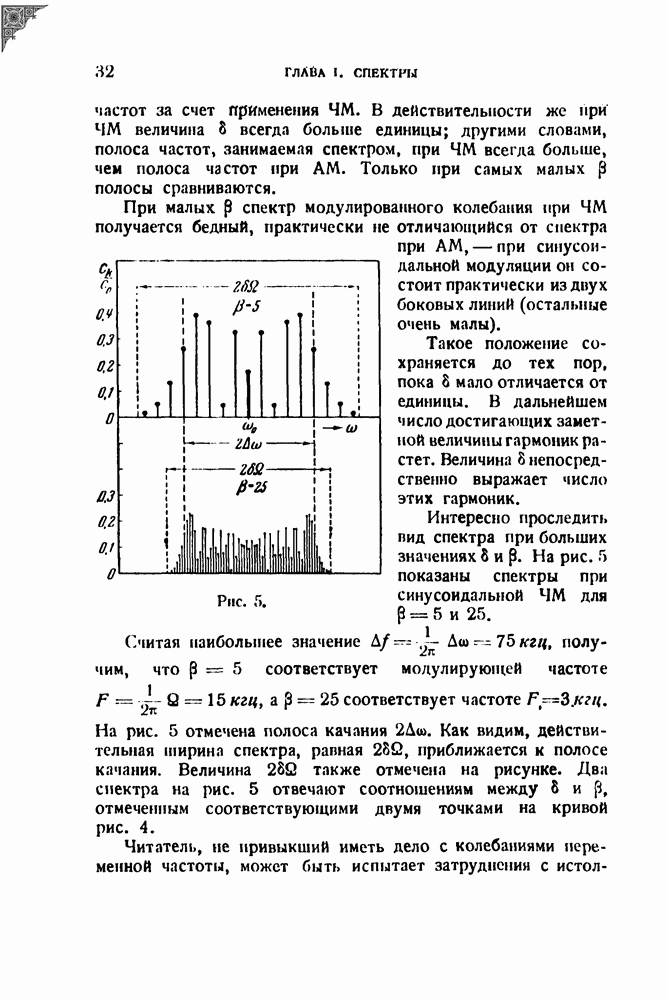
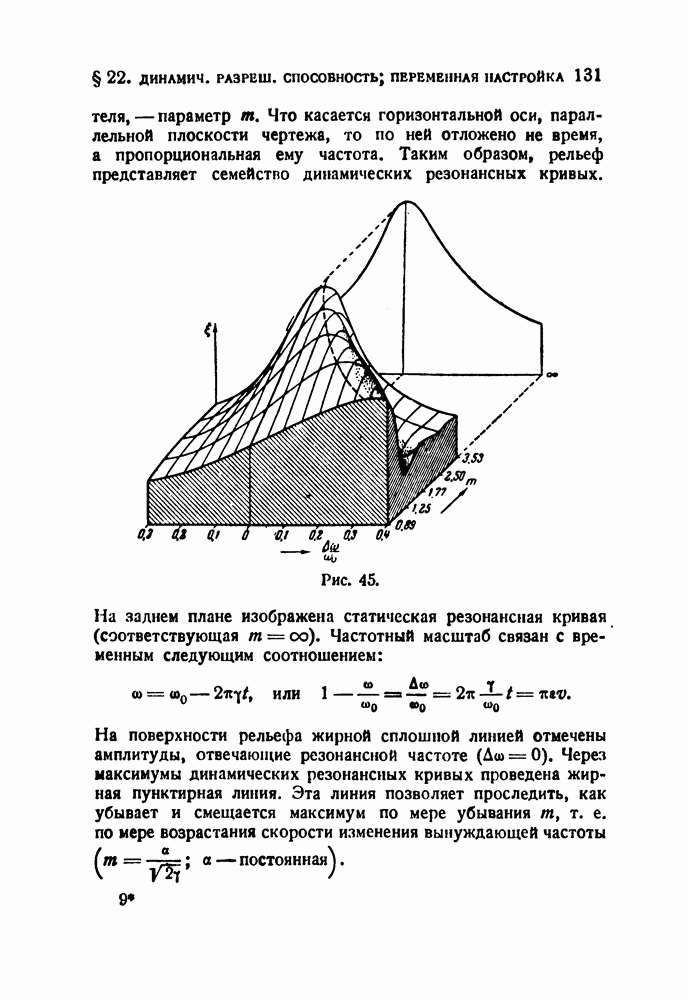
5. Об одном методе сжатия спектра
Рассмотрим метод, состоящий в том, что передача, предварительно записанная, читается движущейся щелью, причем относительная скорость щели меньше скорости, с которой была сделана запись 
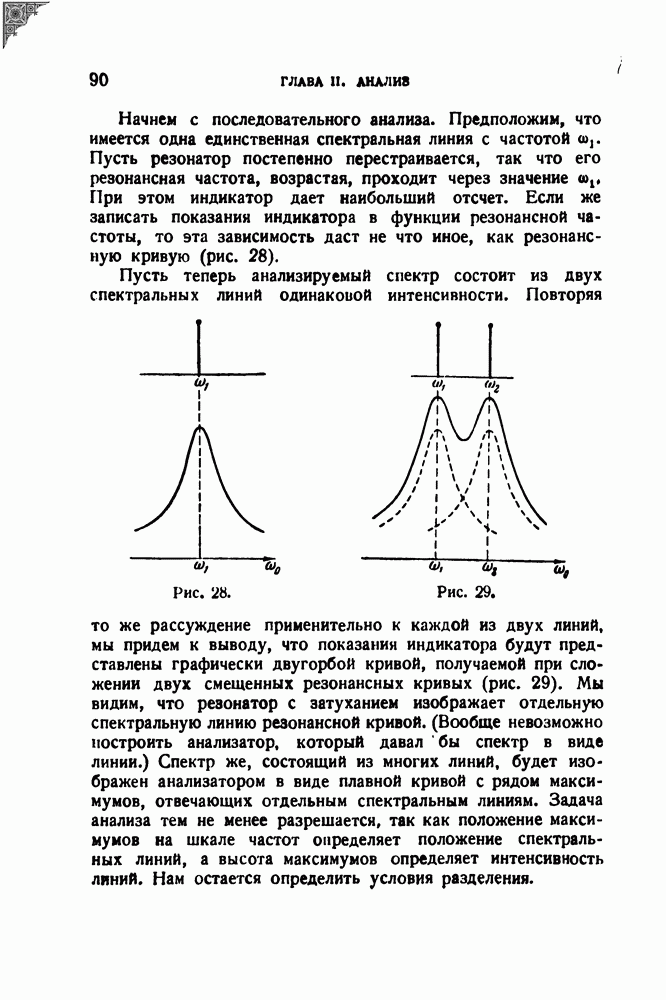
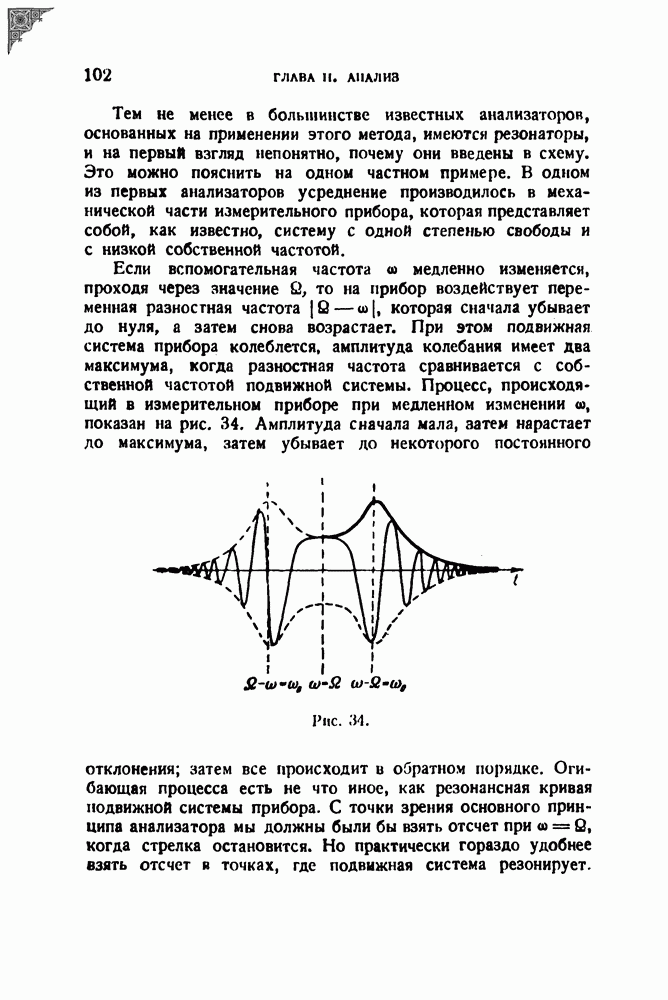
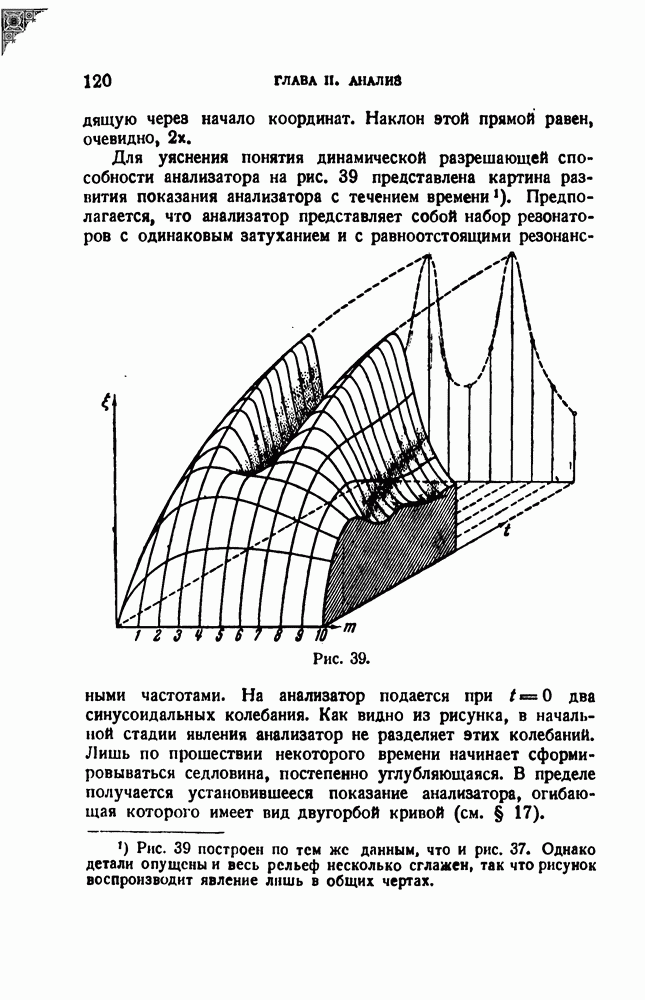
Если бы одна единственная щель равномерно скользила вдоль записи на всем ее протяжении, то это было бы совершенно равносильно замедленному воспроизведению, — случай, который мы уже рассмотрели. Однако описываемое устройство осуществлено при помощи нескольких, поочередно вступающих в действие щелей. Это устройство изображено схематически на рис. 56 в фотооптическом варианте.

Рис. 56.
Внутри вращающегося барабана 1 со щелями 2 помещен источник света 3. Фонограмма 4 проходит перед окном 5. Свет, прошедший через щель и фонограмму в пределах окна, попадает на фотоэлемент 6. Суть дела заключается в том, что щель движется с линейной скоростью  в том же направлении, что и фонограмма, скорость которой обозначена через
в том же направлении, что и фонограмма, скорость которой обозначена через  Таким образом, относительная скорость щели и фонограммы равна
Таким образом, относительная скорость щели и фонограммы равна

Когда одна щель, пробежав окно, уходит за его пределы,
на ее место с другой стороны вступает следующая щель, и процесс повторяется циклически.
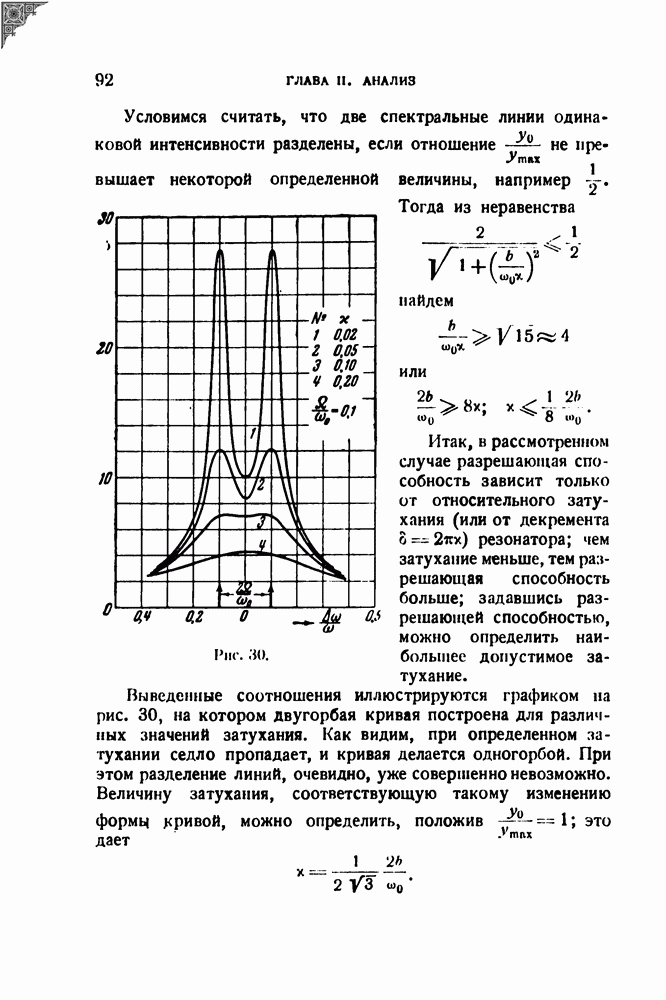
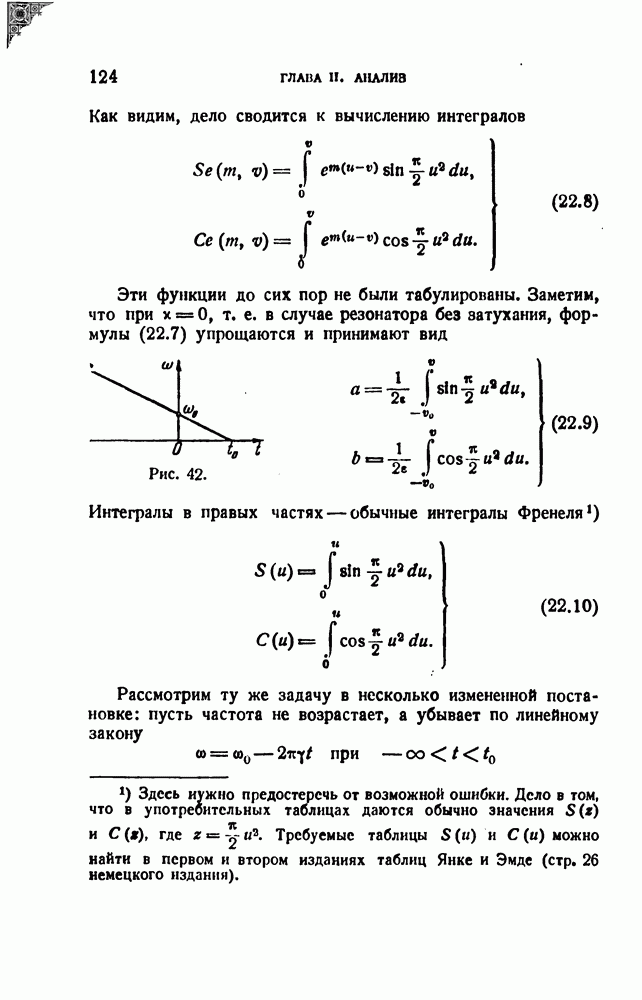
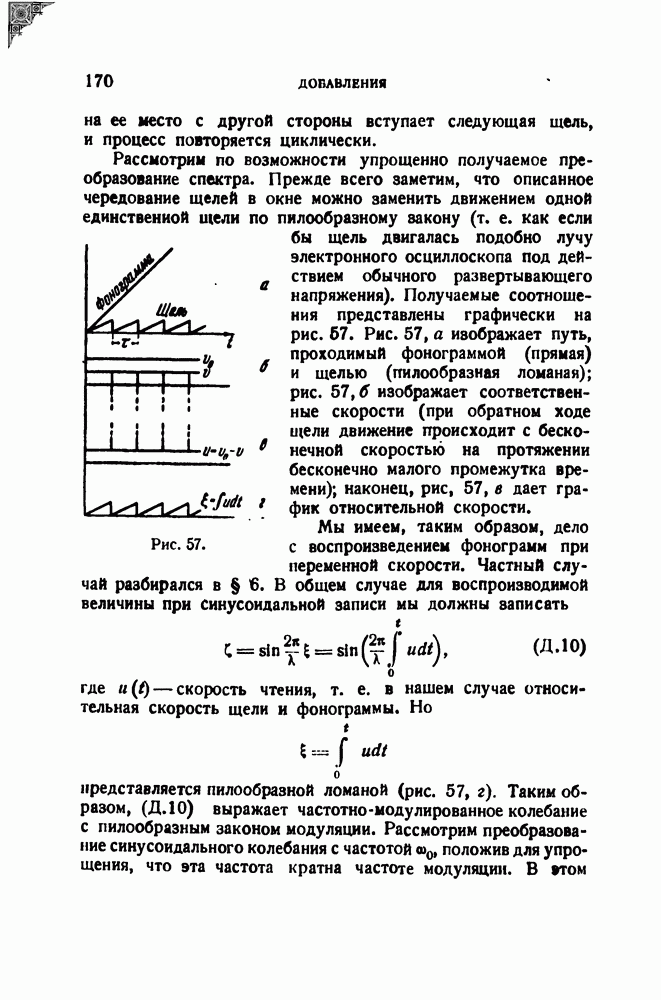
Рассмотрим по возможности упрощенно получаемое преобразование спектра. Прежде всего заметим, что описанное чередование щелей в окне можно заменить движением одной единственной щели по пилообразному эакону (т. е. как если бы щель двигалась подобно лучу электронного осциллоскопа под действием обычного развертывающего напряжения). Получаемые соотношения представлены графически на рис. 57. Рис. 57, а изображает путь, проходимый фонограммой (прямая) и щелью (пилообразная ломаная); рис. 57, б изображает соответственные скорости (при обратном ходе щели движение происходит с бесконечной скоростью на протяжении бесконечно малого промежутка времени); наконец, рис, 57, в дает график относительной скорости.

Рис. 57.
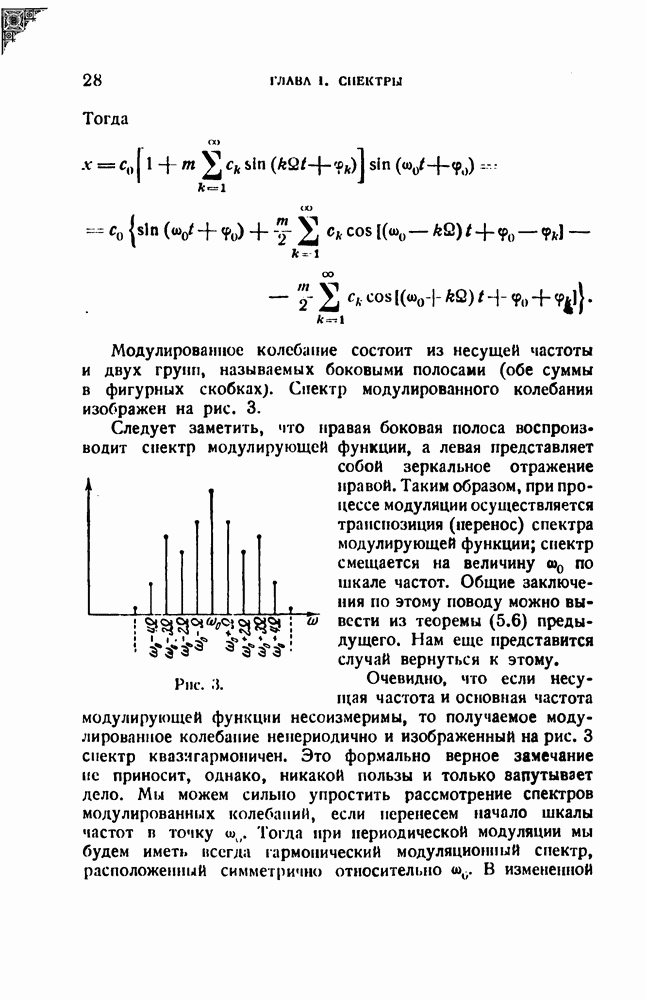
Мы имеем, таким образом, дело с воспроизведением фонограмм при переменной скорости. Частный случай разбирался в § 6. В общем случае для воспроизводимой величины при синусоидальной записи мы должны записать

где  — скорость чтения, т. е. в нашем случае относительная скорость щели и фонограммы. Но
— скорость чтения, т. е. в нашем случае относительная скорость щели и фонограммы. Но

представляется пилообразной ломаной (рис. 57, г). Таким образом, (Д.10) выражает частотно - модулированное колебание с пилообразным законом модуляции. Рассмотрим преобразование синусоидального колебания с частотой  положив для упрощения, что эта частота кратна частоте модуляции. В этом
положив для упрощения, что эта частота кратна частоте модуляции. В этом
случае получается периодический процесс с основной частотой

и мы легко можем вычислить спектр. На протяжении промежутка — синусоида с частотой  читается с постоянной скоростью
читается с постоянной скоростью  Кажущаяся частота составляет при этом
Кажущаяся частота составляет при этом

Для амплитуды  гармоники имеем
гармоники имеем

Из этого выражения видно, что характер получаемого спектра зависит от отношения

Если  равно целому числу, и только в этом случае, — преобразованный спектр состоит из одной единственной спектральной линии с частотой
равно целому числу, и только в этом случае, — преобразованный спектр состоит из одной единственной спектральной линии с частотой  и с амплитудой
и с амплитудой  . Во всех остальных случаях получается линейчатый спектр, наиболее богатый при
. Во всех остальных случаях получается линейчатый спектр, наиболее богатый при  равном целому числу с половиной. При этом, однако, максимум огибающей спектра сохраняет свое положение на шкале частот. Таким образом, единственная спектральная линия с частотой
равном целому числу с половиной. При этом, однако, максимум огибающей спектра сохраняет свое положение на шкале частот. Таким образом, единственная спектральная линия с частотой  представлявшая первоначальный спектр, преобразована в линейчатый спектр с максимумом на частоте
представлявшая первоначальный спектр, преобразована в линейчатый спектр с максимумом на частоте

Специальными мерами, в частности применением окна переменной прозрачности, можно обеспечить получение более узкого спектра после преобразования, так что можно сказать,
что дискретная частота  заменяется узкой полосой около более низкой частоты
заменяется узкой полосой около более низкой частоты  причем коэффициент
причем коэффициент  выражающей понижение частоты, зависит от нашего усмотрения. Таким образом, сжатие диапазона, хотя и управляемое довольно сложными закономерностями, описанным методом осуществляется.
выражающей понижение частоты, зависит от нашего усмотрения. Таким образом, сжатие диапазона, хотя и управляемое довольно сложными закономерностями, описанным методом осуществляется.
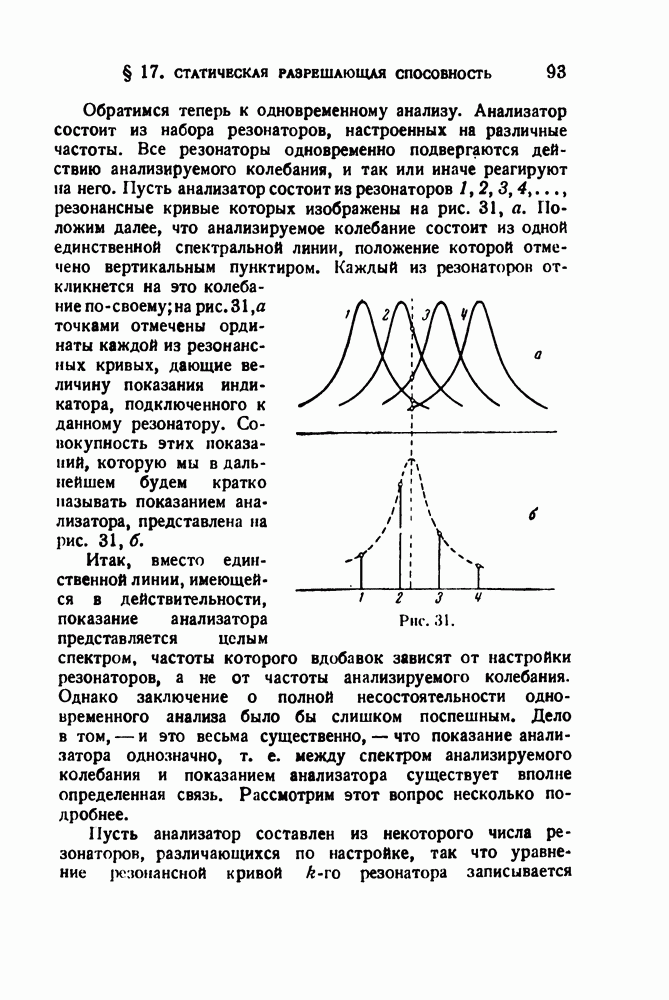
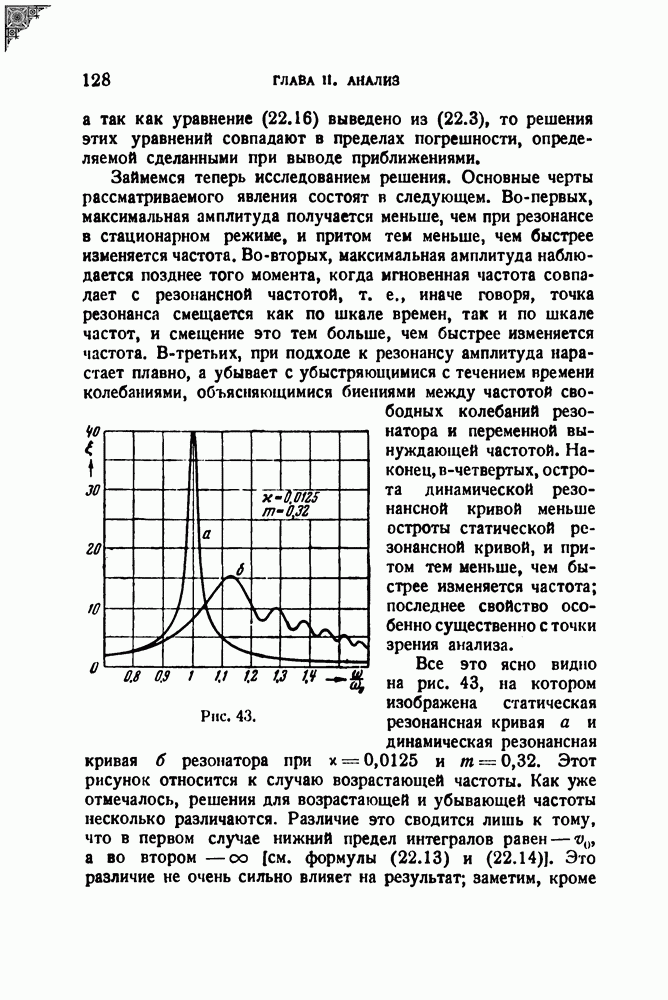
Рассмотрим вопрос о возможности восстановления первоначального спектра, т. е. об обратимости описанного процесса. Процесс преобразования частоты можно пояснить следующим образом.

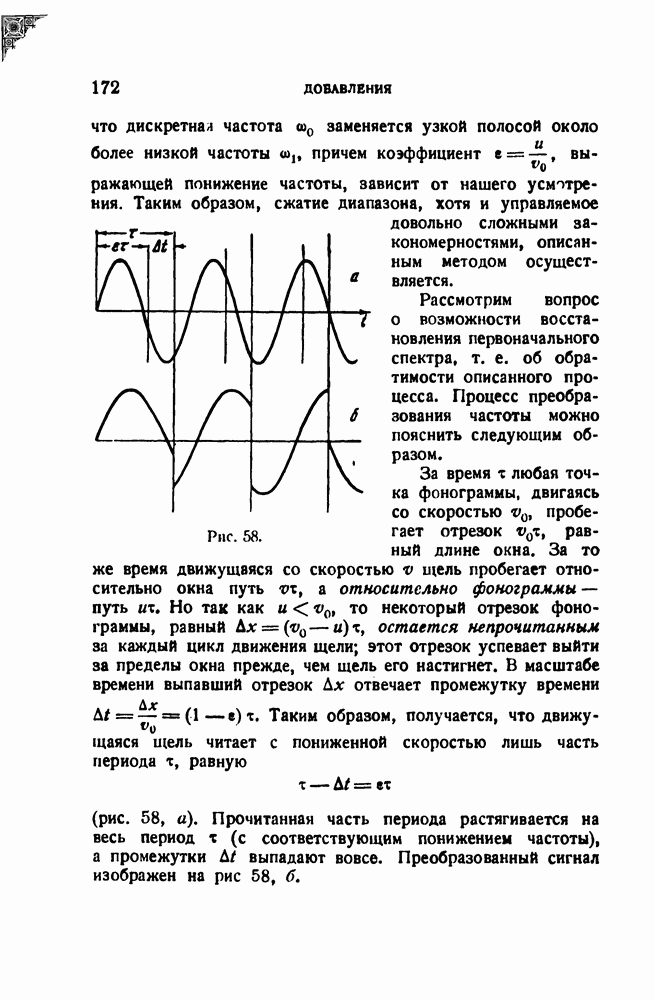
Рис. 58.
За время х любая точка фонограммы, двигаясь со скоростью  пробегает отрезок
пробегает отрезок  равный длине окна. За то же время движущаяся со скоростью
равный длине окна. За то же время движущаяся со скоростью  щель пробегает относительно окна путь
щель пробегает относительно окна путь  а относительно фонограммы — путь их. Но так как
а относительно фонограммы — путь их. Но так как  то некоторый отрезок фонограммы, равный
то некоторый отрезок фонограммы, равный  остается непрочитанным за каждый цикл движения щели; этот отрезок успевает выйти за пределы окна прежде, чем щель его настигнет. В масштабе времени выпавший отрезок
остается непрочитанным за каждый цикл движения щели; этот отрезок успевает выйти за пределы окна прежде, чем щель его настигнет. В масштабе времени выпавший отрезок  отвечает промежутку времени
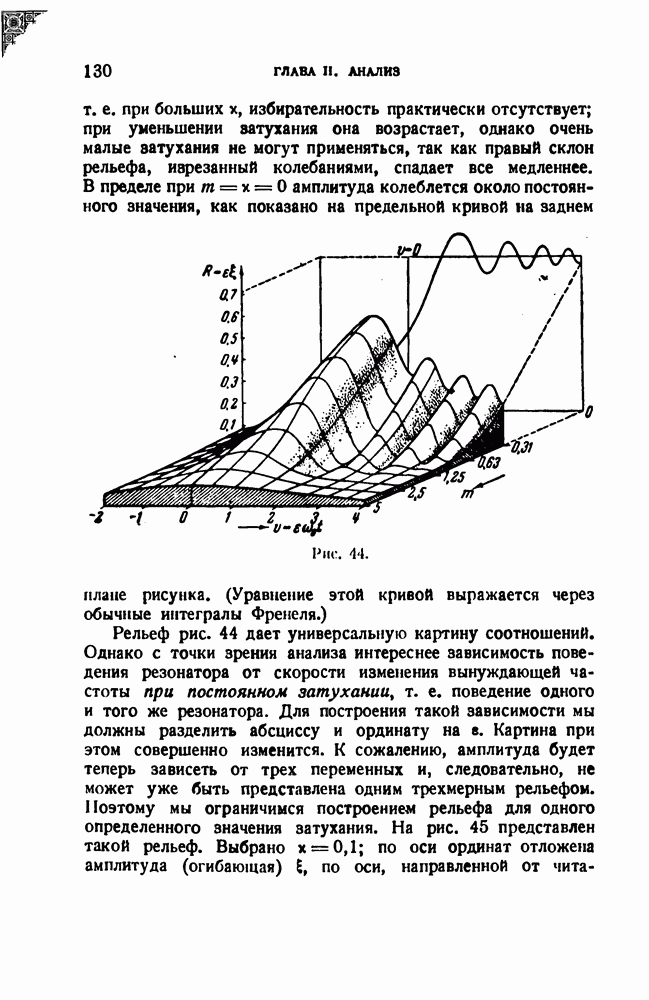
отвечает промежутку времени  . Таким образом, получается, что движущаяся щель читает с пониженной скоростью лишь часть периода х, равную
. Таким образом, получается, что движущаяся щель читает с пониженной скоростью лишь часть периода х, равную

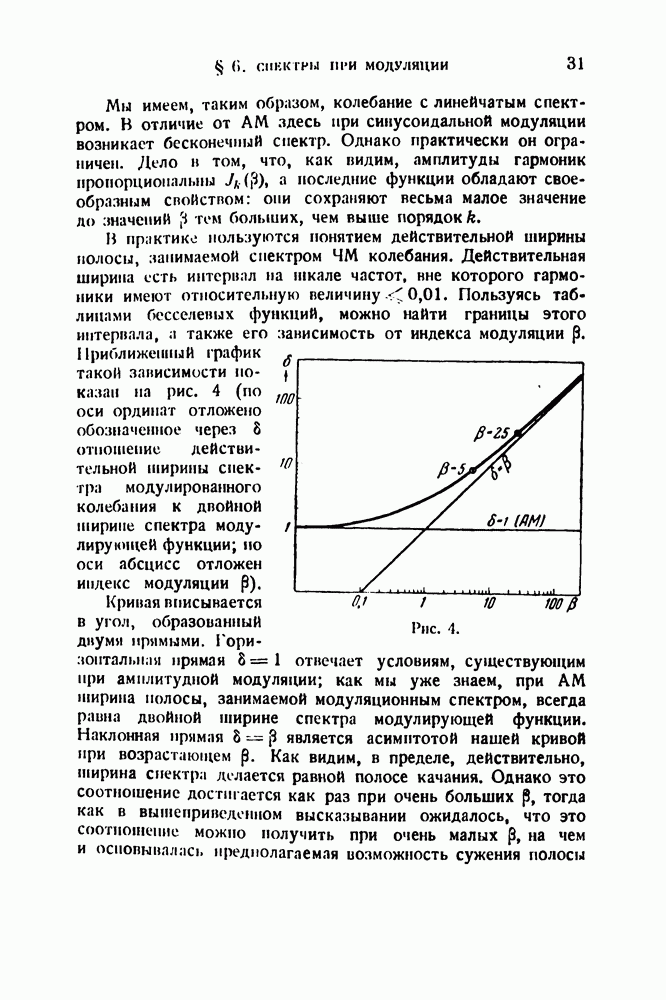
(рис. 58, а). Прочитанная часть периода растягивается на весь период х (с соответствующим понижением частоты), а промежутки  выпадают вовсе. Преобразованный сигнал изображен на рис 58, б.
выпадают вовсе. Преобразованный сигнал изображен на рис 58, б.
Для того чтобы понять непоправимость такого искажения, достаточно представить себе, например, что передача состоит из отдельных слогов, причем на период  приходится по два слога и
приходится по два слога и  Тогда, очевидно, в результате описанной операции сжатия безвозвратно выпадет ровно половина слогов.
Тогда, очевидно, в результате описанной операции сжатия безвозвратно выпадет ровно половина слогов.
Мы убеждаемся на примере рассмотренного устройства в том, что сжатие диапазона эквивалентно сокращению времени, т. е. что если происходит уменьшение площади на диаграмме  то безразлично, за счет ли сокращения
то безразлично, за счет ли сокращения  или за счет сокращения Т.
или за счет сокращения Т.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
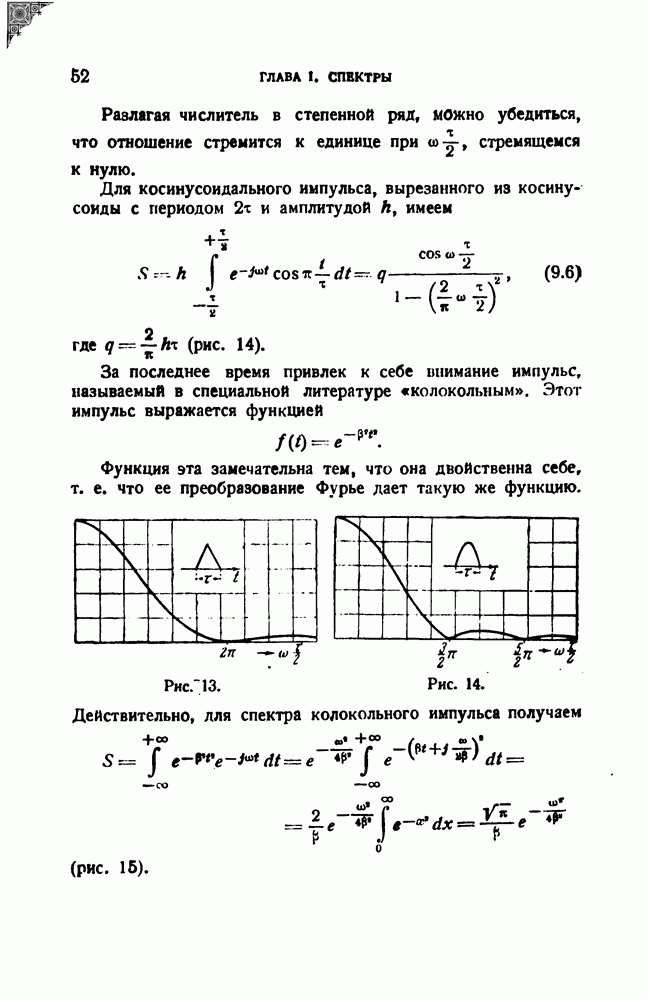
- § 9. Спектры некоторых импульсов
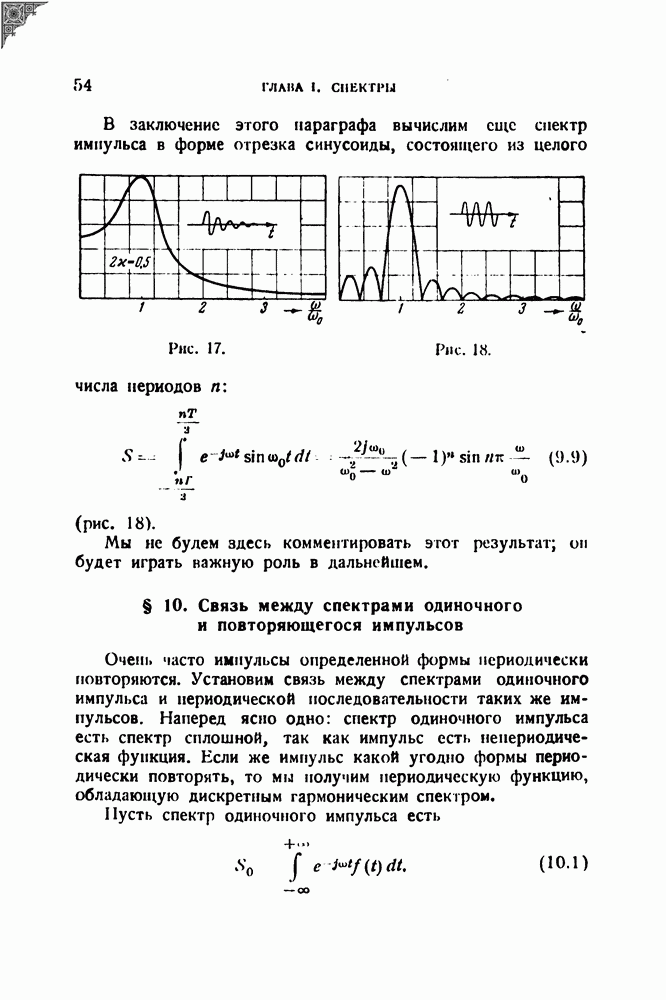
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
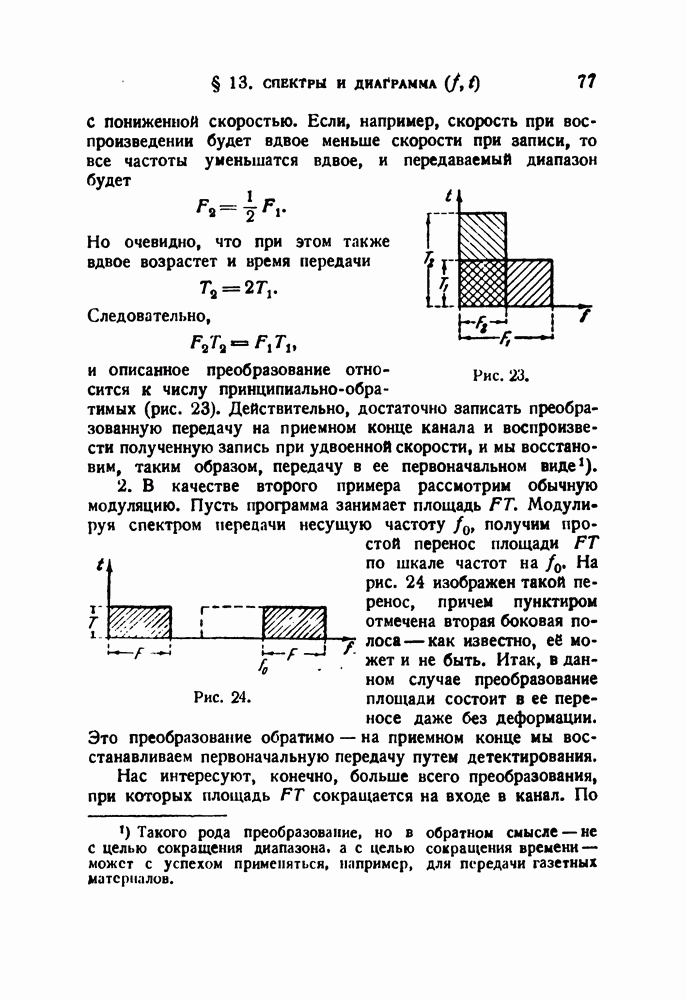
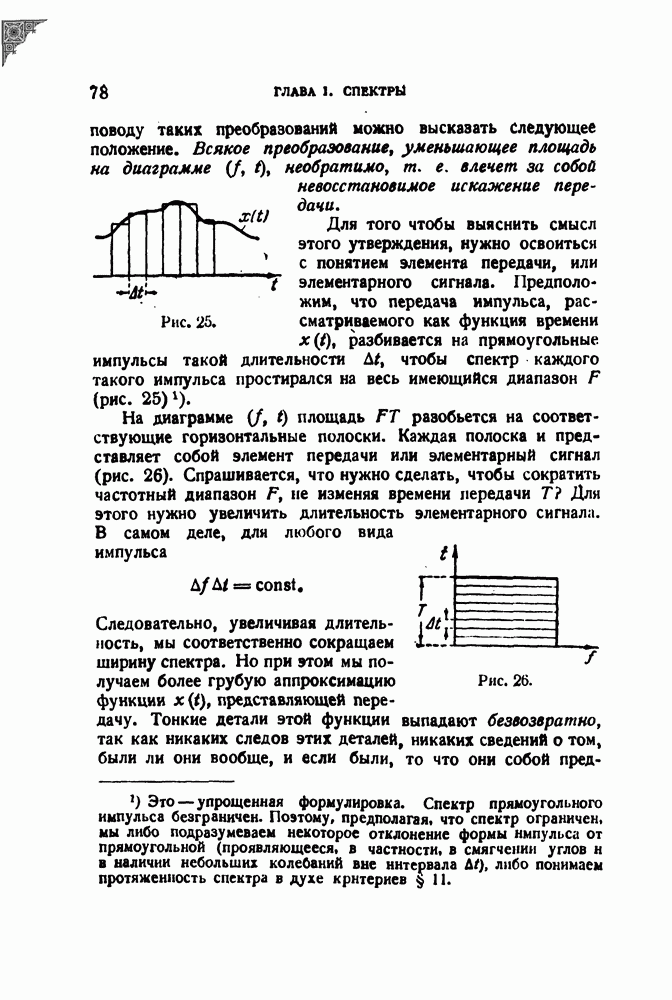
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
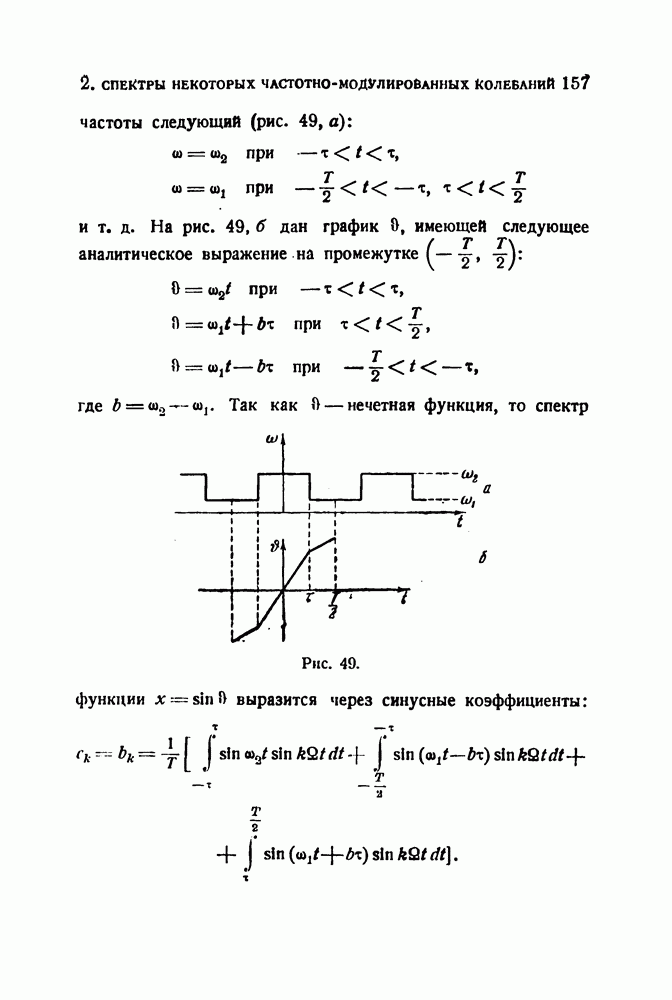
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА