| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Некоторые теоремы о спектрах
Мы выведем теперь несколько общих теорем о спектрах, основанных на свойствах преобразования Фурье. Эти теоремы сходны с теоремами операционного исчисления и выводятся аналогичным путем: ведь преобразование Фурье и преобразование Лапласа, составляющее основу операционного исчисления, находятся в близком родстве между собой.
Прежде нсего отметим, что преобразование Фурье линейно. Из этого непосредственно следует, что к нему применим принцип наложения. Это обстоятельство можно выразить следующим соотношением:

Смысл соотношения (5.1) может быть кратко выражен так: спектр суммы равен сумме спектров.
Теперь докажем теорему о спектре производной: если комплексный спектр функции  есть
есть  то комплексный спектр — есть
то комплексный спектр — есть  комплексный спектр производной получается из комплексного спектра функции умножением на
комплексный спектр производной получается из комплексного спектра функции умножением на 
Для доказательства составим выражение

и проинтегрируем его но частям. Получим

Так как функция, представимая интегралом Фурье, обращается в нуль при  то имеем
то имеем

Это доказательство может быть распространено на случай  производной. Проделав интегрирование по частям
производной. Проделав интегрирование по частям  раз, получим комплексный спектр
раз, получим комплексный спектр  производной (при условии, что все производные функции до
производной (при условии, что все производные функции до  порядка включительно обращаются в нуль при
порядка включительно обращаются в нуль при 

Подобным же образом может быть выведено выражение для комплексного спектра интеграла от данной функции. Составляя выражение

и интегрируя его по частям, находим

при условии, что

Это условие выполняется, например, для всякой нечетной функции, интегрируемой в бесконечных пределах.
Выведем теперь выражение для комплексного спектра функции, отличающейся от исходной запаздыванием на время т. Мы можем записать

Путем простой замены переменной по формуле  мы приходим к результату
мы приходим к результату

Нели в этом соотношении перейти от комплексных спектров к их модулям, то получим

т. е. при запаздывании — или вообще при смещении функции но шкале времен — спектр ее остается неизменным. Иначе говоря, спектр не зависит от выбора начального момента для отсчета времен, чего и следовало ожидать.
Следующая теорема относится к транспозиции (переносу) спектров. Вопрос ставится следующим образом: какой функции соответствует спектр, смещенный но шкале частот на  ? Так как
? Так как

то, следовательно, требуемого вида комплексным спектром обладает функция

Выведем некоторые более сложные соотношения. Возьмем выражение интеграла Фурье

умножим обе части на  и проинтегрируем по
и проинтегрируем по  в пределах
в пределах  Получим
Получим

Изменим порядок интегрирования в правой части:

Таким образом,

Эта известная формула аналогична операционному соотношению, выведенному Римским-Корсаковым [19]. Ома годится, например, для вычисления энергии, если известны спектры скорости и силы или тока и напряжения, или любых двух других функций, произведение которых выражает мощность.
В вещественной форме формула (5.7) может быть представлена в виде (учитывая, что 

для частного случая 

Последнее соотношение известно под названием теоремы Рэйли. Нам предстоит им пользоваться в дальнейшем.
Далее, перепишем формулу (5.7) в новых обозначениях

и определим функцию  соотношением
соотношением

Если обозначить через  спектр функции
спектр функции  то на основании теоремы (5.6) будем иметь
то на основании теоремы (5.6) будем иметь

и, следовательно,

Таким образом, если  — соответственно спектры функций
— соответственно спектры функций  — спектр произведения
— спектр произведения  то имеем
то имеем

Это соотношение, подобное операционной теореме Гринберга [9], выражает спектр произведения двух функций через спектры каждой из них.
Выведем, наконец, еще одну формулу. Обозначим

и вычислим спектр этой функции

Здесь после перемены порядка интегрирования сделана замена переменной по формуле 
Итак, спектр функции  есть
есть

Соотношение (5.11) подобно известной из операционного исчисления теореме свертывания, или теореме Бореля. Это соотношение дает возможность найти функцию времени, спектр которой известен и выражается произведением спектров двух функций.
Применение соотношений (5.1) — (5.11) может в значительной степени облегчить вычисление спектров различных функций.
В заключение настоящего параграфа следует указать на одно интересное обстоятельство. Применяя разложение Фурье, мы имеем дело с парой преобразований Фурье:

В этих формулах обращает на себя внимание то, что время  и круговая частота
и круговая частота  входят в них симметричным
входят в них симметричным
образом на равных началах. Но из полной симметрии формул (5.12) следует также, что всякая теорема теории спектров имеет парную теорему, не требующую особого доказательства и получаемую из данной теоремы простой формальной заменой переменной  переменной
переменной  и функций времени — соответствующими спектральными плотностями.
и функций времени — соответствующими спектральными плотностями.
Пересматривая теоремы настоящего параграфа, мы убеждаемся в том, что они имеют парный характер. Для иллюстрации этого можно записать некоторые из них в форме таблицы:
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
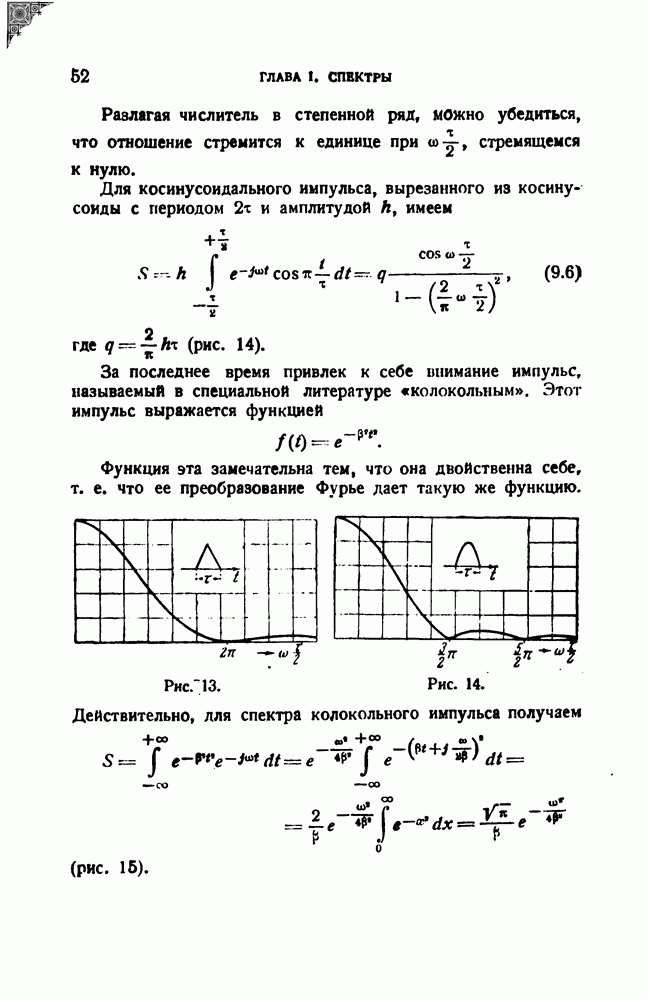
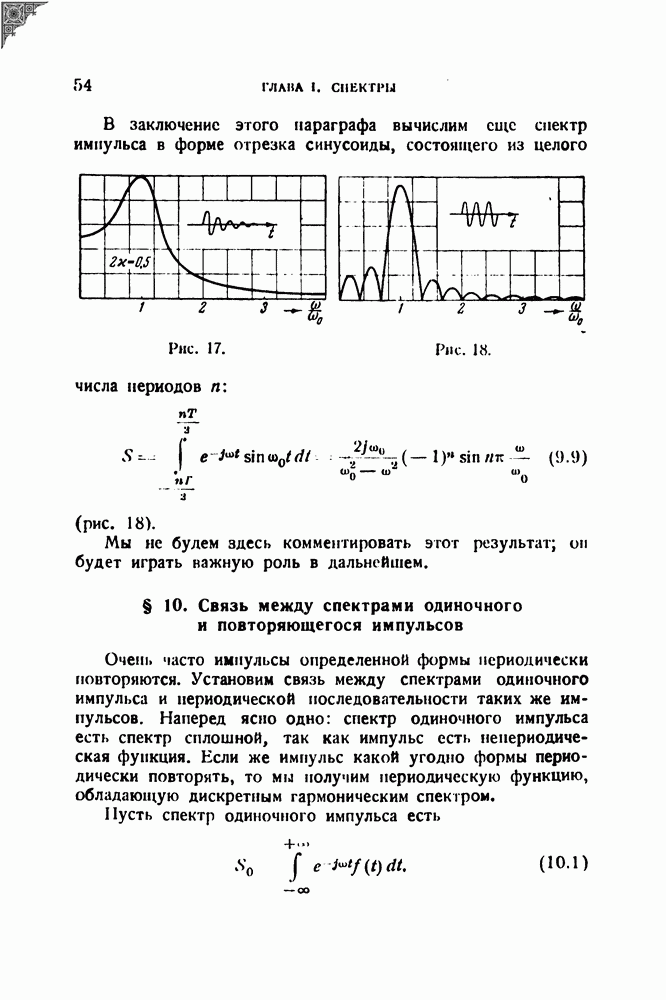
- § 9. Спектры некоторых импульсов
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
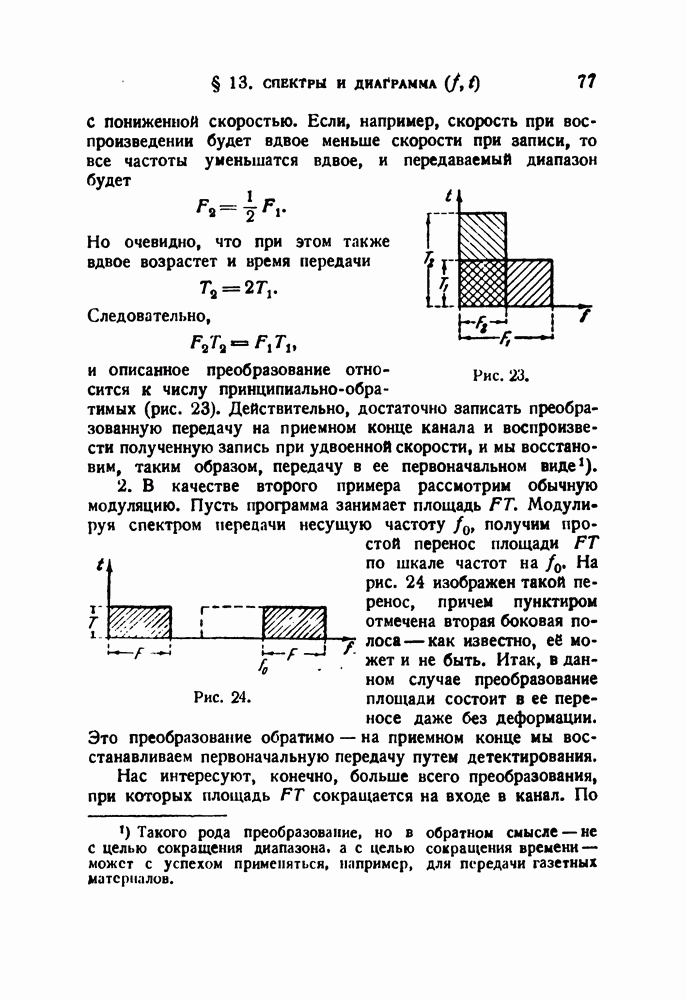
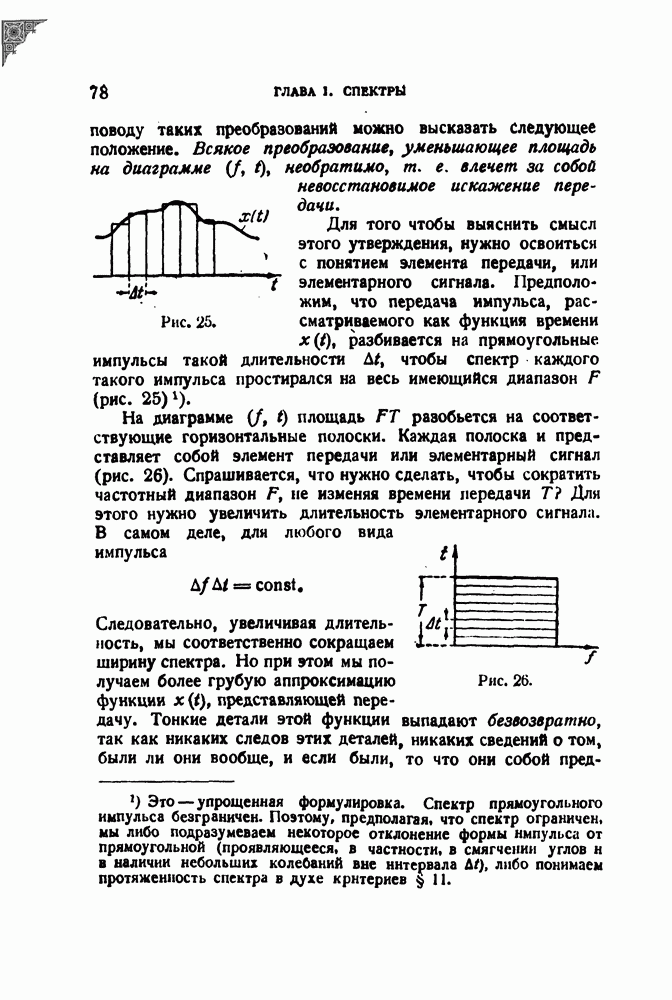
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА