| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Преобразование спектров при детектировании
Если некоторое периодическое колебание х подвергнуть нелинейной операции

то полученное в результате этой операции колебание у будет обладать спектром, отличным от спектра  , как правило, более богатым. Так, например, если первоначальное колебание представляет собой сумму двух синусоид
, как правило, более богатым. Так, например, если первоначальное колебание представляет собой сумму двух синусоид

и, следовательно, имеет спектр, состоящий из двух спектральных линий, то после нелинейной операции  мы получим в составе колебания у спектральные составляющие с частотами
мы получим в составе колебания у спектральные составляющие с частотами

где  в общем случае любые положительные целые числа. Такого рода спектр носит название комбинационного, а частоты
в общем случае любые положительные целые числа. Такого рода спектр носит название комбинационного, а частоты  называются комбинационными частотами.
называются комбинационными частотами.
Таким изменением спектра пользуются для измерения степени отклонения данной системы от линейности. На вход системы подается колебание  изучается спектр получаемого на выходе колебания у. Комбинационные частоты не возникают в том единственном случае, когда 9 (выражающая в данном случае характеристику исследуемой системы) — линейная функция.
изучается спектр получаемого на выходе колебания у. Комбинационные частоты не возникают в том единственном случае, когда 9 (выражающая в данном случае характеристику исследуемой системы) — линейная функция.
Специальный вид нелинейной операции, преобразовывающей спектр, называется детектированием. В составе модулированного колебания составляющей с частотой модуляции нет. Но эта составляющая нам нужна, так как она - то и представляет собой передаваемый сигнал. Для того чтобы она вновь появилась, нужно подвергнуть модулированное колебание некоторой нелинейной операции. Эта операция, имеющая целью образование составляющей с частотой модуляции, и носит название детектирования (детектирование — обнаружение). В результате детектирования получается сложное колебание, в состав которого входит в качестве одной из составляющих интересующее нас колебание с частотой модуляции. Дальнейшее разделение слагаемых не представляет уже никаких затруднений.
Рассмотрение вопросов детектирования в общем виде было бы очень громоздким; мы ограничимся несколькими простейшими примерами.
Рассмотрим простое АМ колебание при синусоидальной модуляции. Первоначально мы имели колебание несущей частоты  и модулирующее колебание
и модулирующее колебание  . В результате нелинейной операции, которую мы называем модуляцией, оба эти колебания оказываются перемноженными, и мы имеем
. В результате нелинейной операции, которую мы называем модуляцией, оба эти колебания оказываются перемноженными, и мы имеем

В составе полезного колебания, как мы знаем, уже нет составляющей с частотой  ; спектр
; спектр  состоит из трех линий с частотами
состоит из трех линий с частотами 
Если мы желаем теперь снова получить колебание с частотой  , то мы должны соответствующим образом продетектировать х.
, то мы должны соответствующим образом продетектировать х.
Операция детектирования в данном случае выполняет действие, обратное операции модуляции, поэтому в применении к модулированным сигналам детектирование называют иногда демодуляцией. Мы будем рассматривать только два основных вида детекторов: «линейный» детектор

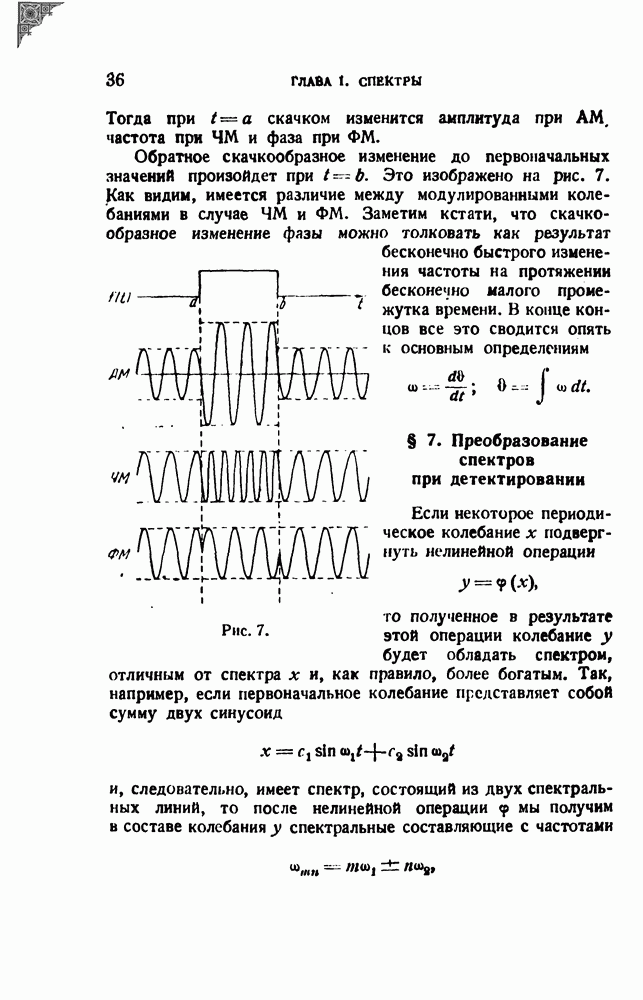
(рис. 8, а) и квадратичный детектор

(рис. 8, б). Слово линейный поставлено для первого раза в кавычки, чтобы подчеркнуть, что на самом деле линейный детектор нелинеен, и что линейный в подлинном смысле детектор невозможен (т. е. линейная система не детектирует).

Рис. 8.
Для детектирования модулированного колебания пригодно линейное детектирование. Воспользовавшись тем, что абсолютная величина произведения равна произведению абсолютных величин сомножителей, можем записать

Но функция  может быть представлена следующим рядом Фурье:
может быть представлена следующим рядом Фурье:

откуда

В этом выражении первый член (в квадратных скобках) — модулирующая функция, которую мы и стремились получить; второй член объединяет под энаком суммы составляющие высоких частот  которые нетрудно отделить.
которые нетрудно отделить.
Если бы мы подвергли модулированное колебание квадратичному детектированию, то получили бы

Таким образом, в этом случае кроме постоянной составляющей  и пяти спектральных линий с высокими частотами
и пяти спектральных линий с высокими частотами

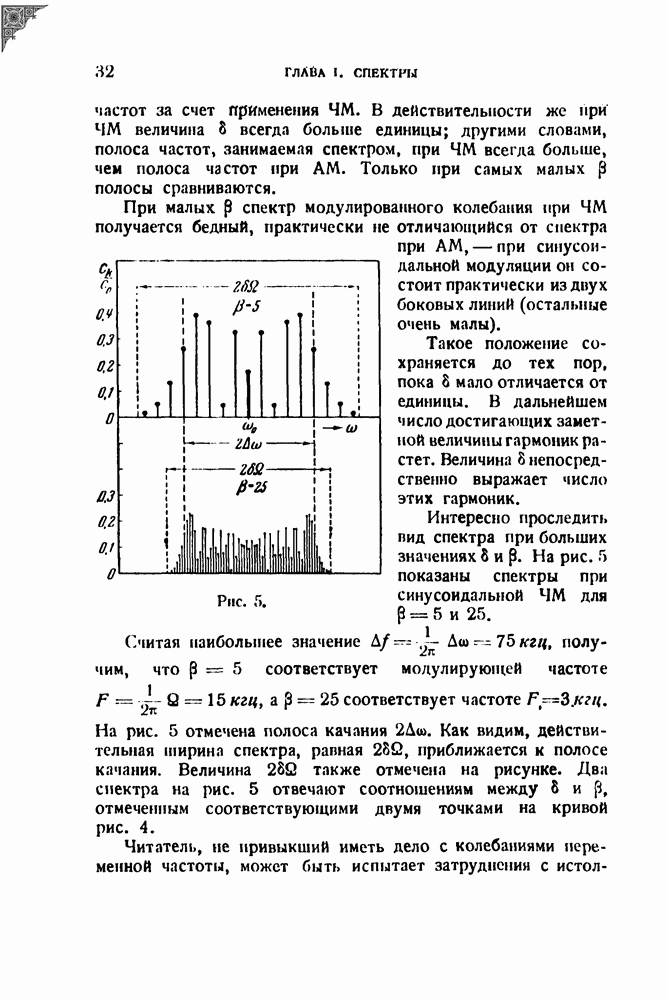
мы получаем две спектральные линии с низкими частотами 9 и 29. Следовательно, спектр модулирующего колебания, состоявший первоначально из одной линии с частотой О, оказывается искаженным, и данный вид детектирования может применяться только при очень малой глубине модуляции (так как отношение амплитуд второй и первой гармоник равно 
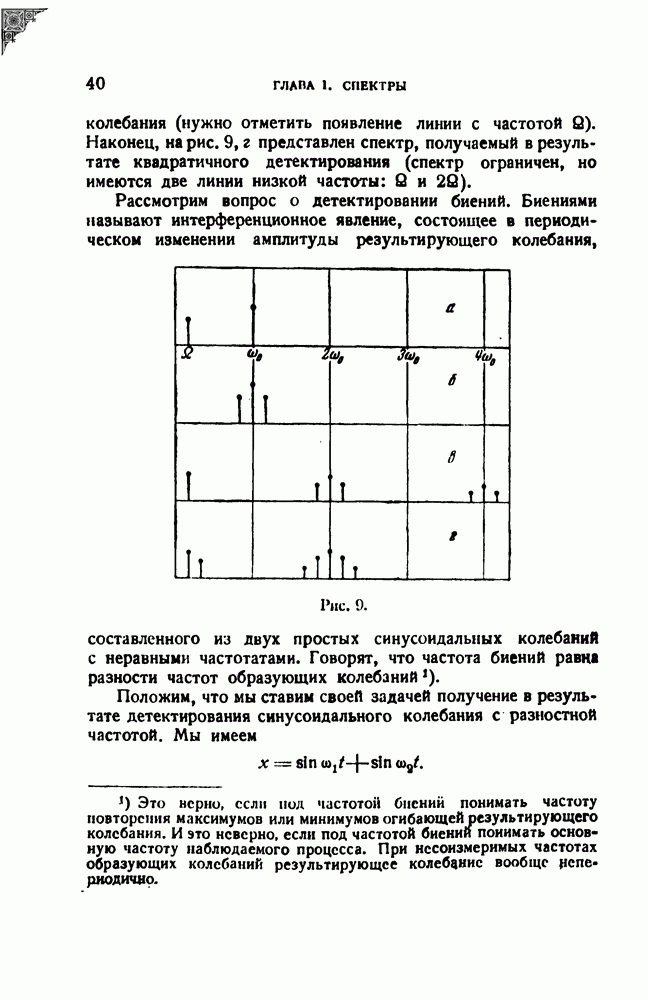
На рис. 9 изображены разобранные случаи. На рис. 9, а представлены два исходных колебания — несущая частота  и модулирующая частота
и модулирующая частота  на рис. 9, б изображен спектр модулированного колебания — несущая частота и два спутника, на рис. 9, в представлен спектр колебания, получаемого в результате линейного детектирования модулированного
на рис. 9, б изображен спектр модулированного колебания — несущая частота и два спутника, на рис. 9, в представлен спектр колебания, получаемого в результате линейного детектирования модулированного
колебания (нужно отметить появление линии с частотой  Наконец, на рис. 9, г представлен спектр, получаемый в результате квадратичного детектирования (спектр ограничен, но имеются две линии низкой частоты:
Наконец, на рис. 9, г представлен спектр, получаемый в результате квадратичного детектирования (спектр ограничен, но имеются две линии низкой частоты:  и
и 
Рассмотрим вопрос о детектировании биений. Биениями называют интерференционное явление, состоящее в периодическом изменении амплитуды результирующего колебания, составленного из двух простых синусоидальных колебаний с неравными частотатами. Говорят, что частота биений равна разности частот образующих колебаний
Рис. 9. (см. скан)
Положим, что мы ставим своей задачей получение в результате детектирования синусоидального колебания с разностной частотой. Мы имеем

В данном случае следует применить квадратичное детектирование, которое дает

Как видим, мы получили кроме постоянной составляющей и высоких частот  требуемое колебание с частотой
требуемое колебание с частотой  Линейное детектирование этого не дает. Мы получили бы, применив линейное детектирование,
Линейное детектирование этого не дает. Мы получили бы, применив линейное детектирование,

т. е. кроме постоянной составляющей и высоких частот мы имели бы бесконечный спектр низкочастотных слагаемых с частотами 
Квадратичное детектирование дает при детектировании биений нужный результат и в том более сложном случае, когда амплитуды образующих колебаний не равны, т. е. когда

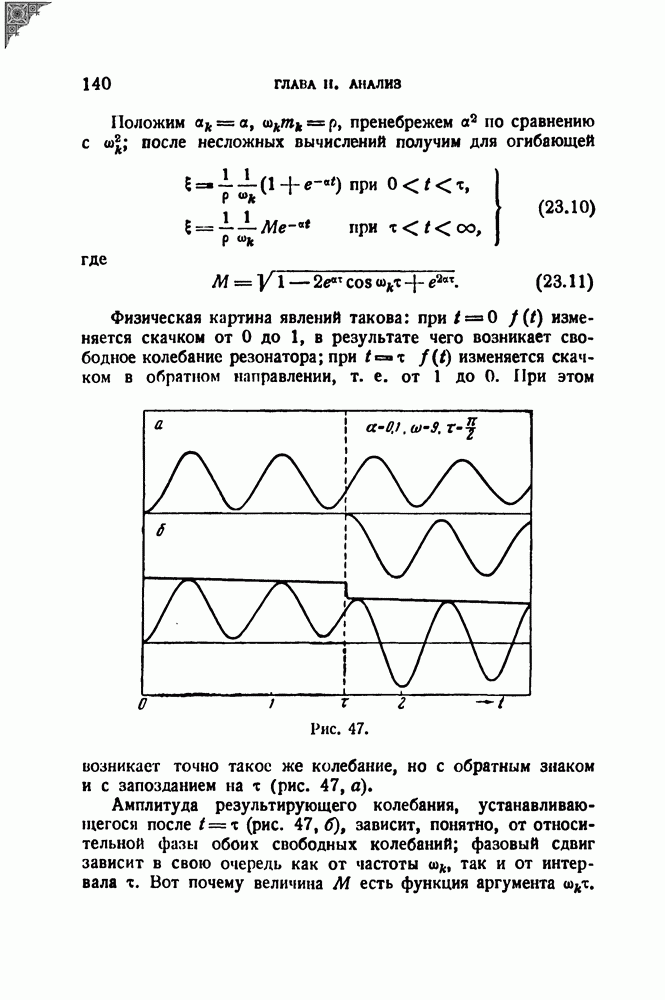
 Форма результирующего колебания в этом случае настолько сходна с формой модулированного колебания, что естественно возникает вопрос: в чем же разница между этими двумя видами колебаний? Разница заключается в огибающих. В то время как огибающая модулированного колебания воспроизводит форму модулирующей функции и, значит, при синусоидальной модуляции эта огибающая синусоидальна, огибающая биений несинусоидальна. Выражение для огибающей
Форма результирующего колебания в этом случае настолько сходна с формой модулированного колебания, что естественно возникает вопрос: в чем же разница между этими двумя видами колебаний? Разница заключается в огибающих. В то время как огибающая модулированного колебания воспроизводит форму модулирующей функции и, значит, при синусоидальной модуляции эта огибающая синусоидальна, огибающая биений несинусоидальна. Выражение для огибающей
биений при равенстве амплитуд есть

Если возвести эту величину в квадрат, то получим

Если амплитуды не равны, то для огибающей получается

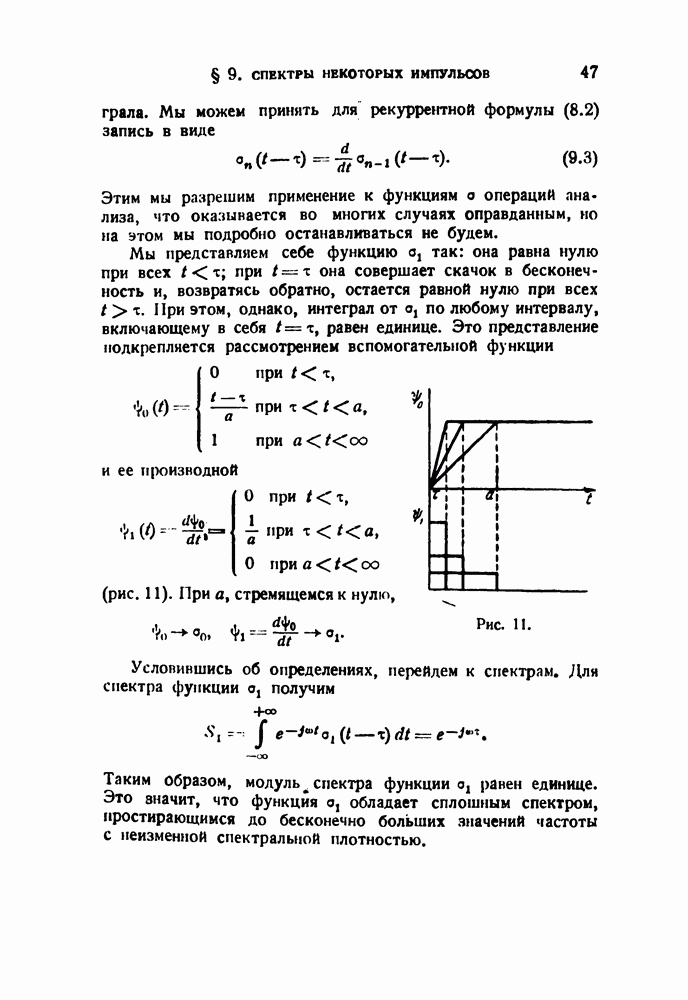
Это выражение проще всего получить из построения (рис. 10). Возводя в квадрат, получаем

Только в пределе при очень малых или очень больших  огибающая биений приближается к синусоиде. При
огибающая биений приближается к синусоиде. При 

и следовательно, при таких условиях можно применять и линейное детектирование. Кривая биений при этом не отличается от кривой синусоидально - модулированного колебания при малой глубине модуляции. Совершенно так же обстоит дело и при  .
.

В общем, можно кратко сказать, что при детектировании по закону  мы получаем в составе колебания слагаемое
мы получаем в составе колебания слагаемое  где
где  — огибающая детектируемого колебания.
— огибающая детектируемого колебания.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
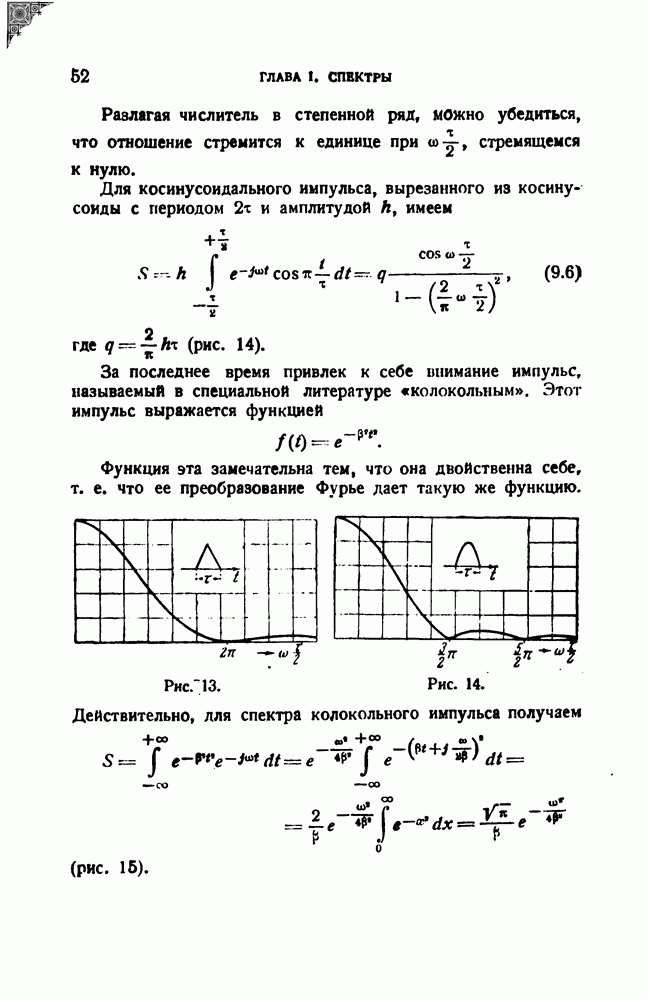
- § 9. Спектры некоторых импульсов
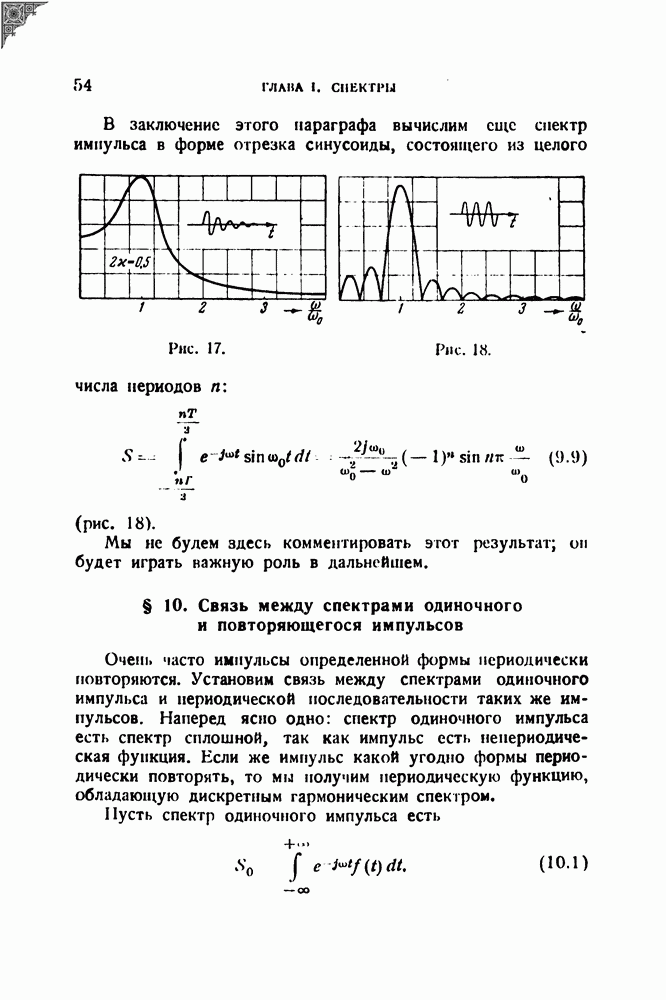
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
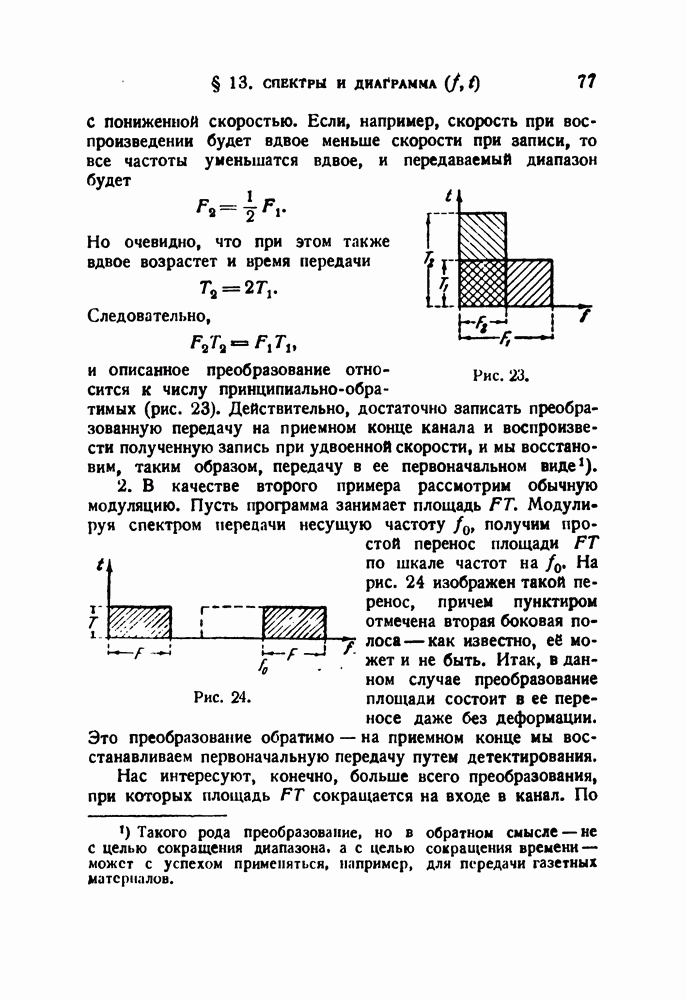
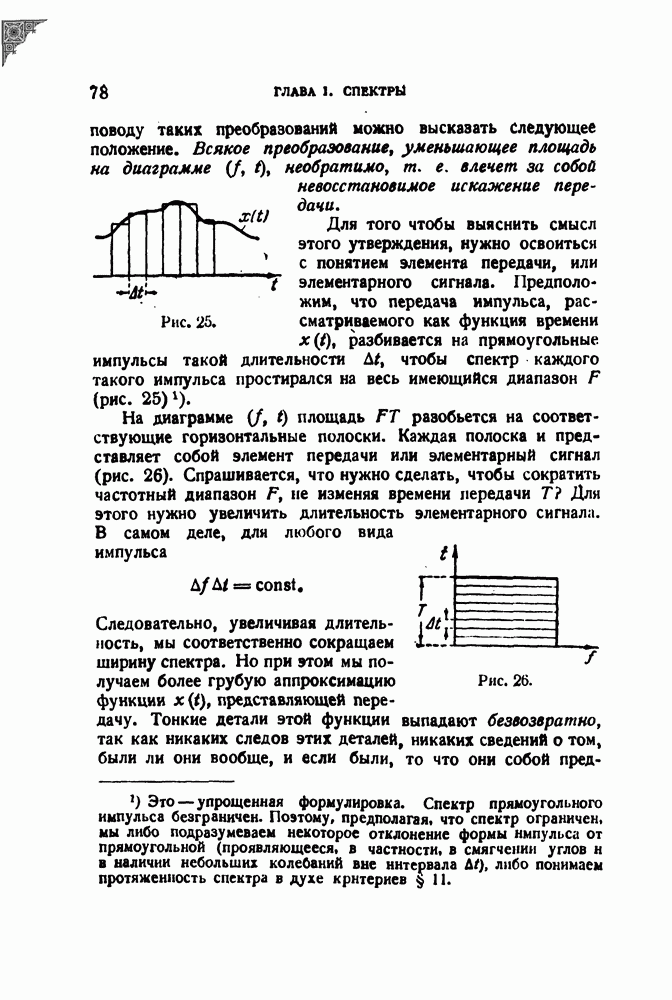
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
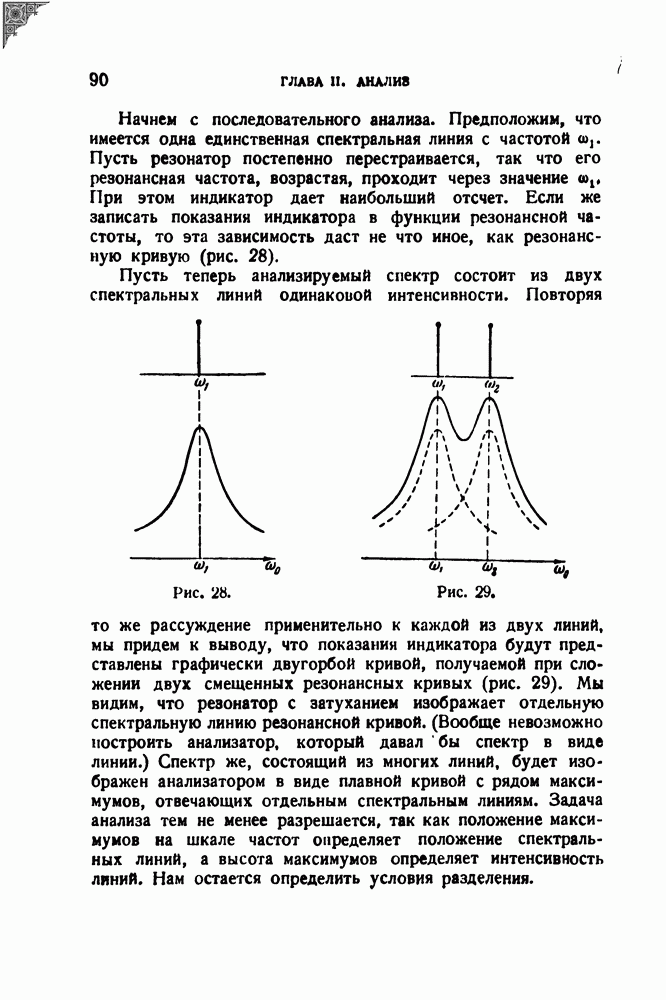
- § 16. Одновременный и последовательный анализ
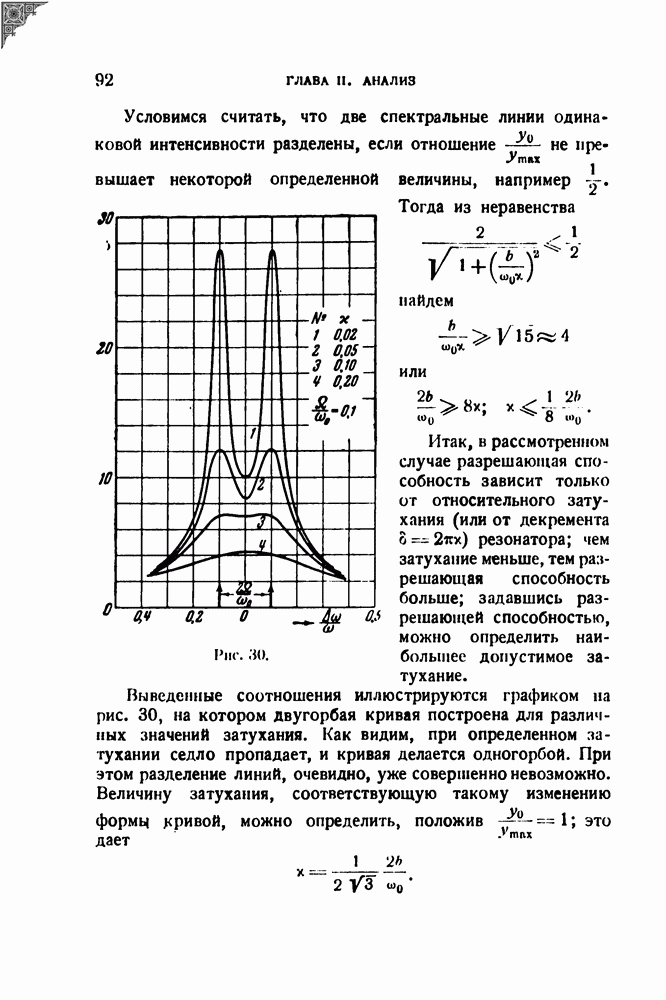
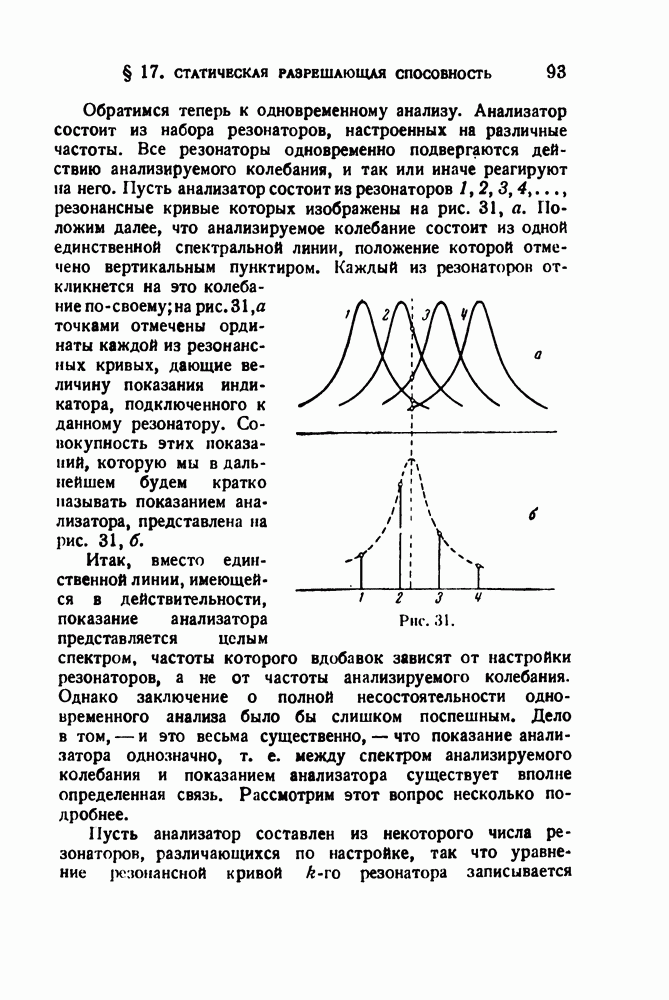
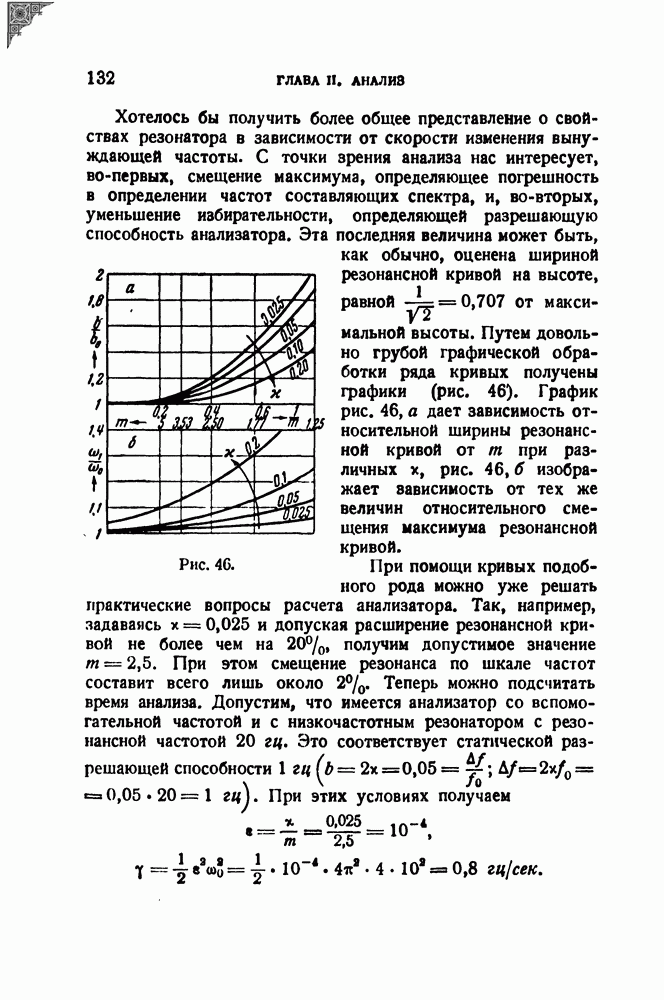
- § 17. Статическая разрешающая способность и погрешность анализатора
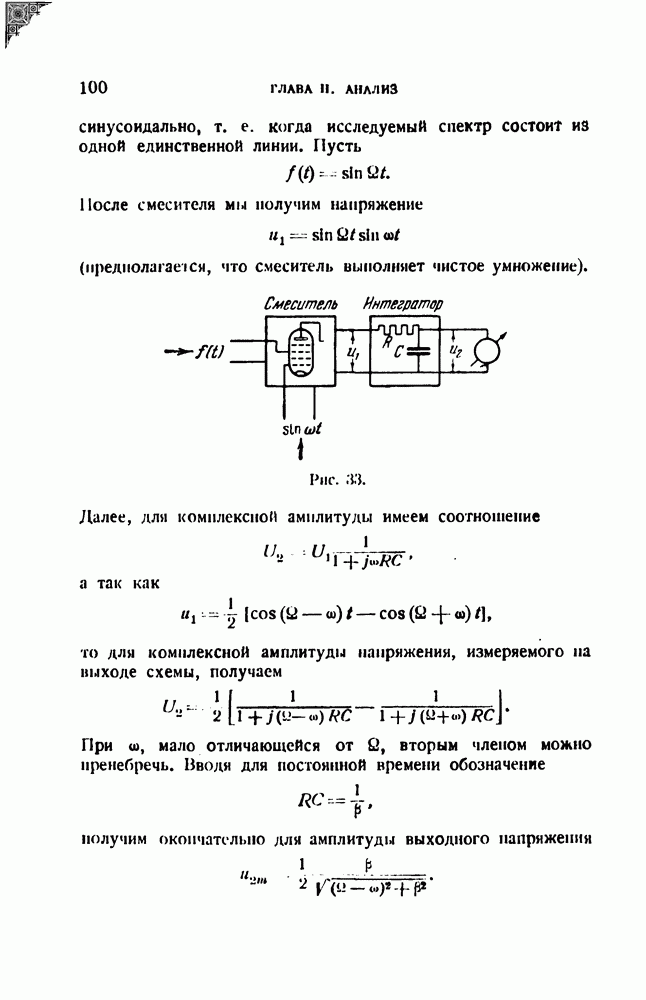
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
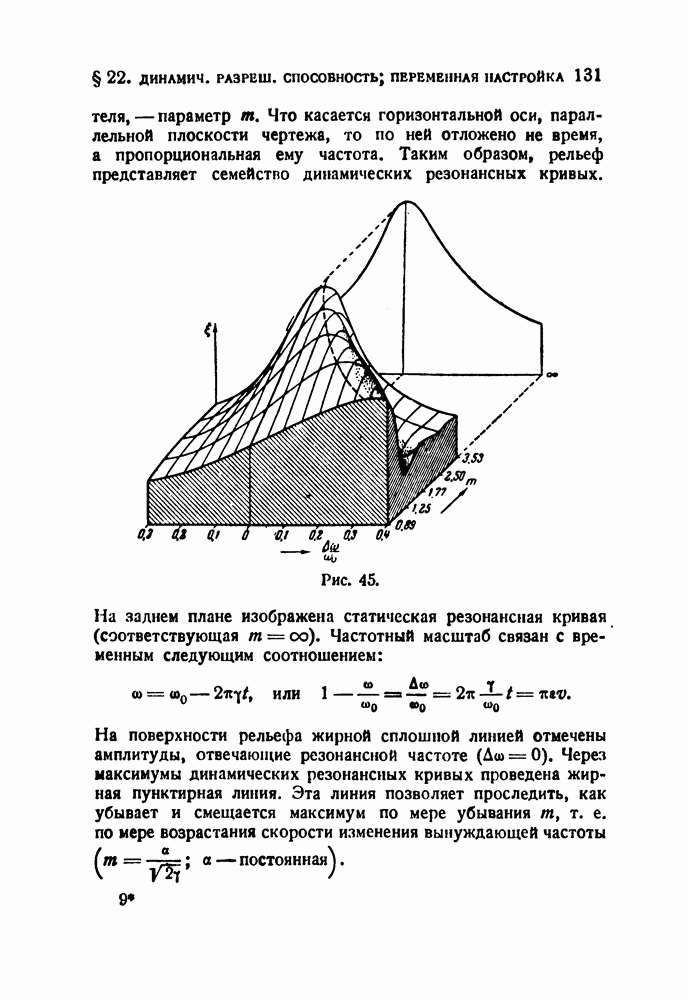
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
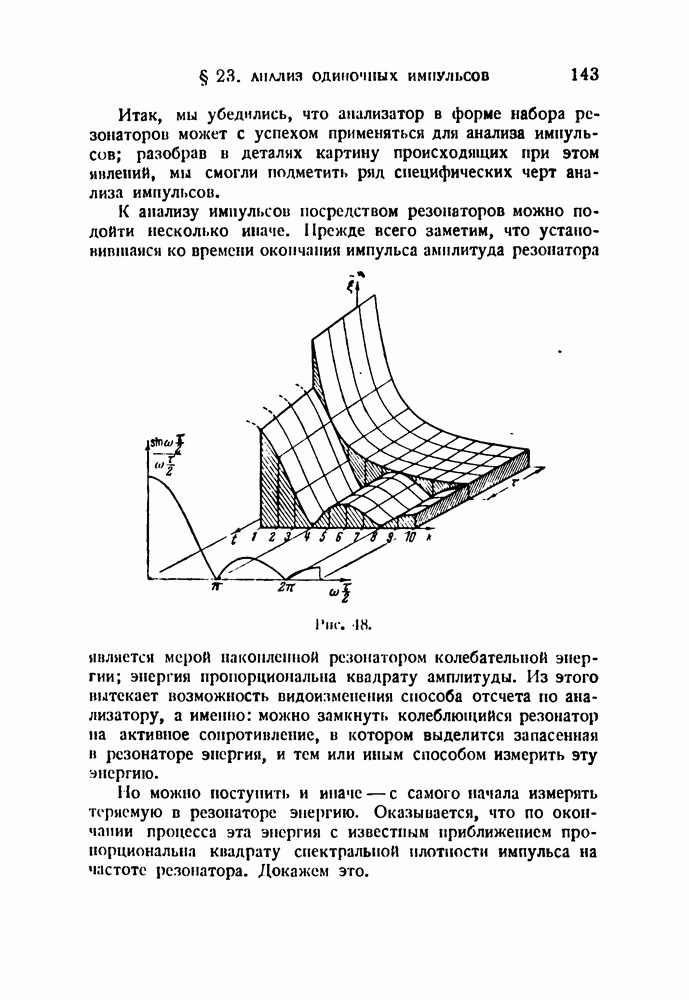
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
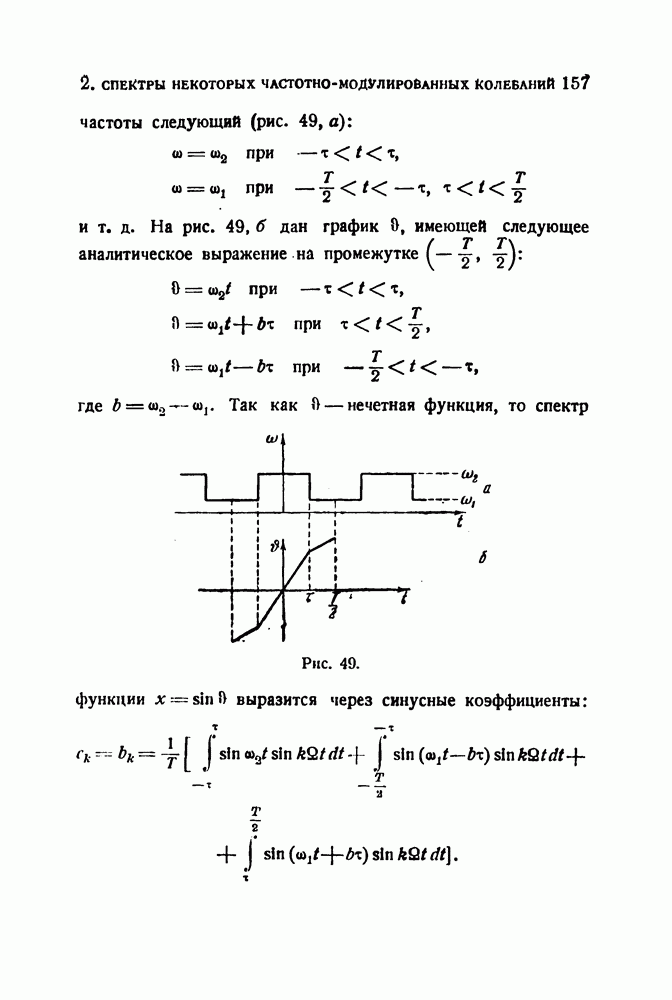
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
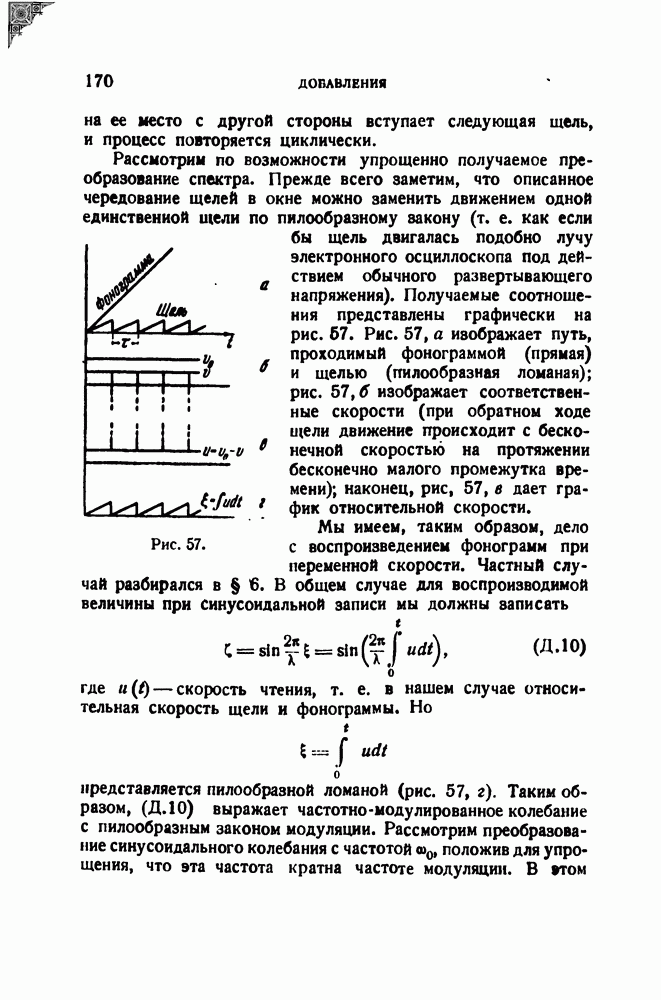
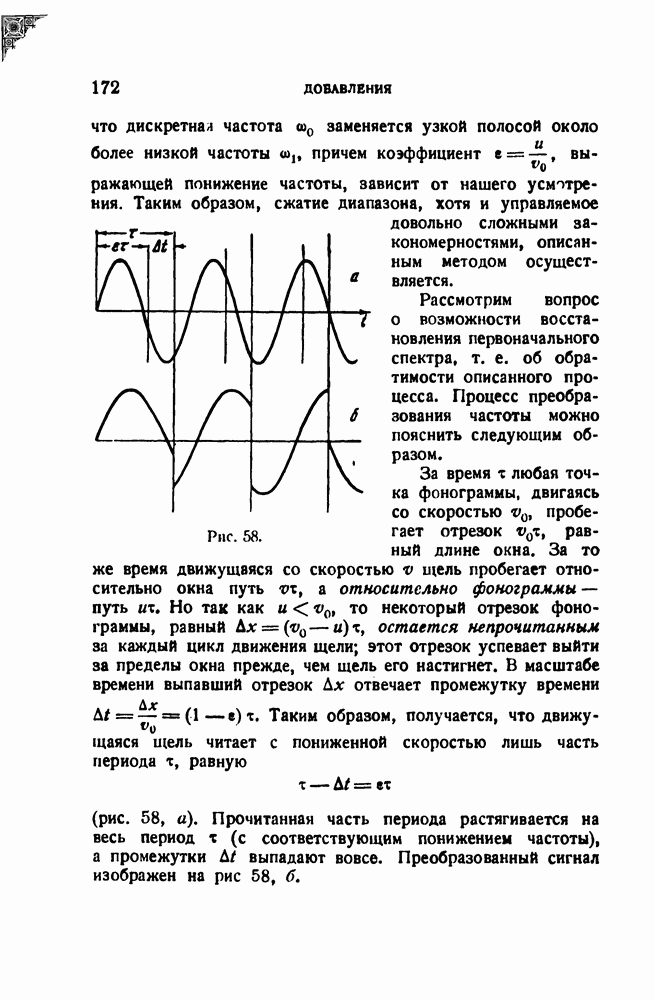
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА