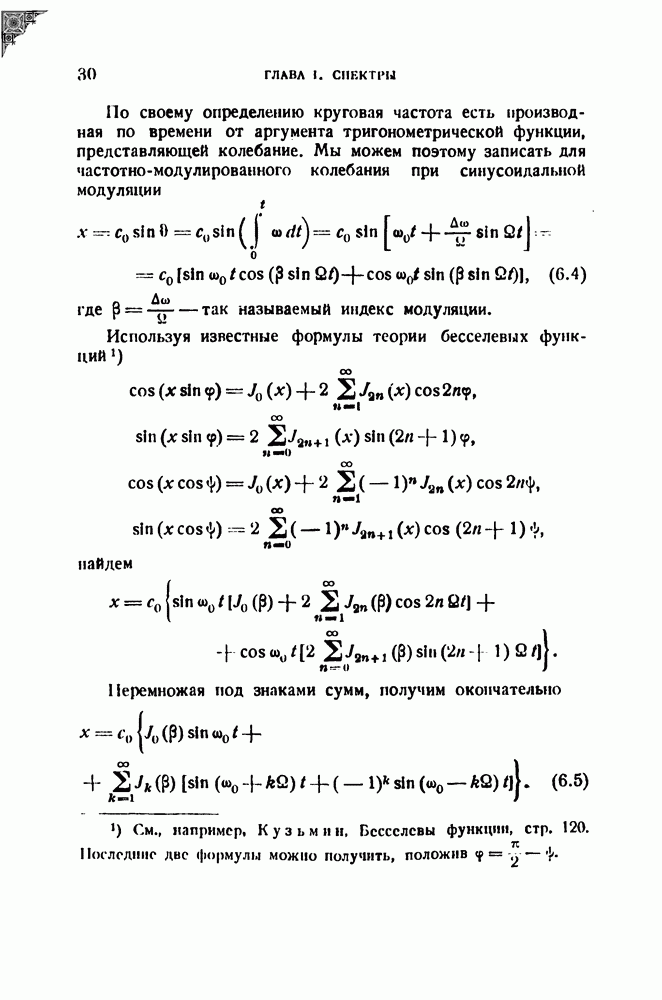| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 17. Статическая разрешающая способность и погрешность анализатора
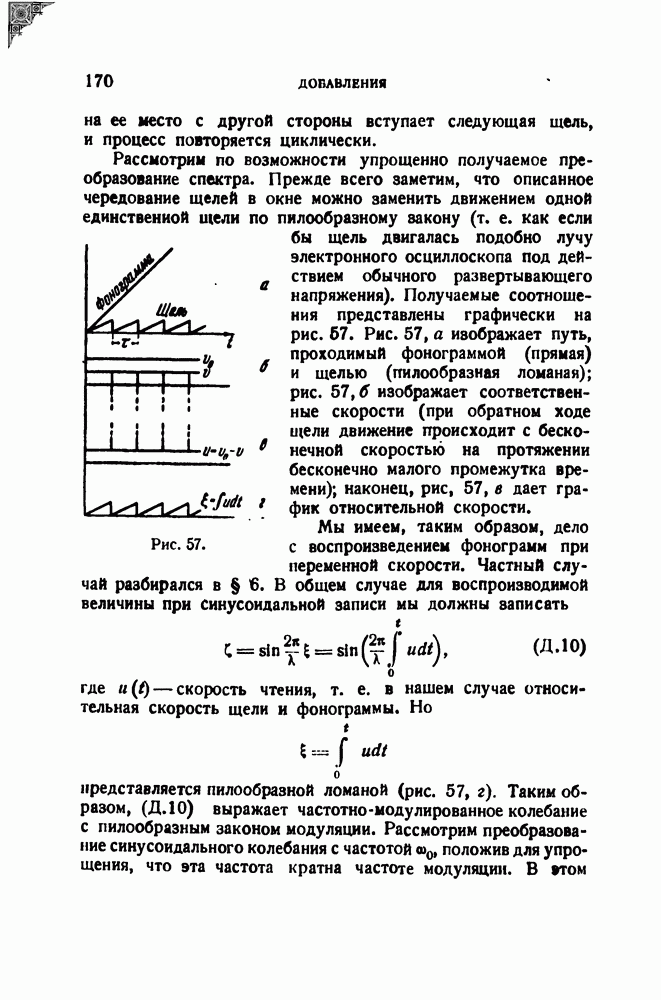
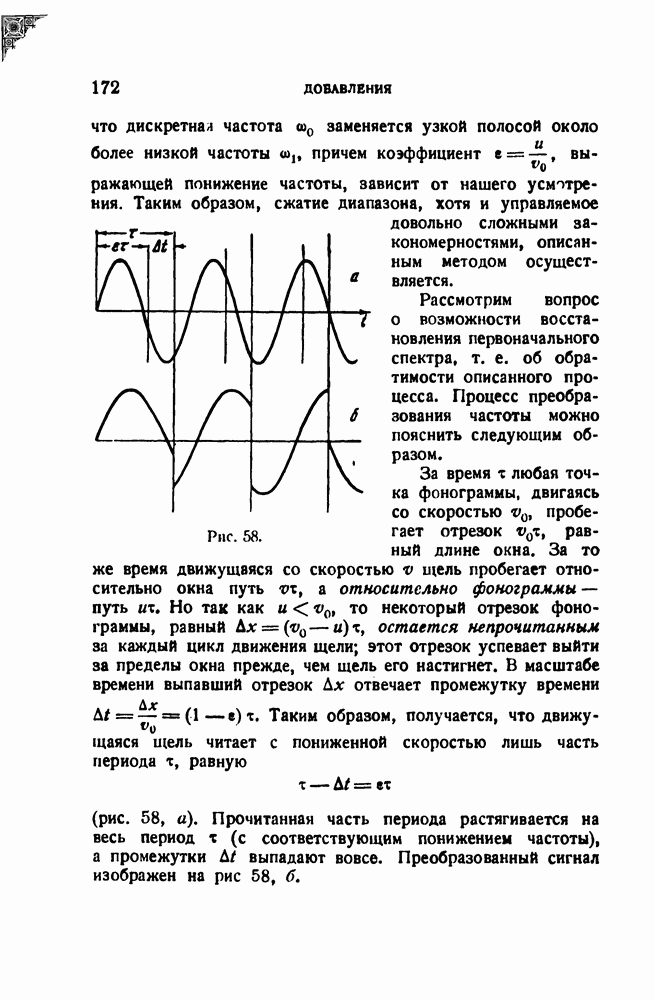
Разрешающая способность — важнейшая метрологическая характеристика анализатора. Под разрешающей способностью анализатора понимается вообще способность его разрешить (или разделить) две соседние спектральные линии. Количественной мерой разрешающей способности является наименьший интервал по частоте между двумя спектральными линиями, при котором они еще разделяются анализатором. Нужно определенным образом условиться, при каких обстоятельствах мы будем считать линии разделенными. Для этого нужно рассмотреть процесс анализа подробнее.
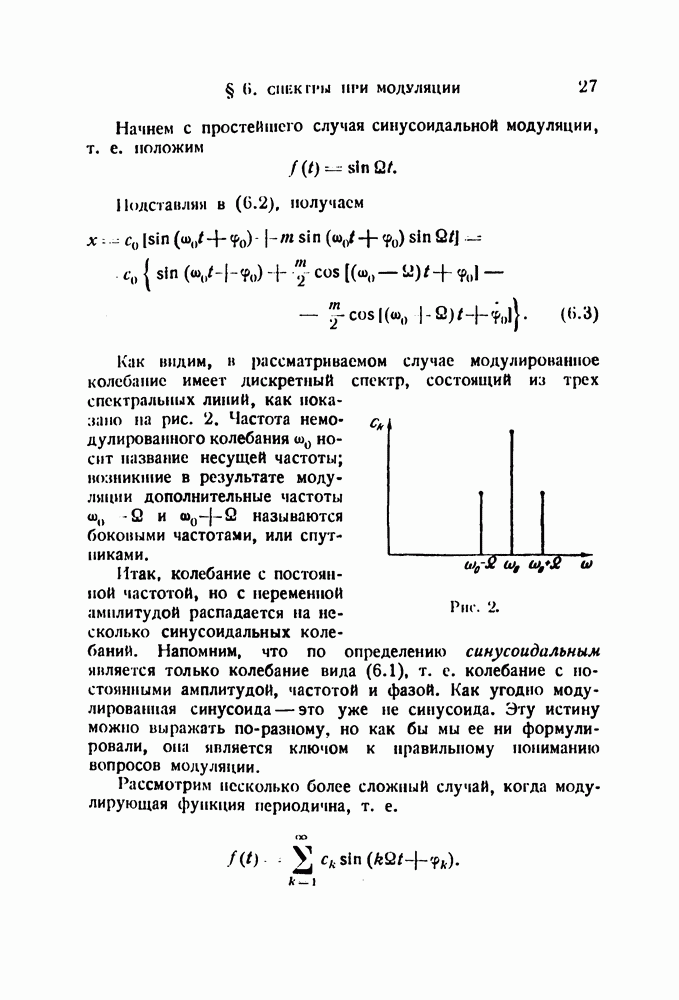
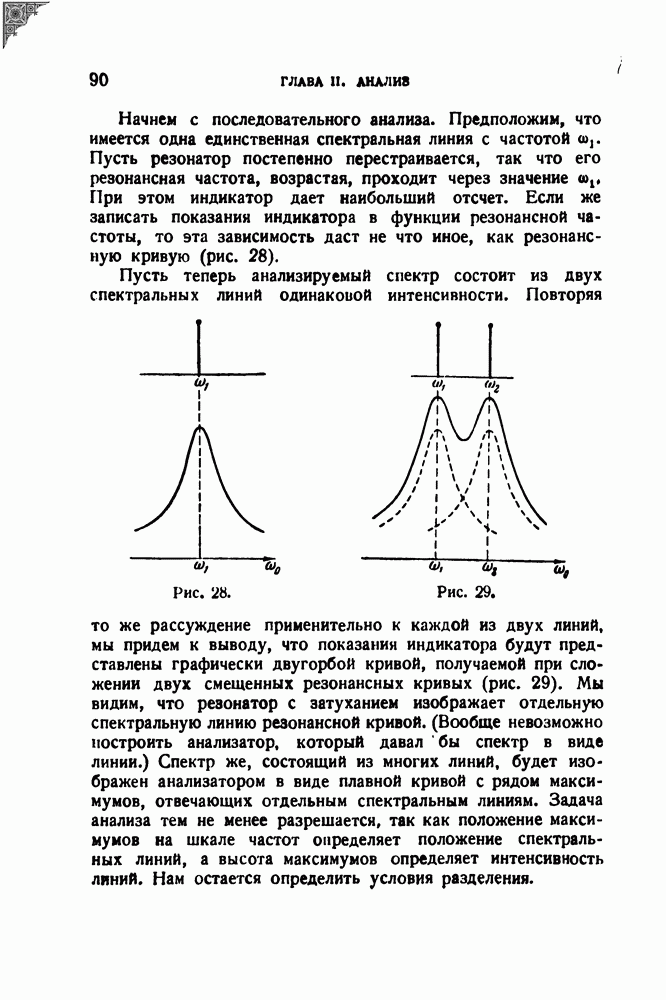
Начнем с последовательного анализа. Предположим, что имеется одна единственная спектральная линия с частотой  Пусть резонатор постепенно перестраивается, так что его резонансная частота, возрастая, проходит через значение
Пусть резонатор постепенно перестраивается, так что его резонансная частота, возрастая, проходит через значение  При этом индикатор дает наибольший отсчет. Если же записать показания индикатора в функции резонансной частоты, то эта зависимость даст не что иное, как резонансную кривую (рис. 28).
При этом индикатор дает наибольший отсчет. Если же записать показания индикатора в функции резонансной частоты, то эта зависимость даст не что иное, как резонансную кривую (рис. 28).

Рис. 28.

Рис. 29.
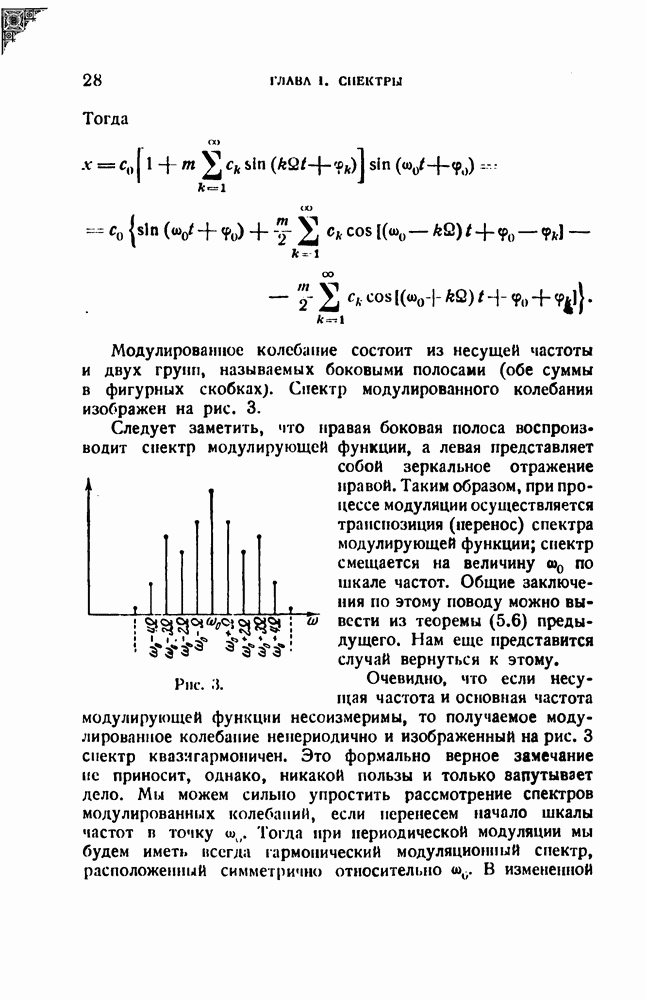
Пусть теперь анализируемый спектр состоит из двух спектральных линий одинаковой интенсивности. Повторяя то же рассуждение применительно к каждой из двух линий, мы придем к выводу, что показания индикатора будут представлены графически двугорбой кривой, получаемой при сложении двух смещенных резонансных кривых (рис. 29). Мы видим, что резонатор с затуханием изображает отдельную спектральную линию резонансной кривой. (Вообще невозможно построить анализатор, который давал бы спектр в виде линии.) Спектр же, состоящий из многих линий, будет изо-бражен анализатором в виде плавной кривой с рядом максимумов, отвечающих отдельным спектральным линиям. Задача анализа тем не менее разрешается, так как положение максимумов на шкале частот определяет положение спектральных линий, а высота максимумов определяет интенсивность линий. Нам остается определить условия разделения.
Для двух резонансных кривых рис. 29 можно записать

где х — относительное затухание резонатора. Введем

Тогда

и уравнение двугорбой кривой есть

При небольшом затухании максимумы кривой будут расположены на частотах  т. е. при
т. е. при  величина максимума приближенно равна
величина максимума приближенно равна

а ордината седловины, т. е. величина у при  или
или  равна
равна

Отношение ординаты седла к величине максимума равно

Мы видим, что отношение это зависит как от относительного расстояния между линиями  так и от затухания
так и от затухания  причем увеличение расстояния равносильно уменьшению затухания, и обратно.
причем увеличение расстояния равносильно уменьшению затухания, и обратно.
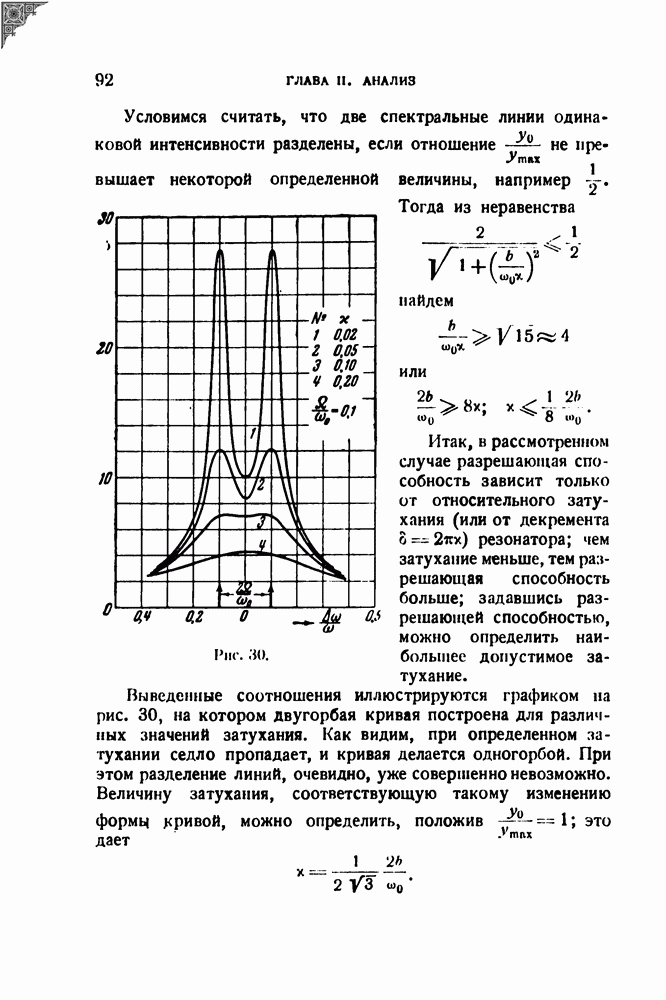
Условимся считать, что две спектральные линии одинаковой интенсивности разделены, если отношение  не превышает некоторой определенной величины, например
не превышает некоторой определенной величины, например 
Тогда из неравенства

найдем

или

Итак, в рассмотренном случае разрешающая способность зависит только  относительного затухания (или от декремента
относительного затухания (или от декремента  ) резонатора; чем затухание меньше, тем разрешающая способность больше; задавшись разрешающей способностью, можно определить наибольшее допустимое затухание.
) резонатора; чем затухание меньше, тем разрешающая способность больше; задавшись разрешающей способностью, можно определить наибольшее допустимое затухание.
Рис. 30. (см. скан)
Выведенные соотношения иллюстрируются графиком на рис. 30, на котором двугорбая кривая построена для различных значений затухания. Как видим, при определенном затухании седло пропадает, и кривая делается одногорбой. При этом разделение линий, очевидно, уже совершенно невозможно. Величину затухания, соответствующую такому изменению формы кривой, можно определить, положив  это дает
это дает

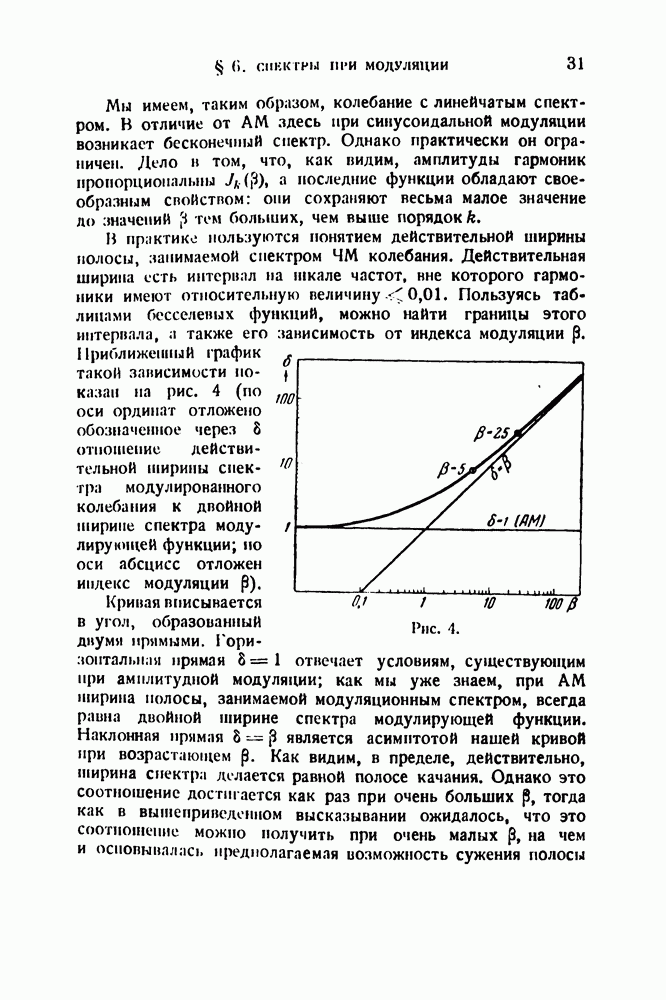
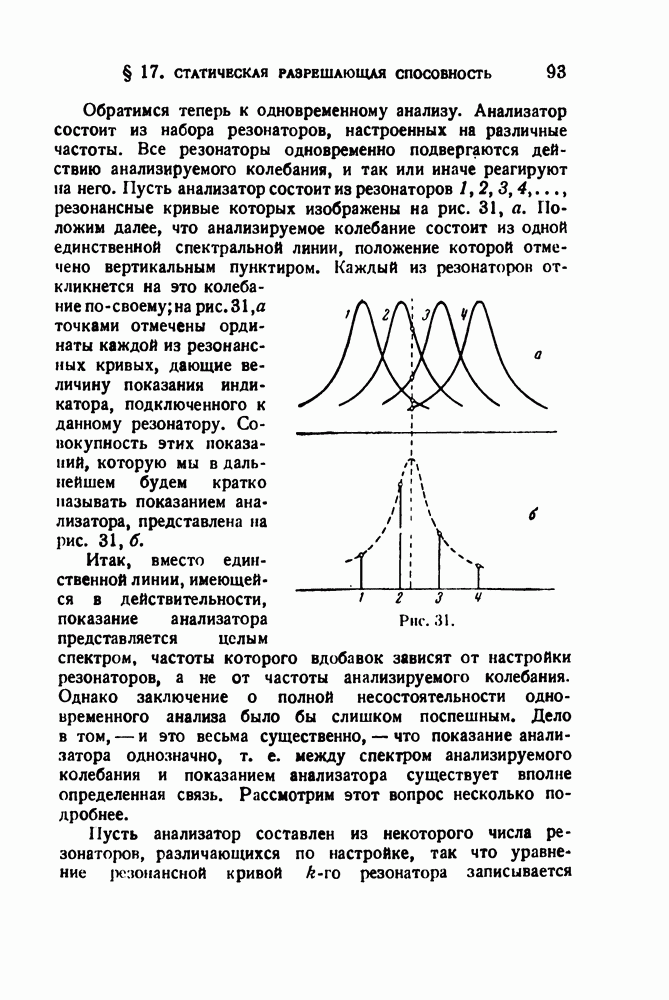
Обратимся теперь к одновременному анализу. Анализатор состоит из набора резонаторов, настроенных на различные частоты. Все резонаторы одновременно подвергаются действию анализируемого колебания, и так или иначе реагируют на него. Пусть анализатор состоит из резонаторов 1, 2, 3, 4,..., резонансные кривые которых изображены на рис. 31, а. Положим далее, что анализируемое колебание состоит из одной единственной спектральной линии, положение которой отмечено вертикальным пунктиром. Каждый из резонаторов откликнется на это колебание посвоему; на рис. 31, а точками отмечены ординаты каждой из резонансных кривых, дающие величину показания индикатора, подключенного к данному резонатору. Совокупность этих показаний, которую мы в дальнейшем будем кратко называть показанием анализатора, представлена на рис. 31, б.

Рис. 31
Итак, вместо единственной линии, имеющейся в действительности, показание анализатора представляется целым спектром, частоты которого вдобавок зависят от настройки резонаторов, а не от частоты анализируемого колебания. Однако заключение о полной несостоятельности одновременного анализа было бы слишком поспешным. Дело в том, — и это весьма существенно, — что показание анализатора однозначно, т. е. между спектром анализируемого колебания и показанием анализатора существует вполне определенная связь. Рассмотрим этот вопрос несколько подробнее.
Пусть анализатор составлен из некоторого числа резонаторов, различающихся по настройке, так что уравнение резонансной кривой  резонатора записывается
резонатора записывается
в виде

где  — резонансная частота. Под воздействием синусоидального колебания с частотой
— резонансная частота. Под воздействием синусоидального колебания с частотой  показание анализатора представится совокупностью величин
показание анализатора представится совокупностью величин

Но в силу тех же самых приближений, при помощи которых выводится выражение для резонансной кривой, последнее соотношение можно переписать в виде

а это выражение означает, что показание анализатора представляется совокупностью линий с частотами  вписанных в такую же резонансную кривую, но с резонансом при
вписанных в такую же резонансную кривую, но с резонансом при  Последняя резонансная кривая на рис. 31, б намечена пунктиром.
Последняя резонансная кривая на рис. 31, б намечена пунктиром.
Из этого следует, что если мы составим анализатор из большого числа резонаторов с часто и равномерно расположенными по шкале частот резонансными частотами, то показание такого анализатора даст столь же частый спектр, так что определить по нему положение максимума станет уже
возможным. При таком положении можно говорить о разрешающей способности анализатора при одновременном анализе совершенно так же, как и применительно к последовательному анализу. Можно также рассматривать кривую, изображающую показание последовательного анализатора, как предельный случай показания одновременного анализатора при неограниченном увеличении числа резонаторов. Выражая это же соотношение еще иначе, можно сказать, что показание при последовательном и одновременном анализе соотносятся так же, как спектры одиночного и периодически повторяемого импульса: первый спектр — сплошной, второй — линейчатый, вписывающийся в первый.
Возможность хорошего разрешения при помощи одновременного анализа можно иллюстрировать ссылкой на общеизвестный технический язычковый частотомер. Этот прибор состоит из набора механических резонаторов, обладающих большой селективностью. Если настройка выполнена, как обычно, с шагом 1 гц, то частота может быть уверенно отсчитана с точностью до 0,5 гц, так как, когда частота попадает в середину интервала между частотами двух соседних язычков, они колеблются одновременно с равными амплитудами.

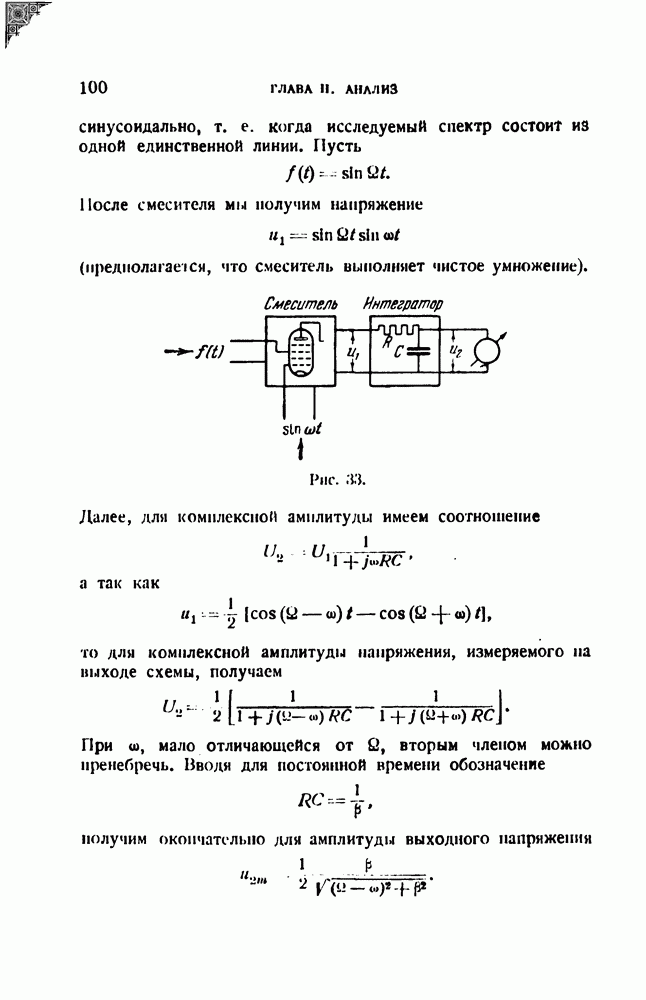
Рис. 32.
Возможна принципиально иная постановка вопроса об анализе, особенно уместная в применении к одновременному анализу. Представим себе, что анализатор составлен из набора не обычных резонаторов, а идеальных полосовых фильтров с тесно примыкающими границами (рис. 32, а). Тогда при наличии одной спектральной линии (рис. 32, б) показание анализатора будет однозначным: на колебание, отвечающее этой линии, откликнется только тот фильтр, в пределах полосы пропускания которого лежит возбуждающая частота. Показание анализатора изображено условно на рис. 32, в. Однако ясно, что значение частоты не определяется точно; мы можем лишь утверждать, что она находится в пределах той или иной полосы.
Так же ясно, что мерой разрешающей способности такого полосового анализатора является ширина полосы. Если в пределах одной и той же полосы оказывается более чем одна линия исследуемого спектра, то анализатор их не разделяет; он дает лишь некоторое суммарное значение для всех составляющих, частоты которых лежат в пределах той или иной полосы. При таких обстоятельствах естественно заставить полосовой анализатор измерять мощность, так как мощность в полосе выразится простой арифметической суммой мощности отдельных составляющих.
В заключение настоящего параграфа рассмотрим вопрос о погрешности анализатора. Если исследуемое колебание синусоидально, то амплитуда и частота колебания могут быть в принципе определены при помощи анализатора точно. Если же анализируется сложное колебание, то возникает неустранимая погрешность. Погрешность эта обусловлена тем, что на резонатор воздействуют одновременно все составляющие сложного колебания, и мы не в состоянии разделить их влияние, а следовательно, и определить амплитуду и частоту каждой составляющей в отдельности.
Пусть комплексная амплитуда  резонатора под действием
резонатора под действием  гармоники спектра есть
гармоники спектра есть

где  — частота гармоники,
— частота гармоники,  — ее амплитуда,
— ее амплитуда,  — резонансная частота данного резонатора. Под действием всего спектра амплитуда резонатора будет
— резонансная частота данного резонатора. Под действием всего спектра амплитуда резонатора будет

Предположим, что резонатор настроен точно на частоту одной из гармоник. Выделив слагаемое, относящееся к этой гармонике, получим

В остающейся здесь сумме суммирование производится по всем остальным гармоникам, т. е. по всем  не равным к. Положим теперь, что спектр гармоничен, т. е. что
не равным к. Положим теперь, что спектр гармоничен, т. е. что

где  — основная частота. Кроме того, примем, что относительное затухание для всех резонаторов одинаково, т. е. положим
— основная частота. Кроме того, примем, что относительное затухание для всех резонаторов одинаково, т. е. положим

Тогда

Последнее выражение показывает, что отсчет по резонатору пропорционален амплитуде гармоники, т. е.

только при условии, что суммой в правой части можно пренебречь. Таким обравом, эта сумма и представляет собой погрешность, совершаемую при анализе.
Рассматривая формулу, мы видим, что погрешность тем меньше, чем реже спектр, т. е. чем больше основная частота  Кроме того, относительная погрешность убывает с уменьшением затухания ( т. е. с увеличением разрешающей способности), потому что при этом возрастает первый член в правой части по сравнению с суммой.
Кроме того, относительная погрешность убывает с уменьшением затухания ( т. е. с увеличением разрешающей способности), потому что при этом возрастает первый член в правой части по сравнению с суммой.
Все эти соображения применимы в равной мере как к одновременному, так и к последовательному анализу.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
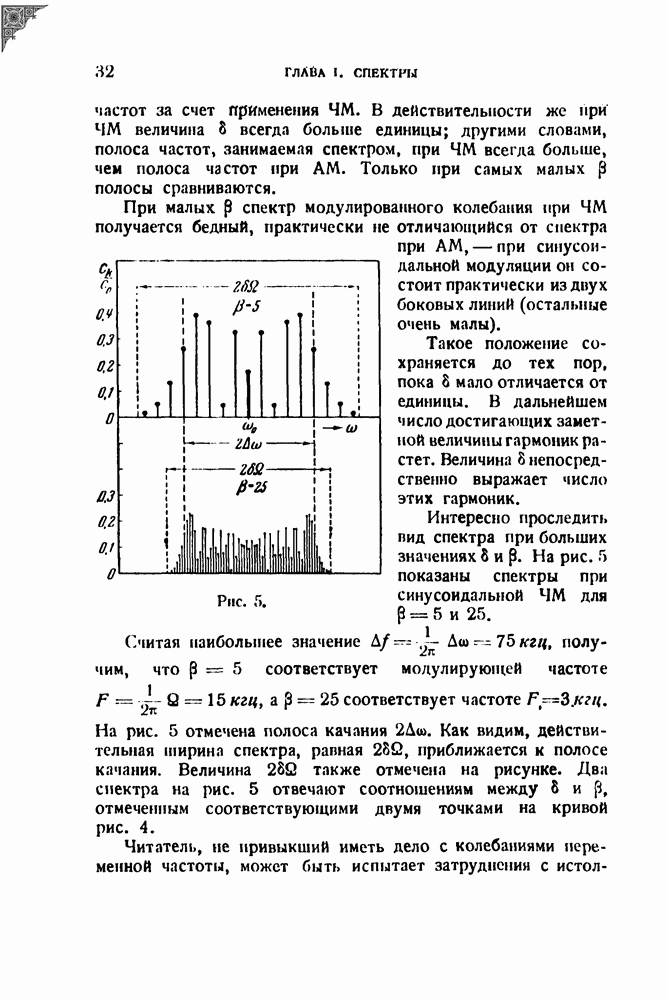
- § 6. Спектры при модуляции
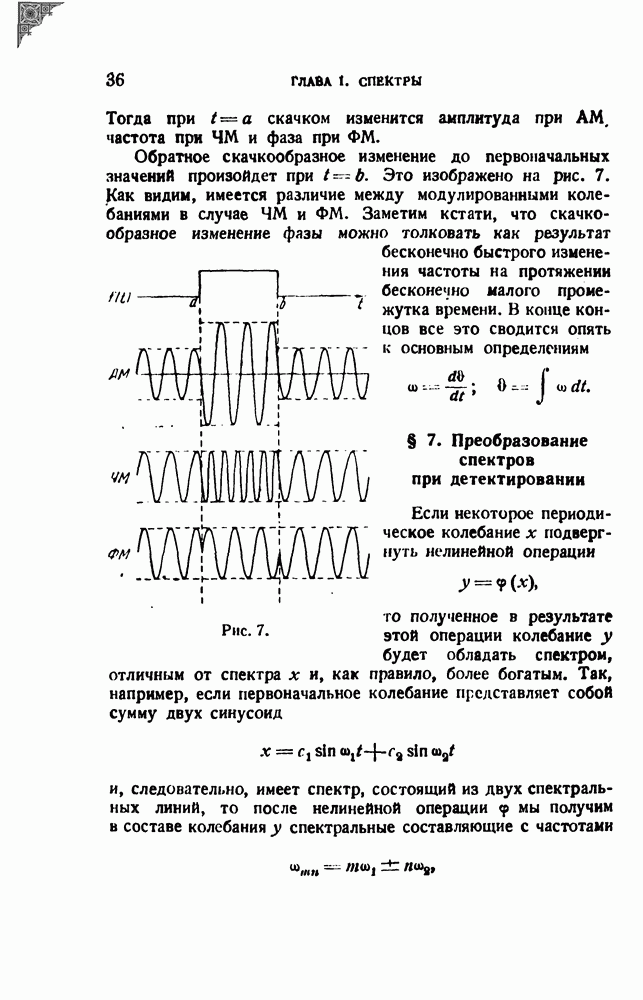
- § 7. Преобразование спектров при детектировании
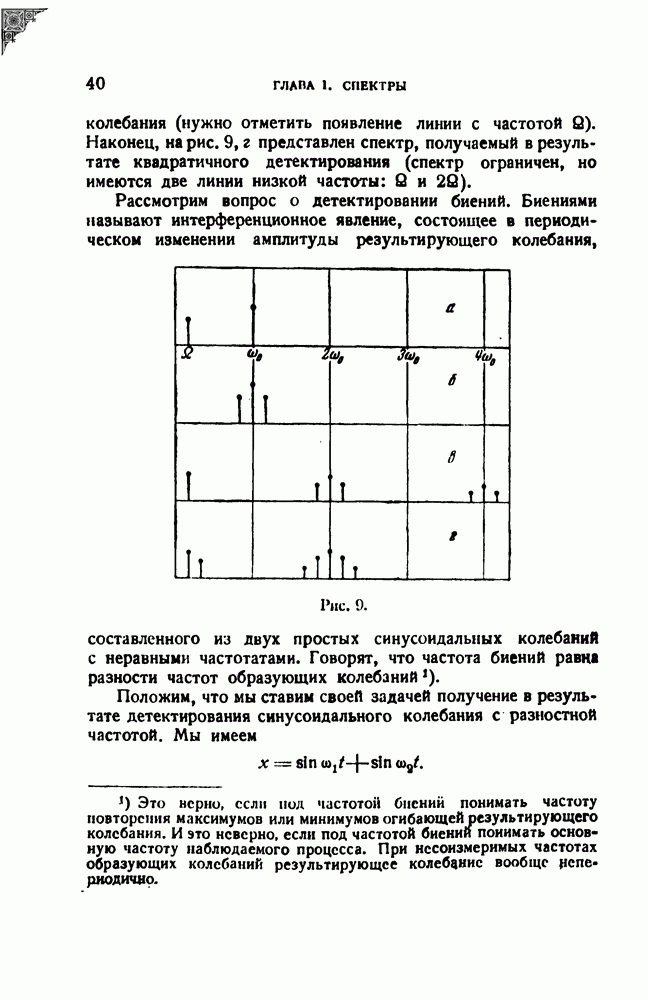
- § 8. Спектр суммы периодических функций
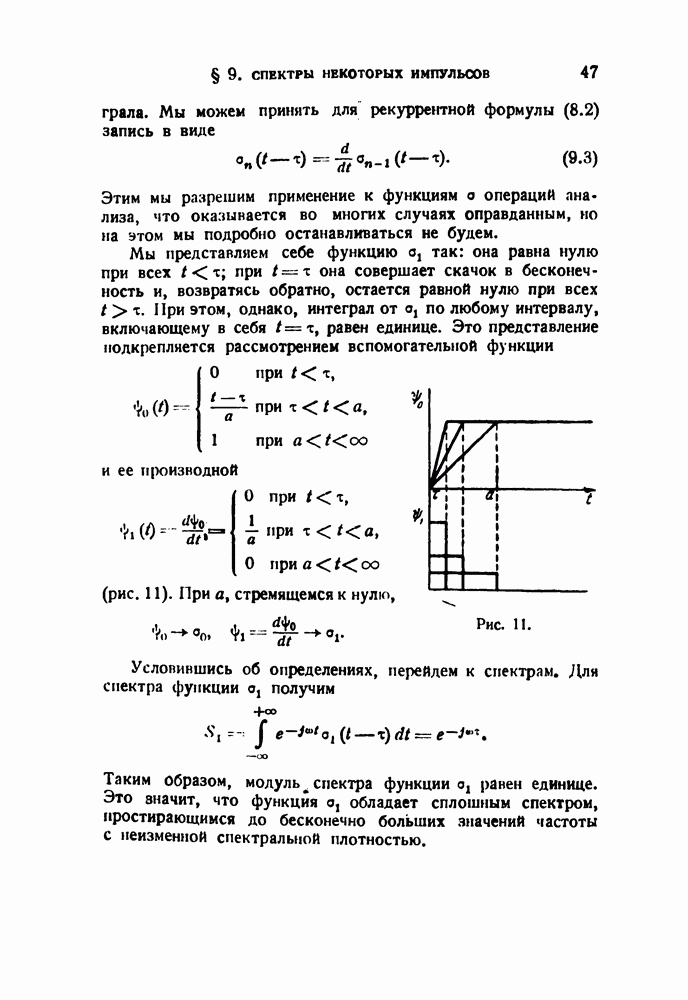
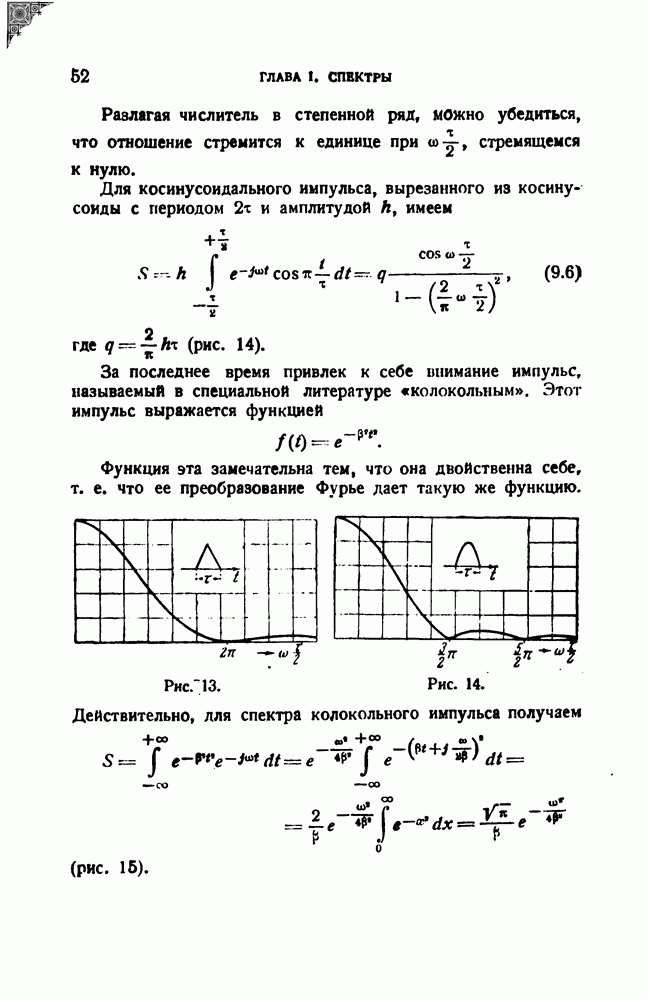
- § 9. Спектры некоторых импульсов
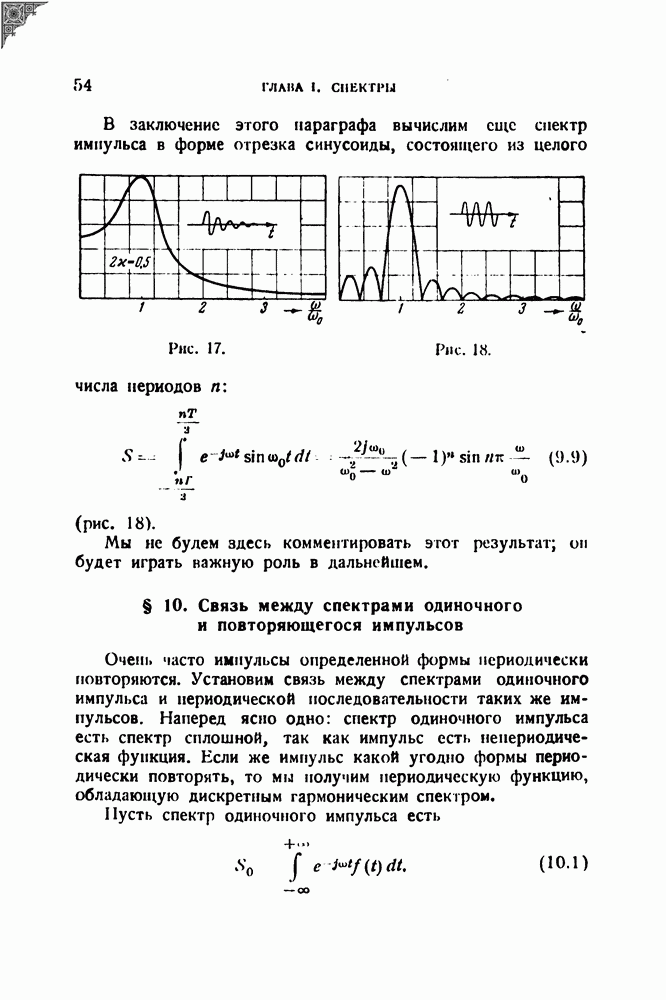
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
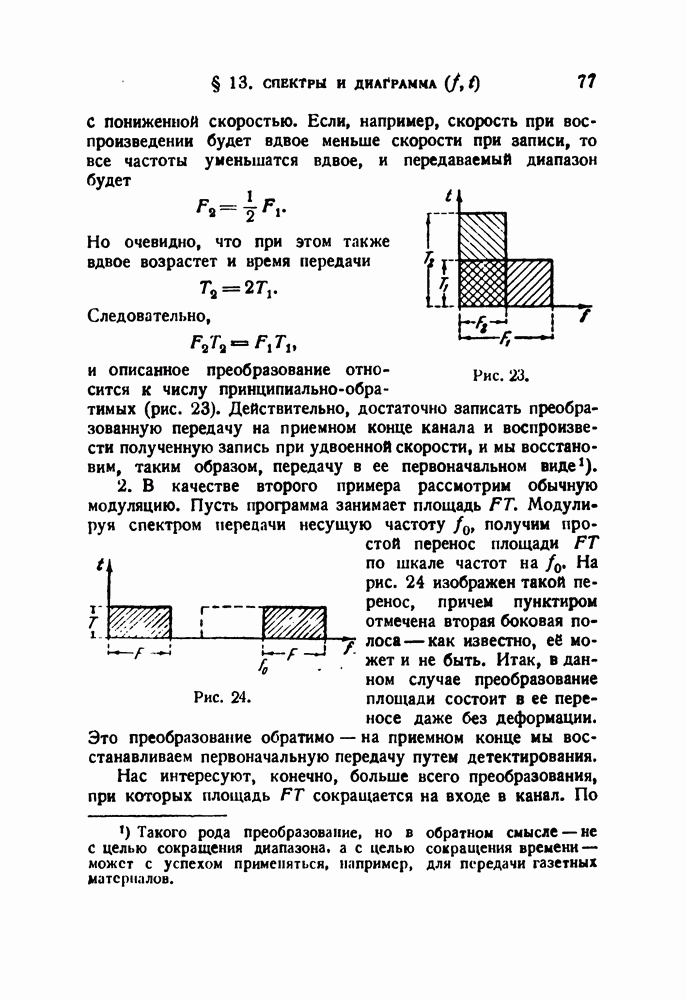
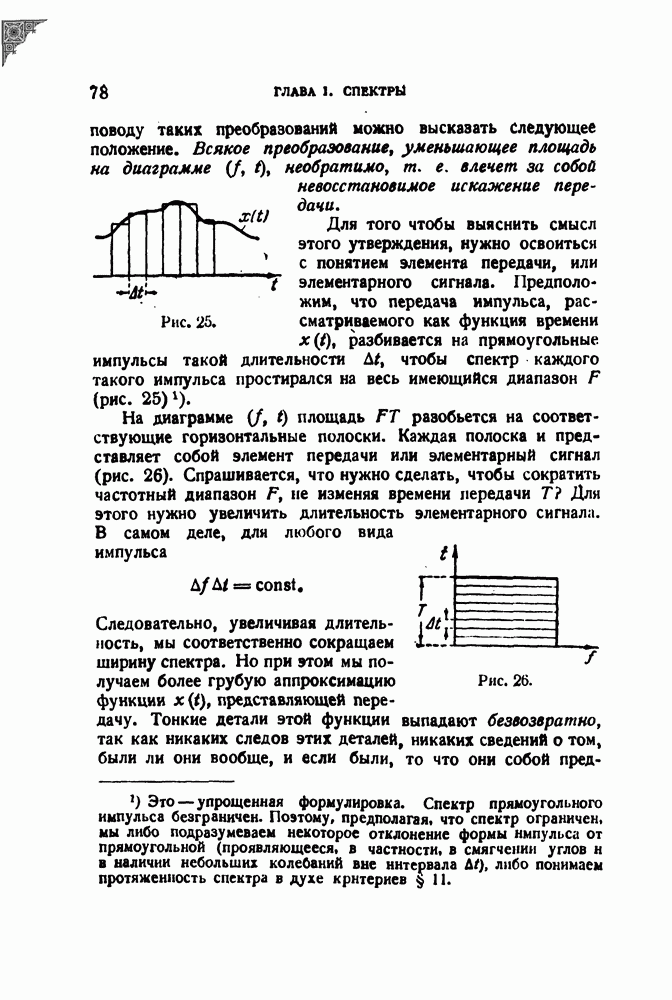
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
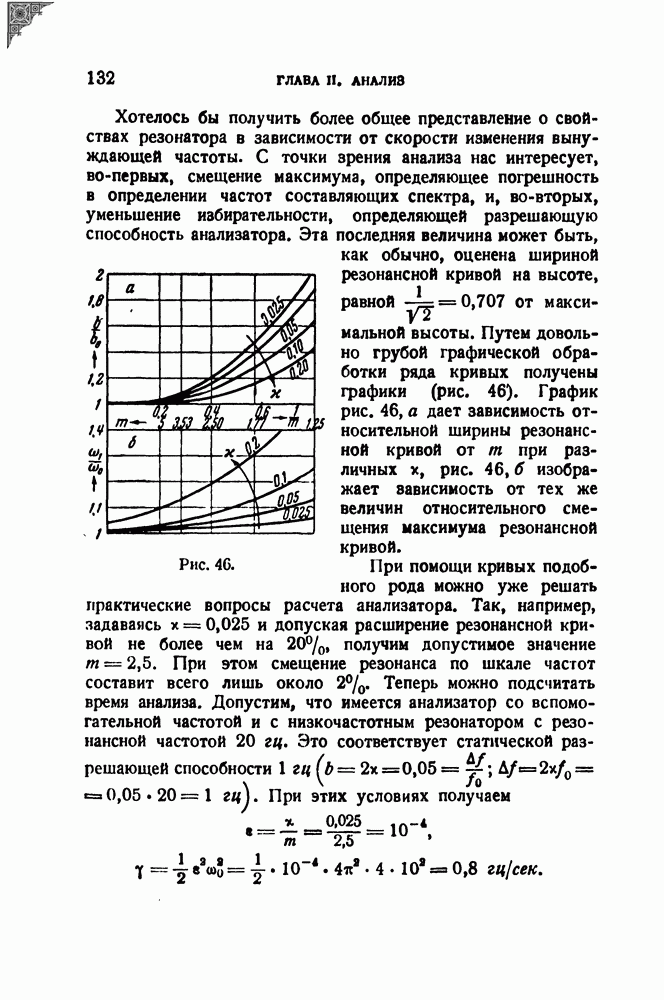
- § 20. Связь между разрешающей способностью анализатора и временем анализа
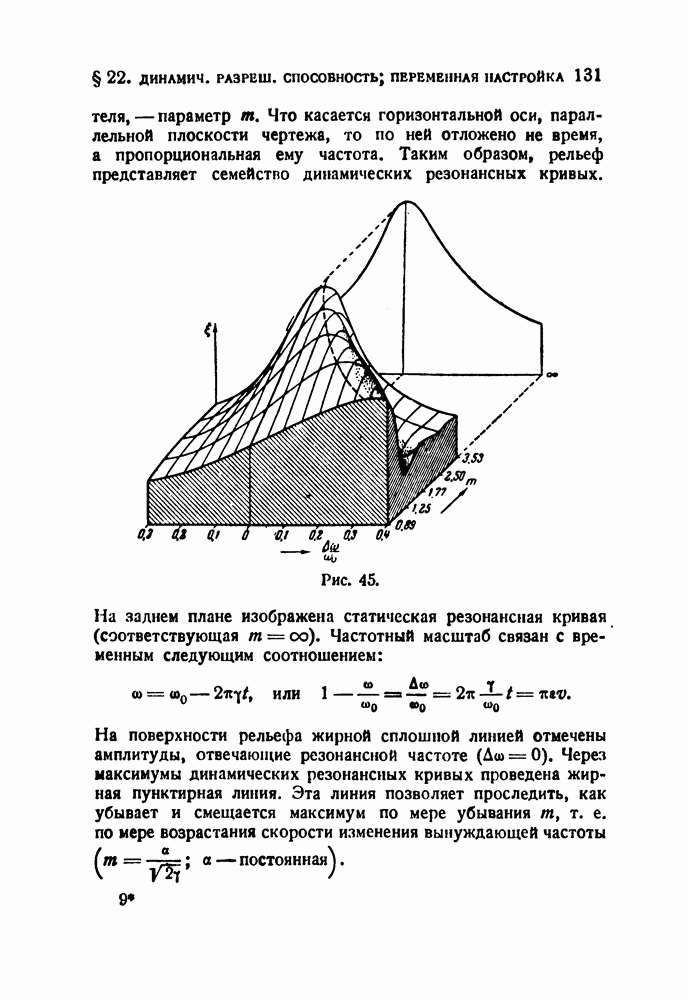
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
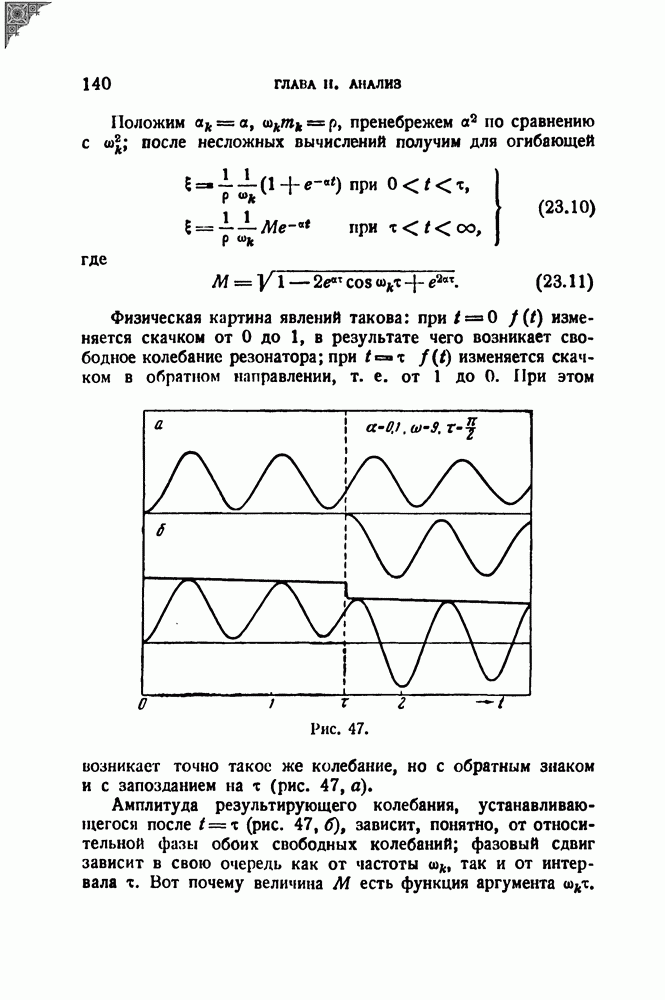
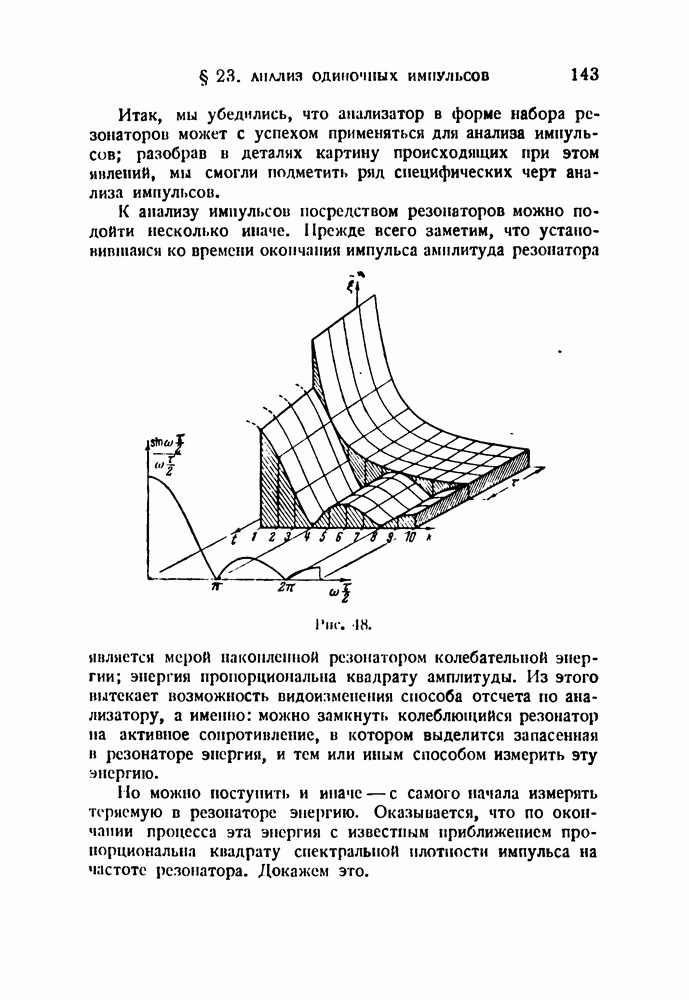
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА