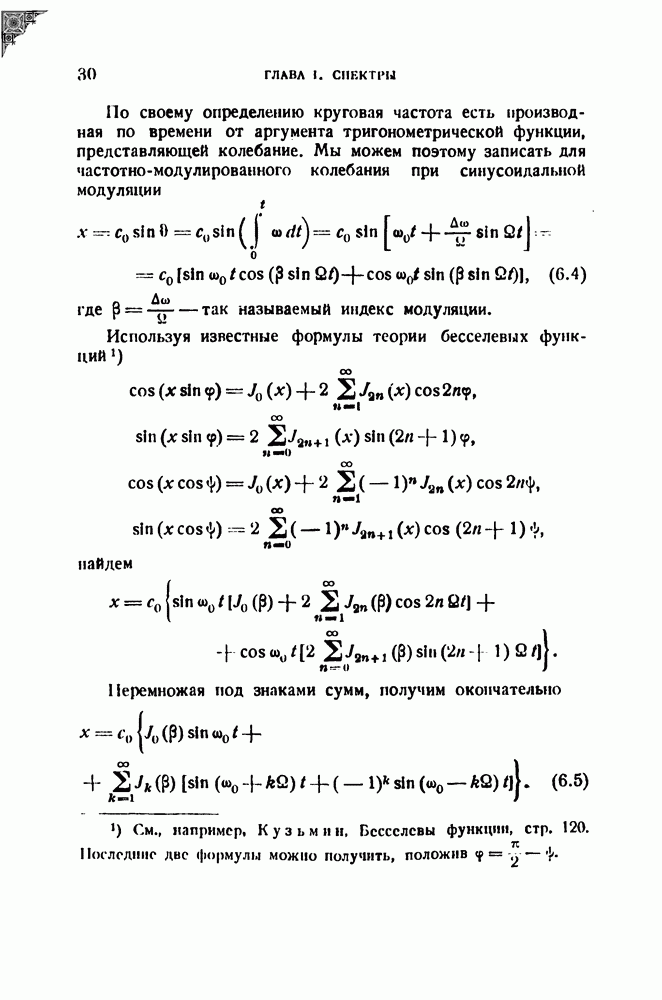| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. К вопросу о динамических характеристиках резонатора
Вопрос о динамических характеристиках резонатора рассмотрен в § 21 с временной точки зрения, т. е. требуемый результат получен путем исследования устанавливающегося режима резонатора. Тот же вопрос мог бы быть изложен на чисто спектральном языке следующим образом.
Будем решать задачу о поведении резонатора как стационарную, т. е. положим, что приложенное напряжение представлено суммой синусоидальных напряжений. Воспользуемся процедурой, изложенной в § 12, т. е. применим к уравнению резонатора

преобразование Фурье. Мы получим

где  — соответственно, спектры напряжения и тока. Далее,
— соответственно, спектры напряжения и тока. Далее,

Но в рассматриваемом случае спектральная плотность является функцией не только частоты, но и времени. В самом деле, приложенное напряжение  предполагается синусоидальным, но включается на анализатор в момент
предполагается синусоидальным, но включается на анализатор в момент  Следовательно, для каждого данного момента времени
Следовательно, для каждого данного момента времени  напряжение, воздействующее на анализатор, представляется следующей функцией:
напряжение, воздействующее на анализатор, представляется следующей функцией:

и спектр этой функции в данный момент, т. е. текущий спектр, выражается формулой

где  — текущая частота спектра,
— текущая частота спектра,  — текущее время, и — переменная интегрирования. Таким образом, получаем для
— текущее время, и — переменная интегрирования. Таким образом, получаем для

Подинтегральная функция имеет два простых сопряженных полюса, лежащих над вещественной осью:

(Точки  не являются полюсами, в чем легко убедиться, раскрыв получающуюся неопределенность.) Вычеты подинтегральной функции равны
не являются полюсами, в чем легко убедиться, раскрыв получающуюся неопределенность.) Вычеты подинтегральной функции равны

Выполнив вычисление, находим (положив  )
)

Эта формула представляет собой точное решение задачи, совпадающее, разумеется, с решением, полученным любым другим способом. Вычислив огибающую, найдем

Это выражение несколько отличается от (21.4) вследствие того, что формула (21.4) не является точной; она получена из укороченных уравнений (21.3). Интересно заметить, что в точном решении аргумент косинуса имеет более простой вид.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
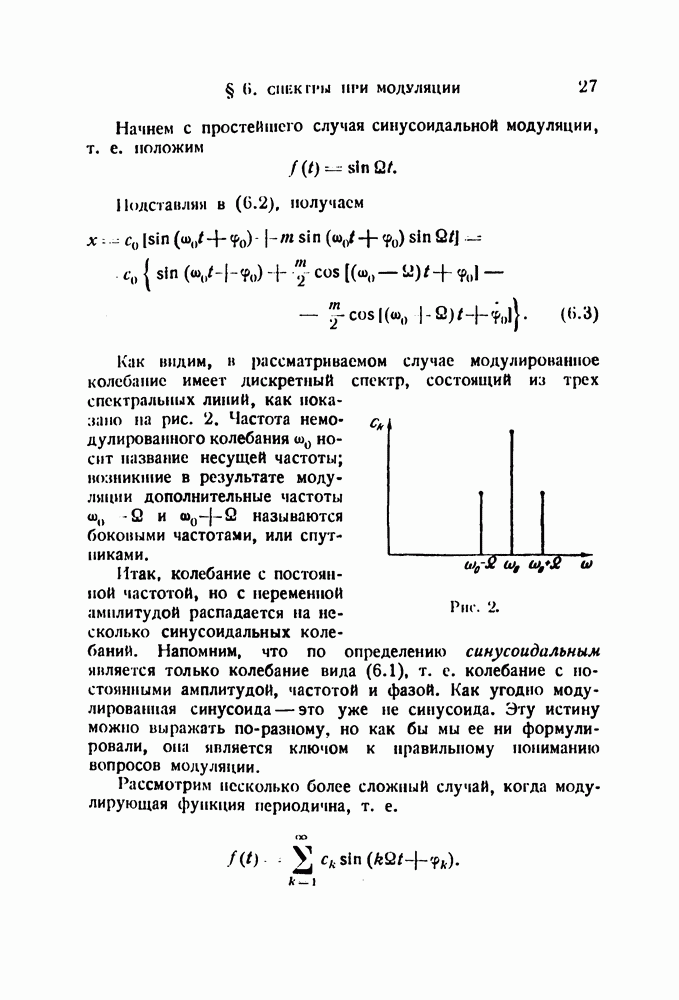
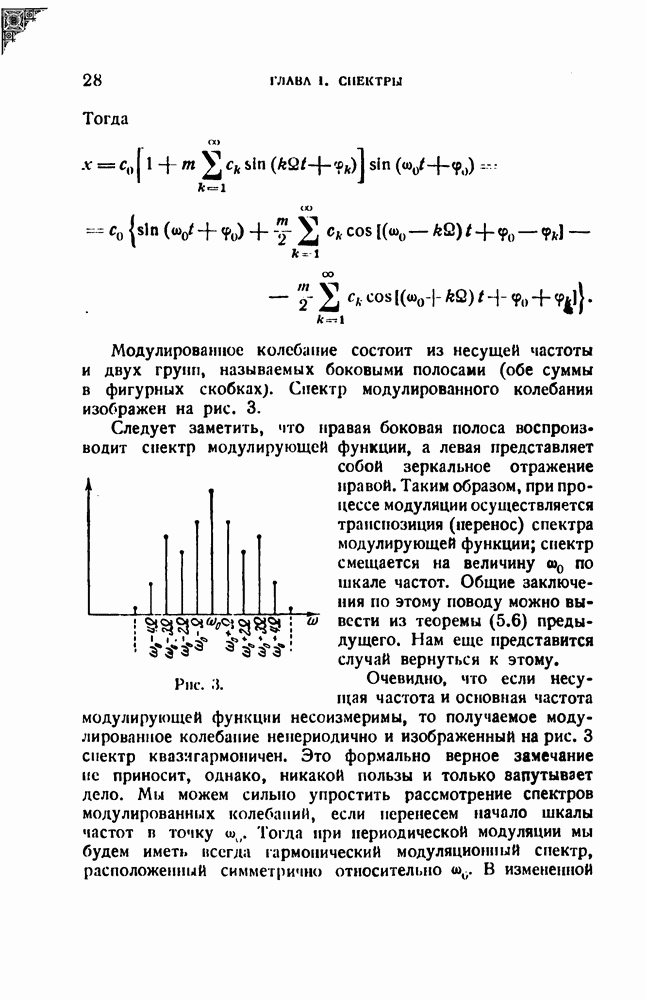
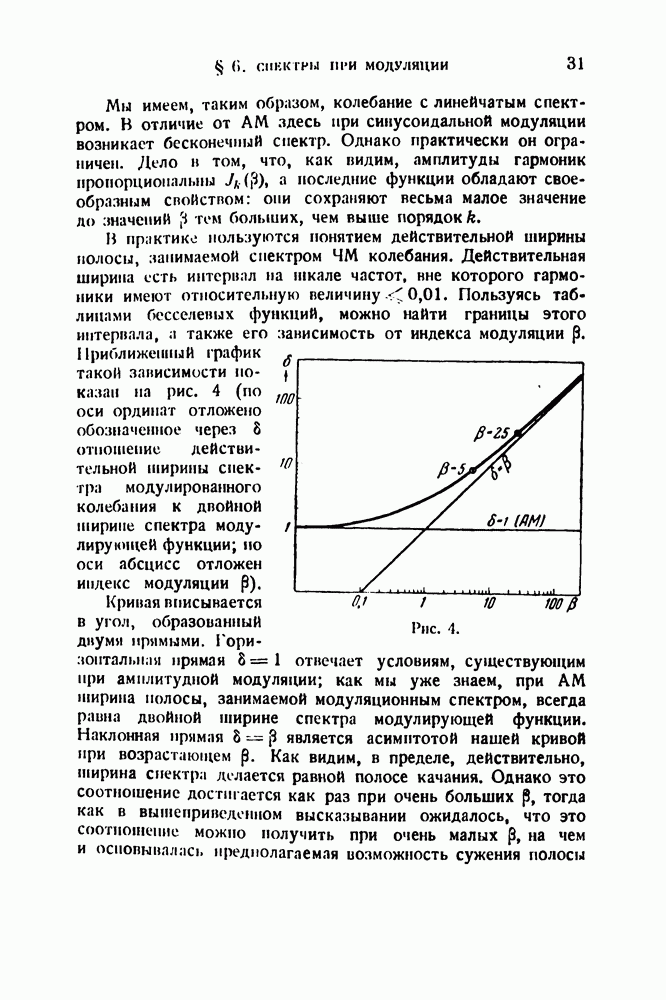
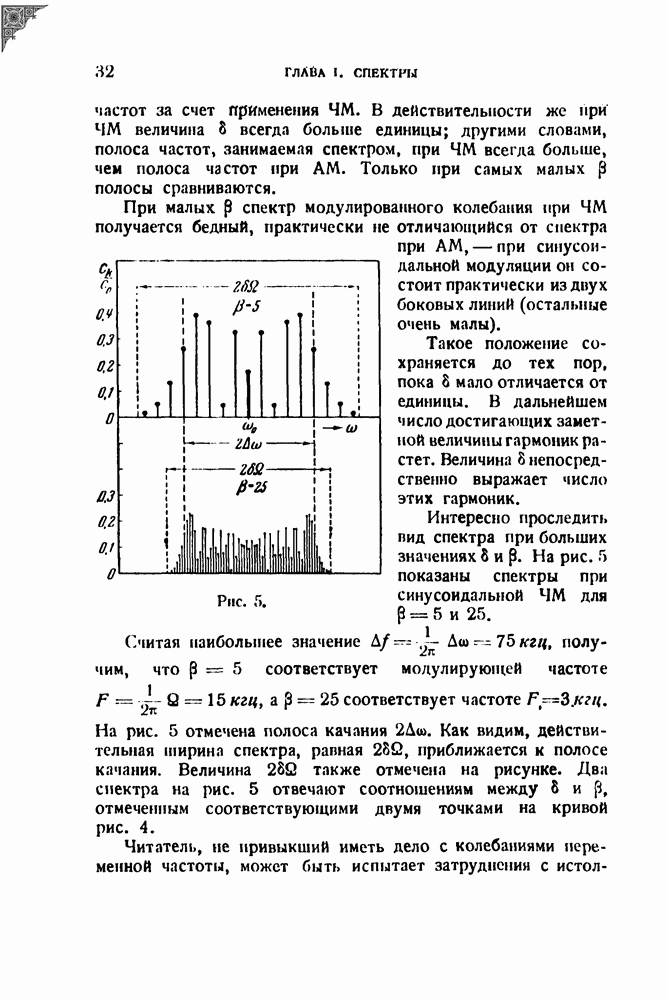
- § 6. Спектры при модуляции
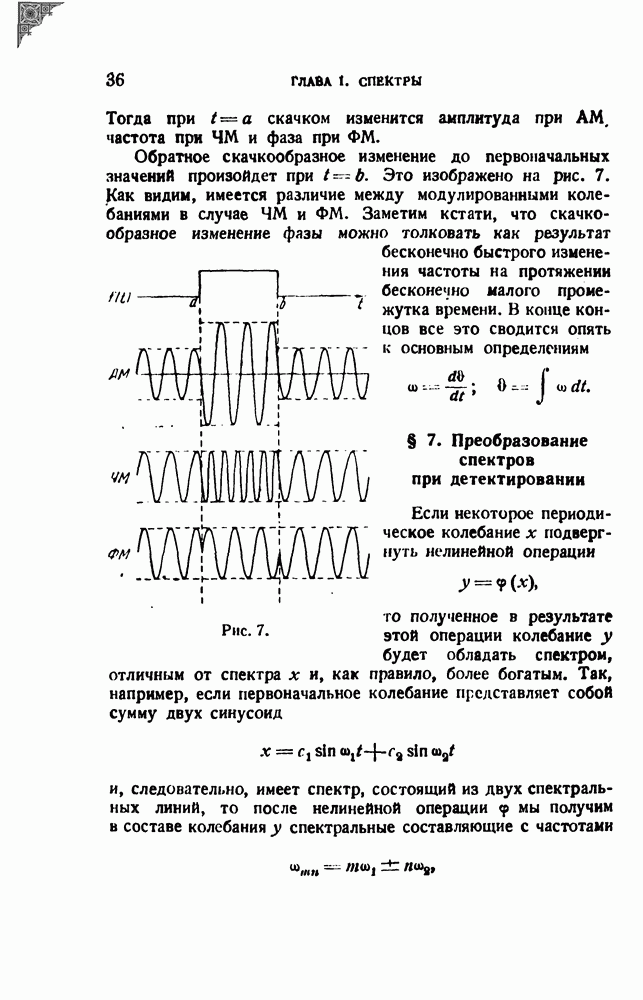
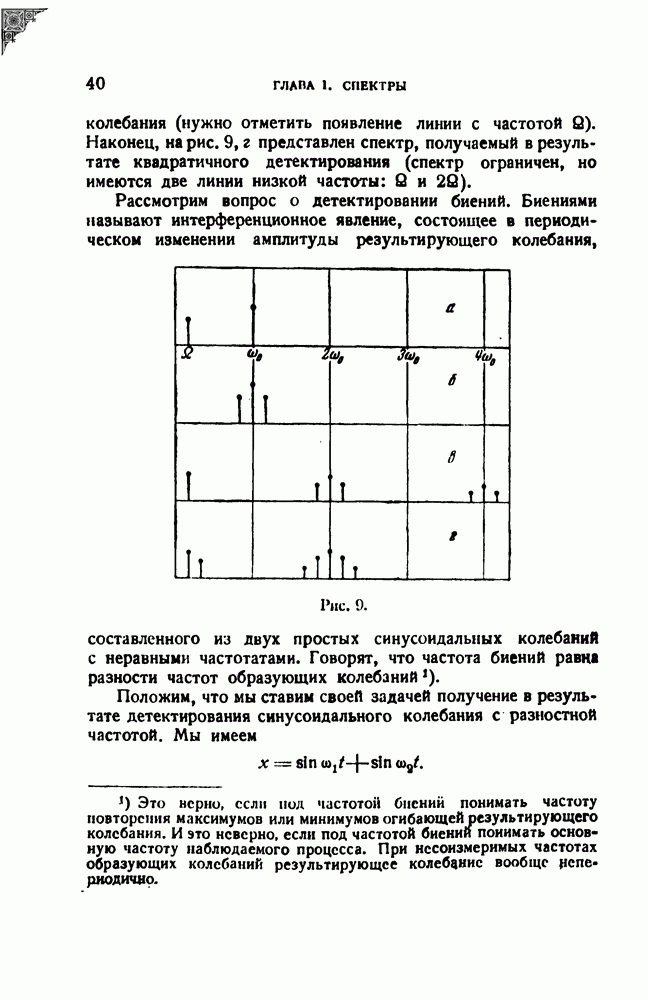
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
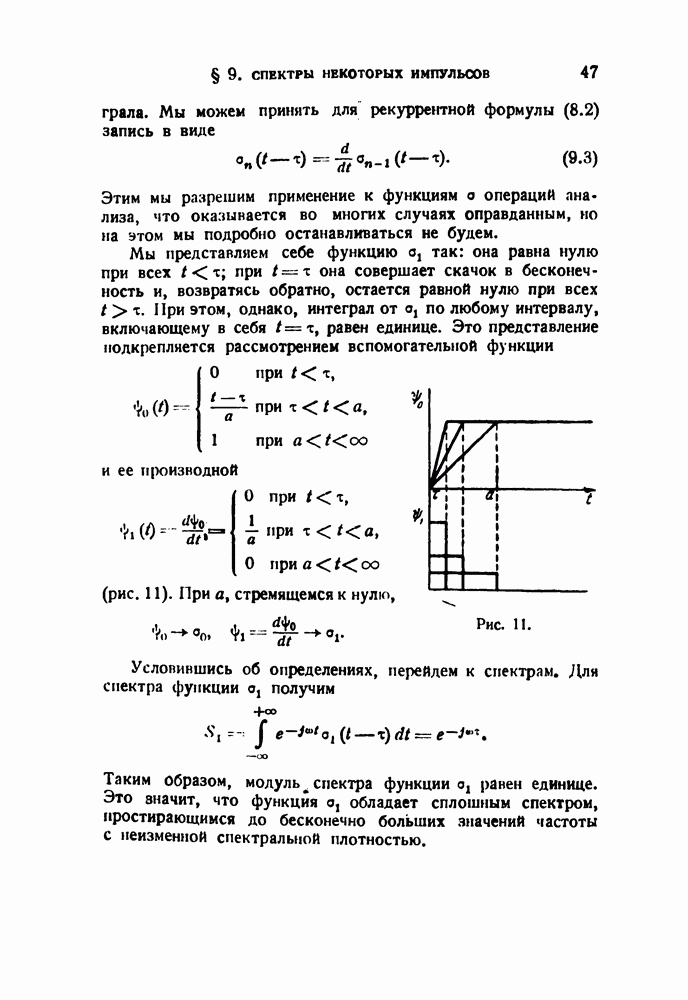
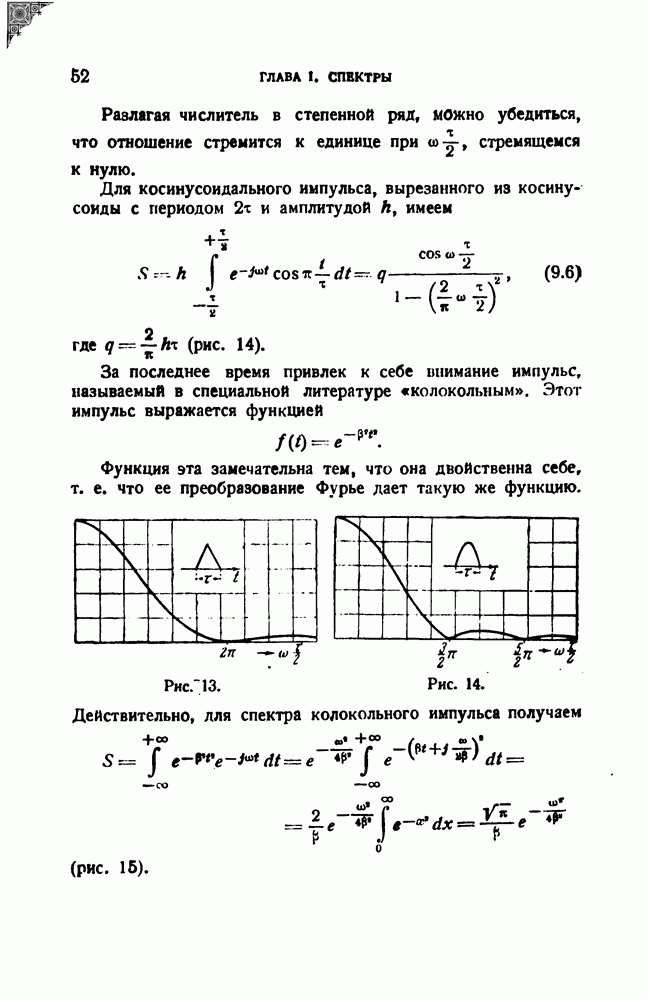
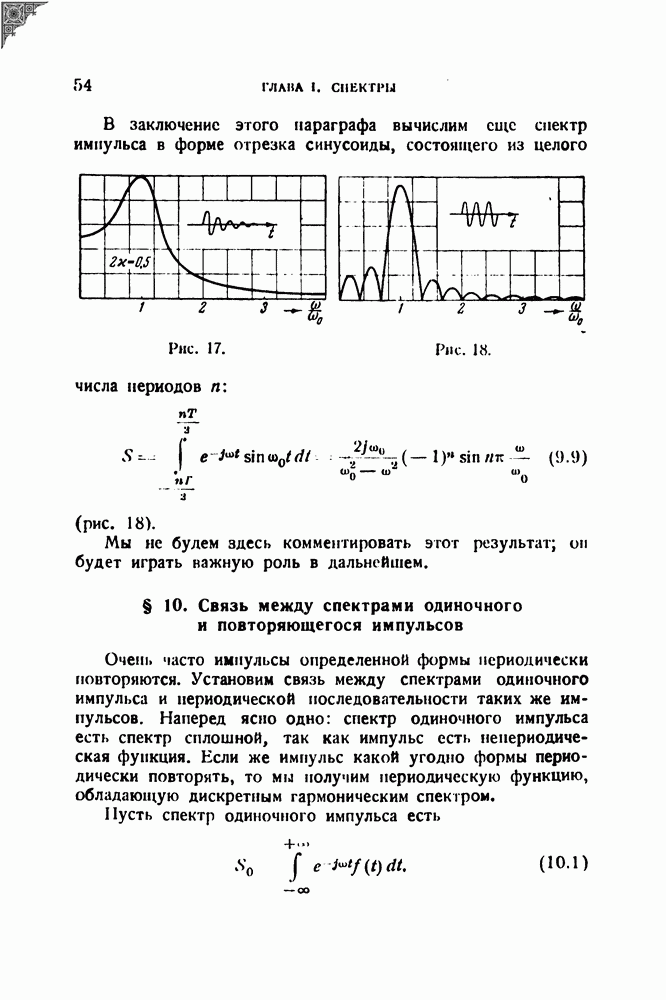
- § 9. Спектры некоторых импульсов
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
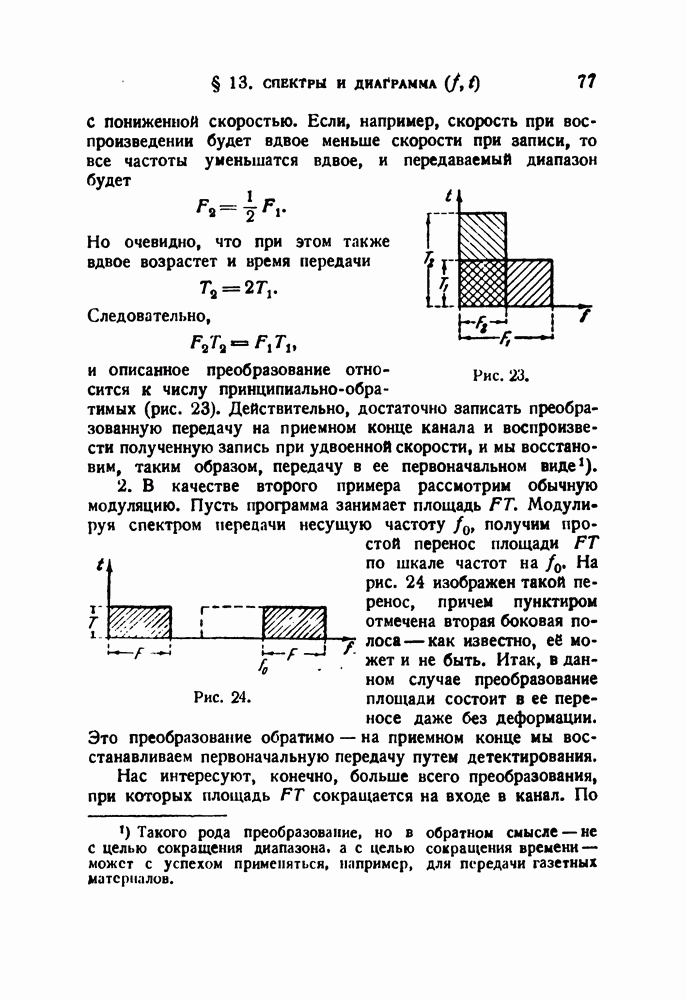
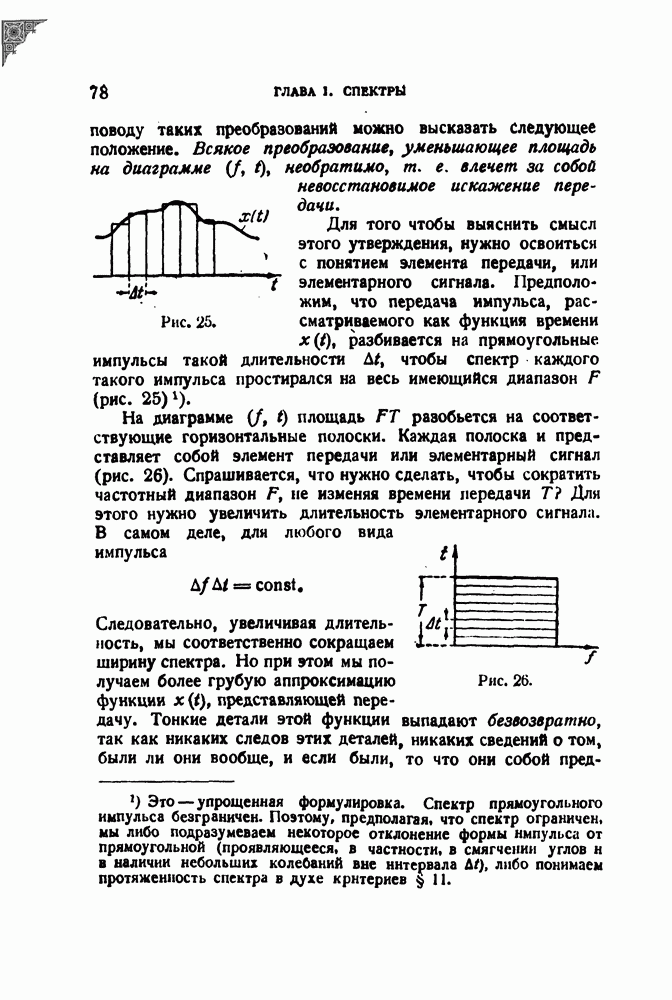
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА