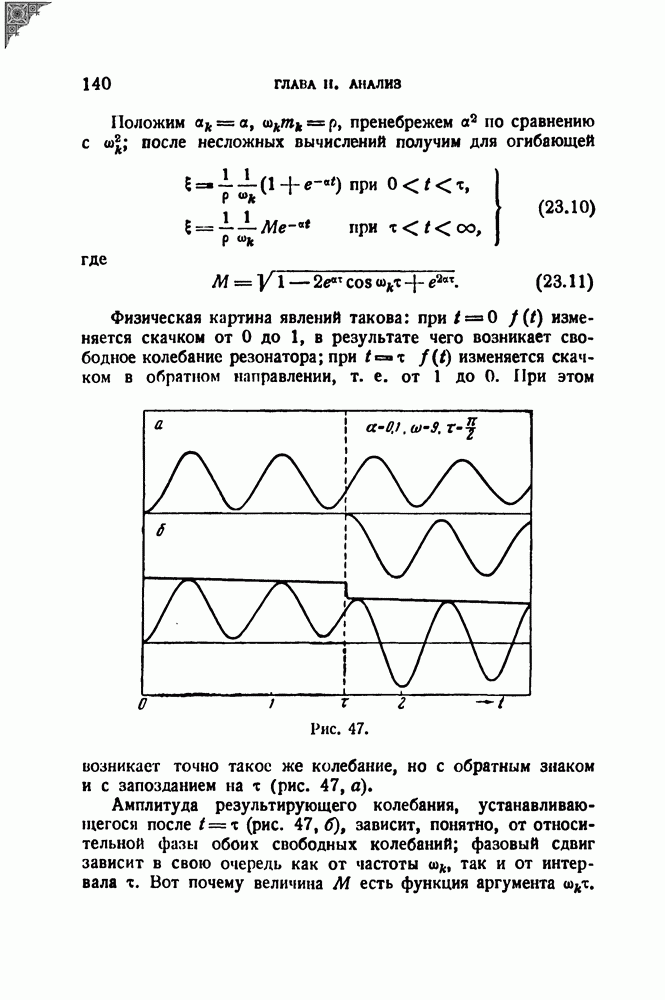
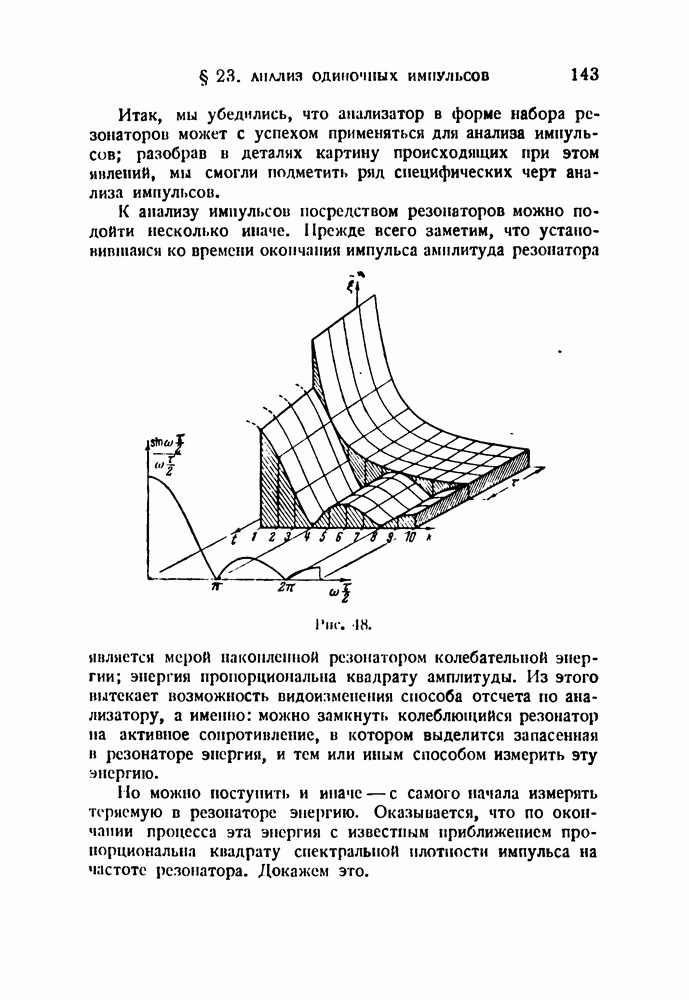
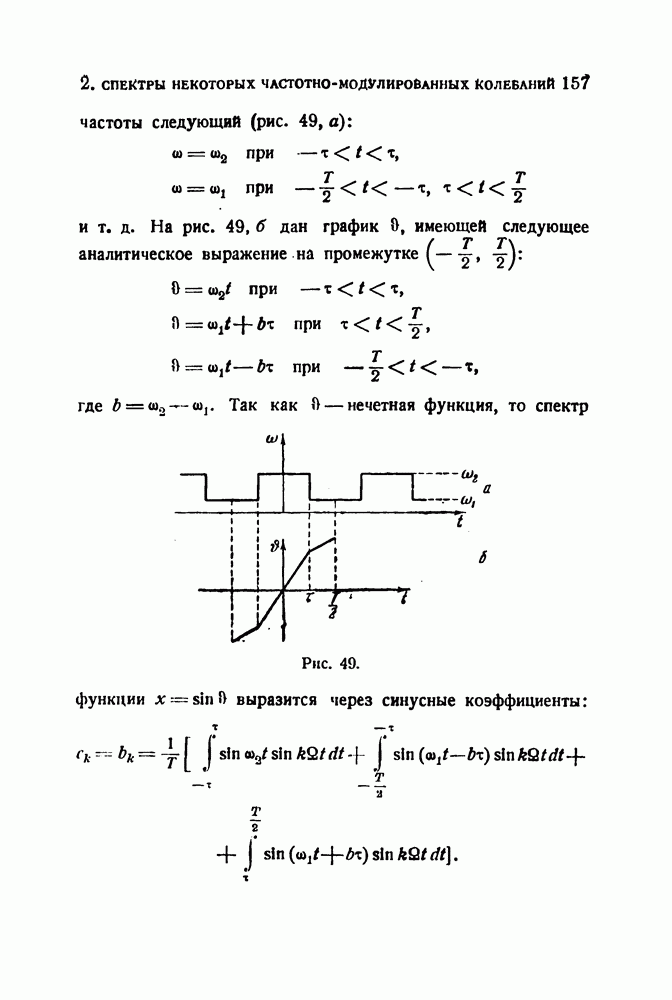
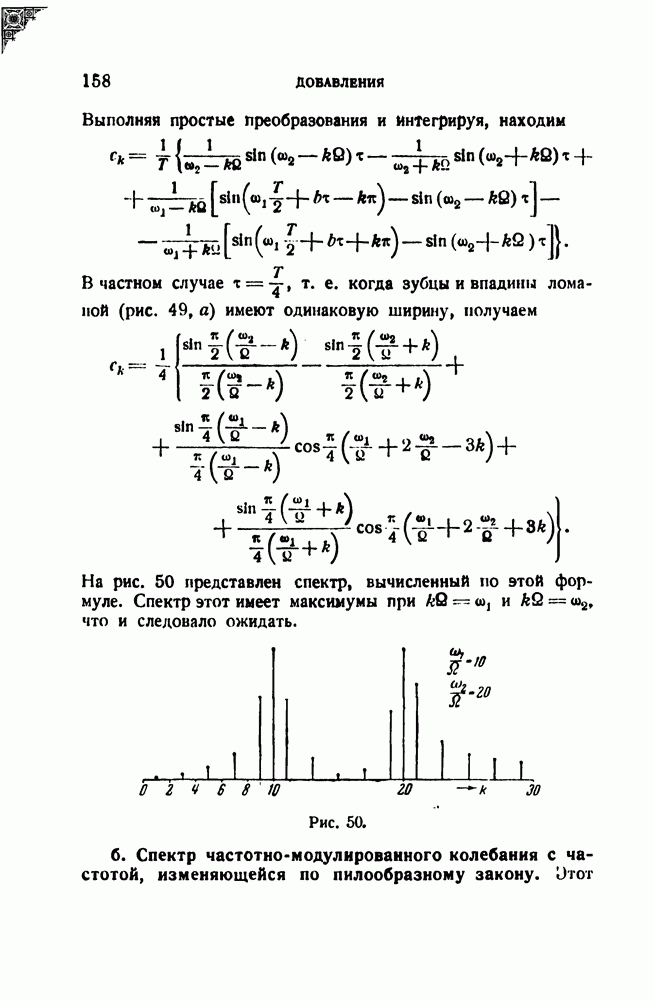
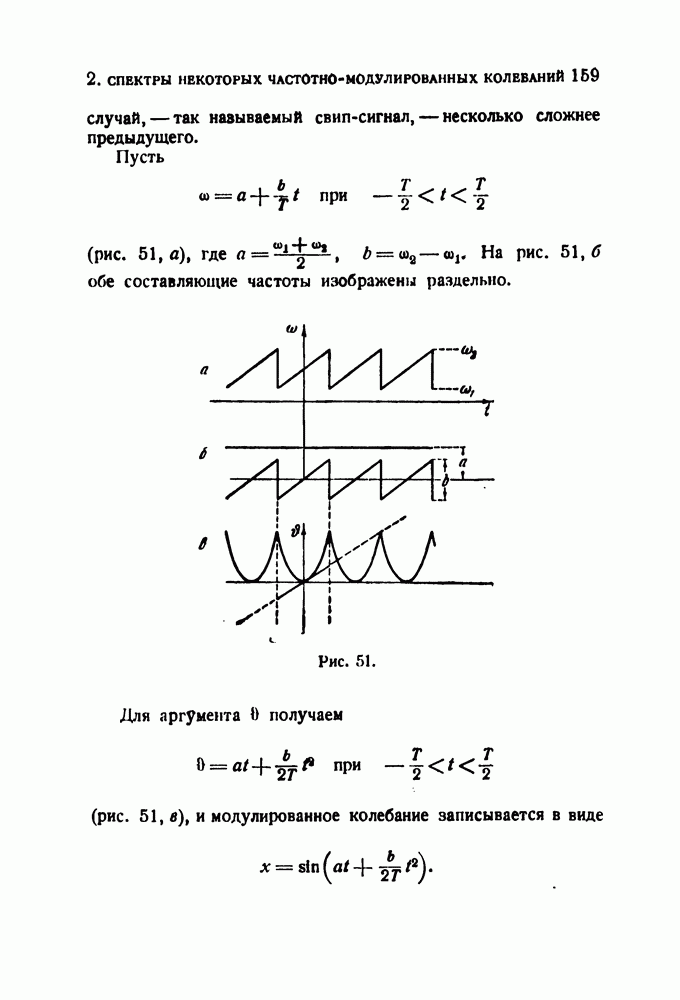
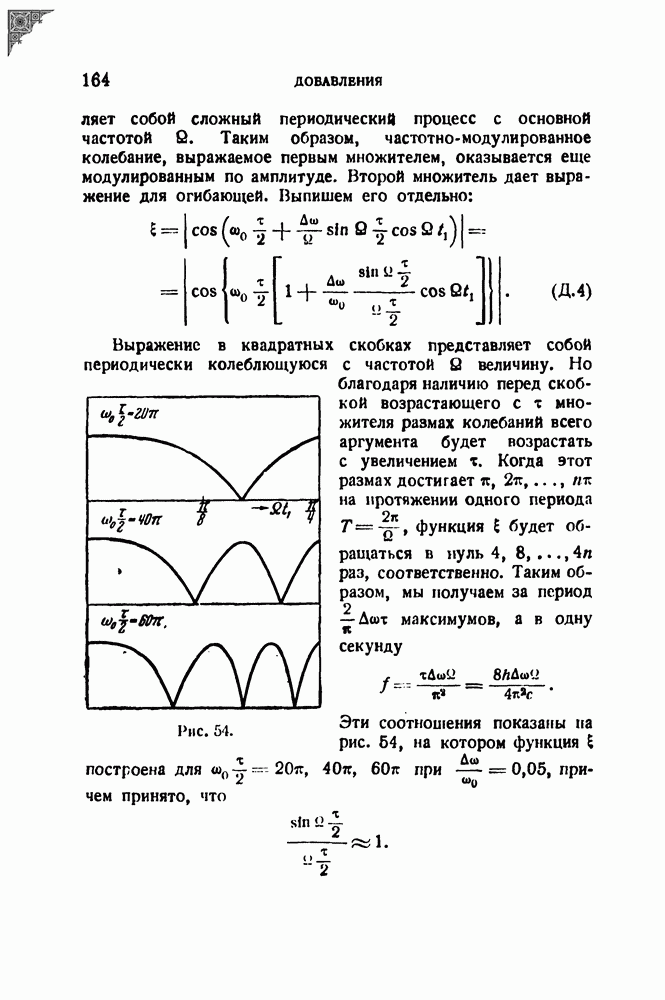
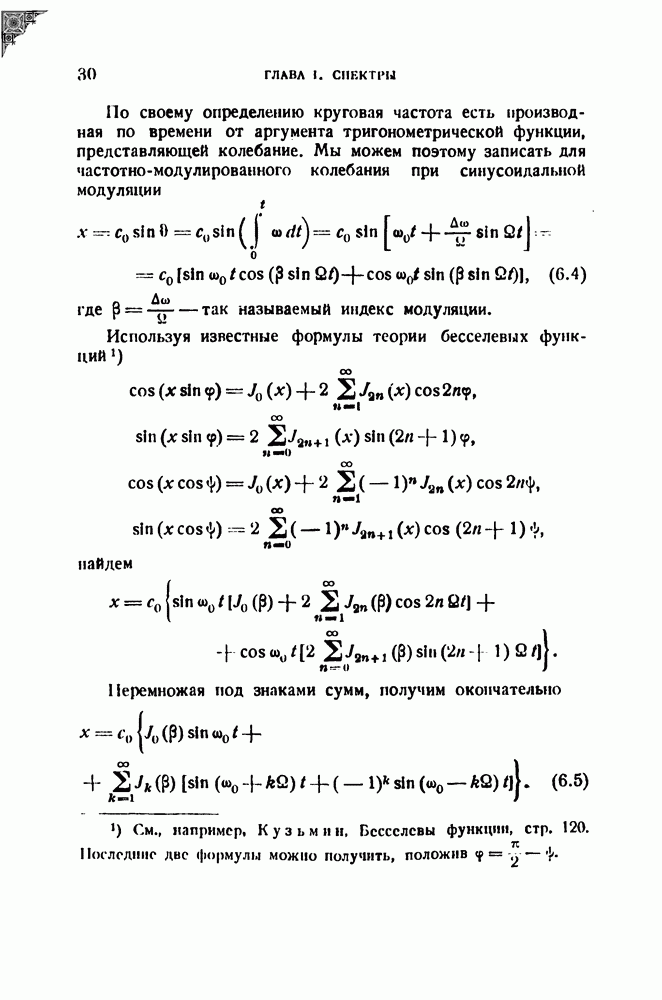| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 22. Динамическая разрешающая способность резонатора; переменная настройка
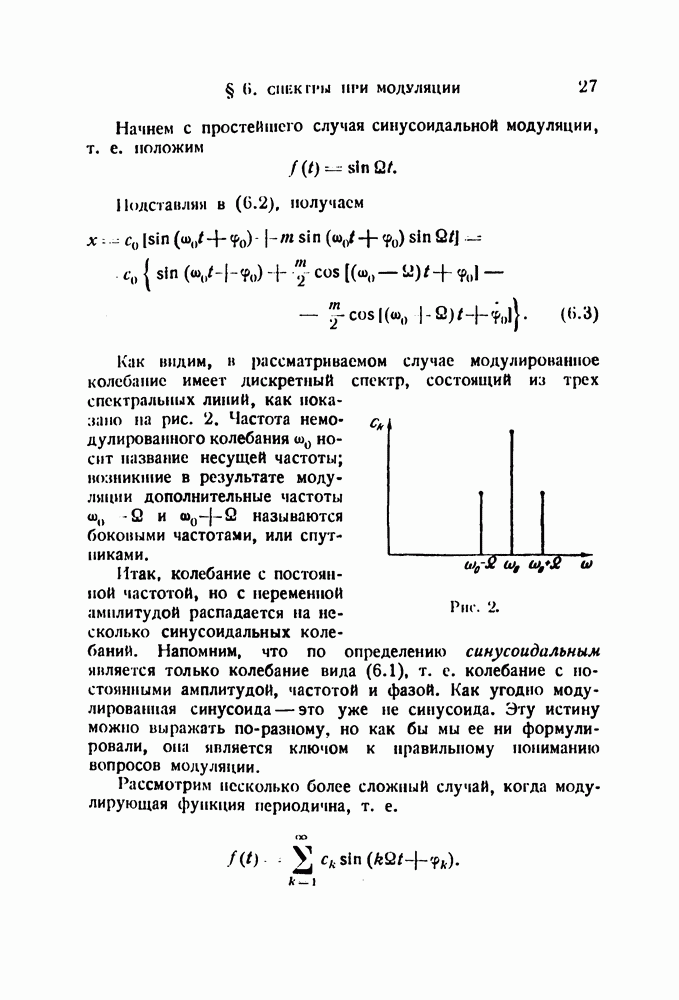
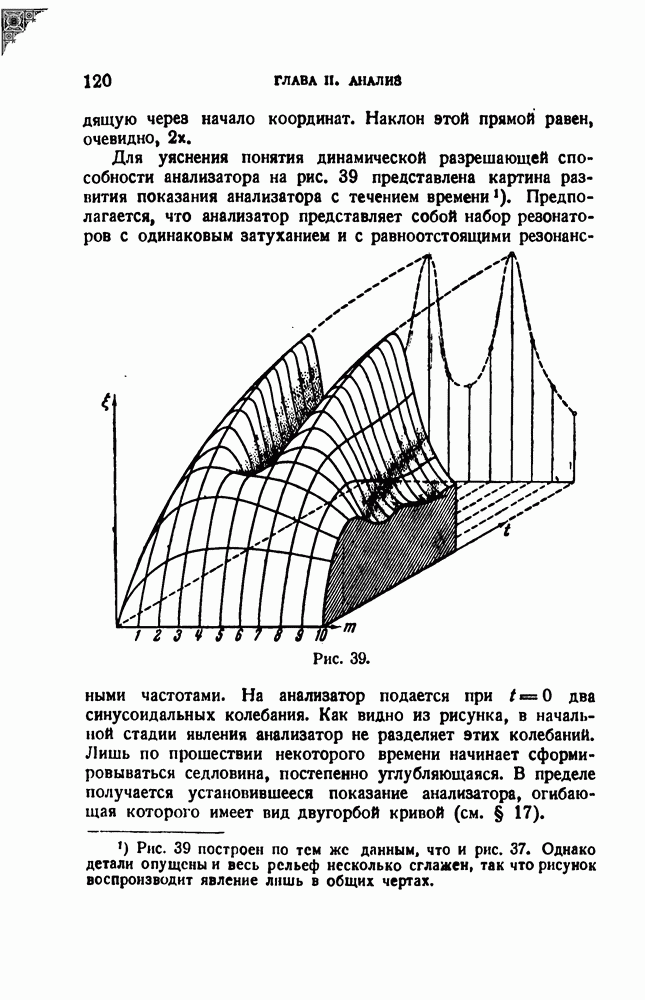
В предыдущем параграфе был рассмотрен вопрос о динамической разрешающей способности резонатора в системе одновременного анализа. Теперь мы разберем соотношения при последовательном анализе, т. е. когда меняется либо настройка резонатора, либо возбуждающая резонатор частота. Вопросу о вынужденных колебаниях при переменной частоте посвящен ряд работ, в том числе и новейших. Обзор этих работ дан в добавлении.
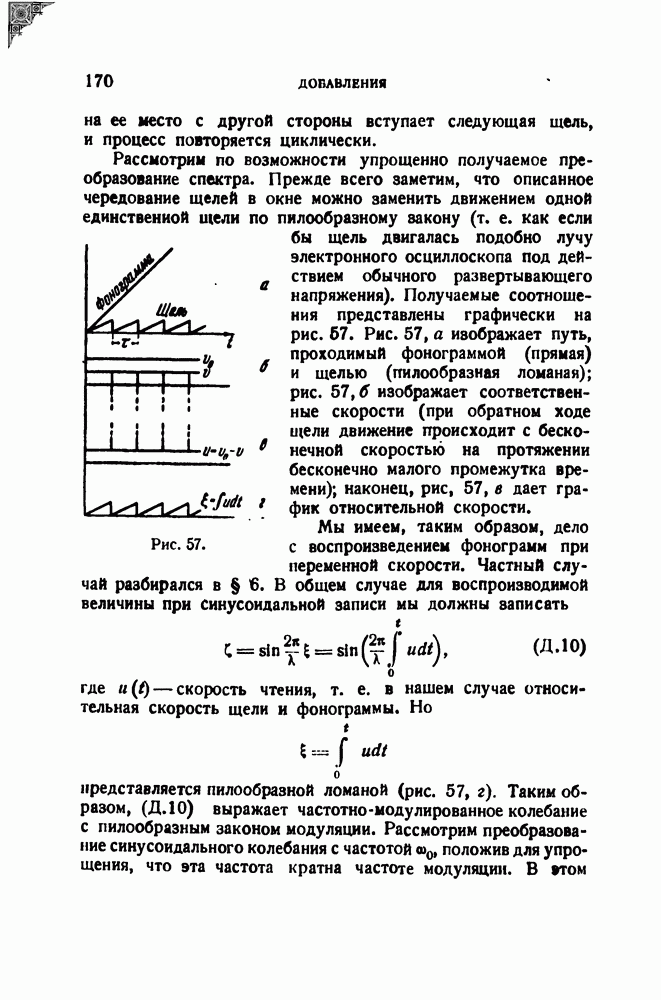
Рассмотрим сначала поведение резонатора под воздействием колебания с частотой, возрастающей со временем по линейному закону. Пусть

(рис. 40). В этой формуле выражает скорость изменения частоты (в герцах в секунду).

Рис. 40.

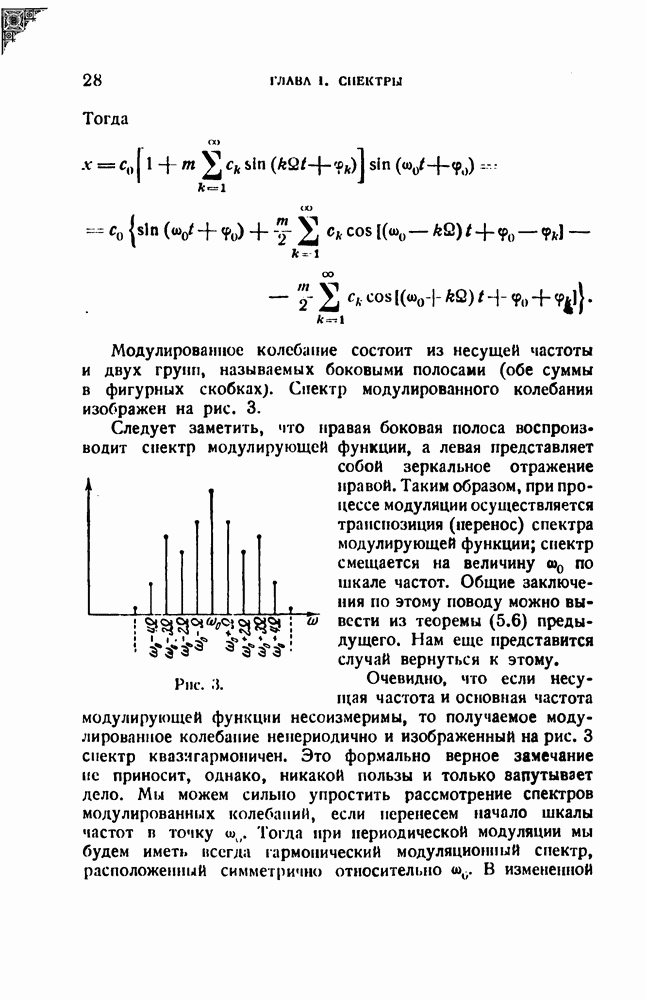
Рис. 41.
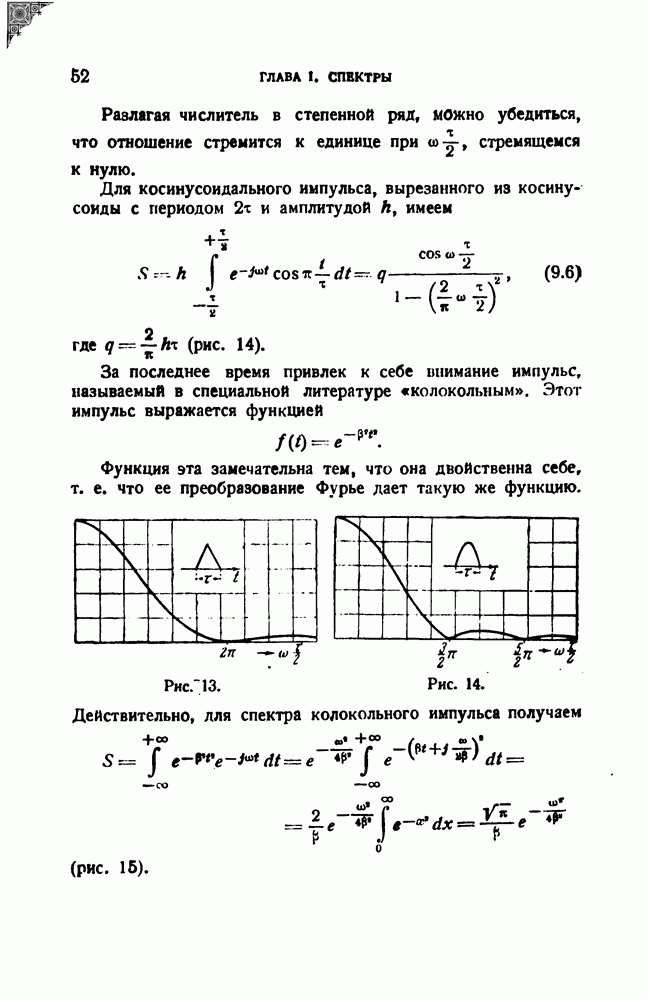
Воздействие на резонатор может быть представлено в виде

Представим себе резонатор в виде электрической цепи, показанной на рис. 41, и обозначим  Тогда уравнение вынужденных колебаний примет вид
Тогда уравнение вынужденных колебаний примет вид

Выберем начало отсчета времени так, чтобы при  изменяющаяся частота
изменяющаяся частота  совпадала с резонансной частотой; иначе говоря, положим
совпадала с резонансной частотой; иначе говоря, положим  Уравнение (22.2)
Уравнение (22.2)
перепишется при этом условии в виде

Нам нужно найти не полное решение этого уравнении, а лишь значение изменяющейся во времени амплитуды, т. е. выражение для огибающей. Поэтому и в данном случае уместно воспользоваться методом § 21. Предположим решение в виде

где  — медленно меняющиеся функции времени. Представим множитель в правой части (22-3) в виде
— медленно меняющиеся функции времени. Представим множитель в правой части (22-3) в виде

После этого, продифференцировав (22.4) дважды, подставив в (22.3) и приравняв коэффициенты при синусе и косинусе, получим два уравнения:

Члены левых частей этих уравнений имеют различный порядок малости; вторые производные функций а и  имеют второй порядок малости в силу исходного предположения о медленности этих функций. Второй порядок малости имеют также члены, содержащие произведения производных функций а и
имеют второй порядок малости в силу исходного предположения о медленности этих функций. Второй порядок малости имеют также члены, содержащие произведения производных функций а и  на показатель затухания. Это обусловлено тем, что мы рассматриваем резонатор с малым затуханием
на показатель затухания. Это обусловлено тем, что мы рассматриваем резонатор с малым затуханием  так как только такой резонатор и пригоден для целей анализа.
так как только такой резонатор и пригоден для целей анализа.
Отбрасывая члены второго порядка, получаем укороченные уравнения

Решение этих уравнений можно получить при помощи теоремы свертывания. Для этого нужно сначала найти переходную амплитуду (по терминологии Н. Н. Крылова [13]), определяемую уравнением

или в операционной форме

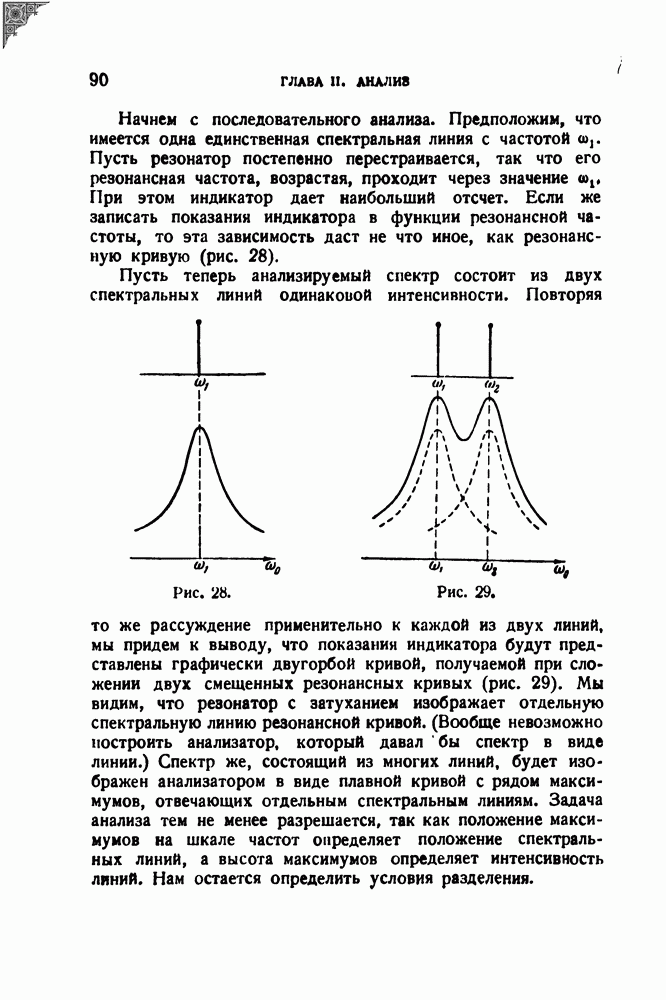
откуда

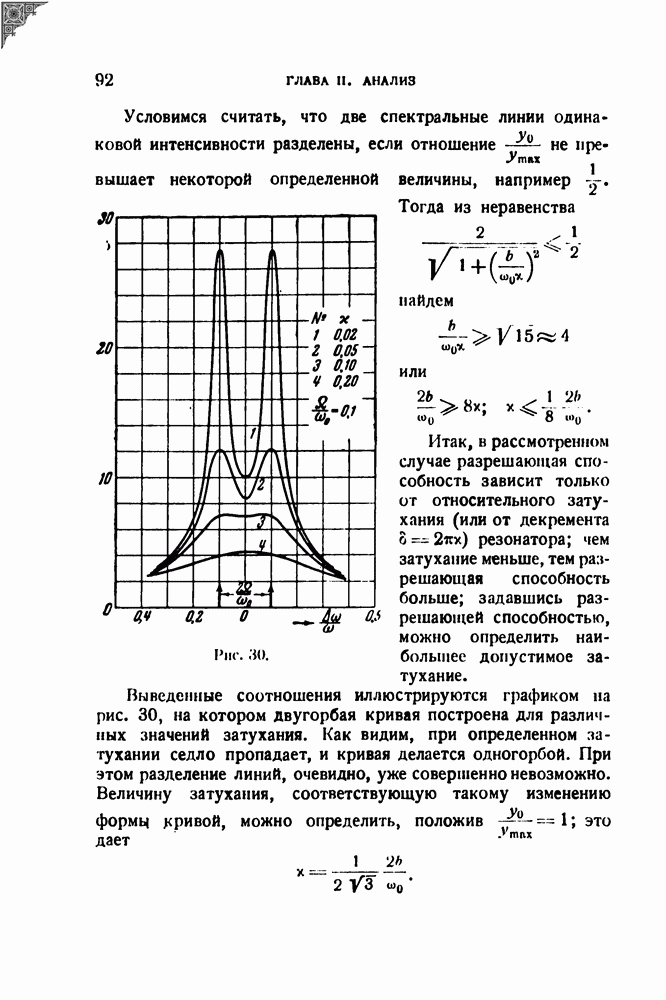
а для производной переходной амплитуды

Теперь по теореме свертывания !), принимая во внимание, что возмущение начало действовать при  когда система находилась в покое, получаем
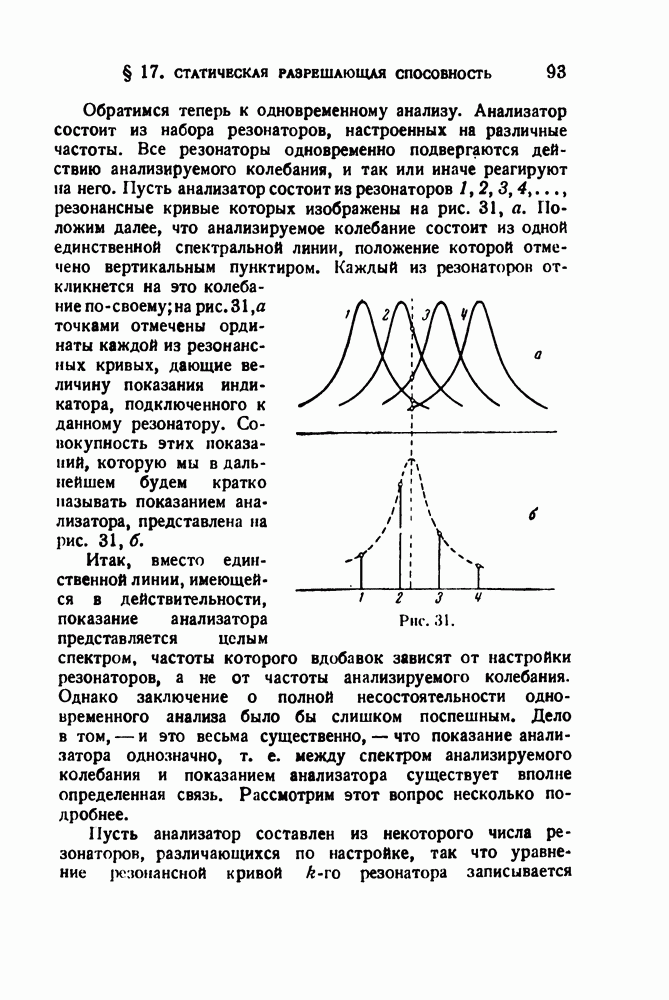
когда система находилась в покое, получаем

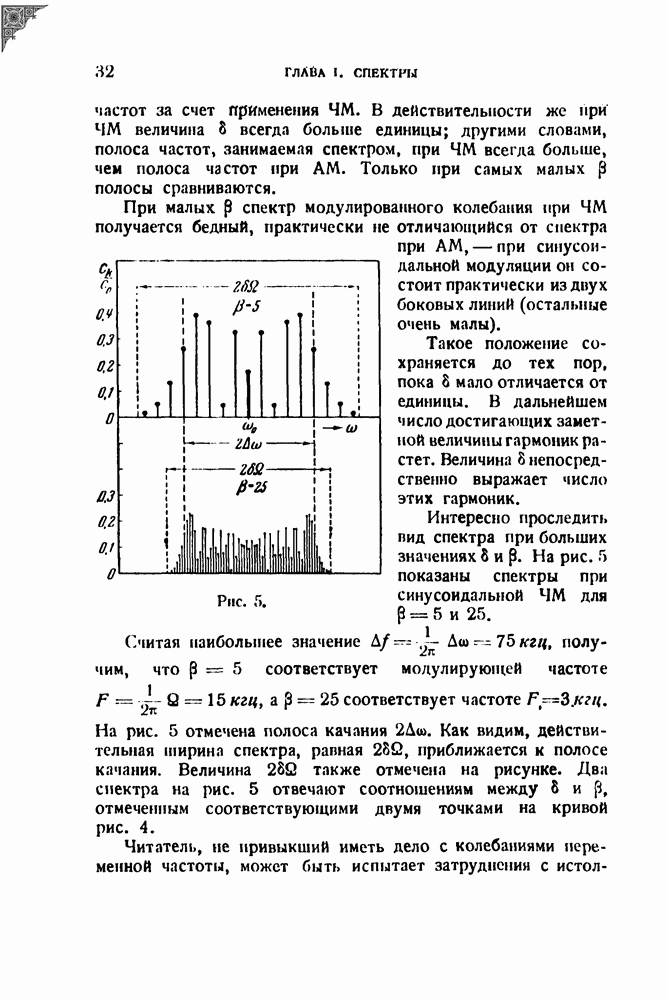
Эти формулы дают уже решение задачи. Но мы сделаем еще замену переменных по формулам

и введем обозначения для безразмерных величин

Тогда формулы (22.6) примут вид

Как видим, дело сводится к вычислению интегралов

Эти функции до сих пор не были табулированы. Заметим, что при  т. е. в случае резонатора без затухания, формулы (22.7) упрощаются и принимают вид
т. е. в случае резонатора без затухания, формулы (22.7) упрощаются и принимают вид

Интегралы в правых частях — обычные интегралы Френеля

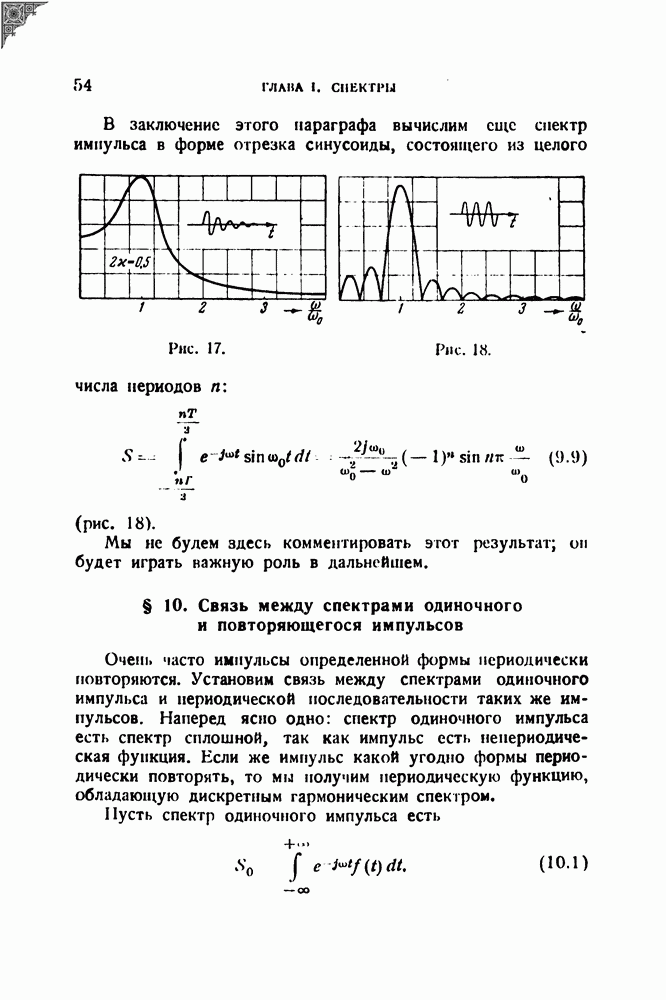
Рассмотрим ту же задачу в несколько измененной постановке: пусть частота не возрастает, а убывает по линейному закону


Рис. 42.
(рис. 42). Тогда

а дальше все выкладки повторяются в том же порядке и приводят к результатам, аналогичным (22.7), с той лишь разницей, что в выражении для а появляется знак минус (не существенный для дальнейшего) и, кроме того, нижний предел интегралов становится рапным минус бесконечности:

Пользуясь обозначениями (22.8), можно представить формулы (22.7) и (22.12) в случае возрастающей частоты в следующем виде:

а в случае убывающей частоты:

Итак, как в случае возрастающей, так и в случае убывающей частоты, ход функций а и  аргумента
аргумента  (пропорционального времени) в окрестности значения
(пропорционального времени) в окрестности значения  (принятого за начало отсчета времен) определяется только первыми членами в квадратных скобках. Эти члены в формулах (22.13) и (22.14) одинаковы; различаются в этих формулах только вторые члены в квадратных скобках, представляющие собой постоянные величины. Заметим, что для формул (22.14) эти вторые члены
(принятого за начало отсчета времен) определяется только первыми членами в квадратных скобках. Эти члены в формулах (22.13) и (22.14) одинаковы; различаются в этих формулах только вторые члены в квадратных скобках, представляющие собой постоянные величины. Заметим, что для формул (22.14) эти вторые члены
легко вычисляются. Мы имеем

В этих формулах

Рассмотрим также случай экспоненциального закона изменения частоты во времени. Пусть

Если скорость изменения частоты, определяемая показателем  , невелика, то в окрестности
, невелика, то в окрестности  можно представить а приближенным выражением
можно представить а приближенным выражением

Таким образом, случай экспоненциального изменения частоты сводится к уже рассмотренному случаю линейного изменения частоты, если положить

Обратимся теперь к случаю, когда возбуждающая частота неизменна, а меняется настройка резонатора. Соотношения для этого случая оказываются аналогичными выведенным ранее. Это можно показать следующим образом.
Перепишем уравнение (22.3), отбросив несущественное слагаемое  в аргументе правой части,
в аргументе правой части,

и заменим переменную по формуле

Составляя производные по новой независимой переменной, отбросим член, зависящий от  полагая эту величину малой. Мы имеем
полагая эту величину малой. Мы имеем

и приближенно

Теперь уравнение относительно переменной  принимает вид
принимает вид

или

где

Таким образом, уравнение (22.16) представляет собой уравнение вынужденных колебаний контура с индуктивностью и емкостью, изменяющимися по закону

а так как уравнение (22.16) выведено из (22.3), то решения этих уравнений совпадают в пределах погрешности, определяемой сделанными при выводе приближениями.
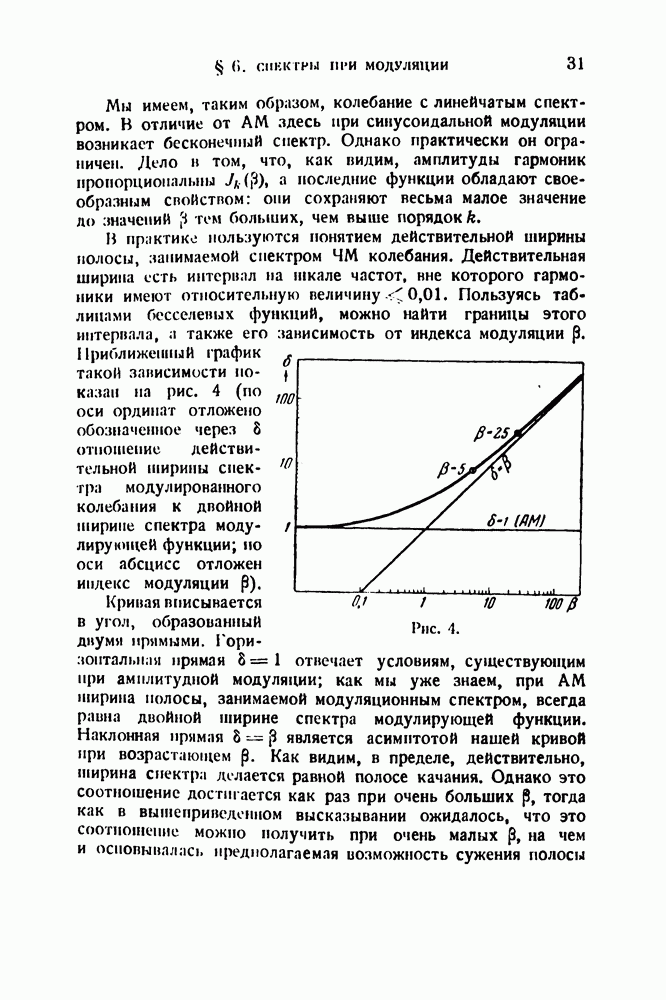
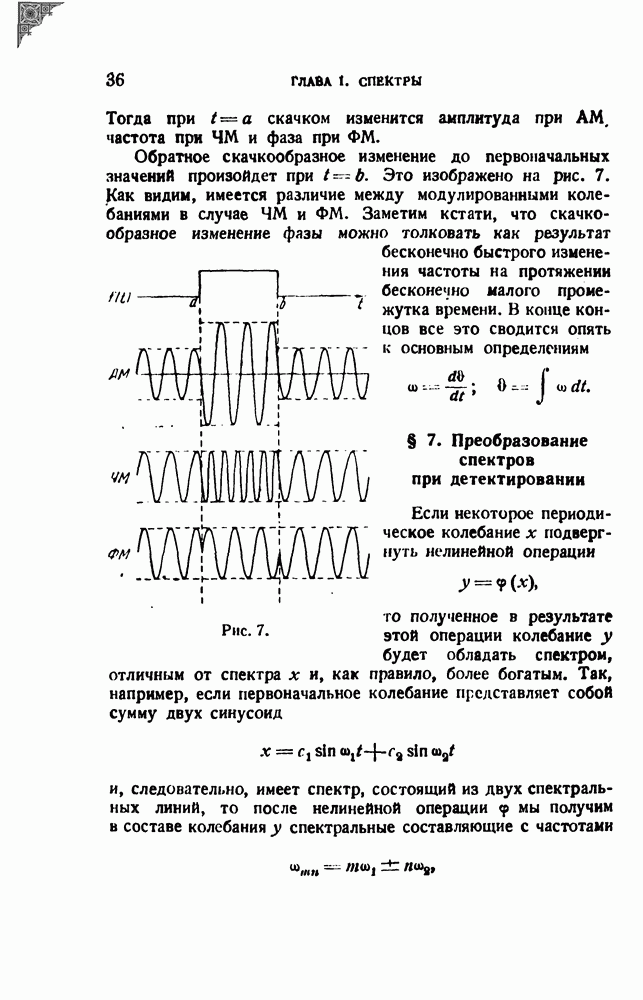
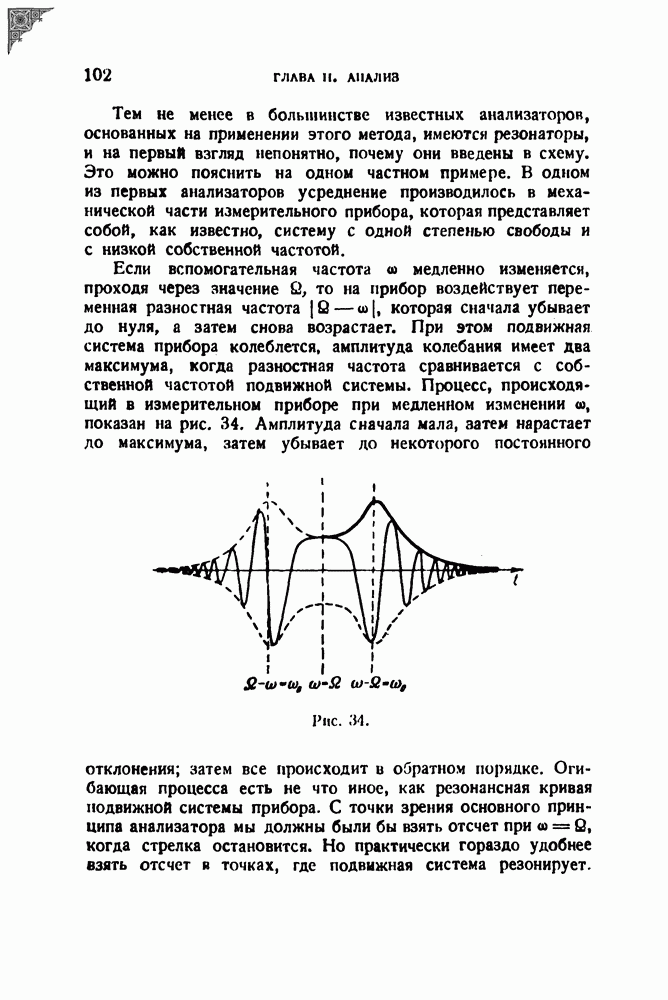
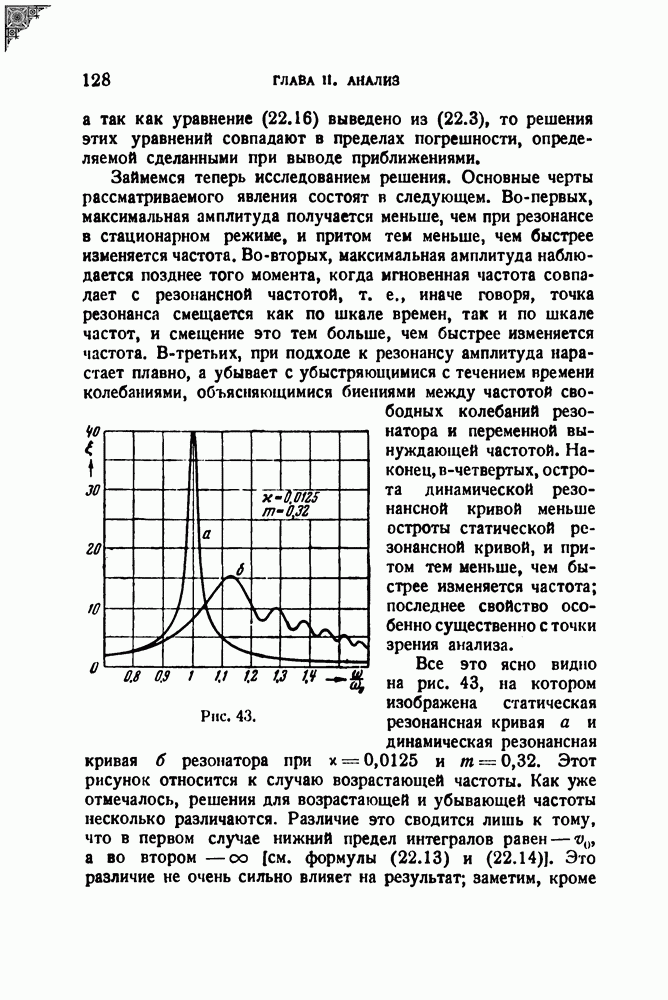
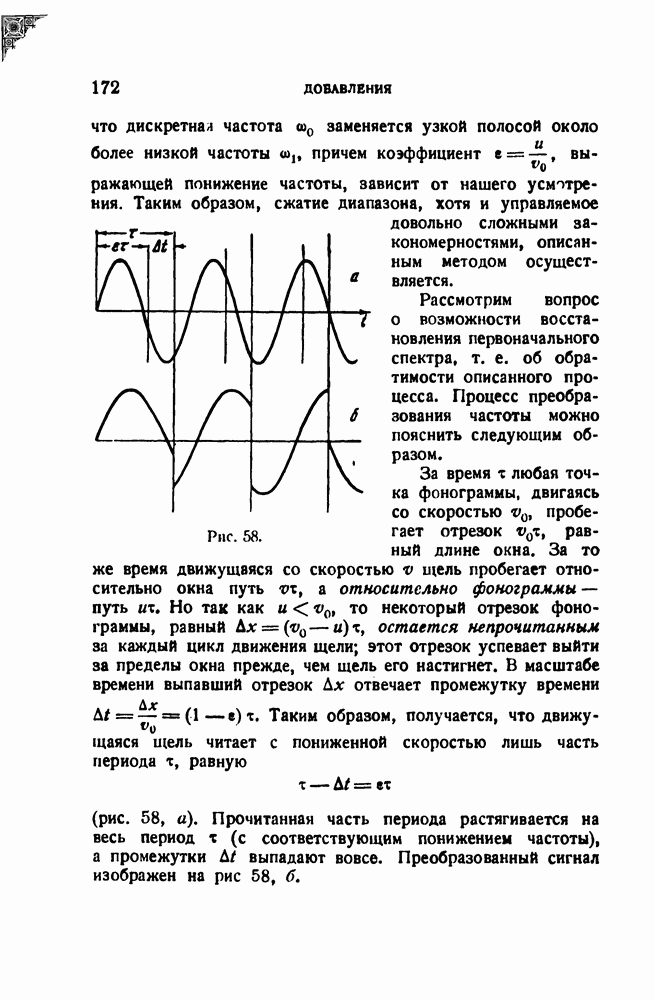
Займемся теперь исследованием решения. Основные черты рассматриваемого явления состоят в следующем. Во-первых, максимальная амплитуда получается меньше, чем при резонансе в стационарном режиме, и притом тем меньше, чем быстрее изменяется частота. Во-вторых, максимальная амплитуда наблюдается позднее того момента, когда мгновенная частота совпадает с резонансной частотой, т. е., иначе говоря, точка резонанса смещается как по шкале времен, так и по шкале частот, и смещение это тем больше, чем быстрее изменяется частота. В-третьих, при подходе к резонансу амплитуда нарастает плавно, а убывает с убыстряющимися с течением времени колебаниями, объясняющимися биениями между частотой свободных колебаний резонатора и переменной вынуждающей частотой. Наконец, в-четвертых, острота динамической резонансной кривой меньше остроты статической резонансной кривой, и притом тем меньше, чем быстрее изменяется частота; последнее свойство особенно существенно с точки зрения анализа.

Рис. 43.
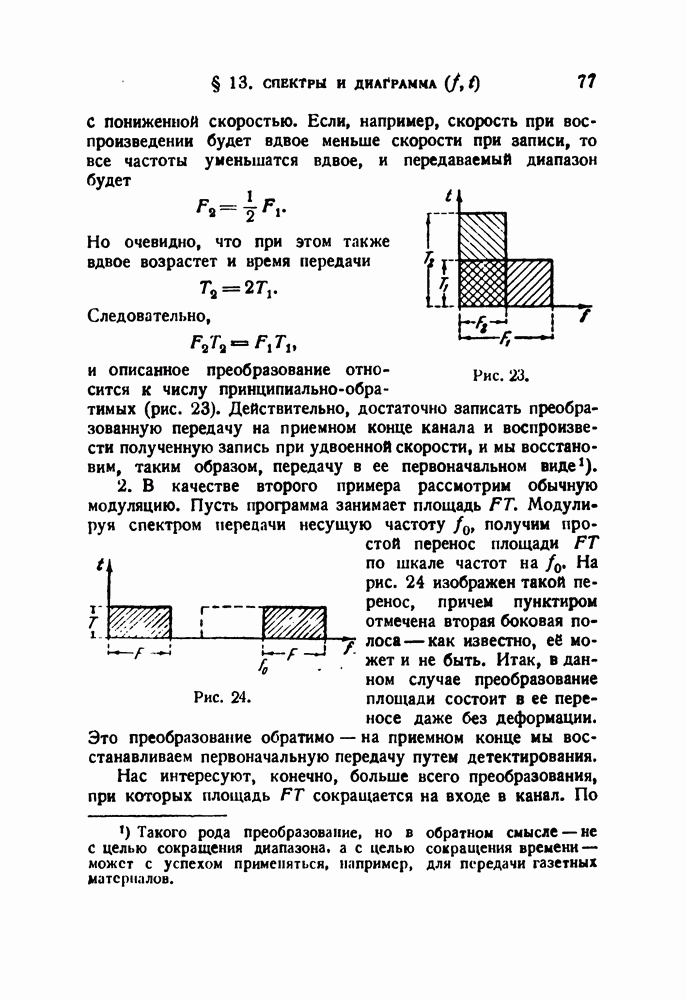
Все это ясно видно на рис. 43, на котором изображена статическая резонансная кривая а и динамическая резонансная кривая  резонатора при
резонатора при  Этот рисунок относится к случаю возрастающей частоты. Как уже отмечалось, решения для возрастающей и убывающей частоты несколько различаются. Различие это сводится лишь к тому, что в первом случае нижний предел интегралов равен —
Этот рисунок относится к случаю возрастающей частоты. Как уже отмечалось, решения для возрастающей и убывающей частоты несколько различаются. Различие это сводится лишь к тому, что в первом случае нижний предел интегралов равен —  а во втором
а во втором  [см. формулы (22.13) и (22.14)]. Это различие не очень сильно влияет на результат; заметим, кроме
[см. формулы (22.13) и (22.14)]. Это различие не очень сильно влияет на результат; заметим, кроме
того, что

т.е.  тем больше, чем медленнее изменяется частота. Следовательно, и различие в решениях для случаев возрастающей и убывающей частоты тем меньше, чем меньше
тем больше, чем медленнее изменяется частота. Следовательно, и различие в решениях для случаев возрастающей и убывающей частоты тем меньше, чем меньше  а так как
а так как  применении к анализу нас интересуют именно процессы с относительно медленным изменением частоты, то можно
применении к анализу нас интересуют именно процессы с относительно медленным изменением частоты, то можно  большой погрешности применять одно и то же решение для обоих случаев. Очевидно, следует выбрать для этой цели формулы (22.14) для убывающей частоты, как более простые.
большой погрешности применять одно и то же решение для обоих случаев. Очевидно, следует выбрать для этой цели формулы (22.14) для убывающей частоты, как более простые.
Таким образом, решение, которым мы будем в дальнейшем пользоваться, может быть на основании формул (22,14) записано в виде

Как видим, огибающая  зависит от
зависит от  и
и  Если теперь рассматривать вместо
Если теперь рассматривать вместо 

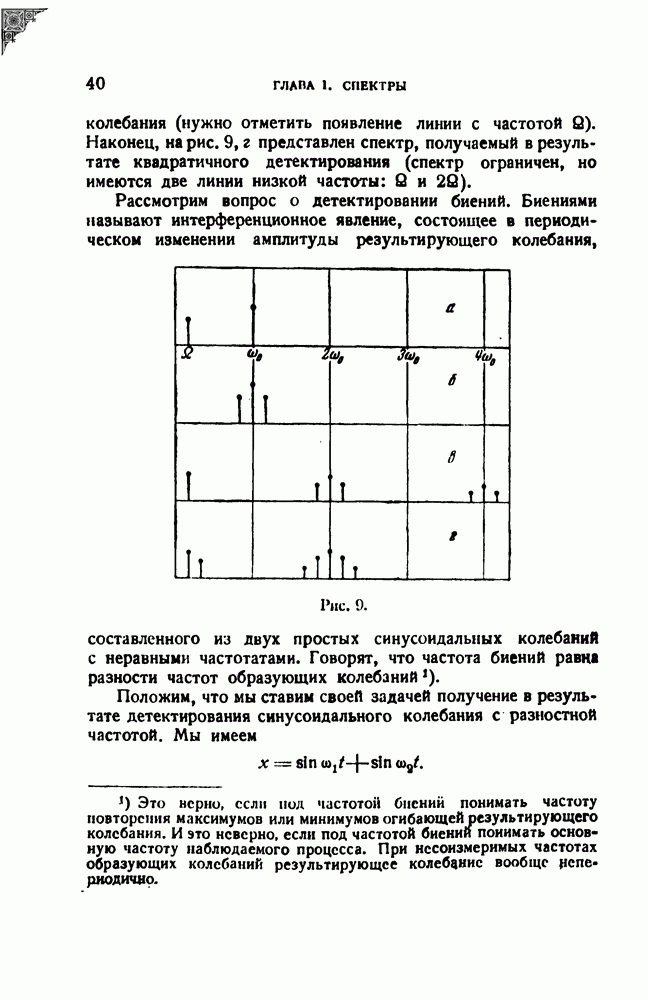
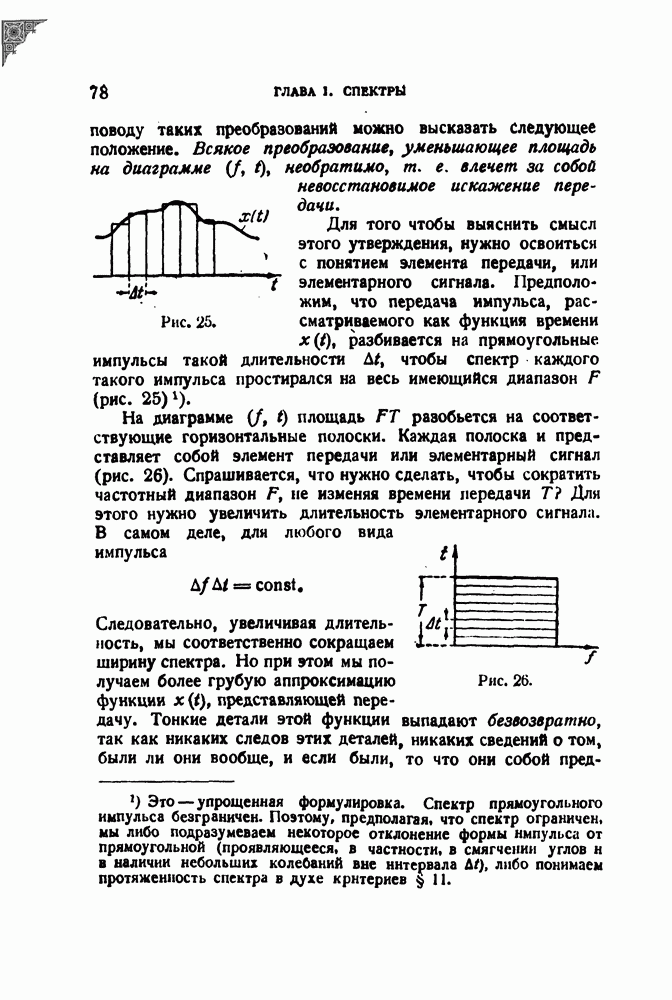
то эта величина зависит уже только от двух переменных  и, следовательно, может быть представлена графически одним семейством кривых. Такое семейство изображено в виде рельефа на рис. 44. По оси ординат отложена величина
и, следовательно, может быть представлена графически одним семейством кривых. Такое семейство изображено в виде рельефа на рис. 44. По оси ординат отложена величина  по горизонтальной оси параллельной плоскости чертежа, отложена величина
по горизонтальной оси параллельной плоскости чертежа, отложена величина

По третьей оси, направленной к читателю, отложена величина

Рельеф в таких координатах дает представление об изменении поведения резонатора в зависимости от изменения затухания при постоянной скорости изменения вынуждающей частоты (т. е. при постоянных  ). Как видим, при больших
). Как видим, при больших 
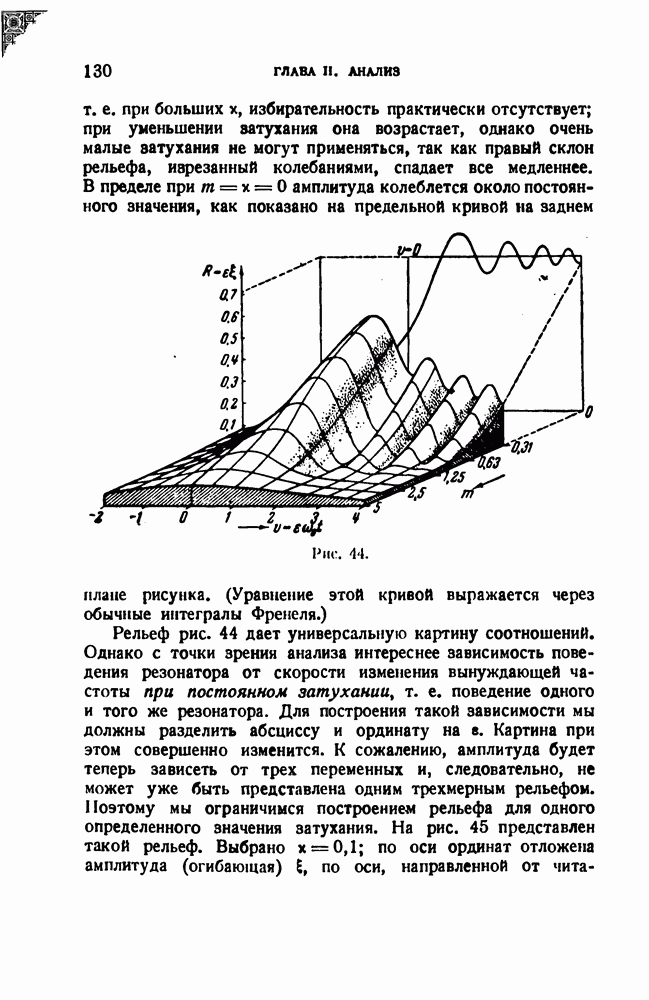
т. е. при больших х, избирательность практически отсутствует; при уменьшении затухания она возрастает, однако очень малые затухания не могут применяться, так как правый склон рельефа, изрезанный колебаниями, спадает все медленнее. В пределе при  амплитуда колеблется около постоянного значения, как показано на предельной кривой на заднем плане рисунка. (Уравнение этой кривой выражается через обычные интегралы Френеля.)
амплитуда колеблется около постоянного значения, как показано на предельной кривой на заднем плане рисунка. (Уравнение этой кривой выражается через обычные интегралы Френеля.)

Рис. 44.
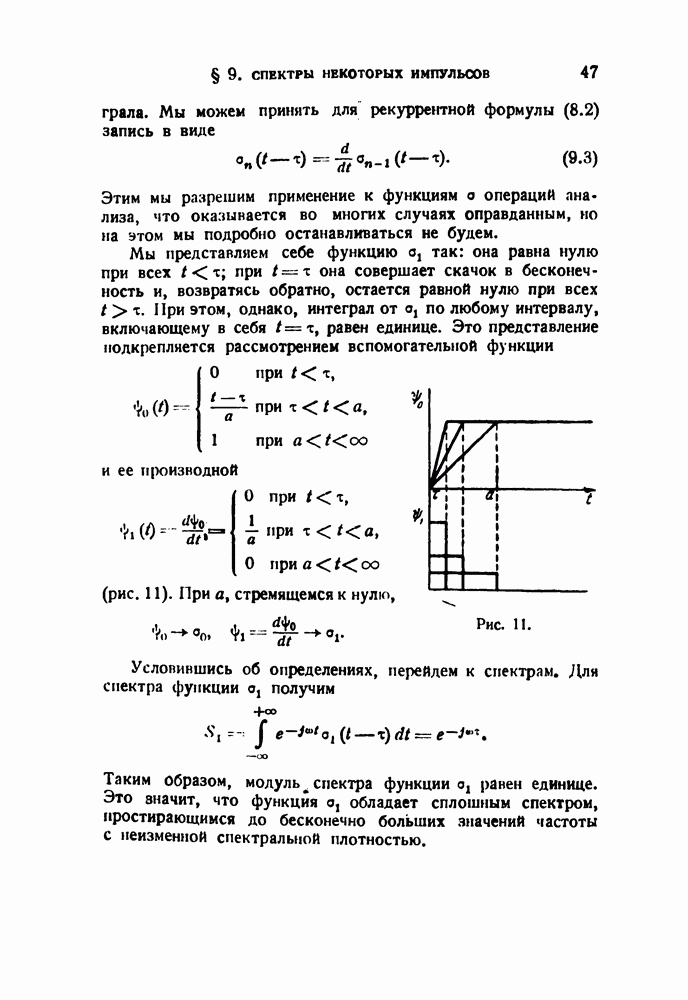
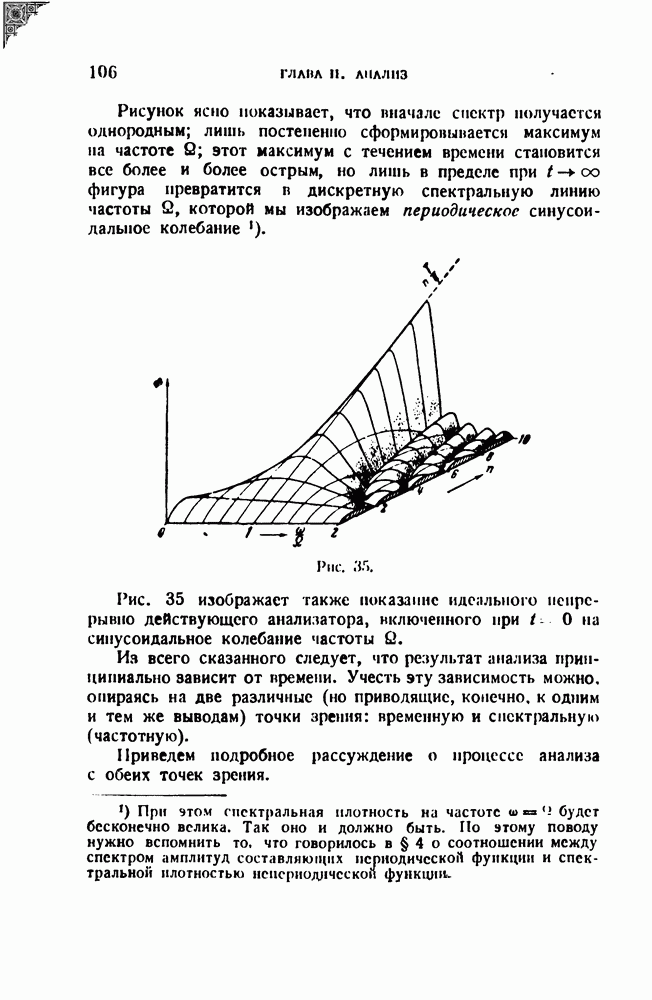
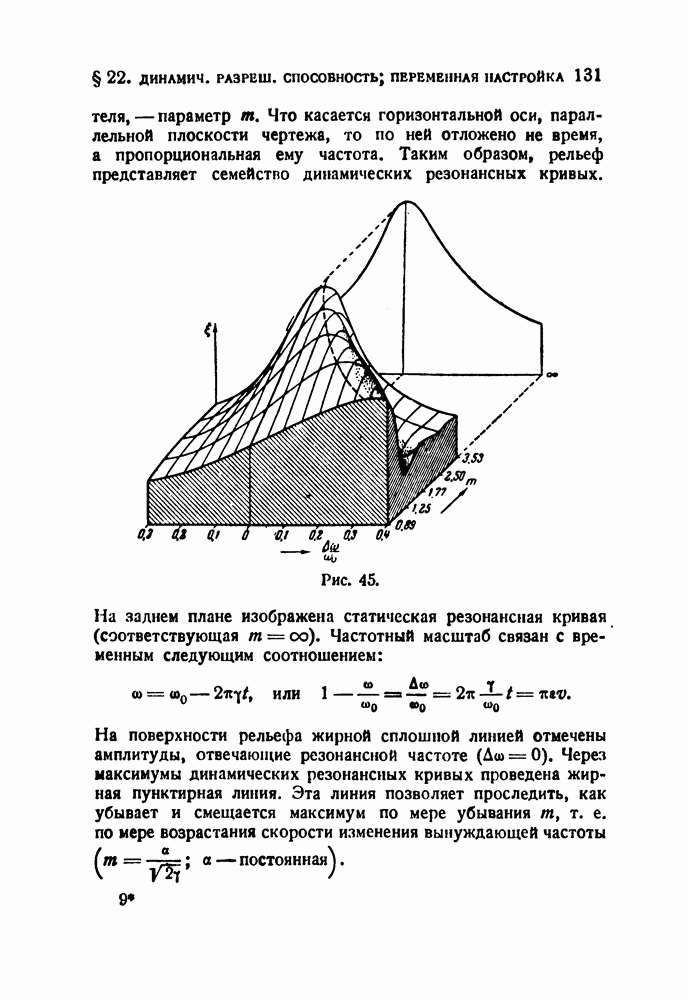
Рельеф рис. 44 дает универсальную картину соотношений. Однако с точки зрения анализа интереснее зависимость поведения резонатора от скорости изменения вынуждающей частоты при постоянном затухании, т. е. поведение одного и того же резонатора. Для построения такой зависимости мы должны разделить абсциссу и ординату на в. Картина при этом совершенно изменится. К сожалению, амплитуда будет теперь зависеть от трех переменных и, следовательно, не может уже быть представлена одним трехмерным рельефом. Поэтому мы ограничимся построением рельефа для одного определенного значения затухания. На рис. 45 представлен такой рельеф. Выбрано  по оси ординат отложена амплитуда (огибающая)
по оси ординат отложена амплитуда (огибающая)  по оси, направленной от
по оси, направленной от
читателя, — параметр  Что касается горизонтальной оси, параллельной плоскости чертежа, то по ней отложено не время, а пропорциональная ему частота. Таким образом, рельеф представляет семейство динамических резонансных кривых.
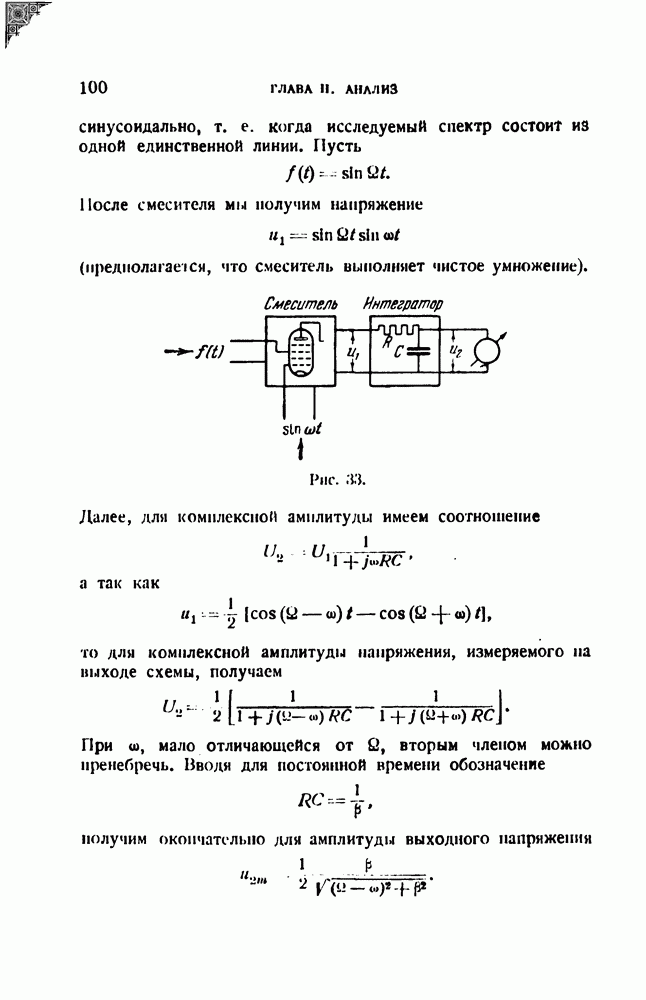
Что касается горизонтальной оси, параллельной плоскости чертежа, то по ней отложено не время, а пропорциональная ему частота. Таким образом, рельеф представляет семейство динамических резонансных кривых.

Рис. 45.
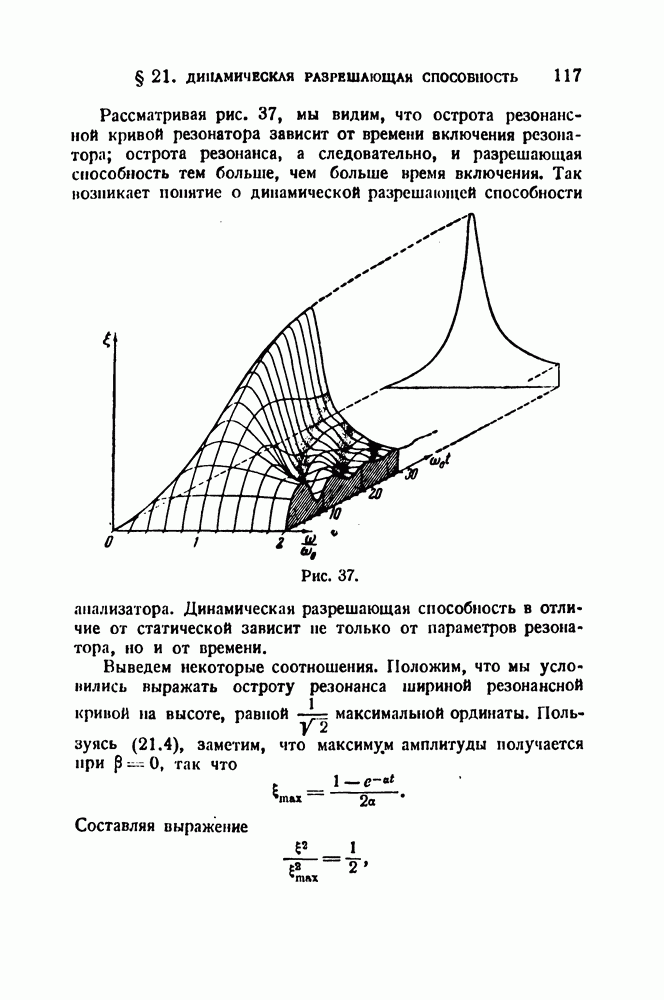
На заднем плане изображена статическая резонансная кривая (соответствующая  Частотный масштаб связан с временным следующим соотношением:
Частотный масштаб связан с временным следующим соотношением:

На поверхности рельефа жирной сплошной линией отмечены амплитуды, отвечающие резонансной частоте  Через максимумы динамических резонансных кривых проведена жирная пунктирная линия. Эта линия позволяет проследить, как убывает и смещается максимум по мере убывания
Через максимумы динамических резонансных кривых проведена жирная пунктирная линия. Эта линия позволяет проследить, как убывает и смещается максимум по мере убывания  т. е. по мере возрастания скорости изменения вынуждающей частоты (
т. е. по мере возрастания скорости изменения вынуждающей частоты ( — постоянная).
— постоянная).
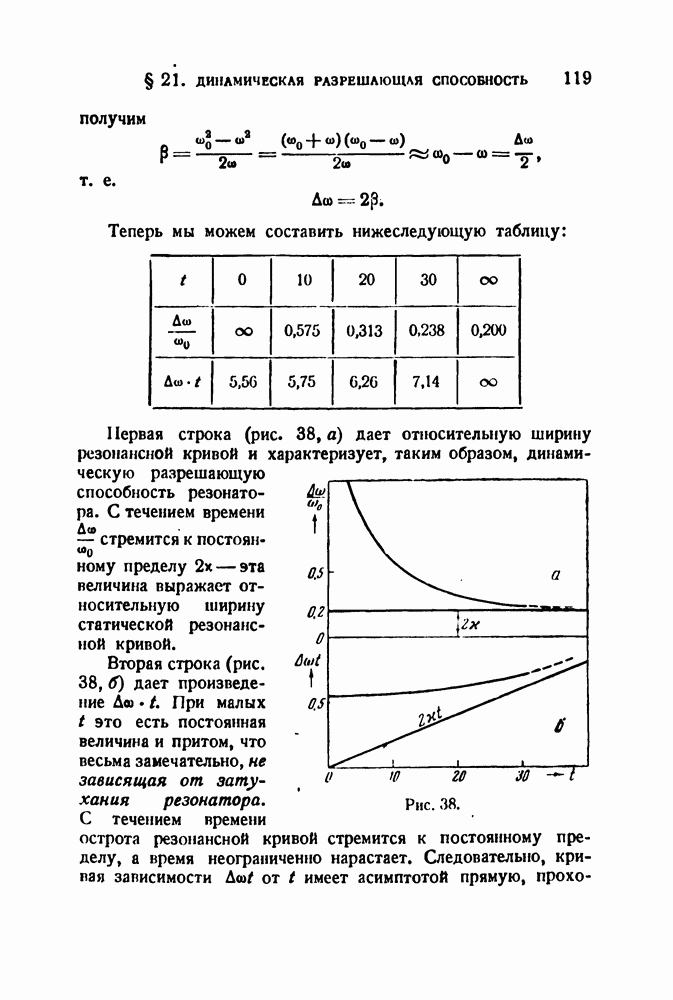
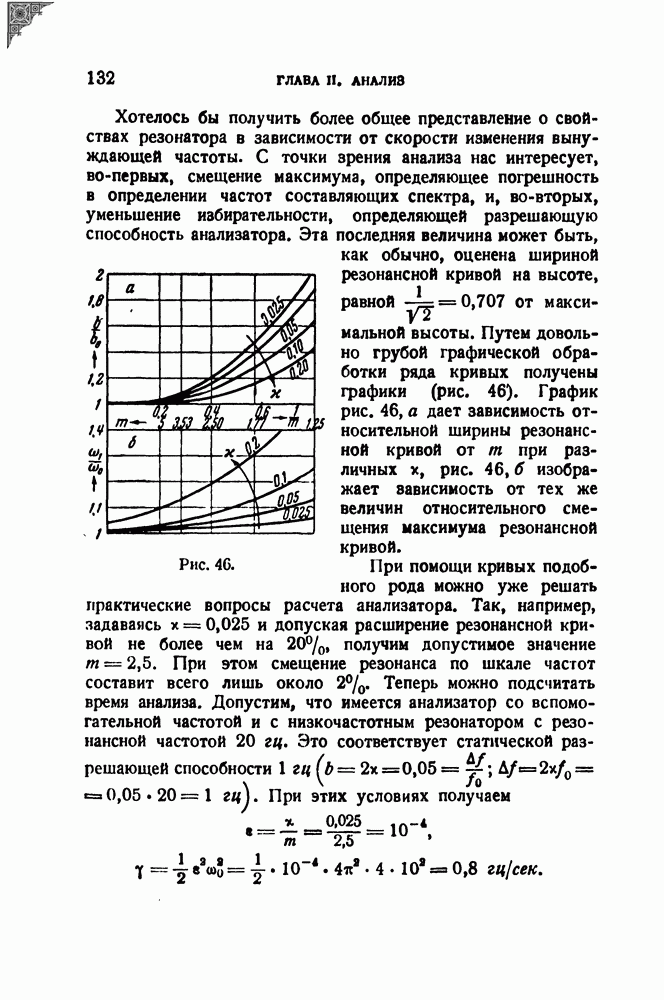
Хотелось бы получить более общее представление о свойствах резонатора в зависимости от скорости изменения вынуждающей частоты. С точки зрения анализа нас интересует, во-первых, смещение максимума, определяющее погрешность в определении частот составляющих спектра, и, во-вторых, уменьшение избирательности, определяющей разрешающую способность анализатора. Эта последняя величина может быть, как обычно, оценена шириной резонансной кривой на высоте, равной  от максимальной высоты. Путем довольно грубой графической обработки ряда кривых получены графики (рис. 46). График рис. 46, а дает зависимость относительной ширины резонансной кривой от
от максимальной высоты. Путем довольно грубой графической обработки ряда кривых получены графики (рис. 46). График рис. 46, а дает зависимость относительной ширины резонансной кривой от  при различных х, рис.
при различных х, рис.  изображает зависимость от тех же величин относительного смещения максимума резонансной кривой.
изображает зависимость от тех же величин относительного смещения максимума резонансной кривой.

Рис. 46.
При помощи кривых подобного рода можно уже решать практические вопросы расчета анализатора. Так, например, задаваясь  и допуская расширение резонансной кривой не более чем на 20%. получим допустимое значение
и допуская расширение резонансной кривой не более чем на 20%. получим допустимое значение  При этом смещение резонанса по шкале частот составит всего лишь около
При этом смещение резонанса по шкале частот составит всего лишь около  Теперь можно подсчитать время анализа. Допустим, что имеется анализатор со вспомогательной частотой и с низкочастотным резонатором с резонансной частотой 20 гц. Это соответствует статической разрешающей способности 1 гц
Теперь можно подсчитать время анализа. Допустим, что имеется анализатор со вспомогательной частотой и с низкочастотным резонатором с резонансной частотой 20 гц. Это соответствует статической разрешающей способности 1 гц  . При этих условиях получаем
. При этих условиях получаем

Для анализа в звуковом диапазоне  потребуется время
потребуется время

Этот обескураживающий результат показывает, как осмотри тельно нужно ставить требования к анализатору. Достаточно выбрать статическую разрешающую способность 10 гц (при этом динамическая разрешающая способность будет 12 гц — увеличение на  при данном
при данном  чтобы время анализа сократилось в 100 раз, т. е. до 2 мин.
чтобы время анализа сократилось в 100 раз, т. е. до 2 мин.
В заключение настоящего параграфа рассмотрим вопрос о соблюдении соотношения  Мы подойдем к этому вопросу следующим образом: под
Мы подойдем к этому вопросу следующим образом: под  будем понимать динамическую разрешающую способность, т. е. ширину динамической резонансной кривой; под
будем понимать динамическую разрешающую способность, т. е. ширину динамической резонансной кривой; под  будем понимать время, затрачиваемое на прохождение соответствующего частотного интервала. Очевидно, что при очень малой скорости изменения частоты динамическая разрешающая способность в пределе стремится к статической, т. е. к постоянной величине, а следовательно, произведение
будем понимать время, затрачиваемое на прохождение соответствующего частотного интервала. Очевидно, что при очень малой скорости изменения частоты динамическая разрешающая способность в пределе стремится к статической, т. е. к постоянной величине, а следовательно, произведение  стремится к бесконечности. Это заключение аналогично тому, которое было сделано в § 20 для случая постоянной относительной настройки. Таким образом, можно ожидать, что в рассматриваемом случае соотношение
стремится к бесконечности. Это заключение аналогично тому, которое было сделано в § 20 для случая постоянной относительной настройки. Таким образом, можно ожидать, что в рассматриваемом случае соотношение  будет осуществлено в пределе при весьма больших скоростях изменения частоты.
будет осуществлено в пределе при весьма больших скоростях изменения частоты.
Проверим это. Прежде всего отметим, что при 

а следовательно, выражения для компонент огибающей упрощаются и принимают вид [см. формулы (22.7)]

Из этого следует, что огибающая колебания

будет зависеть только от  если не считать масштабного множителя
если не считать масштабного множителя  Особенность рассматриваемого случая состоит в том, что одна и та же функция
Особенность рассматриваемого случая состоит в том, что одна и та же функция  представляет собой как частотную, так и временную зависимость. Предположим, что мы, опираясь на тот или иной критерий, установили ширину кривой
представляет собой как частотную, так и временную зависимость. Предположим, что мы, опираясь на тот или иной критерий, установили ширину кривой  и обозначили ее через
и обозначили ее через  Эта величина является постоянной, т. е. не зависящей от скорости изменения частоты (поскольку мы рассматриваем соотношения для больших скоростей, когда Е зависит только от
Эта величина является постоянной, т. е. не зависящей от скорости изменения частоты (поскольку мы рассматриваем соотношения для больших скоростей, когда Е зависит только от  Теперь нам нужно выразить
Теперь нам нужно выразить  через
через  Мы имеем
Мы имеем

откуда

с другой стороны,

откуда

Таким образом,

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
- § 9. Спектры некоторых импульсов
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА