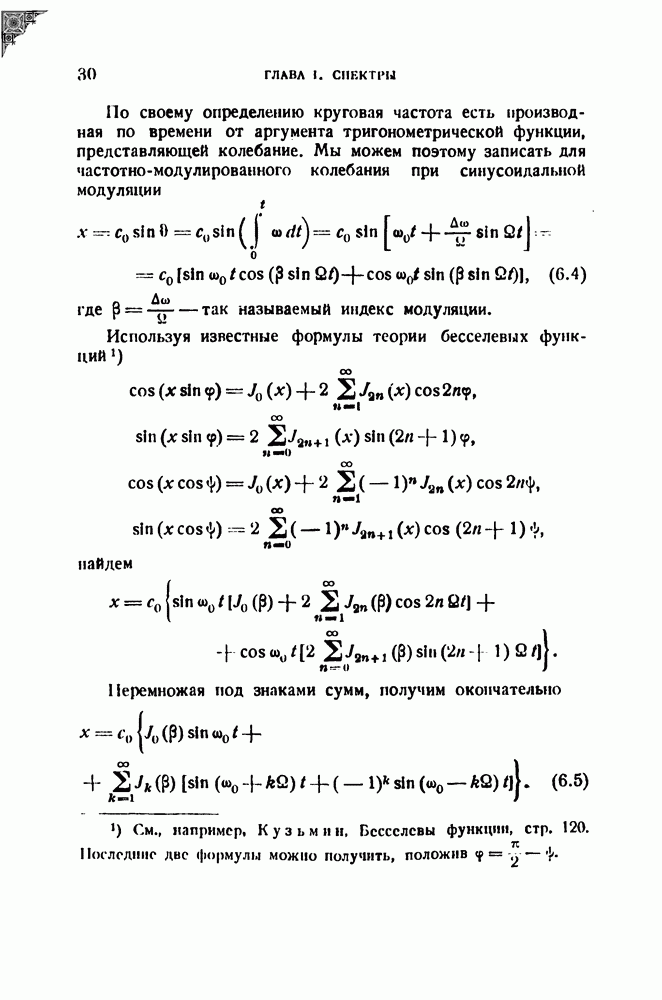| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
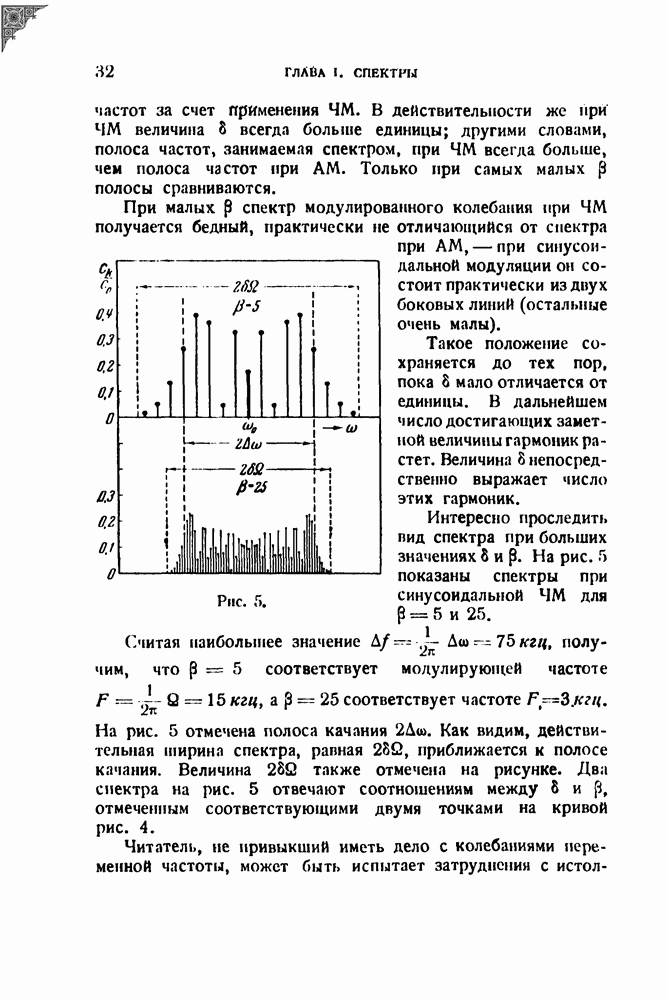
§ 13. Спектры и диаграмма (f, t)
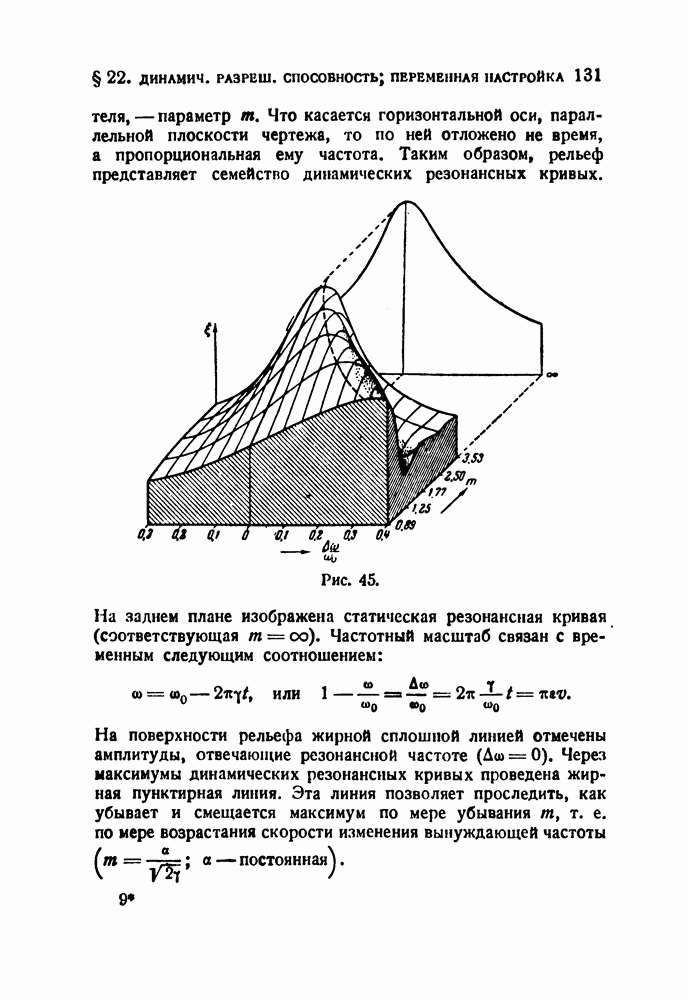
Технику связи давно уже интересовал вопрос о возможности сокращения диапазона частот, занимаемого передачей. Эта возможность позволила бы произвести дальнейшее «уплотнение эфира», увеличить нагрузку проводных линий связи и т.  По этому важному вопросу можно высказать некоторые общие соображения.
По этому важному вопросу можно высказать некоторые общие соображения.
В теории связи предложено характеризовать емкость канала связи некоторой площадью на диаграмме, на которой частота  и время
и время  приняты за прямоугольные координаты. Такую диаграмму мы будем в дальнейшем называть диаграммой
приняты за прямоугольные координаты. Такую диаграмму мы будем в дальнейшем называть диаграммой  Если капал пропускает диапазон
Если капал пропускает диапазон  и если он может быть использован в течение времени
и если он может быть использован в течение времени 
то емкость канала может быть выражена произведением  (рис. 22).
(рис. 22).
Рассмотрим вопрос о закономерностях, имеющих место при преобразовании площадей на диаграмме  . В частности, попытаемся выяснить, обратимы ли те или иные преобразования. Смысл этого вопроса состоит в следующем.
. В частности, попытаемся выяснить, обратимы ли те или иные преобразования. Смысл этого вопроса состоит в следующем.

Рис. 22.
Пусть данная передача требует диапазона  и времени занимая на диаграмме площадь
и времени занимая на диаграмме площадь  Предположим, что тем или иным способом мы изменили одну из этих величин (или обе) на передающем конце канала с целью получить более выгодные условия его работы. Это, конечно, связано с изменением характера сигнала, т. е. с его искажением. На приемном конце необходимо произвести обратное преобразование, т. е. восстановить сигнал в его первоначальном виде. Под обратимостью и понимается возможность двух взаимно компенсирующих друг друга преобразований.
Предположим, что тем или иным способом мы изменили одну из этих величин (или обе) на передающем конце канала с целью получить более выгодные условия его работы. Это, конечно, связано с изменением характера сигнала, т. е. с его искажением. На приемном конце необходимо произвести обратное преобразование, т. е. восстановить сигнал в его первоначальном виде. Под обратимостью и понимается возможность двух взаимно компенсирующих друг друга преобразований.
Можно высказать в качестве постулата следующее положение.
Принципиально обратимыми являются такие преобразования на диаграмме  которые не изменяют величины площади. К сожалению, это как раз те преобразования, которые не открывают для техники связи никаких новых возможностей. Поясним понятие об обратимых преобразованиях на двух простых примерах.
которые не изменяют величины площади. К сожалению, это как раз те преобразования, которые не открывают для техники связи никаких новых возможностей. Поясним понятие об обратимых преобразованиях на двух простых примерах.
1. Предположим, что имеется программа, занимающая диапазон  и время
и время  Простейший способ сокращения диапазона состоит в том, что программа предварительно записывается и передается по каналу путем воспроизведения
Простейший способ сокращения диапазона состоит в том, что программа предварительно записывается и передается по каналу путем воспроизведения
С пониженной скоростью. Если, например, скорость при воспроизведении будет вдвое меньше скорости при записи, то все частоты уменьшатся вдвое, и передаваемый диапазон будет

Но очевидно, что при этом также вдвое возрастет и время передачи

Следовательно,

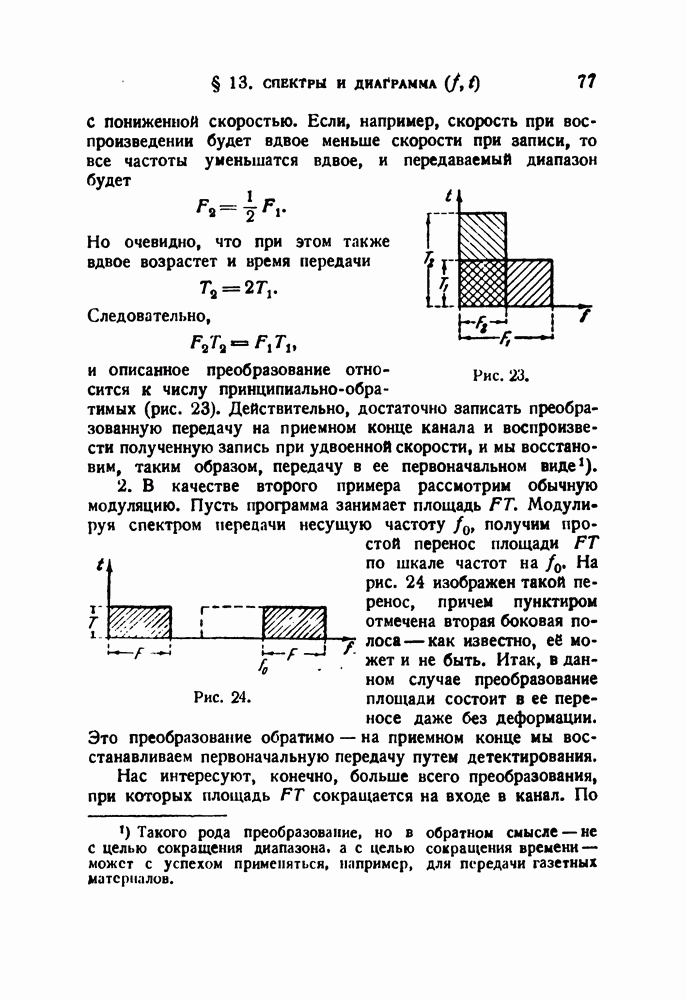
и описанное преобразование относится к числу принципиально - обратимых (рис. 23). Действительно, достаточно записать преобразованную передачу на приемном конце канала и воспроизвести полученную запись при удвоенной скорости, и мы восстановим, таким образом, передачу в ее первоначальном виде.

Рис. 23.
2. В качестве второго примера рассмотрим обычную модуляцию. Пусть программа занимает площадь  Модулируя спектром передачи несущую частоту
Модулируя спектром передачи несущую частоту  получим простой перенос площади
получим простой перенос площади  по шкале частот на
по шкале частот на  На рис. 24 изображен такой перенос, причем пунктиром отмечена вторая боковая полоса — как известно, её может и не быть. Итак, в данном случае преобразование площади состоит в ее переносе даже без деформации. Это преобразование обратимо — на приемном конце мы восстанавливаем первоначальную передачу путем детектирования.
На рис. 24 изображен такой перенос, причем пунктиром отмечена вторая боковая полоса — как известно, её может и не быть. Итак, в данном случае преобразование площади состоит в ее переносе даже без деформации. Это преобразование обратимо — на приемном конце мы восстанавливаем первоначальную передачу путем детектирования.

Рис. 24.
Нас интересуют, конечно, больше всего преобразования, при которых площадь  сокращается на входе в канал. По
сокращается на входе в канал. По
поводу таких преобразований можно высказать следующее положение. Всякое преобразование, уменьшающее площадь на диаграмме  необратимо, т. е. влечет за собой невосстановимое искажение передачи.
необратимо, т. е. влечет за собой невосстановимое искажение передачи.

Рис. 25.
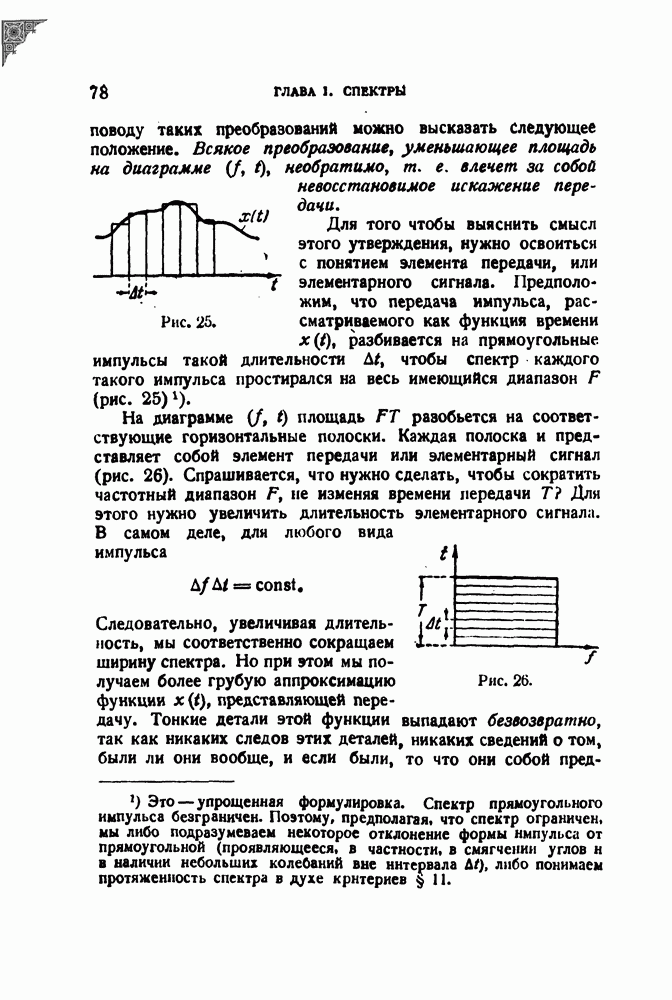
Для того чтобы выяснить смысл этого утверждения, нужно освоиться с понятием элемента передачи, или элементарного сигнала. Предположим, что передача импульса, рассматриваемого как функция времени  разбивается на прямоугольные импульсы такой длительности
разбивается на прямоугольные импульсы такой длительности  чтобы спектр каждого такого импульса простирался на весь имеющийся диапазон
чтобы спектр каждого такого импульса простирался на весь имеющийся диапазон  (рис. 25).
(рис. 25).
На диаграмме  площадь
площадь  разобьется на соответствующие горизонтальные полоски. Каждая полоска и представляет собой элемент передачи или элементарный сигнал (рис. 26). Спрашивается, что нужно сделать, чтобы сократить частотный диапазон
разобьется на соответствующие горизонтальные полоски. Каждая полоска и представляет собой элемент передачи или элементарный сигнал (рис. 26). Спрашивается, что нужно сделать, чтобы сократить частотный диапазон  не изменяя времени передачи Т? Для этого нужно увеличить длительность элементарного сигнала. В самом деле, для любого вида импульса
не изменяя времени передачи Т? Для этого нужно увеличить длительность элементарного сигнала. В самом деле, для любого вида импульса


Рис. 26.
Следовательно, увеличивая длительность, мы соответственно сокращаем ширину спектра. Но при этом мы получаем более грубую аппроксимацию функции  представляющей передачу. Тонкие детали этой функции выпадают безвозвратно, так как никаких следов этих деталей, никаких сведений о том, были ли они вообще, и если были, то что они собой
представляющей передачу. Тонкие детали этой функции выпадают безвозвратно, так как никаких следов этих деталей, никаких сведений о том, были ли они вообще, и если были, то что они собой
представляли, у нас не остается. В этом и состоит необратимое искажение передачи.
По этому поводу нужно сделать два замечания.
Во-первых, из сказанного ясно, что точное изображение данной функции  мы могли бы получить только путем построения ее из бесконечно коротких импульсов. Но бесконечно короткие импульсы обладают бесконечно протяженным спектром. Следовательно, то обстоятельство, что на передачу опускается конечный, ограниченный диапазон, уже предполагает некоторое, считаемое допустимым, искажение передачи. Всякое дальнейшее ограничение диапазона вызывает дальнейшее увеличение искажения.
мы могли бы получить только путем построения ее из бесконечно коротких импульсов. Но бесконечно короткие импульсы обладают бесконечно протяженным спектром. Следовательно, то обстоятельство, что на передачу опускается конечный, ограниченный диапазон, уже предполагает некоторое, считаемое допустимым, искажение передачи. Всякое дальнейшее ограничение диапазона вызывает дальнейшее увеличение искажения.
Во-вторых, следует подчеркнуть различие между искажениями, проявляющимися в нарушении первоначального распределения спектральной плотности, — этот вид искажений обусловлен непрямолинейностью частотной характеристики тракта — и искажениями, проявляющимися в полном устранении спектральных компонент в пределах некоторой полосы частот. У нас речь идет именно о втором виде искажений. Первый вид не изменяет площади на диаграмме и является обратимым в том смысле, что внесенные трактом искажения могут быть скомпенсированы корректорами с надлежащим образом подобранными характеристиками.

Рис. 27.
К аналогичным заключениям мы пришли бы и в том случае, если бы разбили площадь  на элементы другим способом, а именно, если бы мы разделили диапазон
на элементы другим способом, а именно, если бы мы разделили диапазон  на соответствующее число полосок
на соответствующее число полосок  (рис. 27).
(рис. 27).
Из предыдущего рассуждения следует тот, имеющий большое принципиальное значение вывод, что пути сокращения площади  за счет сокращения диапазона
за счет сокращения диапазона  или за счет времени Т эквивалентны — и в том и в другом случае возникает необратимое искажение, состоящее в выпадении деталей передаваемого сигнала. Прекрасной иллюстрацией к этому выводу служит одна довольно замысловатая (но не дающая ничего хорошего) система сжатия спектра, подробно рассмотренная в добавлении. Мы приходим, таким
или за счет времени Т эквивалентны — и в том и в другом случае возникает необратимое искажение, состоящее в выпадении деталей передаваемого сигнала. Прекрасной иллюстрацией к этому выводу служит одна довольно замысловатая (но не дающая ничего хорошего) система сжатия спектра, подробно рассмотренная в добавлении. Мы приходим, таким
образом, к неутешительному заключению о том, что проблема обратимого сжатия спектра (без изменения времени) в рамках наших теперешних представлений неразрешима.
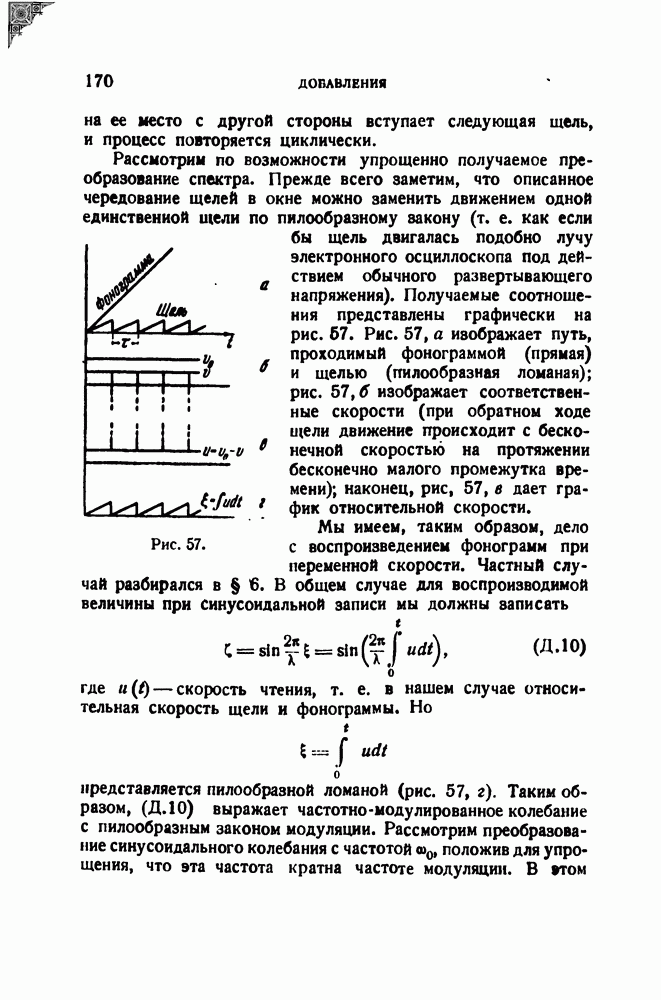
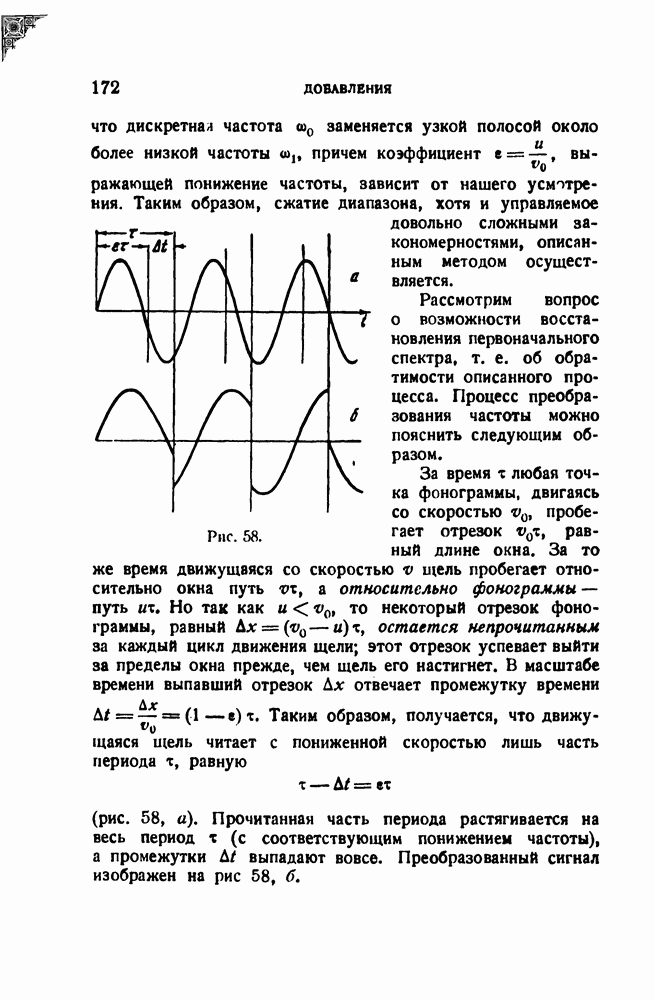
Существует, однако, одна совершенно специальная возможность, которая здесь будет описана в самых общих чертах. Представим себе, что задача состоит в передаче синусоидально - модулированного по амплитуде колебания, спектр которого состоит, как известно, из трех линий: несущей и двух спутников. Но, вместо того чтобы передавать ьтот сигнал по каналу связи, перенесем генератор несущей частоты и модулятор на приемный конец, а по каналу направим лишь модулирующую синусоиду. Таким образом, подлежащий передаче сигнал синтезируется на приемном конце, а канал связи соответственно разгружается, поскольку вместо спектра из трех линий по каналу передается только одна — модулирующая частота. Аналогично обстоит дело и в случае частотной модуляции, причем в случае ЧМ получаемый выигрыш еще Солее очевиден, так как простой синусоидальной модуляции соответствует густой спектр модулированного сигнала. Более общий вид сигнала представляет собой колебание, модулированное одновременно как по амплитуде, так и по частоте. Такое колебание тоже можно получить путем синтеза на приемном конце, так сказать, «из местного сырья», для чего достаточно передать по каналу связи две модулирующие функции.
На подобного рода идеях основан принцип «синтетической телефонии». На приемном конце расположены генераторы, имитирующие звук голосовых связок и дающие белый шум, а также формантные фильтры и управляющие элементы. По каналу связи посылаются только командные сигналы, получаемые путем соответствующей обработки звуков естественной речи. Эти командные сигналы только управляют процессом синтеза, т. е. высотой, силой тона, ритмом речи, спектральным составом и т. д.
Очевидно, что емкость канала, необходимая для передачи командных сигналов, может быть значительно меньше, чем для передачи всего действительного состава звуков речи. Действительно, в одном из осуществленных устройств, так называемом «Вокодере», управление выполняется по 10 цепям, каждая из которых требует лишь  так что весь
так что весь
диапазон, необходимый для передачи командных импульсов, составляет лишь 250 гц.
Не нужно, однако, думать, что описанная возможность представляет собой что-либо принципиально новое с точки зрения способов связи в общем смысле: ведь в сущности речь идет о передаче своеобразным кодом. Различные кеды издавна применялись для ускорения передачи информации. Применение кодов позволяет очень существенно увеличить нагрузку канала связи. Однако вдаваться здесь в этот обширный и специальный вопрос нет возможности.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
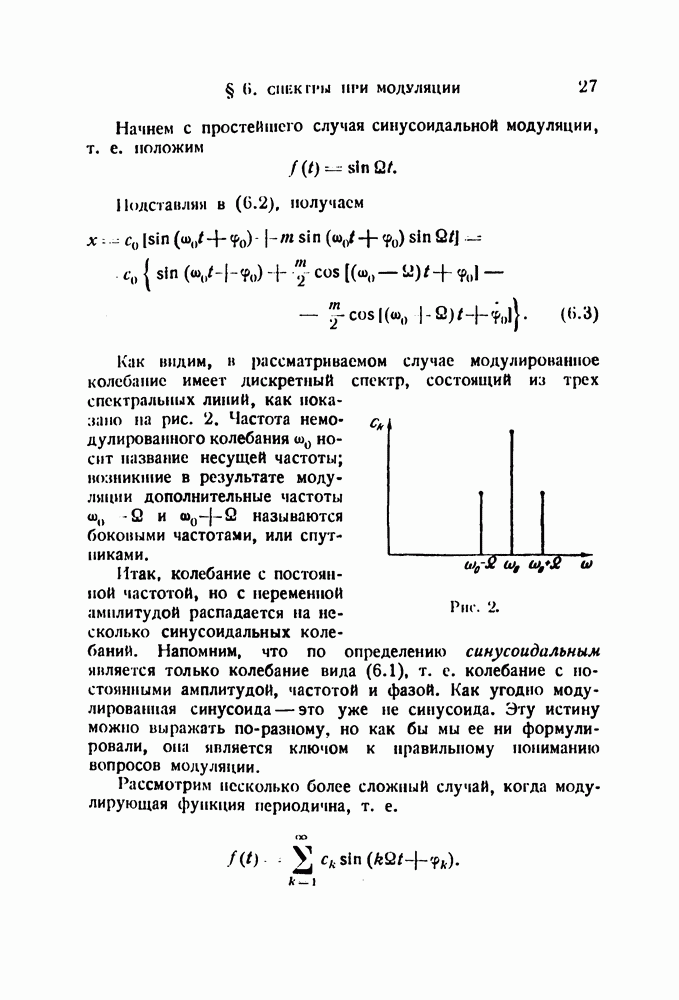
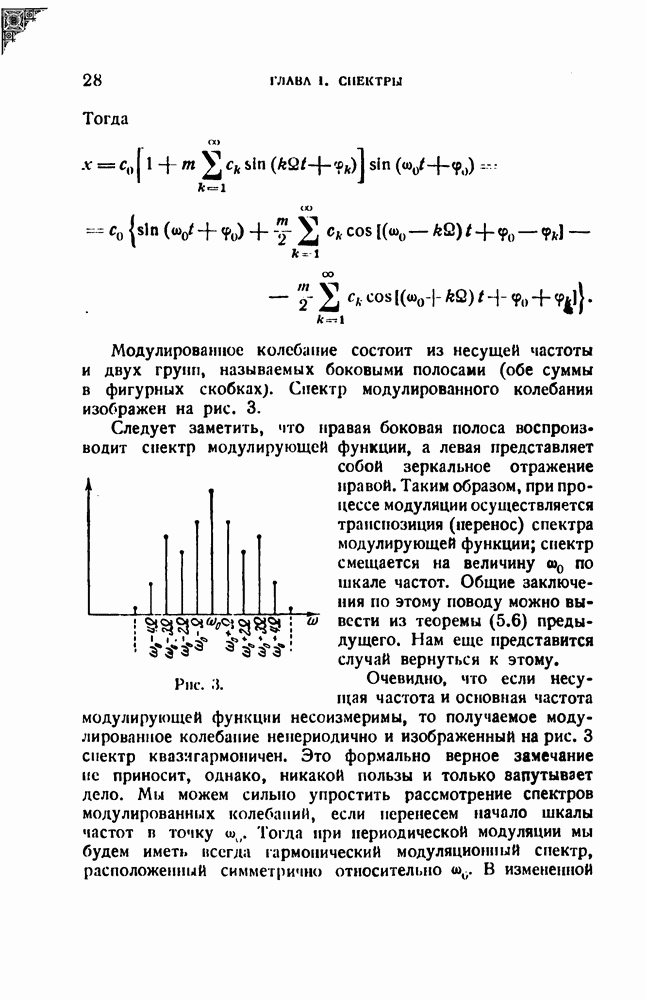
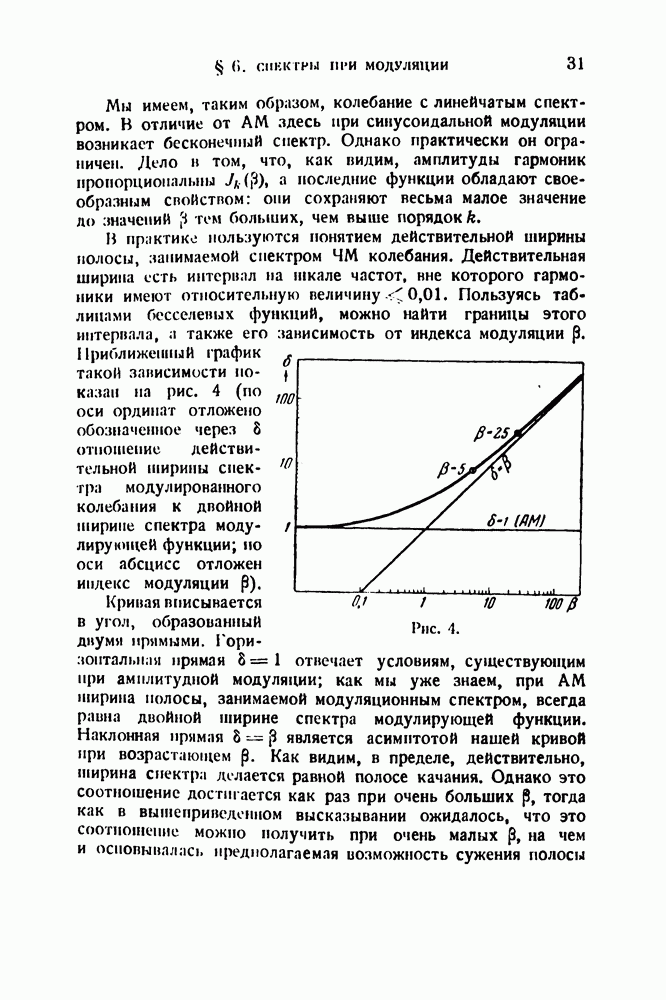
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
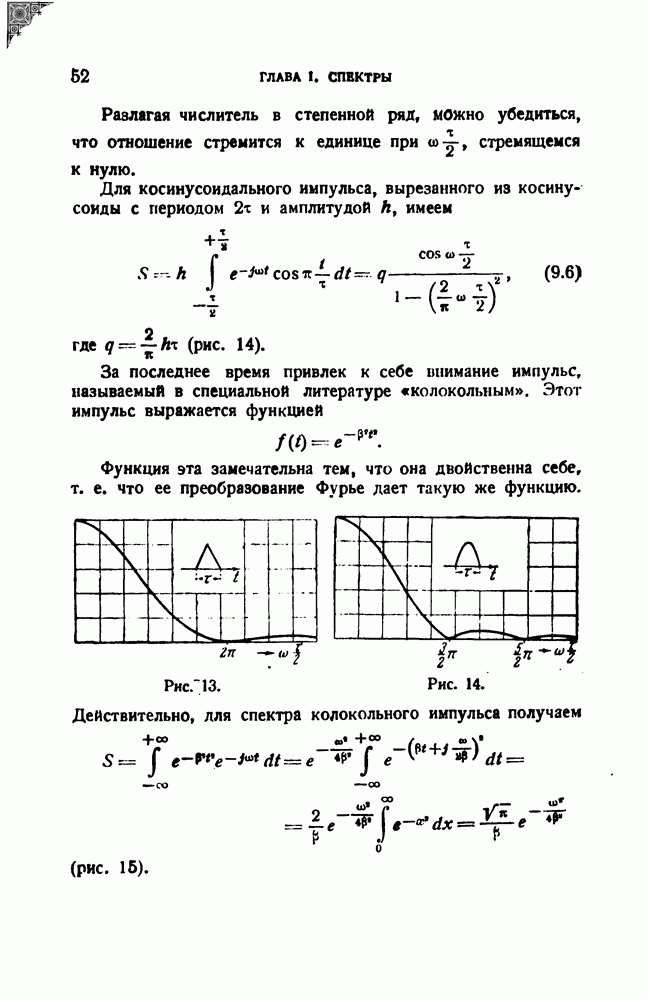
- § 9. Спектры некоторых импульсов
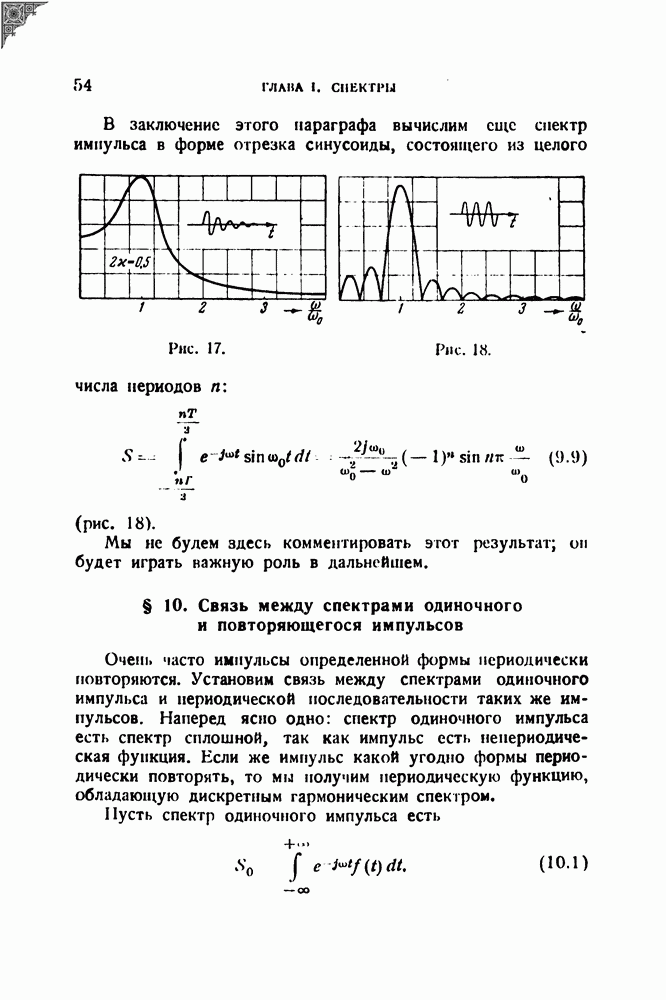
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
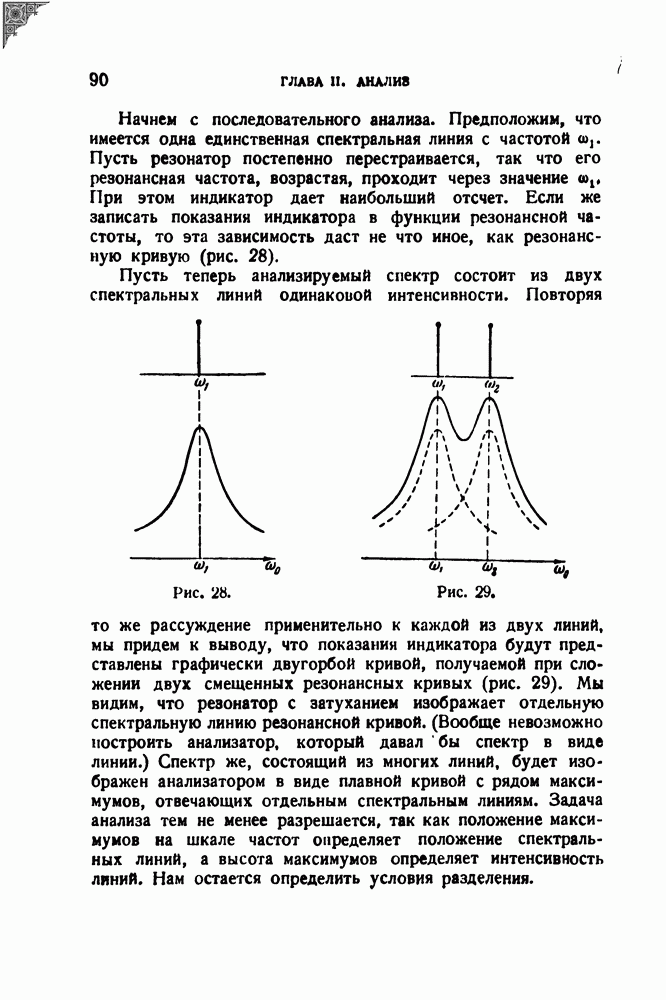
- § 16. Одновременный и последовательный анализ
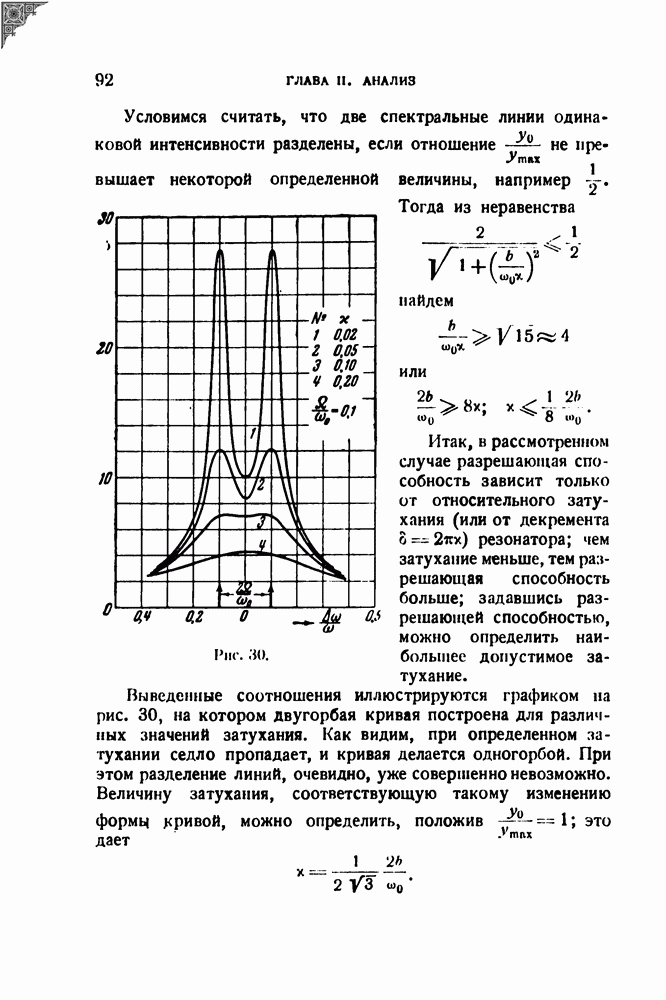
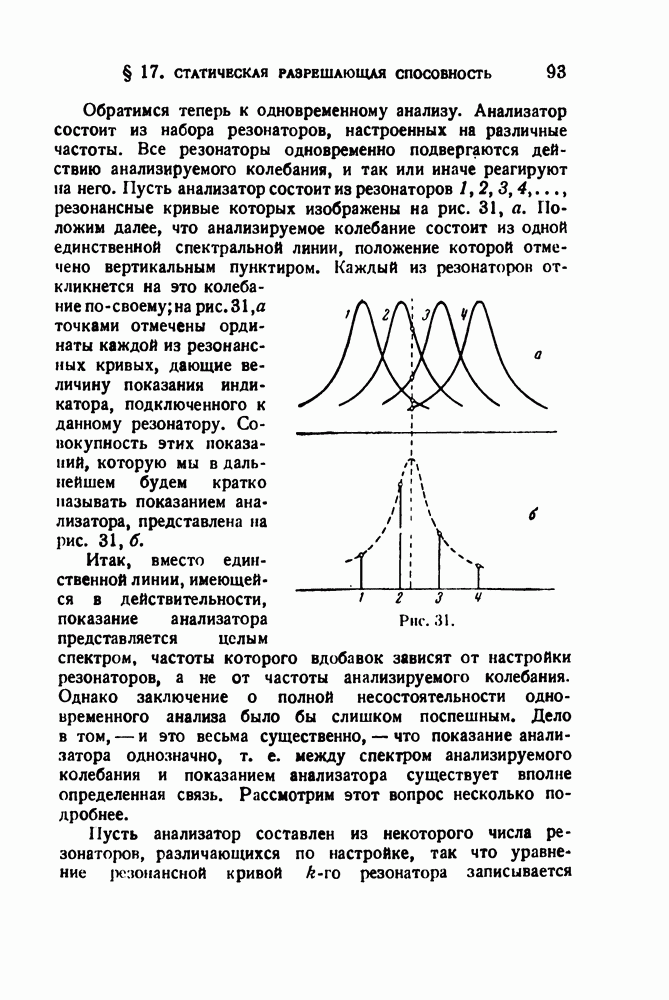
- § 17. Статическая разрешающая способность и погрешность анализатора
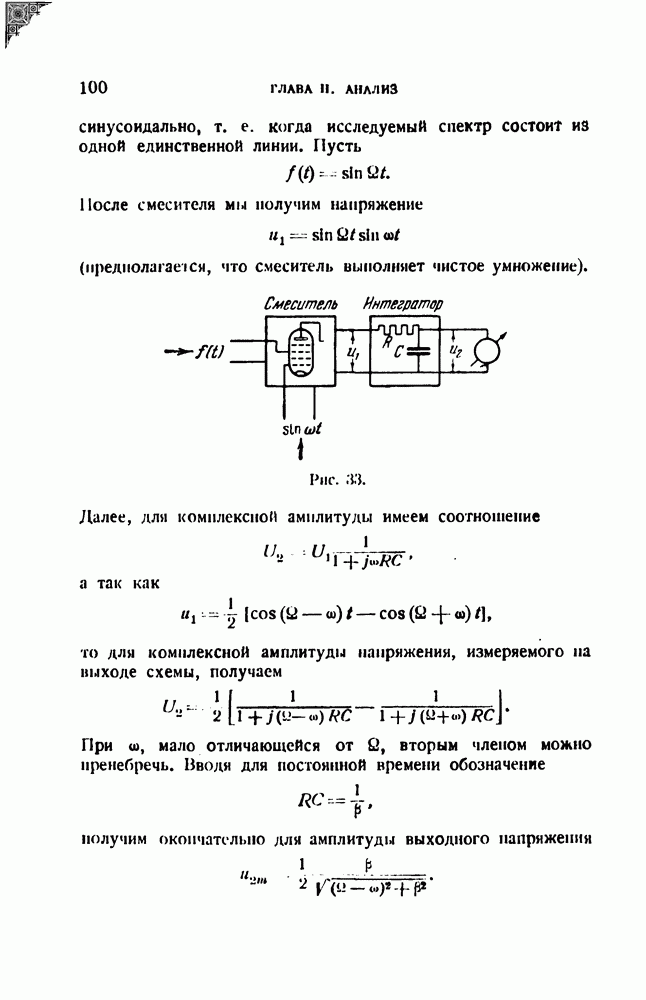
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
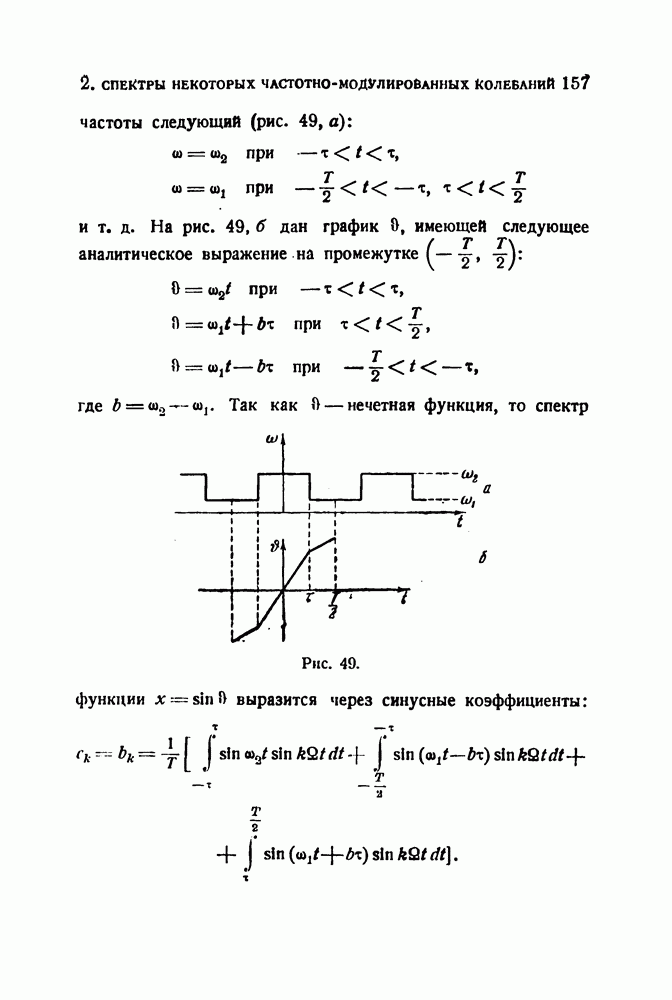
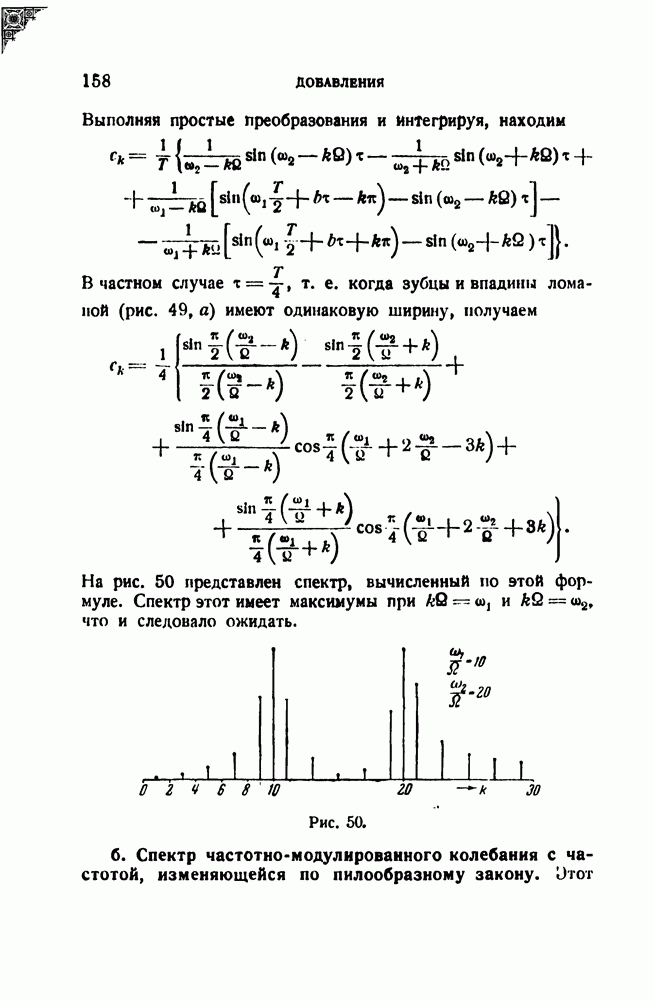
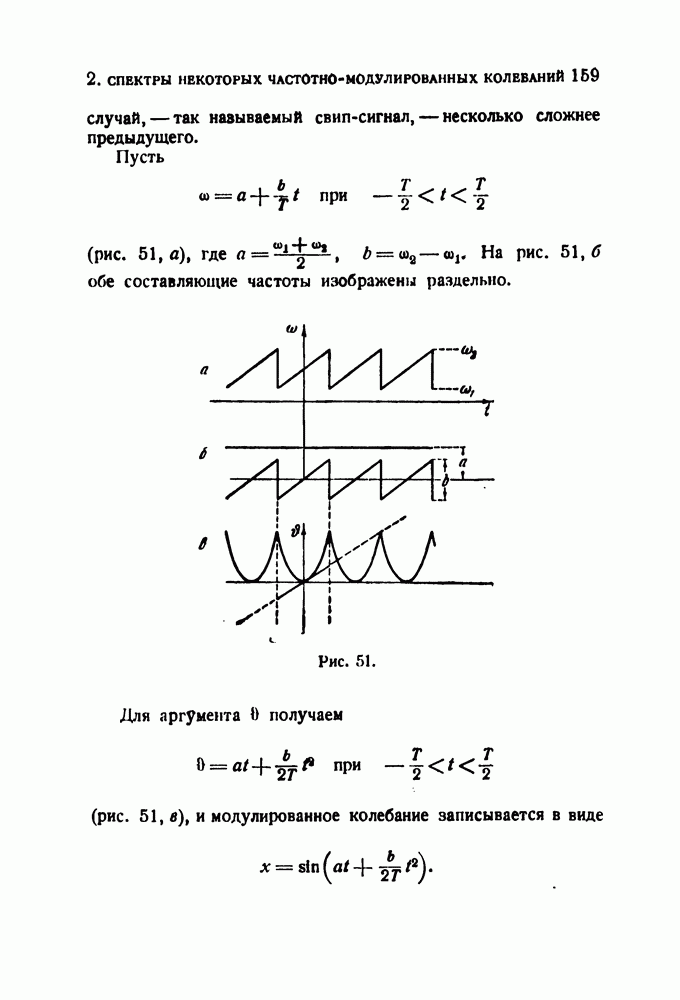
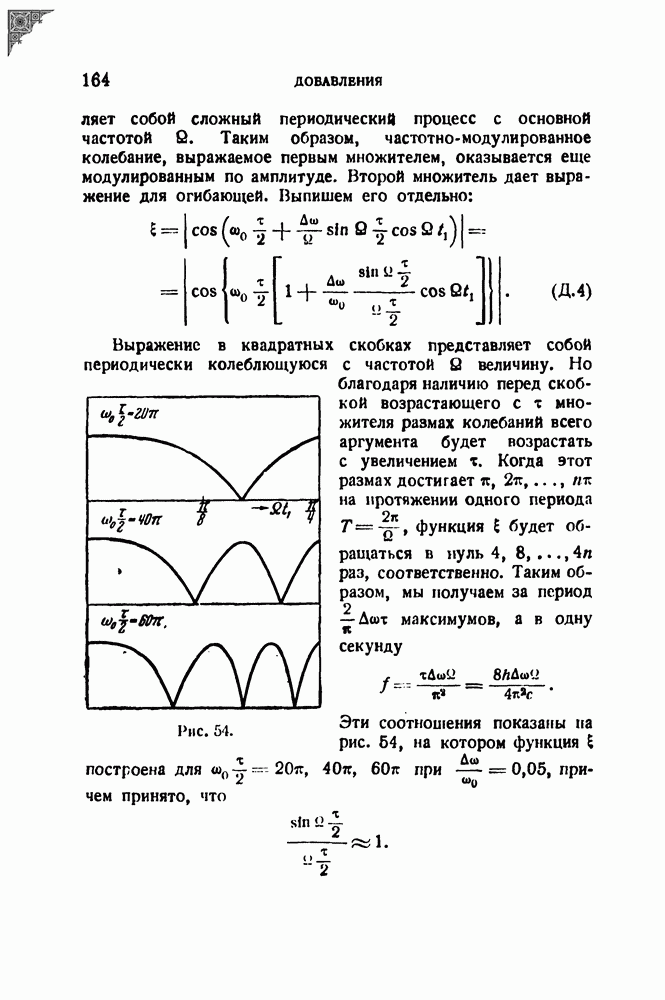
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА