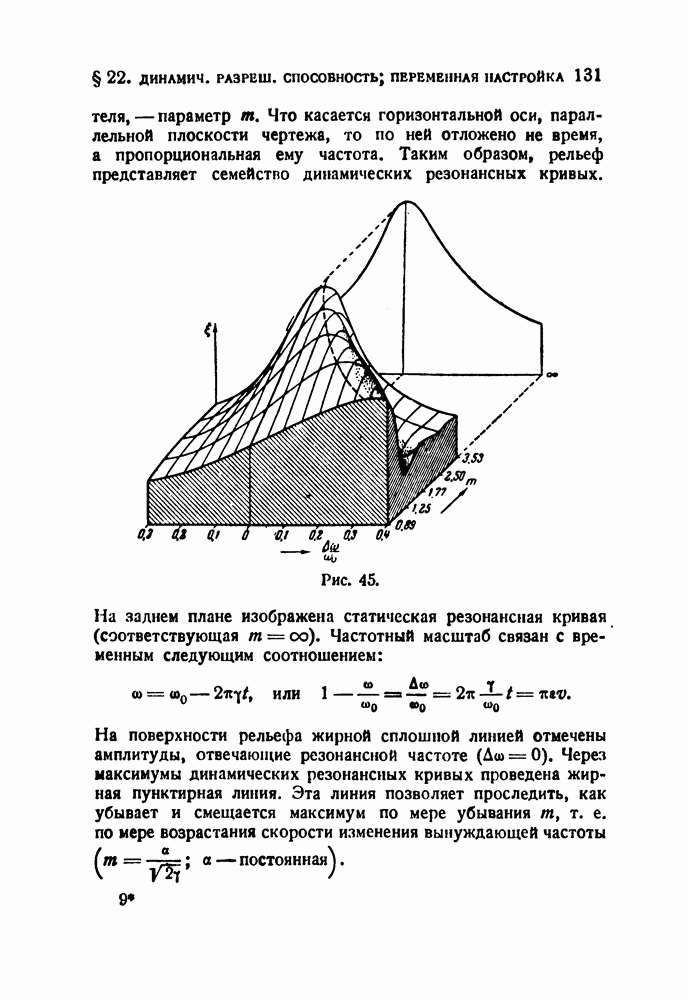
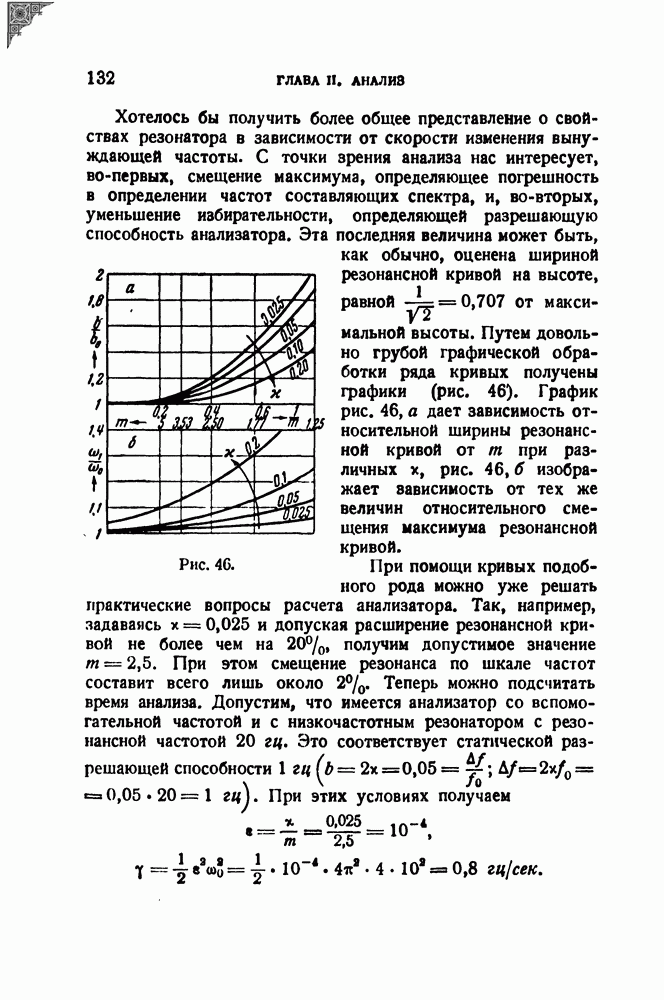
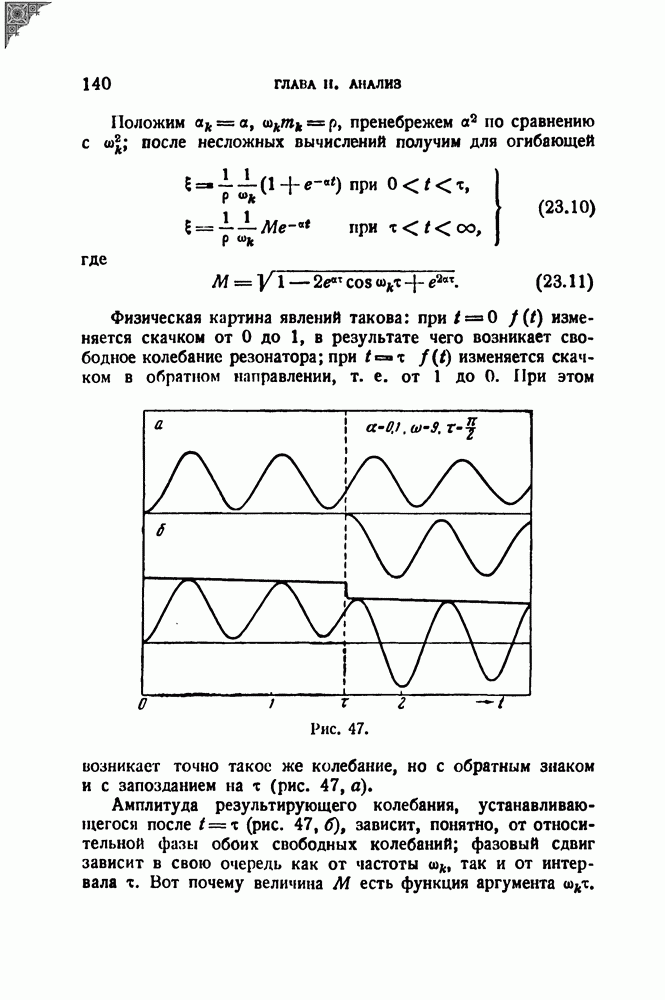
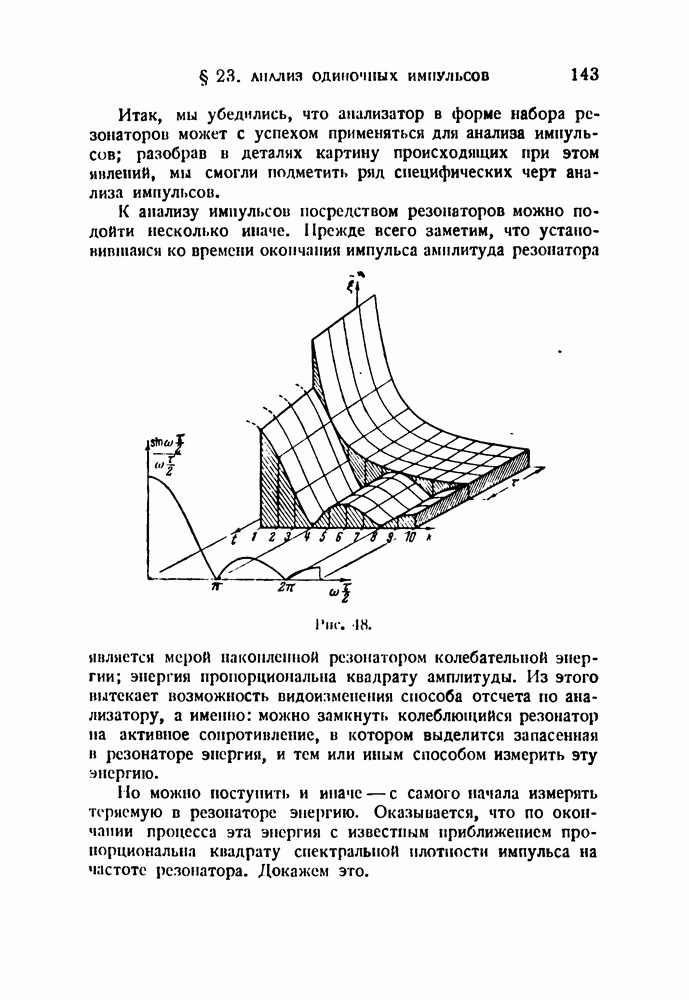
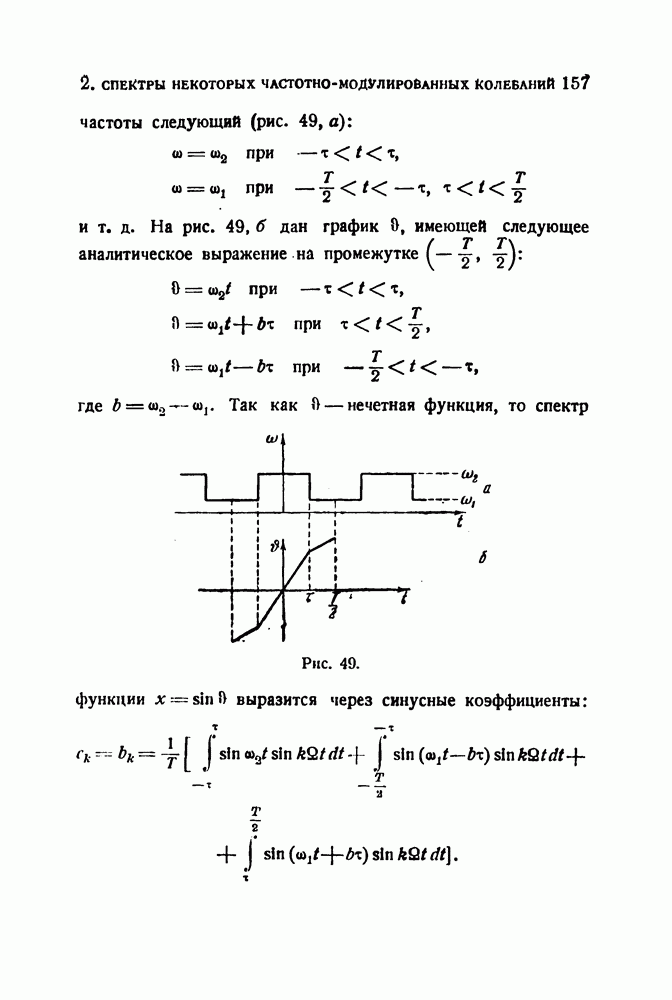
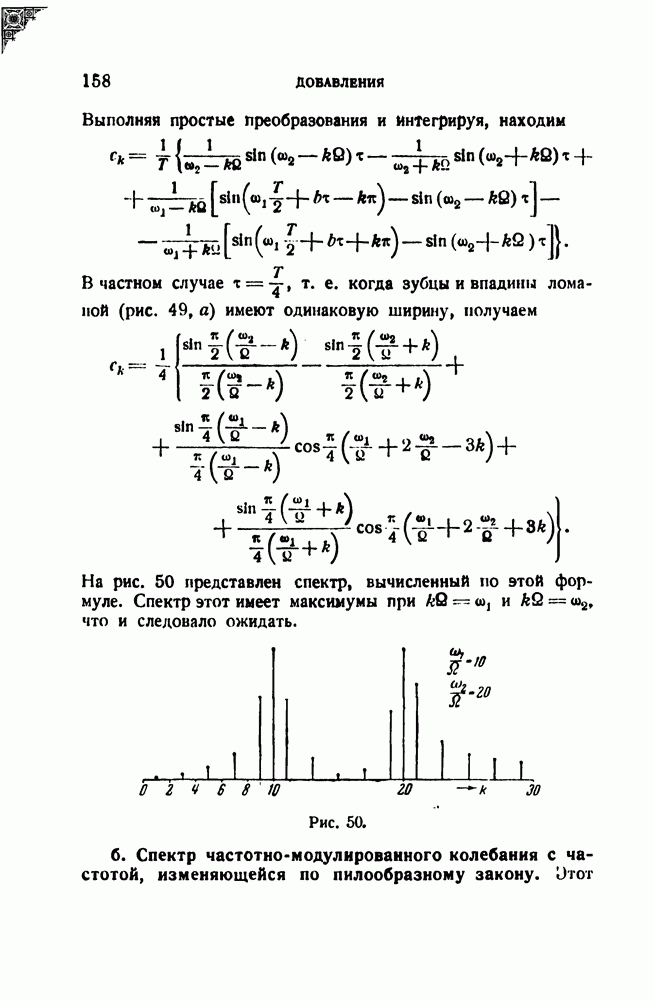
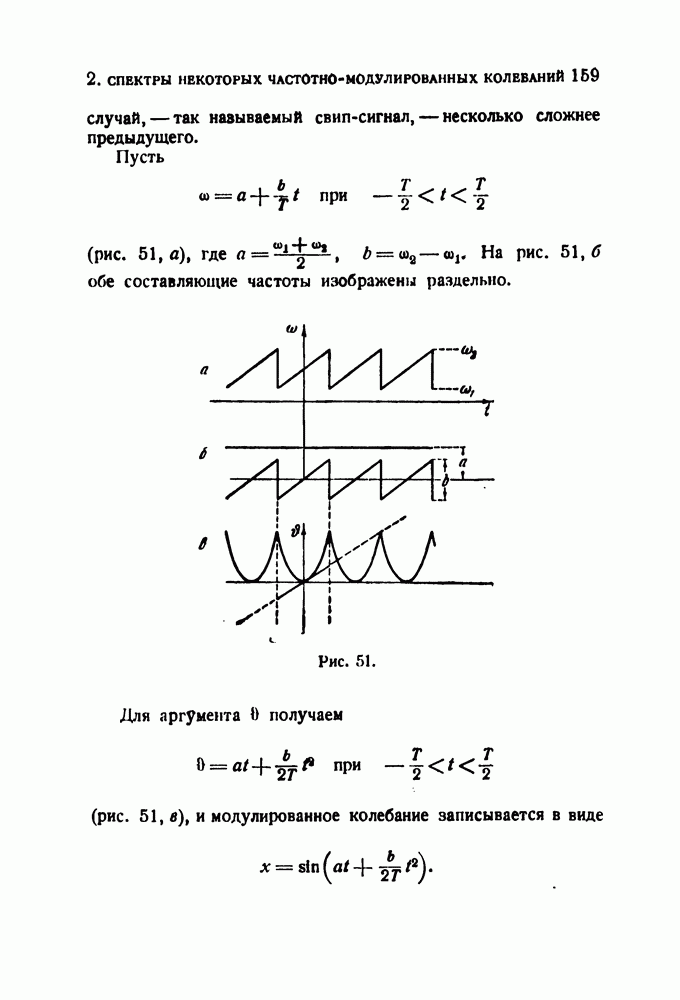
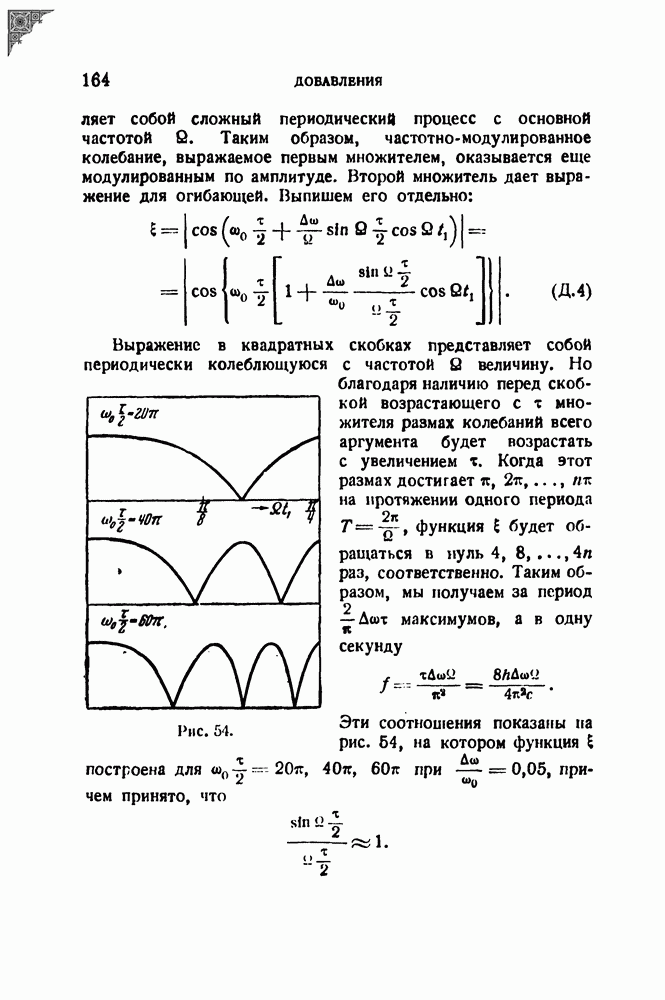
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Спектры при модуляции
Мы переходим  общих соотношений к ряду приложений и займемся прежде всего вопросом о модуляции, играющим в современной технике очень важную роль.
общих соотношений к ряду приложений и займемся прежде всего вопросом о модуляции, играющим в современной технике очень важную роль.
Наибольшее значение имеет модуляция в технике связи. Всякий сигнал радиосвязи — будь то сигнал телеграфный, телефонный, телевизионный или любой другой — получается путем модуляции. Излучение радиостанции без модуляции подобно чистой странице, модулированное излучение подобно странице, на которой напечатаны те или иные буквы или знаки.
Большое значение имеет модуляция и в современной измерительной технике и в ряде специальных отраслей.
Под модуляцией в общем смысле понимают такое воздействие на некоторую постоянную величину, в результате которого эта величина перестает быть постоянной и начинает изменяться в соответствии с оказываемым на нее воздействием. В более специальном понимании объектом модуляции является синусоидальное колебание. Запишем аналитическое выражение такого колебания

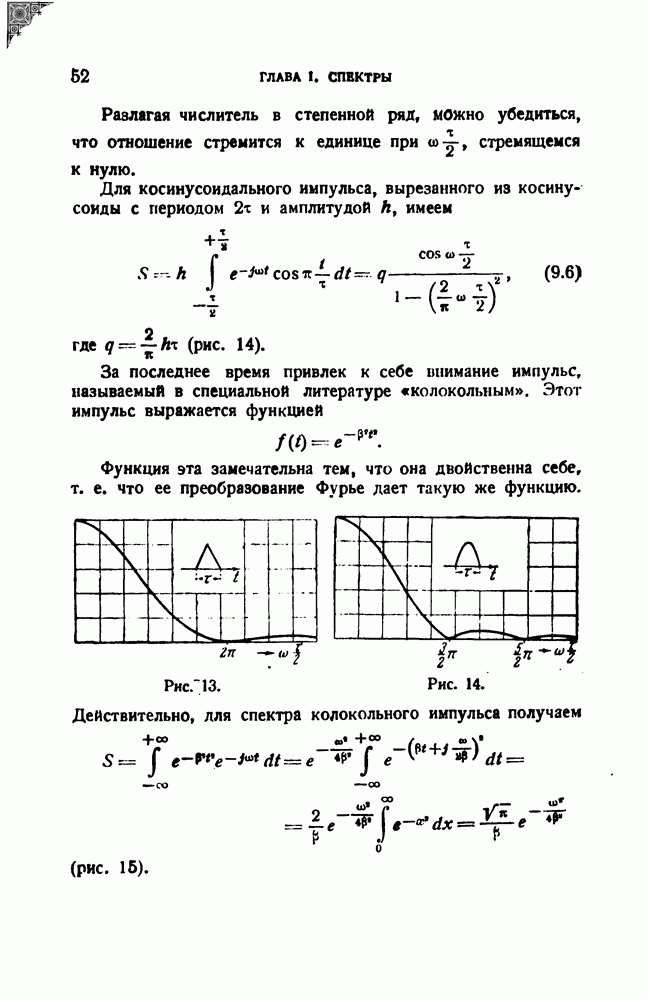
Здесь  — амплитуда,
— амплитуда,  - частота,
- частота,  - начальная фаза. В немодулированном колебании эти три величины, полностью определяющие колебание, постоянны. В принципе возможно модулировать каждую из трех названных постоянных величин; мы будем иметь соответственно амплитудную модуляцию (АМ) , частотную модуляцию (ЧМ) и фазовую модуляцию (ФМ). Разберем каждый вид модуляции подробно.
- начальная фаза. В немодулированном колебании эти три величины, полностью определяющие колебание, постоянны. В принципе возможно модулировать каждую из трех названных постоянных величин; мы будем иметь соответственно амплитудную модуляцию (АМ) , частотную модуляцию (ЧМ) и фазовую модуляцию (ФМ). Разберем каждый вид модуляции подробно.
Воздействие, называемое модуляцией, мы можем характеризовать как умножение модулируемой величины на множитель

где  — модулирующая функция, определяемая так, чтобы
— модулирующая функция, определяемая так, чтобы  — величина, характеризующая степень воздействия, могущая принимать значения от 0 до 1 и называемая глубиной модуляции.
— величина, характеризующая степень воздействия, могущая принимать значения от 0 до 1 и называемая глубиной модуляции.
При амплитудной модуляции модулированное колебание принимает вид

Начнем с простейшего случая синусоидальной модуляции, т. е. положим

Подставляя в (0.2), получаем 

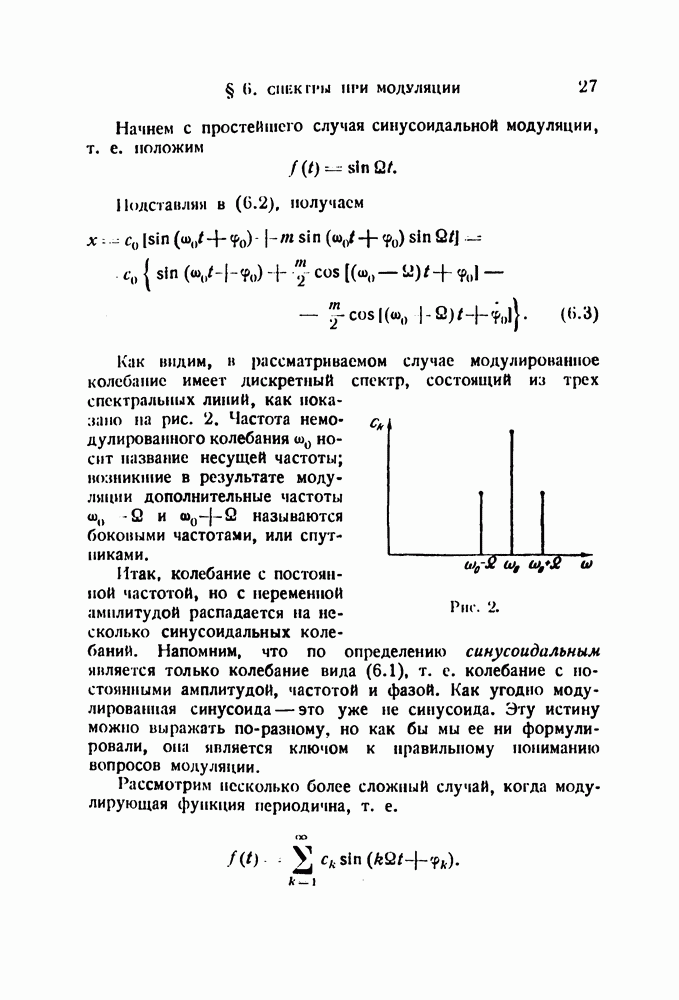
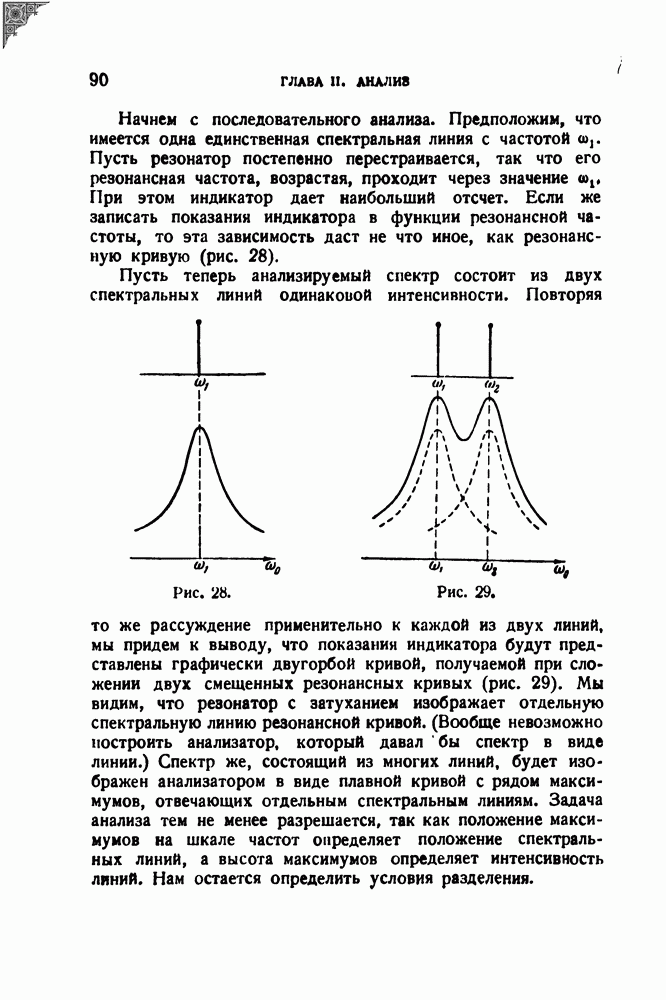
Как видим, в рассматриваемом случае модулированное колебание имеет дискретный спектр, состоящий из трех спектральных линий, как показано на рис. 2. Частота немодулированного колебания  носит название несущей частоты; возникшие в результате модуляции дополнительные частоты
носит название несущей частоты; возникшие в результате модуляции дополнительные частоты  называются боковыми частотами, или спутниками.
называются боковыми частотами, или спутниками.

Рис.
Итак, колебание с постоянной частотой, но с переменной амплитудой распадается на несколько синусоидальных колебаний. Напомним, что по определению синусоидальным является только колебание вида (6.1), т. е. колебание с постоянными амплитудой, частотой и фазой. Как угодно модулированная синусоида — это уже не синусоида. Эту истину можно выражать по-разному, но как бы мы ее ни формулировали, она является ключом к правильному пониманию вопросов модуляции.
Рассмотрим несколько более сложный случай, когда модулирующая функция периодична, т. е.

Тогда

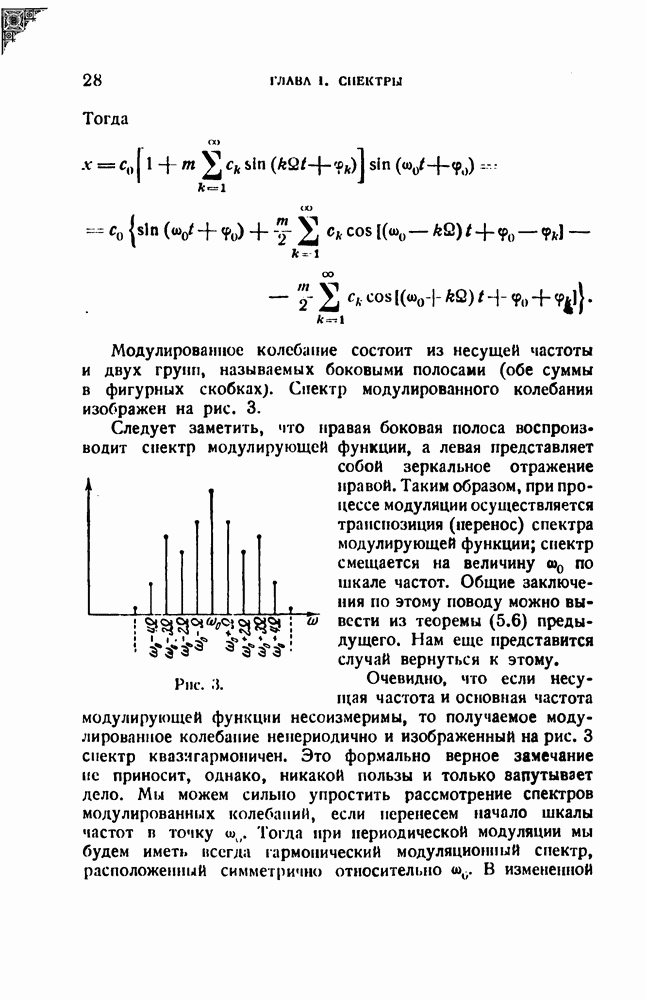
Модулированное колебание состоит из несущей частоты и двух групп, называемых боковыми полосами (обе суммы в фигурных скобках). Спектр модулированного колебания изображен на рис. 3.
Следует заметить, что правая боковая полоса воспроиз водит спектр модулирующей функции, а левая представляет собой зеркальное отражение правой. Таким образом, при процессе модуляции осуществляется транспозиция (перенос) спектра модулирующей функции; спектр смещается на величину  по шкале частот. Общие заключения по этому поводу можно вывести из теоремы (5.6) предыдущего. Нам еще представится случай вернуться к этому.
по шкале частот. Общие заключения по этому поводу можно вывести из теоремы (5.6) предыдущего. Нам еще представится случай вернуться к этому.

Рис. 3.
Очевидно, что если несущая частота и основная частота модулирующей функции несоизмеримы, то получаемое модулированное колебание непериодично и изображенный на рис. 3 спектр квазигармоничен. Это формально верное замечание не приносит, однако, никакой пользы и только вапутывзет дело. Мы можем сильно упростить рассмотрение спектров модулированных колебаний, если перенесем начало шкалы частот  точку
точку  Тогда при периодической модуляции мы будем иметь всегда гармонический модуляционный спектр, расположенный симметрично относительно
Тогда при периодической модуляции мы будем иметь всегда гармонический модуляционный спектр, расположенный симметрично относительно  . В измененной
. В измененной
таким образом системе координат колебание несущей частоты займет место постоянной составляющей. Сказанное по поводу гармоничности модуляционного спектра будет иметь силу при том всегда выполняемом на практике условии, что частота наивысшей гармоники модулирующей функции меньше несущей частоты.
Перейдем к несколько более трудному вопросу о частотной модуляции. Нужно сказать, что история развития теории модуляции дает наибольшее количество примеров путаницы в понятиях, связанной с неправильным применением спектрального воззрения на колебания. Даже сравнительно простая амплитудная модуляция послужила (и притом не так давно) поводом для совершенно ошибочных высказываний в заграничной печати. Еще хуже обстояло дело с частотной модуляцией. Сущности дела долго не понимали инженеры и исследователи. Поучительно воспроизвести распространенное в свое время рассуждение о свойствах частотной модуляции: при частотной модуляции мы имеем колебание, частота которого непрерывно изменяется в пределах заданного нами интервала  от частоты модуляции
от частоты модуляции  зависит частота изменения несущей частоты, но не величина этого изменения. Стало быть, спектр колебания должен быть сплошным (так как частота пробегает все значения в пределах интервала
зависит частота изменения несущей частоты, но не величина этого изменения. Стало быть, спектр колебания должен быть сплошным (так как частота пробегает все значения в пределах интервала  ), а ширина спектра должна составлять
), а ширина спектра должна составлять  . А так как эта ширина назначается нами произвольно, то можно сократить полосу, занимаемую на шкале частот передающей радиостанцией.
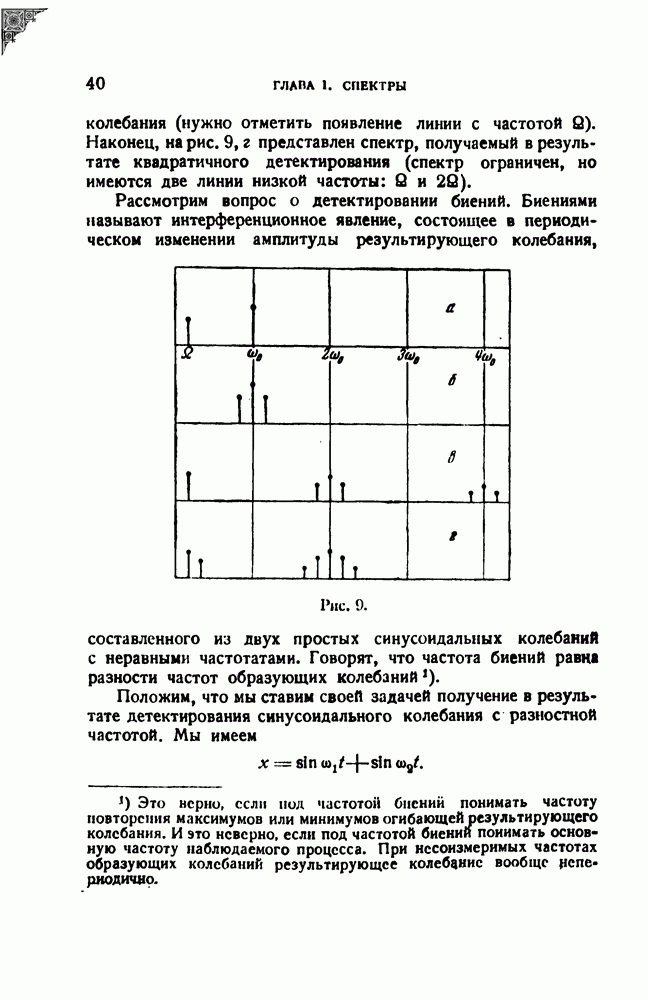
. А так как эта ширина назначается нами произвольно, то можно сократить полосу, занимаемую на шкале частот передающей радиостанцией.
Все здесь неверно: и спектр получается не сплошной, а дискретный, и ширина его при узком интервале  (так называемая полоса качания) не зависит вовсе от величины этого интервала, а определяется, как и в случае АМ, шириной спектра модулирующей функции. Наконец, когда ЧМ получила практическое применение, то оказалось, что, имея значительные специфические преимущества, она требует полосы раз в 15—20 более широкой, чем та, которая отпускается по международным правилам на
(так называемая полоса качания) не зависит вовсе от величины этого интервала, а определяется, как и в случае АМ, шириной спектра модулирующей функции. Наконец, когда ЧМ получила практическое применение, то оказалось, что, имея значительные специфические преимущества, она требует полосы раз в 15—20 более широкой, чем та, которая отпускается по международным правилам на 
Выведем теперь основные соотношения. Предположим, что частота модулируется по косинусоидальному закону

По своему определению круговая частота есть производная по времени от аргумента тригонометрической функции, представляющей колебание. Мы можем поэтому записать для частотно - модулированного колебания при синусоидальной модуляции

где  называемый индекс модуляции.
называемый индекс модуляции.
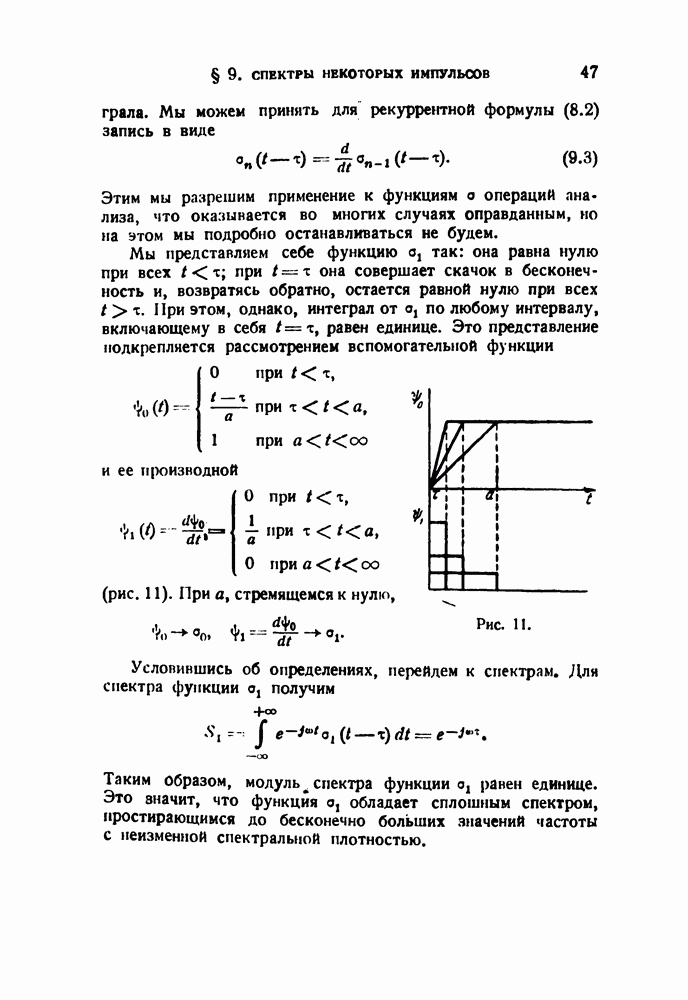
Используя известные формулы теории бесселевых функций

найдем

Перемножая под знаками сумм, получим окончательно

Мы имеем, таким образом, колебание с линейчатым спектром. В отличие от  здесь при синусоидальной модуляции возникает бесконечный спектр. Однако практически он ограничен. Дело в том, что, как видим, амплитуды гармоник пропорциональны
здесь при синусоидальной модуляции возникает бесконечный спектр. Однако практически он ограничен. Дело в том, что, как видим, амплитуды гармоник пропорциональны  а последние функции обладают своеобразным спойстпом: они сохраняют весьма малое значение до значений
а последние функции обладают своеобразным спойстпом: они сохраняют весьма малое значение до значений  тем больших, чем выше порядок
тем больших, чем выше порядок 
И практике пользуются понятием действительной ширины полосы, занимаемой спектром ЧМ колебания. Действительная ширина есть интервал на шкале частот, вне которого гармоники имеют относительную величину  . Пользуясь таблицами бесселевых функций, можно найти границы этого интервала, а также его зависимость от индекса модуляции
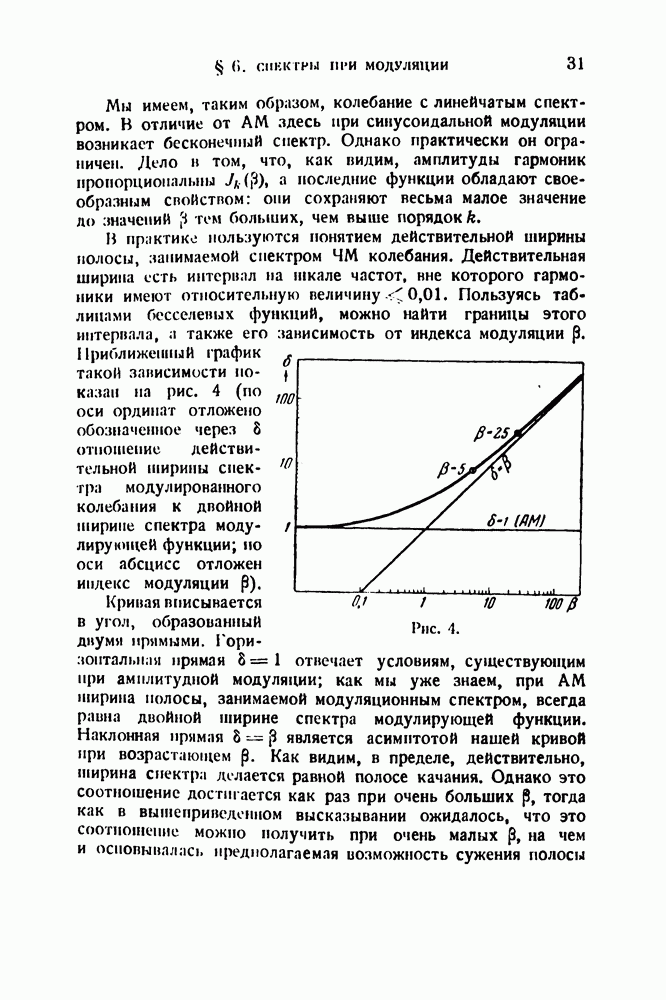
. Пользуясь таблицами бесселевых функций, можно найти границы этого интервала, а также его зависимость от индекса модуляции  Приближенный график такой зависимости показан на рис. 4 (по оси ординат отложено обозначенное через 8 отношение действительной ширины спектра модулированного колебания к двойной ширине спектра модулирующей функции; но оси абсцисс отложен индекс модуляции Р).
Приближенный график такой зависимости показан на рис. 4 (по оси ординат отложено обозначенное через 8 отношение действительной ширины спектра модулированного колебания к двойной ширине спектра модулирующей функции; но оси абсцисс отложен индекс модуляции Р).

Рис. 4.
Кривая вписывается в угол, образованный днуми прямыми. Горизонтальная прямая  отвечает условиям, существующим при амплитудной модуляции; как мы уже знаем, при
отвечает условиям, существующим при амплитудной модуляции; как мы уже знаем, при  ширина полосы, занимаемой модуляционным спектром, всегда равна двойной ширине спектра модулирующей функции. Наклонная прямая
ширина полосы, занимаемой модуляционным спектром, всегда равна двойной ширине спектра модулирующей функции. Наклонная прямая  является асимптотой нашей кривой при возрастающем
является асимптотой нашей кривой при возрастающем  Как видим, в пределе, действительно, ширина спектра делается равной полосе качания. Однако это соотношение достигается как раз при очень больших
Как видим, в пределе, действительно, ширина спектра делается равной полосе качания. Однако это соотношение достигается как раз при очень больших  тогда как в вышеприведенном высказывании ожидалось, что это соотношение можно получить при очень малых
тогда как в вышеприведенном высказывании ожидалось, что это соотношение можно получить при очень малых  на чем и основывалась предполагаемая возможность сужения полосы
на чем и основывалась предполагаемая возможность сужения полосы
частот за счет применения ЧМ. В действительности же при ЧМ величина  всегда больше единицы; другими словами, полоса частот, занимаемая спектром, при ЧМ всегда больше, чем полоса частот при АМ. Только при самых малых (3 полосы сравниваются.
всегда больше единицы; другими словами, полоса частот, занимаемая спектром, при ЧМ всегда больше, чем полоса частот при АМ. Только при самых малых (3 полосы сравниваются.
При малых  спектр модулированного колебания при ЧМ получается бедный, практически не отличающийся от спектра при АМ, — при синусоидальной модуляции он состоит практически из двух боковых линий (остальные очень малы).
спектр модулированного колебания при ЧМ получается бедный, практически не отличающийся от спектра при АМ, — при синусоидальной модуляции он состоит практически из двух боковых линий (остальные очень малы).
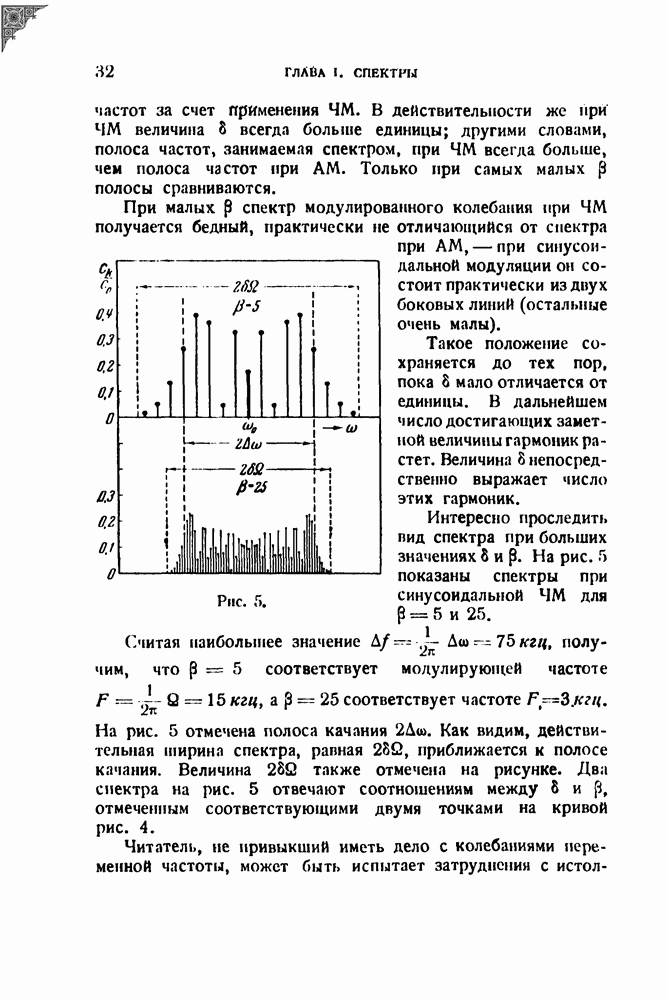
Такое положение сохраняется до тех пор, пока 8 мало отличается от единицы. В дальнейшем число достигающих заметной величины гармоник растет. Величина 8 непосредственно выражает число этих гармоник.

Рис. 5.
Интересно проследить вид спектра при больших значениях 8 и  На рис. 5 показаны спектры при синусоидальной ЧМ для
На рис. 5 показаны спектры при синусоидальной ЧМ для  и 25.
и 25.
Считая наибольшее значение  получим, что
получим, что  соответствует модулирующей частоте
соответствует модулирующей частоте  соответствует частоте
соответствует частоте  На рис. 5 отмечена полоса качания
На рис. 5 отмечена полоса качания  Как видим, действительная ширина спектра, равная
Как видим, действительная ширина спектра, равная  приближается к полосе качания. Величина
приближается к полосе качания. Величина  также отмечена на рисунке. Два спектра на рис. 5 отвечают соотношениям между 8 и
также отмечена на рисунке. Два спектра на рис. 5 отвечают соотношениям между 8 и  отмеченным соответствующими двумя точками на кривой рис. 4.
отмеченным соответствующими двумя точками на кривой рис. 4.
Читатель, не привыкший иметь дело с колебаниями переменной частоты, может быть испытает затруднения с
истолкованием выражения

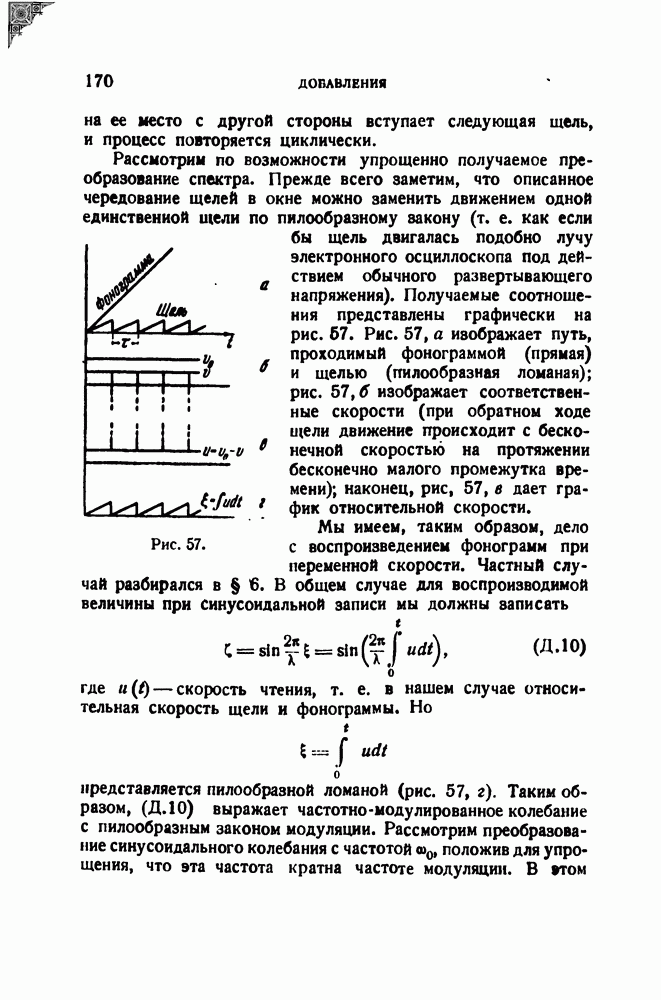
Мы поясним этот пункт, рассмотрев простой пример. Предположим, что имеется правильно записанная фонограмма чистого тона, т. е. синусоидального колебания. Пусть теперь эта фонограмма воспроизводится на аппарате, в котором линейная скорость продвижения фонограммы непостоянна. Возникающие при этом искажения представляют собой, как известно, не что иное, как результат частотной модуляции.
Выведем соответствующие соотношения. Положим, что записано колебание

Фонограмма, сделанная при постоянной линейной скорости  выражается формулой
выражается формулой

где  координата, отсчитываемая вдоль фонограммы,
координата, отсчитываемая вдоль фонограммы,  длина записанной волны. Пусть теперь при воспроизведении фонограмма движется с переменной скоростью
длина записанной волны. Пусть теперь при воспроизведении фонограмма движется с переменной скоростью  Читающий орган, например оптическая щель, воспринимает величину
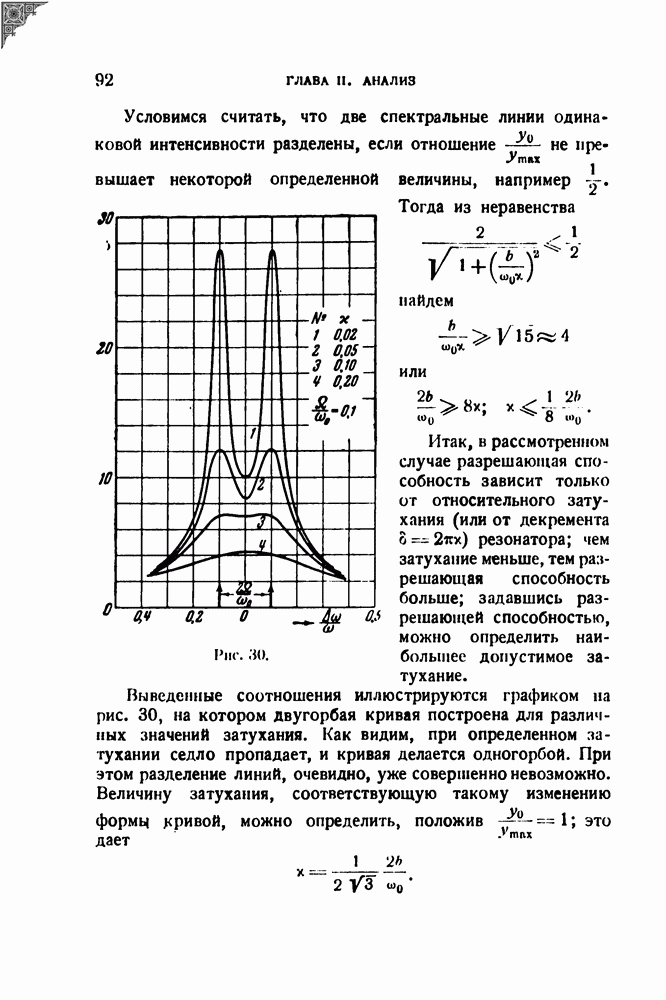
Читающий орган, например оптическая щель, воспринимает величину

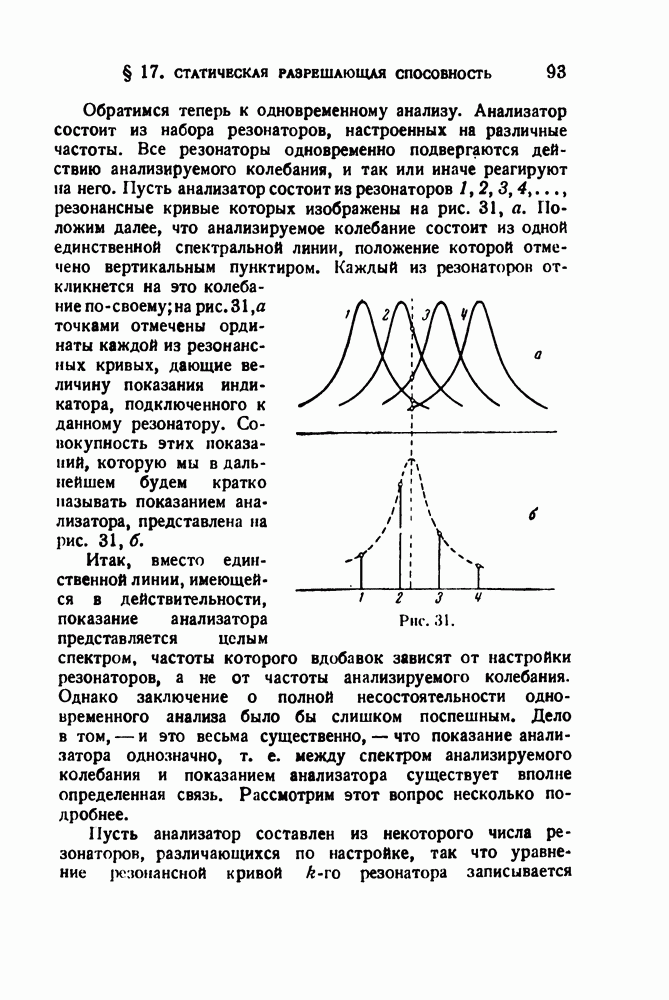
где  — ордината фонограммы в точке
— ордината фонограммы в точке  — путь, пройденный щелью относительно фонограммы (рис. 6). Но этот путь, очевидно, равен
— путь, пройденный щелью относительно фонограммы (рис. 6). Но этот путь, очевидно, равен

и, следовательно,


Рис. 6.
[Это совершенно аналогично выражению  Ведь
Ведь  — это угол, на который поворачивается за время
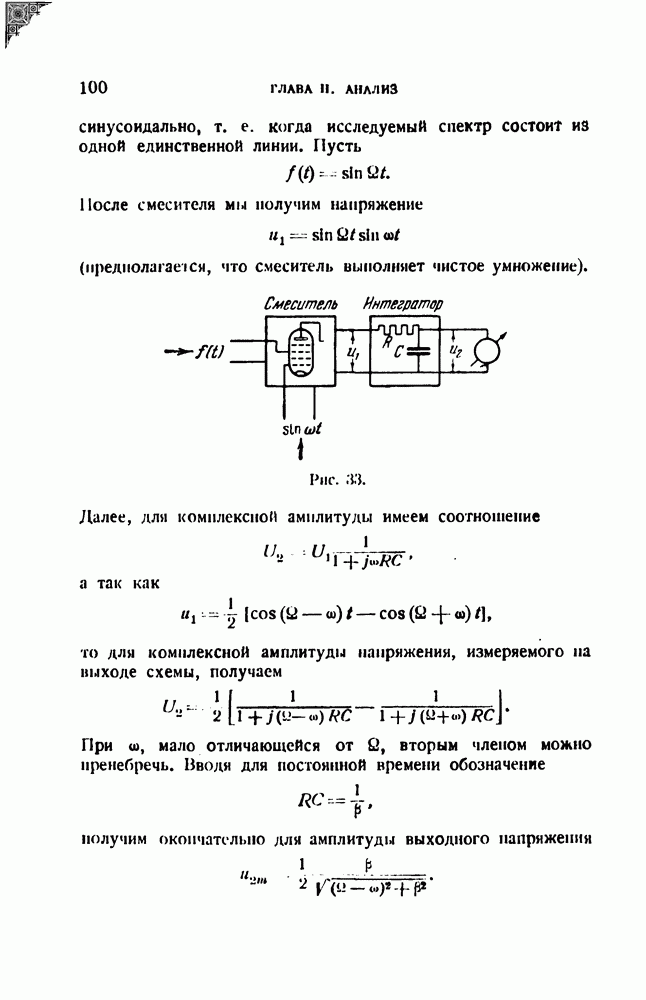
— это угол, на который поворачивается за время  вектор, вращающийся с переменной угловой скоростью
вектор, вращающийся с переменной угловой скоростью  ] Если, например,
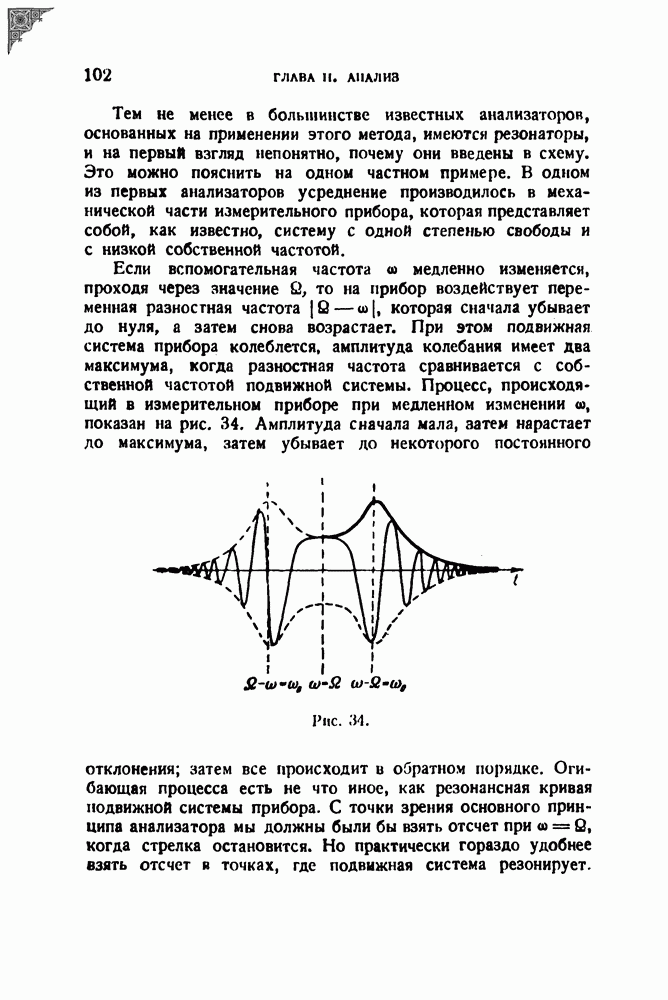
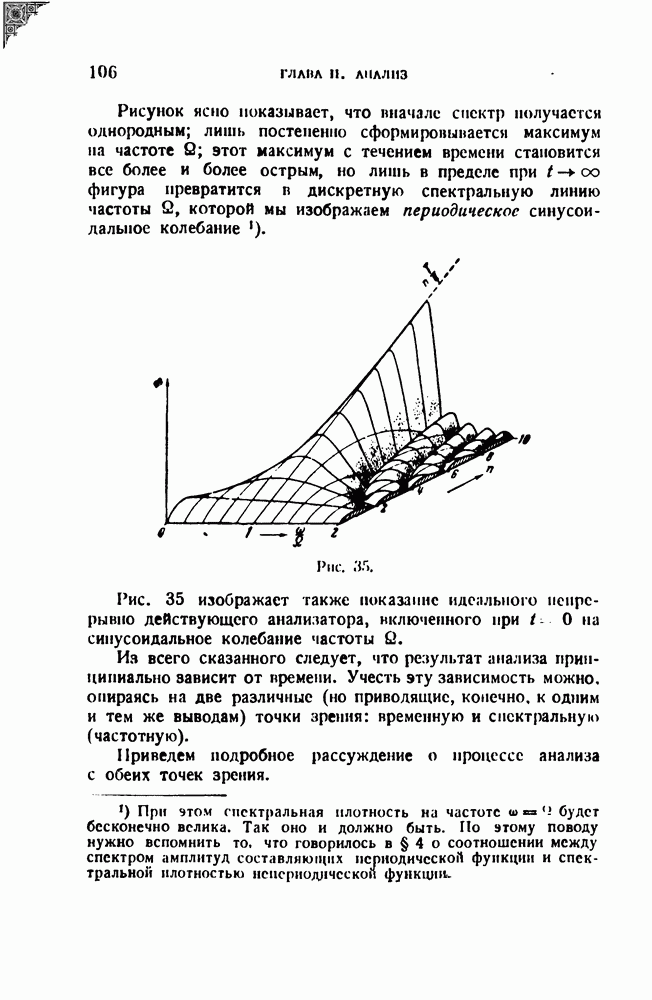
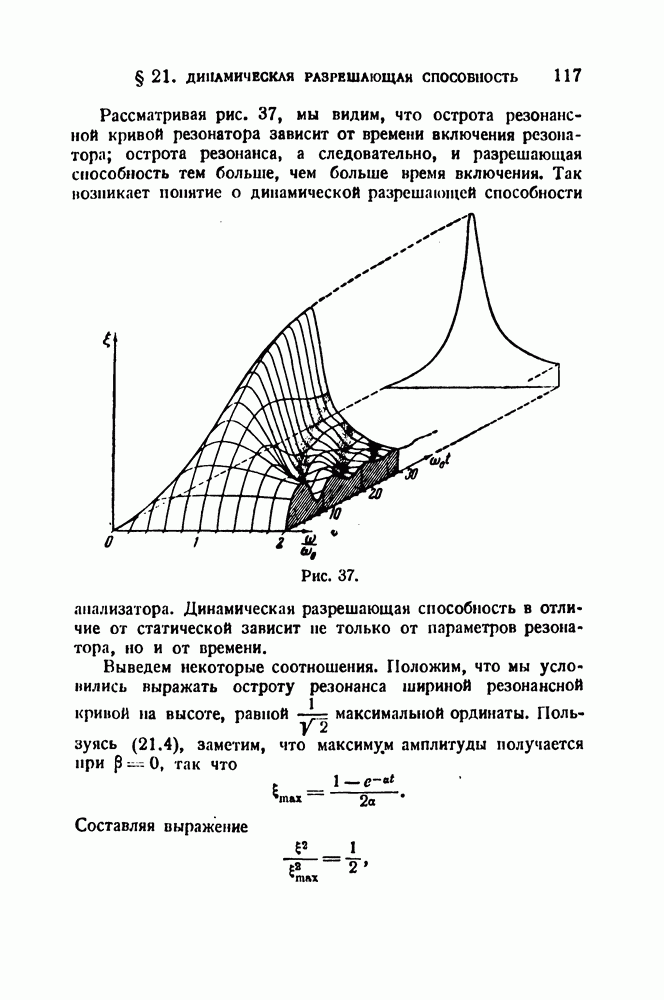
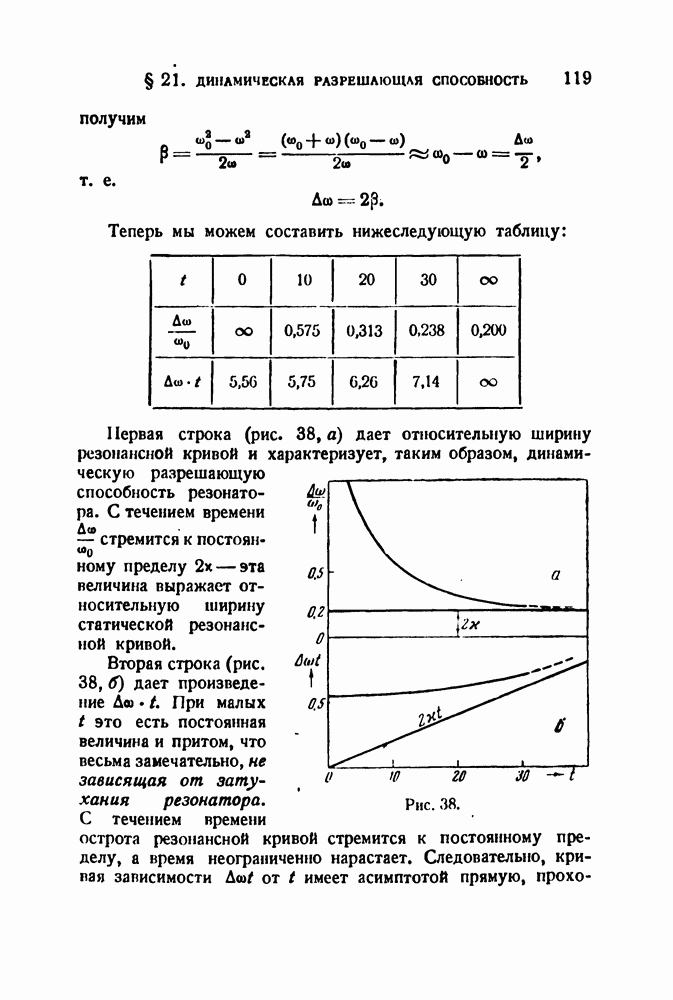
] Если, например,

то

т. e. имеется типичное частотно - модулированное колебание (ср. (6.4)]. В этом выражении

Обратимся теперь к фазовой модуляции. По общему определению мы должны, взяв немодулированное колебание

заменить в нем  величиной
величиной

Тогда мы получим

Для частотной модуляции, вводя переменную частоту

мы получили бы

Сравнивая (6.6) и (6.7), видим, что ФМ и ЧМ в сущности дают совершенно одинакового вида колебания. Разница заключается лишь в том, что при ФМ в аргумент синусоидальной функции входит модулирующая функция  а при ЧМ — ее интеграл.
а при ЧМ — ее интеграл.
Если модуляция синусоидальна, то разницы в форме модулированных колебаний и их спектрах вообще усмотреть нельзя, так как интеграл от синусоиды есть косинусоида, т. е. опять-таки синусоида, лишь сдвинутая по фазе на  .
.
Различие все же есть, но более тонкое. Дело в том, что если

то

Поянление множителя  означает необходимость введения соответствующих корректирующих цепей.
означает необходимость введения соответствующих корректирующих цепей.
Если предположить, что дискриминаторы, т. е. элементы, превращающие ФМ и ЧМ в АМ, ведут себя одинаково, то и дальнейшей схеме приемника ФМ должно быть одно интегрирующее звено по сравнению с аналогичной схемой приемника ЧМ.
Дальнейшее сравнение ФМ и ЧМ завело бы нас очень далеко в специальные области современной радиотехники. Мы ограничимся высказанными общими соображениями и попытаемся лишь в заключение пояснить различие между всеми гремя видами модуляции по возможности наглядным образом.
Как уже говорилось, при синусоидальной ЧМ и ФМ различия в форме модулированных колебаний усмотреть нельзя. Но различие это обнаруживается при более сложном законе модуляции, т. е. когда модулирующая функция обладает более или менее богатым спектром.
Предположим, что модулирующая функция представляет собой импульс следующего вида:

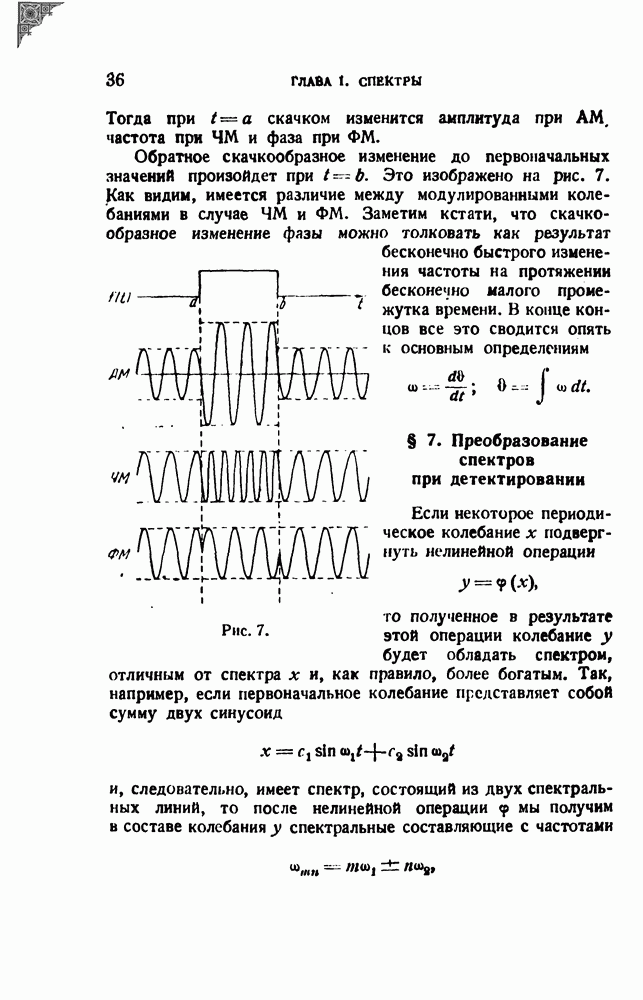
Тогда при  скачком изменится амплитуда при АМ, частота при ЧМ и фаза при ФМ.
скачком изменится амплитуда при АМ, частота при ЧМ и фаза при ФМ.
Обратное скачкообразное изменение до первоначальных значений произойдет при  Это изображено на рис. 7. Как видим, имеется различие между модулированными колебаниями в случае ЧМ и ФМ. Заметим кстати, что скачкообразное изменение фазы можно толковать как результат бесконечно быстрого изменения частоты на протяжении бесконечно малого промежутка времени. В конце концов все это сводится опять к основным определениям
Это изображено на рис. 7. Как видим, имеется различие между модулированными колебаниями в случае ЧМ и ФМ. Заметим кстати, что скачкообразное изменение фазы можно толковать как результат бесконечно быстрого изменения частоты на протяжении бесконечно малого промежутка времени. В конце концов все это сводится опять к основным определениям


Рис. 7.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
- § 9. Спектры некоторых импульсов
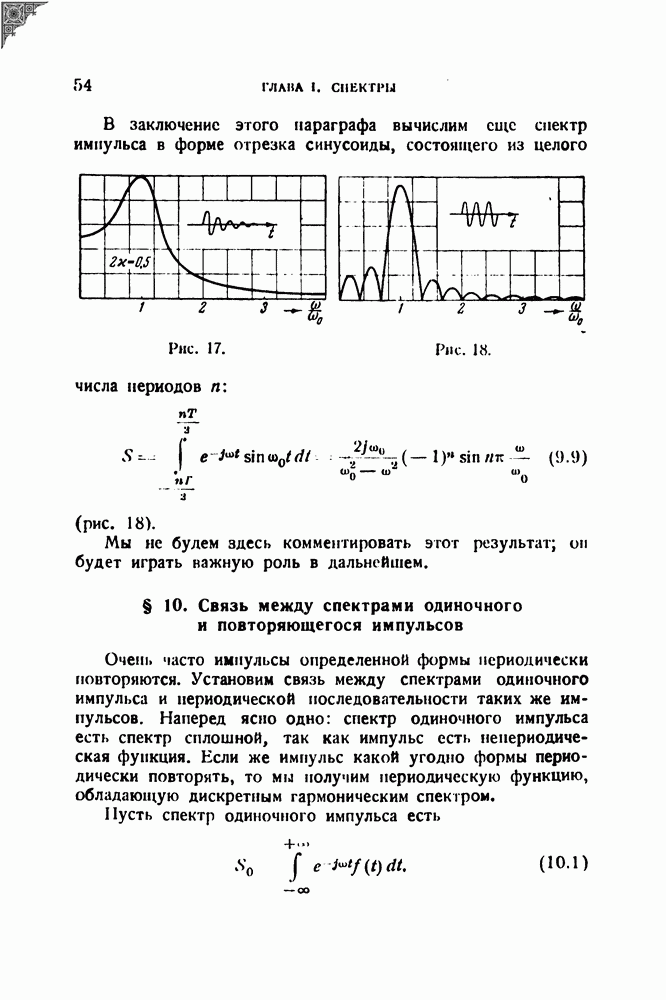
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
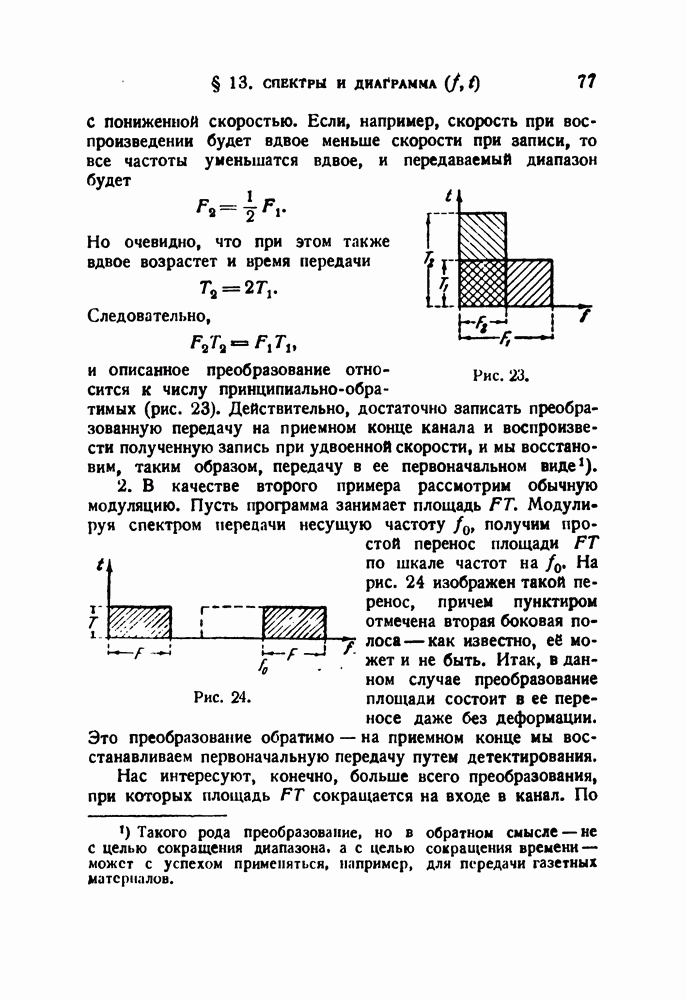
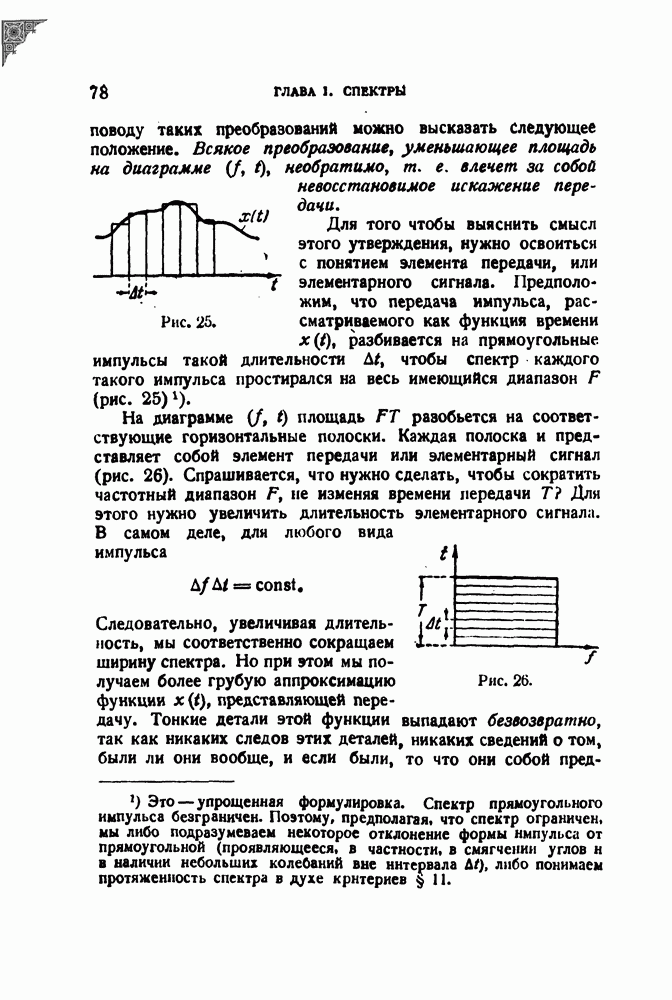
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
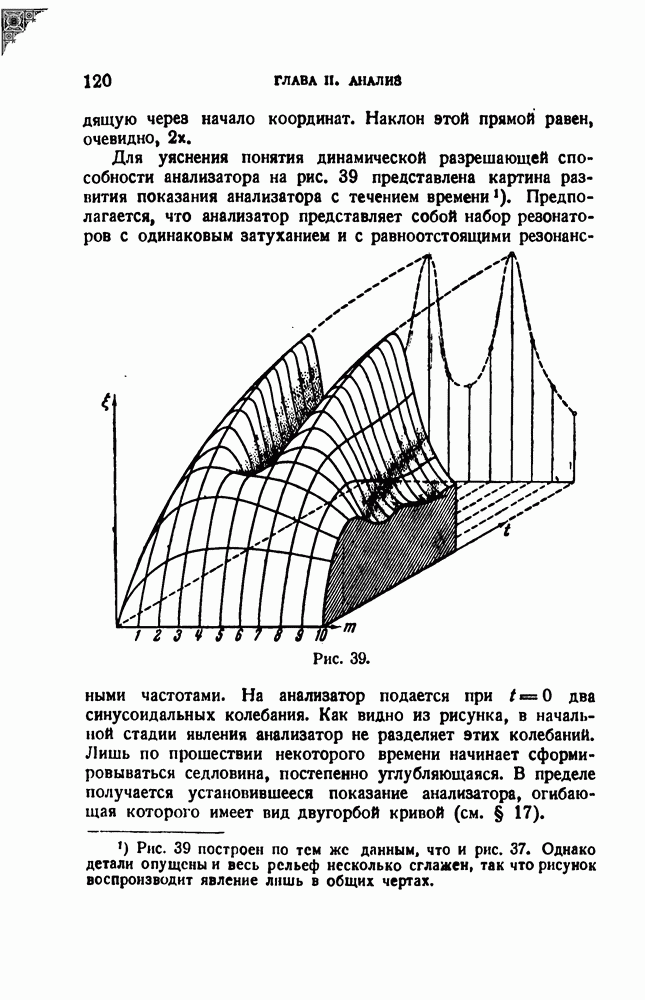
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
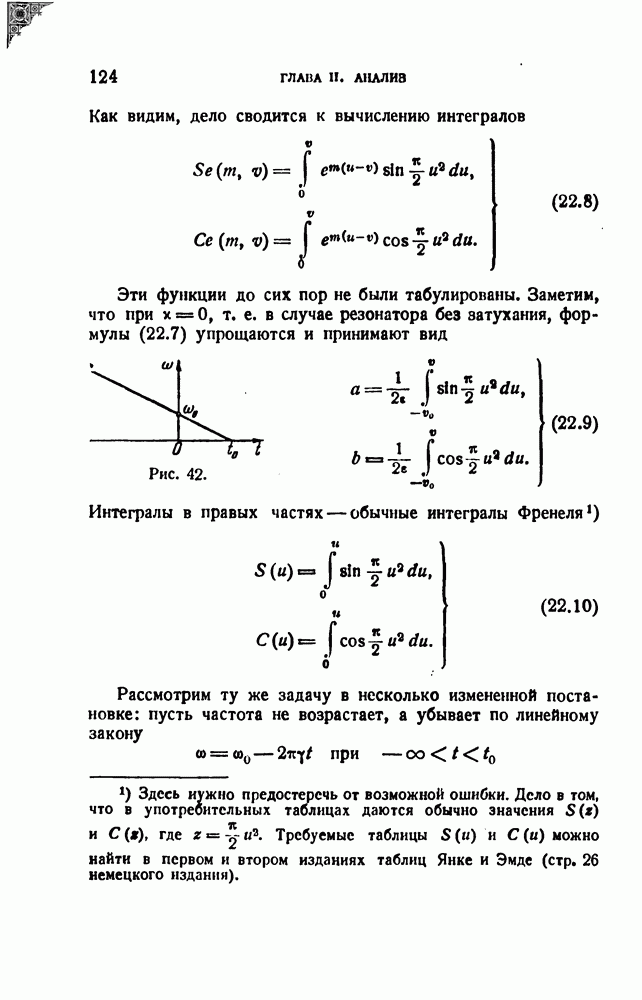
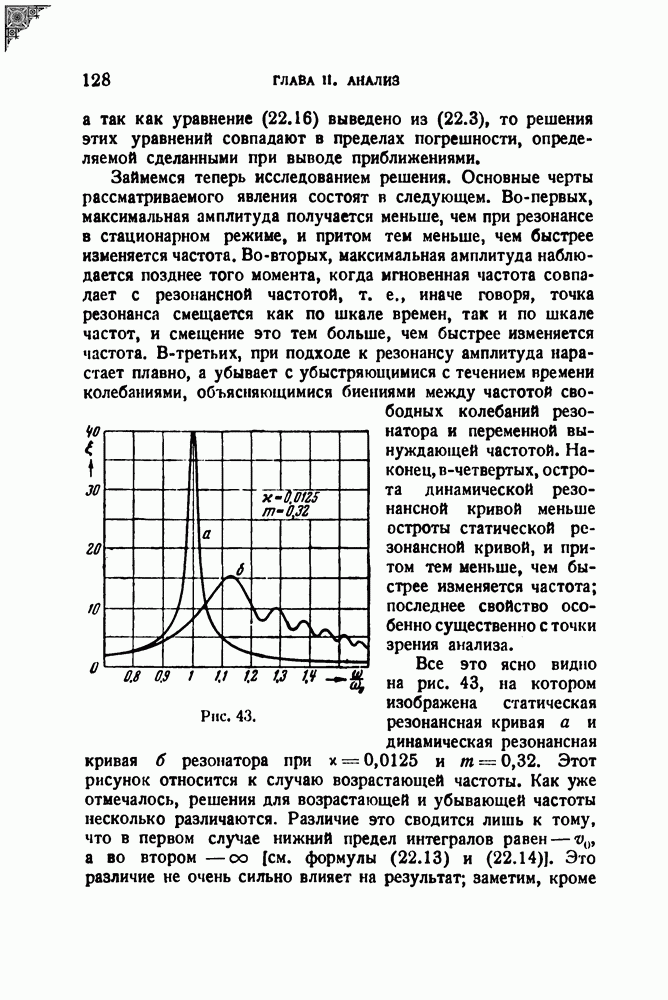
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
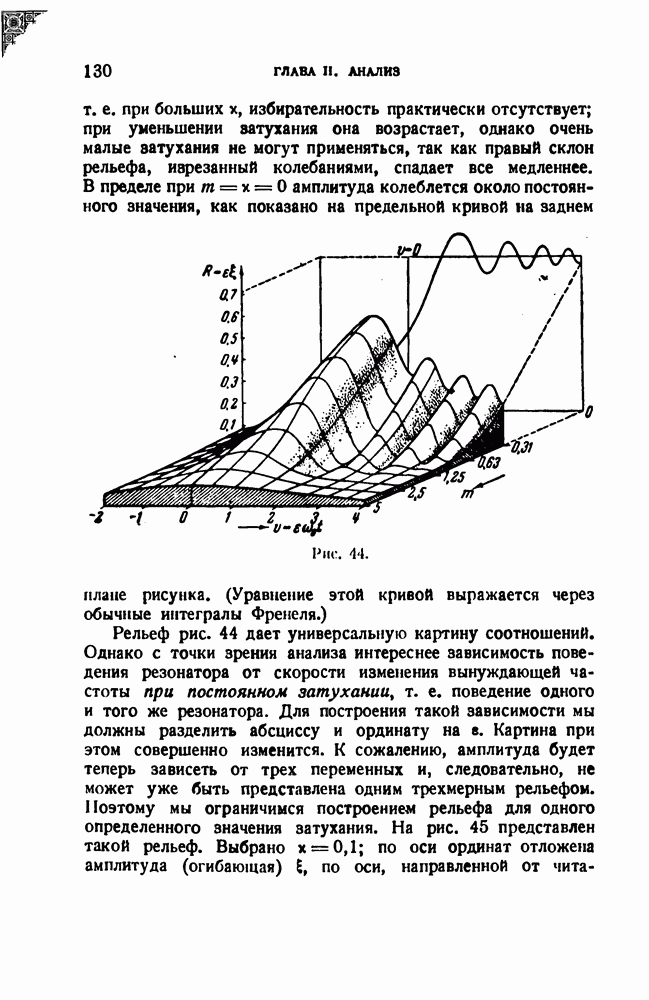
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА