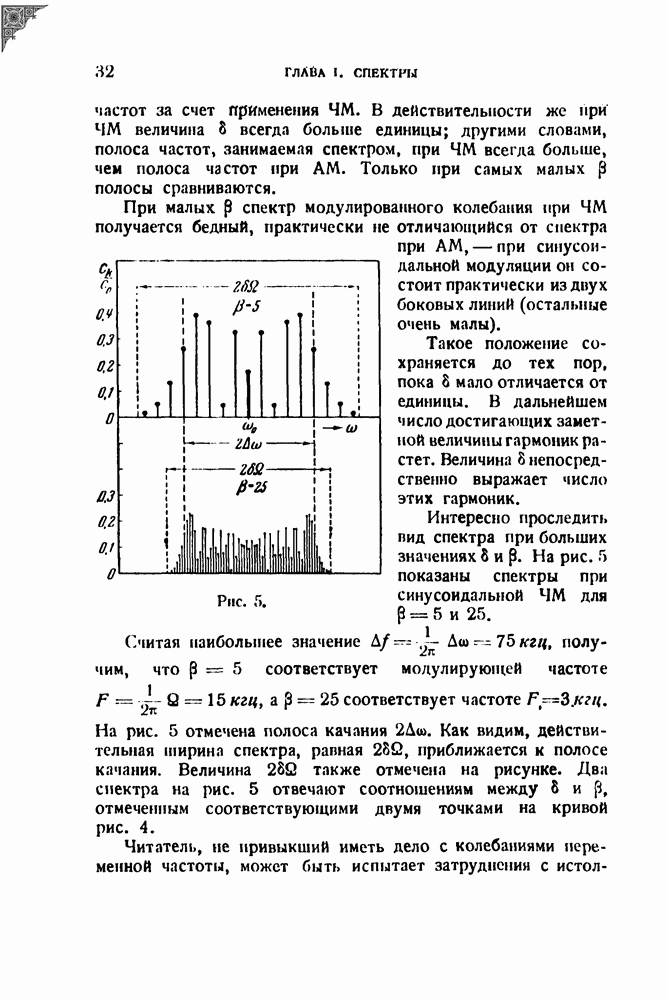
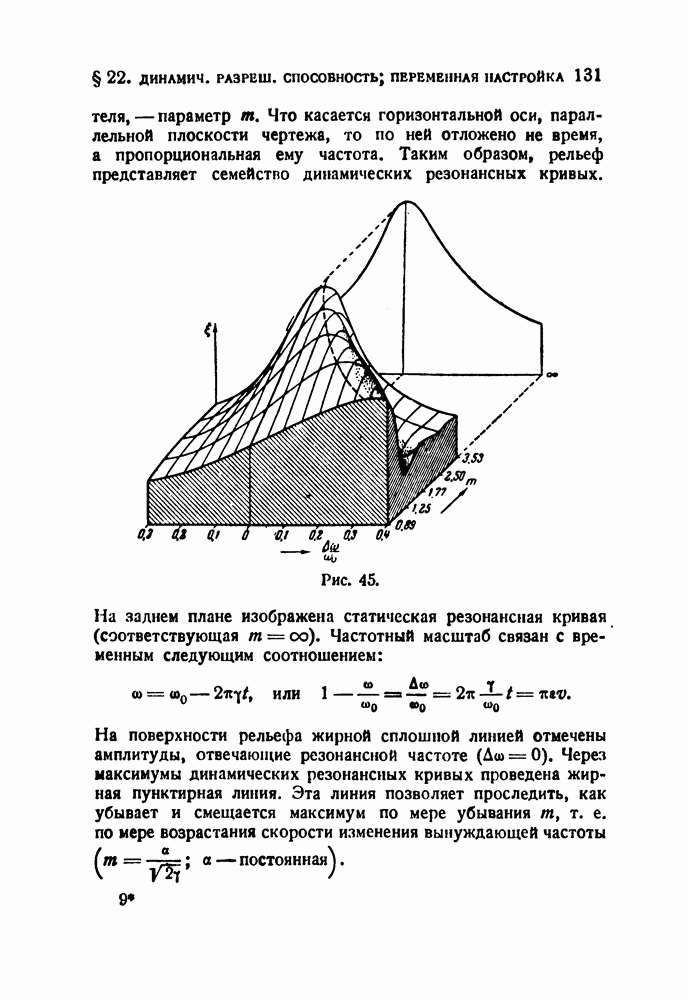
2. Спектры некоторых частотно-модулированных колебаний

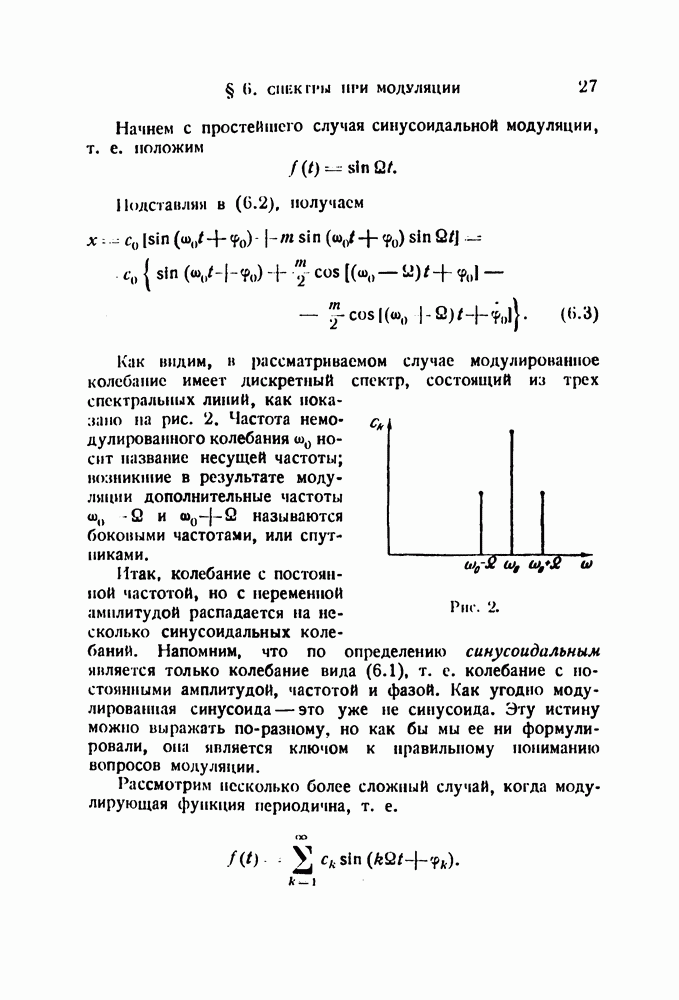
В § 6 вычислен спектр для простейшего случая синусоидальной ЧМ

Общий случай ЧМ может быть записан в виде

откуда

где

Так как модулированное колебание имеет вид

то очевидно, что представление функции каким бы то ни было (например, степенным или тригонометрическим) рядом ни к чему хорошему не приведет. Необходимо стараться представить в конечной форме, и притом таким образом, чтобы интеграл, которым выражается спектр, мог быть вычислен. Мы приведем здесь два примера такого рода вычислений.

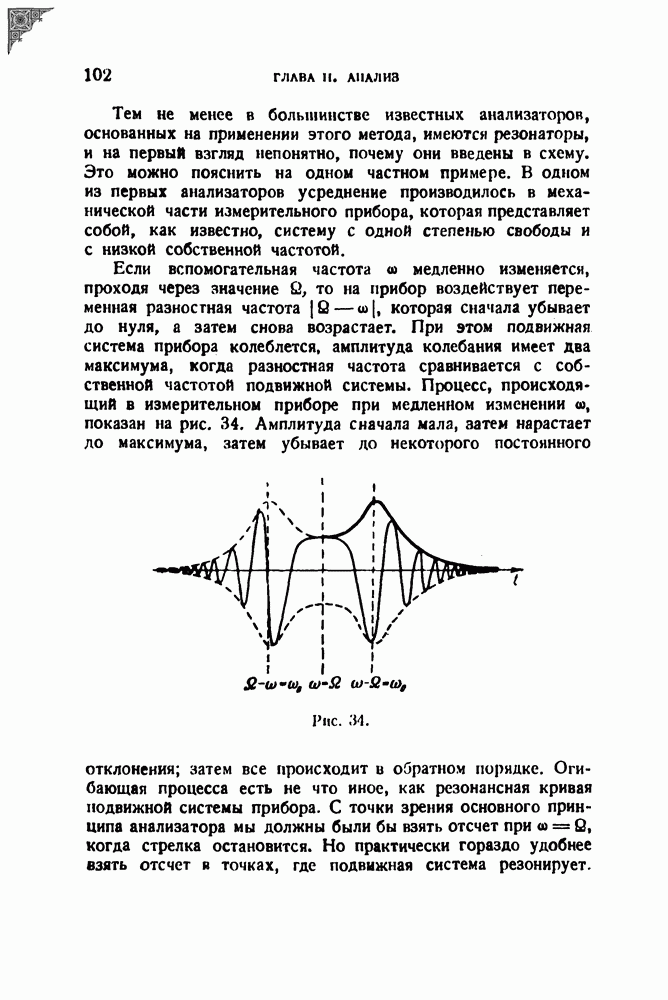
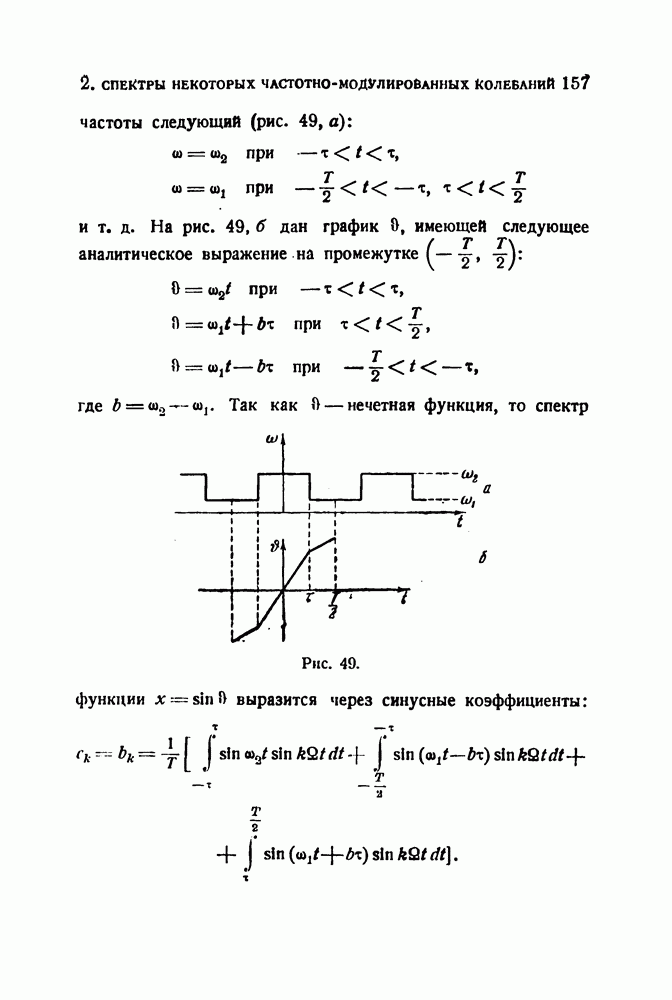
а. Спектр колебания с частотой, модулированной по закону прямоугольной ломаной линии. Закон изменения

(см. скан)

Выполняя простые преобразования и интегрируя, находим

В частном случае когда зубцы и впадины ломаной (рис. 49, а) имеют одинаковую ширину, получаем

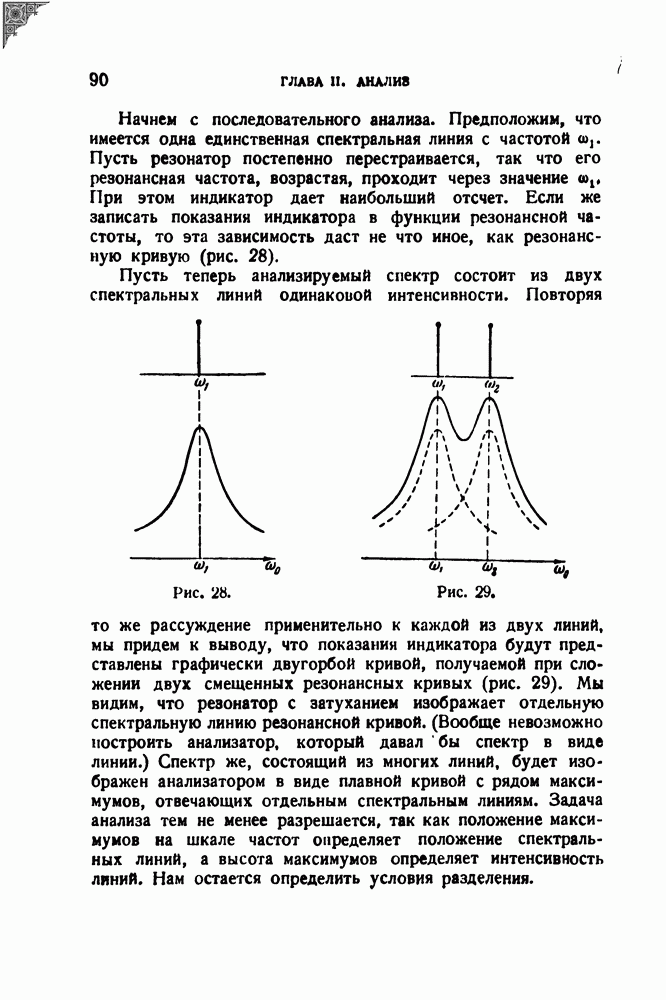
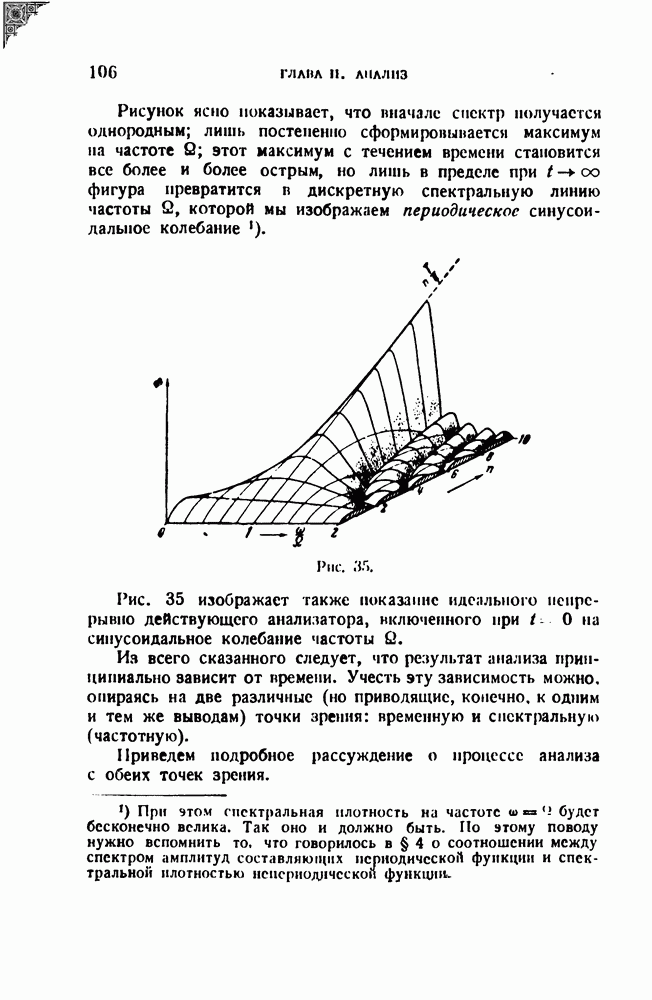
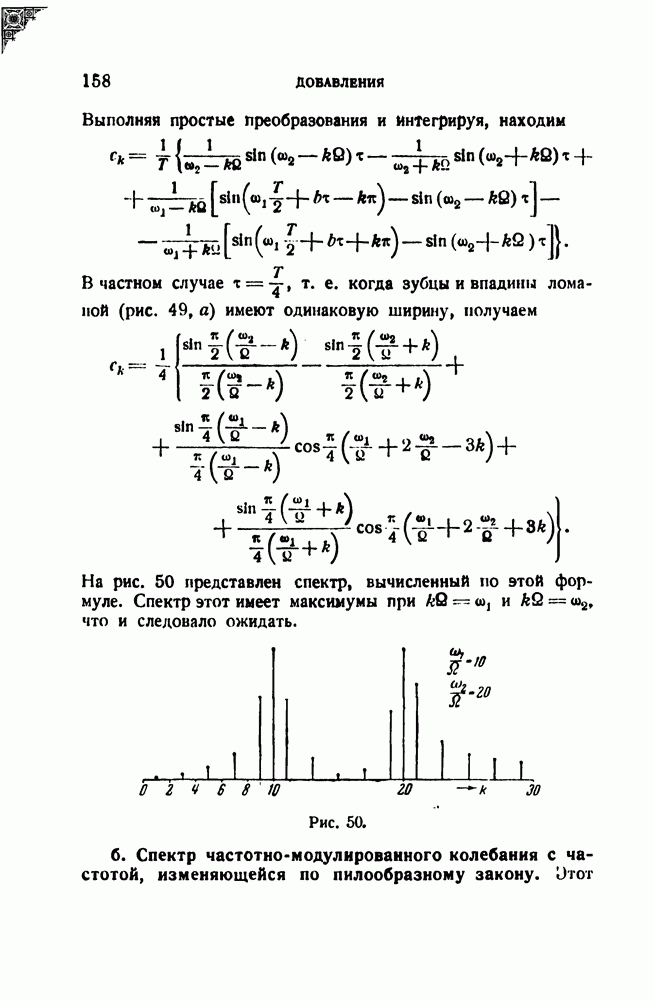
На рис. 50 представлен спектр, вычисленный по этой формуле. Спектр этот имеет максимумы при что и следовало ожидать.

Рис. 50.

б. Спектр частотно - модулированного колебания с частотой, изменяющейся по пилообразному закону. Этот

случай, — так называемый свип-сигнал, — несколько сложнее предыдущего.

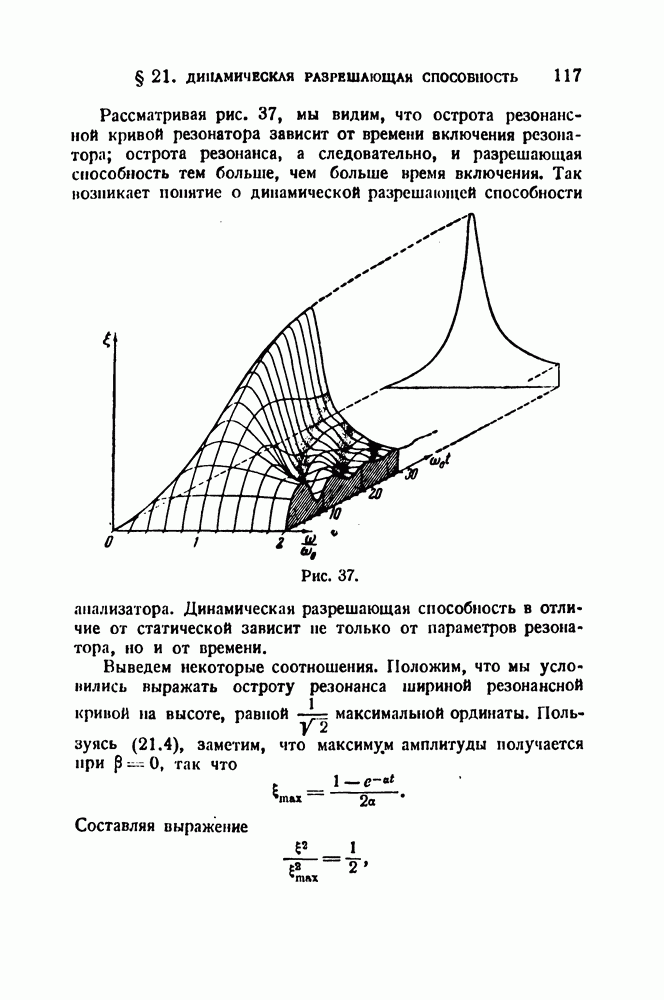
Пусть

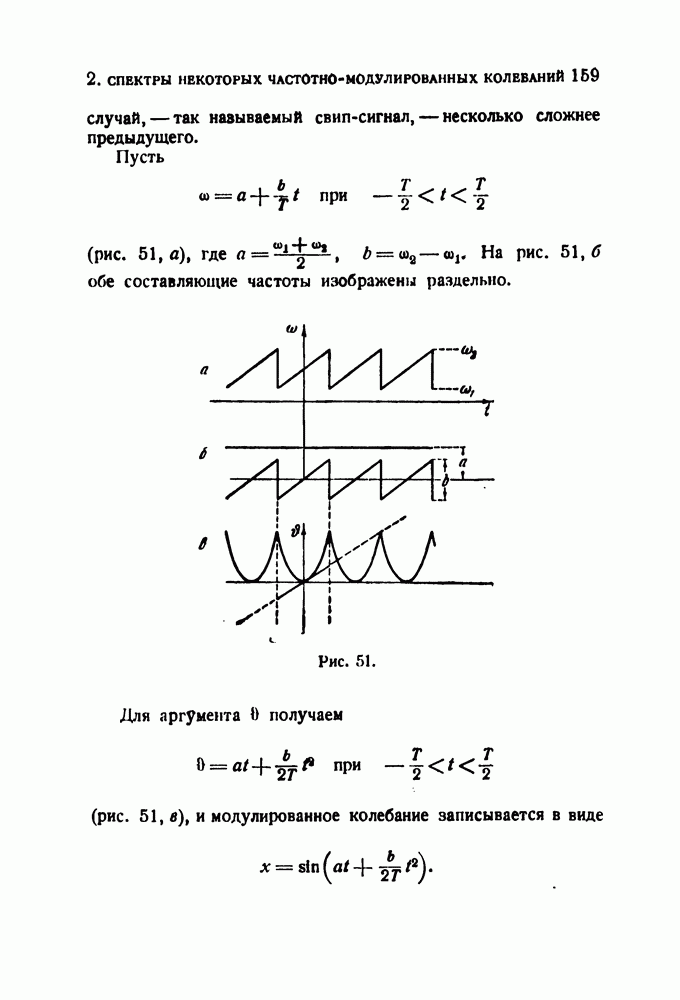
(рис. 51, а), где На рис. 51, б обе составляющие частоты изображены раздельно.

Рис. 51.

Для аргумента получаем

(рис. 51, в), и модулированное колебание записывается в виде

Вычислим компоненты спектра:

Для вычисления этих интегралов нужно сначала сделать тригонометрические преобразования.

Например, для получим

где обозначено для сокращения

В этой форме нужно дополнить аргумент до полного квадрата, прибавляя и вычитая соответственно Затем, разлагая снова синусы разности, найдем

Здесь применены следующие обозначения:

Аналогичная формула получается и для

Нас интересует амплитудный спектр. Амплитуда гармоники равна

Проделав вычисления, получим