| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.1. Элементы кристаллографии
Кристаллическая решетка.
В кристалле элементарные частицы (ионы, атомы, молекулы), из которых построен кристалл, сближены до соприкосновения и располагаются различно, но закономерно по разным направлениям (рис. 1.3, а). Для упрощения пространственное изображение заменяют схемами (рис. 1.3, б6), отмечая точками центры тяжести частиц.
Если в кристалле провести три направления х, у, z, не лежащих в одной плоскости, то расстояния между частицами, расположенными по этим направлениям, в общем случае неодинаковы и соответственно равны а, Ь, с.
Плоскости, параллельные координатным плоскостям, находящиеся на расстоянии а, Ь, с друг от друга, разбивают кристалл на множество параллелепипедов, равных и параллельно ориентированных. Наименьший параллелепипед называют элементарной ячейкой. Последовательное перемещение его

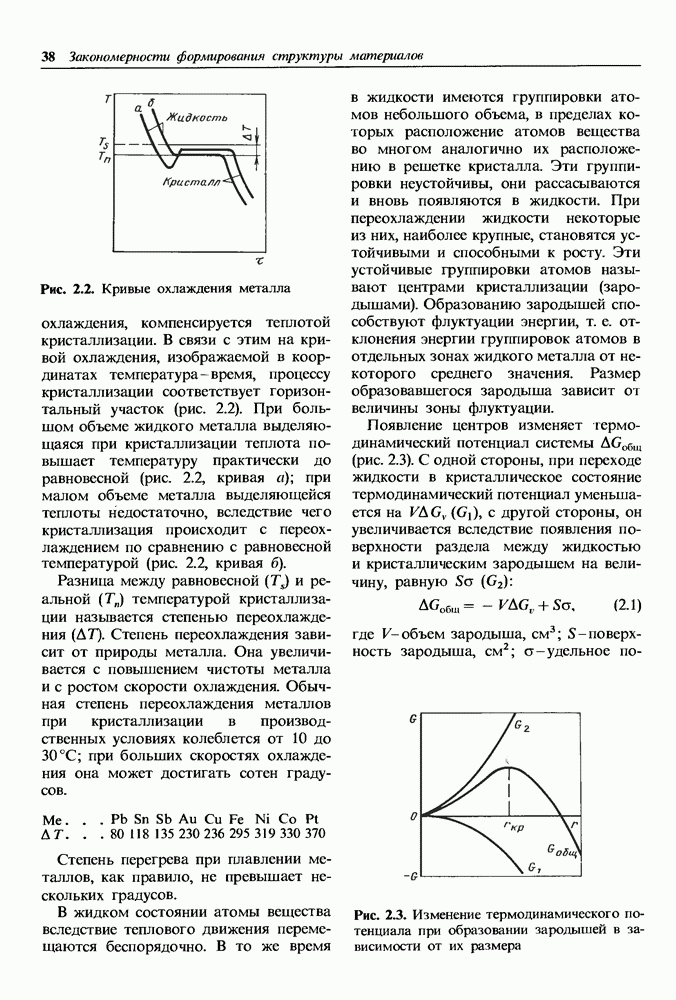
Рис. 1.3. Расположение элементарных частиц в кристалле: а — пространственное изображение; б — схема
ТАБЛИЦА 1.1. Кристаллические системы элементов

образует пространственную кристаллическую решетку. Вершины параллелепипеда называют узлами пространственной решетки. С этими узлами совпадают центры тяжести элементарных частиц, из которых построен кристалл.
Пространственные кристаллические решетки полностью определяют строение кристалла.
Для описания элементарной ячейки кристаллической решетки используют шесть величин: три отрезка, равные расстояниям до ближайших элементарных частиц по осям координат  , и три угла между этими отрезками а, Р, у.
, и три угла между этими отрезками а, Р, у.
Соотношения между этими величинами определяют форму ячейки. По форме элементарных ячеек все кристаллы подразделяют на семь систем (табл. 1.1).
Размер элементарной ячейки кристаллической решетки оценивают отрезки а, Ь, с. Их называют периодами решетки. Зная периоды решетки, можно определить ионный или атомный радиус элемента. Он равен половине наименьшего расстояния между частицами в решетке.
В большинстве случаев решетки сложны, так как элементарные частицы находятся не только в узлах кристаллической решетки, но и на ее гранях или в центре решетки (рис. 1.4). О степени сложности судят по числу частиц. приходящихся на одну элементарную ячейку. В простой пространственной решетке (рис. 1.4, о) всегда на одну ячейку приходится одна частица. В каждой ячейке имеется восемь вершин, но каждая частица в вершине относится, в свою очередь, к восьми ячейкам; таким образом, от узла на долю каждой ячейки приходится 1/8 объема, а всего узлов в ячейке восемь, следовательно, на ячейку приходится одна элементарная частица.
В сложной пространственной решетке на одну ячейку всегда приходится больше одной частицы. На объемно-центрированную ячейку (рис. 1.4, б) приходится две частицы: одна от вершины и другая центрирующая, которая относится только к данной ячейке. В гранецентрированной ячейке (рис. 1.4, в) имеется четыре частицы: одна от вершнн и три от шести центрированных плоскостей, так как элементарная частица, находящаяся в центре плоскости, относится одновременно к двум ячейкам.
Система, период, число частиц, приходящихся на элементарную ячейку, полностью определяют расположение элементарных частиц в кристалле.
В ряде случаев используют дополнительные характеристики кристаллической решетки, вытекающие из ее геометрии и отражающие плотность упаковки элементарных частиц в кристалле. Такими характеристиками являются координационное число и коэффициент компактности.
Число ближайших равноудаленных элементарных частиц определяет координационное число. Например, в решетке объемно-центрированного куба  для каждого атома число таких соседей будет равно восьми
для каждого атома число таких соседей будет равно восьми  Для простой кубической решетки координационное число будет
Для простой кубической решетки координационное число будет  Для гранецентрированной кубической решетки
Для гранецентрированной кубической решетки

Рис. 1.4. Типы элементарных ячеек кристаллических решеток: а — простая; б, в — сложные

Рис. 1.5. Октаэдрические (а) и тетраэдрические (б) поры в металлах с ГЦК решеткой
(ГЦК) координационное число равно 12 (К 12).
Отношение объема всех элементарных частиц, приходящихся на одну элементарную ячейку, ко всему объему элементарной ячейки определяет коэффициент компактности. Для простой кубической решетки этот коэффициент равен 0,52, для  и
и 
Оставшееся пространство образуют поры, которые дифференцируют на октаэдрические и тетраэдрические.
Центры этих пор показаны маленькими точками на решетке ГЦК (рис. 1.5). Радиус октаэдрической поры составляет 0.41 радиуса элементарной частицы, а радиус тетраэдрической поры - лишь 0,22.
Для многих кристаллов характерна плотная упаковка элементарных частиц. Если элементарные частицы изобразить в виде шаров, а для большинства частиц это справедливо, так как они обладают шаровой симметрией. то при упаковке получаются структуры, показанные на рис. 1.6.

Рис. 1.6. Плотная упаковка атомов в кристаллах
На первый слой шаров, обозначенных А, в лунки 1 накладывается второй слой шаров, обозначенных В. Для следующего слоя шаров возможны два варианта: если шары укладываются над первым слоем, то решетка получается гексагональная (внизу); если третий слой шаров С укладывается на второй слой над лунками 2 и только четвертый слой шаров повторяет первый слой шаров А, то получается гранецентрированная кубическая решетка (вверху).
Шестигранная призма на рис. 1.7 изображает гексагональную плотноупакованную кристаллическую решетку ГПУ. Такое изображение подчеркивает, что решетка гексагональная (шестиугольная). Однако элементарной ячейкой является элемент, выделенный жирными линиями. В нем  Исходя из чисто
Исходя из чисто

Рис. 1.7. Элементарные ячейки кристаллических решеток: а, г - - ГПУ; б, д - ГЦК; в, е - ОЦК
геометрических соображений, можно определить отношение периодов  если элементарные частицы обладают сферической симметрией. Оно равно 1,633.
если элементарные частицы обладают сферической симметрией. Оно равно 1,633.
На этом же рисунке отмечены частицы, обозначенные на рис. 1.6 буквами А и В. Для гранецентрированной кубической решетки шары А принадлежат первому слою, шары В к С соответственно второму и третьему слоям. Оба эти слоя заштрихованы. Только четвертый слой повторяет первый. Заштрихованные плоскости - это плоскости плотной упаковки.
При отклонении элементарных частиц от сферической симметрии возможно образование гексагональных структур с отношением параметров, отличающихся от значения 1,633, а также структуры объемно-центрированного куба (см. рис. 1.7).
Кристаллографические индексы.
По параллельным направлениям свойства одинаковы, поэтому достаточно указать для всего семейства параллельных прямых одно направление, проходящее через начало координат. Это дает возможность определить направление прямой только одной точкой, так как другой всегда служит начало координат. Такой точкой является узел кристаллической решетки, занимаемый элементарной частицей. Координаты этого узла выражают целыми числами  в единицах отрезков
в единицах отрезков  , заключают в квадратные скобки
, заключают в квадратные скобки  и называют индексами направления. Их всегда выражают целыми числами, а отрицательное значение индекса обозначается знаком минус над индексом (рис. 1.8, а).
и называют индексами направления. Их всегда выражают целыми числами, а отрицательное значение индекса обозначается знаком минус над индексом (рис. 1.8, а).
Положение плоскости в пространстве определяется отрезками, отсекаемыми плоскостью по осям  Эти отрезки выражают целыми числами
Эти отрезки выражают целыми числами  в единицах отрезков а, Ь, с. Принято за индексы плоскостей брать обратные отрезки:
в единицах отрезков а, Ь, с. Принято за индексы плоскостей брать обратные отрезки:  Три этих числа
Три этих числа  , заключенные в круглые скобки, называют индексами плоскости (рис. 1.8, б). Если плоскость отсекает по осям отрицательные отрезки, то это отмечается знаком минус над соответствующим индексом.
, заключенные в круглые скобки, называют индексами плоскости (рис. 1.8, б). Если плоскость отсекает по осям отрицательные отрезки, то это отмечается знаком минус над соответствующим индексом.
Плоскости плотной упаковки (см. рис. 1.7, заштрихованные плоскости) называют плоскостями скольжения, так как по этим плоскостям смещаются атомы при пластической деформации кристалла.
Для кристаллов с ГЦК решеткой плоскостями скольжения будут плоскости семейства (111). Для кристаллов с ГПУ решеткой с отношением  плоскостью скольжения будет плоскость базиса шестигранного основания призмы. При отношении
плоскостью скольжения будет плоскость базиса шестигранного основания призмы. При отношении  плоскостями скольжения будут также и плоскости призмы.
плоскостями скольжения будут также и плоскости призмы.
Анизотропия.
Это зависимость свойств кристалла от направления, возникающая в результате упорядоченного расположения атомов (ионов, молекул) в пространстве.
Свойства кристаллов определяются взаимодействием атомов. В кристалле расстояния между атомами в различных кристаллографических направлениях различны, а поэтому различны и свойства.
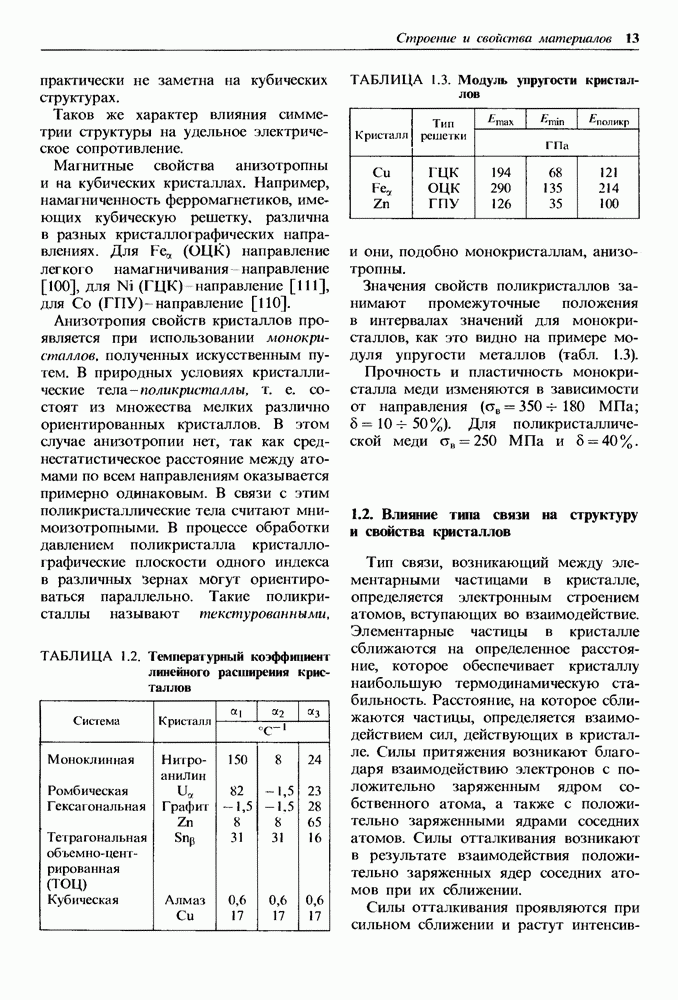
Анизотропия присуща всем свойствам кристаллов. Наиболее сильно она проявляется в кристаллах со структурами, обладающими малой симметрией (табл. 1.2).
Из приведенных значений температурных коэффициентов линейного расширения в кристаллах по трем взаимно перпендикулярным осям видно, что анизотропия резко проявляется на структурах моноклинной и ромбической, но

Рис. 1.8. Кристаллографические индексы направлений (а) и плоскостей (б)
практически не заметна на кубических структурах.
Таков же характер влияния симметрии структуры на удельное электрическое сопротивление.
Магнитные свойства анизотропны и на кубических кристаллах. Например, намагниченность ферромагнетиков, имеющих кубическую решетку, различна в разных кристаллографических направлениях. Для  направление легкого намагничивания направление [100], для
направление легкого намагничивания направление [100], для  направление [111], для
направление [111], для  .
.
Анизотропия свойств кристаллов проявляется при использовании монокристаллов, полученных искусственным путем. В природных условиях кристаллические тела - поликристаллы, т. е. состоят из множества мелких различно ориентированных кристаллов. В этом случае анизотропии нет, так как среднестатистическое расстояние между атомами по всем направлениям оказывается примерно одинаковым. В связи с этим поликристаллические тела считают мнимоизотропными. В процессе обработки давлением поликристалла кристаллографические плоскости одного индекса в различных зернах могут ориентироваться параллельно. Такие поликристаллы называют текстурованными, и они, подобно монокристаллам, анизотропны.
ТАБЛИЦА 1.2. Температурный коэффициент линейного расширения кристаллов

ТАБЛИЦА 1.3. Модуль упругости кристаллов

Значения свойств поликристаллов занимают промежуточные положения в интервалах значений для монокристаллов, как это видно на примере модуля упругости металлов (табл. 1.3).
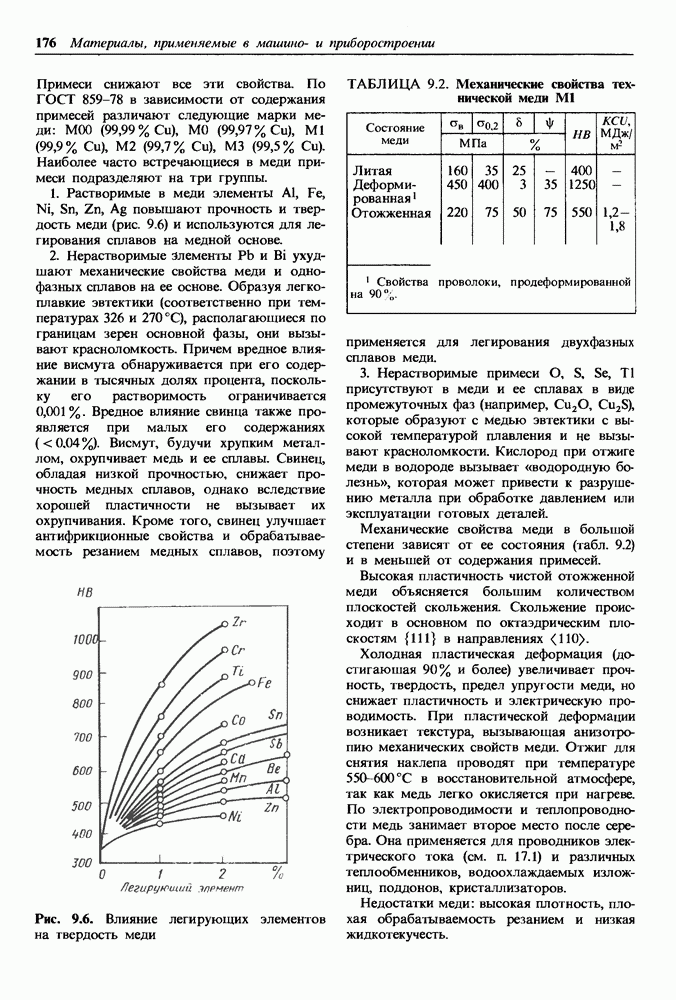
Прочность и пластичность монокристалла меди изменяются в зависимости от направления  Для поликристаллической меди
Для поликристаллической меди 
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. СТРОЕНИЕ И СВОЙСТВА МАТЕРИАЛОВ
- 1.1. Элементы кристаллографии
- 1.2. Влияние типа связи на структуру и свойства кристаллов
- Молекулярные кристаллы.
- Ковалентные кристаллы.
- Металлические кристаллы.
- Ионные кристаллы.
- 1.3. Фазовый состав сплавов
- Твердые растворы.
- Промежуточные фазы.
- 1.4. Дефекты кристаллов
- Линейные дефекты.
- Поверхностные дефекты.
- 1.5. Диффузия в металлах и сплавах
- 1.6. Жидкие кристаллы
- 1.7. Структура полимеров, стекла и керамики
- Глава 2. ФОРМИРОВАНИЕ СТРУКТУРЫ ЛИТЫХ МАТЕРИАЛОВ
- 2.1. Самопроизвольная кристаллизация
- 2.2. Несамопроизвольная кристаллизация
- 2.3. Форма кристаллов и строение слитков
- 2.4. Получение монокристаллов
- 2.5. Аморфное состояние металлов
- Глава 3. ВЛИЯНИЕ ХИМИЧЕСКОГО СОСТАВА НА РАВНОВЕСНУЮ СТРУКТУРУ СПЛАВОВ
- 3.1. Методы построения диаграмм состояния
- 3.2. Основные равновесные диаграммы состояния двойных сплавов
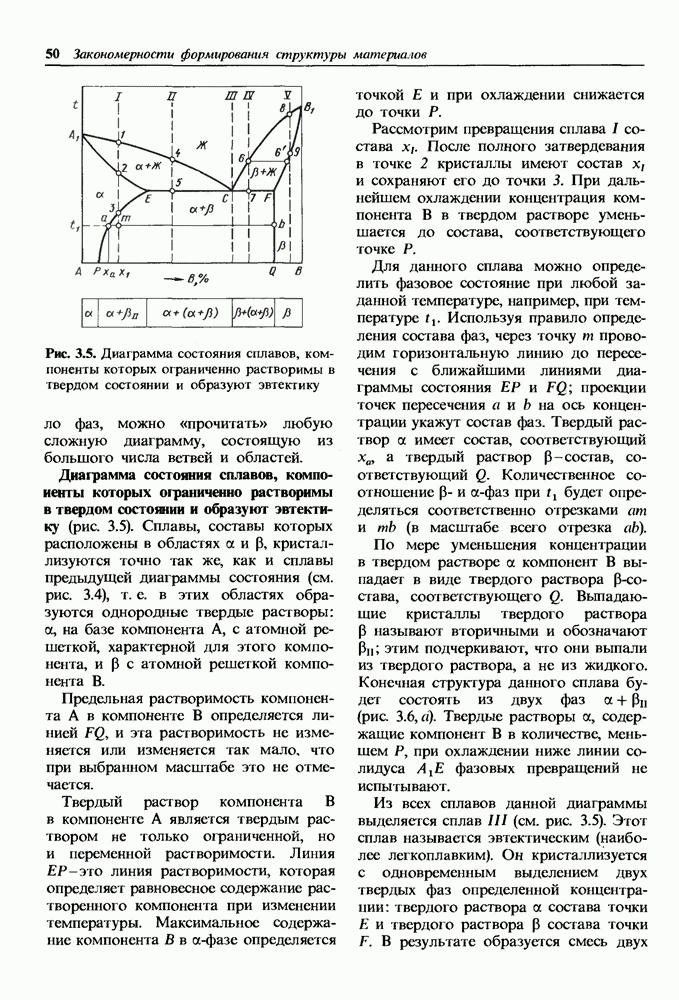
- Диаграмма состояния сплавов, компоненты которых ограниченно растворимы в твердом состоянии и образуют эвтектику
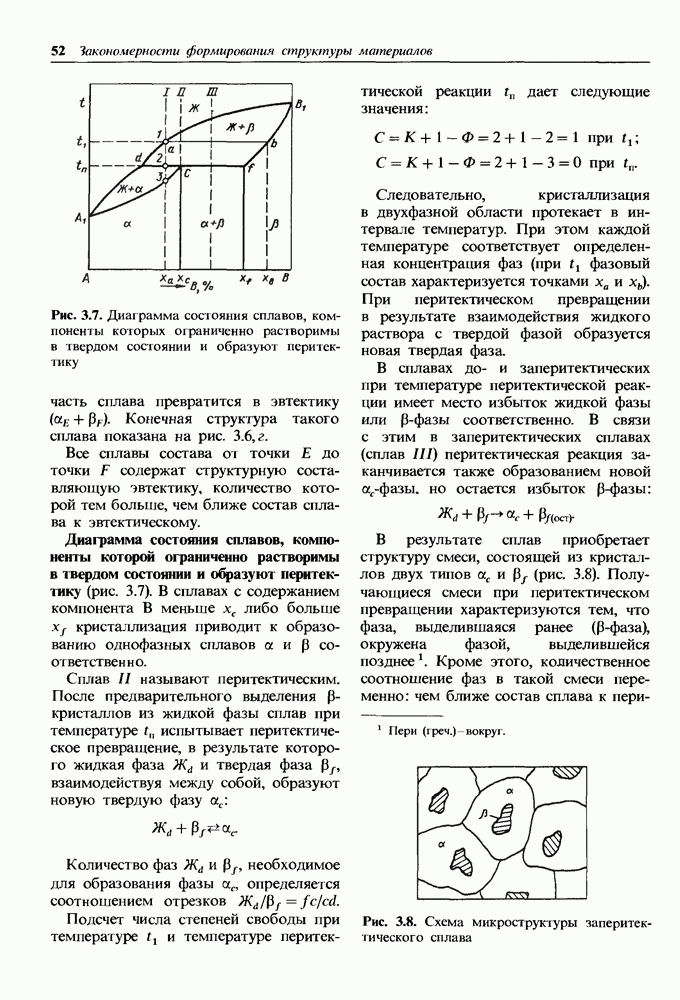
- Диаграмма состояния сплавов, компоненты которой ограниченно растворимы в твердом состоянии и образую! перитектику
- Диаграмма состояния сплавов с полиморфным превращением одного из компонентов.
- Диаграмма состояния сплавов с полиморфными превращениями компонентов и эвтектоидным превращением.
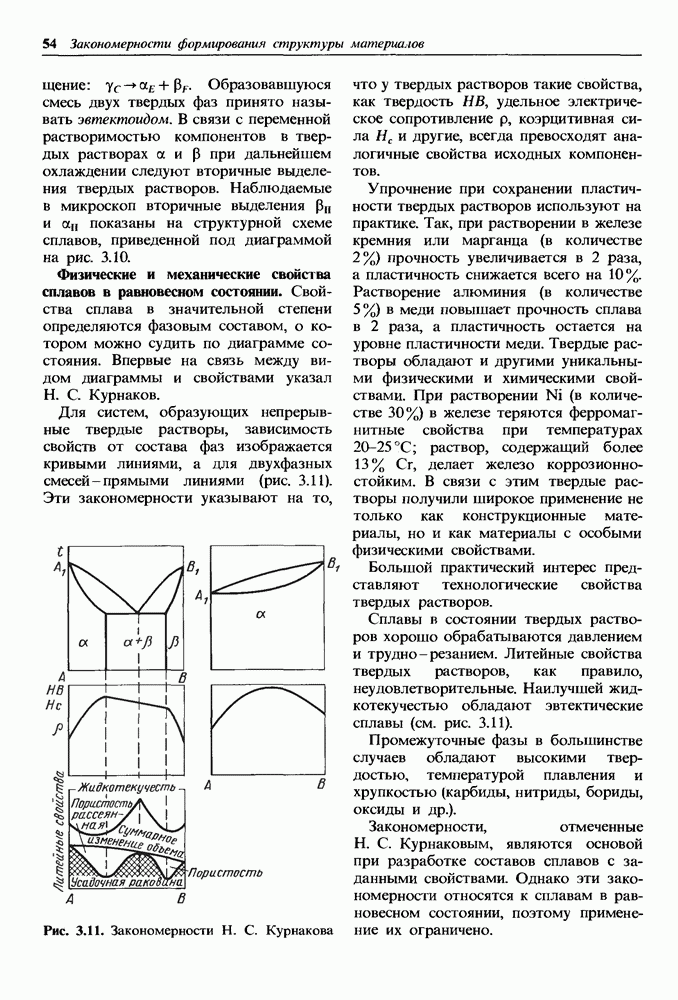
- Физические и механические свойства сплавов в равновесном состоянии.
- 3.3. Диаграмма состояния железоуглеродистых сплавов
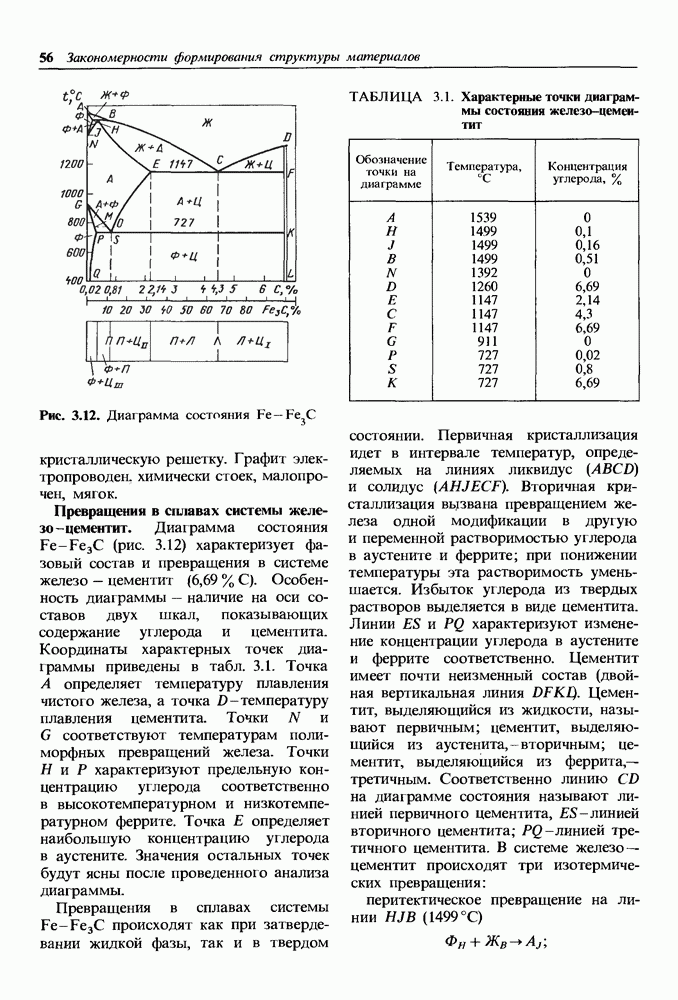
- Превращения в сплавах системы железо-цементит.
- Превращения в сплавах системы железо-графит.
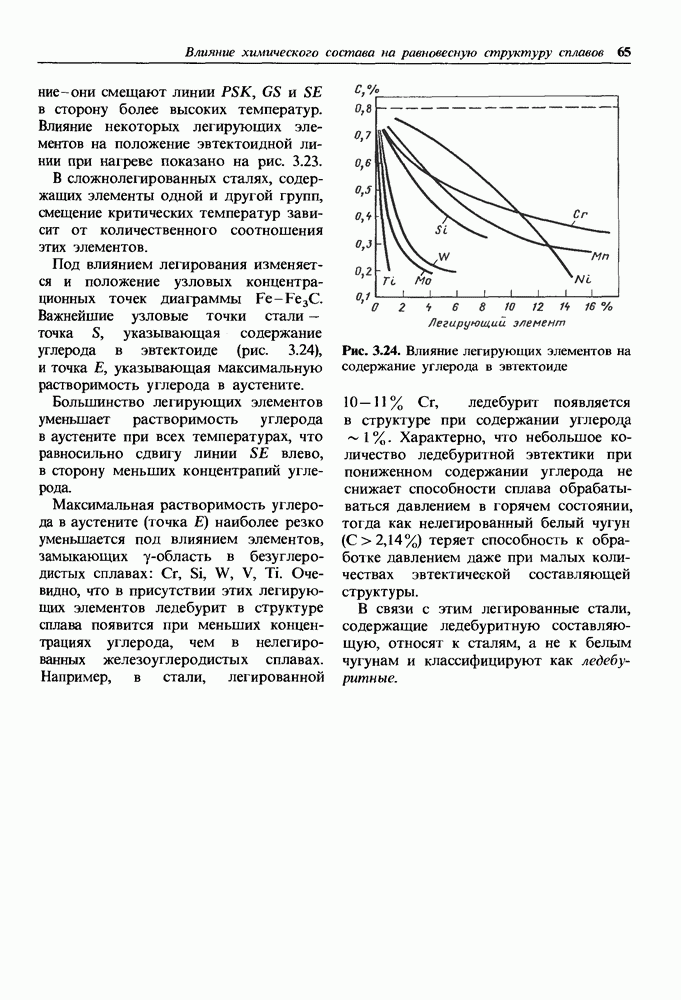
- 3.4. Влияние легирующих элементов на равновесную структуру сталей
- Карбиды в легированных сталях.
- Влияние легирующих элементов на температуры фазовых превращений сталей при нагреве и на состав точек S и Е диаграммы.
- Глава 4. ФОРМИРОВАНИЕ СТРУКТУРЫ ДЕФОРМИРОВАННЫХ МЕТАЛЛОВ И СПЛАВОВ
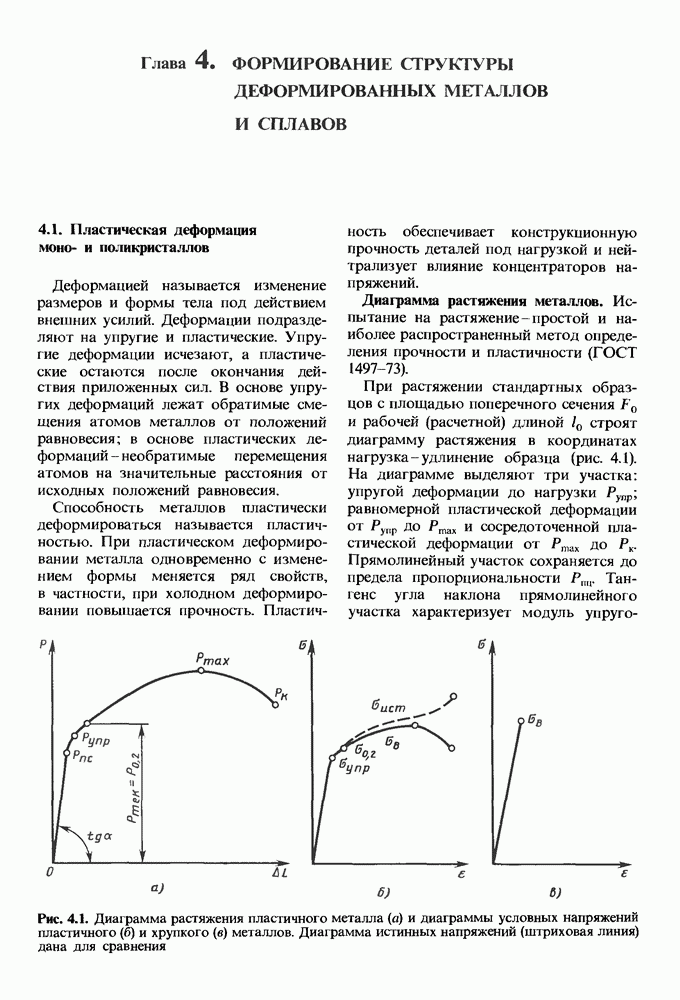
- 4.1. Пластическая деформация моно- и поликристаллов
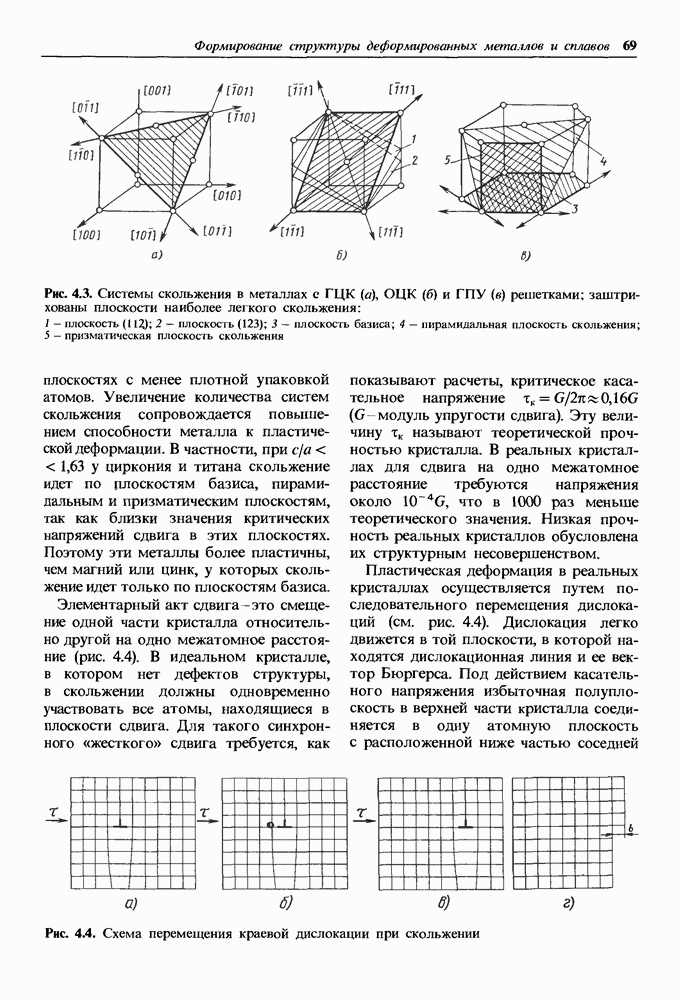
- Механизм пластической деформации
- Пластическая деформация поликристаллических металлов.
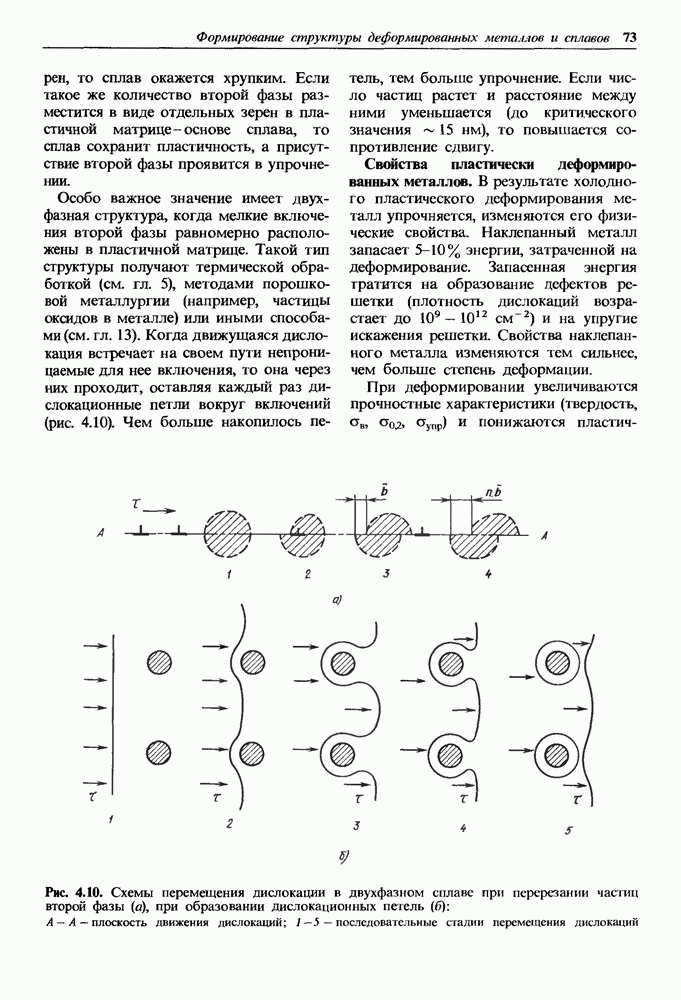
- Деформирование двухфазных сплавов оказывается более сложным.
- Свойства наклепанного металла изменяются тем сильнее, чем больше степень деформации.
- 4.2. Возврат и рекристаллизация
- Глава 5. ТЕРМИЧЕСКАЯ ОБРАБОТКА МЕТАЛЛОВ И СПЛАВОВ
- 5.2. Основное оборудование для термической обработки
- 5.3. Термическая обработка сплавов, не связанная с фазовыми превращениями в твердом состоянии
- Рекристаллизационный отжиг.
- Диффузионный отжиг (гомогенизация).
- 5.4. Термическая обработка сплавов с переменной растворимостью компонентов в твердом состоянии
- 5.5. Термическая обработка сталей с эвтектоидным превращением
- Превращения аустенита при различных степенях переохлаждения.
- 5.6. Основные виды термической обработки стали
- Нормализация сталей.
- Закалка сталей.
- Закаливаемость в прокаливаемость сталей.
- Отпуск закаленных сталей.
- Глава 6. ХИМИКО-ТЕРМИЧЕСКАЯ ОБРАБОТКА МЕТАЛЛОВ И СПЛАВОВ
- 6.2. Диффузионное насыщение углеродом и азотом
- Азотирование стали.
- Ионное азотирование и цементация.
- Одновременное насыщение поверхности стали углеродом и азотом.
- 6.3. Диффузионное насыщение сплавов металлами и неметаллами
- Раздел первый. Конструкционные материалы
- 7.1. Общие требования, предъявляемые к конструкционным материалам
- 7.2. Конструкционная прочность материалов и критерии ее оценки
- 7.3. Методы повышения конструкционной прочности
- 7.4. Классификация конструкционных материалов
- Глава 8. СТАЛИ, ОБЕСПЕЧИВАЮЩИЕ ЖЕСТКОСТЬ, СТАТИЧЕСКУЮ И ЦИКЛИЧЕСКУЮ ПРОЧНОСТЬ
- 8.1. Классификация конструкционных сталей
- 8.2. Влияние углерода и постоянных примесей на свойства стали
- 8.3. Углеродистые стали
- 8.4. Легированные стали
- Легированные стали нормальной и повышенной статической прочности.
- Легированные высокопрочные стали.
- Легированные стали с повышенной циклической прочностью.
- Глава 9. МАТЕРИАЛЫ С ОСОБЫМИ ТЕХНОЛОГИЧЕСКИМИ СВОЙСТВАМИ
- 9.1. Стали с улучшенной обрабатываемостью резанием
- 9.2. Стали с высокое технологической пластичностью и свариваемостью
- 9.3. Железоуглеродистые сплавы с высокими литейными свойствами
- Серые чугуны.
- Высокопрочные чугуны.
- Ковкие чугуны.
- 9.4. Медные сплавы
- Общая характеристика и классификация медных сплавов.
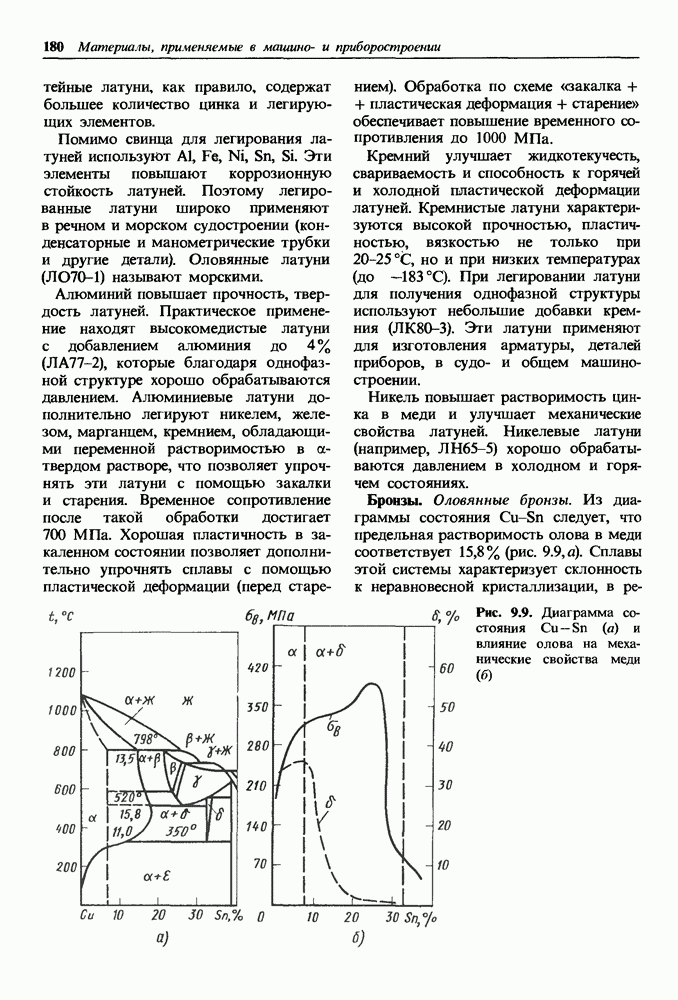
- Латуни.
- Бронзы.
- Глава 10. ИЗНОСОСТОЙКИЕ МАТЕРИАЛЫ
- 10.2. Закономерности изнашивания деталей, образующих пары трения, и пути уменьшения их износа
- 10.3. Материалы с высокой твердостью поверхности
- Материалы, устойчивые к усталостному виду изнашивания.
- Материалы, устойчивые к изнашиванию в условиях больших давлений и ударных нагрузок.
- 10.4. Антифрикционные материалы
- Неметаллические материалы.
- Комбинированные материалы.
- Минералы.
- 10.5. Фрикционные материалы
- Глава 11. МАТЕРИАЛЫ С ВЫСОКИМИ УПРУГИМИ СВОЙСТВАМИ
- 11.1. Рессорно-пружинные стали
- 11.2. Пружинные материалы приборостроения
- Глава 12. МАТЕРИАЛЫ С МАЛОЙ ПЛОТНОСТЬЮ
- 12.1. Сплавы на основе алюминия
- Общая характеристика и классификация алюминиевых сплавов.
- Деформируемые алюминиевые сплавы.
- Литейные алюминиевые сплавы.
- Гранулированные сплавы.
- 12.2. Сплавы на основе магния
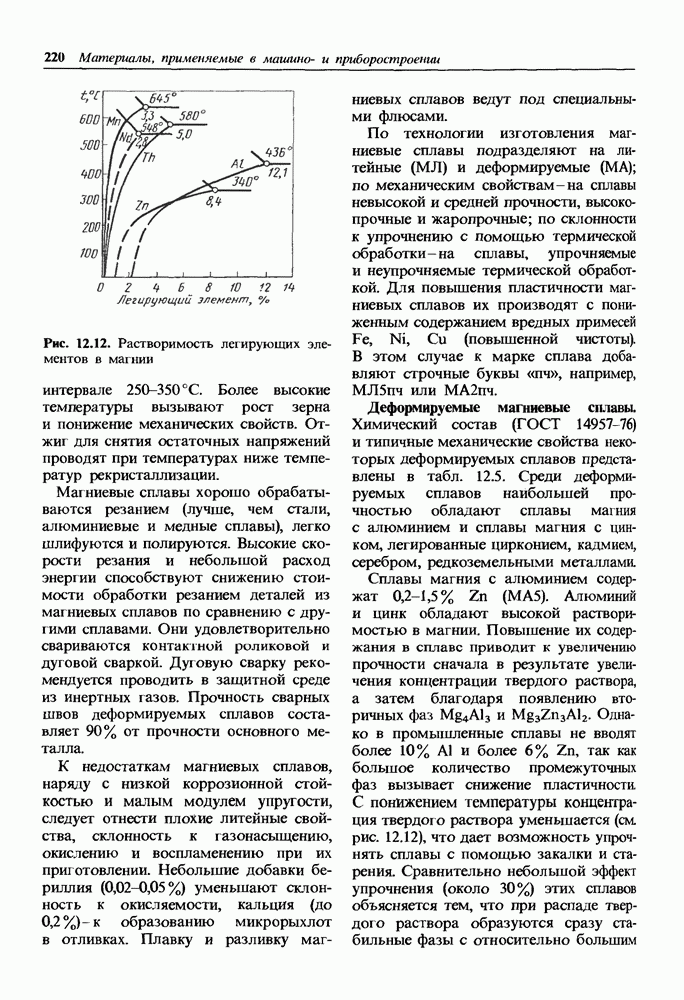
- Общая характеристика и классификация магниевых сплавов.
- Деформируемые магниевые сплавы.
- Литейные магниевые сплавы.
- 12.3. Неметаллические материалы
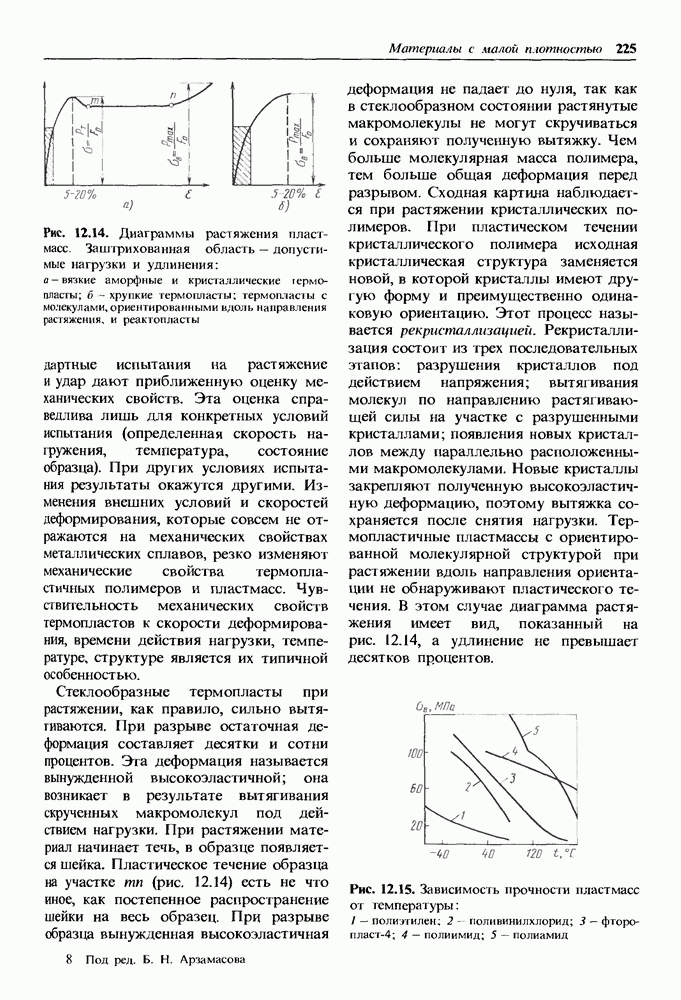
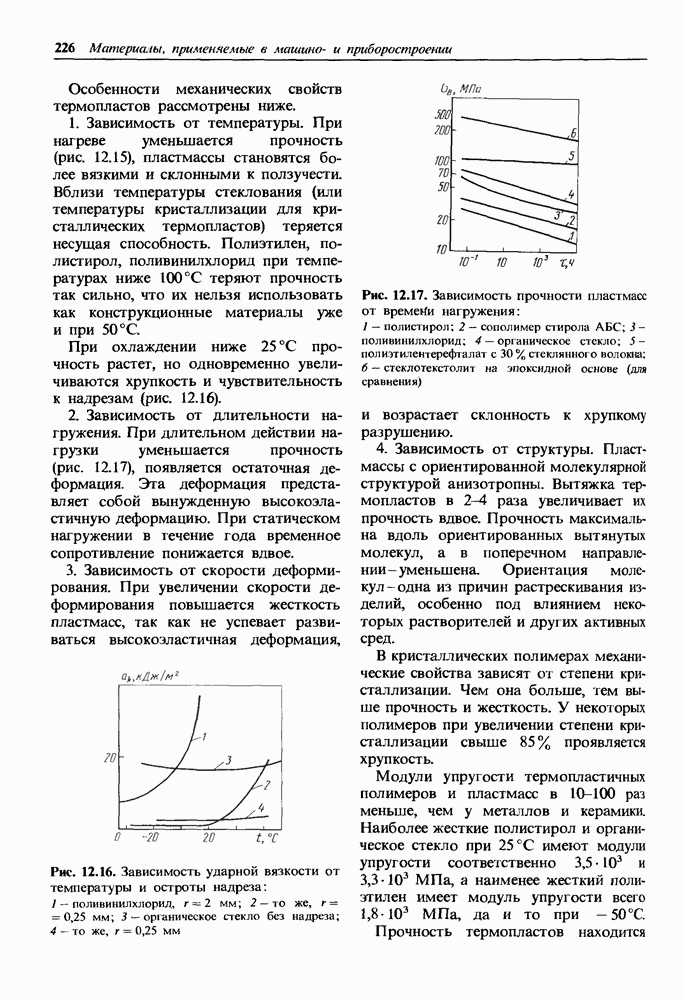
- Механические свойства термопластичных пластмасс.
- Механические свойства термореактивных пластмасс.
- Глава 13. МАТЕРИАЛЫ С ВЫСОКОЙ УДЕЛЬНОЙ ПРОЧНОСТЬЮ
- 13.1. Титан и сплавы на его основе
- Влияние легирующих элементов на структуру и свойства титановых сплавов.
- Особенности термической обработки титановых сплавов.
- Промышленные титановые сплавы.
- 13.2. Бериллий и сплавы на его основе
- Бериллиевые сплавы.
- 13.3. Композиционные материалы
- Дисперсно-упрочненные композиционные материалы.
- Волокнистые композиционные материалы.
- Композиционные материалы на неметаллической основе.
- Композиционные материалы на металлической основе.
- Глава 14. МАТЕРИАЛЫ, УСТОЙЧИВЫЕ К ВОЗДЕЙСТВИЮ ТЕМПЕРАТУРЫ И РАБОЧЕЙ СРЕДЫ
- 14.1. Коррозионно-стойкие материалы
- Коррозионно-стойкие непассивирующиеся металлы.
- Коррозионностойкие пассивирующиеси металлы.
- Коррозионно-стойкие покрытия.
- 14.2. Жаростойкие материалы
- Жаростойкость металлов.
- Жаростойкость сплавов.
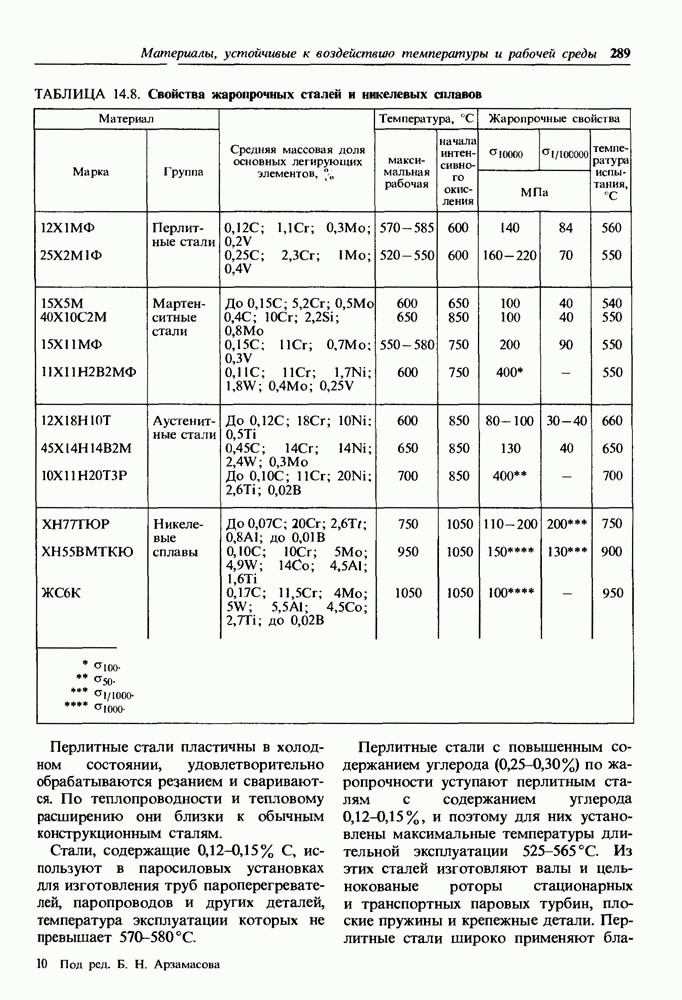
- 14.3. Жаропрочные материалы
- Основные группы жаропрочных материалов.
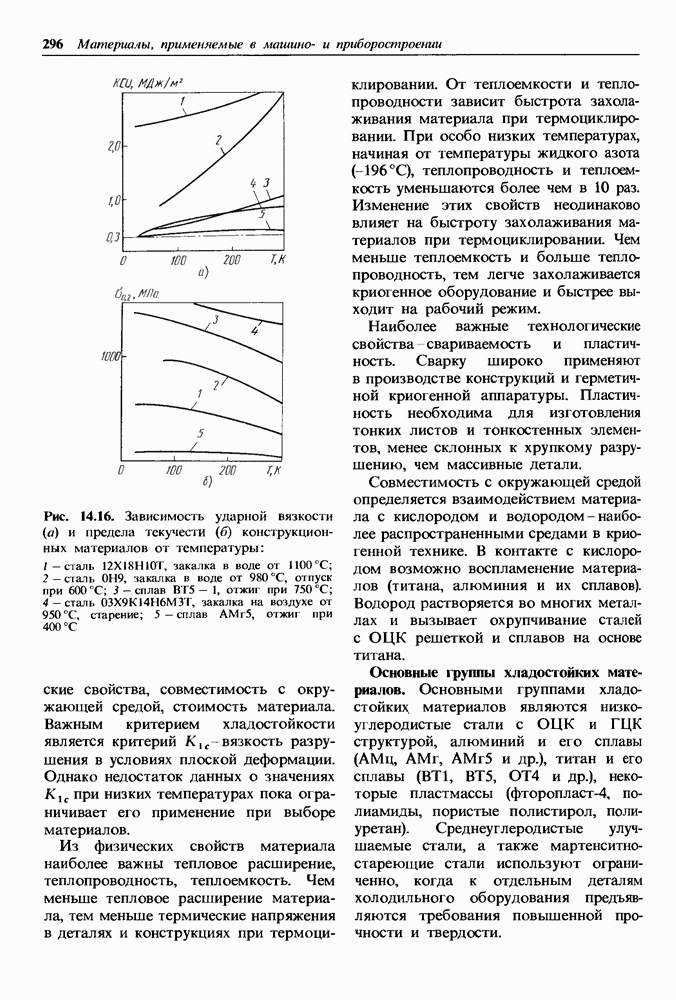
- 14.4. Хладостойкие материалы
- Основные группы хладостойких материалов.
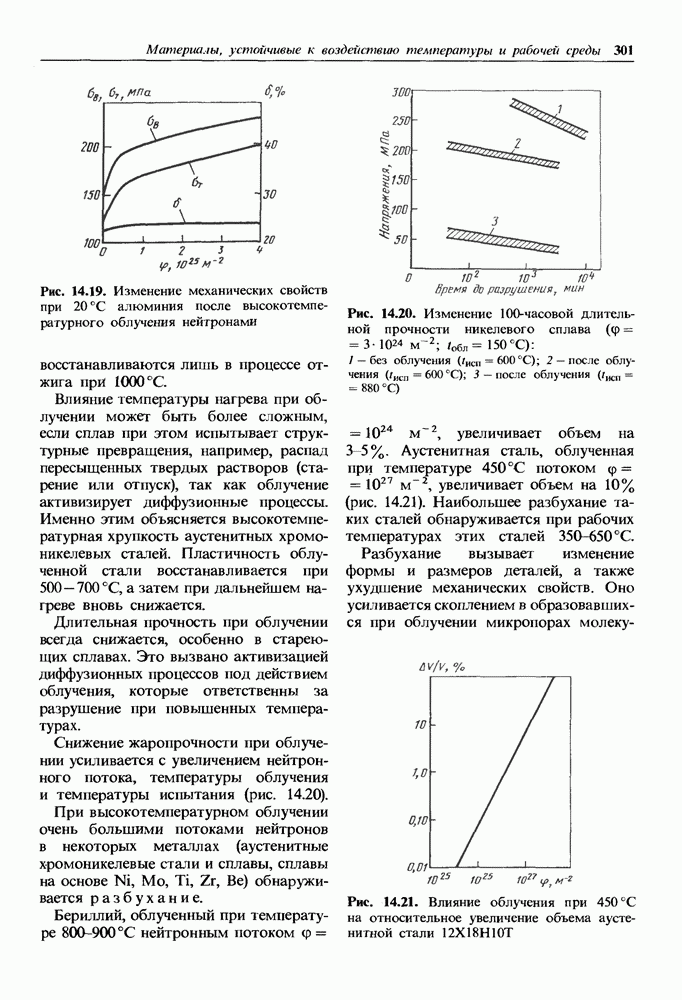
- 14.5. Радиационно-стойкие материалы
- Влияние облучения на коррозионную стойкость.
- Раздел второй. Материалы с особыми физическими свойствами
- 15.1. Общие сведения о ферромагнетиках
- 15.2. Магнитно-мягкие материалы
- Низкочастотные магнитно-мягкие материалы
- Высокочастотные магнитно-мягкие материалы.
- Материалы со специальными магнитными свойствами.
- 15.3. Магнитно-твердые материалы
- Магнитно-твердые лнтые материалы.
- Порошковые магнитно-твердые материалы.
- Деформируемые магнитно-твердые сплавы.
- Глава 16. МАТЕРИАЛЫ С ОСОБЫМИ ТЕПЛОВЫМИ СВОЙСТВАМИ
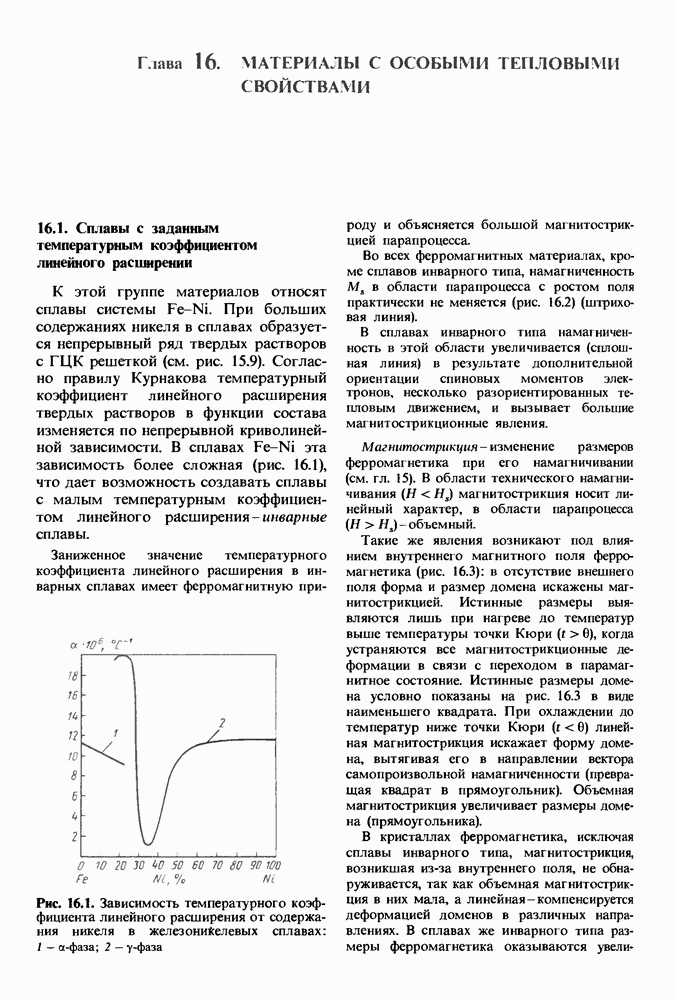
- 16.1. Сплавы с заданным температурным коэффициентом линейного расширении
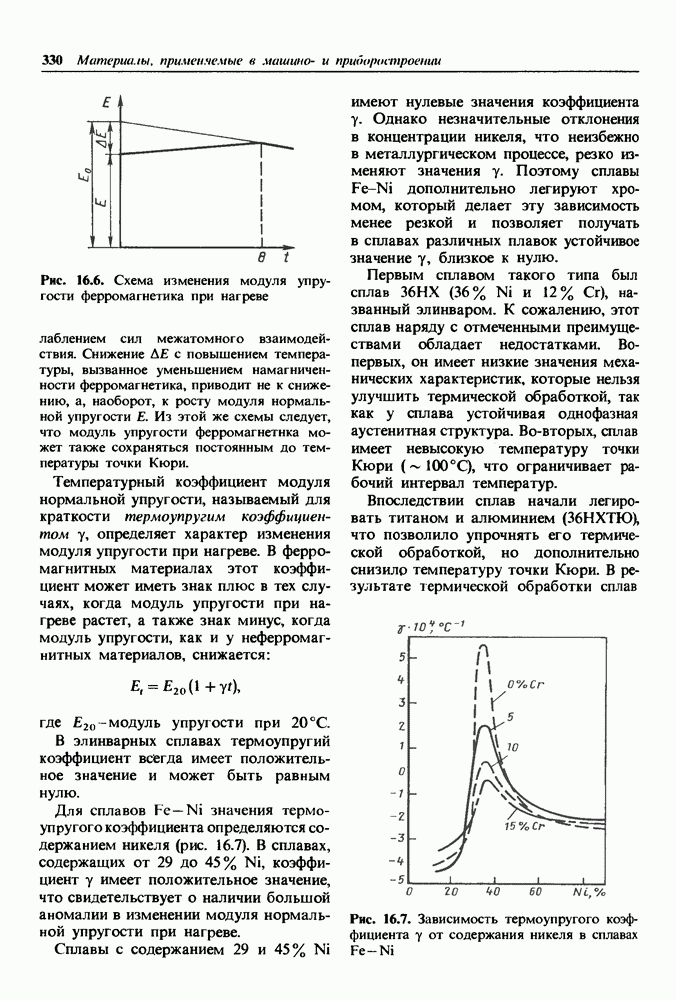
- 16.2. Сплавы с заданным температурным коэффициентом модуля упругости
- Глава 17. МАТЕРИАЛЫ С ОСОБЫМИ ЭЛЕКТРИЧЕСКИМИ СВОЙСТВАМИ
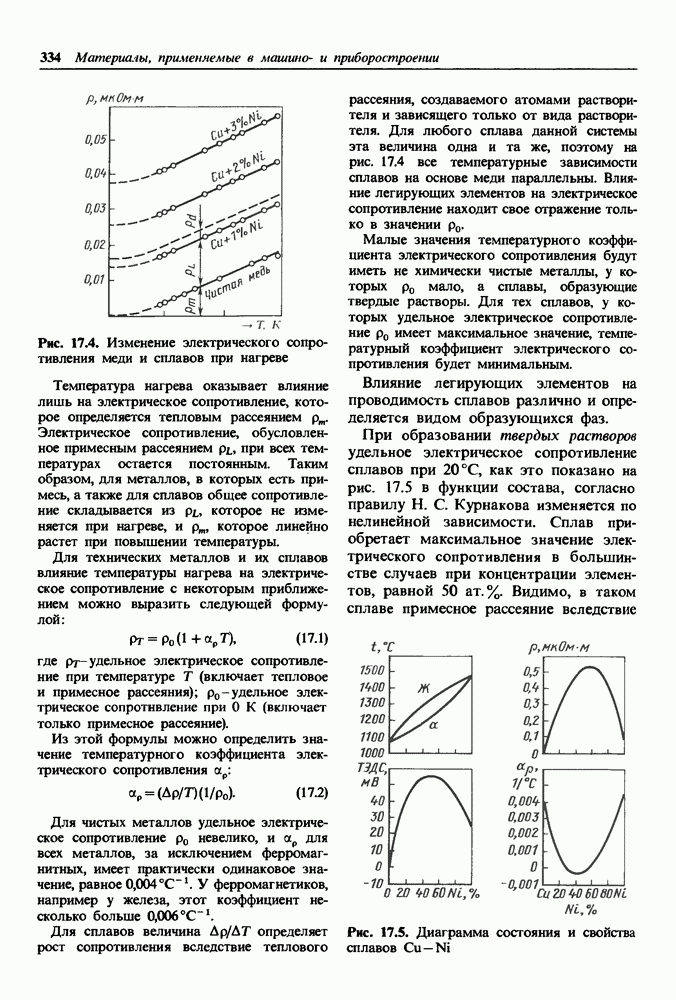
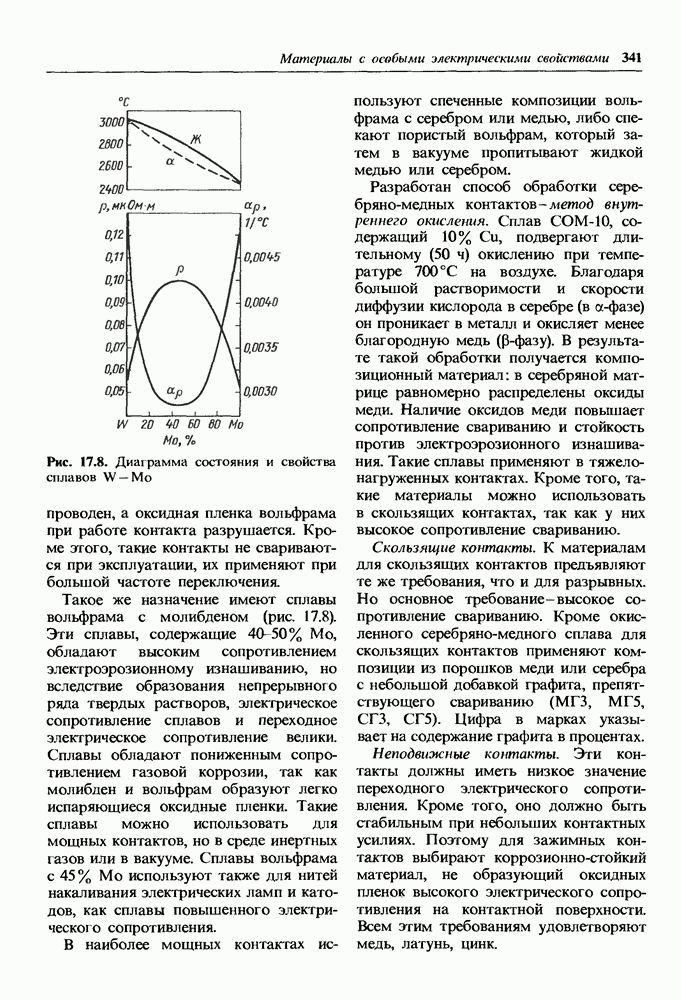
- 17.1. Материалы высокой электрической проводимости
- Проводниковые материалы.
- 17.2. Полупроводниковые материалы
- Кристаллофизические методы получения сверхчистых материалов.
- Легирование полупроводников и получение p-n-переходов.
- 17.3. Диэлектрики
- Раздел третий. Инструментальные материалы
- Глава 18. МАТЕРИАЛЫ ДЛЯ РЕЖУЩИХ И ИЗМЕРИТЕЛЬНЫХ ИНСТРУМЕНТОВ
- 18.1. Материалы для режущих инструментов
- Низколегированные стали.
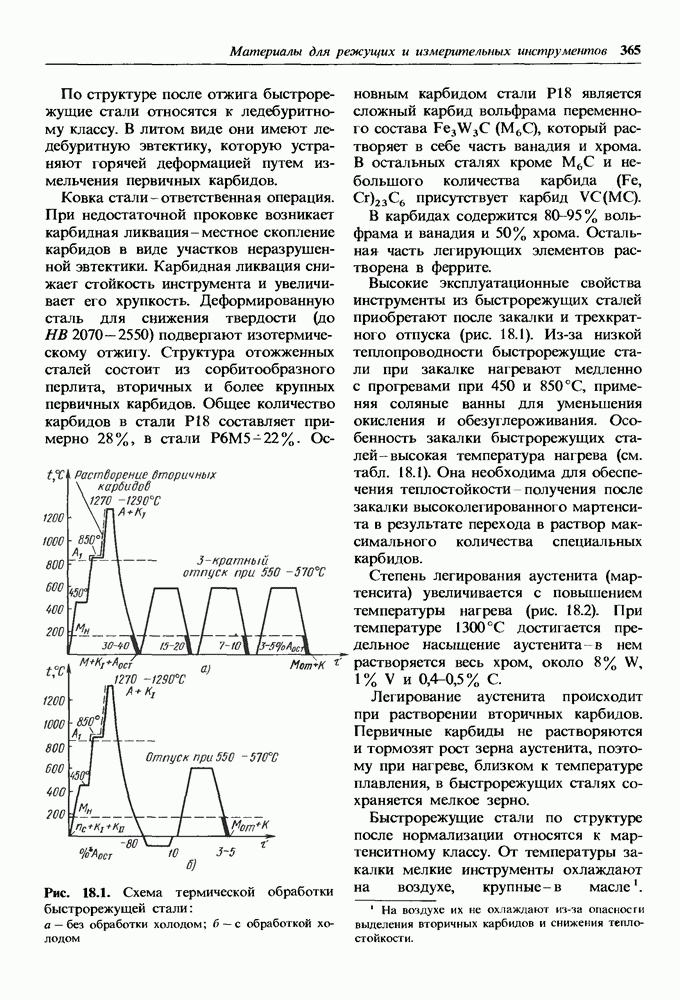
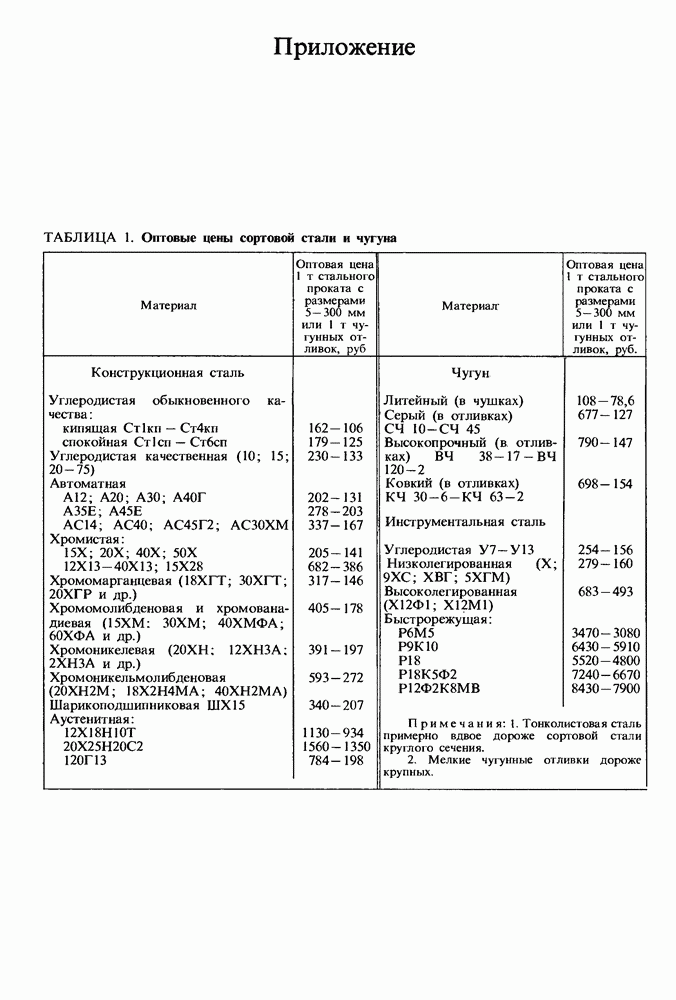
- Быстрорежущие стали.
- Спеченные твердые сплавы.
- Сверхтвердые материалы.
- 18.2. Стали для измерительных инструментов
- Глава 19. СТАЛИ ДЛЯ ИНСТРУМЕНТОВ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ
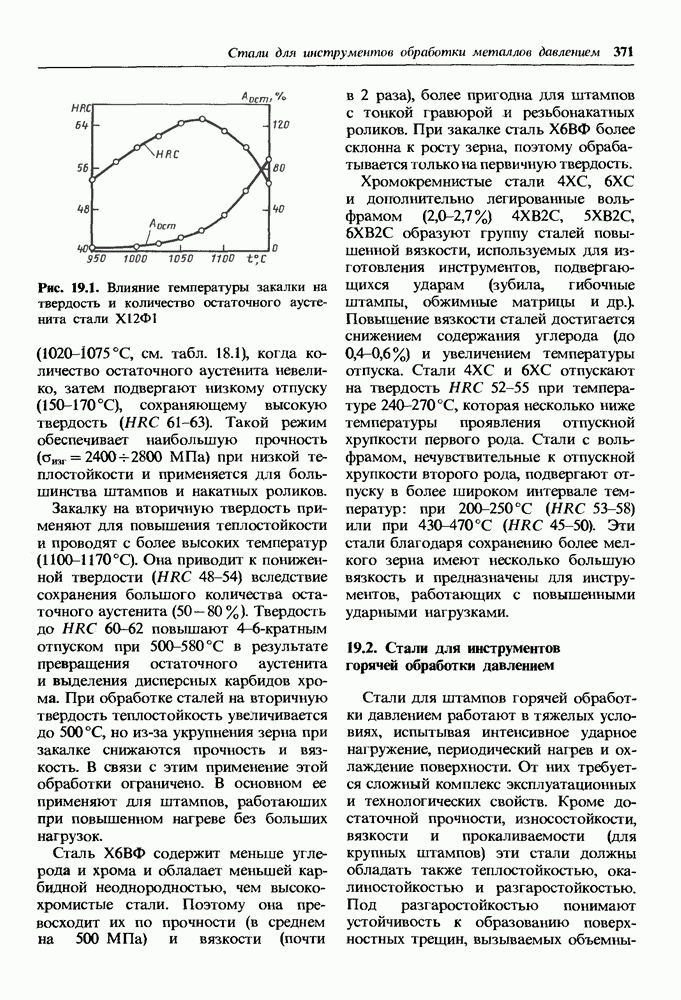
- 19.1. Стали для инструментов холодной обработки давлением
- 19.2. Стали для инструментов горячей обработки давлением
- Приложение
- Список литературы