| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.2. Схемы фильтров
В этом разделе приведены схемы фильтров первого и второго порядков. Схемы сгруппированы по типам фильтров — фильтры нижних частот, фильтры верхних частот, полосовые фильтры и  Отметим, что под мальм значением Q подразумевается
Отметим, что под мальм значением Q подразумевается  среднее Q соответствует значениям
среднее Q соответствует значениям  большое Q означает
большое Q означает 
Схемы фильтров нижних частот
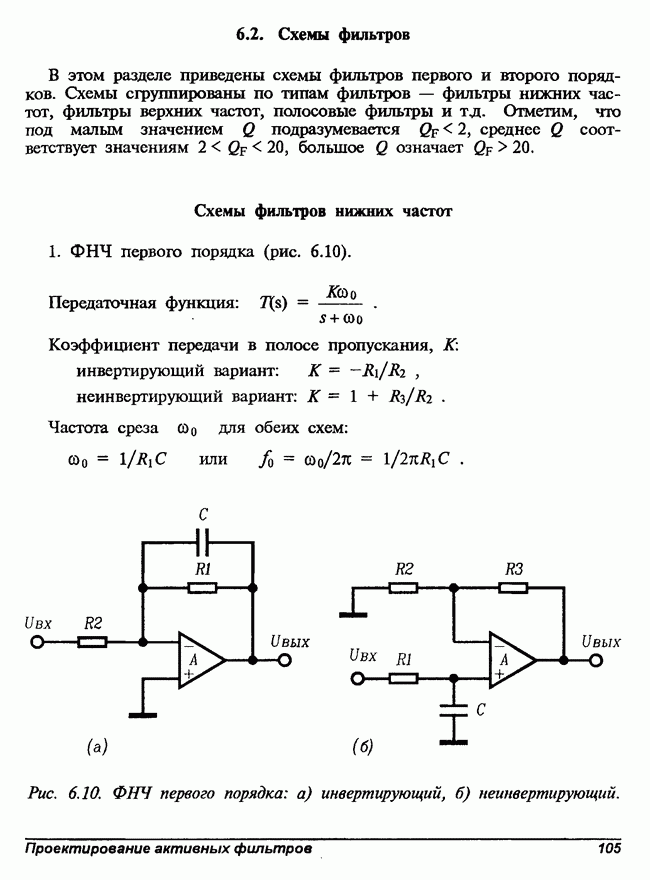
1. ФНЧ первого порядка (рис. 6.10).
Передаточная функция: 
Коэффициент передачи в полосе пропускания, К:

Частота среза  для обеих схем:
для обеих схем:


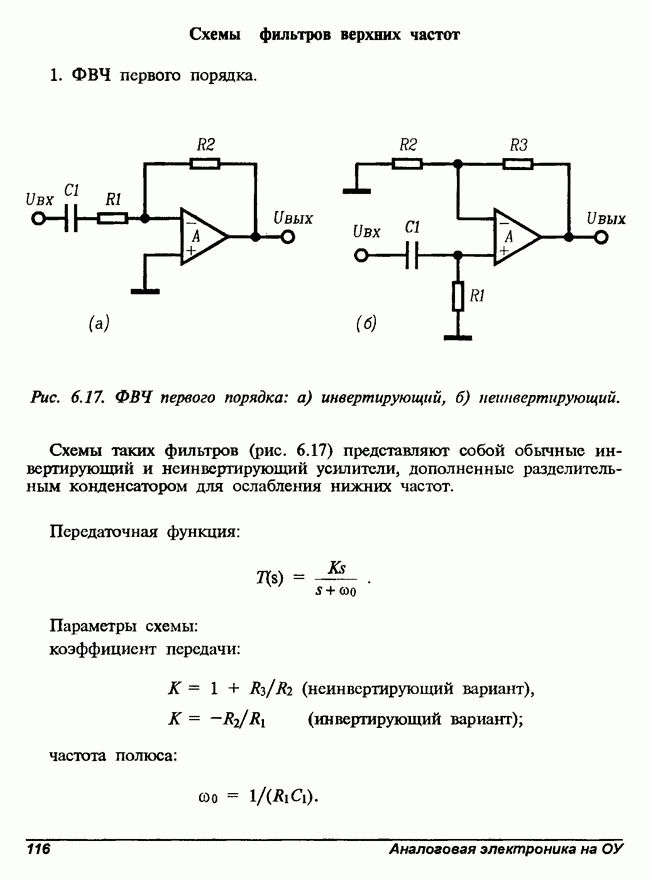
Рис. 6.10. ФНЧ первого порядка: а) инвертирующий, б) неинвертирующий.
По существу, эти схемы представляют собой усилители напряжения на одном ОУ с дополнительным конденсатором, включенным для получения требуемой АЧХ первого порядка. Неинвертирующая схема имеет высокое входное сопротивление во всей полосе пропускания и не нагружает выход предыдущего каскада.
2. ФНЧ Саллена-Кея (рис. 6.11).


Рис. 6.11. Фильтр нижних частот Саллена-Кея.
Передаточная функция:

Параметры схемы:

Номиналы элементов по приведенным формулам можно вычислить разными способами, причем каждый из них обеспечивает тот или иной компромисс между чувствительностью к разбросу значений элементов, "удобством" номиналов и сложностью вычислений. Можно воспользоваться двумя методами.
1-й метод.
Пусть  , тогда
, тогда

Выбираем значение R или С. После выбора одного из них второе находится из соотношения  Значение
Значение  определяется по величине К для постоянного тока.
определяется по величине К для постоянного тока.
Этот метод чрезвычайно прост и не накладывает ограничений на возможные номиналы резисторов и конденсаторов, но  могут сильно зависеть от допусков элементов, кроме того, добротность
могут сильно зависеть от допусков элементов, кроме того, добротность  и коэффициент передачи К оказываются связанньми друг с другом. Если задан коэффициент передачи, то, возможно, окажется необходимым выбрать
и коэффициент передачи К оказываются связанньми друг с другом. Если задан коэффициент передачи, то, возможно, окажется необходимым выбрать  или
или  . В этом случае целесообразнее сделать
. В этом случае целесообразнее сделать  поскольку ряд номинальных значений резисторов более "плотный" и доступный. Кроме того, конденсаторы имеют большие температурные коэффициенты, чем резисторы, поэтому, выбирая конденсаторы одинаковой емкости, можно выбрать их и одного типа, уменьшив тем самым температурные колебания добротности
поскольку ряд номинальных значений резисторов более "плотный" и доступный. Кроме того, конденсаторы имеют большие температурные коэффициенты, чем резисторы, поэтому, выбирая конденсаторы одинаковой емкости, можно выбрать их и одного типа, уменьшив тем самым температурные колебания добротности 
2-й метод.
Зададим 
Тогда

и

Заметим, что вещественные сопротивления резисторов получатся при  (приближенно).
(приближенно).
Если  , то лучше задать равные сопротивления резисторов и вычислить значения емкостей конденсаторов.
, то лучше задать равные сопротивления резисторов и вычислить значения емкостей конденсаторов.
При  получим:
получим:

и

Коэффициент передачи фильтра в полосе пропускания можно уменьшить, заменив  двумя резисторами
двумя резисторами  как это показано пунктиром на рис. 6.11, при этом должно выполняться условие:
как это показано пунктиром на рис. 6.11, при этом должно выполняться условие:  коэффициент передачи будет равен:
коэффициент передачи будет равен:

Применение аттенюатора на входе приводит к тому, что коэффициент передачи  ) неинвергирующего усилителя должен быть больше (чем фильтра в целом — прим. ред.), что может ухудшить характеристики схемы на высоких частотах (т.е. там, где происходит спад собственного коэффициента усиления ОУ — прим. ред.). Кроме того, несколько увеличиваются выходное напряжение смещения, его дрейф и шумы.
) неинвергирующего усилителя должен быть больше (чем фильтра в целом — прим. ред.), что может ухудшить характеристики схемы на высоких частотах (т.е. там, где происходит спад собственного коэффициента усиления ОУ — прим. ред.). Кроме того, несколько увеличиваются выходное напряжение смещения, его дрейф и шумы.
Настройка.
Независимая настройка всех параметров, к сожалению, невозможна. Обычно  настраиваются с помощью R] и
настраиваются с помощью R] и  Точное значение коэффициента передачи можно установить в других каскадах проектируемого устройства.
Точное значение коэффициента передачи можно установить в других каскадах проектируемого устройства.
Чувствительность к значениям элементов.
При больших значениях  и большом коэффициенте усиления эта схема оказывается весьма чувствительной к отклонениям значений элементов от номинальных. Отклонения
и большом коэффициенте усиления эта схема оказывается весьма чувствительной к отклонениям значений элементов от номинальных. Отклонения  при изменениях R и С намного больше самих этих изменений.
при изменениях R и С намного больше самих этих изменений.
В прецизионных фильтрах могут возникнуть дополнительные погрешности, связанные с конечной шириной полосы пропускания ОУ. Эту погрешность можно уменьшить почти на порядок, разделив  на две части и сформировав таким образом корректирующую цепь по опережению (рис. 6.12); при этом должны выполняться условия:
на две части и сформировав таким образом корректирующую цепь по опережению (рис. 6.12); при этом должны выполняться условия:

где  — произведение коэффициента усиления на ширину полосы пропускания ОУ.
— произведение коэффициента усиления на ширину полосы пропускания ОУ.
При построении фильтра Батгерворта второго порядка схему на рис. 6.11 можно упростить, положив  Значение
Значение  оказывается равным нулю, и резистор не требуется. Схема такого ФНЧ Батгерворта с частотой среза по уровню -3 дБ равной
оказывается равным нулю, и резистор не требуется. Схема такого ФНЧ Батгерворта с частотой среза по уровню -3 дБ равной  рад/с приведена на рис. 6.13.
рад/с приведена на рис. 6.13.

Рис. 6.12. Уменьшение погрешностей, обусловленных конечной шириной полосы пропускания ОУ.

Рис. 6.13. ФНЧ Баттерворта второго порядка (структура Саллсна-Ёея).
3. ФНЧ с многопетлевой обратной связью.


Рис. 6.14. ФНЧ с многопетлевой обратной связью.
Передаточная функция:

Параметры схемы:

Расчет номиналов элементов.
Выбираем Q и  отметим, что для получения вещественных значений
отметим, что для получения вещественных значений  должно выполняться условие:
должно выполняться условие:

тогда

Настройка.
Если Ъажны все три параметра  , то настройка оказывается достаточно сложной, поскольку они зависят от значений всех трех резисторов
, то настройка оказывается достаточно сложной, поскольку они зависят от значений всех трех резисторов  . Если же величина К не столь важна, как остальные, то
. Если же величина К не столь важна, как остальные, то  можно настроить с помощью
можно настроить с помощью  или
или  — с помощью
— с помощью 
Схема обладает относительно малой (меньшей единицы) чувствительностью параметров  и К) к неточностям значений элементов.
и К) к неточностям значений элементов.
Расплачиваться за это приходится большим диапазоном номиналов элементов при увеличении QF или коэффициента передачи К, причем растет он в обоих случаях. На практике применение таких схем ограничивается фильтрами, для которых произведение К на QF не превышает 100, т.е.  С ростом
С ростом  важное значение приобретает частотная характеристика ОУ. Ограниченная полоса пропускания ОУ вызывает погрешности в значениях
важное значение приобретает частотная характеристика ОУ. Ограниченная полоса пропускания ОУ вызывает погрешности в значениях 
4. ФНЧ с нулевьм смещением.

Рис. 6.15. ФНЧ с нулевьм смещением.


Коэффициент передачи:

Частота полюса:

Добротность:

Выходное сопротивление:

Расчет номиналов элементов.
Выбираем  тогда
тогда

Значения  следует выбрать так, чтобы
следует выбрать так, чтобы  (которое определяет выходное сопротивление схемы) было минимальным.
(которое определяет выходное сопротивление схемы) было минимальным.
Настройка.
Коэффициент усиления фильтра равен единице, изменить его невозможно. Значения  зависят от
зависят от  поэтому настройка заключается в подборе методом последовательных приближений резисторов
поэтому настройка заключается в подборе методом последовательных приближений резисторов 
Достоинство схемы состоит в том, что ОУ полностью развязан по постоянному току с трактом сигнала и не может внести никакого дополнительного смещения. Расплачиваться за это приходится высоким выходным сопротивлением схемы, равным значению резистора  . Частотный диапазон фильтра ограничен полосой пропускания ОУ, который создает в высокочастотной области дополнительный полюс, а также комплексно сопряженную пару нулей вблизи мнимой оси.
. Частотный диапазон фильтра ограничен полосой пропускания ОУ, который создает в высокочастотной области дополнительный полюс, а также комплексно сопряженную пару нулей вблизи мнимой оси.
Передаточная функция фильтра:
5. ФНЧ на основе конверторов полного сопротивления.

Рис. 6.16. ФНЧ на основе конверторов полного сопротивления.

Передаточная функция:

Параметры схемы:
коэффициент передачи:

частота полюса:

добротность:

Номиналы элементов.
Несмотря на наличие пяти резисторов и двух конденсаторов, расчет элементов по приведенным формулам оказывается довольно простым.
Настройка.
Коэффициент усиления устанавливается резистором 
Частота  устанавливается резистором
устанавливается резистором 
Добротность  устанавливается резистором
устанавливается резистором 
Эта схема особенно хороша для построения фильтров с высокой добротностью  поскольку она некритична к отклонениям значений элементов от номинальных и проста в настройке.
поскольку она некритична к отклонениям значений элементов от номинальных и проста в настройке.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- 1. Измерительные усилители
- 1.1. Измерительные усилители на одном операционном усилителе
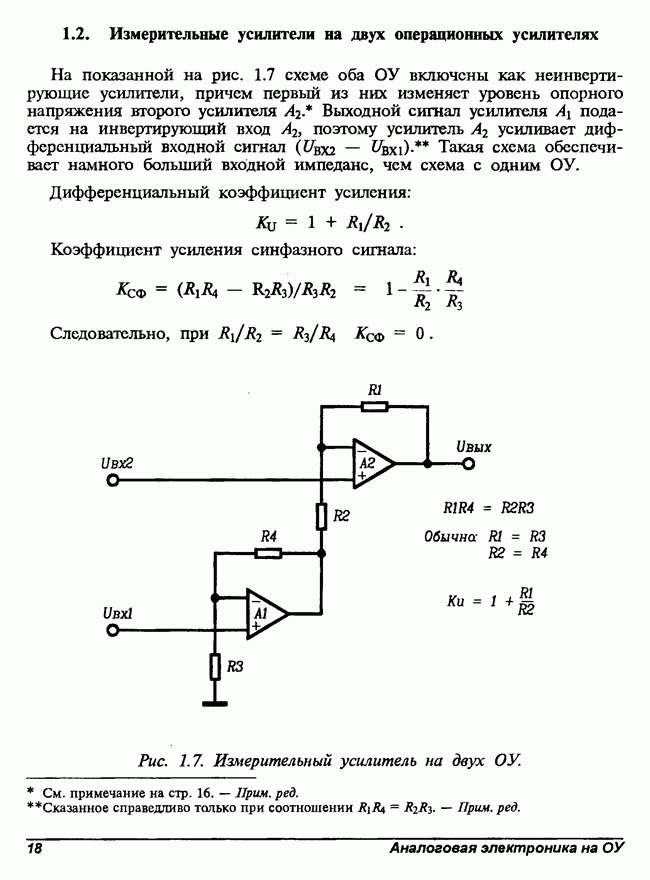
- 1.2. Измерительные усилители на двух операционных усилителях
- 1.3. Измерительные усилители на трех операционных усилителях
- 1.4. Измерительные усилители с согласованными транзисторами
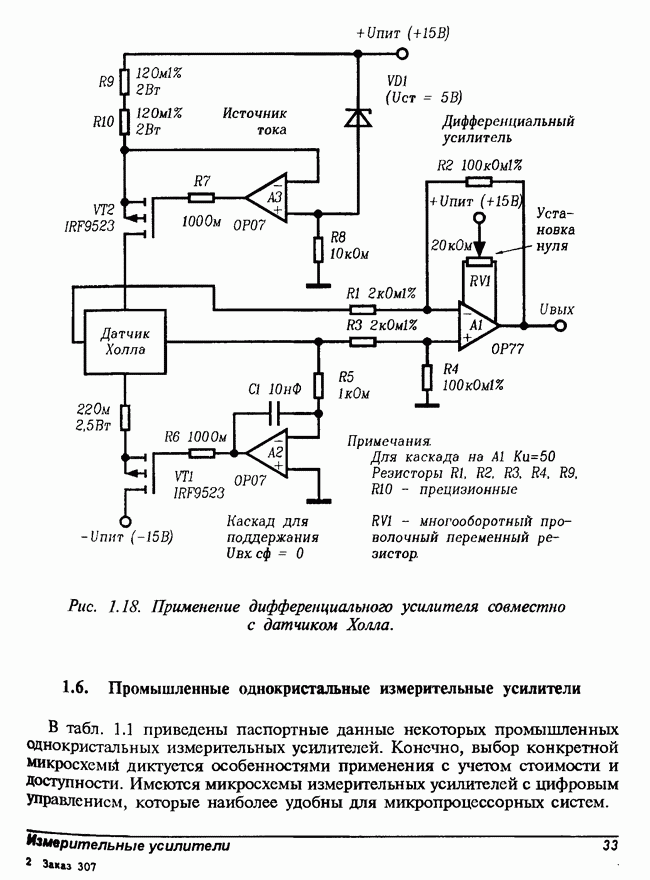
- 1.5. Использование измерительных усилителей совместно с датчиками
- 1.6. Промышленные однокристальные измерительные усилители
- 2. Развязывающие усилители
- 2.1. Развязывающий усилитель с модуляцией/демодуляцией (МДМ)
- 2.2. Развязывающий усилитель с линеаризующей обратной связью
- 2.3. Промышленные развязывающие усилители
- 3. Усилители заряда
- 3.2. Усилитель заряда с высокоимпедансным входом
- 4. Преобразователи тока в напряжение и напряжения в ток
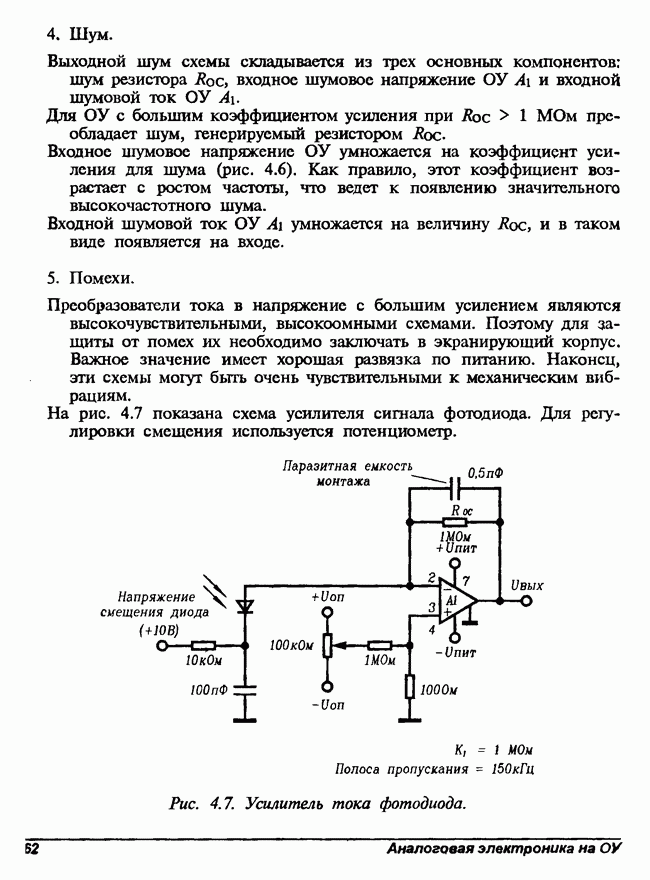
- 4.2. Преобразователь тока в напряжение на одном операционном усилителе
- 4.3. Преобразователь напряжения в ток на одном операционном усилителе
- 4.4. Однополярные источники тока
- 4.5. Преобразователь напряжения в ток с дифференциальным входом
- 4.6. Интегральные микросхемы ПНТ
- 5. Управляемые усилители
- 5.2. Промышленные управляемые напряжением усилители
- 5.3. Автоматическая регулировка усиления (АРУ)
- 5.4. Усилители с цифровым управлением
- 6. Проектирование активных фильтров
- 6.1. Передаточные функции фильтров
- 6.2. Схемы фильтров
- Схемы фильтров верхних частот
- Схемы полосовых фильтров
- Полосно-подавляющие фильтры
- Схемы фазовых фильтров
- Фильтры с переменными параметрами
- 6.3. Управляемые фильтры
- Фильтры, управляемые напряжением
- Фильтры с цифровым управлением
- Применение коммутируемых конденсаторов
- 6.4. Практические вопросы проектирования фильтров
- Настройка
- Выбор элементов
- Устойчивость фильтров
- 6.5 Проектирование фильтров высоких порядков
- Определение требуемой передаточной функции
- Другие типы фильтров.
- Передаточные функции.
- Преобразование и масштабирование
- Переход от передаточной функции к схеме
- 7. Интеграторы и дифференциаторы
- Рекомецдации по выбору элементов
- 7.2. Дифференциаторы
- Рекомендации по выбору элементов
- 8. Логарифмирующие и экспоненциальные преобразователи
- 8.2. Экспоненциальные преобразователи
- 8.3. Промышленные логарифмирующие и экспоненциальные преобразователи
- 9. Арифметические операции
- 9.2. Умножители
- Делитель на основе умножителя
- Распространенные схемы умножителей
- Умножители на основе управляемых источников тока
- Умножители с логарифмированием и антилогарифмированием сигналов
- Импульсные умножители
- Умножители с применением ЦАП и АЦП
- 9.3. Промышленные микросхемы аналоговых умножителей
- 10. Функциональные преобразователи
- 10.2. Логарифмирующие и экспоненциальные функциональные преобразователи
- 10.3. Функциональные преобразователи с кусочно-линейной аппроксимацией
- 10.4. Схемы функциональных преобразователей с использованием АЦП и ЦАП
- 11. Ограничители, пиковые детекторы и выпрямители
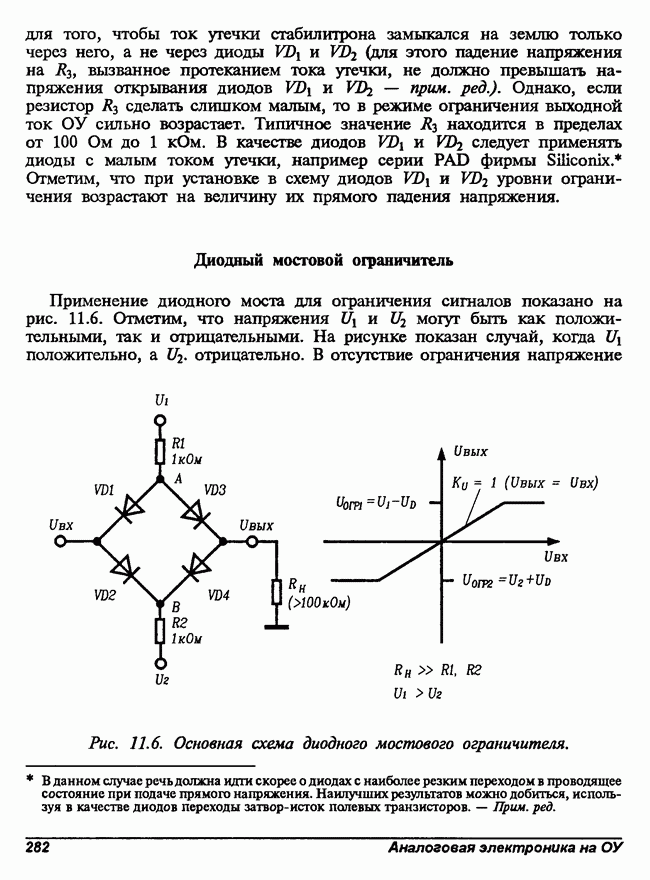
- Диодный мостовой ограничитель
- Управляемый напряжением ограничитель на ОУ
- 11.2. Пиковые детекторы
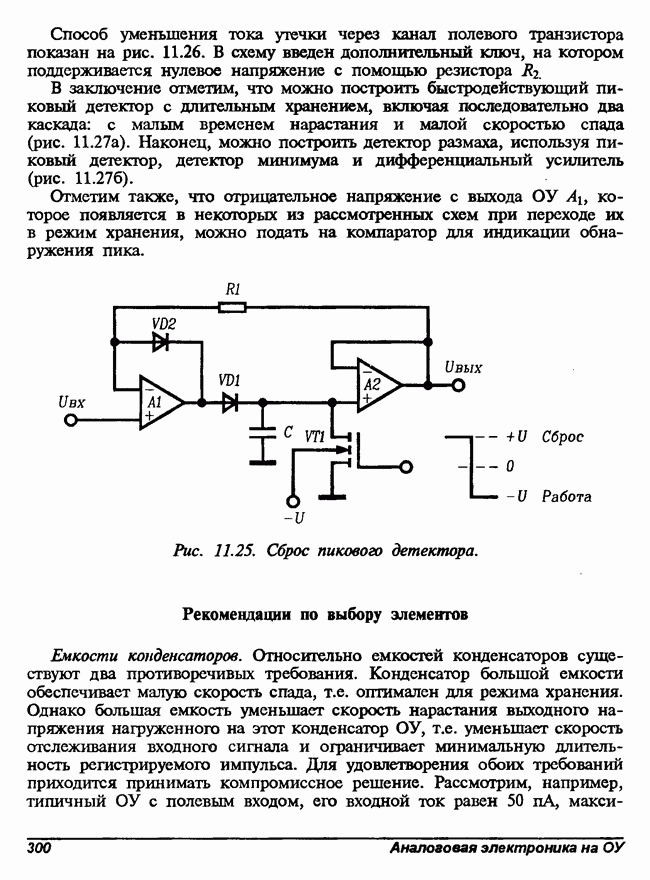
- Двухкаскадные пиковые детекторы
- Пиковый детектор с общей обратной связью
- Улучшение характеристик виковых детекторов
- Рекомендации по выбору элементов
- Пиковые детекторы на базе микросхем
- 11.3. Прецизионные однополупериодные выпрямители
- 11.4. Двухполупериодные выпрямители
- Двухполупериодный выпрямитель с токовым выходом
- Двухполупериодный выпрямитель с токовым входом
- Двухполупериодный выпрямитель на двух ОУ с минимальным числом элементов
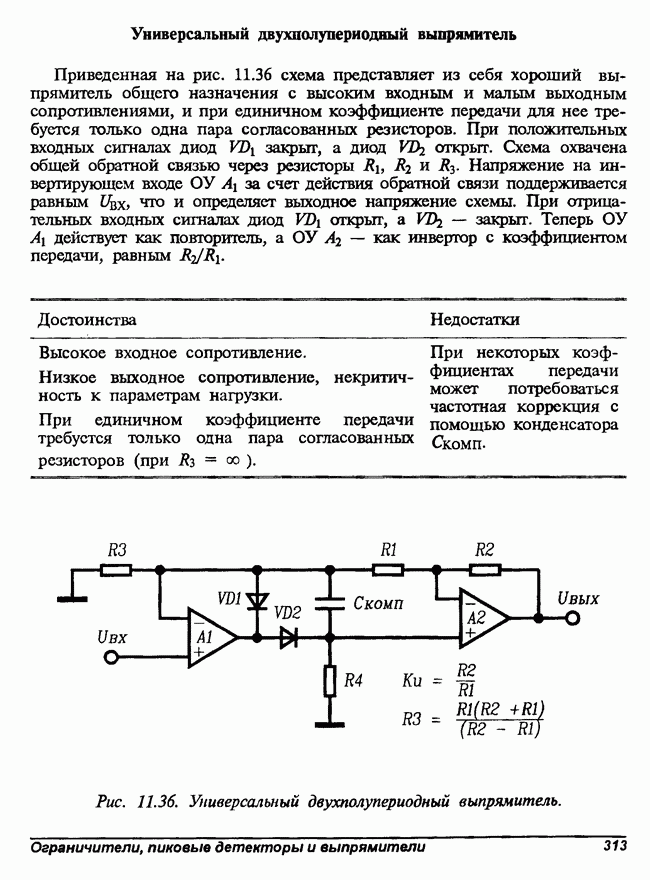
- Универсальный двухполупериодный выпрямитель
- Двухполупериодный выпрямитель с суммированием токов
- Общие рекомендации по схемам выпрямителей
- 12. Измерение пикового, среднего и эффективного значений
- 12.1. Схемы для измерения пиковых значений
- 12.2. Схемы для измерения средневыпрямленного значения
- 12.3. Схемы для измерения средеквадратичного значения
- 12.4. Тепловые преобразователи