| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Фильтры с переменными параметрами
Такие схемы (рис. 6.34) имеют несколько выходов, причем их передаточные функции соответствуют различным типам фильтров — ФНЧ, ФВЧ и ПФ. Название этих устройств связано с методом решения дифференциальных уравнений, использовавшимся в аналоговых вычислительным машинах. Строятся они на основе интеграторов и сумматоров.
Передаточные функции по выходам:


Рис. 6.34. Базовая схема фильтра с переменными параметрами.



где

Схема состоит из сумматора на элементах  и двух интеграторов —
и двух интеграторов —  и
и  с постоянными времени
с постоянными времени  соответственно. Как видно из приведенных выражений, номиналы элементов вычисляются достаточно просто. Настройка схемы сводится к следующим операциям:
соответственно. Как видно из приведенных выражений, номиналы элементов вычисляются достаточно просто. Настройка схемы сводится к следующим операциям:
— установить  с помощью
с помощью 
— установить  с помощью или
с помощью или 
Процедура настройки несколько усложняется, если необходимо также установить точное значение К.
В схемах с большими значениями добротности необходимо следить за тем, чтобы ОУ не входили в насыщение. Конечная ширина полосы пропускания
операционных усилителей может стать причиной ухудшения характеристик фильтра на высоких частотах. При использовании ОУ с одинаковыми произведениями коэффициента усиления на ширину полосы пропускания  рад/с (
рад/с ( прим. ред.)
прим. ред.)

где  — фактически получающиеся значения частоты полюса и добротности. Конечная ширина полосы пропускания ОУ снижает значение
— фактически получающиеся значения частоты полюса и добротности. Конечная ширина полосы пропускания ОУ снижает значение  . При больших добротностях
. При больших добротностях  схема может стать неустойчивой. Чтобы избежать этого, можно ввести в схему корректирующую цепь, разделив входной резистор одного из интеграторов
схема может стать неустойчивой. Чтобы избежать этого, можно ввести в схему корректирующую цепь, разделив входной резистор одного из интеграторов  или
или  на две части, одна из которых
на две части, одна из которых  включается последовательно с конденсатором обратной связи (рис. 6.35). При этом
включается последовательно с конденсатором обратной связи (рис. 6.35). При этом  Если в схеме используются только выходы ФНЧ и ПФ, из нее можно исключить сумматор, оставив только два интегратора (рис. 6.36). Такая схема описывается следующими выражениями:
Если в схеме используются только выходы ФНЧ и ПФ, из нее можно исключить сумматор, оставив только два интегратора (рис. 6.36). Такая схема описывается следующими выражениями:


Рис. 6.35. Частотная коррекция схем с высокой добротностью.

Рис. 6.36. Схема с двумя выходами (ФНЧ и ПФ).
Дополнив исходную схему еще одним ОУ, можно получить полосно-подавляющий фильтр. Дополнительный ОУ выполняет функцию сумматора сигналов с выходов ФНЧ и ФВЧ (рис. 6.37). В качестве активных элементов можно использовать микросхему счетверенного ОУ. Приведем выражения для параметров этой схемы, учитывая, что 

где

Таблица 6.1. Сводка характеристик фильтров


Рис. 6.37. ППФ на основе фильтра с переменными параметрами.
Продолжение таблицы 6.1

Заключение
Рассмотренные схемы фильтров сгруппированы по передаточным функциям (ФНЧ, ФВЧ, ПФ и др.), но их можно также сгруппировать по структуре схем, используемых для каждого фильтра. В табл. 6.1 приведены общие свойства фильтров второго порядка с различными структурами.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- 1. Измерительные усилители
- 1.1. Измерительные усилители на одном операционном усилителе
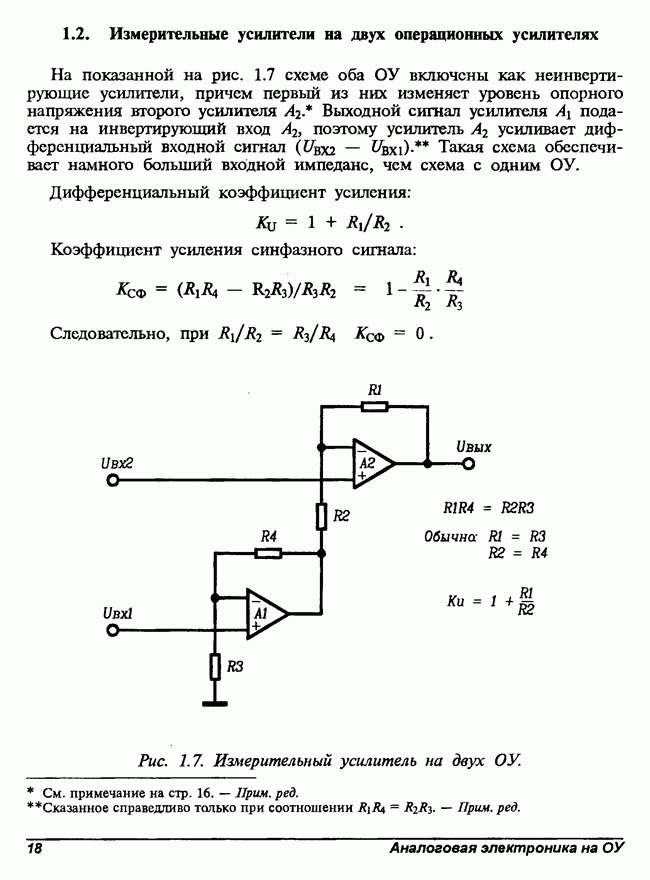
- 1.2. Измерительные усилители на двух операционных усилителях
- 1.3. Измерительные усилители на трех операционных усилителях
- 1.4. Измерительные усилители с согласованными транзисторами
- 1.5. Использование измерительных усилителей совместно с датчиками
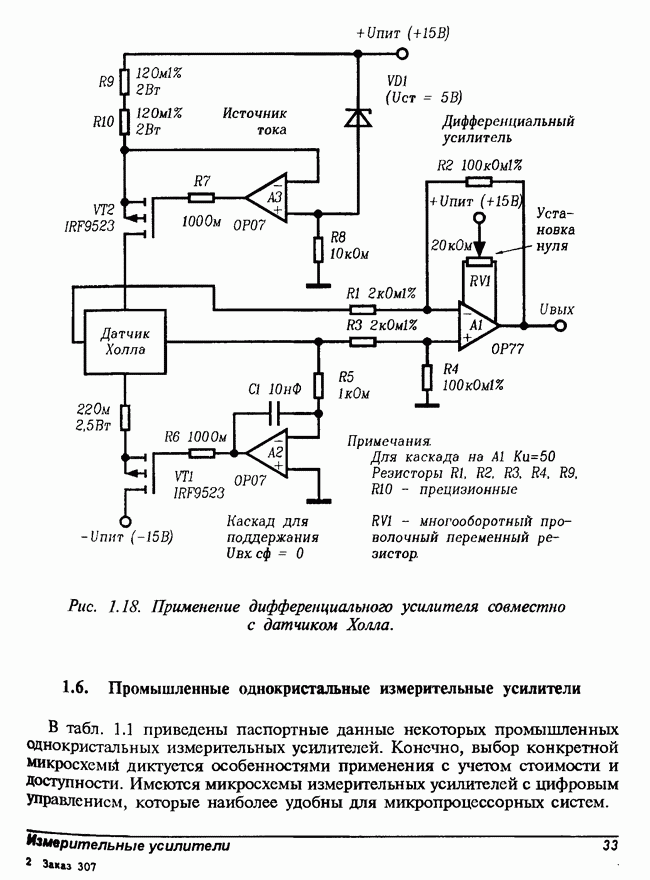
- 1.6. Промышленные однокристальные измерительные усилители
- 2. Развязывающие усилители
- 2.1. Развязывающий усилитель с модуляцией/демодуляцией (МДМ)
- 2.2. Развязывающий усилитель с линеаризующей обратной связью
- 2.3. Промышленные развязывающие усилители
- 3. Усилители заряда
- 3.2. Усилитель заряда с высокоимпедансным входом
- 4. Преобразователи тока в напряжение и напряжения в ток
- 4.2. Преобразователь тока в напряжение на одном операционном усилителе
- 4.3. Преобразователь напряжения в ток на одном операционном усилителе
- 4.4. Однополярные источники тока
- 4.5. Преобразователь напряжения в ток с дифференциальным входом
- 4.6. Интегральные микросхемы ПНТ
- 5. Управляемые усилители
- 5.2. Промышленные управляемые напряжением усилители
- 5.3. Автоматическая регулировка усиления (АРУ)
- 5.4. Усилители с цифровым управлением
- 6. Проектирование активных фильтров
- 6.1. Передаточные функции фильтров
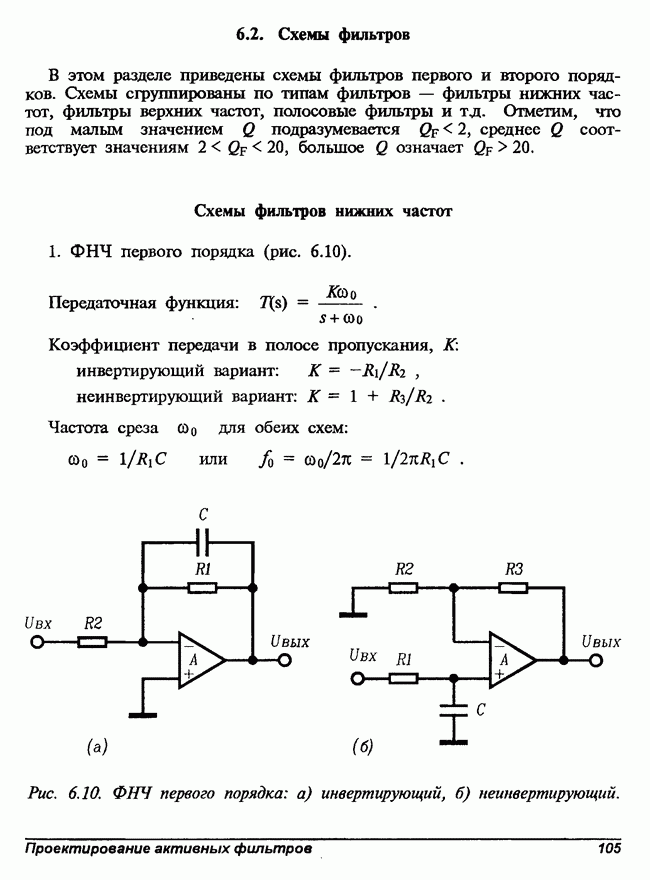
- 6.2. Схемы фильтров
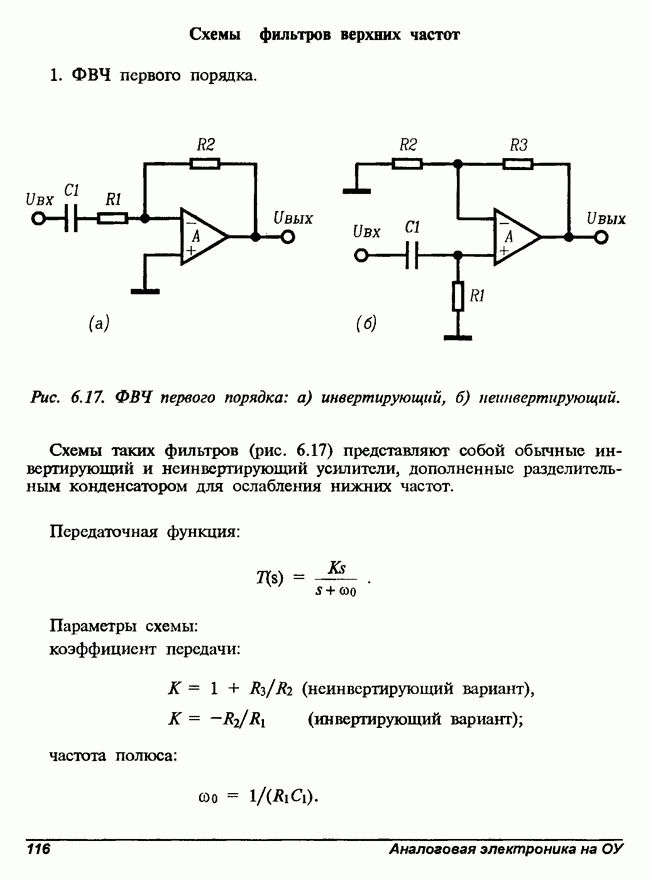
- Схемы фильтров верхних частот
- Схемы полосовых фильтров
- Полосно-подавляющие фильтры
- Схемы фазовых фильтров
- Фильтры с переменными параметрами
- 6.3. Управляемые фильтры
- Фильтры, управляемые напряжением
- Фильтры с цифровым управлением
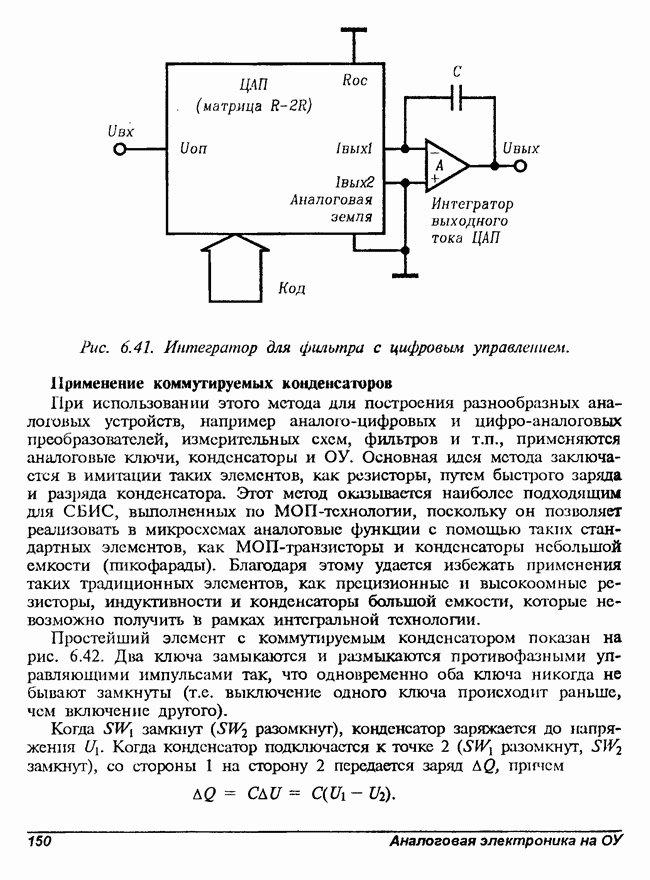
- Применение коммутируемых конденсаторов
- 6.4. Практические вопросы проектирования фильтров
- Настройка
- Выбор элементов
- Устойчивость фильтров
- 6.5 Проектирование фильтров высоких порядков
- Определение требуемой передаточной функции
- Другие типы фильтров.
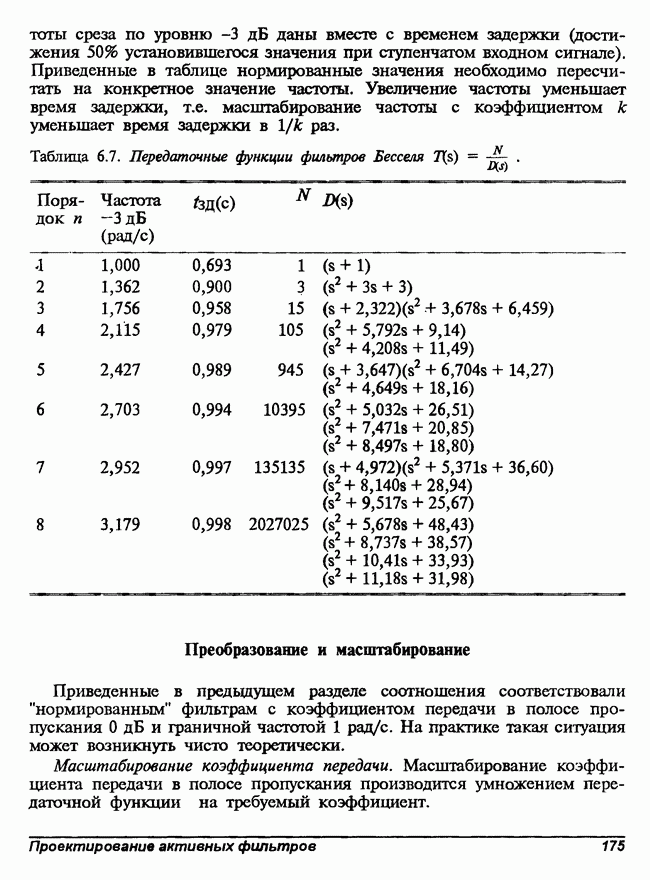
- Передаточные функции.
- Преобразование и масштабирование
- Переход от передаточной функции к схеме
- 7. Интеграторы и дифференциаторы
- Рекомецдации по выбору элементов
- 7.2. Дифференциаторы
- Рекомендации по выбору элементов
- 8. Логарифмирующие и экспоненциальные преобразователи
- 8.2. Экспоненциальные преобразователи
- 8.3. Промышленные логарифмирующие и экспоненциальные преобразователи
- 9. Арифметические операции
- 9.2. Умножители
- Делитель на основе умножителя
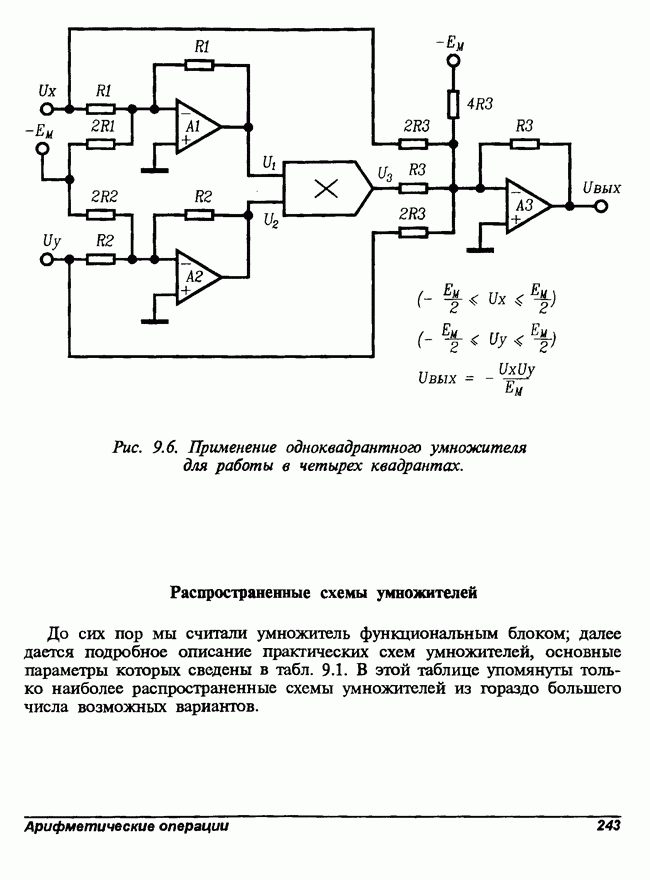
- Распространенные схемы умножителей
- Умножители на основе управляемых источников тока
- Умножители с логарифмированием и антилогарифмированием сигналов
- Импульсные умножители
- Умножители с применением ЦАП и АЦП
- 9.3. Промышленные микросхемы аналоговых умножителей
- 10. Функциональные преобразователи
- 10.2. Логарифмирующие и экспоненциальные функциональные преобразователи
- 10.3. Функциональные преобразователи с кусочно-линейной аппроксимацией
- 10.4. Схемы функциональных преобразователей с использованием АЦП и ЦАП
- 11. Ограничители, пиковые детекторы и выпрямители
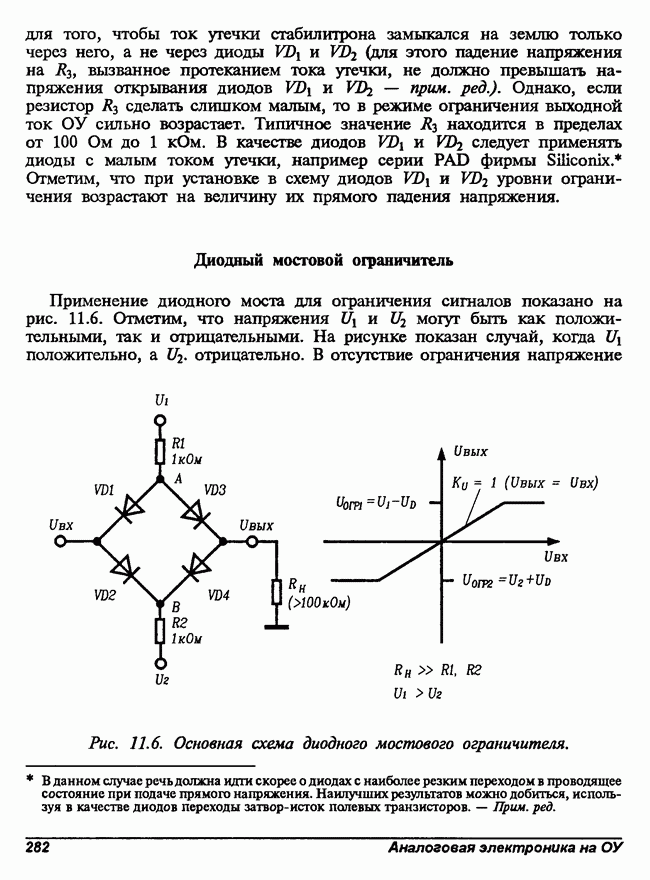
- Диодный мостовой ограничитель
- Управляемый напряжением ограничитель на ОУ
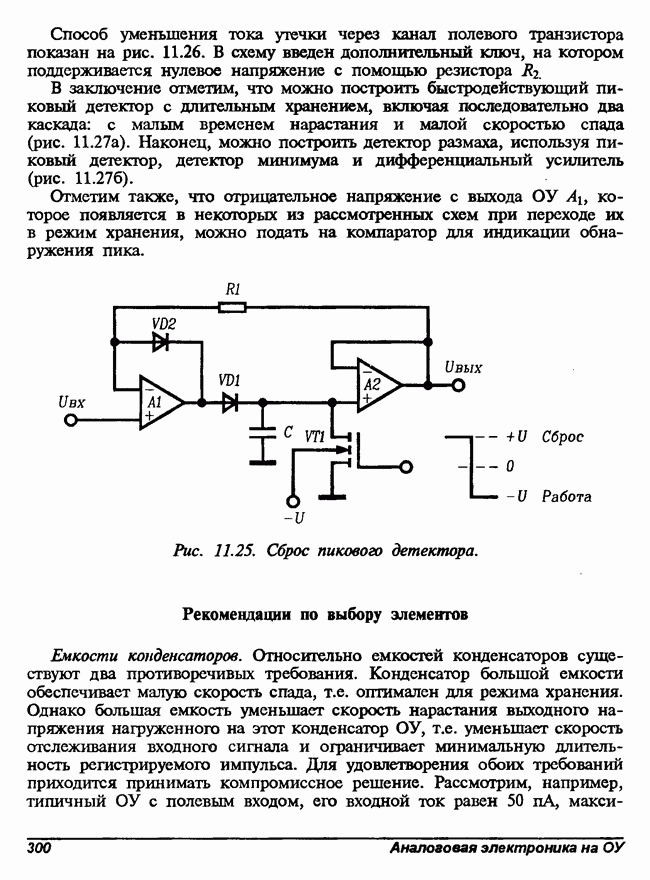
- 11.2. Пиковые детекторы
- Двухкаскадные пиковые детекторы
- Пиковый детектор с общей обратной связью
- Улучшение характеристик виковых детекторов
- Рекомендации по выбору элементов
- Пиковые детекторы на базе микросхем
- 11.3. Прецизионные однополупериодные выпрямители
- 11.4. Двухполупериодные выпрямители
- Двухполупериодный выпрямитель с токовым выходом
- Двухполупериодный выпрямитель с токовым входом
- Двухполупериодный выпрямитель на двух ОУ с минимальным числом элементов
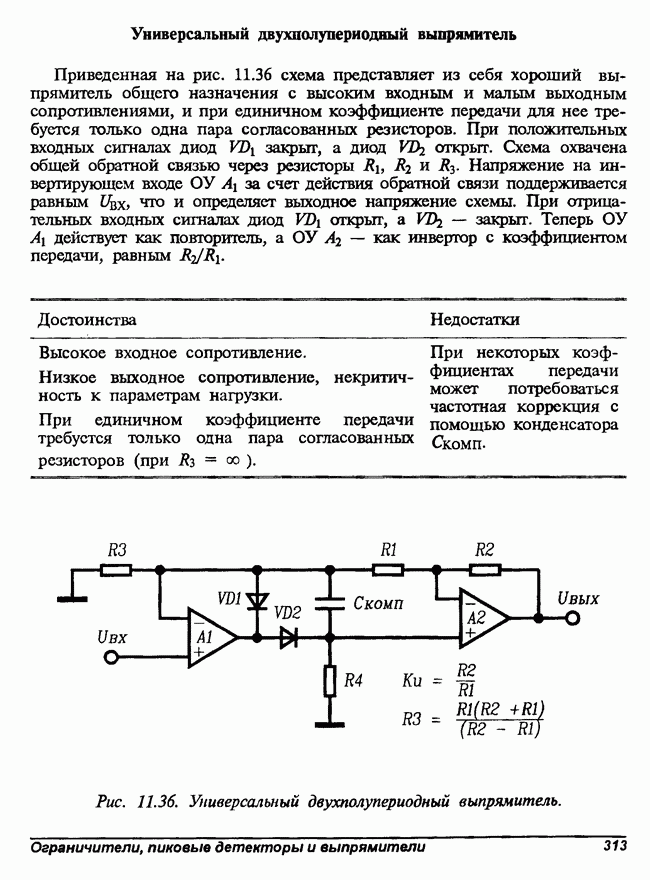
- Универсальный двухполупериодный выпрямитель
- Двухполупериодный выпрямитель с суммированием токов
- Общие рекомендации по схемам выпрямителей
- 12. Измерение пикового, среднего и эффективного значений
- 12.1. Схемы для измерения пиковых значений
- 12.2. Схемы для измерения средневыпрямленного значения
- 12.3. Схемы для измерения средеквадратичного значения
- 12.4. Тепловые преобразователи