| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.1. Передаточные функции фильтров
В одной главе невозможно подробно изложить основы теории фильтров, но мы постараемся в данном разделе дать ее основные положения и выводы. Здесь и далее 5 означает оператор Лапласа,

Активные RC-фильтры принадлежат к классу линейных схем с сосредоточенными параметрами. Передаточная функция линейной цепи  порядка с сосредоточенными параметрами описывается следующим выражением (порядок цепи определяется степенью полинома знаменателя):
порядка с сосредоточенными параметрами описывается следующим выражением (порядок цепи определяется степенью полинома знаменателя):

где  — полином числителя,
— полином числителя,  — полином знаменателя,
— полином знаменателя,  — вещественные коэффициенты,
— вещественные коэффициенты,  — передаточная функция схемы.
— передаточная функция схемы.
Заметим, что для реальных схем 
Полиномы  можно разложить на множители первого и второго порядков с вещественными коэффициентами. Следовательно, нужную характеристику можно получить, включив последовательно несколько фильтров первого и второго порядков. Рассмотрим далее передаточные функции таких фильтров.
можно разложить на множители первого и второго порядков с вещественными коэффициентами. Следовательно, нужную характеристику можно получить, включив последовательно несколько фильтров первого и второго порядков. Рассмотрим далее передаточные функции таких фильтров.
1. Характеристика ФНЧ первого порядка (рис. 6.2). Эта характеристика описывается простым выражением:

где  — коэффициент передачи на постоянном токе,
— коэффициент передачи на постоянном токе,  — частота полюса, которая в данном случае равна частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с
— частота полюса, которая в данном случае равна частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с 

Рис. 6.2. Частотная характеристика ФНЧ первого порядка.
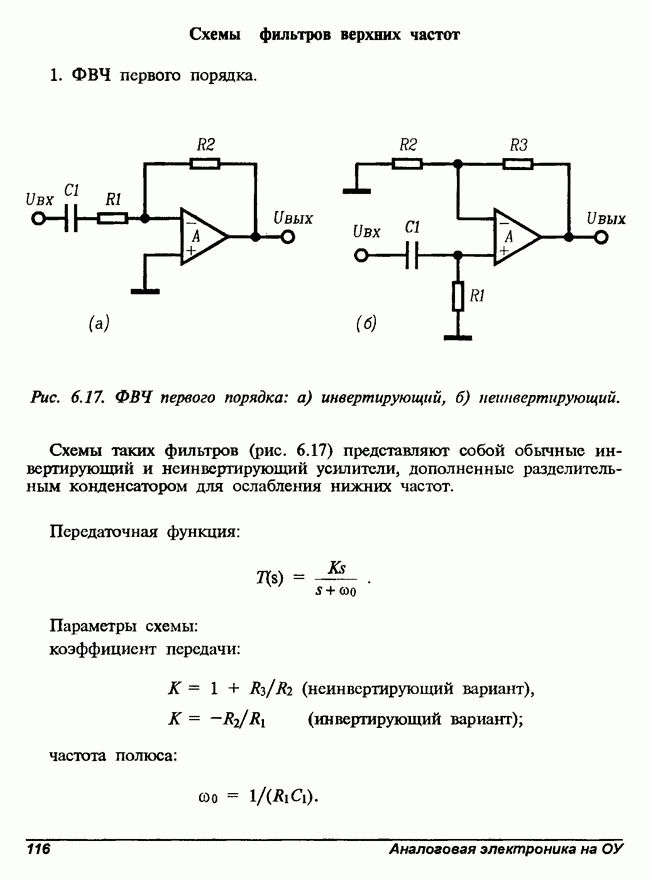
2. Характеристика ФВЧ первого порядка (рис. 6.3). Эта харакгеристика также довольно простая:

где  — коэффициент передачи на высоких частотах,
— коэффициент передачи на высоких частотах,  — частота полюса, равная частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с
— частота полюса, равная частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с 
3. Характеристика фазового фильтра (ФФ) первого порядка (рис. 6.4). Коэффициент передачи этого фильтра имеет постоянное значение во всем частотном диапазоне, изменяется лишь вносимый фазовый сдвиг (временная задержка).
Характеристика фазового фильтра первого порядка:

где  — модуль коэффициента передачи,
— модуль коэффициента передачи,  — частота, на которой фазовый сдвиг равен 90°.
— частота, на которой фазовый сдвиг равен 90°.

Рис. 6.3. Частотная характеристика ФВЧ первого порядка.

Рис. 6.4. Частотная характеристика ФФ первого порядка.
4. Характеристика ФНЧ второго порядка (рис. 6.5). Эта характеристика имеет вид:

где  — коэффициент передачи на постоянном токе,
— коэффициент передачи на постоянном токе,  — частота полюса,
— частота полюса,  — добротность фильтра.
— добротность фильтра.
При  на амплитудно-частотной характеристике (АЧХ) появляется выброс на частоте:
на амплитудно-частотной характеристике (АЧХ) появляется выброс на частоте:

и значение коэффициента передачи на этой частоте равно:

причем частота среза по уровню -3 дБ составляет:

Для ФНЧ, характеристика которого показана на рис. 6.5, при малых  (т.е.
(т.е.  ) полюса передаточной функции вещественные, и его АЧХ оказывается плоской. Выражение для характеристики второго порядка можно разложить на два сомножителя первого порядка. Когда же
) полюса передаточной функции вещественные, и его АЧХ оказывается плоской. Выражение для характеристики второго порядка можно разложить на два сомножителя первого порядка. Когда же  превышает
превышает  на АЧХ появляется "выпуклость". Амплитудно-частотная характеристика схем с большой добротностью имеет значительный выброс.
на АЧХ появляется "выпуклость". Амплитудно-частотная характеристика схем с большой добротностью имеет значительный выброс.

Рис. 6.5. Частотная характеристика ФНЧ второго порядка.
5. Характеристика ФВЧ второго порядка (рис. 6.6). Эта характеристика описывается выражением:

где  — коэффициент передачи на высокой частоте,
— коэффициент передачи на высокой частоте,  — частота полюса,
— частота полюса,  — добротность фильтра.
— добротность фильтра.
Максимальный коэффициент передачи (в точке выброса — прим. ред.) при больших значениях  равен
равен  .
.

Рис. 6.6. Частотная характеристика ФВЧ второго порядка. Выброс на АЧХ возникает при  на частоте:
на частоте:

и значение коэффициента передачи при этом равно:

Частота среза по уровню —3 дБ равна:


Рис. 6.7. Частотная характеристика ПФ второго порядка.
6. Характеристика ПФ второго порядка (рис. 6.7). Эта характеристика описывается выражением:

ее можно представить в другом виде:

где  — коэффициент передачи на центральной частоте
— коэффициент передачи на центральной частоте  ,
,  — добротность фильтра.
— добротность фильтра.
Заметим, что  , где
, где  — частоты, на которых коэффициент передачи снижается на -3 дБ по сравнению с
— частоты, на которых коэффициент передачи снижается на -3 дБ по сравнению с 
Можно показать, что:

Ширина полосы пропускания по уровню -3 дБ составляет:

При малых добротностях  знаменатель передаточной функции можно разложить на два сомножителя с вещественными коэффициентами (т.е. передаточная функция может быть представлена в виде произведения двух функций первого порядка — прим. ред.), поэтому АЧХ и фазочастотная характеристика (ФЧХ) на рис. 6.7 выглядят достаточно пологими. При
знаменатель передаточной функции можно разложить на два сомножителя с вещественными коэффициентами (т.е. передаточная функция может быть представлена в виде произведения двух функций первого порядка — прим. ред.), поэтому АЧХ и фазочастотная характеристика (ФЧХ) на рис. 6.7 выглядят достаточно пологими. При  полюса передаточной функции становятся комплексными. С увеличением
полюса передаточной функции становятся комплексными. С увеличением  полоса пропускания сужается и характеристика фильтра становится более избирательной.
полоса пропускания сужается и характеристика фильтра становится более избирательной.
7. Характеристика ППФ (РФ или фильтра-"пробки") второго порядка (рис. 6.8). Передаточная функция описывается выражением:

где  — коэффициент передачи на постоянном токе и на высокой частоте,
— коэффициент передачи на постоянном токе и на высокой частоте,  — центральная частота полосы подавления,
— центральная частота полосы подавления,  — добротность фильтра.
— добротность фильтра.

Рис. 6.8. Частотная характеристика ППФ.
Приведенное выше выражение можно записать по-другому:

т.е. в виде разности постоянного коэффициента передачи  и коэффициента передачи ПФ.
и коэффициента передачи ПФ.
Частоты среза по уровню -3 дБ такие же, как у полосового фильтра:

Ширина полосы подавления по уровню -3 дБ равна

8. Характеристика ФФ второго порядка (рис. 6.9). Характеристика фазового фильтра второго порядка описывается выражением:

Его можно переписать в следующем виде:

т.е. постоянный коэффициент минус удвоенная передаточная характеристика полосового фильтра.

Рис. 6.9. Частотная характеристика ФФ второго порядка.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- 1. Измерительные усилители
- 1.1. Измерительные усилители на одном операционном усилителе
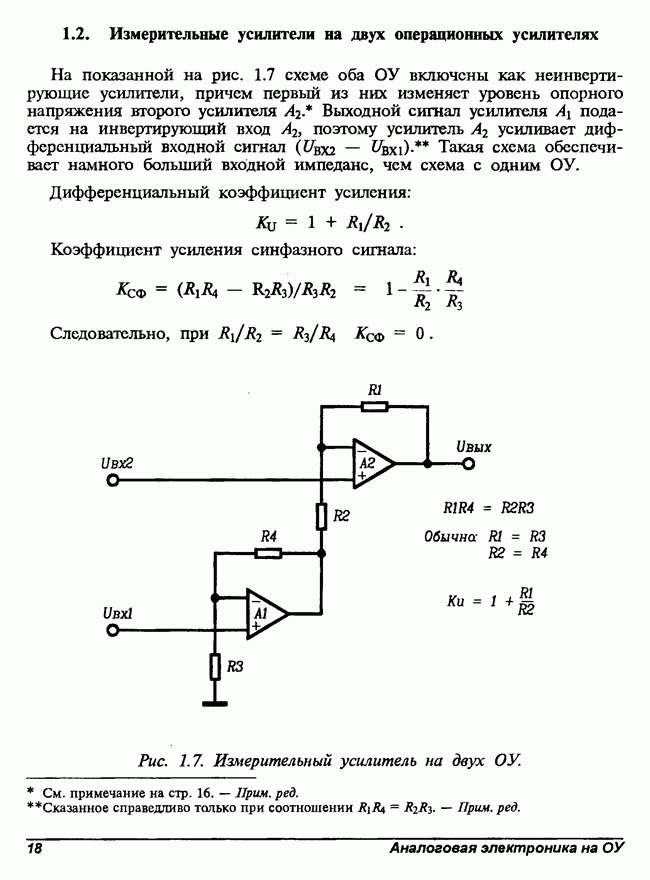
- 1.2. Измерительные усилители на двух операционных усилителях
- 1.3. Измерительные усилители на трех операционных усилителях
- 1.4. Измерительные усилители с согласованными транзисторами
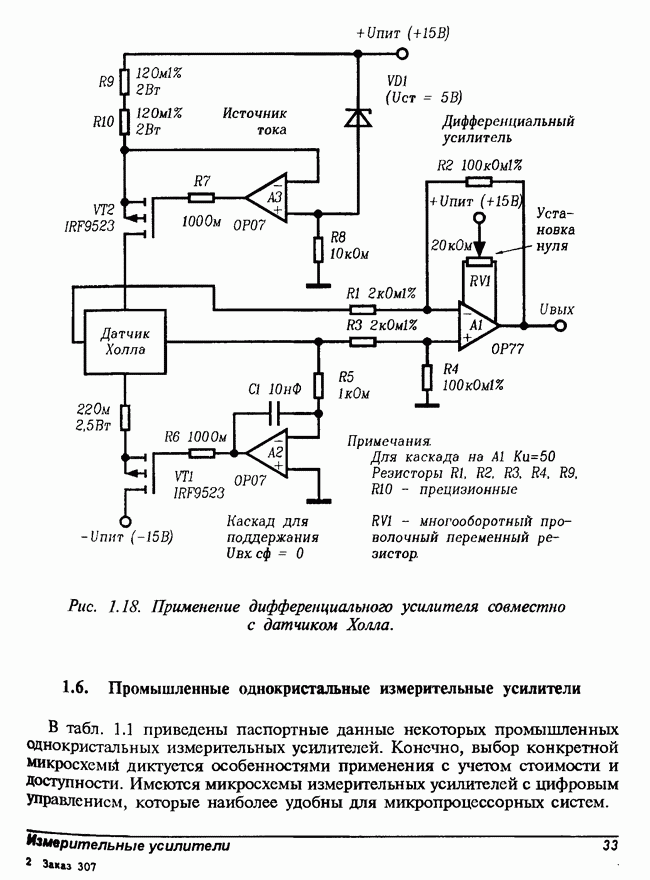
- 1.5. Использование измерительных усилителей совместно с датчиками
- 1.6. Промышленные однокристальные измерительные усилители
- 2. Развязывающие усилители
- 2.1. Развязывающий усилитель с модуляцией/демодуляцией (МДМ)
- 2.2. Развязывающий усилитель с линеаризующей обратной связью
- 2.3. Промышленные развязывающие усилители
- 3. Усилители заряда
- 3.2. Усилитель заряда с высокоимпедансным входом
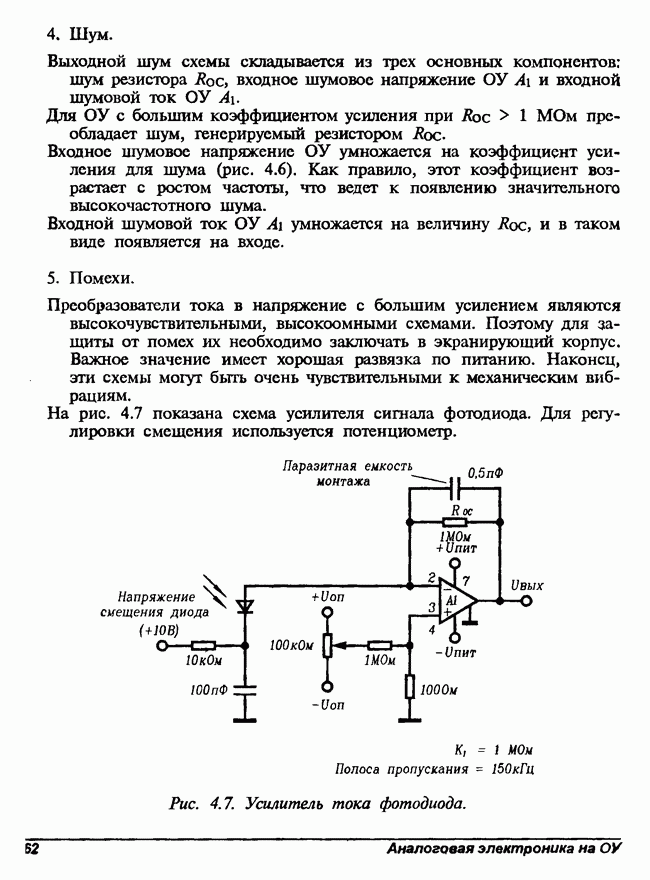
- 4. Преобразователи тока в напряжение и напряжения в ток
- 4.2. Преобразователь тока в напряжение на одном операционном усилителе
- 4.3. Преобразователь напряжения в ток на одном операционном усилителе
- 4.4. Однополярные источники тока
- 4.5. Преобразователь напряжения в ток с дифференциальным входом
- 4.6. Интегральные микросхемы ПНТ
- 5. Управляемые усилители
- 5.2. Промышленные управляемые напряжением усилители
- 5.3. Автоматическая регулировка усиления (АРУ)
- 5.4. Усилители с цифровым управлением
- 6. Проектирование активных фильтров
- 6.1. Передаточные функции фильтров
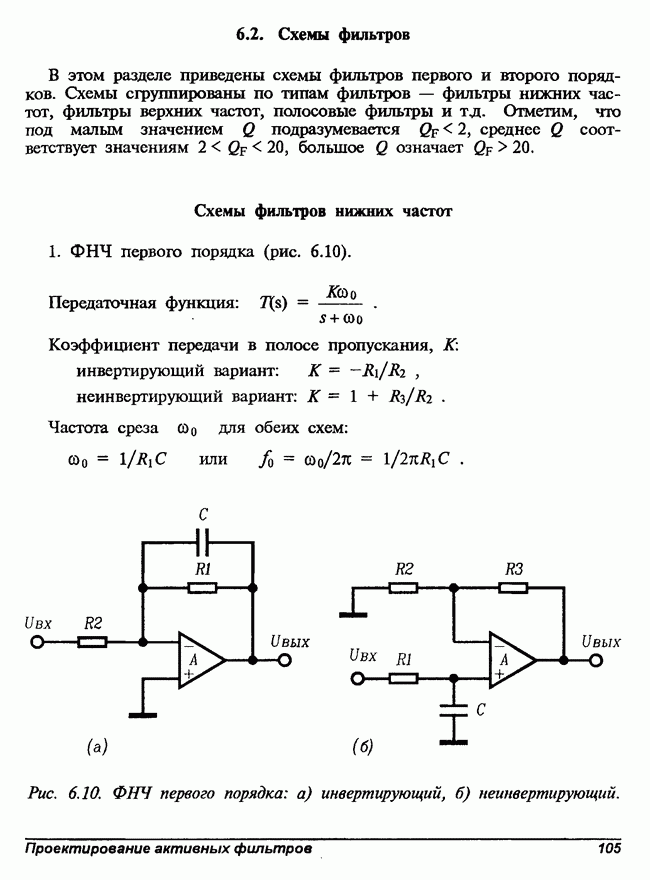
- 6.2. Схемы фильтров
- Схемы фильтров верхних частот
- Схемы полосовых фильтров
- Полосно-подавляющие фильтры
- Схемы фазовых фильтров
- Фильтры с переменными параметрами
- 6.3. Управляемые фильтры
- Фильтры, управляемые напряжением
- Фильтры с цифровым управлением
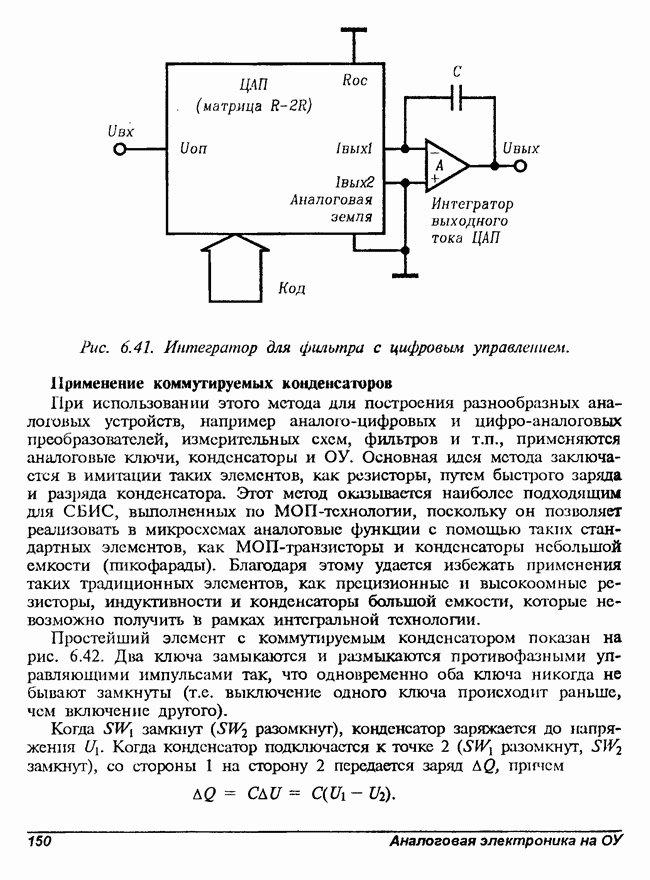
- Применение коммутируемых конденсаторов
- 6.4. Практические вопросы проектирования фильтров
- Настройка
- Выбор элементов
- Устойчивость фильтров
- 6.5 Проектирование фильтров высоких порядков
- Определение требуемой передаточной функции
- Другие типы фильтров.
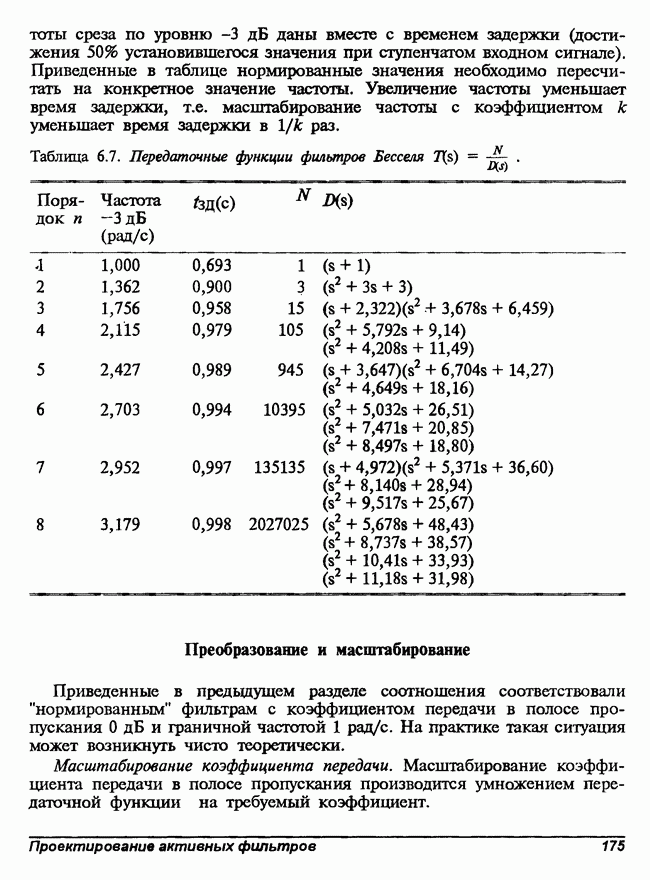
- Передаточные функции.
- Преобразование и масштабирование
- Переход от передаточной функции к схеме
- 7. Интеграторы и дифференциаторы
- Рекомецдации по выбору элементов
- 7.2. Дифференциаторы
- Рекомендации по выбору элементов
- 8. Логарифмирующие и экспоненциальные преобразователи
- 8.2. Экспоненциальные преобразователи
- 8.3. Промышленные логарифмирующие и экспоненциальные преобразователи
- 9. Арифметические операции
- 9.2. Умножители
- Делитель на основе умножителя
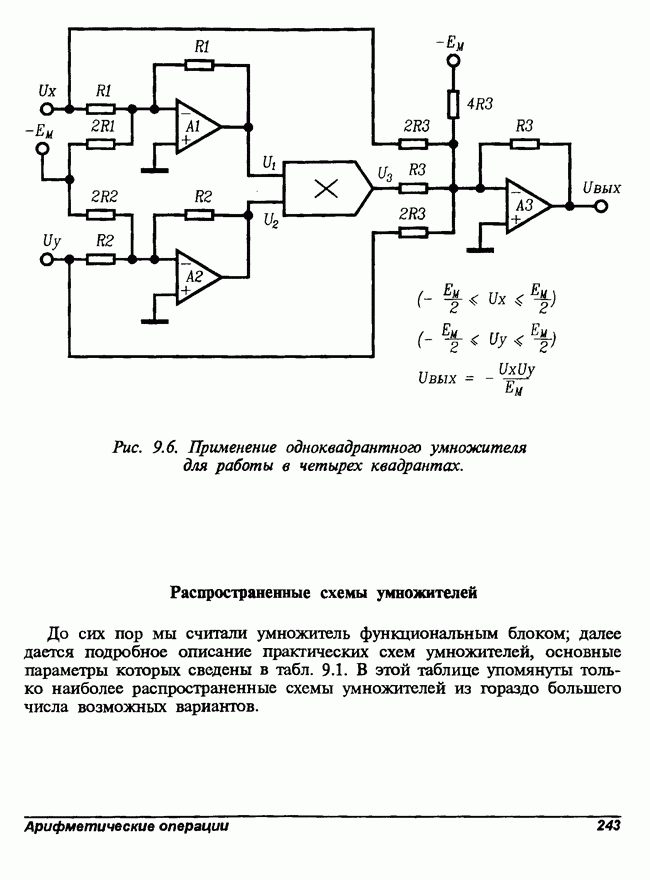
- Распространенные схемы умножителей
- Умножители на основе управляемых источников тока
- Умножители с логарифмированием и антилогарифмированием сигналов
- Импульсные умножители
- Умножители с применением ЦАП и АЦП
- 9.3. Промышленные микросхемы аналоговых умножителей
- 10. Функциональные преобразователи
- 10.2. Логарифмирующие и экспоненциальные функциональные преобразователи
- 10.3. Функциональные преобразователи с кусочно-линейной аппроксимацией
- 10.4. Схемы функциональных преобразователей с использованием АЦП и ЦАП
- 11. Ограничители, пиковые детекторы и выпрямители
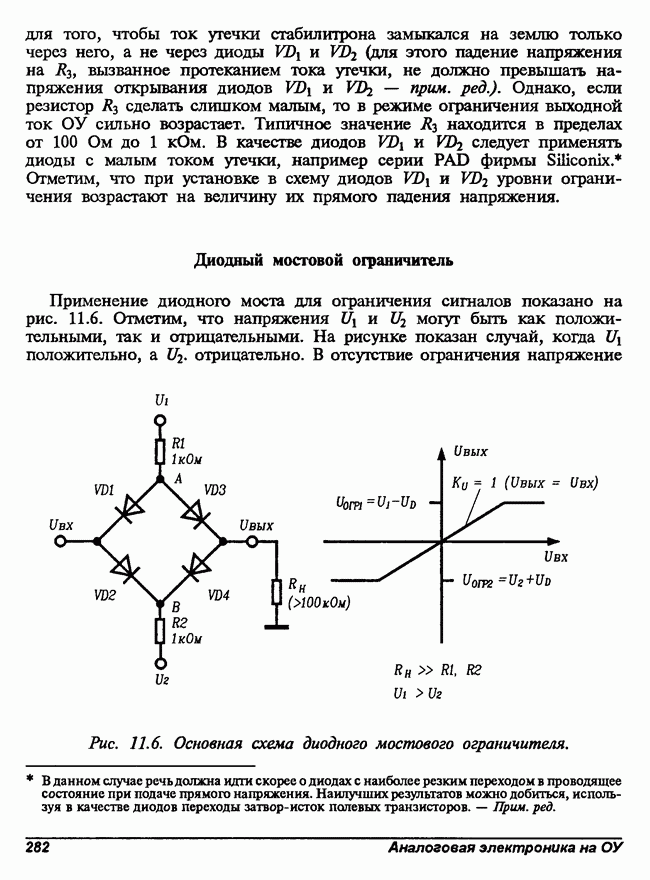
- Диодный мостовой ограничитель
- Управляемый напряжением ограничитель на ОУ
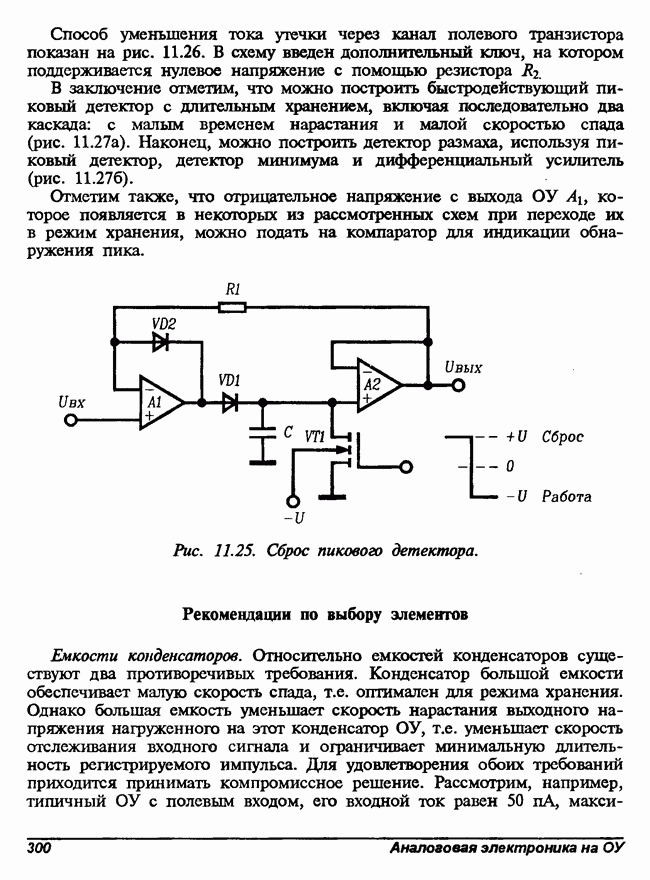
- 11.2. Пиковые детекторы
- Двухкаскадные пиковые детекторы
- Пиковый детектор с общей обратной связью
- Улучшение характеристик виковых детекторов
- Рекомендации по выбору элементов
- Пиковые детекторы на базе микросхем
- 11.3. Прецизионные однополупериодные выпрямители
- 11.4. Двухполупериодные выпрямители
- Двухполупериодный выпрямитель с токовым выходом
- Двухполупериодный выпрямитель с токовым входом
- Двухполупериодный выпрямитель на двух ОУ с минимальным числом элементов
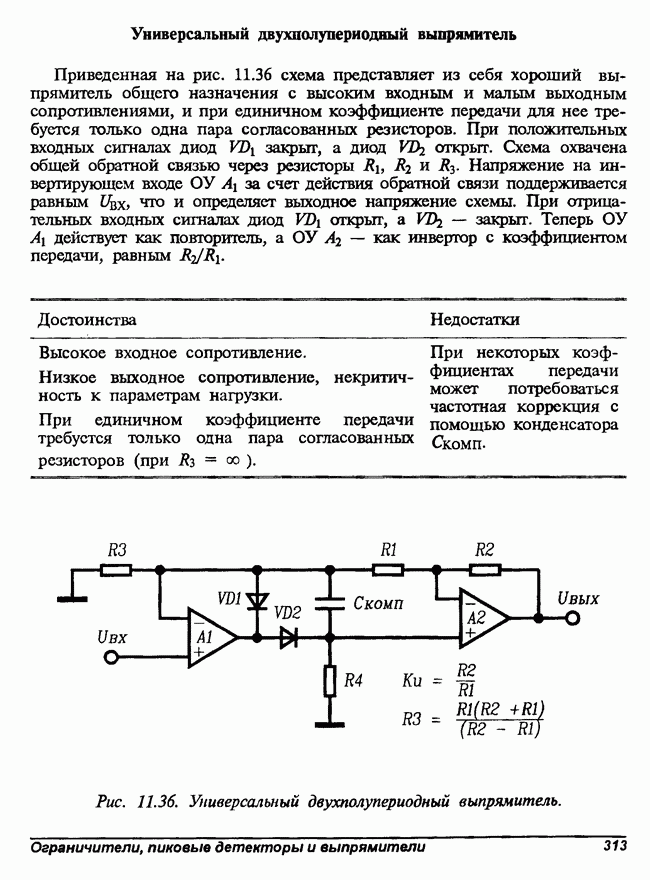
- Универсальный двухполупериодный выпрямитель
- Двухполупериодный выпрямитель с суммированием токов
- Общие рекомендации по схемам выпрямителей
- 12. Измерение пикового, среднего и эффективного значений
- 12.1. Схемы для измерения пиковых значений
- 12.2. Схемы для измерения средневыпрямленного значения
- 12.3. Схемы для измерения средеквадратичного значения
- 12.4. Тепловые преобразователи