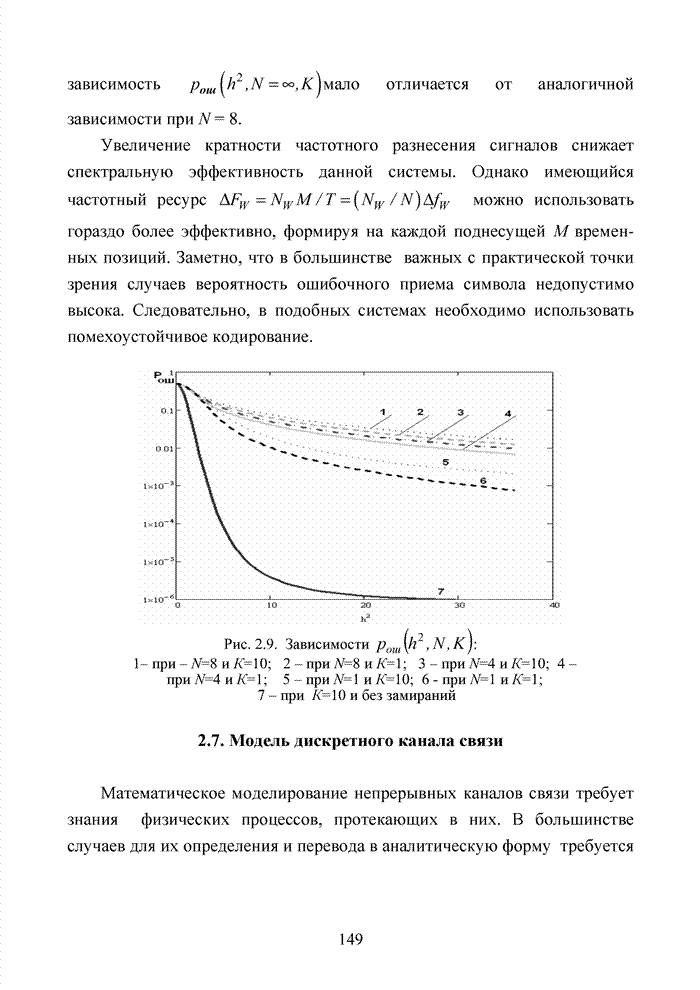
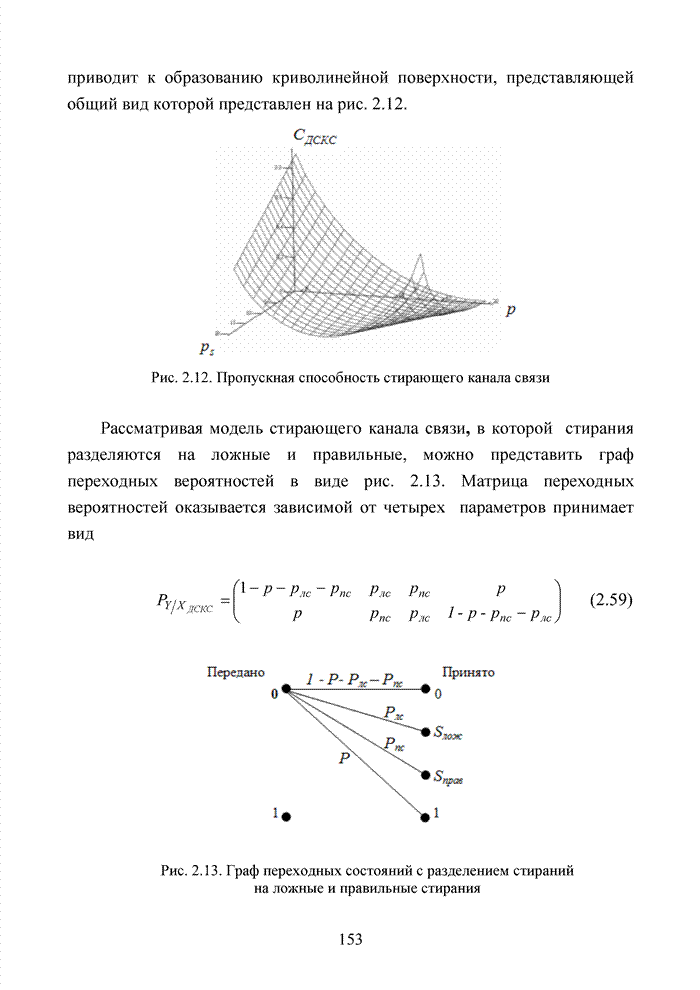
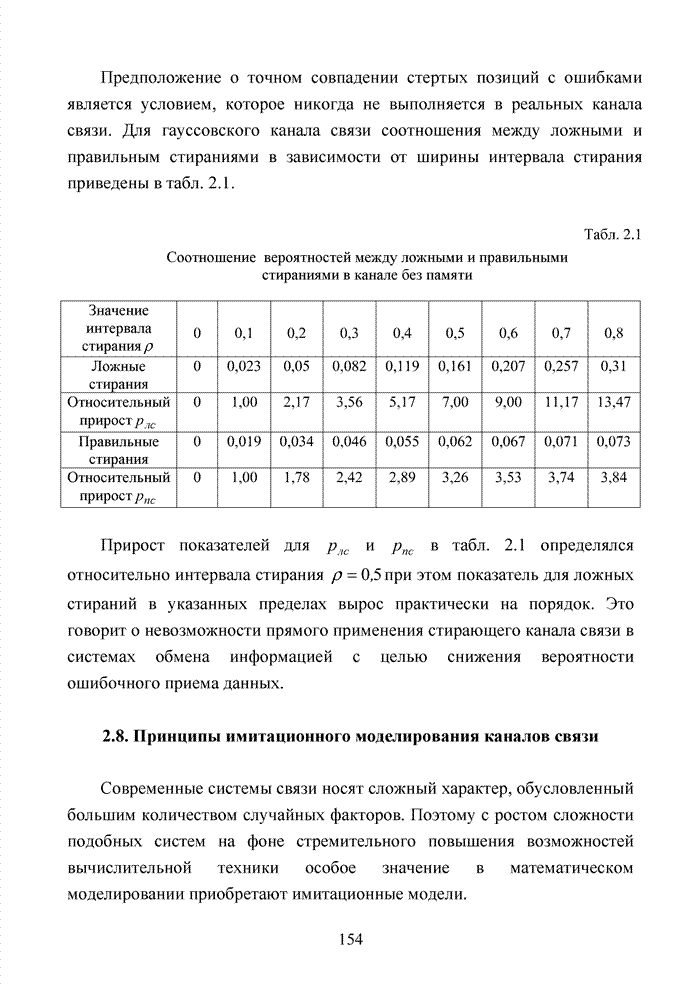
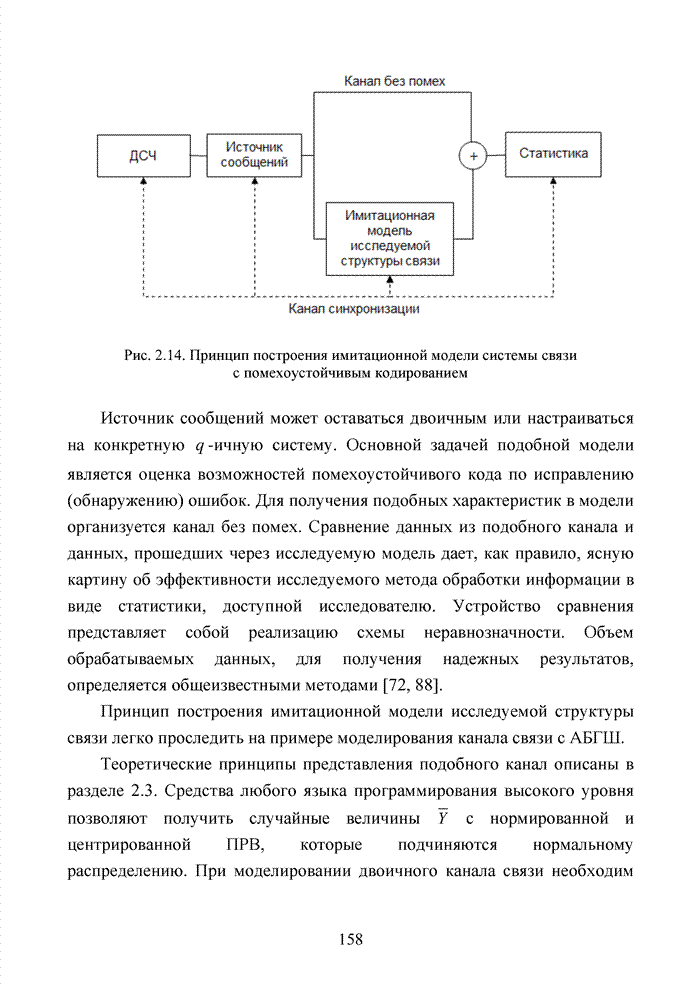
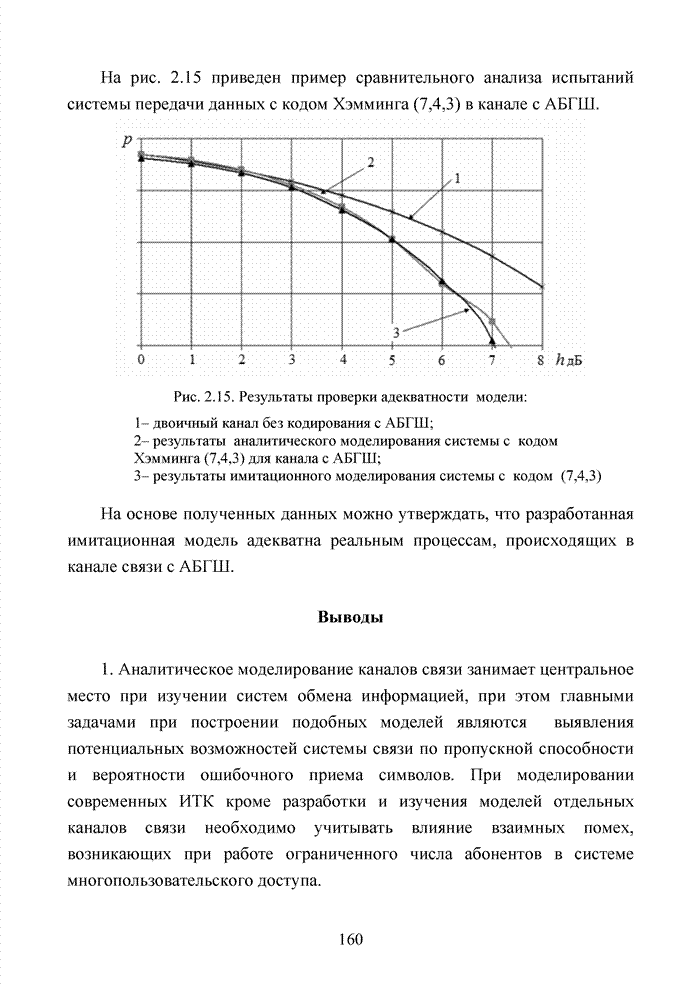
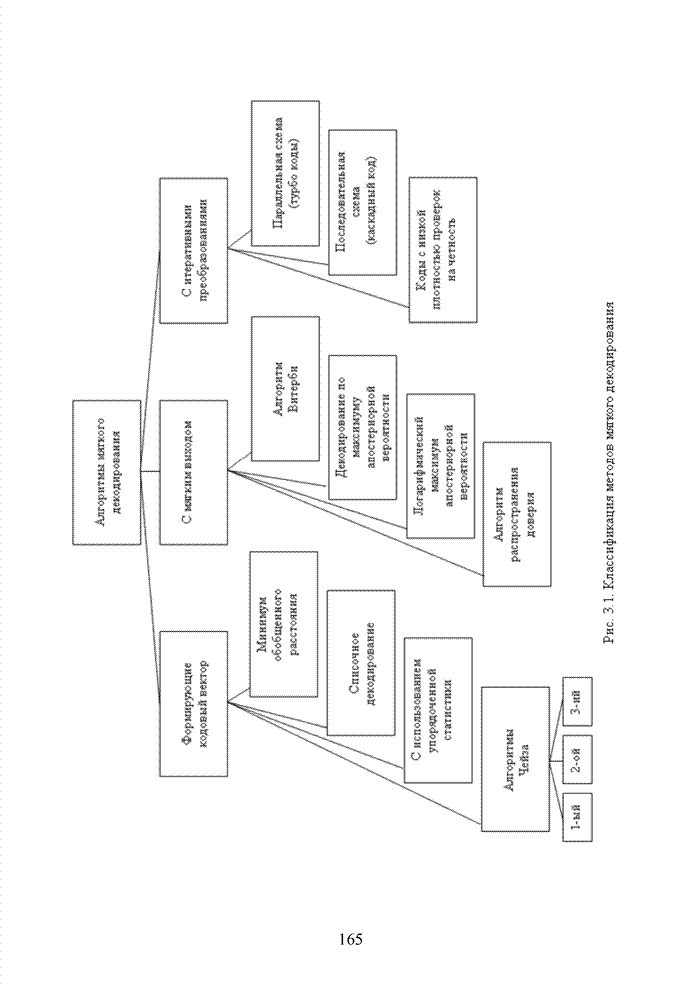
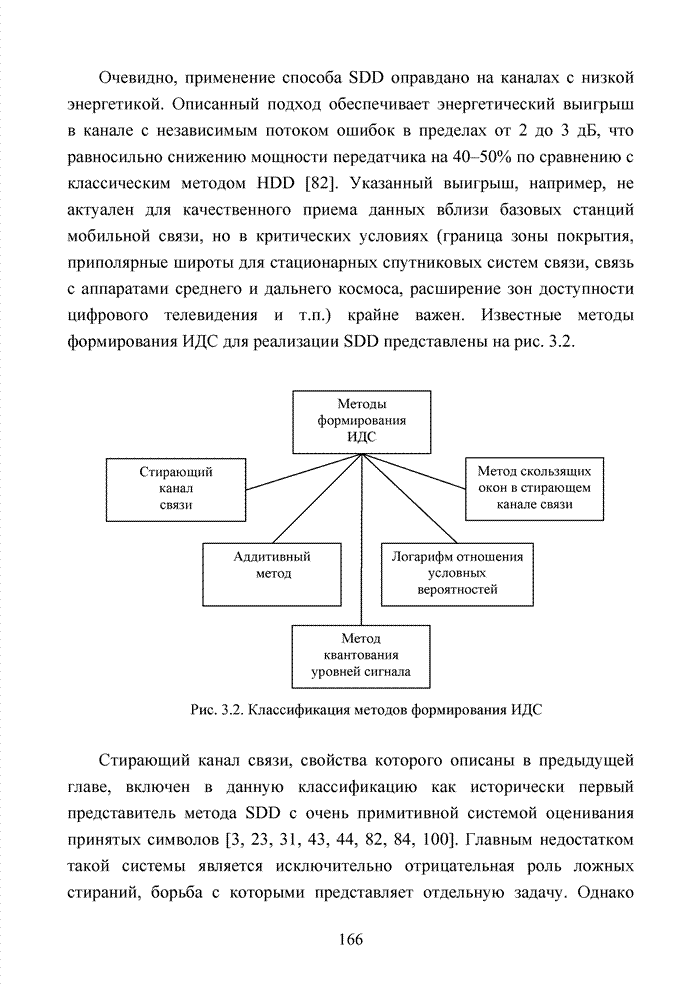
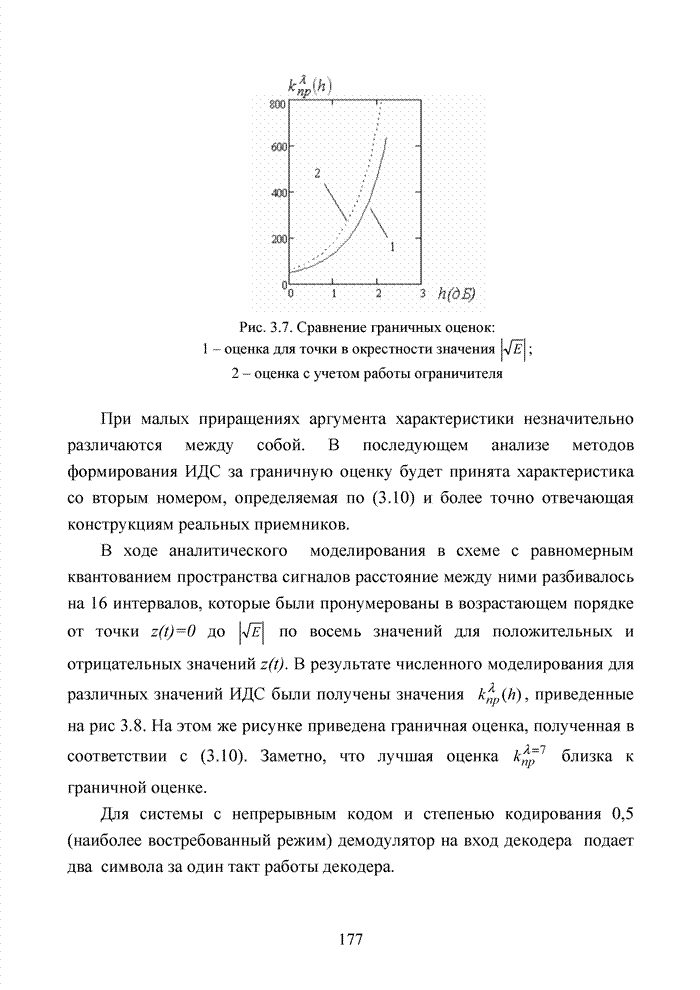
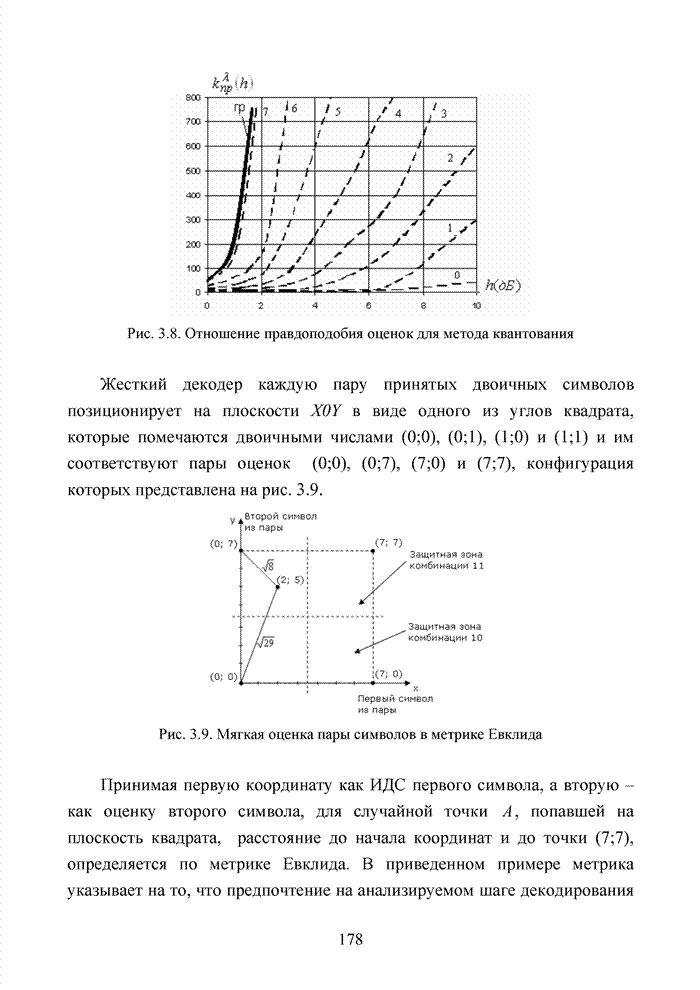
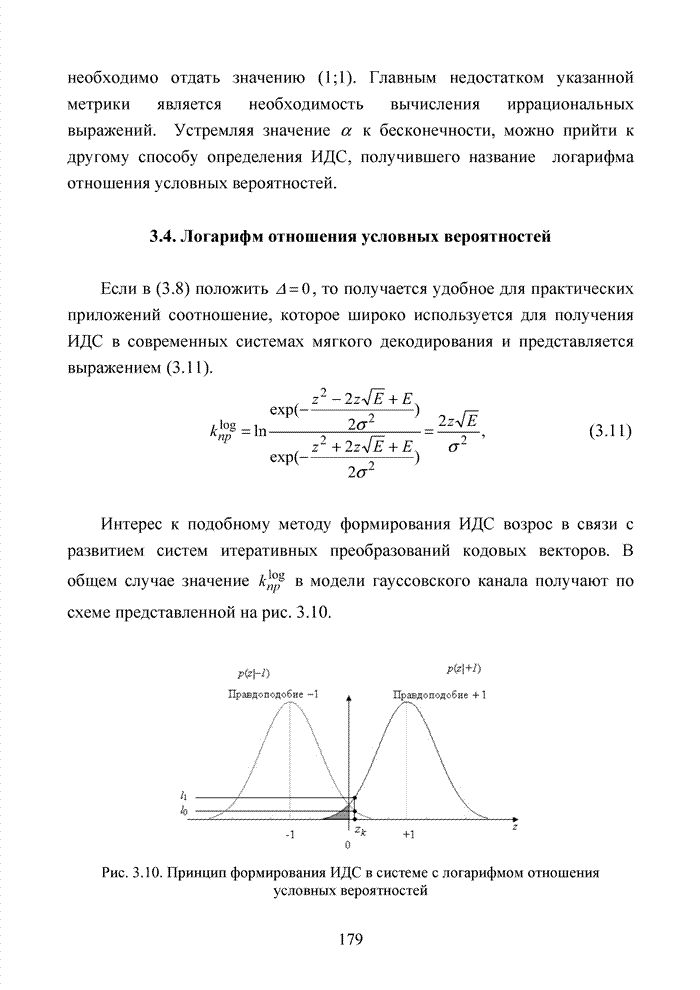
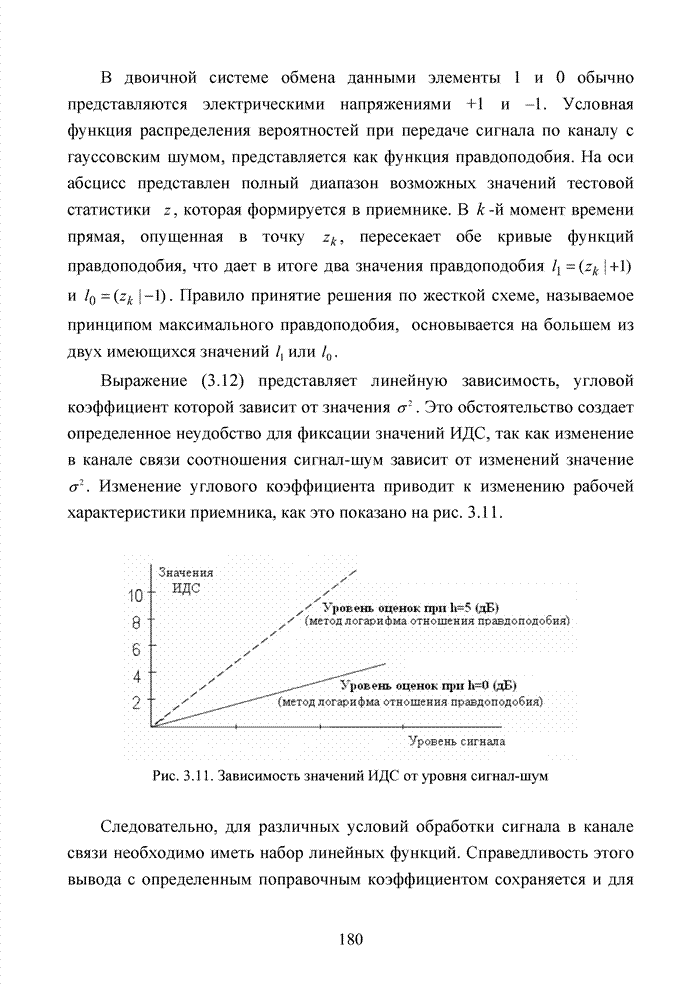
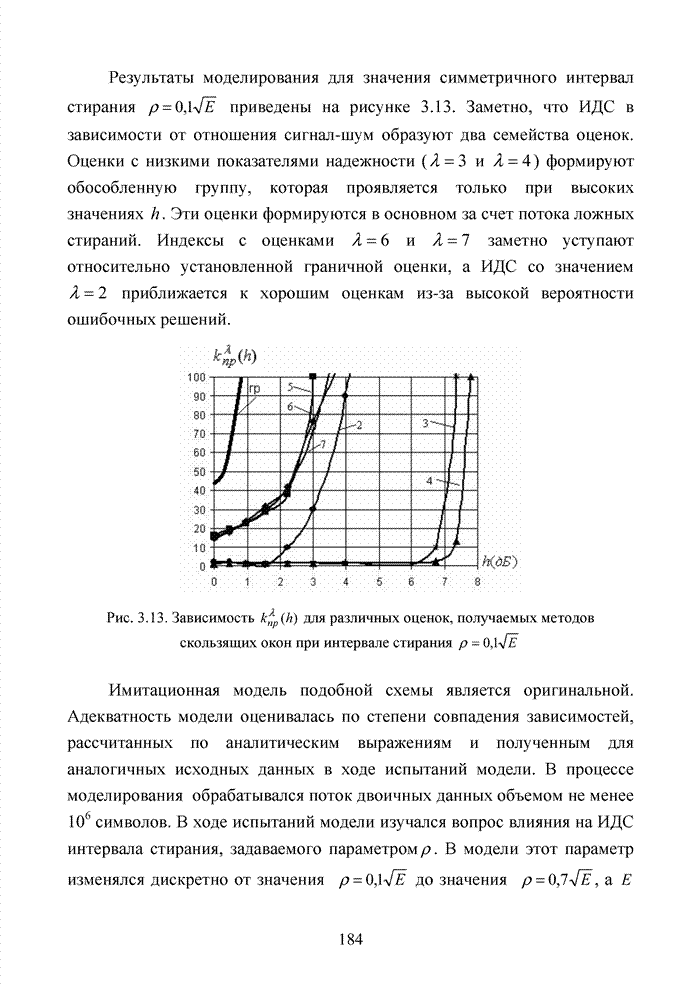
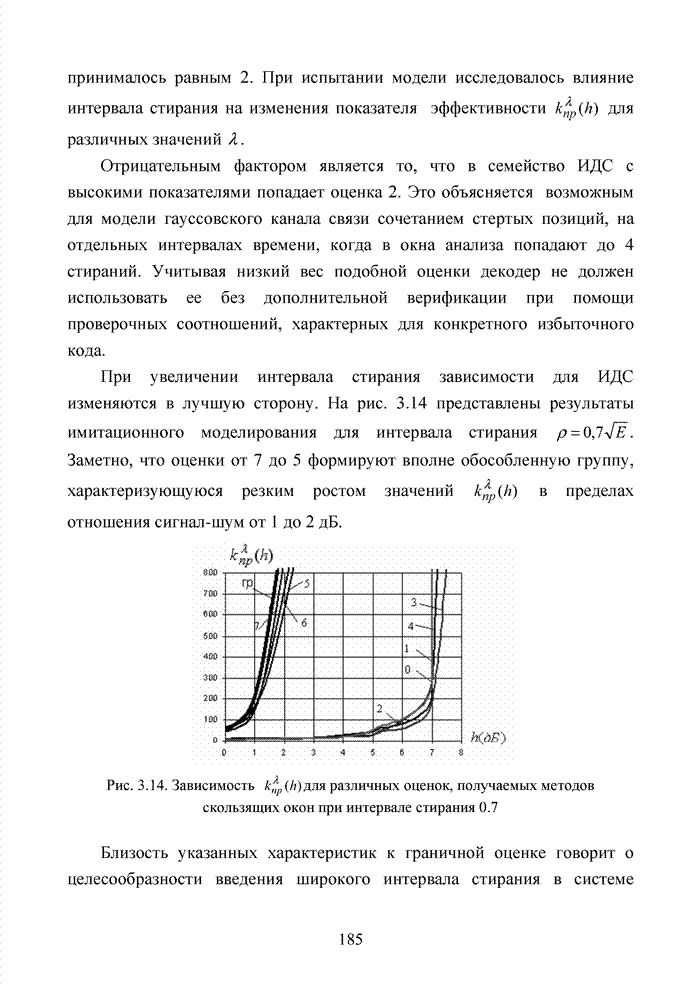
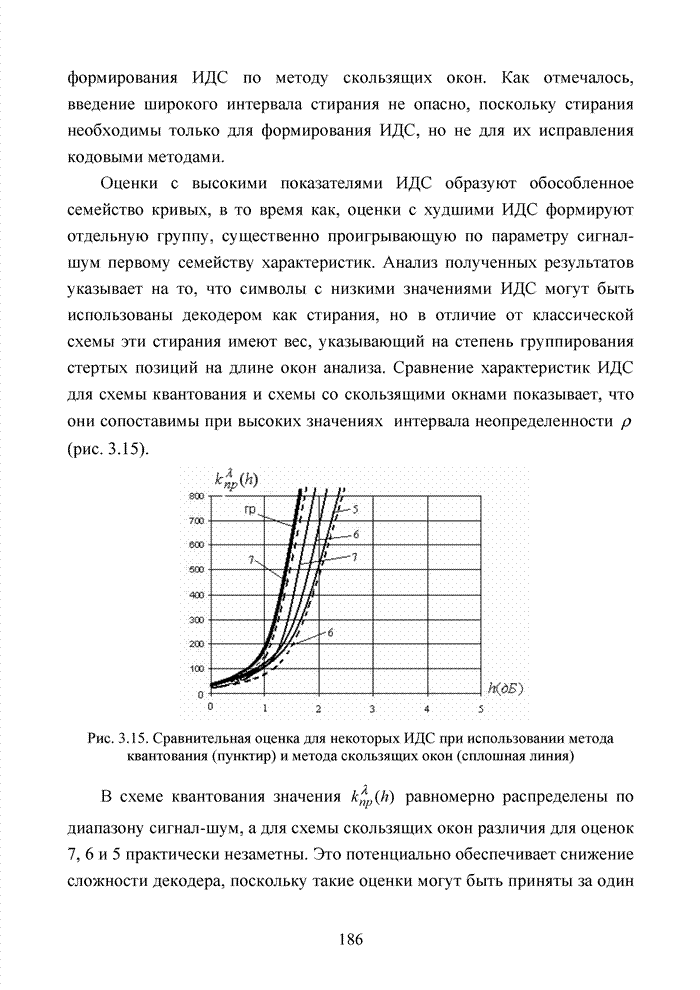
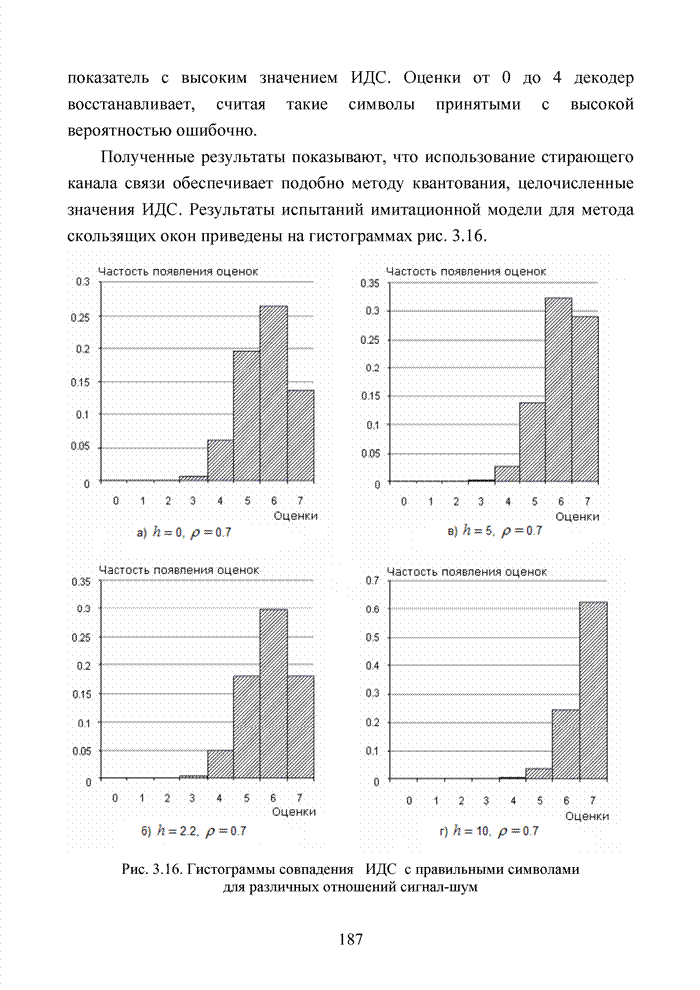
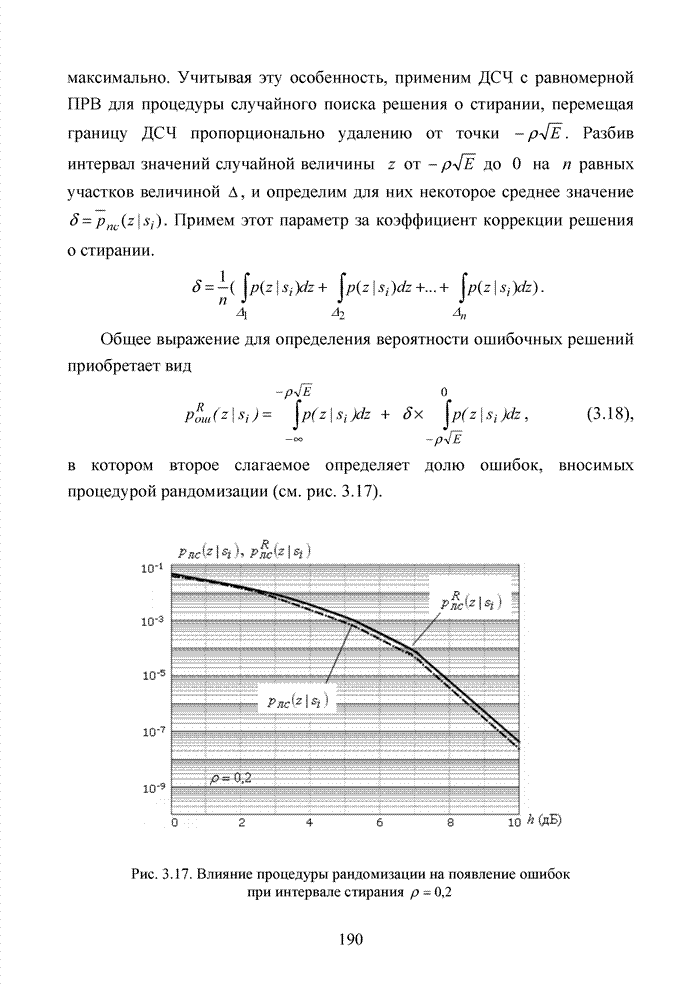
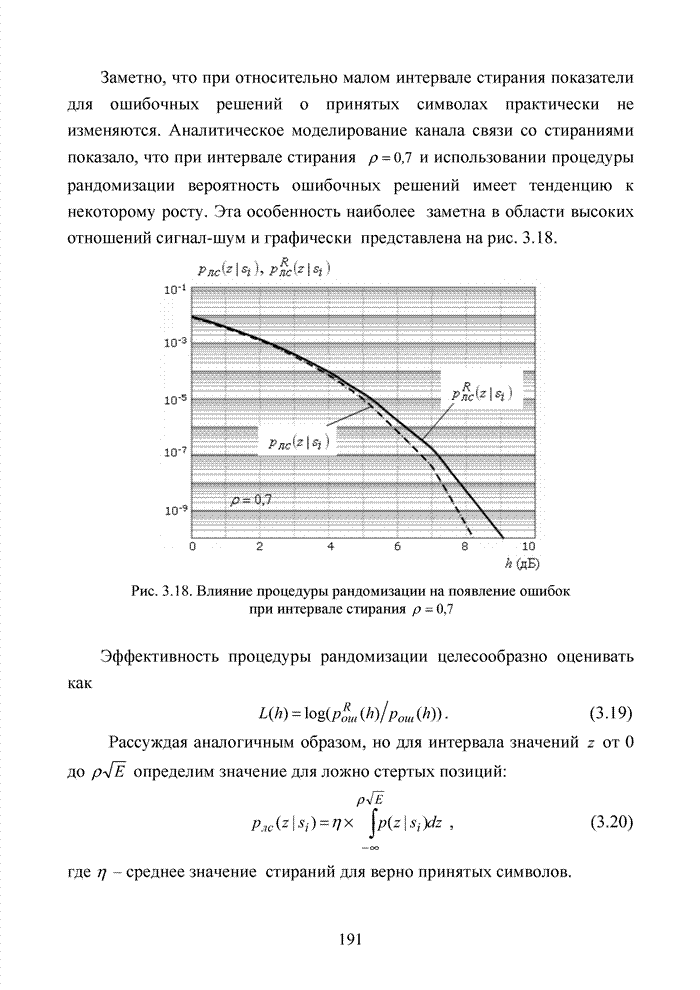
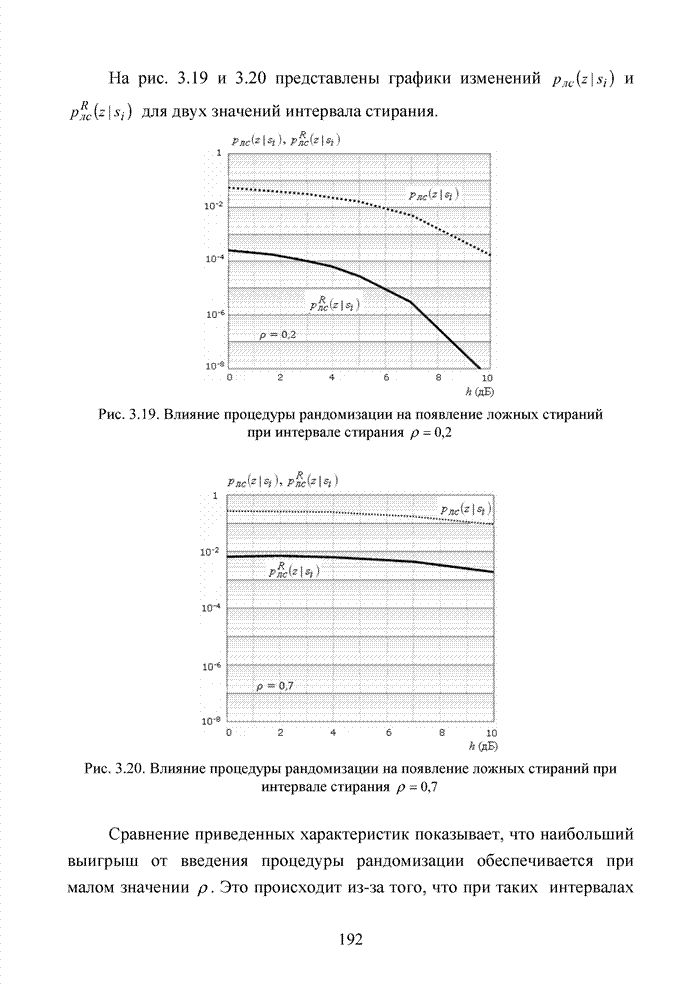
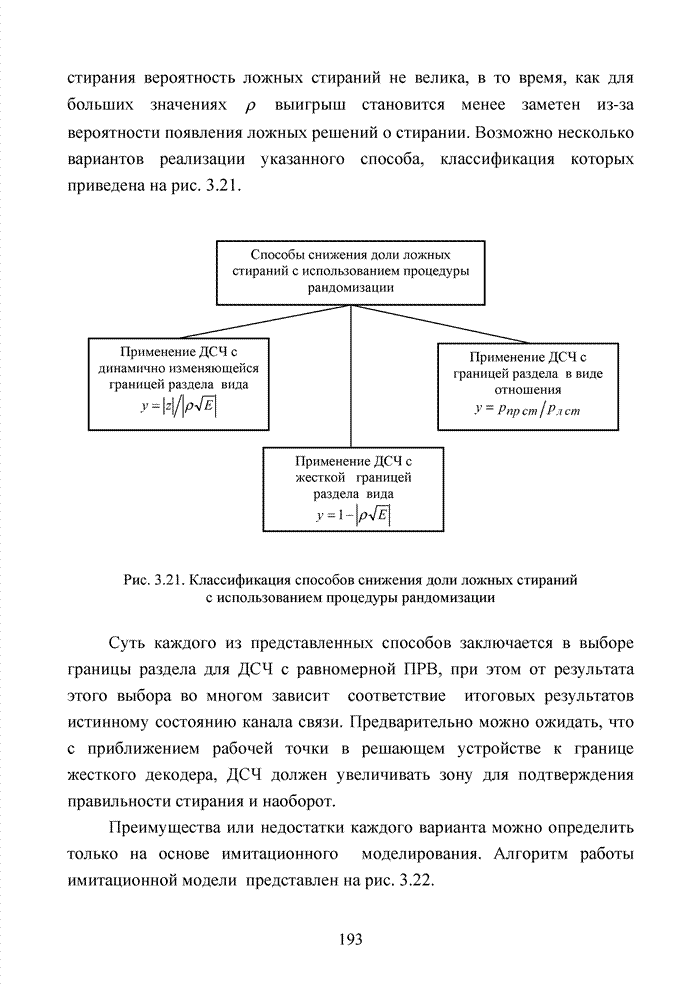
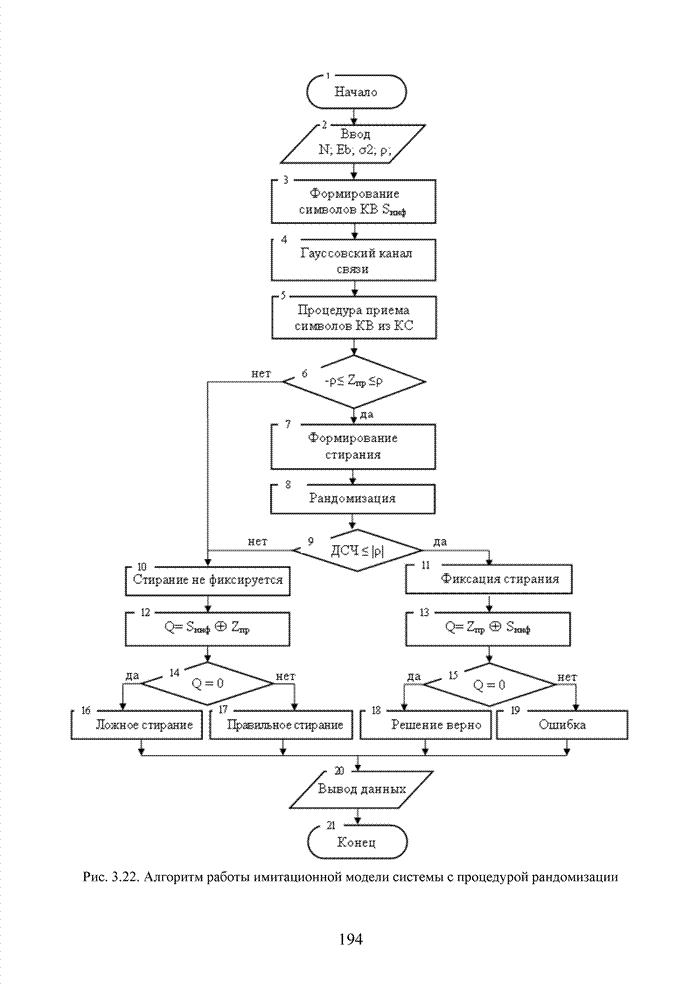
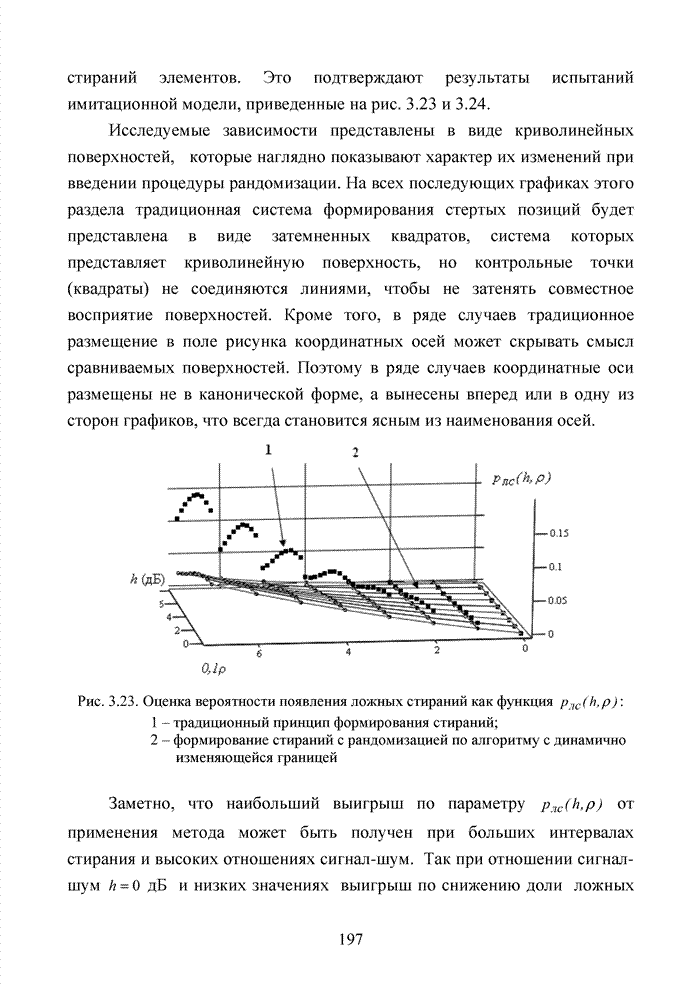
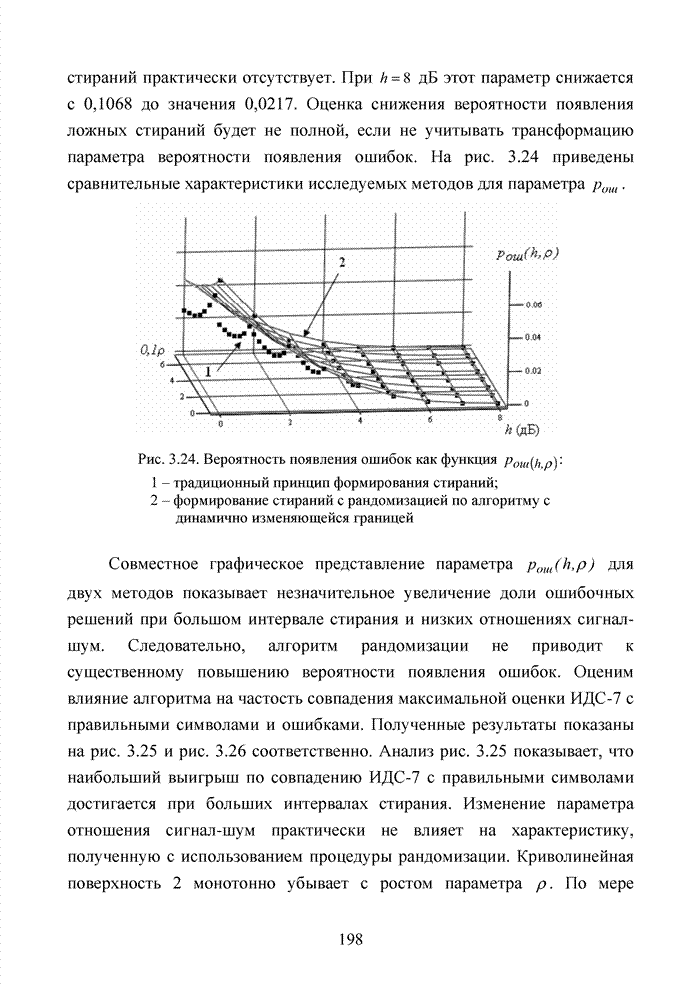
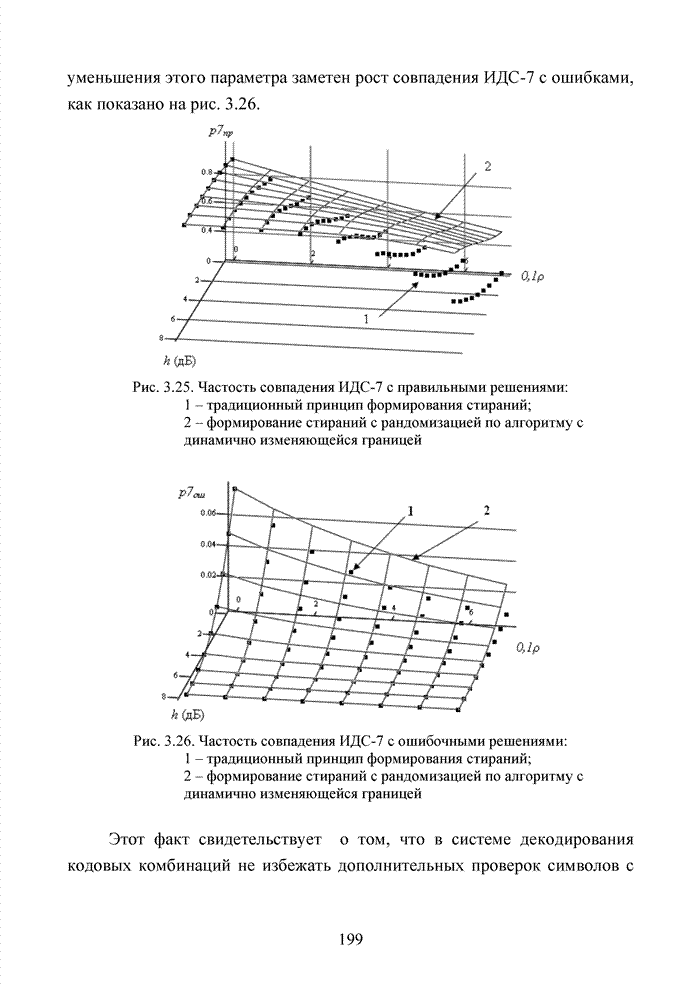
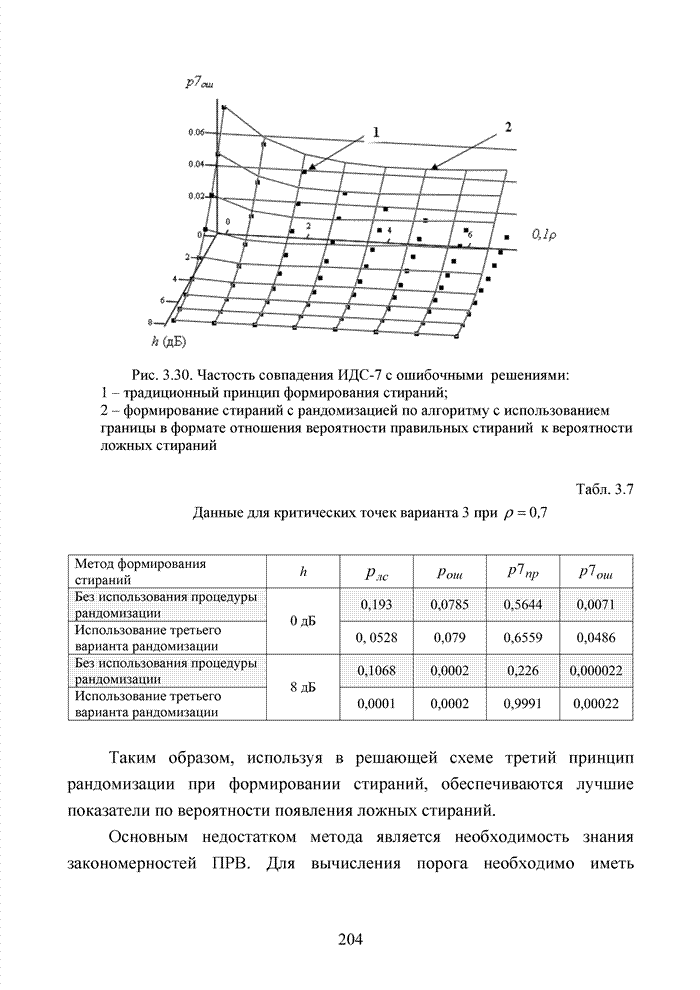
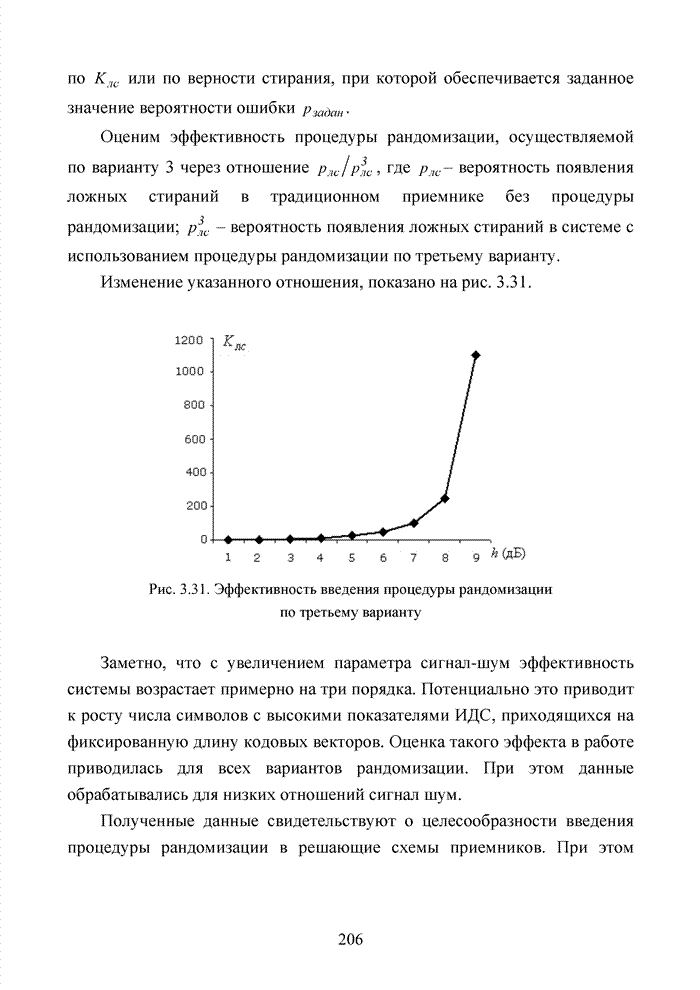
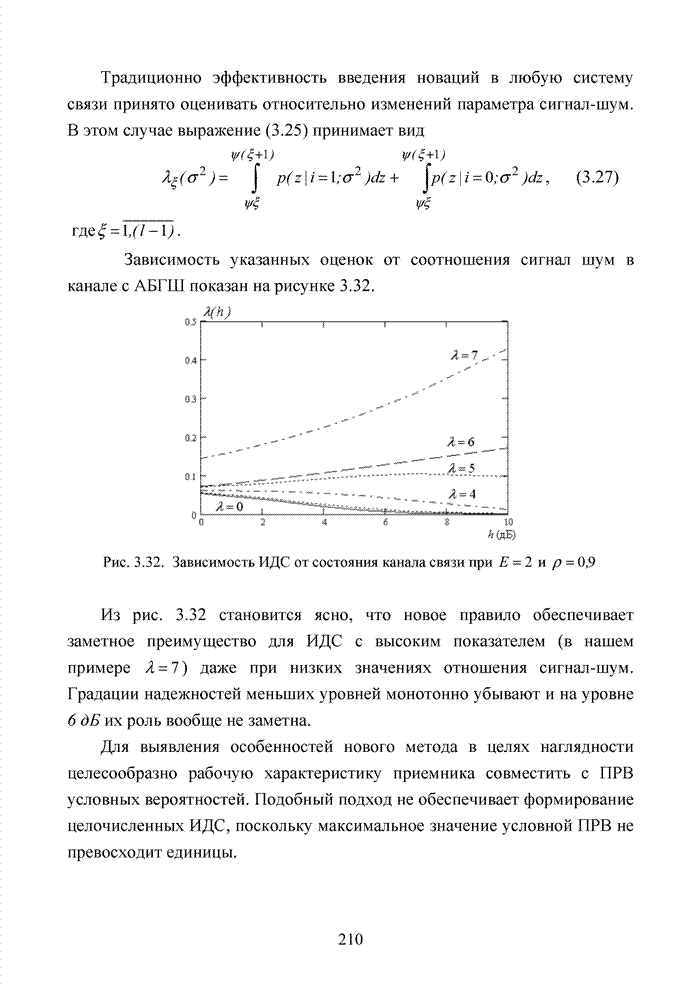
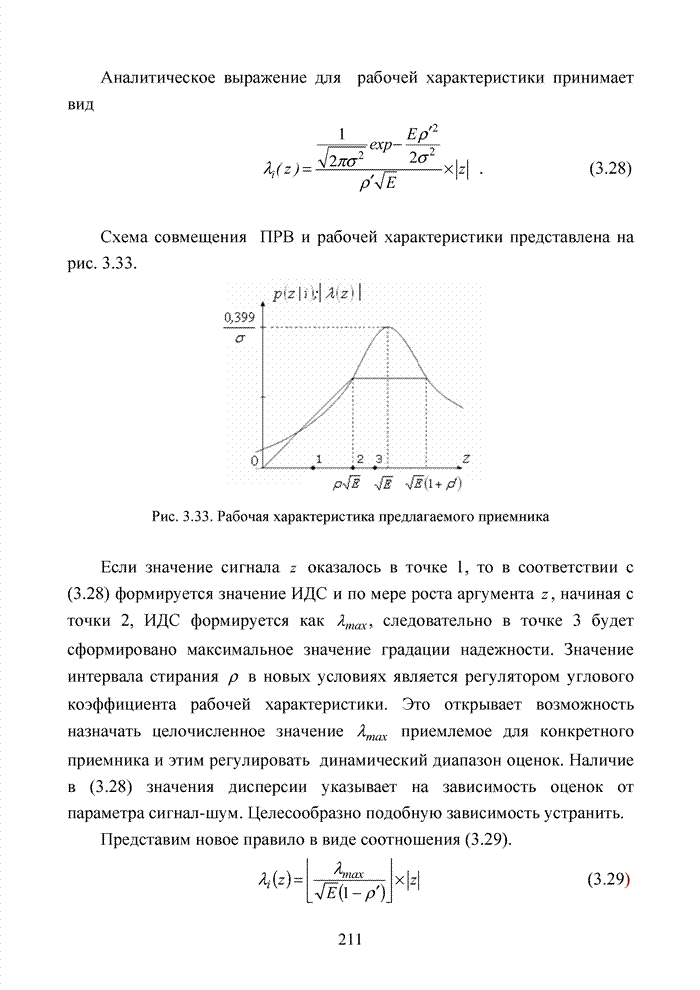
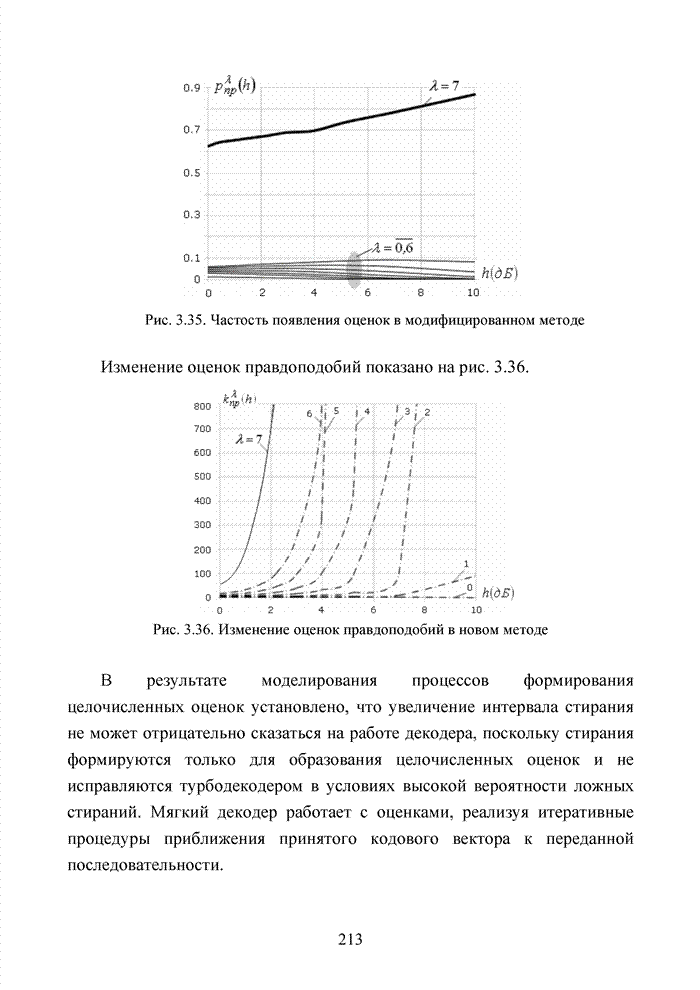
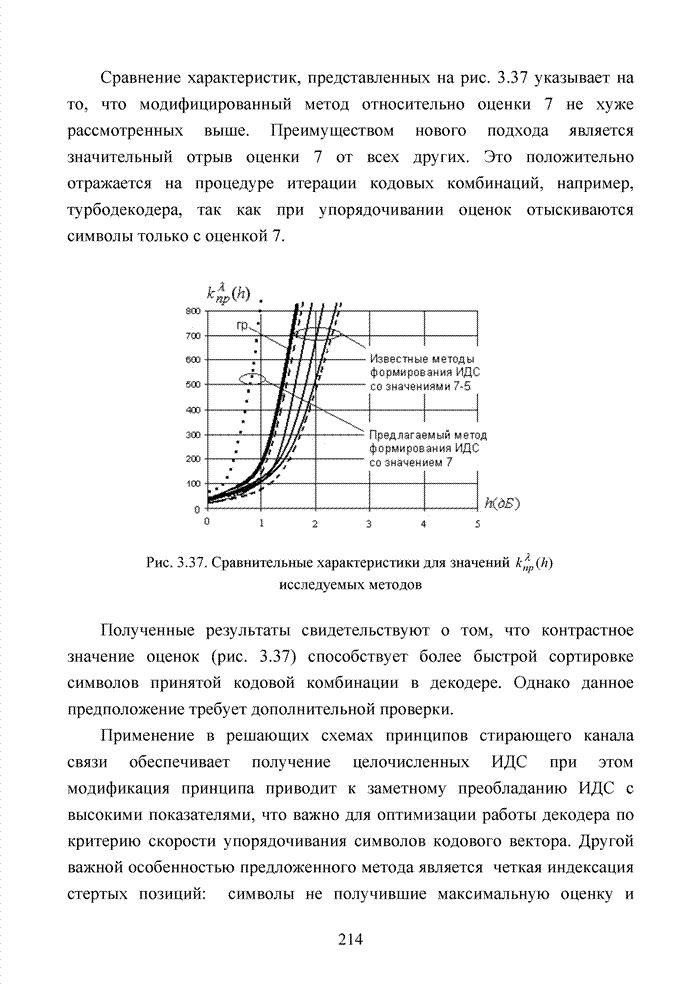
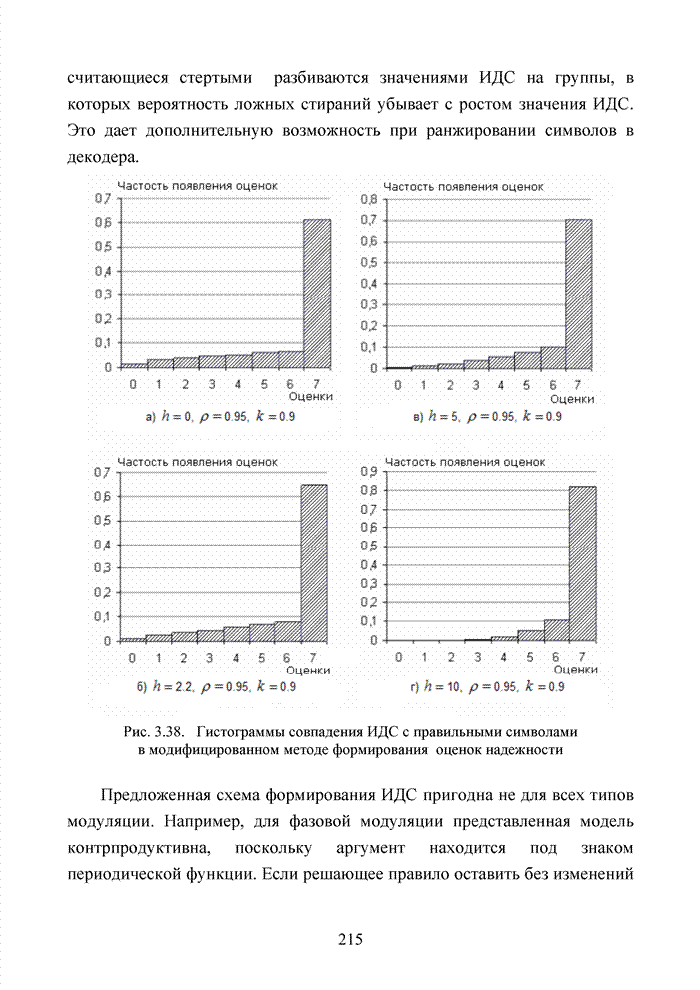
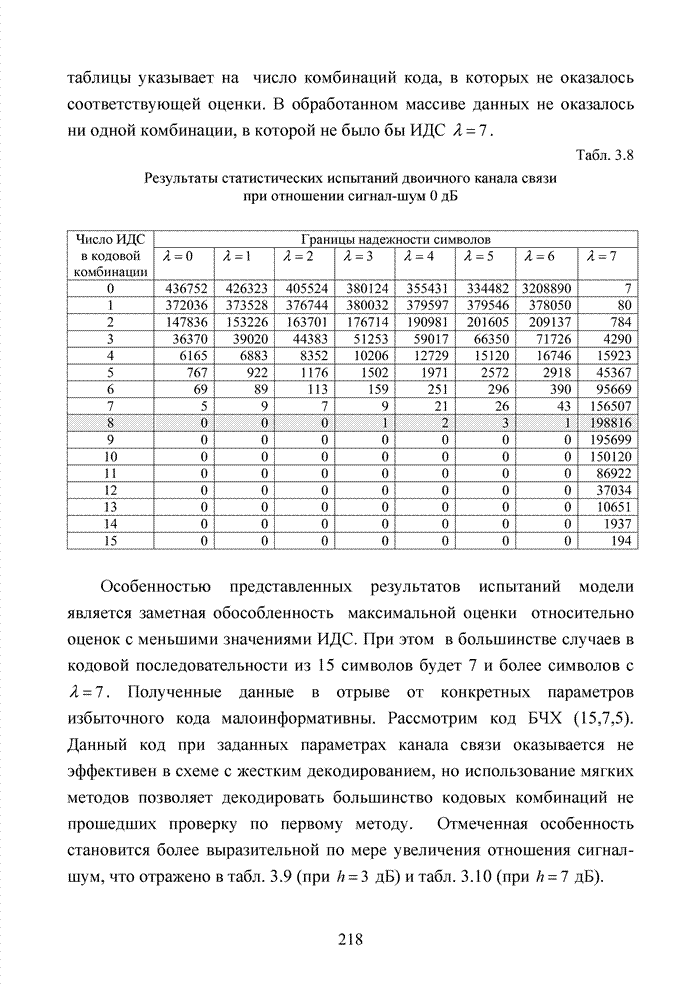
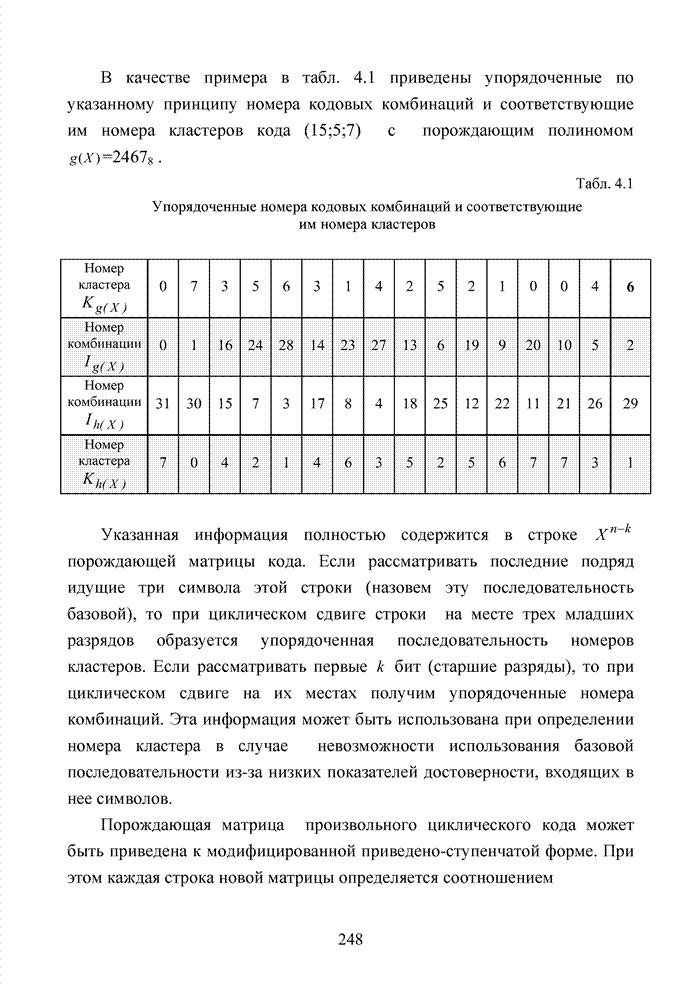
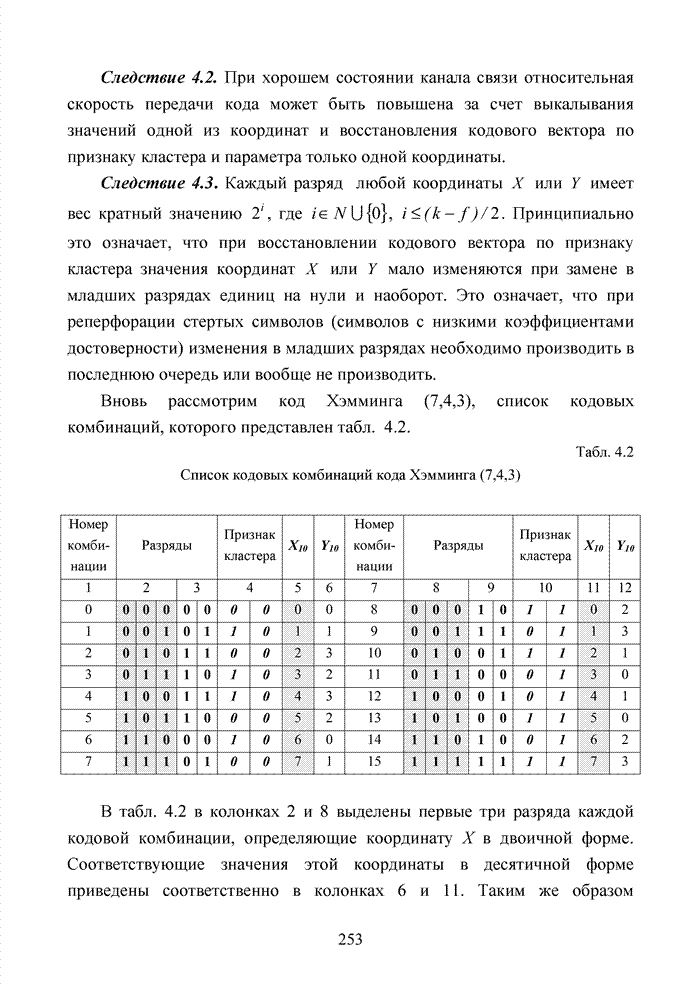
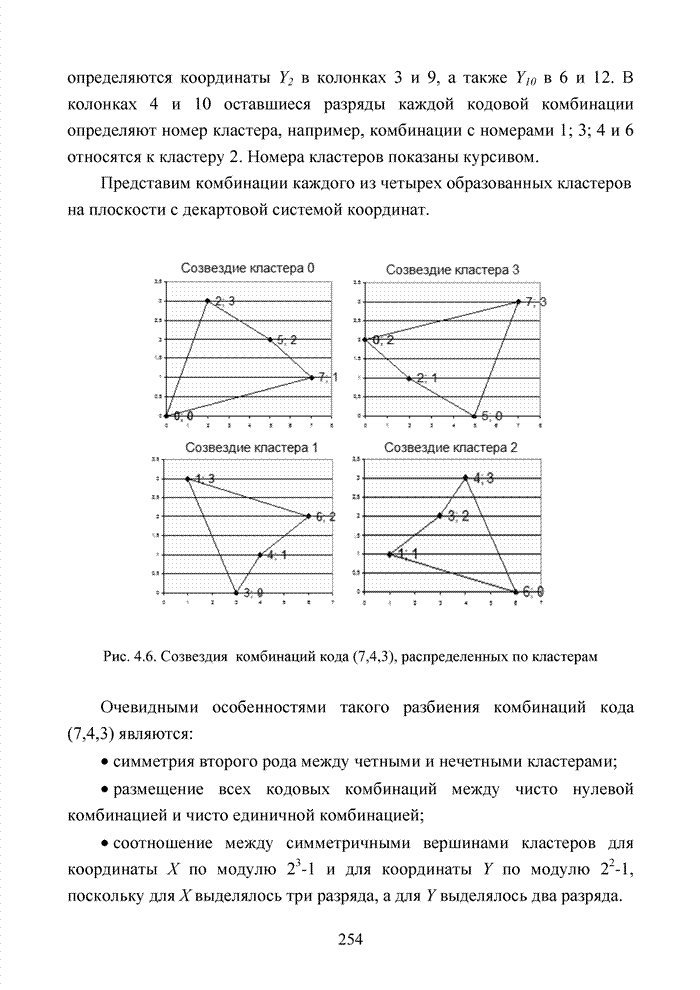
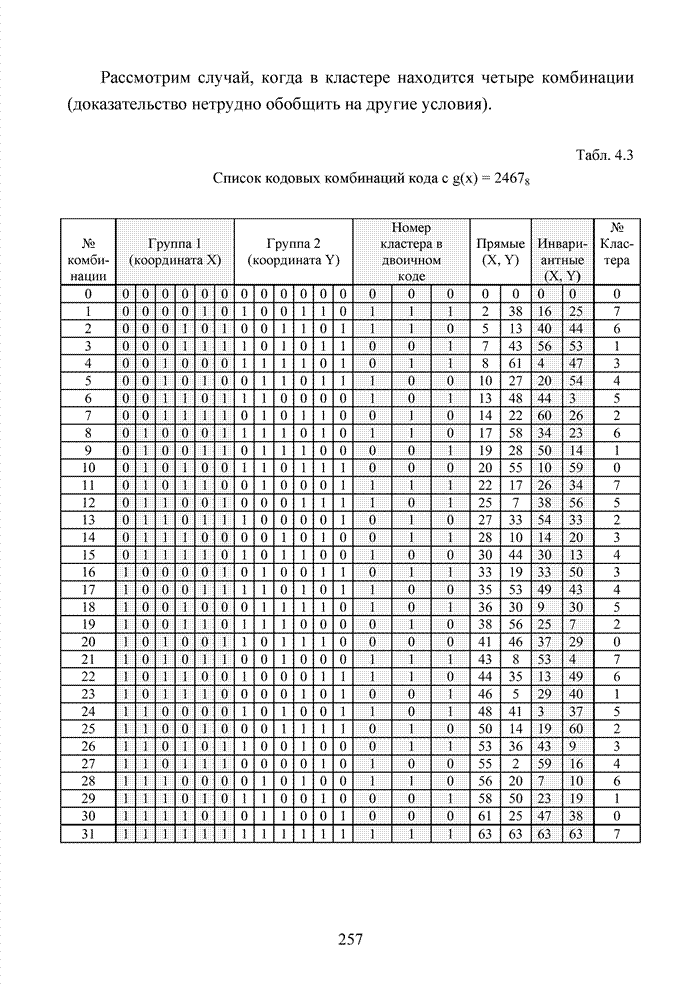
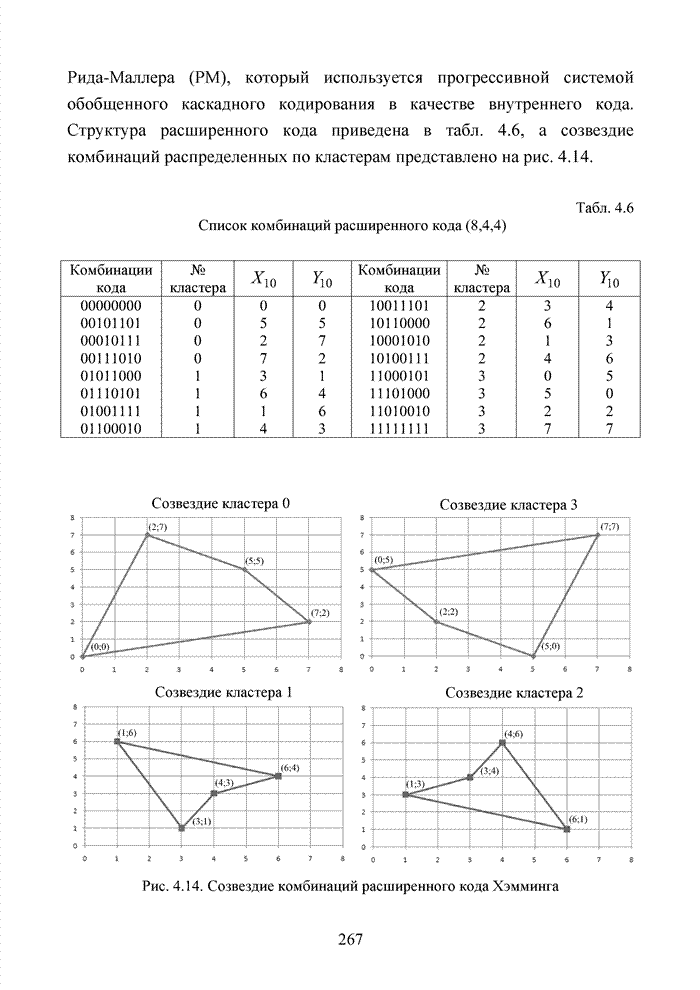
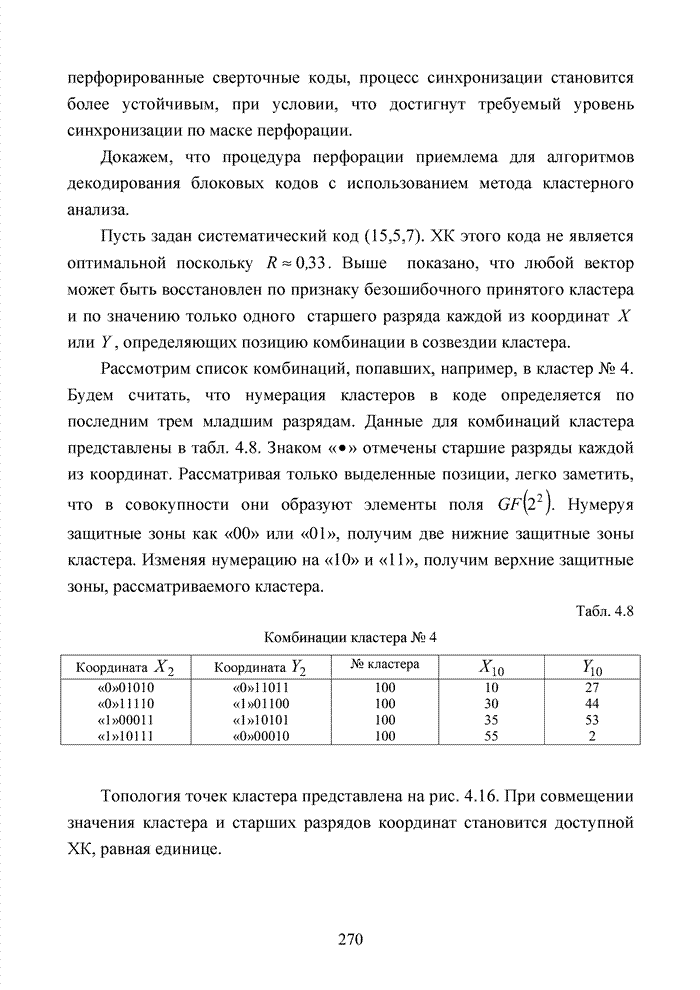
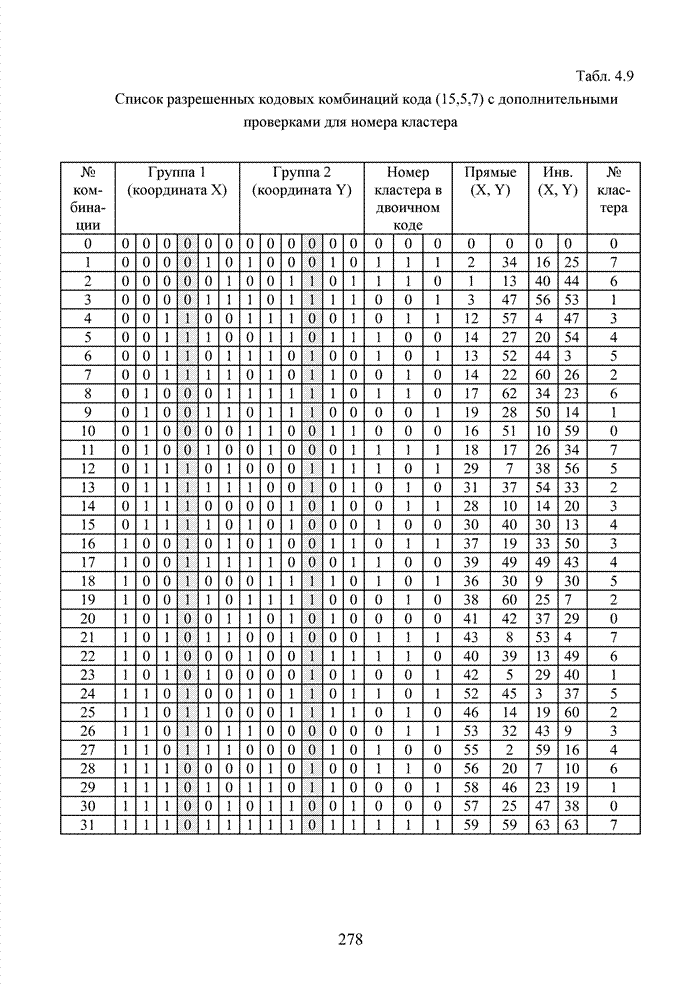
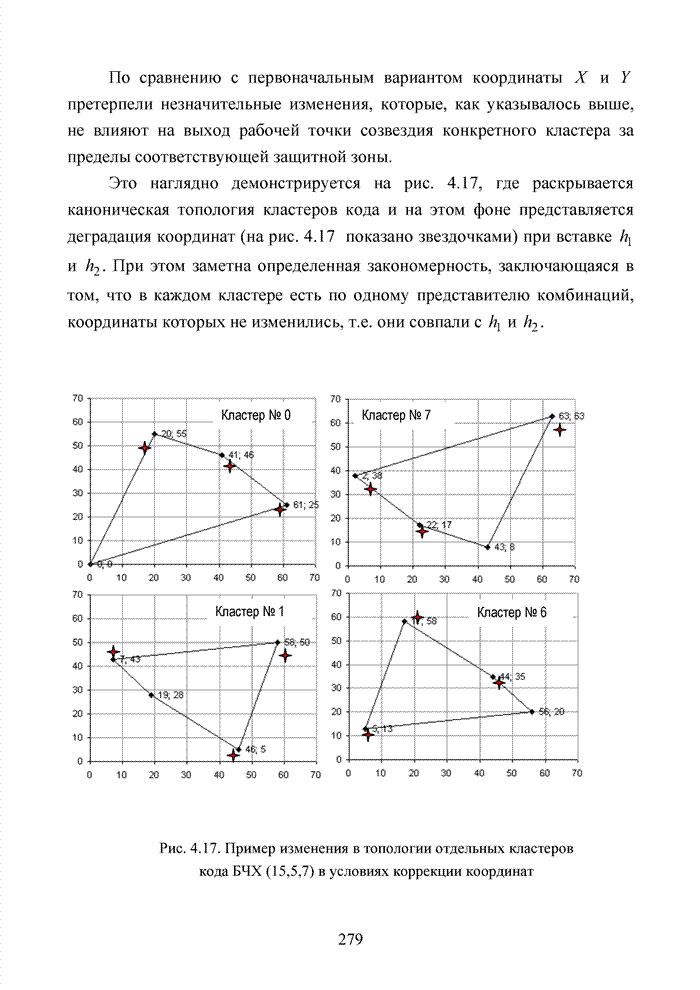
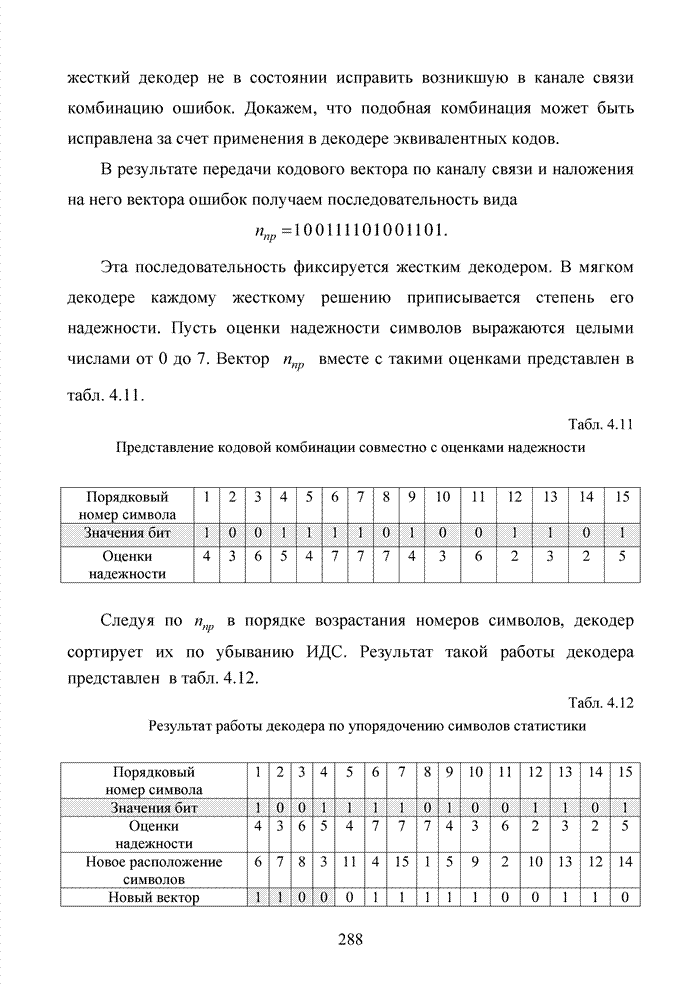
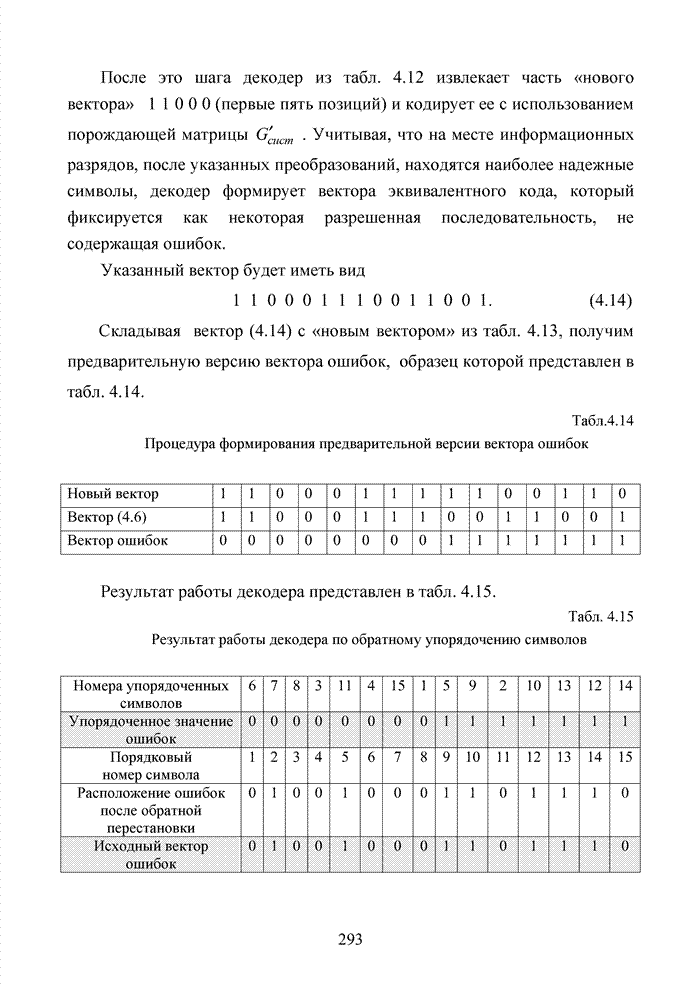
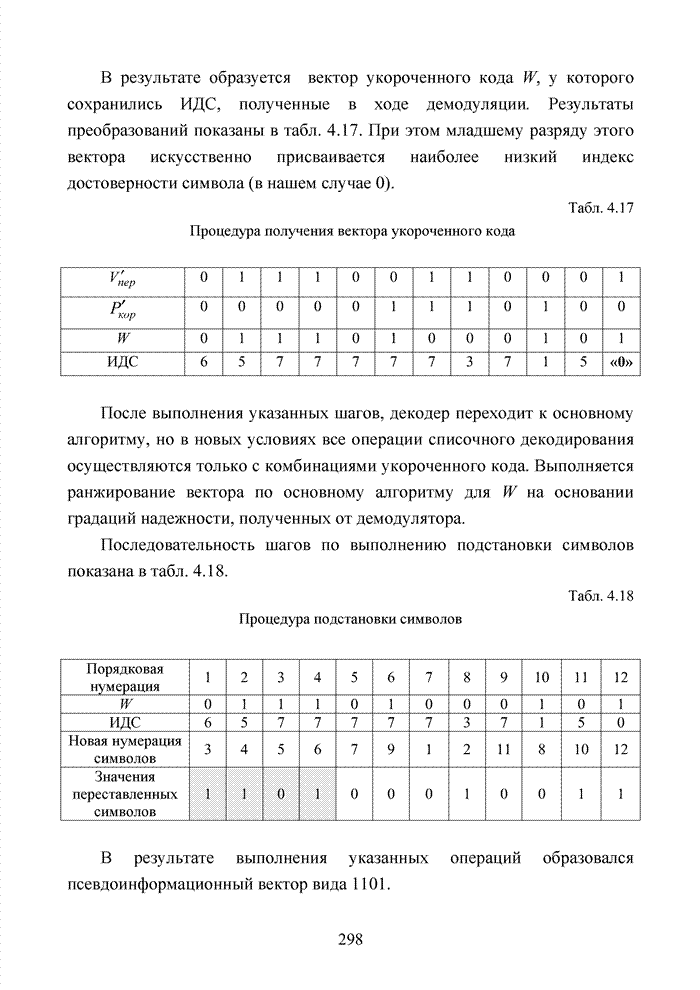
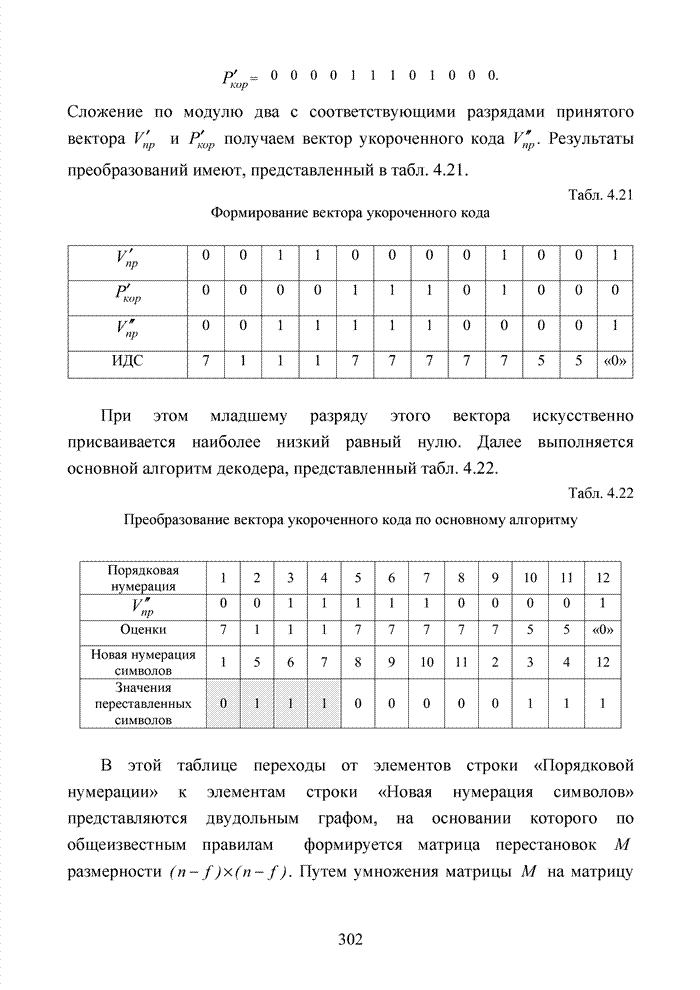
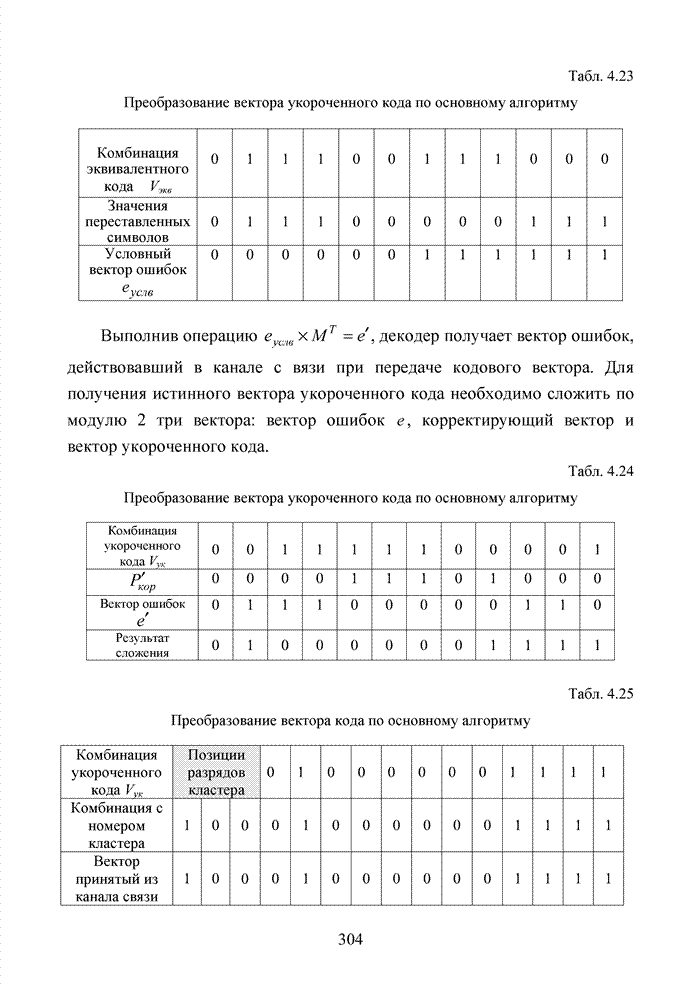
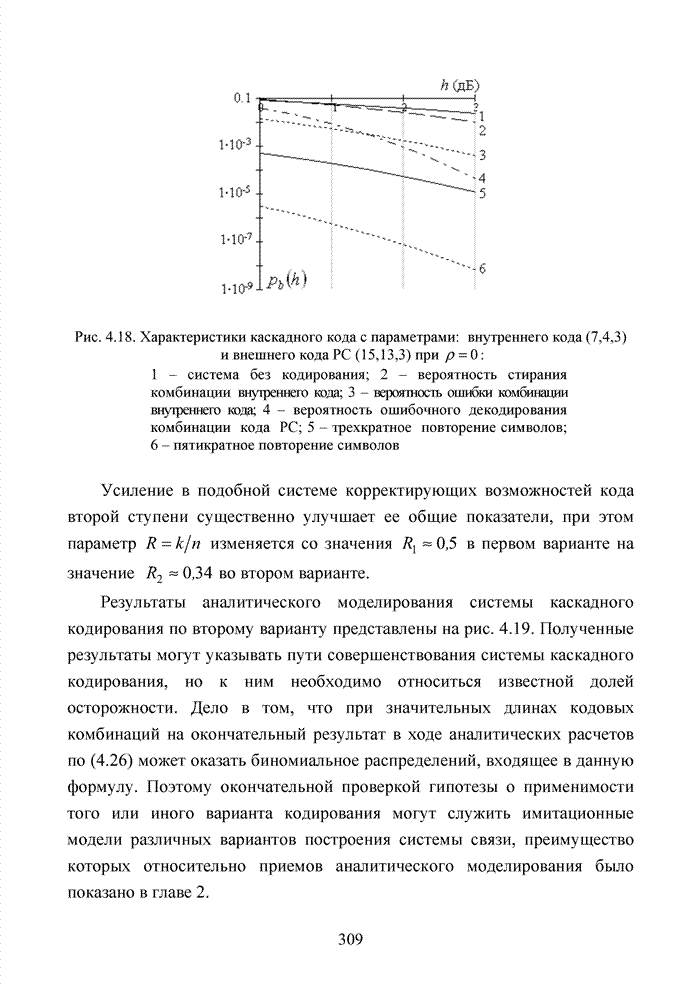
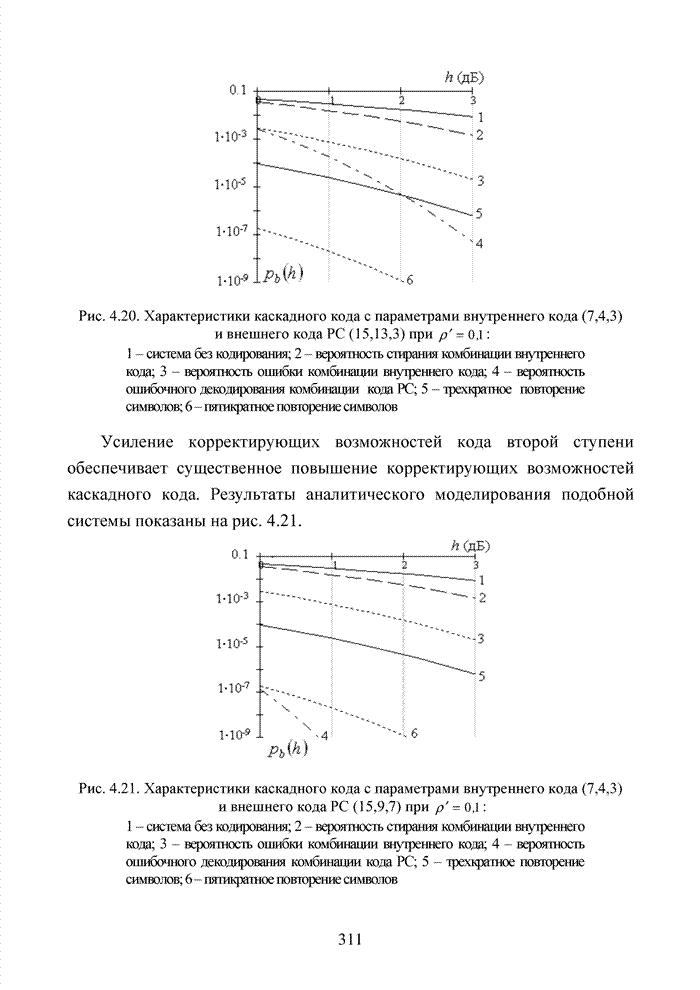
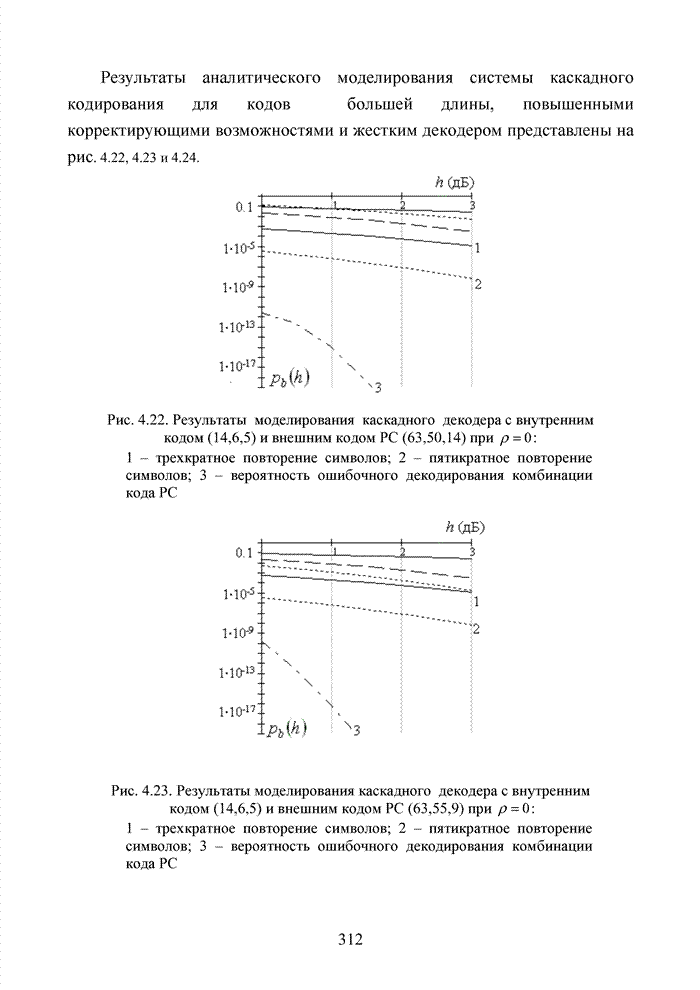
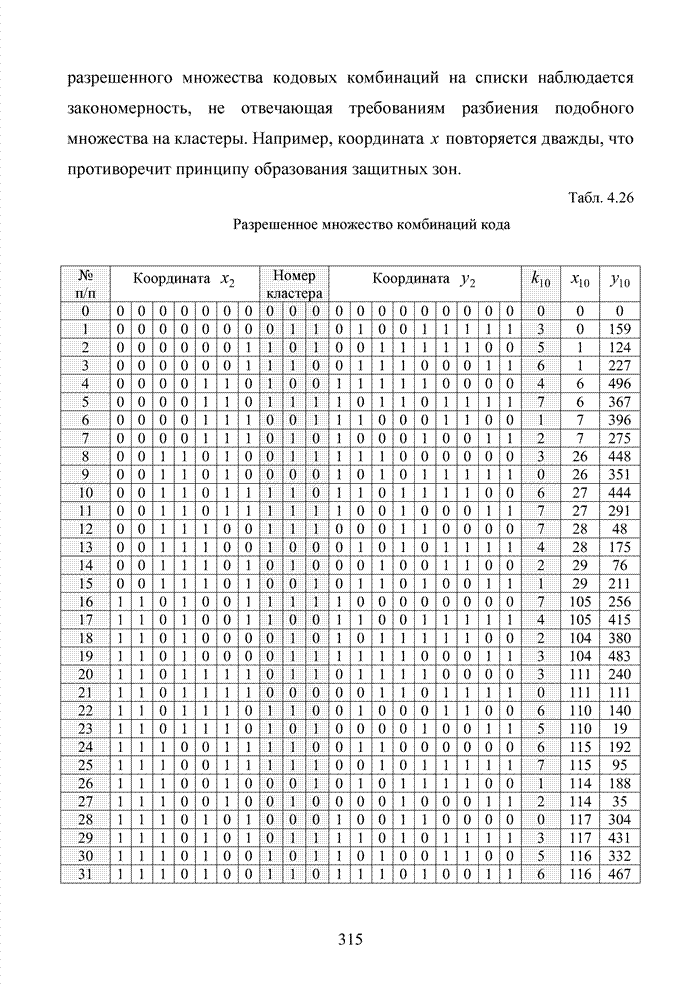
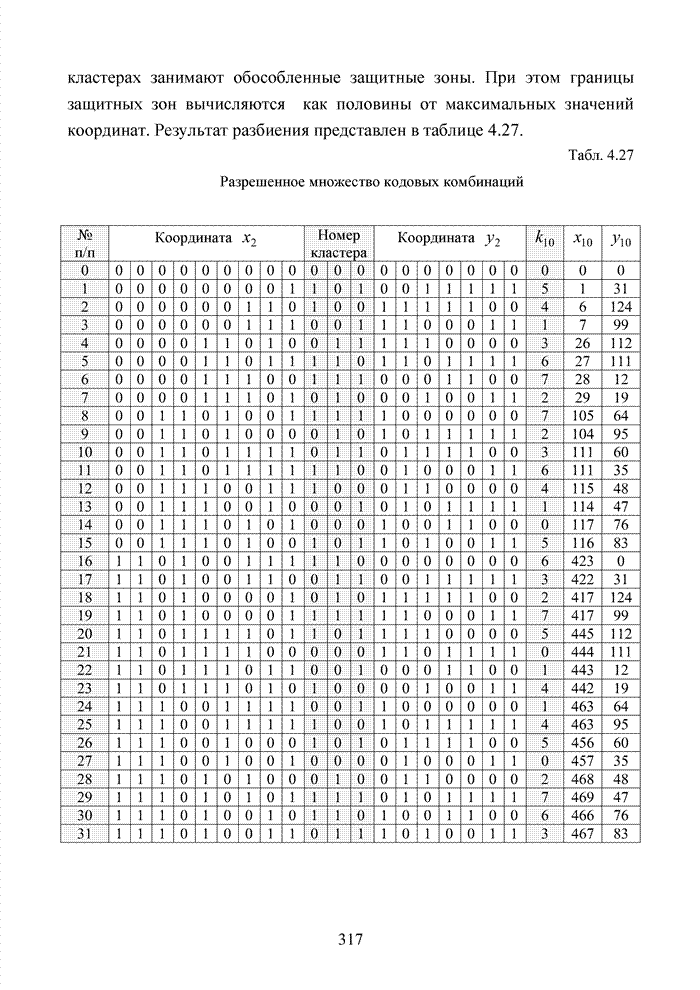
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.9. Поле как алгебраическая структура
Группы можно получать, задавая на множествах несколько операций. Но множества с несколькими операциями возникали и раньше, причем более «естественно», чем в случае групп, и первым из таких множеств было множество целых чисел.
На множестве целых чисел существует две наиболее важные и наиболее естественные операции: сложение и умножение. Каждую из этих операций в отдельности мы уже рассматривали и знаем, что целые числа образуют (коммутативную) группу по сложению и (также коммутативную) группу по умножению. Но известно также, что на множестве целых чисел операция сложения связана с операцией умножения законом дистрибутивности (правило раскрытия скобок), то есть для любых трех целых чисел а, b и с выполняется соотношение (а + b)c = ac + bc.
Объекты с двумя заданными на них операциями, удовлетворяющими этим условиям, называются кольцами. Если операция умножения коммутативна, то говорят, что кольцо коммутативно.
Рассмотрим множество четных чисел. На подобном множестве обычно принято рассматривать операции сложение и умножение. Известно, что четные числа образуют группу по сложению и по умножению, так как произведение двух четных чисел – число четное, а умножение – ассоциативно. Поскольку сложение и умножение четных чисел связаны законом дистрибутивности (так как этот закон выполняется для любых трех четных чисел), то мы действительно получаем кольцо, причем, как очевидно, коммутативное кольцо.
Все действительные числа образуют кольцо относительно обычных операций сложения и умножения. Все положительные и отрицательные целые числа вместе с нолем также образуют кольцо относительно обычных операций сложения им умножения. Оба эти кольца коммутативны.
Совокупность всех квадратных матриц некоторого порядка с целыми и действительными элементами является кольцом относительно операций матричного сложения и матричного умножения, причем это кольцо некоммутативно.
Совокупность всех многочленов с целыми коэффициентами и одним
неизвестным (или переменным является коммутативным кольцом.) Выражения вида ![]() , где a0, a1,
…, an являются целыми числами, называются
многочленами с целочисленными коэффициентами. Задание операций на множестве
многочленов существенно упрощается, если члены многочлена записать в обратном
порядке:
, где a0, a1,
…, an являются целыми числами, называются
многочленами с целочисленными коэффициентами. Задание операций на множестве
многочленов существенно упрощается, если члены многочлена записать в обратном
порядке: ![]() и,
кроме того, не обращать внимание на степень многочлена.
и,
кроме того, не обращать внимание на степень многочлена.
Говорят, что многочлен f(x) совпадает с многочленом ![]() , если равенства b0 = a0, b1 = a1,… выполняются до тех пор, пока существуют как
коэффициенты bi ,
так и коэффициенты ai; если же какой-нибудь из коэффициентов ai или bi не существует, то коэффициент
другого многочлена с тем же номером либо также не существует, либо равен нулю.
, если равенства b0 = a0, b1 = a1,… выполняются до тех пор, пока существуют как
коэффициенты bi ,
так и коэффициенты ai; если же какой-нибудь из коэффициентов ai или bi не существует, то коэффициент
другого многочлена с тем же номером либо также не существует, либо равен нулю.
Суммой h(x) = f(x) + g(x) многочленов f(x) и g(x) называется многочлен
![]() ,
,
при этом предполагается, что n
≥ k и в многочлене g(x)
«отсутствующие» коэффициенты заменены нулями. Относительно определенной таким
образом операции сложения многочлены образуют коммутативную группу, поскольку
при любом ![]() может
стоять произвольное целое число, а целые числа образуют кольцо.
может
стоять произвольное целое число, а целые числа образуют кольцо.
Произведением k(x) = f(x)g(x) многочленов f (x) и g(x) называется многочлен
![]() .
.
Можно доказать, что введенная подобным образом операция умножения многочленов ассоциативна.
Известно, что любое целое число можно (по существу единственным способом) представить в виде произведения простых чисел. Решение алгебраических уравнений высоких степеней весьма упрощается тем, что многочлены допускают аналогичные разложения. Всякий многочлен (например, с рациональными коэффициентами) можно представить в виде произведения неразложимых далее многочленов (также с рациональными коэффициентами), причём это разложение в определённом смысле единственно. Известно, что для любых двух целых чисел существует наибольший общий делитель: аналогичное утверждение справедливо и для любых двух многочленов. Известно также, что во множестве целых чисел деление без остатка может оказаться невыполнимой операцией, но всегда выполнимо деление с остатком. Аналогичное утверждение можно доказать и для многочленов. Все это свидетельствует о том, кольца целых чисел и многочленов, обладают выраженным сходством.
К наиболее важным общим
свойствам относится разложение целых чисел в произведение простых чисел и
разложением многочленов в произведение неразложимых множителей. Оба разложения
следует из осуществимости операции «деление с остатком» на множествах целых
чисел и многочленов. Для любого целого числа ![]() и отличного от нуля целого числа
и отличного от нуля целого числа ![]() всегда найдутся такие
целые числа
всегда найдутся такие
целые числа ![]() и
и
![]() , что
, что
![]() при этом
при этом ![]() .
.
По аналогии. Для любого
многочлена ![]() и
не обращающегося тождественно в ноль многочлена
и
не обращающегося тождественно в ноль многочлена ![]() существуют такие многочлены
существуют такие многочлены ![]() и
и ![]() , что
, что ![]() , где степень многочлена
, где степень многочлена ![]() меньше степени
многочлена
меньше степени
многочлена ![]() или
или
![]() , т.е. все коэффициенты
многочлена
, т.е. все коэффициенты
многочлена ![]() равны
нулю.
равны
нулю.
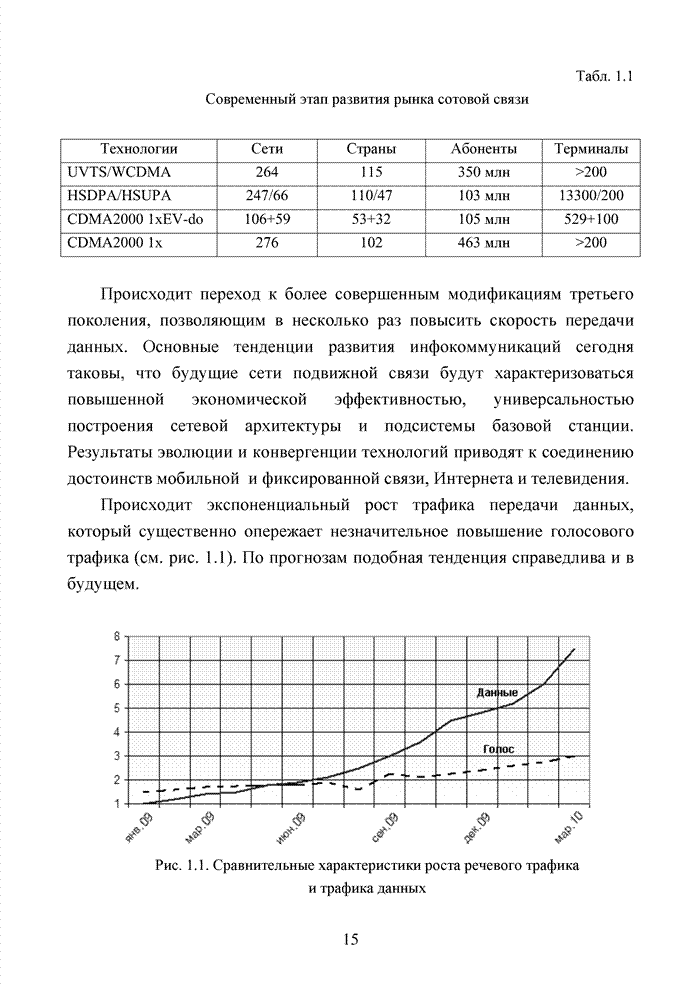
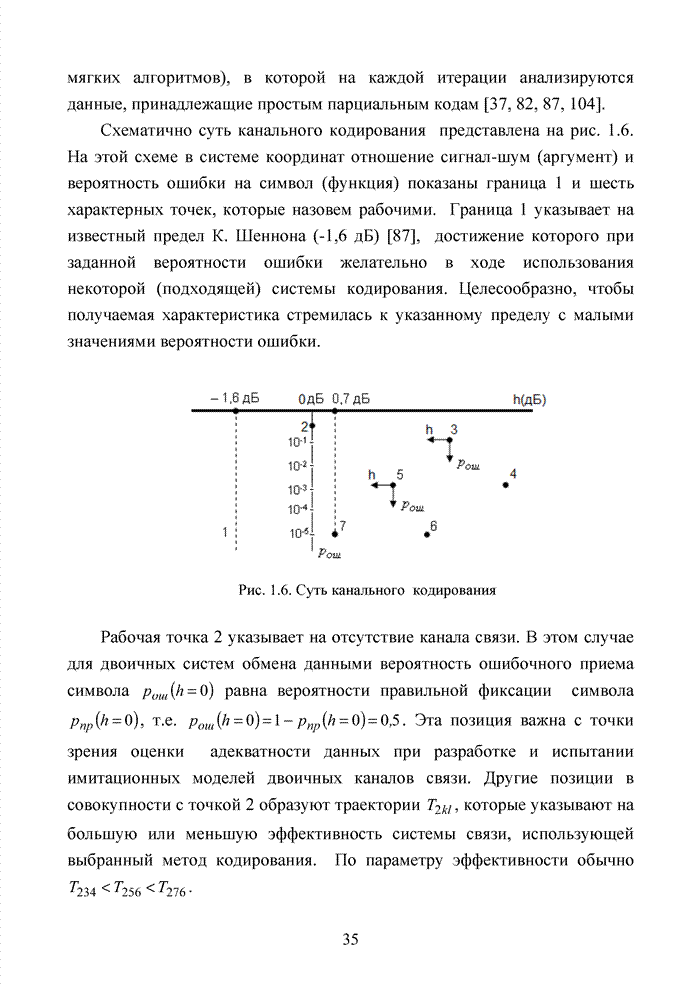
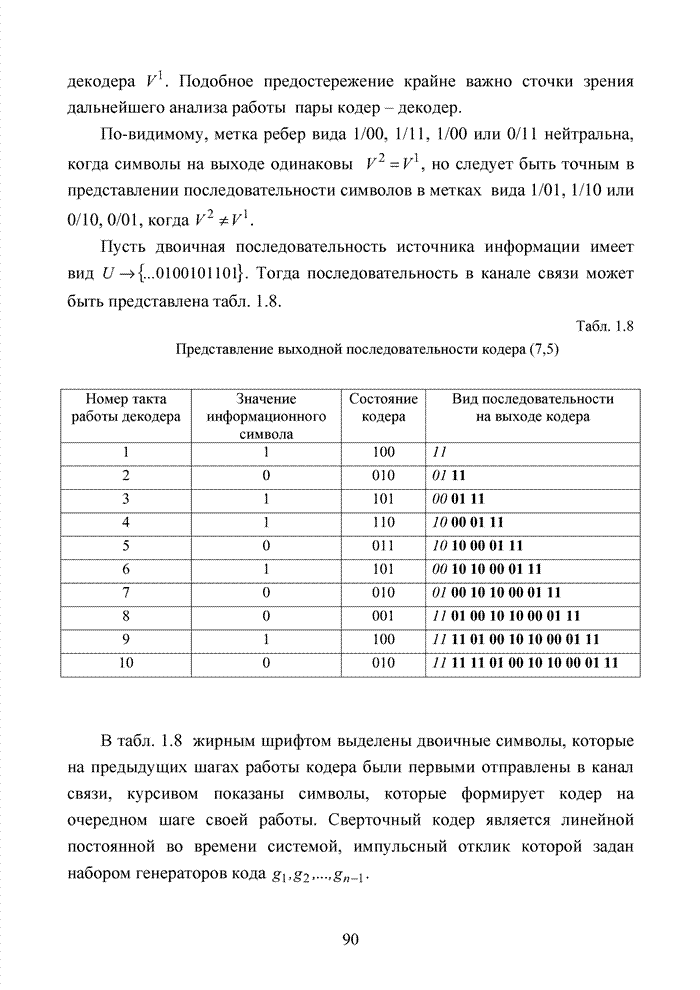
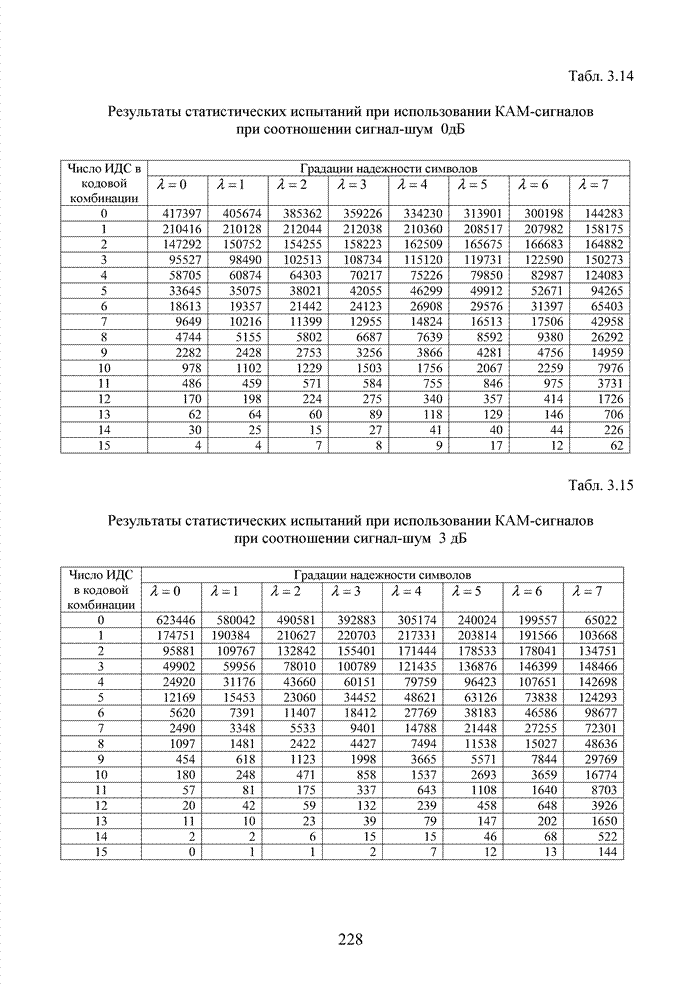
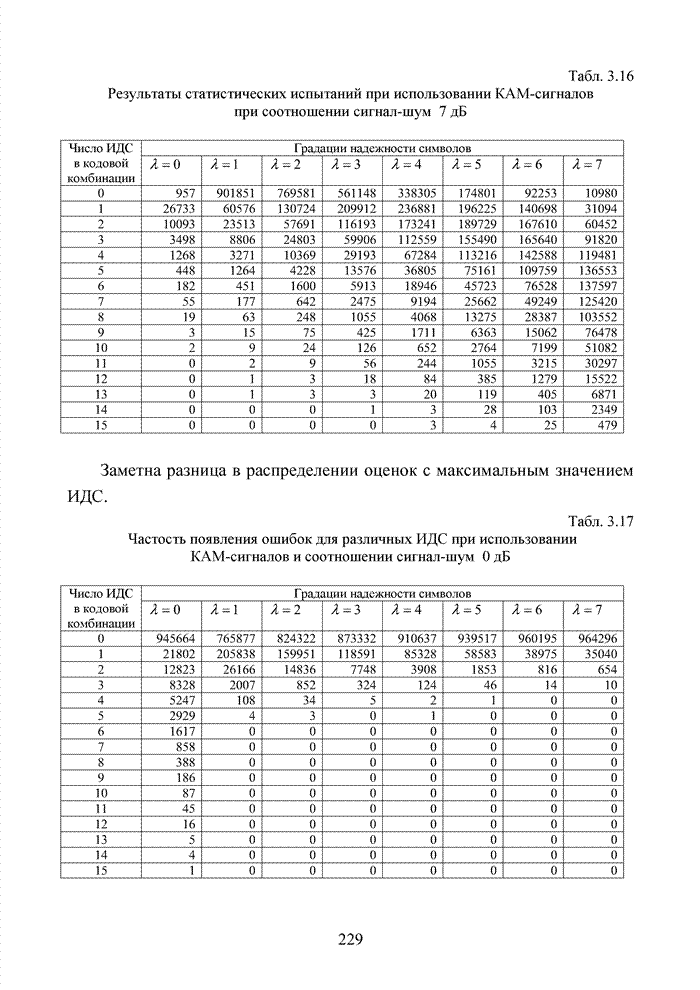
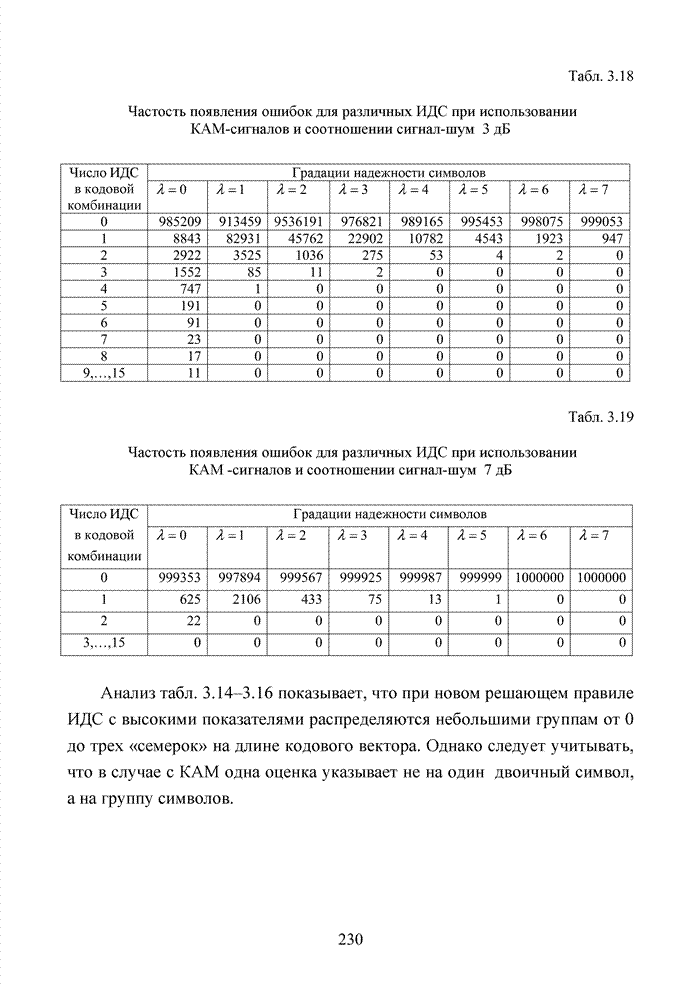
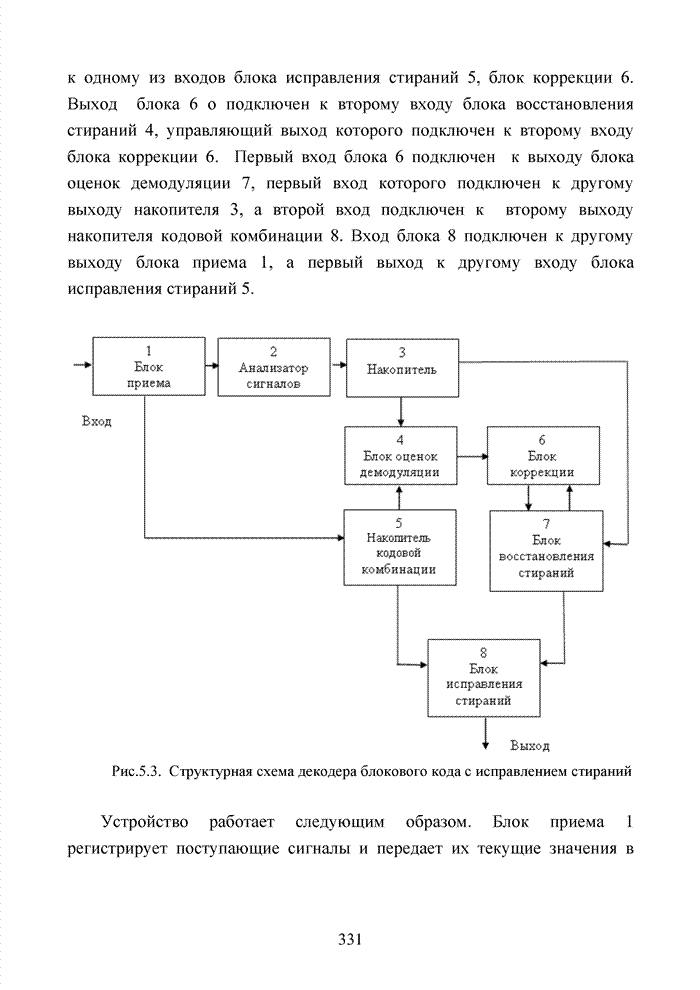
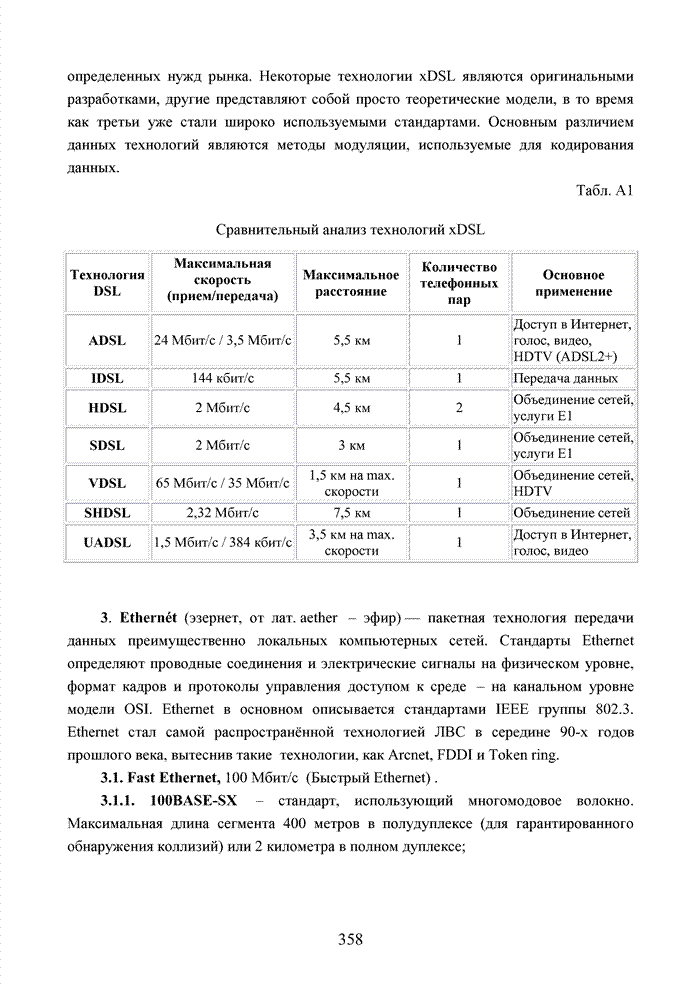
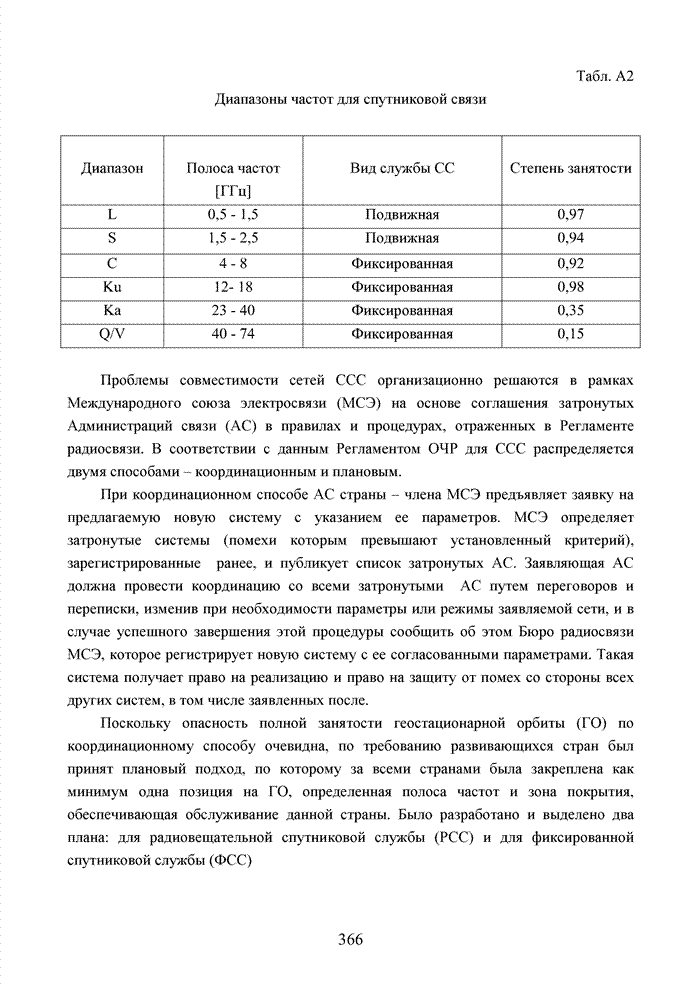
В современных системах кодирования информации широко используются недвоичные коды [105]. Это связано с тем, что подобные коды в наибольшей степени отвечают передовым методам формирования сигналов в виде сигнально-кодовых конструкций, позволяющих существенно повысить общую эффективность системы связи. Практика применения таких кодов опирается на алгебраическую систему, которая получила название поле. В поле, как и в кольце, определены две основные операции (сложение и умножение) и для каждой из них обратные операции (вычитание и деление).
Полем называется коммутативное кольцо с единичным элементом относительно умножения (единичный мультипликативный элемент кольца), в котором каждый ненулевой элемент имеет мультипликативный обратный элемент (т.е. обратный по умножению).
Ненулевые элементы поля
удовлетворяют всем аксиомам группы и, следовательно, образуют мультипликативную
группу (т.е. группу относительно умножения). Для любого числа ![]() , являющегося степенью
простого числа, существует поле, содержащее
, являющегося степенью
простого числа, существует поле, содержащее ![]() элементов. Это означает, что
минимальное число элементов, образующих поле должно быть всего два.
Действительно, вместе значения 0 и 1 образуют поле. При этом поле содержит два
единичных элемента: 0 относительно операции сложения и 1 относительно операции
умножения. Однако множество элементов кольца относительно операции сложения
коммутативно и образует группу, следовательно, должно выполняться свойство замкнутости,
характерное аддитивной группе. Но 1+1=2, и, следовательно, указанное свойство
нарушается до тех пор, пока операция сложения не будет уточнена как сложение
по
элементов. Это означает, что
минимальное число элементов, образующих поле должно быть всего два.
Действительно, вместе значения 0 и 1 образуют поле. При этом поле содержит два
единичных элемента: 0 относительно операции сложения и 1 относительно операции
умножения. Однако множество элементов кольца относительно операции сложения
коммутативно и образует группу, следовательно, должно выполняться свойство замкнутости,
характерное аддитивной группе. Но 1+1=2, и, следовательно, указанное свойство
нарушается до тех пор, пока операция сложения не будет уточнена как сложение
по ![]() 2, т.е.
2, т.е. ![]() . И поскольку в общем
случае в кольце должно выполняться
. И поскольку в общем
случае в кольце должно выполняться ![]() , то (0)(1)=0, а (1)(1)=1.
, то (0)(1)=0, а (1)(1)=1.
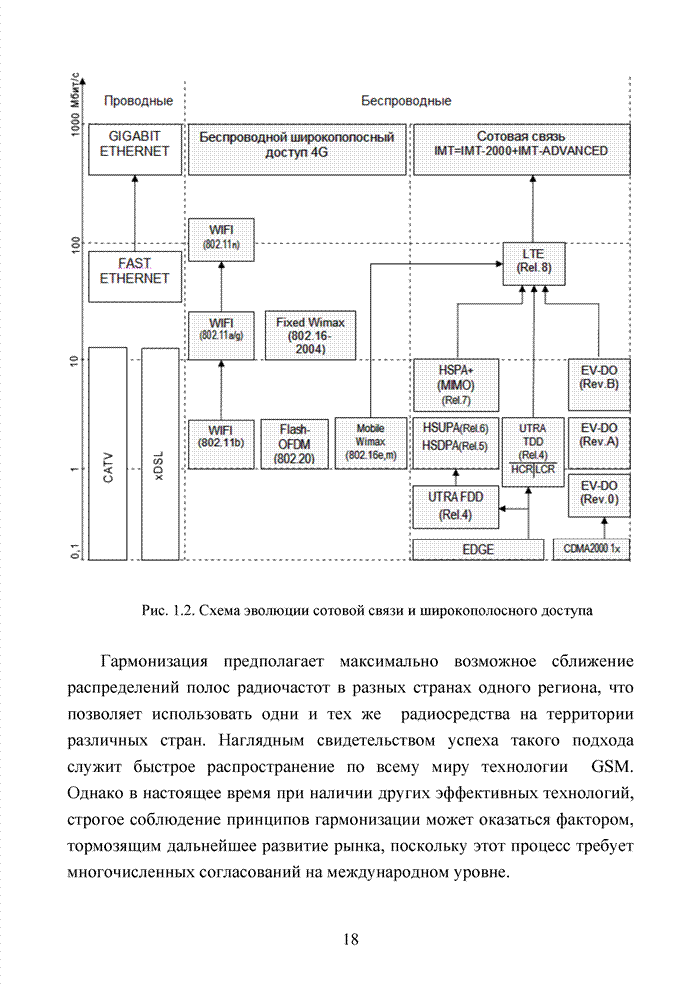
Расширениями поля
рациональных чисел являются поля вещественных и комплексных чисел, которые
содержат бесконечное множество элементов. В каналах связи множество
передаваемых сигналов конечно, поэтому в системах канального кодирования и в
системах записи информации на носители используются поля, содержащие
ограниченное число элементов. Приведенное выше простейшее поле получило
название двоичного поля Галуа и его принято обозначать через ![]() . В высшей алгебре
доказывается, что число элементов
. В высшей алгебре
доказывается, что число элементов ![]() конечного поля всегда удовлетворяет
условию
конечного поля всегда удовлетворяет
условию ![]() , где
, где
![]() – простое, а
– простое, а
![]() Значение
Значение ![]() называют
характеристикой поля [8, 15, 80]. Невозможно образовать поле с числом
элементов, равным
называют
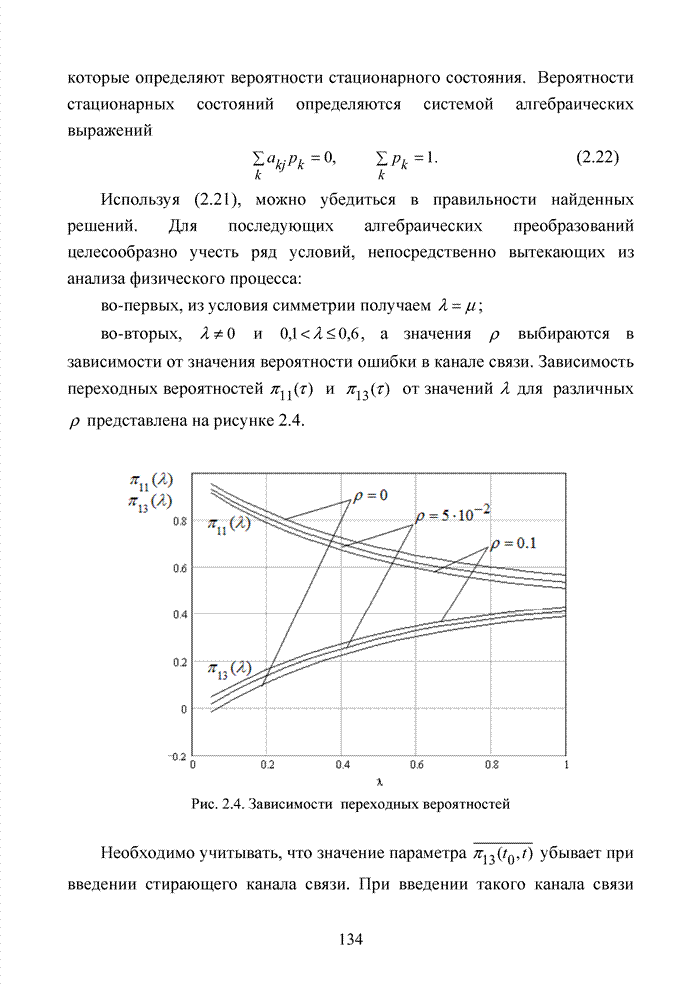
характеристикой поля [8, 15, 80]. Невозможно образовать поле с числом
элементов, равным ![]() или
или
![]() , или
, или ![]() и т.п. Можно построить
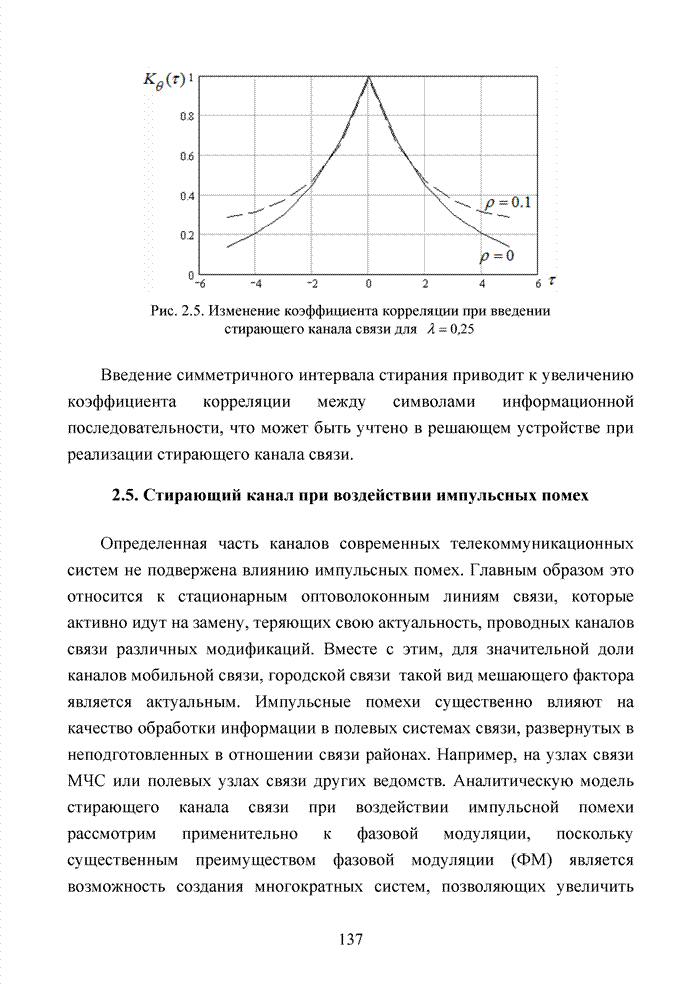
поле с числом элементов равным
и т.п. Можно построить
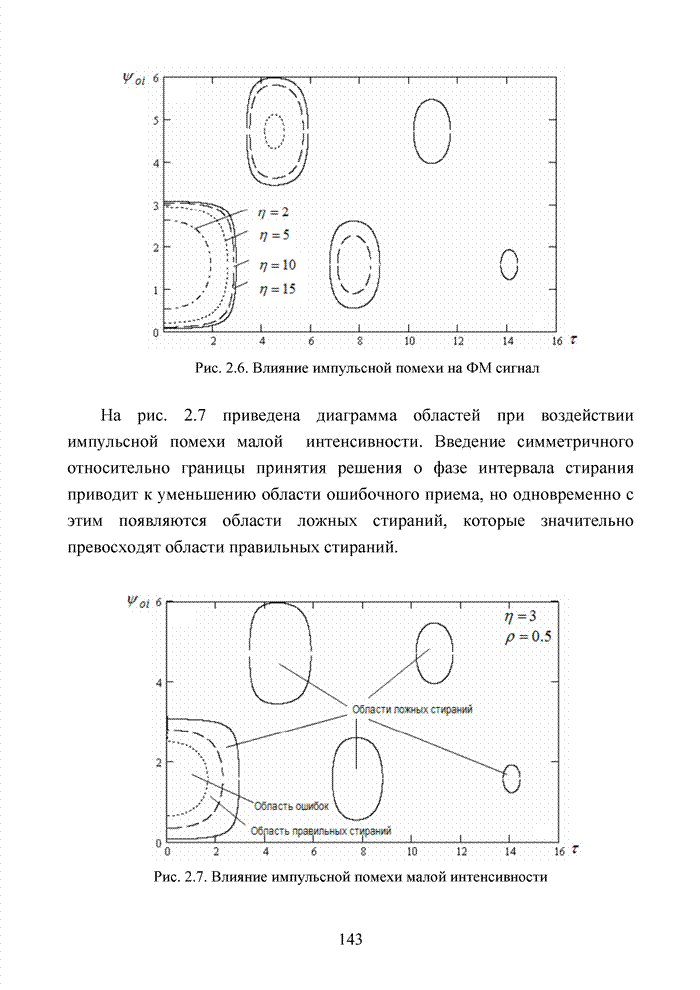
поле с числом элементов равным ![]() ;
; ![]() ;
; ![]() ;
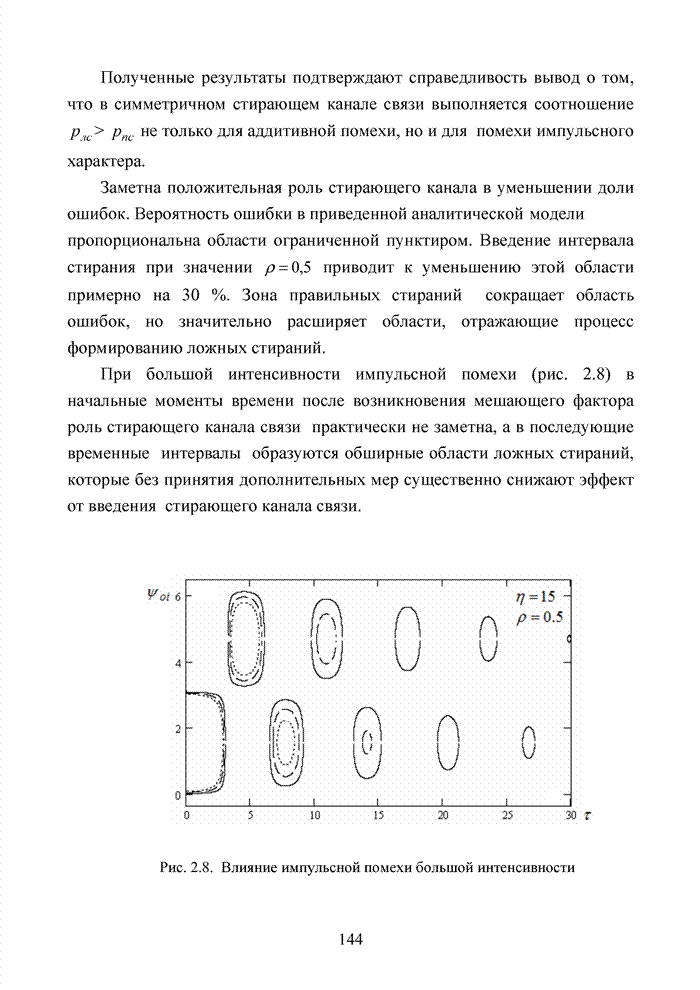
; ![]() и т.п.
и т.п.
Если число элементов ![]() некоторого множества
этому условию не удовлетворяет, то для такого множества невозможно определить
операции сложения и умножения в поле. Для простоты положим
некоторого множества
этому условию не удовлетворяет, то для такого множества невозможно определить
операции сложения и умножения в поле. Для простоты положим ![]() , тогда операции сложения и
умножения выполняются по mod
, тогда операции сложения и
умножения выполняются по mod ![]() . Пусть
. Пусть ![]() , тогда результаты
сложения двух любых элементов поля
, тогда результаты
сложения двух любых элементов поля ![]() (mod 7) и результаты умножения чисел
(mod 7) и результаты умножения чисел ![]() (mod 7) удобно представить в виде схем, показанных на рис.
1.11.
(mod 7) удобно представить в виде схем, показанных на рис.
1.11.


Рис. 1.11. Схемы сложения и умножения в поле q=7
Из теории полей Галуа
известно, что в поле, содержащем q элементов, существует, по крайней мере один примитивный элемент ![]() такой, что каждый
ненулевой элемент из
такой, что каждый
ненулевой элемент из ![]() может
быть представлен как некоторая степень этого элемента
может
быть представлен как некоторая степень этого элемента ![]() .
.
Это утверждение указывает
на то, что примитивных элементов может быть несколько. Оценим возможность
использовать простые числа 2, 3 и 5 в качестве примитивных элементов поля
характеристики 7. Пусть примитивами будут ![]() ;
; ![]() ; и
; и ![]() . Техника представления элементов поля
показана в табл. 1.6.
. Техника представления элементов поля
показана в табл. 1.6.
Табл.1.6 Представление
элементов поля ![]() через
примитивные элементы
через
примитивные элементы
|
|
|
|
|
20 = 1 |
30 = 1 |
50 = 1 |
|
21 = 2 |
31 = 3 |
51 = 5 |
|
22 = 4 |
32 = 9 (mod 7) = 2 |
52 = 25 (mod 7) = 4 |
|
23 = 8 (mod 7) = 1 |
33 = 27 (mod 7) = 6 |
53 = 125 (mod 7) = 6 |
|
24 = 16(mod 7) = 4 |
34 = 81 (mod 7) = 4 |
54 = 625 (mod 7) = 2 |
|
25 =32(mod 7) = 4 |
35 = 243 (mod 7) = 5 |
55 = 3125 (mod 7) = 3 |
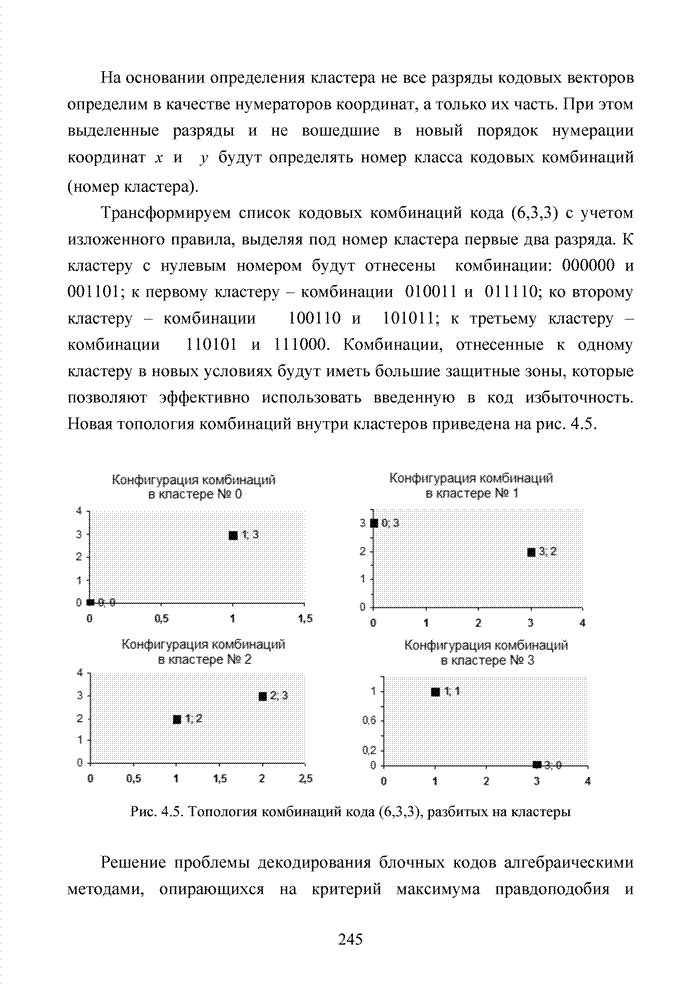
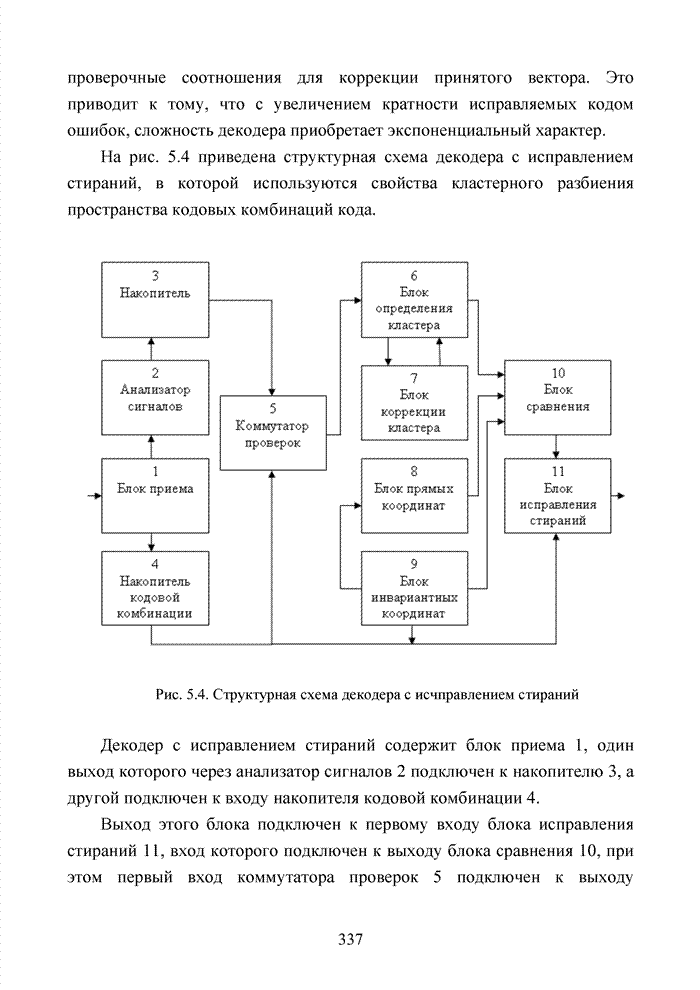
Становится ясно, что не
каждое простое число может являться примитивным элементом поля некоторой
характеристики. Поскольку теория кодирования оперирует главным образом полем
характеристики 2, рассмотрим методы построения двоичных полей Галуа степени
расширения ![]() ,
т.е.
,
т.е. ![]() . Каждый
элемент
. Каждый
элемент ![]() представляется
в виде полиномов с двоичными коэффициентами, степень которых не превосходит
представляется
в виде полиномов с двоичными коэффициентами, степень которых не превосходит ![]() . Сложение многочленов
выполняется по правилу сложения в
. Сложение многочленов
выполняется по правилу сложения в ![]() , а умножение элементов определяется как
умножение представляющих эти элементы многочленов по модулю некоторого
заданного неприводимого многочлена над
, а умножение элементов определяется как
умножение представляющих эти элементы многочленов по модулю некоторого
заданного неприводимого многочлена над ![]() . Например, для
. Например, для ![]() из 24 элементов
может быть образовано как поле многочленов над полем характеристики 2 по модулю
многочлена
из 24 элементов
может быть образовано как поле многочленов над полем характеристики 2 по модулю
многочлена ![]() .
Тогда корнем этого многочлена является примитивный элемент
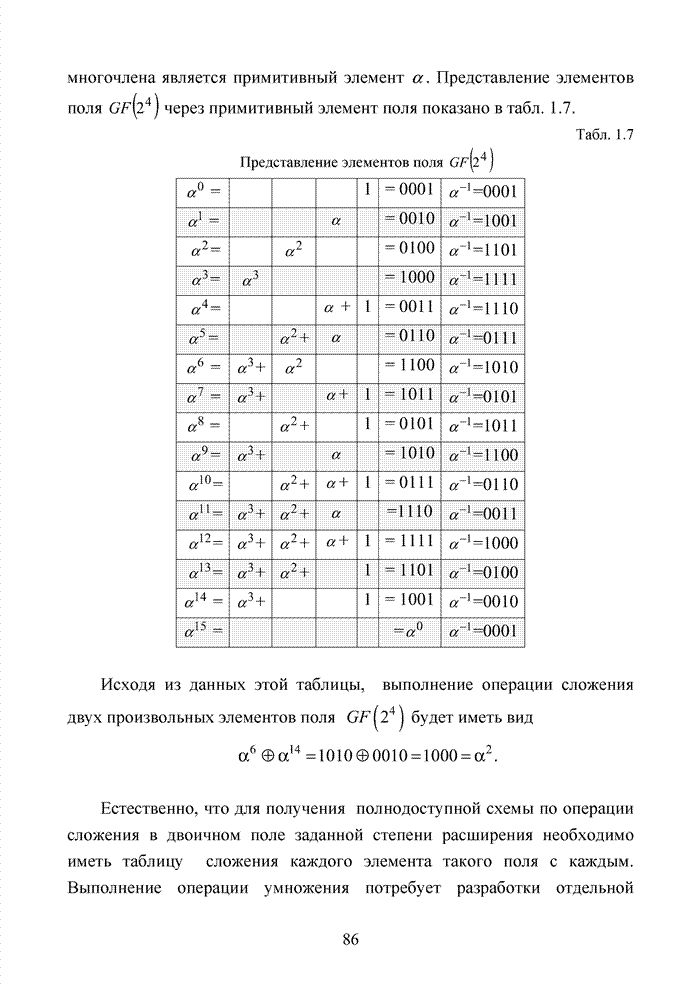
.
Тогда корнем этого многочлена является примитивный элемент ![]() . Представление элементов поля
. Представление элементов поля ![]() через примитивный
элемент поля показано в табл. 1.7.
через примитивный
элемент поля показано в табл. 1.7.
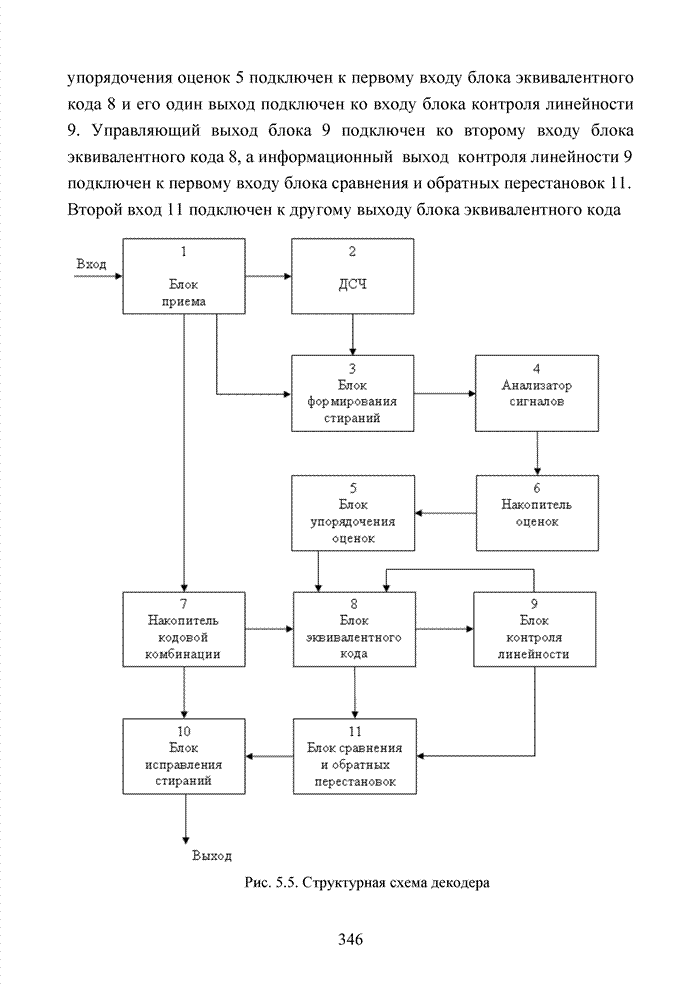
Табл. 1.7 Представление элементов поля ![]()
|
|
|
|
|
1 |
= 0001 |
|
|
|
|
|
|
|
= 0010 |
|
|
|
|
|
|
|
= 0100 |
|
|
|
|
|
|
|
= 1000 |
|
|
|
|
|
|
1 |
= 0011 |
|
|
|
|
|
|
|
= 0110 |
|
|
|
|
|
|
|
= 1100 |
|
|
|
|
|
|
1 |
= 1011 |
|
|
|
|
|
|
1 |
= 0101 |
|
|
|
|
|
|
|
= 1010 |
|
|
|
|
|
|
1 |
= 0111 |
|
|
|
|
|
|
|
=1110 |
|
|
|
|
|
|
1 |
= 1111 |
|
|
|
|
|
|
1 |
= 1101 |
|
|
|
|
|
|
1 |
= 1001 |
|
|
|
|
|
|
|
= |
|
Исходя из данных этой
таблицы, выполнение операции сложения двух произвольных элементов поля ![]() будет иметь вид
будет иметь вид
![]() .
.
Естественно, что для получения полнодоступной схемы по операции сложения в двоичном поле заданной степени расширения необходимо иметь таблицу сложения каждого элемента такого поля с каждым. Выполнение операции умножения потребует разработки отдельной таблицы. Применение табличных значений способствует повышению скорости реализации процедуры кодирования (декодирования). Процедура сложения полиномов в реальных декодерах не вызывает принципиальных трудностей, однако, для выполнения операции умножения в поле некоторой характеристики используют табличное представление многочленов в виде целочисленных значений.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
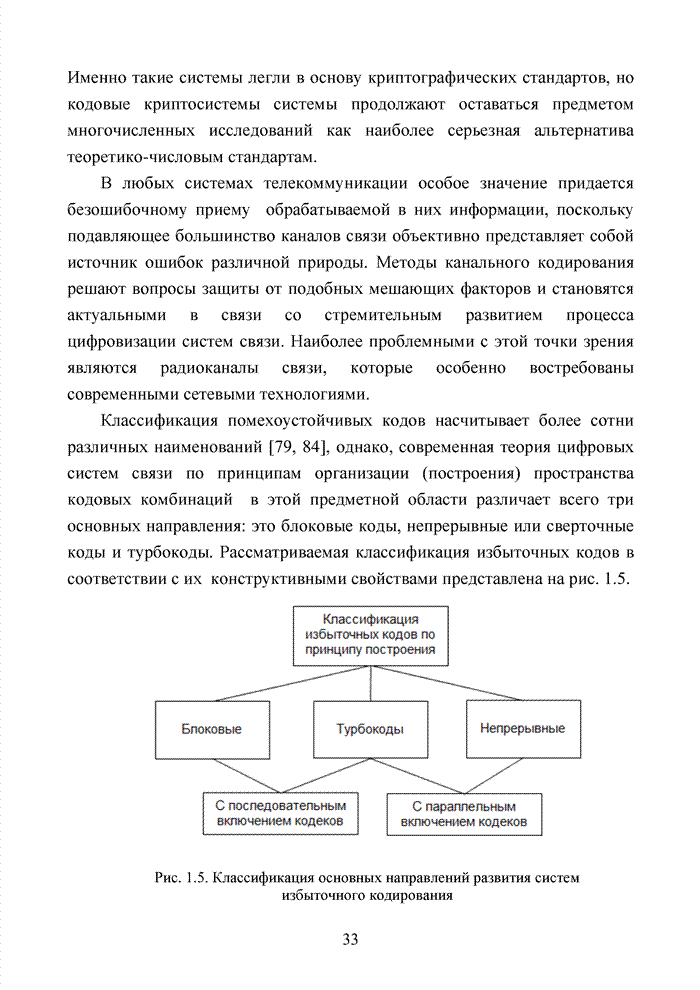
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
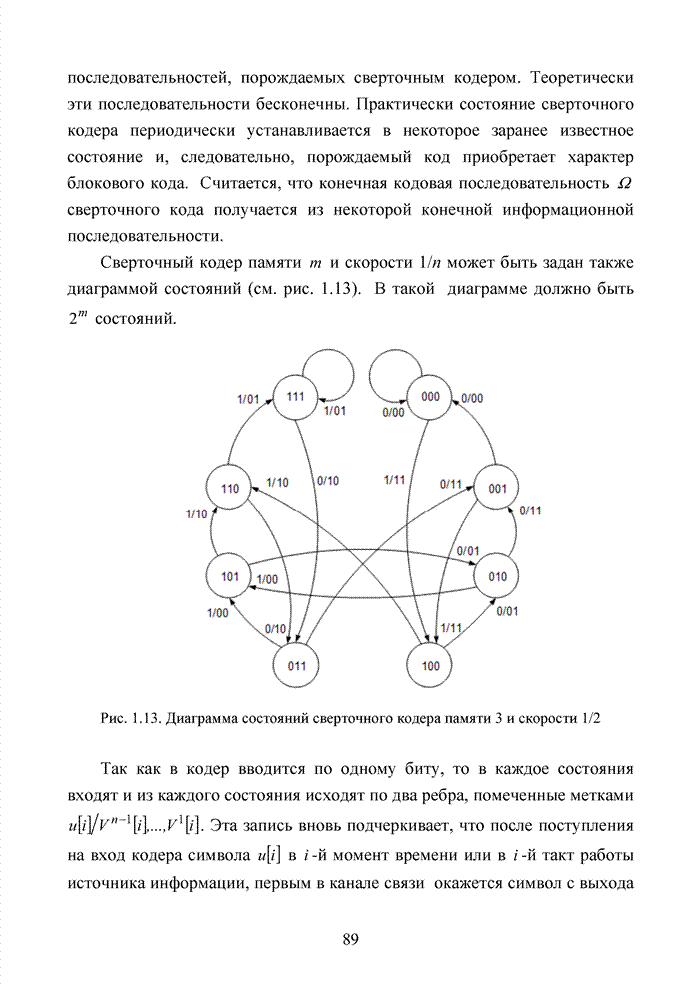
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
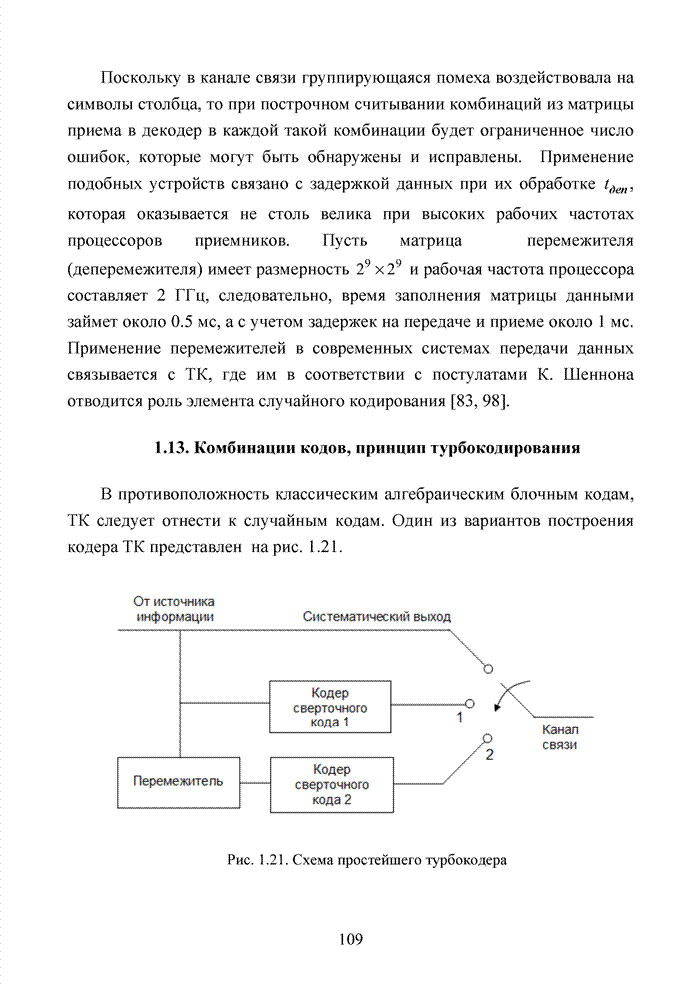
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
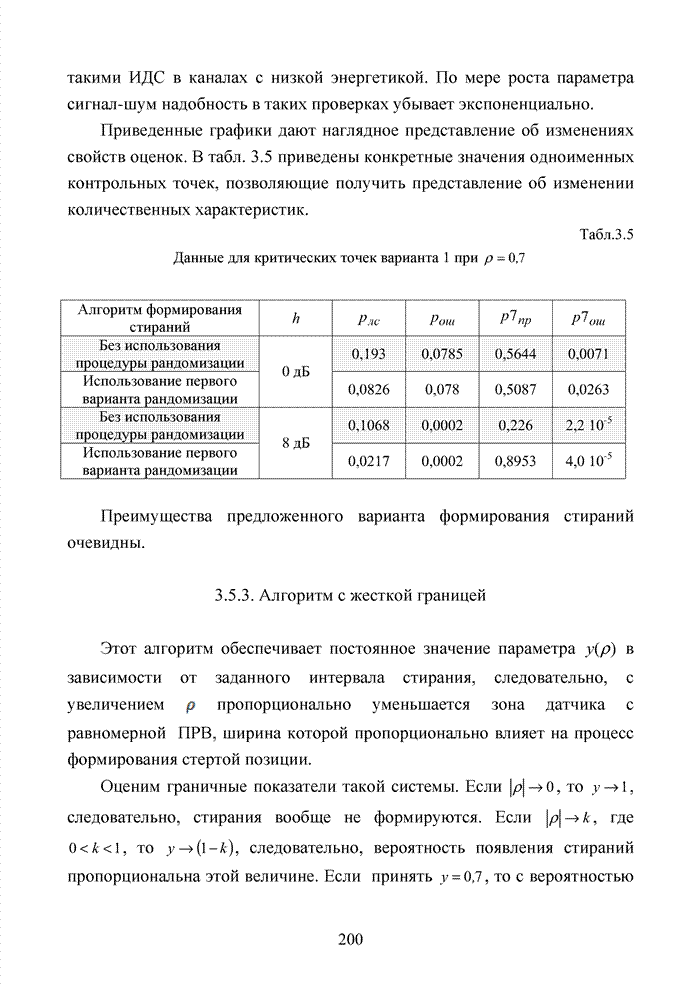
- 3.5.2. Алгоритм с динамично изменяющейся границей
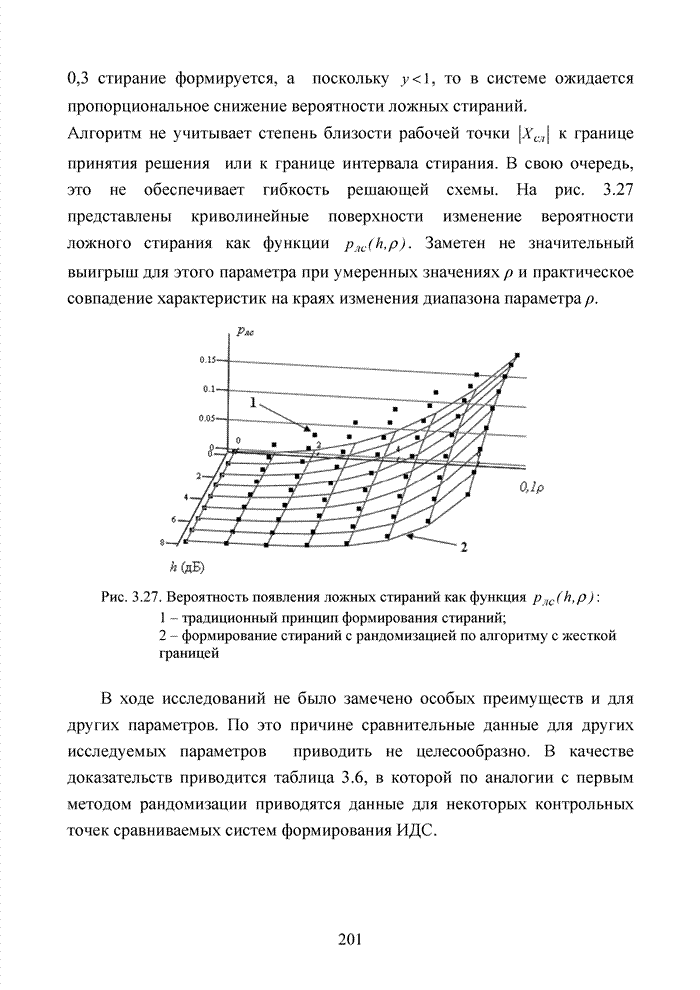
- 3.5.3. Алгоритм с жесткой границей
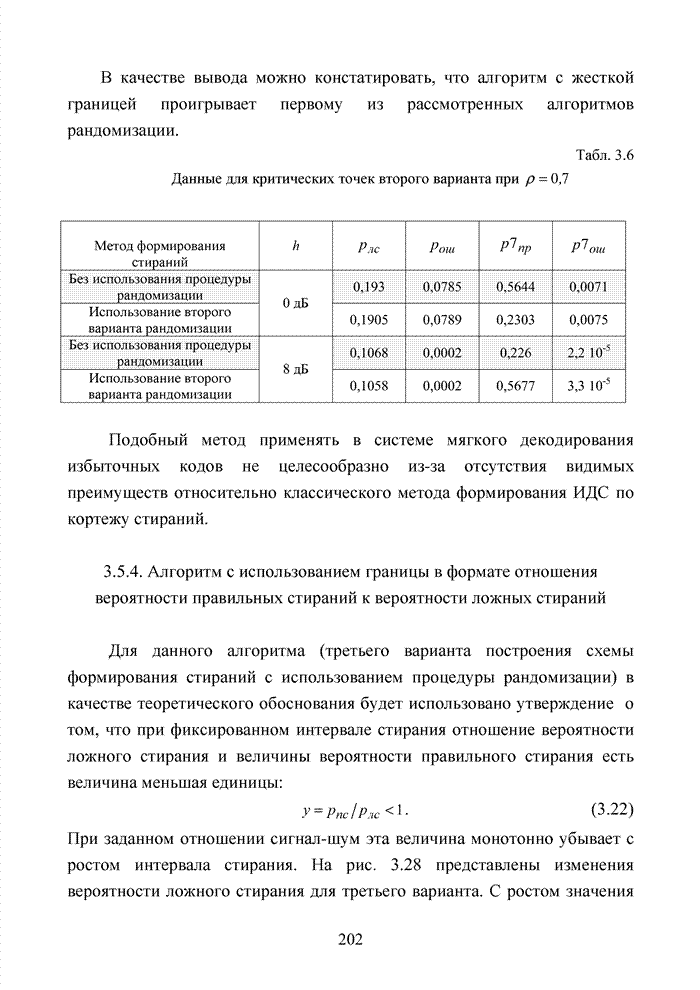
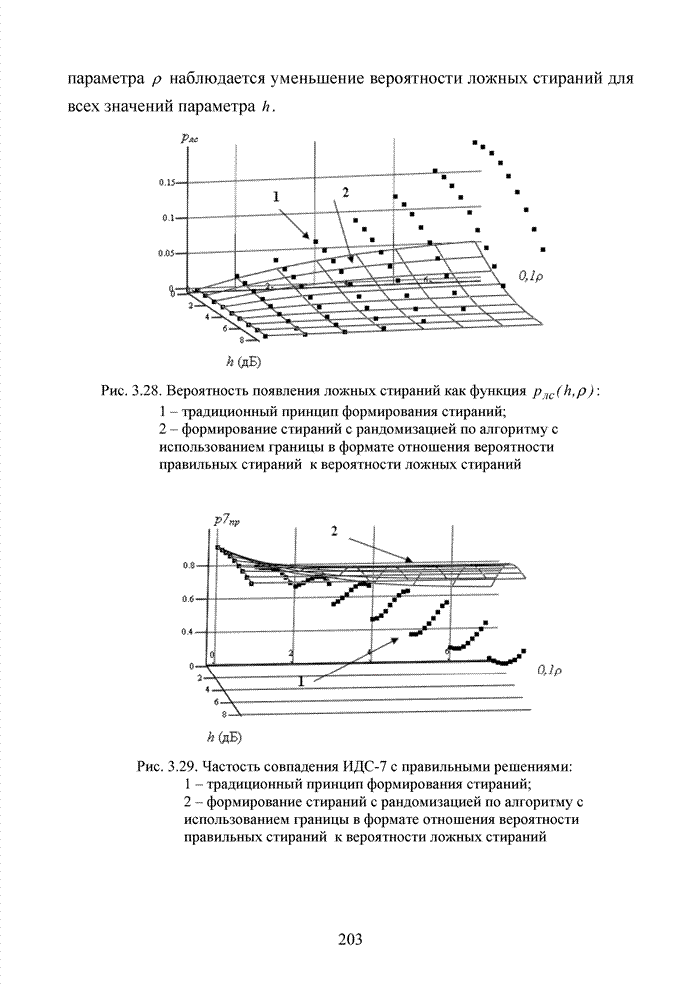
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
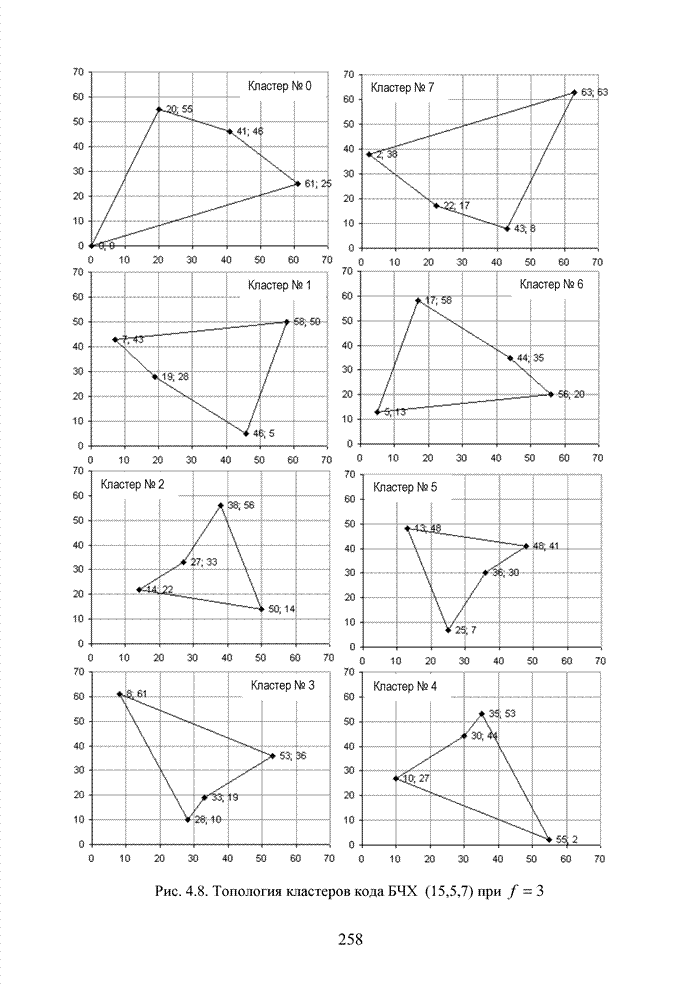
- 4.2. Кластерный подход к декодированию полиномиальных кодов
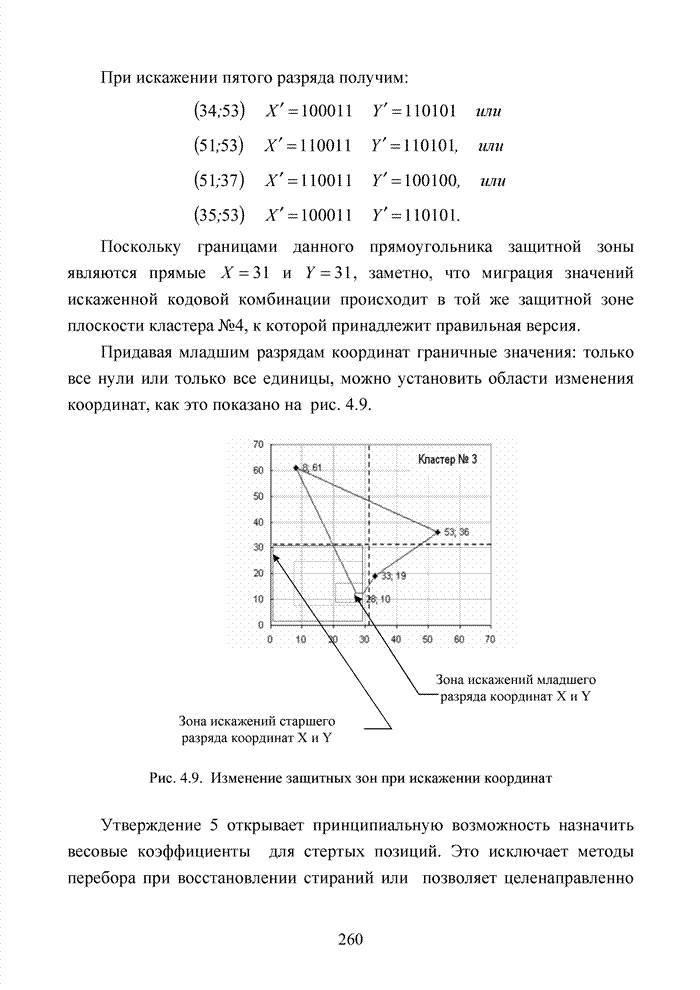
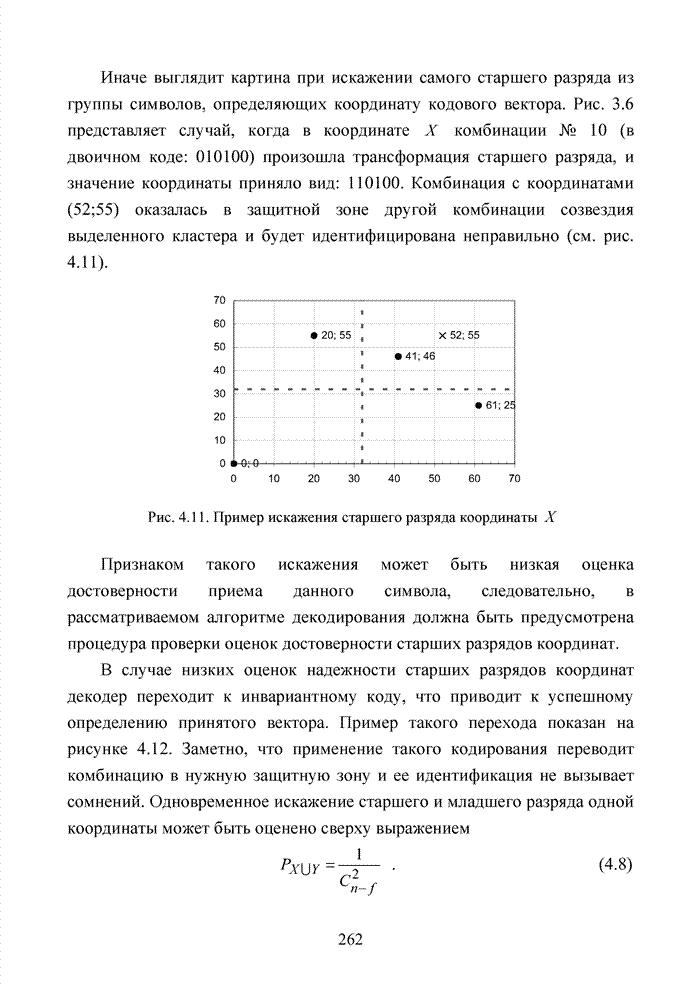
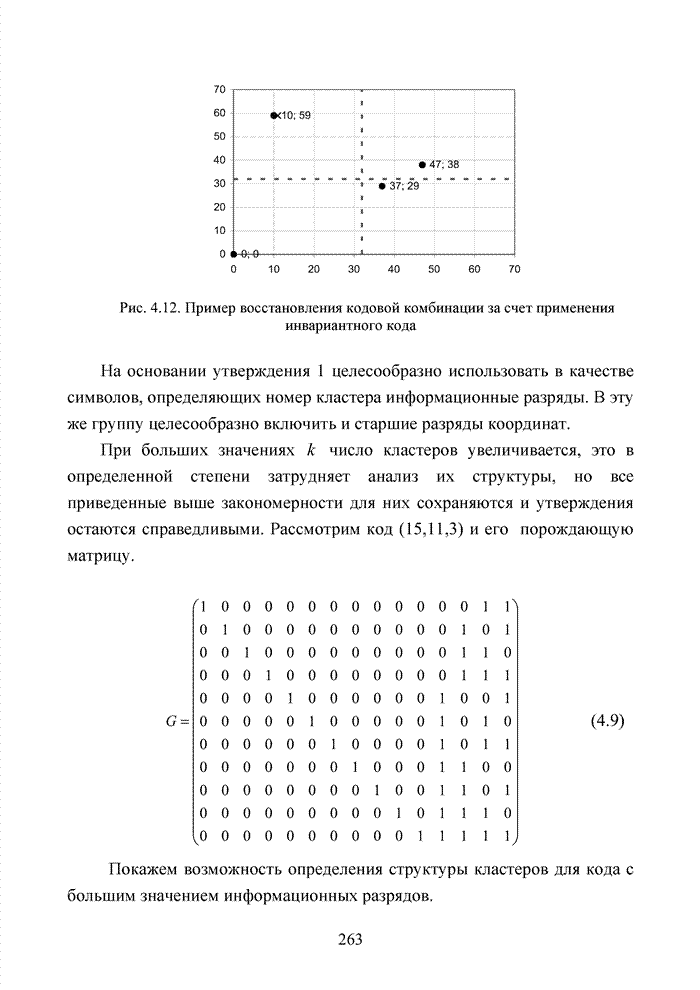
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
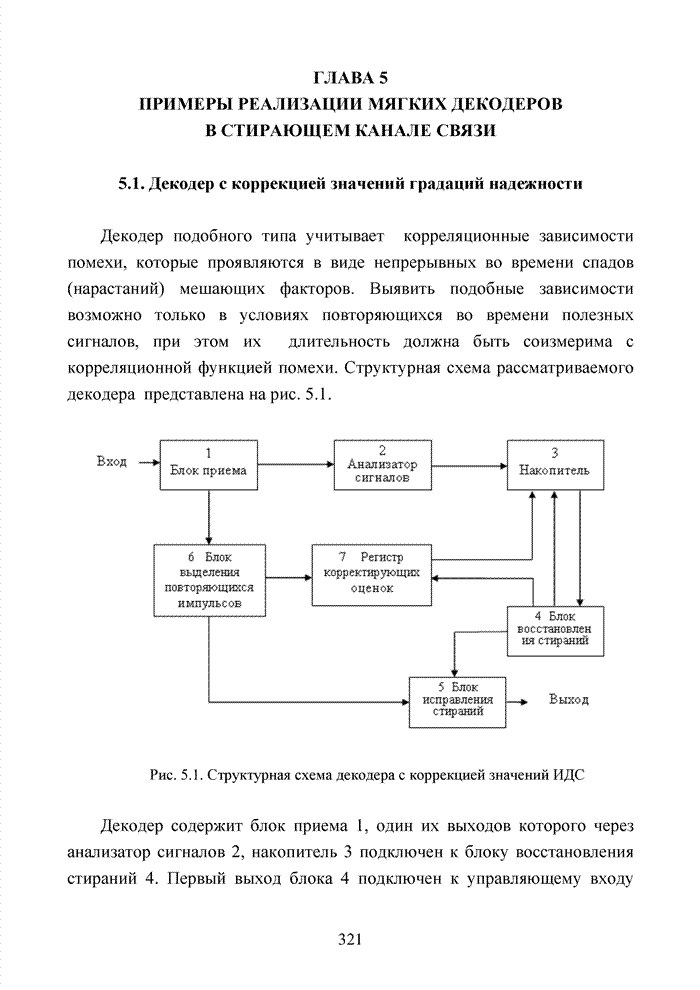
- 5.1. Декодер с коррекцией значений градаций надежности
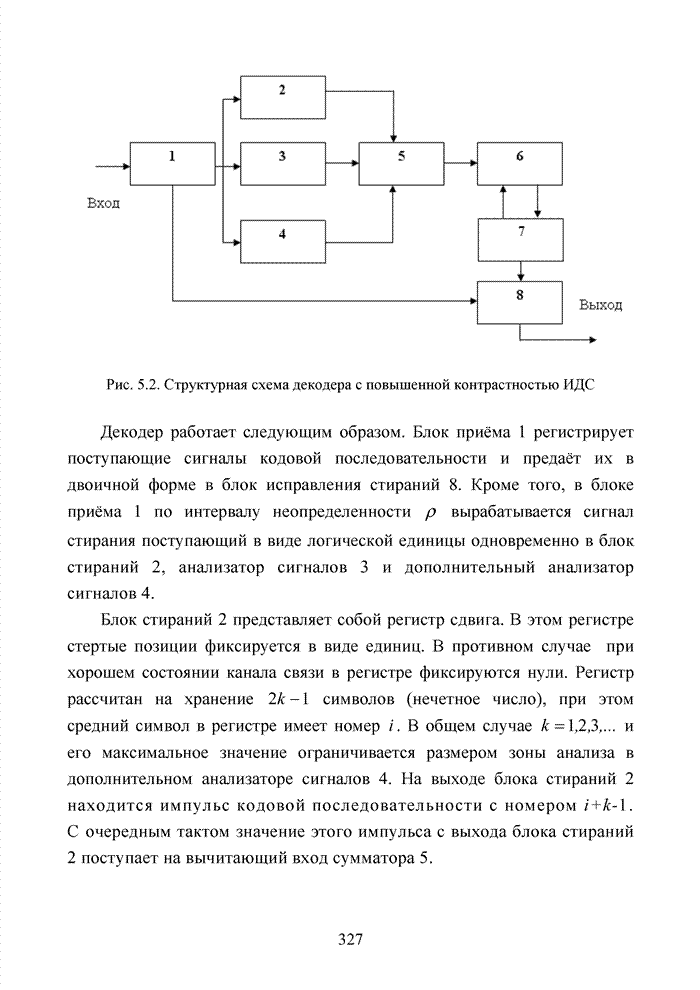
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
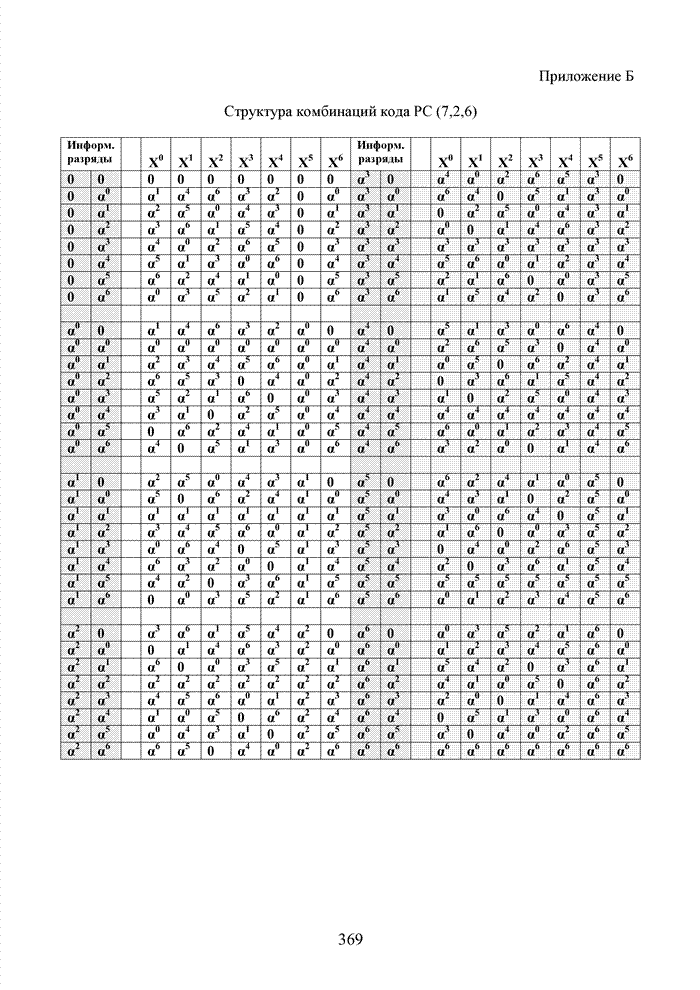
- Приложение Б Структура комбинаций кода РС (7,2,6)
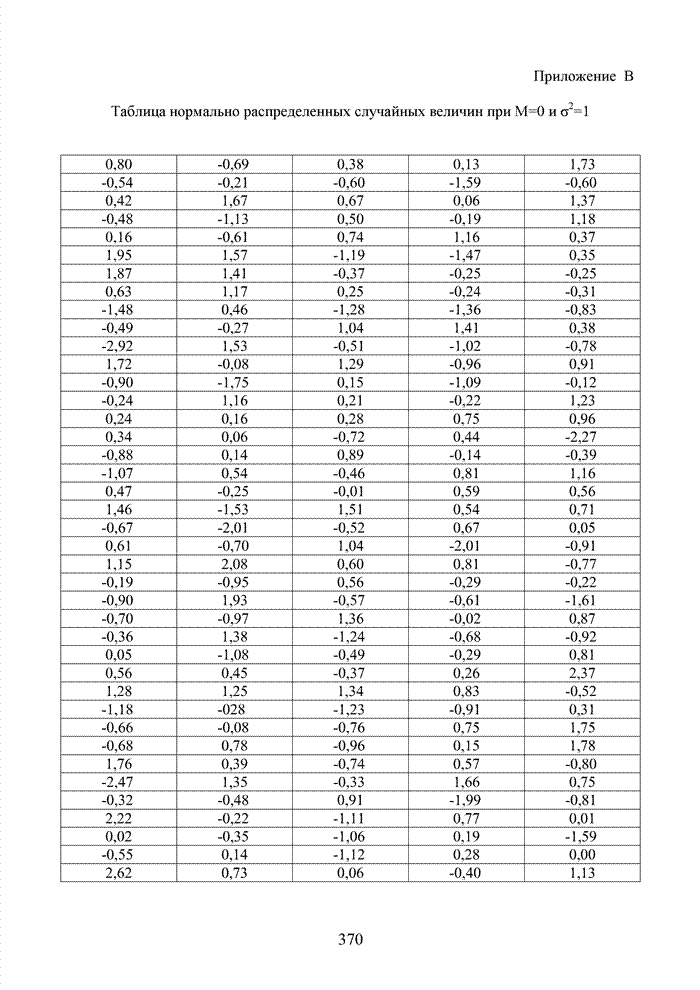
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК