| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
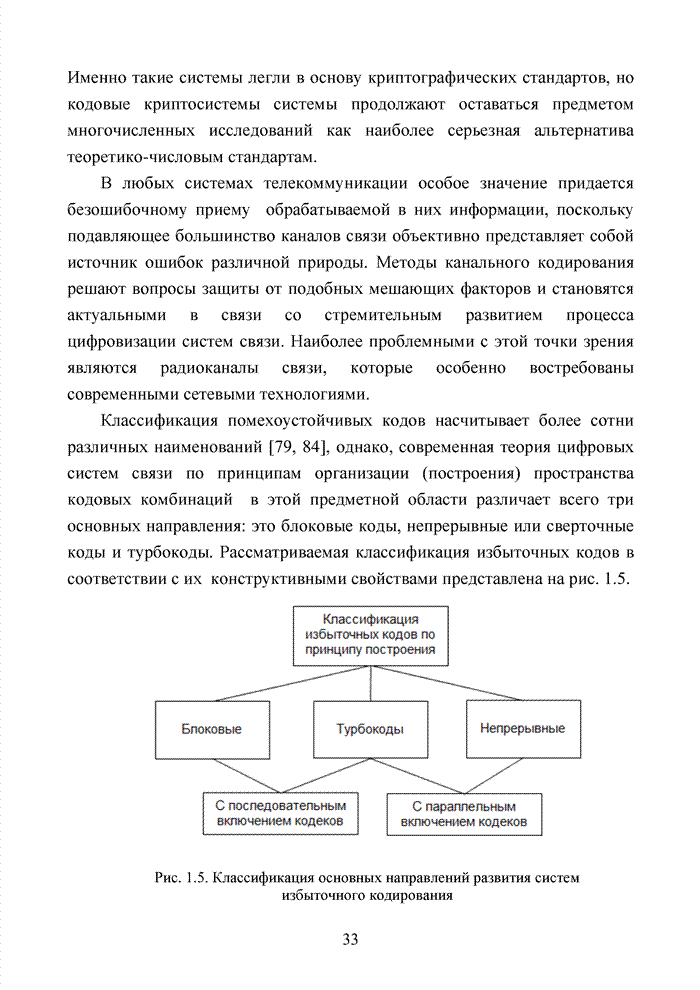
1.10. Непрерывные (сверточные) коды
Сверточные коды это коды, исправляющие ошибки, которые используют непрерывную, или последовательную, обработку информации короткими фрагментами (блоками). Сверточный кодер обладает памятью в том смысле, что символы на его выходе зависят не только от (очередного фрагмента) информационных символов на входе, но и предыдущих символов на его входе. Другими словами, кодер представляет собой последовательную машину или автомат с конечным числом состояний. Состояние кодера определяется содержимым его памяти.
Кодер использует ![]() элементов памяти
элементов памяти ![]() , при этом ясно, что скорость
кода равна 1/2, так как на каждый введенный информационный символ
выдаются два кодовых символа. Кодер, использующий т элементов памяти,
называется в дальнейшем кодер памяти т. В
общем случае, сверточный кодер скорости k/п использует к регистров сдвига, один регистр на
один вводимый информационный символ. Под скоростью кода в теории кодирования
понимается отношение
, при этом ясно, что скорость
кода равна 1/2, так как на каждый введенный информационный символ
выдаются два кодовых символа. Кодер, использующий т элементов памяти,
называется в дальнейшем кодер памяти т. В
общем случае, сверточный кодер скорости k/п использует к регистров сдвига, один регистр на
один вводимый информационный символ. Под скоростью кода в теории кодирования
понимается отношение ![]() .
Более точное наименование параметра
.
Более точное наименование параметра ![]() – относительная скорость кода [69, 94],
поскольку за единицу времени кодер принимает на вход
– относительная скорость кода [69, 94],
поскольку за единицу времени кодер принимает на вход ![]() информационных разрядов и
трансформирует их в
информационных разрядов и
трансформирует их в ![]() разрядов
избыточного кода. Кодер памяти
разрядов
избыточного кода. Кодер памяти ![]() и скорости
и скорости ![]() двоичного сверточного кода можно
рассматривать также как дискретную линейную инвариантную во времени систему.
Это означает, что отклик кодера на нулевую последовательность, в которой
имеется единственная единица, т.е. выход кодера, полученный для входной
последовательности
двоичного сверточного кода можно
рассматривать также как дискретную линейную инвариантную во времени систему.
Это означает, что отклик кодера на нулевую последовательность, в которой
имеется единственная единица, т.е. выход кодера, полученный для входной
последовательности ![]() , полностью определяет код. Стрелка вправо
символизирует, что единица от источника информации первой поступит на вход
кодера. Рассмотрим сверточный кодер, показанный на рис. 1.12.
, полностью определяет код. Стрелка вправо
символизирует, что единица от источника информации первой поступит на вход
кодера. Рассмотрим сверточный кодер, показанный на рис. 1.12.

Рис. 1.12. Кодер сверточного кода
Имеется ![]() импульсных
откликов сверточного кодера скорости
импульсных
откликов сверточного кодера скорости ![]() , по одному на каждый выход
, по одному на каждый выход ![]() , где
, где ![]() . По мере того, как
импульс проходит через память кодера, он отражает связи между элементами памяти
и выходом. Обозначим
. По мере того, как
импульс проходит через память кодера, он отражает связи между элементами памяти
и выходом. Обозначим ![]() набор импульсных откликов сверточного
кодера скорости
набор импульсных откликов сверточного
кодера скорости ![]() ,
получивших название порождающих последовательностей или генераторов кода,
которые задают действительные (физические) связи кодера. Кодер на рис. 1
порождает генераторы
,
получивших название порождающих последовательностей или генераторов кода,
которые задают действительные (физические) связи кодера. Кодер на рис. 1
порождает генераторы ![]() и
и
![]() , поскольку
на каждом их выходов кодера через
, поскольку
на каждом их выходов кодера через ![]() тактов формируются последовательности с
нулевыми хвостами, при этом
тактов формируются последовательности с
нулевыми хвостами, при этом ![]() , а
, а ![]() . Обычно, говоря о сверточном коде,
генераторы записывают в восьмеричной системе счисления. Для рассматриваемого
кодера эта запись имеет вид (7,5).
. Обычно, говоря о сверточном коде,
генераторы записывают в восьмеричной системе счисления. Для рассматриваемого
кодера эта запись имеет вид (7,5).
Общая длина регистров сдвига, используемых кодером, называется
памятью кода. Сверточный код образуется множеством всех двоичных
последовательностей, порождаемых сверточным кодером. Теоретически эти
последовательности бесконечны. Практически состояние сверточного кодера
периодически устанавливается в некоторое заранее известное состояние и, следовательно,
порождаемый код приобретает характер блокового кода. Считается,
что конечная кодовая последовательность ![]() сверточного кода получается из некоторой конечной
информационной последовательности.
сверточного кода получается из некоторой конечной
информационной последовательности.
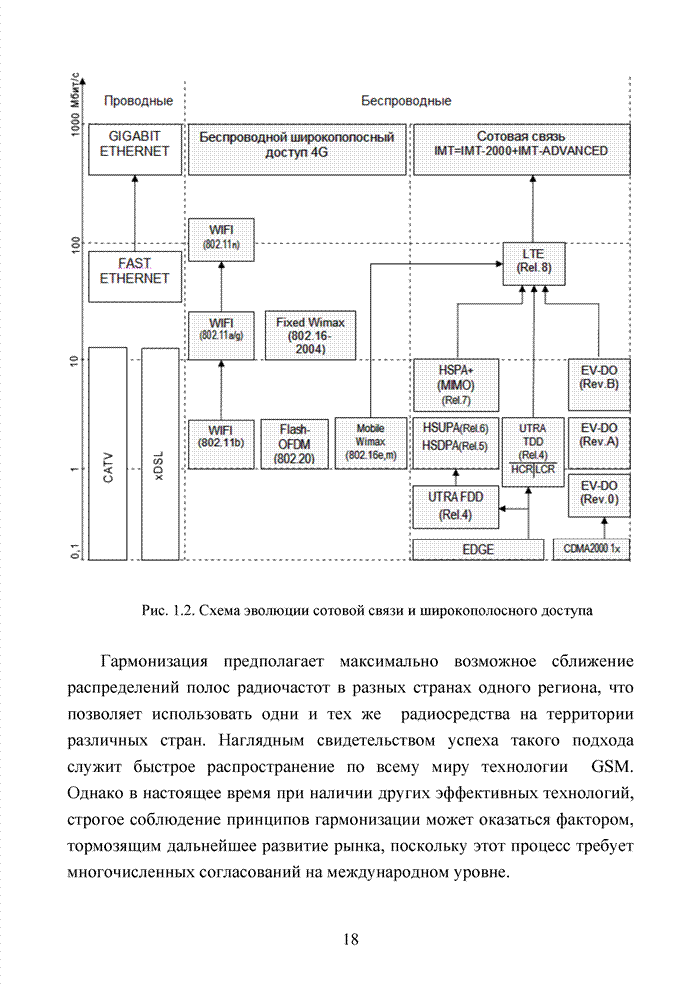
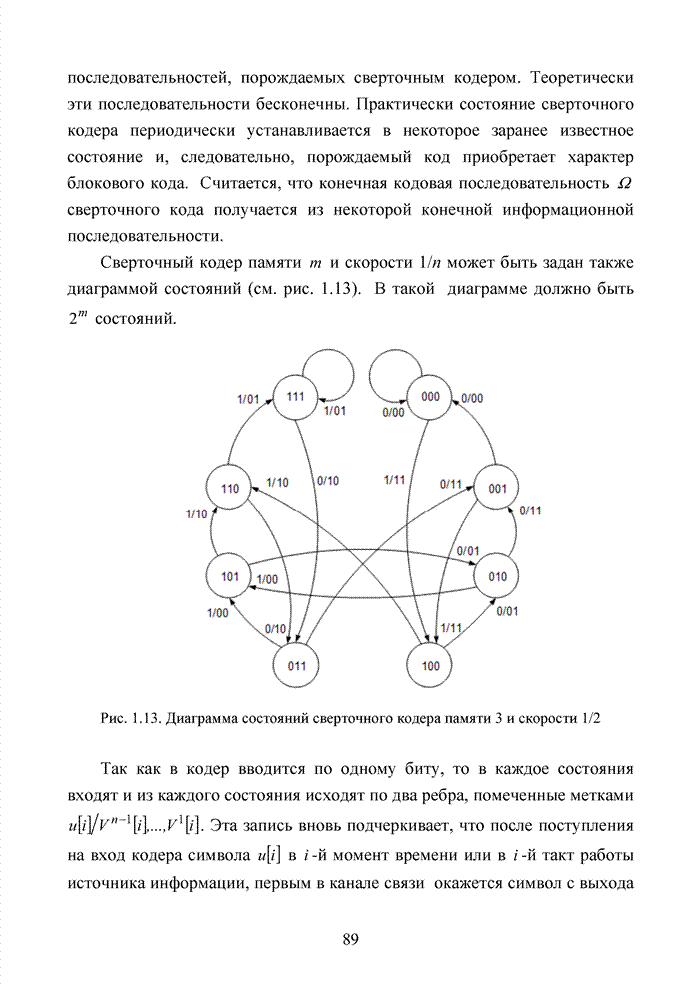
Сверточный кодер памяти ![]() и скорости 1/n может быть задан также диаграммой
состояний (см. рис. 1.13). В такой диаграмме должно быть
и скорости 1/n может быть задан также диаграммой
состояний (см. рис. 1.13). В такой диаграмме должно быть ![]() состояний.
состояний.

Рис. 1.13. Диаграмма состояний сверточного кодера памяти 3 и скорости 1/2
Так как в кодер вводится по одному биту, то в каждое состояния
входят и из каждого состояния исходят по два ребра, помеченные метками ![]() . Эта запись вновь
подчеркивает, что после поступления на вход кодера символа
. Эта запись вновь
подчеркивает, что после поступления на вход кодера символа ![]() в
в ![]() -й момент времени или в
-й момент времени или в ![]() -й такт работы
источника информации, первым в канале связи окажется символ с выхода декодера
-й такт работы
источника информации, первым в канале связи окажется символ с выхода декодера ![]() . Подобное
предостережение крайне важно сточки зрения дальнейшего анализа работы пары
кодер – декодер.
. Подобное
предостережение крайне важно сточки зрения дальнейшего анализа работы пары
кодер – декодер.
По-видимому, метка ребер вида 1/00, 1/11, 1/00 или 0/11
нейтральна, когда символы на выходе одинаковы ![]() , но следует быть точным в представлении
последовательности символов в метках вида 1/01, 1/10 или 0/10, 0/01, когда
, но следует быть точным в представлении
последовательности символов в метках вида 1/01, 1/10 или 0/10, 0/01, когда ![]() .
.
Пусть двоичная последовательность
источника информации имеет вид ![]() . Тогда последовательность в канале связи
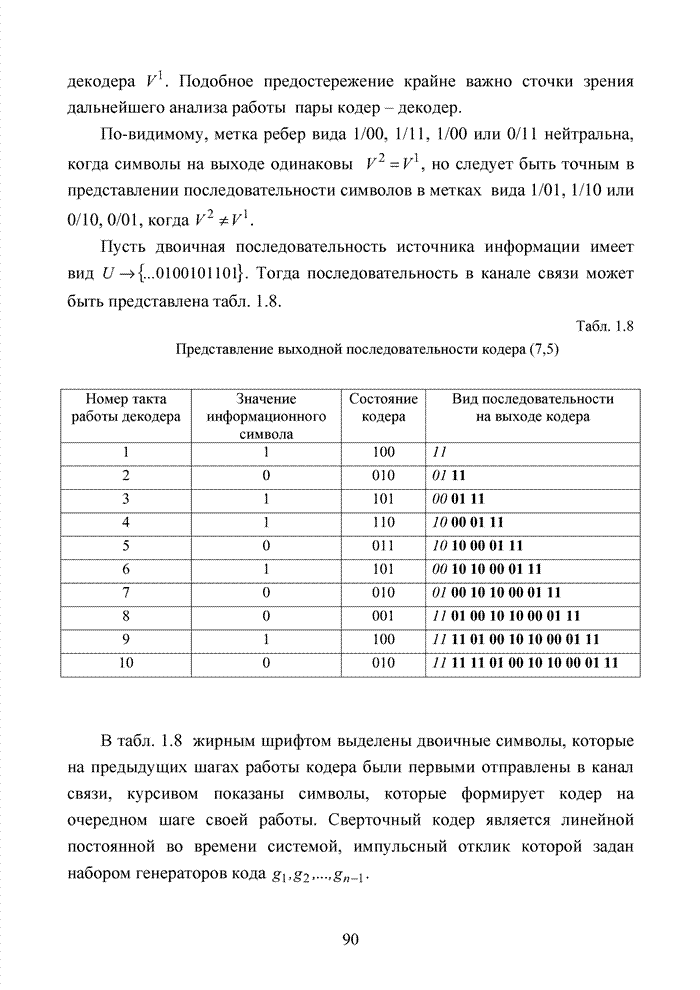
может быть представлена табл. 1.8.
. Тогда последовательность в канале связи
может быть представлена табл. 1.8.
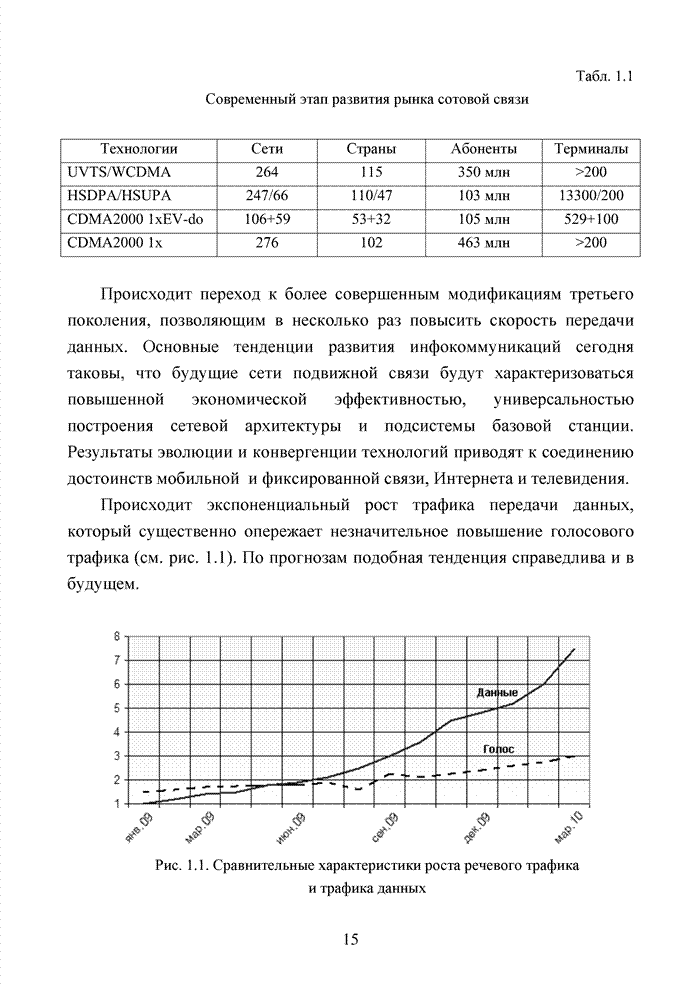
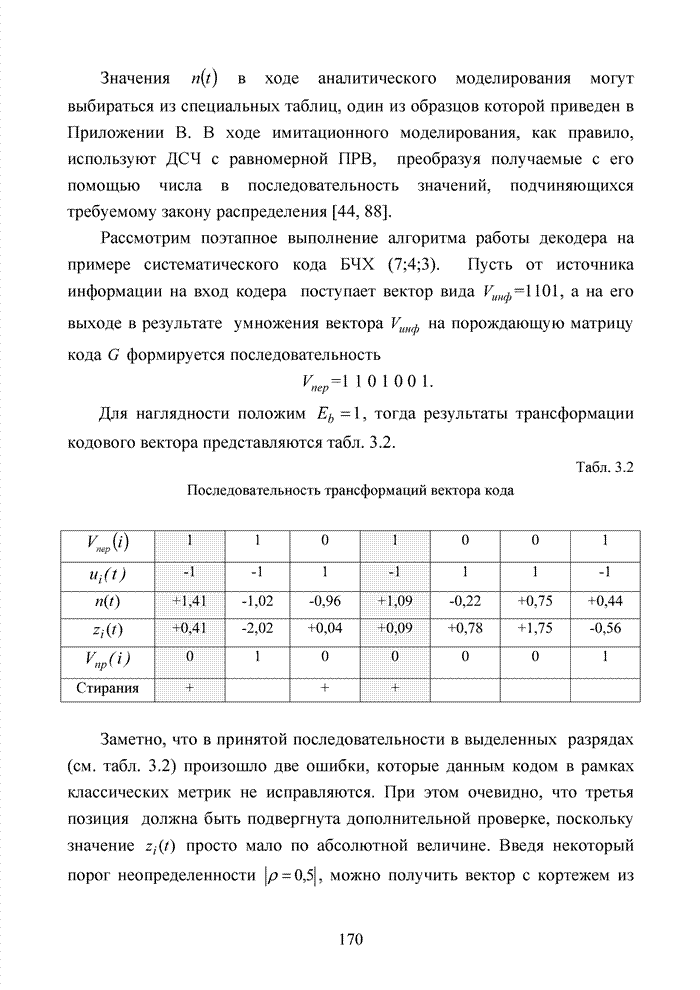
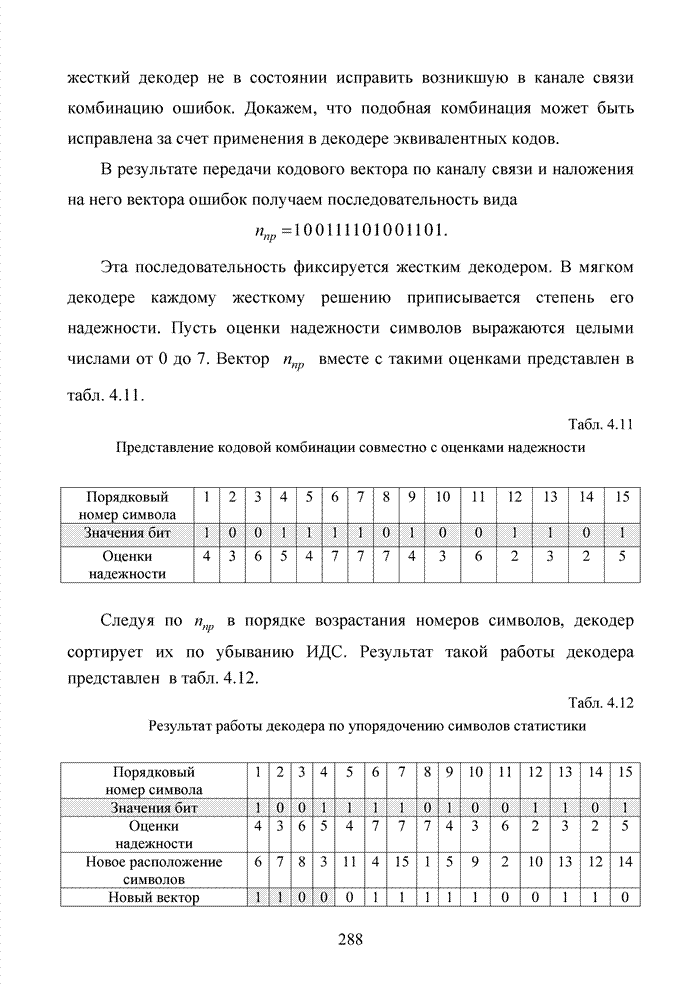
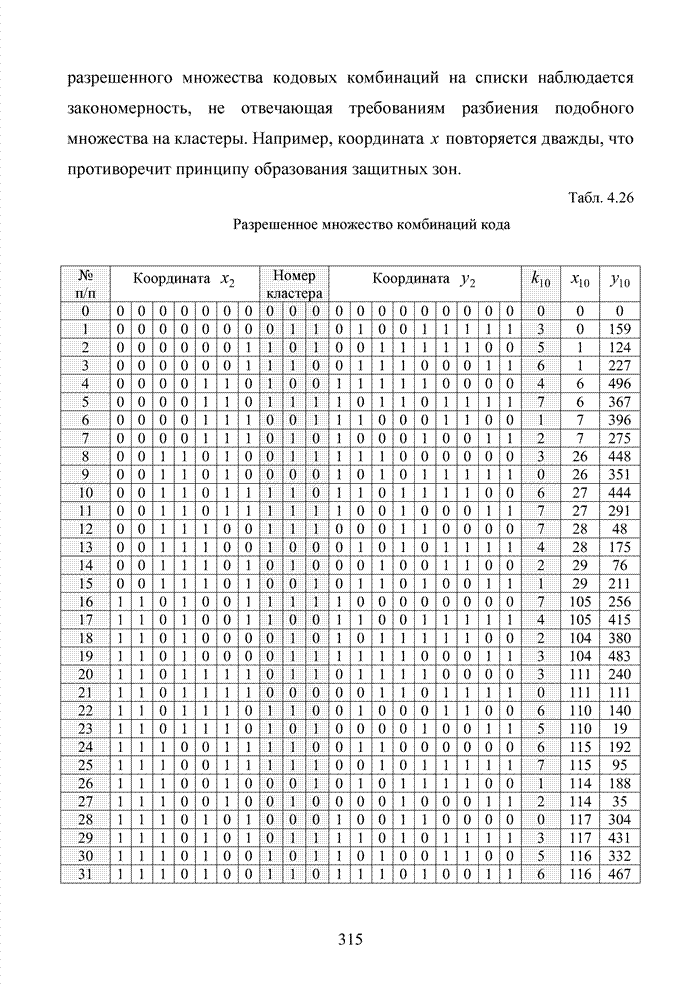
Табл. 1.8 Представление выходной последовательности кодера (7,5)
|
Номер такта работы декодера |
Значение информационного символа |
Состояние кодера |
Вид последовательности на выходе кодера |
|
1 |
1 |
100 |
11 |
|
2 |
0 |
010 |
01 11 |
|
3 |
1 |
101 |
00 01 11 |
|
4 |
1 |
110 |
10 00 01 11 |
|
5 |
0 |
011 |
10 10 00 01 11 |
|
6 |
1 |
101 |
00 10 10 00 01 11 |
|
7 |
0 |
010 |
01 00 10 10 00 01 11 |
|
8 |
0 |
001 |
11 01 00 10 10 00 01 11 |
|
9 |
1 |
100 |
11 11 01 00 10 10 00 01 11 |
|
10 |
0 |
010 |
11 11 11 01 00 10 10 00 01 11 |
В табл. 1.8 жирным
шрифтом выделены двоичные символы, которые на предыдущих шагах работы кодера
были первыми отправлены в канал связи, курсивом показаны символы, которые формирует
кодер на очередном шаге своей работы. Сверточный кодер является линейной постоянной
во времени системой, импульсный отклик которой задан набором
генераторов кода ![]() .
.
Тогда общее значение
импульсного отклика должно соответствовать композиции элементов ![]() , относящихся к одному
показателю переменной
, относящихся к одному
показателю переменной ![]() . Следовательно,
. Следовательно,
![]()
для ![]() . С помощью этих генераторов
выходную последовательность кода можно записать как
. С помощью этих генераторов
выходную последовательность кода можно записать как
 при
при
![]() (1.18)
(1.18)
Выходные
последовательности ![]() ,
равны дискретной свертке входной последовательности
,
равны дискретной свертке входной последовательности ![]() с генераторами кода
с генераторами кода ![]() . Уравнение
(1.2) в матричной форме имеет вид
. Уравнение
(1.2) в матричной форме имеет вид
![]() , (1.19)
, (1.19)
![]()
где G – порождающая матрица сверточного кода.
В частности, для сверточного кода памяти т и скорости 1/2 имеем
 .
.
Это, так называемая, ленточная матрица с шириной ленты
равной тп, для кода памяти т и скорости 1/п. В
представленной матрице сохраняется требование об очередности следования
двоичных символов в канал связи. Поэтому первый элемент матрицы находится в
первой строке справа. Поступления новых значений ![]() приводит к наращиванию номеров столбцов матрицы
слева, а номера строк увеличиваются снизу. Например, для кодера,
представленного на рис. 1.10, и
приводит к наращиванию номеров столбцов матрицы
слева, а номера строк увеличиваются снизу. Например, для кодера,
представленного на рис. 1.10, и ![]() порождающая матрица имеет вид
порождающая матрица имеет вид
 .
(1.20)
.
(1.20)
Пусть информационная
последовательность имеет вид: ![]() , тогда произведение вектора
, тогда произведение вектора ![]() на матрицу
на матрицу ![]() представляется
последовательность двоичных символов (1.21)
представляется
последовательность двоичных символов (1.21)
 , (1.21)
, (1.21)
что соответствует данным на пятом шаге работы кодера, которые приведены в табл. 1.8. Кодирование данных может осуществляться на основе решетчатых диаграмм (треллис-диаграмм). Тогда соответствующая выходная (кодовая) последовательность может быть получена непосредственно как выделенный путь диаграммы, показанный на рис. 1.14.

Рис. 1.14. Путь на треллис-диаграмме сверточного кода при m = 3
Преимуществом такого
подхода к описанию работы кодера является идентичность методов анализа работы
декодера на приемной стороне. Кроме того, нет необходимости вычислять параметры
матрицы ![]() при
изменении информационной последовательности
при
изменении информационной последовательности ![]() .
.
Рассмотрим кодер,
представленный на рис. 1.10, и входную последовательность ![]() . Принцип построения подобной
диаграммы заключается в том, что слева показываются состояния последних
. Принцип построения подобной
диаграммы заключается в том, что слева показываются состояния последних ![]() ячеек памяти. Это
определяет число горизонтальных ярусов треллис-диаграммы, которое равно
ячеек памяти. Это
определяет число горизонтальных ярусов треллис-диаграммы, которое равно ![]() . В используемом в
данном разделе примере, показывается состояние ячеек
. В используемом в
данном разделе примере, показывается состояние ячеек ![]() -значного регистра памяти для
-значного регистра памяти для ![]() и
и ![]() .
.
Состояние элемента памяти
![]() изменяется
под воздействием бит от источника информации. Данные, поступающие в канал связи
на каждом шаге диаграммы сохраняют временную последовательность, как это
показано на первом шаге диаграммы. В ходе обработки любых данных кодер начинает
свою работу в точке 00. Дальнейшее движение по диаграмме зависит от данных
источника информации. Приняв от него на первом шаге 1, регистр памяти переходит
в состояние 100. Как было показано выше, в канал связи будут переданы данные
сначала с выхода кодера
изменяется
под воздействием бит от источника информации. Данные, поступающие в канал связи
на каждом шаге диаграммы сохраняют временную последовательность, как это
показано на первом шаге диаграммы. В ходе обработки любых данных кодер начинает
свою работу в точке 00. Дальнейшее движение по диаграмме зависит от данных
источника информации. Приняв от него на первом шаге 1, регистр памяти переходит
в состояние 100. Как было показано выше, в канал связи будут переданы данные
сначала с выхода кодера ![]() и только потом с выхода
и только потом с выхода ![]() . После отправки данных
в канал связи информация в регистре сдвигается на один шаг вправо,
следовательно, последние две ячейки памяти будут иметь состояние 10, что
отражает ребро графа переходных состояний кодера. Следует заметить, что сигналы
на выходе элемента памяти
. После отправки данных
в канал связи информация в регистре сдвигается на один шаг вправо,
следовательно, последние две ячейки памяти будут иметь состояние 10, что
отражает ребро графа переходных состояний кодера. Следует заметить, что сигналы
на выходе элемента памяти ![]() компенсируются специальной схемой гашения
и в дальнейшей работе кодера участия не принимают.
компенсируются специальной схемой гашения
и в дальнейшей работе кодера участия не принимают.
Если предположить, что в канале
связи помехи не действуют, то полученный на диаграмме путь (рис. 1.14) должен
повторить декодер приемника. Принцип его работы заключается в поиске непрерывного
пути наименьшего веса среди множества возможных путей для сверточного кода с определенными
для него параметрами. Треллис-диаграмма приемника в общих чертах соответствует
диаграмме, которая описывает работу кодера. Особенностями диаграммы являются
представители поля ![]() ,
которые характеризуют конкретное заполнение элементов памяти кодера на
различных этапах его работы.
,
которые характеризуют конкретное заполнение элементов памяти кодера на
различных этапах его работы.
Принцип работы декодера иллюстрируется на рис. 1.15.

Рис. 1.15. Принцип работы декодера сверточного кода
Элементы поля показаны парами на схеме слева во
вспомогательных таблицах и соответствуют одному из ![]() уровней, при этом заметно, что
последние два элемента повторяют нумерацию уровней на передаче, а первый
элемент в каждой таблице представляет либо 0, либо 1.
уровней, при этом заметно, что
последние два элемента повторяют нумерацию уровней на передаче, а первый
элемент в каждой таблице представляет либо 0, либо 1.
Для дальнейшего анализа работы декодера необходимо установить
соглашение: если обрабатывается нулевой элемент, то на диаграмме переходных
состояний ребро графа представляется пунктиром, в противном случае – сплошной
линией. В любой точке диаграммы декодер анализирует возможные два исхода по
декодированию принятой информации в предположении, что на ![]() -м шаге на вход кодера поступил
ноль или единица. Следовательно, из любой точки диаграммы исходит два пути и в
целом анализу подвергаются
-м шаге на вход кодера поступил
ноль или единица. Следовательно, из любой точки диаграммы исходит два пути и в
целом анализу подвергаются ![]() возможных вариантов декодирования принятой
информации на
возможных вариантов декодирования принятой
информации на ![]() -м
шаге.
-м
шаге.
Работа декодера начинается с левого верхнего узла решетки
(также как и работа кодера). В этой точке треллис-диаграммы декодер анализирует
ситуацию, когда кодер мог находиться в состоянии 000 и на его входе появился 0.
Таким образом, в канал связи кодер мог отправить значения 00. Сравнивая эти
показатели с показателями, которые реально принял приемник (данные из канала
связи соответствуют значениям 11), декодер устанавливает вес этого пути. Это
осуществляется путем поразрядного сложения по ![]() 2 данных из канала связи и данных
выработанных декодером для данного ребра, т.е. 11
2 данных из канала связи и данных
выработанных декодером для данного ребра, т.е. 11![]() 00=11 и вес этого пути равен 2 (в
результате сложения оказалось, что оба разряда равны единице).
00=11 и вес этого пути равен 2 (в
результате сложения оказалось, что оба разряда равны единице).
Декодер проверяет второй предположительный вариант действия кодера, когда состояние его элементов памяти могло соответствовать значениям 100. В этой ситуации кодер должен был отправить в канал связи пару бит 11. Тогда вес этого ребра равен 0, т.е. зафиксировано полное совпадение информации, принятой из канала связи и информации, которая появляется на выходе декодера в состоянии 100.
На первых дух шагах подобному анализу поверглось всего два
ребра графа, на втором шаге четыре ребра и после этого анализу повергаются все ![]() ребра. Из диаграммы
заметно, что при анализе всех возможных
ребра. Из диаграммы
заметно, что при анализе всех возможных ![]() путей на очередном шаге появляется пара направлений,
вес которых оказывается равен 0. В этом случае предпочтение отдается тому пути,
который продолжает предшествующий шаг пути минимального веса.
путей на очередном шаге появляется пара направлений,
вес которых оказывается равен 0. В этом случае предпочтение отдается тому пути,
который продолжает предшествующий шаг пути минимального веса.
С учетом пунктирных и сплошных линий устанавливается значение бита, который должен быть выдан приемнику сообщений. В отличие от блочных алгебраических кодов, декодирование сверточных кодов с мягкими решениями не вызывает затруднений. Именно это обстоятельство позволяет успешно использовать сверточные коды в современных системах связи.
На практике для декодирования сверточных кодов наибольшее распространение получил алгоритм Витерби, предложенный в 70-х годах прошлого столетия, и несколько модификаций алгоритма последовательного декодирования. Подобные коды используются практически во всех стандартах консорциума DVB (Digital Video Broadcasting) и являются стандартом для многих спутниковых цифровых систем (например, Inmarsat и Intelsat).
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
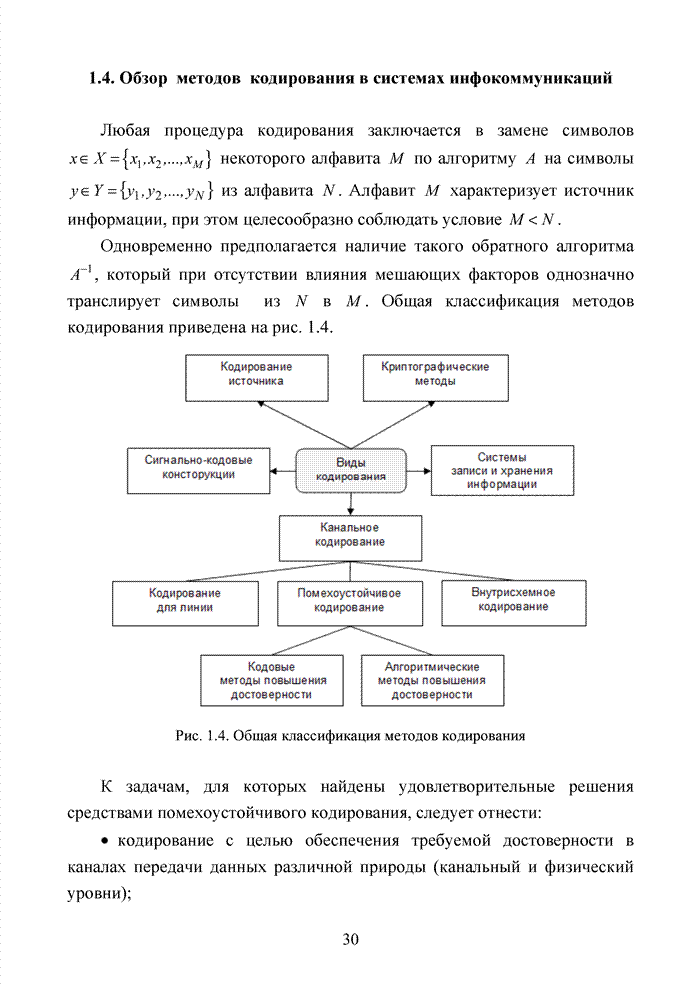
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
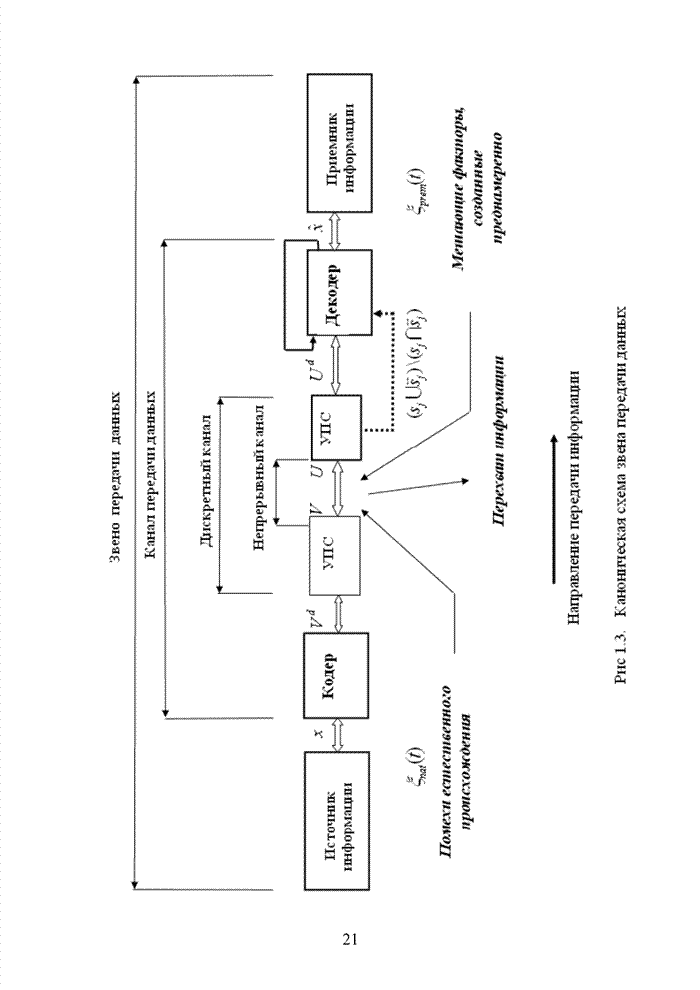
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
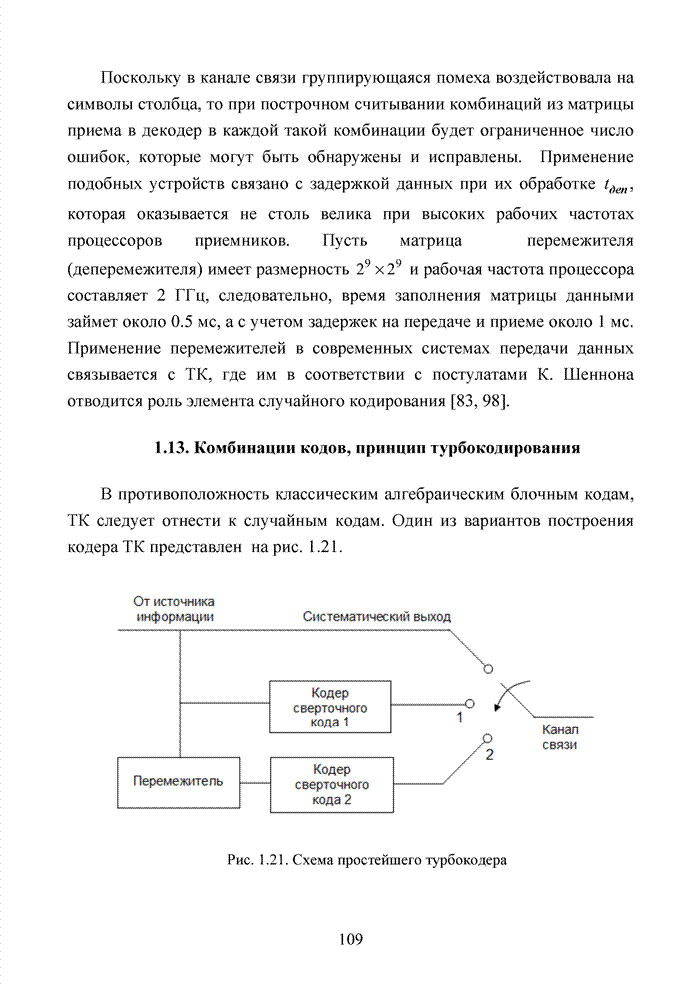
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
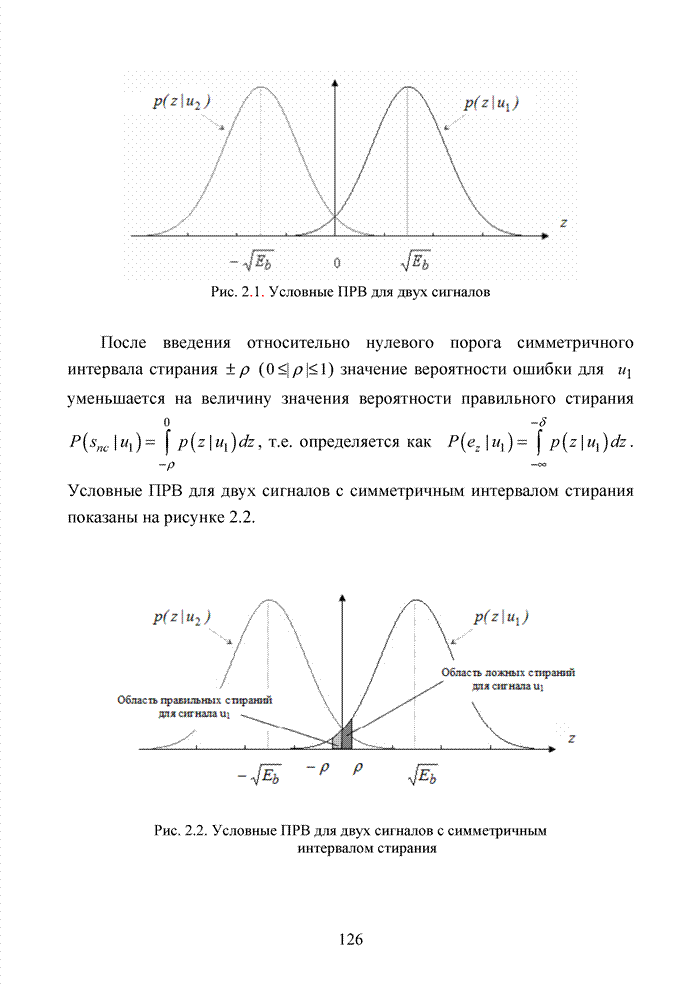
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
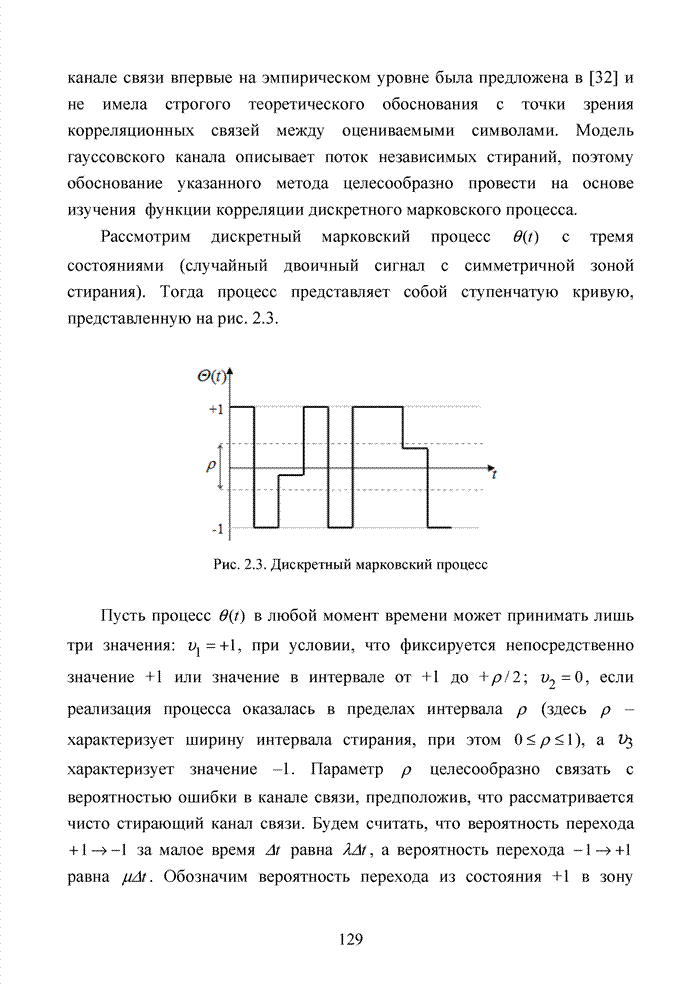
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
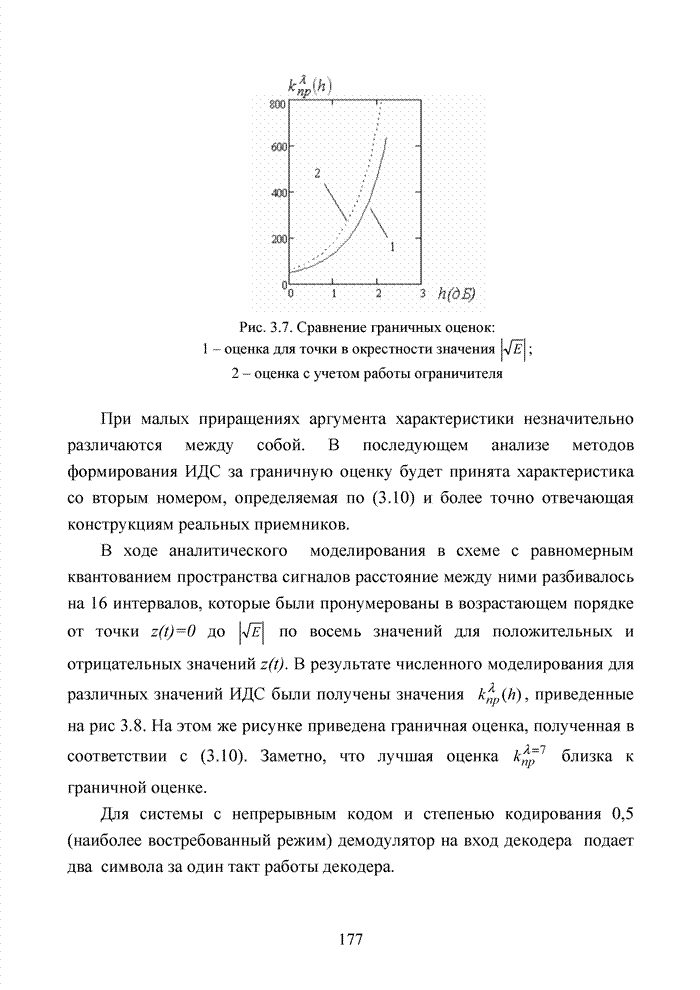
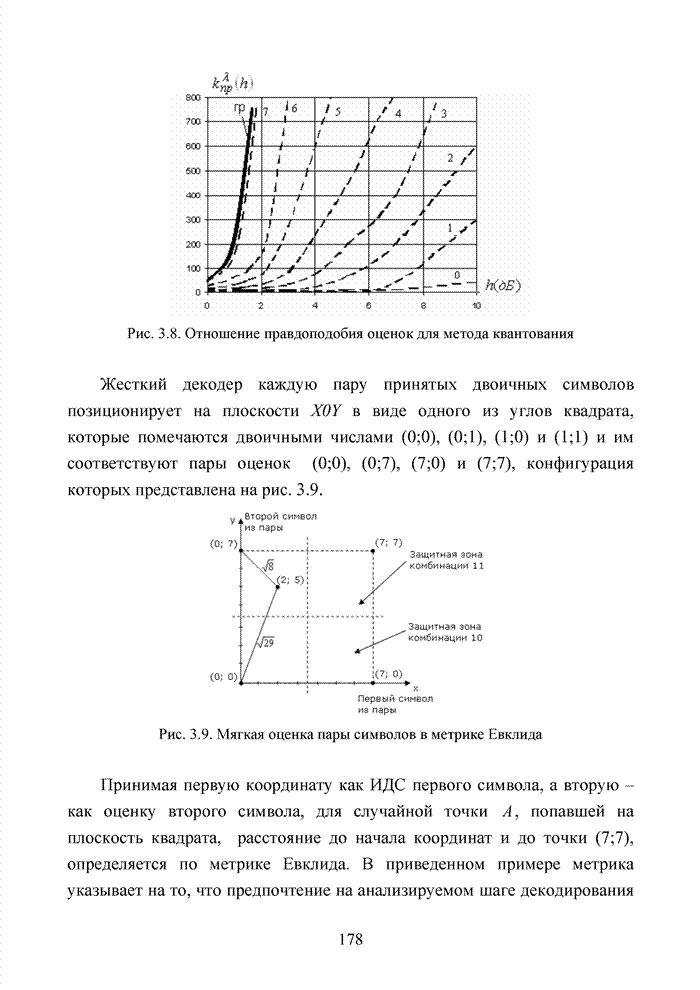
- 3.3. Метод квантования уровней сигнала
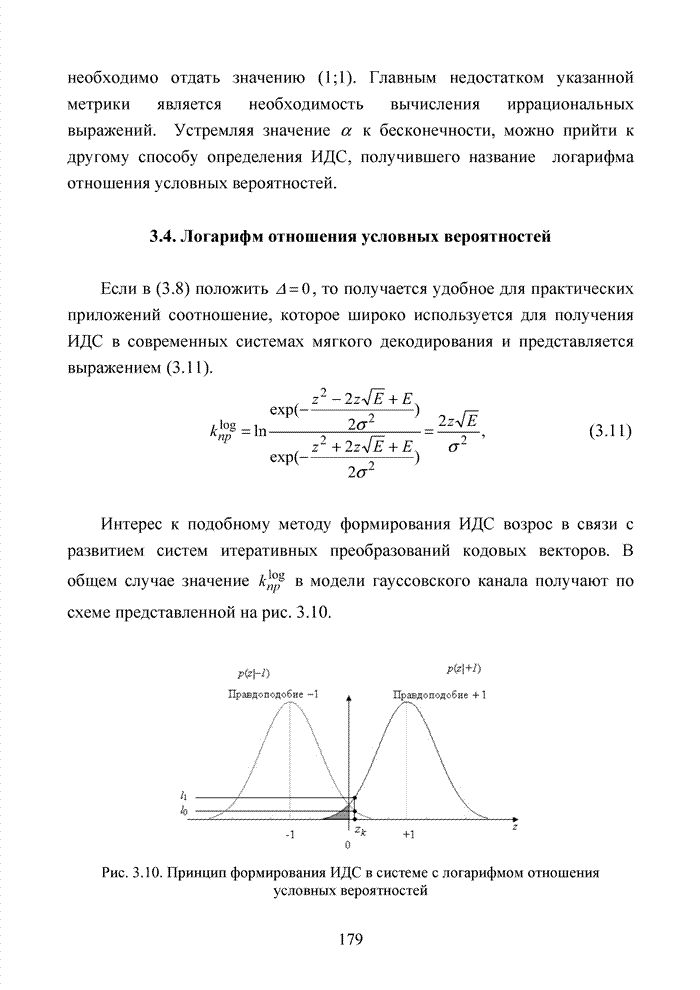
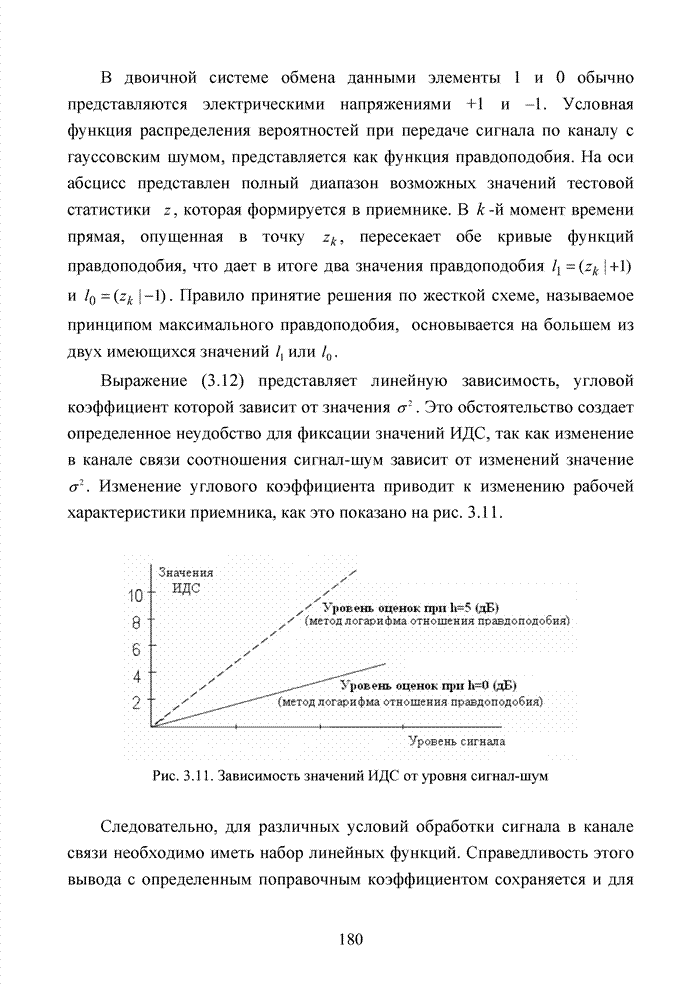
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
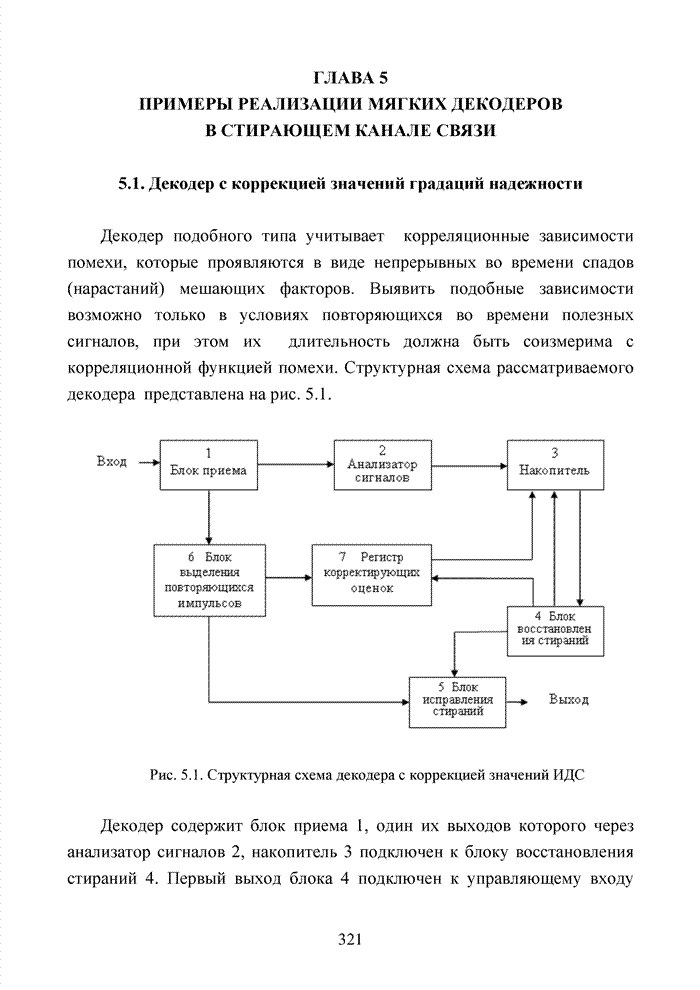
- 5.1. Декодер с коррекцией значений градаций надежности
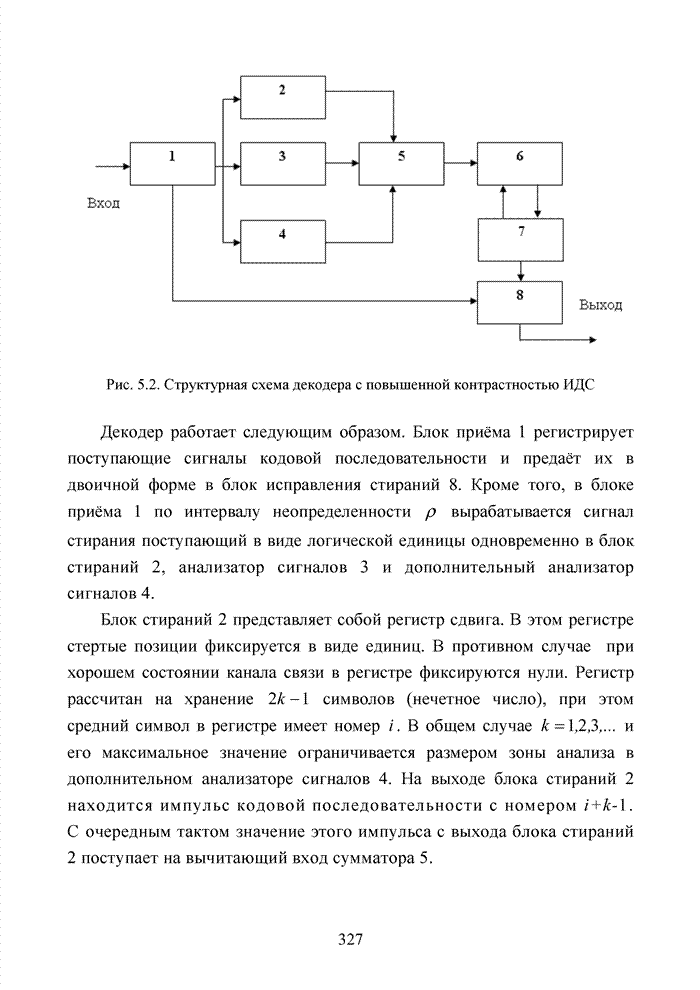
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
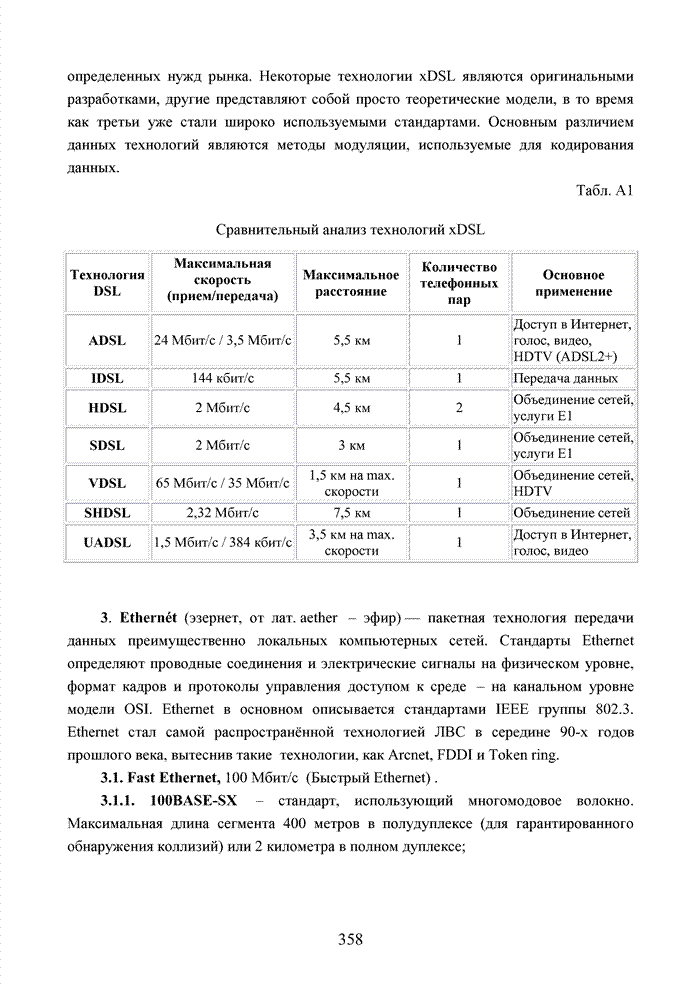
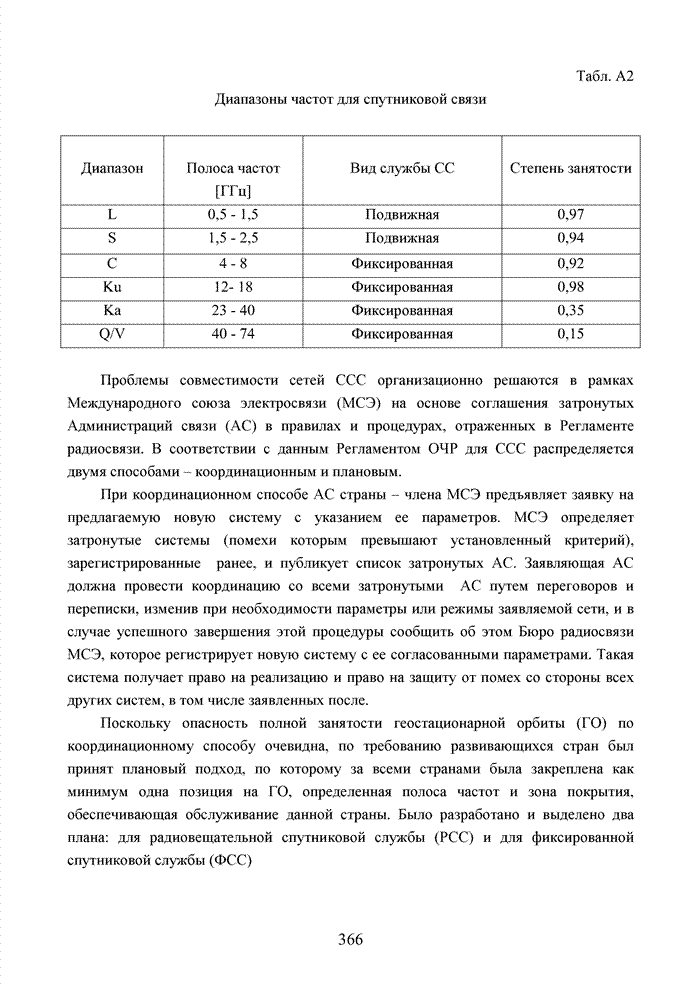
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
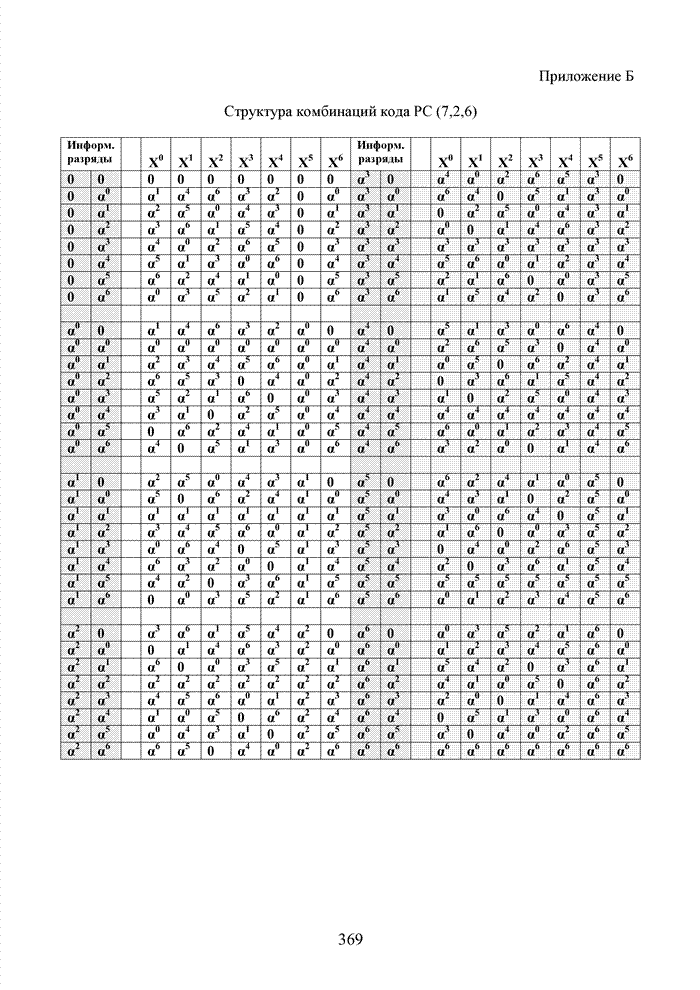
- Приложение Б Структура комбинаций кода РС (7,2,6)
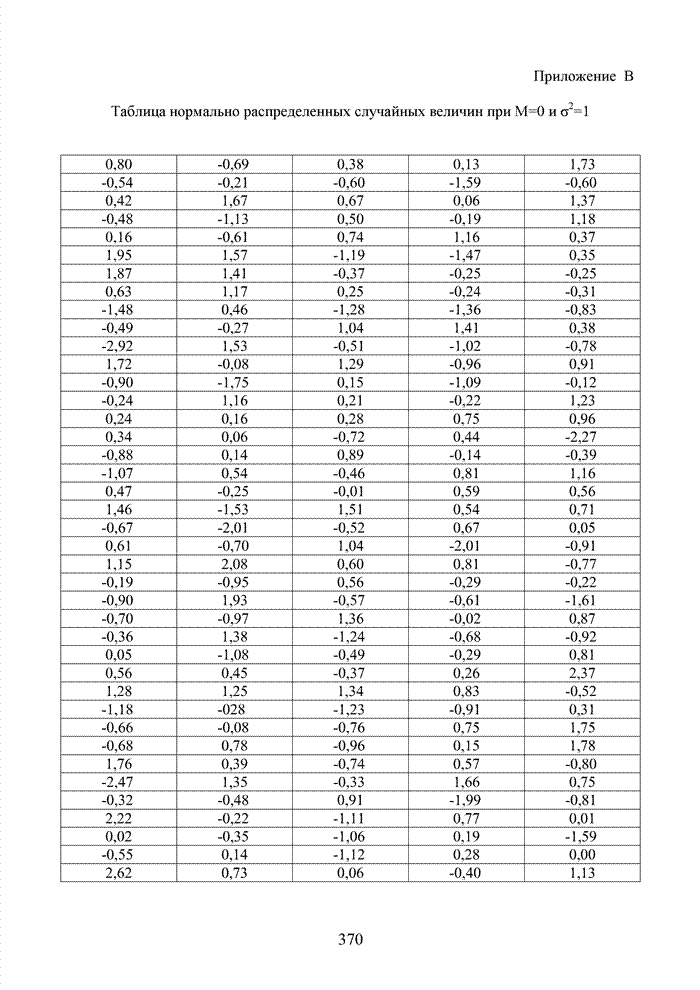
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК