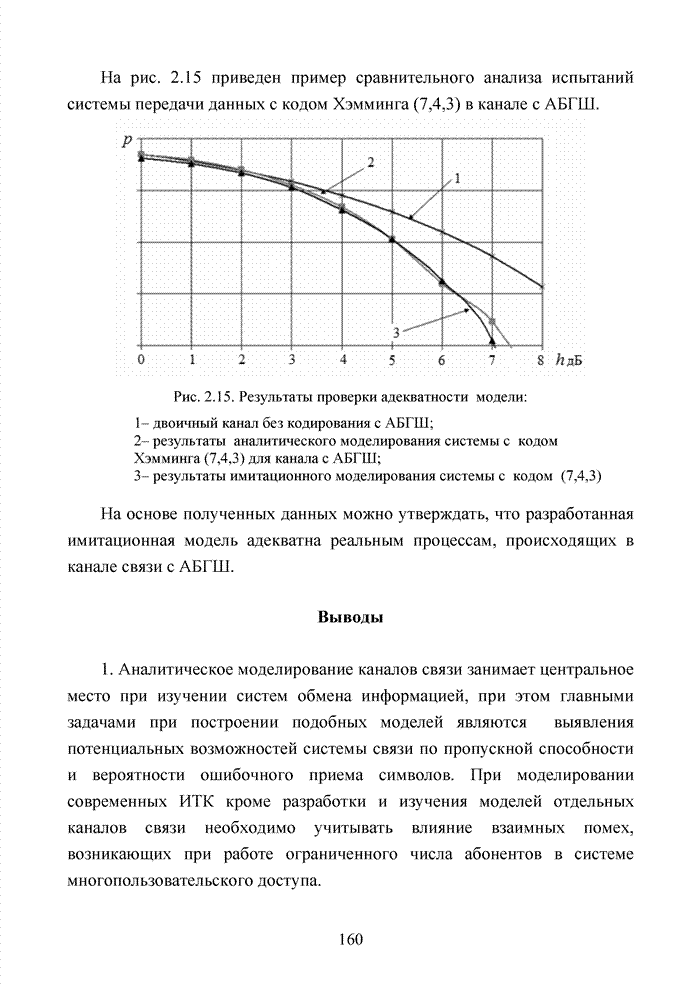
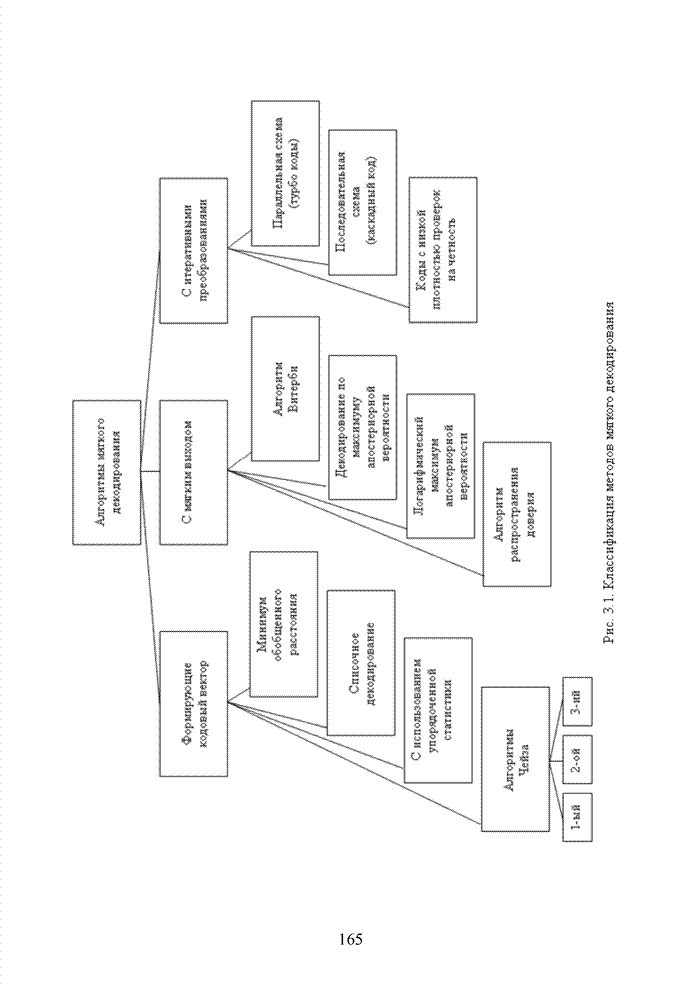
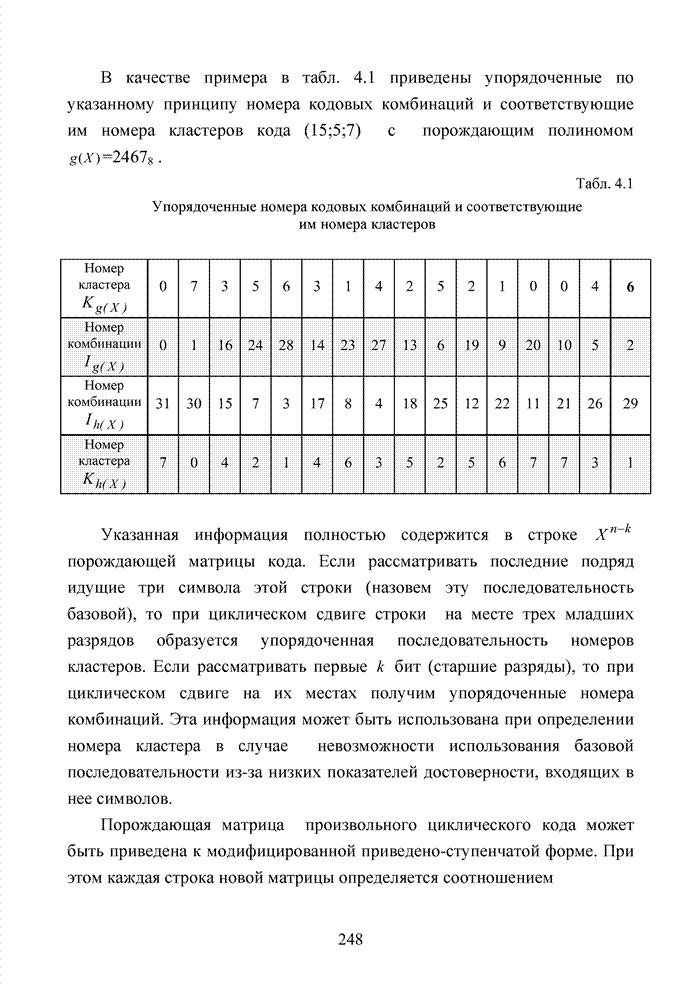
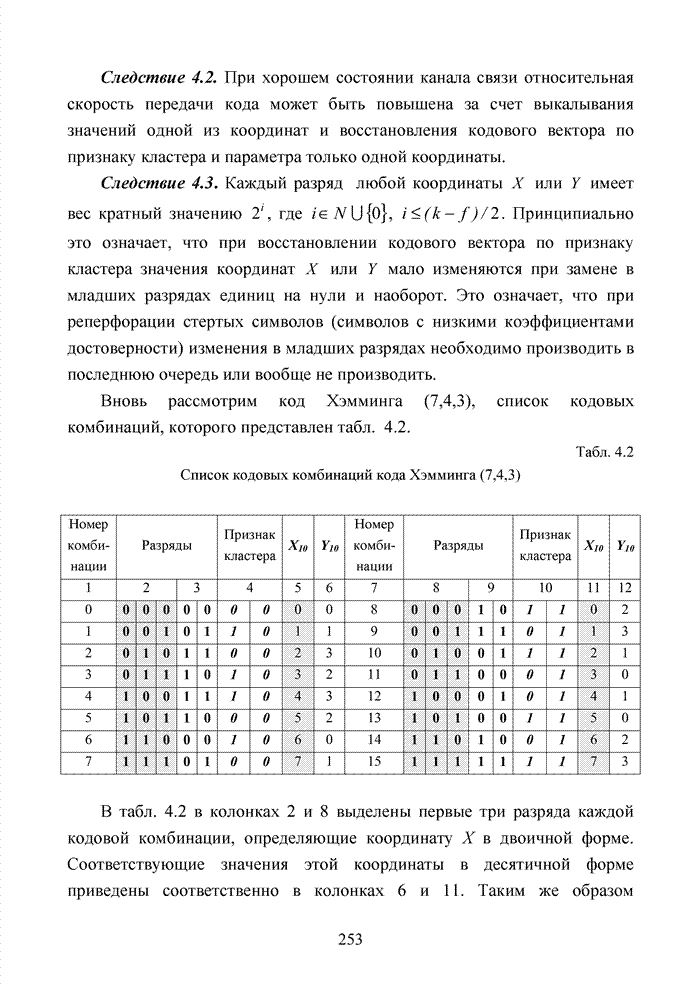
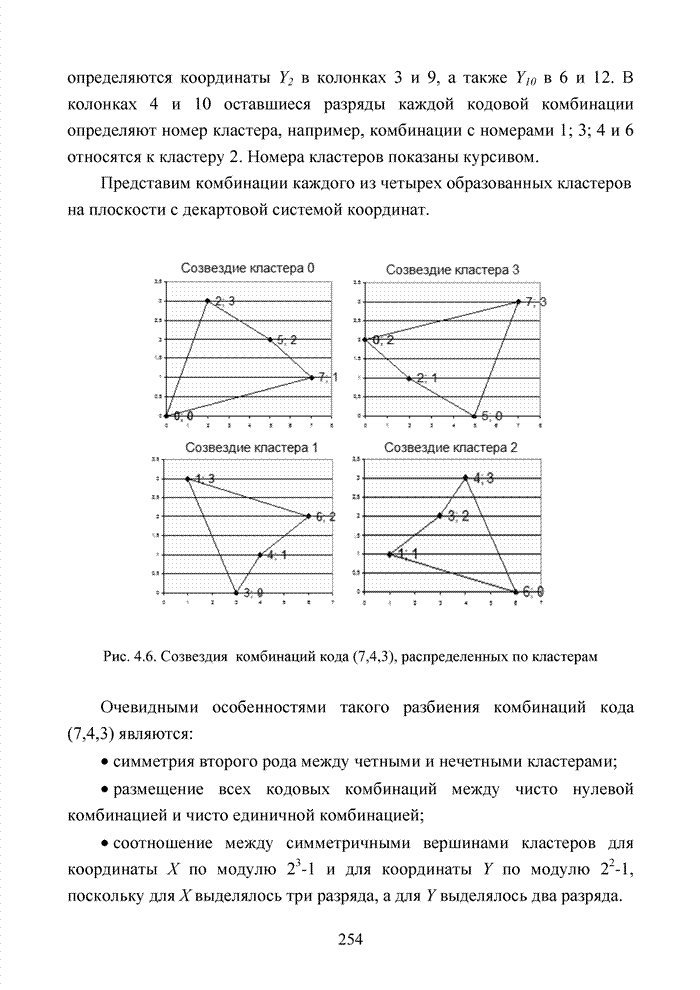
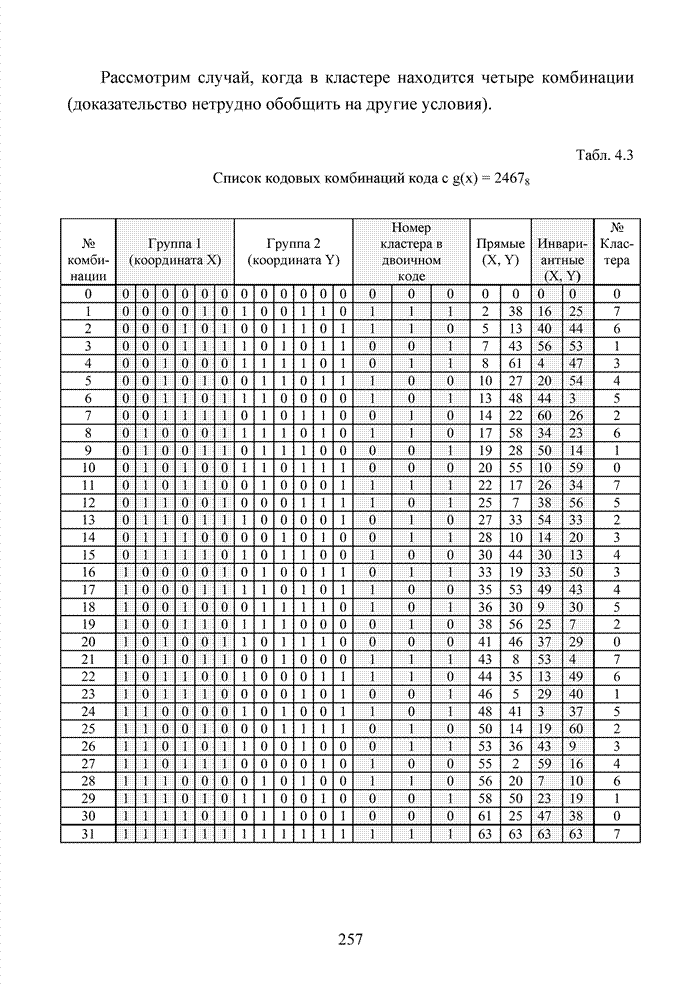
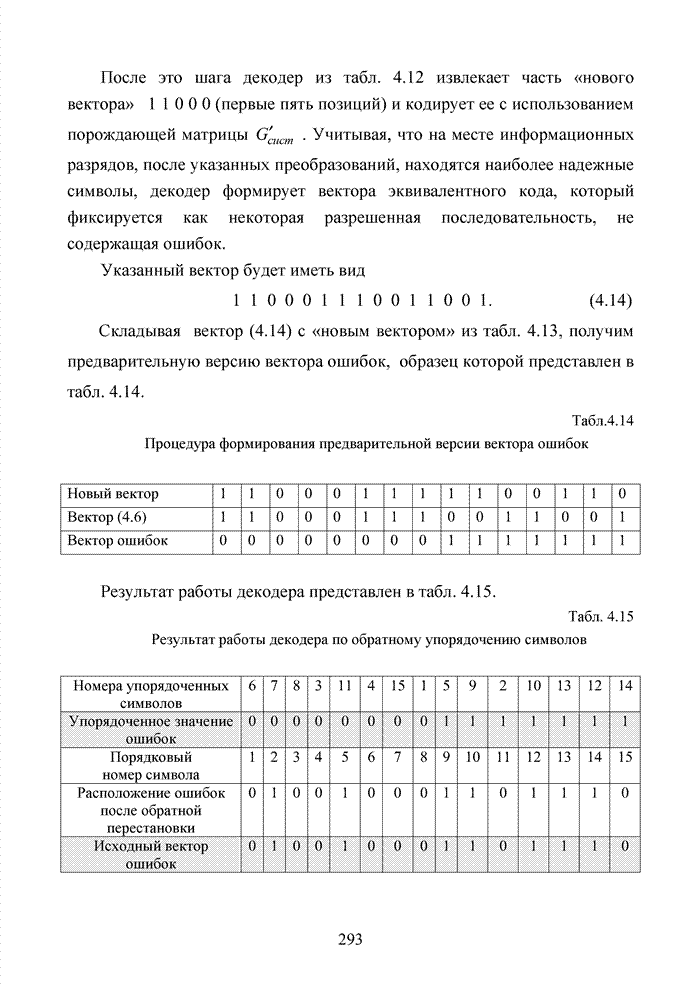
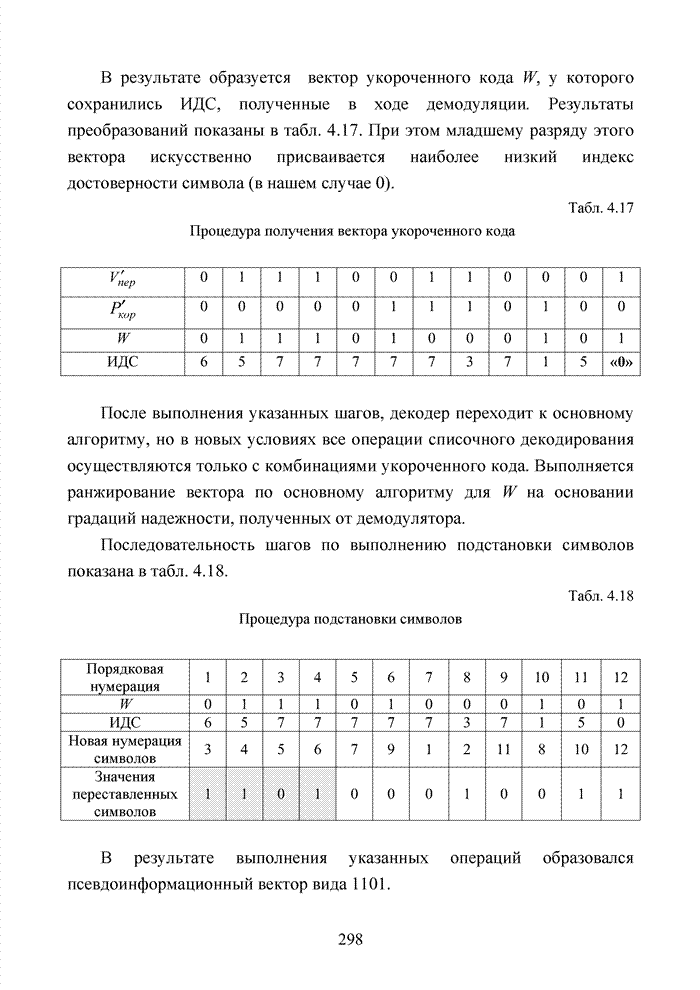
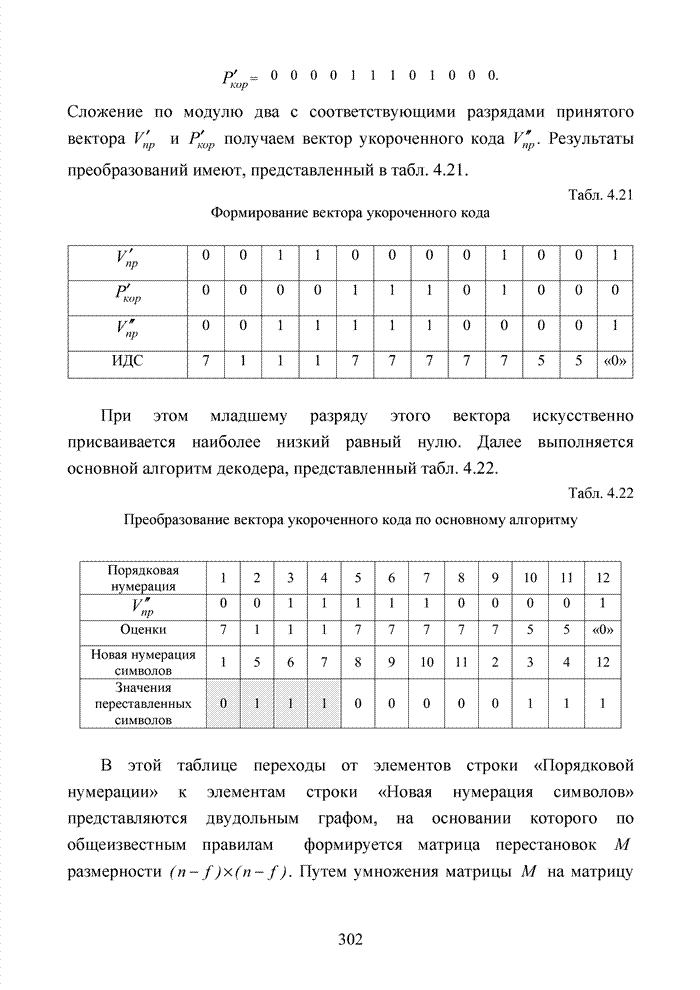
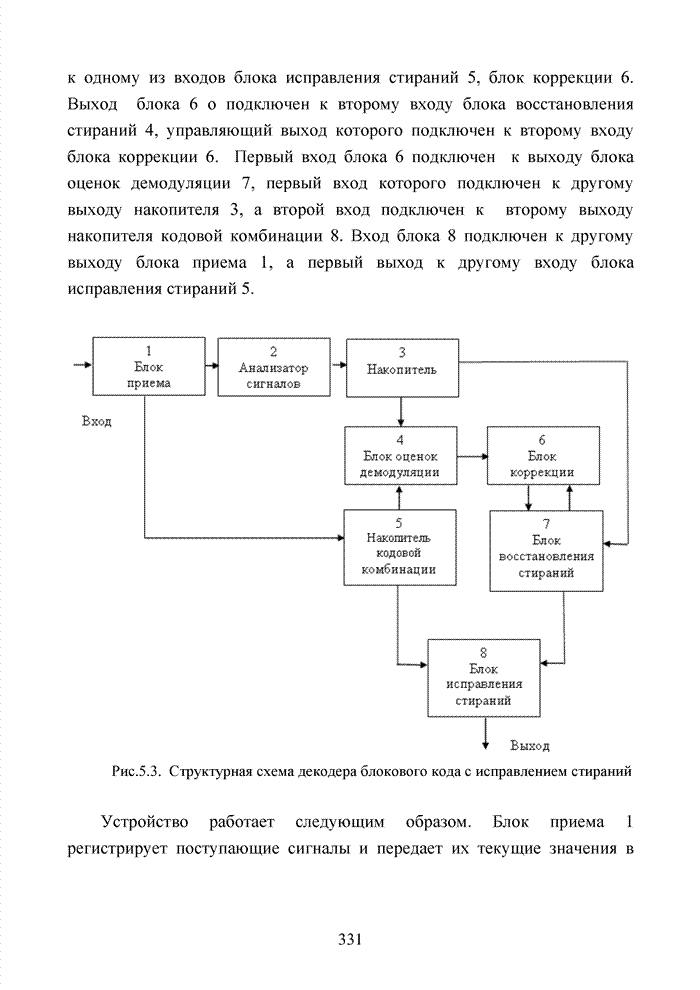
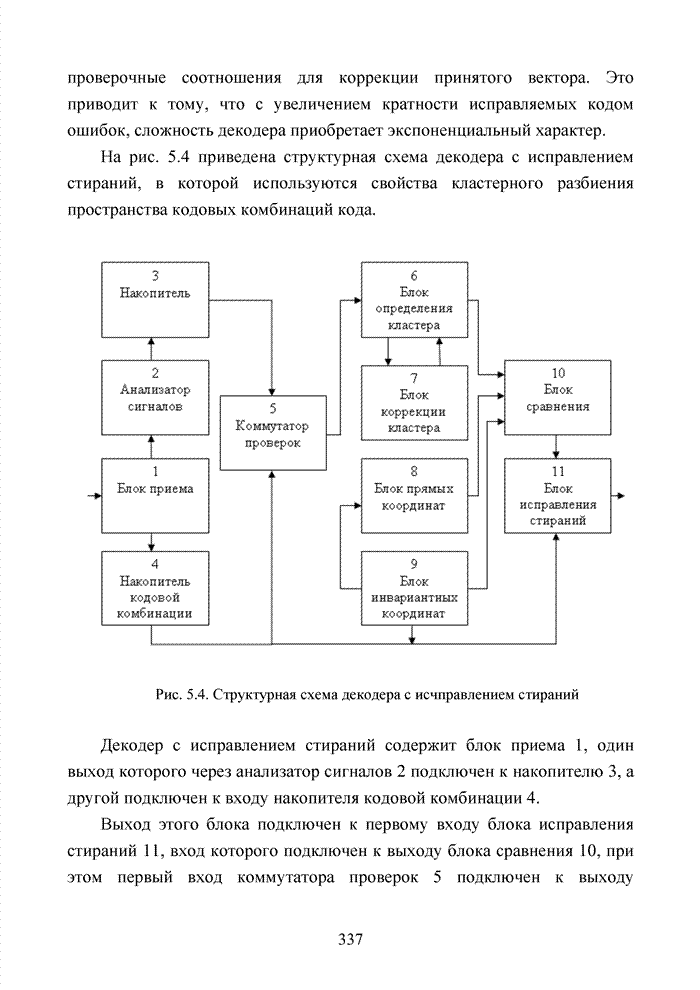
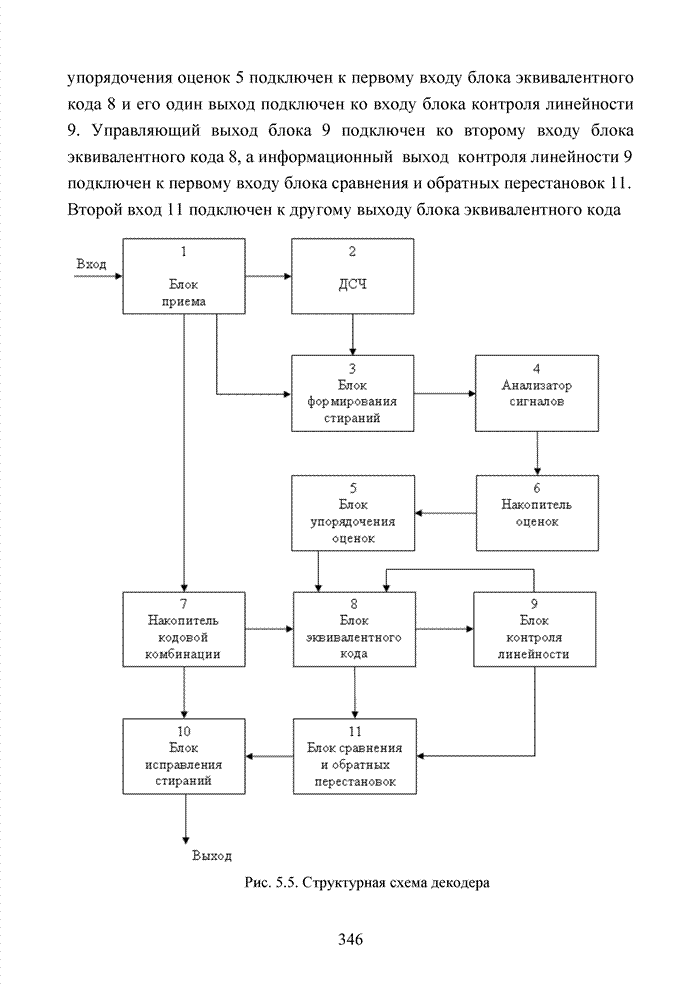
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
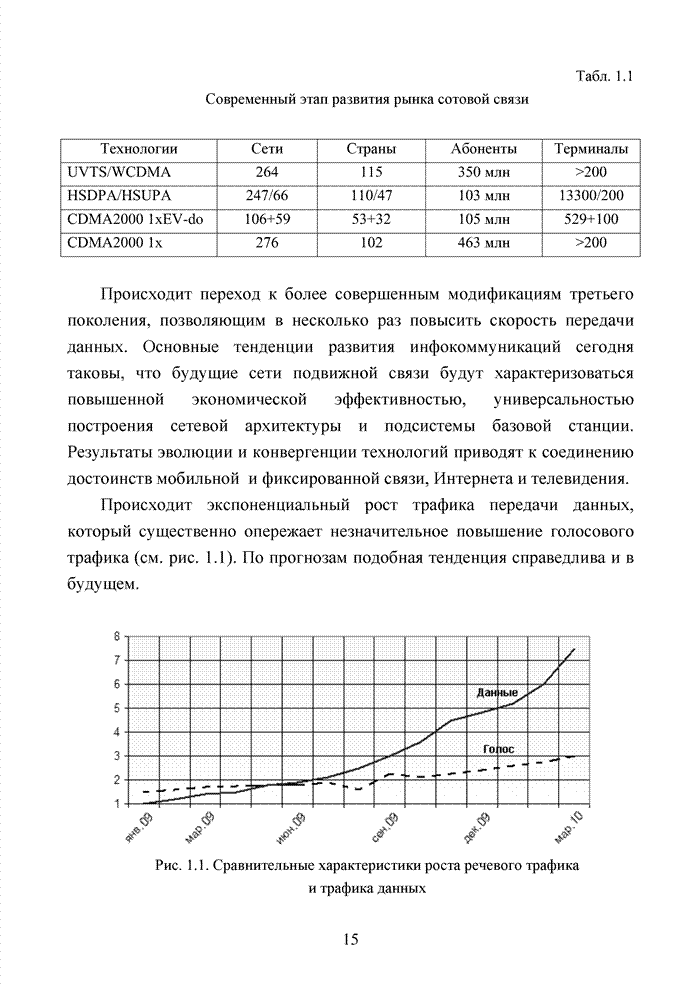
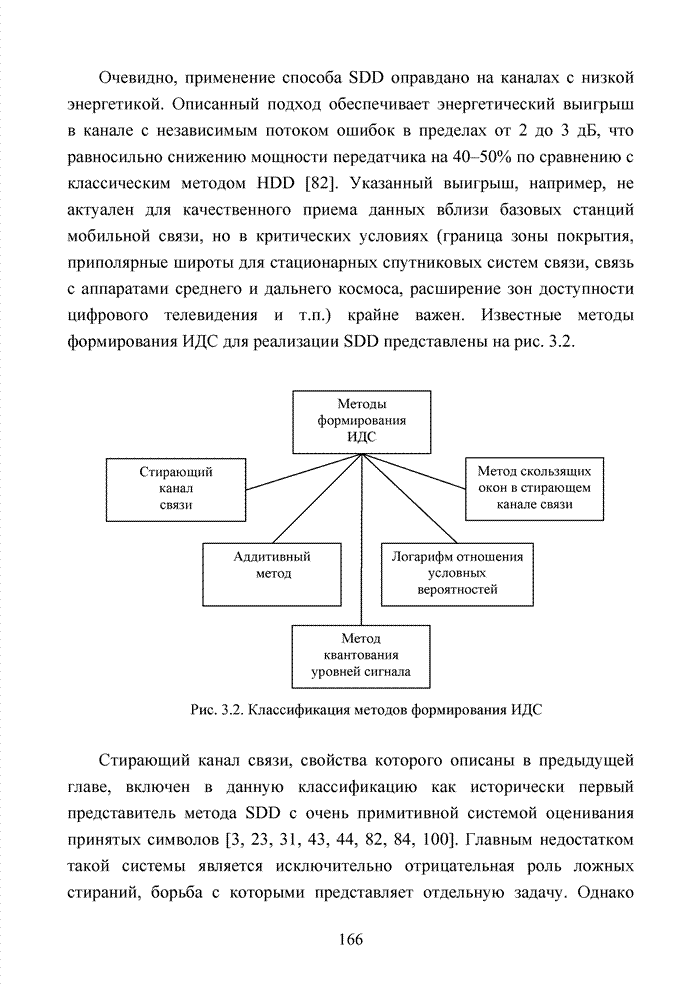
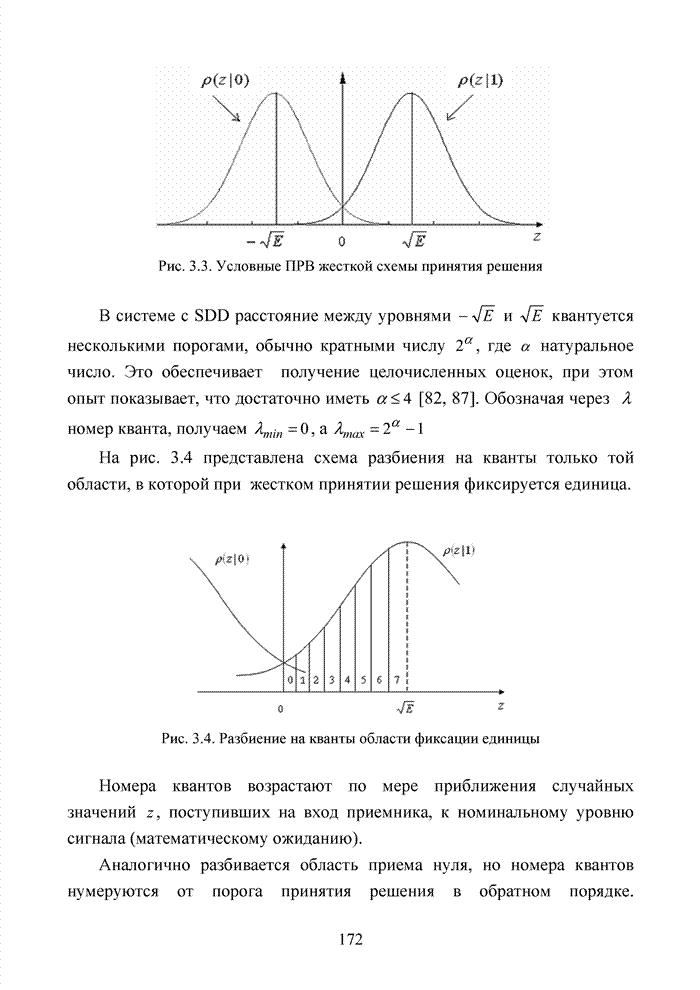
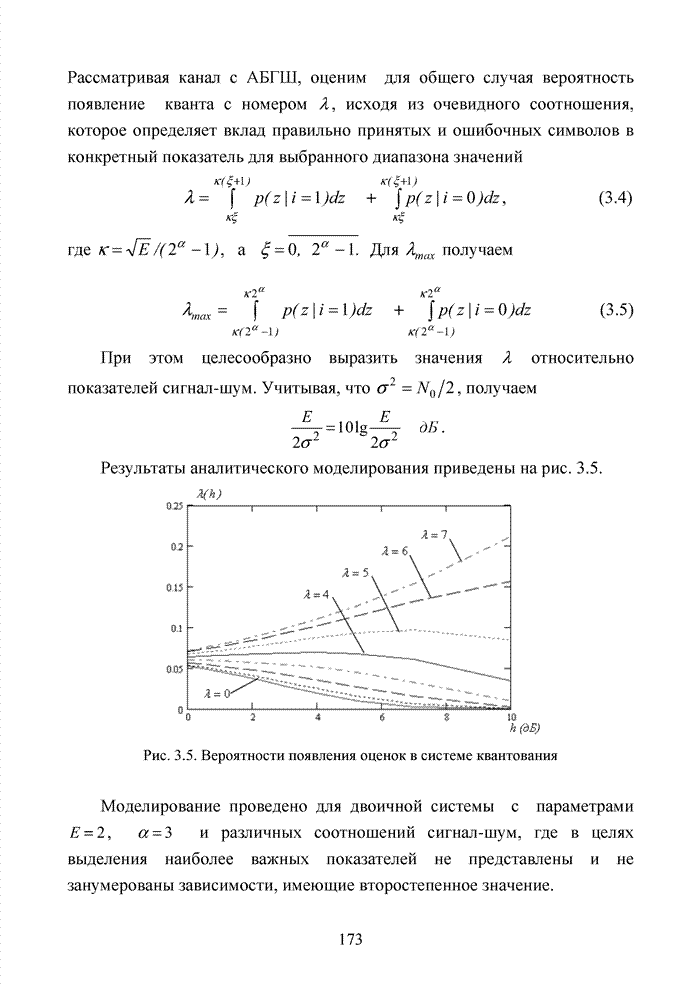
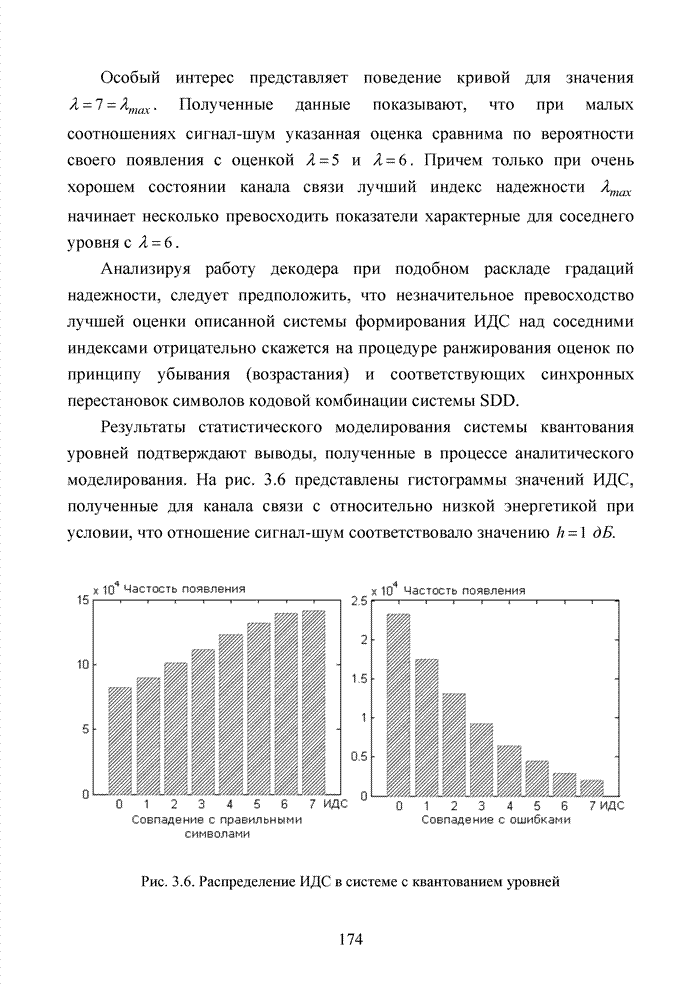
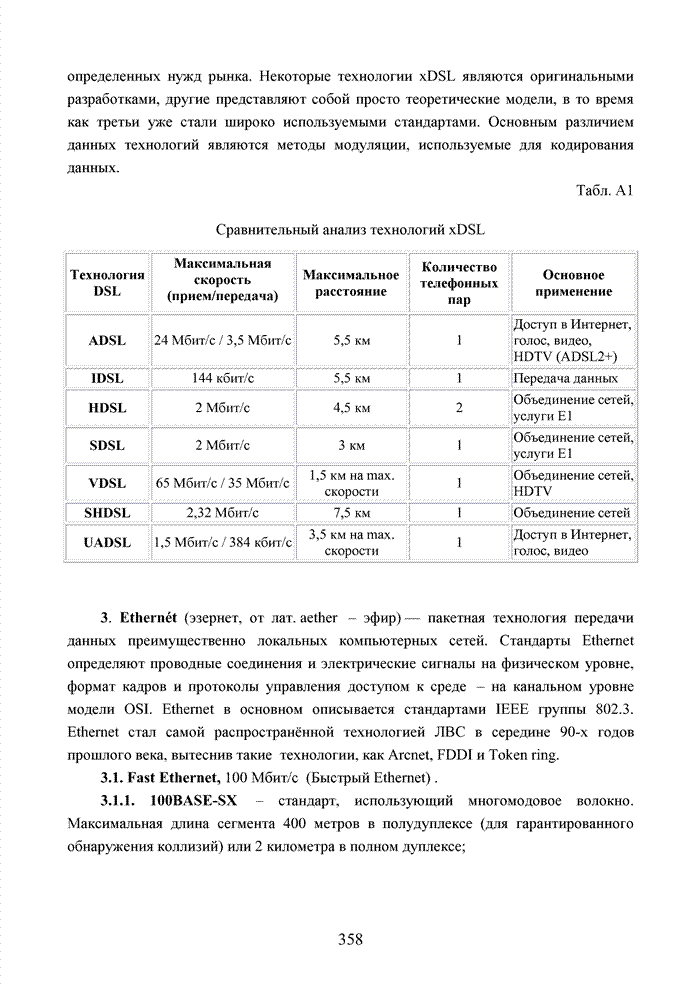
3.2. Аддитивный метод
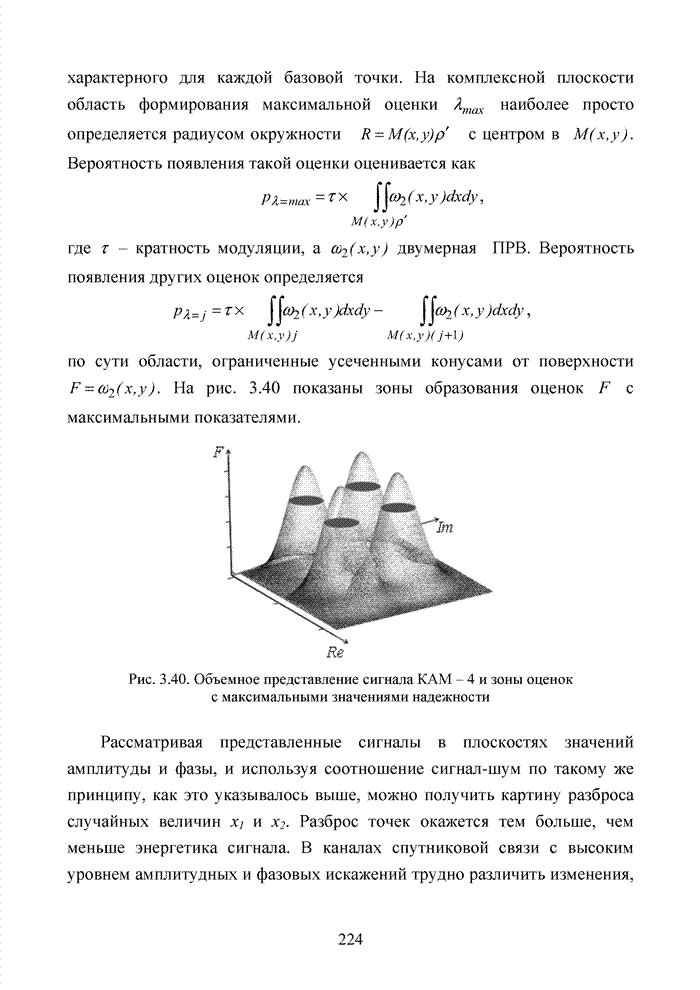
Исходя из принципов минимаксного подхода к решению задачи формирования ИДС, необходимо добиться максимального совпадения ошибочных символов с низкими оценками. По сути, необходимо оценить степень надежности вырабатываемого жесткого решения относительно элементов принимаемой двоичной последовательности или элементов сигнально-кодовой конструкции, обеспечивающего наиболее вероятное совпадение высоких значений ИДС, выраженных в том или ином формате, с кортежем правильно принятых символов.
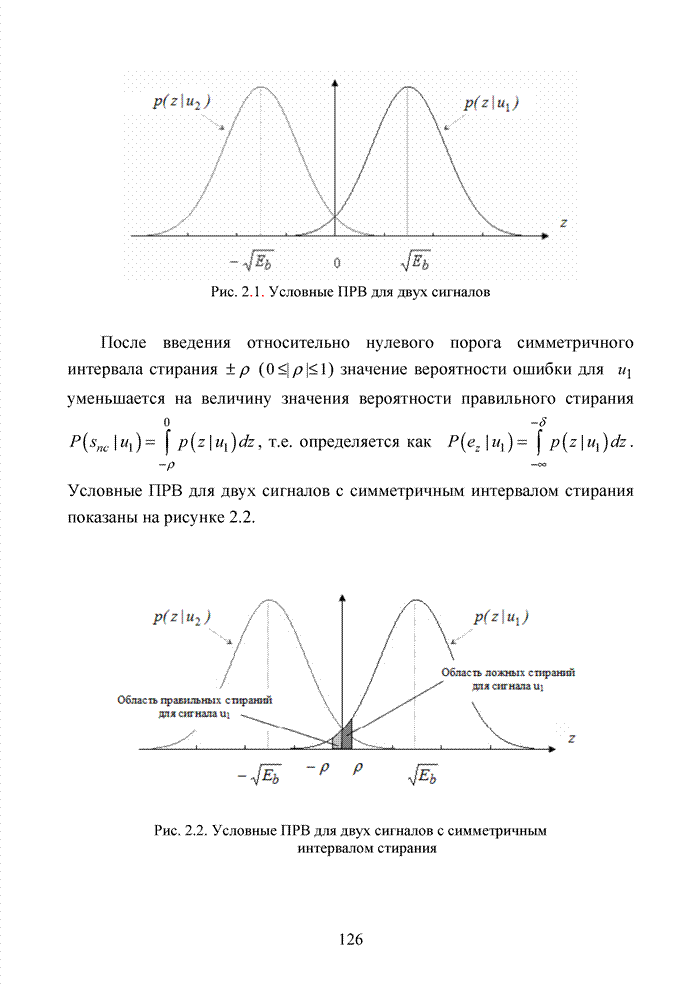
Решение поставленной задачи выполняется на основе аналитического моделирования непрерывного канала связи для выявления потенциальных возможностей исследуемых схем приема с последующим имитационным моделированием процедуры принятия решения и оценки степени приближения различных методов формирования ИДС к полученной границе. Пусть в месте приема наблюдается сигнал
![]() (3.1)
(3.1)
где ![]() – двоичный сигнал передатчика,
принимающий при i=1 значение –1, а при
– двоичный сигнал передатчика,
принимающий при i=1 значение –1, а при ![]() – значение 1,
– значение 1, ![]() – аддитивная помеха. Если
– аддитивная помеха. Если ![]() энергия переданного сигнала, а
энергия переданного сигнала, а ![]() временно представить
равной нулю, то
временно представить
равной нулю, то
![]()
 (3.2)
(3.2)
Часто ![]() для двоичных систем модуляции
представляют в форме [89]
для двоичных систем модуляции
представляют в форме [89]
![]() .
(3.3)
.
(3.3)
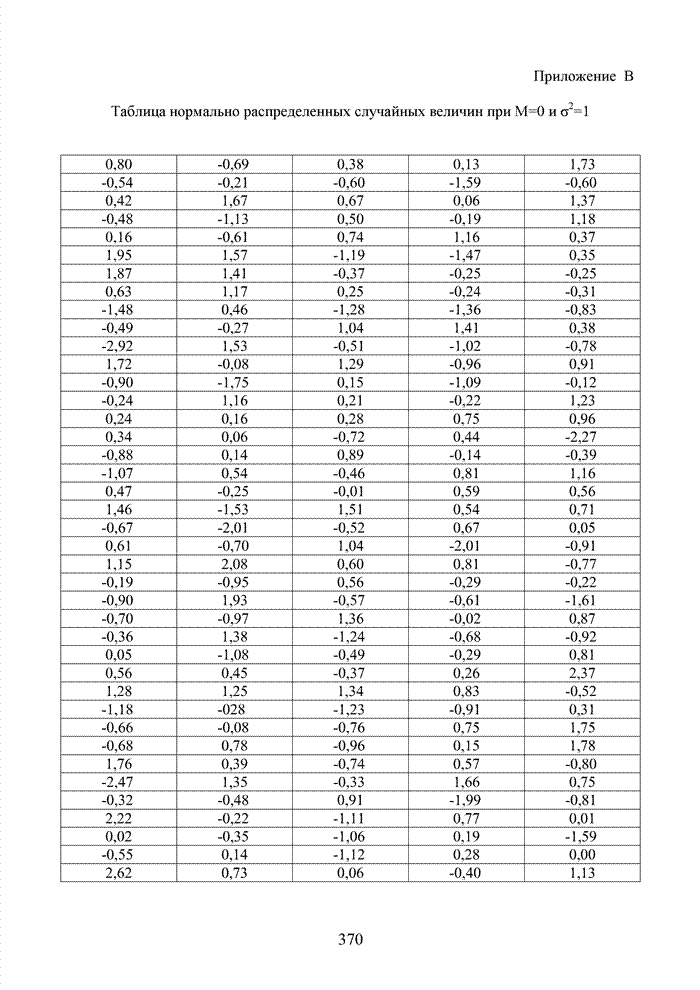
Значения ![]() в ходе аналитического
моделирования могут выбираться из специальных таблиц, один из образцов которой
приведен в Приложении В. В ходе имитационного моделирования, как правило,
используют ДСЧ с равномерной ПРВ, преобразуя получаемые с его помощью числа в
последовательность значений, подчиняющихся требуемому закону распределения [44,
88].
в ходе аналитического
моделирования могут выбираться из специальных таблиц, один из образцов которой
приведен в Приложении В. В ходе имитационного моделирования, как правило,
используют ДСЧ с равномерной ПРВ, преобразуя получаемые с его помощью числа в
последовательность значений, подчиняющихся требуемому закону распределения [44,
88].
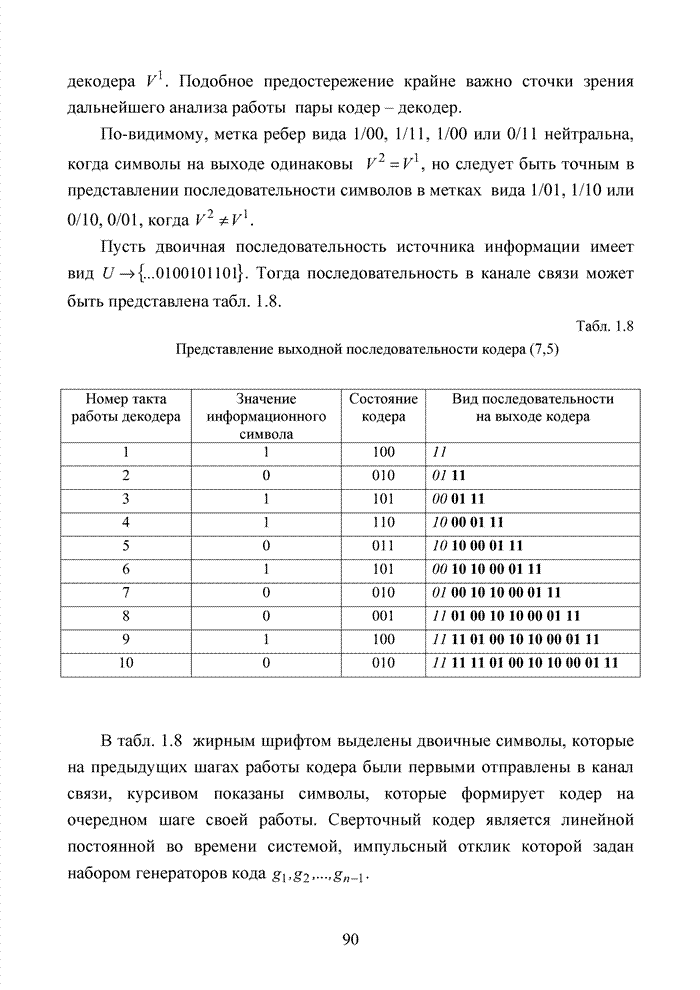
Рассмотрим
поэтапное выполнение алгоритма работы декодера на примере систематического кода
БЧХ (7;4;3). Пусть от
источника информации на вход кодера поступает вектор вида ![]() =1101, а на его выходе в
результате умножения вектора
=1101, а на его выходе в
результате умножения вектора ![]() на порождающую матрицу кода
на порождающую матрицу кода ![]() формируется
последовательность
формируется
последовательность
![]() =1 1 0 1 0 0 1.
=1 1 0 1 0 0 1.
Для наглядности положим ![]() , тогда результаты
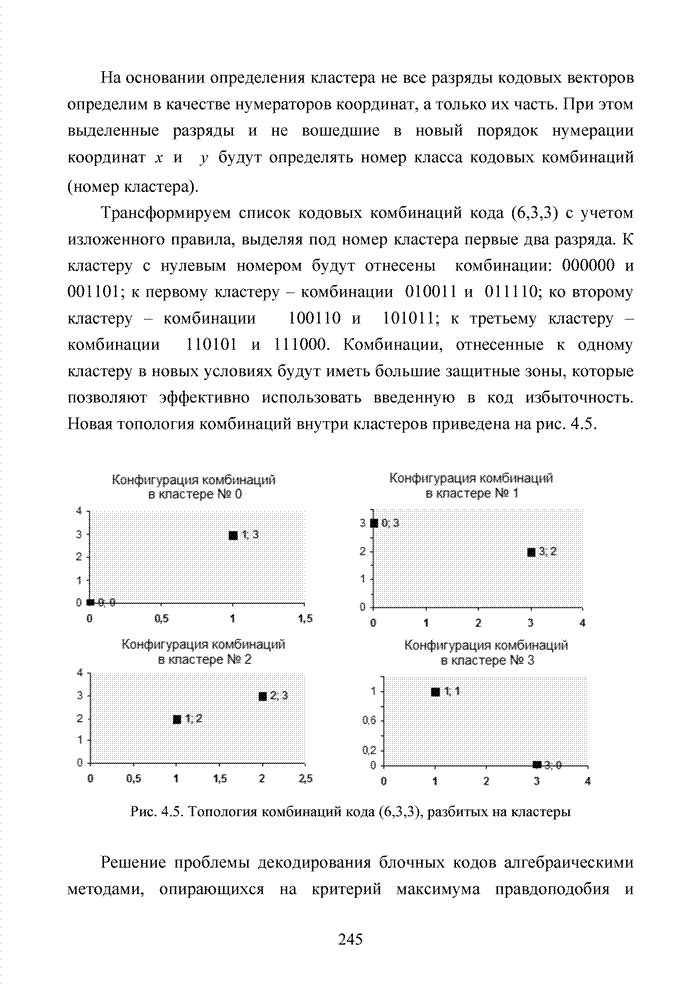
трансформации кодового вектора представляются табл. 3.2.
, тогда результаты
трансформации кодового вектора представляются табл. 3.2.
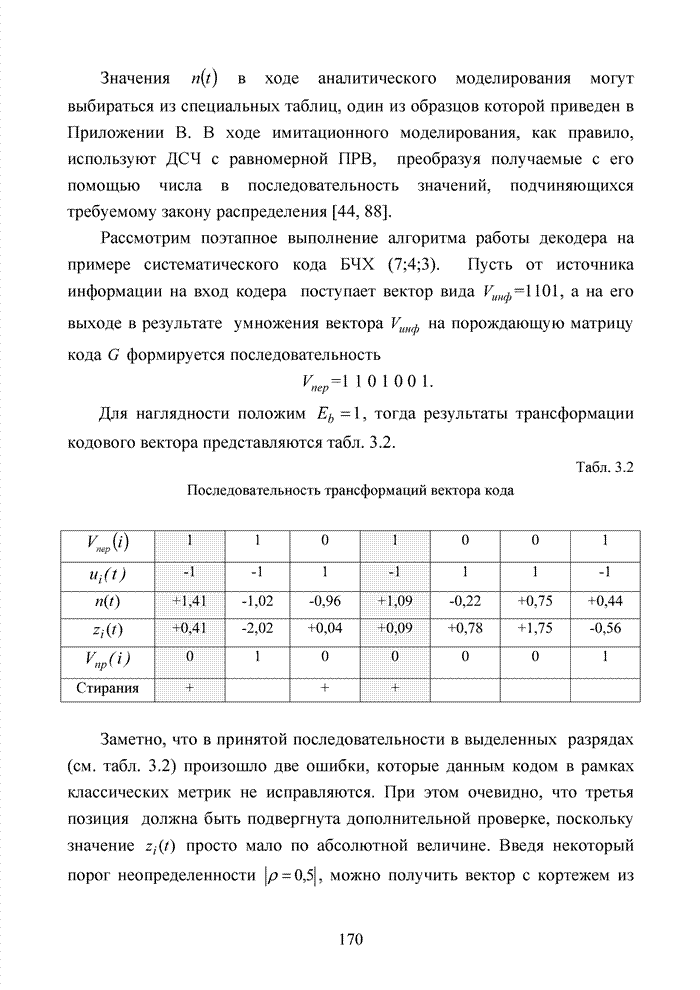
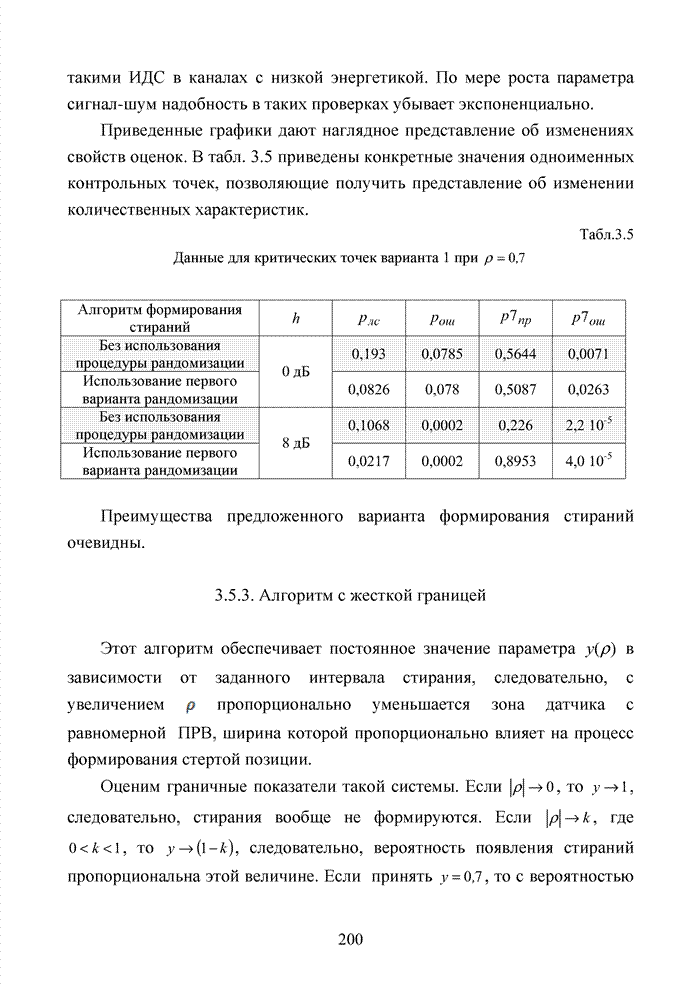
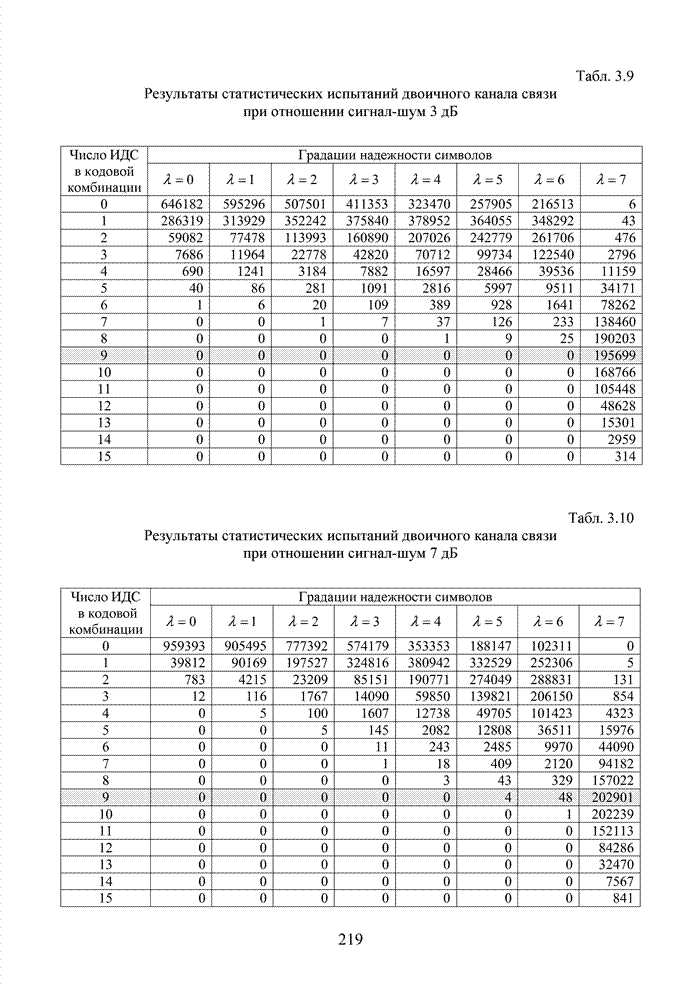
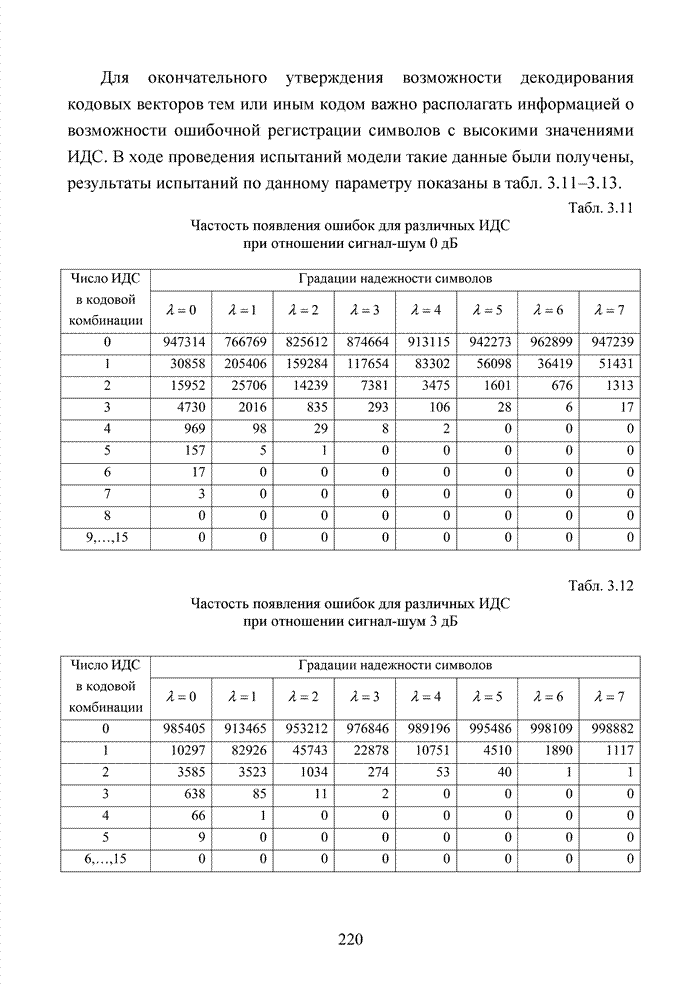
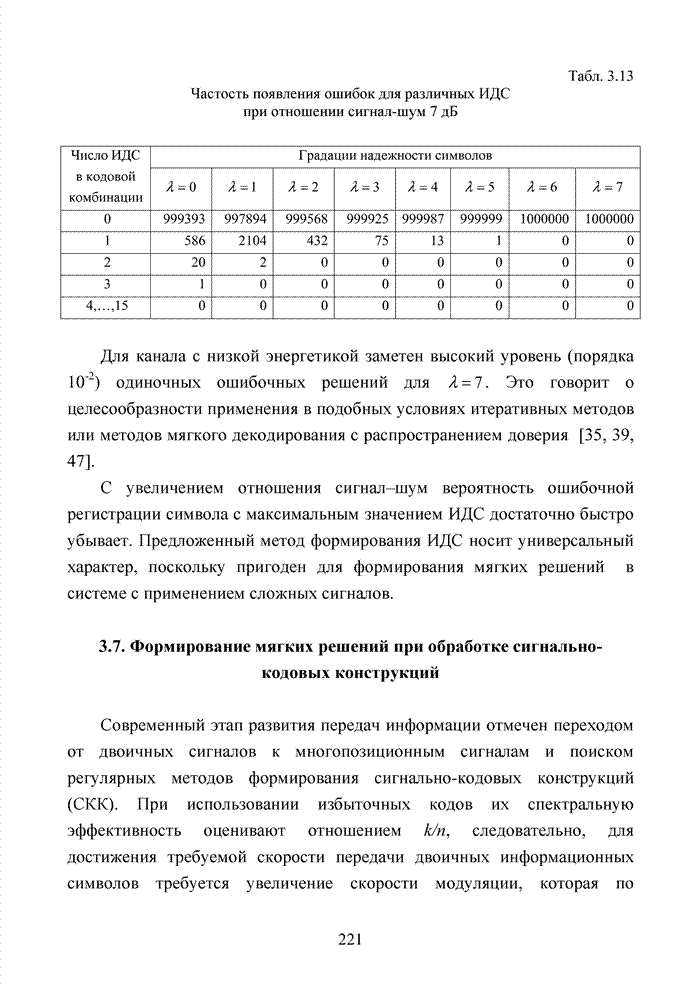
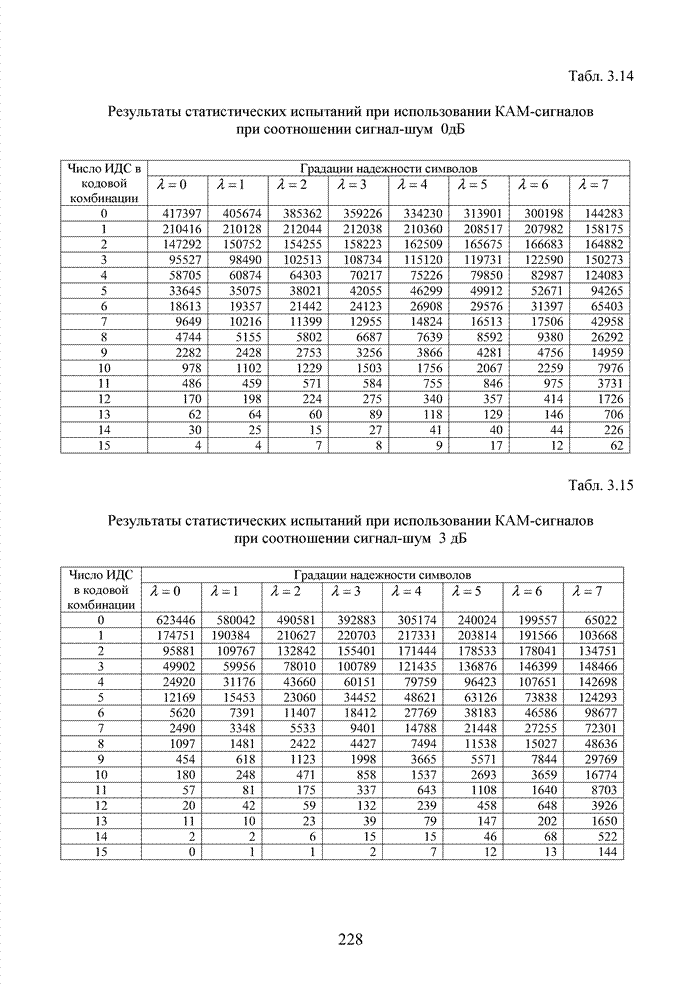
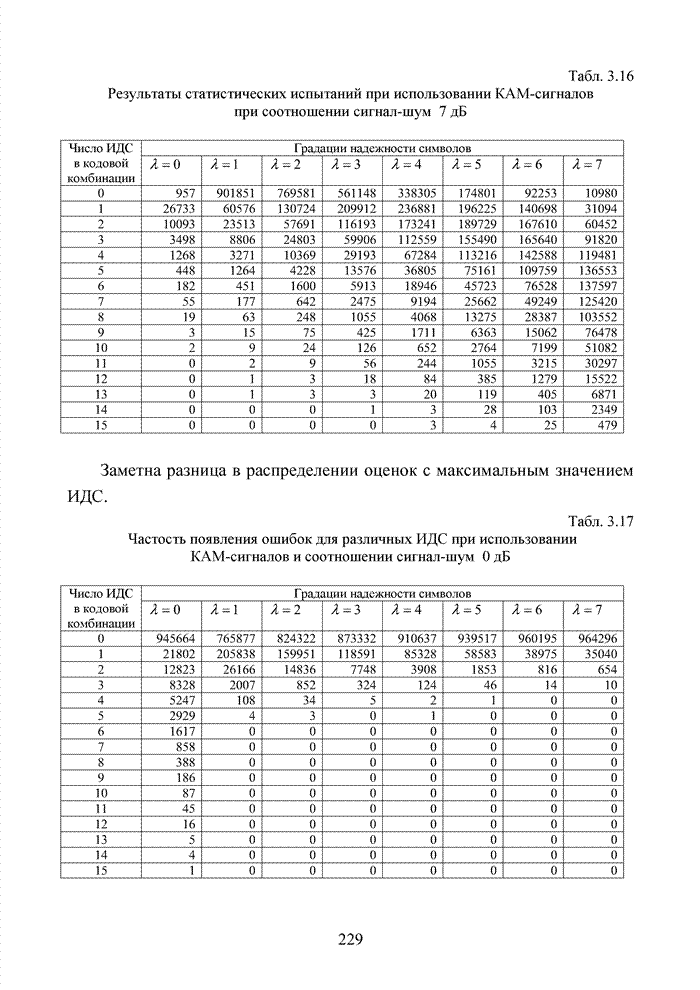
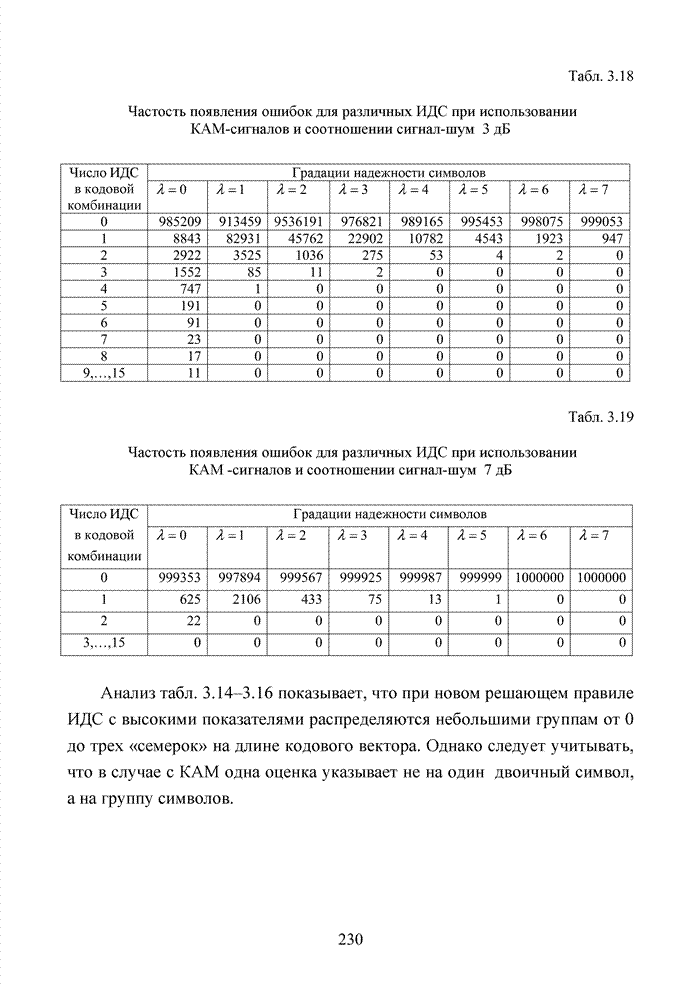
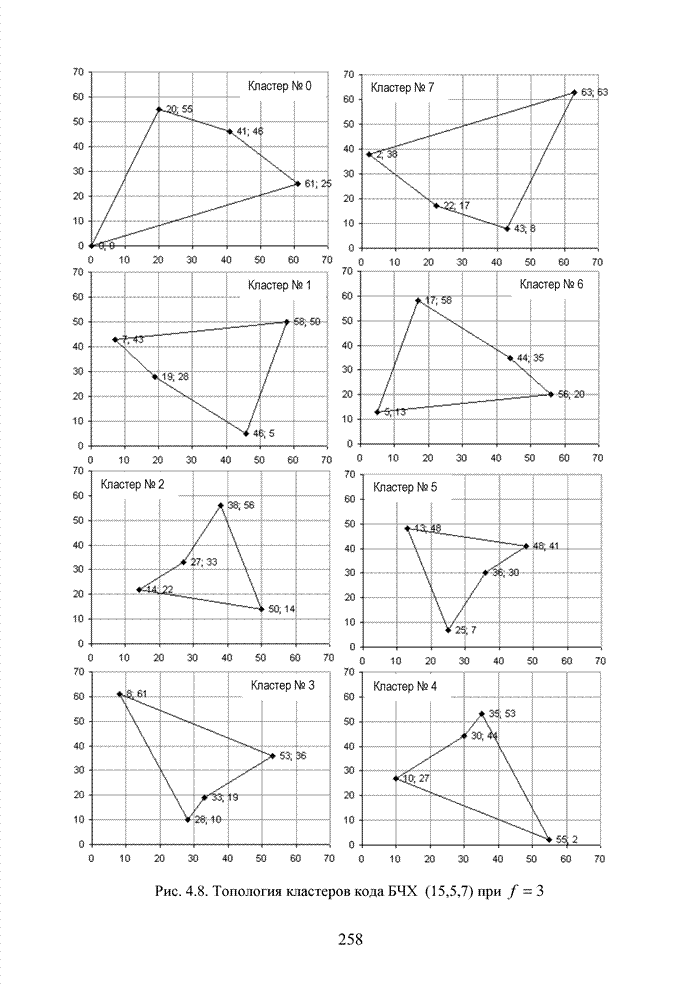
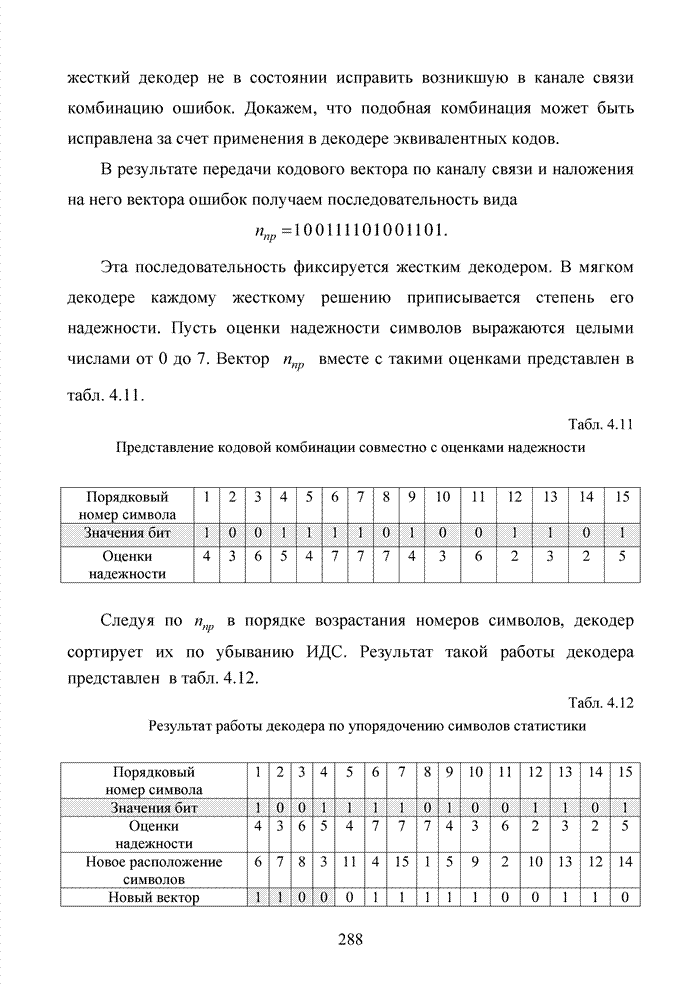
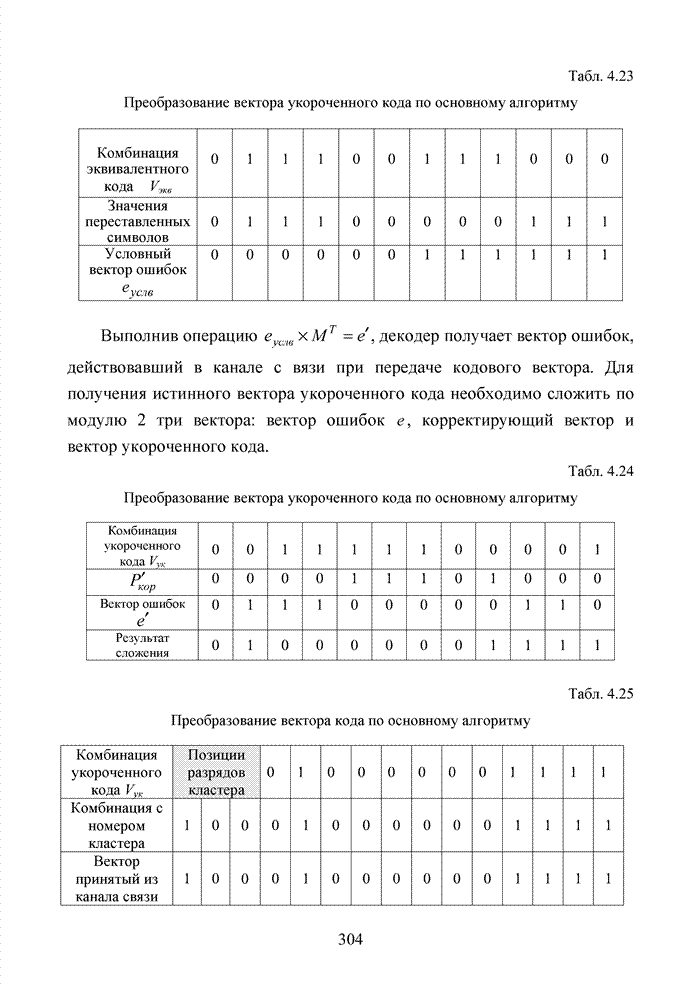
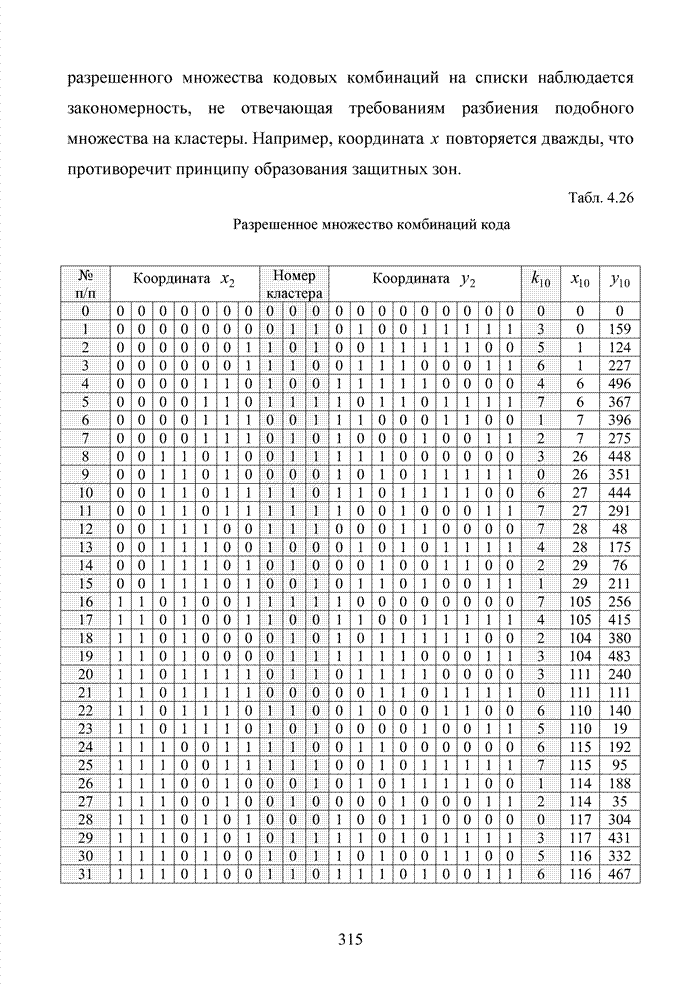
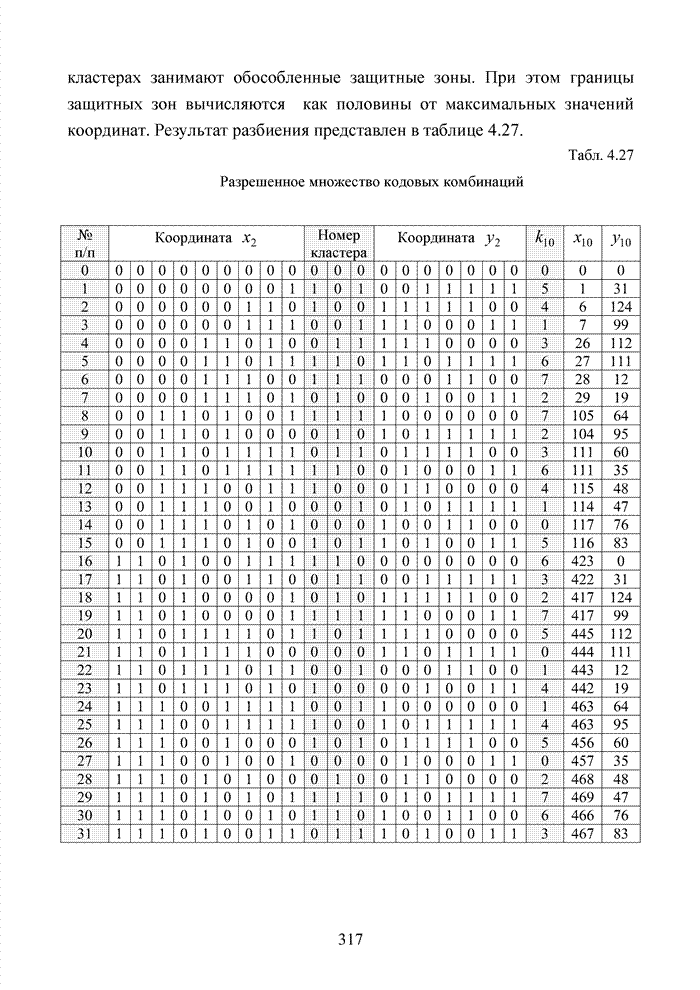
Табл. 3.2 Последовательность трансформаций вектора кода
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
-1 |
-1 |
1 |
-1 |
1 |
1 |
-1 |
|
|
+1,41 |
-1,02 |
-0,96 |
+1,09 |
-0,22 |
+0,75 |
+0,44 |
|
|
+0,41 |
-2,02 |
+0,04 |
+0,09 |
+0,78 |
+1,75 |
-0,56 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
Стирания |
+ |
|
+ |
+ |
|
|
|
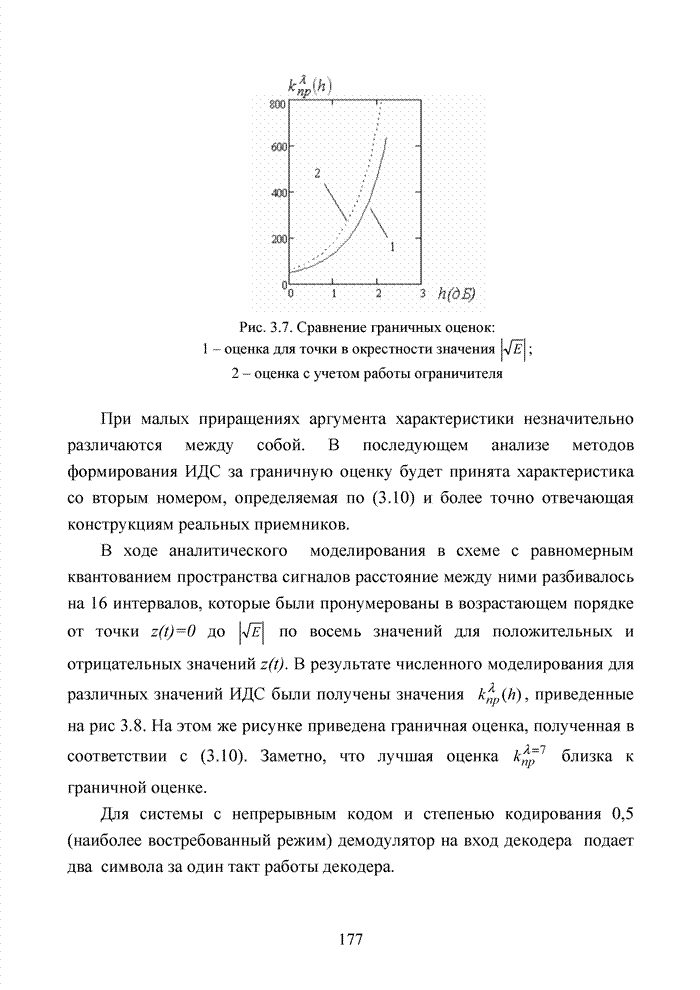
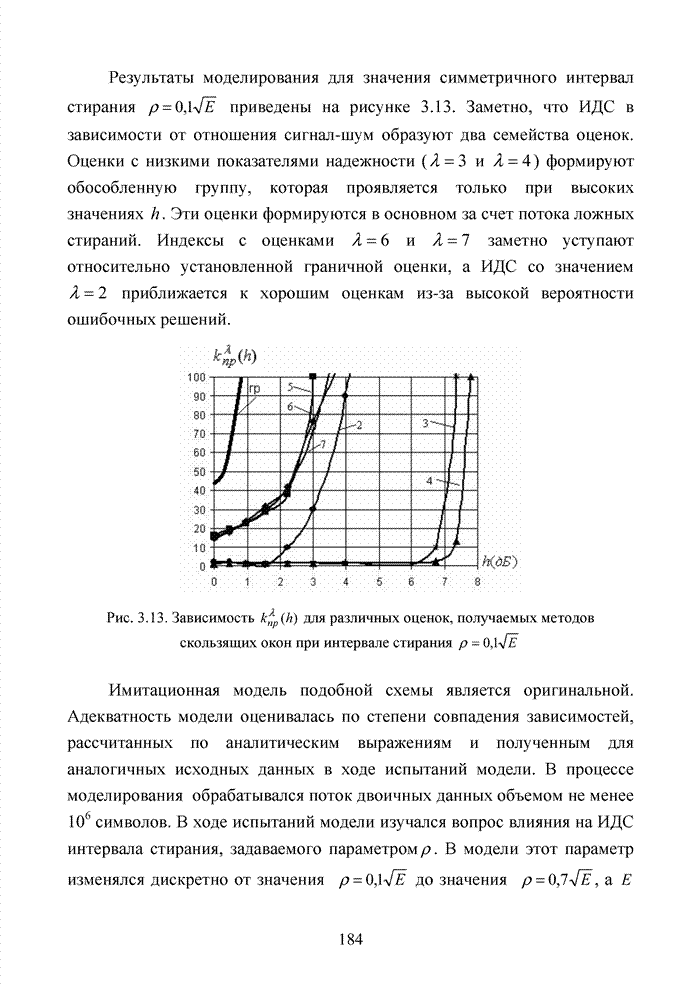
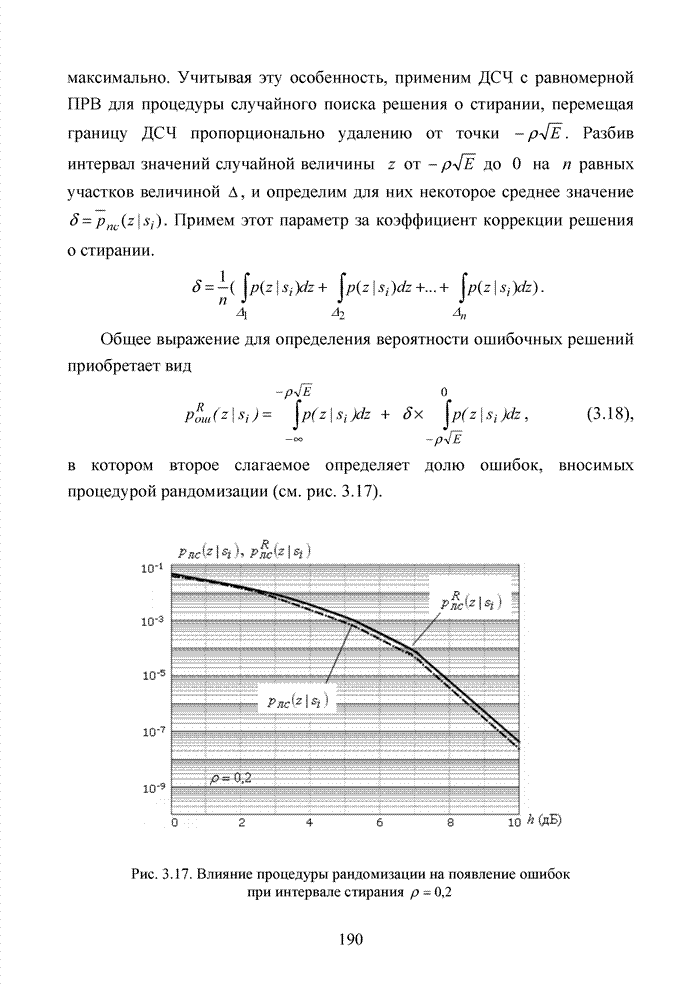
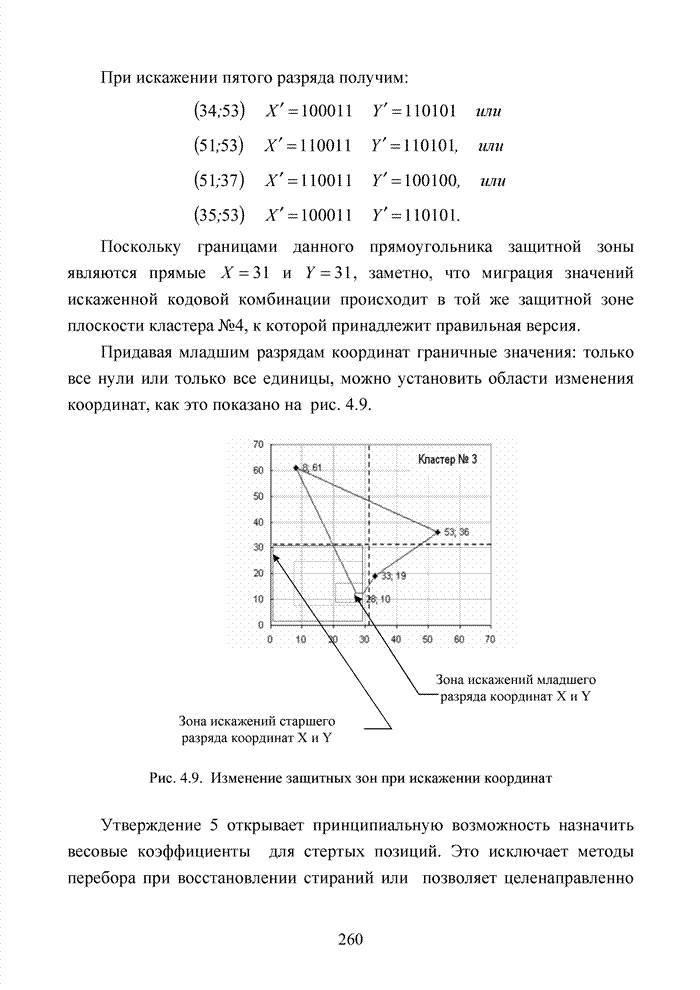
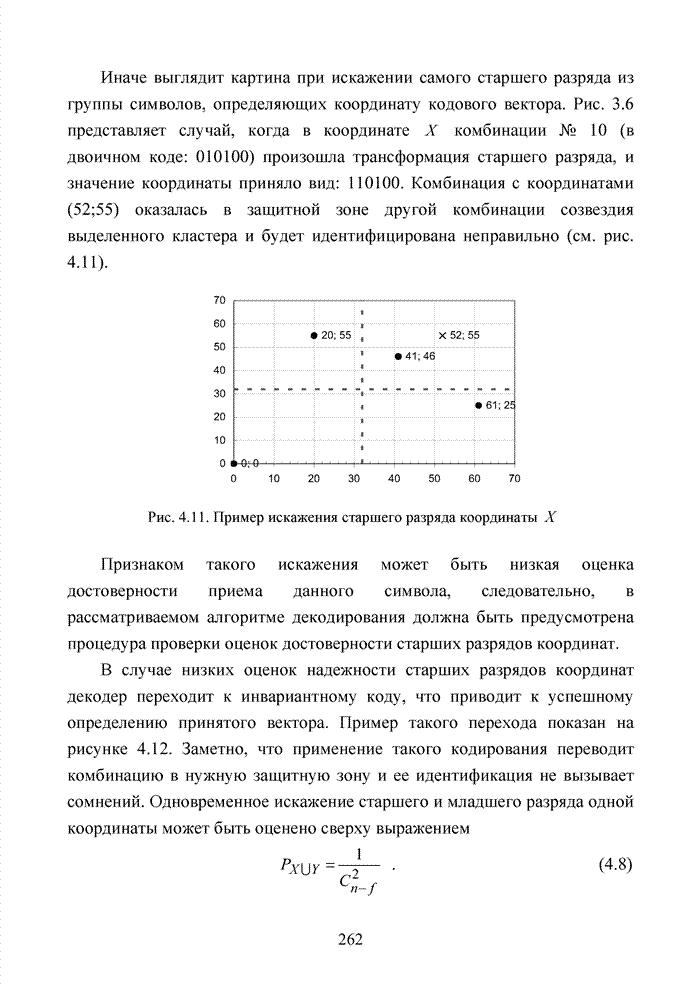
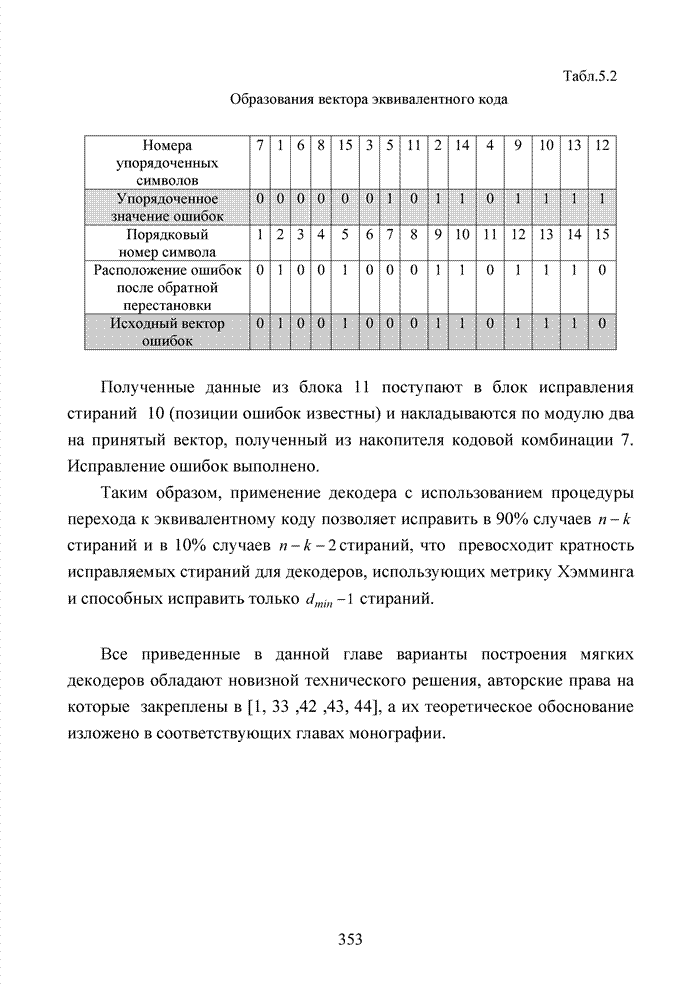
Заметно, что в принятой
последовательности в выделенных разрядах (см. табл. 3.2) произошло две ошибки,
которые данным кодом в рамках классических метрик не исправляются. При этом очевидно,
что третья позиция должна быть подвергнута дополнительной проверке, поскольку
значение ![]() просто
мало по абсолютной величине. Введя некоторый порог неопределенности
просто
мало по абсолютной величине. Введя некоторый порог неопределенности ![]() , можно получить вектор
с кортежем из трех стертых позиций, но подобная комбинация стираний в рамках
тех же классических метрик, используемых в теории кодирования, однозначно
восстановлена быть тоже не может.
, можно получить вектор
с кортежем из трех стертых позиций, но подобная комбинация стираний в рамках
тех же классических метрик, используемых в теории кодирования, однозначно
восстановлена быть тоже не может.
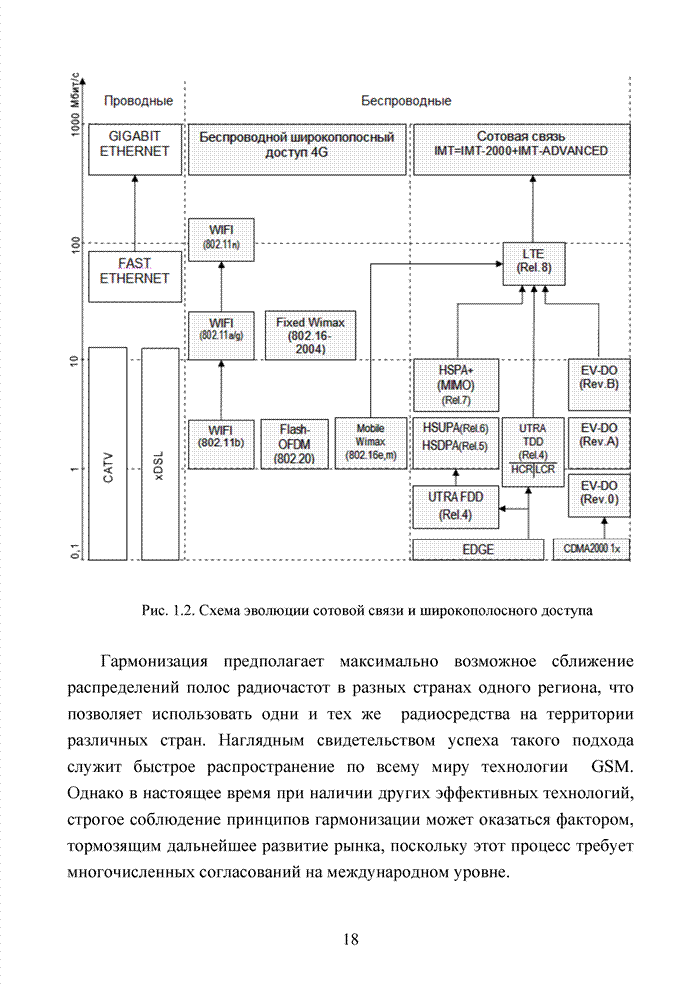
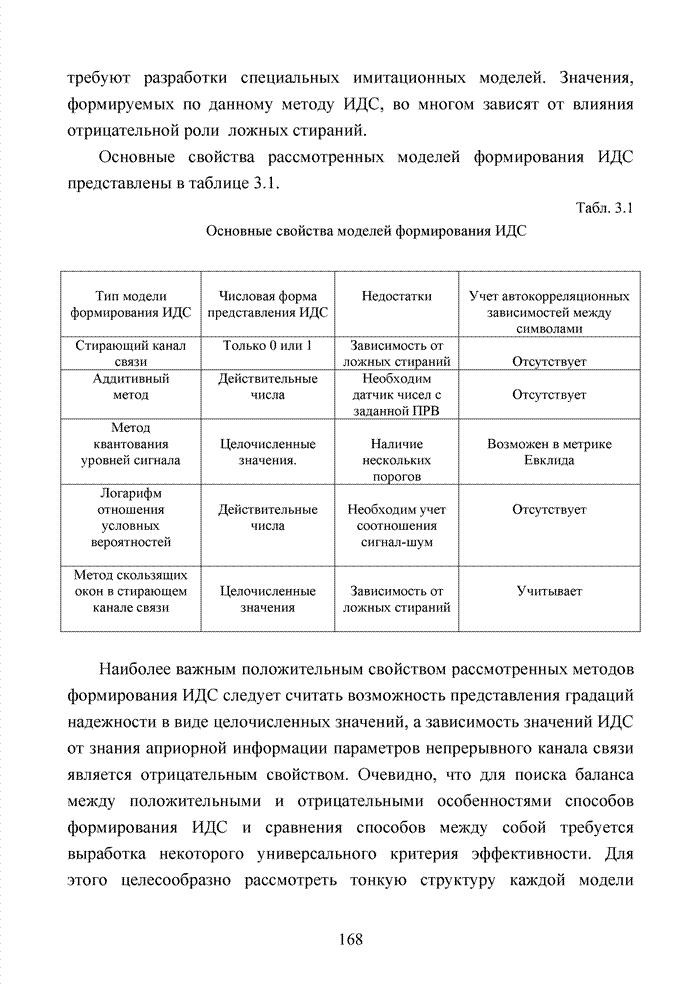
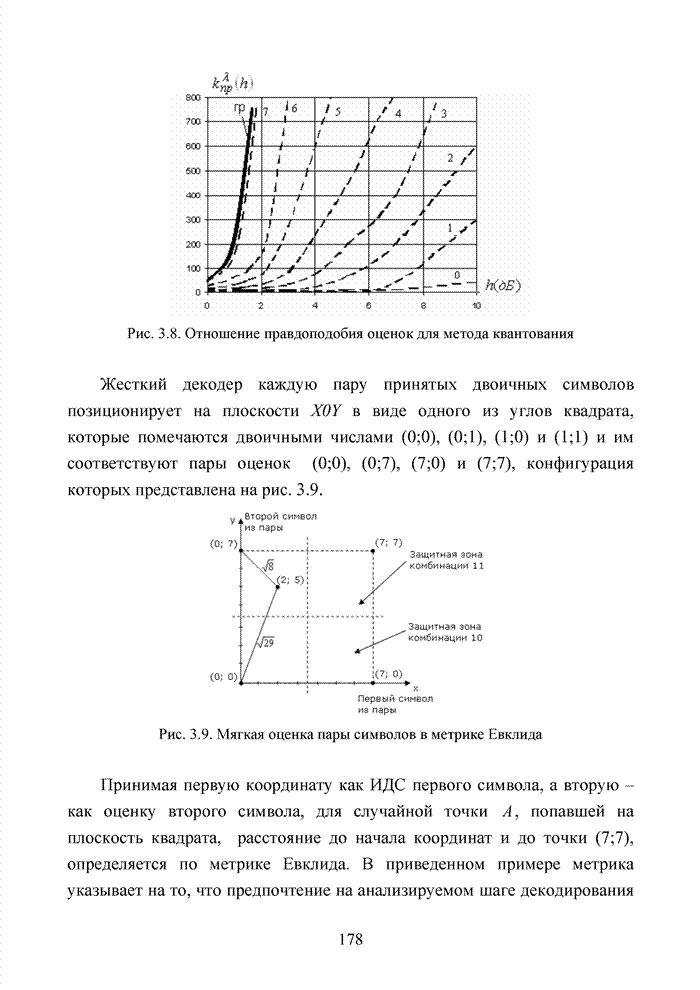
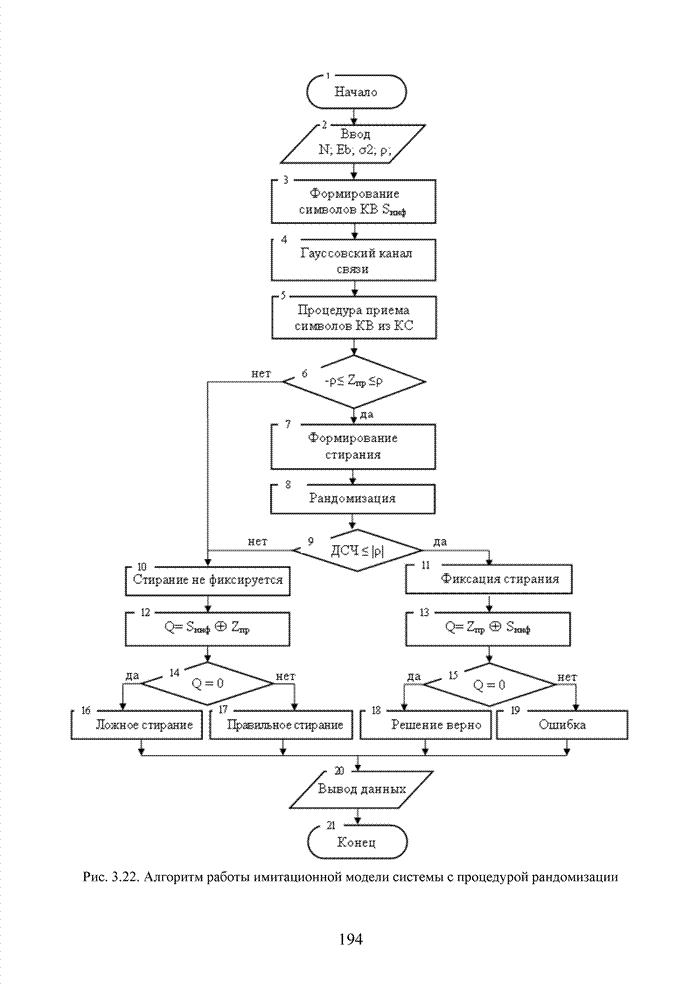
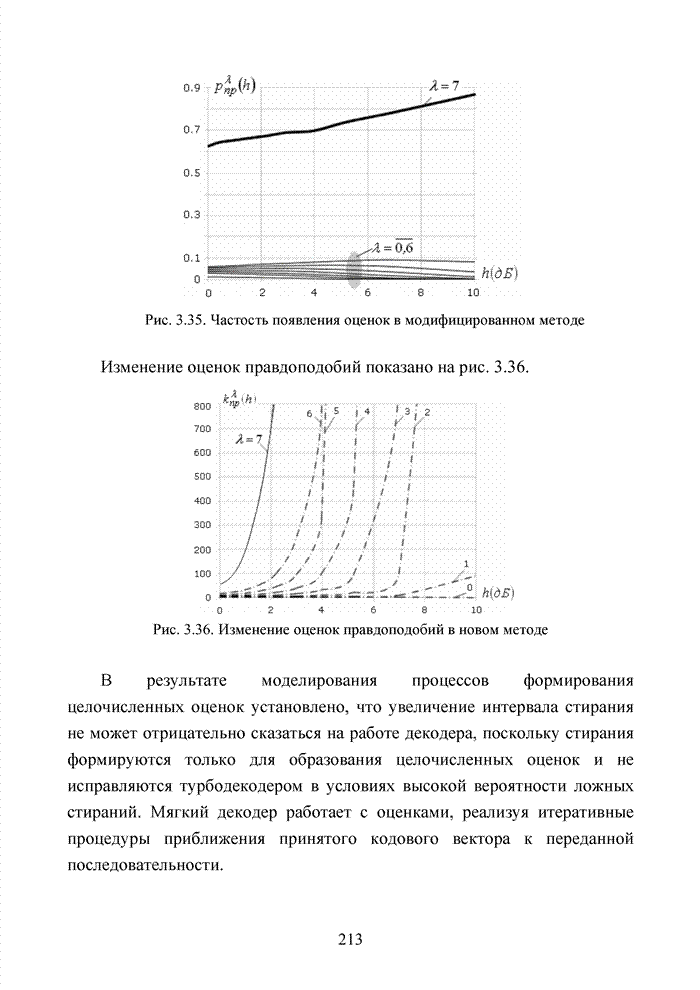
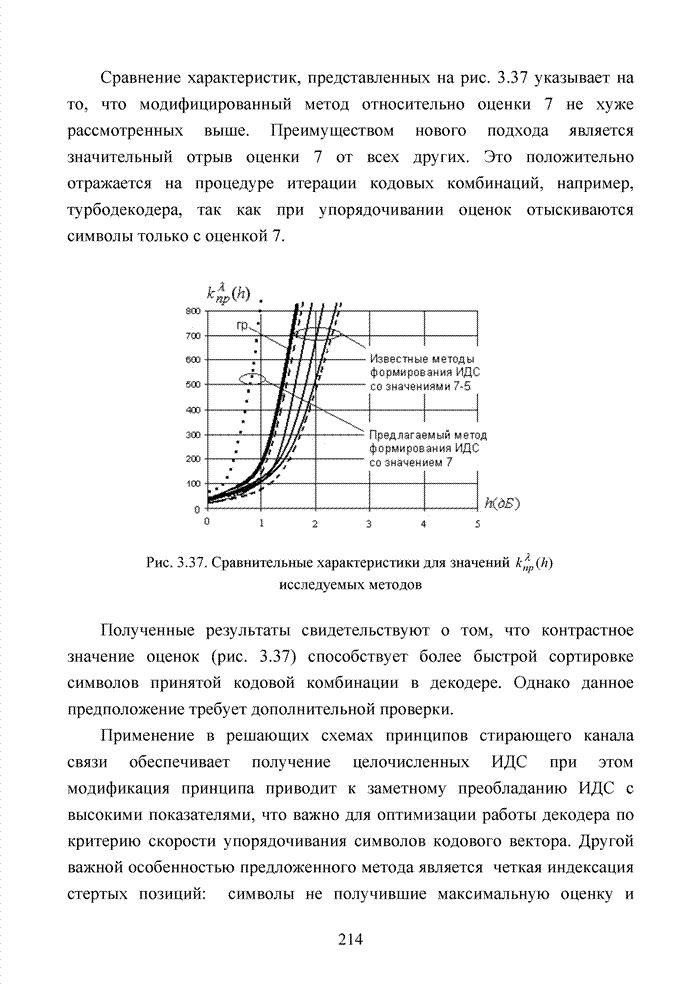
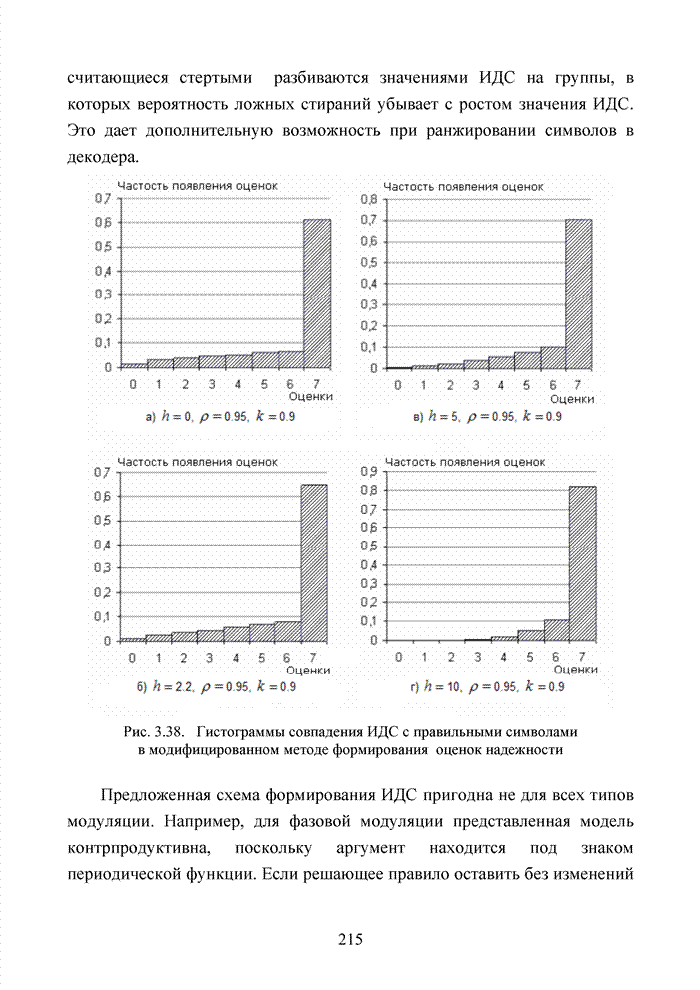
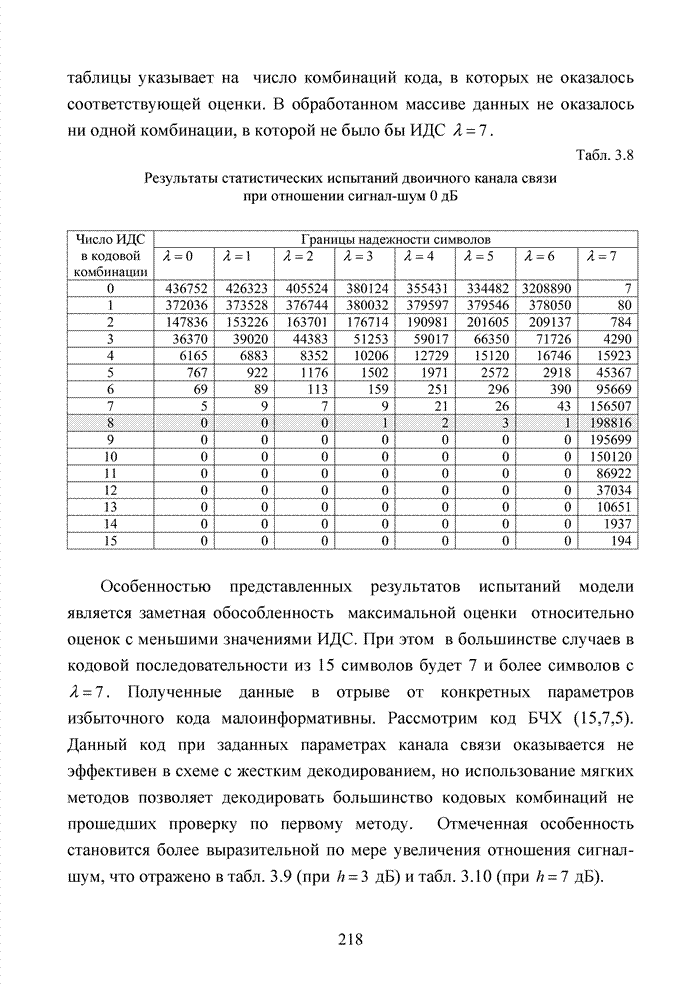
Большинство декодеров современных систем связи обрабатывают поступающую на их вход информацию в реальном масштабе времени. Это обстоятельство требует системного подхода в реализации всей последовательности шагов обработки данных. По крайней мере, при построении мягкого декодера должен соблюдаться принцип приоритета глобальной цели (повышение достоверности передаваемой информации), принцип совместного анализа системы декодирования как целого и как совокупности элементов, а также принцип связности, исходя из которого, анализ работы любой части мягкого декодера выполняется с учетом всех его связей. Получив мягкие решения, декодер сортирует их в порядке возрастания (убывания) и данные табл. 3.2 наглядно показывают, что действительные числа при их упорядочении потребуют больших вычислительных затрат и ресурсов памяти, чем выполнение процедуры сортировки целых чисел. Округление полученных значений ИДС при использовании данного метода до целых значений позволяет снизить сложность реализации процессора приемника.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
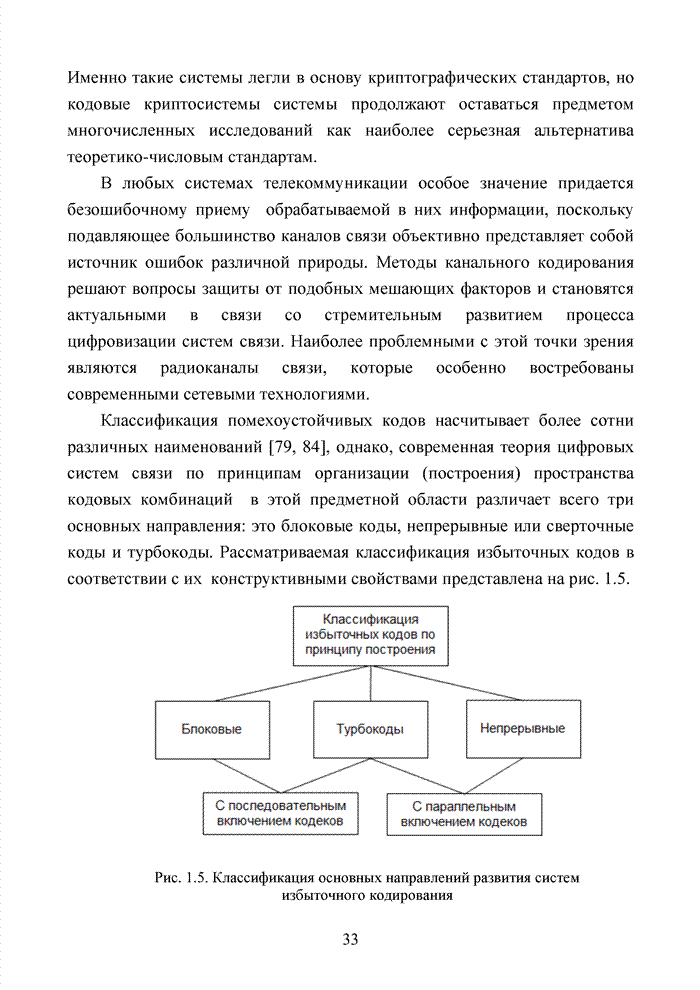
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
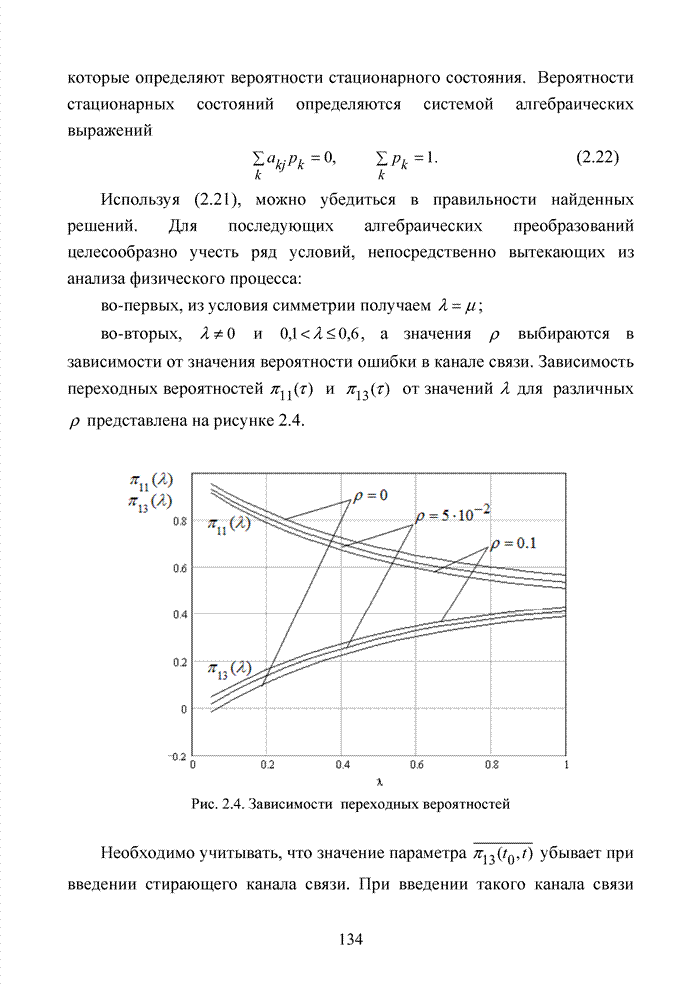
- 1.1. Инфокоммуникационные технологии нового поколения
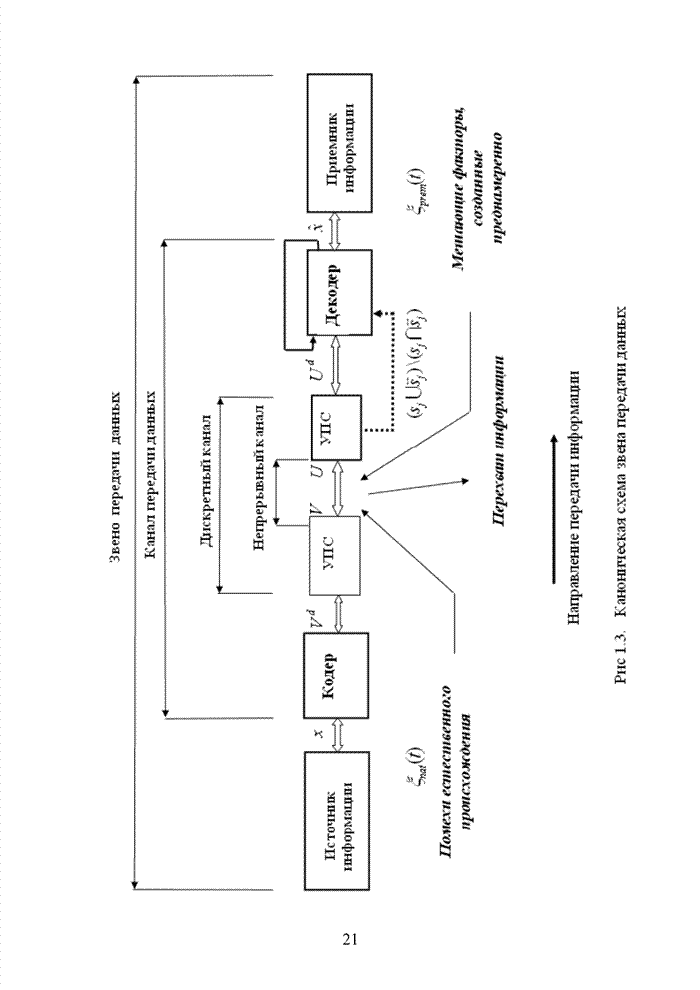
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
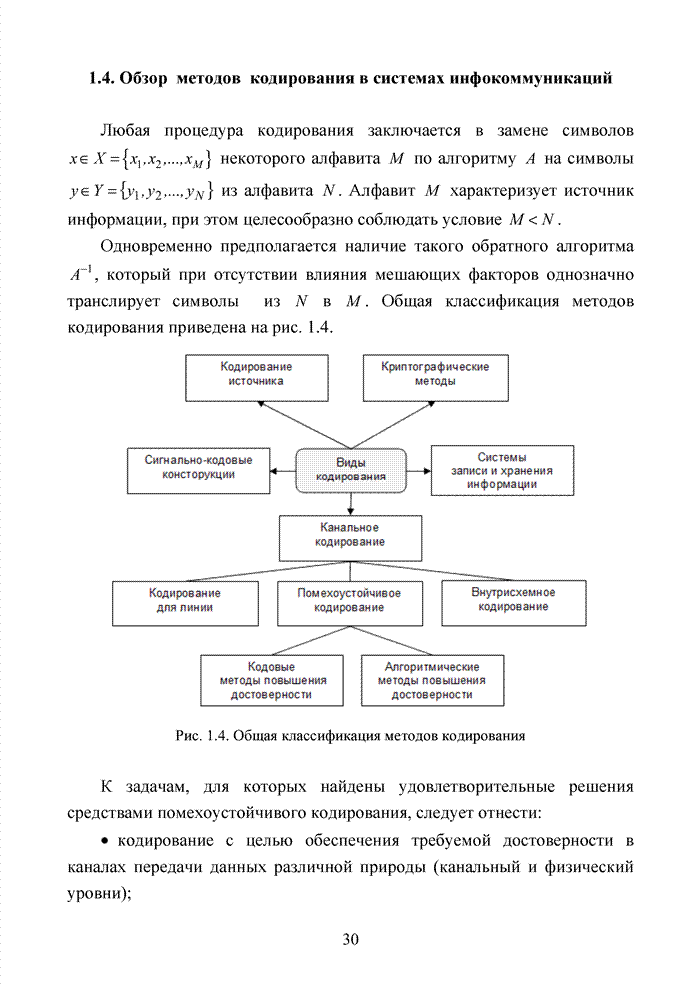
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
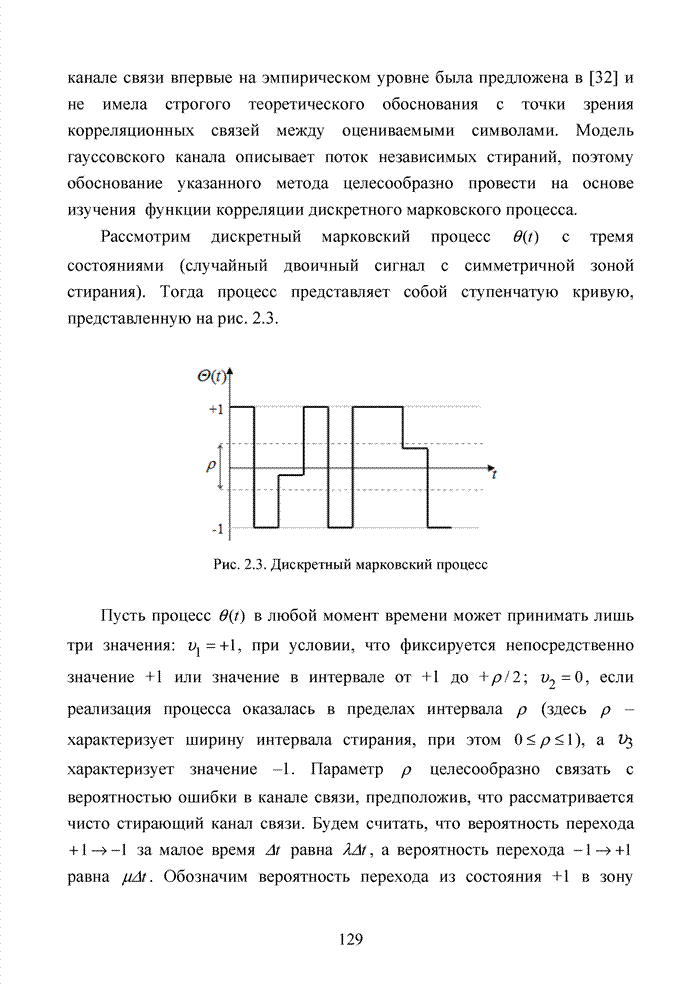
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
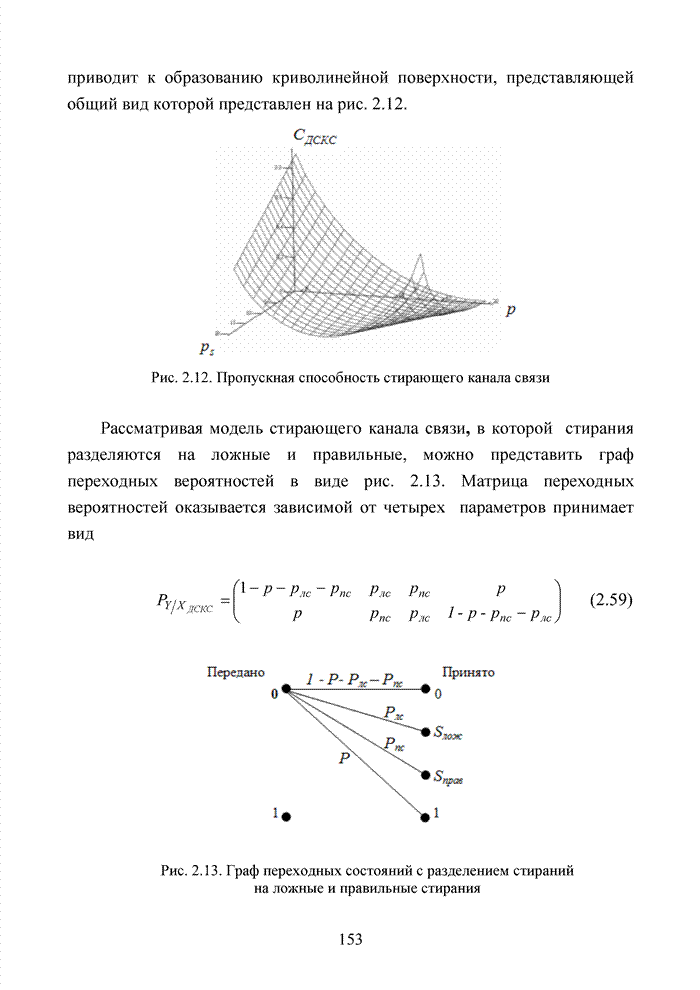
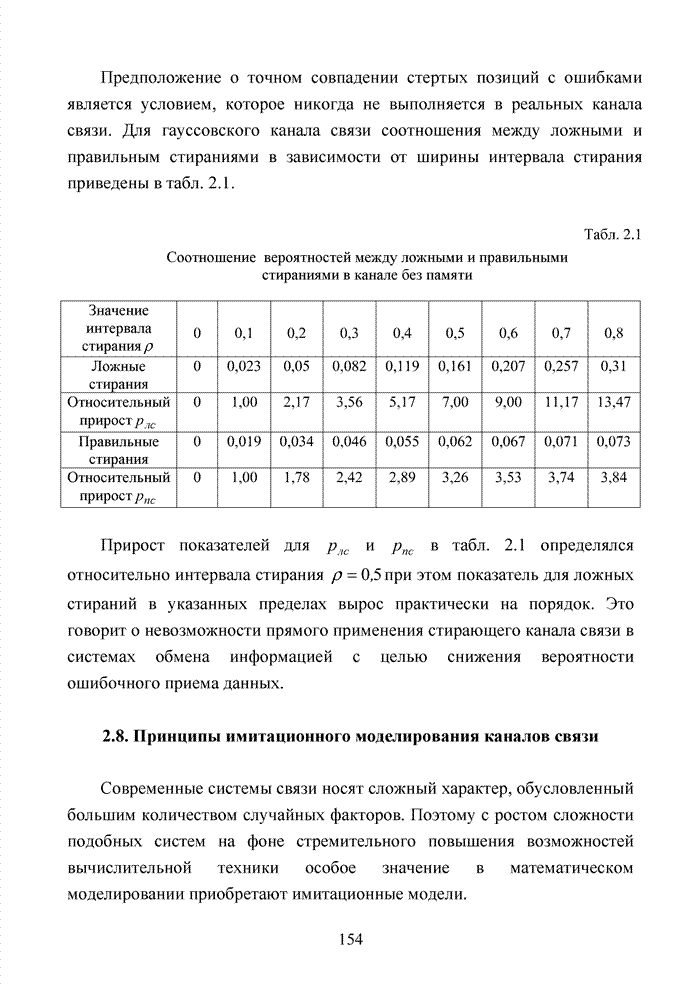
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
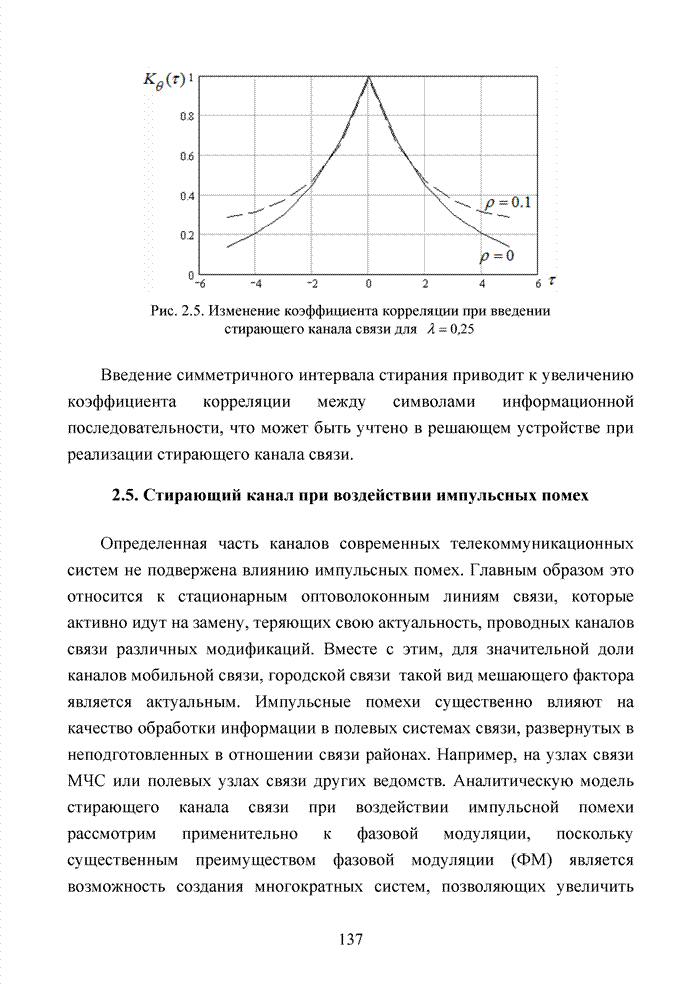
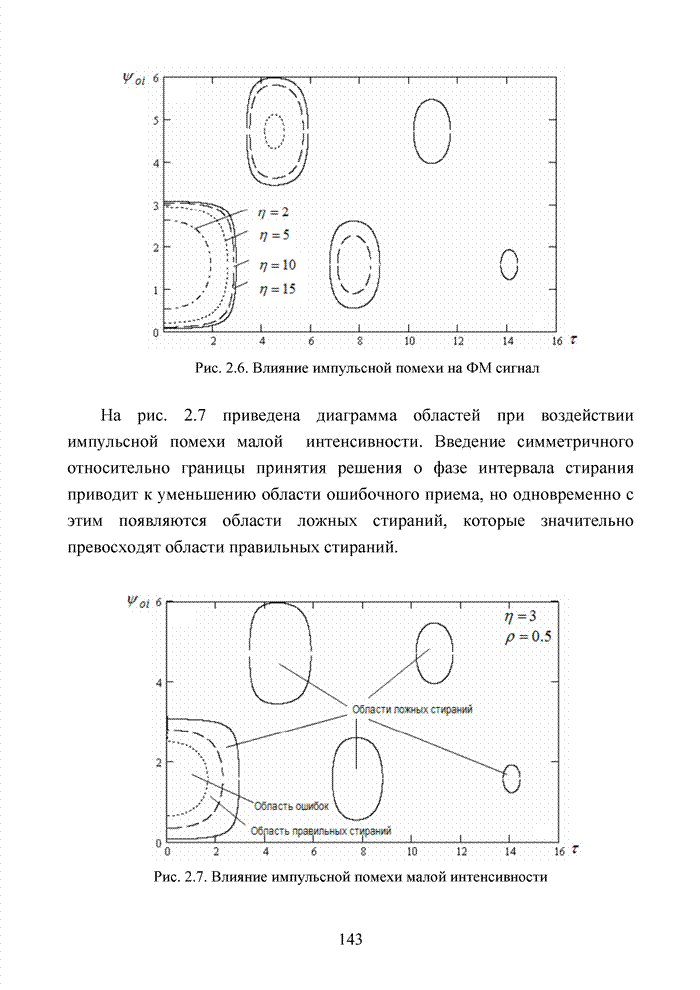
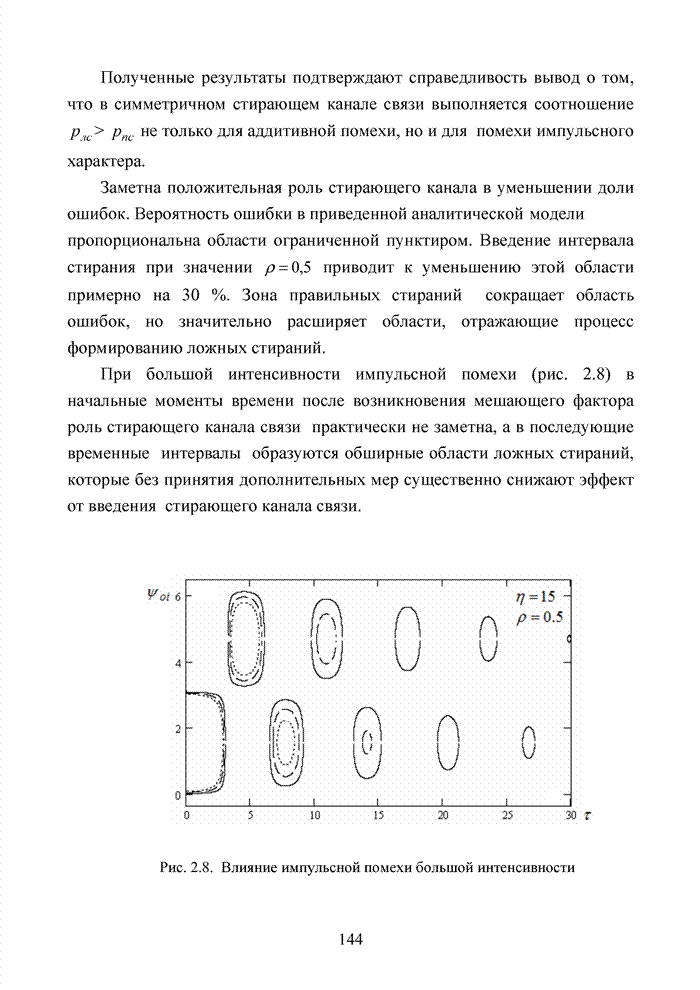
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
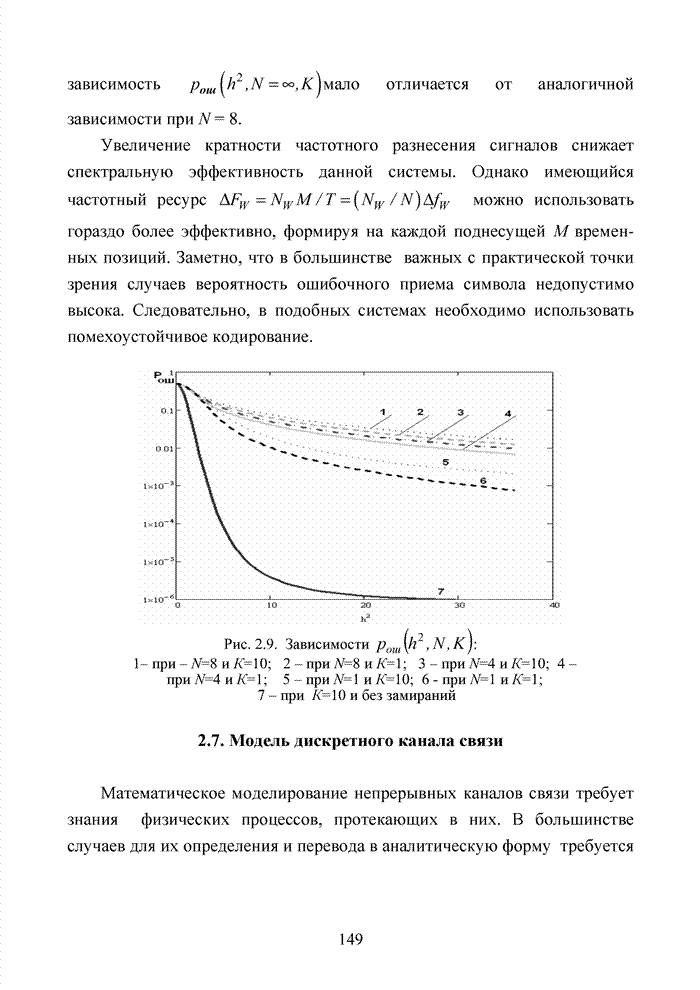
- 2.7. Модель дискретного канала связи
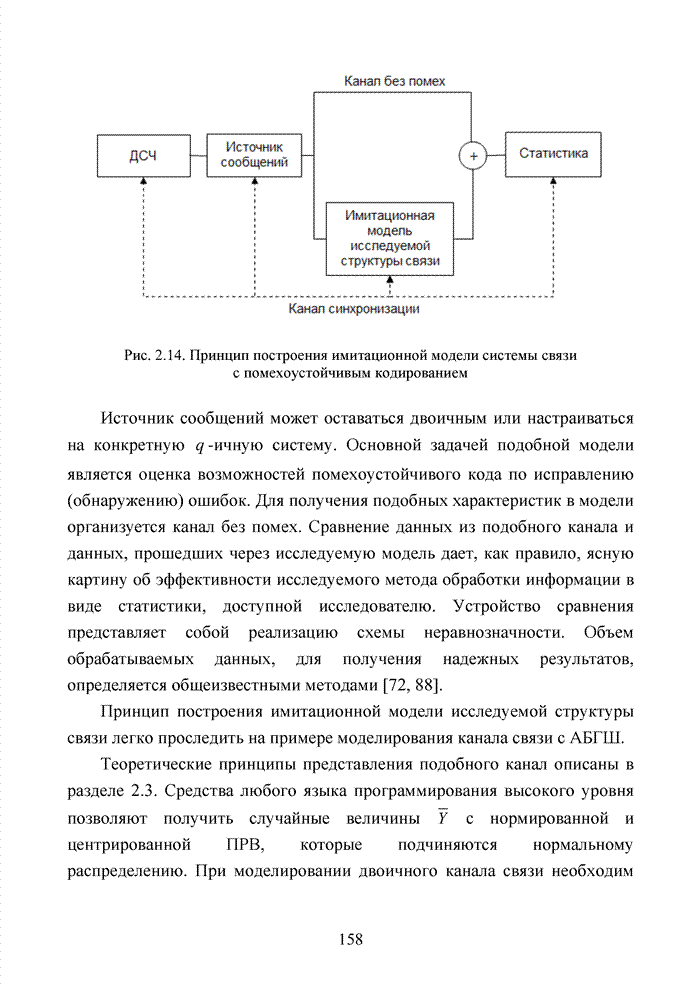
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
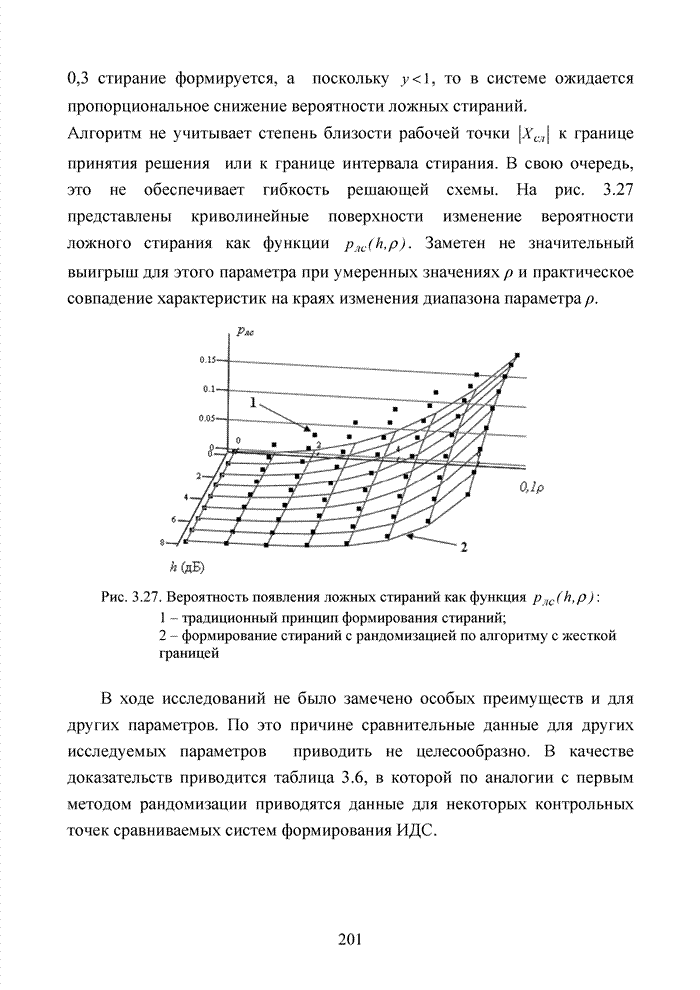
- 3.5.3. Алгоритм с жесткой границей
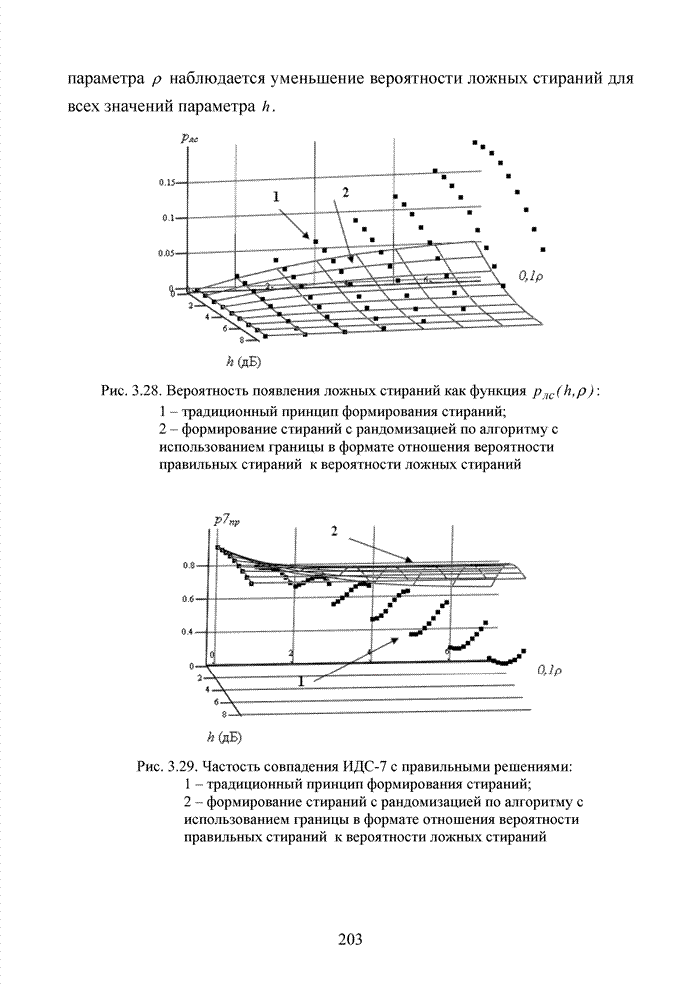
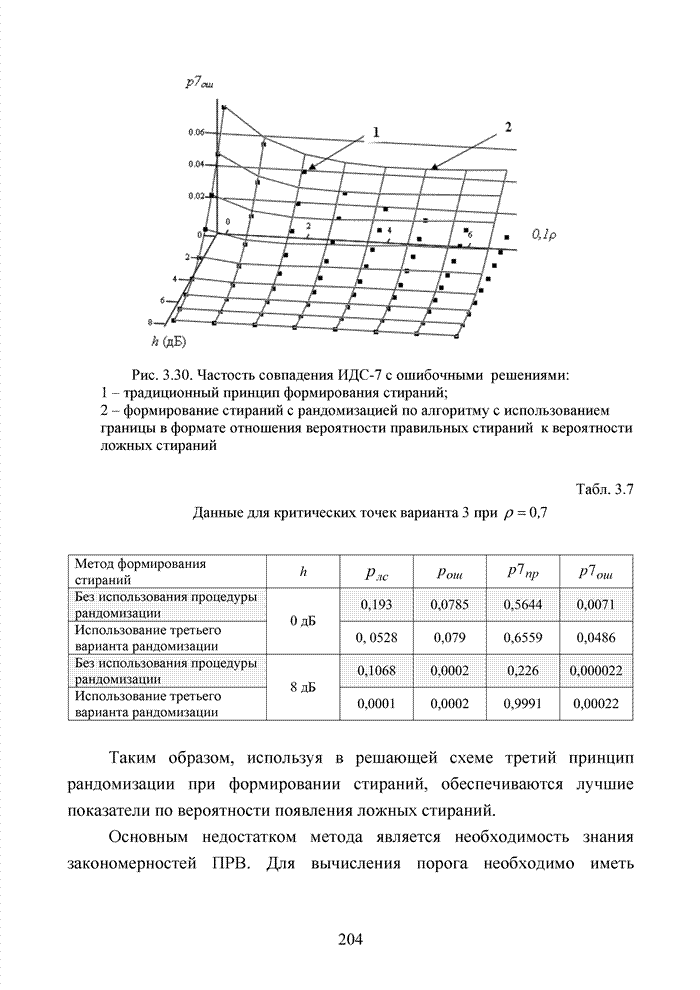
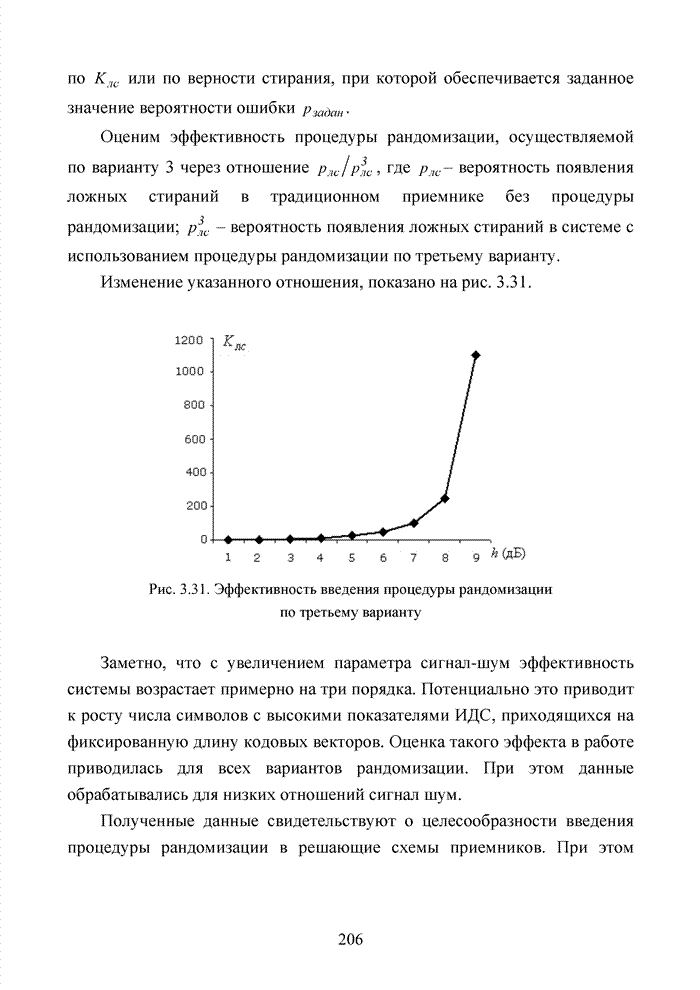
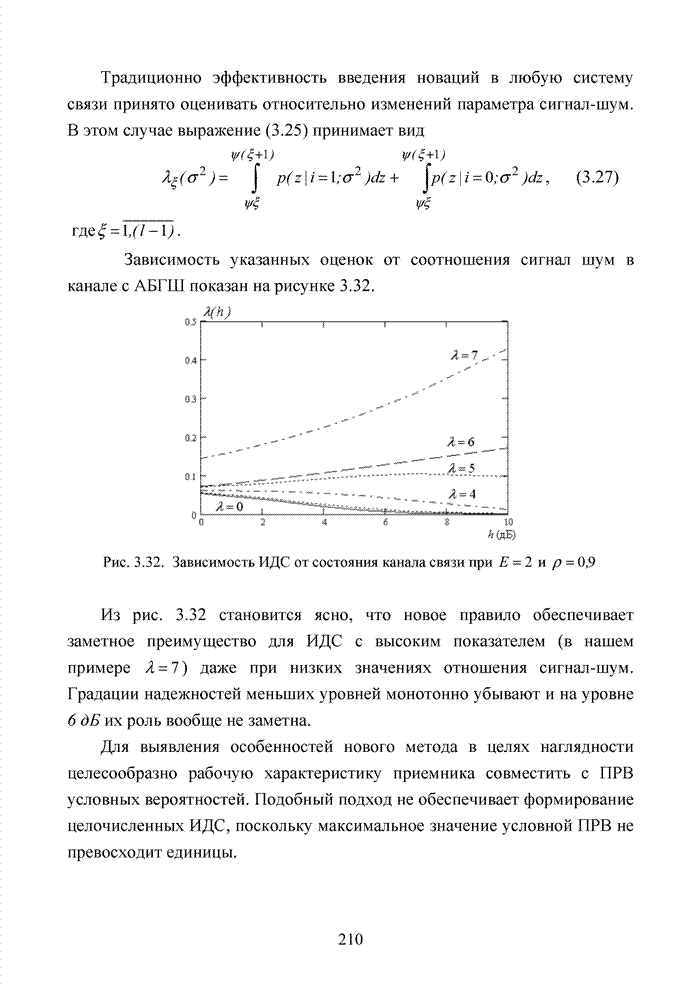
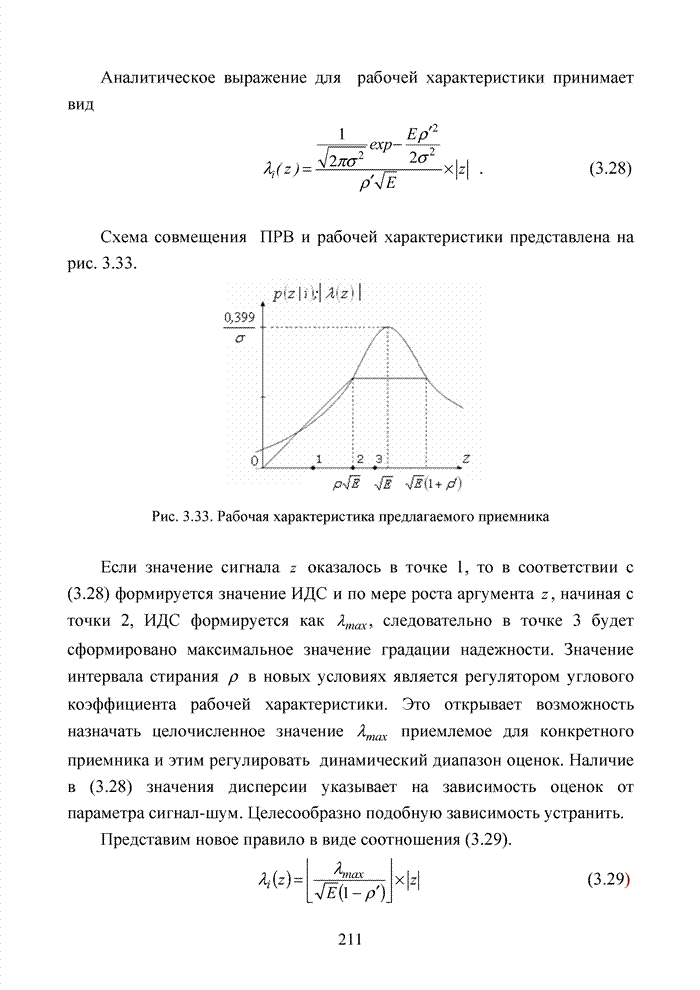
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
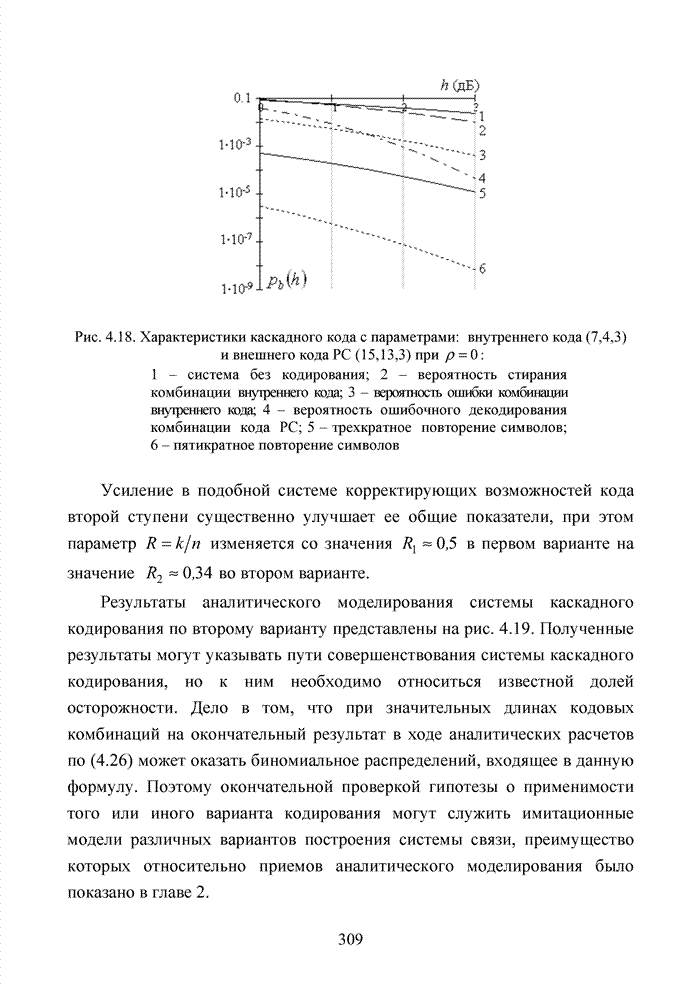
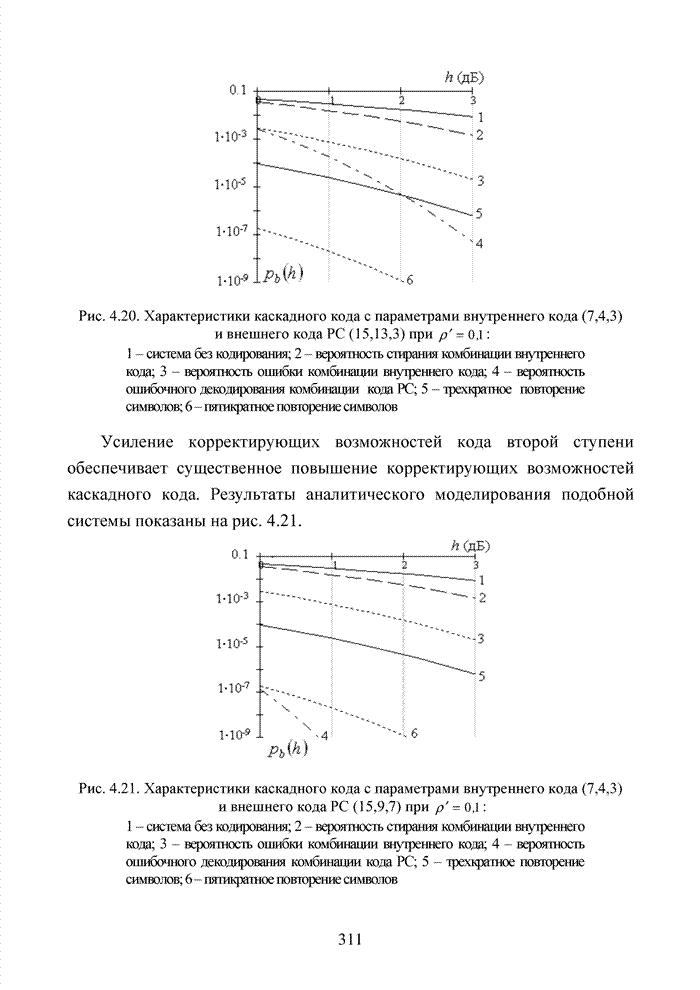
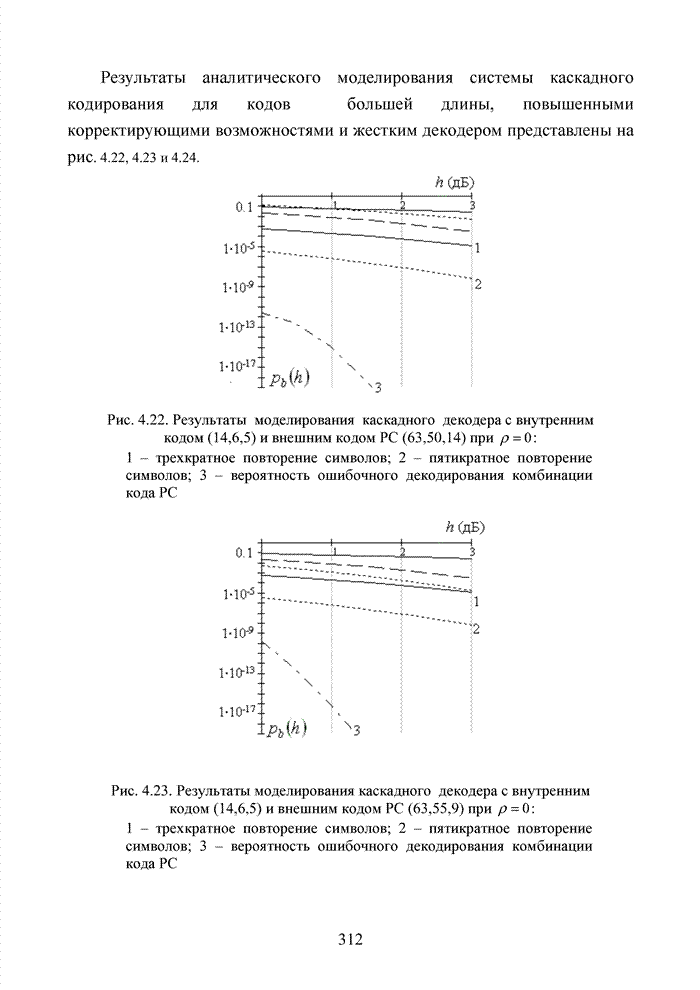
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
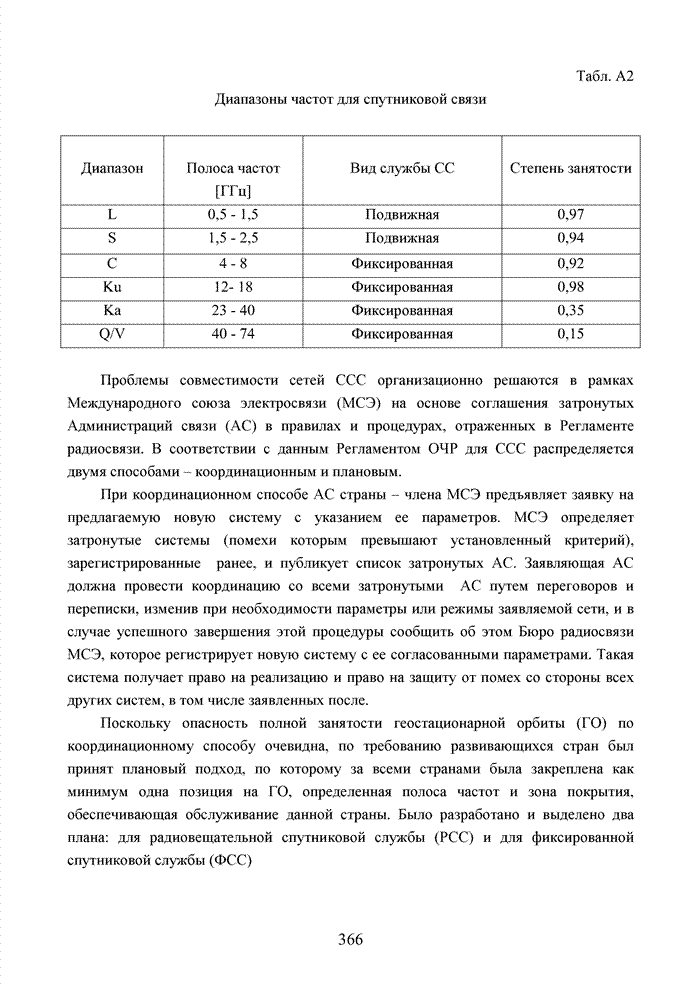
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
- Приложение Б Структура комбинаций кода РС (7,2,6)
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК