| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
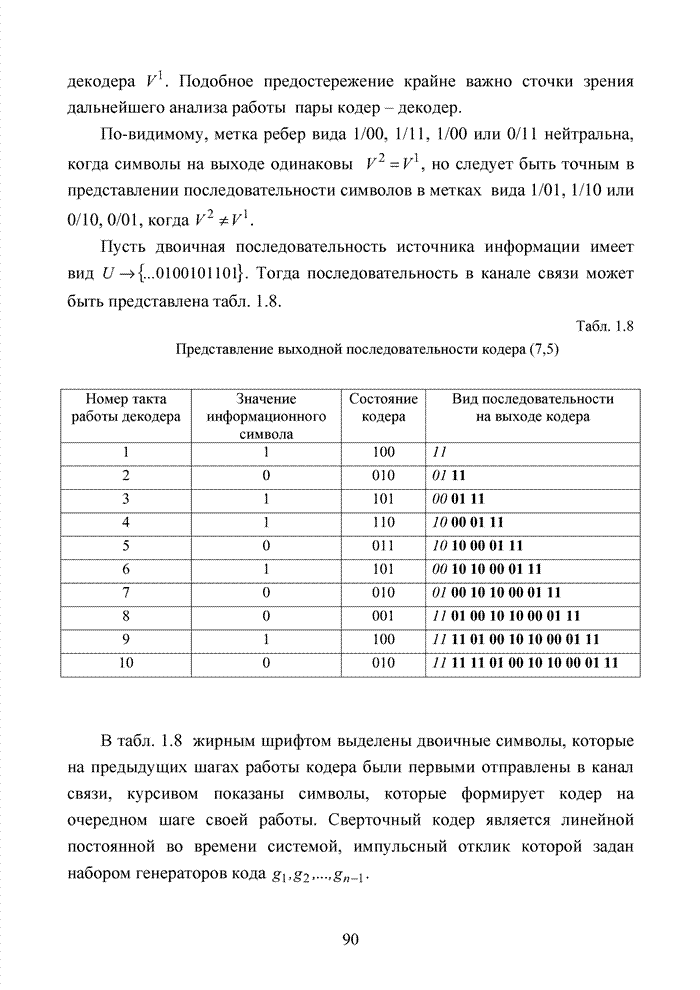
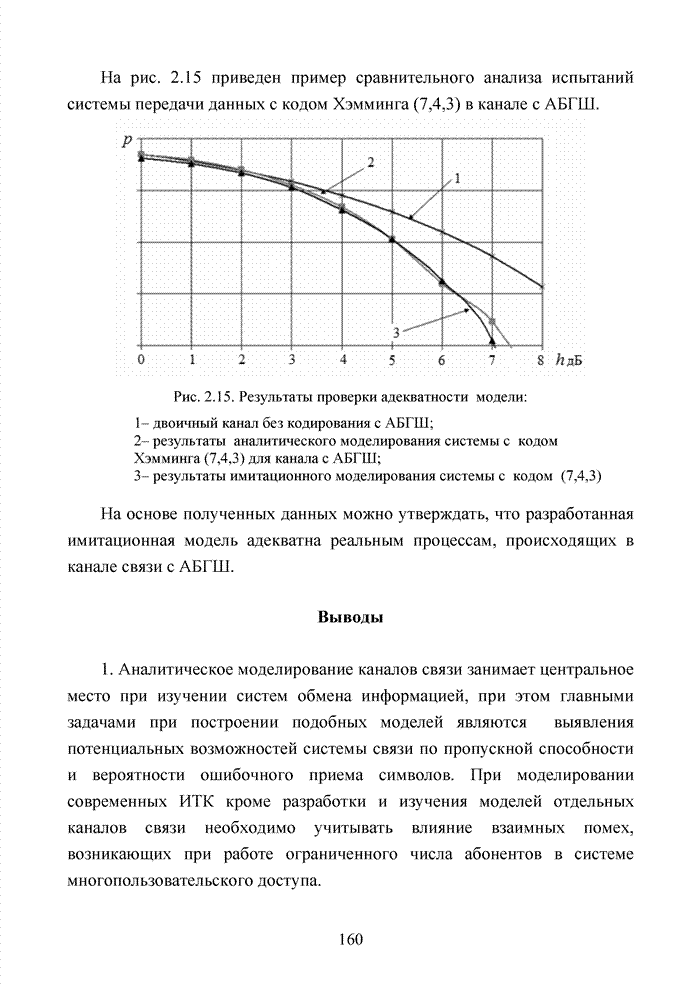
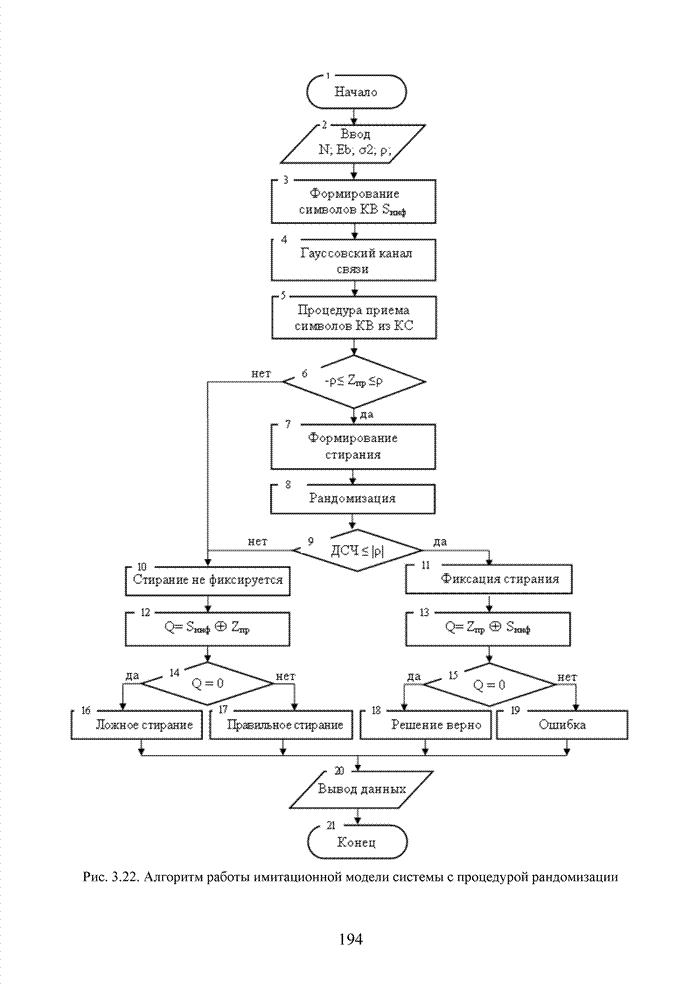
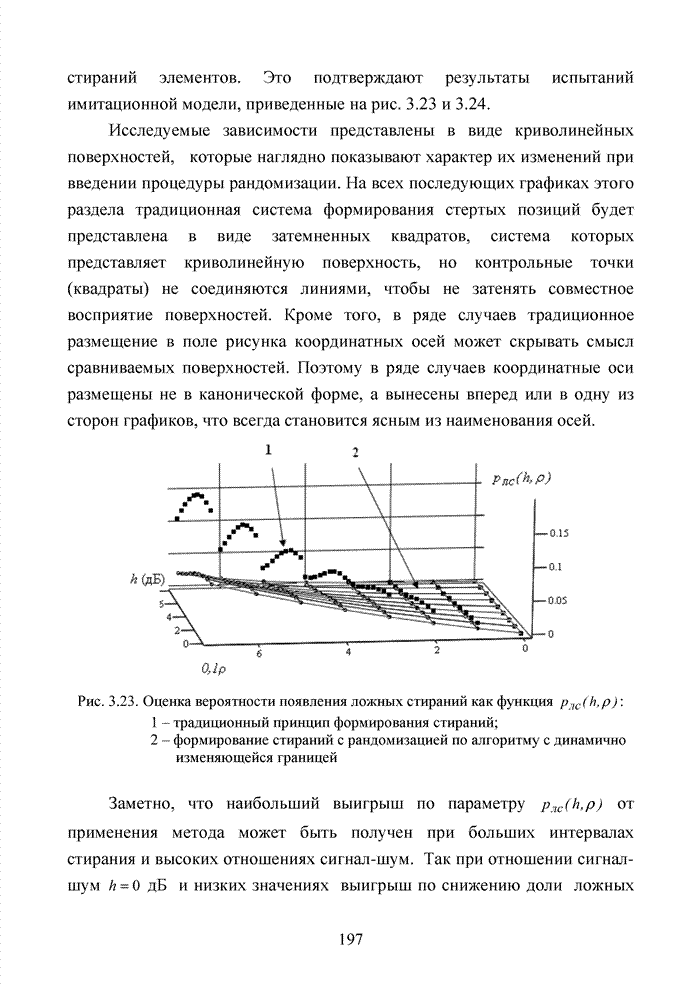
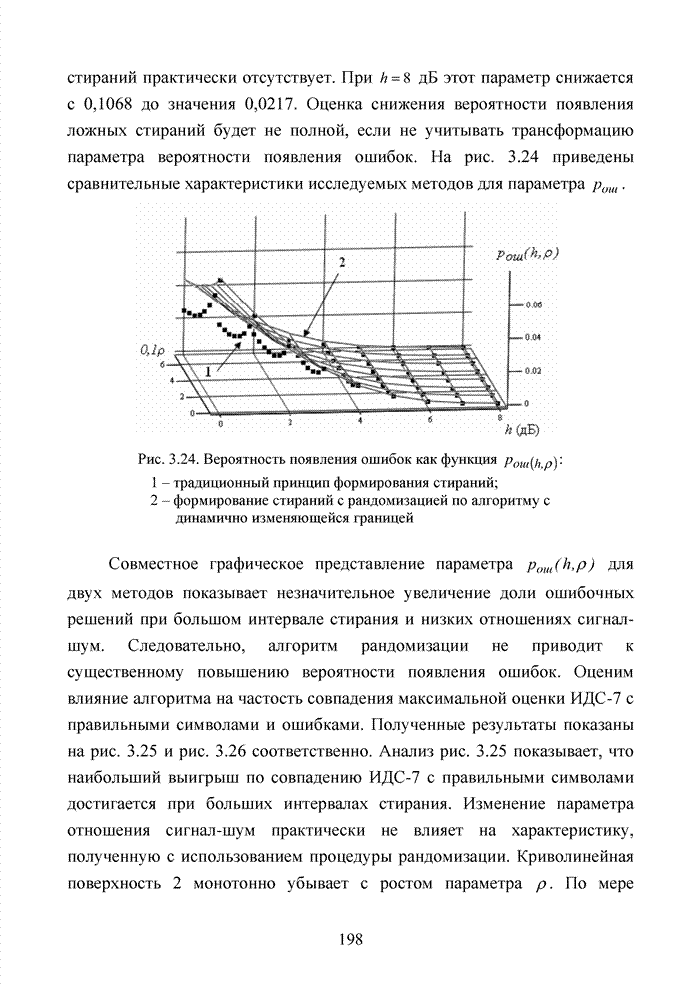
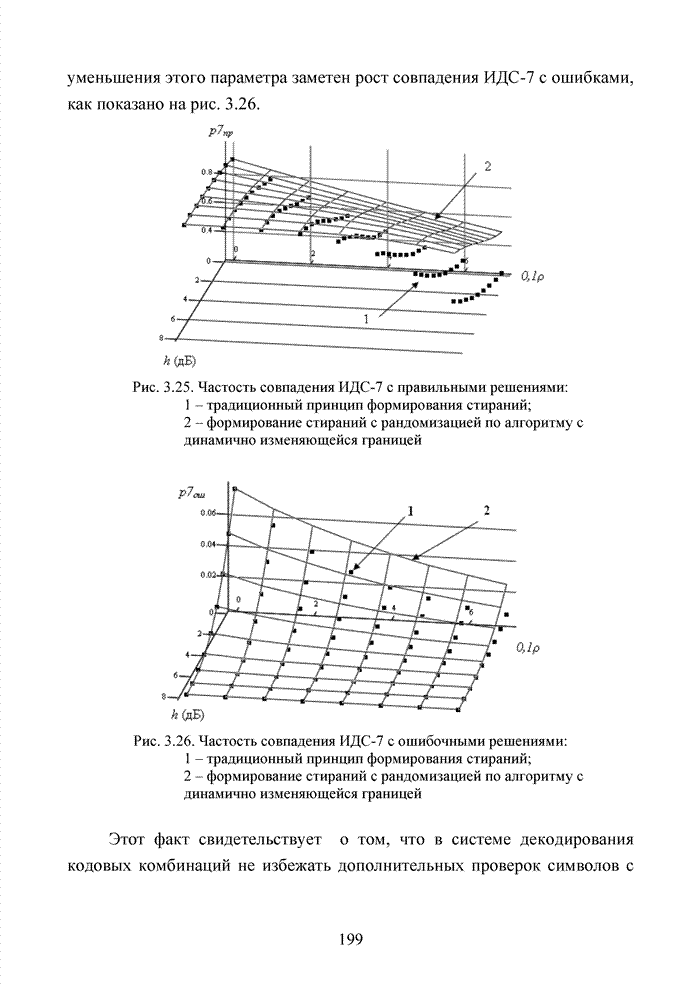
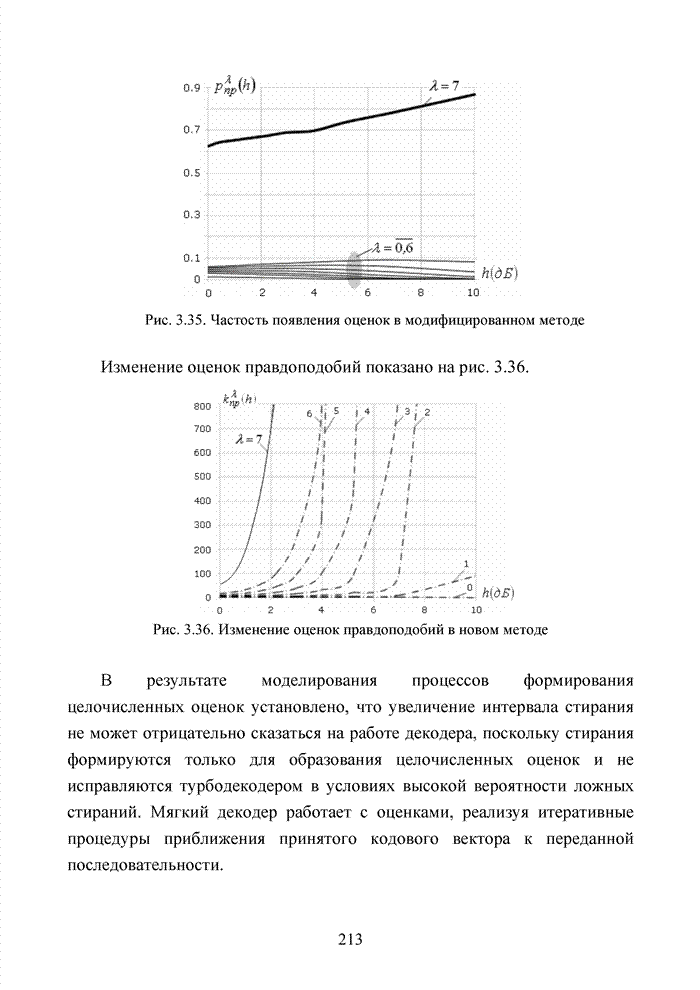
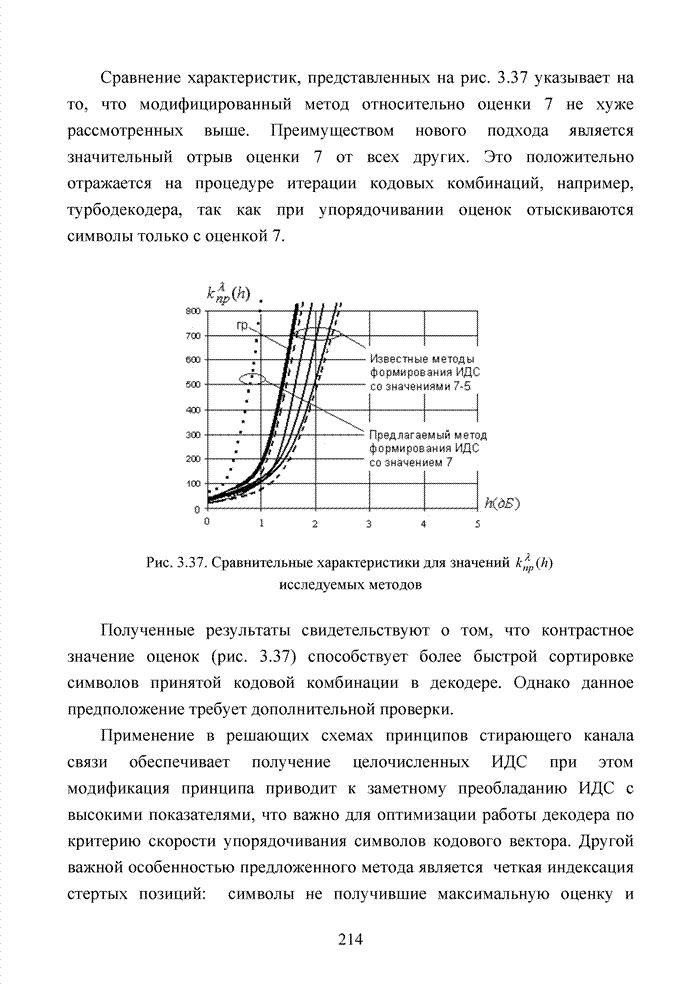
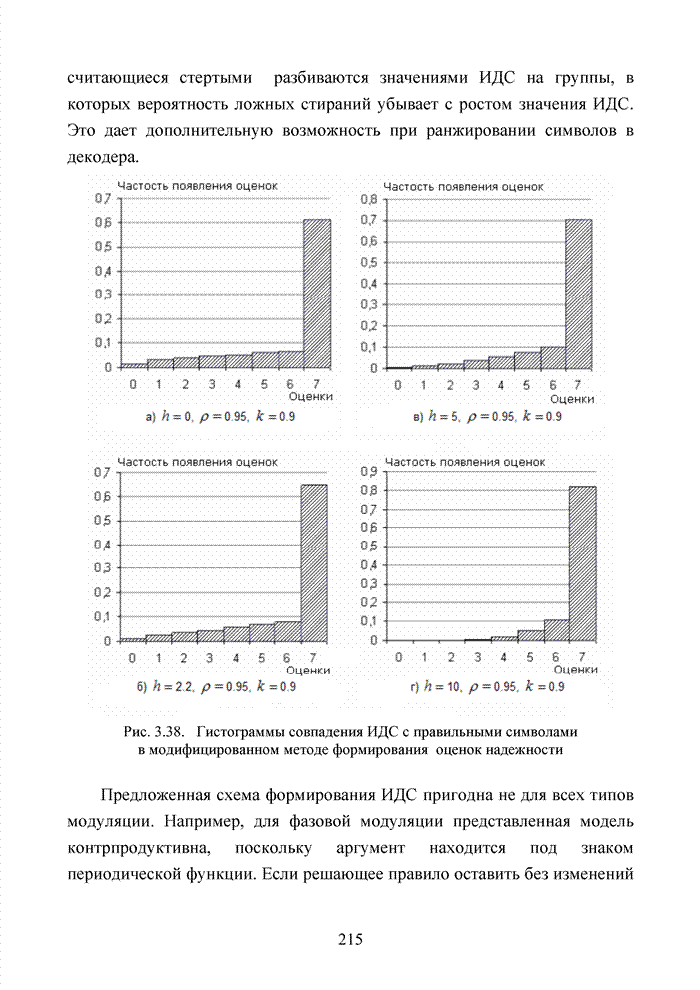
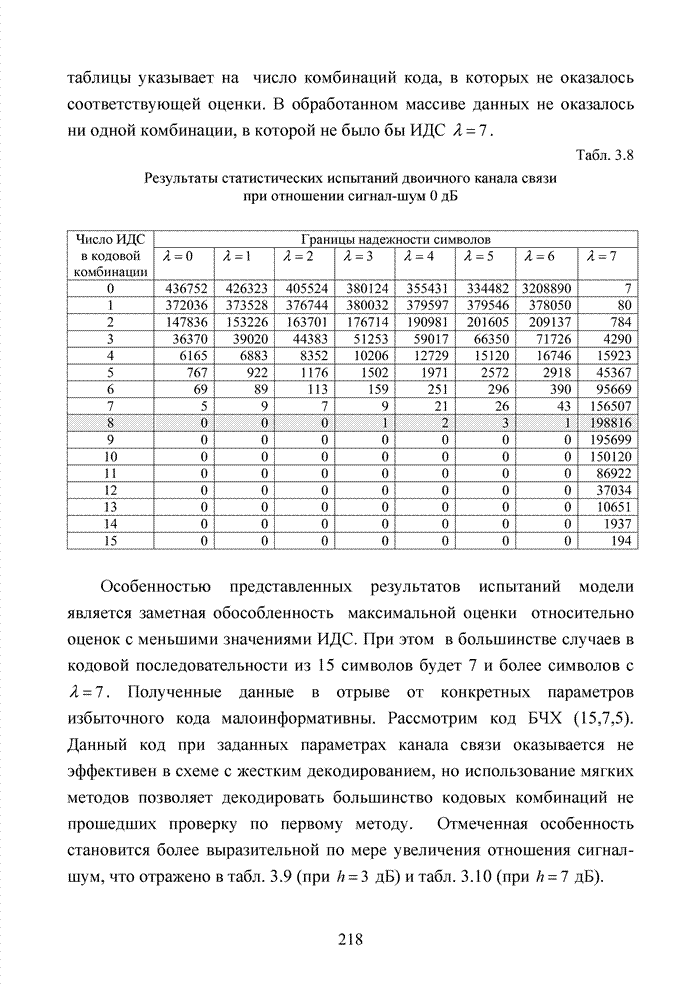
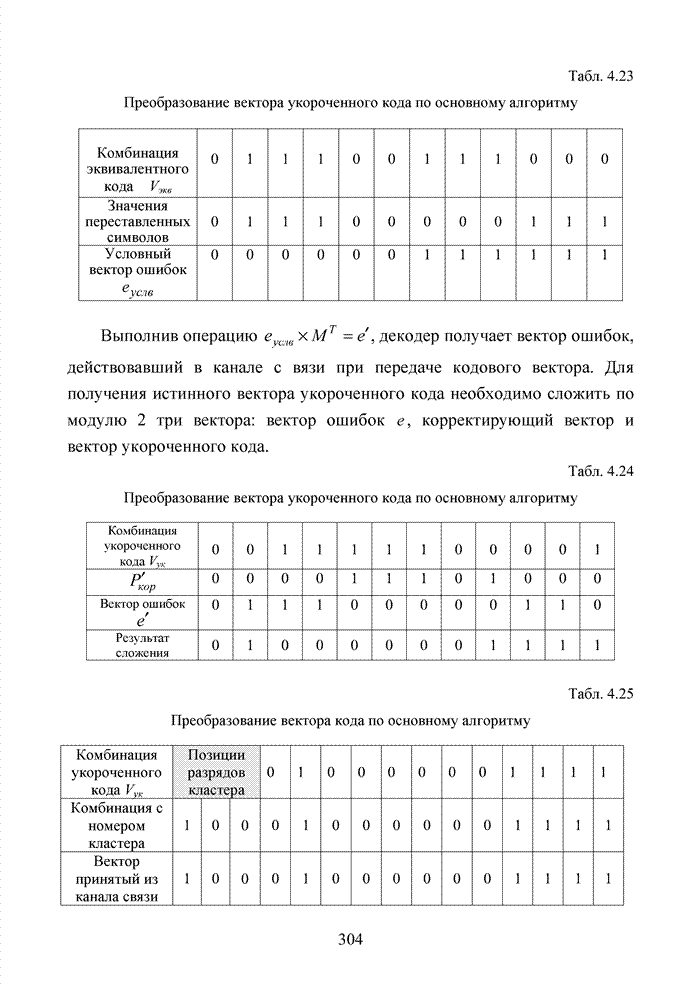
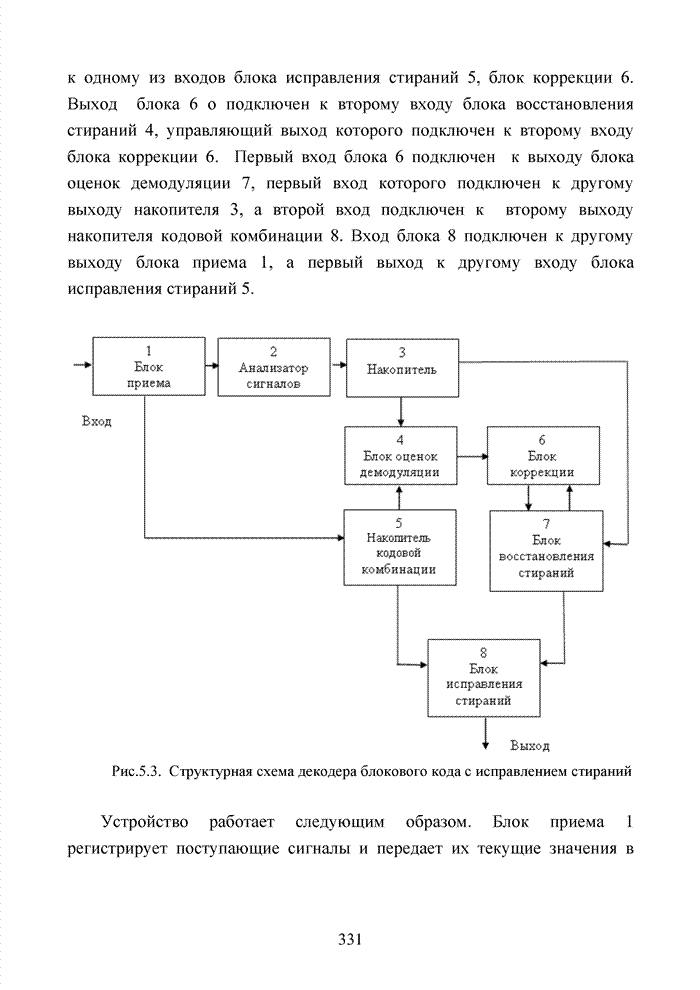
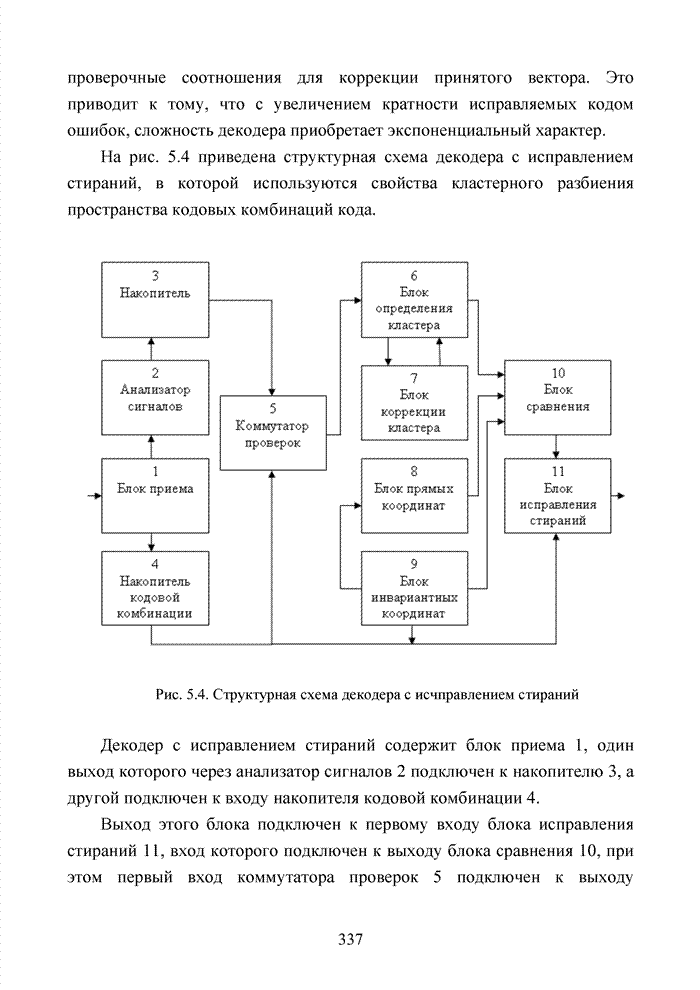
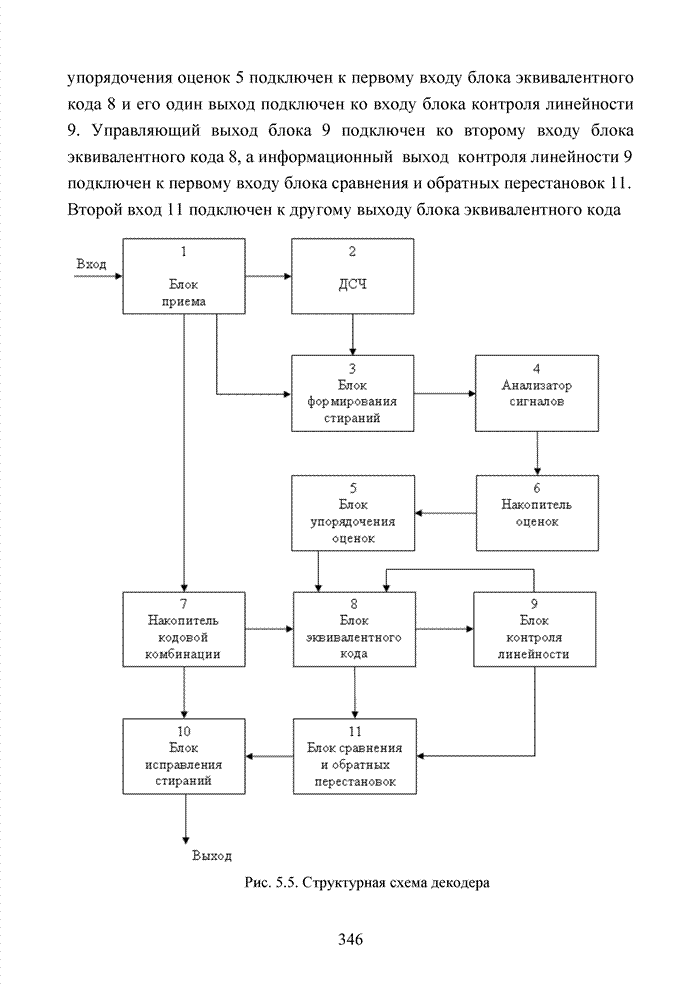
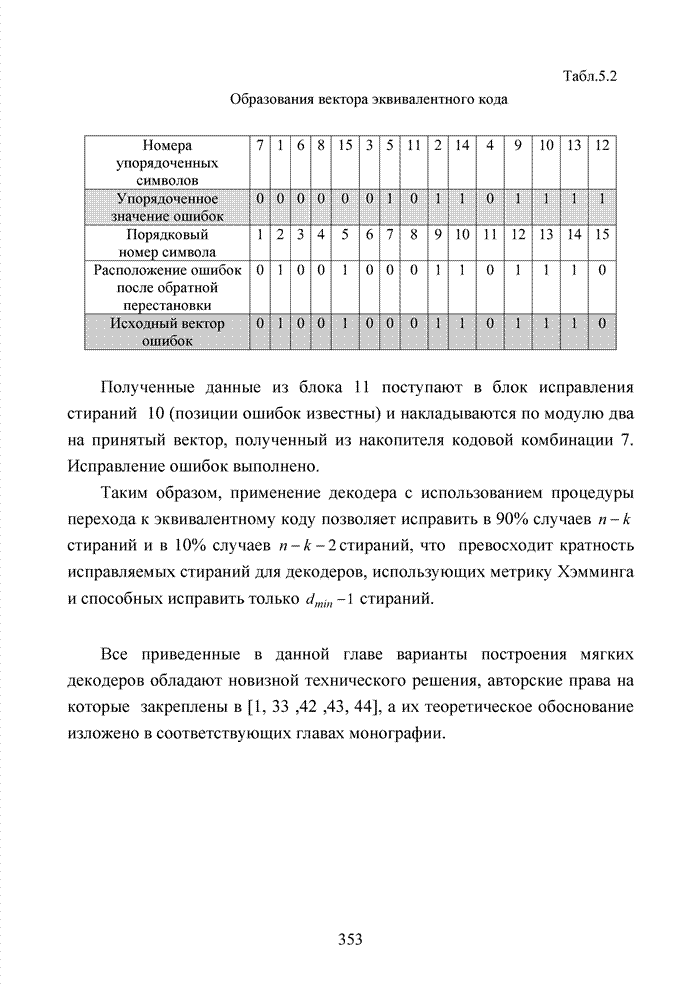
4.3. Модификация кодов при декодировании по кластерам
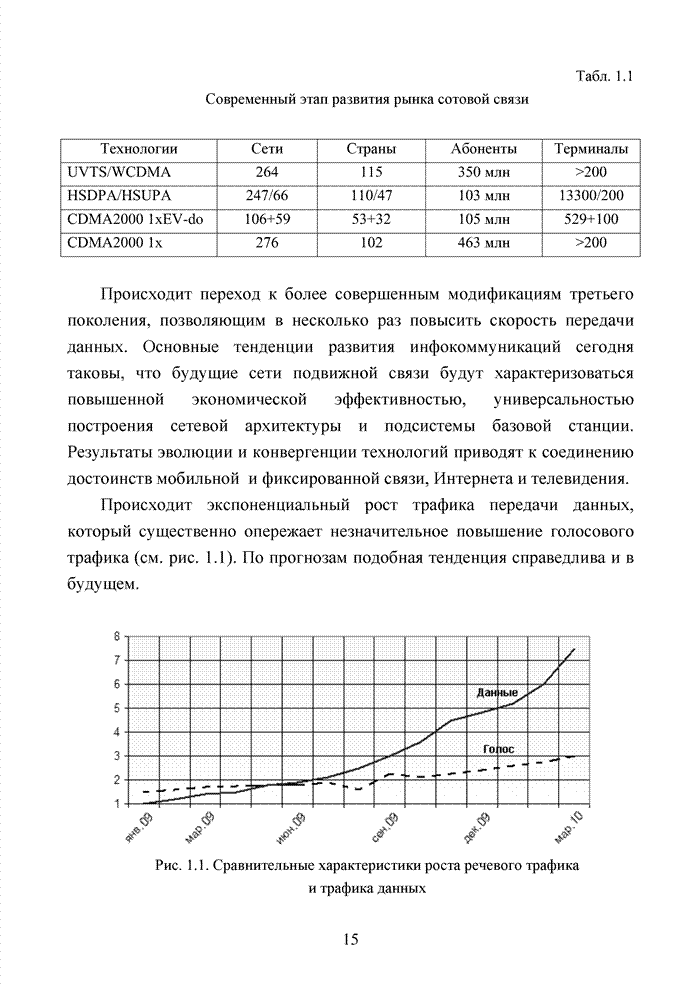
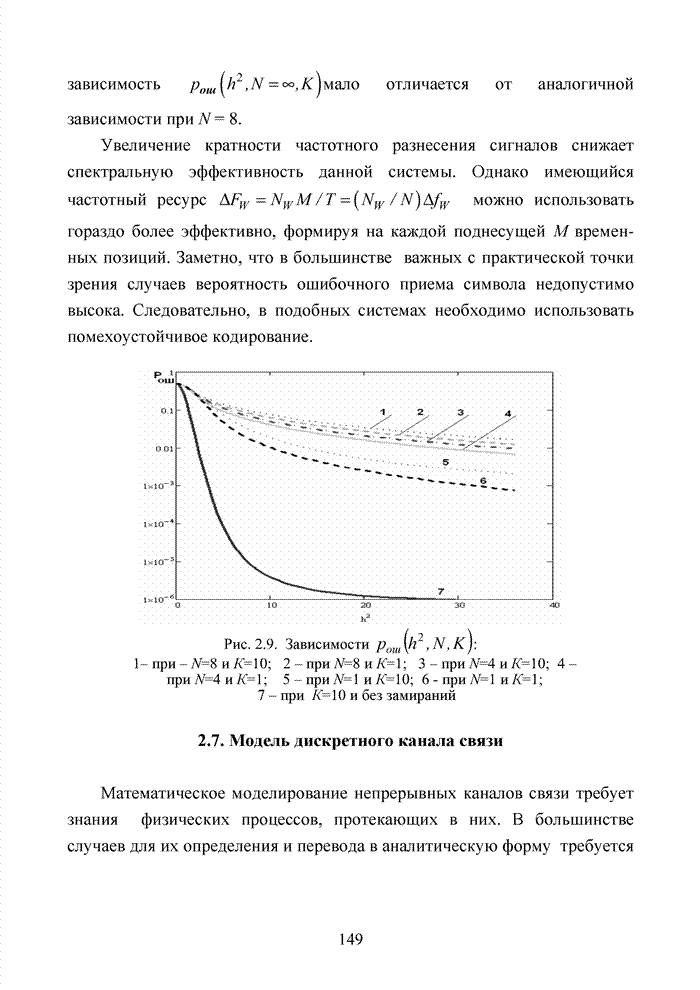
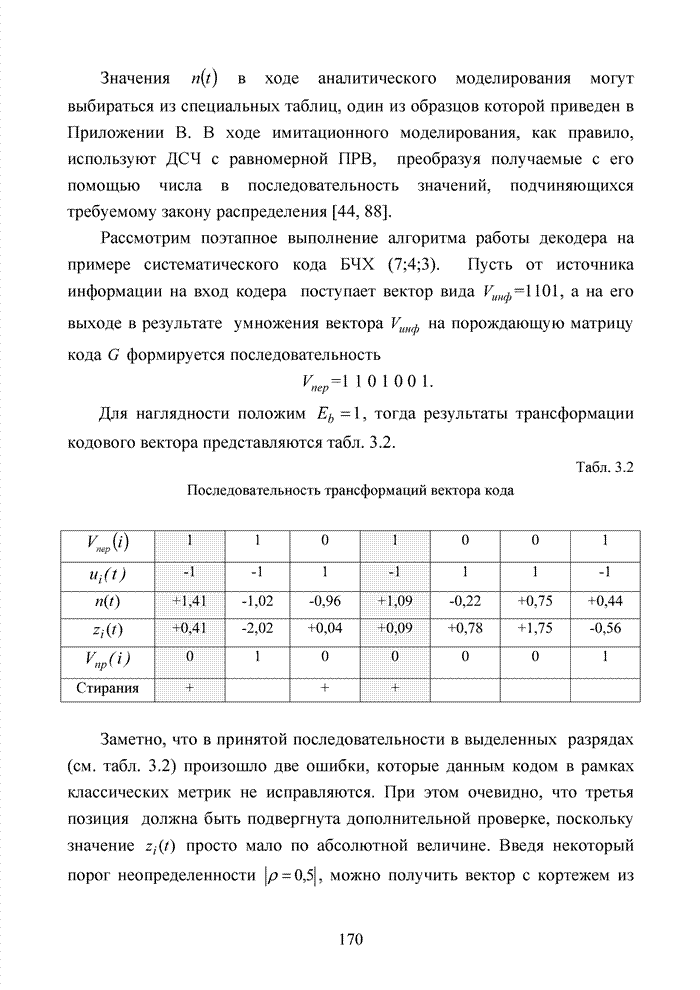
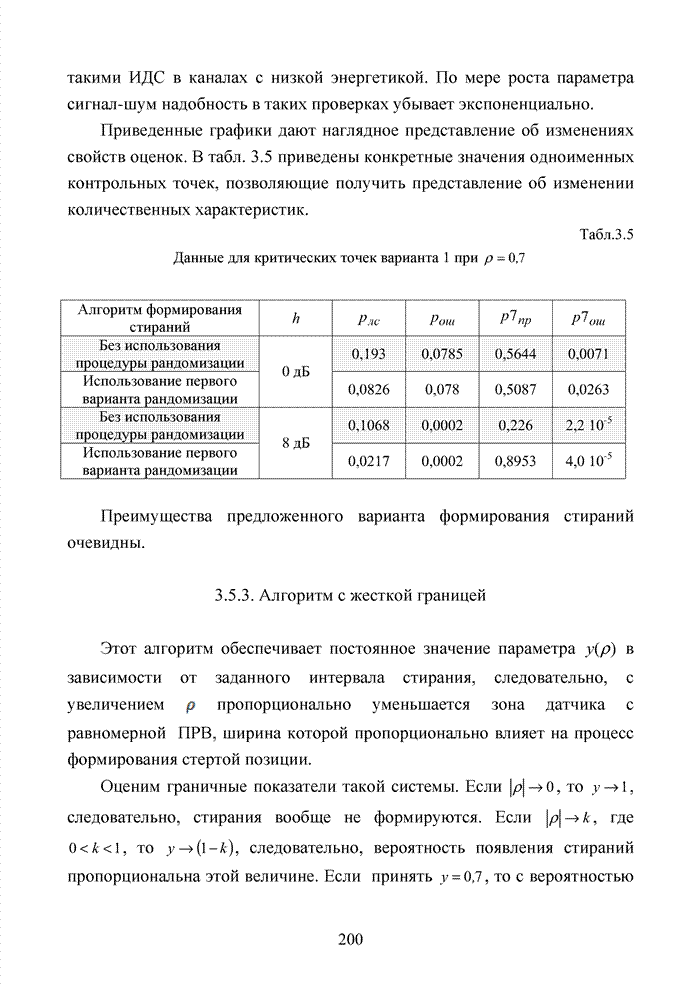
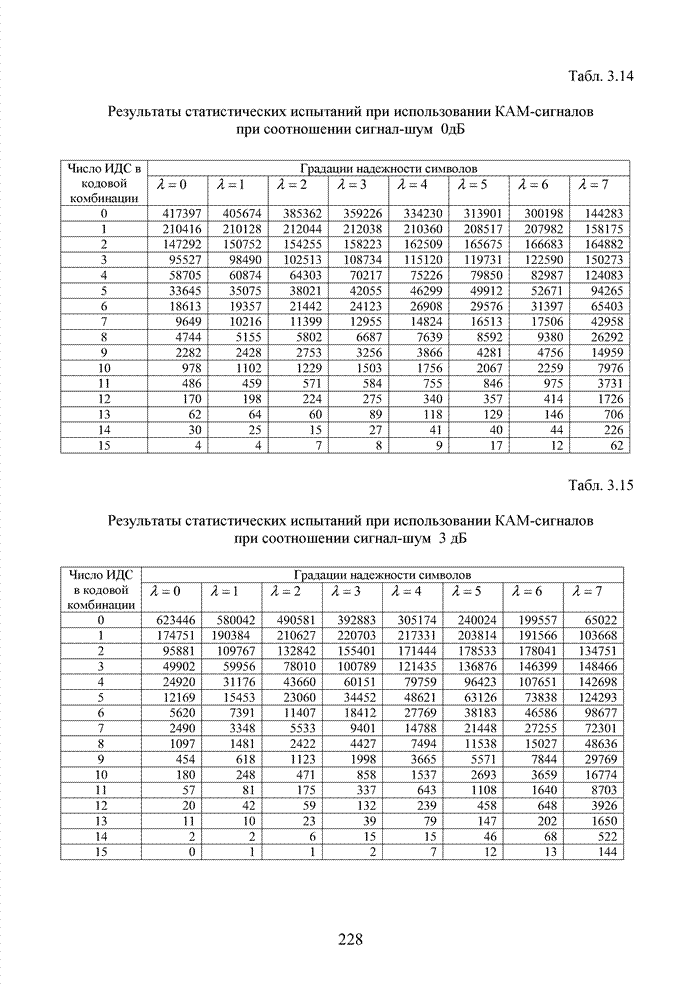
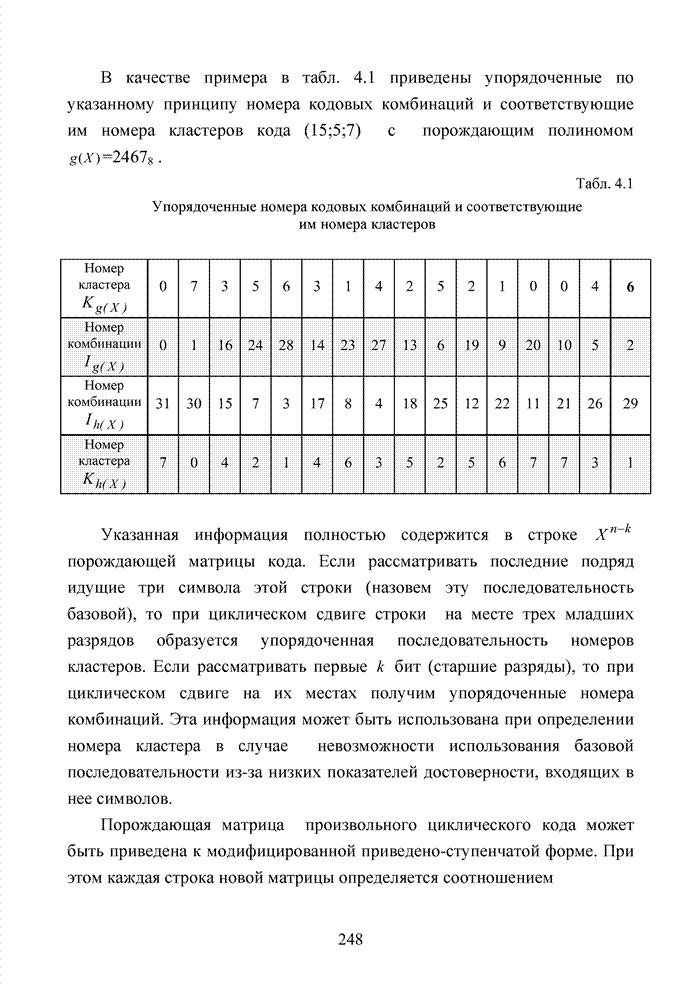
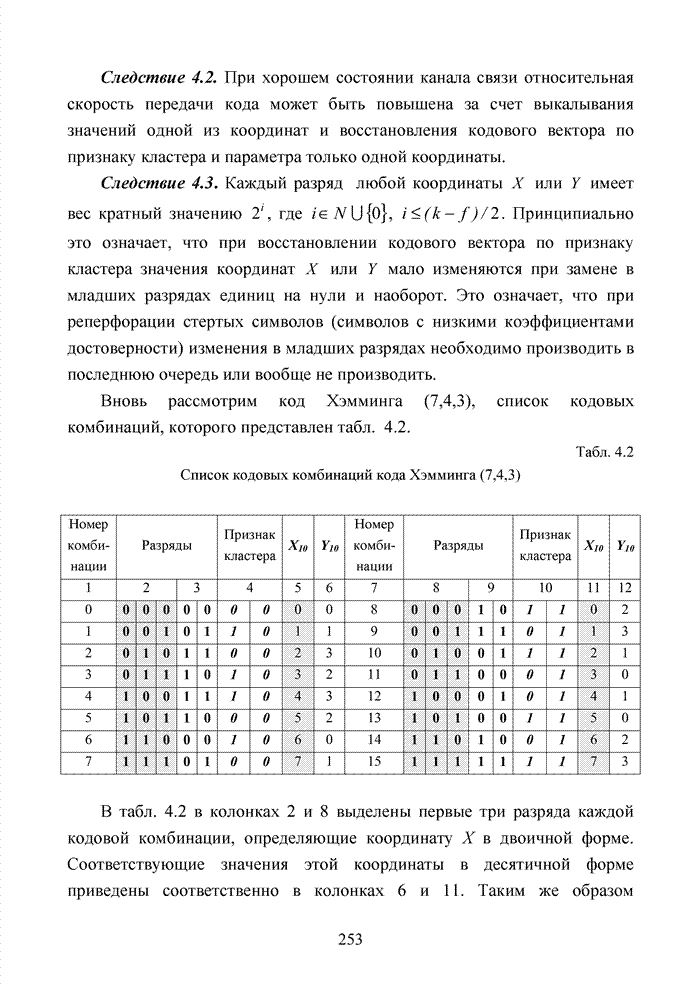
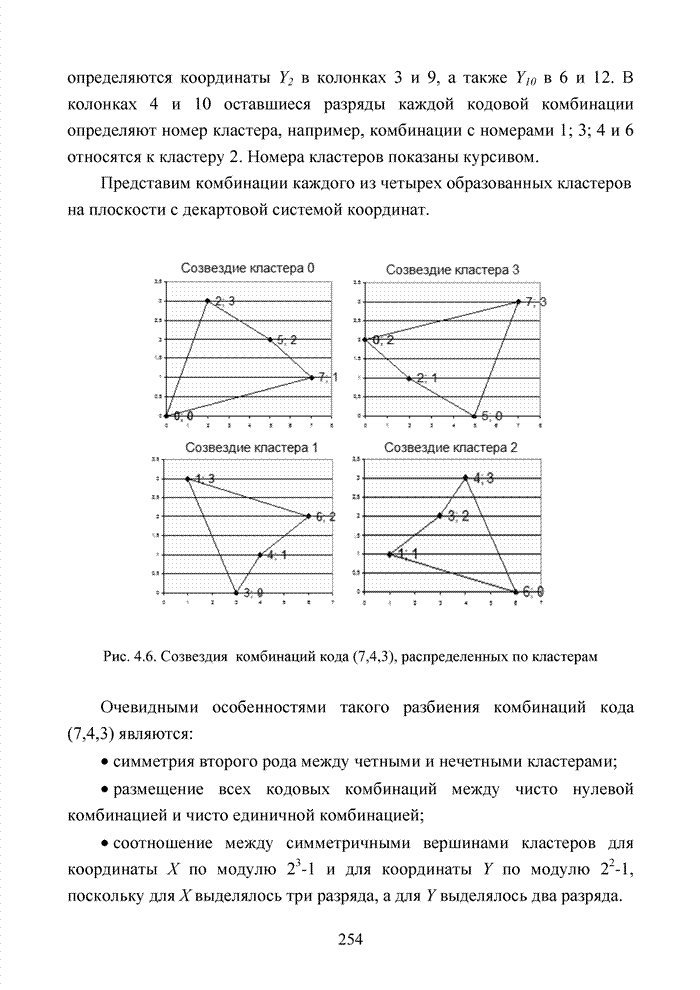
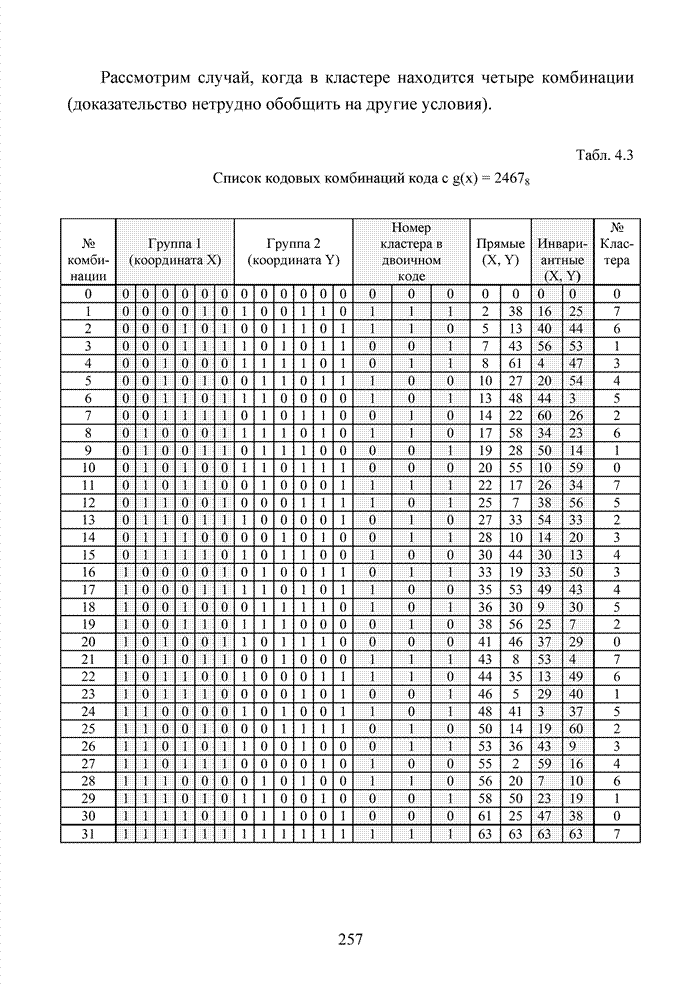
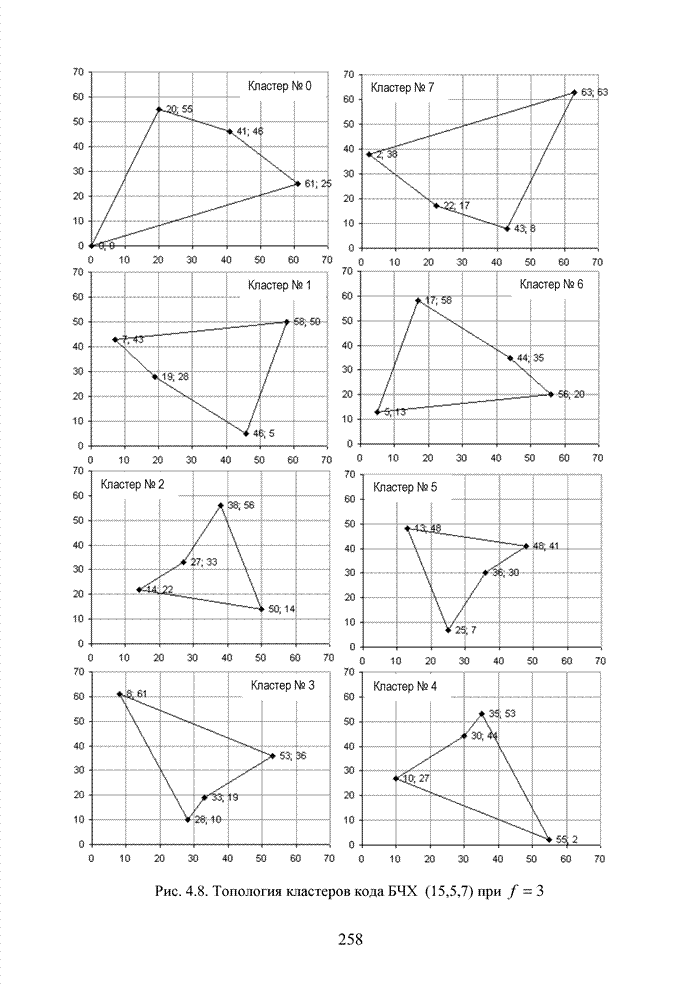
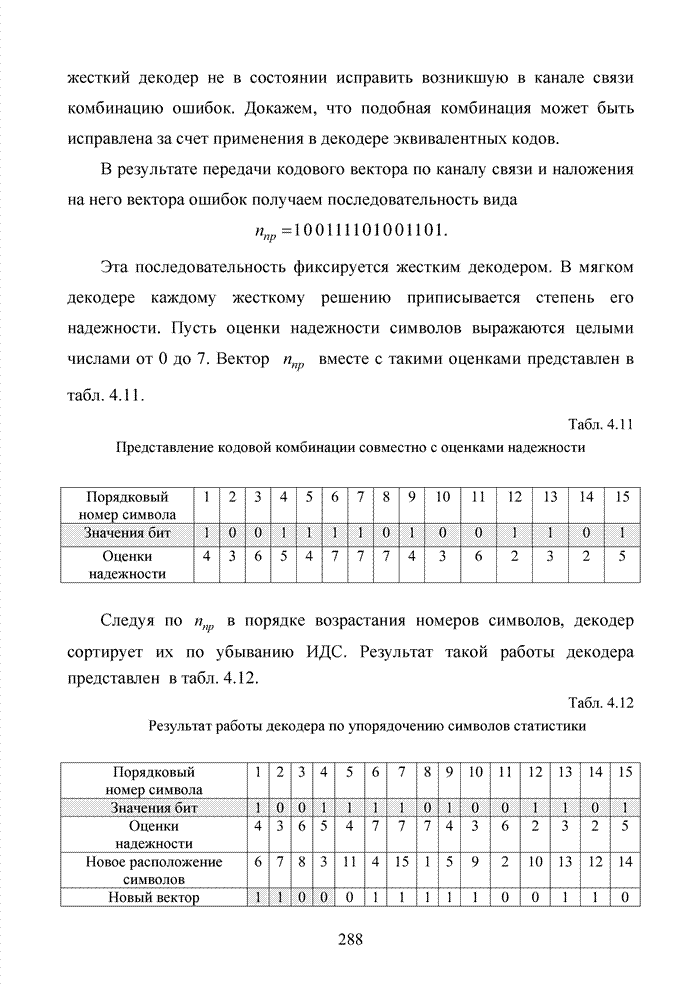
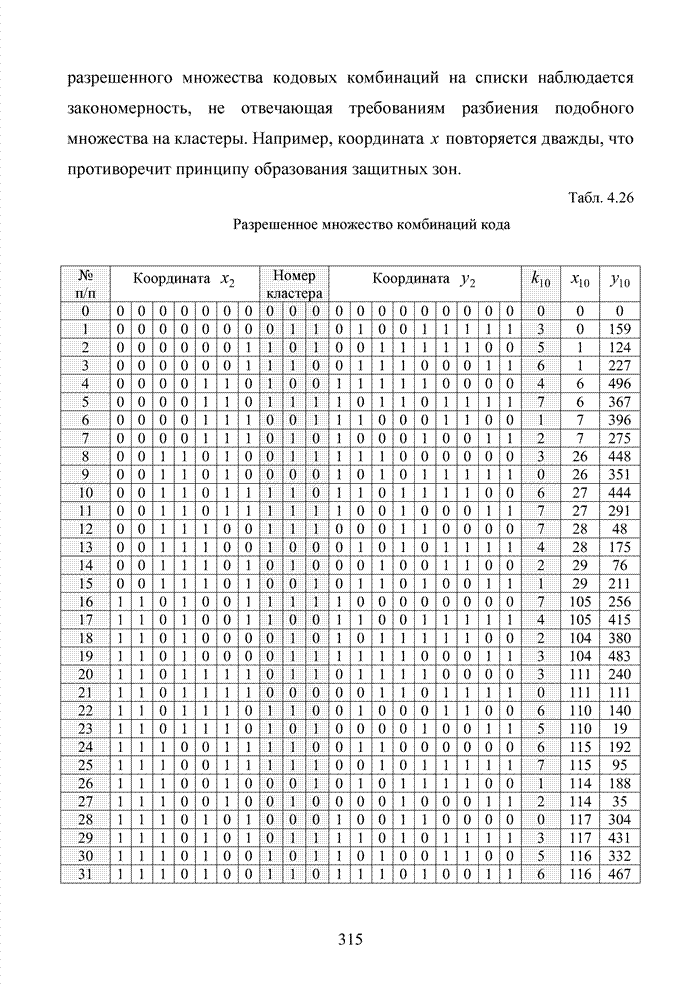
Как было отмечено выше, в системах помехоустойчивого кодирования широко используются различные способы модификации параметров избыточных кодов, призванных повысить гибкость в конструировании систем связи. Рассмотрим влияние указанных процедур на метод декодирования систематических блоковых кодов с использованием кластерного подхода. Анализ проведем на основе кода (7,4,3), полное представление комбинаций которого приведено в табл. 4.2.
4.3.1. Процедура расширения кода
Процедура расширения кода
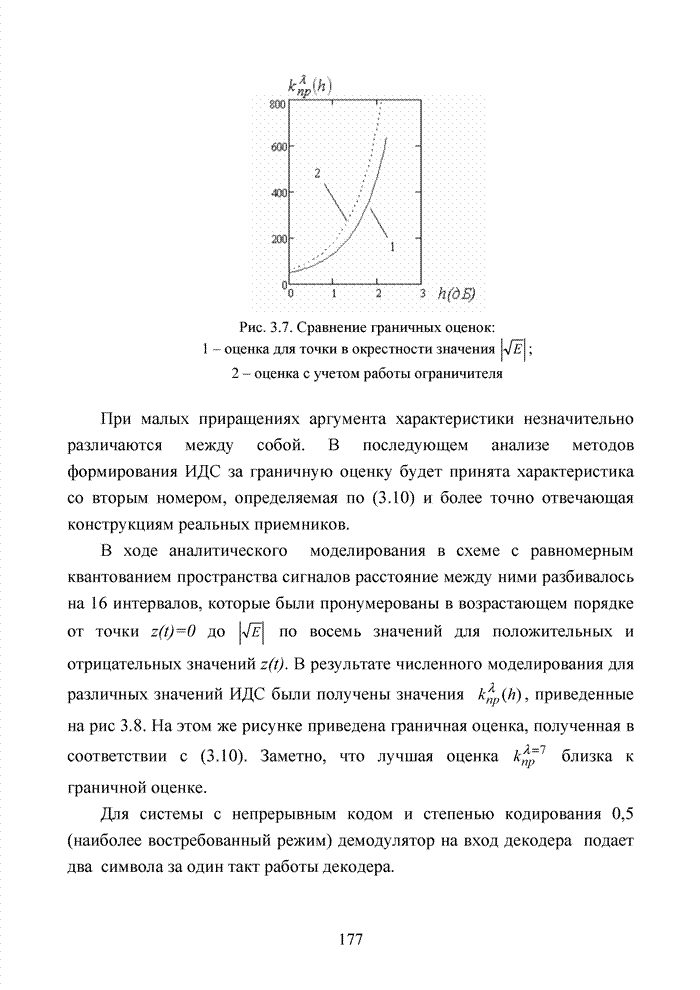
(7,4,3) приводит к образованию кода (8,4,4), что приводит к увеличению метрики
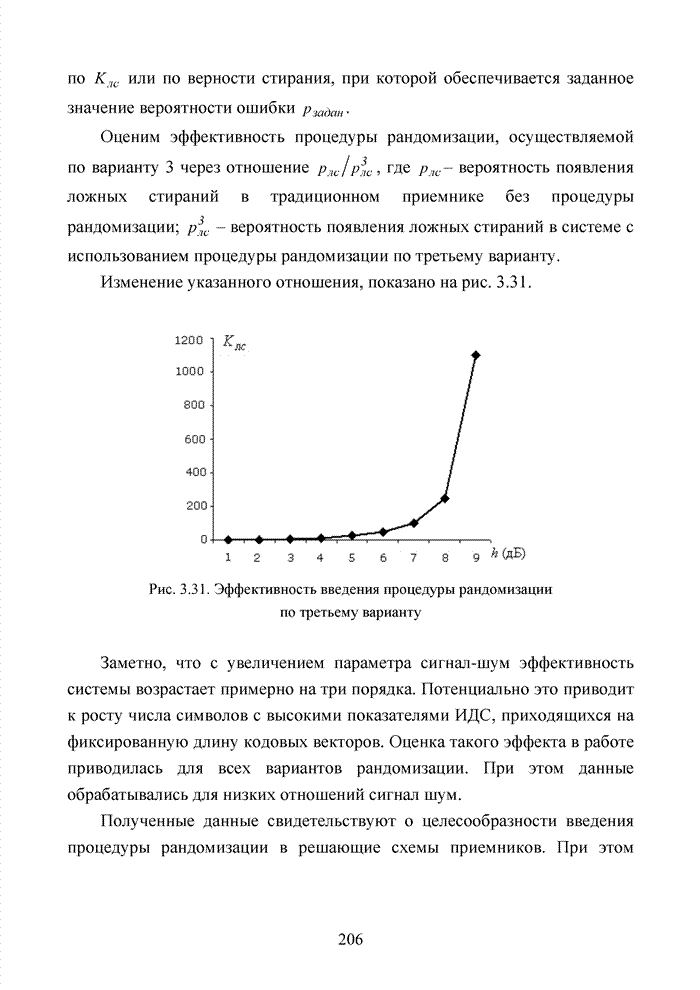
Хэмминга ![]() и
повышению исправляющей способности кода по восстановлению стираний. Кроме того,
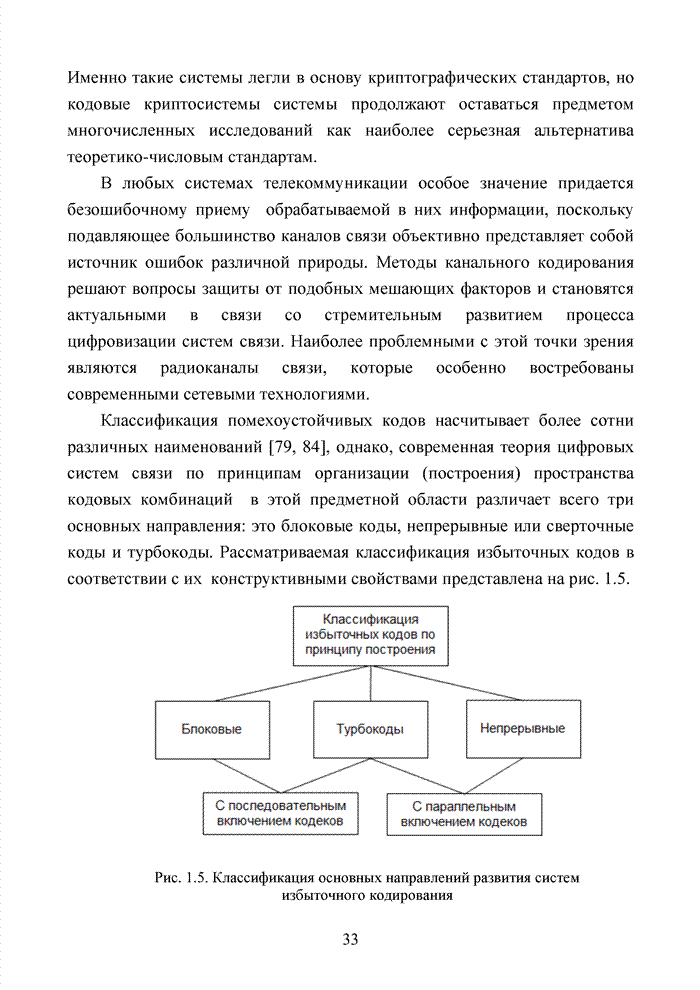
расширение кода обеспечивает получение кода Рида-Маллера (РМ), который
используется прогрессивной системой обобщенного каскадного кодирования в
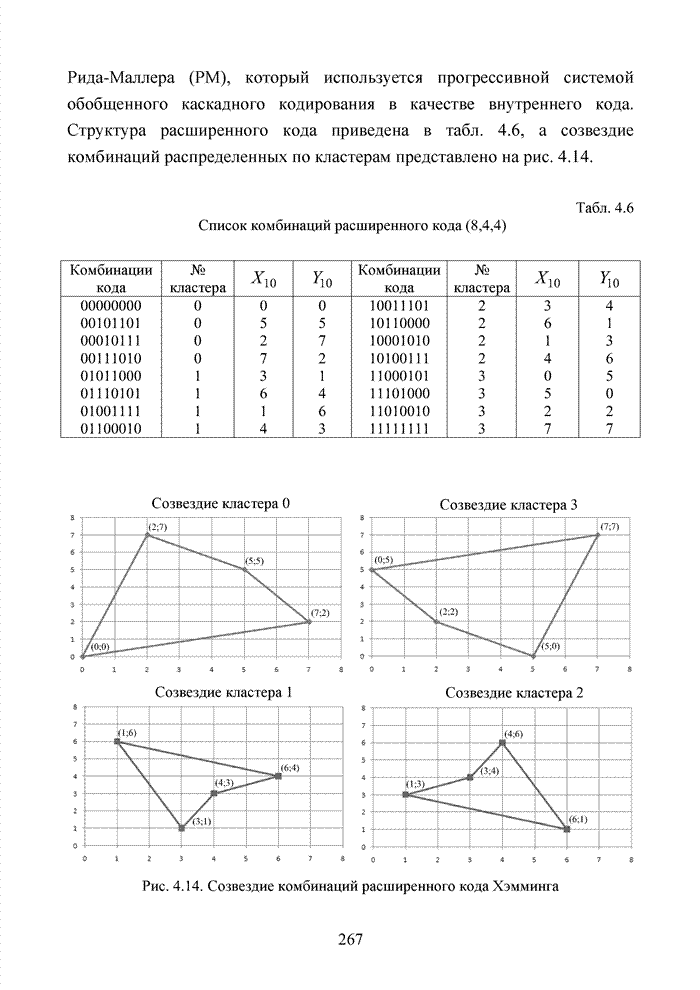
качестве внутреннего кода. Структура расширенного кода приведена в табл. 4.6, а
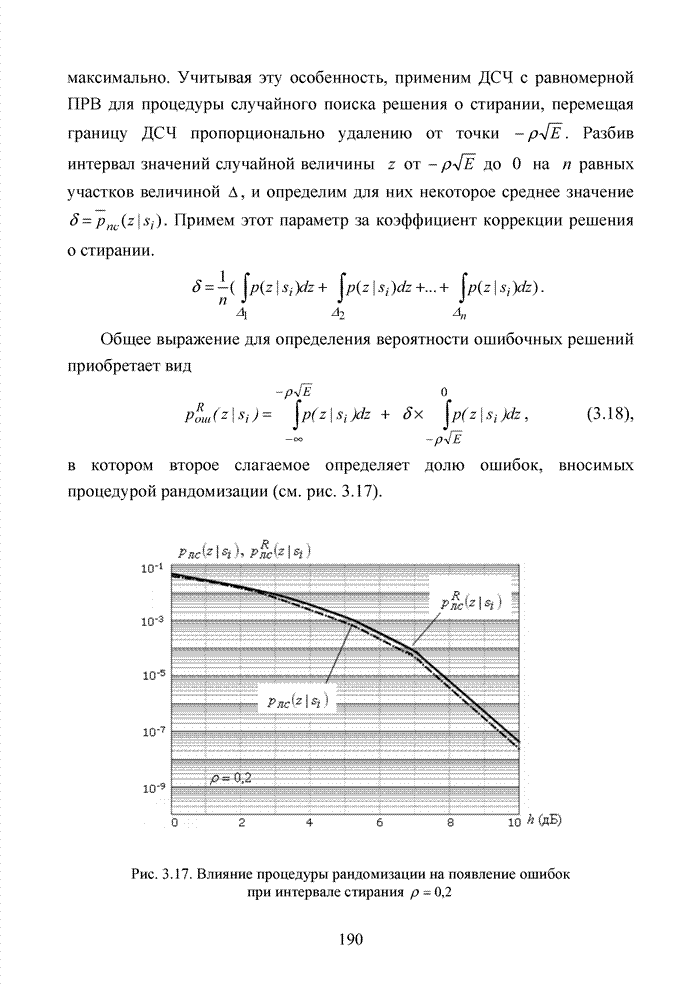
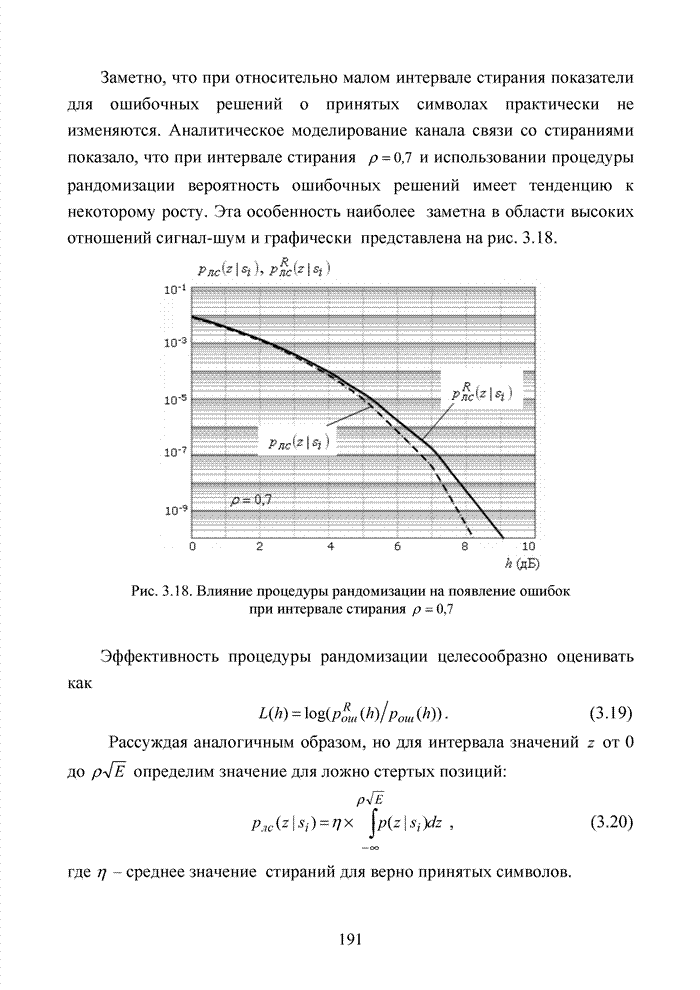
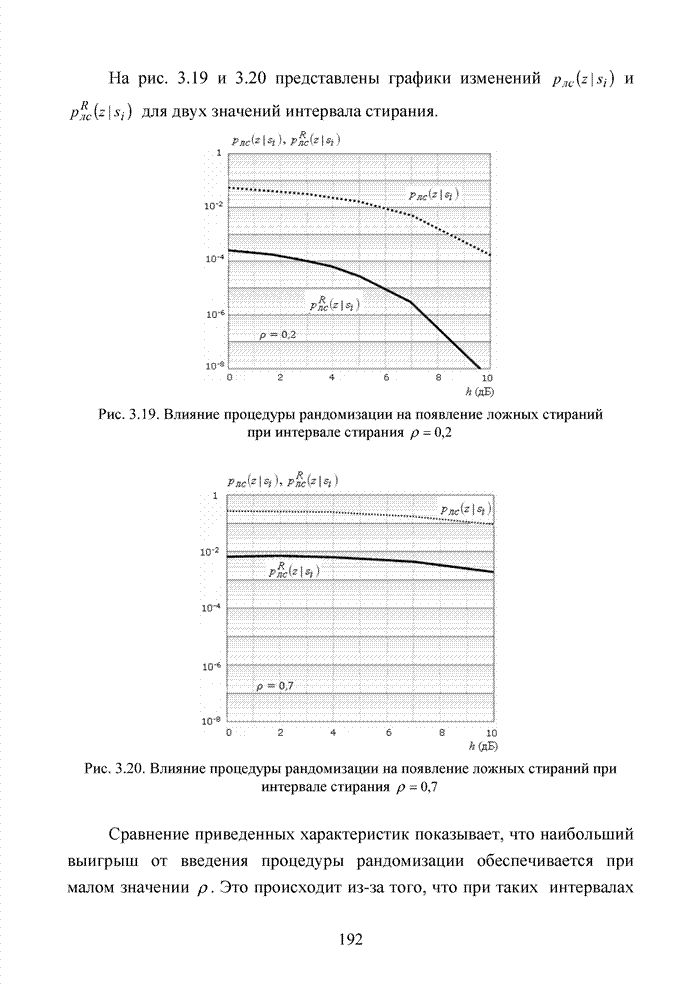
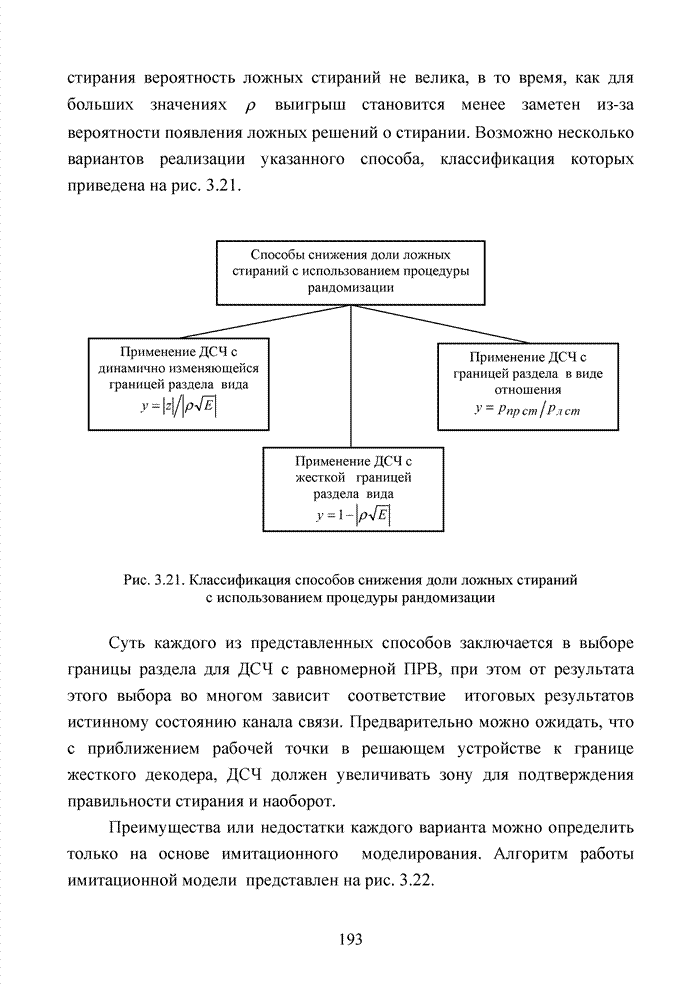
созвездие комбинаций распределенных по кластерам представлено на рис. 4.14.
и
повышению исправляющей способности кода по восстановлению стираний. Кроме того,
расширение кода обеспечивает получение кода Рида-Маллера (РМ), который
используется прогрессивной системой обобщенного каскадного кодирования в
качестве внутреннего кода. Структура расширенного кода приведена в табл. 4.6, а
созвездие комбинаций распределенных по кластерам представлено на рис. 4.14.
Табл. 4.6 Список комбинаций расширенного кода (8,4,4)
|
Комбинации кода |
№ кластера |
|
|
Комбинации кода |
№ кластера |
|
|
|
00000000 00101101 00010111 00111010 01011000 01110101 01001111 01100010 |
0 0 0 0 1 1 1 1 |
0 5 2 7 3 6 1 4 |
0 5 7 2 1 4 6 3 |
10011101 10110000 10001010 10100111 11000101 11101000 11010010 11111111 |
2 2 2 2 3 3 3 3 |
3 6 1 4 0 5 2 7 |
4 1 3 6 5 0 2 7 |

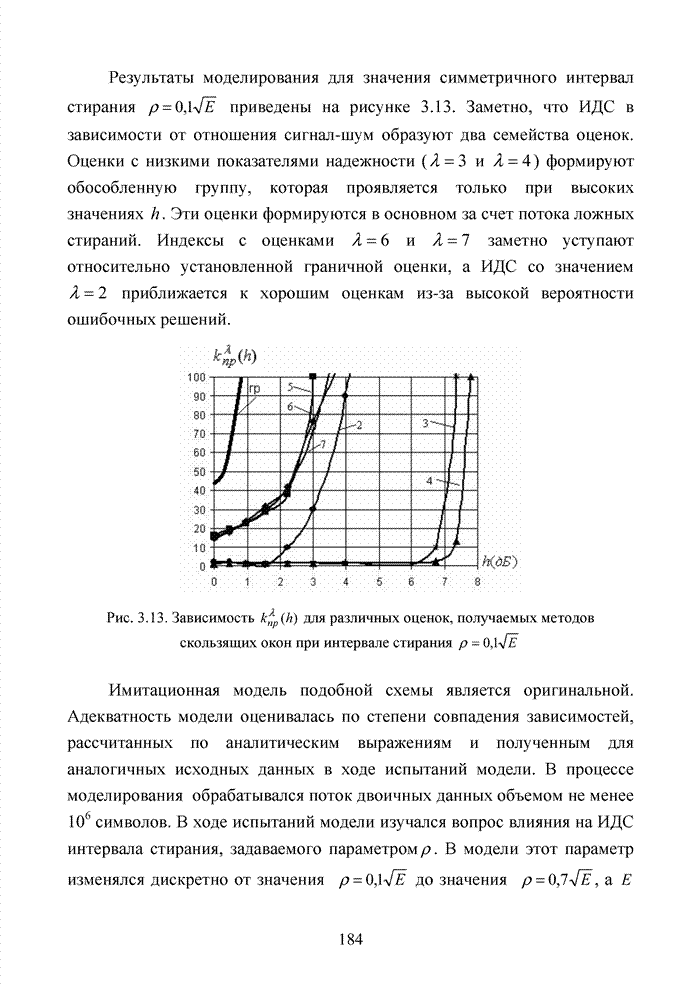
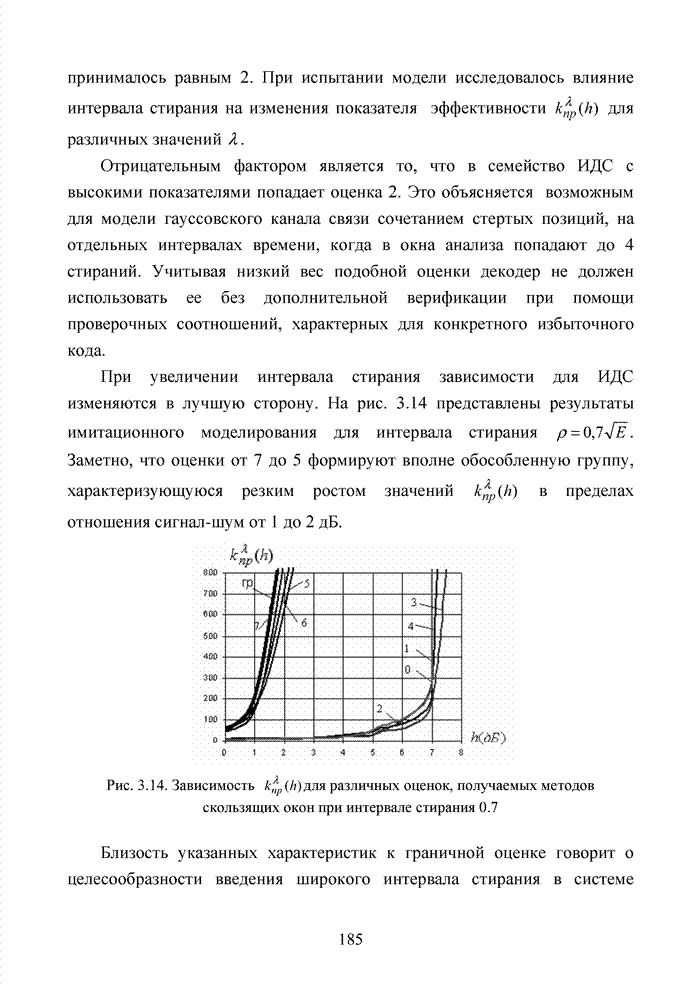
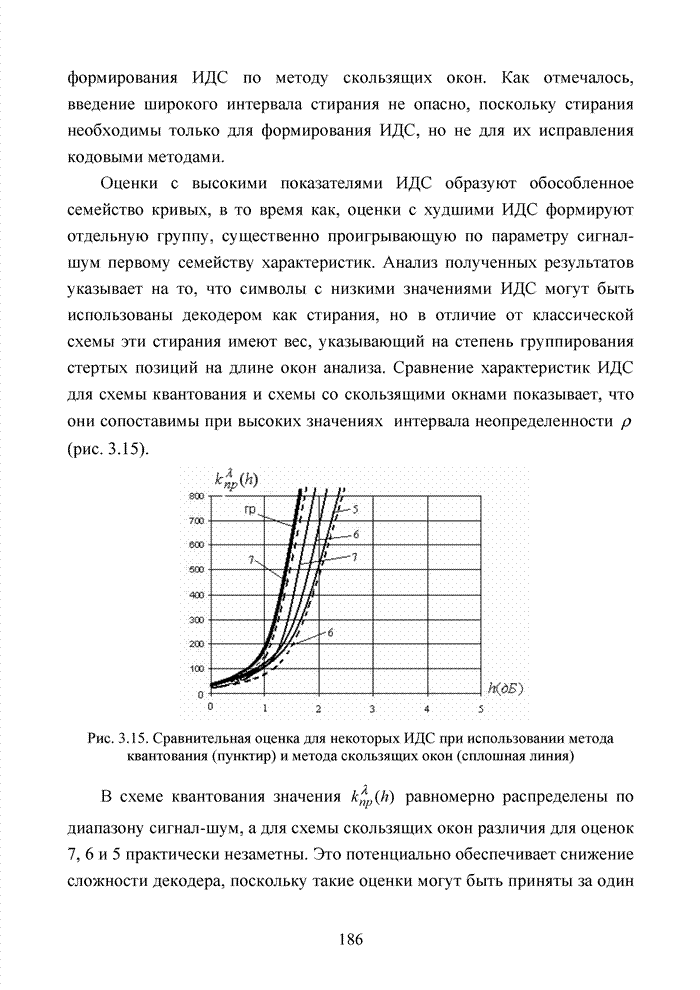
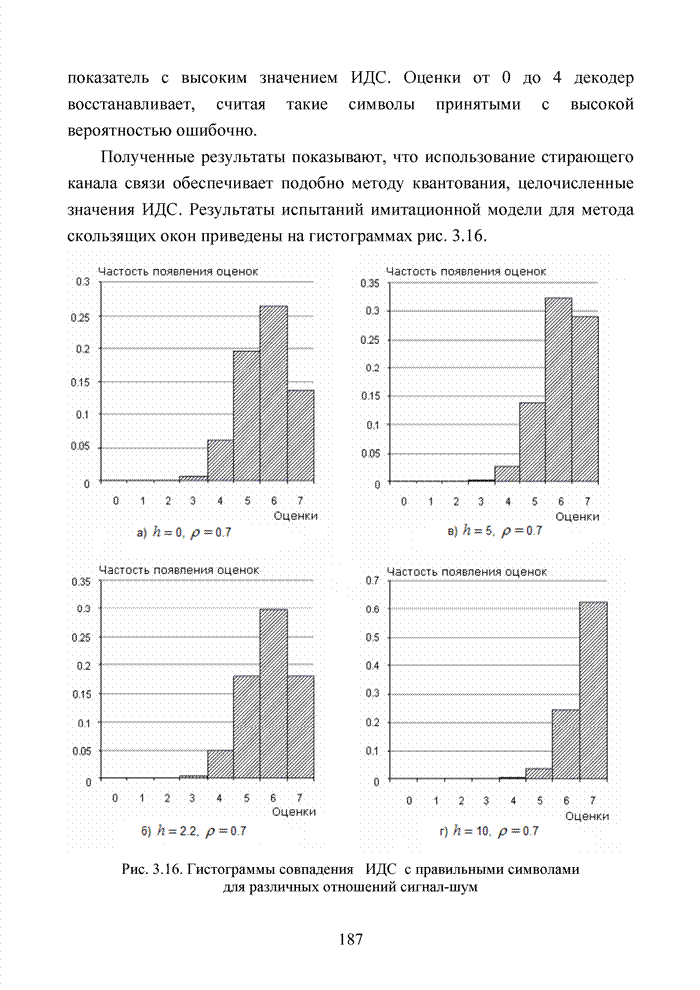
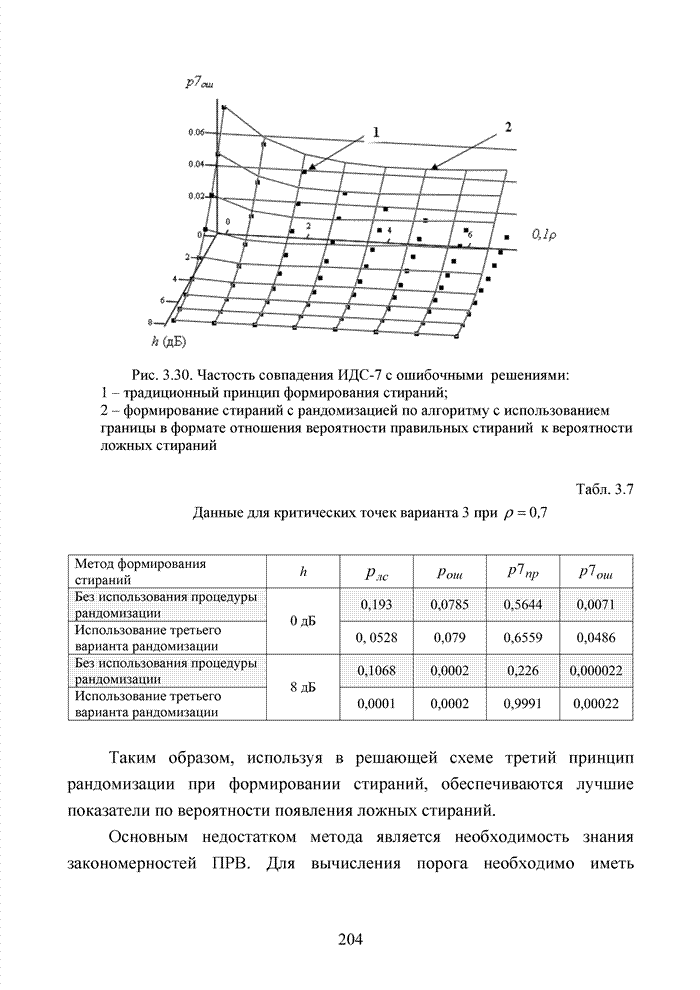
Рис. 4.14. Созвездие комбинаций расширенного кода Хэмминга
Выполненная процедура
обеспечила сохранение всех отмеченные ранее свойства кластерного подхода к
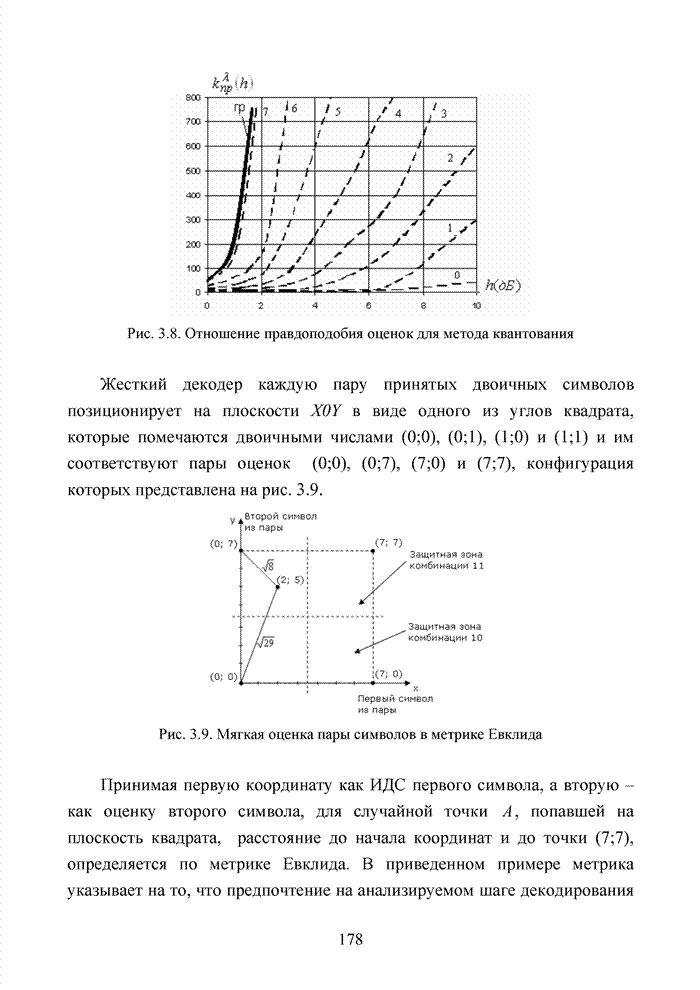
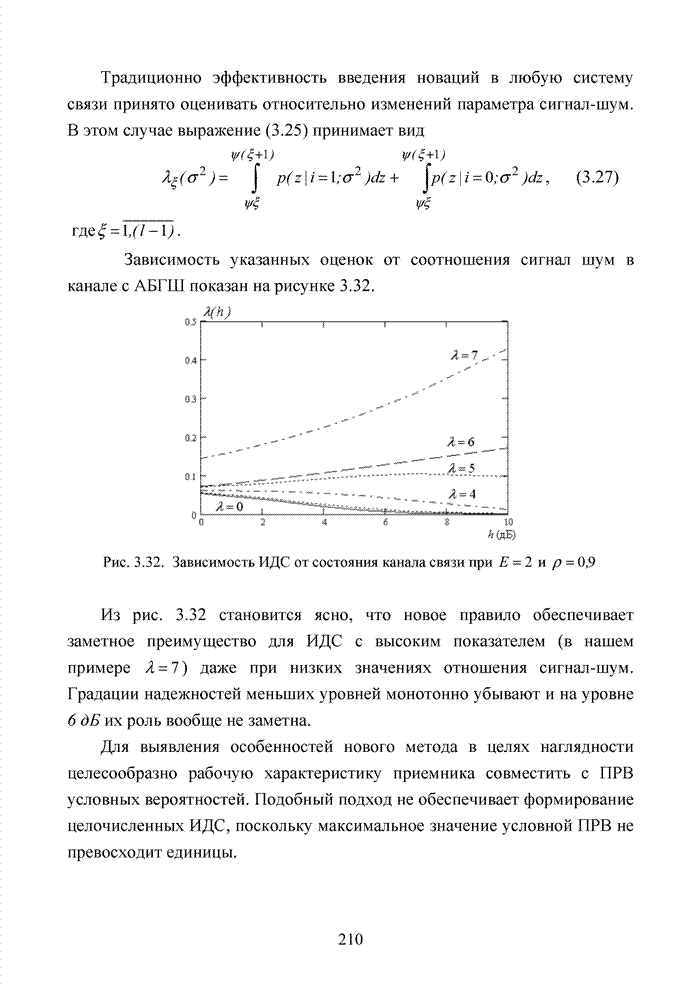
анализу подобных кодов. В связи с увеличением значений координаты ![]() на один разряд увеличивается Евклидова метрика между точками
созвездий, что обеспечивает повышение корректирующей способности кода.
на один разряд увеличивается Евклидова метрика между точками
созвездий, что обеспечивает повышение корректирующей способности кода.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
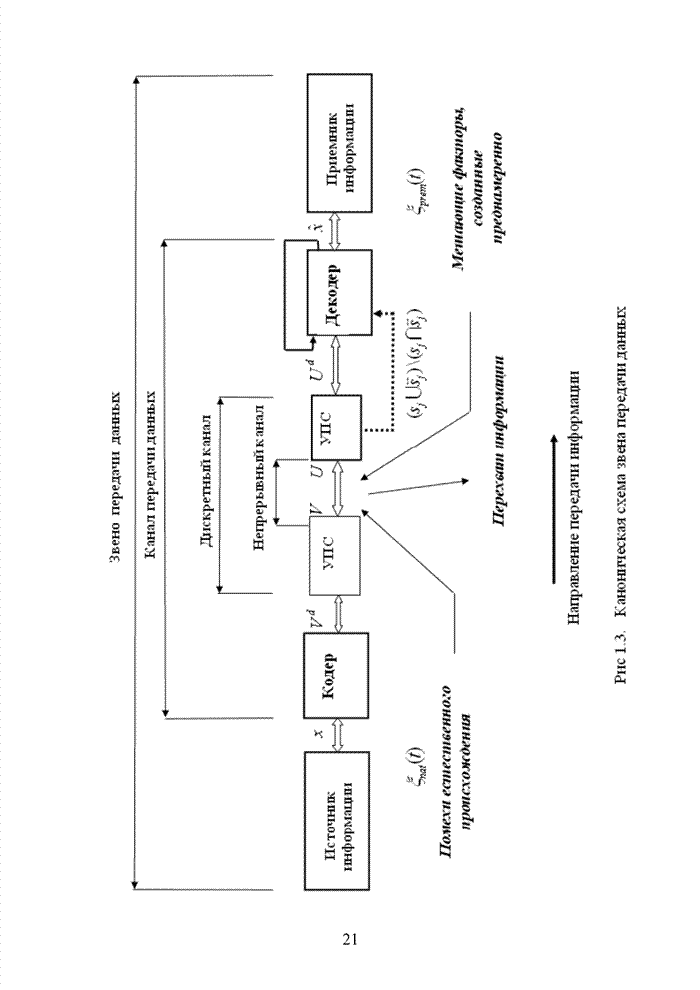
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
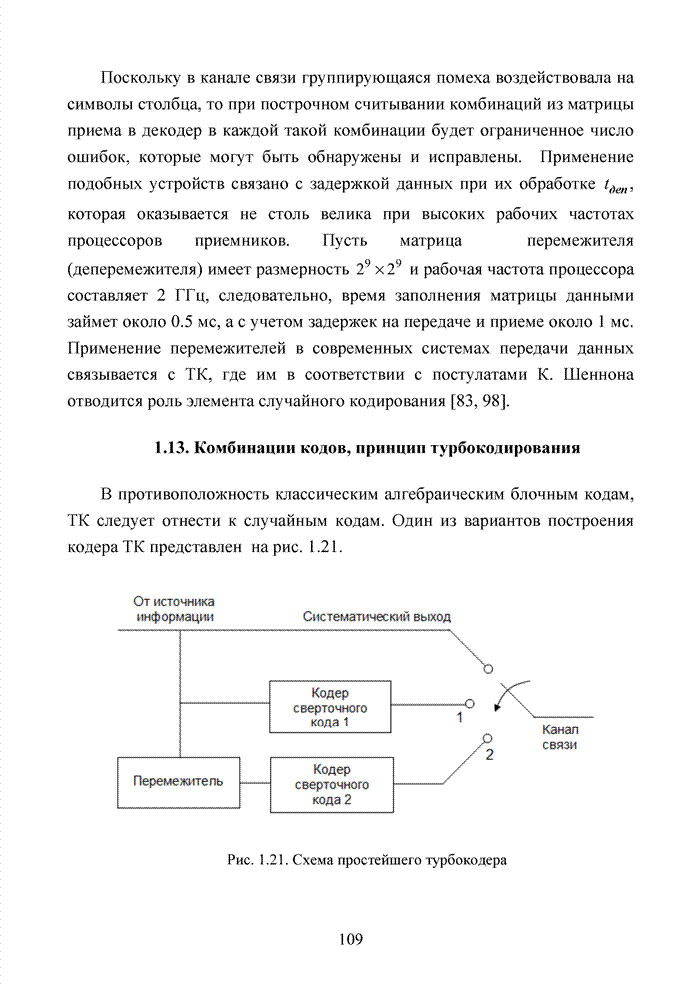
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
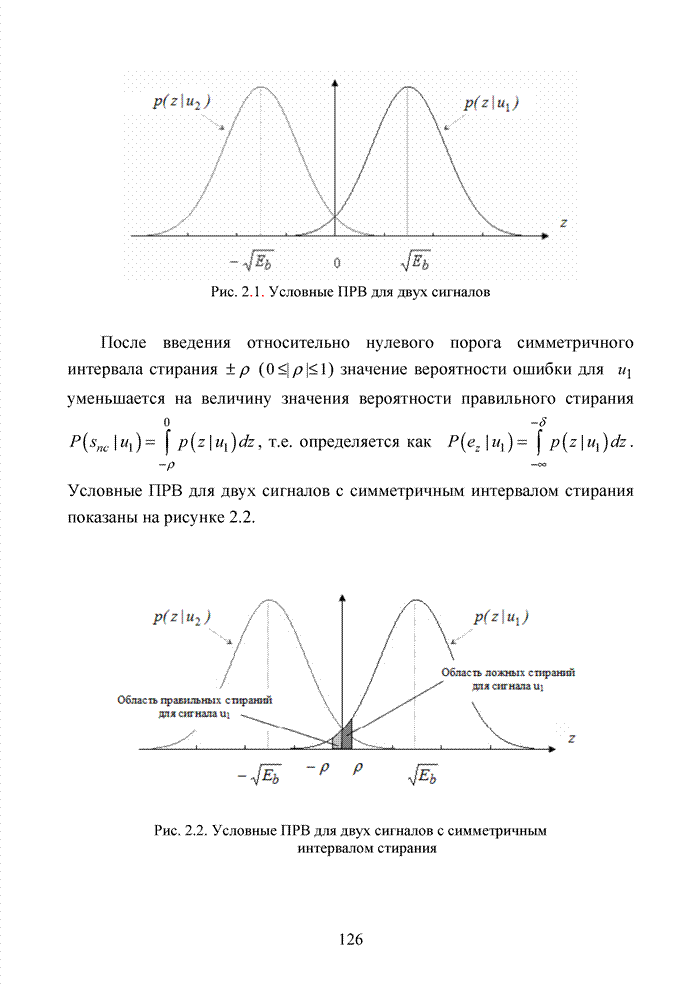
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
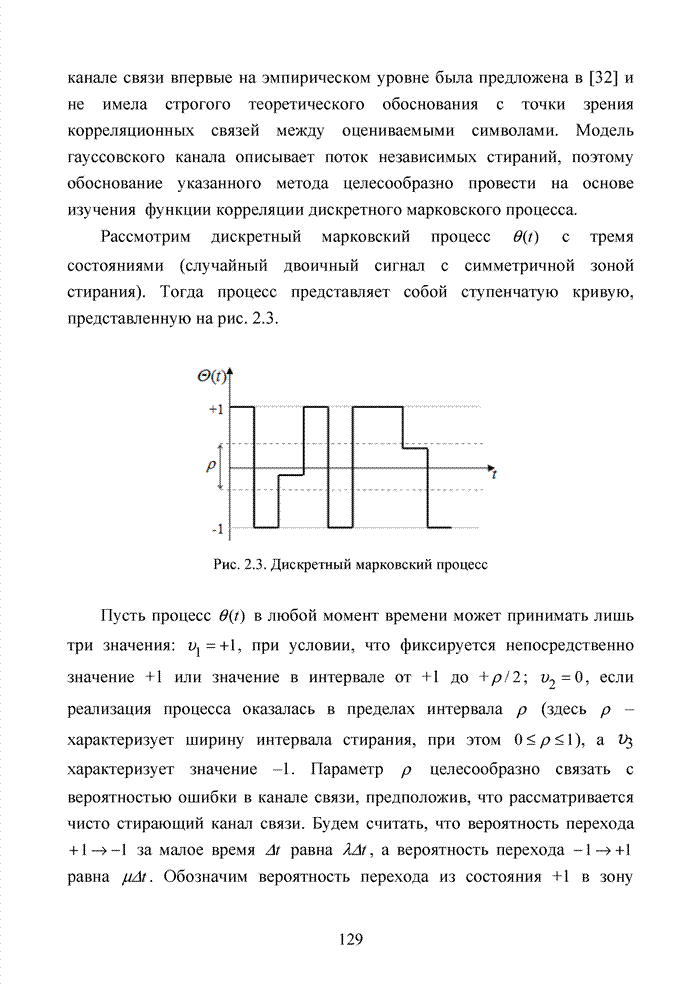
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
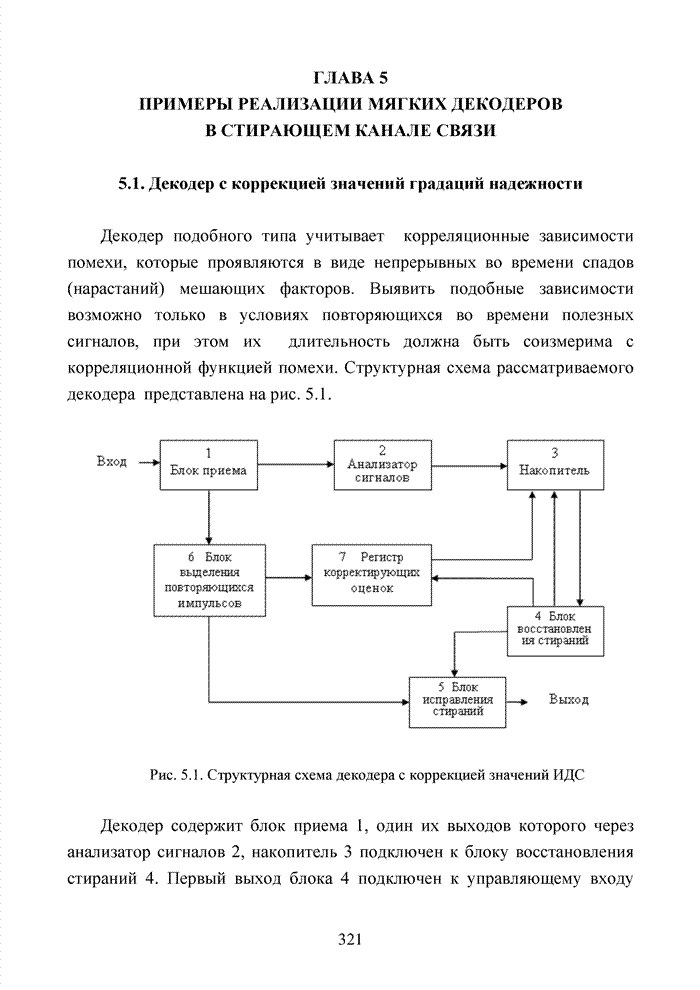
- 5.1. Декодер с коррекцией значений градаций надежности
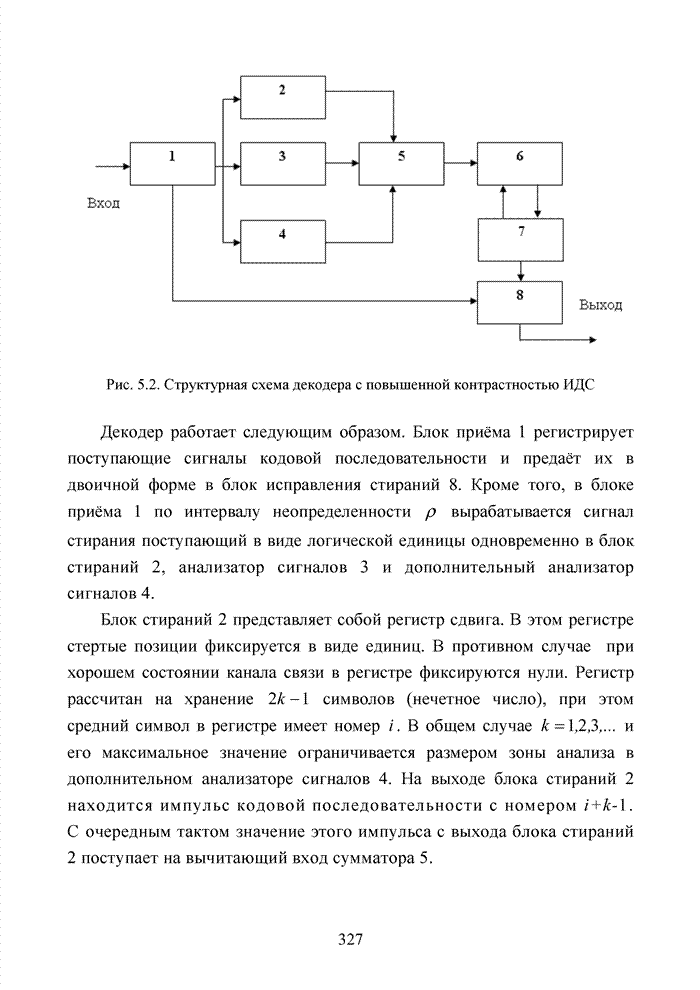
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
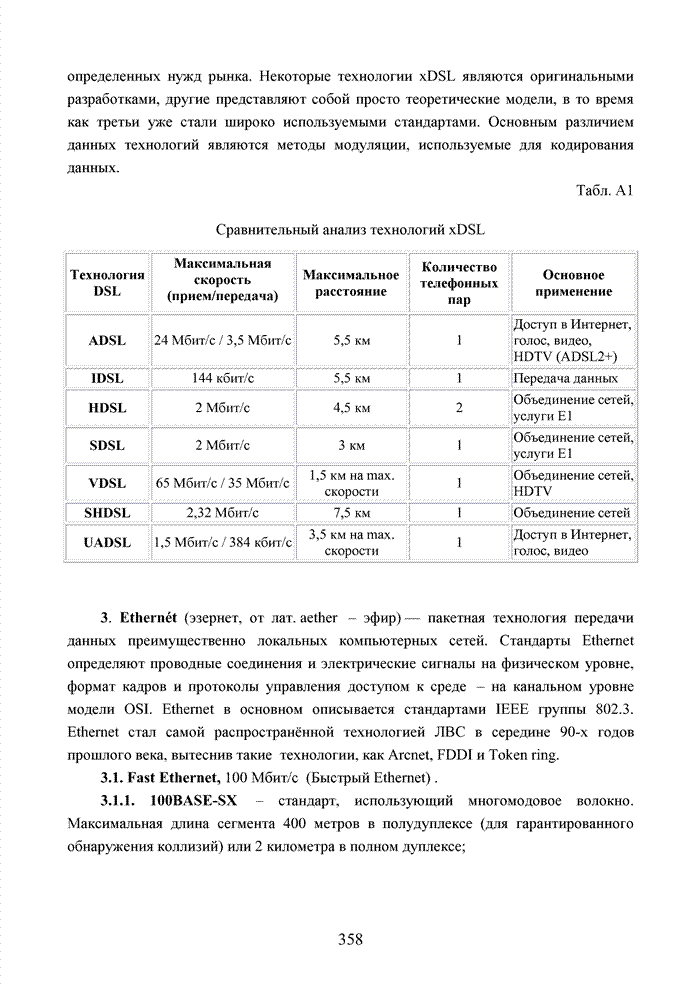
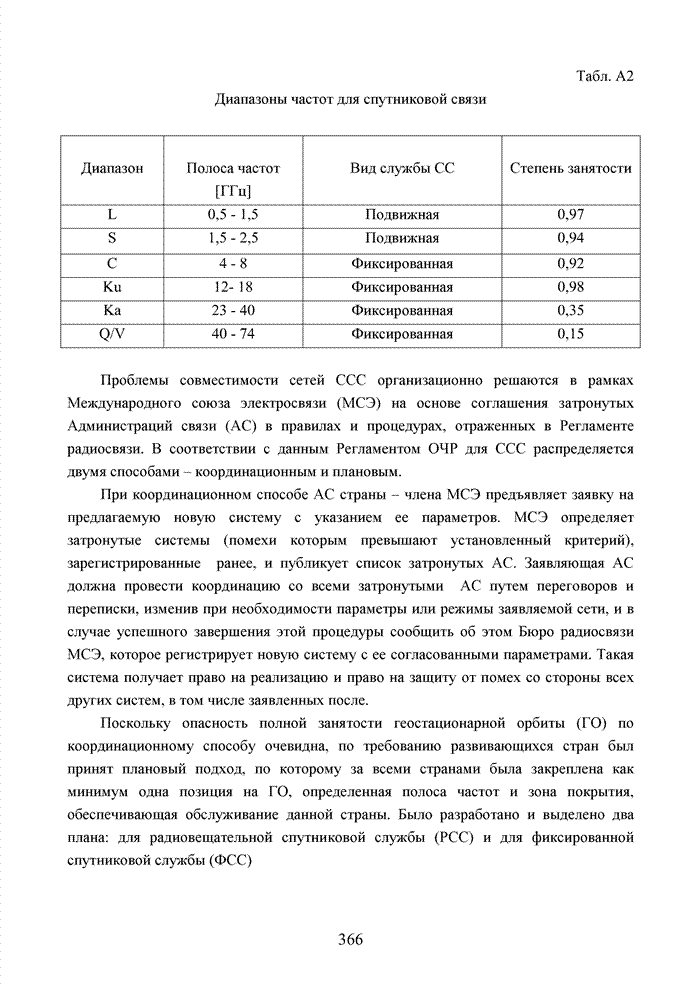
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
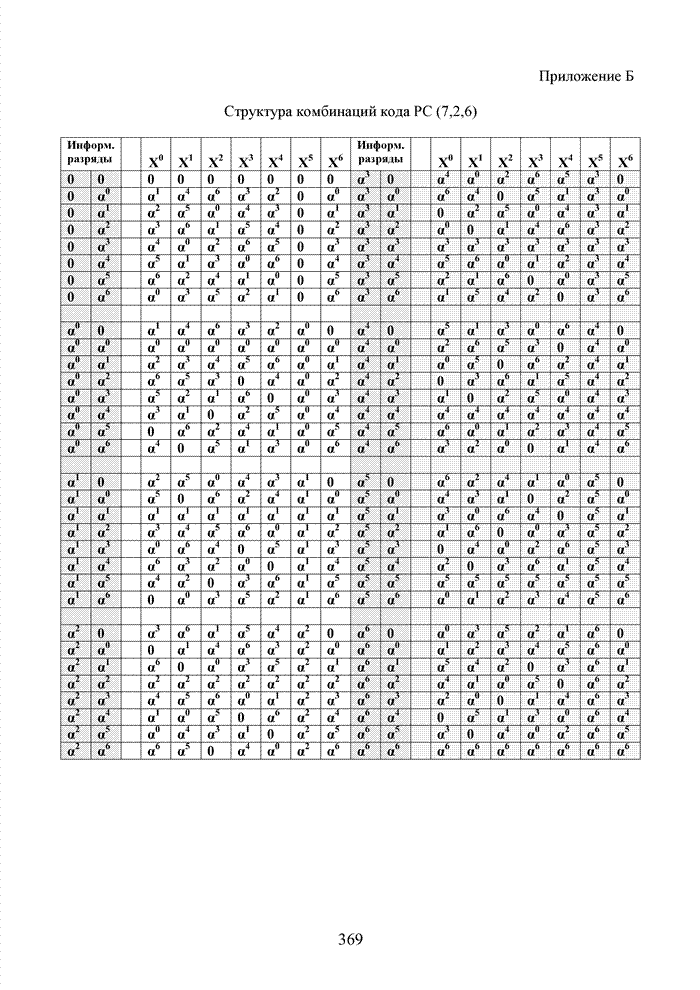
- Приложение Б Структура комбинаций кода РС (7,2,6)
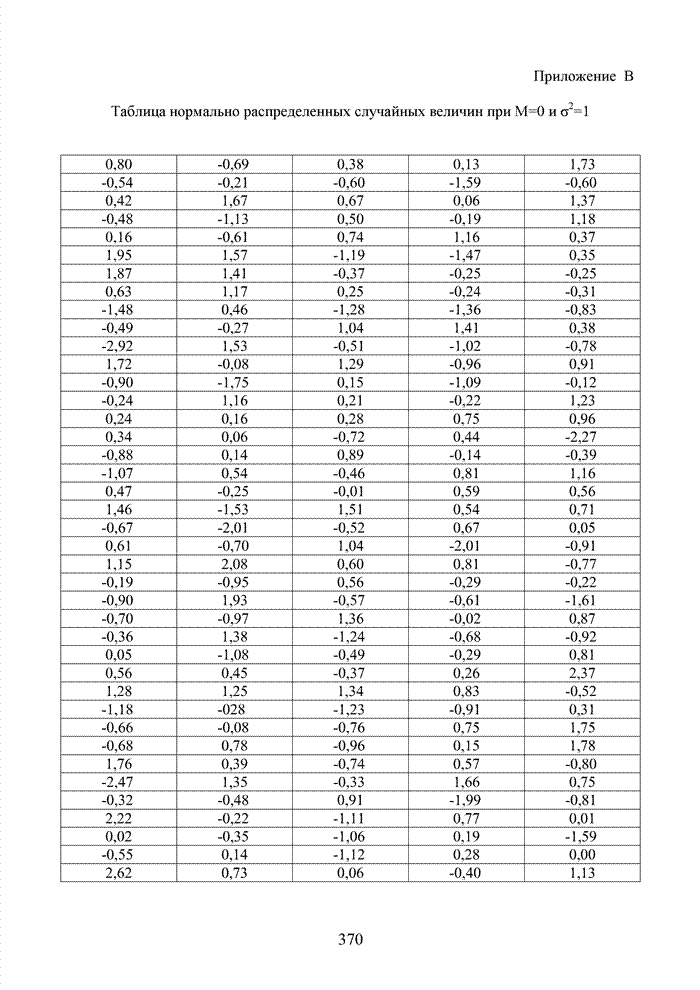
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК