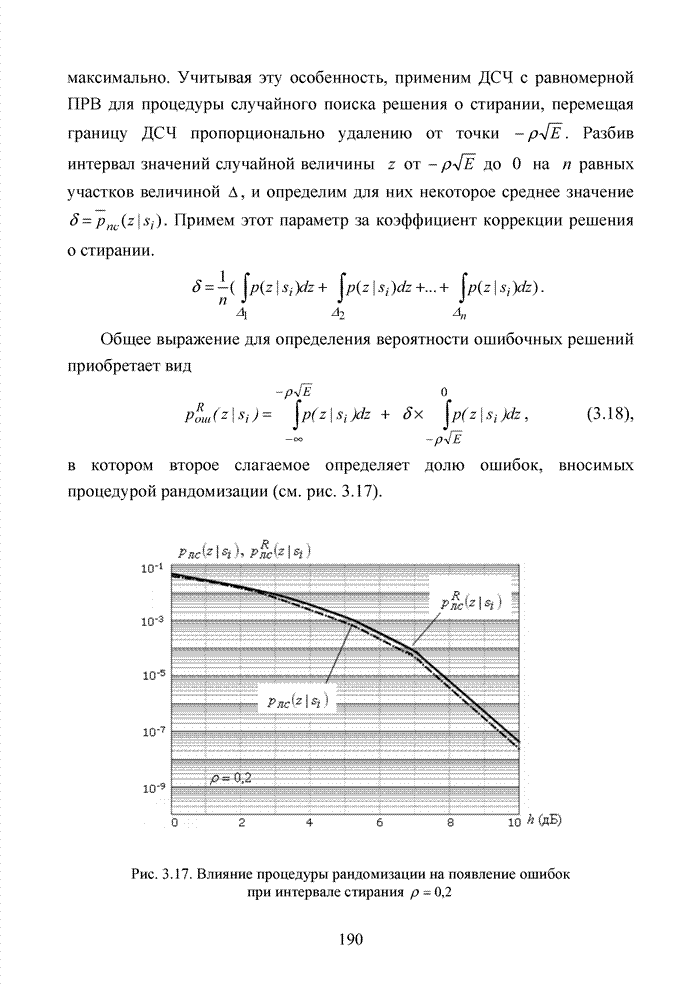
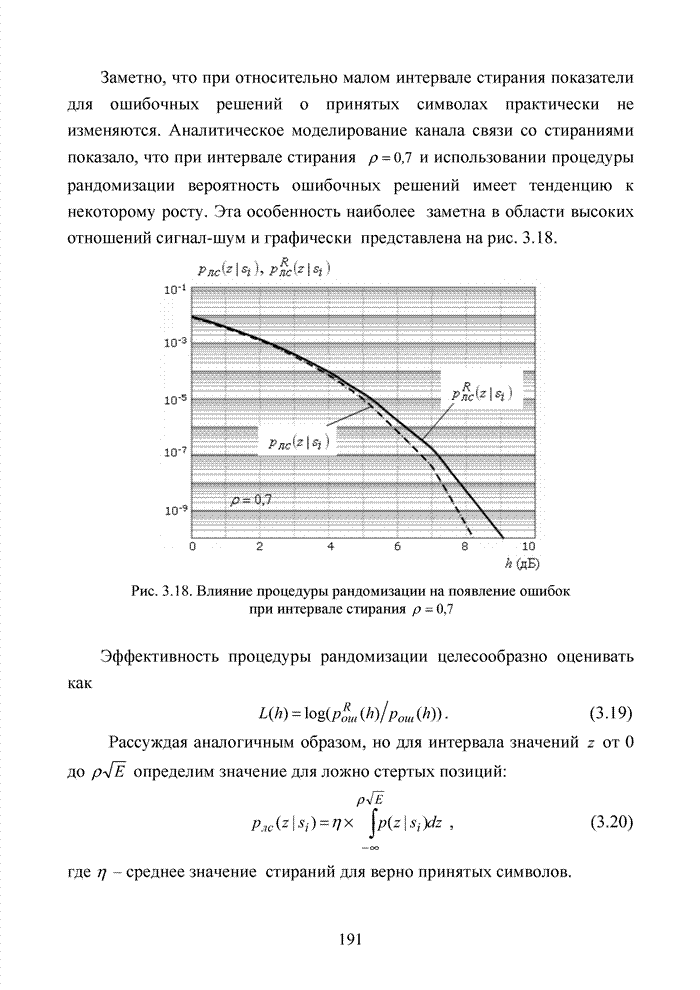
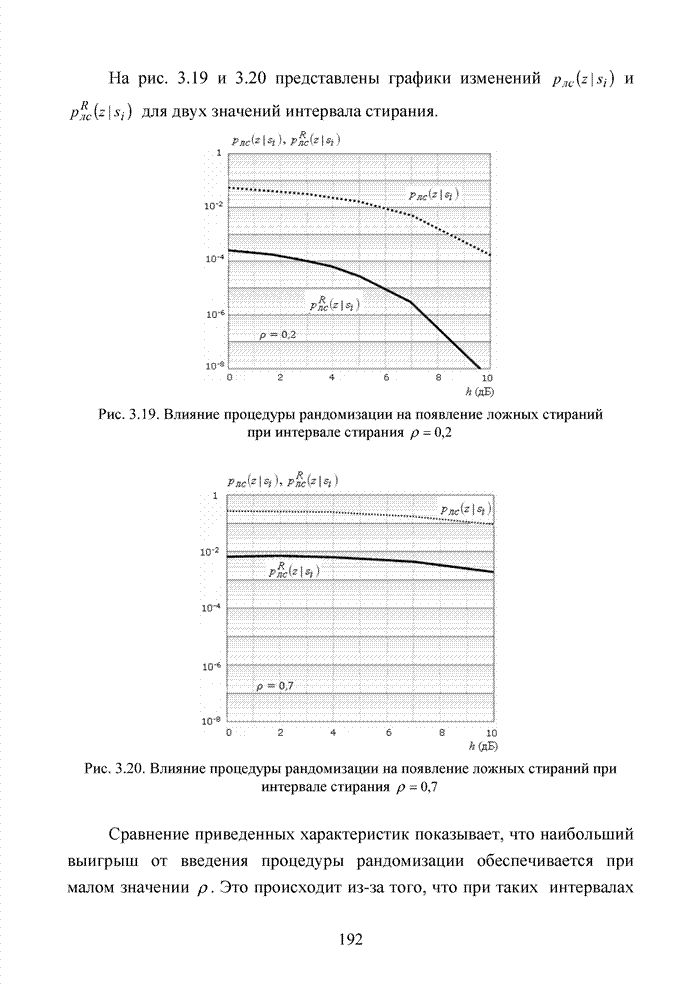
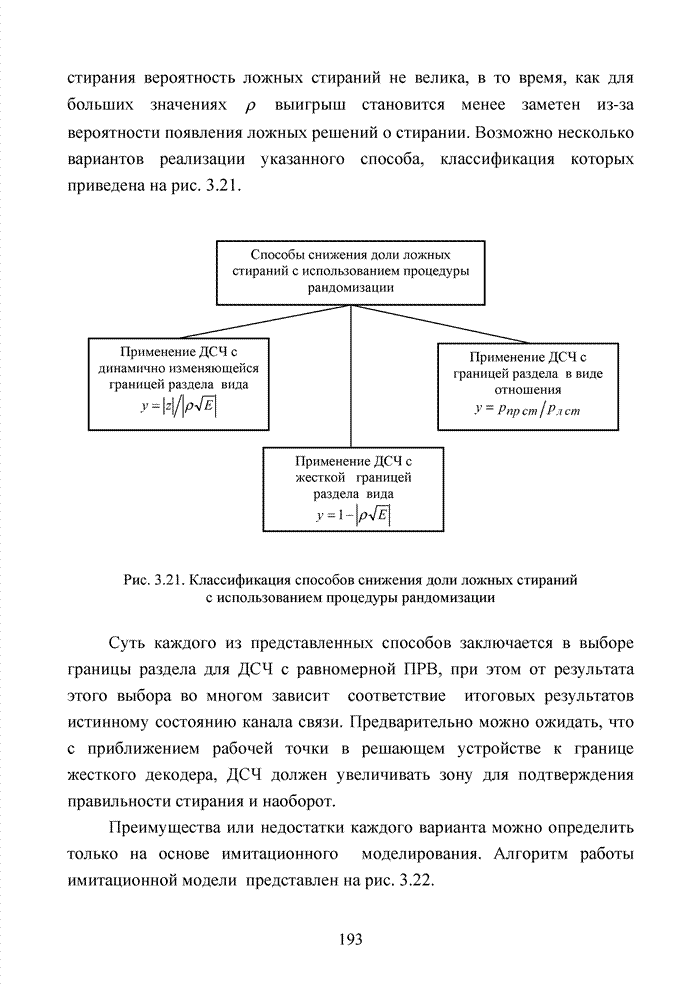
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
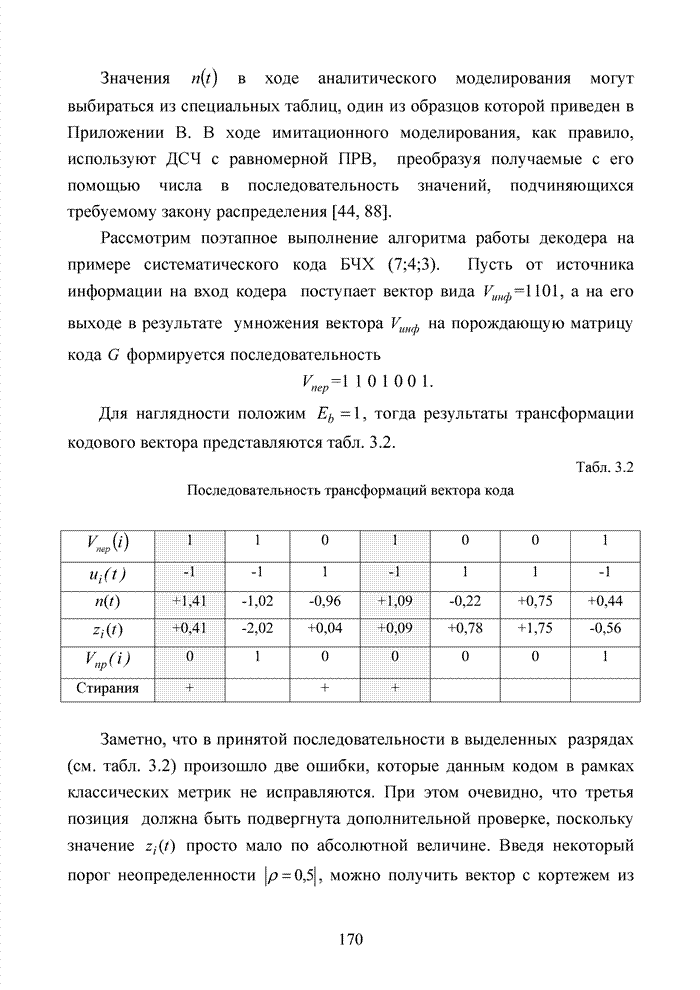
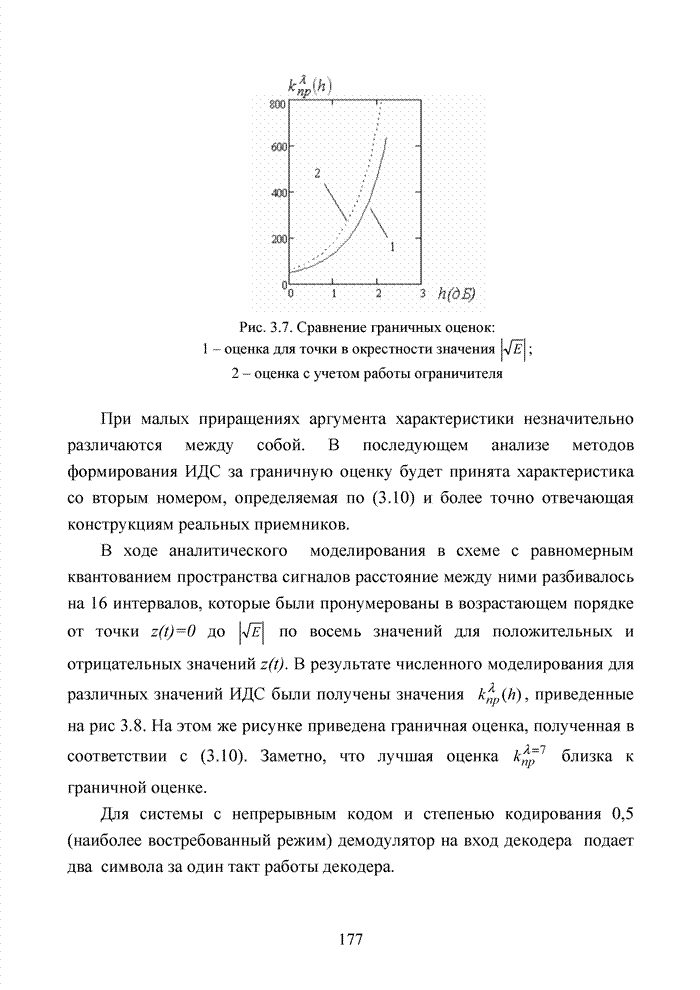
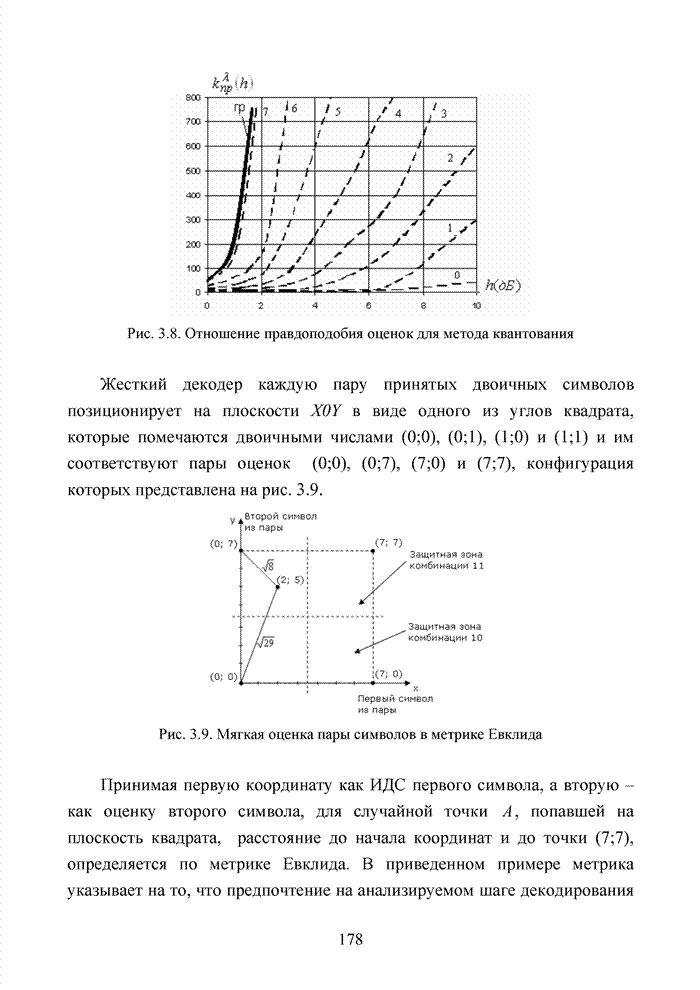
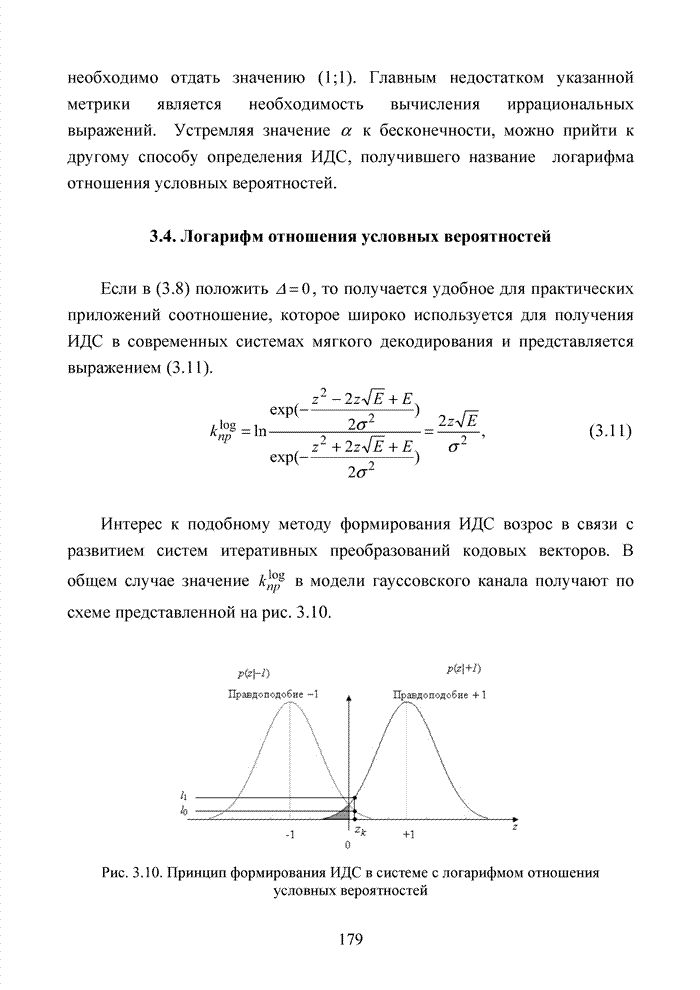
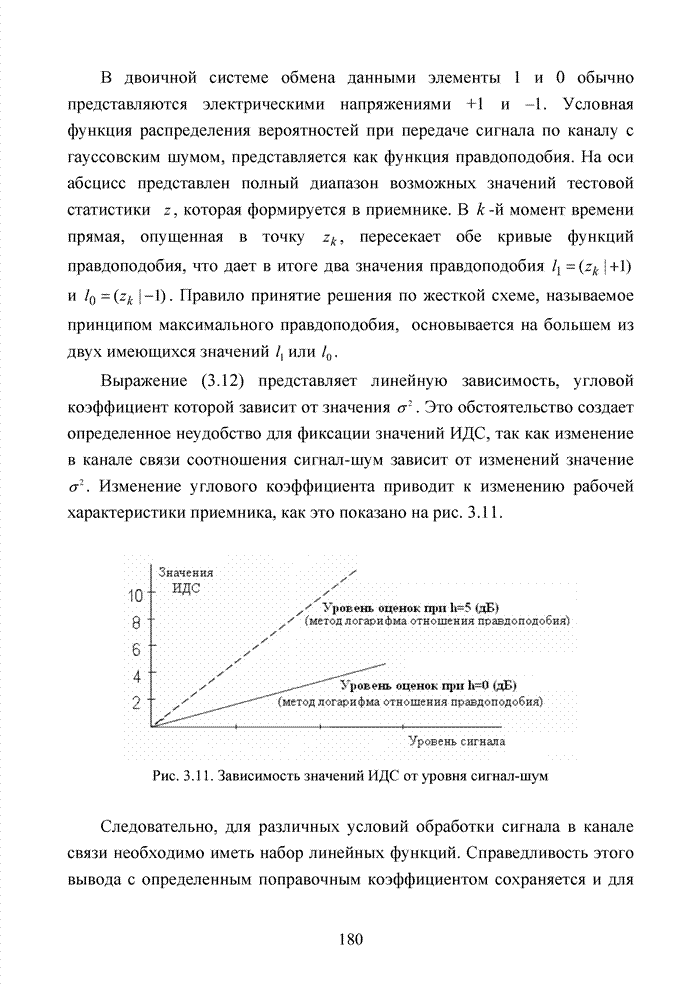
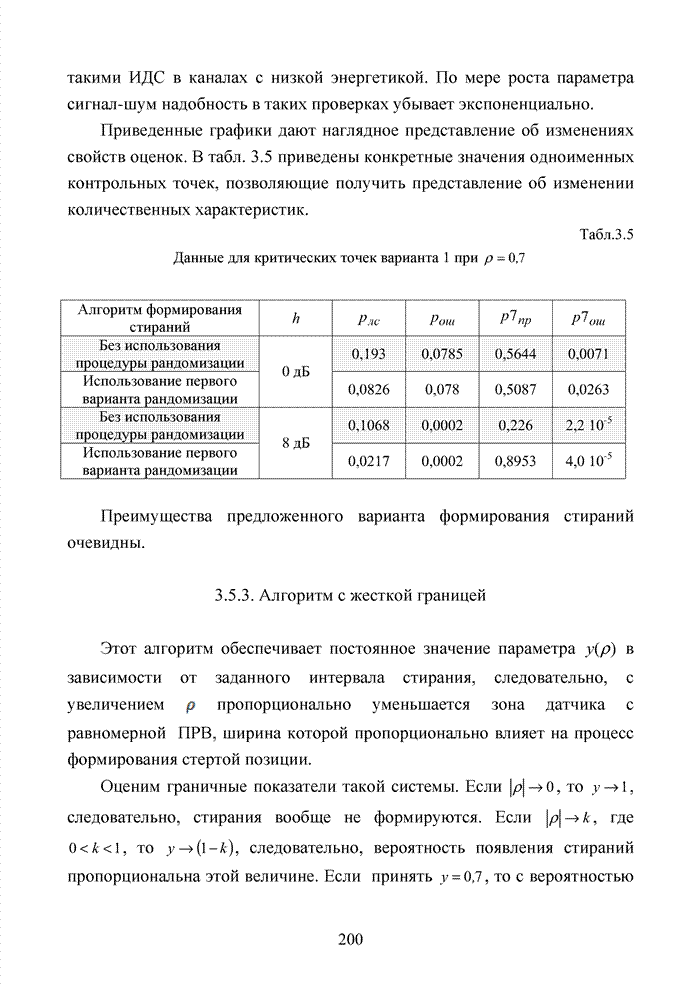
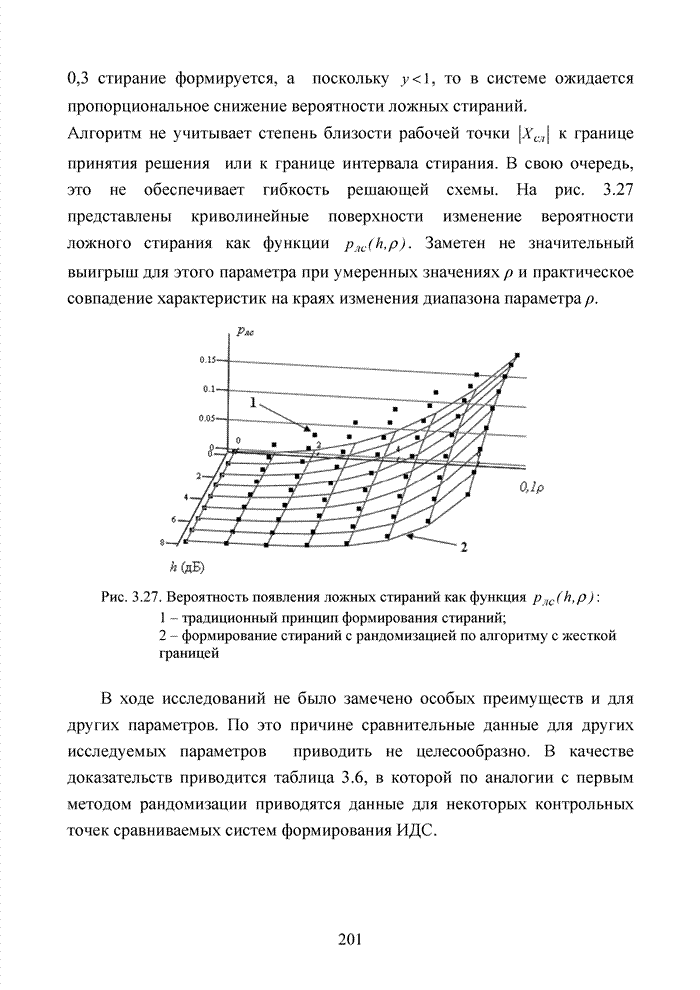
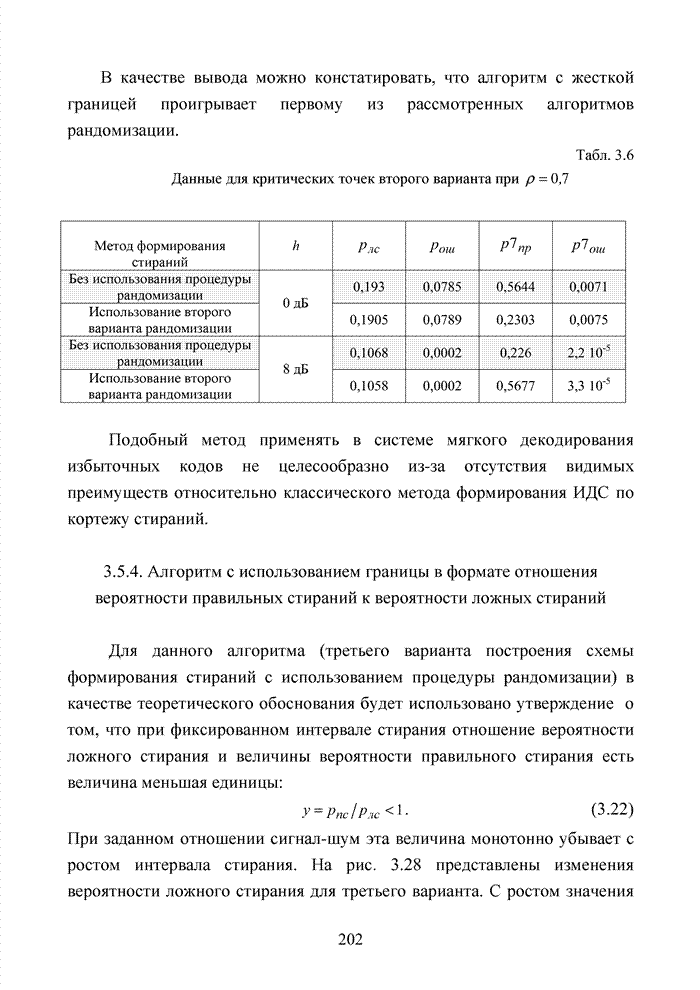
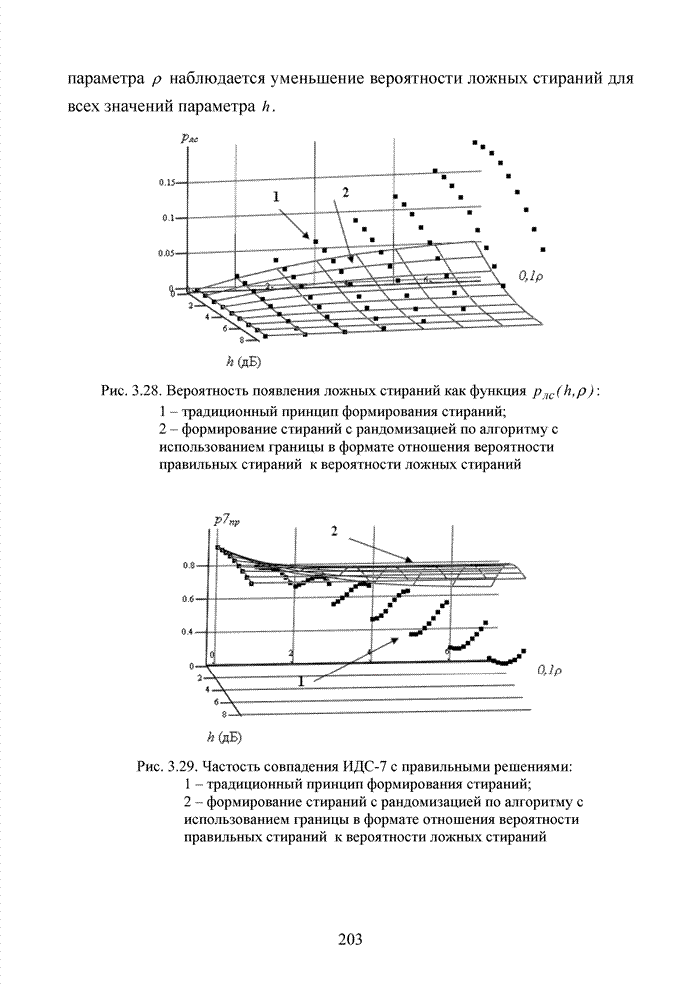
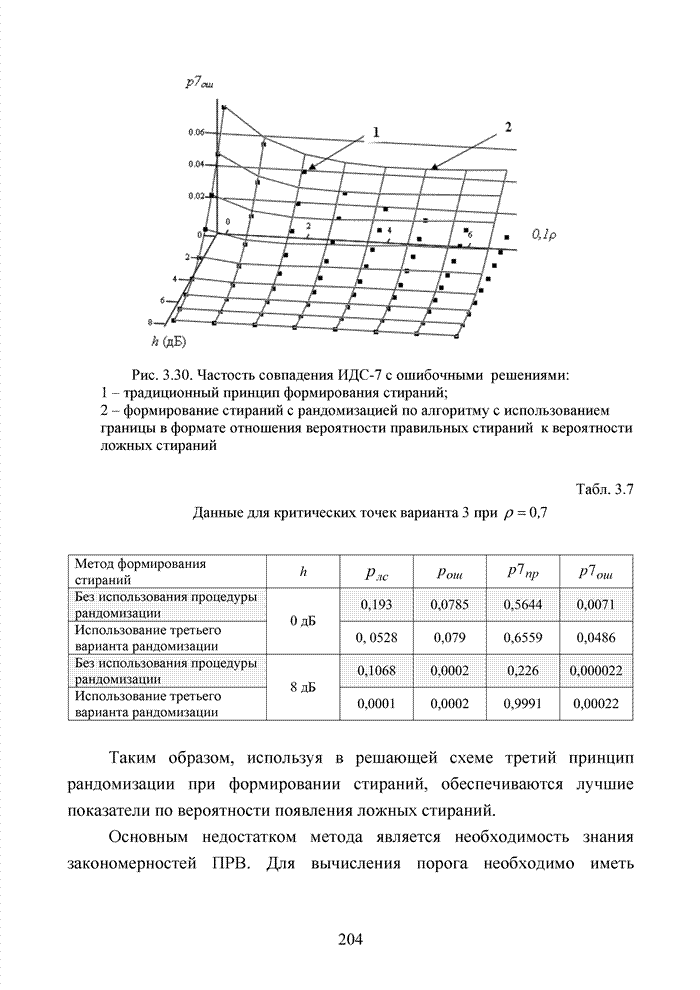
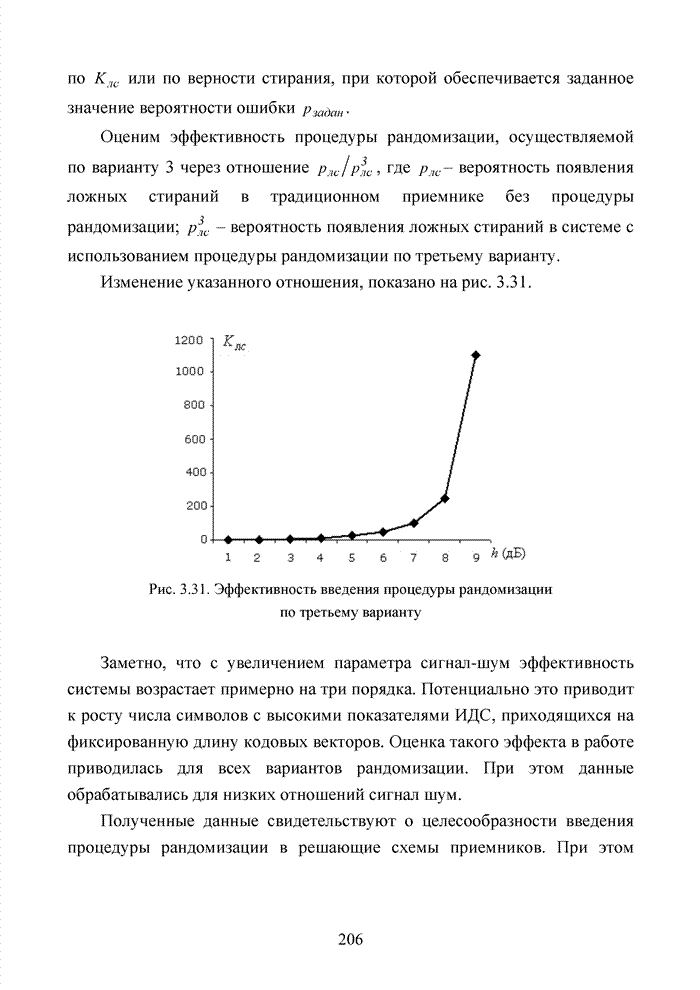
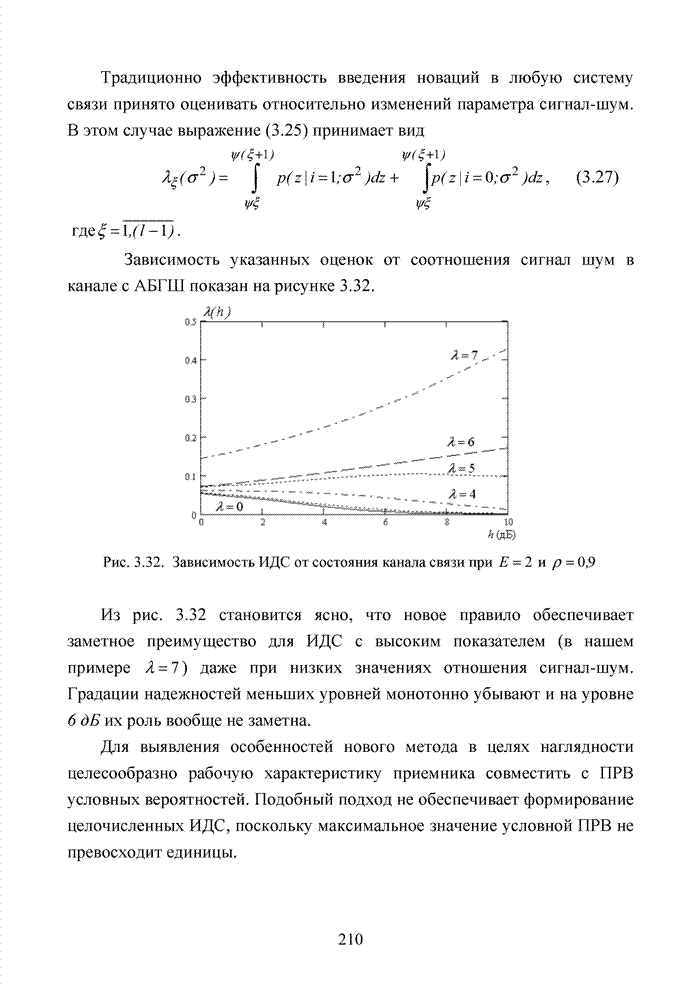
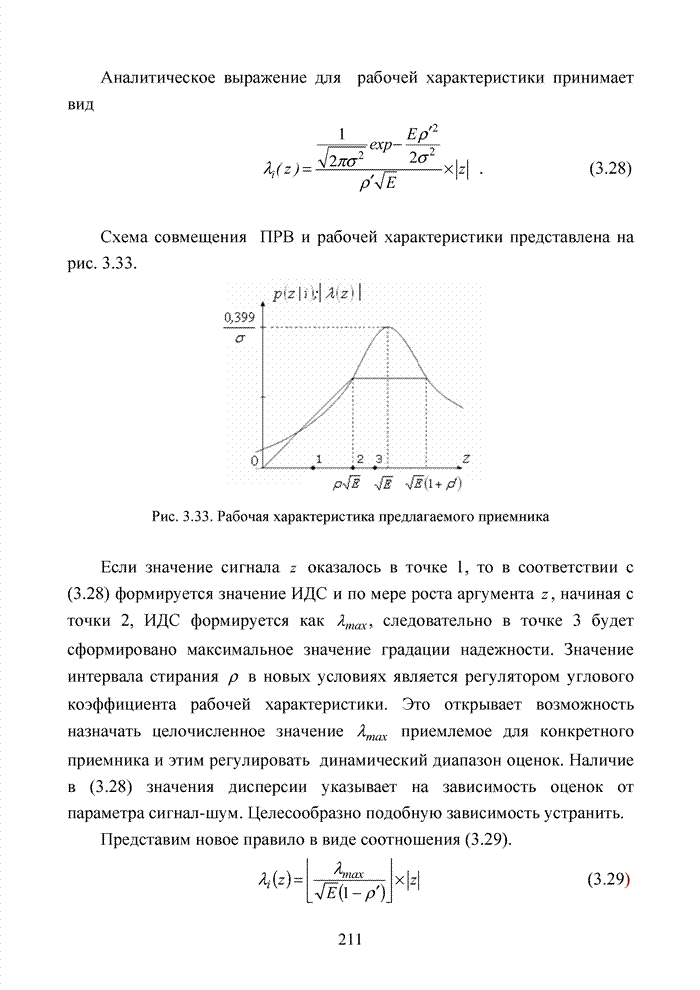
3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
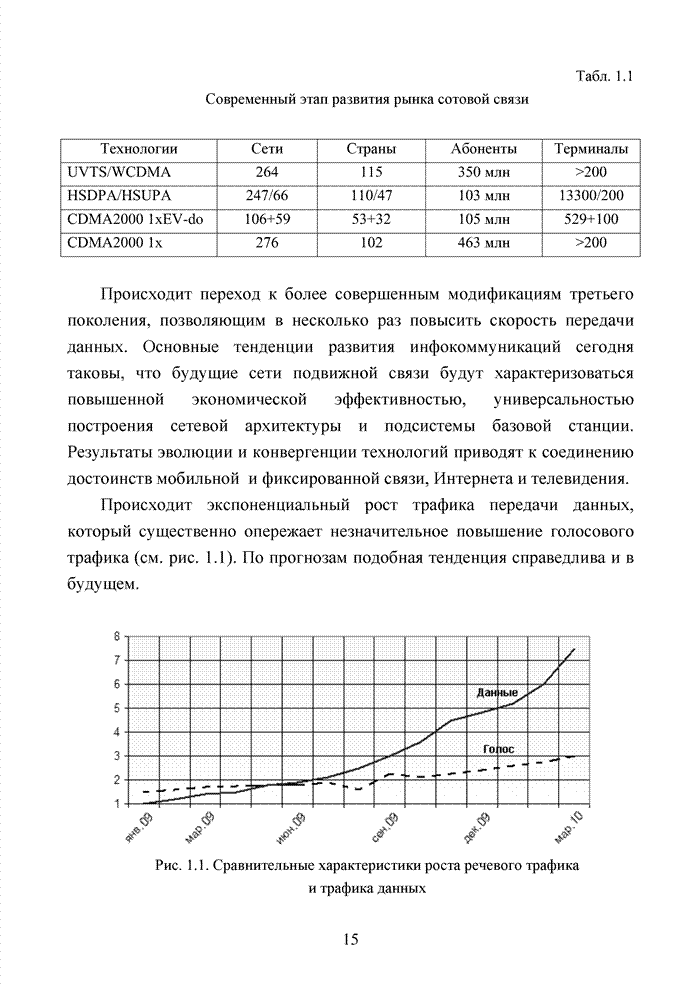
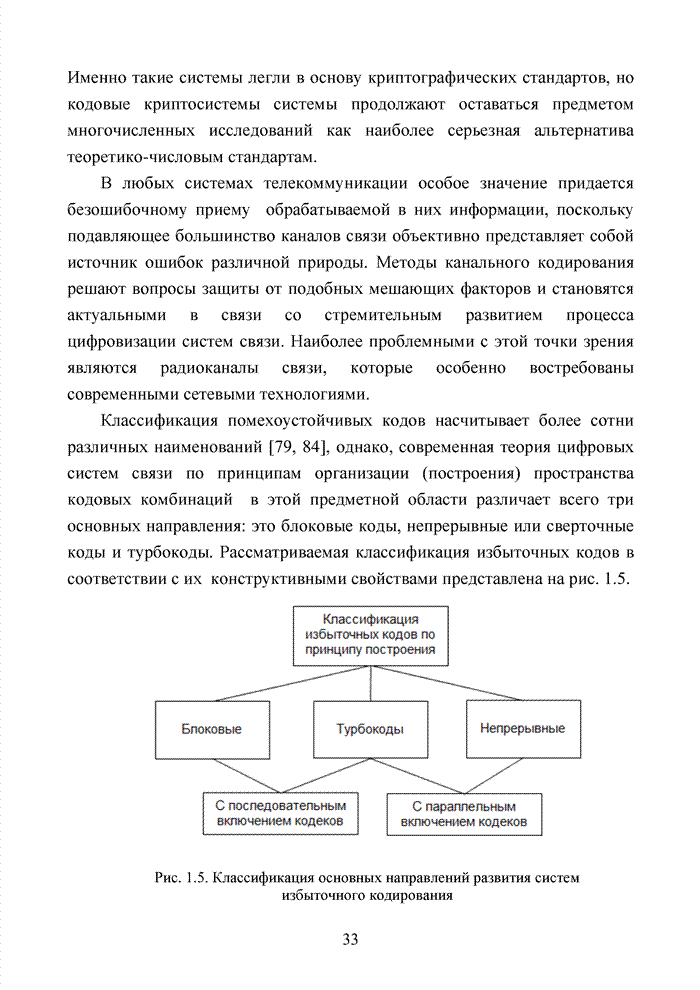
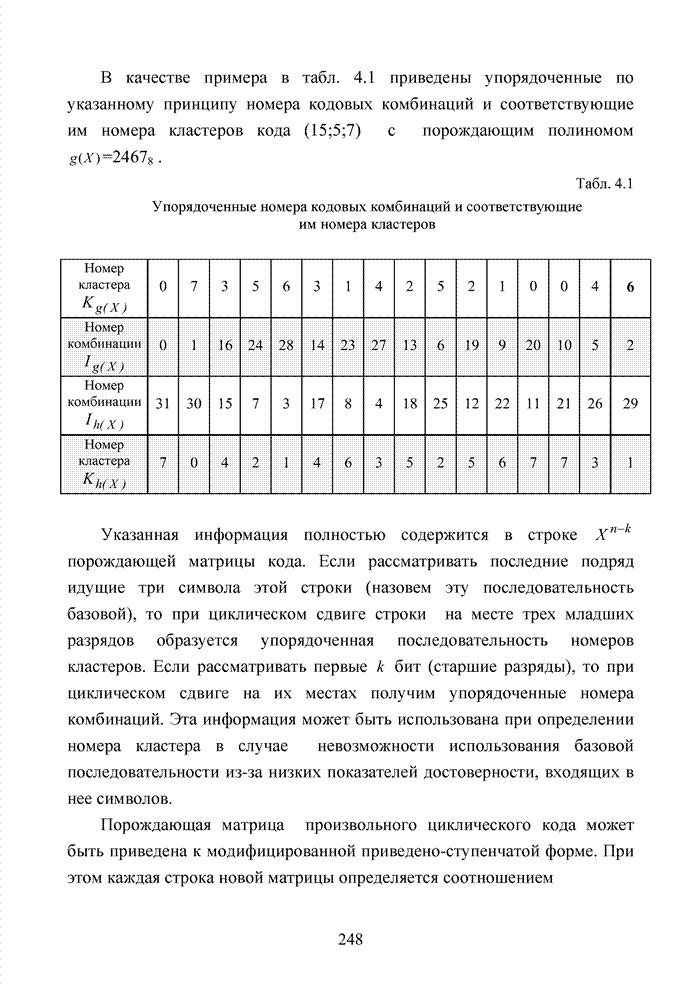
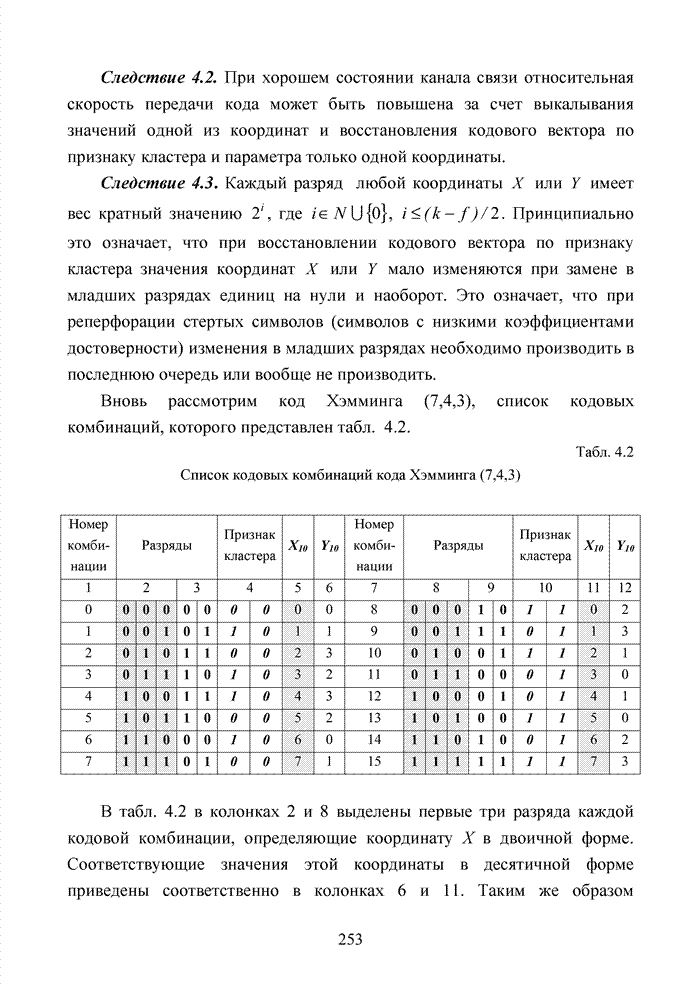
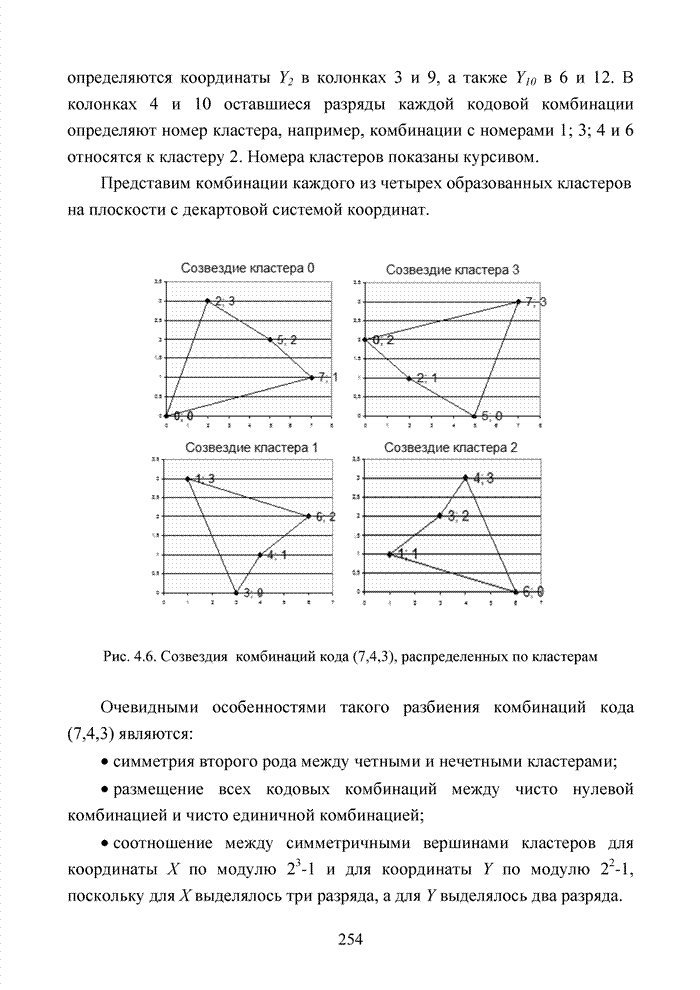
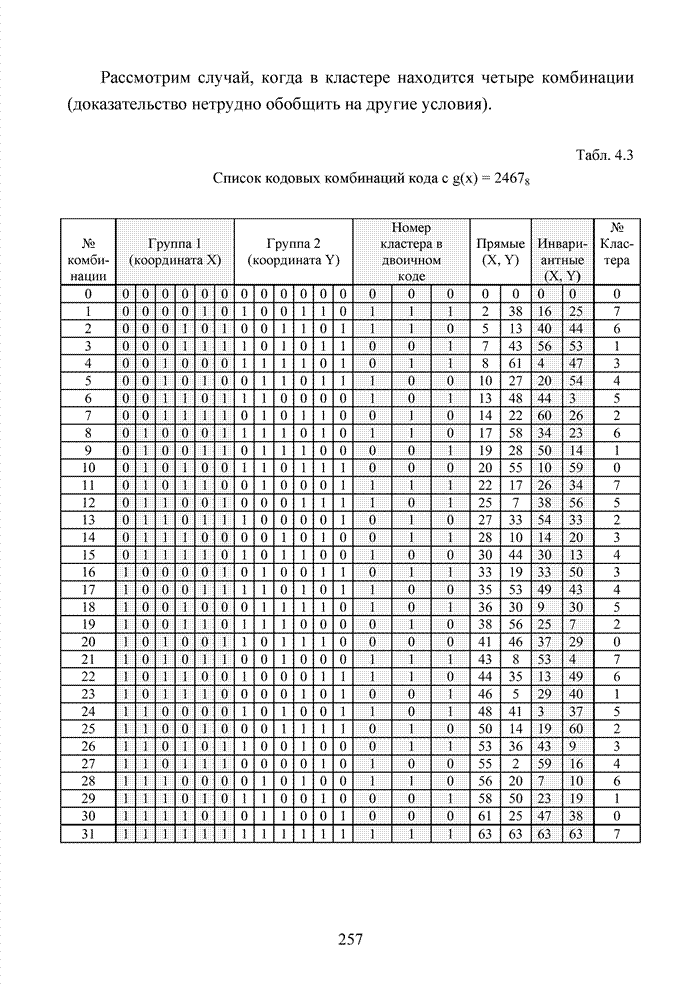
Современный этап развития передач информации отмечен переходом от двоичных сигналов к многопозиционным сигналам и поиском регулярных методов формирования сигнально-кодовых конструкций (СКК). При использовании избыточных кодов их спектральную эффективность оценивают отношением k/n, следовательно, для достижения требуемой скорости передачи двоичных информационных символов требуется увеличение скорости модуляции, которая по критерию Найквиста неизбежно [94] приводит к увеличению полосы пропускания. Чтобы этого избежать, расширяют множество сигналов [87]. Наибольший эффект указанная процедура обеспечивается в сочетании с применением помехоустойчивого кодирования, следовательно, вполне очевидна целесообразность использования мягких декодеров и в этих случаях, например, в асимметричных цифровых абонентских линиях. В таких линиях действует сочетание многообразных мешающих факторов, которые, с одной стороны, трудно поддаются прогнозам, а, с другой стороны, динамично изменяются во времени. К таким факторам относят затухание в линии, баланс кабеля, интерференцию радиочастот и перекрестные помехи на ближнем или на дальнем конце канала. Основная трудность при этом заключается в расчете показателей отклонения сигнала от базовых точек, которые не могут быть определены тривиальным способом, описанным для двоичного гауссовского канала связи. Это не позволяет напрямую применить метод формирования целочисленных ИДС по стираниям и восстанавливать стирания неэффективными переборными методами среди возможных сочетаний нескольких q-ичных символов. Для сложных видов модуляции применимы многомерные ПРВ.
Важнейшим для
практических приложений является n-мерный
нормальный закон распределения совокупности случайных величин ![]() . Соответствующая
нормальному закону n-мерная
функция распределения по определению равна [76].
. Соответствующая
нормальному закону n-мерная
функция распределения по определению равна [76].
 .
.
Здесь ![]() - произвольные действительные числа,
- произвольные действительные числа, ![]() , D -
определитель n-го порядка.
, D -
определитель n-го порядка.
В современных системах
связи объем передаваемой информации увеличивается за счет изменения как
амплитуды, так фазовый компонент несущего колебания. Наиболее общей формой фазы
амплитудной модуляции является квадратурная амплитудная модуляция (КАМ), сигнал
которой формируется путем сложения амплитудно-модулированных сигналов,
смещенных по фазе на ![]() .
Полная совокупность сигналов состоит и прямоугольной сетки сигнальных точек
(базовых точек). Наиболее простая форма КАМ включает всего четыре различных
сигнала, и поэтому может кодировать пары входных бит (рис. 3.39).
.
Полная совокупность сигналов состоит и прямоугольной сетки сигнальных точек
(базовых точек). Наиболее простая форма КАМ включает всего четыре различных
сигнала, и поэтому может кодировать пары входных бит (рис. 3.39).

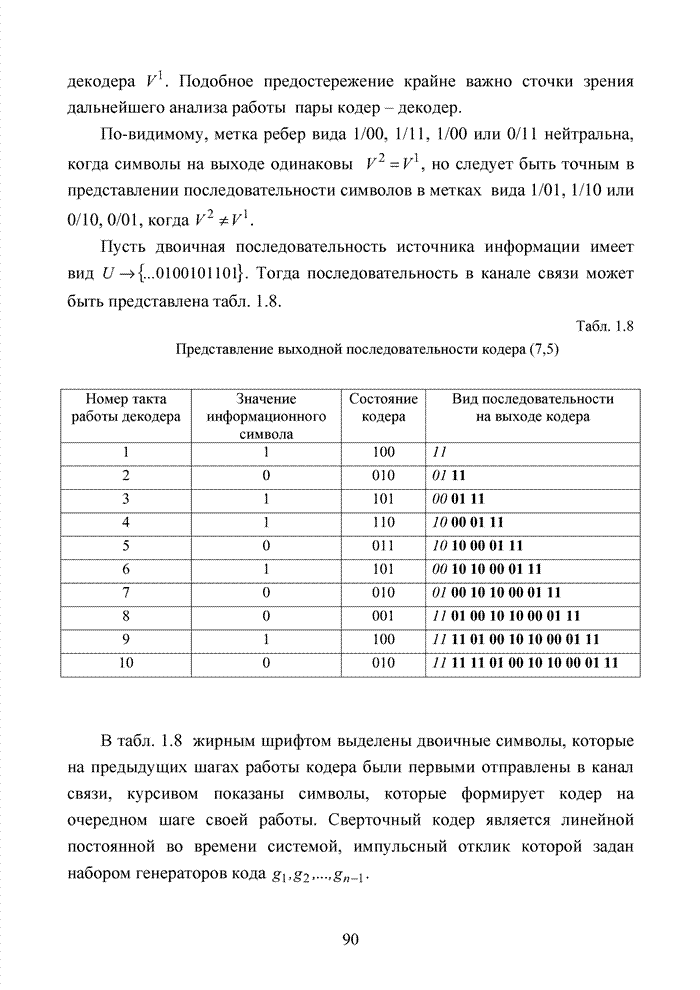
Рис. 3.39. Структура сигнала КАМ-4
Из рис. 3.39 становится ясно, что расстояние от одних точек до других не является одинаковым: по сторонам образовавшегося квадрата это расстояние меньше, чем расстояние по диагонали квадрата. Именно это обстоятельство указывает на невозможность использовать классические методы организации стирающего канала по принципу двоичного канала в системах с КАМ-сигналами.
Рассматривая точки, находящиеся на одной стороне квадрата комплексной плоскости, можно использовать аппарат многомерной нормальной функции распределения для оценки вероятности ошибки в такой системе. Этот подход не является продуктивным, поскольку для диагонали квадрата параметры модели отсчетов изменяются.
Для решения задачи в
общем виде целесообразно применить метод описанный в разделе 3.6, когда отсчет
интервала стирания ведется от позиции, определяющей математическое ожидание
сигналов, характерного для каждой базовой точки. На комплексной плоскости
область формирования максимальной оценки ![]() наиболее просто определяется радиусом
окружности
наиболее просто определяется радиусом
окружности ![]() с
центром в
с
центром в ![]() .
Вероятность появления такой оценки оценивается как
.
Вероятность появления такой оценки оценивается как
 ,
,
где ![]() – кратность модуляции, а
– кратность модуляции, а ![]() двумерная ПРВ.
Вероятность появления других оценок определяется
двумерная ПРВ.
Вероятность появления других оценок определяется
 ,
,
по сути области, ограниченные
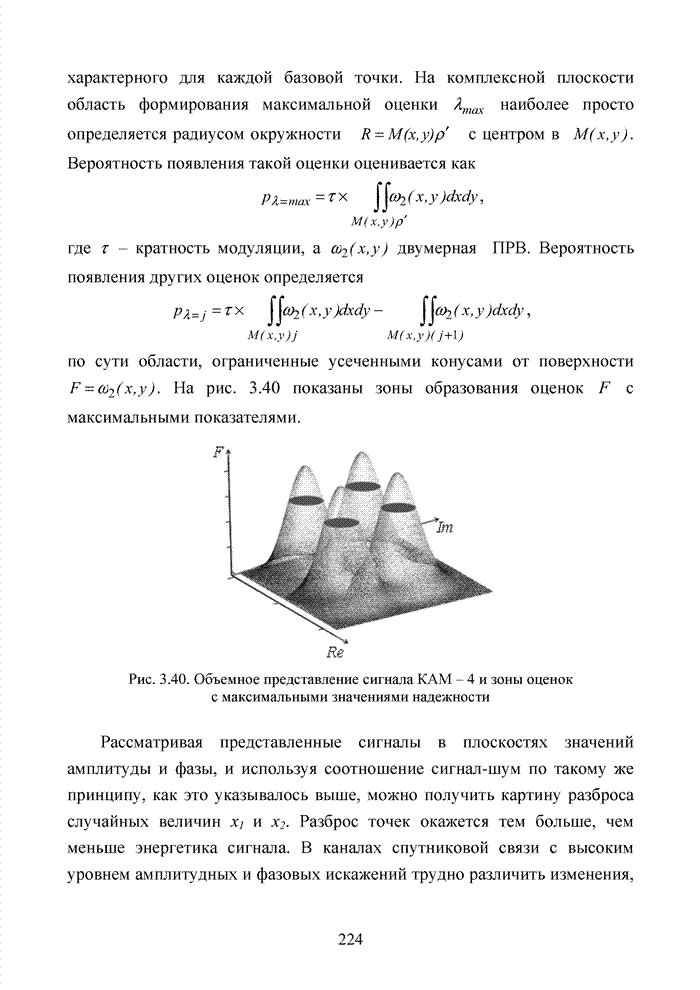
усеченными конусами от поверхности ![]() . На рис. 3.40 показаны зоны образования
оценок
. На рис. 3.40 показаны зоны образования
оценок ![]() с
максимальными показателями.
с
максимальными показателями.

Рис. 3.40. Объемное представление сигнала КАМ – 4 и зоны оценок с максимальными значениями надежности
Рассматривая представленные сигналы в плоскостях значений амплитуды и фазы, и используя соотношение сигнал-шум по такому же принципу, как это указывалось выше, можно получить картину разброса случайных величин x1 и x2. Разброс точек окажется тем больше, чем меньше энергетика сигнала. В каналах спутниковой связи с высоким уровнем амплитудных и фазовых искажений трудно различить изменения, введенные в передаваемый сигнал каналом, от изменений, введенных передатчиком. Поэтому сигнальные точки при использовании КАМ защищаются с помощью манипуляционного кода Грея [87], как показано на рис. 3.41.

Рис. 3.41. Нумерация созвездия сигнальных точек при КАМ-16
Из рисунка видно, что соседние точки вершин квадрата, принадлежащие одной стороне отличаются друг от друга только в одном бите. Это обстоятельство дает возможность организовать стирающий канал при КАМ-модуляции.
Пусть приемник обеспечивает линейный квадратурный прием и регистрацию сигнального созвездия в виде последовательности комплексных отсчетов сигнала в n-й момент времени на комплексной плоскости {z1, z2,…,zm} и любая точка определяется приемником как комплексное число Zn. На этой плоскости приемнику известно подмножество точек, содержащее пронумерованные комплексные числа {Ci} (i=1,2,…,2m), которые соответствуют m-ичным блокам многоуровневых сигналов и которые кодируются в образованном подмножестве кодом Грея так, чтобы соседние символы отличались друг от друга только в одном бите. При этом на комплексной плоскости при любом m > 1 можно выделить четыре соседние точки, которые образуют квадрат, как показано на рис.3.40. Если любую точку созвездия в n-й момент времени занумеровать через Ci, то соседние точки по вершинам квадрата будут иметь номер Ci,j, где j = 0;3. При j = 0 образуется номер исходной точки. Особенностью любого выделенного квадрата является то, что сложение по модулю два значений точек, лежащих на одной стороне квадрата, приводит к образованию одного неопределенного двоичного символа, что вытекает из свойств кода Грея.
При приеме текущего значения сигнала Zn приемник выполняет проверку принадлежности Zn к некоторой точке из множества {Ci}. Для этого назначается некоторый радиус R, значение которого могут зависеть от ПРВ (в конечном счете от отношения сигнал-шум).
Сигнал считается принятым верно, если координаты зафиксированной пороговым блоком точки Zn соответствуют условию │Zn-Ci│≤ R. Следовательно, если условие │Zn-Ci│≤ R выполнено приемник по двум наименьшим rij формирует сигнал со стиранием, за счет сложения конкурирующих комбинаций по модулю 2. Например, за счет сложения С3,1 и С3,2. Таким образом будет сформирована последовательность 000X. Это означает, что вместо четырех стираний XXXX в потоке данных будет сформировано одно стирание, которое может быть использовано для формирования целочисленных ИДС методом скользящих окон. Процессор приемника в таком варианте построения схемы формирования ИДС достаточно сложен, но развитие микропроцессорных технологий позволяет рассматривать подобную схему как некоторую перспективу в развитии мягких декодеров.
Принципиально значение rij могут служить дополнительной информацией для формирования метрики пути восстановление стираний, т.е. Pвос0000 > Pвос0001 > Pвос0010. Располагая указанной информацией декодер исключает процедуру полного перебора q-ичных символов, тем самым, увеличивая скорость обработки данных в декодере.
Обращаясь к рис. 3.34, можно установить разницу между схемой формирования ИДС по принципу разбиения пространства сигналов на кванты и предложенной схемой формирования градаций надежности. Основным достоинством модифицированного метода является наличие всего одного порога, в то время, как в методе разбиения на кванты необходимо оценивать рабочую точку по нескольким границам, как это показано для сигнала с КАМ на рис. 3.42.

Рис. 3.42. Принцип получения ИДС в системе КАМ-сигналов
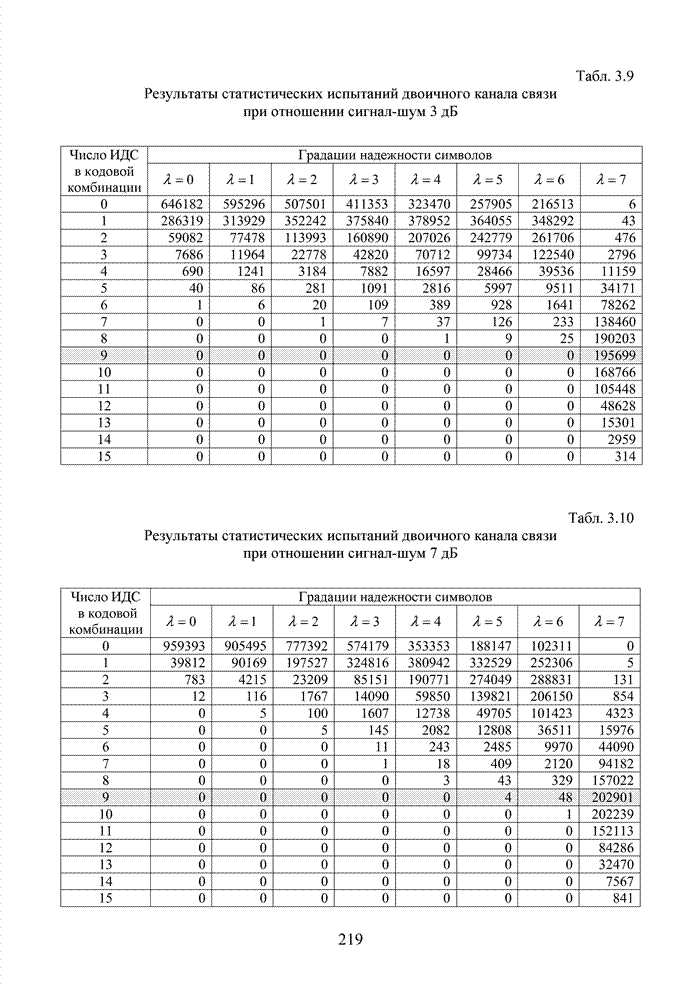
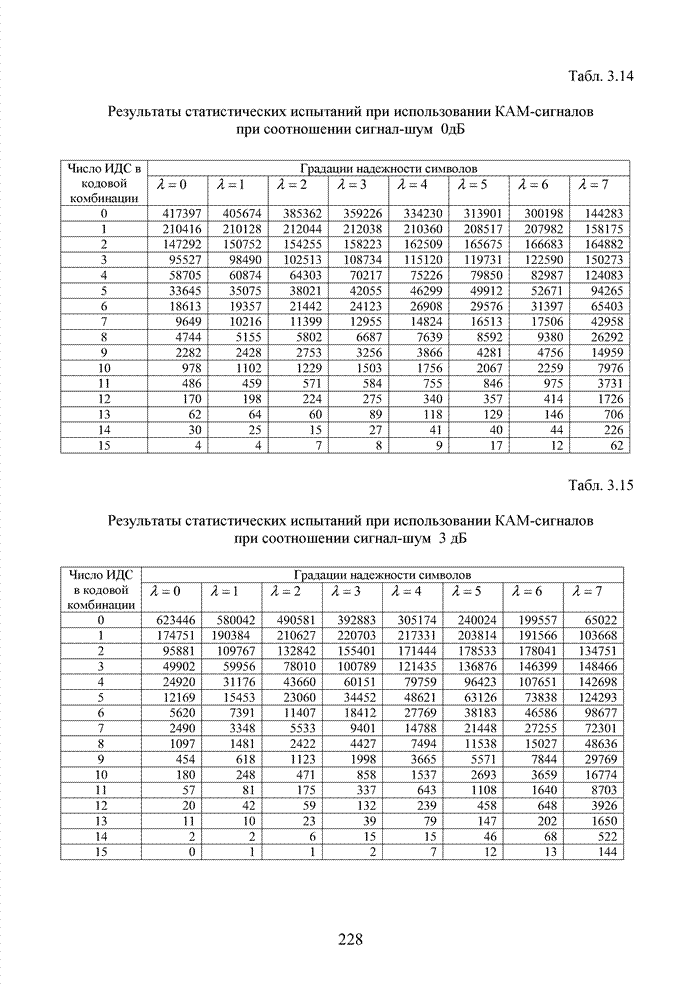
Для сравнения с ранее полученными данными (см. табл. 3.8 – 3.13) в табл. 3.14 – 3.19 приведены результаты оценки системы связи при применении КАМ-сигналов. В ходе испытаний использовался блоковый код с длиной комбинации 15 символов.
Анализ полученных результатов свидетельствует о том, при очень слабом сигнале на общей длине кодовой комбинации в различной степени формируются значения всех заданных в системе ИДС. При этом количественно оценки распределены относительно равномерно в виде убывающих последовательностей (отсутствуют явные максимумы). Подобная статистика отрицательно сказывается на последующей процедуре сортировки оценок в декодере. С ростом отношения сигнал-шум преобладание ИДС с высокими значениями увеличивается, однако, общий итог образования градаций надежности представляется не столь контрастным, как в случае кодирования линии или использования широкополосных сигналов.
Табл. 3.14 Результаты статистических испытаний при использовании КАМ-сигналов при соотношении сигнал-шум 0дБ
|
Число ИДС в кодовой комбинации |
Градации надежности символов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
417397 |
405674 |
385362 |
359226 |
334230 |
313901 |
300198 |
144283 |
|
1 |
210416 |
210128 |
212044 |
212038 |
210360 |
208517 |
207982 |
158175 |
|
2 |
147292 |
150752 |
154255 |
158223 |
162509 |
165675 |
166683 |
164882 |
|
3 |
95527 |
98490 |
102513 |
108734 |
115120 |
119731 |
122590 |
150273 |
|
4 |
58705 |
60874 |
64303 |
70217 |
75226 |
79850 |
82987 |
124083 |
|
5 |
33645 |
35075 |
38021 |
42055 |
46299 |
49912 |
52671 |
94265 |
|
6 |
18613 |
19357 |
21442 |
24123 |
26908 |
29576 |
31397 |
65403 |
|
7 |
9649 |
10216 |
11399 |
12955 |
14824 |
16513 |
17506 |
42958 |
|
8 |
4744 |
5155 |
5802 |
6687 |
7639 |
8592 |
9380 |
26292 |
|
9 |
2282 |
2428 |
2753 |
3256 |
3866 |
4281 |
4756 |
14959 |
|
10 |
978 |
1102 |
1229 |
1503 |
1756 |
2067 |
2259 |
7976 |
|
11 |
486 |
459 |
571 |
584 |
755 |
846 |
975 |
3731 |
|
12 |
170 |
198 |
224 |
275 |
340 |
357 |
414 |
1726 |
|
13 |
62 |
64 |
60 |
89 |
118 |
129 |
146 |
706 |
|
14 |
30 |
25 |
15 |
27 |
41 |
40 |
44 |
226 |
|
15 |
4 |
4 |
7 |
8 |
9 |
17 |
12 |
62 |
Табл. 3.15 Результаты статистических испытаний при использовании КАМ-сигналов при соотношении сигнал-шум 3 дБ
|
Число ИДС в кодовой комбинации |
Градации надежности символов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
623446 |
580042 |
490581 |
392883 |
305174 |
240024 |
199557 |
65022 |
|
1 |
174751 |
190384 |
210627 |
220703 |
217331 |
203814 |
191566 |
103668 |
|
2 |
95881 |
109767 |
132842 |
155401 |
171444 |
178533 |
178041 |
134751 |
|
3 |
49902 |
59956 |
78010 |
100789 |
121435 |
136876 |
146399 |
148466 |
|
4 |
24920 |
31176 |
43660 |
60151 |
79759 |
96423 |
107651 |
142698 |
|
5 |
12169 |
15453 |
23060 |
34452 |
48621 |
63126 |
73838 |
124293 |
|
6 |
5620 |
7391 |
11407 |
18412 |
27769 |
38183 |
46586 |
98677 |
|
7 |
2490 |
3348 |
5533 |
9401 |
14788 |
21448 |
27255 |
72301 |
|
8 |
1097 |
1481 |
2422 |
4427 |
7494 |
11538 |
15027 |
48636 |
|
9 |
454 |
618 |
1123 |
1998 |
3665 |
5571 |
7844 |
29769 |
|
10 |
180 |
248 |
471 |
858 |
1537 |
2693 |
3659 |
16774 |
|
11 |
57 |
81 |
175 |
337 |
643 |
1108 |
1640 |
8703 |
|
12 |
20 |
42 |
59 |
132 |
239 |
458 |
648 |
3926 |
|
13 |
11 |
10 |
23 |
39 |
79 |
147 |
202 |
1650 |
|
14 |
2 |
2 |
6 |
15 |
15 |
46 |
68 |
522 |
|
15 |
0 |
1 |
1 |
2 |
7 |
12 |
13 |
144 |
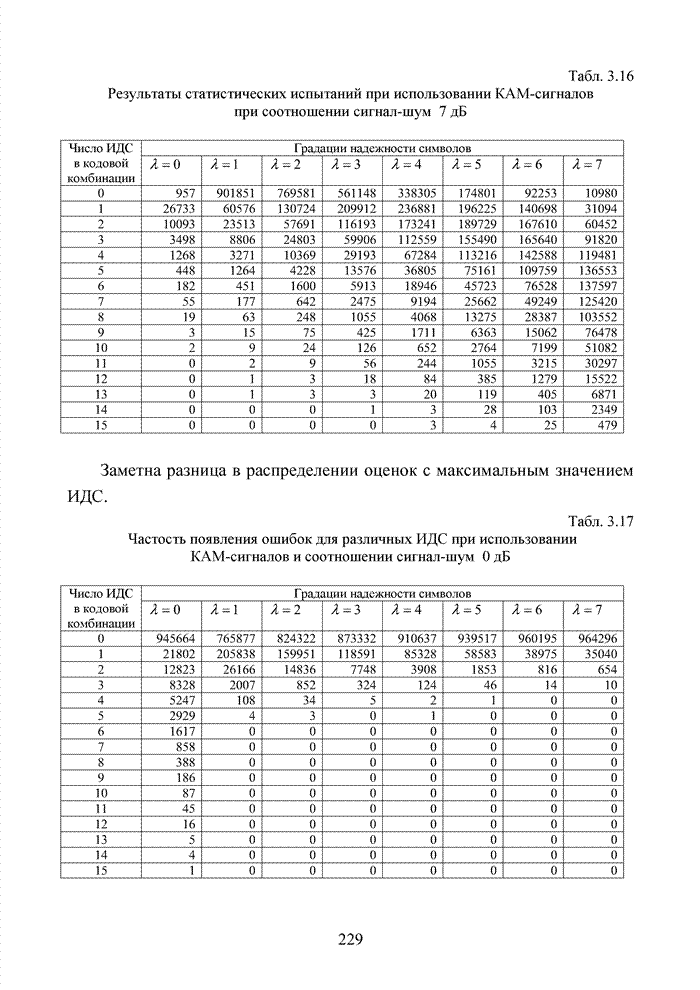
Табл. 3.16 Результаты статистических испытаний при использовании КАМ-сигналов при соотношении сигнал-шум 7 дБ
|
Число ИДС в кодовой комбинации |
Градации надежности символов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
957 |
901851 |
769581 |
561148 |
338305 |
174801 |
92253 |
10980 |
|
1 |
26733 |
60576 |
130724 |
209912 |
236881 |
196225 |
140698 |
31094 |
|
2 |
10093 |
23513 |
57691 |
116193 |
173241 |
189729 |
167610 |
60452 |
|
3 |
3498 |
8806 |
24803 |
59906 |
112559 |
155490 |
165640 |
91820 |
|
4 |
1268 |
3271 |
10369 |
29193 |
67284 |
113216 |
142588 |
119481 |
|
5 |
448 |
1264 |
4228 |
13576 |
36805 |
75161 |
109759 |
136553 |
|
6 |
182 |
451 |
1600 |
5913 |
18946 |
45723 |
76528 |
137597 |
|
7 |
55 |
177 |
642 |
2475 |
9194 |
25662 |
49249 |
125420 |
|
8 |
19 |
63 |
248 |
1055 |
4068 |
13275 |
28387 |
103552 |
|
9 |
3 |
15 |
75 |
425 |
1711 |
6363 |
15062 |
76478 |
|
10 |
2 |
9 |
24 |
126 |
652 |
2764 |
7199 |
51082 |
|
11 |
0 |
2 |
9 |
56 |
244 |
1055 |
3215 |
30297 |
|
12 |
0 |
1 |
3 |
18 |
84 |
385 |
1279 |
15522 |
|
13 |
0 |
1 |
3 |
3 |
20 |
119 |
405 |
6871 |
|
14 |
0 |
0 |
0 |
1 |
3 |
28 |
103 |
2349 |
|
15 |
0 |
0 |
0 |
0 |
3 |
4 |
25 |
479 |
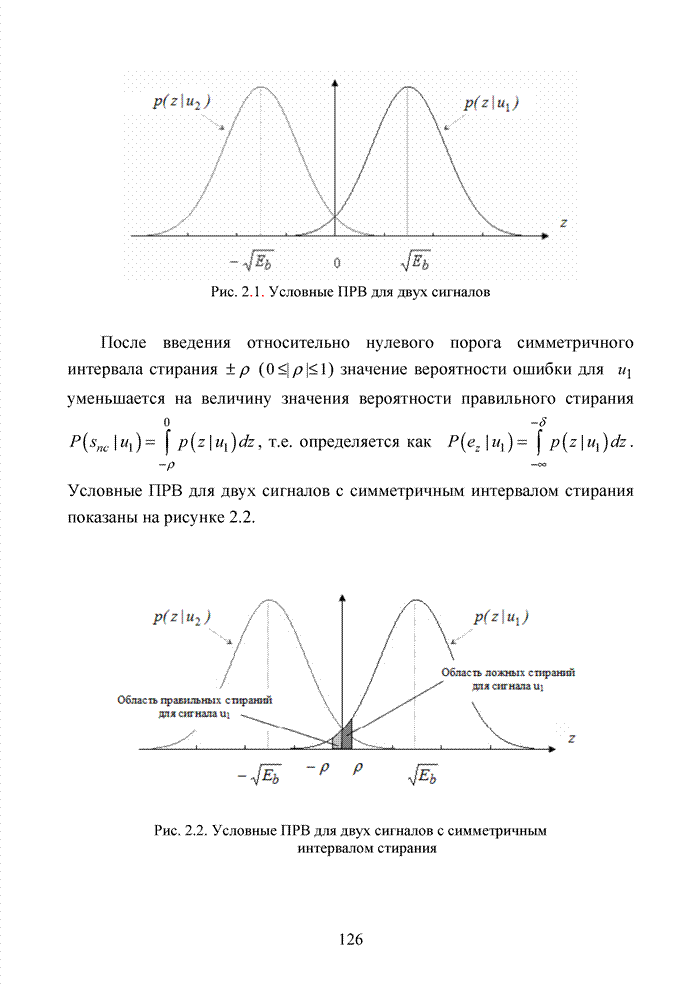
Заметна разница в распределении оценок с максимальным значением ИДС.
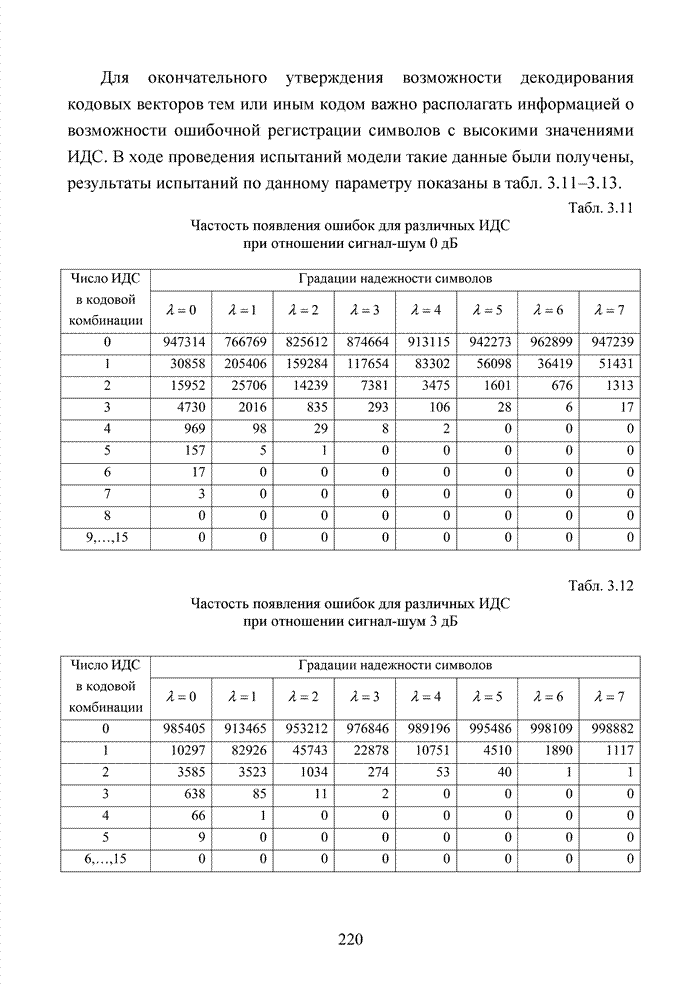
Табл. 3.17 Частость появления ошибок для различных ИДС при использовании КАМ-сигналов и соотношении сигнал-шум 0 дБ
|
Число ИДС в кодовой комбинации |
Градации надежности символов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
945664 |
765877 |
824322 |
873332 |
910637 |
939517 |
960195 |
964296 |
|
1 |
21802 |
205838 |
159951 |
118591 |
85328 |
58583 |
38975 |
35040 |
|
2 |
12823 |
26166 |
14836 |
7748 |
3908 |
1853 |
816 |
654 |
|
3 |
8328 |
2007 |
852 |
324 |
124 |
46 |
14 |
10 |
|
4 |
5247 |
108 |
34 |
5 |
2 |
1 |
0 |
0 |
|
5 |
2929 |
4 |
3 |
0 |
1 |
0 |
0 |
0 |
|
6 |
1617 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
858 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
388 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
186 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
87 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
11 |
45 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
12 |
16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
13 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
14 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
15 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
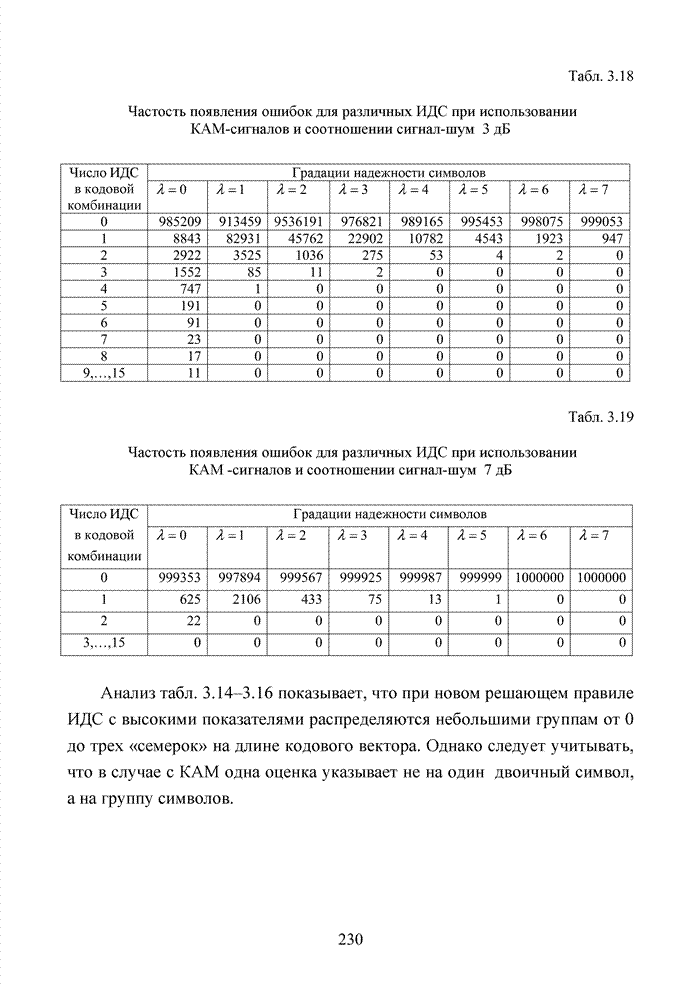
Табл. 3.18 Частость появления ошибок для различных ИДС при использовании КАМ-сигналов и соотношении сигнал-шум 3 дБ
|
Число ИДС в кодовой комбинации |
Градации надежности символов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
985209 |
913459 |
9536191 |
976821 |
989165 |
995453 |
998075 |
999053 |
|
1 |
8843 |
82931 |
45762 |
22902 |
10782 |
4543 |
1923 |
947 |
|
2 |
2922 |
3525 |
1036 |
275 |
53 |
4 |
2 |
0 |
|
3 |
1552 |
85 |
11 |
2 |
0 |
0 |
0 |
0 |
|
4 |
747 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
191 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
91 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
23 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9,…,15 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
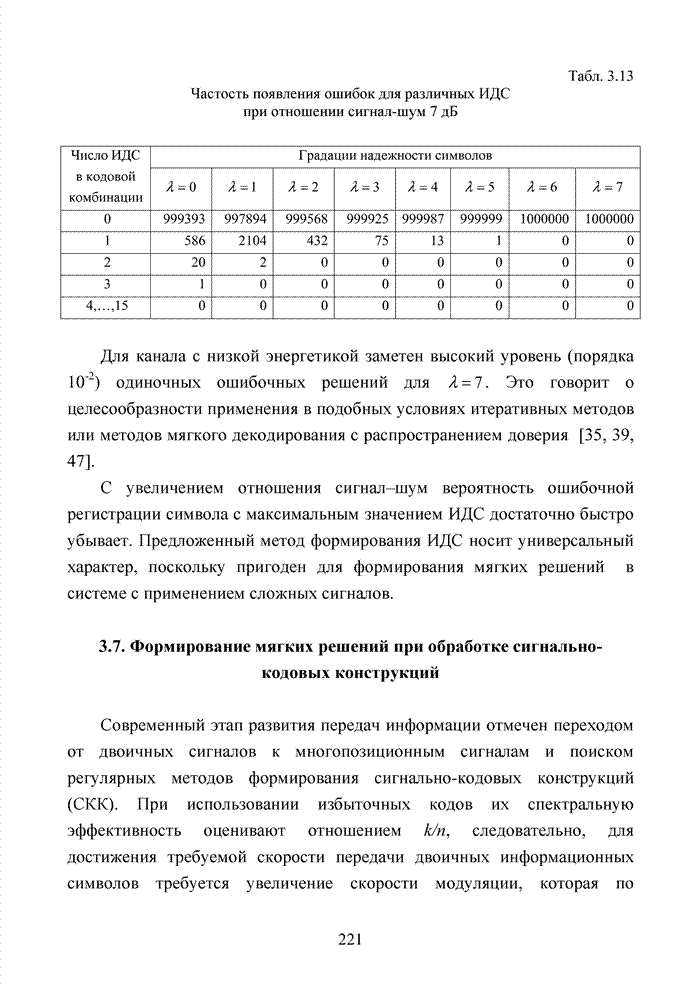
Табл. 3.19 Частость появления ошибок для различных ИДС при использовании КАМ -сигналов и соотношении сигнал-шум 7 дБ
|
Число ИДС в кодовой комбинации |
Градации надежности символов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
999353 |
997894 |
999567 |
999925 |
999987 |
999999 |
1000000 |
1000000 |
|
1 |
625 |
2106 |
433 |
75 |
13 |
1 |
0 |
0 |
|
2 |
22 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3,…,15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
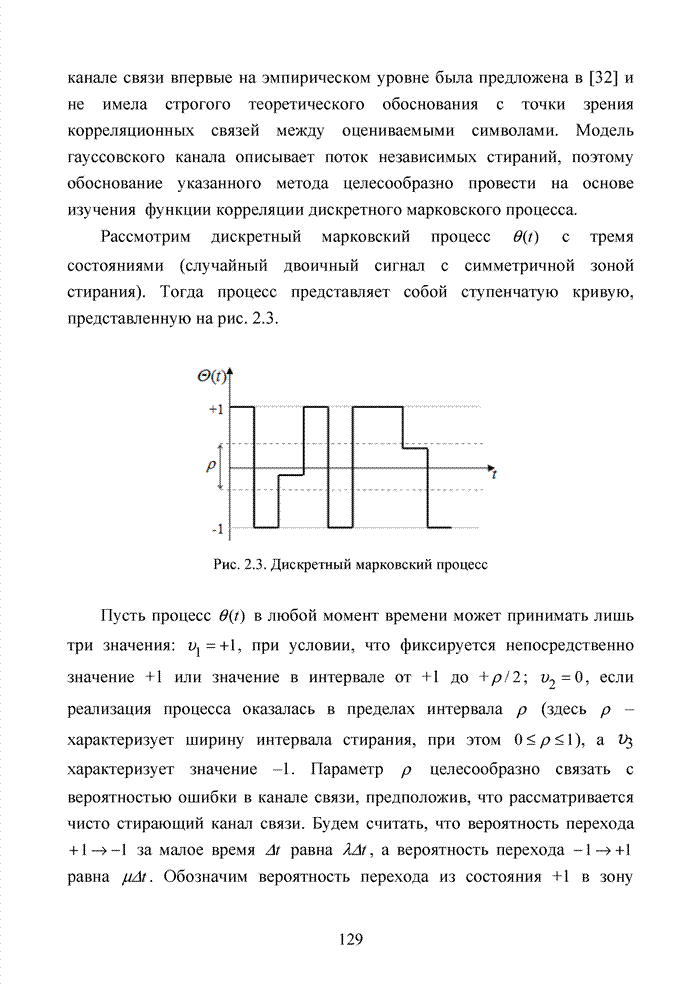
Анализ табл. 3.14–3.16 показывает, что при новом решающем правиле ИДС с высокими показателями распределяются небольшими группам от 0 до трех «семерок» на длине кодового вектора. Однако следует учитывать, что в случае с КАМ одна оценка указывает не на один двоичный символ, а на группу символов.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
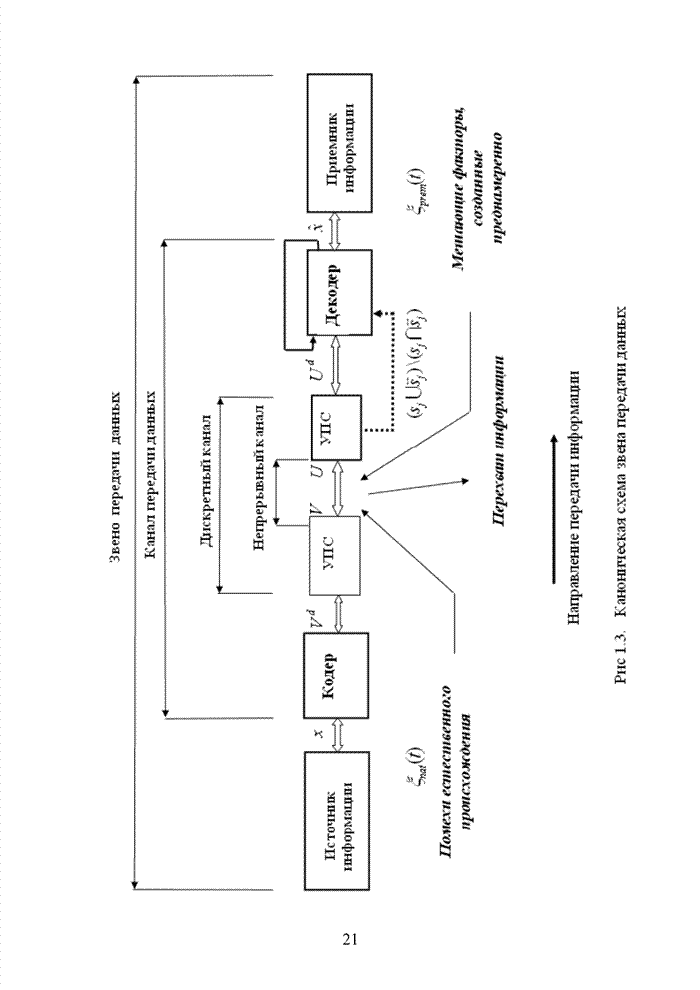
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
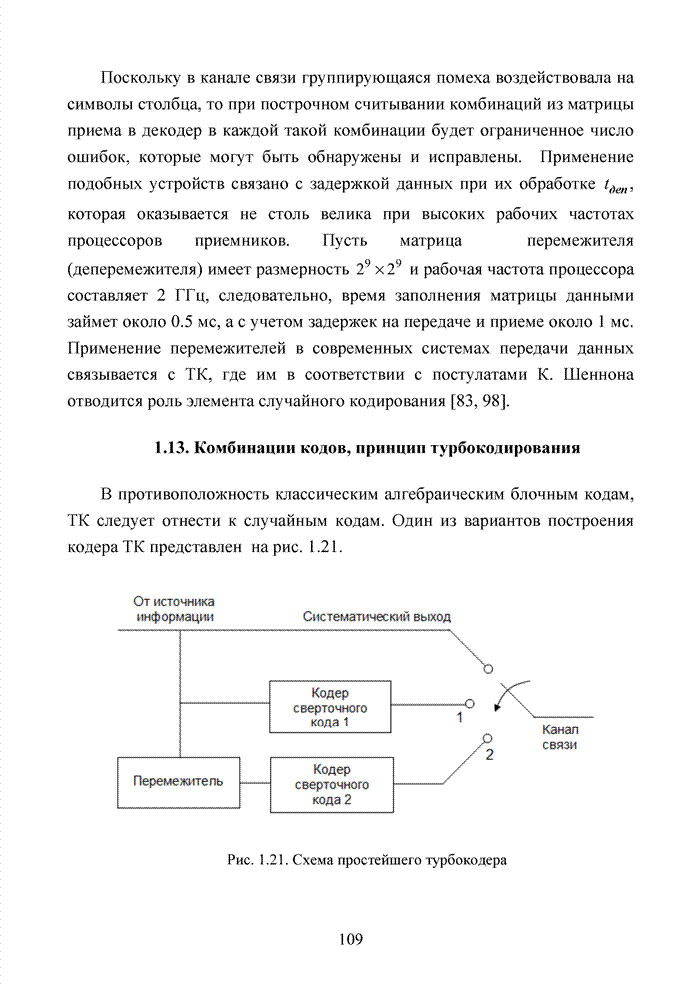
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
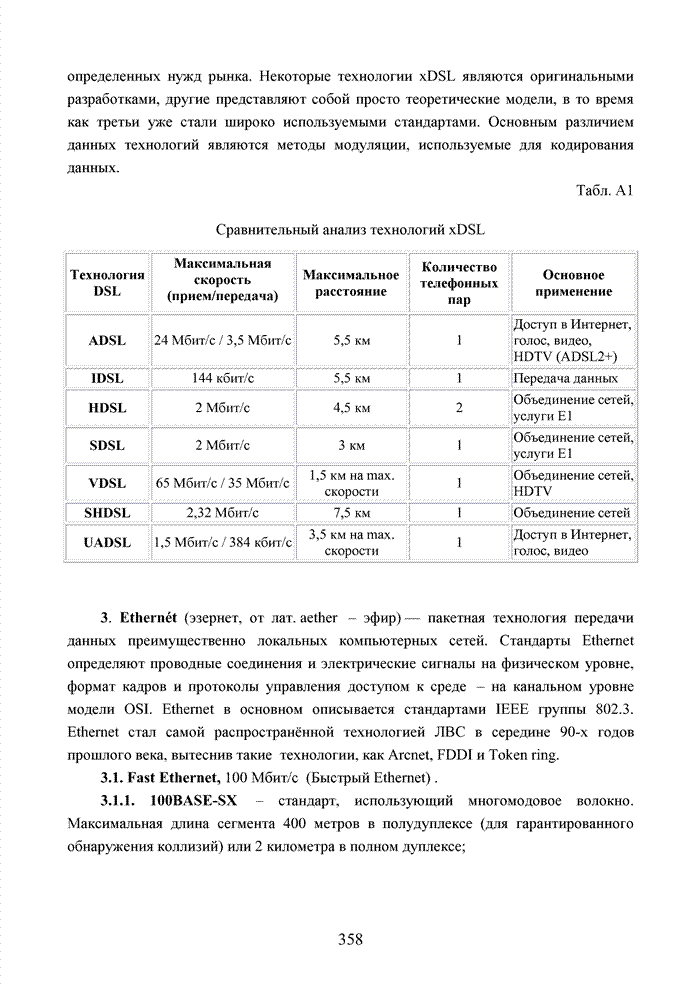
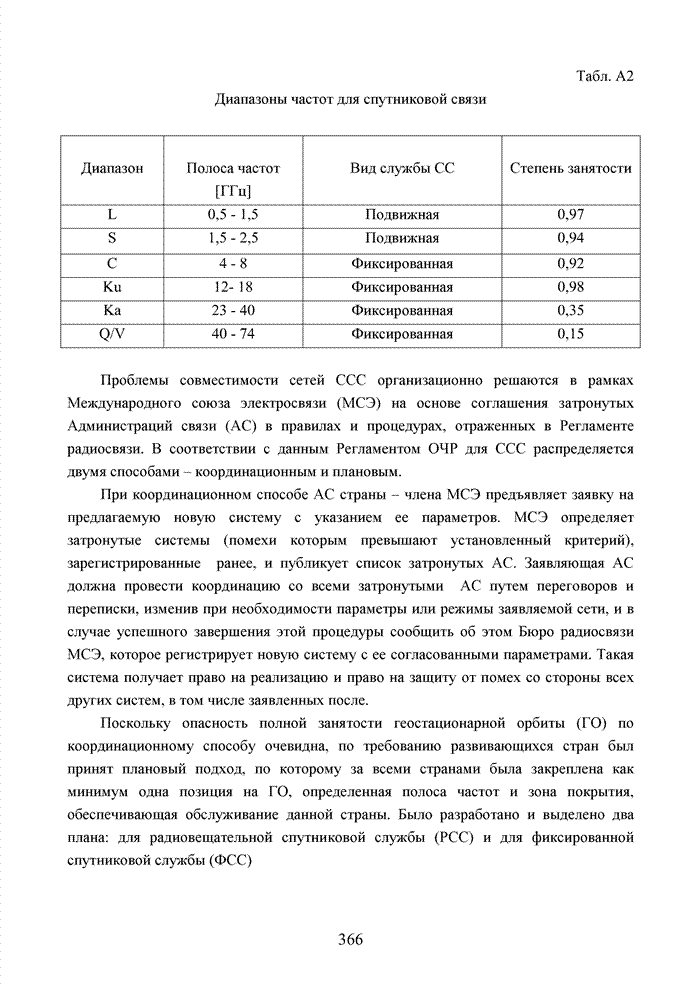
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
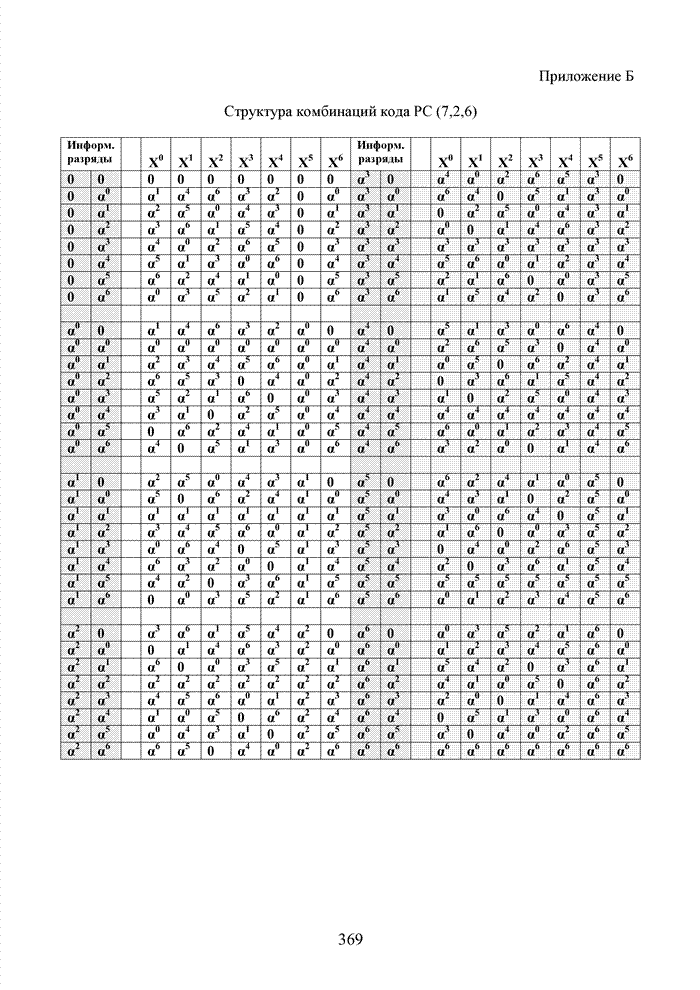
- Приложение Б Структура комбинаций кода РС (7,2,6)
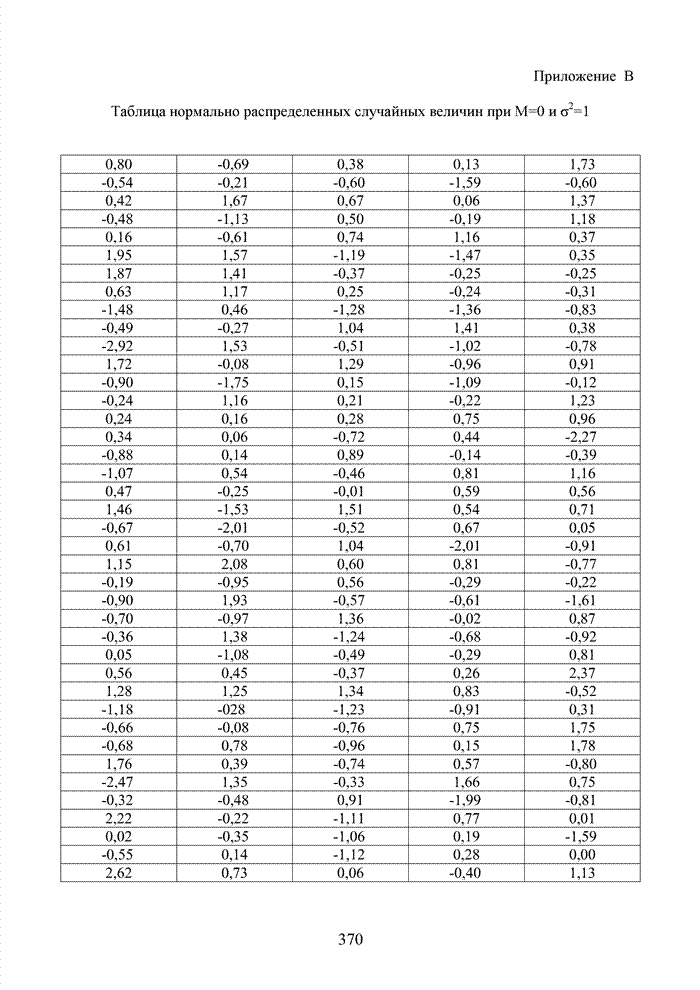
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК