| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.6. Декодирование на основе упорядоченной статистики
Исправление определенной части ошибок за пределами метрики Хэмминга возможно не только при использовании метода кластерного анализа. Одним из таких способов является декодирование на основе упорядоченной статистки.
Использование
упорядоченной статистики при декодировании блоковых кодов позволяет повысить
кратность исправляемых стираний до значения ![]() , где
, где ![]() – общая длина кодовой комбинации, а
– общая длина кодовой комбинации, а ![]() – число информационных разрядов. Докажем,
что повышение кратности исправляемых стираний не является экзотической задачей,
а реализуется за счет использования в системе эквивалентных кодов и разделения
символов кодовой комбинации на две группы за счет использования ИДС, при этом в
первую группу собираются наиболее надежные символы, тогда как ко второй группе
относятся наименее надежные символы. В обеих группах символы ранжируются по
убыванию значений ИДС.
– число информационных разрядов. Докажем,
что повышение кратности исправляемых стираний не является экзотической задачей,
а реализуется за счет использования в системе эквивалентных кодов и разделения
символов кодовой комбинации на две группы за счет использования ИДС, при этом в
первую группу собираются наиболее надежные символы, тогда как ко второй группе
относятся наименее надежные символы. В обеих группах символы ранжируются по
убыванию значений ИДС.
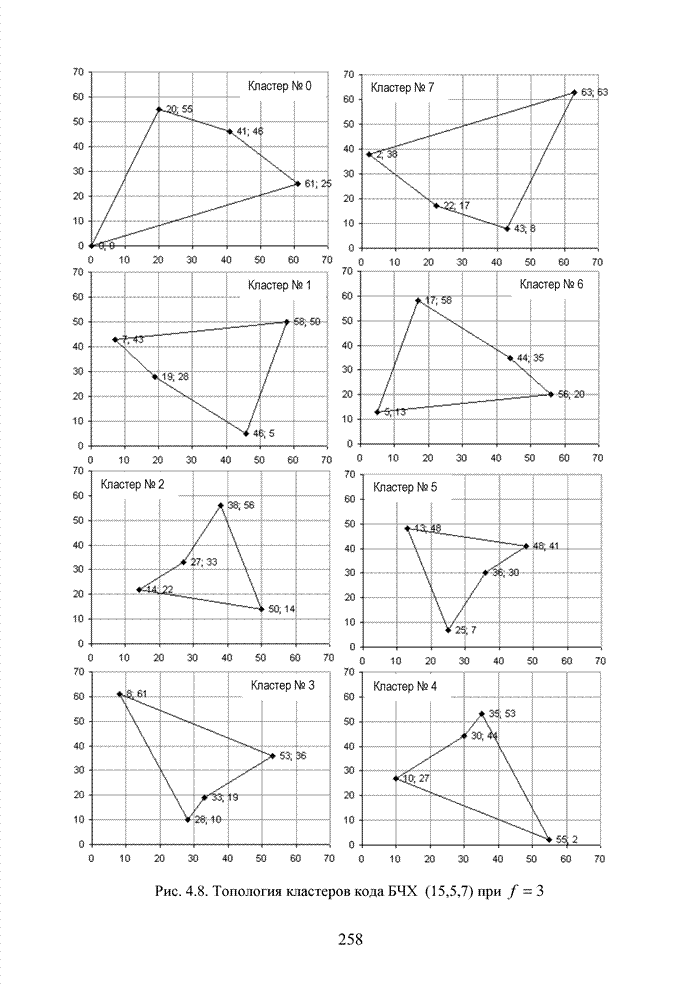
Алгоритм работы такого декодера (назовем его основным) рассмотрим на примере кода БЧХ (15;5;7). Порождающая матрица кода в систематической форме приведена в (4.5) и будет представлена здесь для удобства
 .
.
Пусть от источника информации на вход кодера поступает вектор вида 1 1 0 1 0 .
В результате умножения вектора на порождающую матрицу на выходе кодера формируется последовательность:
![]() 1 1 0 1 0 1 1 0 0 1 0 0
0 1 1.
1 1 0 1 0 1 1 0 0 1 0 0
0 1 1.
После передачи этой последовательности по каналу связи принимается вектор, в котором в соответствии с вероятностью ошибки на бит, характерной данному каналу связи, возможно появление ошибок. Пусть образец ошибок имеет вид
![]() .
.
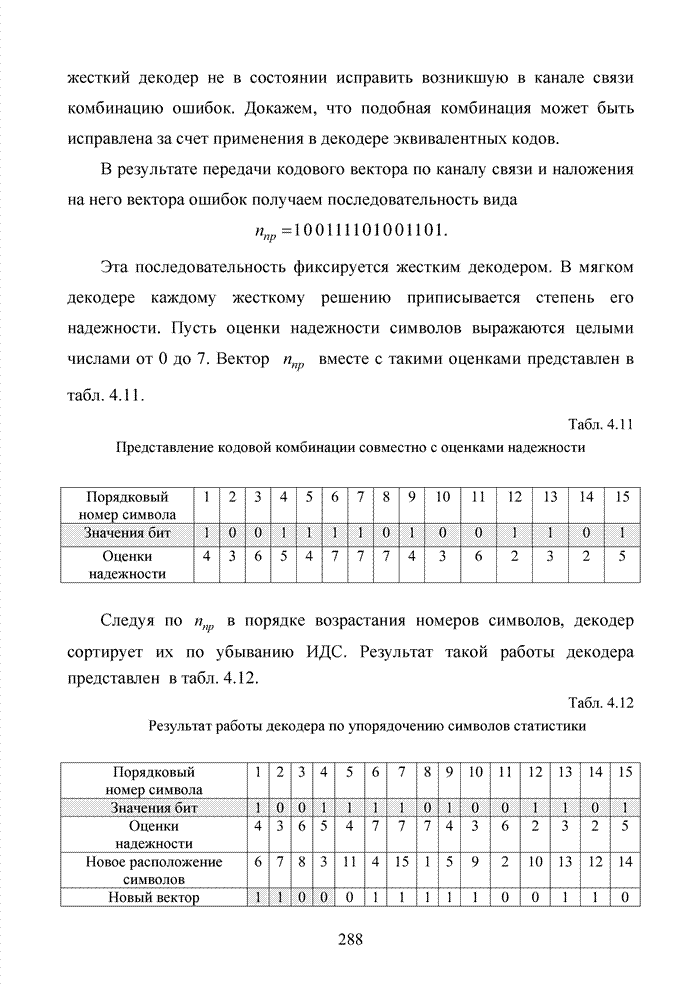
Заметно, что представленный объем ошибочных символов превосходит исправляющую способность кода по восстановлению не только ошибочно принятых символов, но и стираний. Естественно, что жесткий декодер не в состоянии исправить возникшую в канале связи комбинацию ошибок. Докажем, что подобная комбинация может быть исправлена за счет применения в декодере эквивалентных кодов.
В результате передачи кодового вектора по каналу связи и наложения на него вектора ошибок получаем последовательность вида
![]() .
.
Эта последовательность
фиксируется жестким декодером. В мягком декодере каждому жесткому решению
приписывается степень его надежности. Пусть оценки надежности символов
выражаются целыми числами от 0 до 7. Вектор![]()
![]() вместе с такими оценками представлен в
табл. 4.11.
вместе с такими оценками представлен в
табл. 4.11.
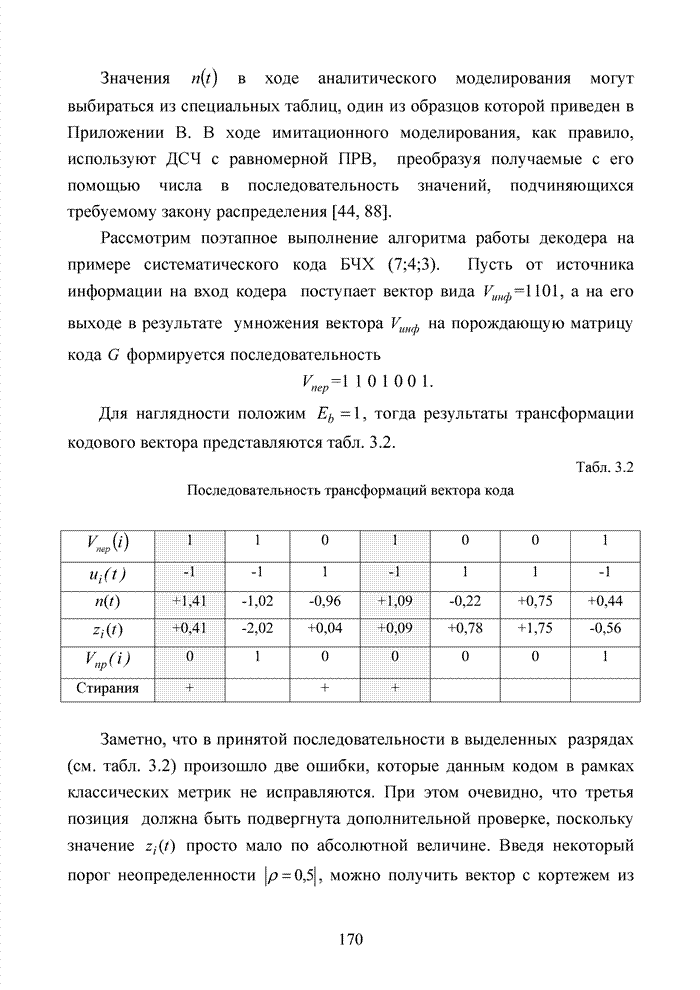
Табл. 4.11 Представление кодовой комбинации совместно с оценками надежности
|
Порядковый номер символа |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Значения бит |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
Оценки надежности |
4 |
3 |
6 |
5 |
4 |
7 |
7 |
7 |
4 |
3 |
6 |
2 |
3 |
2 |
5 |
Следуя по ![]() в порядке возрастания
номеров символов, декодер сортирует их по убыванию ИДС. Результат такой работы
декодера представлен в табл. 4.12.
в порядке возрастания
номеров символов, декодер сортирует их по убыванию ИДС. Результат такой работы
декодера представлен в табл. 4.12.
Табл. 4.12 Результат работы декодера по упорядочению символов статистики
|
Порядковый номер символа |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Значения бит |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
Оценки надежности |
4 |
3 |
6 |
5 |
4 |
7 |
7 |
7 |
4 |
3 |
6 |
2 |
3 |
2 |
5 |
|
Новое расположение символов |
6 |
7 |
8 |
3 |
11 |
4 |
15 |
1 |
5 |
9 |
2 |
10 |
13 |
12 |
14 |
|
Новый вектор |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
Заметно, что на первых ![]() позициях оказались
наиболее надежные символы, значения которых в последующем будут использованы
для создания эквивалентного кода.
позициях оказались
наиболее надежные символы, значения которых в последующем будут использованы
для создания эквивалентного кода.
Для создания подобного
кода необходимо найти его порождающую матрицу. Для этого, используя матрицу
перехода, выполним умножение истинной порождающей матрицы ![]() на матрицу перехода
на матрицу перехода ![]() , которая формируется в
соответствии с табл. 4.12 и для данной конфигурации ИДС имеет вид
, которая формируется в
соответствии с табл. 4.12 и для данной конфигурации ИДС имеет вид

Выполняя ![]() , получим новую
матрицу
, получим новую
матрицу ![]() размерности
размерности![]()
![]()
![]()
 .
.
В этой матрице может быть утрачено свойство линейной независимости строк, которое обязательно для образования эквивалентного кода.
Для проверки линейной
независимости строк в матрице ![]() декодер выделяет квадратную матрицу
размерности
декодер выделяет квадратную матрицу
размерности ![]() и
вычисляет ее детерминант. Признаком линейной зависимости строк является
равенство детерминанта квадратной матрицы нулю. При отсутствии подобного
условия признак линейной независимости строк сохраняется. В случае линейной
зависимости строк необходимо поменять местами столбцы с номерами
и
вычисляет ее детерминант. Признаком линейной зависимости строк является
равенство детерминанта квадратной матрицы нулю. При отсутствии подобного
условия признак линейной независимости строк сохраняется. В случае линейной
зависимости строк необходимо поменять местами столбцы с номерами ![]() и
и ![]() в
в ![]() .
.
Принципиально эта
процедура легко программируется для процессора приемника, однако объем
вычислений существенно увеличивается с ростом ![]() . В приведенном примере матрица
. В приведенном примере матрица ![]() из
из ![]() имеет вид
имеет вид
 .
.
Поскольку ![]() , то полученную на
предыдущем шаге алгоритма матрицу
, то полученную на
предыдущем шаге алгоритма матрицу ![]() возможно привести к систематической форме
и на этой основе получить порождающую матрицу
возможно привести к систематической форме
и на этой основе получить порождающую матрицу ![]() эквивалентного кода в систематической
форме.
эквивалентного кода в систематической
форме.
Вычисление детерминанта
квадратной матрицы является достаточно емкой процедурой с точки зрения объема
вычислений. Оценим максимальное число операций, необходимых для определения
детерминанта квадратных матриц заданной размерности и полученные для различных значений
![]() результаты
сведем в табл. 4.13.
результаты
сведем в табл. 4.13.
Первоначально рассмотрим
матрицу размерности ![]() .
Число операций, необходимых для вычисления определителя подобной матрицы
составляет: две операции умножения и одна операция вычитания (обратное действие
операции сложения).
.
Число операций, необходимых для вычисления определителя подобной матрицы
составляет: две операции умножения и одна операция вычитания (обратное действие
операции сложения).
 .
.
Современные процессоры тратят на операцию сложения до 2 нс, а на операцию умножения – до 180 нс. в декодере осуществляется умножение единиц и нулей, будем считать, с некоторой долей условности, что на операцию умножения операндов будет тратиться тоже 2 нс. Таким образом, на вычисление указанного определителя будет потрачено порядка 6 нс. Исходя из этих условий, в табл. 4.13 представлены данные оценки временных затрат при вычислении определителей других размерностей.
Табл. 4.13 Временные интервалы для оценки определителей
|
Размерность
матрицы |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из табл. 4.13 следует, что незначительное увеличение размерности квадратной матрицы приводит к существенному увеличению времени вычисления определителя.
Получив
удовлетворительный результат по вычислению ![]() , декодер должен выполнить регулярную
процедуру по вычислению матрицы
, декодер должен выполнить регулярную
процедуру по вычислению матрицы ![]() . Известно, что произведение матрицы
. Известно, что произведение матрицы ![]() на ее обратное
отображение
на ее обратное
отображение ![]() обеспечивает
получение единичной матрицы
обеспечивает
получение единичной матрицы ![]() . Выполнив действие
. Выполнив действие ![]() , декодер вычисляет обратную
матрицу, которая точно указывает на порядок сложения строк матрицы
, декодер вычисляет обратную
матрицу, которая точно указывает на порядок сложения строк матрицы ![]() для получения новой
порождающей матрицы в систематической форме
для получения новой
порождающей матрицы в систематической форме![]() .
.
 .
.
Поскольку все действия
декодер выполняет в двоичном поле, то в обратной матрице ![]() четные показатели строк
(столбцов) необходимо заменить на нули. Таким образом, в рассматриваемом
примере, для получения матрицы в систематической форме, необходимо четвертую
строку из матрицы
четные показатели строк
(столбцов) необходимо заменить на нули. Таким образом, в рассматриваемом
примере, для получения матрицы в систематической форме, необходимо четвертую
строку из матрицы ![]() взять
как первую строку новой матирцы. Для получения второй строки необходимо сложить
первую и вторую строку матрицы
взять
как первую строку новой матирцы. Для получения второй строки необходимо сложить
первую и вторую строку матрицы ![]() . Для получения третьей строки необходимо
сложить вторую, четвертую и пятую строки указанной матрицы. Аналогично,
для получения четвертой строки с учетом свойств двоичного поля, требуется
сложить все строки матрицы, исключив вторую строку. Для пятой строки требуется
комбинация первой, второй и пятой строки матрицы
. Для получения третьей строки необходимо
сложить вторую, четвертую и пятую строки указанной матрицы. Аналогично,
для получения четвертой строки с учетом свойств двоичного поля, требуется
сложить все строки матрицы, исключив вторую строку. Для пятой строки требуется
комбинация первой, второй и пятой строки матрицы ![]() . Изложенная схема является математической
основой для реализации процедуры получения эквивалентного кода.
. Изложенная схема является математической
основой для реализации процедуры получения эквивалентного кода.
Исследования показали,
что в обратной матрице ![]() могут появиться значения, равные,
например,
могут появиться значения, равные,
например, ![]() ,
тогда в соответствии с концепцией выполнения арифметических действий в поле
,
тогда в соответствии с концепцией выполнения арифметических действий в поле ![]() , соответствующая позиция
строки порождающей матрицы
, соответствующая позиция
строки порождающей матрицы ![]() считается активной. В результате
преобразований получим порождающую матрицу эквивалентного кода, которая после
выполнения указанных преобразований принимает вид
считается активной. В результате
преобразований получим порождающую матрицу эквивалентного кода, которая после
выполнения указанных преобразований принимает вид
 .
.
После это шага декодер из
табл. 4.12 извлекает часть «нового вектора» 1 1 0 0 0 (первые пять позиций) и
кодирует ее с использованием порождающей матрицы ![]() . Учитывая, что на месте
информационных разрядов, после указанных преобразований, находятся наиболее
надежные символы, декодер формирует вектора эквивалентного кода, который
фиксируется как некоторая разрешенная последовательность, не содержащая ошибок.
. Учитывая, что на месте
информационных разрядов, после указанных преобразований, находятся наиболее
надежные символы, декодер формирует вектора эквивалентного кода, который
фиксируется как некоторая разрешенная последовательность, не содержащая ошибок.
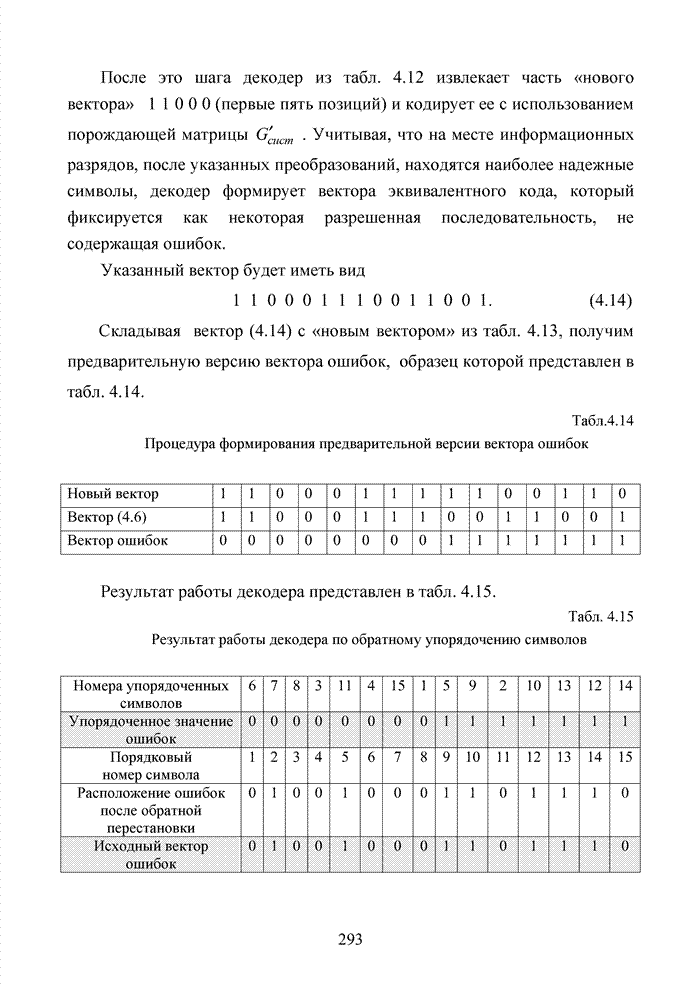
Указанный вектор будет иметь вид
1 1 0 0 0 1 1 1 0 0 1 1 0 0 1. (4.14)
Складывая вектор (4.14) с «новым вектором» из табл. 4.13, получим предварительную версию вектора ошибок, образец которой представлен в табл. 4.14.
Табл.4.14 Процедура формирования предварительной версии вектора ошибок
|
Новый вектор |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
Вектор (4.6) |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
Вектор ошибок |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
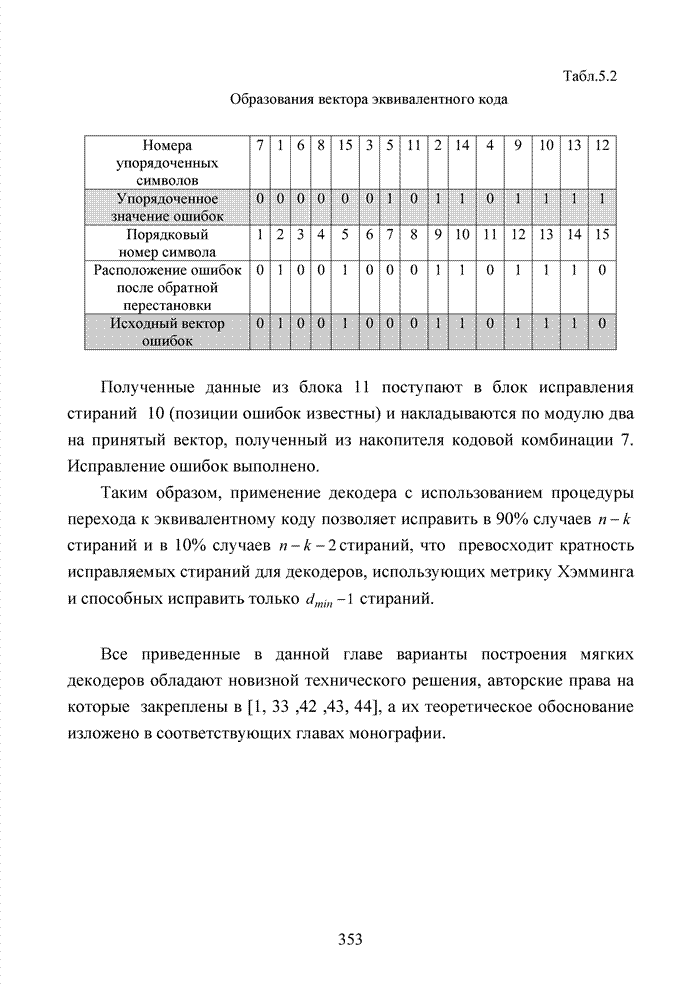
Результат работы декодера представлен в табл. 4.15.
Табл. 4.15 Результат работы декодера по обратному упорядочению символов
|
Номера упорядоченных символов |
6 |
7 |
8 |
3 |
11 |
4 |
15 |
1 |
5 |
9 |
2 |
10 |
13 |
12 |
14 |
|
Упорядоченное значение ошибок |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Порядковый номер символа |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Расположение ошибок после обратной перестановки |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
Исходный вектор ошибок |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
В таком представлении
вектор ошибок не соответствует комбинации ошибок, действовавшей в канале связи
в момент передачи кодового вектора ![]() . Для получения истинной комбинации ошибок
необходимо данный вектор умножить на транспонированную перестановочную матрицу
. Для получения истинной комбинации ошибок
необходимо данный вектор умножить на транспонированную перестановочную матрицу ![]() . Заметно, что после
обратной перестановки символов вектора ошибок полученное расположение ошибок
полностью соответствует исходному вектору ошибок.
. Заметно, что после
обратной перестановки символов вектора ошибок полученное расположение ошибок
полностью соответствует исходному вектору ошибок.
Анализ полученного
алгоритма показывает, что эквивалентный код в ряде случаев не может быть
получен сразу после выполнения перестановок, т.к. проверка на нелинейность
столбцов порождающей матрицы эквивалентного кода не всегда заканчивается
успешно. Это связано с тем, что после перестановки возможны ситуации, когда в
одной строке или столбце окажутся только нули или только единицы. В этом случае
декодер «занимает» подходящий столбец из ближайших столбцов, превосходящих
значения ![]() .
Эта операция приводит к замене надежного символа из
.
Эта операция приводит к замене надежного символа из ![]() отобранных первоначально на
менее надежный символ, который может оказаться пораженным ошибкой. В предельном
случае в матрице
отобранных первоначально на
менее надежный символ, который может оказаться пораженным ошибкой. В предельном
случае в матрице ![]() может
оказаться до двух столбцов (строк), которые нарушают свойства нелинейности.
Процедура перестановки столбцов после сортировки столбцов несколько снижает
значения асимптотической оценки. Целесообразно оценить отрицательное влияние
линейно зависимых комбинаций на эффективность рассматриваемого алгоритма.
может
оказаться до двух столбцов (строк), которые нарушают свойства нелинейности.
Процедура перестановки столбцов после сортировки столбцов несколько снижает
значения асимптотической оценки. Целесообразно оценить отрицательное влияние
линейно зависимых комбинаций на эффективность рассматриваемого алгоритма.
Пусть известна весовая
структура кода (как правило, для коротких кодов весовой спектр кода известен).
Код БЧХ (15,5,7) имеет кроме чисто нулевого и чисто единичного вектора по 15
векторов веса 7 и 8. Обозначим представители указанных значений, как ![]() и
и ![]() .
.
Оценим появление чисто
единичной строки и чисто нулевой строки в матрице размерности ![]() при упорядочивании
статистики. Очевидно, для первой строки число возможных вариантов сочетаний
нулей определяется выражением
при упорядочивании
статистики. Очевидно, для первой строки число возможных вариантов сочетаний
нулей определяется выражением ![]() , а для единиц – выражением
, а для единиц – выражением ![]() . Всего нежелательных
вариантов для первой строки оказывается 77. Обозначим число нежелательных
вариантов для первой строки порождающей матрицы через
. Всего нежелательных
вариантов для первой строки оказывается 77. Обозначим число нежелательных
вариантов для первой строки порождающей матрицы через ![]() . Тогда в общем случае число
таких вариантов оценивается выражением
. Тогда в общем случае число
таких вариантов оценивается выражением
 ,
,
при ![]() = 7; 8.
= 7; 8.
Для кода БЧХ (15,5,7) ![]() = 385 при общем числе
вариантов
= 385 при общем числе
вариантов ![]() ,
что составляет 12,8 %. Следовательно, повторный поиск нелинейного соотношения
строк порождающей матрицы не приводит к существенному снижению показателей
эффективности разработанного алгоритма. С увеличением
,
что составляет 12,8 %. Следовательно, повторный поиск нелинейного соотношения
строк порождающей матрицы не приводит к существенному снижению показателей
эффективности разработанного алгоритма. С увеличением ![]() это влияние уменьшается.
это влияние уменьшается.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
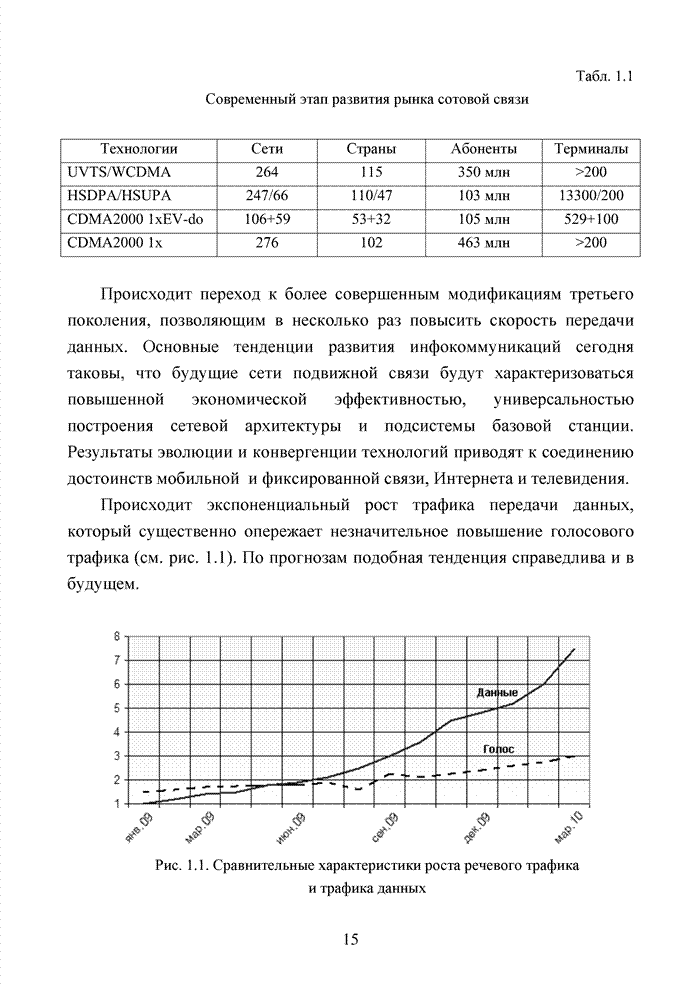
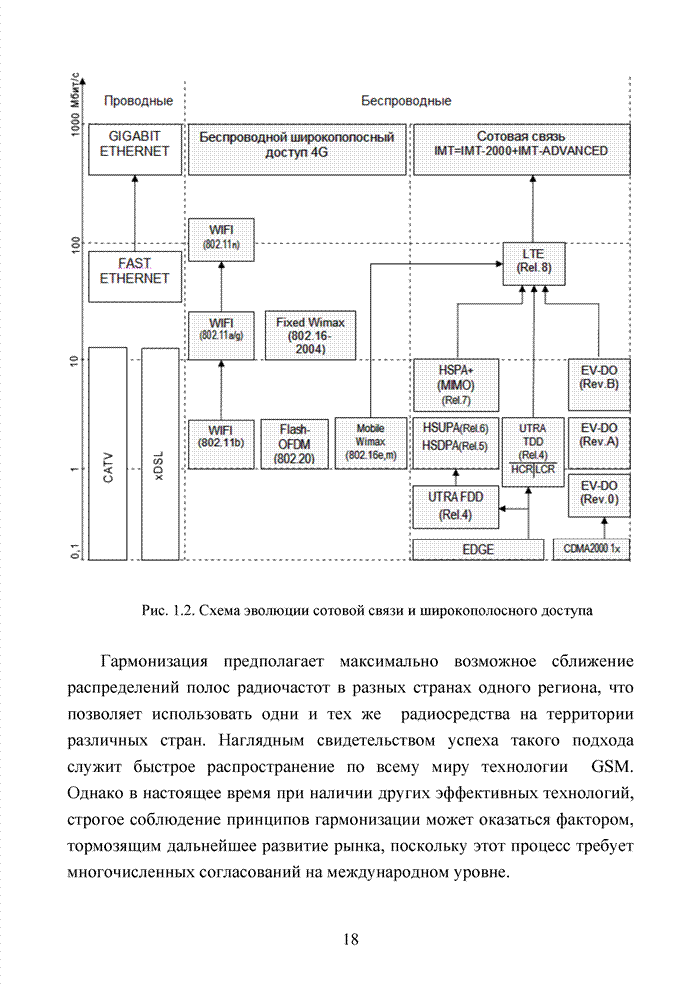
- 1.1. Инфокоммуникационные технологии нового поколения
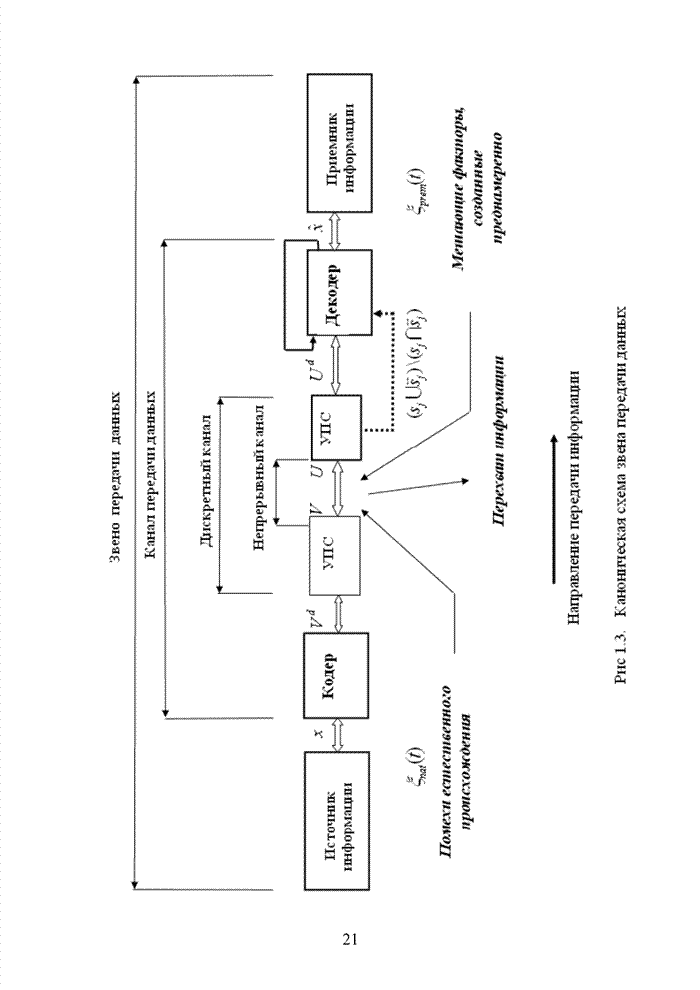
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
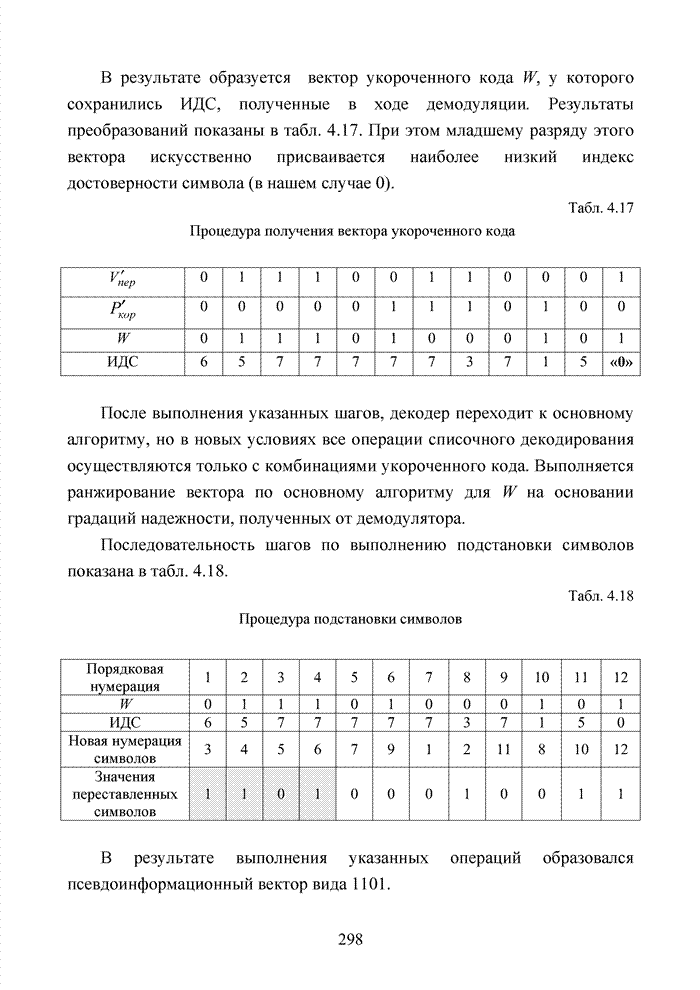
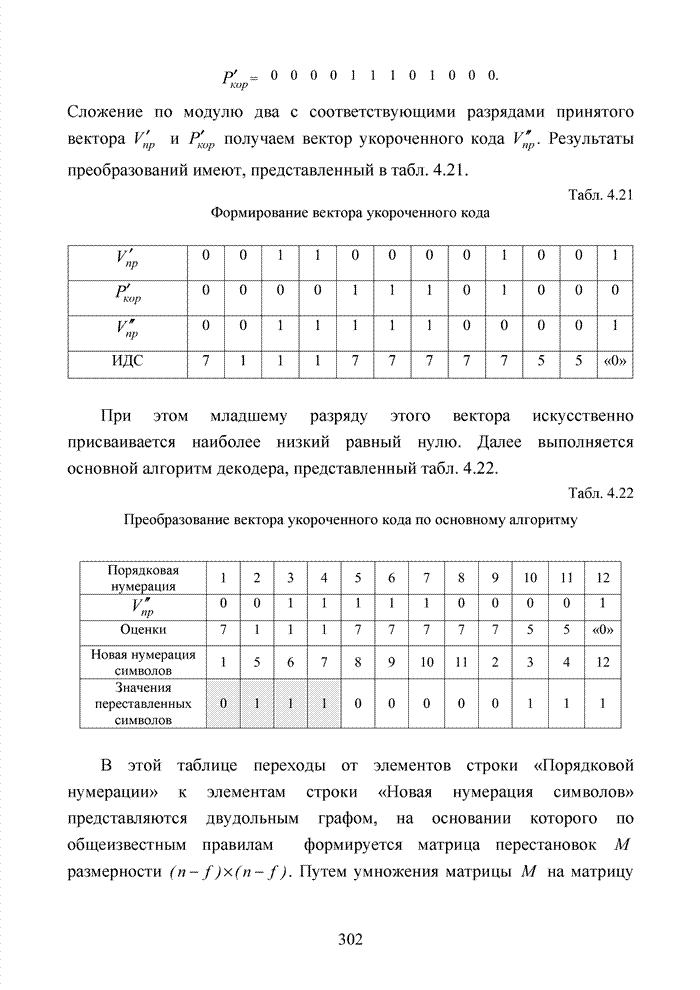
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
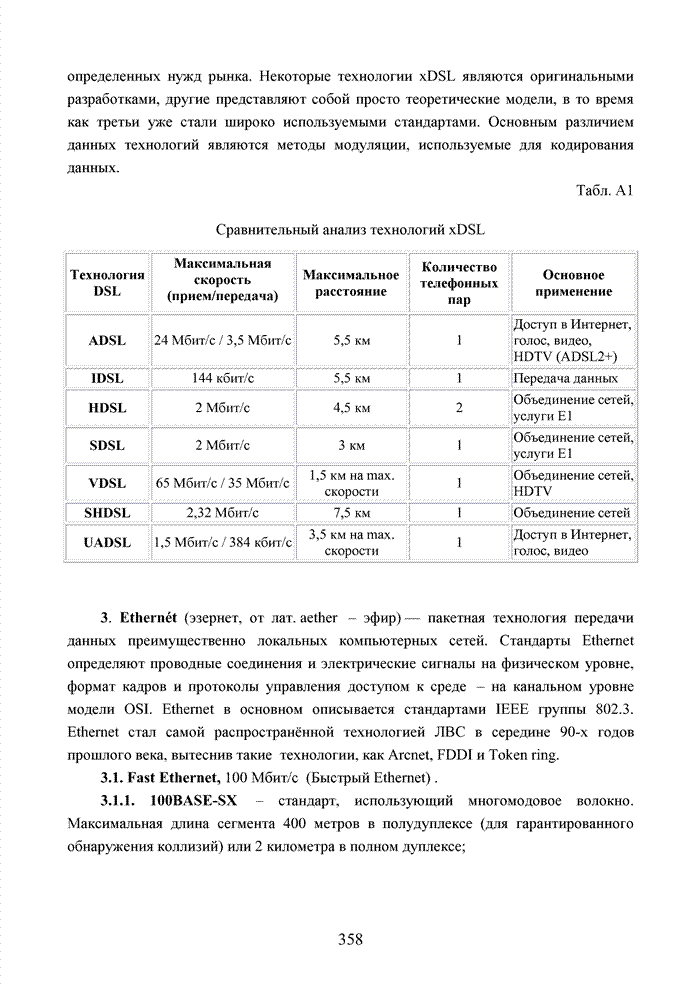
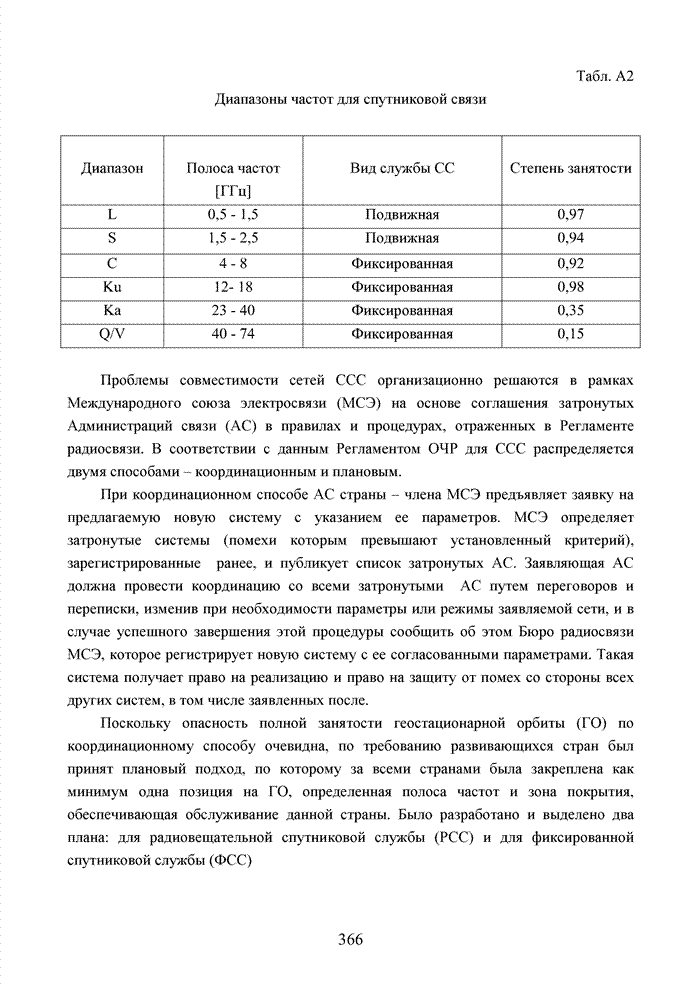
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
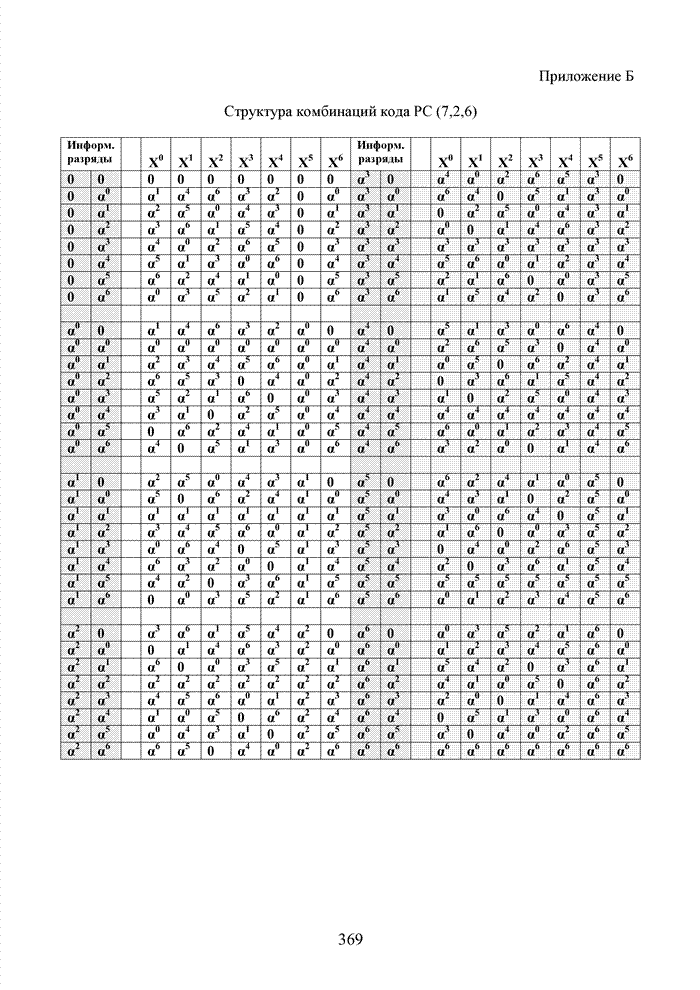
- Приложение Б Структура комбинаций кода РС (7,2,6)
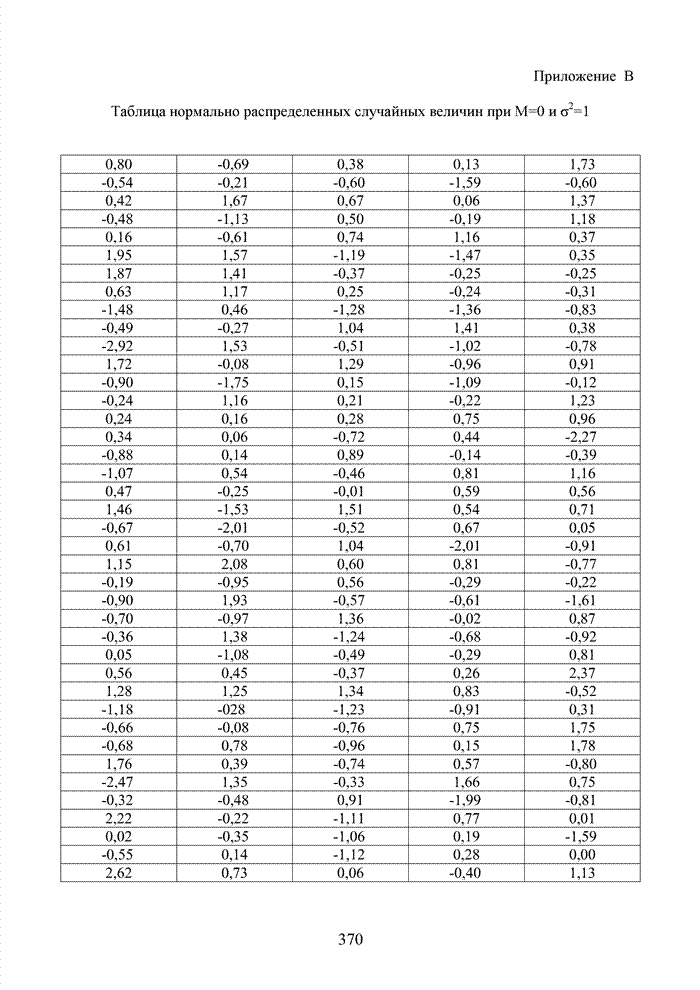
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК