| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
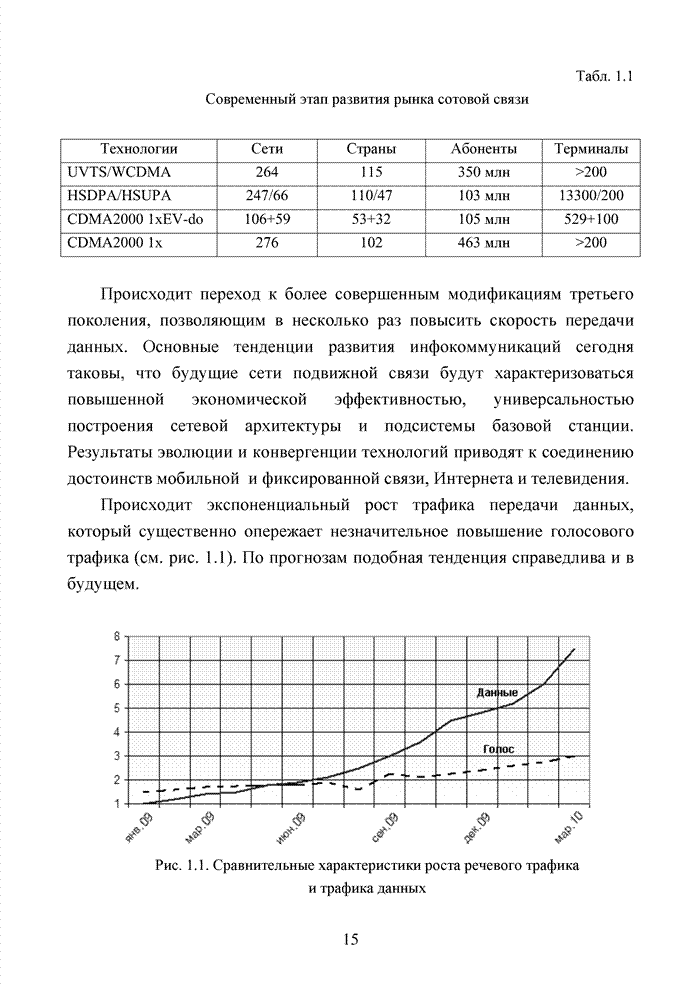
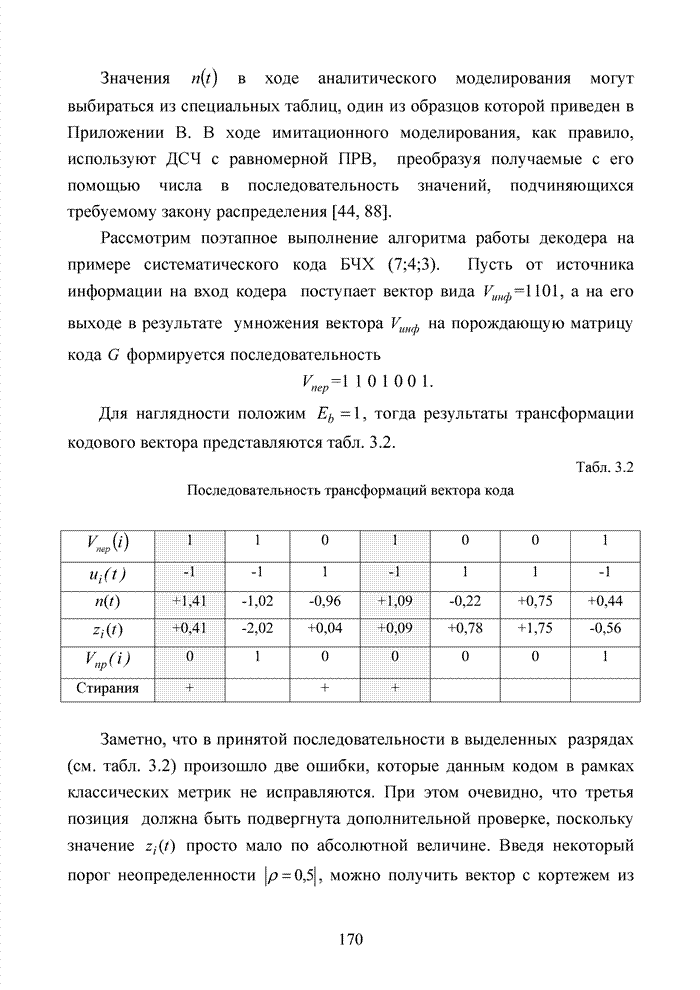
1.8. Модулярное представление блоковых кодов и их эквивалентность
Пусть ![]() – порождающая матрица линейного
– порождающая матрица линейного
![]() -кода. Эта
матрица по определению имеет
-кода. Эта
матрица по определению имеет ![]() строк и
строк и ![]() столбцов, при этом существует всего
столбцов, при этом существует всего ![]() различных типов
возможных столбцов (чисто нулевой столбец из анализа исключается, поскольку он
не информативен). Если задать произвольный порядок расположения столбцов, то
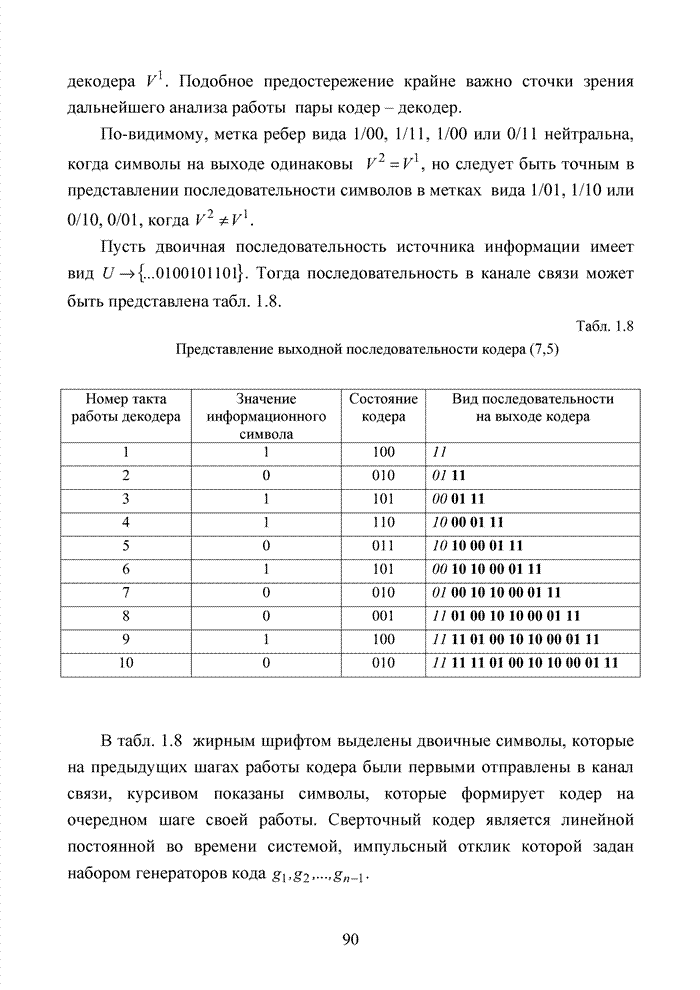
код можно задать указанием числа столбцов каждого типа. Подобный способ задания
кода получил название модулярного представления. Он оказывается продуктивным
при реализации мягких методов декодирования систематических блоковых кодов.
различных типов
возможных столбцов (чисто нулевой столбец из анализа исключается, поскольку он
не информативен). Если задать произвольный порядок расположения столбцов, то
код можно задать указанием числа столбцов каждого типа. Подобный способ задания
кода получил название модулярного представления. Он оказывается продуктивным
при реализации мягких методов декодирования систематических блоковых кодов.
Пусть задана специальная
матрица ![]() размерности
размерности
![]() , содержащая
в качестве столбцов все возможные векторы из
, содержащая
в качестве столбцов все возможные векторы из ![]() двоичных элементов, исключая нулевой
вектор. Тогда j-й столбец
матрицы
двоичных элементов, исключая нулевой
вектор. Тогда j-й столбец
матрицы ![]() можно
рассматривать как столбец типа j, а код может быть задан вектором, образованным
можно
рассматривать как столбец типа j, а код может быть задан вектором, образованным ![]() положительными целыми числами.
Пусть
положительными целыми числами.
Пусть![]() , где
, где ![]() – число столбцов типа i. Известно [8, 15, 84], что матрица
– число столбцов типа i. Известно [8, 15, 84], что матрица
![]() размерности
размерности ![]() в качестве строк
содержит все возможные ненулевые линейные комбинации строк матрицы
в качестве строк
содержит все возможные ненулевые линейные комбинации строк матрицы ![]() . Следовательно,
строками матрицы
. Следовательно,
строками матрицы ![]() являются
все ненулевые кодовые векторы.
являются
все ненулевые кодовые векторы.
Важным случаем является
матрица, которая содержит весь код, задаваемый матрицей ![]() , если ее рассматривать как
порождающую матрицу кода
, если ее рассматривать как
порождающую матрицу кода ![]() . Пусть используется двоичный код,
у которого
. Пусть используется двоичный код,
у которого ![]() ,
тогда
,
тогда ![]() может
быть представлена как
может
быть представлена как

и пусть задана порождающая матрица укороченного кода Хэмминга (6,3,3)
 .
.
Тогда ![]() , поскольку в
матрице
, поскольку в
матрице ![]() имеется
весь набор чисел, кроме 3. Оценка произведения
имеется
весь набор чисел, кроме 3. Оценка произведения ![]() дает следующий результат
дает следующий результат
 .
.
Отсюда вектор весового
спектра определяется как вес каждой строки ![]() матрицы
матрицы ![]() . Аналогичный результат можно получить,
вычислив
. Аналогичный результат можно получить,
вычислив ![]() и
далее
и
далее ![]() .
.
Таким образом, если
имеется совокупность весов кодовых слов, упорядоченных так же, как кодовые
слова в соотношении ![]() ,
то можно найти вектор модулярного представления и тем самым определить код с
точностью до перестановки столбцов. Именно такую процедуру предполагают
отдельные методы мягкого декодирования кодов.
,
то можно найти вектор модулярного представления и тем самым определить код с
точностью до перестановки столбцов. Именно такую процедуру предполагают
отдельные методы мягкого декодирования кодов.
При изучении свойств кодов, в которых расположение столбцов несущественно, т.е. свойств, общих для эквивалентных кодов, особенно удобно пользоваться модулярным представлением. Существует много различных способов выбора базиса для одного и того же кода, и, следовательно, много различных порождающих матриц. Вообще говоря. Различные порождающие матрицы будут приводить к различным векторам модулярного представления, и желательно знать, когда модулярные представления описывают эквивалентные коды [84].
Существует два очевидных
необходимых условия. Если два столбца для некоторого кода совпадают, то они
будут совпадать при любом выборе базиса, и поэтому если некоторый столбец типа ![]() появляется
появляется ![]() раз в одном
представлении, то в любом другом представлении того же самого или
эквивалентного кода столбец некоторого другого типа появляется так же
раз в одном
представлении, то в любом другом представлении того же самого или
эквивалентного кода столбец некоторого другого типа появляется так же ![]() раз. Таким образом,
компоненты вектора
раз. Таким образом,
компоненты вектора ![]() могут меняться местами, но не
заменяться другими числами. Аналогично компоненты весового вектора
могут меняться местами, но не
заменяться другими числами. Аналогично компоненты весового вектора ![]() могут меняться
местами, но не заменяться другими числами. Теперь задача сводится к описанию
перестановок.
могут меняться
местами, но не заменяться другими числами. Теперь задача сводится к описанию
перестановок.
Пусть ![]() – любая невырожденная матрица
размерности
– любая невырожденная матрица
размерности ![]() .
Если vi и vj – векторы с
.
Если vi и vj – векторы с ![]() компонентами каждый, то vi
компонентами каждый, то vi![]() vj
vj![]() (vi
(vi![]() vj)
vj)![]() есть линейная комбинация строк матрицы
есть линейная комбинация строк матрицы ![]() , и поскольку строки матрицы
, и поскольку строки матрицы ![]() линейно зависимы, то
(vi
линейно зависимы, то
(vi![]() vj)
vj)![]() тогда и только тогда, когда (vi
тогда и только тогда, когда (vi![]() vj)=0. Поэтому если векторы vi и vj не совпадают, то не совпадают и векторы
vi
vj)=0. Поэтому если векторы vi и vj не совпадают, то не совпадают и векторы
vi![]() и vj
и vj![]() . Следовательно, все
. Следовательно, все ![]() строк матрицы
строк матрицы ![]() будут различны.
будут различны.
Так как имеется ровно ![]() различных ненулевых
векторов, то матрица
различных ненулевых
векторов, то матрица ![]() должна
отличаться от матрицы
должна
отличаться от матрицы ![]() только расстановкой строк
только расстановкой строк
![]() ,
,
где ![]() – некоторая матрица перестановки.
– некоторая матрица перестановки.
Если ![]() и
и ![]() – невырожденные матрицы размерности
– невырожденные матрицы размерности ![]() , то
, то
![]() ,
,
т.е. произведению ![]() соответствует перестановка
соответствует перестановка ![]() . Отсюда следует, что
рассматриваемые перестановки образуют группу, изоморфную (т.е. обладающую той
же самой структурой) группе невырожденных матриц размерности
. Отсюда следует, что
рассматриваемые перестановки образуют группу, изоморфную (т.е. обладающую той
же самой структурой) группе невырожденных матриц размерности ![]() .
.
Выбор нового базиса и
порождающей матрицы для группового кода соответствует умножению слева
порождающей матрицы на некоторую невырожденную матрицу ![]() . Ненулевые кодовые векторы для
порождающей матрицы
. Ненулевые кодовые векторы для
порождающей матрицы ![]() являются
строками матрицы
являются
строками матрицы
![]() ,
,
т.е. строками матрицы ![]() , перестановленными с
помощью
, перестановленными с
помощью ![]() .
Таким образом, выбор ново базиса эквивалентен применению перестановки к кодовым
словам. Очевидно, что эти рассуждения могут быть проведены в обратную сторону.
.
Таким образом, выбор ново базиса эквивалентен применению перестановки к кодовым
словам. Очевидно, что эти рассуждения могут быть проведены в обратную сторону.
Итак, две различные порождающие матрицы приводят к модулярным представлениям, которые отличаются перестановкой.
Пусть задана перестановка вида
![]() ,
,
с соответствующей матрицей
перестановки ![]() .
Пусть задана порождающая матрица (6,3,3)-кода вида
.
Пусть задана порождающая матрица (6,3,3)-кода вида
 .
.
Заметно, что нумераторы
столбцов матрицы ![]() совпадают
с операндом перестановки
совпадают
с операндом перестановки ![]() . Результатом произведения
. Результатом произведения ![]() будет новая матрица
будет новая матрица ![]() .
.
 ,
,
но эта матрица представлена в несистематической
форме. Складывая поразрядно первую строку матрицы ![]() со второй строкой, и первую
строку с третьей строкой получим, матрицу в систематической форме
со второй строкой, и первую
строку с третьей строкой получим, матрицу в систематической форме ![]()
 .
.
Совпадение вторых строк матрицы ![]() и
и ![]() следует считать случайным.
следует считать случайным.
Сравним результаты
произведений ![]() и
и
![]() :
:
 ;
;  .
.
![]() .
. ![]()
Обе матрицы ![]() и
и ![]() представляют один и тот же код,
но с разными проверочными соотношениями. Заметно, что весовые значения
векторов в
представляют один и тот же код,
но с разными проверочными соотношениями. Заметно, что весовые значения
векторов в ![]() и
и
![]() распределены
не одинаково, поэтому обратные преобразования в
распределены
не одинаково, поэтому обратные преобразования в ![]() должны в первую очередь соответствовать
весовым показателям в
должны в первую очередь соответствовать
весовым показателям в ![]() . Рассмотрим вектор vi =
. Рассмотрим вектор vi =![]() из
из ![]() . Выполнив vi
. Выполнив vi![]() , получим значение vj =
, получим значение vj =![]() из
из ![]() . Из рис. 1.10 становится ясно, что
эквивалентные коды образуют множество подстановок вида
. Из рис. 1.10 становится ясно, что
эквивалентные коды образуют множество подстановок вида
![]() !
!
поскольку векторы веса ![]() могут перейти только в
векторы аналогичного веса, при этом значение
могут перейти только в
векторы аналогичного веса, при этом значение ![]() !.
!.

Рис. 1.10. Принцип подстановок в эквивалентных кодах
Таким образом, если ![]() пространство строк
матрицы
пространство строк
матрицы ![]() , то
код
, то
код ![]() эквивалентен
коду
эквивалентен
коду ![]() тогда и
только тогда, когда
тогда и
только тогда, когда ![]() –
пространство строк матрицы
–
пространство строк матрицы ![]() , полученной из матрицы
, полученной из матрицы ![]() подстановкой столбцов.
Подстановка столбцов порождающей матрицы кода приводит к порождающей матрице
для эквивалентного кода.
подстановкой столбцов.
Подстановка столбцов порождающей матрицы кода приводит к порождающей матрице
для эквивалентного кода.
В описанном процессе
представления кода через его эквивалентные аналоги наиболее сложным шагом
является переход от произвольной матрицы ![]() к матрице
к матрице ![]() в систематической форме. Действительно
подстановка
в систематической форме. Действительно
подстановка ![]() может
быть такой, что линейная независимость строк матрицы
может
быть такой, что линейная независимость строк матрицы ![]() может не соблюдаться. При таких
условиях эквивалентный код получить невозможно. Пусть некоторая подстановка
может не соблюдаться. При таких
условиях эквивалентный код получить невозможно. Пусть некоторая подстановка ![]() принимает вид:
принимает вид:
![]() .
.
После применения подстановки к порождающей матрице кода получим
 .
.
Выделяя из матрицы ![]() первые
первые ![]() столбцов, получим
квадратную матрицу размерности
столбцов, получим
квадратную матрицу размерности ![]() , которая является индикатором возможности
получения из
, которая является индикатором возможности
получения из ![]() матрицы
в систематической форме. Оценим пространство кодовых последовательностей,
которое образуется при умножении
матрицы
в систематической форме. Оценим пространство кодовых последовательностей,
которое образуется при умножении ![]() .
.
 и
и ![]() .
.
Назовем подобную матрицу
тестовой. Заметно, что полученная квадратная матрица является вырожденной,
следовательно, эквивалентный код при заданной подстановке ![]() не может быть получен.
не может быть получен.
Весовые показатели
остались неизменными, но в первых ![]() столбцах
столбцах ![]() заметен повтор отдельных наборов,
например, 110; 011 и 101. Именно в этом проявляется линейная зависимость строк
матрицы
заметен повтор отдельных наборов,
например, 110; 011 и 101. Именно в этом проявляется линейная зависимость строк
матрицы ![]() .
Поскольку весовые показатели матрицы
.
Поскольку весовые показатели матрицы ![]() остались неизменными, то для получения
эквивалентного кода необходимо изменить подстановку (изменить порядок
следования столбцов в произведении
остались неизменными, то для получения
эквивалентного кода необходимо изменить подстановку (изменить порядок
следования столбцов в произведении ![]() ). Эту процедуру можно выполнить
нескольким путями.
). Эту процедуру можно выполнить
нескольким путями.
Во-первых, осуществить
циклический сдвиг столбцов в матрице ![]() на
на ![]() шагов вправо. Новая конфигурация столбцов
будет представлять вариант подстановки вида
шагов вправо. Новая конфигурация столбцов
будет представлять вариант подстановки вида
![]() .
.
Во-вторых, возможно
получить невырожденную матрицу, если выполнить транспозицию ![]() -го элемента подстановки
-го элемента подстановки ![]() с
с ![]() -м элементом.
-м элементом.
В первом случае циклический сдвиг результата подстановки (элементов второй строки) может привести к обработке ненадежных позиций, но для решения задач мягкого декодирования одних кодовых методов может оказаться недостаточно. В подобной ситуации целесообразно использовать итеративные преобразования кодовых комбинаций.
Во втором случае
процедура транспозиции может дать отрицательный результат, если нулевая строка
в тестовой матрице в результате транспозиции не будет ликвидирована. В подобной
ситуации необходимо повторить операцию транспозиции, но вместо ![]() -го элемента
использовать
-го элемента
использовать ![]() -й
элемент.
-й
элемент.
Оценим вероятность
неблагоприятного исхода при использовании некоторой подстановки к столбцам
порождающей матрицы кода ![]() . Если
. Если ![]() -я строка матрицы
-я строка матрицы ![]() имеет вес равный
имеет вес равный ![]() , то число
отрицательных исходов (получение невырожденной матрицы) при формировании
порождающей матрицы эквивалентного кода будет определяться возможностью
образования в квадратной матрице размерности
, то число
отрицательных исходов (получение невырожденной матрицы) при формировании
порождающей матрицы эквивалентного кода будет определяться возможностью
образования в квадратной матрице размерности ![]() чисто нулевой строки как результат
выполнения подстановки.
чисто нулевой строки как результат
выполнения подстановки. ![]()
Общее число отрицательных исходов может быть найдено из выражения
![]()
![]() ,
,
тогда суммирование по всем строкам
матрицы ![]() определит
общее число отрицательных исходов
определит
общее число отрицательных исходов
![]()
 при
при ![]() .
.
Вероятность перехода к итеративным преобразованиям матрицы эквивалентного кода будет определяться как
![]() .
.
Например, для кода
(7,4,3) с ![]() значение
значение
![]() составит
составит ![]() , здесь
, здесь ![]() – весовая матрица
порождающей матрицы кода.
– весовая матрица
порождающей матрицы кода.
Приведенные соотношения прямо указывают на то, что при использовании блоковых кодов целесообразно использовать укороченные коды, которые обеспечивают снижение общего числа нулевых позиций за счет их вычеркивания в первых столбцах исходной порождающей матрицы кода в систематической форме.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
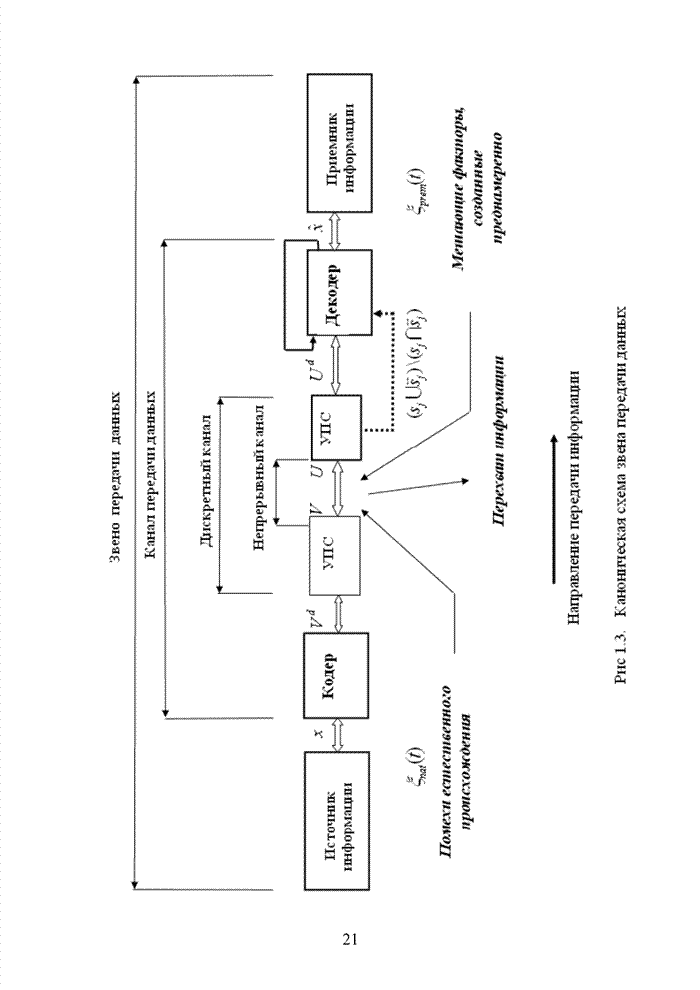
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
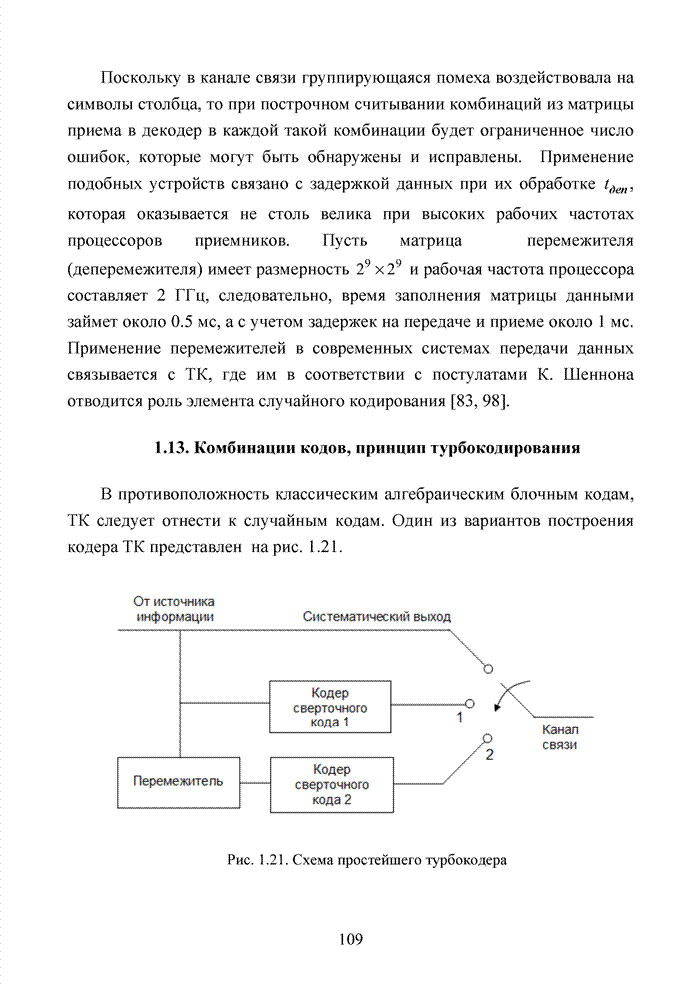
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
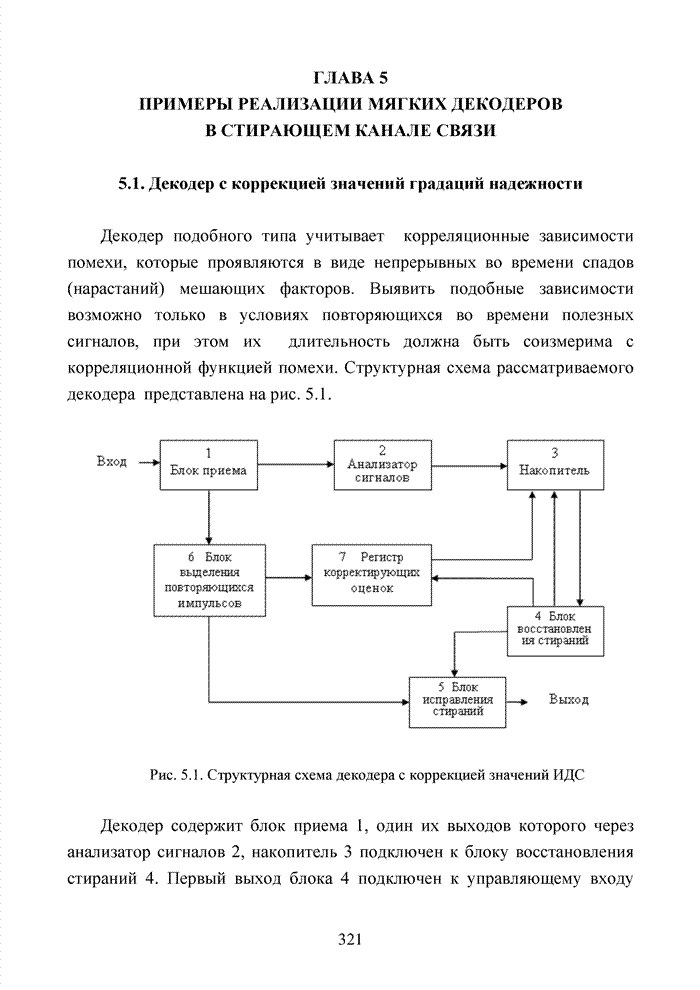
- 5.1. Декодер с коррекцией значений градаций надежности
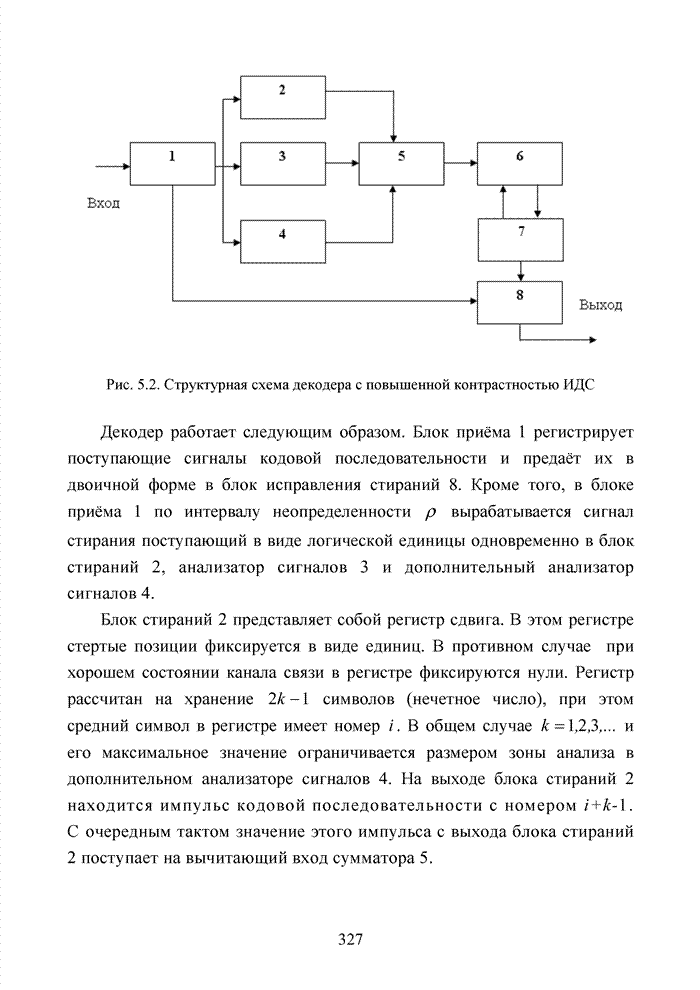
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
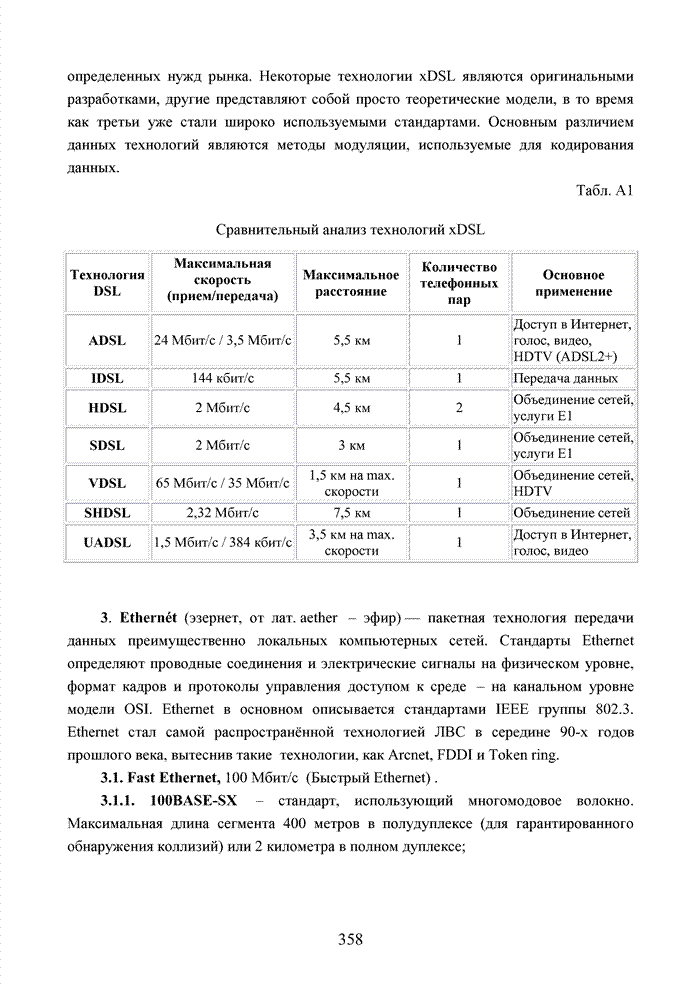
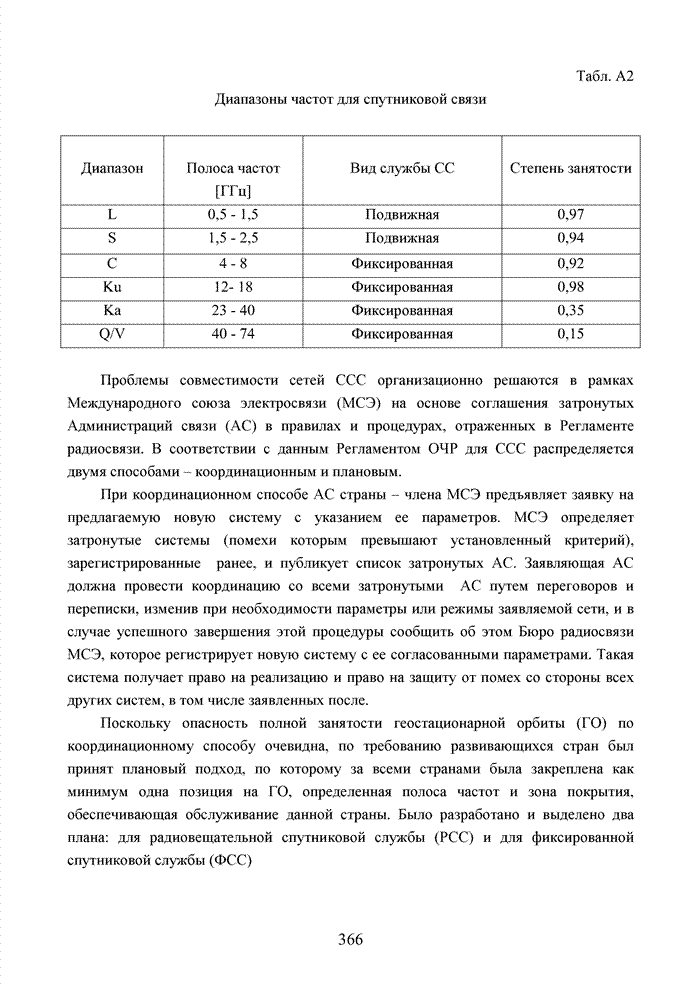
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
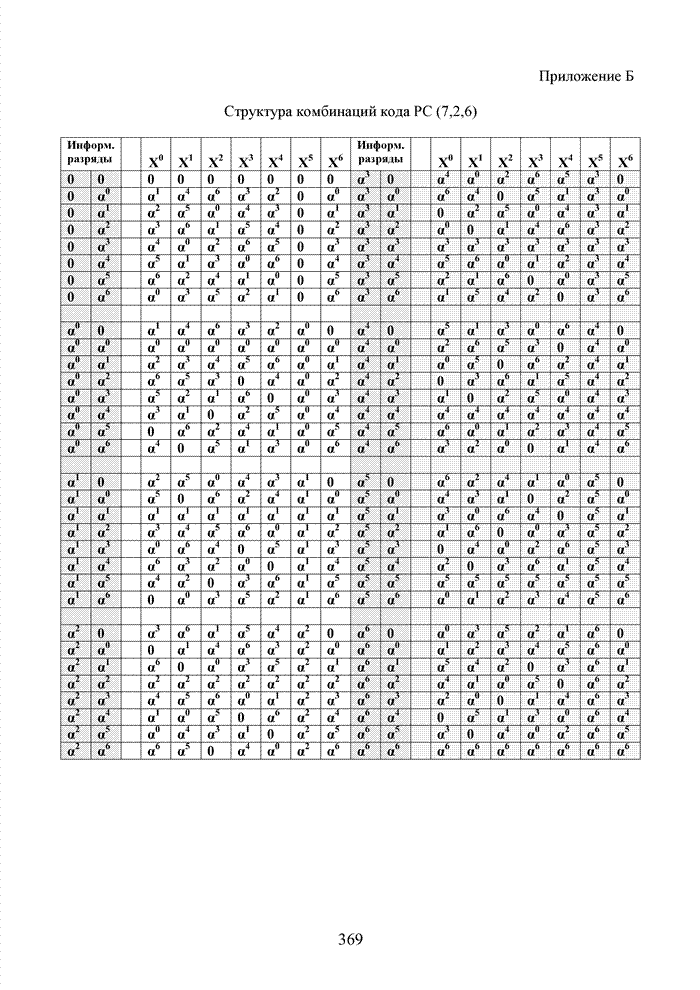
- Приложение Б Структура комбинаций кода РС (7,2,6)
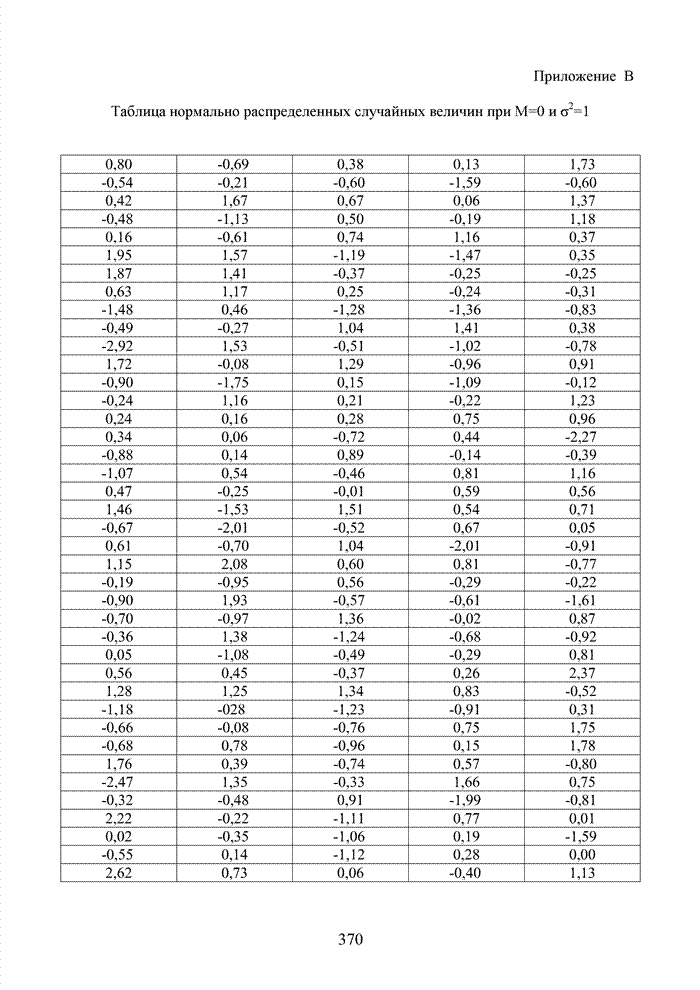
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК