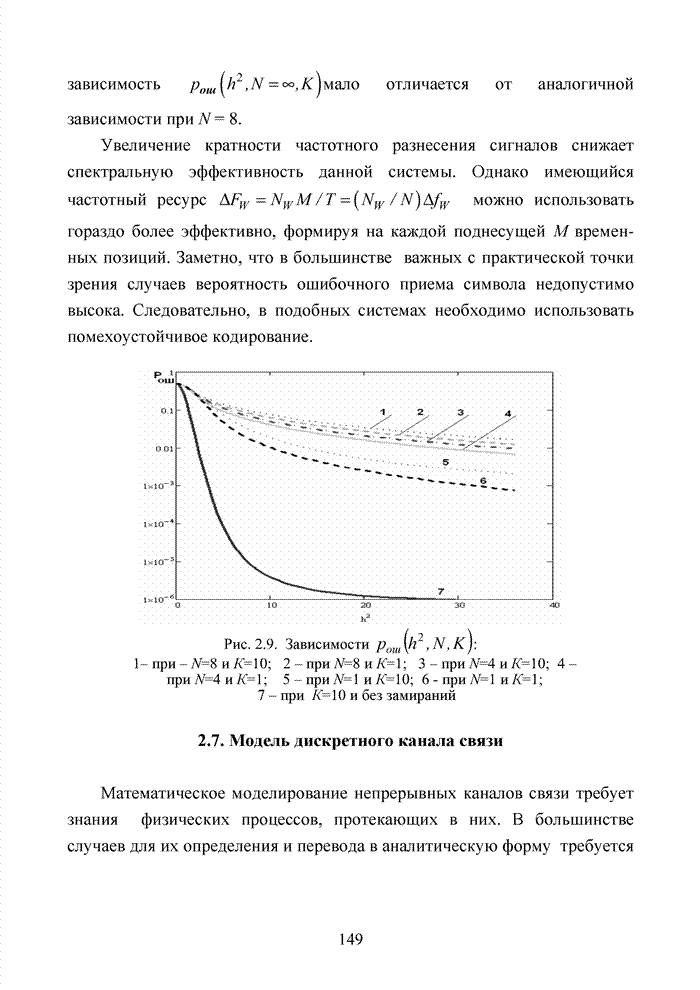
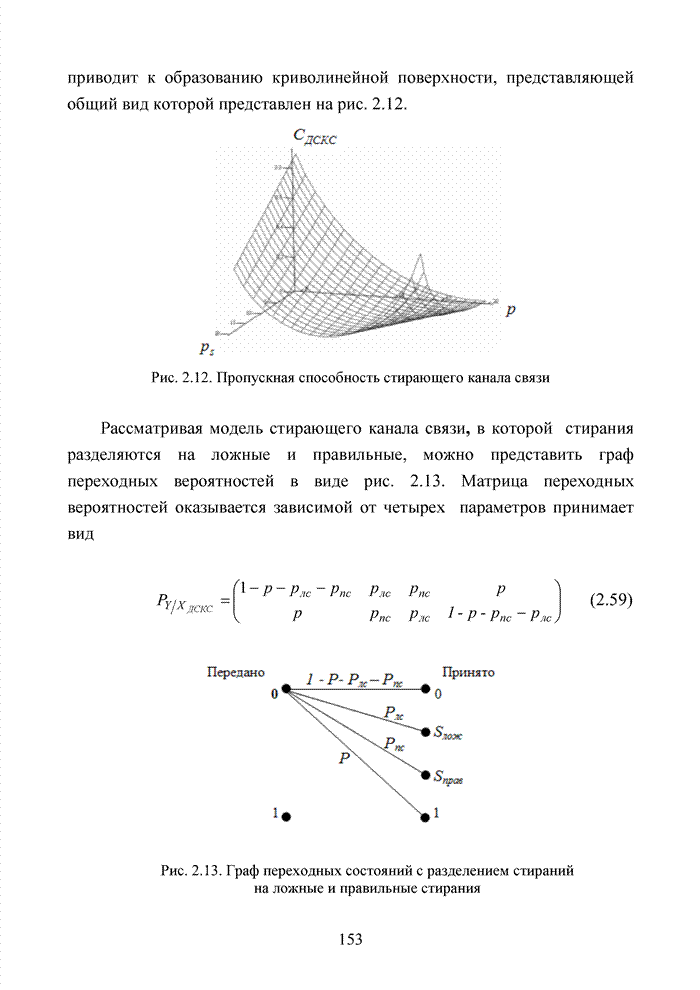
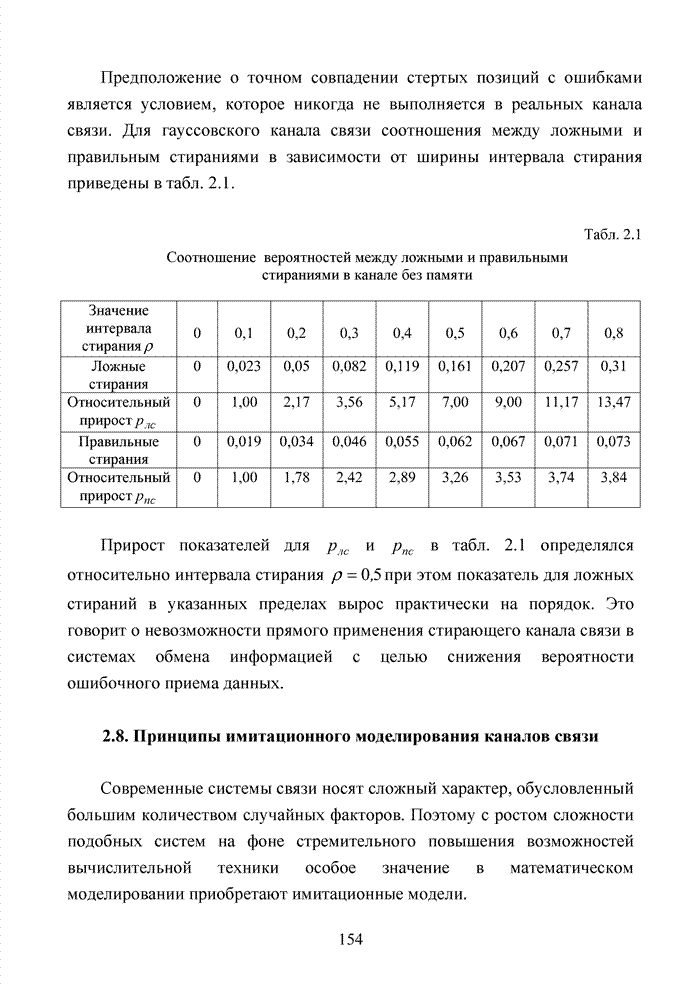
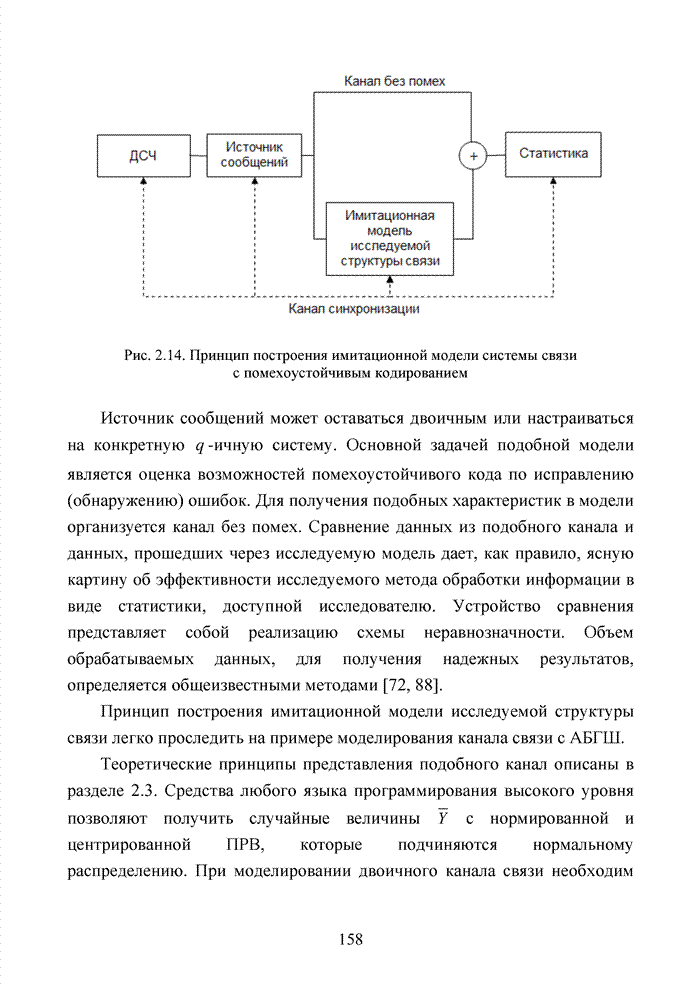
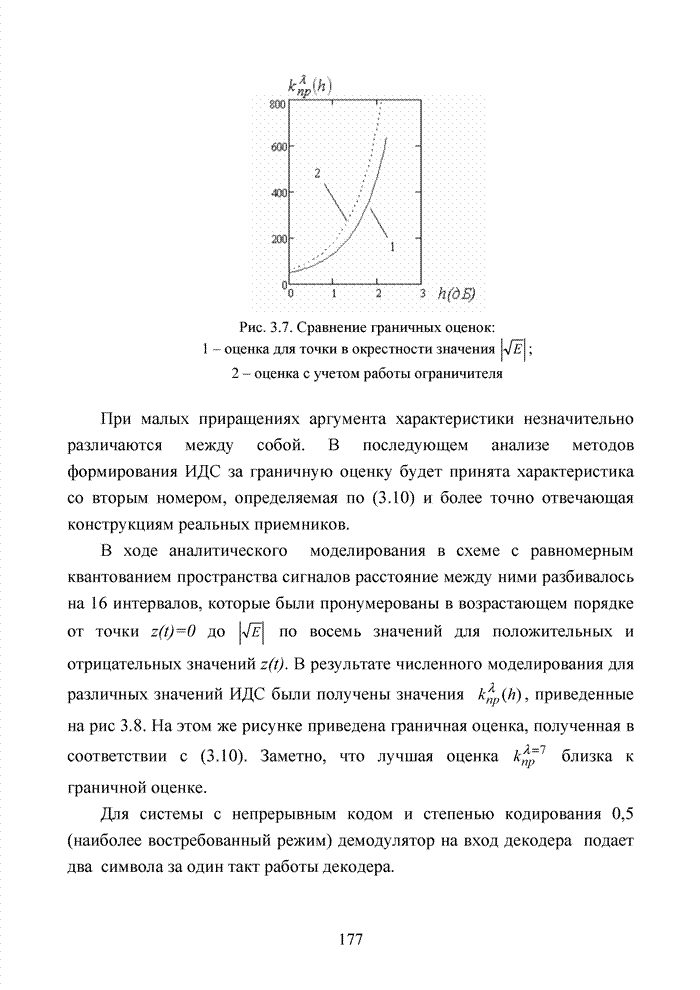
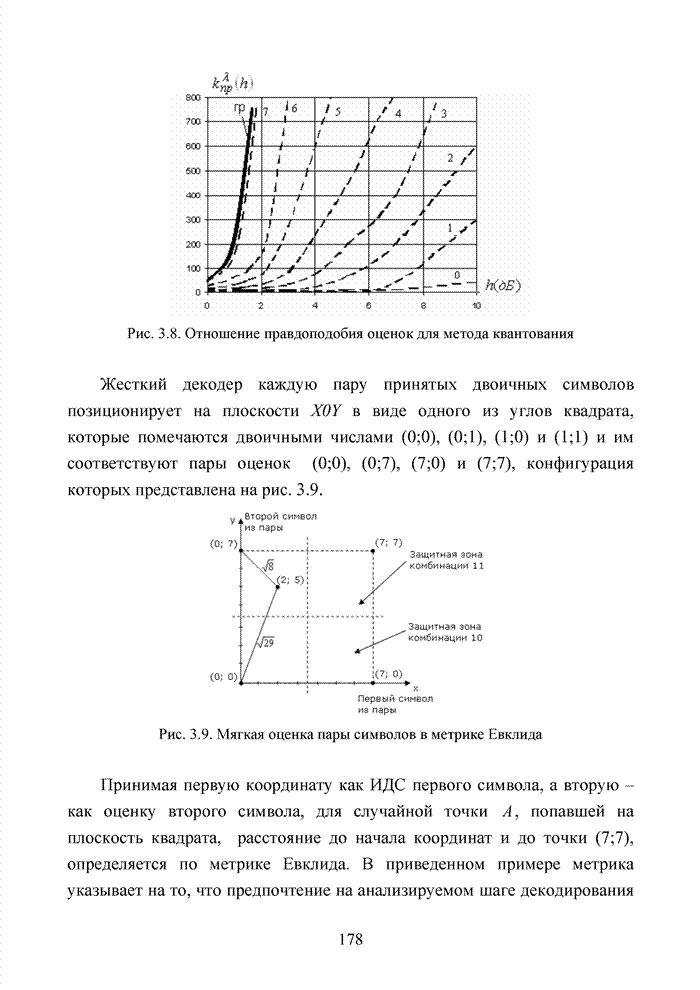
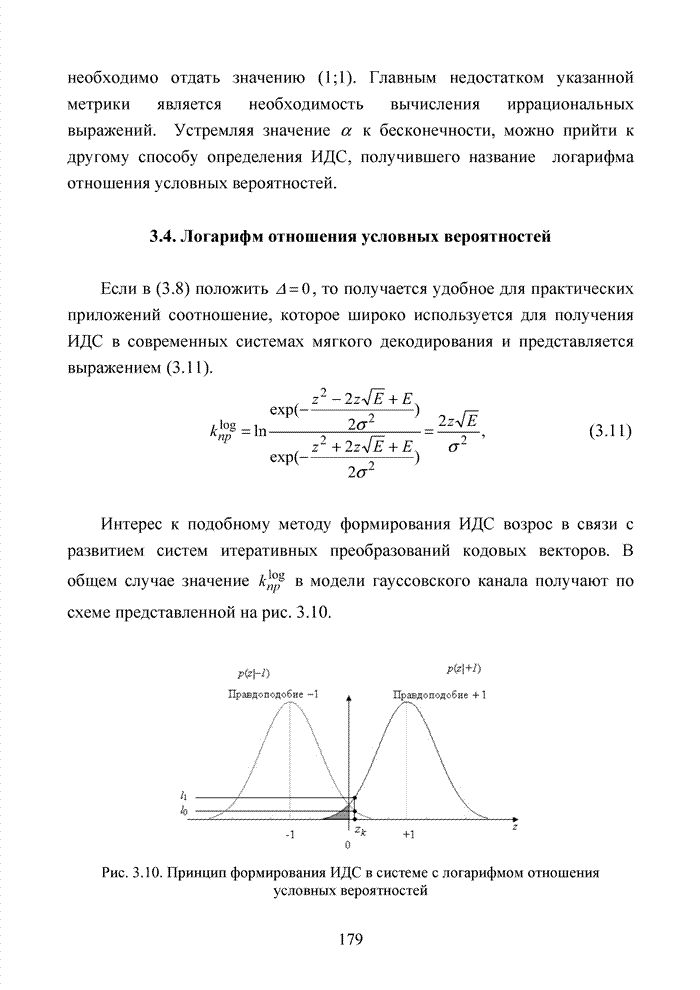
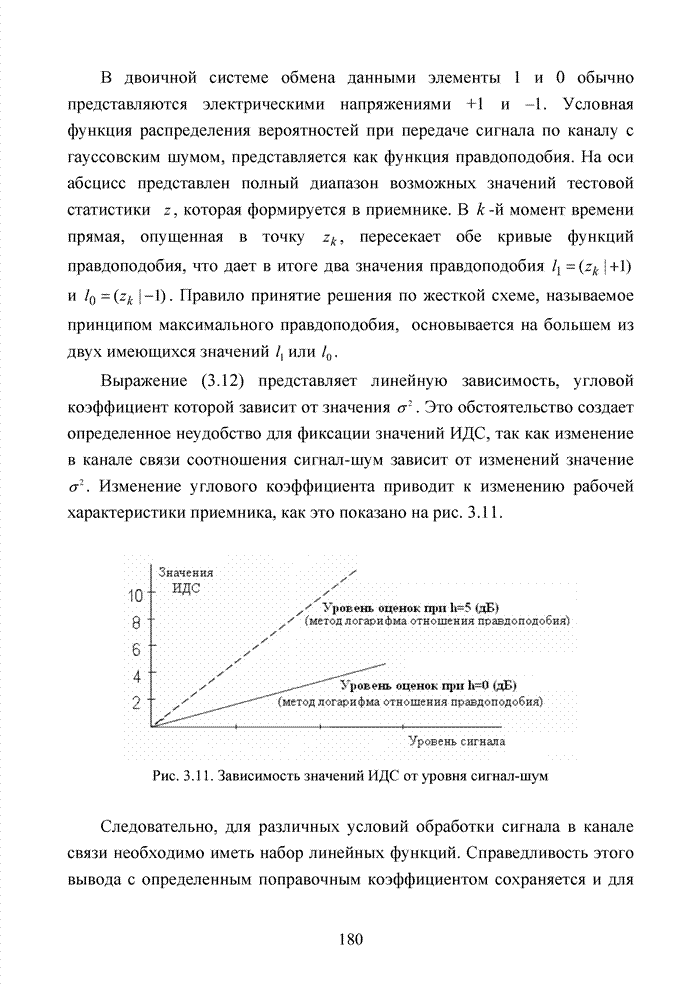
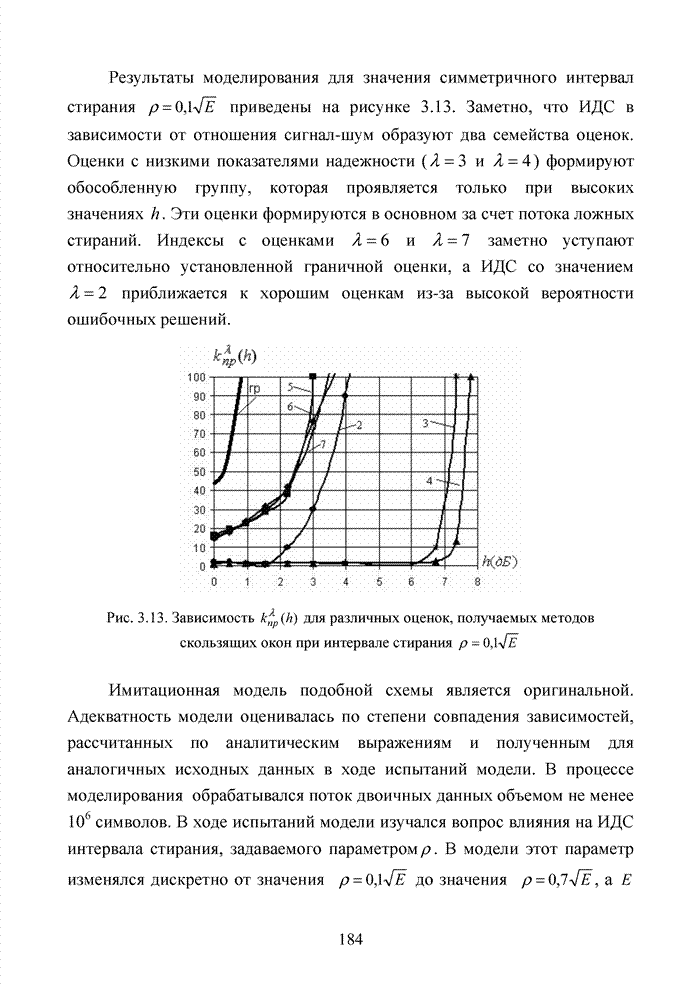
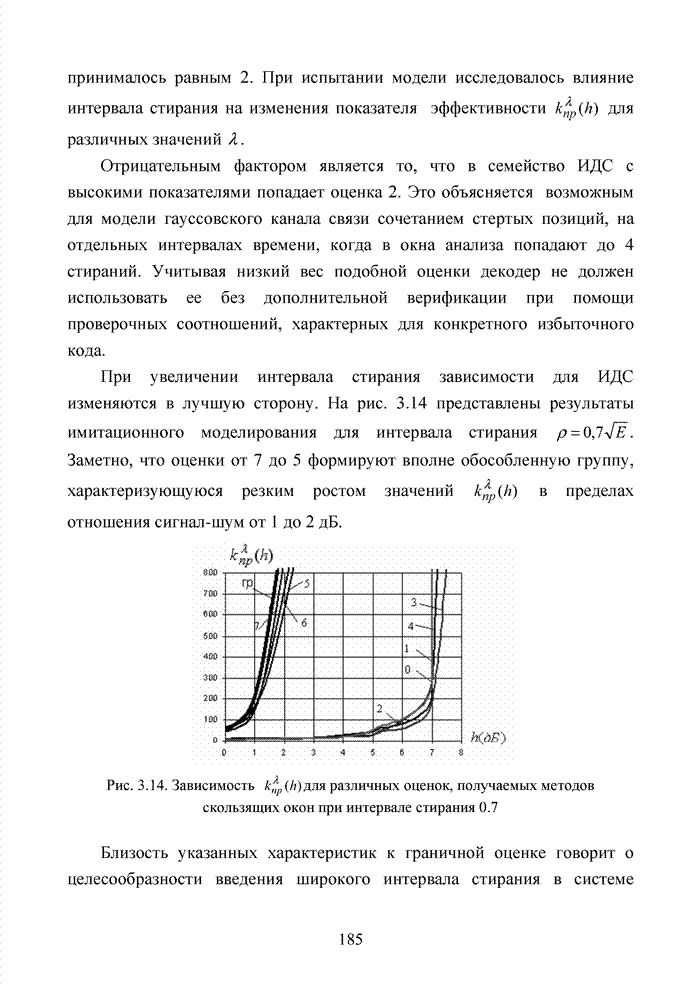
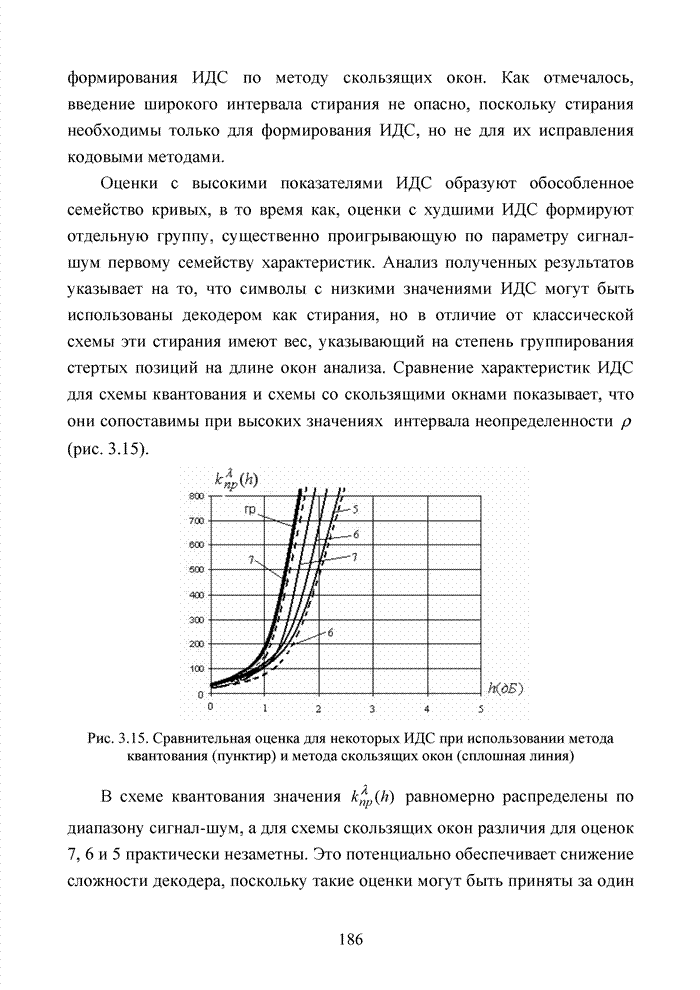
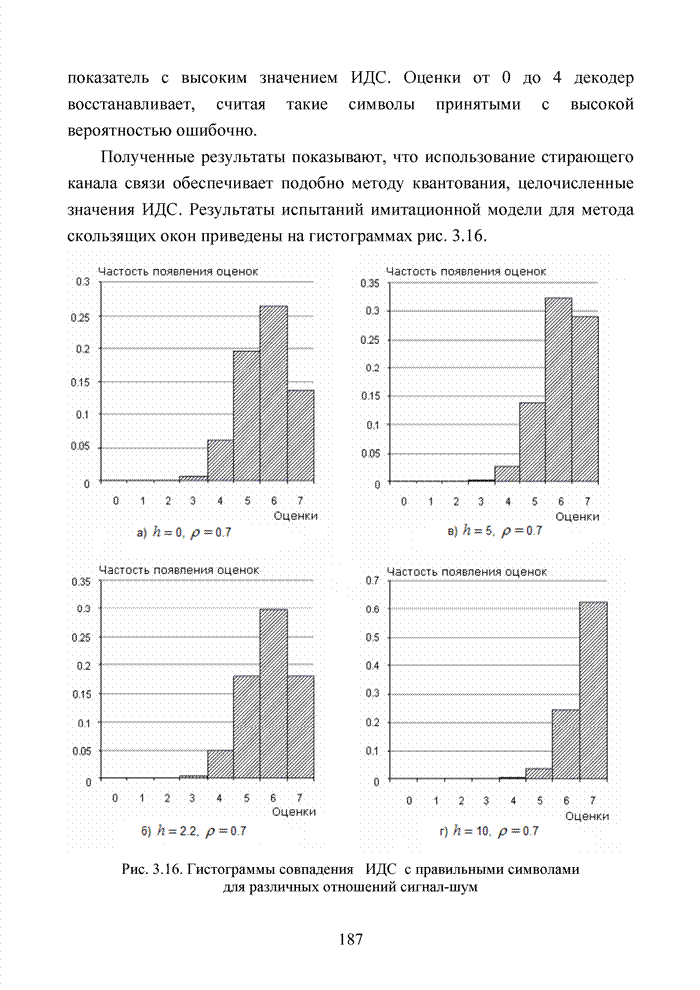
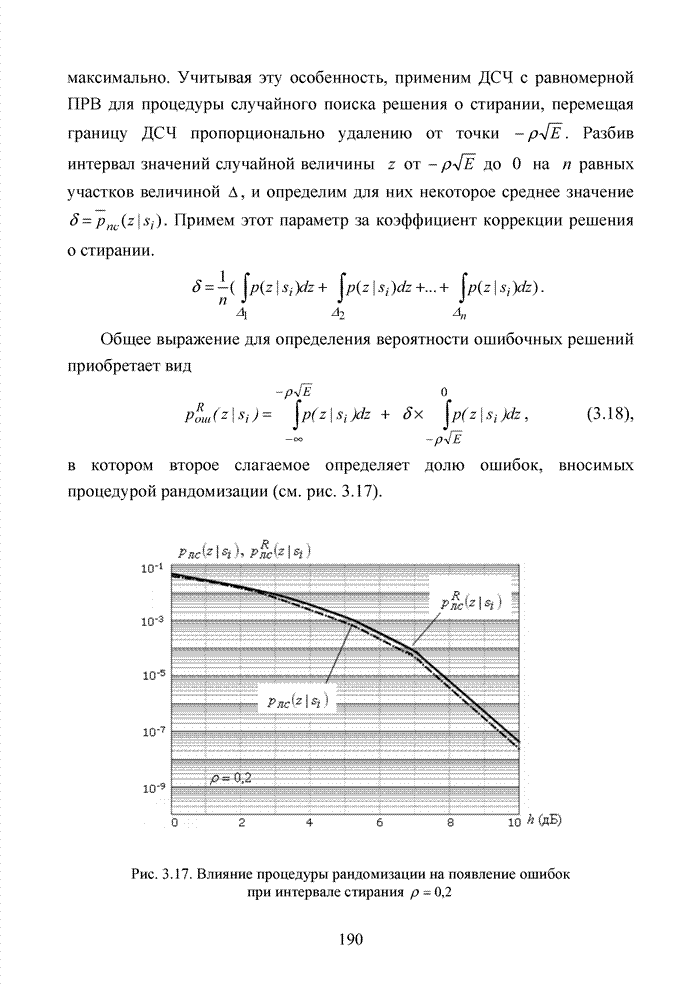
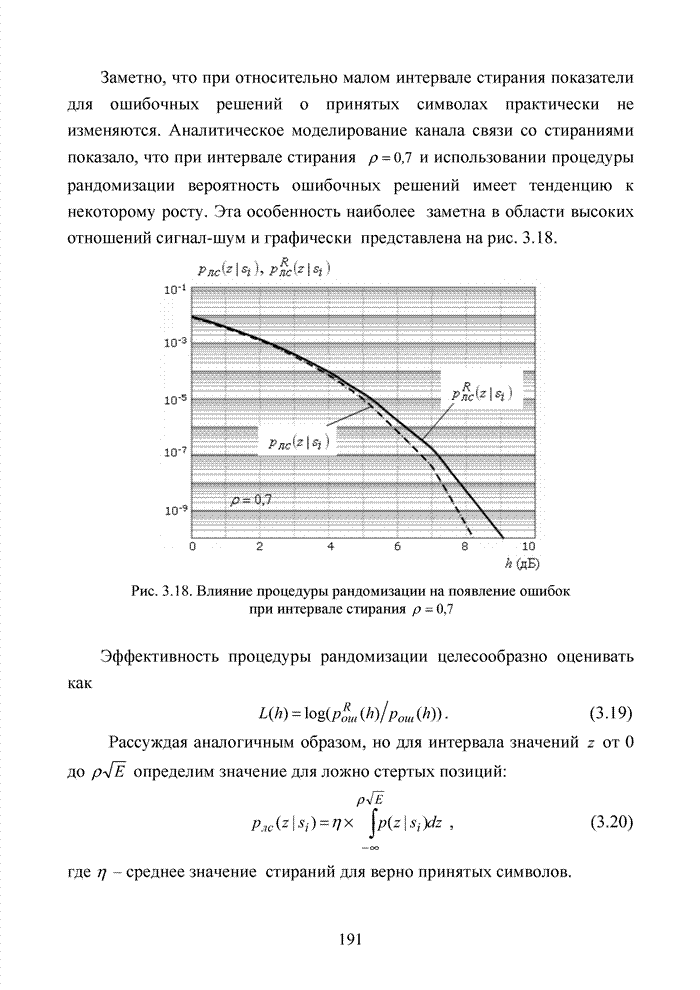
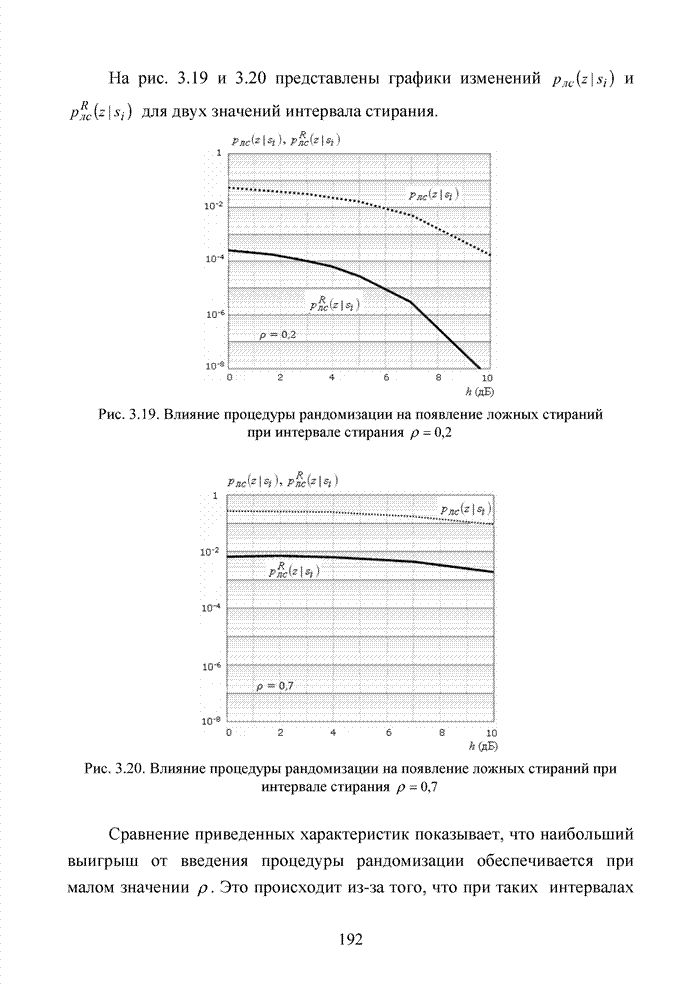
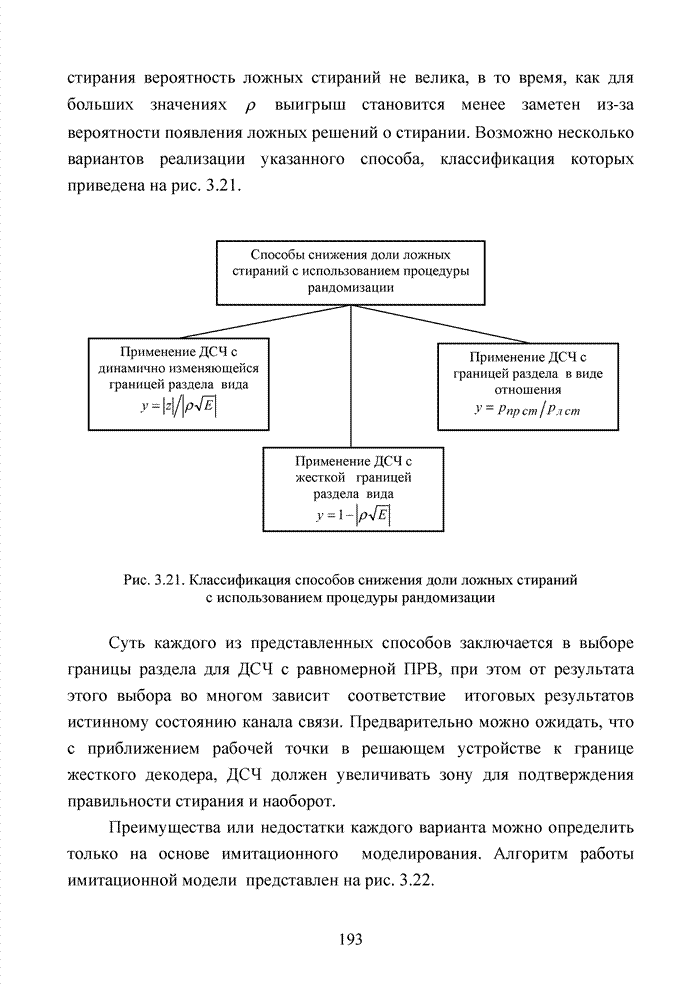
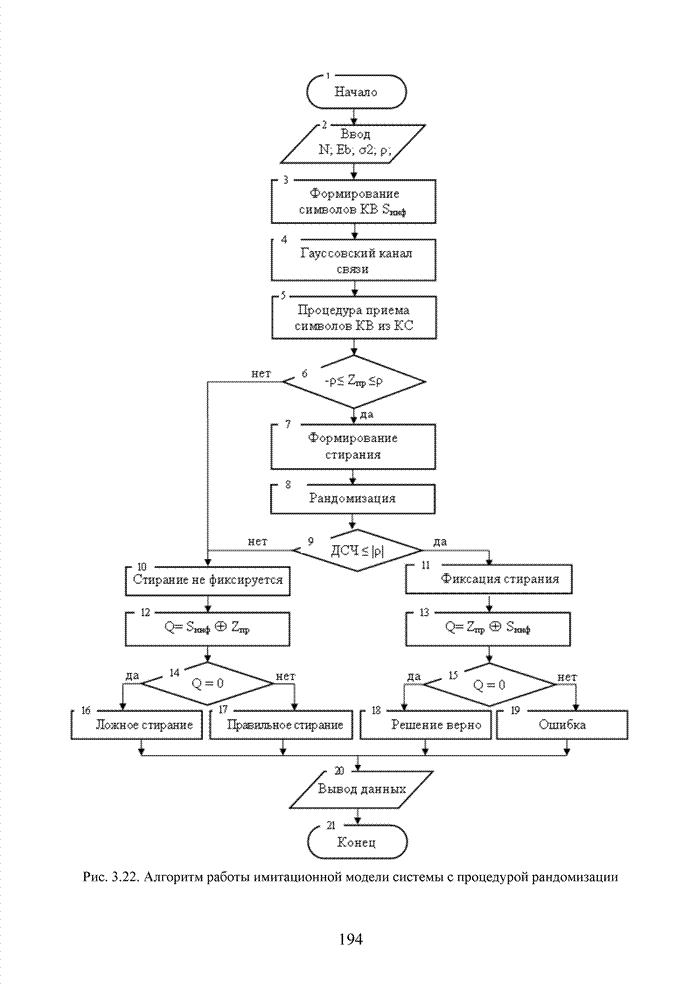
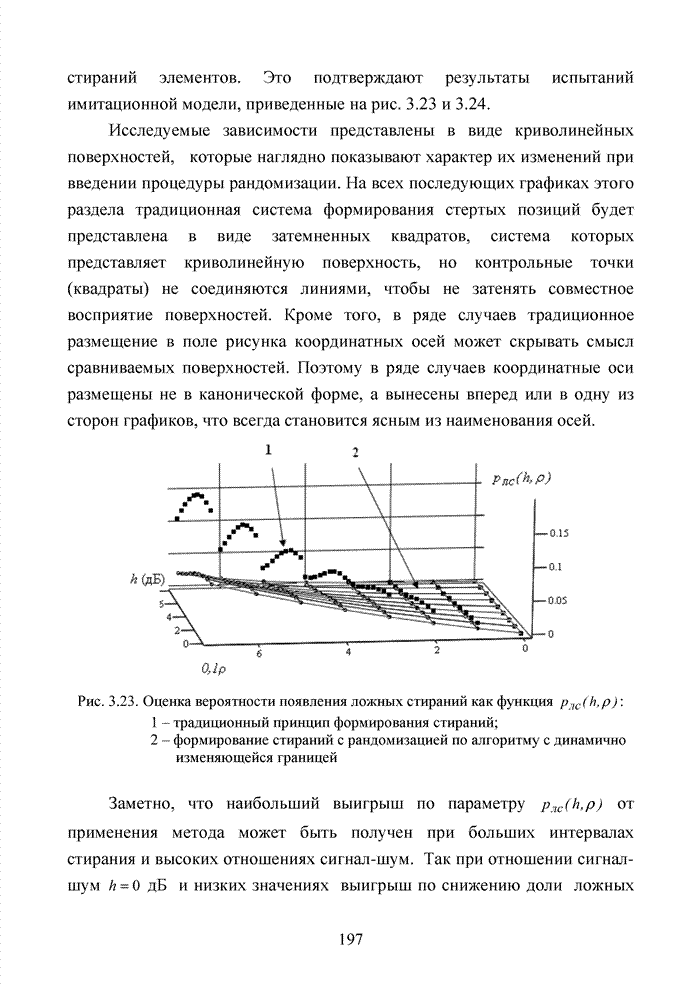
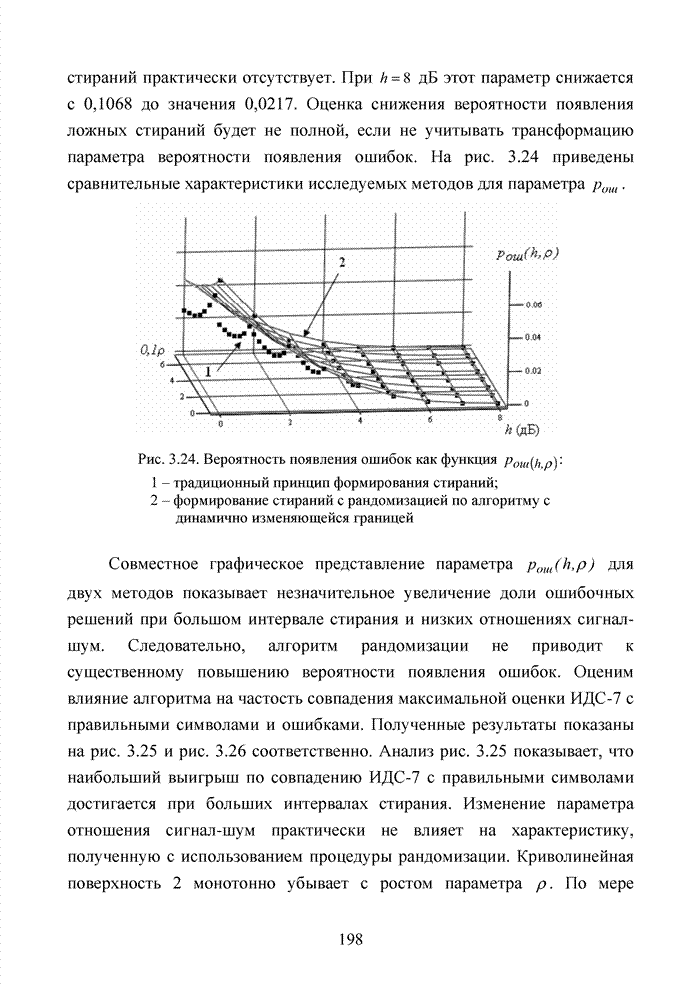
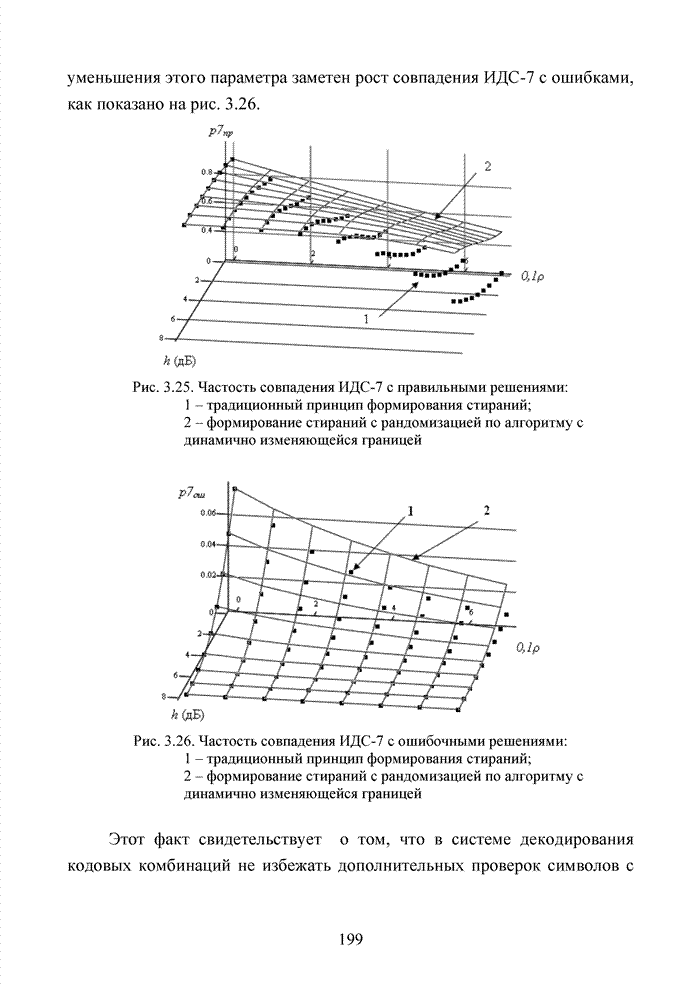
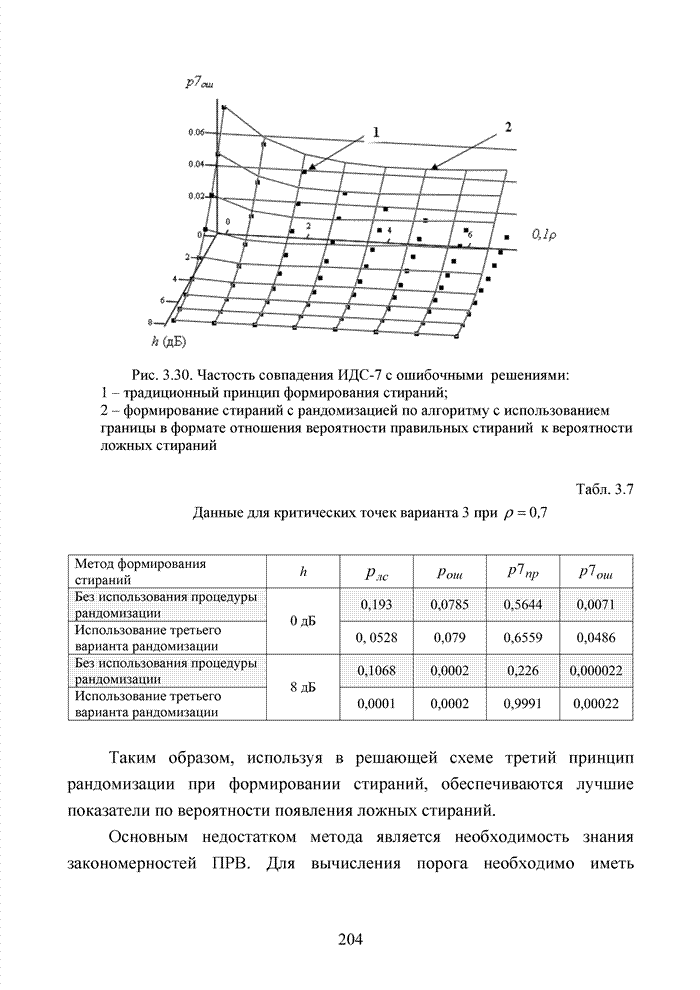
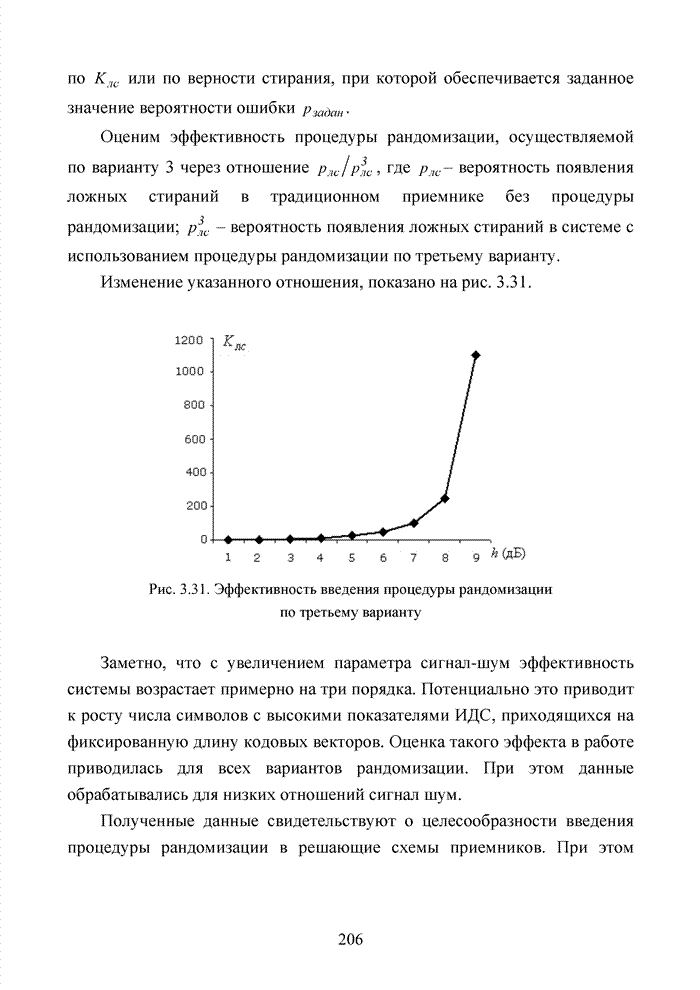
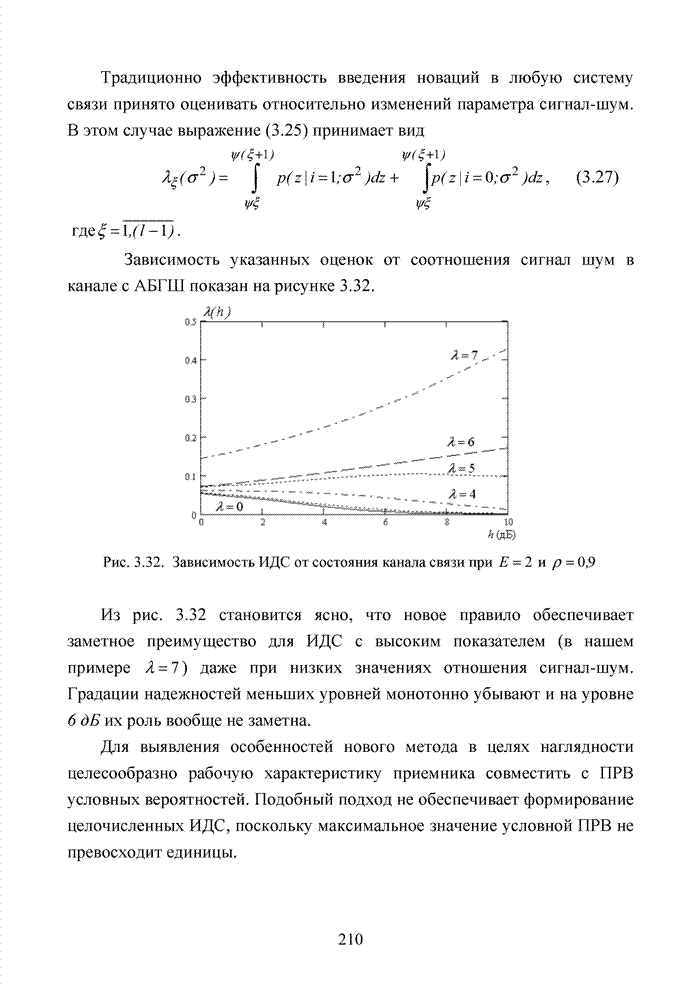
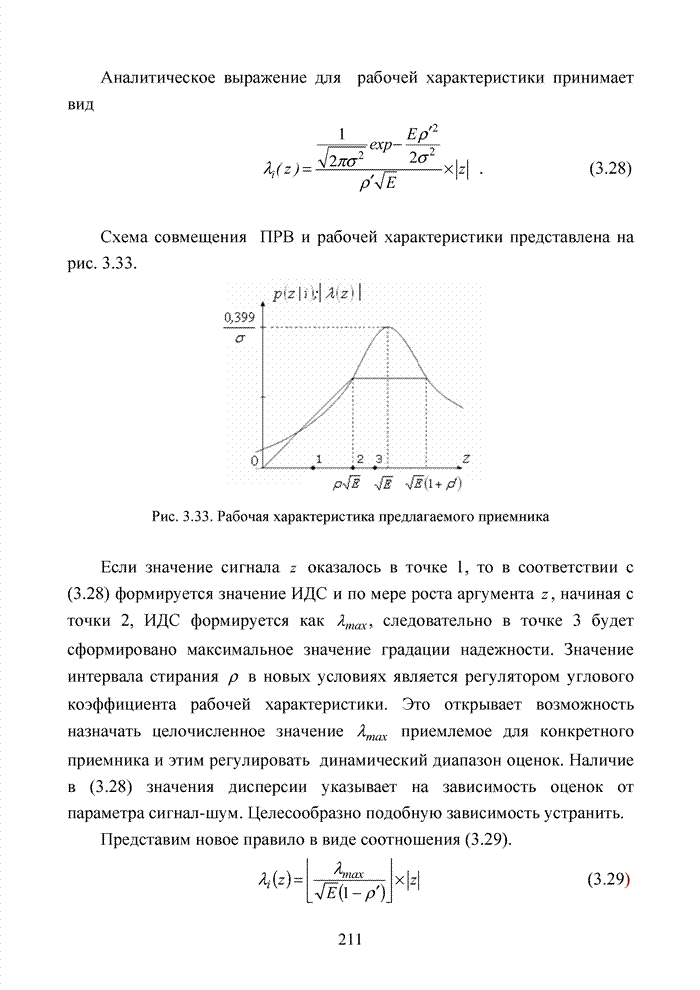
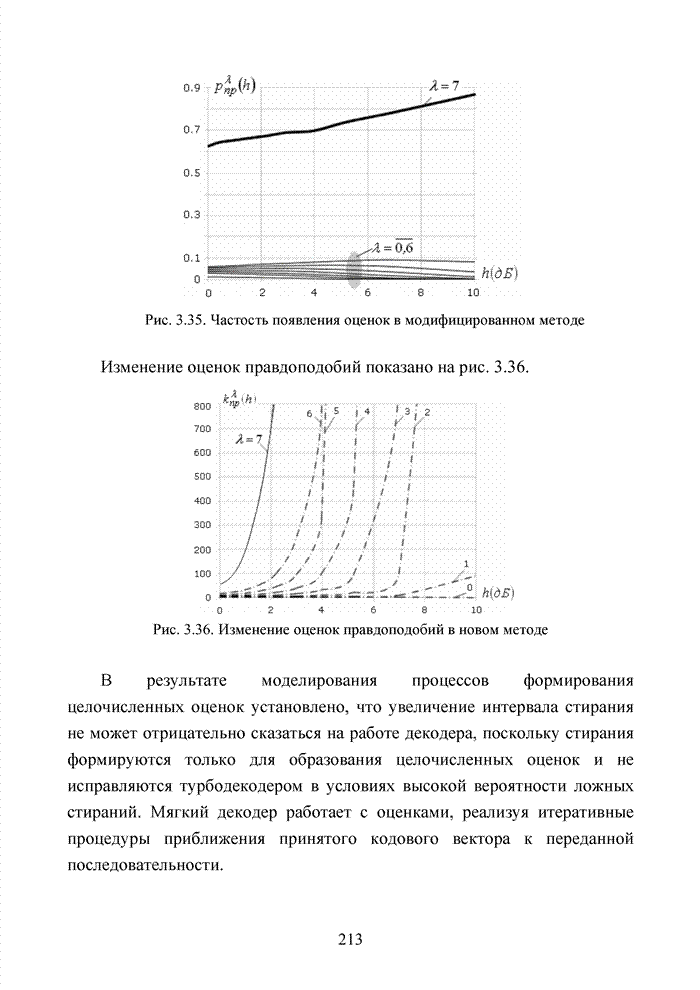
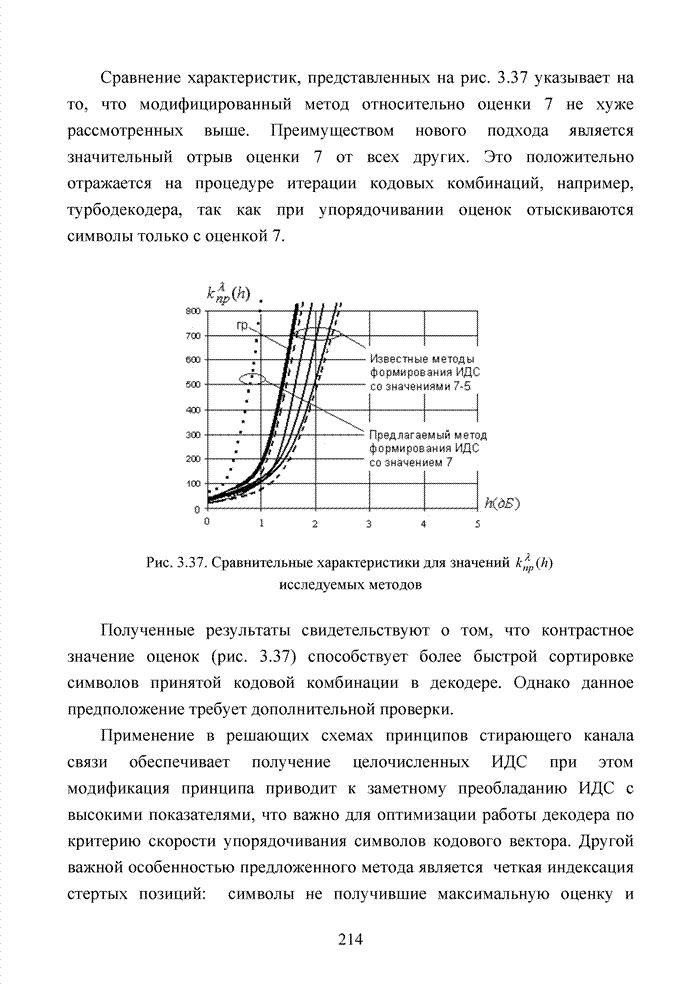
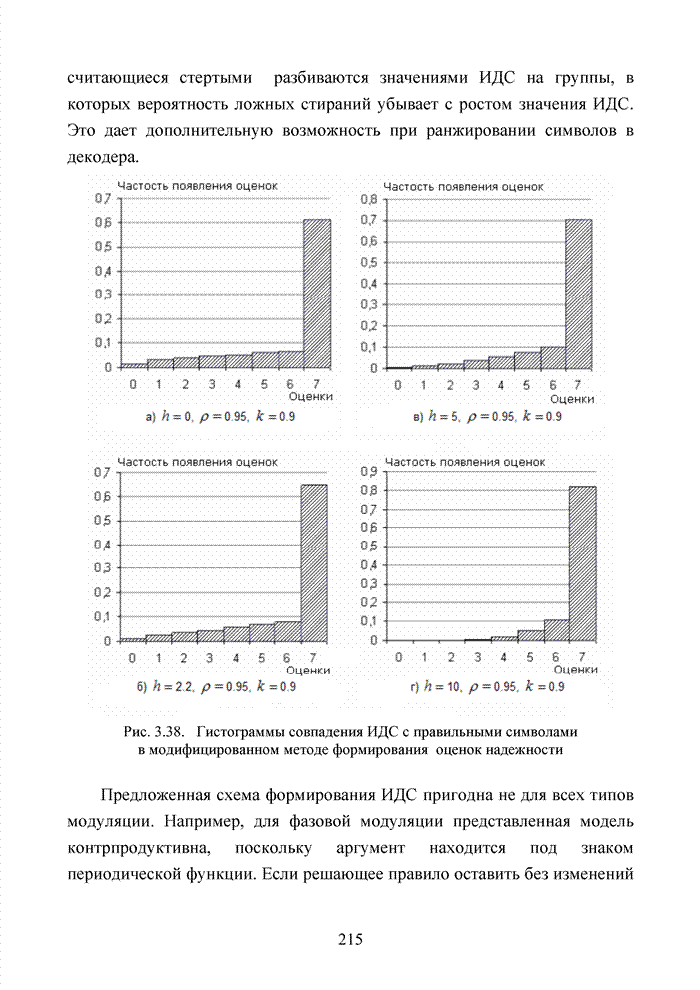
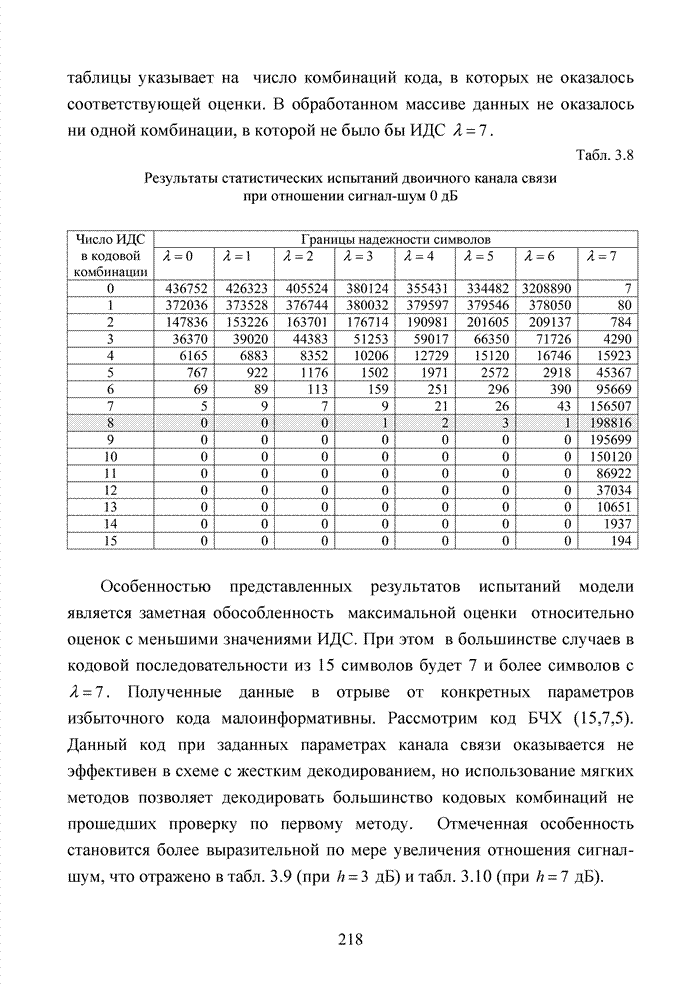
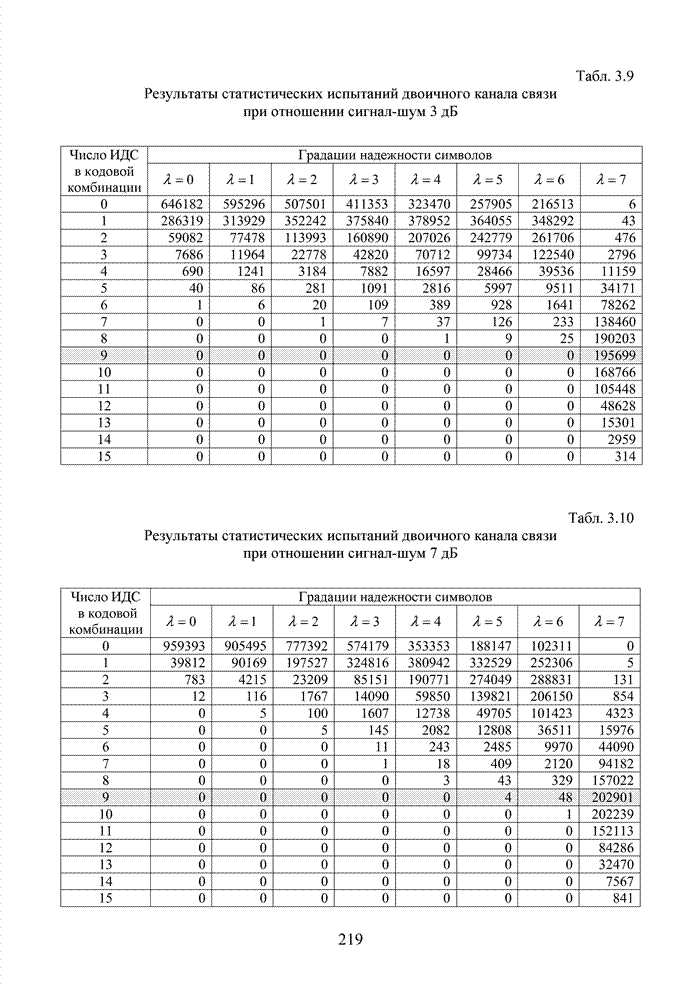
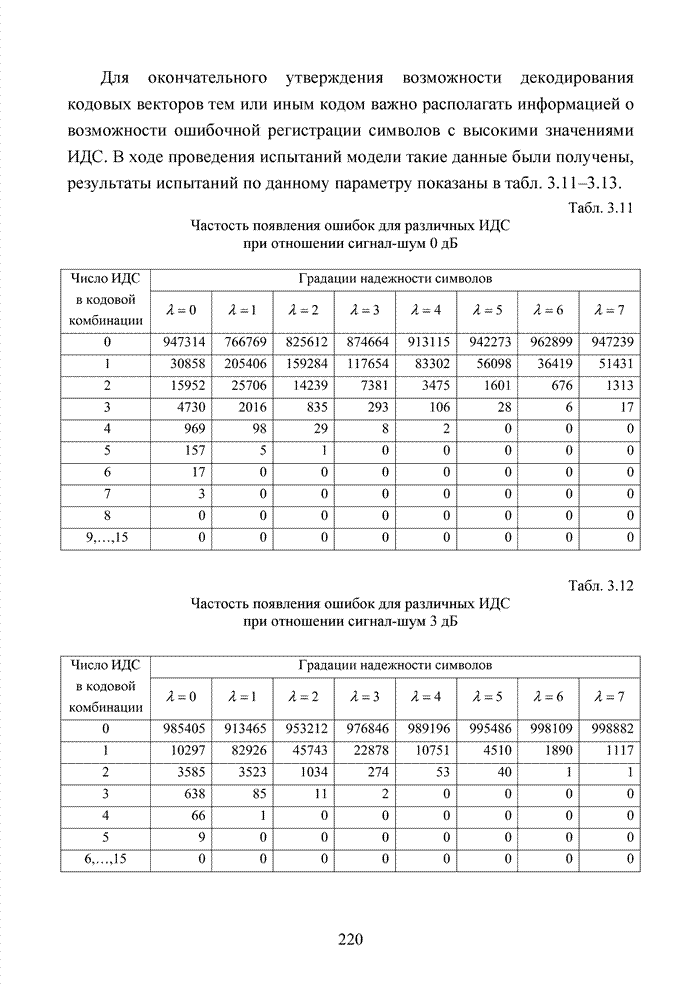
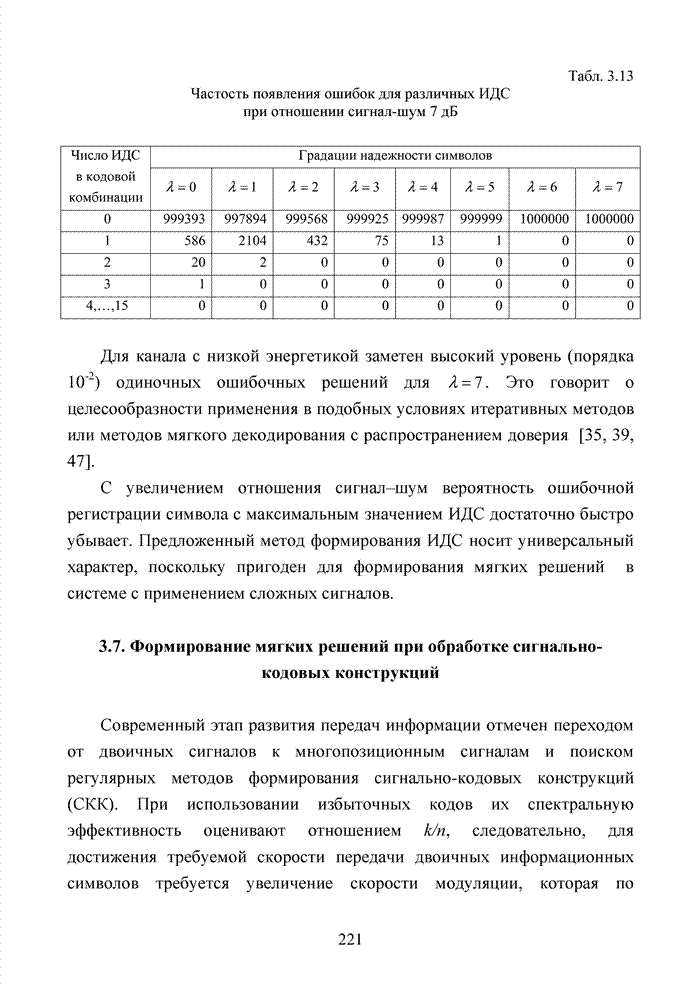
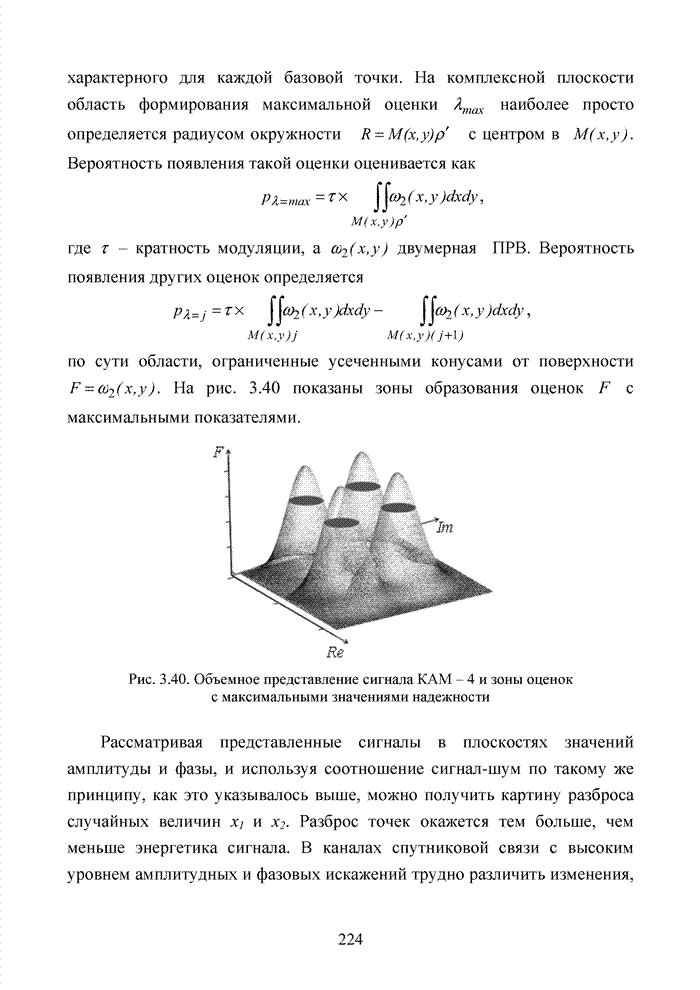
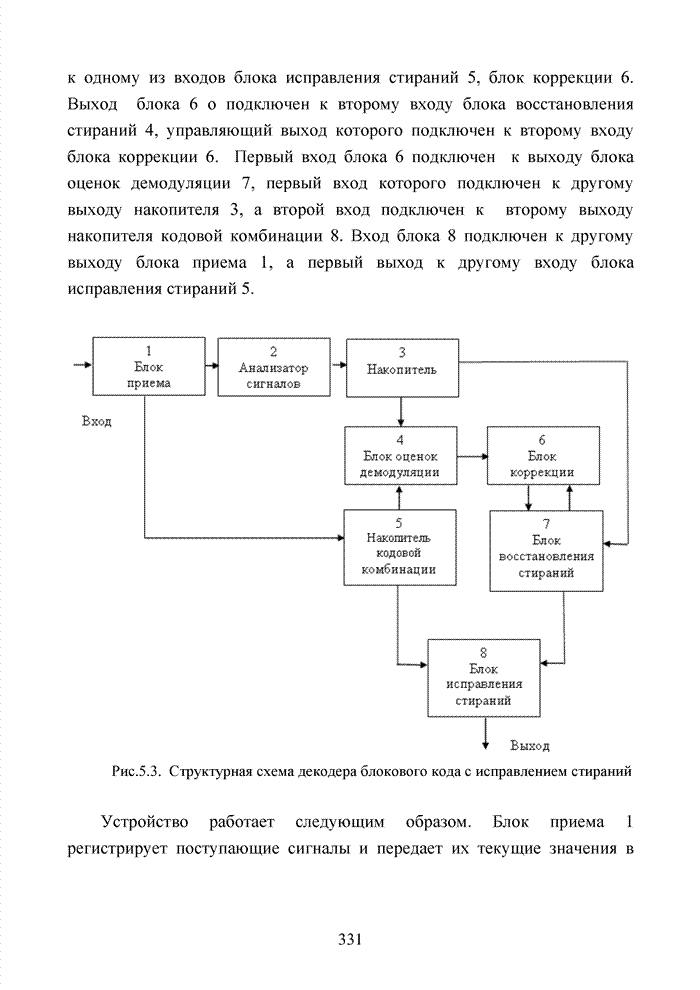
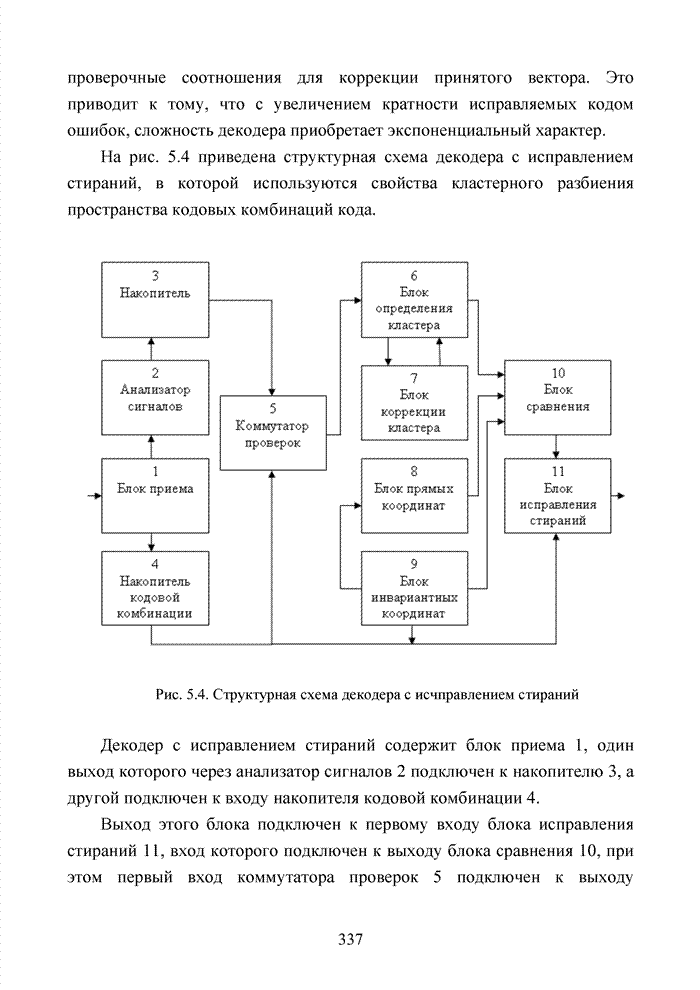
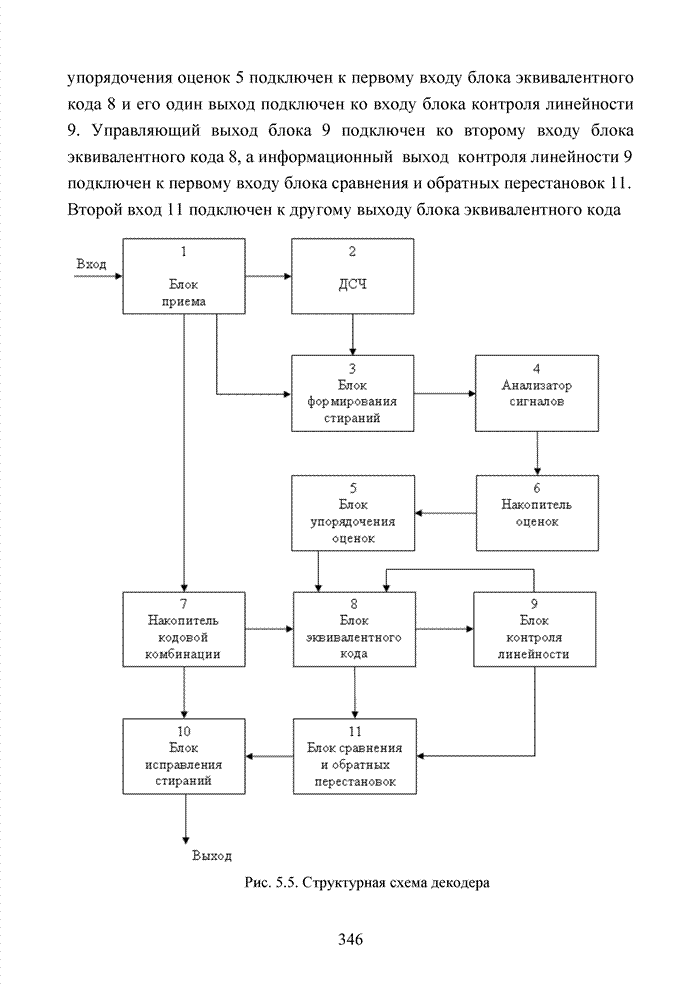
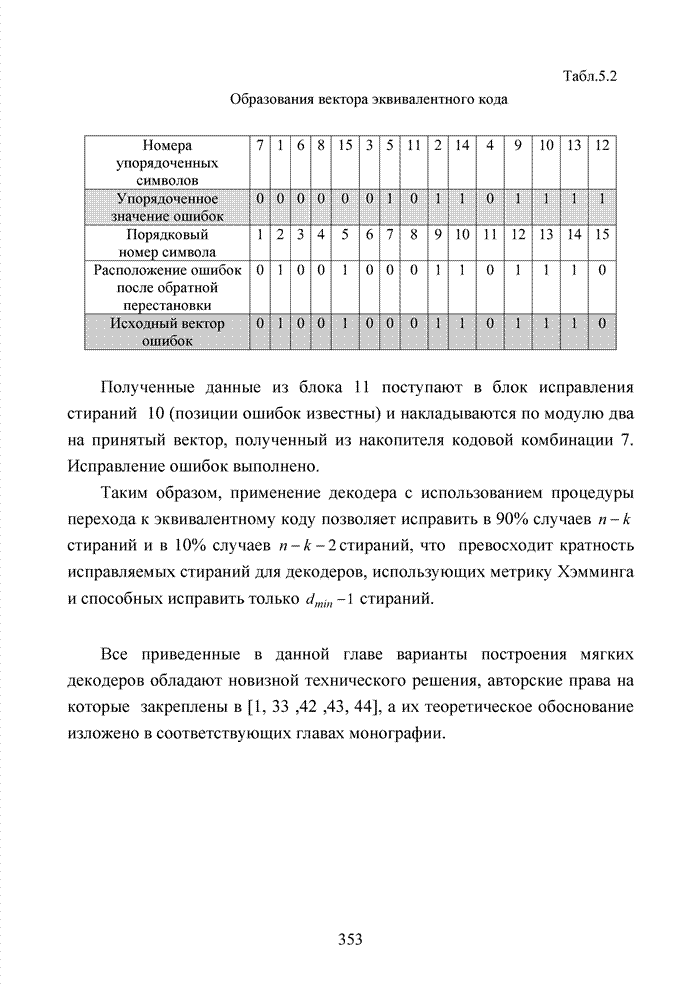
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
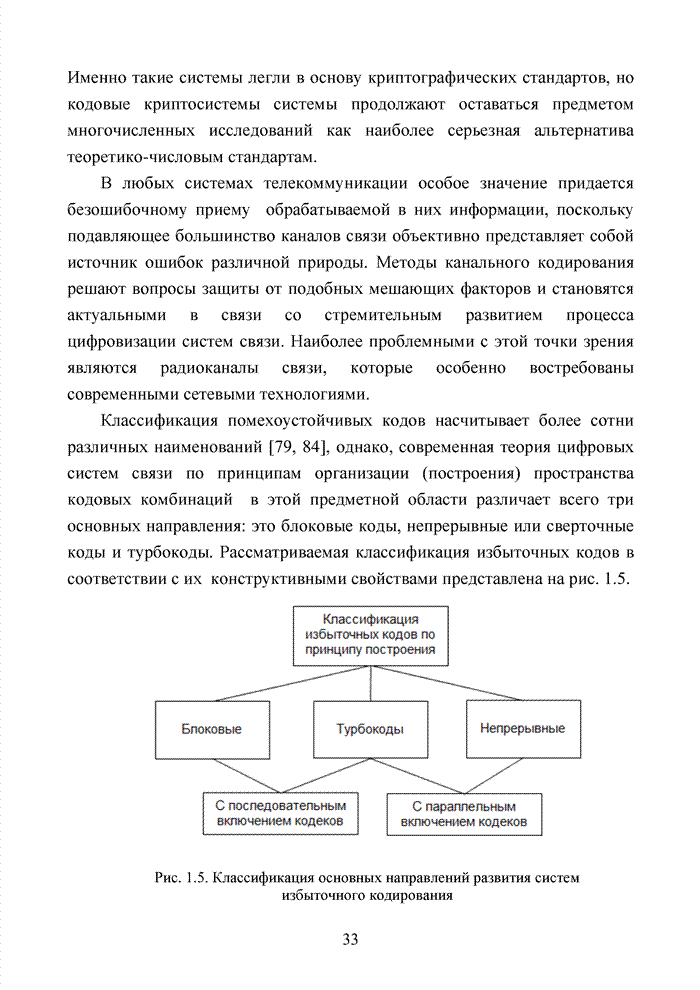
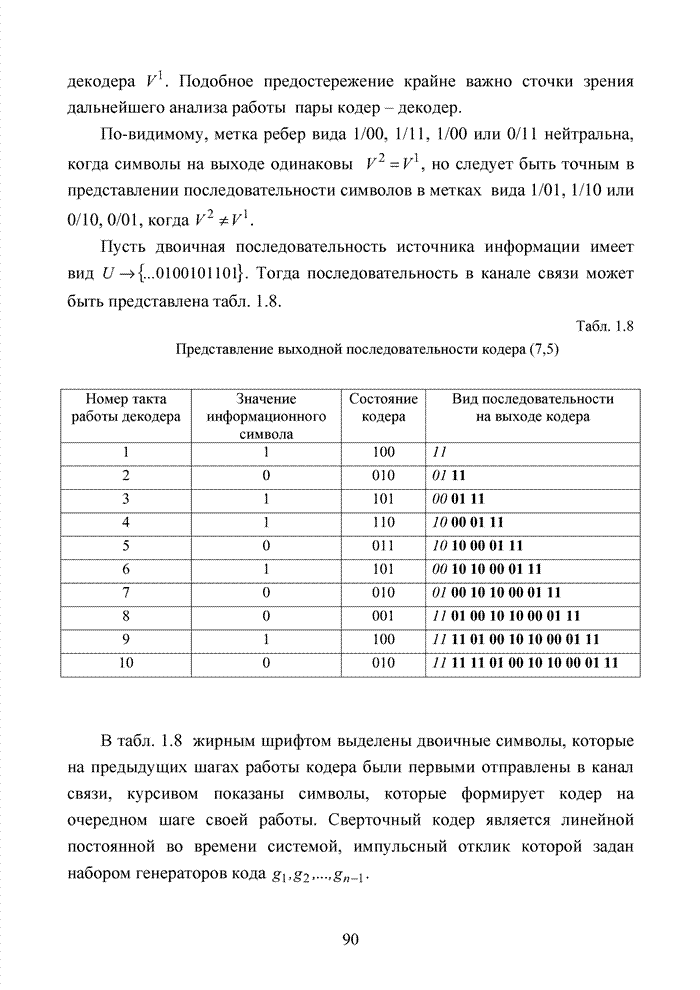
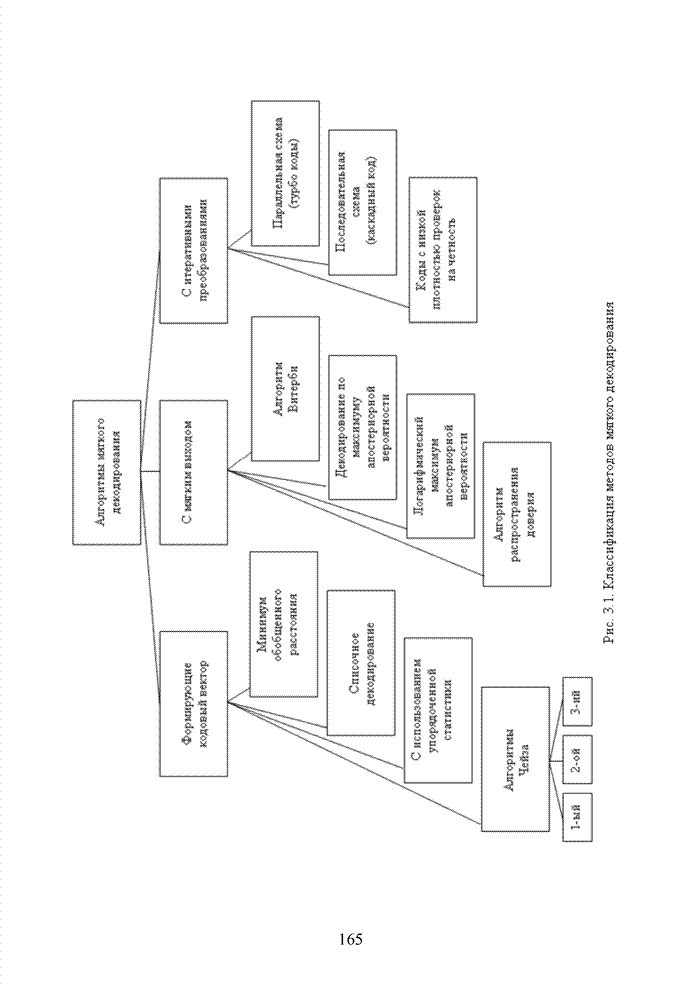
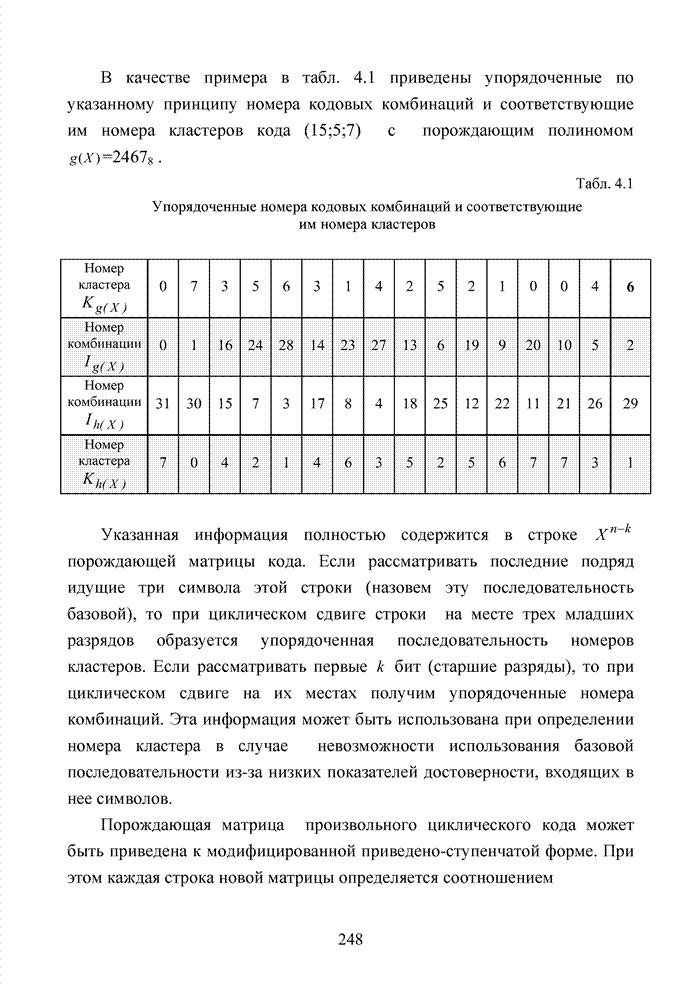
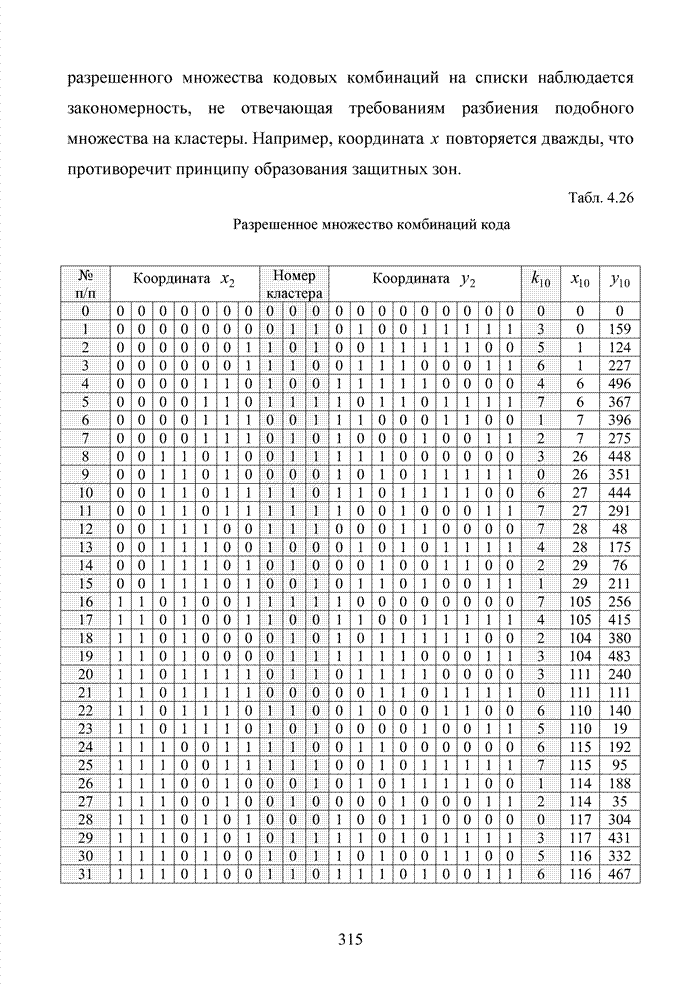
4.5. Декодирование циклических кодов на основе кластерного подхода
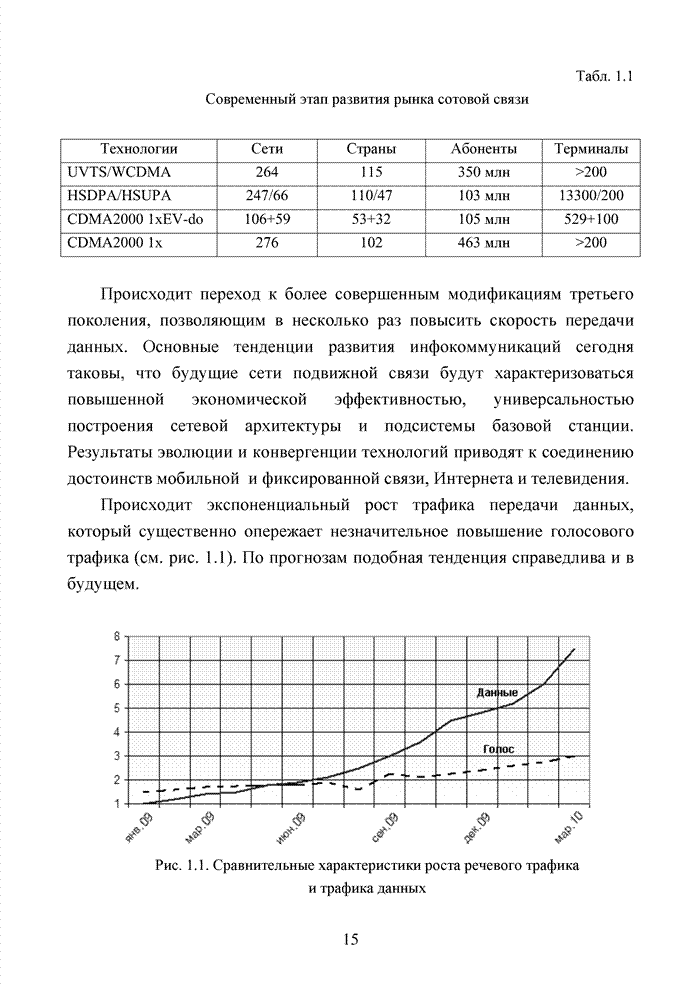
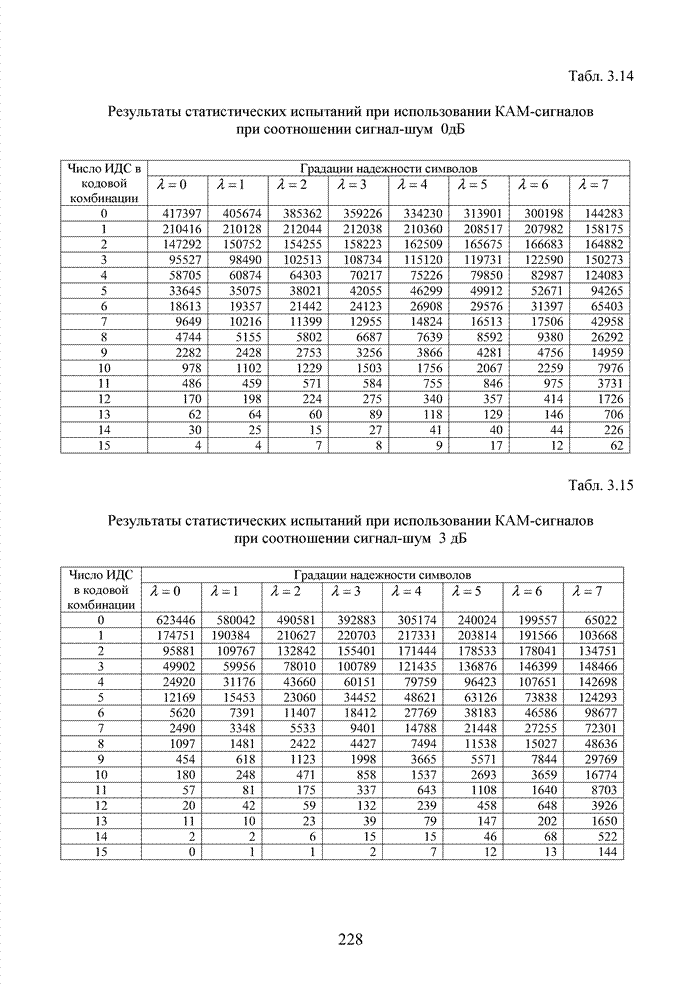
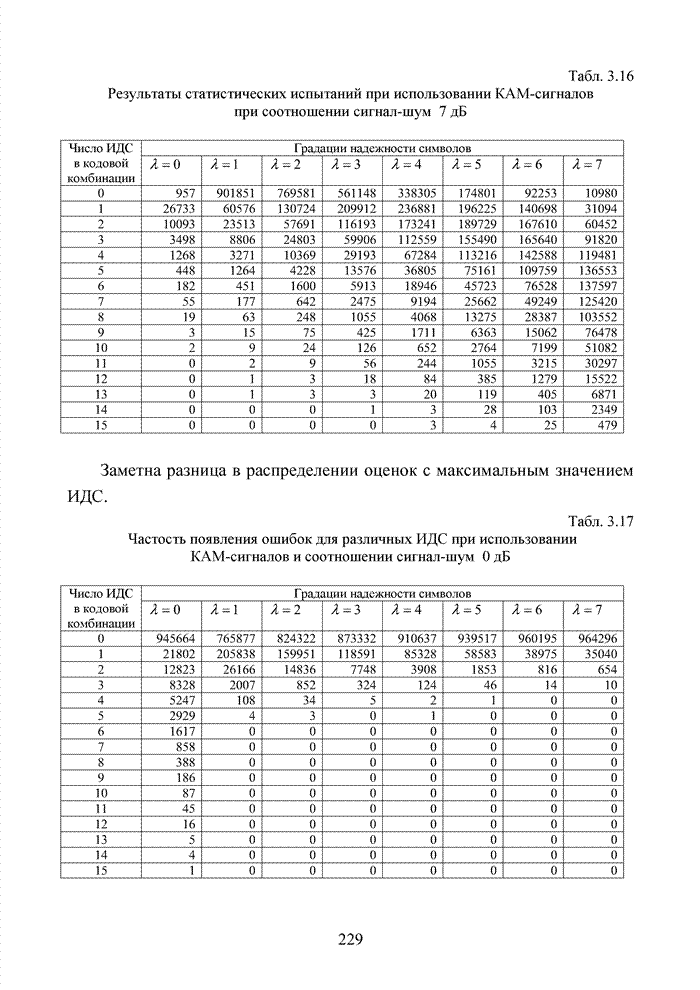
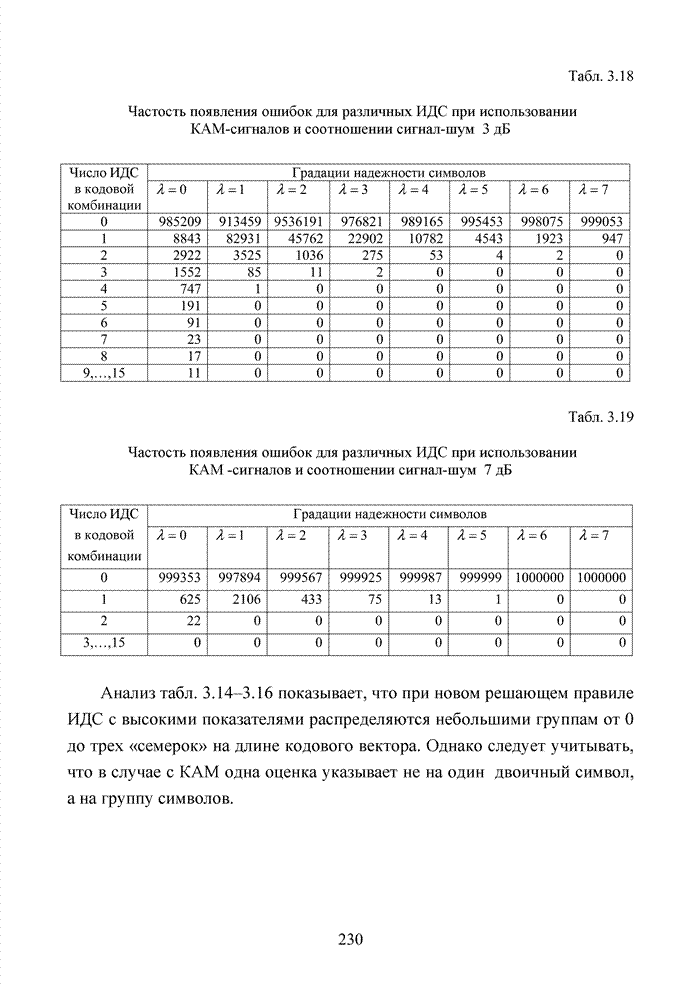
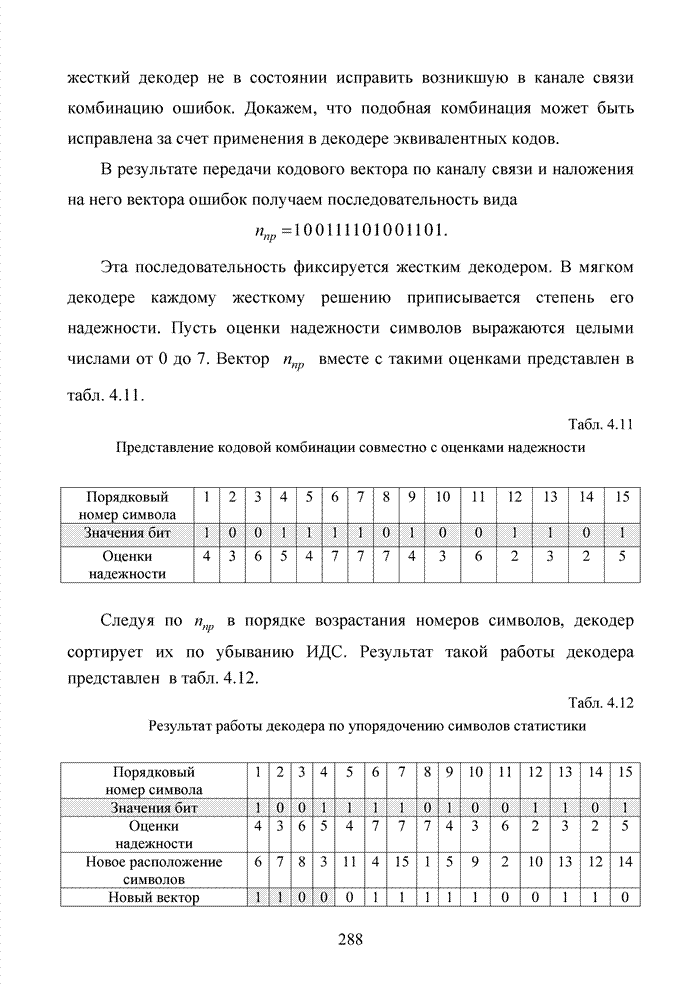
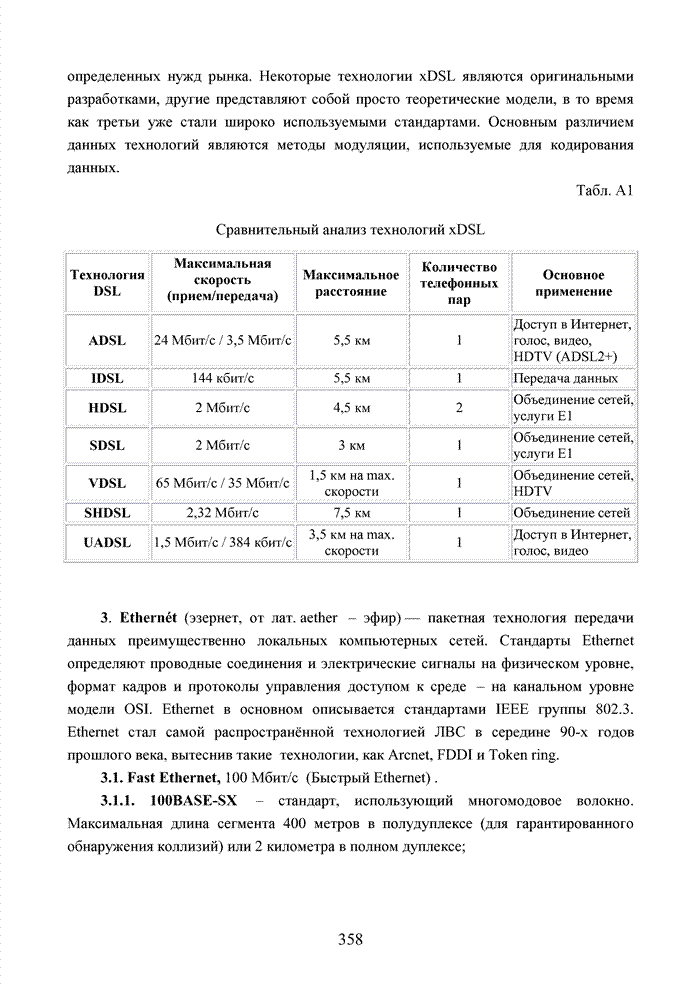
Циклические коды нашли широкое применение в современных системах обмена данными. Особенно удачно эти коды используются для оценки достоверности информации размещенных в заголовках пакетов данных. Применение циклических кодов в современных технологиях представлено в табл. 4.10.
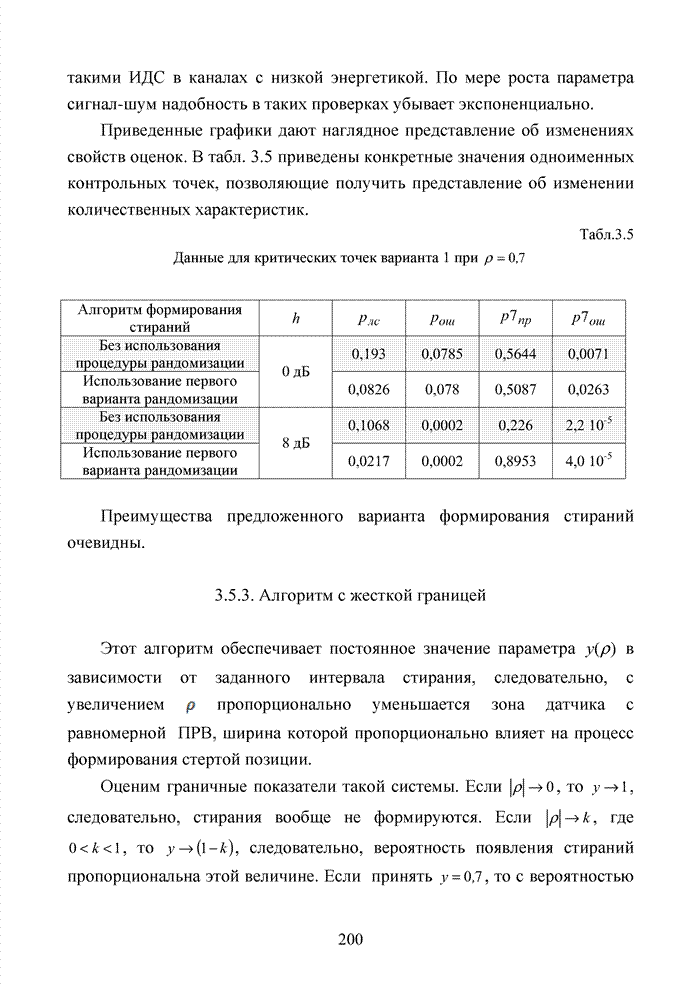
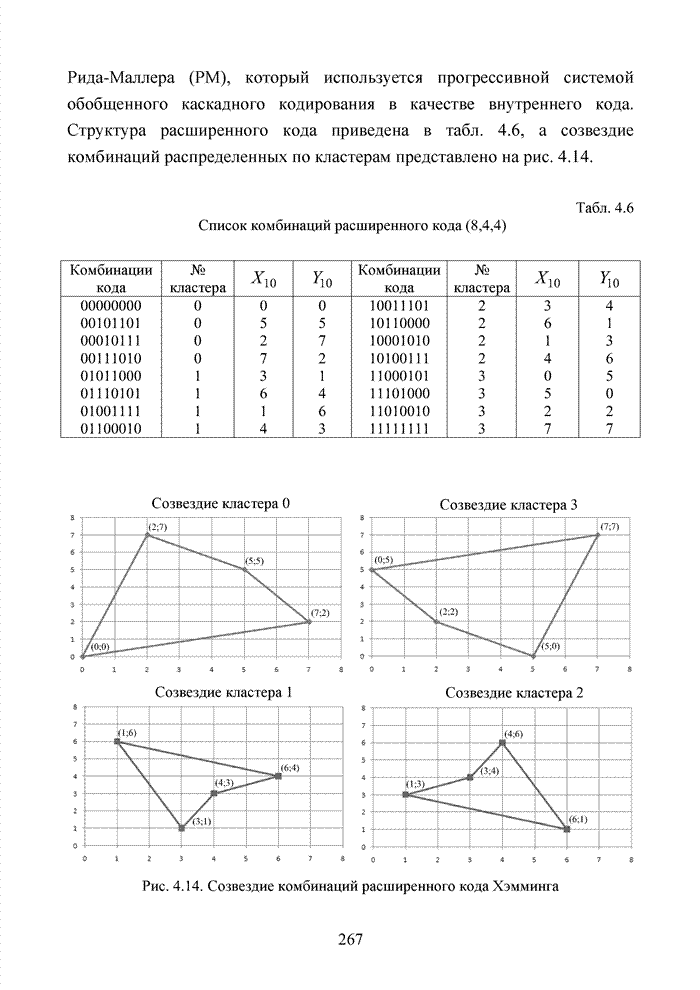
Табл.4.10 Сведения о циклических кодах современных технологий обмена данными
|
Тип циклического кода |
Порождающий многочлен |
Тип технологии |
|
CRC-4 |
|
ISDN |
|
CRC-8 |
|
ATM |
|
CRC-12 |
|
IBM |
|
CRC-16 |
|
IBM |
|
CRC-16 |
|
HDLC и LAPD |
|
CRC-32 |
|
HDLC |
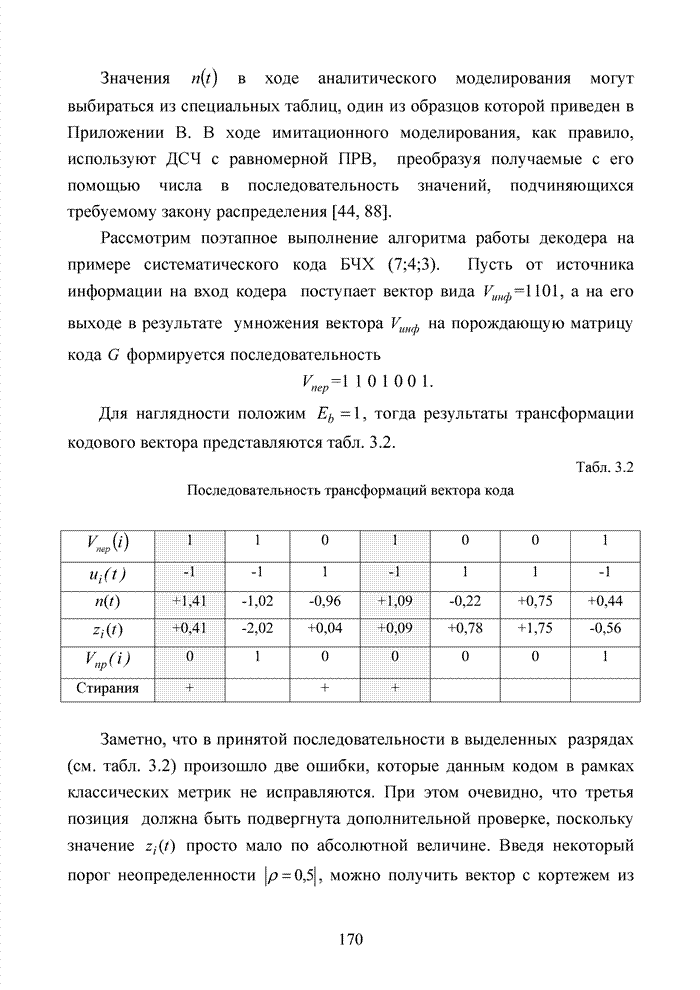
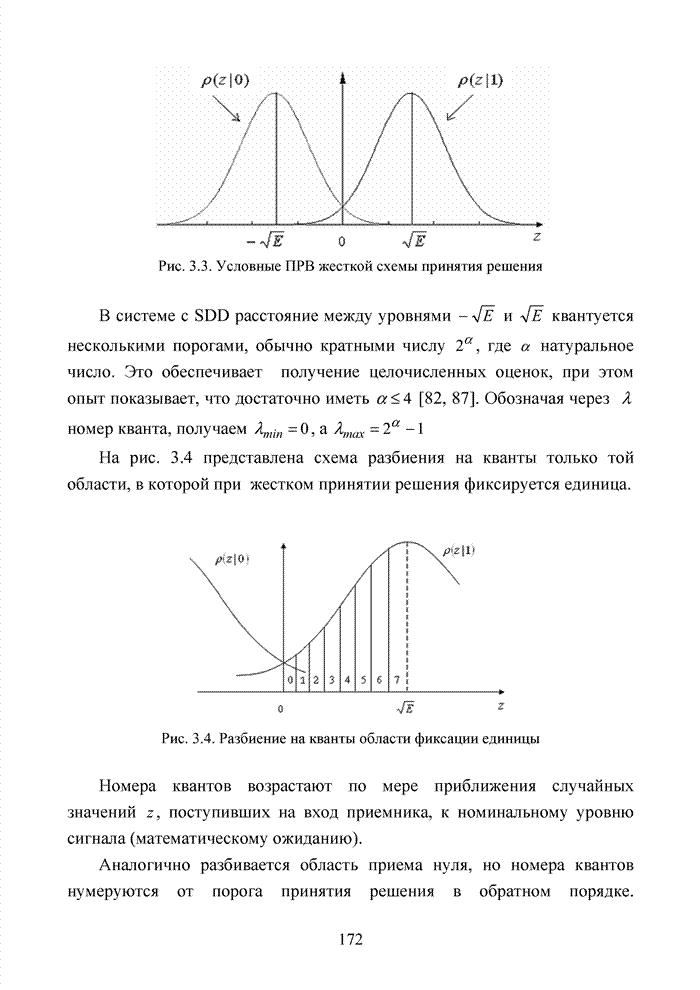
Пусть
задан двоичный циклический ![]() код с порождающим полиномом вида
код с порождающим полиномом вида
![]() ,
,
где ![]() – коэффициенты из
– коэффициенты из ![]() .
.
Пусть весовой спектр кода определен как множество векторов кода
![]() ,
,
здесь через ![]() обозначены
представители прямого кода, задаваемые полиномом
обозначены
представители прямого кода, задаваемые полиномом ![]() , а через
, а через ![]() показаны представители дуального кода,
формируемого порождающим полиномом по схеме
показаны представители дуального кода,
формируемого порождающим полиномом по схеме ![]() .
.
Назначим
произвольно![]() номеров
(
номеров
(![]() ) двоичных
символов для всего разрешенного множества кодовых комбинаций, которые будут
определять признак группы комбинаций (кластера). Тогда число комбинаций такого
кода, входящих в кластер одного признака, определяется соотношением
) двоичных
символов для всего разрешенного множества кодовых комбинаций, которые будут
определять признак группы комбинаций (кластера). Тогда число комбинаций такого
кода, входящих в кластер одного признака, определяется соотношением ![]() . При
. При ![]() все кодовые векторы
входят в один кластер (система обычного алгебраического декодирования). При
выборе
все кодовые векторы
входят в один кластер (система обычного алгебраического декодирования). При
выборе ![]() образуется
совокупность
образуется
совокупность ![]() кластеров.
кластеров.
Из
любого циклического кода путем линейных преобразований над строками
порождающей матрицы ![]()
![]() кода можно образовать систематический код с матрицей
кода можно образовать систематический код с матрицей ![]() , порождающей тот же код. В единичной
матрице
, порождающей тот же код. В единичной
матрице ![]() при
при ![]() матрицы
матрицы ![]() всегда можно выделить
единичную матрицу меньшей размерности
всегда можно выделить
единичную матрицу меньшей размерности ![]() . Путем линейных преобразований над
строками матрицы
. Путем линейных преобразований над
строками матрицы ![]() ,
можно получить двоичное поле Галуа степени расширения
,
можно получить двоичное поле Галуа степени расширения ![]() , при этом комбинации поля
, при этом комбинации поля ![]() будут определять
признак кластера или его номер. Поле
будут определять
признак кластера или его номер. Поле ![]() содержится в поле
содержится в поле ![]() ровно
ровно ![]() раз, следовательно, число
кодовых комбинаций в одном кластере будет определяться этим же соотношением.
При
раз, следовательно, число
кодовых комбинаций в одном кластере будет определяться этим же соотношением.
При ![]() число
кластеров равно числу разрешенных кодовых комбинаций, т.е. в кластер входит
только одна кодовая комбинация.
число
кластеров равно числу разрешенных кодовых комбинаций, т.е. в кластер входит
только одна кодовая комбинация.
Следует
отметить важное для декодера свойство: при разбиении пространства кодовых
векторов двоичного циклического кода на кластеры значения координат кодовых
векторов остаются неизменными в пределах каждого кластера при условии, что
сохраняется заданная конфигурация следования номеров символов, определяющих
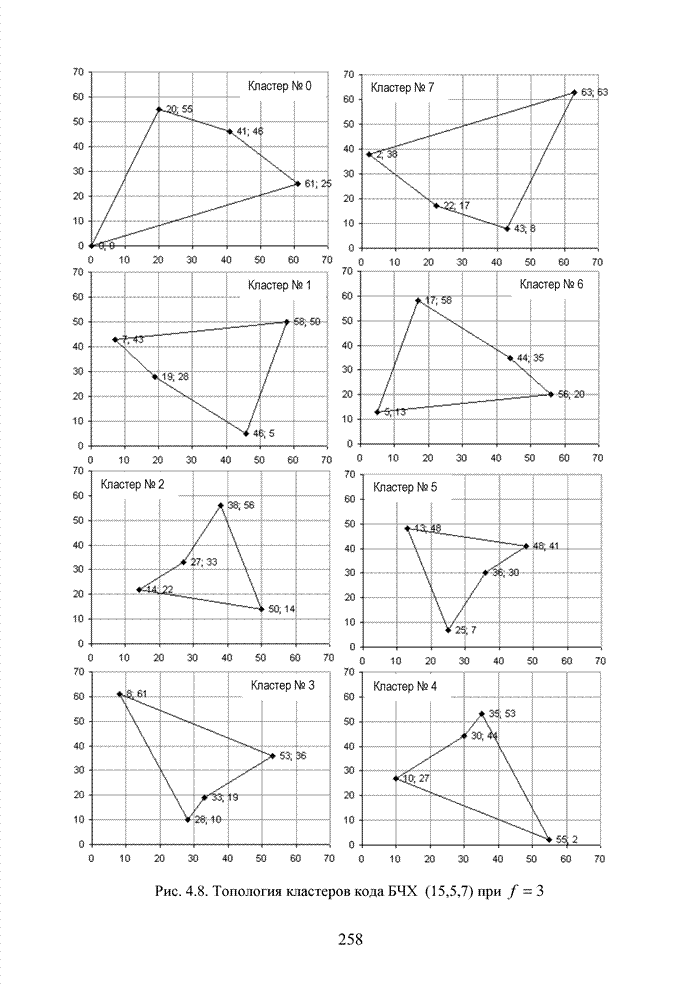
признак кластера. Пусть для кода БЧХ (15,5) при ![]() признак кластера определяется разрядами
признак кластера определяется разрядами ![]() , а оставшиеся разряды,
разбитые на две части, определяют координаты векторов на плоскости кластера.
Если в качестве признака кластера в новых условиях выбрать разряды
, а оставшиеся разряды,
разбитые на две части, определяют координаты векторов на плоскости кластера.
Если в качестве признака кластера в новых условиях выбрать разряды ![]() или
или ![]() , то координаты
векторов кластеров не претерпят никаких изменений. Указанный признак следует
из свойств цикличности кода.
, то координаты
векторов кластеров не претерпят никаких изменений. Указанный признак следует
из свойств цикличности кода.
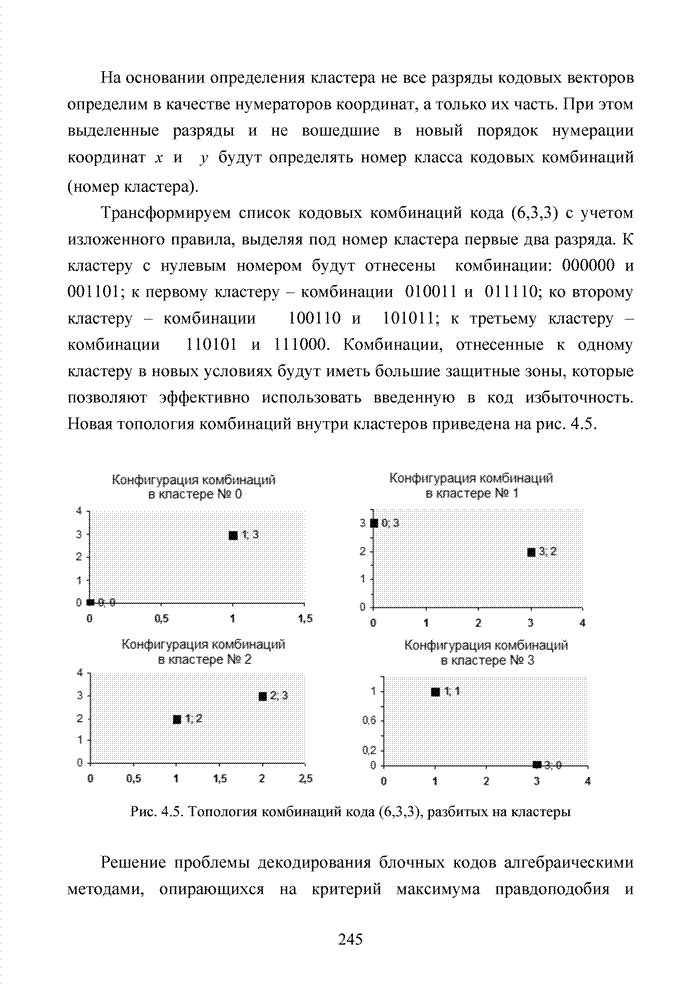
Комбинация
кода, содержащая ![]() и
входящая в
и
входящая в ![]() ,
на местах старших разрядов должна содержать
,
на местах старших разрядов должна содержать ![]() нулевых символов. Не теряя общности
рассуждений предположим, что
нулевых символов. Не теряя общности
рассуждений предположим, что ![]() . Тогда номер кластера по первым
. Тогда номер кластера по первым ![]() разрядам для
рассматриваемой комбинации в
разрядам для
рассматриваемой комбинации в ![]() -значной системе счисления будет иметь
вид
-значной системе счисления будет иметь
вид ![]() .
.
Выполним
циклический сдвиг данной кодовой комбинации на один двоичный символ влево и
вновь, выделяя ![]() разрядов,
получим номер кластера в двоичной системе счисления вида
разрядов,
получим номер кластера в двоичной системе счисления вида ![]() . Затем
. Затем
![]()
и далее до завершения цикла.
Таким
образом, номера кластеров будут упорядочены в соответствии с особенностями
распределения единичных коэффициентов ![]() в порождающем полиноме
в порождающем полиноме ![]() , а в окончательном
виде результат может быть представлен детерминированной для данных
, а в окончательном
виде результат может быть представлен детерминированной для данных ![]() и
и ![]() последовательностью чисел
последовательностью чисел
![]()
![]()
![]()
![]() …
… ![]() .
.
Назовем
полученную на основе комбинации порождающего полинома последовательность
номеров кластеров базовой и обозначим ее как ![]() . Циклическое смещение номеров базовой
последовательности кластеров приведет к новой комбинации кластеров,
принадлежащей данному коду. Она будет иметь вид
. Циклическое смещение номеров базовой
последовательности кластеров приведет к новой комбинации кластеров,
принадлежащей данному коду. Она будет иметь вид
![]()
![]()
![]() …
… ![]()
![]() .
.
Предположим,
что группа векторов веса ![]() определят общее число кодовых векторов
данного веса, а другие представители весов прямого кода отсутствуют. Исключим
из дальнейшего анализа чисто нулевой вектор, который при любом сочетании из
определят общее число кодовых векторов
данного веса, а другие представители весов прямого кода отсутствуют. Исключим
из дальнейшего анализа чисто нулевой вектор, который при любом сочетании из ![]() разрядов определяет
номер нулевого кластера, а так же единичный элемент группы, который при любом
сочетании из
разрядов определяет
номер нулевого кластера, а так же единичный элемент группы, который при любом
сочетании из ![]() разрядов
однозначно обеспечивает получение кластера с номером
разрядов
однозначно обеспечивает получение кластера с номером ![]() . Циклические сдвиги вектора
веса
. Циклические сдвиги вектора
веса ![]() приведет
к образованию
приведет
к образованию ![]() циклически
сдвинутых последовательностей номеров кластеров представителя данного веса.
циклически
сдвинутых последовательностей номеров кластеров представителя данного веса.
В
комбинациях производных от полинома ![]() будет ровно
будет ровно ![]() одинаковых номеров кластеров, а другая
половина кластеров с таким же номером будет в составе комбинаций, образованных
от циклических трансформаций порождающего полинома
одинаковых номеров кластеров, а другая
половина кластеров с таким же номером будет в составе комбинаций, образованных
от циклических трансформаций порождающего полинома ![]() дуального кода.
дуального кода.
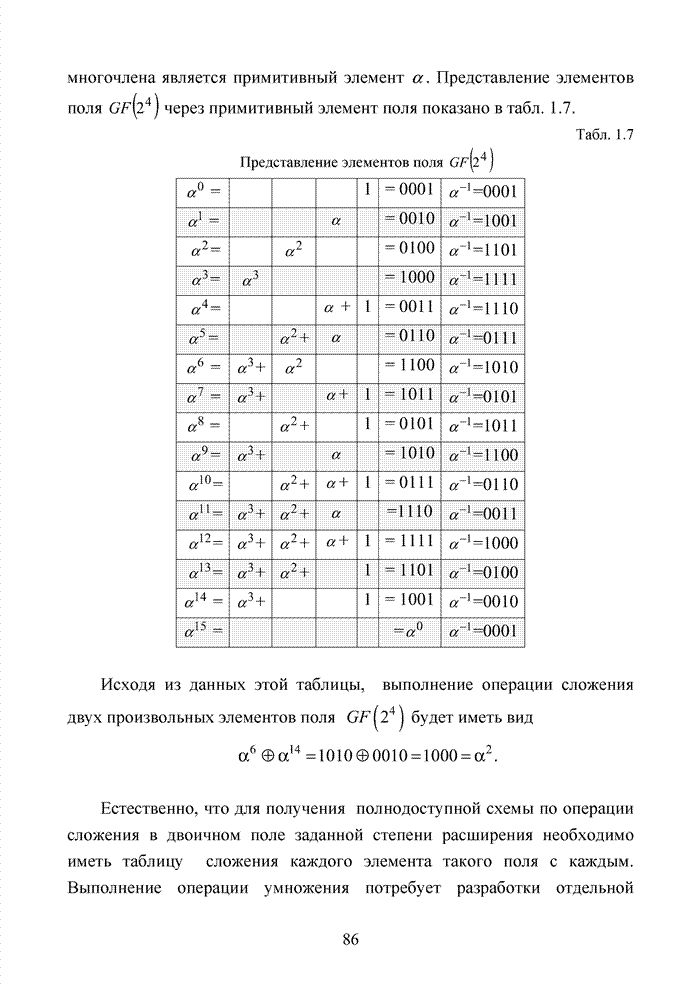
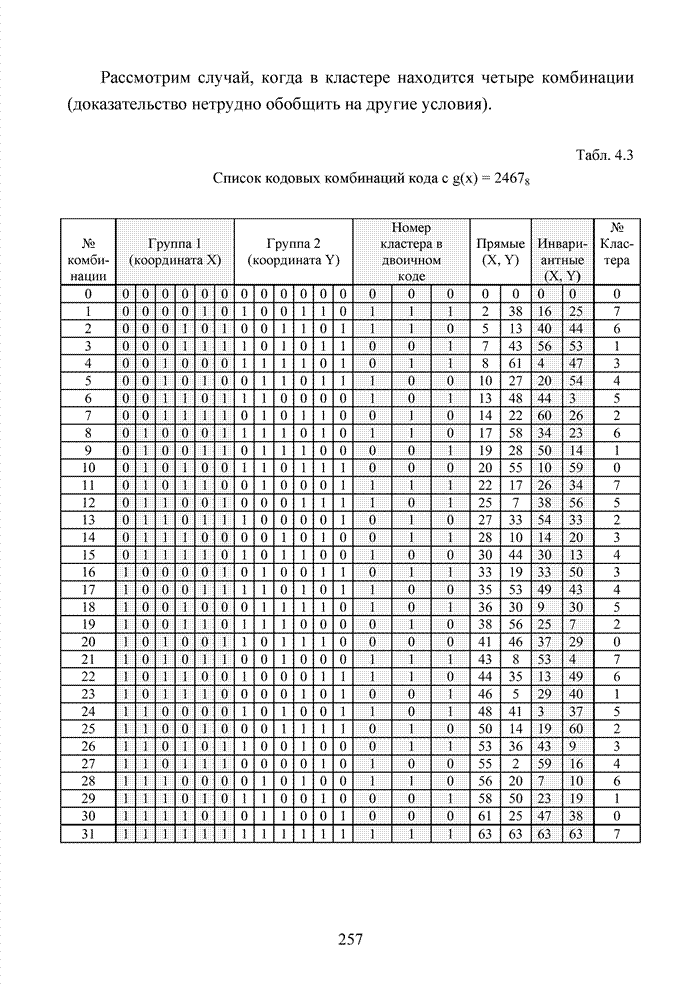
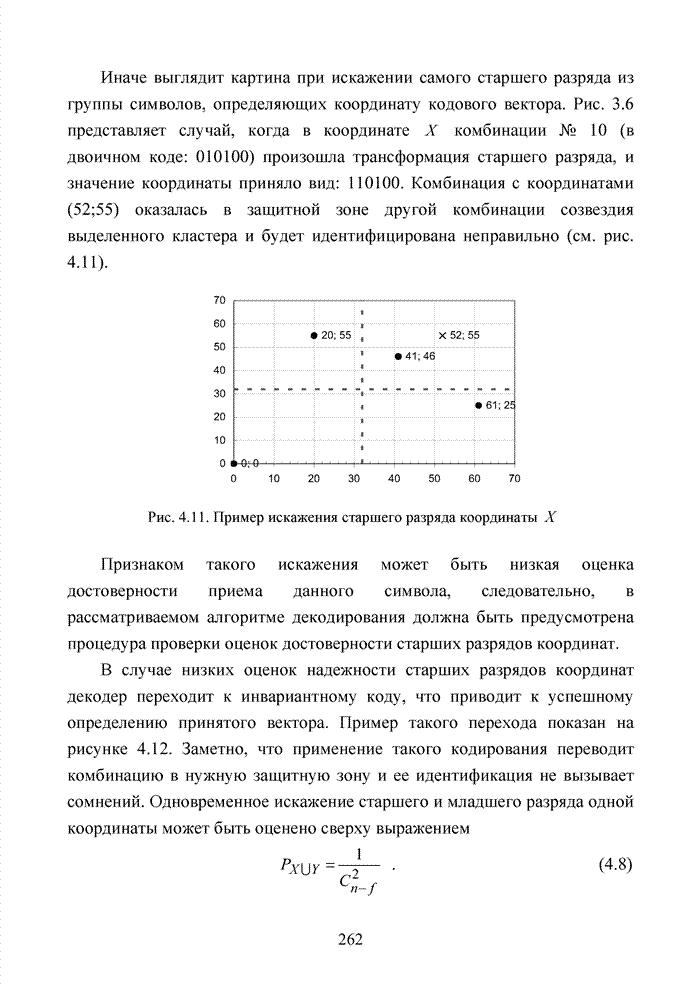
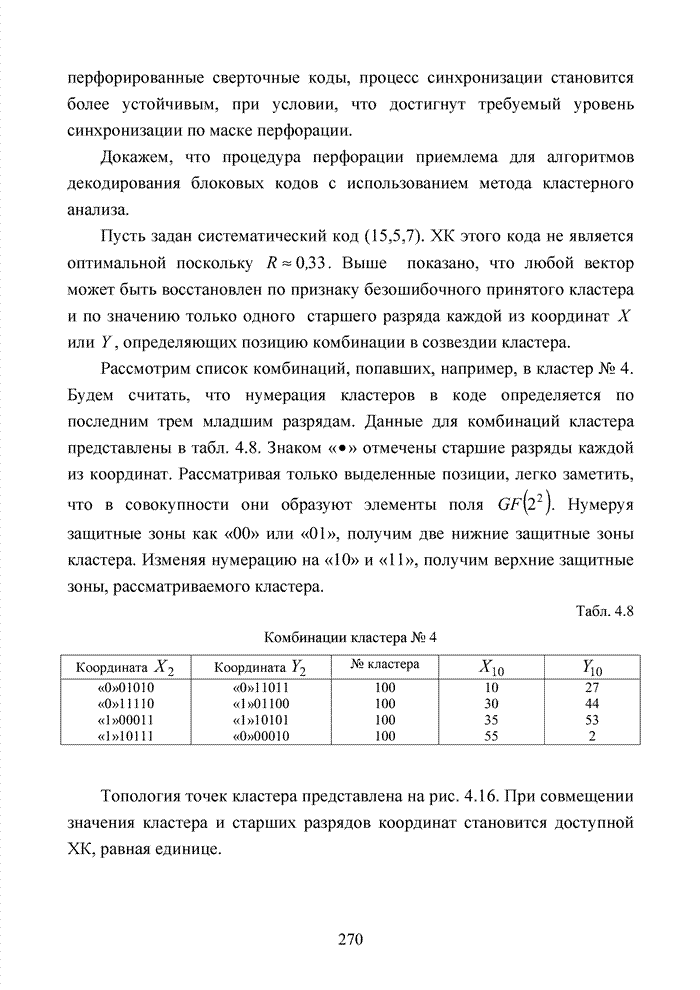
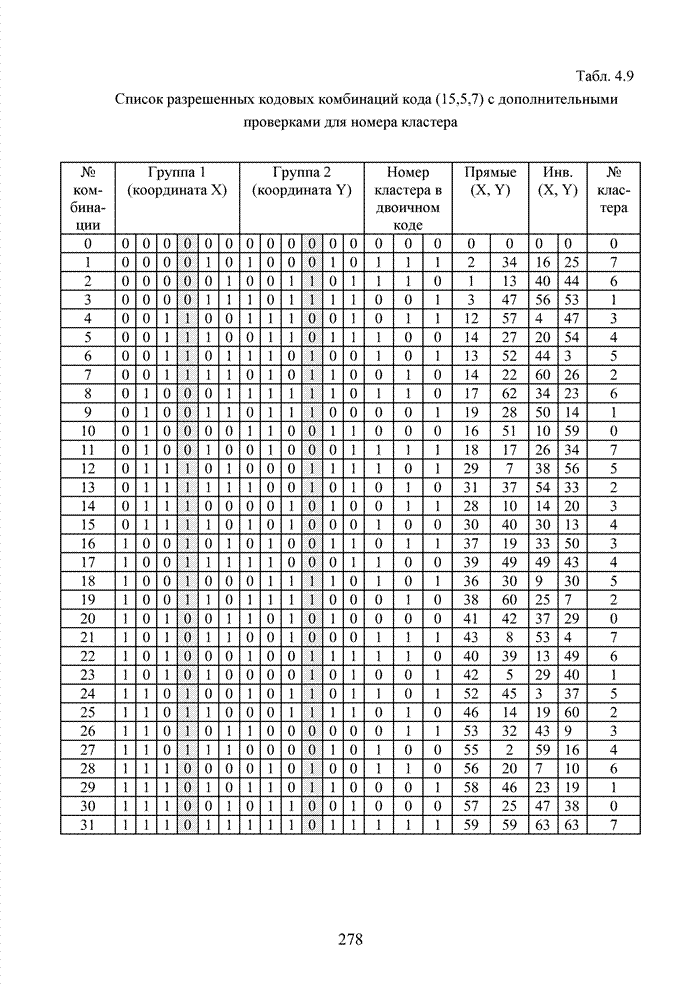
Рассмотрим
порождающий полином кода БЧХ (15,5), заданный в виде 24678.
Определим ![]() и
выделим три бита указанной кодовой комбинации, находящиеся в левых разрядах.
Тогда получим значение
и
выделим три бита указанной кодовой комбинации, находящиеся в левых разрядах.
Тогда получим значение ![]() . Значение
. Значение ![]() после смещения на один разряд вправо
принимает вид
после смещения на один разряд вправо
принимает вид ![]() .
Представляя подобным образом другие значения
.
Представляя подобным образом другие значения ![]()
![]() в десятичной системе счисления, получим
последовательность номеров кластеров в виде ряда
в десятичной системе счисления, получим
последовательность номеров кластеров в виде ряда
{0 0 1 2 5 2 4 1 3 6 5 3 7 6 4}.
Важным
свойством такой последовательности является строгая зависимость в смене номеров
кластеров, зависящая только от структуры порождающего полинома ![]() . Аналогичную последовательность
следует получить и для дуального кода, вытекающую из особенностей
. Аналогичную последовательность
следует получить и для дуального кода, вытекающую из особенностей ![]() . При этом номера
кластеров определяются по модулю числа
. При этом номера
кластеров определяются по модулю числа ![]() , т.е.
, т.е.
{7 7 6 5 2 5 3 6 4 1 2 4 0 1 3}.
Приемнику
известны обе последовательности номеров, поэтому он способен восстановить
номер переданного кластера в случае искажения его помехой. Действительно, если
по индексам достоверности символов становится ясно, что позиции разрядов
кластера искажены (они оказались приняты с низкими оценками надежности) декодер
в принятом кодов векторе определяет ![]() надежных разрядов и, выполняя
циклические сдвиги, осуществляет подсчет числа шагов до оговоренных с
передатчиком позиций, определяющих номера кластеров.
надежных разрядов и, выполняя
циклические сдвиги, осуществляет подсчет числа шагов до оговоренных с
передатчиком позиций, определяющих номера кластеров.
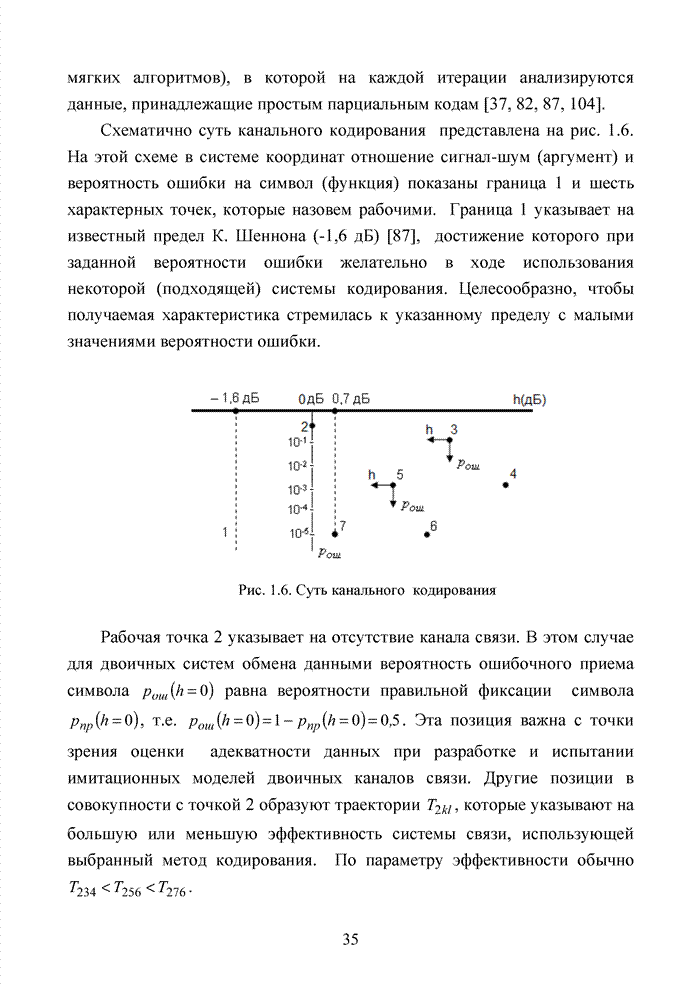
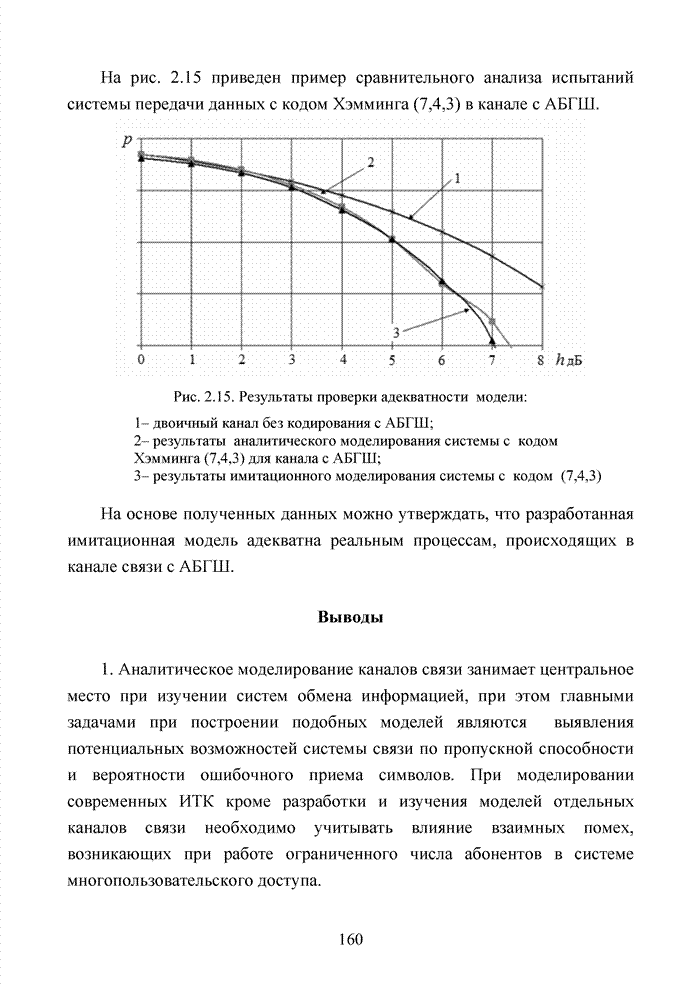
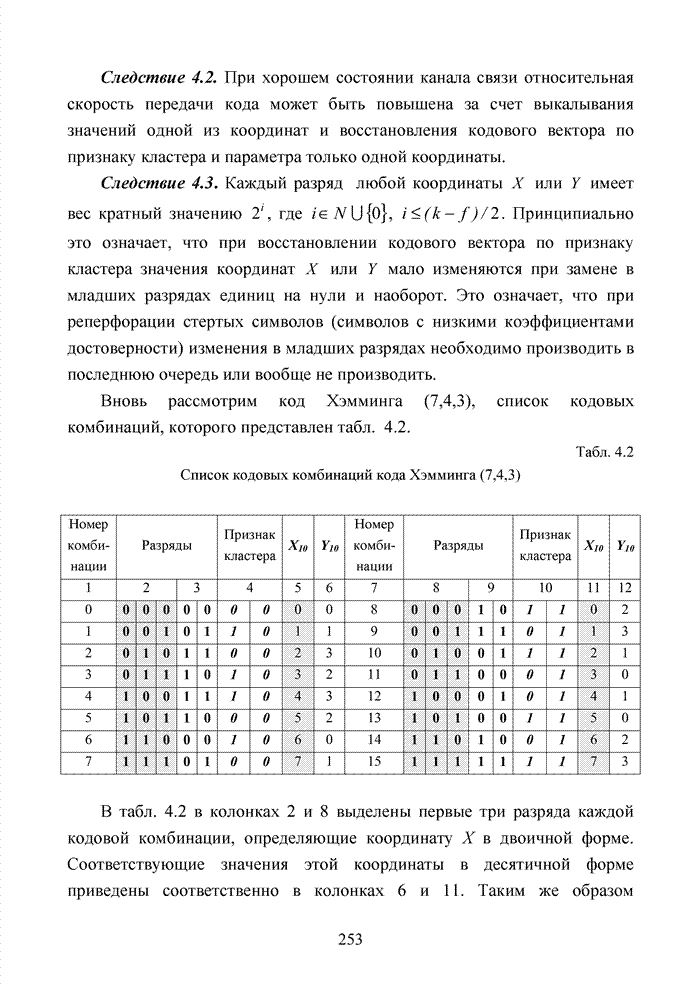
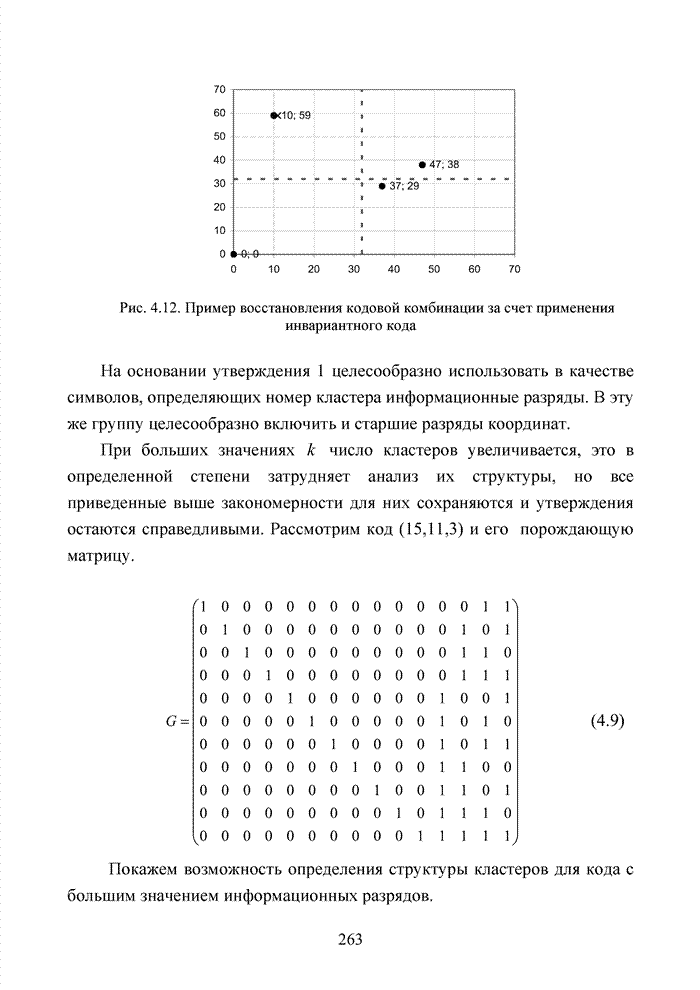
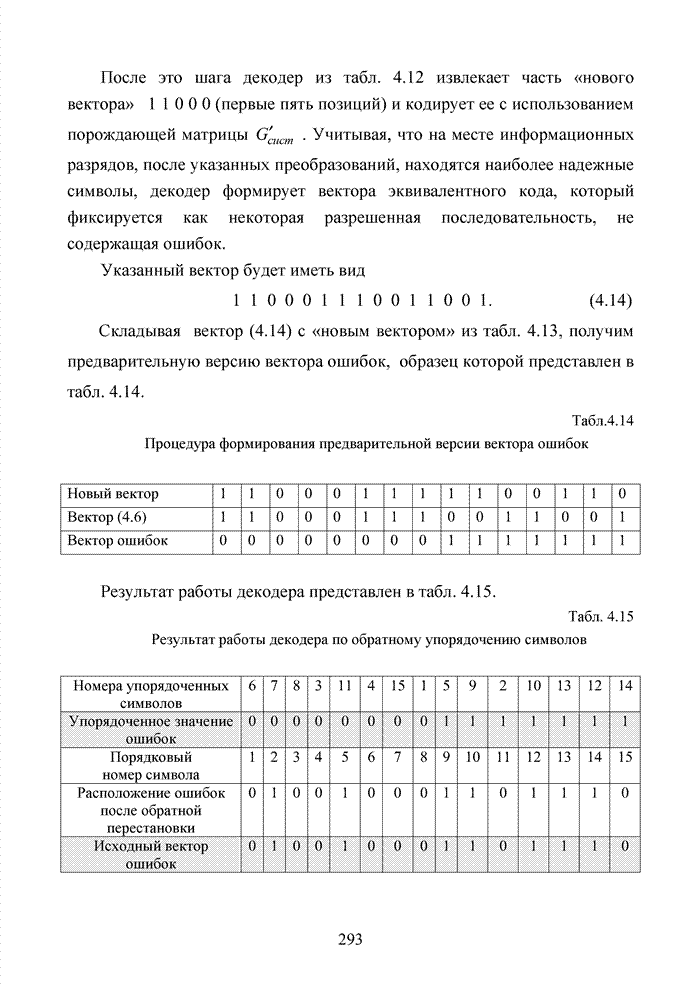
Например, если в канонической системе обмена данными номера кластеров определялись правыми разрядами, а надежно приняты позиции, соответствующие кластеру 6, находящемуся между 3 и 5 кластерами (выделено жирным), то, выполнив пять шагов вправо, декодер устанавливает, что это был кластер 4. Следовательно, группа комбинаций, принадлежащих данному кластеру, устанавливается сразу, а не по алгоритму последовательного анализа комбинация за комбинацией, как это осуществляется при классическом списочном декодировании.
Можно
утверждать, что информация о кластере находится в любой группе, состоящей из ![]() надежно принятых
символов кодового вектора, не обязательно следующих друг за другом.
надежно принятых
символов кодового вектора, не обязательно следующих друг за другом.
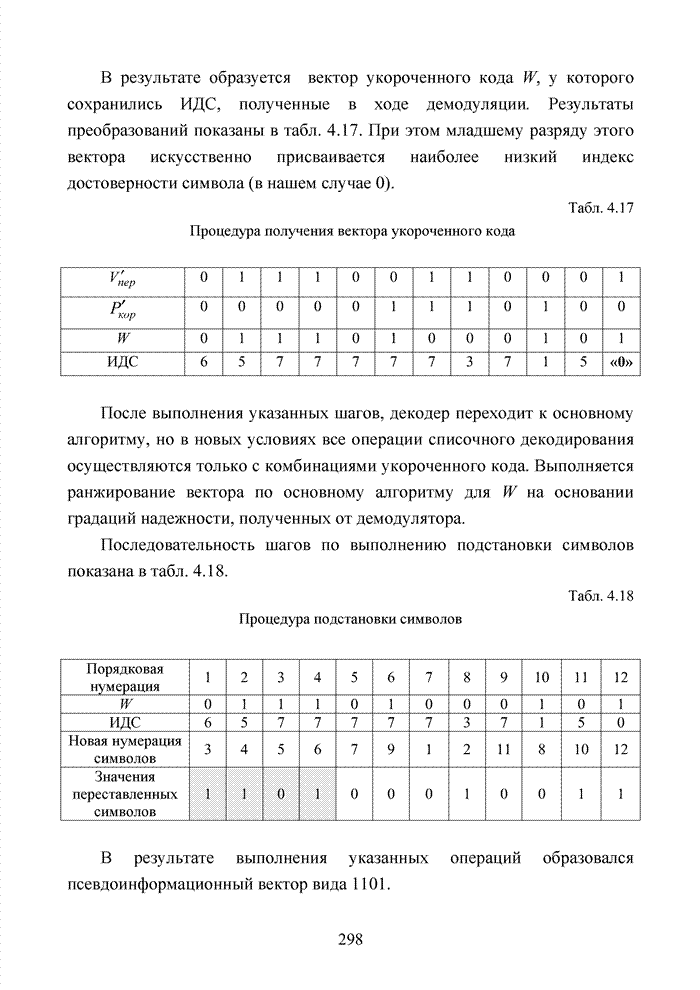
Описанный
алгоритм выявления номера параллельной группы (номера кластера) не является
безупречным, поскольку эти номера определяются безызбыточным кодом и искажение
одного из ![]() символов
немедленно влечет неправильное определение номера группы (соответственно
списка). Поэтому необходимы дополнительные проверки с использованием
проверочных соотношений проверочной матрицы кода.
символов
немедленно влечет неправильное определение номера группы (соответственно
списка). Поэтому необходимы дополнительные проверки с использованием
проверочных соотношений проверочной матрицы кода.
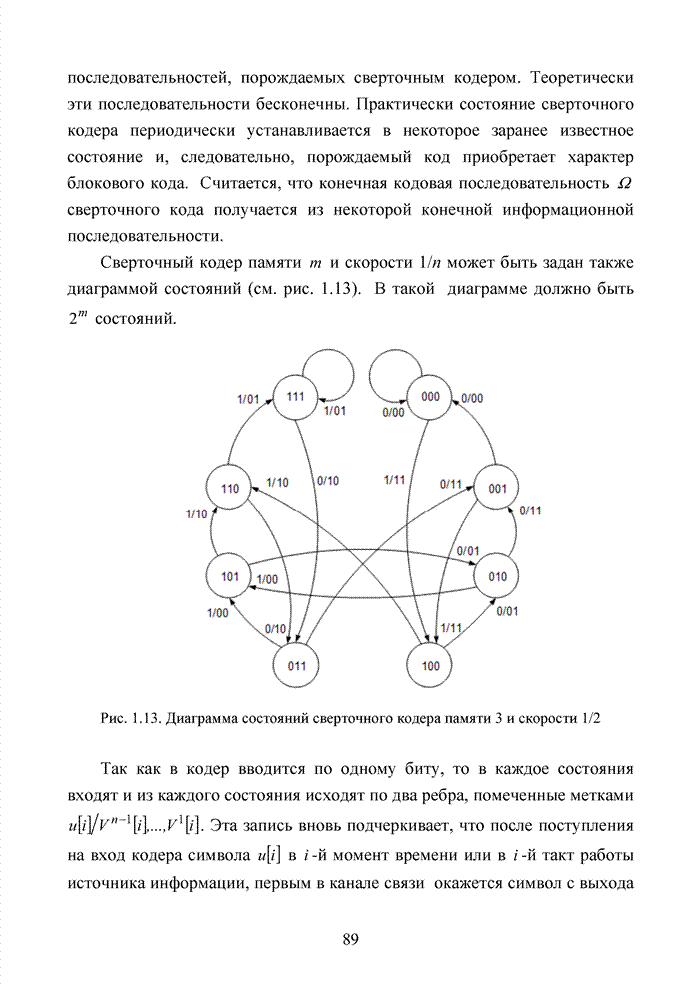
Рассмотрим алгоритм декодирования принятой кодовой комбинации циклического кода по идентификации номера кластера.
Шаг
1. Декодер по мягким
решениям определяет ![]() наиболее
надежных позиций в принятом кодовом векторе.
наиболее
надежных позиций в принятом кодовом векторе.
Шаг 2. Определяется группа подряд идущих надежных позиций. Если такая группа существует, то декодер приступает к поиску номера кластера, выполняя шаг 4. Если надежные символы следуют в разбивку, декодер выполняет шаг 3.
Шаг
3. Декодер смещает
группу надежных символов в зону информационных разрядов и выполняет проверки по
проверочным соотношениям, восстанавливая, те символы, которые могут образовать ![]() надежных позиций. При
этом используются свойства графа Таннера. Делается обратный отсчет и
выполняется шаг 2.
надежных позиций. При
этом используются свойства графа Таннера. Делается обратный отсчет и
выполняется шаг 2.
Шаг
4. Используя
циклические сдвиги ![]() и
и
![]() в кластерном
представлении, декодер определяет номер кластера и старшие разряды координат
принятого кодового вектора. Декодирование завершается.
в кластерном
представлении, декодер определяет номер кластера и старшие разряды координат
принятого кодового вектора. Декодирование завершается.
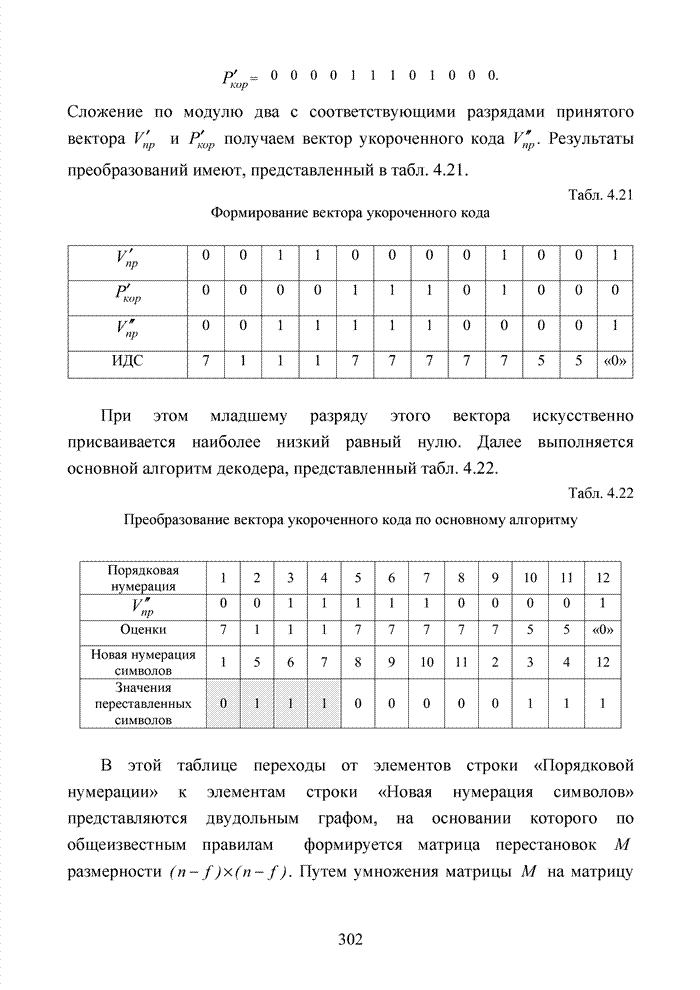
Параметр
![]() можно
подобрать таким образом, чтобы совместно с необходимыми шагами по определению
номера кластера выявить весь информационный вектор.
можно
подобрать таким образом, чтобы совместно с необходимыми шагами по определению
номера кластера выявить весь информационный вектор.
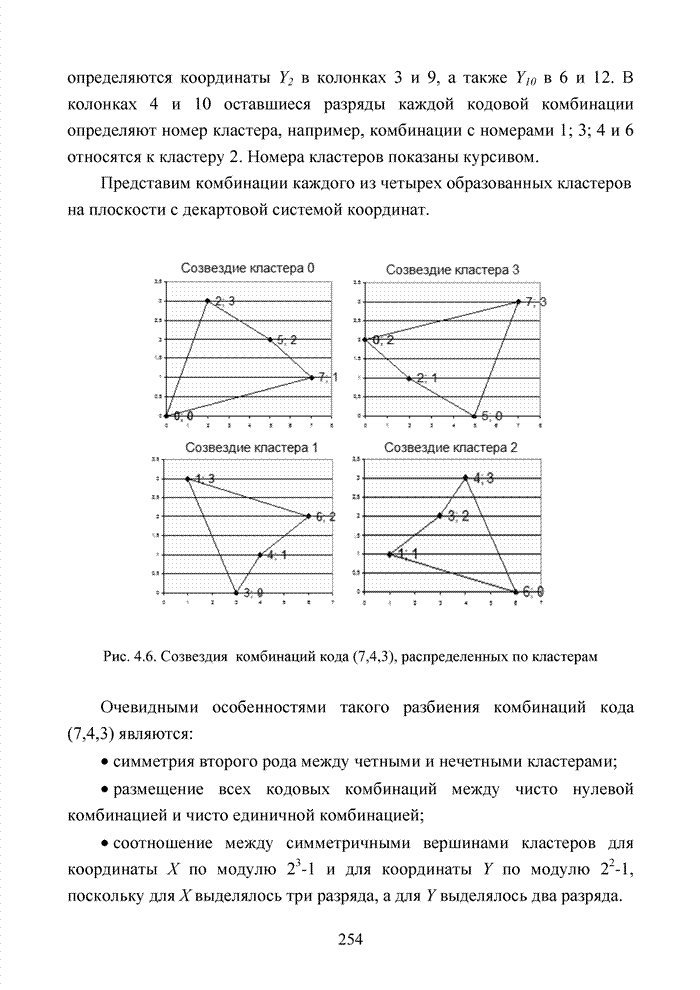
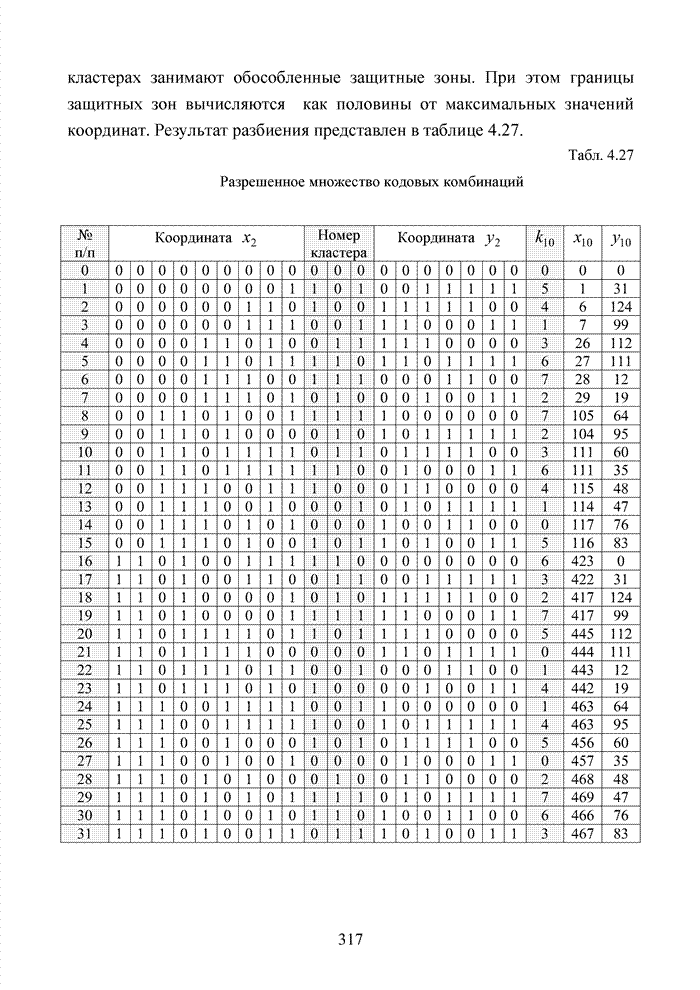
Декодер, применяя циклические сдвиги, решает задачу декодирования, не используя метрику Хэмминга. В качестве метрики выступают защитные зоны кодовых комбинаций, которые в плоскости кластера имеют вид примыкающих друг к другу прямоугольников.
В общем
случае для ![]() двоичных
разрядов координат
двоичных
разрядов координат ![]() и
и
![]() вес старшего
разряда равен
вес старшего
разряда равен ![]() .
Новая метрика в форме прямоугольной защитной зоны будет определяться
уравнениями
.
Новая метрика в форме прямоугольной защитной зоны будет определяться
уравнениями ![]() .
.
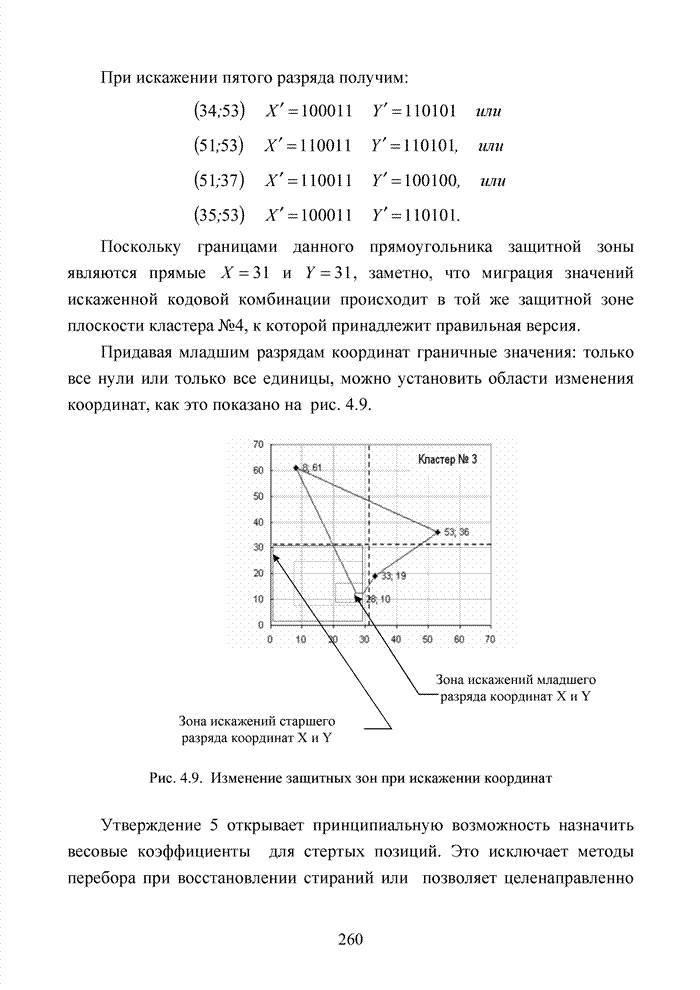
При
этом искажение младших разрядов координат кодового вектора не приводит к выходу
вектора за пределы защитной зоны. Нарушение защитной зоны произойдет только при
искажении старшего разряда любой координаты. Например, для кода (15,5)
целесообразно выбрать ![]() , тогда выполняя поиск номера кластера,
декодер в циклической последовательности
, тогда выполняя поиск номера кластера,
декодер в циклической последовательности ![]() или
или ![]() проверяет два следующих номера, например,
в
проверяет два следующих номера, например,
в ![]() 6; 5; 2 и
точно определяет не только номер кластера, но и выявляет переданный
информационный вектор. В совокупности номер кластера и старшие разряды
координат образуют ровно
6; 5; 2 и
точно определяет не только номер кластера, но и выявляет переданный
информационный вектор. В совокупности номер кластера и старшие разряды
координат образуют ровно ![]() символов. Следовательно, код способен в
системе мягкого декодирования восстановить
символов. Следовательно, код способен в
системе мягкого декодирования восстановить ![]() стираний.
стираний.
При
таком подходе асимптотическая эффективность декодера может быть оценена по
формуле ![]() ,
которая демонстрирует отсутствие какого-либо энергетического выигрыша при
передаче безызбыточных сообщений, когда
,
которая демонстрирует отсутствие какого-либо энергетического выигрыша при
передаче безызбыточных сообщений, когда ![]() , т.е.
, т.е. ![]() .
.
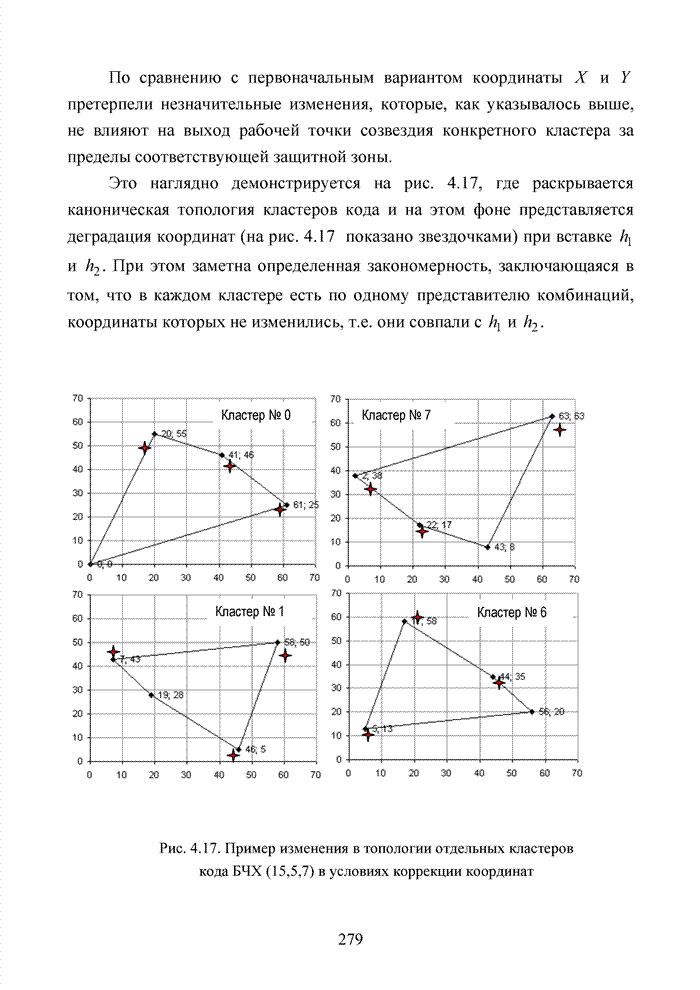
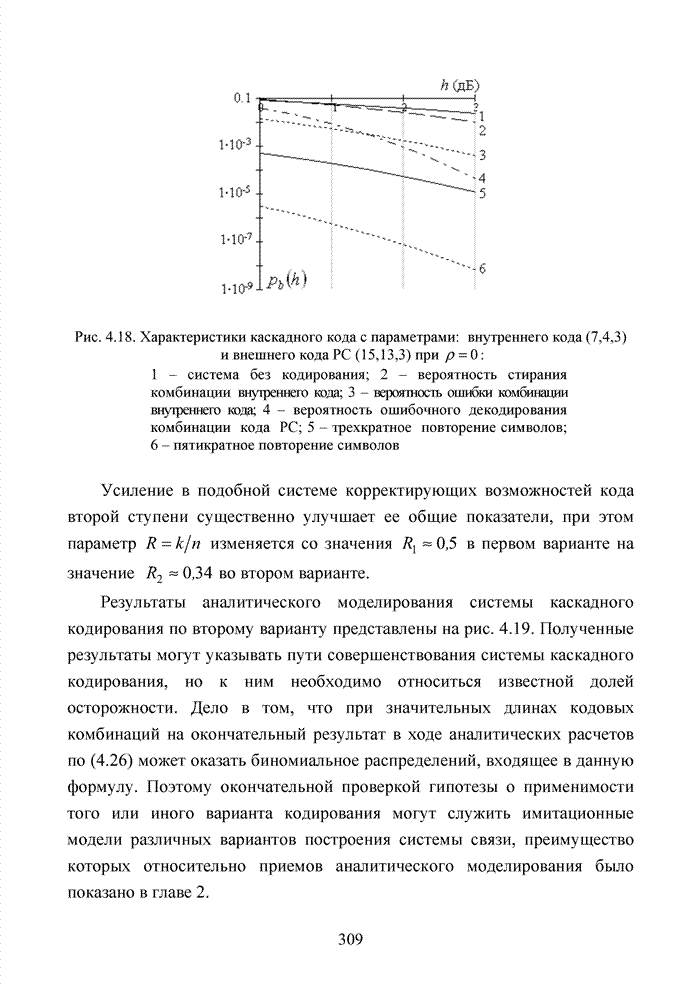
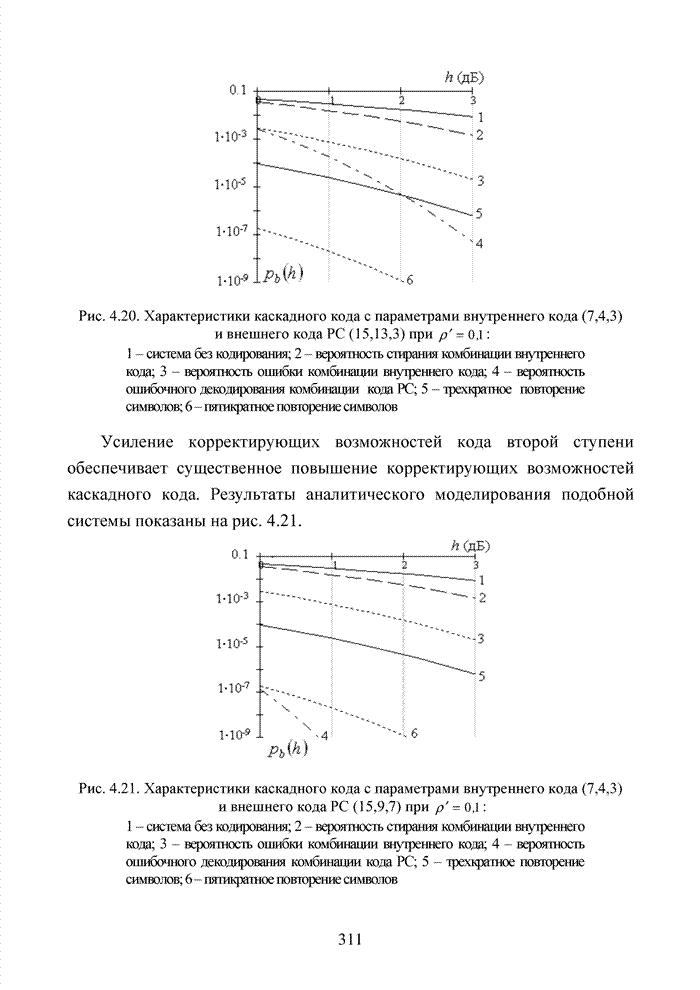
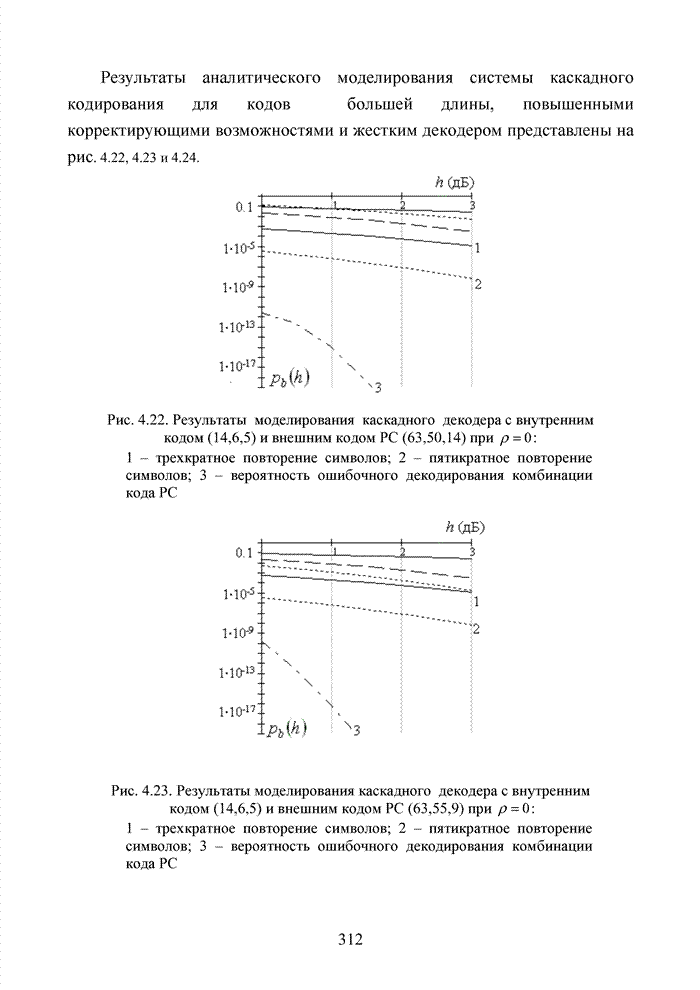
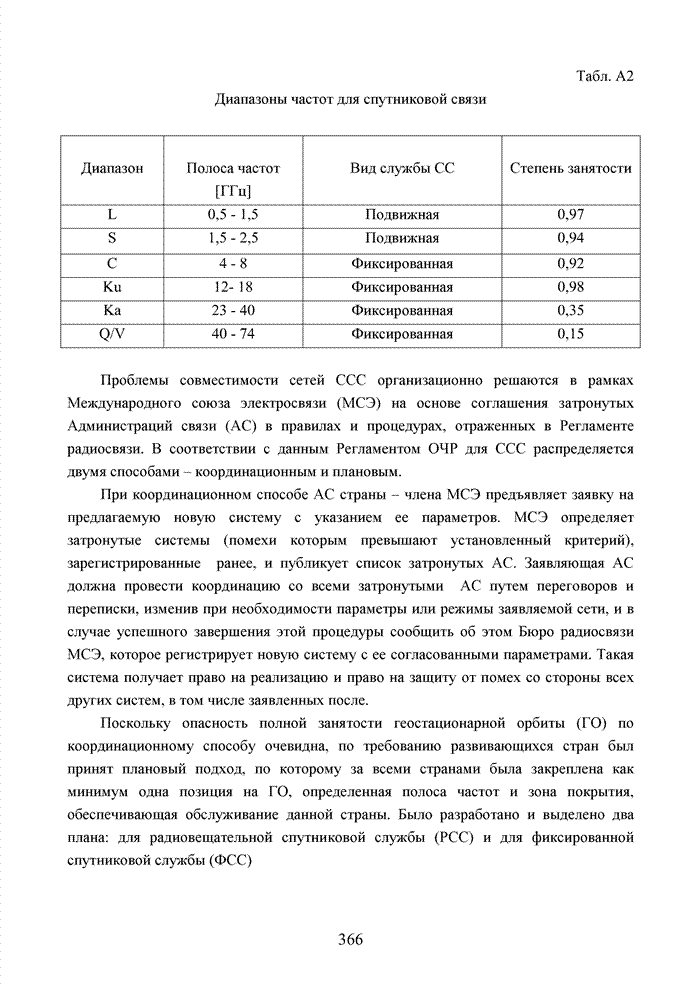
Асимптотическая оценка энергетического выигрыша представленного способа для кодов БЧХ указывает на возможность получения дополнительного выигрыша до 3 дБ по отношению к мягкому декодеру. Очевидно, что в подобной ситуации номер кластера должен определяться безошибочно. На практике добиться подобной ситуации невозможно, поэтому метод кластерного анализа целесообразно применять в рамках последовательного каскадного кодирования или использовать в качестве вспомогательного для совершенствования известных алгоритмов мягкого декодирования блоковых кодов.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
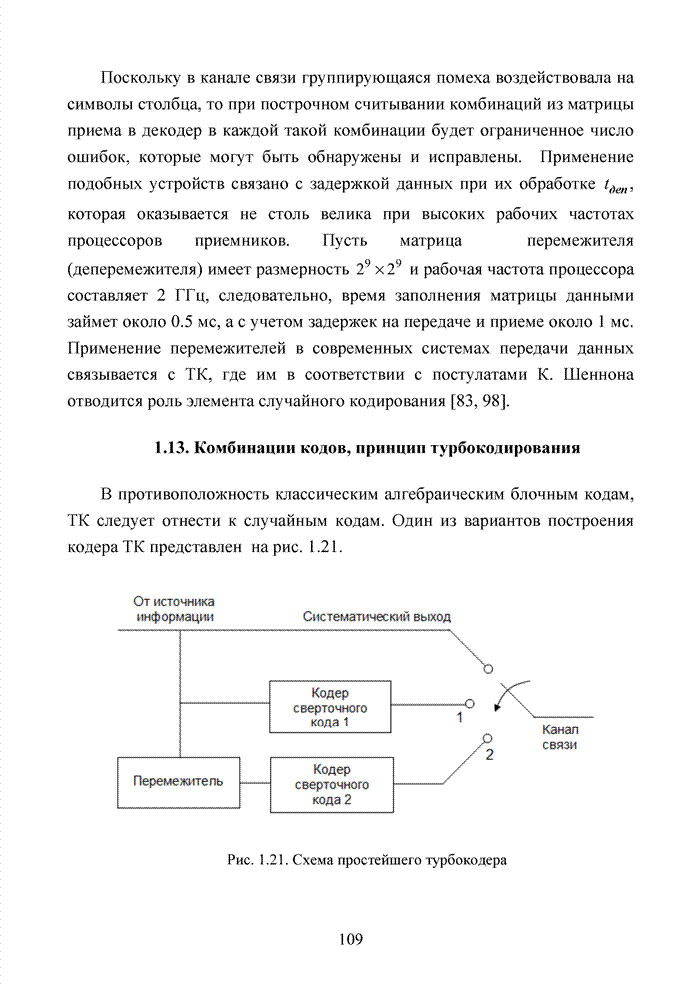
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
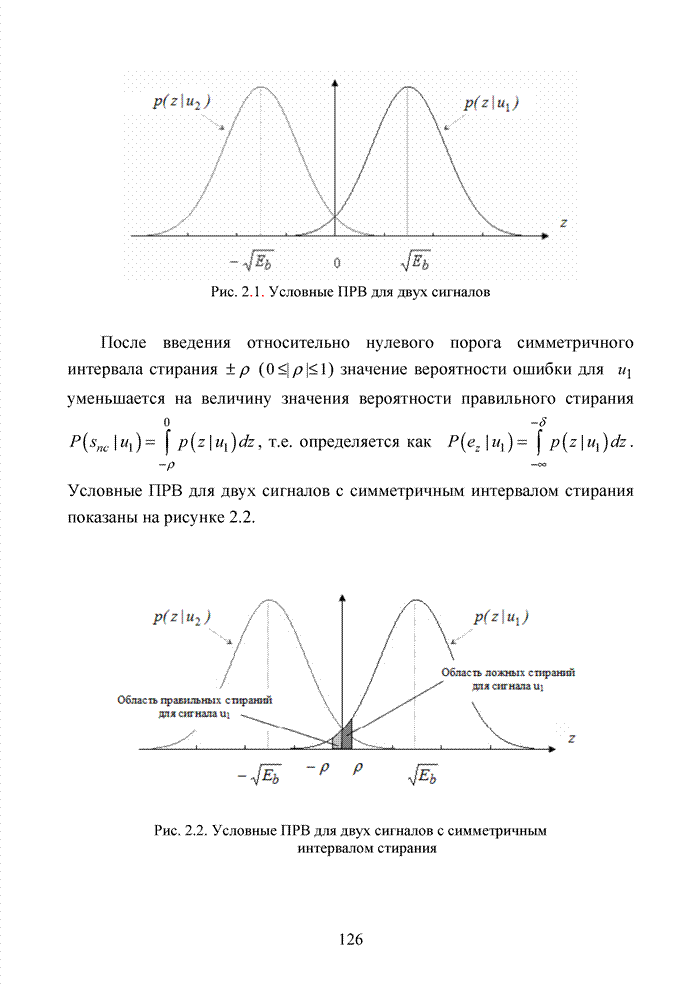
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
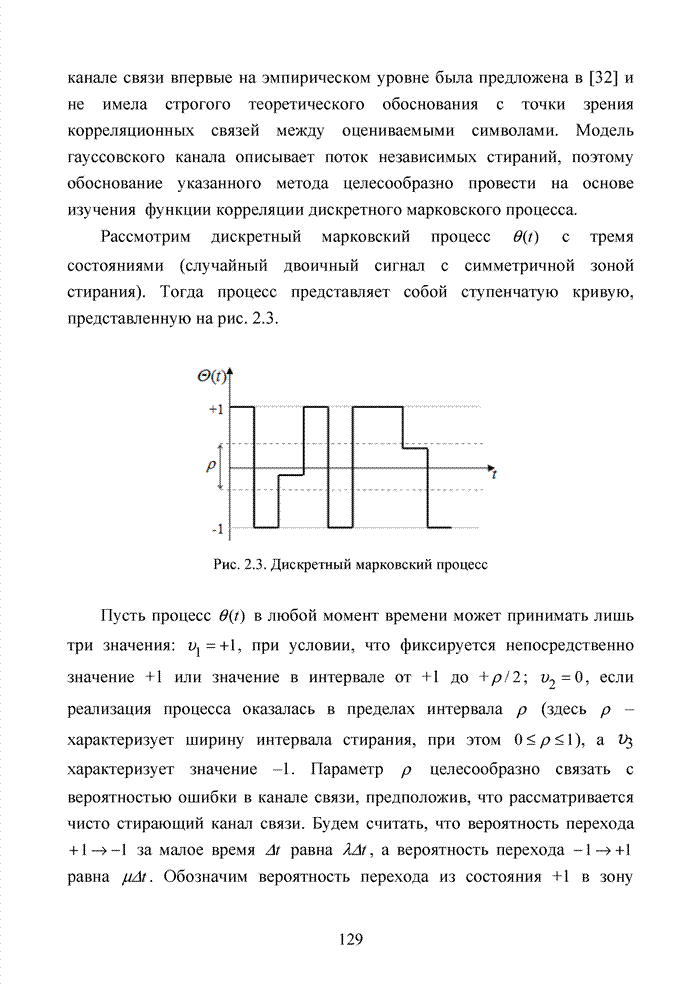
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
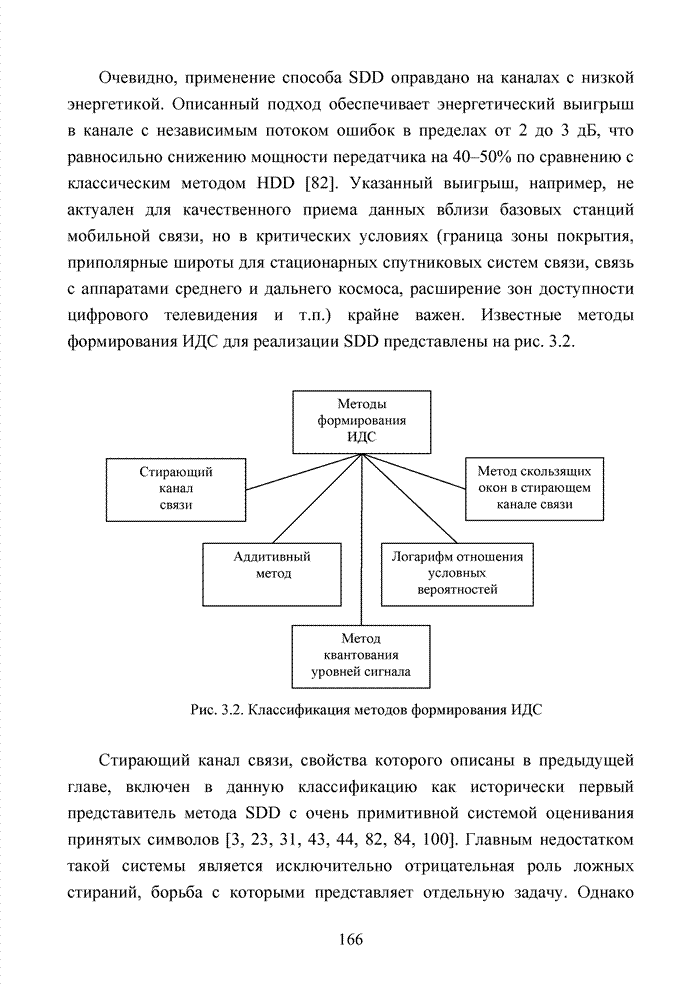
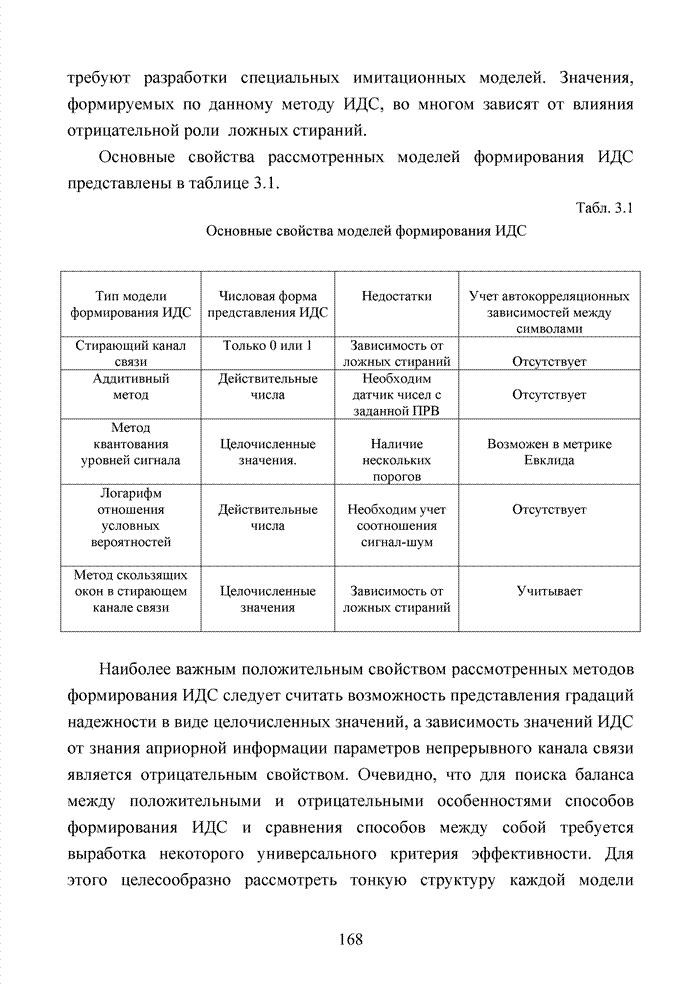
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
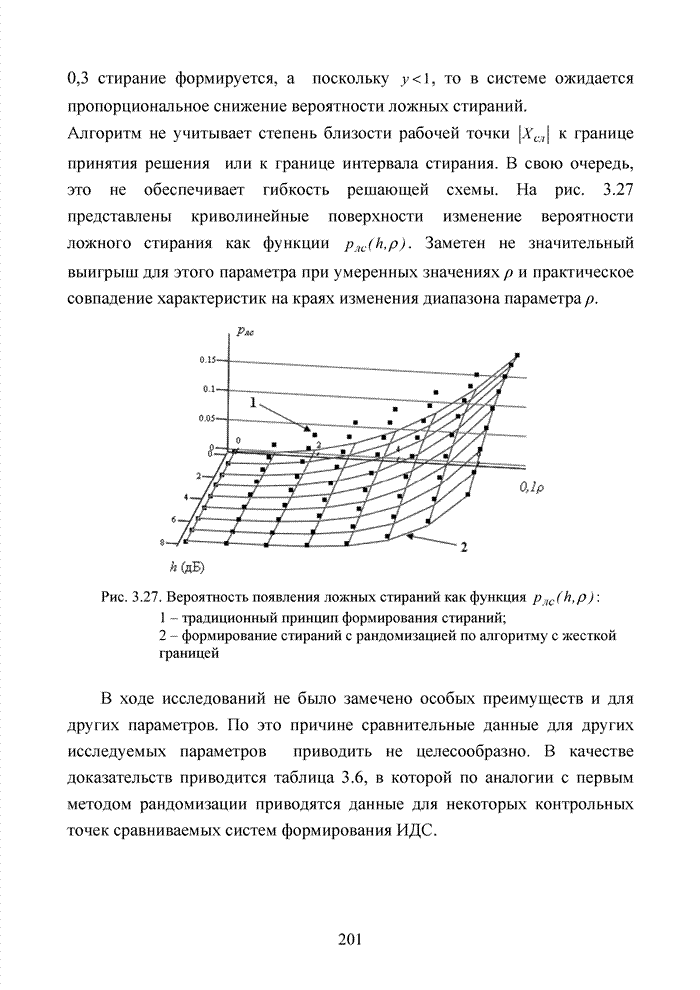
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
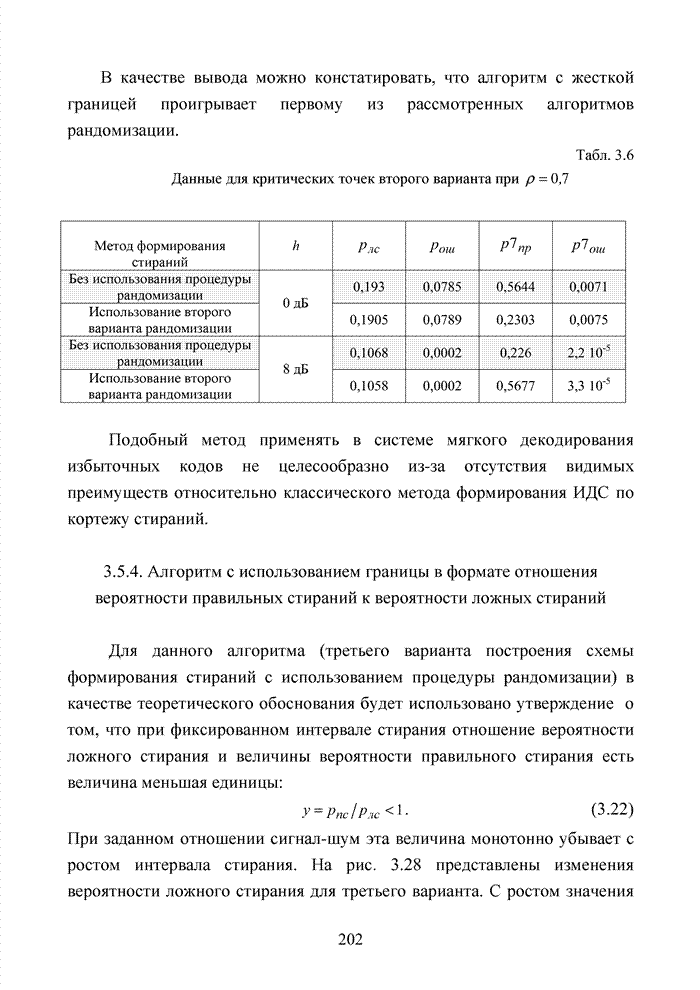
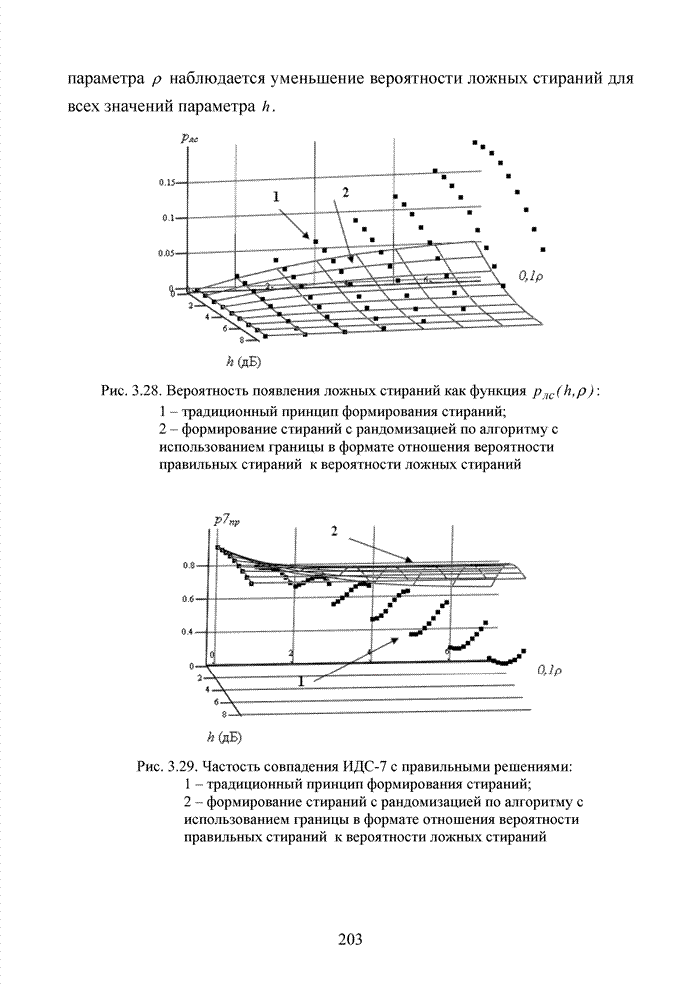
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
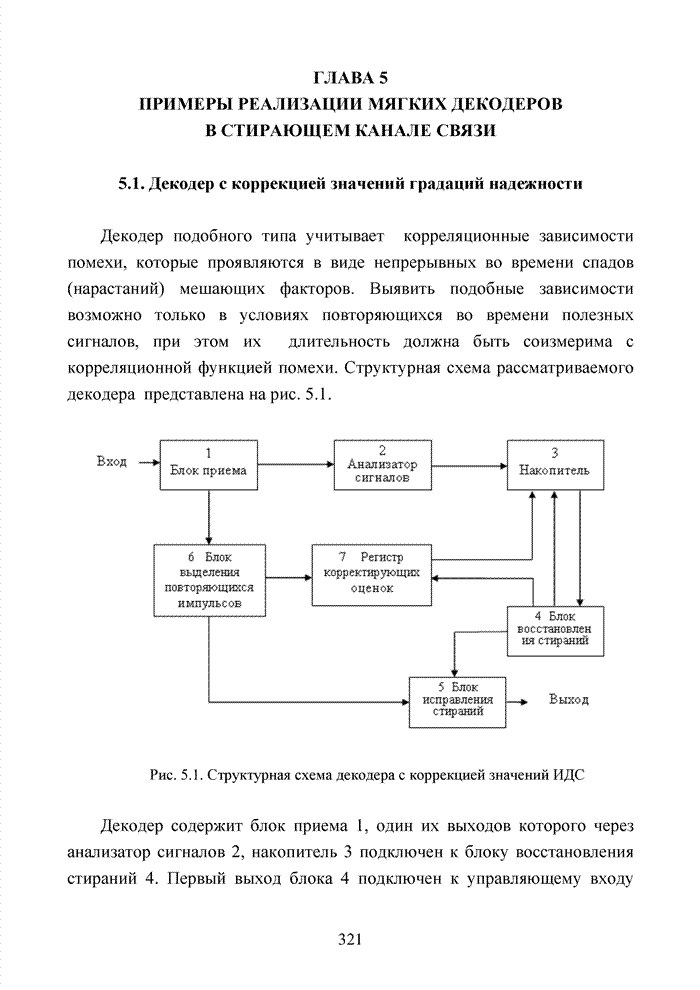
- 5.1. Декодер с коррекцией значений градаций надежности
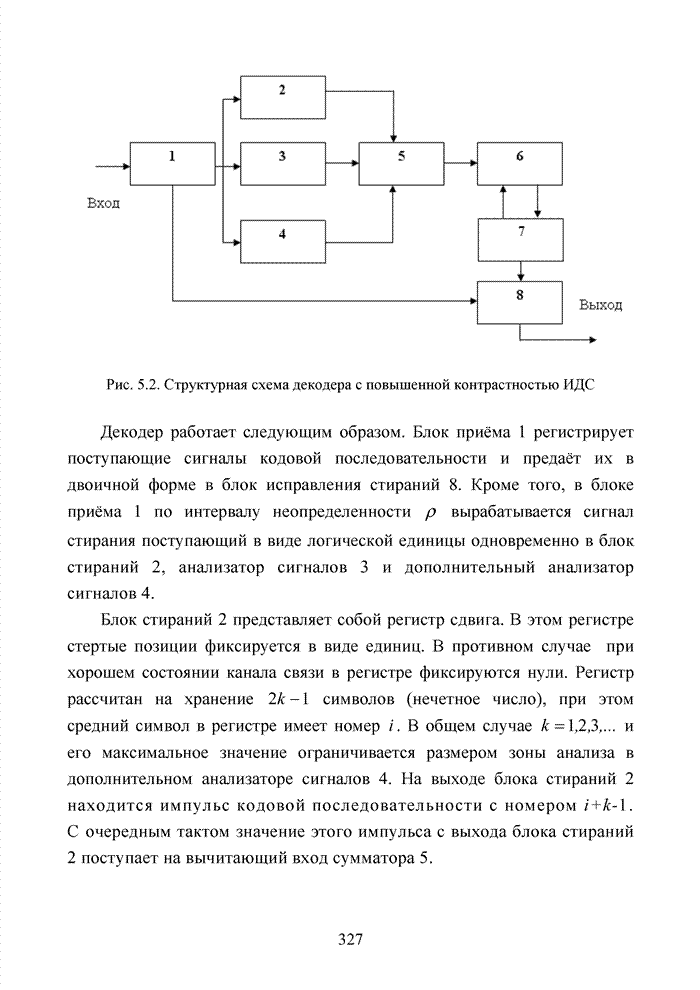
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
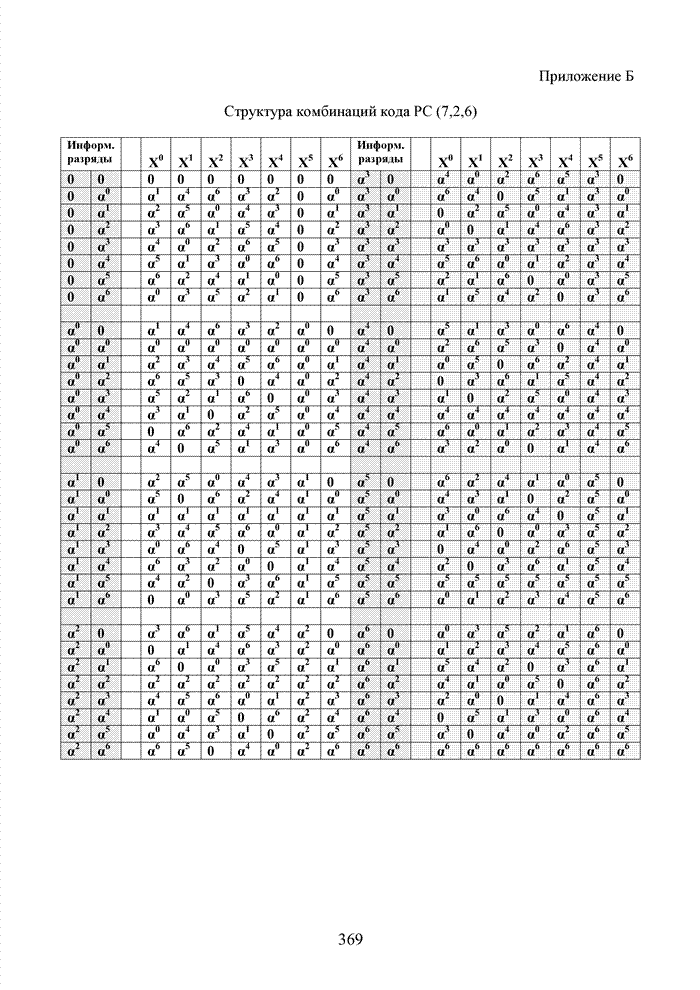
- Приложение Б Структура комбинаций кода РС (7,2,6)
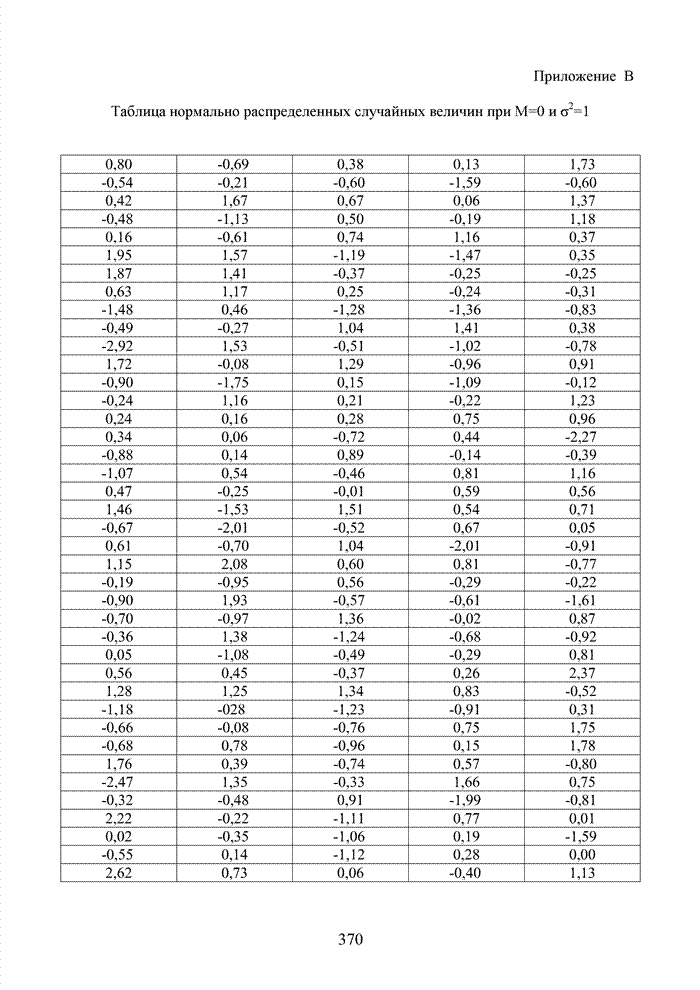
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК