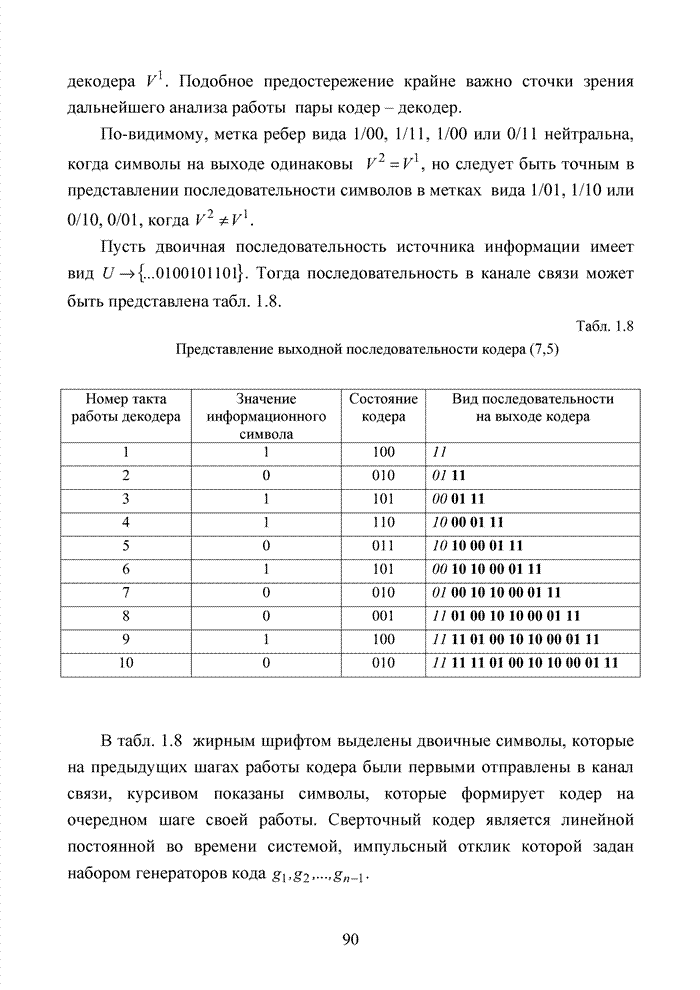
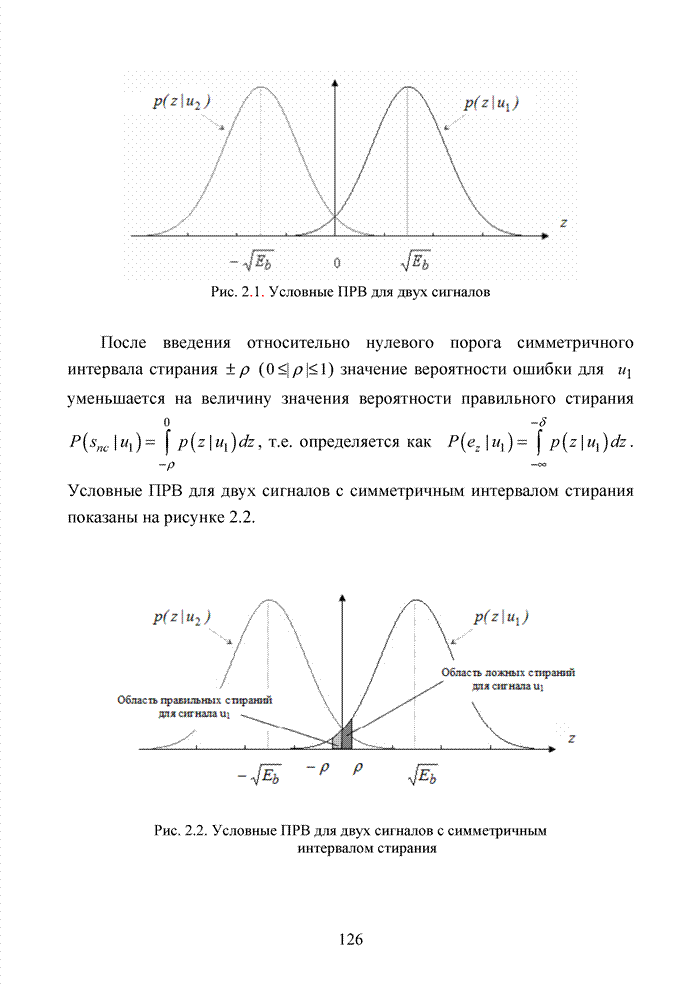
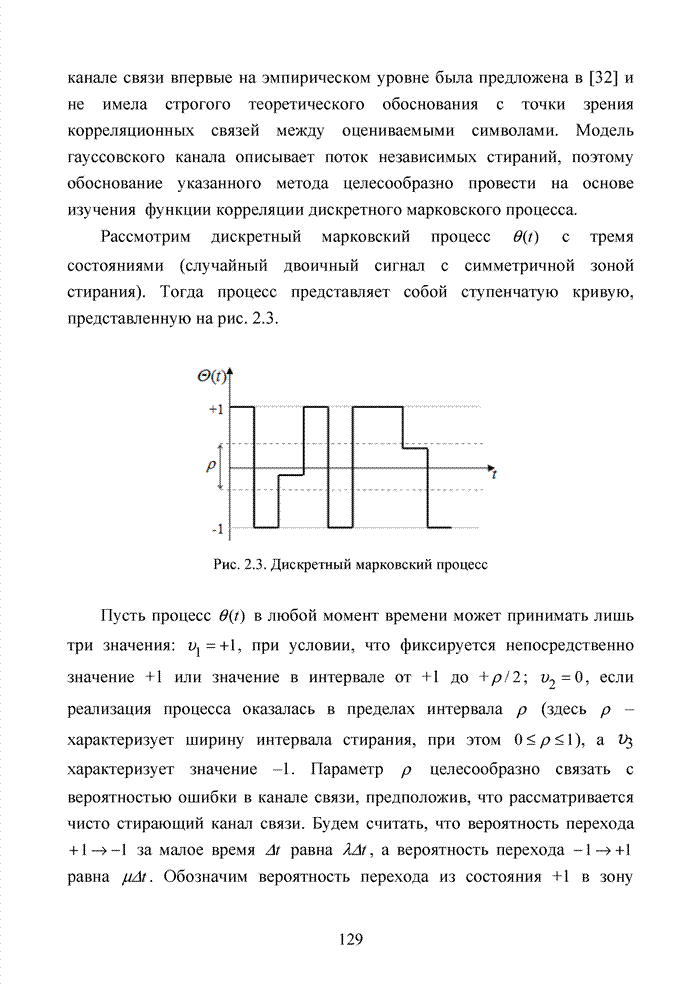
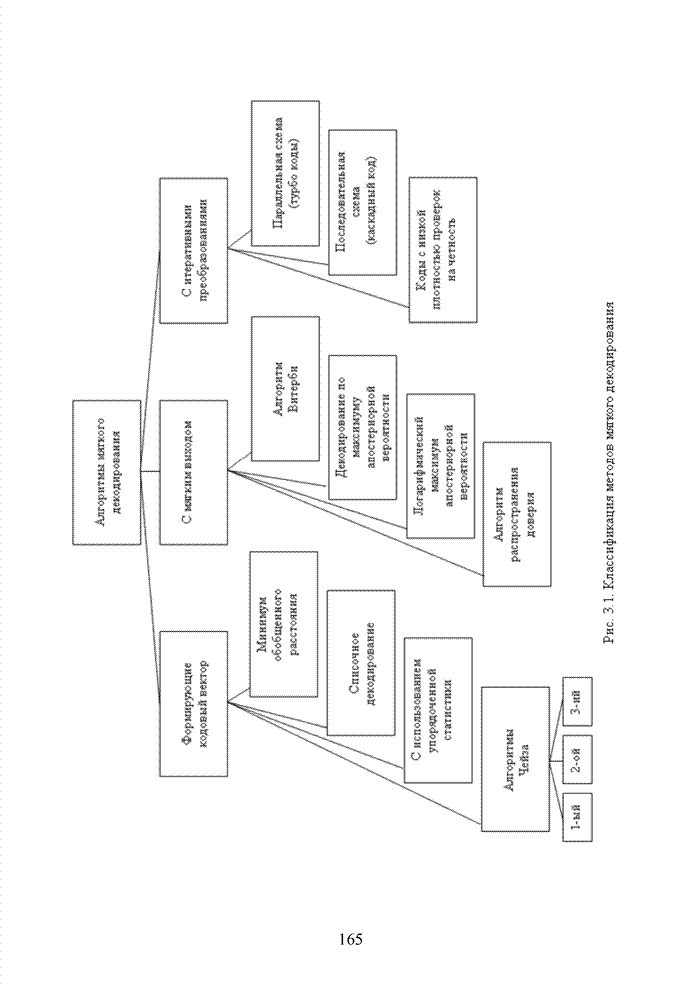
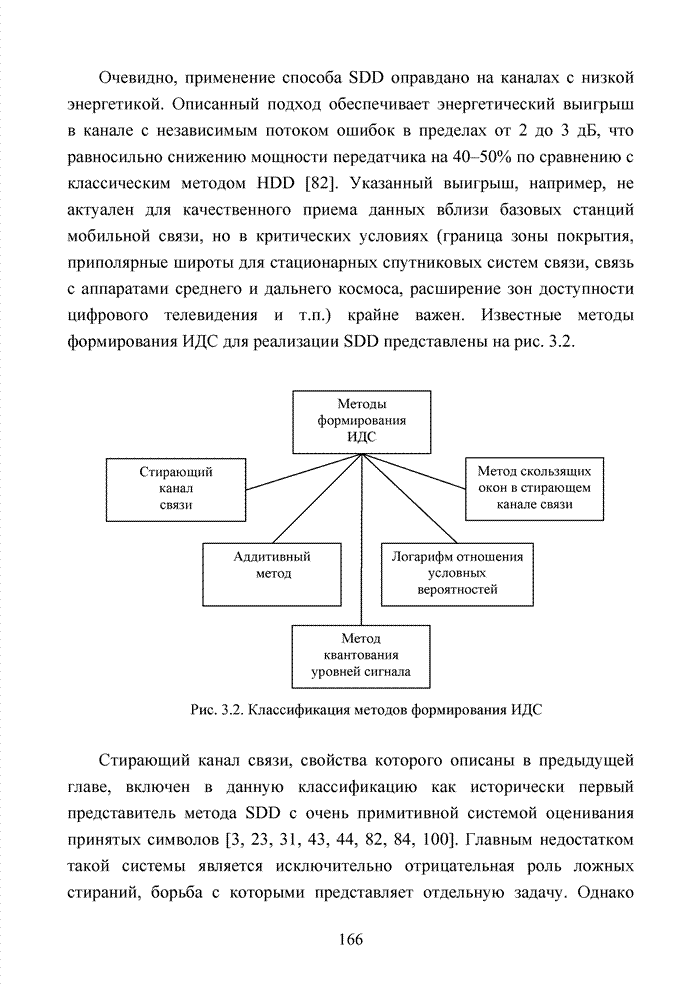
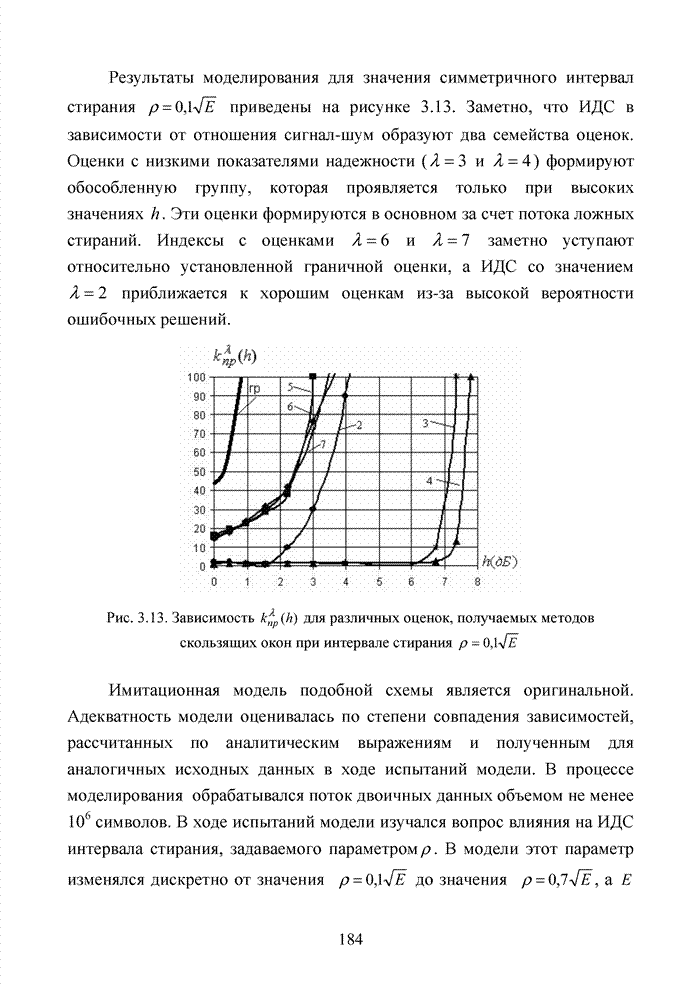
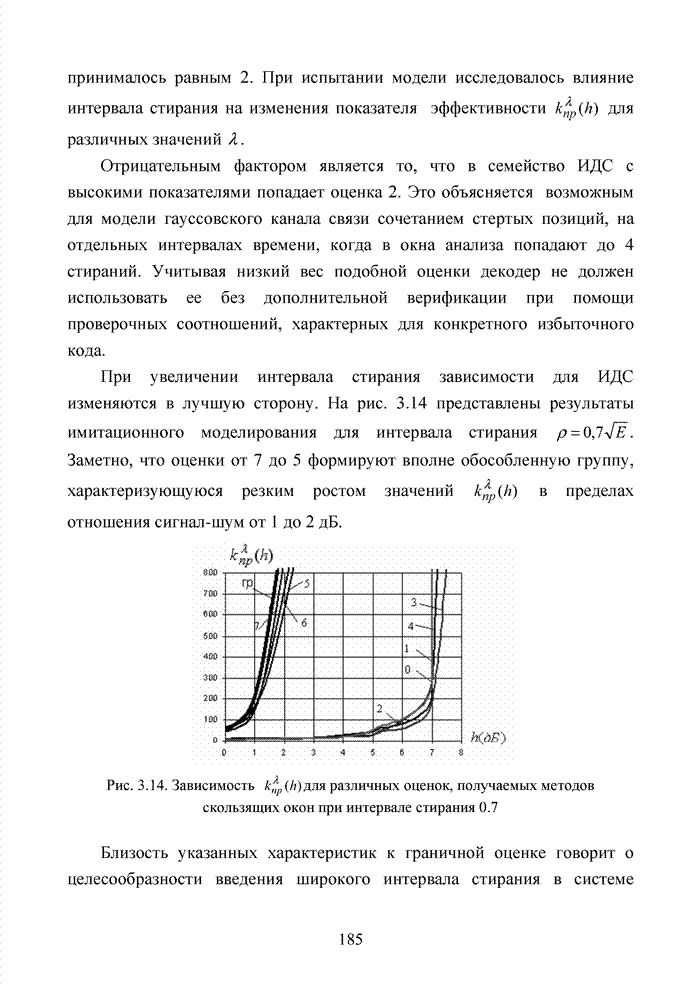
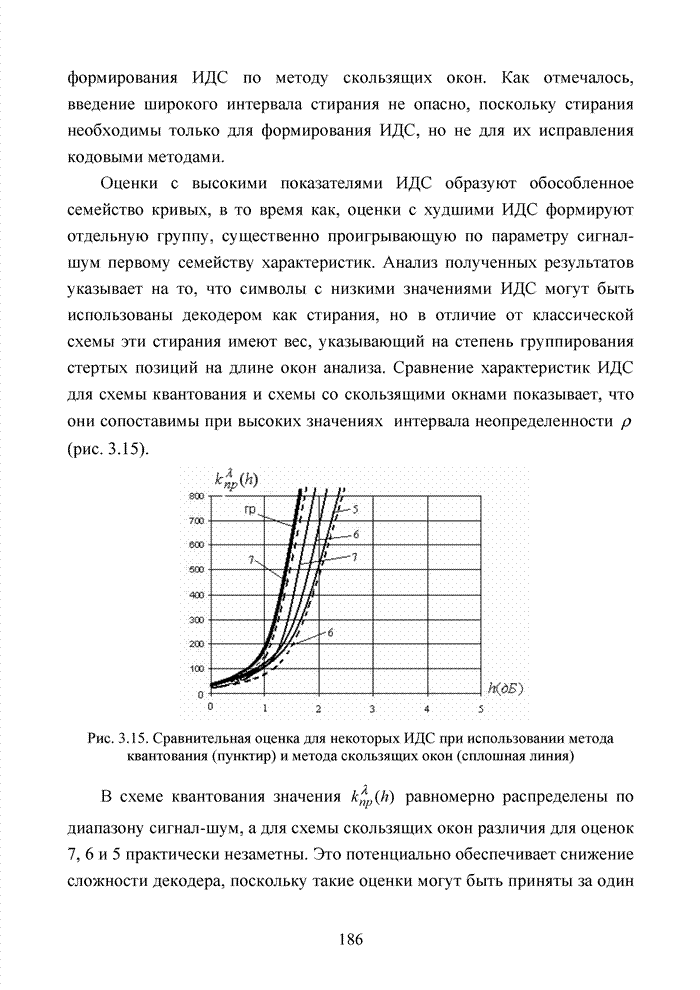
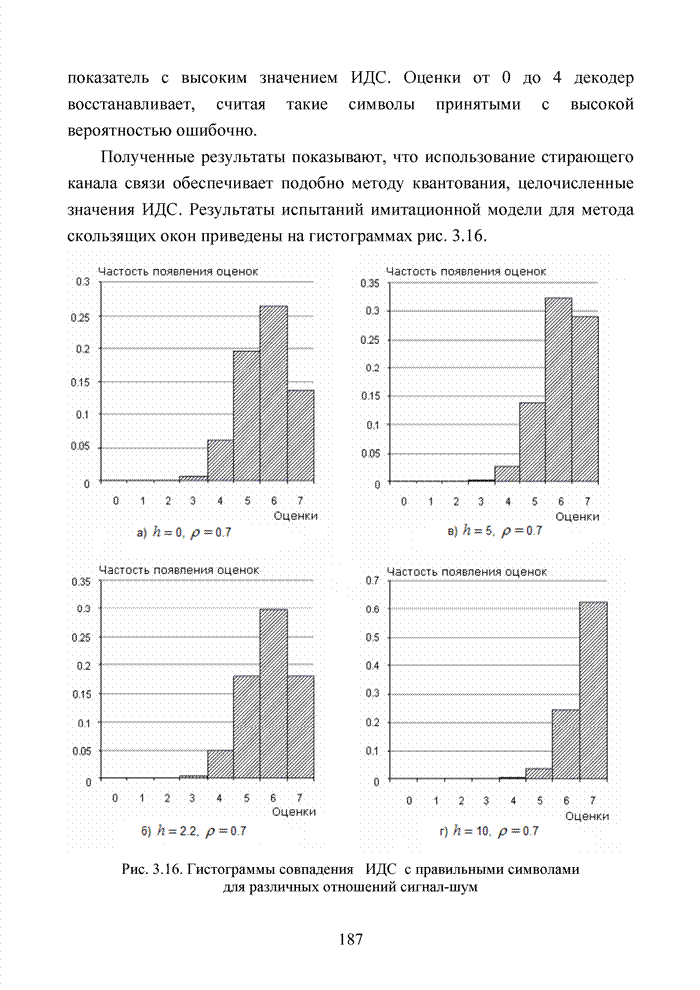
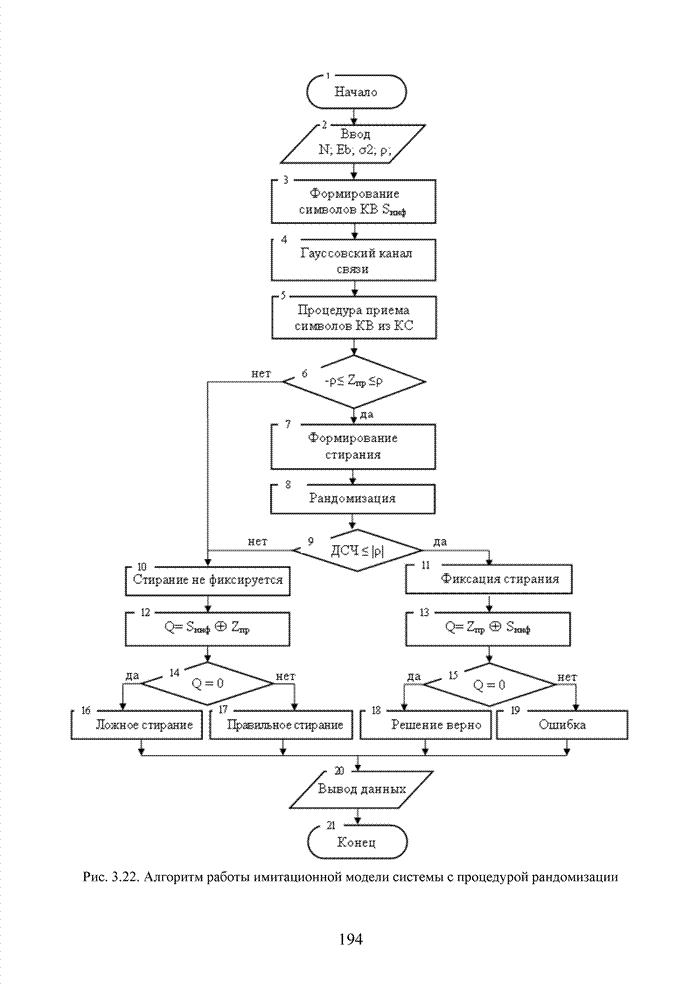
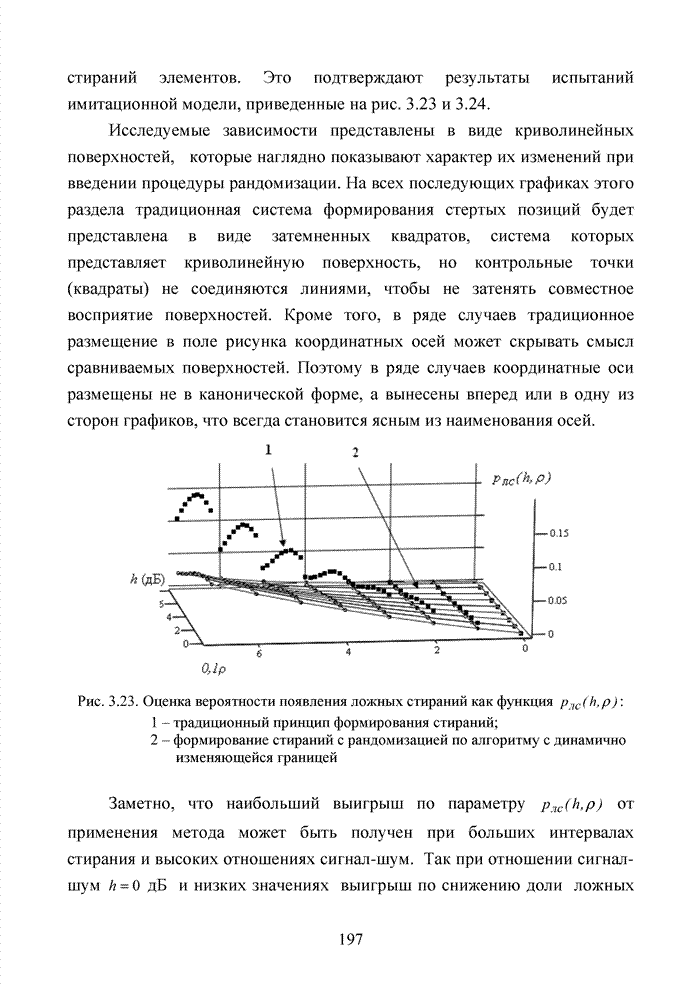
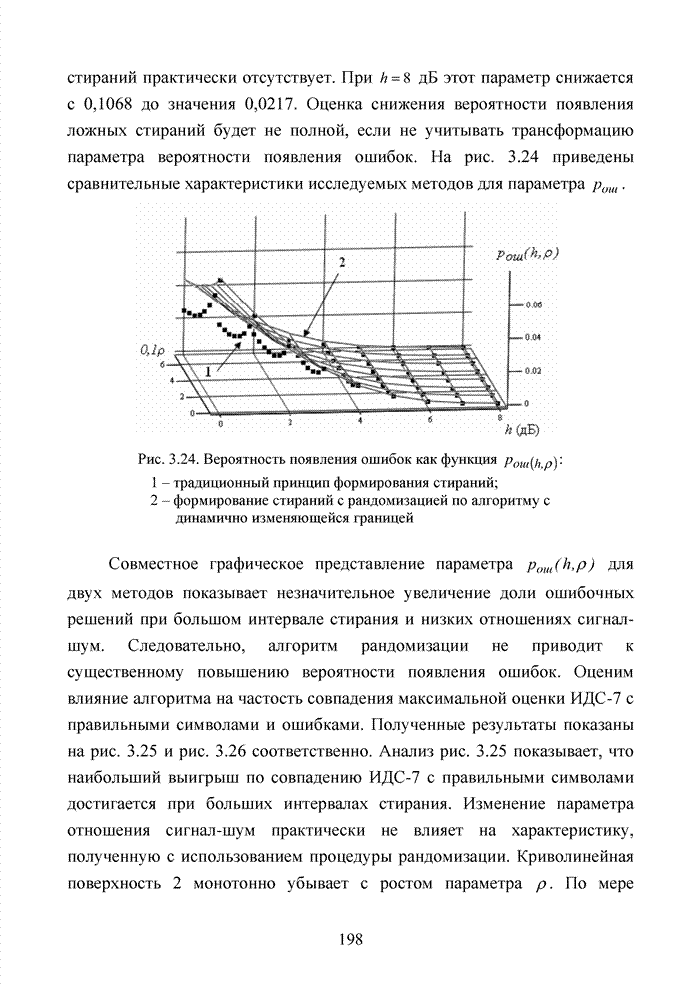
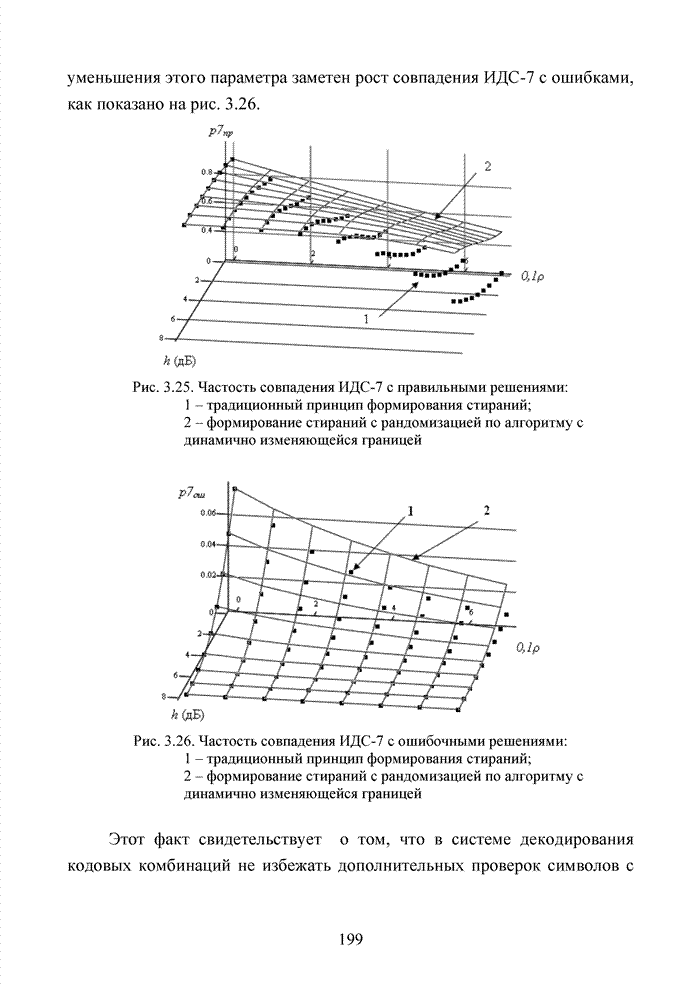
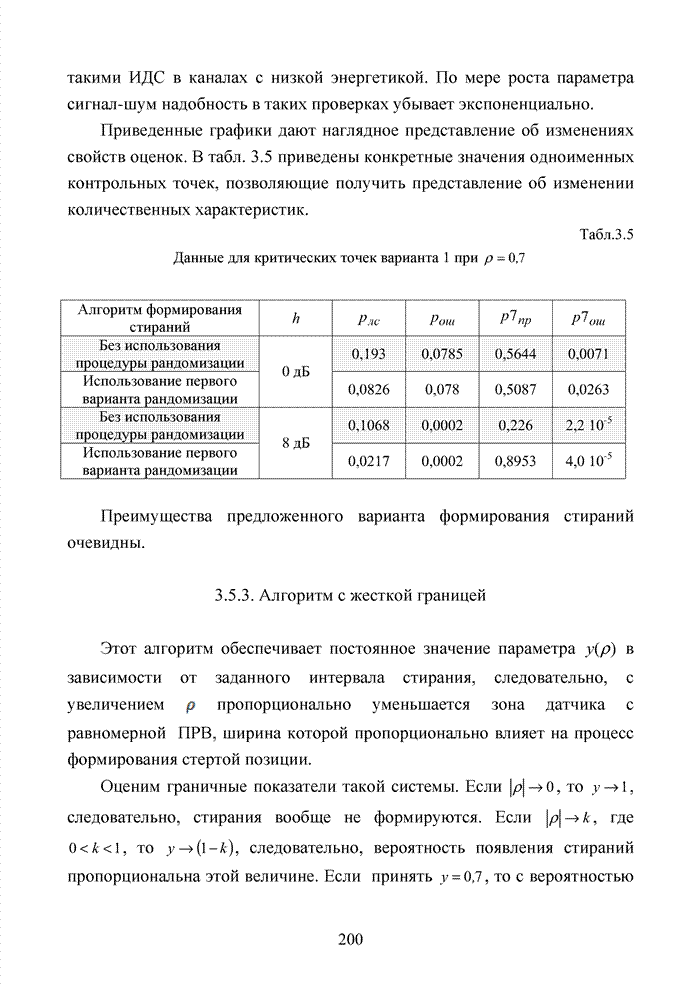
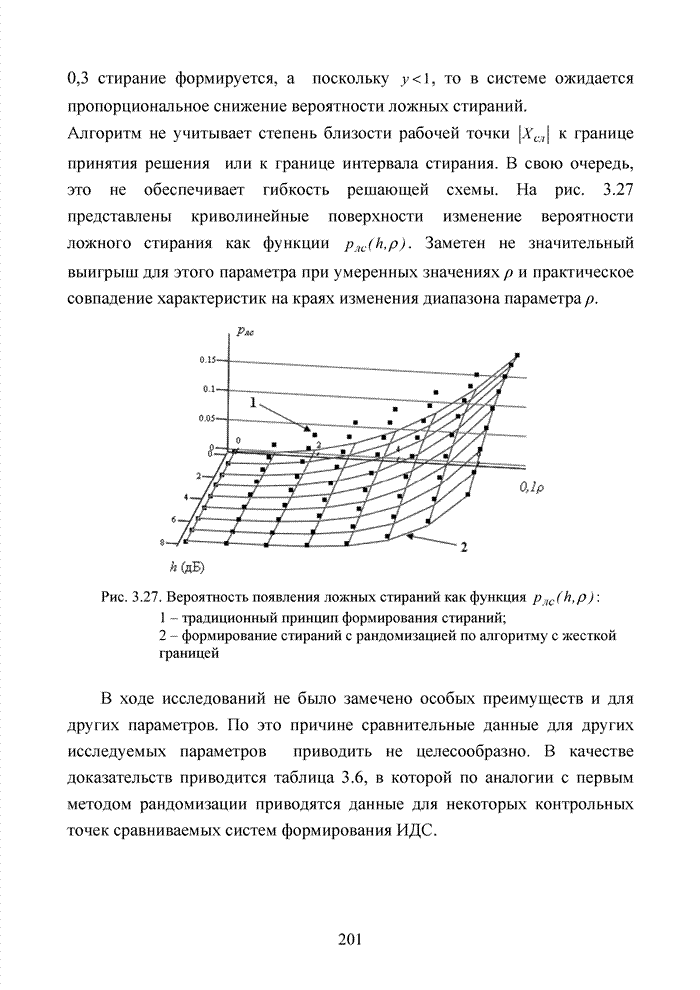
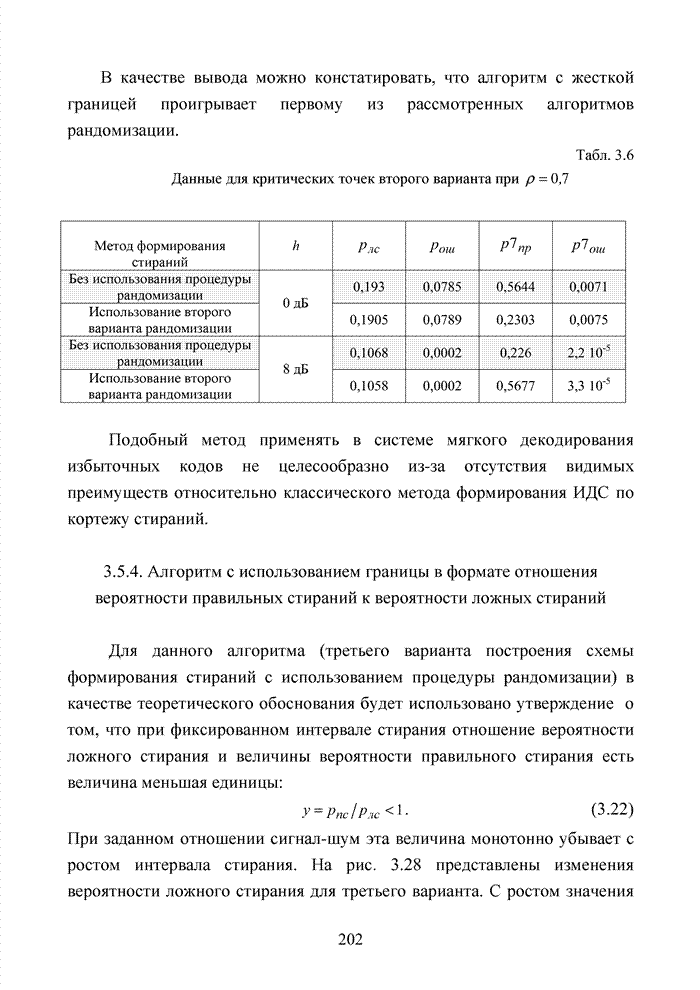
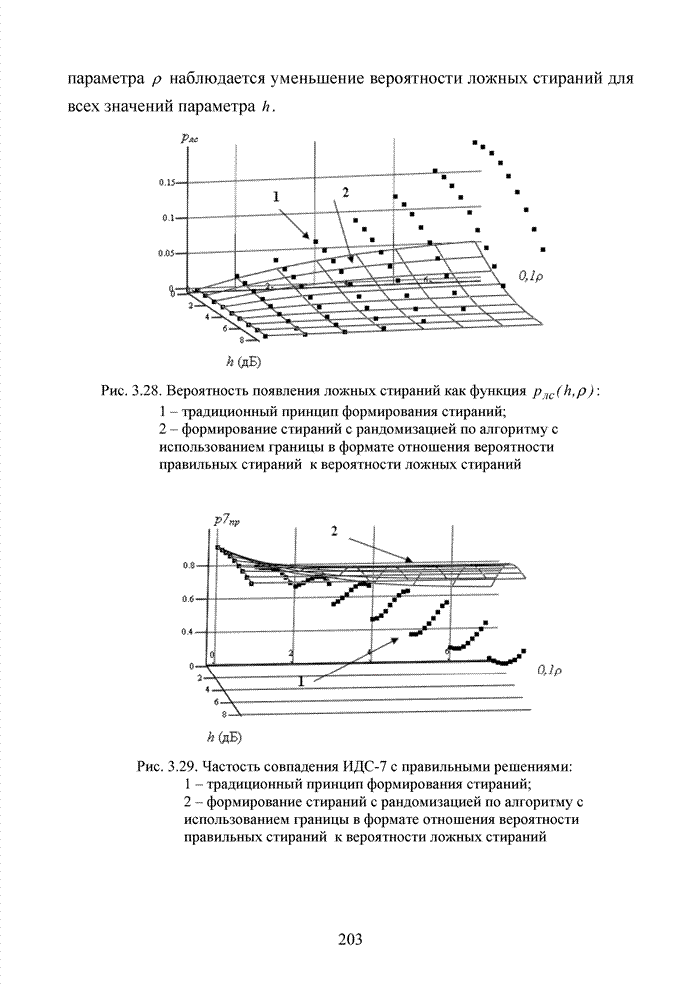
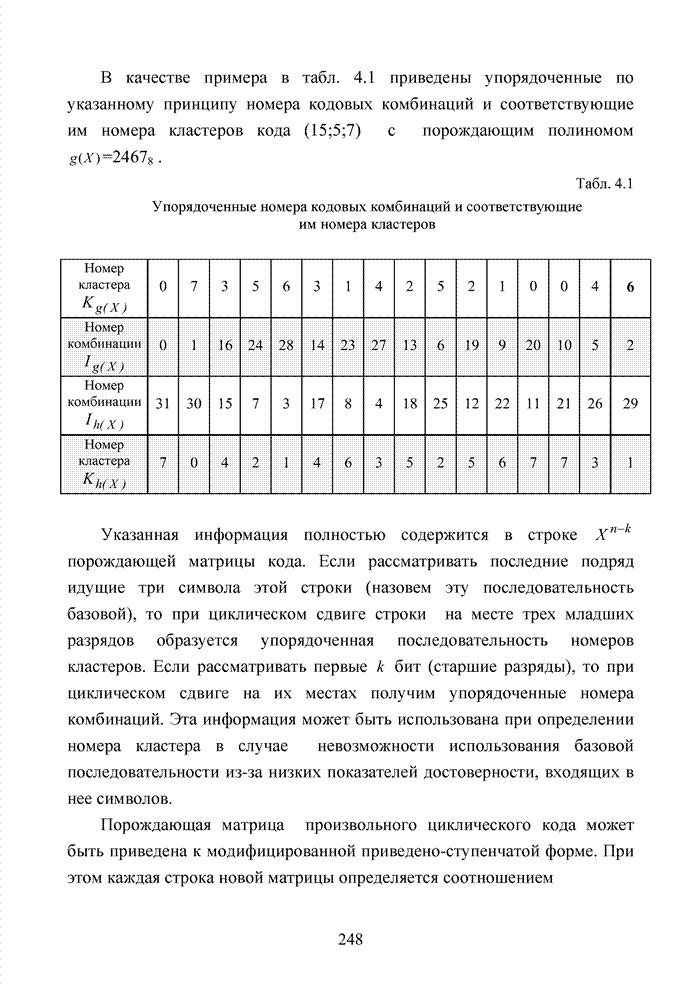
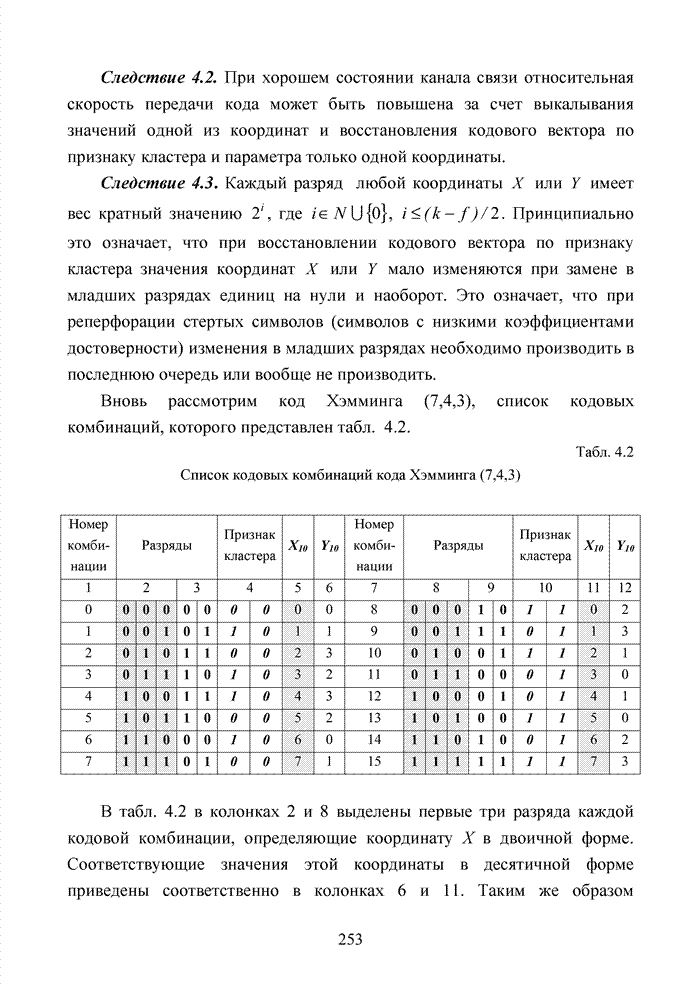
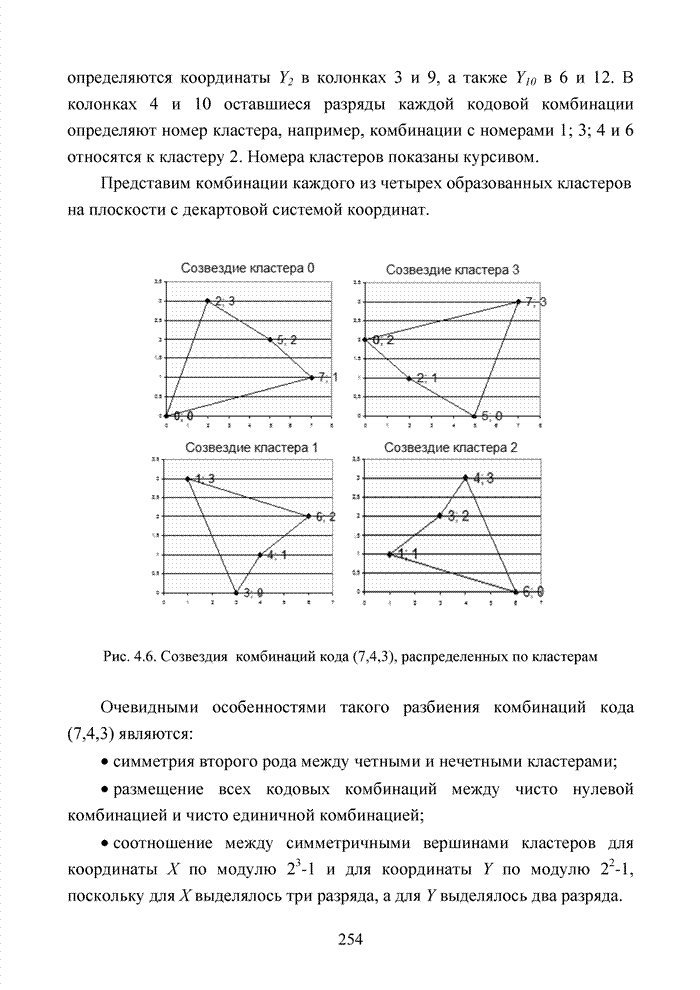
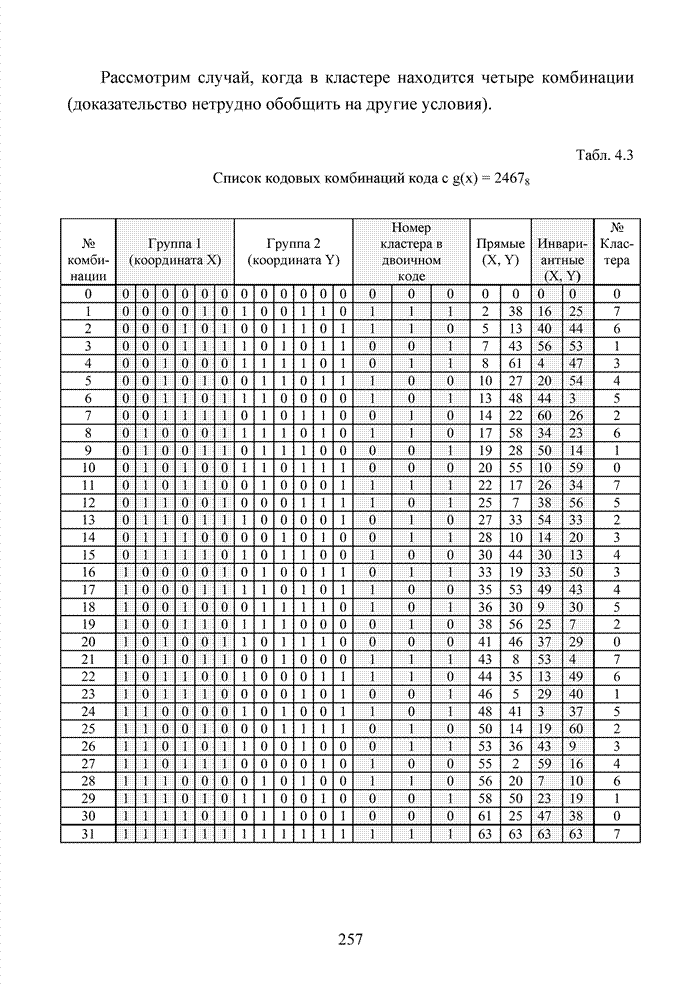
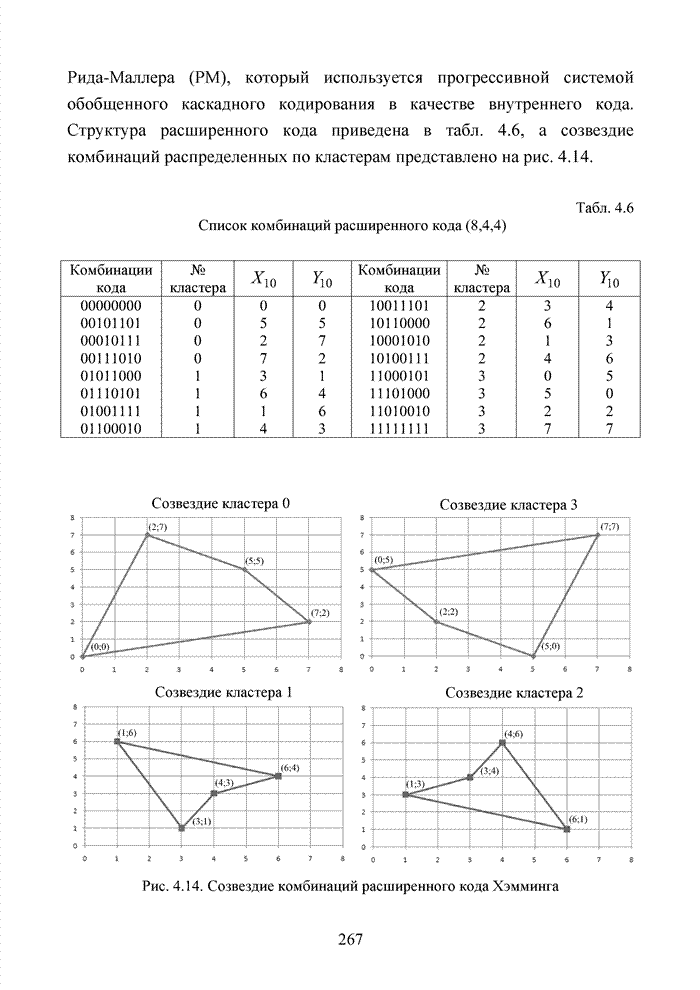
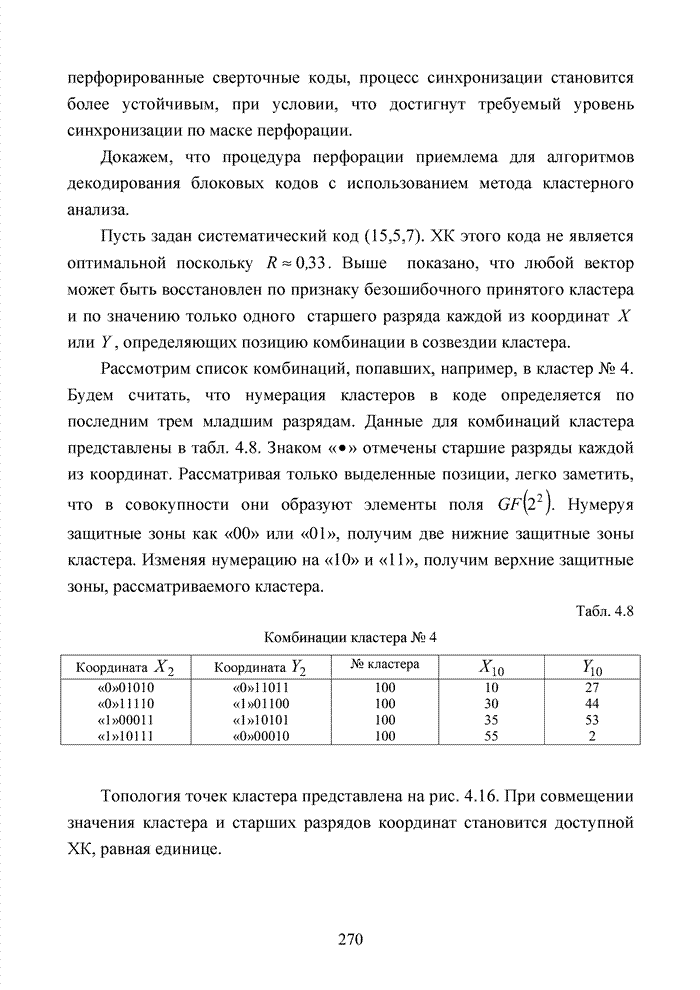
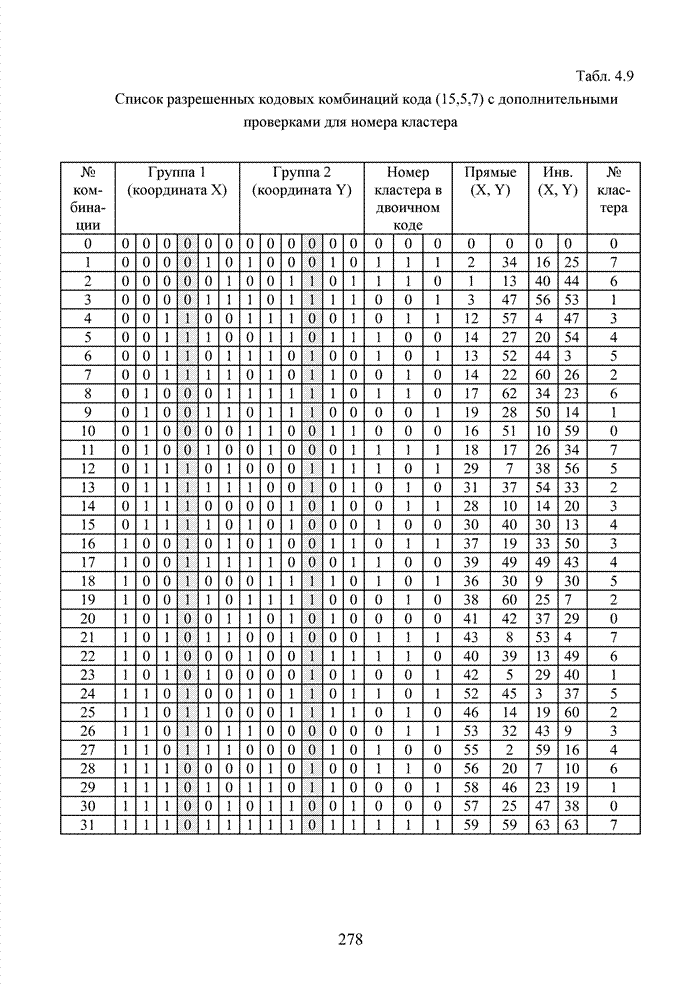
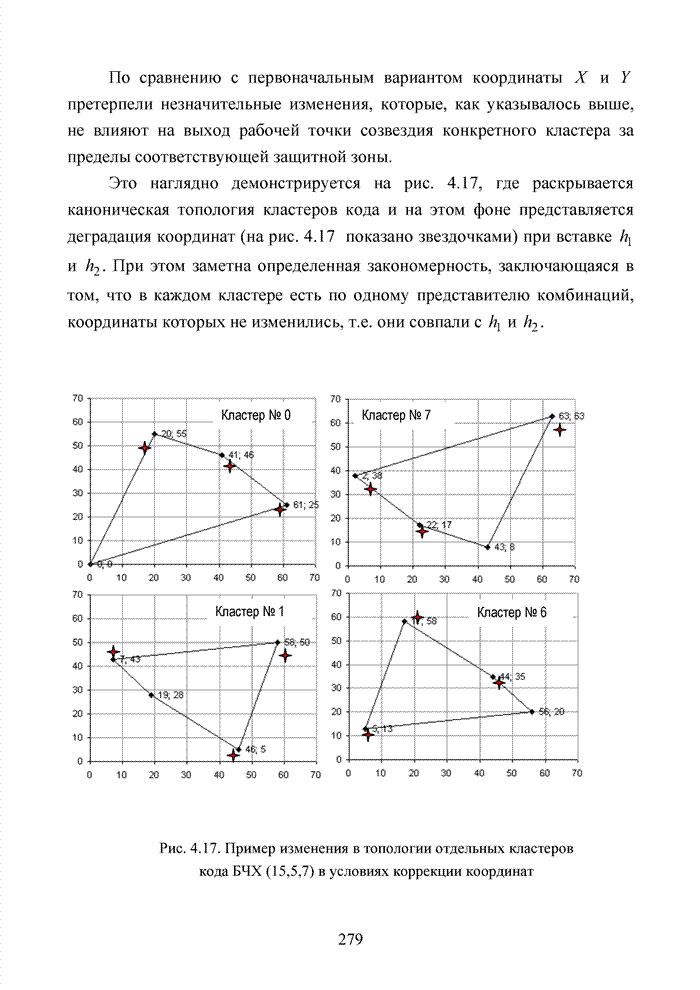
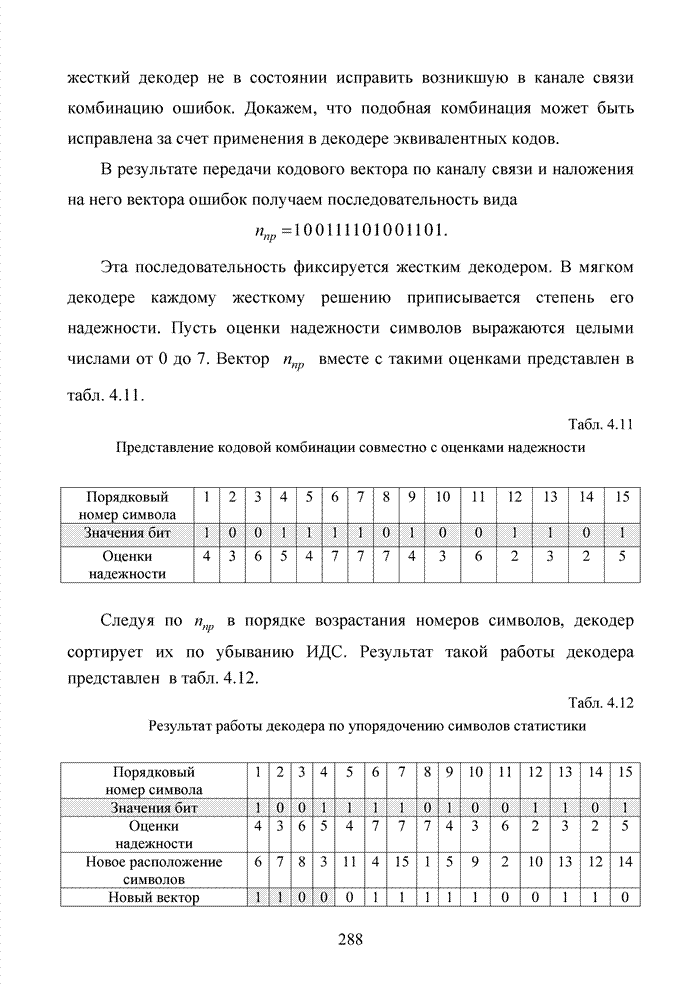
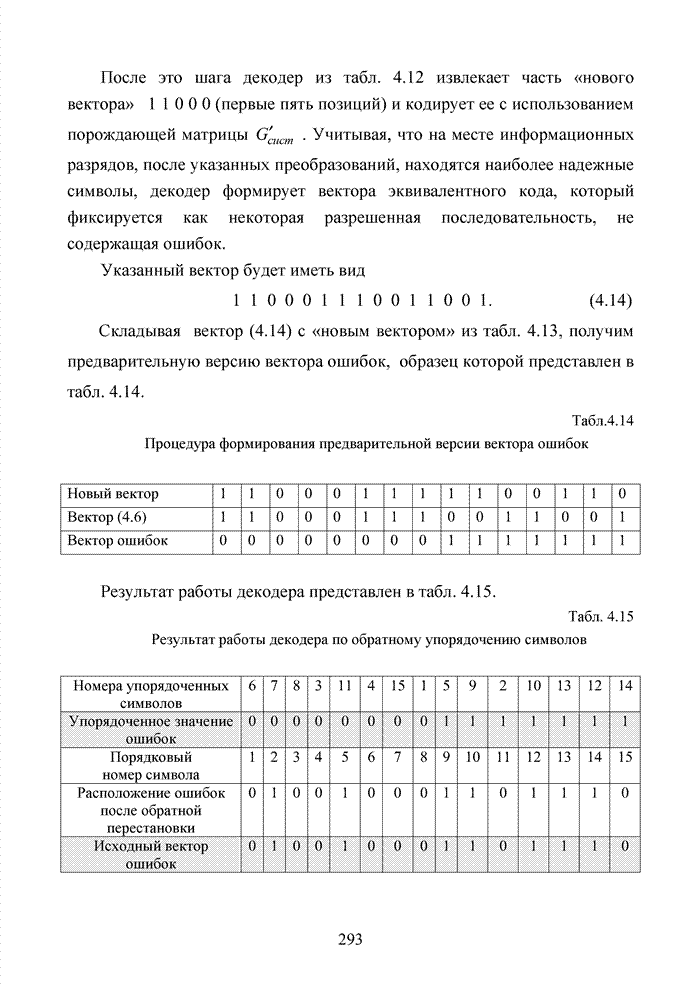
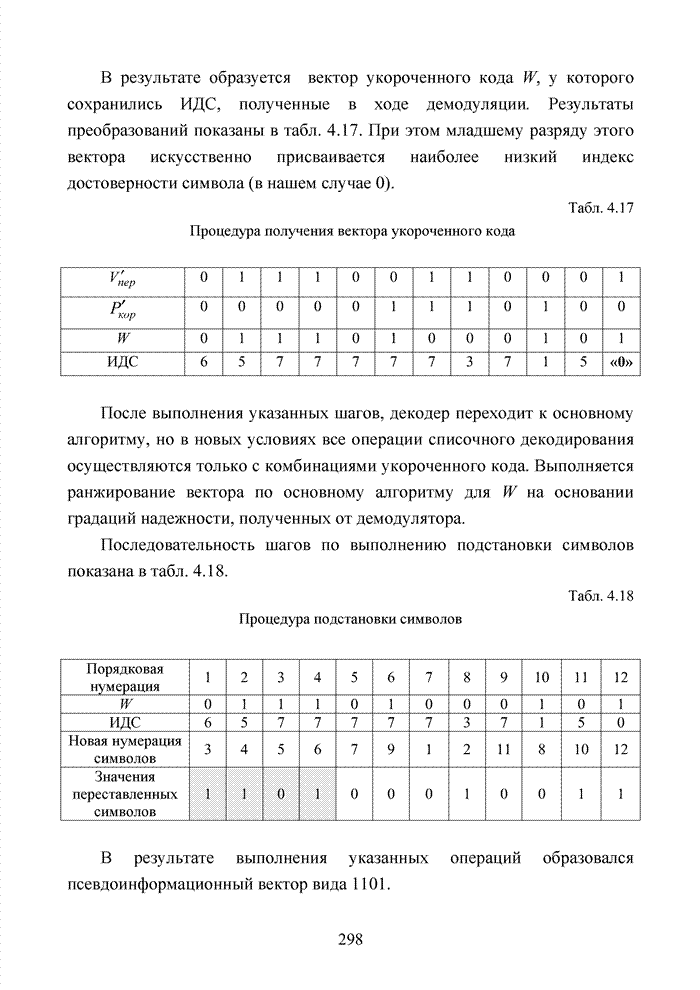
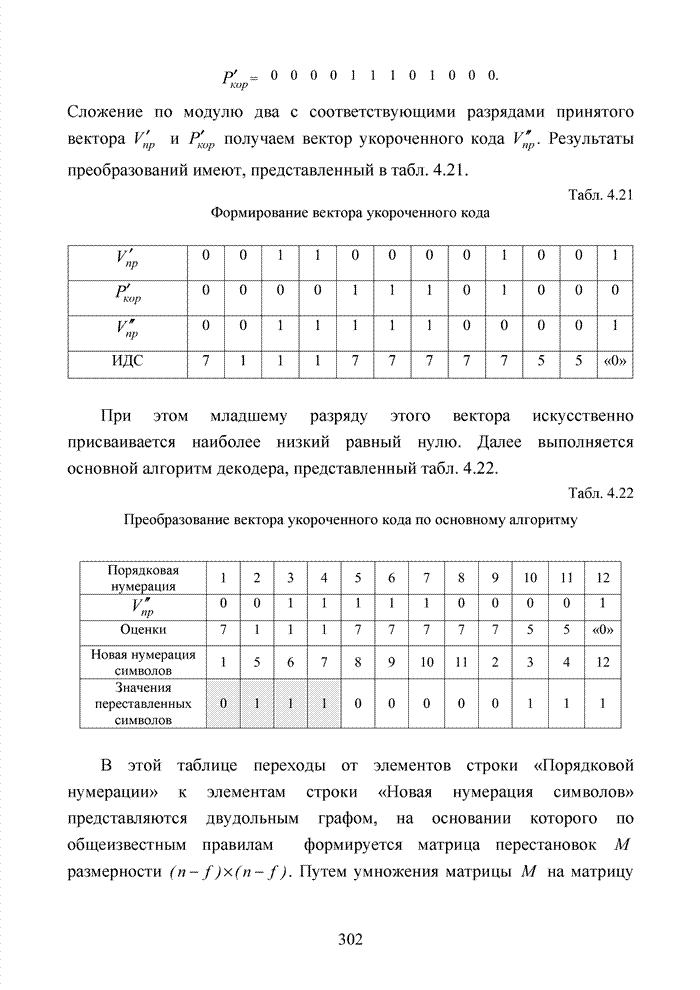
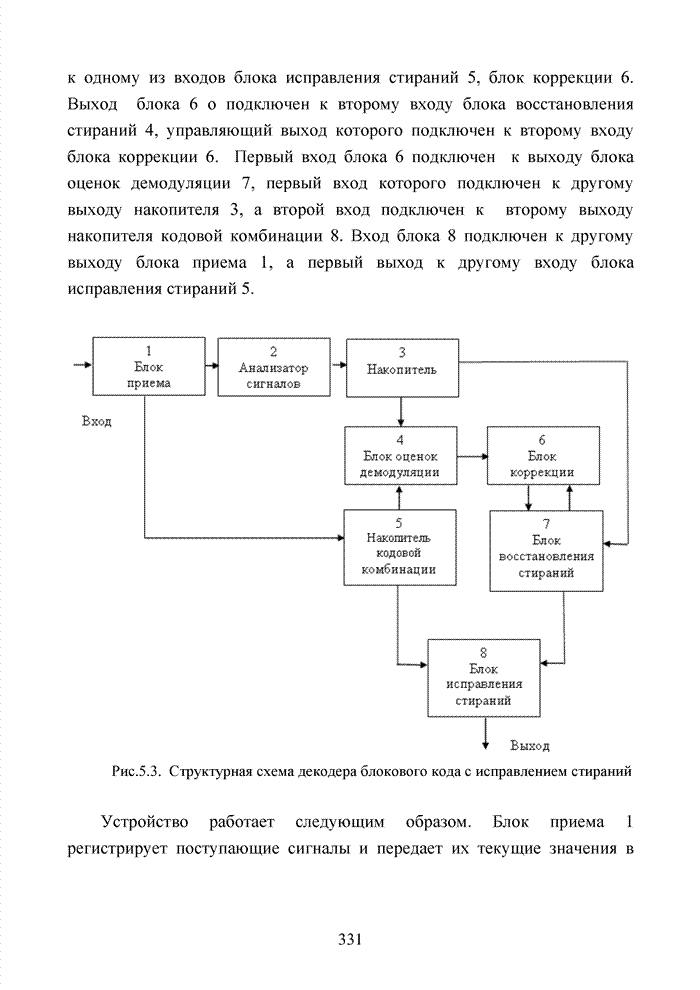
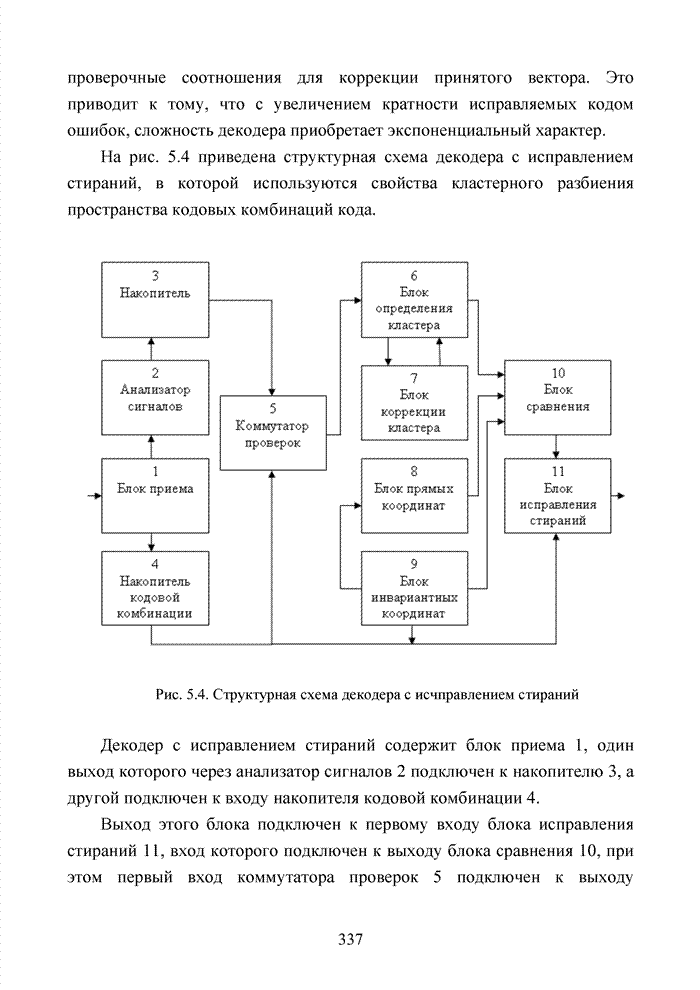
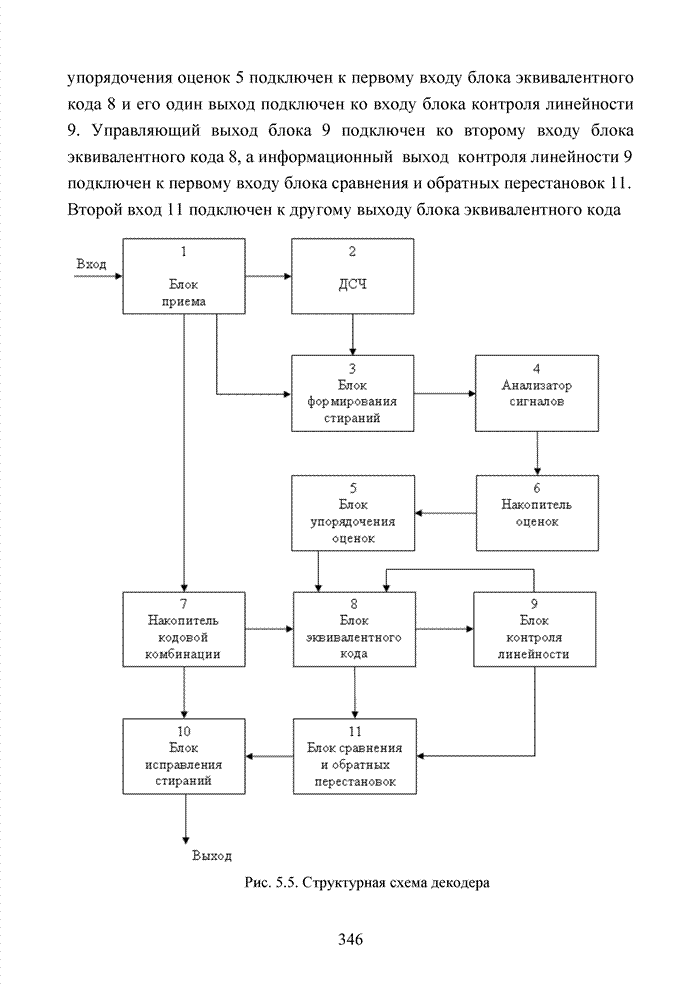
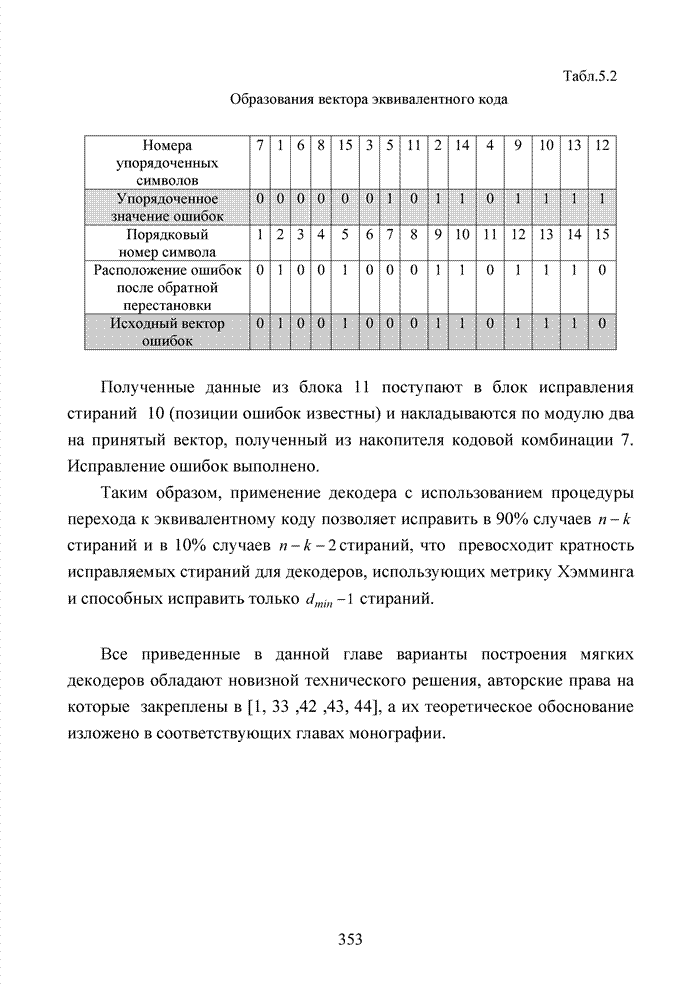
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
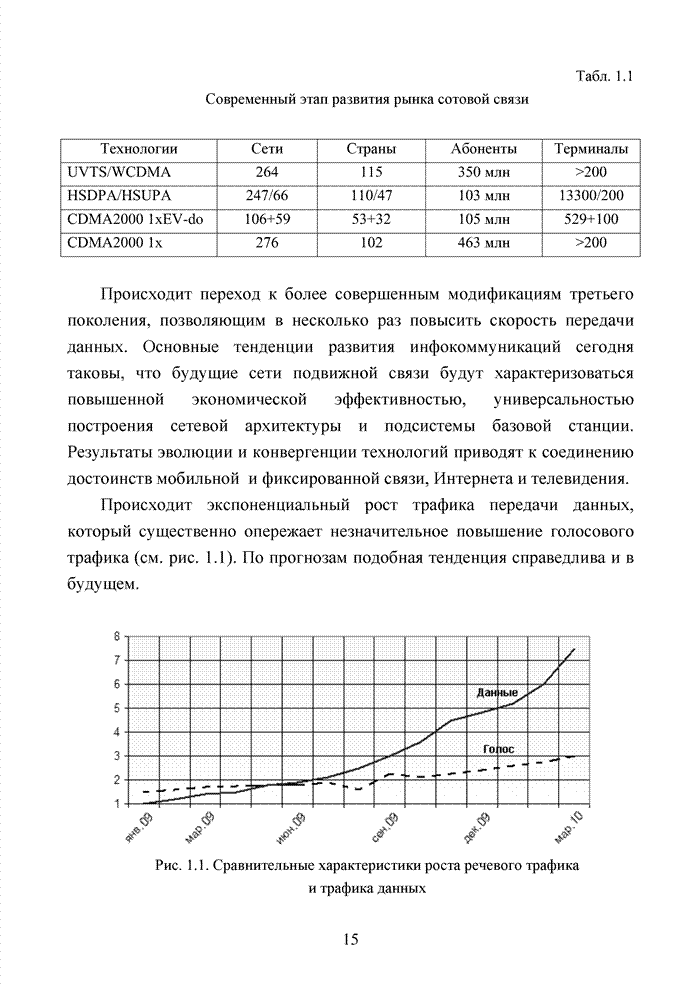
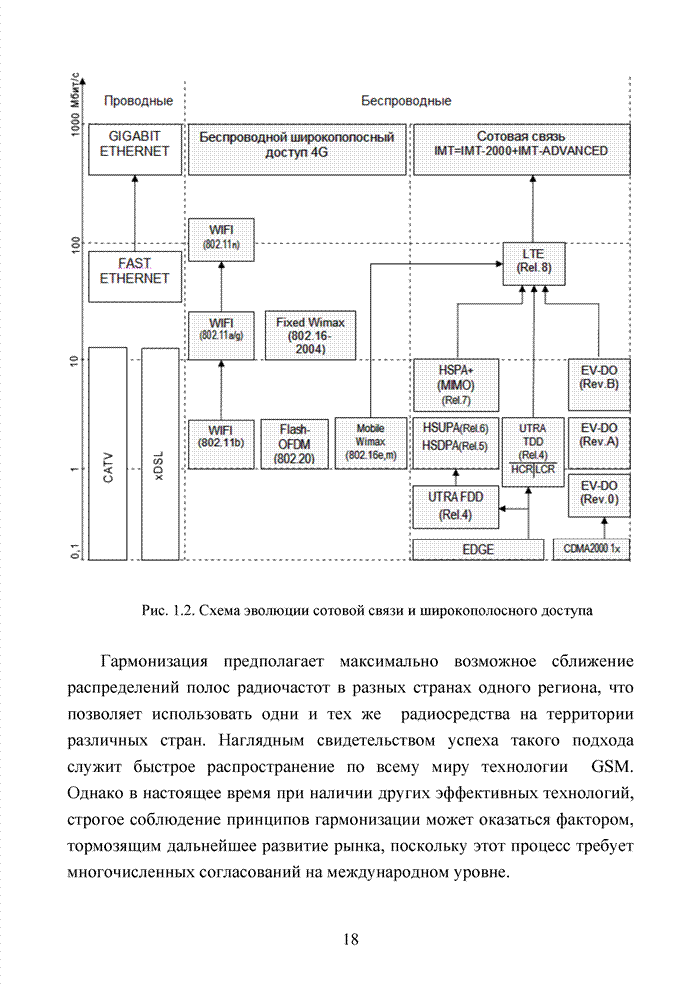
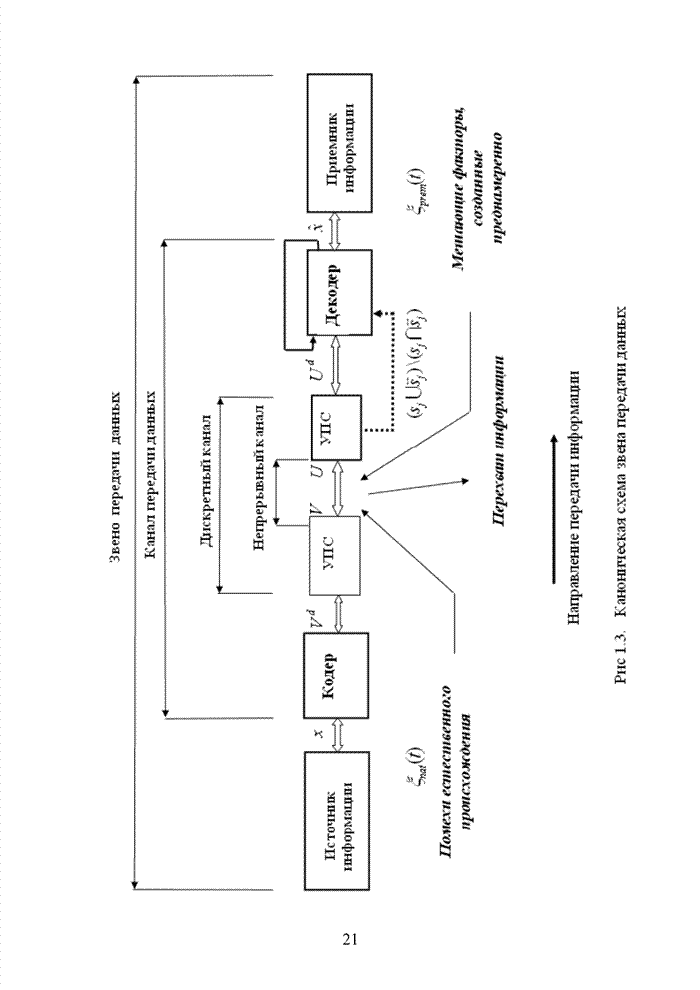
1.5. Алгебраические системы. Понятие группы
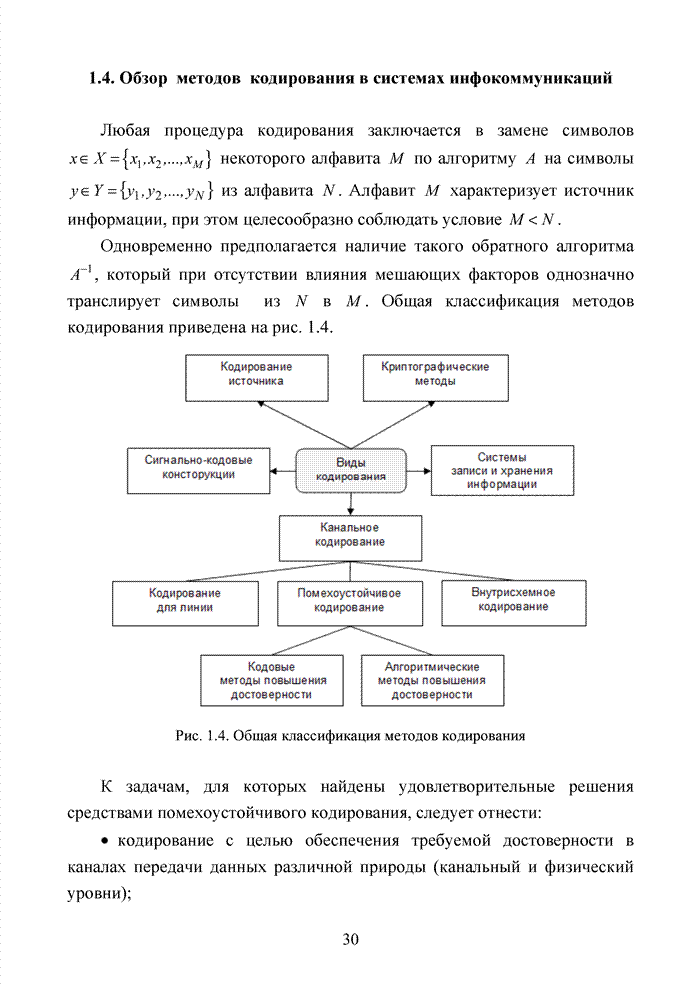
Тория помехоустойчивого кодирования опирается на существование особых структурных закономерностей, которые описываются алгебраическими системами. В этом разделе вводятся наиболее важные понятия абстрактной алгебры (прикладной комбинаторики), которые активно используются в последующих главах, для строго обоснования приведенных в них утверждений и доказательства работоспособности представленных алгоритмов. Поэтому в отличие специальной литературы, посвященной исключительно математическим аспектам рассматриваемой предметной области, излагаемый материал будет носить прикладной характер и иллюстрироваться примерами, непосредственно относящимися к теории помехоустойчивого кодирования.
Известным направлением комбинаторики является изучение свойств перестановок и подстановок. Под перестановками некоторых элементов (чаще всего чисел) принято понимать все возможные способы, которыми эти элементы можно выстроить в ряд. Подсчет числа таких способов представляет собой задачу комбинаторики.
Числа 1, 2 и 3 можно выстроить в ряд следующими способами
123, 132, 213, 231, 312, 321.
В общем случае число
перестановок из ![]() элементов
равно произведению всех целых чисел от 1 до
элементов
равно произведению всех целых чисел от 1 до ![]() или
или ![]() !. Подстановкой называется биекция (взаимно
однозначное соответствие) конечного множества R на себя. Подстановку часто изображают в виде
двудольного графа (см. рис. 1.7).
!. Подстановкой называется биекция (взаимно
однозначное соответствие) конечного множества R на себя. Подстановку часто изображают в виде
двудольного графа (см. рис. 1.7).

Рис. 1.7. Представление подстановки в виде графа
Другими словами, подстановка – это операция, изменяющая порядок элементов в перестановке.
Подстановку часто изображают в виде соответствия между двумя строками
![]() ,
,
верхнюю строку называют «операндом»,
нижнюю – «результатом». Подстановку можно представить, выписывая в строку ![]() элементов R и подписывая под каждым из них его
образ при биекции.
элементов R и подписывая под каждым из них его
образ при биекции.
Перестановкой множества R называется вполне упорядоченное
множество, состоящее из всех элементов R. Если R состоит
из ![]() элементов,
то имеется
элементов,
то имеется ![]() !
таких множеств. Таким образом, подстановку можно охарактеризовать
перестановкой, задаваемой нижней строкой. Исходя из этого в ряде работ термины
«перестановка» и «подстановка» трактуются без особых отличий между собой,
например, в [79, 84].
!
таких множеств. Таким образом, подстановку можно охарактеризовать
перестановкой, задаваемой нижней строкой. Исходя из этого в ряде работ термины
«перестановка» и «подстановка» трактуются без особых отличий между собой,
например, в [79, 84].
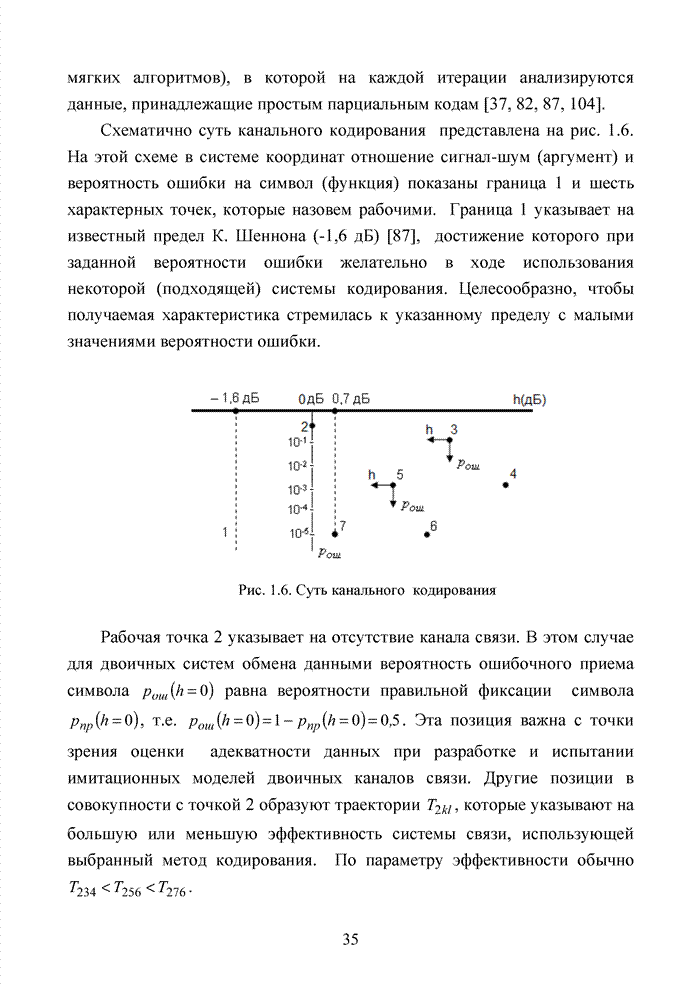
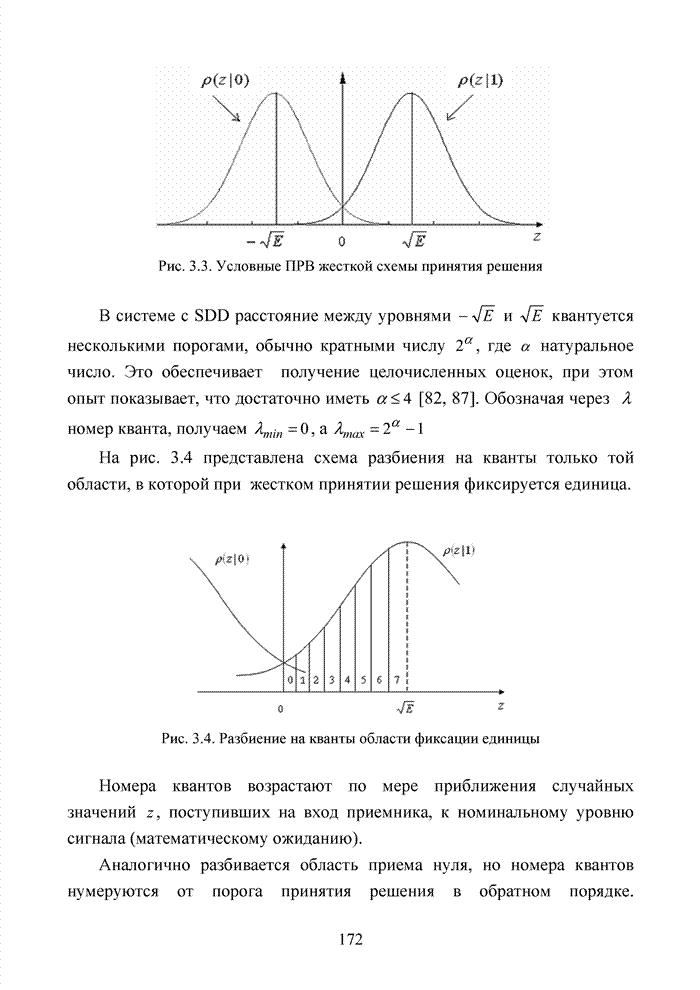
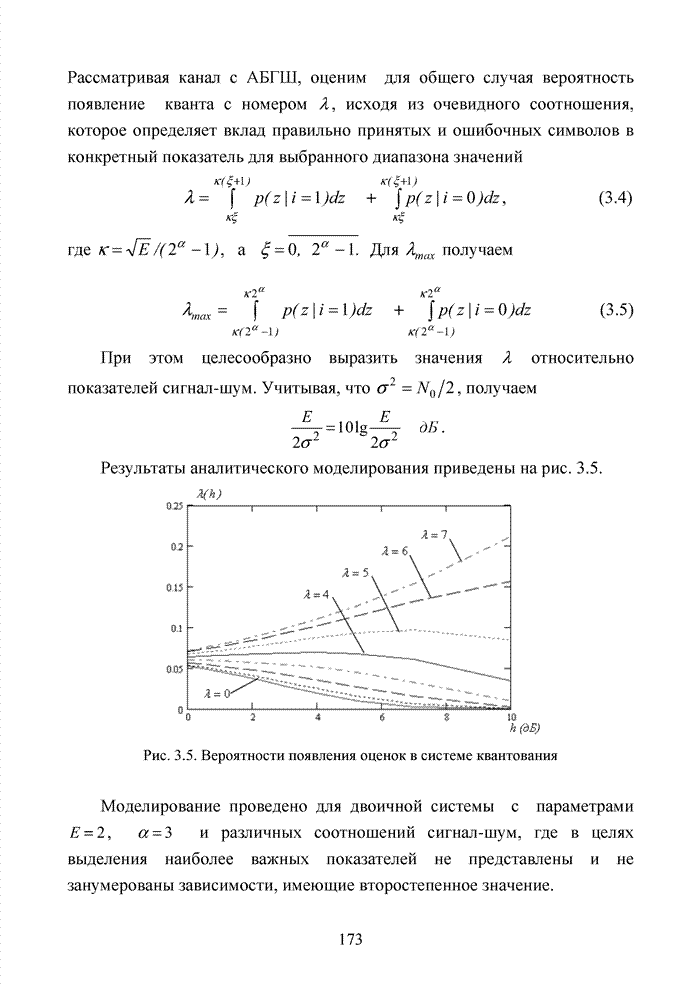
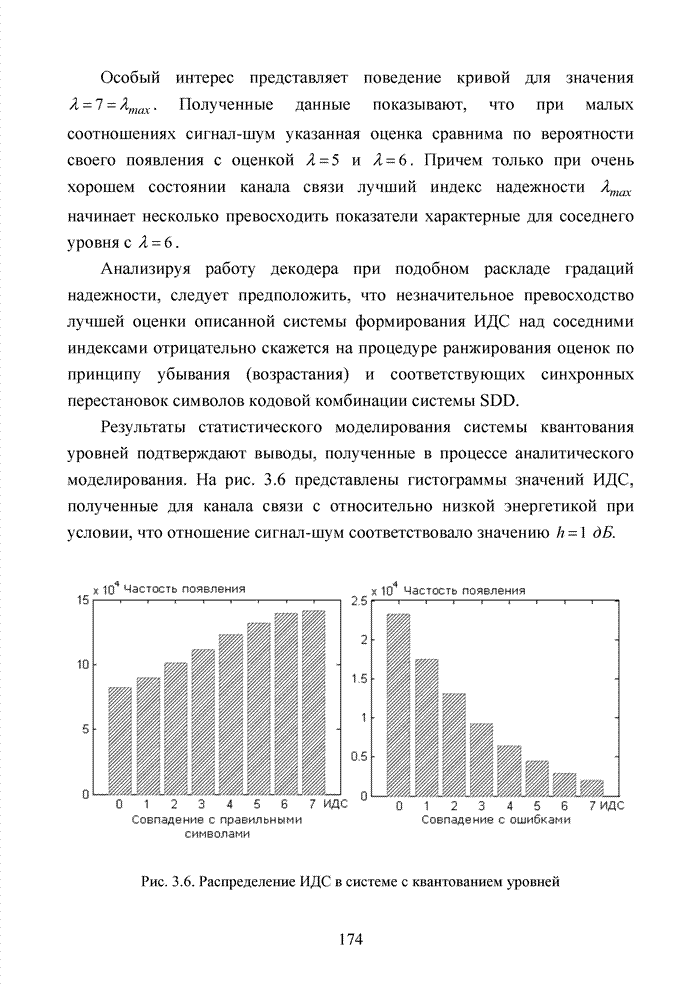
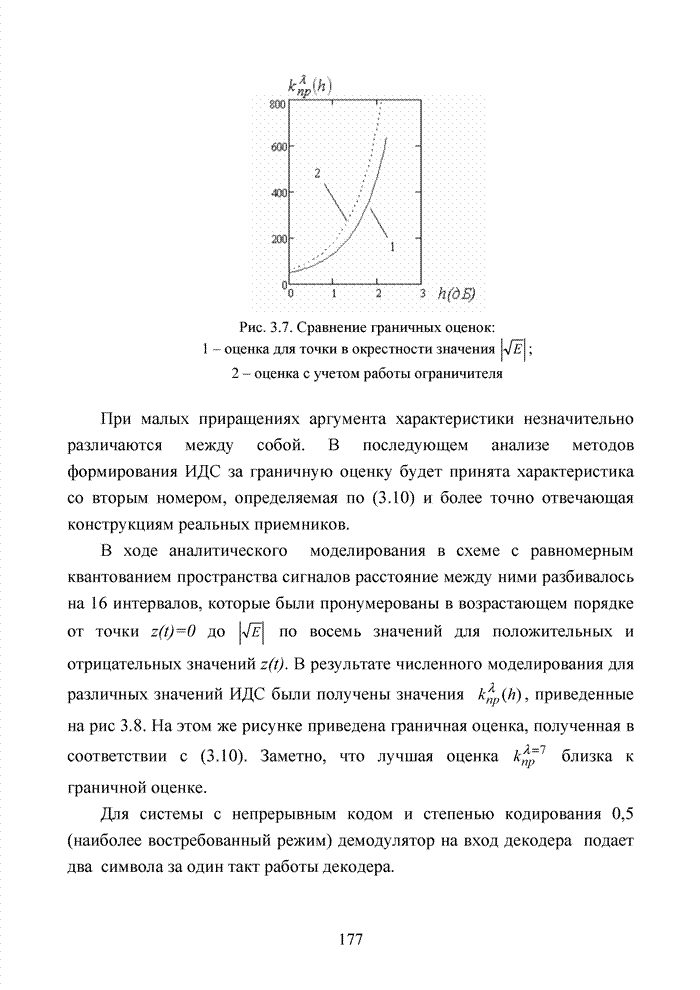
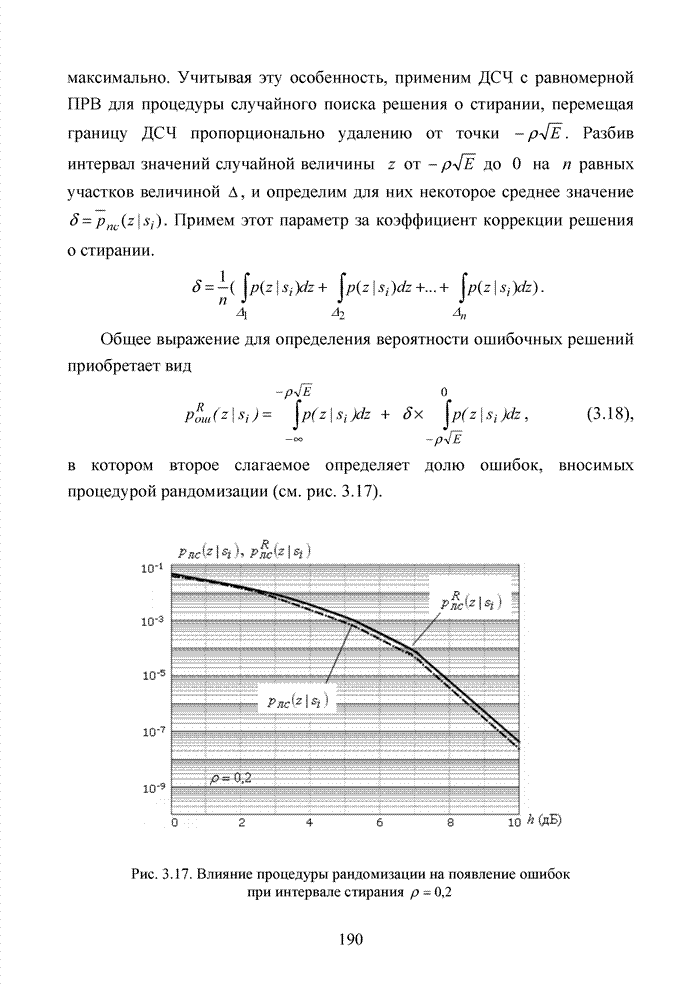
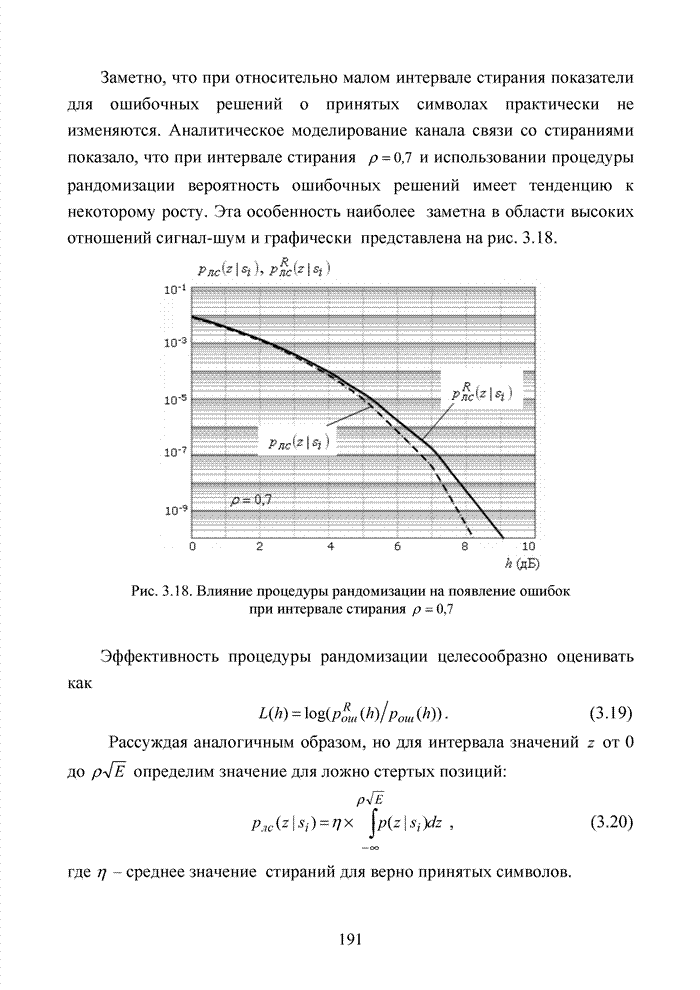
Приведенные простые правила используются в системах мягкого декодирования в качестве основы при сортировке символов кодовых комбинаций по убыванию или возрастанию оценок надежности. Подобную сортировку часто называют упорядоченной статистикой. Не рассматривая подробно на данном этапе изложения материала принципы формирования оценок надежности символов кодовых комбинаций, будем считать, что приемник формирует для каждого символа некоторую градацию надежности в виде целых чисел от 0 до 7. Таким образом, значение R определяется длиной кодового вектора, поэтому упорядочиваются не сами оценки надежности, а их номера в кодовом блоке.
Пусть в порядке
возрастания номеров были зафиксированы ![]() символов. Обозначим через
символов. Обозначим через ![]()
![]() -й символ, которому приемник в
ходе обработки присвоил градацию надежности
-й символ, которому приемник в
ходе обработки присвоил градацию надежности ![]() , причем
, причем ![]() , а
, а ![]() может принимать любые целые значения из
множества
может принимать любые целые значения из
множества ![]() ,
которые на длине
,
которые на длине ![]() могут
повторяться. Пусть
могут
повторяться. Пусть ![]() ,
и пусть последовательность имеет вид
,
и пусть последовательность имеет вид
![]() .
.
Упорядочим последовательность принятых символов в порядке убывания градаций надежности символов
![]() .
.
Следовательно, операнд и результат подстановки будут иметь вид
![]() .
.
На основании этого в
декодере формируется перестановочная матрица ![]() .
.
 .
.
Подобная матрица необходима для дальнейшей обработки кодовой комбинации, поскольку умножение кодового вектора на матрицу приводит к биекции элементов кодовой комбинации в соответствии с результатом перестановки.
Действительно:
![]()
и
![]() .
.
Для того чтобы подстановка была полностью задана необходимо:
- задать всю совокупность элементов, над которыми производится подстановка, то есть конечное множество, называемое областью определения подстановки;
- задать алгоритм подстановки, то есть для каждого элемента, принадлежащего области определения подстановки указать тот элемент, в который он переходит под действием подстановки, причем так, чтобы различные элементы при подстановке переходили в другие отличные от исходных.
Две подстановки называются одинаковыми, если их области определения совпадают и каждый элемент, принадлежащий совместной области определения, они переводят в один и тот же элемент.
Пусть ![]() R,
R, ![]() – образ элемента
– образ элемента ![]() при подстановке
при подстановке ![]() , и пусть
, и пусть ![]() R
R![]() , – образ элемента
, – образ элемента ![]() при подстановке
при подстановке ![]() .
.
Определим подстановку
![]() .
.
Если после любой
подстановки ![]() выполнить
подстановку
выполнить
подстановку ![]() получится
подстановка, которая называется произведением подстановок
получится
подстановка, которая называется произведением подстановок ![]() и
и ![]() , обозначаемое через
, обозначаемое через ![]() .
.
Например, если
![]() и
и ![]() то
то
![]() .
.
Последовательное выполнение подстановок, называемое «умножением», не означает, что для этого «умножения» справедливы все правила обычного умножения. В обычном умножении (умножении чисел) произведение не зависит от порядка сомножителей. Для умножения подстановок подобное утверждение не верно. Действительно
![]() .
.
Полученный результат заведомо
отличается от результата, приведенного выше. Следовательно, свойство
коммутативности (переместительный закон) умножения подстановок не выполняется. Только
при одинаковых сомножителях ![]() или
или ![]() умножение подстановок оказывается
коммутативным.
умножение подстановок оказывается
коммутативным.
За единичную подстановку принимают перестановку, которая не приводит к перестановке элементов, например,
![]() .
.
Заданная на некотором множестве подстановка называется единичной или тождественной, если под действием ее все элементы множества переходят в себя. Единичная подстановка играет во множестве подстановок такую же роль, какая отведена в умножении чисел единице.
Если в любой подстановке
поменять местами операнд и результат, то получается обратная перестановка,
которую принято обозначать как ![]() для подстановки
для подстановки ![]() или
или ![]() для подстановки
для подстановки ![]() .
.
В теории кодирования особое значение имеют операции на множестве перестановок, которые подчиняются трем свойствам:
- ассоциативности;
- наличию единичного элемента;
- существование обратного элемента.
Операция ассоциативна, то
есть для любых трех подстановок ![]() и
и ![]() выполняется соотношение
выполняется соотношение ![]() . Ассоциативность
означает, что произведение трех сомножителей не зависит от того, в каком
порядке производится умножение.
. Ассоциативность
означает, что произведение трех сомножителей не зависит от того, в каком
порядке производится умножение.
Существование единичного
элемента означает, что есть такая подстановка ![]() , которая для любой подстановки
, которая для любой подстановки ![]() приводит к равенству
вида
приводит к равенству
вида ![]() .
.
Существование обратного
элемента указывает на то, что для любой подстановки ![]() можно найти такой однозначно
определенный элемент
можно найти такой однозначно
определенный элемент ![]() ,
что
,
что ![]() .
.
На других множествах, так же как и на множестве подстановок можно задать операции, обладающие указанными свойствами. В таких случаях принято говорить, что выбранное множество с заданной на нем операцией образует группу.
Пример 1. Рассмотрим множество целых чисел. В таком множестве умножение всегда выполнимо, поскольку произведение двух целых чисел также является целым числом. Остается лишь проверить, обладает ли оно тремя свойствами группового умножения.
Во-первых, умножение ассоциативно.
Во-вторых, существует
такое целое число ![]() ,
что при любом целом числе
,
что при любом целом числе ![]() выполняется соотношение
выполняется соотношение ![]() , следовательно,
, следовательно, ![]() . Действительно, если
. Действительно, если ![]() – такое число, что при
любом отличном от нуля числе
– такое число, что при
любом отличном от нуля числе ![]() выполняется соотношение
выполняется соотношение ![]() , то это возможно лишь в
одном случае: при
, то это возможно лишь в
одном случае: при ![]() .
С другой стороны, если рассматриваемое множество чисел содержит единицу, то все
входящие в него числа удовлетворяют соотношениям
.
С другой стороны, если рассматриваемое множество чисел содержит единицу, то все
входящие в него числа удовлетворяют соотношениям ![]() . Следовательно, для множества целых чисел
с обычным умножением в качестве предполагаемого группового умножения проверка
второго свойства с водится к ответу на вопрос, принадлежит ли единица к
интересующему нас множеству. Единственное исключение составляет множество,
содержащее только один элемент – ноль.
. Следовательно, для множества целых чисел
с обычным умножением в качестве предполагаемого группового умножения проверка
второго свойства с водится к ответу на вопрос, принадлежит ли единица к
интересующему нас множеству. Единственное исключение составляет множество,
содержащее только один элемент – ноль.
В третьих, обратный
элемент не существует. Например, для числа 2 невозможно указать такое число ![]() , которое удовлетворяло
бы соотношению
, которое удовлетворяло
бы соотношению ![]() ,
так как в левой части стояло бы четное, а в правой – нечетное число. Во
множестве целых чисел деление выполнимо не во всех случаях. Таким образом,
необходимым условием существования группы по умножению является выполнимость
обратной операции – операции деления.
,
так как в левой части стояло бы четное, а в правой – нечетное число. Во
множестве целых чисел деление выполнимо не во всех случаях. Таким образом,
необходимым условием существования группы по умножению является выполнимость
обратной операции – операции деления.
Вывод: целые числа не образуют группу по умножению.
Пример 2. Рассмотрим множество рациональных чисел. Поскольку произведение двух рациональных чисел – число рациональное, то обычное умножение не выводит результат умножения за пределы множества рациональных чисел.
Проверим выполнение всех групповых свойств. Ассоциативность в проверке не нуждается, так же как и наличие единичного элемента (единица – рациональное число). Проверка выполнения третьего условия дает неудовлетворительный результат. Если рациональное число умножить на обратное число (дробь), то результат окажется равным единице. Известно, что обратные числа существуют почти для всех рациональных чисел, и единственное исключение составляет ноль. При умножении его на любое другое число всегда получается ноль. Это означает, что произведение двух сомножителей, один из которых равен нолю, никак не может равняться единице. Поэтому во множестве рациональных чисел с заданным на нем умножением обратный элемент существует не для всех элементов.
Вывод: рациональные числа не образуют группу по умножению.
Пример 3. Рассмотрим множество рациональных чисел, отличных от нуля. Произведение двух рациональных чисел, отличных от нуля, не равно нулю и рационально. Результат умножения не выходит за пределы рассматриваемого множества чисел. Единица рациональное число, следовательно, остается проверить, выполнение третьего условия. Было показано, что для чисел, отличных от нуля, всегда существует обратные числа. Эти обратные числа также рациональны и отличны от нуля.
Вывод: отличные от нуля рациональные числа образуют группу по умножению.
Пример 4. Рассмотрим множество положительных рациональных чисел. Из предыдущих примеров ясно, что необходима проверка только третьего условия. Поскольку число, обратное положительному числу, также положительно и рационально, то проверяемое условие выполняется.
Вывод: положительные рациональные числа образуют группу по умножению.
Используя приведенную методику, можно показать, что числа +1 и -1 образуют группу по умножению, а отрицательные рациональные числа не образуют группу по умножению, поскольку умножение двух отрицательных чисел уводит результат за пределы множества отрицательных рациональных чисел.
Приведенные рассуждения касались тех групп, в которых за основную операцию была принята арифметическая операция – умножение. Такие образования получили название мультипликативных групп. Оценим возможность образования группы, если за основную операцию принять операцию сложения. Такие группы называются аддитивными. При этом, если в мультипликативной группе обратной операцией для умножения была необходима операция деления, то в аддитивной группе такой операцией должна служить операция вычитания.
Условиями образования аддитивных групп являются:
- выполнение требований ассоциативности;
- наличие единичного элемента относительно операции сложения;
- наличие обратного элемента.
Операция сложения ассоциативна, поэтому первое свойство выполняется всегда.
Единицей относительно
сложения может быть такой элемент ![]() , который при любом элементе
, который при любом элементе ![]() , принадлежащем
рассматриваемому множеству чисел, удовлетворяет соотношению
, принадлежащем
рассматриваемому множеству чисел, удовлетворяет соотношению ![]() . Это условие выполняется только,
если
. Это условие выполняется только,
если ![]() .
Действительно, для любого элемента множества удовлетворяется условие
.
Действительно, для любого элемента множества удовлетворяется условие ![]() , при этом необходимо
проверять, принадлежит ли нуль рассматриваемому множеству чисел.
, при этом необходимо
проверять, принадлежит ли нуль рассматриваемому множеству чисел.
Числом обратным числу ![]() при сложении служит
число
при сложении служит
число ![]() ,
удовлетворяющее соотношению
,
удовлетворяющее соотношению ![]() . Таким числом может быть лишь
. Таким числом может быть лишь ![]() . Для него выполняется
условие
. Для него выполняется
условие ![]() . В
этом случае достаточно каждый раз проверять, содержит ли рассматриваемое
множество чисел вместе с каждым принадлежащим числом то же число, взятое со
знаком минус.
. В
этом случае достаточно каждый раз проверять, содержит ли рассматриваемое
множество чисел вместе с каждым принадлежащим числом то же число, взятое со
знаком минус.
Пример 5. Рассмотрим множество целых чисел. Сумма двух целых чисел также является целым числом, то выполнение операции сложения не выводит результат сложения за пределы рассматриваемого множества. Поскольку ноль – целое число и любое целое число, взятое со знаком минус, является также целым числом, то сложение, заданное на множестве целых чисел, обладает всеми свойствами группового сложения.
Вывод: целые числа образуют группу по сложению.
Проводя аналогичные рассуждения по указанной схеме, легко доказать, что рациональные числа и ноль, представленный как единичное множество, образуют группу по сложению. Напротив, рациональные числа, отличные от ноля, положительные рациональные числа, неотрицательные рациональные числа, числа -1 и +1 не образуют группу по сложению.
Аналогичные рассуждения можно проводить относительно любого множества чисел: вещественных (положительных или отрицательных), комплексных, целых положительных степени двойки и т.п.
Рассмотренные примеры показывают, как часто встречаются множества с заданными на них ассоциативными операциями, относительно которых существует единичный элемент, и все элементы имеют обратные элементы. В таких случаях говорят, что соответствующие множества образуют группы относительно заданных на них операций. Множество всех целых чисел может и быть группой и не быть группой в зависимости от того, какая операция будет задана на ней: сложение или умножение чисел.
Пара ![]() , состоящая из множества
, состоящая из множества ![]() и двухместной (или
бинарной) операции
и двухместной (или
бинарной) операции ![]() ,
называется группой, если операция
,
называется группой, если операция ![]() удовлетворяет следующим аксиомам.
удовлетворяет следующим аксиомам.
I. Операция ![]() ассоциативна, то есть для любых элементов
ассоциативна, то есть для любых элементов ![]() ,
, ![]() и
и ![]() множества
множества ![]() выполняется
выполняется ![]() .
.
II. Существует единичный элемент ![]() множества
множества ![]() такой, что для любого
элемента
такой, что для любого
элемента ![]() из
из ![]() выполняется условие
выполняется условие![]() .
.
III. Существует обратный элемент, то
есть для любого элемента ![]() множества
множества ![]() можно найти такой элемент
можно найти такой элемент ![]() , что
, что ![]() .
.
Операция ![]() называется групповой
операцией, а элементы множества
называется групповой
операцией, а элементы множества ![]() – элементами группы.
– элементами группы.
Многие группы обладают тем свойством, что любые два их элемента можно менять местами и при этом получать одинаковое решение. Таковы, например, группы чисел как по сложению, так и по умножению. Именно такие группы находят широкое применение в теории кодирования.
Группа ![]() называется
коммутативной, или абелевой, если операция
называется
коммутативной, или абелевой, если операция ![]() коммутативна, то есть для любых двух
элементов
коммутативна, то есть для любых двух
элементов ![]() и
и ![]() группы
группы ![]() выполняется равенство
выполняется равенство ![]() .
.
Необходимо сделать ряд
специальных замечаний, связанных с особенностями теории групп, который
позволит обосновать отдельные алгоритмы обработки кодовых комбинаций. В ряде
задач перечисление группы может осуществляться лексикографическим порядком,
т.е. порядком, принятым в словарях. Выборка размерности ![]()
![]() предшествует
предшествует ![]() -й выборке
-й выборке ![]() , если
, если ![]() первых элементов (считая слева направо или
справа налево, по соглашению) этих
первых элементов (считая слева направо или
справа налево, по соглашению) этих ![]() выборок равны, а
выборок равны, а ![]() -й элемент первой предшествует
-й элемент первой предшествует ![]() -му элементу второй.
Например,
-му элементу второй.
Например, ![]() предшествует
предшествует
![]() . Разумеется,
отношение порядка может быть произвольным.
. Разумеется,
отношение порядка может быть произвольным.
Для удобства аксиомы группы сведены в табл. 1.2.
Табл. 1.2 Основные аксиомы групп
|
Основные аксиомы группы |
Аддитивная группа |
Мультипликативная группа |
|
Замкнутость |
Если
|
Если
|
|
Ассоциативный закон |
|
|
|
Существование единичного элемента |
|
|
|
Существование обратного элемента |
или |
|
|
Коммутативность |
|
|
Другим примером группы являются векторы на плоскости (операция сложения векторов). При сложении любых двух векторов результатом этой операции является новый вектор. Следовательно, в этом случае операция не выходит за пределы рассматриваемого множества. Операция сложения векторов ассоциативна. Единичным элементом служит нулевой вектор, а элементом обратным данному вектору – противоположный вектор (т.е. вектор, занимающий то же положение и имеющий ту же длину, что и данный вектор, но направленный в противоположную сторону). Таким образом, групповые свойства операции подтверждаются.
Особое место в групповых операциях занимают движения на плоскости.
Преобразование плоскости называется движением, если:
- между точками плоскости до преобразования и теми точками, в которые они переходят под действием преобразования, существует взаимно-однозначное соответствие;
- расстояние между любыми двумя точками плоскости совпадает с расстоянием между соответствующими им точками.
Каждому движению на плоскости соответствует свое отображение. Одни движения сводятся к сдвигам, другие – к повороту на 180° вокруг прямой, лежащей в плоскости (то есть к отражению относительно этой прямой).
Движение ![]() переводит каждую точку
переводит каждую точку ![]() плоскости в однозначно
определенную точку
плоскости в однозначно
определенную точку ![]() ,
а в общем случае по этому принципу различные точки могут переходить в различные
другие точки. Кроме того, если движение
,
а в общем случае по этому принципу различные точки могут переходить в различные
другие точки. Кроме того, если движение ![]() переводит точку
переводит точку ![]() в
в ![]() , то расстояние между точками
, то расстояние между точками ![]() и
и ![]() совпадает с расстоянием между
точками
совпадает с расстоянием между
точками ![]() и
и ![]() . Точку, в которую
преобразование
. Точку, в которую
преобразование ![]() переводит
точку
переводит
точку ![]() ,
обозначают
,
обозначают ![]() .
.
В целях иллюстрации применимости принципов алгебраических систем к теории построения помехоустойчивых кодов введем понятие линейного блокового кода, при этом комментарии по отдельным параметрам и свойствам таких кодов будут вводиться по мере изложения теоретического материала.
Пусть необходимо
закодировать ![]() информационных
двоичных разряда, которые обозначим через
информационных
двоичных разряда, которые обозначим через ![]() , где
, где ![]() . Линейный код представляет собой множество
комбинаций
. Линейный код представляет собой множество
комбинаций ![]() ,
полученных в результате линейного преобразования
,
полученных в результате линейного преобразования ![]() -значных комбинаций в
-значных комбинаций в ![]() -значные (для двоичных кодов
линейное преобразование имеет смысл умножения и сложения по mod 2). Полученный код, содержащий
-значные (для двоичных кодов
линейное преобразование имеет смысл умножения и сложения по mod 2). Полученный код, содержащий ![]() блоков длиной
блоков длиной ![]() , обозначают
, обозначают ![]() .
.
Множество ![]() -элементных разрешенных
комбинаций линейного кода может быть представлено (аналог представления
функции) тремя способами:
-элементных разрешенных
комбинаций линейного кода может быть представлено (аналог представления
функции) тремя способами:
- полным перечислением всех разрешенных кодовых комбинаций;
-
через
порождающую матрицу кода
 ;
;
-
через
порождающий полином кода
 .
.
Пусть процедура получения
проверочных символов кода ![]() , число которых составляет
, число которых составляет ![]() , задается уравнениями
вида
, задается уравнениями
вида
 ,
,
тогда множество разрешенных кодовых комбинаций может быть представлено табл. 1.3.
Табл. 1.3 Разрешенное множество комбинаций блокового кода (7,4)
|
Кодируемое число |
Двоичное представление числа |
Комбинация (n,k) кода |
Кодируемое число |
Двоичное представление числа |
Комбинация (n,k) кода |
|
010 |
00002 |
0000 000 |
810 |
10002 |
1000 101 |
|
110 |
00012 |
0001 011 |
910 |
10012 |
1001 110 |
|
210 |
00102 |
0010 110 |
1010 |
10102 |
1010 011 |
|
310 |
00112 |
0011 101 |
1110 |
10112 |
1011 000 |
|
410 |
01002 |
0100 111 |
1210 |
11002 |
1100 010 |
|
510 |
01012 |
0101 100 |
1310 |
11012 |
1101 001 |
|
610 |
01102 |
0110 001 |
1410 |
11102 |
1110 100 |
|
710 |
01112 |
0111 010 |
1510 |
11112 |
1111 111 |
Перечисление разрешенного
множества комбинаций по первому способу допустимо при небольших значениях параметра
![]() . Но если
. Но если ![]() , подобная процедура при
ручном счете становится громоздкой. Метод прямого перебора комбинаций
используют при решении отдельных задач кодирования с привлечением
вычислительной техники, например, для точного определения весового спектра
кода.
, подобная процедура при
ручном счете становится громоздкой. Метод прямого перебора комбинаций
используют при решении отдельных задач кодирования с привлечением
вычислительной техники, например, для точного определения весового спектра
кода.
Второй способ представления кодовых комбинаций является более рациональным. Для описания кода он занимает значительно меньшее время, хотя в порождающей матрице по-прежнему содержится вся информация о пространстве разрешенных кодовых комбинаций.
Третий способ описания
кодов через их порождающие полиномы ![]() наиболее удобен, поскольку имеет
компактную форму записи, но через нее возможно получение порождающей матрицы
наиболее удобен, поскольку имеет
компактную форму записи, но через нее возможно получение порождающей матрицы ![]() , и, следовательно,
всего пространства разрешенных кодовых комбинаций.
, и, следовательно,
всего пространства разрешенных кодовых комбинаций.
Порождающая матрица кода
![]() в
систематической форме имеет вид:
в
систематической форме имеет вид:
 ,
,
а порождающий полином кода ![]() представлен нижней
строкой этой матрицы и записывается как
представлен нижней
строкой этой матрицы и записывается как ![]() . Представленная матрица в первых
. Представленная матрица в первых ![]() столбцах содержит
единичную матрицу
столбцах содержит
единичную матрицу ![]() размерности
размерности
![]() , при этом
оставшаяся подматрица
, при этом
оставшаяся подматрица ![]() размерности
размерности
![]() играет важную
роль в процедуре декодирования и будет описана ниже. Таким образом,
играет важную
роль в процедуре декодирования и будет описана ниже. Таким образом,
![]() . (1.13)
. (1.13)
В самом общем случае, в
качестве порождающей матрицы можно использовать любые ![]() разрешенные комбинации кода. При
этом может быть образован тот же код, но матрица
разрешенные комбинации кода. При
этом может быть образован тот же код, но матрица ![]() в систематической форме и порождаемый с
ее помощью систематический код отличаются большим количеством полезных
свойств, чем произвольно взятый набор строк и формируемый с их помощью код. Из
матрицы
в систематической форме и порождаемый с
ее помощью систематический код отличаются большим количеством полезных
свойств, чем произвольно взятый набор строк и формируемый с их помощью код. Из
матрицы ![]() в
систематической форме сравнительно просто может быть образована проверочная
матрица кода
в
систематической форме сравнительно просто может быть образована проверочная
матрица кода ![]() .
.
![]() , (1.14)
, (1.14)
при этом обязательно выполняется условие
![]() .
(1.15)
.
(1.15)
Представленное в табл.
1.3 множество кодовых комбинаций является аддитивной группой. Если единичный
элемент е=0000000, то обратным элементом для произвольной кодовой
комбинации в коде является эта же комбинация. Представленное множество нельзя
классифицировать как мультипликативную группу, поскольку для произвольной
кодовой комбинации (кроме комбинации 1111111) невозможно отыскать обратный
элемент по умножению. Анализ табл. 1.3 показывает, что если выполняется
соотношение ![]() ,
комбинации
,
комбинации ![]() и
и ![]() оказываются инверсными.
Например, если
оказываются инверсными.
Например, если ![]() и
и
![]() , то
, то ![]() =15, следовательно,
=15, следовательно, ![]() и
и ![]() . Число единиц в кодовом векторе
принято называть весом кодовой комбинации, а общее количество таких комбинаций,
входящих в разрешенное множество кодовых комбинаций, принято назвать весовым
спектром. Весовой спектр, представленного в табл. 1.3 кода, показан на рис. 1.8.
. Число единиц в кодовом векторе
принято называть весом кодовой комбинации, а общее количество таких комбинаций,
входящих в разрешенное множество кодовых комбинаций, принято назвать весовым
спектром. Весовой спектр, представленного в табл. 1.3 кода, показан на рис. 1.8.

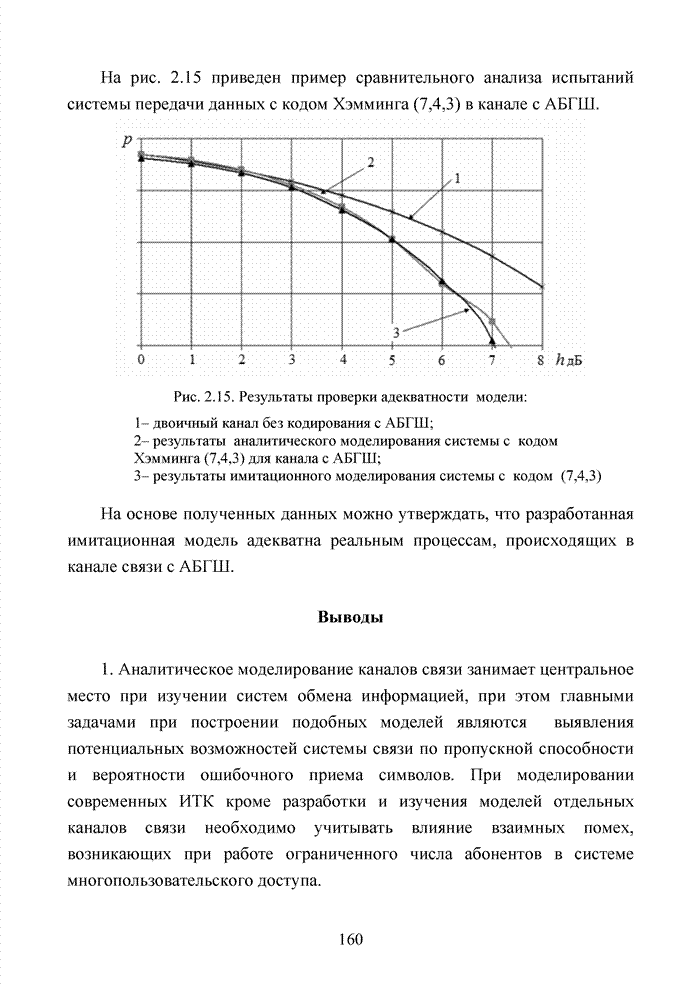
Рис. 1.8. Весовой спектр кода (7,4,3)
Если в кодовой комбинации
общее число единичных элементов оказывается равным ![]() , то комбинацию c таким же числом единичных элементов обозначают через значение
, то комбинацию c таким же числом единичных элементов обозначают через значение
![]() .
.
В ряде полезных для практики случаев знание весового спектра кода позволяет более точно оценить возможности кода по обнаружению или исправлению ошибок. Аналитическими методами точные значения весового спектра кода могут быть определены только для узкого круга типов кодов.
Как правило, для
большинства кодов применяется переборный метод, возможности которого по
понятным причинам ограничены. Наибольшее значение из всего множества
разрешенных кодовых комбинаций имеют комбинации с минимальным весом, т.е.
когда ![]() , при
этом комбинация, состоящая из одних нулей (единичный элемент аддитивной
группы), в расчет не принимается. Комбинации минимального веса дают непосредственное
представление о том, какое количество
, при
этом комбинация, состоящая из одних нулей (единичный элемент аддитивной
группы), в расчет не принимается. Комбинации минимального веса дают непосредственное
представление о том, какое количество ![]() ошибок код гарантирует исправить или
какое количество
ошибок код гарантирует исправить или
какое количество ![]() ошибок
обнаружить. Минимальный вес кодовой комбинации получил наименование метрики
Хэмминга и обозначается как
ошибок
обнаружить. Минимальный вес кодовой комбинации получил наименование метрики
Хэмминга и обозначается как ![]() или просто
или просто ![]() . Тогда свойства любого группового кода становятся
представимы всего через три параметра n, k и d
и формально такой код записывается как
. Тогда свойства любого группового кода становятся
представимы всего через три параметра n, k и d
и формально такой код записывается как ![]() . Любой групповой
. Любой групповой ![]() код способен исправить
код способен исправить ![]() ошибок, при этом тот же
код способен обнаружить
ошибок, при этом тот же
код способен обнаружить ![]() ошибок. Обнаружение ошибок является менее
сложной вычислительной процедурой относительно варианта с их исправлением. В
последнем случае от декодера требуется в принятой с ошибками кодовой
комбинации, прежде всего, найти ошибочные разряды и только после этого
выполнить их исправление.
ошибок. Обнаружение ошибок является менее
сложной вычислительной процедурой относительно варианта с их исправлением. В
последнем случае от декодера требуется в принятой с ошибками кодовой
комбинации, прежде всего, найти ошибочные разряды и только после этого
выполнить их исправление.
Предположим, что
приемнику в ходе обработки символов кодовой комбинации удалось отметить
каким-либо образом те разряды, которые по принятым в схеме демодуляции
критериям фиксируются как ненадежные. При таком подходе сложная задача поиска
ошибочных разрядов считается решенной, следовательно, остается решить вторую и
более простую часть общей задачи: исправить ![]() отмеченных ошибок. При этом корректирующая
способность кода косвенно повышается в два раза, что является несомненным преимуществом.
отмеченных ошибок. При этом корректирующая
способность кода косвенно повышается в два раза, что является несомненным преимуществом.
Выберем из множества
разрешенных кодовых комбинаций некоторого корректирующего кода две кодовые
комбинации с номерами ![]() и
и
![]() , вес которых
удовлетворяет значению
, вес которых
удовлетворяет значению ![]() . Такой код способен исправить только две
ошибки. Действительно, как это следует из анализа рис. 1.9, защитная зона
каждой кодовой комбинации составляет
. Такой код способен исправить только две
ошибки. Действительно, как это следует из анализа рис. 1.9, защитная зона
каждой кодовой комбинации составляет ![]() единицы.
единицы.

Рис. 1.9. Схеме образования защитных зон комбинаций
Если в результате
передачи по каналу связи комбинации ![]() ее значение оказалось переведенным в
состояние 1 или 2, то декодер примет верное решение, указав на комбинацию
ее значение оказалось переведенным в
состояние 1 или 2, то декодер примет верное решение, указав на комбинацию ![]() . В случае перевода
комбинации
. В случае перевода
комбинации ![]() в
точку 3 решение будет в пользу комбинации
в
точку 3 решение будет в пользу комбинации ![]() , поскольку точка 3 оказывается в защитной
зоне, принадлежащей комбинации
, поскольку точка 3 оказывается в защитной
зоне, принадлежащей комбинации ![]() . Изображая защитные зоны комбинаций в виде
сфер, в центре которых находятся кодовые комбинации, получим представление о
сферах Хэмминга, позволяющих выявить принципы существования кодов с заданными
параметрами.
. Изображая защитные зоны комбинаций в виде
сфер, в центре которых находятся кодовые комбинации, получим представление о
сферах Хэмминга, позволяющих выявить принципы существования кодов с заданными
параметрами.
В случае установки режима
обнаружения ошибок декодер не принимает решения о том, какой разрешенной комбинации
соответствует принятая с ошибками последовательность. Находясь в любой
промежуточной точке расстояния между центрами комбинаций ![]() и
и ![]() , декодер указывает, на выявленное несоответствие,
которое не дает возможности однозначно идентифицировать ни комбинацию
, декодер указывает, на выявленное несоответствие,
которое не дает возможности однозначно идентифицировать ни комбинацию ![]() , ни комбинацию
, ни комбинацию ![]() . Режим обнаружения
ошибок более прост относительно режима их исправления и широко используется при
реализации алгоритмических методов защиты информации от ошибок. Из рис. 1.9
становится ясным, что при реализации режима исправления ошибок целесообразно
выбирать нечетное значение параметра
. Режим обнаружения
ошибок более прост относительно режима их исправления и широко используется при
реализации алгоритмических методов защиты информации от ошибок. Из рис. 1.9
становится ясным, что при реализации режима исправления ошибок целесообразно
выбирать нечетное значение параметра ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
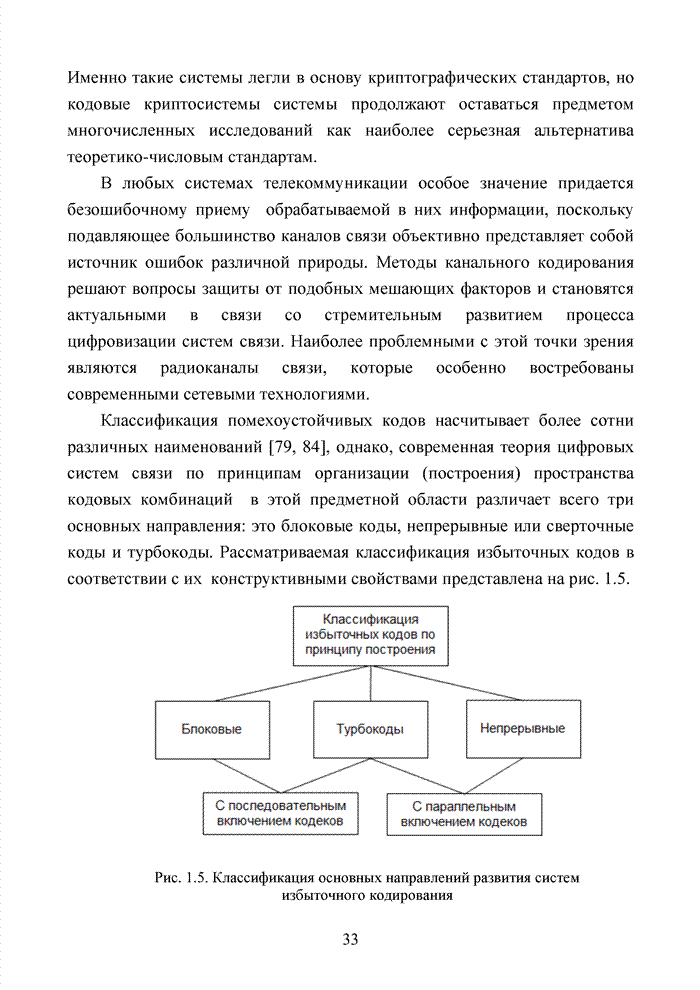
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
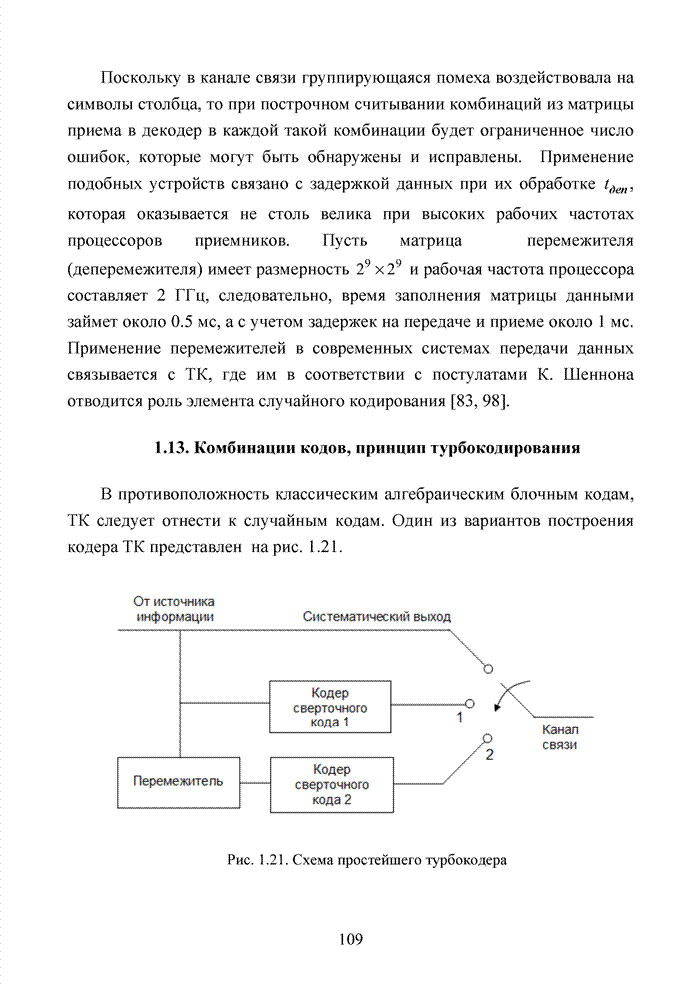
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
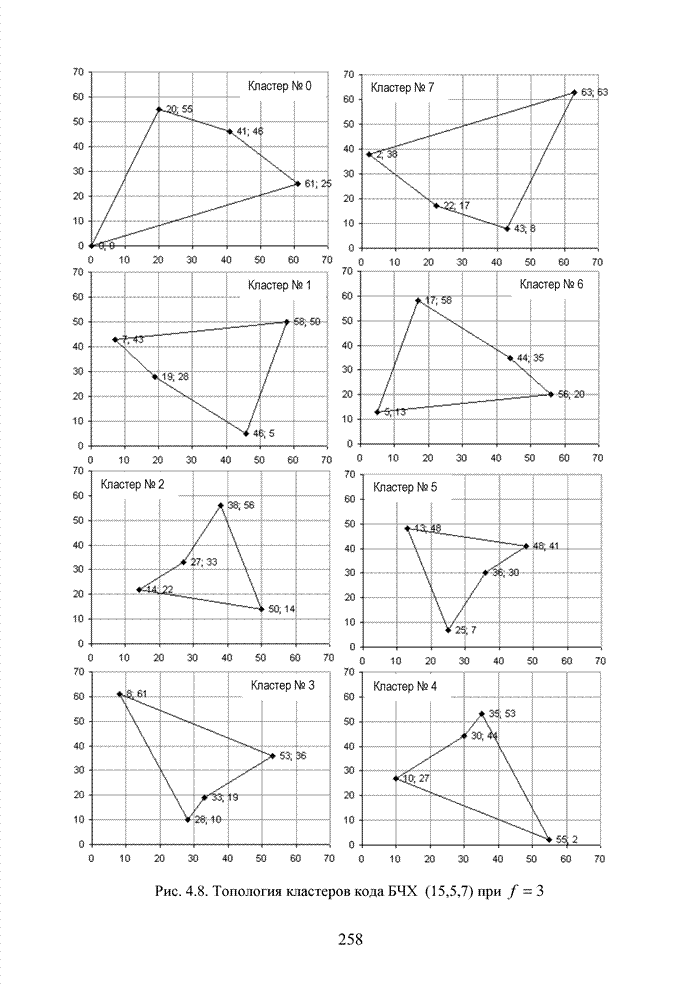
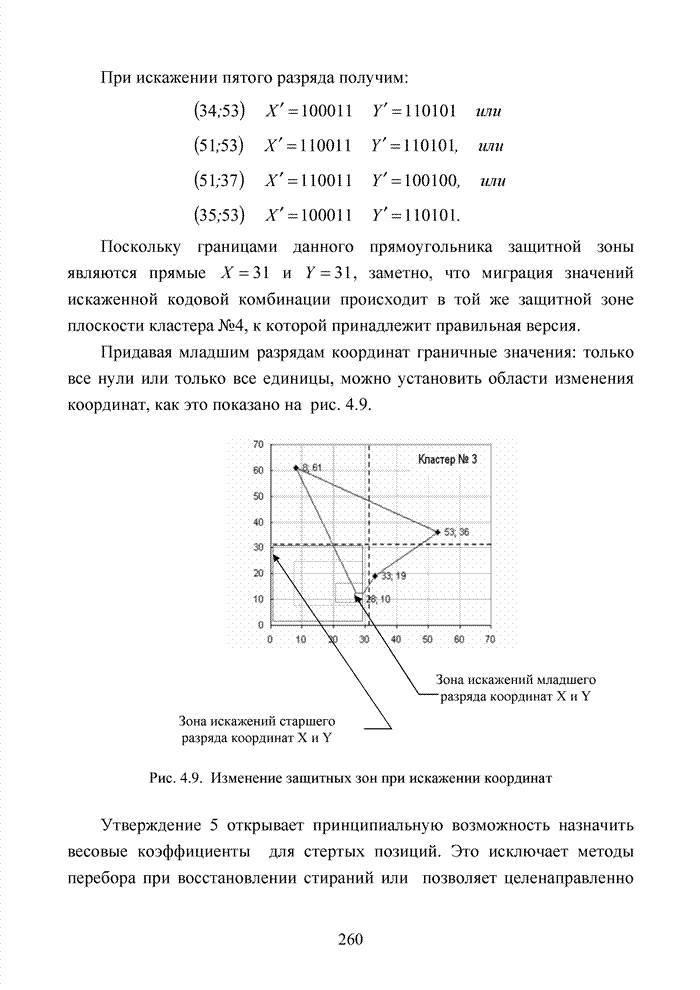
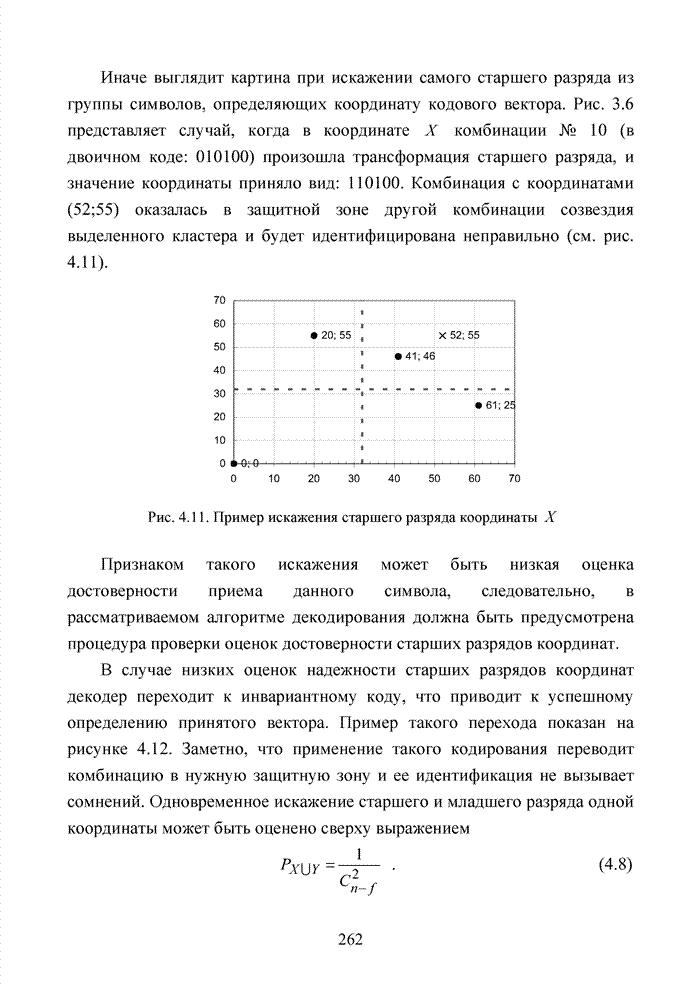
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
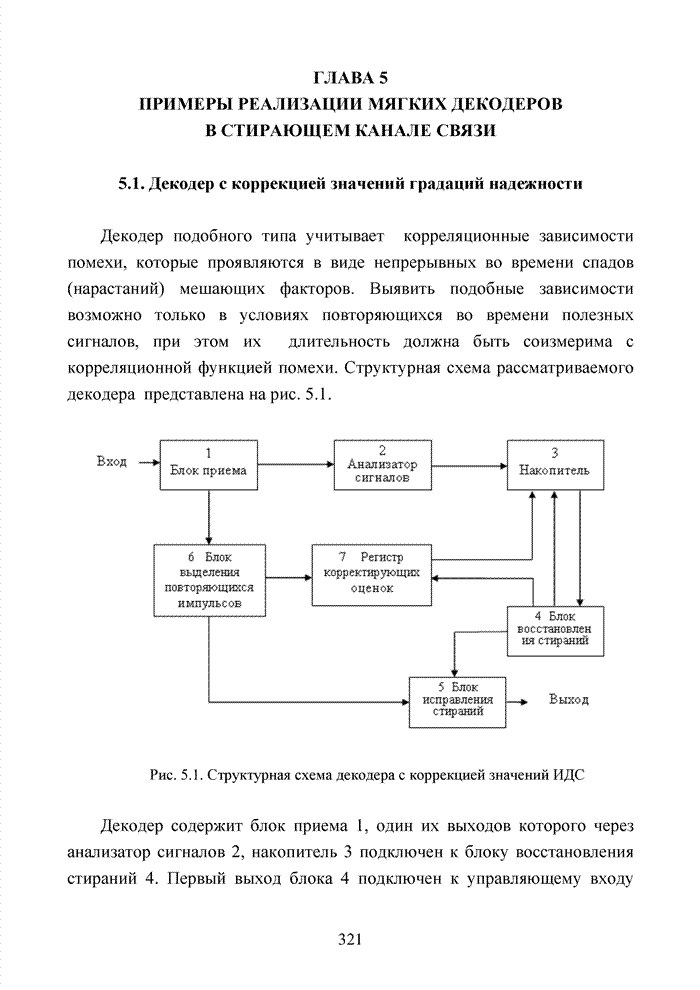
- 5.1. Декодер с коррекцией значений градаций надежности
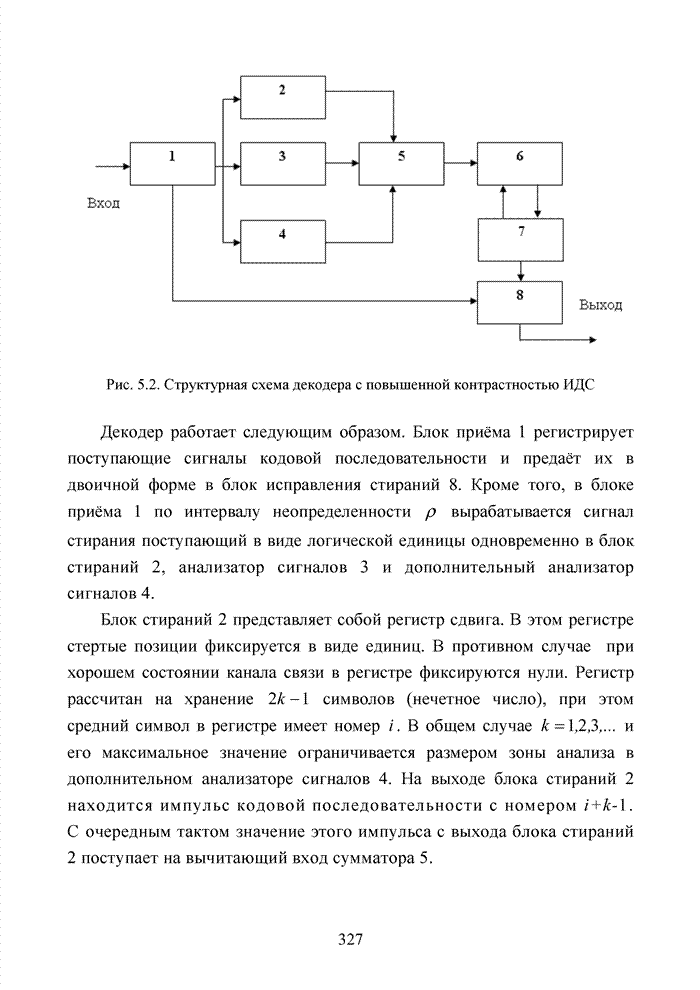
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
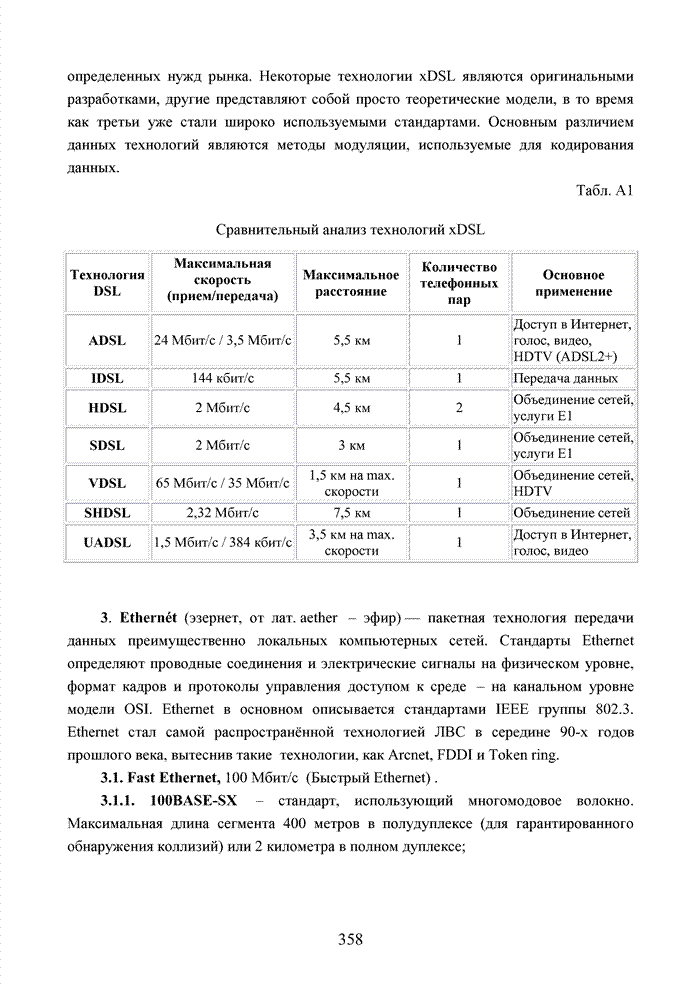
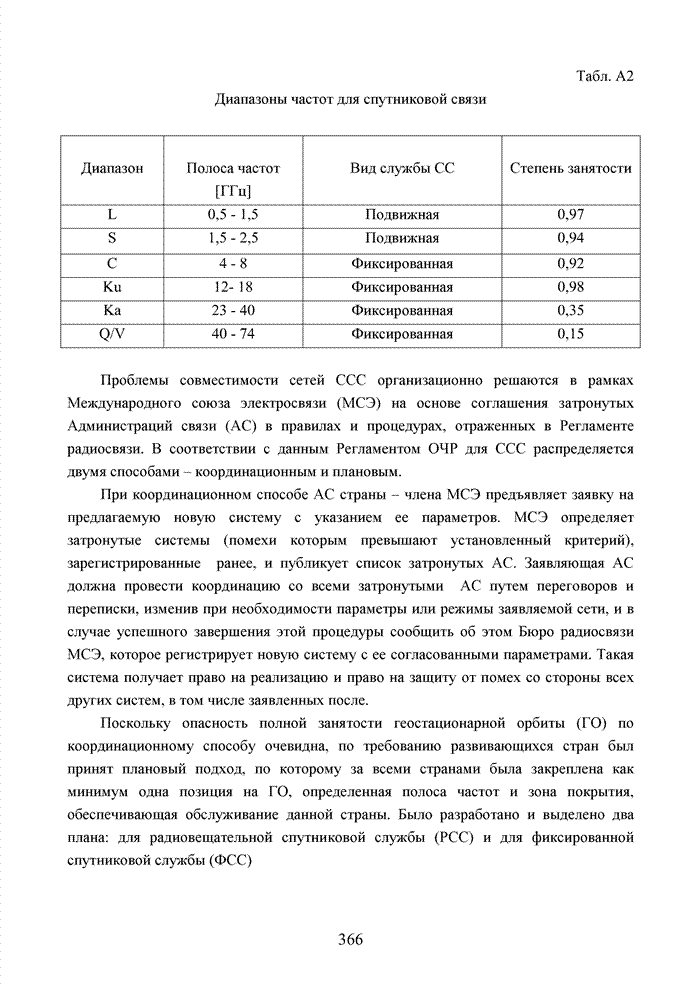
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
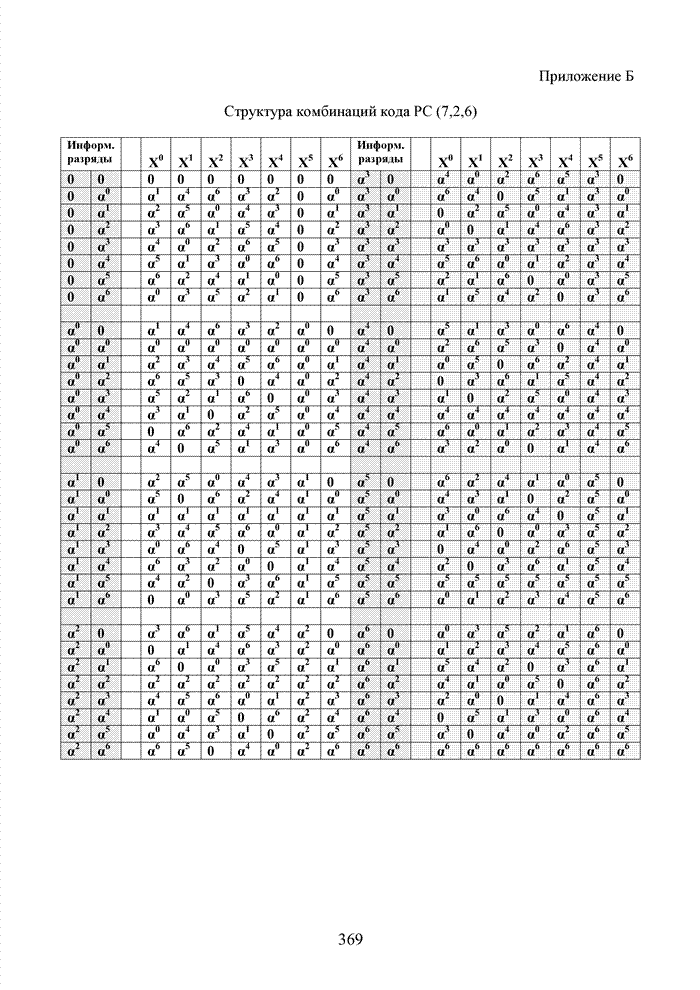
- Приложение Б Структура комбинаций кода РС (7,2,6)
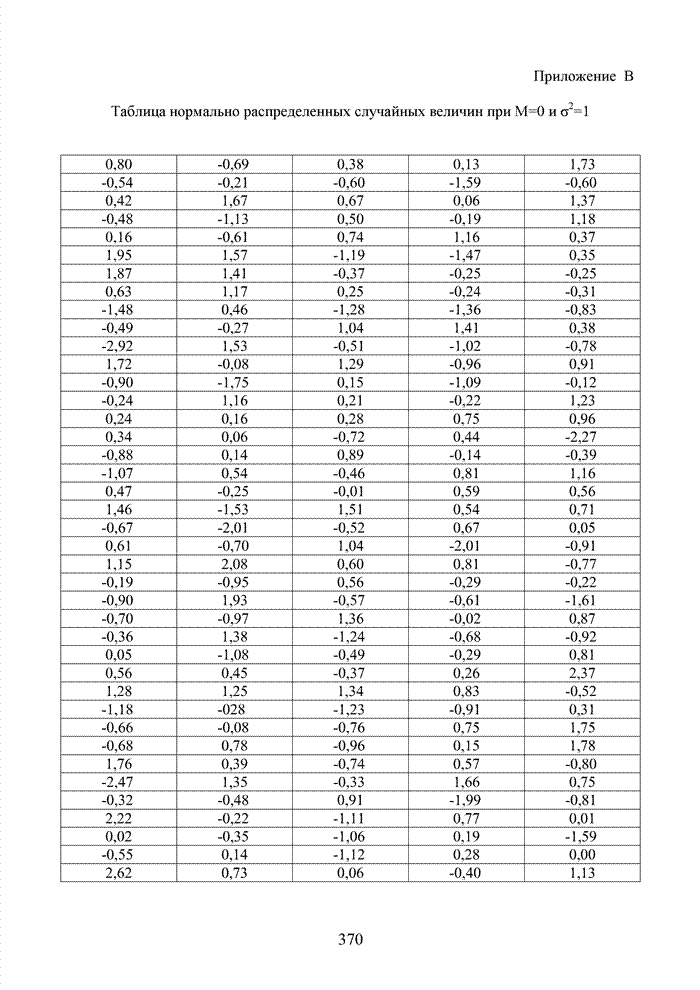
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК