| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
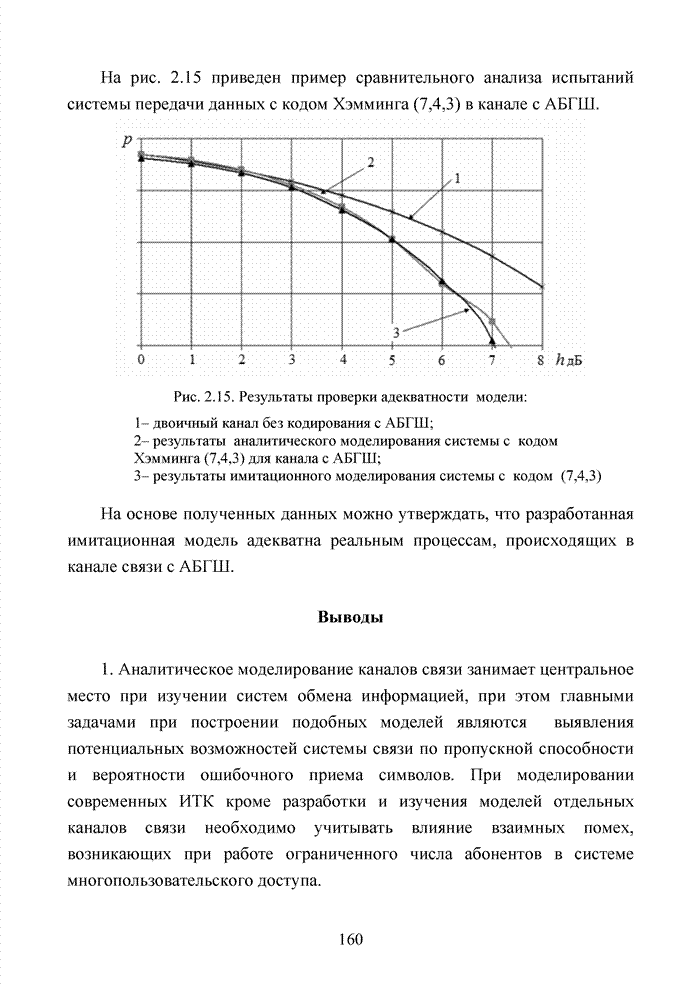
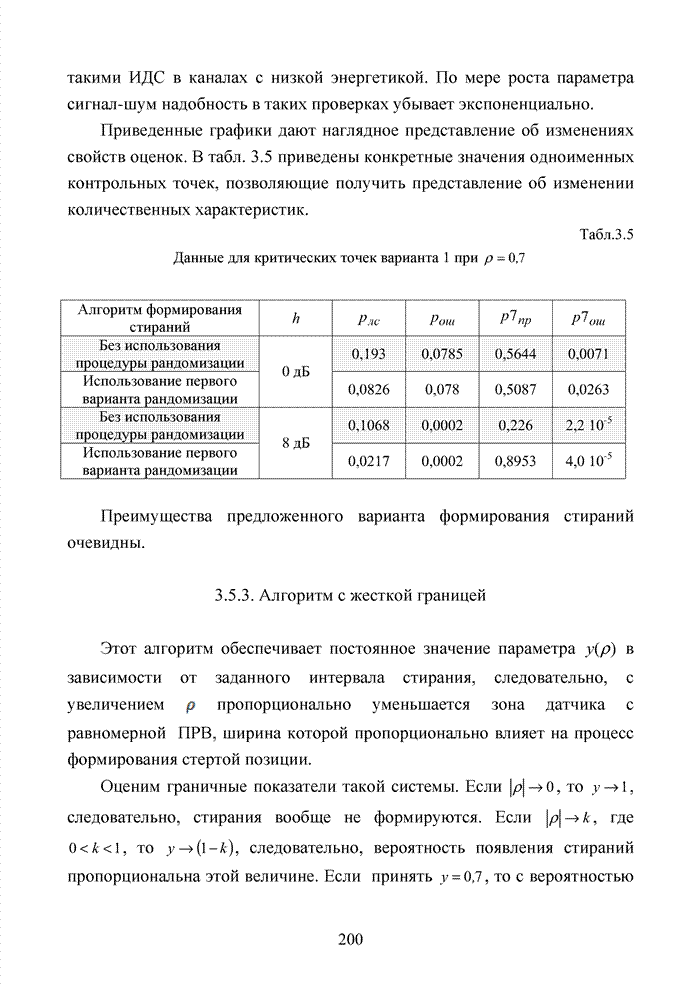
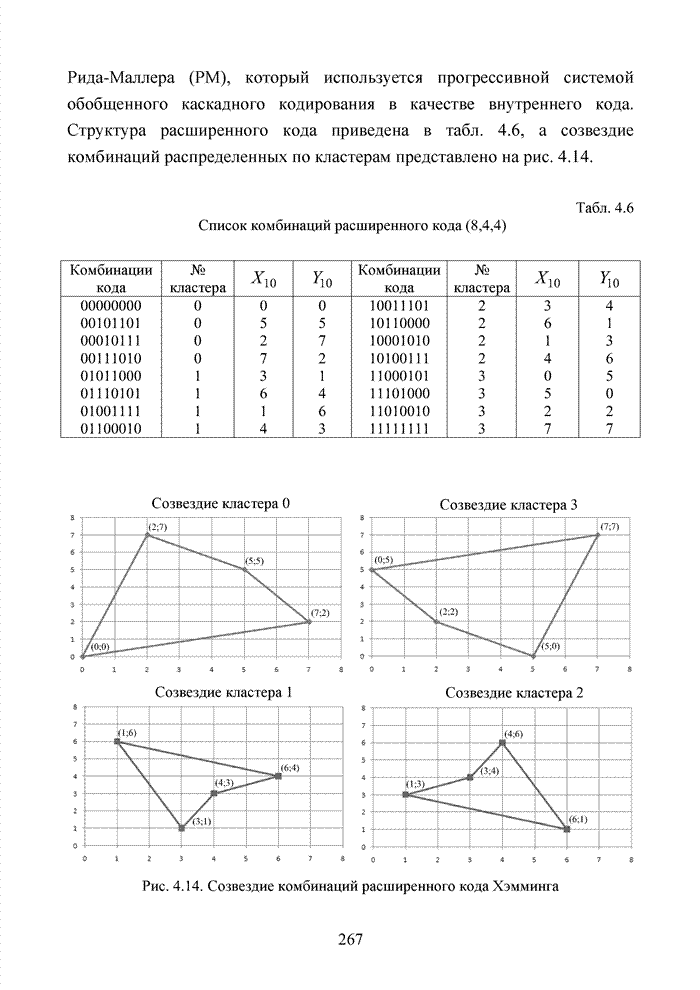
4.7. Способ списочного декодирования с защитой номера кластера
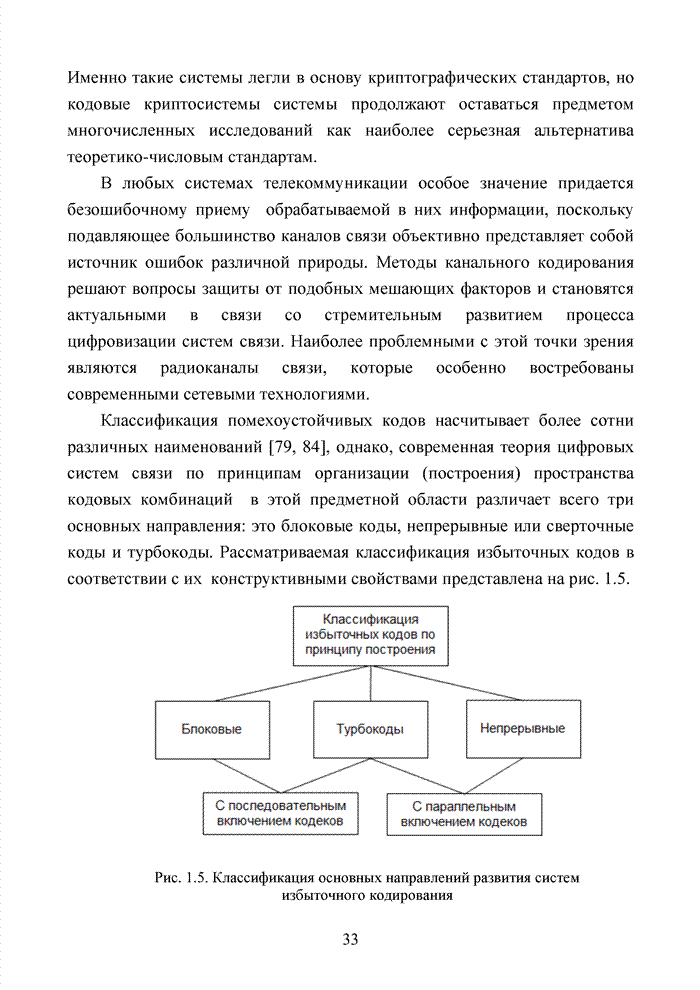
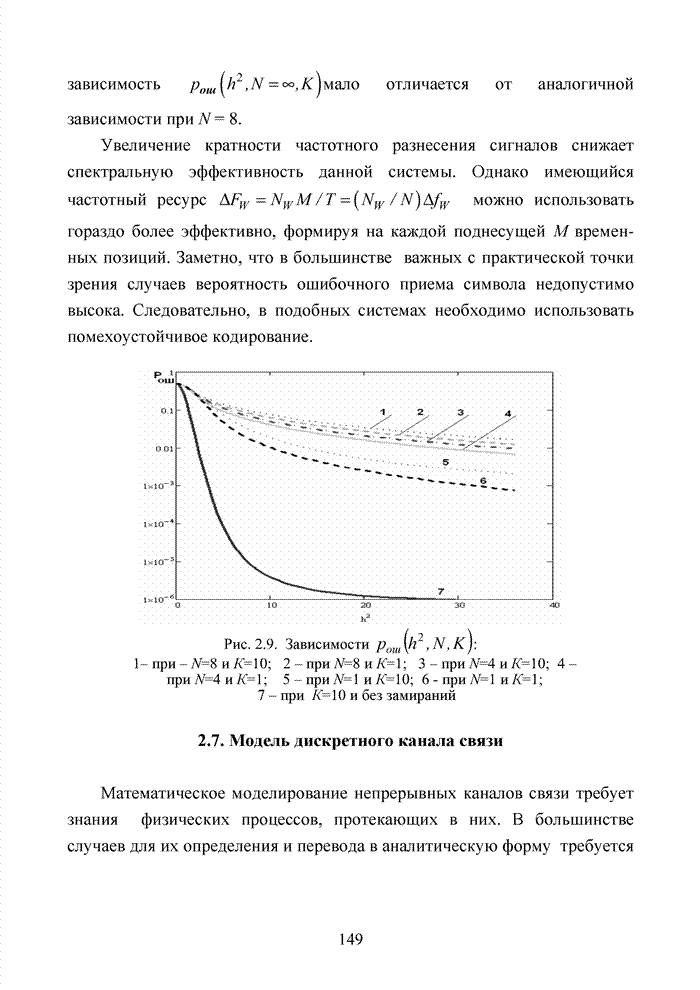
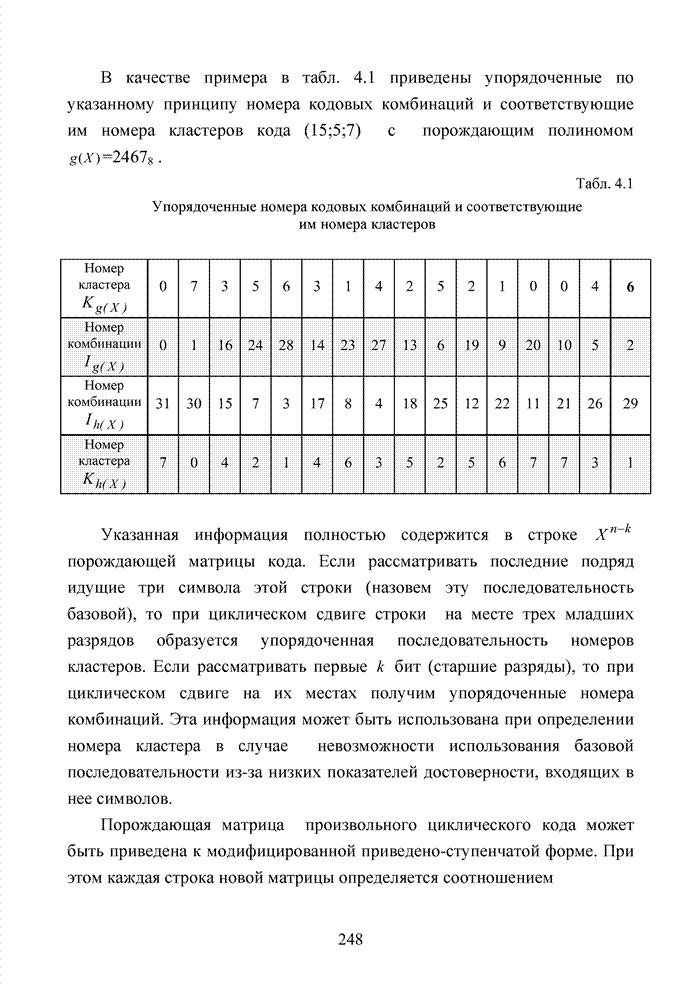
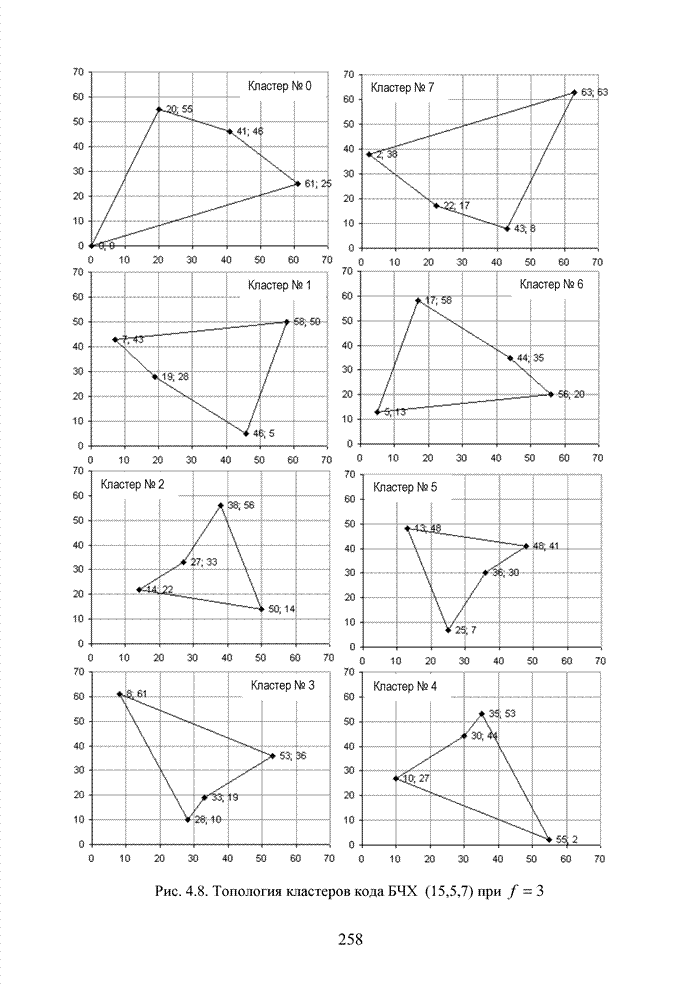
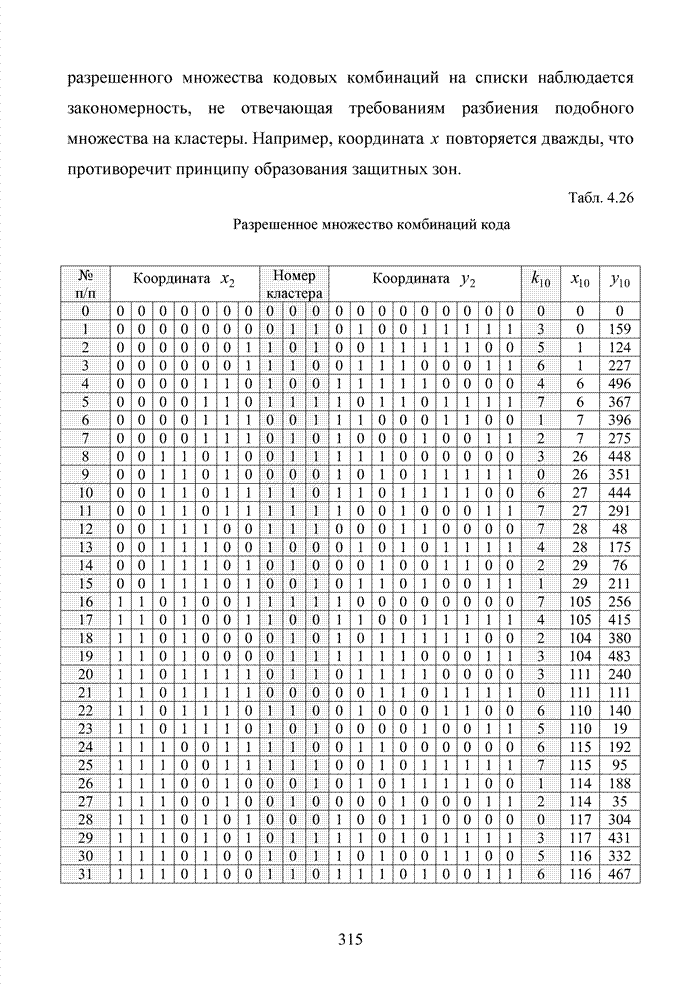
Списочное декодирование блоковых кодов на основе выделения в кодовой комбинации номера кластера открывает принципиальную возможность сократить объем вычислений в достаточно эффективном алгоритме мягкого декодирования с использованием упорядоченной статистики. Оценим применение метода для кода БЧХ (15,7,5). Использование такого кода оправдано с точки зрения получения максимального ЭЭ выигрыша, возможной для любого кода при относительной скорости кода, равной 0,5.
4.7.1. Описание алгоритма при отсутствии ошибок
Пусть задан блоковый код ![]() с порождающим
полиномом g(x)=7218 и пусть с выхода источника информации
на вход кодера поступила комбинация вида
с порождающим
полиномом g(x)=7218 и пусть с выхода источника информации
на вход кодера поступила комбинация вида
0 1 0 0 1 1 1.
Представим порождающую матрицу кода в систематической форме.
 . (4.15)
. (4.15)
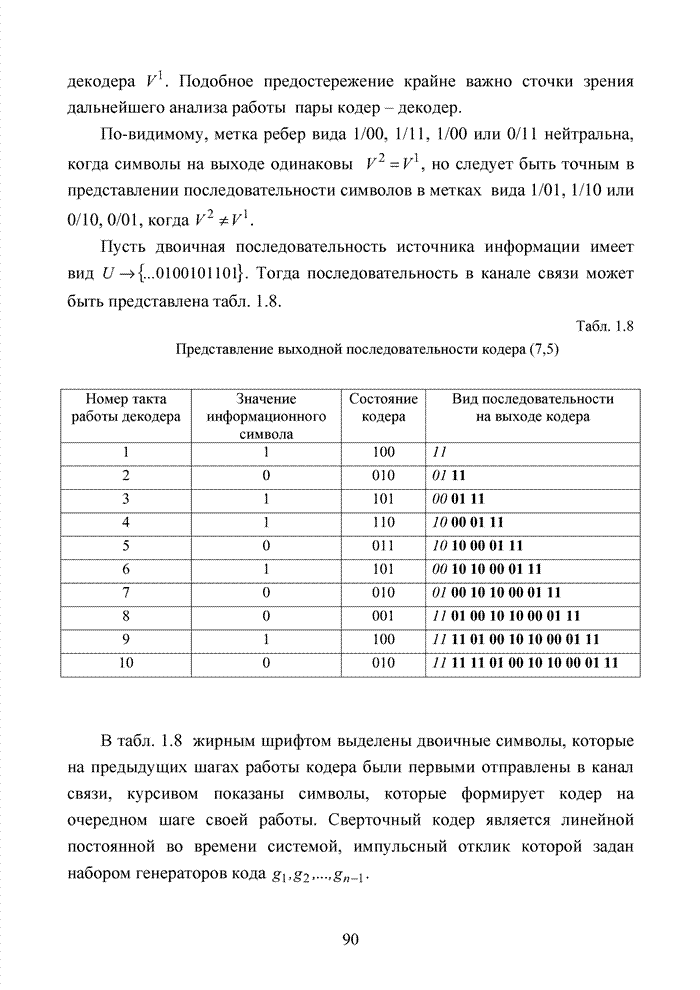
Тогда на выходе кодера образуется вектор вида:
![]() .
.
Предварительно установим,
что за номер кластера принимаются первые три (слева) символа. Следовательно, ![]() принадлежит кластеру с номером 2. Осуществляя
дополнительную защиту номера кластера, передатчик выкалывает последний символ
кодовой комбинации и на его место устанавливает проверку четности номера
кластера. Следовательно, в канал связи будет передан вектор
принадлежит кластеру с номером 2. Осуществляя
дополнительную защиту номера кластера, передатчик выкалывает последний символ
кодовой комбинации и на его место устанавливает проверку четности номера
кластера. Следовательно, в канал связи будет передан вектор
![]() .
.
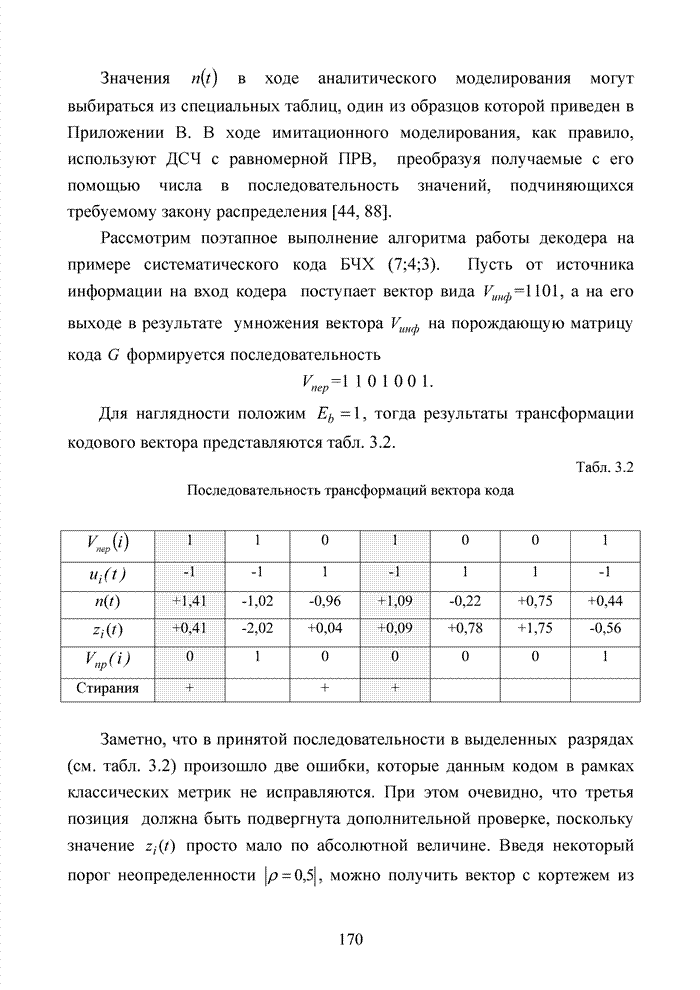
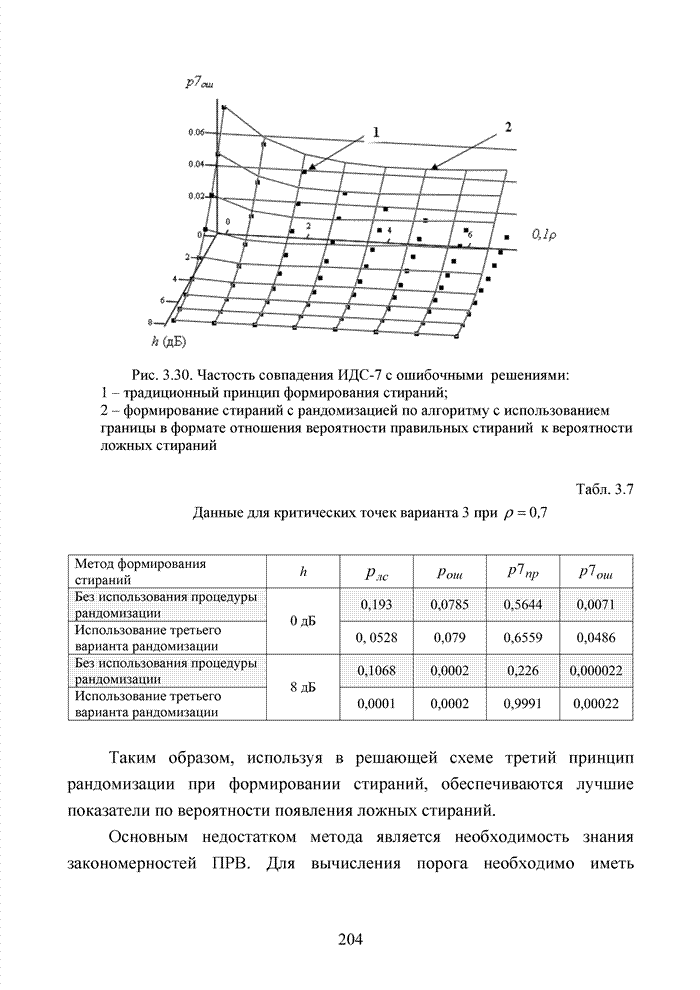
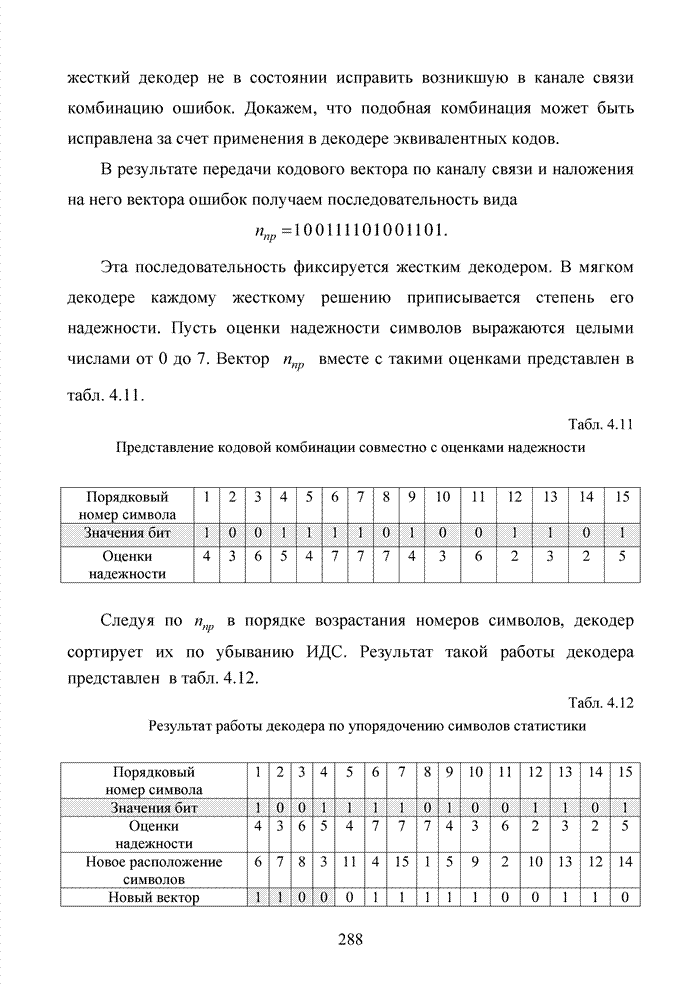
Приемник обрабатывает вектор, устанавливая для каждого символа градацию надежности. В табл. 4.16 в качестве примера представлены оценки надежности, принадлежащие каждому принятому символу.
Табл. 4.16 Соответствие символов и их градаций надежности
|
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
ИДС |
7 |
7 |
7 |
6 |
5 |
7 |
7 |
7 |
7 |
7 |
3 |
7 |
1 |
5 |
7 |
Если кластер вектора ![]() идентифицирован верно, то возможна эффективная
реализация перехода от кода
идентифицирован верно, то возможна эффективная
реализация перехода от кода ![]() к укороченному коду
к укороченному коду ![]() . Действительно, номер кластера
определяет комбинацию первых
. Действительно, номер кластера
определяет комбинацию первых ![]() строк матрицы
строк матрицы ![]() . Это означает, что при удалении
сочетания символов, отвечающих за подобную комбинацию декодер должен обрабатывать
комбинации только кода
. Это означает, что при удалении
сочетания символов, отвечающих за подобную комбинацию декодер должен обрабатывать
комбинации только кода ![]() , что приводит к сокращению объема
вычислений. Следовательно, приняв вектор
, что приводит к сокращению объема
вычислений. Следовательно, приняв вектор ![]() декодер проверяет выполнение четности для символов, определяющих номер
кластера, и преобразует порождающую матрицу G в матрицу укороченного (12,4,5) кода
декодер проверяет выполнение четности для символов, определяющих номер
кластера, и преобразует порождающую матрицу G в матрицу укороченного (12,4,5) кода ![]() . Принцип декодирования
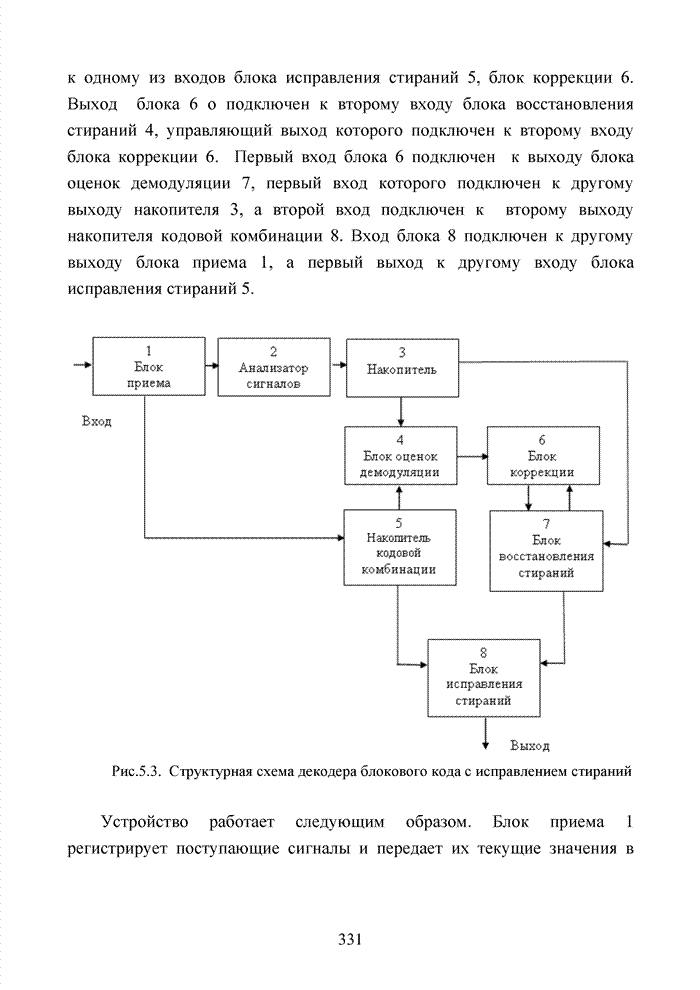
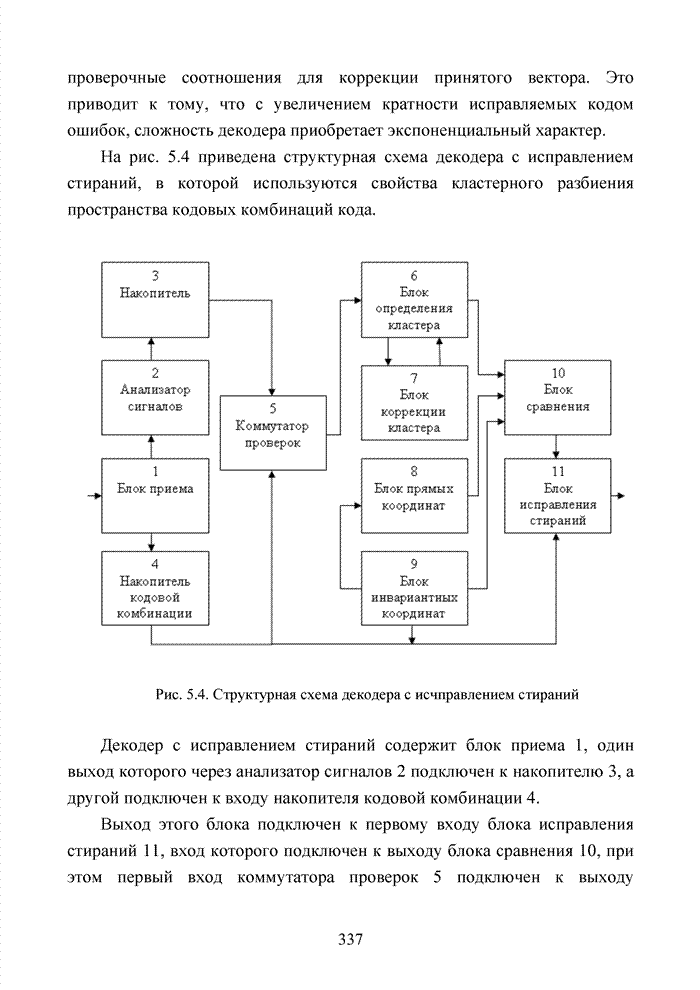
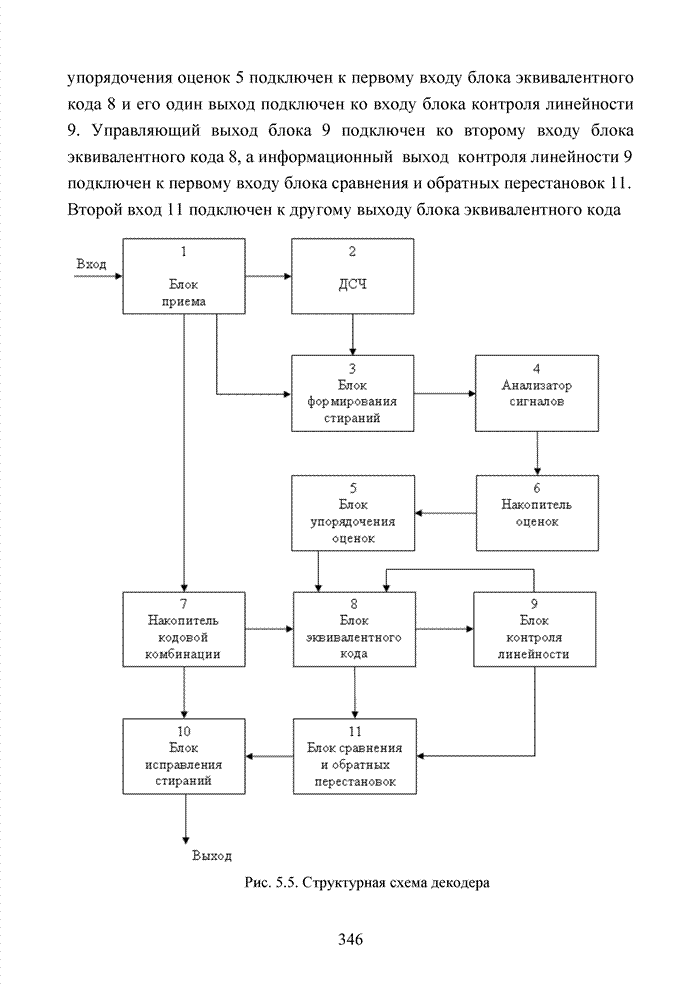
систематического кода с использованием номера кластера представлен на рис.
4.18.
. Принцип декодирования
систематического кода с использованием номера кластера представлен на рис.
4.18.

Рис. 4.18. Схема перехода к укороченному коду
 .
(4.16)
.
(4.16)
Далее в декодере формируется
корректирующий вектор ![]() путем умножения номера кластера на первые
три строки порождающей матрицы G .
путем умножения номера кластера на первые
три строки порождающей матрицы G .
|
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
Декодер исключает символы
номера кластера из вектора ![]() и полученный вектор
и полученный вектор ![]() складывает с соответствующими
разрядами принятого вектора
складывает с соответствующими
разрядами принятого вектора ![]() .
.
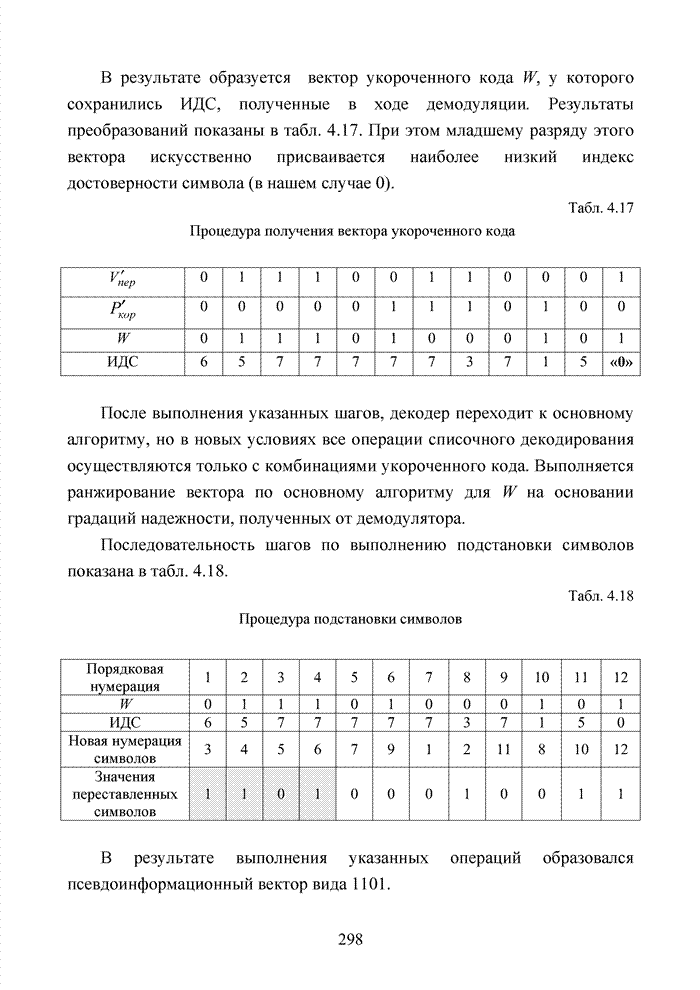
В результате образуется вектор укороченного кода W, у которого сохранились ИДС, полученные в ходе демодуляции. Результаты преобразований показаны в табл. 4.17. При этом младшему разряду этого вектора искусственно присваивается наиболее низкий индекс достоверности символа (в нашем случае 0).
Табл. 4.17 Процедура получения вектора укороченного кода
|
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
W |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
ИДС |
6 |
5 |
7 |
7 |
7 |
7 |
7 |
3 |
7 |
1 |
5 |
«0» |
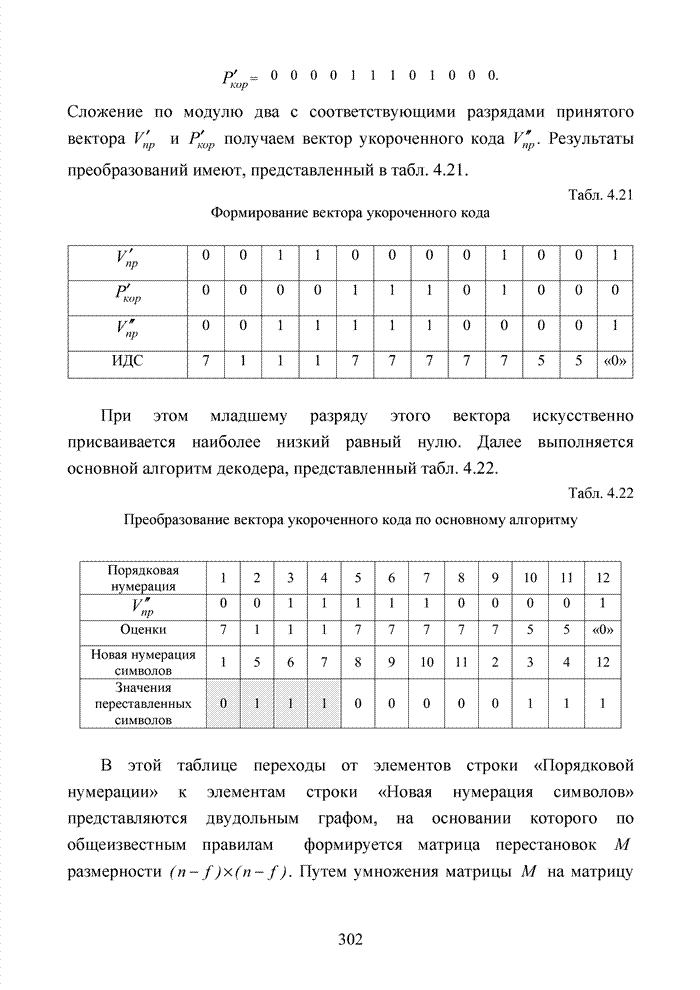
После выполнения указанных шагов, декодер переходит к основному алгоритму, но в новых условиях все операции списочного декодирования осуществляются только с комбинациями укороченного кода. Выполняется ранжирование вектора по основному алгоритму для W на основании градаций надежности, полученных от демодулятора.
Последовательность шагов по выполнению подстановки символов показана в табл. 4.18.
Табл. 4.18 Процедура подстановки символов
|
Порядковая нумерация |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
W |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
ИДС |
6 |
5 |
7 |
7 |
7 |
7 |
7 |
3 |
7 |
1 |
5 |
0 |
|
Новая нумерация символов |
3 |
4 |
5 |
6 |
7 |
9 |
1 |
2 |
11 |
8 |
10 |
12 |
|
Значения переставленных символов |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
В результате выполнения указанных операций образовался псевдоинформационный вектор вида 1101.
На основании выполненной
подстановки формируется перестановочная матрица М. Путем умножения
матрицы М на матрицу Gук декодер получает
предварительный результат преобразования в виде матрицы ![]() , структура которой оценивается
с точки зрения сохранения свойств нелинейности ее строк.
, структура которой оценивается
с точки зрения сохранения свойств нелинейности ее строк.

Очевидно, что детерминант
квадратной матрицы, составленной из первых ![]() столбцов окажется равным нулю из-за
нулевой первой строки этой матрицы. По этой же причине замена четвертого
столбца на пятый приведет к аналогичному результату. Удачной окажется следующий
шаг итерации (замена четвертого столбца на шестой). Порождающая матрица
принимает вид
столбцов окажется равным нулю из-за
нулевой первой строки этой матрицы. По этой же причине замена четвертого
столбца на пятый приведет к аналогичному результату. Удачной окажется следующий
шаг итерации (замена четвертого столбца на шестой). Порождающая матрица
принимает вид
 . (4.17)
. (4.17)
Следует учитывать, что
простановка столбцов должна быть адекватно отражена в перестановочной матрице ![]() . Последующие
преобразования представлены в табл. 4.19 и табл. 4.20.
. Последующие
преобразования представлены в табл. 4.19 и табл. 4.20.
Табл. 4.19 Процедура подстановки символов (продолжение)
|
Порядковая нумерация |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
W |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
ИДС |
6 |
5 |
7 |
7 |
7 |
7 |
7 |
3 |
7 |
1 |
5 |
0 |
|
Новая нумерация символов |
3 |
4 |
5 |
9 |
7 |
6 |
1 |
2 |
11 |
8 |
10 |
12 |
|
Значения переставленных символов |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
Выделяя из (4.19) матрицу
![]() , и выполнив
, и выполнив
![]() , получим
обратную матрицу для
, получим
обратную матрицу для ![]() ,
которая точно указывает на порядок последующих действий над строками матрицы
,
которая точно указывает на порядок последующих действий над строками матрицы ![]() для получения
порождающей матрицы в систематической форме. Отсюда
для получения
порождающей матрицы в систематической форме. Отсюда
 и
и  .
.
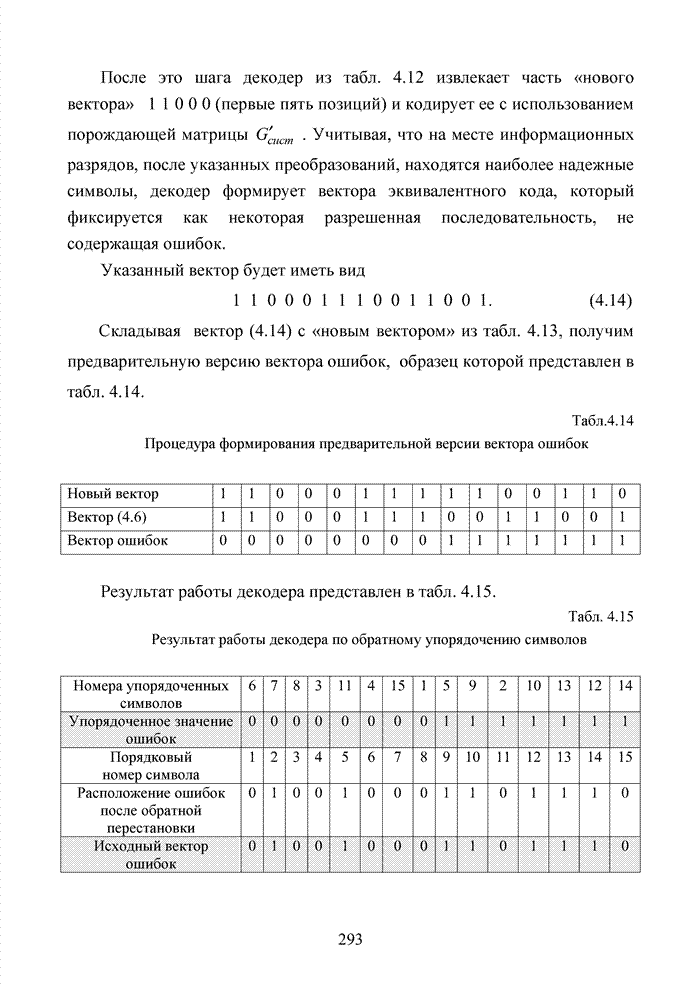
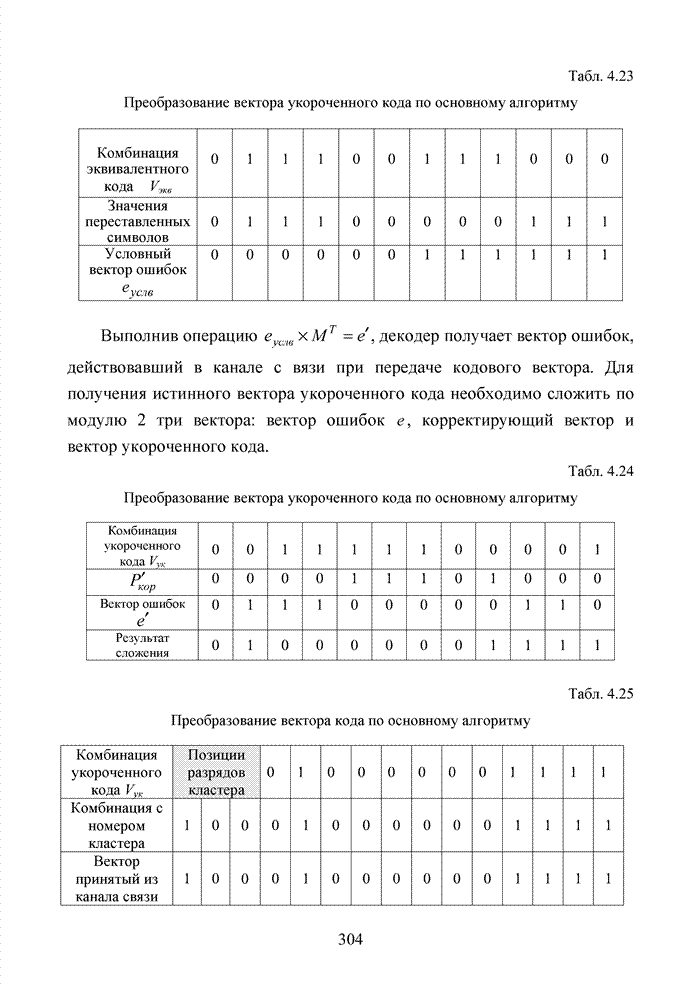
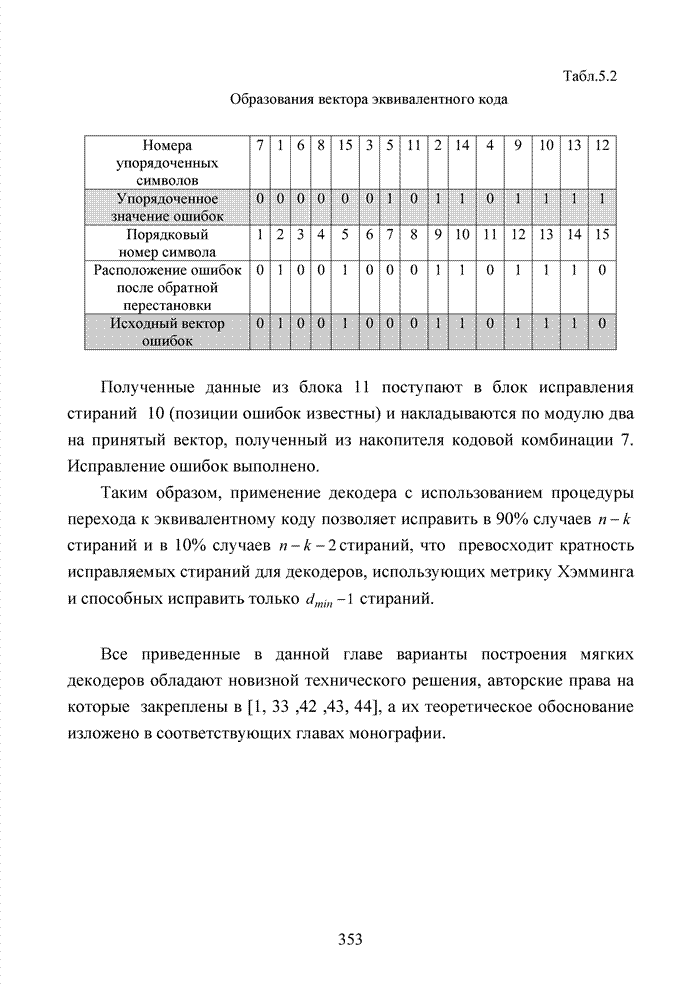
Табл. 4.20 Формирование вектора ошибок
|
Комбинация эквивалентного кода |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
Значения переставленных символов |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
Вектор ошибок
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
«1» |
Полученный результат
свидетельствует о результативности алгоритма. Вектор ошибок содержит
единственную ошибку в младшем разряде, которая изначально определялась
передатчиком как условие защиты номера кластера от искажений. Для получения
вектора ![]() необходимо
сложить три вектора: вектор ошибок
необходимо
сложить три вектора: вектор ошибок ![]() , корректирующий вектор
, корректирующий вектор ![]() и вектор укороченного
кода
и вектор укороченного
кода ![]() :
: ![]() . После размещения
символов номера кластера декодер получает вектор
. После размещения
символов номера кластера декодер получает вектор ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
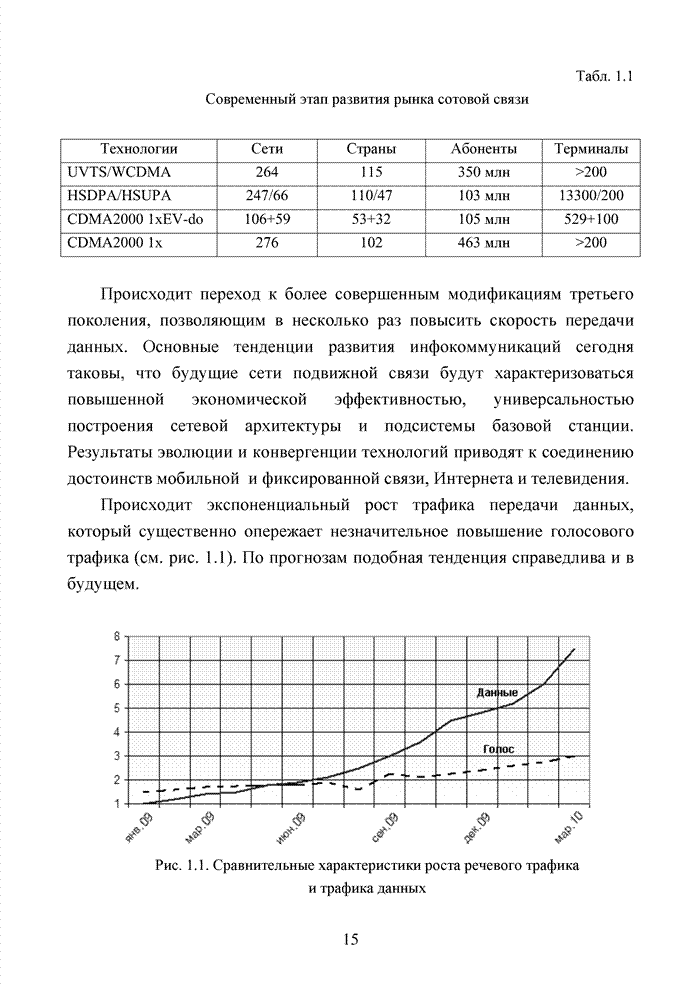
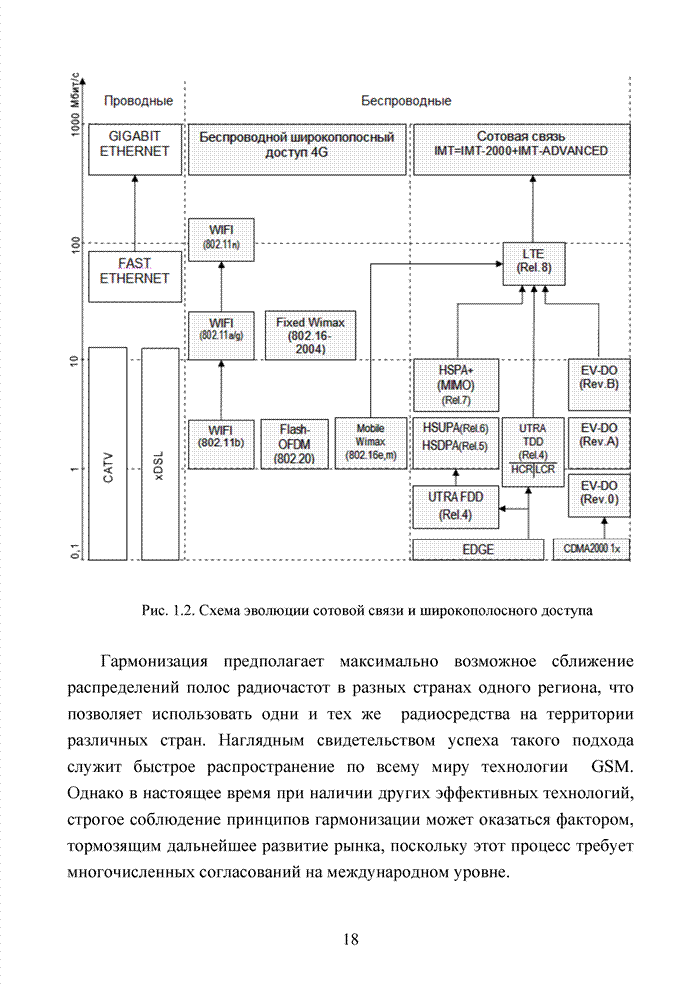
- 1.1. Инфокоммуникационные технологии нового поколения
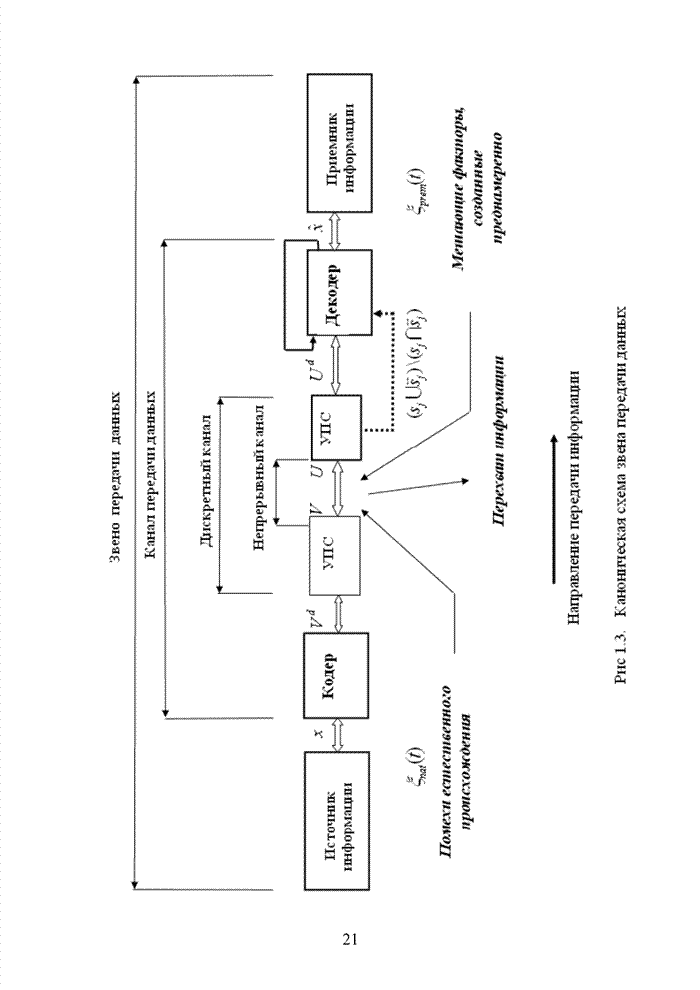
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
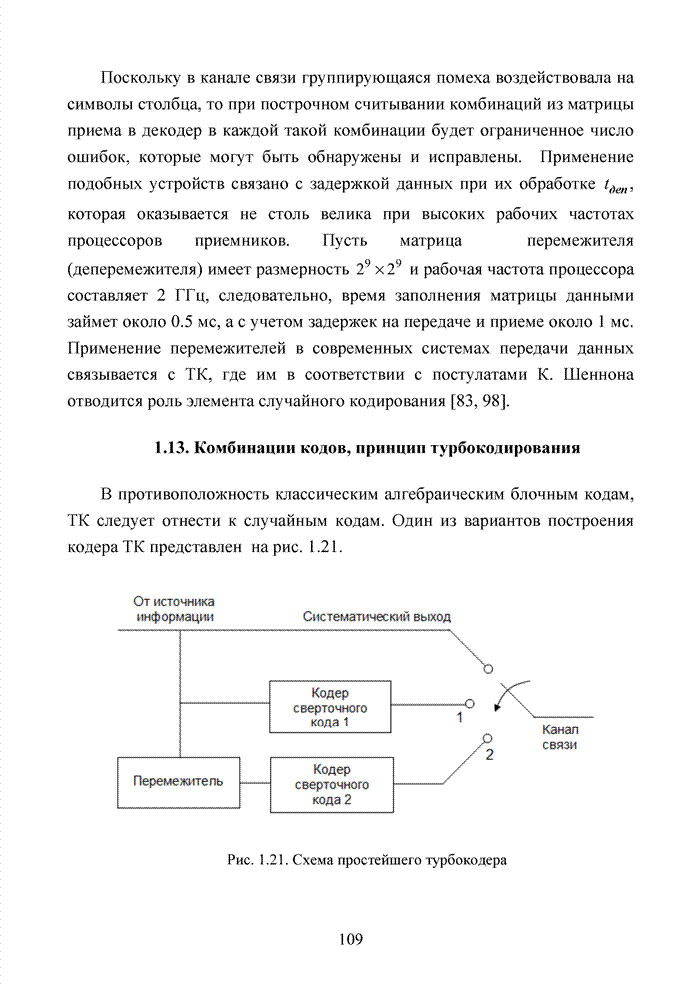
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
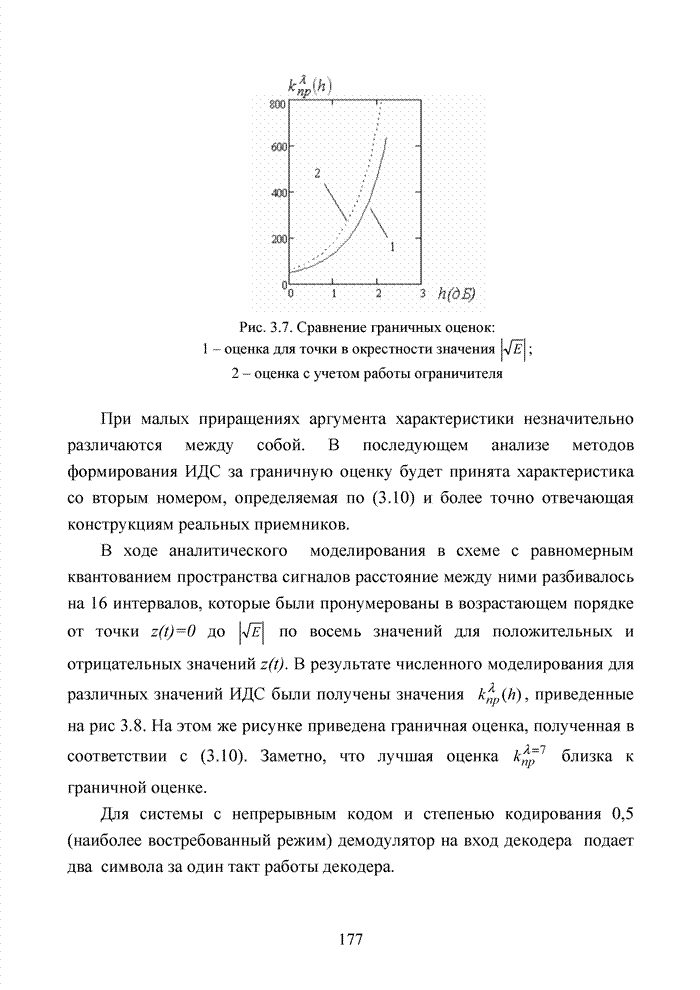
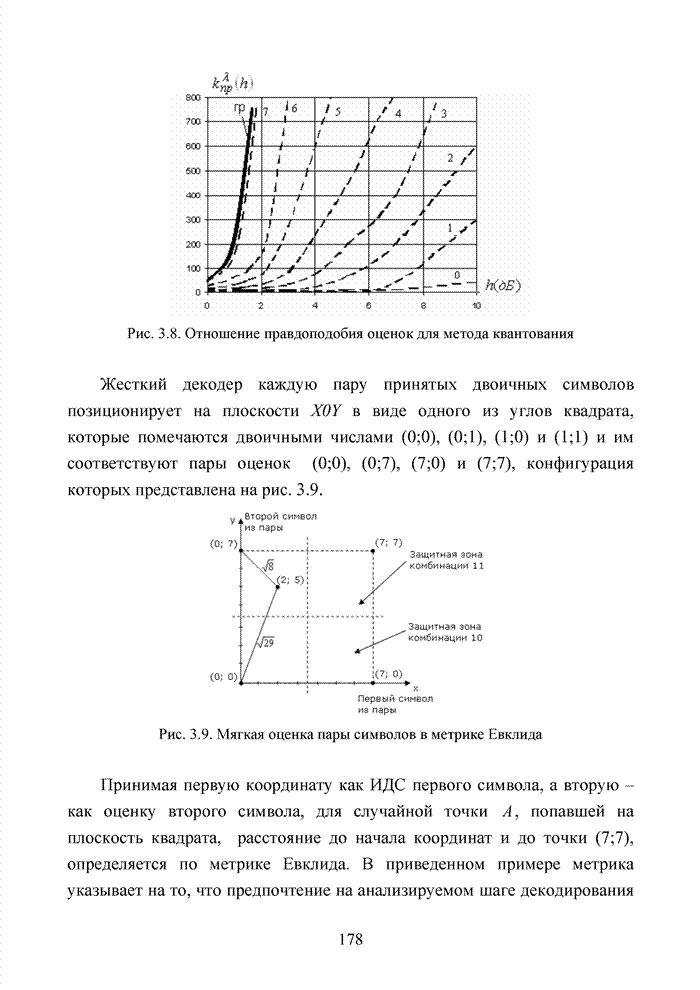
- 3.3. Метод квантования уровней сигнала
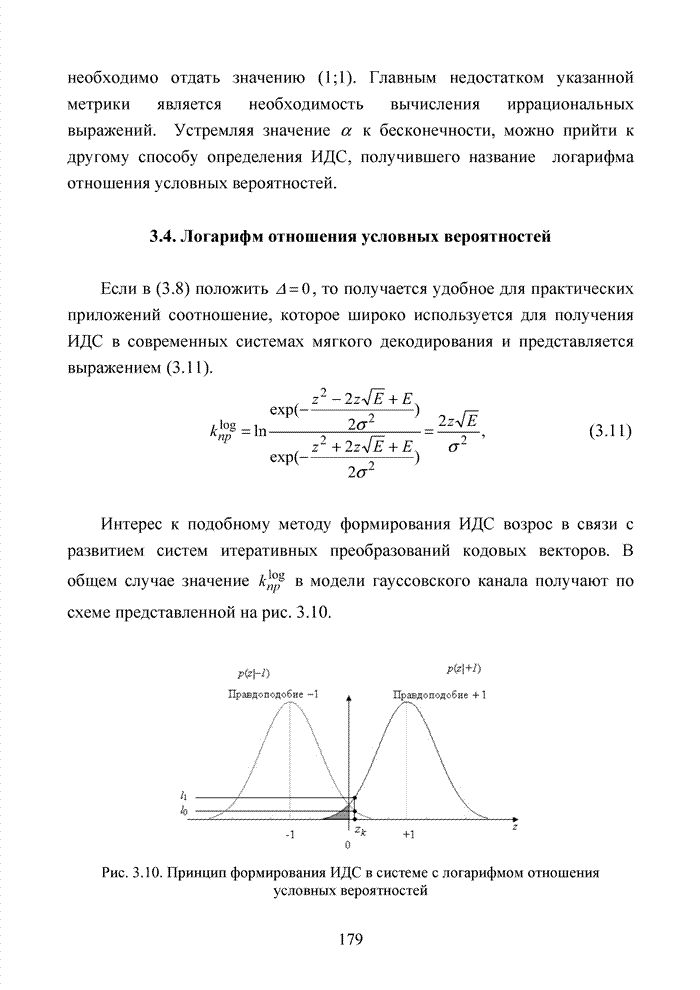
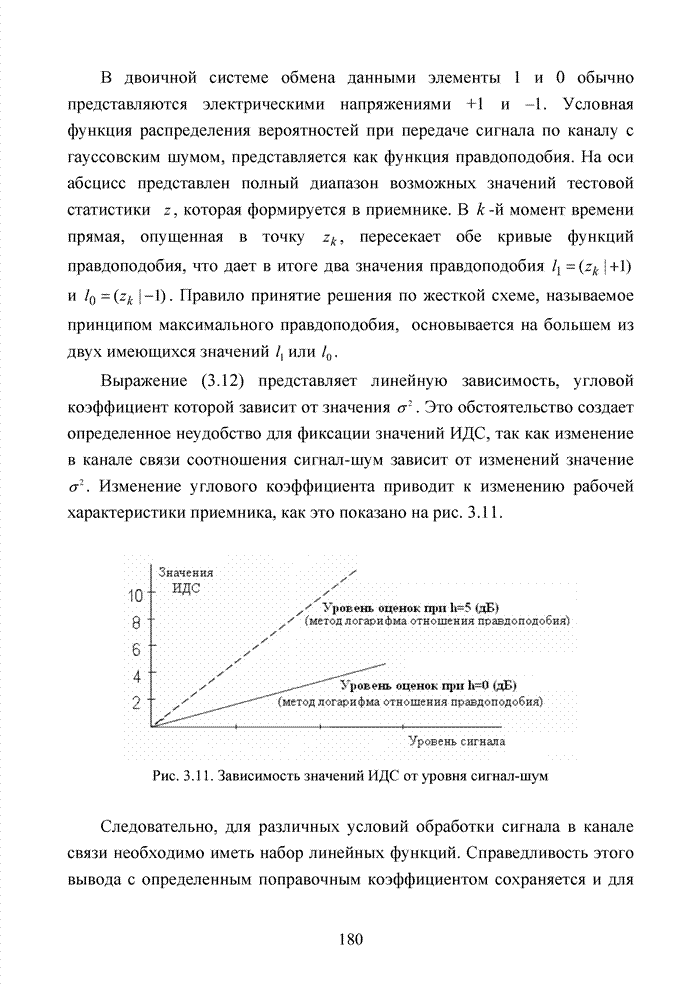
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
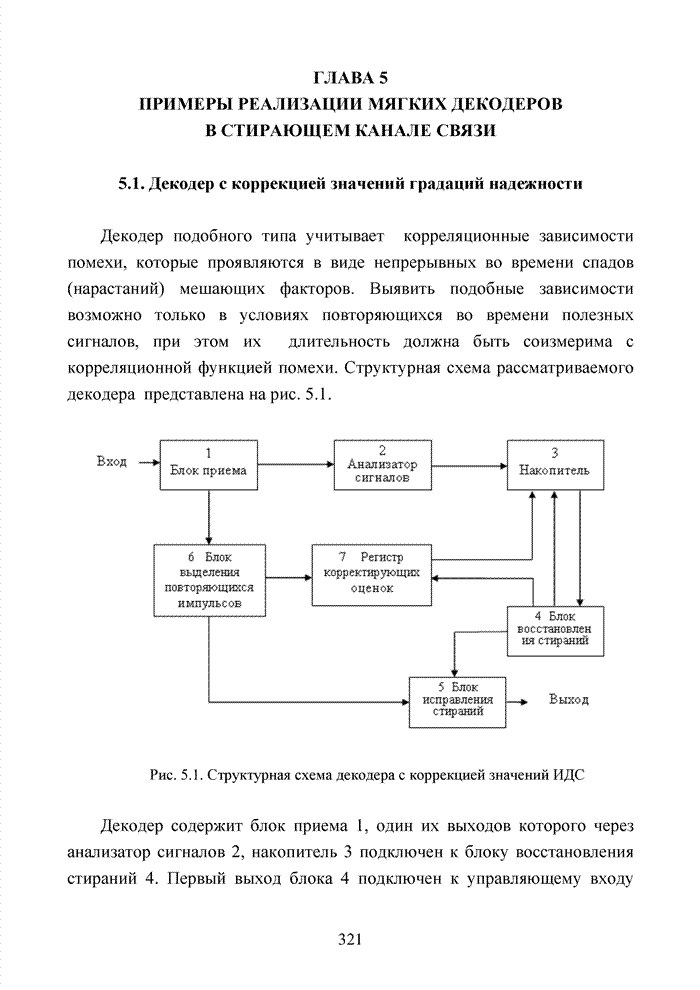
- 5.1. Декодер с коррекцией значений градаций надежности
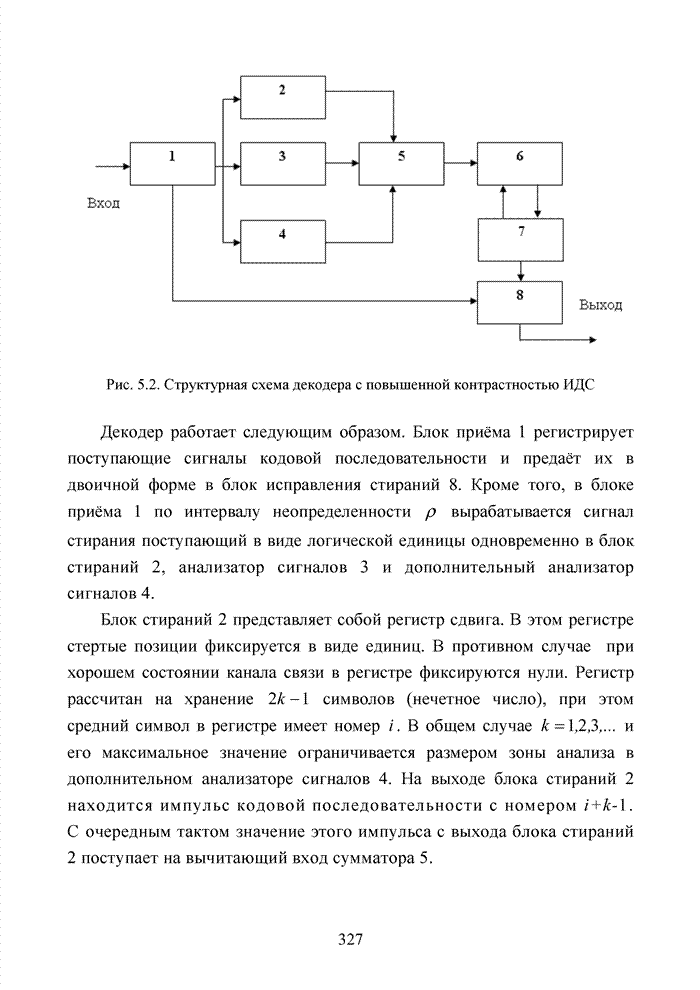
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
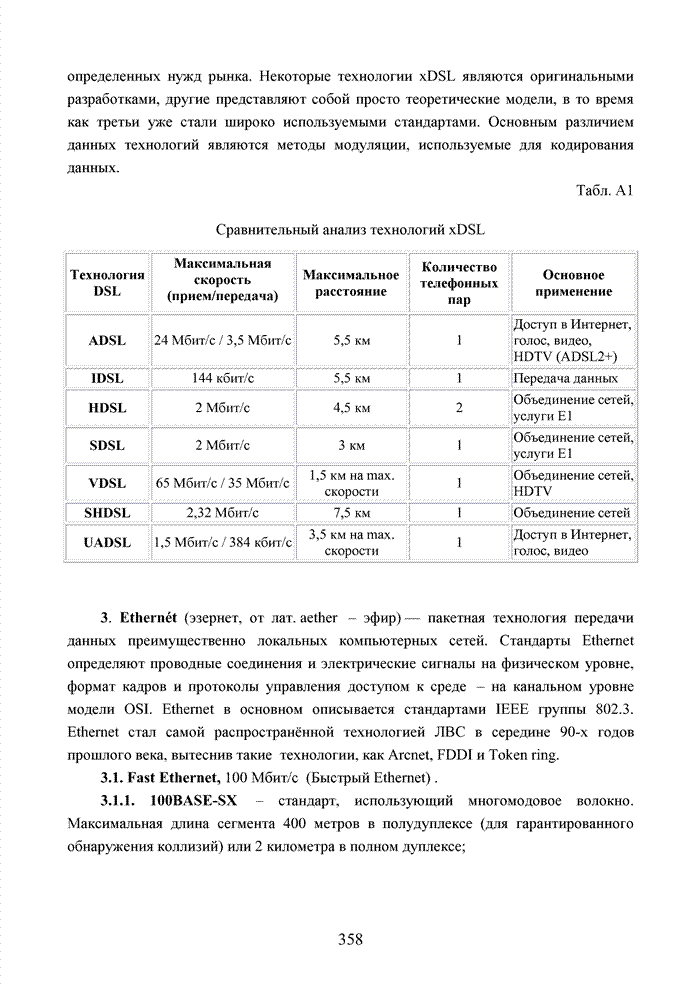
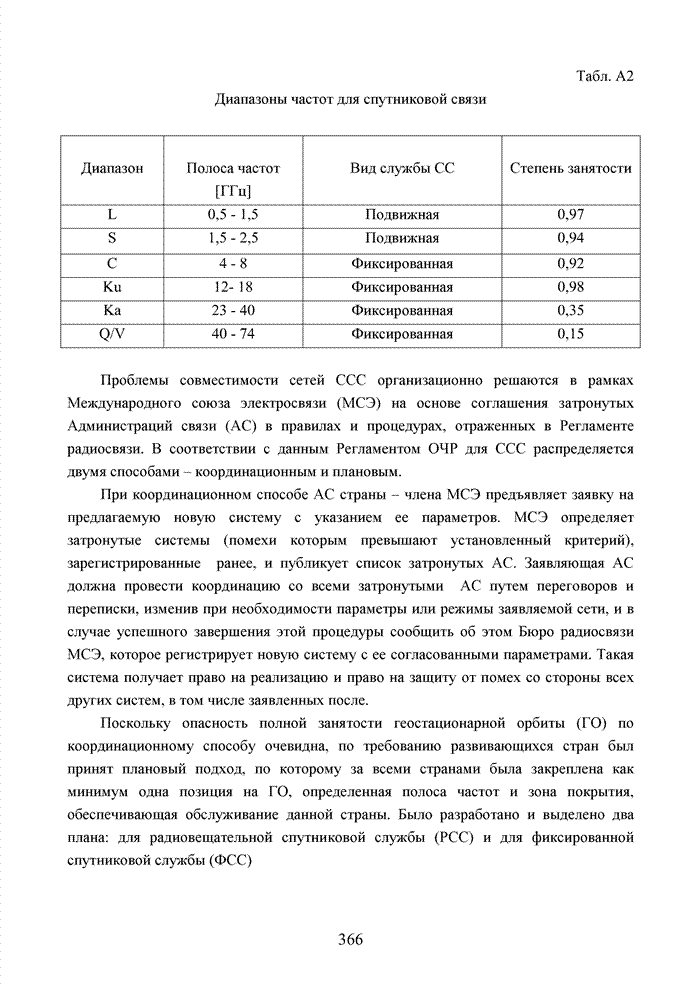
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
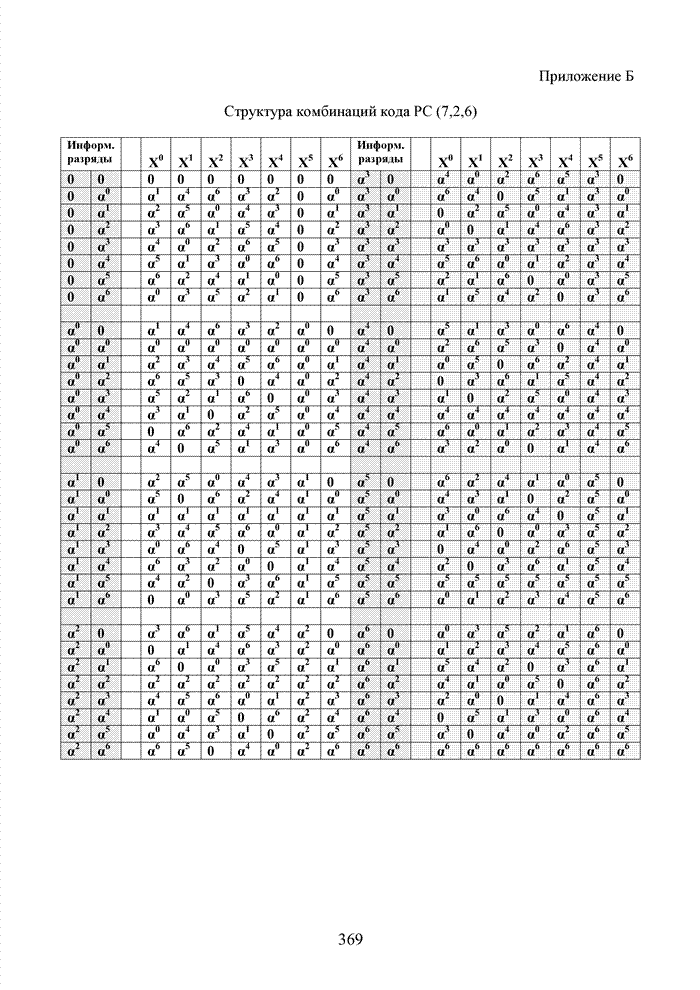
- Приложение Б Структура комбинаций кода РС (7,2,6)
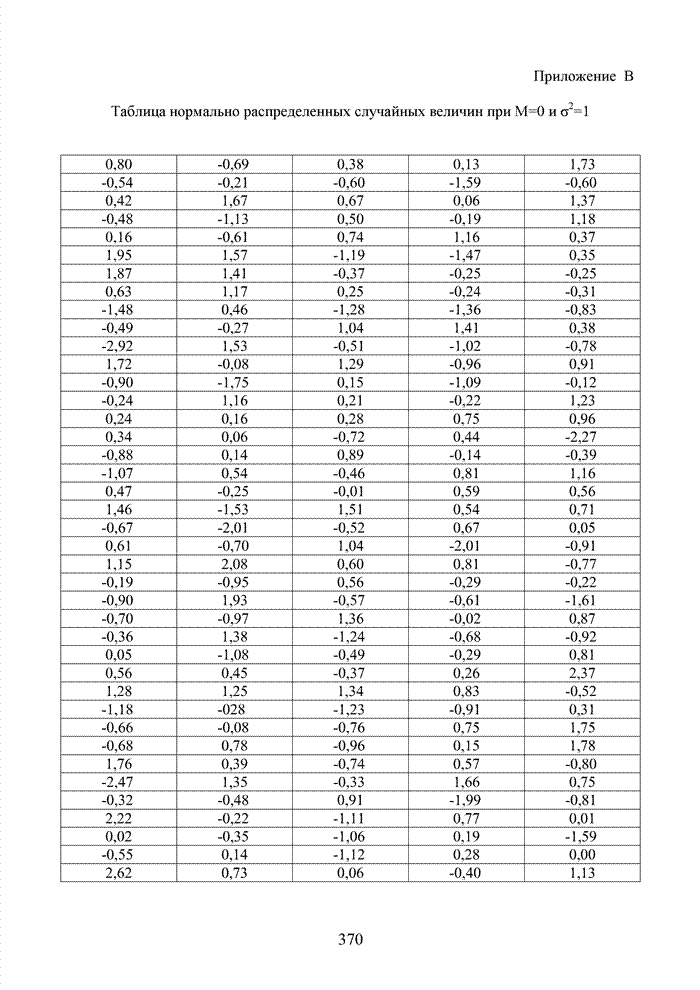
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК