| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
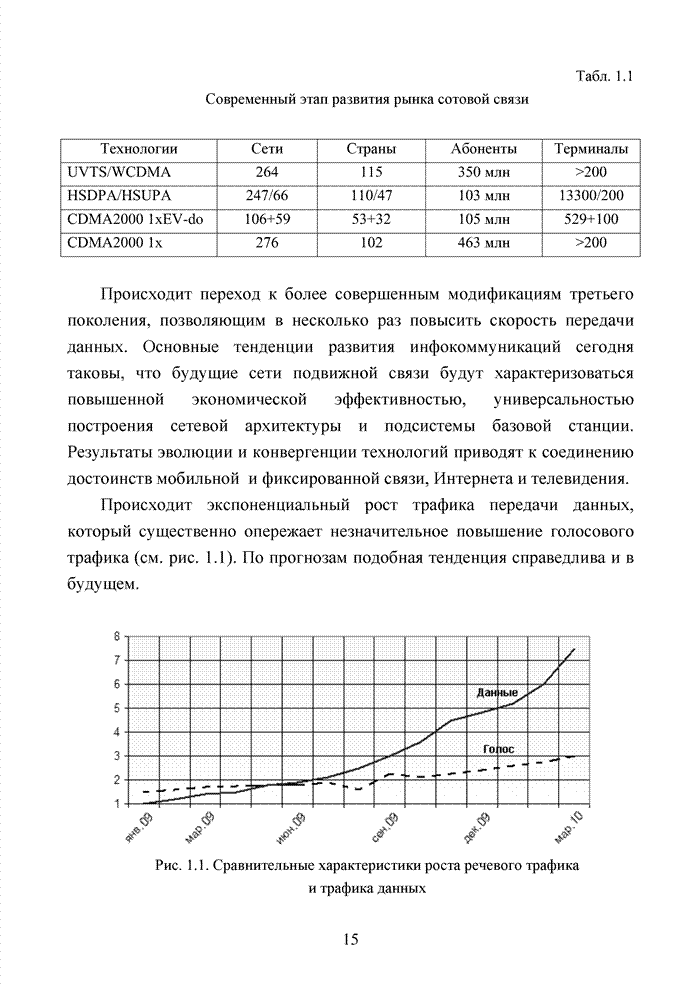
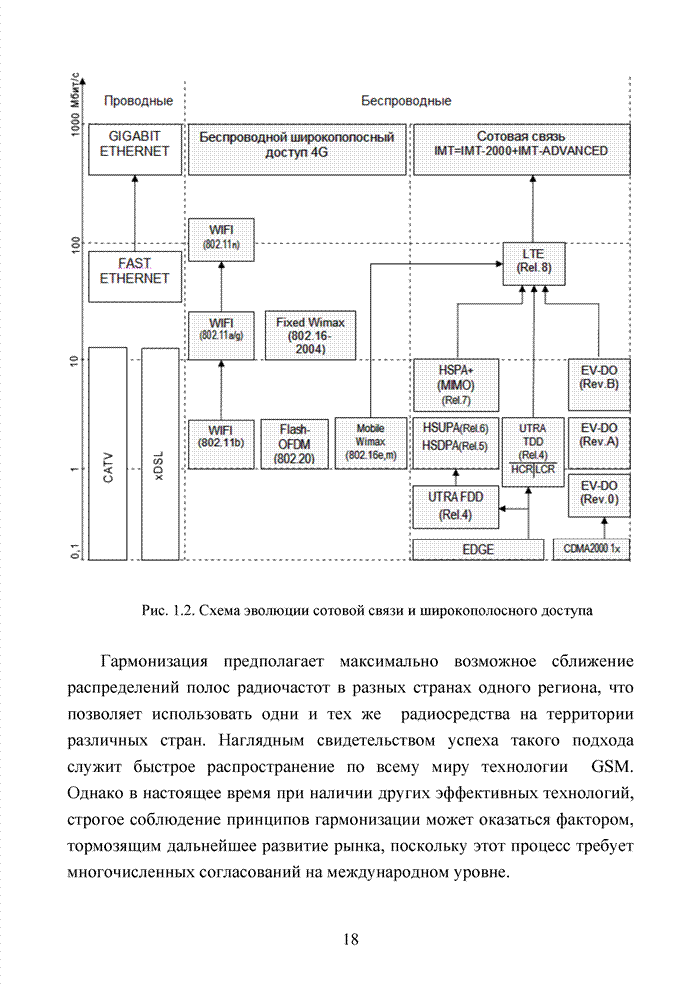
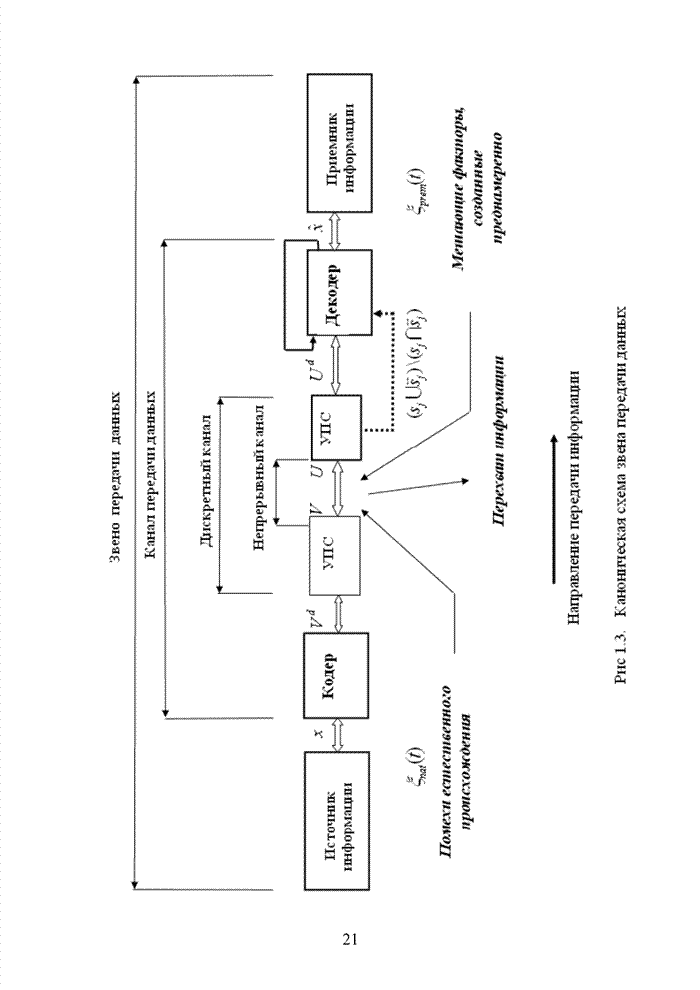
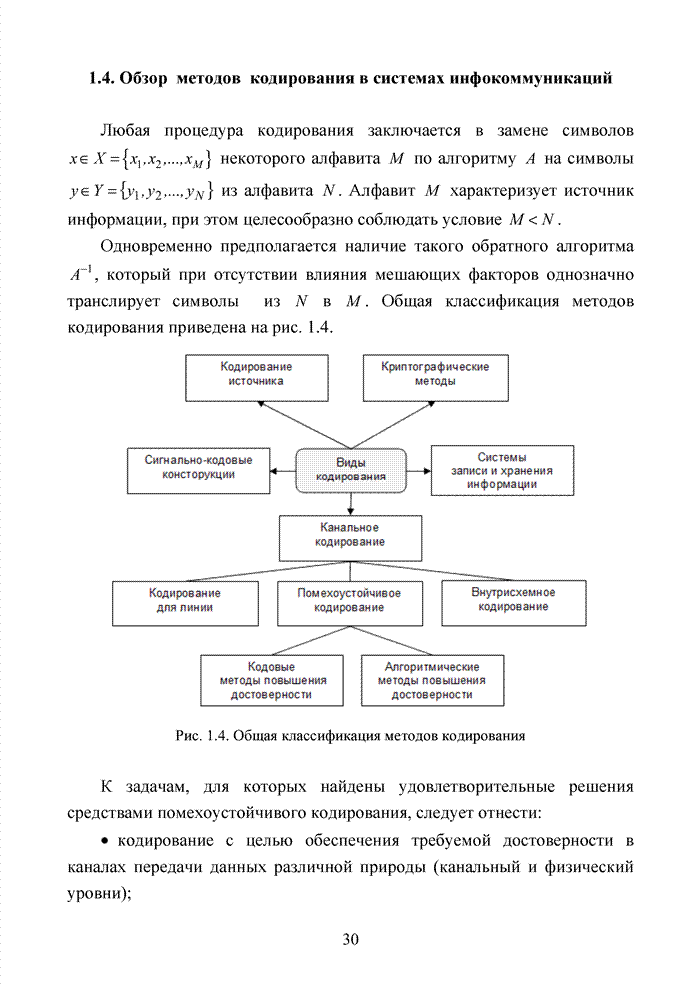
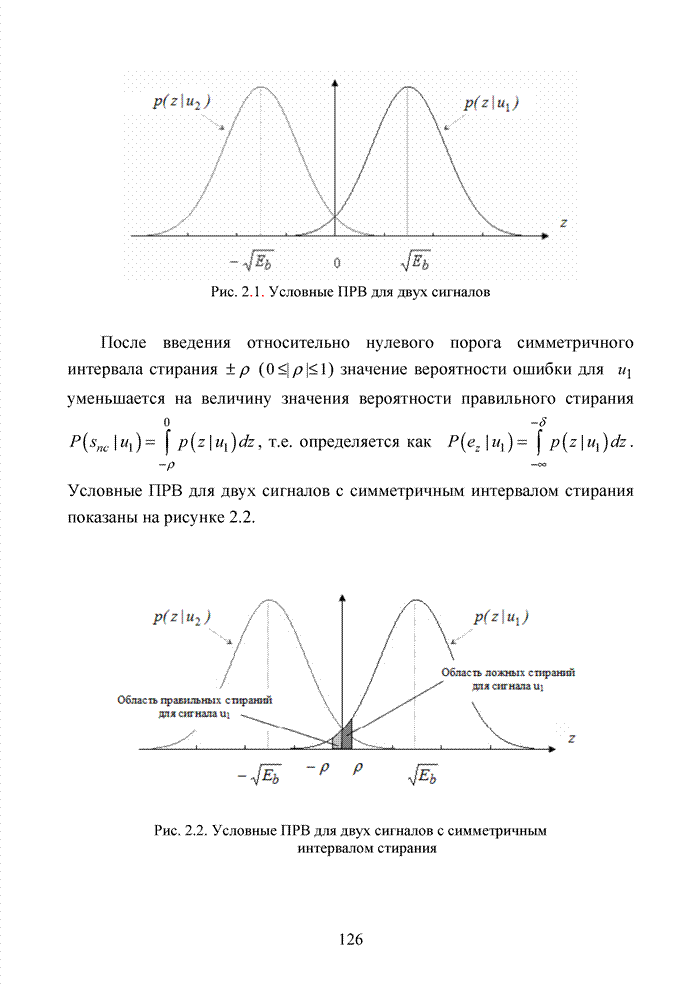
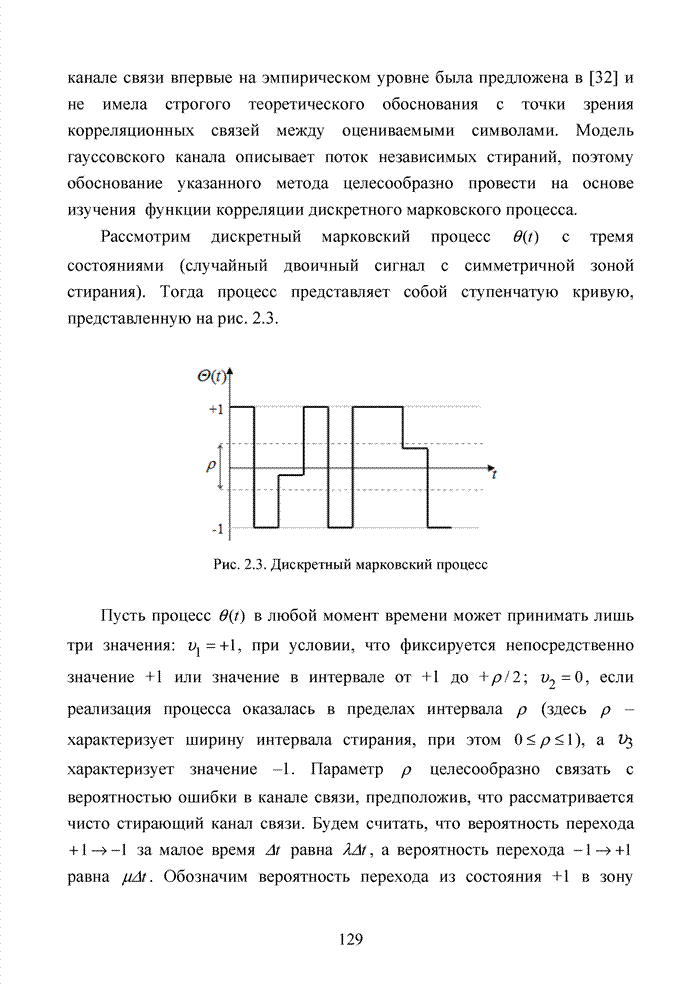
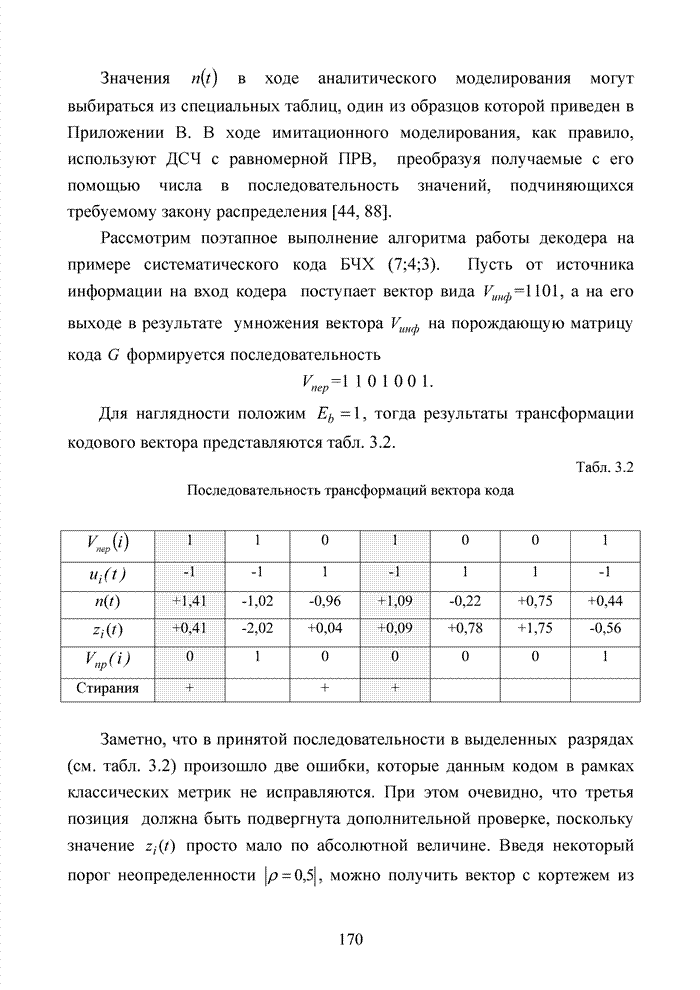
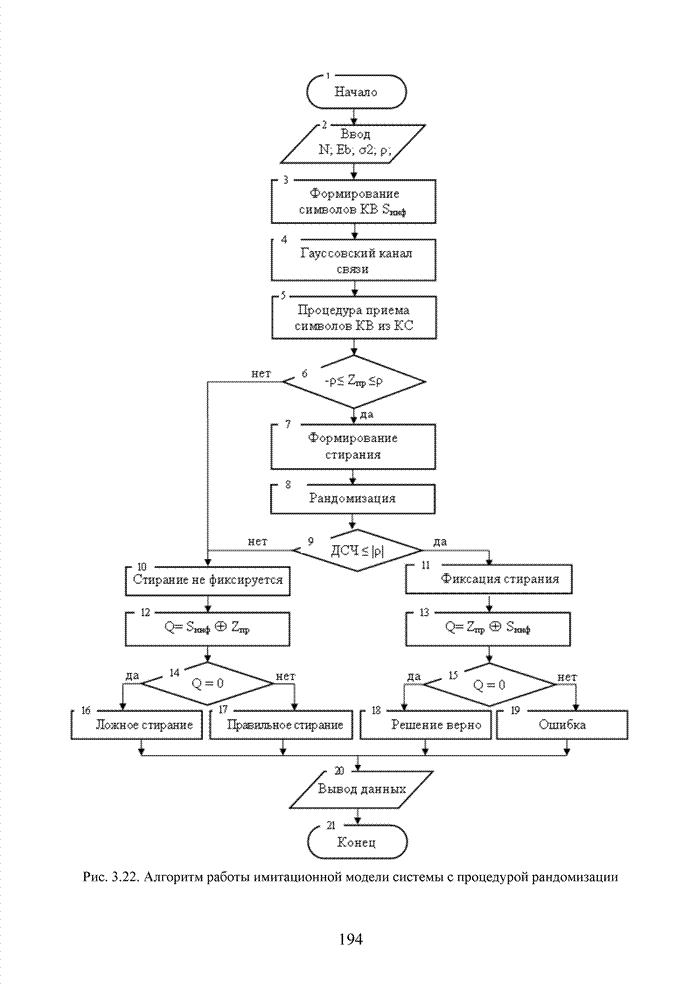
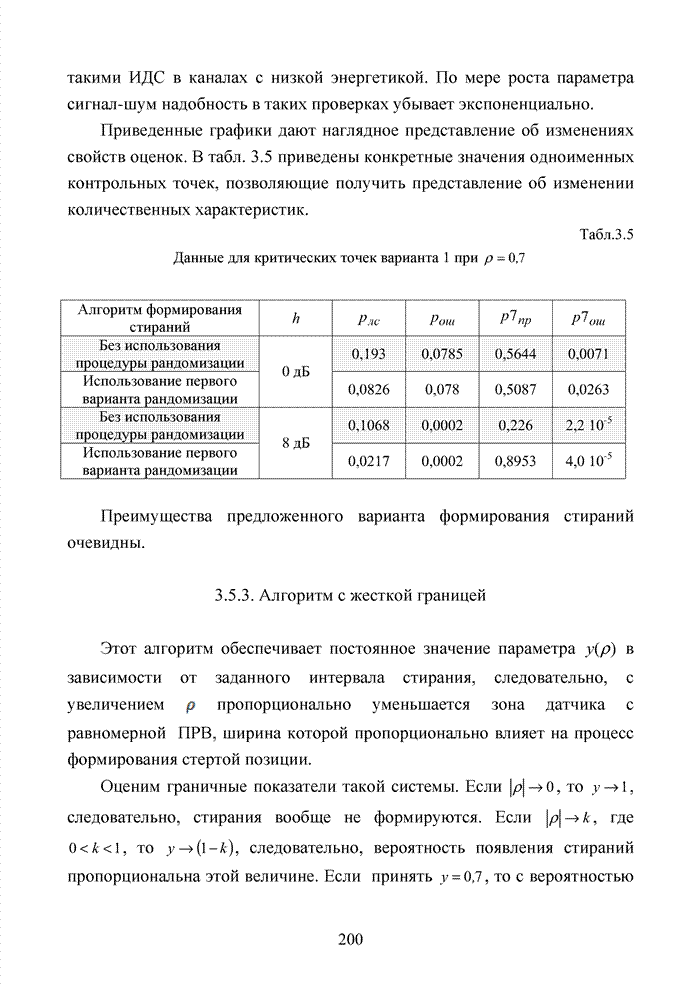
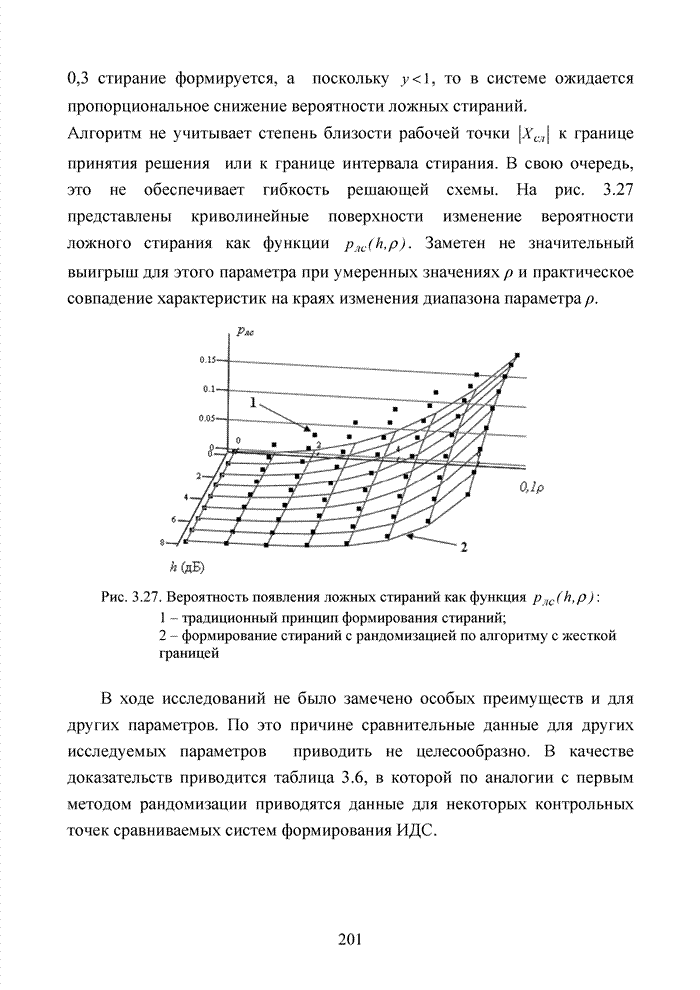
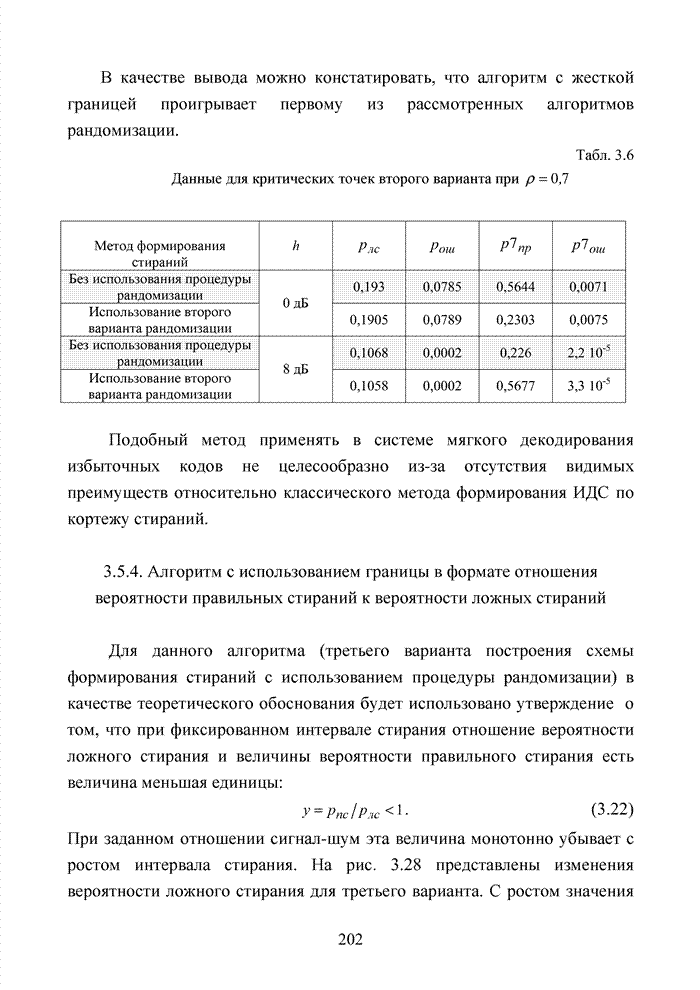
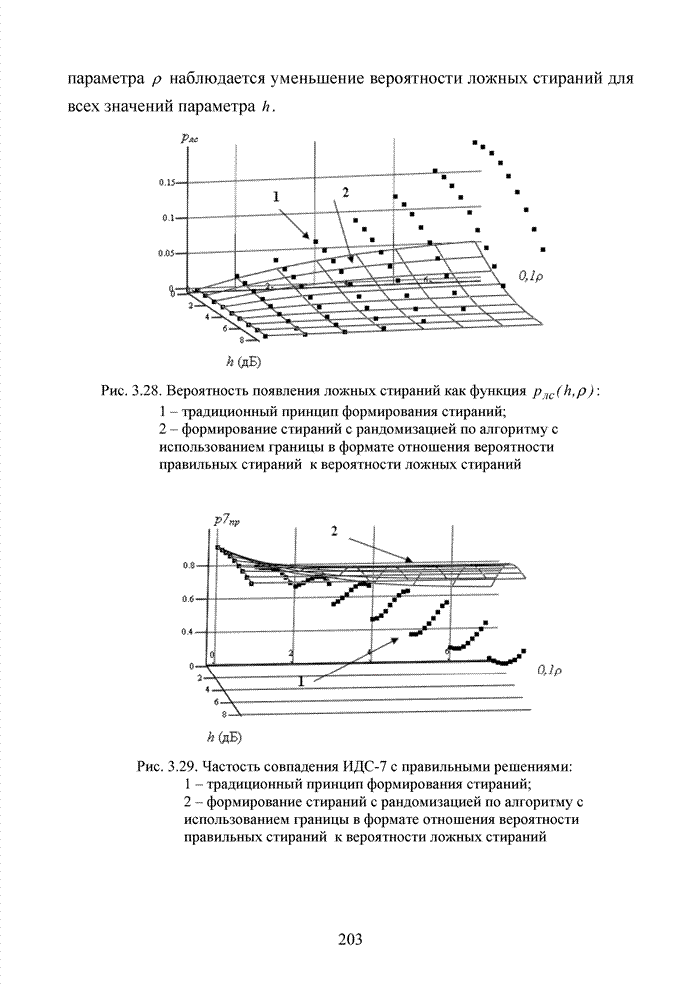
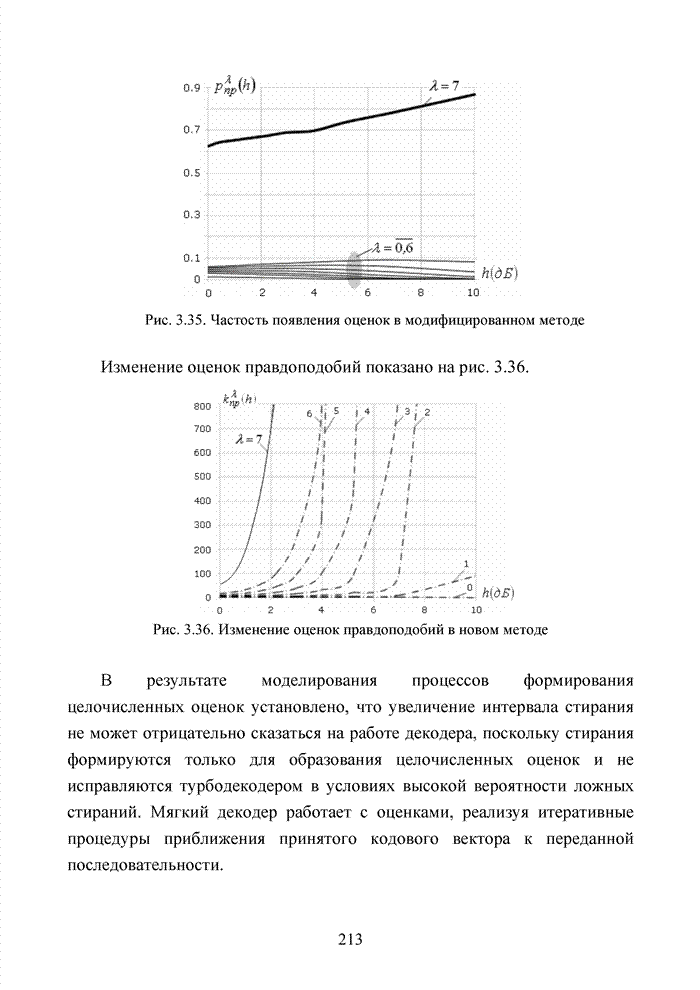
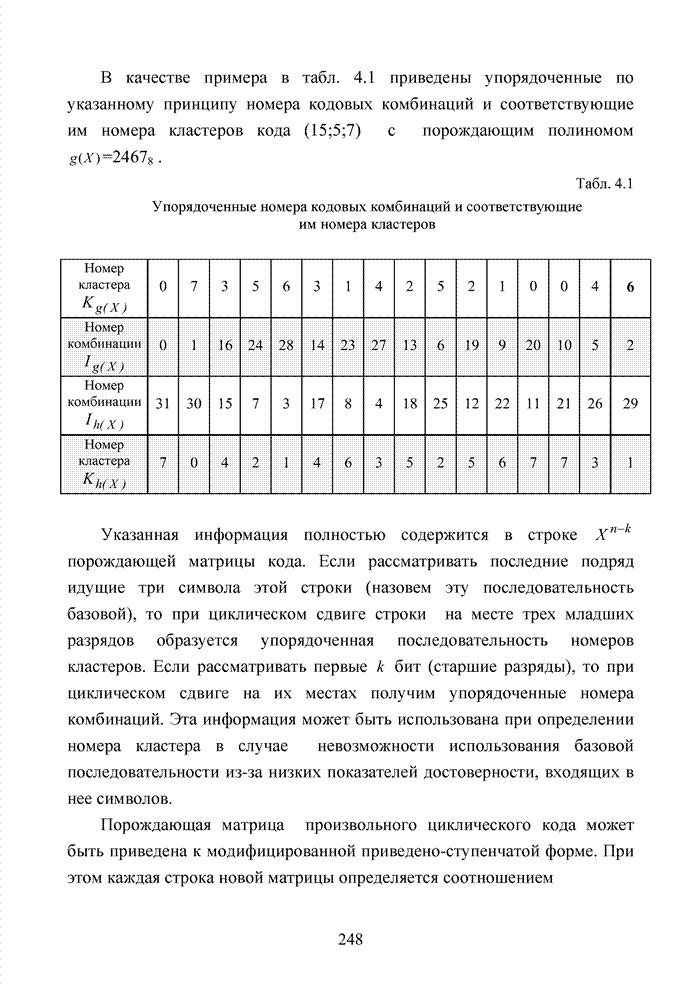
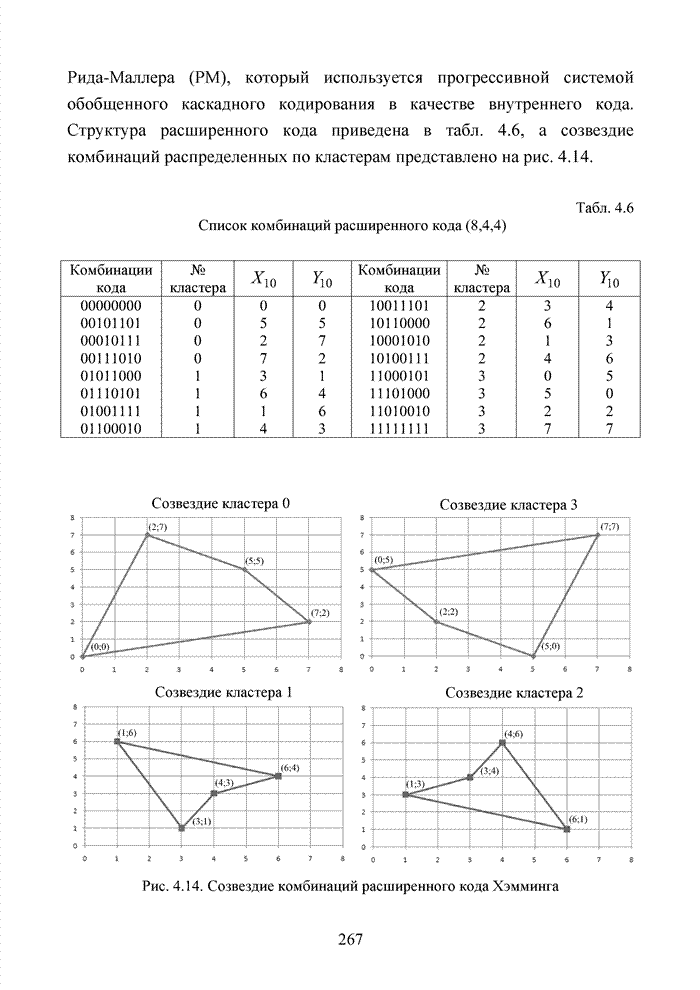
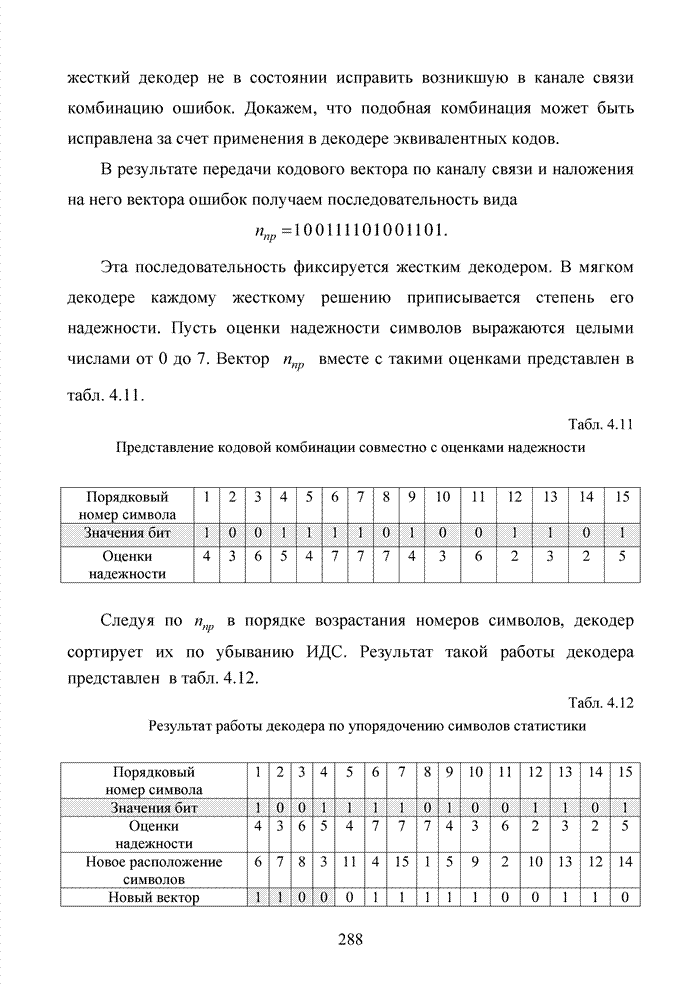
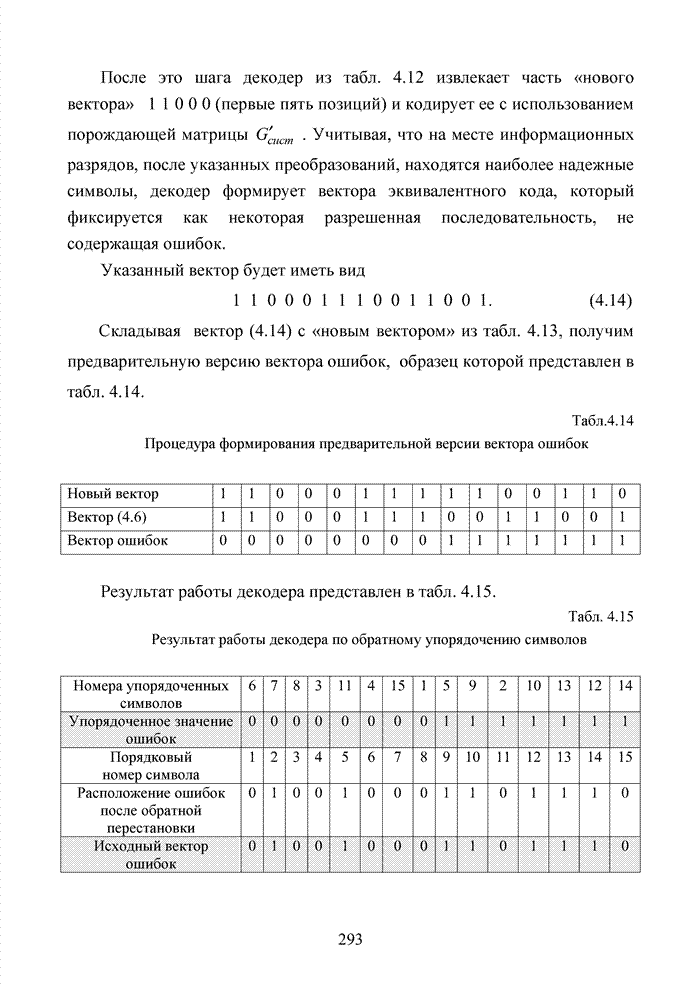
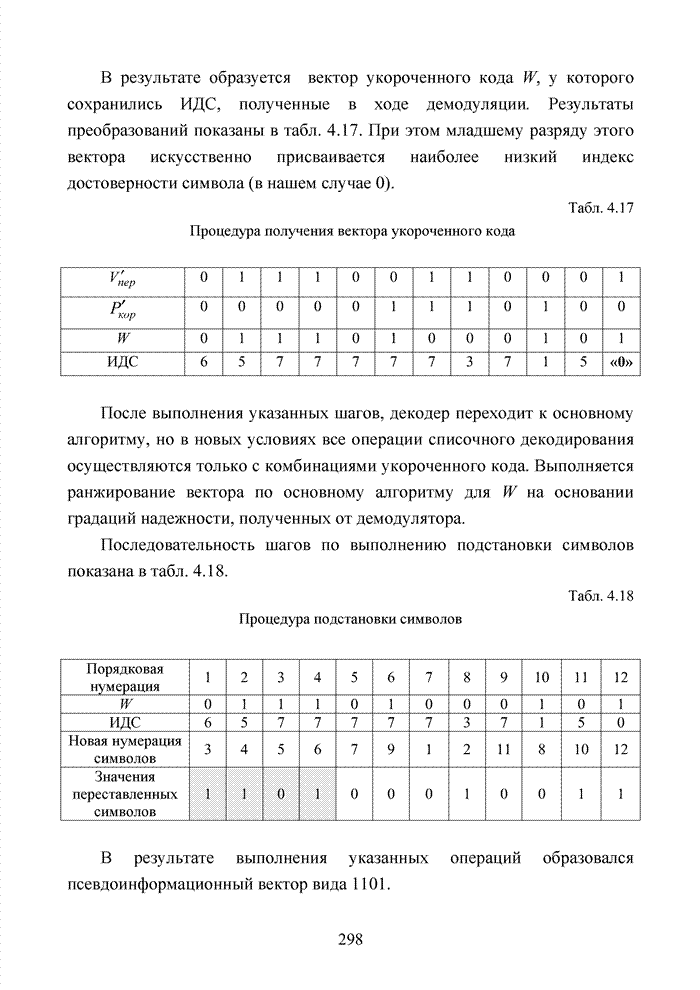
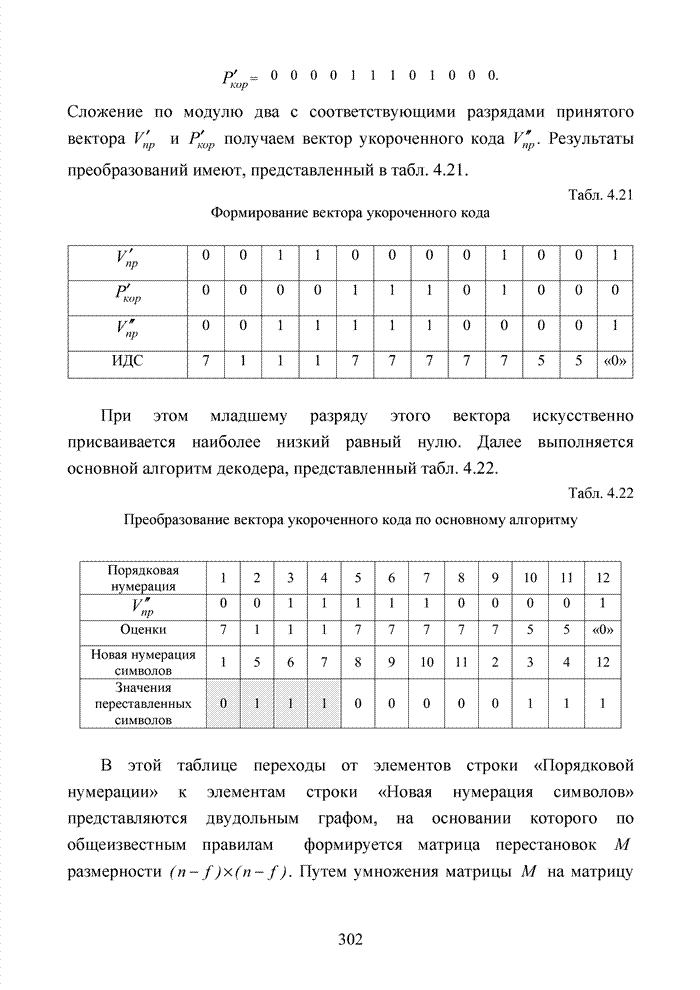
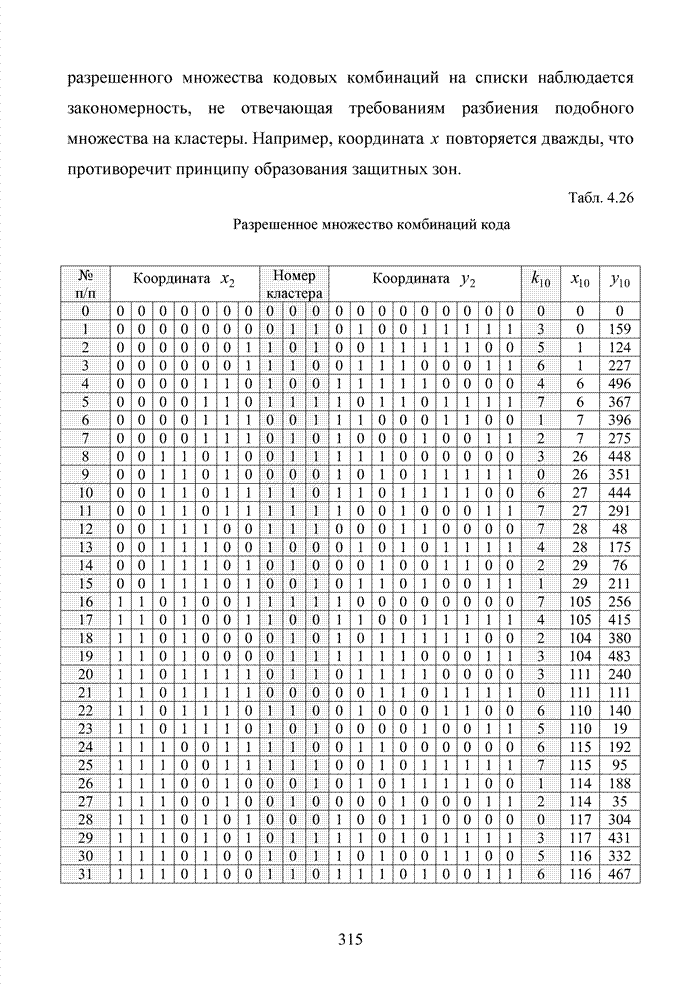
2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
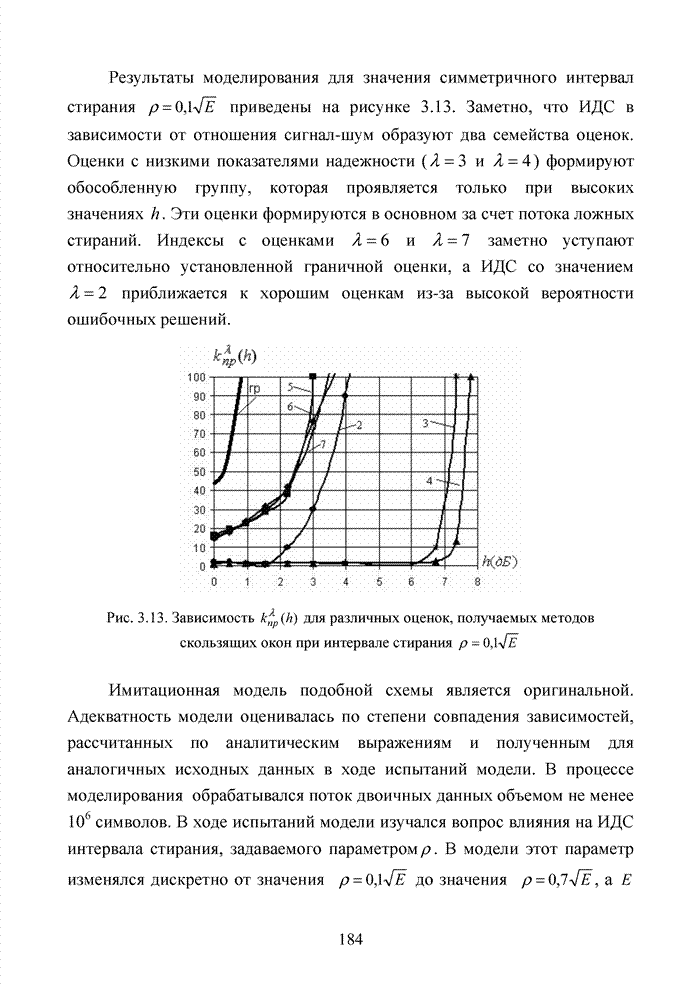
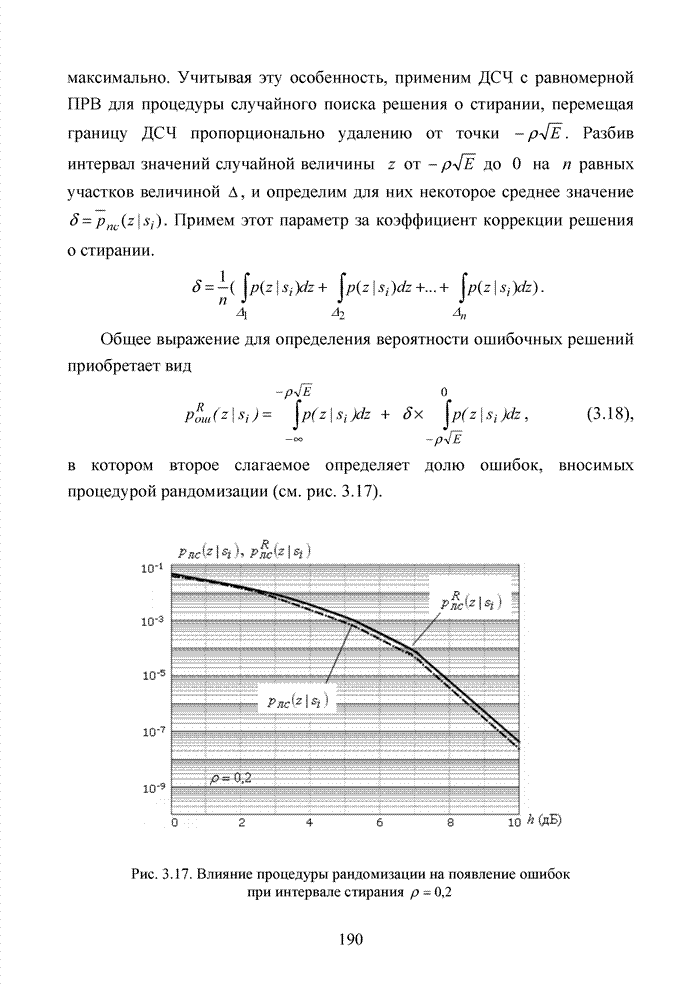
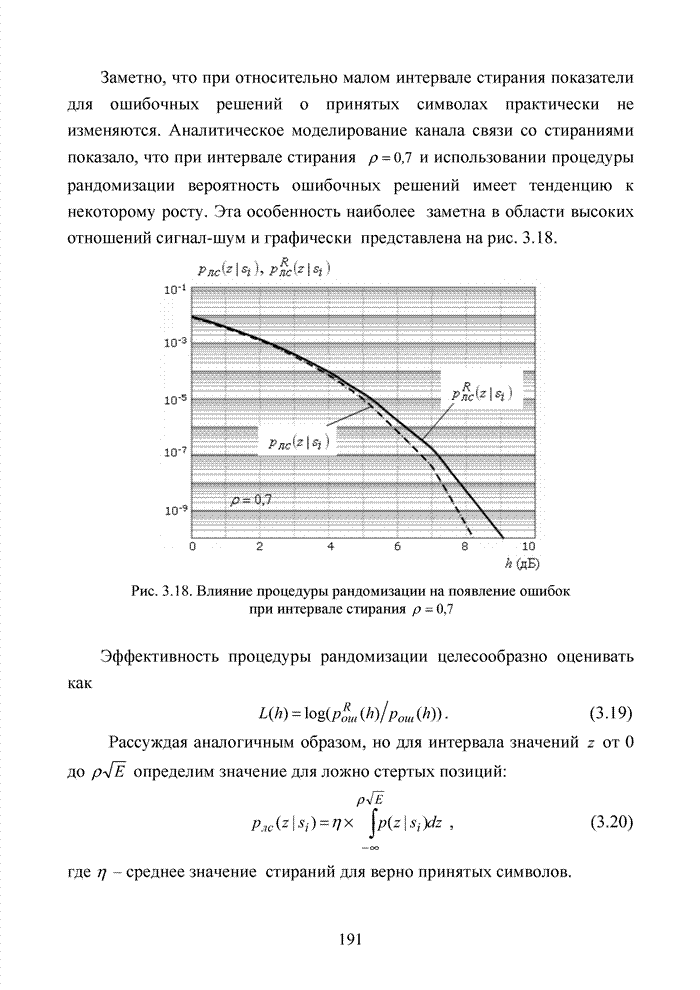
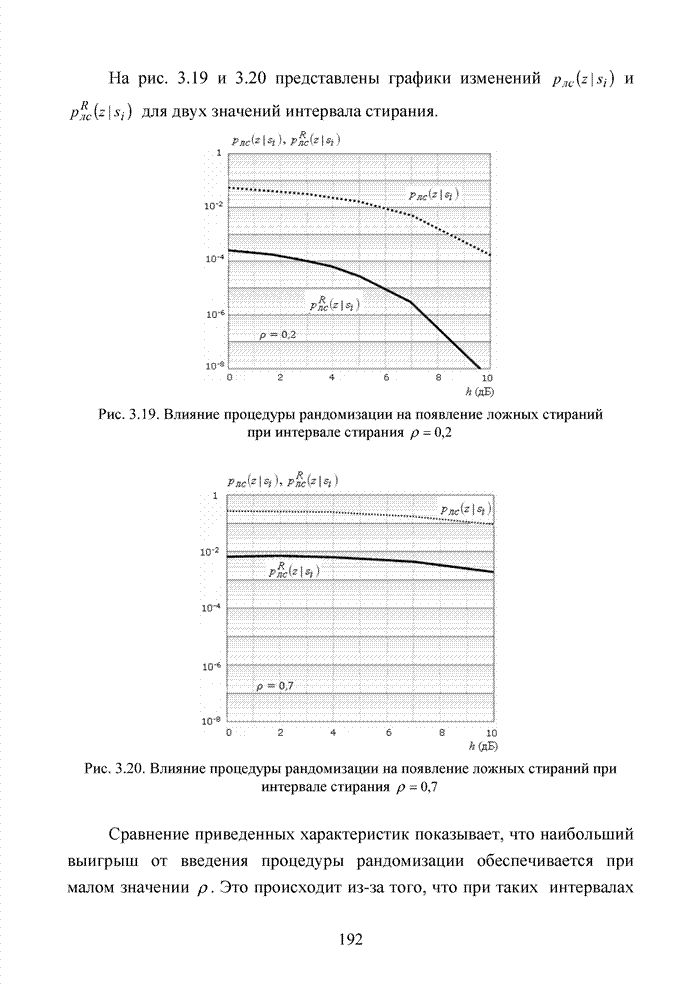
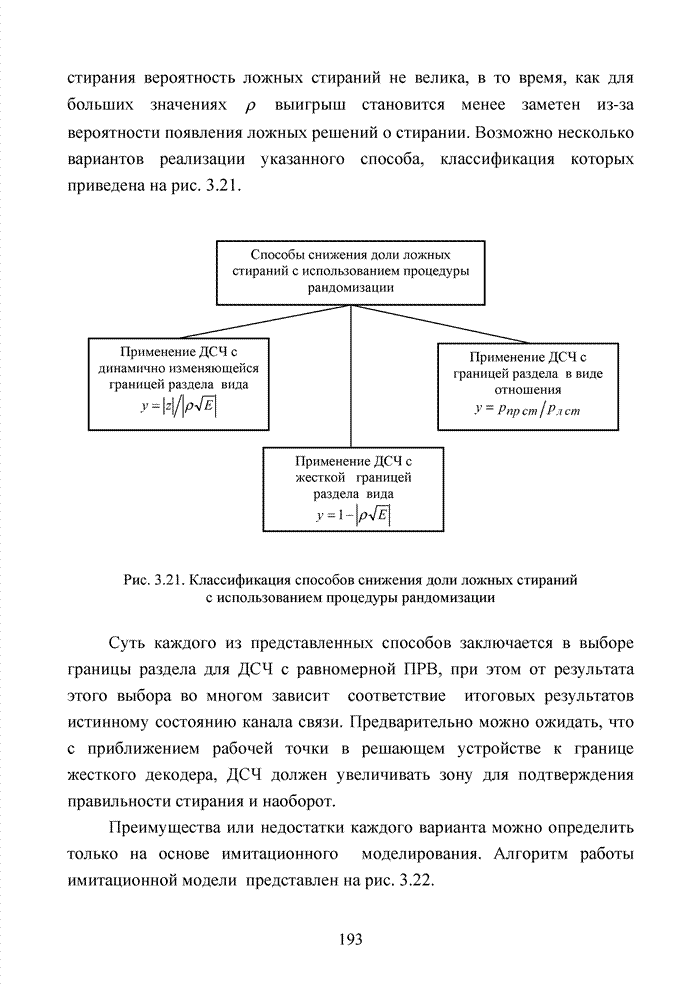
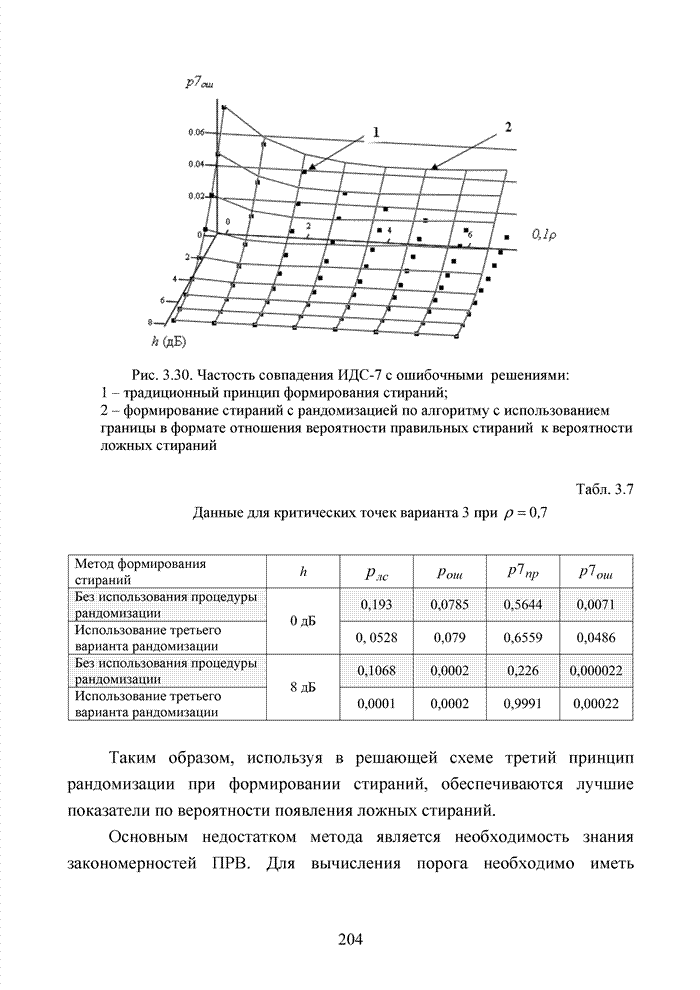
При беспроводной передаче сигналов один и тот же сигнал в результате многократных отражений может поступать в приемник различными путями. Поэтому в точке приема результирующий сигнал представляет собой суперпозицию (интерференцию) многих сигналов с различными амплитудами и начальными фазами. Применительно к многолучевой интерференции, возникающей при передаче сигналов, различают два крайних случая. В первом случае максимальная задержка между различными сигналами не превышает длительности одного символа, и интерференция возникает в пределах одного передаваемого символа. Во втором случае максимальная задержка между различными сигналами больше длительности одного символа, и в результате интерференции складываются сигналы, представляющие разные символы. Вследствие этого возникает межсимвольная интерференция, которая наиболее сильно сказывается на искажении сигнала. Для того, чтобы частично компенсировать эффект многолучевого распространения, применяют частотные эквалайзеры, однако по мере роста скорости передачи данных либо за счет увеличения символьной скорости, либо за счет усложнения схемы кодирования, эффективность их применения падает. Поэтому для достижения высокой, скорости передачи данных используют другой подход, состоящий в том, что поток передаваемых данных распределяется по множеству частотных подканалов и передача ведется параллельно на всех этих подканалах. При этом достигается высокая скорость передачи за счет одновременной передачи данных по всем каналам, причем скорость передачи в отдельном подканале может быть и невысокой. Это создает предпосылки для эффективного подавления межсимвольной интерференции. При частотном разделении каналов необходимо, чтобы ширина каждого канала была, с одной стороны, достаточно узкой для минимизации искажения сигнала в его пределах, а с другой - достаточно широкой для обеспечения требуемой скорости передачи. Кроме того, для экономного использования всей полосы канала, разделяемого на подканалы, желательно как можно плотнее расположить частотные подканалы, но при этом избежать межканальной интерференции для того, чтобы обеспечить полную независимость каналов друг от друга.
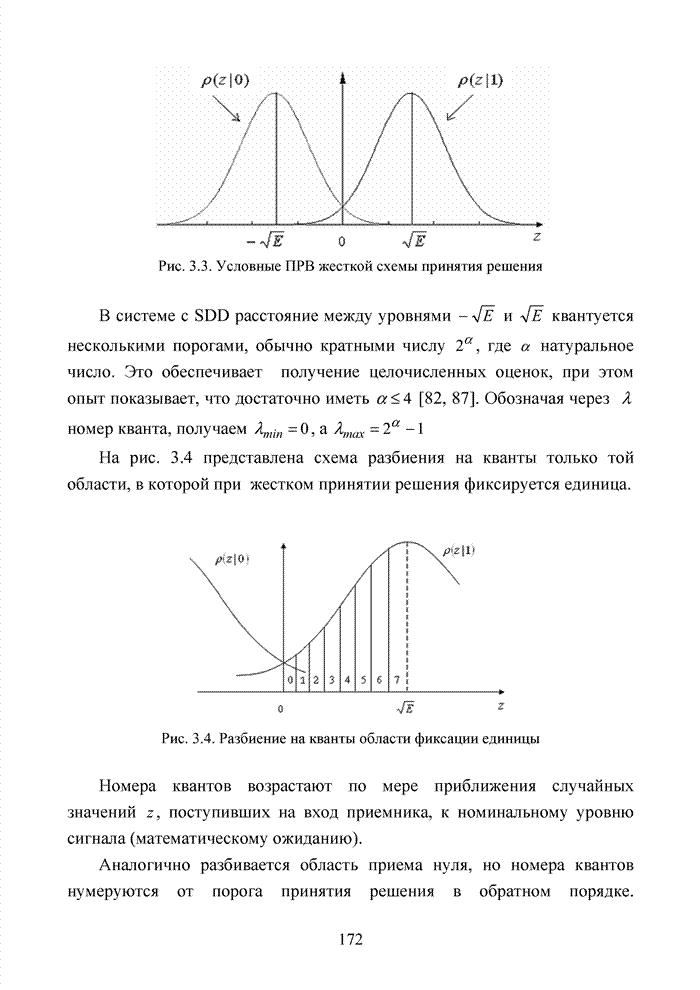
Перечисленным требованиям удовлетворяют ортогональные частотные каналы. Функции, описывающие несущие сигналы всех этих каналов, ортогональны друг другу, т.е. для них выполняется условие:
 , при
, при ![]() ,
(2.47)
,
(2.47)
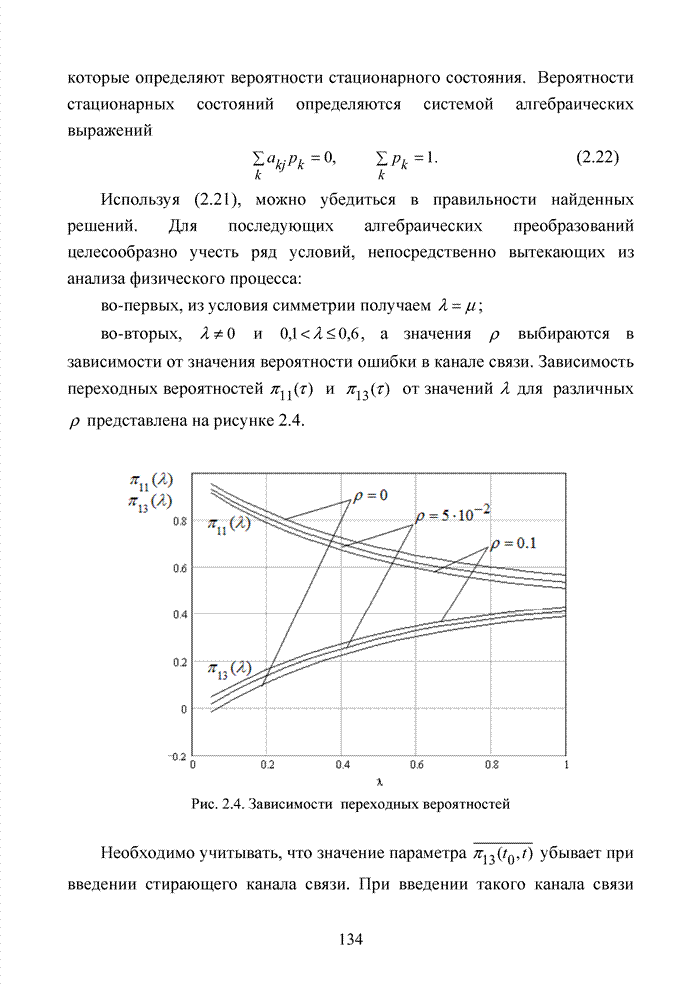
где T – длительность передаваемого символа, ![]() и
и ![]() – частоты l-го и k-го несущих сигналов соответственно. Ортогональность
несущих сигналов обеспечивает частотную независимость каналов друг от друга и,
следовательно, отсутствие межканальной интерференции. Рассмотренный способ
деления широкополосного канала на ортогональные частотные подканалы называется
ортогональным частотным разделением с мультиплексированием или
OFDM-модуляцией.
– частоты l-го и k-го несущих сигналов соответственно. Ортогональность
несущих сигналов обеспечивает частотную независимость каналов друг от друга и,
следовательно, отсутствие межканальной интерференции. Рассмотренный способ
деления широкополосного канала на ортогональные частотные подканалы называется
ортогональным частотным разделением с мультиплексированием или
OFDM-модуляцией.
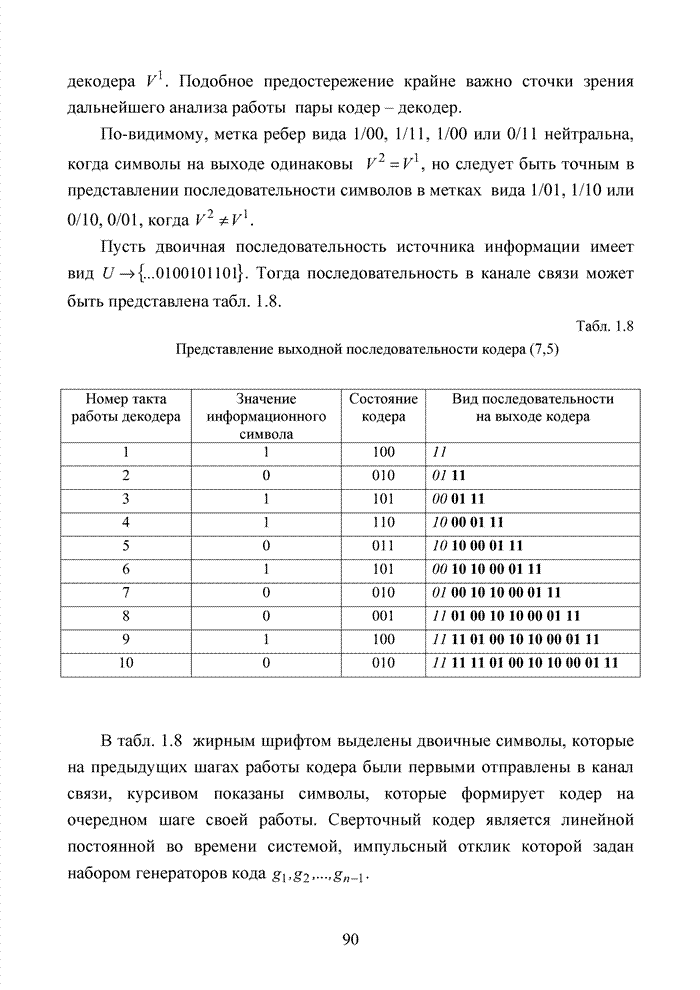
Рассмотрим широкополосные сигналы, состоящие из N поднесущих, когда входной высокоскоростной поток данных разделятся на множество низкоскоростных потоков, каждый из которых независимо модулируется на одной из поднесущих частот.
Пусть каждой поднесущей в
течение времени Т передается последовательно М псевдослучайных
чисел, которые образуются как результат деления исходного информационного
потока на субканалы. Очевидно, что в полосе ![]() сигналы ортогональны на каждом из интервалов Т. При разных значениях
уровня помех (например, К одновременно работающих абонентов) и
коэффициенте передачи канала
сигналы ортогональны на каждом из интервалов Т. При разных значениях
уровня помех (например, К одновременно работающих абонентов) и
коэффициенте передачи канала ![]() величины псевдослучайных чисел взаимно независимы, т.е. вероятность появления символов ±1
равняется 0,5.
величины псевдослучайных чисел взаимно независимы, т.е. вероятность появления символов ±1
равняется 0,5.
В [14] рассматривается способ обработки данных, при котором вероятность ошибки оценивается выражением
![]() (2.48)
(2.48)
где ![]() , а
, а ![]() – отношение полной средней энергии принимаемого полезного сигнала к спектральной мощности гауссовского шума,
– отношение полной средней энергии принимаемого полезного сигнала к спектральной мощности гауссовского шума, ![]() – база сигнала.
– база сигнала.
При отсутствии замираний
коэффициент передачи канала ![]() , а значение
, а значение ![]() определяется из соотношения
определяется из соотношения ![]() . При больших значениях
. При больших значениях ![]() получим
получим ![]() т.е. отношение
сигнал-шум на входе
решающего устройства не зависит от отношения мощности сигнала к мощности
гауссовского шума и равно отношению базы широкополосного сигнала к числу
радиопомех (или числу других абонентов, работающих в системе широкополосных
многочастотных сигналов) и мешающих приему полезного сигнала
т.е. отношение
сигнал-шум на входе
решающего устройства не зависит от отношения мощности сигнала к мощности
гауссовского шума и равно отношению базы широкополосного сигнала к числу
радиопомех (или числу других абонентов, работающих в системе широкополосных
многочастотных сигналов) и мешающих приему полезного сигнала ![]() . Если сигнал
. Если сигнал ![]() распространяется по
многолучевому каналу, в котором
распространяется по
многолучевому каналу, в котором
 ,
,
получаем ![]() и
и ![]() . Если сигналы
. Если сигналы ![]() передаются разными
радиопередатчиками, то коэффициент передачи принимает вид
передаются разными
радиопередатчиками, то коэффициент передачи принимает вид
 ,
(2.49)
,
(2.49)
что представляет собой сумму
большого числа случайных величин. При больших значениях K она имеет
среднее значение 1 и малую дисперсию, равную . Принимая
. Принимая ![]() , получаем выражение для
, получаем выражение для ![]() .
.
Расчетная формула для
определения ![]() должна в
комплексе учитывать влияние замираний полезного сигнала и радиопомех на
помехоустойчивость приема информационного символа
должна в
комплексе учитывать влияние замираний полезного сигнала и радиопомех на
помехоустойчивость приема информационного символа ![]() . Для этого вычислим среднее значение
. Для этого вычислим среднее значение ![]() с учетом
распределения вероятностей случайной величины z, которое имеет вид
с учетом
распределения вероятностей случайной величины z, которое имеет вид
![]() .
(2.50)
.
(2.50)
После чего получаем
![]() ,
,
где
![]() ,
,
и ![]() .
.
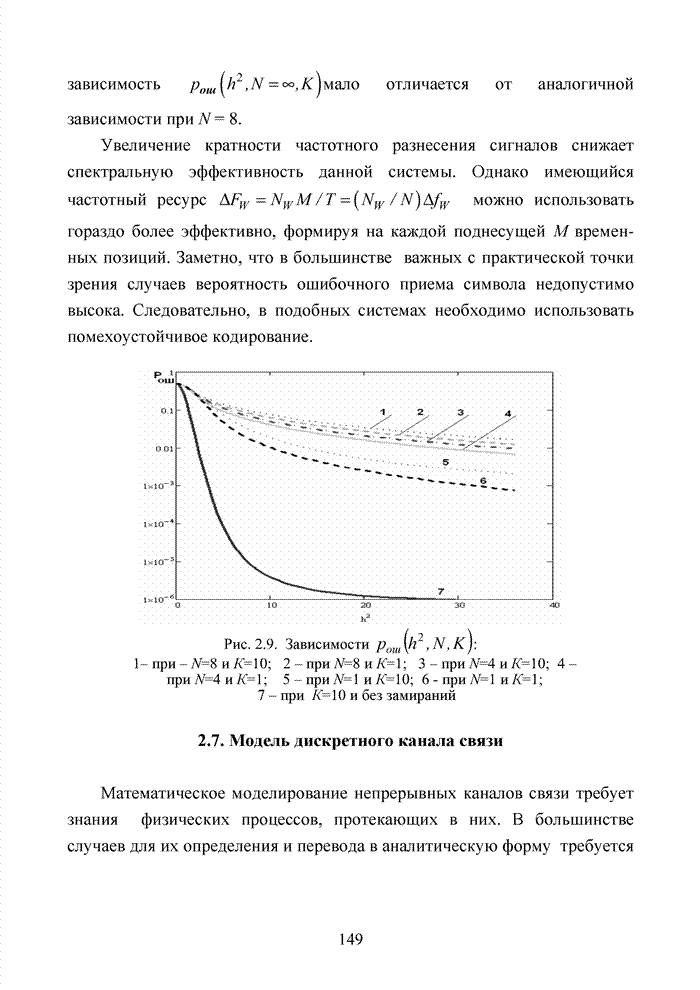
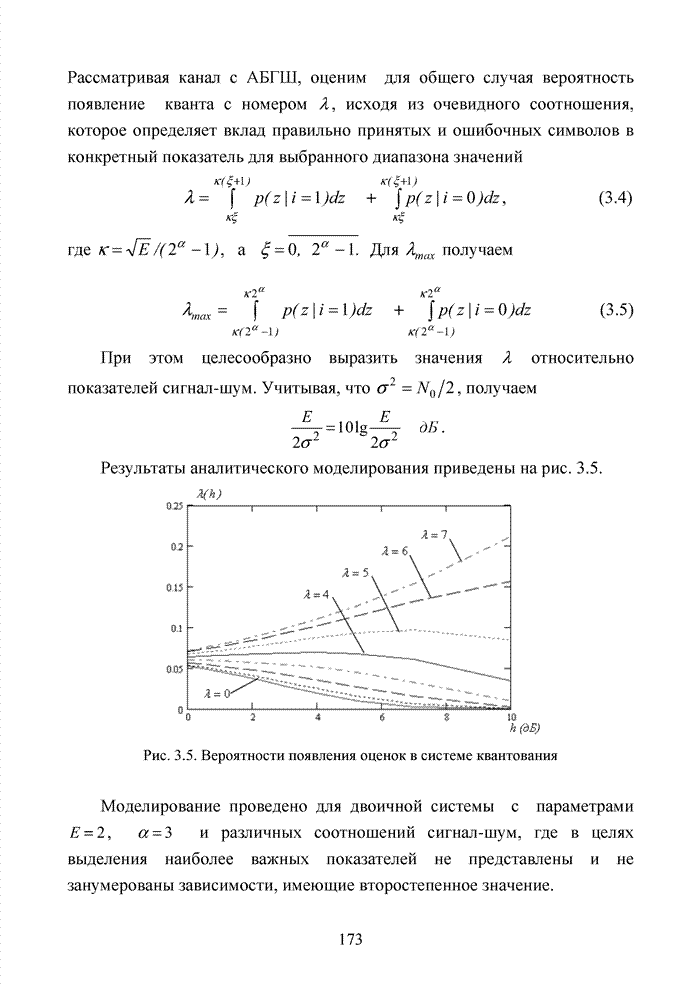
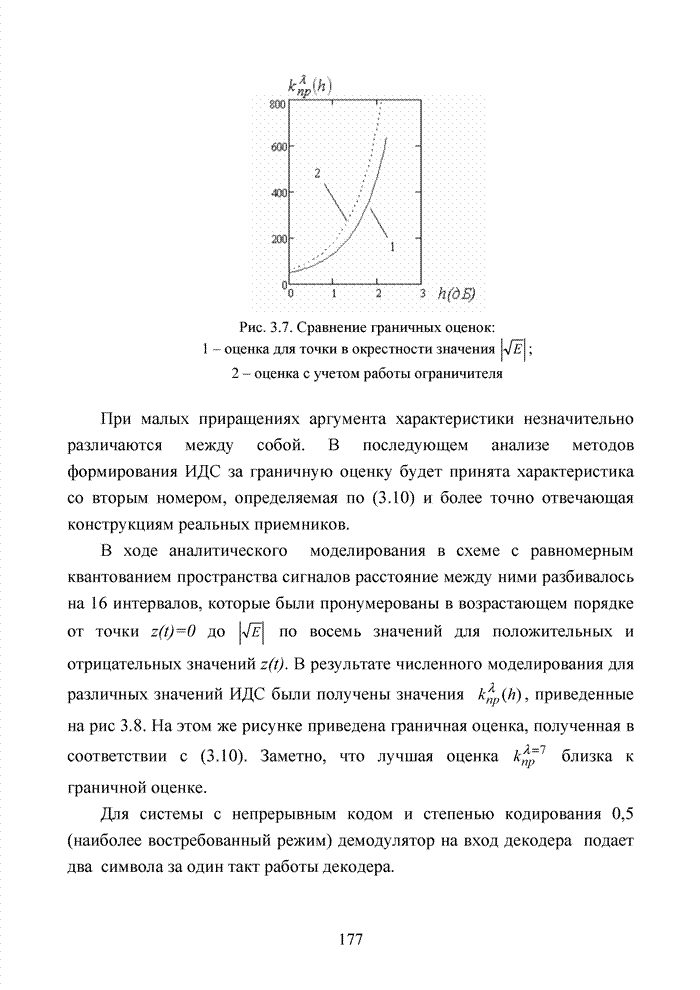
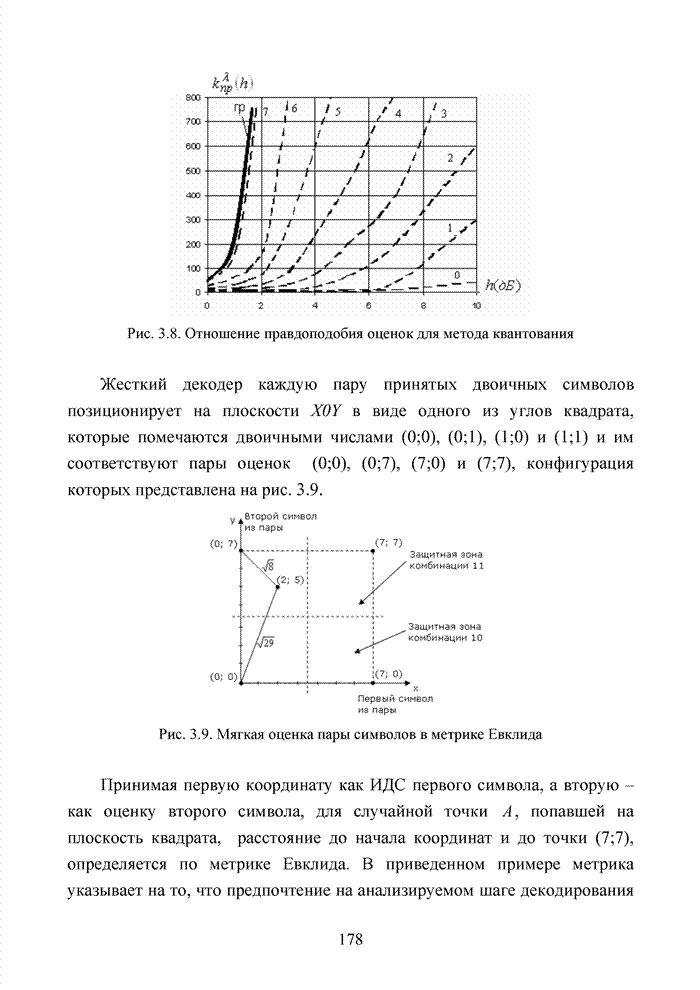
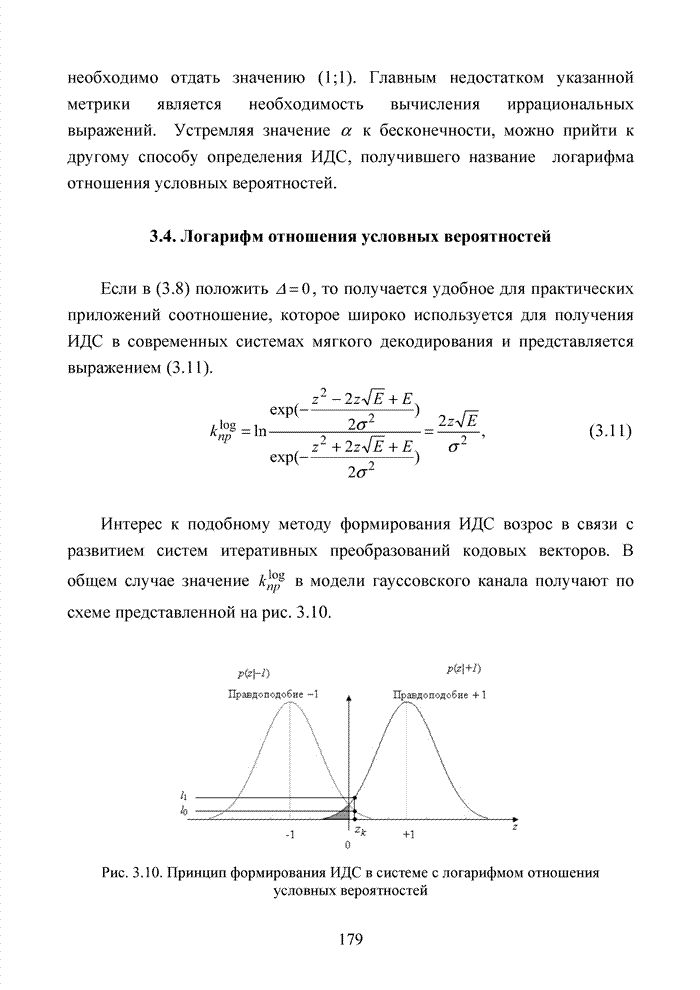
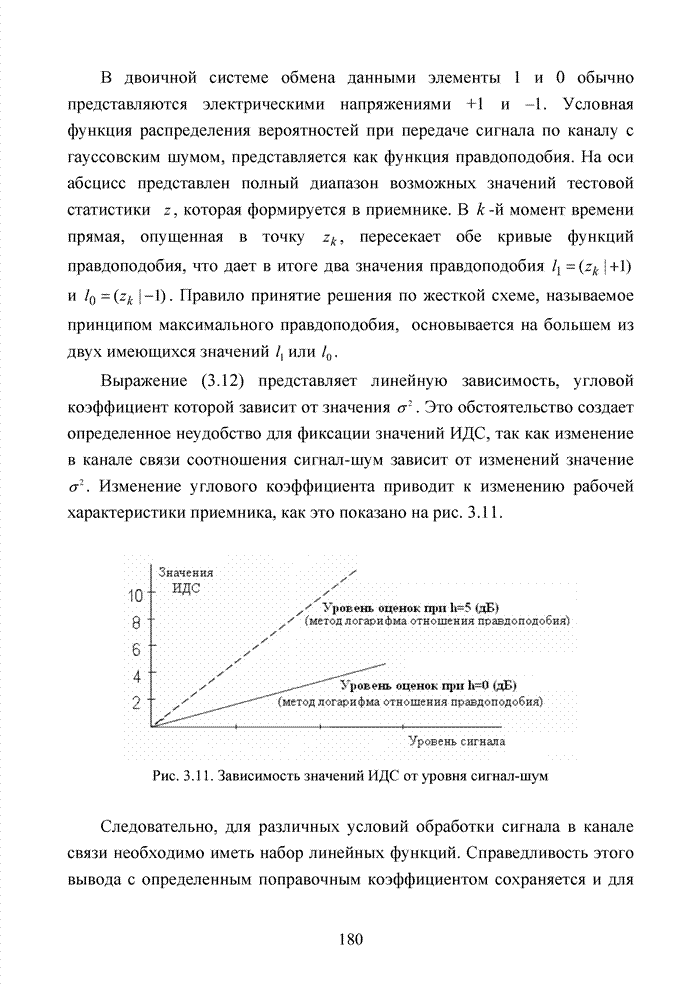
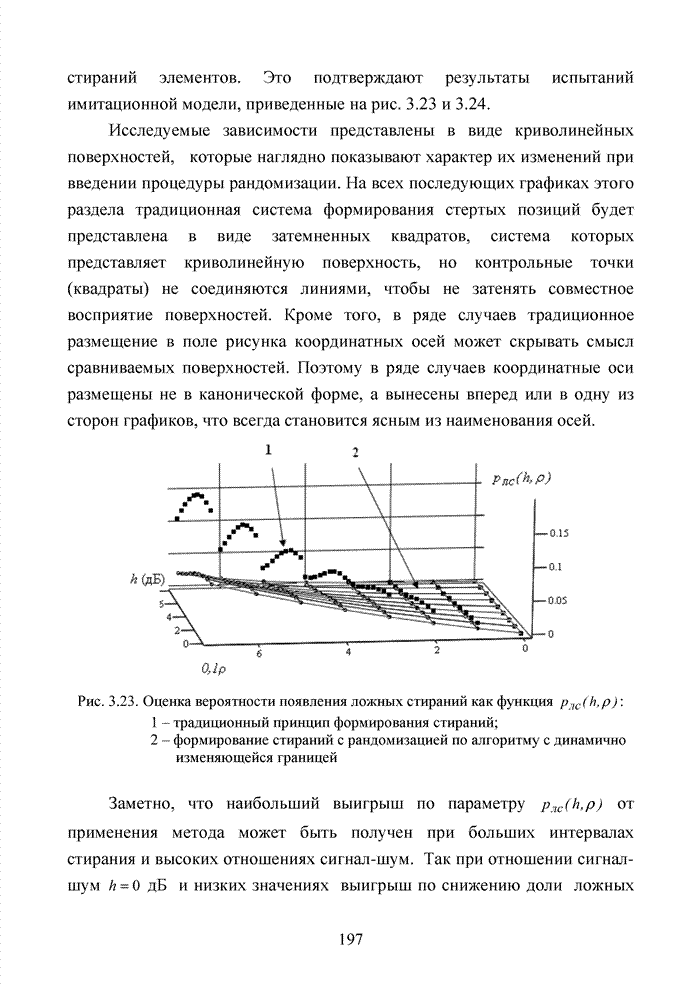
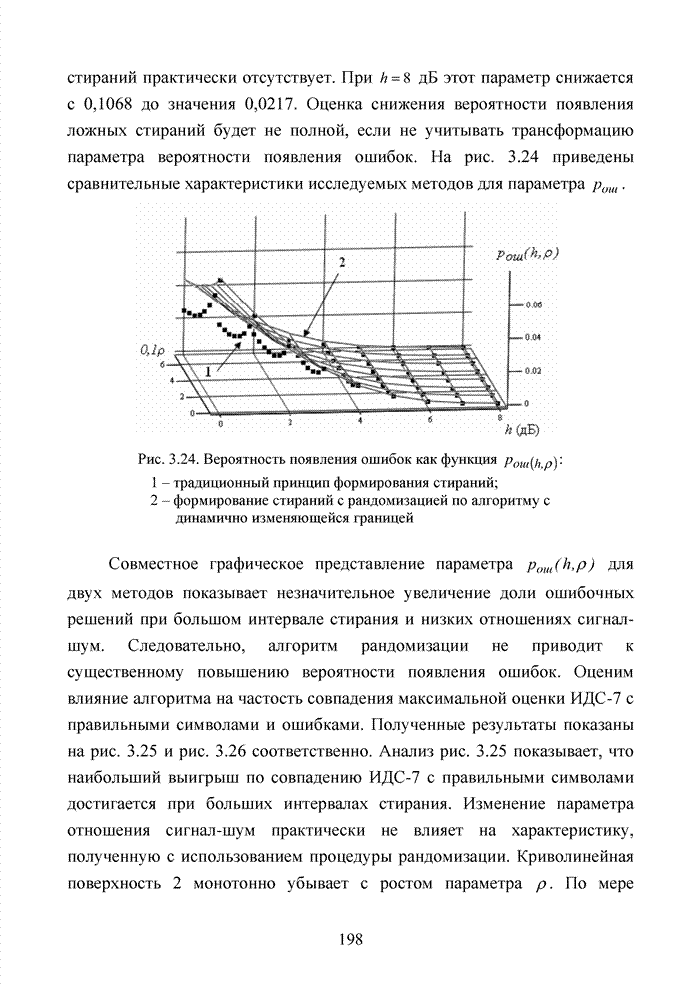
Используя численный метод, получим семейство характеристик, представленное на рис. 2.9.
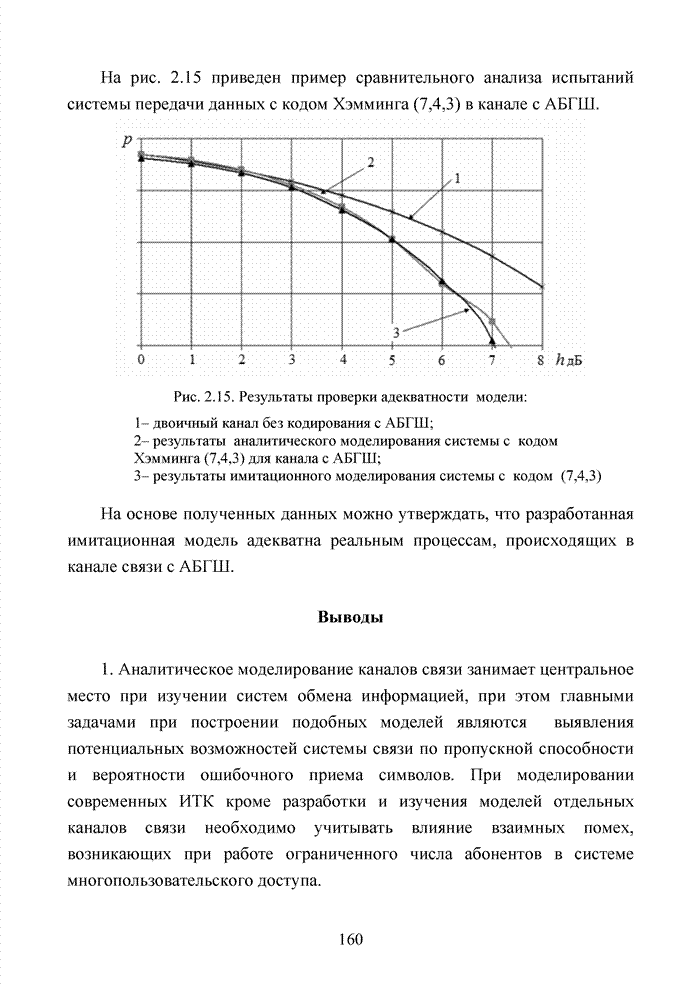
Анализ полученных кривых показывает, что наличие радиопомех от других абонентских терминалов существенно ухудшает помехоустойчивость приема и чем выше кратность разнесенного приема, тем ситуация хуже.
Так, при N = 1
отличие между кривыми ![]() для
K= 1 и 10 незначительно. Оно становится ощутимым при N = 4 и еще
в большей степени при N = 8, а также в том случае, когда замираний сигнала
нет.
для
K= 1 и 10 незначительно. Оно становится ощутимым при N = 4 и еще
в большей степени при N = 8, а также в том случае, когда замираний сигнала
нет.
При K = 10
различие в помехоустойчивости приема при 4-х и 8-ми кратном разнесенном приеме
невелико. Для случая, когда замираний нет, зависимость ![]() мало отличается от аналогичной
зависимости при N = 8.
мало отличается от аналогичной
зависимости при N = 8.
Увеличение кратности
частотного разнесения сигналов снижает спектральную эффективность данной системы.
Однако имеющийся частотный ресурс ![]() можно использовать гораздо более
эффективно, формируя на каждой поднесущей М временных позиций. Заметно,
что в большинстве важных с практической точки зрения случаев вероятность ошибочного
приема символа недопустимо высока. Следовательно, в подобных системах
необходимо использовать помехоустойчивое кодирование.
можно использовать гораздо более
эффективно, формируя на каждой поднесущей М временных позиций. Заметно,
что в большинстве важных с практической точки зрения случаев вероятность ошибочного
приема символа недопустимо высока. Следовательно, в подобных системах
необходимо использовать помехоустойчивое кодирование.

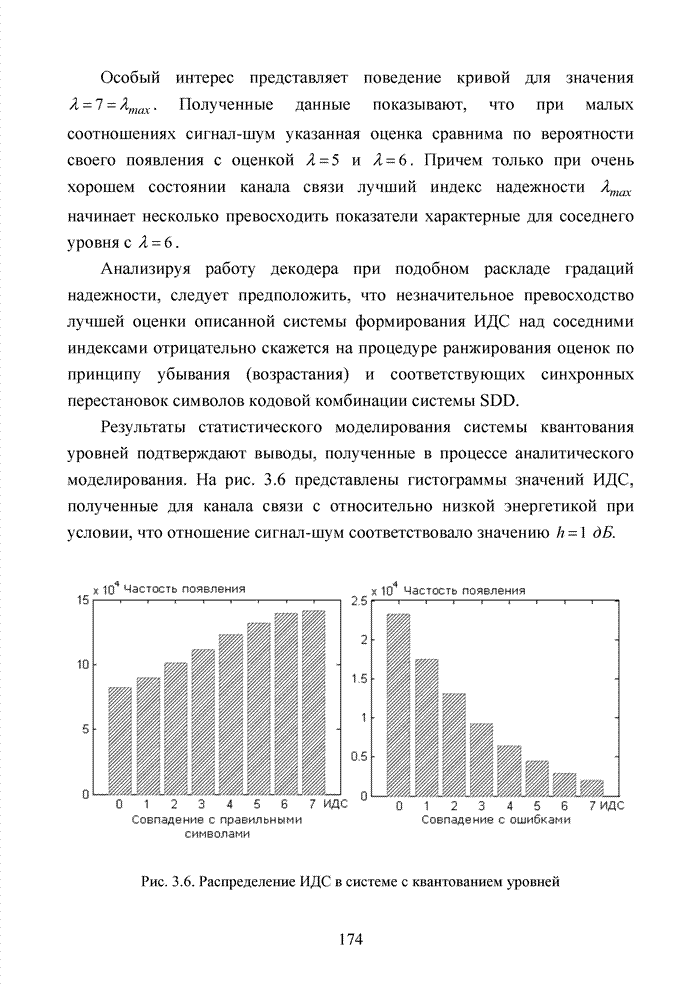
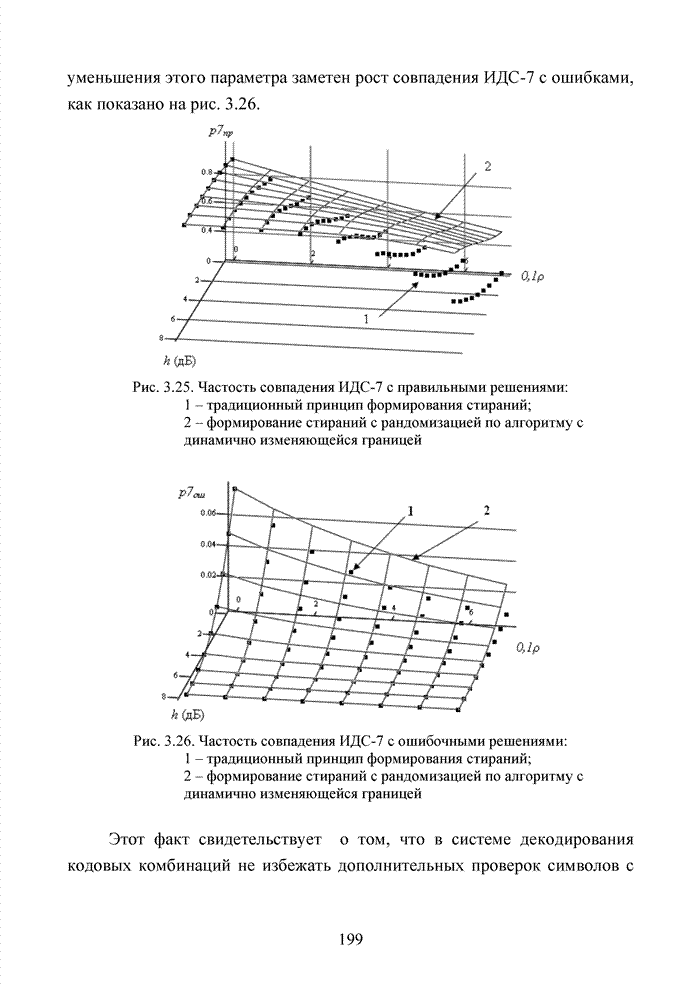
Рис. 2.9. Зависимости ![]() :
:
1– при – N=8 и К=10; 2 – при N=8 и К=1; 3 – при N=4 и К=10; 4 – при N=4 и К=1; 5 – при N=1 и К=10; 6 - при N=1 и К=1;
7 – при К=10 и без замираний
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
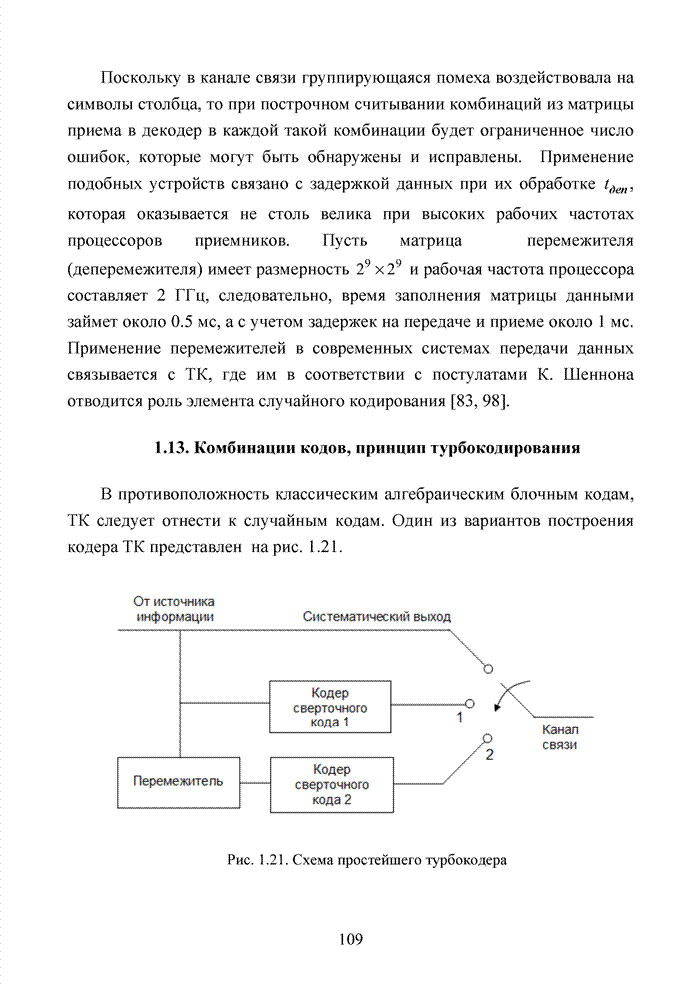
- 1.13. Комбинации кодов, принцип турбокодирования
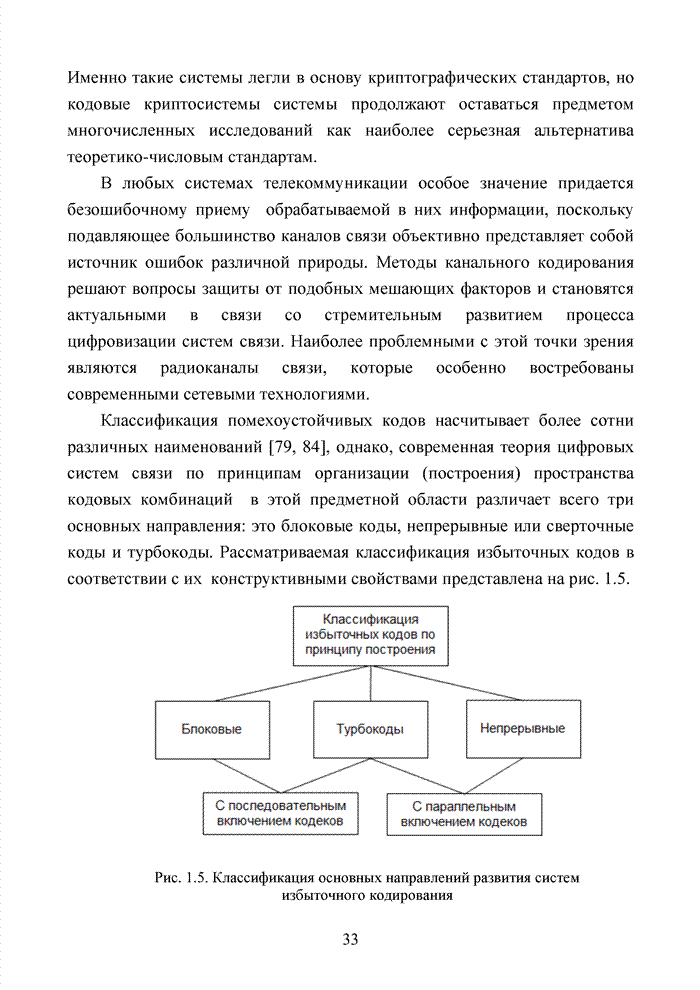
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
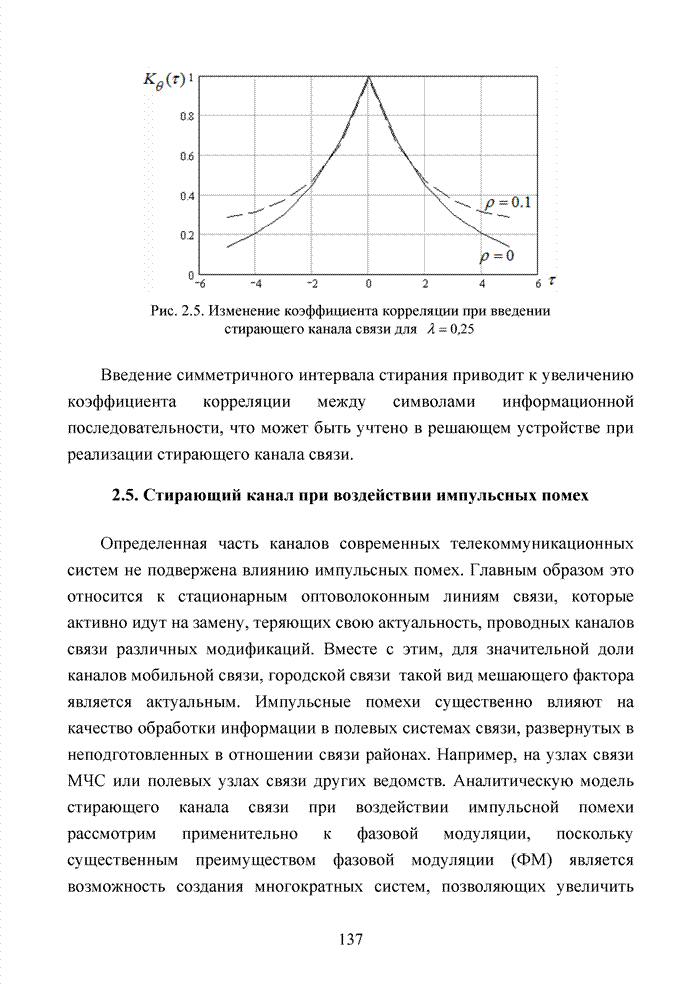
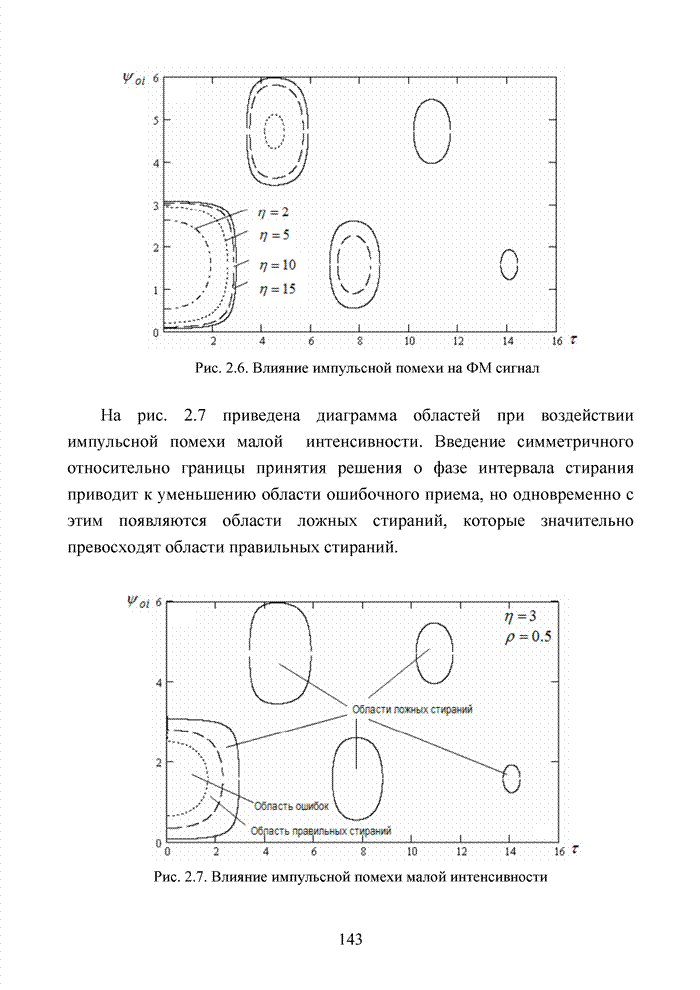
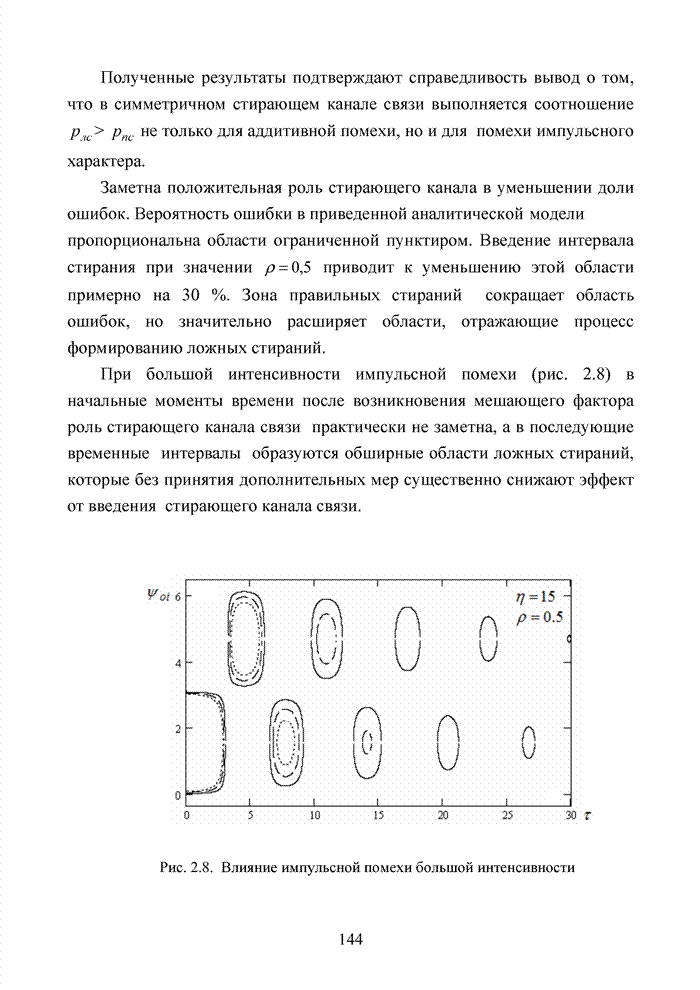
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
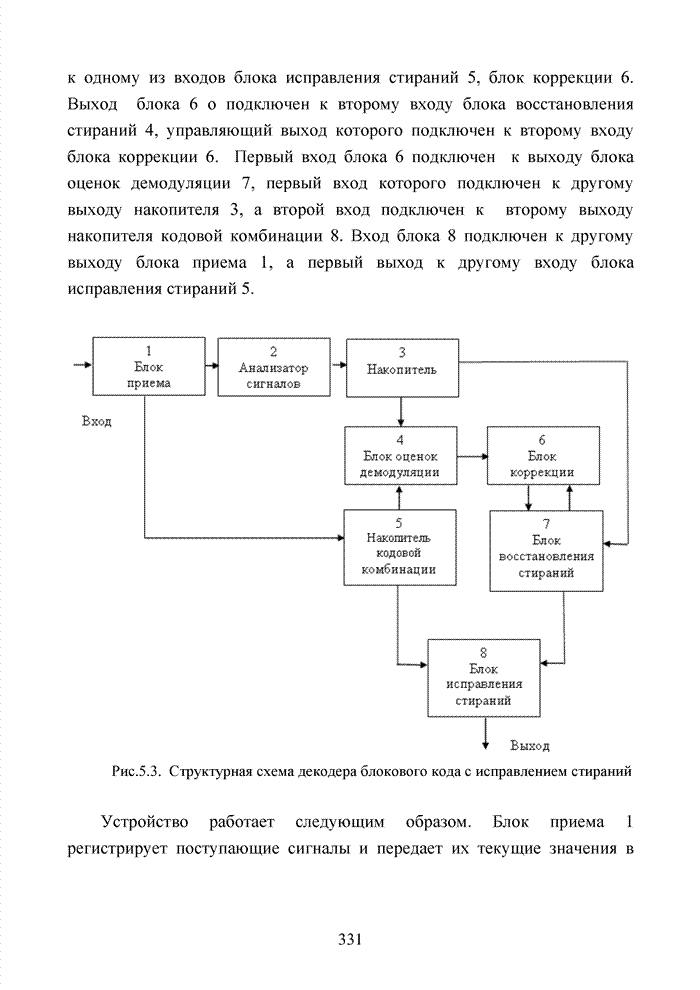
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
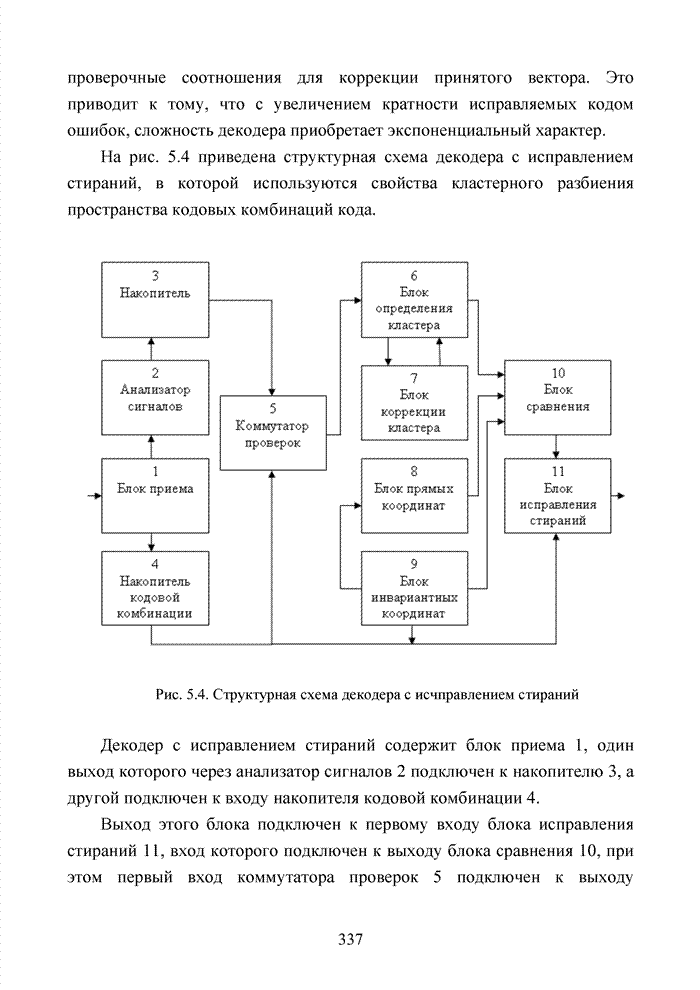
- 5.4. Декодирование с использованием списков на основе кластеров
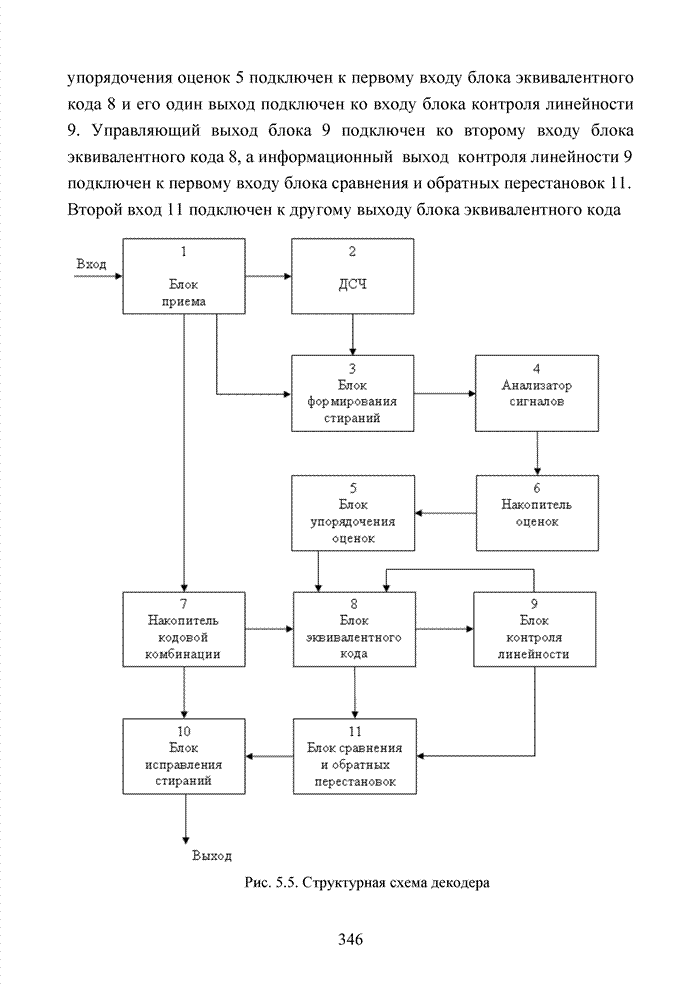
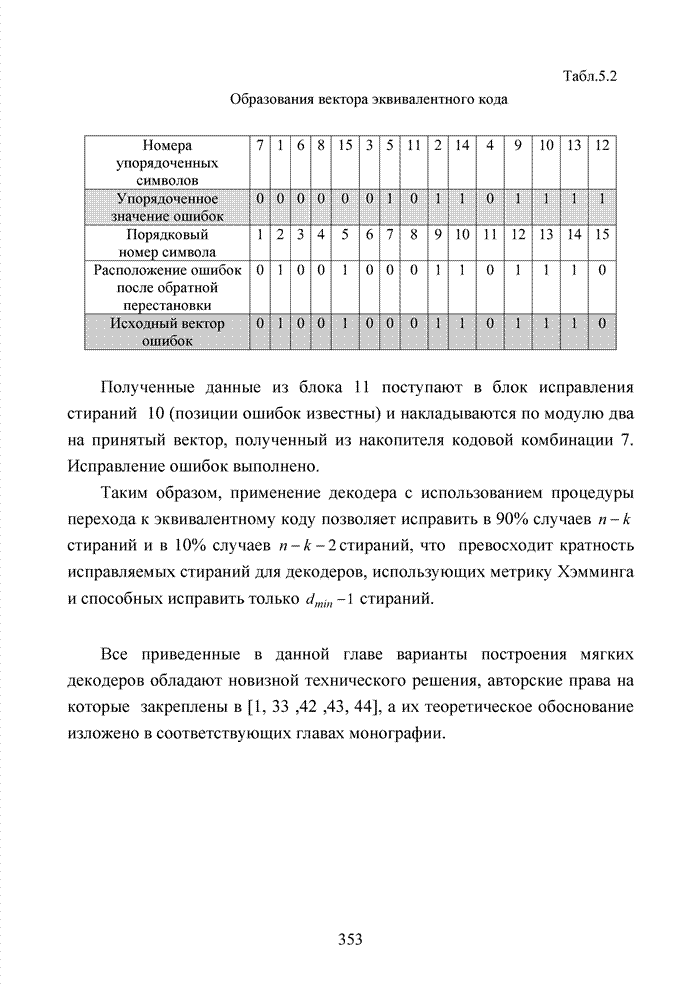
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
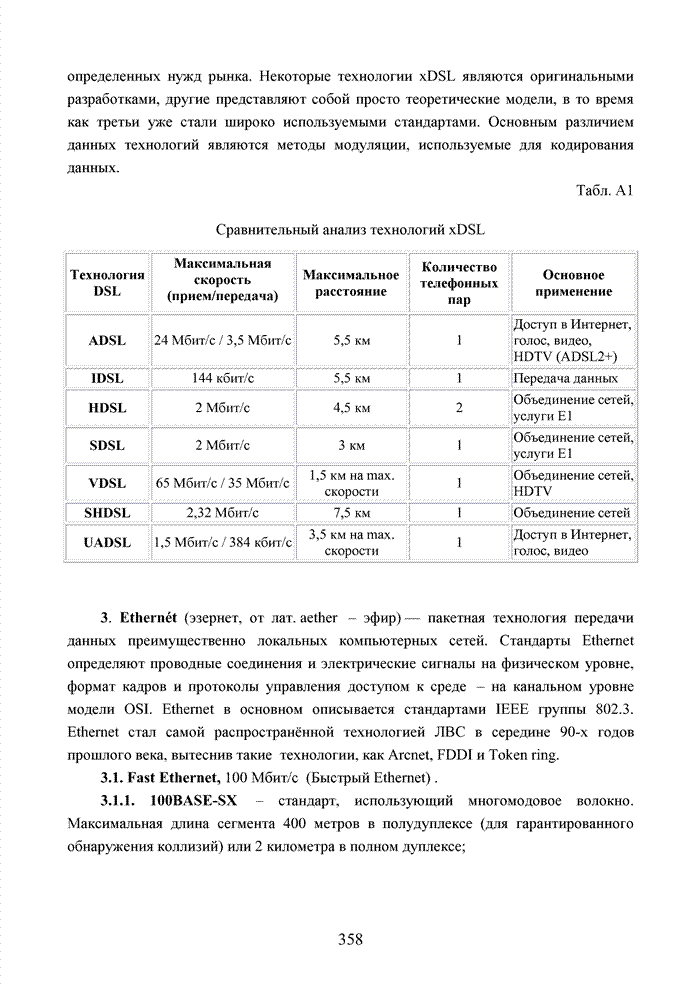
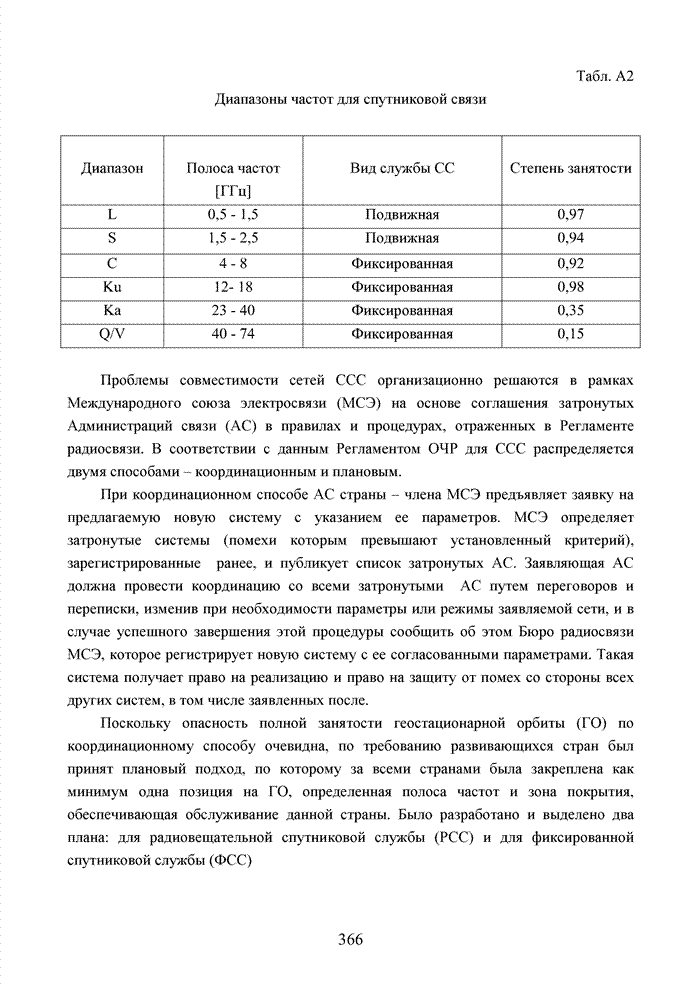
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
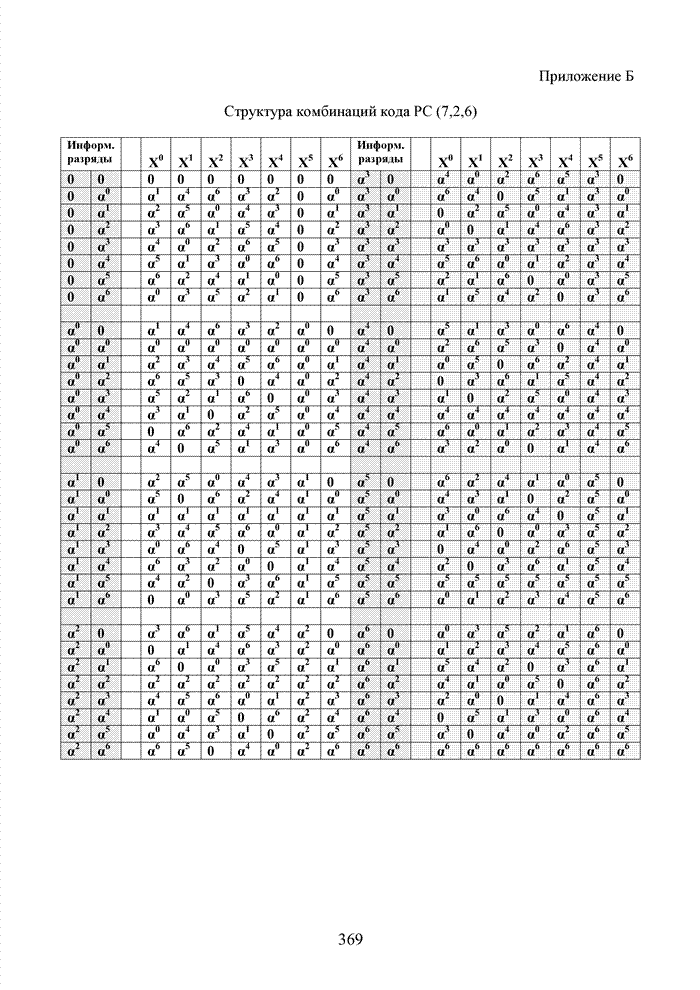
- Приложение Б Структура комбинаций кода РС (7,2,6)
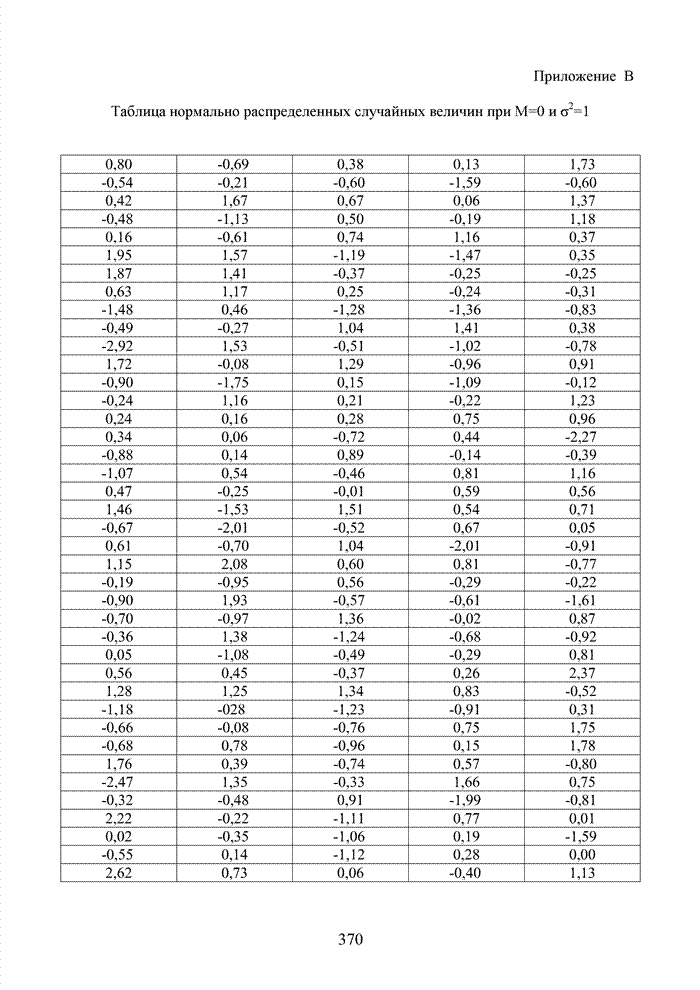
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК