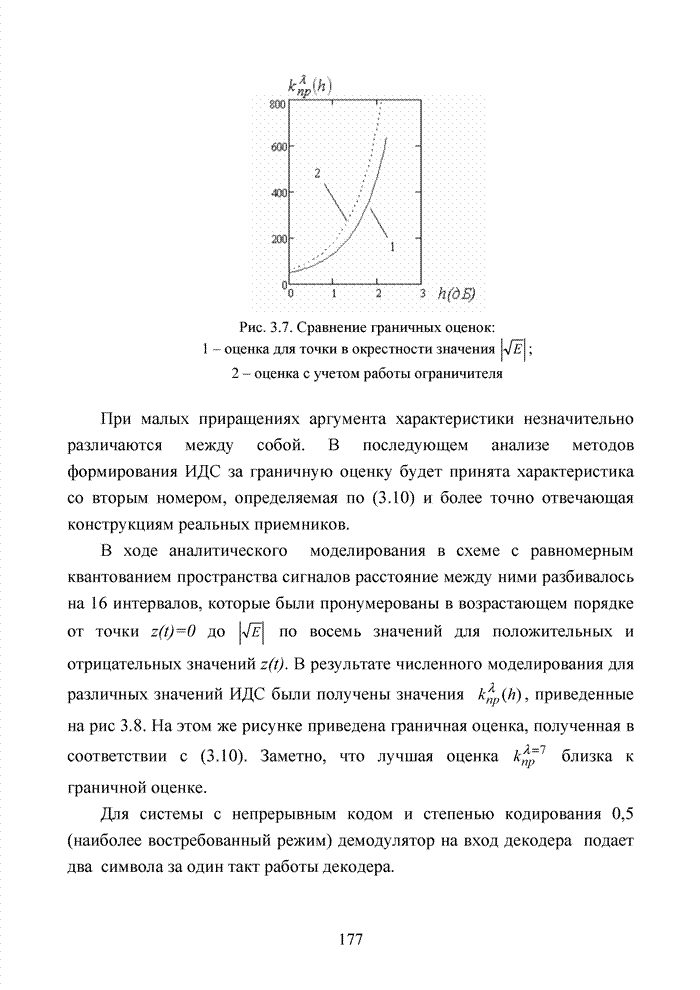
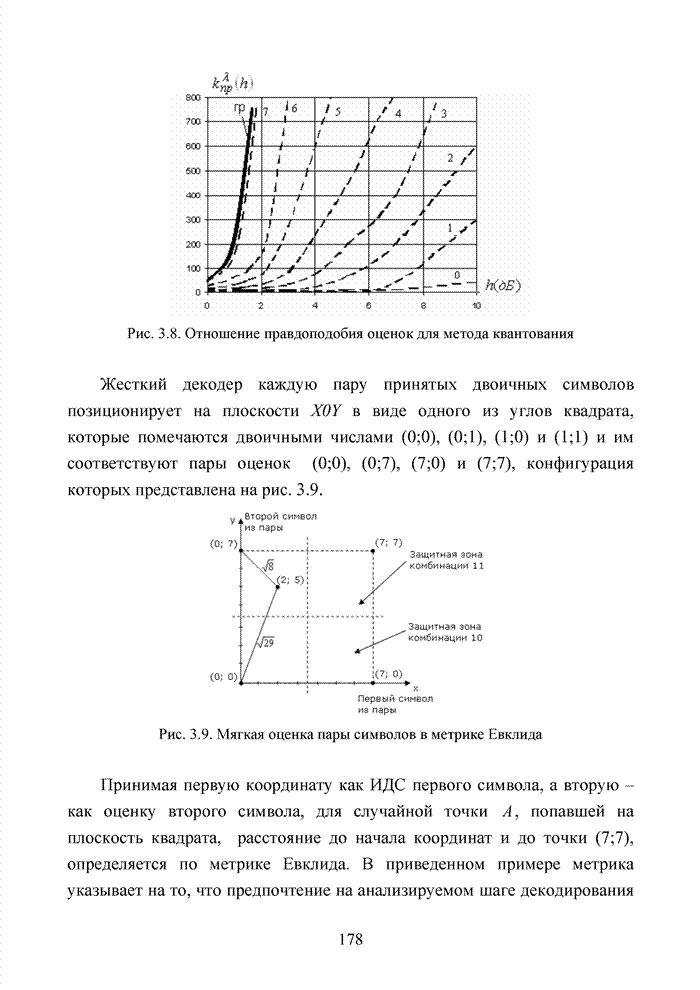
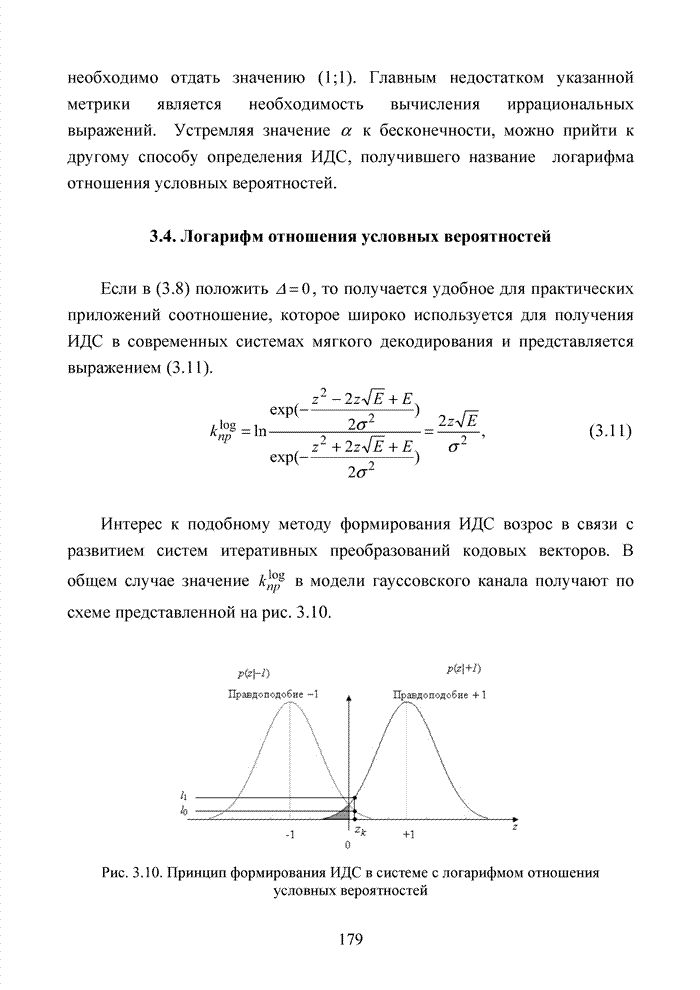
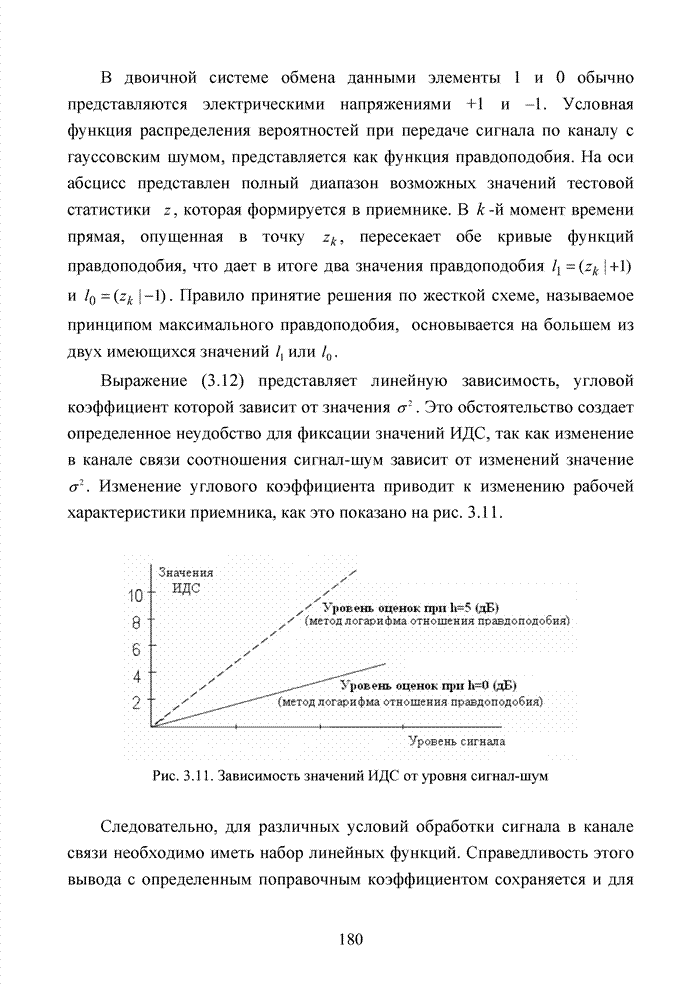
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
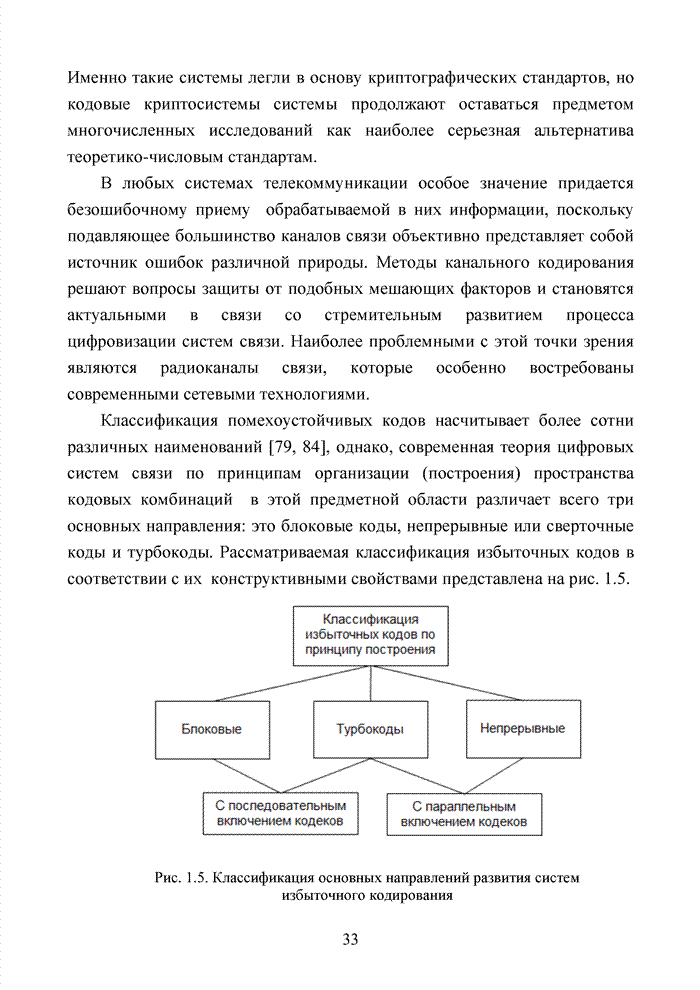
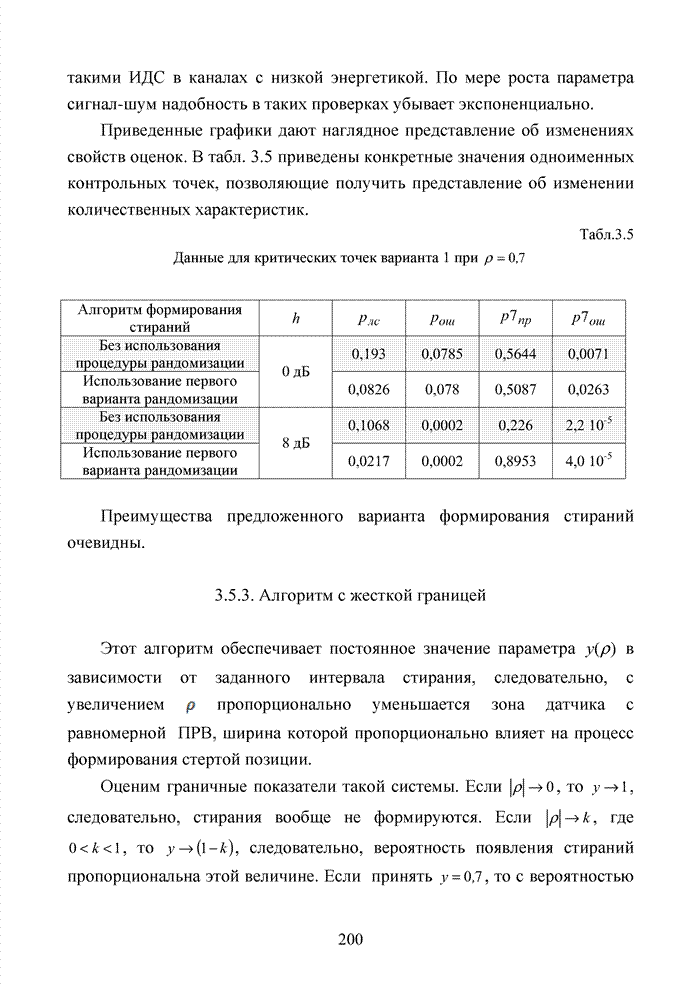
1.12. Комбинации кодов, принцип каскадного кодирования
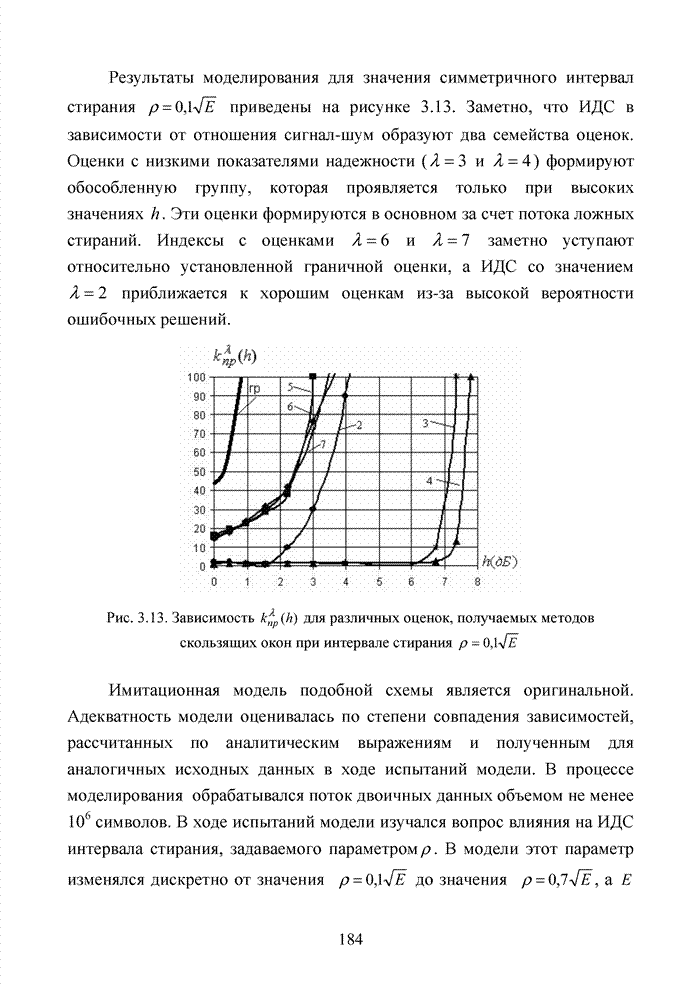
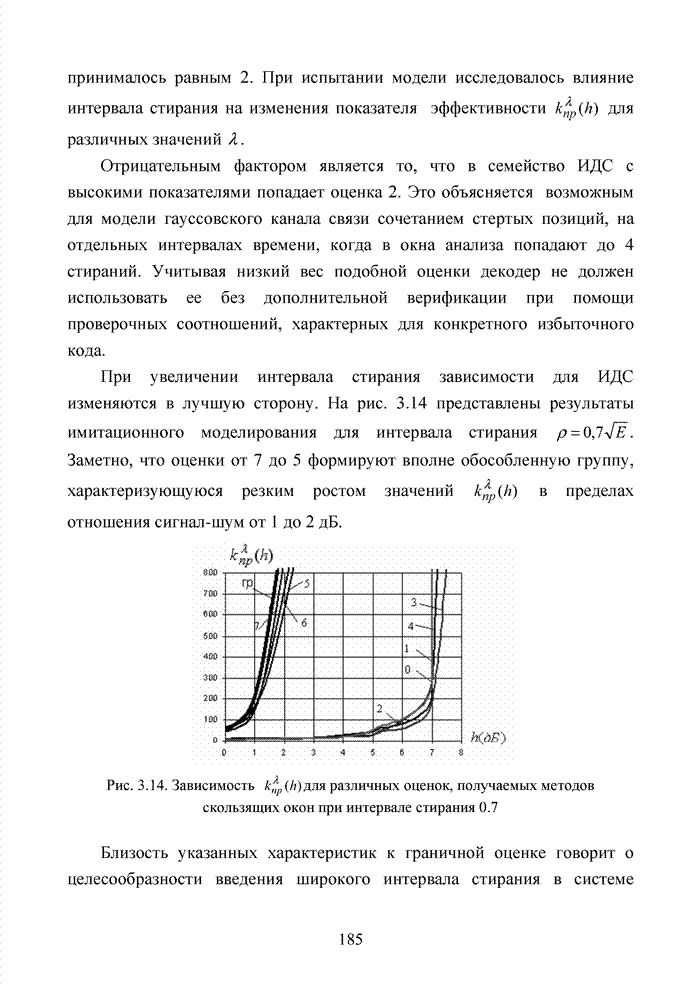
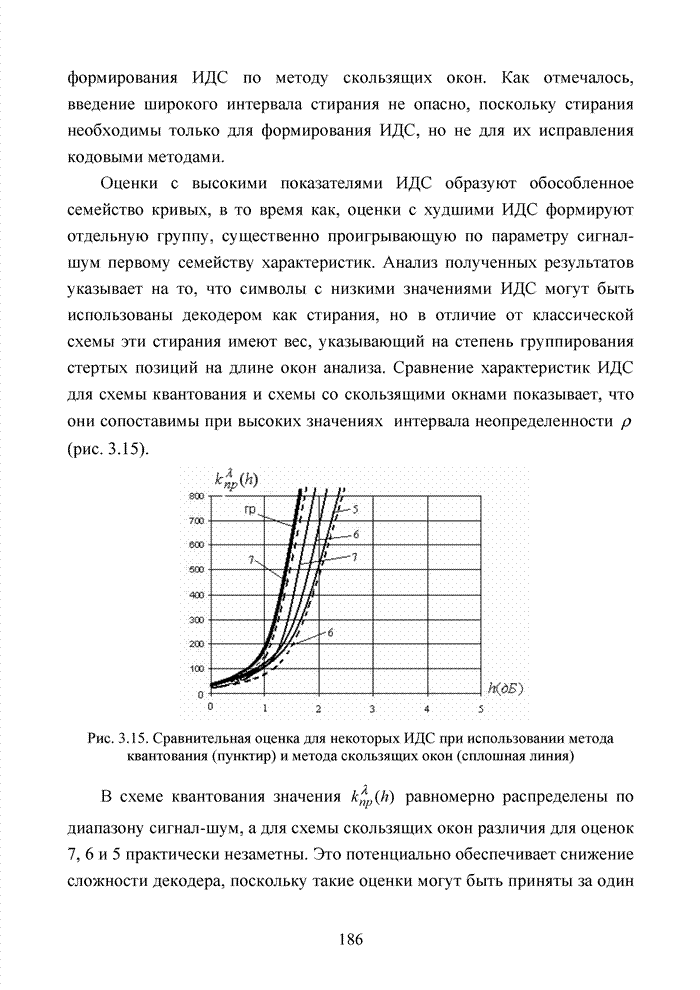
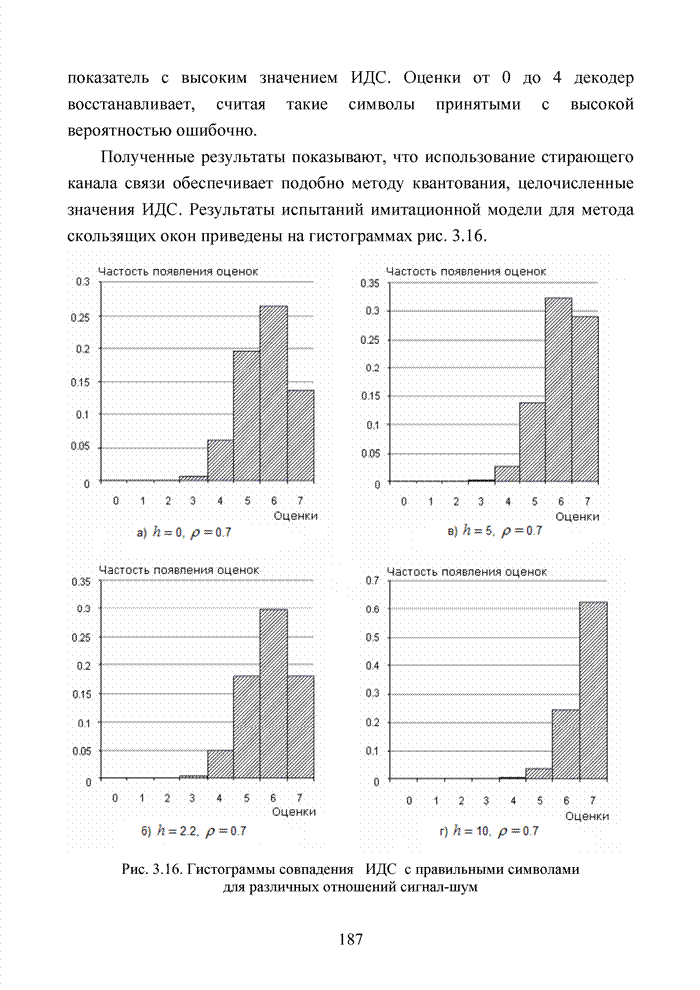
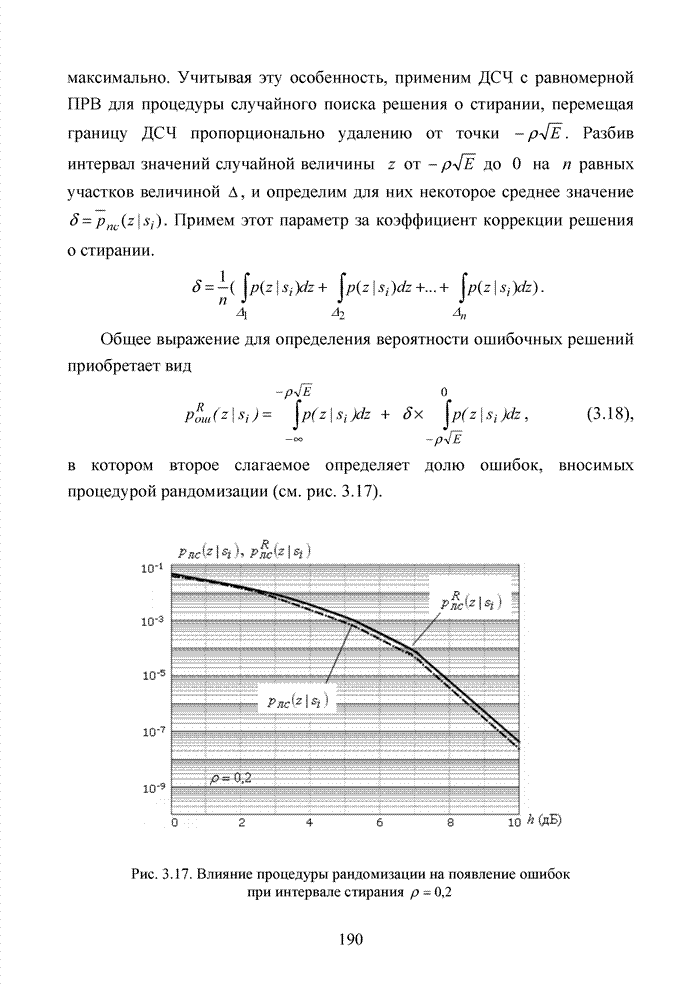
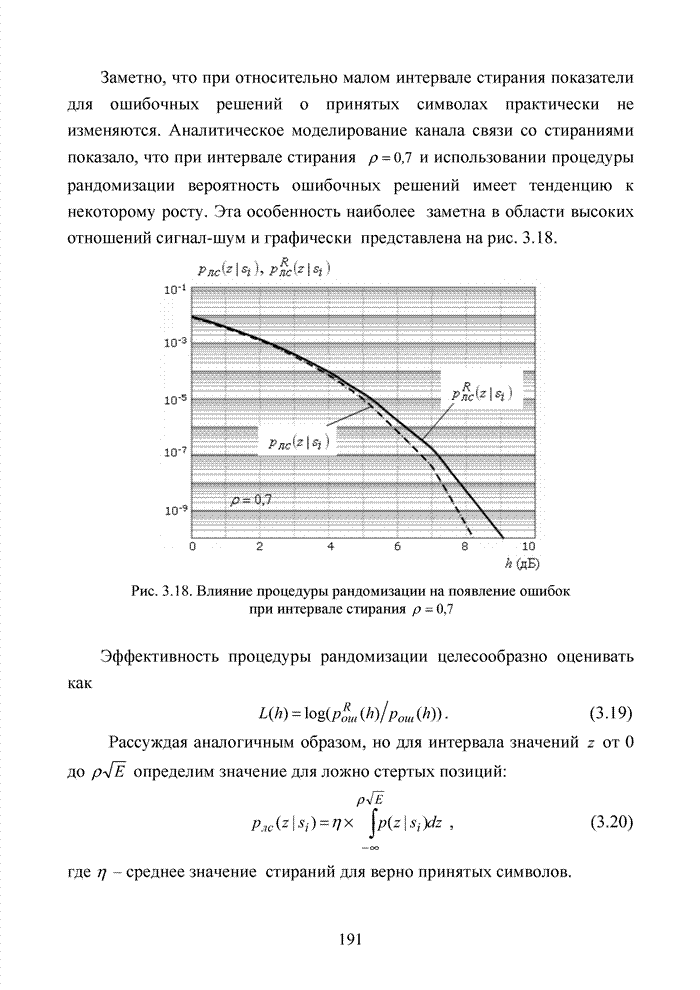
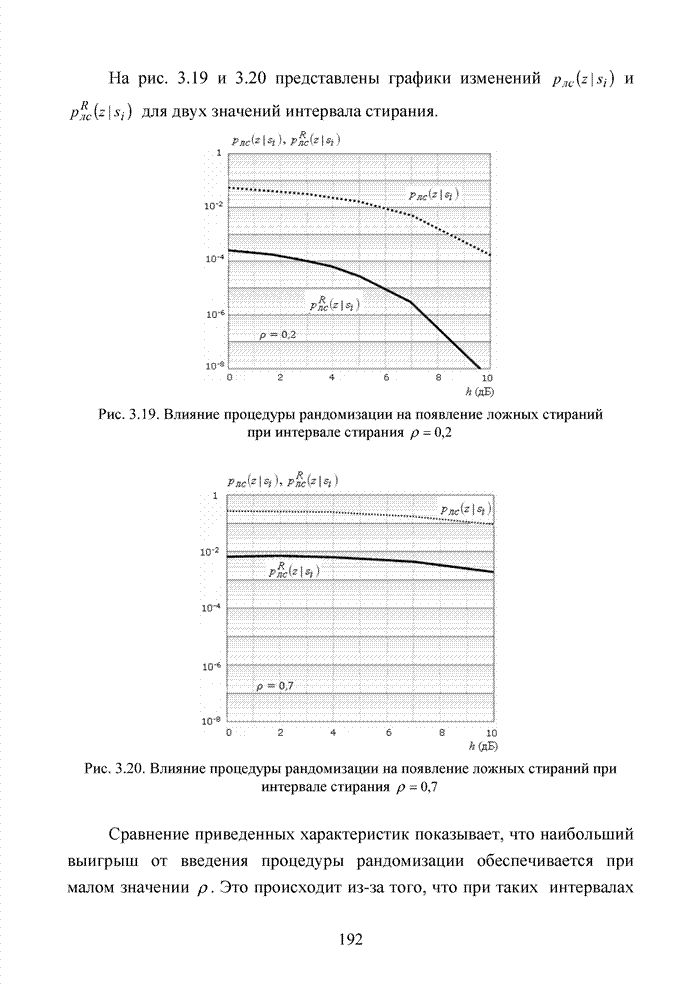
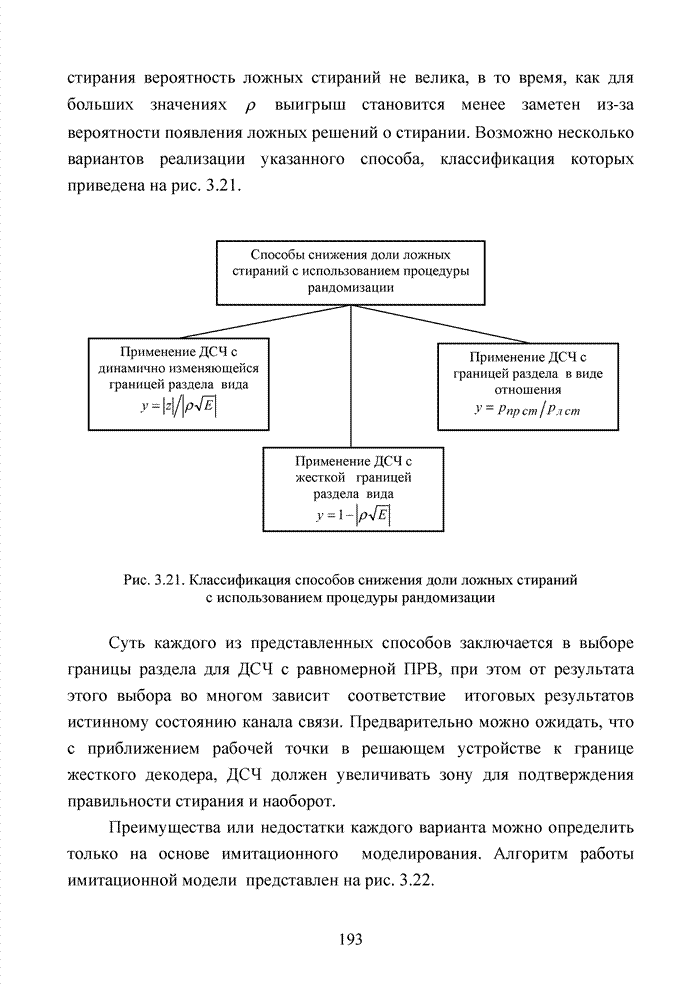
Развитие теории помехоустойчивого кодирования показало, что использование любых классов кодов наталкивается на принципиальные трудности, связанные с многообразием условий их применения, а так же с экспоненциальным ростом сложности декодеров при увеличении краткости, исправляемых избыточным кодом ошибок. Для достижения известной гибкости в конструировании избыточных кодов прибегают к их модификациям или комбинированию. Наилучшие на сегодня коды получены не как представители того или иного семейства кодов, а с помощью процедуры модификации и комбинирования. В современных телекоммуникационных системах предъявляются достаточно высокие требования к достоверности передачи информации с вероятность ошибки на символ не хуже 10-9.
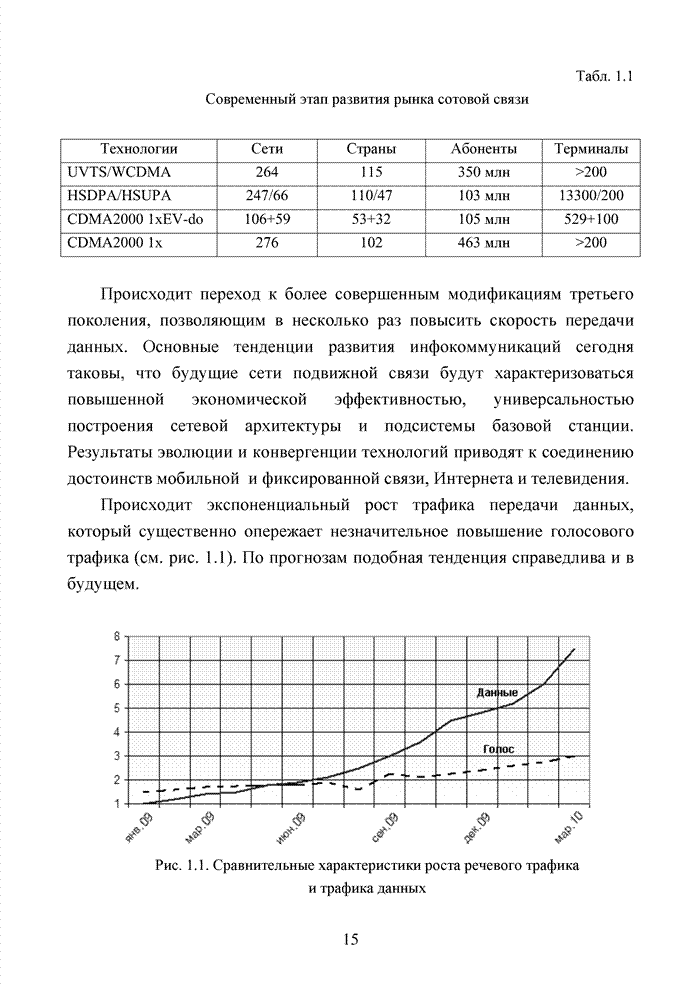
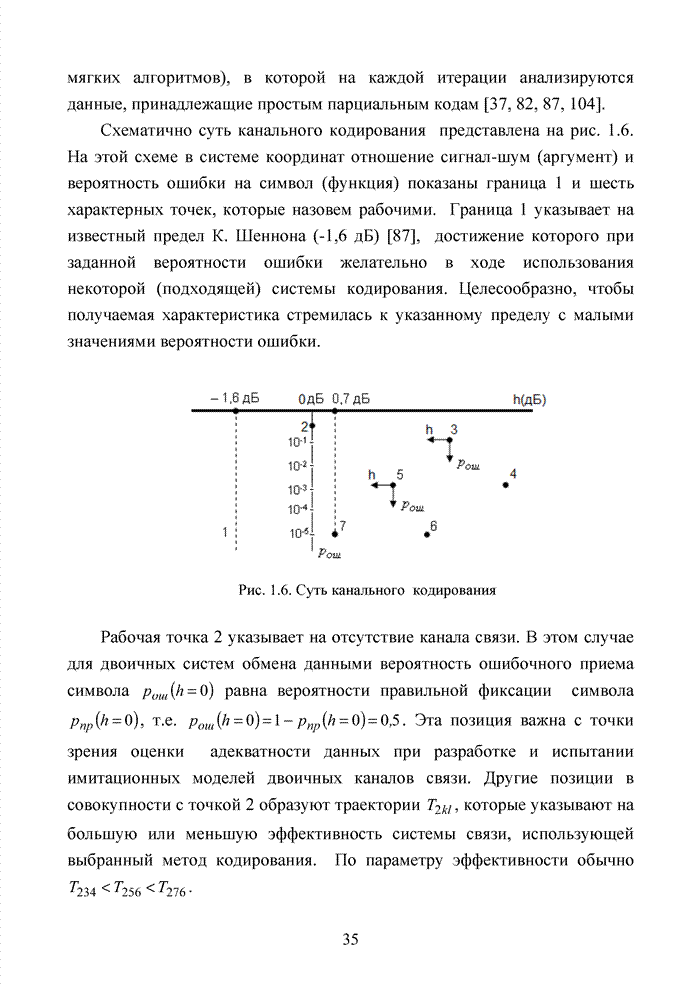
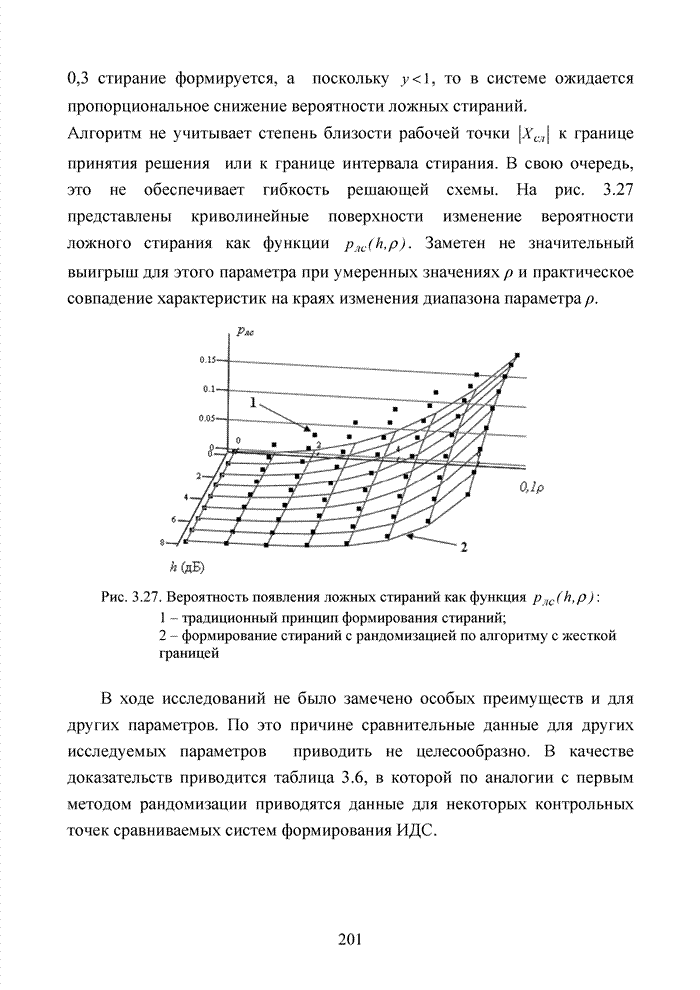
В беспроводных каналах связи такую достоверность практически не возможно получить без применения помехоустойчивого кодирования. Однако применение мощных кодов с высокой исправляющей способность ограничено высокой сложностью реализации оптимальных декодеров, обеспечивающих минимальную вероятность ошибочного декодирования кодовых блоков. При выборе методов кодирования и главным образом методов декодирования, руководствуются многими факторами, которые делятся на три основные группы, взаимосвязь между которыми показана на рис. 1.17.

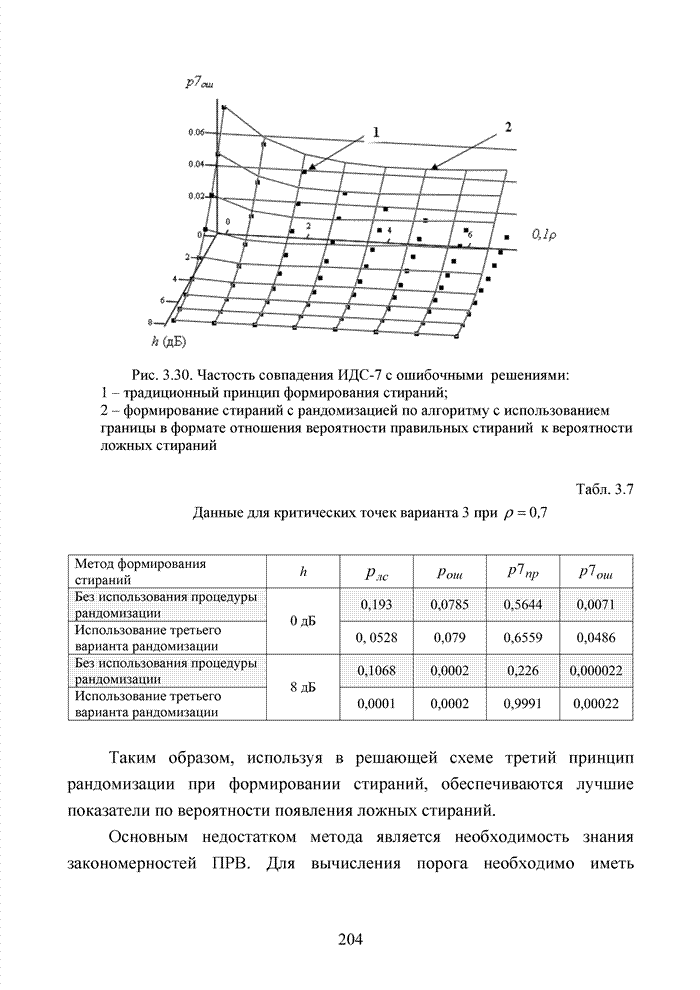
Рис. 1.17. Взаимосвязь между параметрами кодовых конструкций
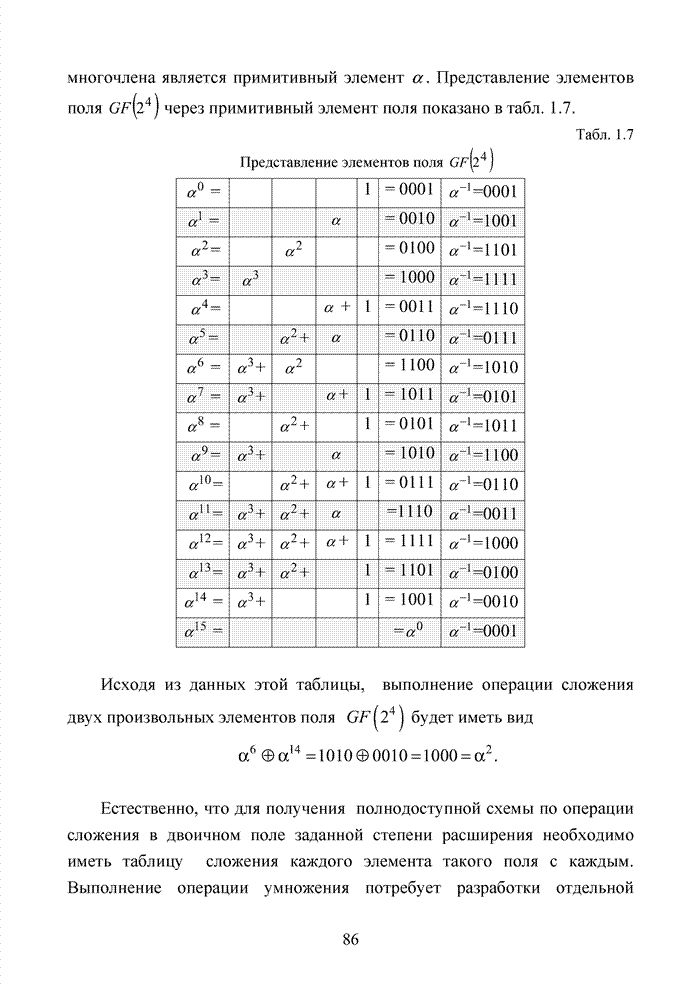
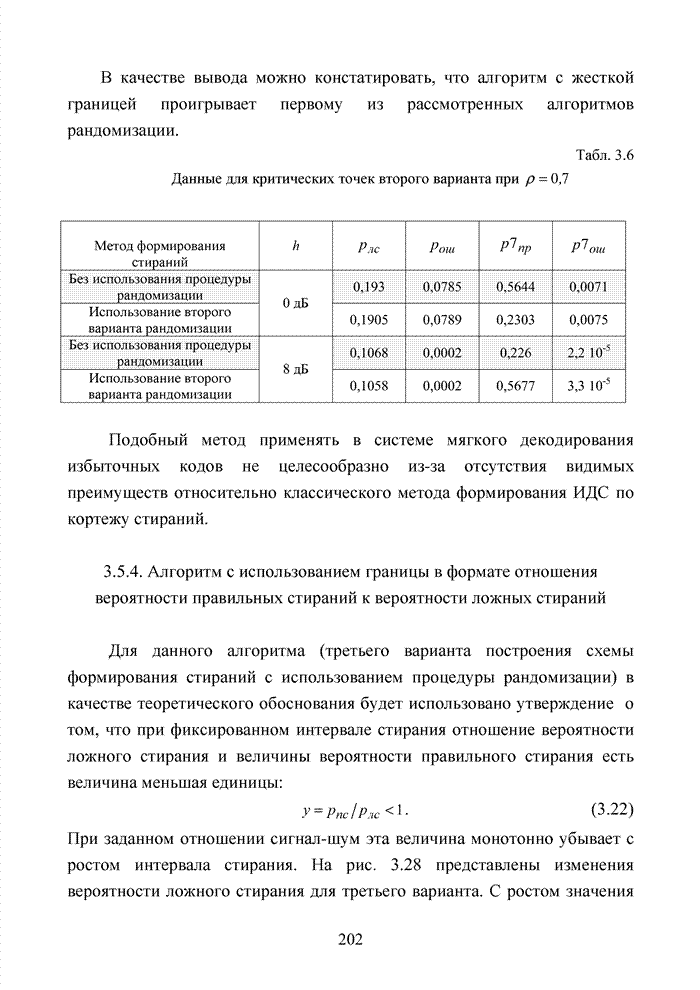
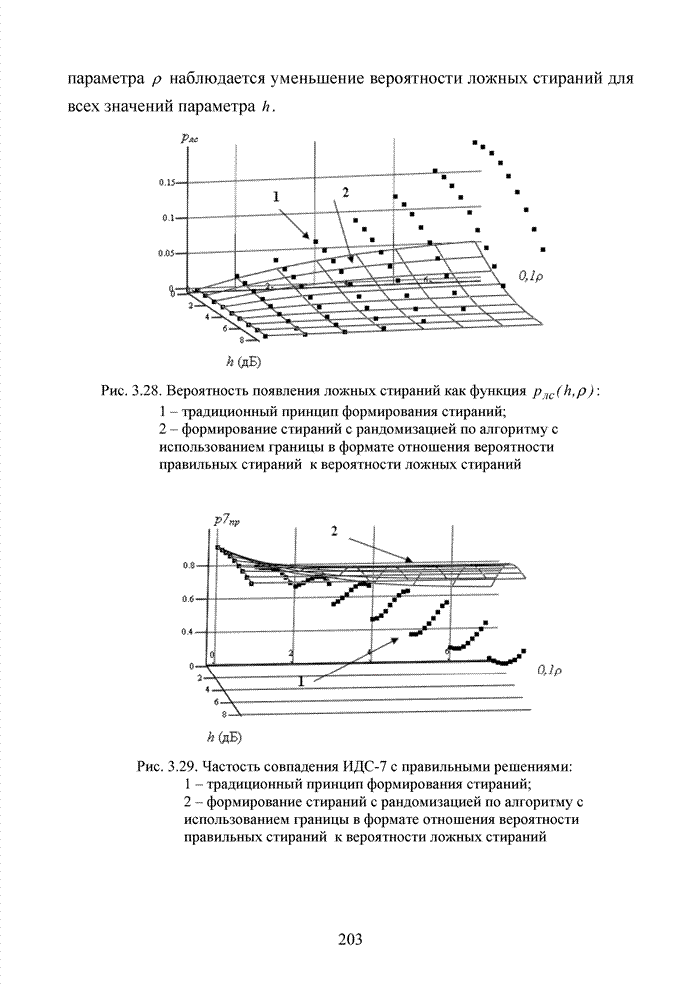
Под сложностью реализации понимают аппаратные и программные затраты, стоимость микросхем и микропроцессоров, стоимость памяти для хранения данных и т.п. Под пропускной способностью, в данном контексте, понимают не только объемы полезной информации и избыточности, но и объемы служебной информации. Подобные сведения необходимы для установления и поддержания синхронизации передатчика и приемника, а также для управления элементами звена передачи данных. На практике чаще всего используются составные или каскадные коды. Метод каскадного кодирования был предложен в работе [95]. На рис 1.18 представлен канал связи, в котором используется каскадный код.

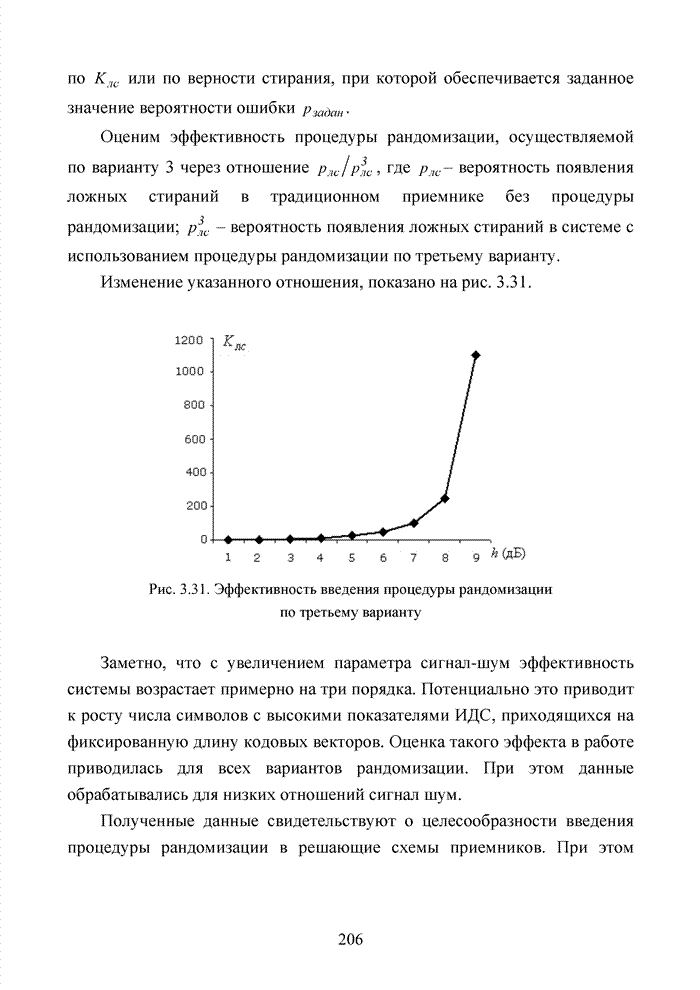
Рис. 1.18. Канал связи с использованием каскадного кода
Возможны различные
варианты реализации каскадного принципа кодирования. Первоначально
последовательность из ![]() =
=![]() двоичных символов, являющихся
информационными разбивается на
двоичных символов, являющихся
информационными разбивается на ![]() подблоков по
подблоков по ![]() =
=![]() символов в каждом. Эти подблоки
рассматриваются над двоичным полем Галуа степени расширения
символов в каждом. Эти подблоки
рассматриваются над двоичным полем Галуа степени расширения ![]() , образуя группу
информационных символов внешнего кода. Множество всех таких символов
определяется
, образуя группу
информационных символов внешнего кода. Множество всех таких символов
определяется ![]() .
Внешний код формирует на основе
.
Внешний код формирует на основе ![]() проверочные символы. Если в
качестве внешнего кода используется код РС, то корректирующие возможности
такого кода определяются выражением
проверочные символы. Если в
качестве внешнего кода используется код РС, то корректирующие возможности
такого кода определяются выражением ![]() [68]. Проверочные символы этого кода являются
элементами поля
[68]. Проверочные символы этого кода являются
элементами поля![]() .
Все
.
Все ![]() -ичные символы комбинации кода (n2, k2) кодируются внутренним (n1, k1) кодом. В результате получается
двоичный блоковый код длины
-ичные символы комбинации кода (n2, k2) кодируются внутренним (n1, k1) кодом. В результате получается
двоичный блоковый код длины ![]() содержащий
содержащий ![]() информационных двоичных
символов с общим минимальным расстоянием
информационных двоичных
символов с общим минимальным расстоянием ![]() , где
, где ![]() минимальное расстояние внутреннего кода.
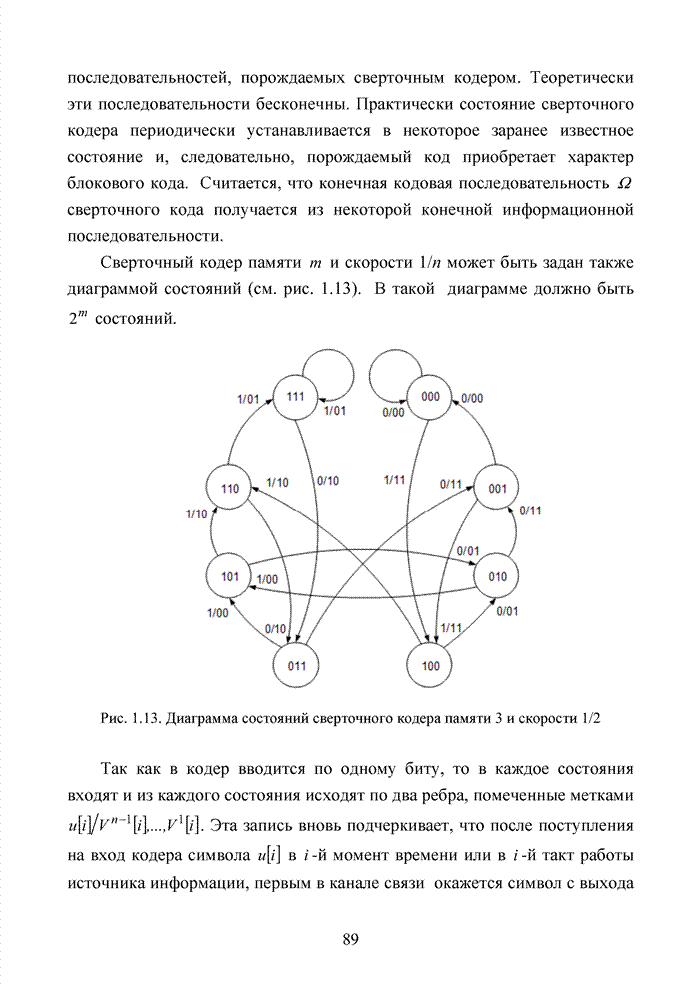
На рис. 1.19 представлена схема образования слова каскадного кода на основе
кода РС.
минимальное расстояние внутреннего кода.
На рис. 1.19 представлена схема образования слова каскадного кода на основе
кода РС.

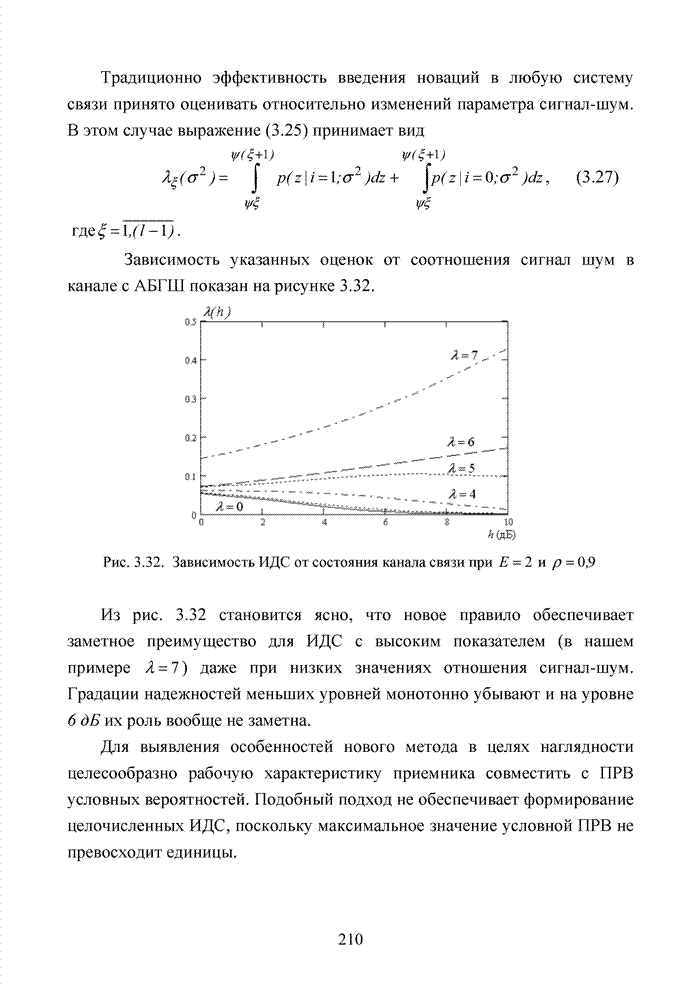
Рис. 1.19. Схема образования слова каскадного кода
Достоинством каскадных
кодов является то, что они позволяют заменить декодирование длинного (n1, n2, k1, k2) кода декодированием двух
значительно более коротких кодов – внутреннего двоичного (n1, k1) кода и внешнего (n2,k2) кода. Это позволяет говорить о
линейном росте сложности декодера в зависимости от кратности исправляемых
ошибок [55, 63]. Каскадные коды позволяют реализовать достаточно большое
значение ![]() , поэтому их применение имеет смысл в каналах с
группирующимися ошибками.
, поэтому их применение имеет смысл в каналах с
группирующимися ошибками.
Другое преимущество каскадных кодов состоит в том, что при исправлении ошибок внутренним кодом можно использовать не только различные конструктивные методы исправления независимых ошибок, но и оптимальные переборные методы, если (n1,k1) маломощный код [55]. Свойство может быть использовано при декодировании блочных кодов, методом кластерного анализа [62]. Этот алгоритм декодирования подобен декодированию по списку, когда в кластер (список) входят наиболее вероятные образцы ошибок.
В работе [96] показано, что сложность декодера как функция числа исправляемых кодом ошибок в системе с каскадным кодированием растет линейно тогда, как при использовании обычных кодов эта зависимость носит экспоненциальный характер.
Основная причина такого эффекта заключается в том, что при декодировании комбинаций внутреннего кода он не исправляет ошибки, а формирует стирания при обнаружении ошибки.
Стертые позиции восстанавливаются кодом РС, и поскольку стирания достаточно хорошо указывают на ошибочные позиции, корректирующие возможности кода используются не поиск ошибок, а на исправление стертых позиций.
Коды РС сроятся над конечными полями. Как было отмечено, такое поле может быть образовано для любого простого p и обозначается как GF(p). Понятие GF(p) обобщается на поле из pm элементов, именуемые полем расширением поля GF(p) степени расширения GF (pm). Поле GF (pm) содержит в качестве подмножества все элементы GF(p). Символы из поля расширения GF (2m) используются при построении кода РС.
Общепринятым [72]
считается представление кода РС через параметры ![]() и некоторое
и некоторое ![]() , здесь
, здесь ![]() – число, исправляемых кодом ошибок, при
этом
– число, исправляемых кодом ошибок, при
этом ![]() . Генерирующий полином для кода РС
имеет вид:
. Генерирующий полином для кода РС
имеет вид:
![]() .
.
Общее число информационных символов кода РС над двоичным полем GF (2m) оценивается выражением:
![]() .
.
Предположим что ![]() , а m =
3, тогда K = 64. При этом образуется
, а m =
3, тогда K = 64. При этом образуется ![]() групп комбинаций, в
которых на первом месте среди информационных разрядов систематического кода РС
будет находиться один и тот же представитель поля GF (2m) от 0 до
групп комбинаций, в
которых на первом месте среди информационных разрядов систематического кода РС
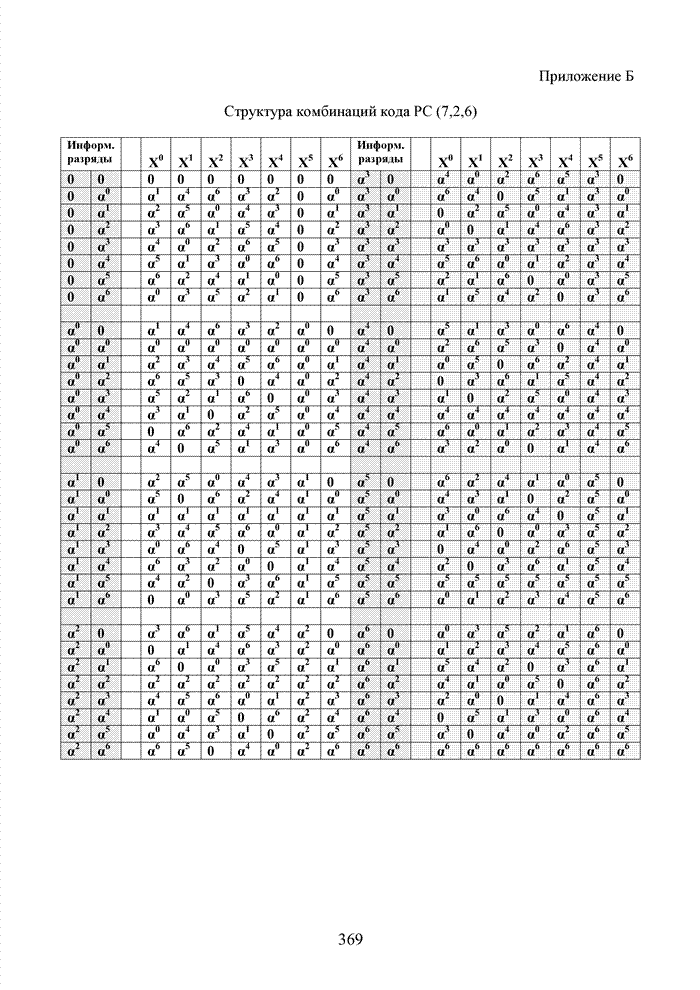
будет находиться один и тот же представитель поля GF (2m) от 0 до ![]() . Пример такого разбиения кода РС
представлен в Приложении Б.
. Пример такого разбиения кода РС
представлен в Приложении Б.
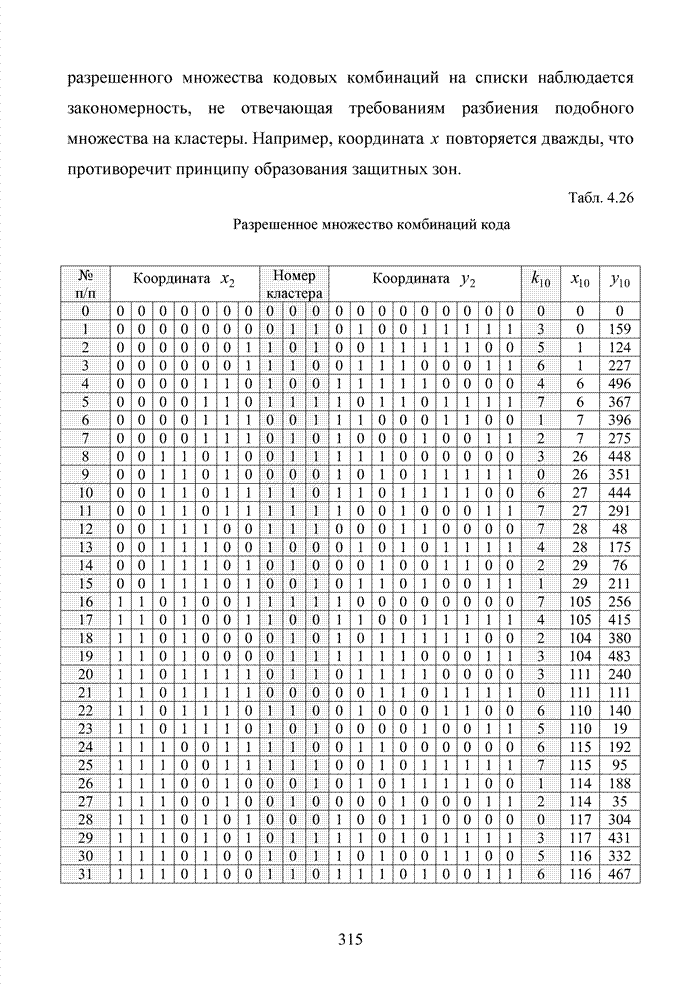
Заметно, что разряд X5 всех кодовых комбинаций (таблица представляет код РС с n2 = 7, k2 = 2) определяют конкретную группу комбинаций, которую назовем кластером. Номера кластеров определим как степень примитивного элемента базового поля на месте разряда X5. Порождающий полином кода определен как:

здесь учтено, что операции сложения и вычитания в двоичном поле равнозначны. Кроме общеизвестных свойств кода РС выделим несколько важных с точки зрения последующих рассуждений.
Свойство 1. Любой систематический код РС в своем
составе имеет ![]() комбинаций, состоящих из n2 одинаковых q-ичных элементов. Так же как двоичный
групповой код содержит чисто единичный элемент (единичную комбинацию), q-ичный код должен содержать
комбинации, состоящие из одинаковых элементов поля GF (2m), например,
комбинаций, состоящих из n2 одинаковых q-ичных элементов. Так же как двоичный
групповой код содержит чисто единичный элемент (единичную комбинацию), q-ичный код должен содержать
комбинации, состоящие из одинаковых элементов поля GF (2m), например, ![]() . В рамках параметров рассматриваемого
кода первые пять символов являются проверочными, а последние два символа
являются информационными разрядами. В [88] доказывается, что аналогичная картина
сохраняется и для несистематических кодов РС (см. Приложение Б). Рассмотренное
свойство может быть использовано для реализации метода синхронного накопления
данных и декодирования кодовых комбинаций мажоритарным методом (за счет
применения кодов повторителей), причем применение таких кодов является
обязательным условием в процедуре реализации обобщенных каскадных кодов.
. В рамках параметров рассматриваемого
кода первые пять символов являются проверочными, а последние два символа
являются информационными разрядами. В [88] доказывается, что аналогичная картина
сохраняется и для несистематических кодов РС (см. Приложение Б). Рассмотренное
свойство может быть использовано для реализации метода синхронного накопления
данных и декодирования кодовых комбинаций мажоритарным методом (за счет
применения кодов повторителей), причем применение таких кодов является
обязательным условием в процедуре реализации обобщенных каскадных кодов.
Свойство 2. Все множество V кодовых комбинаций кода РС для
каждого разряда ![]() порождающего
полинома содержит одинаковое число элементов из поля
порождающего
полинома содержит одинаковое число элементов из поля ![]() . Другими словами каждый элемент
поля распределен по каждому разряду Xi общего множества кодовых комбинации
кода РС с одинаковой плотностью. Например, в рассматриваемом коде РС (7,2,6),
для разряда Х0 элемент
. Другими словами каждый элемент
поля распределен по каждому разряду Xi общего множества кодовых комбинации
кода РС с одинаковой плотностью. Например, в рассматриваемом коде РС (7,2,6),
для разряда Х0 элемент ![]() или любой другой элемент базового поля
повторяется только q
раз. Исключение составляют только те разряды, которые совпадают с номером
кластера. Следствием данного свойства является тот факт, что искажение символа
в каждом разряде кодовой комбинации может произойти с вероятностью
или любой другой элемент базового поля
повторяется только q
раз. Исключение составляют только те разряды, которые совпадают с номером
кластера. Следствием данного свойства является тот факт, что искажение символа
в каждом разряде кодовой комбинации может произойти с вероятностью![]() .
.
Свойство 3. В любой комбинации систематического
(несистематического) кода РС, не отвечающей свойству 1, отсутствует один из
элементов поля, который заменяется нулевым элементом поля. Это свойство
вытекает из определения длины кодовой комбинации кода РС, определяемой как ![]() , и свойства цикличности.
, и свойства цикличности.
На основании
представленных свойств множества кодовых комбинаций кода РС возможна оценка
верхней границы для вероятности ошибочного декодирования комбинаций такого
кода. В качестве предварительного замечания отметим, что любой код с метрикой
Хемминга ![]() способен
исправить
способен
исправить ![]() ошибок
и стираний, здесь
ошибок
и стираний, здесь ![]() –
число ошибок в кодовой комбинации, а
–
число ошибок в кодовой комбинации, а ![]() – число стираний. При исправлении
стираний целесообразно принять значение
– число стираний. При исправлении
стираний целесообразно принять значение ![]() равным единице. Это связано с
тем, что среди символов с ИДС равных максимальной оценке с определенной долей
вероятности не исключены ошибочные символы. Принимая
равным единице. Это связано с
тем, что среди символов с ИДС равных максимальной оценке с определенной долей
вероятности не исключены ошибочные символы. Принимая ![]() , получаем некоторый запас по
коррекции стираний. Тогда
, получаем некоторый запас по
коррекции стираний. Тогда ![]() и окончательно
и окончательно ![]() . Это число стираний, исправляемых
кодом и обеспечивающее запас корректирующей способности в случае возникновения
не выявленной ошибки. Пусть внутренним кодом обнаруживаются ошибки и q-ичные символы (подблоки) с
обнаруженными ошибками стираются, если число стертых подблоков больше
. Это число стираний, исправляемых
кодом и обеспечивающее запас корректирующей способности в случае возникновения
не выявленной ошибки. Пусть внутренним кодом обнаруживаются ошибки и q-ичные символы (подблоки) с
обнаруженными ошибками стираются, если число стертых подблоков больше ![]() , то стирается вся комбинация кода РС, а если число стираний
меньше или равно
, то стирается вся комбинация кода РС, а если число стираний
меньше или равно ![]() , то стирания исправляются кодом РС.
Внешний код не обнаруживает ошибку в случае, если нестертые q-ичные символы совпадут в
соответствующих местах с символами одной из кодовых комбинаций, отличной от
переданной.
, то стирания исправляются кодом РС.
Внешний код не обнаруживает ошибку в случае, если нестертые q-ичные символы совпадут в
соответствующих местах с символами одной из кодовых комбинаций, отличной от
переданной.
В такой конструкции проявляются два очень важных свойства. Первое из них заключается в том, что при использовании адаптивных режимов в условиях высокого качества канала связи может быть повышена скорость кода за счет выкалывания проверочных символов, относящихся к проверочным разрядам внешнего кода, т.е. выкалывание (перфорация) символов, относящихся к проверкам проверок. Конструкция кодового слова каскадного кода показана на рис. 1.20.

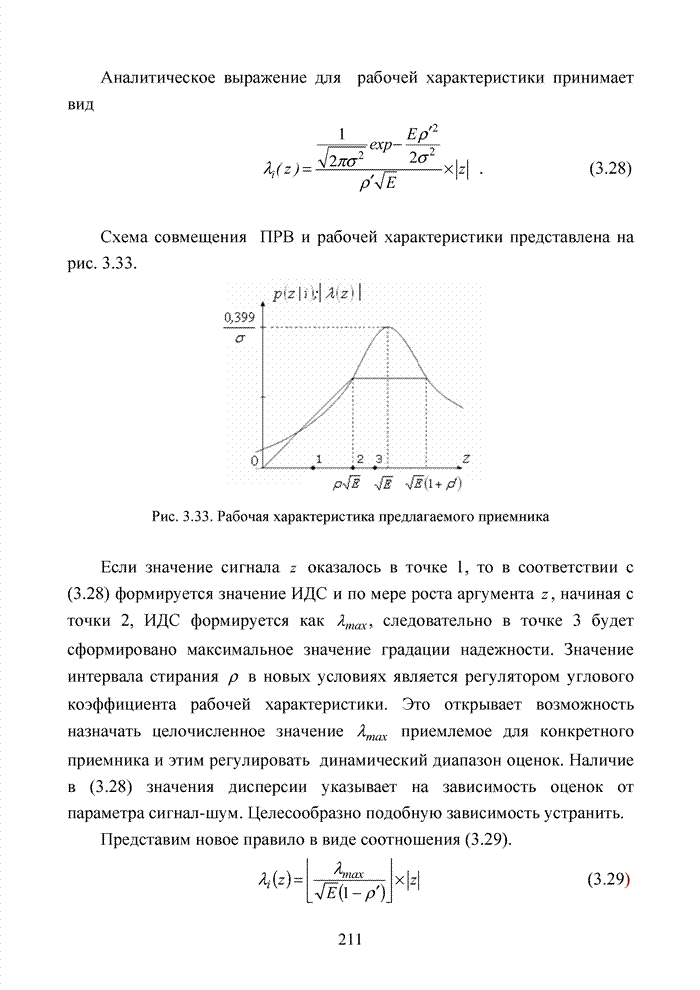
Рис. 1.20. Конструкция слова каскадного кода
Вторым положительным
свойством конструкции слова каскадного кода является возможность применения
напрямую процедуры перемежения символов непосредственно к матрице, с помощью которой
это слово представляется. Процедура перемежения символов заключается в
предварительном заполнении информационными разрядами матрицы памяти некоторой
размерности. Если запись данных от источника информации в указанную матрицу
осуществляется по строкам, то после ее заполнения считывание данных в канал
связи выполняется по столбцам. Это делается для того, чтобы противостоять
наиболее сложному виду помехи, которая в канале связи проявляется в виде
группирующихся ошибок. Если известна средняя вероятность ошибки на символ в
данном типе канала связи ![]() , то внутри пачки ошибок значение этого
параметра
, то внутри пачки ошибок значение этого
параметра ![]() ,
при этом
,
при этом ![]() . Подобные
устройства описаны в [94] и имели название декоррелятора ошибок, что более
точно отражает их суть. Приемник последовательно фиксирует столбцы данных и
записывает их в виде столбцов в матрицу памяти аналогичную по размерности
матрице на передаче. После заполнения матрицы приема, данные в декодер
списываются построчно.
. Подобные
устройства описаны в [94] и имели название декоррелятора ошибок, что более
точно отражает их суть. Приемник последовательно фиксирует столбцы данных и
записывает их в виде столбцов в матрицу памяти аналогичную по размерности
матрице на передаче. После заполнения матрицы приема, данные в декодер
списываются построчно.
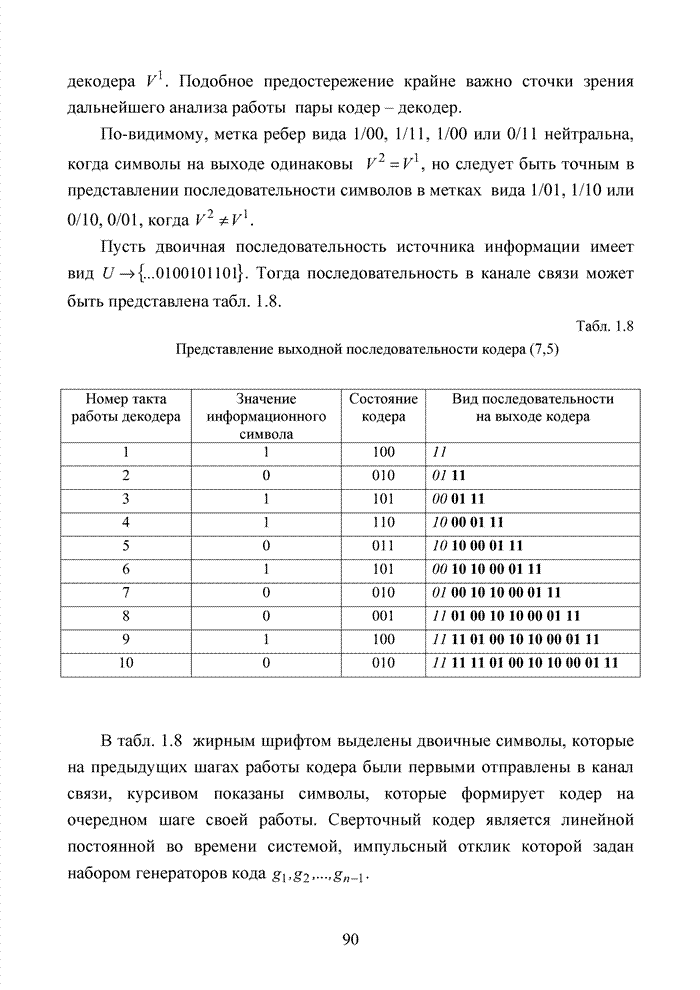
Поскольку в канале связи
группирующаяся помеха воздействовала на символы столбца, то при построчном
считывании комбинаций из матрицы приема в декодер в каждой такой комбинации
будет ограниченное число ошибок, которые могут быть обнаружены и исправлены. Применение
подобных устройств связано с задержкой данных при их обработке ![]() , которая оказывается
не столь велика при высоких рабочих частотах процессоров приемников. Пусть
матрица перемежителя (деперемежителя) имеет размерность
, которая оказывается
не столь велика при высоких рабочих частотах процессоров приемников. Пусть
матрица перемежителя (деперемежителя) имеет размерность ![]() и рабочая частота процессора составляет
2 ГГц, следовательно, время заполнения матрицы данными займет около 0.5 мс, а с
учетом задержек на передаче и приеме около 1 мс. Применение перемежителей в
современных системах передачи данных связывается с ТК, где им в соответствии с
постулатами К. Шеннона отводится роль элемента случайного кодирования [83, 98].
и рабочая частота процессора составляет
2 ГГц, следовательно, время заполнения матрицы данными займет около 0.5 мс, а с
учетом задержек на передаче и приеме около 1 мс. Применение перемежителей в
современных системах передачи данных связывается с ТК, где им в соответствии с
постулатами К. Шеннона отводится роль элемента случайного кодирования [83, 98].
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
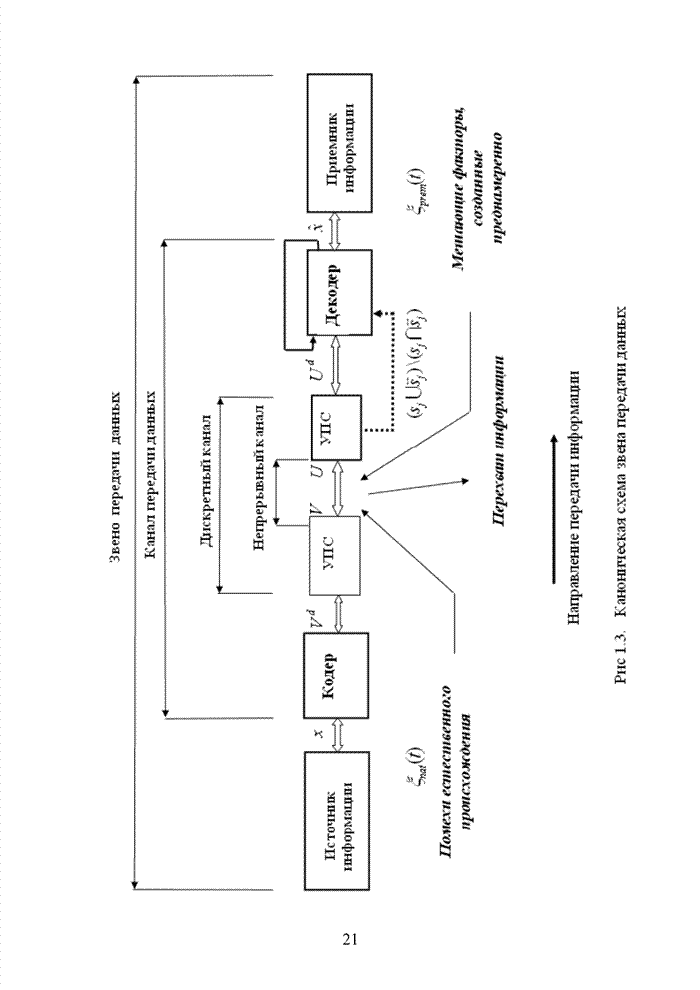
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
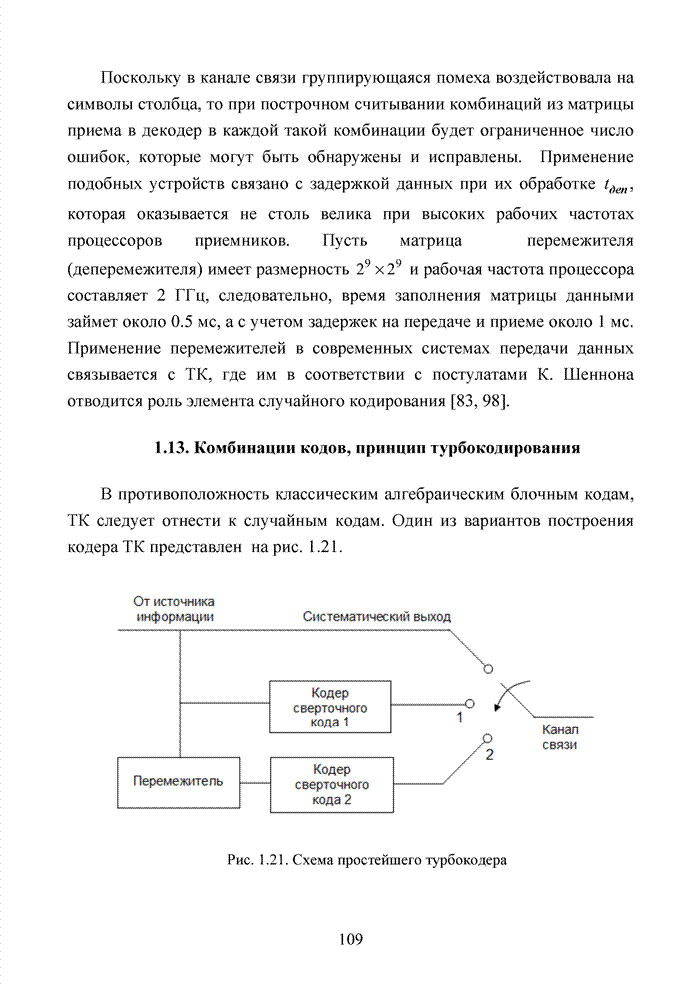
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
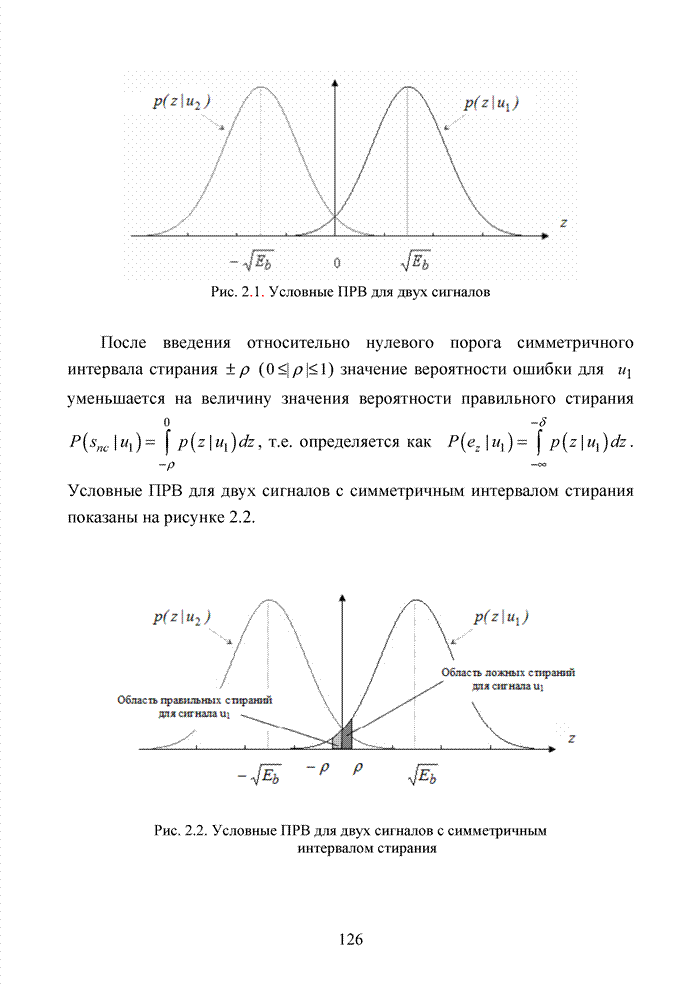
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
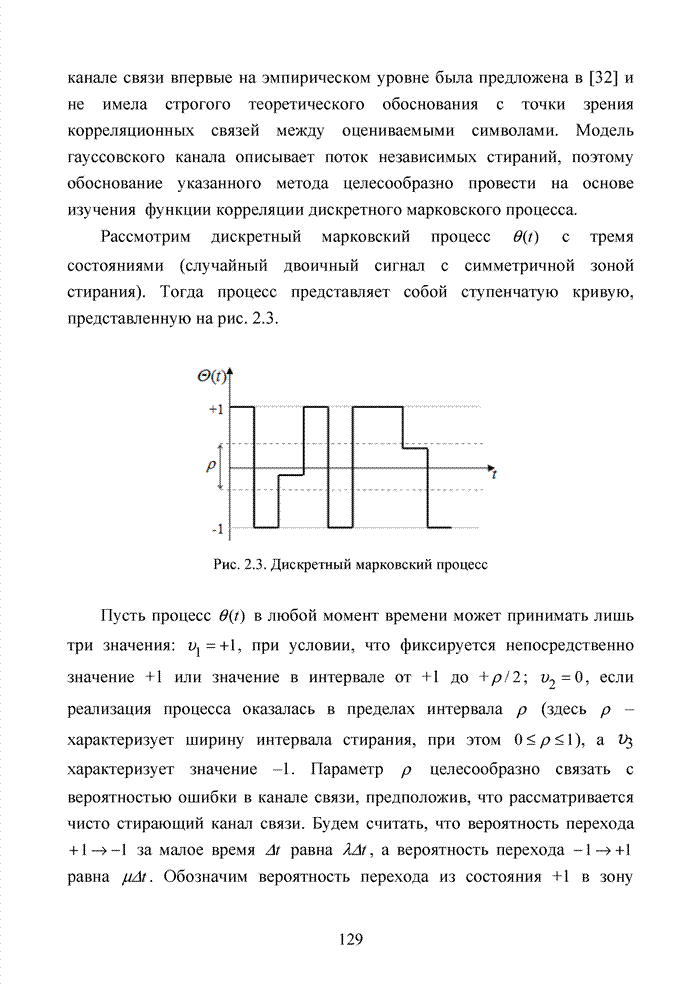
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
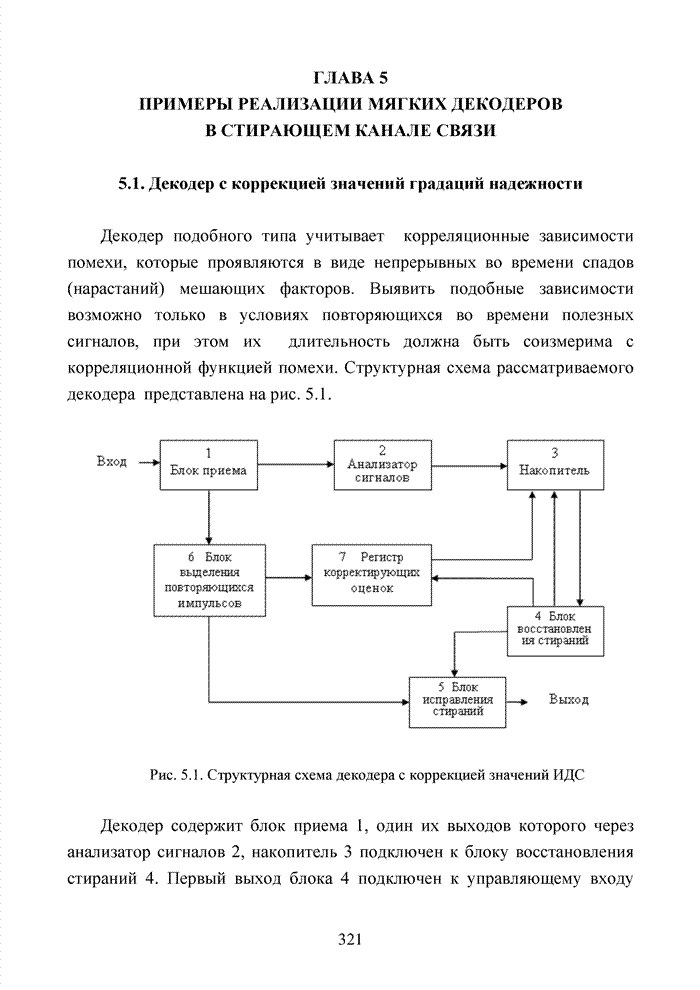
- 5.1. Декодер с коррекцией значений градаций надежности
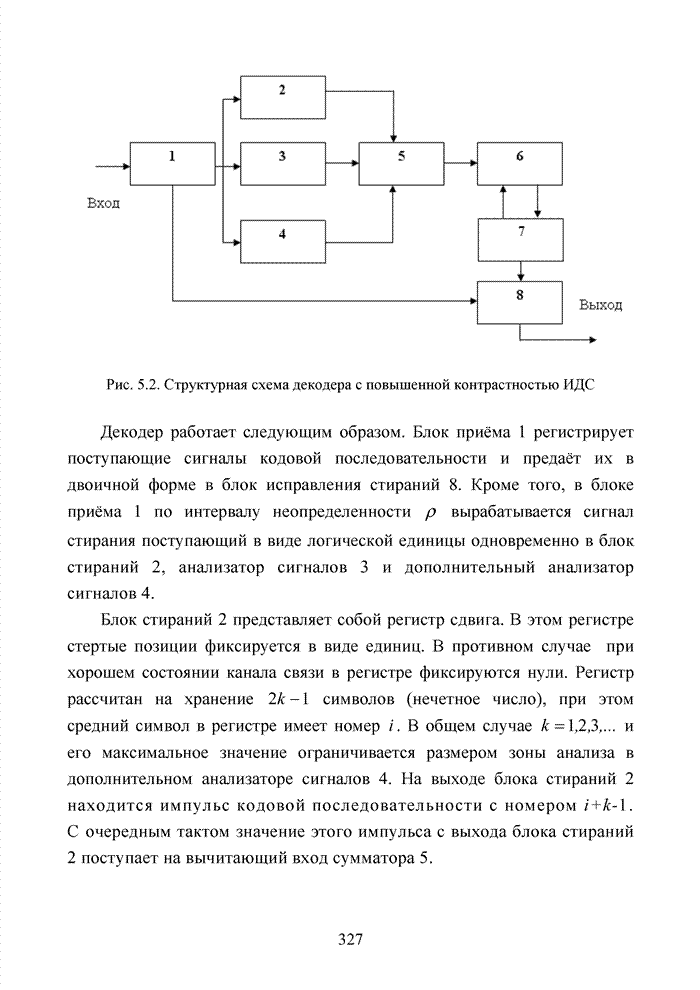
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
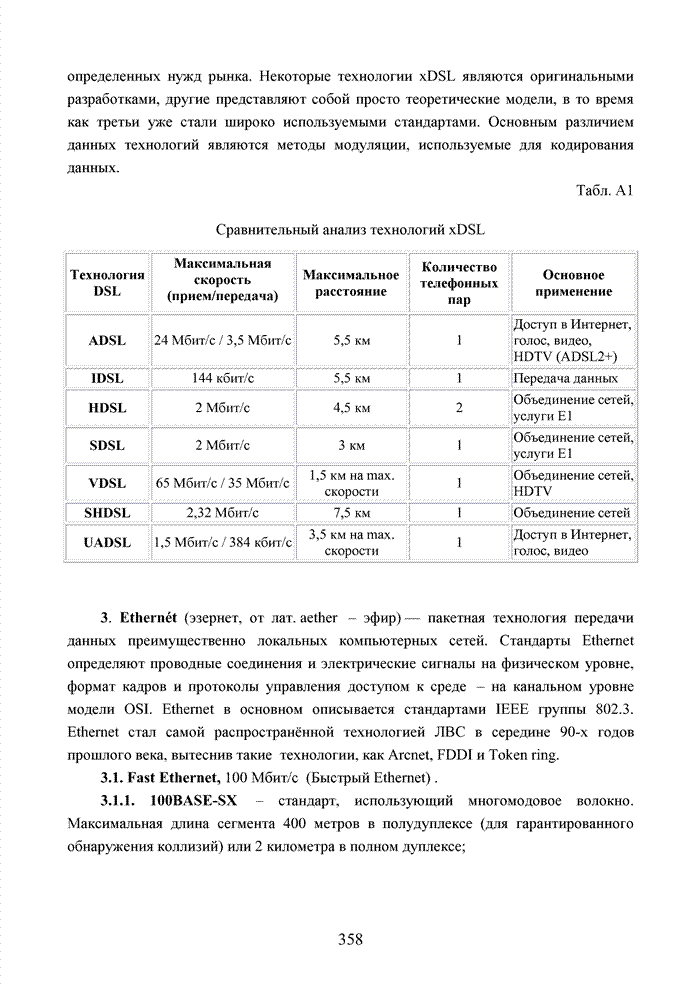
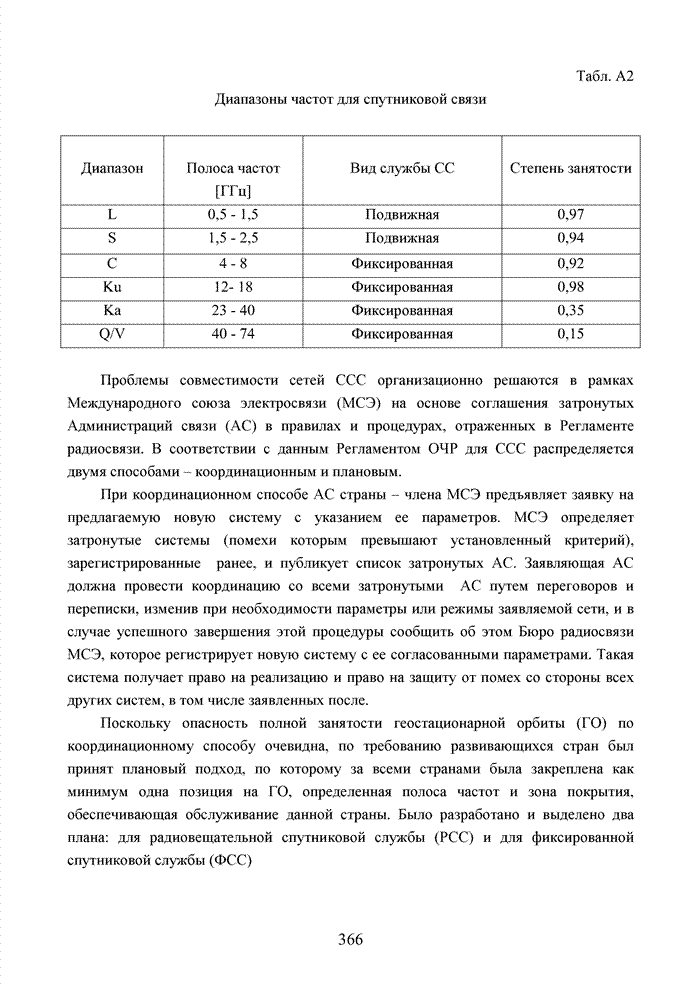
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
- Приложение Б Структура комбинаций кода РС (7,2,6)
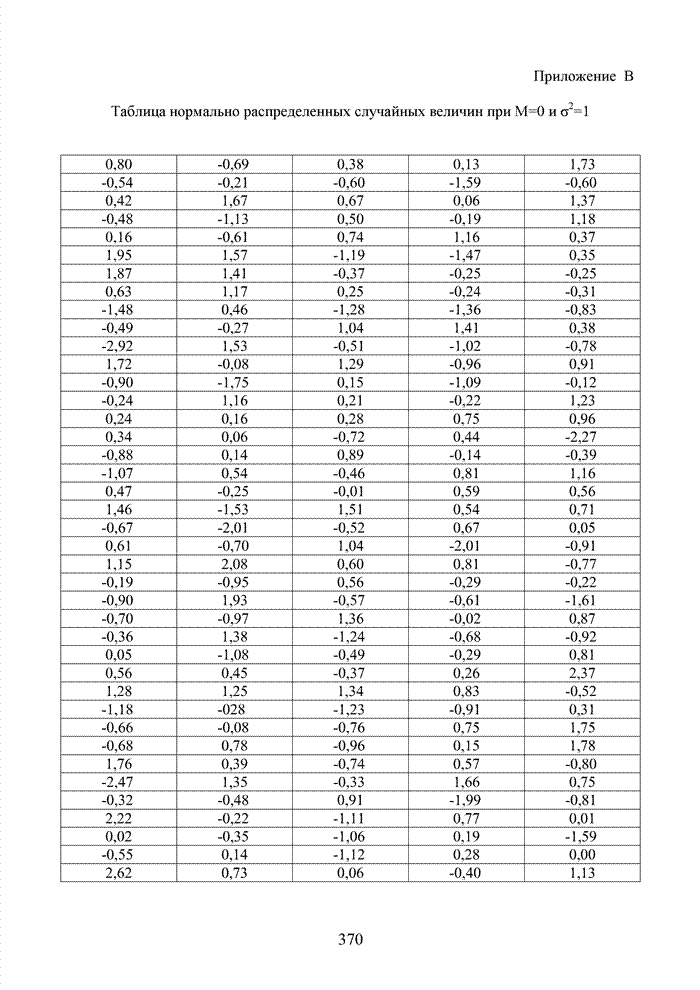
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК