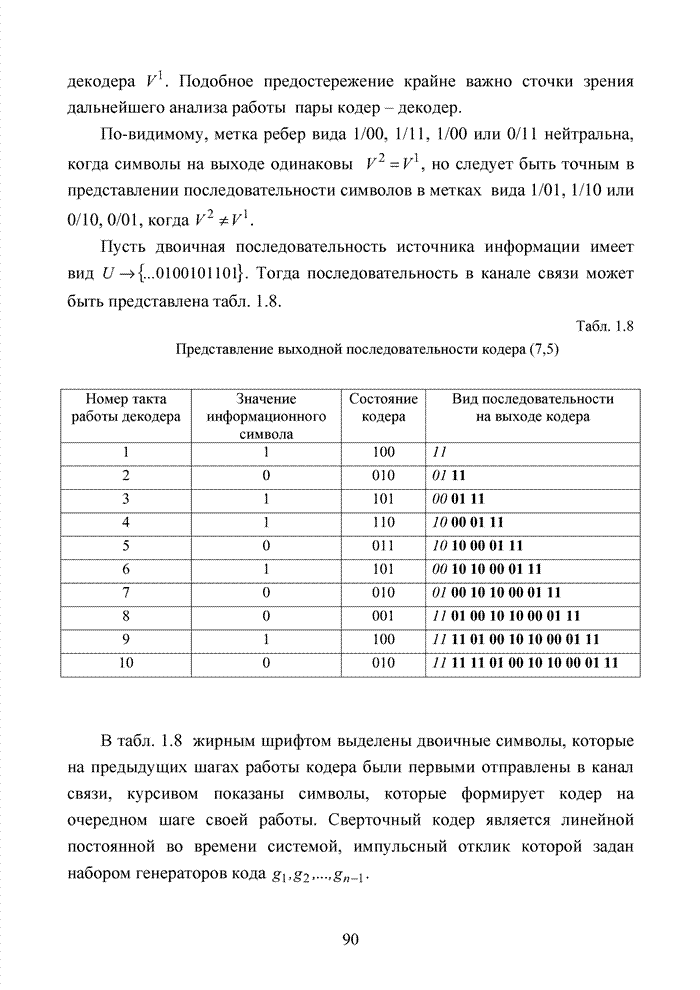
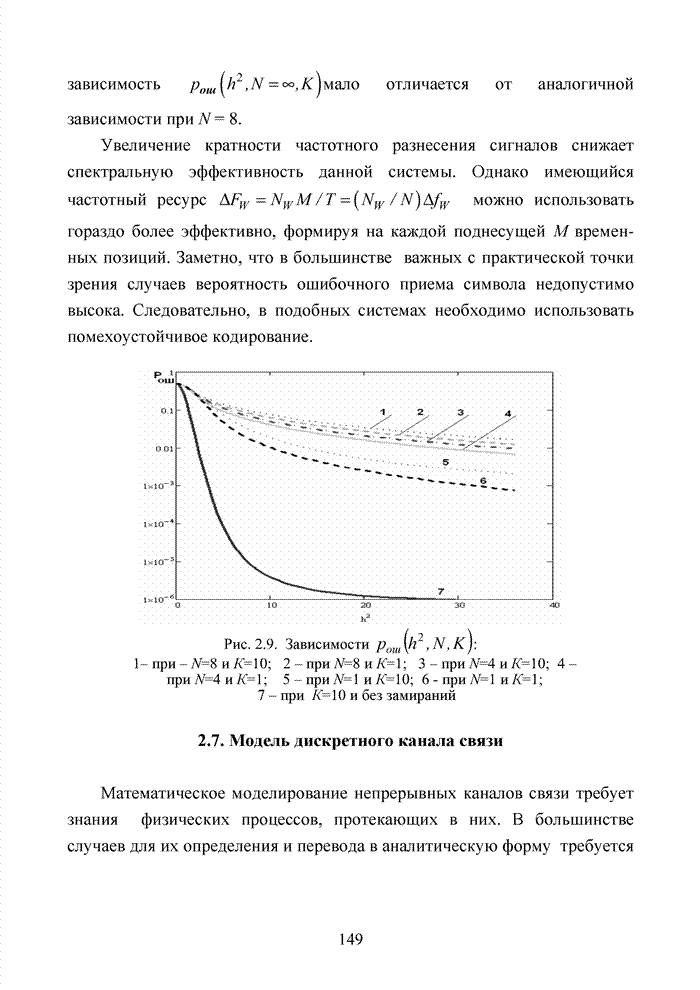
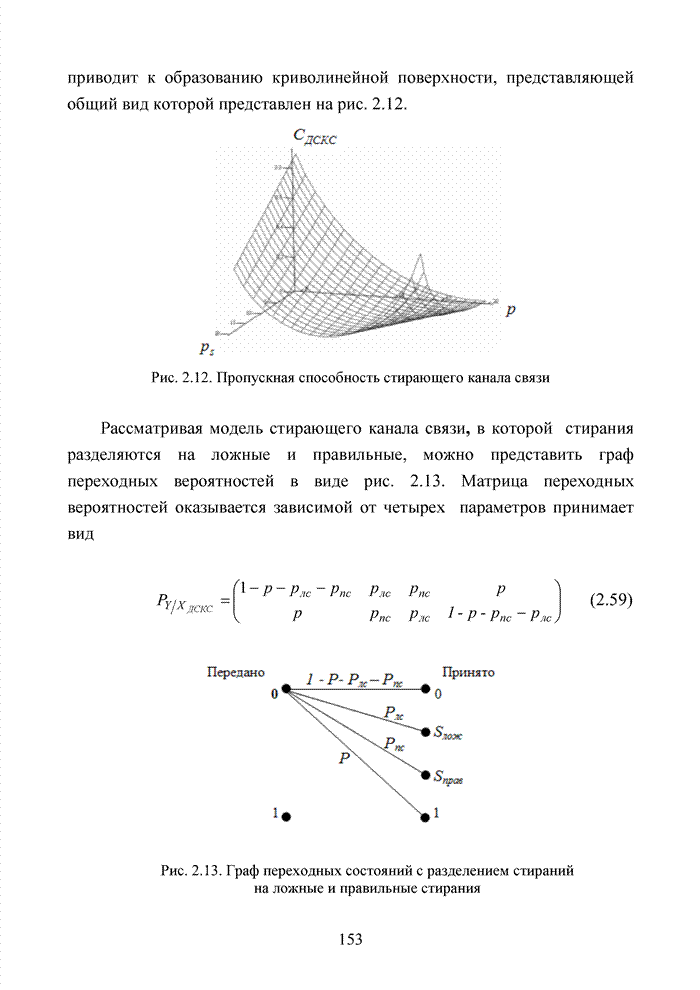
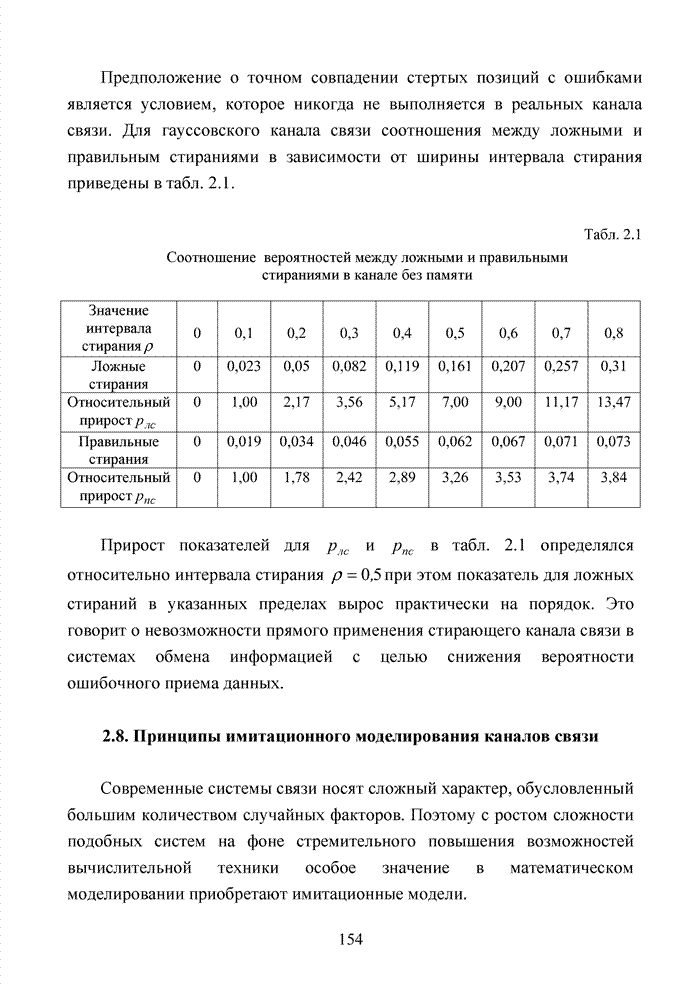
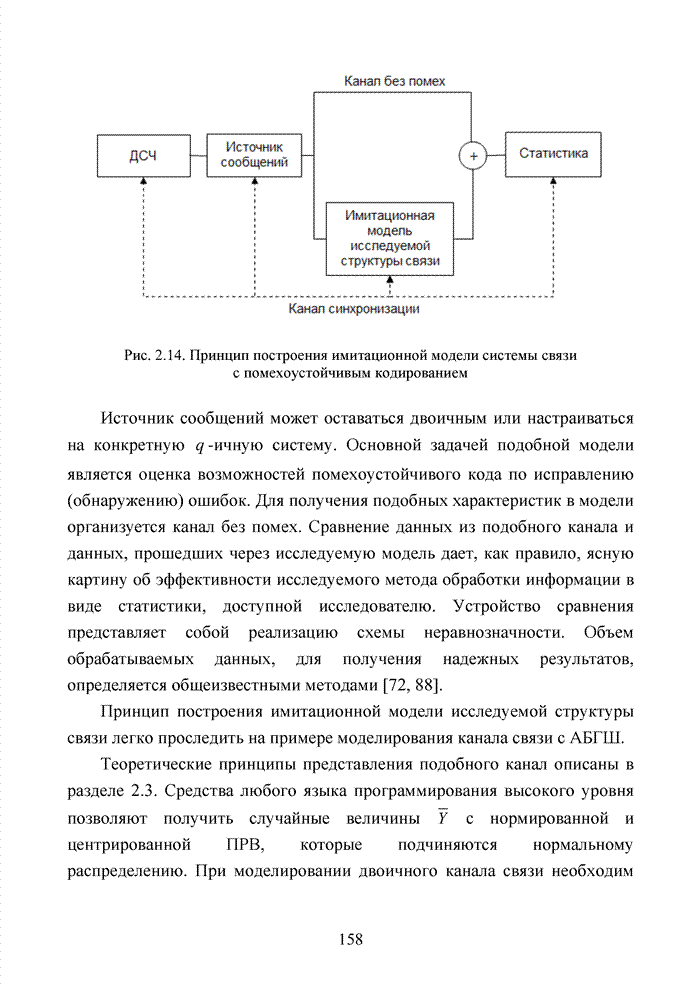
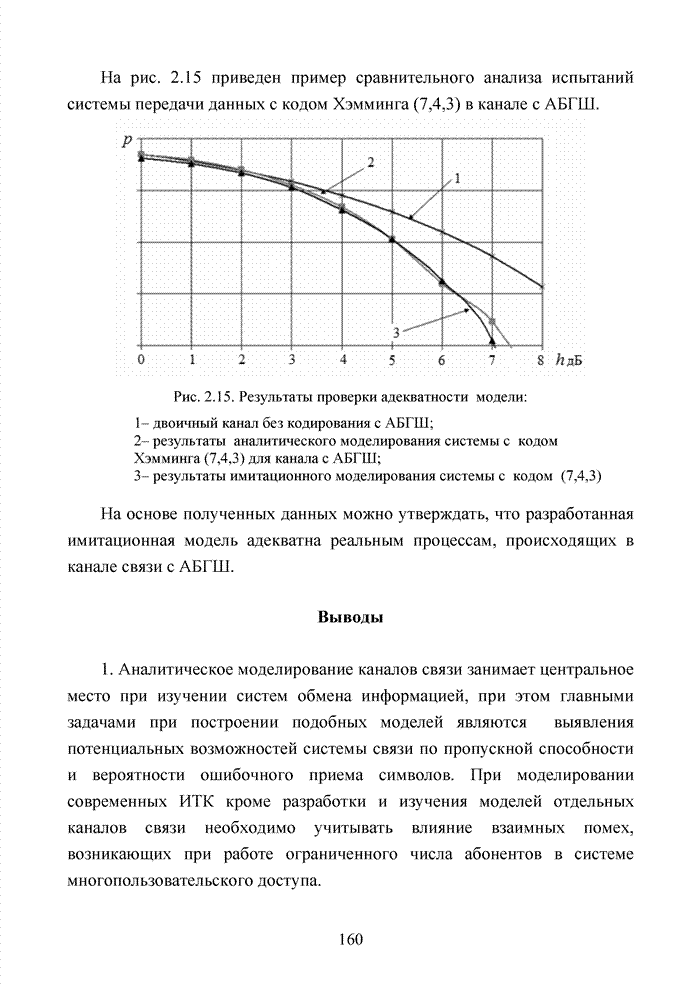
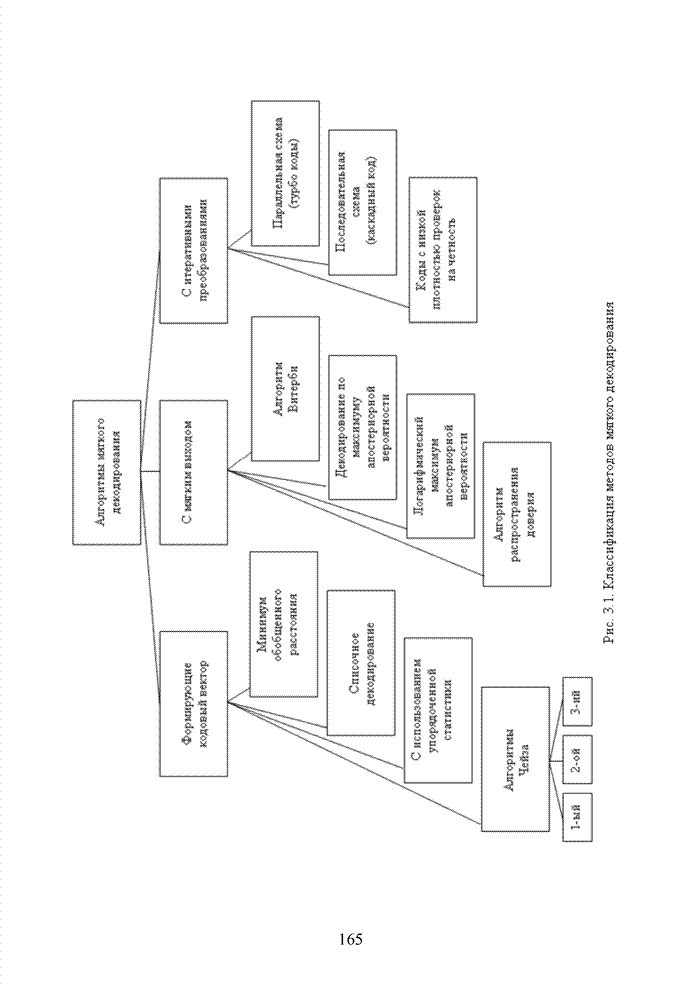
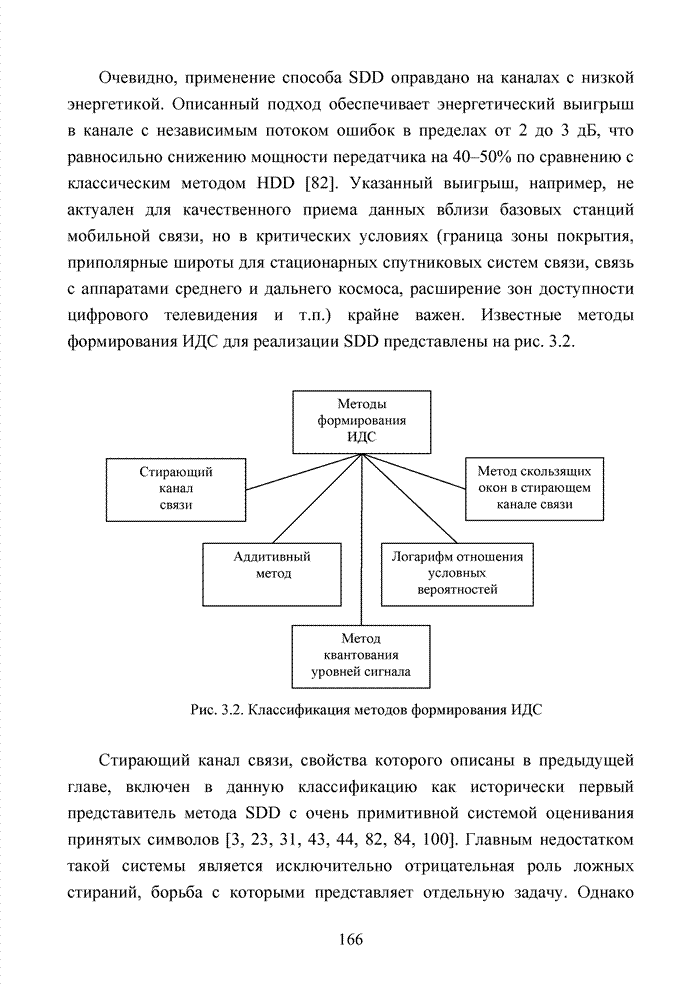
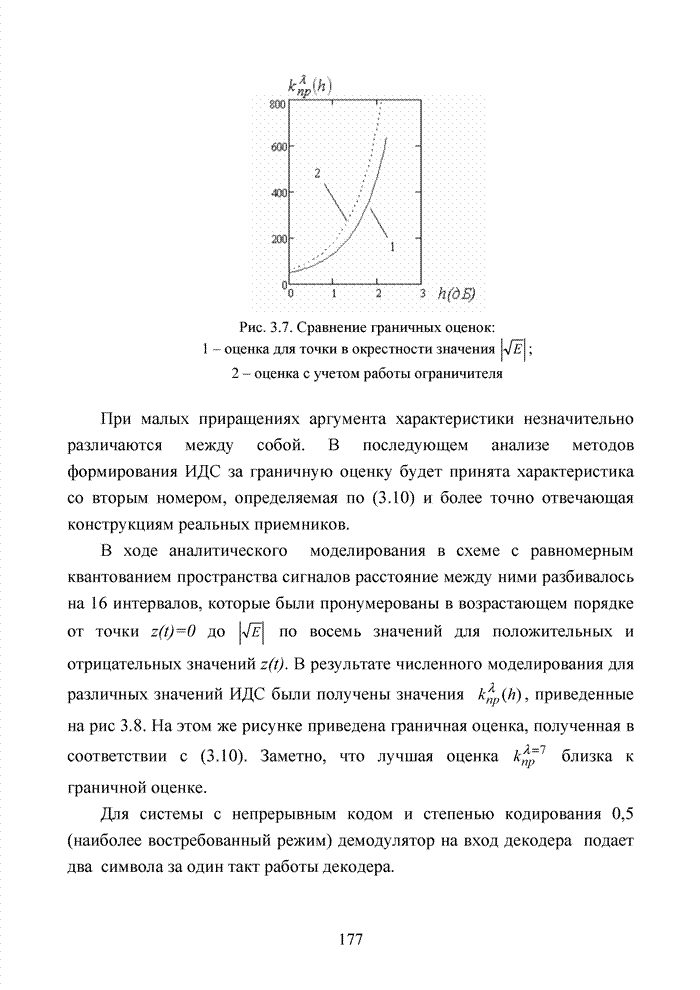
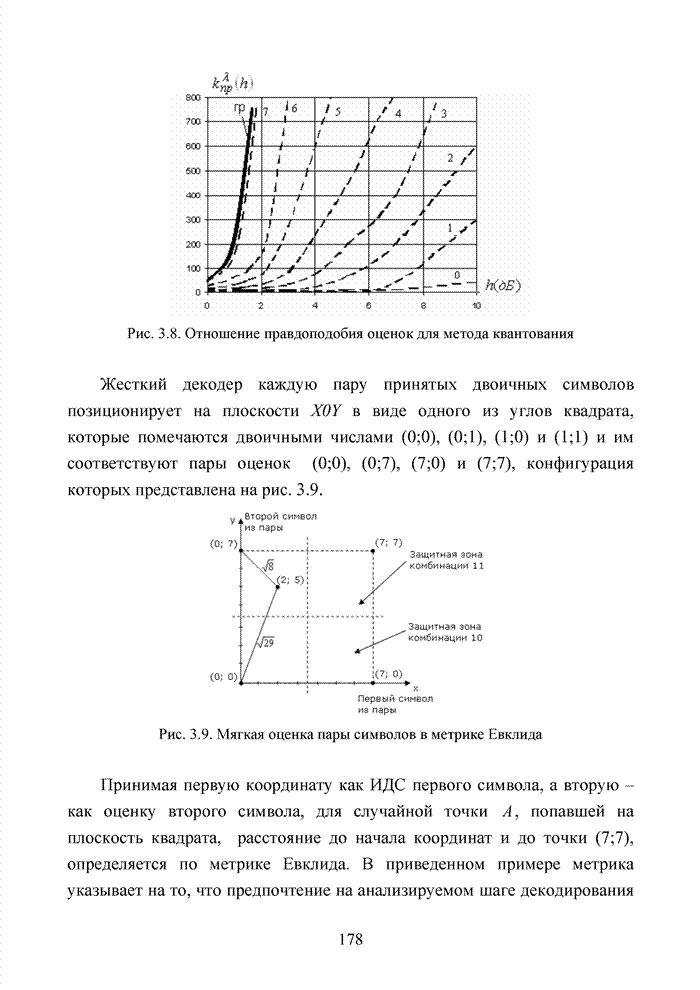
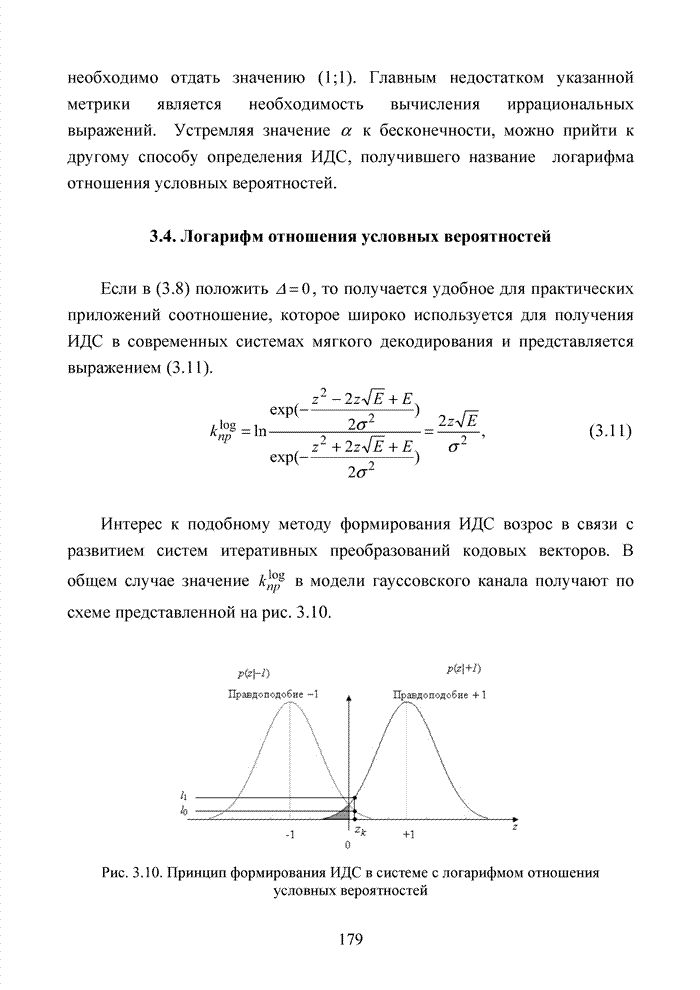
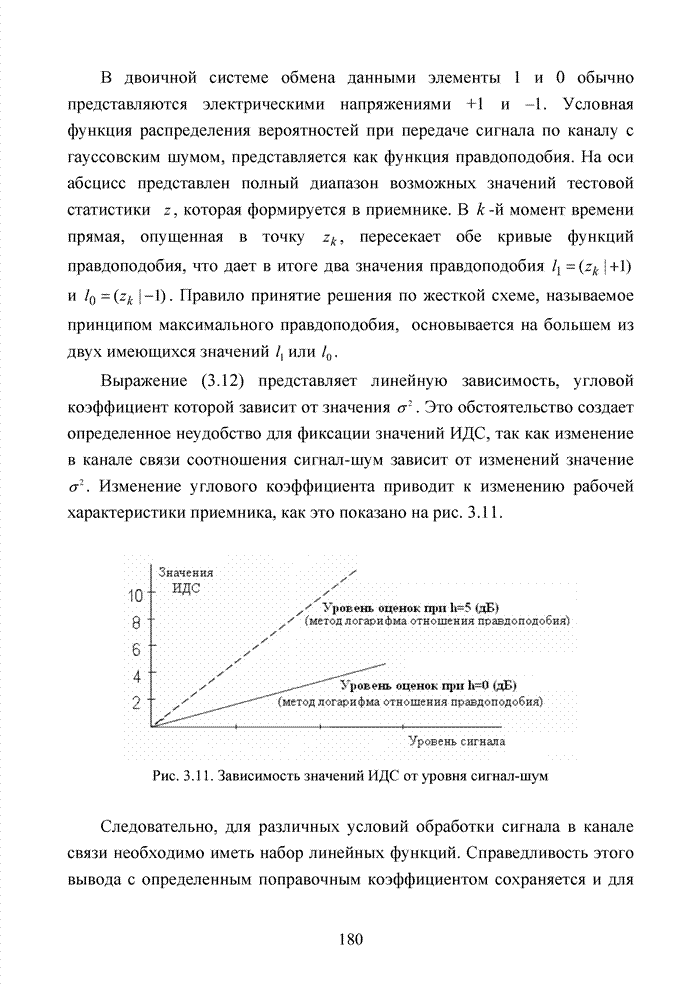
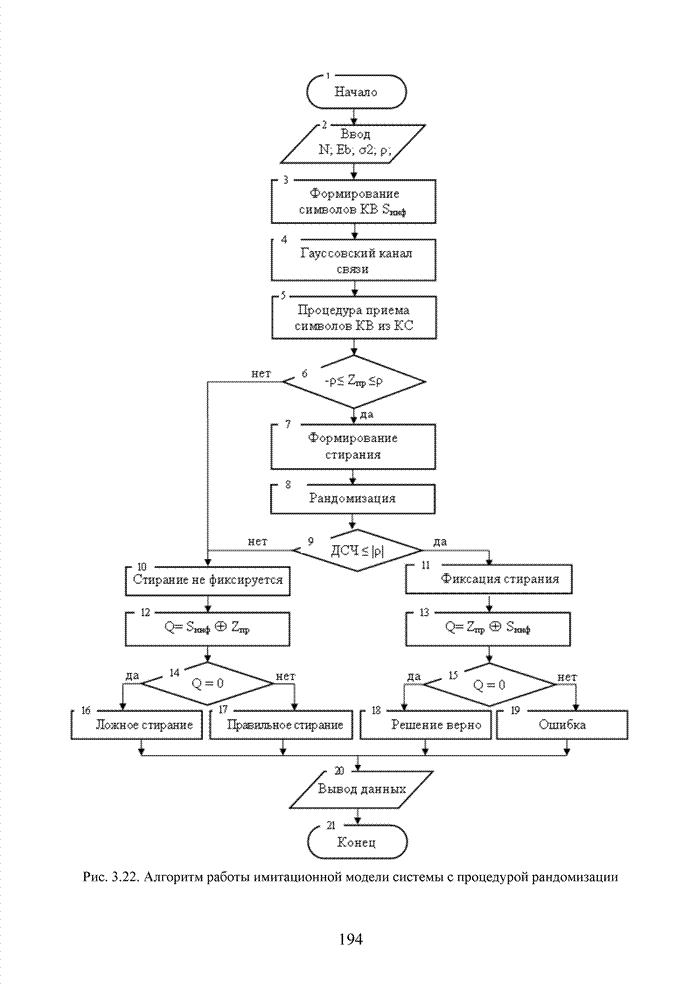
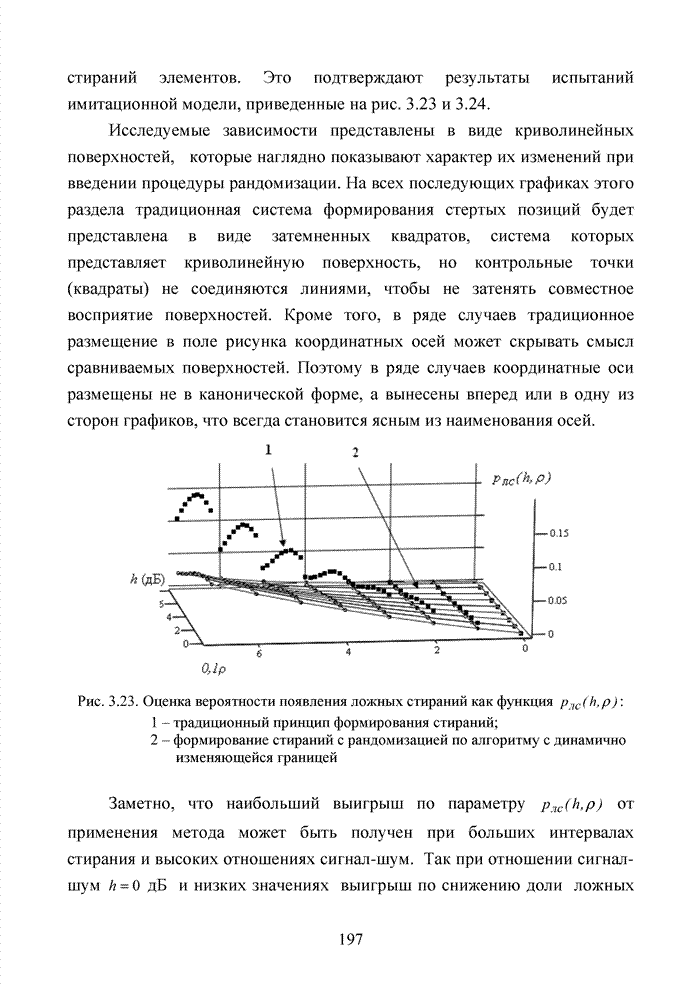
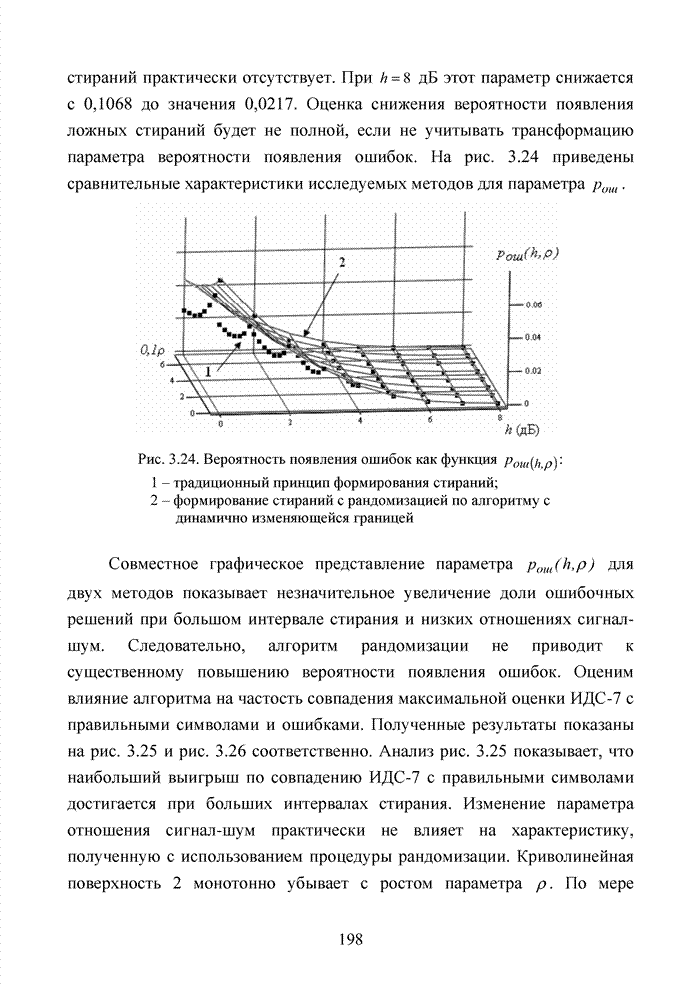
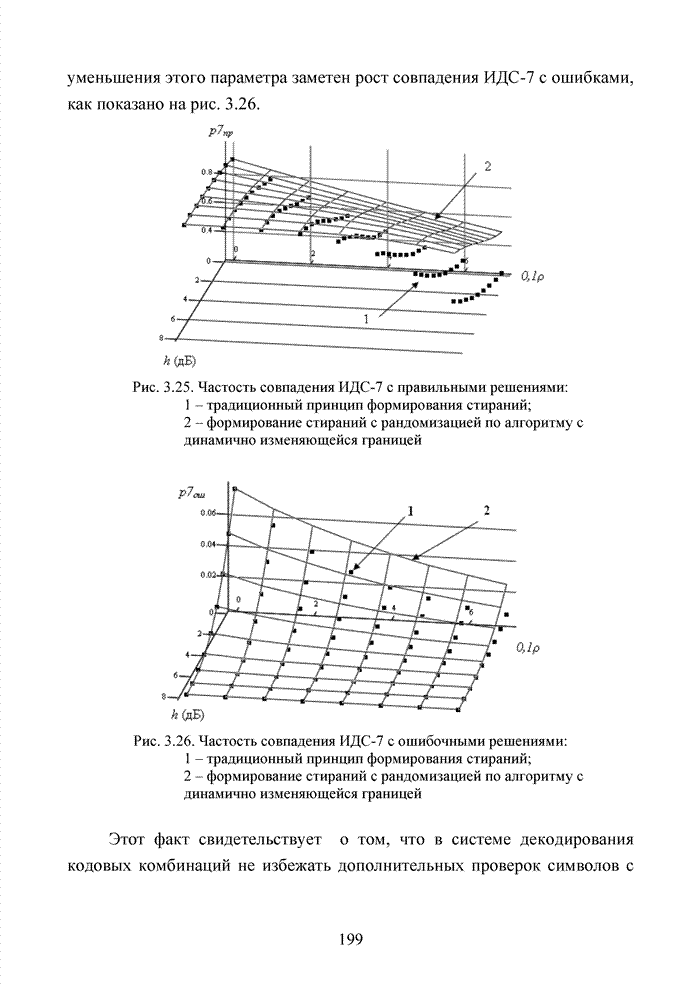
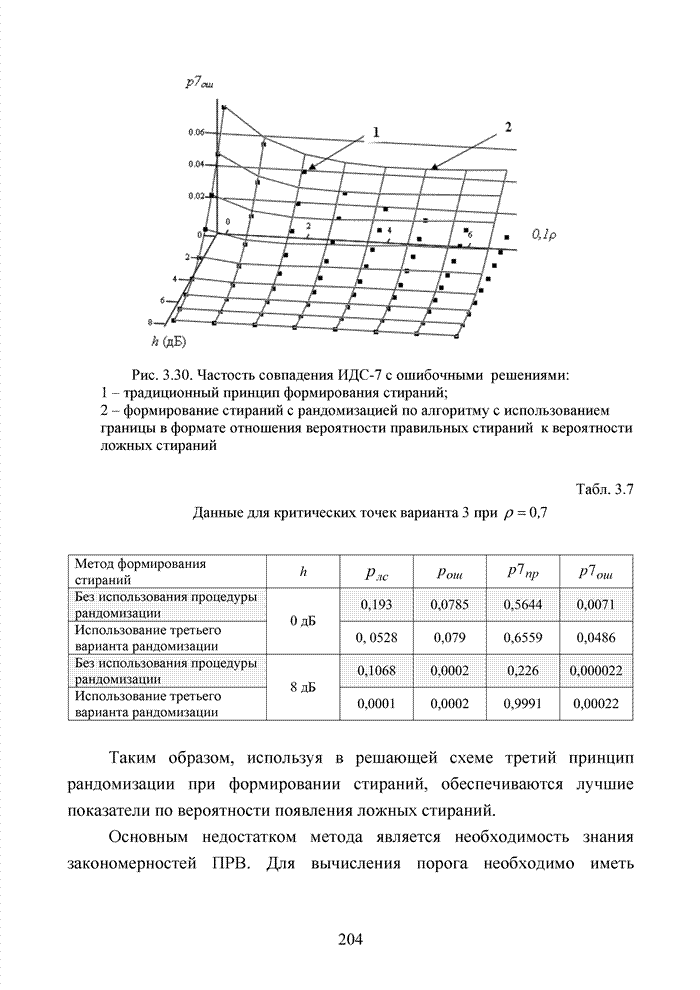
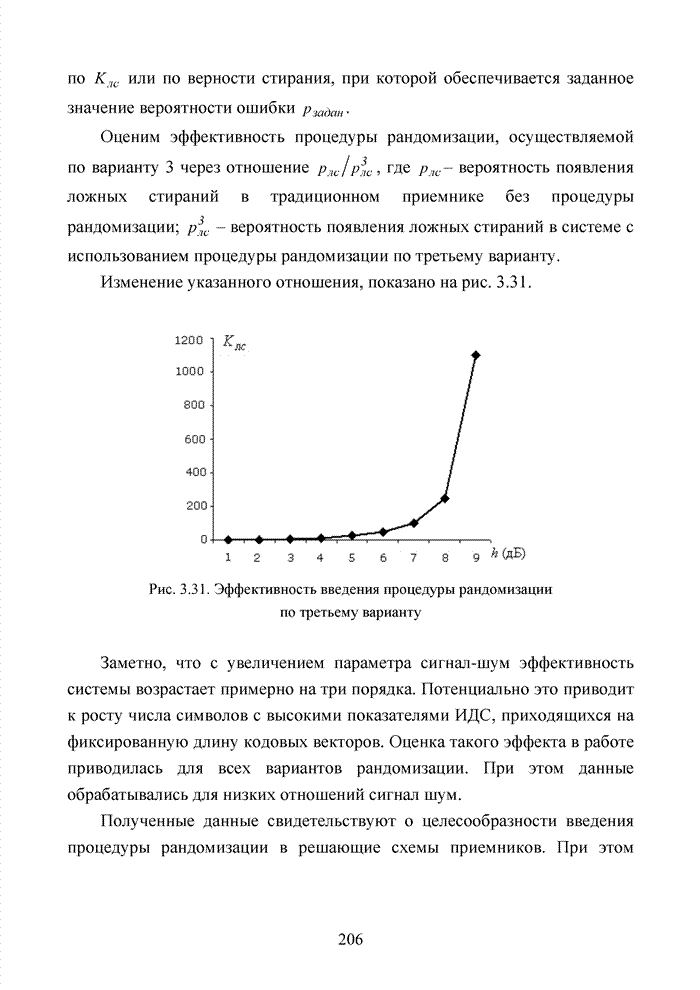
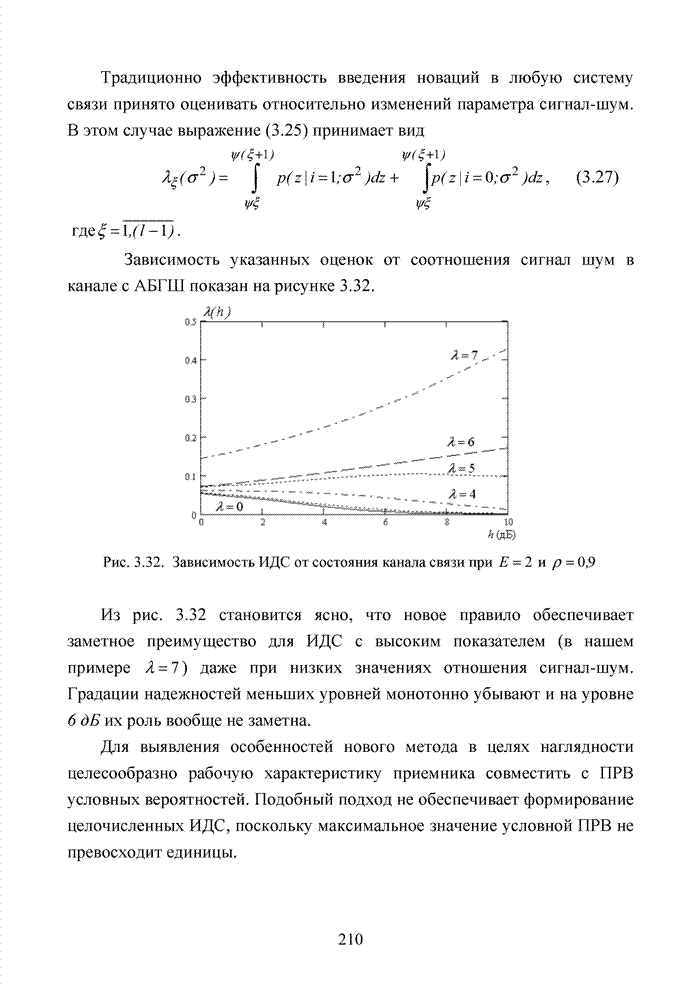
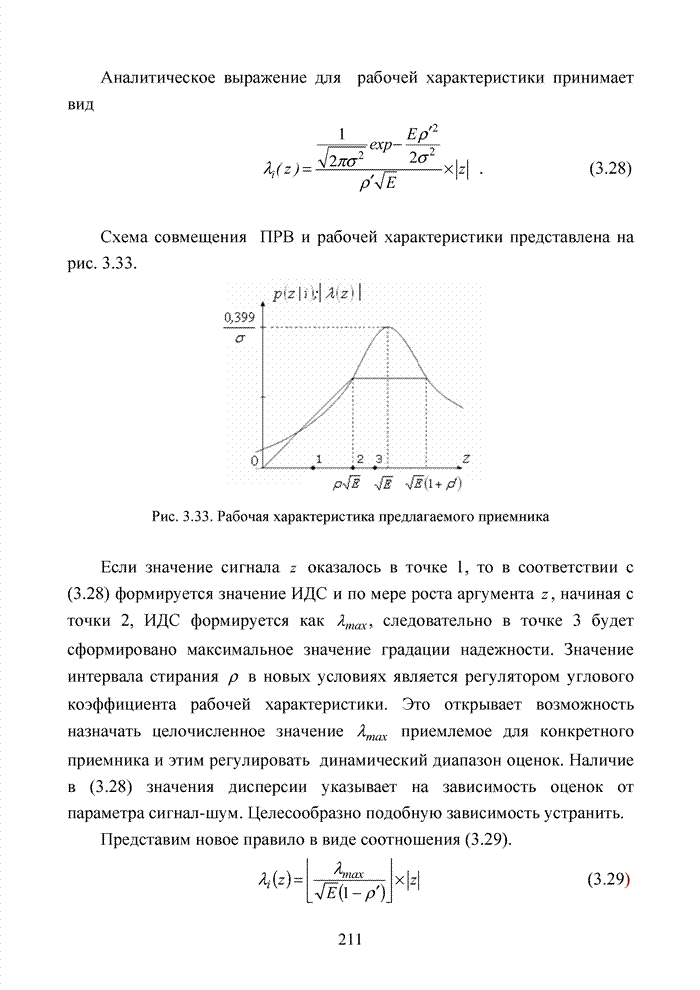
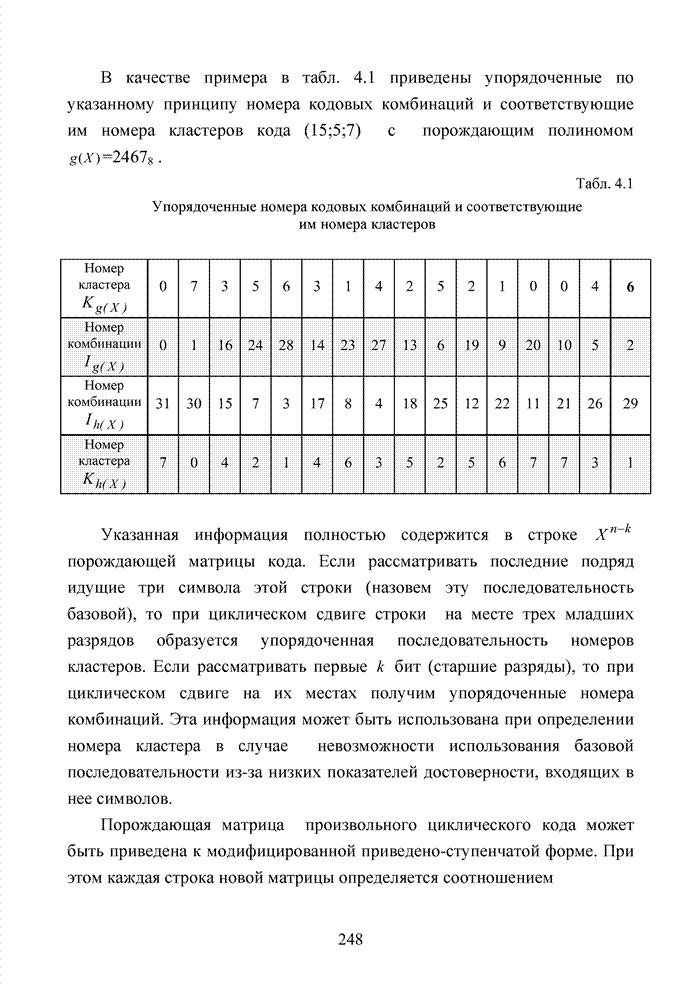
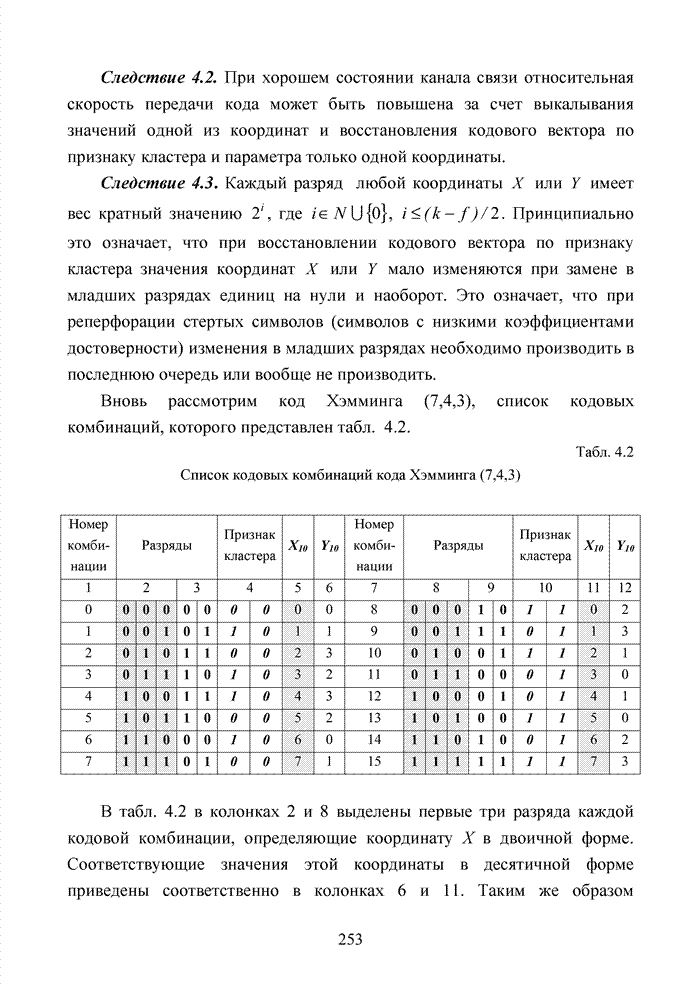
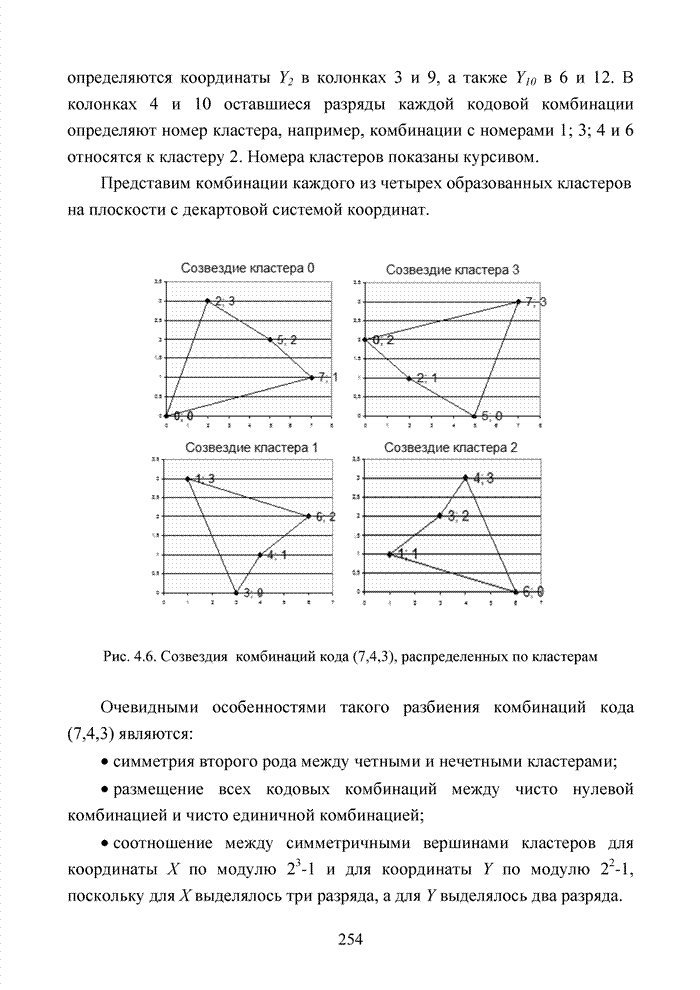
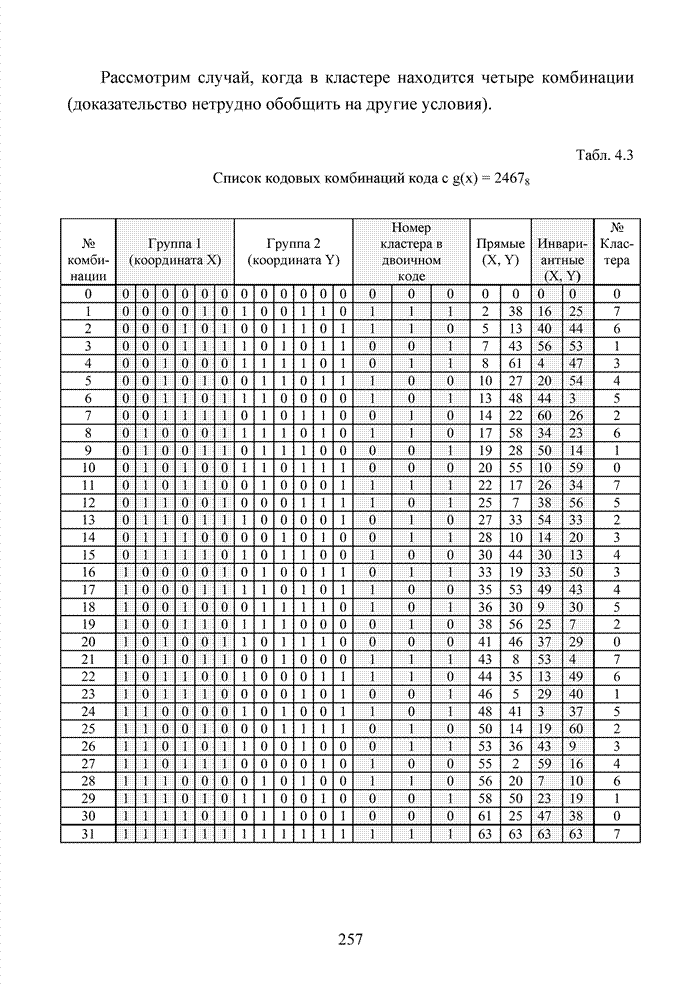
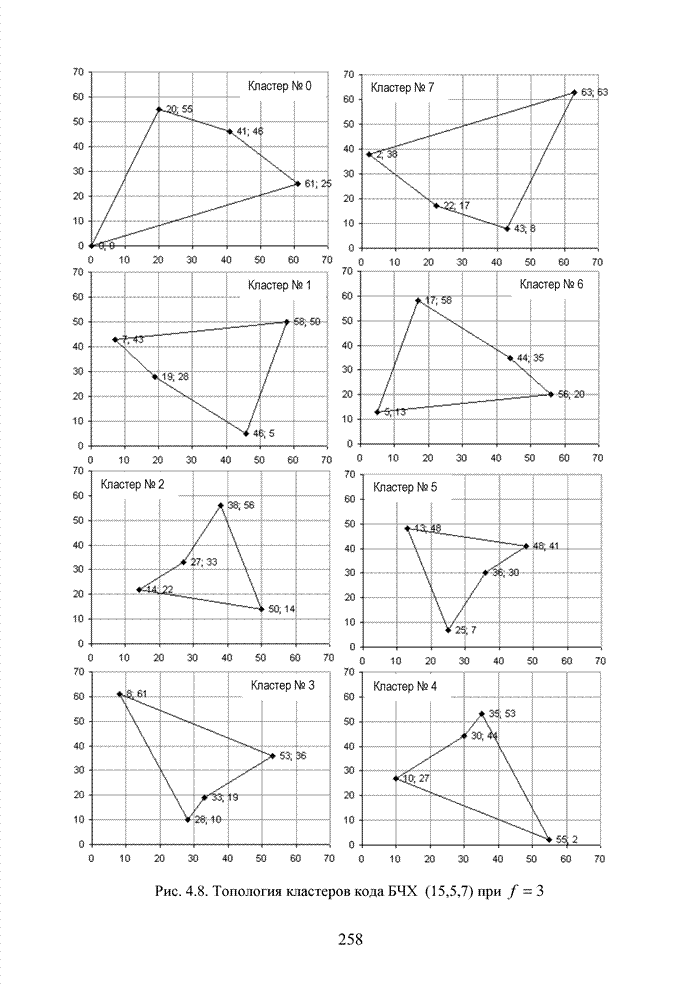
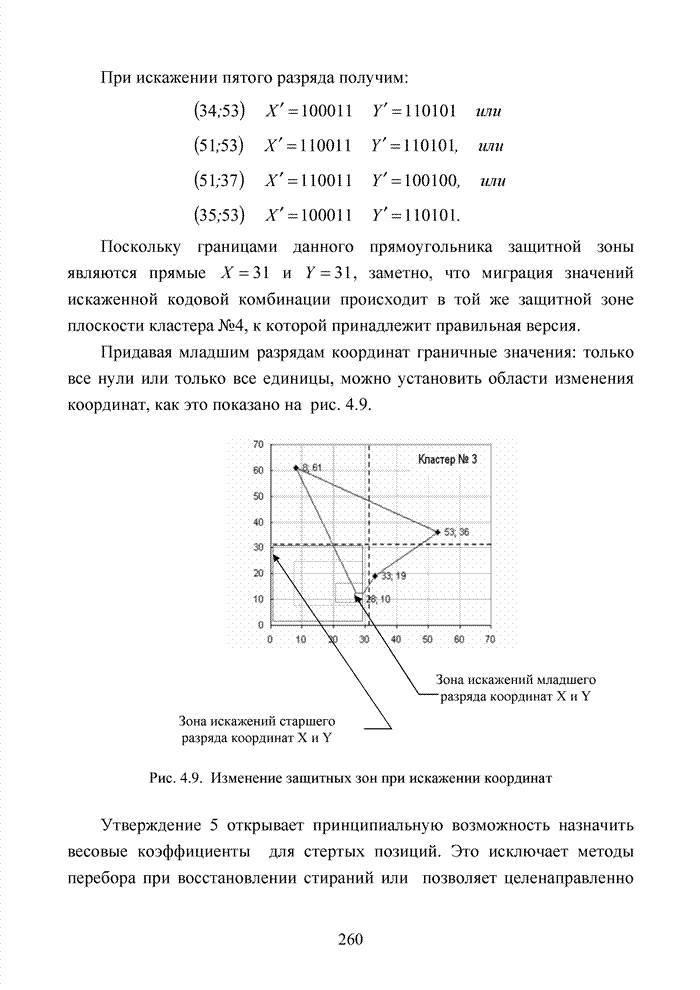
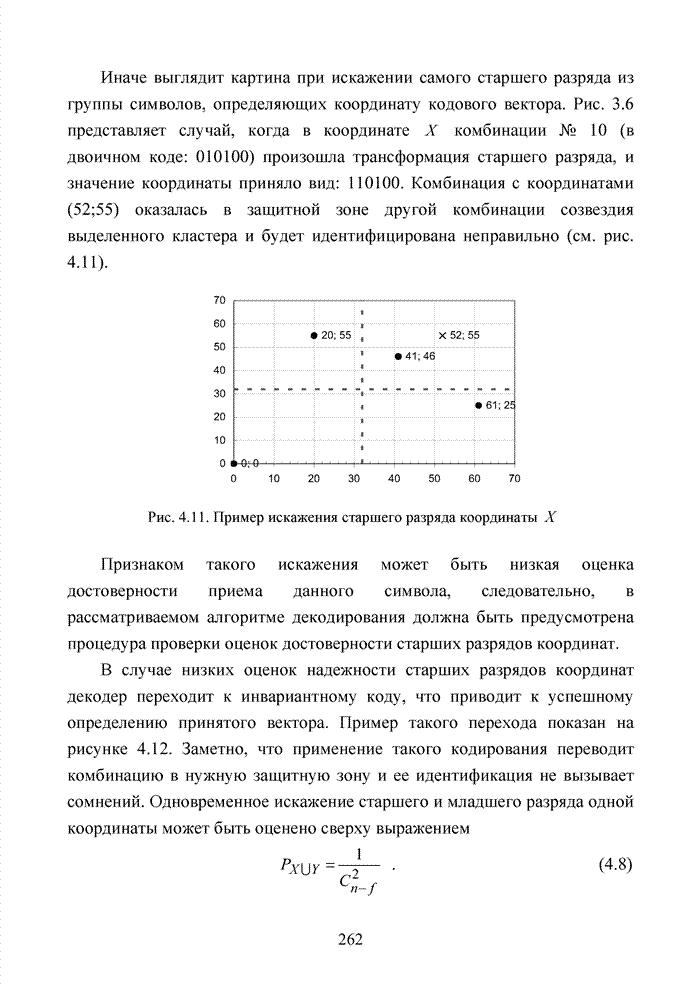
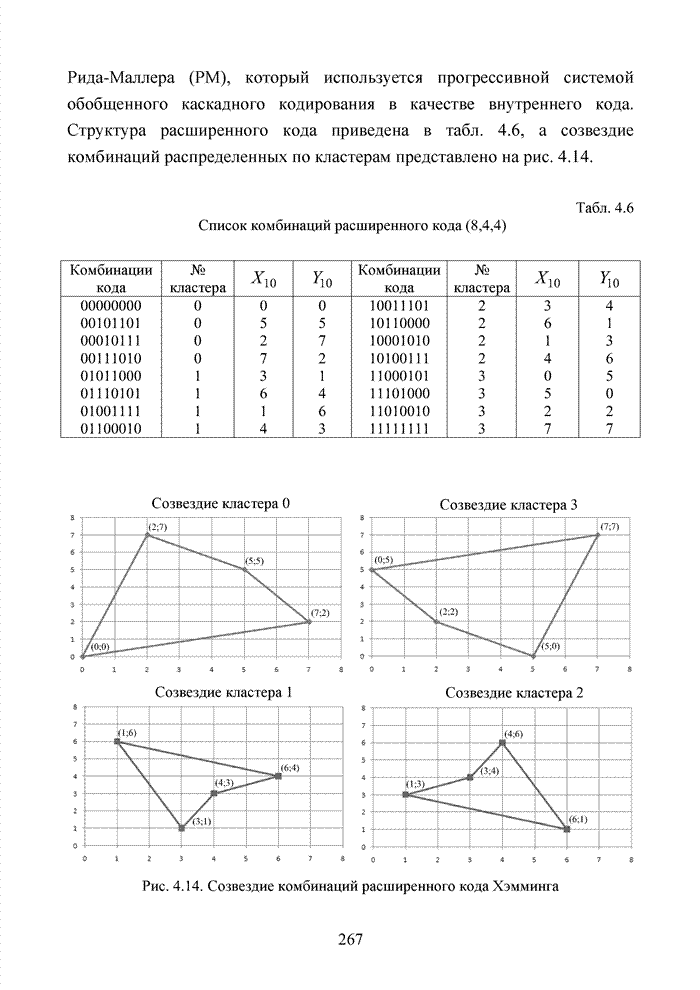
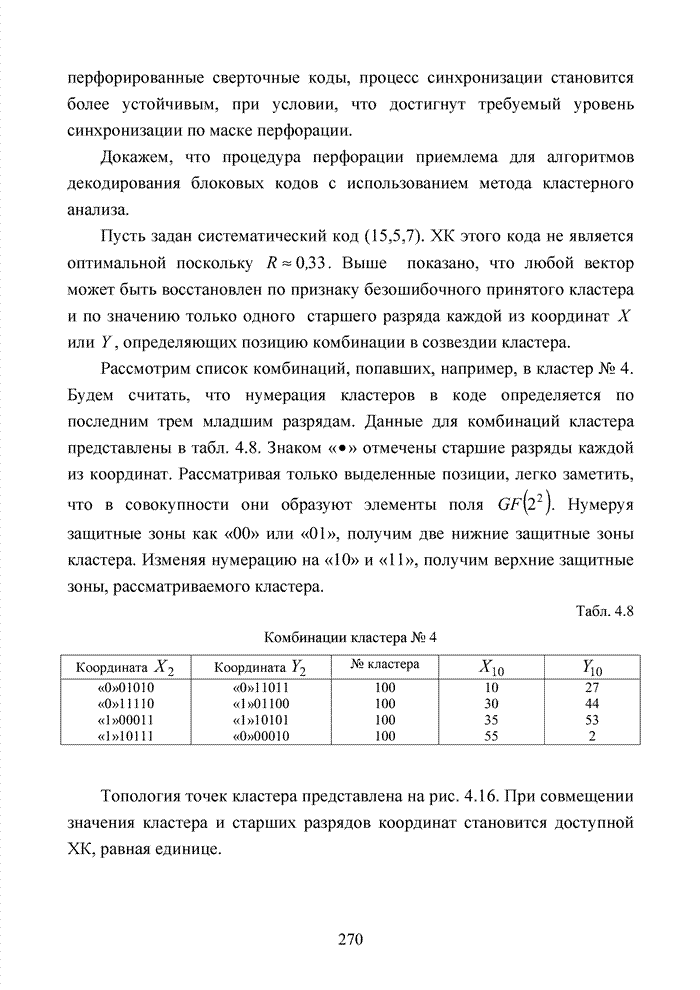
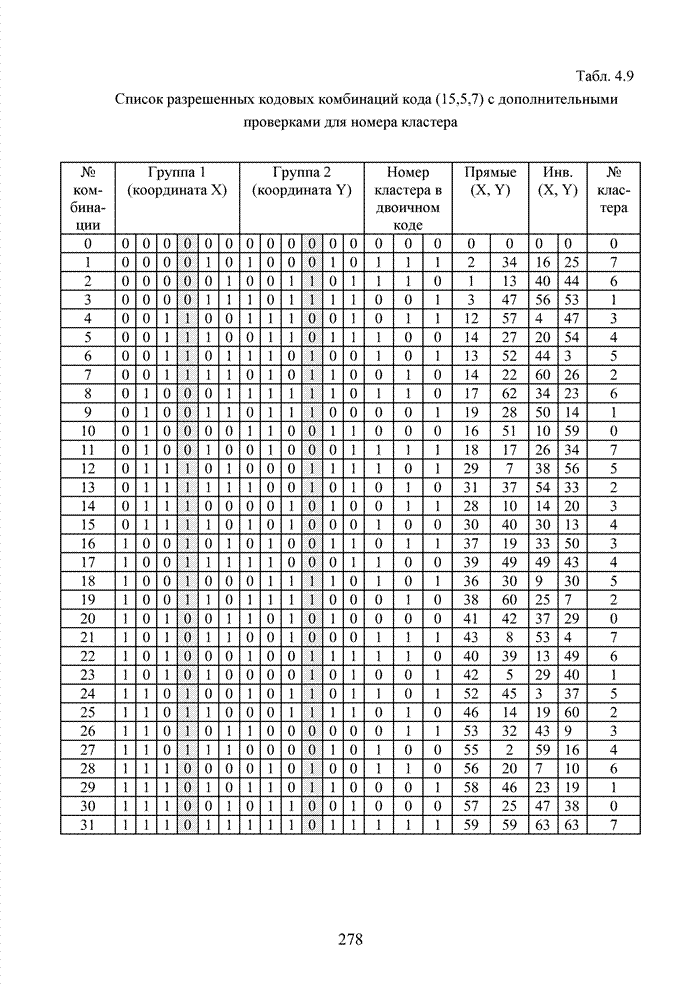
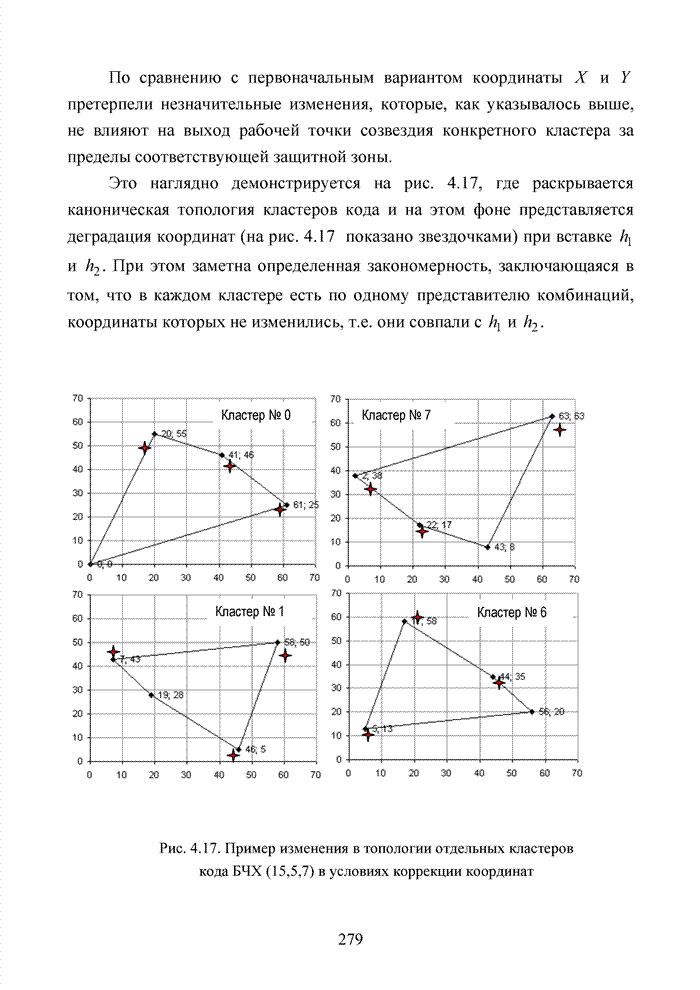
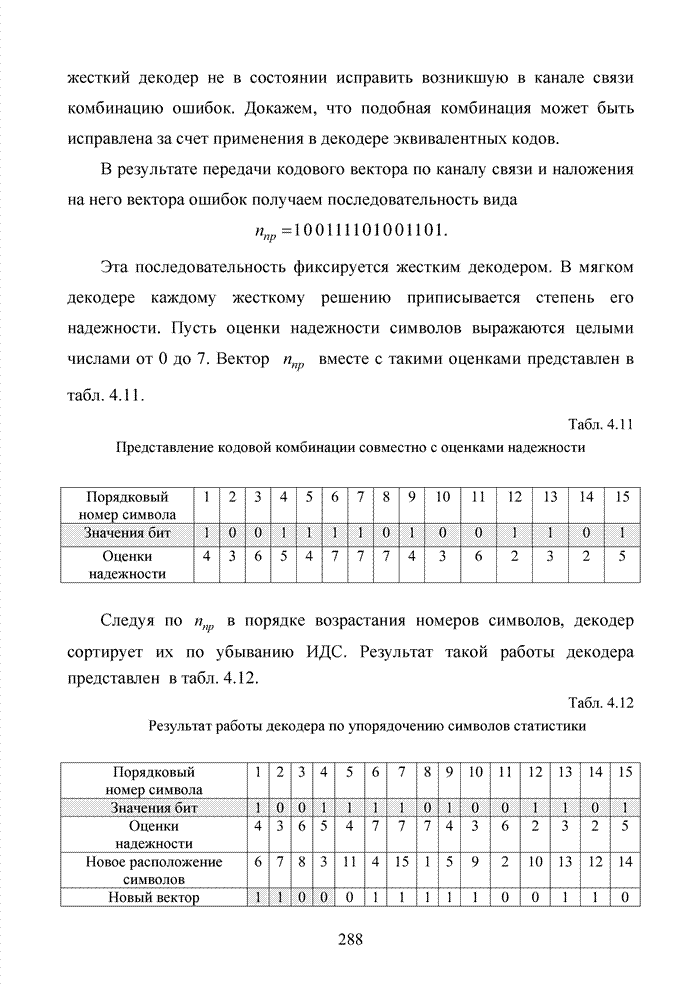
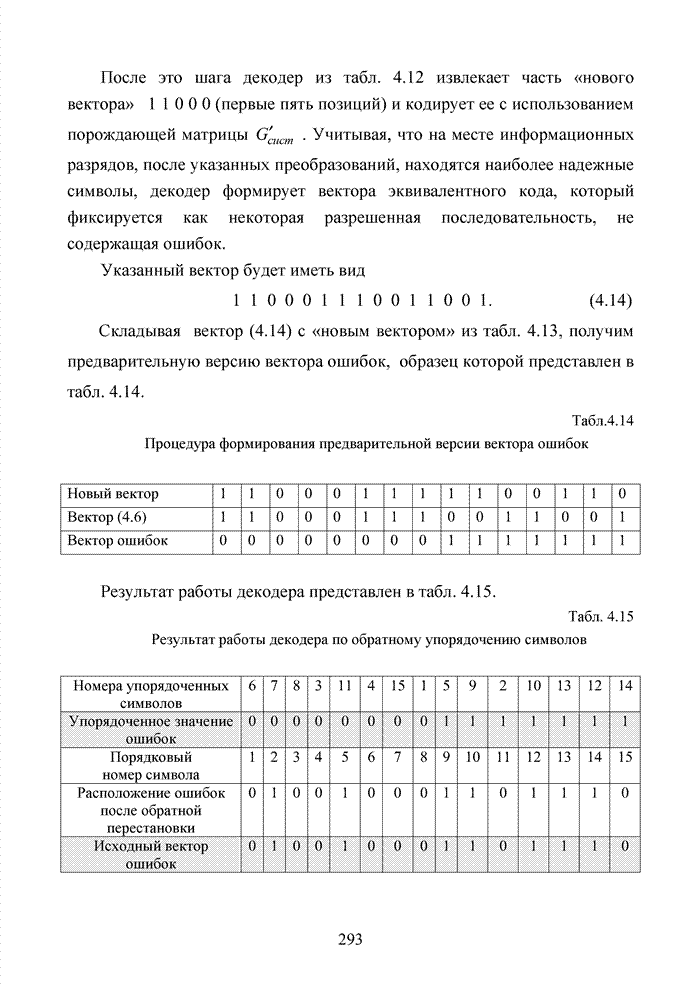
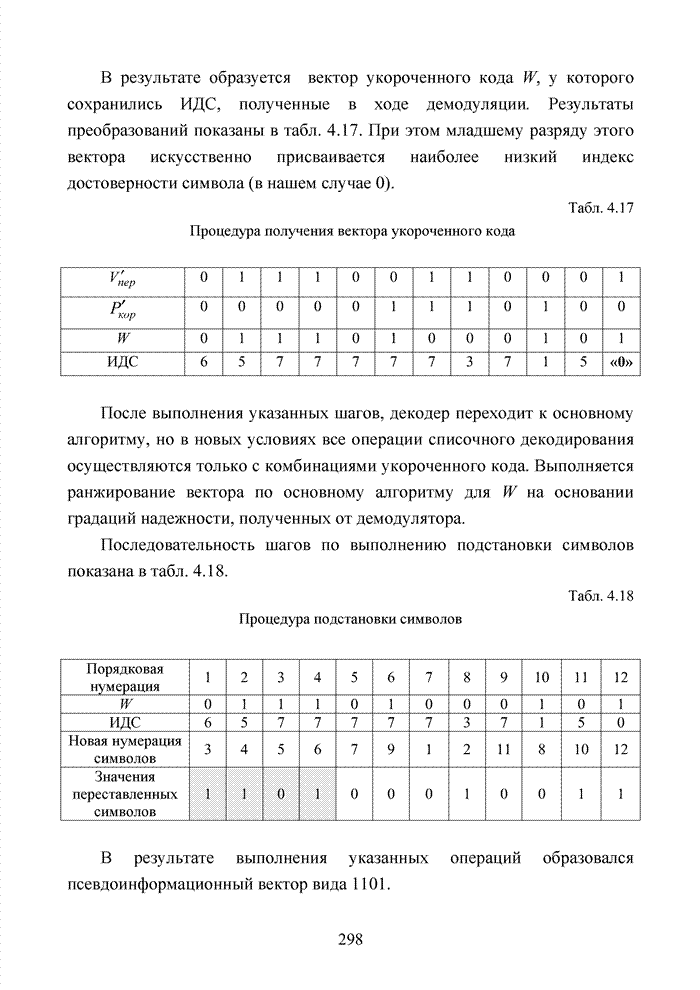
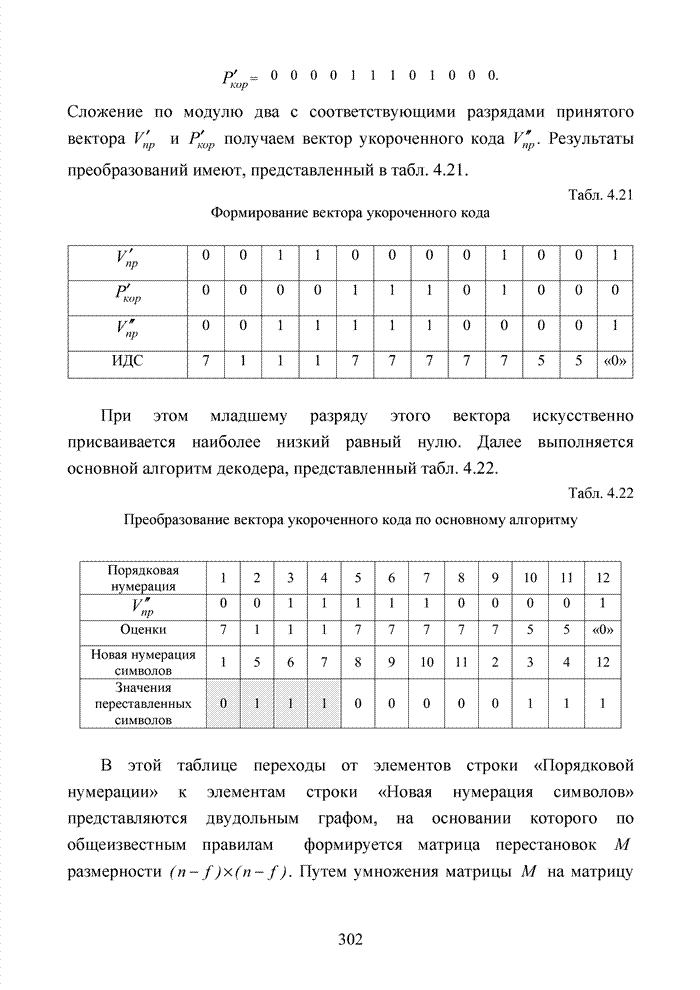
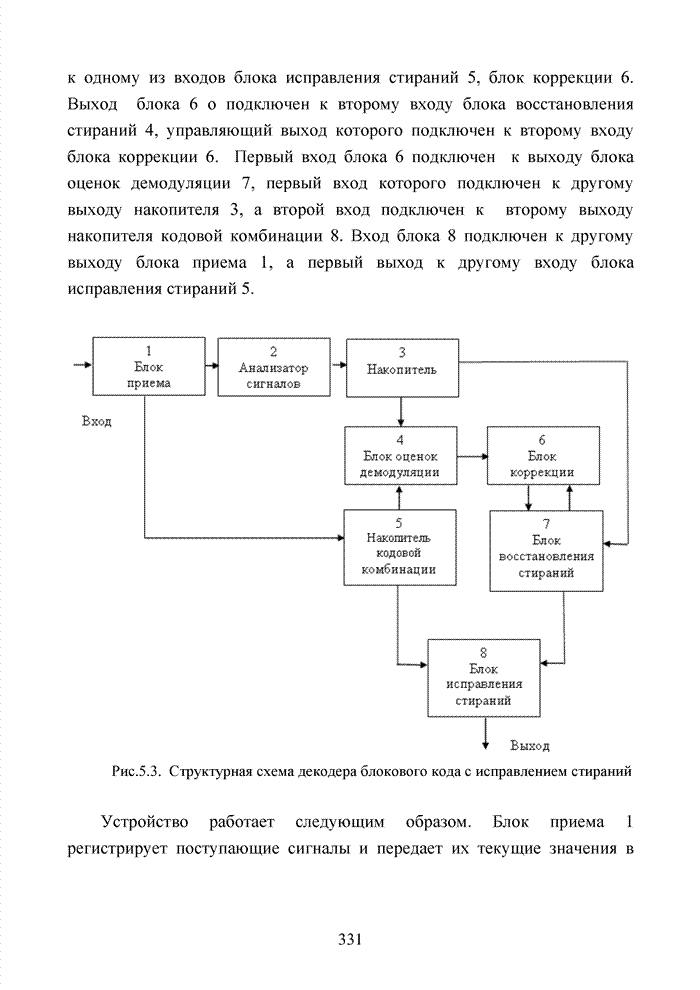
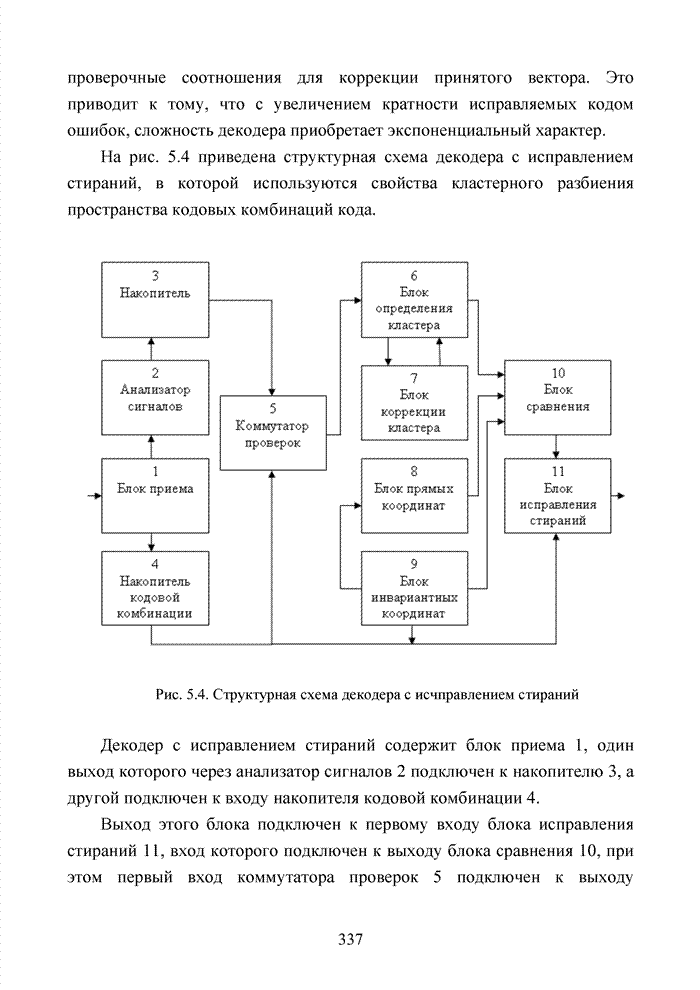
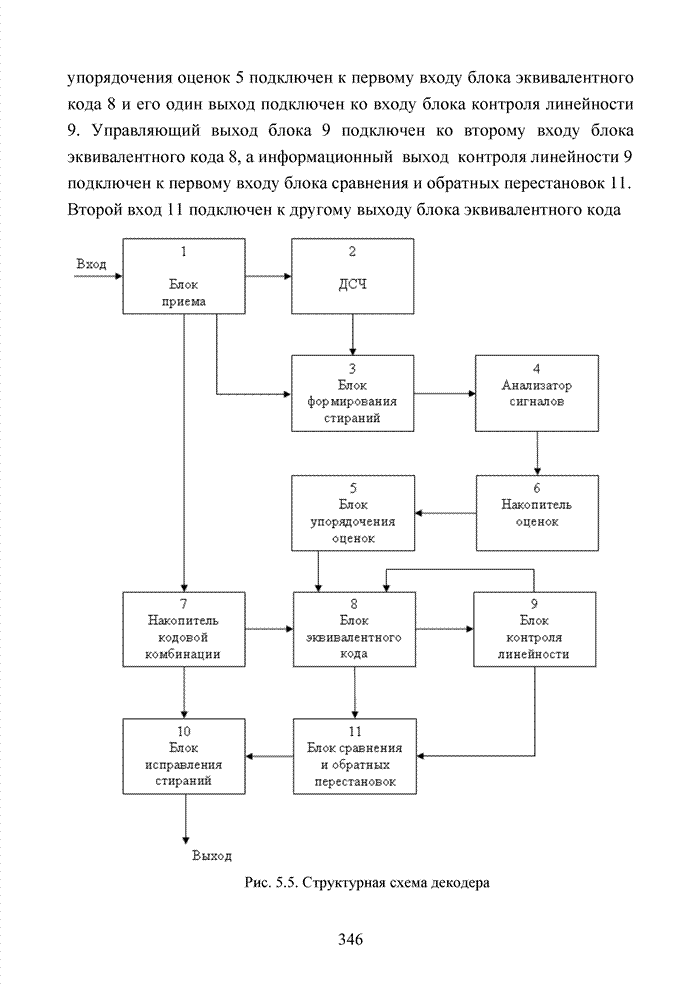
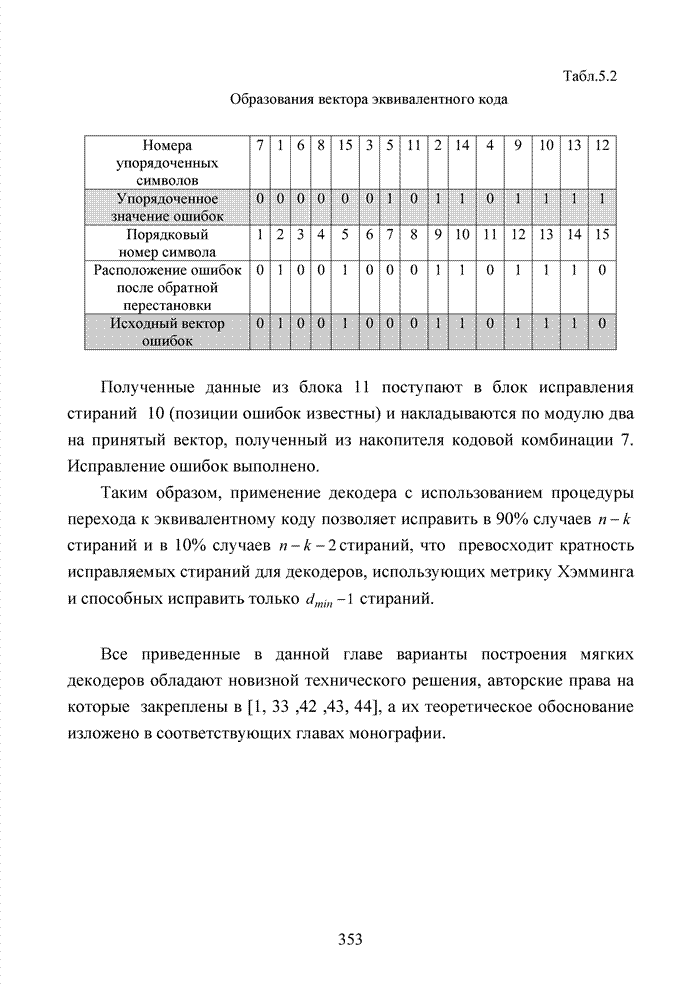
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
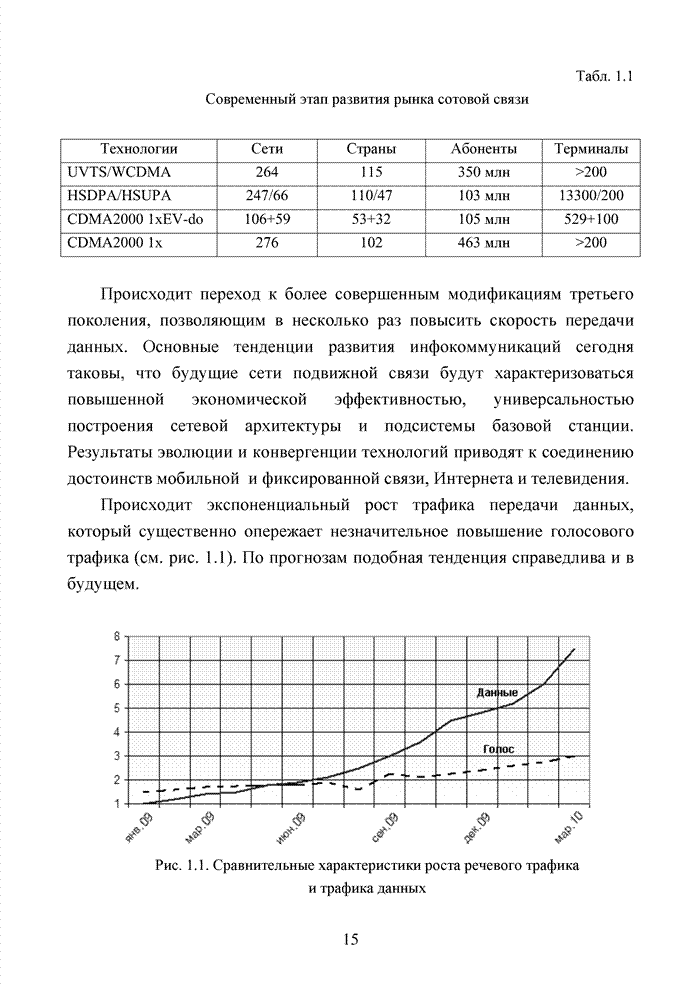
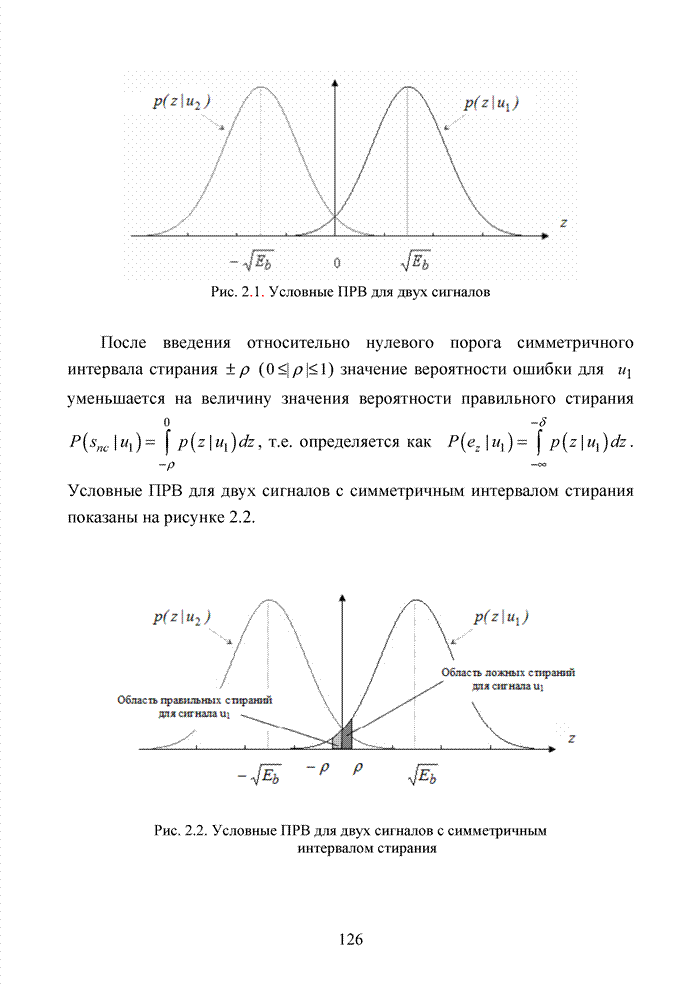
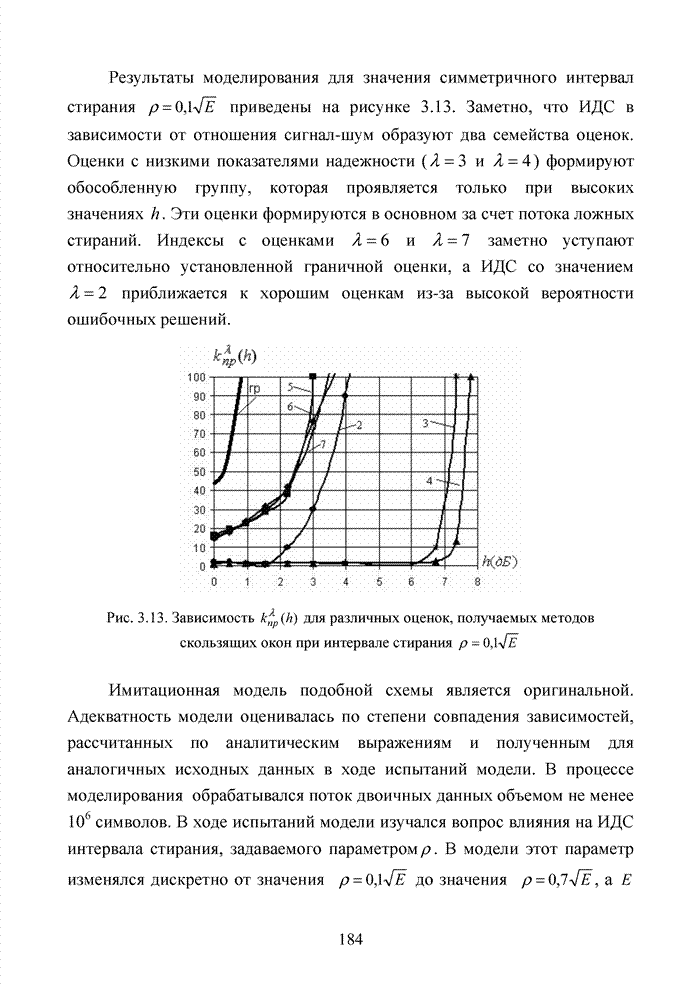
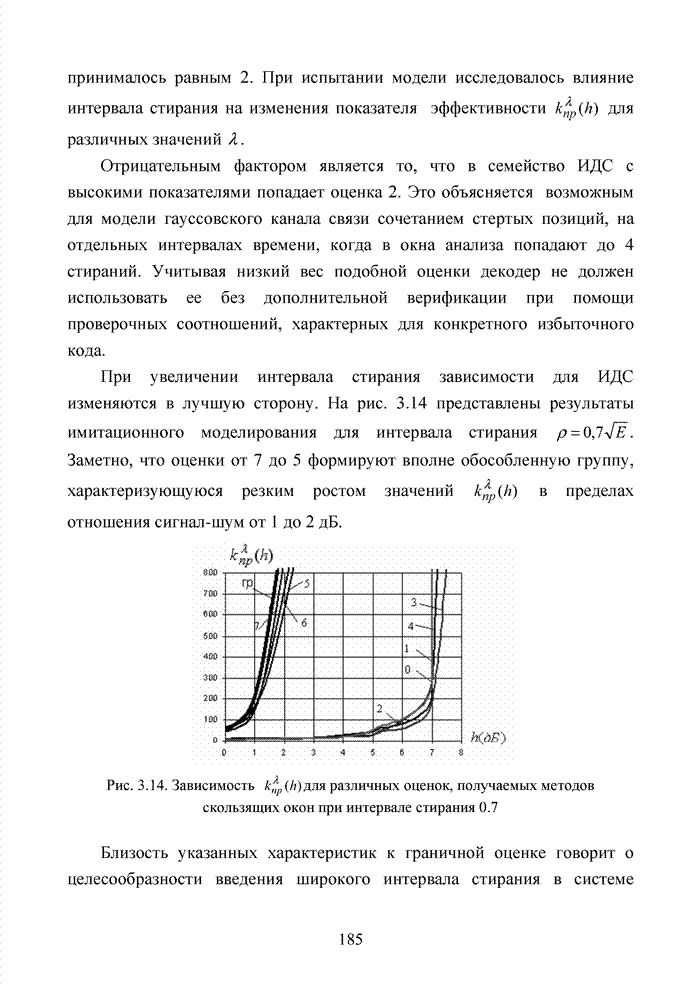
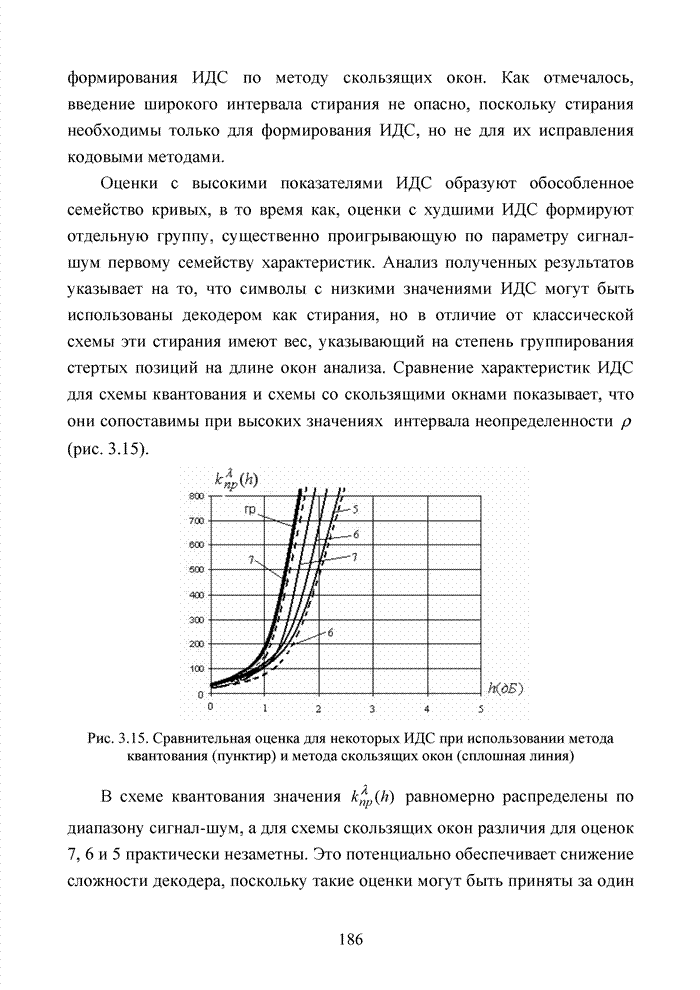
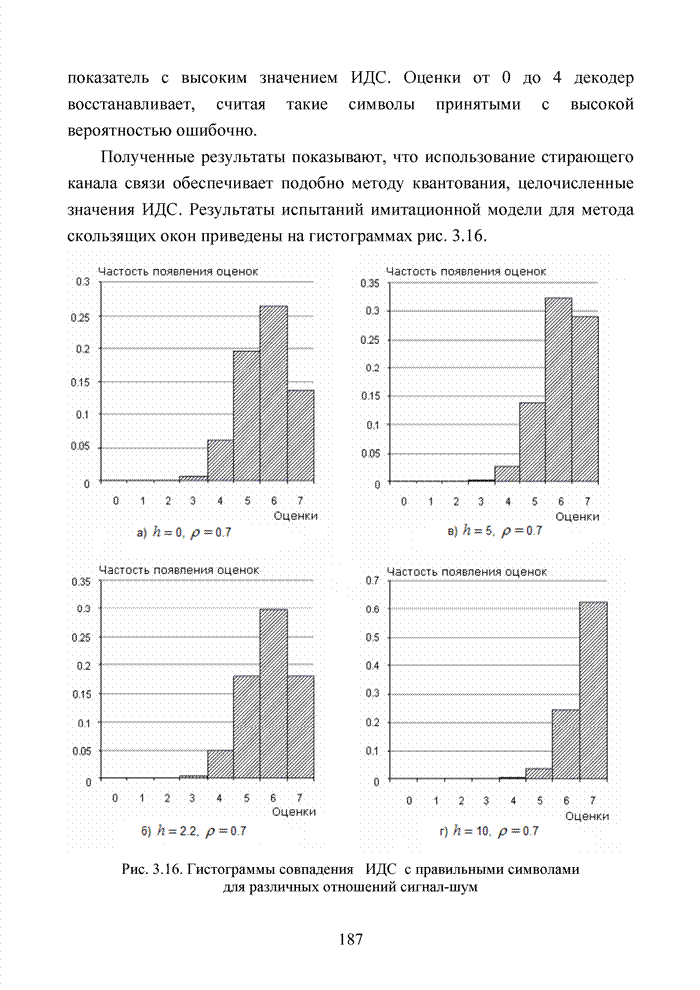
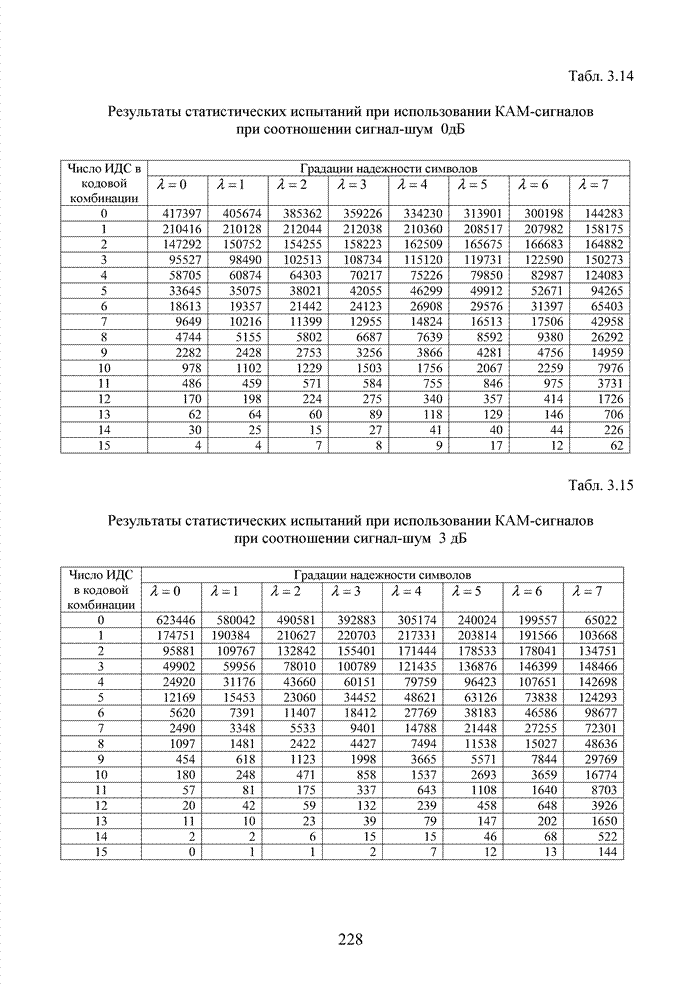
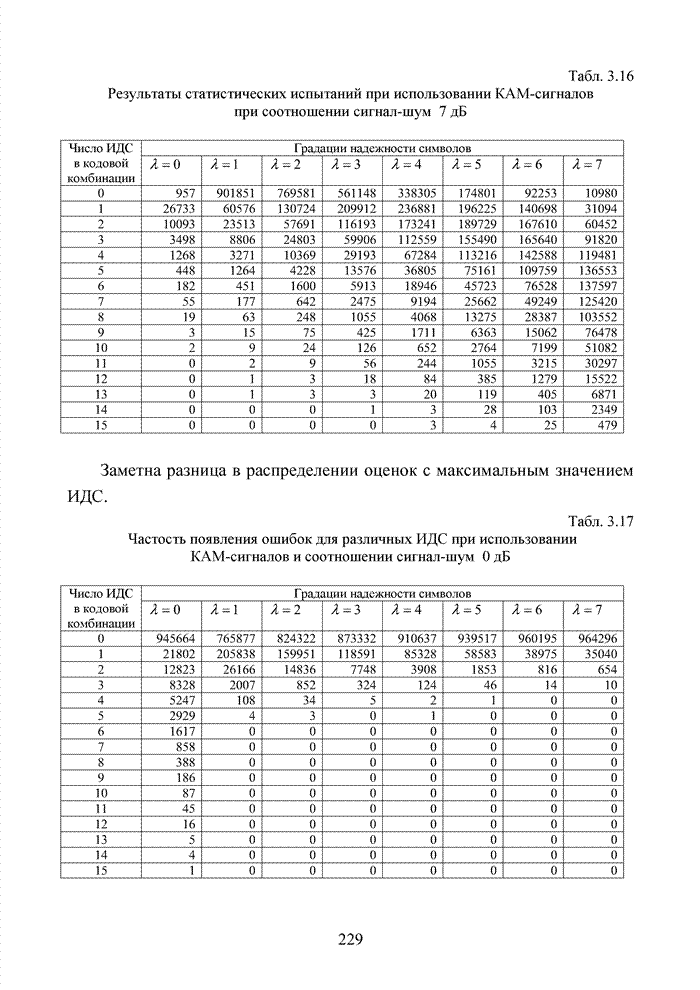
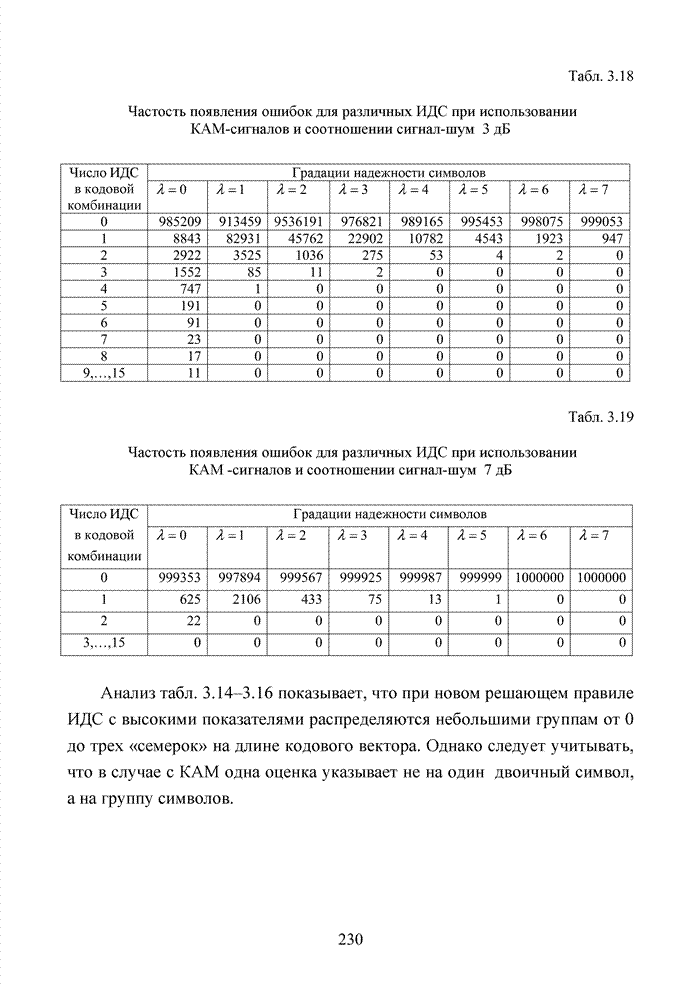
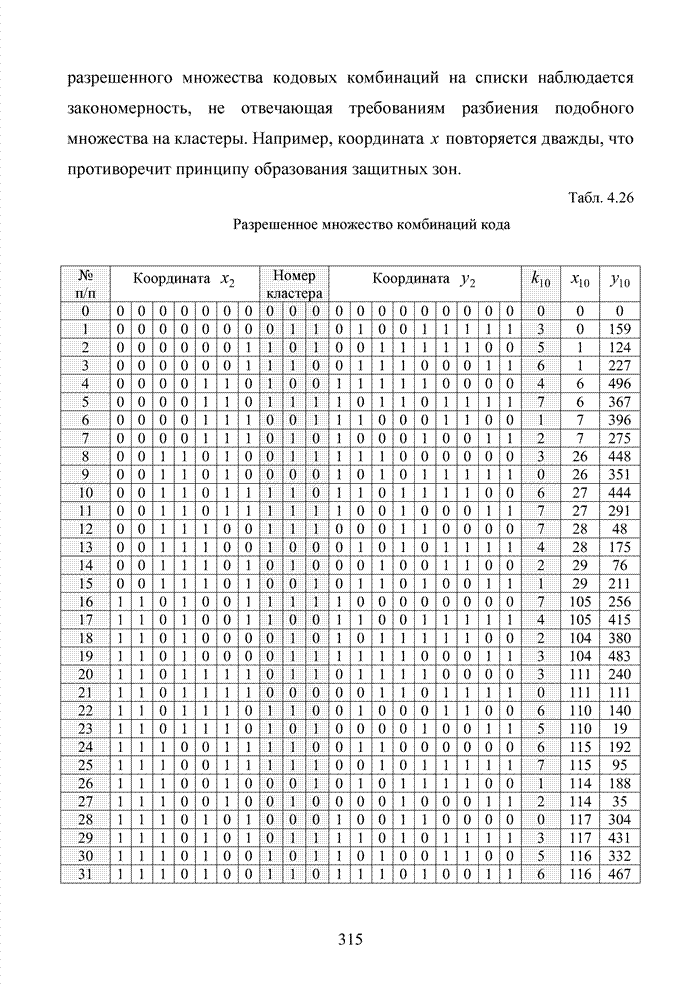
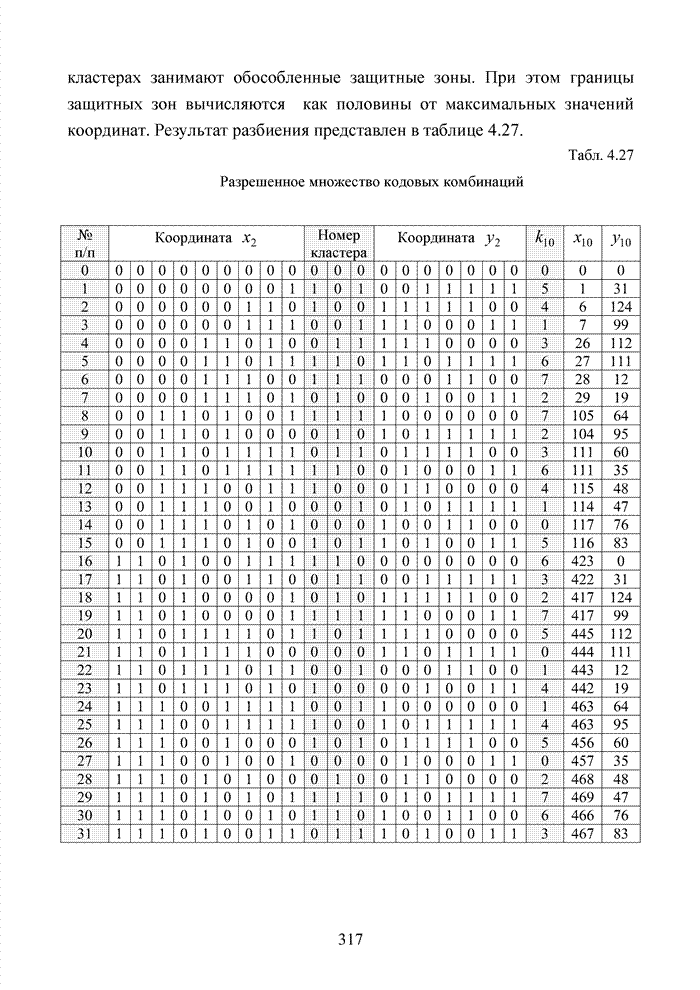
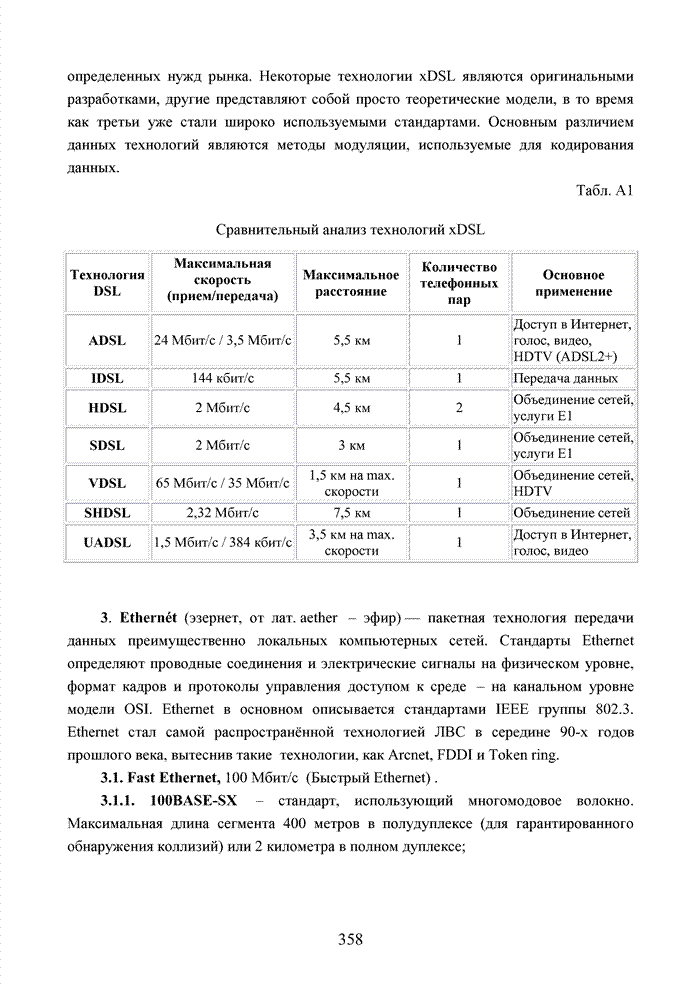
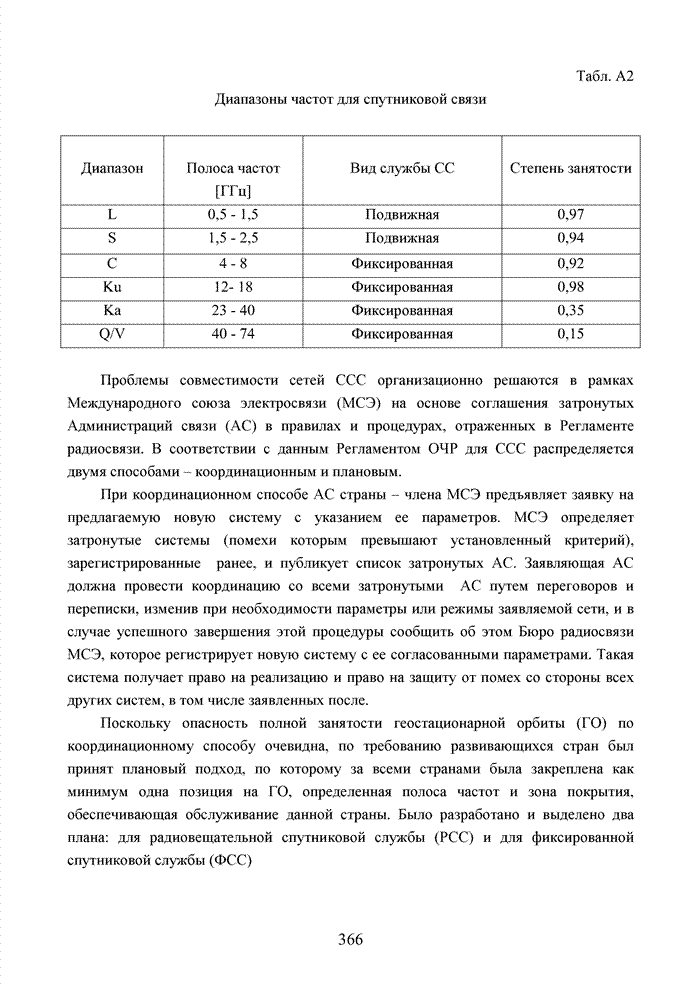
2.4. Модель марковского двоичного канала со стираниями
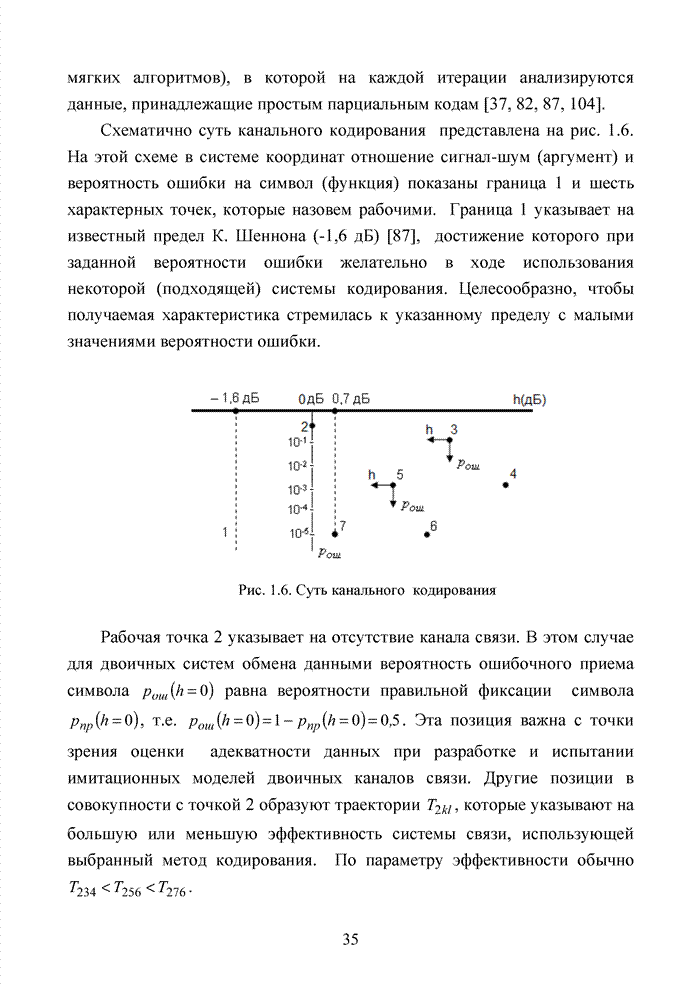
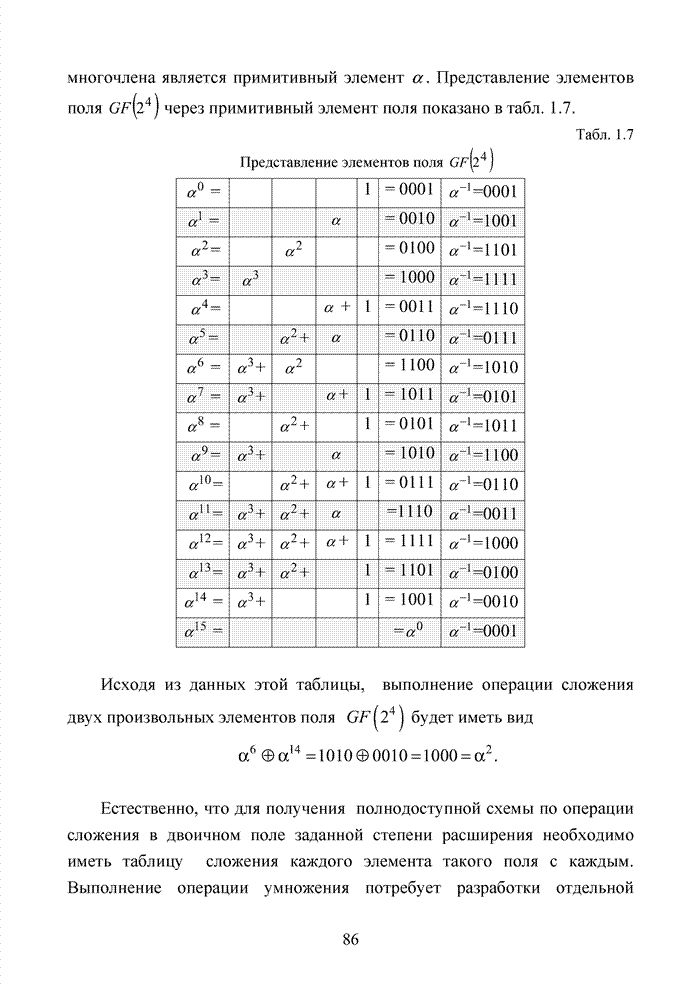
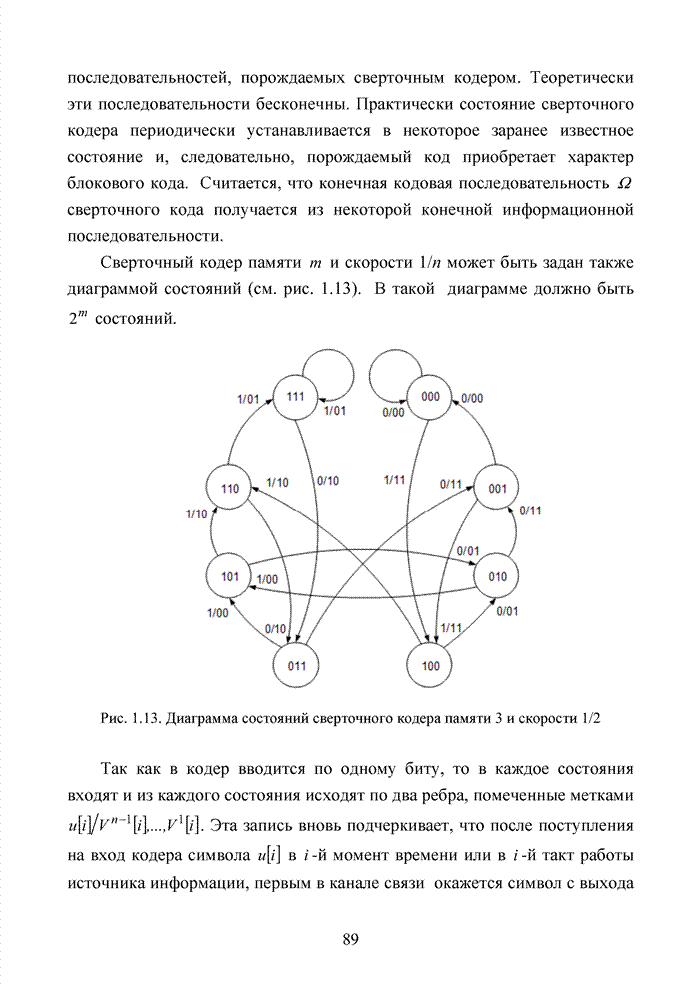
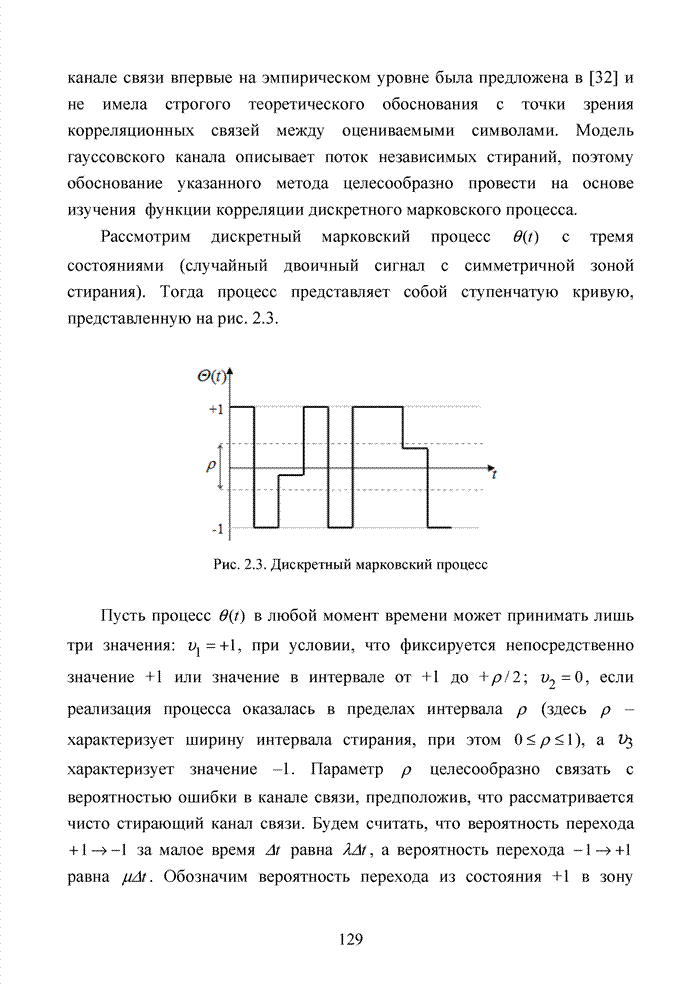
Для многих практически важных приложений и особенно в мобильной связи, стремятся минимизировать стоимость декодера. Декодер в современных системах связи представляет собой интегральную схему, размещенную в одном чипе. Очень важную роль играют так же надежность в эксплуатации, потребляемая энергия и минимальная мощность принимаемого сигнала. Указанный комплекс требований удается реализовать при применении целочисленных оценок надежности символов. Возможность получения целочисленных оценок в стирающем канале связи впервые на эмпирическом уровне была предложена в [32] и не имела строгого теоретического обоснования с точки зрения корреляционных связей между оцениваемыми символами. Модель гауссовского канала описывает поток независимых стираний, поэтому обоснование указанного метода целесообразно провести на основе изучения функции корреляции дискретного марковского процесса.
Рассмотрим дискретный
марковский процесс ![]() с
тремя состояниями (случайный двоичный сигнал с симметричной зоной стирания).
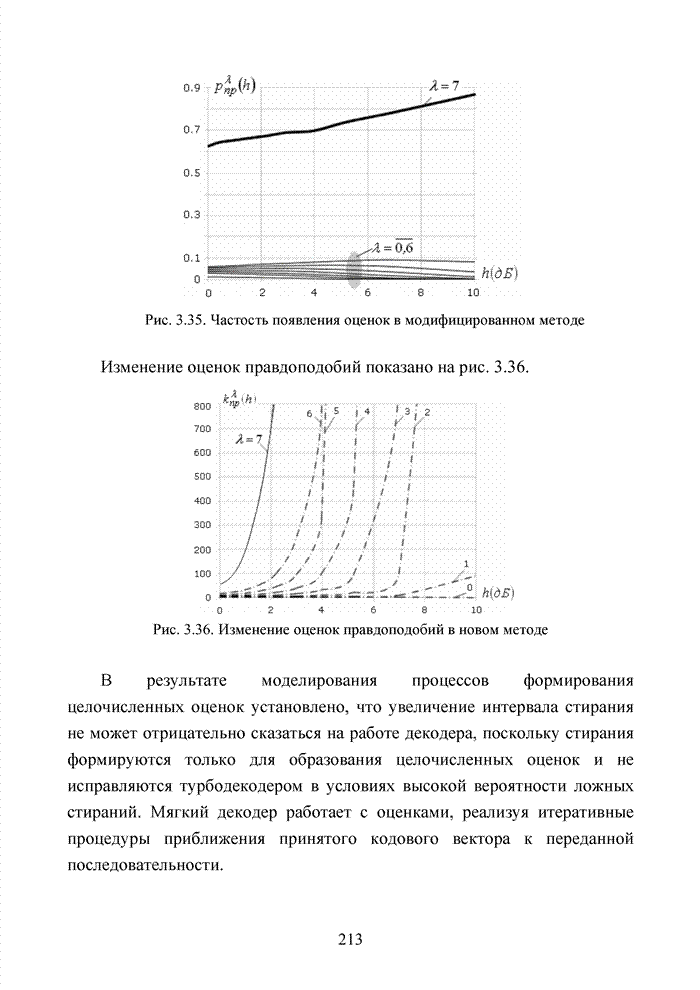
Тогда процесс представляет собой ступенчатую кривую, представленную на рис. 2.3.
с
тремя состояниями (случайный двоичный сигнал с симметричной зоной стирания).
Тогда процесс представляет собой ступенчатую кривую, представленную на рис. 2.3.

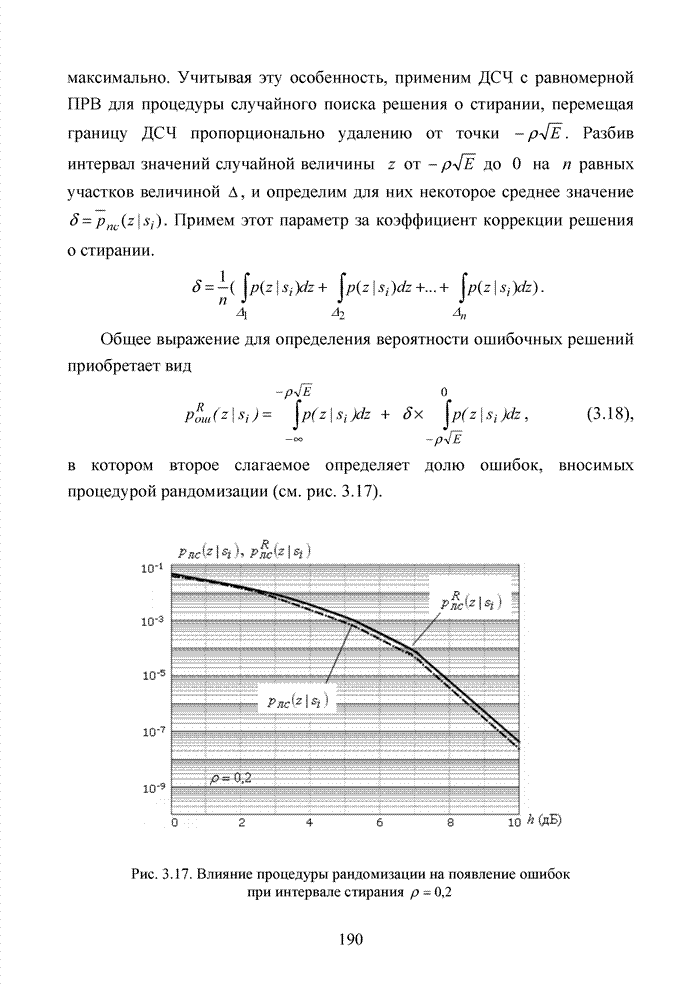
Рис. 2.3. Дискретный марковский процесс
Пусть процесс ![]() в любой момент времени
может принимать лишь три значения:
в любой момент времени
может принимать лишь три значения: ![]() , при условии, что фиксируется
непосредственно значение +1 или значение в интервале от +1 до +
, при условии, что фиксируется
непосредственно значение +1 или значение в интервале от +1 до +![]() ;
; ![]() , если реализация процесса
оказалась в пределах интервала
, если реализация процесса
оказалась в пределах интервала ![]() (здесь
(здесь ![]() – характеризует ширину интервала
стирания, при этом
– характеризует ширину интервала
стирания, при этом ![]() ),
а
),
а ![]() характеризует
значение –1. Параметр
характеризует
значение –1. Параметр ![]() целесообразно связать с вероятностью
ошибки в канале связи, предположив, что рассматривается чисто стирающий канал
связи. Будем считать, что вероятность перехода
целесообразно связать с вероятностью
ошибки в канале связи, предположив, что рассматривается чисто стирающий канал
связи. Будем считать, что вероятность перехода ![]() за малое время
за малое время ![]() равна
равна ![]() , а вероятность перехода
, а вероятность перехода ![]() равна
равна ![]() . Обозначим вероятность
перехода из состояния +1 в зону стирания за время
. Обозначим вероятность
перехода из состояния +1 в зону стирания за время ![]() или из состояния -1 в ту же зону через
или из состояния -1 в ту же зону через ![]() Пусть для такого
процесса известны вероятности начального состояния
Пусть для такого
процесса известны вероятности начального состояния
![]() ,
, ![]() и
и ![]() .
.
Определим вероятности
перехода ![]() (где
(где
![]() ,
, ![]() ,
, ![]() ,
, ![]() ), здесь
), здесь ![]() условные вероятности нахождения системы
в состоянии
условные вероятности нахождения системы
в состоянии ![]() в
момент времени
в
момент времени ![]() ,
если известно, что в предшествующий момент времени
,
если известно, что в предшествующий момент времени ![]() она находилась в состоянии
она находилась в состоянии ![]() . Если принять
. Если принять ![]() , то канала вырождается
в двоичный канал и описывается марковским процессом с двумя состояниями. Если
параметр
, то канала вырождается
в двоичный канал и описывается марковским процессом с двумя состояниями. Если
параметр ![]() и
составляет долю интервала от +1 до -1, то вероятности перехода
и
составляет долю интервала от +1 до -1, то вероятности перехода ![]() и
и ![]() изменятся пропорционально
принятому значению
изменятся пропорционально
принятому значению ![]() .
При
.
При ![]() канал не
имеет смысла, поскольку вырождается в чисто стирающий. Условие нормировки
процесса определяется выражением
канал не
имеет смысла, поскольку вырождается в чисто стирающий. Условие нормировки
процесса определяется выражением
 ,
, ![]() ,
, ![]() . (2.12)
. (2.12)
Обычно [92] вероятности
перехода из одного состояния в другое неотрицательны (![]() ). С учетом условий нормировки
(2.12) получаем, что
). С учетом условий нормировки
(2.12) получаем, что ![]() . Переходя к пределу при
. Переходя к пределу при ![]() , для стирающего канала
с тремя состояниями получим систему линейных дифференциальных уравнений
, для стирающего канала
с тремя состояниями получим систему линейных дифференциальных уравнений
 ,
, ![]() (2.13)
(2.13)
В случае разрывных
марковских процессов для малых временных интервалов ![]() и
и ![]() вероятности перехода
вероятности перехода ![]() примут вид:
примут вид: ![]() ,
, ![]() . Отсюда находим
. Отсюда находим ![]() .
. ![]() Так как все коэффициента
Так как все коэффициента ![]() – постоянные величины,
не зависящие от времени, то процесс
– постоянные величины,
не зависящие от времени, то процесс ![]() является однородным. Аналогично для
является однородным. Аналогично для ![]() получаем:
получаем: ![]() ,
, ![]() и
и ![]() . Для
. Для ![]() значения
значения ![]() будут иметь вид:
будут иметь вид: ![]() ,
, ![]() и
и ![]() .
.
Дифференциальные
уравнения, описывающие процесс перехода из одного состояния в такое же
состояние (![]() )
принимают вид:
)
принимают вид:
![]() ,
,
![]() , (2.14)
, (2.14)
![]() .
.
Всего при ![]() получаем систему,
состоящую из девяти дифференциальных уравнений. Условие нормировки для первого
из уравнений (2.14) имеет вид
получаем систему,
состоящую из девяти дифференциальных уравнений. Условие нормировки для первого
из уравнений (2.14) имеет вид ![]() .
.
Для вычисления любого из ![]() соотношений (2.13)
необходимо третье дополнительное условие. Определим его для
соотношений (2.13)
необходимо третье дополнительное условие. Определим его для ![]() , исходя из следующих
соображений.
, исходя из следующих
соображений.
Введение симметричного
интервала стирания приводит к снижению условных вероятностей ![]() и
и ![]() , определенных для канала без
стирания символов. Предположим, что величина указанных изменений пропорциональна
ширине интервала стирания. Тогда
, определенных для канала без
стирания символов. Предположим, что величина указанных изменений пропорциональна
ширине интервала стирания. Тогда
![]() . (2.15)
. (2.15)
Собственно ![]()
![]() , но
, но ![]()
![]() , следовательно
, следовательно ![]() .
.
Тогда ![]() В таком случае первое
из уравнений (2.14) можно записать иначе
В таком случае первое
из уравнений (2.14) можно записать иначе
 (2.16)
(2.16)
Начальные условия для дискретного марковского процесса при решении дифференциальных уравнений определяются как
![]()
Общее решение линейного
неоднородного дифференциального уравнения первого порядка (2.16) с начальным
условием ![]() имеет
вид
имеет
вид
 (2.17)
(2.17)
Здесь ![]() .
.
Если ввести обозначение ![]() , то (2.16) принимает
более удобный вид
, то (2.16) принимает
более удобный вид
 .
(2.18)
.
(2.18)
При ![]() получим значение
получим значение ![]() для двоичного
симметричного канала связи.
для двоичного
симметричного канала связи.
Значение для ![]() найдем с учетом (2.15)
и (2.18).
найдем с учетом (2.15)
и (2.18).

Здесь ![]() . Поскольку
. Поскольку ![]() , то, принимая
, то, принимая ![]() получаем
получаем ![]() и
и
![]()
Отсюда: ![]() Тогда
Тогда ![]() .
.
Оставшиеся значения переходных вероятностей находим аналогичным образом
![]()
 (2.19)
(2.19)
 (2.20)
(2.20)
Отсюда видно, что
рассматриваемый марковский процесс с тремя состояниями является однородным, так
как вероятности перехода зависят только от разности фигурирующих в них времен.
Кроме этого, процесс эргодичен, поскольку при ![]() существуют предельные значения
вероятностей перехода
существуют предельные значения
вероятностей перехода

![]() ;
;  ,
(2.21)
,
(2.21)
которые определяют вероятности стационарного состояния. Вероятности стационарных состояний определяются системой алгебраических выражений
![]()
![]() (2.22)
(2.22)
Используя (2.21), можно убедиться в правильности найденных решений. Для последующих алгебраических преобразований целесообразно учесть ряд условий, непосредственно вытекающих из анализа физического процесса:
во-первых, из условия
симметрии получаем ![]() ;
;
во-вторых, ![]() и
и ![]() , а значения
, а значения ![]() выбираются в зависимости от
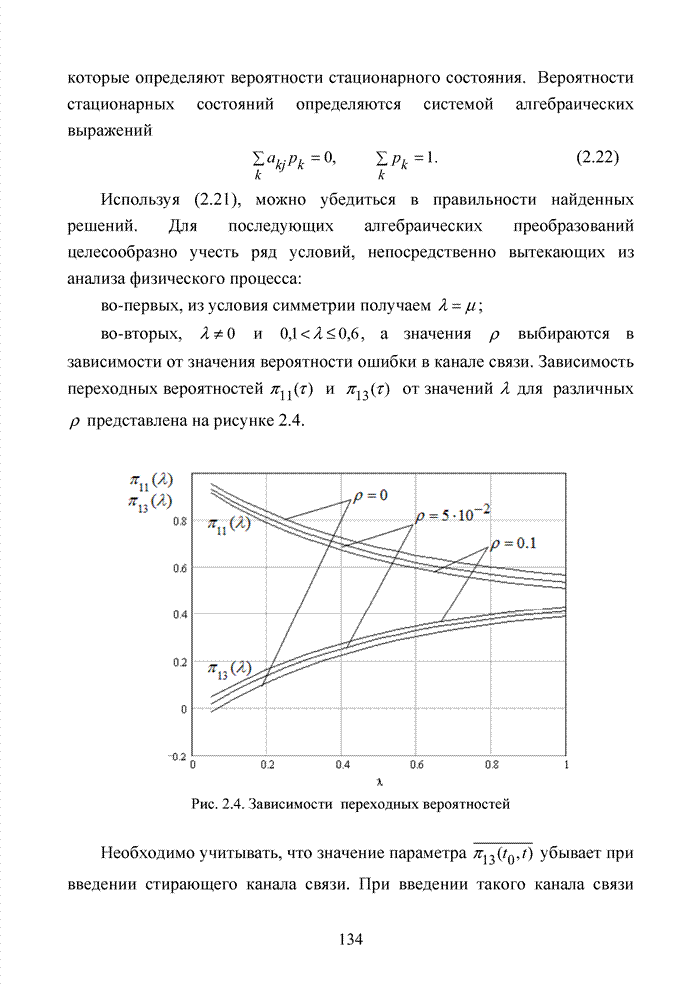
значения вероятности ошибки в канале связи. Зависимость переходных вероятностей
выбираются в зависимости от
значения вероятности ошибки в канале связи. Зависимость переходных вероятностей
![]() и
и ![]() от значений
от значений ![]() для различных
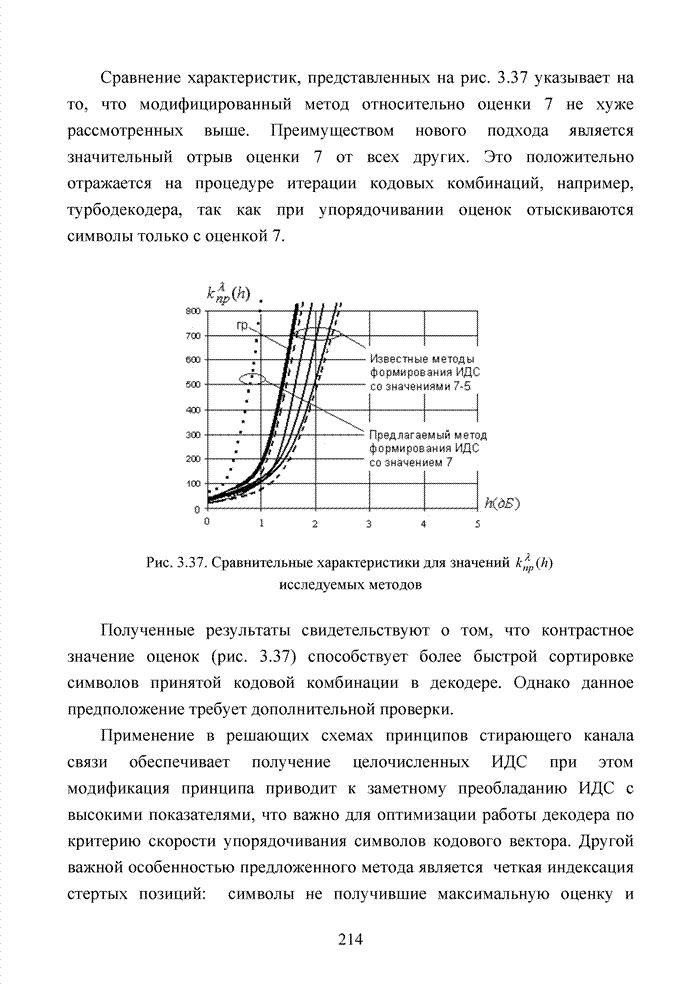
для различных ![]() представлена на
рисунке 2.4.
представлена на
рисунке 2.4.

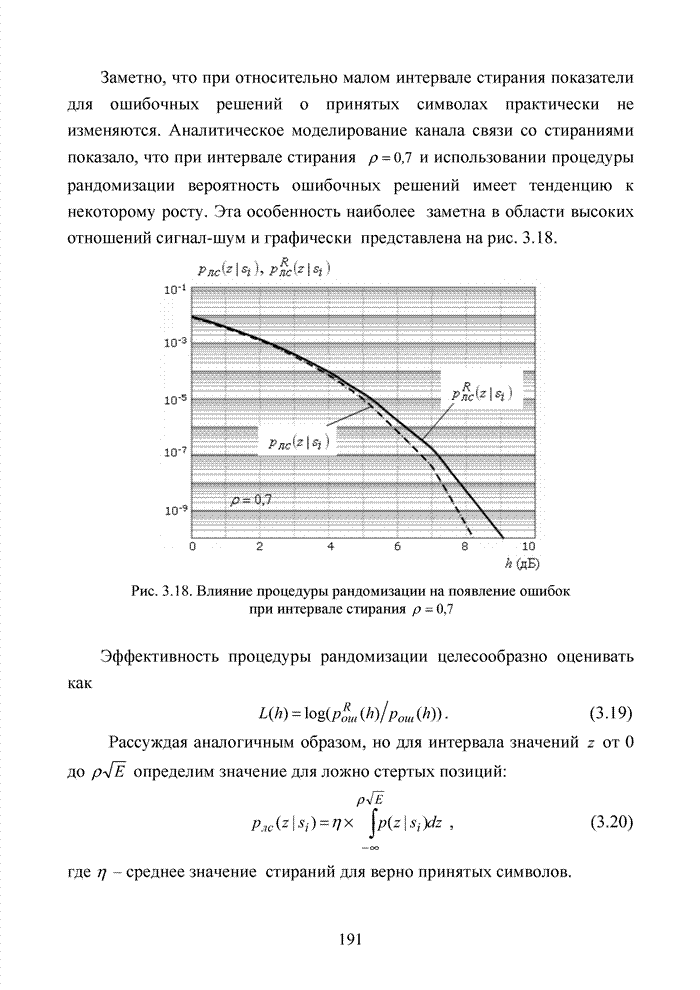
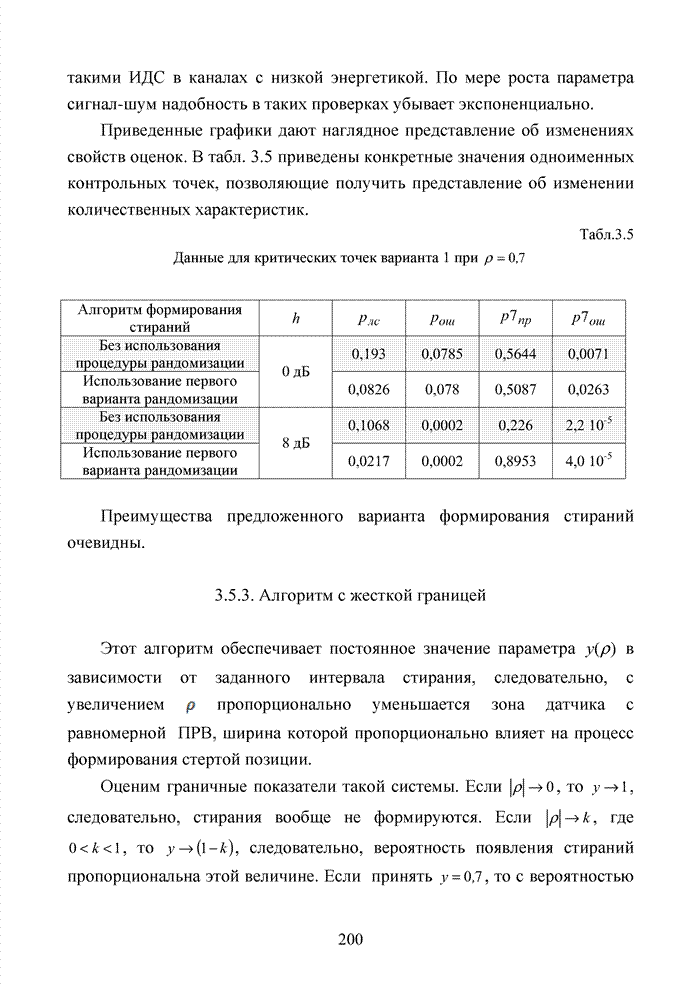
Рис. 2.4. Зависимости переходных вероятностей
Необходимо учитывать, что
значение параметра ![]() убывает
при введении стирающего канала связи. При введении такого канала связи
необходимо проверять выполнение соотношения
убывает
при введении стирающего канала связи. При введении такого канала связи
необходимо проверять выполнение соотношения ![]() . Приведенное соотношение может нарушаться
при незначительных значениях
. Приведенное соотношение может нарушаться
при незначительных значениях ![]() , обычно не встречающихся на практике.
, обычно не встречающихся на практике.
Зная вероятности начального состояния и вероятности перехода, находим общие выражения для абсолютных вероятностей состояний
 (2.23)
(2.23)
 (2.24)
(2.24)
Здесь учтено, что ![]() и
и ![]() – вероятность стационарного
состояния. По определению, среднее значение процесса
– вероятность стационарного
состояния. По определению, среднее значение процесса ![]() при указанных условиях равно
при указанных условиях равно
 (2.25)
(2.25)
Подставим соответствующие выражения вероятностей перехода и получим

![]() . (2.26)
. (2.26)
Корреляционная функция процесса имеет вид:
![]() ,
, ![]() .
.
Расписав, по определению, среднее значение произведения, имеем

учтено, что
![]() и
и ![]() .
(2.27)
.
(2.27)
Отсюда:
 (2.28)
(2.28)
Здесь в качестве
вероятности начального состояния взята вероятность стационарного состояния ![]() . В данном случае
процесс
. В данном случае
процесс ![]() будет
стационарным с момента времени
будет
стационарным с момента времени ![]() .
.
На основании четности
корреляционной функции стационарного процесса ![]() приходим к следующей окончательной
формуле, справедливой для положительных и отрицательных значений
приходим к следующей окончательной
формуле, справедливой для положительных и отрицательных значений ![]() ,
,
![]()
 . (2.29)
. (2.29)
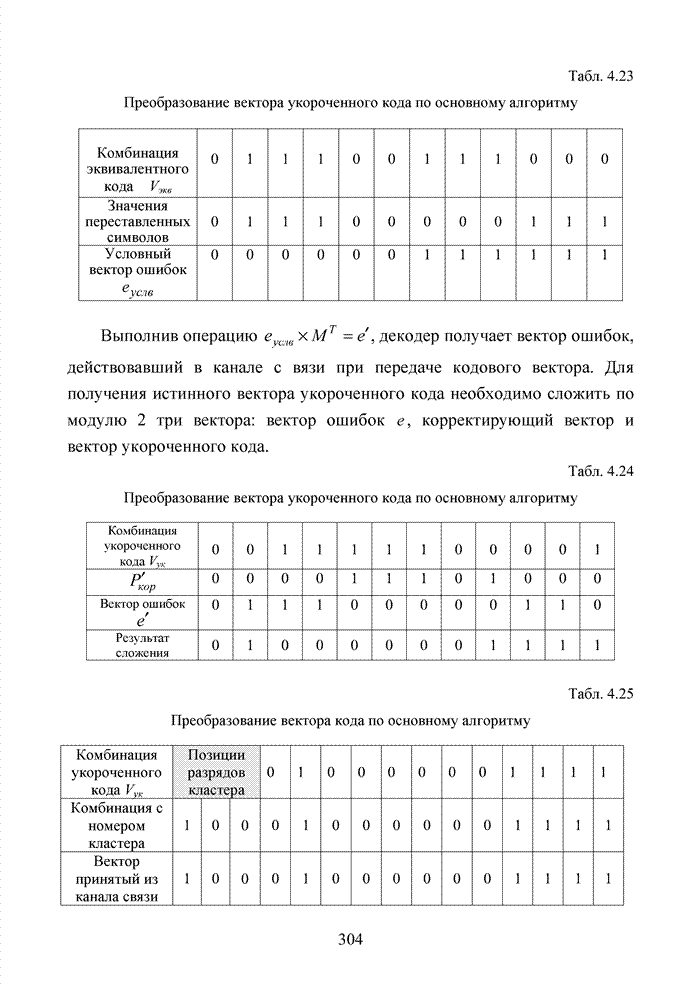
Полученное выражение имеет относительно сложный вид, однако по мере улучшения характеристик канала связи (уменьшения вероятности ошибки) значение (2.29) быстро сходится к выражению вида
![]() ,
(2.30)
,
(2.30)
поскольку ![]() и
и ![]() стремятся к 0. Корреляционная функция
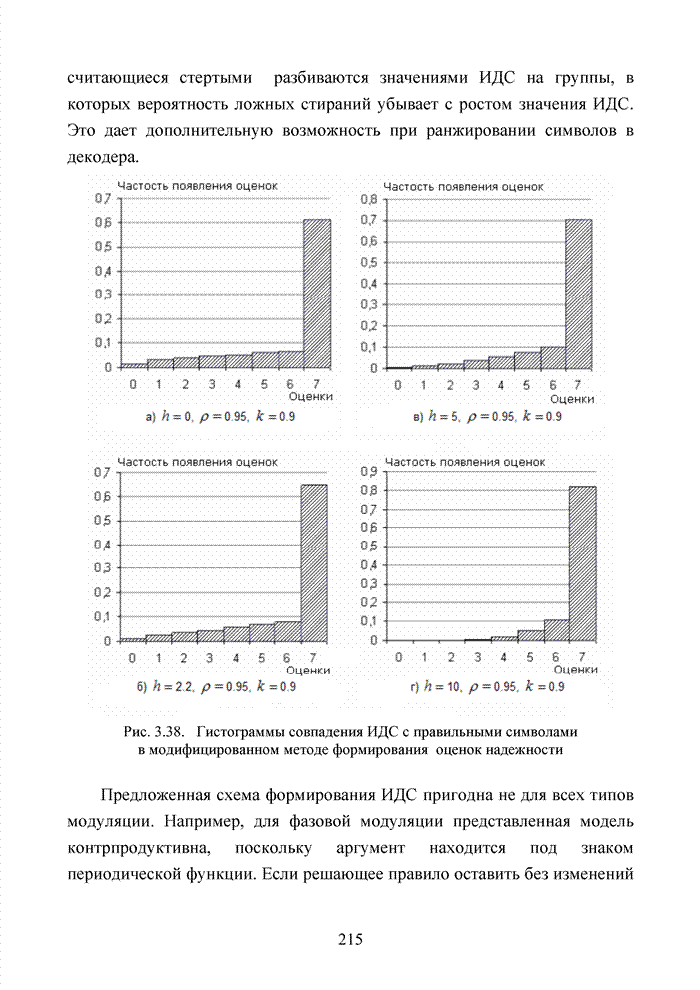
стремятся к 0. Корреляционная функция ![]() для характерных
значений
для характерных
значений ![]() имеет
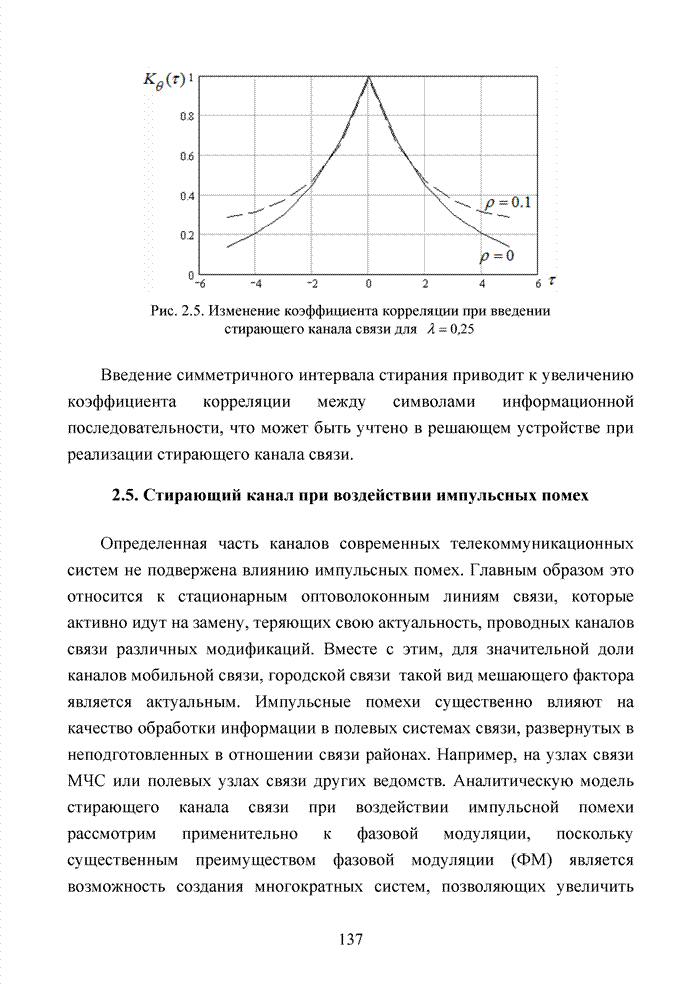
вид, представленный на рис. 2.5.
имеет
вид, представленный на рис. 2.5.

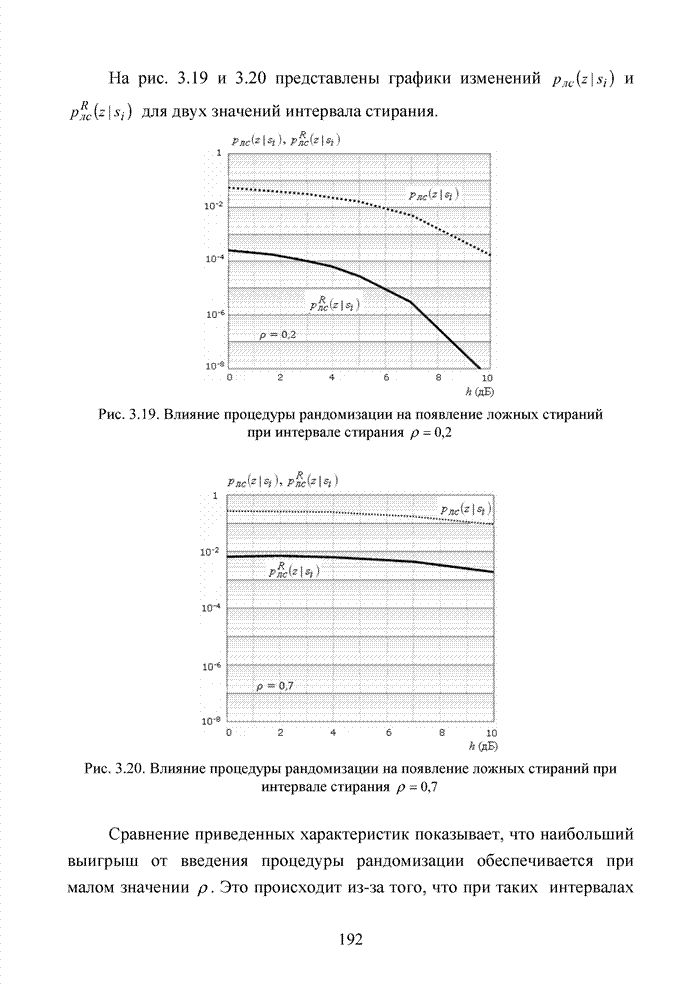
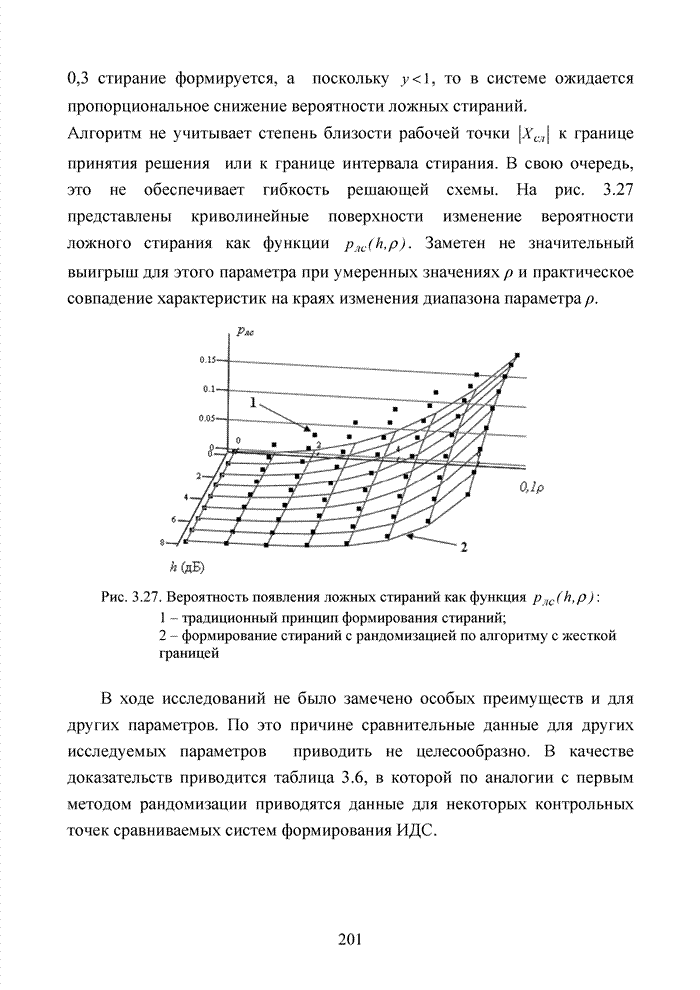
Рис. 2.5. Изменение коэффициента корреляции при
введении
стирающего канала связи для ![]()
Введение симметричного интервала стирания приводит к увеличению коэффициента корреляции между символами информационной последовательности, что может быть учтено в решающем устройстве при реализации стирающего канала связи.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
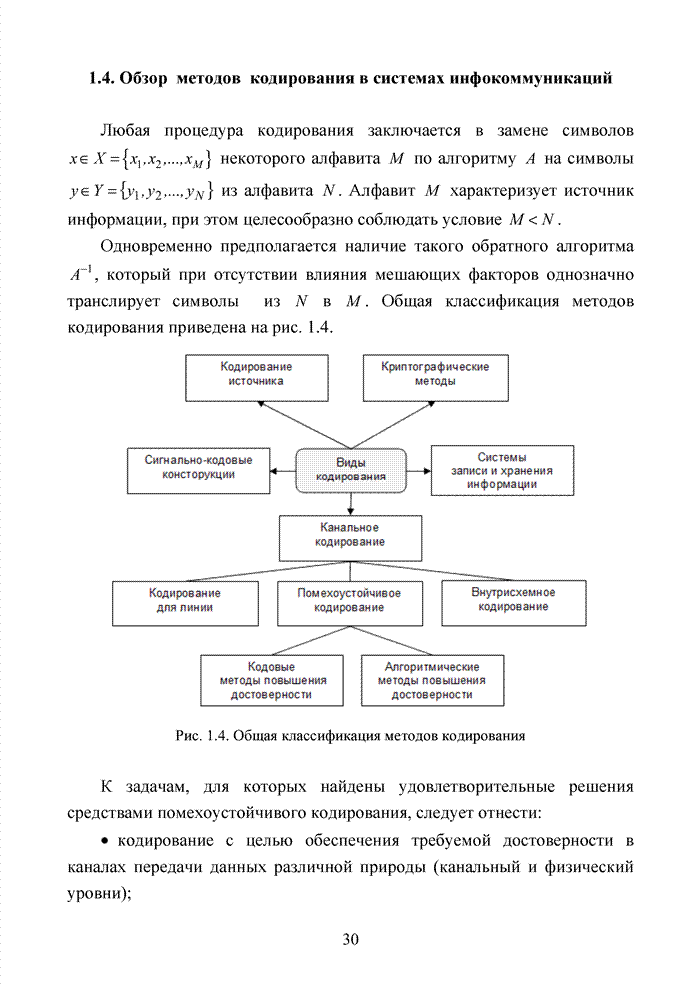
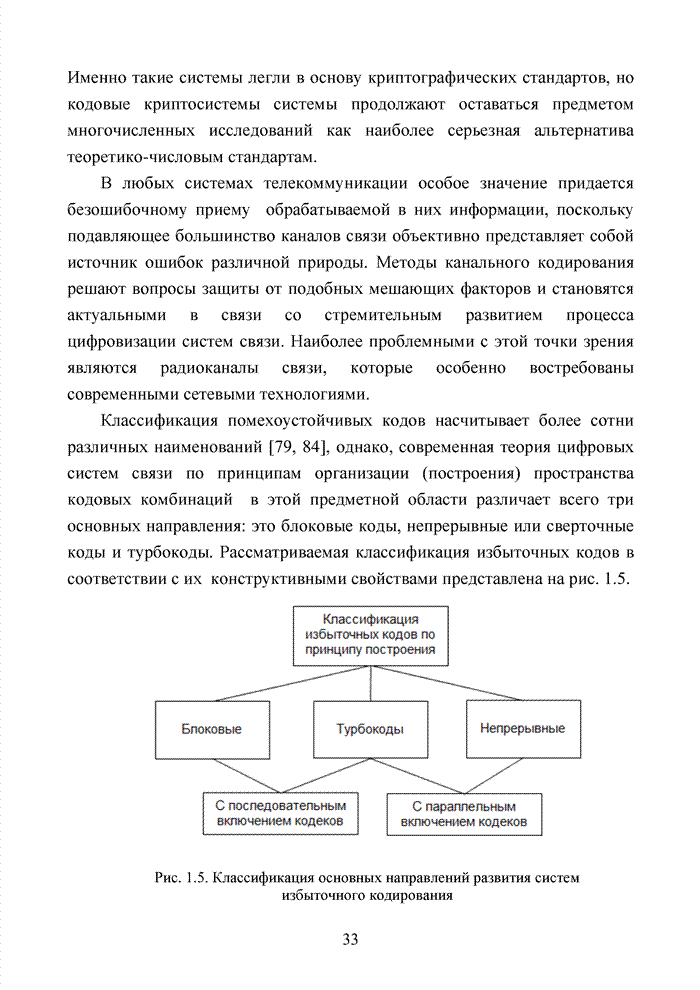
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
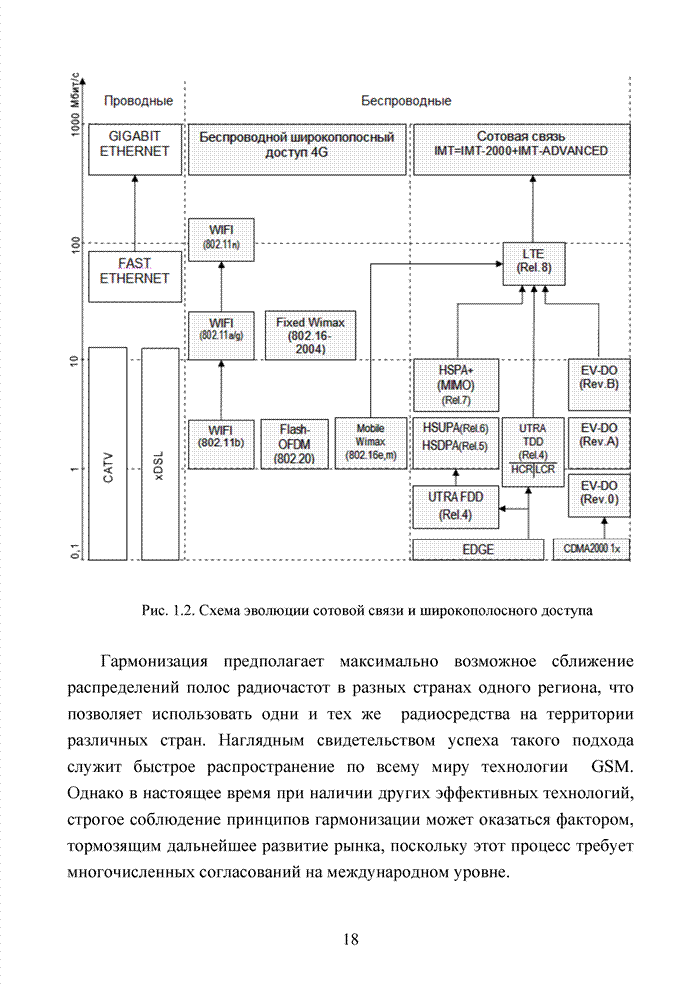
- 1.1. Инфокоммуникационные технологии нового поколения
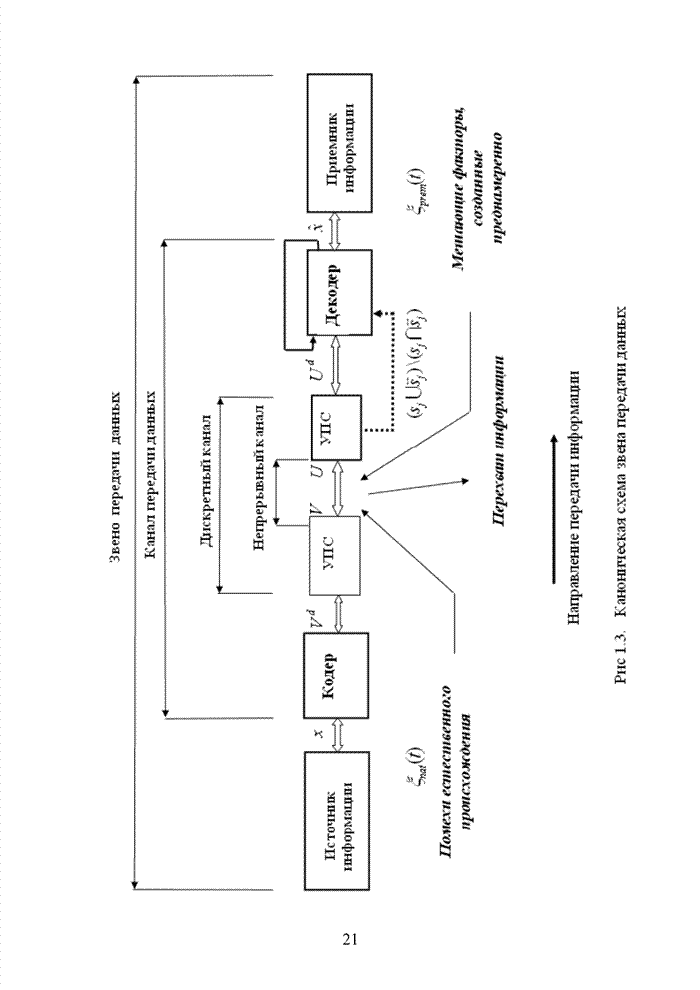
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
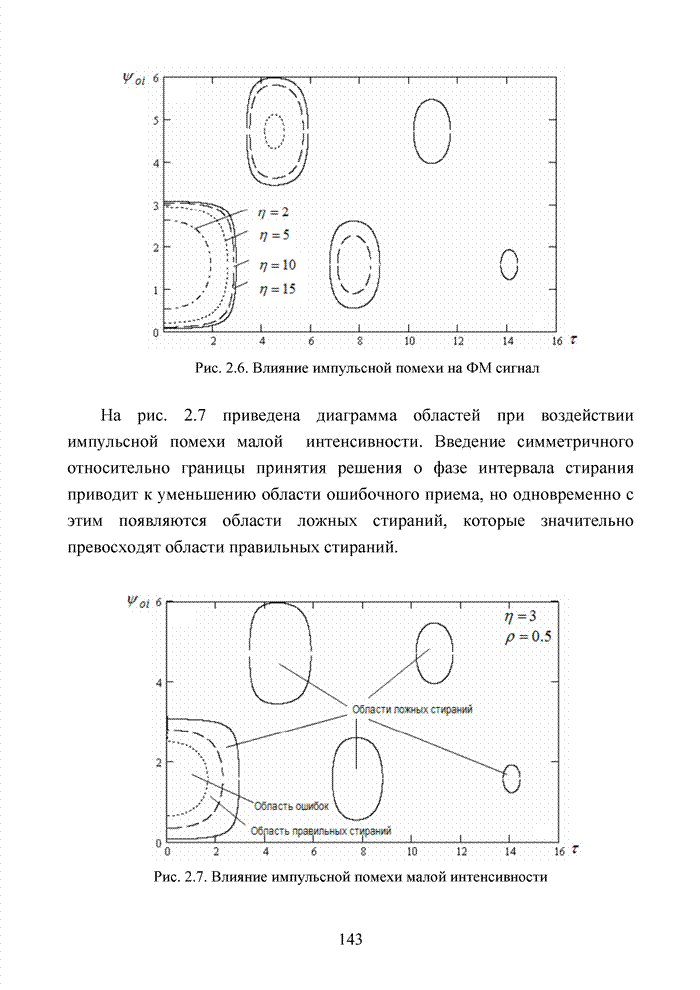
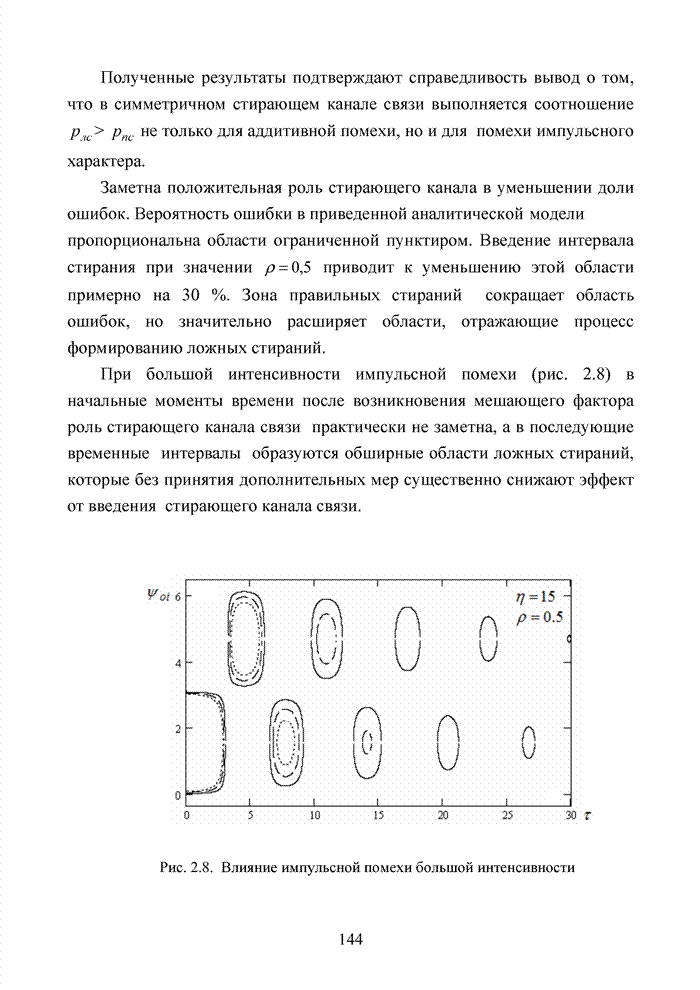
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
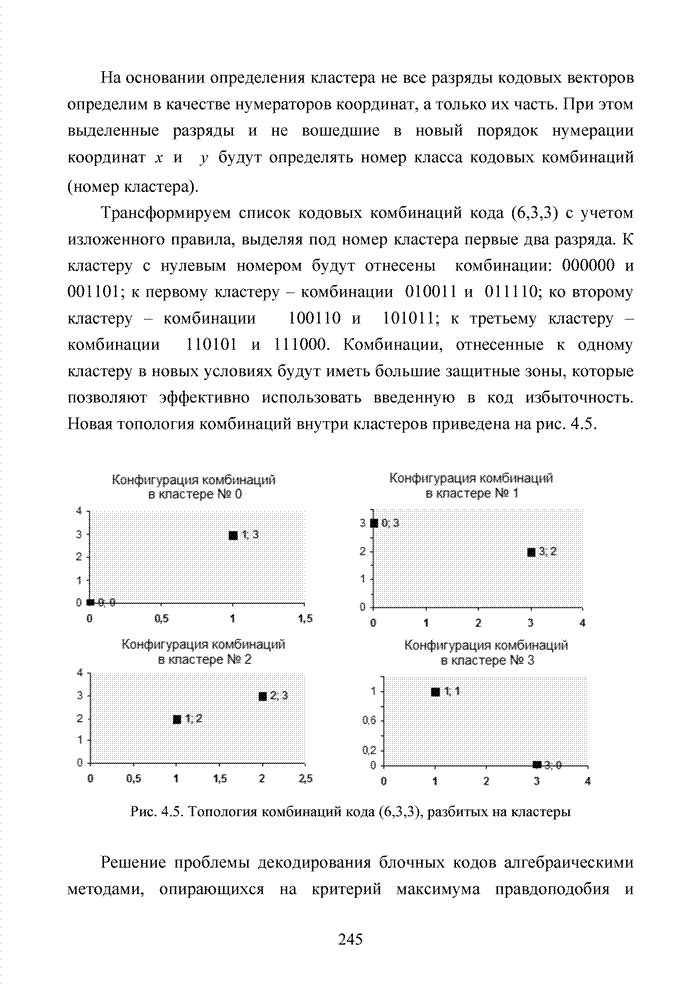
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
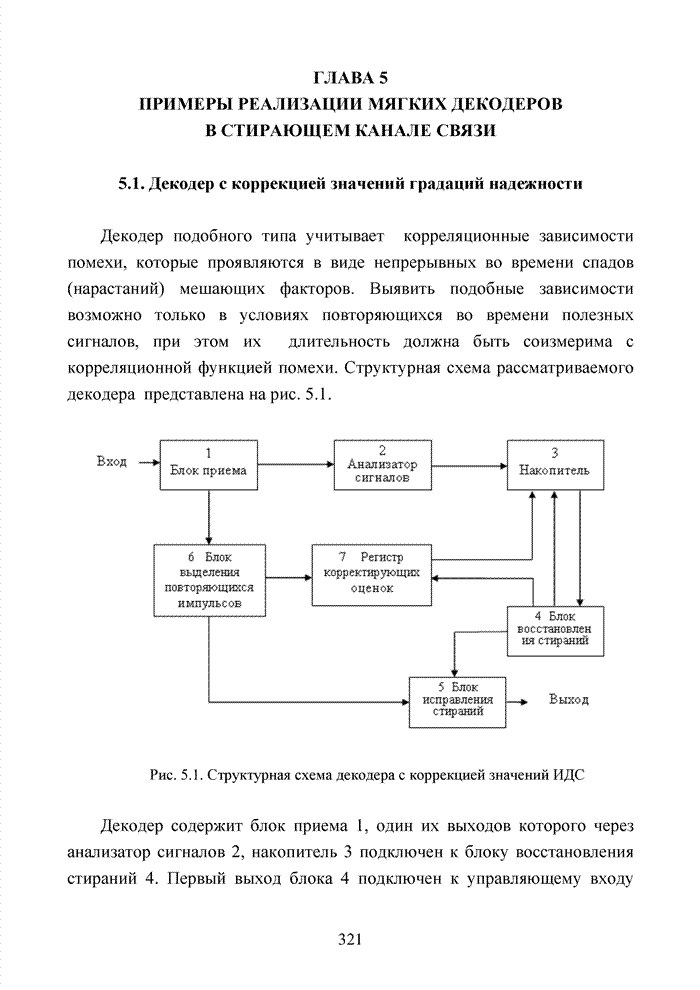
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
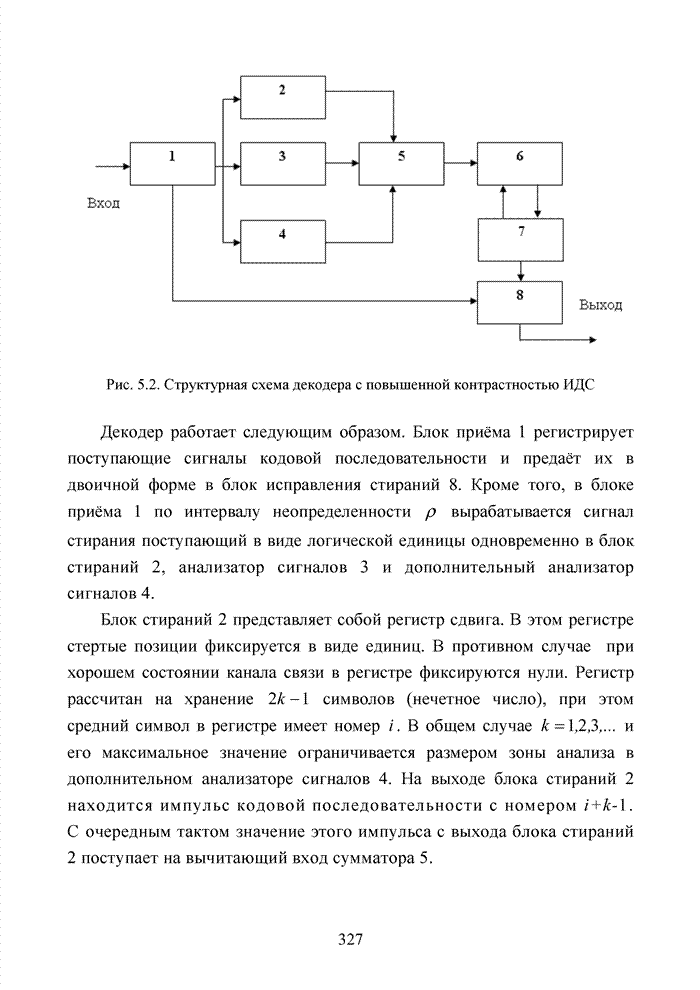
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
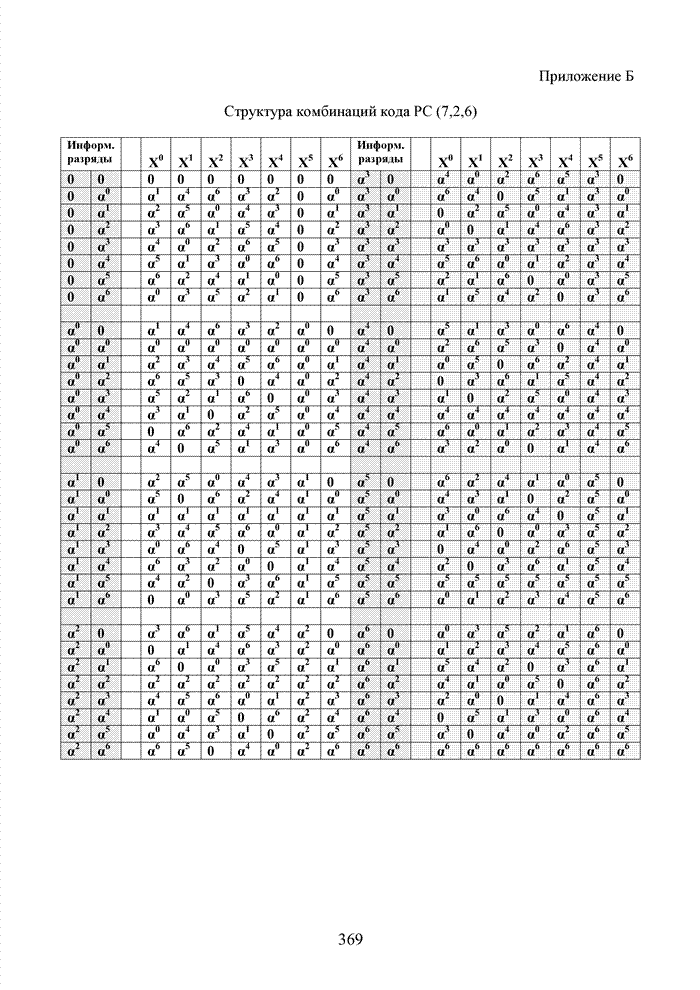
- Приложение Б Структура комбинаций кода РС (7,2,6)
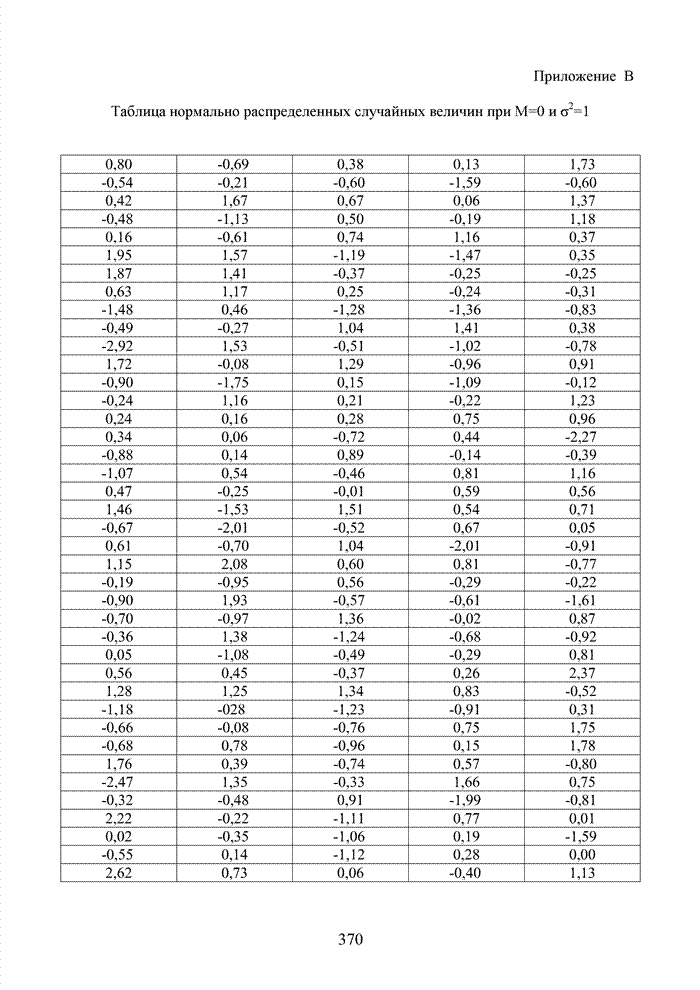
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК