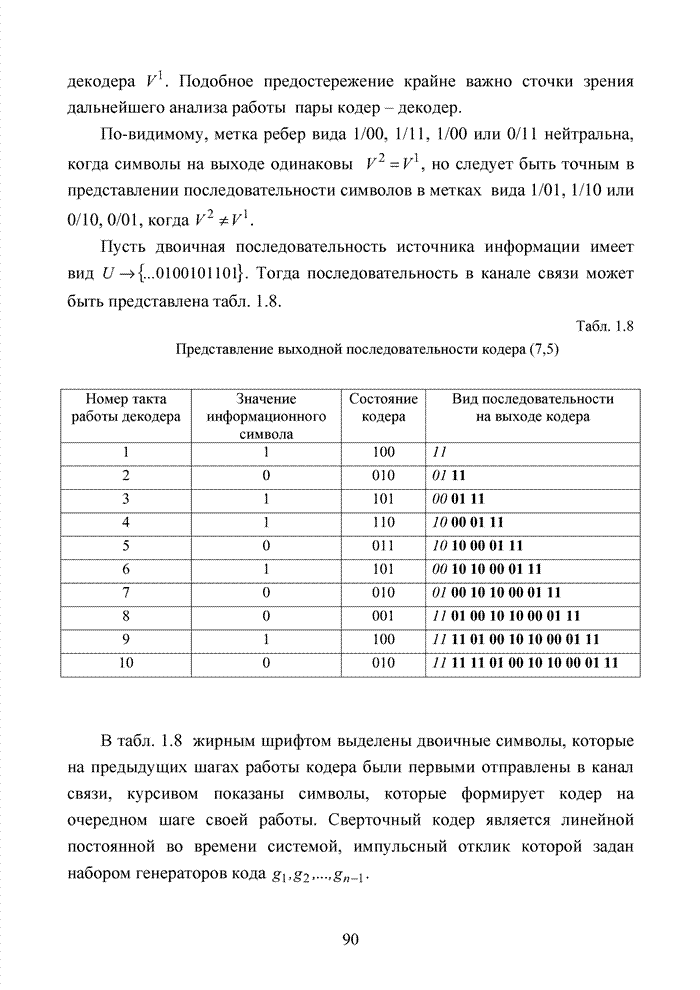
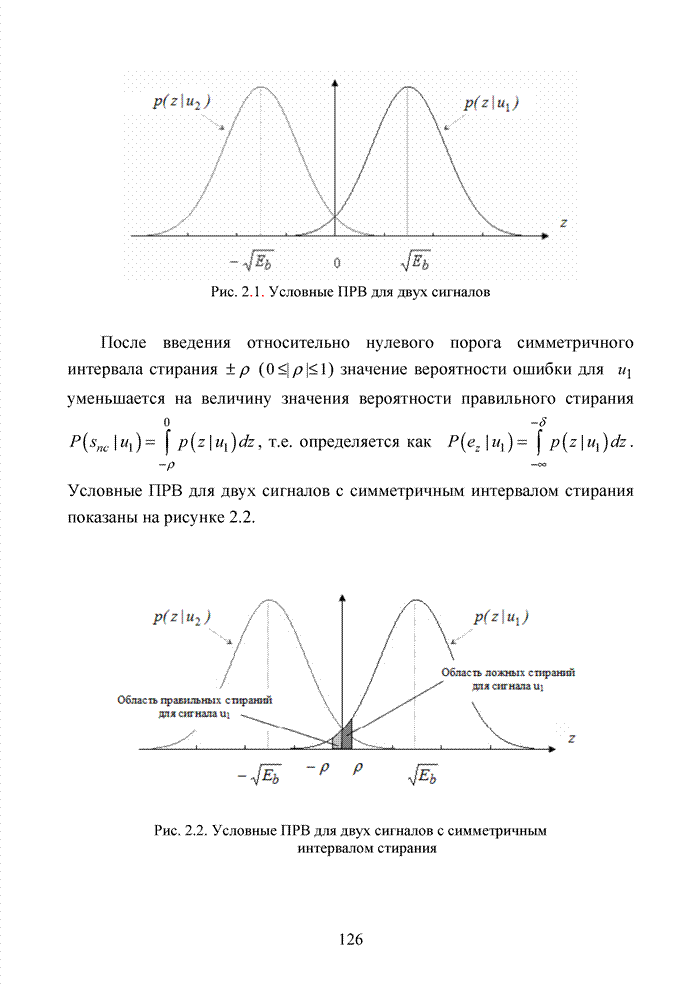
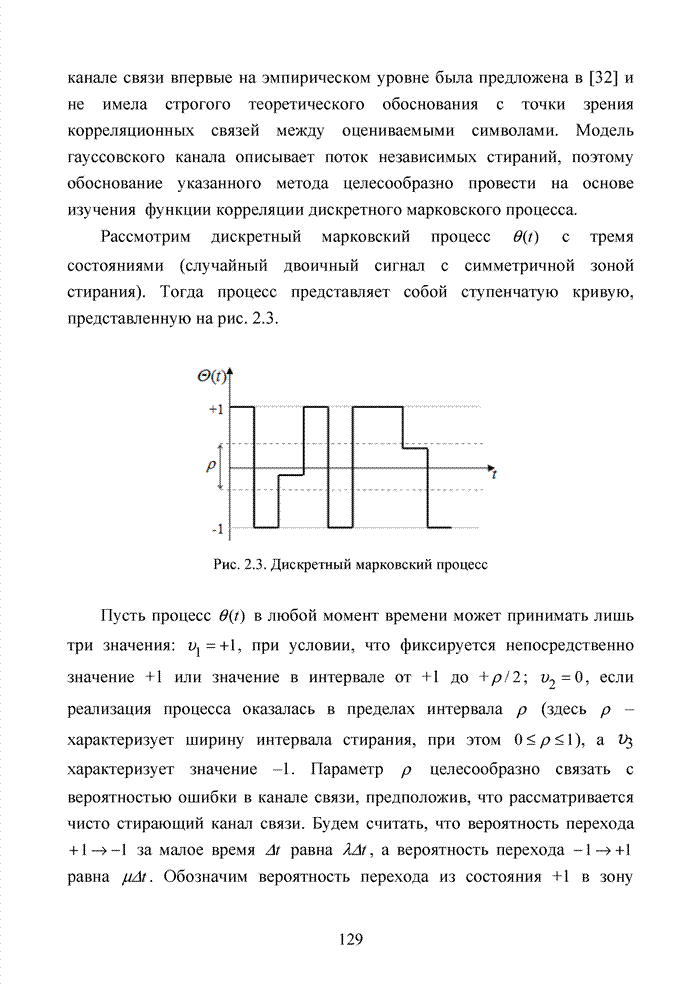
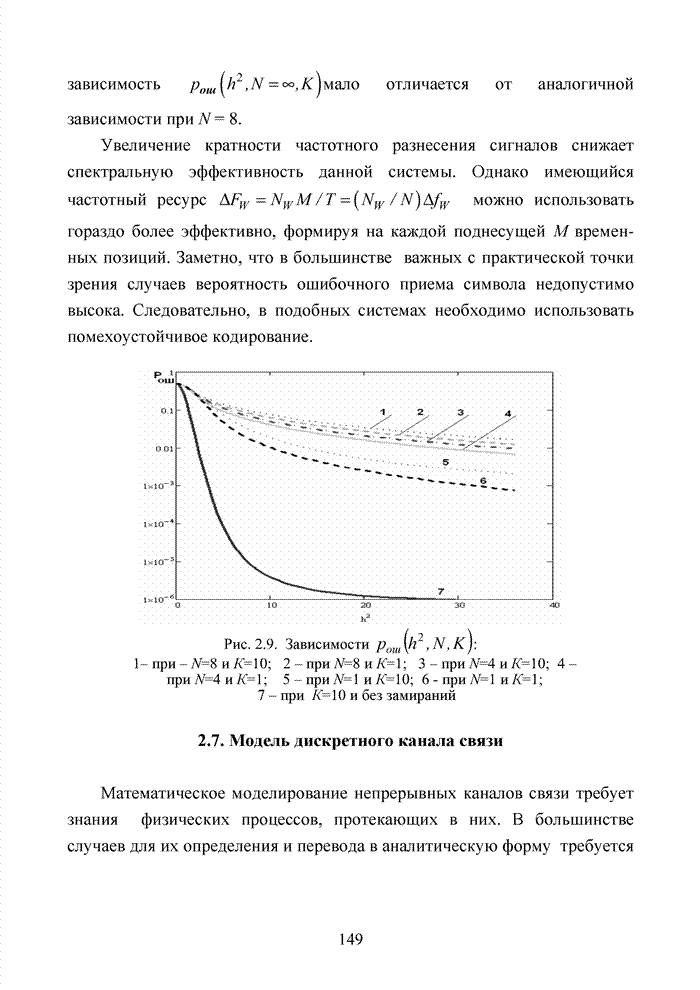
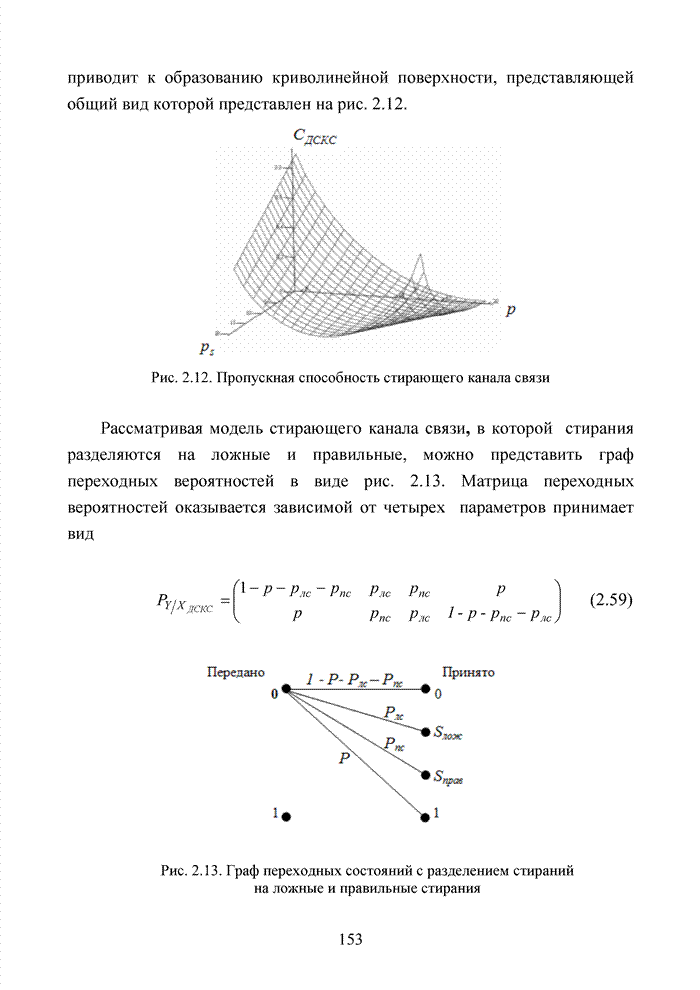
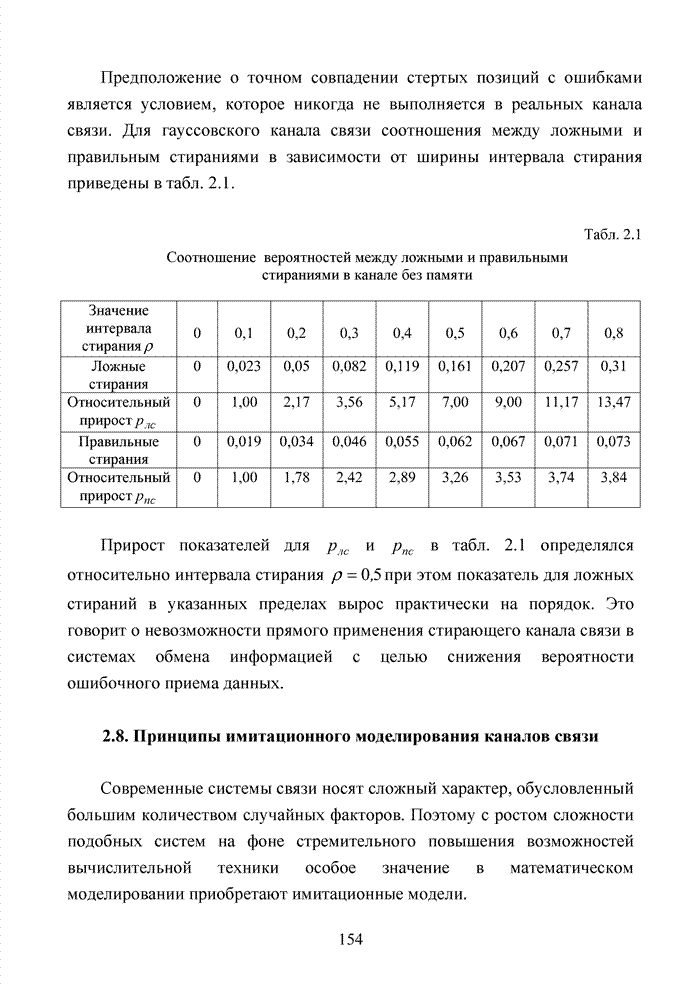
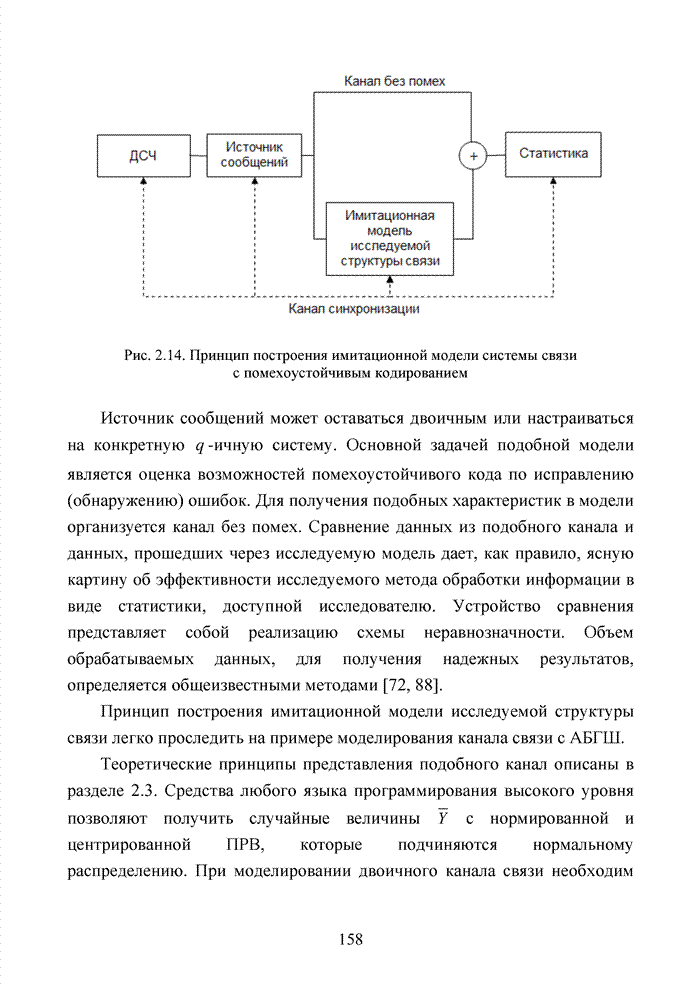
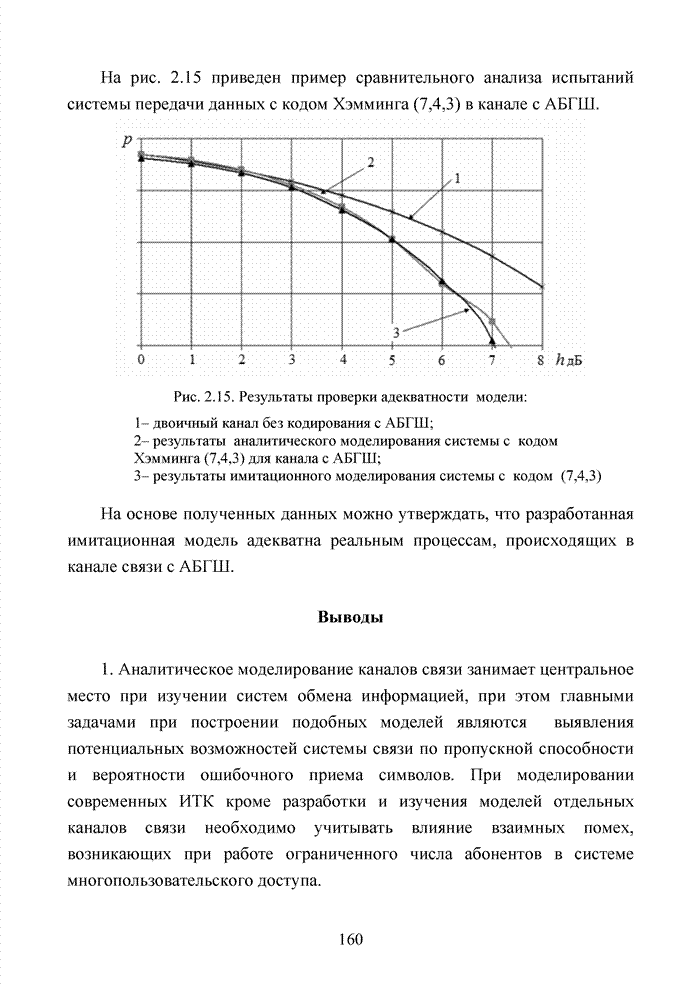
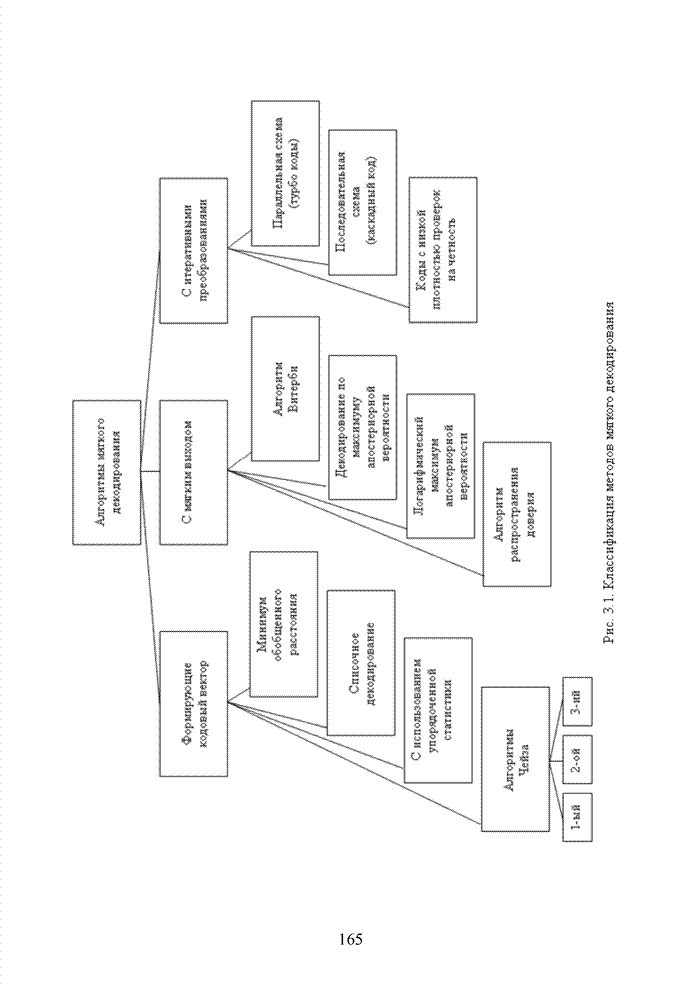
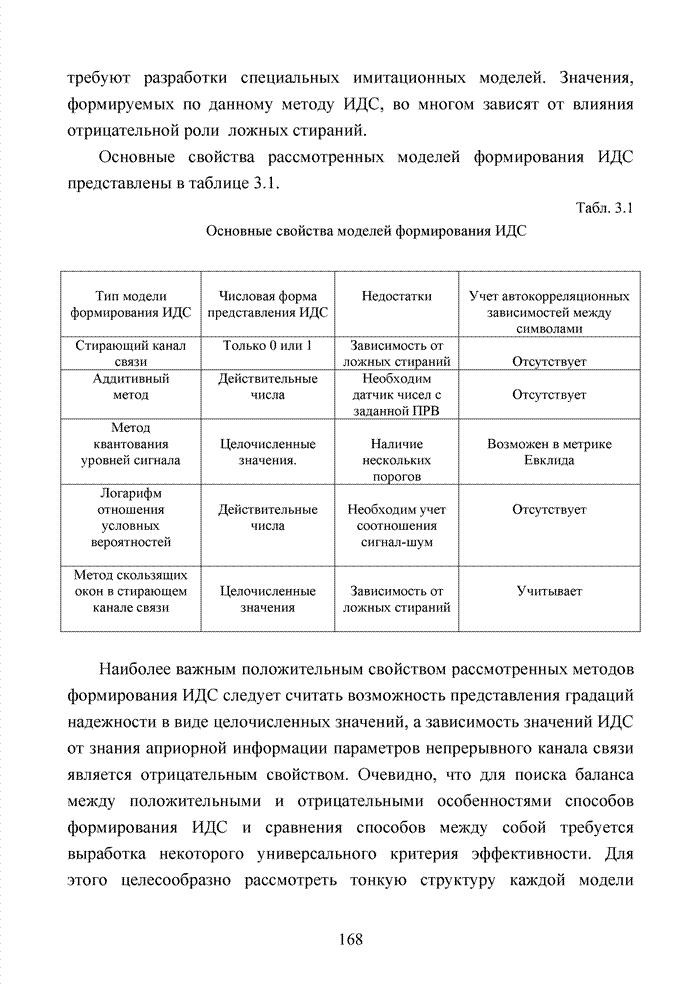
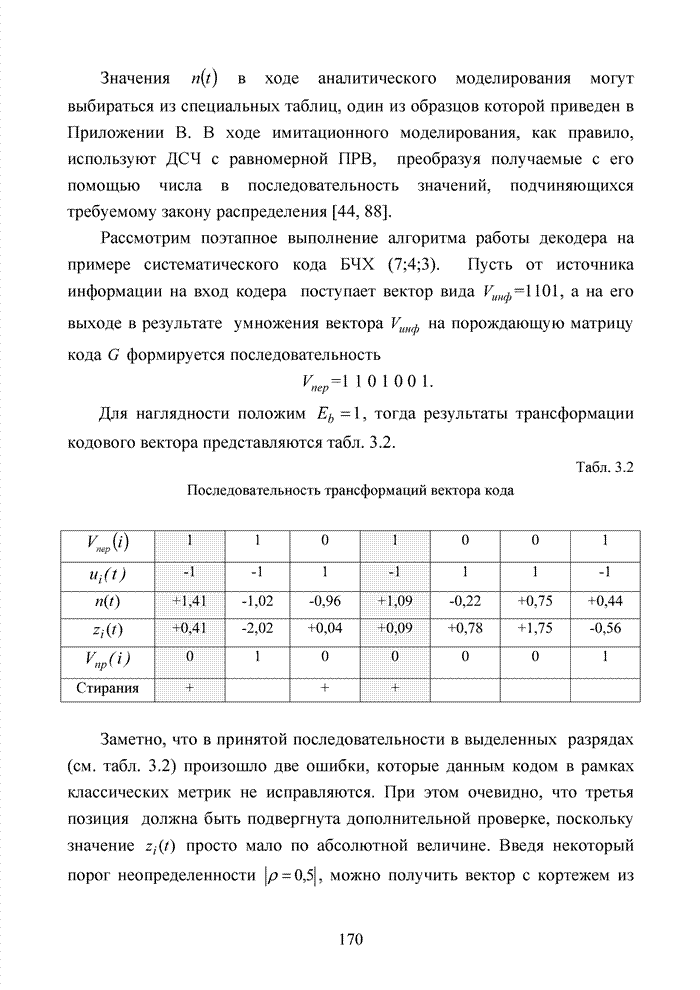
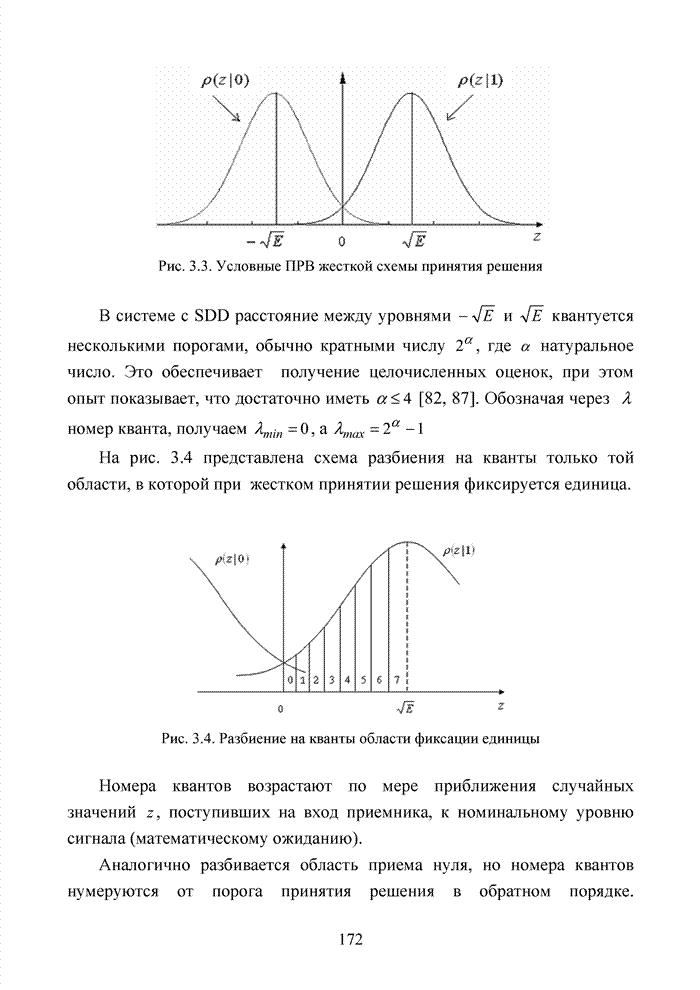
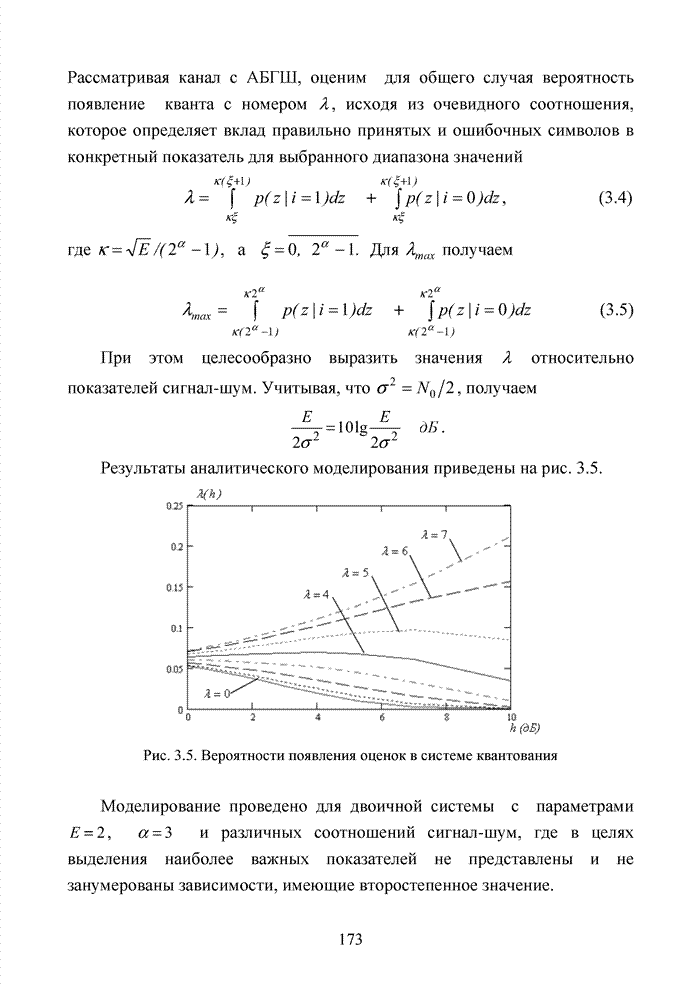
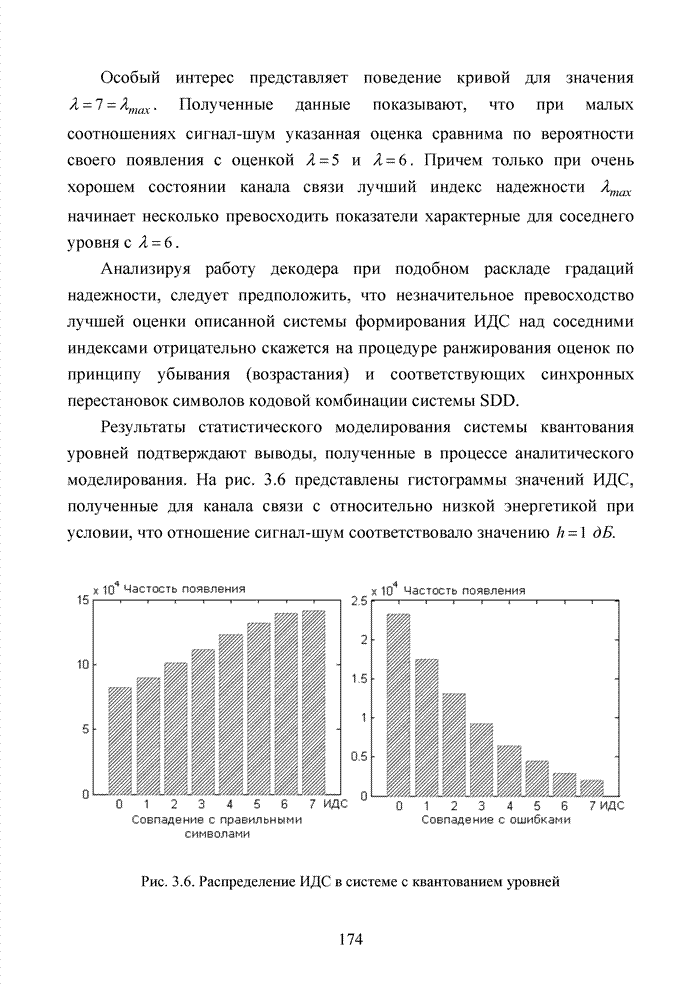
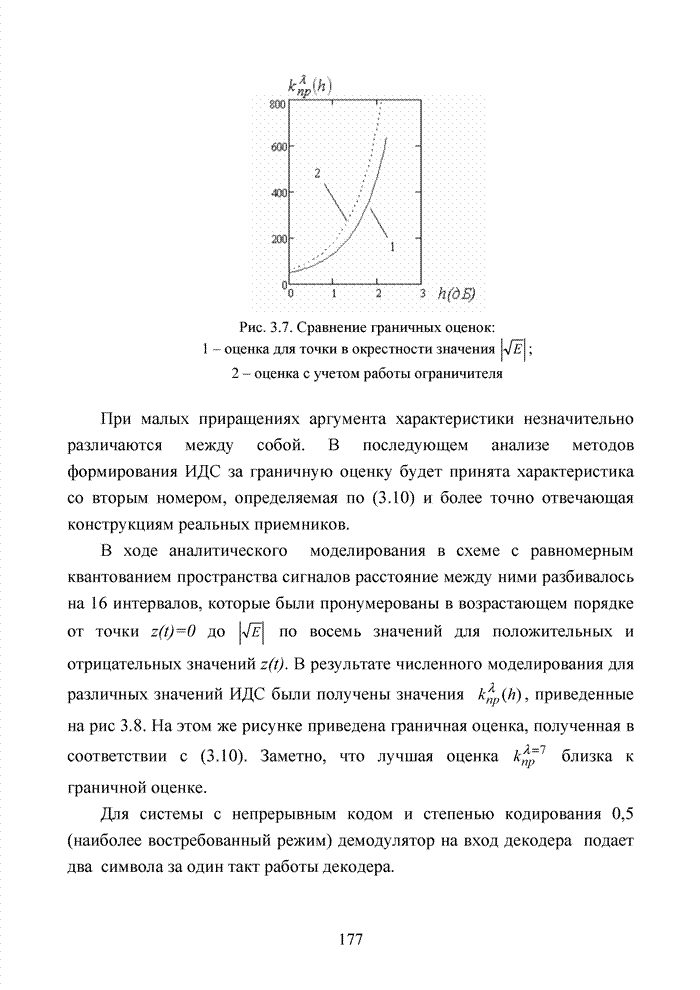
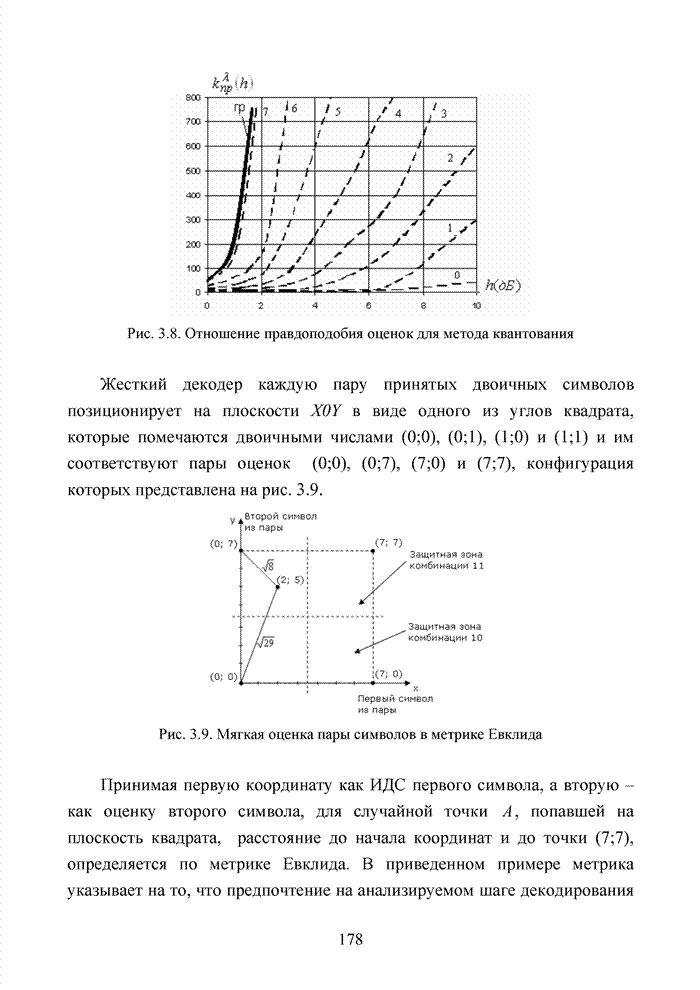
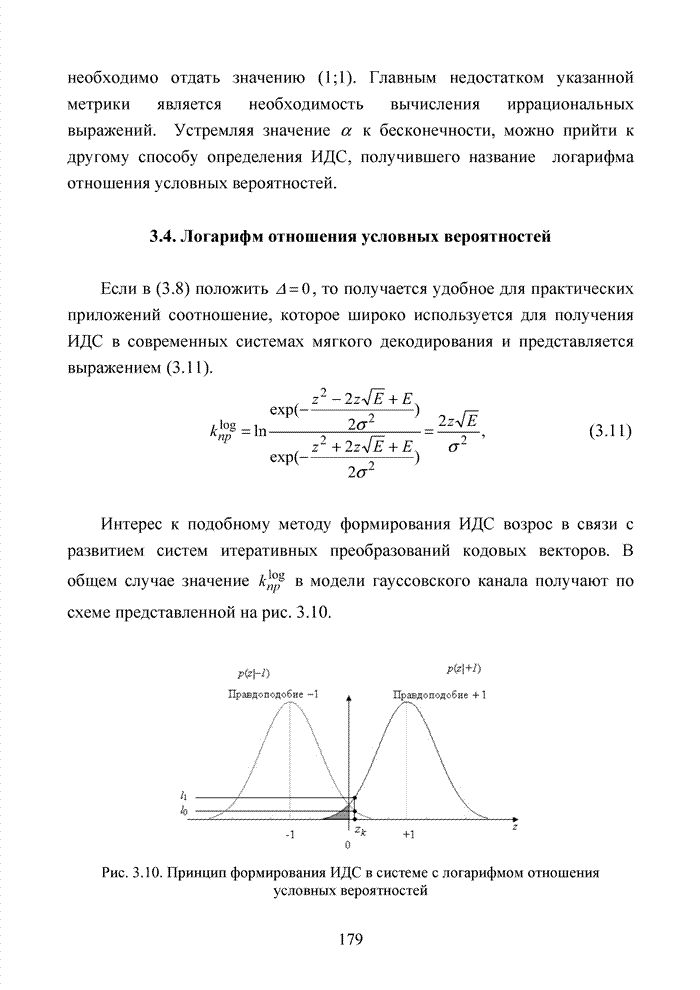
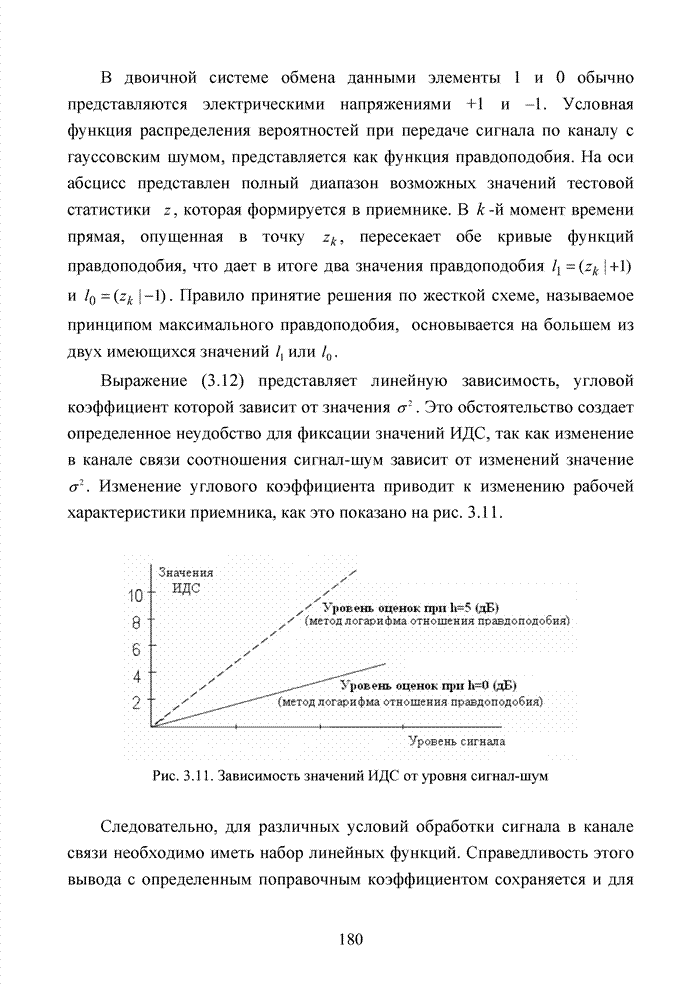
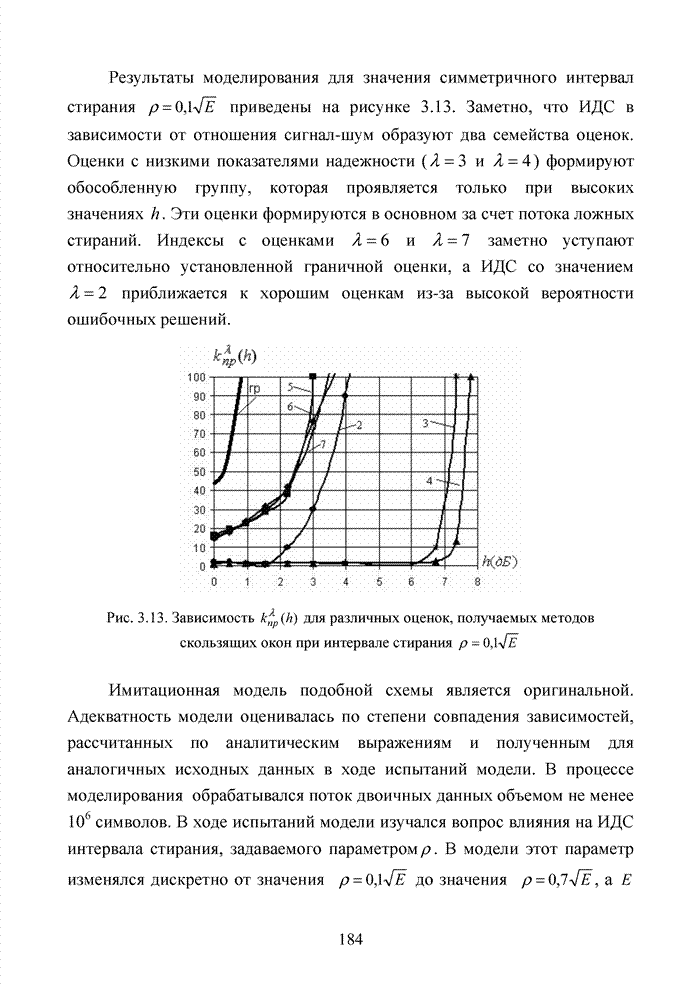
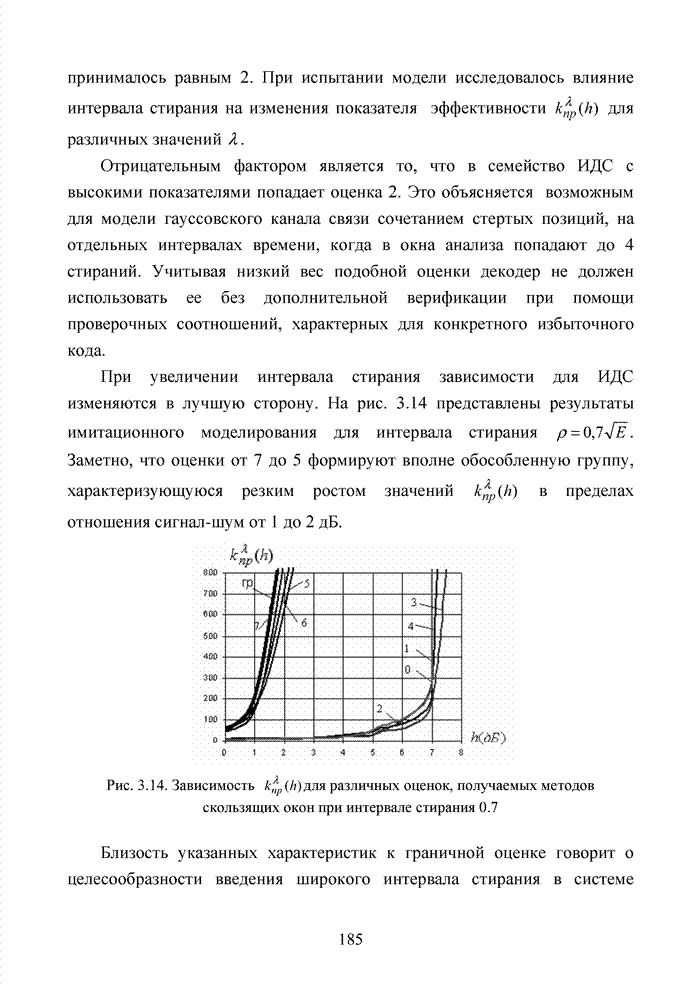
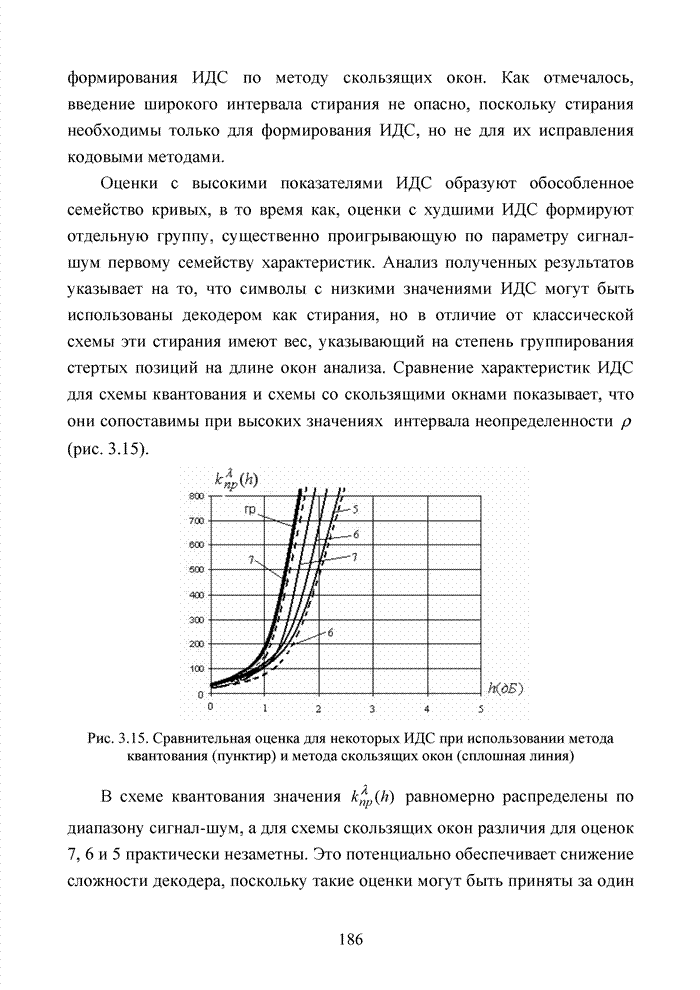
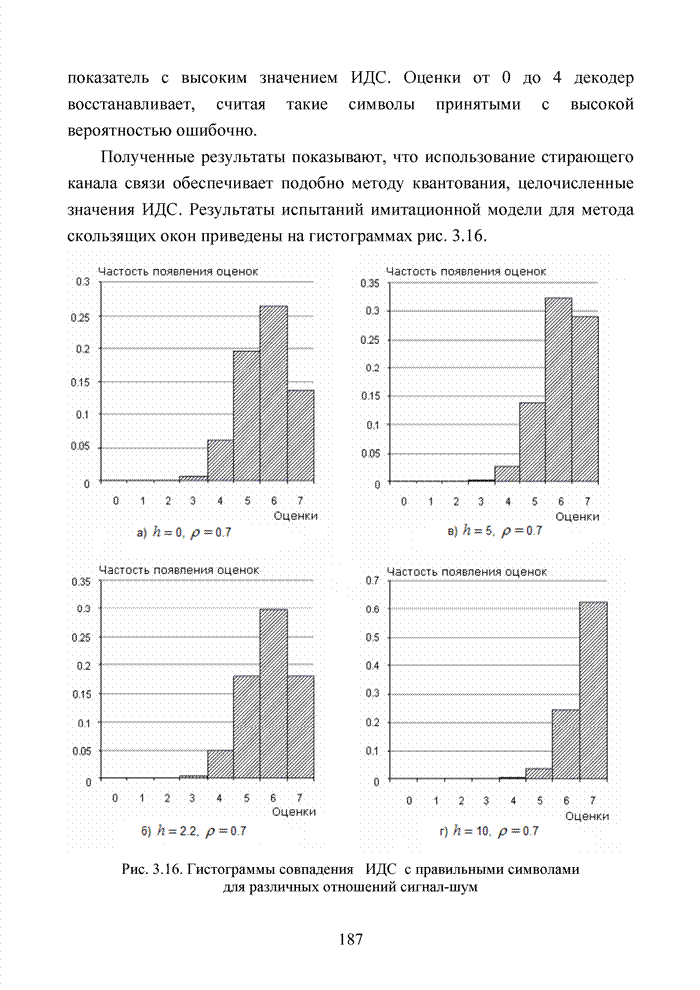
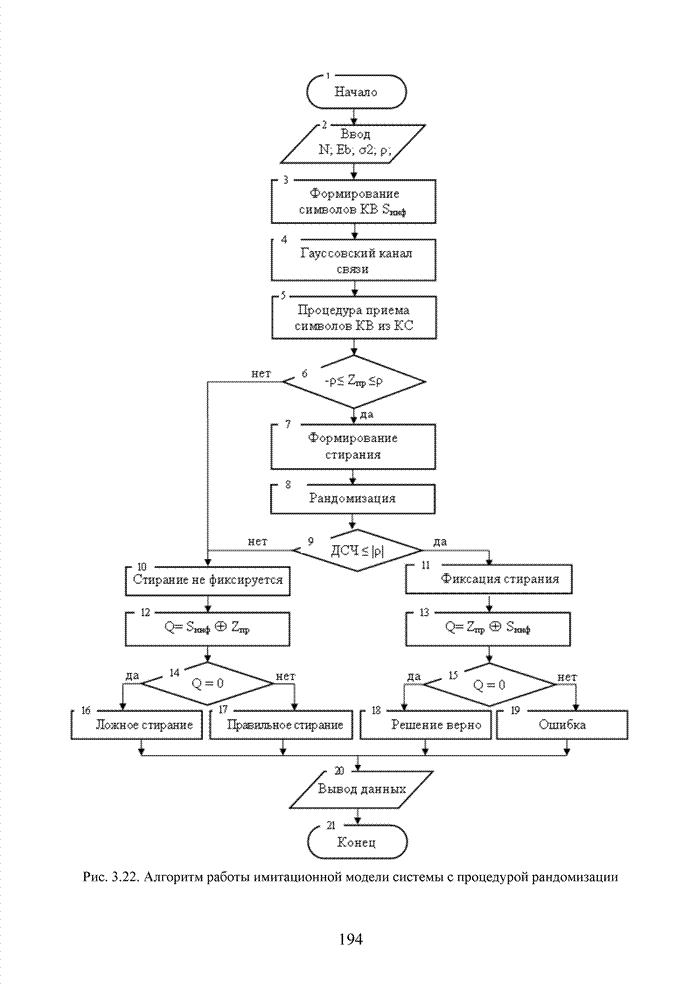
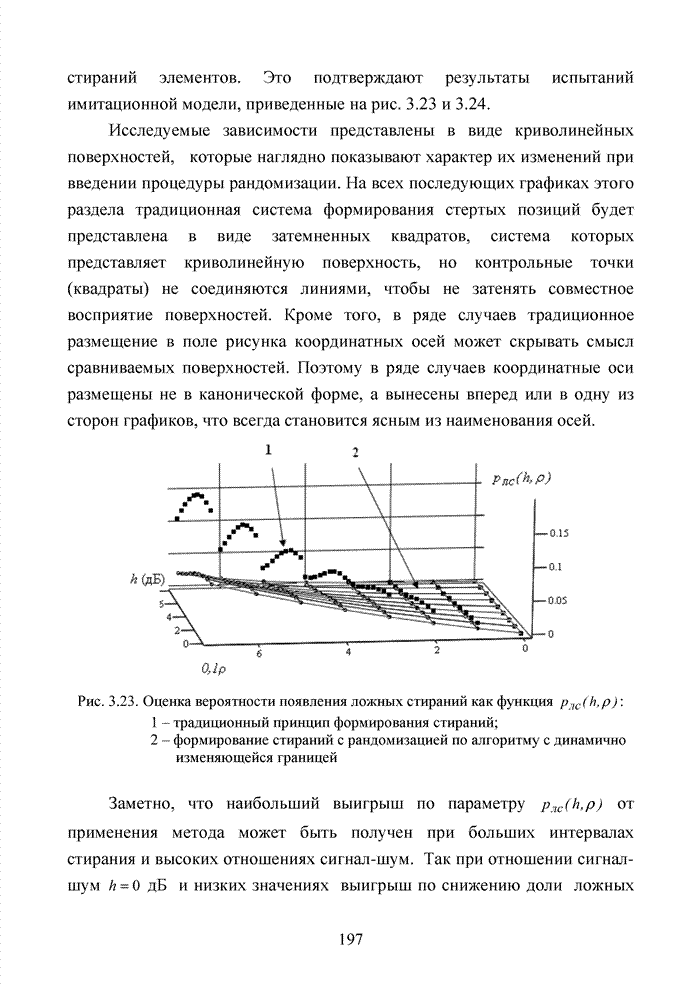
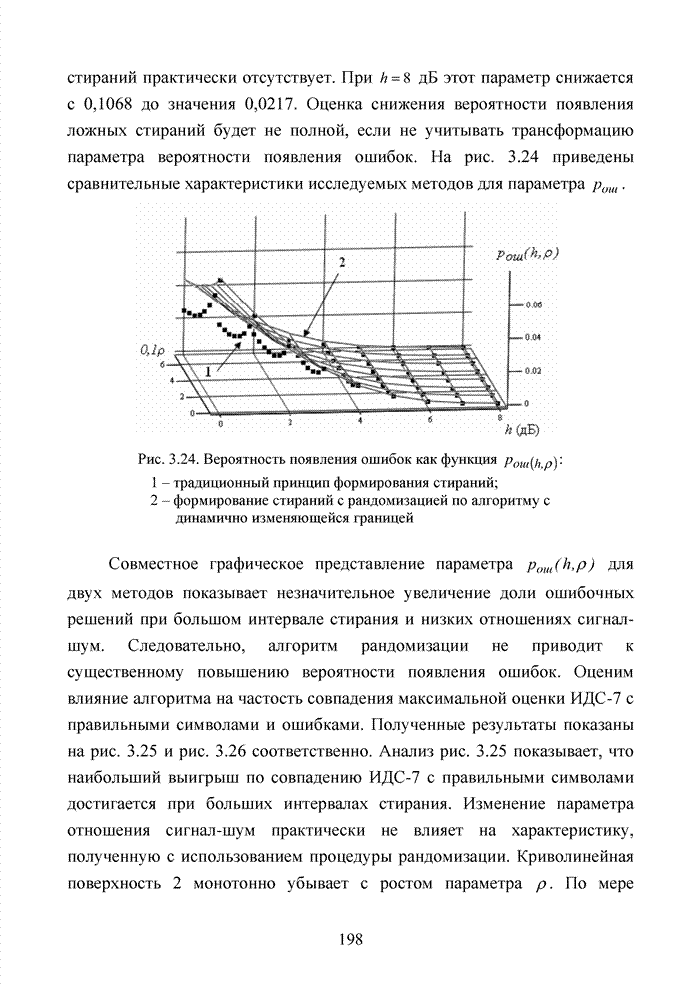
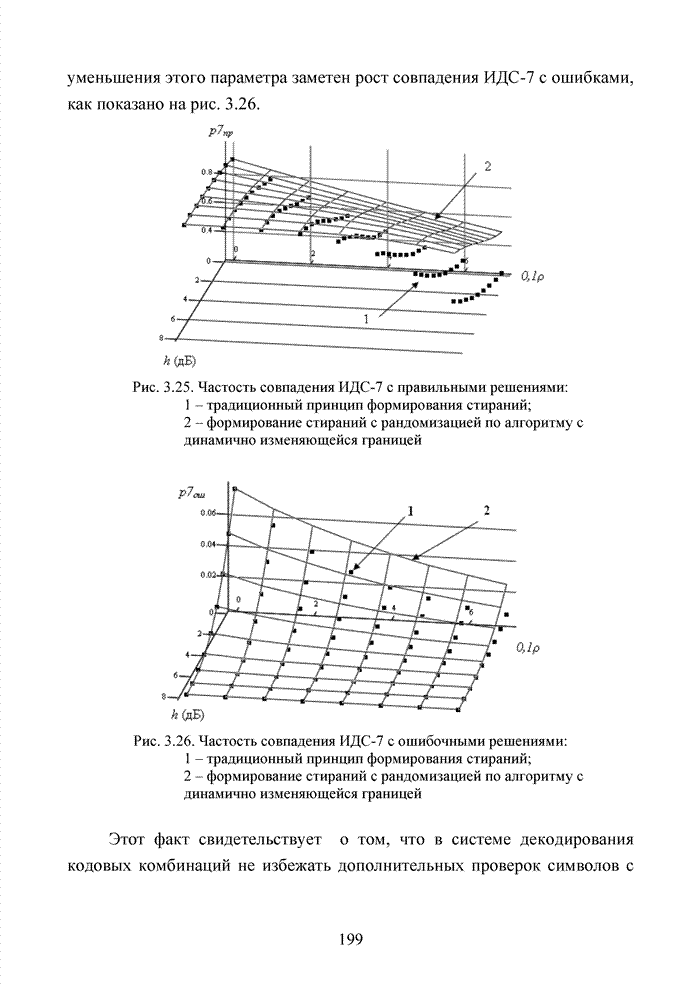
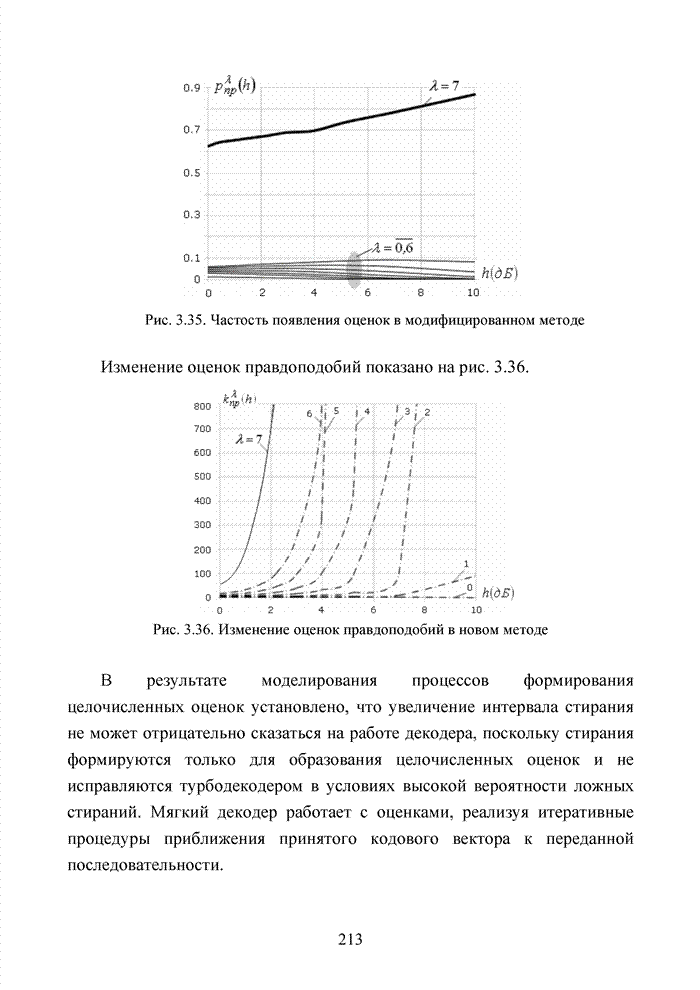
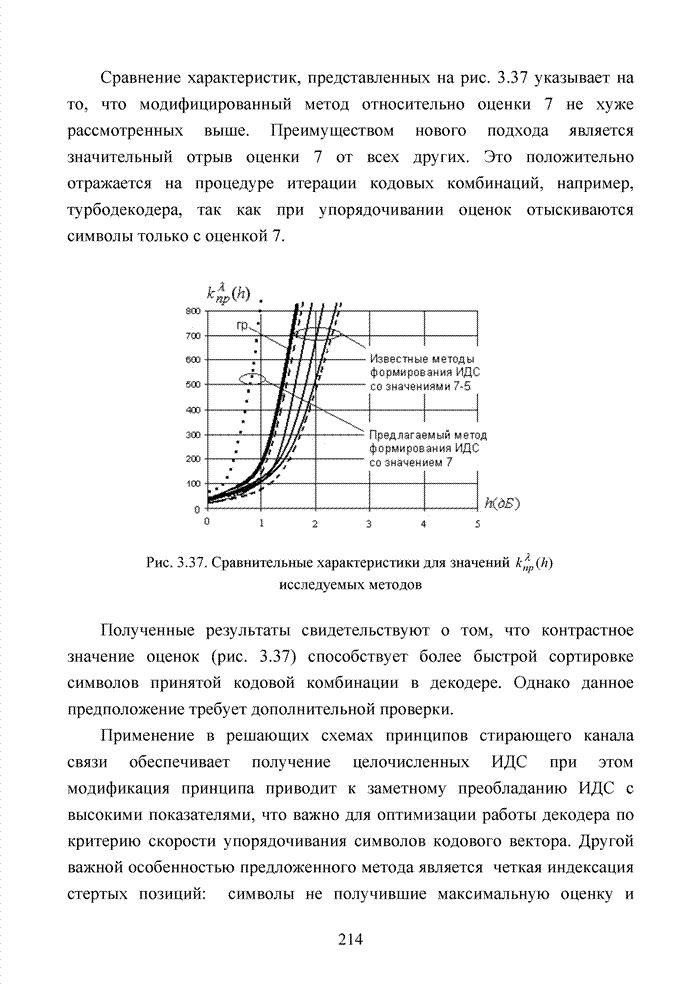
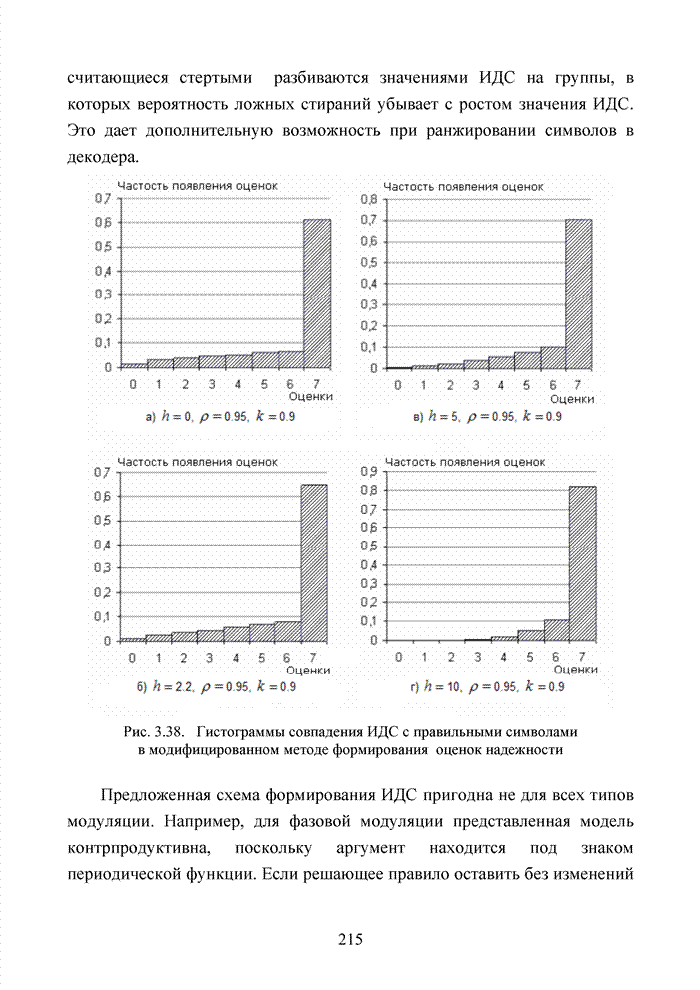
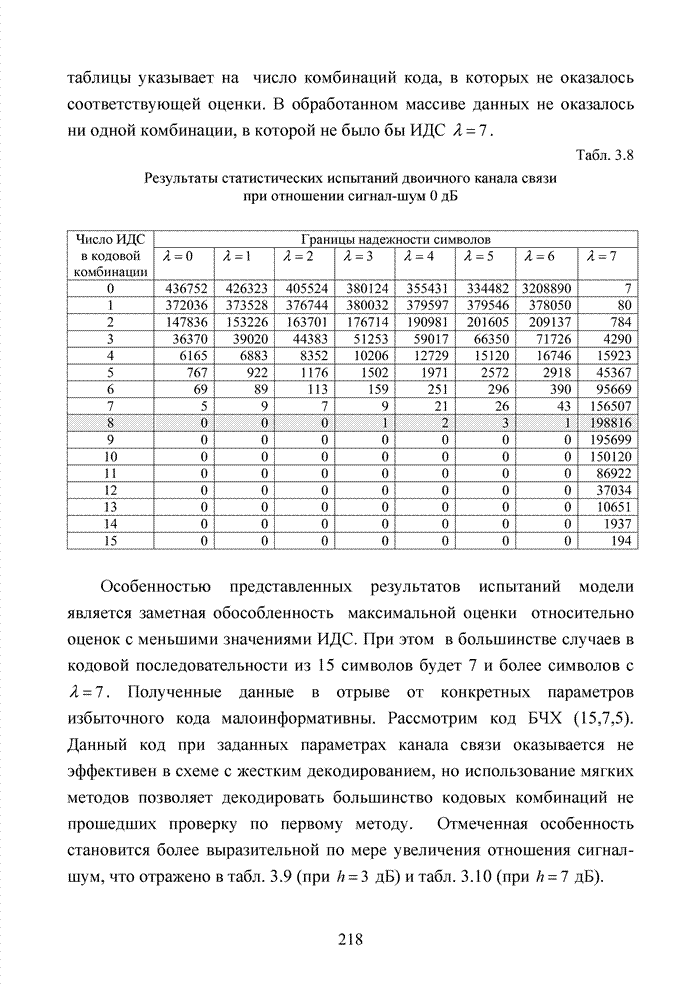
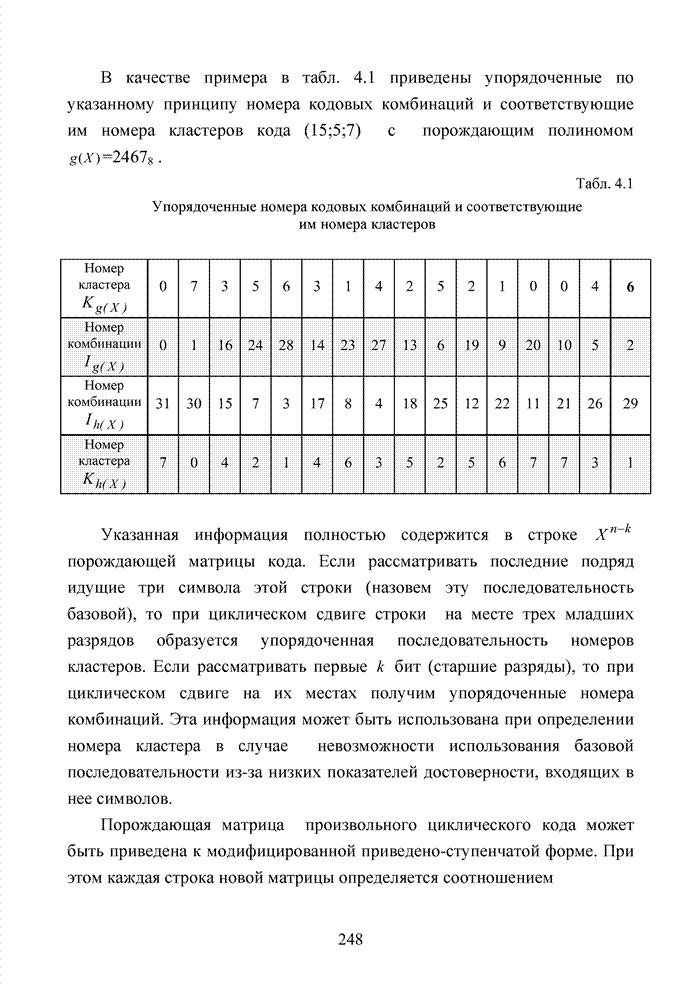
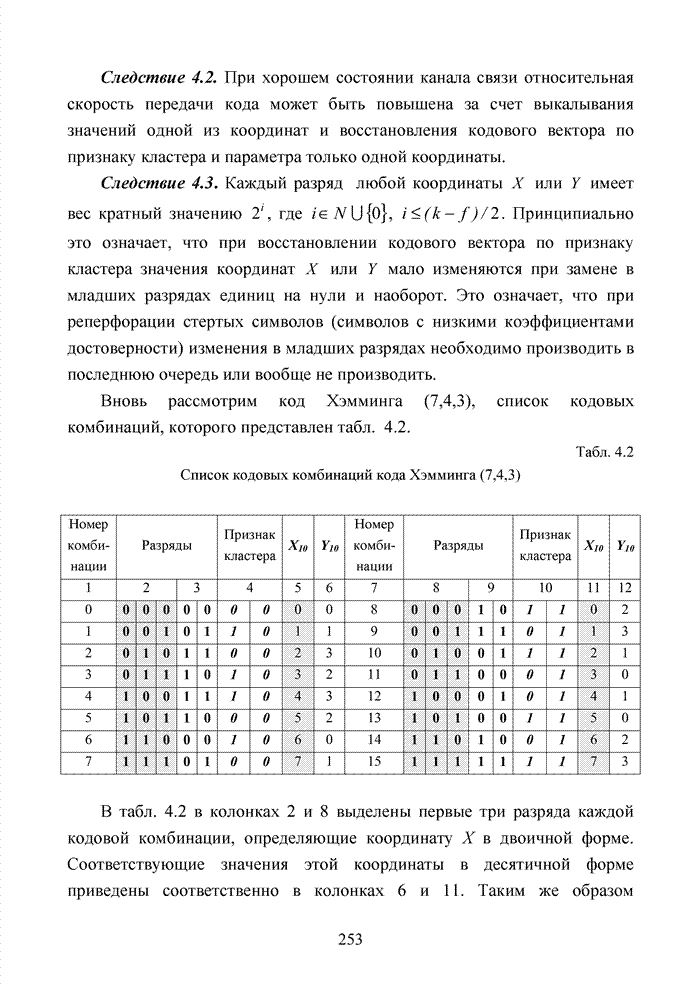
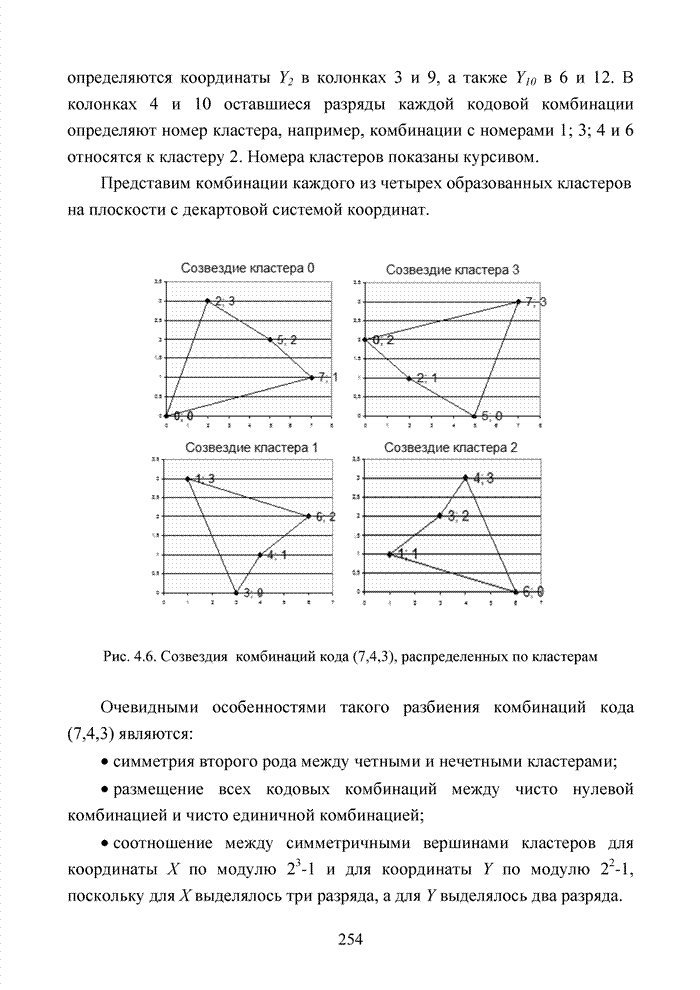
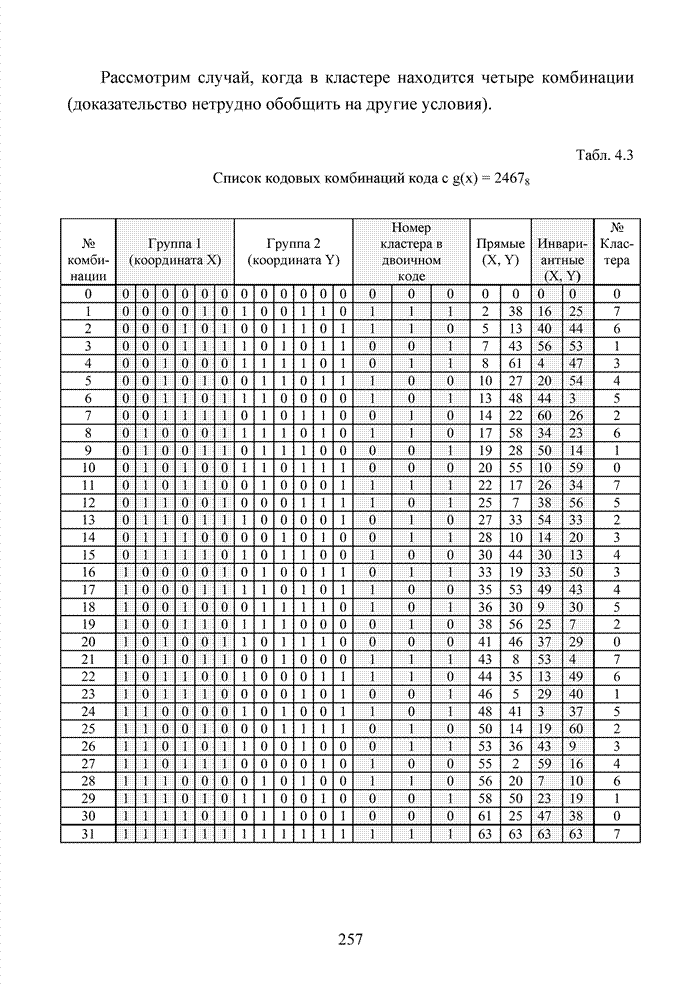
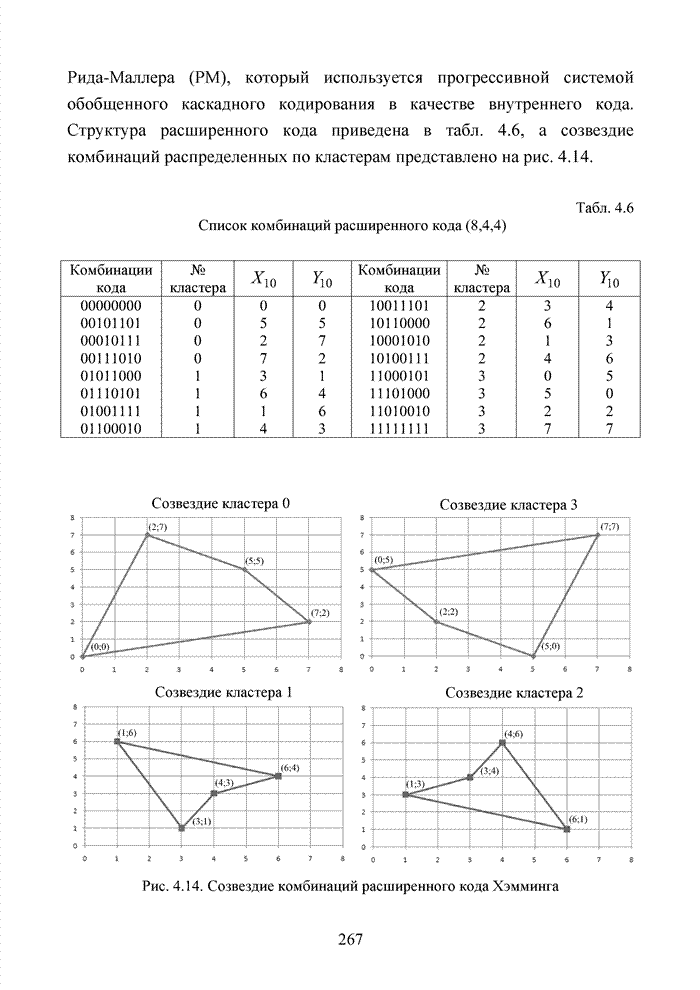
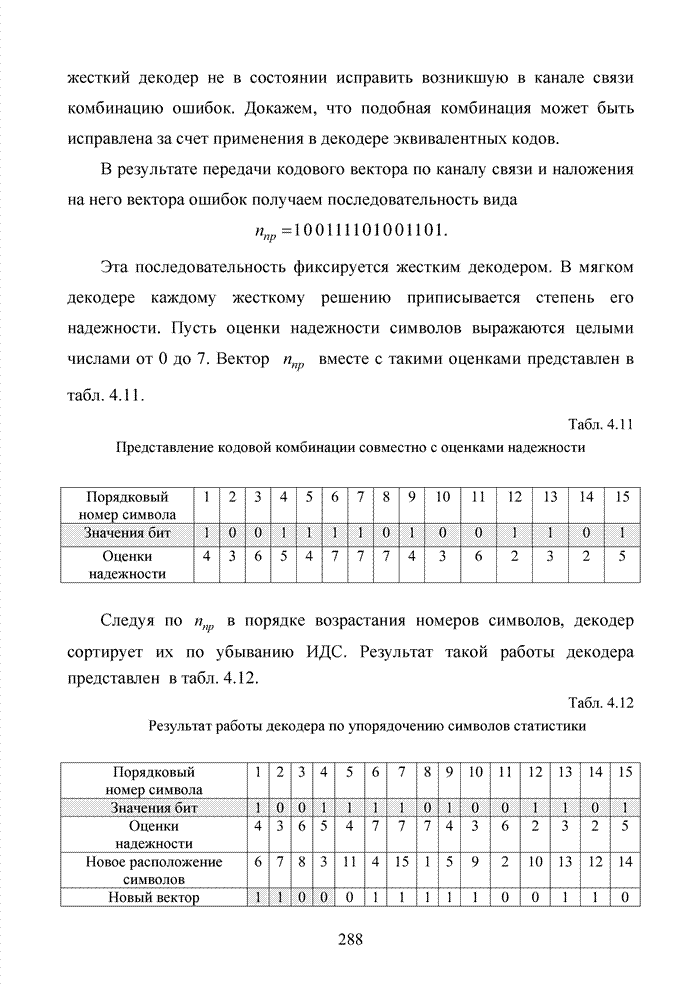
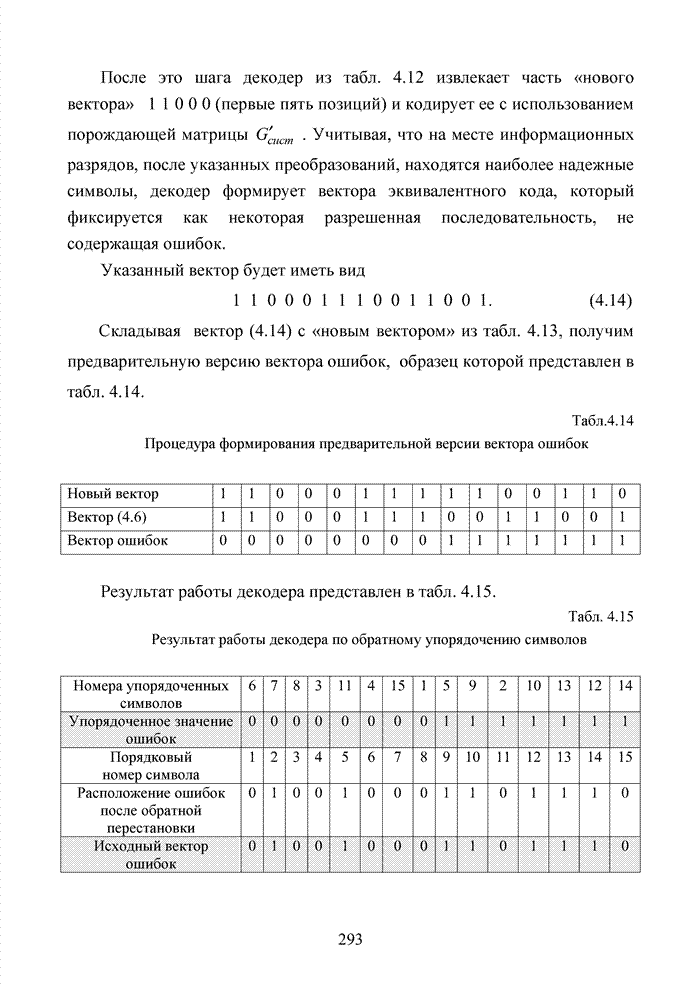
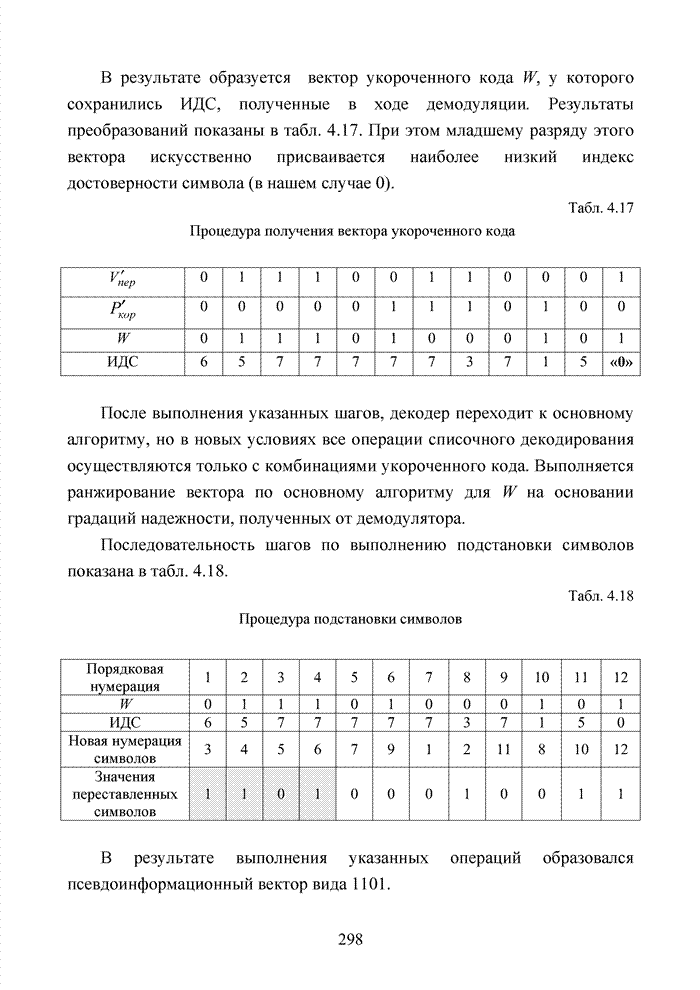
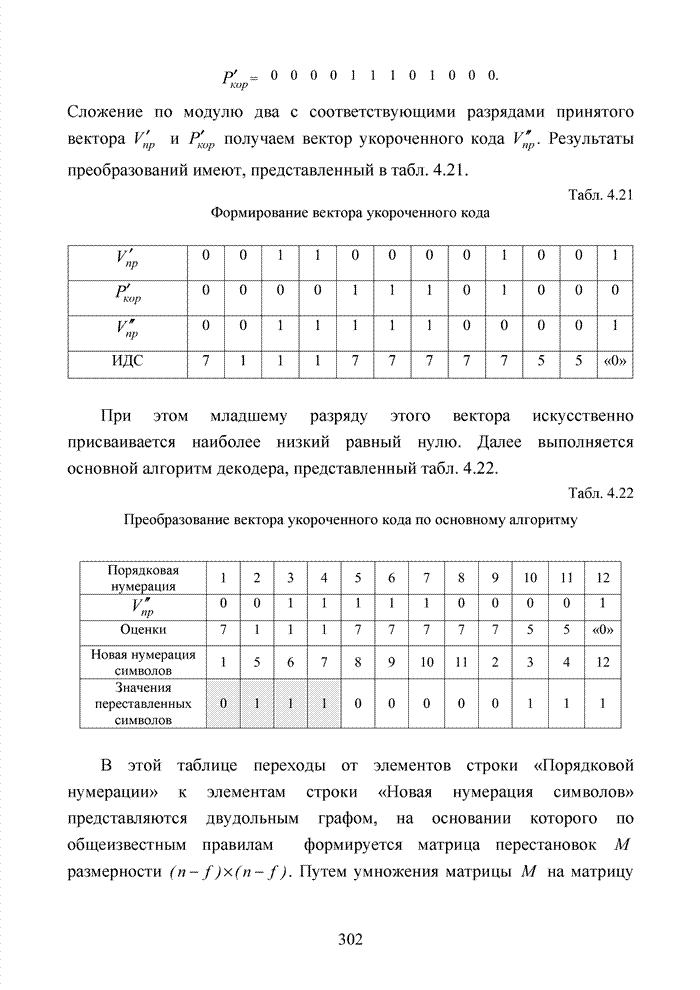
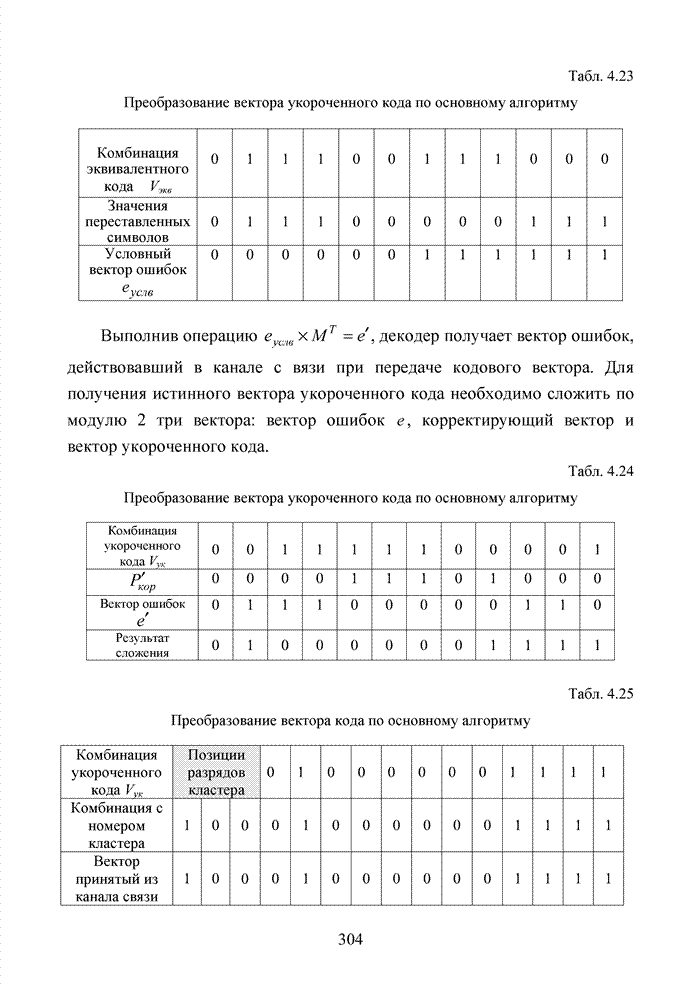
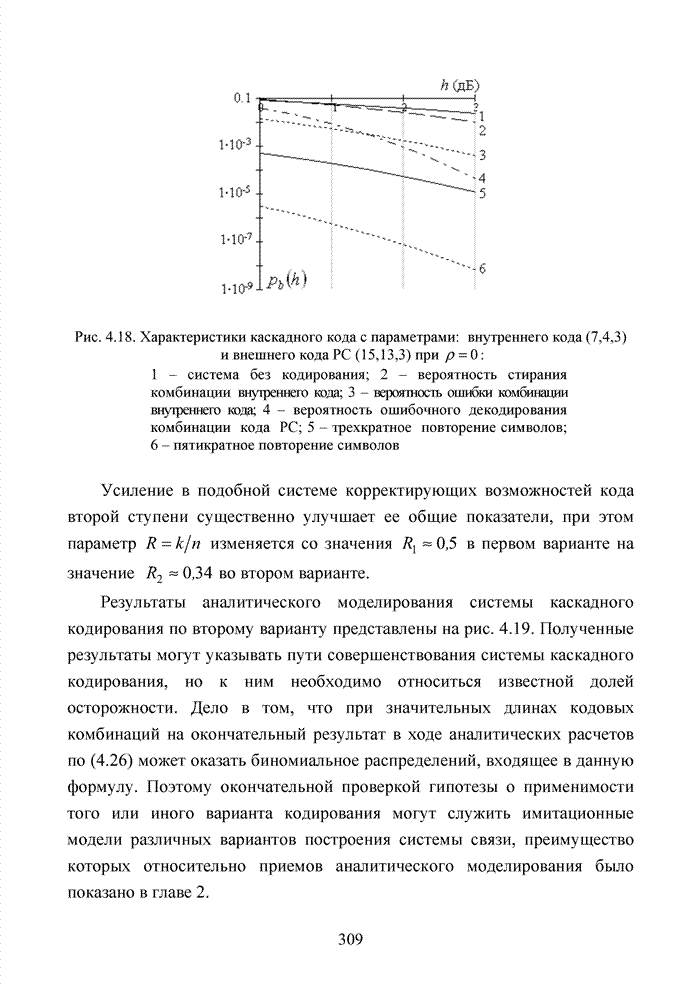
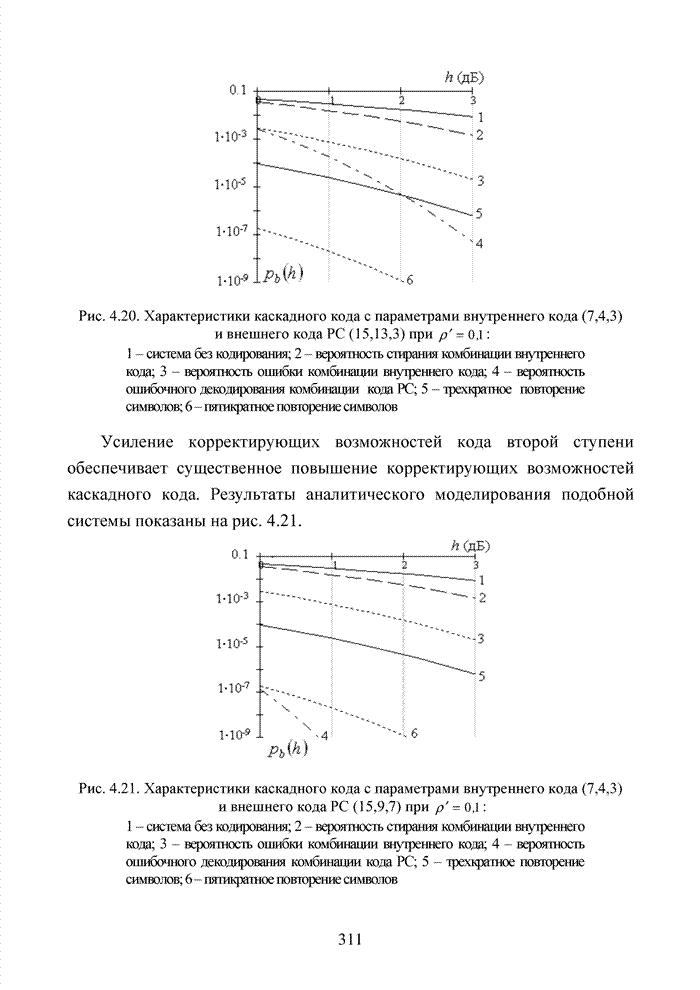
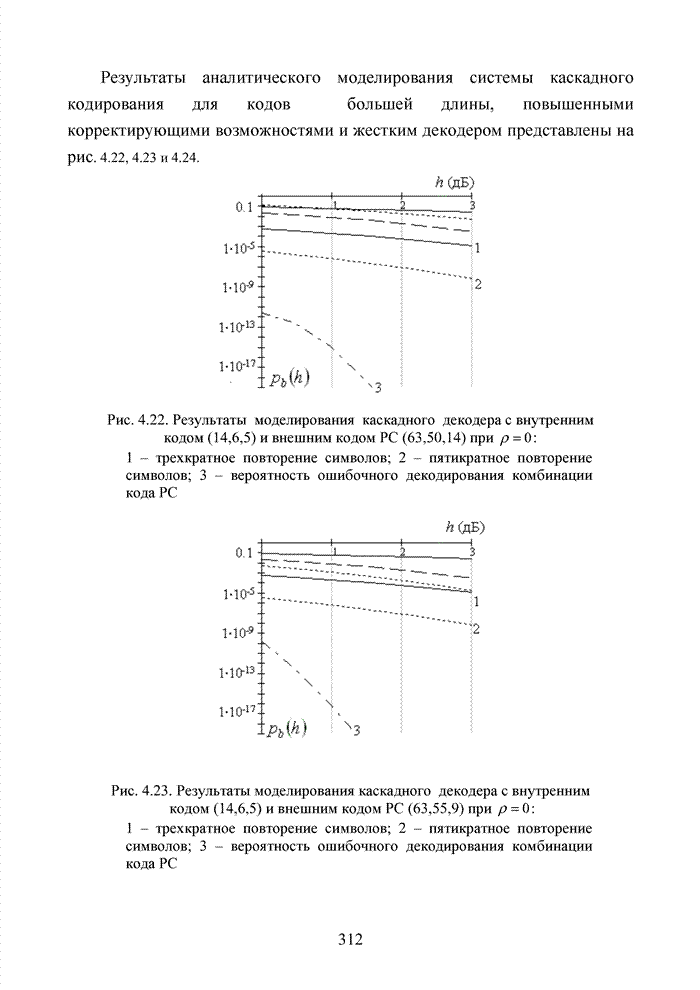
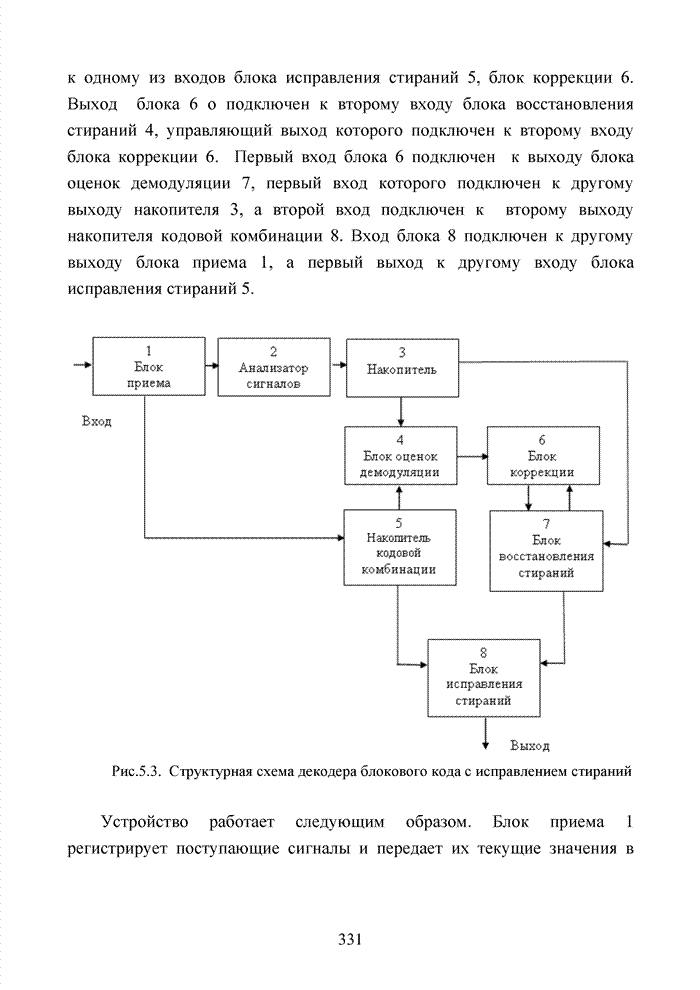
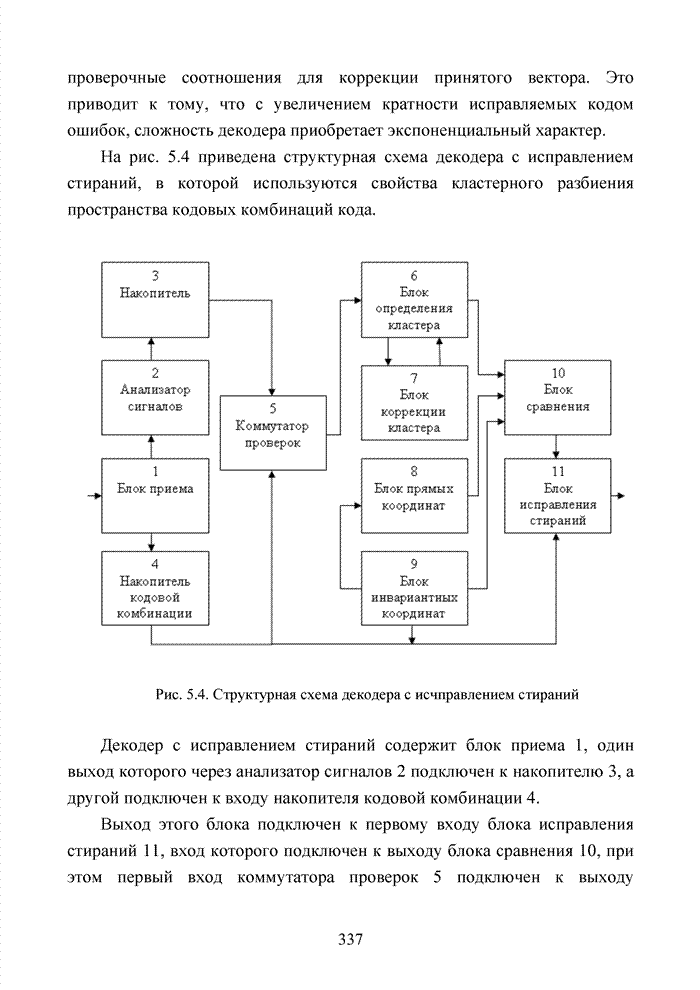
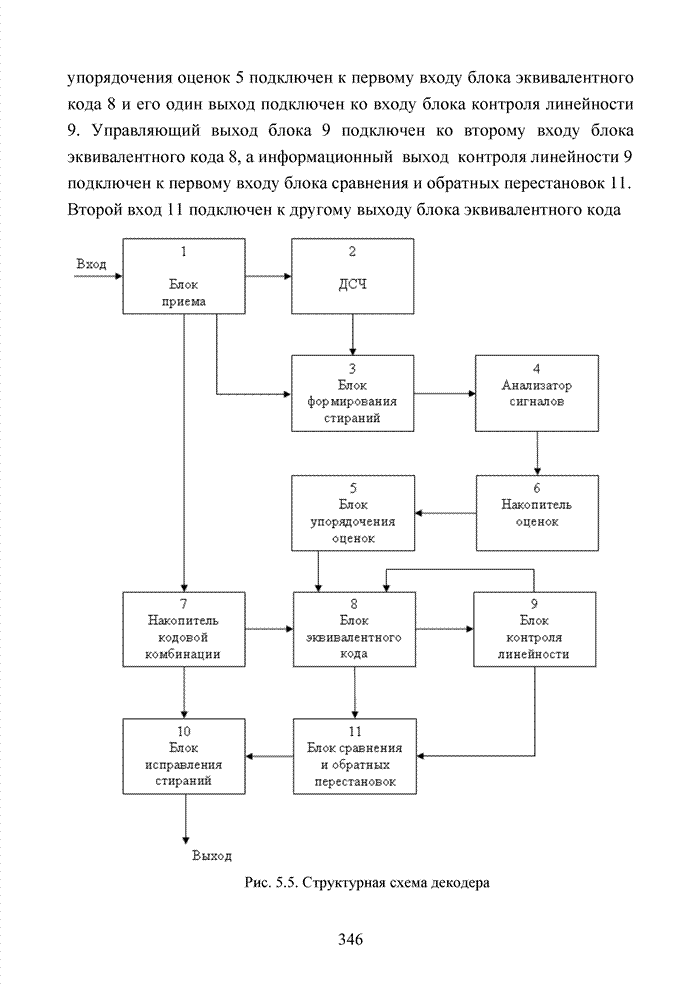
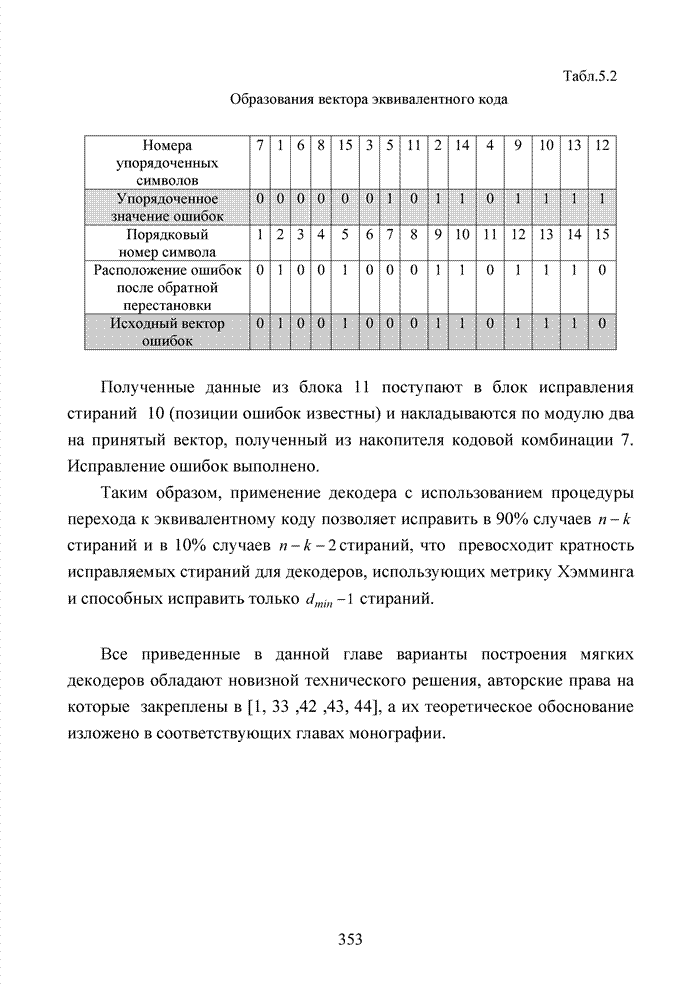
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
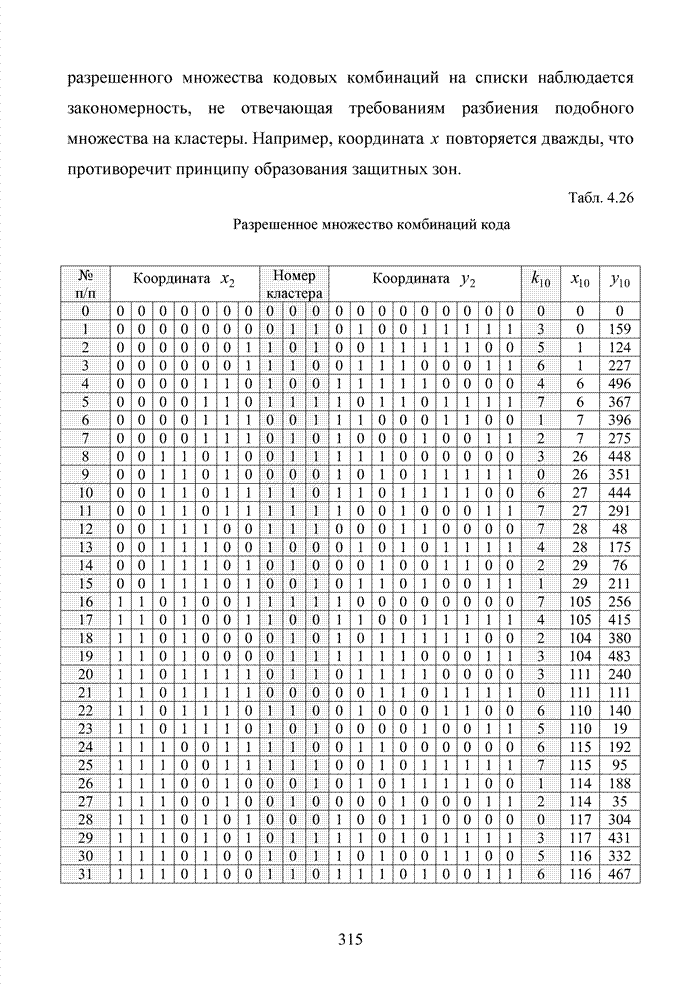
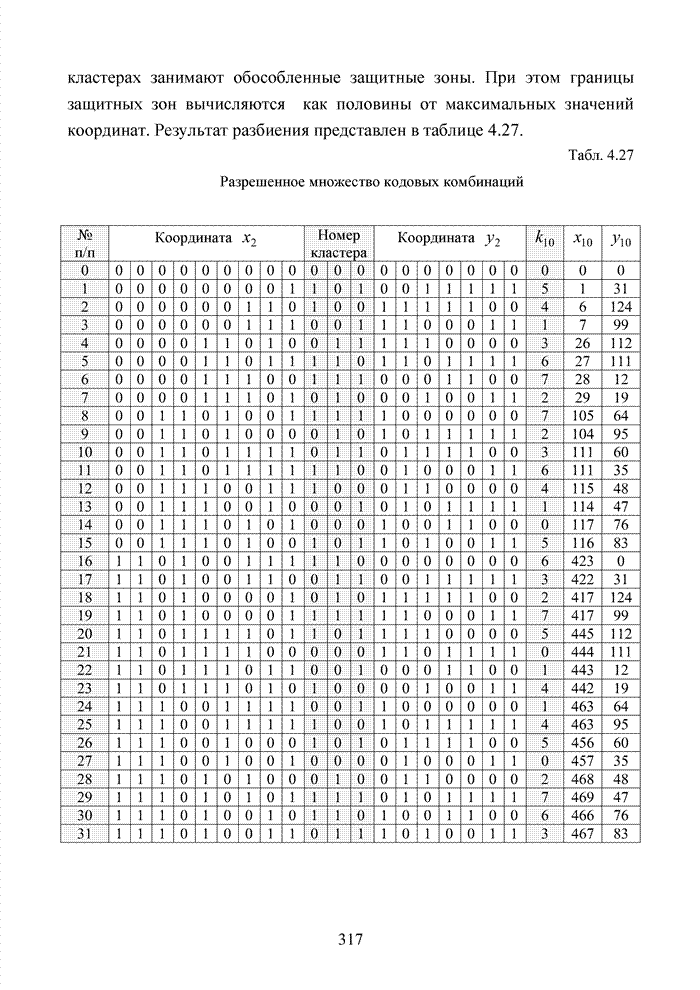
ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
Введение
Неалгебраические методы
декодирования помехоустойчивых кодов появились сразу, как только стало ясно,
что методы декодирования, опирающиеся на строгие нормы алгебраической теории групп,
колец и полей существенно усложняют конструкцию декодера. На начальных этапах
своего становления технология кодирования и декодирования использовала
относительно простые сдвиговые регистры. Обратные связи и сумматоры таких
регистров отражали структуру порождающего полинома ![]() на передаче и структуру
порождающего полинома
на передаче и структуру
порождающего полинома ![]() дуального кода на приеме. Подобные
устройства не позволяли достаточно просто применить в системах обмена данными
дуального кода на приеме. Подобные
устройства не позволяли достаточно просто применить в системах обмена данными ![]() -ичные коды,
преимущества которых к этому моменту были очевидны [7].
-ичные коды,
преимущества которых к этому моменту были очевидны [7].
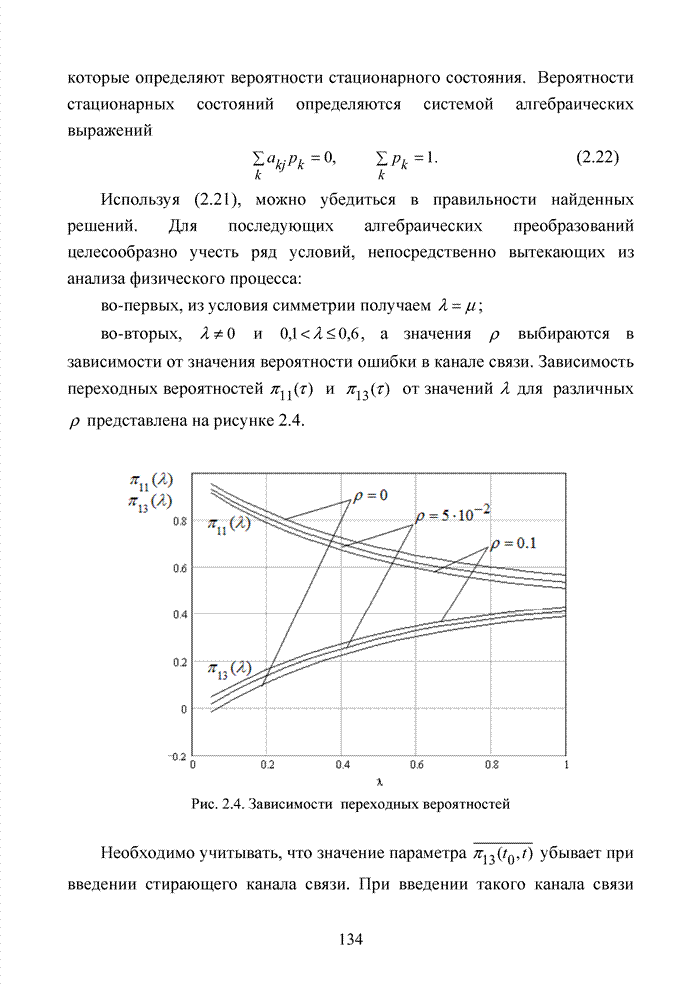
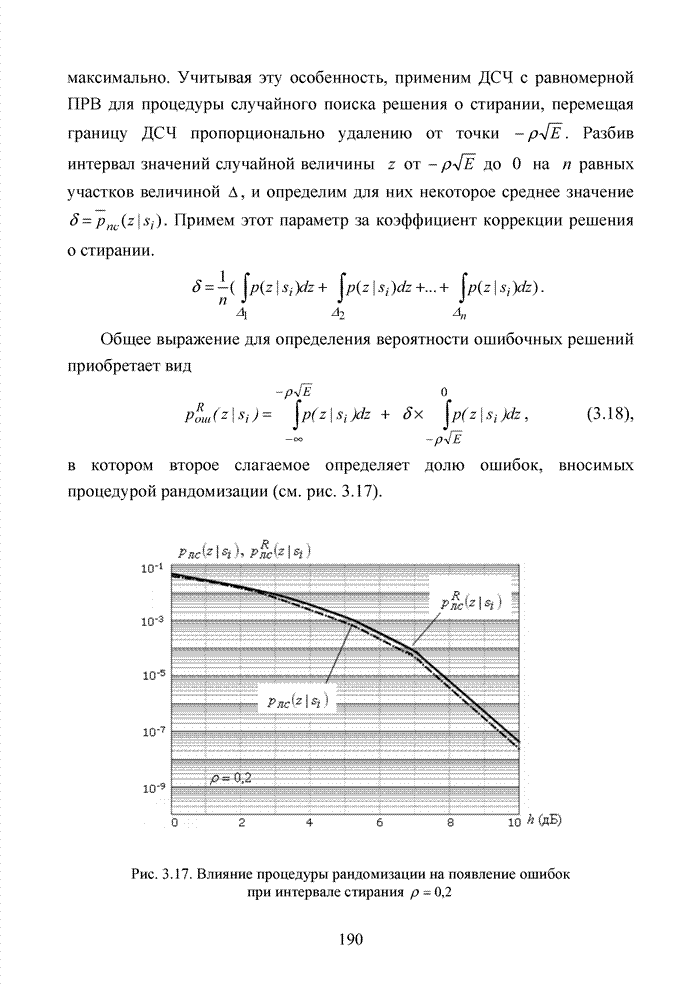
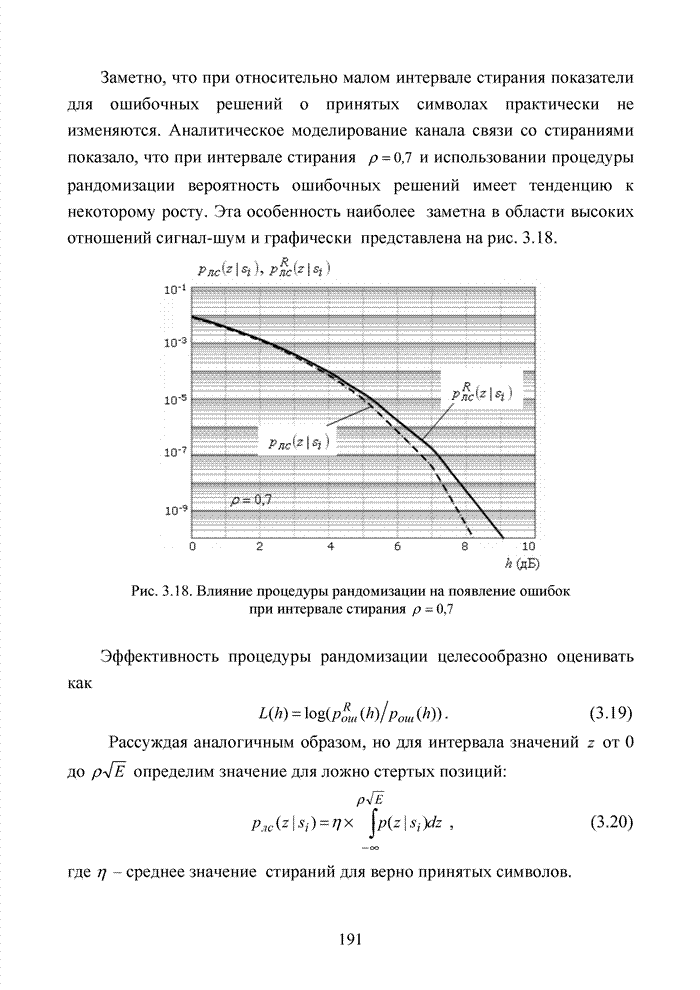
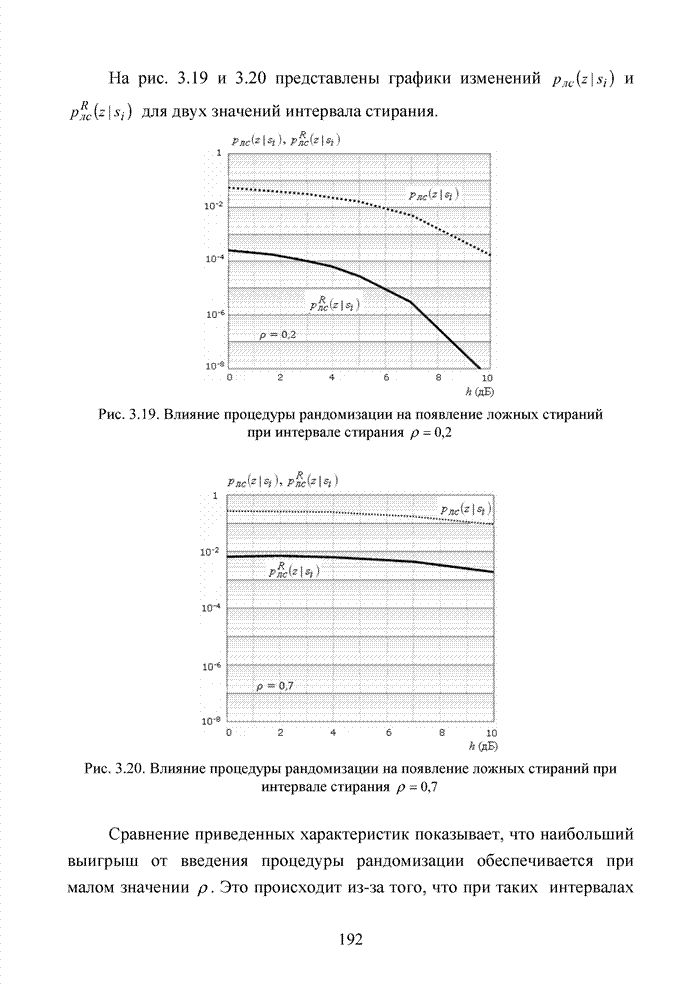
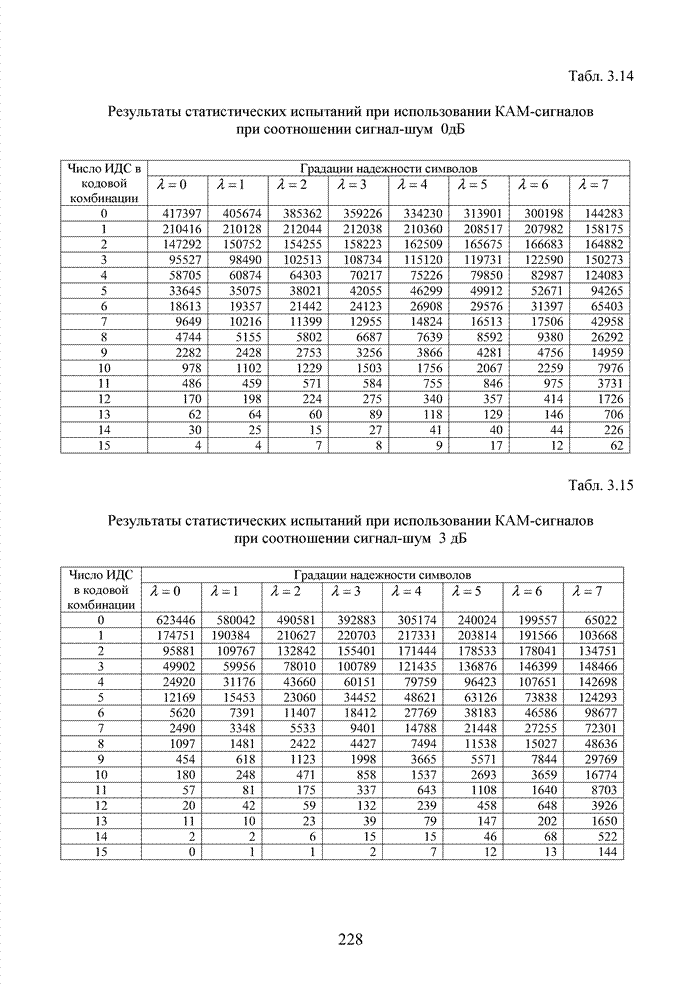
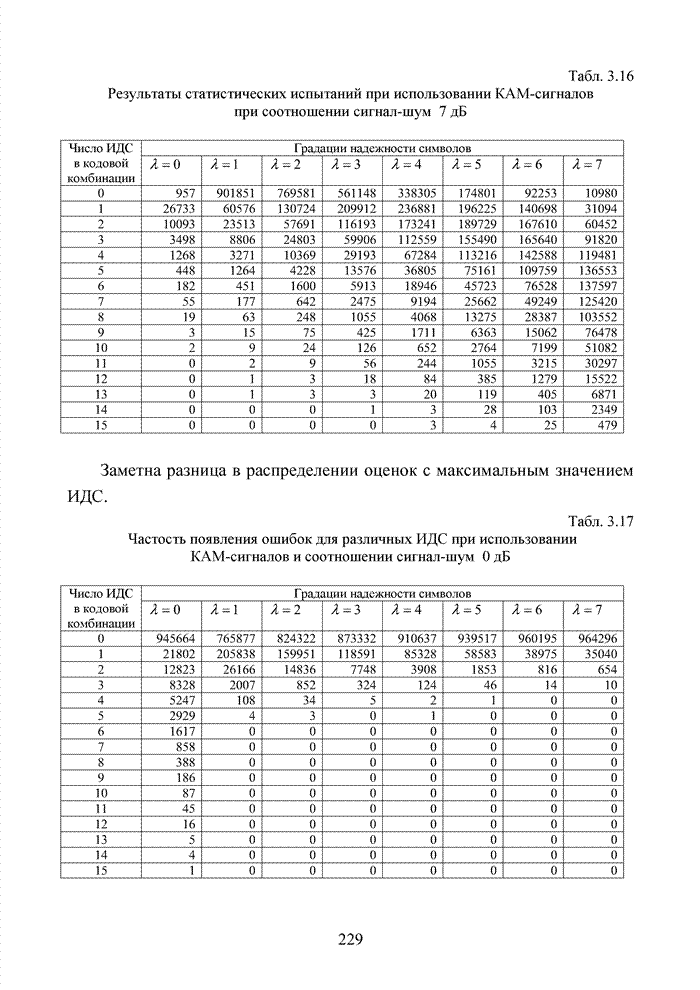
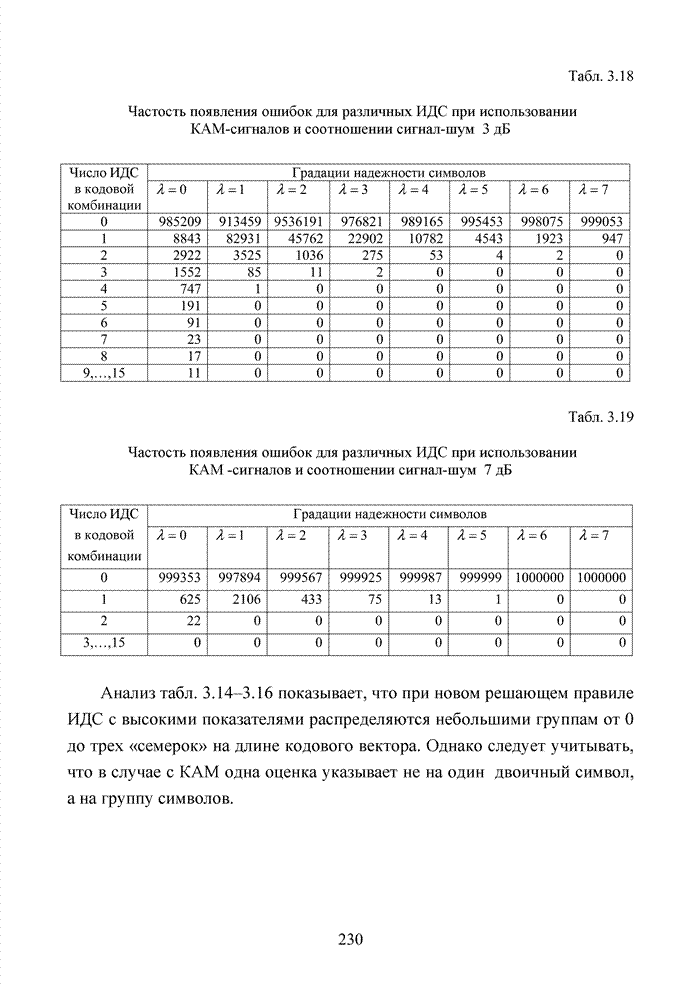
Большинство специалистов по теории помехоустойчивого кодирования считают, что первым устройством, в котором была реализована идея неалгебраического декодирования циклических кодов, был декодер Меггита [65, 74]. Подобная конструкция являлась декодером максимального правдоподобия и рассчитывалась на обработку только жестких решений. Было установлено, что сложность такого декодера с ростом числа исправляемых ошибок растет экспоненциально, поэтому он предназначался для коррекции ошибок небольшой кратности (до трех включительно).
Как указывалось выше, для
циклических кодов существует взаимно однозначное соответствие между множеством
всех исправляемых ошибок и множеством всех синдромов. Если ![]() – синдром, соответствующий
многочлену ошибок
– синдром, соответствующий
многочлену ошибок ![]() ,
то
,
то ![]() –
синдром, соответствующий
–
синдром, соответствующий ![]() Из этого следует важное для последующих
рассуждений свойство: все возможные синдромы можно разбить на непересекающиеся
множества (классы эквивалентности), каждый из которых соответствует
циклическому сдвигу одной и той же комбинации ошибок. Декодер запоминает в
специальной таблице только синдромы, представляющие исправляемые комбинации
ошибок, имеющие единицу в старшем разряде. В результате, процесс декодирования
кодового блока можно разбить на
Из этого следует важное для последующих
рассуждений свойство: все возможные синдромы можно разбить на непересекающиеся
множества (классы эквивалентности), каждый из которых соответствует
циклическому сдвигу одной и той же комбинации ошибок. Декодер запоминает в
специальной таблице только синдромы, представляющие исправляемые комбинации
ошибок, имеющие единицу в старшем разряде. В результате, процесс декодирования
кодового блока можно разбить на ![]() шагов, на каждом из которых текущее
значение синдрома сравнивается с табличным значением. В случае определенного совпадения,
изменяется старший бит кодового блока. После этого содержимое синдрома
сдвигается с помощью регистра с обратными связями и начинается следующий шаг
декодирования. Например, при декодировании кодов Хэмминга необходимо запомнить
всего одно значение синдрома, поскольку для этого кода возможно исправление
только одной ошибки.
шагов, на каждом из которых текущее
значение синдрома сравнивается с табличным значением. В случае определенного совпадения,
изменяется старший бит кодового блока. После этого содержимое синдрома
сдвигается с помощью регистра с обратными связями и начинается следующий шаг
декодирования. Например, при декодировании кодов Хэмминга необходимо запомнить
всего одно значение синдрома, поскольку для этого кода возможно исправление
только одной ошибки.
Использование
информационных множеств для построения алгоритмов декодирования групповых кодов
было предложено Прейнджем [65, 73]. Информационным множеством группового (n,k) – кода называется любое множество k символов кодового слова, которые
можно задавать независимо. Остальные ![]() символов называются проверочным
множеством. Для систематических кодов в порождающей матрице G единичная матрица
символов называются проверочным
множеством. Для систематических кодов в порождающей матрице G единичная матрица ![]() образует
информационное множество. Путем линейных комбинаций над строками и столбцами
матрицы G можно добиться другой конфигурации
информационного множества. Информационных множеств создается несколько.
Принятое кодовое слово с ошибкой сравнивается с каждым из них, затем по
наименьшему расстоянию результатов сравнения принимают решение о принятом
слове. Общий алгоритм декодирования на основе информационных множеств может выглядеть
следующим образом.
образует
информационное множество. Путем линейных комбинаций над строками и столбцами
матрицы G можно добиться другой конфигурации
информационного множества. Информационных множеств создается несколько.
Принятое кодовое слово с ошибкой сравнивается с каждым из них, затем по
наименьшему расстоянию результатов сравнения принимают решение о принятом
слове. Общий алгоритм декодирования на основе информационных множеств может выглядеть
следующим образом.
Шаг 1. Выбрать несколько различных информационных множеств в соответствии с некоторым правилом.
Шаг 2. Построить кодовое слово для каждого из множеств, предположив, что символы информационного множества приняты без ошибок.
Шаг 3. Сравнить каждое гипотетическое кодовое слово с принятой последовательностью и выбрать ближайшее кодовое слово (находящееся на наименьшем расстоянии).
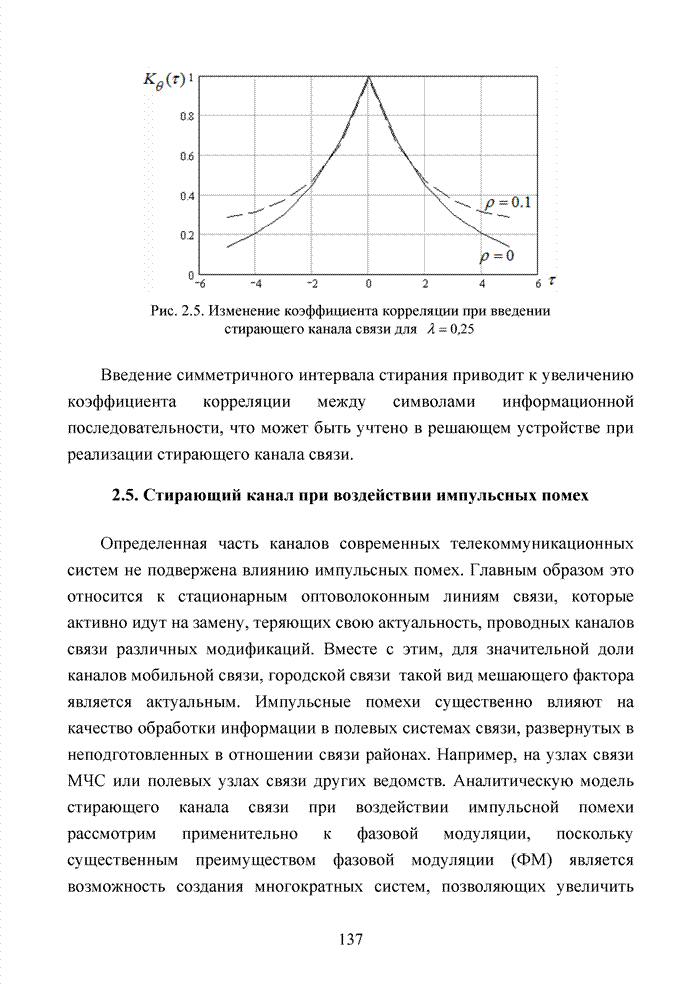
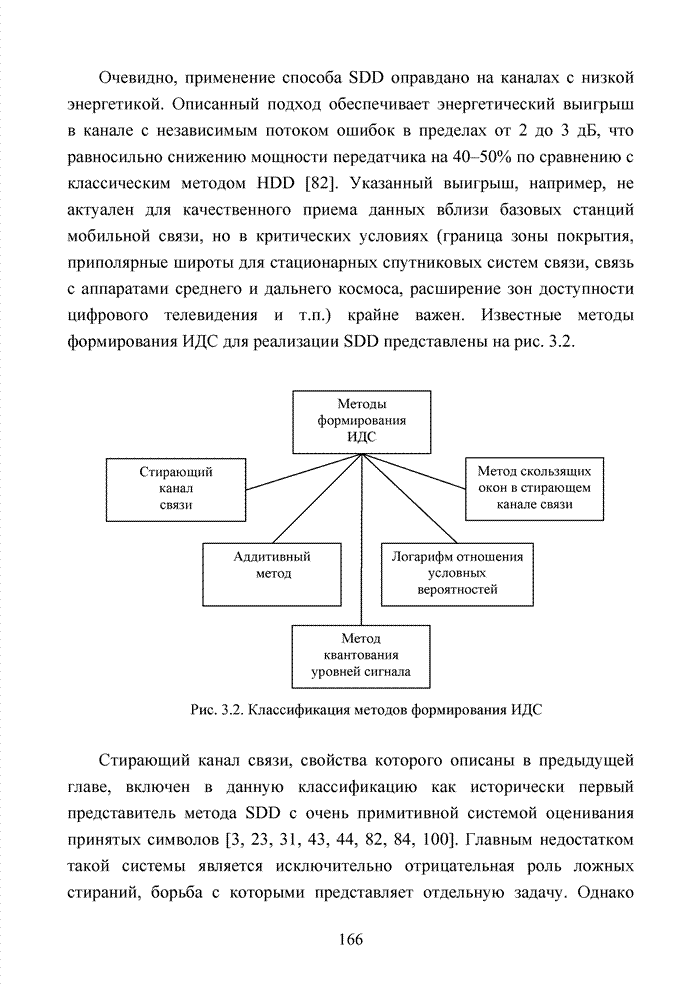
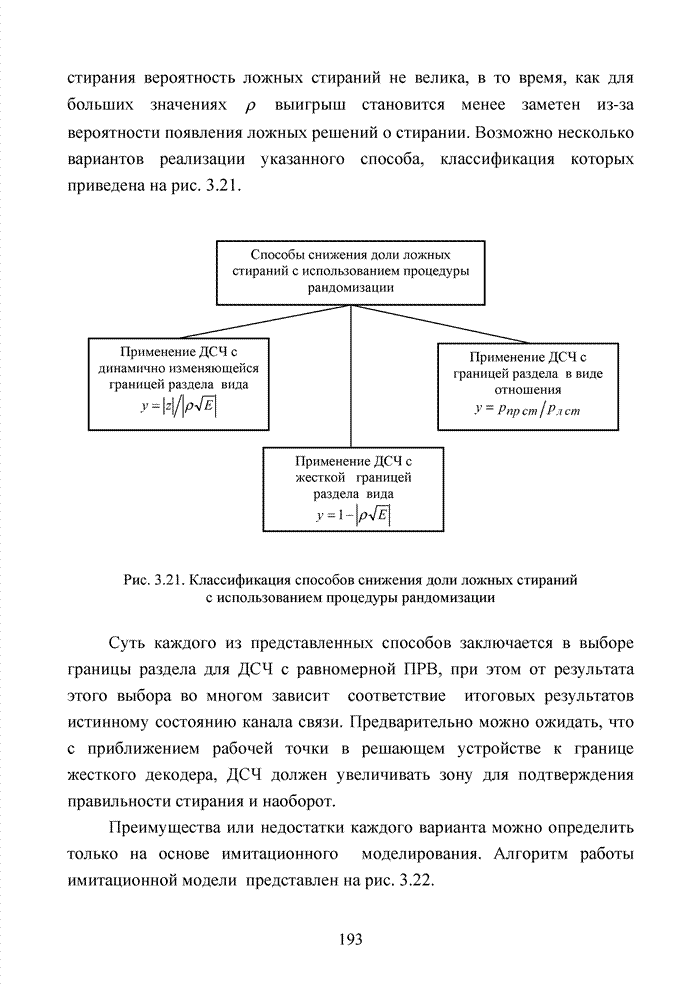
Другим направлением является перестановочное декодирование, которое возможно реализовать как с использованием порождающей матрицы G, так и с помощью проверочной матрицы H [77, 78, 89]. Комбинация ошибок будет определена, если удается найти проверочное множество целиком, содержащее эту комбинацию. Такое проверочное множество называется покрывающим комбинацию ошибок. Набор проверочных множеств, покрывающим комбинацию ошибок данного типа, называется покрытием. Задача декодера состоит в том, чтобы найти проверочное множество, которое покрывает данную неизвестную комбинацию ошибок.
При использовании заранее выбранного покрывающего множества возникает два важных вопроса. Первый из них состоит в том, каково минимальное число различных проверочных множеств, необходимых для исправления данного числа ошибок, второй – как найти эти множества. Ни на один из этих вопросов нет вполне удовлетворительного ответа.
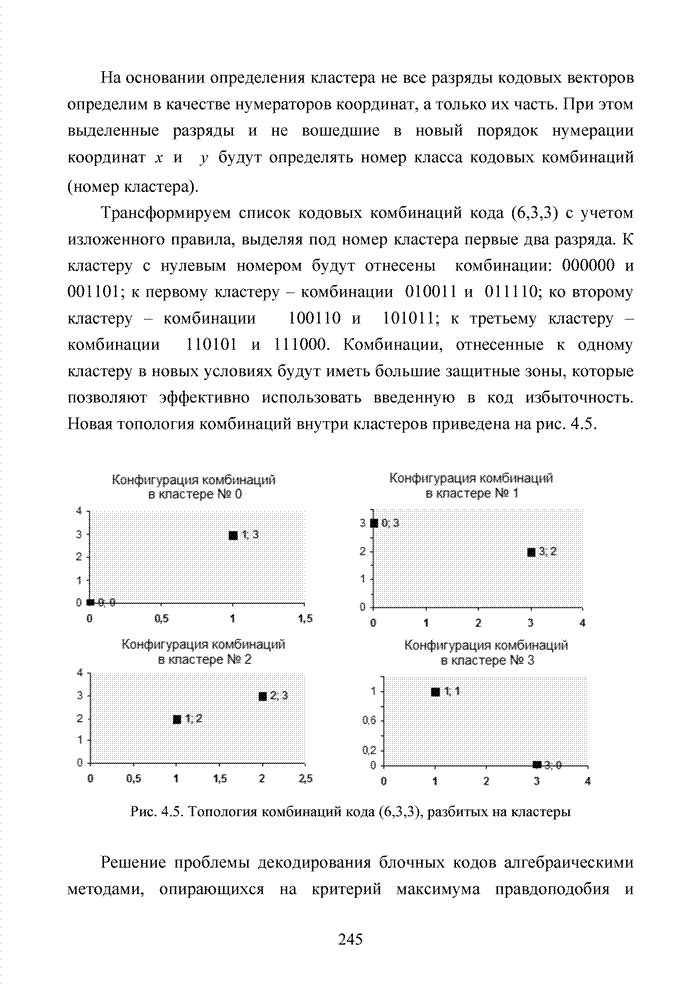
Благодаря усилиям отечественных авторов: В.В. Золотареву, Г.В. Овечкину и др., активно развивается концепция многопорогового декодирования, берущая свое начало от порогового декодирования Меггита [54, 55]. Такой метод декодирования применим не только к групповым кодам, но и к непрерывным кодам, однако этот метод целесообразно применять к кодам определенной структуры: к мажоритарно декодируемым кодам или к самоортоганальным кодам.
Сложность порогового декодера пропорциональна кодовому расстоянию, следовательно, быстрое увеличение этого параметра оказывается малоэффективным. Кроме того, при фиксированном значении кодового расстояния лучшими энергетическими характеристиками обладать коды с большей кодовой скоростью.
Многопороговый декодер
самоортоганальных кодов является развитием простейшего порогового декодера и
позволяет декодировать очень длинные коды с линейной от длины кода сложностью
исполнения. Важно отметить, что в основе такого устройства лежит принцип
итеративного приближения к окончательному выбору решения о принятом векторе.
Основной шаг декодирования заключается в том, что для произвольного взятого
символа uj вычисляется функция правдоподобия Lj , от относящихся к нему проверок ![]() и j-го элемента разностного вектора
и j-го элемента разностного вектора ![]() , который получается в
результате итеративных преобразований исходной информации. Основным свойством
такого декодера является постоянная сходимость его решения к решению
оптимального по максимуму правдоподобия декодера.
, который получается в
результате итеративных преобразований исходной информации. Основным свойством
такого декодера является постоянная сходимость его решения к решению
оптимального по максимуму правдоподобия декодера.
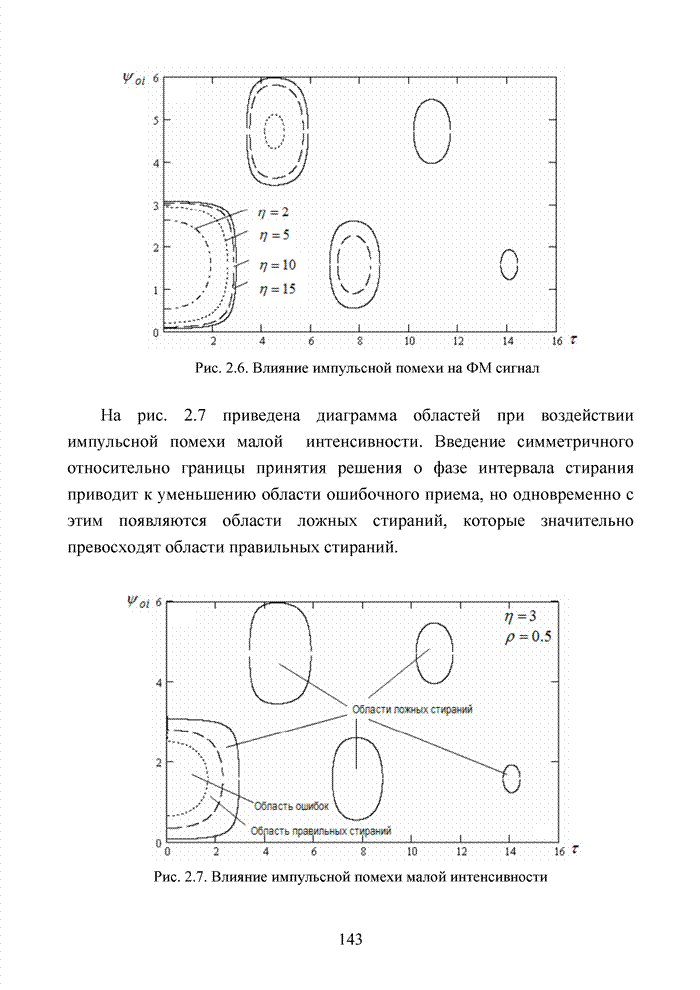
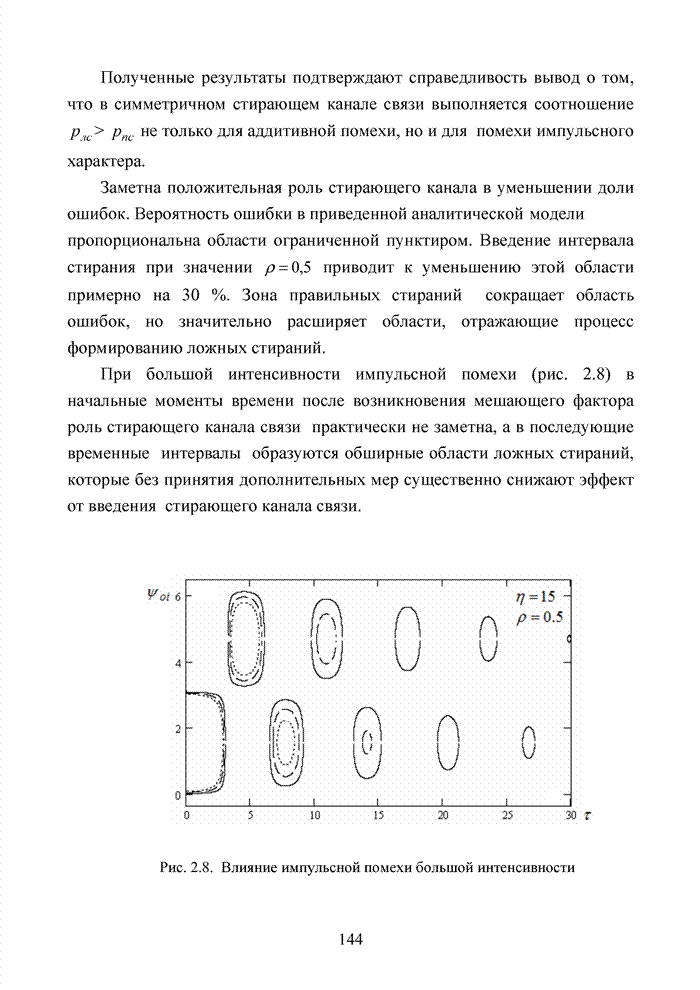
Подобная ситуация активизировала поиски иных подходов к процедуре декодирования помехоустойчивых кодов. Одним из таких направлений явилось списочное декодирование. Именно к таким методам следует отнести, прежде всего, приемы списочного декодирования, которые были введены Элайесом и Возенкрафтом [40, 59, 65, 74]. Алгоритм списочного декодирования имеет самостоятельное значение при решении различных задач. Списочный декодер вместо единственного решения выдает получателю список предполагаемых решений о передаваемом сообщении. Ошибкой является такой результат декодирования, когда в списке нет правильного сообщения. Понятно, что вероятность ошибки такого списочного декодера много меньше вероятности ошибки обычного декодера.
Наиболее очевидное применение этого подхода возможно в системах с каскадным кодированием. Результатом декодирования внутреннего кода является список решений, а декодер внешнего кода устраняет оставшуюся неопределенность.
Алгоритм декодирования, основанный на списках, обеспечивает лучшее соотношение между сложностью и вероятностью ошибки, чем другие известные алгоритмы. Это справедливо в асимптотике при увеличении кодового ограничения кода, а также при использовании конкретных конструкций кодов конечной длины.
Научный поиск в области построения эффективных избыточных кодов и каскадных конструкций на их основе продолжается. Развитие технологии реализации устройств кодирования и декодирования на базе интегральных микросхем и сигнальных процессоров существенно расширяет круг технически реализуемых решений. Этим стимулируется интерес к исследованиям в данной области.
Списочное
декодирование ![]() -ичных
кодов стало объектом пристального внимания, вызванного рядом публикаций,
указывающих на возможности таких кодов реализовать корректирующие способности
за пределами их конструктивной способности [109]. Поэтому в данной главе особое
место отведено результатам исследований направленных на поиск и обоснование
метрик, отличных от метрики Хэмминга, которые показали, что и для двоичных
кодов возможно в полной мере использовать введенную в них избыточность.
-ичных
кодов стало объектом пристального внимания, вызванного рядом публикаций,
указывающих на возможности таких кодов реализовать корректирующие способности
за пределами их конструктивной способности [109]. Поэтому в данной главе особое
место отведено результатам исследований направленных на поиск и обоснование
метрик, отличных от метрики Хэмминга, которые показали, что и для двоичных
кодов возможно в полной мере использовать введенную в них избыточность.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
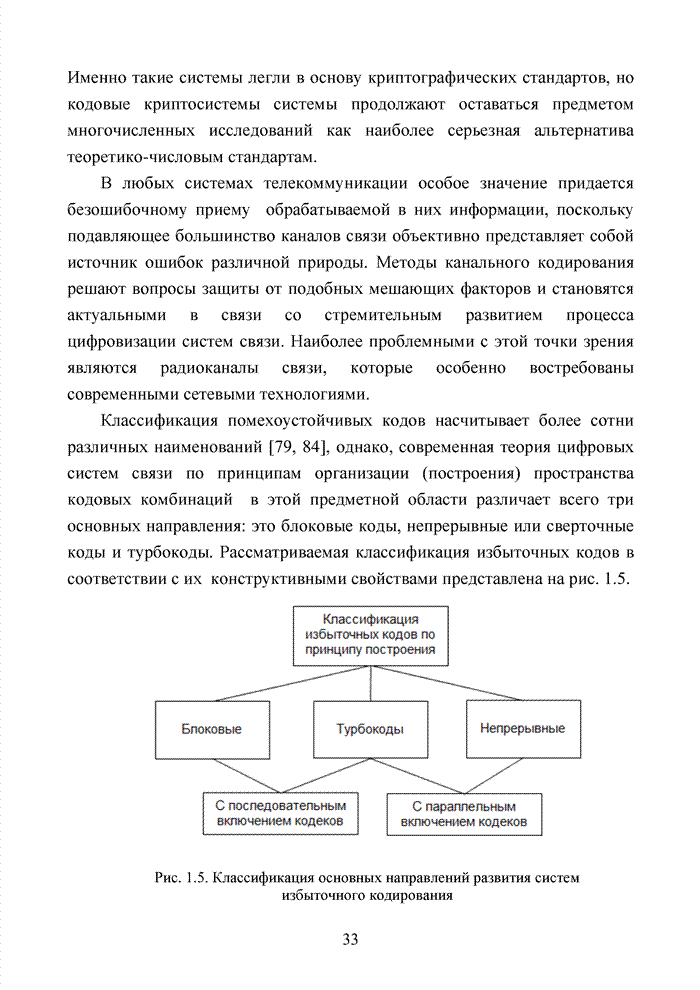
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
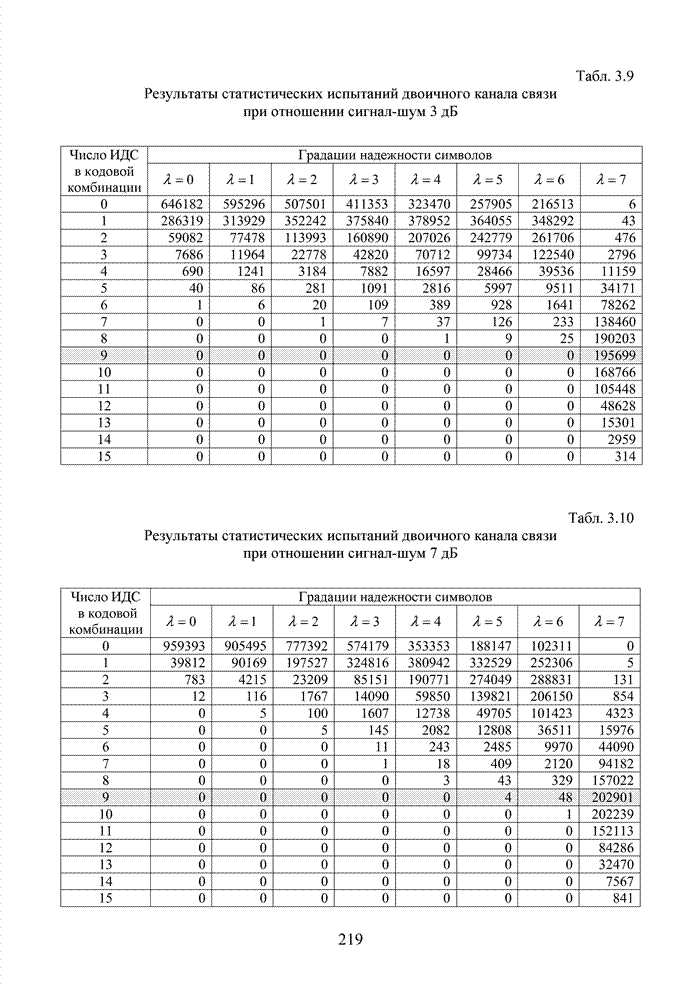
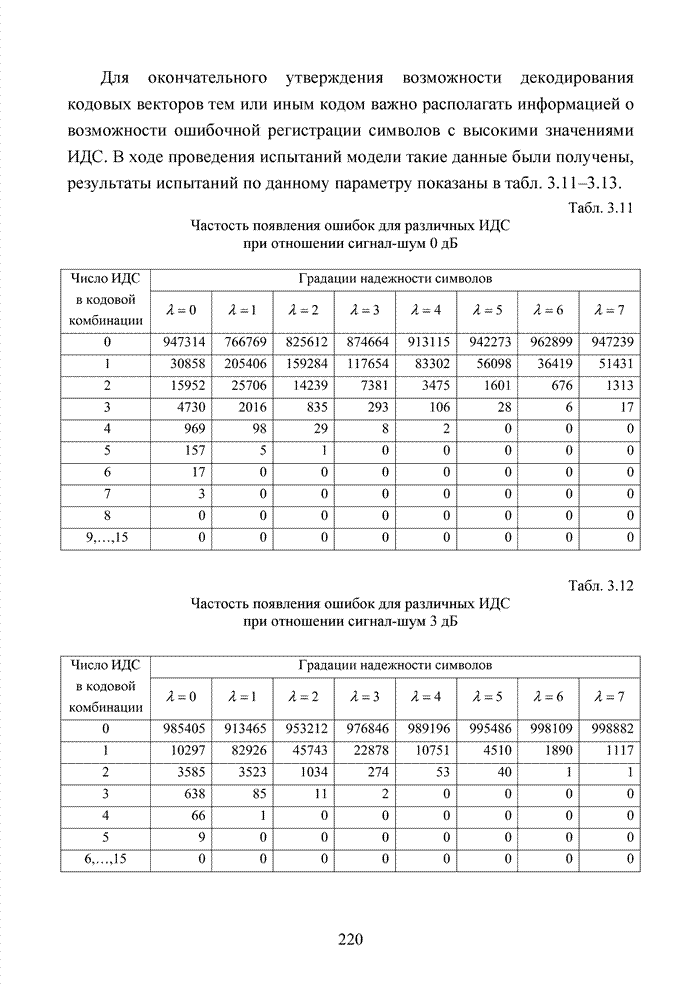
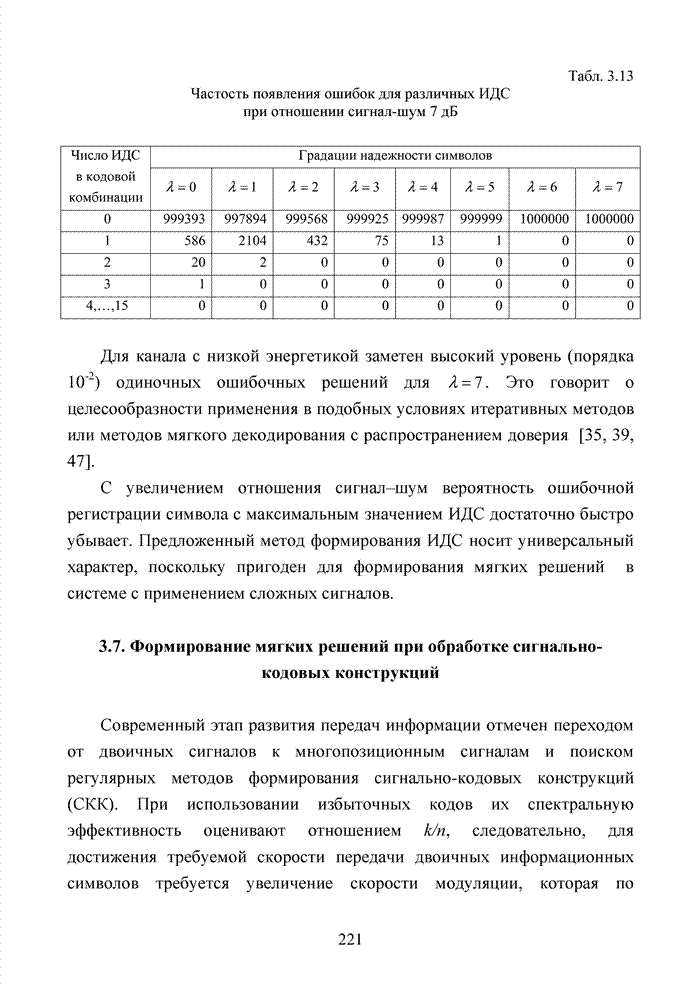
- 3.5. Метод скользящих окон в стирающем канале связи
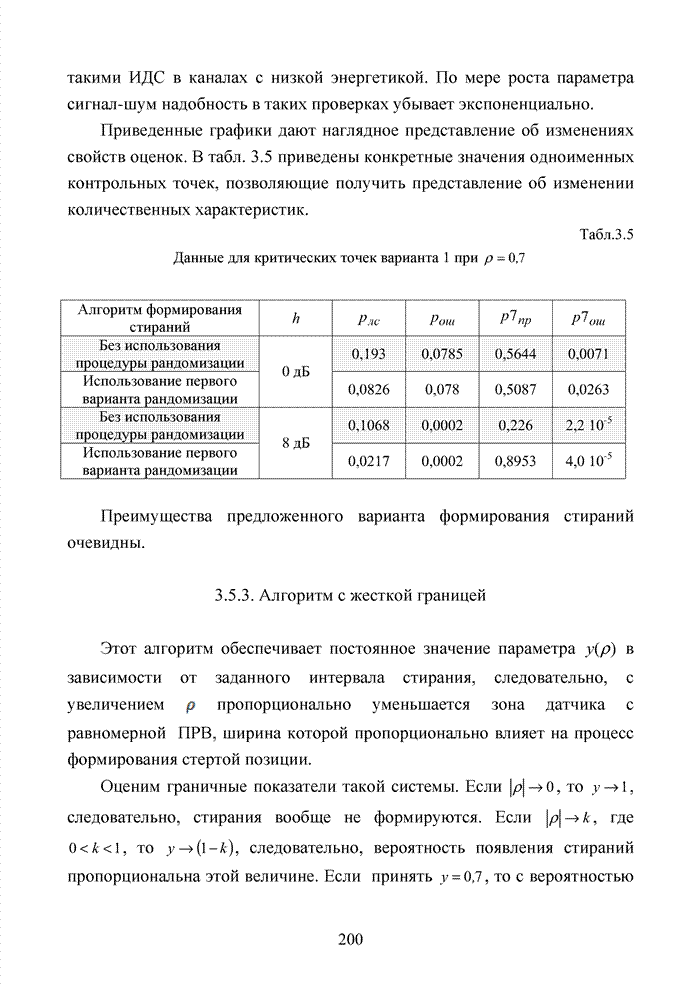
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
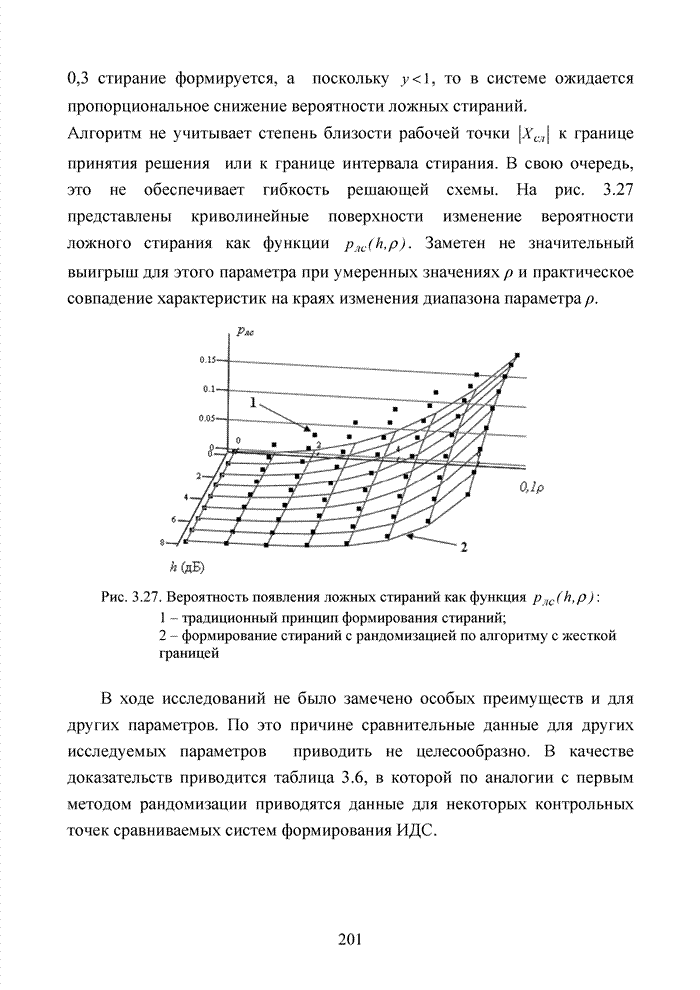
- 3.5.3. Алгоритм с жесткой границей
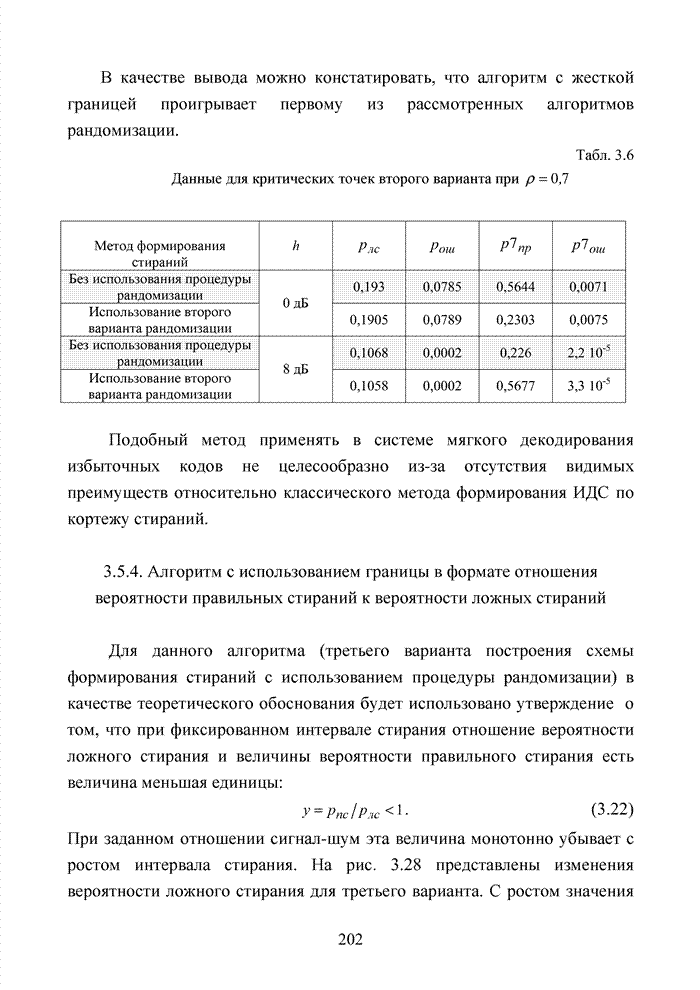
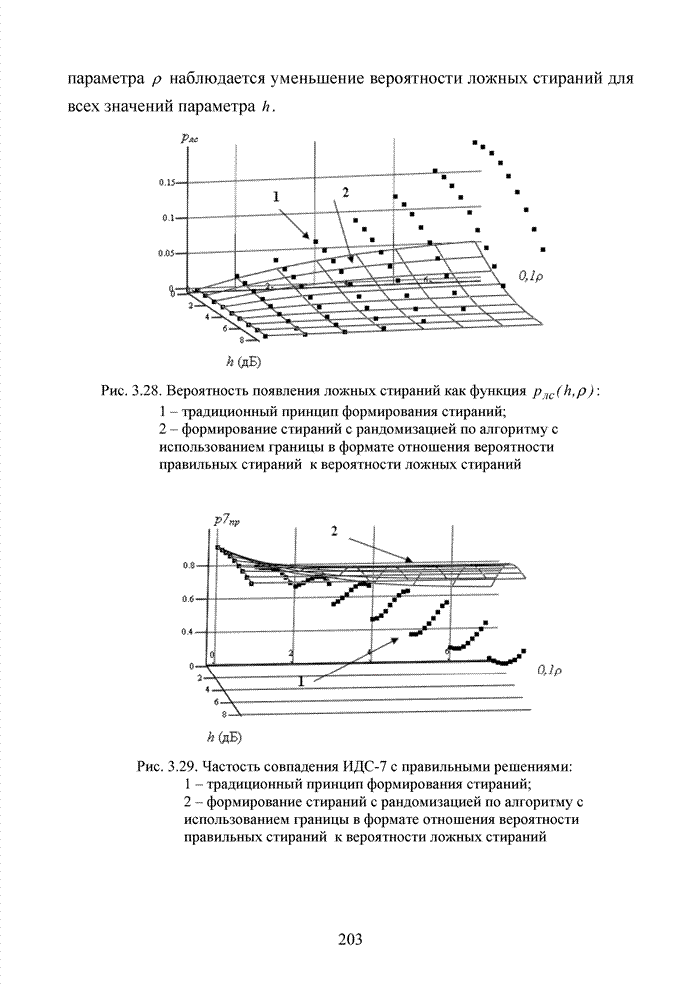
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
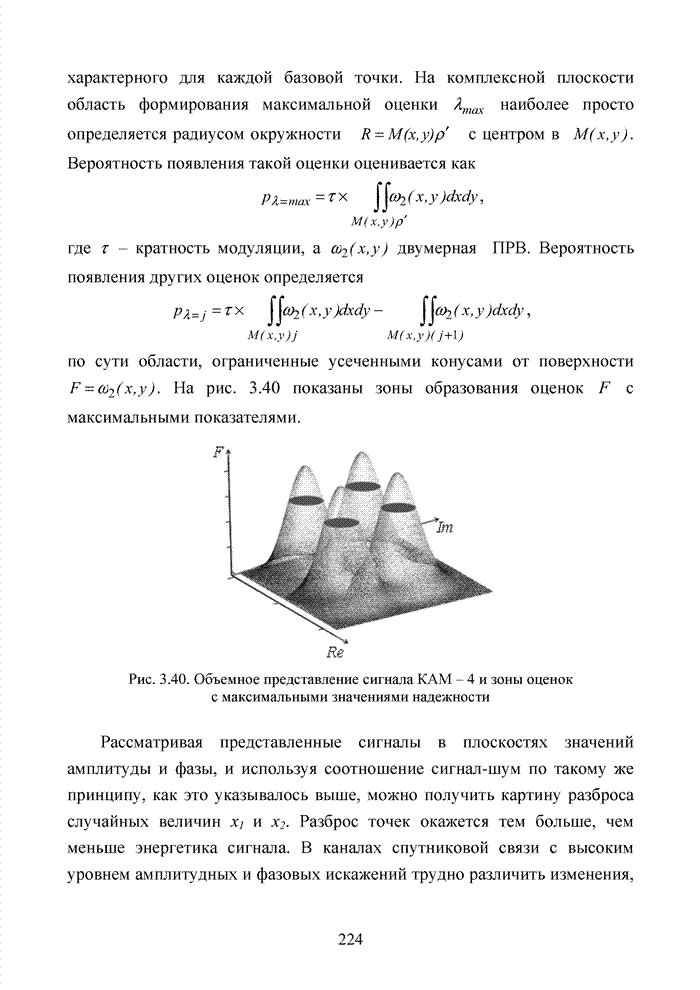
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
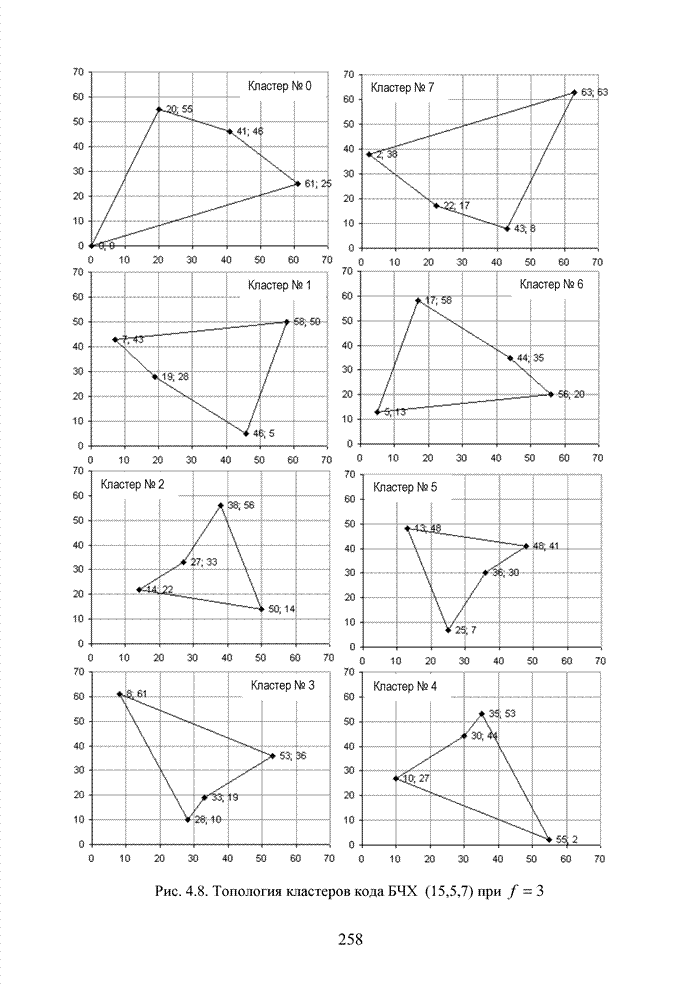
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
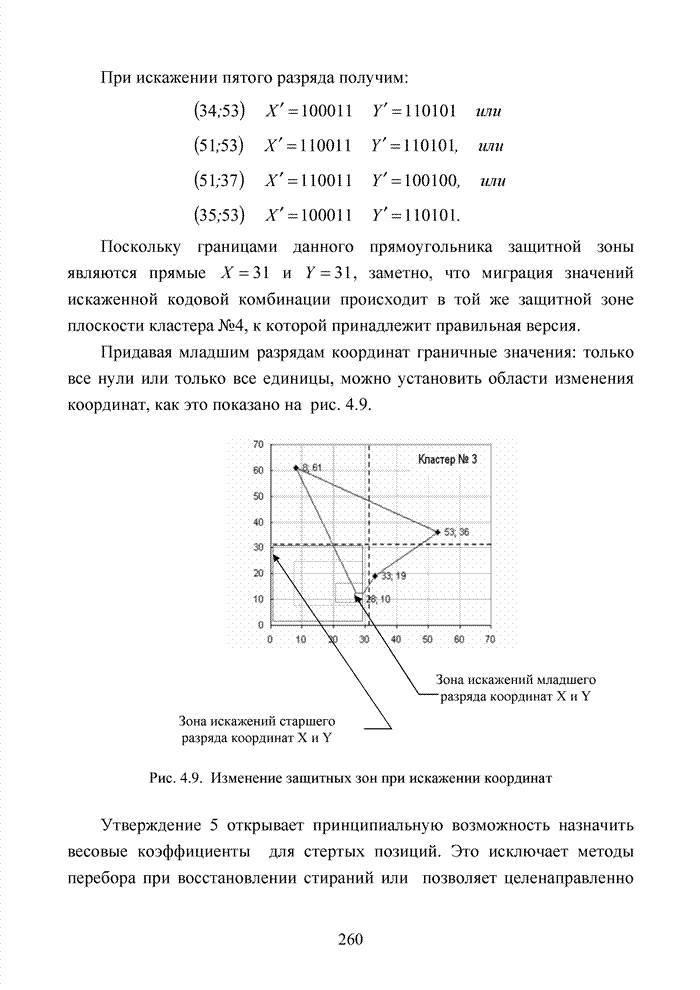
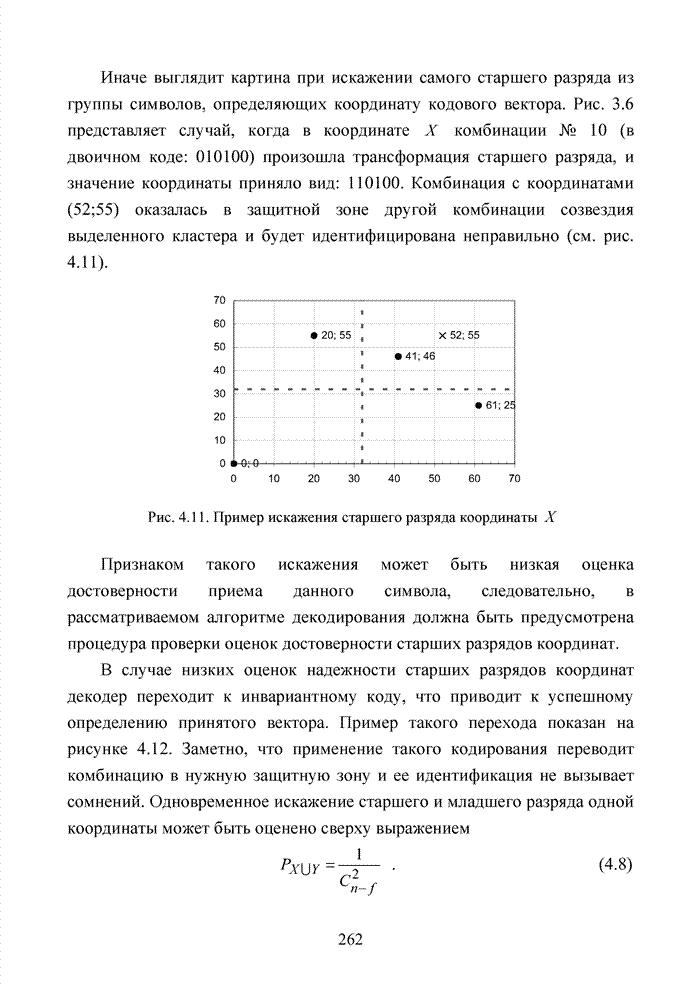
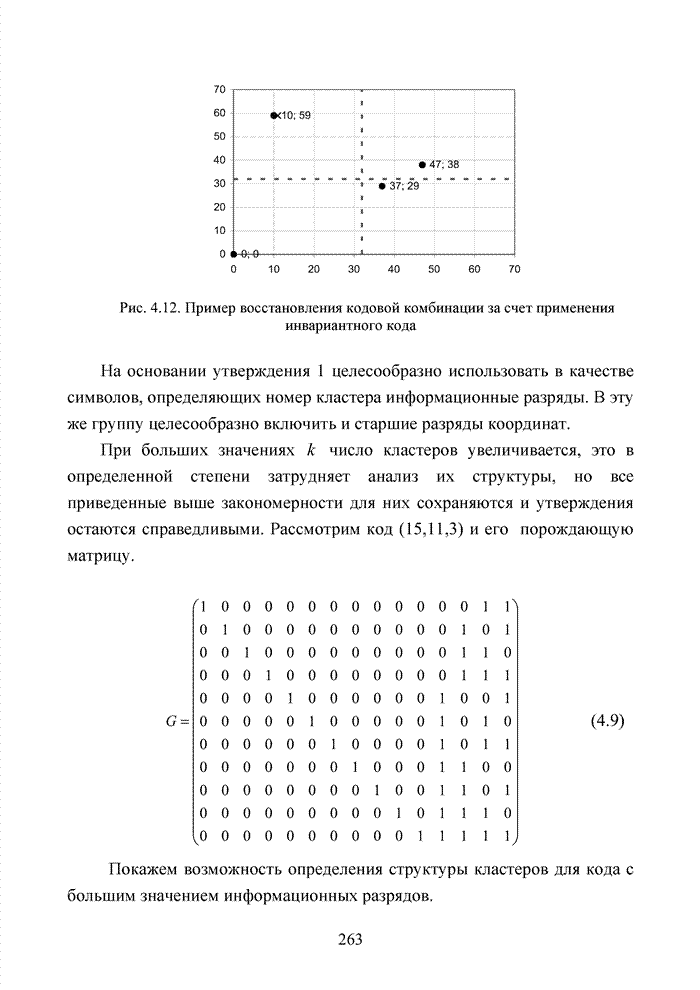
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
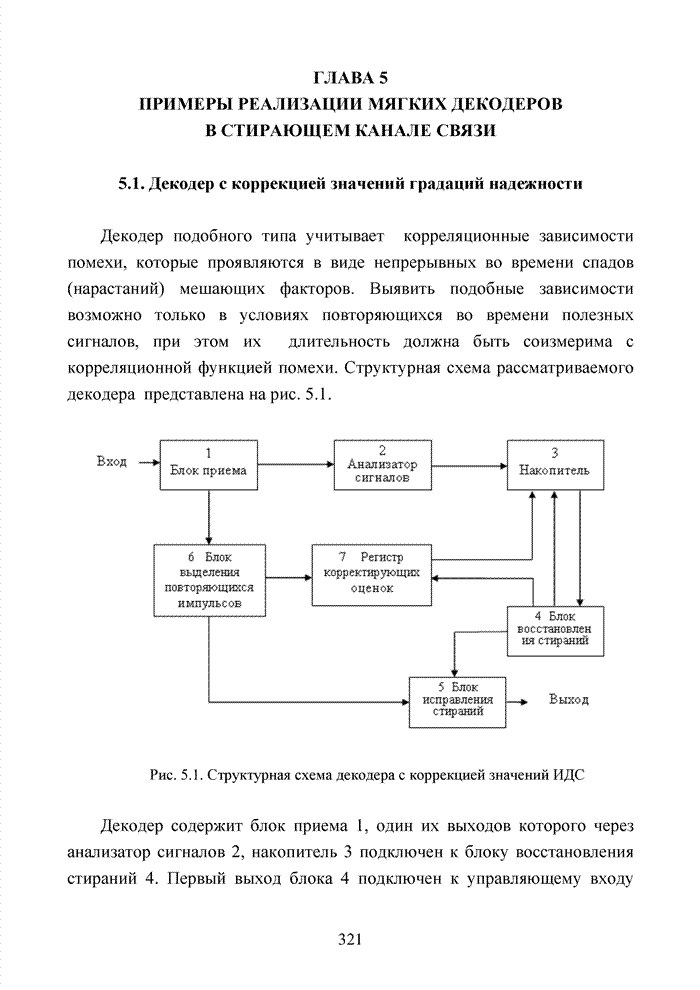
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
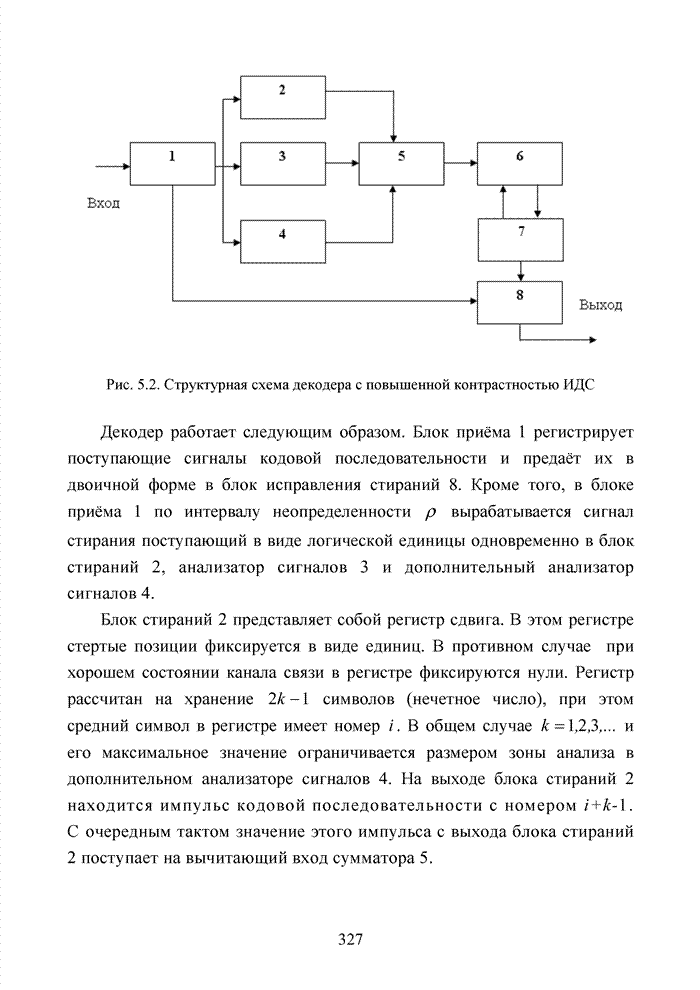
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
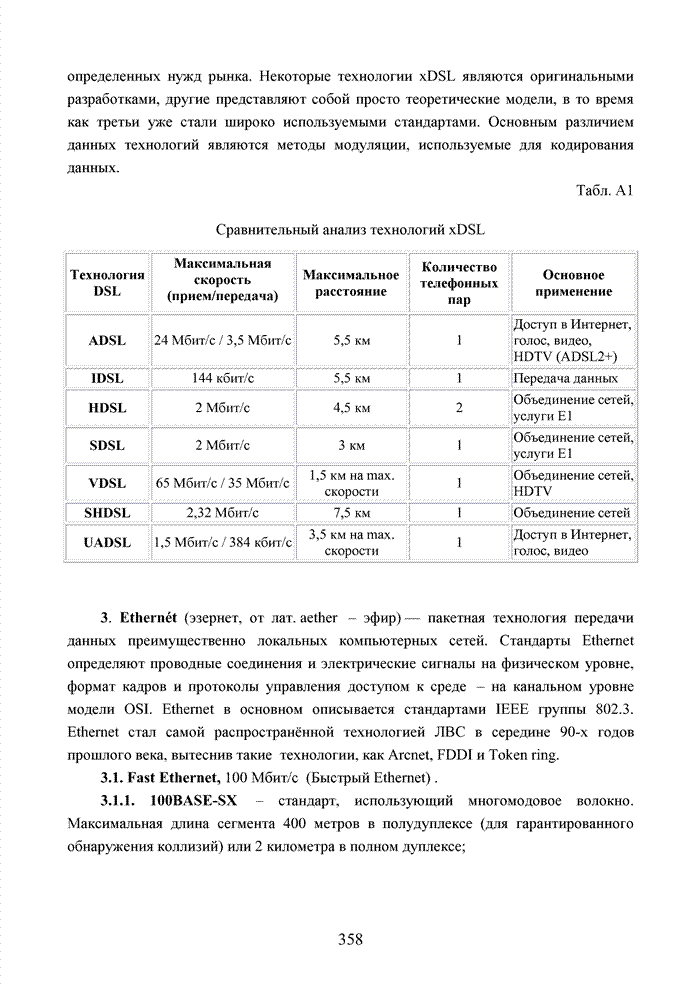
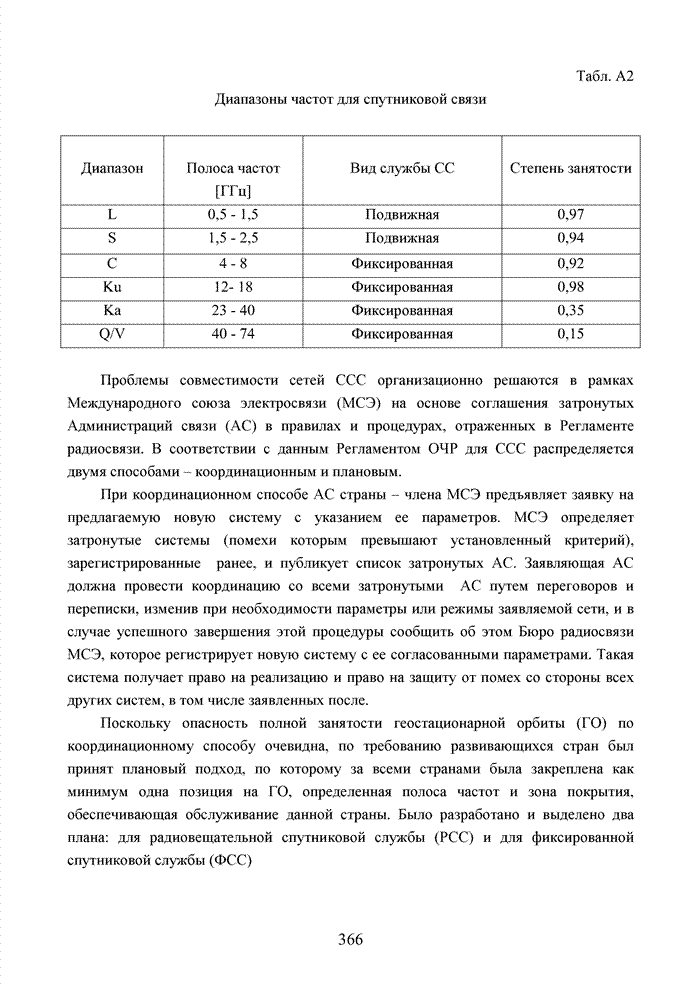
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
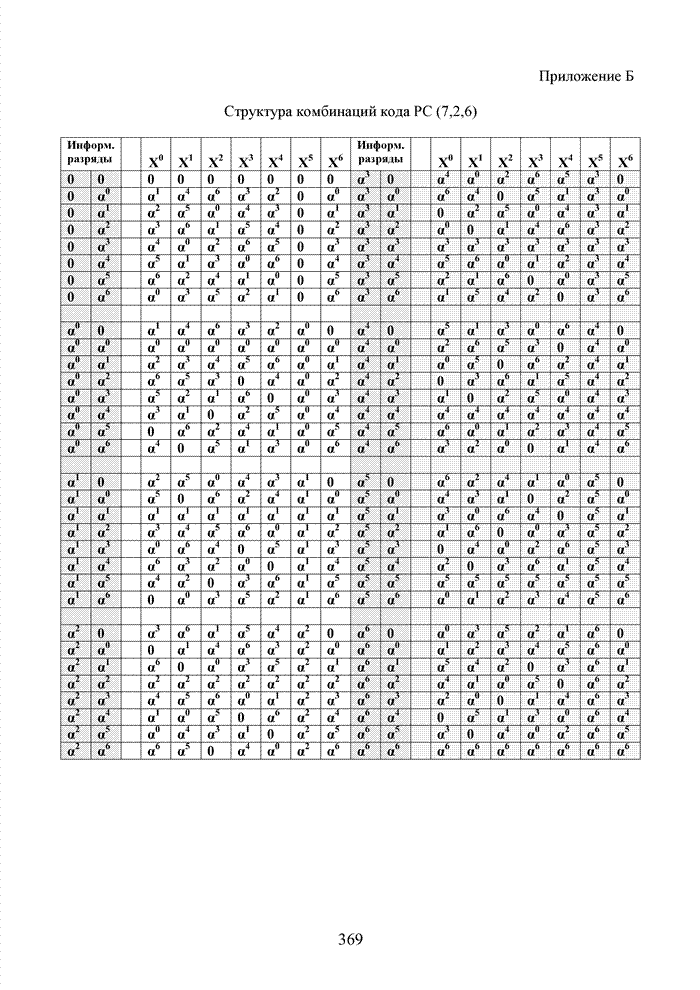
- Приложение Б Структура комбинаций кода РС (7,2,6)
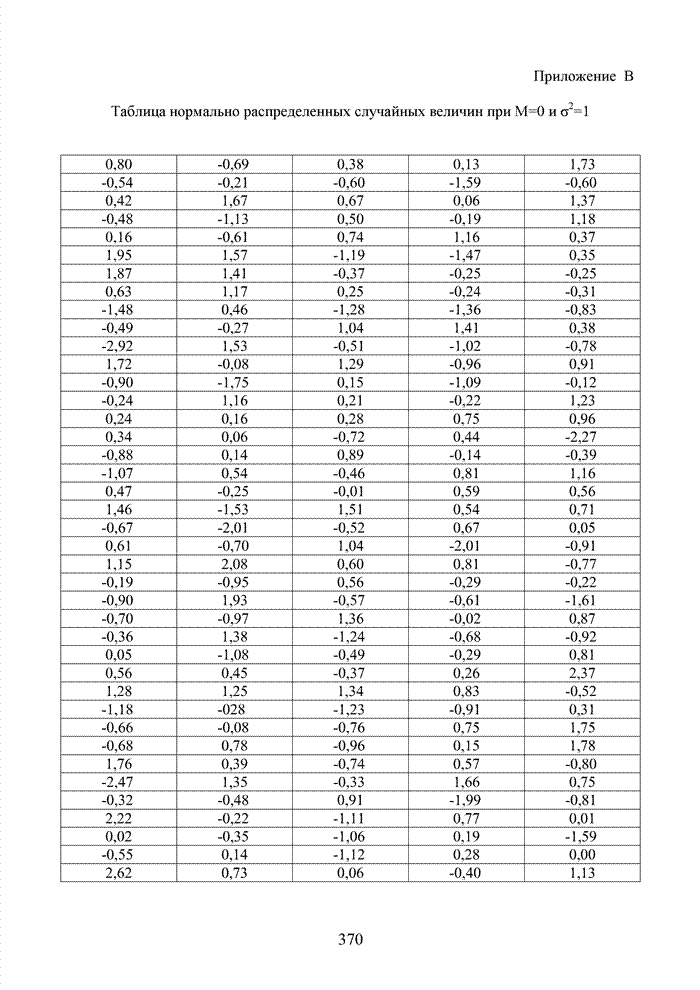
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК