| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
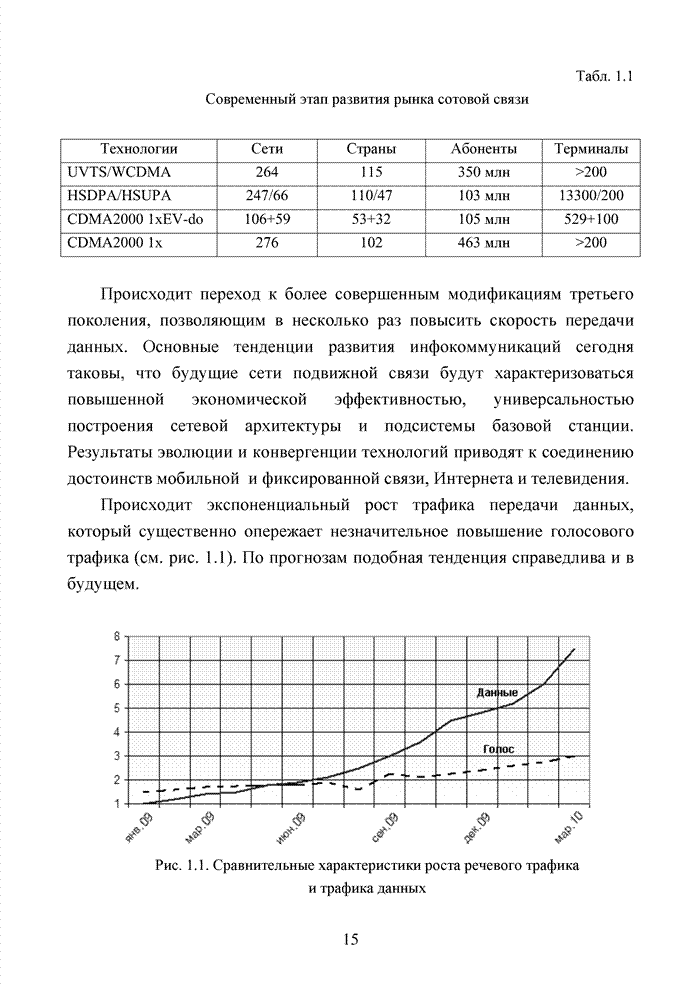
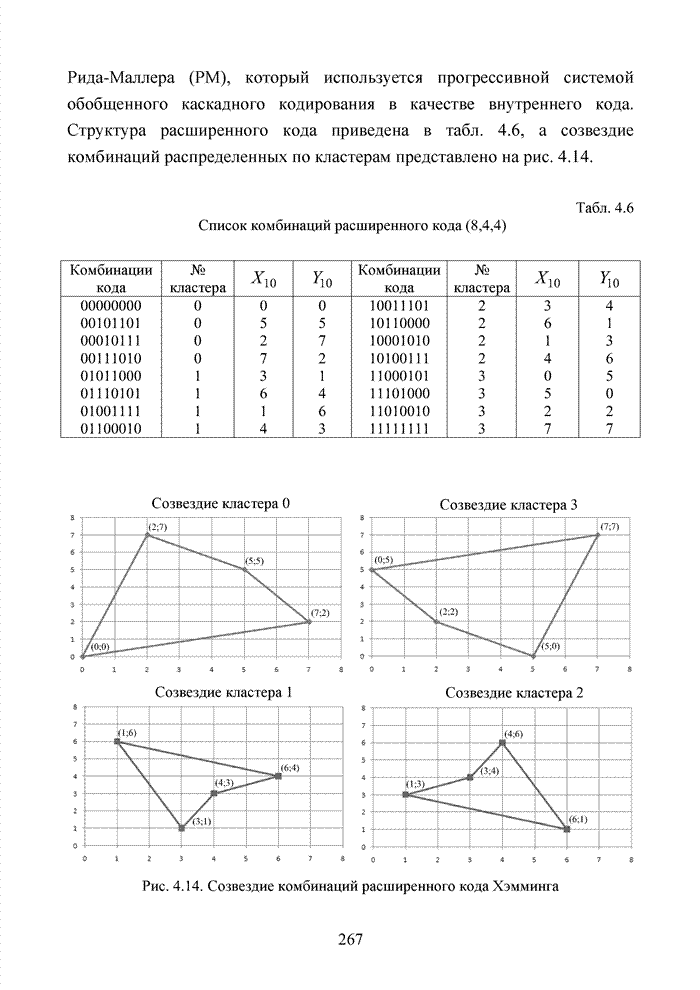
4.4. Система кодирования с надежной защитой номера кластера
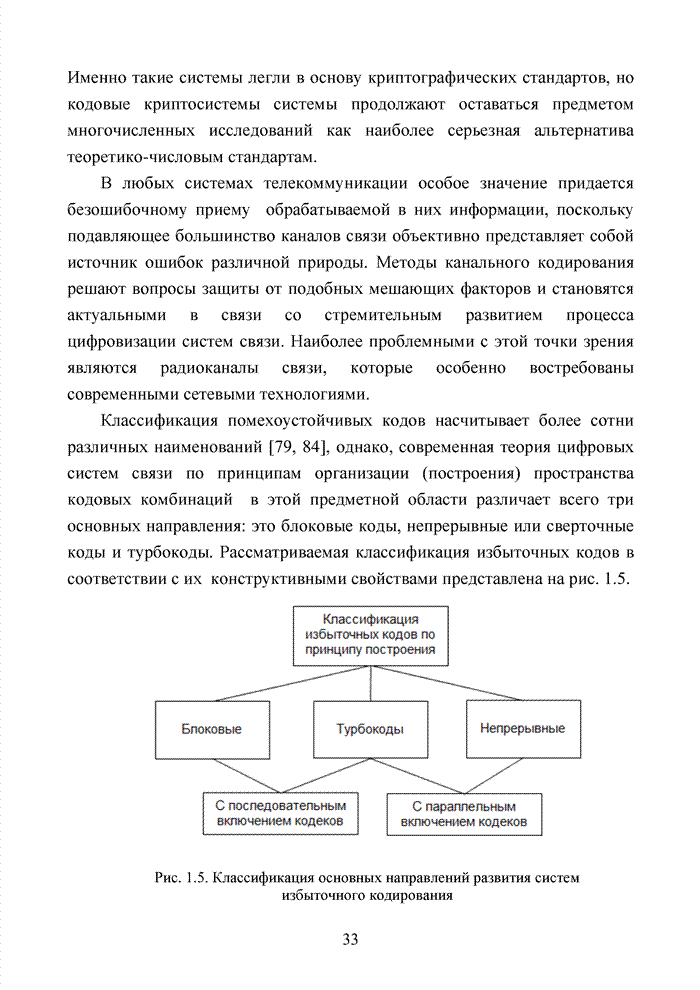
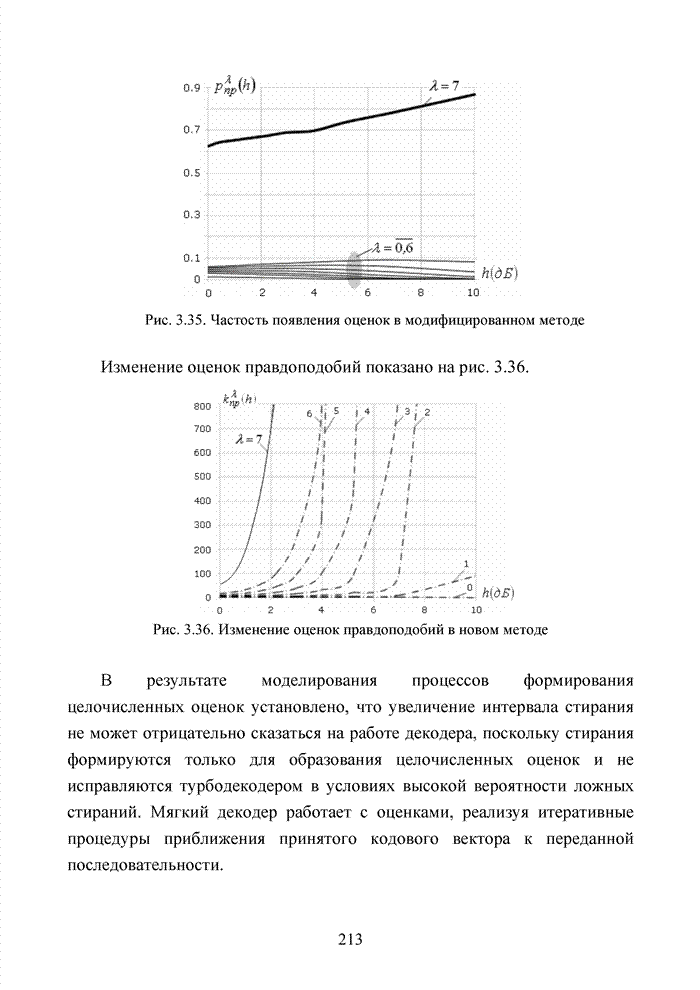
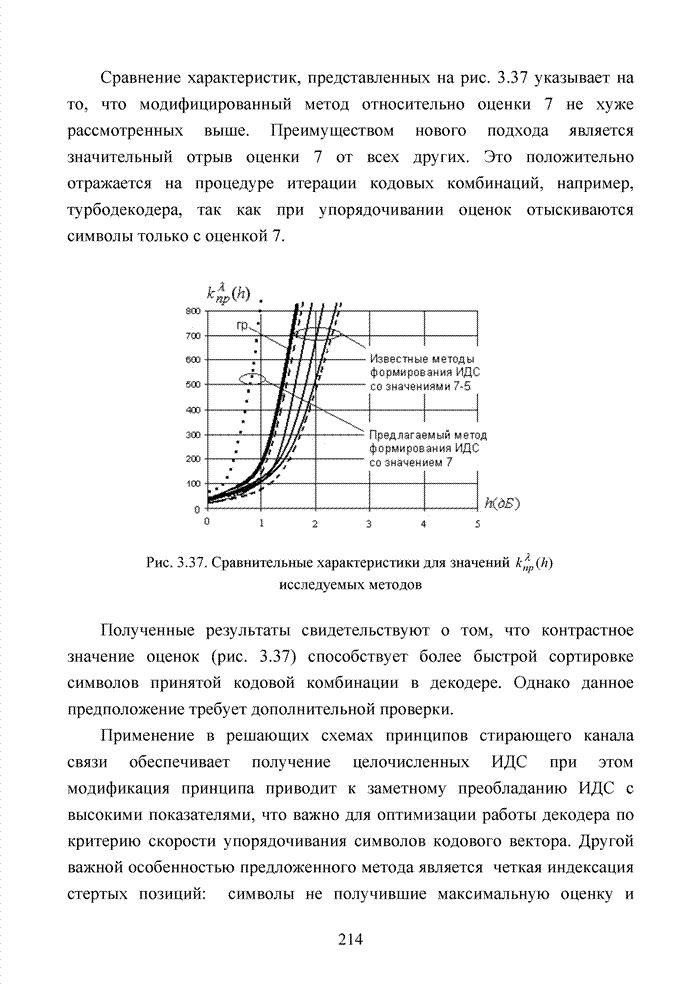
Рассмотренные принципы обработки кодовых комбинаций, использующие элементы кластерного анализа, показывают, что указанный метод декодирования может быть успешно реализован при условии надежного определения номера кластера. Решить эту задачу удается тремя путями:
- использовать циклические сдвиги принятого кодового вектора для определения группы символов с надежными ИДС;
- использовать алгоритм повышения ИДС отдельных символов, входящих в конкретные проверочные соотношения;
- использовать метод выкалывания символов, полученный в ходе стандартной процедуры кодирования и замены их на проверочные символы, определяющие дополнительные проверки для символов, определяющих номер кластера.
Исследования показали,
что использование первого способа необходимо связать с весовой структурой кода,
поскольку циклические сдвиги возможны только в комбинации определенного веса.
Так, в коде (7,4,3) необходимо выделить комбинации веса 3 и веса 4. Причем
первая группа символов определяется порождающим полиномом ![]() , а вторая группа является
циклическим сдвигом порождающего полинома дуального кода
, а вторая группа является
циклическим сдвигом порождающего полинома дуального кода ![]() . Вторым недостатком является
наличие в алгоритме процедуры перебора, которая усиливает неравномерность
времени декодирования комбинации.
. Вторым недостатком является
наличие в алгоритме процедуры перебора, которая усиливает неравномерность
времени декодирования комбинации.
Более надежным является второй способ, который лег в основу устройства, получившего положительное решение на выдачу патента. Суть метода заключается в том, что для повышения ИДС ненадежно принятого символа используется система проверочных соотношений, которая включает корректируемый бит. Алгоритм коррекции заключается в выборе проверочного соотношения, у которого проверочный бит, принят с наибольшим значением ИДС. Затем в выбранном проверочном соотношении вычеркиваются данные с ненадежными оценками. При этом учитывается знак вычеркиваемого бита, который влияет на четность результирующей оценки. При вычеркивании нуля коррекция знака проверочного символа не производится. При вычеркивании единицы проверочный бит корректируется. В [1, 3, 34, 81, 86] показано, что для статистических независимых данных сумма двух отношений правдоподобия определяется выражением:
 (4.11)
(4.11)
По сути, ![]() является ИДС символа, который подлежит коррекции, а
является ИДС символа, который подлежит коррекции, а ![]() является ИДС проверочного соотношения, на
основании которого осуществляется коррекция. Кроме значения ИДС символа
обозначение вида
является ИДС проверочного соотношения, на
основании которого осуществляется коррекция. Кроме значения ИДС символа
обозначение вида ![]() несет
информационную нагрузку, которая выражаются через знак
несет
информационную нагрузку, которая выражаются через знак ![]() для единиц и через знак
для единиц и через знак ![]() для нулей. Выражение (4.11) может быть использовано для
коррекции двоичных символов, определяющих номер кластера.
для нулей. Выражение (4.11) может быть использовано для
коррекции двоичных символов, определяющих номер кластера.
Известны свойства суммы двух логарифмических отношений правдоподобия [86]
![]() и
и ![]() .
.
Это означает, что при надежном приеме проверочного разряда возможна коррекция информационного символа вплоть до исправления ошибки, т.е. знака символа. По сути, представленная процедура используется для любых систем с итеративными методами обработки принятой информации 1, 27, 40, 47, 50, 71, 86, 108, 110].
Покажем, что выражение (4.11) при определенных условиях справедливо для блоковых кодов. Используя критерий максимума правдоподобия и соотношение (4.11) возможно декодирование на основе лучших показателей градаций надежности принятых символов [1]. Такое декодирование получило название декодирования с итеративным распространением доверия или итеративным вероятностным декодированием.
Предварительно докажем ряд утверждений, определяющих процедуру такого декодирования применительно для целочисленных ИДС.
Утверждение 8. Применение целочисленных ИДС для системы двоичного кодирования сокращает число итераций относительно возможных рациональных показателей надежности.
Пусть задана процедура
(4.11) для пространства трех сигналов ![]() ;
; ![]() ;
;![]() и пусть
и пусть ![]() является проверкой на четность для
символов
является проверкой на четность для
символов ![]() и
и ![]() , которая выполняется при условии,
что
, которая выполняется при условии,
что ![]() . Тогда
в соответствии с принципом Байеса для первого шага итераций имеем:
. Тогда
в соответствии с принципом Байеса для первого шага итераций имеем:
![]() , поскольку
, поскольку ![]() ,
,
![]() , поскольку
, поскольку ![]() .
.
После выполнения второго шага получаем:
![]() ;
;
![]() ,
,
где ![]() – корректирующие оценки.
– корректирующие оценки.
Пусть ![]() имеет максимальное целочисленное
значение ИДС
имеет максимальное целочисленное
значение ИДС ![]() .
Если
.
Если ![]() , что с
высокой долей вероятности выполняется при средних значениях отношения сигнал
шум, то для получения корректирующих оценок
, что с
высокой долей вероятности выполняется при средних значениях отношения сигнал
шум, то для получения корректирующих оценок ![]() и
и ![]() необходим минимум итераций. Условие
необходим минимум итераций. Условие ![]() будет выполнено, например, при
будет выполнено, например, при ![]() и
и ![]() .
.
Пусть в новых условиях в
системе с рациональными показателями значение ![]() , а остальные значения остались
неизменными, тогда для достижения
, а остальные значения остались
неизменными, тогда для достижения ![]() необходимы три шага итераций.
необходимы три шага итераций.
Допустим, что выполняются
условия ![]() и
и ![]() , тогда
, тогда
![]() ;
;
![]() .
.
После выполнения второго шага итераций получаем:
![]() ;
;
![]() ,
,
поскольку необходимо выполнить
условие (4.11): ![]() Дальнейшее выполнение шагов не имеет
смысла, т.к. результаты второго шага будут повторяться из-за условия
Дальнейшее выполнение шагов не имеет
смысла, т.к. результаты второго шага будут повторяться из-за условия ![]() . Таким образом, использование целочисленных ИДС сокращает
число итераций, уменьшая общее время декодирования.
. Таким образом, использование целочисленных ИДС сокращает
число итераций, уменьшая общее время декодирования.
Утверждение 9. При выполнении условий ![]() и
и ![]() , при одновременном выполнении
проверки на четность значение ИДС проверочного бита может быть
откорректировано за счет ИДС информационных битов. Пусть
, при одновременном выполнении
проверки на четность значение ИДС проверочного бита может быть
откорректировано за счет ИДС информационных битов. Пусть
![]() (4.12)
(4.12)
На данном этапе рассуждений не будет
учитывать значение ИДС, а знак ![]() означает сложение по
означает сложение по ![]() . Условие (4.12) определяет
очередное сложение в соответствие с теорией групп в двоичном поле
. Условие (4.12) определяет
очередное сложение в соответствие с теорией групп в двоичном поле ![]() . В этом поле операции
сложения и вычитания адекватны, следовательно:
. В этом поле операции
сложения и вычитания адекватны, следовательно:
![]()
![]()
Следствие 9.1. Если приемник зафиксировал проверочный бит с низким значением ИДС, но определившие его по проверке на четность биты имеют высокие показатели надежности, то ИДС проверочного бита может быть повышен путем перестановки.
Пример. Пусть ![]() . Тогда
. Тогда
![]() .
.
С учетом множителя ![]() в (4.11) имеем
в (4.11) имеем



Выполнение третьего шага
итераций не имеет смысла в соответствии с утверждением 8 . Здесь ![]() .
.
Выполняем коррекцию символов:

Возвращаясь к исходному
выражению, получаем: ![]() Проверочный символ откорректирован.
Проверочный символ откорректирован.
Утверждение 10. При правильном выполнении коррекции
ИДС на втором шаге итерации выполняется условие: ![]() .
.
Действительно,
корректируемые символы должны увеличивается по абсолютной величине,
следовательно, для ![]()
![]() и
и ![]() признак отсутствия ошибки в
корректируемой группе символов проявляется в явном виде.
признак отсутствия ошибки в
корректируемой группе символов проявляется в явном виде.
Следствие 10.1. Если одно из условий не выполняется,
необходимо сменить знак при ![]() , что адекватно исправлению ошибки.
, что адекватно исправлению ошибки.
Утверждение 11. Если в принятой кодовой комбинации
зафиксировано ![]() ошибок, число которых может быть исправлено с учетом метрики
Хэмминга, то утверждение 10. может не выполняться, поскольку значение
ошибок, число которых может быть исправлено с учетом метрики
Хэмминга, то утверждение 10. может не выполняться, поскольку значение ![]() корректирует ошибочное значение
корректирует ошибочное значение ![]() .
.
Действительно, ошибочные
биты имеют искаженные знаки ![]() и исправление знака происходит за счет
параметра
и исправление знака происходит за счет
параметра ![]() ,
имеющего знак противоположный
,
имеющего знак противоположный![]() .
.
Для выполнения коррекции
требуется больше двух шагов. Поскольку именно на втором шаге проявляется
тенденция для значений ![]() и
и ![]() в соответствии с утверждением 10. Для
коррекции символа
в соответствии с утверждением 10. Для
коррекции символа ![]() необходим
хотя бы один дополнительный шаг для подтверждения выявленной тенденции.
необходим
хотя бы один дополнительный шаг для подтверждения выявленной тенденции.
Следствие 11.1. В случае выполнения условия по утверждению 10 на втором шаге итерации целесообразно изменить знак у слабого ИДС и проверить правильность действий посредством выполнения четности для других проверочных соотношений.
Утверждение 12. При выборе символов, подлежащих
коррекции, и последующее удаление ИДС символа из проверочного соотношения с
положительным знаком требует изменения показателя степени у основания ![]() с единицы на
с единицы на ![]() , где
, где ![]() – число удаленных (свернутых) символов со знаком
– число удаленных (свернутых) символов со знаком ![]() . Выполнение условия
четности для проверочного символа не должно нарушаться, удаляя из проверочного
соотношения хотя бы одну единицу (ИДС со знаком
. Выполнение условия
четности для проверочного символа не должно нарушаться, удаляя из проверочного
соотношения хотя бы одну единицу (ИДС со знаком![]() ) требует коррекции правой части выражения
(4.11), а удаление ИДС с отрицательным знаком не требует коррекции правой части
этого уравнения . Из-за этого выражение (4.11) принимает вид
) требует коррекции правой части выражения
(4.11), а удаление ИДС с отрицательным знаком не требует коррекции правой части
этого уравнения . Из-за этого выражение (4.11) принимает вид
 (4.13)
(4.13)
Приведенные соотношения
позволяют предложить новый алгоритм декодирования блоковых кодов с
использованием метода кластерного анализа. Его суть заключается в том, что
передатчик выделяет разряды кластера и на их основе получает два проверочных
бита ![]() и
и ![]() . Сама кодовая
комбинация образуется или с использованием процедуры умножения кодового вектора
на порождающую матрицу
. Сама кодовая
комбинация образуется или с использованием процедуры умножения кодового вектора
на порождающую матрицу ![]() или с использованием схемы сдвигового регистра.
Учитывая свойства кода восстанавливать перфорированные символы, в разрядах,
определяющих координаты вектора, выкалываются позиции, находящиеся в средней
части одной из координат. На место выколотых символов вставляются символы
или с использованием схемы сдвигового регистра.
Учитывая свойства кода восстанавливать перфорированные символы, в разрядах,
определяющих координаты вектора, выкалываются позиции, находящиеся в средней
части одной из координат. На место выколотых символов вставляются символы ![]() и
и ![]() , которые используются для
проверки символов кластера по принципу
, которые используются для
проверки символов кластера по принципу
![]() и
и ![]()
Включение дополнительной проверки позволяет снизить вероятность искажения номера кластера, что важно для дальнейшей работы декодера. Указанные проверки могут быть усилены за счет использования вычислений апостериорных вероятностей.
Рассмотрим внедрение
проверочных разрядов ![]() и
и
![]() на примере
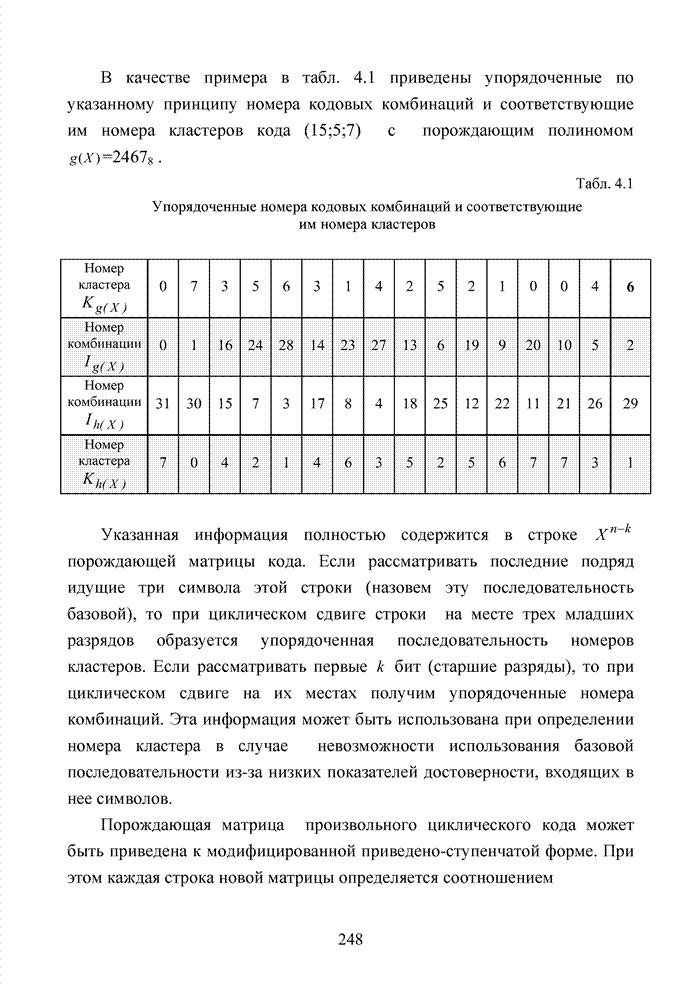
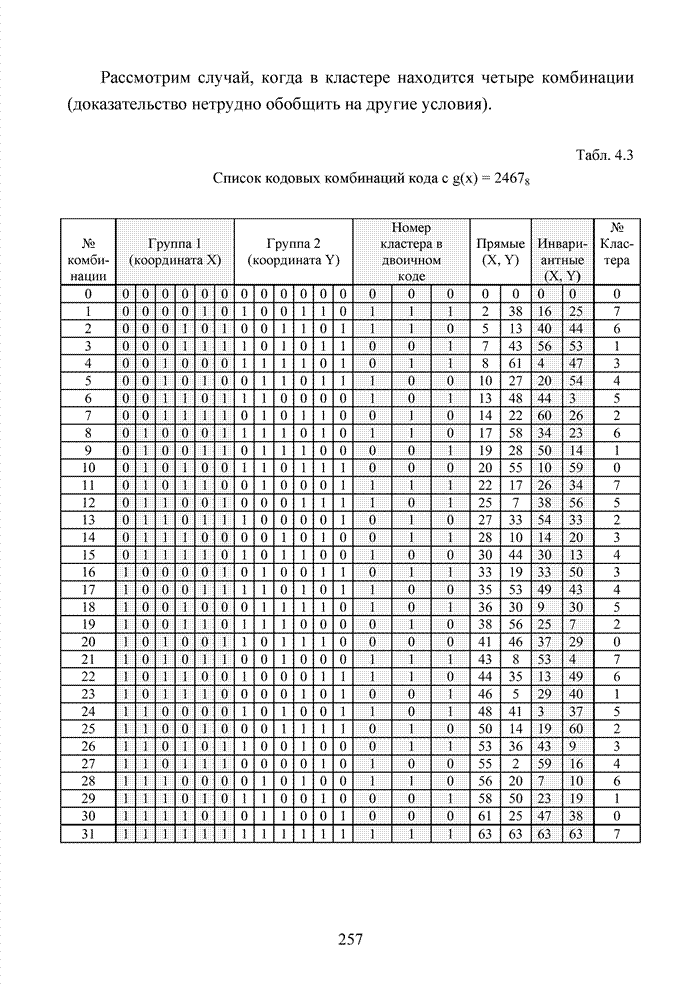
кода (15,5,7). Напомним, что в табл. 4.3 представлен канонический список
кодовых комбинаций кода. В этом списке приводятся прямые координаты комбинаций
кластеров и их инвариантные аналоги. Представим третьи младшие разряды
координат
на примере
кода (15,5,7). Напомним, что в табл. 4.3 представлен канонический список
кодовых комбинаций кода. В этом списке приводятся прямые координаты комбинаций
кластеров и их инвариантные аналоги. Представим третьи младшие разряды
координат ![]() и
и ![]() в форме проверочных
разрядов
в форме проверочных
разрядов ![]() и
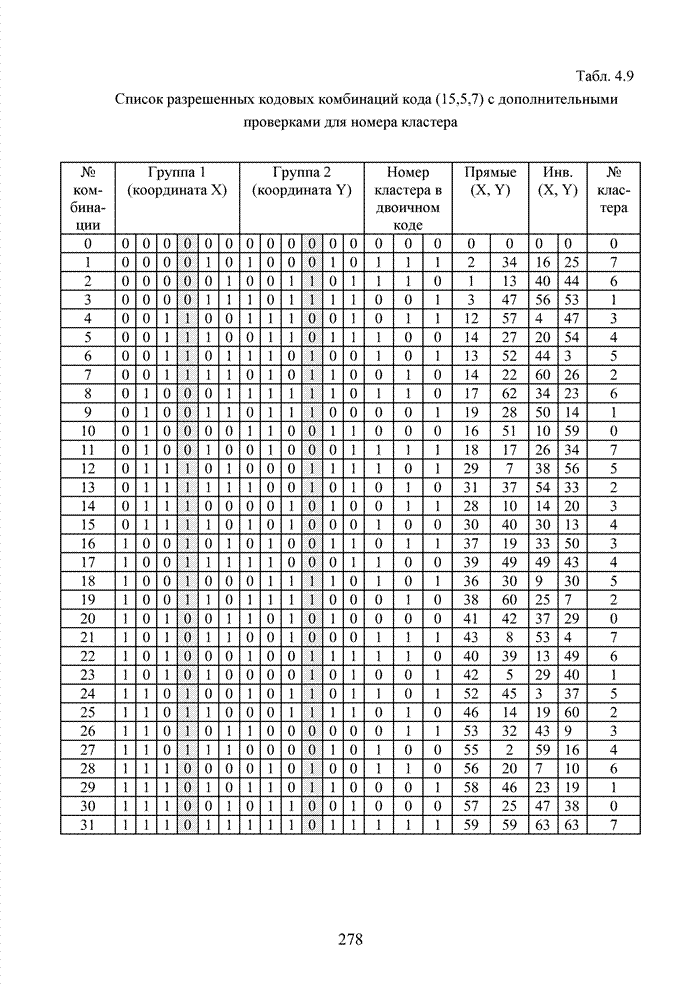
и ![]() . Список таких
комбинаций приведен в табл. 4.9.
. Список таких
комбинаций приведен в табл. 4.9.
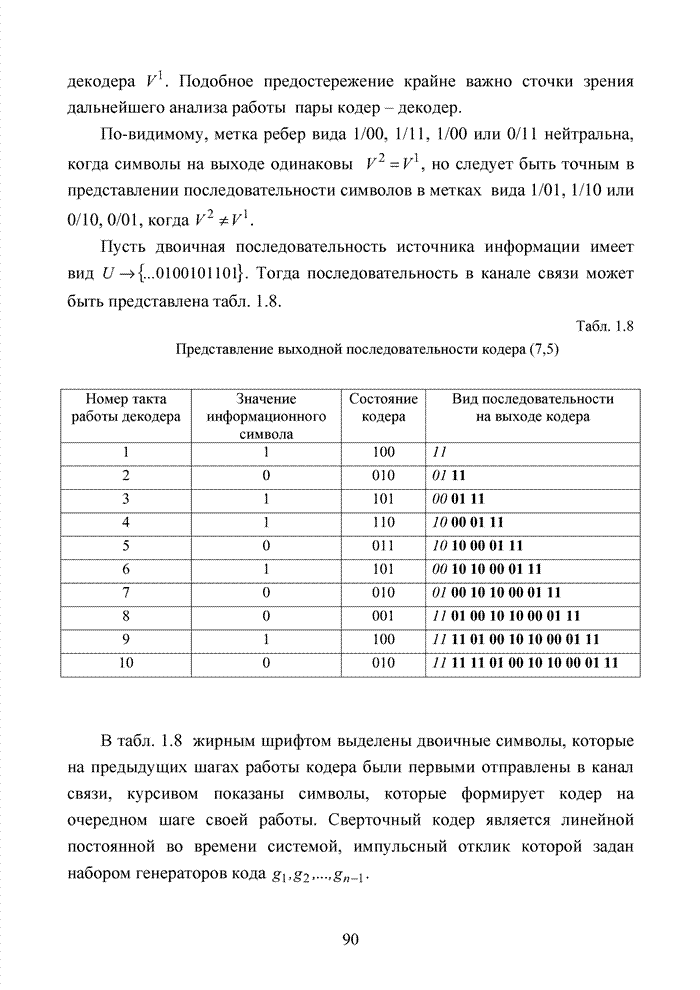
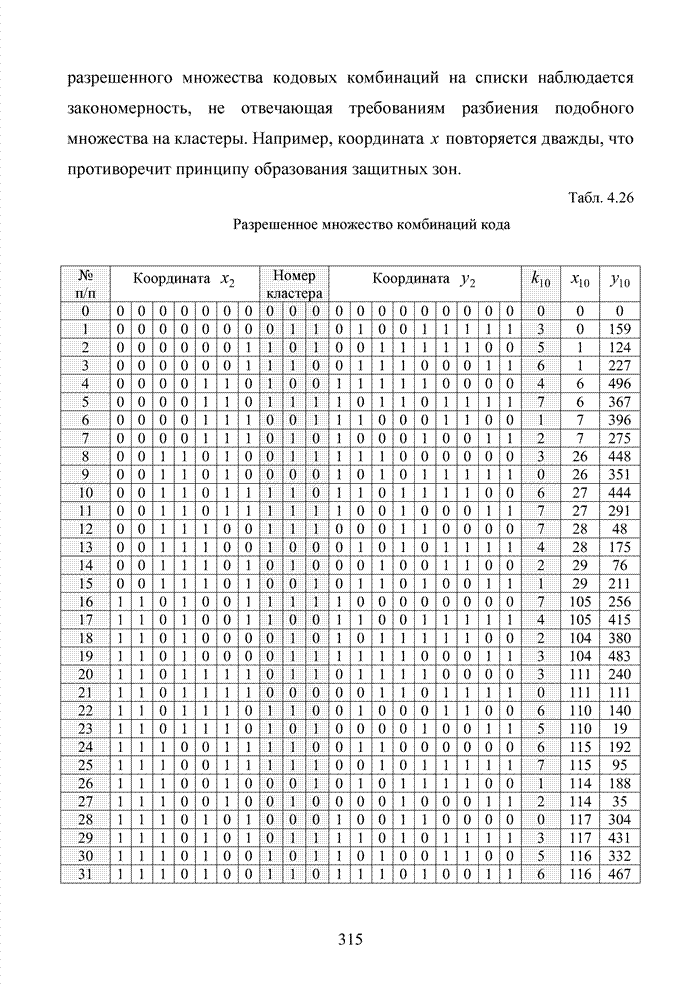
Табл. 4.9 Список разрешенных кодовых комбинаций кода (15,5,7) с дополнительными проверками для номера кластера
|
№ ком- бина-ции |
Группа 1 (координата Х) |
Группа 2 (координата Y) |
Номер кластера в двоичном коде |
Прямые (X, Y) |
Инв. (X, Y) |
№ клас-тера |
||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
2 |
34 |
16 |
25 |
7 |
|
2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
13 |
40 |
44 |
6 |
|
3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
3 |
47 |
56 |
53 |
1 |
|
4 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
12 |
57 |
4 |
47 |
3 |
|
5 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
14 |
27 |
20 |
54 |
4 |
|
6 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
13 |
52 |
44 |
3 |
5 |
|
7 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
14 |
22 |
60 |
26 |
2 |
|
8 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
17 |
62 |
34 |
23 |
6 |
|
9 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
19 |
28 |
50 |
14 |
1 |
|
10 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
16 |
51 |
10 |
59 |
0 |
|
11 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
18 |
17 |
26 |
34 |
7 |
|
12 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
29 |
7 |
38 |
56 |
5 |
|
13 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
31 |
37 |
54 |
33 |
2 |
|
14 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
28 |
10 |
14 |
20 |
3 |
|
15 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
30 |
40 |
30 |
13 |
4 |
|
16 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
37 |
19 |
33 |
50 |
3 |
|
17 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
39 |
49 |
49 |
43 |
4 |
|
18 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
36 |
30 |
9 |
30 |
5 |
|
19 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
38 |
60 |
25 |
7 |
2 |
|
20 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
41 |
42 |
37 |
29 |
0 |
|
21 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
43 |
8 |
53 |
4 |
7 |
|
22 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
40 |
39 |
13 |
49 |
6 |
|
23 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
42 |
5 |
29 |
40 |
1 |
|
24 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
52 |
45 |
3 |
37 |
5 |
|
25 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
46 |
14 |
19 |
60 |
2 |
|
26 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
53 |
32 |
43 |
9 |
3 |
|
27 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
55 |
2 |
59 |
16 |
4 |
|
28 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
56 |
20 |
7 |
10 |
6 |
|
29 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
58 |
46 |
23 |
19 |
1 |
|
30 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
57 |
25 |
47 |
38 |
0 |
|
31 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
59 |
59 |
63 |
63 |
7 |
По сравнению с
первоначальным вариантом координаты ![]() и
и ![]() претерпели незначительные изменения, которые, как
указывалось выше, не влияют на выход рабочей точки созвездия конкретного
кластера за пределы соответствующей защитной зоны.
претерпели незначительные изменения, которые, как
указывалось выше, не влияют на выход рабочей точки созвездия конкретного
кластера за пределы соответствующей защитной зоны.
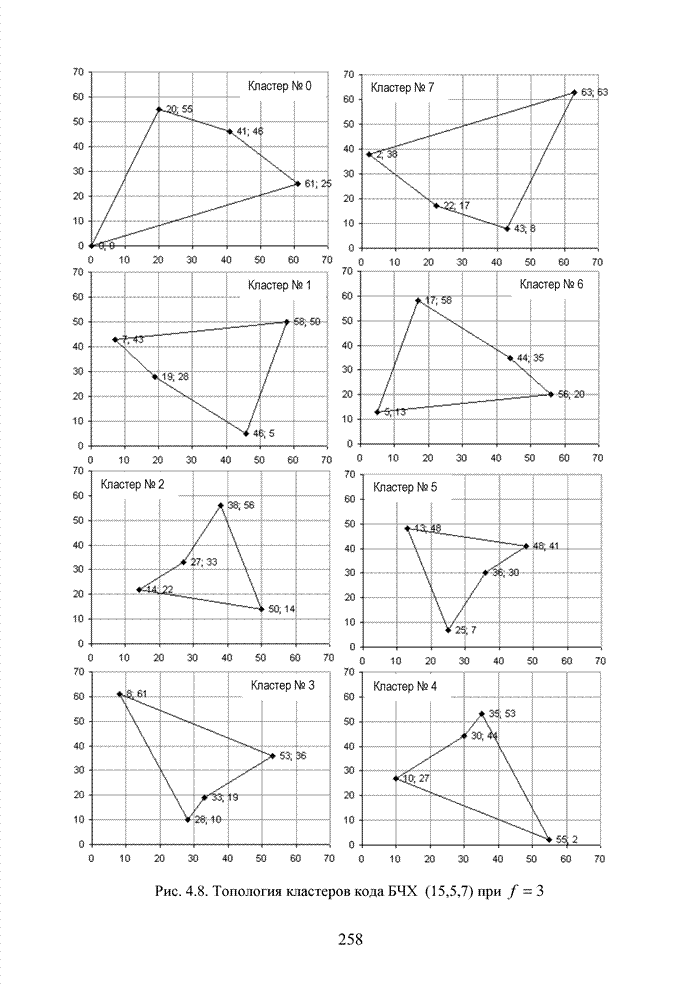
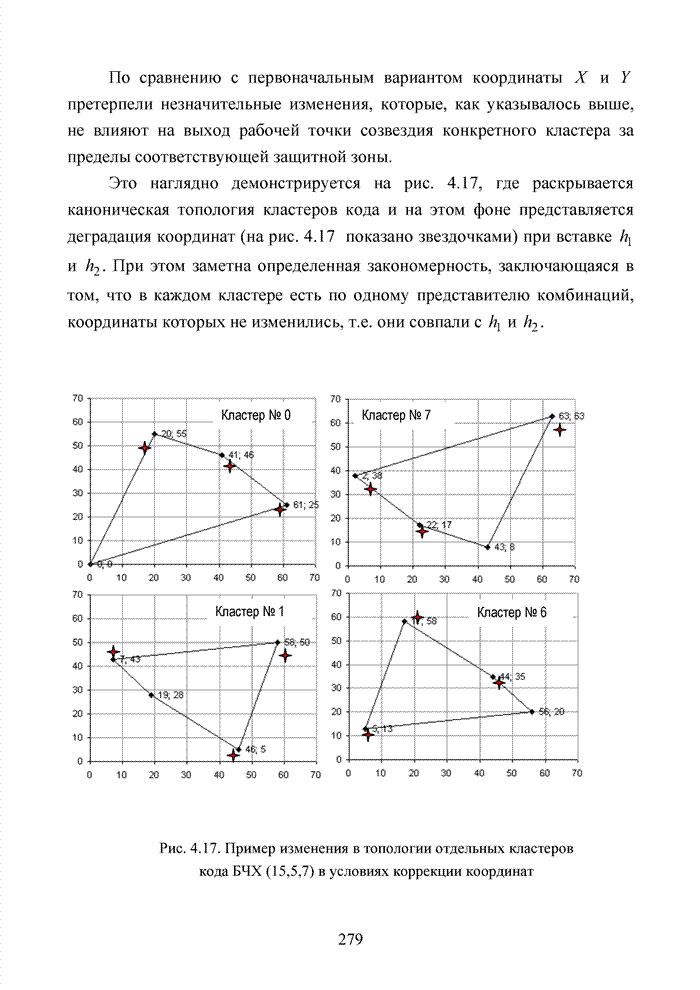
Это наглядно
демонстрируется на рис. 4.17, где раскрывается каноническая топология кластеров
кода и на этом фоне представляется деградация координат (на рис. 4.17 показано
звездочками) при вставке ![]() и
и ![]() . При этом заметна определенная
закономерность, заключающаяся в том, что в каждом кластере есть по одному
представителю комбинаций, координаты которых не изменились, т.е. они совпали с
. При этом заметна определенная
закономерность, заключающаяся в том, что в каждом кластере есть по одному
представителю комбинаций, координаты которых не изменились, т.е. они совпали с ![]() и
и ![]() .
.

Рис. 4.17. Пример изменения в топологии отдельных кластеров кода БЧХ (15,5,7) в условиях коррекции координат
В указанной схеме
обработки кодовых векторов перфорируются центральные символы разрядов координат
![]() и
и ![]() . Это сделано для того, чтобы не нарушать формулу способа, в
соответствии с которой при искажении старших разрядов координат декодер
переходит к инвариантному коду, при котором координаты
. Это сделано для того, чтобы не нарушать формулу способа, в
соответствии с которой при искажении старших разрядов координат декодер
переходит к инвариантному коду, при котором координаты ![]() и
и ![]() будут определяться по принципу, когда старшие разряды
находятся справа.
будут определяться по принципу, когда старшие разряды
находятся справа.
При определении номера кластера с использованием дополнительных проверочных символов старшие разряды координат могут быть определены с использованием проверочных соотношений проверочной матрицы кода.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
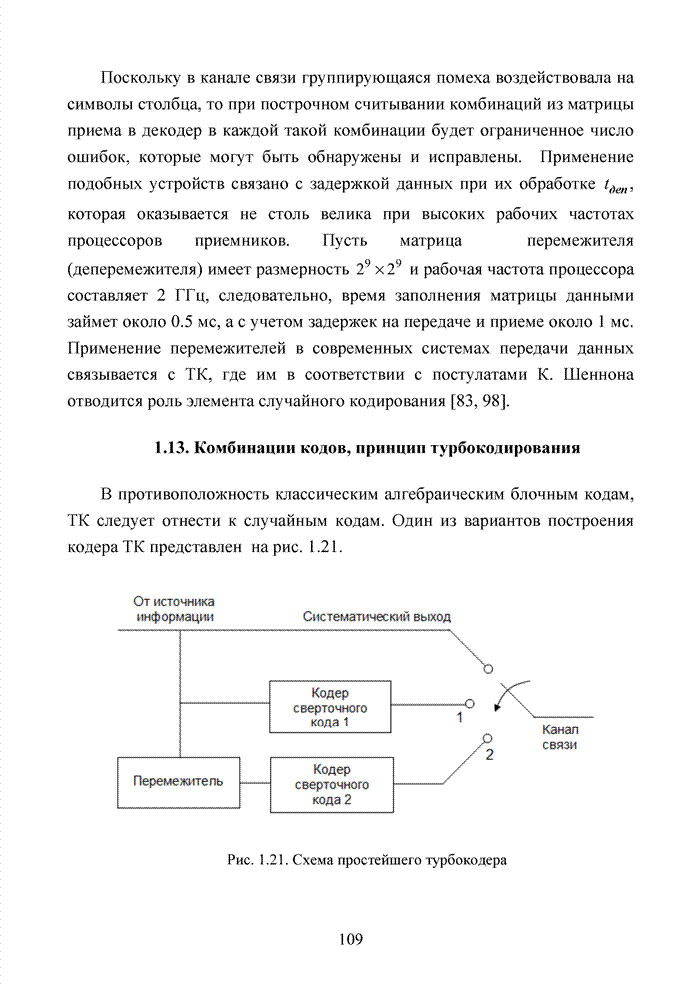
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
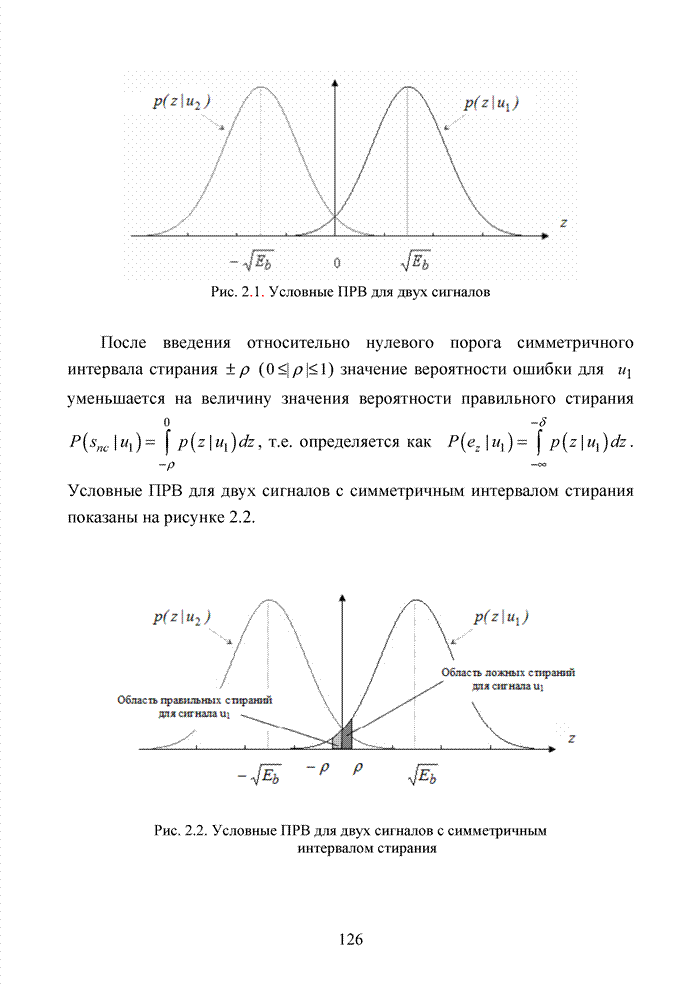
- 2.3. Модель канала связи со стиранием элементов
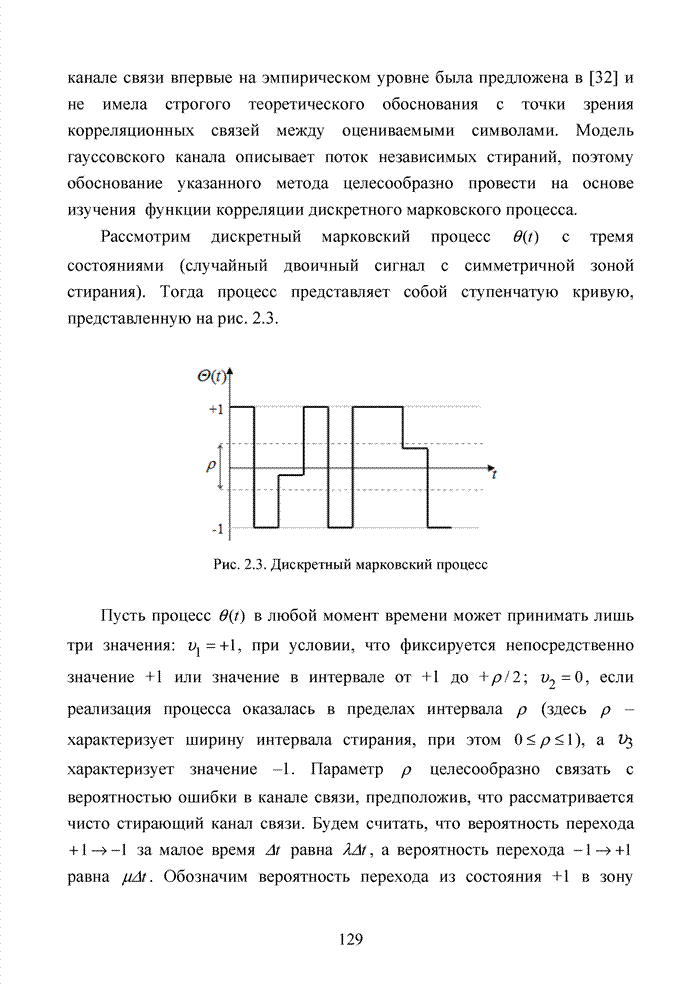
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
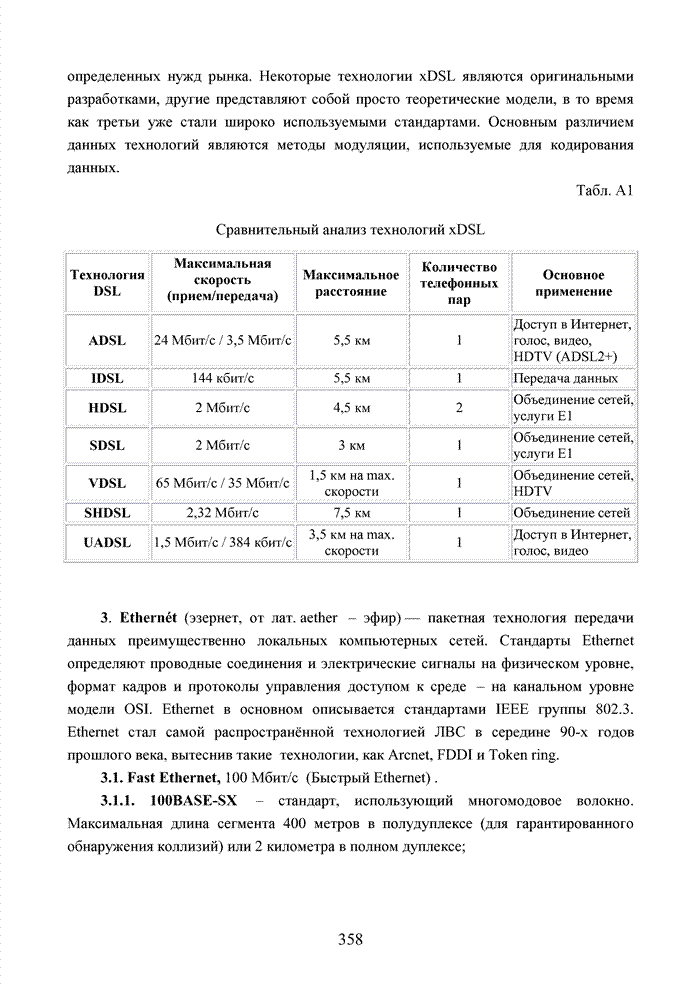
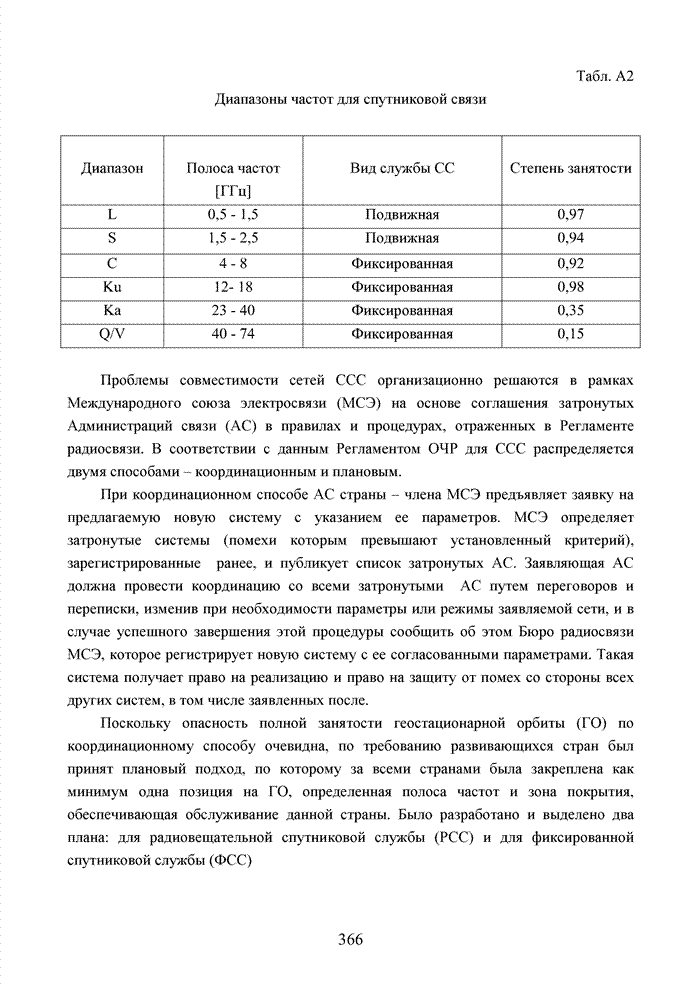
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
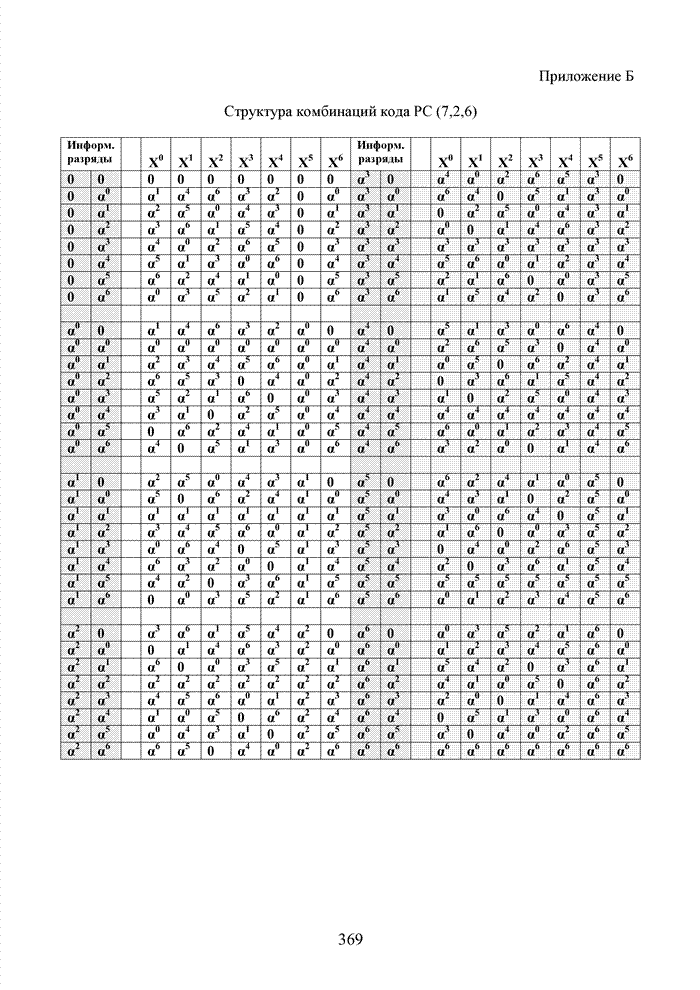
- Приложение Б Структура комбинаций кода РС (7,2,6)
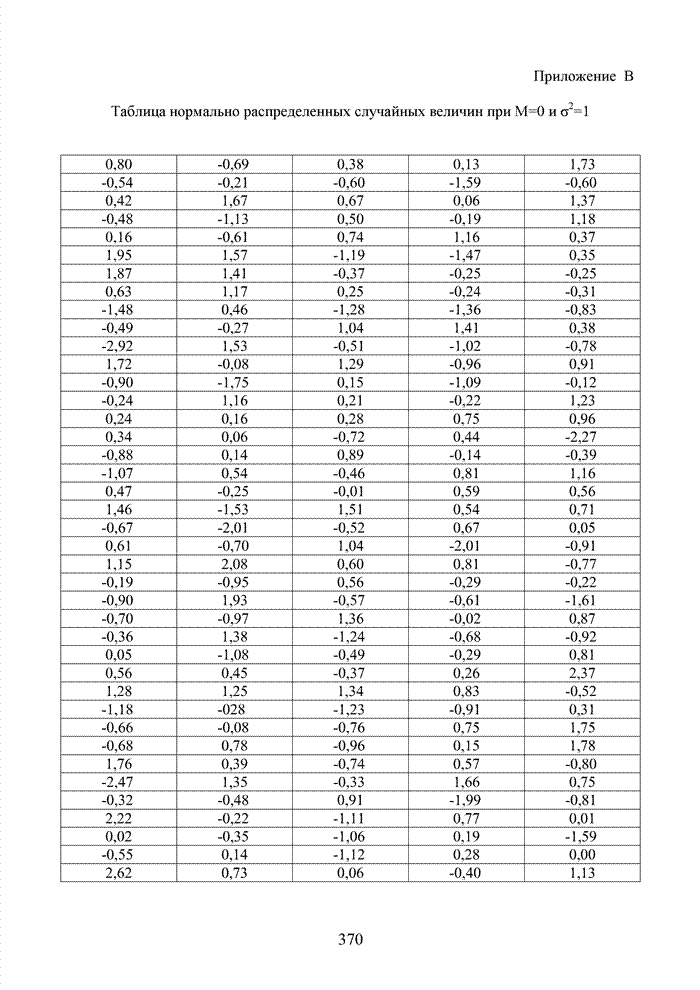
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК