| << Предыдущий параграф | Следующий параграф >> |
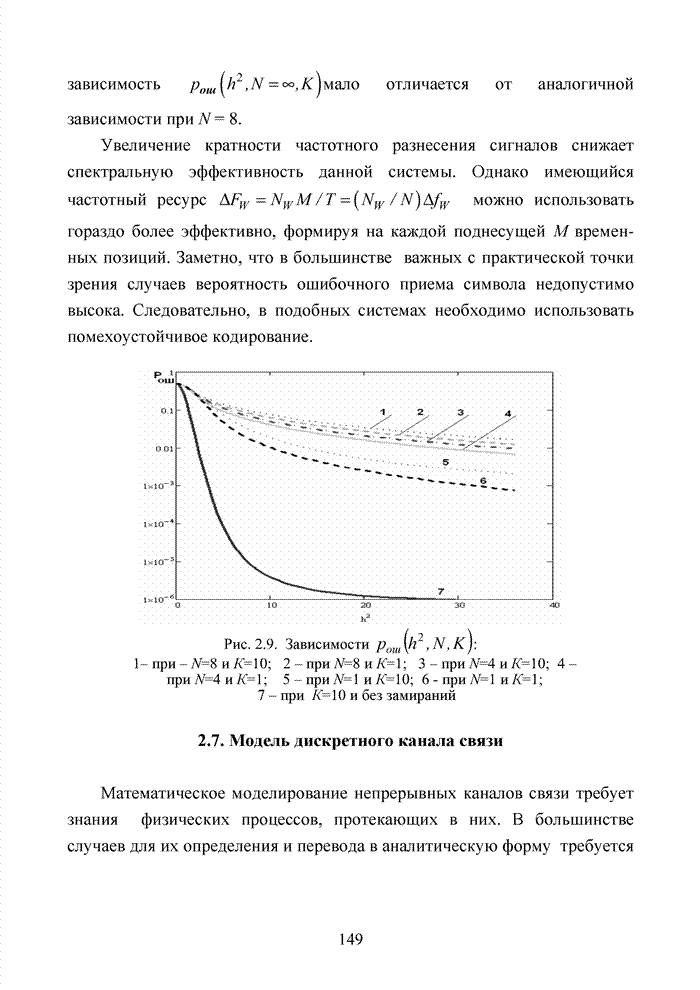
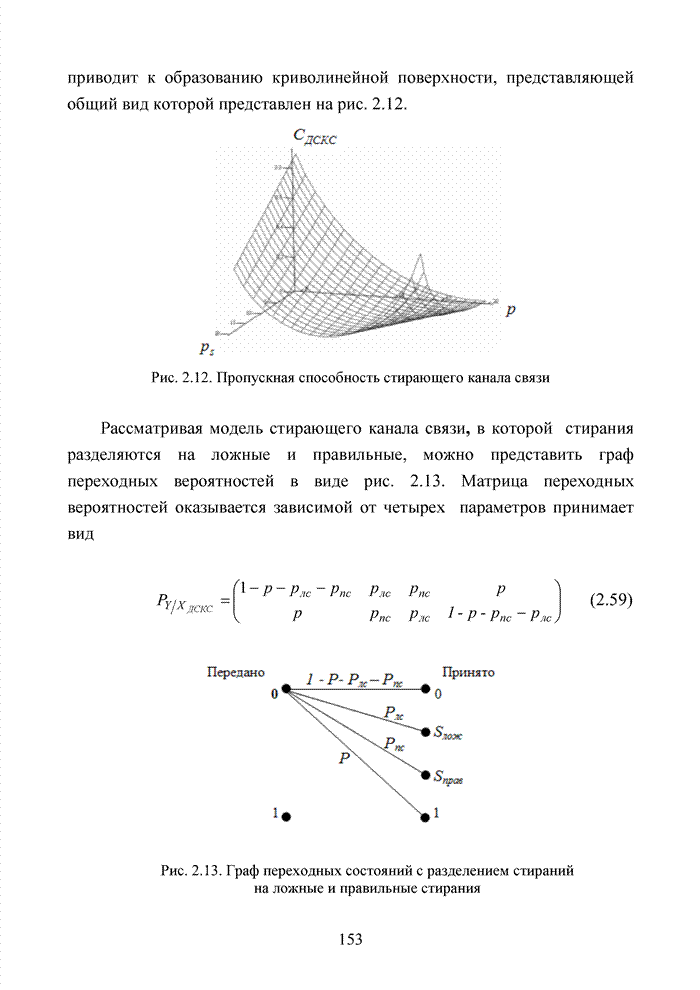
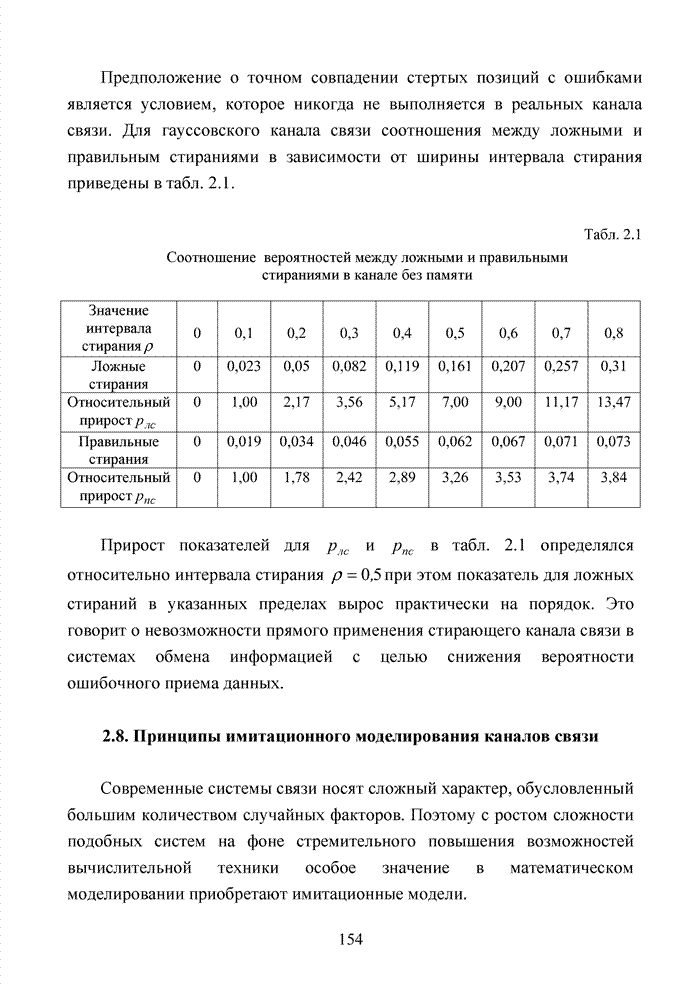
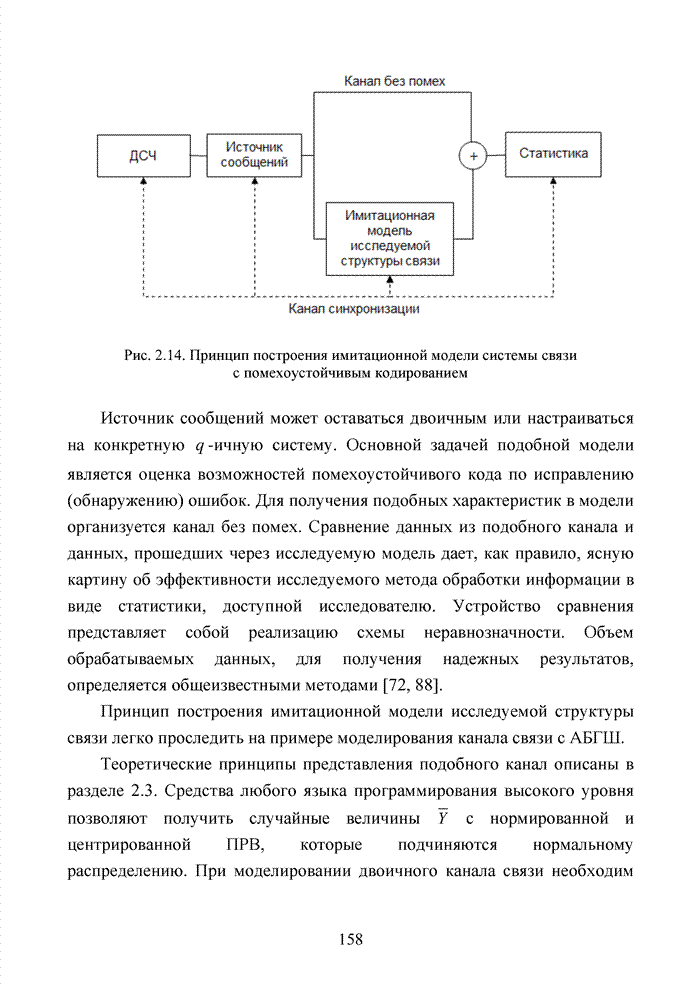
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
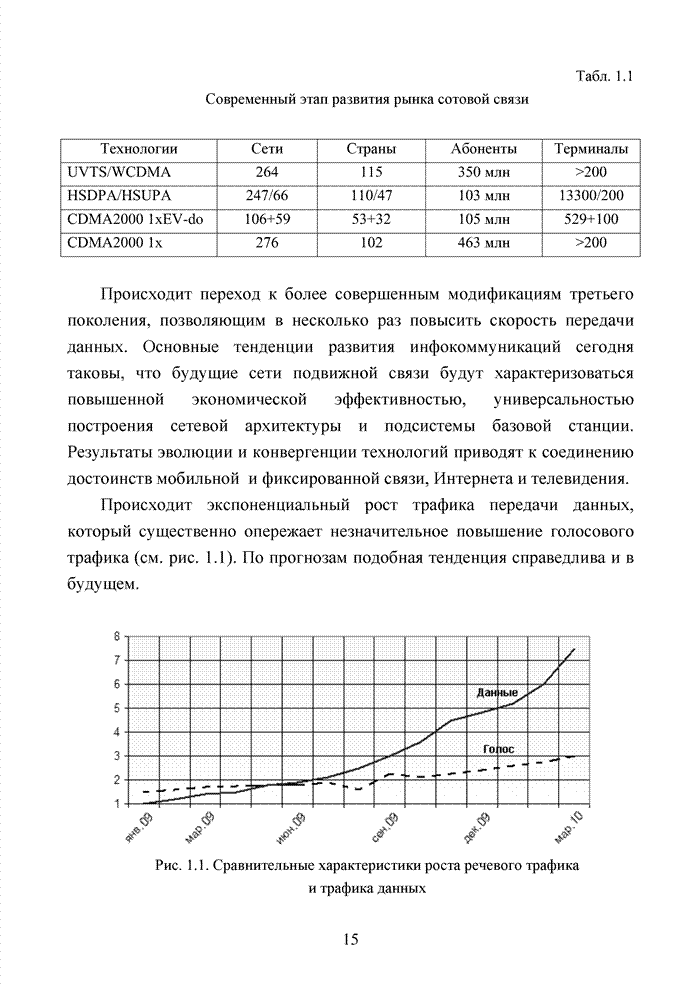
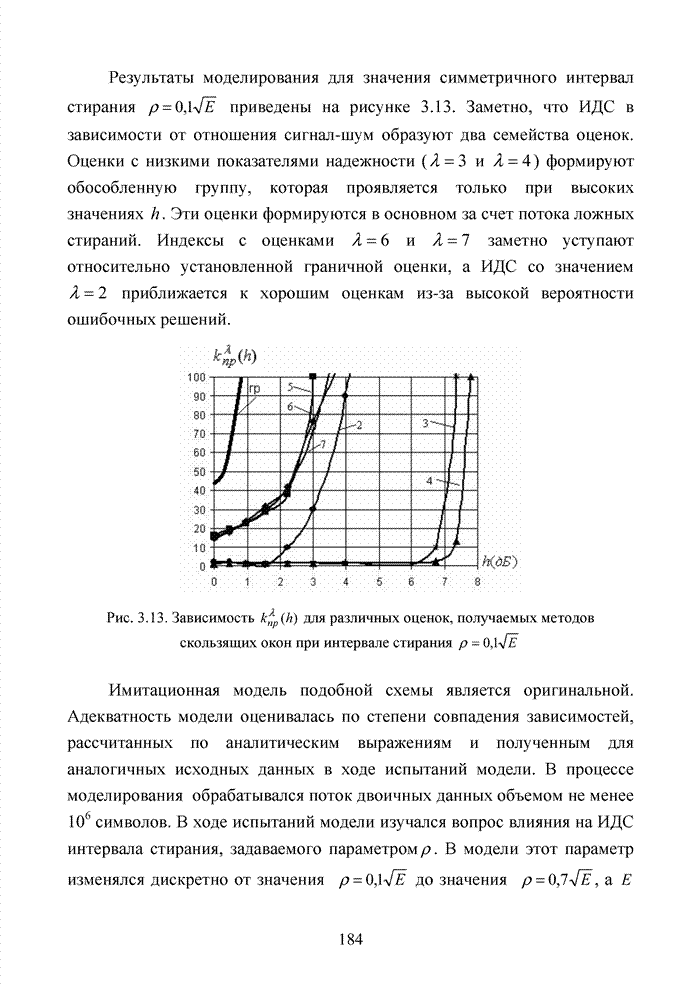
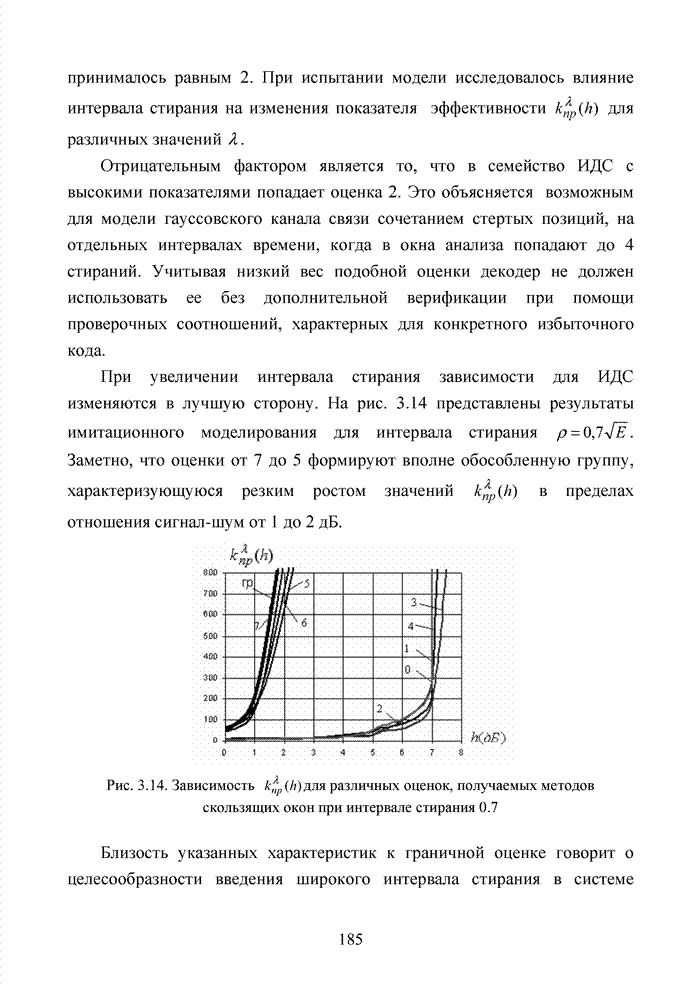
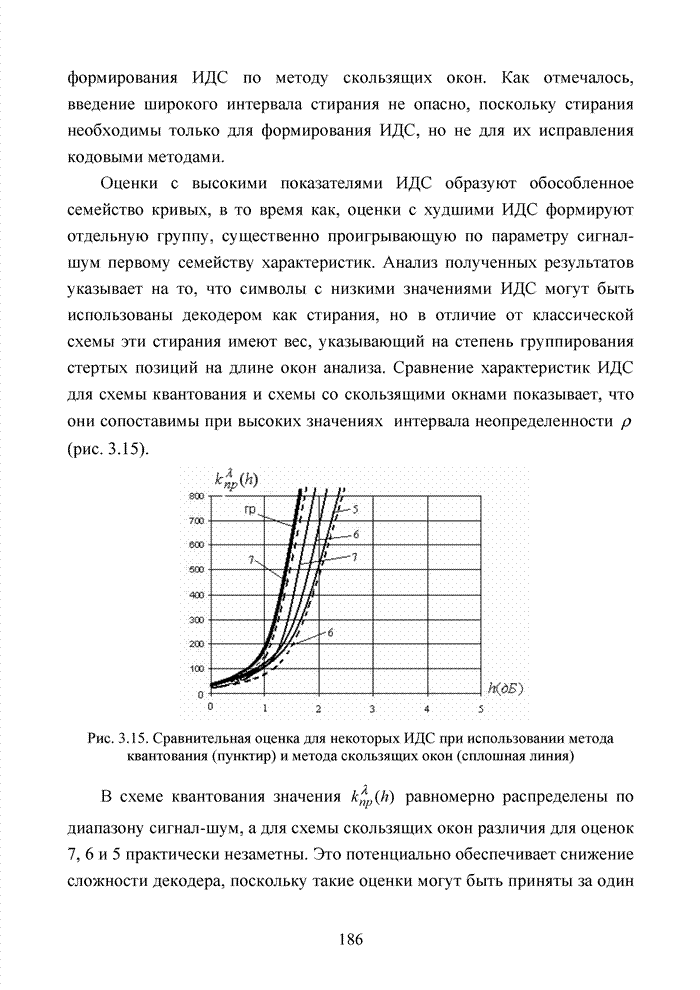
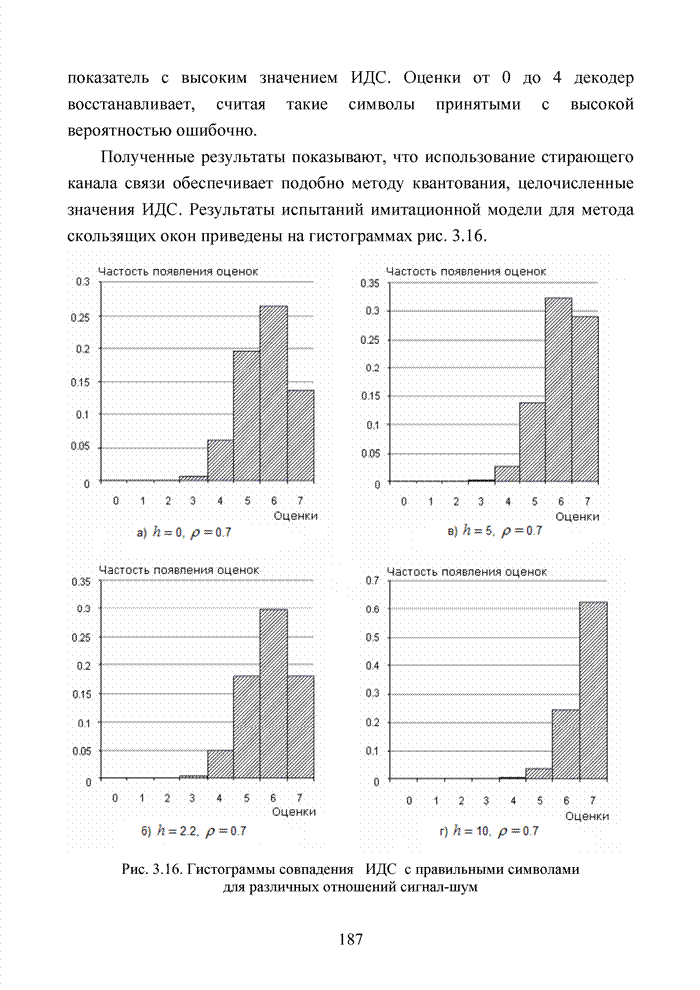
4.2. Кластерный подход к декодированию полиномиальных кодов
Одной из распространенных
метрик, используемой при декодировании помехоустойчивых кодов, является метрика
Евклида. Если обозначить переданный вектор через ![]() , а принятый вектор через
, а принятый вектор через ![]() , то при декодировании
по максимуму правдоподобия расстояние между указанными векторами определяется
как
, то при декодировании
по максимуму правдоподобия расстояние между указанными векторами определяется
как
 .
(4.4)
.
(4.4)
Применяя данный подход к
двумерной декартовой плоскости, можно отобразить ![]() и
и ![]() в виде точек на ее поверхности. Для этого
вектор из двоичной формы необходимо перевести в любую позиционную систему
счисления (например, десятичную). Представим полный список укороченного код
Хэмминга (6,3,3), имеющего порождающую и проверочную матрицу вида
в виде точек на ее поверхности. Для этого
вектор из двоичной формы необходимо перевести в любую позиционную систему
счисления (например, десятичную). Представим полный список укороченного код
Хэмминга (6,3,3), имеющего порождающую и проверочную матрицу вида
 ,
, ![]()
 .
.
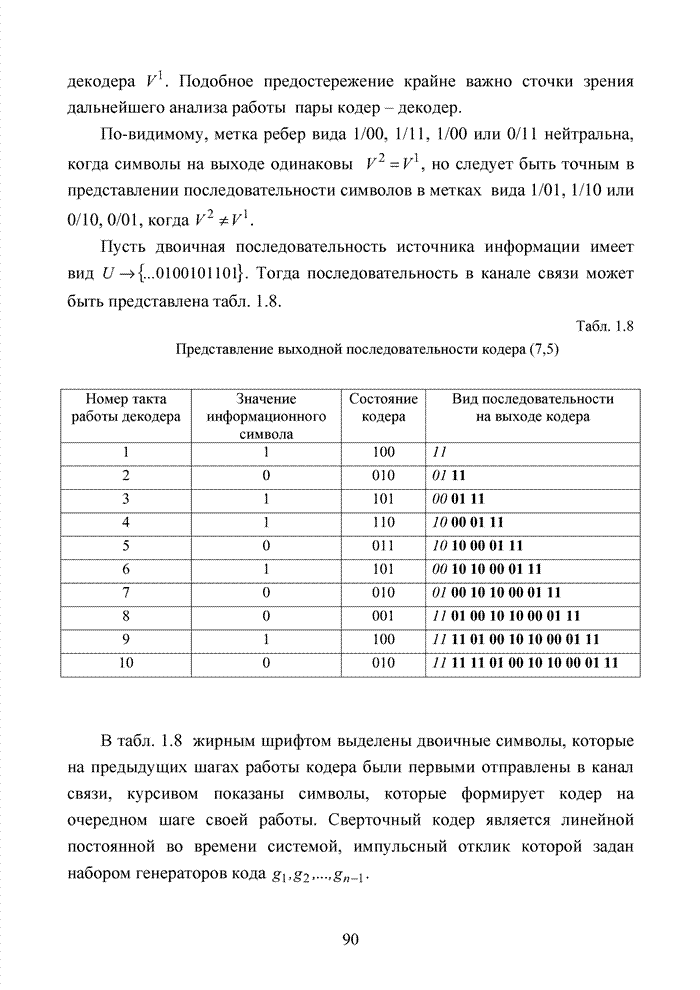
Непосредственное вычисление кодовых векторов дает их значения: 0000002; 0011012; 0100112; 0111102; 1001102; 1010112; 1101012; 1110002.
Разделим двоичные символы
каждого вектора на две части. Первую часть символов примем за координату ![]() , а вторую часть
символов примем за координату
, а вторую часть
символов примем за координату ![]() . Тогда значения тех же векторов можно
представить в десятичной системе счисления в виде (0;0)10; (1;5)10;
(2;3)10; (3;6)10; (4;6)10; (5;3)10;
(6;5)10; (7;0)10. Геометрическая интерпретация для всех
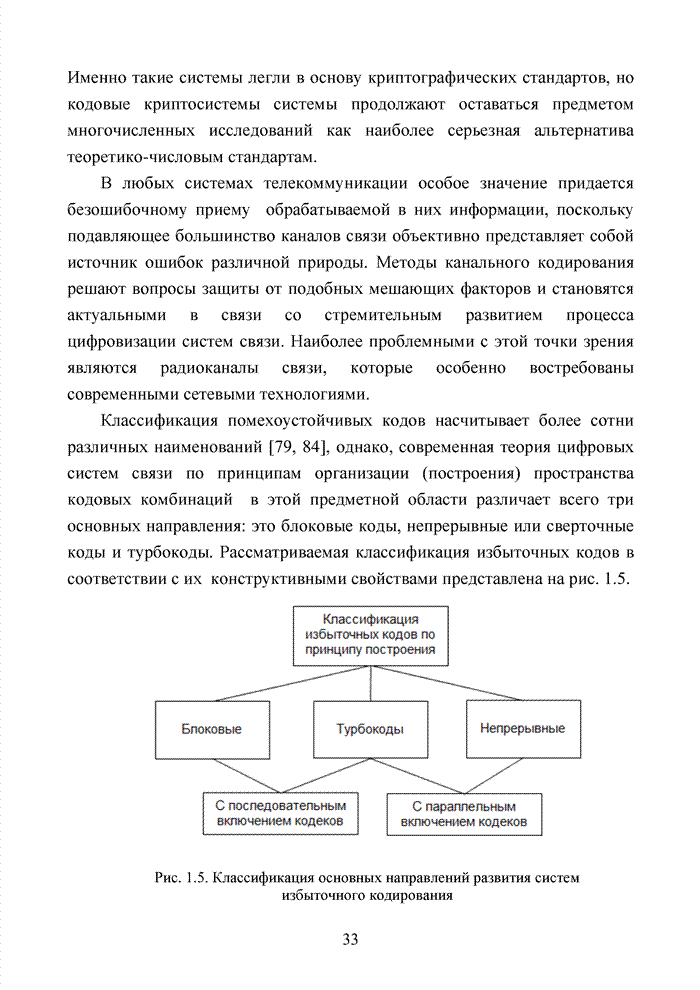
комбинаций кода на плоскости будет иметь вид, показанный на рис. 4.2.
. Тогда значения тех же векторов можно
представить в десятичной системе счисления в виде (0;0)10; (1;5)10;
(2;3)10; (3;6)10; (4;6)10; (5;3)10;
(6;5)10; (7;0)10. Геометрическая интерпретация для всех
комбинаций кода на плоскости будет иметь вид, показанный на рис. 4.2.

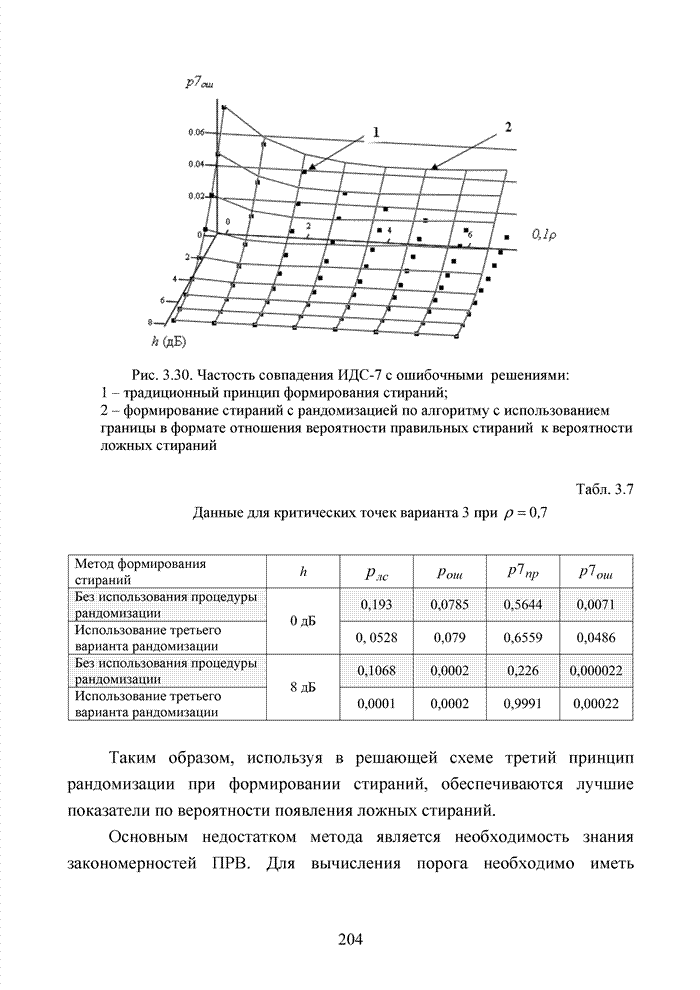
Рис. 4.2. Геометрическое представление на плоскости комбинаций кода (6,3,3)
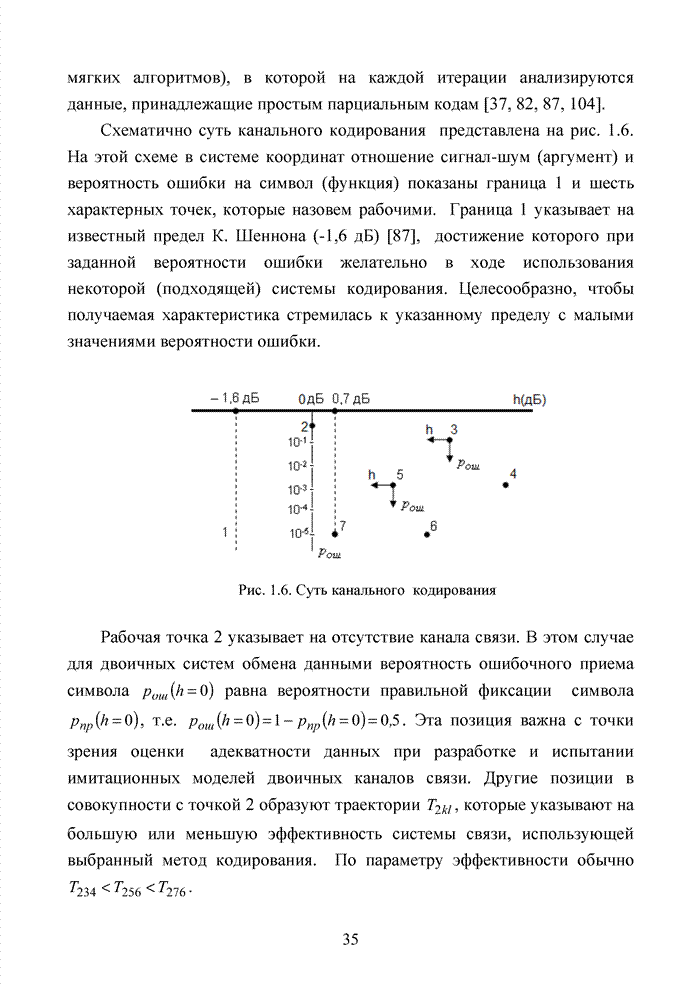
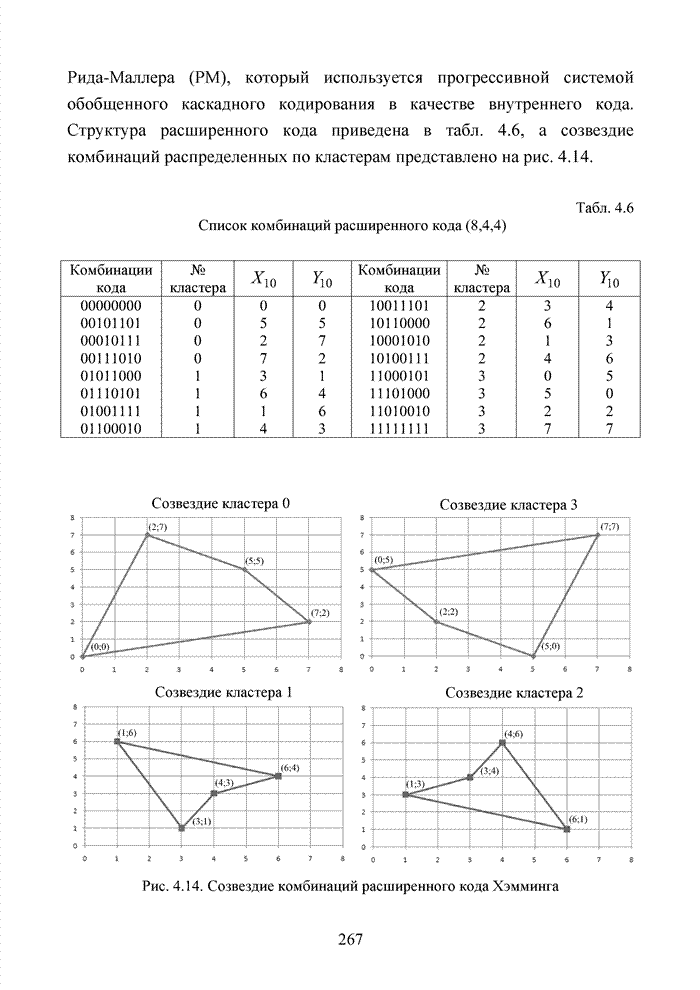
Поскольку групповой код (6,3,3) является укороченным, в нем отсутствует единичный элемент группы с координатами (7;7)10. Используя данную методику, представим для наглядности в подобной форме (см. рис. 4.3) множество комбинаций кода БЧХ (15,7,5).

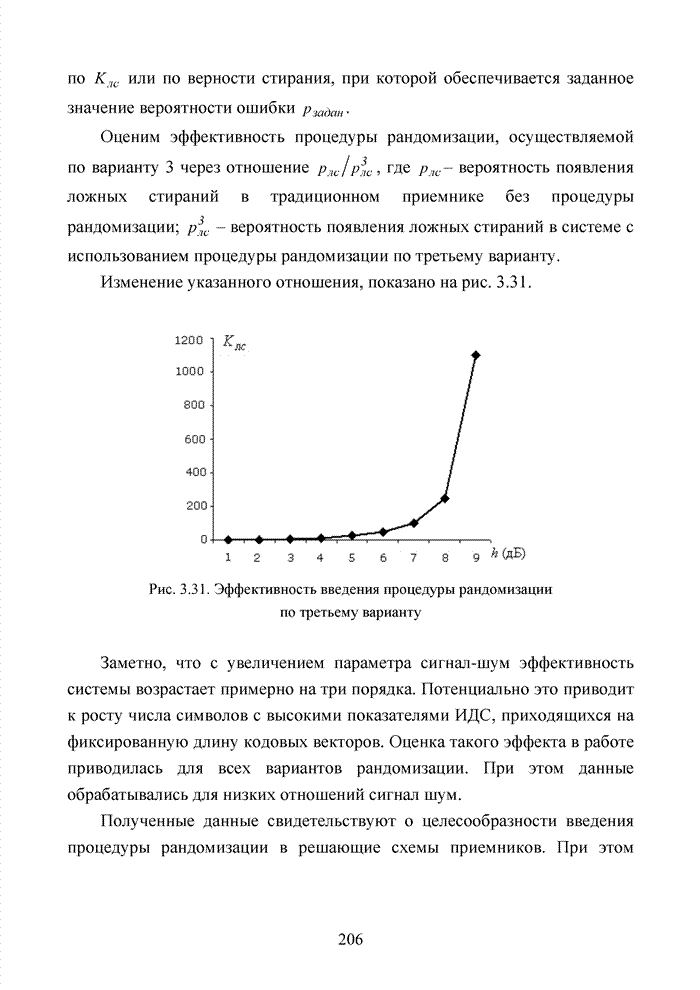
Рис. 4.3. Топология комбинаций кода БЧХ (15,7,5)
Укороченный код обеспечивает получение более ясной картины и поэтому будет использован для дальнейших рассуждений. Полученная конфигурация кодовых комбинаций говорит о центральной симметрии значений кодовых векторов, которая непосредственно вытекает из свойств прямого и дуального кода. Расстояние между комбинациями на плоскости не может быть истолковано как метрика Хэмминга, поэтому удаление одной комбинации относительно других на плоскости не является мерой их защищенности, а метрика Евклида оказывается справедливой только при представлении принятого вектора (возможно искаженного) в выбранной системе счисления.
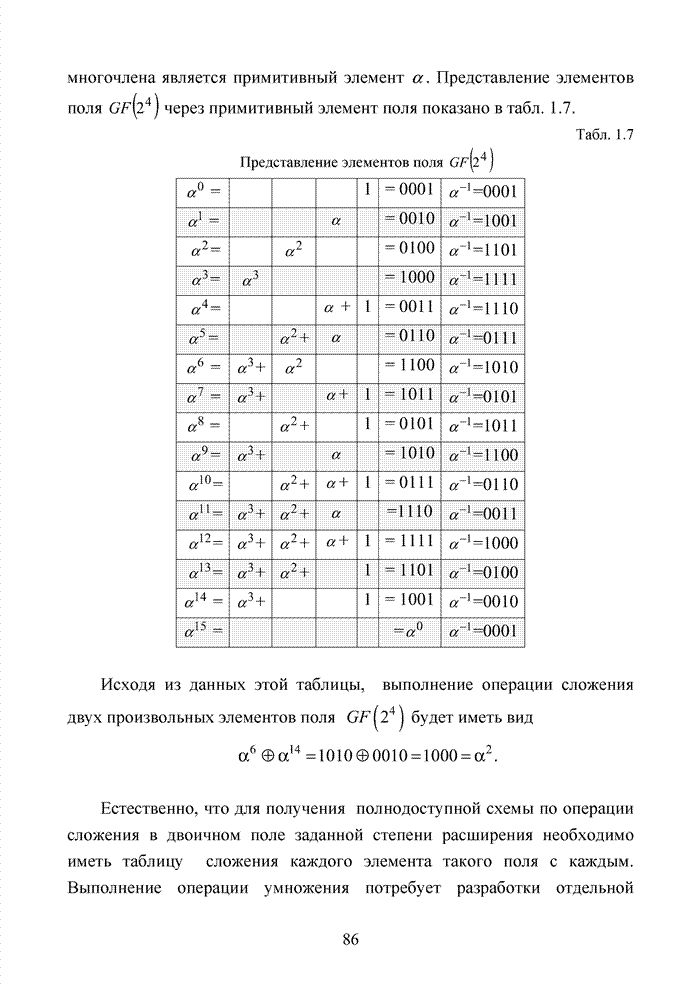
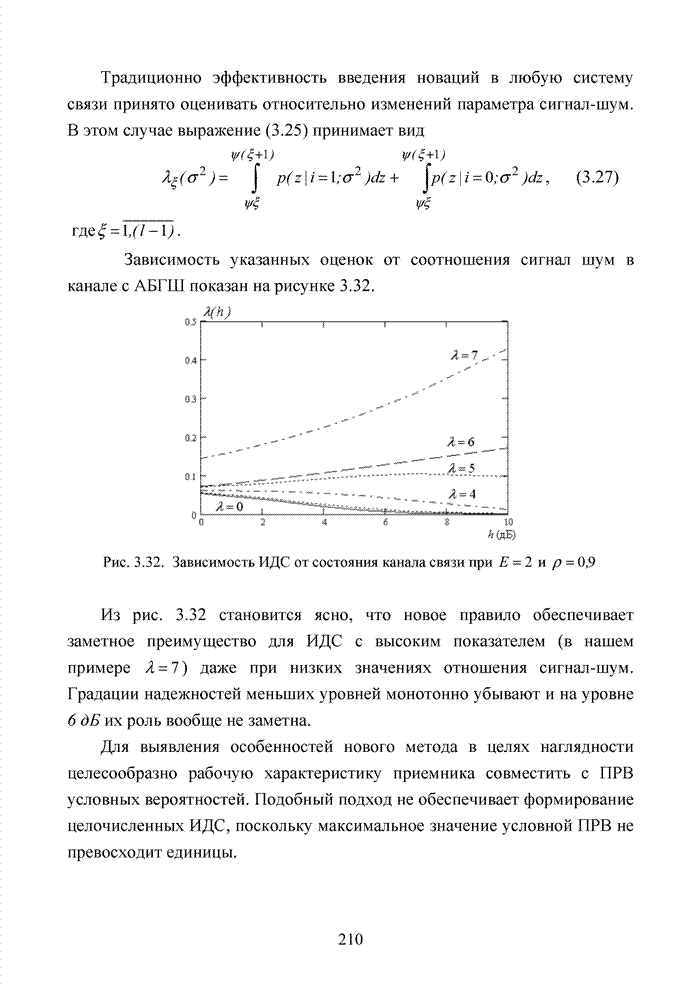
На рис. 4.4 точками
показана каноническая топология кодовых комбинаций кода (6,3,3), а
треугольниками показаны координаты точек при искажении младших разрядов
нулевого вектора. При этом заметно, что возможные варианты искажений двух самых
младших разрядов координаты ![]() и
и ![]() формируют прямоугольную зону, углы
которой соответствуют координатам (0;0), (0;1), (1;1) и (1;0).
формируют прямоугольную зону, углы
которой соответствуют координатам (0;0), (0;1), (1;1) и (1;0).
Выделенное пространство не включает в себя ни одного разрешенного кодового вектора и представленные искажения могут быть интерпретированы как стирания, которые данный код гарантированно исправляет.

Рис. 4.4. Конфигурация нулевого вектора при искажении его младших разрядов
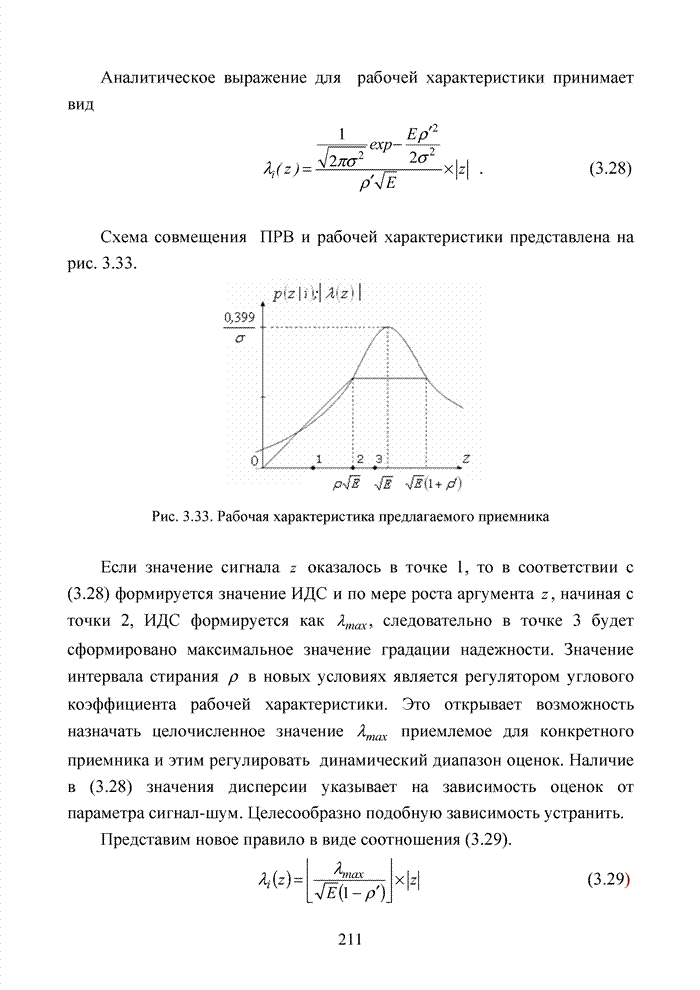
При искажении двух младших разрядов координат прямоугольник увеличивает свою площадь и в новых условиях ограничивается точкам с координатами (0;0), (0;3), (3;3) и (3;0), при этом в защитную зону нулевого вектора попадает разрешенная комбинация кода (2;3).
Поиск защитных зон для вектора
(2;3) по аналогичной схеме показывает, что эти зоны будут совпадать с
прямоугольником, определенным для нулевого вектора. Для исключения подобного
совпадения целесообразно применить метод кластерного анализа, который позволяет
разбить исследуемую совокупность объектов на группы похожих по каким-либо
признакам объектов, называемых кластерами. Кластерный анализ предполагает, что
выделенные в один класс объекты должны находиться на близких расстояниях
относительно друг друга, а объекты разных классов на относительно отдаленных
расстояниях. При этом каждый объект ![]() рассматривается как точка в
рассматривается как точка в ![]() -мерном пространстве.
Выбор способа вычисления расстояний или близости между объектами и признаками
является узловым моментом исследования, от которого в основном зависит
окончательный варианта разбиения объектов на классы.
-мерном пространстве.
Выбор способа вычисления расстояний или близости между объектами и признаками
является узловым моментом исследования, от которого в основном зависит
окончательный варианта разбиения объектов на классы.
На основании определения
кластера не все разряды кодовых векторов определим в качестве нумераторов
координат, а только их часть. При этом выделенные разряды и не вошедшие в новый
порядок нумерации координат ![]() и
и ![]() будут определять номер класса кодовых
комбинаций (номер кластера).
будут определять номер класса кодовых
комбинаций (номер кластера).
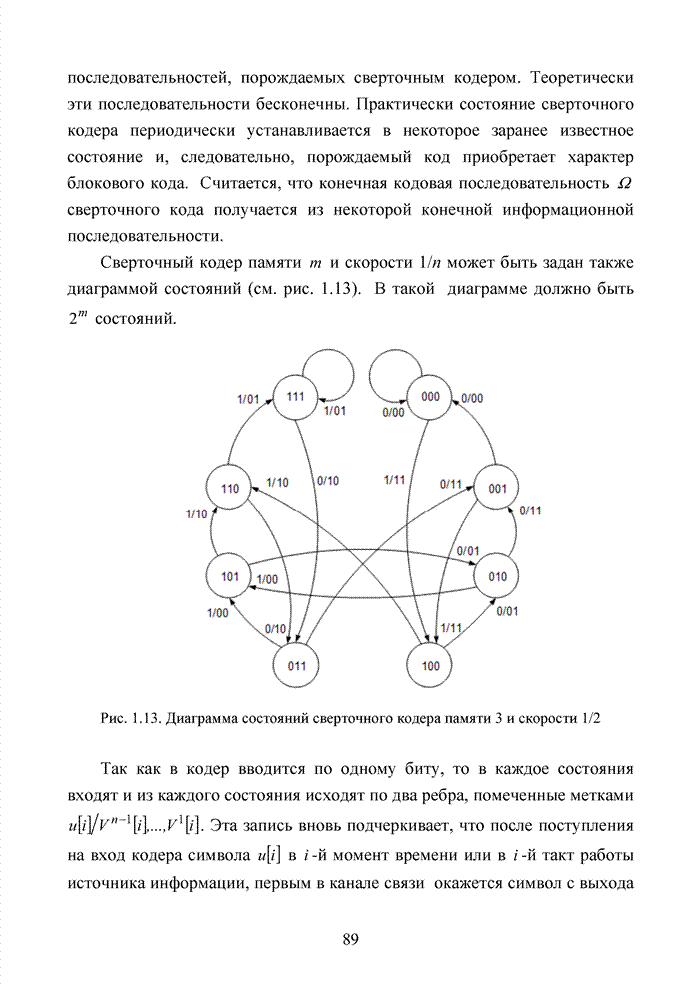
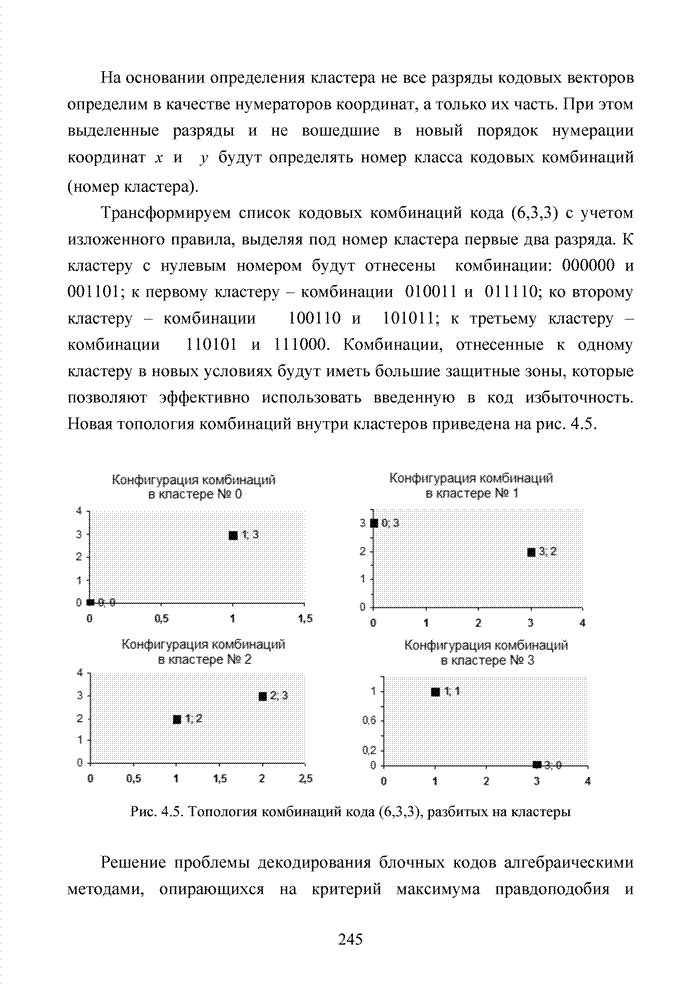
Трансформируем список кодовых комбинаций кода (6,3,3) с учетом изложенного правила, выделяя под номер кластера первые два разряда. К кластеру с нулевым номером будут отнесены комбинации: 000000 и 001101; к первому кластеру – комбинации 010011 и 011110; ко второму кластеру – комбинации 100110 и 101011; к третьему кластеру – комбинации 110101 и 111000. Комбинации, отнесенные к одному кластеру в новых условиях будут иметь большие защитные зоны, которые позволяют эффективно использовать введенную в код избыточность. Новая топология комбинаций внутри кластеров приведена на рис. 4.5.

Рис. 4.5. Топология комбинаций кода (6,3,3), разбитых на кластеры
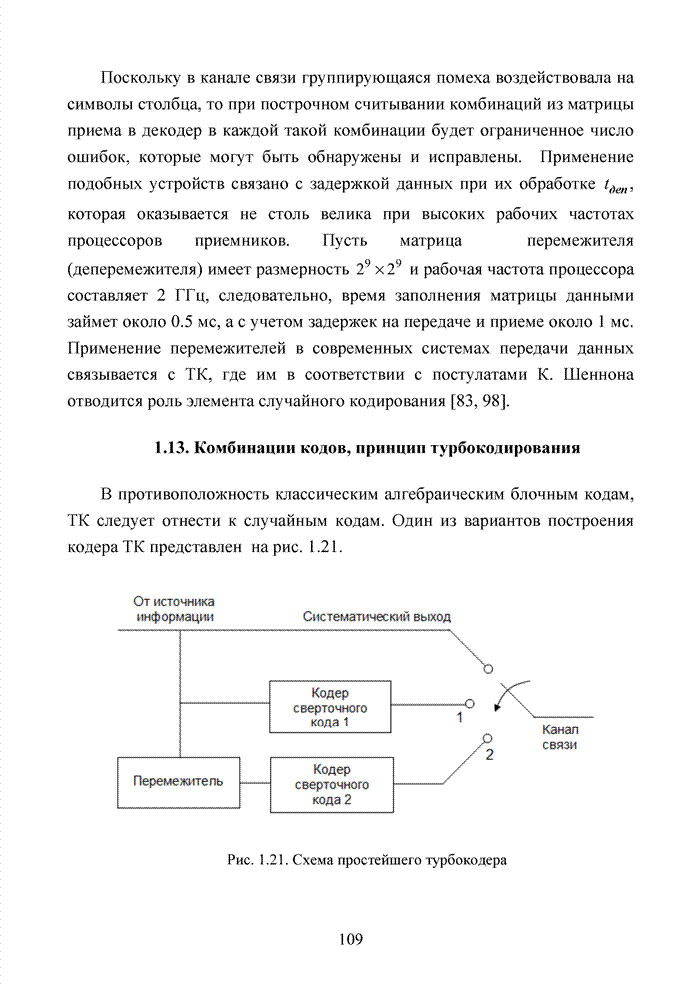
Решение проблемы декодирования блочных кодов алгебраическими методами, опирающихся на критерий максимума правдоподобия и метрику Хэмминга натолкнулась на проблему сложности декодера, исправляющего от трех и более ошибок. После указанного порога, трудности технической реализации декодера возрастают экспоненциально относительно кратности исправляемых ошибок. Это привело к созданию неалгебраических методов исправления ошибок, построению каскадных схем кодирования – декодирования с последовательным включением декодеров и схем турбо кодирования с параллельным включением декодеров.
Суть рассматриваемого в работе способа обработки кодовых векторов заключается в том, что все множество разрешенных комбинаций блокового кода разбивается на подмножества (кластеры), определяемые по заранее оговоренном принципу, с последующим определением принятого вектора по метрике Евклида внутри кластера. Для этого символы кодовой комбинации разбиваются на две группы, каждая из которых образуют координаты по двум осям координатной плоскости. Такое разбиение приводит к размещению разрешенных комбинаций кода в трехмерном пространстве, при этом номера кластеров образуют плоскости, для которых известны координаты кодовых векторов, принадлежащие данному кластеру. Применение на практике данного метода требует доказательства ряда утверждений, основанных на алгебраической теории групп, колец и полей.
Пусть общее число
комбинаций группового кода равно ![]() . Из любого циклического кода путем
регулярных преобразований или линейных преобразований над строками порождающей
матрицы
. Из любого циклического кода путем
регулярных преобразований или линейных преобразований над строками порождающей
матрицы ![]() можно
образовать систематический код с матрицей
можно
образовать систематический код с матрицей ![]() , порождающей тот же код. В единичной
матрице
, порождающей тот же код. В единичной
матрице ![]() всегда
можно выделить единичную матрицу меньшей размерности
всегда
можно выделить единичную матрицу меньшей размерности ![]() , где
, где ![]() . Путем линейных преобразований
над строками выделенной матрицы
. Путем линейных преобразований
над строками выделенной матрицы ![]() , можно получить двоичное поле Галуа
степени расширения
, можно получить двоичное поле Галуа
степени расширения ![]() ,
при этом комбинации поля
,
при этом комбинации поля ![]() будут определять признак кластера или
его номер. Поле
будут определять признак кластера или
его номер. Поле ![]() содержится
в поле
содержится
в поле ![]() ровно
ровно
![]() раз,
следовательно, число кодовых комбинаций в одном кластере будет определяться
этим же соотношением. Отсюда вытекает.
раз,
следовательно, число кодовых комбинаций в одном кластере будет определяться
этим же соотношением. Отсюда вытекает.
Утверждение 1. Если число двоичных символов, определяющих признак
кластера равно ![]() и
и
![]() , где
, где ![]() – число информационных
символов в кодовом векторе циклического кода, то число комбинаций такого кода,
входящих в кластер одного признака, определяется соотношением
– число информационных
символов в кодовом векторе циклического кода, то число комбинаций такого кода,
входящих в кластер одного признака, определяется соотношением ![]() . При
. При ![]() все кодовые векторы
входят в один кластер. При этом процедура обработки кодового вектора сводится к
обычной системе алгебраического декодирования.
все кодовые векторы
входят в один кластер. При этом процедура обработки кодового вектора сводится к
обычной системе алгебраического декодирования.
Следствие 1.1. При ![]() число кластеров равно числу разрешенных
кодовых комбинаций, т.е. в кластер входит только одна кодовая комбинация.
число кластеров равно числу разрешенных
кодовых комбинаций, т.е. в кластер входит только одна кодовая комбинация.
В множество комбинаций
при циклическом сдвиге любого ![]() -мерного вектора образуется всего
-мерного вектора образуется всего ![]() , а с учетом нулевого
и единичного элемента группы получим значение
, а с учетом нулевого
и единичного элемента группы получим значение ![]() . Остальные элементы кода получаем за счет
инверсии циклических сдвигов комбинации с номером
. Остальные элементы кода получаем за счет
инверсии циклических сдвигов комбинации с номером ![]() матрицы
матрицы ![]() .
.
Действительно, ![]() , что эквивалентно
, что эквивалентно ![]()
![]() , т.е. полином
, т.е. полином ![]() и полином
и полином ![]() , порождающий дуальный
код ортогональны. Отсюда вытекает.
, порождающий дуальный
код ортогональны. Отсюда вытекает.
Утверждение 2. Циклический сдвиг строки с номером ![]() матрицы
матрицы ![]() характеризует только
характеризует только ![]() комбинации из
разрешенного множества.
комбинации из
разрешенного множества.
Следствие 2.1. Номера комбинаций прямого и дуального циклического
кода, упорядоченные по циклическим сдвигам строки с номером ![]() матрицы
матрицы ![]() , подчиняются соотношению
, подчиняются соотношению ![]() , а номера их
кластеров
, а номера их
кластеров ![]() .
.
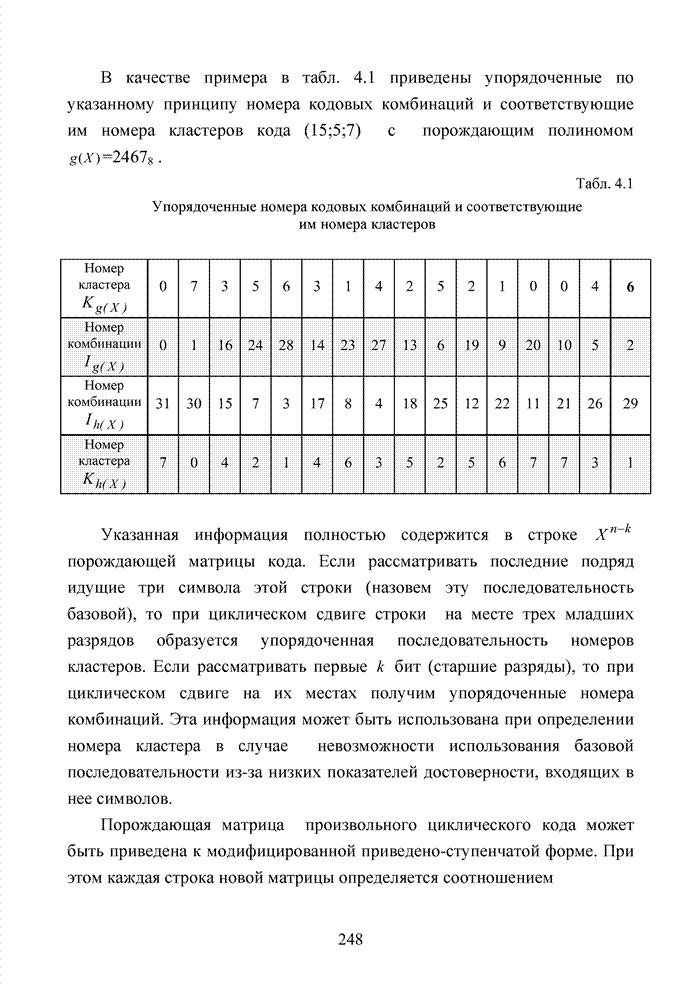
В качестве примера в
табл. 4.1 приведены упорядоченные по указанному принципу номера кодовых
комбинаций и соответствующие им номера кластеров кода (15;5;7) с порождающим
полиномом ![]() =24678
.
=24678
.
Табл. 4.1 Упорядоченные номера кодовых комбинаций и соответствующие им номера кластеров
|
Номер кластера |
0 |
7 |
3 |
5 |
6 |
3 |
1 |
4 |
2 |
5 |
2
|
1 |
0 |
0 |
4 |
6 |
|
Номер комбинации
|
0 |
1 |
16 |
24 |
28 |
14 |
23 |
27 |
13 |
6 |
19 |
9 |
20 |
10 |
5 |
2 |
|
Номер комбинации
|
31 |
30 |
15 |
7 |
3 |
17 |
8 |
4 |
18 |
25 |
12 |
22 |
11 |
21 |
26 |
29 |
|
Номер кластера
|
7 |
0 |
4 |
2 |
1 |
4 |
6 |
3 |
5 |
2 |
5 |
6 |
7 |
7 |
3 |
1 |
Указанная информация
полностью содержится в строке ![]() порождающей матрицы кода. Если
рассматривать последние подряд идущие три символа этой строки (назовем эту
последовательность базовой), то при циклическом сдвиге строки на месте трех
младших разрядов образуется упорядоченная последовательность номеров кластеров.
Если рассматривать первые
порождающей матрицы кода. Если
рассматривать последние подряд идущие три символа этой строки (назовем эту
последовательность базовой), то при циклическом сдвиге строки на месте трех
младших разрядов образуется упорядоченная последовательность номеров кластеров.
Если рассматривать первые ![]() бит (старшие разряды), то при циклическом
сдвиге на их местах получим упорядоченные номера комбинаций. Эта информация
может быть использована при определении номера кластера в случае невозможности
использования базовой последовательности из-за низких показателей
достоверности, входящих в нее символов.
бит (старшие разряды), то при циклическом
сдвиге на их местах получим упорядоченные номера комбинаций. Эта информация
может быть использована при определении номера кластера в случае невозможности
использования базовой последовательности из-за низких показателей
достоверности, входящих в нее символов.
Порождающая матрица произвольного циклического кода может быть приведена к модифицированной приведено-ступенчатой форме. При этом каждая строка новой матрицы определяется соотношением
![]() ,
,
где ![]() – остаток от деления
– остаток от деления ![]() на порождающий многочлен
на порождающий многочлен ![]() , а
, а ![]() пробегает значения от
пробегает значения от ![]() до
до ![]() .
.
Поскольку степень ![]()
![]() равна
равна ![]() , то последняя строка новой
матрицы
, то последняя строка новой
матрицы ![]() будет
иметь вид
будет
иметь вид ![]() ,
здесь
,
здесь ![]() –
по-прежнему единичная матрица размерности
–
по-прежнему единичная матрица размерности ![]() , а
, а ![]() – матрица размерности
– матрица размерности ![]() ,
, ![]() -й строкой которой является вектор из
коэффициентов многочлена
-й строкой которой является вектор из
коэффициентов многочлена ![]()
В алгебре многочленов по
модулю ![]() подпространство
является циклическим подпространством тогда и только тогда, когда оно является
идеалом. В таком случае умножение вектора избыточного кода на
подпространство
является циклическим подпространством тогда и только тогда, когда оно является
идеалом. В таком случае умножение вектора избыточного кода на ![]() эквивалентно
циклическом сдвигу этого вектора на шаг вправо.
эквивалентно
циклическом сдвигу этого вектора на шаг вправо.
В систематическом коде
порядковый номер информационного вектора автоматически переносится на порядковый
номер разрешенного вектор избыточного кода. Выделим ![]() старших разрядов строки матрицы
старших разрядов строки матрицы
![]() с номером
с номером ![]() и проследим за
трансформаций двоичных чисел в выделенных разрядах. Пусть
и проследим за
трансформаций двоичных чисел в выделенных разрядах. Пусть ![]() , тогда в исходном состоянии
номер этой строки равен единице. Умножение этой строки на
, тогда в исходном состоянии
номер этой строки равен единице. Умножение этой строки на ![]() приводит к циклическому сдвигу
ее элементов вправо на один шаг. При этом на место старшего разряда среди
выделенных
приводит к циклическому сдвигу
ее элементов вправо на один шаг. При этом на место старшего разряда среди
выделенных ![]() разрядов
приходит младший разряд порождающего полинома
разрядов
приходит младший разряд порождающего полинома ![]() . Любой
. Любой ![]() является неприводимым многочленом над
полем
является неприводимым многочленом над
полем ![]() ,
следовательно, на месте старшего разряда при первом циклическом сдвиге
появится единица. Дальнейшие изменения будут зависеть от структуры порождающего
полинома, но они вполне закономерны и могут быть определены регулярными
методами.
,
следовательно, на месте старшего разряда при первом циклическом сдвиге
появится единица. Дальнейшие изменения будут зависеть от структуры порождающего
полинома, но они вполне закономерны и могут быть определены регулярными
методами.
Умножение на ![]() приводит к
приводит к ![]() циклическим шагам
циклическим шагам ![]() вправо и
соответствующей трансформации номера вектора, определяемого выделенными
вправо и
соответствующей трансформации номера вектора, определяемого выделенными ![]() разрядами.
Следовательно, количество сдвигов
разрядами.
Следовательно, количество сдвигов ![]() соответствует номеру некоторого
вектора избыточного кода.
соответствует номеру некоторого
вектора избыточного кода.
Если ![]() , для точной идентификации
кластера необходимо
, для точной идентификации
кластера необходимо ![]() шагов.
Это связано с последовательным, по мере увеличения числа шагов, расширением
поля
шагов.
Это связано с последовательным, по мере увеличения числа шагов, расширением
поля ![]() до
размеров поля
до
размеров поля ![]() .
.
Утверждение 3. Для любого двоичного циклического кода с установленной базовой структурой бит, определяющей номер кластера, возможна однозначная идентификация номера кластера по любой другой группе двоичных символов адекватной базовой структуре.
Рассмотренное свойство позволяет установить номер кластера зафиксированного приемником кодового вектора в случае его искажения при передаче по каналу связи. Для этого может быть использована другая группа разрядов той же кодовой комбинации, которые оказались принятыми с высокими значениями ИДС. Подобный подход не исключает применения и итеративных преобразований разрядов кодового вектора в комплексе с известными проверочными соотношениями.
Пример. Пусть задан циклический код
(15;5;7). Представляя его в двоичной форме, получим ![]() =101001101112.
Порождающая матрица этого кода в приведенно-ступенчатой форме имеет вид:
=101001101112.
Порождающая матрица этого кода в приведенно-ступенчатой форме имеет вид:
 .
(4.5)
.
(4.5)
Выделим последнюю строку
матрицы, отделив условно ![]() старших разрядов.
старших разрядов.

Умножая этот вектор на ![]() , получим 10000
010011011. Таким образом, номер вектора со значения 1 сменился на значение
16. Вновь умножая вектор с номером 16 на
, получим 10000
010011011. Таким образом, номер вектора со значения 1 сменился на значение
16. Вновь умножая вектор с номером 16 на ![]() , получим значение 24 и т.д. Результатом
, получим значение 24 и т.д. Результатом ![]() последовательных
сдвигов вправо является образование последовательности номеров кодовых
комбинаций, которая приведена в табл. 4.1:
последовательных
сдвигов вправо является образование последовательности номеров кодовых
комбинаций, которая приведена в табл. 4.1:
1; 16; 24; 28; 14; 23; 27; 13; 6; 19; 9; 20; 10; 5; 2.
Эта последовательность может быть использована для восстановления признака кластера в случае поражения символов, определяющих признак кластера, помехой.
Пусть был передан вектор
с номером 19: 100110111000010 и пусть установленная структура символов для определения
номера кластера представляется тремя последними подряд, идущими символами (![]() ) вектора 100110111000010,
т.е. кодовая комбинация принадлежит кластеру № 2. Предположим, что в результате
прохождения вектора по каналу связи с помехами именно эти символы оказались
принятыми с минимальными оценками достоверности, что не позволяет надежно
причислить его к одному из кластеров.
) вектора 100110111000010,
т.е. кодовая комбинация принадлежит кластеру № 2. Предположим, что в результате
прохождения вектора по каналу связи с помехами именно эти символы оказались
принятыми с минимальными оценками достоверности, что не позволяет надежно
причислить его к одному из кластеров.
Пусть структура вектора
на приеме имеет вид: 10011Х111000ХХХ, где символом Х отмечены стертые
символы, принятые с наименьшими оценками достоверности. Приемник в сложившейся
ситуации оценивает первые три подряд идущих символа (структура бит,
определяющих номер кластера, не меняется) с получением № 4. Поскольку эти
символы представляют циклический сдвиг последних разрядов на три шага вправо,
то в последовательности номеров образованных при циклических сдвигах последней
строки ![]() необходимо
сделать три шага влево. Все действия над элементами осуществляются в поле
необходимо
сделать три шага влево. Все действия над элементами осуществляются в поле ![]() , следовательно
возникает ситуация неопределенность, так как при движении влево, в
рассматриваемом примере, получается
, следовательно
возникает ситуация неопределенность, так как при движении влево, в
рассматриваемом примере, получается ![]() различных кластеров. Перемещение признака
кластера в принятом векторе на разряд вправо, уменьшает неопределенность до
двух кластеров. И еще одно перемещение приводит к решению задачи.
различных кластеров. Перемещение признака
кластера в принятом векторе на разряд вправо, уменьшает неопределенность до
двух кластеров. И еще одно перемещение приводит к решению задачи.
Упорядочим разрешенное
множество кодовых комбинаций корректирующего кода в порядке возрастания номеров
комбинаций безызбыточного кода. Примем эти номера за часть разрядов координат
для ![]() . На одну
координату приходится (
. На одну
координату приходится (![]() )/2=
)/2=![]()
![]() разрядов кодового вектора. Первоначально
выберем первые
разрядов кодового вектора. Первоначально
выберем первые ![]() разрядов
в любых двух векторах отличающихся друг от друга всего на единицу. Тогда,
например, для координаты
разрядов
в любых двух векторах отличающихся друг от друга всего на единицу. Тогда,
например, для координаты ![]() и векторов с № 1 и с номером №2 имеем:
и векторов с № 1 и с номером №2 имеем:
![]()
![]()
![]()
![]() .
.
Здесь коэффициенты ![]() – нули, а
– нули, а ![]() – суть единицы для
двоичных кодов. Добавление справа в позиционной системе счисления одного
разряда эквивалентно умножению каждой последовательности, определяющей эти
вектора, на
– суть единицы для
двоичных кодов. Добавление справа в позиционной системе счисления одного
разряда эквивалентно умножению каждой последовательности, определяющей эти
вектора, на ![]() ,
что означает сохранение различий между ними. Разряд добавляется для всех
номеров, следовательно, различия остаются для всего подмножества координат
,
что означает сохранение различий между ними. Разряд добавляется для всех
номеров, следовательно, различия остаются для всего подмножества координат ![]() . Легко убедиться в
том, что разница между векторами в зависимости от комбинации единиц в последних
двух разрядах будет составлять 1, 2 или 3. Добавление справа ко всем векторам
еще одного разряда приводит к аналогичным последствиям.
. Легко убедиться в
том, что разница между векторами в зависимости от комбинации единиц в последних
двух разрядах будет составлять 1, 2 или 3. Добавление справа ко всем векторам
еще одного разряда приводит к аналогичным последствиям.
В циклических кодах часть
кодового вектора, принадлежащая координате ![]() , циклически смещается вправо и через
определенное число тактов занимает разряды, отведенные для координаты
, циклически смещается вправо и через
определенное число тактов занимает разряды, отведенные для координаты ![]() . Следовательно,
получаем.
. Следовательно,
получаем.
Утверждение 4. При разбиении множества кодовых комбинаций на
кластеры ни одно значение координат взятых отдельно по подмножеству ![]() или
или ![]() для всей совокупности
комбинаций не имеет повторяющихся значений.
для всей совокупности
комбинаций не имеет повторяющихся значений.
Следствие 4.1. Любой вектор может быть восстановлен по признаку
кластера и значению только одной из координат ![]() или
или ![]() .
.
Следствие 4.2. При хорошем состоянии канала связи относительная скорость передачи кода может быть повышена за счет выкалывания значений одной из координат и восстановления кодового вектора по признаку кластера и параметра только одной координаты.
Следствие 4.3. Каждый разряд любой координаты ![]() или
или ![]() имеет вес кратный значению
имеет вес кратный значению ![]() , где
, где ![]() ,
, ![]() . Принципиально это означает,
что при восстановлении кодового вектора по признаку кластера значения координат
. Принципиально это означает,
что при восстановлении кодового вектора по признаку кластера значения координат
![]() или
или ![]() мало изменяются при
замене в младших разрядах единиц на нули и наоборот. Это означает, что при
реперфорации стертых символов (символов с низкими коэффициентами достоверности)
изменения в младших разрядах необходимо производить в последнюю очередь или
вообще не производить.
мало изменяются при
замене в младших разрядах единиц на нули и наоборот. Это означает, что при
реперфорации стертых символов (символов с низкими коэффициентами достоверности)
изменения в младших разрядах необходимо производить в последнюю очередь или
вообще не производить.
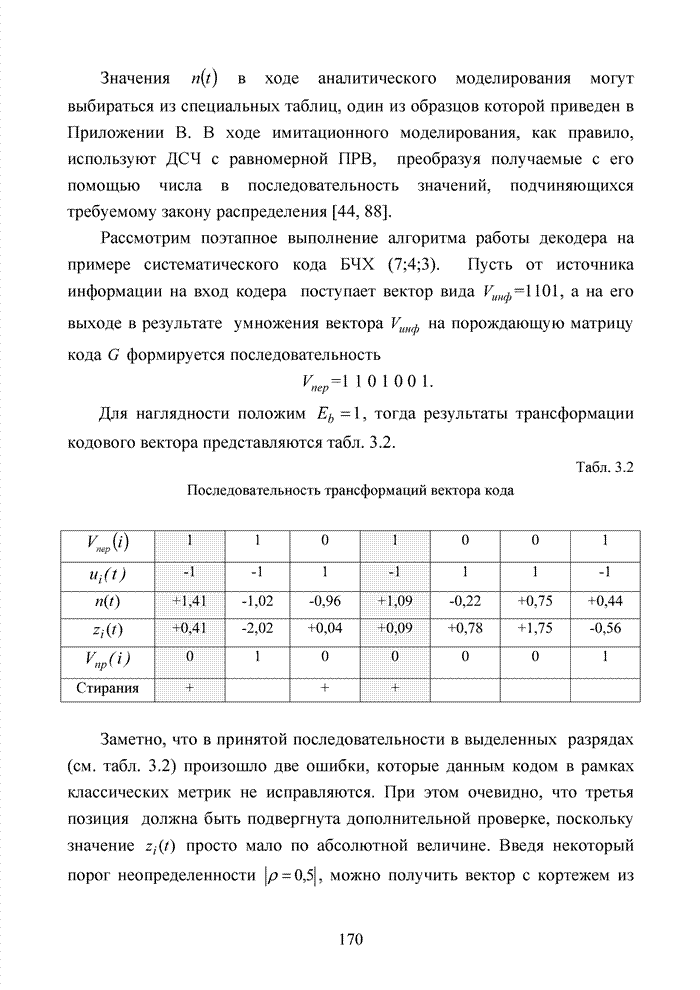
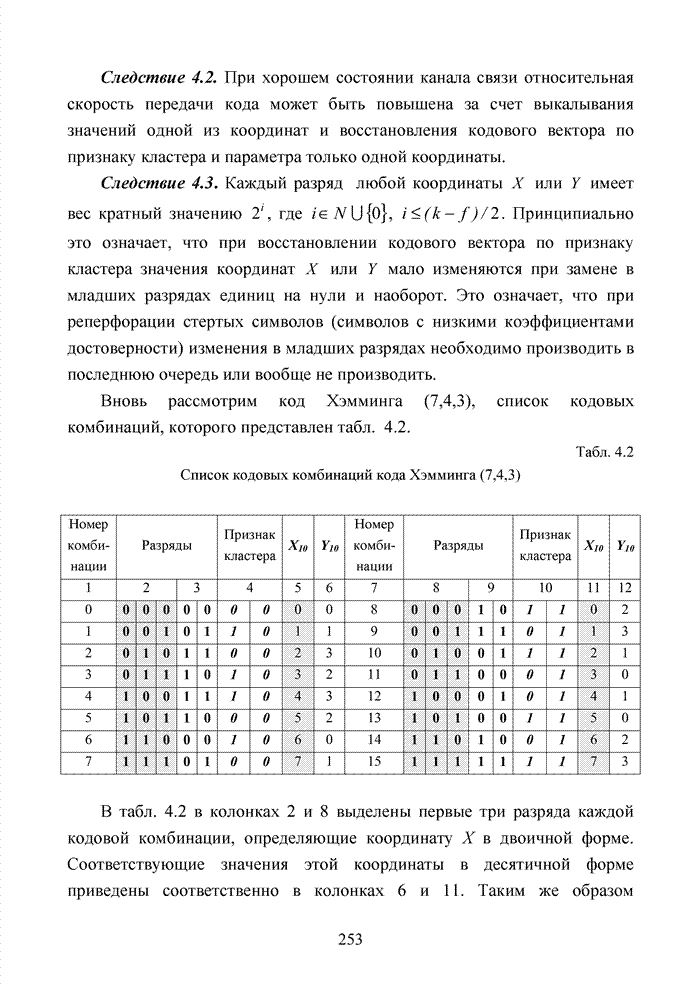
Вновь рассмотрим код Хэмминга (7,4,3), список кодовых комбинаций, которого представлен табл. 4.2.
Табл. 4.2 Список кодовых комбинаций кода Хэмминга (7,4,3)
|
Номер комби-нации |
Разряды |
Признак кластера |
Х10 |
Y10 |
Номер комби-нации |
Разряды |
Признак кластера |
Х10 |
Y10 |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
2 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
9 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
3 |
|
2 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
2 |
3 |
10 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
2 |
1 |
|
3 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
3 |
2 |
11 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
3 |
0 |
|
4 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
4 |
3 |
12 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
4 |
1 |
|
5 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
5 |
2 |
13 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
5 |
0 |
|
6 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
6 |
0 |
14 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
6 |
2 |
|
7 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
7 |
1 |
15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
7 |
3 |
В табл. 4.2 в колонках 2 и 8 выделены первые три разряда каждой кодовой комбинации, определяющие координату Х в двоичной форме. Соответствующие значения этой координаты в десятичной форме приведены соответственно в колонках 6 и 11. Таким же образом определяются координаты Y2 в колонках 3 и 9, а также Y10 в 6 и 12. В колонках 4 и 10 оставшиеся разряды каждой кодовой комбинации определяют номер кластера, например, комбинации с номерами 1; 3; 4 и 6 относятся к кластеру 2. Номера кластеров показаны курсивом.
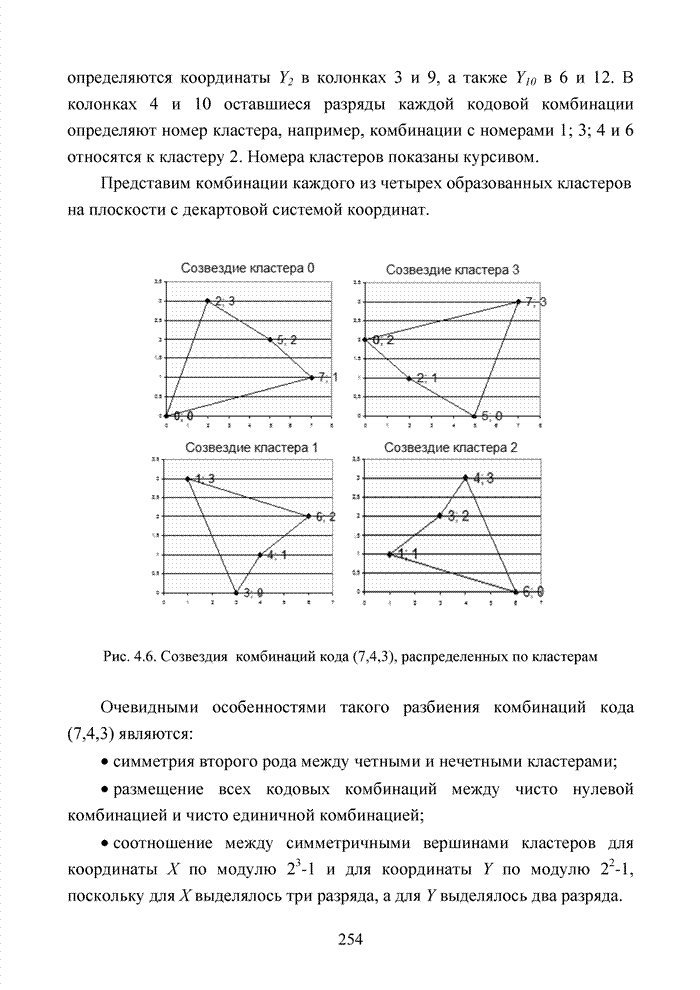
Представим комбинации каждого из четырех образованных кластеров на плоскости с декартовой системой координат.

Рис. 4.6. Созвездия комбинаций кода (7,4,3), распределенных по кластерам
Очевидными особенностями такого разбиения комбинаций кода (7,4,3) являются:
- симметрия второго рода между четными и нечетными кластерами;
- размещение всех кодовых комбинаций между чисто нулевой комбинацией и чисто единичной комбинацией;
- соотношение между симметричными вершинами кластеров для координаты Х по модулю 23-1 и для координаты Y по модулю 22-1, поскольку для Х выделялось три разряда, а для Y выделялось два разряда.
Принципиально под
значения координат при других параметрах кода и иной нумерации кластеров могут
выделяться одинаковое число разрядов. В этом случае значения кодовых комбинаций
с симметричными координатами будут определяться по модулю ![]() .
.
Применение кластерного подхода предполагает декодирование комбинаций по списку. В современных условиях это не является сложной задачей, поскольку прогресс в создании систем памяти значителен, а методы алгебраического декодирования кодов сохранили классическую форму. При алгебраическом декодировании декодер связан обязательной процедурой составления системы линейных уравнений и ее решения. Сложность этой процедуры зависит от конфигурации ошибок и не может быть решена итеративными методами. Предлагаемый подход позволяет повысить корректирующие возможности кода. Код (7,4,3), способен гарантированно исправить одну ошибку или два стирания. Исправление стираний более высокой кратности связано с изучением весовой структуры кода, на основе переборных методов поиска соседних комбинаций относительно исправляемой. При кластерном подходе исключаются методы перебора. Все зависит от правильности определения кластера и старших разрядов координат. Рассмотрим это на примере кластера 1 (см. рис. 4.7).

Рис. 4.7. Расстановка защитных зон в кластере № 1
Если они правильно
идентифицированы, то кластерный подход позволяет игнорировать младшие разряды
при декодировании, т.е. представить их в виде стираний. В этом случае код
исправляет ![]() стираний.
Это связано с защитными зонами для каждой комбинации. При использовании метрики
Хэмминга защитная зона для любой комбинации представляется в виде сферы. При
кластерном анализе защитная зона в пределах кластера определяется
прямоугольником. Задачей декодера в указанных условиях является решение системы
строгих неравенств и определения области, к которой принадлежит вектор.
стираний.
Это связано с защитными зонами для каждой комбинации. При использовании метрики
Хэмминга защитная зона для любой комбинации представляется в виде сферы. При
кластерном анализе защитная зона в пределах кластера определяется
прямоугольником. Задачей декодера в указанных условиях является решение системы
строгих неравенств и определения области, к которой принадлежит вектор.
В общем случае методика
получения защитных зон заключается в определении диапазона изменения допустимых
границ при перемещении кодовой комбинации в ходе искажения младших разрядов.
Поскольку для координаты Х выделяется ![]() разрядов, то при искажении младшего
разряда координаты со значения 0 на значение 1, ее значение увеличивается, либо
уменьшается при переходе 1 в 0. При искажении других разрядов, также могут быть
получены большие или меньшие показатели координат. Аналогичные рассуждения
справедливы и для координаты Y.
разрядов, то при искажении младшего
разряда координаты со значения 0 на значение 1, ее значение увеличивается, либо
уменьшается при переходе 1 в 0. При искажении других разрядов, также могут быть
получены большие или меньшие показатели координат. Аналогичные рассуждения
справедливы и для координаты Y.
В целом сочетания максимальных и минимальных значений координат дают четыре числа, которые определяют границы возможных изменений для данного вектора. Следовательно, любые наборы искажений младших разрядов могут быть исправлены при условии, что номер кластера, к которому принадлежит комбинация и старшие разряды координат определены достоверно. Докажем это свойство более строго.
Утверждение 5. Любые искажения координат,
относящиеся к одной кодовой комбинации и содержащие ![]() разрядов (
разрядов (![]() ) могут быть восстановлены при
условии, что старшие разряды координат
) могут быть восстановлены при
условии, что старшие разряды координат ![]() и
и ![]() приняты достоверно.
приняты достоверно.
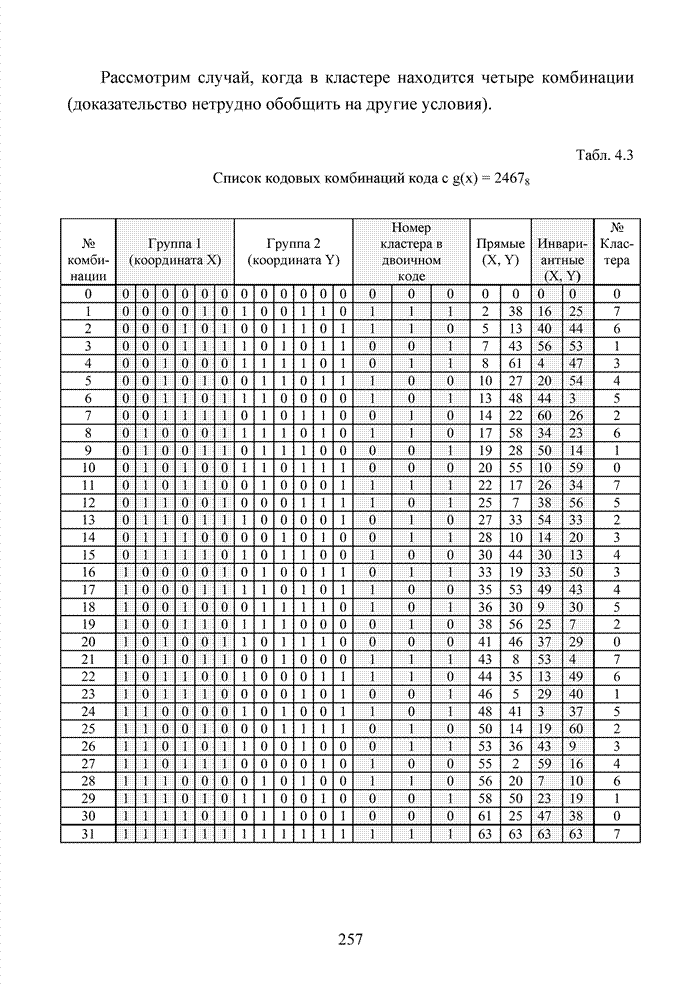
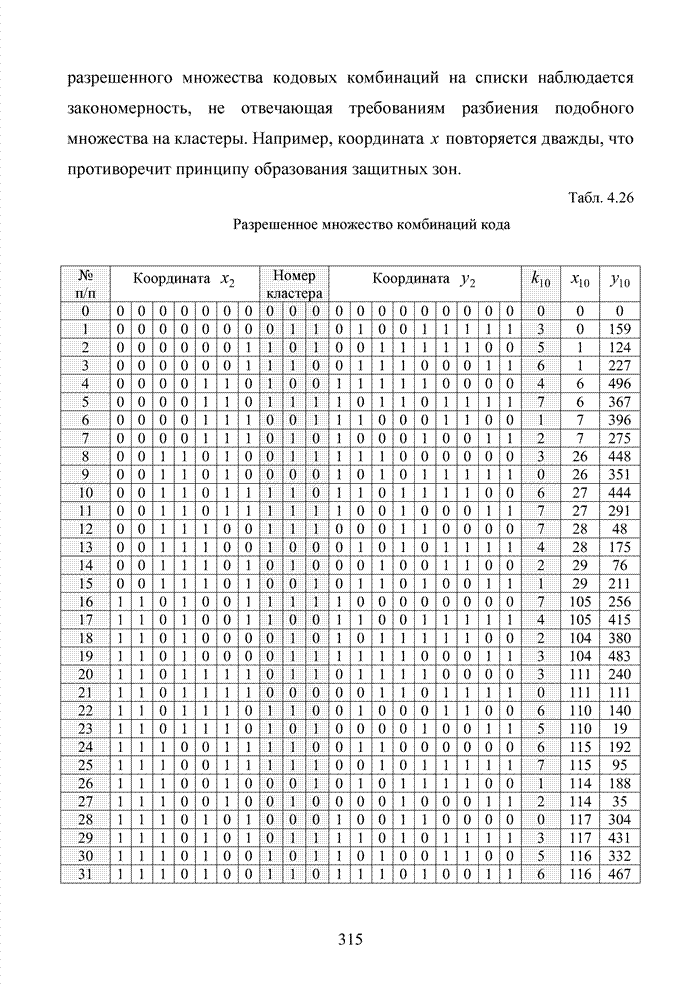
Для доказательства рассмотрим код БЧХ (15,5,7) с порождающим полиномом g(x)=24678. Приведем список кодовых комбинаций и их разбиение на кластеры (таб. 4.3). В этой таблице наряду с прямыми координатами векторов приведены и, так называемые, инвариантные значения координат, суть которых будет показана ниже.
Рассмотрим случай, когда в кластере находится четыре комбинации (доказательство нетрудно обобщить на другие условия).
Табл. 4.3 Список кодовых комбинаций кода с g(x) = 24678
|
№ комби- нации |
Группа 1 (координата Х) |
Группа 2 (координата Y) |
Номер кластера в двоичном коде |
Прямые (X, Y) |
Инвари- антные (X, Y) |
№ Клас- тера |
||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
2 |
38 |
16 |
25 |
7 |
|
2 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
5 |
13 |
40 |
44 |
6 |
|
3 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
7 |
43 |
56 |
53 |
1 |
|
4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
8 |
61 |
4 |
47 |
3 |
|
5 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
10 |
27 |
20 |
54 |
4 |
|
6 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
13 |
48 |
44 |
3 |
5 |
|
7 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
14 |
22 |
60 |
26 |
2 |
|
8 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
17 |
58 |
34 |
23 |
6 |
|
9 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
19 |
28 |
50 |
14 |
1 |
|
10 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
20 |
55 |
10 |
59 |
0 |
|
11 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
22 |
17 |
26 |
34 |
7 |
|
12 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
25 |
7 |
38 |
56 |
5 |
|
13 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
27 |
33 |
54 |
33 |
2 |
|
14 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
28 |
10 |
14 |
20 |
3 |
|
15 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
30 |
44 |
30 |
13 |
4 |
|
16 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
33 |
19 |
33 |
50 |
3 |
|
17 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
35 |
53 |
49 |
43 |
4 |
|
18 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
36 |
30 |
9 |
30 |
5 |
|
19 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
38 |
56 |
25 |
7 |
2 |
|
20 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
41 |
46 |
37 |
29 |
0 |
|
21 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
43 |
8 |
53 |
4 |
7 |
|
22 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
44 |
35 |
13 |
49 |
6 |
|
23 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
46 |
5 |
29 |
40 |
1 |
|
24 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
48 |
41 |
3 |
37 |
5 |
|
25 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
50 |
14 |
19 |
60 |
2 |
|
26 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
53 |
36 |
43 |
9 |
3 |
|
27 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
55 |
2 |
59 |
16 |
4 |
|
28 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
56 |
20 |
7 |
10 |
6 |
|
29 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
58 |
50 |
23 |
19 |
1 |
|
30 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
61 |
25 |
47 |
38 |
0 |
|
31 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
63 |
63 |
63 |
63 |
7 |


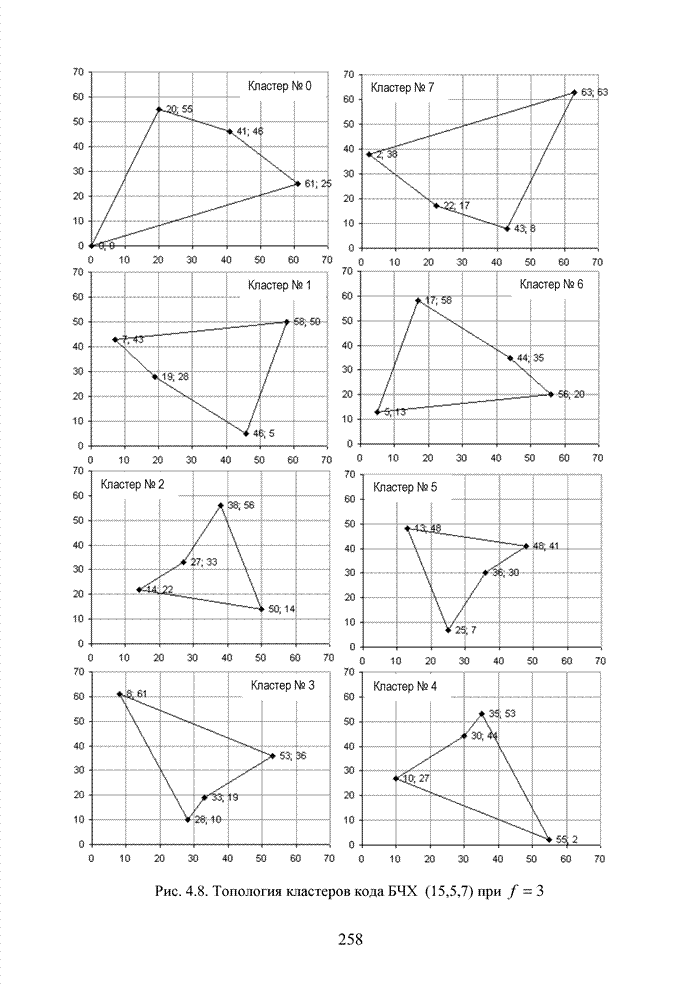
Рис. 4.8.
Топология кластеров кода БЧХ (15,5,7) при ![]()
В приведенном примере
координаты ![]() и
и ![]() содержат по 6 двойных разрядов. Вес младших разрядов
координат при переходе от двоичной системы счисления к десятичной системе
счисления равен
содержат по 6 двойных разрядов. Вес младших разрядов
координат при переходе от двоичной системы счисления к десятичной системе
счисления равен ![]() . Вес следующих разрядов имеет значение
. Вес следующих разрядов имеет значение ![]() , где
, где ![]() . В общем случае для
. В общем случае для ![]() двоичных разрядов
координаты
двоичных разрядов
координаты ![]() и
и ![]() вес старшего разряда равен
вес старшего разряда равен ![]() . Важно отметить, что при кластерном
подходе появляется новая метрика в форме прямоугольной защитной зоны,
определяемой прямыми линиями, проходящими
через пары точек с координатами:
. Важно отметить, что при кластерном
подходе появляется новая метрика в форме прямоугольной защитной зоны,
определяемой прямыми линиями, проходящими
через пары точек с координатами:
для вертикальной границы [(![]() ); 0] и [(
); 0] и [(![]() );
); ![]() ];
. (4.6)
];
. (4.6)
для горизонтальной границы [0; (![]() )] и [
)] и [![]() ;(
;(![]() )]. (4.7)
)]. (4.7)
В приведенном примере легко заметить то, что расстояние между комбинациями кластера № 4 (30;44) и (35;53) минимально, и с точки зрения метрики Евклида эти комбинации могут легко перейти одна в другую.
Применяя метрику
кластерного анализа, покажем, что это произойдет только при искажении старших
разрядов координат. Выберем, например, комбинацию с координатами (35;53) ![]() .
.
Искажение младших разрядов координат приведет к образованию следующих последовательностей:

Заметно, что миграция
рабочей точки в плоскости защитной зоны при переборе всевозможных искажений
младших разрядов координат минимальна, т.к. вес этого разряда при переходе ![]() незначителен. Указанные координаты
определяют зону миграции (зона прямоугольной формы) при искажении младшего
разряда.
незначителен. Указанные координаты
определяют зону миграции (зона прямоугольной формы) при искажении младшего
разряда.
При искажении пятого разряда получим:

Поскольку
границами данного прямоугольника защитной зоны являются прямые ![]() и
и ![]() , заметно, что миграция значений
искаженной кодовой комбинации происходит в той же защитной зоне плоскости
кластера №4, к которой принадлежит правильная версия.
, заметно, что миграция значений
искаженной кодовой комбинации происходит в той же защитной зоне плоскости
кластера №4, к которой принадлежит правильная версия.
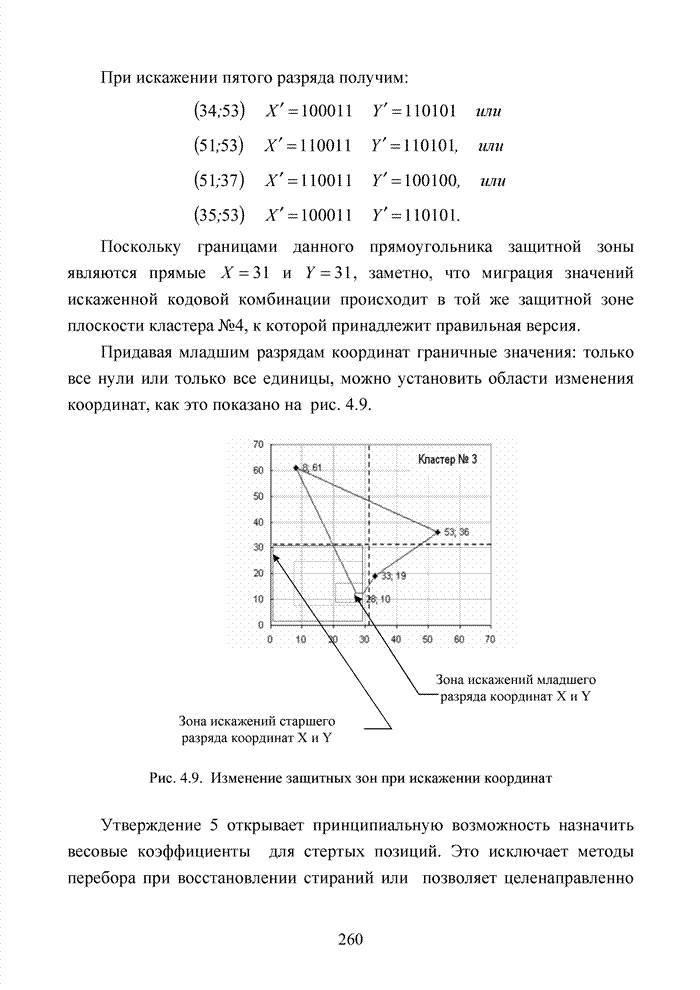
Придавая младшим разрядам координат граничные значения: только все нули или только все единицы, можно установить области изменения координат, как это показано на рис. 4.9.

Рис. 4.9. Изменение защитных зон при искажении координат
Утверждение 5
открывает принципиальную возможность назначить весовые коэффициенты для
стертых позиций. Это исключает методы перебора при восстановлении стираний или
позволяет целенаправленно снижать степень расширения двоичного поля Галуа в
целях сокращения времени при переборе стираний старших разрядов. Указанное
свойство имеет важное прикладное значение. Суть его заключается в том, что при
хорошем состоянии канала связи в каждой координате ![]() и
и ![]() возможна перфорация младших разрядов. Следовательно, ХК
может быть повышена.
возможна перфорация младших разрядов. Следовательно, ХК
может быть повышена.
В случае искажения
старшего разряда одной из координат кодовой комбинации ресурсом декодера
является надежная фиксация другой координаты. При искажении старших разрядов
декодер переходит к инвариантному коду координат. Инвариантным кодом координат
называется такое представление истинных координат, при котором позиция ![]() принимает в
позиционной системе счисления значение
принимает в
позиционной системе счисления значение ![]() , т.е. становится старшим разрядом;
значение
, т.е. становится старшим разрядом;
значение ![]() принимает
значение
принимает
значение ![]() и
т.д. В общем виде позиция
и
т.д. В общем виде позиция ![]() замещается на значение
замещается на значение ![]() . На рис. 4.10 показан
пример искажения координат 10-й комбинации из табл. 4.3. Искажения произошли в
младших разрядах. Созвездие комбинаций представляющее правильные символы
кластера № 0 показаны точками, а искаженная комбинация показана крестиком.
Заметно, что искаженная комбинация не вышла за пределы защитной зоны и поэтому
будет восстановлена правильно при условии точного определения номера кластера.
. На рис. 4.10 показан
пример искажения координат 10-й комбинации из табл. 4.3. Искажения произошли в
младших разрядах. Созвездие комбинаций представляющее правильные символы
кластера № 0 показаны точками, а искаженная комбинация показана крестиком.
Заметно, что искаженная комбинация не вышла за пределы защитной зоны и поэтому
будет восстановлена правильно при условии точного определения номера кластера.

Рис. 4.10. Пример искажений в младших разрядах значений координат
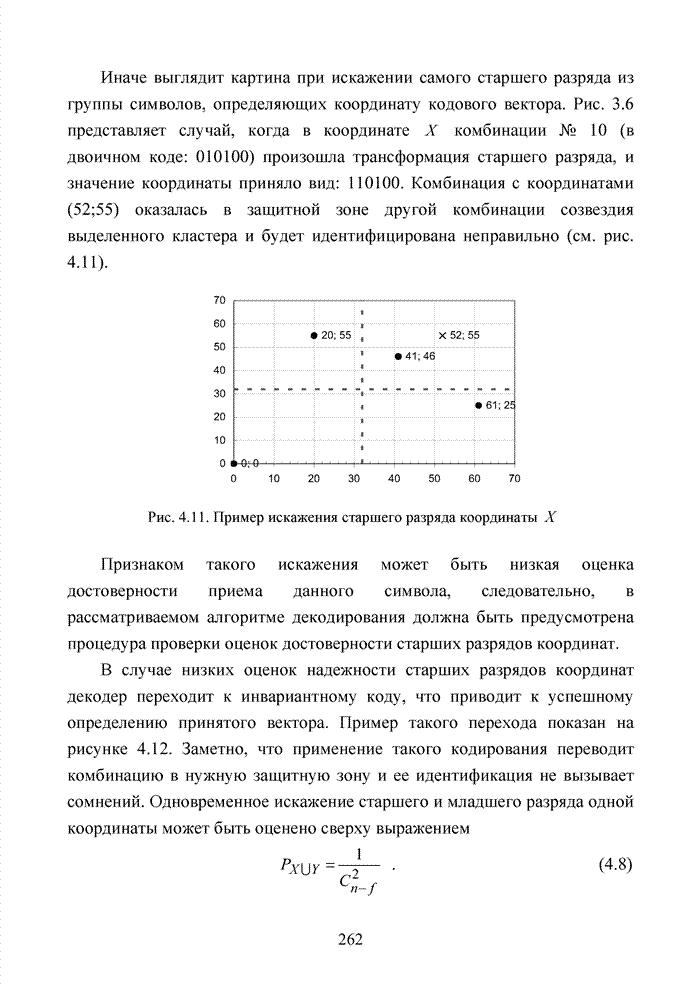
Иначе выглядит картина
при искажении самого старшего разряда из группы символов, определяющих
координату кодового вектора. Рис. 3.6 представляет случай, когда в координате ![]() комбинации № 10 (в
двоичном коде: 010100) произошла трансформация старшего разряда, и значение
координаты приняло вид: 110100. Комбинация с координатами (52;55) оказалась в
защитной зоне другой комбинации созвездия выделенного кластера и будет
идентифицирована неправильно (см. рис. 4.11).
комбинации № 10 (в
двоичном коде: 010100) произошла трансформация старшего разряда, и значение
координаты приняло вид: 110100. Комбинация с координатами (52;55) оказалась в
защитной зоне другой комбинации созвездия выделенного кластера и будет
идентифицирована неправильно (см. рис. 4.11).

Рис.
4.11. Пример искажения старшего разряда координаты ![]()
Признаком такого искажения может быть низкая оценка достоверности приема данного символа, следовательно, в рассматриваемом алгоритме декодирования должна быть предусмотрена процедура проверки оценок достоверности старших разрядов координат.
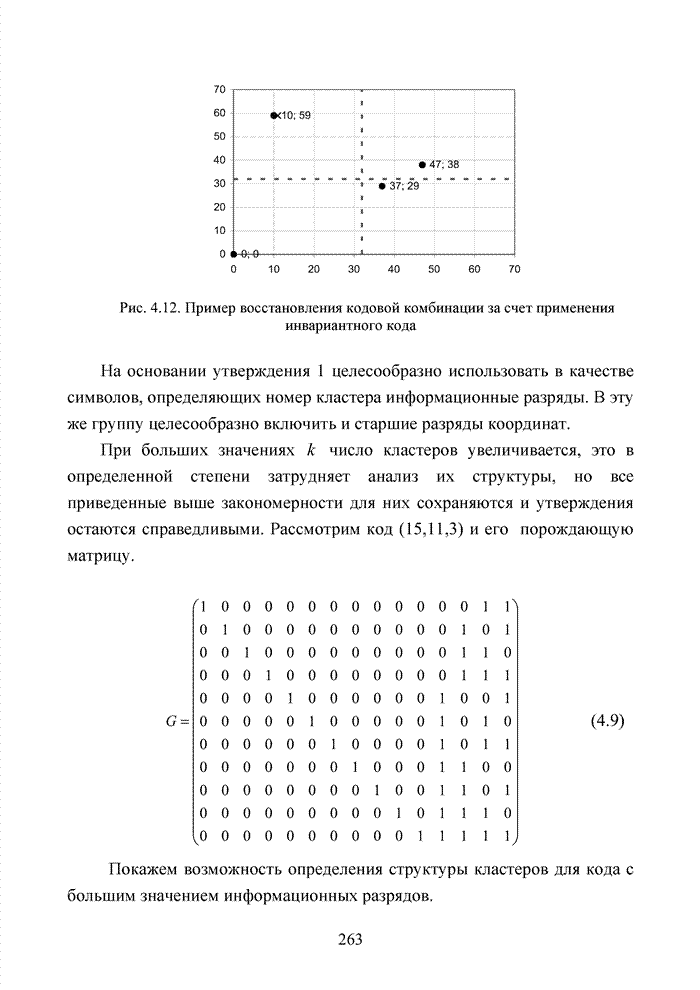
В случае низких оценок надежности старших разрядов координат декодер переходит к инвариантному коду, что приводит к успешному определению принятого вектора. Пример такого перехода показан на рисунке 4.12. Заметно, что применение такого кодирования переводит комбинацию в нужную защитную зону и ее идентификация не вызывает сомнений. Одновременное искажение старшего и младшего разряда одной координаты может быть оценено сверху выражением
 .
(4.8)
.
(4.8)

Рис. 4.12. Пример восстановления кодовой комбинации за счет применения инвариантного кода
На основании утверждения 1 целесообразно использовать в качестве символов, определяющих номер кластера информационные разряды. В эту же группу целесообразно включить и старшие разряды координат.
При больших значениях ![]() число кластеров
увеличивается, это в определенной степени затрудняет анализ их структуры, но
все приведенные выше закономерности для них сохраняются и утверждения остаются
справедливыми. Рассмотрим код (15,11,3) и его порождающую матрицу.
число кластеров
увеличивается, это в определенной степени затрудняет анализ их структуры, но
все приведенные выше закономерности для них сохраняются и утверждения остаются
справедливыми. Рассмотрим код (15,11,3) и его порождающую матрицу.
 (4.9)
(4.9)
Покажем возможность определения структуры кластеров для кода с большим значением информационных разрядов.
Утверждение 6. Полное множество всех возможных
кластеров блокового систематического кода может быть образовано путем линейной
комбинации строк порождающей матрицы. Действительно, определив разряды кодовых
комбинаций, указывающих на номер кластера (параметр ![]() ), выделим в порождающей матрице
), выделим в порождающей матрице ![]() первые
первые ![]() строк. В единичной матрице
строк. В единичной матрице ![]() под последней строкой из выбранных
под последней строкой из выбранных ![]() строк образуется множество
столбцов, содержащих только нули. Строки матрицы
строк образуется множество
столбцов, содержащих только нули. Строки матрицы ![]() с первыми
с первыми ![]() нулями являются кандидатами для
формирования нулевого кластера. Поскольку комбинации всех строк матрицы
нулями являются кандидатами для
формирования нулевого кластера. Поскольку комбинации всех строк матрицы ![]() определяют кластер с
номером
определяют кластер с
номером ![]() , то все другие номера могут быть сформированы путем линейной
комбинации соответствующих строк. Утверждение доказано. Пусть в коде (15;11)
параметр
, то все другие номера могут быть сформированы путем линейной
комбинации соответствующих строк. Утверждение доказано. Пусть в коде (15;11)
параметр ![]() . Тогда образуется
. Тогда образуется ![]() кластеров, причем в каждый кластер войдет
ровно
кластеров, причем в каждый кластер войдет
ровно ![]() комбинации.
Выделяем первые девять строк в матрице (4.7) . Из последних двух строк составим
список комбинаций, входящих в кластер с номером 000000000. Из
комбинации.
Выделяем первые девять строк в матрице (4.7) . Из последних двух строк составим
список комбинаций, входящих в кластер с номером 000000000. Из ![]() выделяем
выделяем
![]() (4.10)
(4.10)
Выражение (4.10) указывает на два представителя кластера с нулевым номером. Линейно комбинируя строки между собой, получаем третий вектор:
000000000110001,
а чисто нулевой вектор дополняет этот кластер до полного множества комбинаций (см. табл. 4.4.).
Табл. 4.4 Комбинации кластера с № 010
|
Номер кластера |
Координата |
Координата |
|
|
|
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 0 0 1 0 1 0 1 1 1 1 0 |
0 0 0 1 1 0 1 1 1 0 0 1 |
0 5 3 6 |
0 6 7 1 |
Выделим кластер с номером
51110 или 1111111112. Для этого необходимо оперировать со
всеми строками матрицы ![]() . Результаты линейных преобразований
показаны в табл. 4.5.
. Результаты линейных преобразований
показаны в табл. 4.5.
Табл. 4.5 Комбинации кластера с № 51110
|
Номер кластера |
Координата |
Координата |
|
|
|
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
1 1 1 1 0 0 0 1 0 0 0 1 |
1 1 1 0 0 0 0 0 1 1 1 0 |
7 4 2 1 |
7 0 1 6 |
Было показано, что все
кластеры группового кода, номера которых в сумме дают значение ![]() , отображают на
двумерной декартовой плоскости фигуры с симметрией второго порядка. Данные из
табл. 4.4 и 4.5 подтверждают этот тезис. Заметно, что комбинации (0;0) и (7;7), (5;6) и (2;1), (3;7) и
(4;0), (6;1) и (1;6) образуют созвездия с указанными свойствами. Наличие в
группе нулевого и единичного элементов однозначно определяет указанное свойство.
Приведенные созвездия для образованных выше кластеров на рис. 4.13 являются
дополнительным подтверждением доказанного свойства.
, отображают на
двумерной декартовой плоскости фигуры с симметрией второго порядка. Данные из
табл. 4.4 и 4.5 подтверждают этот тезис. Заметно, что комбинации (0;0) и (7;7), (5;6) и (2;1), (3;7) и
(4;0), (6;1) и (1;6) образуют созвездия с указанными свойствами. Наличие в
группе нулевого и единичного элементов однозначно определяет указанное свойство.
Приведенные созвездия для образованных выше кластеров на рис. 4.13 являются
дополнительным подтверждением доказанного свойства.

Рис. 4.13. Созвездие комбинаций кластеров 0 и 511
Утверждение 7. Учитывая структуру порождающей матрицы![]() , целесообразно
назначать номера кластеров, начиная с левых столбцов матрицы.
, целесообразно
назначать номера кластеров, начиная с левых столбцов матрицы.
Назначение номеров кластеров
со стороны единичной матрицы, порождающей матрицы ![]() , обеспечивает вложенность кластеров как
подкодов основного кода. Действительно, операция назначения кластеров слева
адекватна операции модификации кода методом его укорочения. Таким образом,
сохраняя систему вложенности кодов возможно использование кластерного подхода в
построении комбинированных декодеров. Назначение номеров кластеров в матрице
, обеспечивает вложенность кластеров как
подкодов основного кода. Действительно, операция назначения кластеров слева
адекватна операции модификации кода методом его укорочения. Таким образом,
сохраняя систему вложенности кодов возможно использование кластерного подхода в
построении комбинированных декодеров. Назначение номеров кластеров в матрице ![]() со стороны проверочных
разрядов матрицы не исключается, но это не обеспечивает свойств вложенности
кодов.
со стороны проверочных
разрядов матрицы не исключается, но это не обеспечивает свойств вложенности
кодов.
| << Предыдущий параграф | Следующий параграф >> |
- СПИСОК СОКРАЩЕНИЙ
- ВВЕДЕНИЕ
- ГЛАВА 1 ПРОБЛЕМА КОДИРОВАНИЯ В СОВРЕМЕННЫХ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМАХ
- Введение
- 1.1. Инфокоммуникационные технологии нового поколения
- 1.2. Каноническая схема построения звена передачи данных
- 1.5. Алгебраические системы. Понятие группы
- 1.6. Групповые конструкции. Подгруппа группы
- 1.7. Стандартное расположение кода
- 1.8. Модулярное представление блоковых кодов и их эквивалентность
- 1.9. Поле как алгебраическая структура
- 1.10. Непрерывные (сверточные) коды
- 1.11. Варианты модификации параметров кодов
- 1.12. Комбинации кодов, принцип каскадного кодирования
- 1.13. Комбинации кодов, принцип турбокодирования
- Выводы
- ГЛАВА 2 ПРИНЦИПЫ МОДЕЛИРОВАНИЯ КАНАЛОВ И СИСТЕМ СВЯЗИ
- Введение
- 2.1. Принципы моделирования непрерывных каналов связи
- 2.2. Субоптимальные отображения каналов связи
- 2.3. Модель канала связи со стиранием элементов
- 2.4. Модель марковского двоичного канала со стираниями
- 2.5. Стирающий канал при воздействии импульсных помех
- 2.6. Аналитическая модель системы связи с ортогональным частотным разделением каналов
- 2.7. Модель дискретного канала связи
- 2.8. Принципы имитационного моделирования каналов связи
- Выводы
- ГЛАВА 3 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ В МОДЕЛИРОВАНИИ ИНДЕКСОВ ДОСТОВЕРНОСТИ СИМВОЛОВ
- Введение
- 3.1. Классификация методов формирования ИДС
- 3.2. Аддитивный метод
- 3.3. Метод квантования уровней сигнала
- 3.4. Логарифм отношения условных вероятностей
- 3.5. Метод скользящих окон в стирающем канале связи
- 3.5.1. Способ снижения доли ложных стираний на основе случайного поиска решения о стирании элемента
- 3.5.2. Алгоритм с динамично изменяющейся границей
- 3.5.3. Алгоритм с жесткой границей
- 3.5.4. Алгоритм с использованием границы в формате отношения вероятности правильных стираний к вероятности ложных стираний
- 3.6. Модификация метода формирования ИДС в стирающем канале связи
- 3.7. Формирование мягких решений при обработке сигнально-кодовых конструкций
- Выводы
- ГЛАВА 4 ПРИНЦИПЫ НЕАЛГЕБРАИЧЕСКОГО ДЕКОДИРОВАНИЯ ИЗБЫТОЧНЫХ КОДОВ
- Введение
- 4.2. Кластерный подход к декодированию полиномиальных кодов
- 4.3. Модификация кодов при декодировании по кластерам
- 4.3.1. Процедура расширения кода
- 4.3.2. Укорочение кода
- 4.3.3. Операция выкалывания
- 4.4. Система кодирования с надежной защитой номера кластера
- 4.5. Декодирование циклических кодов на основе кластерного подхода
- 4.6. Декодирование на основе упорядоченной статистики
- 4.7. Способ списочного декодирования с защитой номера кластера
- 4.7.1. Описание алгоритма при отсутствии ошибок
- 4.9. Оценка возможности применения метода кластерного декодирования к непрерывным кодам
- Выводы
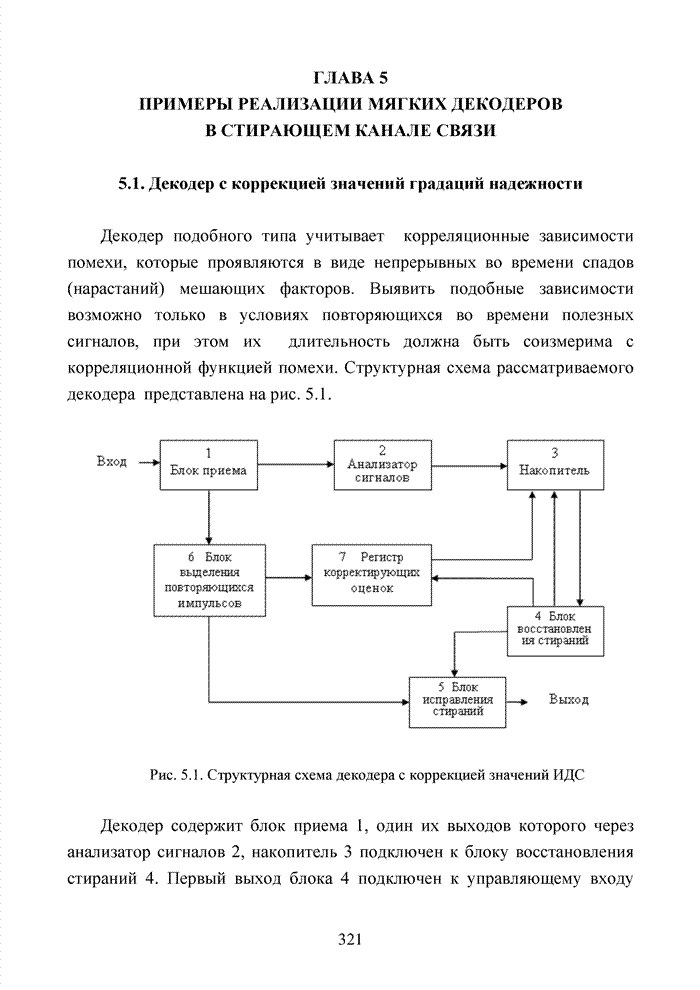
- ГЛАВА 5 ПРИМЕРЫ РЕАЛИЗАЦИИ МЯГКИХ ДЕКОДЕРОВ В СТИРАЮЩЕМ КАНАЛЕ СВЯЗИ
- 5.1. Декодер с коррекцией значений градаций надежности
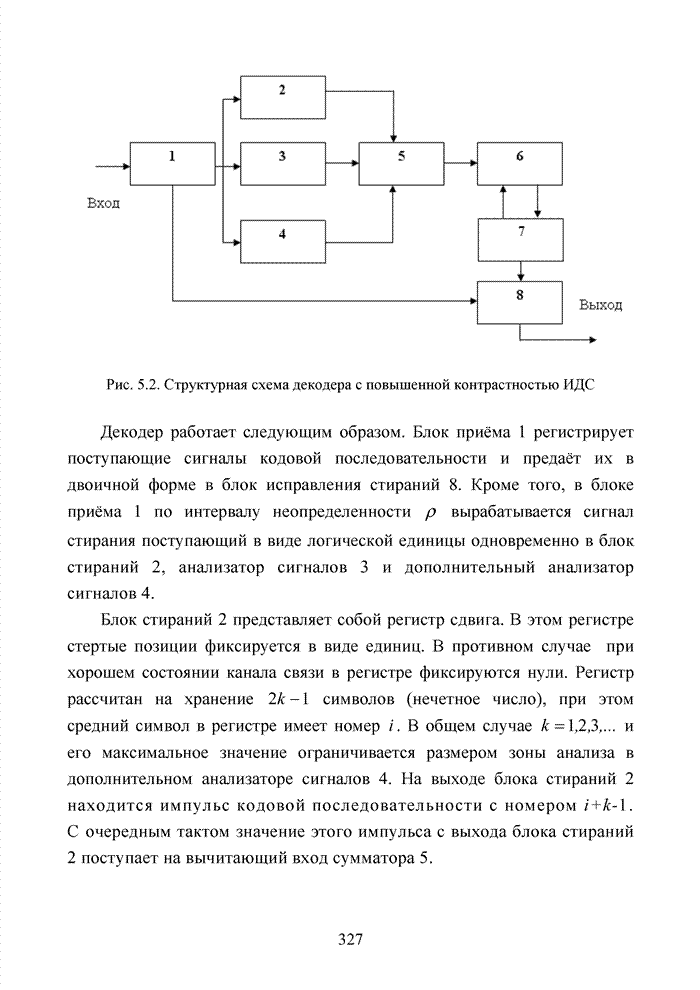
- 5.2. Приемник с повышенной контрастностью оценок надежности
- 5.3. Декодирование на основе лучших показателей ИДС
- 5.4. Декодирование с использованием списков на основе кластеров
- 5.5. Декодер с повышенной корректирующей способностью
- ЗАКЛЮЧЕНИЕ
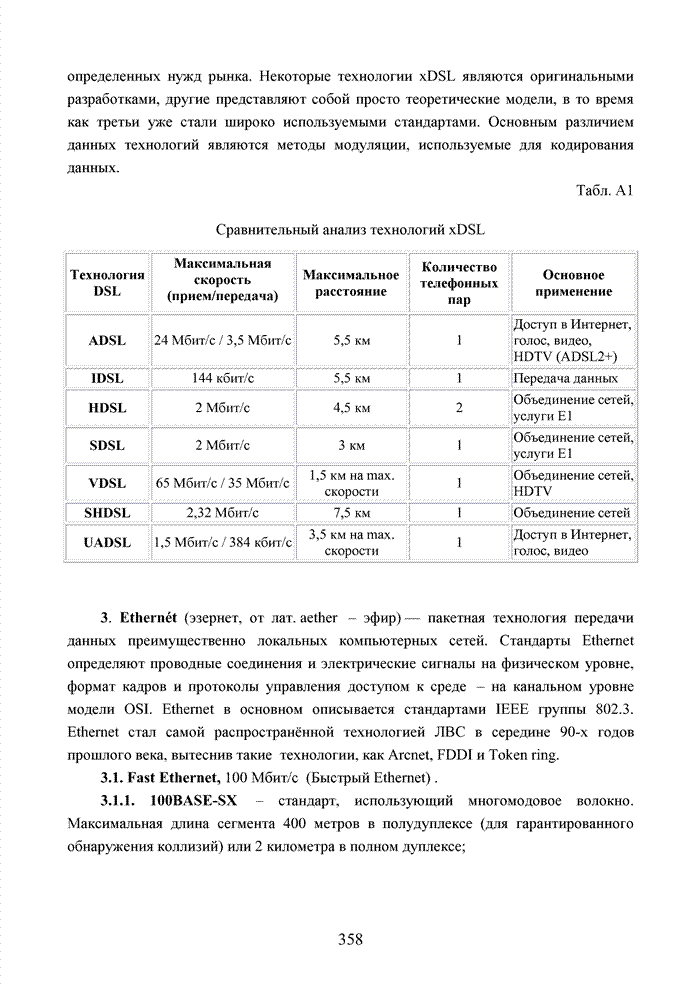
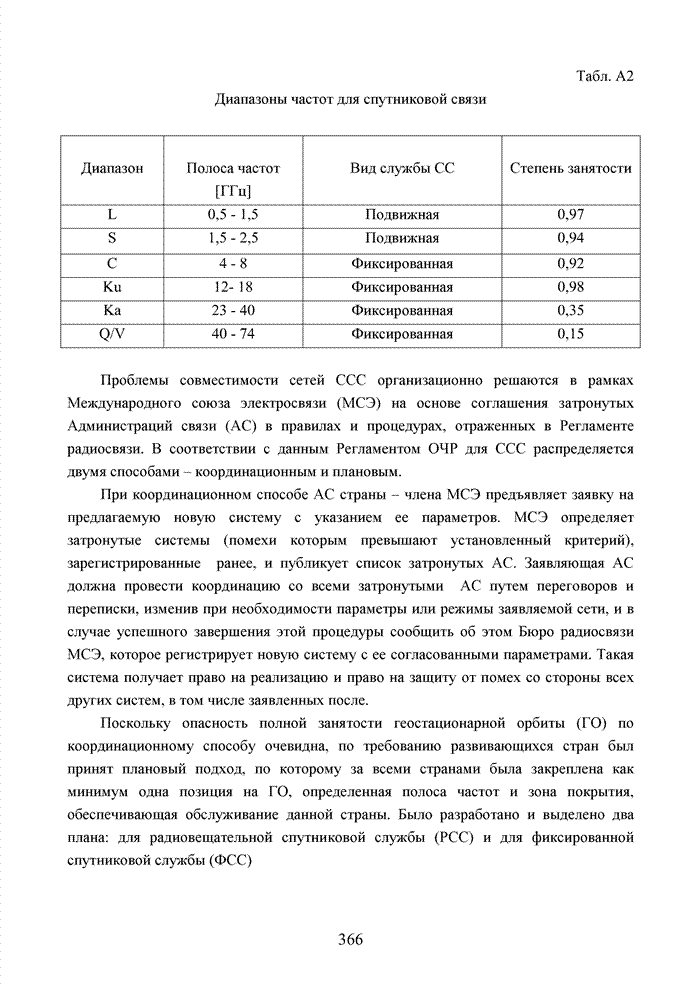
- Приложение А Краткие сведения об основных телекоммуникационных стандартах
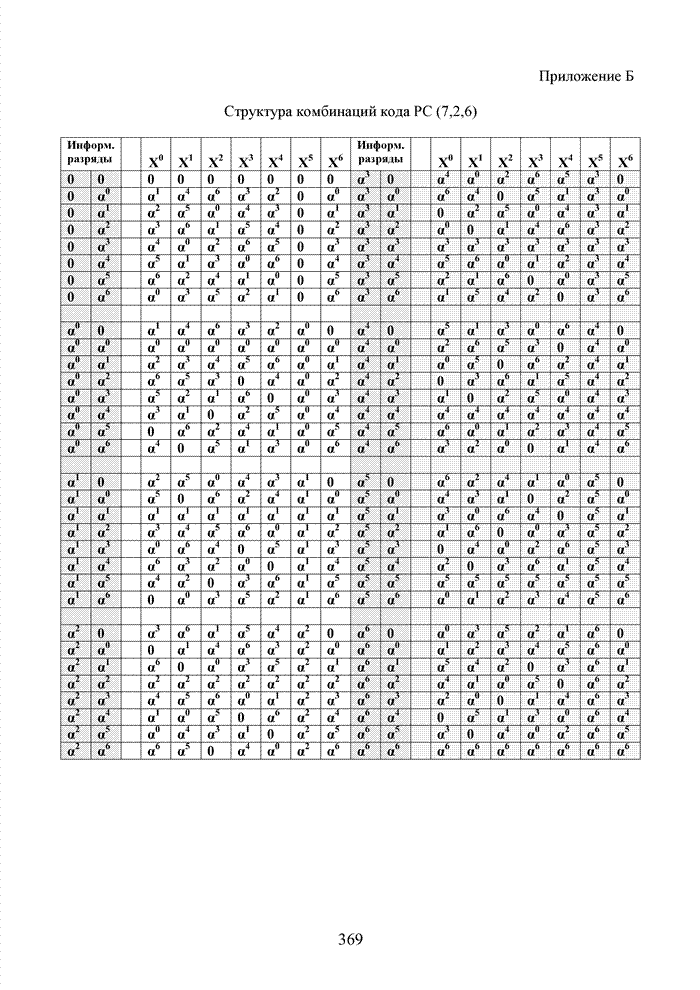
- Приложение Б Структура комбинаций кода РС (7,2,6)
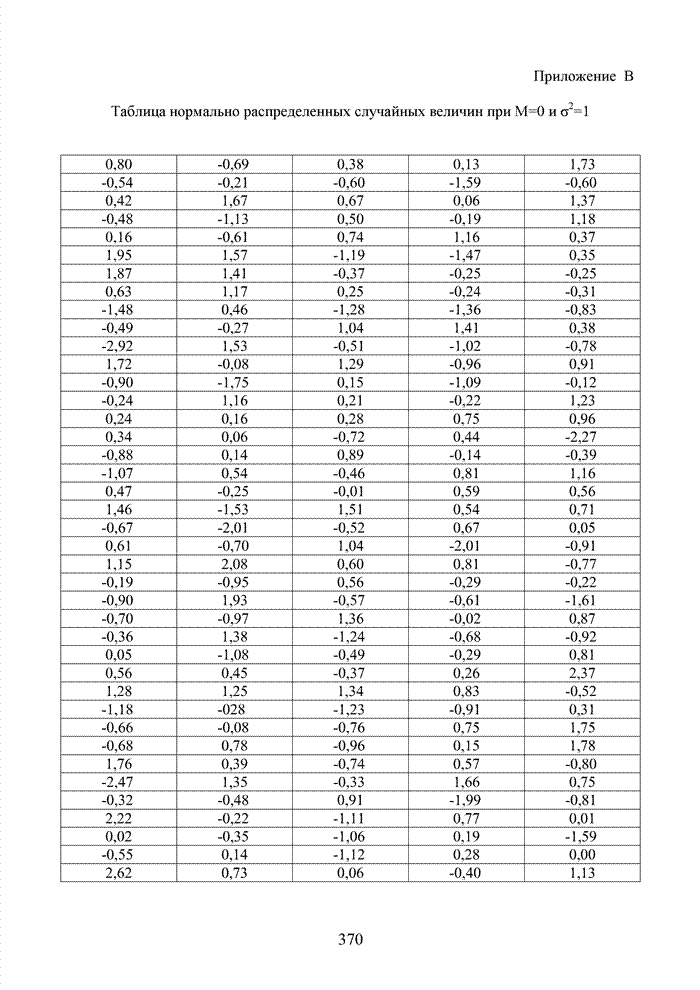
- Приложение В Таблица нормально распределенных случайных величин
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК