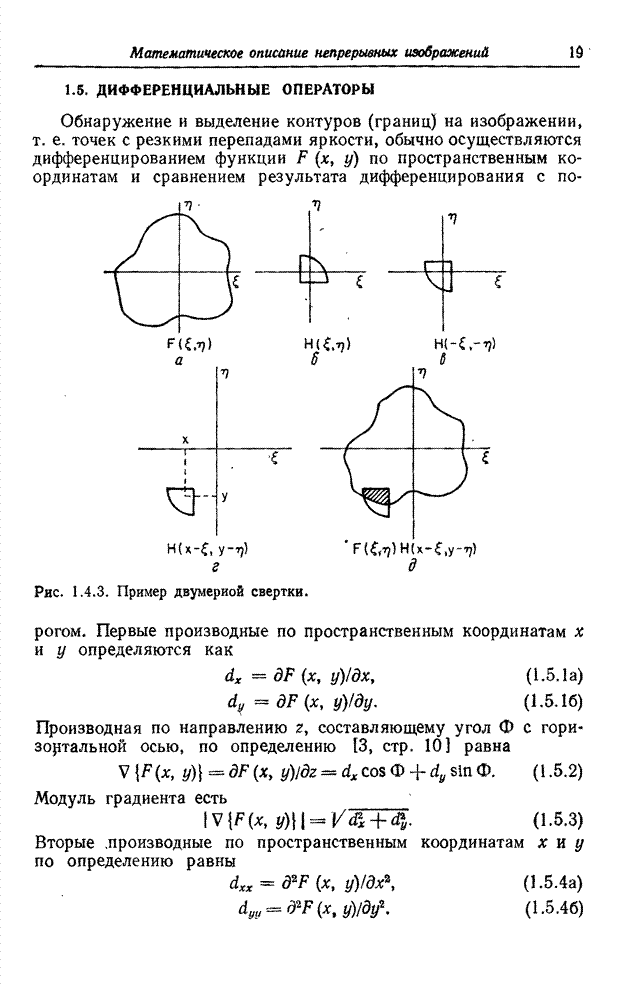
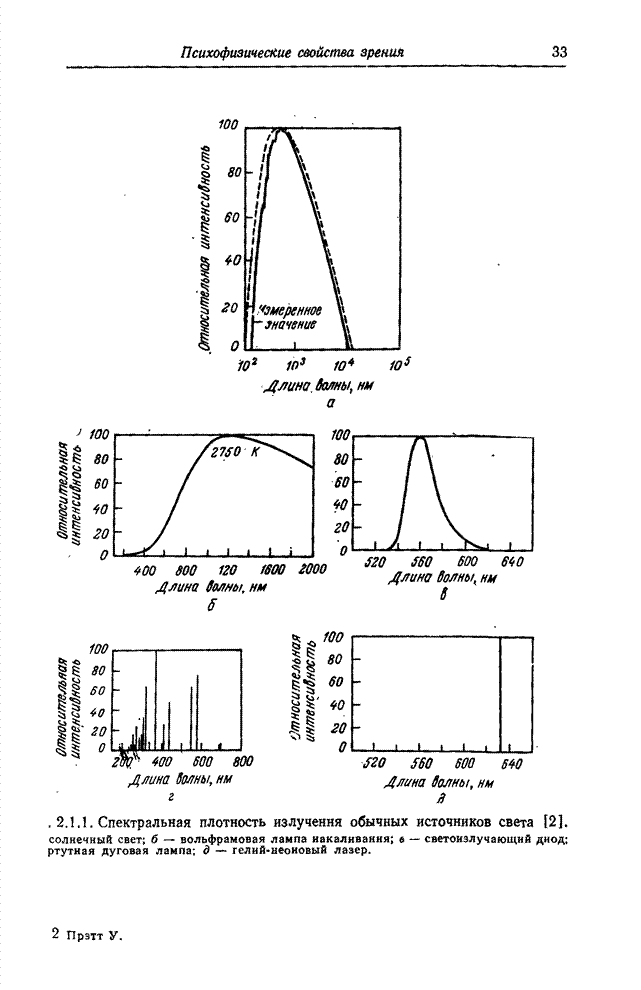
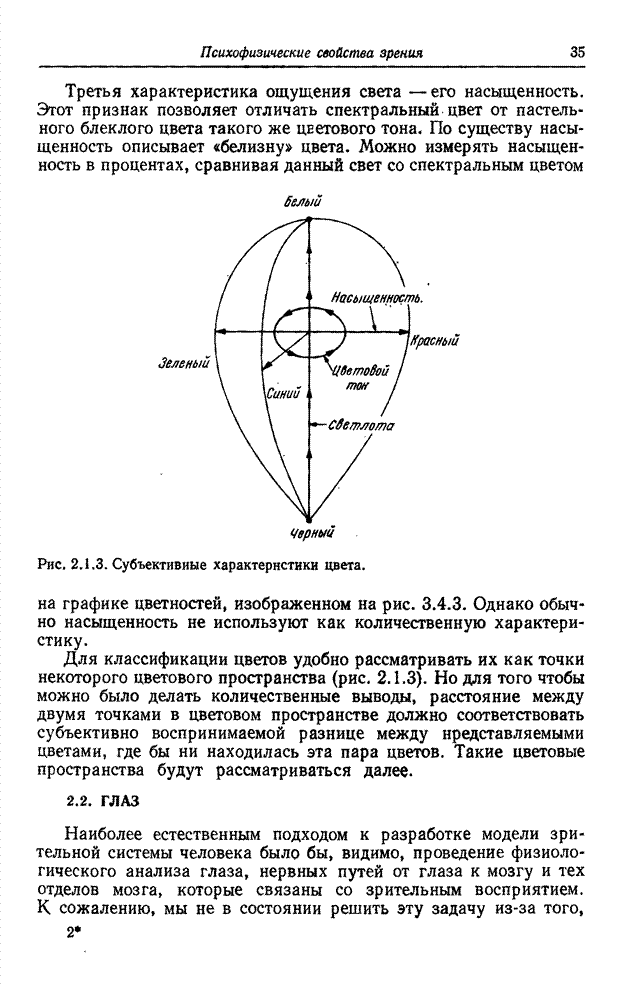
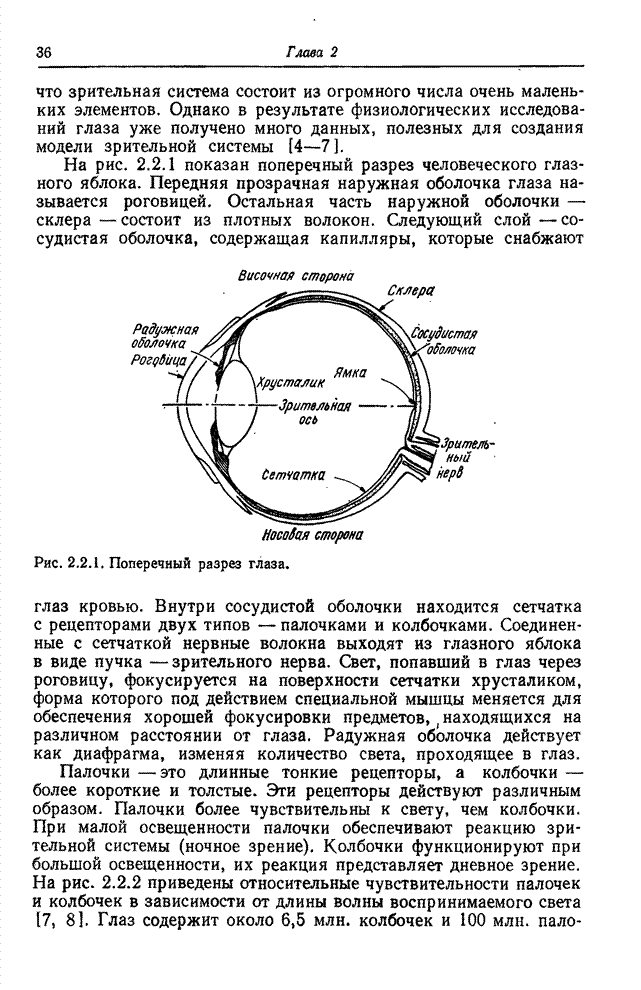
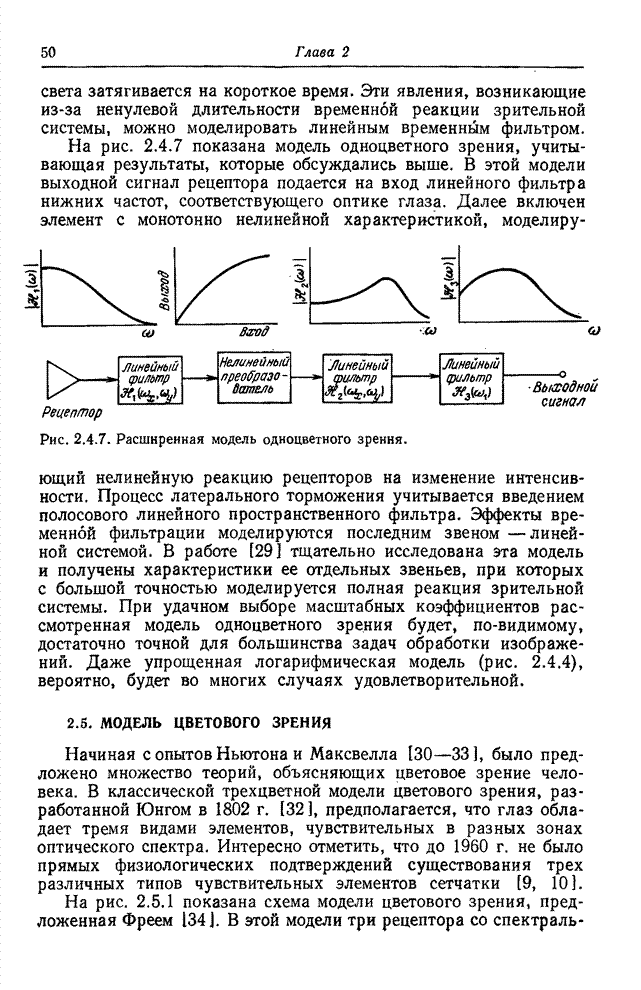
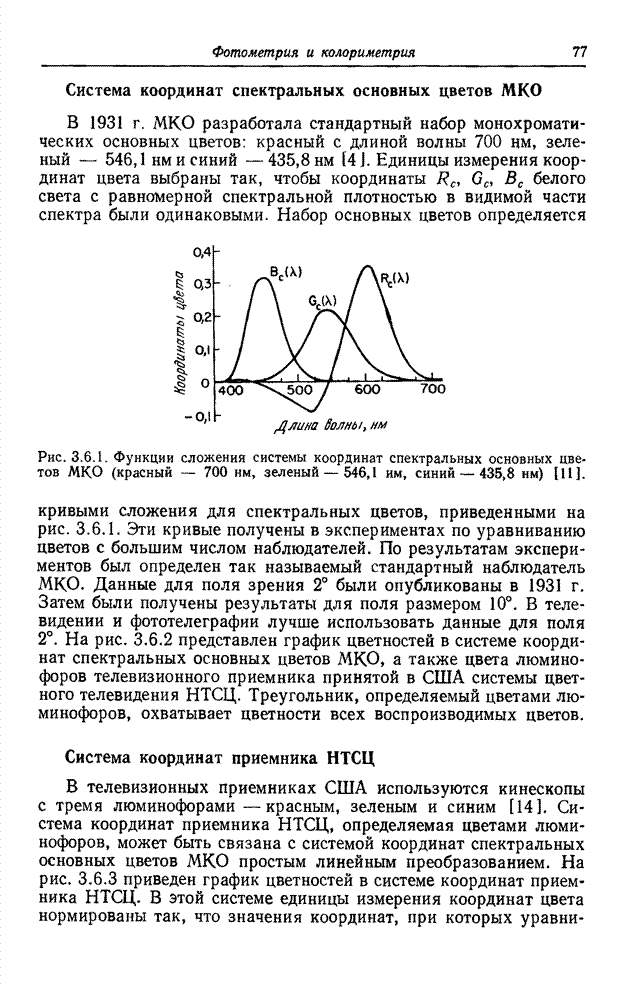
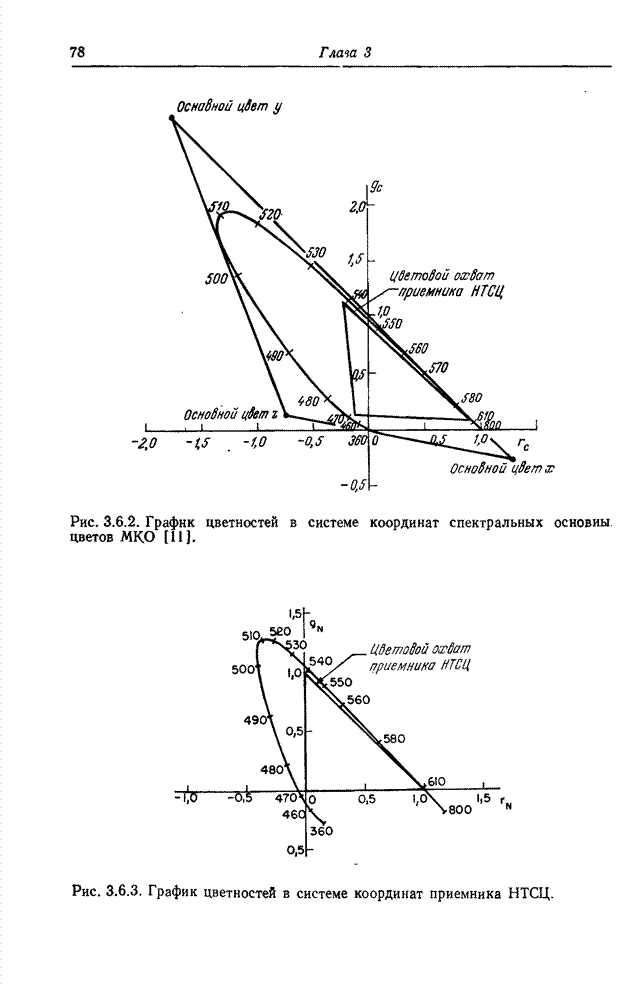
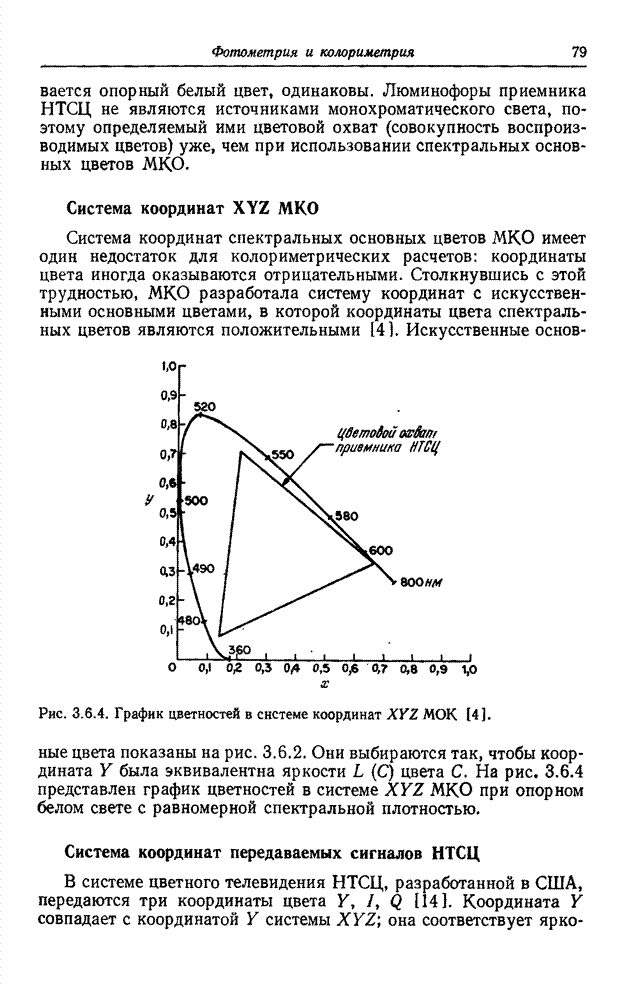
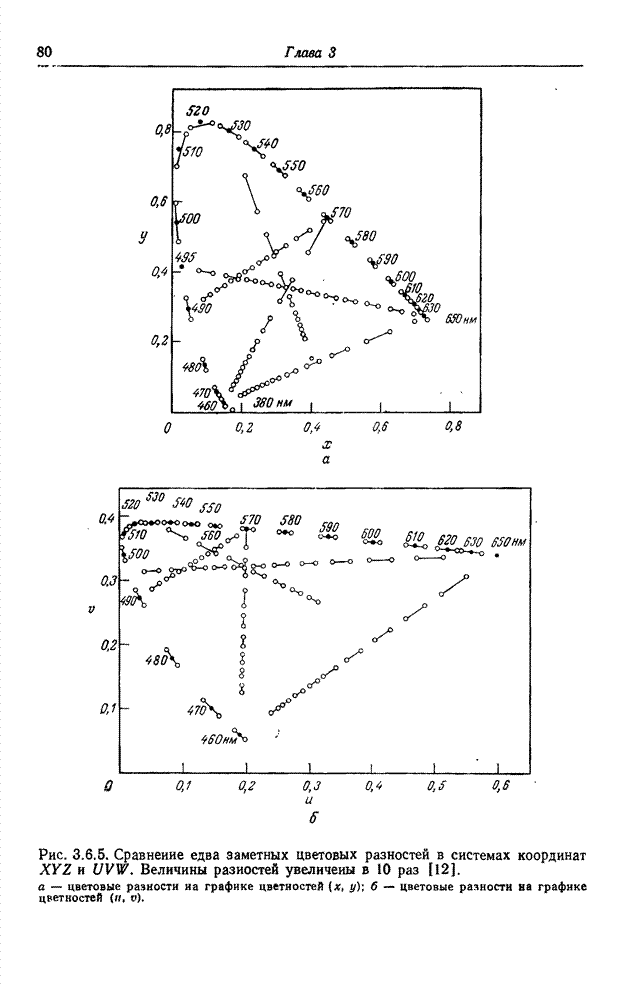
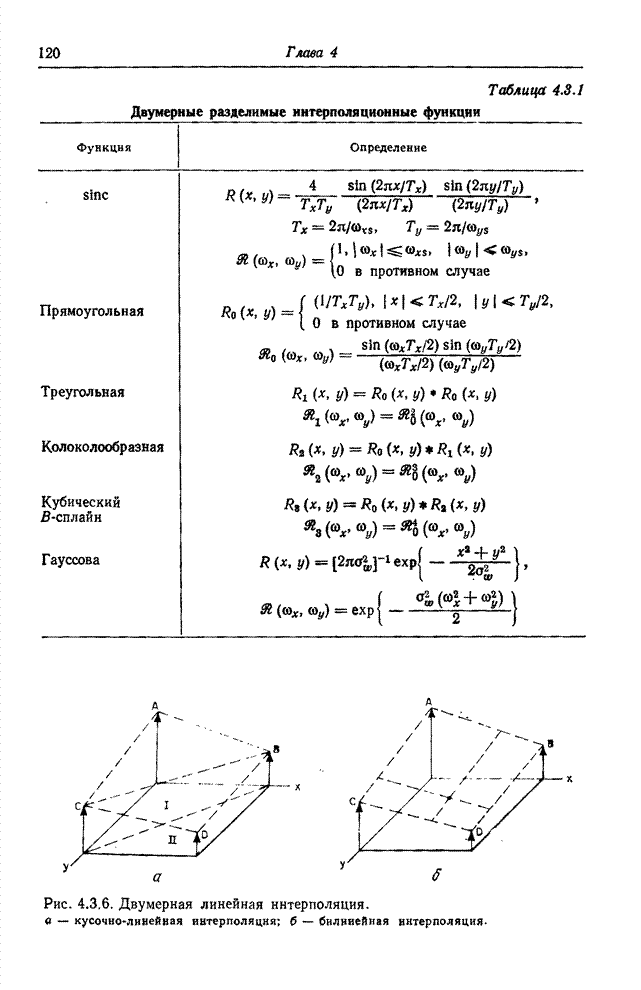
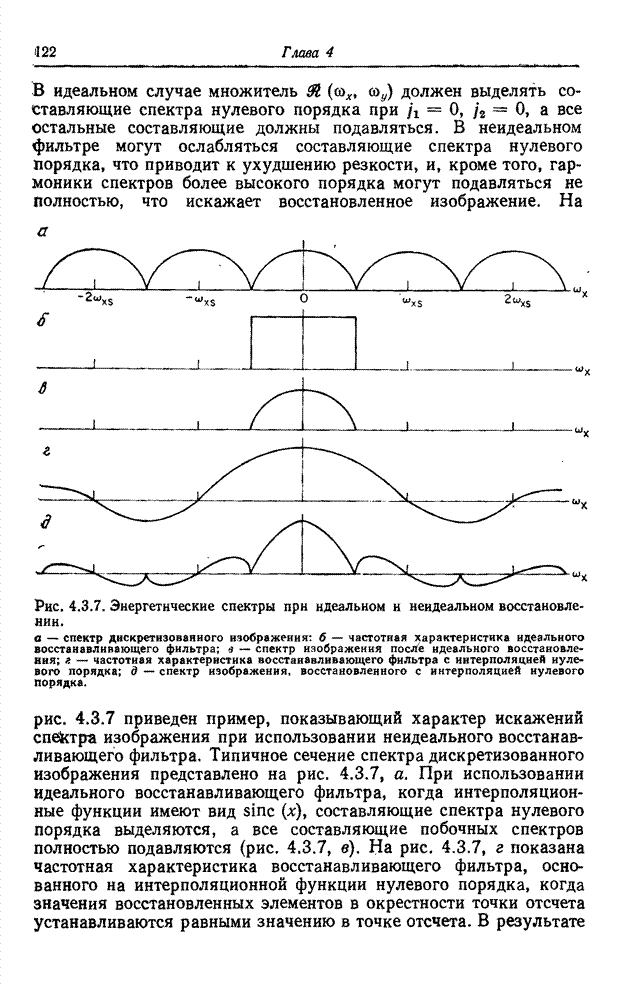
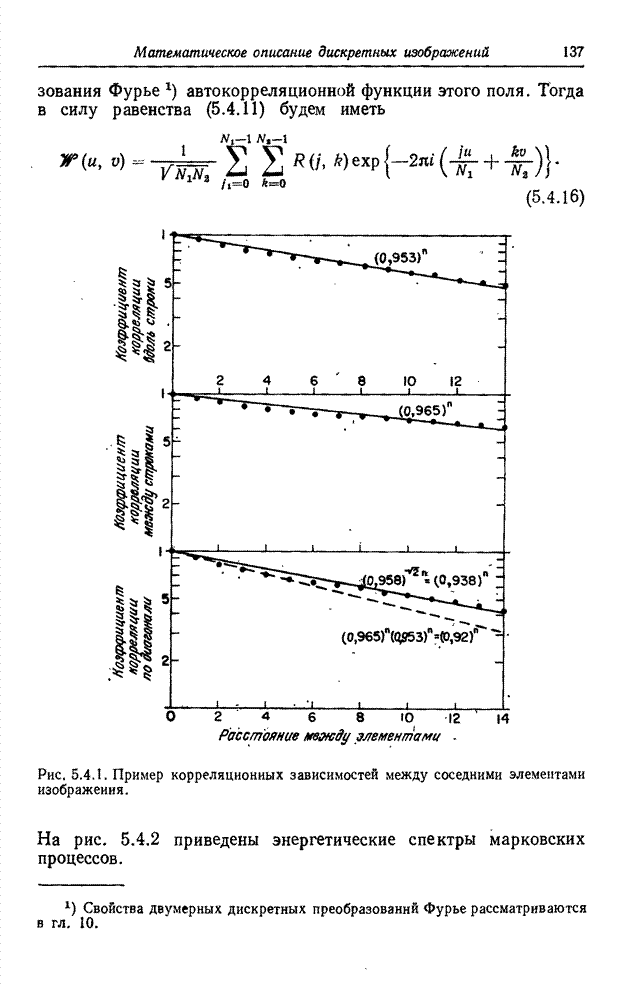
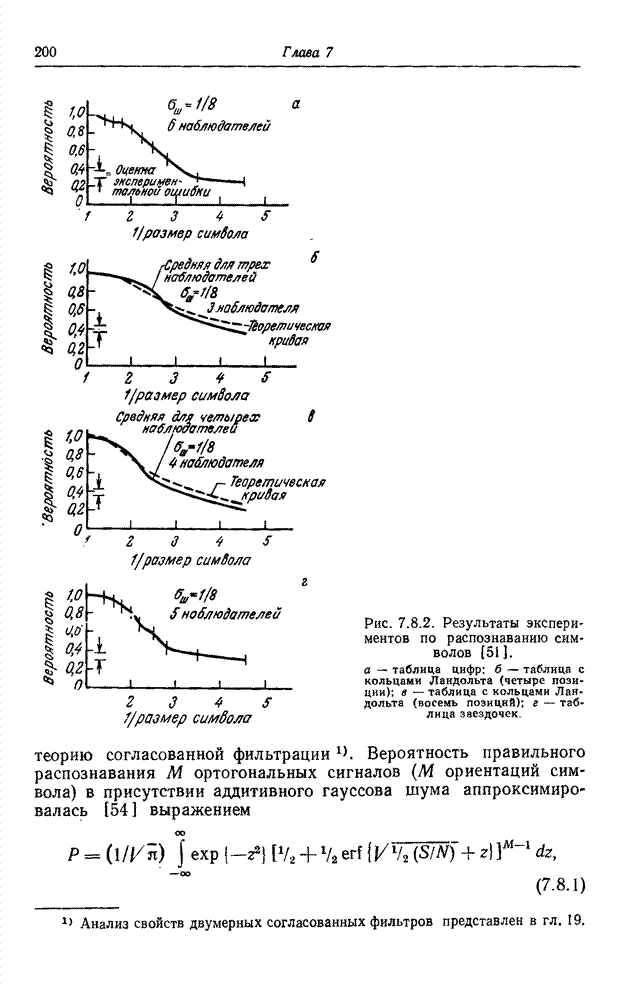
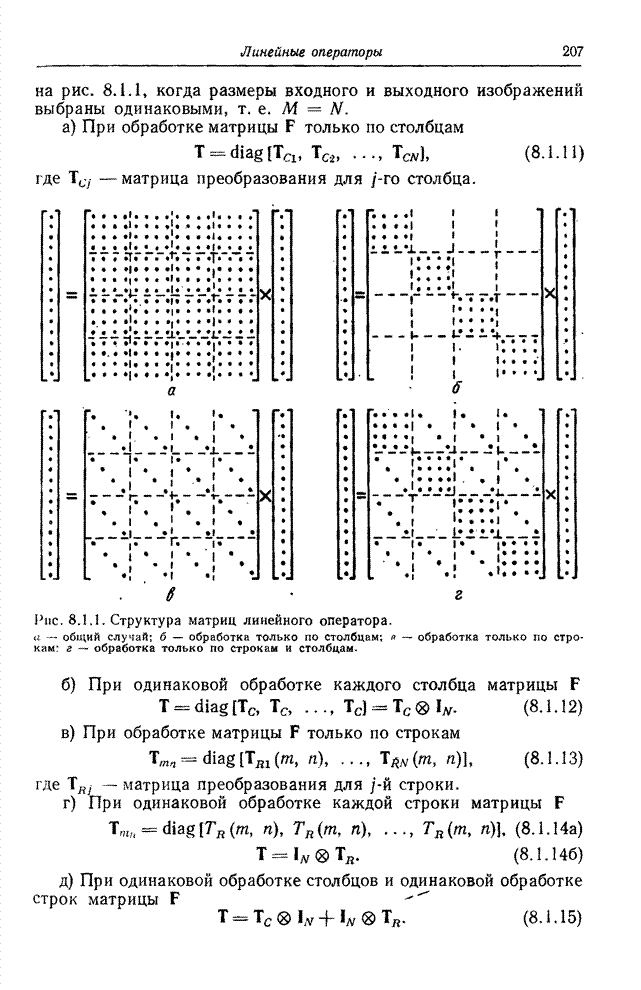
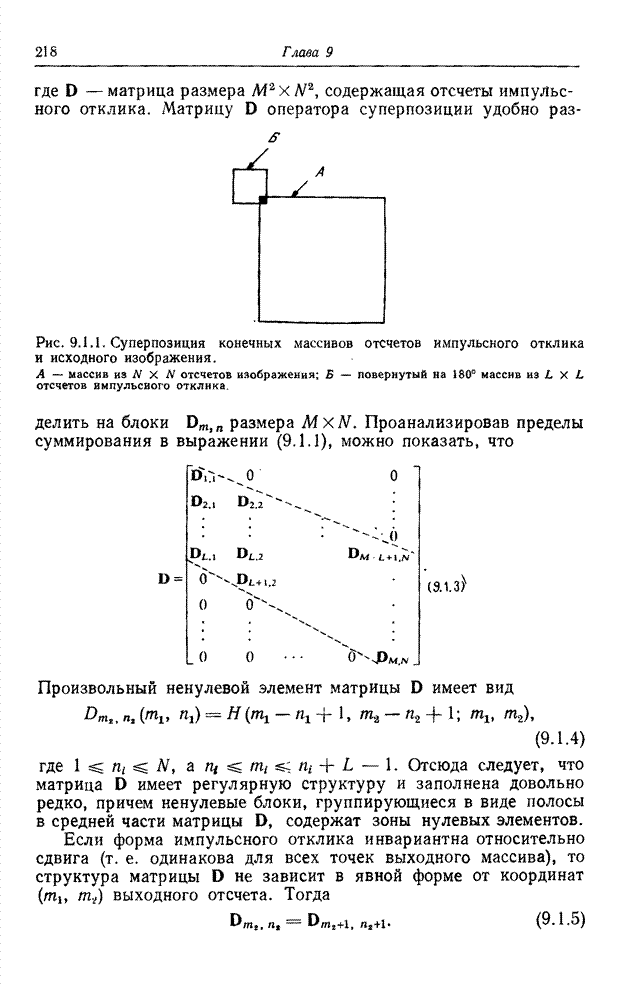
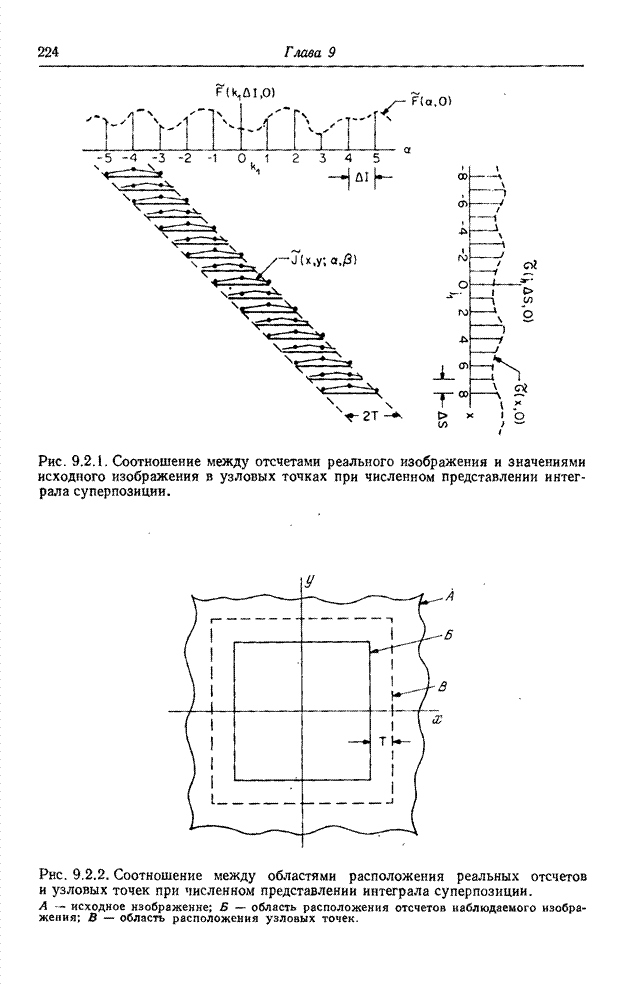
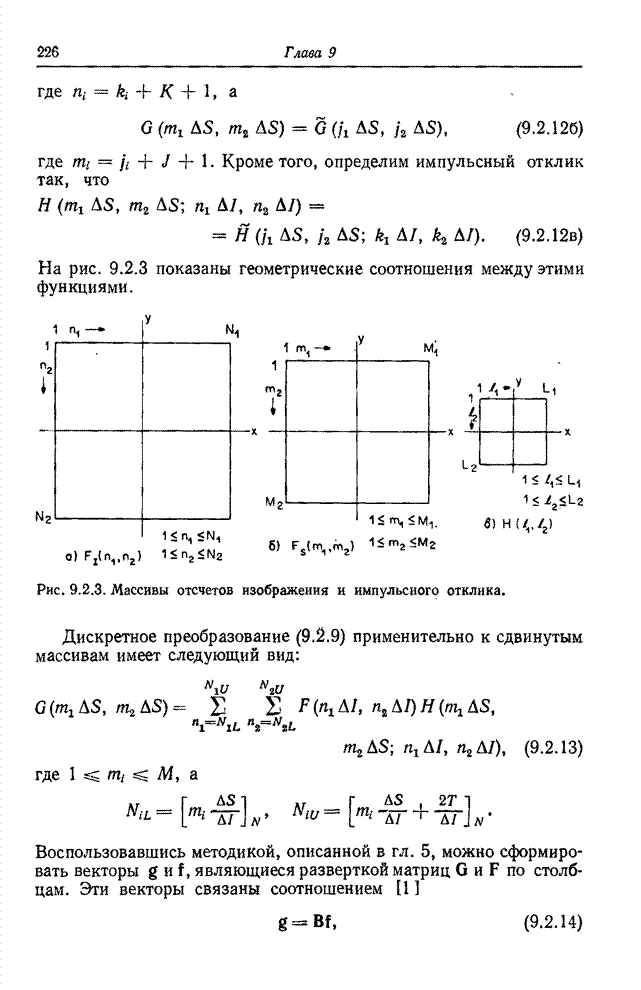
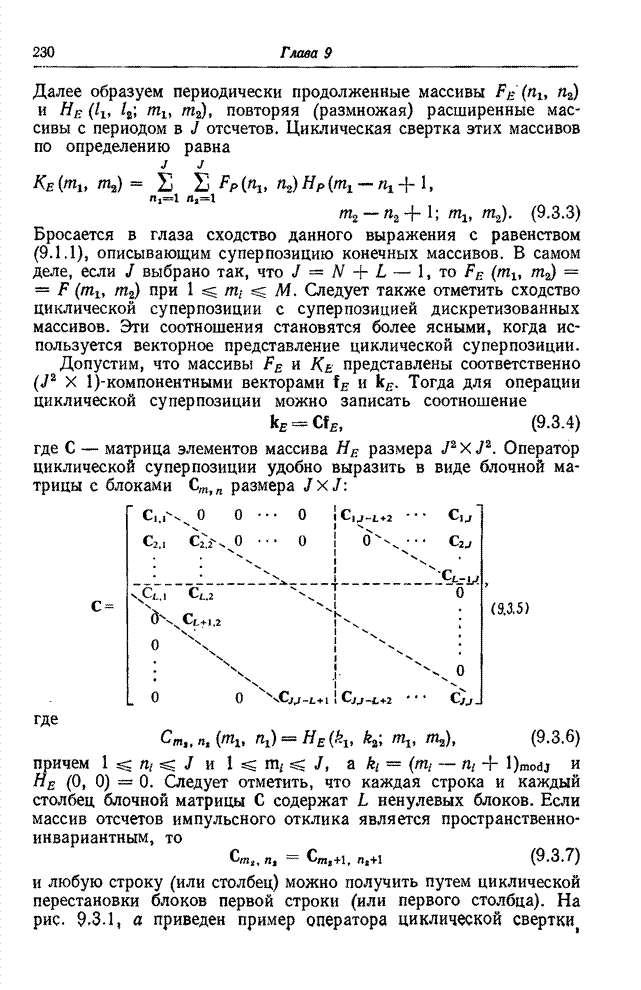
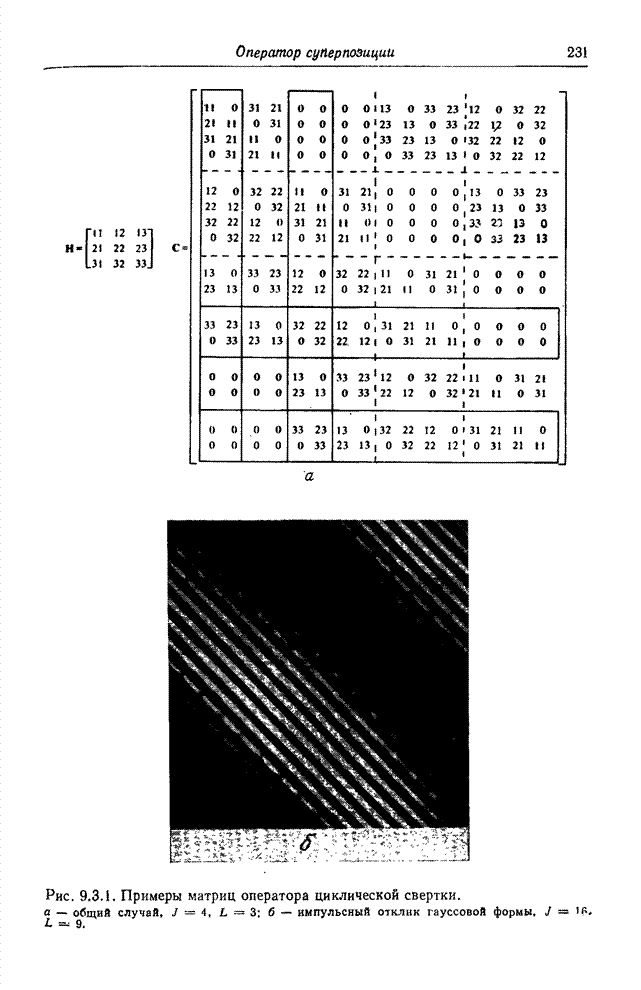
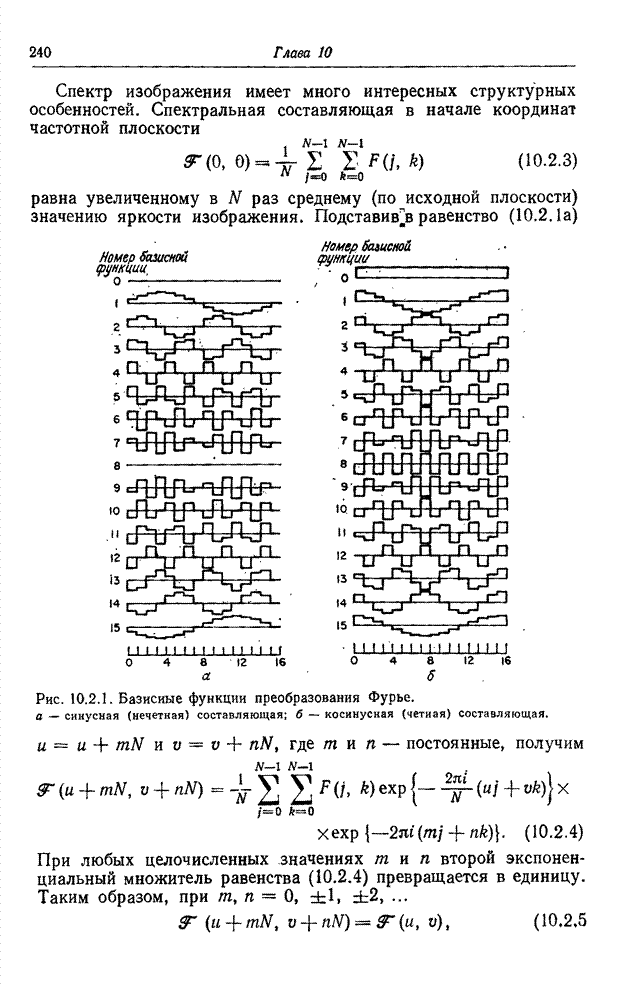
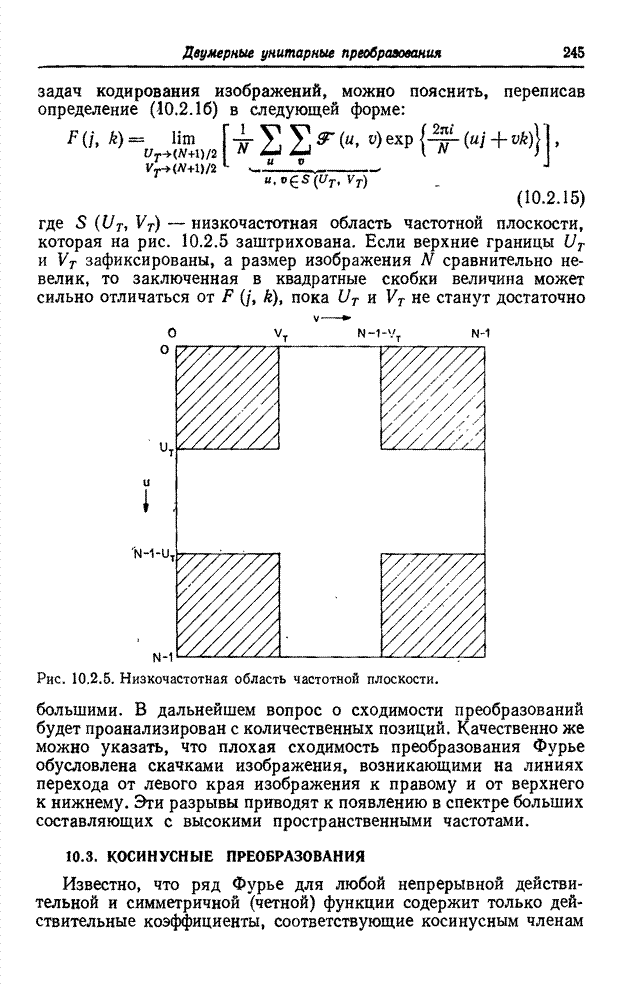
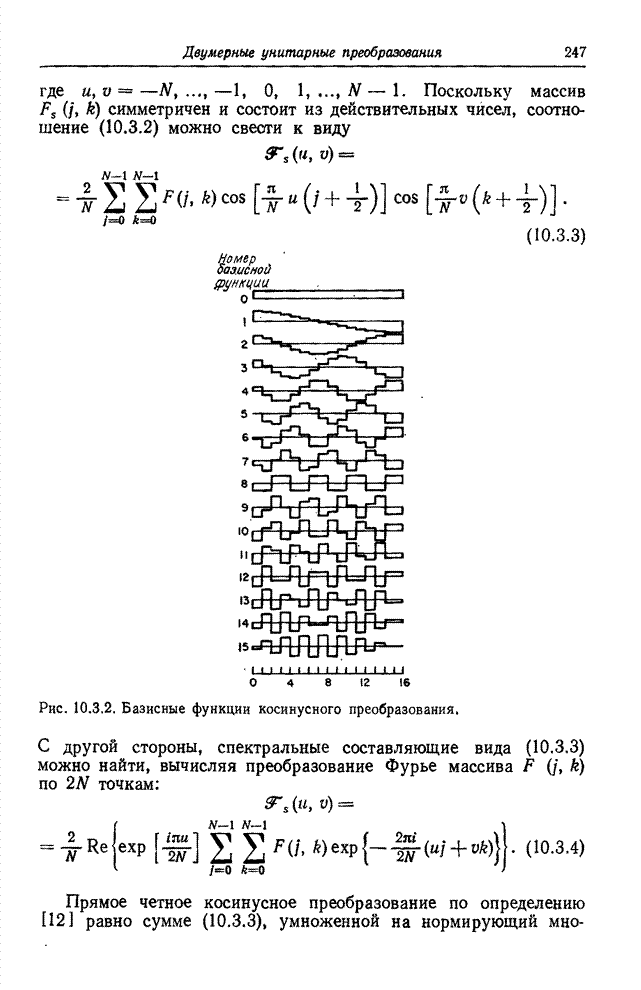
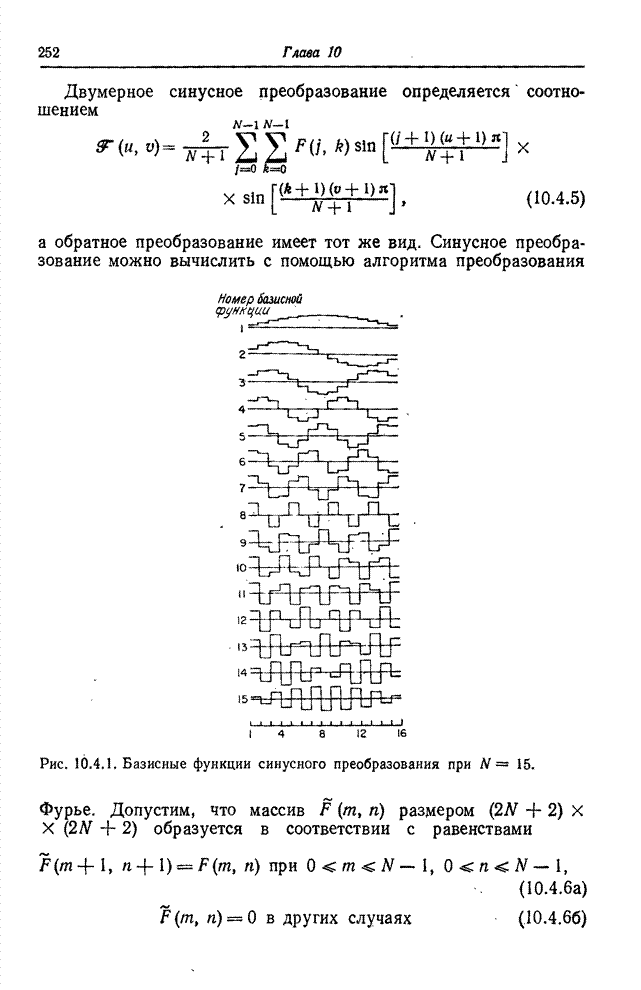
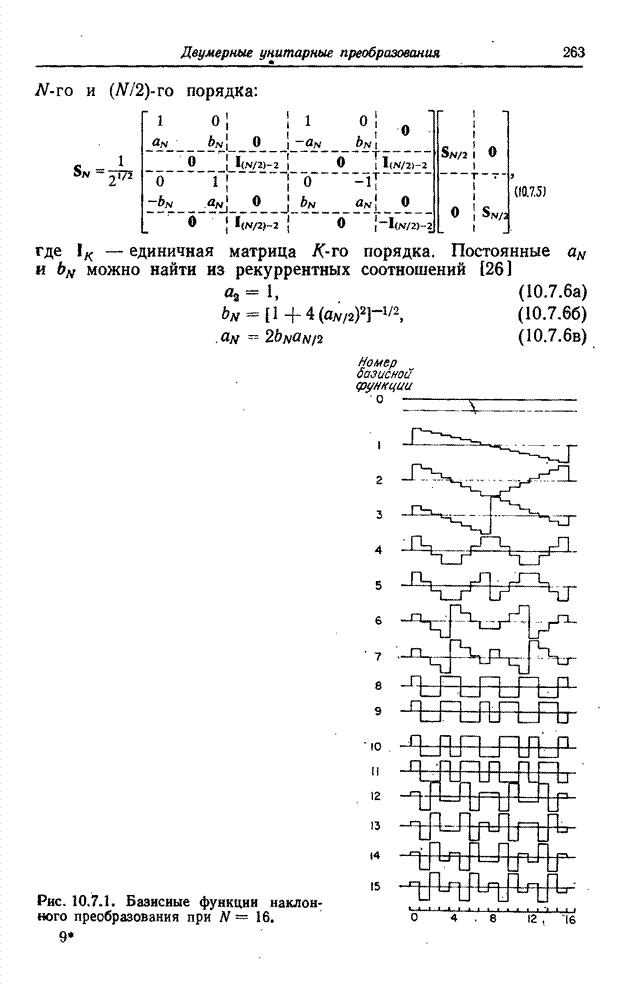
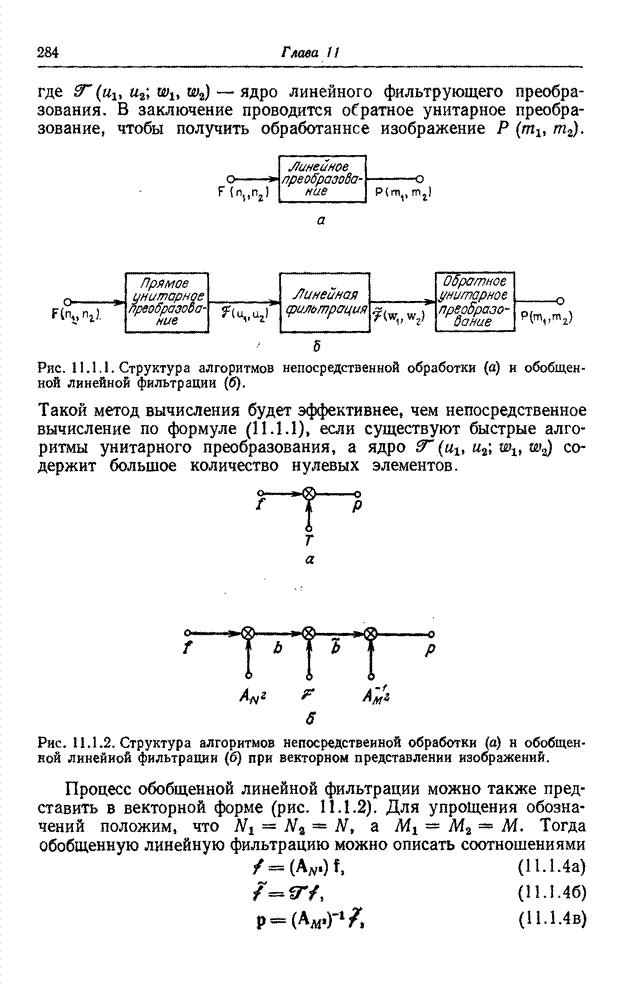
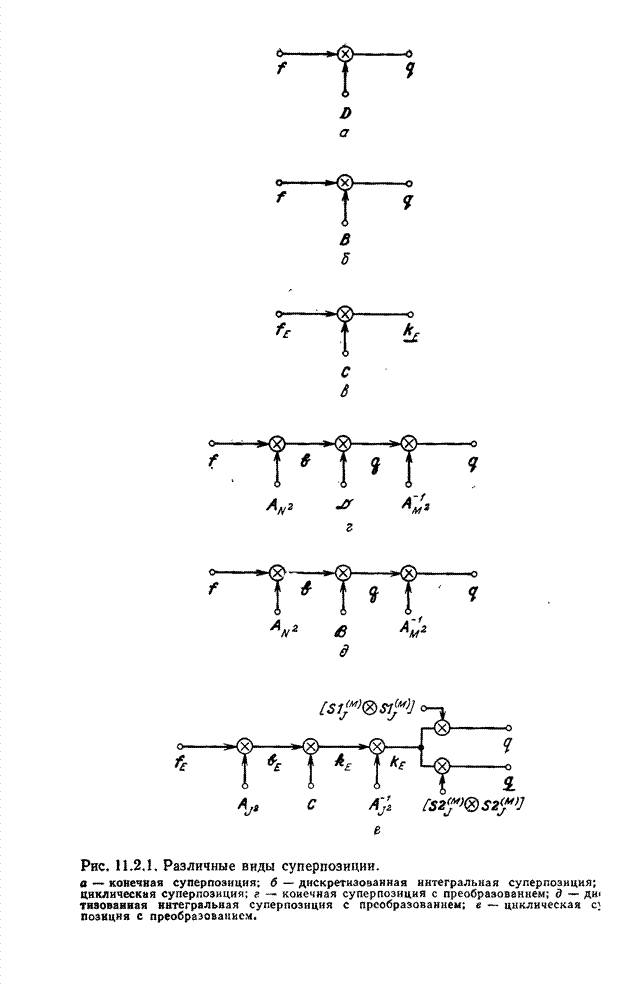
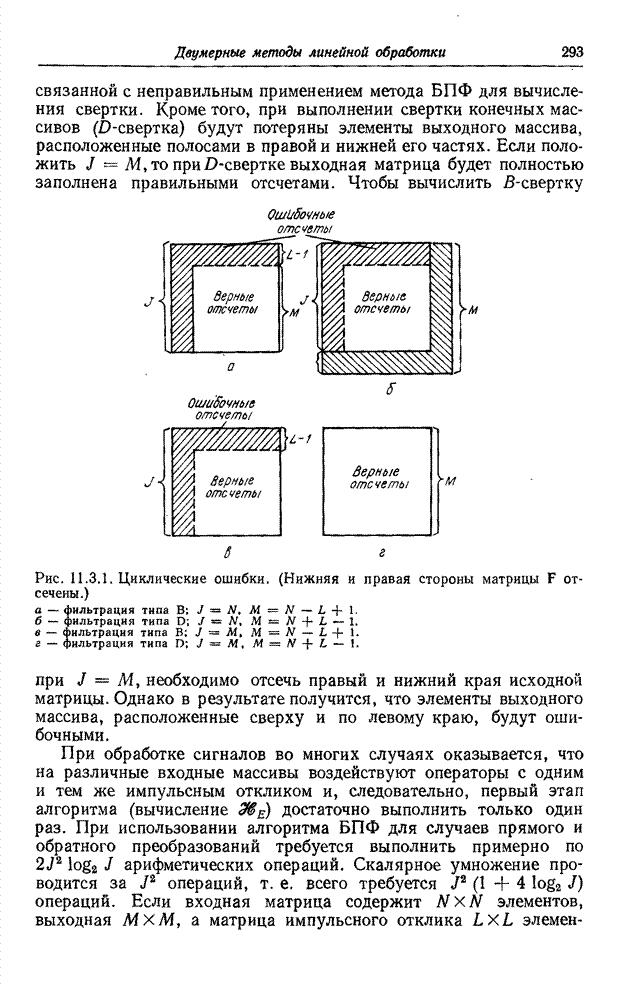
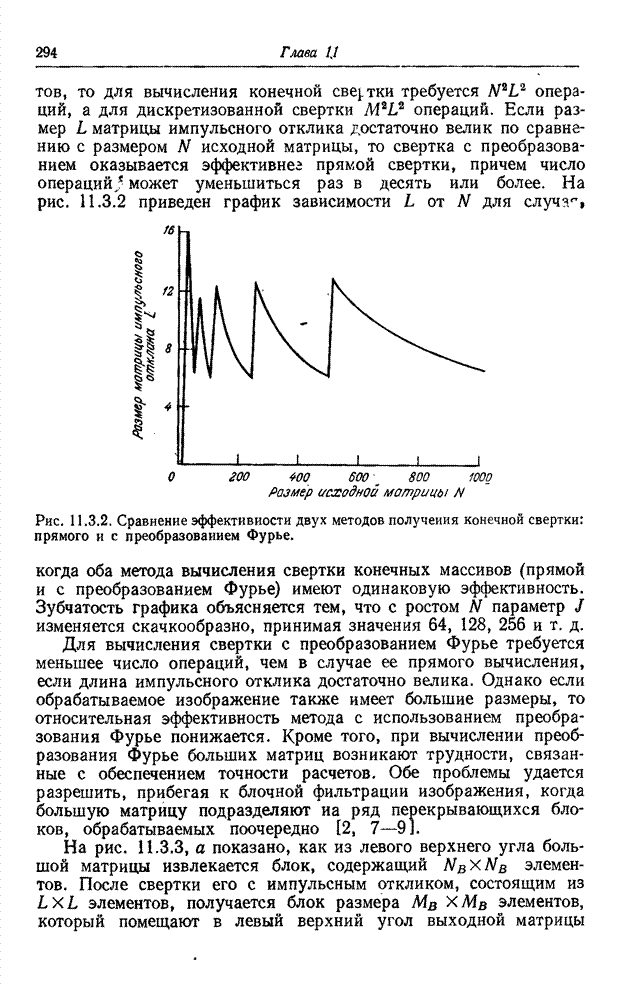
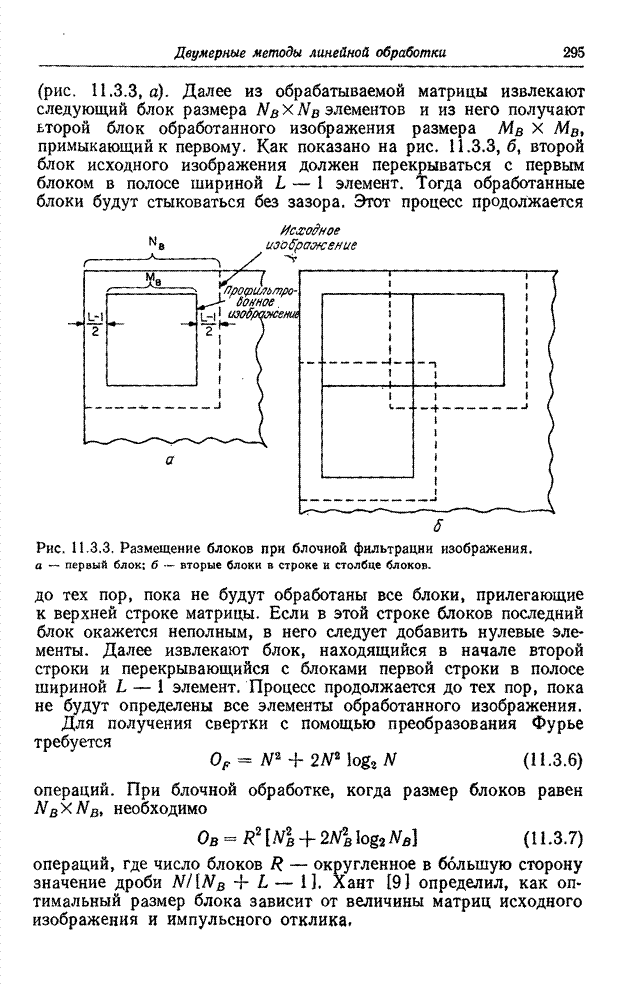
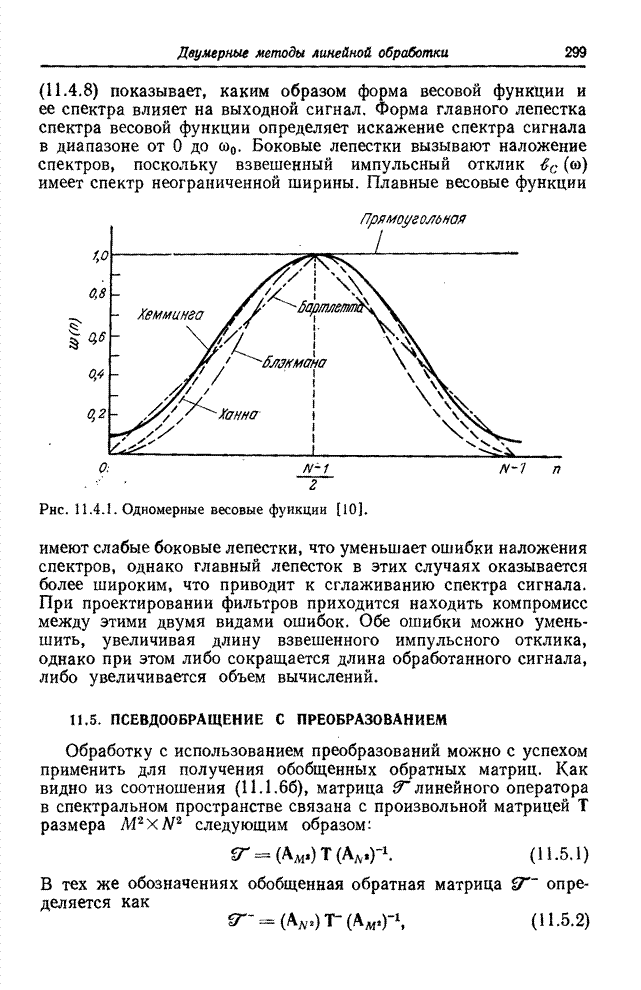
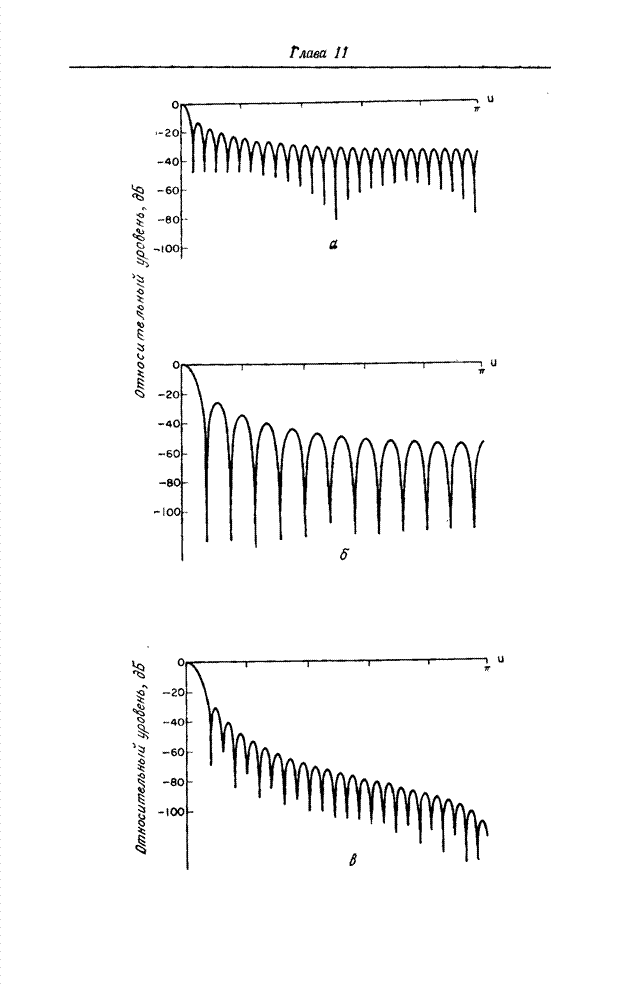
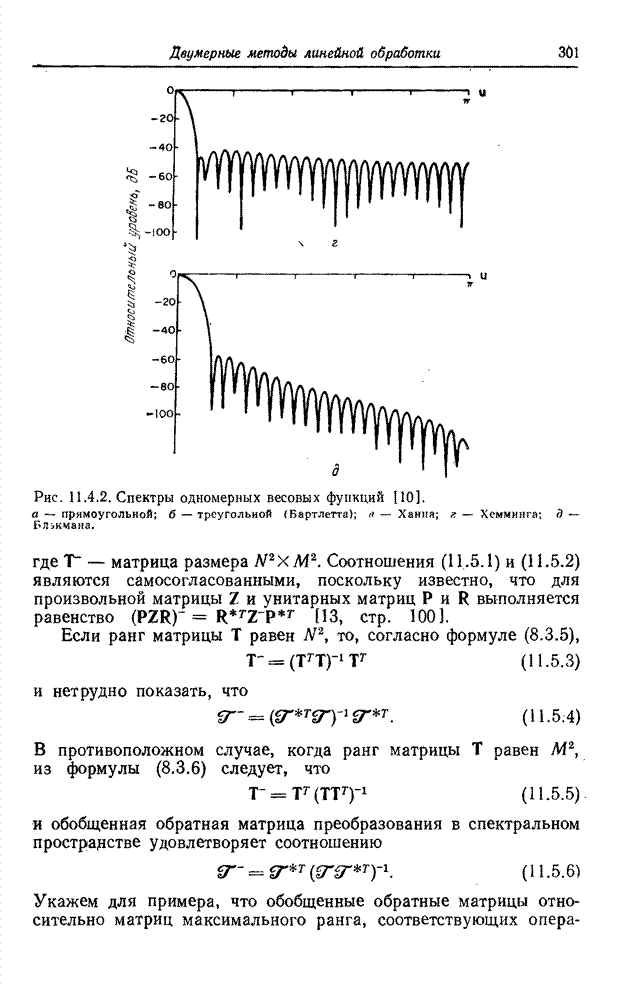
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
В предыдущих разделах данной главы обработка с преобразованием рассматривалась как косвенный метод выполнения двумерной линейной обработки. Было показано, что для обработки с преобразованием часто требуется гораздо меньше арифметических операций, чем при использовании стандартных методов. В данном разделе будет рассмотрен другой способ линейной обработки, называемый рекурсивной фильтрацией [14-16]. Иногда рекурсивная фильтрация оказывается даже более эффективной, чем обработка с преобразованием. Кроме того, в этом случае для хранения данных требуется ЗУ меньшей емкости, чем при обработке с преобразованием.
Рекурсивная фильтрация основывается на рекуррентном соотношении между входными и выходными переменными системы. Для одномерных сигналов подобное рекуррентное соотношение имеет следующий вид [14]:
 , (11.6.1)
, (11.6.1)
где
![]() ,
, ![]() - отсчеты входной
последовательности,
- отсчеты входной
последовательности, ![]() ,
, ![]() - отсчеты выходной
последовательности, а
- отсчеты выходной
последовательности, а ![]() и
и ![]() - весовые множители. Ключевой момент
здесь в том, что
- весовые множители. Ключевой момент
здесь в том, что ![]() -й элемент выходной
последовательности зависит не только от последнего и
-й элемент выходной
последовательности зависит не только от последнего и ![]() предпоследних элементов
входной последовательности, но и от
предпоследних элементов
входной последовательности, но и от ![]() предыдущих элементов выходной
последовательности.
предыдущих элементов выходной
последовательности.
Большинство
методов синтеза и анализа рекурсивных фильтров основано на применении ![]() -преобразования.
По определению [17, 18]
-преобразования.
По определению [17, 18] ![]() -преобразование
-преобразование ![]() -элементной
последовательности
-элементной
последовательности ![]() дает образ
дает образ
![]() . (11.6.2)
. (11.6.2)
Нетрудно
показать, что ![]() -преобразование
выражения (11.6.1) дает образ
-преобразование
выражения (11.6.1) дает образ
![]() , (11.6.3)
, (11.6.3)
где
![]() и
и ![]() - образы
соответствующих последовательностей.
- образы
соответствующих последовательностей.
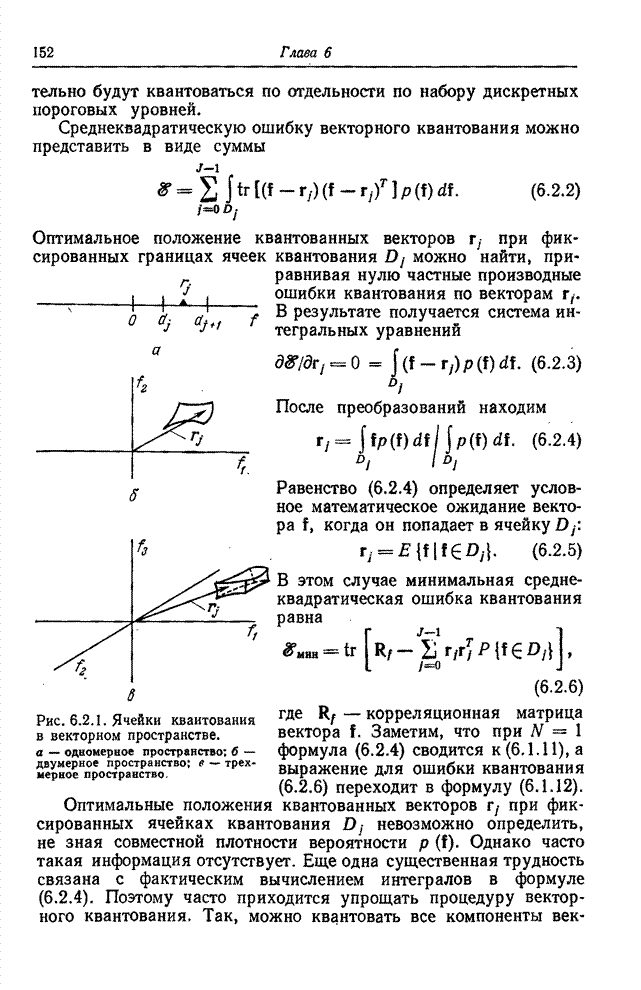
Двумерная рекурсивная фильтрация основана на следующем рекуррентном соотношении между входным и выходным массивами [19, 20]:
 (11.6.4)
(11.6.4)
где
![]() - входной
массив из
- входной
массив из ![]() элементов,
элементов,
![]() -
выходной массив из
-
выходной массив из ![]() элементов, а
элементов, а ![]() и
и ![]() - весовые множители.
Предполагается, что процесс рекурсивной фильтрации начинается с левого верхнего
угла входного массива. С помощью двумерного
- весовые множители.
Предполагается, что процесс рекурсивной фильтрации начинается с левого верхнего
угла входного массива. С помощью двумерного ![]() -преобразования из равенства (11.6.4)
получается
-преобразования из равенства (11.6.4)
получается
![]() , (11.6.5)
, (11.6.5)
где
![]() и
и ![]() - двумерные
образы соответствующих массивов. Так, например,
- двумерные
образы соответствующих массивов. Так, например,
 . (11.6.6)
. (11.6.6)
При
синтезе рекурсивных фильтров требуется выбрать такие массивы весовых множителей
![]() и
и ![]() , чтобы выходной
массив
, чтобы выходной
массив ![]() оказался
эквивалентным массиву, получаемому в результате свертки функции
оказался
эквивалентным массиву, получаемому в результате свертки функции ![]() , описывающей
исходное изображение, с заданным импульсным откликом
, описывающей
исходное изображение, с заданным импульсным откликом ![]() . Как правило, точного
совпадения массивов добиться не удается и при синтезе фильтров приходится
пользоваться приближенными методами [21, 22]. При этом возникает вопрос об
устойчивости рассчитанного рекурсивного фильтра. Если фильтр неустойчив, то
ошибки округления или шум, присутствующий во входном массиве, могут в ходе
обработки не ослабляться, а увеличиваться до очень большого уровня. Рекурсивный
фильтр устойчив [20], если коэффициенты
. Как правило, точного
совпадения массивов добиться не удается и при синтезе фильтров приходится
пользоваться приближенными методами [21, 22]. При этом возникает вопрос об
устойчивости рассчитанного рекурсивного фильтра. Если фильтр неустойчив, то
ошибки округления или шум, присутствующий во входном массиве, могут в ходе
обработки не ослабляться, а увеличиваться до очень большого уровня. Рекурсивный
фильтр устойчив [20], если коэффициенты ![]() разложения частотной характеристики
фильтра в ряд по степеням переменных
разложения частотной характеристики
фильтра в ряд по степеням переменных ![]() и
и ![]()
 (11.6.7)
(11.6.7)
являются абсолютно суммируемыми, т. е. удовлетворяют условию
 . (11.6.8)
. (11.6.8)
Разработано несколько методов проверки рекурсивных фильтров на устойчивость [23-25]. При обработке изображения согласно равенству (11.6.4) требуется выполнить
![]() (11.6.9)
(11.6.9)
арифметических
операций. Здесь ![]() и
и
![]() -
размеры массивов весовых множителей для входного и выходного изображений, a
-
размеры массивов весовых множителей для входного и выходного изображений, a ![]() - размеры
входного изображения. Если изображения и массивы весовых множителей -
квадратные (т. е.
- размеры
входного изображения. Если изображения и массивы весовых множителей -
квадратные (т. е. ![]() ,
, ![]() и
и ![]() ), то при рекурсивной фильтрации
нужно выполнить
), то при рекурсивной фильтрации
нужно выполнить
![]() (11.6.10)
(11.6.10)
операций. Для сравнения укажем, что для получения конечной свертки (см. разд. 9.3) требуется
![]() (11.6.11)
(11.6.11)
операций,
где ![]() -
размер импульсного отклика. Как показано в разд. 11.2, для получения свертки с
применением быстрого преобразования Фурье необходимо примерно
-
размер импульсного отклика. Как показано в разд. 11.2, для получения свертки с
применением быстрого преобразования Фурье необходимо примерно
![]() (11.6.12)
(11.6.12)
операций. Степень относительной эффективности трех типов обработки зависит от размеров массива импульсного отклика [27]. Если эти размеры невелики, то для прямого метода получения свертки и рекурсивной фильтрации требуется почти одинаковое число арифметических операций. В этом случае сравнить эффективность обоих методов с эффективностью получения свертки с использованием БПФ можно с помощью графика на рис. 11.3.2. При больших размерах массива импульсного отклика быстрый метод получения свертки оказался гораздо эффективнее прямого метода. Сравнивая число операций в равенствах (11.6.10) и (11.6.12), можно показать, что при больших размерах импульсного отклика рекурсивная фильтрация оказывается эффективнее быстрого метода получения свертки, если площади массивов коэффициентов рекурсивного фильтра удовлетворяют неравенству
![]() , (11.6.13)
, (11.6.13)
где
![]() -
постоянная, принимающая значения от 1 до 20, причем ее величина зависит от вида
использованного алгоритма БПФ и от того, насколько вычисления с комплексными
числами происходят медленнее, чем с действительными.
-
постоянная, принимающая значения от 1 до 20, причем ее величина зависит от вида
использованного алгоритма БПФ и от того, насколько вычисления с комплексными
числами происходят медленнее, чем с действительными.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
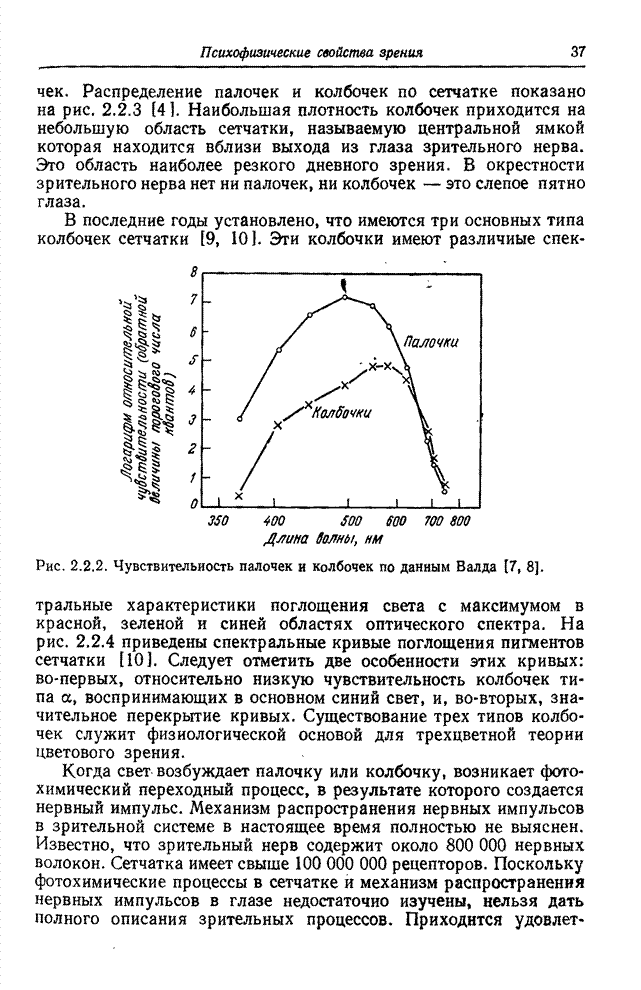
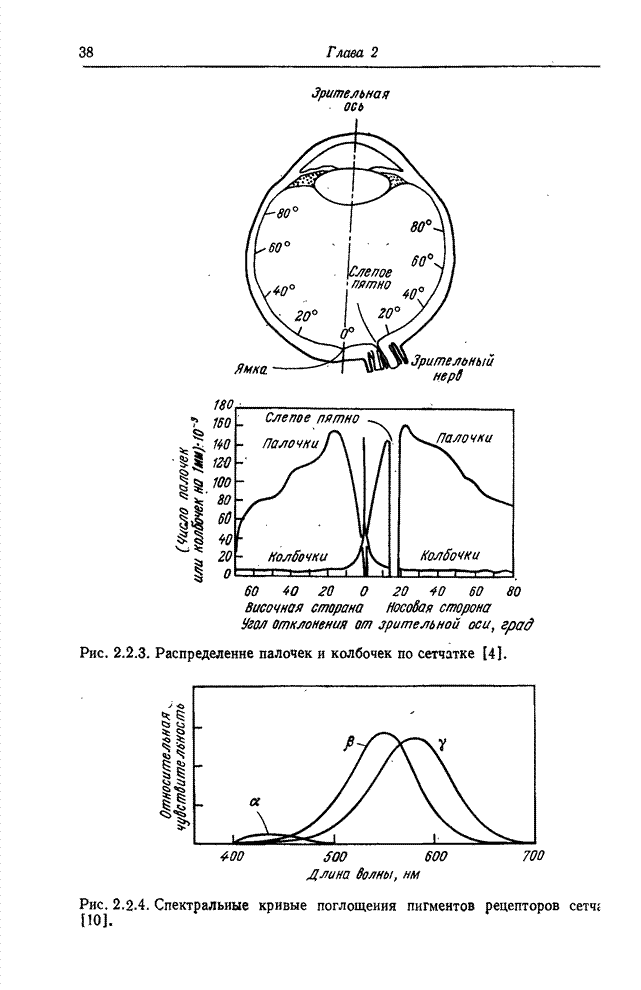
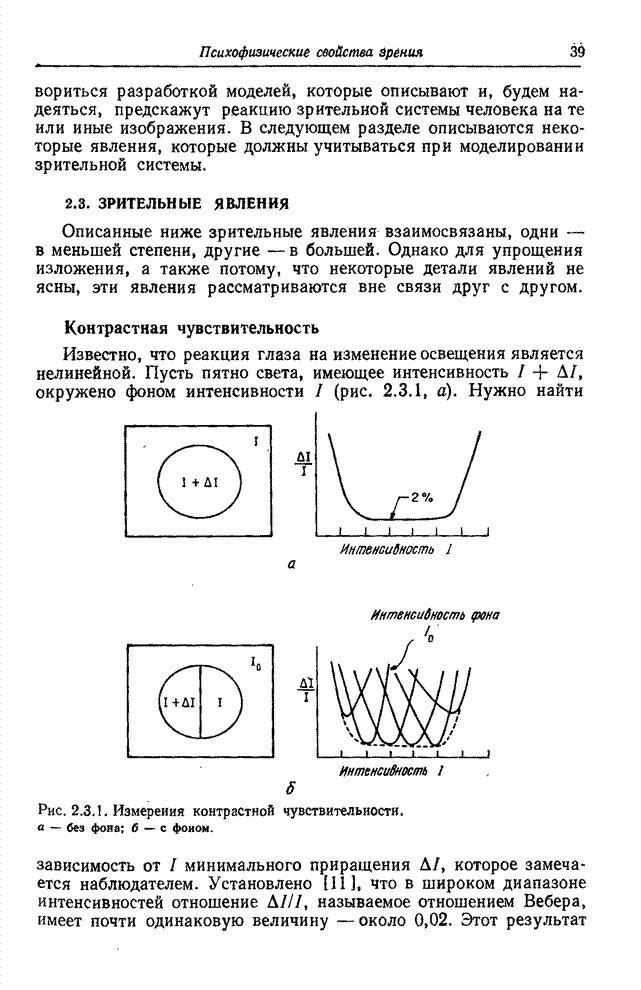
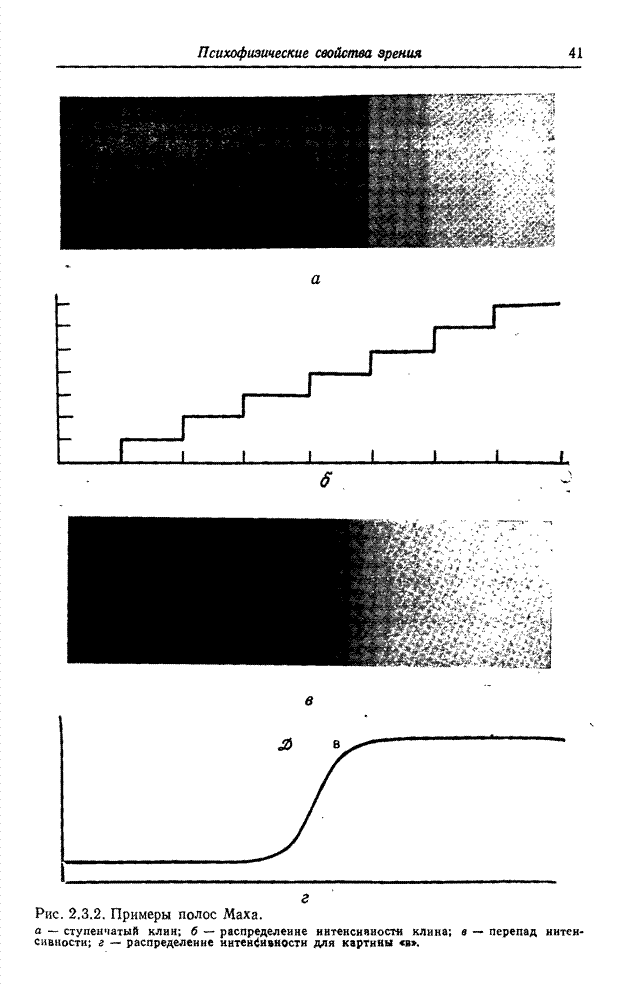
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
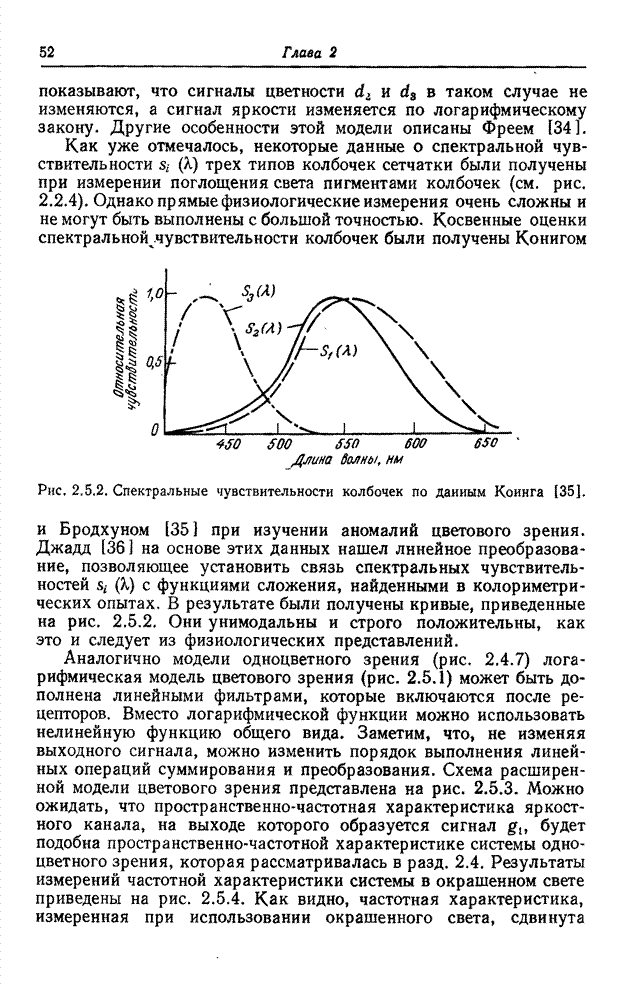
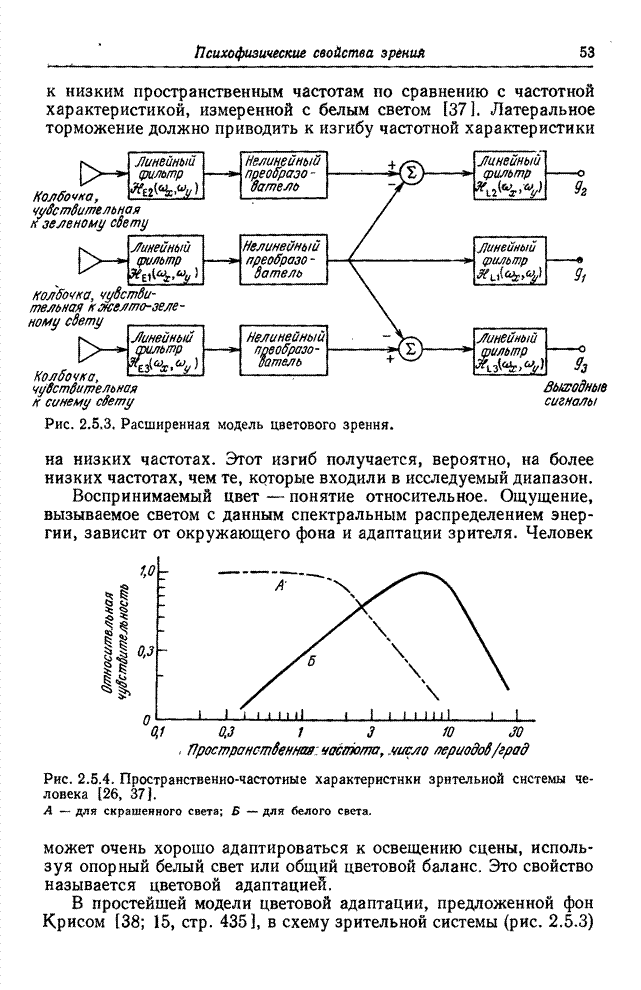
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
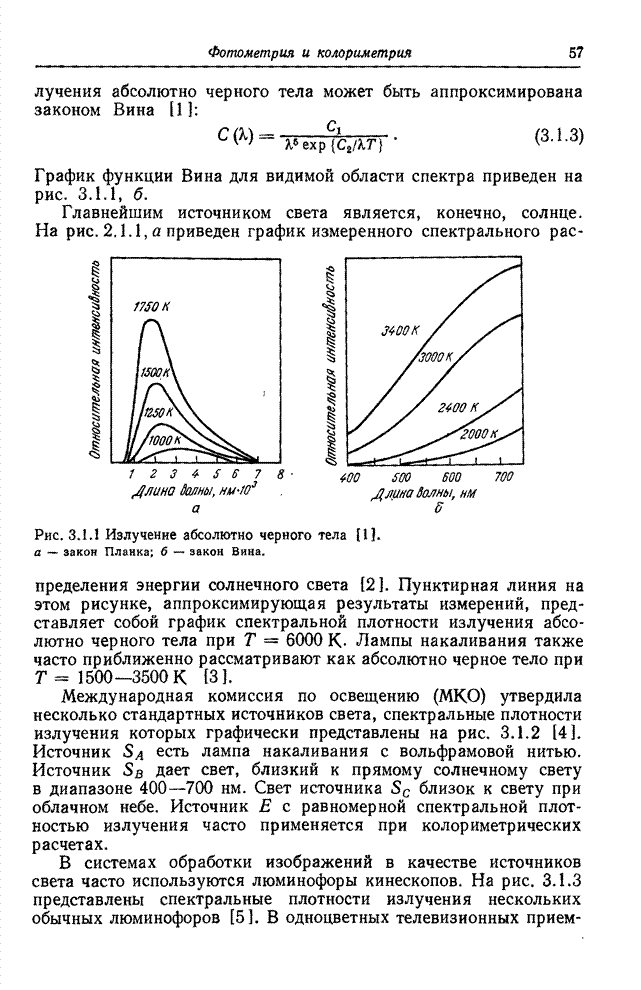
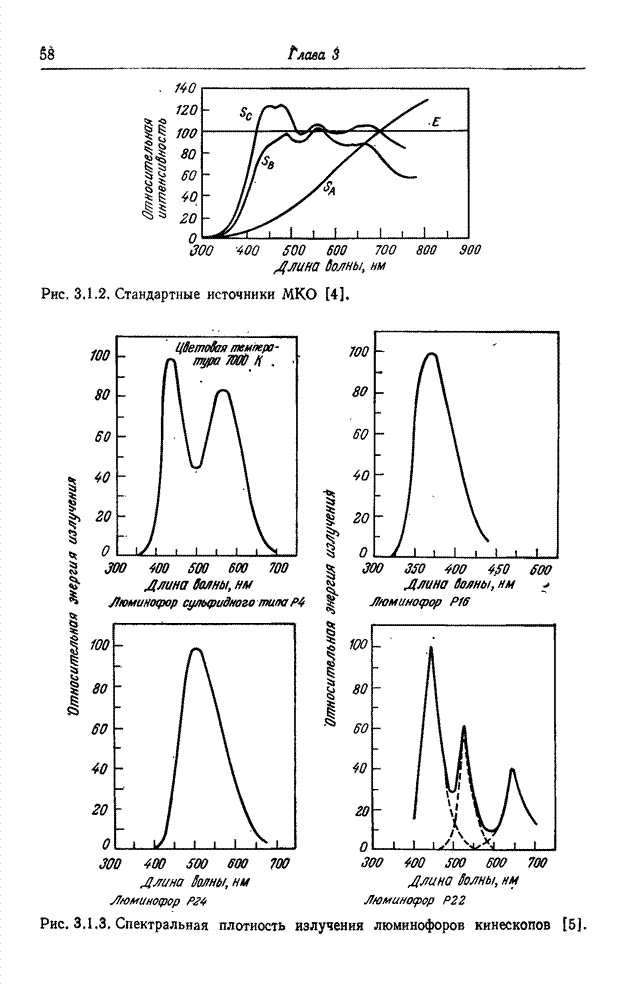
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
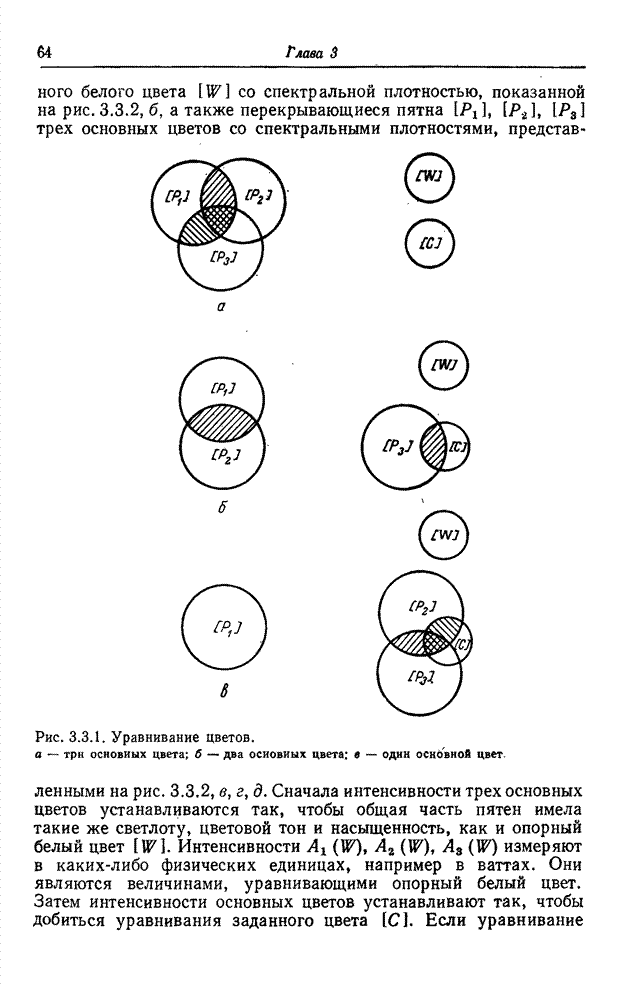
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
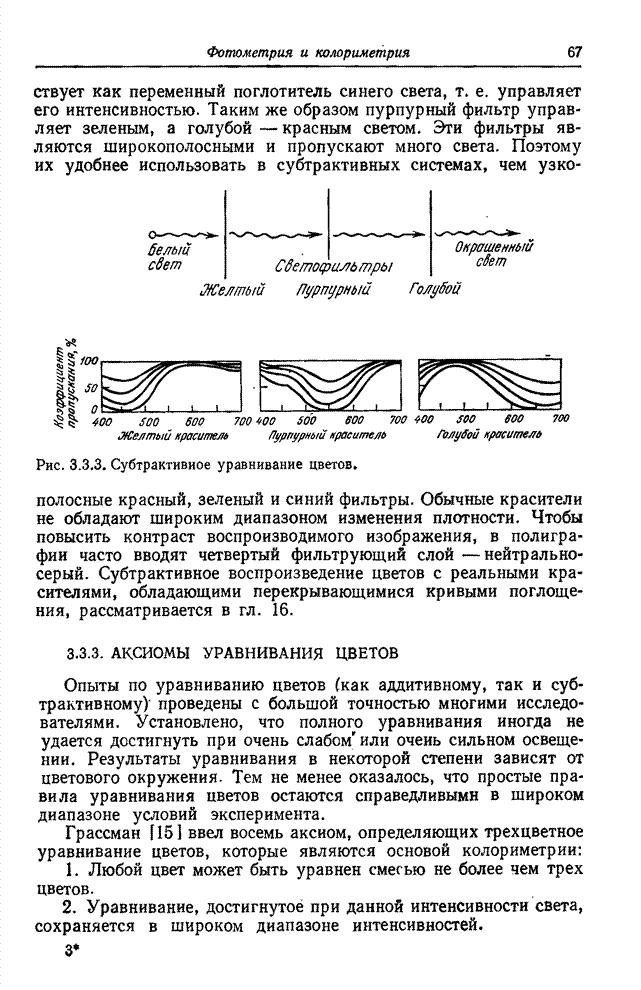
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
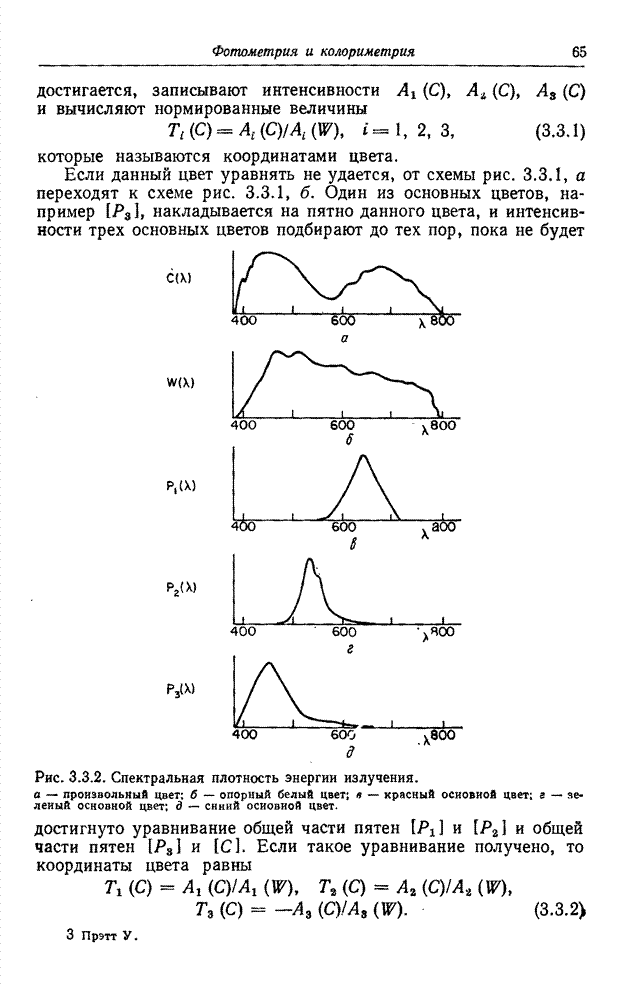
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
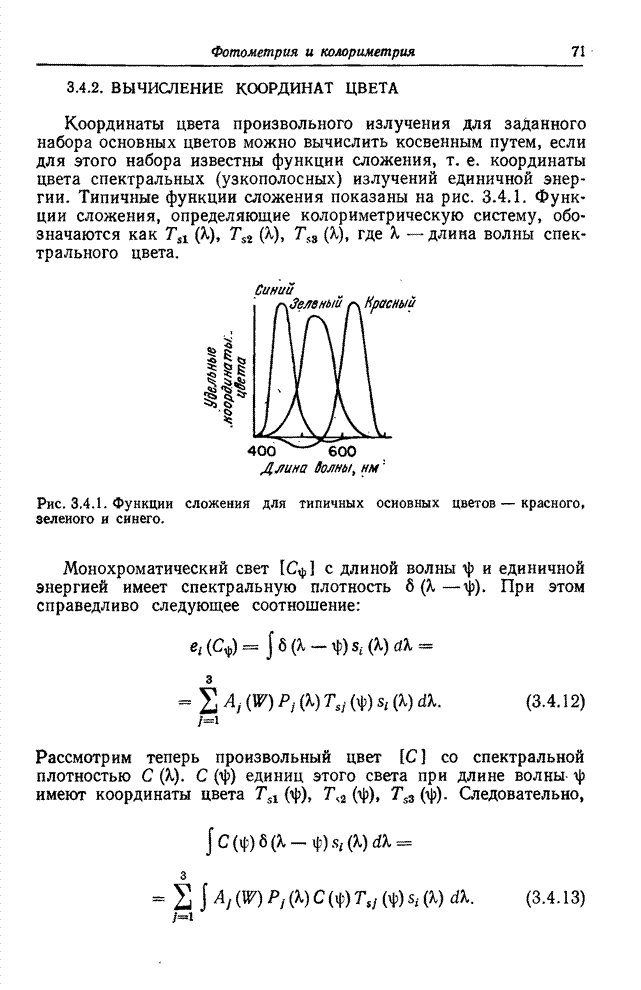
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
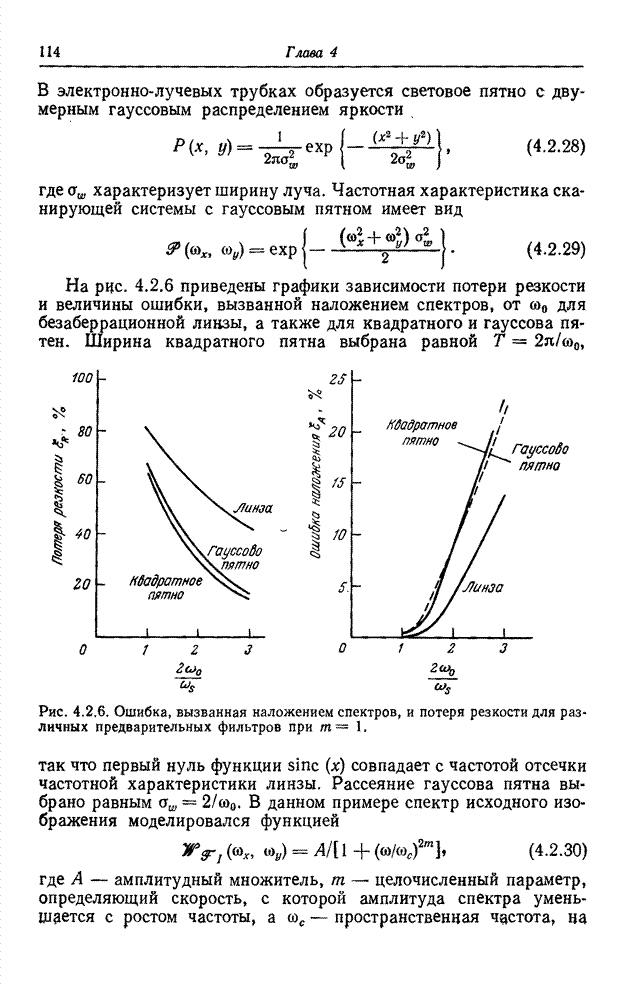
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
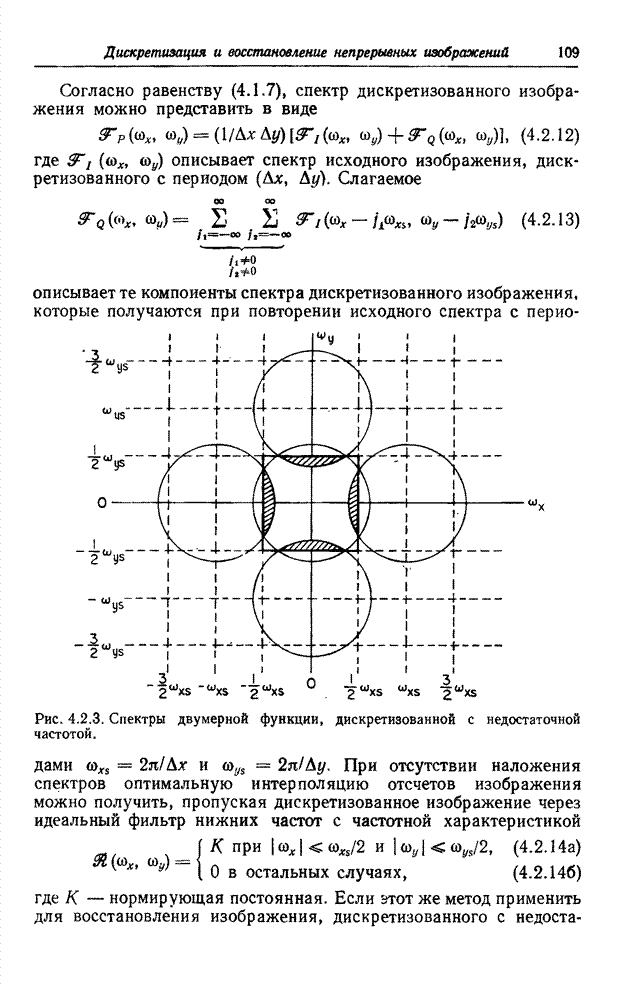
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
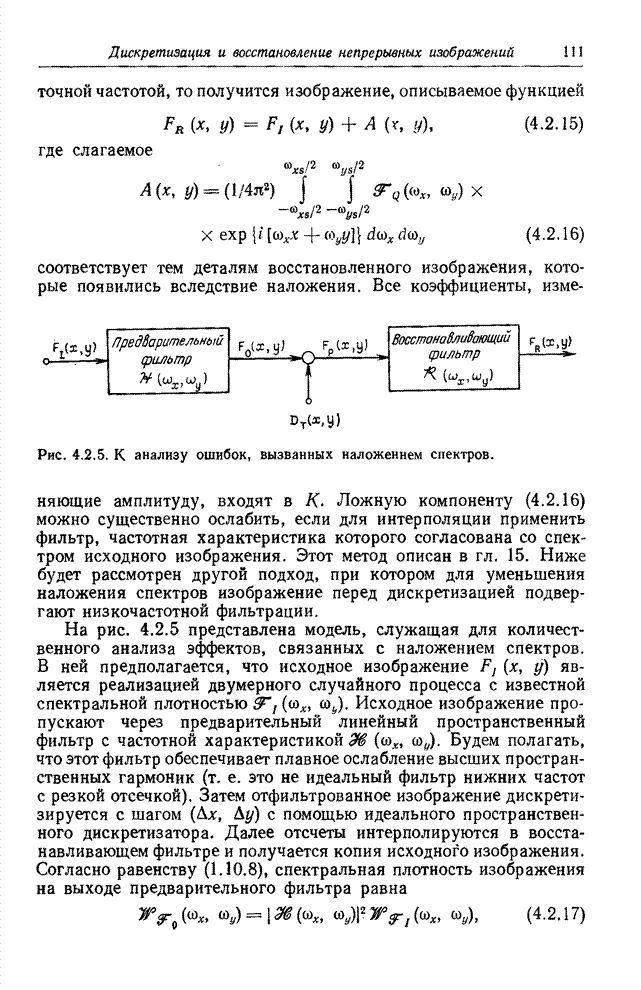
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
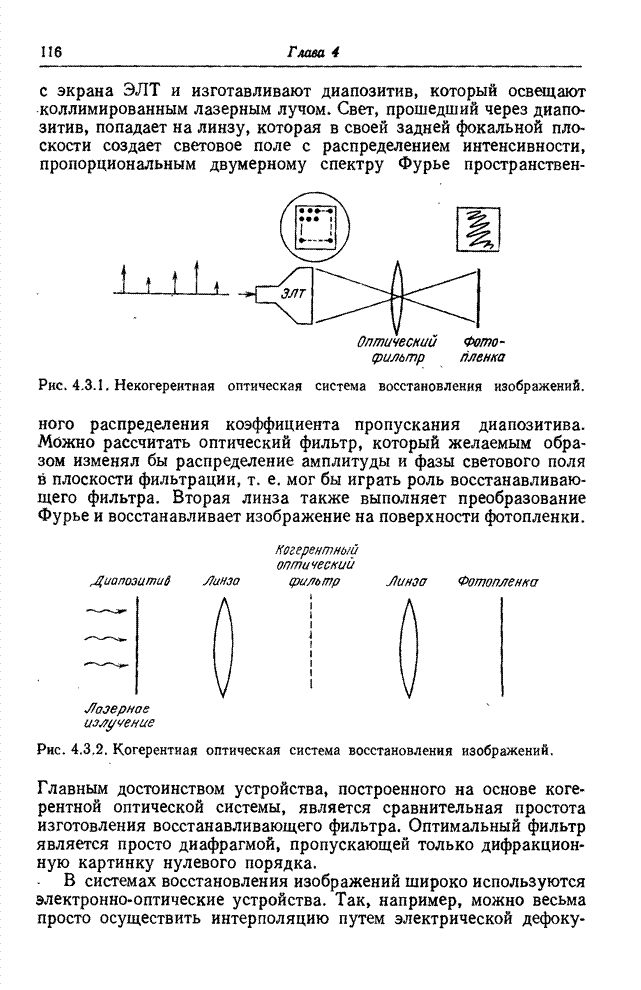
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
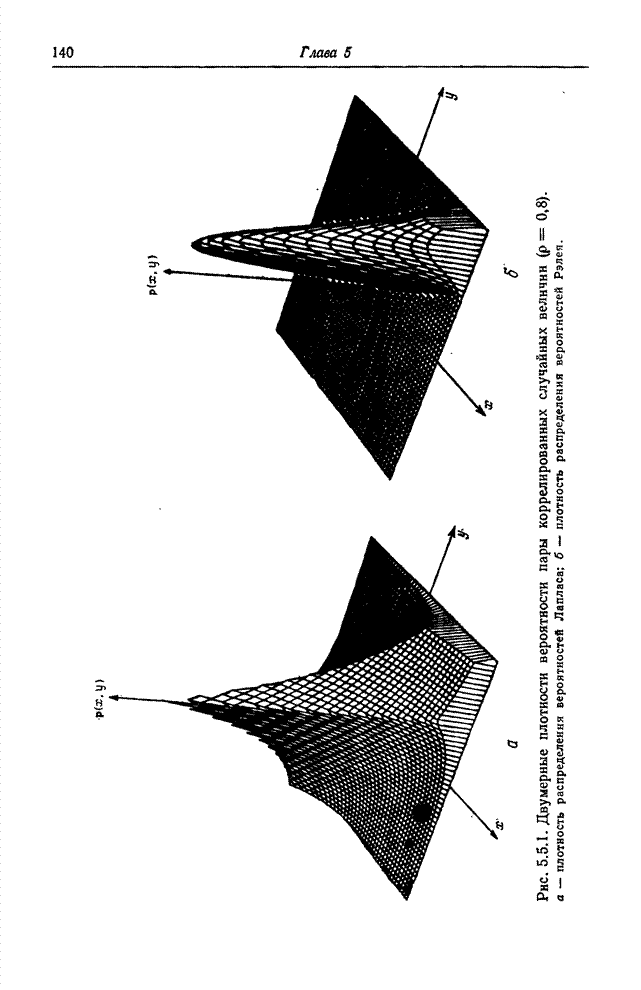
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
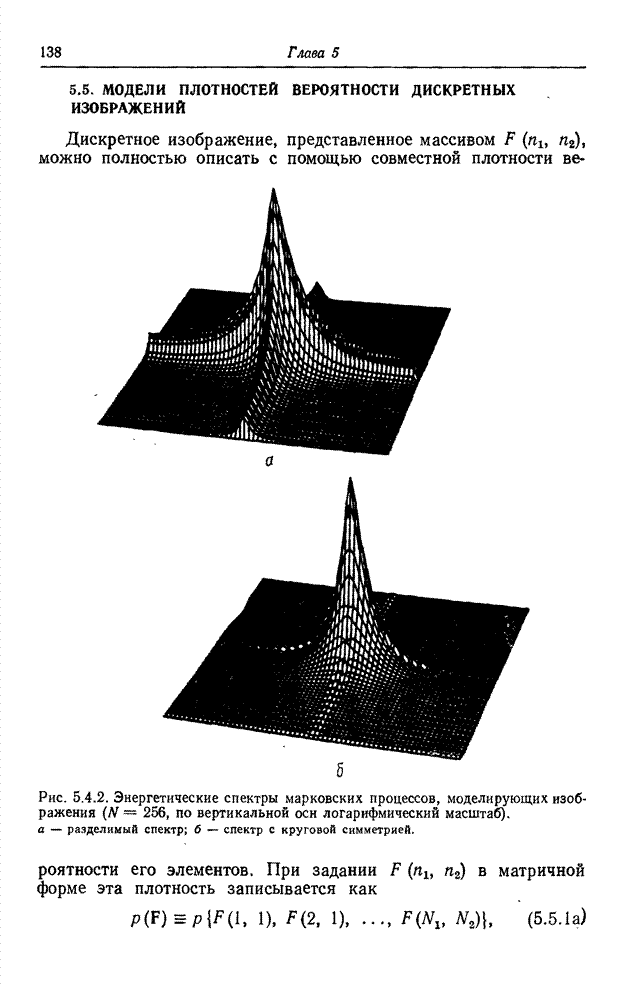
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
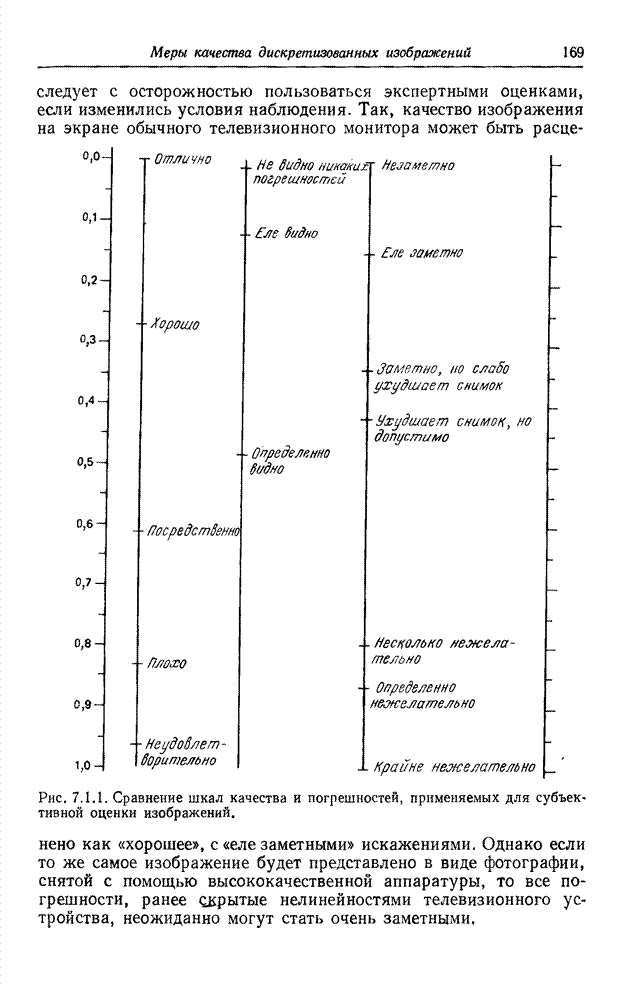
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
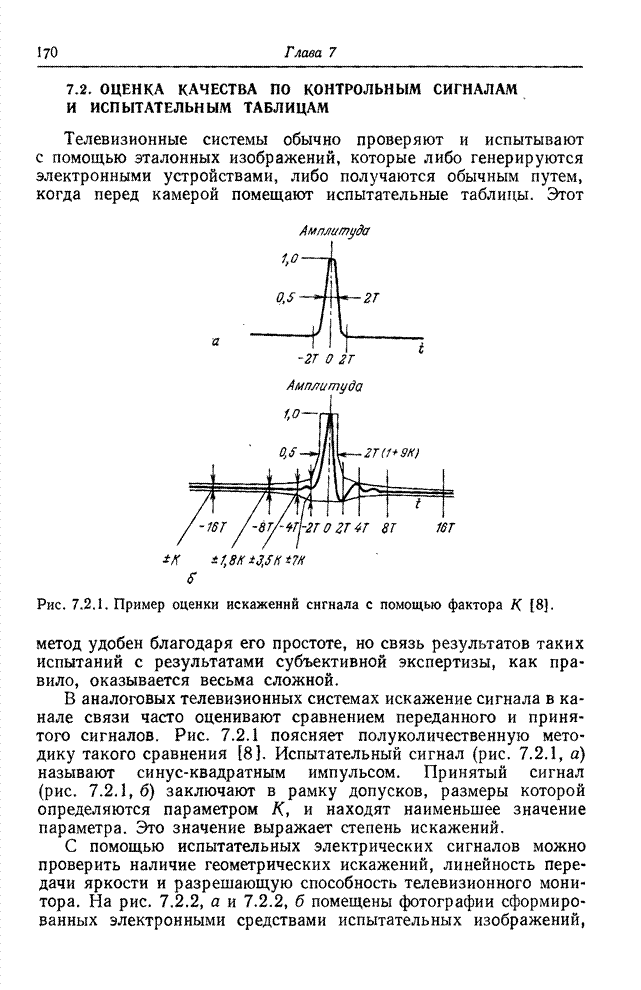
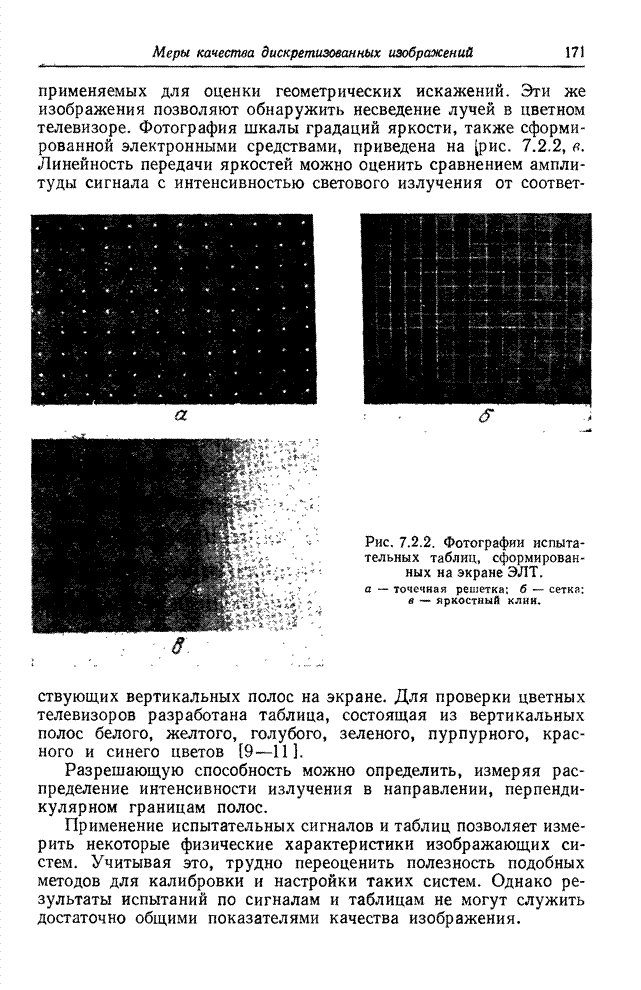
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
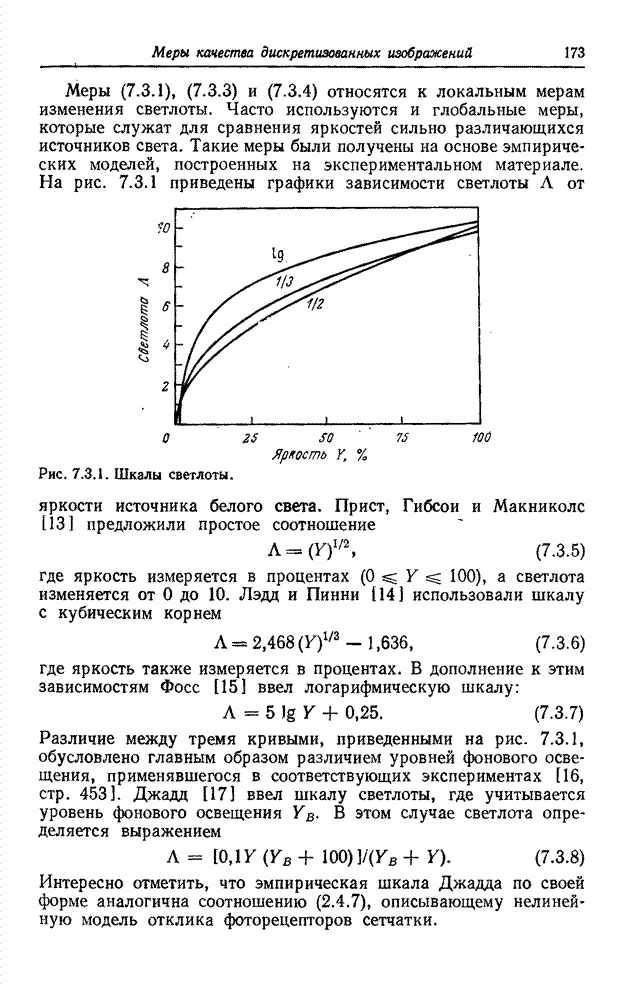
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
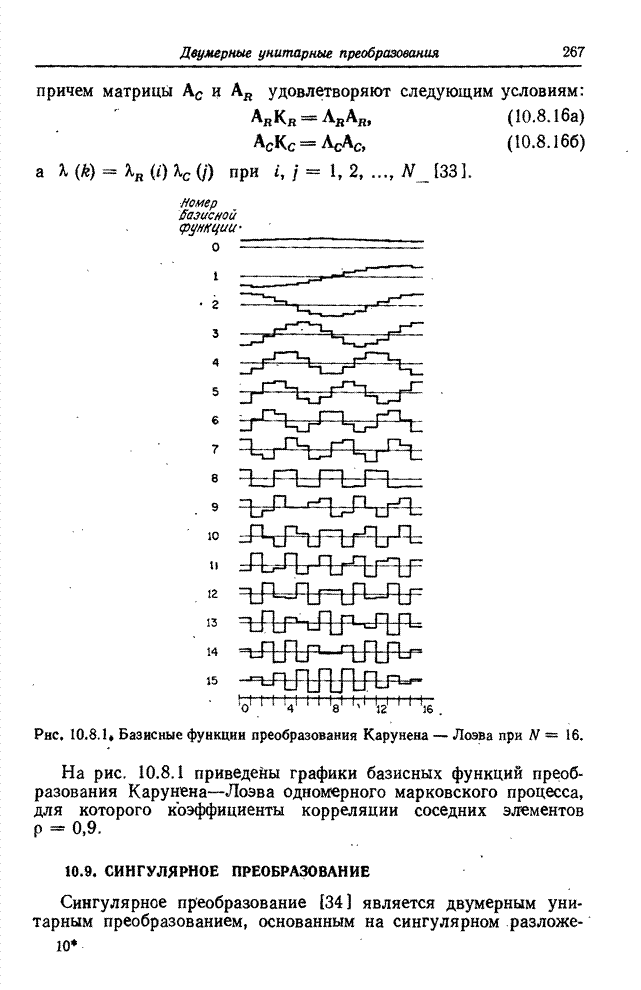
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
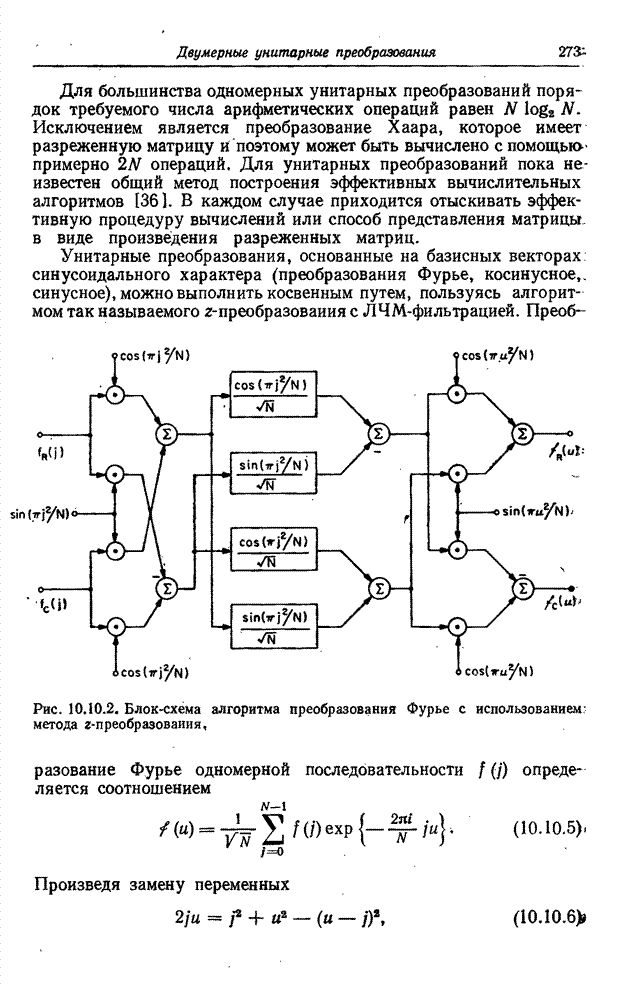
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
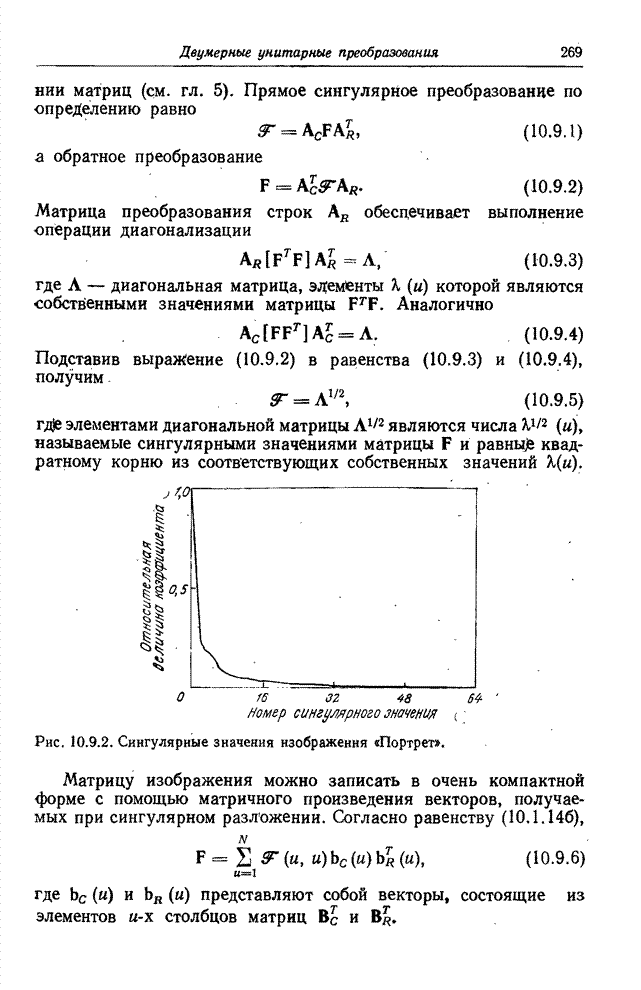
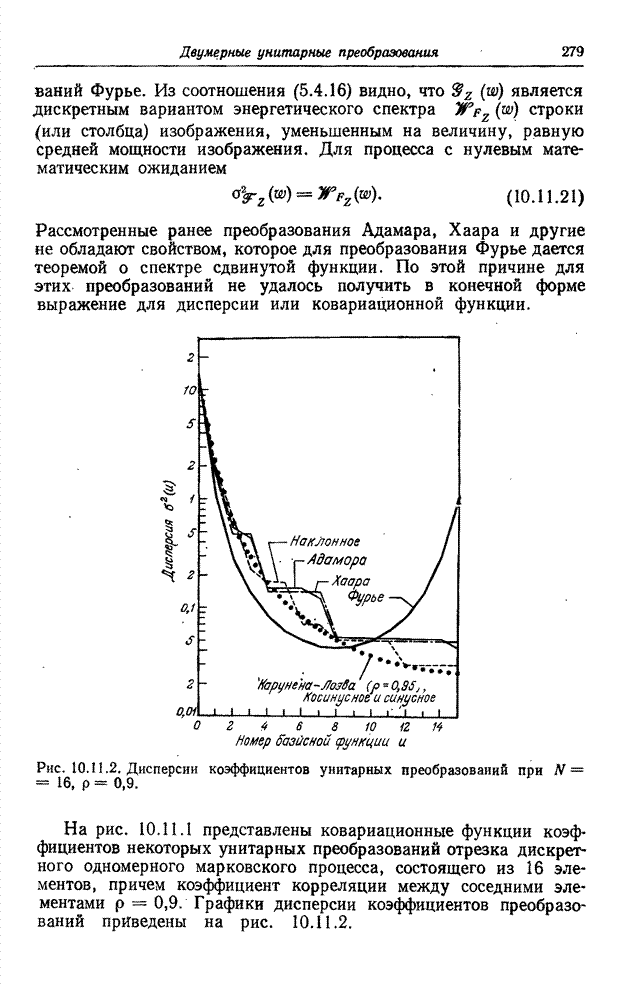
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА