| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
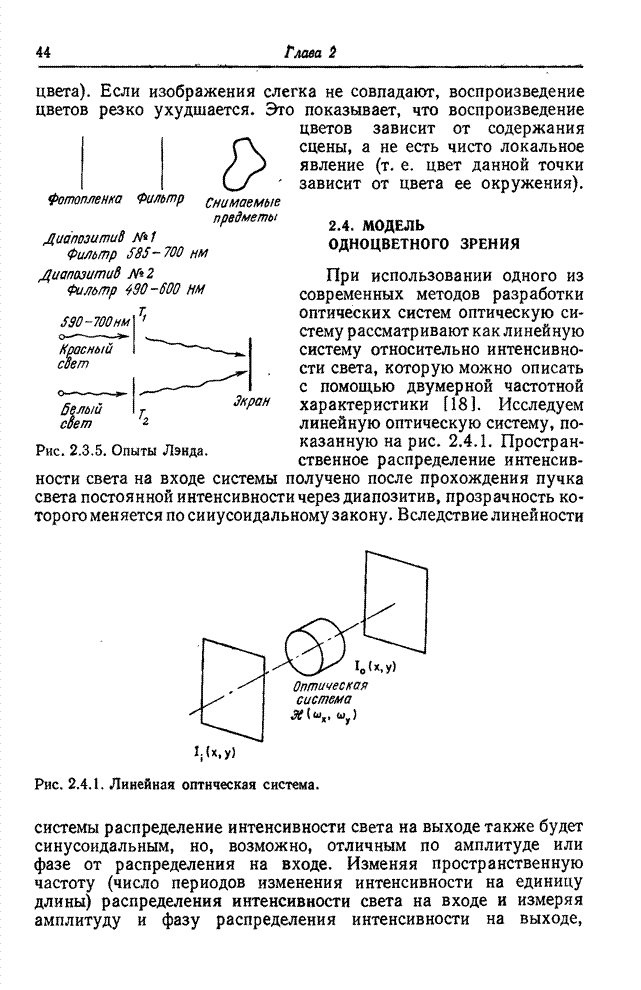
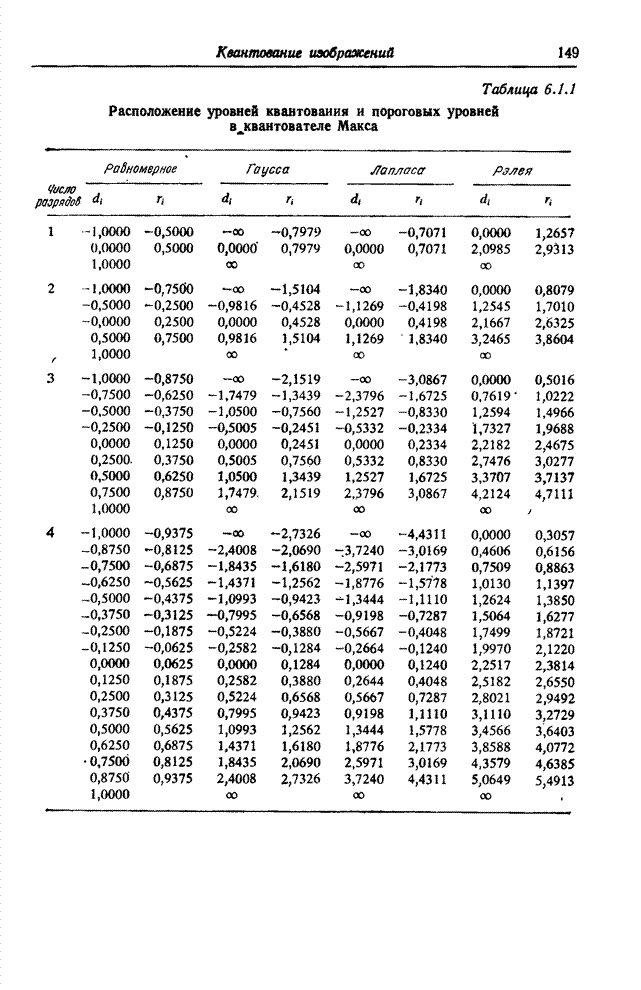
5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
Статистические методы описания непрерывных изображений, приведенные в гл. 1, можно непосредственно применить и для описания дискретных изображений. В данном разделе получены выражения для моментов дискретных изображений. Модели совместных плотностей вероятностей приведены в следующем разделе.
Среднее значение матрицы, описывающей дискретное изображение, представляет собой матрицу
![]() . (5.4.1)
. (5.4.1)
Если эта матрица разверткой по столбцам преобразована в вектор, то среднее значение этого вектора есть
![]() . (5.4.2)
. (5.4.2)
Корреляция
двух элементов изображения с координатами ![]() и
и ![]() определяется
как
определяется
как
![]() . (5.4.3)
. (5.4.3)
Ковариация двух элементов изображения есть
![]() . (5.4.4)
. (5.4.4)
И наконец, дисперсия элемента изображения равна
![]() . (5.4.5)
. (5.4.5)
Если
матрица изображения преобразована в вектор ![]() , то корреляционную матрицу этого
вектора можно выразить через корреляции элементов матрицы
, то корреляционную матрицу этого
вектора можно выразить через корреляции элементов матрицы ![]() :
:
 ,
(5.4.6a)
,
(5.4.6a)
или
![]() . (5.4.6б)
. (5.4.6б)
Выражение
![]() (5.4.7)
(5.4.7)
представляет собой корреляционную матрицу ![]() -го и
-го и ![]() -го столбцов
матрицы
-го столбцов
матрицы ![]() и
имеет размеры
и
имеет размеры ![]() . Следовательно,
. Следовательно, ![]() можно представить в виде блочной матрицы
можно представить в виде блочной матрицы
 (5.4.8)
(5.4.8)
Ковариационную
матрицу вектора ![]() можно
получить на основе его корреляционной матрицы и вектора средних значений с
помощью соотношения
можно
получить на основе его корреляционной матрицы и вектора средних значений с
помощью соотношения
![]() . (5.4.9)
. (5.4.9)
Матрица
дисперсий ![]() массива
чисел
массива
чисел ![]() по определению
является матрицей, элементы которой равны дисперсиям соответствующих элементов
массива. Элементы матрицы
по определению
является матрицей, элементы которой равны дисперсиям соответствующих элементов
массива. Элементы матрицы ![]() можно непосредственно выделить из
блоков матрицы
можно непосредственно выделить из
блоков матрицы ![]() :
:
![]() . (5.4.10)
. (5.4.10)
Если дискретное изображение представляется массивом, стационарным в широком смысле, то его корреляционную функцию можно записать в виде
![]() , (5.4.11)
, (5.4.11)
где
![]() и
и ![]() . Соответственно
блоки ковариационной матрицы (5.4.9) будут связаны соотношениями
. Соответственно
блоки ковариационной матрицы (5.4.9) будут связаны соотношениями
![]() ,
, ![]() ,
(5.4.12а)
,
(5.4.12а)
![]() ,
, ![]() , (5.4.12б)
, (5.4.12б)
где
![]() . Таким образом,
для стационарного в широком смысле массива
. Таким образом,
для стационарного в широком смысле массива
 (5.4.13)
(5.4.13)
Матрица
(5.4.13) является блочно-тёплицевой [11]. Наконец, если корреляционную функцию
изображения можно записать в виде произведения корреляционных функций строк и
столбцов, то ковариационную матрицу вектора ![]() ,
представляющего изображение, можно записать в виде прямого произведения
ковариационных матриц для строк и столбцов:
,
представляющего изображение, можно записать в виде прямого произведения
ковариационных матриц для строк и столбцов:
 (5.4.14)
(5.4.14)
где
![]() -
ковариационная матрица столбцов матрицы
-
ковариационная матрица столбцов матрицы ![]() , имеющая размеры
, имеющая размеры ![]() , а
, а ![]() -
ковариационная матрица строк матрицы
-
ковариационная матрица строк матрицы ![]() с размерами
с размерами ![]() .
.
Рассмотрим
случай, когда ковариационная матрица строк матрицы ![]() имеет следующий вид:
имеет следующий вид:
 (5.4.15)
(5.4.15)
где
![]() -
дисперсия элементов изображения. Эта ковариационная матрица - аналог
непрерывной автоковариационной функции вида
-
дисперсия элементов изображения. Эта ковариационная матрица - аналог
непрерывной автоковариационной функции вида ![]() - описывает
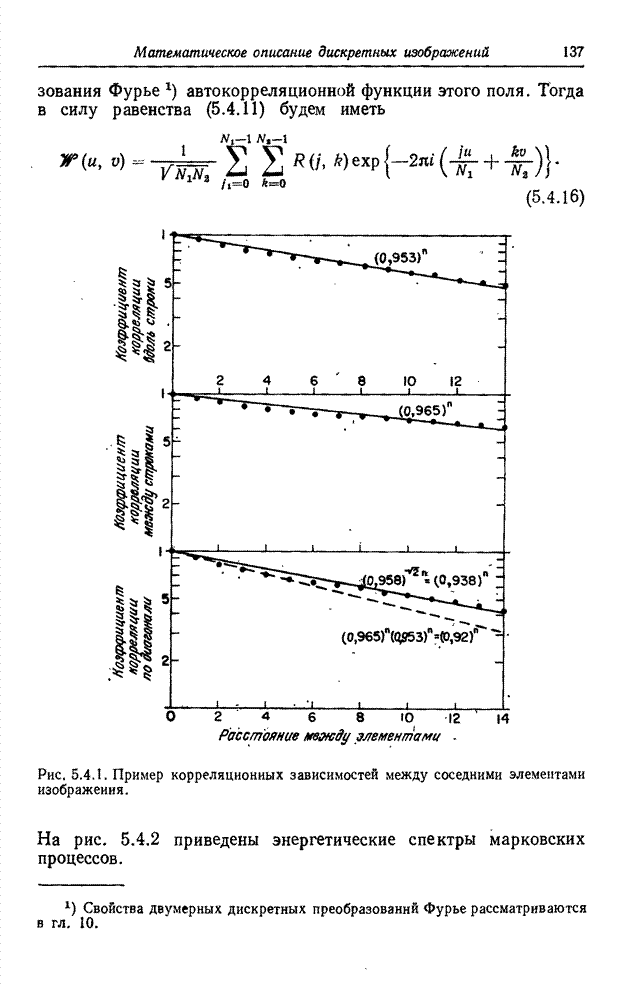
марковский процесс. На рис. 5.4.1 приведены полученные Дэвиссоном [12] значения
коэффициентов корреляции элементов строки типичного изображения.
Экспериментальные точки хорошо аппроксимируются ковариационной функцией
марковского процесса с параметром
- описывает
марковский процесс. На рис. 5.4.1 приведены полученные Дэвиссоном [12] значения
коэффициентов корреляции элементов строки типичного изображения.
Экспериментальные точки хорошо аппроксимируются ковариационной функцией
марковского процесса с параметром ![]() . Аналогично значения коэффициентов
корреляции в направлении, перпендикулярном к строкам, хорошо согласуются с
марковской ковариационной функцией при
. Аналогично значения коэффициентов
корреляции в направлении, перпендикулярном к строкам, хорошо согласуются с
марковской ковариационной функцией при ![]() . Если ковариационная функция может
быть представлена в виде (5.4.14), то коэффициенты корреляции по диагонали
должны быть равны произведению соответствующих коэффициентов корреляции вдоль
строк изображения и в направлении, перпендикулярном к ним. В данном примере
оказалось, что такая аппроксимация является достаточно точной в области от нуля
до пяти шагов дискретизации.
. Если ковариационная функция может
быть представлена в виде (5.4.14), то коэффициенты корреляции по диагонали
должны быть равны произведению соответствующих коэффициентов корреляции вдоль
строк изображения и в направлении, перпендикулярном к ним. В данном примере
оказалось, что такая аппроксимация является достаточно точной в области от нуля
до пяти шагов дискретизации.
По аналогии с непрерывным энергетическим спектром (1.8.11) можно определить дискретную спектральную плотность дискретного стационарного двумерного случайного поля, представляющего изображение, как результат двумерного дискретного преобразования Фурье автокорреляционной функции этого поля. Тогда в силу равенства (5.4.11) будем иметь
 (5.4.16)
(5.4.16)

Рис. 5.4.1. Пример корреляционных зависимостей между соседними элементами изображения.
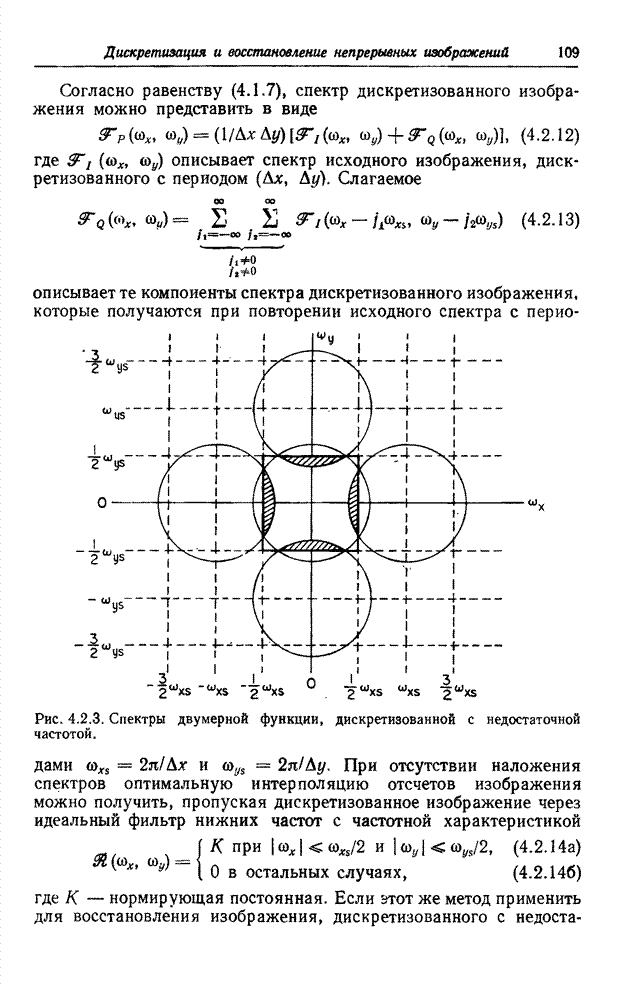
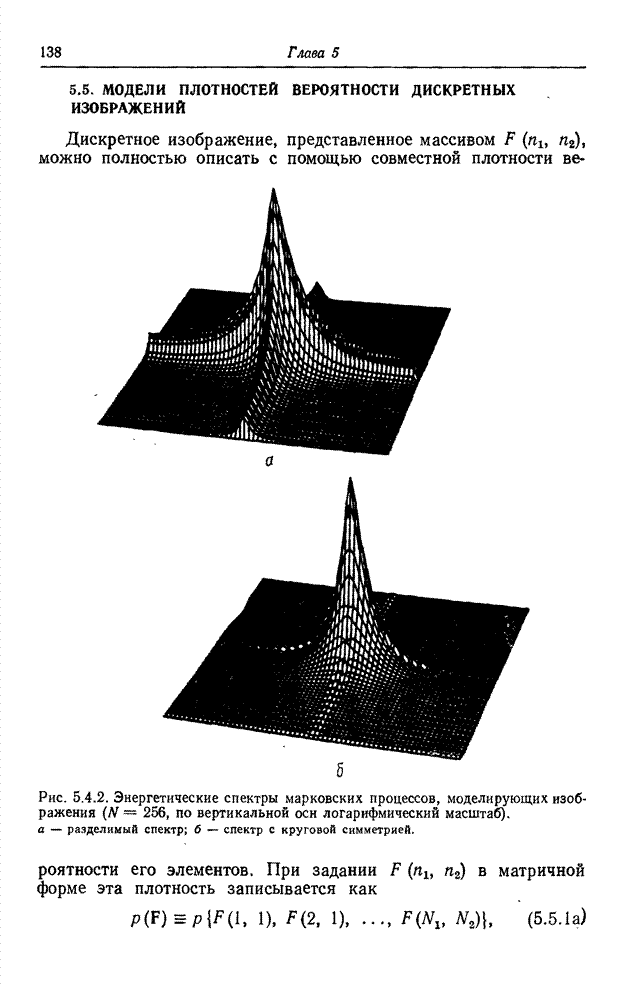
На рис. 5.4.2 приведены энергетические спектры марковских процессов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
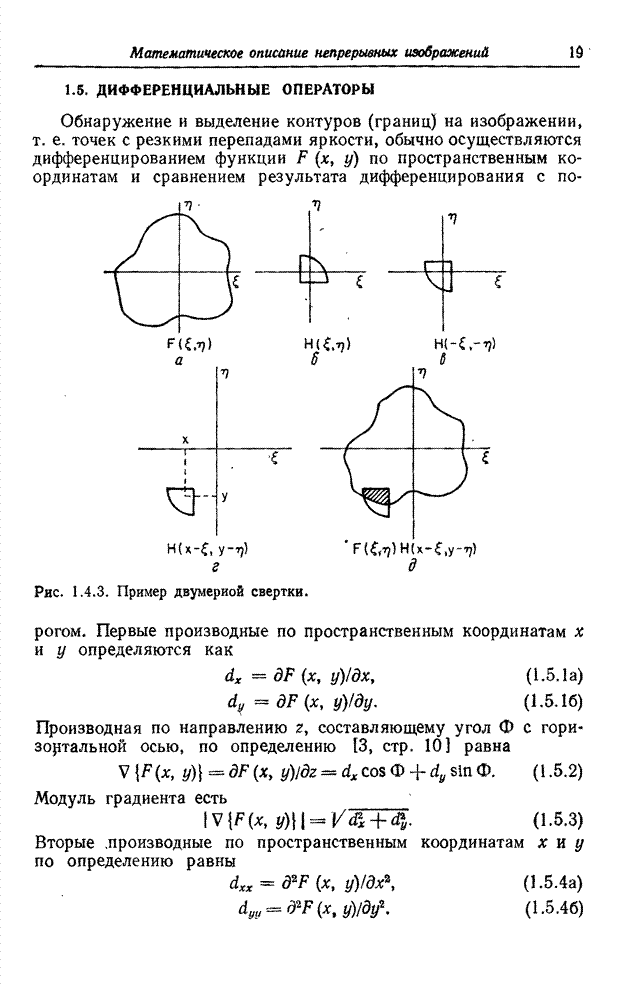
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
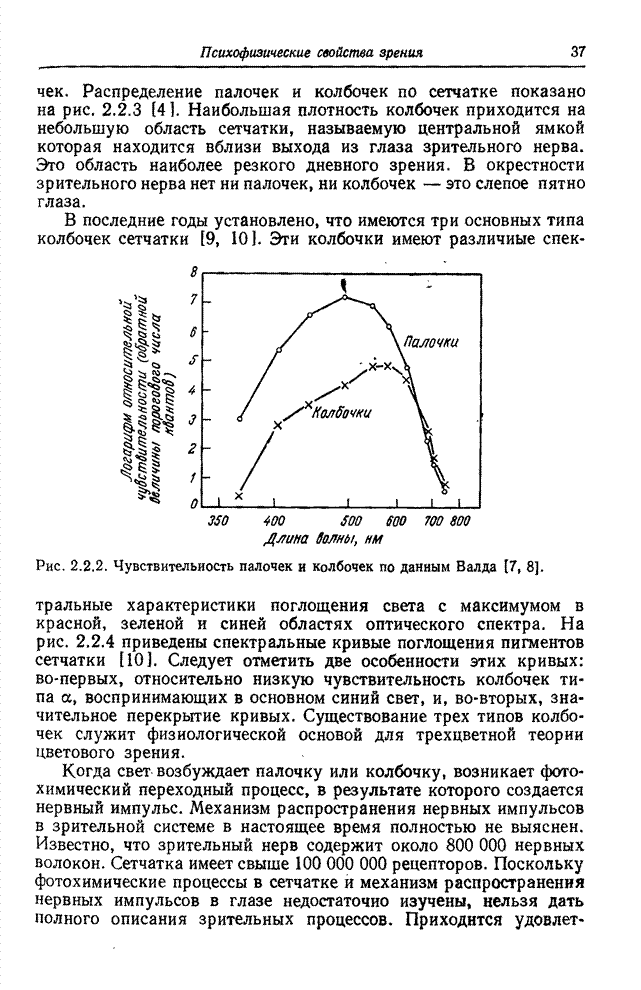
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
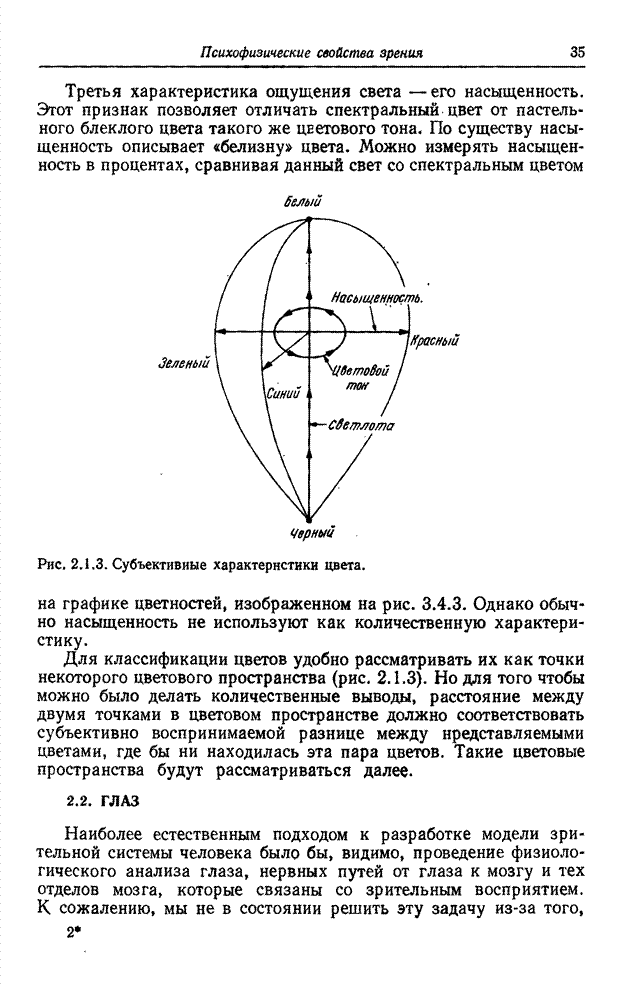
- 2.1. ВОСПРИЯТИЕ СВЕТА
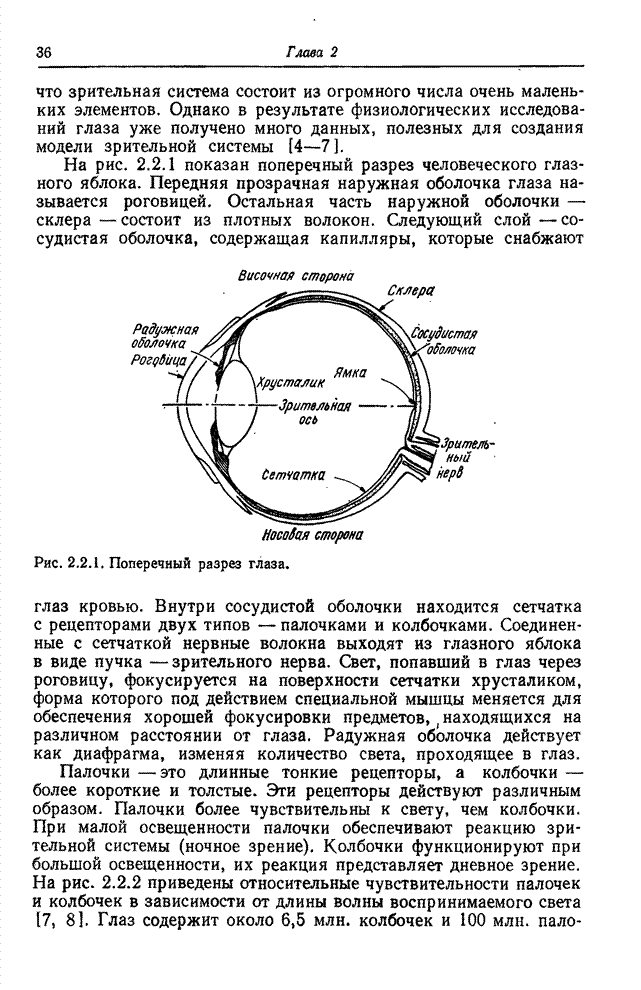
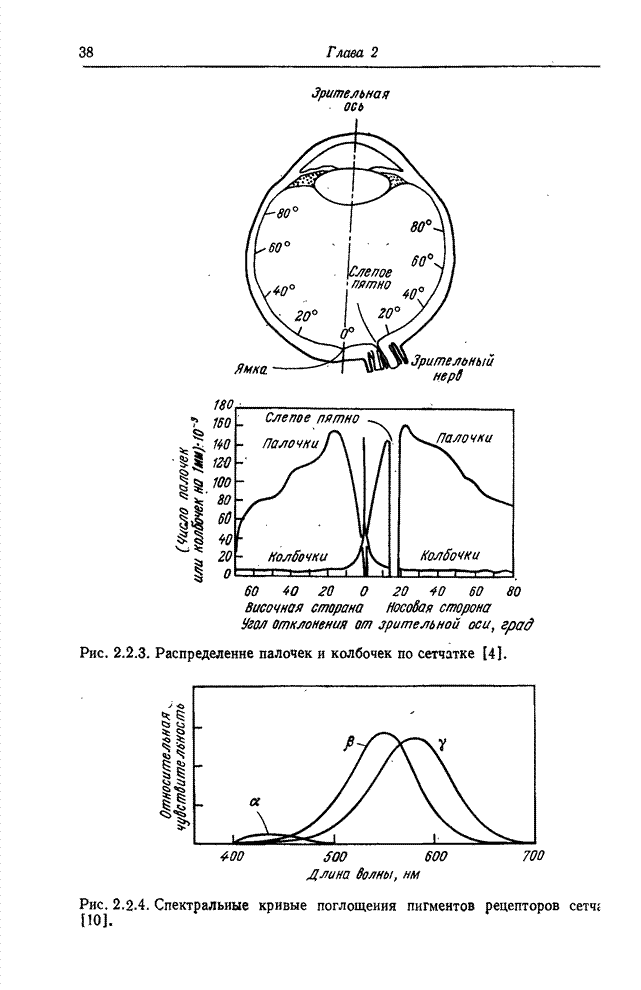
- 2.2. ГЛАЗ
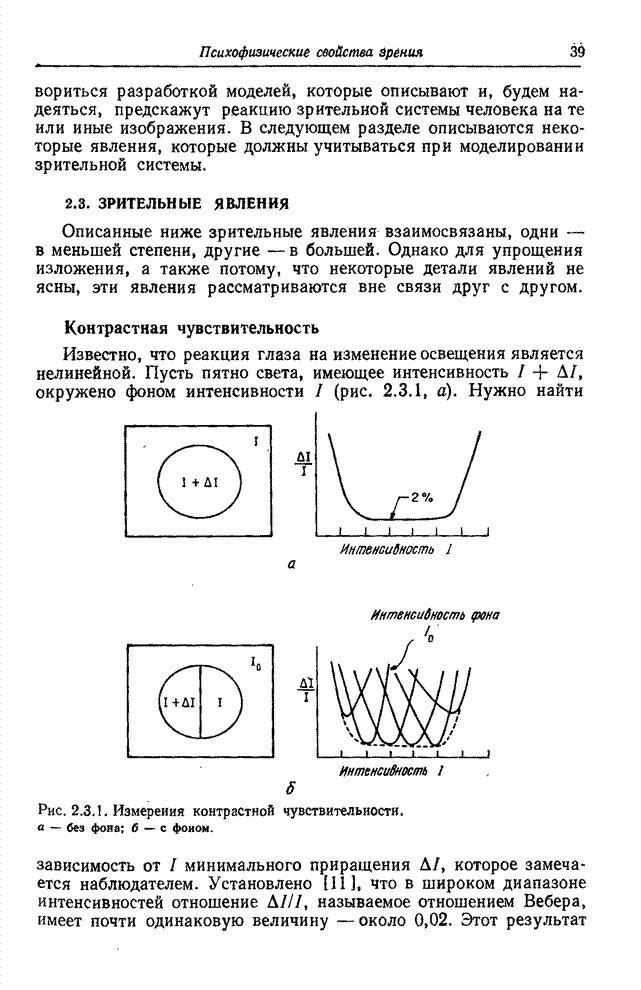
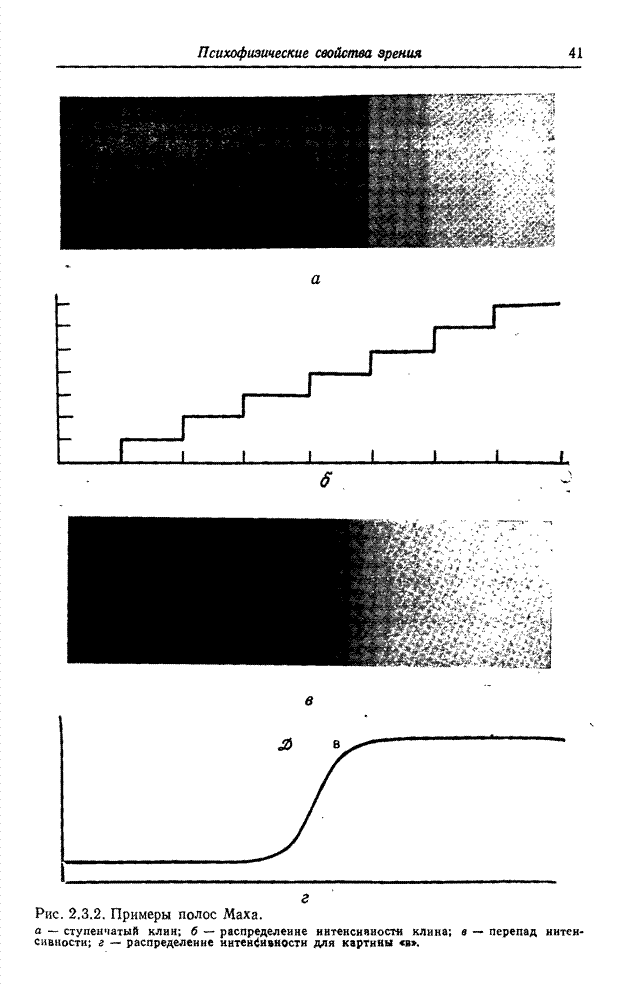
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
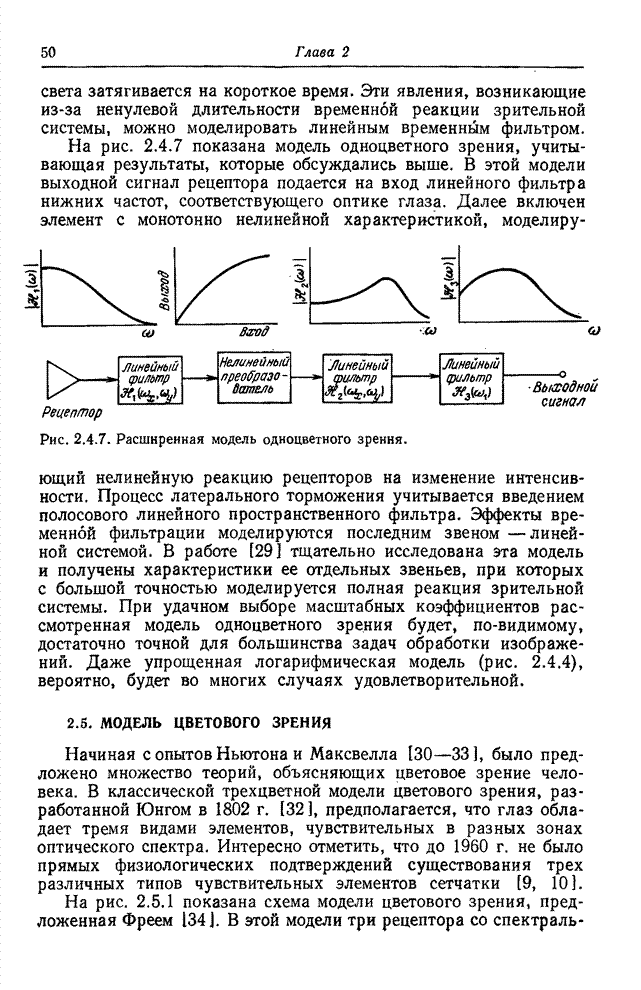
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
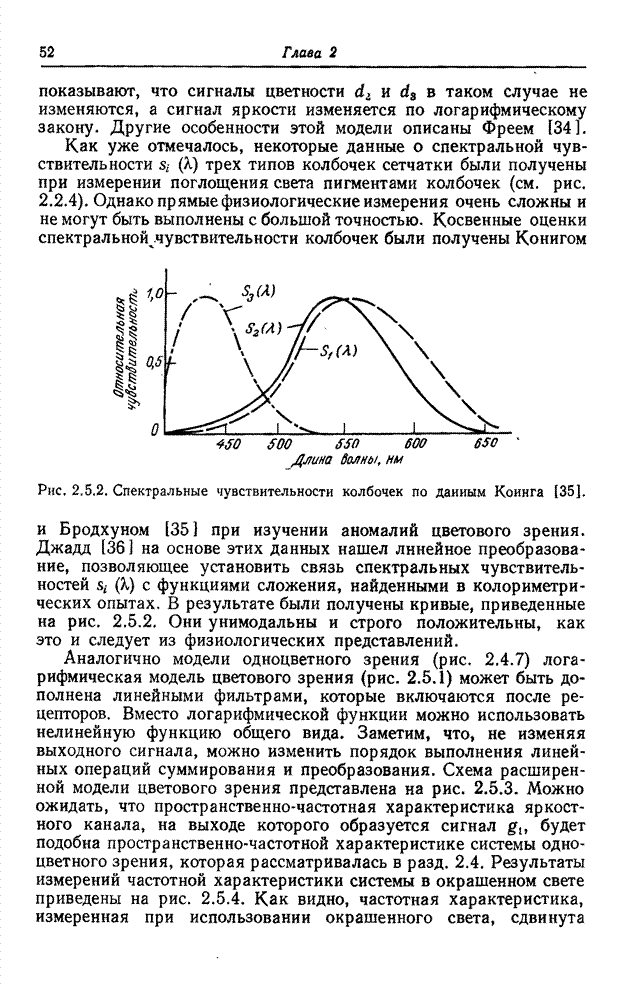
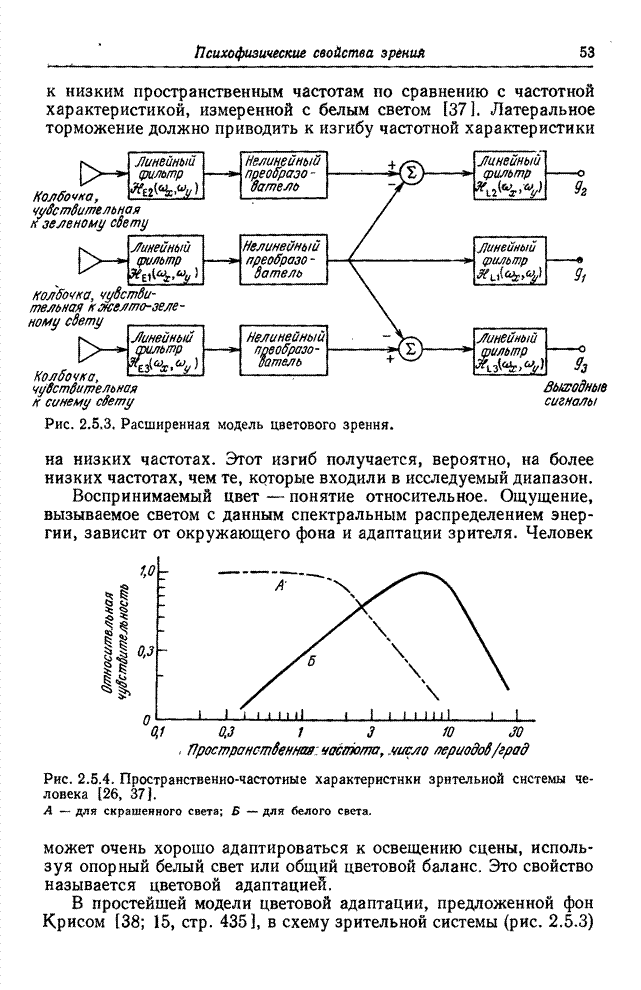
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
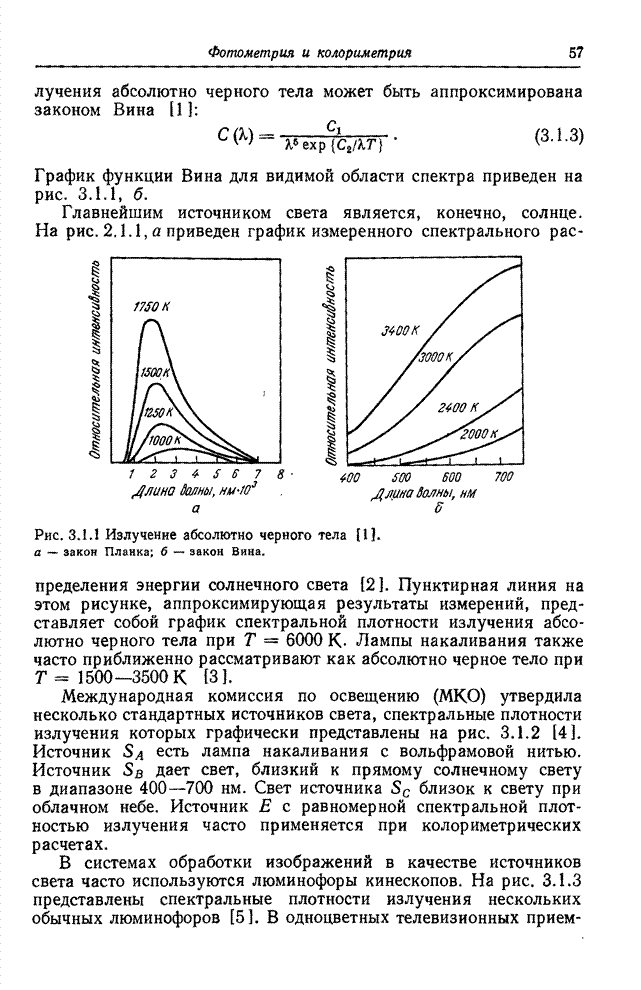
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
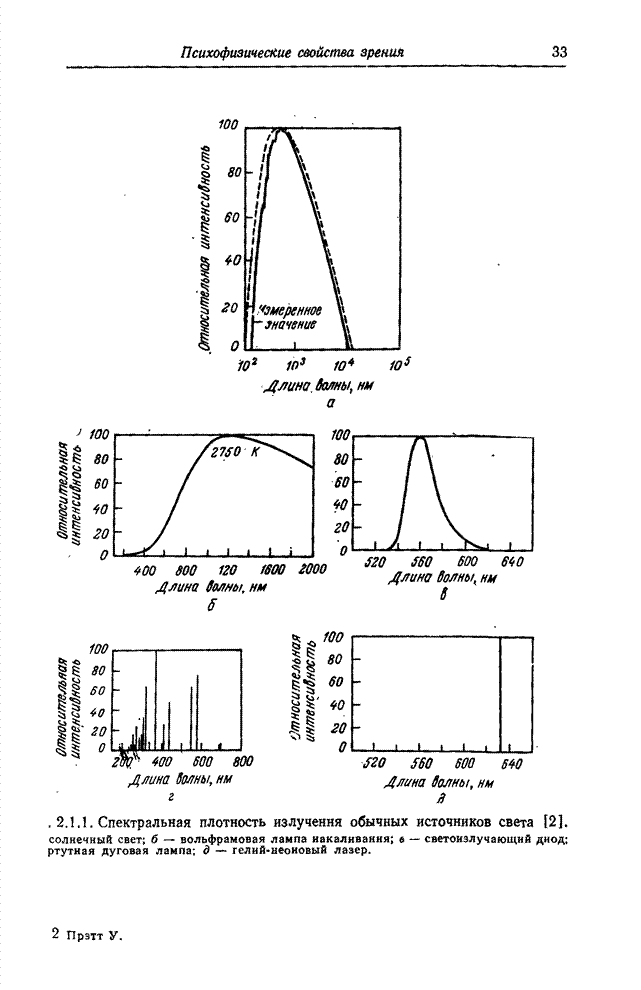
- 3.1. ИСТОЧНИКИ СВЕТА
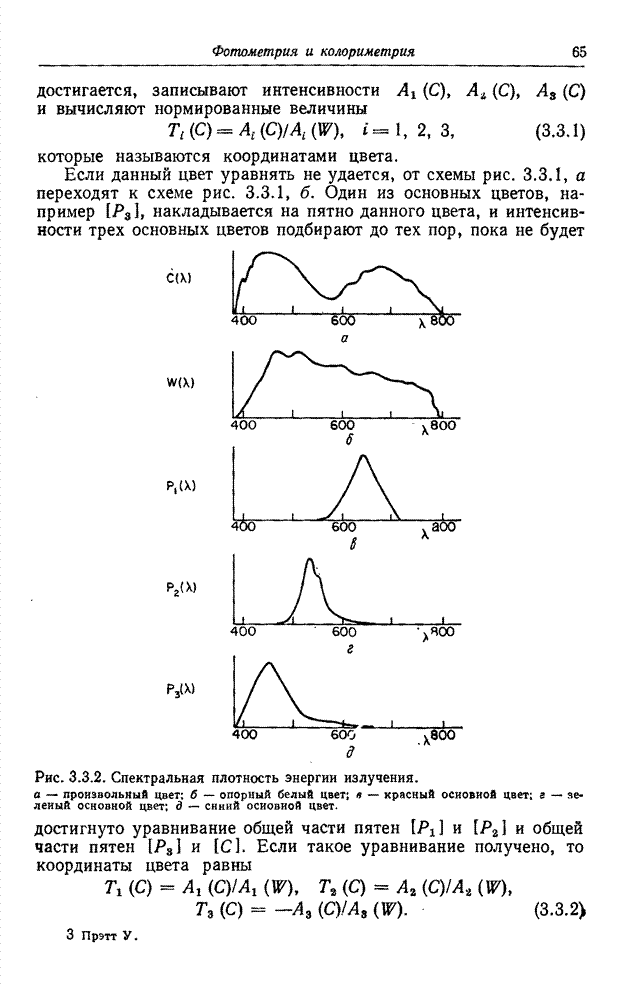
- 3.2. ФОТОМЕТРИЯ
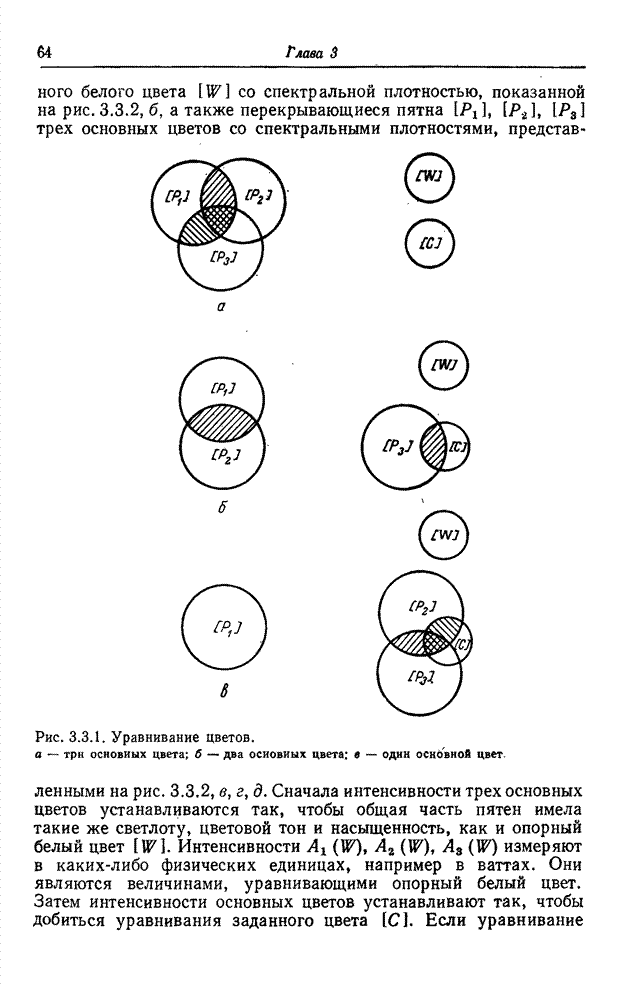
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
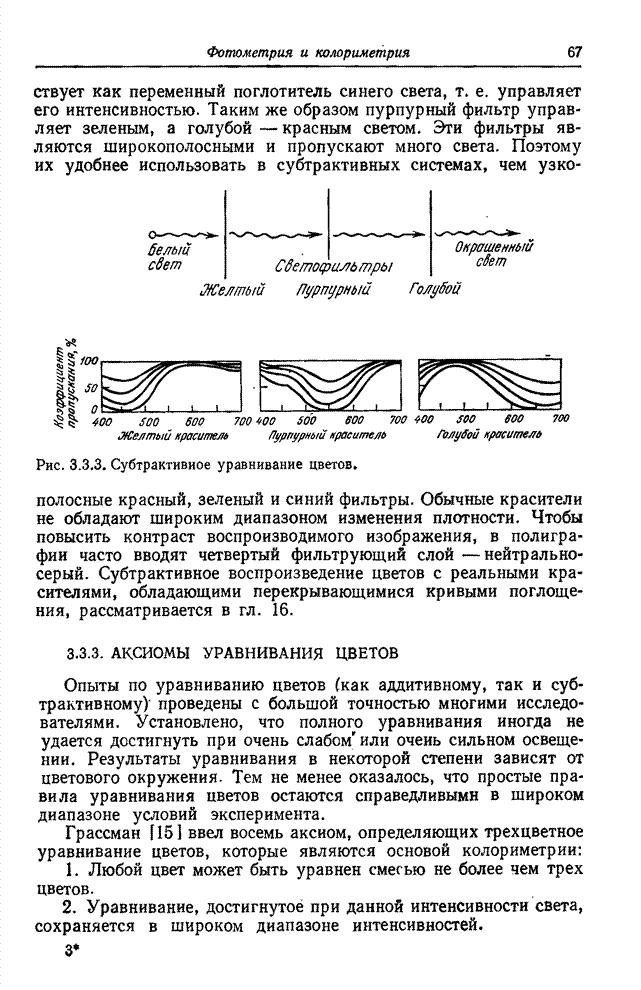
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
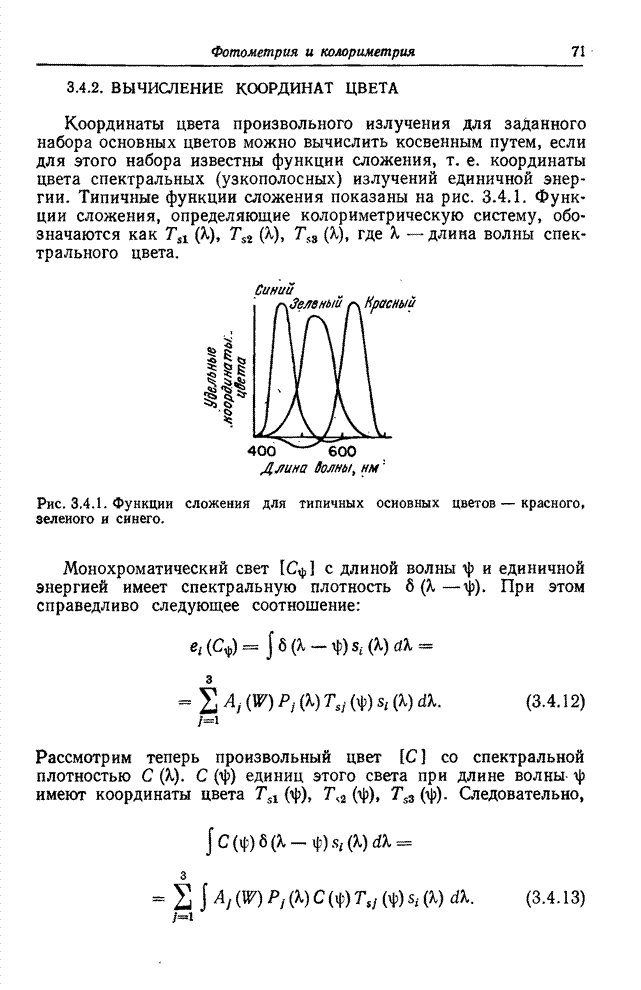
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
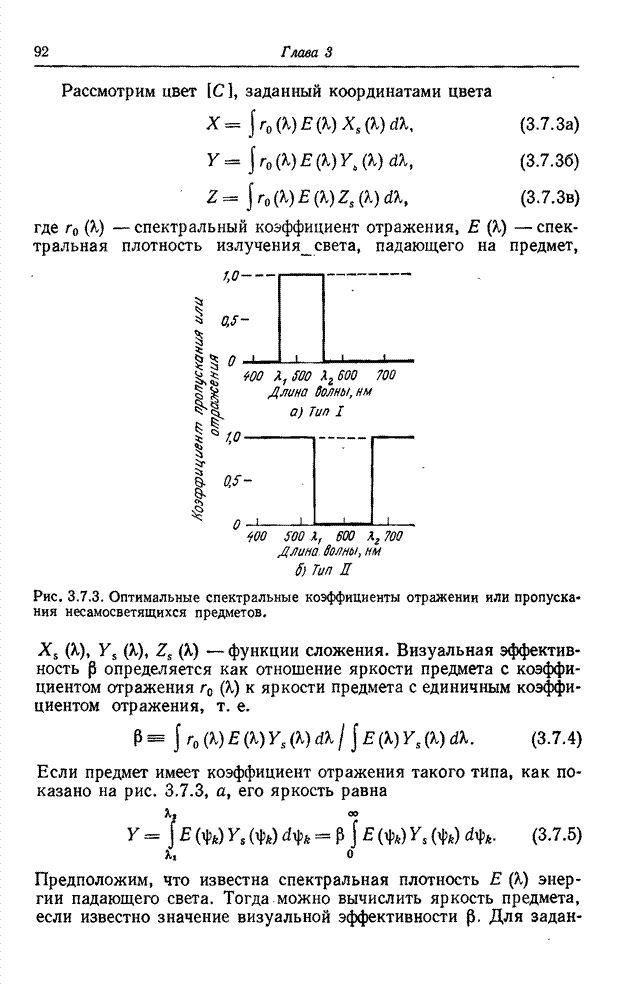
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
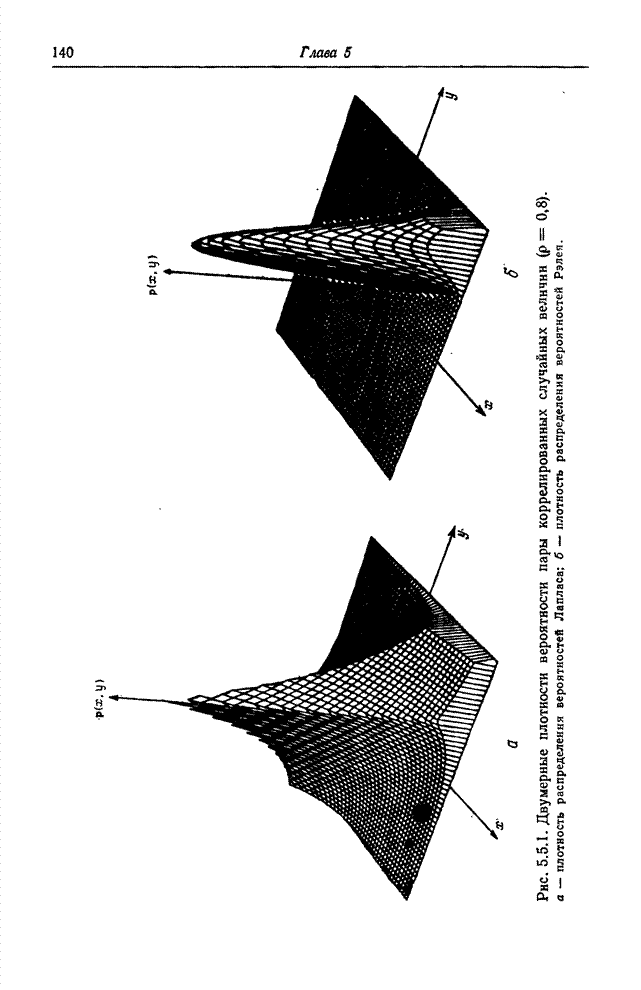
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
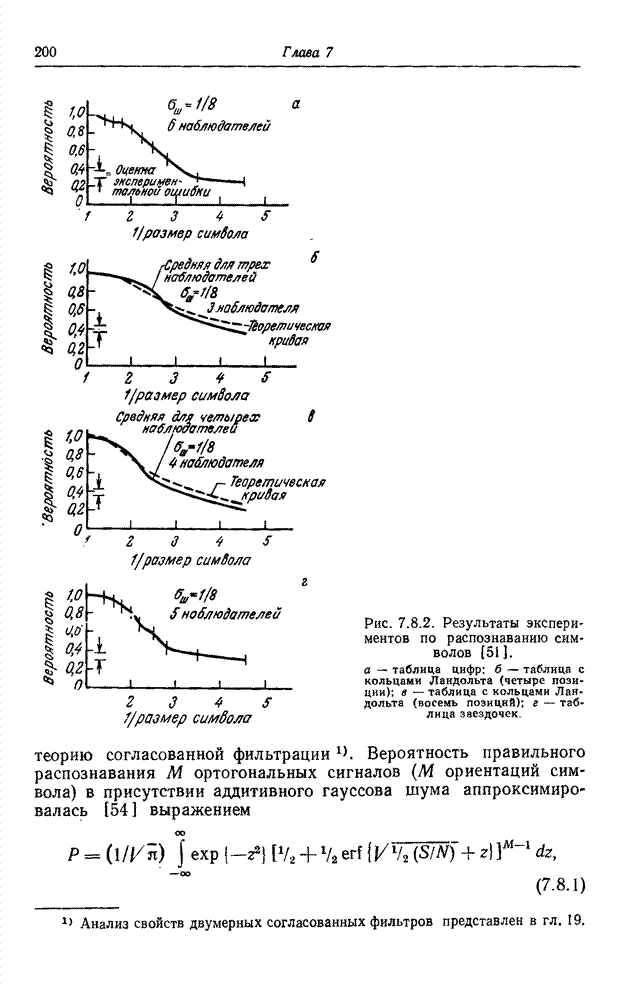
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
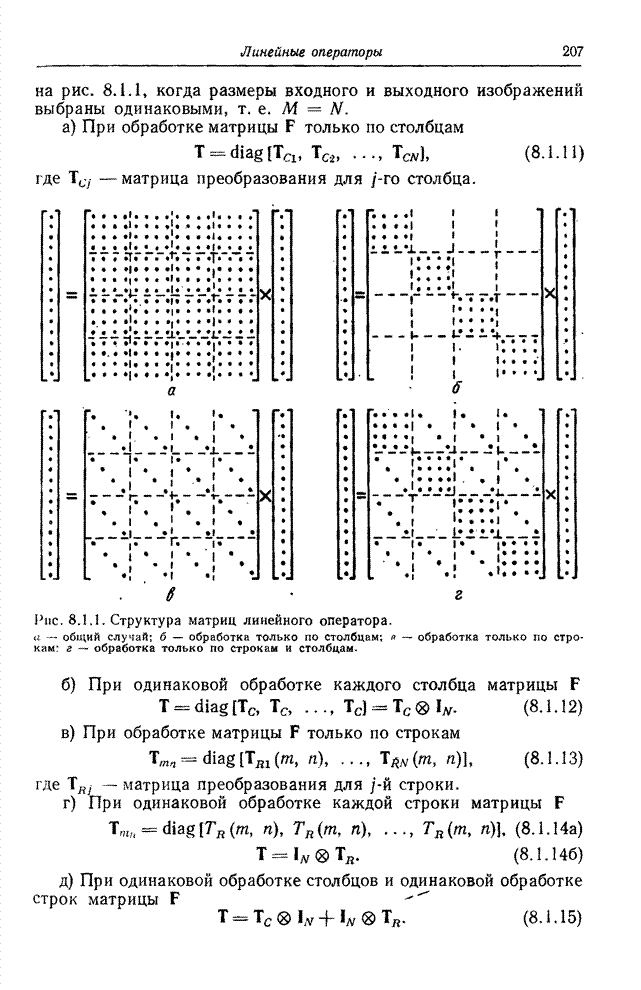
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
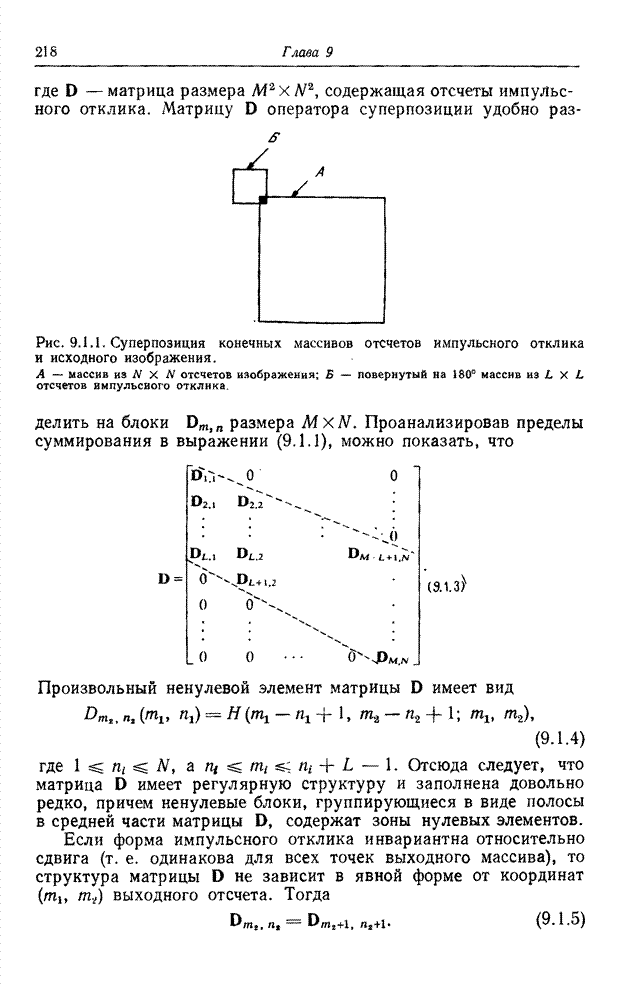
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
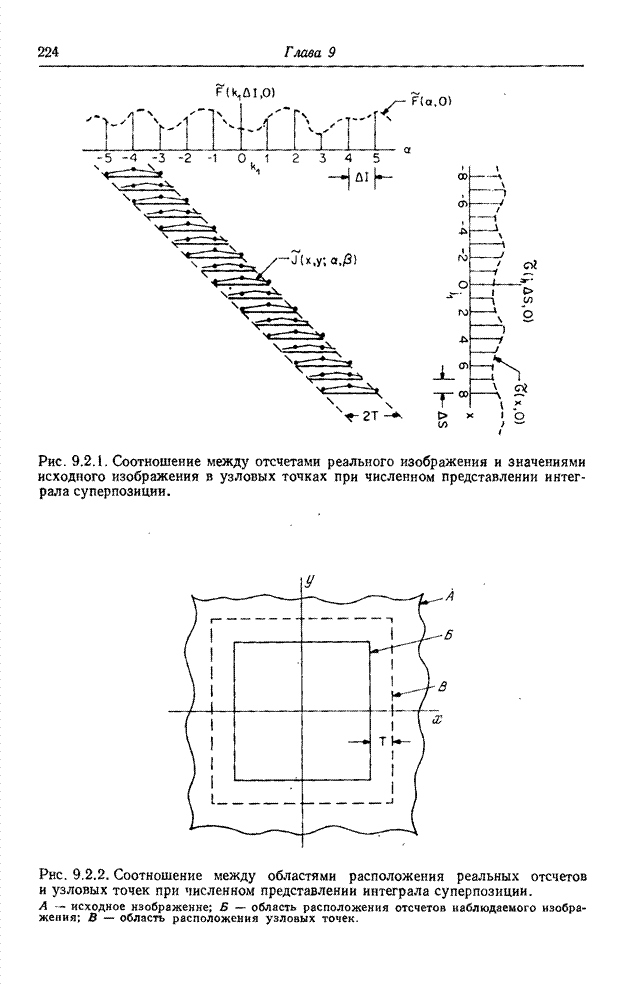
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
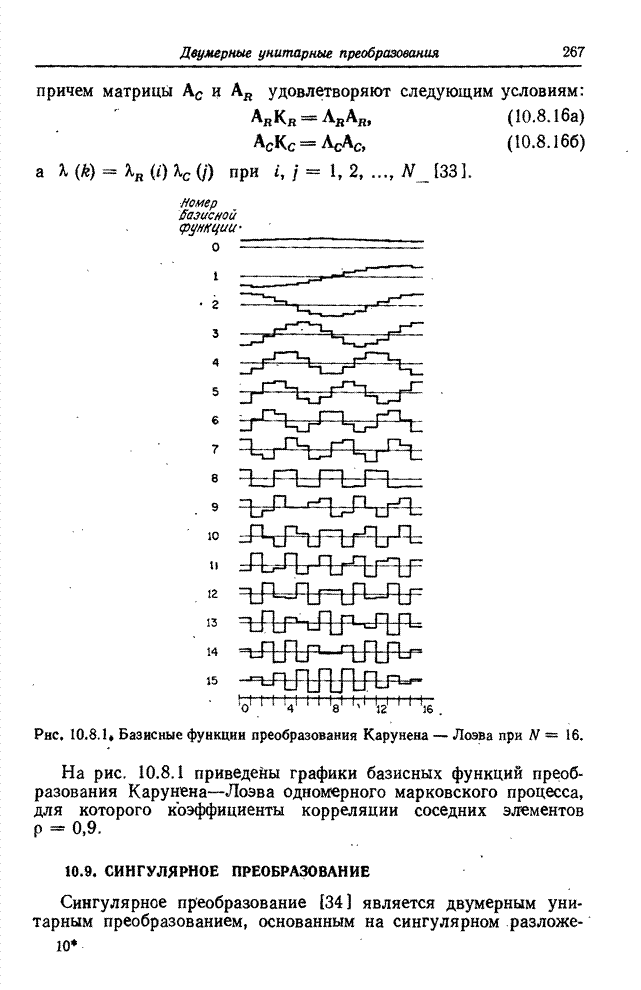
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
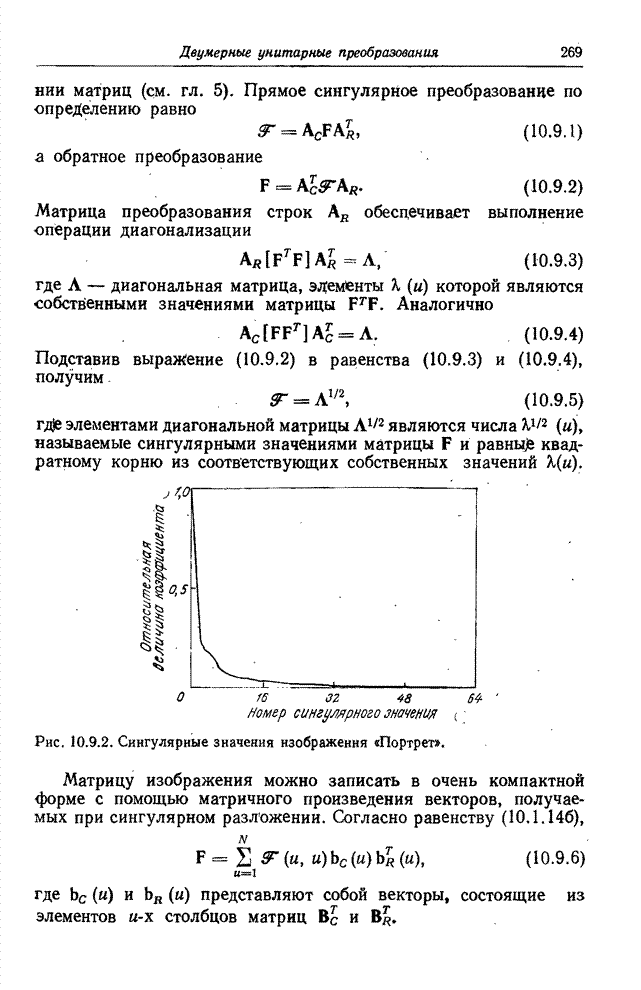
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
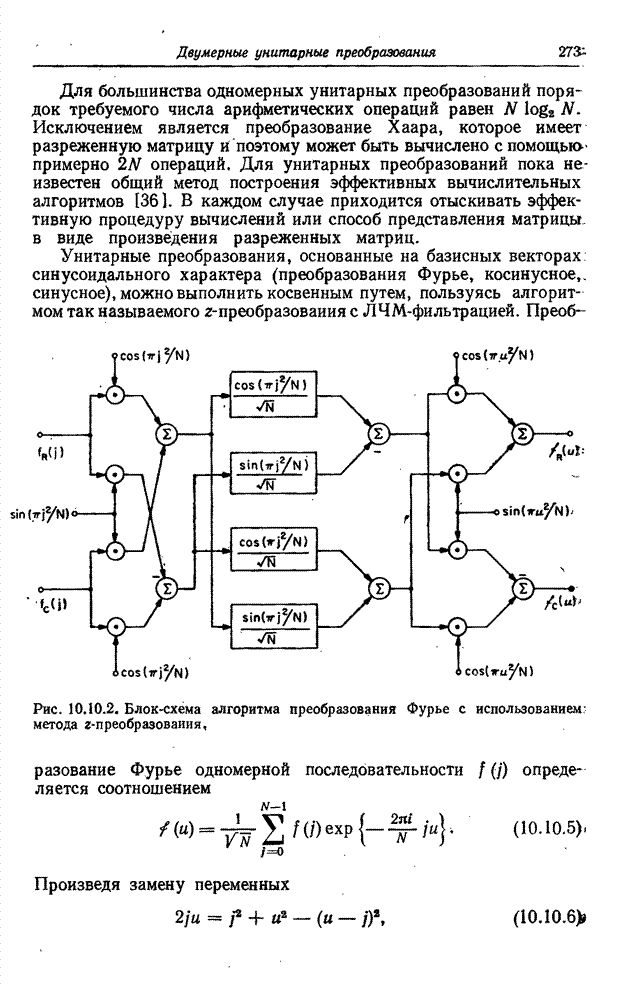
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
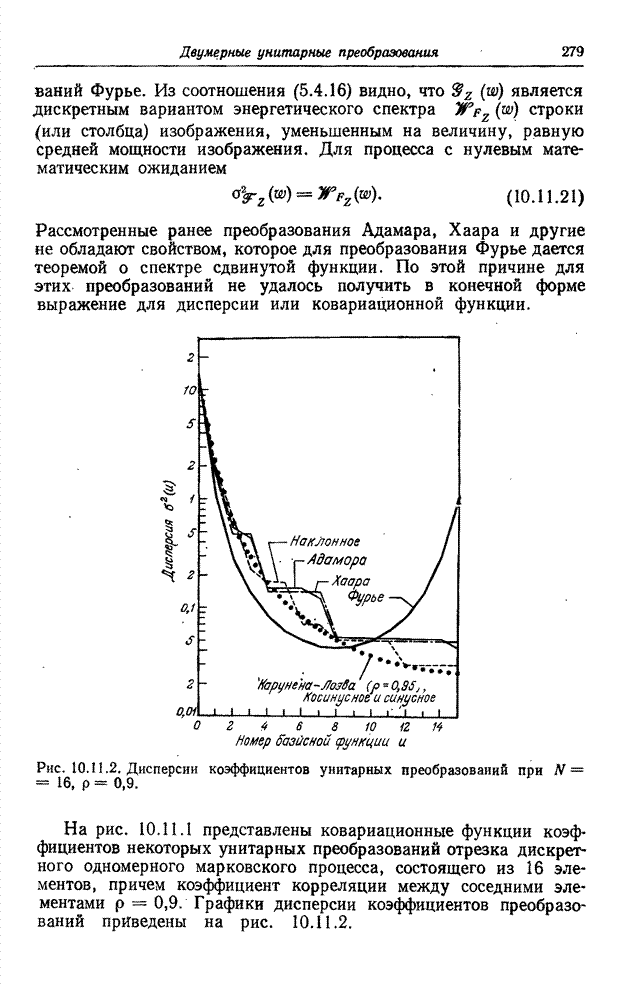
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
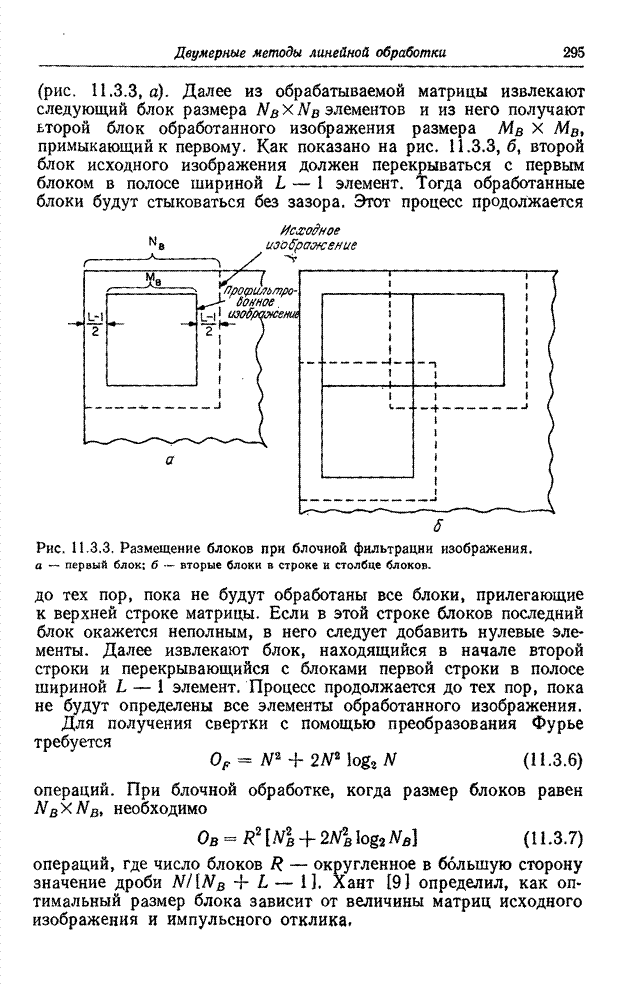
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
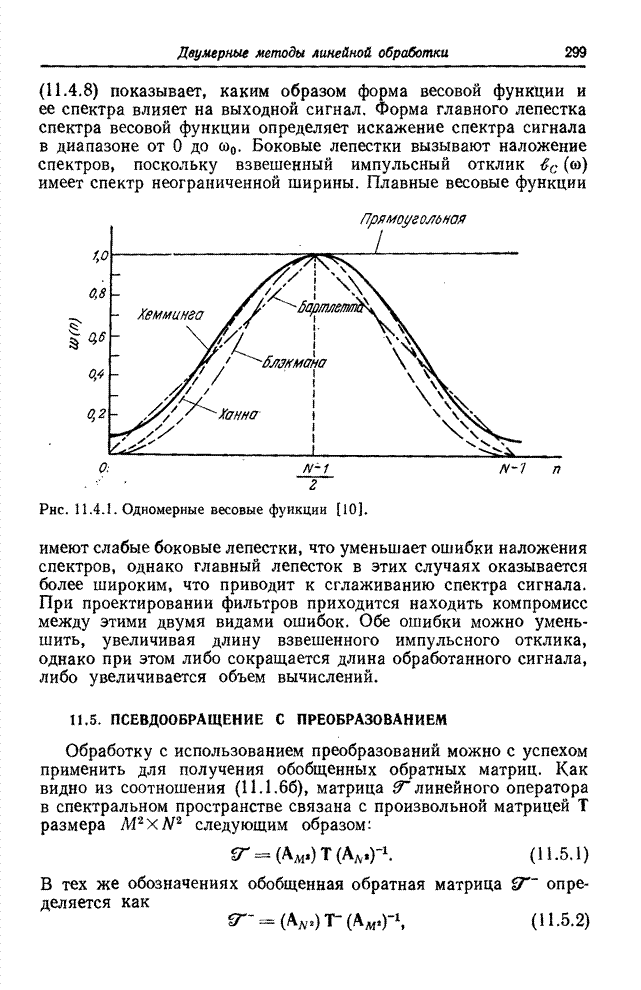
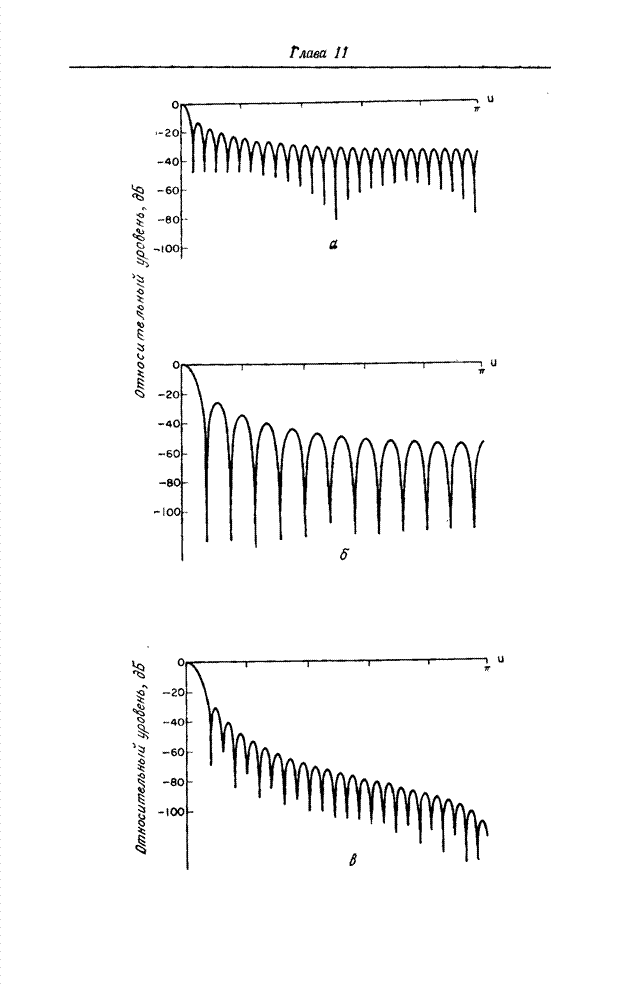
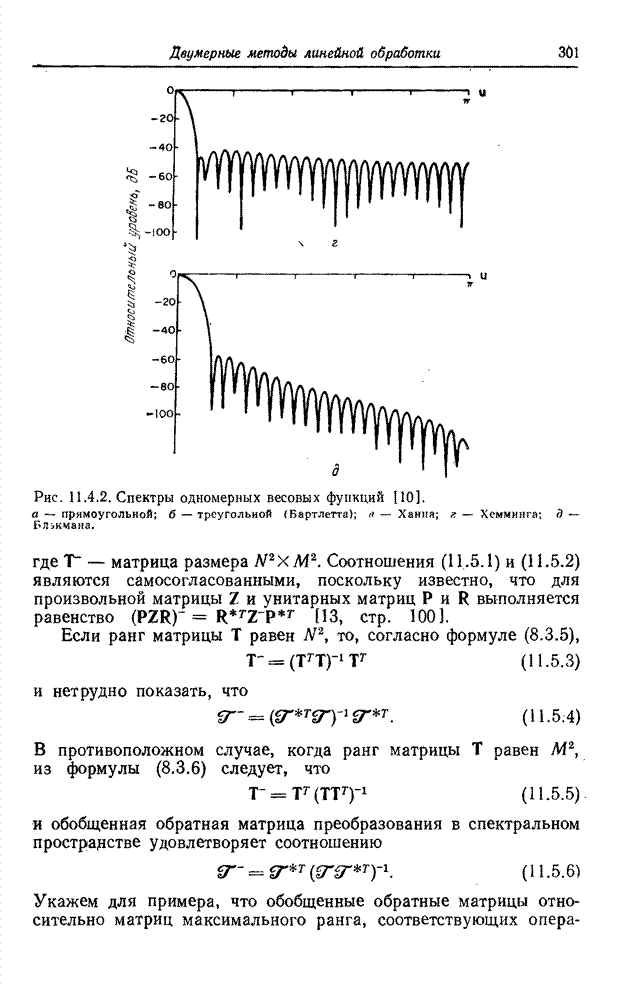
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА