| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
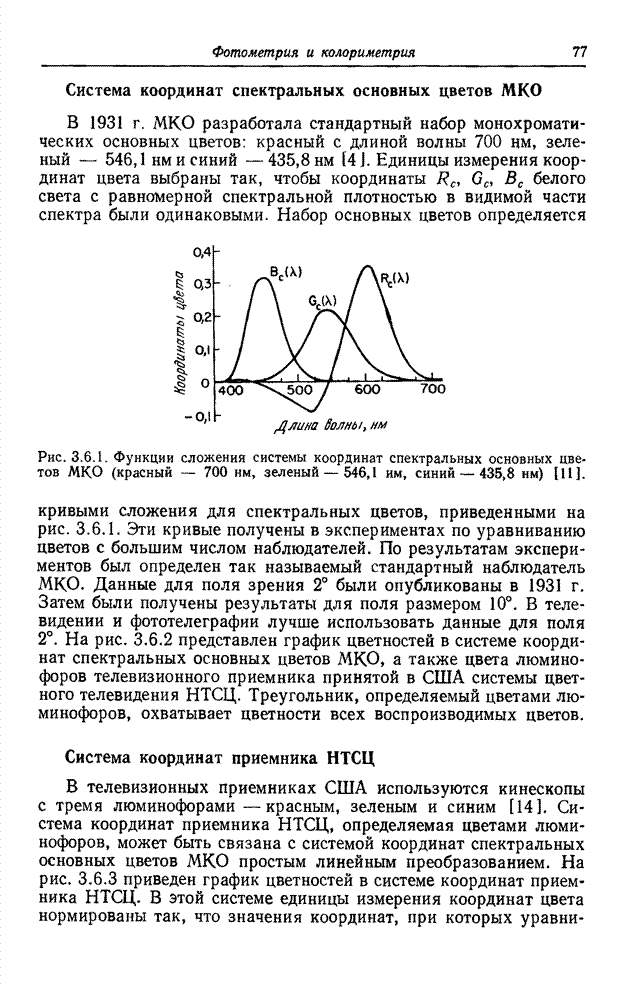
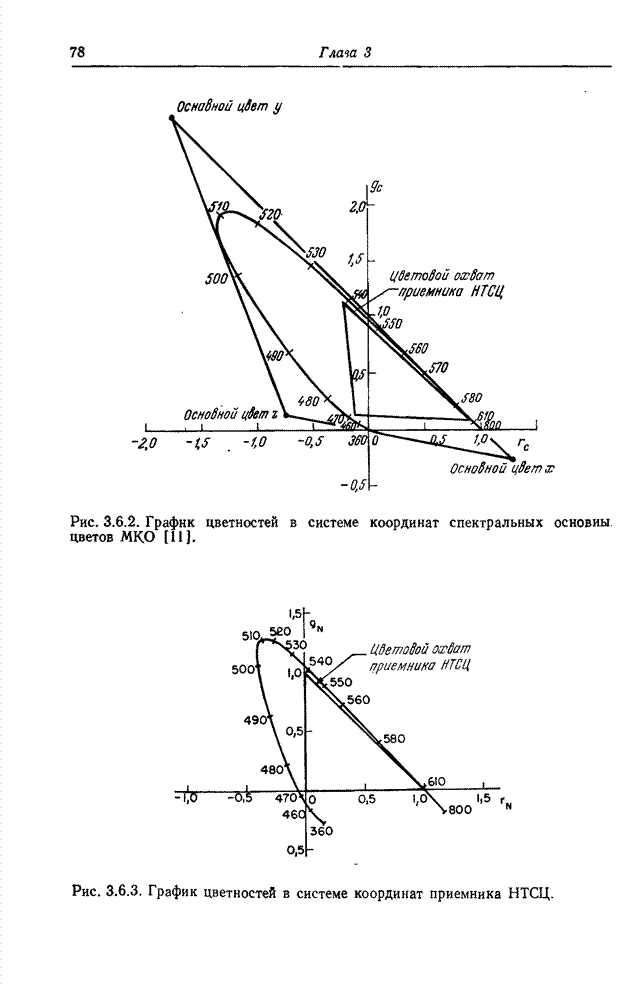
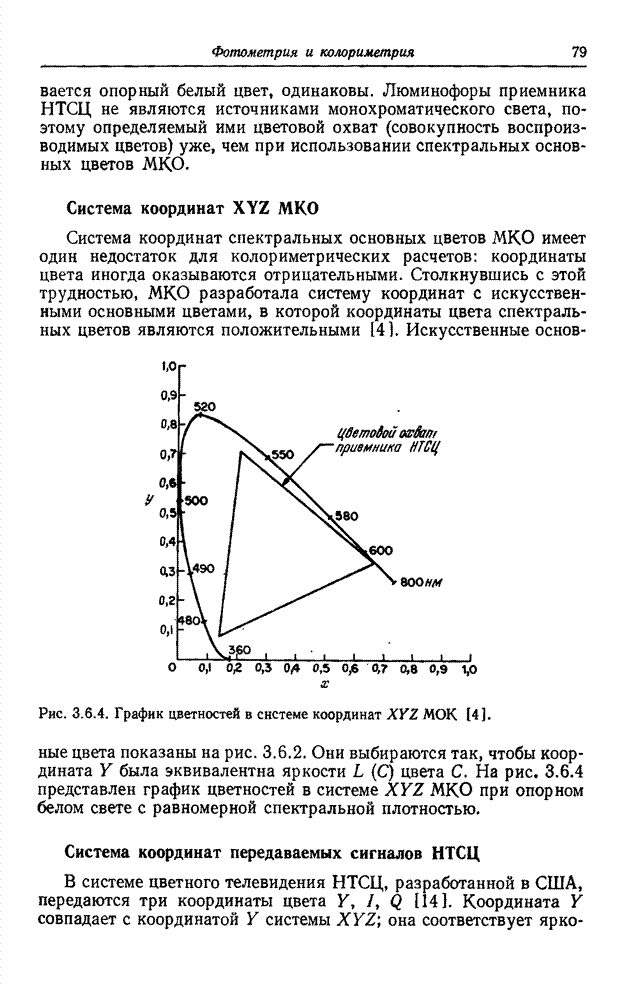
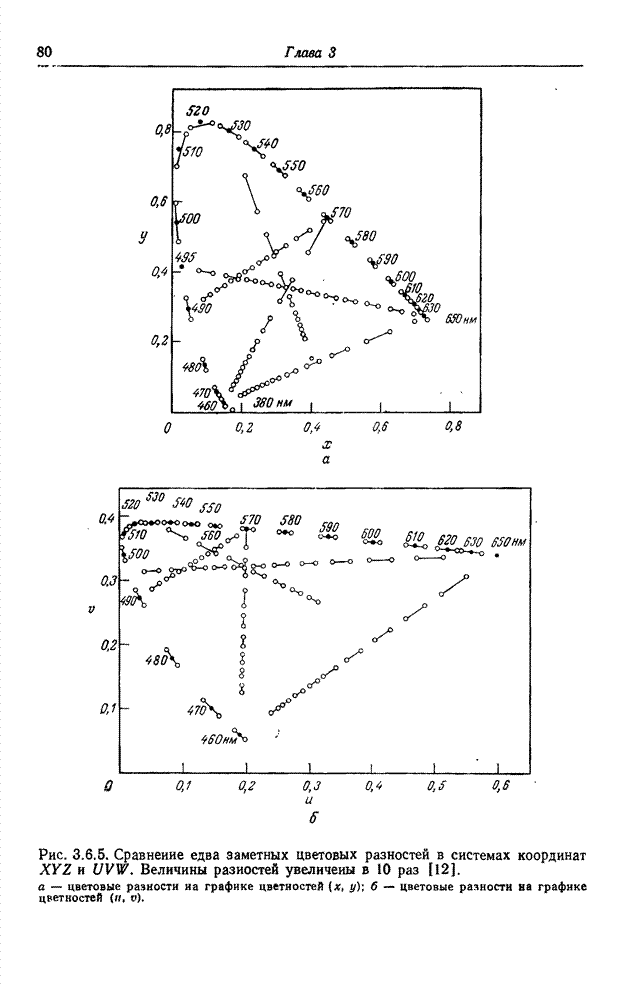
7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
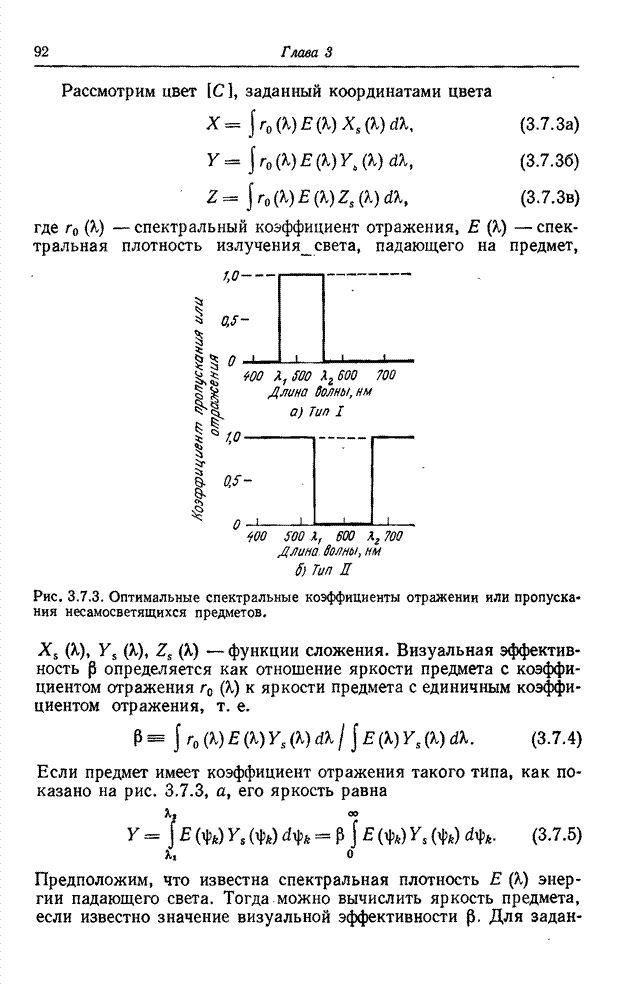
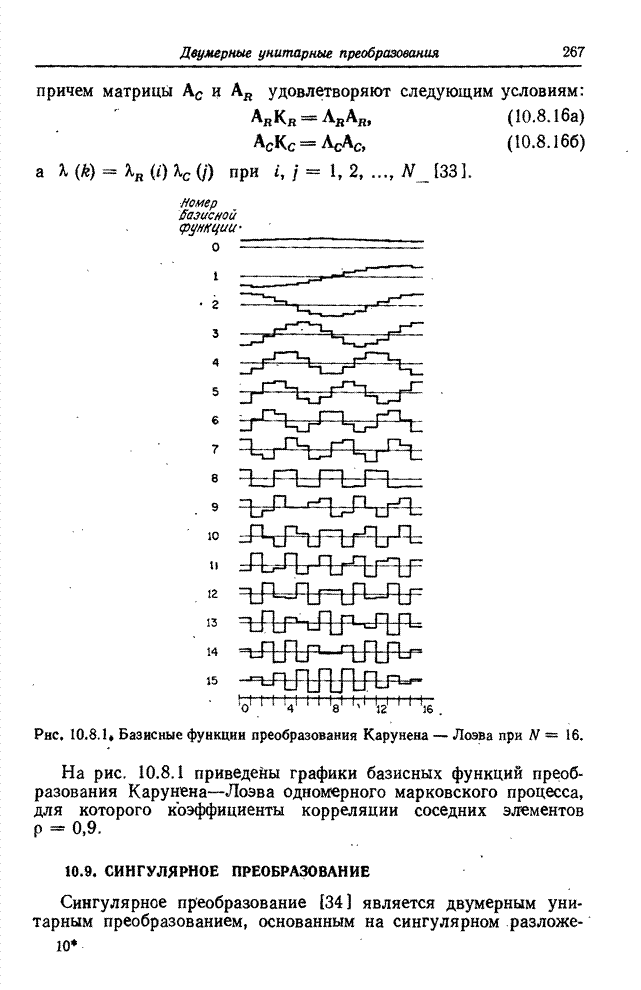
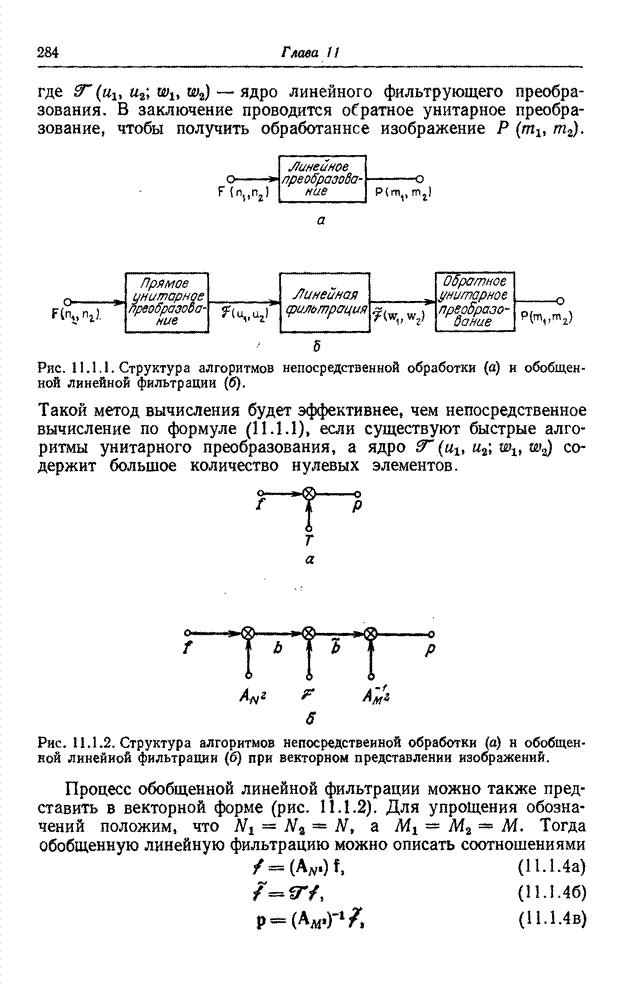
Скорость создания информации некоторым источником определяет минимальную величину пропускной способности канала, которая необходима для передачи сообщения с заданным допустимым уровнем искажений в принятом сообщении относительно переданного [45, 46]. Был предпринят ряд попыток [2, 47-50] приспособить теорию информации к задачам передачи изображений с тем, чтобы определить предельные возможности систем кодирования изображений. В данном разделе приведены основные положения этой теории, сформулированные применительно к изображениям на основе обзорной статьи Дэвиссона [50].

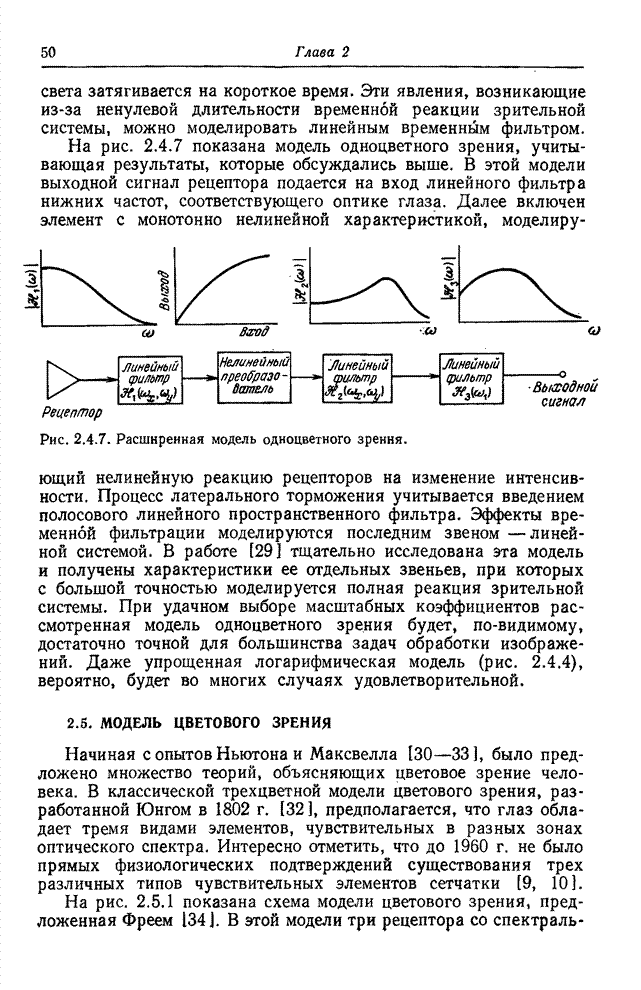
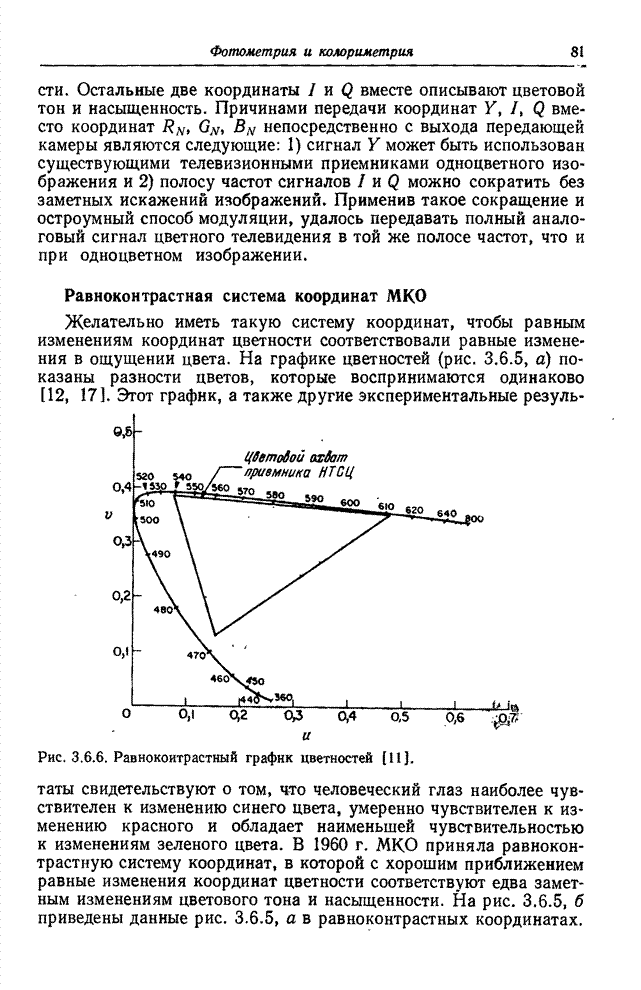
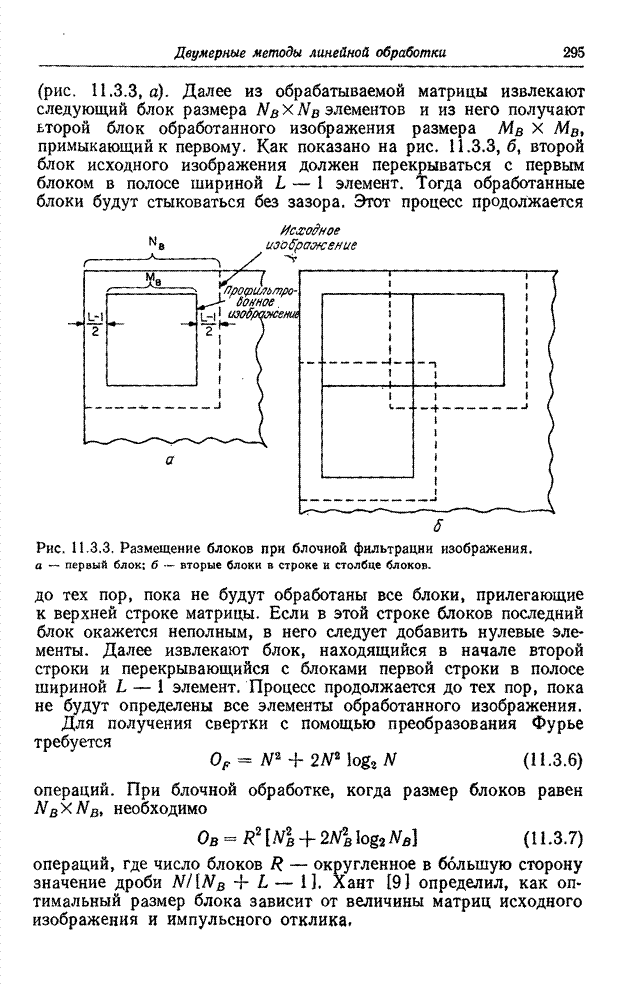
Рис. 7.7.1. Блок-схема системы передачи информации.
На
рис. 7.7.1 приведена упрощенная блок-схема системы передачи изображений.
Источник создает последовательность из ![]() элементов изображения, каждый из
которых квантуется на
элементов изображения, каждый из
которых квантуется на ![]() уровней. Эта последовательность
образует вектор
уровней. Эта последовательность
образует вектор ![]() размера
размера ![]() . В кодере
каждому из
. В кодере
каждому из ![]() возможных
сочетаний яркостей
возможных
сочетаний яркостей ![]() , где
, где ![]() , ставится в
соответствие кодовая комбинация.
, ставится в
соответствие кодовая комбинация.
После
декодирования восстанавливается сочетание яркостей ![]() . Характеристики
системы передачи изображений можно описать с помощью условной вероятности
. Характеристики
системы передачи изображений можно описать с помощью условной вероятности ![]() вектора
вектора ![]() , на выходе при
условии, что кодированию подвергался вектор
, на выходе при
условии, что кодированию подвергался вектор ![]() . Если кодер и
декодер работают без ошибок, то входной и выходной векторы изображения (при
отсутствии ошибок в канале) будут одинаковыми.
. Если кодер и
декодер работают без ошибок, то входной и выходной векторы изображения (при
отсутствии ошибок в канале) будут одинаковыми.
Условная
вероятность ![]() описывает
работу системы передачи изображений при наличии искажений. На основании этой
условной вероятности и распределения априорных вероятностей находим безусловное
распределение вероятностей восстановленных векторов
описывает
работу системы передачи изображений при наличии искажений. На основании этой
условной вероятности и распределения априорных вероятностей находим безусловное
распределение вероятностей восстановленных векторов
![]() . (7.7.1)
. (7.7.1)
Требования к пропускной способности канала определяются количеством взаимной информации, по определению равной
![]() . (7.7.2)
. (7.7.2)
При безошибочном кодировании это выражение упрощается:
![]() , (7.7.3)
, (7.7.3)
т.
е. количество взаимной информации оказывается равным энтропии источника. Если в
процессе кодирования вносятся искажения, то восстановленная последовательность ![]() содержит
неполную информацию о состоянии
содержит
неполную информацию о состоянии ![]() и требования к
пропускной способности канала будут уменьшены.
и требования к
пропускной способности канала будут уменьшены.
Допустим,
что функция ![]() представляет собой
некоторую меру искажений воспроизведенного изображения. Тогда для вектора из
представляет собой
некоторую меру искажений воспроизведенного изображения. Тогда для вектора из ![]() элементов средняя
величина искажений в расчете на один элемент будет определяться равенством
элементов средняя
величина искажений в расчете на один элемент будет определяться равенством
![]() . (7.7.4)
. (7.7.4)
Определим для этого вектора скорость создания информации в расчете на один элемент как
![]() (7.7.5)
(7.7.5)
при
![]() . В принципе
. В принципе ![]() и есть
минимальная пропускная способность канала, необходимая для передачи информации,
создаваемой источником, когда искажения в среднем не должны превышать некоторой
максимальной величины
и есть
минимальная пропускная способность канала, необходимая для передачи информации,
создаваемой источником, когда искажения в среднем не должны превышать некоторой
максимальной величины ![]() . Скорость
создания информации источником
. Скорость
создания информации источником ![]() можно найти,
увеличивая длину вектора до бесконечности:
можно найти,
увеличивая длину вектора до бесконечности:
![]() . (7.7.6)
. (7.7.6)
Как
правило, отыскать минимум количества взаимной информации при условии, что
средняя величина искажений не должна превышать заданного предела ![]() , сложно как
аналитическими, так и численными методами. Получено несколько решений для
каналов связи, используемых на практике. Одно из них относится к источнику с
гауссовым распределением вероятностей при оценке искажений среднеквадратической
мерой. Такое решение нельзя непосредственно применить к задаче о кодировании
яркостей элементов, поскольку яркость — неотрицательная величина. Кроме того,
среднеквадратическая мера искажений может оказаться неподходящей. Однако
решение, полученное для гауссова источника и среднеквадратической меры
искажений, позволяет указать предельные возможности системы кодирования для
любых источников с заданными вторыми моментами. Кроме того, это решение
непосредственно переносится на задачу о кодировании с преобразованием. Поэтому
ниже будут рассмотрены свойства скорости создания информации для случая
гауссова источника и среднеквадратической меры искажений.
, сложно как
аналитическими, так и численными методами. Получено несколько решений для
каналов связи, используемых на практике. Одно из них относится к источнику с
гауссовым распределением вероятностей при оценке искажений среднеквадратической
мерой. Такое решение нельзя непосредственно применить к задаче о кодировании
яркостей элементов, поскольку яркость — неотрицательная величина. Кроме того,
среднеквадратическая мера искажений может оказаться неподходящей. Однако
решение, полученное для гауссова источника и среднеквадратической меры
искажений, позволяет указать предельные возможности системы кодирования для
любых источников с заданными вторыми моментами. Кроме того, это решение
непосредственно переносится на задачу о кодировании с преобразованием. Поэтому
ниже будут рассмотрены свойства скорости создания информации для случая
гауссова источника и среднеквадратической меры искажений.
Рассмотрим
вектор ![]() ,
образованный
,
образованный ![]() независимыми
гауссовыми случайными величинами с нулевыми средними и известной дисперсией
независимыми
гауссовыми случайными величинами с нулевыми средними и известной дисперсией ![]() .
Среднеквадратическая ошибка определяется формулой
.
Среднеквадратическая ошибка определяется формулой
 . (7.7.7)
. (7.7.7)
Было найдено [45], что скорость создания информации

Таким
образом, скорость создания информации равна половине логарифма отношения
мощности сигнала к мощности искажений, если это отношение превышает единицу, и
нулю в противном случае. Если элементы последовательности, создаваемой
гауссовым источником, коррелированы и ковариационная матрица ![]() известна, то
скорость создания информации равна [50]
известна, то
скорость создания информации равна [50]
 , (7.7.9)
, (7.7.9)
где
![]() —
— ![]() -e собственное
значение матрицы
-e собственное
значение матрицы ![]() , а
, а ![]() выбрано так, что
выбрано так, что
 . (7.7.10)
. (7.7.10)
При
обработке изображений представляет интерес частный случай двумерного
разделимого марковского источника, когда все элементы имеют одинаковые
дисперсии, равные ![]() , а коэффициенты
корреляции вдоль строк и столбцов равны соответственно
, а коэффициенты
корреляции вдоль строк и столбцов равны соответственно ![]() и
и ![]() . Если предположить,
что степень искажений невелика, то скорость создания информации для однородного
случая равна [50]
. Если предположить,
что степень искажений невелика, то скорость создания информации для однородного
случая равна [50]
 , (7.7.11)
, (7.7.11)
а в двумерном случае
 . (7.7.12)
. (7.7.12)

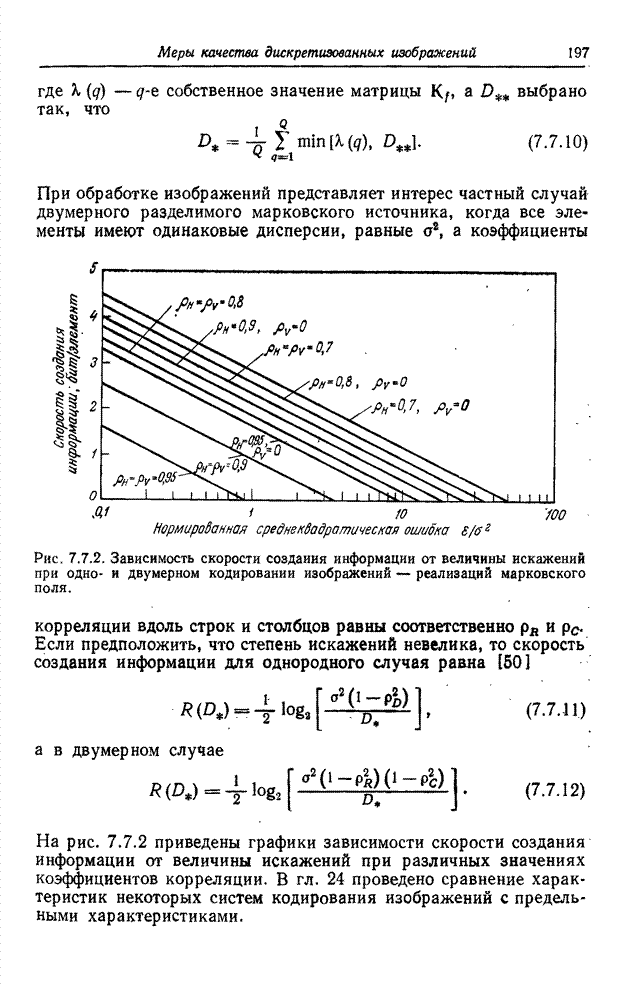
Рис. 7.7.2. Зависимость скорости создания информации от величины искажений при одно- и двумерном кодировании изображений – реализаций марковского поля.
На рис. 7.7.2 приведены графики зависимости скорости создания информации от величины искажений при различных значениях коэффициентов корреляции. В гл. 24 проведено сравнение характеристик некоторых систем кодирования изображений с предельными характеристиками.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
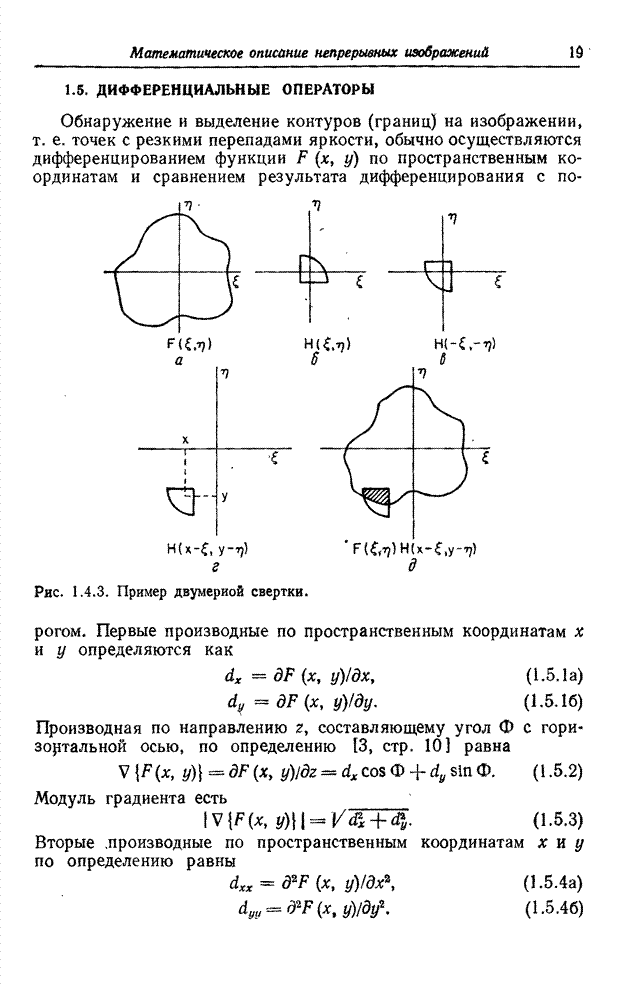
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
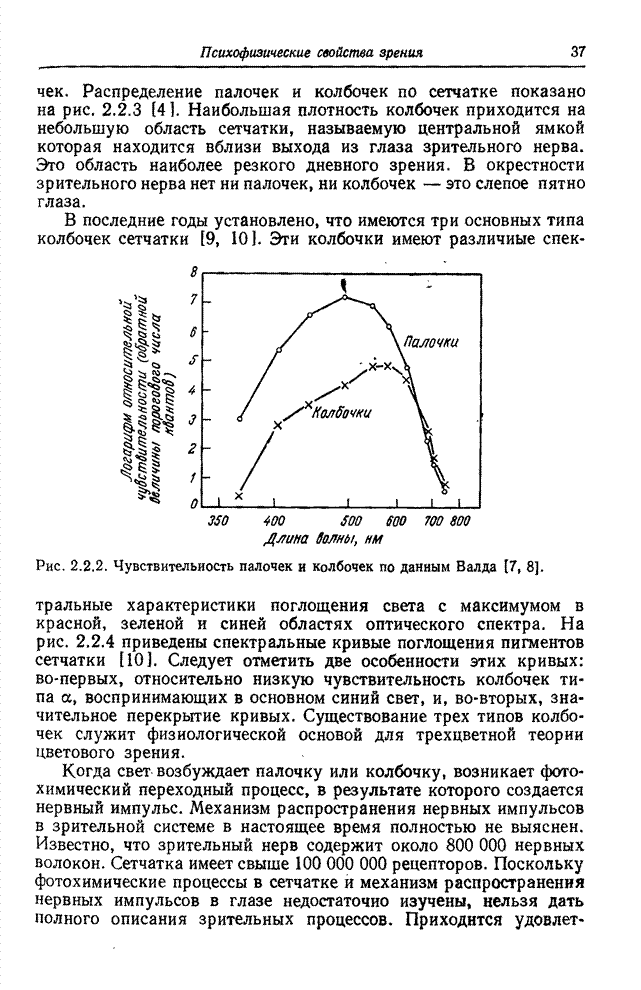
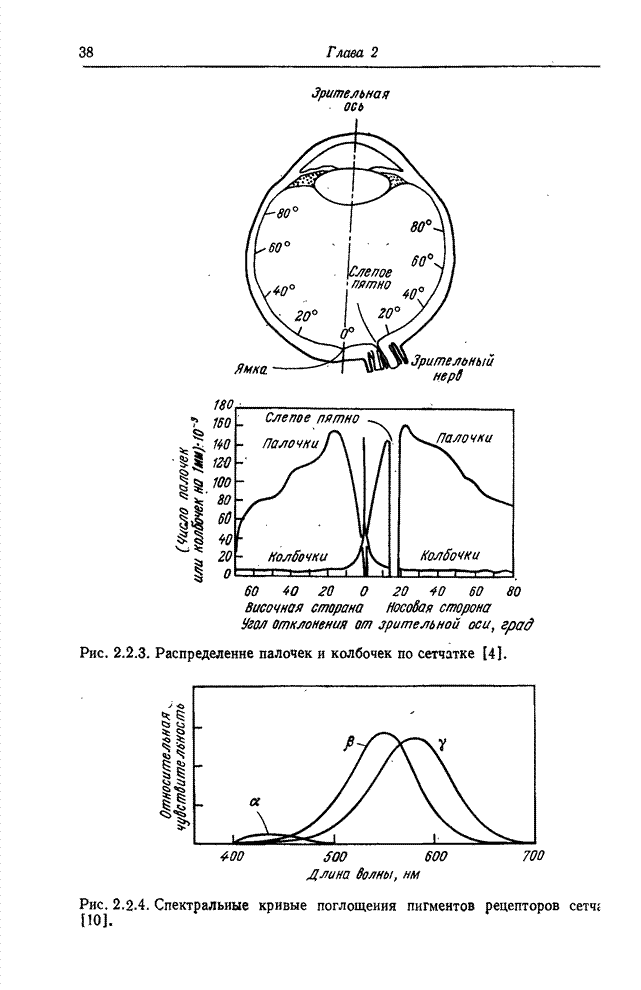
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
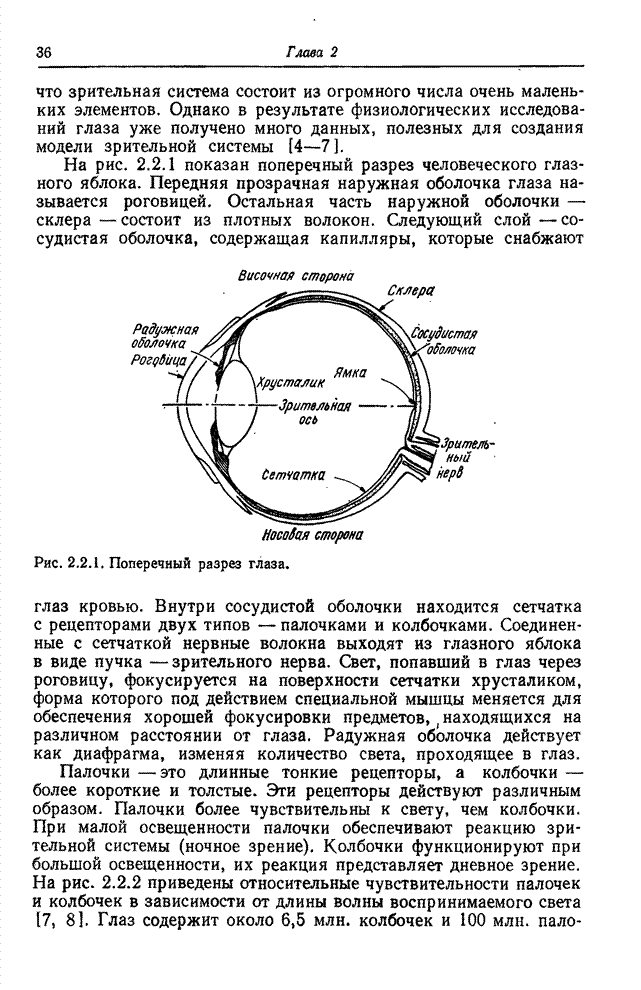
- 2.2. ГЛАЗ
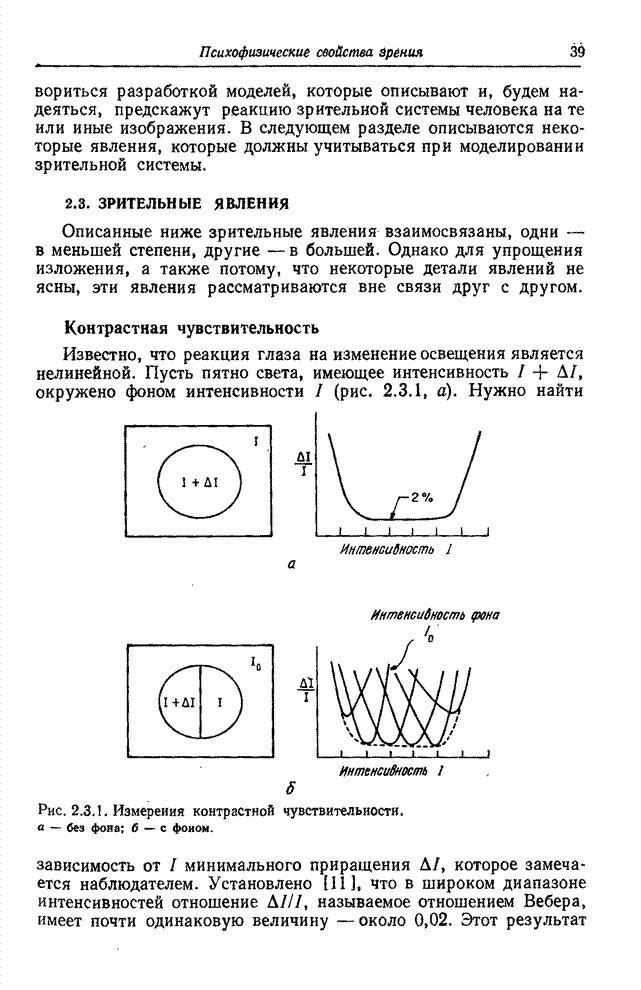
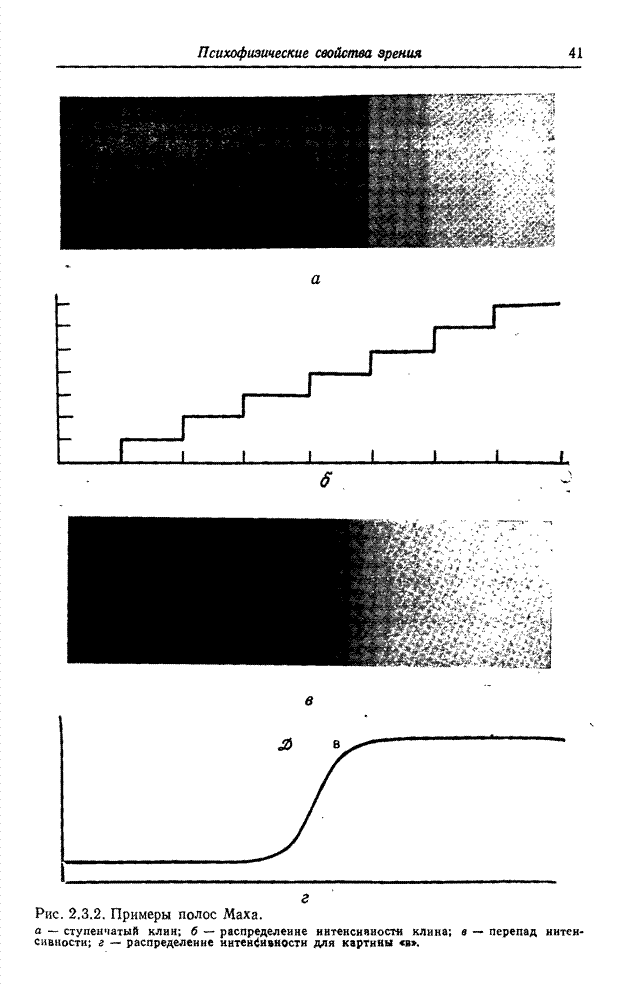
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
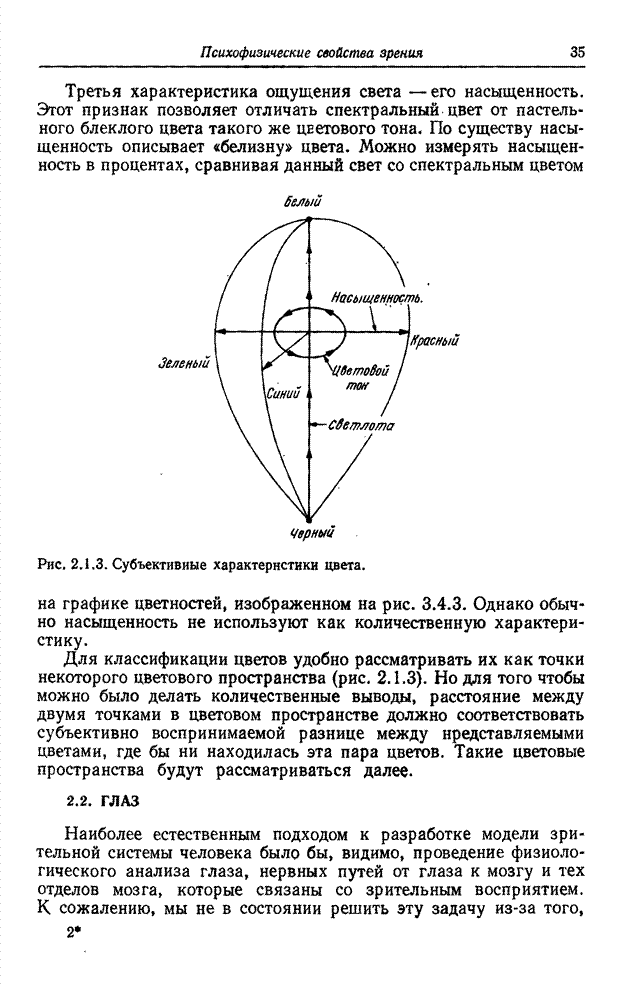
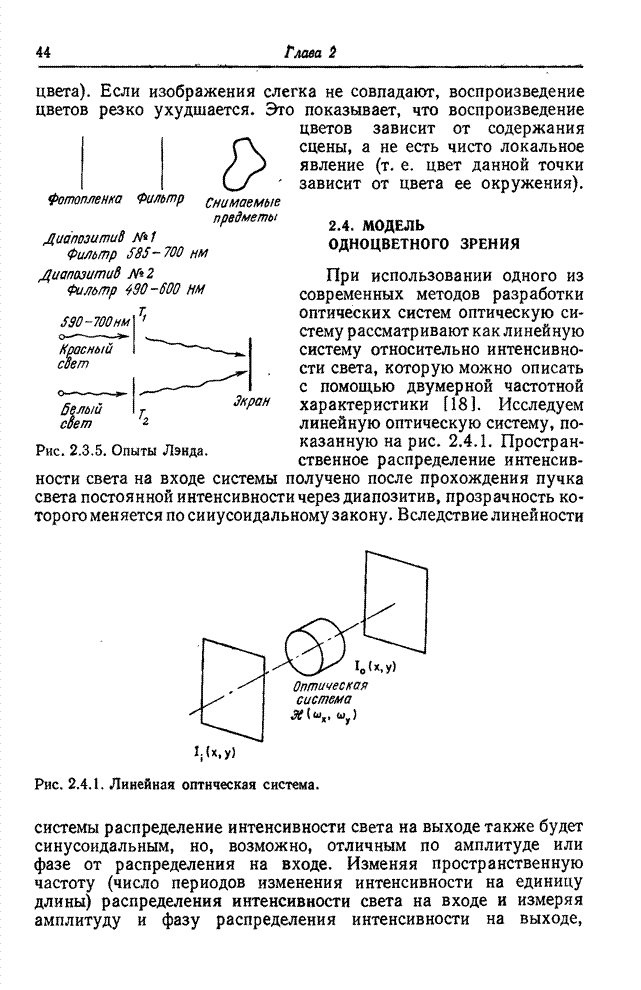
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
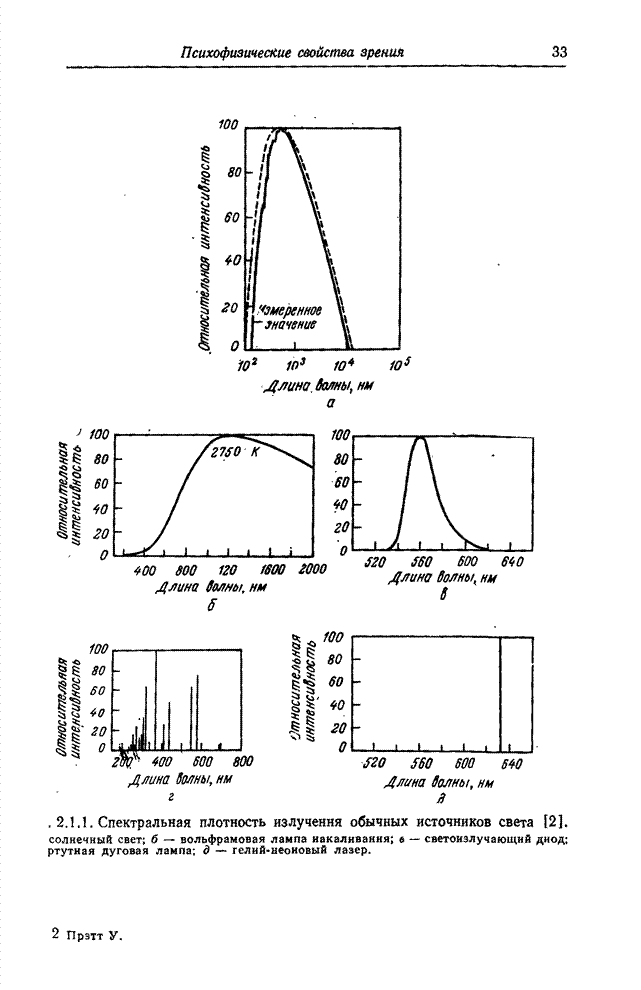
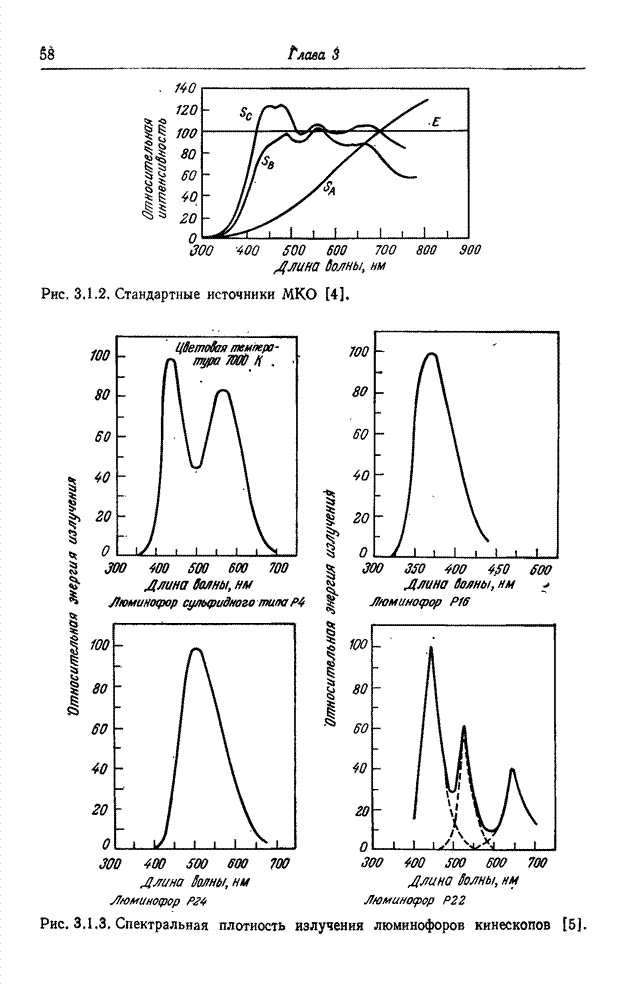
- 3.1. ИСТОЧНИКИ СВЕТА
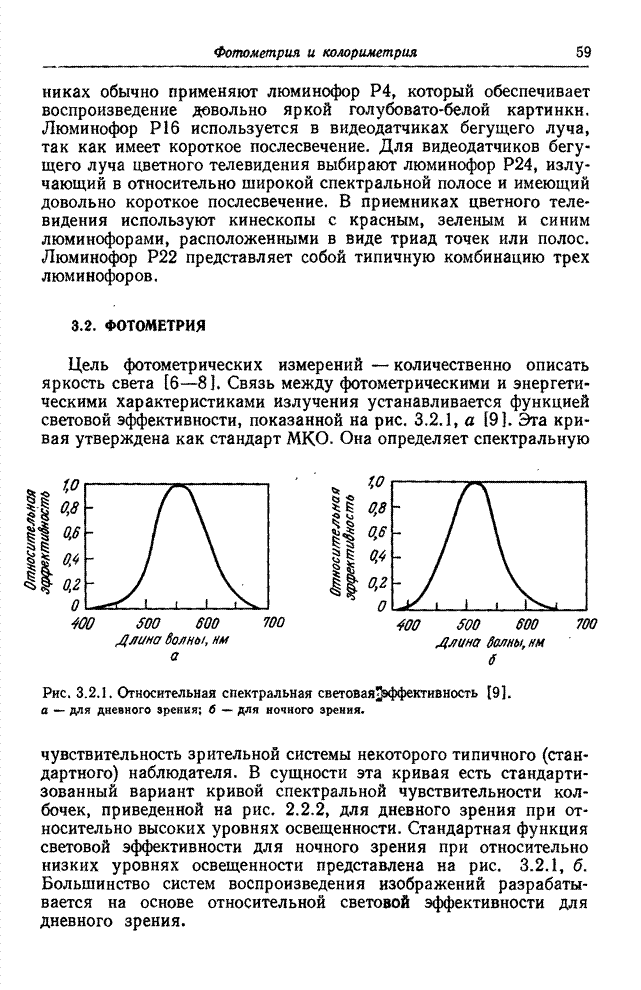
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
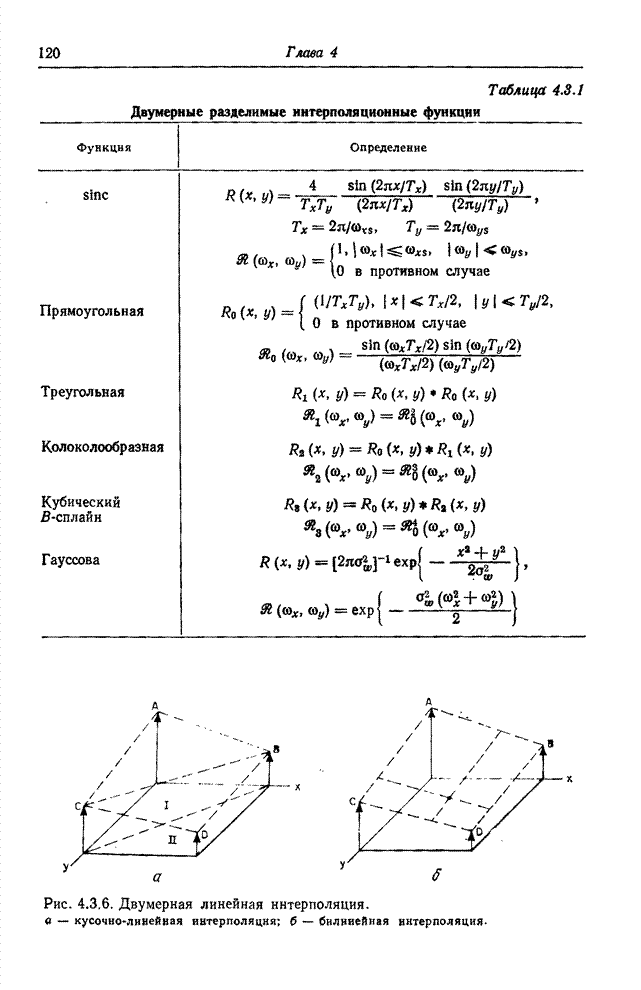
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
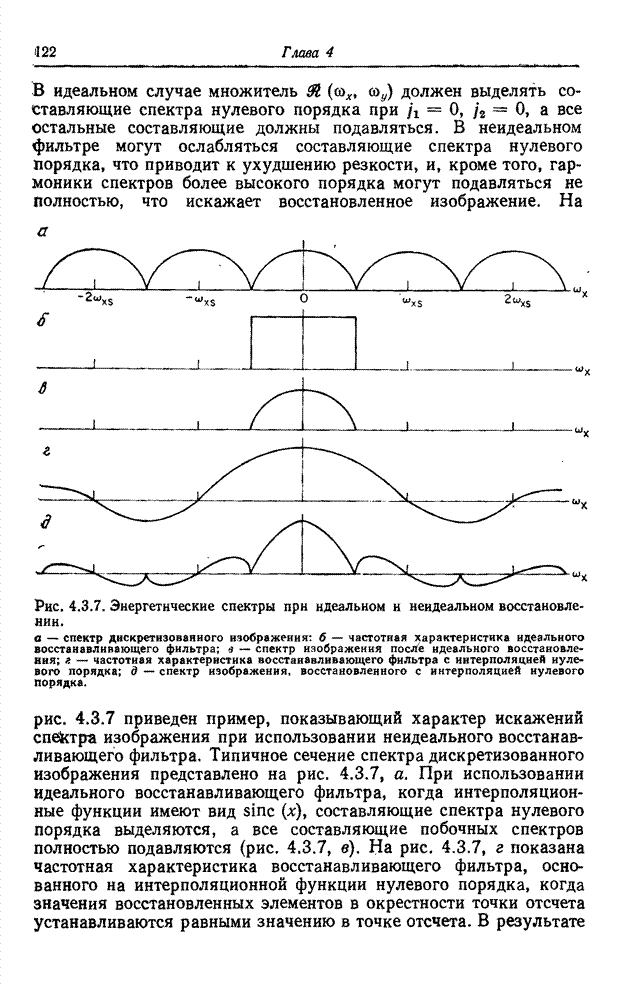
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
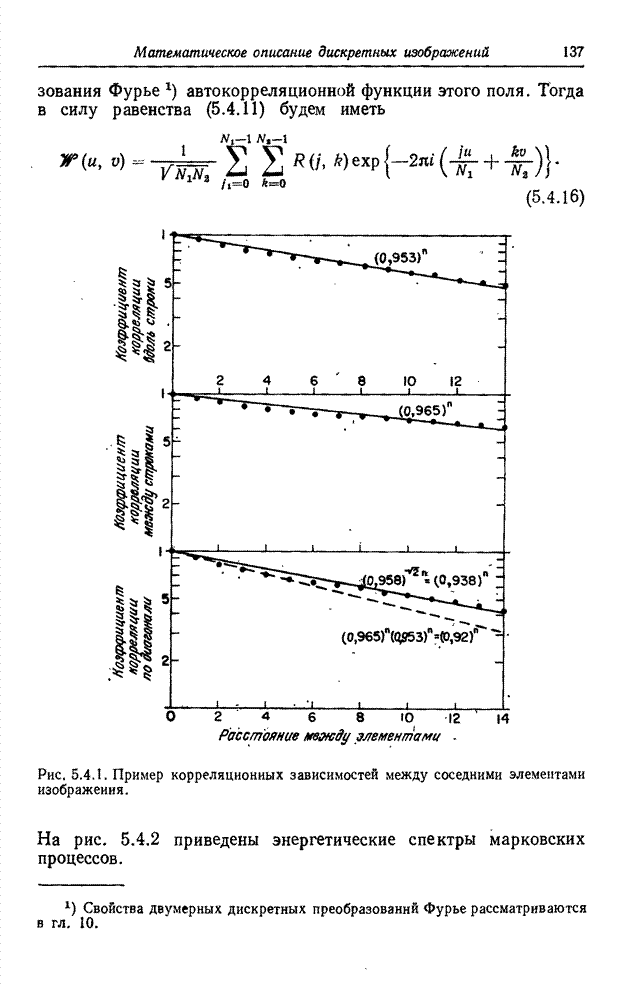
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
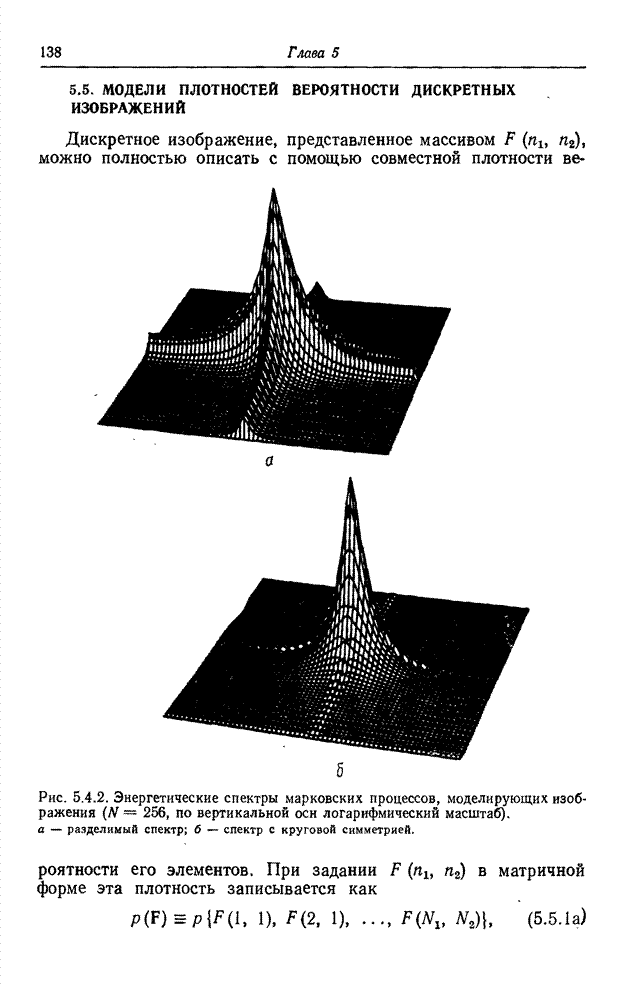
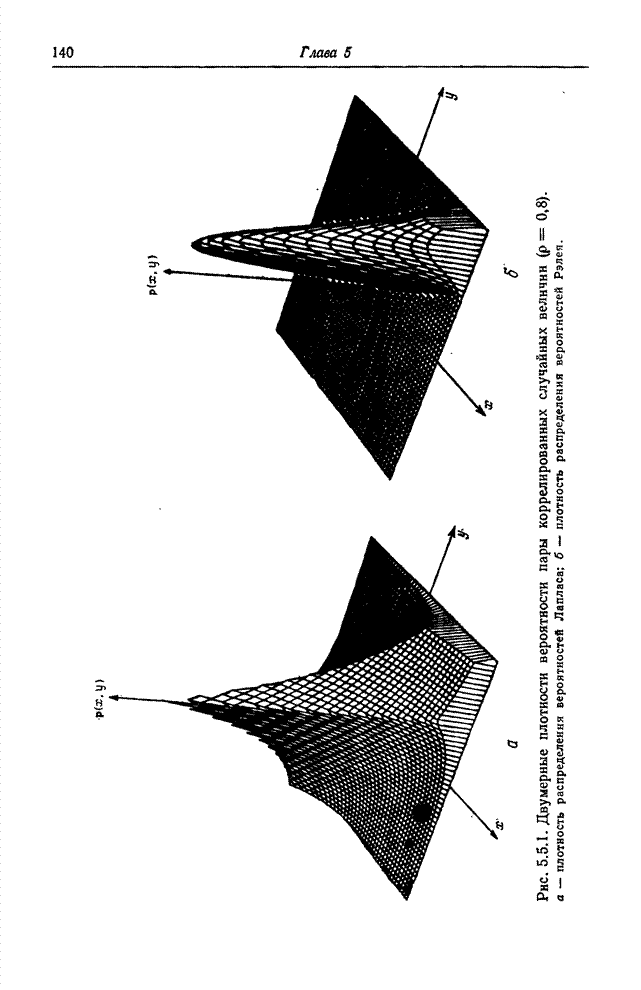
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
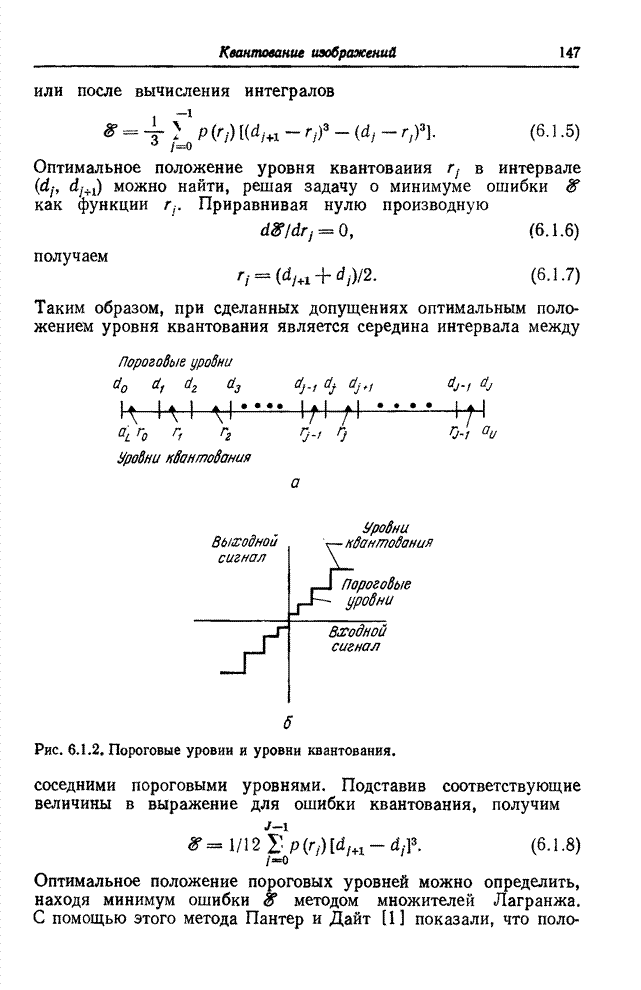
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
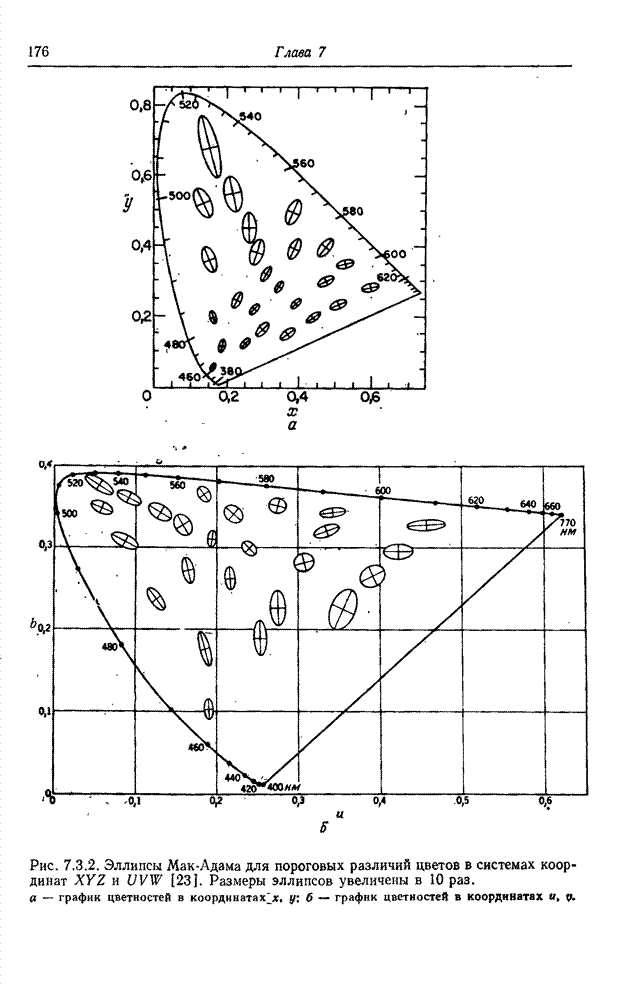
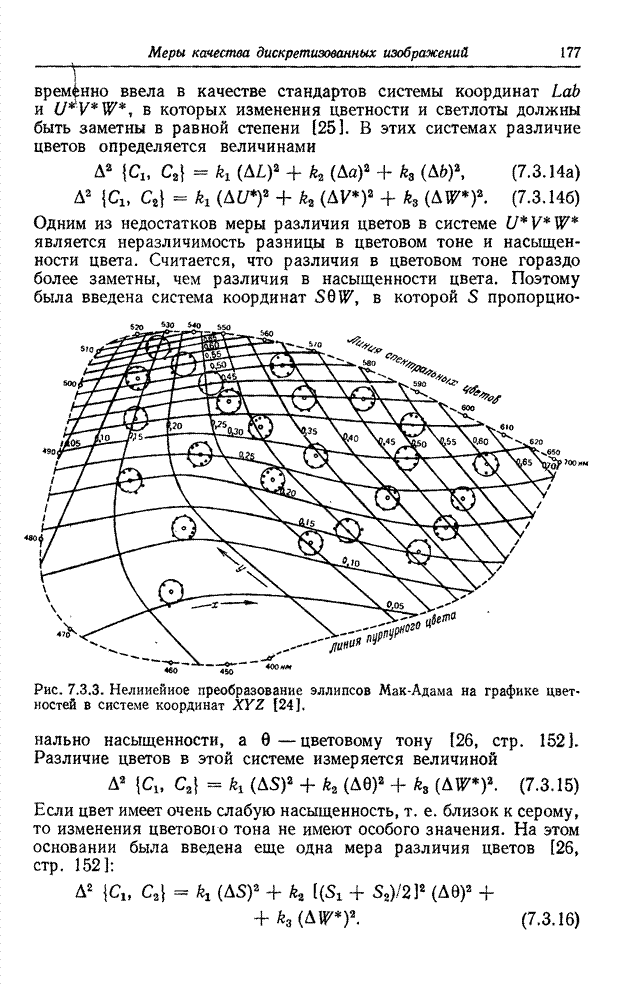
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
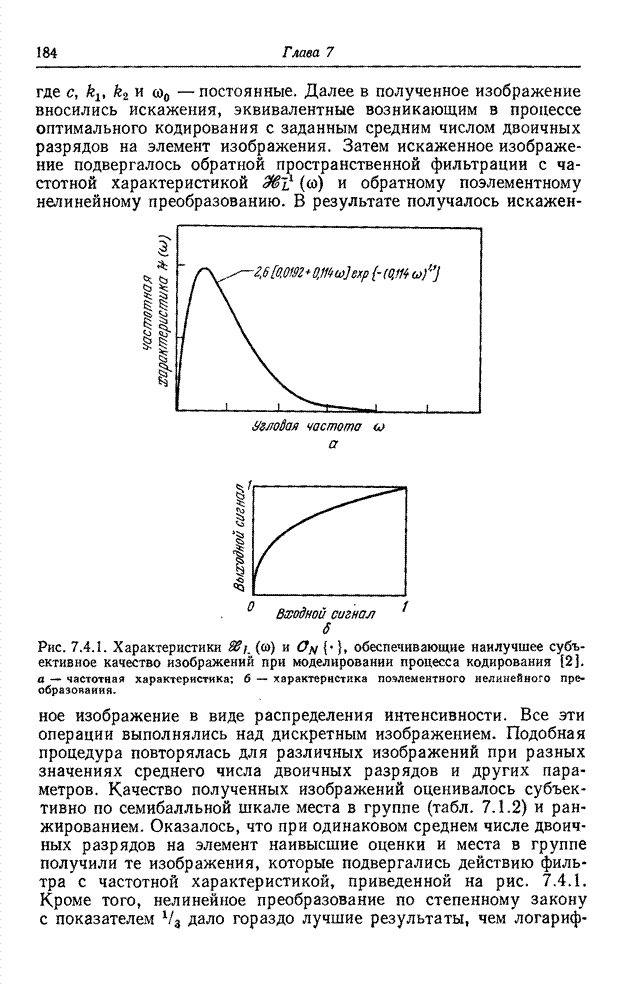
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
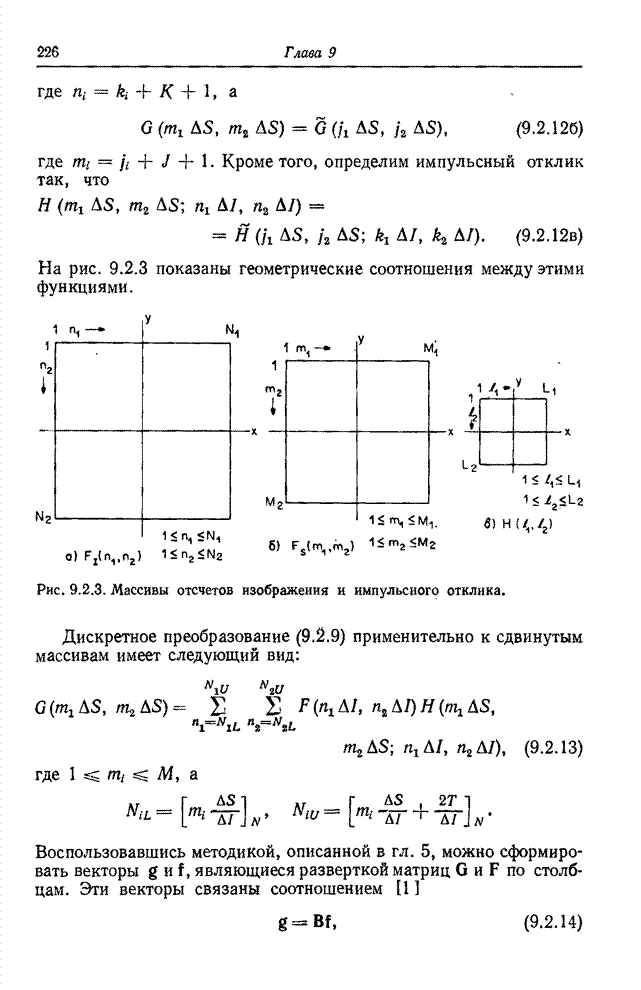
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
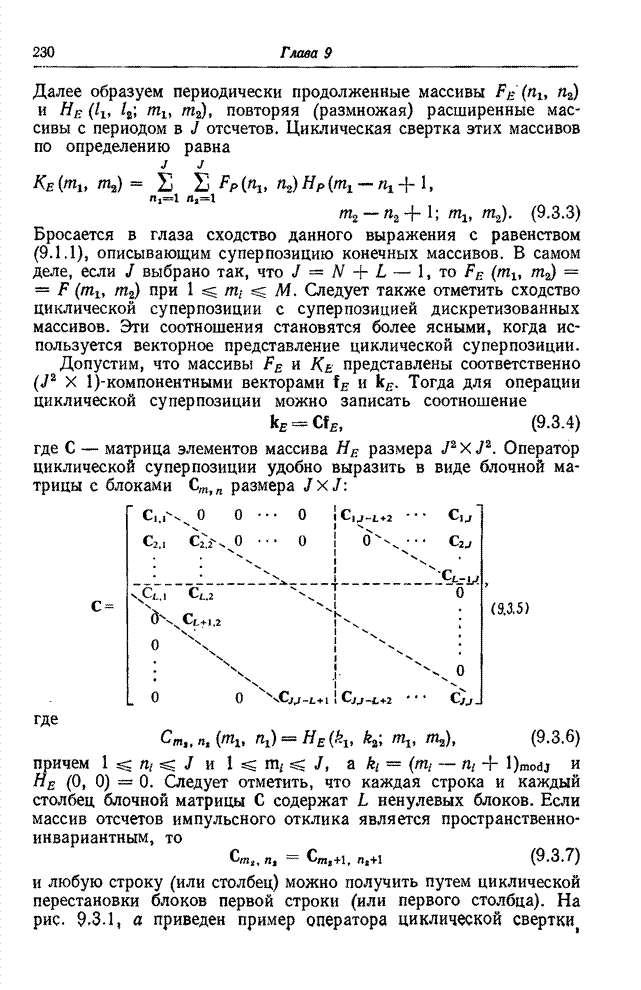
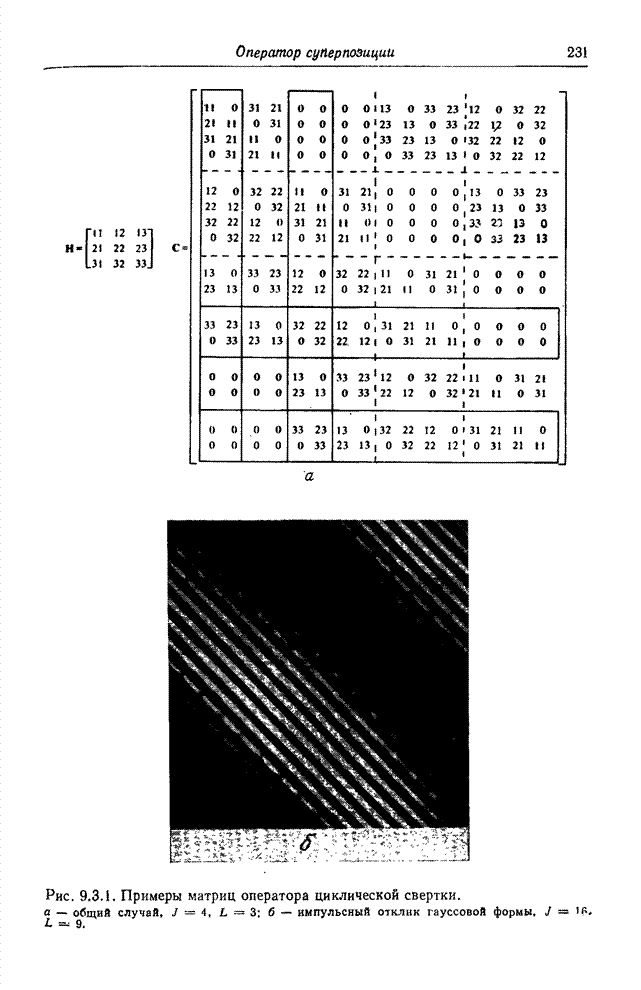
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
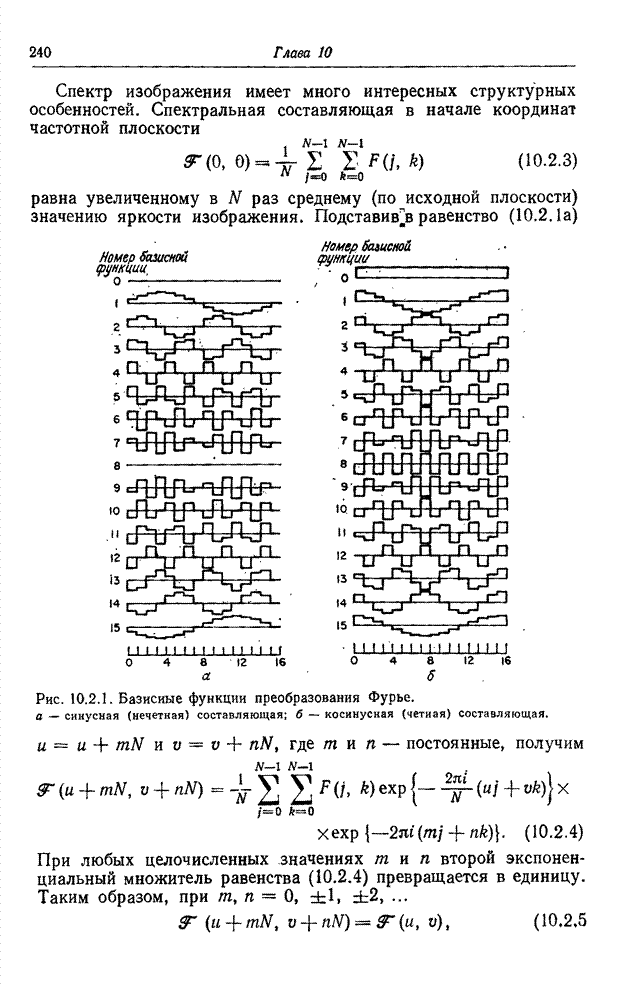
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА