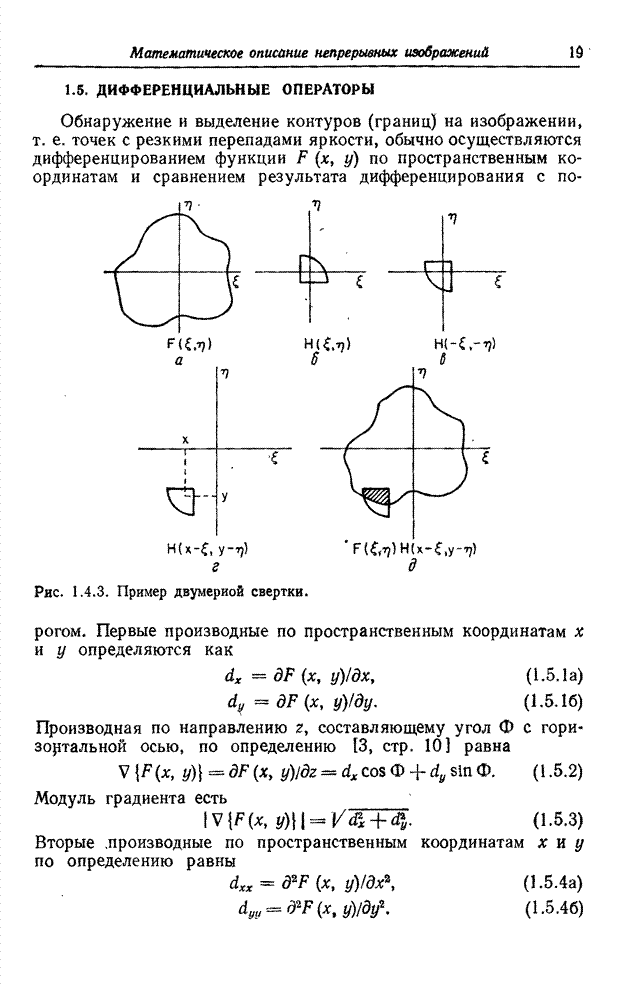
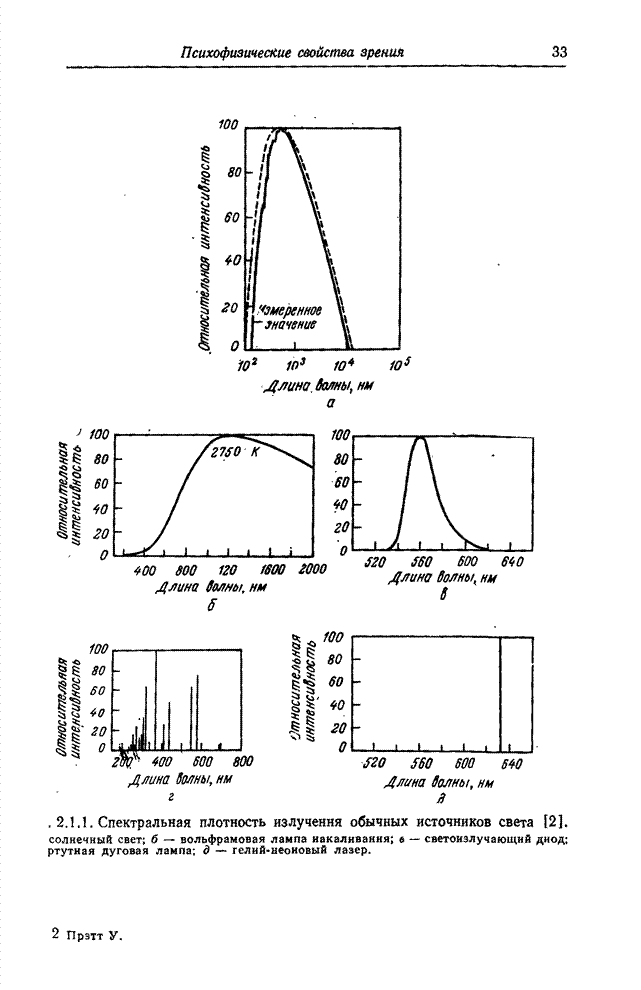
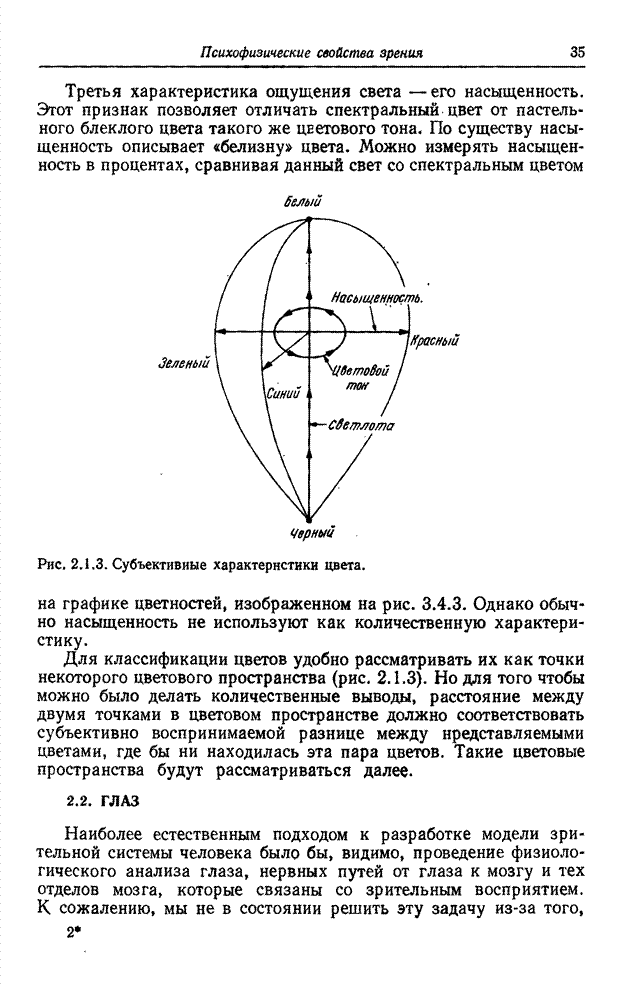
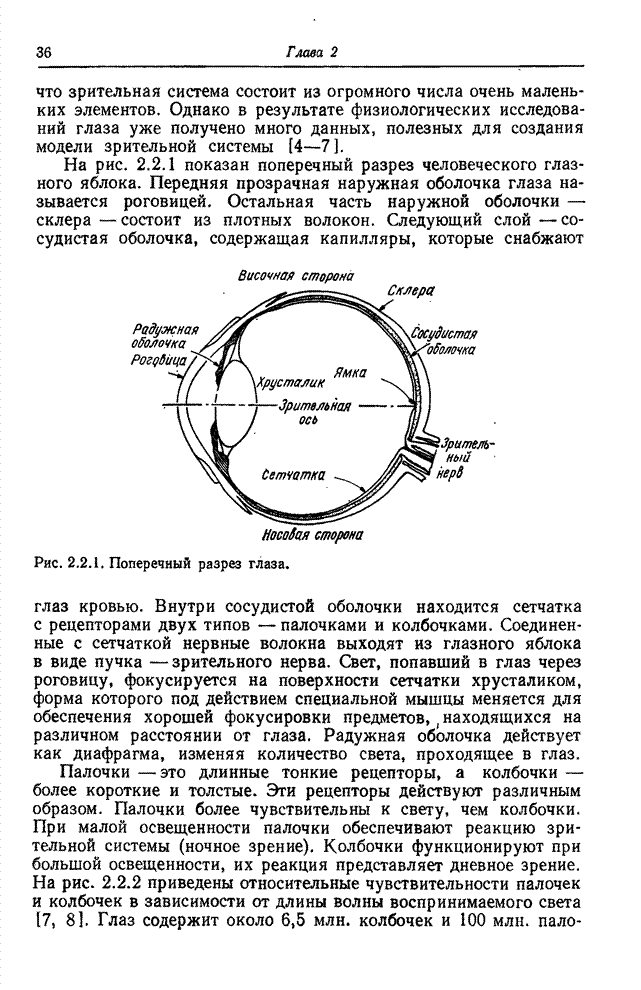
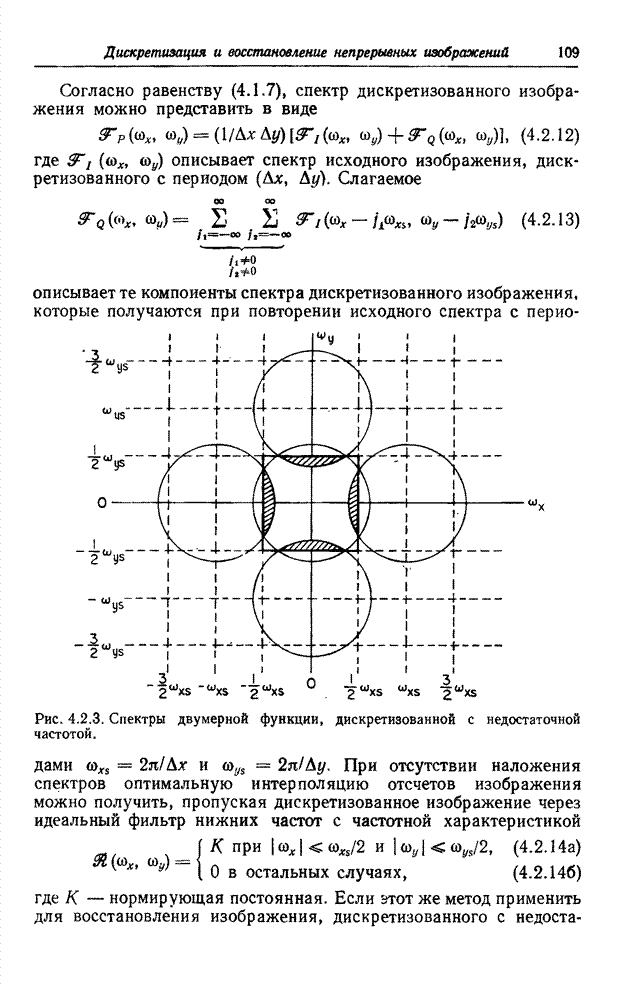
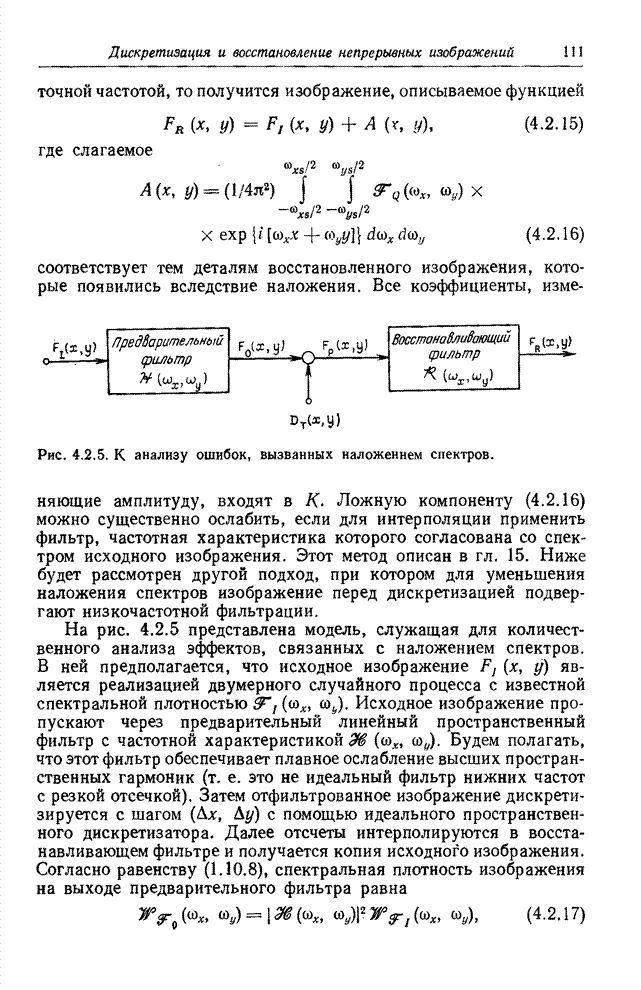
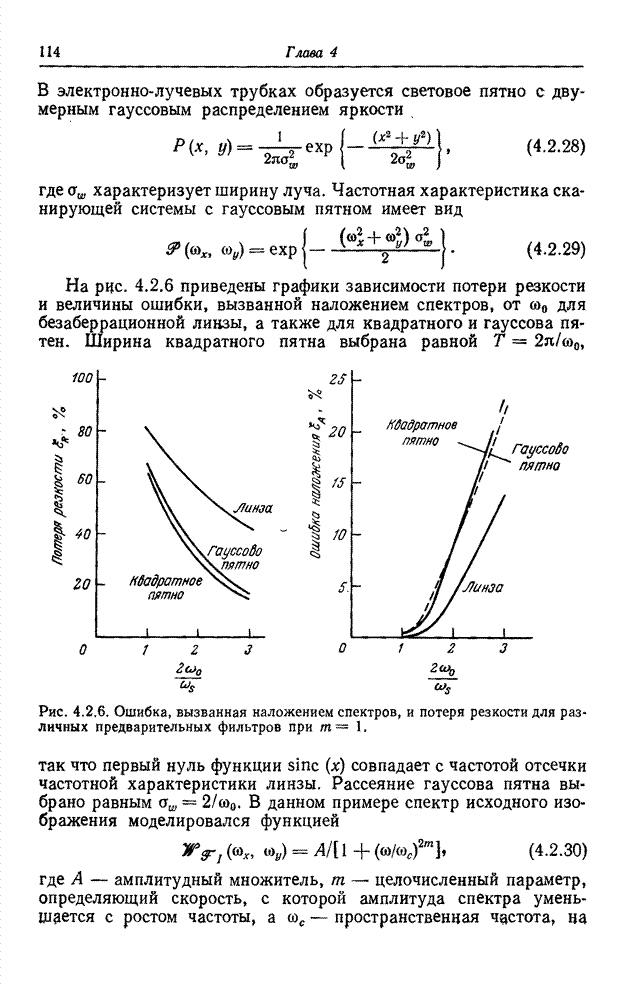
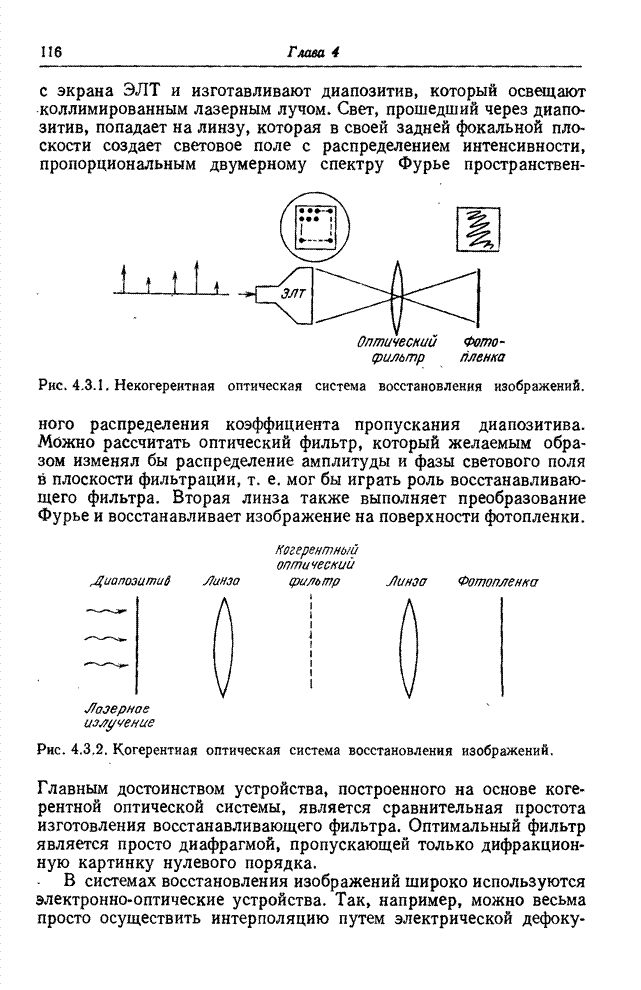
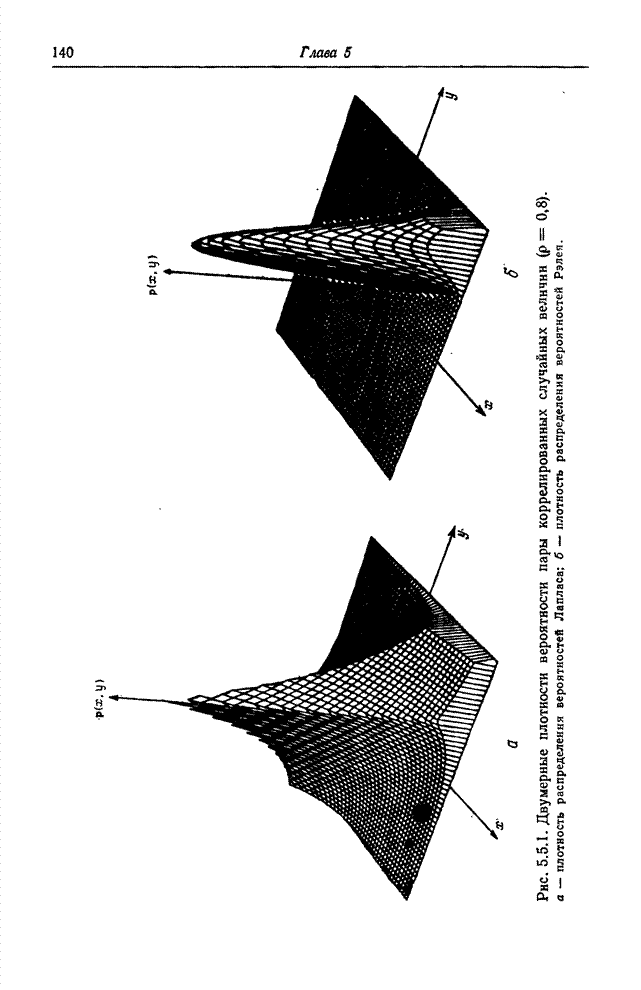
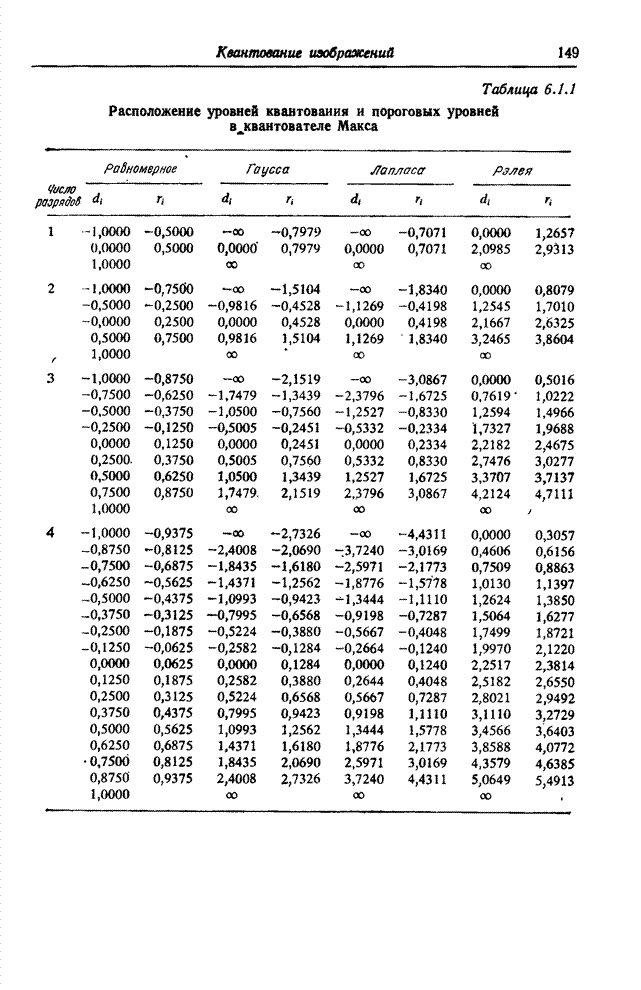
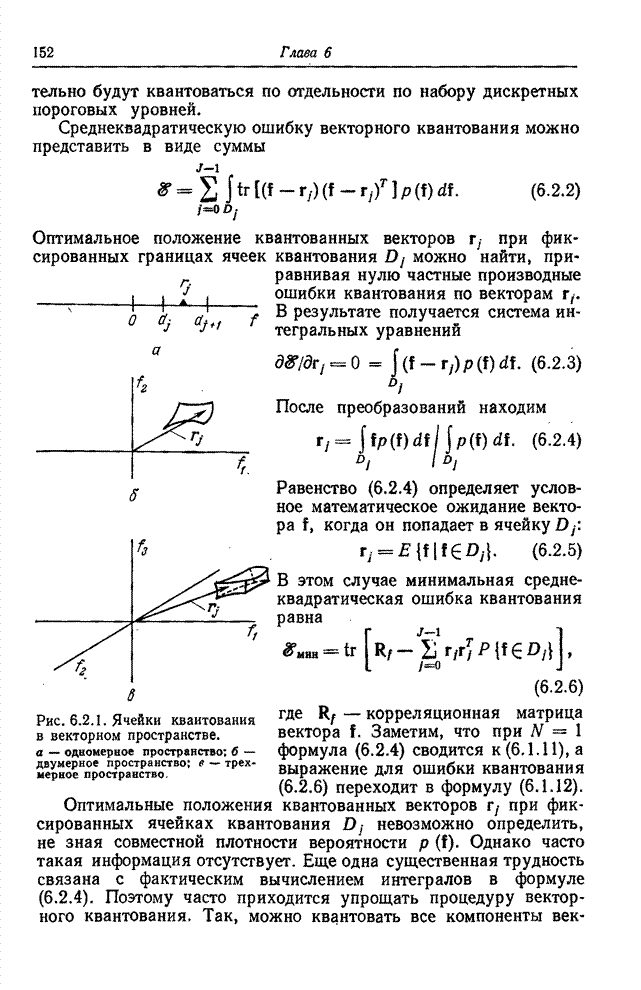
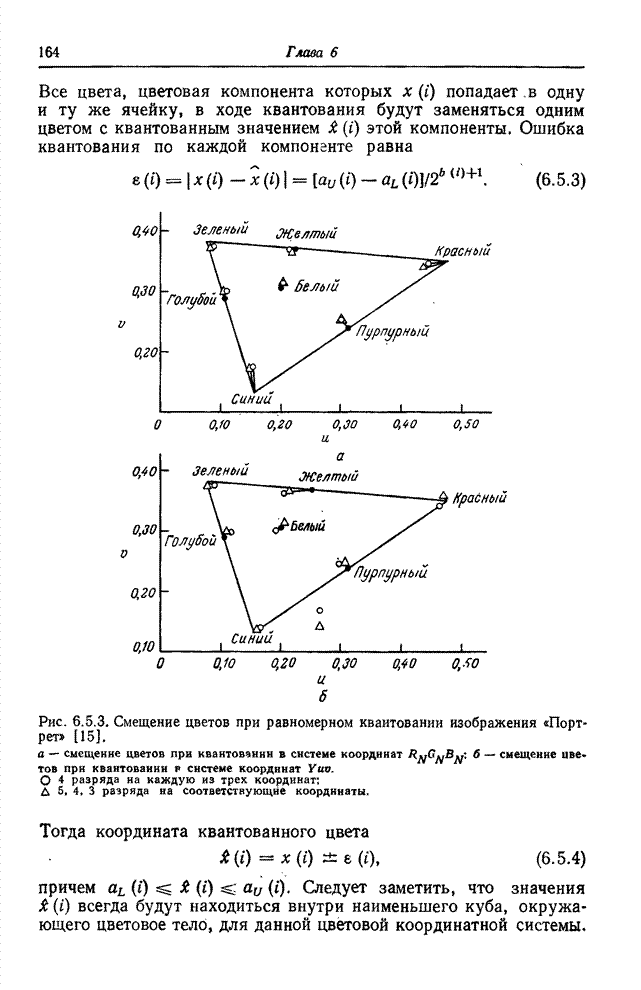
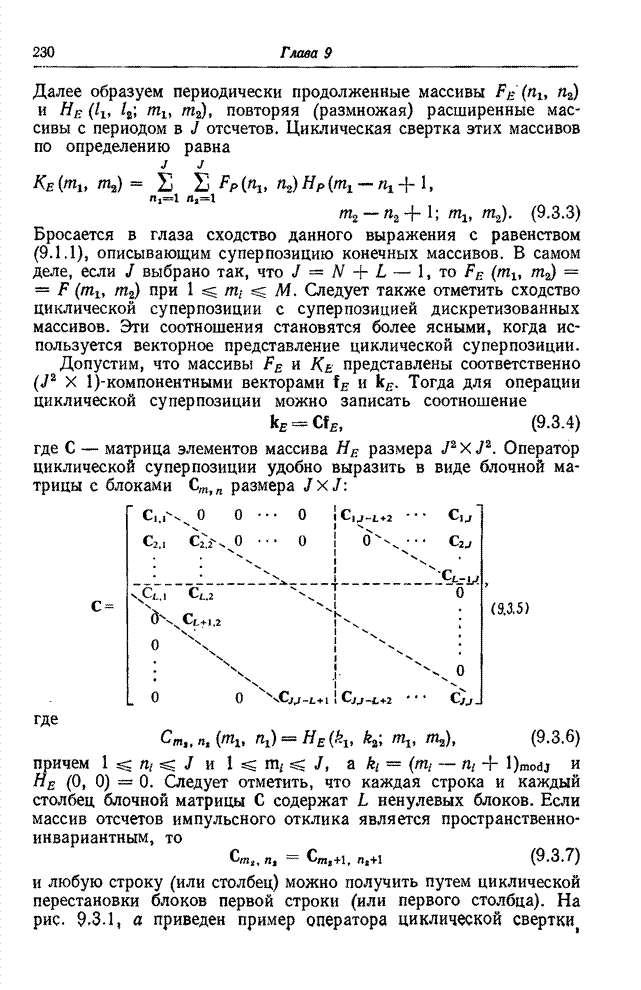
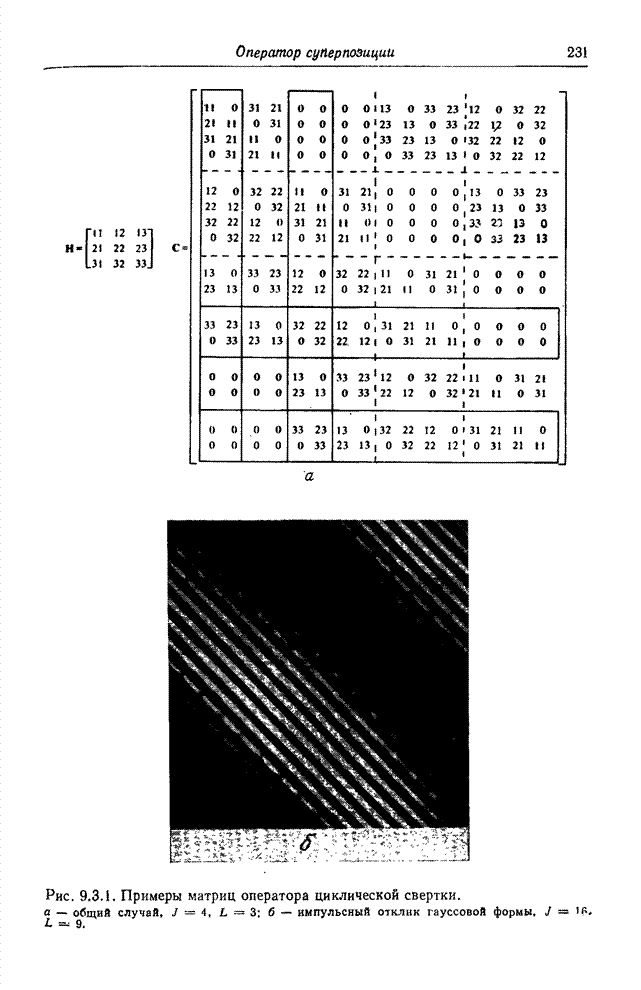
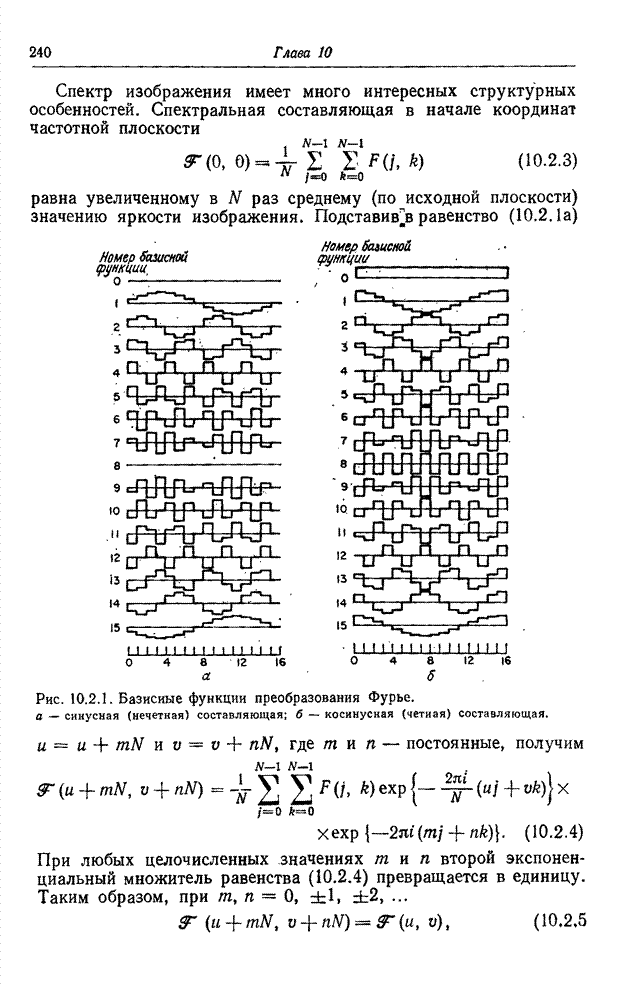
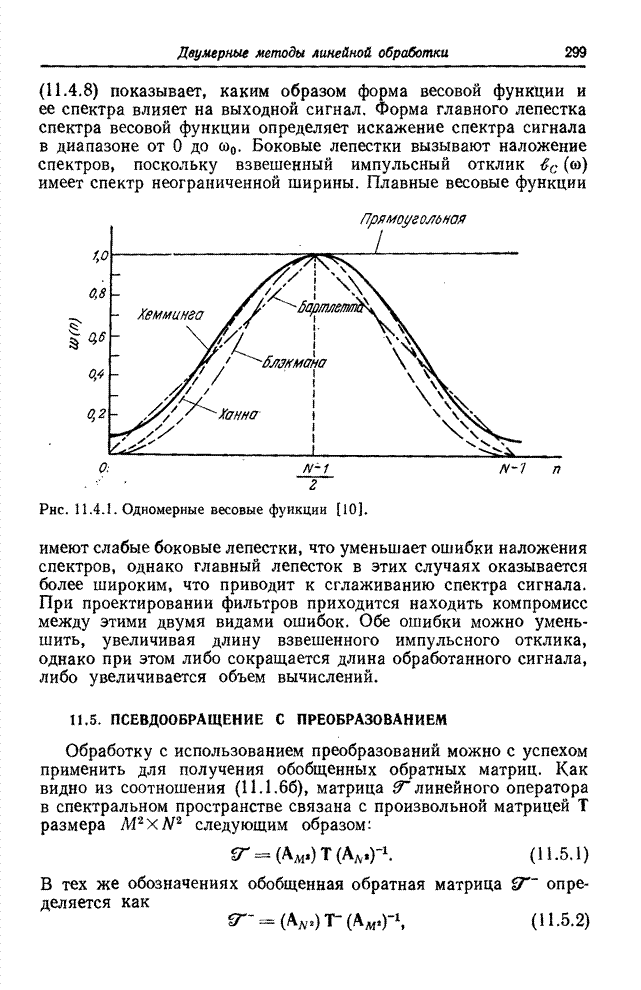
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
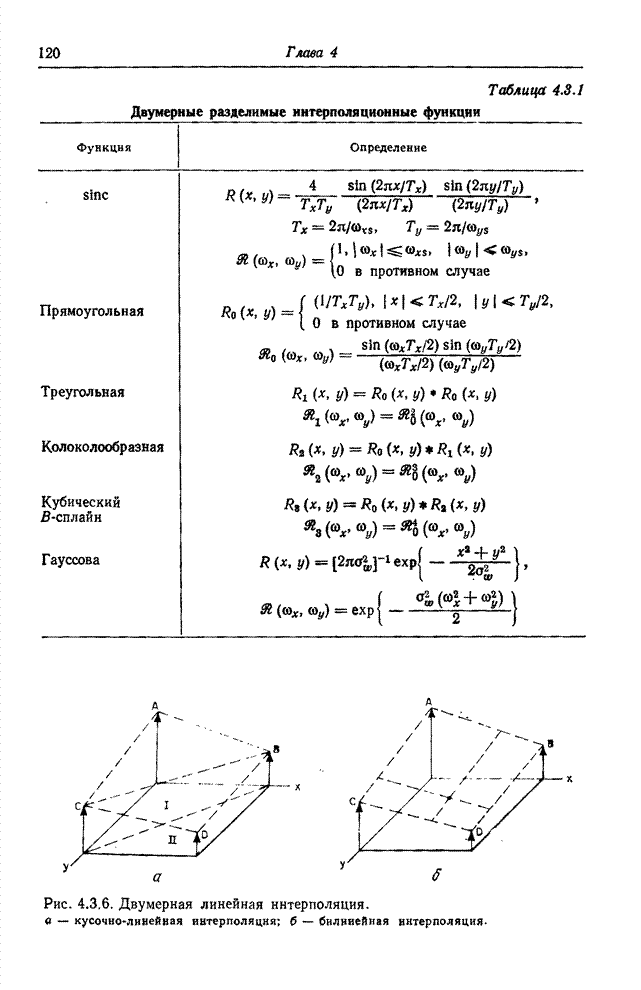
6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
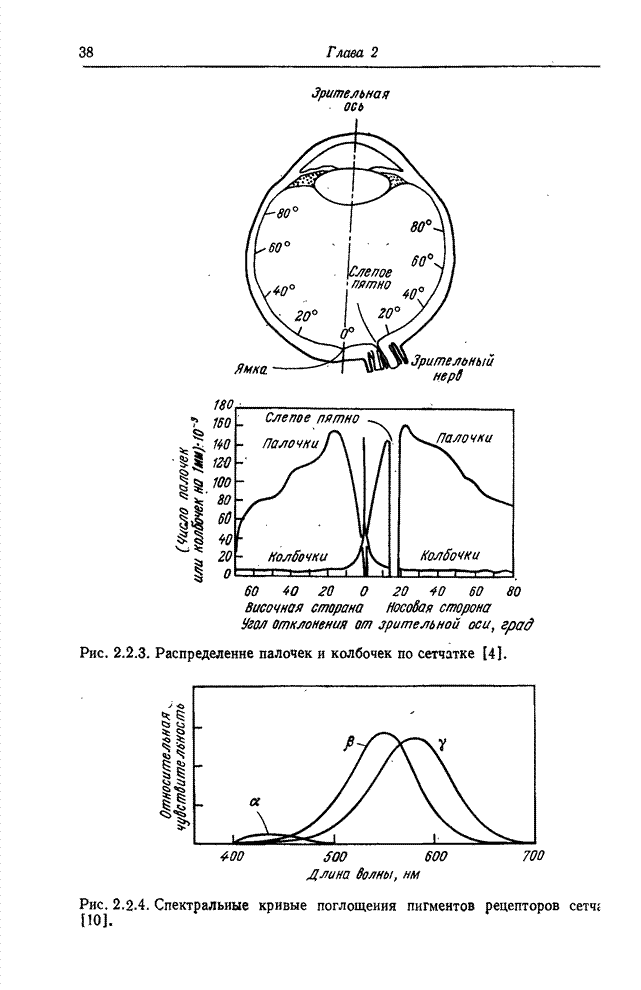
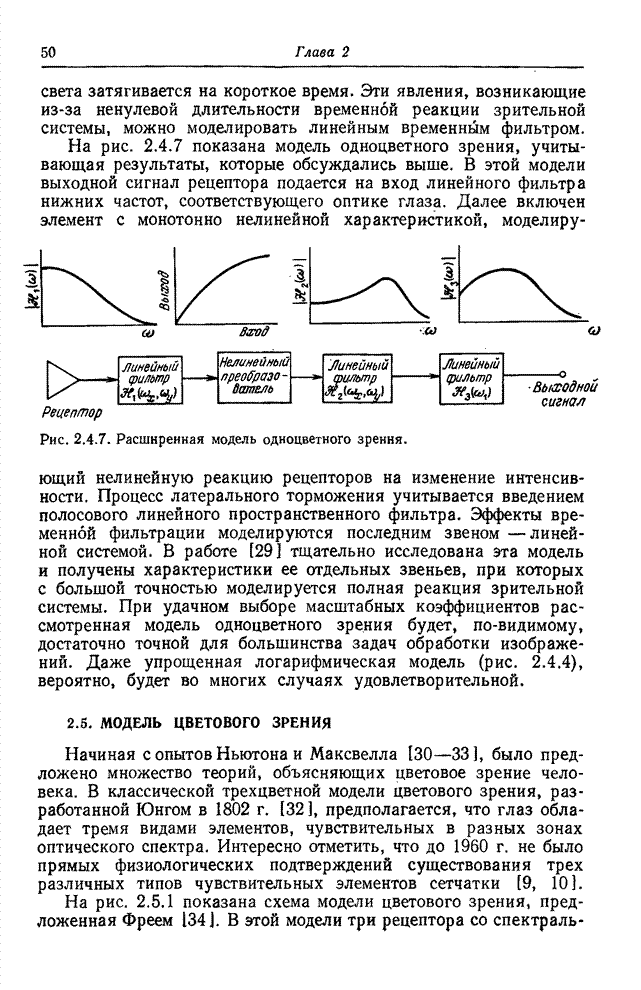
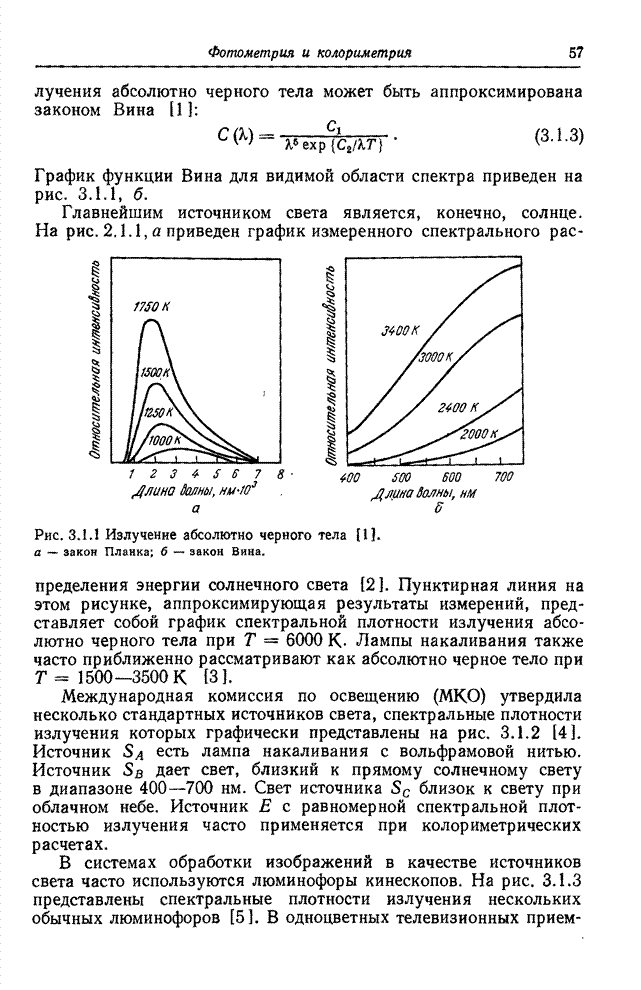
Числа, описывающие изображения (например, представляющие яркость или координаты цвета), обычно вводятся в цифровую вычислительную машину в виде целочисленных кодовых комбинаций, соответствующих уровням квантования отсчетов. Так, яркость одноцветного изображения обычно измеряют с помощью линейной целочисленной шкалы, ограниченной числами 0 (уровень черного) и 255 (уровень белого). Эти целочисленные кодовые комбинации, однако, не следует рассматривать как арифметические величины. Перед обработкой в машине кодовые комбинации следует преобразовать в действительные десятичные числа, соответствующие уровня квантования. Если этого не сделать, то можно получить совершенно неверные результаты. Так, если кодовые комбинации — номера уровней — изменяются вдоль шкалы яркостей немонотонно, то их вообще нельзя использовать для обработки. Рассмотрим теперь, что произойдет, если эти комбинации изменяются монотонно и обрабатываются в ЦВМ без преобразования в десятичные числа — значения уровней квантования.
Существуют
две основные формы представления чисел в цифровых вычислительных машинах: как
целое число и как действительное число. Целые числа изменяются от 0 до
некоторого максимального значения. Так, в 16-разрядной мини-ЭВМ наибольшее
положительное целое число равно 32 768 (![]() ). Если результат арифметической
операции определен как целое число, а в результате получается дробное число, то
дробная часть просто отбрасывается. Отношение 8/3, например, будет представлено
как целое число 2 без десятичной точки и знаков после нее. Если обрабатываемые
величины определены как действительные числа, то дробная часть итога операции
будет сохраняться и содержать столько знаков, сколько позволяет получить
разрядность машины. Отношение действительных чисел 8./3. будет иметь вид
2.66...66.
). Если результат арифметической
операции определен как целое число, а в результате получается дробное число, то
дробная часть просто отбрасывается. Отношение 8/3, например, будет представлено
как целое число 2 без десятичной точки и знаков после нее. Если обрабатываемые
величины определены как действительные числа, то дробная часть итога операции
будет сохраняться и содержать столько знаков, сколько позволяет получить
разрядность машины. Отношение действительных чисел 8./3. будет иметь вид
2.66...66.

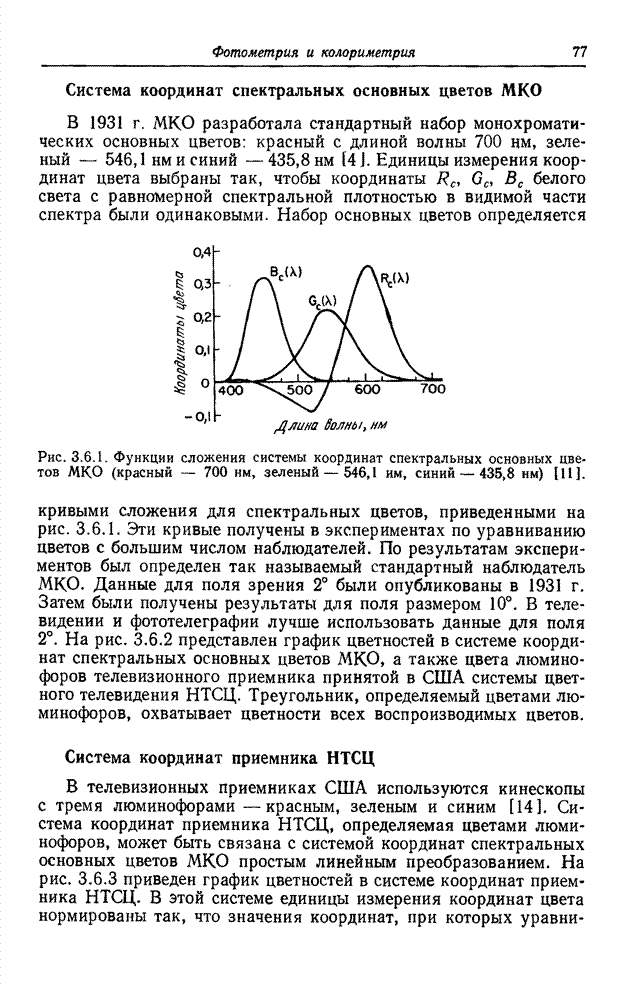
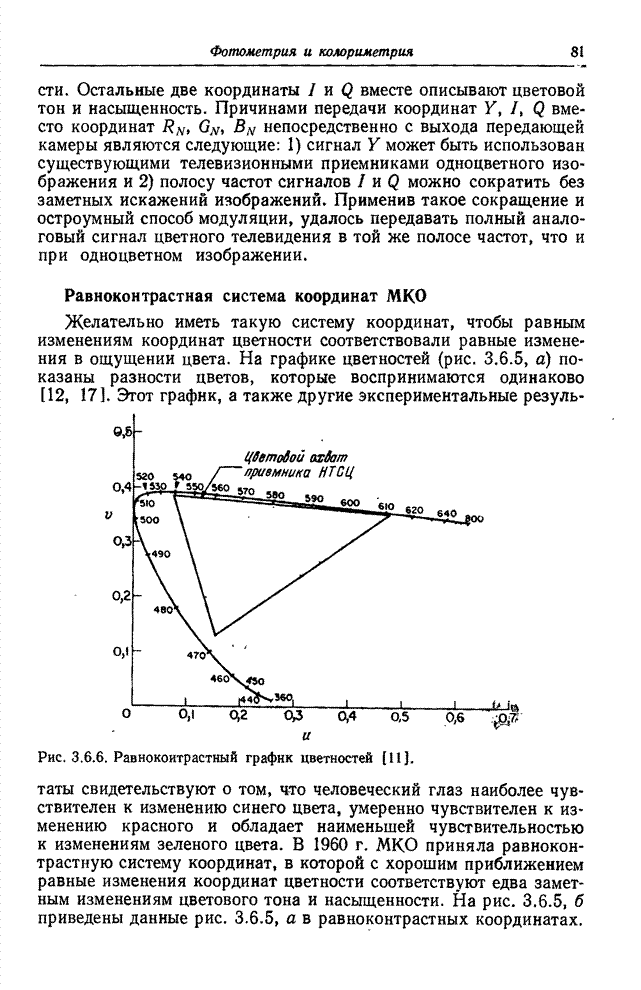
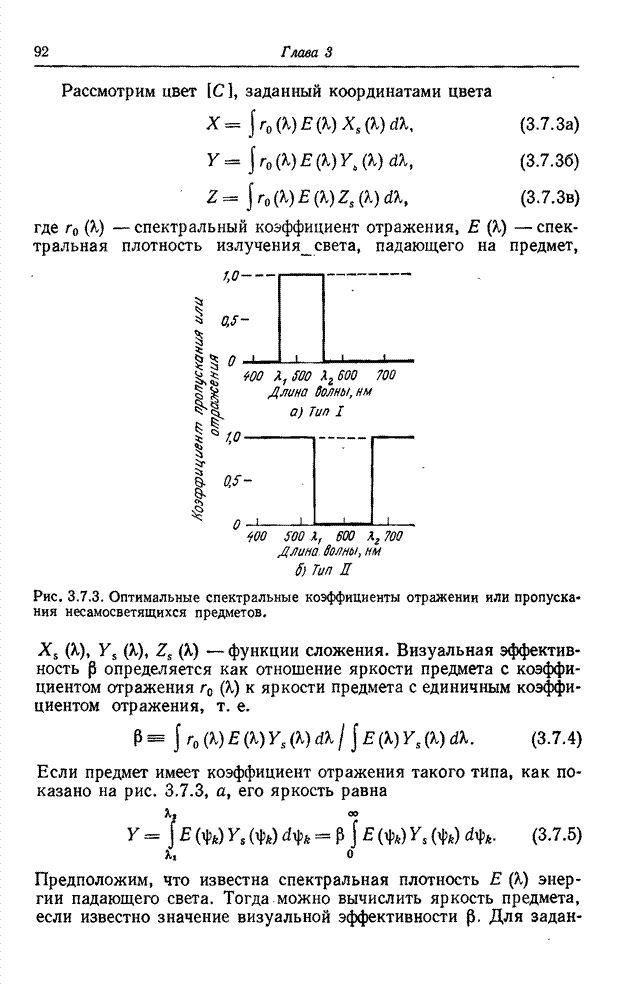
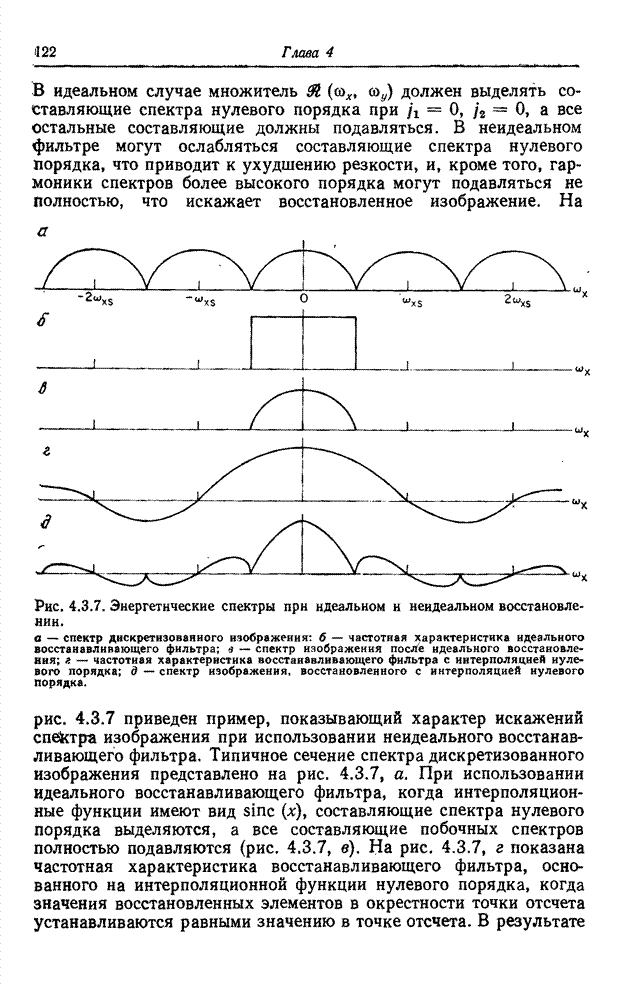
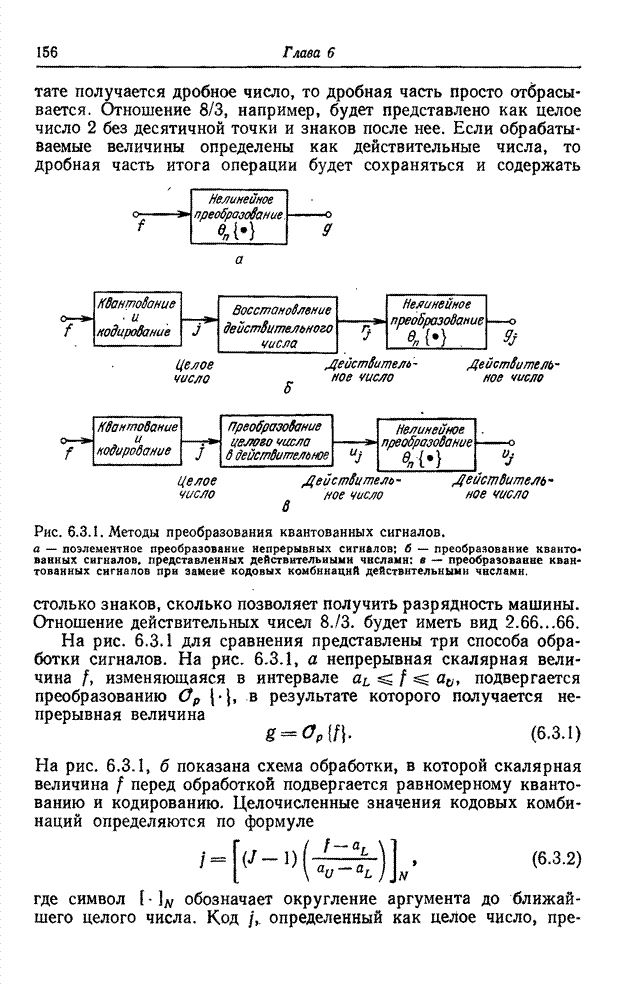
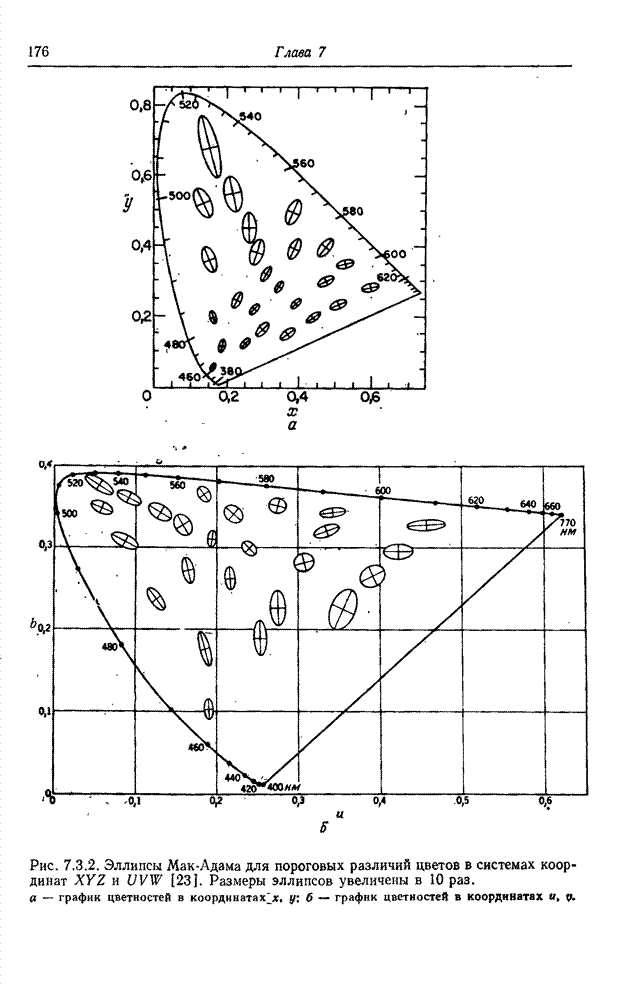
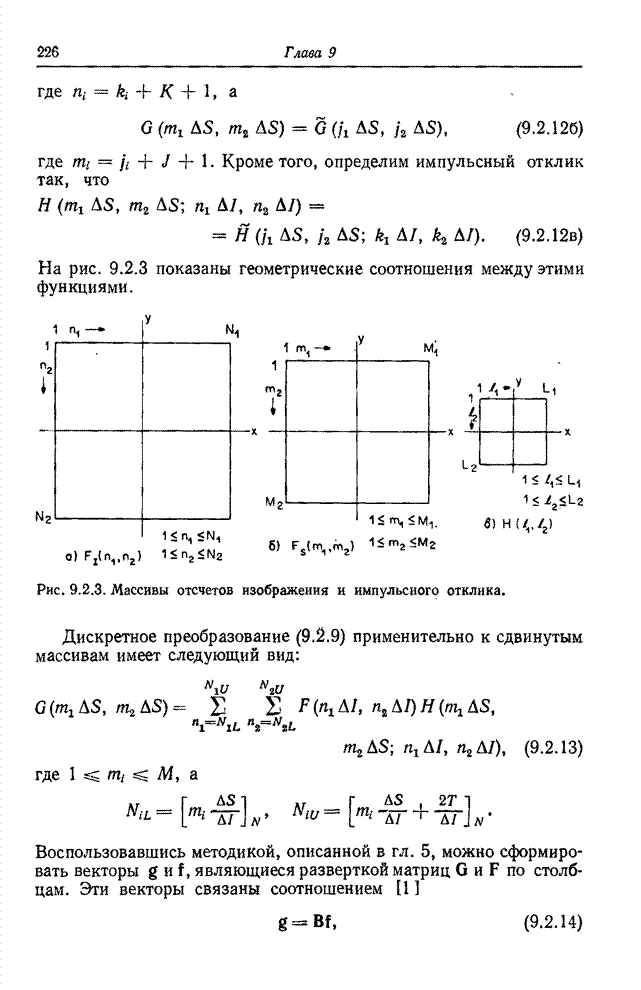
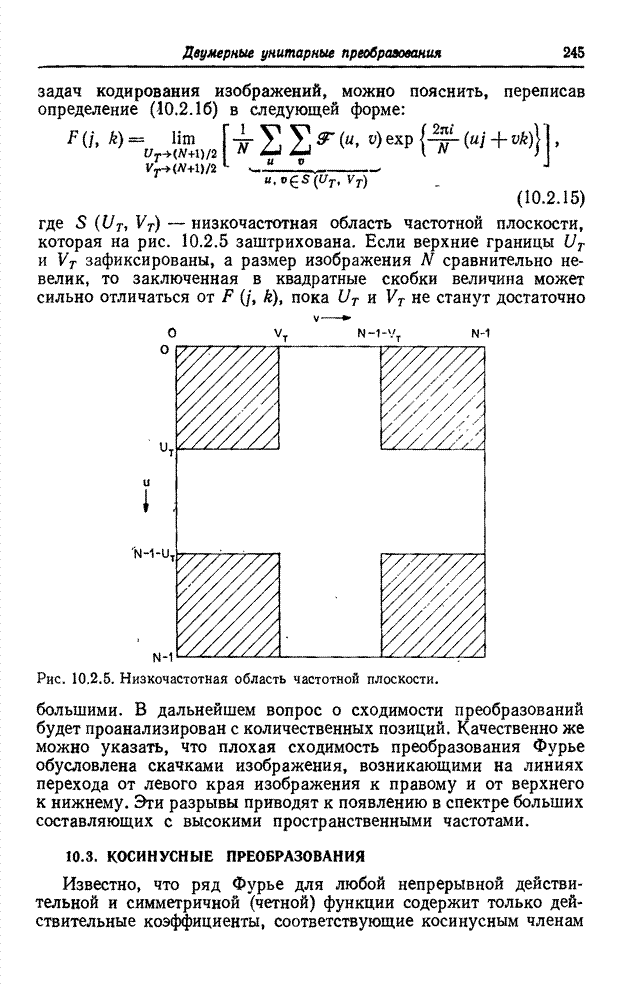
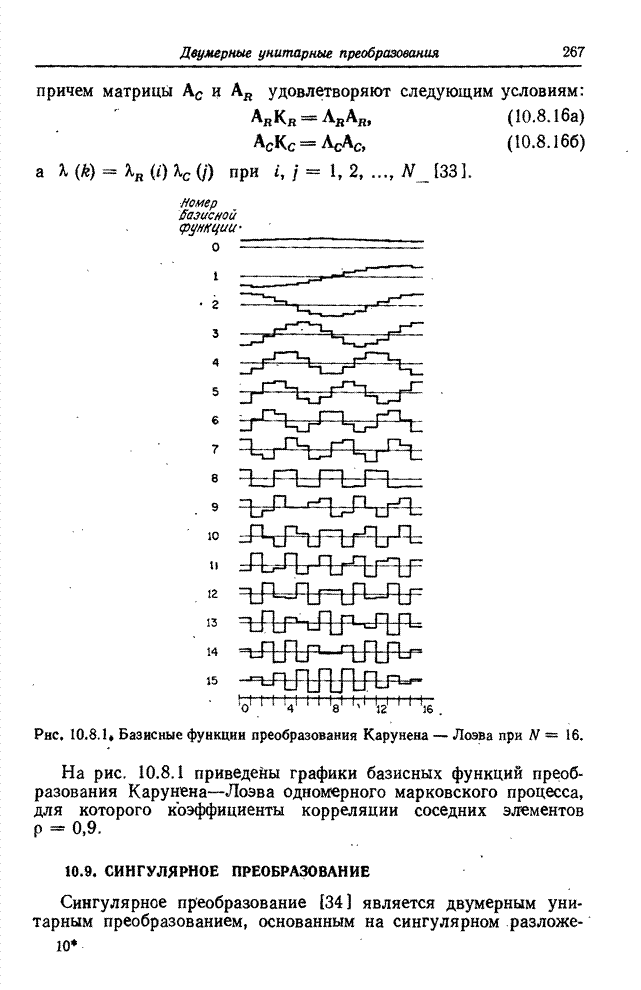
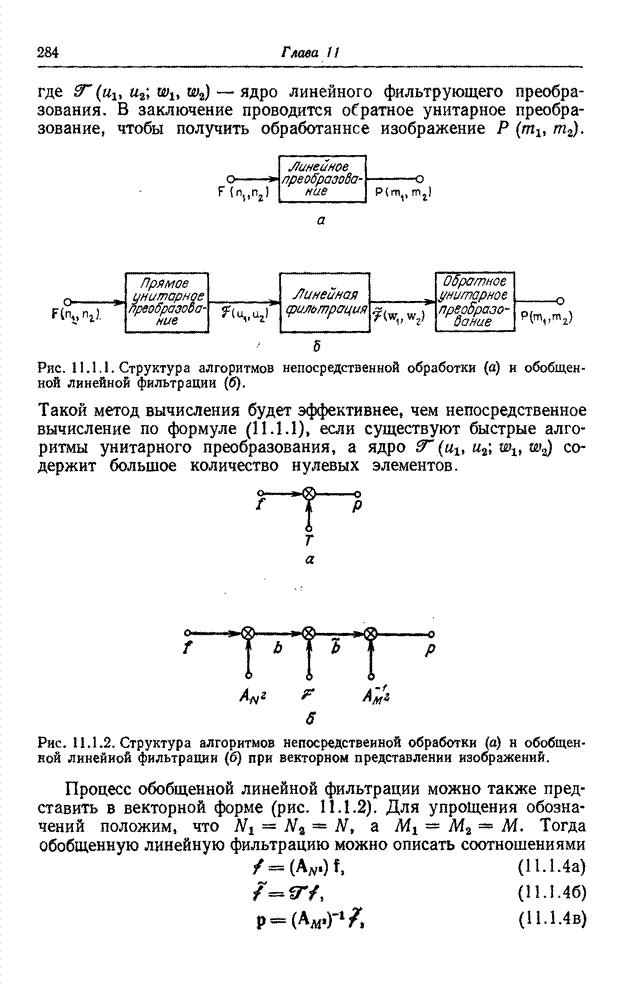
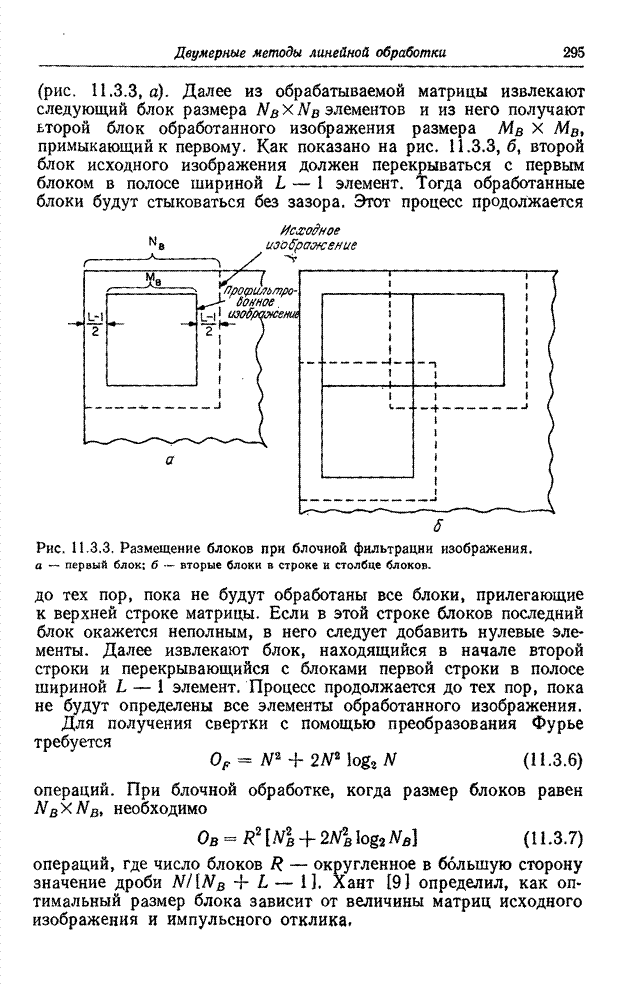
Рис. 6.3.1. Методы преобразования квантованных сигналов: а – поэлементное преобразование непрерывных сигналов; б – преобразование квантованных сигналов, представленных действительными числами; в – преобразование квантованных сигналов при замене кодовых комбинаций действительными числами.
На
рис. 6.3.1 для сравнения представлены три способа обработки сигналов. На рис.
6.3.1, а непрерывная скалярная величина ![]() , изменяющаяся в интервале
, изменяющаяся в интервале ![]() , подвергается
преобразованию
, подвергается
преобразованию ![]() , в результате
которого получается непрерывная величина
, в результате
которого получается непрерывная величина
![]() . (6.3.1)
. (6.3.1)
На
рис. 6.3.1, б показана схема обработки, в которой скалярная величина ![]() перед
обработкой подвергается равномерному квантованию и кодированию. Целочисленные
значения кодовых комбинаций определяются по формуле
перед
обработкой подвергается равномерному квантованию и кодированию. Целочисленные
значения кодовых комбинаций определяются по формуле
 , (6.3.2)
, (6.3.2)
где
символ ![]() ,
обозначает округление аргумента до ближайшего целого числа. Код
,
обозначает округление аргумента до ближайшего целого числа. Код ![]() , определенный как
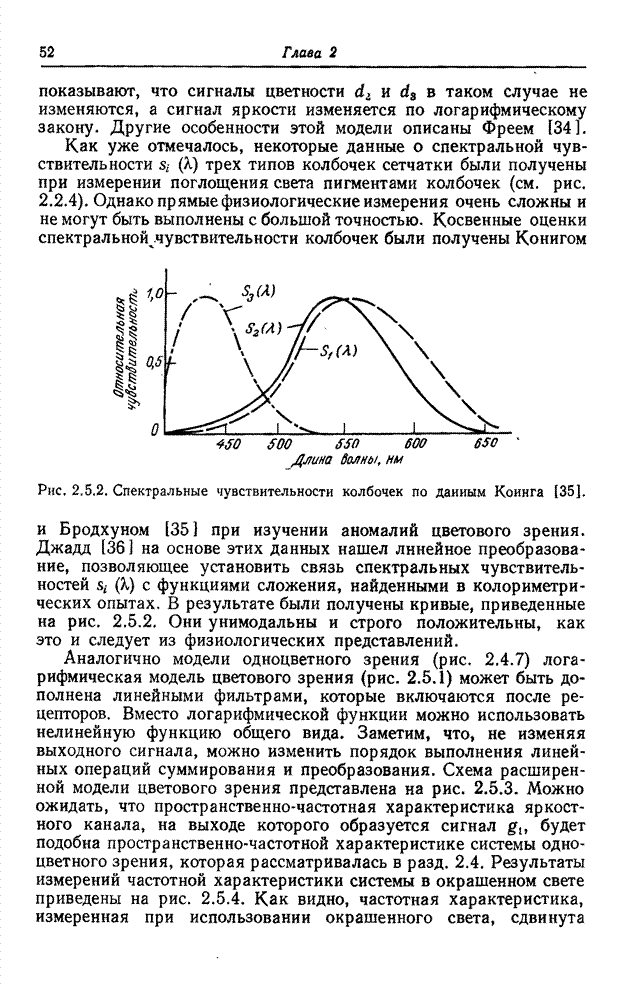
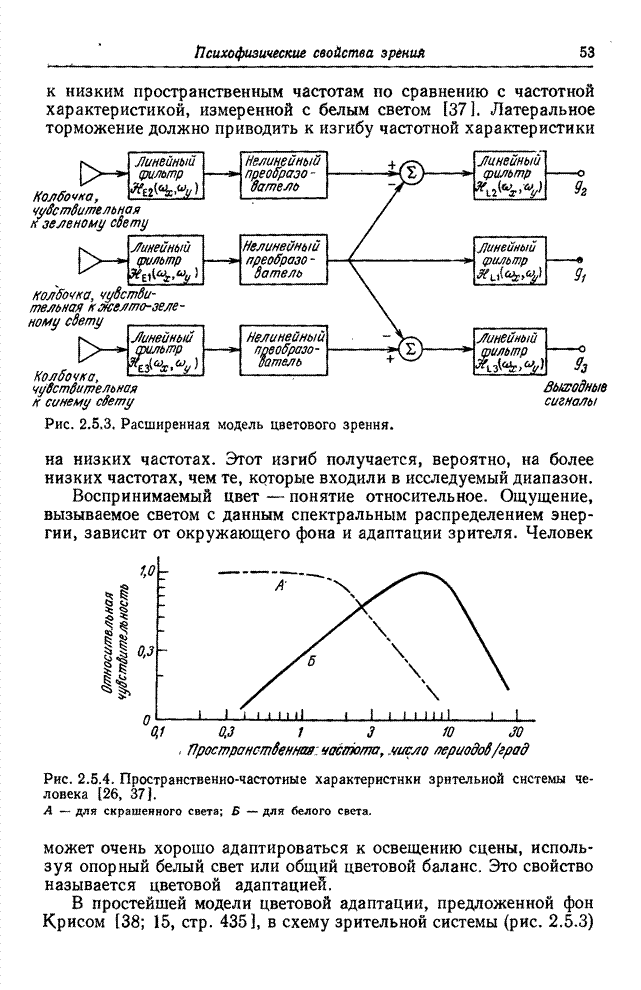
целое число, преобразуется в действительное число
, определенный как
целое число, преобразуется в действительное число ![]() согласно
соотношению
согласно
соотношению
![]() , (6.3.3а)
, (6.3.3а)
или, что то же самое,
![]() . (6.3.3б)
. (6.3.3б)
Далее
с квантованным отсчетом ![]() выполняется необходимая операция и
получается квантованный выходной сигнал
выполняется необходимая операция и
получается квантованный выходной сигнал
![]() , (6.3.4)
, (6.3.4)
отличающийся
от непрерывного выходного сигнала ![]() , фигурирующего в равенстве (6.3.1),
только из-за ошибки квантования исходной величины.
, фигурирующего в равенстве (6.3.1),
только из-за ошибки квантования исходной величины.
К
сожалению, часто обработку квантованных сигналов производят неправильно — по
схеме, приведенной на рис. 6.3.1, в. Кодовая комбинация ![]() , рассматриваемая как целое
число, преобразуется в действительное число
, рассматриваемая как целое
число, преобразуется в действительное число ![]() принимающее
значения
принимающее
значения ![]() . После этого по
формуле
. После этого по
формуле
![]() (6.3.5)
(6.3.5)
вычисляются
значения выходного сигнала ![]() , определяемые как действительные
числа. В общем случае
, определяемые как действительные
числа. В общем случае ![]() имеет и целую,
и дробную части. Если, например
имеет и целую,
и дробную части. Если, например ![]() , то после
преобразования, состоящего в извлечении квадратного корня с точностью до пятого
знака, получается выходной сигнал
, то после
преобразования, состоящего в извлечении квадратного корня с точностью до пятого
знака, получается выходной сигнал ![]() . Ясно, конечно,
что ошибки квантования входного отсчета
. Ясно, конечно,
что ошибки квантования входного отсчета ![]() проявятся и в выходном отсчете
проявятся и в выходном отсчете ![]() . Однако существуют
более серьезные трудности, если считать, что
. Однако существуют
более серьезные трудности, если считать, что ![]() может служить
сравнительно хорошей аппроксимацией непрерывного выходного сигнала
может служить
сравнительно хорошей аппроксимацией непрерывного выходного сигнала ![]() . Предположим, что
число уровней квантования достаточно велико и поэтому
. Предположим, что
число уровней квантования достаточно велико и поэтому
![]() . (6.3.6)
. (6.3.6)
Тогда выходной сигнал будет равен
![]() , (6.3.7)
, (6.3.7)
где постоянные
![]() , (6.3.8а)
, (6.3.8а)
![]() . (6.3.8б)
. (6.3.8б)
Если
преобразование ![]() линейно, то
линейно, то
![]() (6.3.9)
(6.3.9)
и
![]() . (6.3.10)
. (6.3.10)
Таким
образом, выходной сигнал рассматриваемой системы (рис. 6.3.1, в) будет хорошей
аппроксимацией непрерывного выходного сигнала системы с аналоговой обработкой
(рис. 6.3:1, а), если преобразование, выполняемое в системе, является линейным.
С другой стороны, если это преобразование нелинейно, то аппроксимация одного
сигнала другим обычно оказывается очень плохой. Так, например, обычно логарифм
квантованной переменной ![]() существенно отличается от логарифма
действительного числа
существенно отличается от логарифма
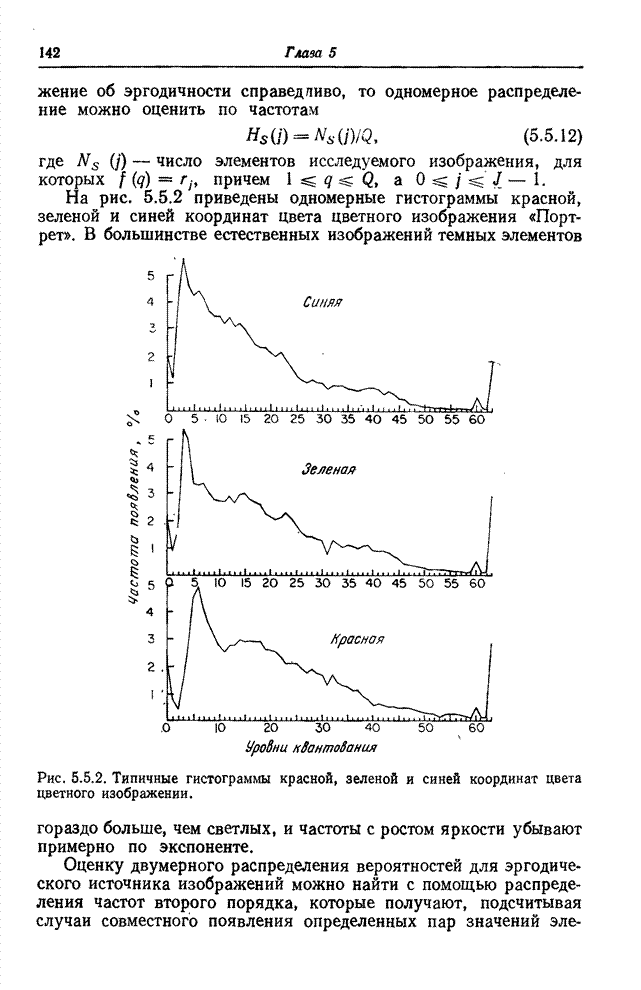
действительного числа ![]() сформированного из кодовой комбинации, которая задает номер уровня квантования для
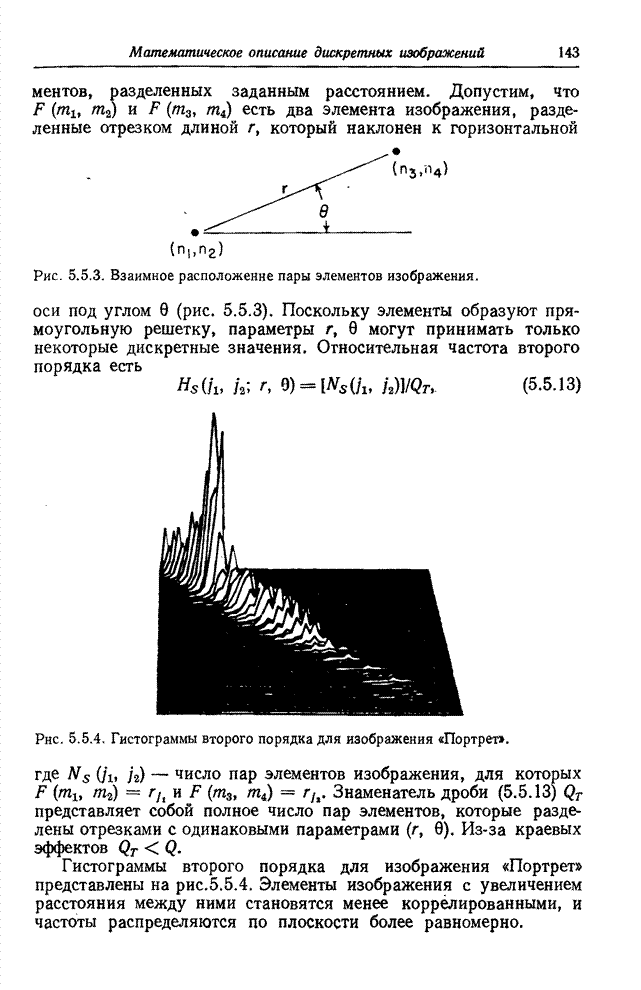
сформированного из кодовой комбинации, которая задает номер уровня квантования для ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
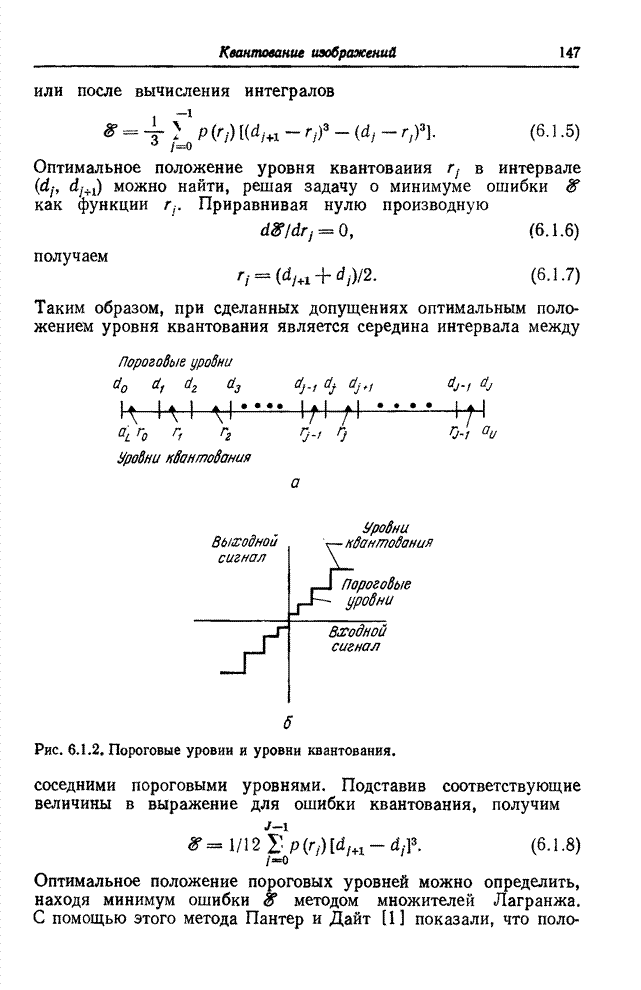
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
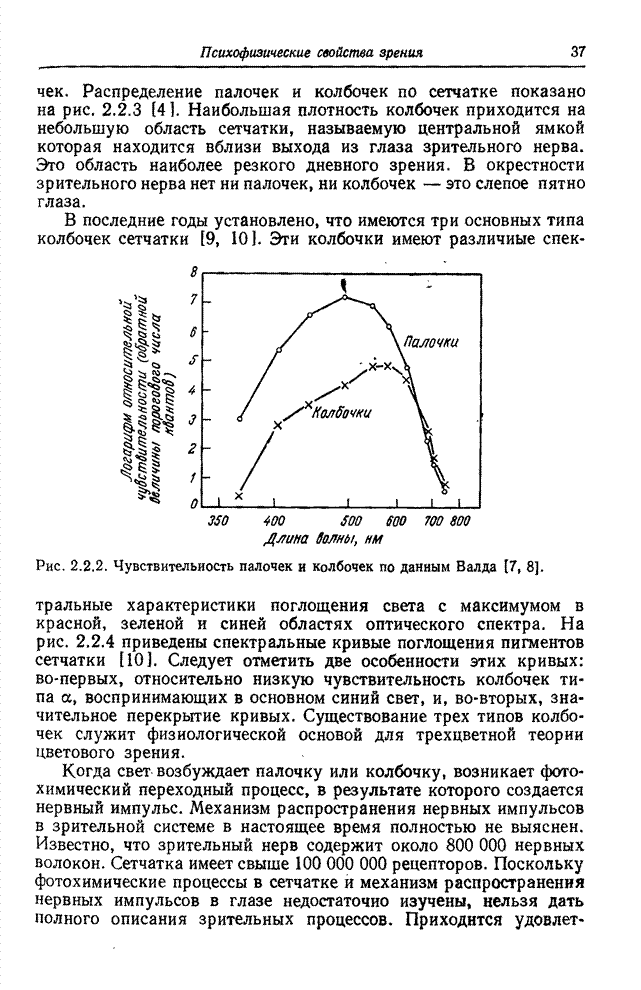
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
- 2.2. ГЛАЗ
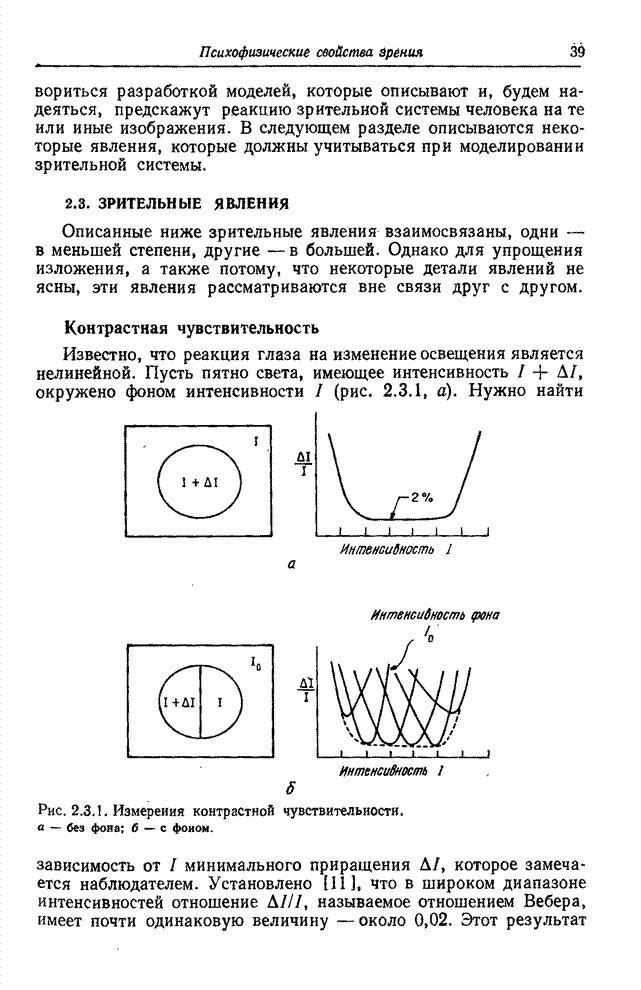
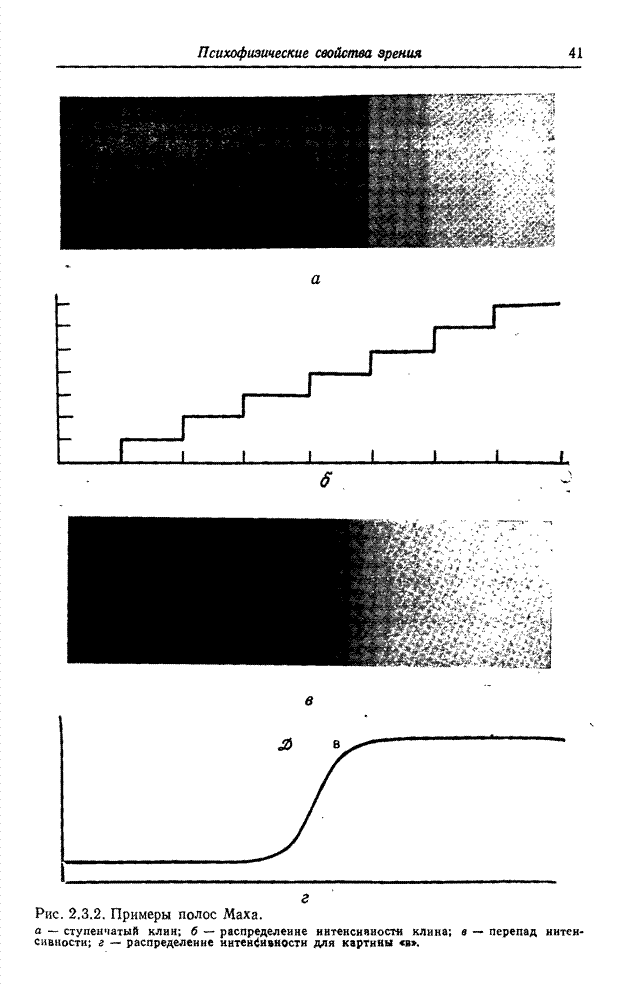
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
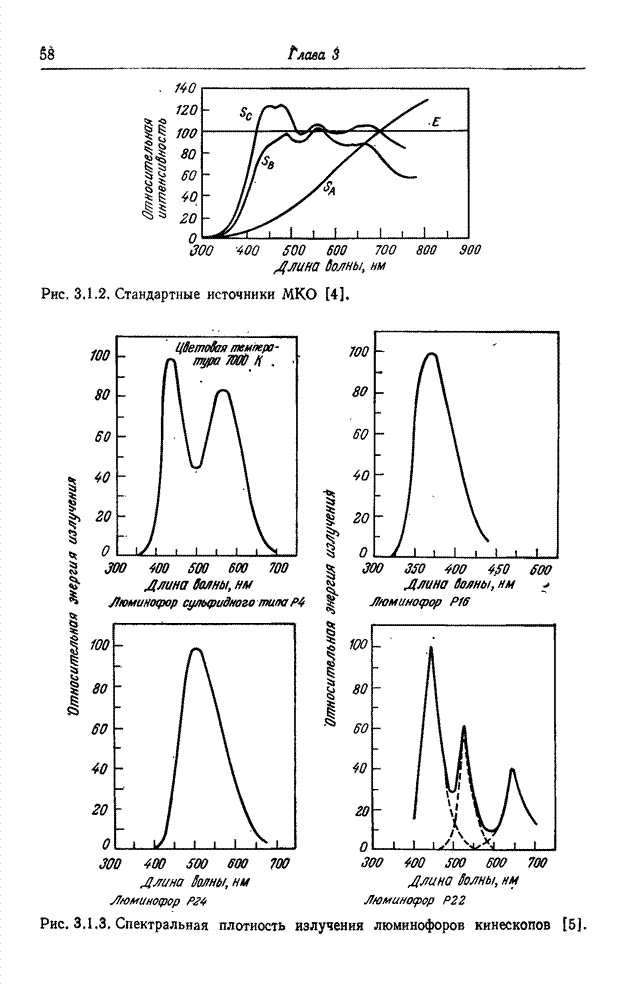
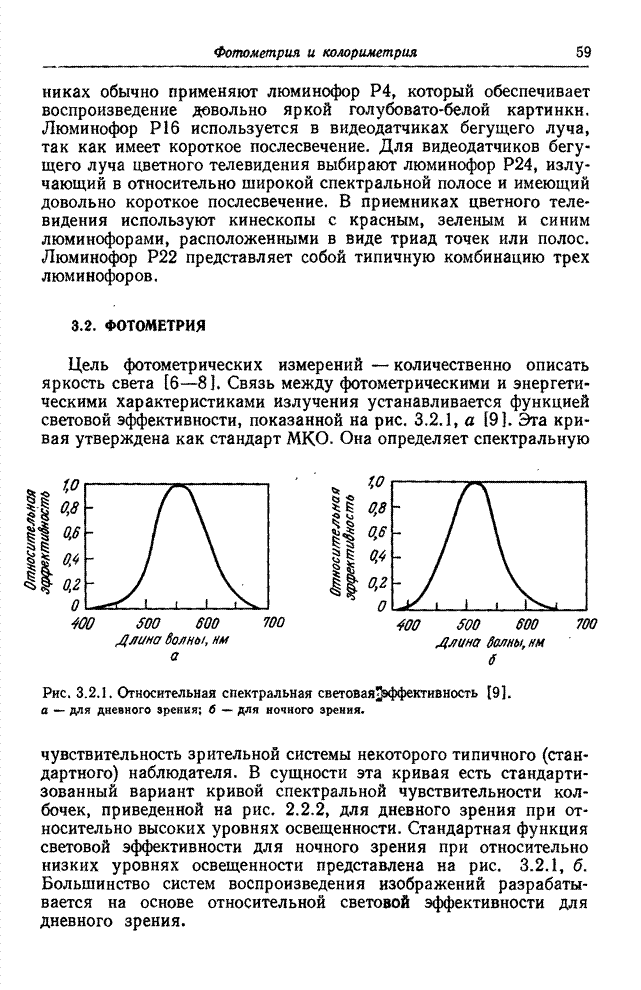
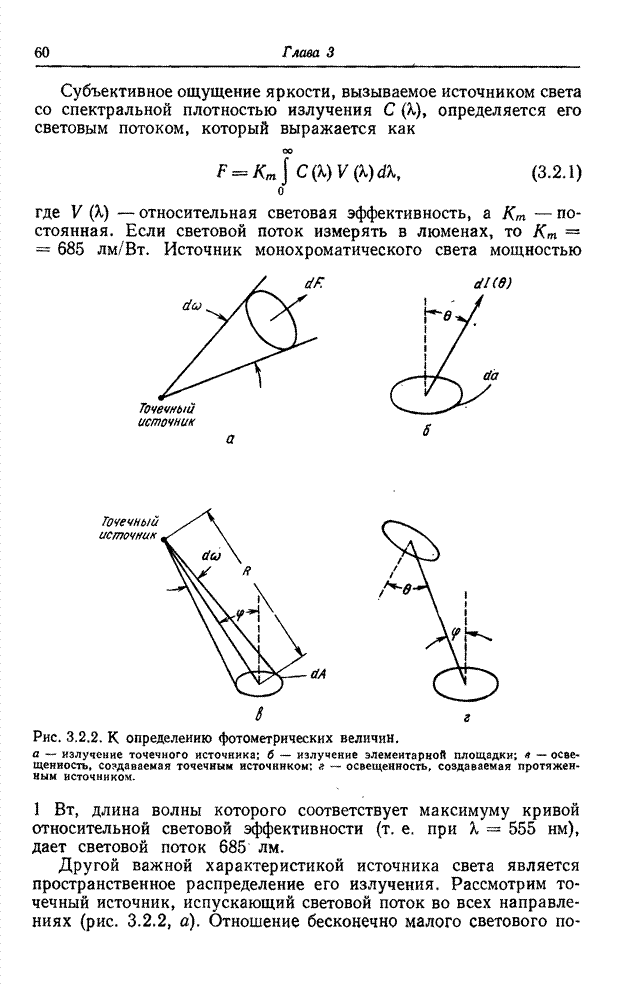
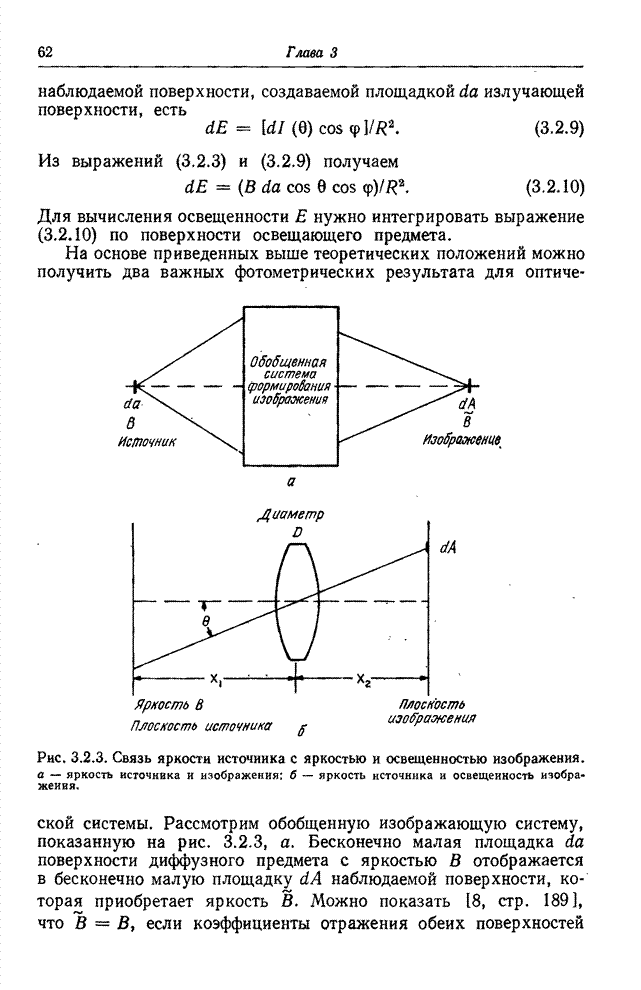
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
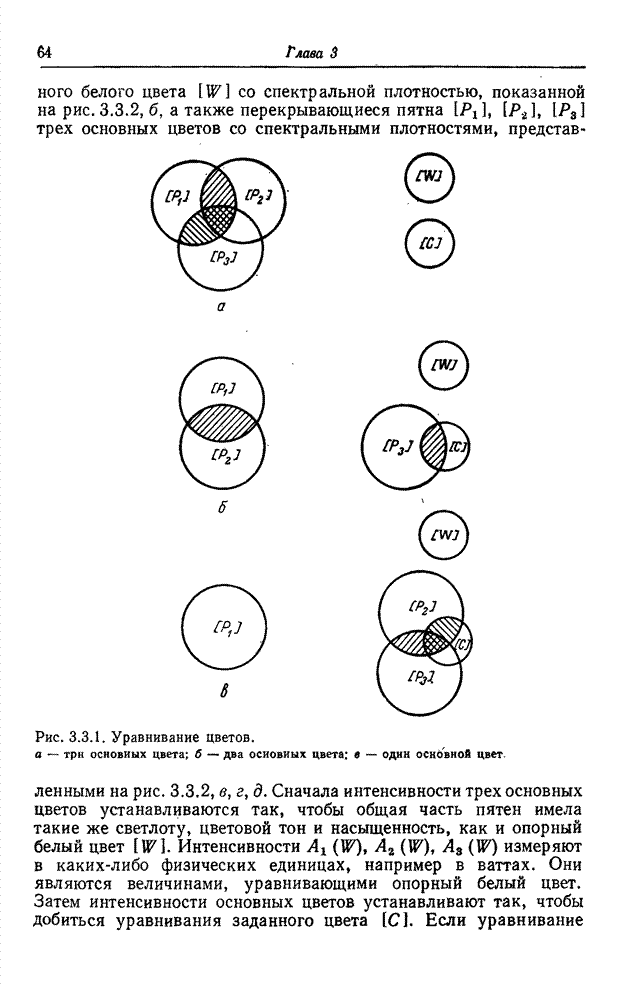
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
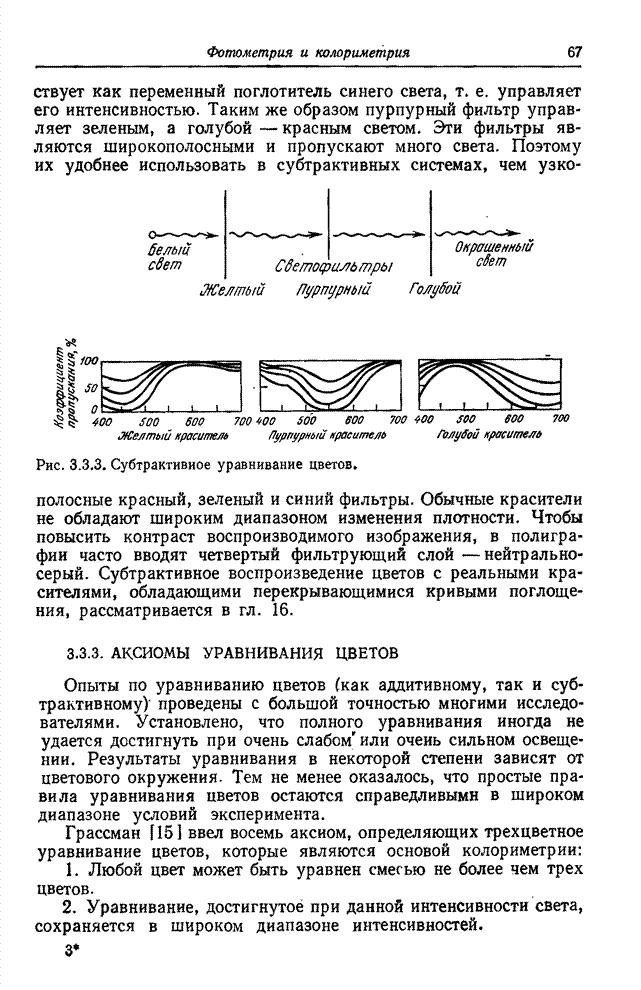
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
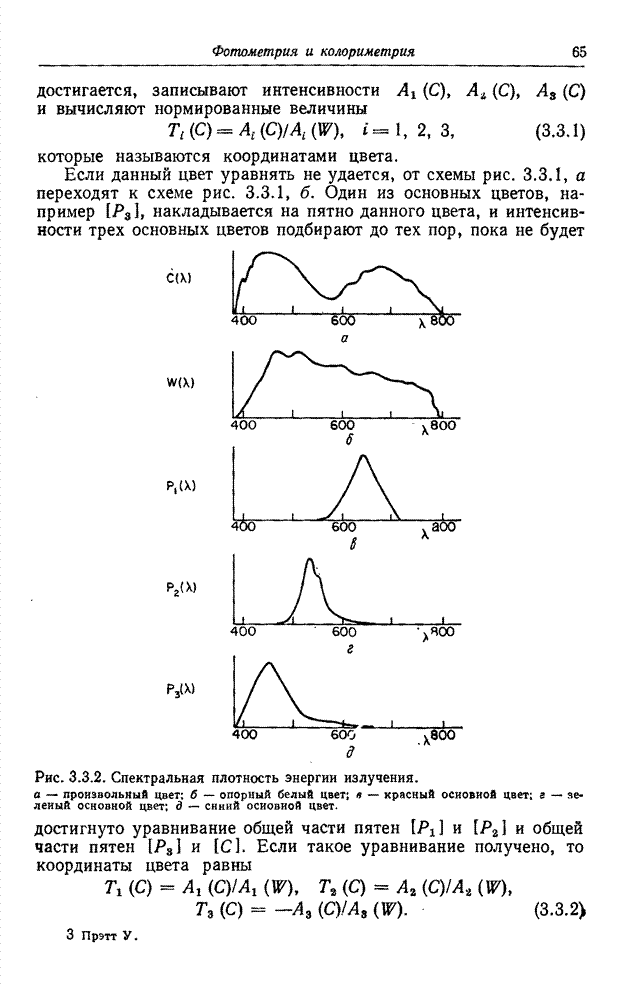
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
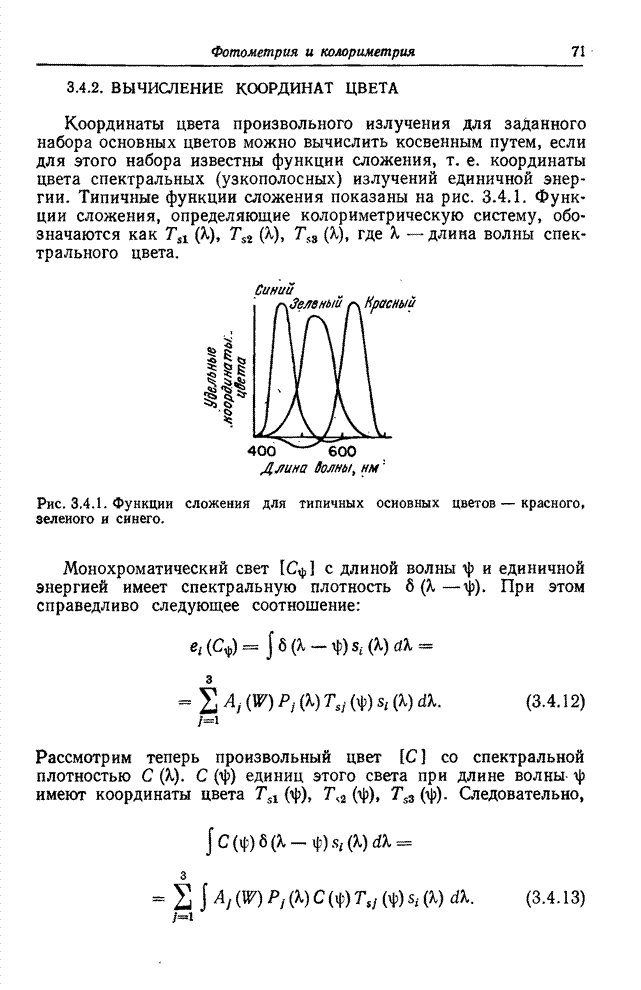
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
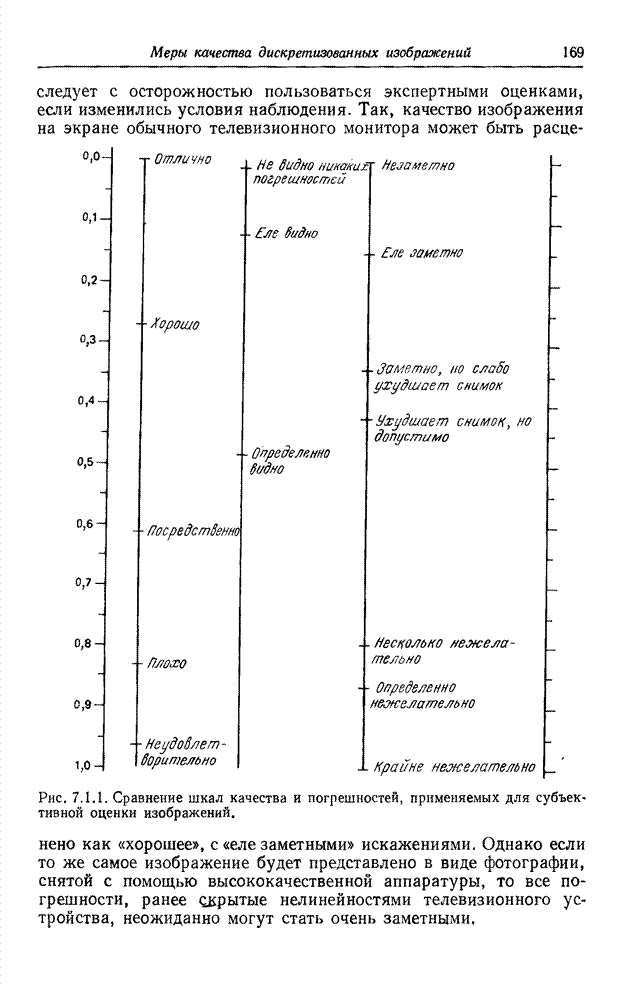
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
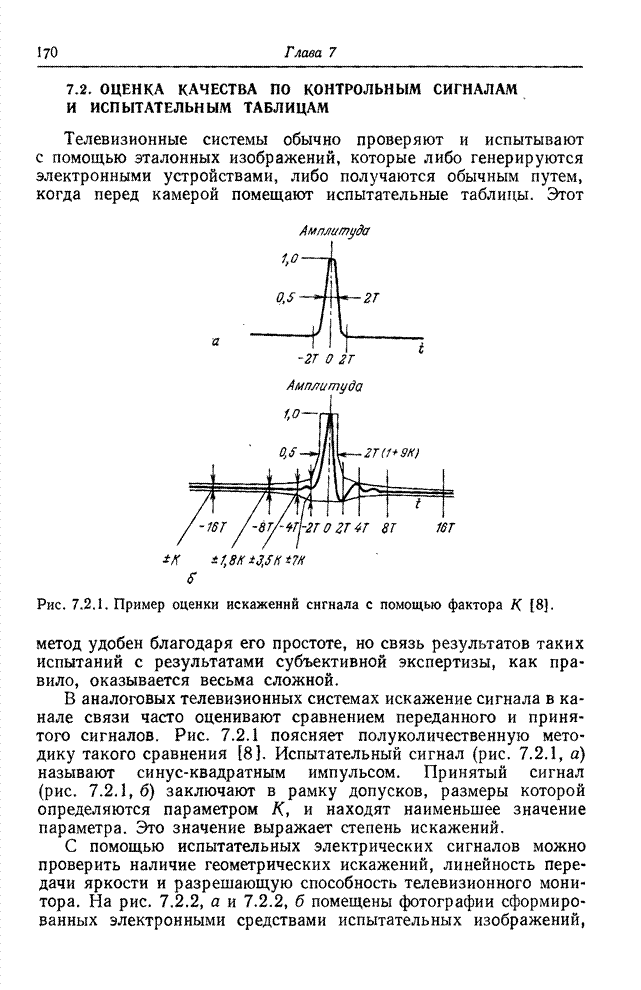
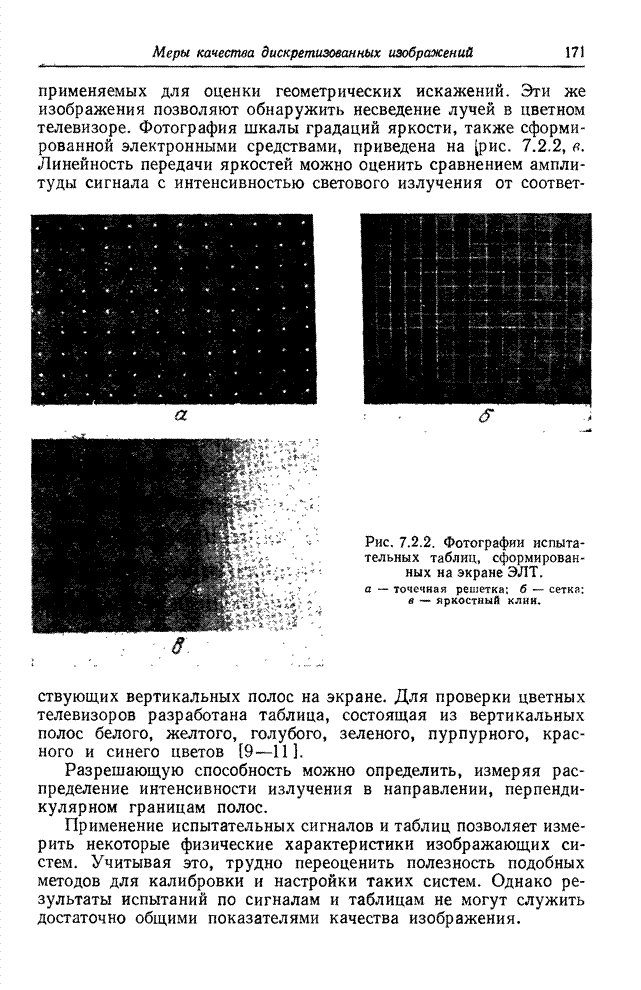
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
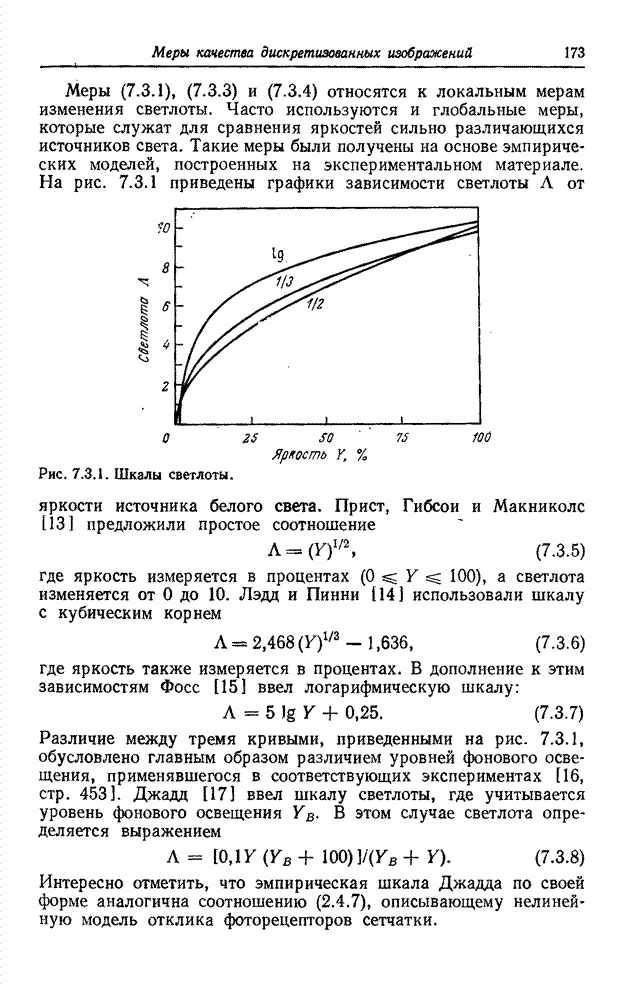
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
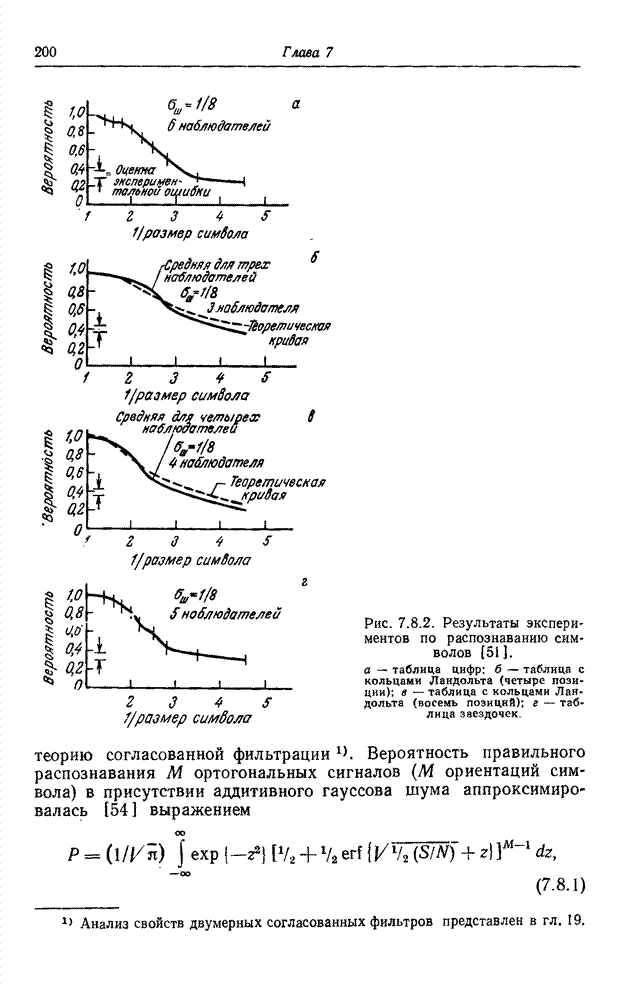
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
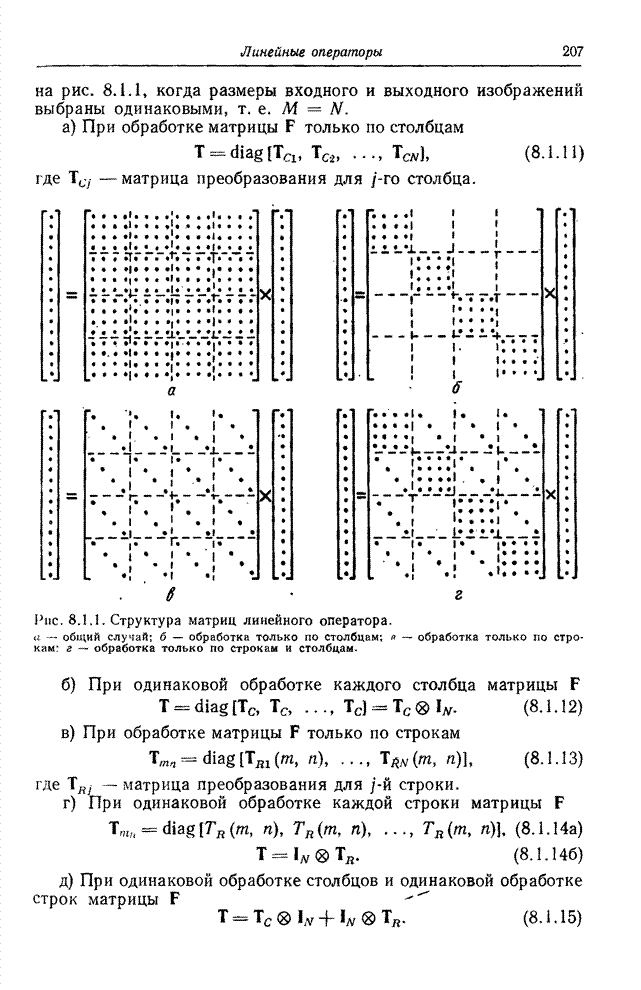
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
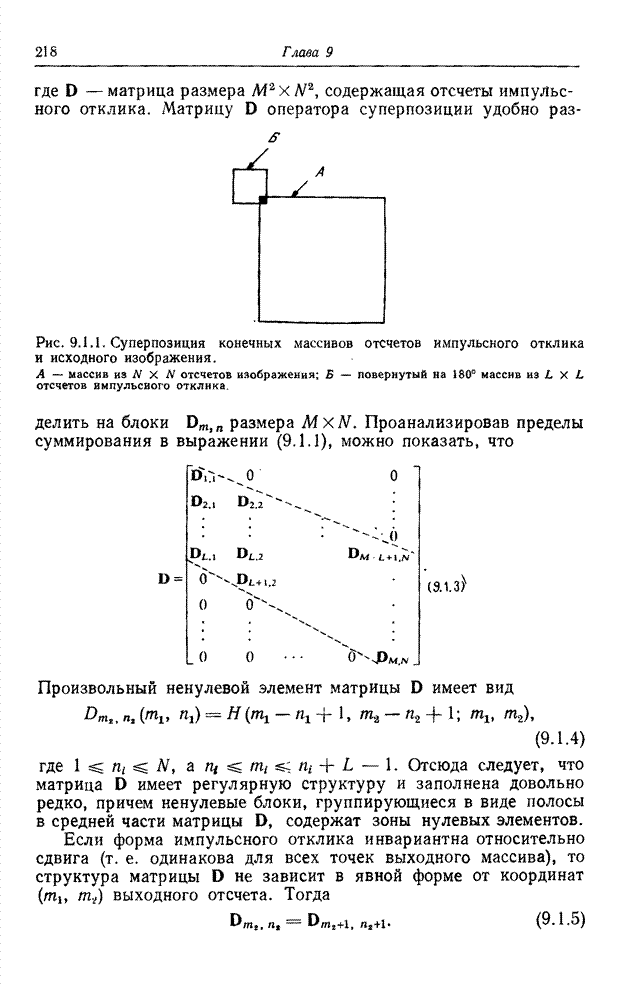
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА