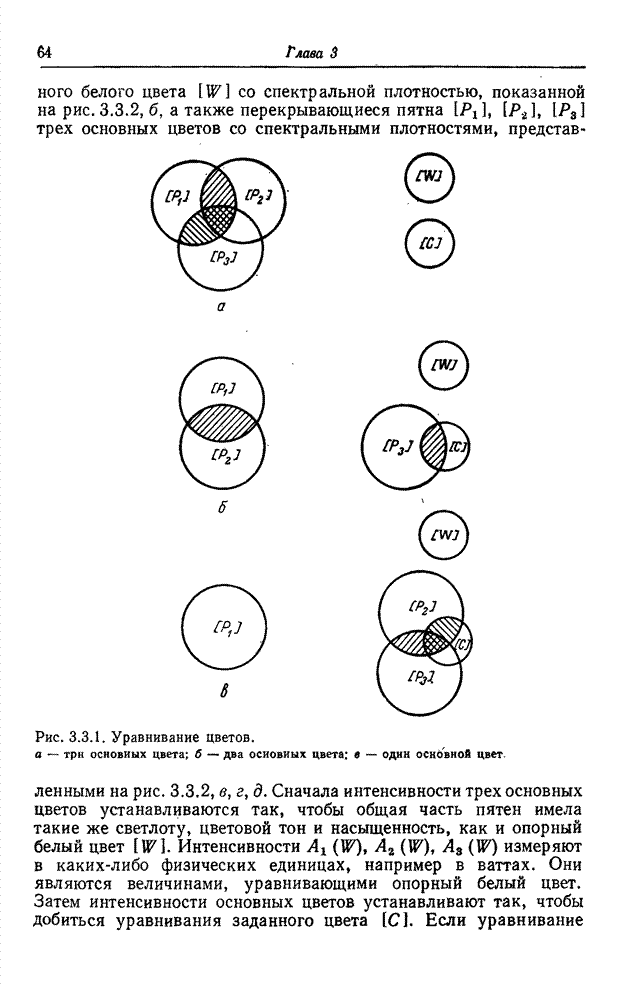
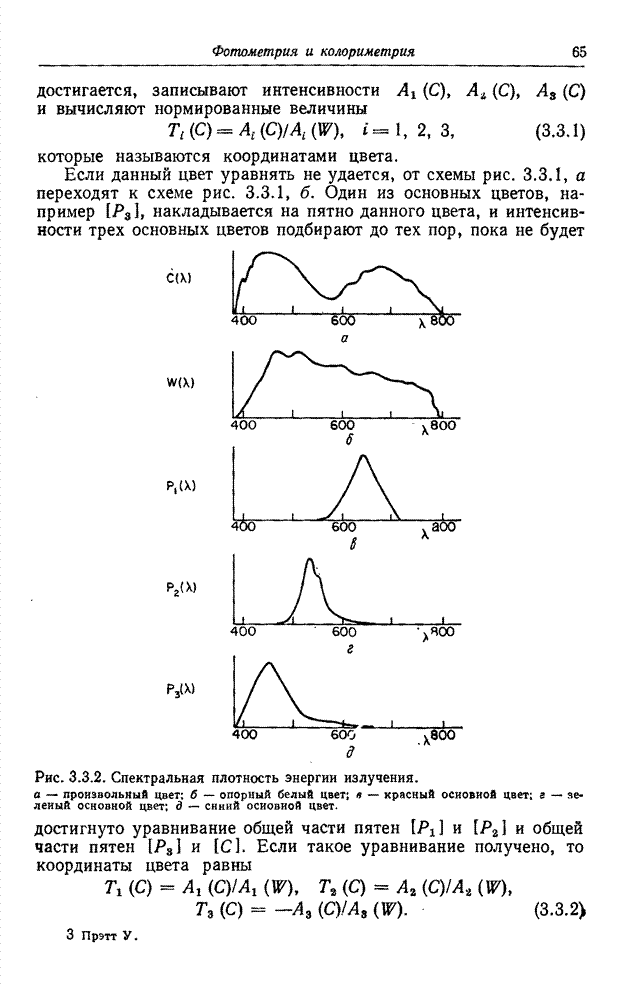
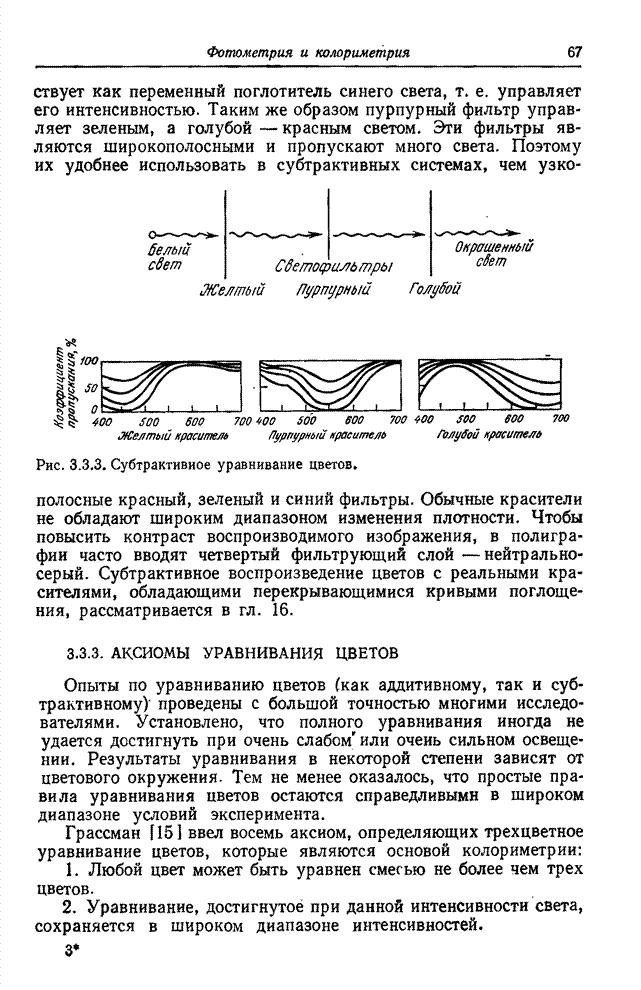
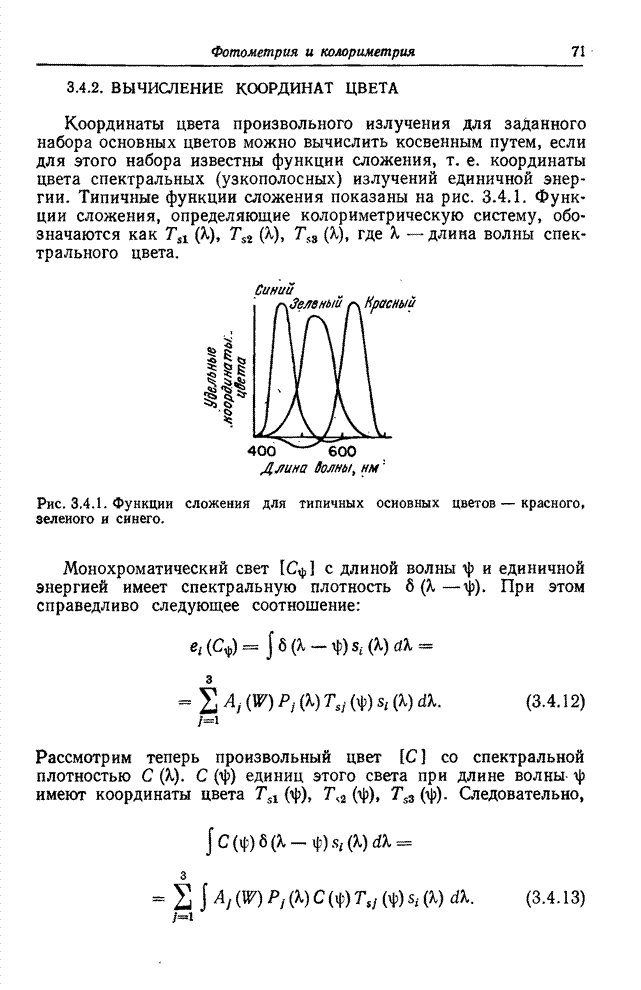
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
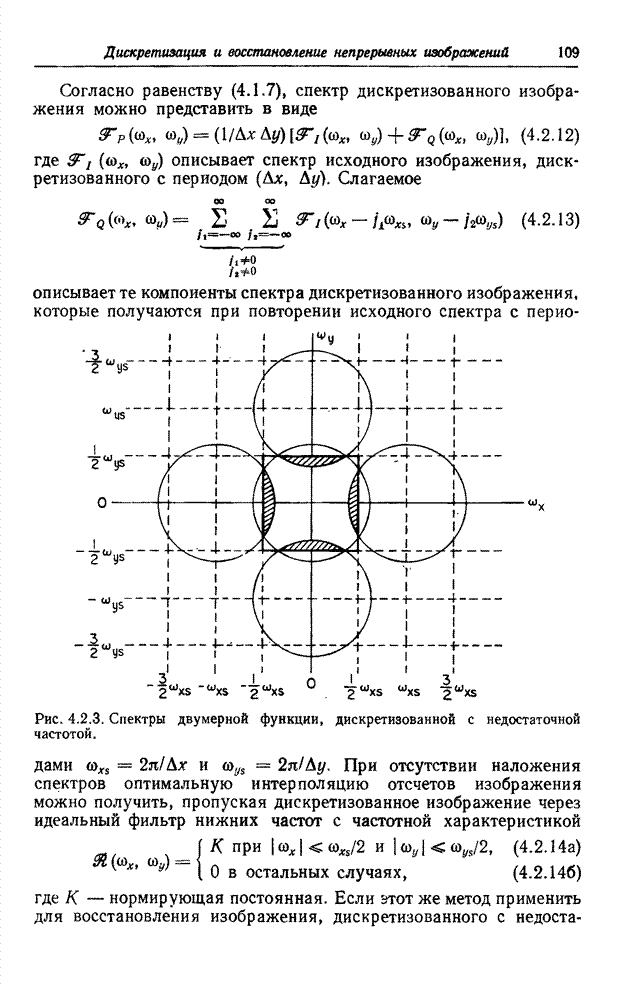
9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
Рассмотрим сначала
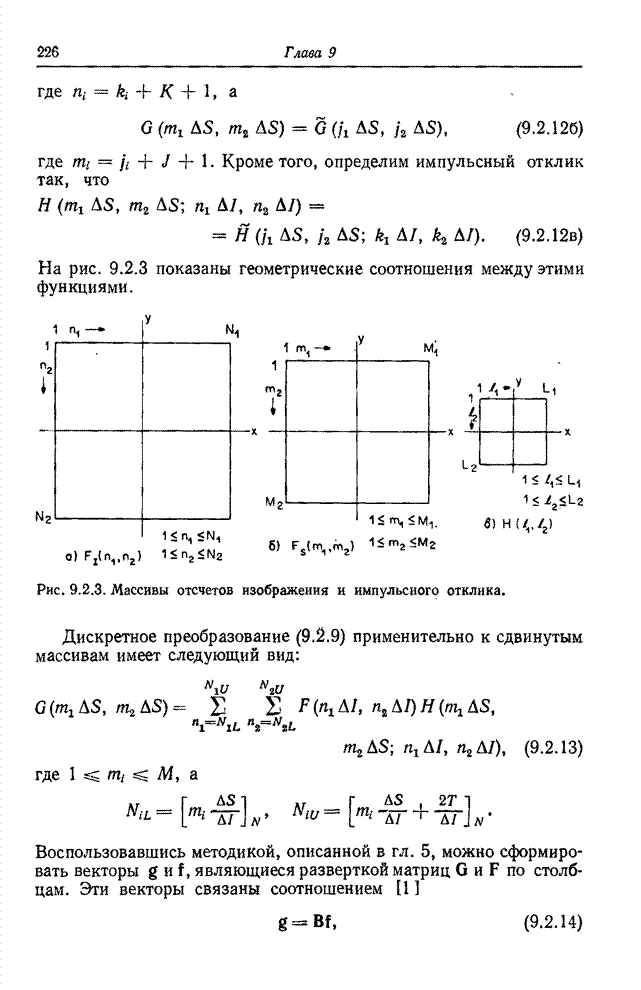
дискретный оператор суперпозиции конечного массива отсчетов
(для простоты обозначений принято, что все массивы отсчетов квадратные) ![]() (где
(где
![]() )
с конечным массивом
)
с конечным массивом ![]() (где
(где ![]() ), играющим роль импульсного
отклика. В общем случае импульсный отклик может изменяться
в зависимости от координат
), играющим роль импульсного
отклика. В общем случае импульсный отклик может изменяться
в зависимости от координат ![]() отсчета в выходном массиве
отсчета в выходном массиве
![]() . Операция суперпозиции в ограниченной области
определяется соотношением
. Операция суперпозиции в ограниченной области
определяется соотношением
 (9.1.1)
(9.1.1)
где ![]() , а массивы
, а массивы ![]() и
и ![]() имеют
нулевые значения вне областей изменения соответствующих
индексов. Анализируя предельные
значения индексов отсчетов импульсного отклика,
можно убедиться, что
имеют
нулевые значения вне областей изменения соответствующих
индексов. Анализируя предельные
значения индексов отсчетов импульсного отклика,
можно убедиться, что ![]() и,
следовательно, выходной массив
и,
следовательно, выходной массив ![]() имеет
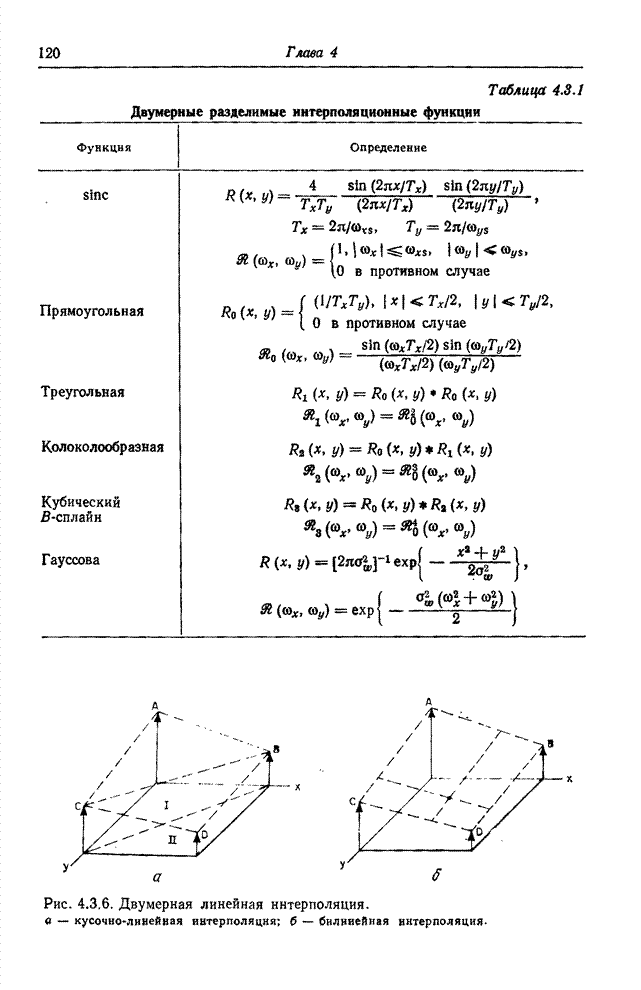
большие размеры, чем исходный (рис.
9.1.1).
имеет
большие размеры, чем исходный (рис.
9.1.1).
Если массивы ![]() и
и
![]() представлены соответственно в виде вектора
представлены соответственно в виде вектора ![]() размера
размера
![]() и вектора
и вектора ![]() размера
размера ![]() , то
преобразование (9.1.1) можно записать
как [1]
, то
преобразование (9.1.1) можно записать
как [1]
![]() , (9.1.2)
, (9.1.2)
где ![]() - матрица размера
- матрица размера ![]() , содержащая отсчеты импульсного отклика. Матрицу
, содержащая отсчеты импульсного отклика. Матрицу ![]() оператора
суперпозиции удобно разделить на блоки
оператора
суперпозиции удобно разделить на блоки ![]() размера
размера ![]() .
.

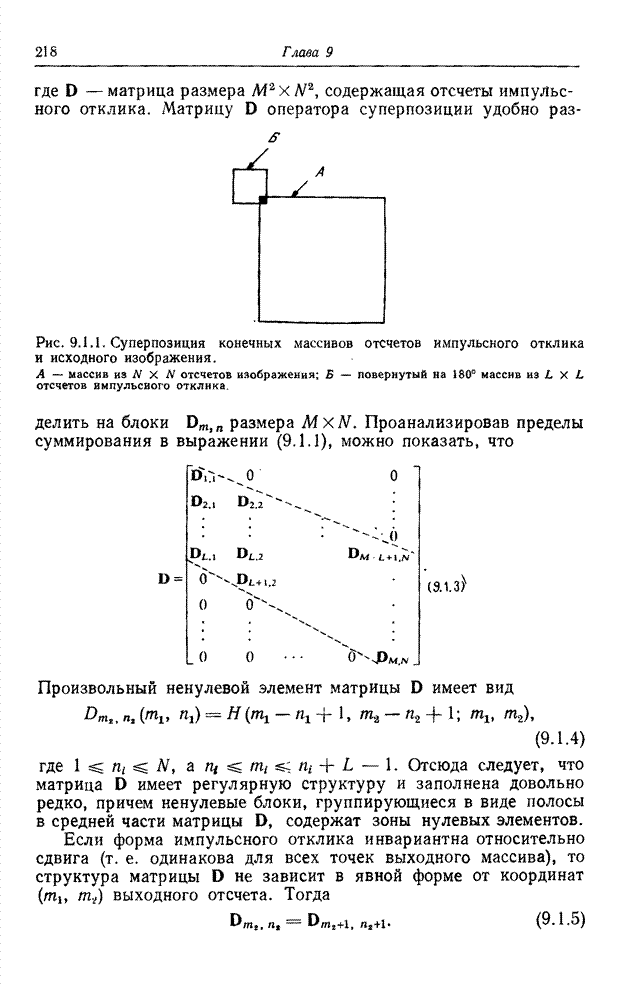
Рис.
9.1.1. Суперпозиция конечных массивов отсчетов импульсного отклика
и исходного изображения: А - пассив
из ![]() отсчетов изображения; Б - повернутый на 180° массив из
отсчетов изображения; Б - повернутый на 180° массив из ![]() отсчетов
импульсного отклика.
отсчетов
импульсного отклика.
Проанализировав пределы суммирования в выражении (9.1.1), можно показать, что
 (9.1.3)
(9.1.3)
Произвольный ненулевой
элемент матрицы ![]() имеет вид
имеет вид
![]() (9.1.4)
(9.1.4)
где ![]() , а
, а ![]() . Отсюда следует, что матрица
. Отсюда следует, что матрица ![]() имеет
регулярную структуру и заполнена довольно редко, причем
ненулевые блоки, группирующиеся в виде полосы в средней
части матрицы
имеет
регулярную структуру и заполнена довольно редко, причем
ненулевые блоки, группирующиеся в виде полосы в средней
части матрицы ![]() , содержат зоны нулевых
элементов.
, содержат зоны нулевых
элементов.
Если форма импульсного
отклика инвариантна относительно сдвига (т. е. одинакова для всех точек выходного массива),
то структура матрицы ![]() не зависит в явной форме
от координат
не зависит в явной форме
от координат ![]() выходного отсчета.
Тогда
выходного отсчета.
Тогда
![]() (9.1.5)
(9.1.5)
Таким образом,
все столбцы матрицы ![]() образуются сдвигом первого столбца. В этом случае оператор суперпозиции
называется оператором свертки конечных массивов. На рис.
9.1.2;а приведены полученные на ЦВМ распечатки
матриц, фигурирующих в операции свертки конечных массивов,
для случая, когда входной массив имеет
размеры
образуются сдвигом первого столбца. В этом случае оператор суперпозиции
называется оператором свертки конечных массивов. На рис.
9.1.2;а приведены полученные на ЦВМ распечатки
матриц, фигурирующих в операции свертки конечных массивов,
для случая, когда входной массив имеет
размеры ![]() (
(![]() ), выходной массив
), выходной массив ![]() (
(![]() ), а массив отсчетов импульсного
отклика
), а массив отсчетов импульсного
отклика ![]() (
(![]() ). Пары целых чисел
). Пары целых чисел ![]() в матрице
в матрице ![]() обозначают
обозначают
![]() -й элемент матрицы
-й элемент матрицы ![]() .
.

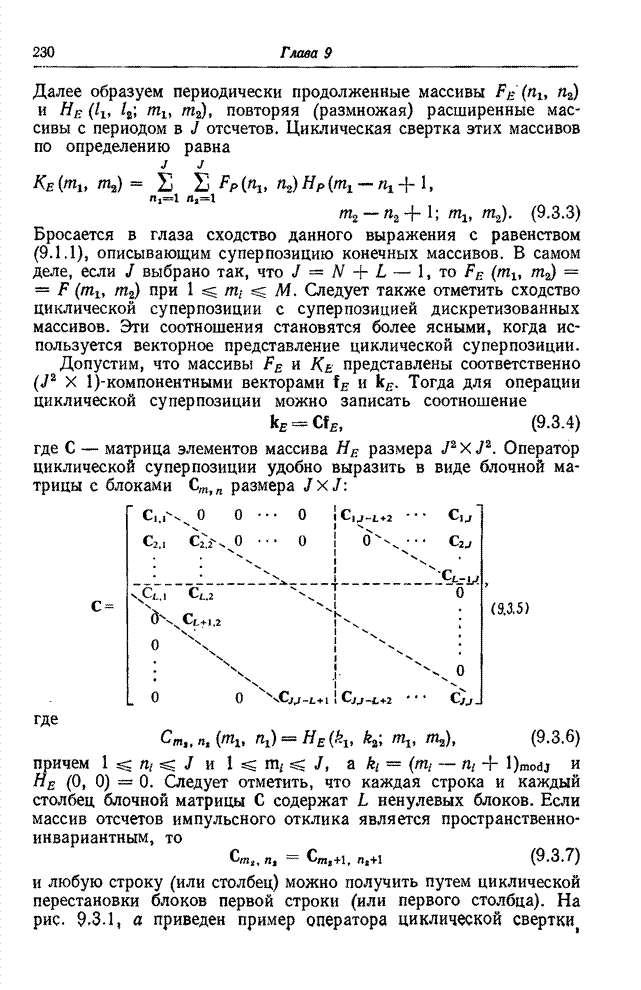
Рис.
9.1.2. Примеры матриц операторов свертки конечных массивов:
а - общий случай, ![]() ,
, ![]() ,
, ![]() ; б
- импульсный отклик гауссовой формы,
; б
- импульсный отклик гауссовой формы, ![]() ,
, ![]() ,
, ![]() .
.
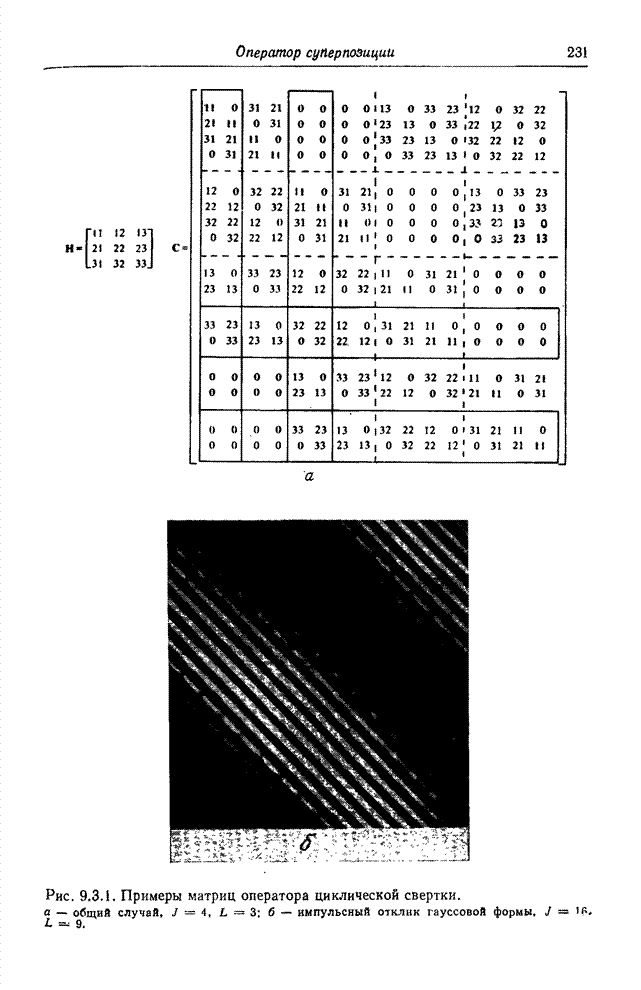
Структура матрицы
![]() лучше видна на примере матрицы большего размера, показанной на рис. 9.1.2, б. В рассматриваемой матрице
лучше видна на примере матрицы большего размера, показанной на рис. 9.1.2, б. В рассматриваемой матрице ![]() ,
, ![]() ,
, ![]() , а импульсный отклик
симметричен и имеет гауссову форму. Заметим, что в данном примере размеры матрицы
, а импульсный отклик
симметричен и имеет гауссову форму. Заметим, что в данном примере размеры матрицы ![]() равны 256
равны 256![]() 64.
64.
Пользуясь методикой, примененной при выводе соотношения (8.1.7), оператор суперпозиции можно представить в матричной форме
![]() (9.1.6)
(9.1.6)
Если импульсный отклик является инвариантным относительно сдвига и разделимым, т. е.
![]() , (9.1.7)
, (9.1.7)
где
![]() и
и ![]() - вектор-столбцы,
описывающие соответственно характер изменения импульсного отклика по столбцам и
строкам, то
- вектор-столбцы,
описывающие соответственно характер изменения импульсного отклика по столбцам и
строкам, то
![]() . (9.1.8)
. (9.1.8)
Матрицы
![]() и
и ![]() имеют размеры
имеют размеры ![]() и структуру вида
и структуру вида
 . (9.1.9)
. (9.1.9)
Операция двумерной свертки в этом случае сводится к последовательному вычислению одномерных сверток по строкам и столбцам. Таким образом,
![]() . (9.1.10)
. (9.1.10)
Для
получения конечной свертки или суперпозиции в общем случае необходимо выполнить
![]() арифметических
операций, причем в это число не входят умножения на нулевые элементы матрицы
арифметических
операций, причем в это число не входят умножения на нулевые элементы матрицы ![]() . Если же оператор
является разделимым, т. е. удовлетворяет равенству (9.1.10), то достаточно
выполнить
. Если же оператор
является разделимым, т. е. удовлетворяет равенству (9.1.10), то достаточно
выполнить ![]() операций.
операций.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
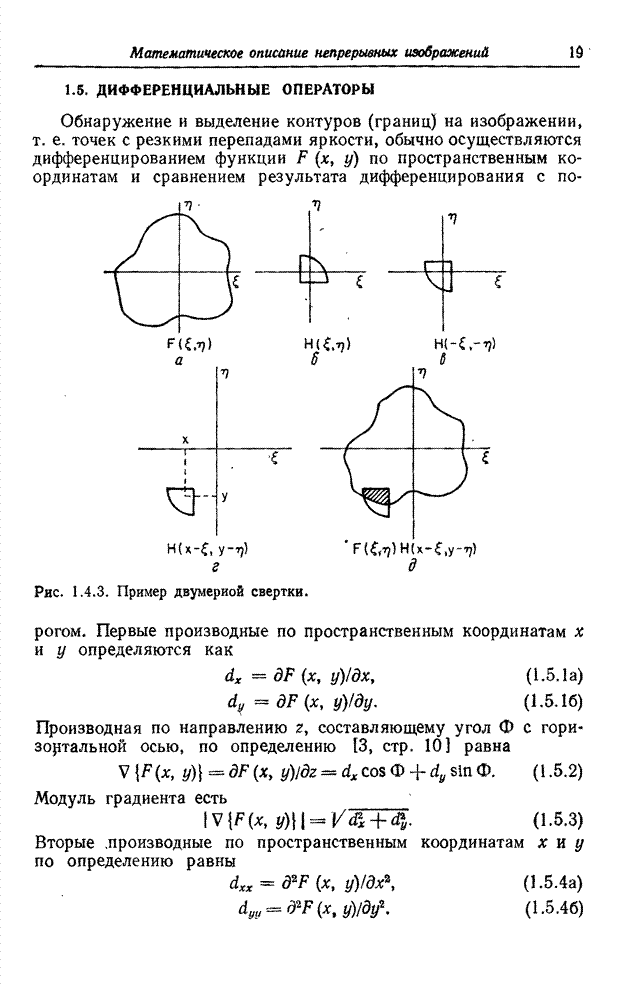
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
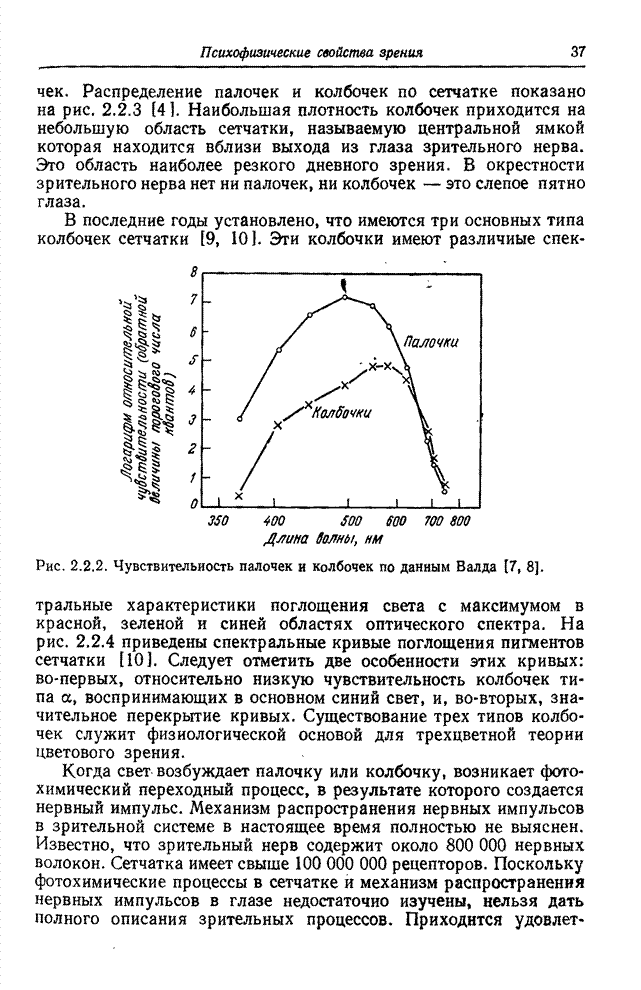
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
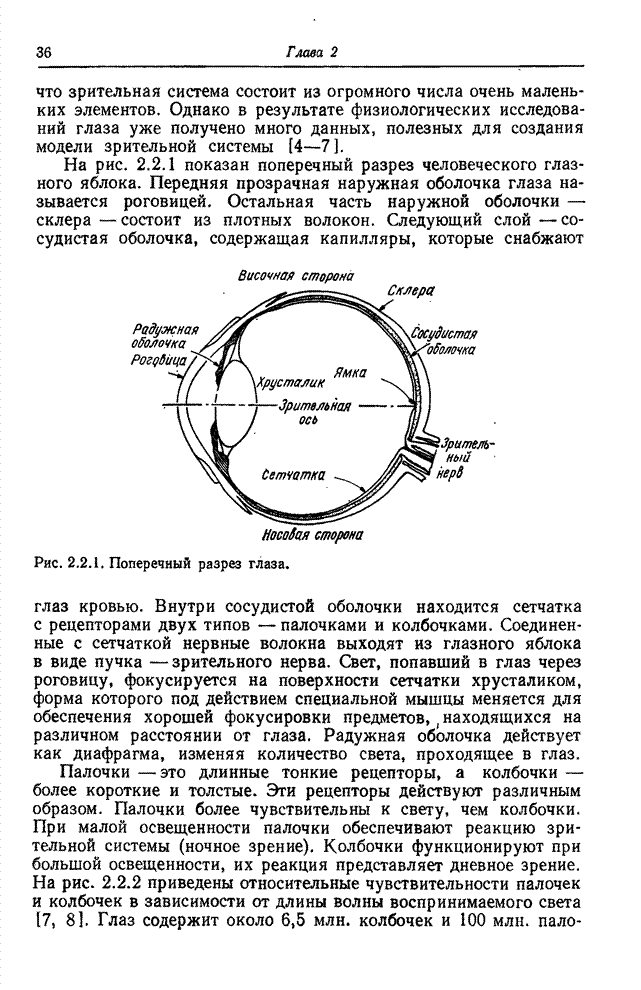
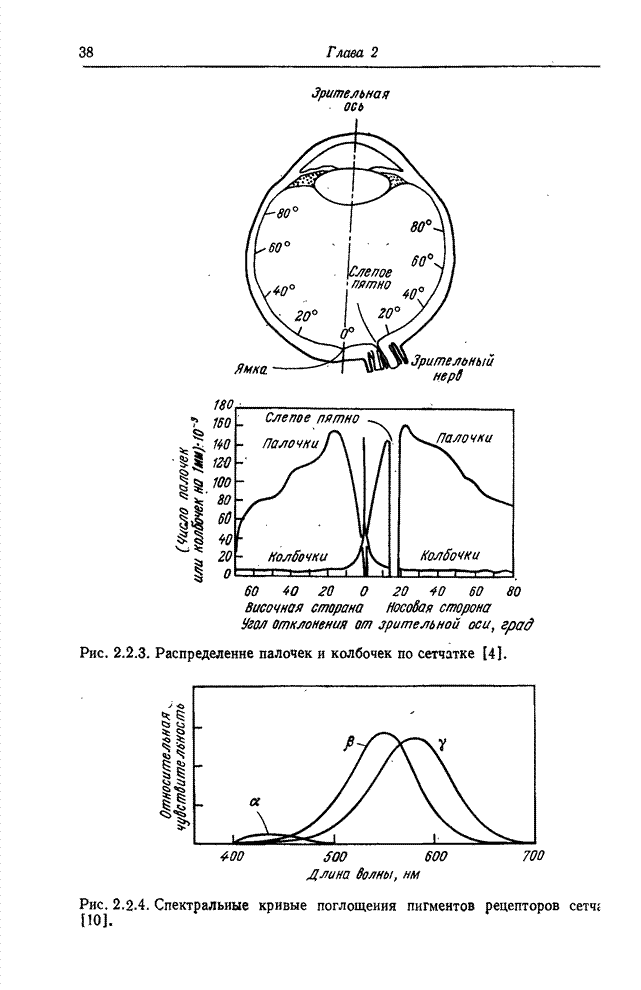
- 2.2. ГЛАЗ
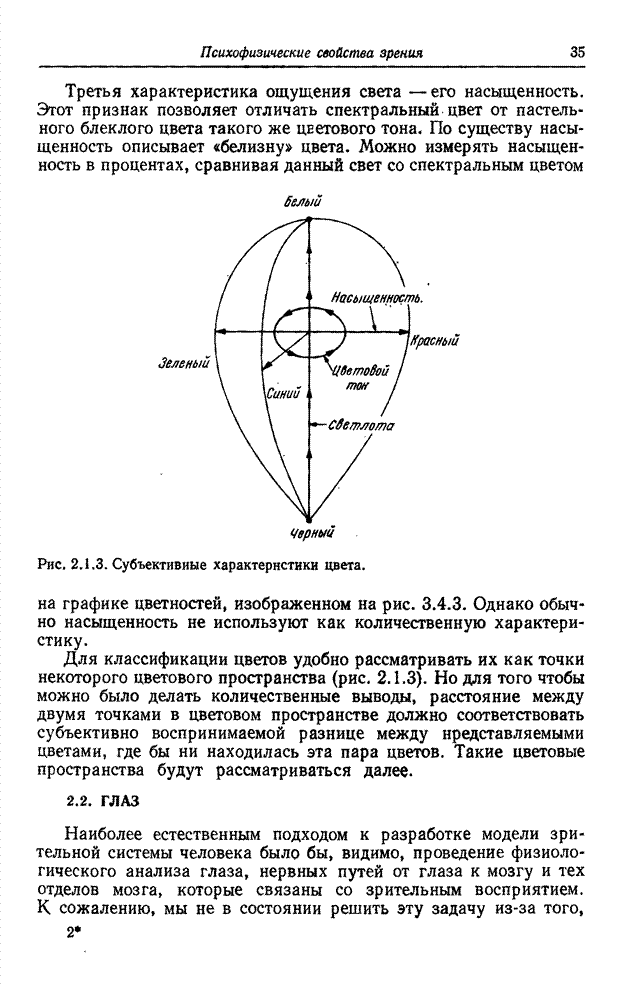
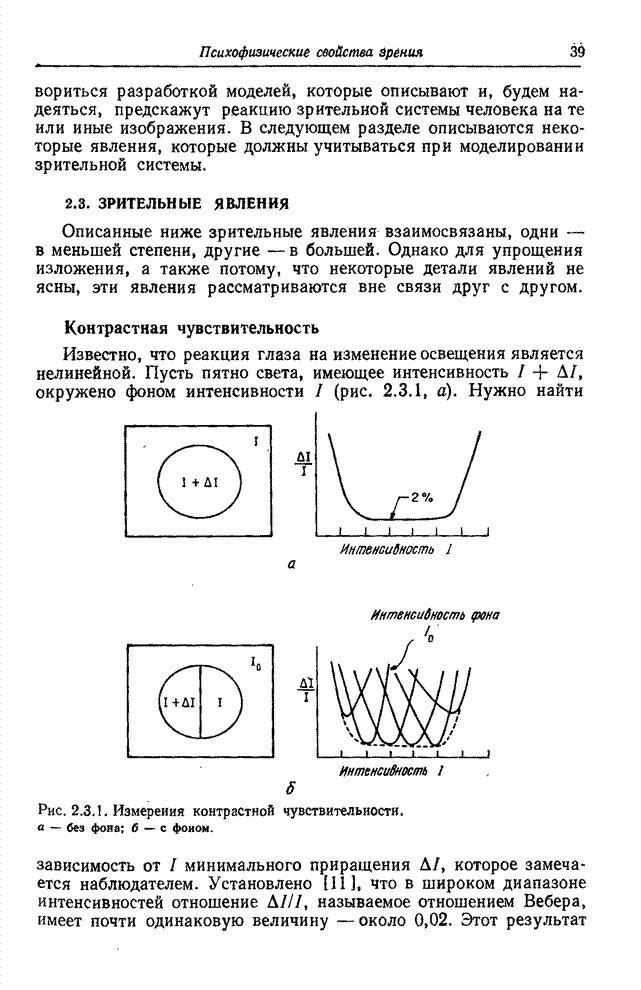
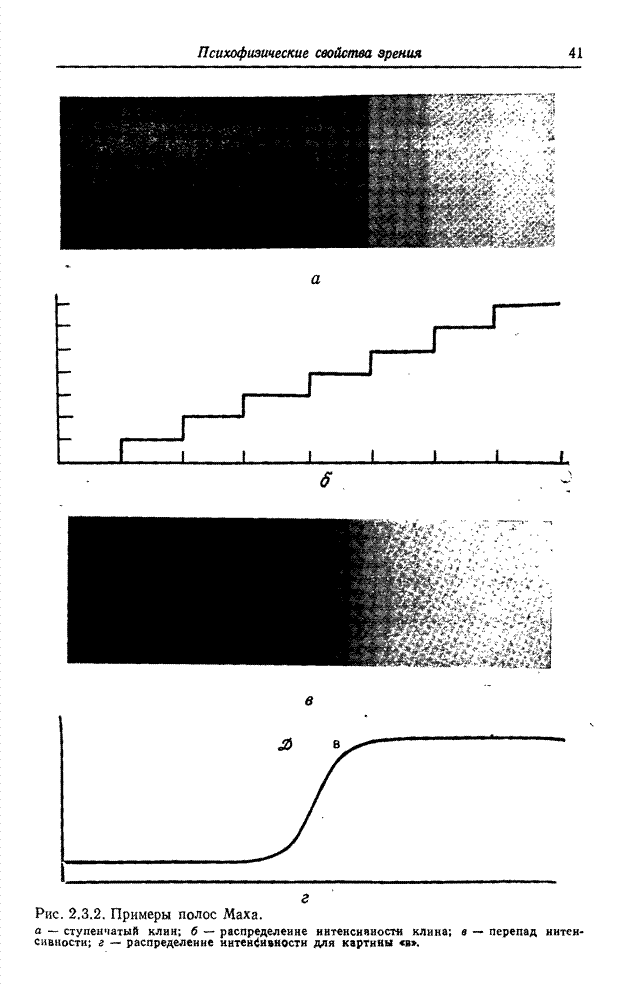
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
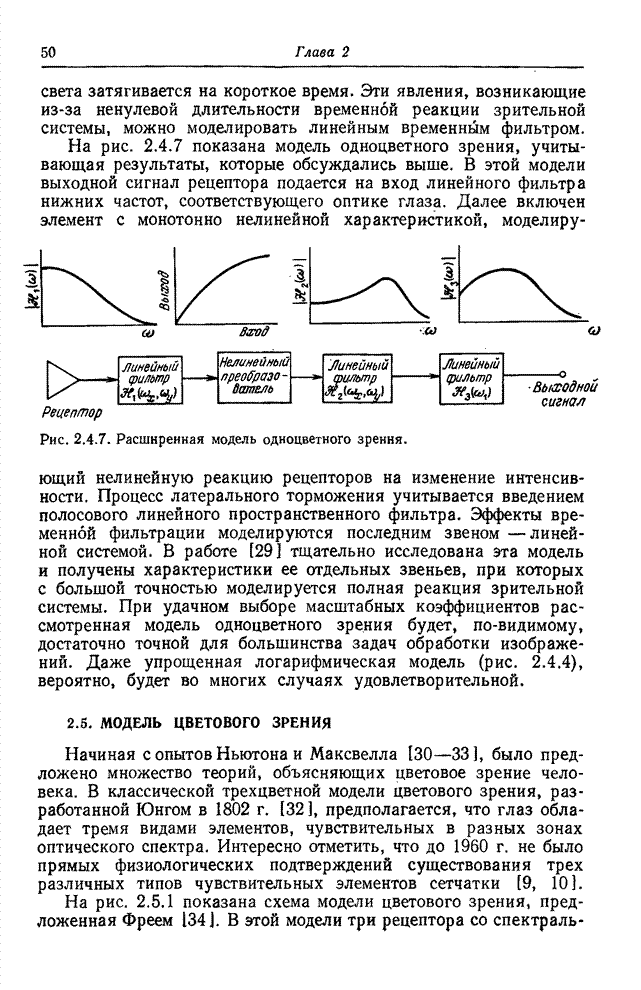
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
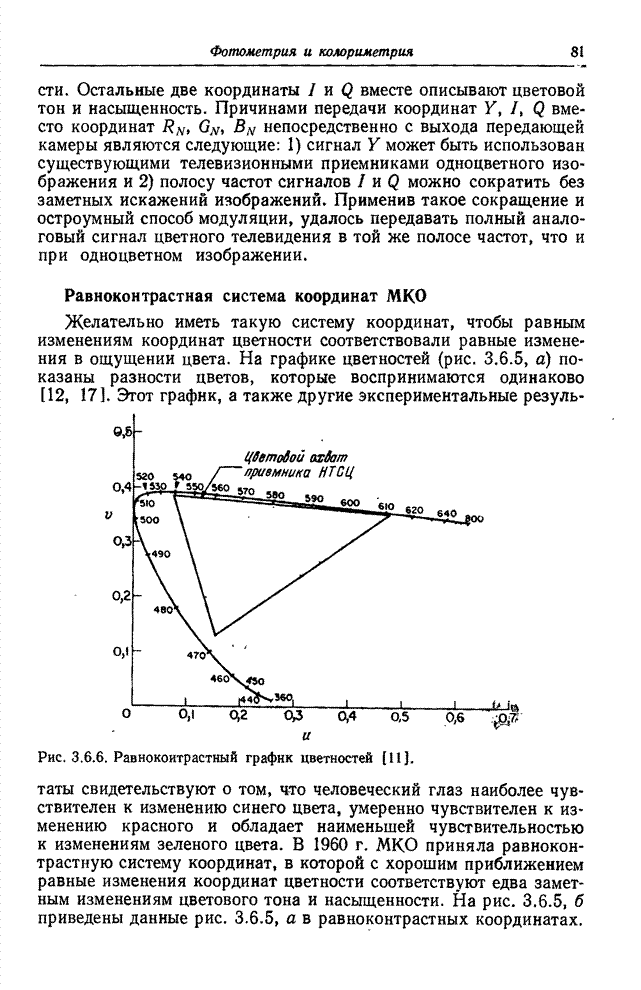
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
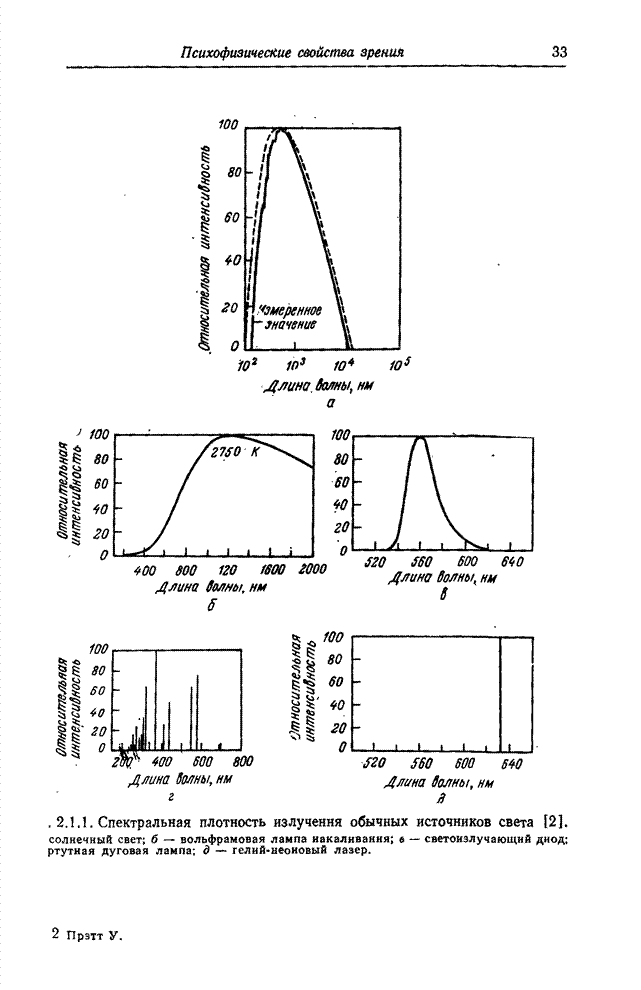
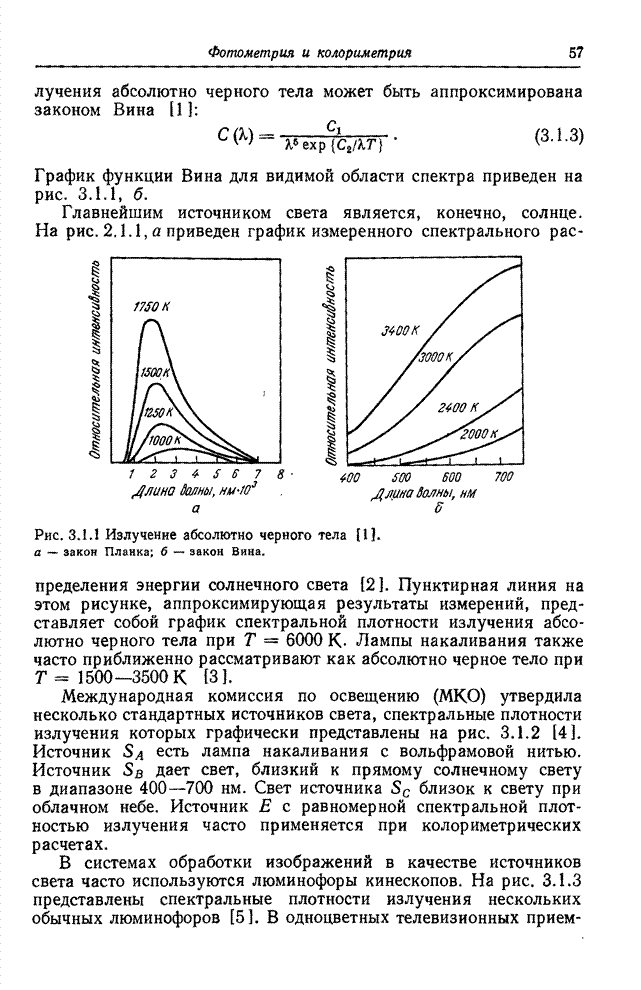
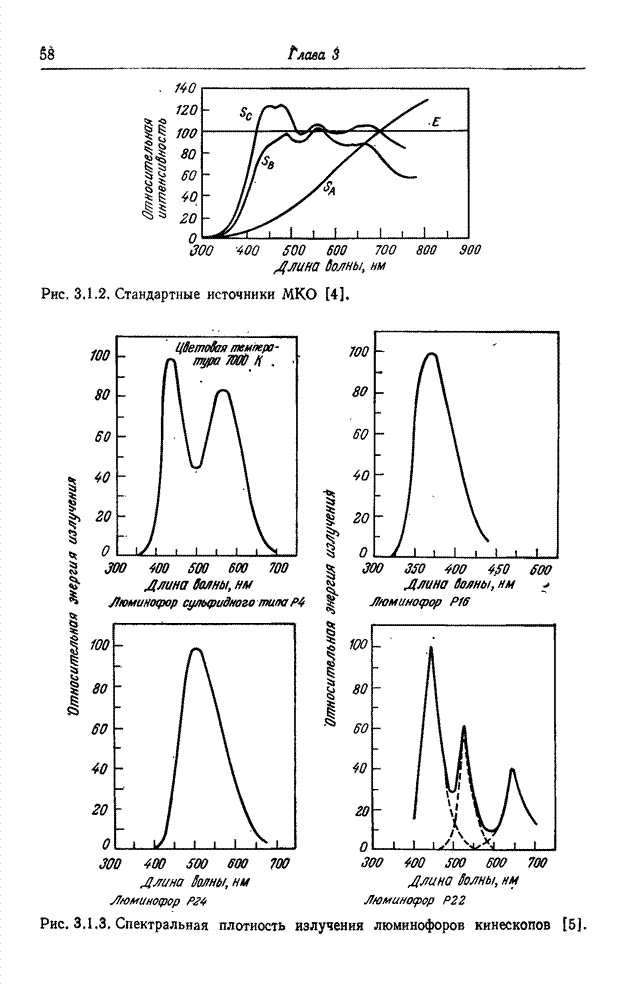
- 3.1. ИСТОЧНИКИ СВЕТА
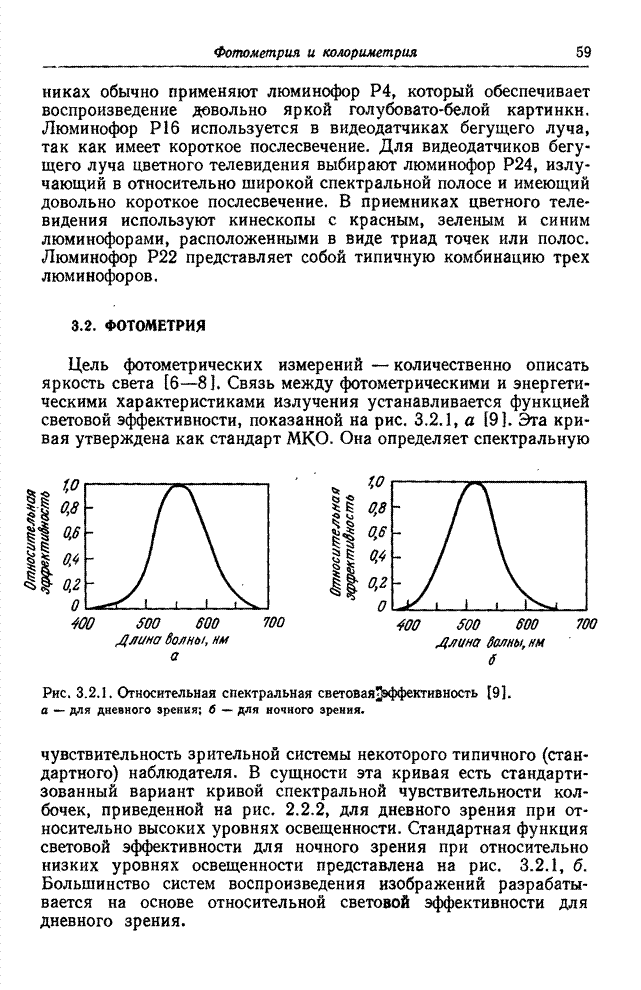
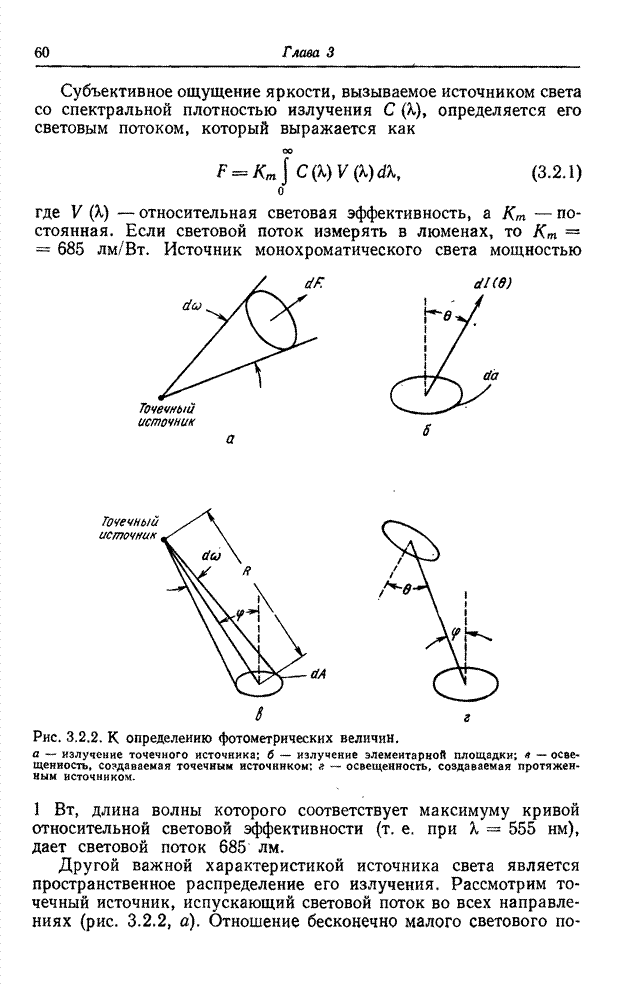
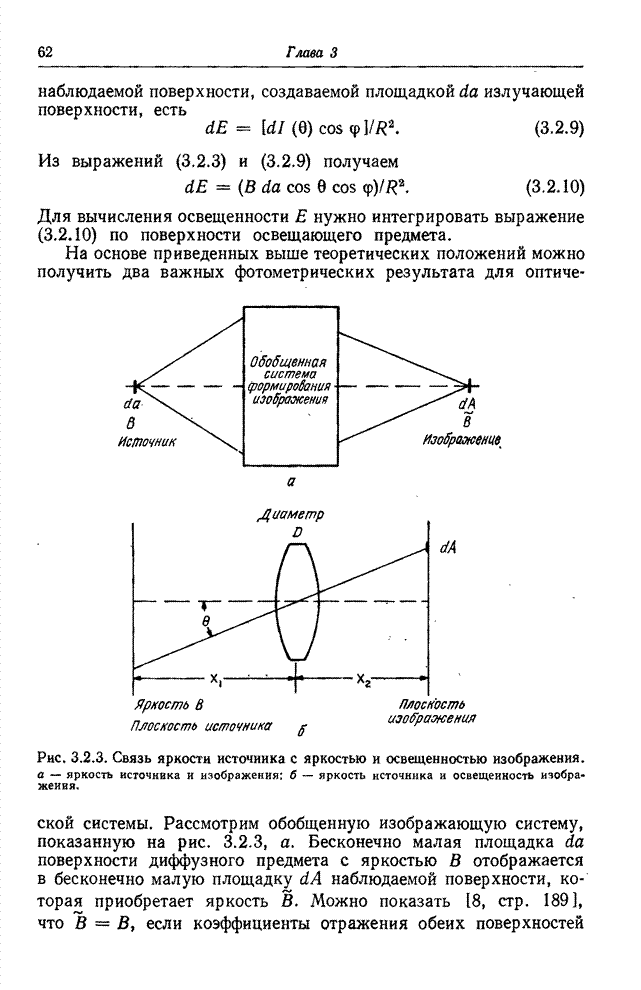
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
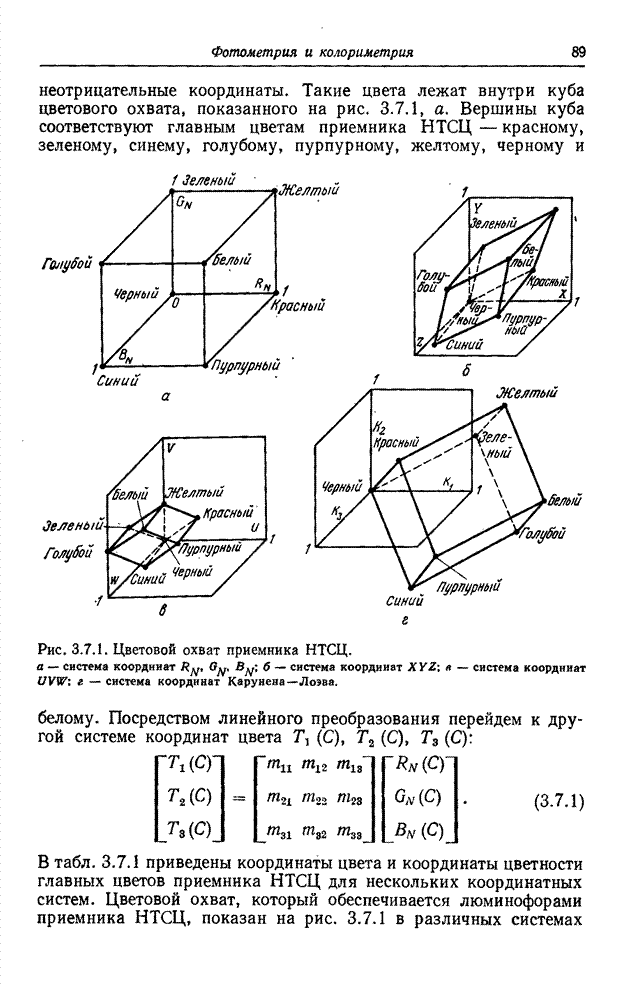
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
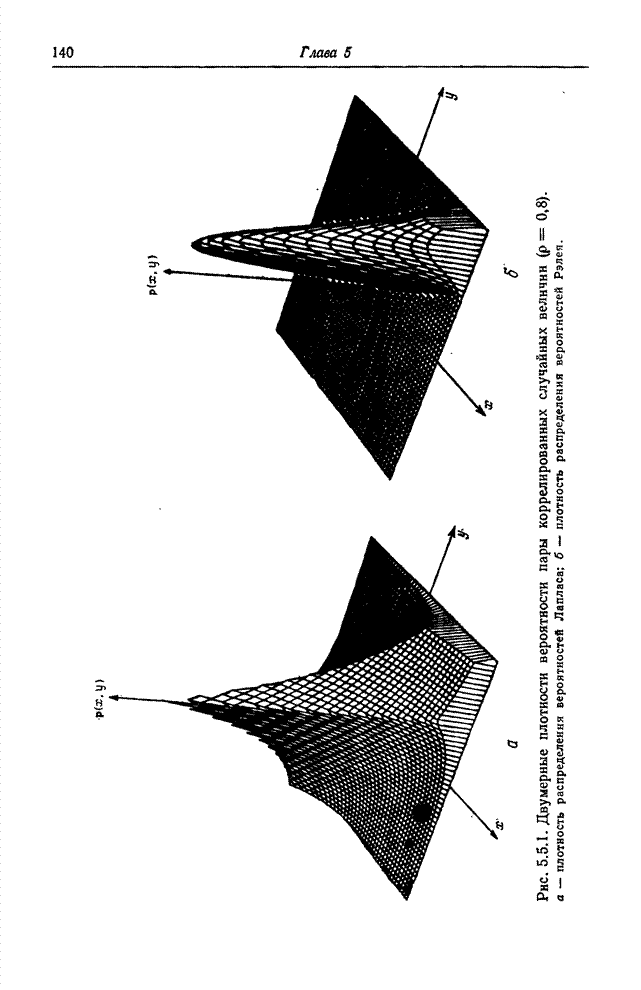
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
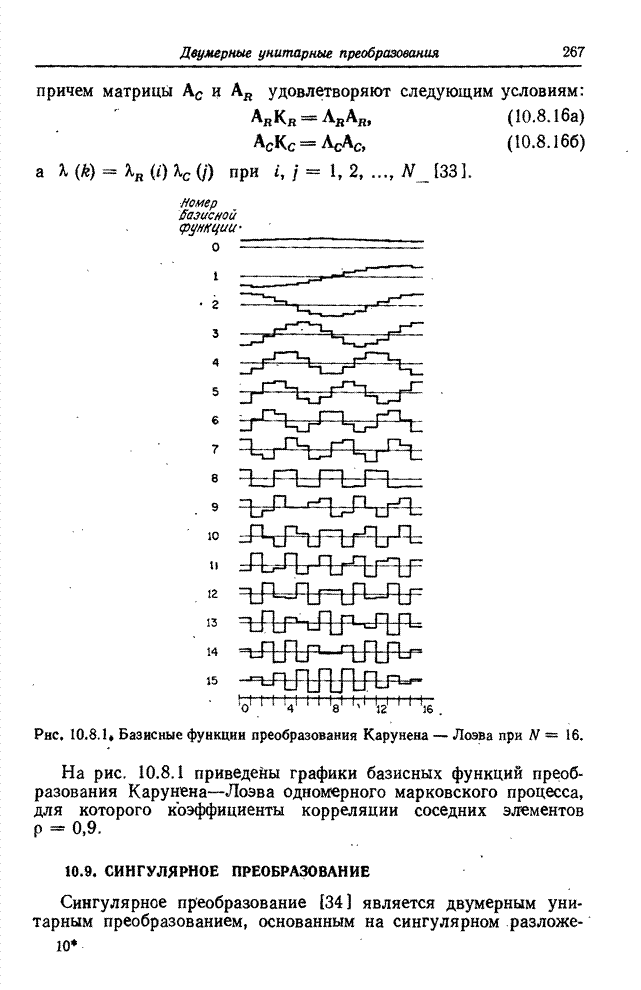
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
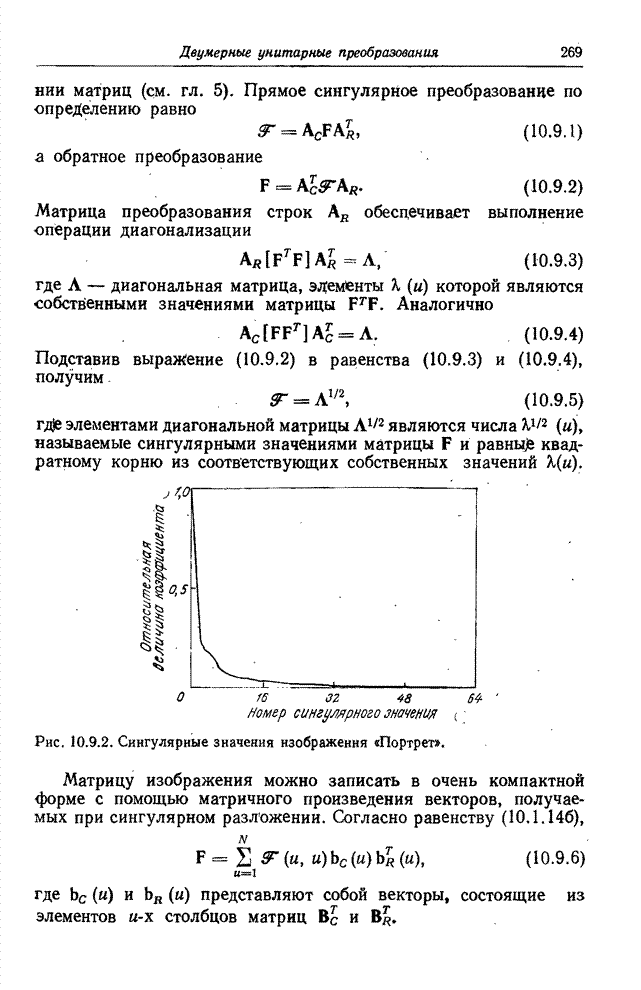
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
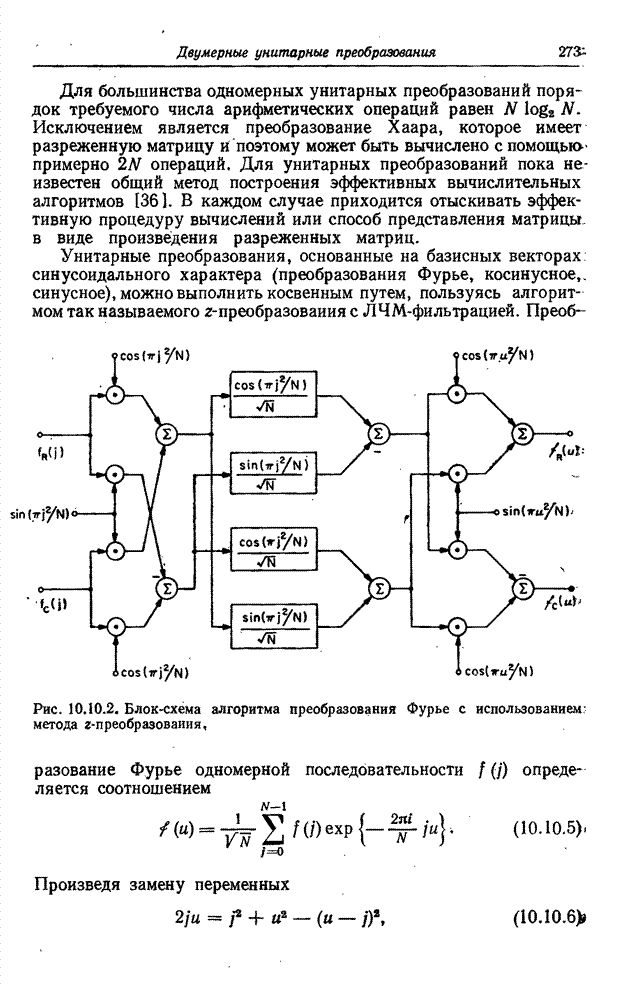
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
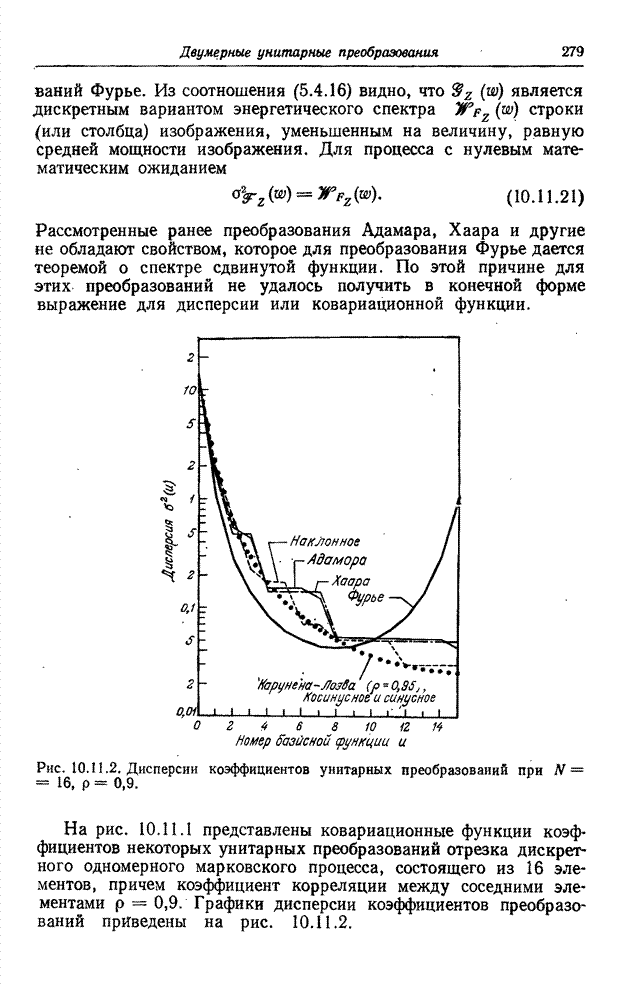
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА