| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
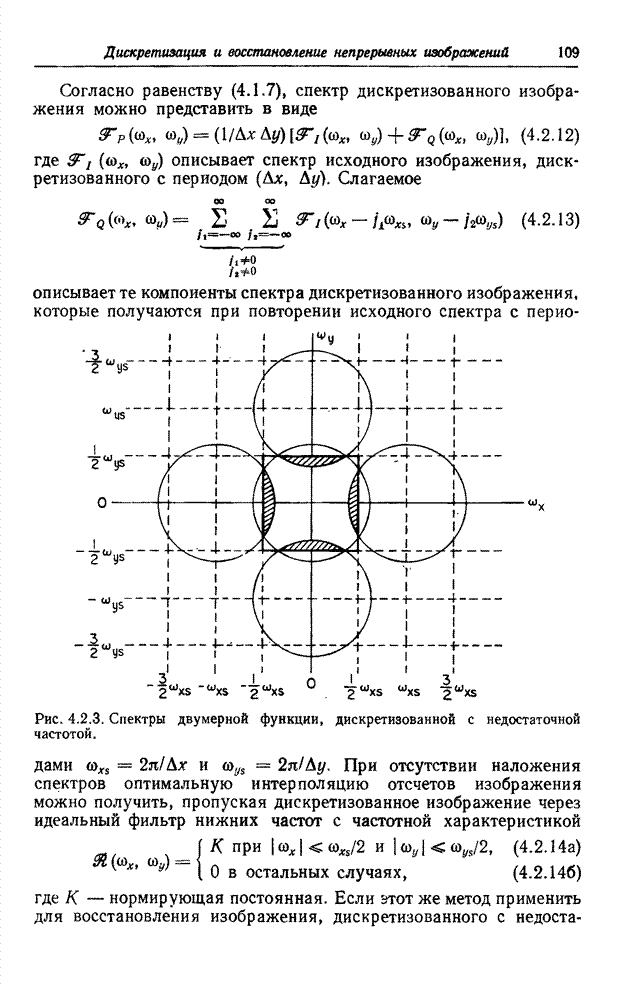
8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
Рассмотрим массив ![]() из
из ![]() элементов, представляющий
исходное (входное) изображение. При воздействии на него обобщенным линейным оператором
получается массив из
элементов, представляющий
исходное (входное) изображение. При воздействии на него обобщенным линейным оператором
получается массив из ![]() элементов, описывающий преобразованное
(выходное) изображение
элементов, описывающий преобразованное
(выходное) изображение
 (8.1.1)
(8.1.1)
где ядро оператора ![]() представляет собой
набор весовых множителей, зависящих в общем случае от координат элементов как входного,
так и выходного изображений.
представляет собой
набор весовых множителей, зависящих в общем случае от координат элементов как входного,
так и выходного изображений.
При анализе линейных операций
по обработке изображений удобно пользоваться векторными представлениями, описанными
в гл. 5 [1]. Поэтому будем полагать, что входной массив ![]() представлен или в виде матрицы
представлен или в виде матрицы
![]() , или в виде
вектора
, или в виде
вектора ![]() ,
полученного разверткой матрицы
,
полученного разверткой матрицы ![]() по столбцам. Аналогичным образом допустим,
что выходной массив
по столбцам. Аналогичным образом допустим,
что выходной массив ![]() может быть представлен либо матрицей
может быть представлен либо матрицей
![]() , либо в виде
ее развертки по столбцам, т. е. вектором
, либо в виде
ее развертки по столбцам, т. е. вектором ![]() . Для упрощения обозначений ниже будет
принято, что матрицы, представляющие входное и выходное изображения, квадратные
с размерами
. Для упрощения обозначений ниже будет
принято, что матрицы, представляющие входное и выходное изображения, квадратные
с размерами ![]()
![]() соответственно. Допустим
теперь, что символ
соответственно. Допустим
теперь, что символ ![]() обозначает матрицу размера
обозначает матрицу размера ![]() , с помощью которой
вектор исходного изображения
, с помощью которой
вектор исходного изображения ![]() размера
размера ![]() линейно преобразуется в вектор
линейно преобразуется в вектор
![]() (8.1.2)
(8.1.2)
выходного изображения размера.
Матрицу ![]() можно
разделить на блоки - матрицы
можно
разделить на блоки - матрицы ![]() размера
размера ![]() (число которых также равно
(число которых также равно ![]() ) - и представить ее
в следующем виде:
) - и представить ее
в следующем виде:
 (8.1.3)
(8.1.3)
В согласии с соотношением
(5.3.3) вектор выходного изображения ![]() можно выразить через матрицу входного
изображения
можно выразить через матрицу входного
изображения ![]() :
:
![]() (8.1.4)
(8.1.4)
Кроме того, с помощью равенства
(5.3.4) матрицу ![]() выходного
изображения можно выразить через вектор p
того
же изображения:
выходного
изображения можно выразить через вектор p
того
же изображения:
![]() (8.1.5)
(8.1.5)
Из этих формул получим выражение, связывающее между собой входную и выходную матрицы:
![]() (8.1.6)
(8.1.6)
Заметим, что операторы ![]() и
и ![]() просто выделяют из
матрицы
просто выделяют из
матрицы ![]() блок
блок
![]() . Следовательно,
. Следовательно,
![]() (8.1.7)
(8.1.7)
Пусть линейное преобразование
является разделимым, т. е. матрицу ![]() можно представить в виде прямого произведения
можно представить в виде прямого произведения
![]() (8.1.8)
(8.1.8)
где ![]() и
и ![]() - операторы преобразования столбцов
и строк матрицы изображения
- операторы преобразования столбцов
и строк матрицы изображения ![]() . В этом случае
. В этом случае
![]() (8.1.9)
(8.1.9)
Следовательно,
![]() (8.1.10)
(8.1.10)
Таким образом, матрицу выходного
изображения ![]() можно
получить путем последовательной обработки матрицы
можно
получить путем последовательной обработки матрицы ![]() по строкам и столбцам.
по строкам и столбцам.
При обработке изображений
во многих случаях оказывается, что оператор линейного преобразования ![]() имеет специфическую
структуру, позволяющую упростить вычислительные операции. Ниже перечислены важные
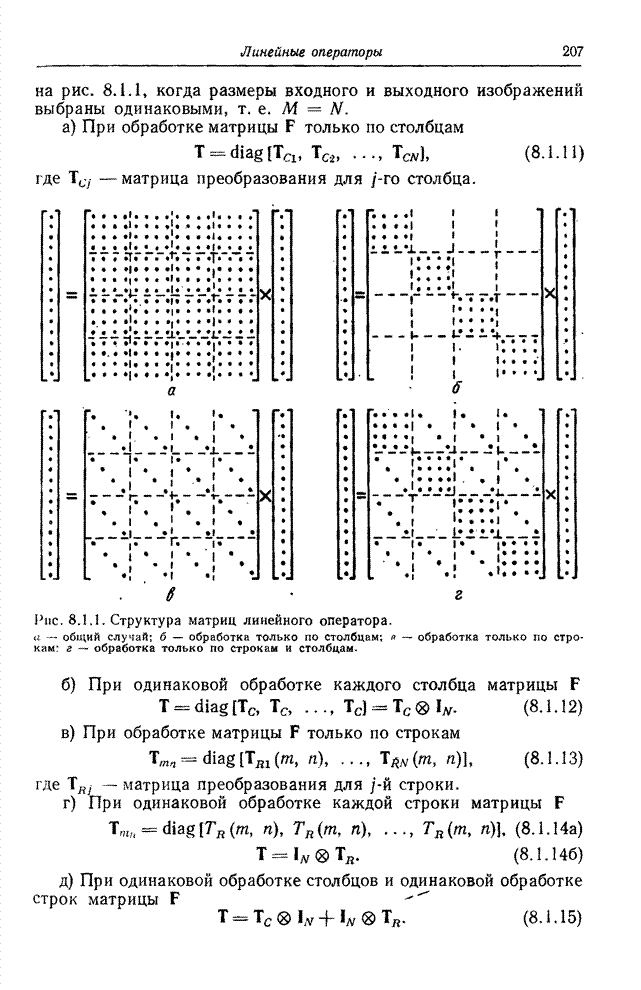
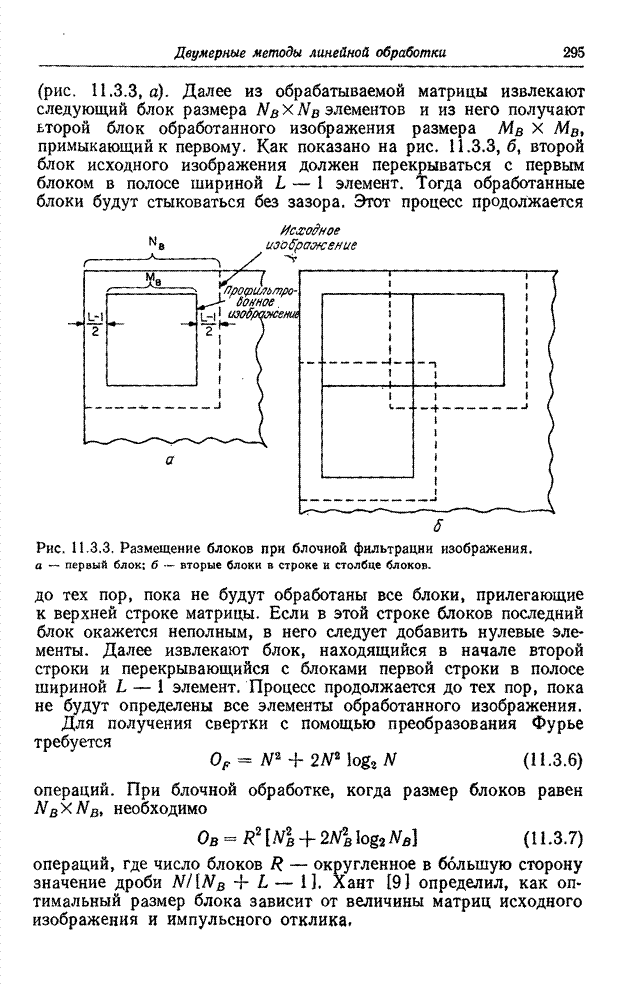
частные случаи, проиллюстрированные на рис. 8.1.1, когда размеры входного и выходного
изображений выбраны одинаковыми, т. е.
имеет специфическую
структуру, позволяющую упростить вычислительные операции. Ниже перечислены важные
частные случаи, проиллюстрированные на рис. 8.1.1, когда размеры входного и выходного
изображений выбраны одинаковыми, т. е. ![]() .
.
а) При обработке матрицы
![]() только по
столбцам
только по
столбцам
![]() (8.1.11)
(8.1.11)
где ![]() - матрица преобразования для
- матрица преобразования для
![]() -го столбца.
-го столбца.
б) При одинаковой обработке
каждого столбца матрицы ![]()
![]() (8.1.12)
(8.1.12)
в) При обработке матрицы
![]() только по
строкам
только по
строкам
![]() (8.1.13)
(8.1.13)
где ![]() - матрица преобразования для
- матрица преобразования для
![]() -й строки.
-й строки.
г) При одинаковой обработке
каждой строки матрицы ![]()
![]() (8.1.14a)
(8.1.14a)
![]() (8.1.14б)
(8.1.14б)
д) При одинаковой обработке
столбцов и одинаковой обработке строк матрицы ![]()
![]() (8.1.15)
(8.1.15)
Число арифметических операций, выполняемых в каждом из этих случаев, указано в табл. 8.1.1.

Рис. 8.1.1. Структура матриц линейного оператора: а – общий случай; б – обработка только по столбцам; в – обработка только строкам; г – обработка только строкам и столбцам.
Таблица 8.1.1. Число арифметических операций при линейном преобразовании
|
Случай |
Число умножений и сложений |
|
Общий Обработка по столбцам Обработка по строкам Обработка по строкам и столбцам Обработка при разделимой матрице |
|
Из соотношения (8.1.10)
видно, что если двумерное линейное преобразование имеет разделимую матрицу, то его
можно выполнить путем последовательной одномерной обработки строк и столбцов массива
отсчетов. Как следует из табл. 8.1.1, для таких преобразований удается существенно
сократить число необходимых вычислительных операций: в общем случае при вычислении
по формуле (8.1.2) требуется ![]() операций, но если можно воспользоваться
формулой (8.1.10), достаточно
операций, но если можно воспользоваться
формулой (8.1.10), достаточно ![]() операций. Более того, в этом случае матрицу
операций. Более того, в этом случае матрицу
![]() можно хранить
в запоминающем устройстве (ЗУ) с последовательным доступом, например на диске или
на барабане, и считывать строка за строкой, т. е. отпадает необходимость хранения
матрицы
можно хранить
в запоминающем устройстве (ЗУ) с последовательным доступом, например на диске или
на барабане, и считывать строка за строкой, т. е. отпадает необходимость хранения
матрицы ![]() в
более дорогостоящем ЗУ с произвольным доступом. Необходимо, однако, транспонировать
результаты преобразований по столбцам с тем, чтобы выполнить построчные преобразования.
В работах [2, 3] описаны алгоритмы транспонирования матриц, записанных в ЗУ с последовательным
доступом.
в
более дорогостоящем ЗУ с произвольным доступом. Необходимо, однако, транспонировать
результаты преобразований по столбцам с тем, чтобы выполнить построчные преобразования.
В работах [2, 3] описаны алгоритмы транспонирования матриц, записанных в ЗУ с последовательным
доступом.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
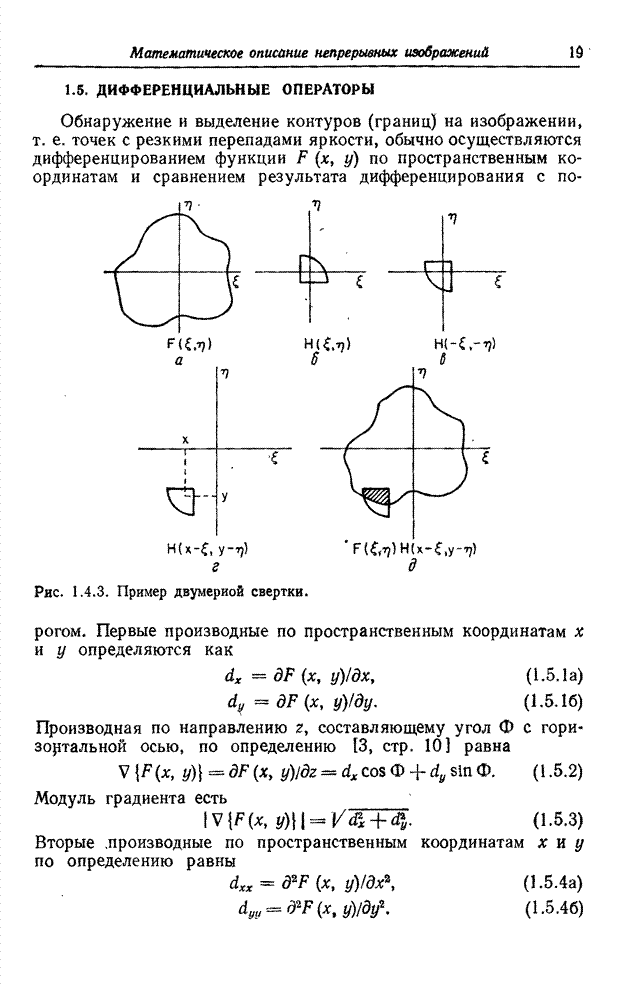
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
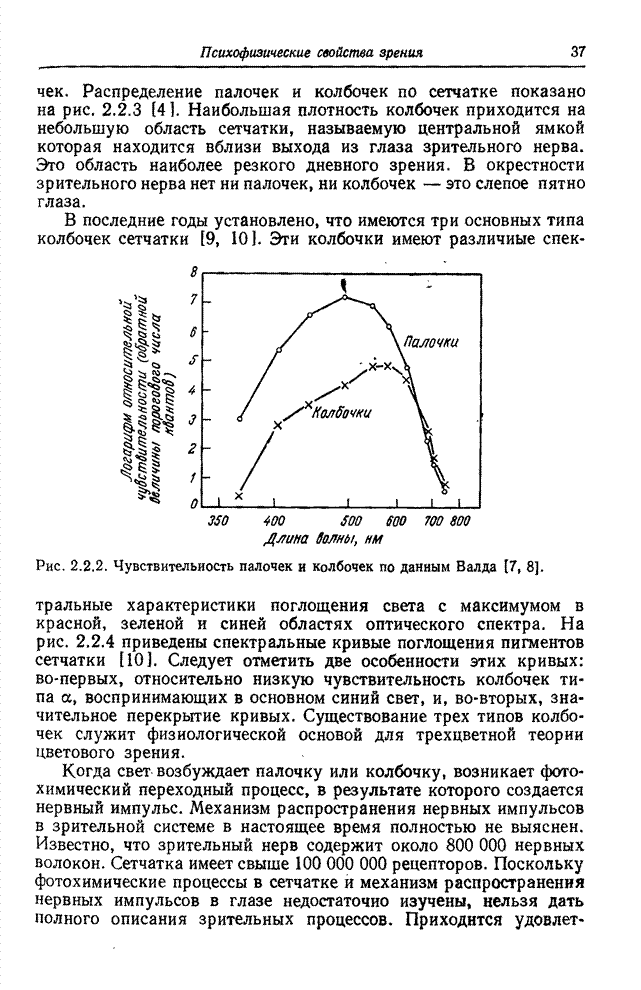
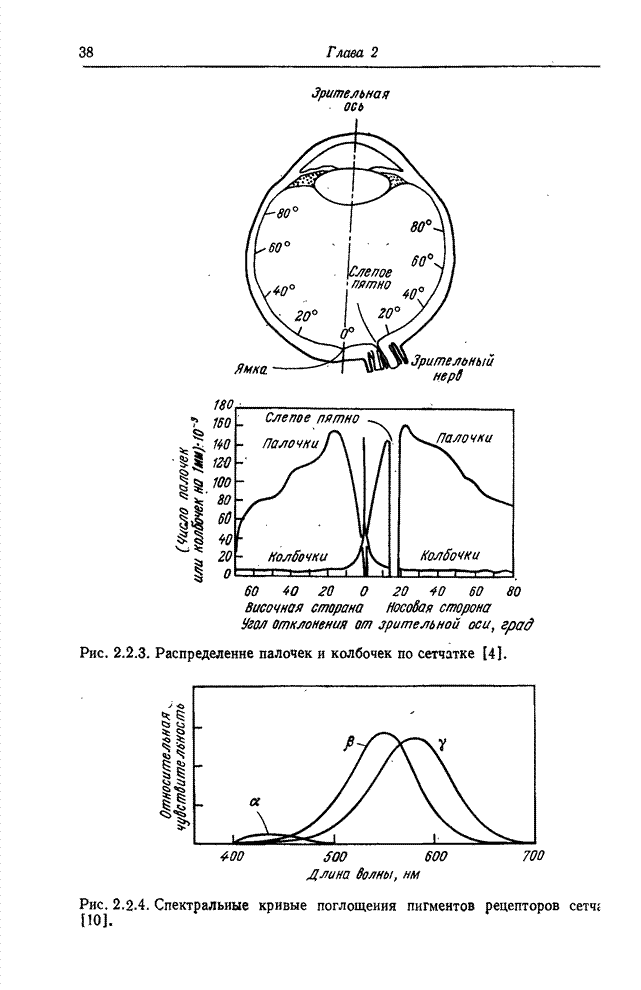
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
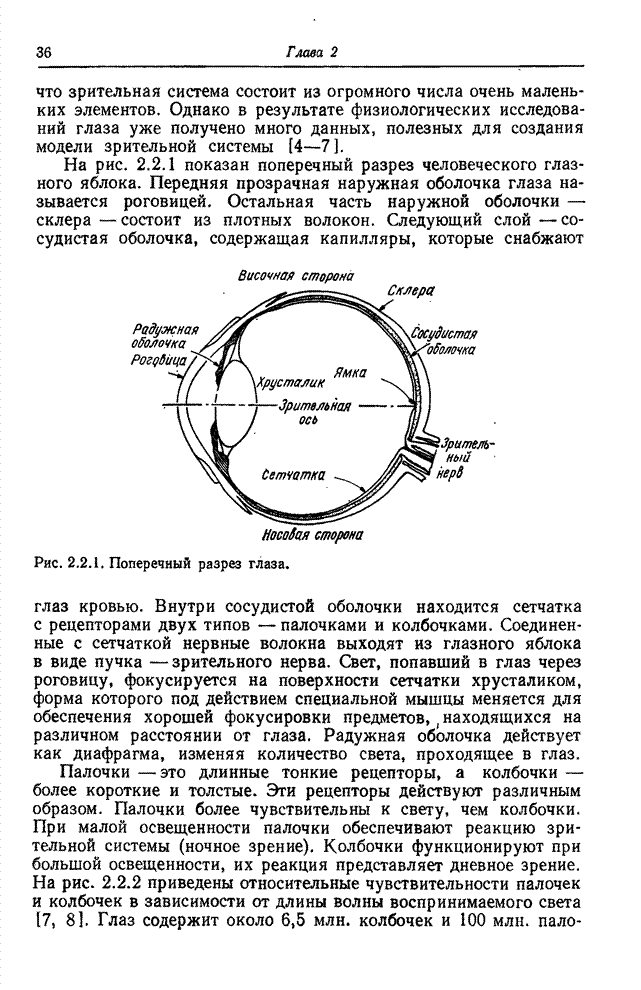
- 2.2. ГЛАЗ
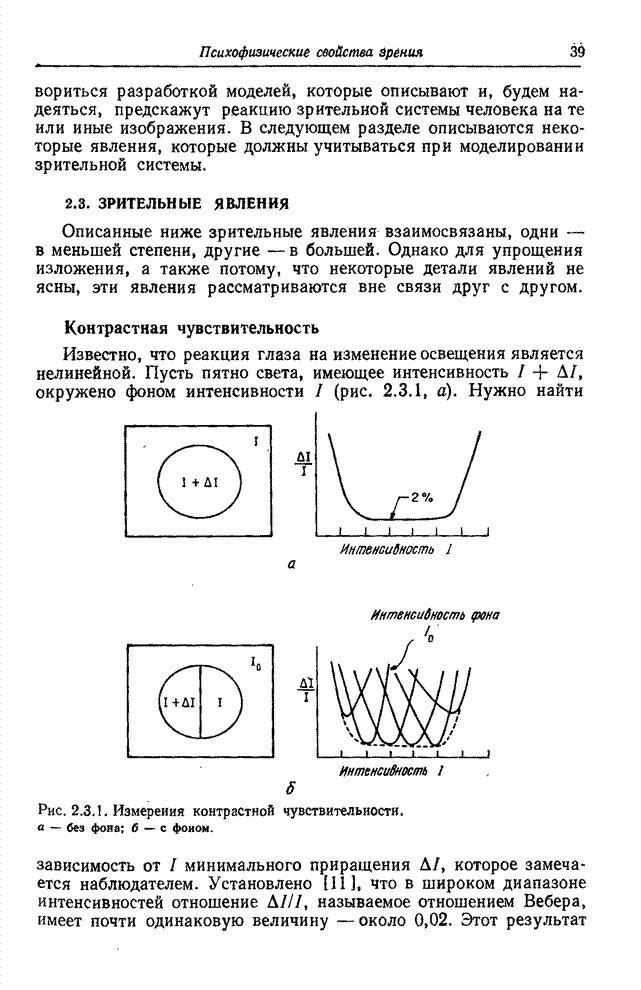
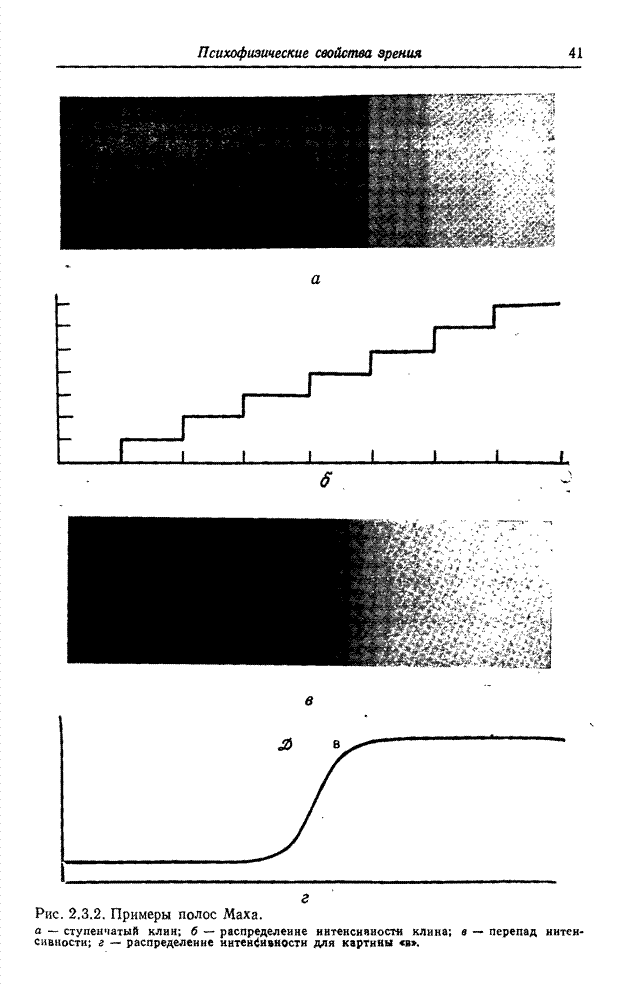
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
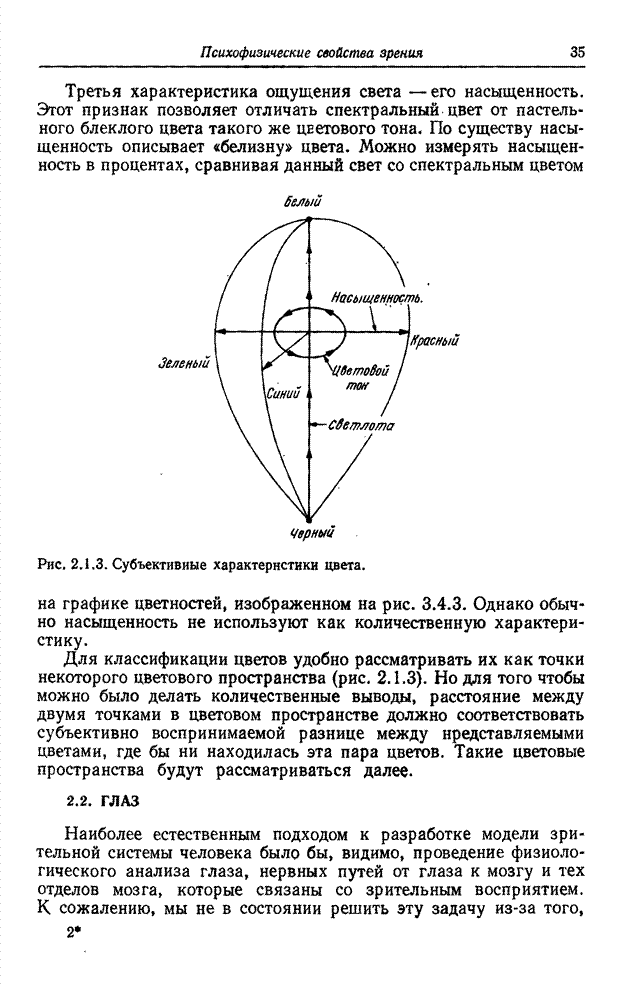
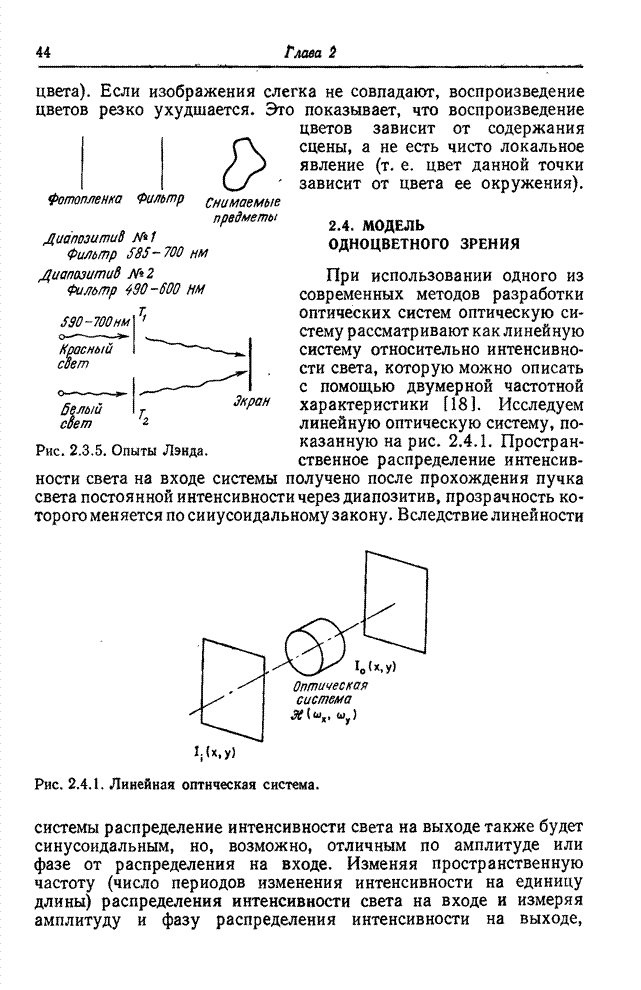
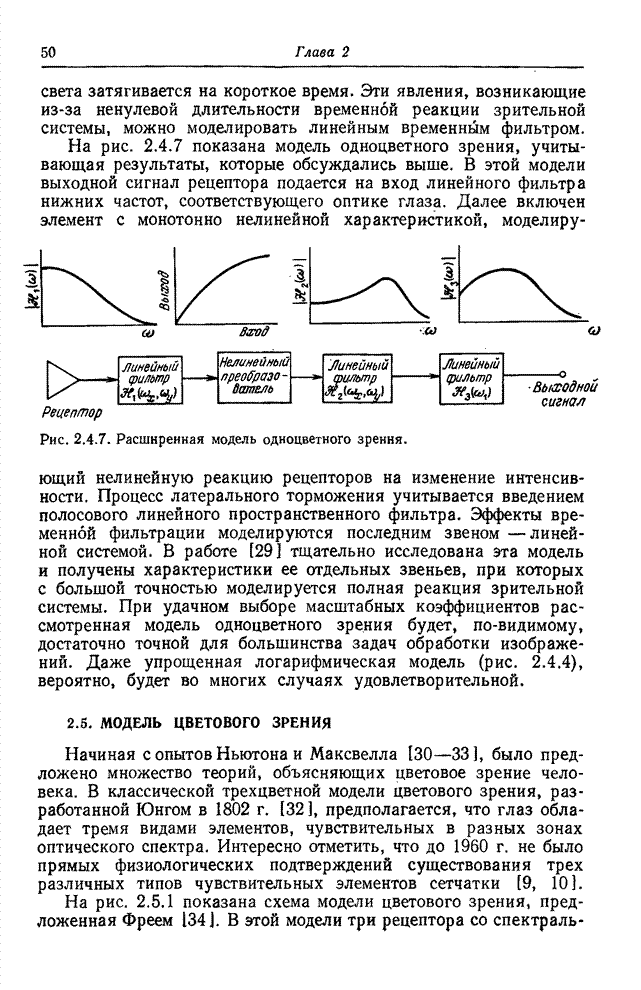
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
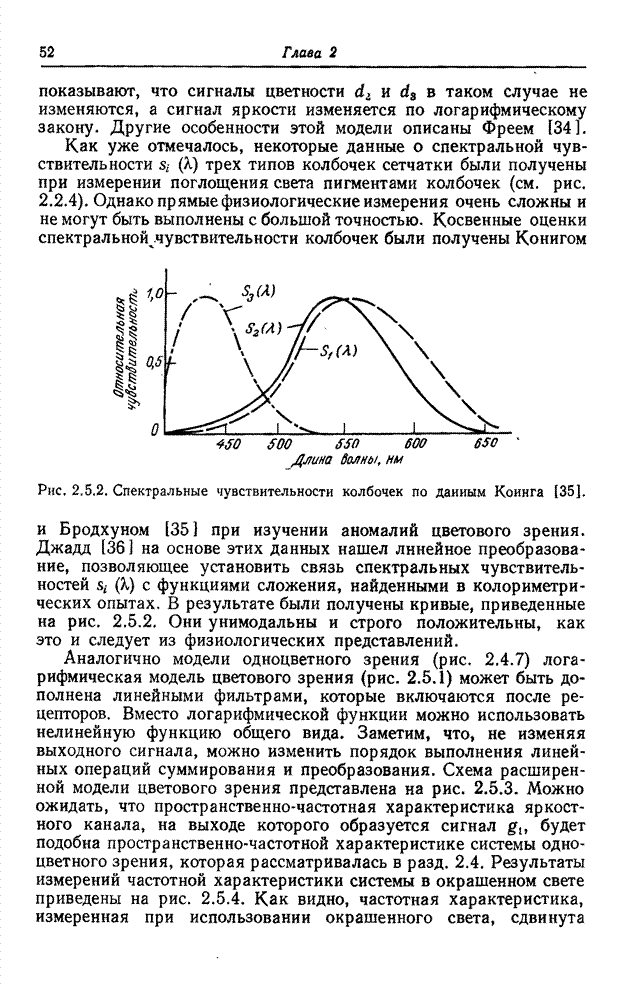
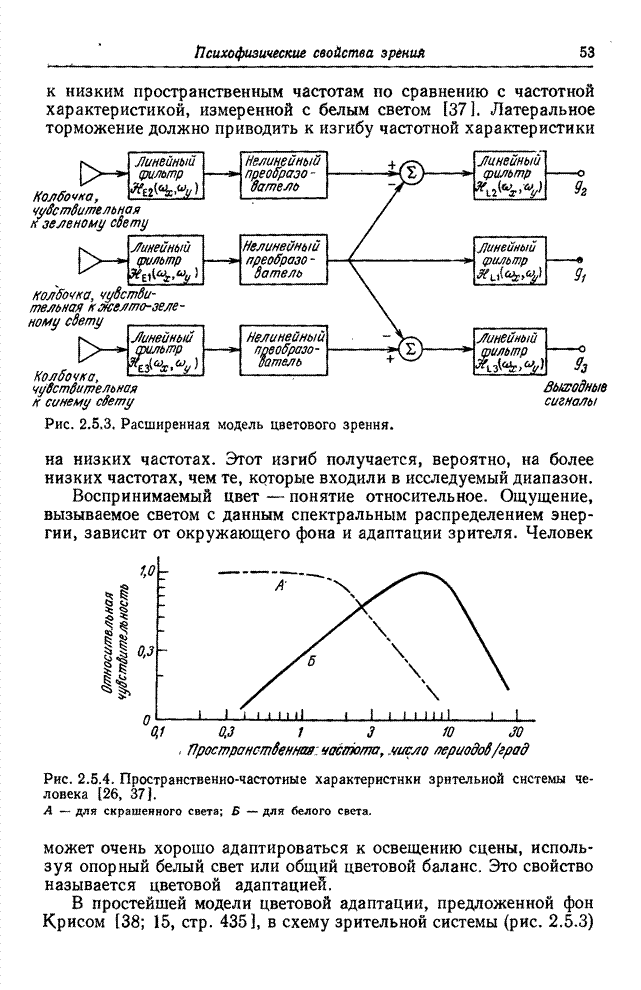
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
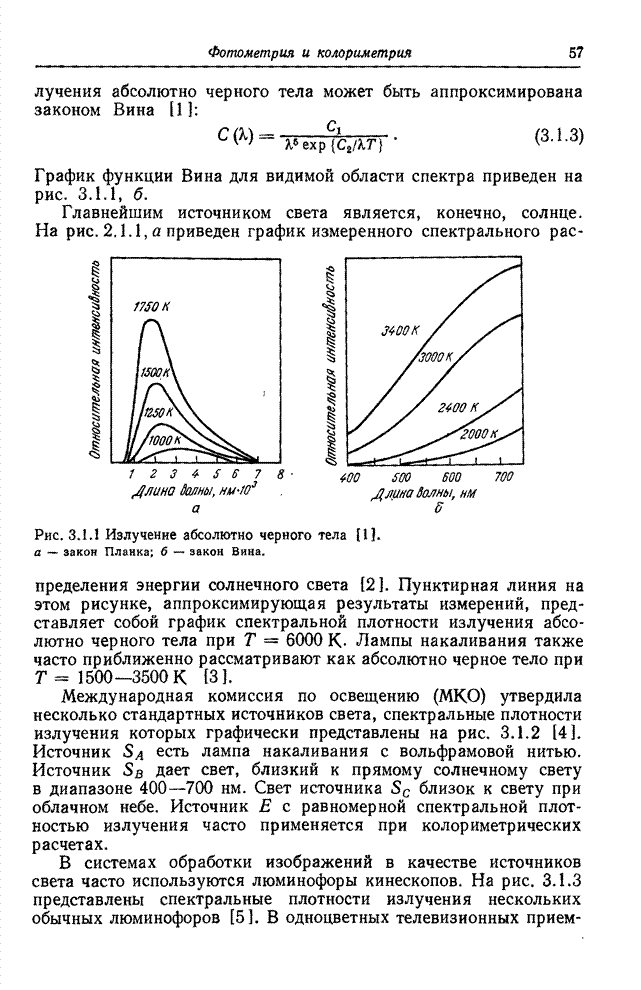
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
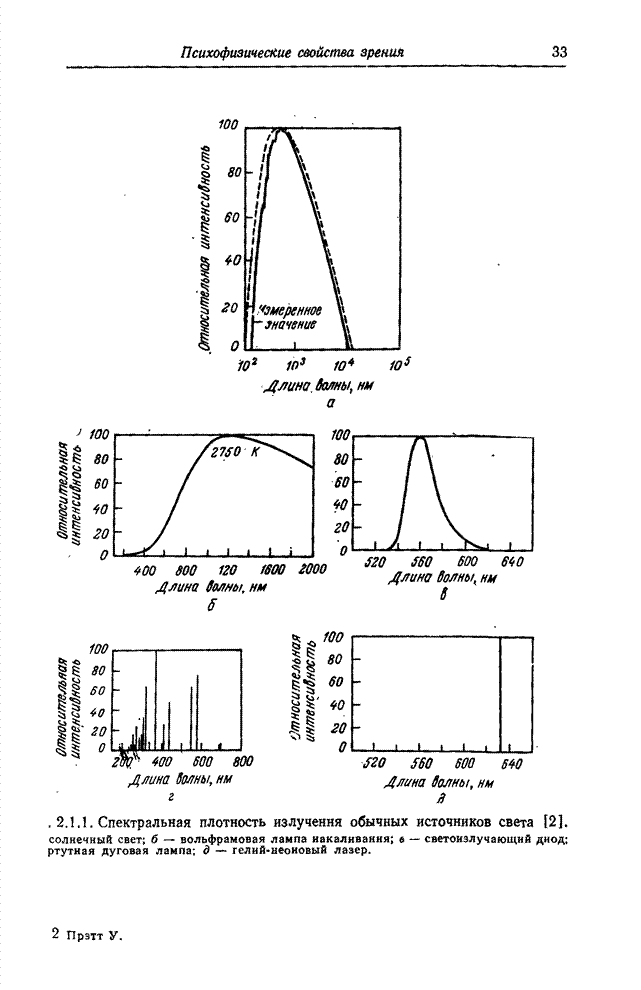
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
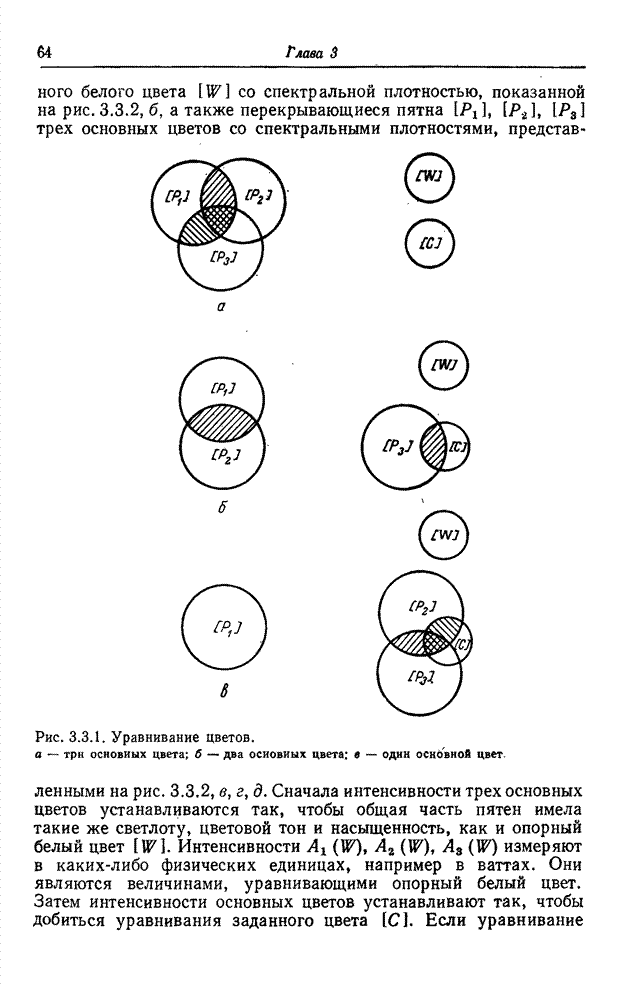
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
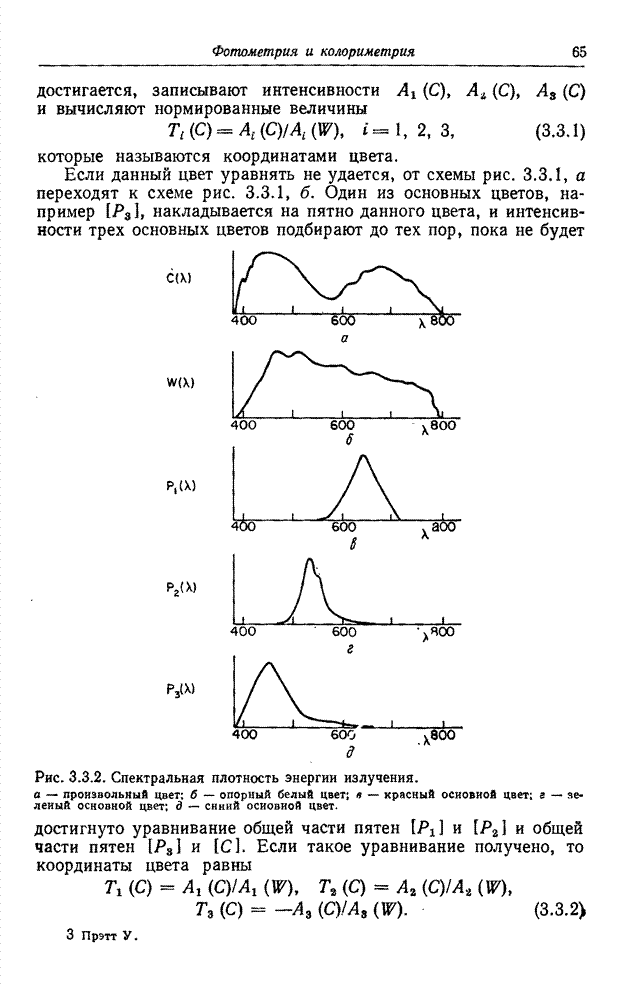
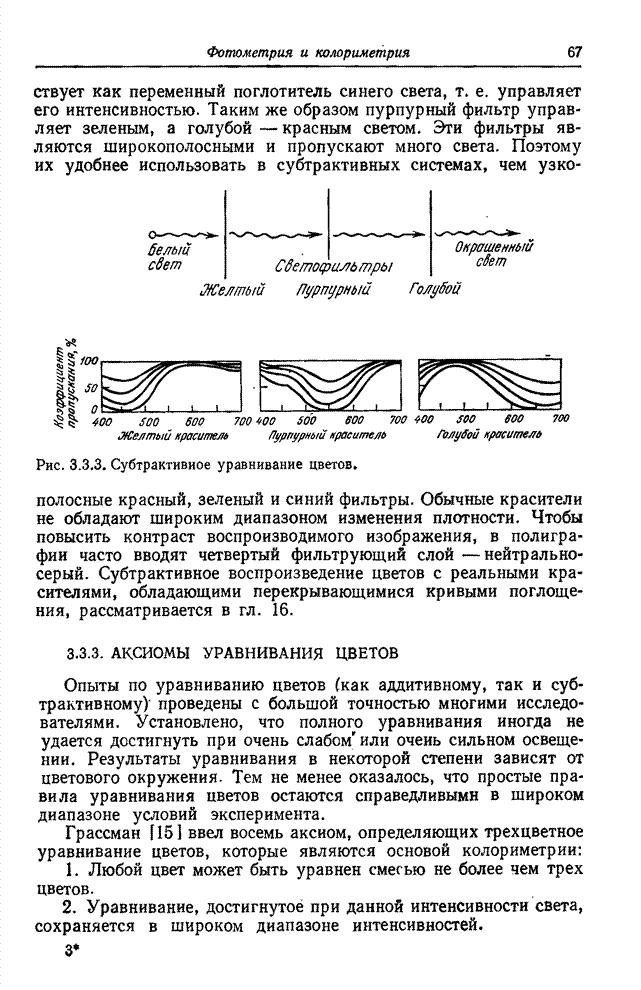
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
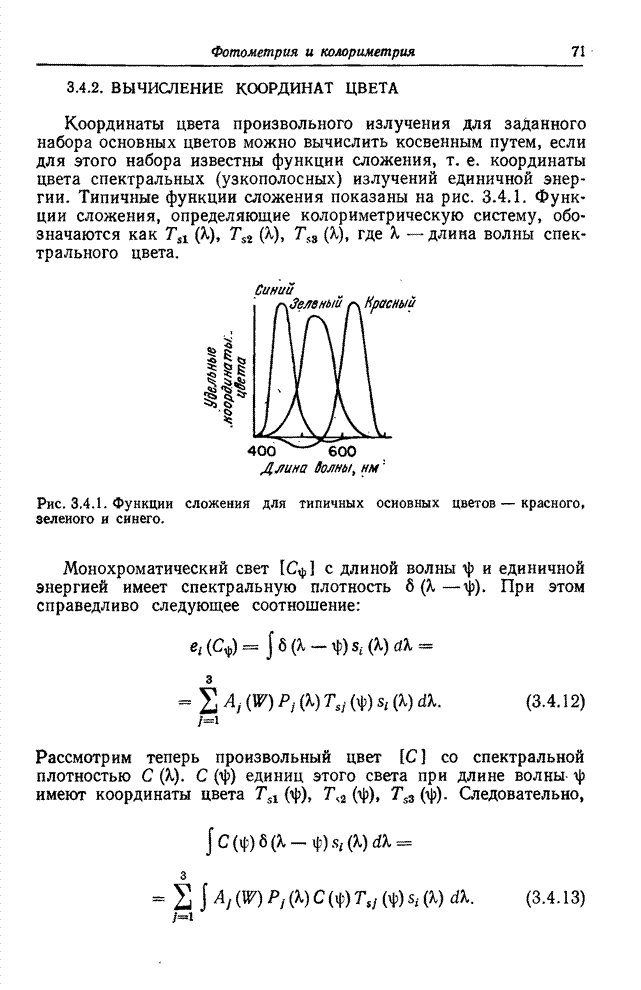
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
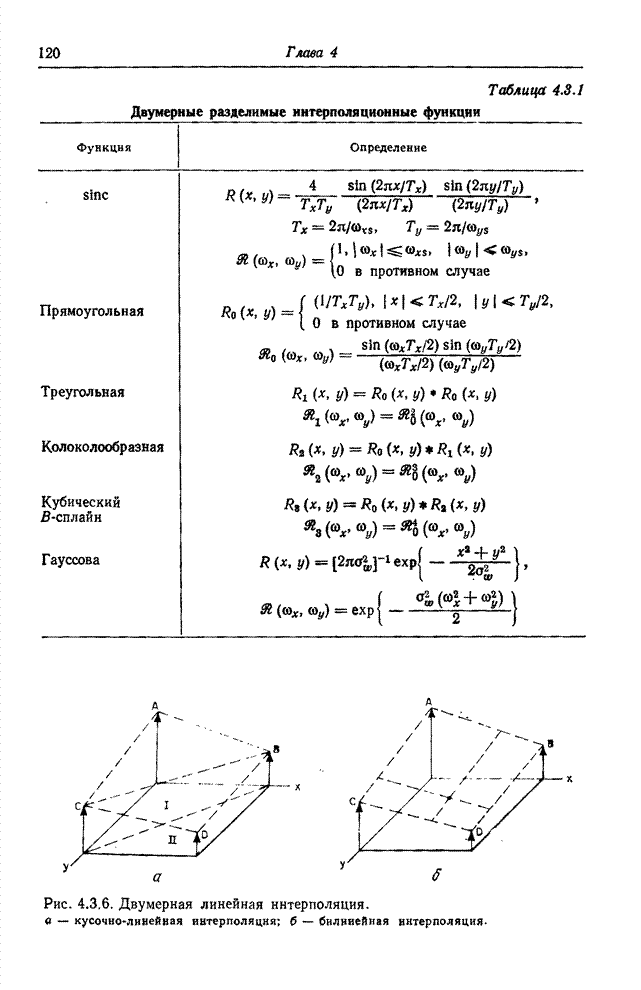
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
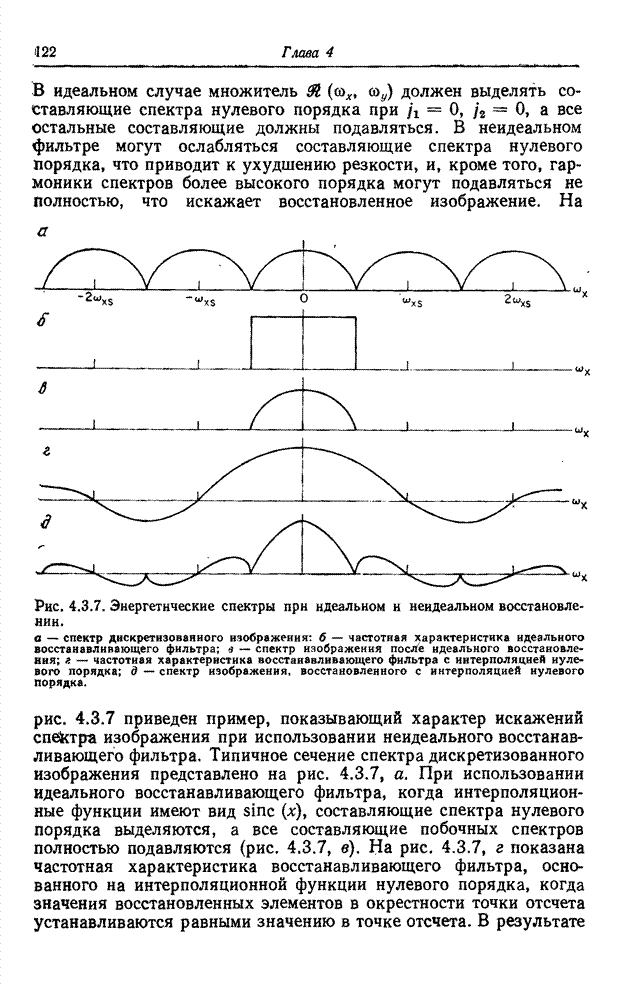
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
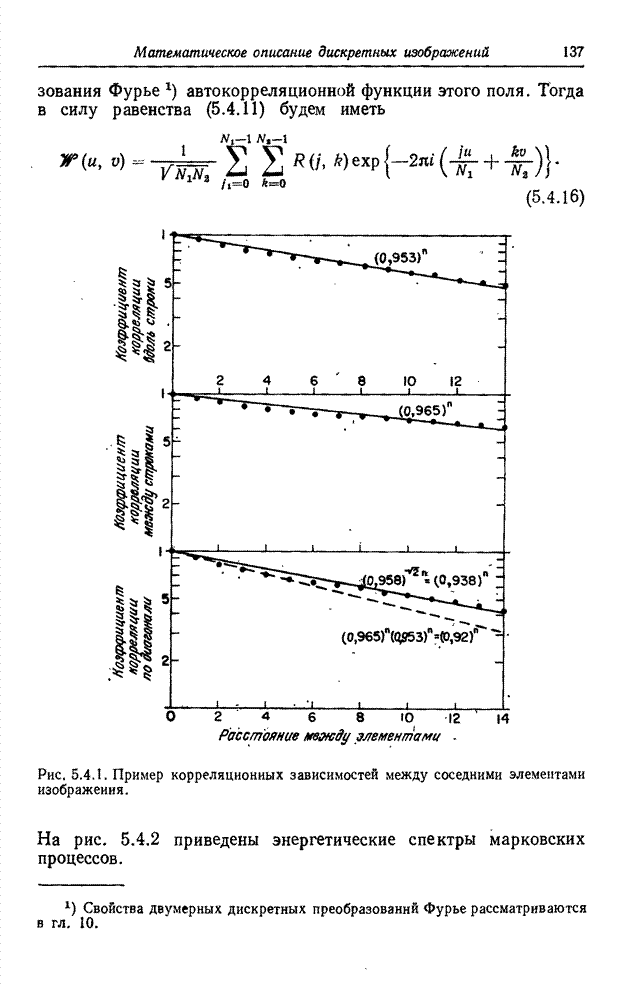
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
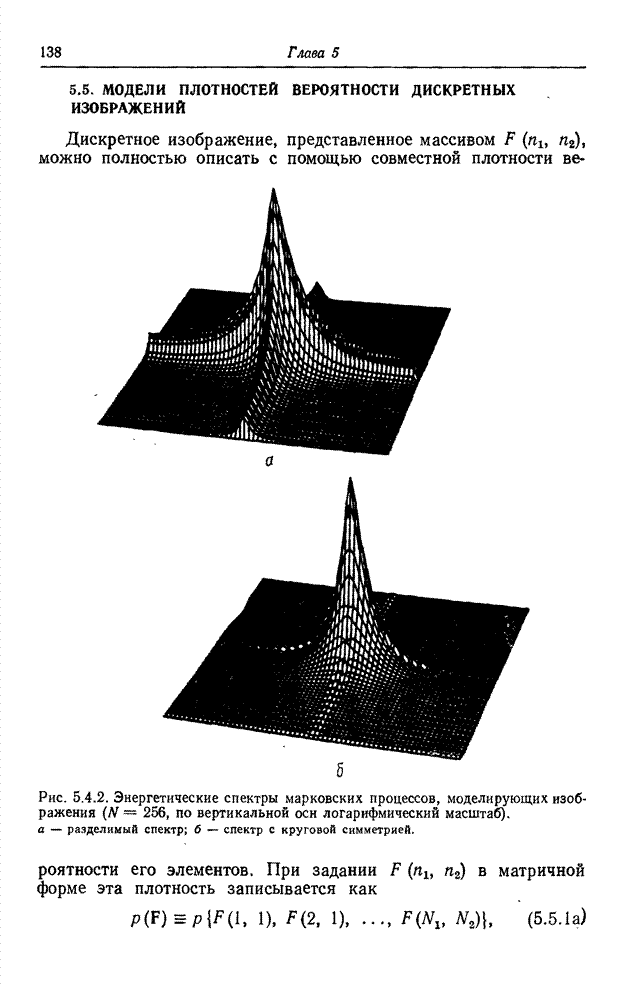
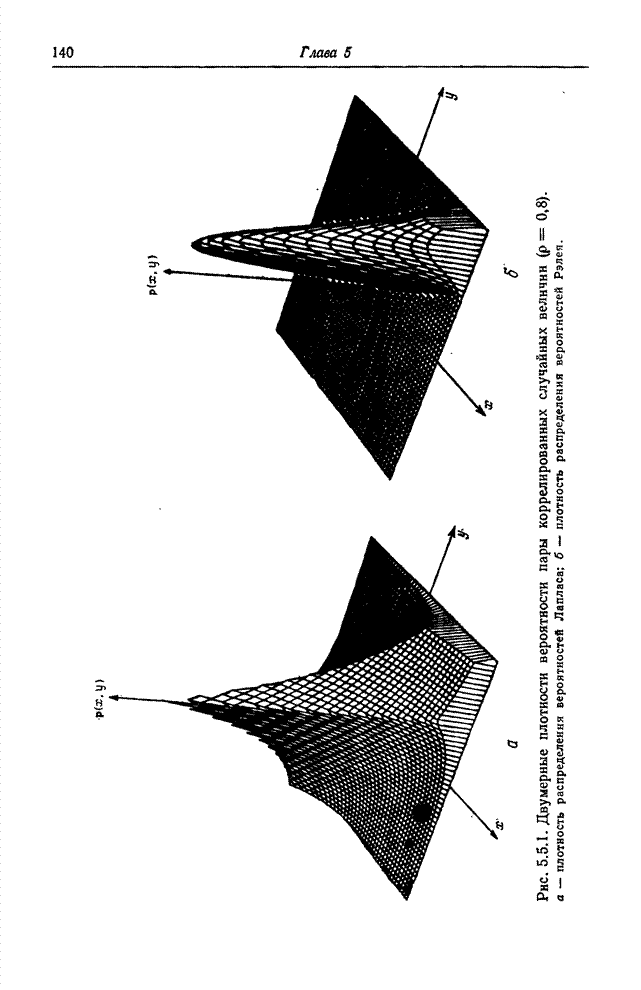
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
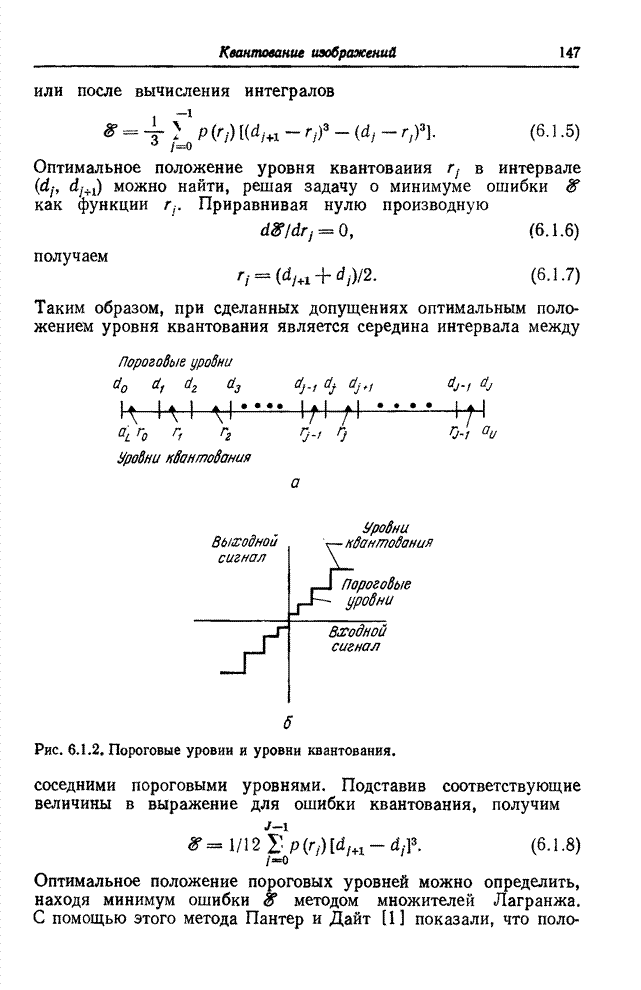
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
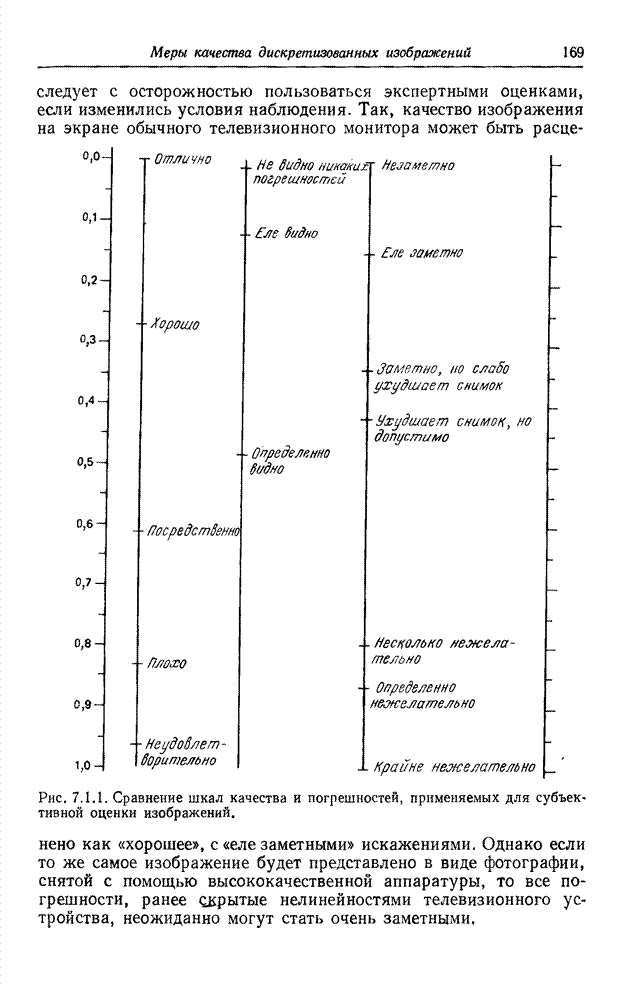
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
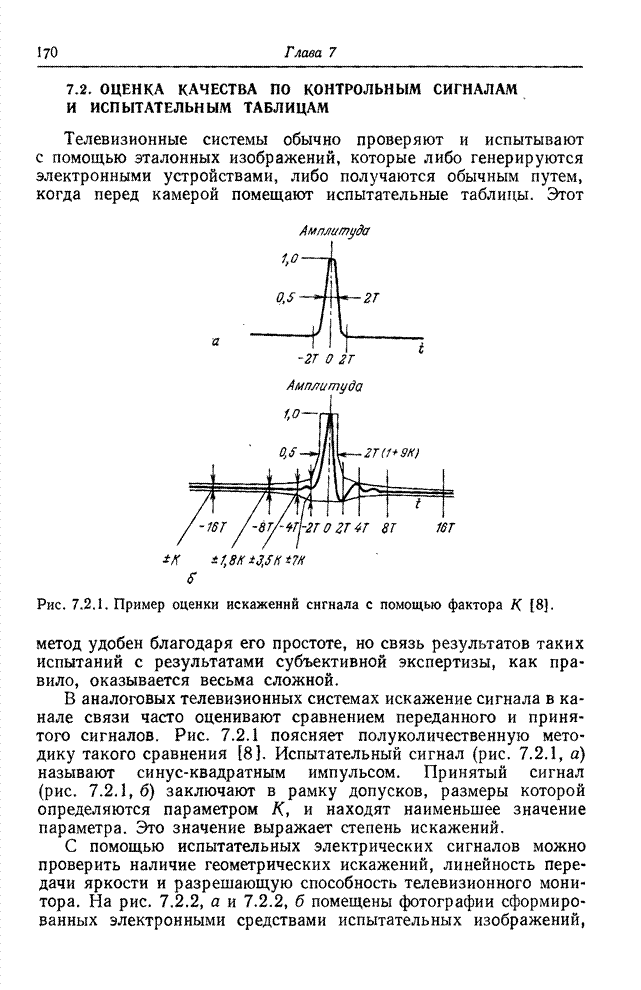
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
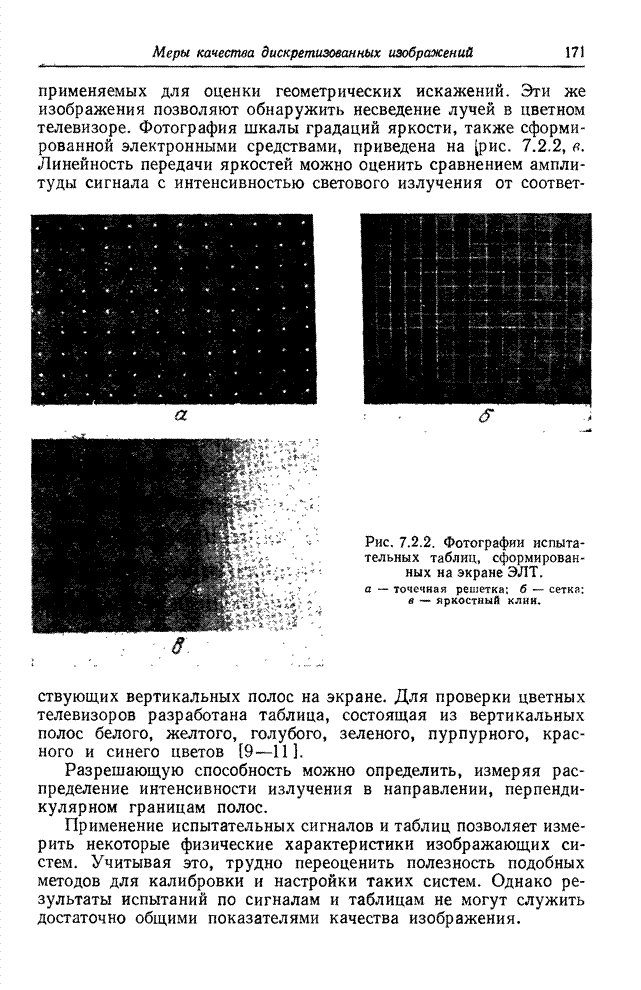
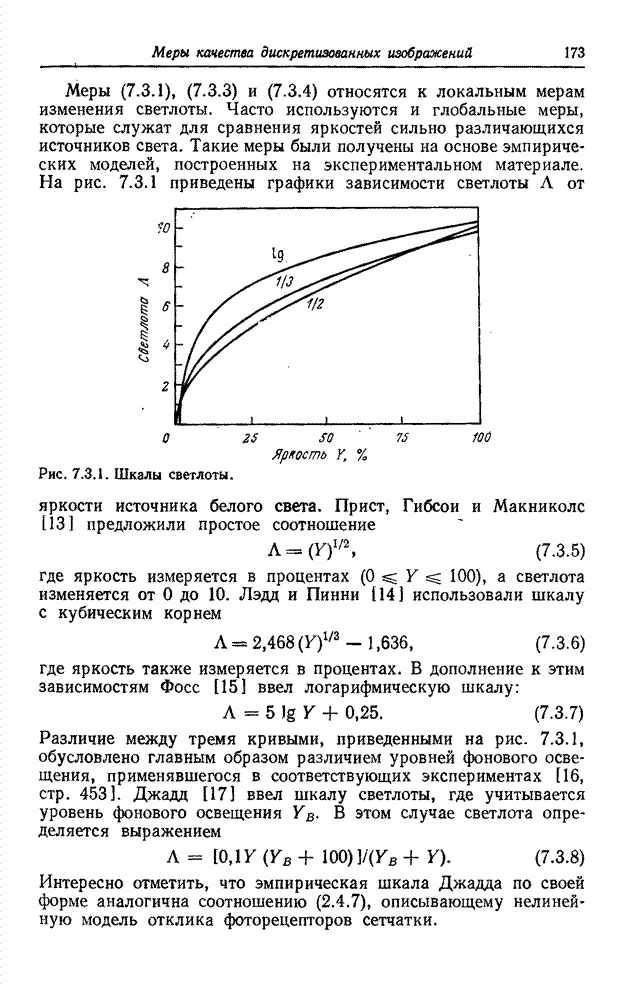
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА