| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
Дискретное
изображение, представленное массивом ![]() , можно
полностью описать с помощью совместной плотности вероятности его элементов. При
задании в матричной форме
эта плотность записывается как
, можно
полностью описать с помощью совместной плотности вероятности его элементов. При
задании в матричной форме
эта плотность записывается как
![]() , (5.5.1а)
, (5.5.1а)
а в векторной форме - как
![]() , (5.5.1б)
, (5.5.1б)
где
![]() определяет
порядок совместной плотности. Если все элементы изображения статистически
независимы, то совместная плотность вероятности равна произведению одномерных
безусловных плотностей
определяет
порядок совместной плотности. Если все элементы изображения статистически
независимы, то совместная плотность вероятности равна произведению одномерных
безусловных плотностей
![]() . (5.5.2)
. (5.5.2)

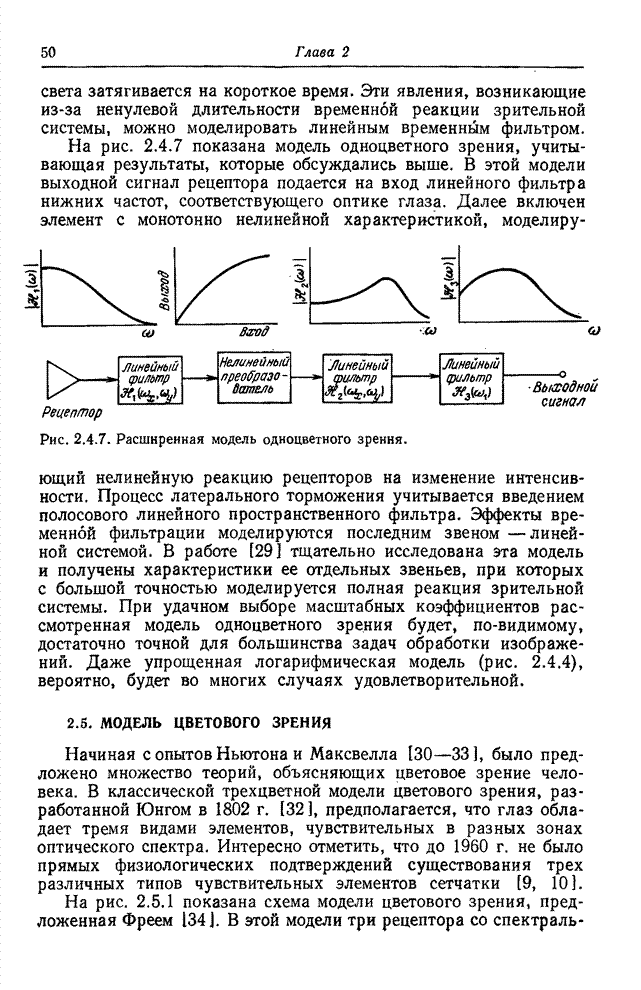
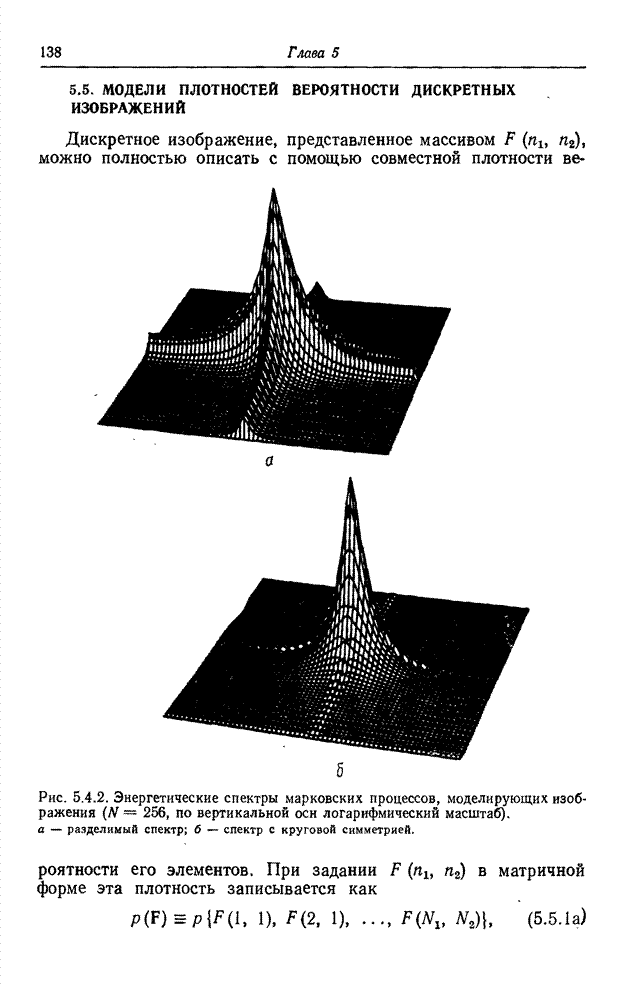
Рис. 5.4.2. Энергетические спектры марковских
процессов, моделирующих изображения (![]() , по вертикальной оси логарифмический
масштаб): а – разделимый спектр; б – спектр с круговой симметрией.
, по вертикальной оси логарифмический
масштаб): а – разделимый спектр; б – спектр с круговой симметрией.
Наиболее распространенным видом совместной плотности вероятности является гауссова плотность
![]() , (5.5.3)
, (5.5.3)
где
![]() -
ковариационная матрица вектора
-
ковариационная матрица вектора ![]() ,
, ![]() - среднее
значение
- среднее
значение ![]() ,
а символом
,
а символом ![]() обозначен
определитель матрицы
обозначен
определитель матрицы ![]() . Гауссова
плотность является полезной моделью совместной плотности вероятности
коэффициентов, полученных в результате унитарных преобразований изображений.
Однако гауссова плотность не подходит для описания яркости элементов
изображения, поскольку яркость может быть только положительной, а гауссовы
случайные величины принимают как положительные, так и отрицательные значения.
. Гауссова
плотность является полезной моделью совместной плотности вероятности
коэффициентов, полученных в результате унитарных преобразований изображений.
Однако гауссова плотность не подходит для описания яркости элементов
изображения, поскольку яркость может быть только положительной, а гауссовы
случайные величины принимают как положительные, так и отрицательные значения.
В
литературе редко встречаются выражения для совместных плотностей, не являющихся
гауссовыми. Хунс [13] разработал методику формирования подобных плотностей
высокого порядка на основе заданной безусловной плотности первого порядка и
заданной ковариационной матрицы элементов ансамбля. Для плотности с нулевым
средним эта процедура сводится к линейному преобразованию набора независимых
случайных величин ![]() , совместную плотность вероятности
которых
, совместную плотность вероятности
которых
![]() (5.5.4)
(5.5.4)
можно записать в виде произведения заданных плотностей первого порядка. Тогда искомая совместная плотность вероятности имеет вид
![]() , (5.5.5)
, (5.5.5)
где
![]() , (5.5.6)
, (5.5.6)
а
![]() обозначает
определитель матрицы
обозначает
определитель матрицы ![]() . Столбцы
матрицы
. Столбцы
матрицы ![]() являются
собственными векторами заданной ковариационной матрицы
являются
собственными векторами заданной ковариационной матрицы ![]() , а матрица
, а матрица ![]() - диагональная и
состоит из собственных значений этой матрицы, причем выполняется соотношение
- диагональная и
состоит из собственных значений этой матрицы, причем выполняется соотношение
![]() . (5.5.7)
. (5.5.7)

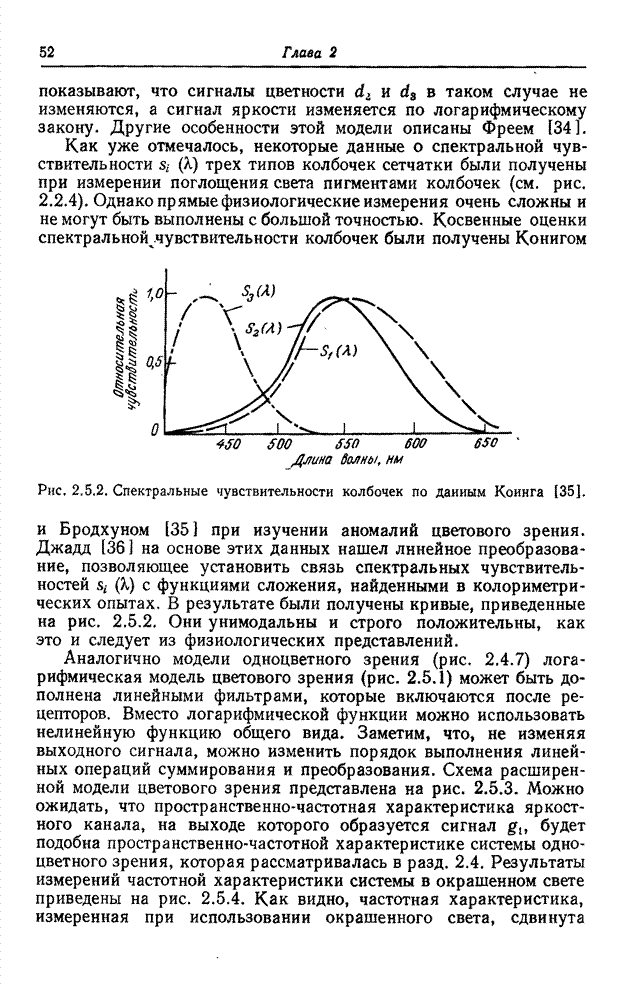
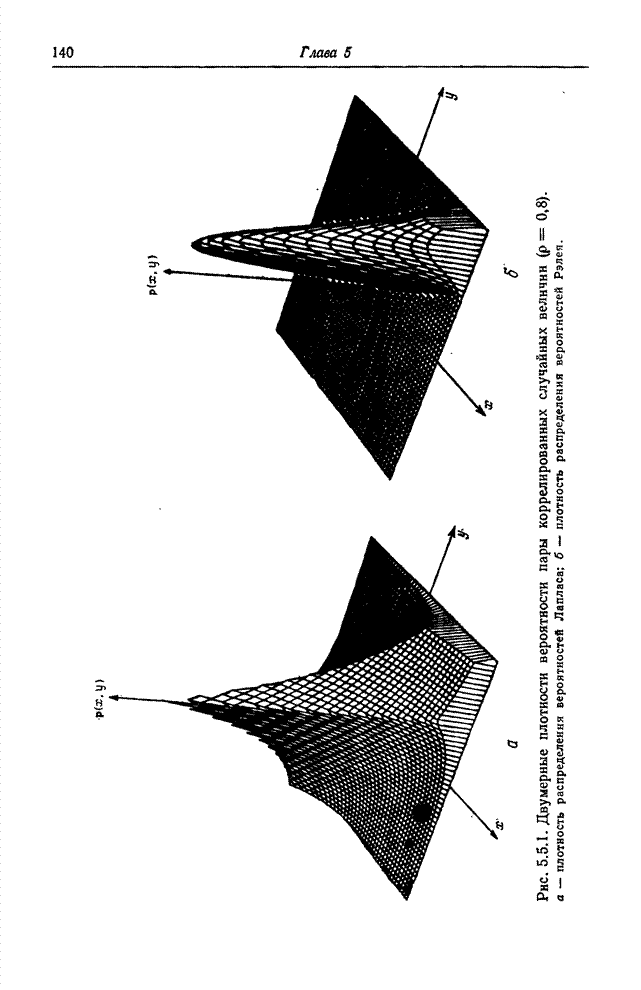
Рис. 5.5.1. Двумерные плотности вероятности пары
коррелированных случайных величин ![]() : а – плотность распределения
вероятностей Лапласа; б – плотность распределения вероятностей Рэлея.
: а – плотность распределения
вероятностей Лапласа; б – плотность распределения вероятностей Рэлея.
На рис. 5.5.1 приведены двумерные плотности вероятности пары коррелированных случайных величин, безусловные распределения которых являются распределениями Рэлея или Лапласа. Многомерная модель с распределением Рэлея полезна при рассмотрении совместной плотности вероятности яркостей элементов изображения, а модель с распределением Лапласа применяется для статистического описания последовательности разностных сигналов, образующихся в системах кодирования изображений методом предсказания.
В
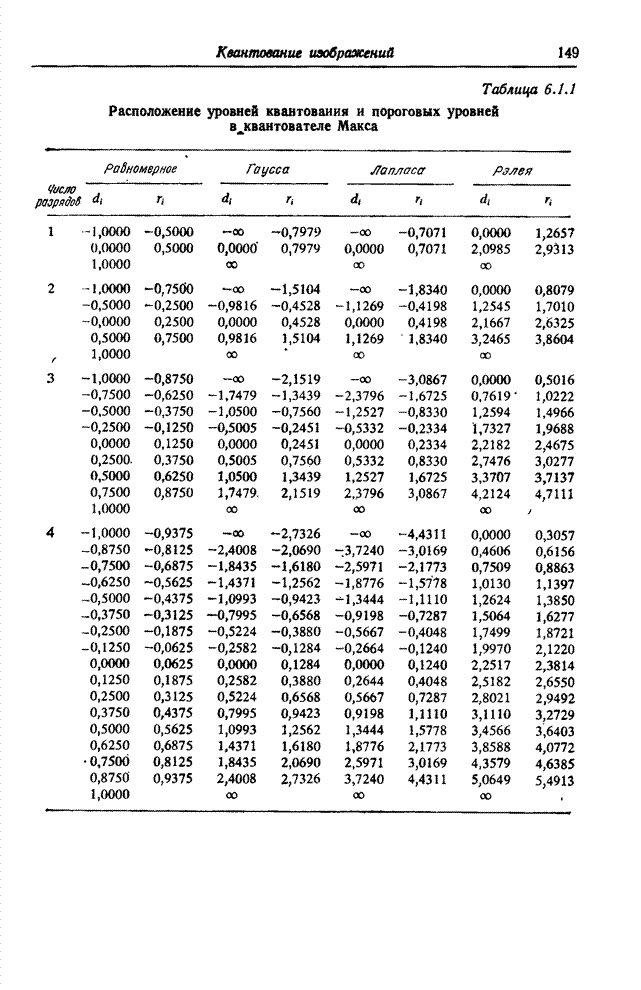
следующей главе рассматривается методика квантования, т. е. представления
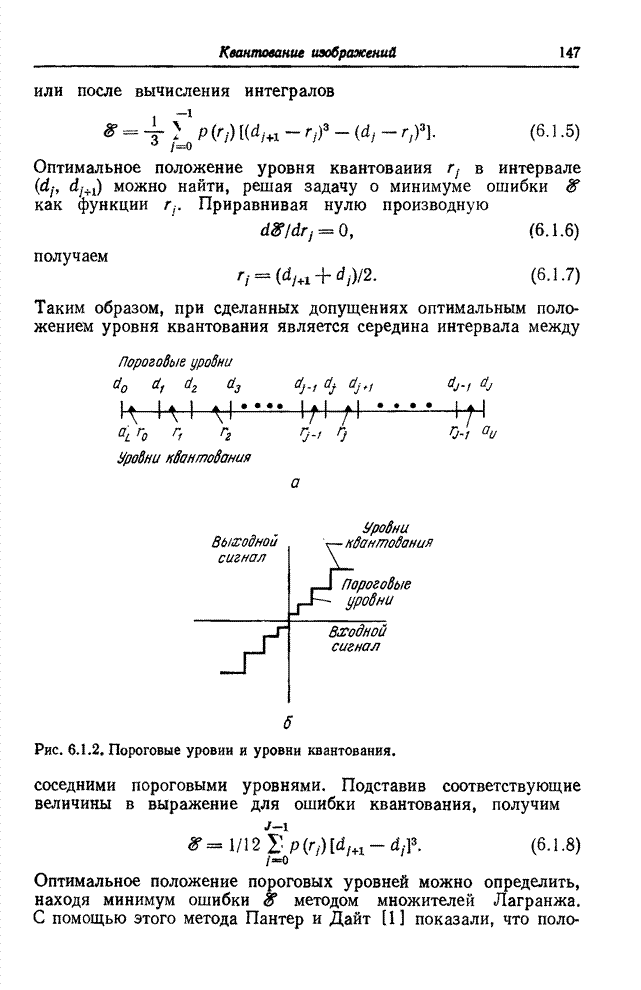
отсчетов с помощью дискретного набора чисел, называемых уровнями квантования.
Пусть ![]() обозначает
обозначает ![]() -й уровень
квантования для элемента изображения, который занимает
-й уровень
квантования для элемента изображения, который занимает ![]() -e место в векторе
изображения
-e место в векторе
изображения ![]() .
Тогда вероятность получения одного из возможных значений вектора
.
Тогда вероятность получения одного из возможных значений вектора ![]() можно выразить
через совместное распределение вероятностей значений отсчетов следующим
образом:
можно выразить
через совместное распределение вероятностей значений отсчетов следующим
образом:
![]() , (5.5.8)
, (5.5.8)
где
![]() . Обычно для
всех компонент вектора выбирают одинаковый набор уровней квантования и
совместное распределение вероятностей принимает вид
. Обычно для
всех компонент вектора выбирают одинаковый набор уровней квантования и
совместное распределение вероятностей принимает вид
![]() . (5.5.9)
. (5.5.9)
Распределения
вероятностей значений отсчетов можно оценить, измеряя соответствующие частоты.
Так, одномерное распределение ![]() -й компоненты вектора
-й компоненты вектора
![]() (5.5.10)
(5.5.10)
можно оценить путем анализа большого набора изображений, относящихся к одному и тому же классу, таких, например, как флюорограммы, аэрофотоснимки полей и т. д. Оценкой одномерного распределения вероятностей служит распределение относительных частот
![]() , (5.5.11)
, (5.5.11)
где
![]() - полное число
исследованных снимков, а
- полное число
исследованных снимков, а ![]() - число
снимков, для которых
- число
снимков, для которых ![]() ,
,![]() . Если источник
изображений является стационарным, то одномерные распределения (5.5.10) будут
одинаковы для всех компонент вектора, т. е. не будут зависеть от
. Если источник
изображений является стационарным, то одномерные распределения (5.5.10) будут
одинаковы для всех компонент вектора, т. е. не будут зависеть от ![]() . Кроме того,
если источник изображений является эргодическим, то усреднение по ансамблю
(измерения при использовании набора снимков) можно заменить усреднением по
пространственным координатам. Если предположение об эргодичности справедливо,
то одномерное распределение можно оценить по частотам
. Кроме того,
если источник изображений является эргодическим, то усреднение по ансамблю
(измерения при использовании набора снимков) можно заменить усреднением по
пространственным координатам. Если предположение об эргодичности справедливо,
то одномерное распределение можно оценить по частотам
![]() , (5.5.12)
, (5.5.12)
где
![]() - число
элементов исследуемого изображения, для которых
- число
элементов исследуемого изображения, для которых ![]() , причем
, причем ![]() , а
, а ![]() .
.
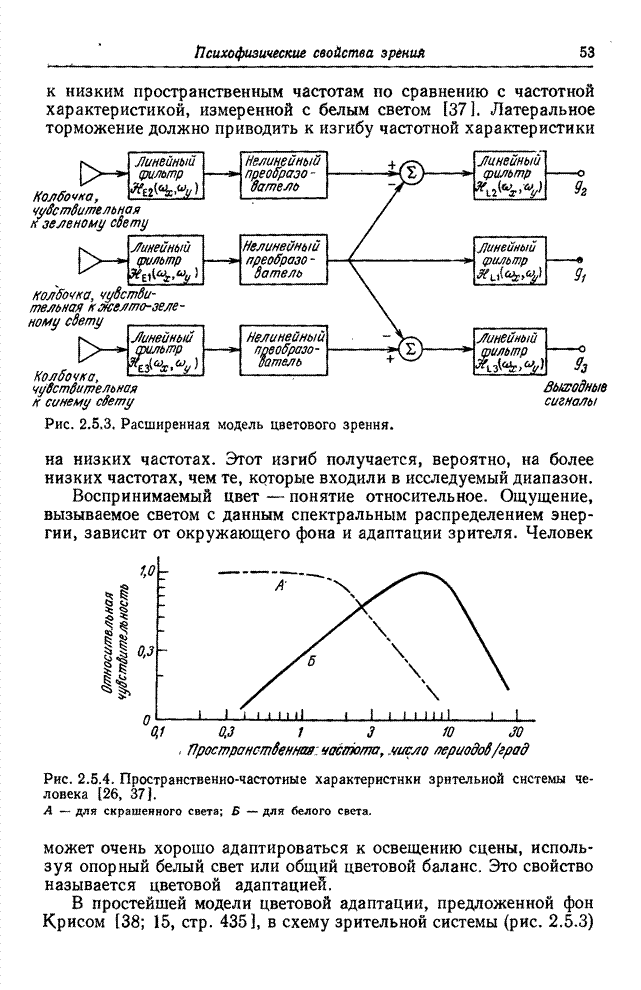
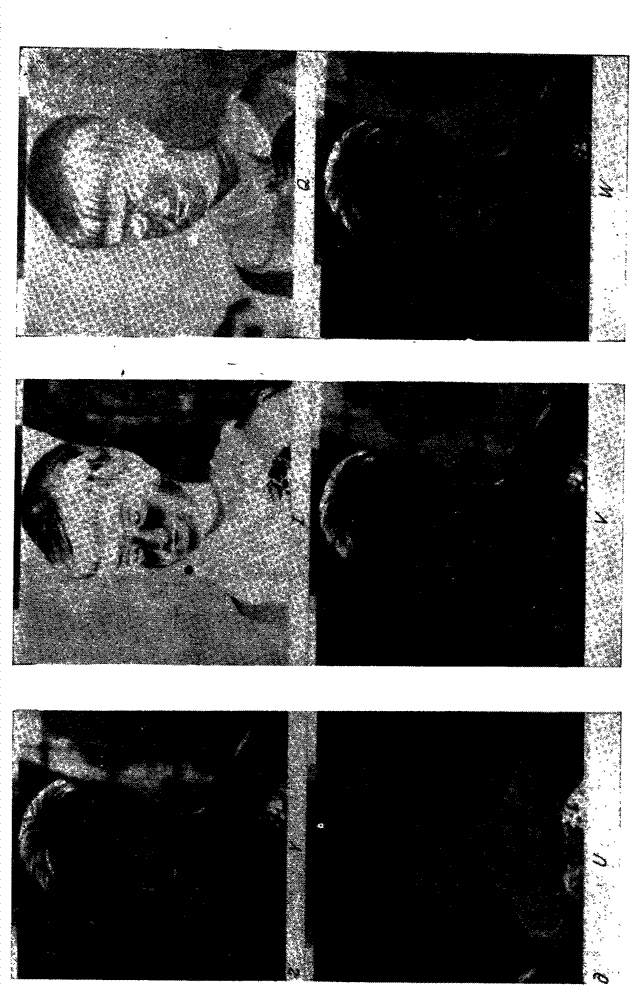
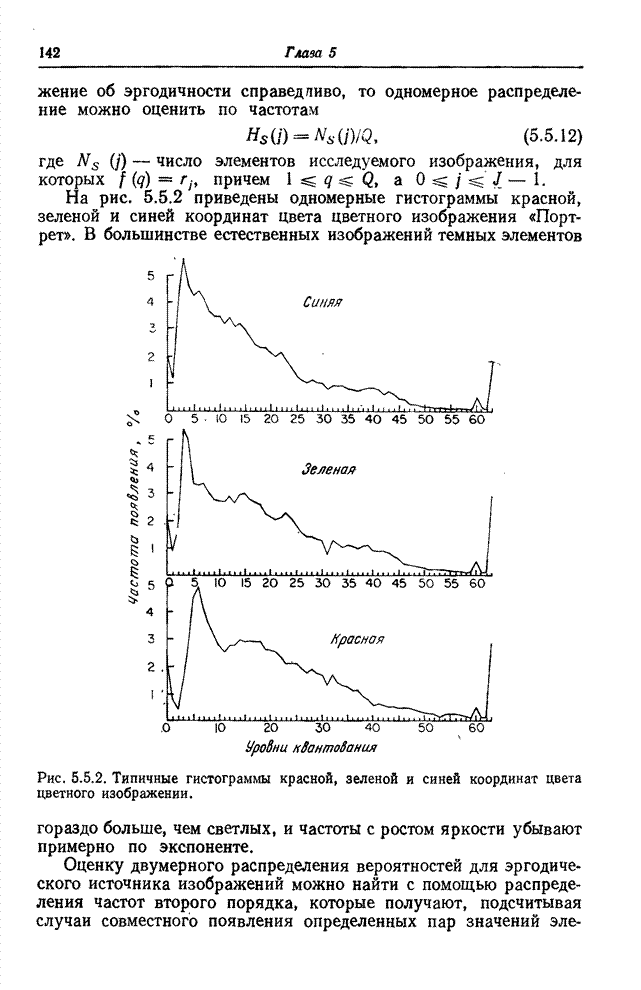
На рис. 5.5.2 приведены одномерные гистограммы красной, зеленой и синей координат цвета цветного изображения «Портрет». В большинстве естественных изображений темных элементов гораздо больше, чем светлых, и частоты с ростом яркости убывают примерно по экспоненте.

Рис. 5.5.2. Типичные гистограммы красной, зеленой и синей координат цвета цветного изображения.
Оценку
двумерного распределения вероятностей для эргодического источника изображений
можно найти с помощью распределения частот второго порядка, которые получают,
подсчитывая случаи совместного появления определенных пар значений элементов,
разделенных заданным расстоянием. Допустим, что ![]() и
и ![]() есть два
элемента изображения, разделенные отрезком длиной
есть два
элемента изображения, разделенные отрезком длиной ![]() , который
наклонен к горизонтальной оси под углом
, который
наклонен к горизонтальной оси под углом ![]() (рис. 5.5.3).
Поскольку элементы образуют прямоугольную решетку, параметры
(рис. 5.5.3).
Поскольку элементы образуют прямоугольную решетку, параметры ![]() ,
, ![]() могут принимать
только некоторые дискретные значения. Относительная частота второго порядка
есть
могут принимать
только некоторые дискретные значения. Относительная частота второго порядка
есть
![]() , (5.5.13)
, (5.5.13)
где
![]() - число пар
элементов изображения, для которых
- число пар
элементов изображения, для которых ![]() и
и ![]() . Знаменатель
дроби (5.5.13)
. Знаменатель
дроби (5.5.13) ![]() представляет
собой полное число пар элементов, которые разделены отрезками с одинаковыми
параметрами
представляет
собой полное число пар элементов, которые разделены отрезками с одинаковыми
параметрами ![]() . Из-за краевых
эффектов
. Из-за краевых
эффектов ![]() .
.

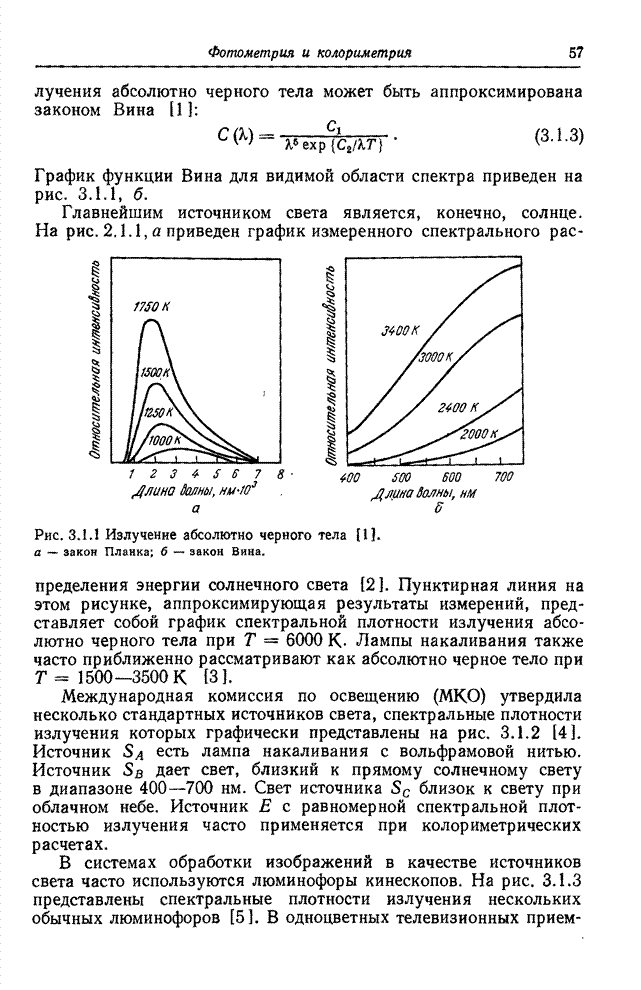
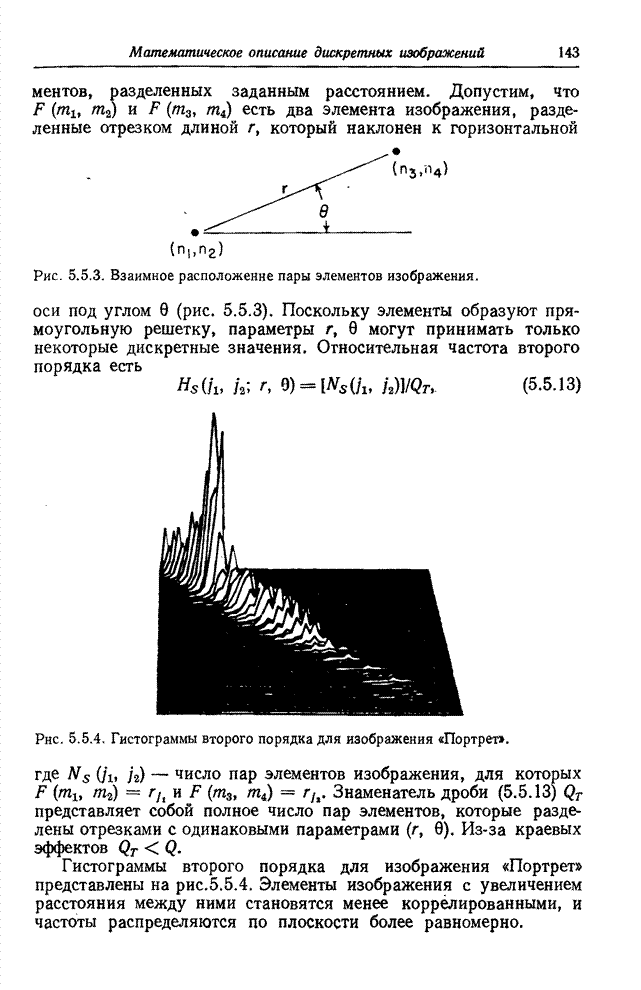
Рис. 5.5.3. Взаимное расположение пары элементов изображения.

Рис. 5.5.4. Гистограммы второго порядка для изображения «Портрет».
Гистограммы второго порядка для изображения «Портрет» представлены на рис.5.5.4. Элементы изображения с увеличением расстояния между ними становятся менее коррелированными, и частоты распределяются по плоскости более равномерно.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
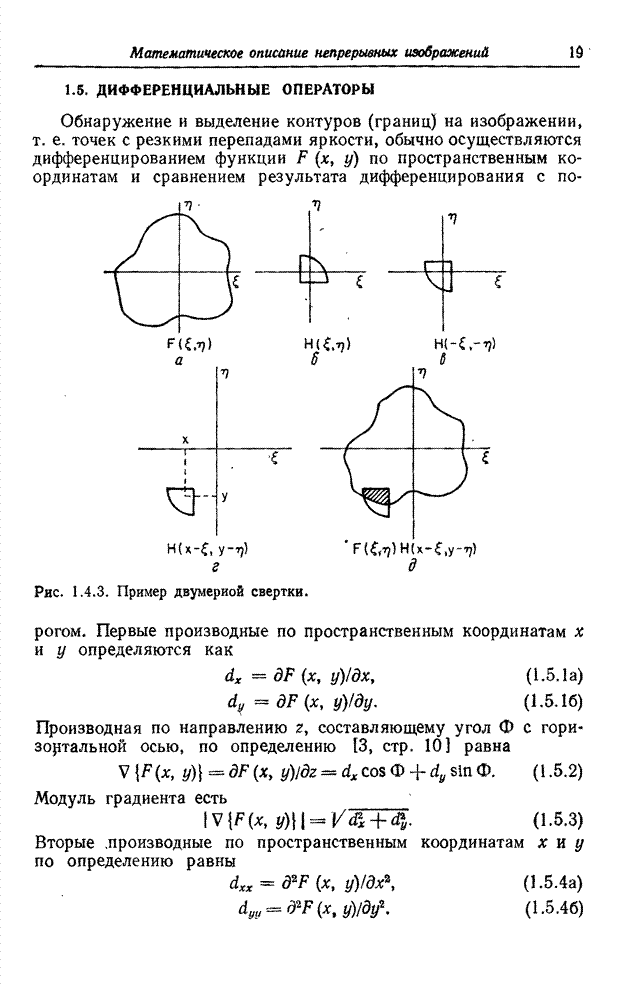
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
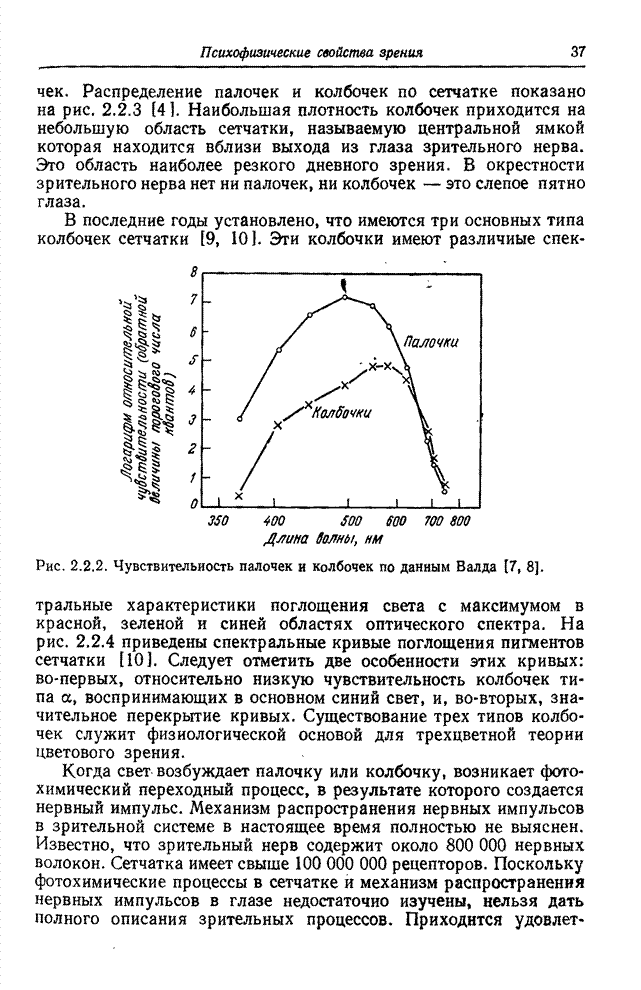
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
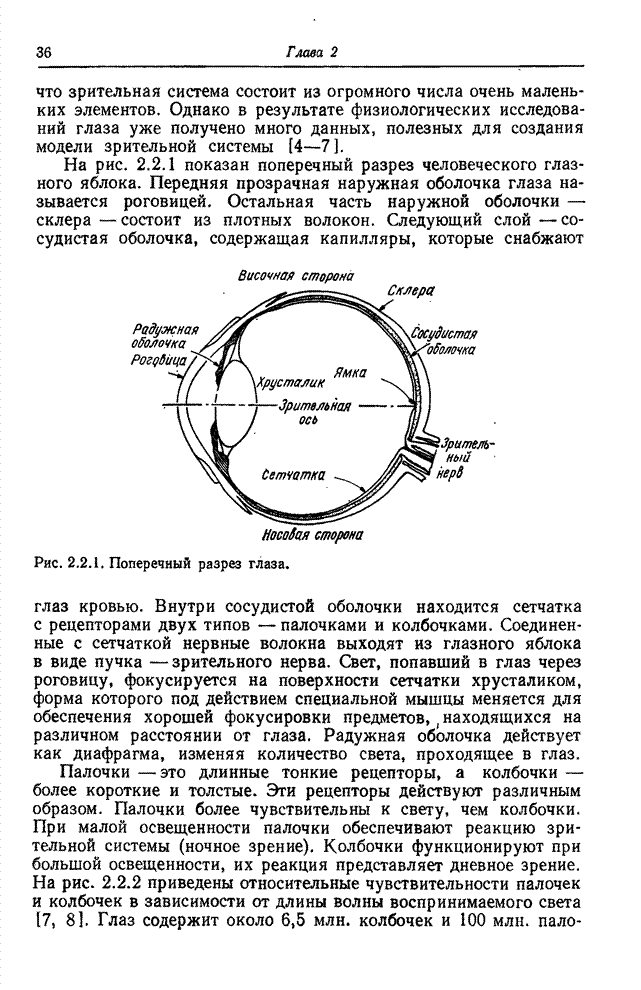
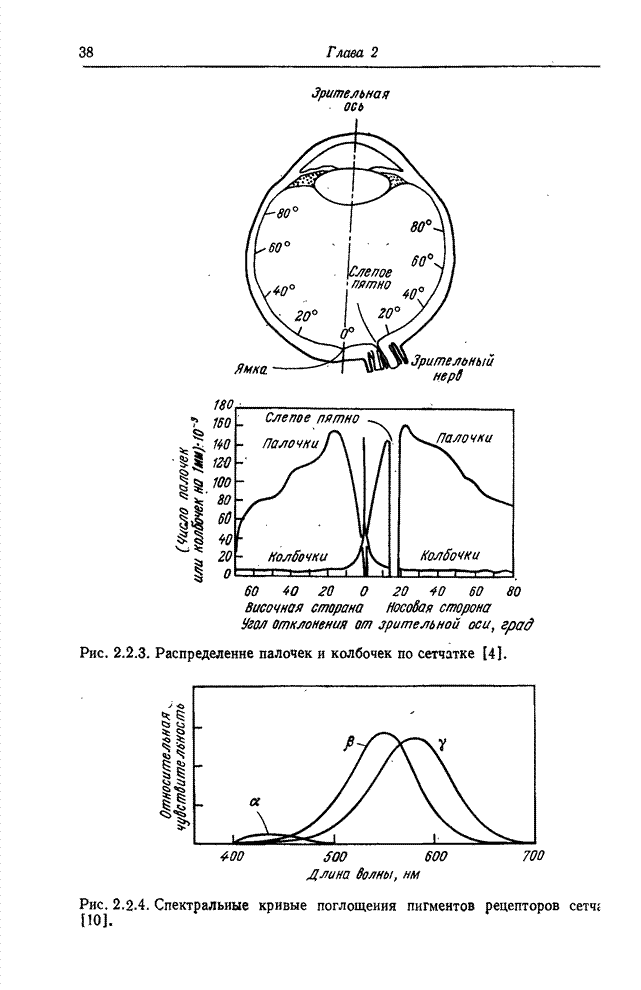
- 2.2. ГЛАЗ
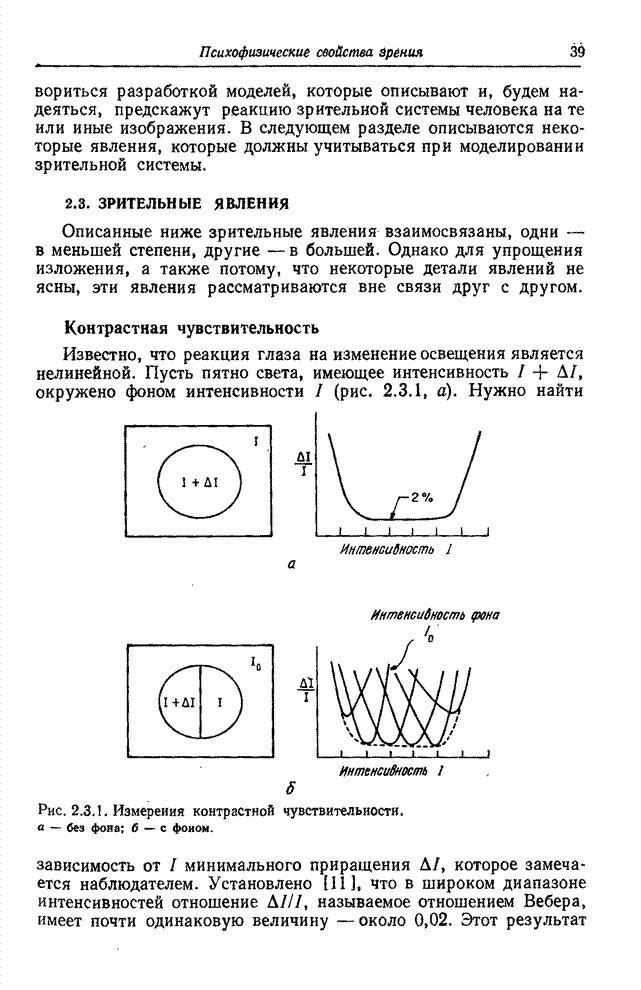
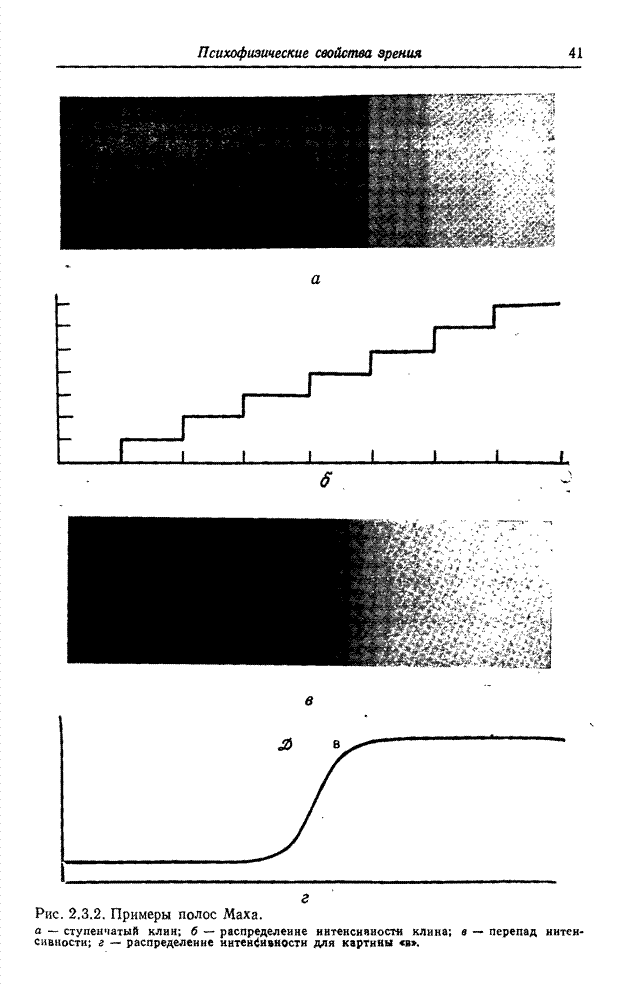
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
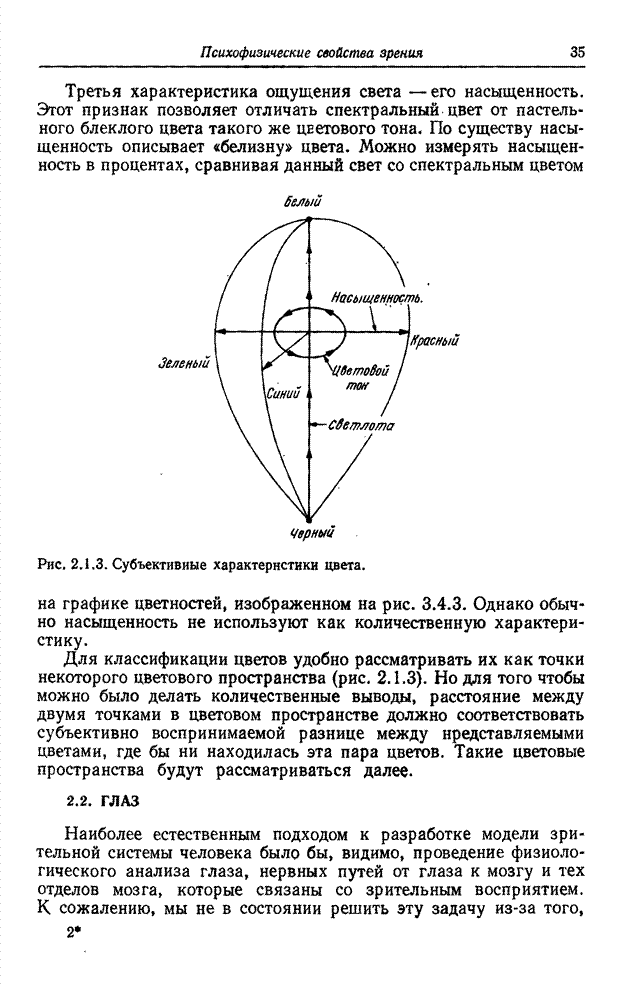
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
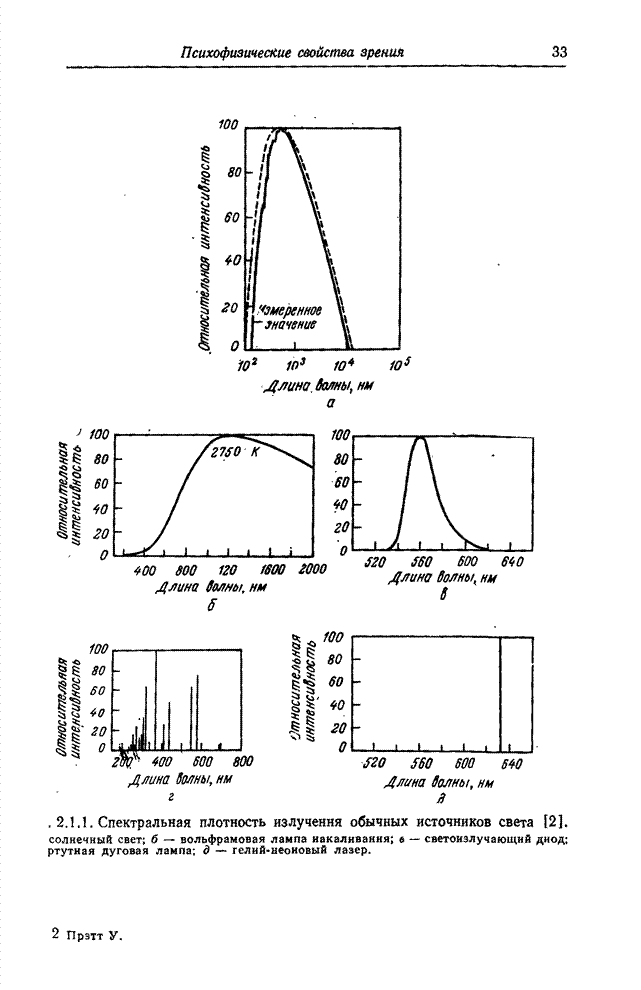
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
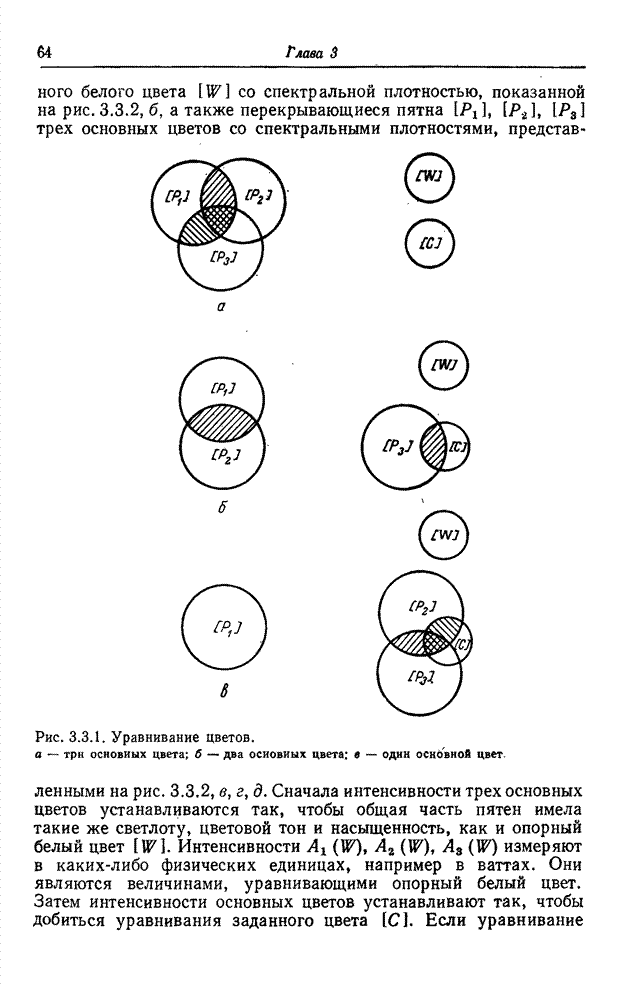
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
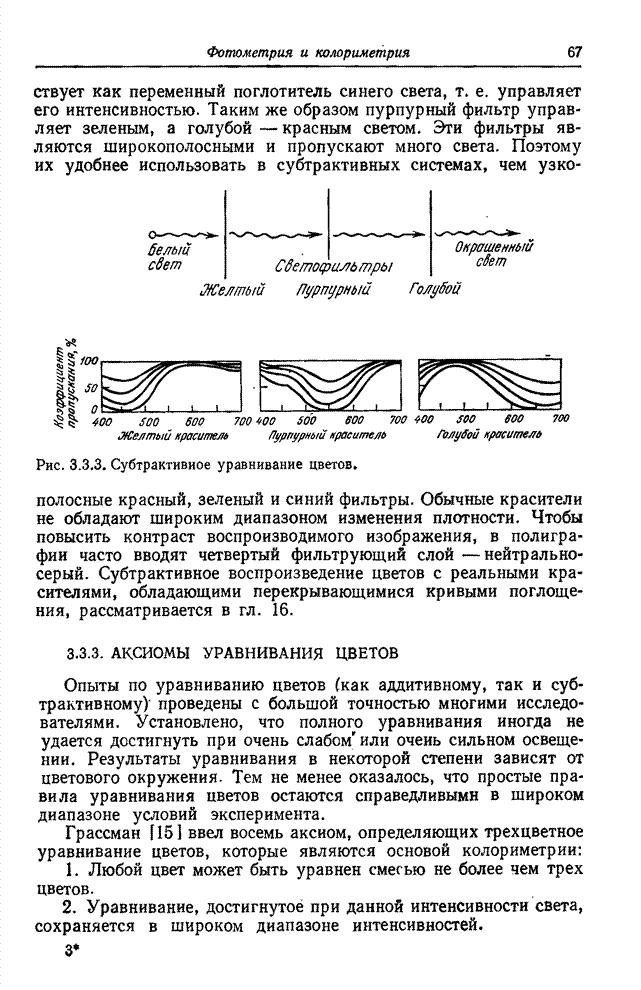
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
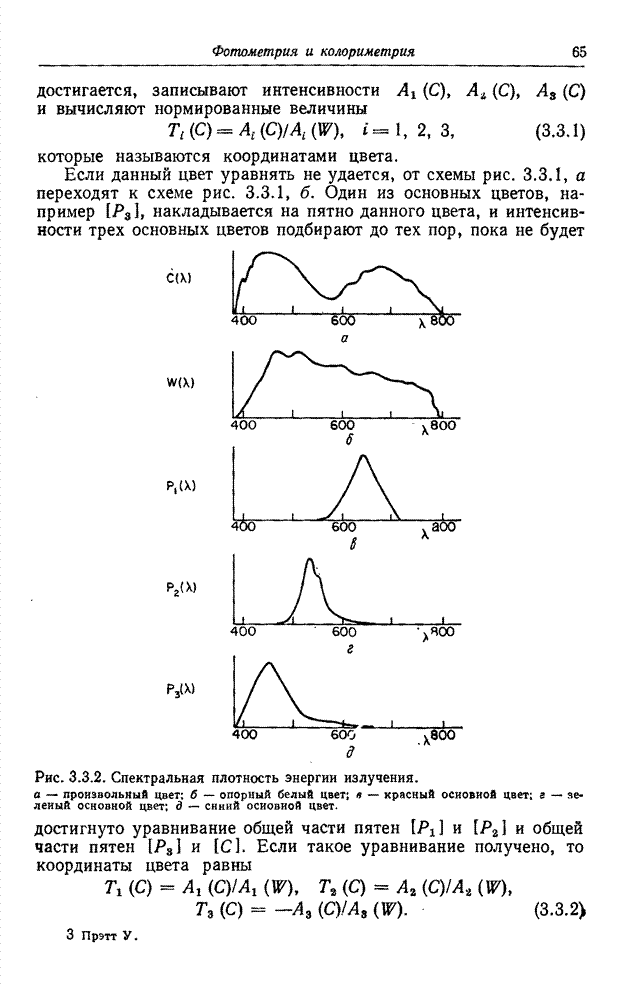
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
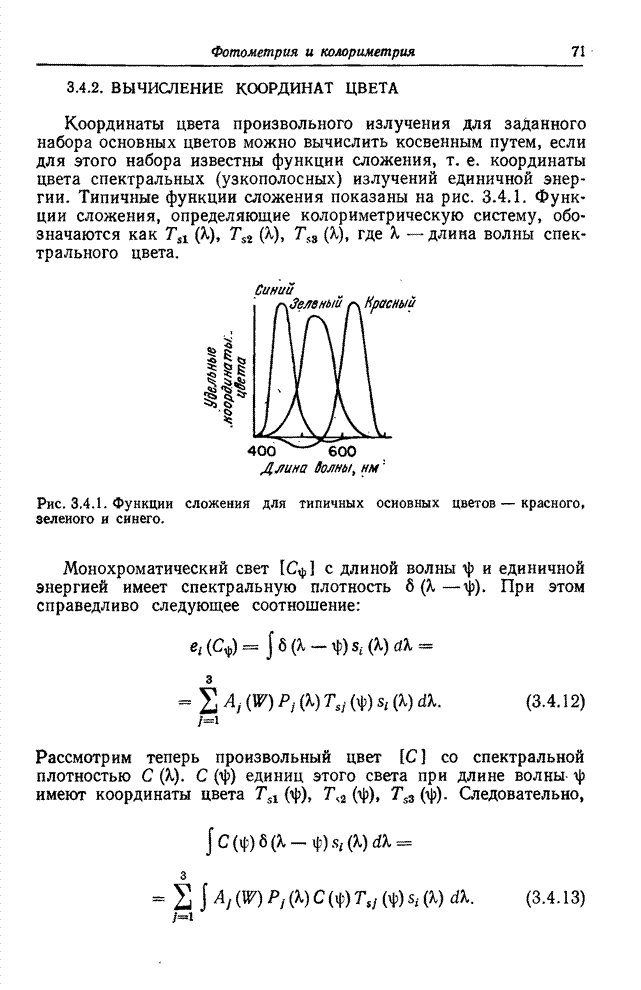
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА