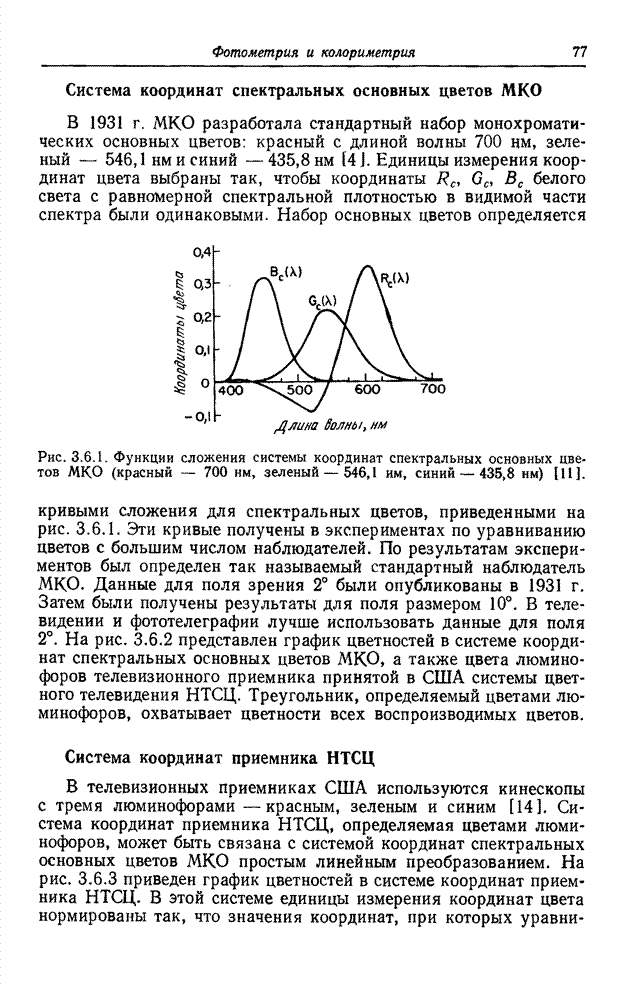
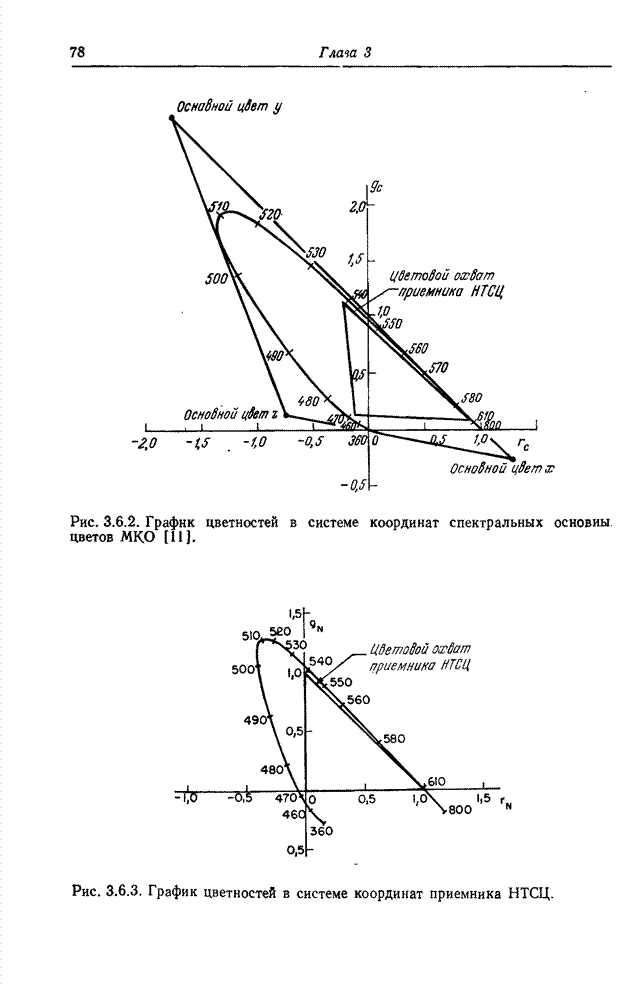
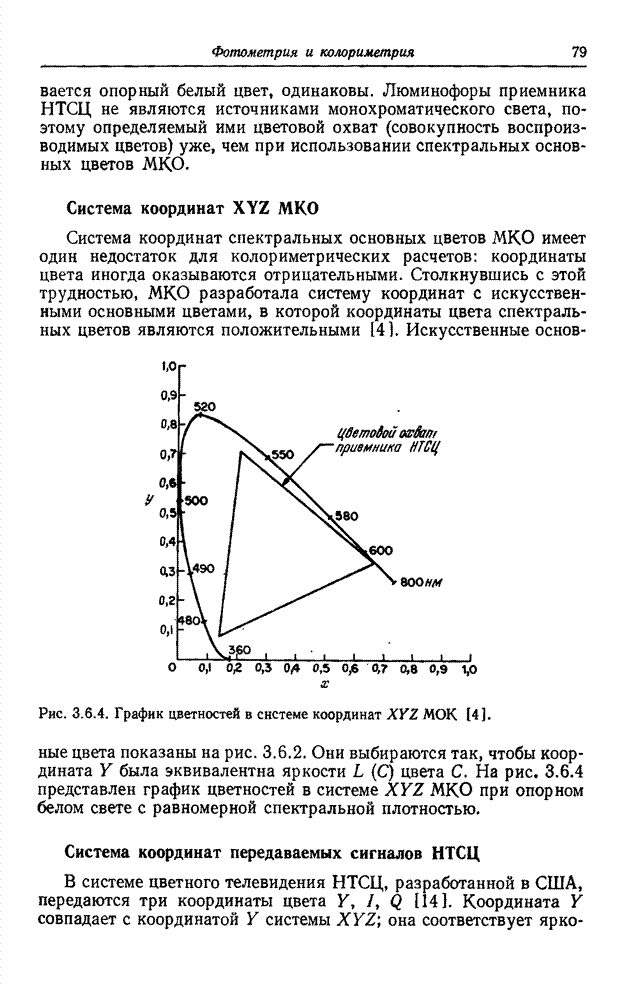
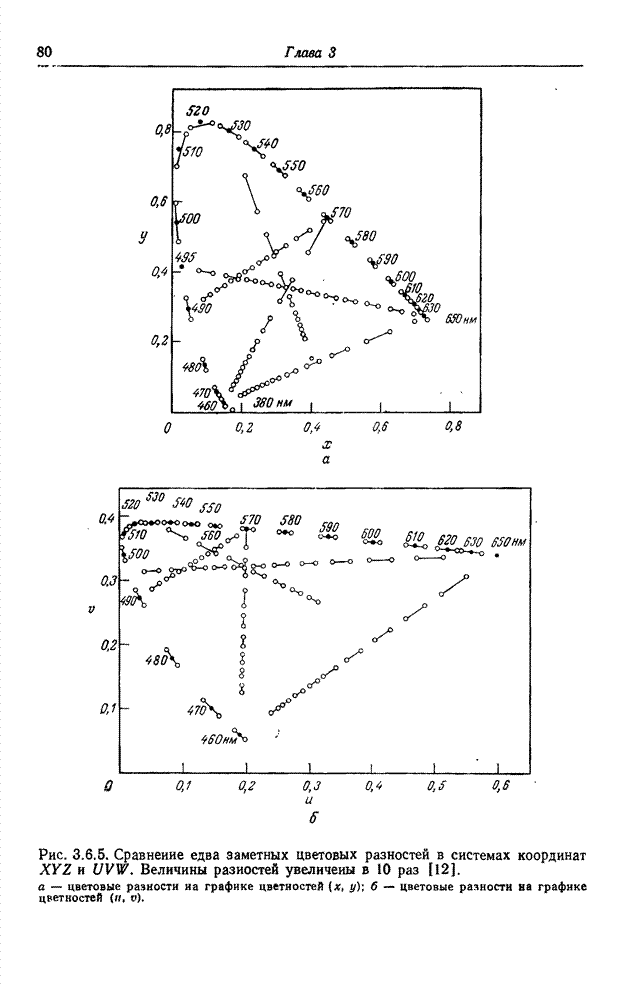
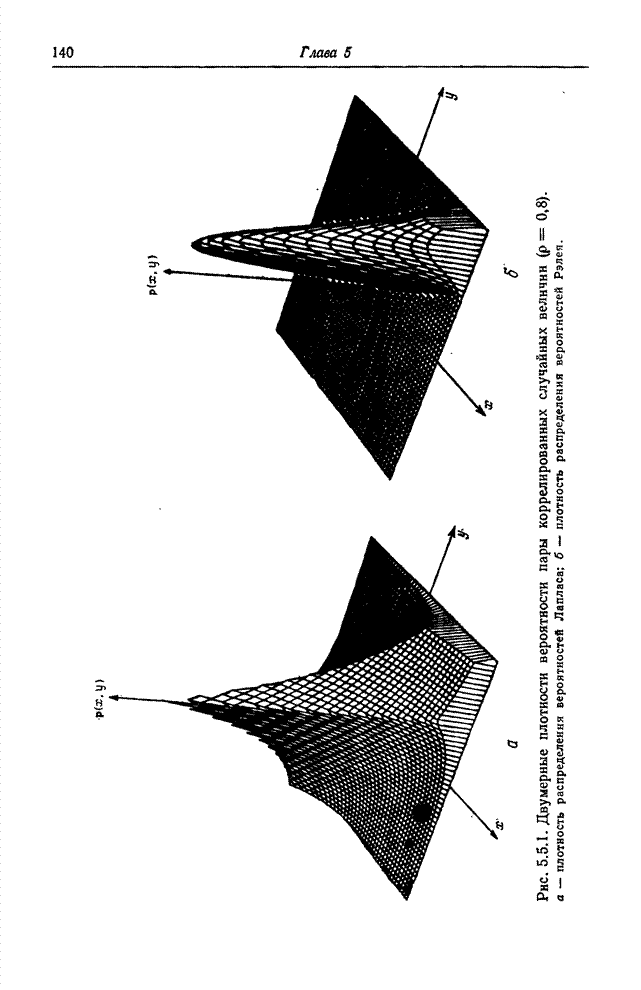
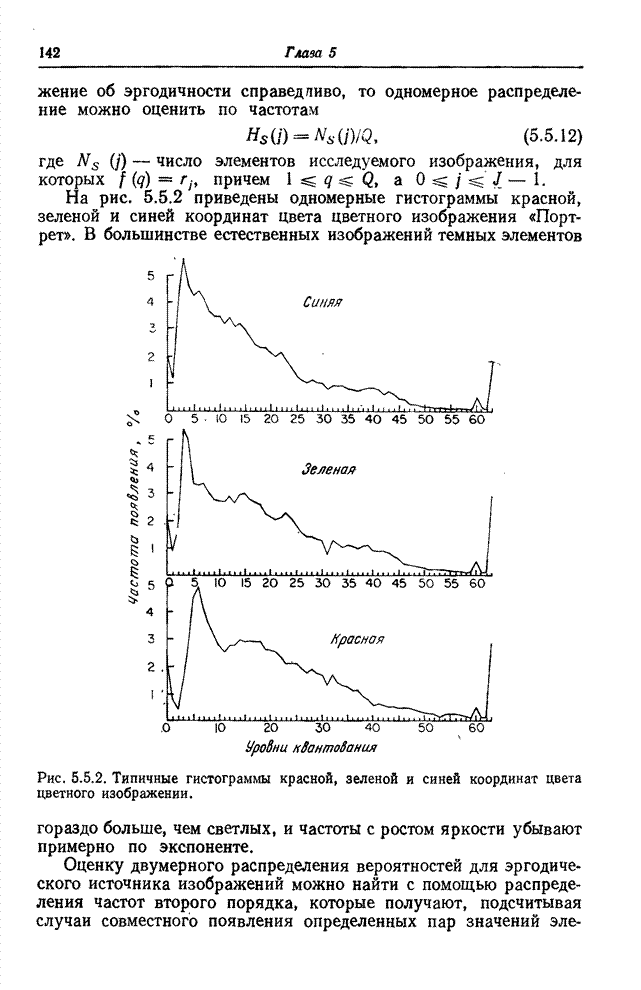
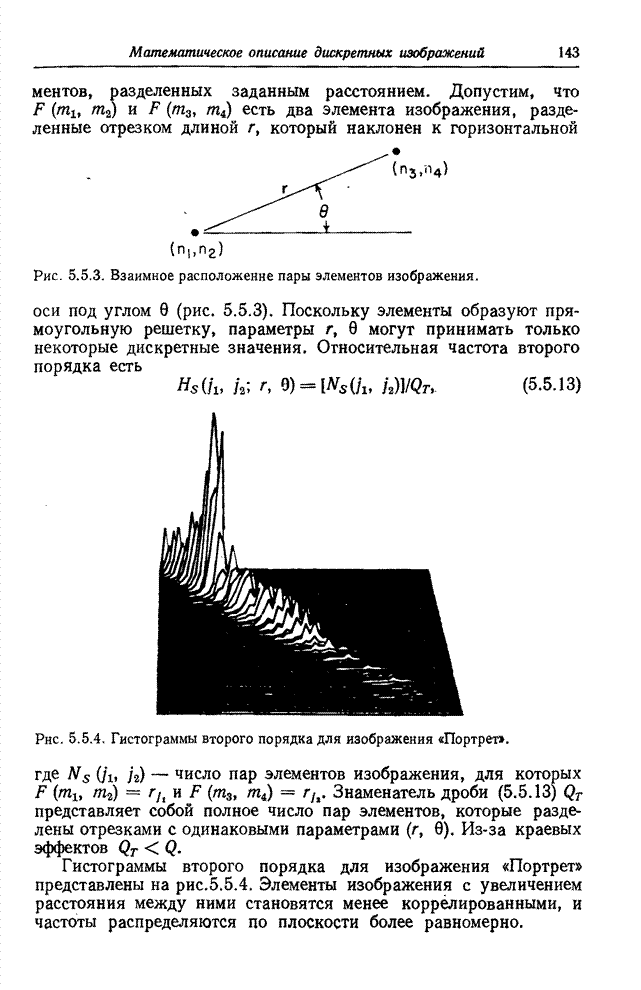
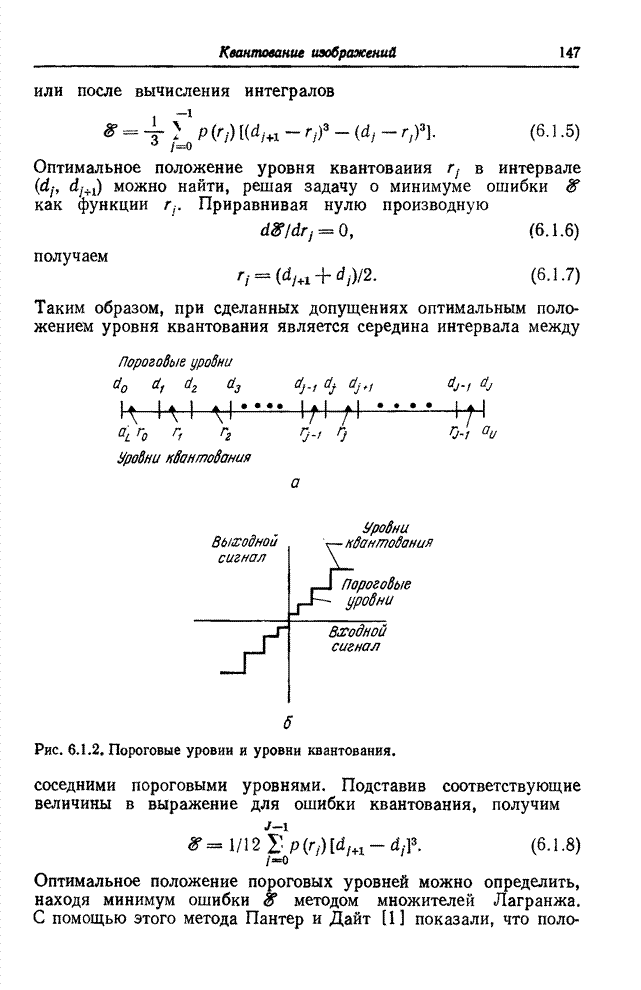
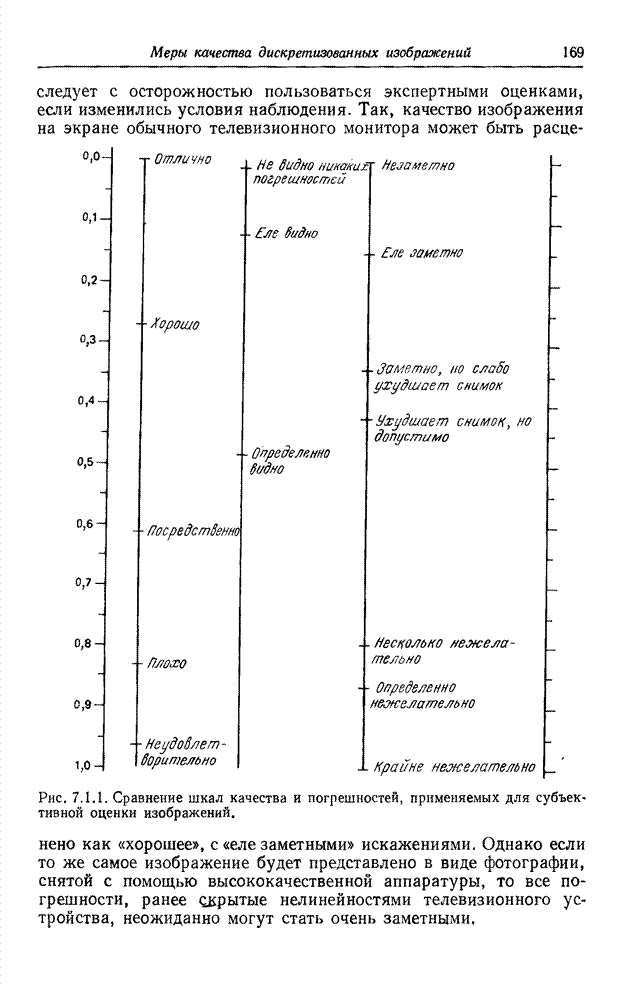
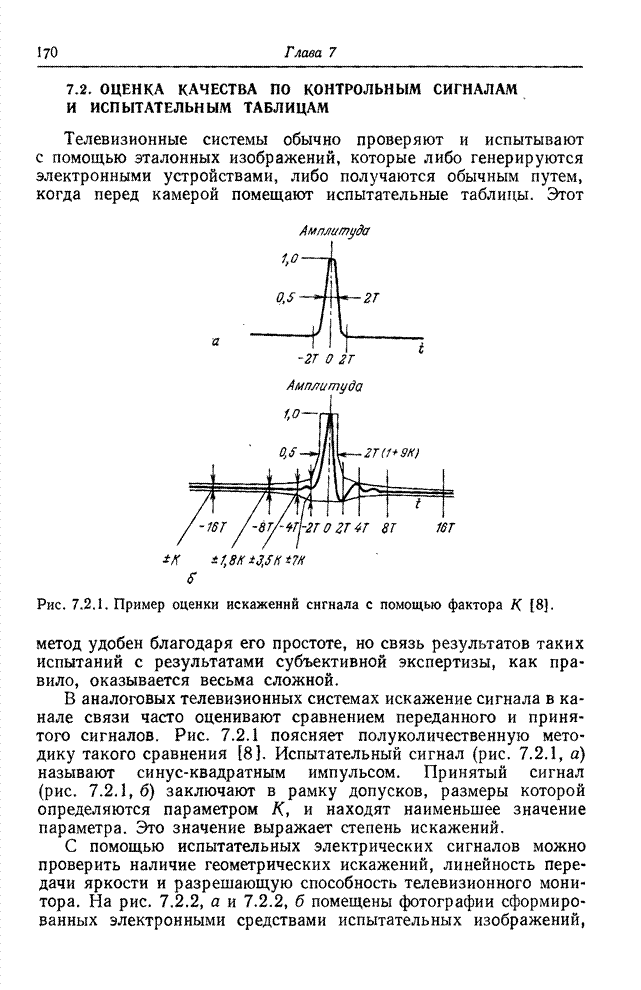
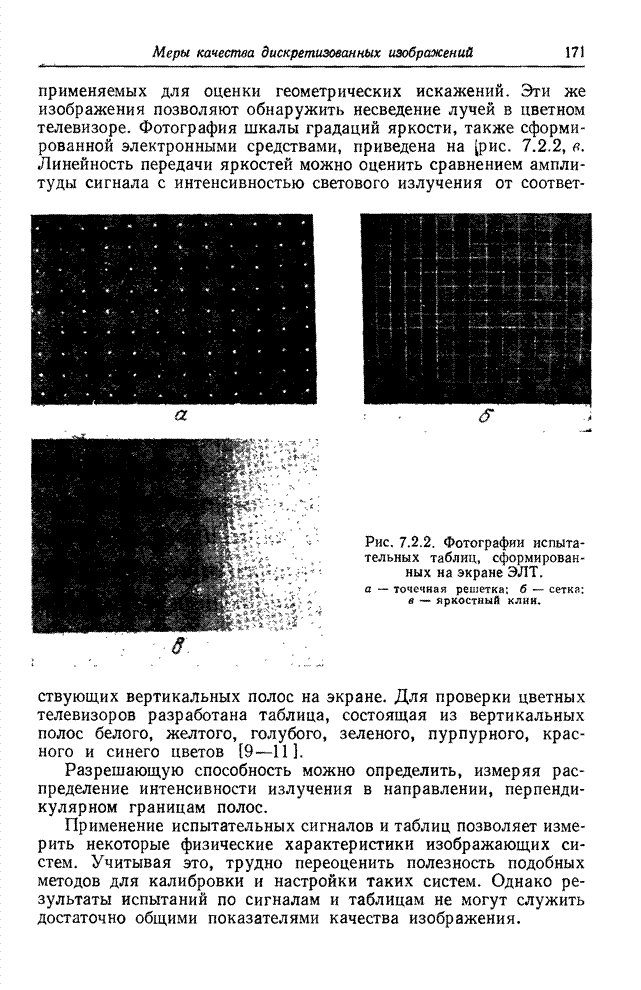
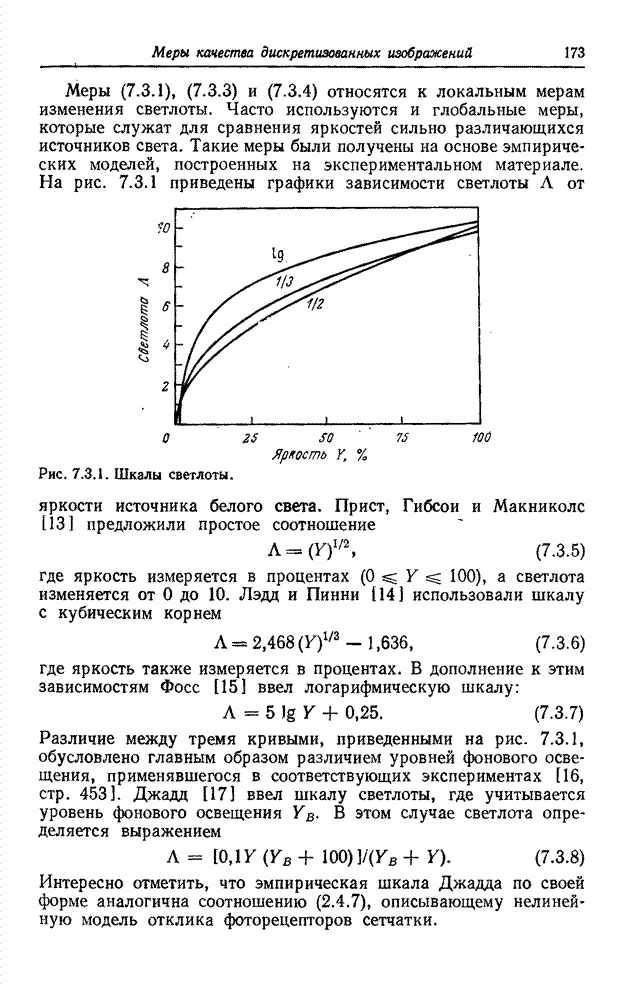
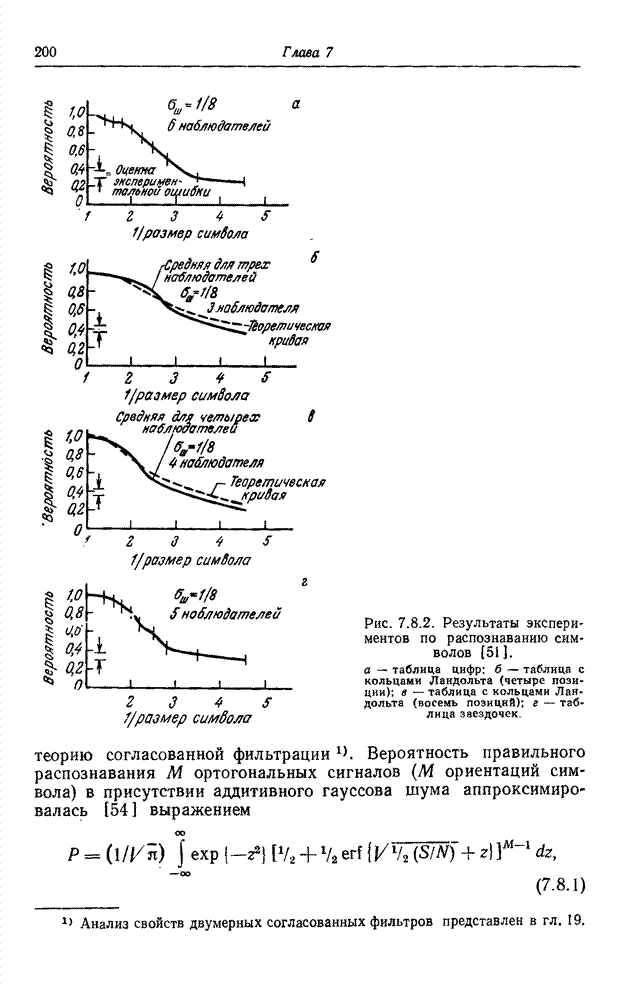
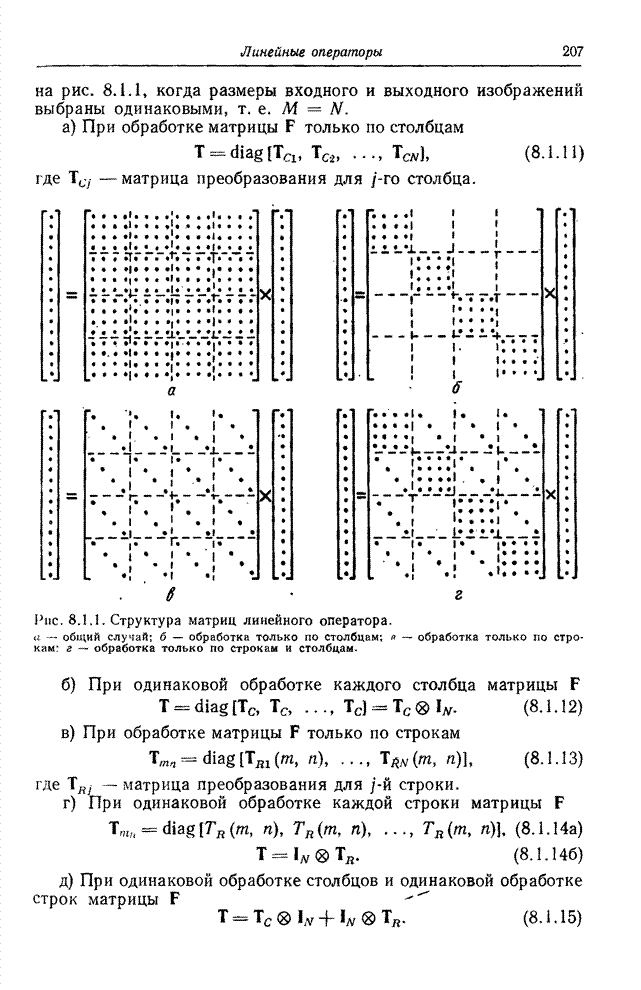
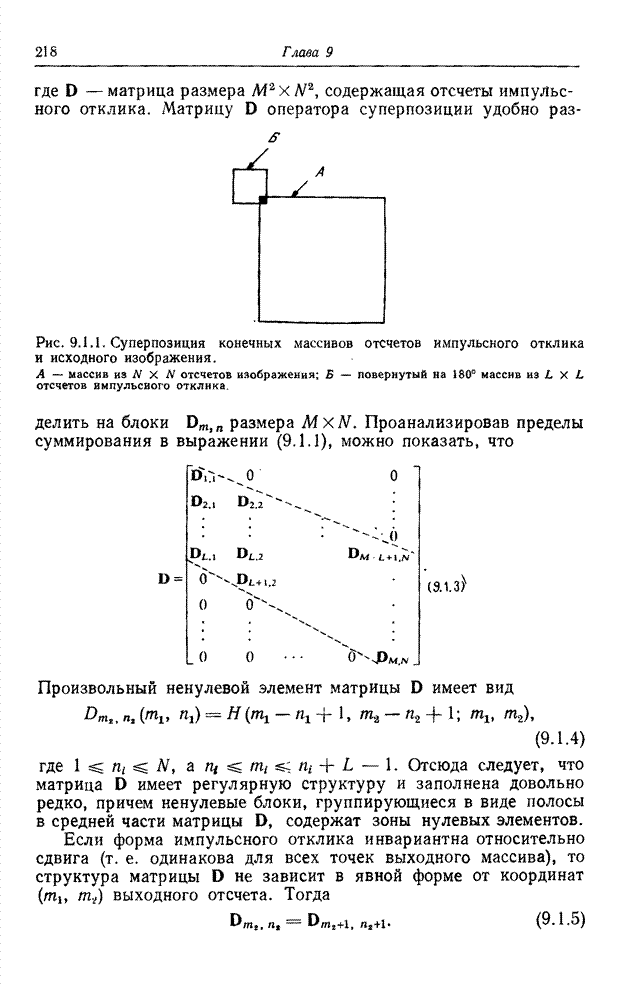
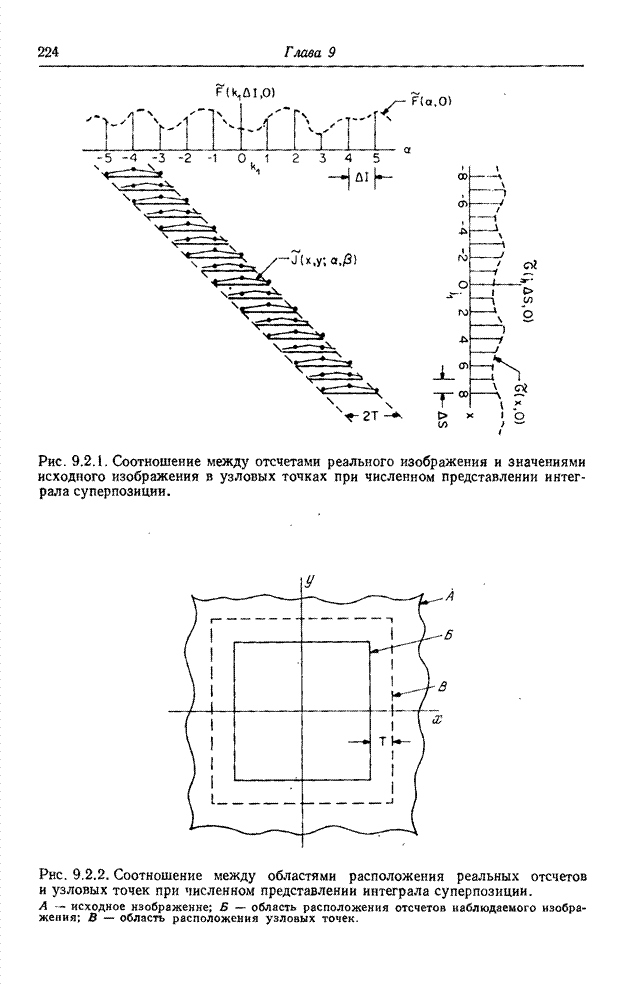
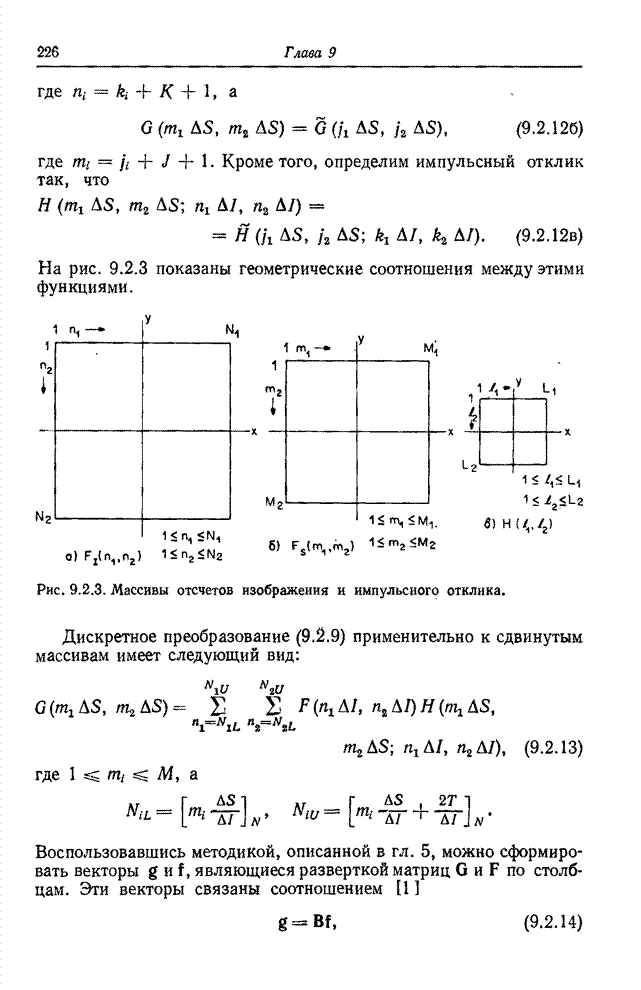
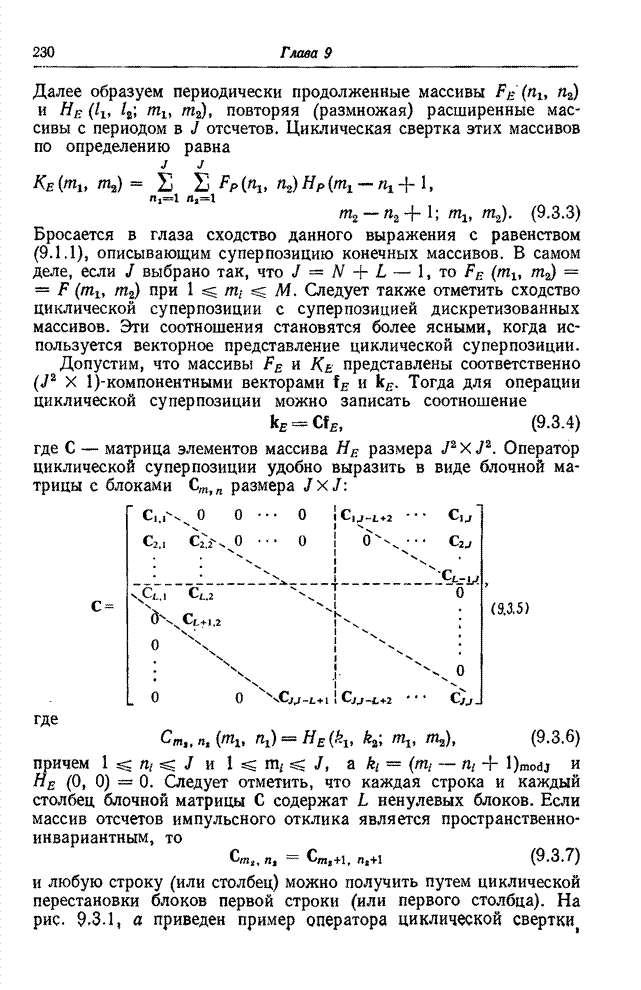
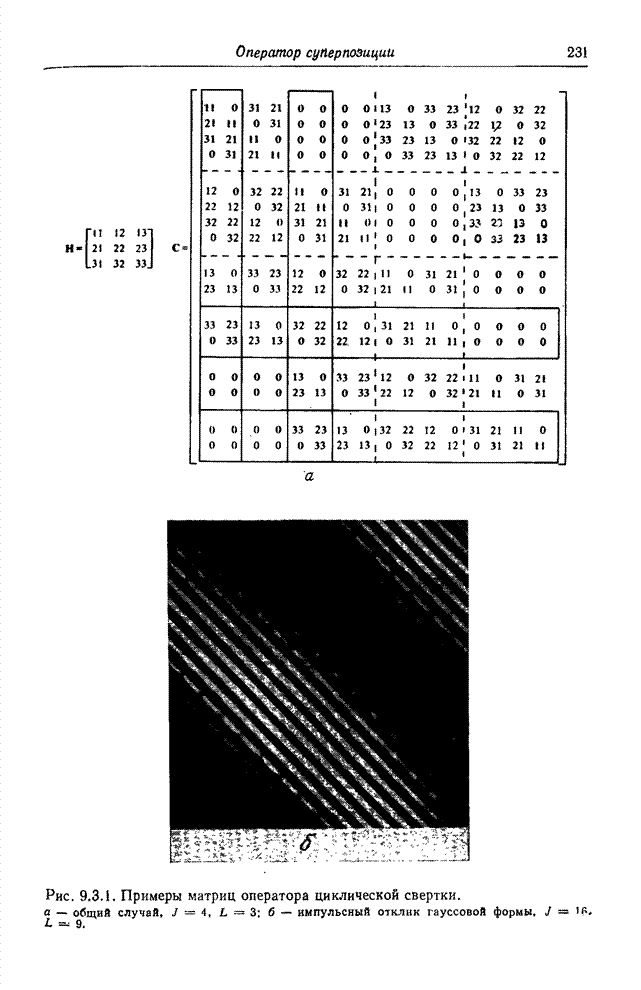
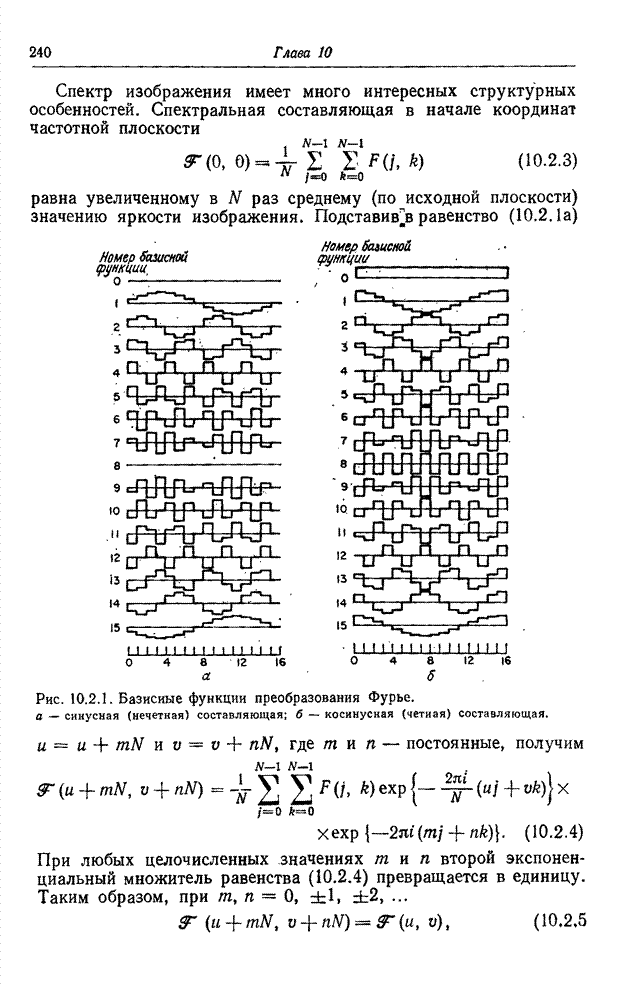
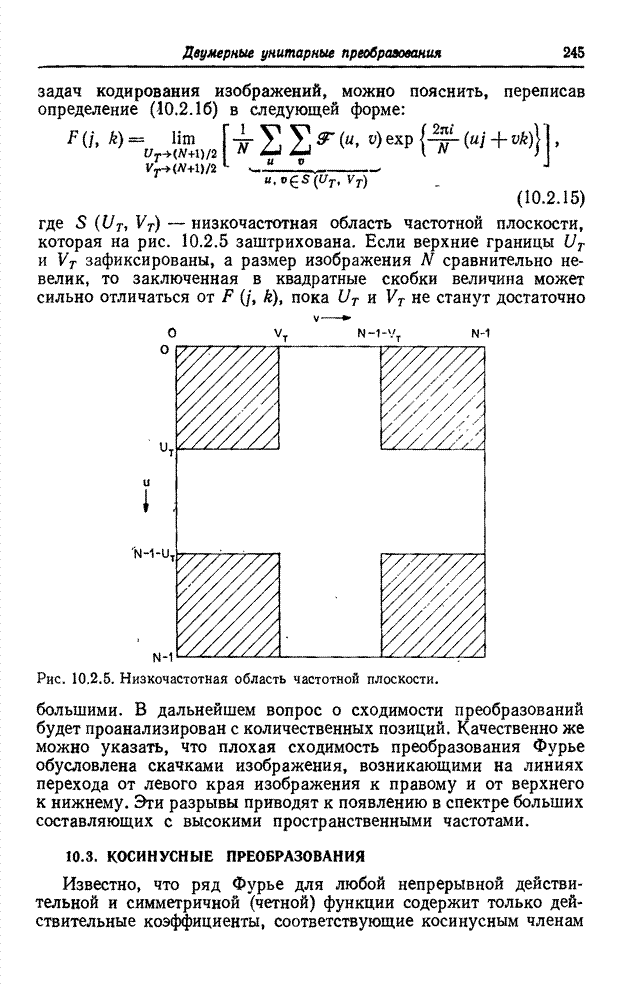
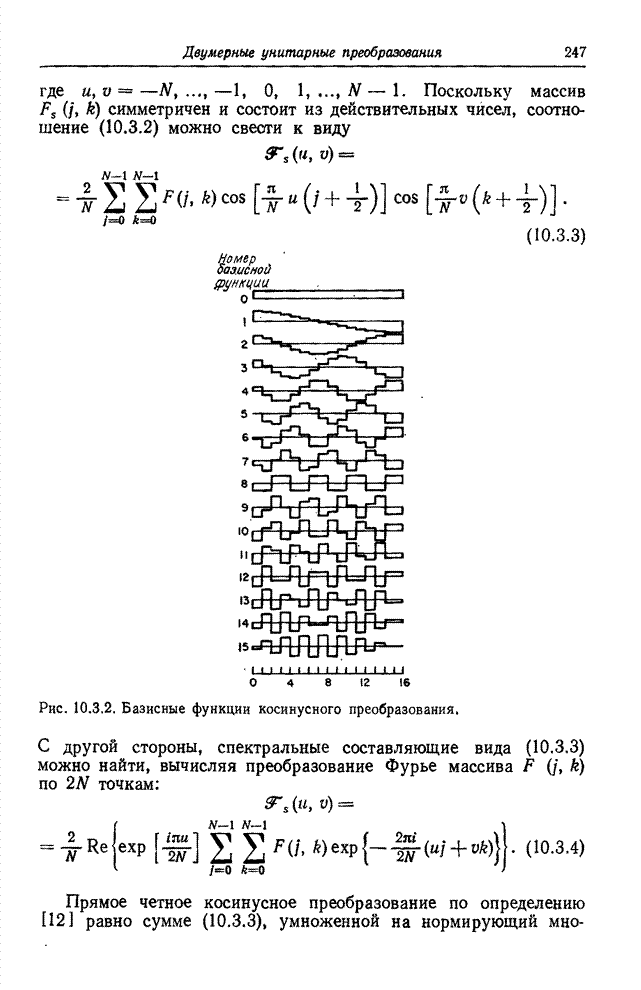
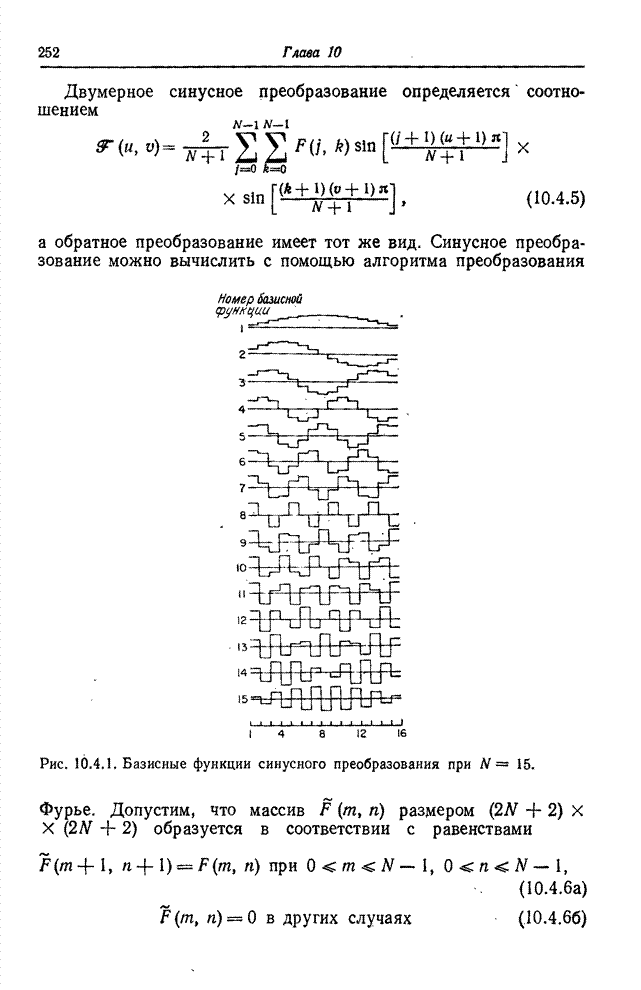
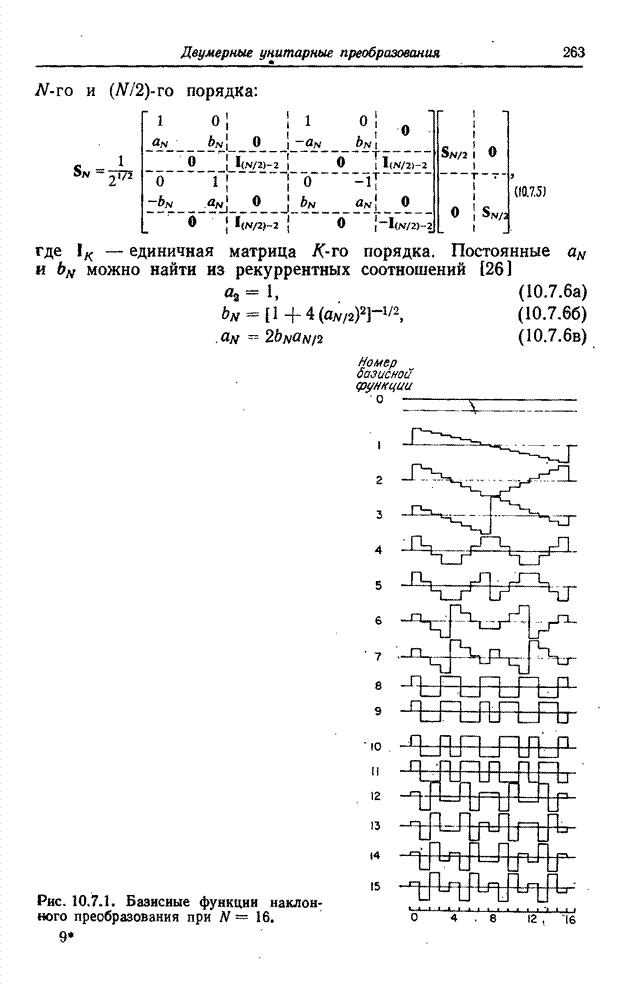
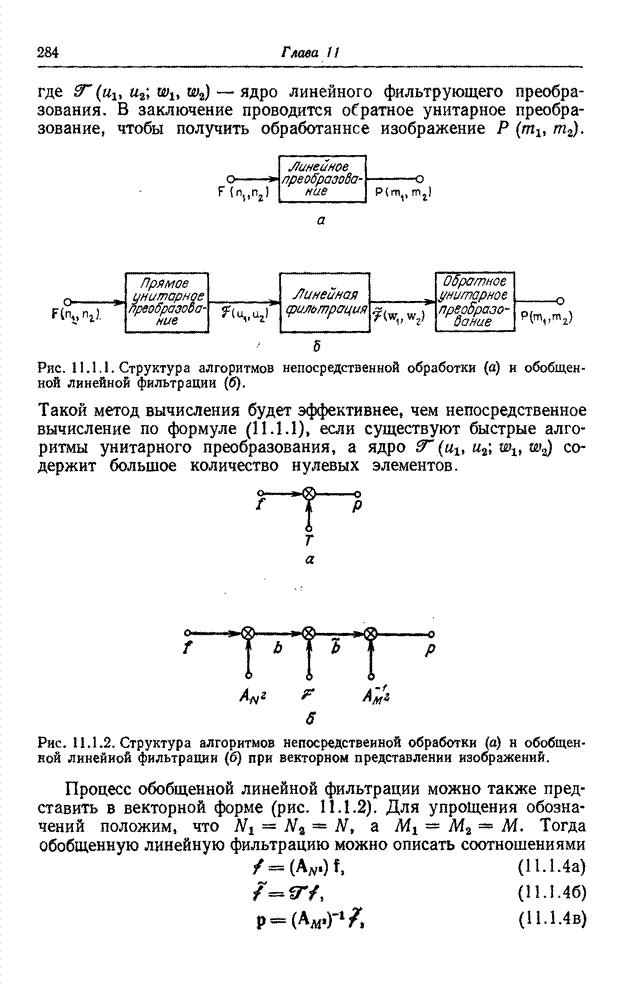
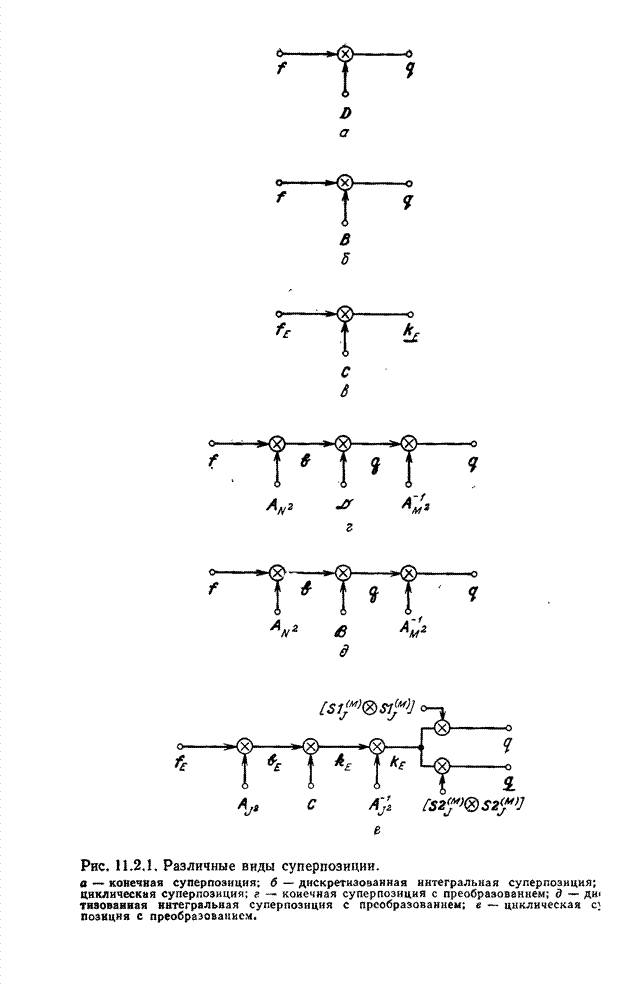
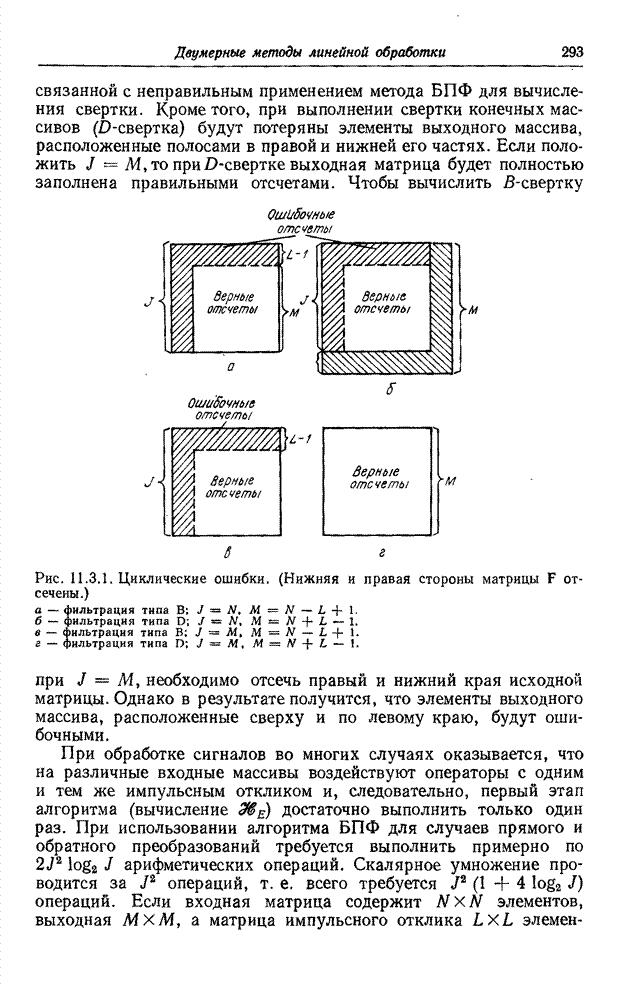
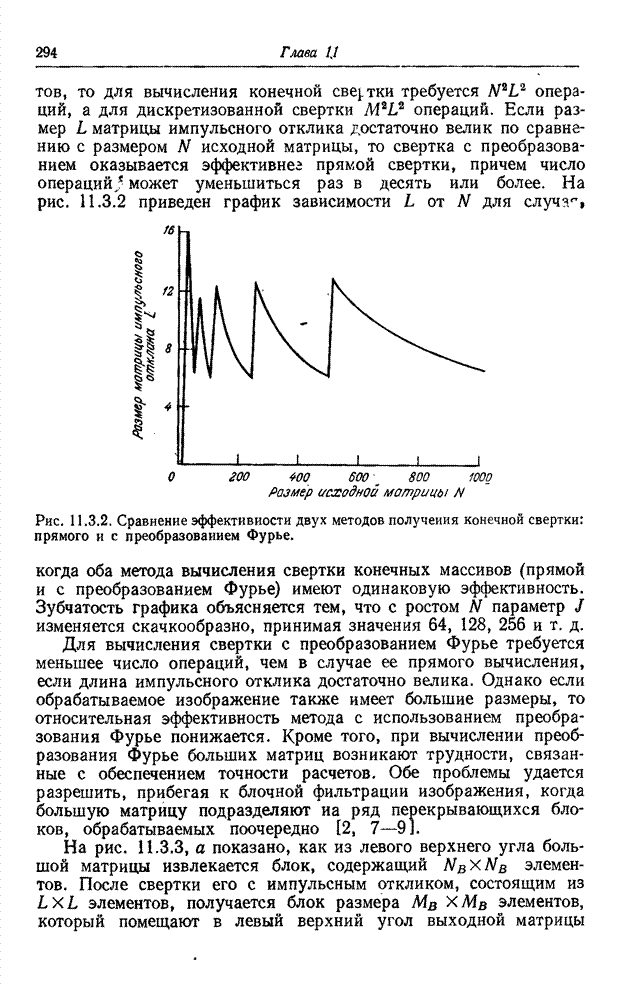
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
Унитарные
преобразования являются частным случаем линейных преобразований, когда линейный
оператор [см. (8.1.1)] точно обратим, а его ядро удовлетворяет условиям
ортогональности [1, 2]. В результате прямого унитарного преобразования матрицы
изображения ![]() размера
размера
![]() образуется
матрица преобразованного изображения того же размера, элементы которой по
определению равны
образуется
матрица преобразованного изображения того же размера, элементы которой по
определению равны
 , (10.1.1)
, (10.1.1)
где
![]() - ядро
прямого преобразования. Исходное изображение можно получить с помощью обратного
преобразования, описываемого соотношением
- ядро
прямого преобразования. Исходное изображение можно получить с помощью обратного
преобразования, описываемого соотношением
 , (10.1.2)
, (10.1.2)
где
![]() - ядро
обратного преобразования. Преобразование является унитарным, если выполняются
следующие условия ортогональности:
- ядро
обратного преобразования. Преобразование является унитарным, если выполняются
следующие условия ортогональности:
 , (10.1.3а)
, (10.1.3а)
 , (10.1.3б)
, (10.1.3б)
 , (10.1.3в)
, (10.1.3в)
 . (10.1.3г)
. (10.1.3г)
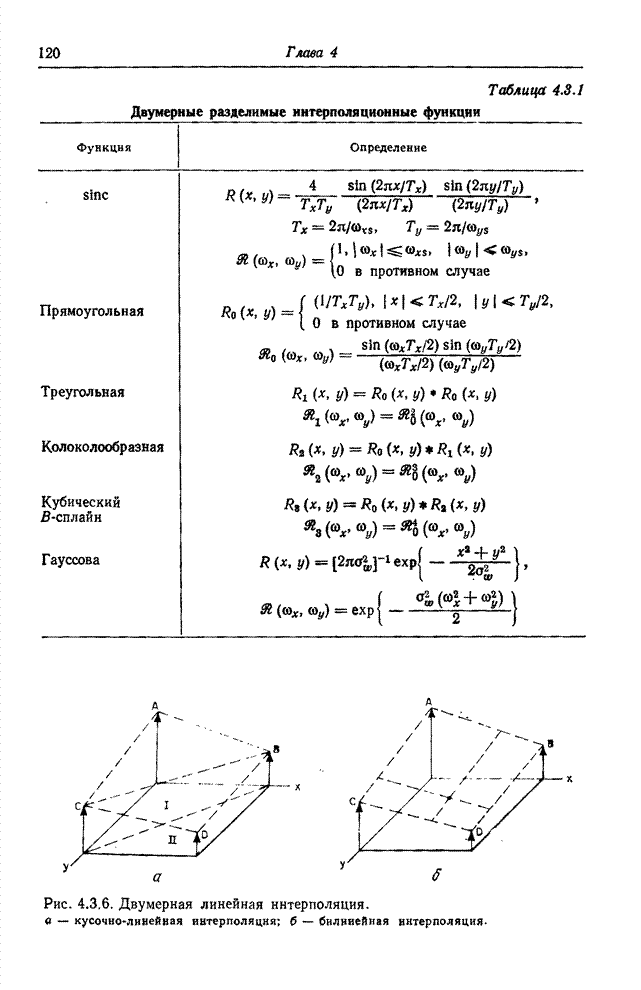
Преобразование называют разделимым, если оба его ядра можно представить в следующей форме:
![]() , (10.1.4а)
, (10.1.4а)
![]() , (10.1.4б)
, (10.1.4б)
где
через ![]() (или
(или
![]() ) и
) и ![]() (или
(или ![]() ) обозначены
соответственно одномерные операторы преобразования столбцов и строк. Результат
воздействия оператора разделимого двумерного унитарного преобразования можно
находить в два этапа. Сначала выполняется одномерное преобразование по всем
столбцам матрицы изображения, причем образуется матрица с элементами
) обозначены
соответственно одномерные операторы преобразования столбцов и строк. Результат
воздействия оператора разделимого двумерного унитарного преобразования можно
находить в два этапа. Сначала выполняется одномерное преобразование по всем
столбцам матрицы изображения, причем образуется матрица с элементами
 . (10.1.5)
. (10.1.5)
Затем выполняется второе одномерное преобразование по всем строкам полученной матрицы, в результате которого образуется массив чисел вида
 . (10.1.6)
. (10.1.6)
Унитарные
преобразования удобно записывать с помощью векторных обозначений [3]. Допустим,
что ![]() и
и ![]() - матричное и
векторное представления массива отсчетов исходного изображения, а
- матричное и
векторное представления массива отсчетов исходного изображения, а ![]() и
и ![]() - матричное и
векторное представления преобразованного изображения. Тогда двумерное унитарное
преобразование в векторной форме выражается соотношением
- матричное и
векторное представления преобразованного изображения. Тогда двумерное унитарное
преобразование в векторной форме выражается соотношением
![]() , (10.1.7)
, (10.1.7)
где
![]() -
матрица прямого преобразования. Обратное преобразование записывается как
-
матрица прямого преобразования. Обратное преобразование записывается как
![]() , (10.1.8)
, (10.1.8)
где
![]() -
матрица обратного преобразования. Очевидно, что
-
матрица обратного преобразования. Очевидно, что
![]() . (10.1.9)
. (10.1.9)
Для унитарных преобразований обратная матрица удовлетворяет соотношению
![]() . (10.1.10)
. (10.1.10)
В
этом случае матрицу ![]() называют унитарной. Действительная
унитарная матрица называется ортогональной матрицей, и для нее справедливо
соотношение
называют унитарной. Действительная
унитарная матрица называется ортогональной матрицей, и для нее справедливо
соотношение
![]() . (10.1.11)
. (10.1.11)
Если ядра преобразования разделимы, так что
![]() , (10.1.12)
, (10.1.12)
где
![]() и
и ![]() - унитарные
матрицы преобразования по строкам и столбцам, то матрицу преобразованного
изображения можно получить из матрицы исходного изображения с помощью равенства
- унитарные
матрицы преобразования по строкам и столбцам, то матрицу преобразованного
изображения можно получить из матрицы исходного изображения с помощью равенства
![]() . (10.1.13а)
. (10.1.13а)
Обратное преобразование определяется соотношением
![]() , (10.1.13б)
, (10.1.13б)
где
![]() и
и ![]() .
.
Разделимые
унитарные преобразования можно также представлять в виде взвешенной суммы
матричных произведений вектор-столбцов, сформированных из элементов матриц.
Пусть ![]() и
и ![]() обозначают
обозначают ![]() -й и
-й и ![]() -й столбцы матриц
-й столбцы матриц ![]() и
и ![]() . Нетрудно
показать, что
. Нетрудно
показать, что
 . (10.1.14а)
. (10.1.14а)
Аналогично
 , (10.1.14б)
, (10.1.14б)
где
![]() и
и ![]() -
- ![]() -й и
-й и ![]() -й столбы матриц
-й столбы матриц ![]() и
и ![]() соответственно.
Матричные произведения векторов, входящие в суммы (10.1.14), образуют
последовательности матриц, называемых базисными матрицами, на основе которых и
производится разложение матрицы
соответственно.
Матричные произведения векторов, входящие в суммы (10.1.14), образуют
последовательности матриц, называемых базисными матрицами, на основе которых и
производится разложение матрицы ![]() исходного изображения или преобразованного
изображения
исходного изображения или преобразованного
изображения ![]() .
.
Возможны
различные интерпретации унитарных преобразований. Преобразование изображения
можно рассматривать как разложение исходного изображения в обобщенный двумерный
спектр [4]. Каждая спектральная составляющая характеризует вклад
соответствующей спектральной (базисной) функции в энергию исходного
изображения. При такой трактовке понятие частоты можно обобщить так, чтобы оно
было применимо не только к синусам и косинусам, но и к другим функциям, на
которых основываются преобразования. Подобный обобщенный спектральный анализ
полезен для изучения тех конкретных разложений, которые в наибольшей мере
подходят для данного класса изображений. Наглядное представление о
преобразованиях изображений можно получить и по-другому, рассматривая
преобразование как поворот многомерной системы координат. Одним из главных
свойств унитарного преобразования является сохранение метрики. Например,
евклидово расстояние между двумя изображениями равно евклидову расстоянию между
их образами. Третья возможность интерпретации преобразований заключается в том,
что равенство (10.1.2) можно рассматривать как способ составления изображения
из набора двумерных функций ![]() , каждая из которых соответствует
определенной точке
, каждая из которых соответствует
определенной точке ![]() плоскости обобщенных частот. В
подобной интерпретации ядро
плоскости обобщенных частот. В
подобной интерпретации ядро ![]() называют двумерной базисной функцией,
а коэффициент
называют двумерной базисной функцией,
а коэффициент ![]() указывает
«вес» этой базисной функции, необходимый для получения рассматриваемого
изображения.
указывает
«вес» этой базисной функции, необходимый для получения рассматриваемого
изображения.
Для
упрощения анализа свойств двумерных унитарных преобразований ниже в этой главе
будет принято, что все массивы являются квадратными и имеют размер ![]() . Кроме того, будут
изменены обозначения и нумерация всех индексов в выражениях вида (10.1.1) и
(10.1.2). Таким образом, массив отсчетов исходного изображения будет обозначен
через
. Кроме того, будут
изменены обозначения и нумерация всех индексов в выражениях вида (10.1.1) и
(10.1.2). Таким образом, массив отсчетов исходного изображения будет обозначен
через ![]() ,
где
,
где ![]() , а
массив коэффициентов преобразования - через
, а
массив коэффициентов преобразования - через ![]() , где
, где ![]() . С учетом этого прямое унитарное
преобразование записывается в следующем виде:
. С учетом этого прямое унитарное
преобразование записывается в следующем виде:
 , (10.1.15а)
, (10.1.15а)
а обратное преобразование - как
![]() . (10.1.15б)
. (10.1.15б)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
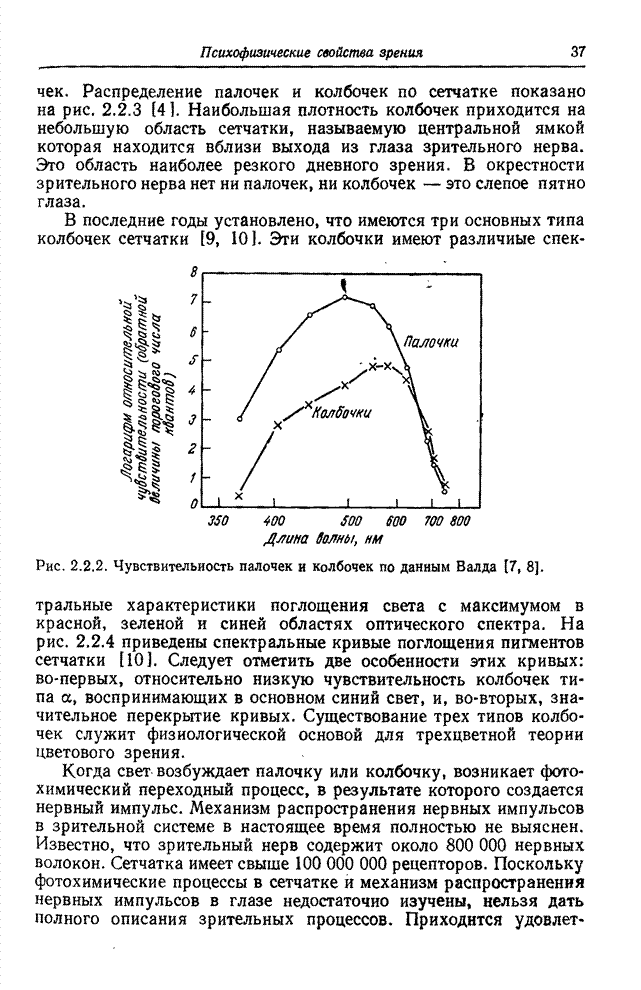
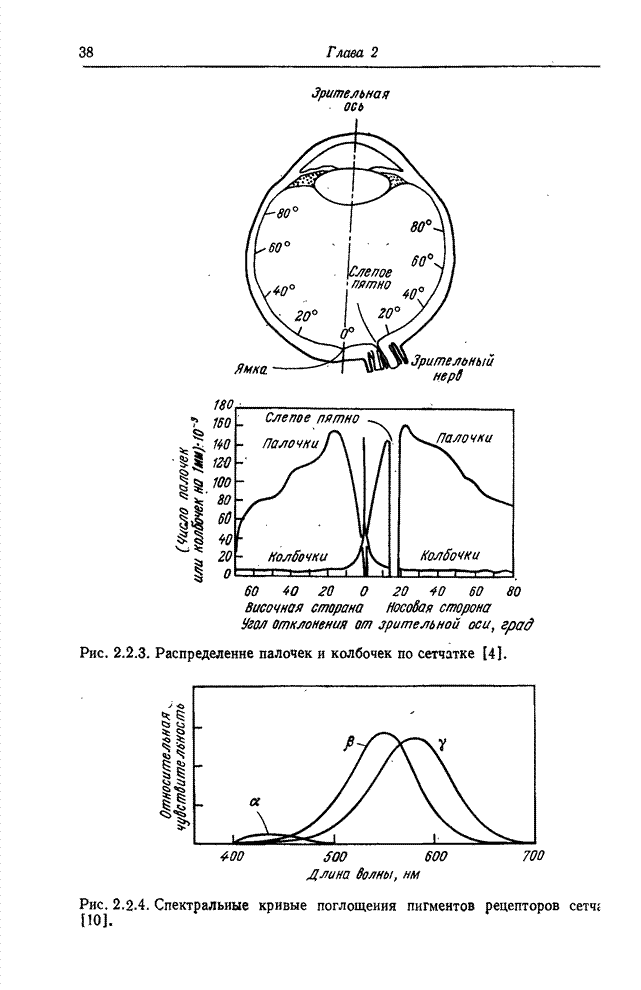
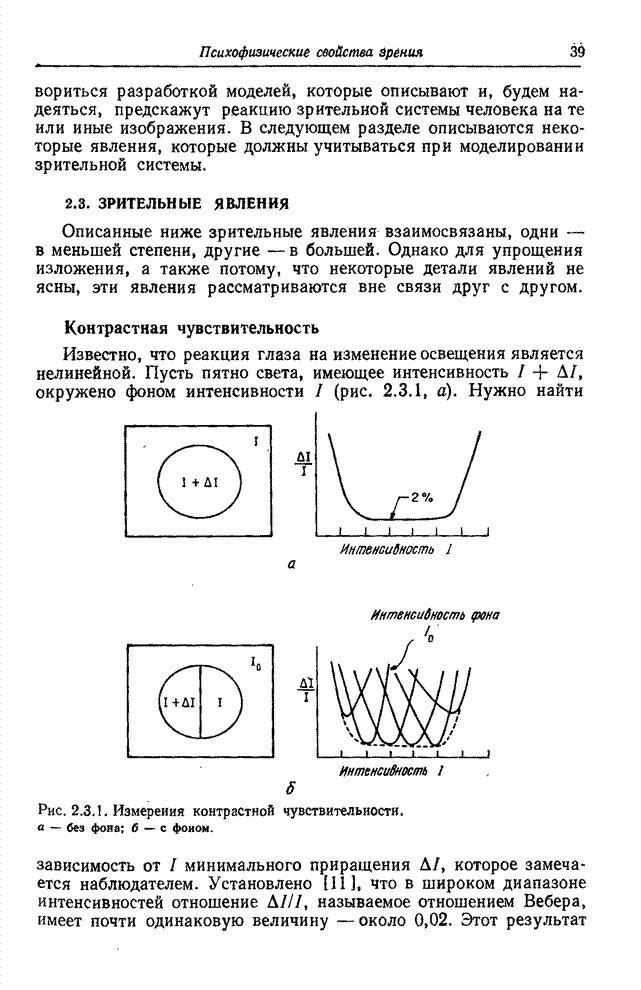
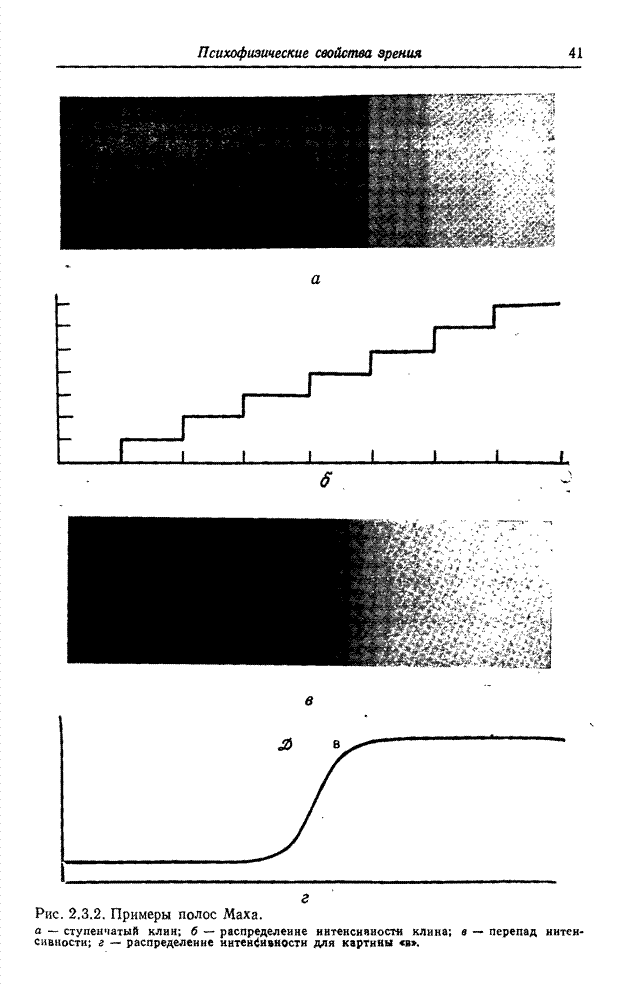
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
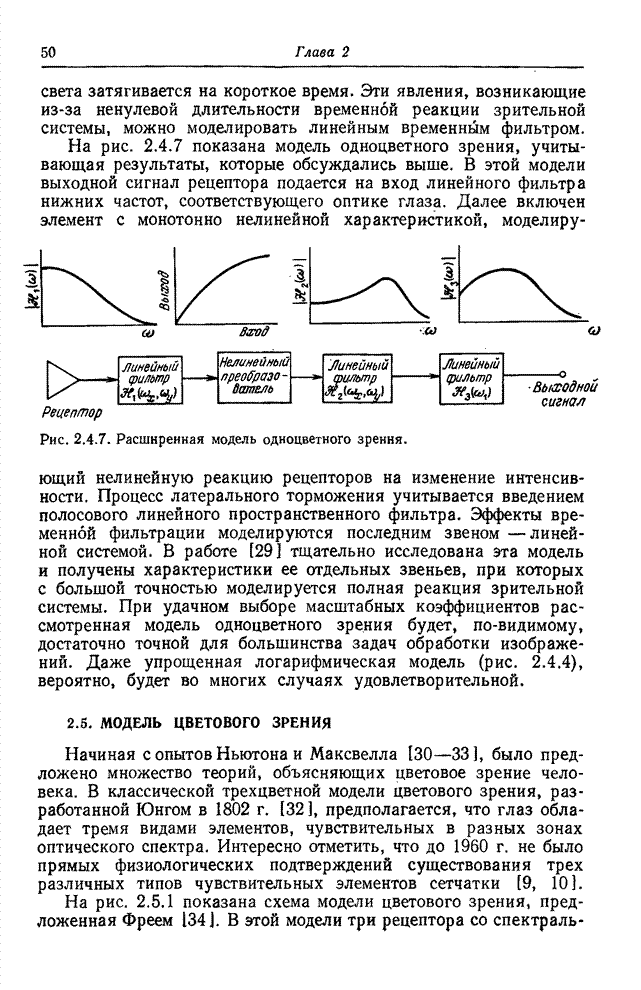
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
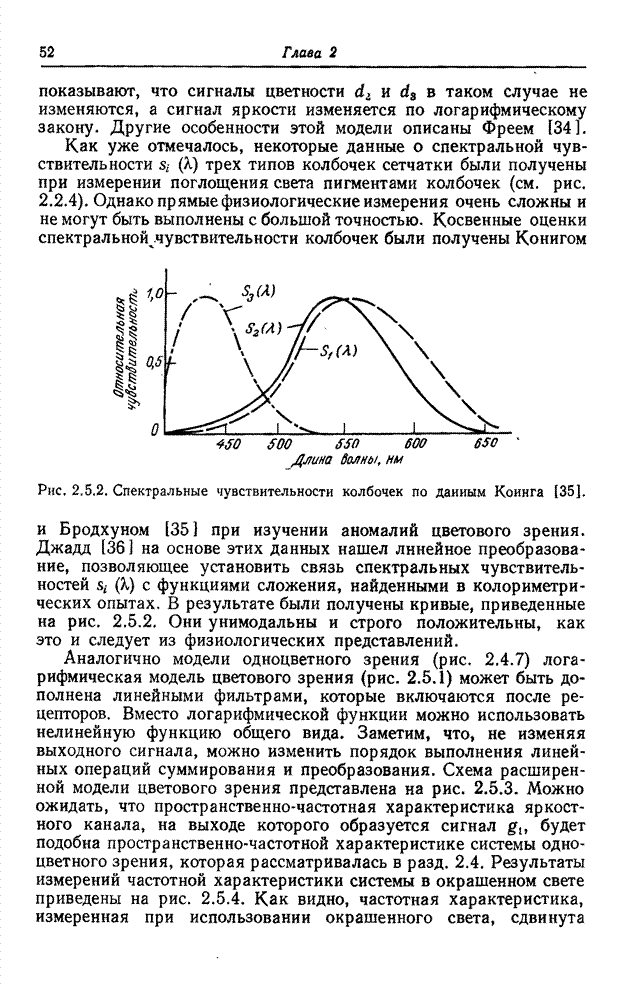
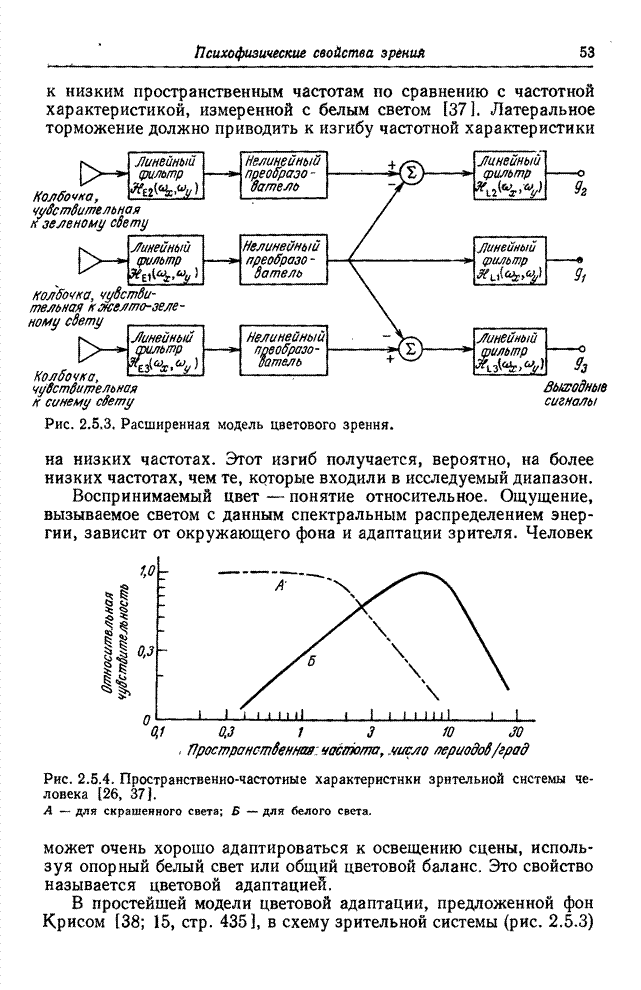
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
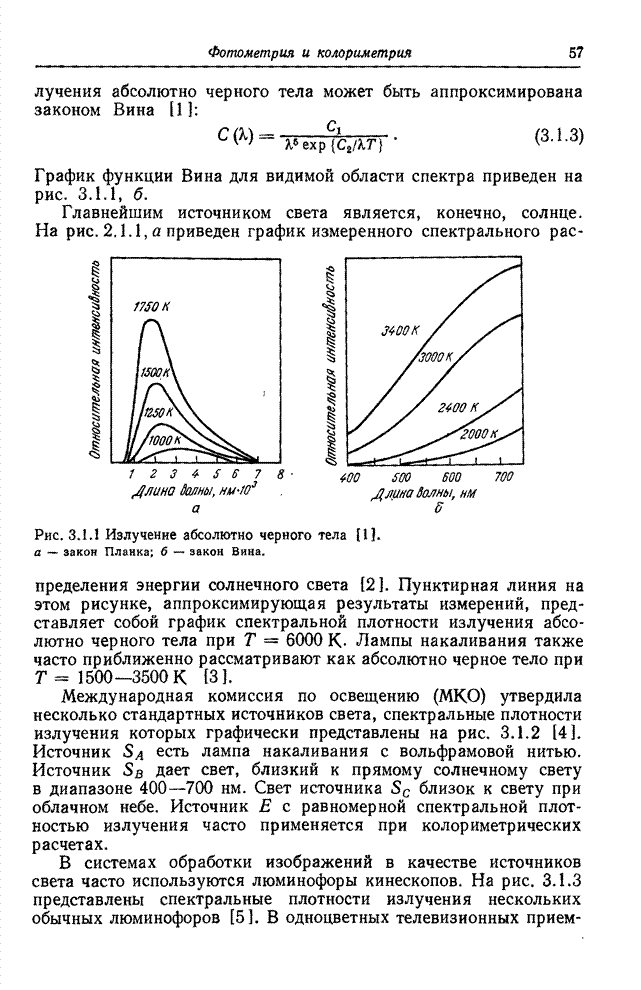
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
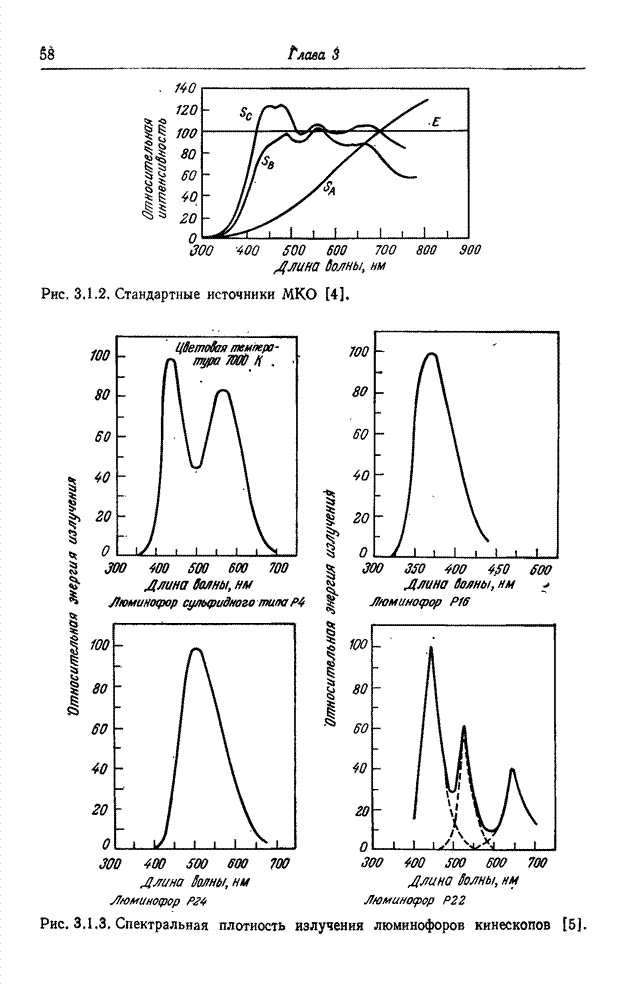
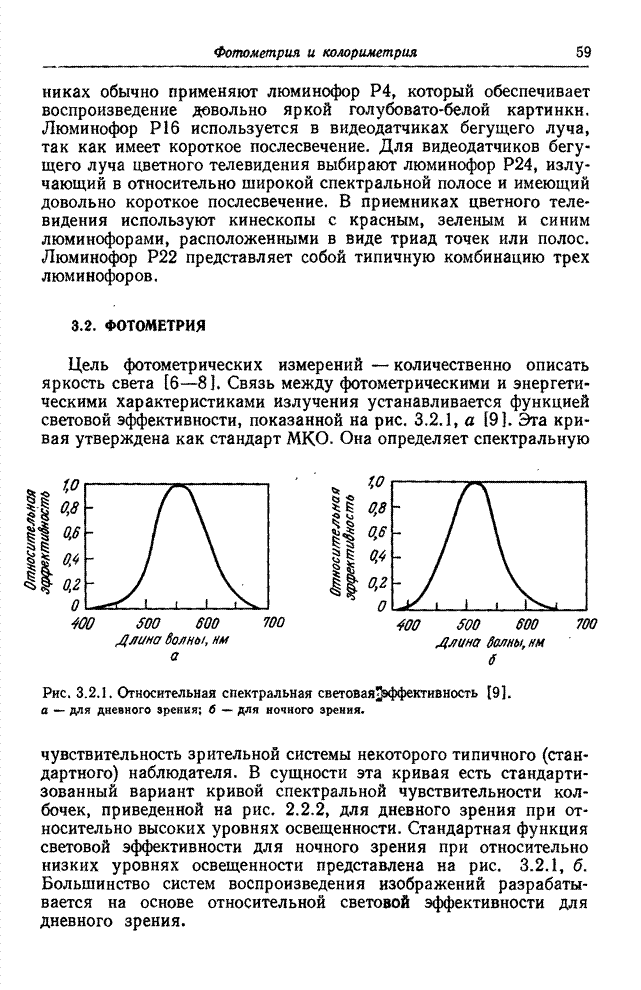
- 3.1. ИСТОЧНИКИ СВЕТА
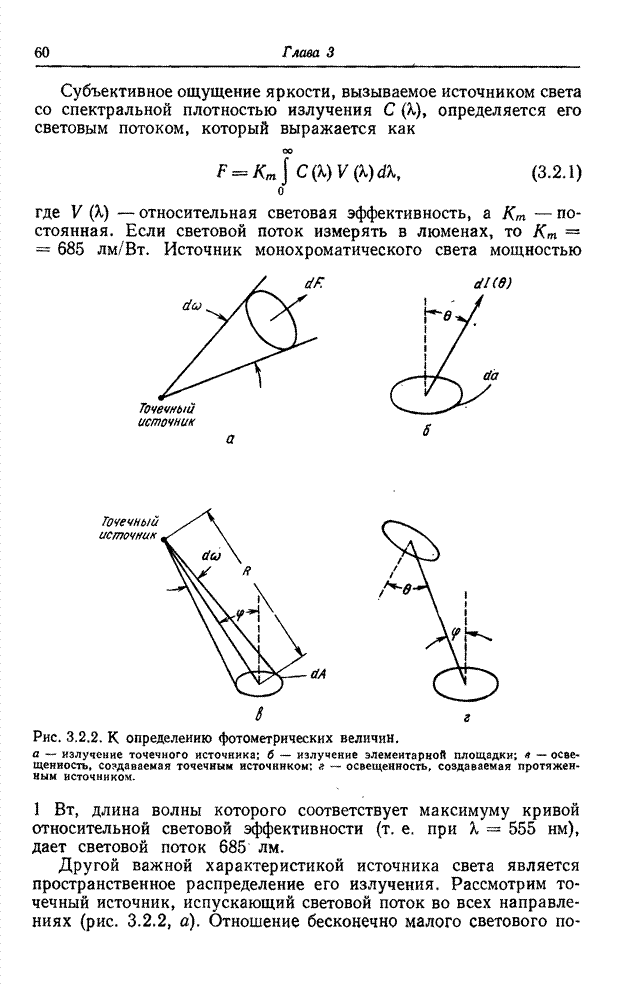
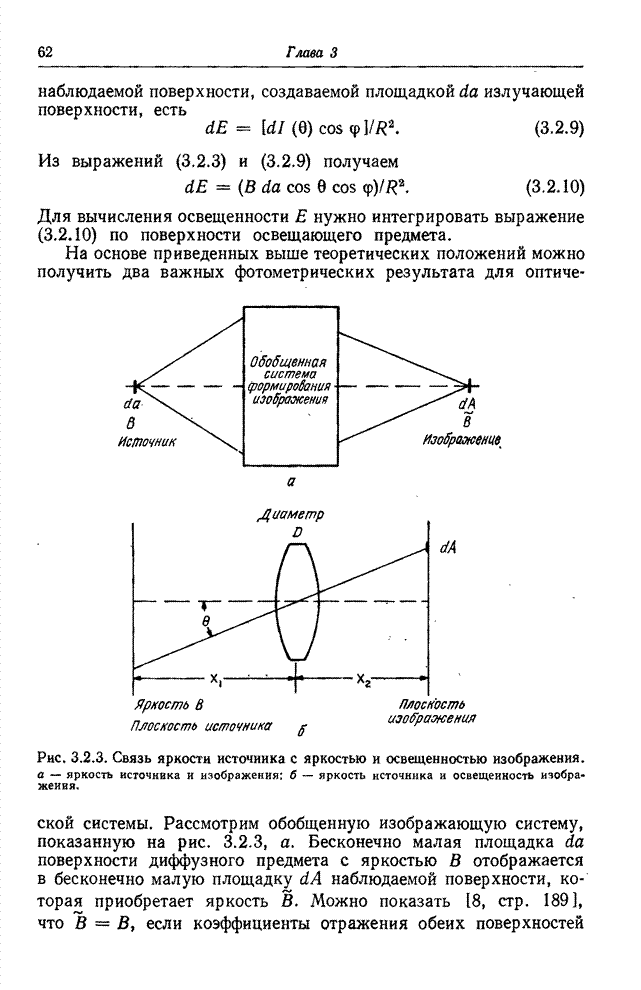
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
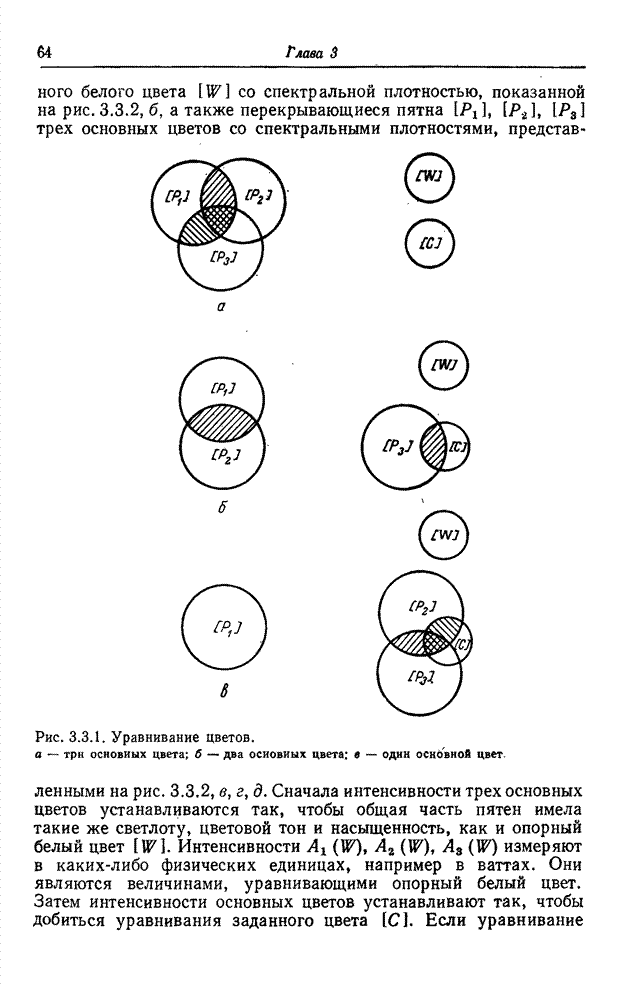
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
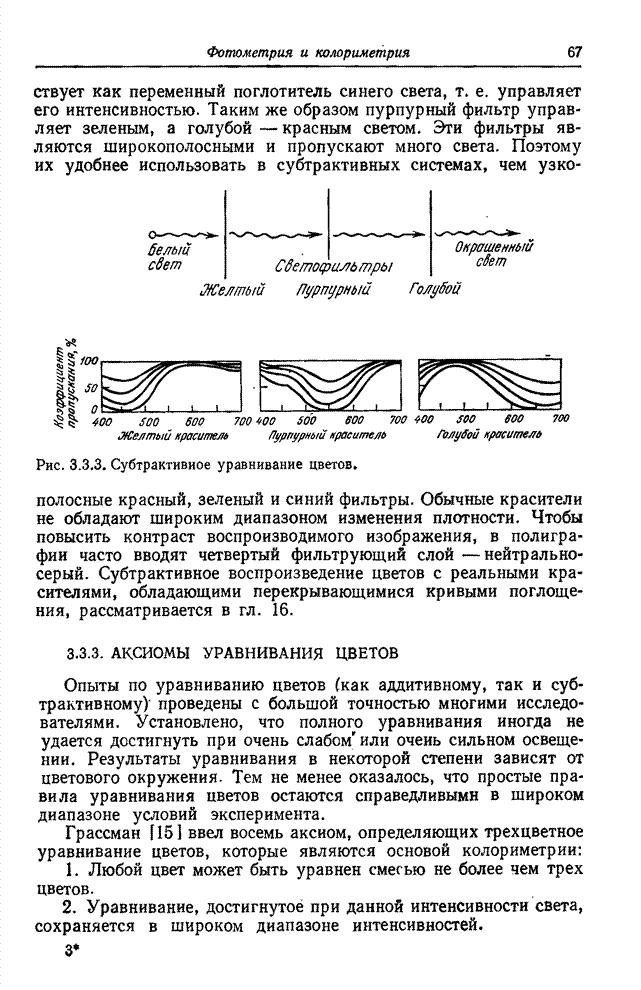
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
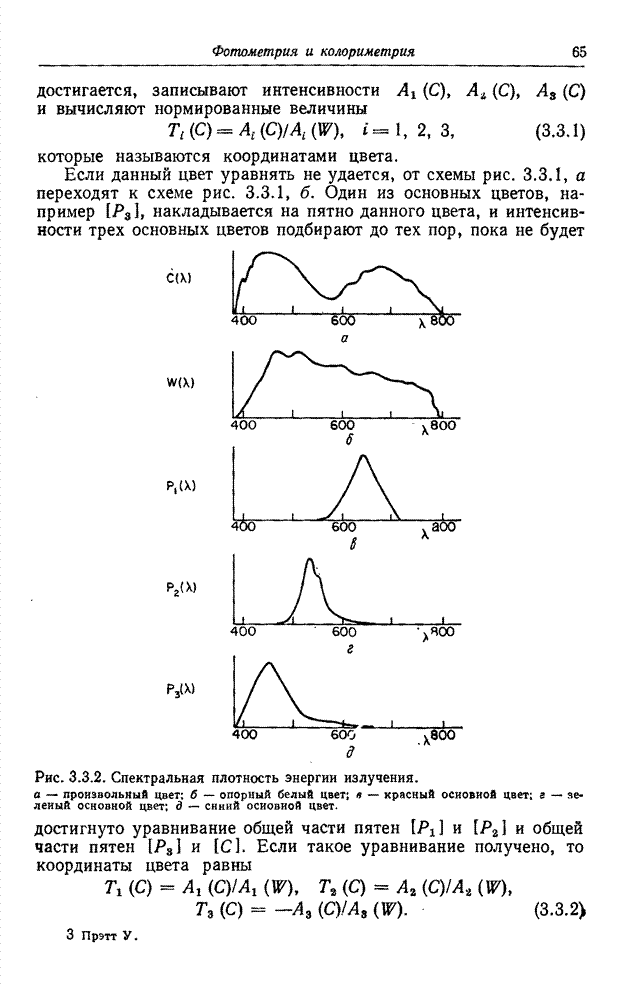
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
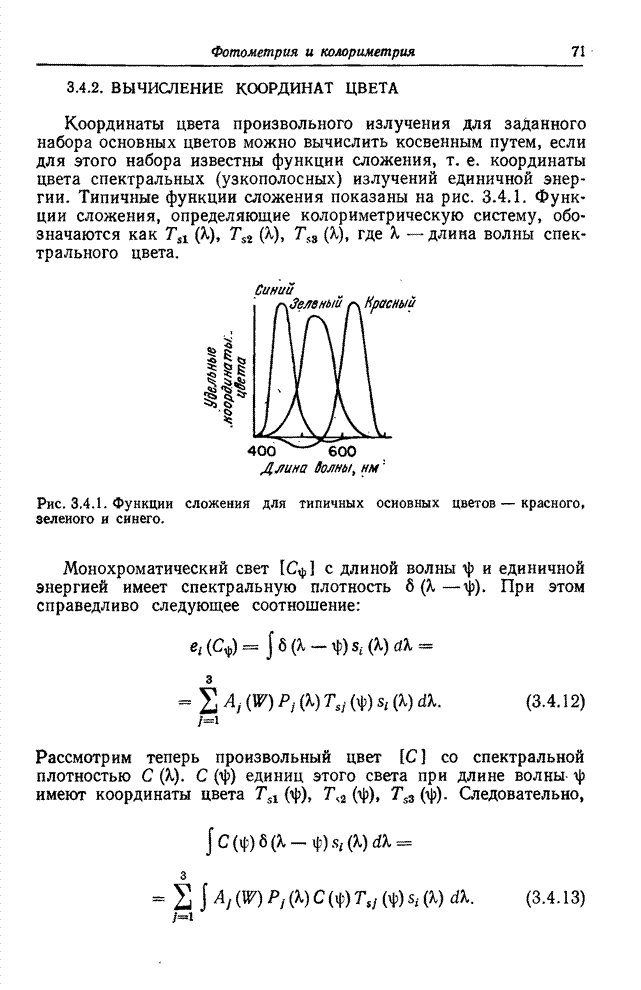
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
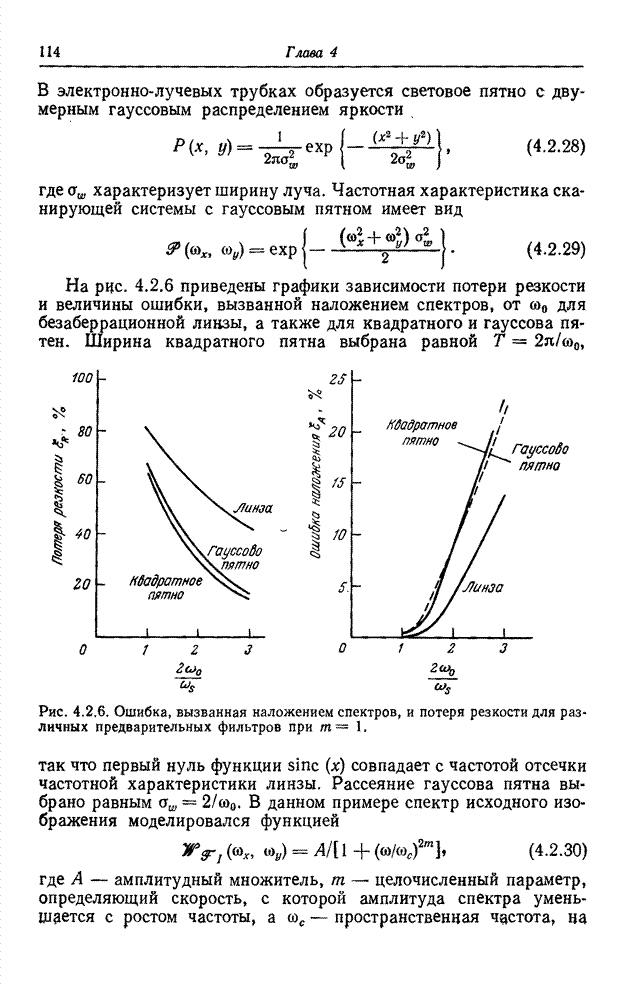
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
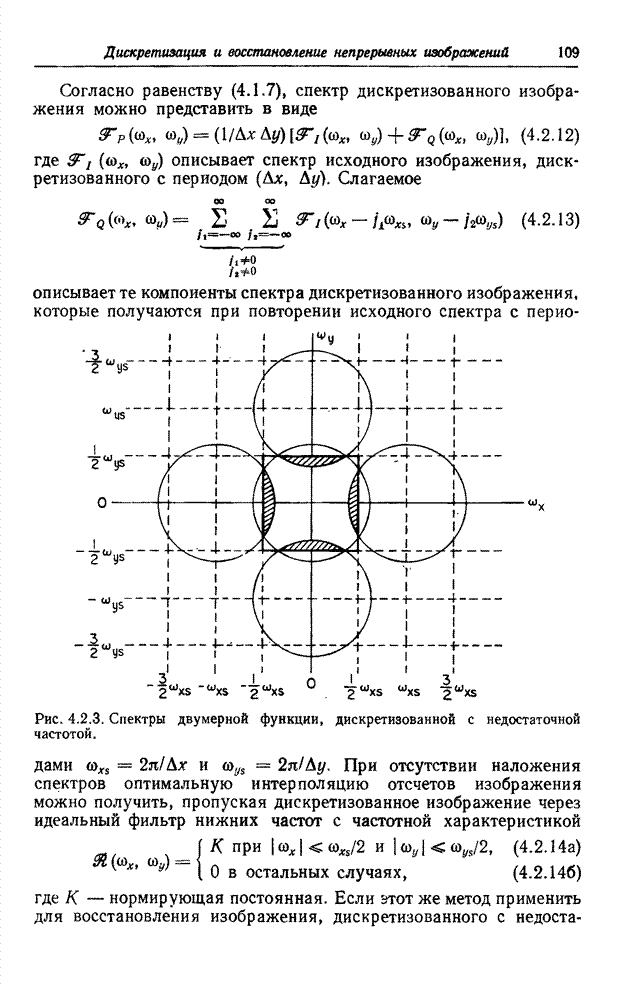
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
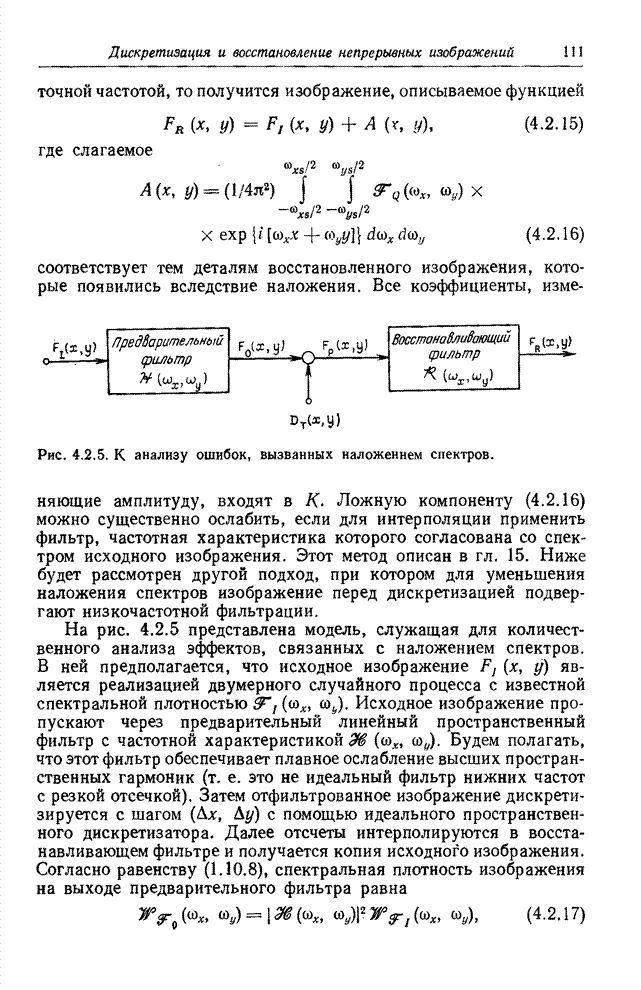
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
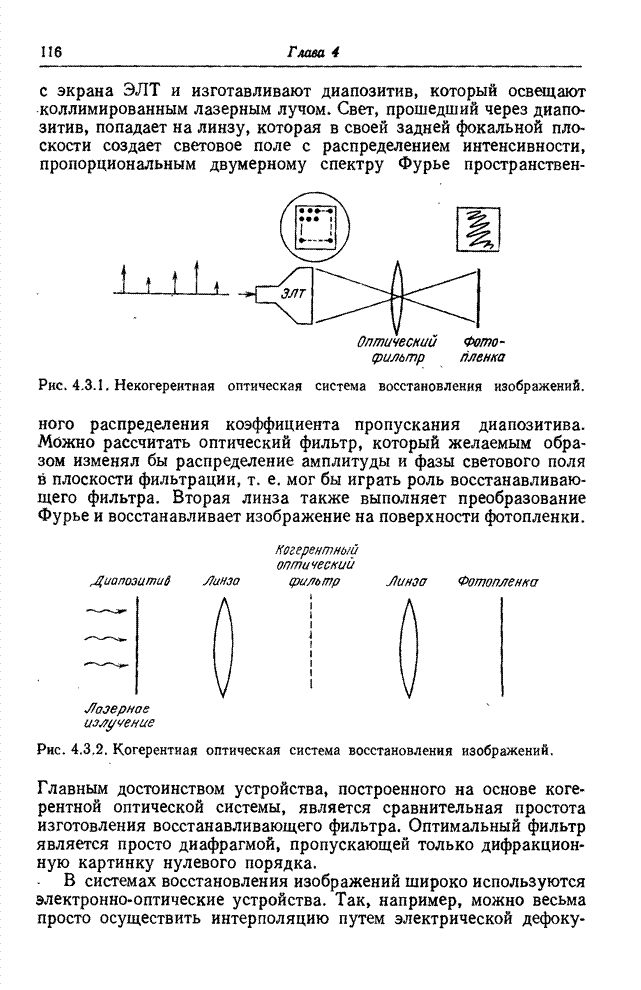
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА