| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Дискретное двумерное преобразование Фурье матрицы отсчетов изображения определяется [5-10] в виде ряда
 , (10.2.1а)
, (10.2.1а)
где
![]() , а
дискретное обратное преобразование имеет вид
, а
дискретное обратное преобразование имеет вид
![]() . (10.2.1б)
. (10.2.1б)
По
аналогии с терминологией непрерывного преобразования Фурье переменные ![]() называют
пространственными частотами. Следует отметить, что не все исследователи пользуются
определением (10.2.1); одни предпочитают помещать все масштабные постоянные в
выражение для обратного преобразования, а другие изменяют знаки в ядрах на
противоположные.
называют
пространственными частотами. Следует отметить, что не все исследователи пользуются
определением (10.2.1); одни предпочитают помещать все масштабные постоянные в
выражение для обратного преобразования, а другие изменяют знаки в ядрах на
противоположные.
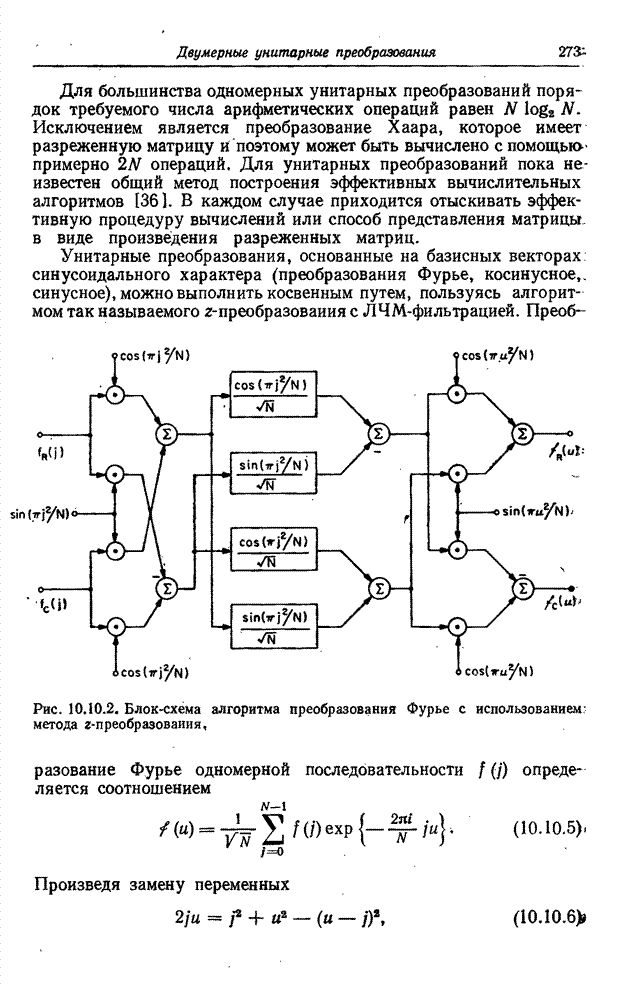
Поскольку ядра преобразования симметричны и разделимы, двумерное преобразование можно выполнить в виде последовательных одномерных преобразований по строкам и столбцам матрицы изображения. Базисными функциями преобразования являются экспоненты с комплексными показателями, которые можно разложить на синусную и косинусную составляющие. Таким образом,
![]() , (10.2.2a)
, (10.2.2a)
![]() . (10.2.2б)
. (10.2.2б)
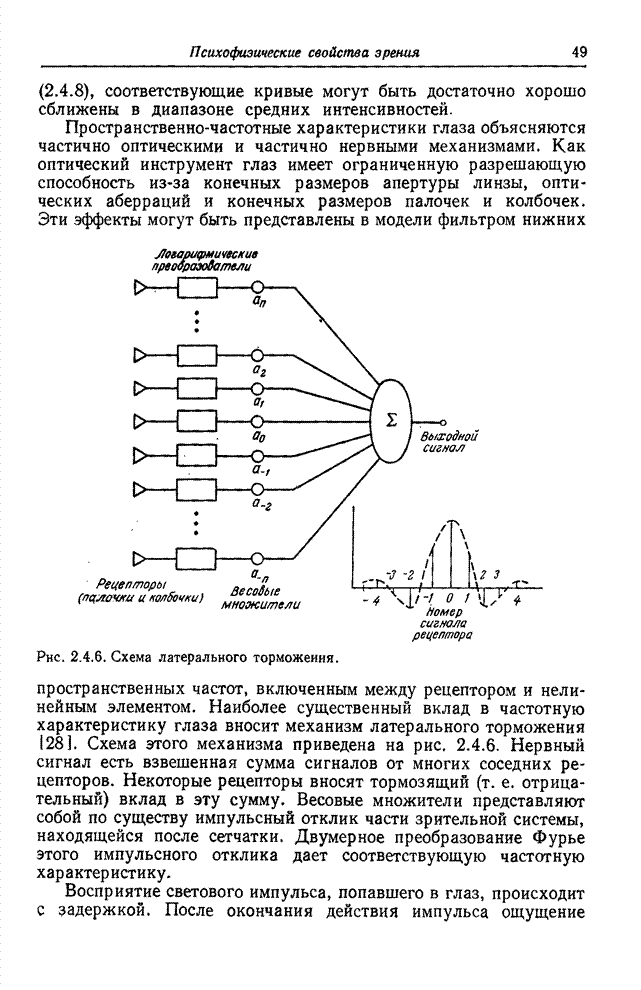
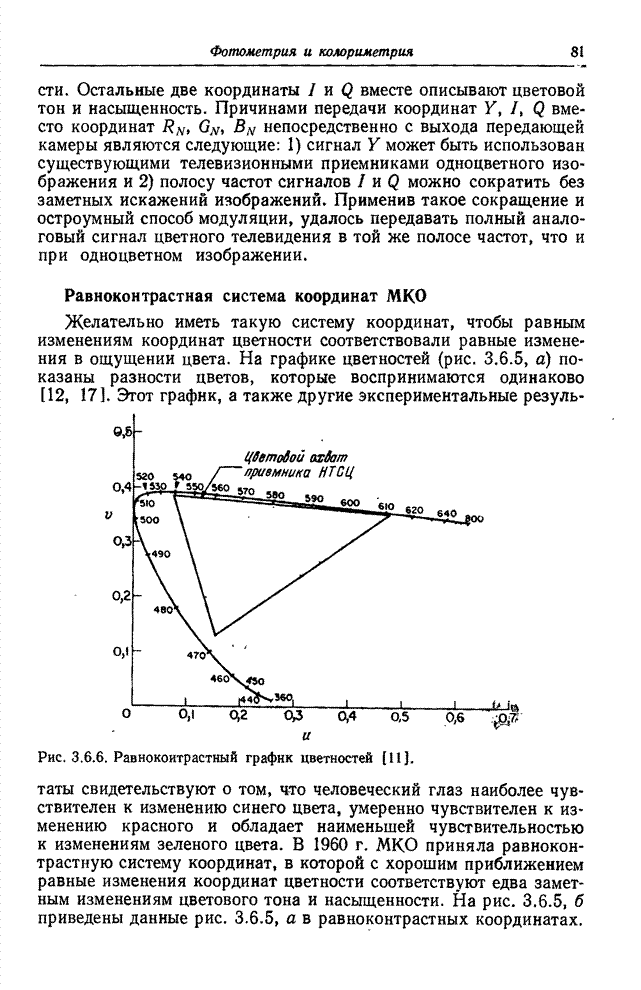
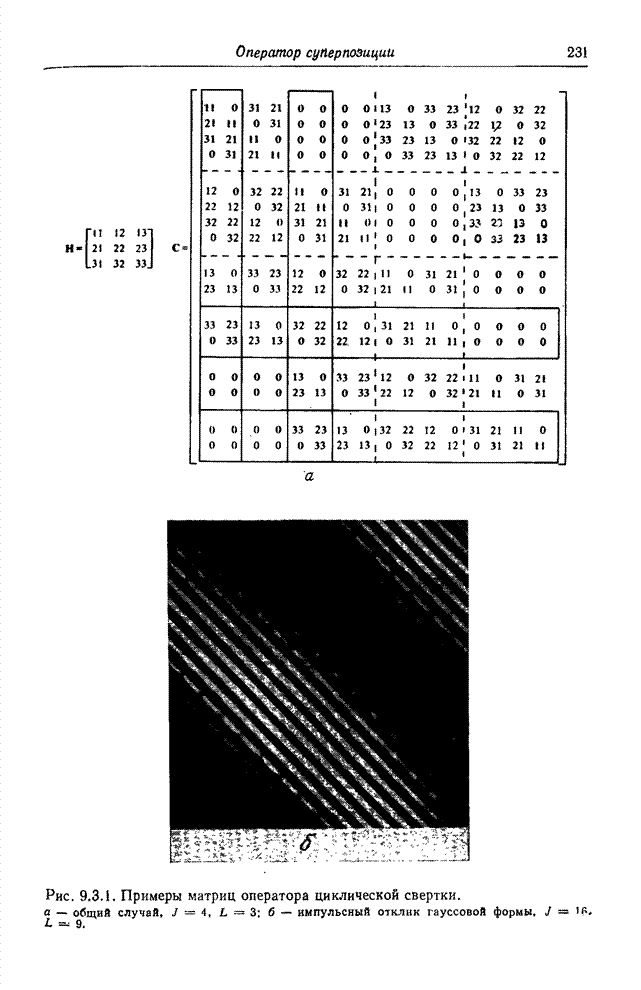
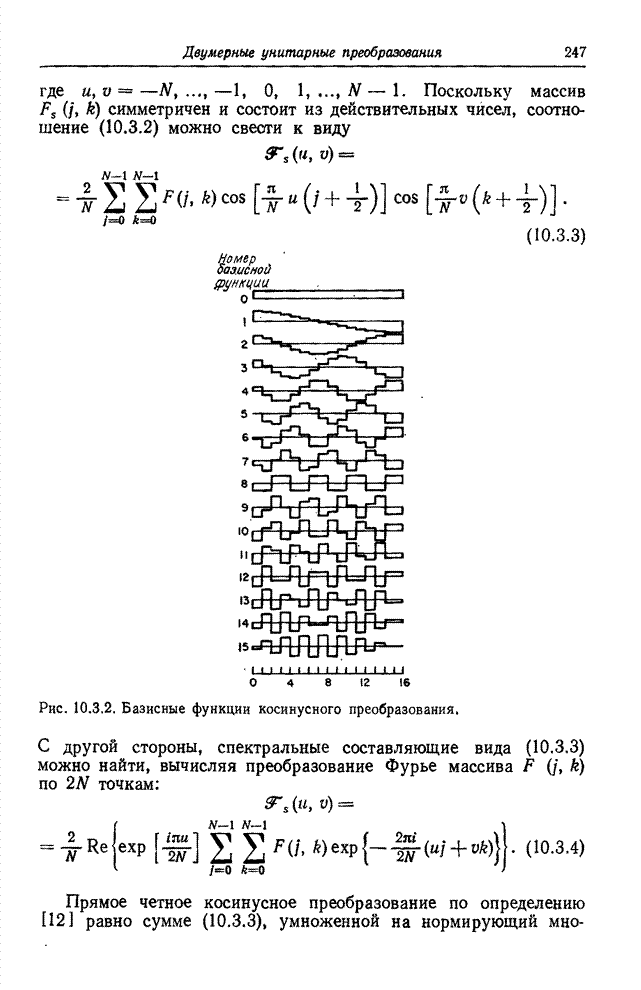
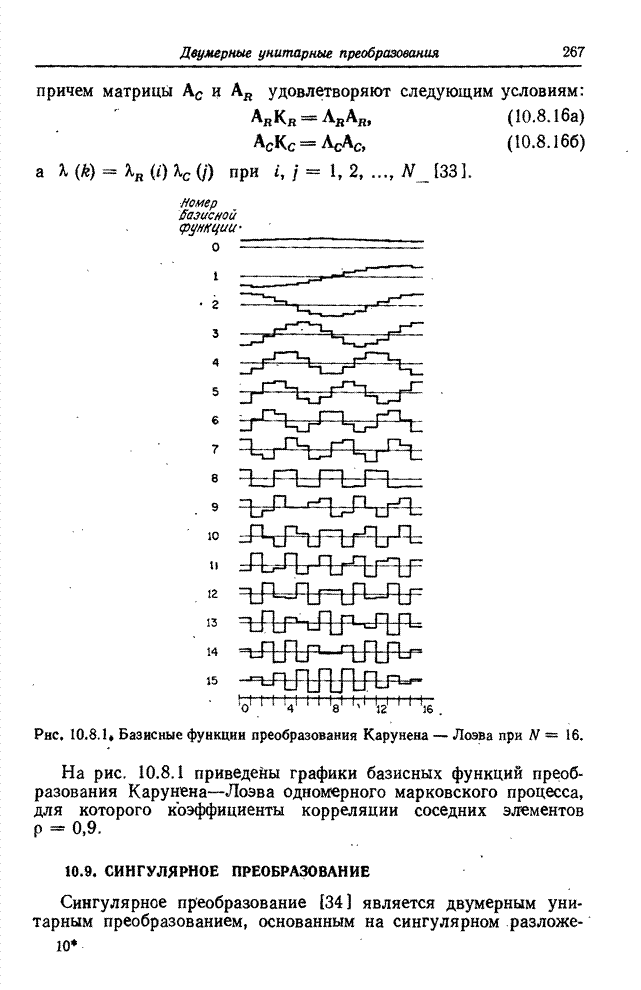
На
рис. 10.2.1 приведены графики синусных и косинусных составляющих одномерных
базисных функций преобразования Фурье для ![]() . Видно, что для низких частот эти
функции являются грубыми аппроксимациями непрерывных синусоид. С повышением
частоты сходство базисных функций с синусоидами теряется. Для наивысшей частоты
базисная функция представляет собой меандр. Можно заметить также избыточность наборов
синусных и косинусных составляющих.
. Видно, что для низких частот эти
функции являются грубыми аппроксимациями непрерывных синусоид. С повышением
частоты сходство базисных функций с синусоидами теряется. Для наивысшей частоты
базисная функция представляет собой меандр. Можно заметить также избыточность наборов
синусных и косинусных составляющих.

Рис. 10.2.1. Базисные функции преобразования Фурье.
а - синусная (нечетная) составляющая; б - косинусная (четная) составляющая.
Спектр изображения имеет много интересных структурных особенностей. Спектральная составляющая в начале координат частотной плоскости
 (10.2.3)
(10.2.3)
равна
увеличенному в ![]() раз
среднему (по исходной плоскости) значению яркости изображения. Подставив в
равенство (10.2.1а)
раз
среднему (по исходной плоскости) значению яркости изображения. Подставив в
равенство (10.2.1а)
![]() и
и
![]() , где
, где ![]() и
и ![]() - постоянные,
получим
- постоянные,
получим
 . (10.2.4)
. (10.2.4)
При
любых целочисленных значениях ![]() и
и ![]() второй экспоненциальный множитель
равенства (10.2.4) превращается в единицу. Таким образом, при
второй экспоненциальный множитель
равенства (10.2.4) превращается в единицу. Таким образом, при ![]()
![]() , (10.2.5)
, (10.2.5)
что свидетельствует о периодичности частотной плоскости. Рис. 10.2.2,а иллюстрирует этот результат.

Рис. 10.2.2. Периодическое продолжение изображения и спектра Фурье.
а - спектр; б - исходное изображение.
Двумерный спектр Фурье изображения является по существу представлением двумерного поля в виде ряда Фурье. Для того чтобы такое представление было справедливым, исходное изображение также должно обладать периодической структурой, т. е. (как показано на рис. 10.2.2,б) иметь рисунок, повторяющийся по вертикали и горизонтали. Таким образом, правый край изображения примыкает к левому, а верхний край - к нижнему. Из-за разрывов значений яркости в этих местах в спектре изображения возникают дополнительные составляющие, лежащие на координатных осях частотной плоскости. Эти составляющие не связаны со значениями яркости внутренних точек изображения, но они необходимы для воспроизведения его резких границ.
Если
массив отсчетов изображения описывает поле яркости, то числа ![]() будут
действительными и положительными. Однако спектр Фурье этого изображения в общем
случае имеет комплексные значения. Поскольку спектр содержит
будут
действительными и положительными. Однако спектр Фурье этого изображения в общем
случае имеет комплексные значения. Поскольку спектр содержит ![]() компонент,
представляющих действительную и мнимую части или фазу и модуль спектральных
составляющих для каждой частоты, может показаться, что преобразование Фурье
увеличивает размерность изображения. Это, однако, не так, поскольку
компонент,
представляющих действительную и мнимую части или фазу и модуль спектральных
составляющих для каждой частоты, может показаться, что преобразование Фурье
увеличивает размерность изображения. Это, однако, не так, поскольку ![]() обладает
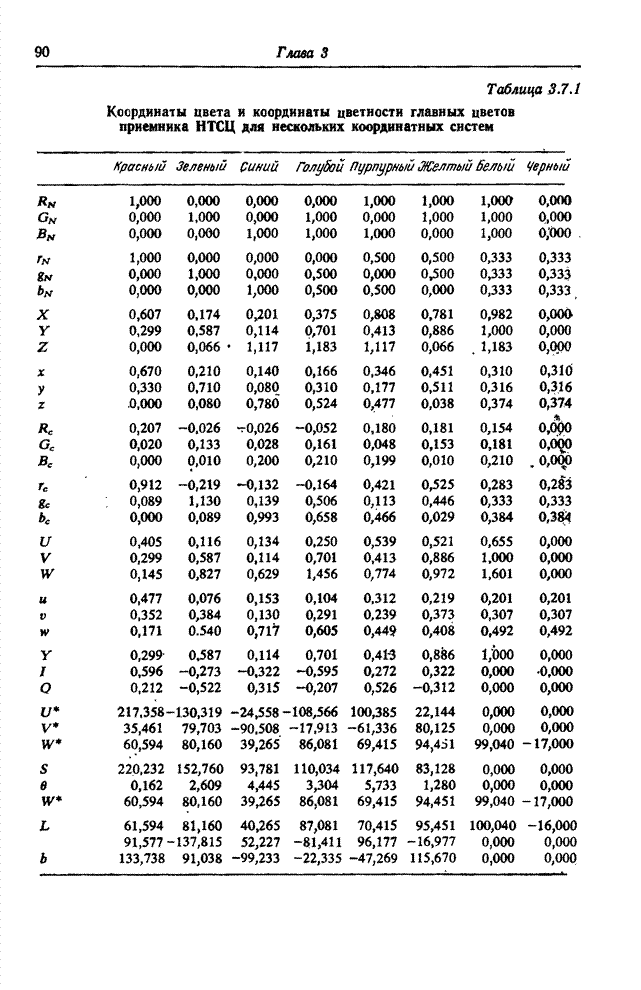
симметрией относительно комплексного сопряжения. Если в равенстве (10.2.4)
положить
обладает
симметрией относительно комплексного сопряжения. Если в равенстве (10.2.4)
положить ![]() и
и
![]() равными
целым числам, то после комплексного сопряжения получится равенство
равными
целым числам, то после комплексного сопряжения получится равенство
 . (10.2.6)
. (10.2.6)
С
помощью подстановки ![]() и
и ![]() можно показать, что
можно показать, что
![]() (10.2.7)
(10.2.7)
при
![]() . Из-за
наличия комплексно-сопряженной симметрии почти половина спектральных составляющих
оказывается избыточной, т. е. их можно сформировать из остальных составляющих.
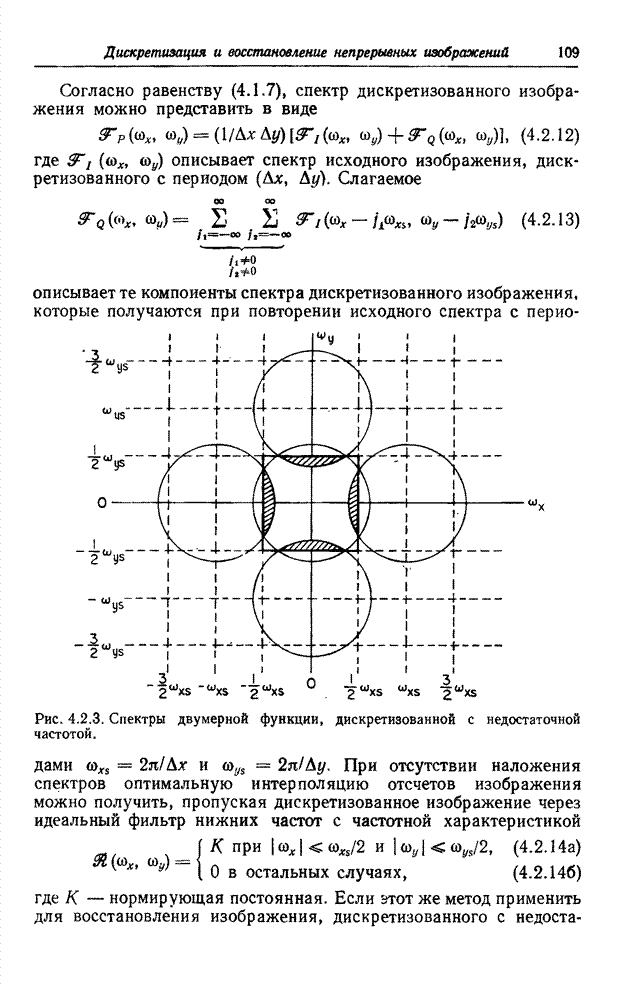
На рис. 10.2.3 области расположения избыточных составляющих спектра на
частотной плоскости заштрихованы. Избыточными составляющими можно, конечно,
считать гармоники, попадающие не в нижнюю, а в правую полуплоскость.
. Из-за
наличия комплексно-сопряженной симметрии почти половина спектральных составляющих
оказывается избыточной, т. е. их можно сформировать из остальных составляющих.
На рис. 10.2.3 области расположения избыточных составляющих спектра на
частотной плоскости заштрихованы. Избыточными составляющими можно, конечно,
считать гармоники, попадающие не в нижнюю, а в правую полуплоскость.

Рис. 10.2.3. Частотная плоскость.
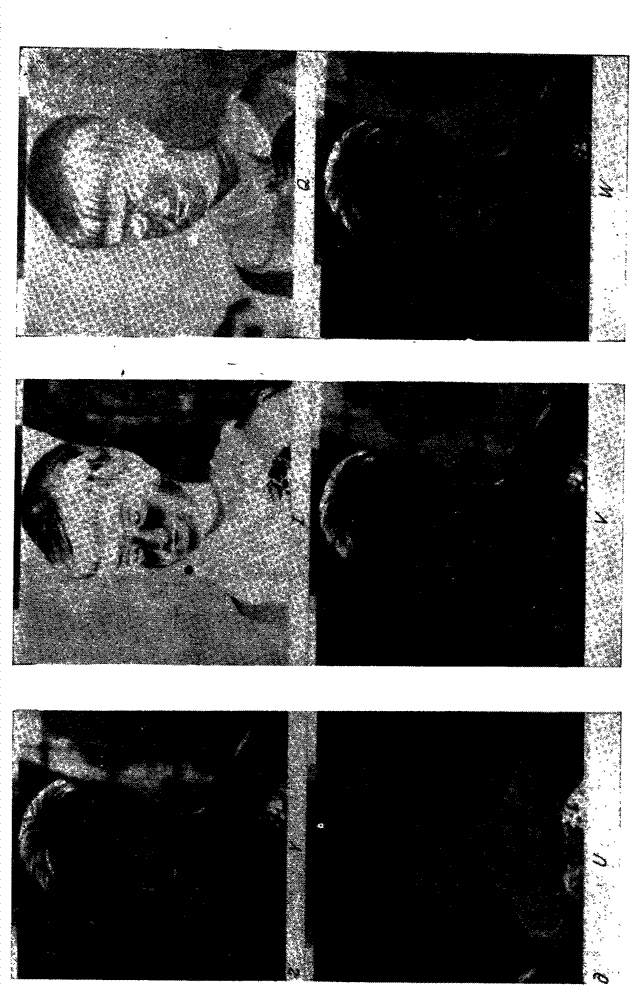
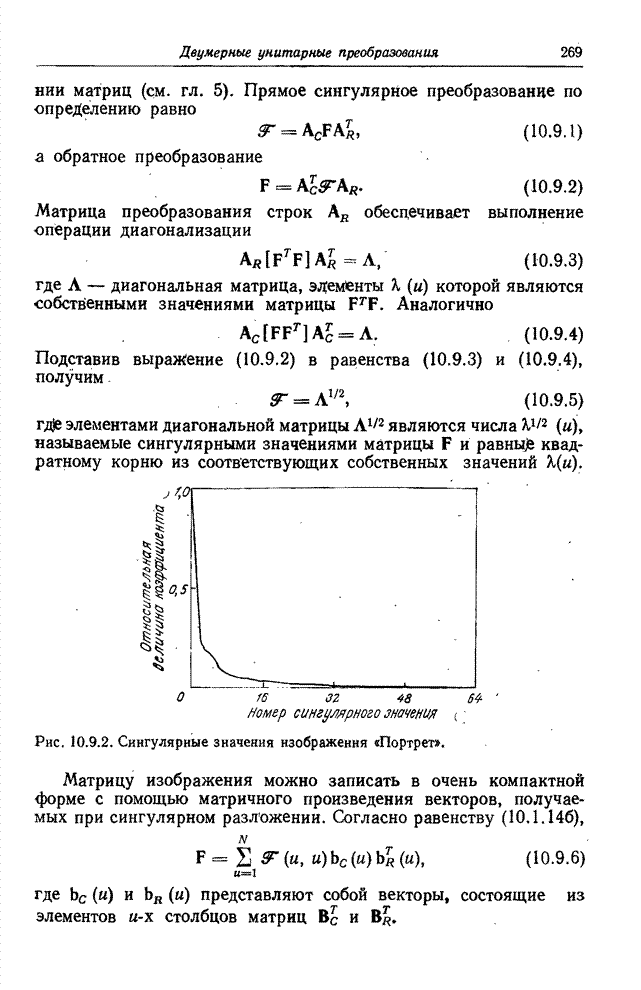
На рис. 10.2.4 приведены фотографии исходного изображения и различных вариантов его Фурье-спектра. Поскольку динамический диапазон составляющих спектра гораздо шире, чем линейный участок интервала экспозиций фотопленки, то спектры необходимо подвергнуть сжатию. Сжатие динамического диапазона можно осуществить путем ограничения больших спектральных составляющих или логарифмическим преобразованием всех составляющих спектра согласно соотношению
![]() , (10.2.8)
, (10.2.8)
где
![]() и
и ![]() - масштабные
постоянные. На рис. 10.2.4,б приведены (в логарифмическом масштабе с
- масштабные
постоянные. На рис. 10.2.4,б приведены (в логарифмическом масштабе с ![]() и
и ![]() ) модули гармоник
спектра, вычисленных в соответствии с равенством (10.2.1а). На рис. 10.2.4,в
показан тот же спектр, в котором наибольшие гармоники, составляющие 25% всех
компонент спектра, были ограничены по величине. При математическом анализе
непрерывных сигналов начало координат частотной плоскости обычно помещают в ее
геометрическом центре. Аналогично в дифракционной картине, полученной с помощью
когерентной оптической системы для диапозитива с коэффициентом пропускания
) модули гармоник
спектра, вычисленных в соответствии с равенством (10.2.1а). На рис. 10.2.4,в
показан тот же спектр, в котором наибольшие гармоники, составляющие 25% всех
компонент спектра, были ограничены по величине. При математическом анализе
непрерывных сигналов начало координат частотной плоскости обычно помещают в ее
геометрическом центре. Аналогично в дифракционной картине, полученной с помощью
когерентной оптической системы для диапозитива с коэффициентом пропускания ![]() , гармоника с
нулевой частотой оказывается в центре. Двумерный дискретный Фурье-спектр,
найденный с помощью вычислительной машины, путем простой перестановки
коэффициентов можно изменить так, чтобы начало координат также оказалось в
центре массива. Тот же результат можно получить по-другому, если отсчеты
изображения предварительно умножить на коэффициенты вида
, гармоника с
нулевой частотой оказывается в центре. Двумерный дискретный Фурье-спектр,
найденный с помощью вычислительной машины, путем простой перестановки
коэффициентов можно изменить так, чтобы начало координат также оказалось в
центре массива. Тот же результат можно получить по-другому, если отсчеты
изображения предварительно умножить на коэффициенты вида ![]() . Тогда квадранты спектра,
рассчитанного согласно формуле (10.2.1а), в процессе вычисления автоматически
меняются местами. Данное утверждение можно доказать с помощью соотношения
(10.2.4), положив в нем
. Тогда квадранты спектра,
рассчитанного согласно формуле (10.2.1а), в процессе вычисления автоматически
меняются местами. Данное утверждение можно доказать с помощью соотношения
(10.2.4), положив в нем ![]() . Тогда в силу тождества
. Тогда в силу тождества
![]() (10.2.9)
(10.2.9)
выражение (10.2.4) можно записать в следующем виде:
 . (10.2.10)
. (10.2.10)
На рис. 10.2.4,г представлен спектр с переставленными гармониками.

Рис. 10.2.4. Преобразование Фурье изображения «Портрет».
а - исходное изображение; б - модули гармоник спектра (в логарифмическом масштабе, без перестановки гармоник); в - спектр с ограниченными наибольшими гармониками (без их перестановки); г - спектр с ограниченными наибольшими гармониками (после их перестановки).
Прямое и обратное преобразования Фурье (10.2.1) можно представить в векторной форме
![]() , (10.2.11а)
, (10.2.11а)
а
![]() , (10.2.11б)
, (10.2.11б)
где
![]() и
и ![]() - векторы,
полученные соответственно путем развертки по столбцам матриц
- векторы,
полученные соответственно путем развертки по столбцам матриц ![]() и
и ![]() . Поскольку матрицу
преобразования
. Поскольку матрицу
преобразования ![]() можно
записать в виде прямого произведения
можно
записать в виде прямого произведения
![]() , (10.2.12)
, (10.2.12)
где
 , (10.2.13)
, (10.2.13)
![]() ,
то матрицы изображения и спектра связаны соотношениями
,
то матрицы изображения и спектра связаны соотношениями
![]() (10.2.14а)
(10.2.14а)
и
![]() . (10.2.14б)
. (10.2.14б)
Понятно, что свойства преобразования Фурье, установленные для рядов (10.2.1), сохраняются и при его матричной записи.
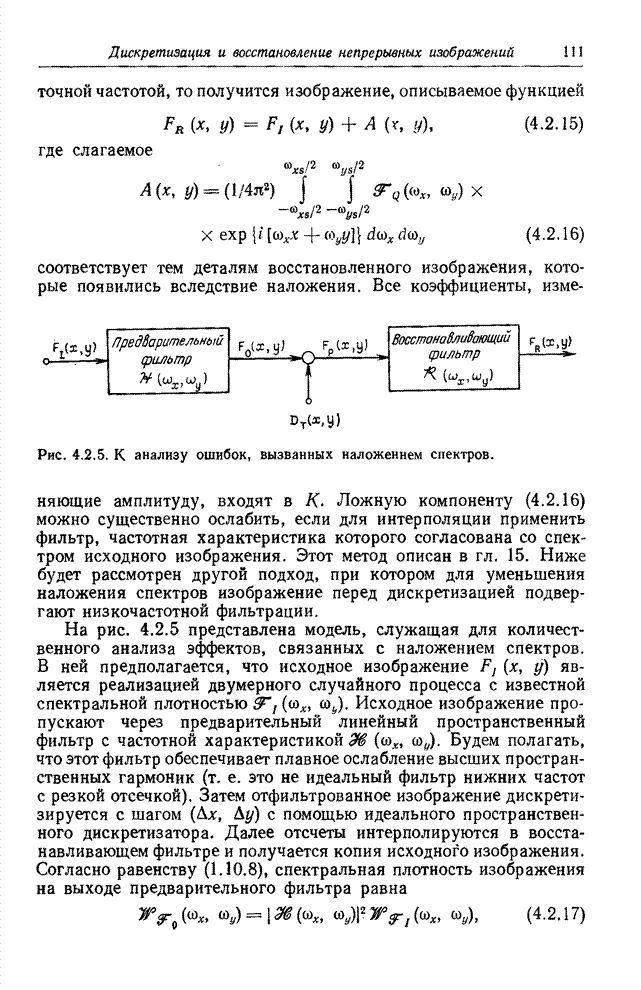
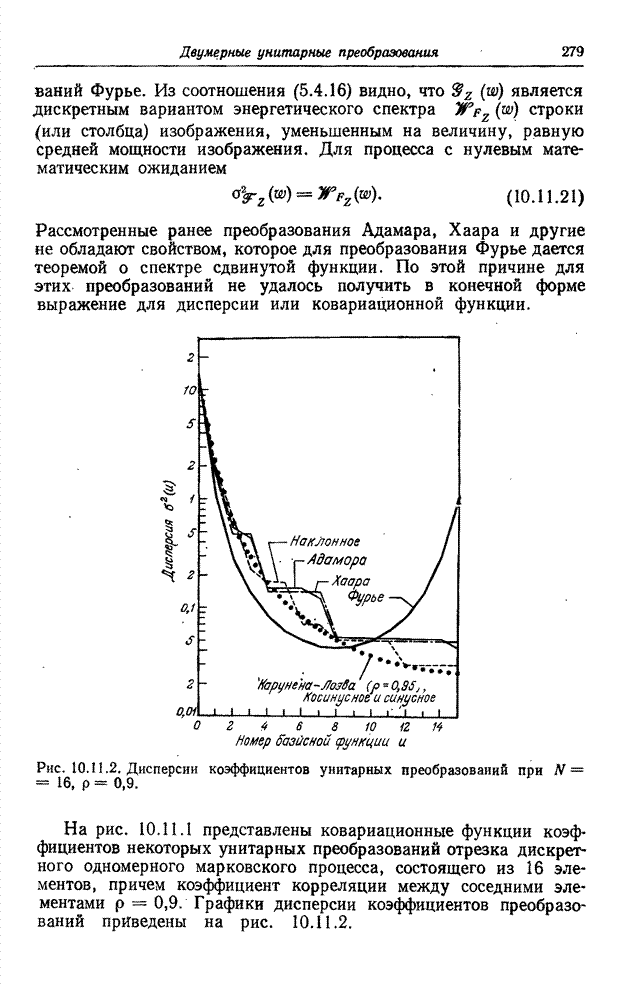
Хотя преобразование Фурье имеет много полезных для анализа свойств, у него есть и два существенных недостатка: во-первых, все вычисления приходится производить не с действительными, а с комплексными числами и, во-вторых, ряды сходятся медленно. Последнее замечание, весьма существенное для задач кодирования изображений, можно пояснить, переписав определение (10.2.1б) в следующей форме:
 , (10.2.15)
, (10.2.15)
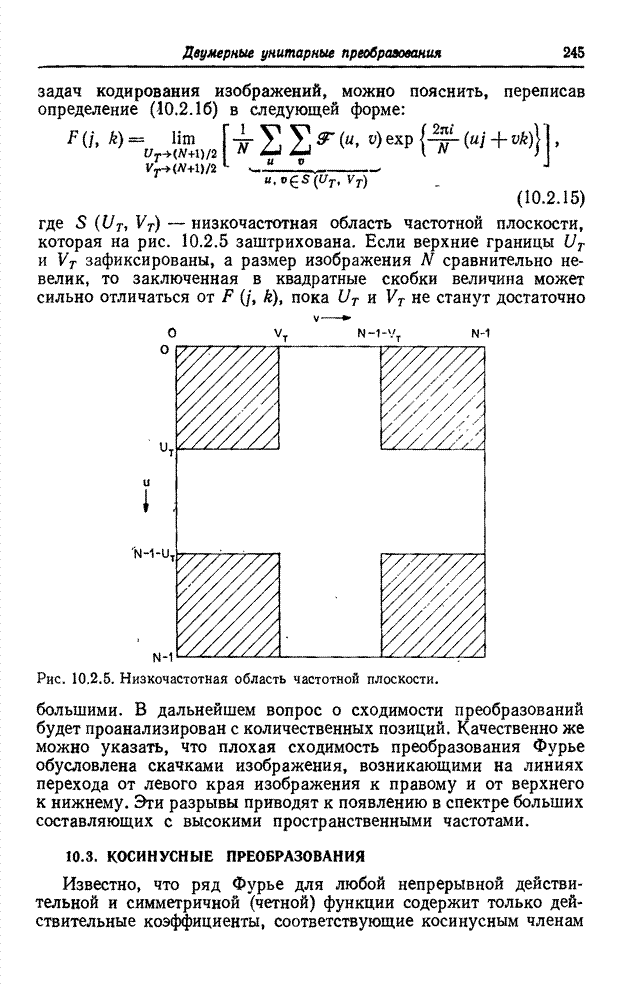
где
![]() -
низкочастотная область частотной плоскости, которая на рис. 10.2.5
заштрихована. Если верхние границы
-
низкочастотная область частотной плоскости, которая на рис. 10.2.5
заштрихована. Если верхние границы ![]() и
и ![]() зафиксированы, а размер изображения
зафиксированы, а размер изображения ![]() сравнительно
невелик, то заключенная в квадратные скобки величина может сильно отличаться от
сравнительно
невелик, то заключенная в квадратные скобки величина может сильно отличаться от
![]() , пока
, пока ![]() и
и ![]() не станут
достаточно большими. В дальнейшем вопрос о сходимости преобразований будет
проанализирован с количественных позиций. Качественно же можно указать, что
плохая сходимость преобразования Фурье обусловлена скачками изображения,
возникающими на линиях перехода от левого края изображения к правому и от
верхнего к нижнему. Эти разрывы приводят к появлению в спектре больших
составляющих с высокими пространственными частотами.
не станут
достаточно большими. В дальнейшем вопрос о сходимости преобразований будет
проанализирован с количественных позиций. Качественно же можно указать, что
плохая сходимость преобразования Фурье обусловлена скачками изображения,
возникающими на линиях перехода от левого края изображения к правому и от
верхнего к нижнему. Эти разрывы приводят к появлению в спектре больших
составляющих с высокими пространственными частотами.

Рис. 10.2.5. Низкочастотная область частотной плоскости.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
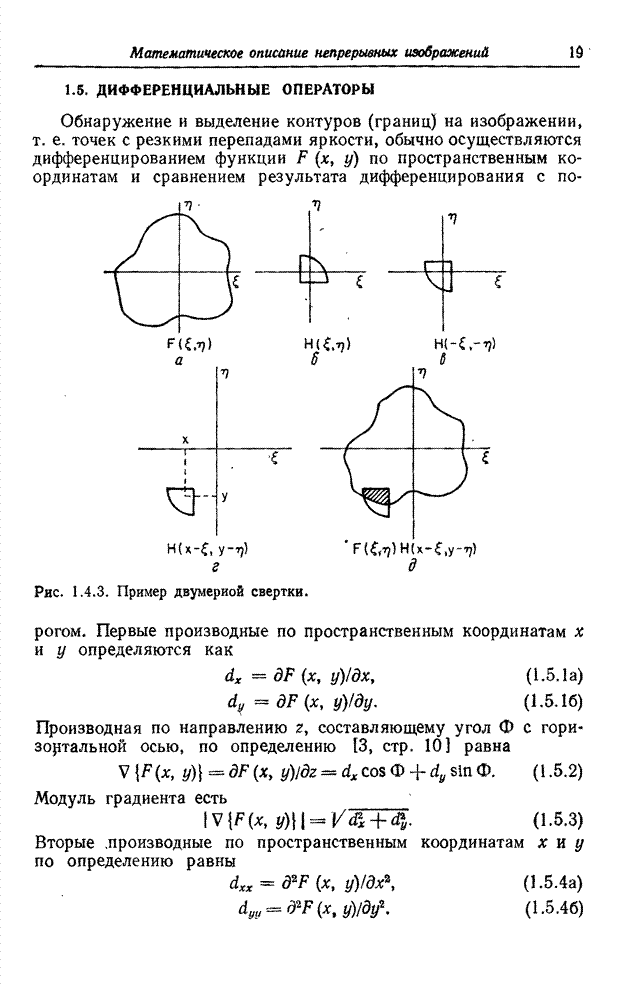
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
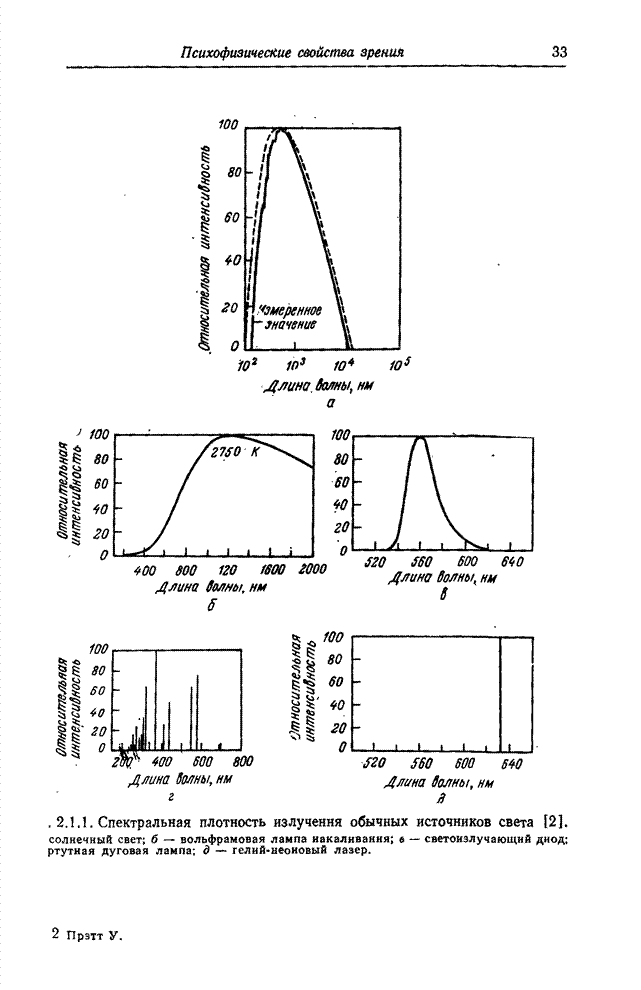
- 2.1. ВОСПРИЯТИЕ СВЕТА
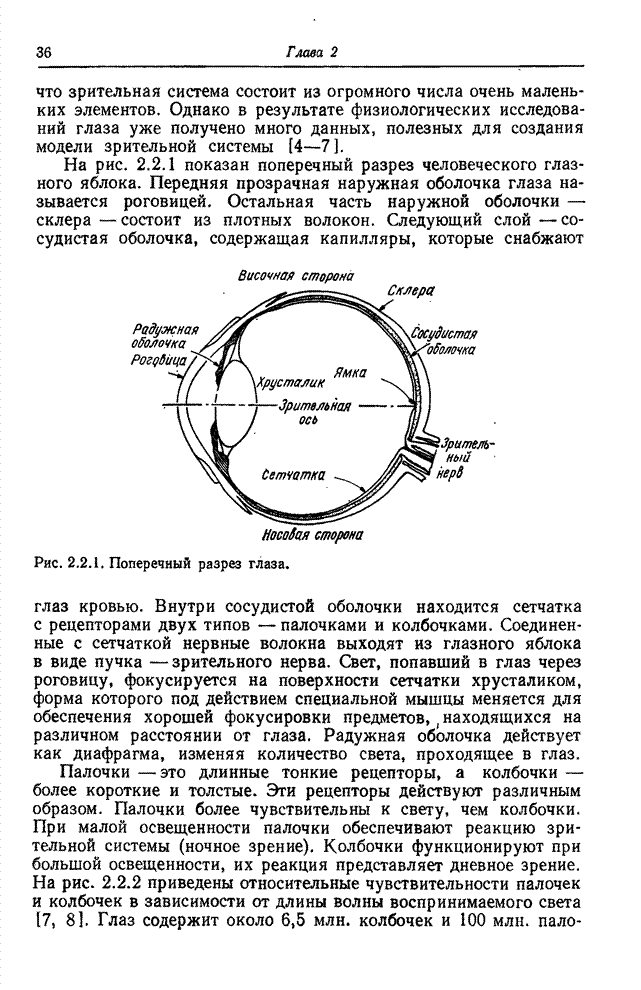
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
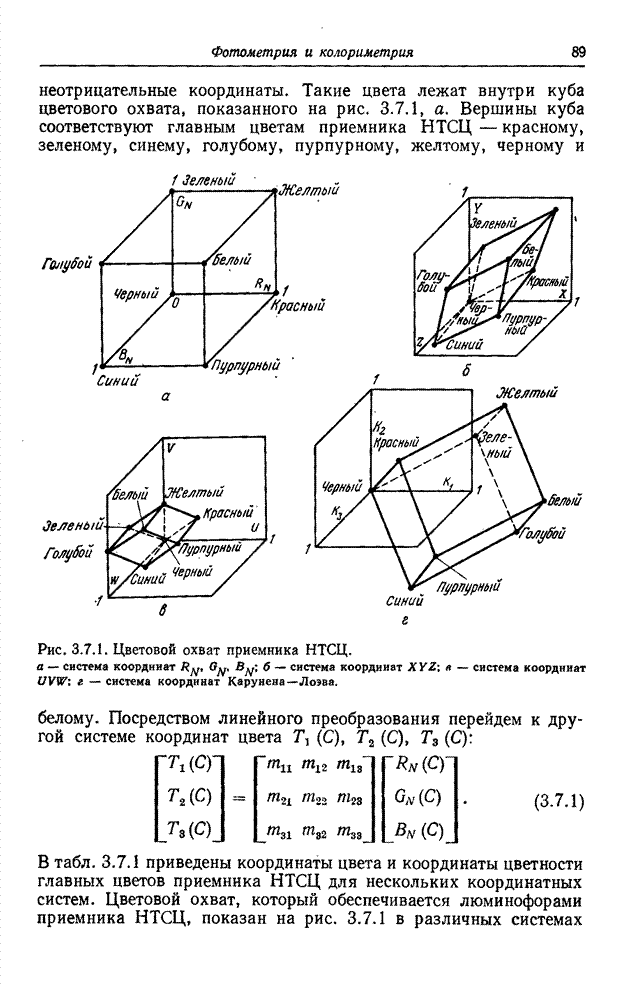
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
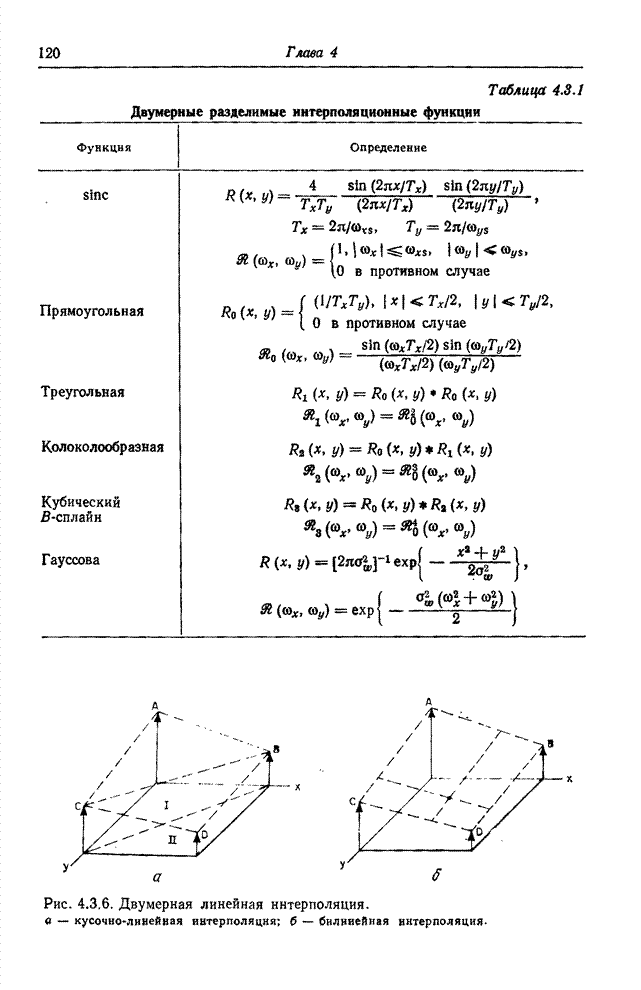
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
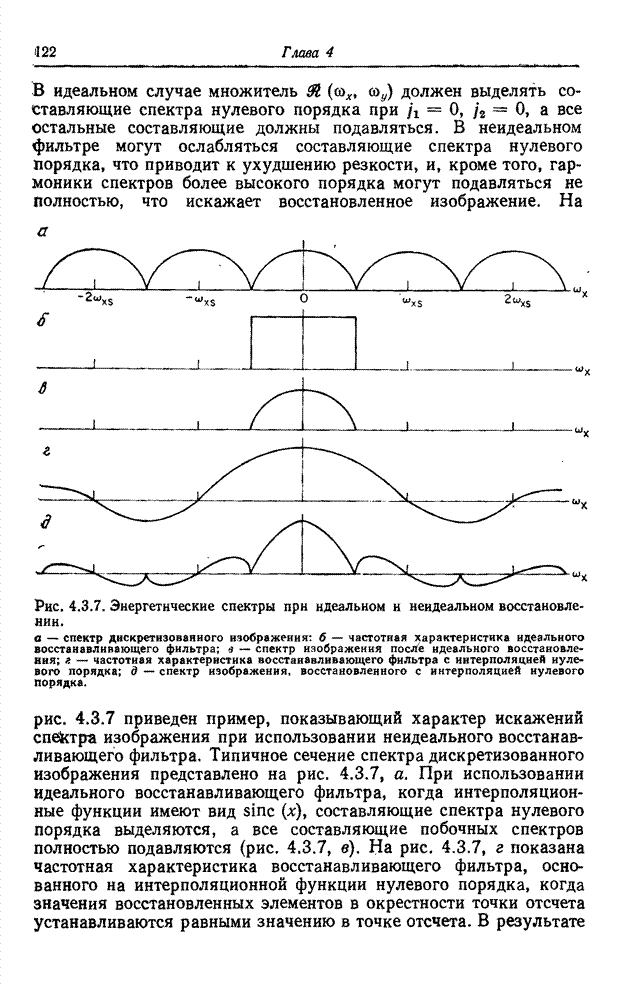
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
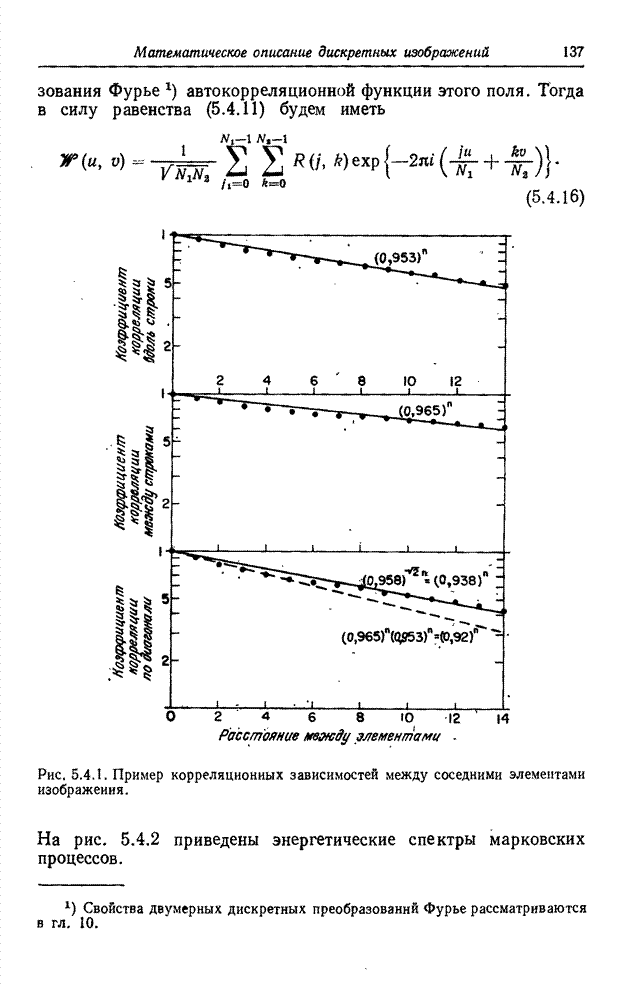
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
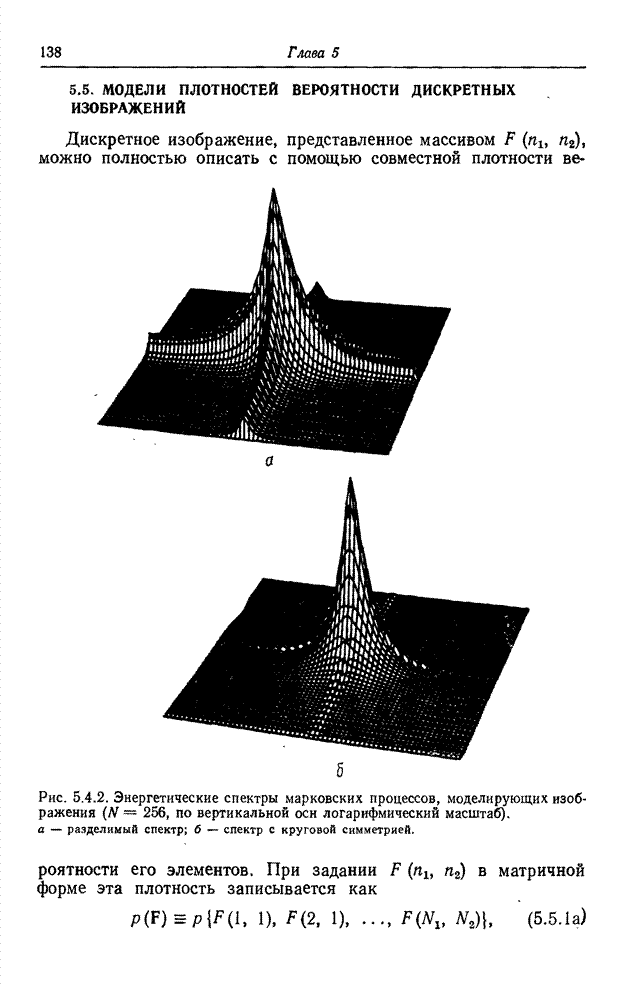
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
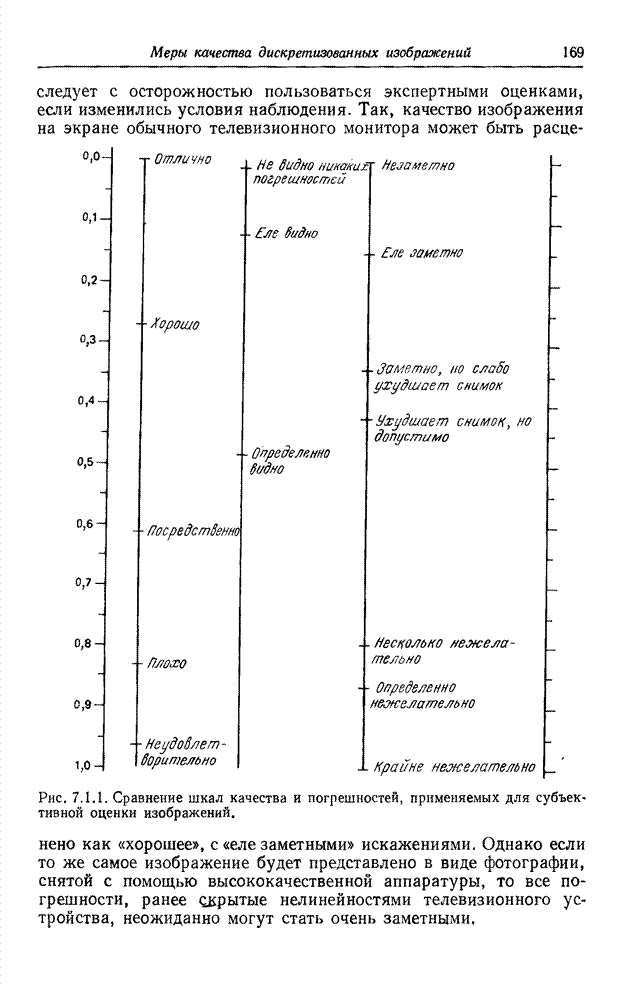
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
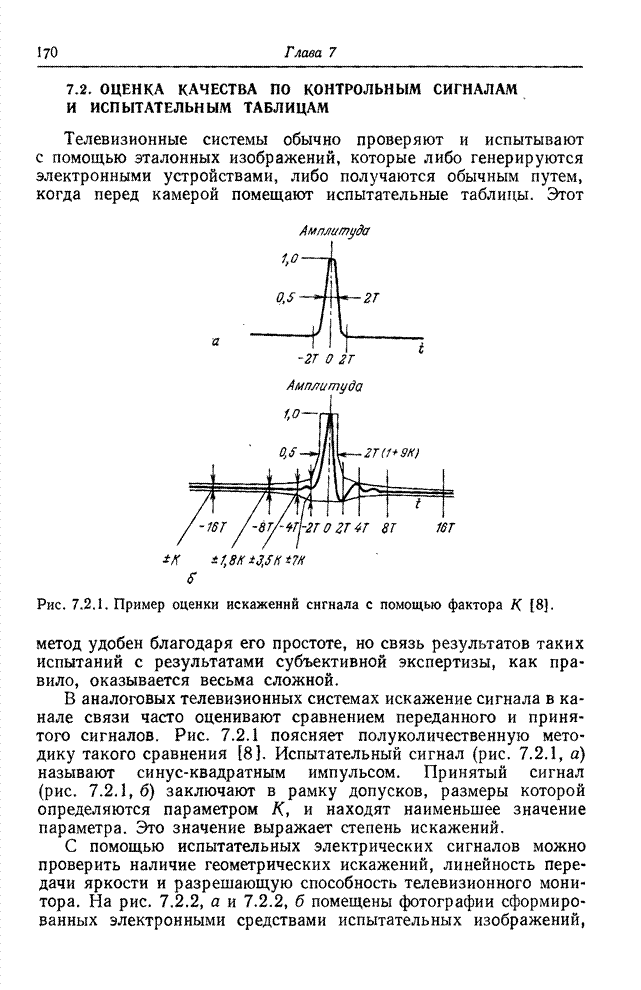
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
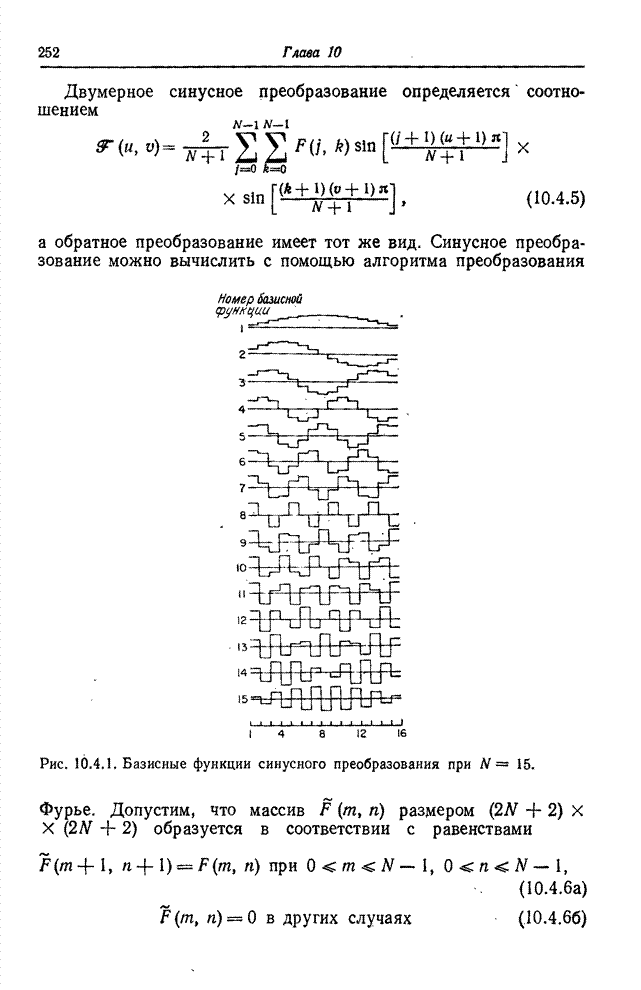
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
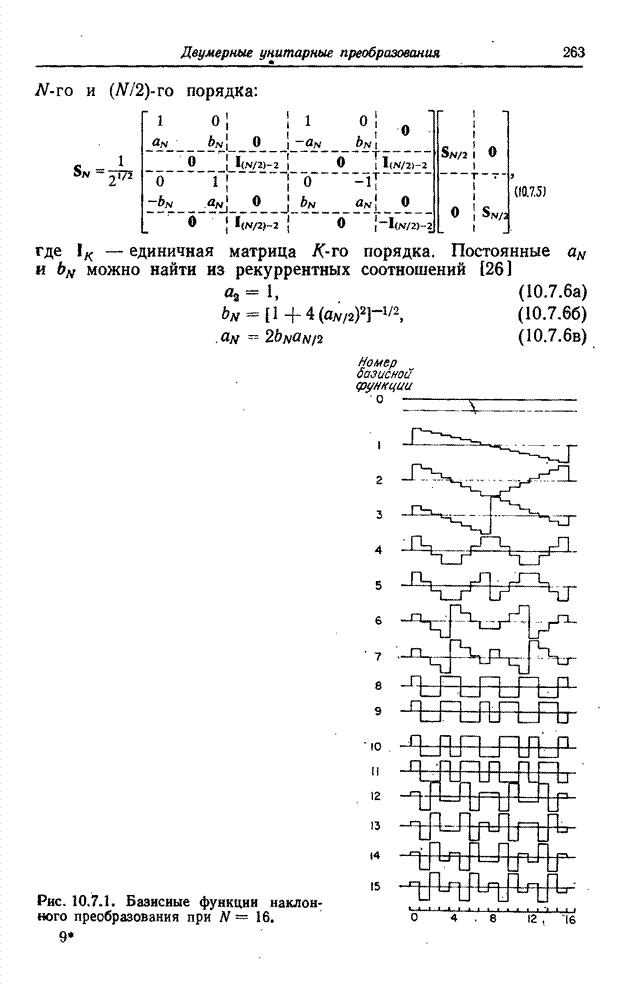
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА