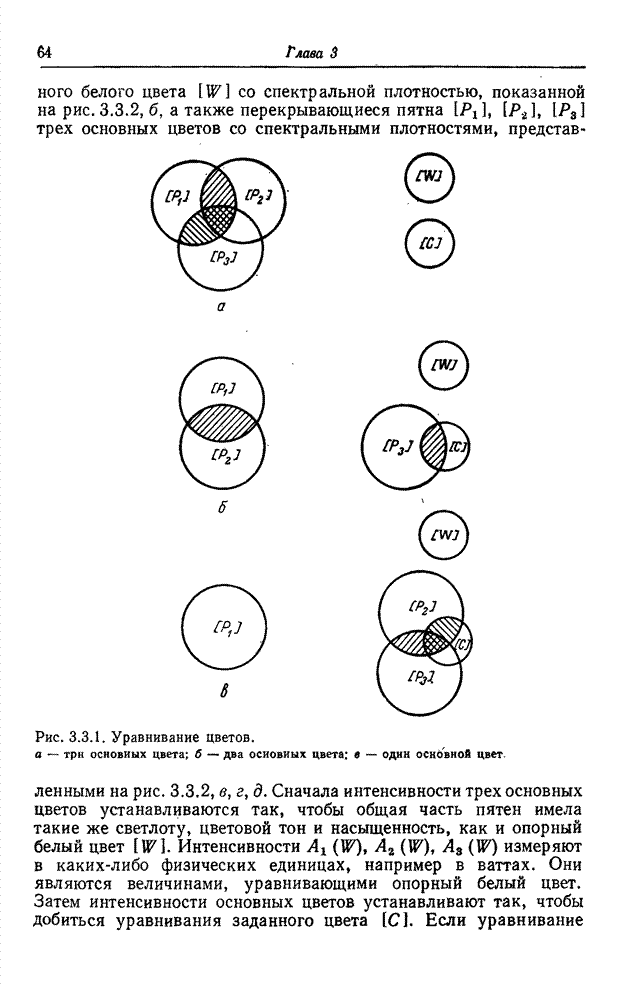
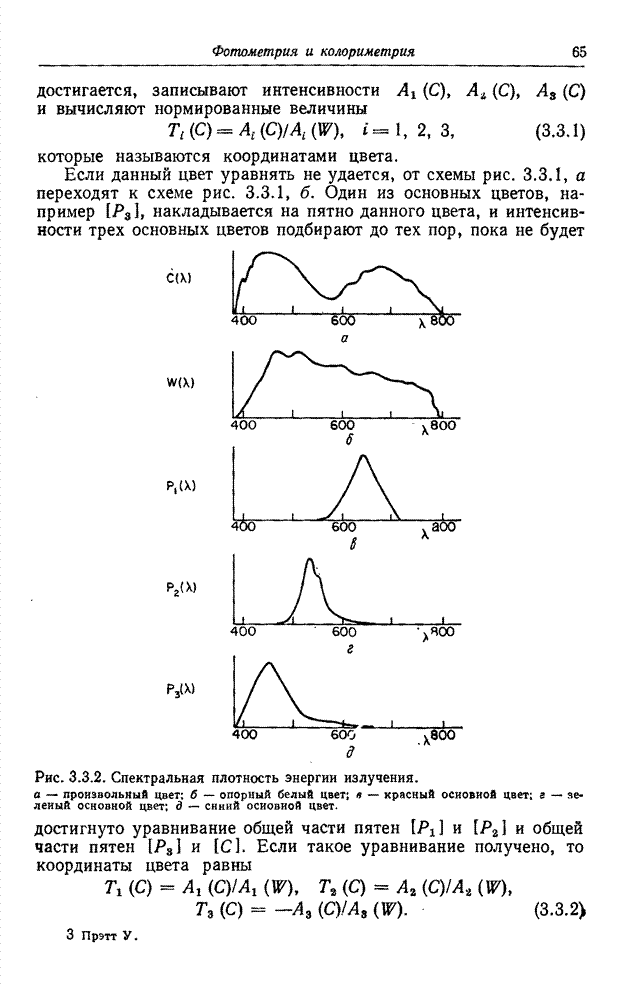
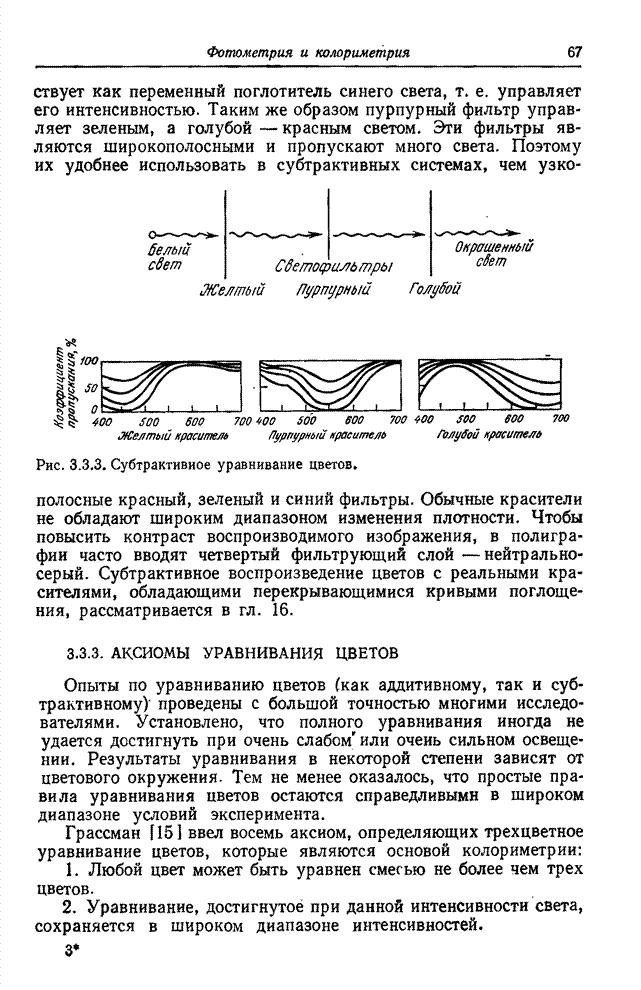
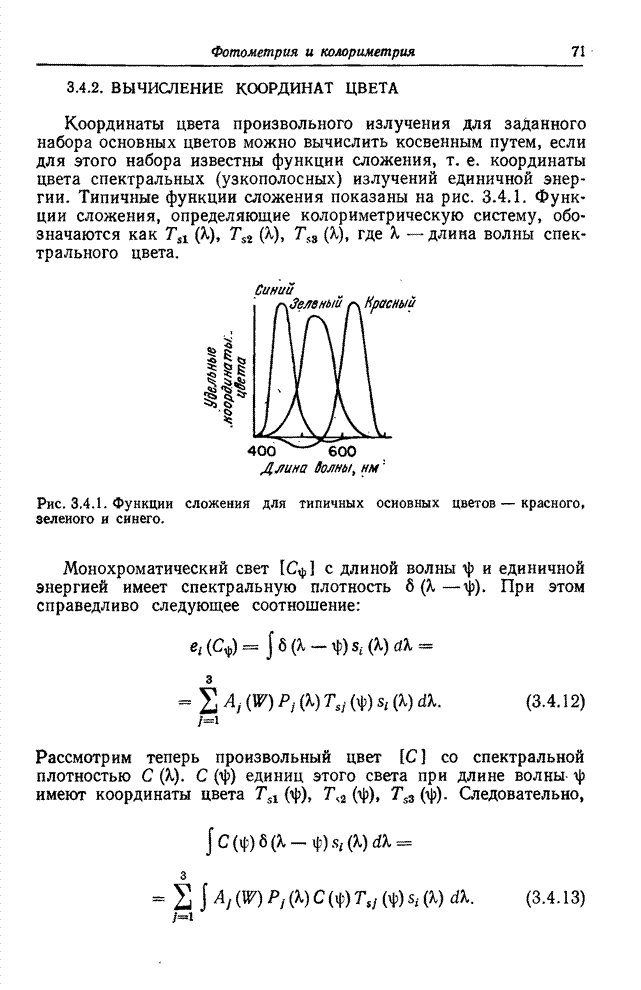
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
В
работах [24-26] предложено ортогональное преобразование, названное наклонным
(slant transform). Это преобразование обладает следующими особенностями: 1) среди
базисных векторов имеется вектор с одинаковыми компонентами (постоянный
базисный вектор); 2) наклонный базисный вектор монотонно убывает от
максимального до минимального значения скачками постоянной величины; 3) матрица
преобразования обладает секвентным свойством; 4) существует быстрый алгоритм
преобразования; 5) обеспечивается высокая степень концентрации энергии
изображения. При длине вектора ![]() наклонное преобразование совпадает с преобразованием Адамара второго порядка. Таким образом,
наклонное преобразование совпадает с преобразованием Адамара второго порядка. Таким образом,
![]() . (10.7.1)
. (10.7.1)
Матрица наклонного преобразования четвертого порядка формируется по следующему правилу:
 , (10.7.2а)
, (10.7.2а)
или
 , (10.7.2б)
, (10.7.2б)
где
![]() и
и ![]() - действительные
коэффициенты, которые следует выбирать так, чтобы матрица
- действительные
коэффициенты, которые следует выбирать так, чтобы матрица ![]() была ортогональной, а
величина скачков при изменении второго наклонного базисного вектора -
постоянной. Из условия постоянства величины скачка можно найти, что
была ортогональной, а
величина скачков при изменении второго наклонного базисного вектора -
постоянной. Из условия постоянства величины скачка можно найти, что ![]() . Из условия
ортогональности
. Из условия
ортогональности ![]() следует,
что
следует,
что ![]() .
Таким образом, матрица наклонного преобразования четвертого порядка имеет вид
.
Таким образом, матрица наклонного преобразования четвертого порядка имеет вид
 . (10.7.3)
. (10.7.3)
Нетрудно
проверить, что матрица ![]() является ортонормальной. Кроме того,
она обладает секвентным свойством: число изменений знака возрастает с
увеличением номера строки от 0 до 3.
является ортонормальной. Кроме того,
она обладает секвентным свойством: число изменений знака возрастает с
увеличением номера строки от 0 до 3.
Матрица
наклонного преобразования при ![]() имеет вид
имеет вид
 . (10.7.4)
. (10.7.4)
Как
и при построении матрицы ![]() , коэффициенты
, коэффициенты ![]() и
и ![]() подбираются так, чтобы
наклонный базисный вектор убывал равномерными скачками, все строки матрицы
являлись ортонормальными векторами, а сама матрица обладала секвентным
свойством.
подбираются так, чтобы
наклонный базисный вектор убывал равномерными скачками, все строки матрицы
являлись ортонормальными векторами, а сама матрица обладала секвентным
свойством.
Обобщая
соотношение (10.7.4), можно получить рекуррентную формулу, связывающую матрицы
наклонного преобразования ![]() -го и
-го и ![]() -го порядка:
-го порядка:
 , (10.7.5)
, (10.7.5)
где
![]() -
единичная матрица
-
единичная матрица ![]() -го порядка. Постоянные
-го порядка. Постоянные ![]() и
и ![]() можно найти из
рекуррентных соотношений [26]
можно найти из
рекуррентных соотношений [26]
![]() , (10.7.6а)
, (10.7.6а)
![]() , (10.7.6б)
, (10.7.6б)
![]() (10.7.6в)
(10.7.6в)
или по формулам
 , (10.7.7а)
, (10.7.7а)
 . (10.7.7б)
. (10.7.7б)
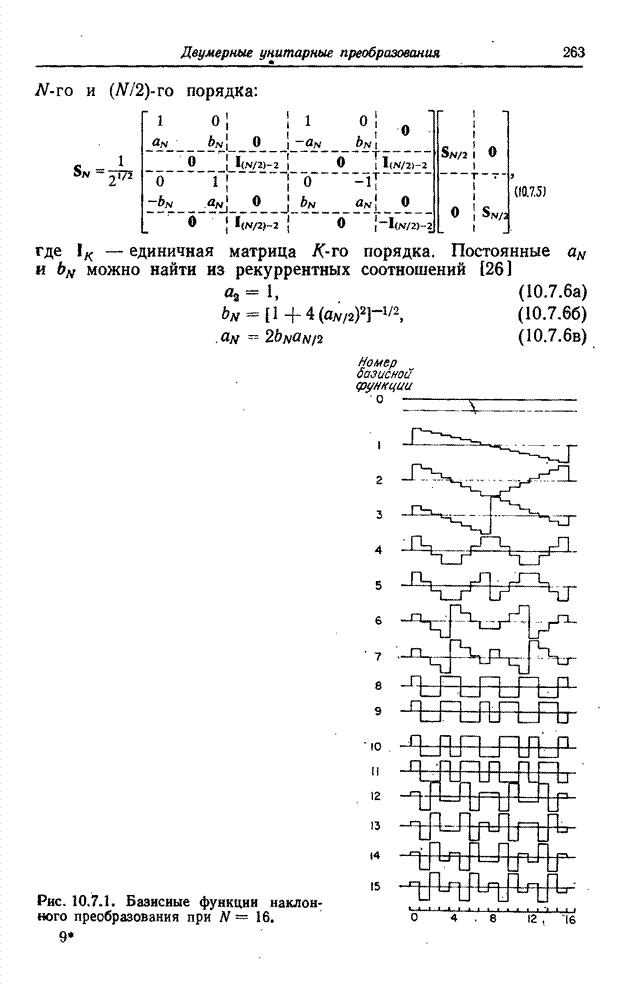
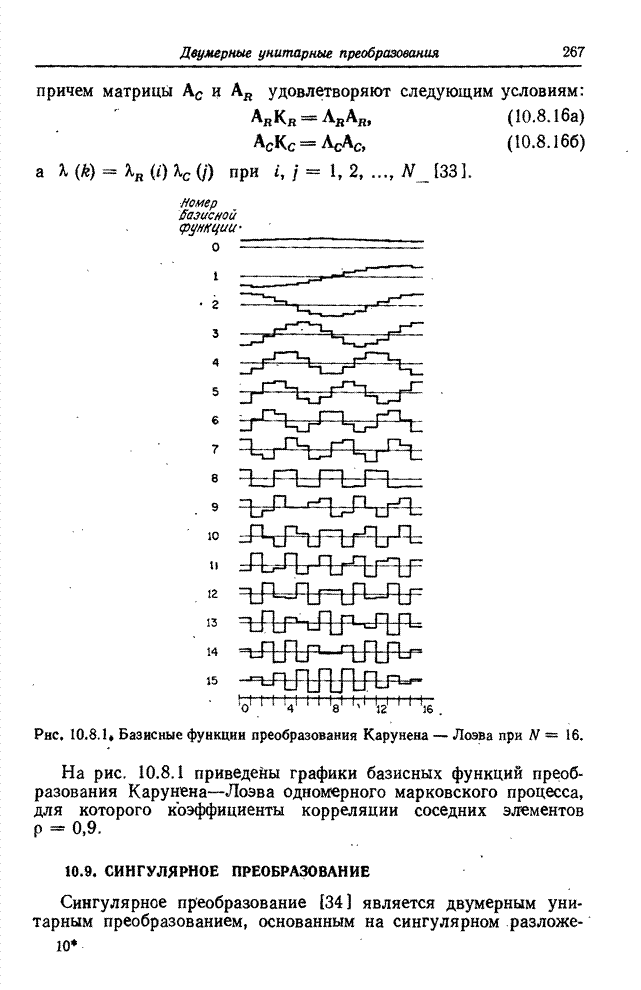
На
рис. 10.7.1 приведены графики базисных функций наклонного преобразования для ![]() . Пример спектра,
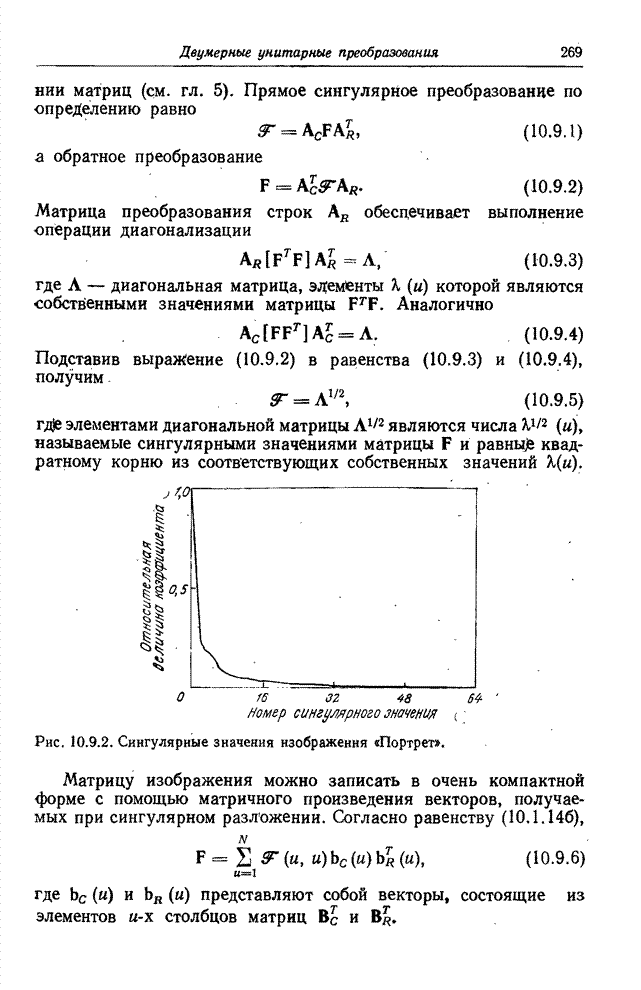
получаемого при таком преобразовании, показан на рис. 10.7.2.
. Пример спектра,
получаемого при таком преобразовании, показан на рис. 10.7.2.

Рис. 10.7.1. Базисные функции
наклонного преобразования при ![]() .
.

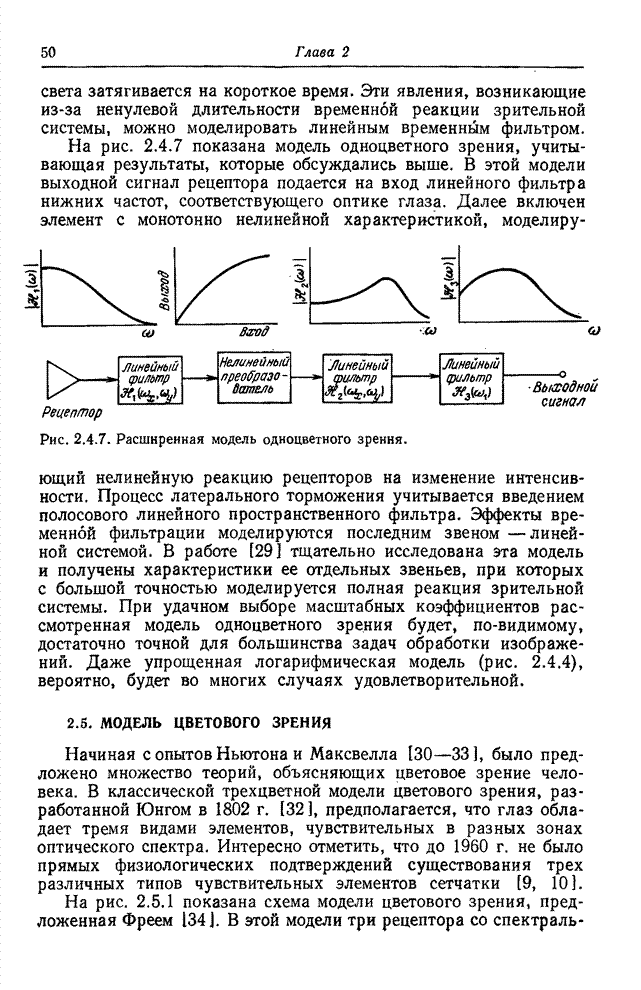
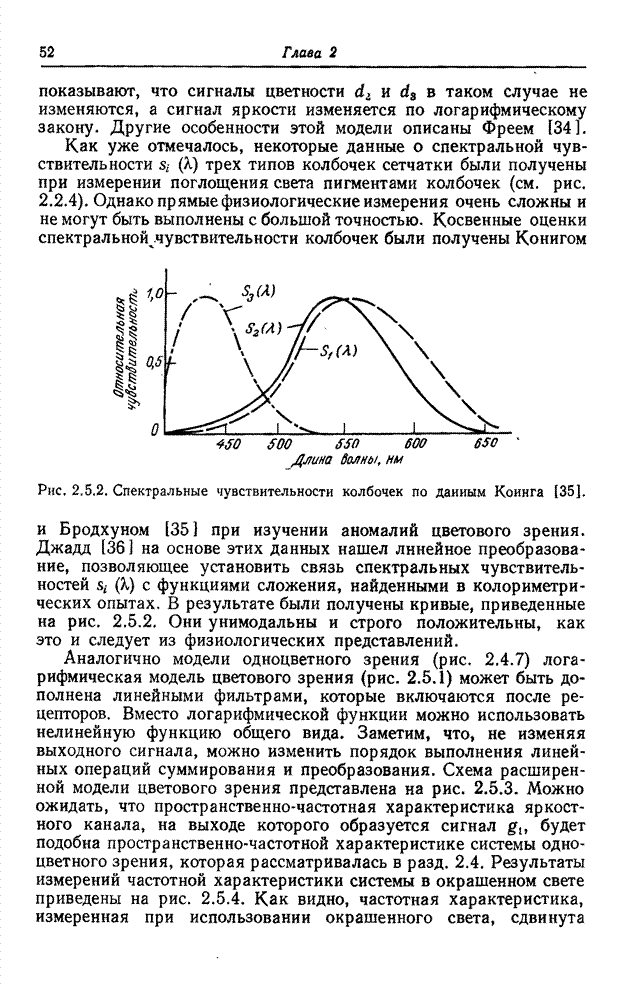
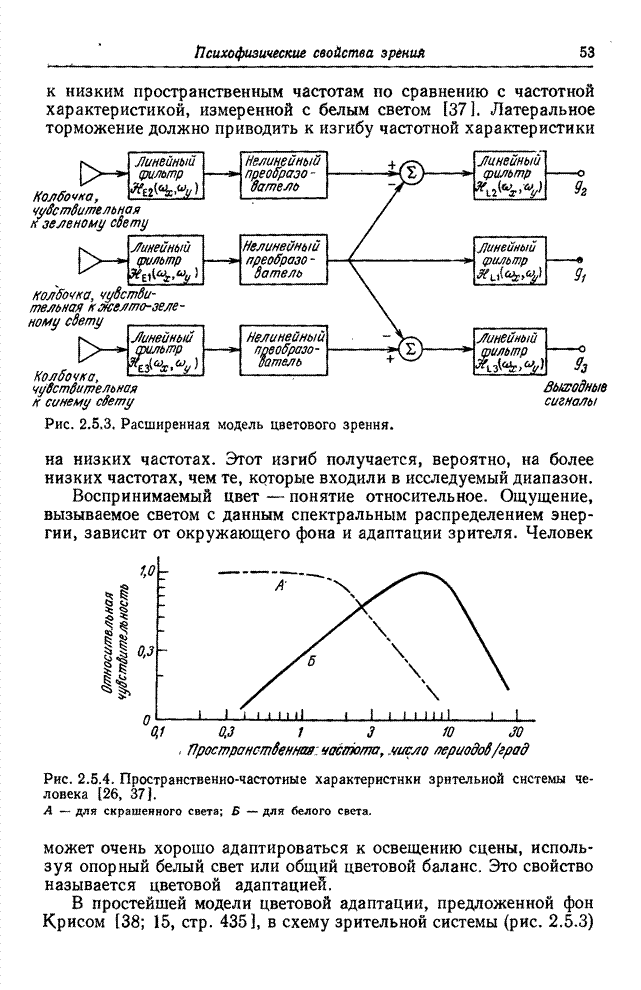
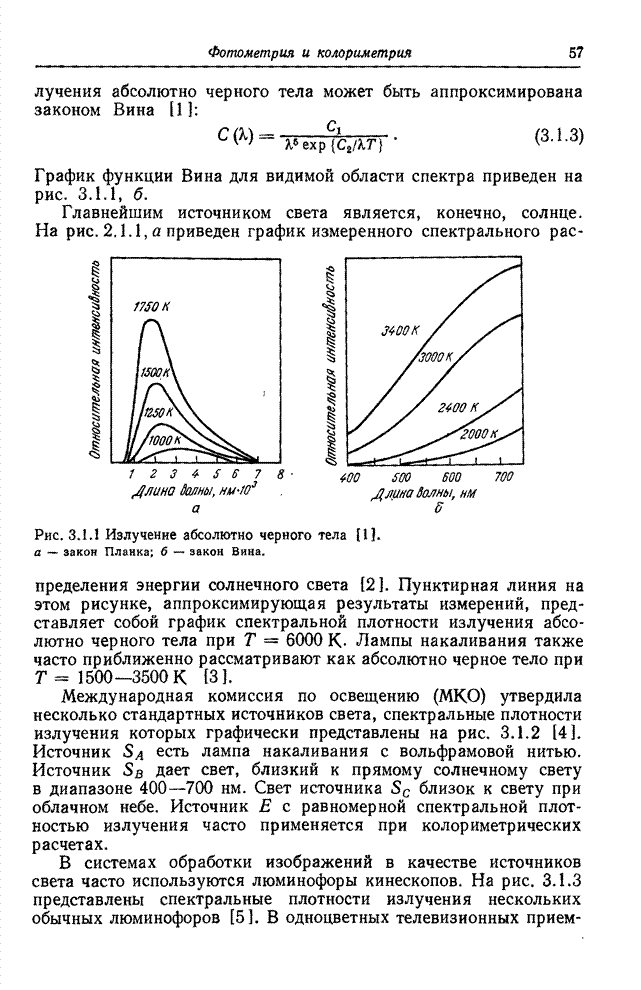
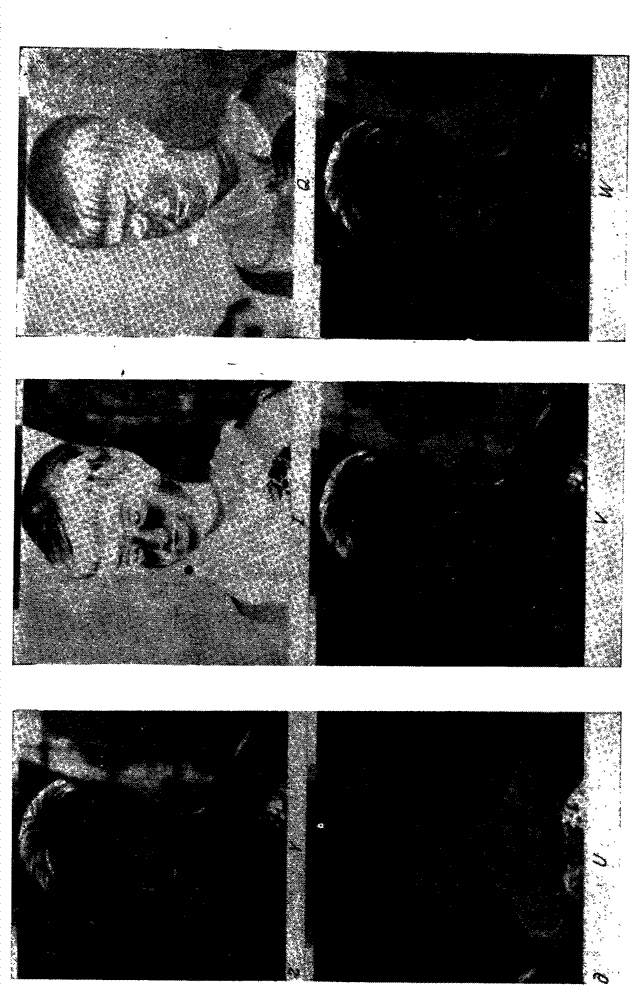
Рис. 10.7.2. Наклонное преобразование изображения «Портрет».
а - исходное изображение; б - результат преобразования в логарифмическом масштабе по оси амплитуд: в - результат преобразования с ограниченными наибольшими гармониками.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
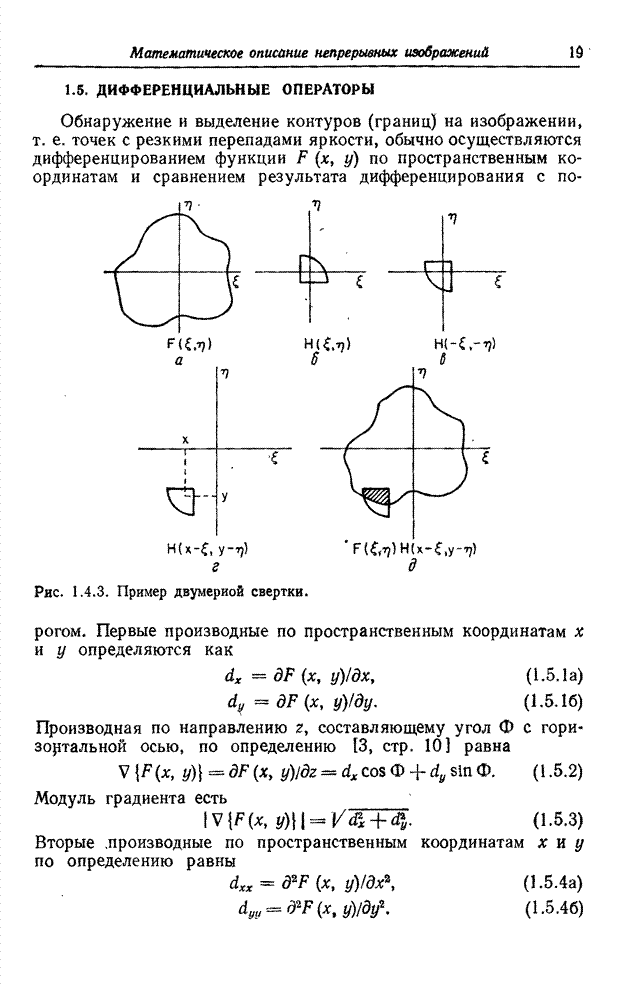
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
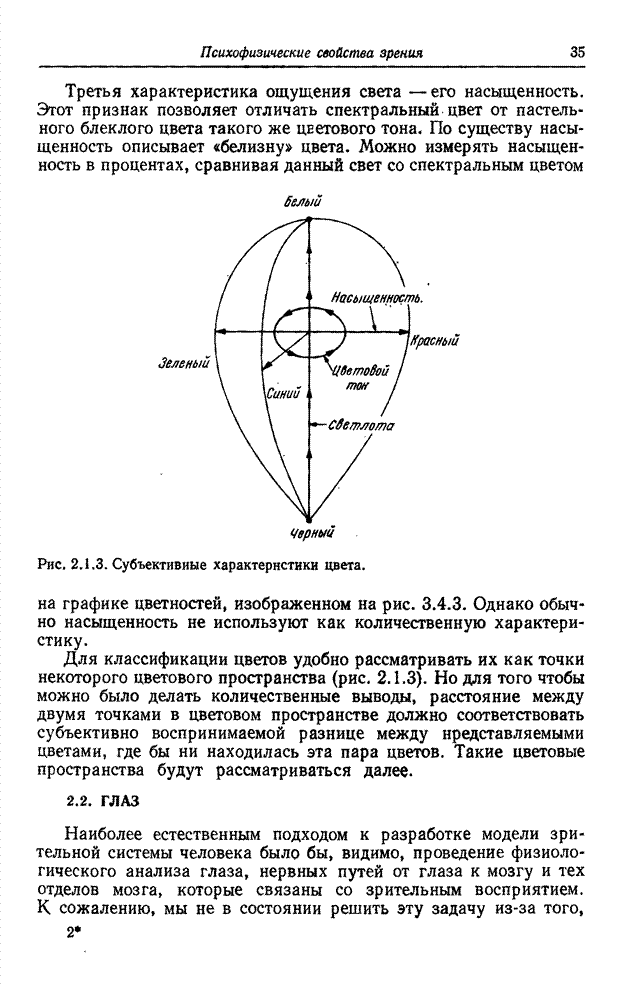
- 2.1. ВОСПРИЯТИЕ СВЕТА
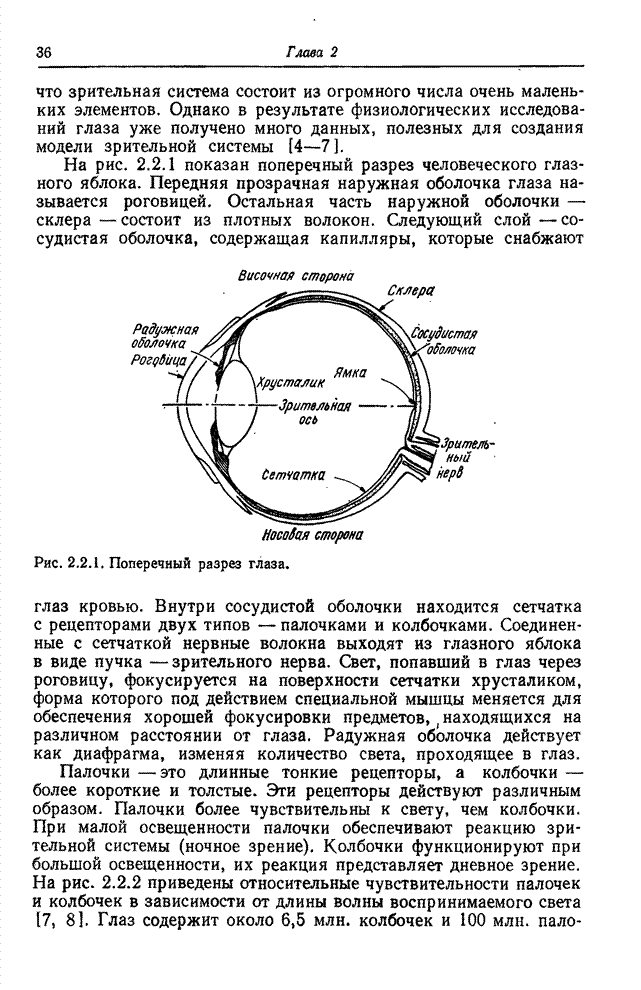
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
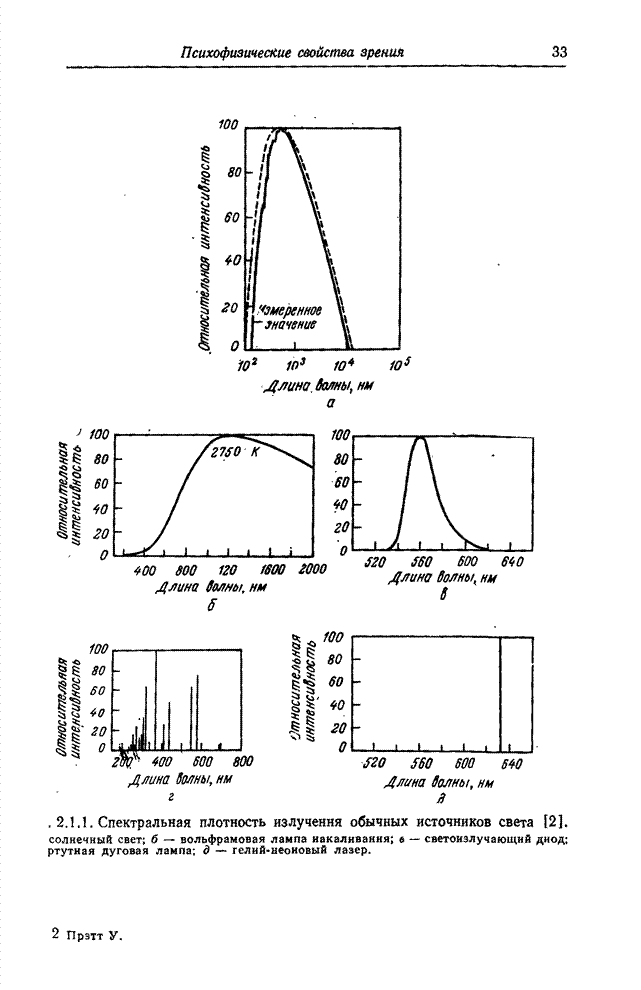
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
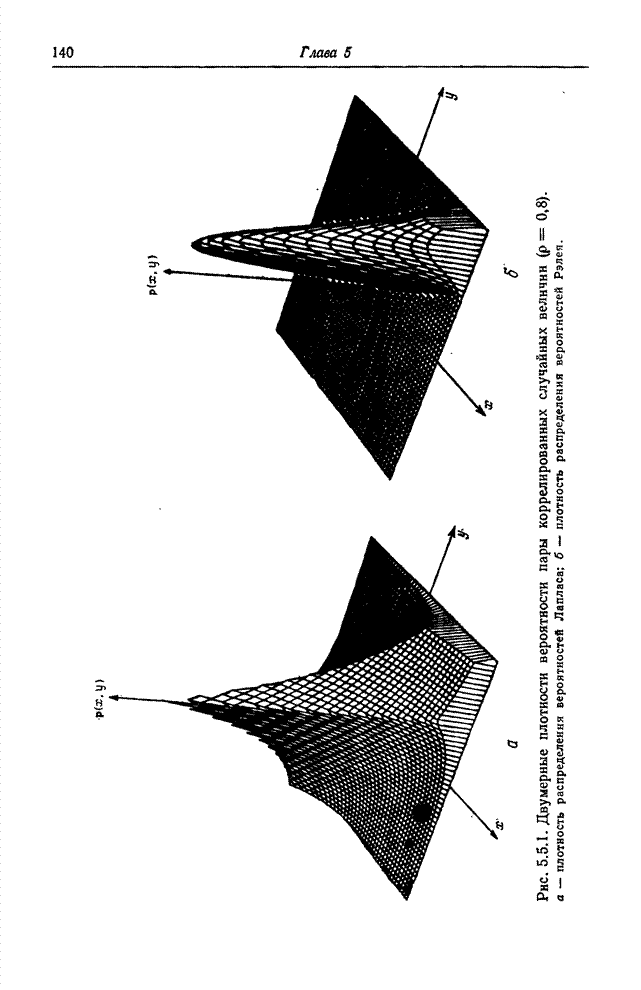
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
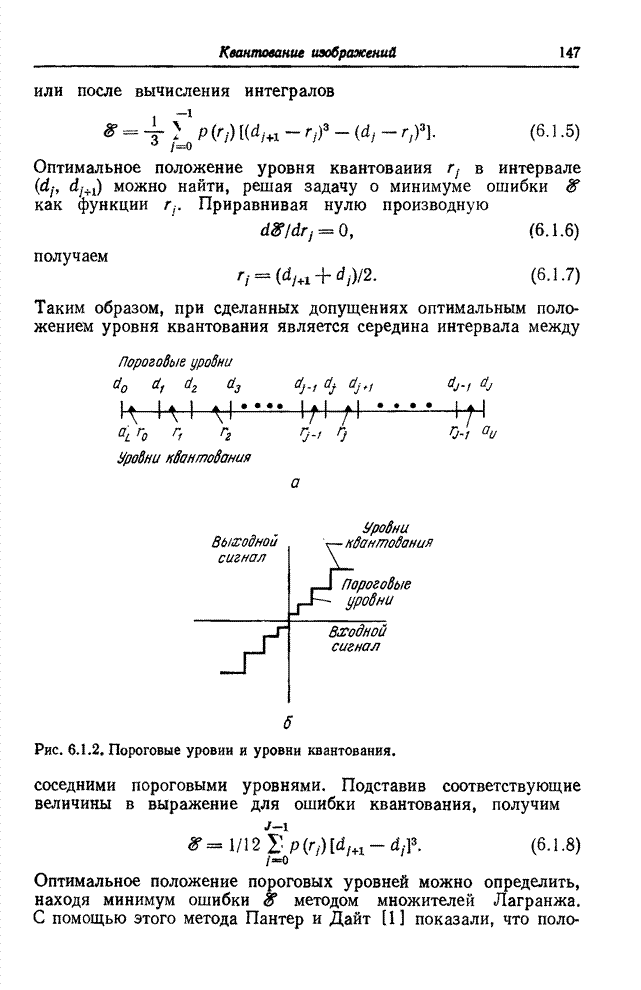
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
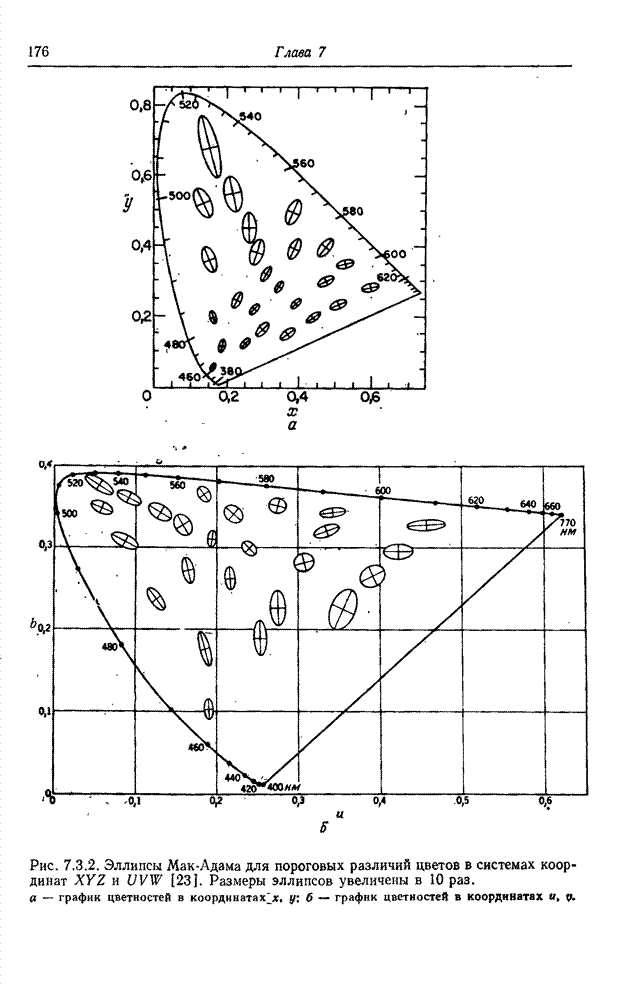
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
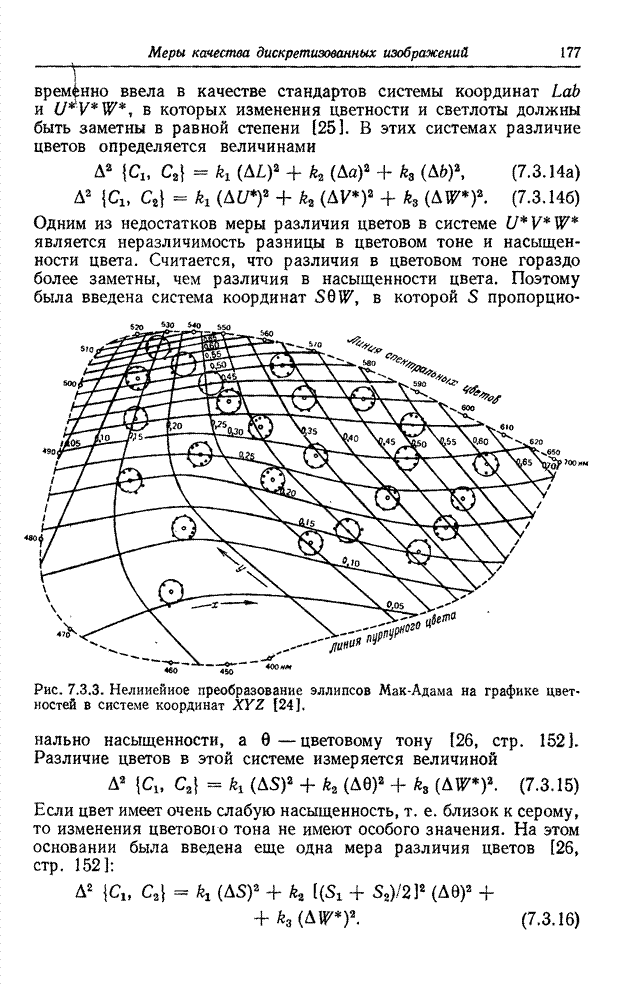
- 7.3.2. МЕТРИКИ ЦВЕТА
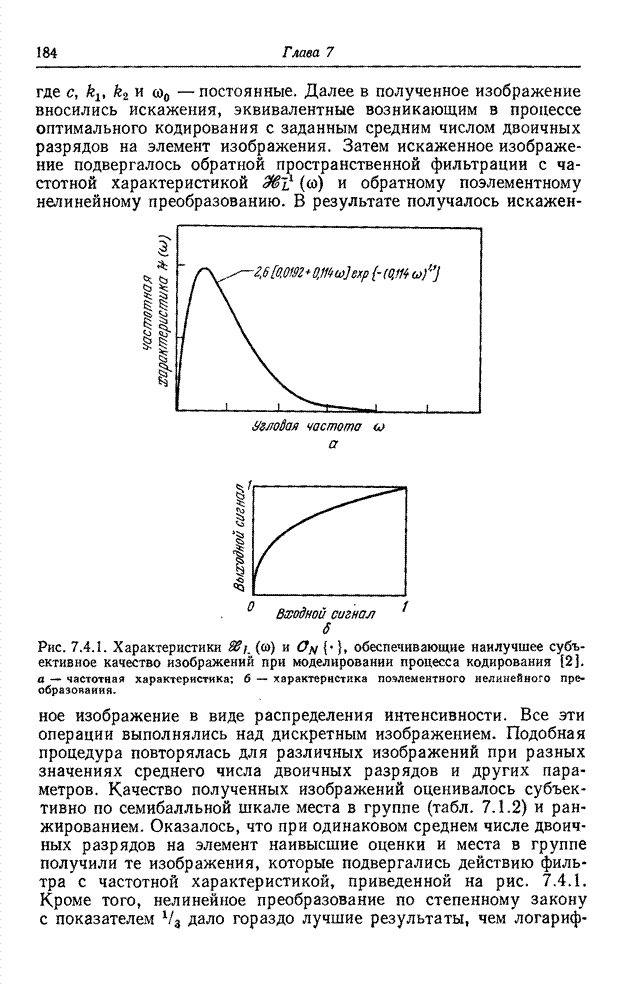
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
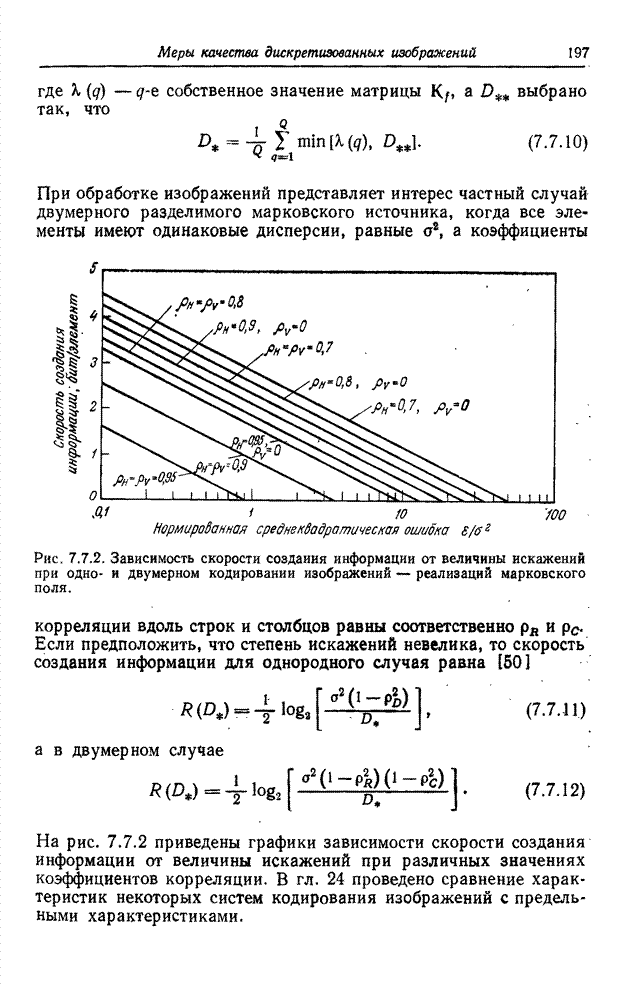
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА