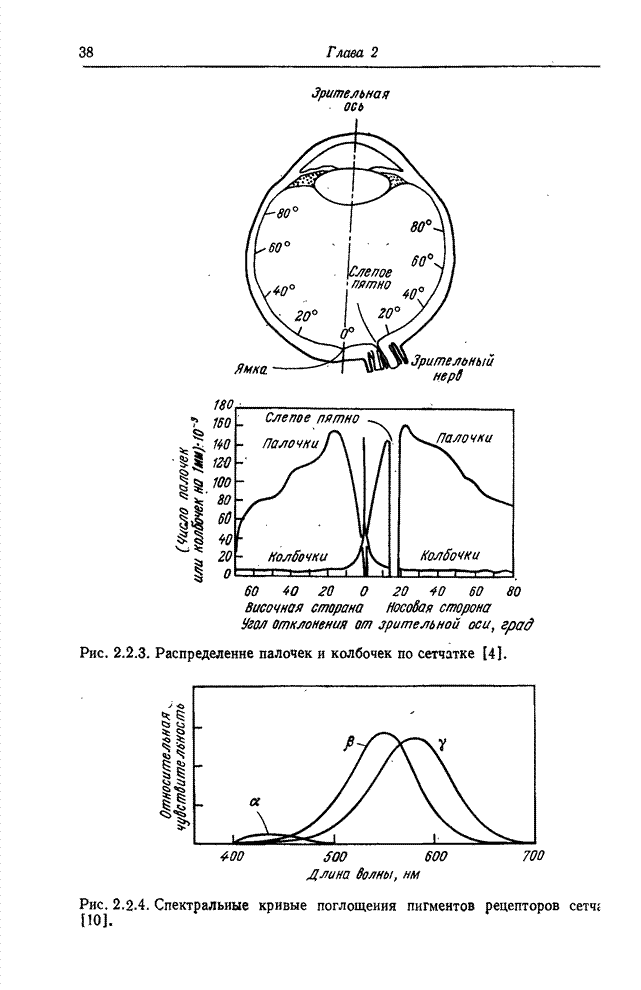
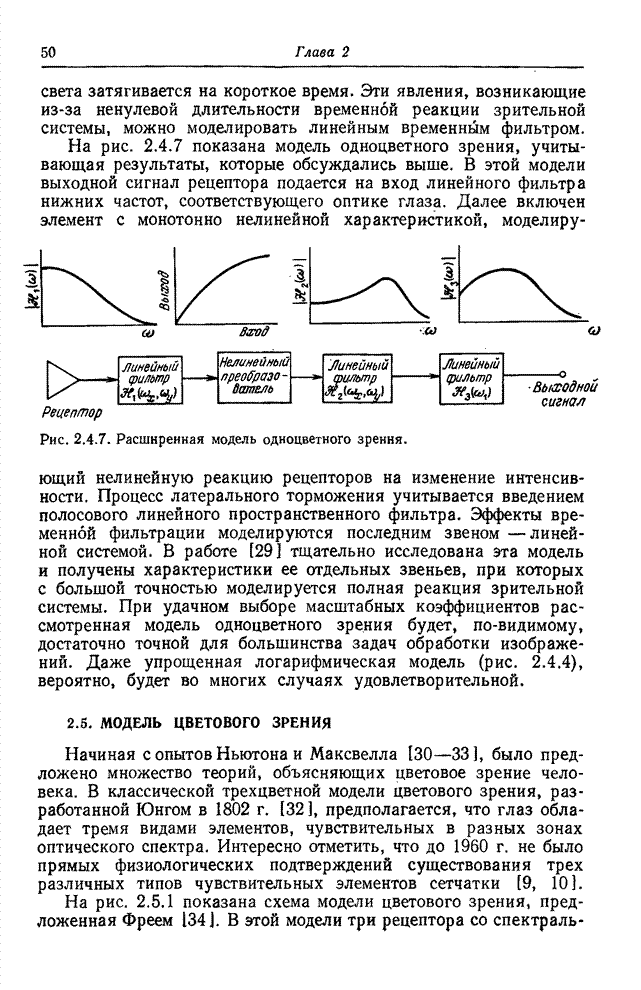
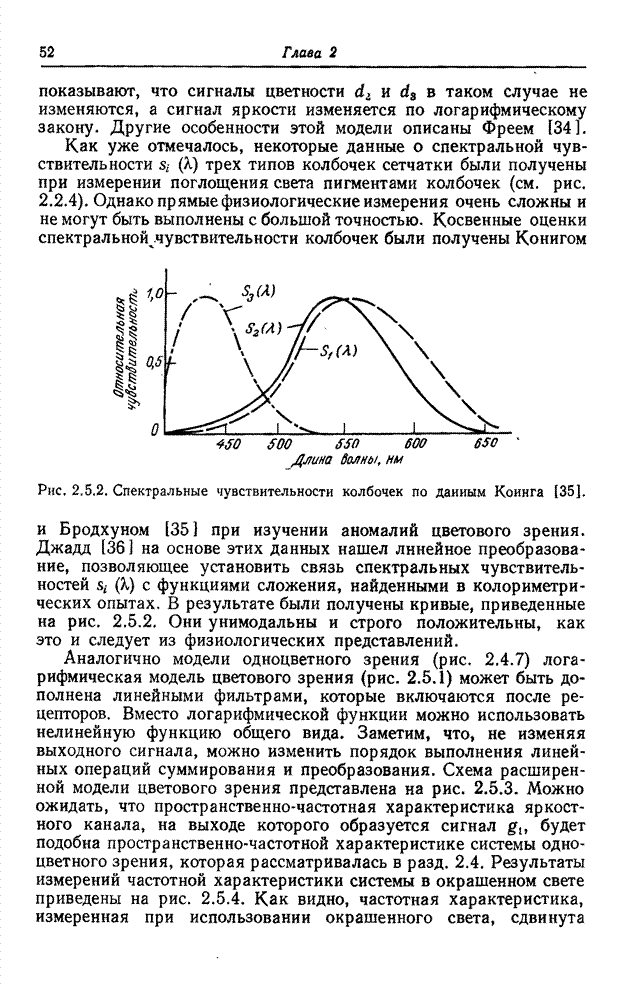
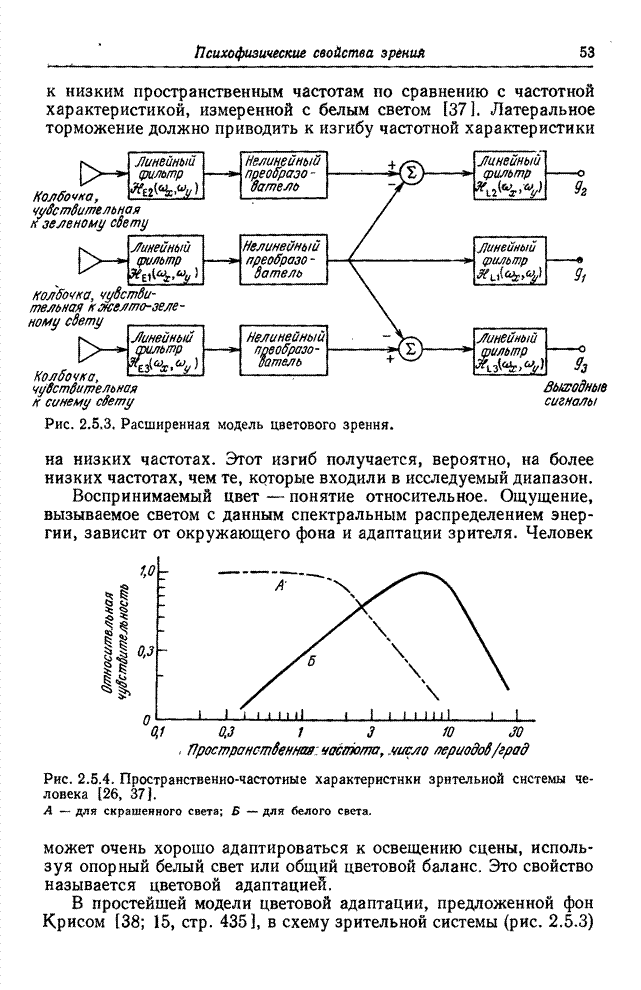
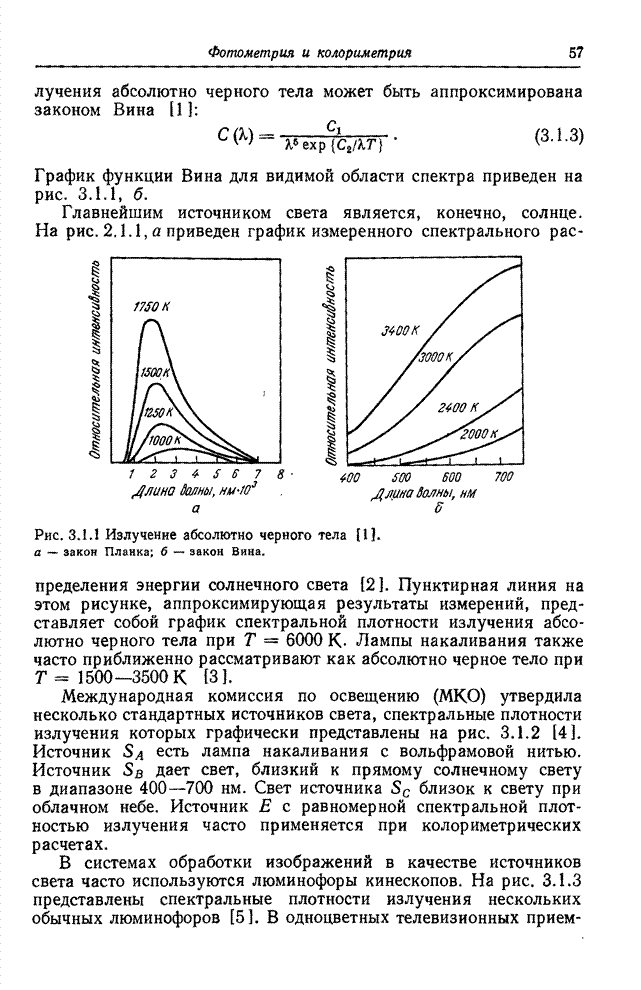
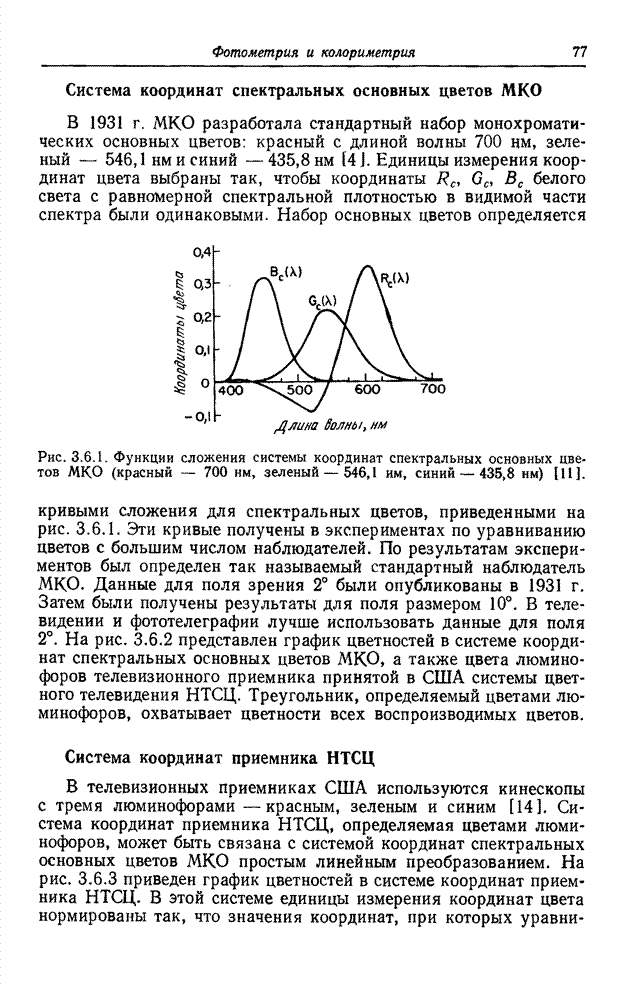
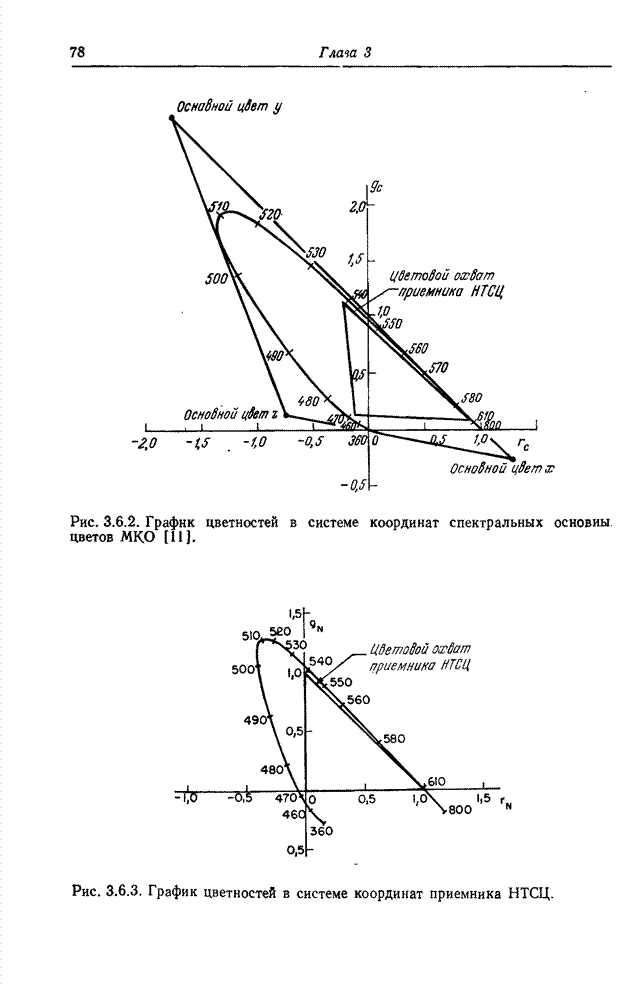
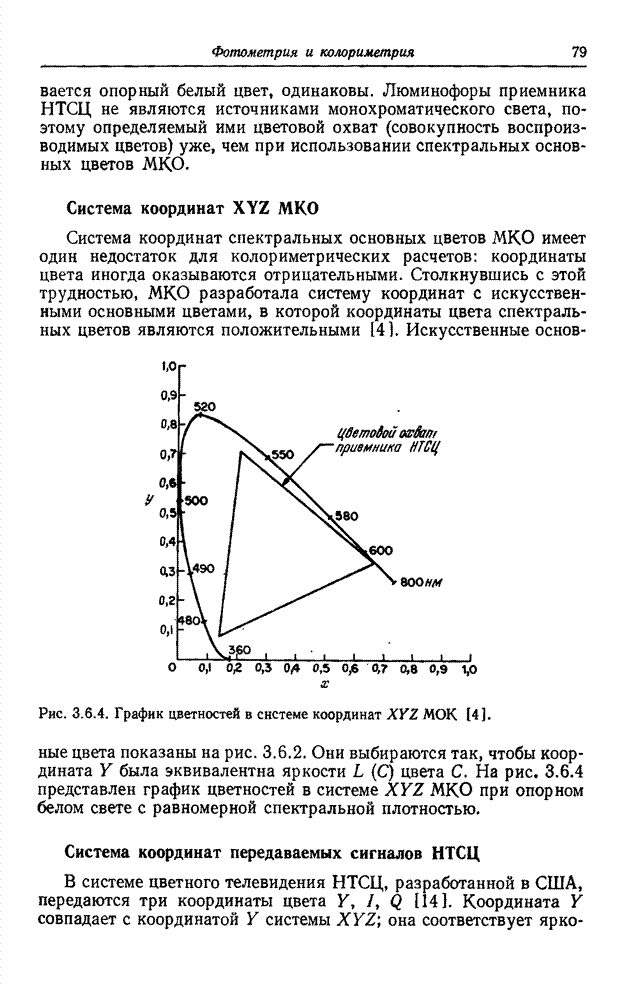
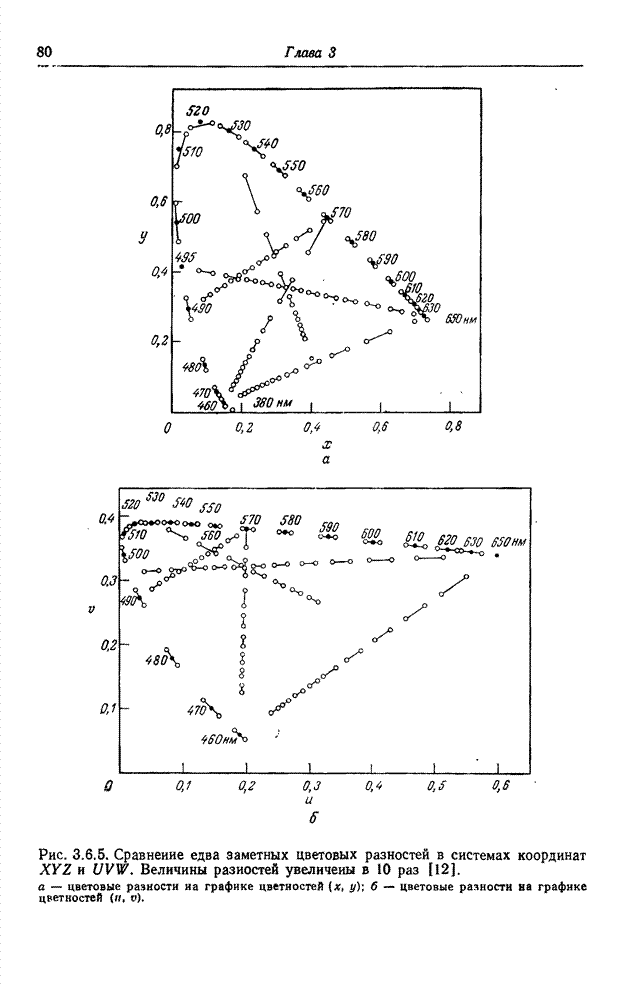
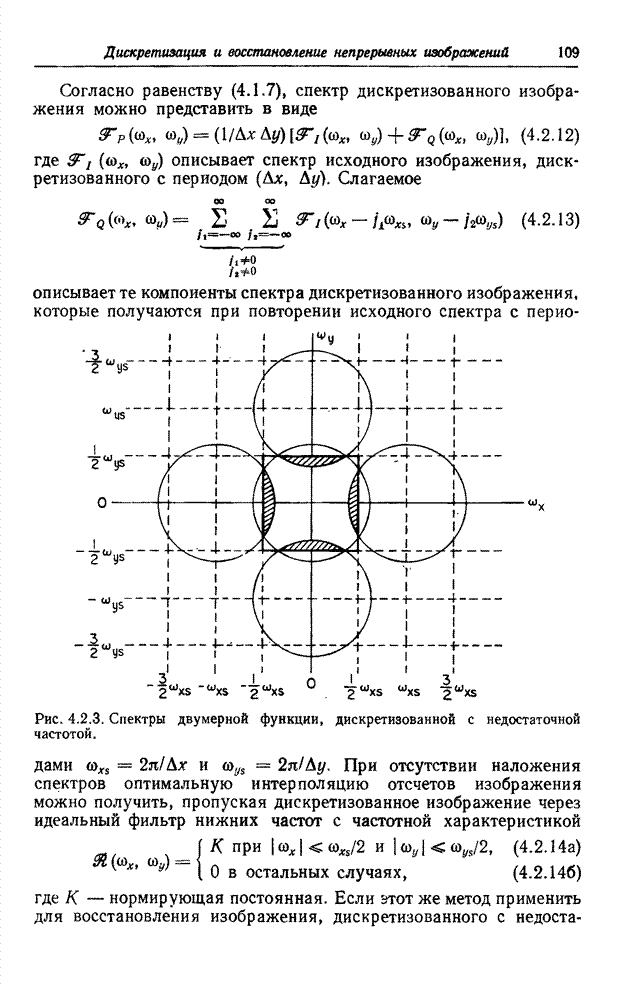
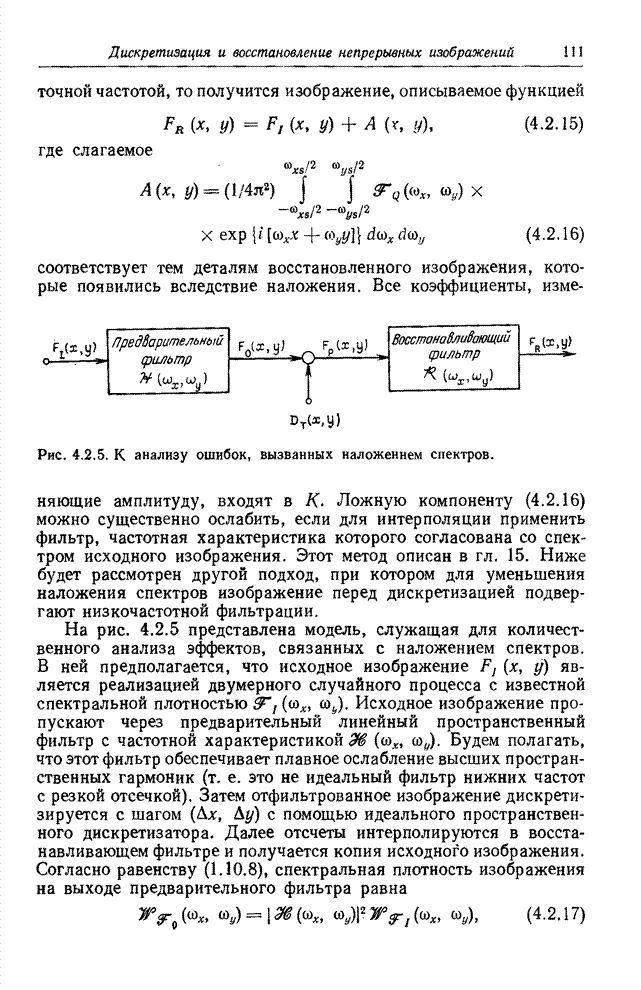
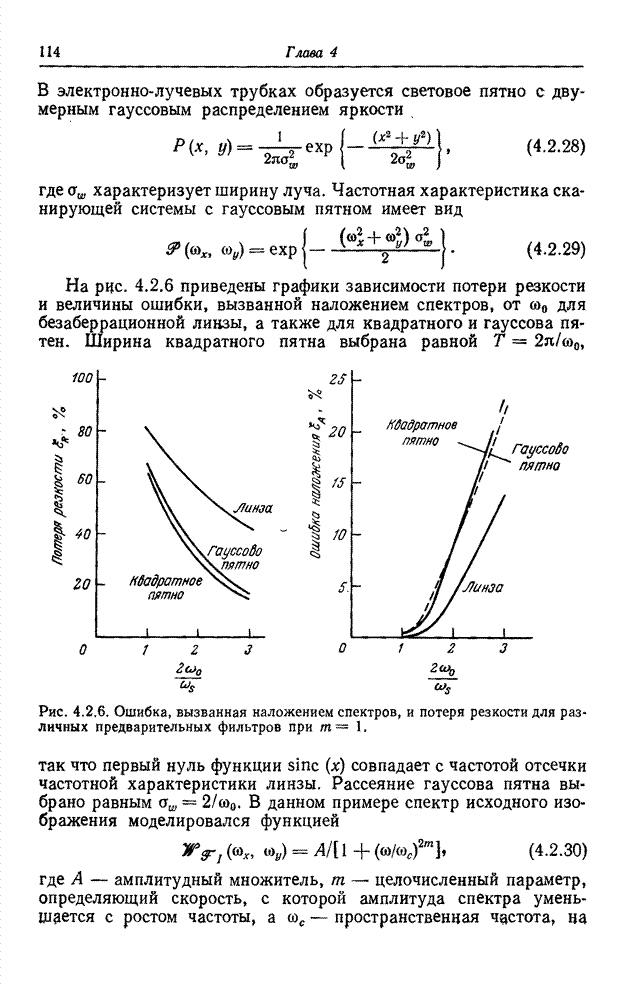
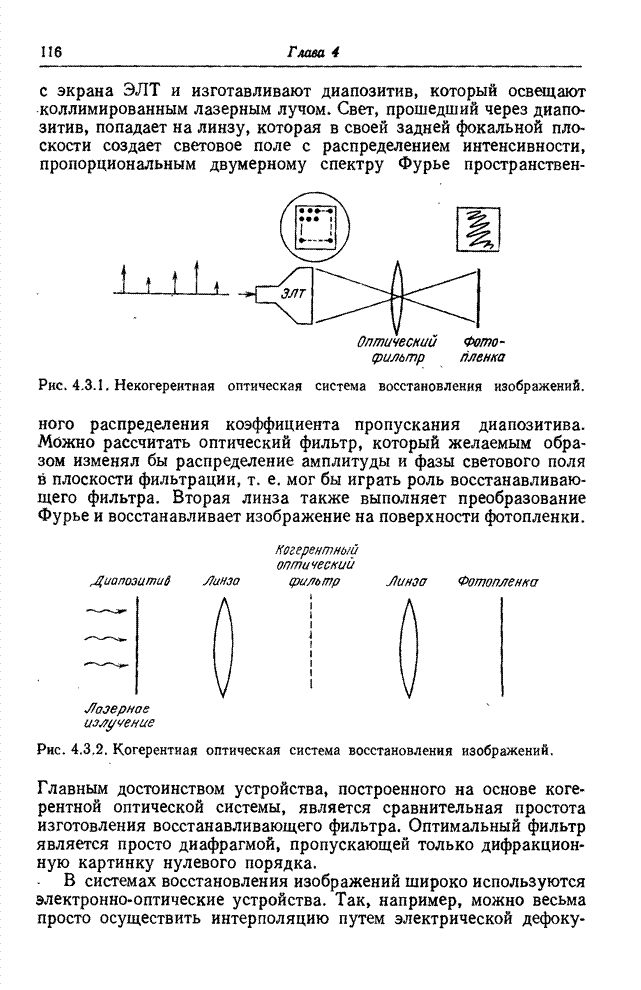
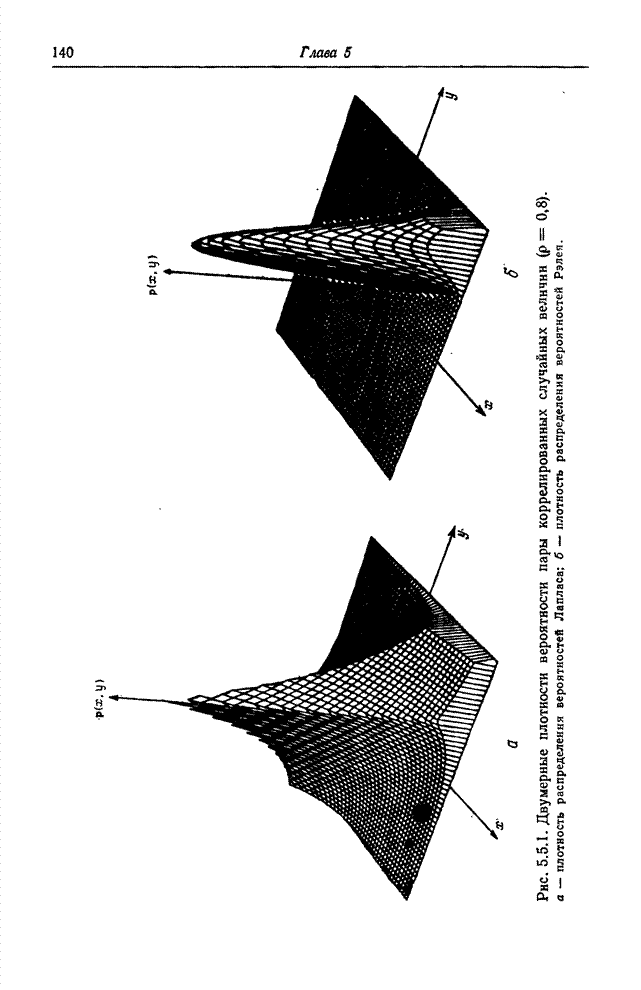
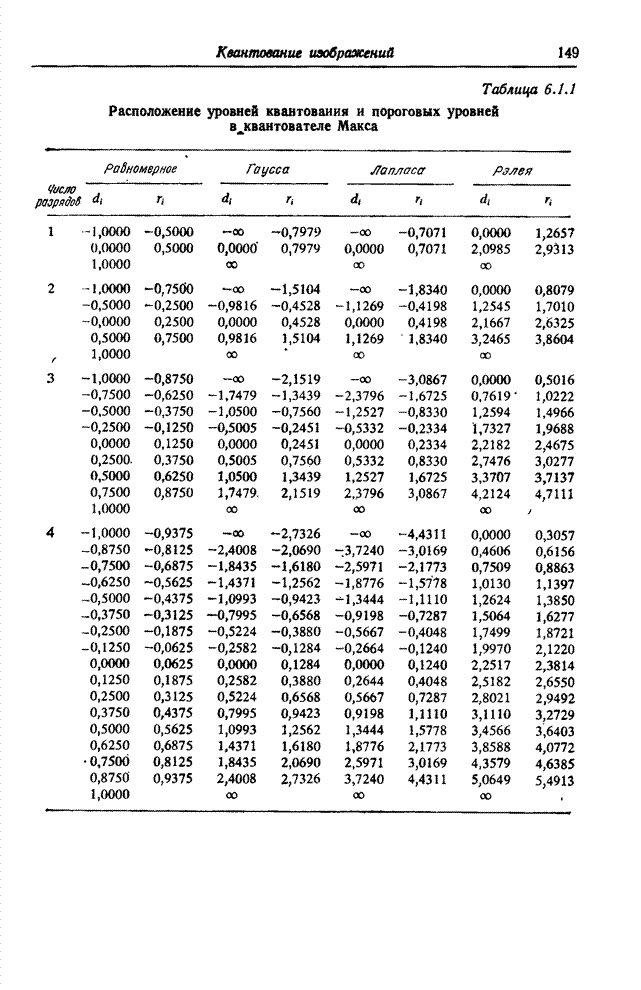
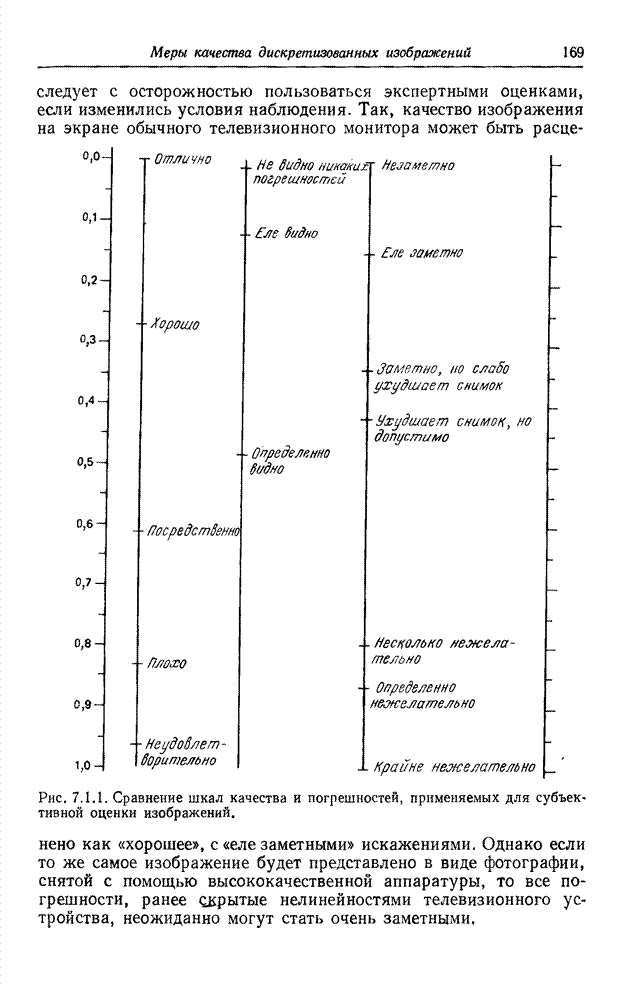
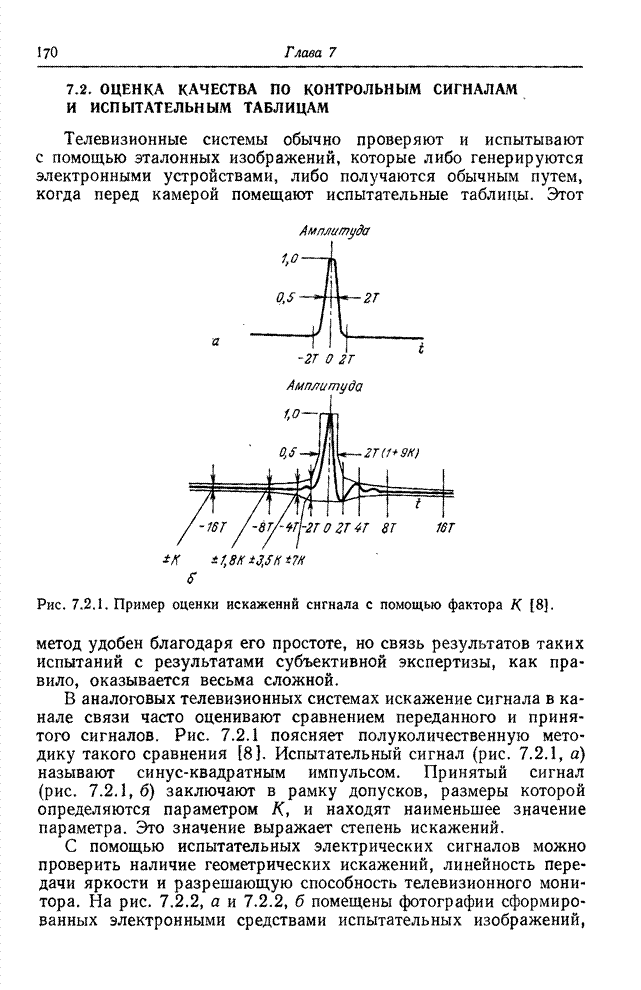
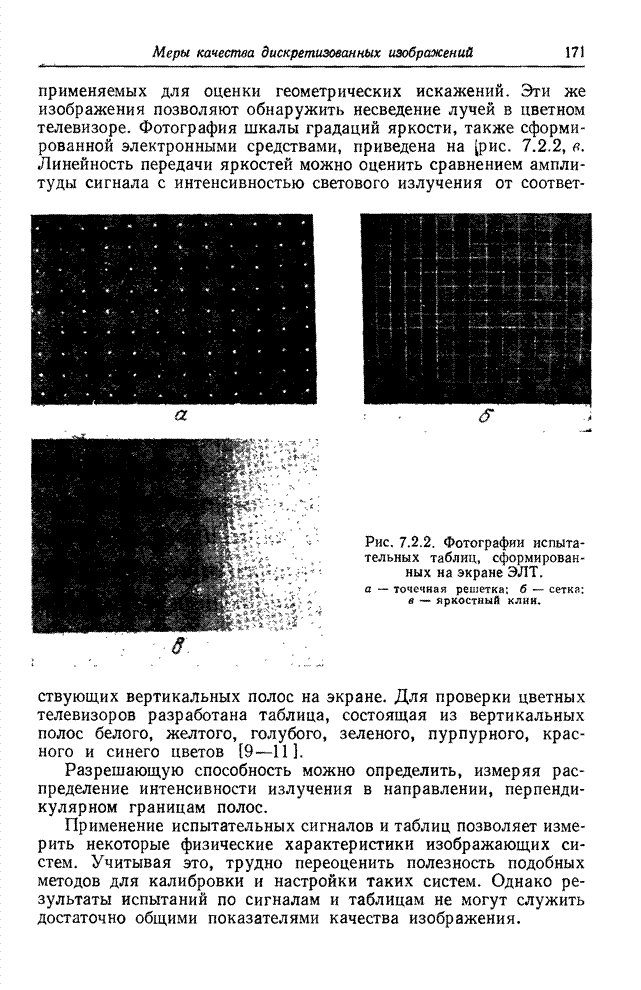
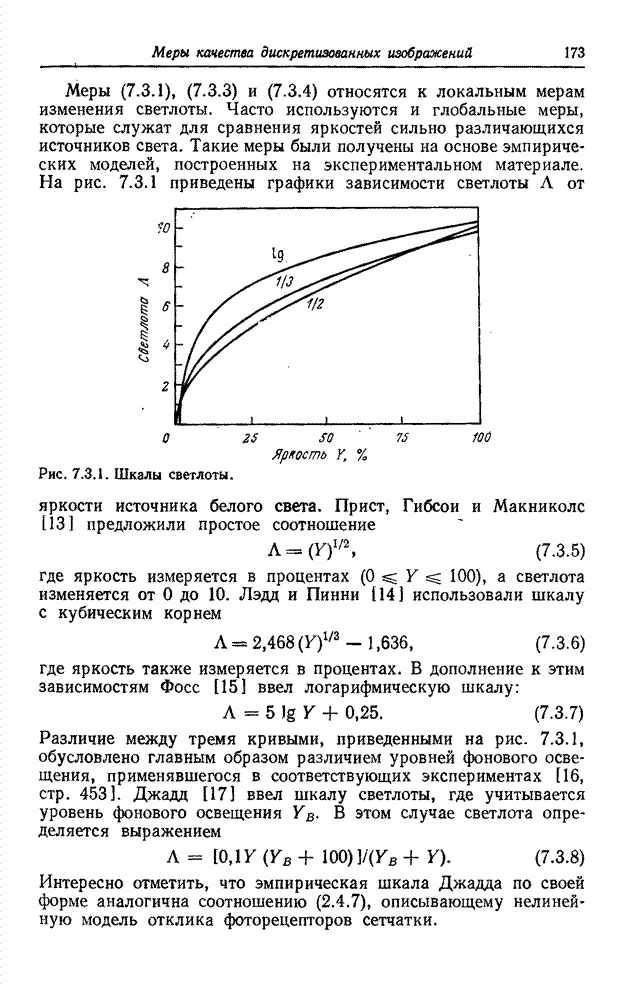
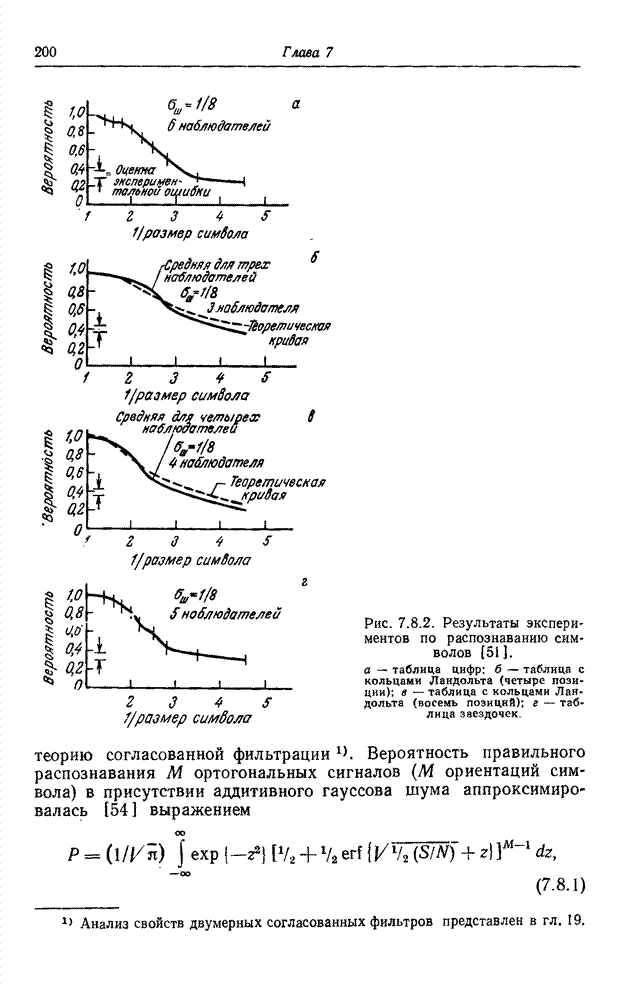
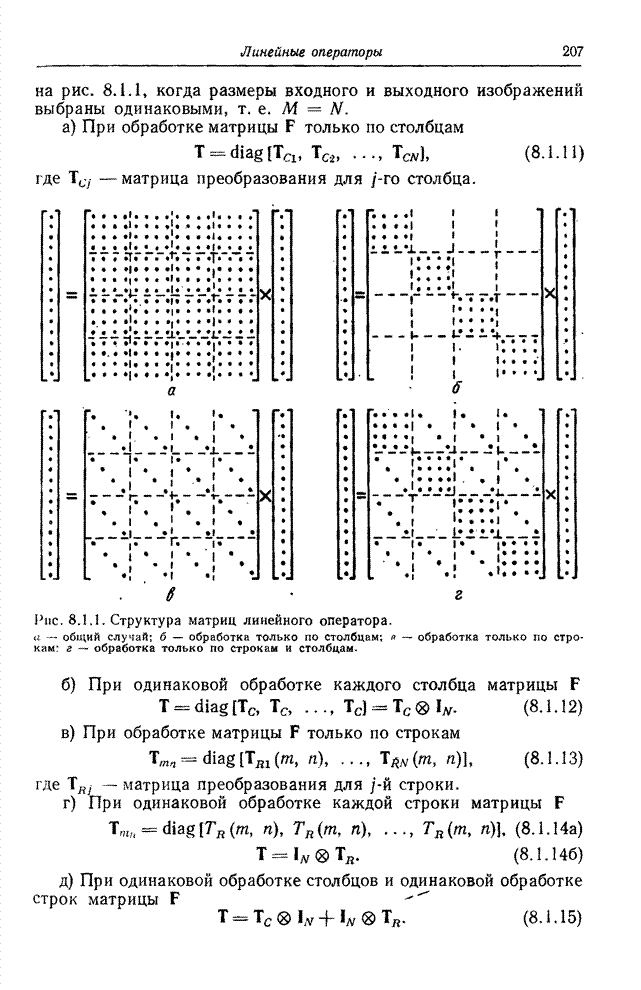
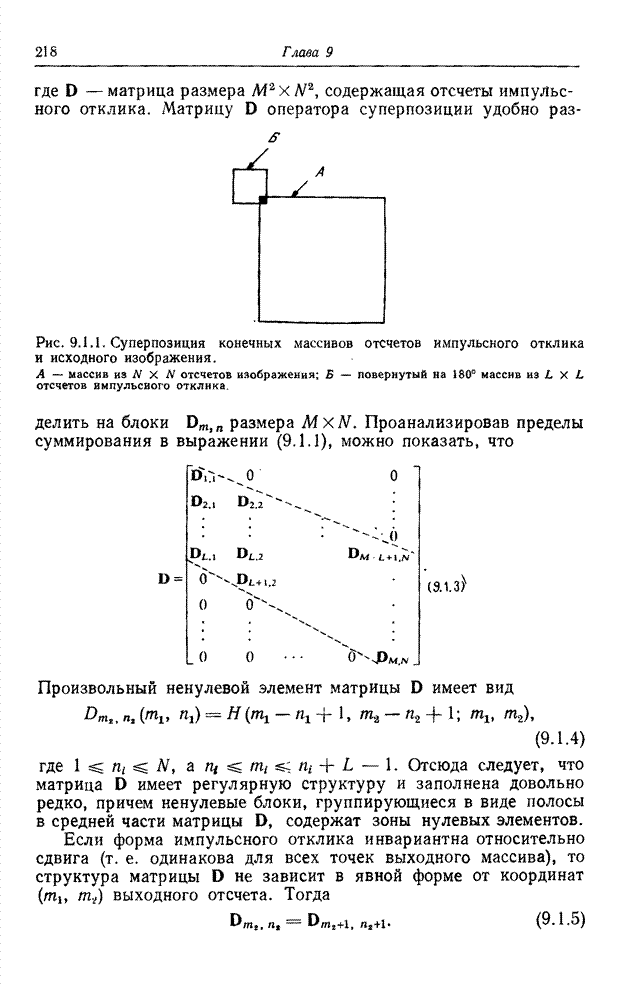
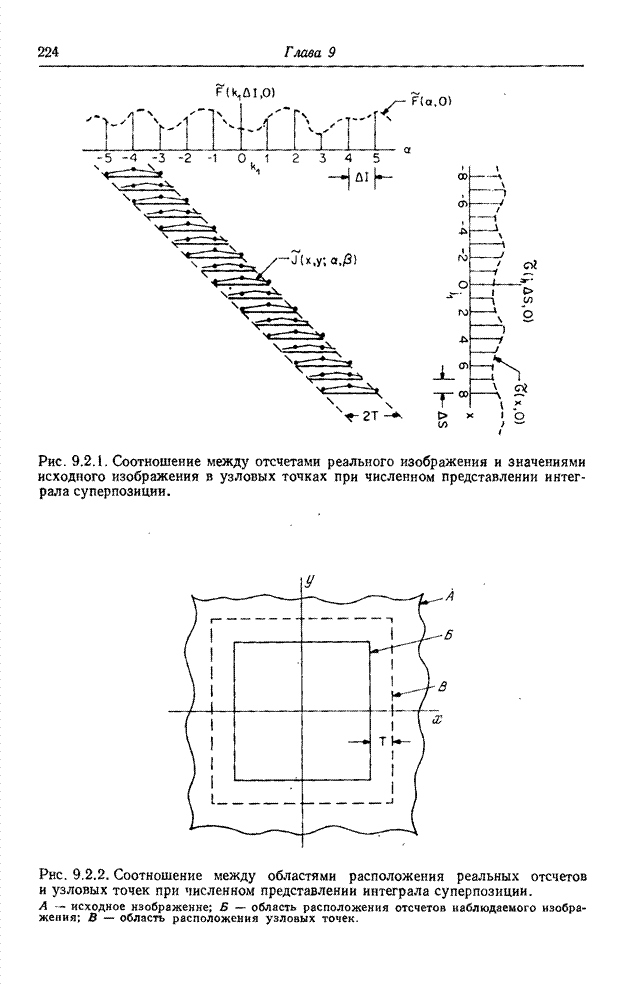
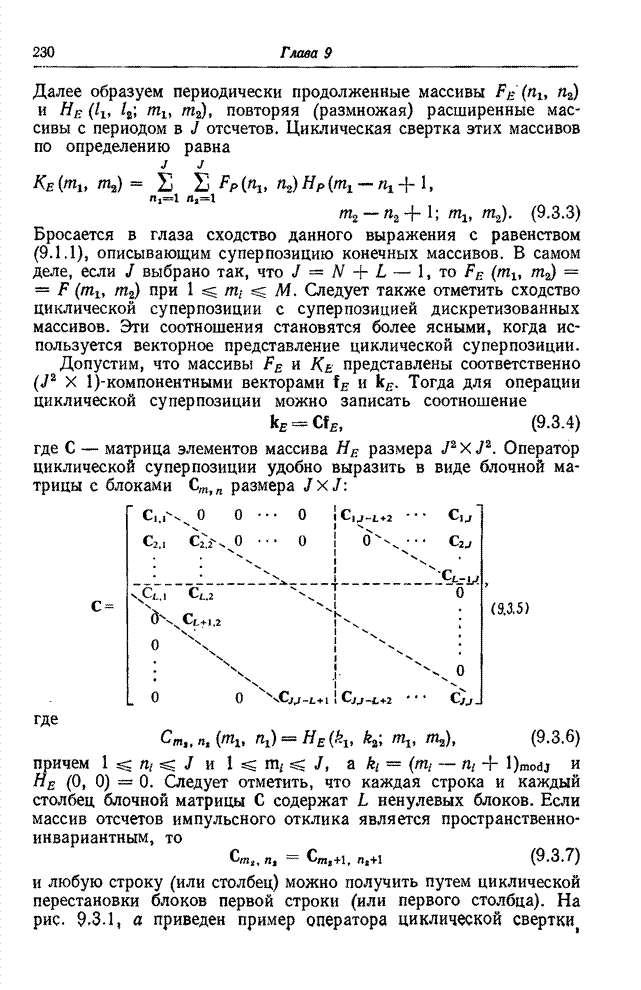
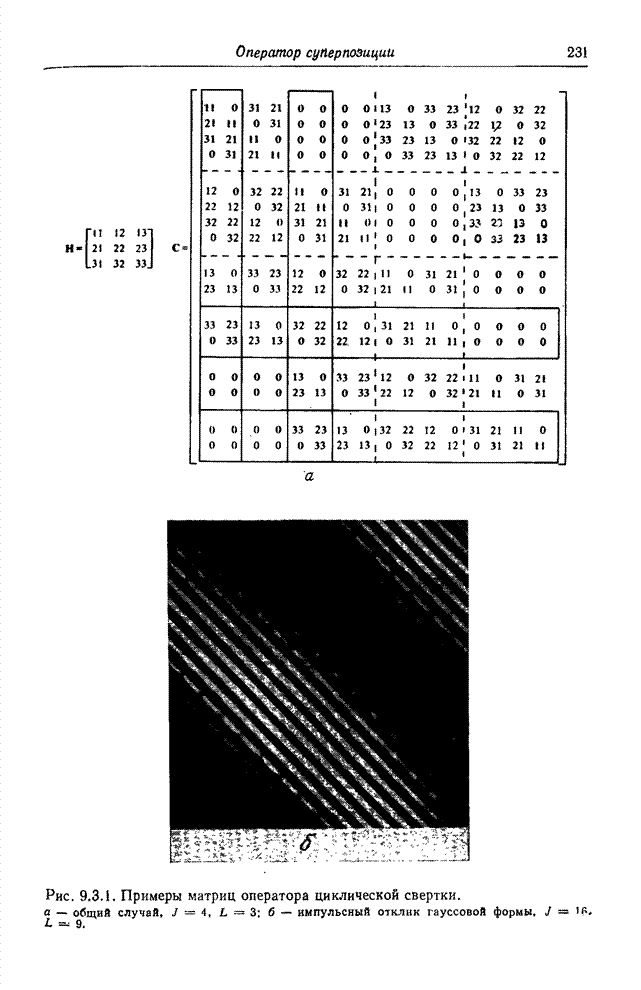
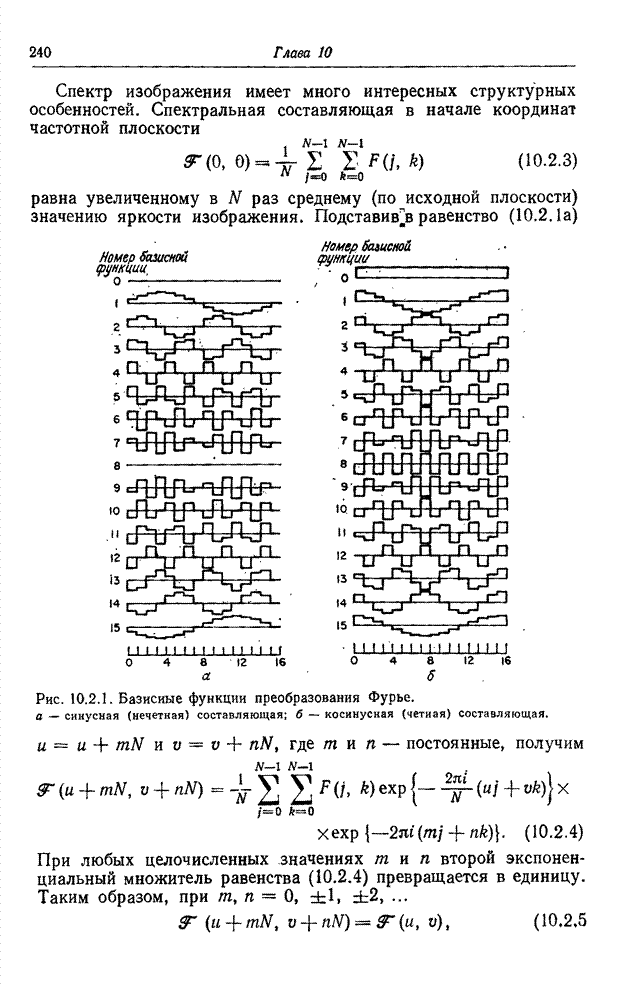
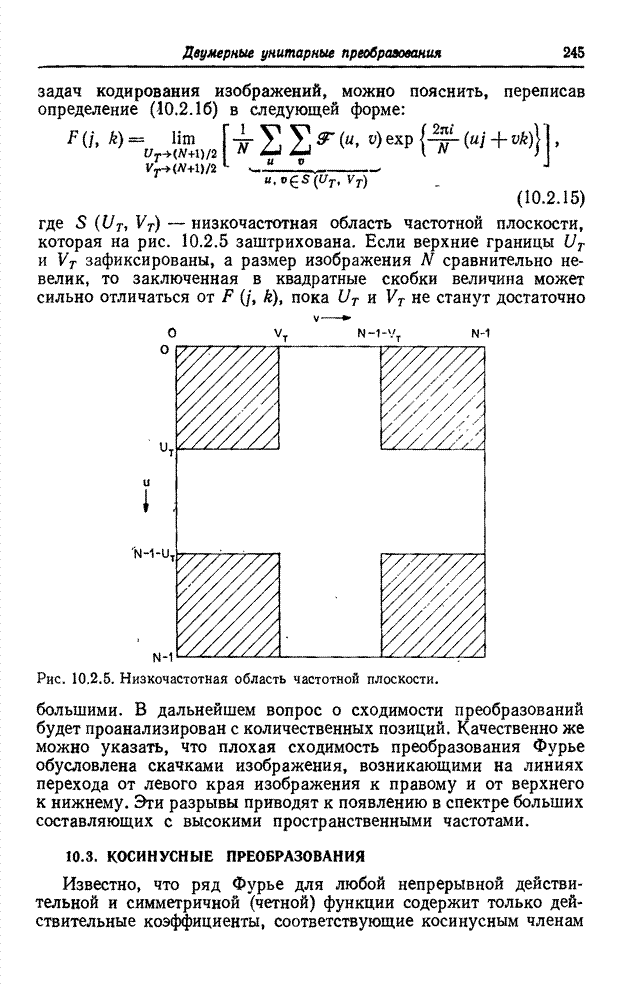
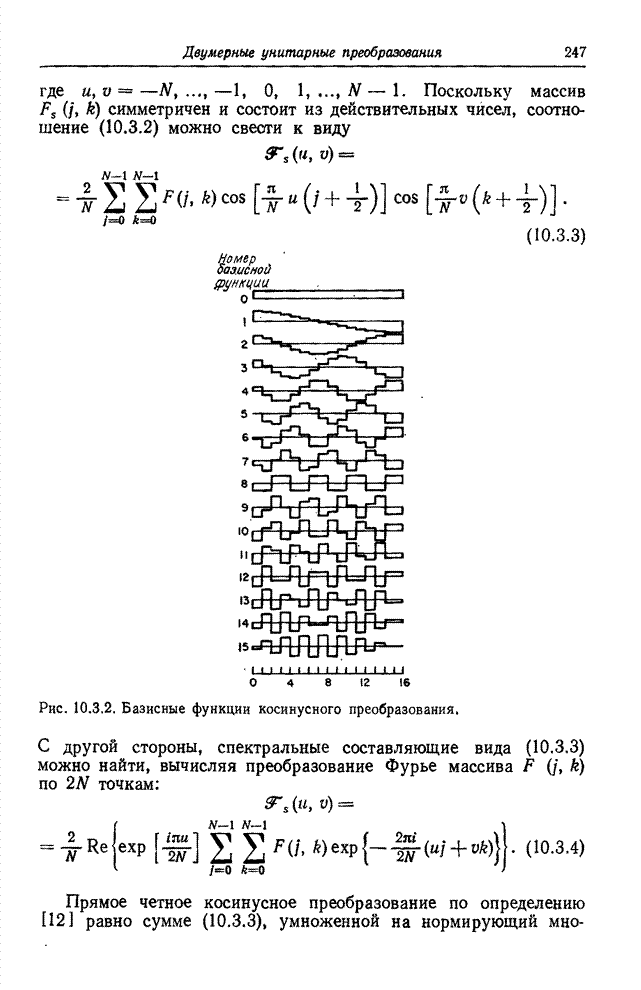
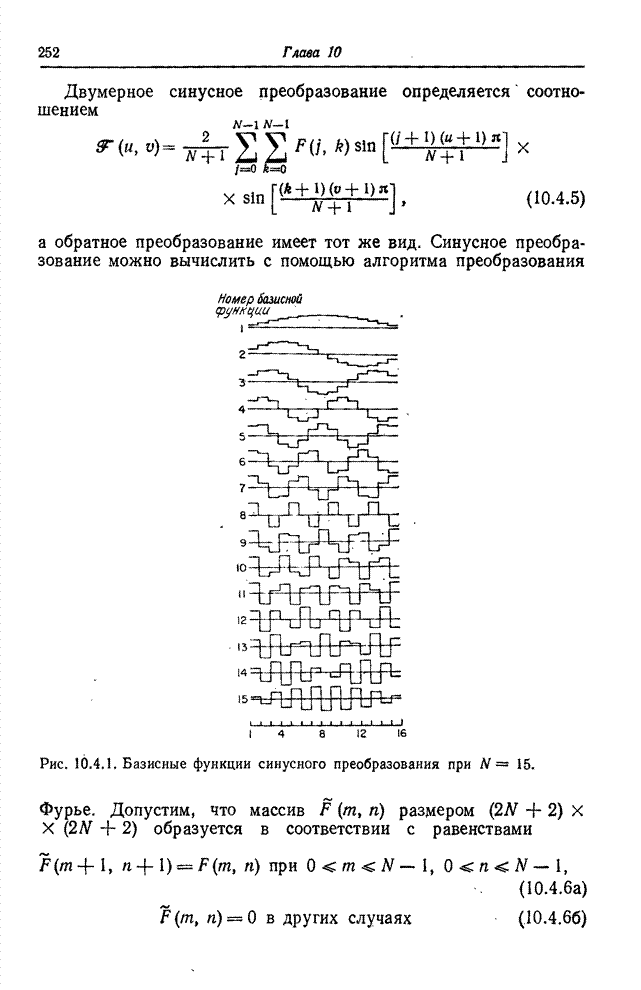
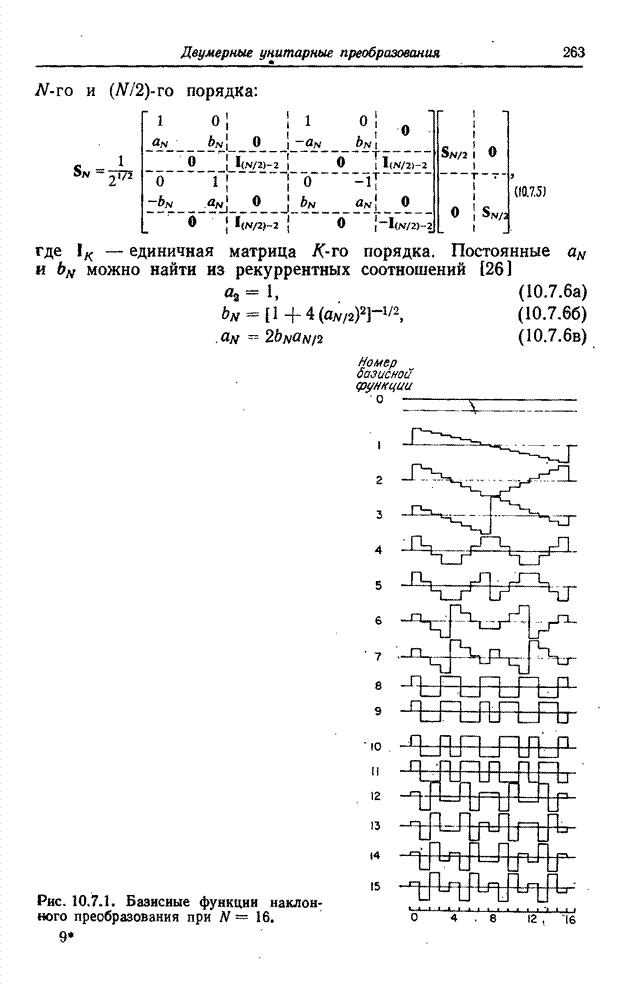
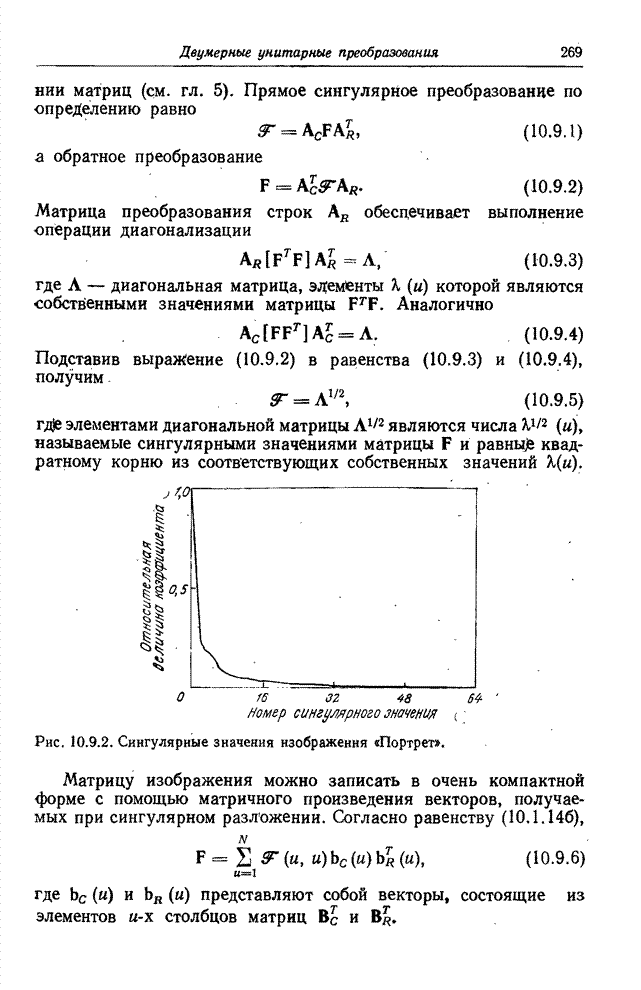
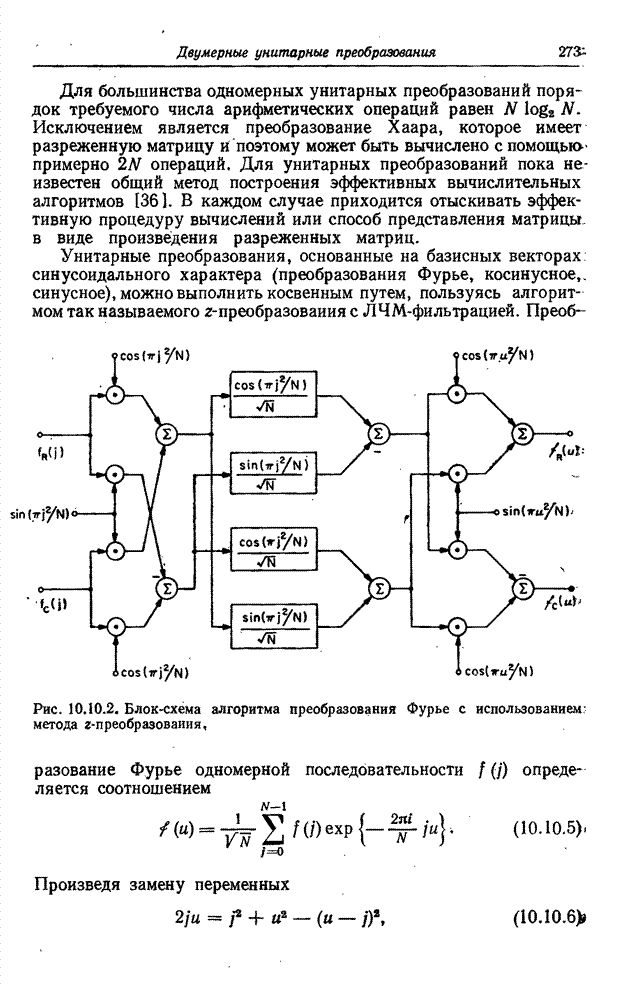
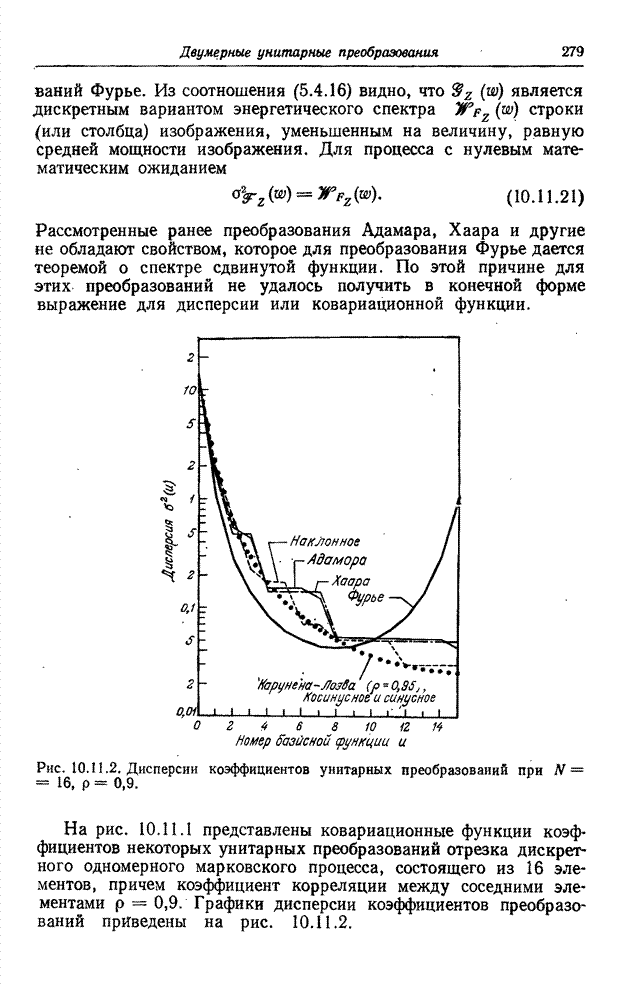
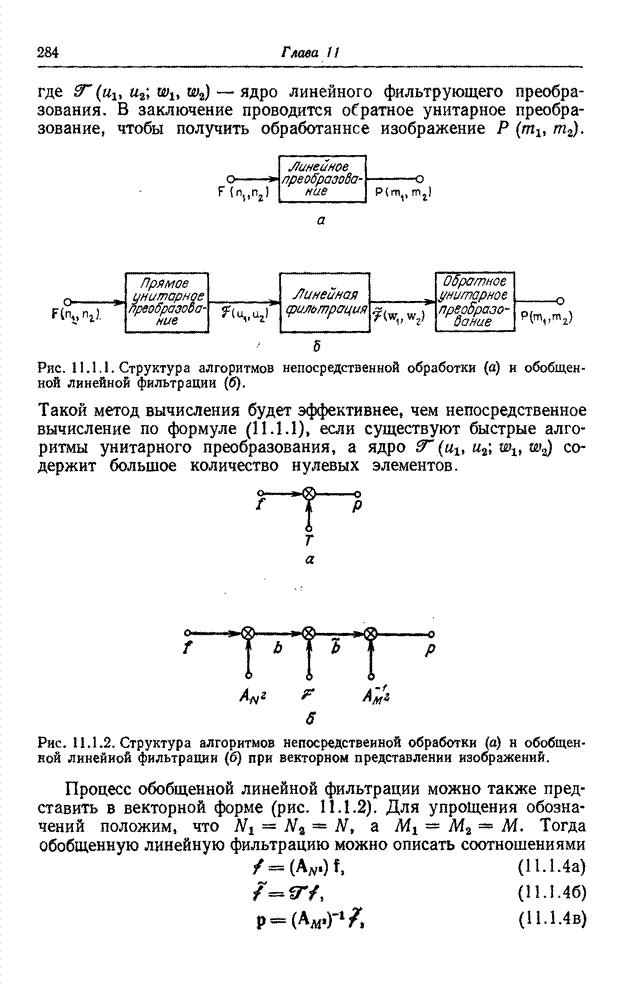
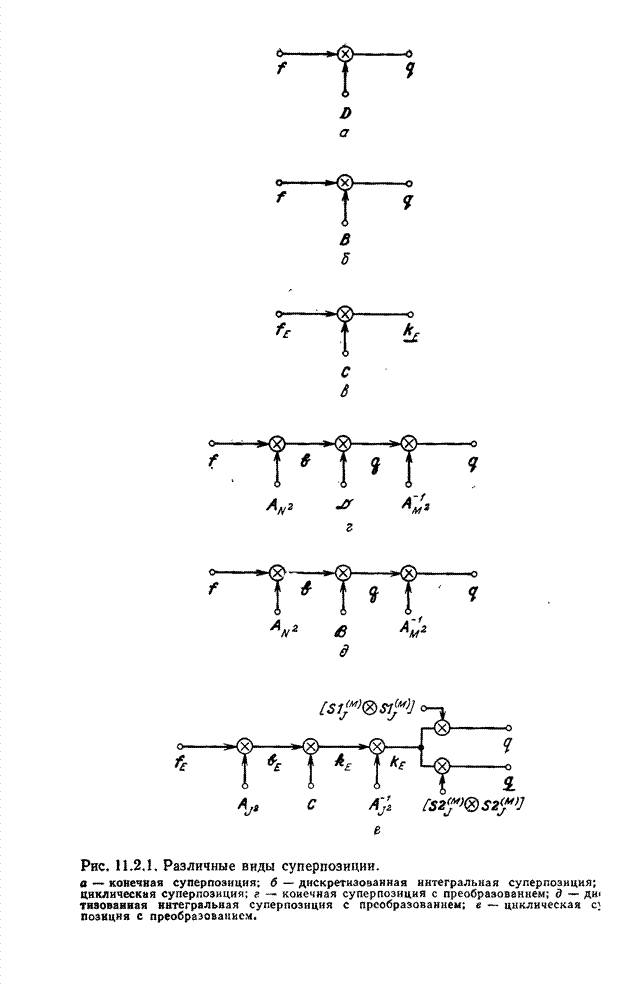
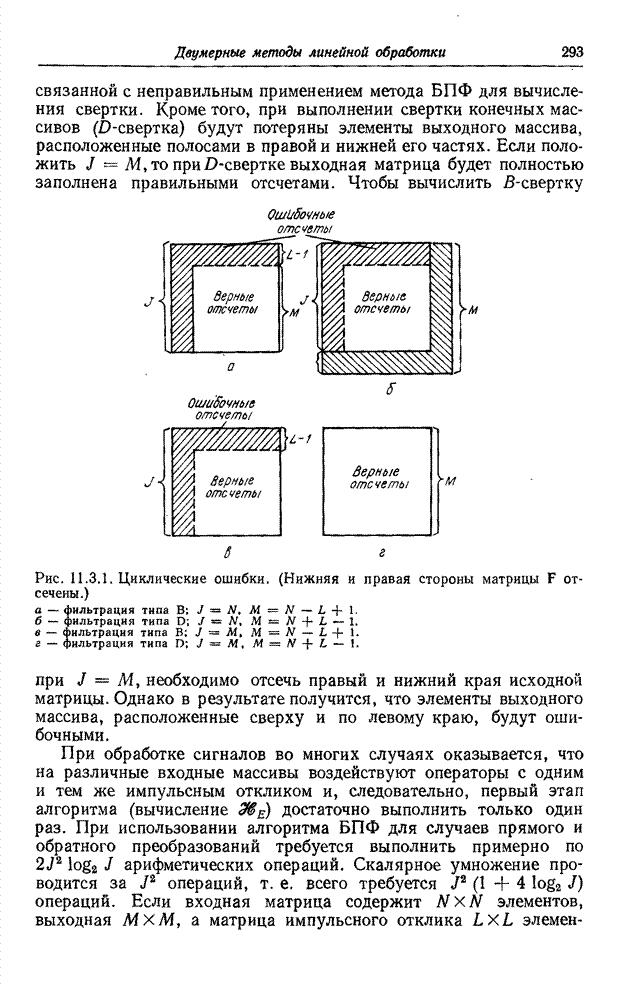
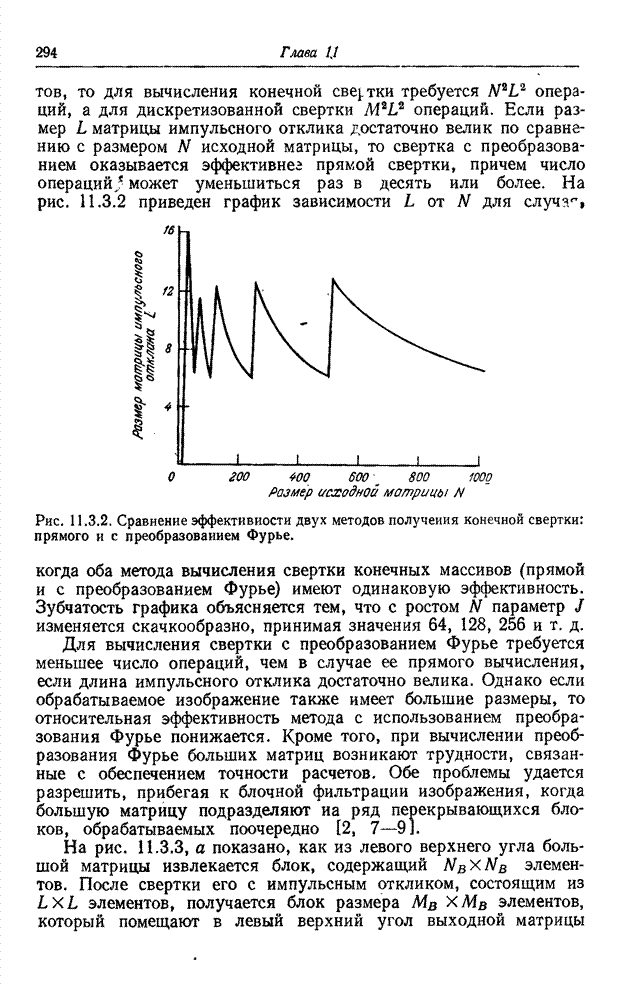
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
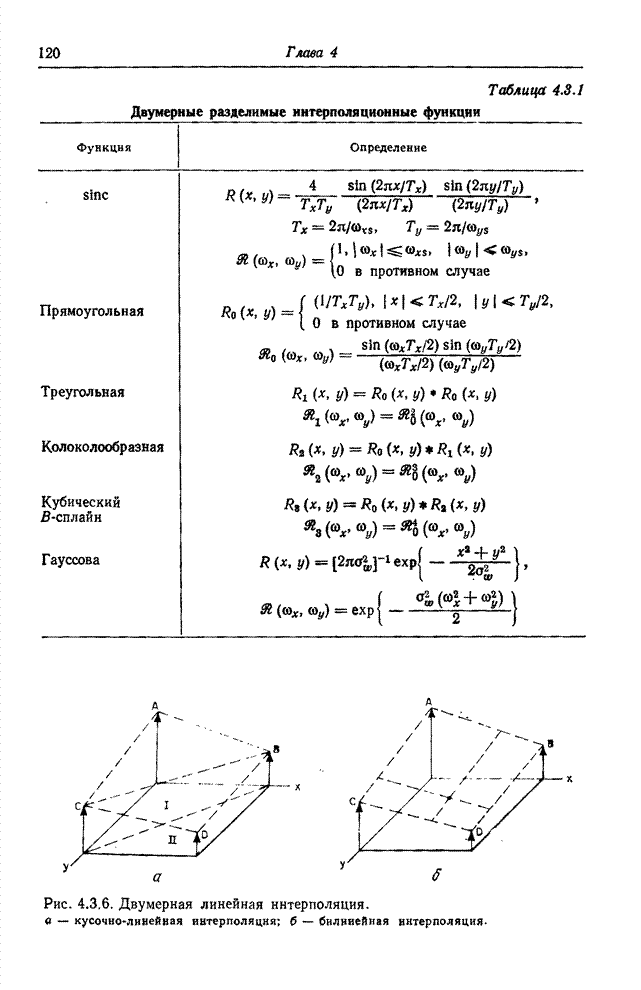
6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
Обычно квантование совокупности отсчетов выполняется последовательно. Каждый отсчет рассматривается как скалярная величина и квантуется независимо от остальных отсчетов с помощью методов, описанных в предыдущем разделе. Однако часто удается уменьшить ошибку квантования, если все отсчеты квантовать совместно.
Рассмотрим
сигнал ![]() ,
представляющий собой вектор размера
,
представляющий собой вектор размера ![]() . Будем
полагать, что этот вектор является реализацией случайного вектора с
. Будем
полагать, что этот вектор является реализацией случайного вектора с ![]() -мерной плотностью
вероятности
-мерной плотностью
вероятности
![]() . (6.2.1)
. (6.2.1)
При
квантовании вектора ![]()
![]() -мерное векторное пространство
разделяют на
-мерное векторное пространство
разделяют на ![]() ячеек
квантования
ячеек
квантования ![]() каждой
из которых соответствует один из
каждой
из которых соответствует один из ![]() квантованных векторов. Векторный
сигнал
квантованных векторов. Векторный
сигнал ![]() заменяется
на квантованный вектор
заменяется
на квантованный вектор ![]() если
если ![]() попадает в ячейку
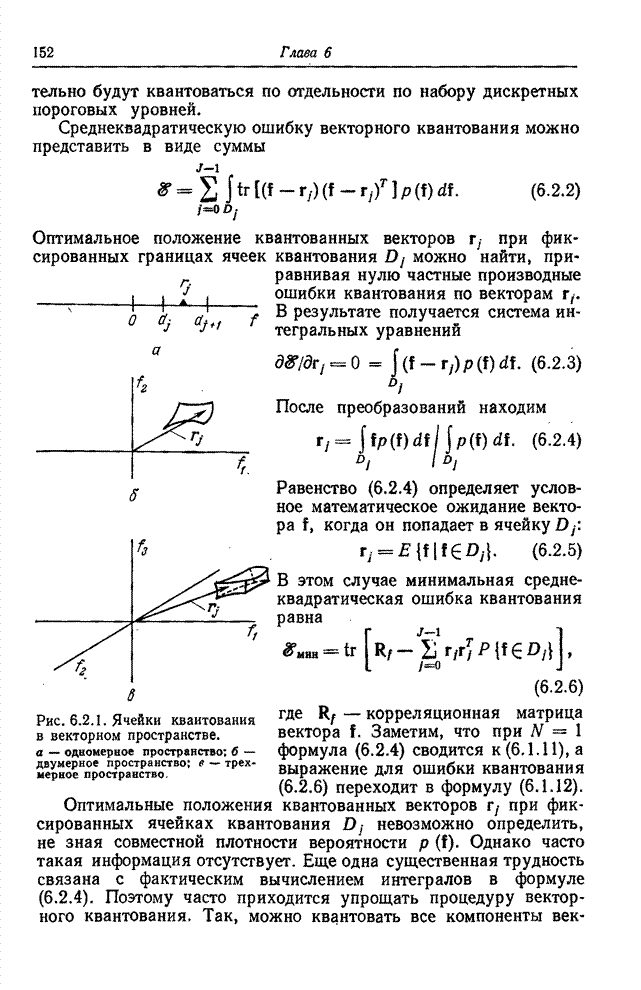
попадает в ячейку ![]() . На рис. 6.2.1
приведены примеры векторного квантования в одно-, двух- и трехмерном
пространствах. В подобной общей постановке задачи о векторном квантовании
векторный сигнал
. На рис. 6.2.1
приведены примеры векторного квантования в одно-, двух- и трехмерном
пространствах. В подобной общей постановке задачи о векторном квантовании
векторный сигнал ![]() преобразуется
в вектор
преобразуется
в вектор ![]() но компоненты
вектора
но компоненты
вектора ![]() при
этом не обязательно будут квантоваться по отдельности по набору дискретных
пороговых уровней.
при
этом не обязательно будут квантоваться по отдельности по набору дискретных
пороговых уровней.

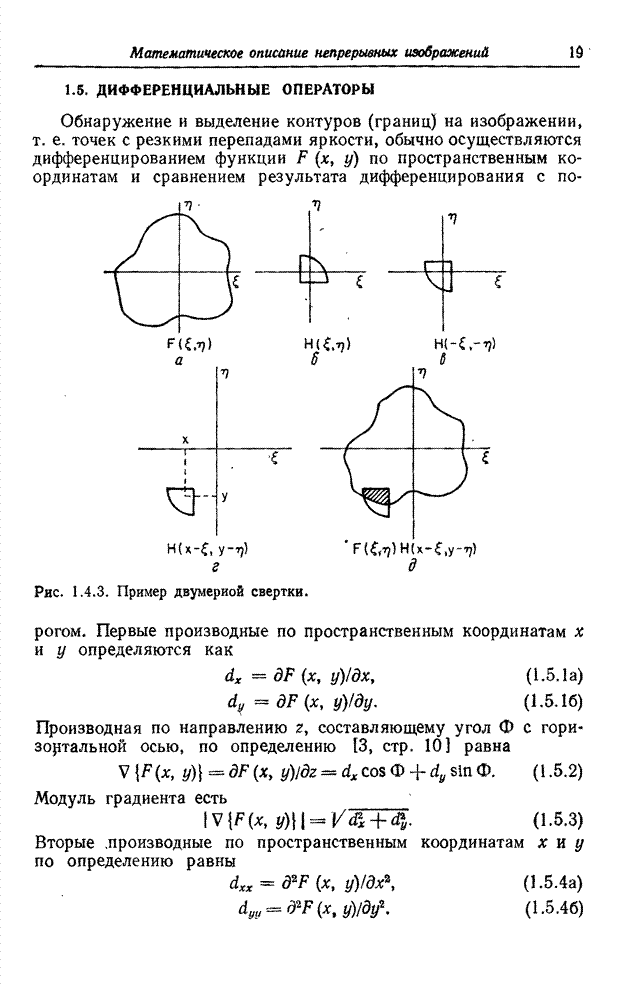
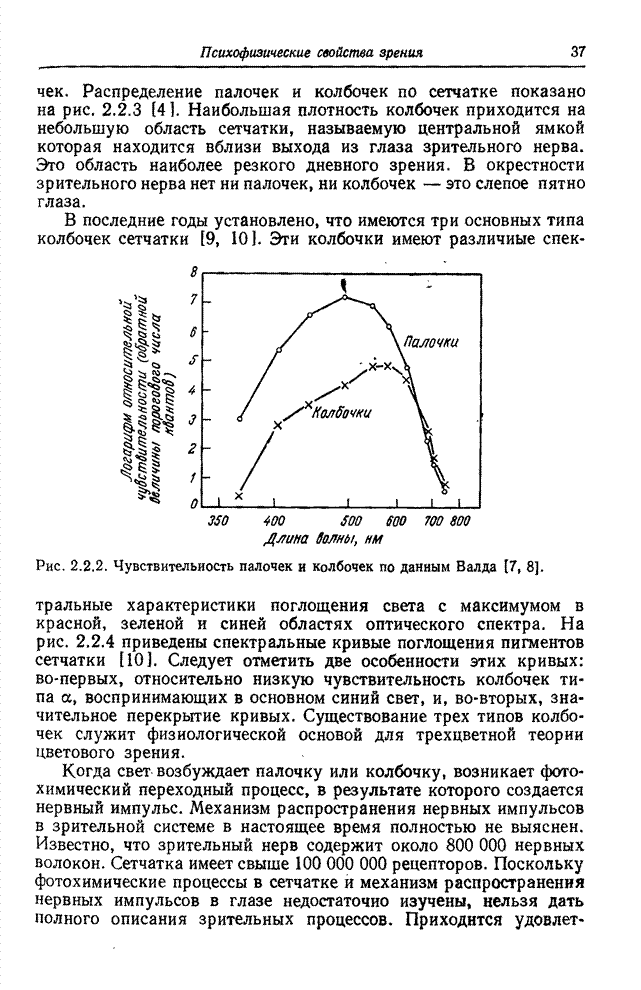
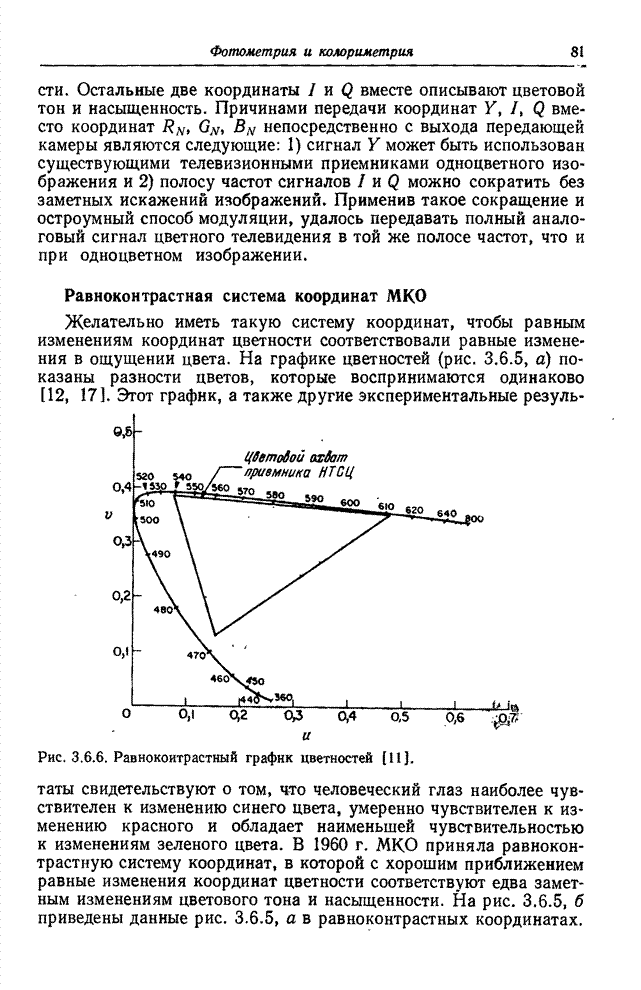
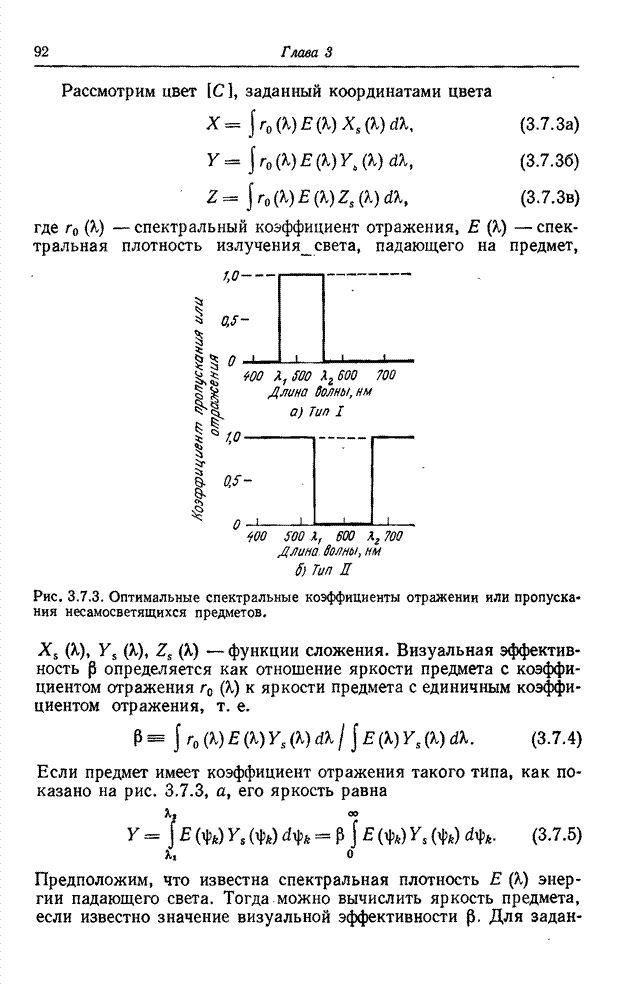
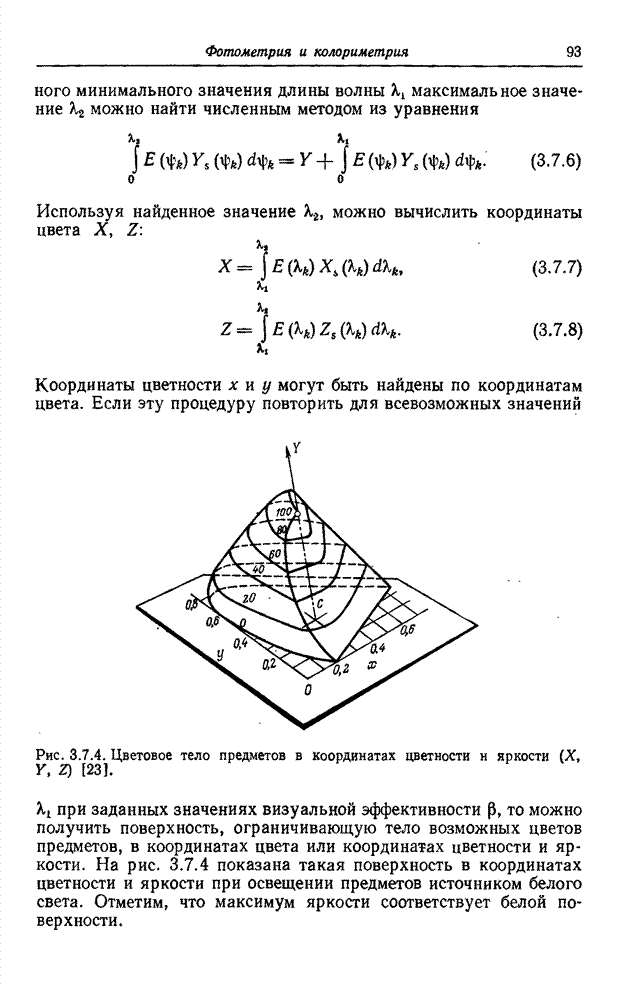
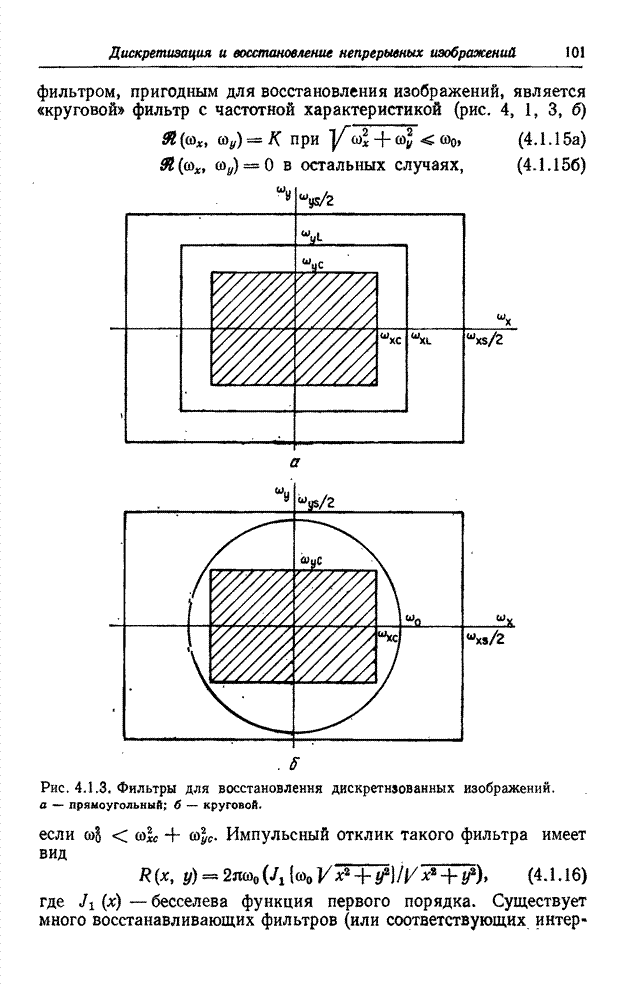
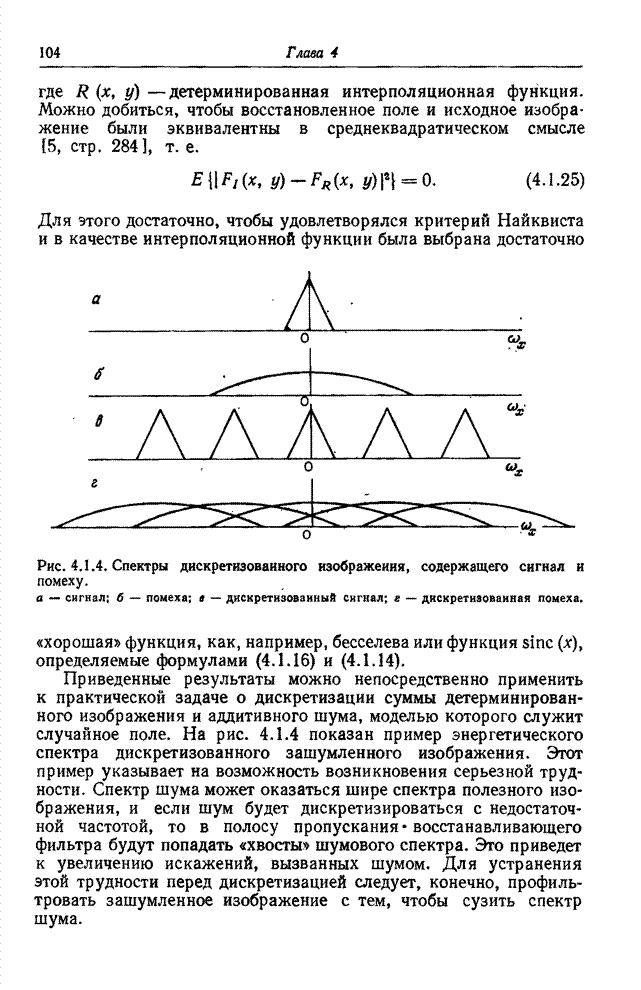
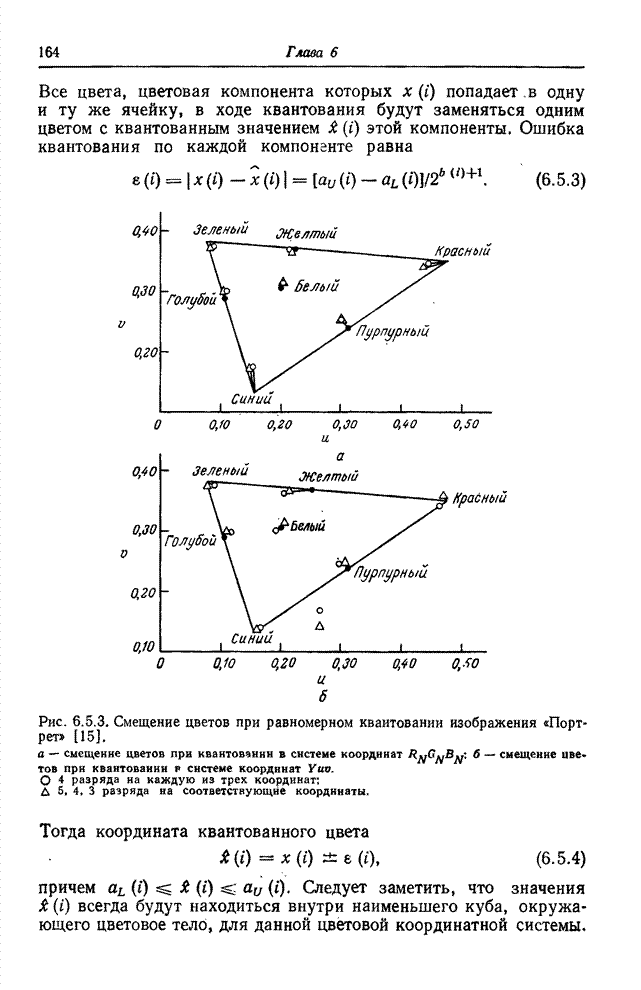
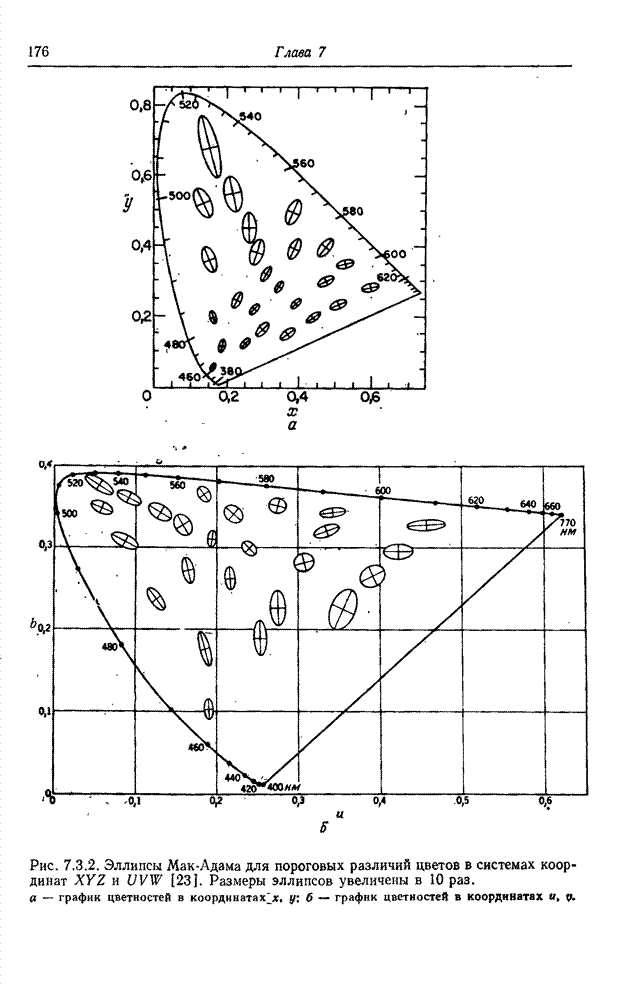
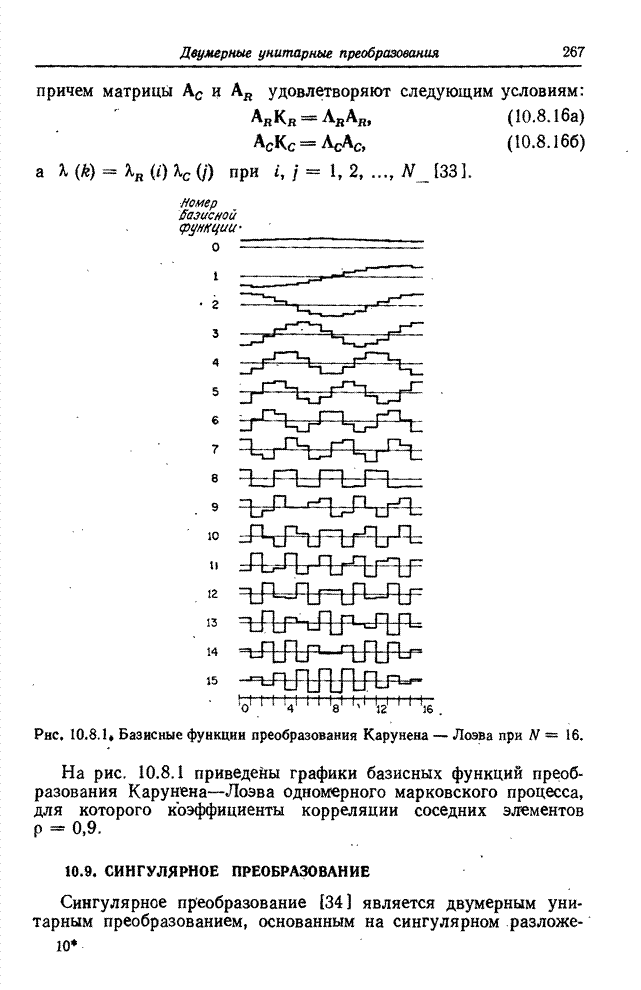
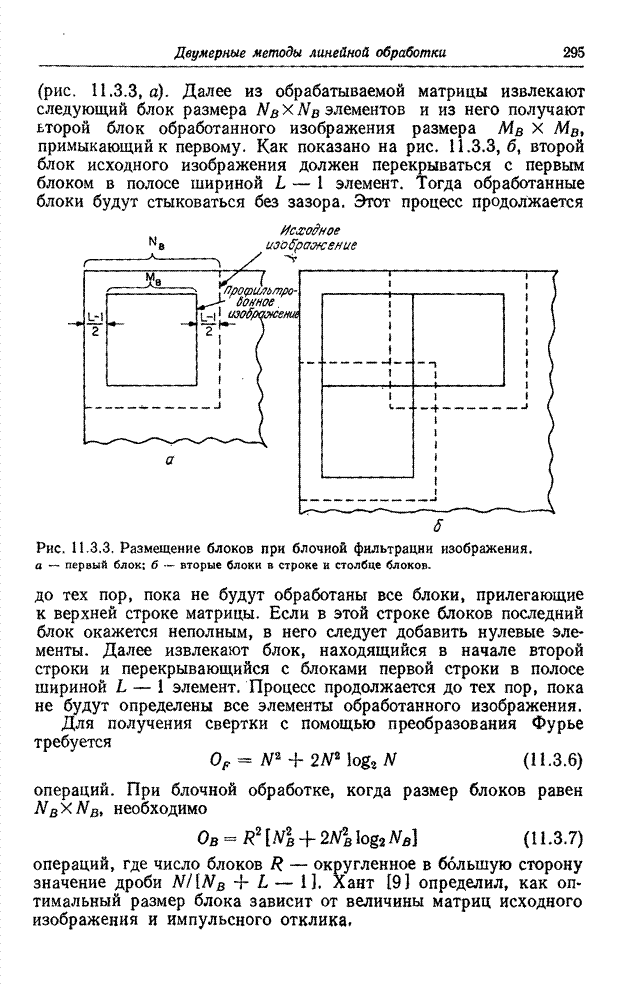
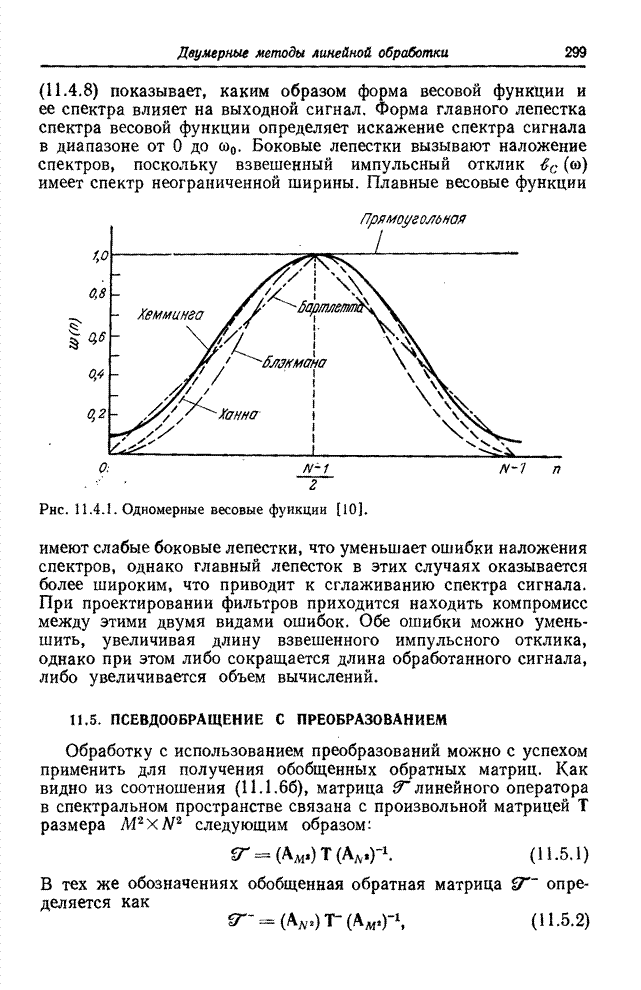
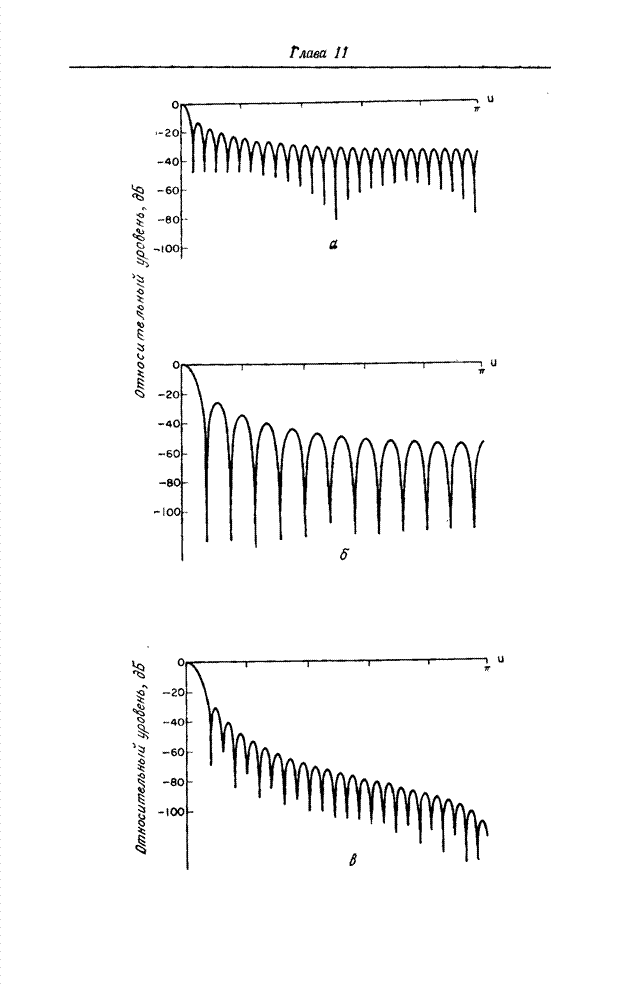
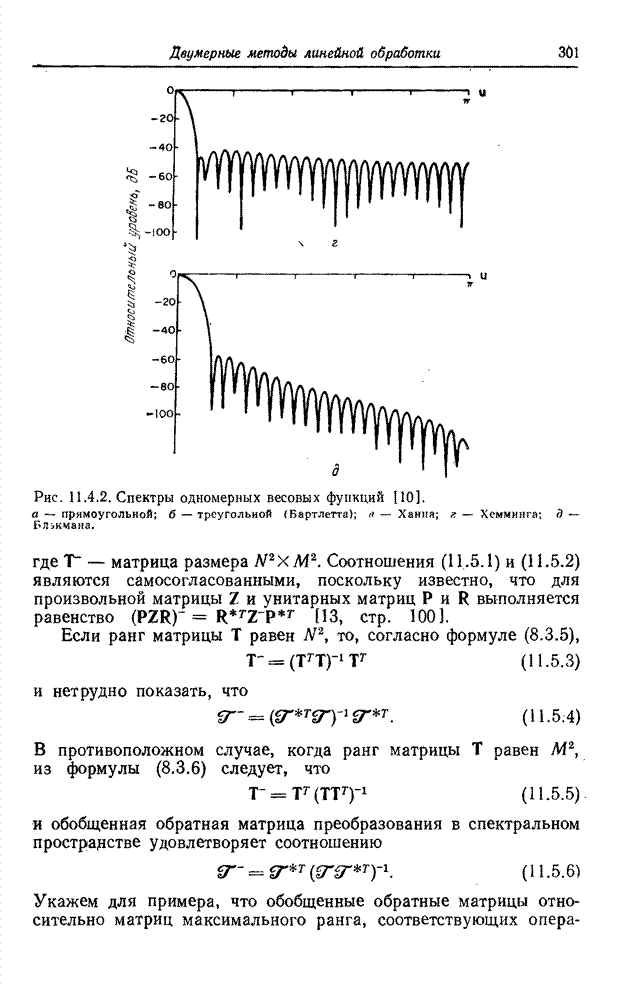
Рис. 6.2.1. Ячейки квантования в векторном пространстве: а – одномерное пространство; б – двумерное пространство; в – трехмерное пространство.
Среднеквадратическую ошибку векторного квантования можно представить в виде суммы
 (6.2.2)
(6.2.2)
Оптимальное
положение квантованных векторов ![]() при фиксированных границах ячеек
квантования можно найти, приравнивая нулю частные производные ошибки
квантования по векторам
при фиксированных границах ячеек
квантования можно найти, приравнивая нулю частные производные ошибки
квантования по векторам ![]() . В результате получается система
интегральных уравнений
. В результате получается система
интегральных уравнений
![]() (6.2.3)
(6.2.3)
После преобразований находим
![]() (6.2.4)
(6.2.4)
Равенство
(6.2.4) определяет условное математическое ожидание вектора ![]() , когда он попадает в ячейку
:
, когда он попадает в ячейку
:
![]() . (6.2.5)
. (6.2.5)
В этом случае минимальная средне-квадратическая ошибка квантования равна
 , (6.2.6)
, (6.2.6)
где
![]() -
корреляционная матрица вектора
-
корреляционная матрица вектора ![]() . Заметим, что
при
. Заметим, что
при ![]() формула (6.2.4)
сводится к (6.1.11), а выражение для ошибки квантования (6.2.6) переходит в
формулу (6.1.12).
формула (6.2.4)
сводится к (6.1.11), а выражение для ошибки квантования (6.2.6) переходит в
формулу (6.1.12).
Оптимальные
положения квантованных векторов ![]() при
фиксированных ячейках квантования
при
фиксированных ячейках квантования ![]() невозможно
определить, не зная совместной плотности вероятности
невозможно
определить, не зная совместной плотности вероятности ![]() . Однако часто такая
информация отсутствует. Еще одна существенная трудность связана с фактическим
вычислением интегралов в формуле (6.2.4). Поэтому часто приходится упрощать
процедуру векторного квантования. Так, можно квантовать все компоненты вектора
. Однако часто такая
информация отсутствует. Еще одна существенная трудность связана с фактическим
вычислением интегралов в формуле (6.2.4). Поэтому часто приходится упрощать
процедуру векторного квантования. Так, можно квантовать все компоненты вектора ![]() по отдельности, но
задавать квантованные векторы
по отдельности, но
задавать квантованные векторы ![]() с помощью ячеек квантования
с помощью ячеек квантования ![]() . Тогда в
трехмерном пространстве ячейки
. Тогда в
трехмерном пространстве ячейки ![]() превращаются в
прямоугольные параллелепипеды. Если при этом компоненты вектора
превращаются в
прямоугольные параллелепипеды. Если при этом компоненты вектора ![]() некоррелированы,
то векторное квантование сводится к последовательному квантованию скалярных
величин. Однако если отсчеты коррелированы, то задача определения оптимального
вектора
некоррелированы,
то векторное квантование сводится к последовательному квантованию скалярных
величин. Однако если отсчеты коррелированы, то задача определения оптимального
вектора ![]() как
правило, не поддается решению без введения дополнительных упрощающих
предположений. Кэри [4] получил решения применительно к совместным гауссовым
плотностям, когда ячейки квантования
как
правило, не поддается решению без введения дополнительных упрощающих
предположений. Кэри [4] получил решения применительно к совместным гауссовым
плотностям, когда ячейки квантования ![]() , достаточно
малы. Хунс [5] исследовал рекуррентный метод решения такой задачи, когда каждая
компонента вектора определяется с помощью последовательных приближений на
основе остальных квантованных компонент вектора. Этот метод позволяет найти
решение задачи для множества различных плотностей вероятности: в части 6 он
рассмотрен как средство уменьшения ошибок квантования в системах, использующих
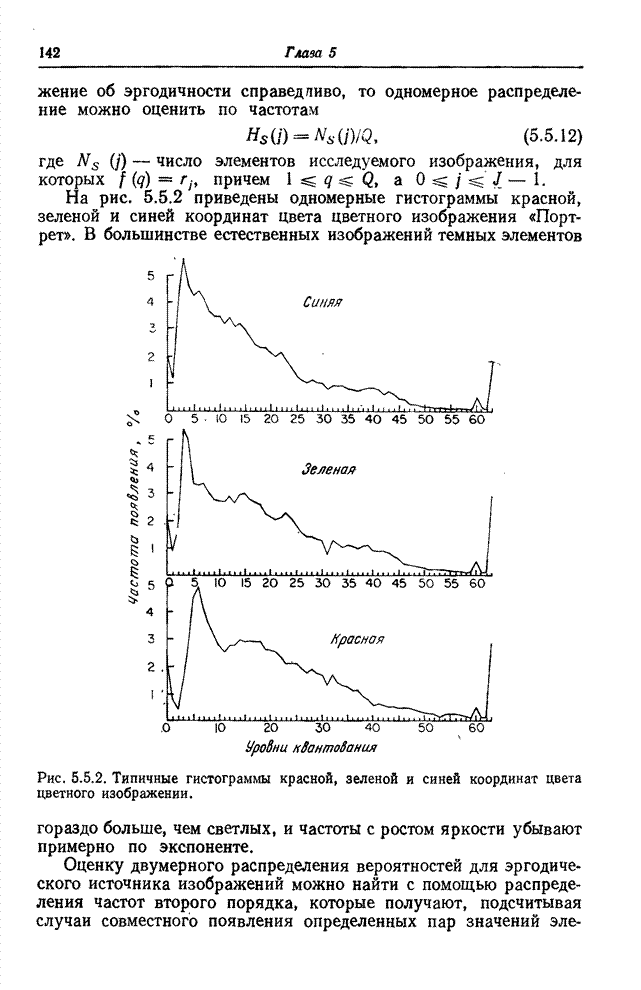
ИКМ и кодирование с преобразованием.
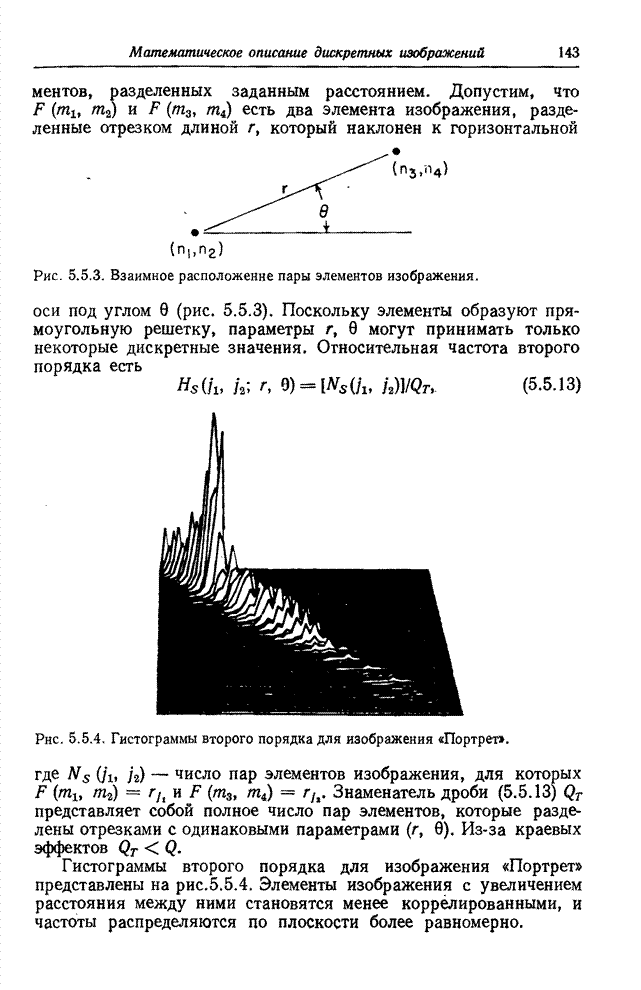
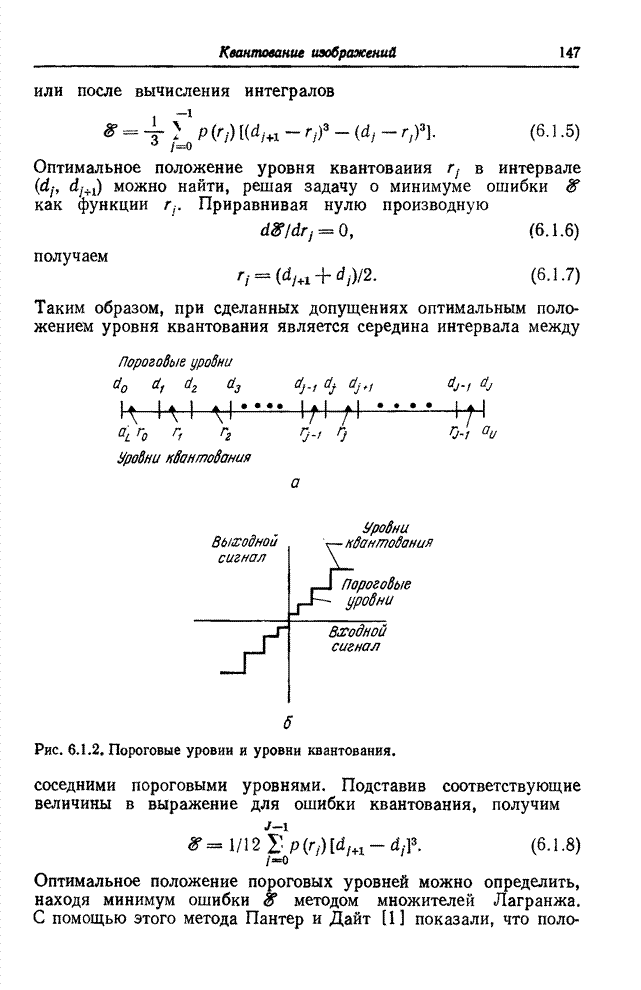
, достаточно
малы. Хунс [5] исследовал рекуррентный метод решения такой задачи, когда каждая
компонента вектора определяется с помощью последовательных приближений на
основе остальных квантованных компонент вектора. Этот метод позволяет найти
решение задачи для множества различных плотностей вероятности: в части 6 он
рассмотрен как средство уменьшения ошибок квантования в системах, использующих
ИКМ и кодирование с преобразованием.
Попытаемся
теперь найти такой набор ячеек квантования ![]() при котором
минимизируется среднеквадрэтическая ошибка квантования. Брюс [6] разработал
метод решения этой задачи, основанный на динамическом программировании. Однако
в общем случае оптимальные формы ячеек квантования сложны и определить их
весьма трудно. Поэтому в большинстве методов векторного квантования
используется субоптимальный подход, когда для каждой компоненты вектора
задается фиксированное число уровней квантовании
при котором
минимизируется среднеквадрэтическая ошибка квантования. Брюс [6] разработал
метод решения этой задачи, основанный на динамическом программировании. Однако
в общем случае оптимальные формы ячеек квантования сложны и определить их
весьма трудно. Поэтому в большинстве методов векторного квантования
используется субоптимальный подход, когда для каждой компоненты вектора
задается фиксированное число уровней квантовании ![]() , где
, где ![]() , и все
компоненты квантуются независимо. Задача оптимизации сводится в этом случае к
выбору величин
, и все
компоненты квантуются независимо. Задача оптимизации сводится в этом случае к
выбору величин ![]() ,
произведение которых
,
произведение которых
 (6.2.7)
(6.2.7)
есть
фиксированное число уровней квантования для данного вектора. Ошибка квантования
![]() -го
отсчета равна
-го
отсчета равна
. . (6.2.8)
. (6.2.8)
В системах с цифровым кодированием число уровней квантования обычно выбирают равным двоичному числу
![]() , (6.2.9)
, (6.2.9)
где
![]() – целое число
кодовых разрядов (бит) для
– целое число
кодовых разрядов (бит) для ![]() -й компоненты вектора. Общее
количество кодовых разрядов должно быть постоянно и равно
-й компоненты вектора. Общее
количество кодовых разрядов должно быть постоянно и равно
![]() . (6.2.10)
. (6.2.10)
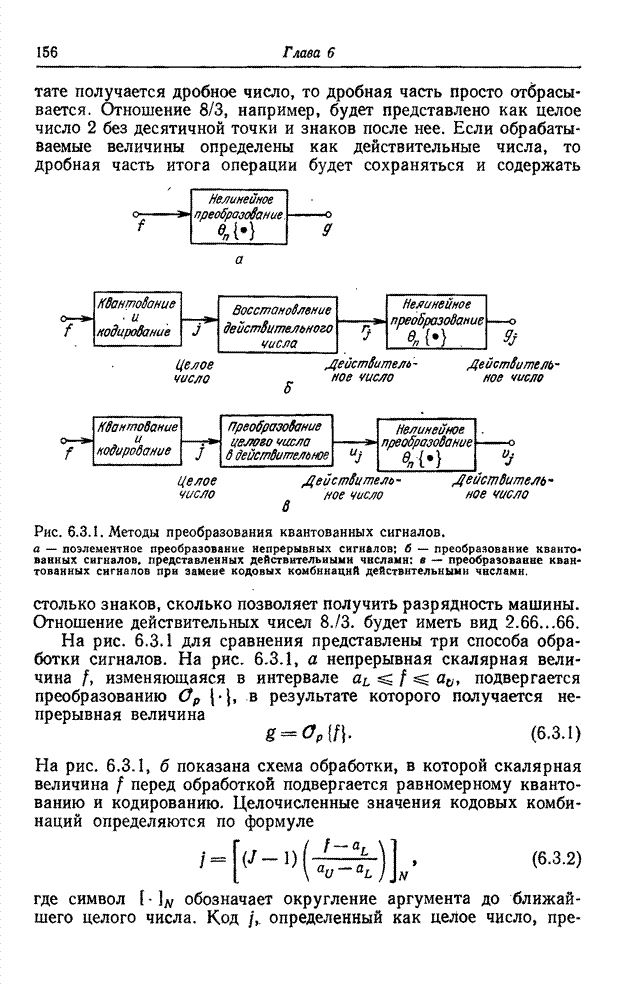
Такой способ квантования называется блочным.
Несколько
специалистов [7-9] разработали алгоритмы распределения числа разрядов ![]() при
фиксированном
при
фиксированном ![]() ,
позволяющие минимизировать среднеквадратическую ошибку квантования. При
использовании алгоритма, предложенного Реди и Уинцем [9] и применяемого для
квантования независимых гауссовых величин по методу Макса, следует выполнить
следующие операции:
,
позволяющие минимизировать среднеквадратическую ошибку квантования. При
использовании алгоритма, предложенного Реди и Уинцем [9] и применяемого для
квантования независимых гауссовых величин по методу Макса, следует выполнить
следующие операции:
1. Вычислить распределение числа разрядов по формуле
![]() , (6.2.11)
, (6.2.11)
где
![]() - дисперсия
- дисперсия ![]() -го отсчета.
-го отсчета.
2.
Округлить каждое из чисел ![]() до ближайшего
целого.
до ближайшего
целого.
3. Изменять полученное распределение, пока не будет выполнено условие (6.2.10)
Вывод
соотношения (6.2.11) основан на экспоненциальной аппроксимации зависимости
(6.1.12), связывающей ошибку квантования ![]() -го отсчета и заданное ему число
разрядов
-го отсчета и заданное ему число
разрядов ![]() .
Если
.
Если ![]() невелико,
то эта аппроксимация оказывается довольно грубой. Более надежные результаты
можно получить, пользуясь разработанным Прэттом [10] методом минимальной
ошибки. Здесь разряды последовательно отводятся отсчетам, которые имеют
наибольшую дифференциальную ошибку (6.2.8). При квантовании величин с нулевым
средним алгоритм состоит из следующих шагов:
невелико,
то эта аппроксимация оказывается довольно грубой. Более надежные результаты
можно получить, пользуясь разработанным Прэттом [10] методом минимальной
ошибки. Здесь разряды последовательно отводятся отсчетам, которые имеют
наибольшую дифференциальную ошибку (6.2.8). При квантовании величин с нулевым
средним алгоритм состоит из следующих шагов:
Шаг 1. Определение начальных условий:
![]() - общее число
разрядов в кодовой комбинации блока,
- общее число
разрядов в кодовой комбинации блока,
![]() - длина блока,
- длина блока,
![]() - дисперсия
компоненты,
- дисперсия
компоненты,
![]() - плотность
вероятности компоненты,
- плотность
вероятности компоненты,
![]() - индекс разряда
(сначала равен нулю).
- индекс разряда
(сначала равен нулю).
Шаг 2. Вычислить и запомнить коэффициенты дифференциальной ошибки
![]() ,
,
где
![]() , а сумма
, а сумма
![]()
определяет коэффициент ошибки для случайных величин с единичной дисперсией, причем знаком тильды (~) отмечены уровни квантования и пороговые уровни, относящиеся к таким величинам.
Шаг
3. Отвести один разряд той компоненте, для которой произведение ![]() имеет
наибольшую величину; увеличить на единицу
имеет
наибольшую величину; увеличить на единицу ![]() и
и ![]() .
.
Шаг
4. Если ![]() , закончить
процедуру; в противном случае повторить шаг 3.
, закончить
процедуру; в противном случае повторить шаг 3.
Коэффициенты
дифференциальной ошибки ![]() , необходимые
для данного алгоритма, можно вычислить заранее и хранить в виде таблицы из
, необходимые
для данного алгоритма, можно вычислить заранее и хранить в виде таблицы из ![]() чисел. В этом
случае алгоритм сводится к
чисел. В этом
случае алгоритм сводится к ![]() последовательным операциям
распределения разрядов. Достоинства алгоритма состоят в том, что здесь не
требуется громоздких вычислений, а также отсутствуют ошибки аппроксимации и
округления, характерные для алгоритма с вычислением логарифмов дисперсий. Кроме
того, метод минимальной ошибки опирается на модель плотности вероятности и
поэтому его можно эффективно применять для распределения разрядов при
неодинаковых плотностях вероятностей отсчетов.
последовательным операциям
распределения разрядов. Достоинства алгоритма состоят в том, что здесь не
требуется громоздких вычислений, а также отсутствуют ошибки аппроксимации и
округления, характерные для алгоритма с вычислением логарифмов дисперсий. Кроме
того, метод минимальной ошибки опирается на модель плотности вероятности и
поэтому его можно эффективно применять для распределения разрядов при
неодинаковых плотностях вероятностей отсчетов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
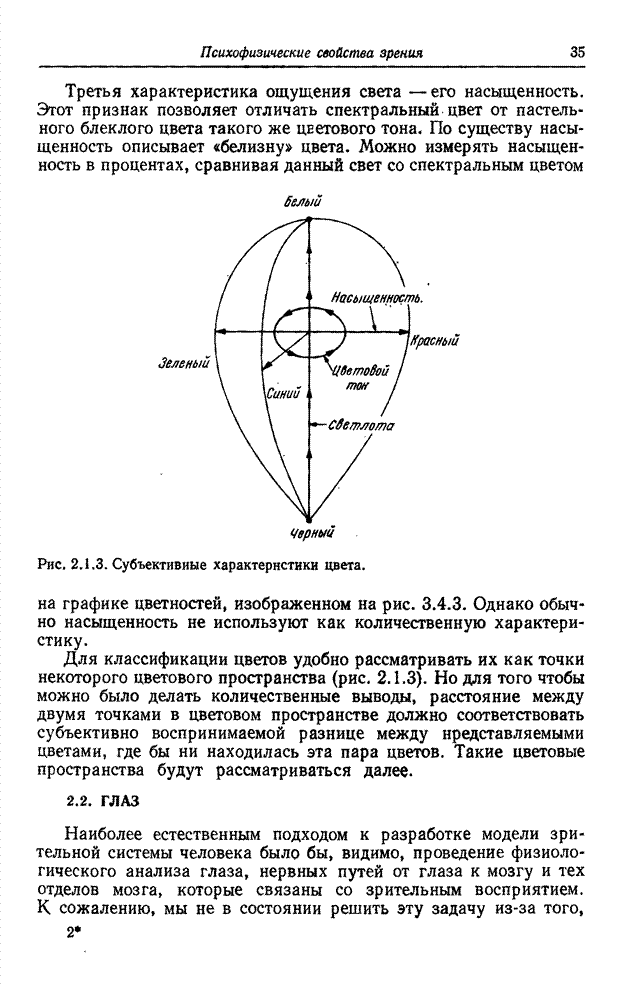
- 2.1. ВОСПРИЯТИЕ СВЕТА
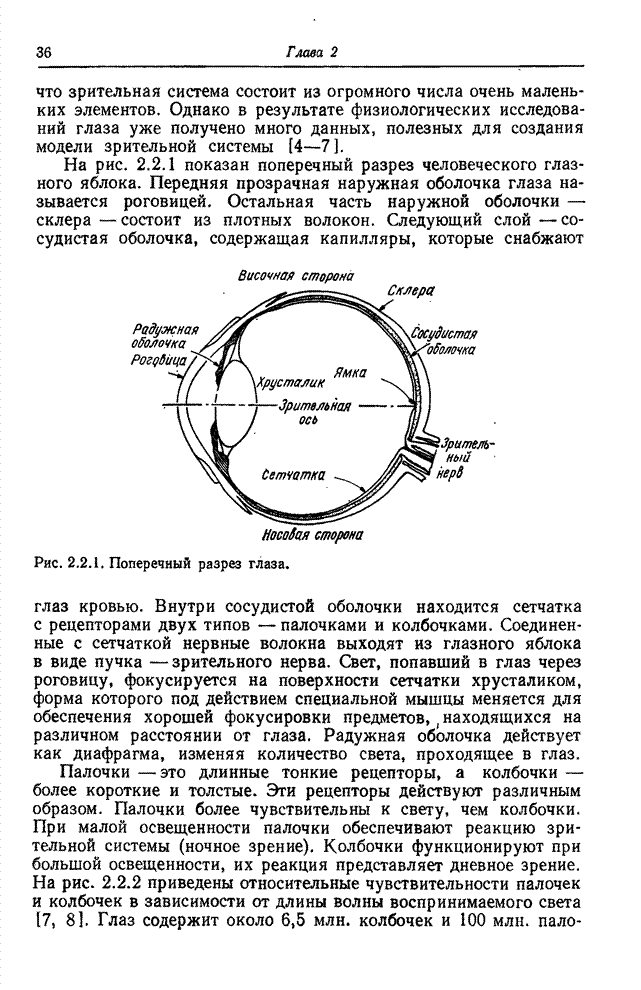
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
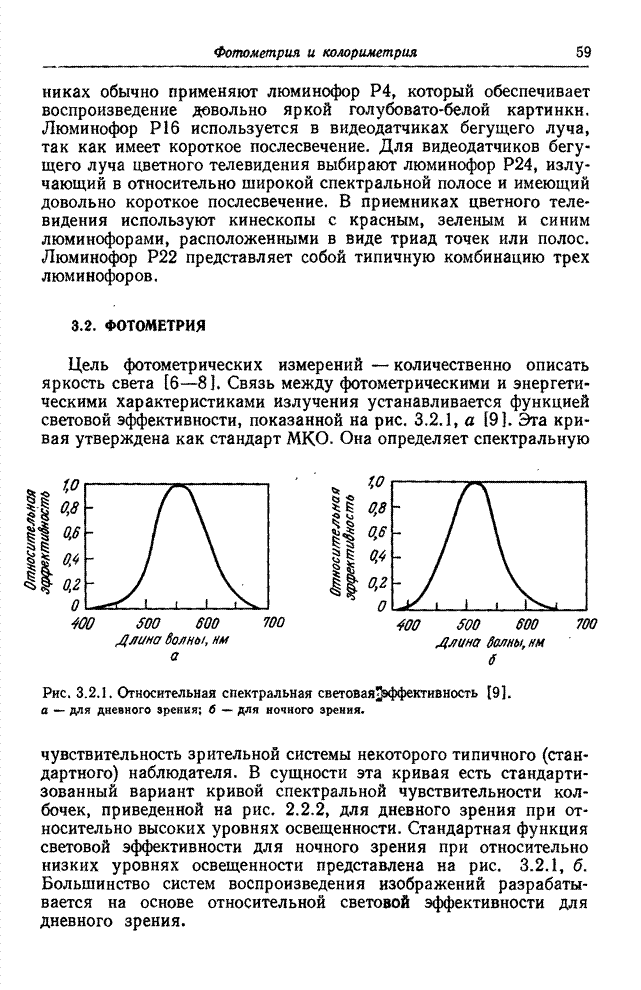
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
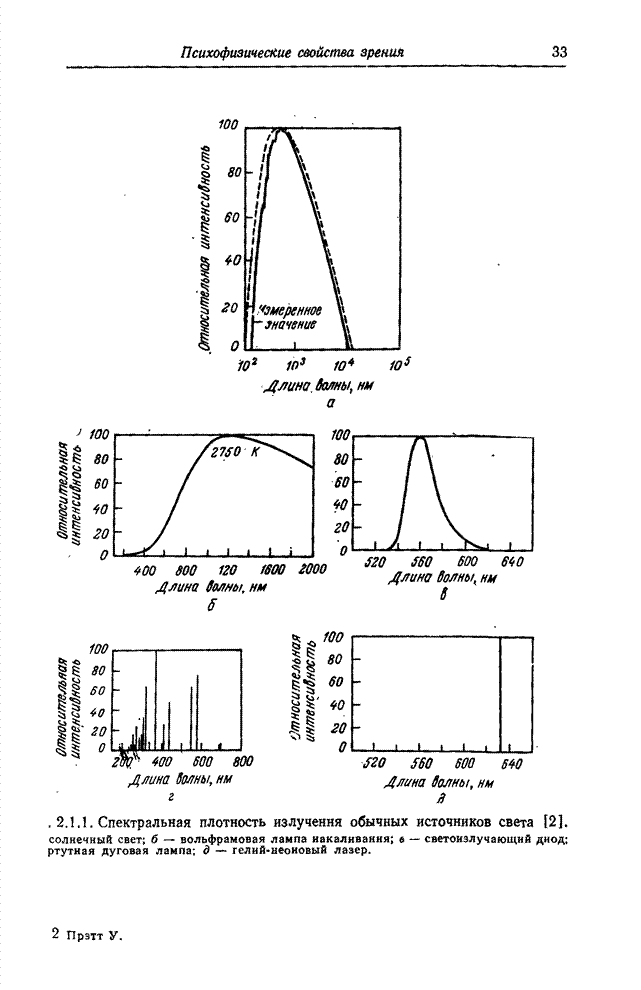
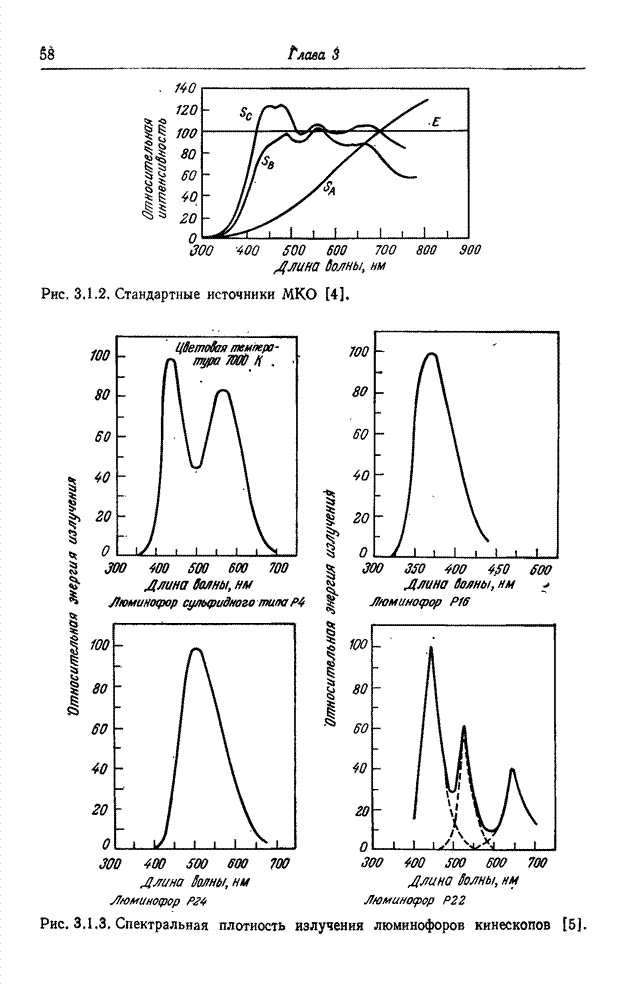
- 3.1. ИСТОЧНИКИ СВЕТА
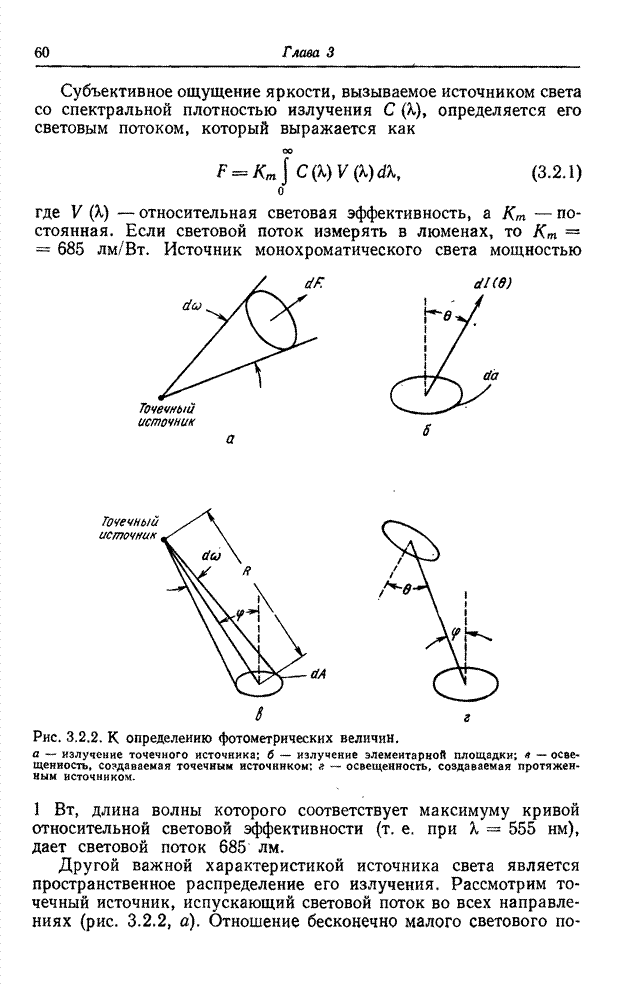
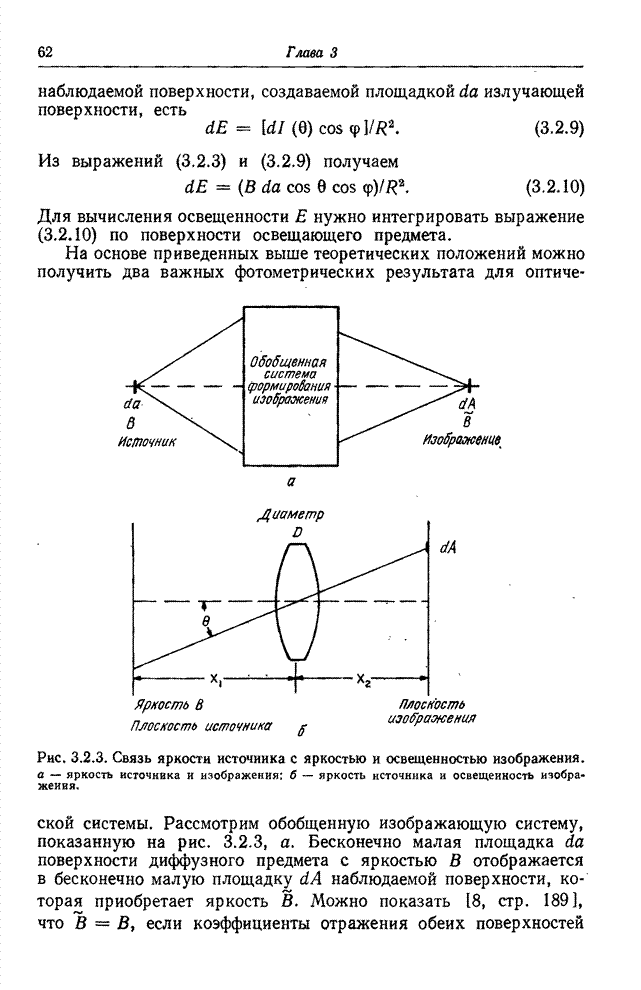
- 3.2. ФОТОМЕТРИЯ
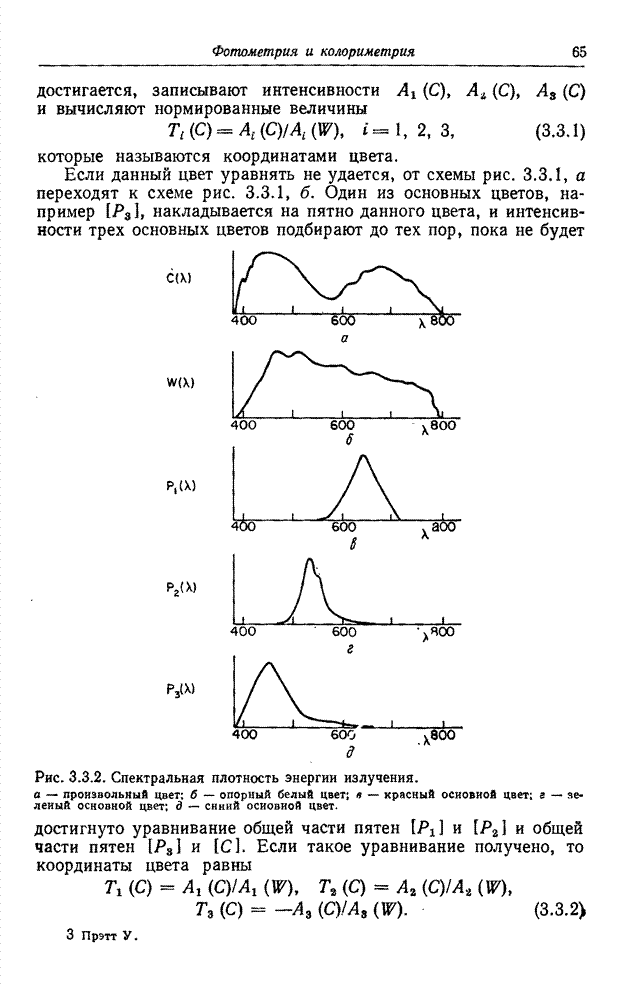
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
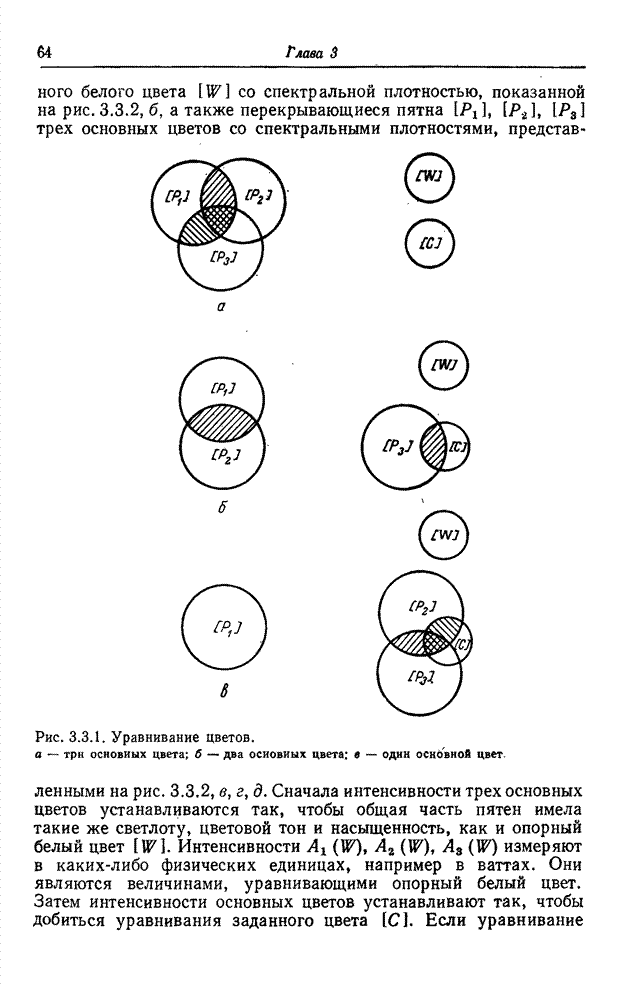
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
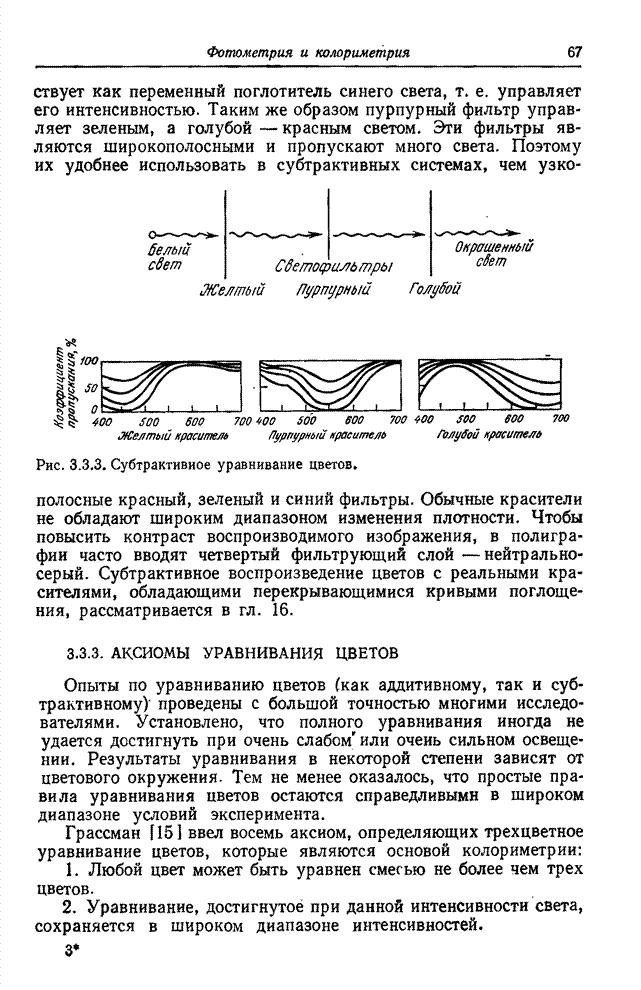
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА