| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
При линейной обработке сигналов часто встречается задача «обращения» преобразования вида
![]() (8.3.1)
(8.3.1)
с тем, чтобы выразить точное значение входного вектора ![]() размера
размера
![]() или некоторую его оценку
или некоторую его оценку ![]() через выходной вектор
p размера
через выходной вектор
p размера ![]() . Если
. Если
![]() -
квадратная матрица, то очевидно,
что
-
квадратная матрица, то очевидно,
что
![]() (8.3.2)
(8.3.2)
если обратная матрица
существует. Если матрица ![]() не квадратная, то для отыскания решения можно воспользоваться
псевдообратной матрицей
не квадратная, то для отыскания решения можно воспользоваться
псевдообратной матрицей ![]() размера
размера ![]() . В
этом случае
. В
этом случае
![]() (8.3.3)
(8.3.3)
Если решение существует
и единственно, то «правильным»
оператором псевдообращения будет тот,
который обеспечивает точную оценку, т.
е. ![]() . Это означает,
что вектор
. Это означает,
что вектор ![]() можно определить по наблюдаемому
вектору
можно определить по наблюдаемому
вектору ![]() без ошибок. Если решение существует, но оно не единственно, то с помощью псевдообратного
оператора можно выбрать решение с минимальной нормой. Если,
наконец, точных решений не существует,
то с помощью оператора псевдообращения
можно найти наилучшее приближенное решение. Более подробно
этот вопрос рассмотрен в последующих разделах. Разъяснения
и доказательства многих из нижеприведенных положений содержатся
в монографиях [4-6].
без ошибок. Если решение существует, но оно не единственно, то с помощью псевдообратного
оператора можно выбрать решение с минимальной нормой. Если,
наконец, точных решений не существует,
то с помощью оператора псевдообращения
можно найти наилучшее приближенное решение. Более подробно
этот вопрос рассмотрен в последующих разделах. Разъяснения
и доказательства многих из нижеприведенных положений содержатся
в монографиях [4-6].
Первым из операторов
псевдообращения будет рассмотрен оператор с обобщенной
обратной матрицей ![]() , для которой выполняются следующие соотношения:
, для которой выполняются следующие соотношения:
![]() (8.3.4а)
(8.3.4а)
![]() (8.3.46)
(8.3.46)
![]() (8.3.4в)
(8.3.4в)
![]() (8.3.4г)
(8.3.4г)
Обобщенная обратная
матрица является единственной и при некоторых условиях
ее можно записать в явном виде. Если ![]() , то
систему уравнений (8.3.1) называют переопределенной,
т. е. число компонент
наблюдаемого вектора
, то
систему уравнений (8.3.1) называют переопределенной,
т. е. число компонент
наблюдаемого вектора ![]() превышает число подлежащих оценке компонент вектора
превышает число подлежащих оценке компонент вектора ![]() . Если при этом
ранг матрицы
. Если при этом
ранг матрицы ![]() равен
равен ![]() , то
обобщенная обратная матрица
, то
обобщенная обратная матрица
![]() (8.3.5)
(8.3.5)
В противоположном
случае, когда ![]() , систему
(8.3.1) называют недоопределенной.
Если при этом ранг матрицы
, систему
(8.3.1) называют недоопределенной.
Если при этом ранг матрицы ![]() равен
равен ![]() , то
обобщенная обратная матрица имеет вид
, то
обобщенная обратная матрица имеет вид
![]() (8.3.6)
(8.3.6)
Нетрудно показать,
что матрицы, определенные соотношениями
(8.3.5) и (8.3.6), удовлетворяют условиям
(8.3.4). Если матрица ![]() может быть представлена
в виде прямого произведения (8.1.8), то обобщенная обратная
матрица имеет вид
может быть представлена
в виде прямого произведения (8.1.8), то обобщенная обратная
матрица имеет вид
![]() (8.3.7)
(8.3.7)
где ![]() и
и
![]() -
обобщенные обратные матрицы для линейных операторов обработки строк
и столбцов. В этом случае сокращается объем вычислений, необходимых для обращения.
-
обобщенные обратные матрицы для линейных операторов обработки строк
и столбцов. В этом случае сокращается объем вычислений, необходимых для обращения.
Еще один тип оператора
псевдообращения имеет матрицу ![]() , называемую матрицей
обращения методом наименьших квадратов, которая определяется
следующими соотношениями:
, называемую матрицей
обращения методом наименьших квадратов, которая определяется
следующими соотношениями:
![]() (8.3.8а)
(8.3.8а)
![]() (8.3.8б)
(8.3.8б)
И наконец,
условно обратная матрица ![]() определяется формулой
определяется формулой
![]() (8.3.9)
(8.3.9)
Анализ определений
всех трех видов оператора псевдообращения показывает, что
обобщенный обратный оператор является оператором обращения
методом наименьших квадратов, а последний - оператором условного обращения. Для любого линейного
оператора с матрицей ![]() всегда существуют
матрица обращения методом наименьших квадратов и условно обратная матрица,
но они могут быть не единственными. Кроме
того, для этих матриц обычно не удается найти явное выражение
в конечной форме.
всегда существуют
матрица обращения методом наименьших квадратов и условно обратная матрица,
но они могут быть не единственными. Кроме
того, для этих матриц обычно не удается найти явное выражение
в конечной форме.
Ниже приведены некоторые
полезные соотношения для матрицы ![]() , которая
является обобщенной обратной матрицей относительно матрицы
, которая
является обобщенной обратной матрицей относительно матрицы
![]() размера
размера ![]() .
.
Обобщенное обращение транспонированной матрицы
![]() (8.3.10)
(8.3.10)
Обобщенное обращение обобщенной обратной матрицы
![]() (8.3.11)
(8.3.11)
Сохранение ранга
![]() (8.3.12)
(8.3.12)
Обобщенное обращение произведения матриц
![]() (8.3.13)
(8.3.13)
![]() (8.3.14)
(8.3.14)
где ![]() и
и
![]() —
матрицы ранга
—
матрицы ранга ![]() , имеющие размеры
, имеющие размеры ![]() и
и
![]() соответственно.
соответственно.
Обобщенное обращение произведения ортогональных матриц
![]() (8.3.15)
(8.3.15)
где ![]() и
и
![]() -
ортогональные матрицы размера
-
ортогональные матрицы размера ![]() и
и ![]() соответственно.
соответственно.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
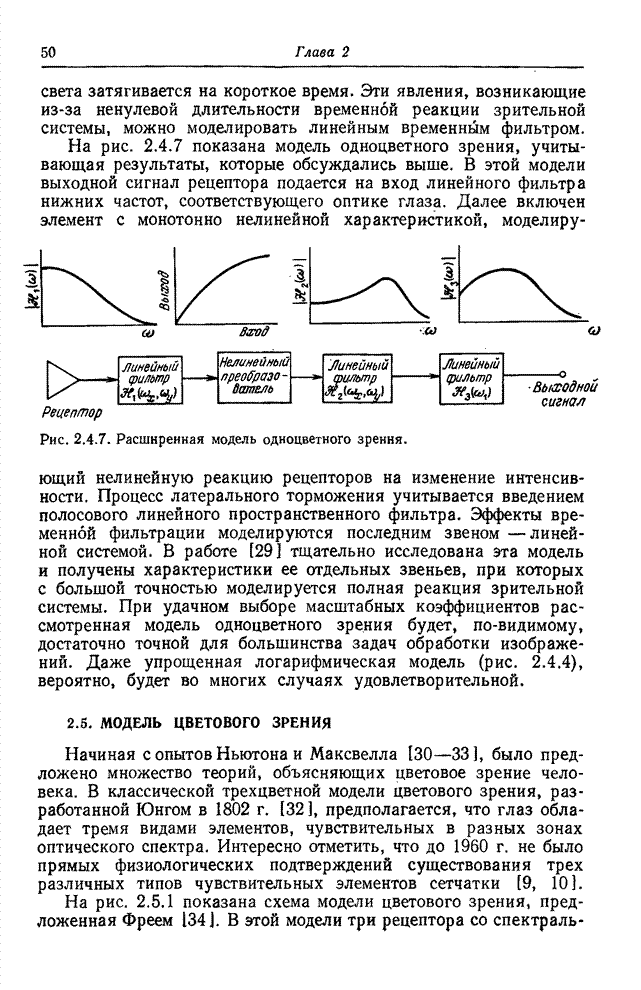
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
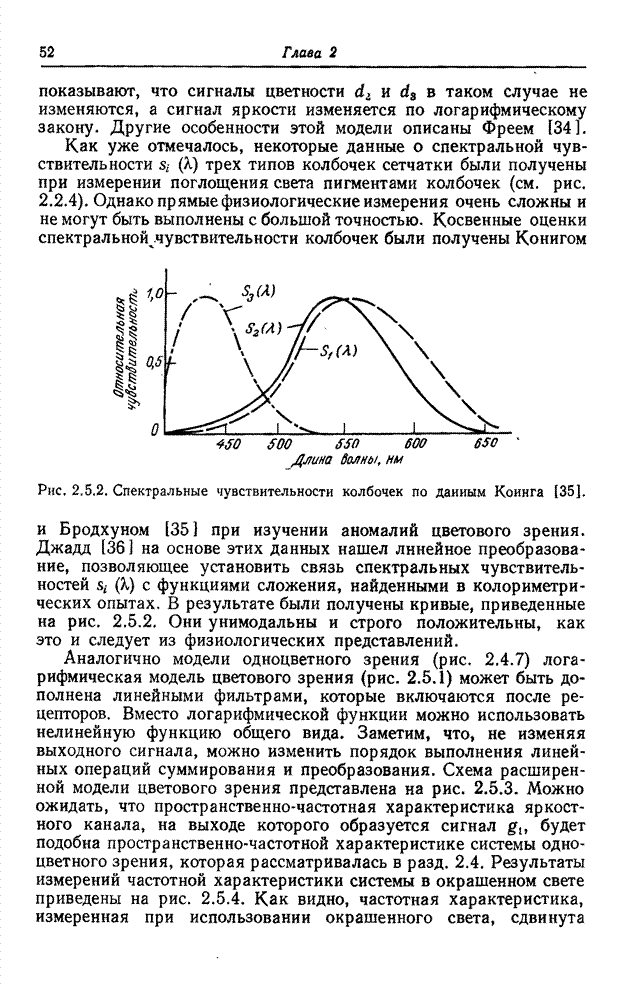
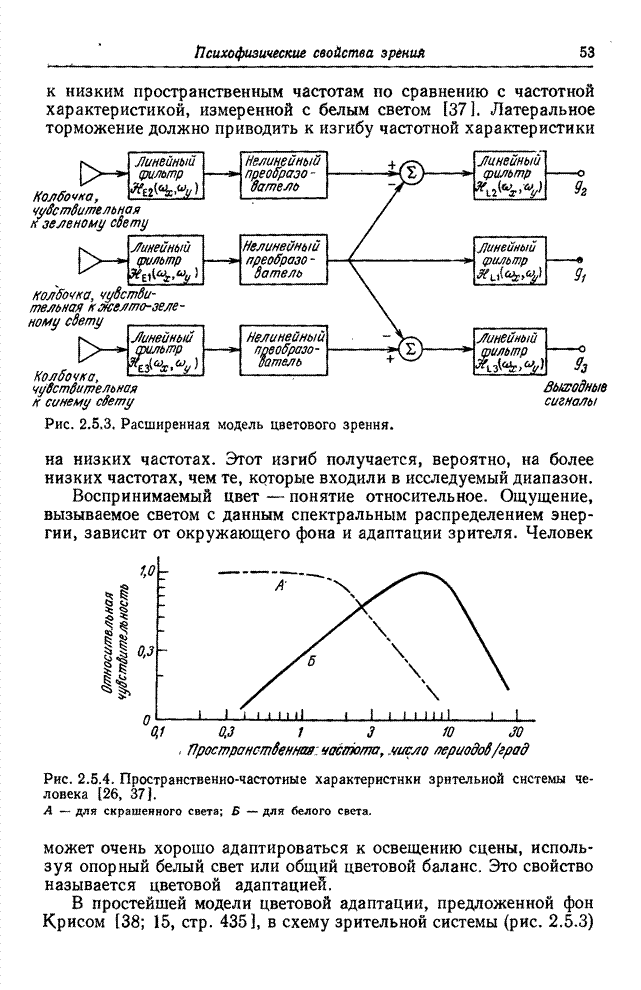
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
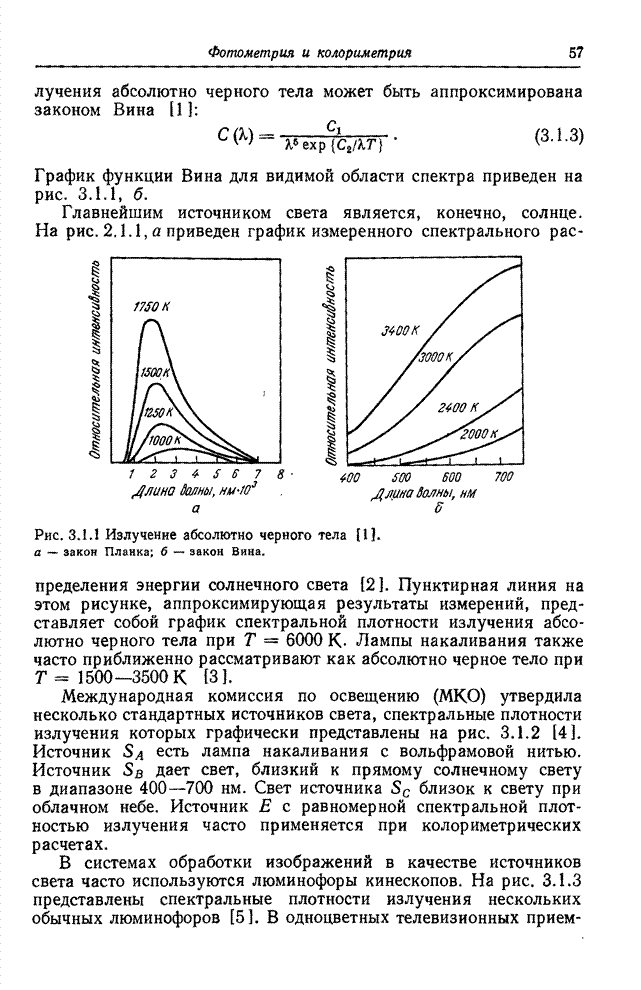
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА