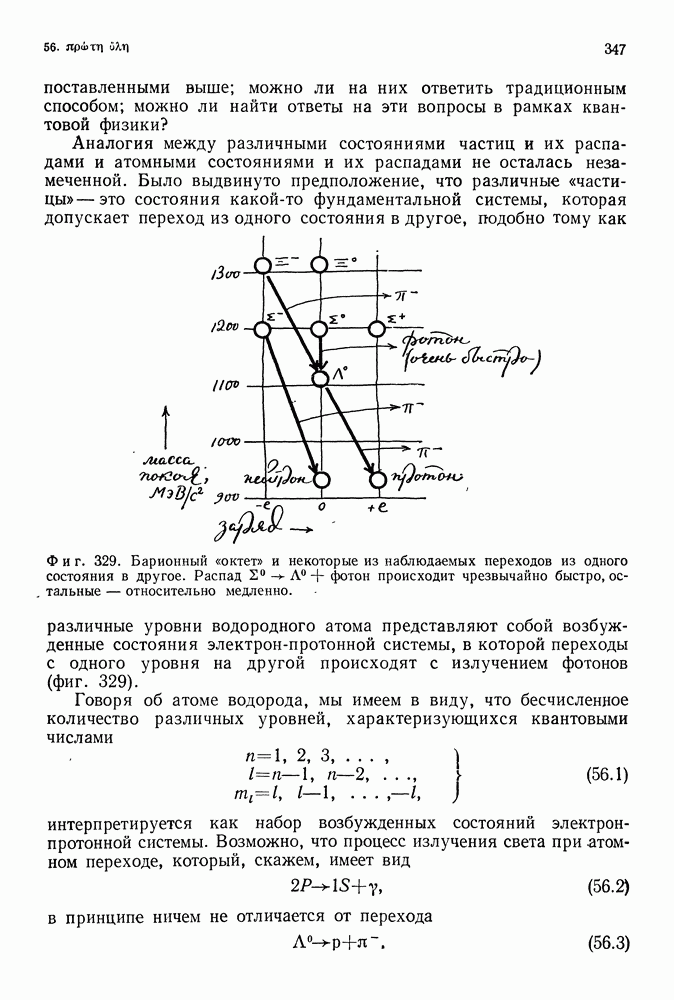
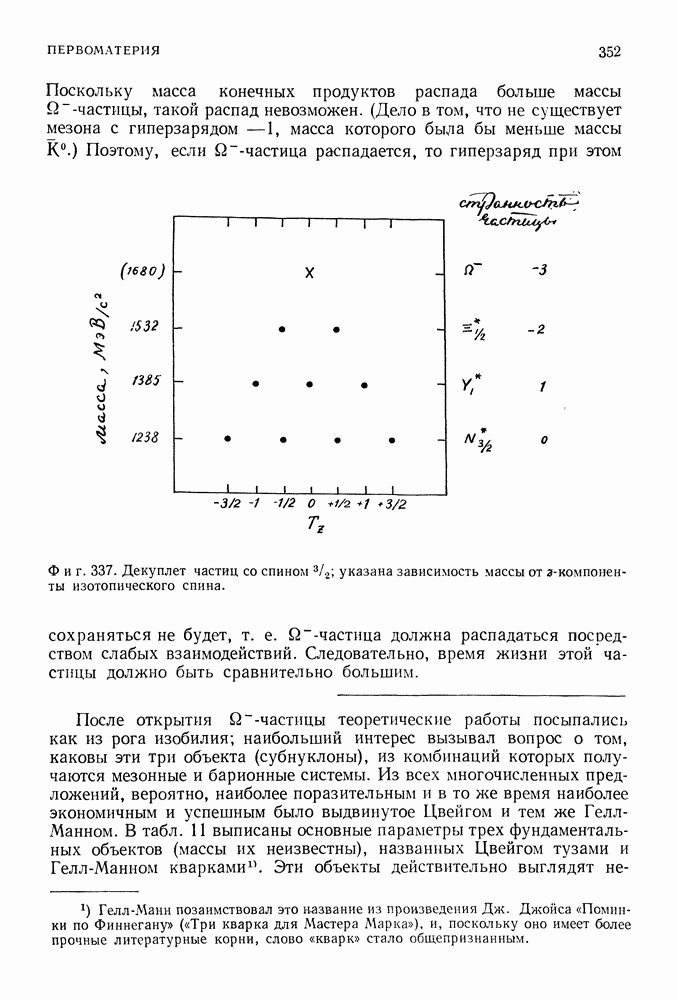
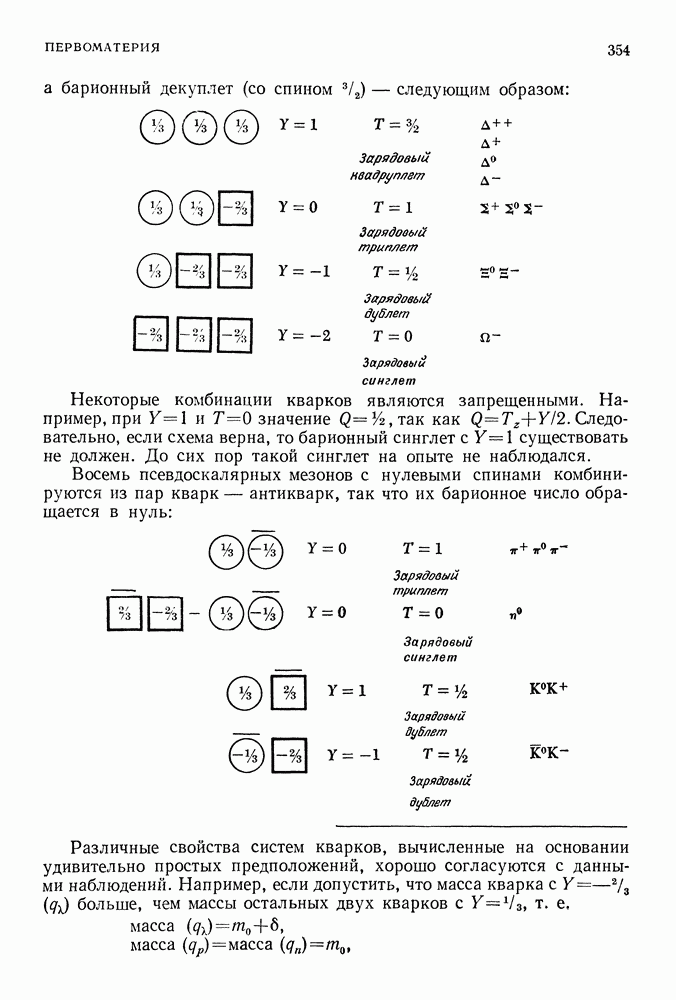
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
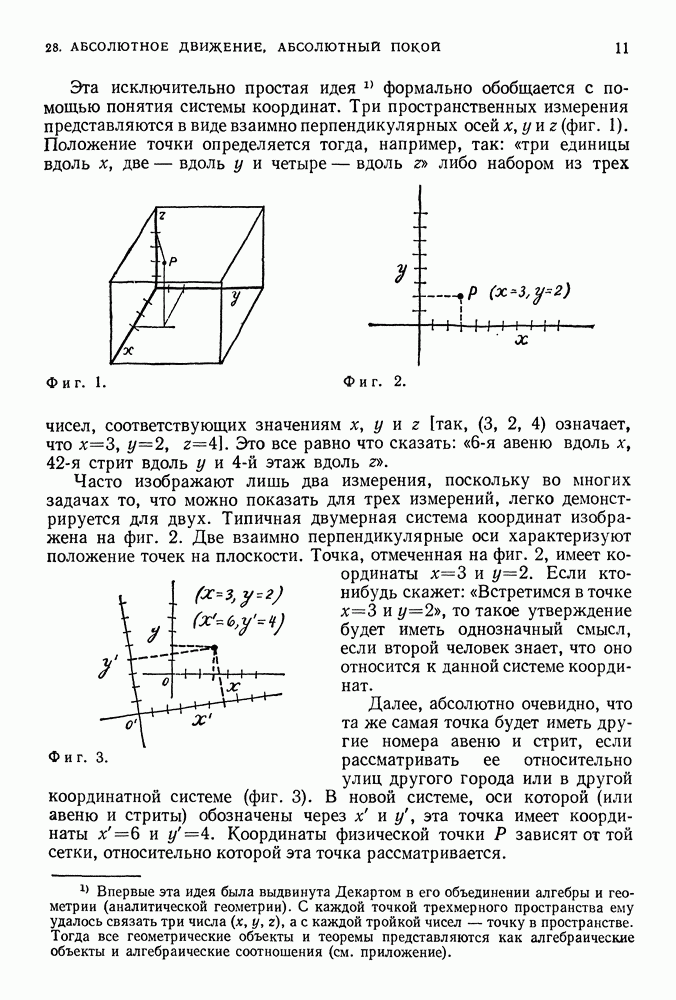
Скорость равна расстоянию, деленному на время. А скорость света, измеренная двумя движущимися друг относительно друга наблюдателями, одна и та же. Если мы согласимся с обоими этими утверждениями, нам придется пересмотреть наши понятия о расстоянии и времени. Сделать такой пересмотр довольно трудно, если не быть последовательным до конца. Наши представления о расстоянии и времени имеют очень глубокие корни. Используя эти представления, мы уже достигли больших успехов в упорядочении опыта нашей обыденной жизни.
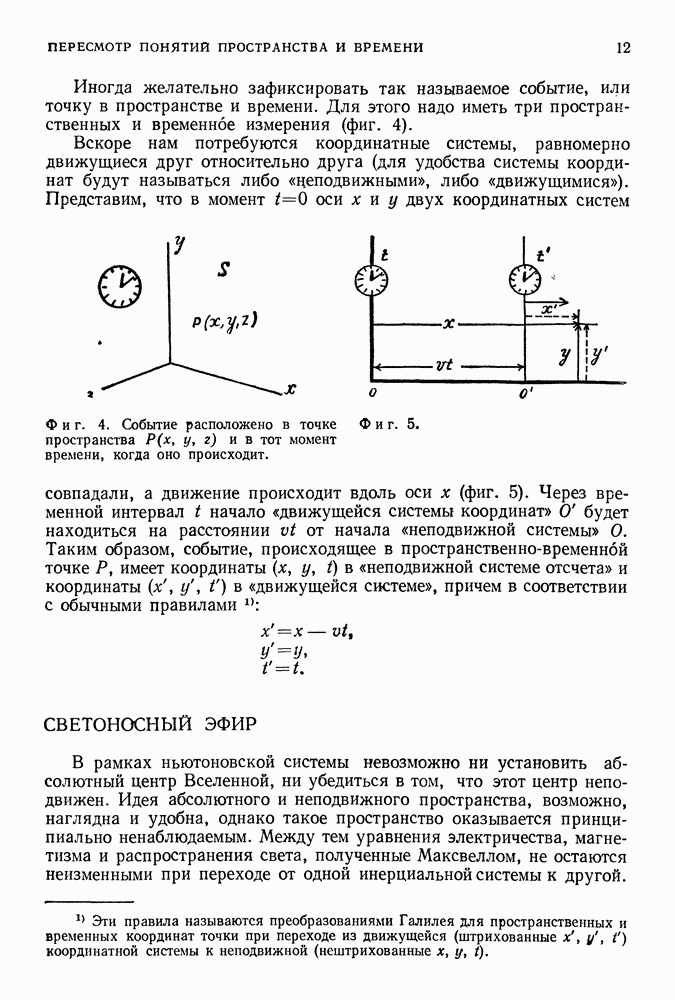
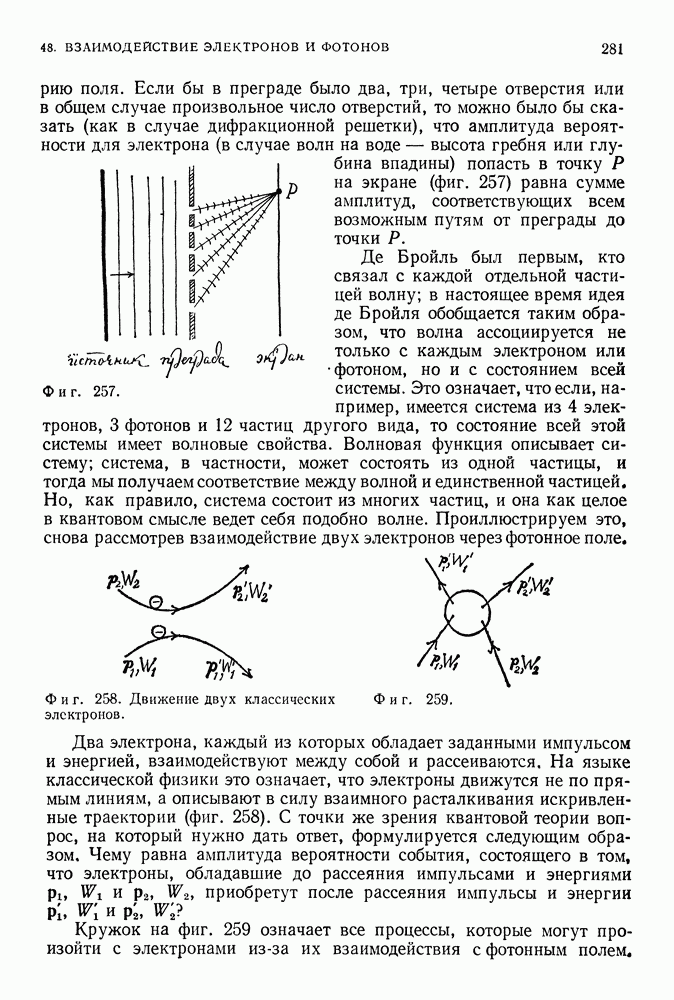
Рассмотрим световой импульс, посылаемый из начала так называемой неподвижной системы координат (система координат  Под этим мы не подразумеваем, что эта система неподвижна в каком-то абсолютном смысле, а имеем лишь в виду, что в этой системе «справедливы уравнения механики» (она является инерциальной), и договариваемся о том, что она неподвижна. В этой системе координат есть обычные, но точные часы, расположенные достаточно удобно, чтобы не приходилось далеко ходить для сверки их с часами, синхронизованными по правилу Эйнштейна (фиг. 25).
Под этим мы не подразумеваем, что эта система неподвижна в каком-то абсолютном смысле, а имеем лишь в виду, что в этой системе «справедливы уравнения механики» (она является инерциальной), и договариваемся о том, что она неподвижна. В этой системе координат есть обычные, но точные часы, расположенные достаточно удобно, чтобы не приходилось далеко ходить для сверки их с часами, синхронизованными по правилу Эйнштейна (фиг. 25).
Представим, что при  из начала координатной системы
из начала координатной системы  испускается световой сигнал, распространяющийся вдоль оси
испускается световой сигнал, распространяющийся вдоль оси
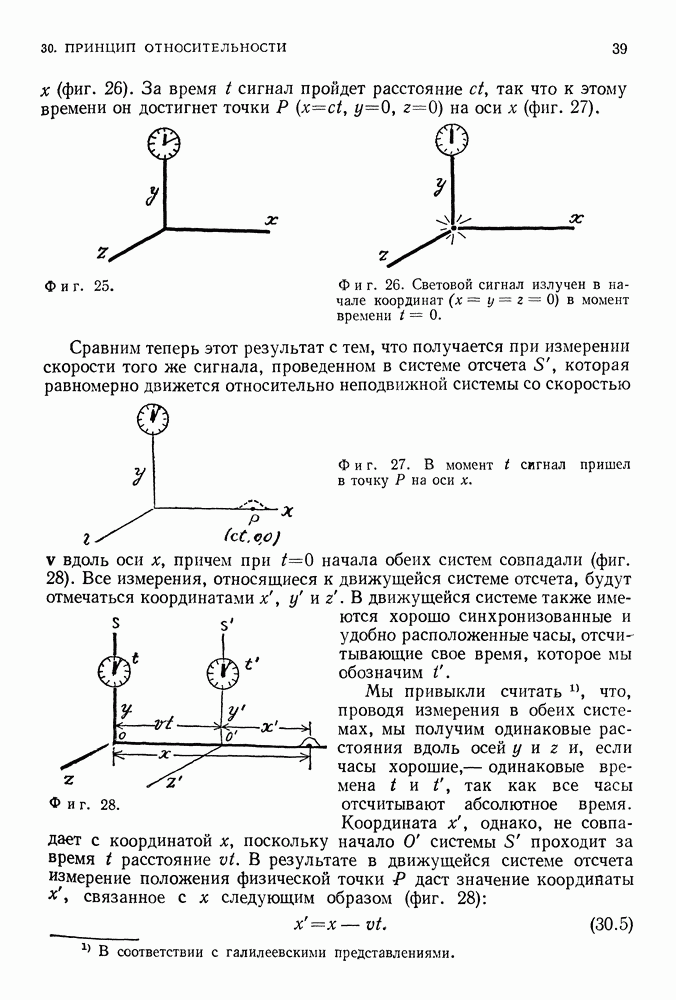
х (фиг. 26). За время  сигнал пройдет расстояние
сигнал пройдет расстояние  так что к этому времени он достигнет точки
так что к этому времени он достигнет точки  на оси
на оси 

Фиг. 25.

Фиг. 26. Световой сигнал излучен в начале координат  в момент времени
в момент времени 
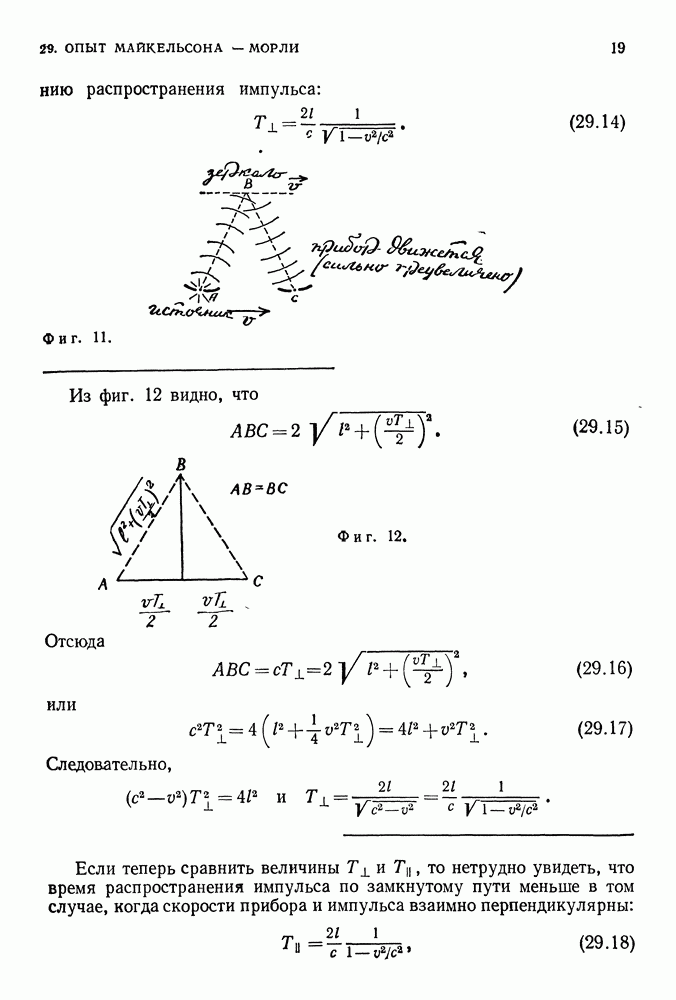
Сравним теперь этот результат с тем, что получается при измерении скорости того же сигнала, проведенном в системе отсчета  которая равномерно движется относительно неподвижной системы со скоростью вдоль оси
которая равномерно движется относительно неподвижной системы со скоростью вдоль оси  причем при начала обеих систем совпадали (фиг. 28).
причем при начала обеих систем совпадали (фиг. 28).

Фиг. 27. В момент  сигнал пришел в точку Р на оси х.
сигнал пришел в точку Р на оси х.
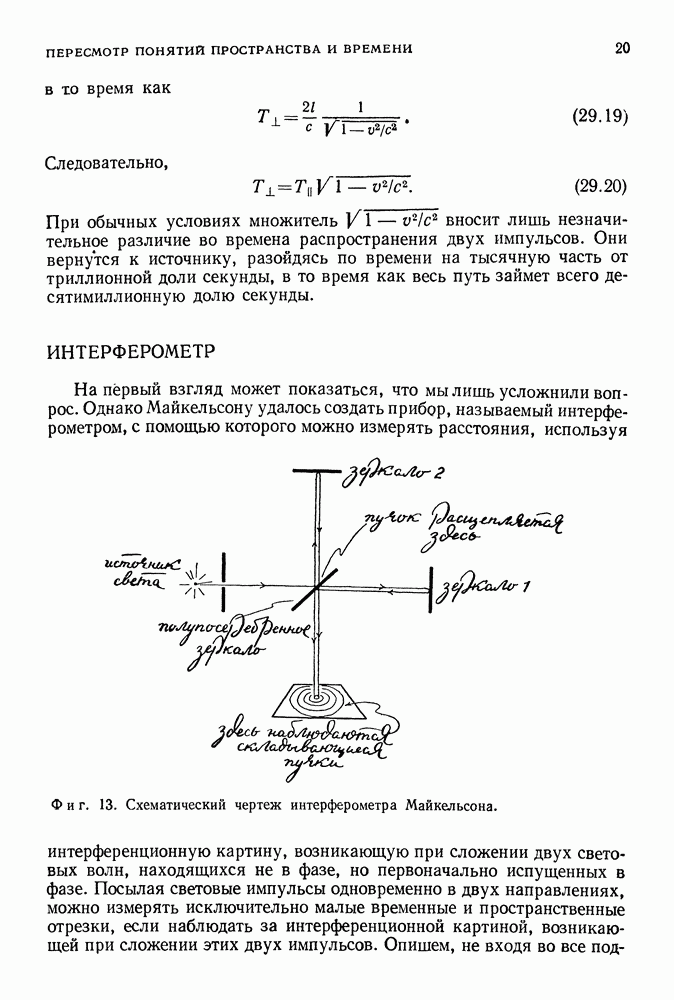
Все измерения, относящиеся к движущейся системе отсчета, будут отмечаться координатами  . В движущейся системе также имеются хорошо синхронизованные и удобно расположенные часы, отсчитывающие свое время, которое мы обозначим С.
. В движущейся системе также имеются хорошо синхронизованные и удобно расположенные часы, отсчитывающие свое время, которое мы обозначим С.

Фиг. 28.
Мы привыкли считать, что, проводя измерения в обеих системах, мы получим одинаковые расстояния вдоль осей у и  , если часы хорошие, — одинаковые времена
, если часы хорошие, — одинаковые времена  так как все часы отсчитывают абсолютное время. Координата
так как все часы отсчитывают абсолютное время. Координата  однако, не совпадает с координатой х, поскольку начало О системы
однако, не совпадает с координатой х, поскольку начало О системы  проходит за время
проходит за время  расстояние
расстояние  . В результате в движущейся системе отсчета измерение положения физической точки «Р даст значение координаты связанное с х следующим образом (фиг. 28):
. В результате в движущейся системе отсчета измерение положения физической точки «Р даст значение координаты связанное с х следующим образом (фиг. 28):

Таким образом, мы привыкли полагать, что соотношения между координатами одной и той же физической точки Р (точка, где находится световой сигнал), наблюдаемой в двух системах отсчета, имеют следующий вид (преобразования Галилея):

С точки зрения наблюдателя, находящегося в движущейся системе отсчета, точка Р отстоит от начала координат не дальше, чем с точки зрения наблюдателя в неподвижной системе, из-за того, что начало О приблизилось к точке Р. Так как вдоль направлений у и  движения не происходит, то
движения не происходит, то  . Как обычно, также
. Как обычно, также  . В результате скорость светового сигнала с точки зрения наблюдателя в движущейся системе отсчета будет равна
. В результате скорость светового сигнала с точки зрения наблюдателя в движущейся системе отсчета будет равна

Это отвечает нашим ожиданиям, но противоречит наблюдениям.
Что это значит? Координата х есть расстояние от О до Р (обозначим его через Г), измеренное в движущейся системе. Координата же х - расстояние от О до Р, измеренное в неподвижной системе. Оно равно расстоянию от О до О (равному  плюс расстояние от О до Р (обозначим его через
плюс расстояние от О до Р (обозначим его через  измеренное в неподвижной системе (фиг. 29).
измеренное в неподвижной системе (фиг. 29).

Фиг. 29.
Обычно мы не испытываем никаких сомнений, полагая, что  т. е. считая, что расстояние между двумя физическими точками (точкой О, где может кто-то находиться, и точкой Р, куда пришел световой сигнал) не зависит от того, измеряем ли мы его в неподвижной или движущейся системе отсчета. Вроде бы для сомнений действительно нет повода: ведь, основываясь на таком предположении, ученые достигли огромных успехов в интерпретации физических явлений. Но мы говорим сейчас не о резонности такого допущения; мы просто констатируем, что мы выдвинули некоторое допущение, неважно, резонное оно или нет, касающееся свойств нашего мира (так же, например, как мы предполагали, что свет распространяется по «прямой линии»), а эти свойства могухоказаться вовсе и не такими.
т. е. считая, что расстояние между двумя физическими точками (точкой О, где может кто-то находиться, и точкой Р, куда пришел световой сигнал) не зависит от того, измеряем ли мы его в неподвижной или движущейся системе отсчета. Вроде бы для сомнений действительно нет повода: ведь, основываясь на таком предположении, ученые достигли огромных успехов в интерпретации физических явлений. Но мы говорим сейчас не о резонности такого допущения; мы просто констатируем, что мы выдвинули некоторое допущение, неважно, резонное оно или нет, касающееся свойств нашего мира (так же, например, как мы предполагали, что свет распространяется по «прямой линии»), а эти свойства могухоказаться вовсе и не такими.
Но если считать, что  то мы получим преобразования Галилея и вывод (не согласующийся с опытом), что скорость света, измеренная в движущейся системе, не равна с. При таких обстоятельствах нам ничего не остается, как только заключить, что либо длина
то мы получим преобразования Галилея и вывод (не согласующийся с опытом), что скорость света, измеренная в движущейся системе, не равна с. При таких обстоятельствах нам ничего не остается, как только заключить, что либо длина
V не равна  либо время
либо время  не равно
не равно  либо и то и другое вместе. Иными словами, наши примитивные предположения, что часы идут одинаково, независимо от того, наблюдаем ли мы их в неподвижной или в движущейся системе, и что линейка сохраняет свою длину, когда начинает двигаться, оказываются противоречащими опыту.
либо и то и другое вместе. Иными словами, наши примитивные предположения, что часы идут одинаково, независимо от того, наблюдаем ли мы их в неподвижной или в движущейся системе, и что линейка сохраняет свою длину, когда начинает двигаться, оказываются противоречащими опыту.
Эту точку зрения и избрал Альберт Эйнштейн в 1905 г. В качестве постулатов, имеющих отношение к «заговору» природы, он выдвинул невозможность измерения абсолютной скорости и постоянство скорости света: «Дальнейшие соображения опираются на принцип относительности и на принцип постоянства скорости света», Эйнштейн затем задается следующим вопросом. Если расстояние V не равно I и если не предполагать, что промежутки времени в движущейся системе совпадают с промежутками в неподвижной системе, то как тогда эти величины связаны между собой? Опираясь на свое определение временных промежутков и на предположения, что скорость света не изменяется в равномерно движущейся системе отсчета и что законы физики не зависят от равномерного движения системы, к которой они отнесены, Эйнштейну удалось получить как следствие этих постулатов соотношения между  Они имеют следующий вид:
Они имеют следующий вид:

Преобразования Галилея таковы:

Рассмотрим обобщение этих преобразований, взяв линейную зависимость между 

где  не зависят от
не зависят от  и
и  [При линейной зависимости мы ограничиваемся рассмотрением систем отсчета, движущихся равномерно друг по отношению к другу. В общей теории относительности рводятся более общие (нелинейные) преобразования, где, например, х может зависеть от
[При линейной зависимости мы ограничиваемся рассмотрением систем отсчета, движущихся равномерно друг по отношению к другу. В общей теории относительности рводятся более общие (нелинейные) преобразования, где, например, х может зависеть от 
Для преобразований Галилея

но в этом случае отношение  не равно с, если
не равно с, если  (скорость света оказывается различной в разных системах).
(скорость света оказывается различной в разных системах).
Эйнштейн ищет такое решение, чтобы и  были бы равные:
были бы равные:

или

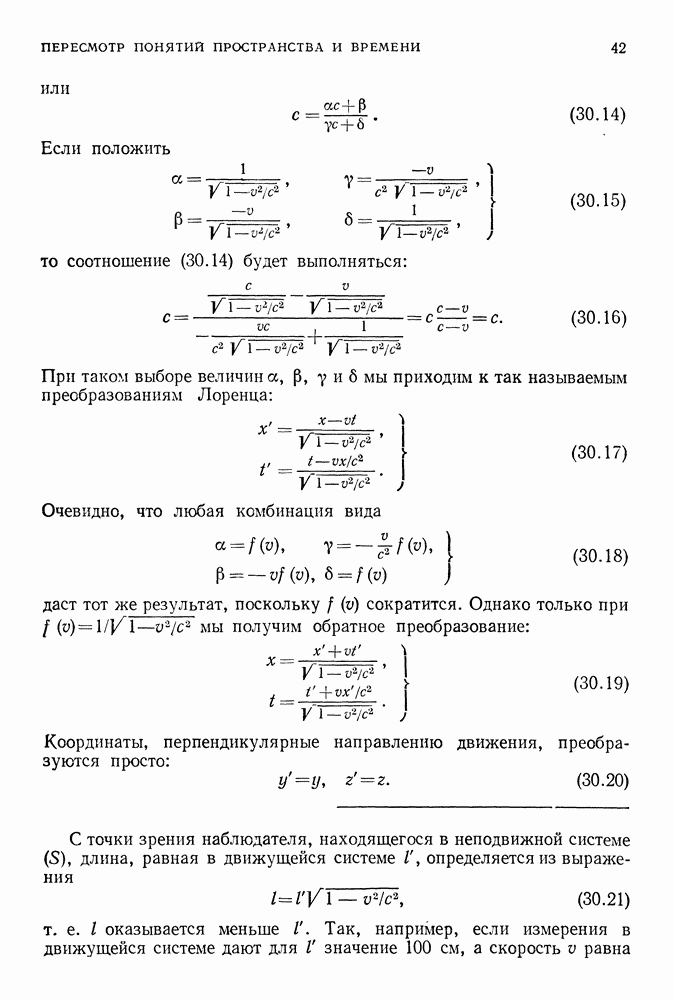
Если положить

то соотношение (30.14) будет выполняться:

При таком выборе величин а, (3, у и  мы приходим к так называемым преобразованиям Лоренца:
мы приходим к так называемым преобразованиям Лоренца:

Очевидно, что любая комбинация вида

даст тот же результат, поскольку  сократится. Однако только при
сократится. Однако только при  мы получим обратное преобразование:
мы получим обратное преобразование:

Координаты, перпендикулярные направлению движения, преобразуются просто:

С точки зрения наблюдателя, находящегося в неподвижной системе  длина, равная в движущейся системе Г, определяется из выражения
длина, равная в движущейся системе Г, определяется из выражения

т. е. I оказывается меньше Так, например, если измерения в движущейся системе дают для Г значение 100 см, а скорость  равна
равна
половине скорости света, то та же длина  с точки зрения наблюдателя, находящегося в неподвижной системе, будет равна
с точки зрения наблюдателя, находящегося в неподвижной системе, будет равна

Наблюдатель в системе  может встать на точку зрения, что покоится он, а наблюдатель в
может встать на точку зрения, что покоится он, а наблюдатель в  движется (в противоположную сторону). Тогда наблюдатель в
движется (в противоположную сторону). Тогда наблюдатель в  заключит, что стержни сократились в системе
заключит, что стержни сократились в системе  Эти наблюдатели пришли к такому кажущемуся противоречию, потому что их часы были не согласованы. То, что происходит «в одно и то же время» в системе
Эти наблюдатели пришли к такому кажущемуся противоречию, потому что их часы были не согласованы. То, что происходит «в одно и то же время» в системе  уже не происходит «в одно и то же время» в системе
уже не происходит «в одно и то же время» в системе  Как только наблюдатели отказались от согласования своих часов, они вынуждены отказаться от согласования длин
Как только наблюдатели отказались от согласования своих часов, они вынуждены отказаться от согласования длин

Фиг. 30.
Недоразумение отчасти объясняется следующим образом. В системе  длцда стержня оказалась равной Г. Наблюдатель в
длцда стержня оказалась равной Г. Наблюдатель в  измеряет длину этого стержня, когда последний движется мимо него. Каким образом? Он видит, что при
измеряет длину этого стержня, когда последний движется мимо него. Каким образом? Он видит, что при  один конец стержня находится при
один конец стержня находится при  а другой — при
а другой — при  Тогда он находит, что
Тогда он находит, что

Наблюдатель в системе  кричит ему: «Ты отмечал положение концов стержня не одновременно! Ты отметил дальний конец слишком рано!» [Из
кричит ему: «Ты отмечал положение концов стержня не одновременно! Ты отметил дальний конец слишком рано!» [Из  при
при  следует, что
следует, что  при
при  при
при  (фиг. 30).] Но к этому времени наблюдатель в
(фиг. 30).] Но к этому времени наблюдатель в  умчался уже далеко вперед.
умчался уже далеко вперед.
При 

С точки зрения наблюдателя из  наблюдатель в
наблюдатель в  отметил правый конец раньше левого, причем разница во времени равна как раз
отметил правый конец раньше левого, причем разница во времени равна как раз

Наблюдатель в  говорит: «Ты отметил правый конец слишком рано. Поэтому длина стержня оказалась у тебя короче». С точки зрения наблюдателя в
говорит: «Ты отметил правый конец слишком рано. Поэтому длина стержня оказалась у тебя короче». С точки зрения наблюдателя в  наблюдатель в
наблюдатель в  получил длину V минус расстояние, проходимое стержнем за отрезок времени (30.25):
получил длину V минус расстояние, проходимое стержнем за отрезок времени (30.25):

или

Анализируя так подробно процедуру измерения длины стержня наблюдателями обеих систем, мы в конце концов убеждаемся (часто, однако, не более чем на полминуты, что выдвинутый новый набор соглашений является согласованным. Сейчас мы попытаемся показать, почему эти соглашения удобны.

Фиг. 31.
Сфера, покоящаяся в движущейся системе отсчета  выглядит с точки зрения наблюдателя в неподвижной системе как эллипсоид, сплющенный в направлении движения (фиг. 31), так как
выглядит с точки зрения наблюдателя в неподвижной системе как эллипсоид, сплющенный в направлении движения (фиг. 31), так как
 в то время как размеры шара (а следовательно, и всякого другого твердого тела любой формы) по осям у и
в то время как размеры шара (а следовательно, и всякого другого твердого тела любой формы) по осям у и  от движения не изменяются, размеры по оси х сокращаются в отношении
от движения не изменяются, размеры по оси х сокращаются в отношении  и тем сильнее, чем больше
и тем сильнее, чем больше  При
При  все движущиеся объекты, наблюдаемые из «покоящейся» системы, сплющиваются и превращаются в плоские фигуры. Для скоростей, превышающих скорость света, наши рассуждения теряют смысл» [11].
все движущиеся объекты, наблюдаемые из «покоящейся» системы, сплющиваются и превращаются в плоские фигуры. Для скоростей, превышающих скорость света, наши рассуждения теряют смысл» [11].
Соотношение между  и
и  выглядит еще более странным. Часы не только ходят по-разному в различных движущихся системах, но их невозможно правильно синхронизовать. Дело в том, что показания часов зависят от их положения в пространстве; то, что одновременно в одной системе, не одновременно в другой.
выглядит еще более странным. Часы не только ходят по-разному в различных движущихся системах, но их невозможно правильно синхронизовать. Дело в том, что показания часов зависят от их положения в пространстве; то, что одновременно в одной системе, не одновременно в другой.
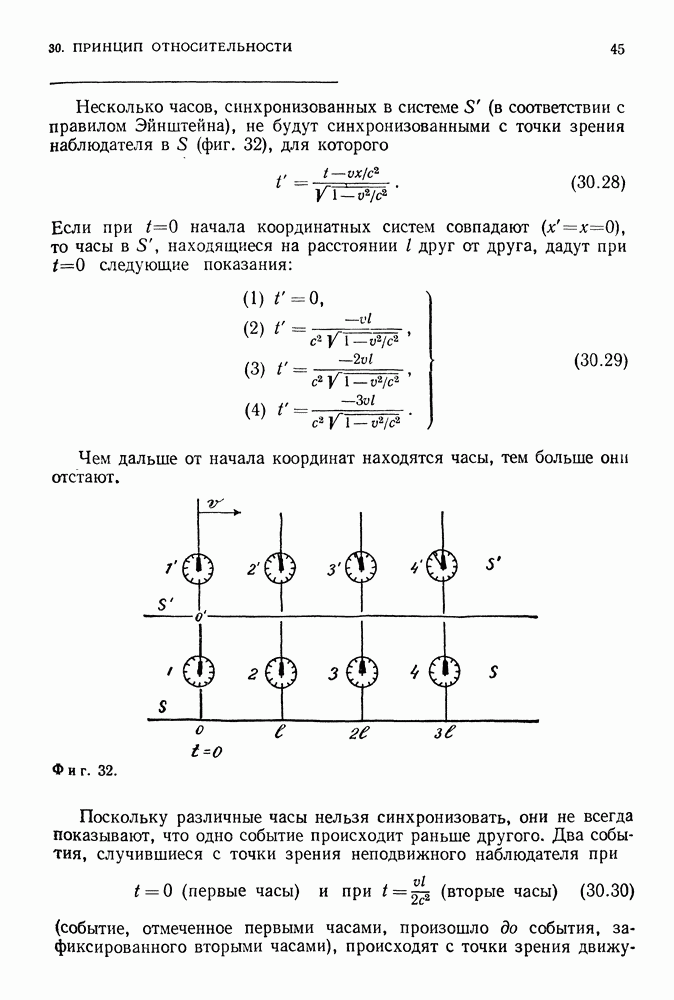
Несколько часов, синхронизованных в системе  (в соответствии с правилом Эйнштейна), не будут синхронизованными с точки зрения наблюдателя в
(в соответствии с правилом Эйнштейна), не будут синхронизованными с точки зрения наблюдателя в  (фиг. 32), для которого
(фиг. 32), для которого

Если при  начала координатных систем совпадают
начала координатных систем совпадают  то часы в
то часы в  находящиеся на расстоянии
находящиеся на расстоянии  друг от друга, дадут при
друг от друга, дадут при  следующие показания:
следующие показания:

Чем дальше от начала координат находятся часы, тем больше они отстают.

Фиг. 32.
Поскольку различные часы нельзя синхронизовать, они не всегда показывают, что одно событие происходит раньше другого. Два события, случившиеся с точки зрения неподвижного наблюдателя при

(событие, отмеченное первыми часами, произошло до события, зафиксированного вторыми часами), происходят с точки зрения движущегося
наблюдателя при

(событие, отмеченное первыми часами, произошло после события, зафиксированного вторыми часами).
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
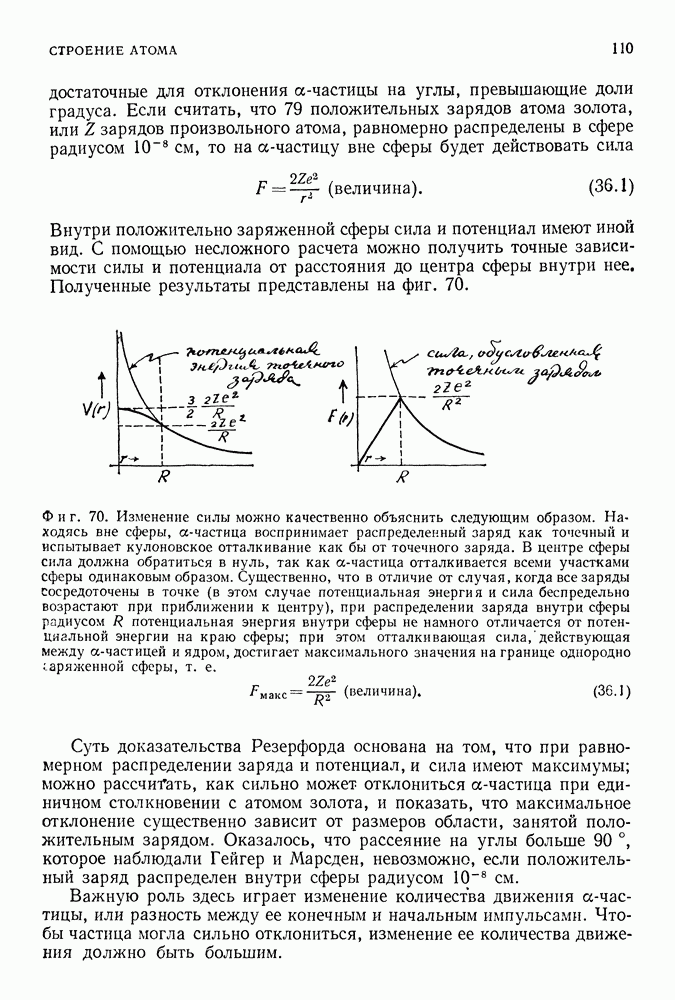
- 36. АТОМ РЕЗЕРФОРДА
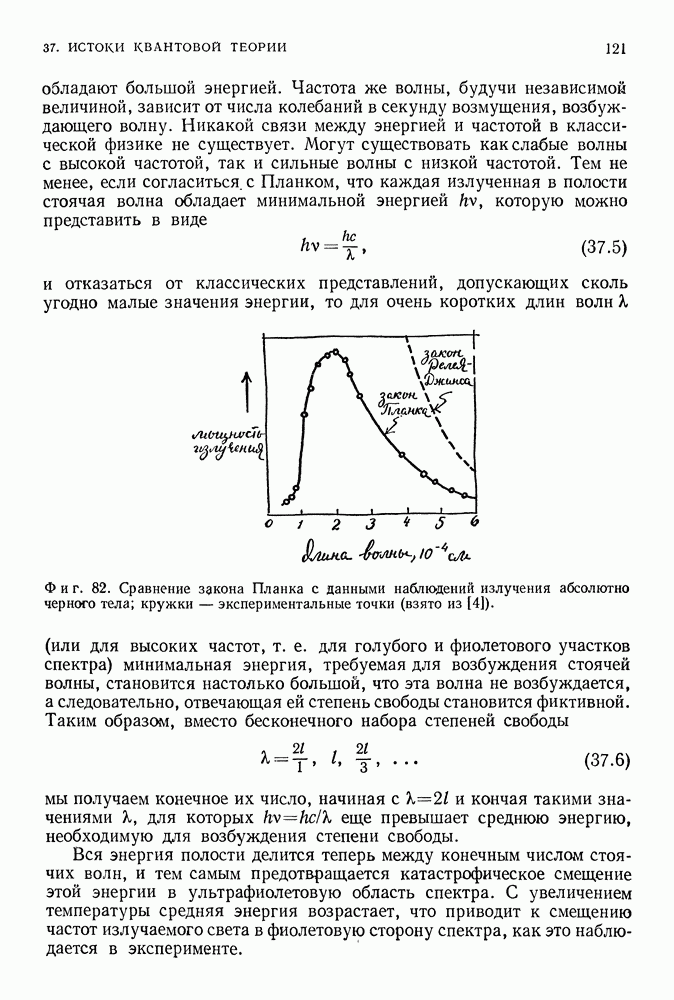
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
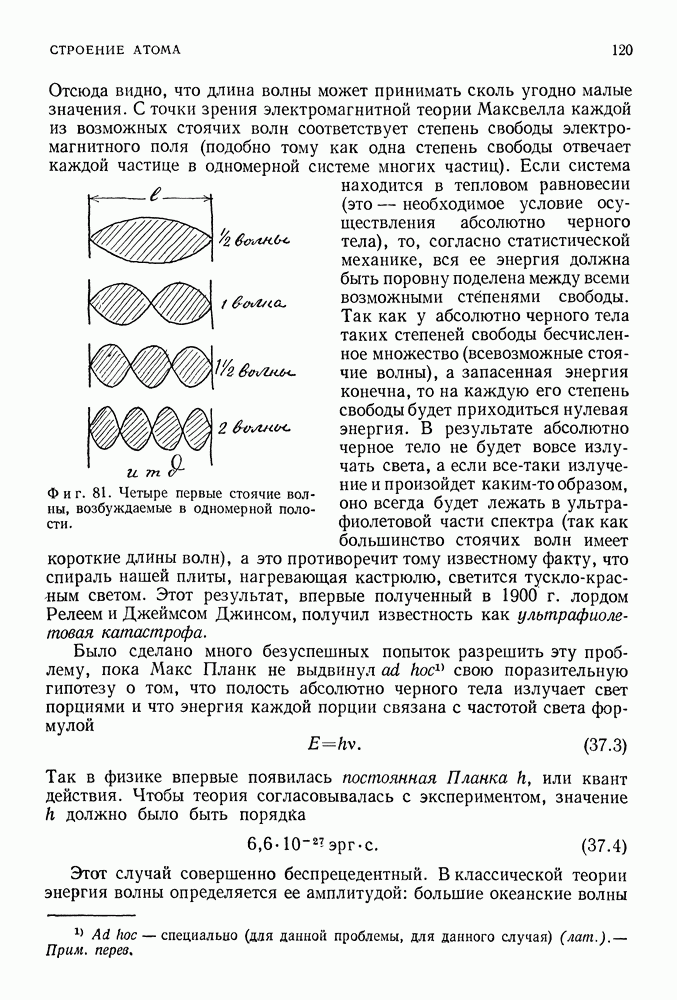
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
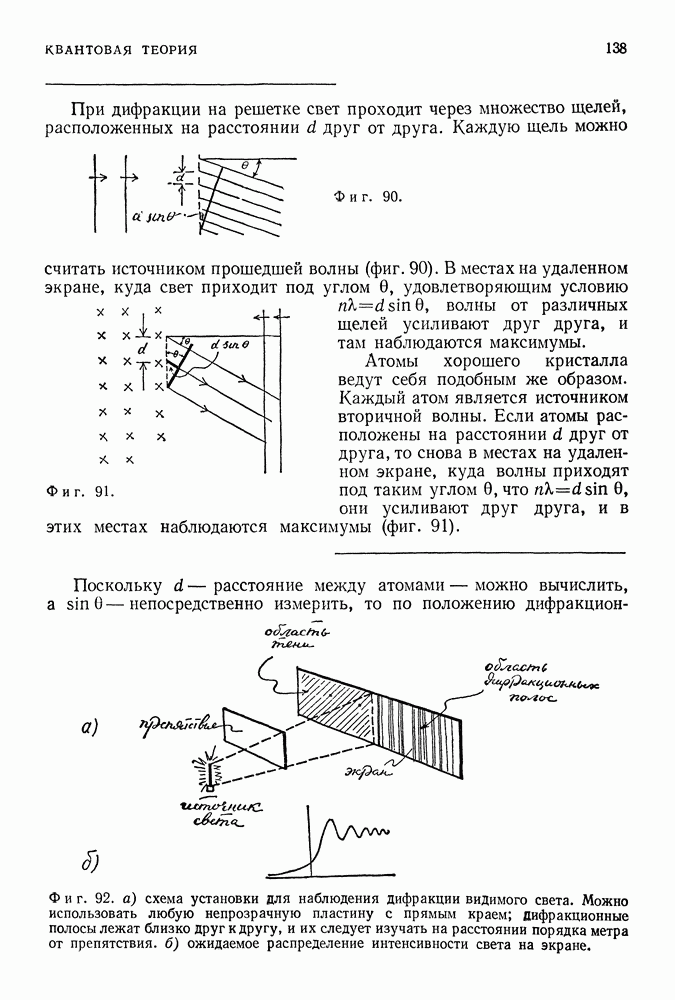
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА