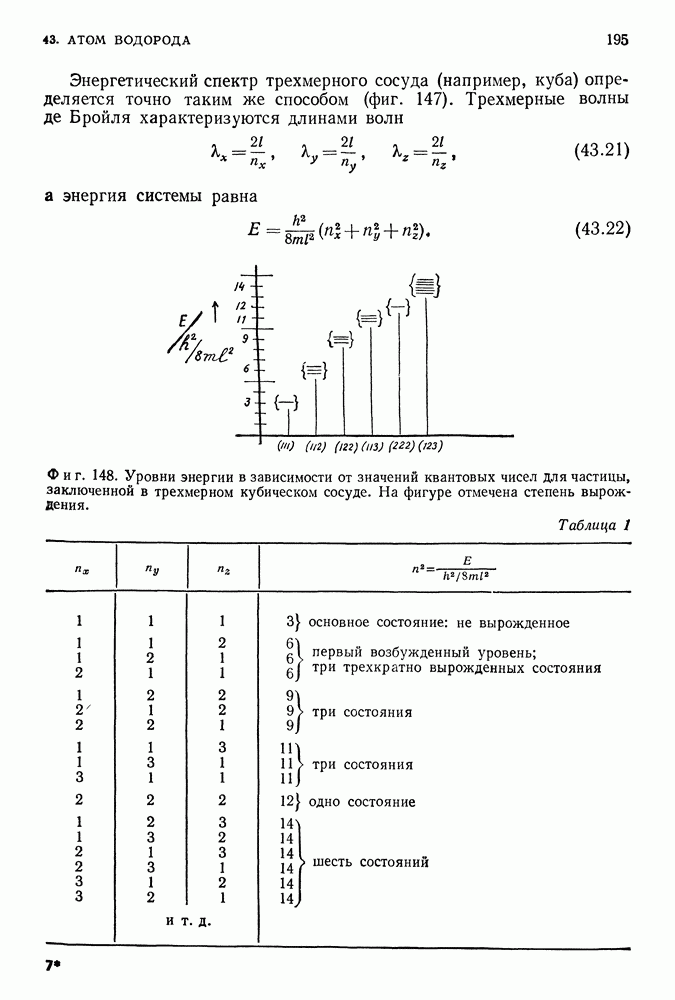
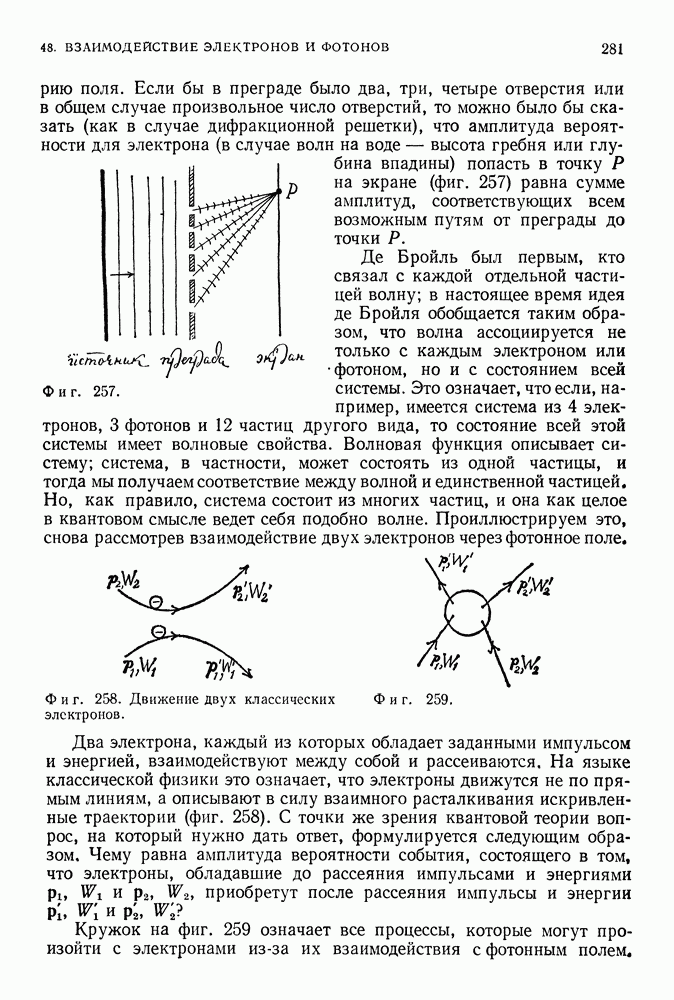
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
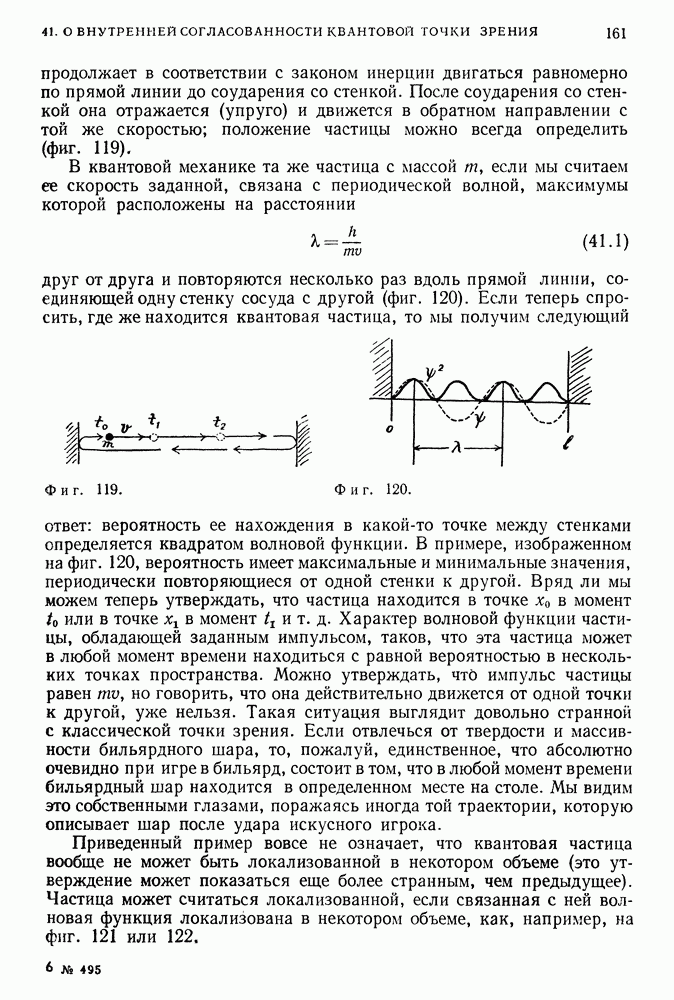
В самом начале развития квантовой теории поля (1930-1935 гг.) были рассчитаны такие процессы, как рассеяние электрона на электроне с обменом одним фотоном (кулоновское рассеяние) и рассеяние фотона на электроне (эффект Комптона). Эти расчеты показали, что если наряду с веществом включить в рассмотрение антивещество, т. е. принять во внимание состояния, которые отвечают отсутствующим электронам с отрицательной энергией (позитронам), то получаются однозначные результаты, хорошо согласующиеся с данными экспериментов.

Фиг. 267.

Фиг. 268.
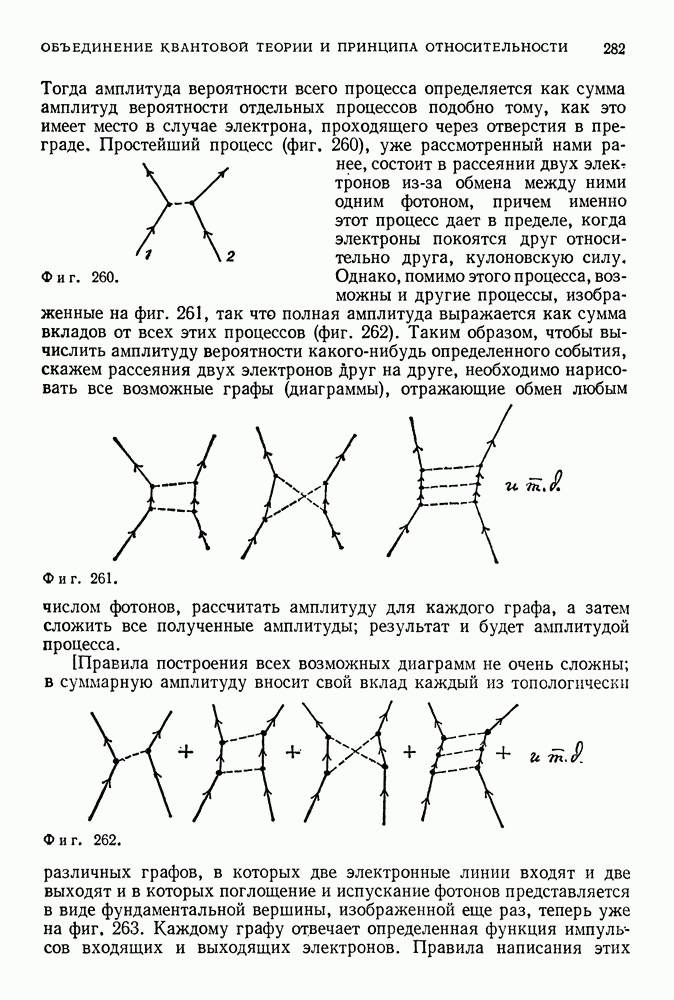
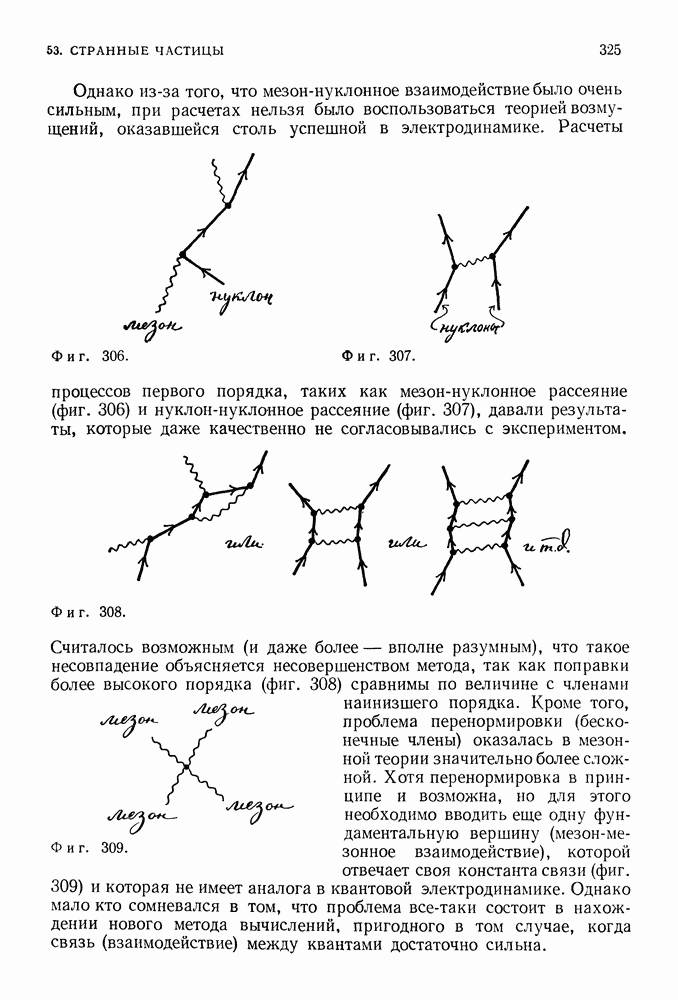
Однако, когда были предприняты попытки рассчитать процессы более высоких порядков (поправки к эффектам наинизшего порядка, соответствующие обменам дополнительными фотонами), очень скоро выяснилось, что получаются бесконечные по величине и, стало быть, бессмысленные результаты.
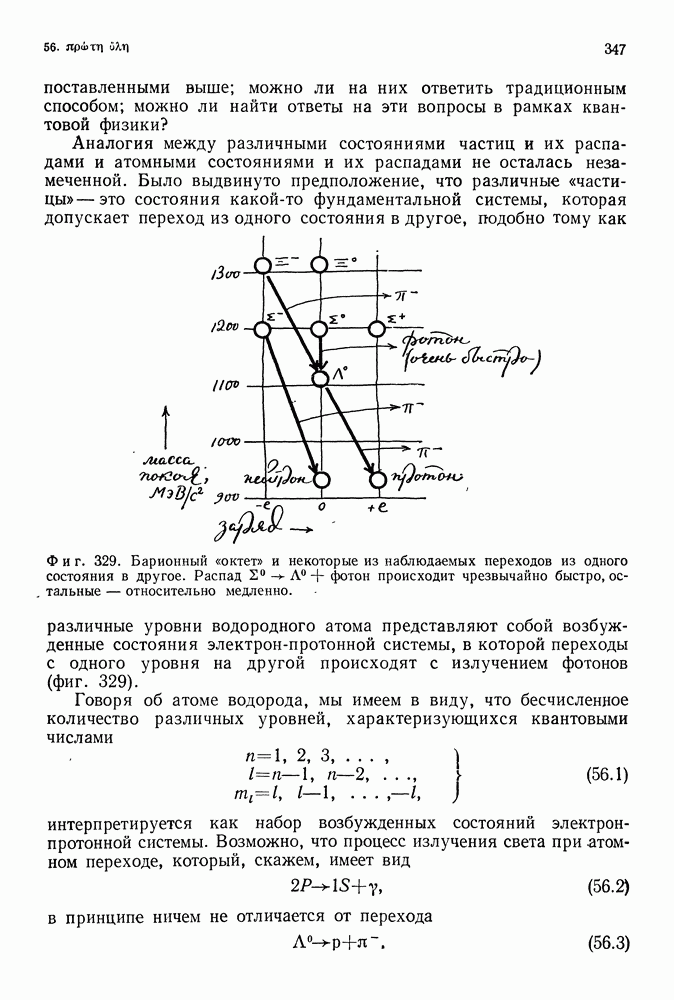
На фиг. 267 представлена диаграмма Фейнмана для рассеяния электрона на фотоне [амплитуда вероятности события, состоящего в том, что фотон  и электрон
и электрон  будут после рассеяния обладать импульсами и энергиями
будут после рассеяния обладать импульсами и энергиями  Этот граф дает конечный результат, прекрасно согласующийся с данными наблюдений. Вклад же графа более высокого порядка (фиг. 268), даже с учетом множителя 1/137, оказывается бесконечно большим.
Этот граф дает конечный результат, прекрасно согласующийся с данными наблюдений. Вклад же графа более высокого порядка (фиг. 268), даже с учетом множителя 1/137, оказывается бесконечно большим.
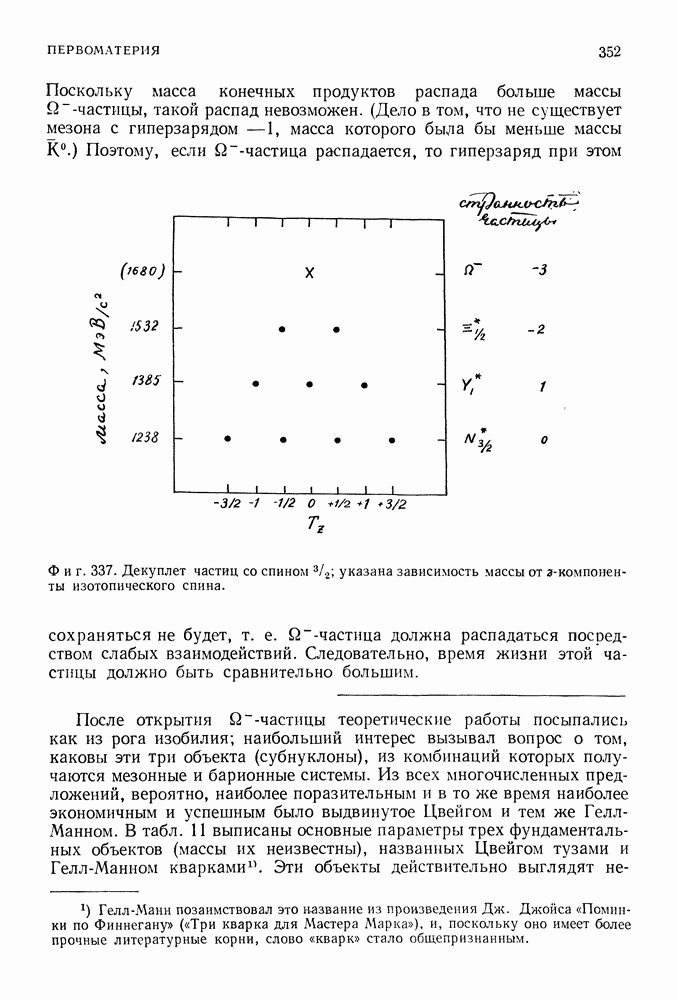
Эту проблему можно понять, рассмотрев наиболее простой процесс взаимодействия электрона с самим собой. На фиг. 269 изображена
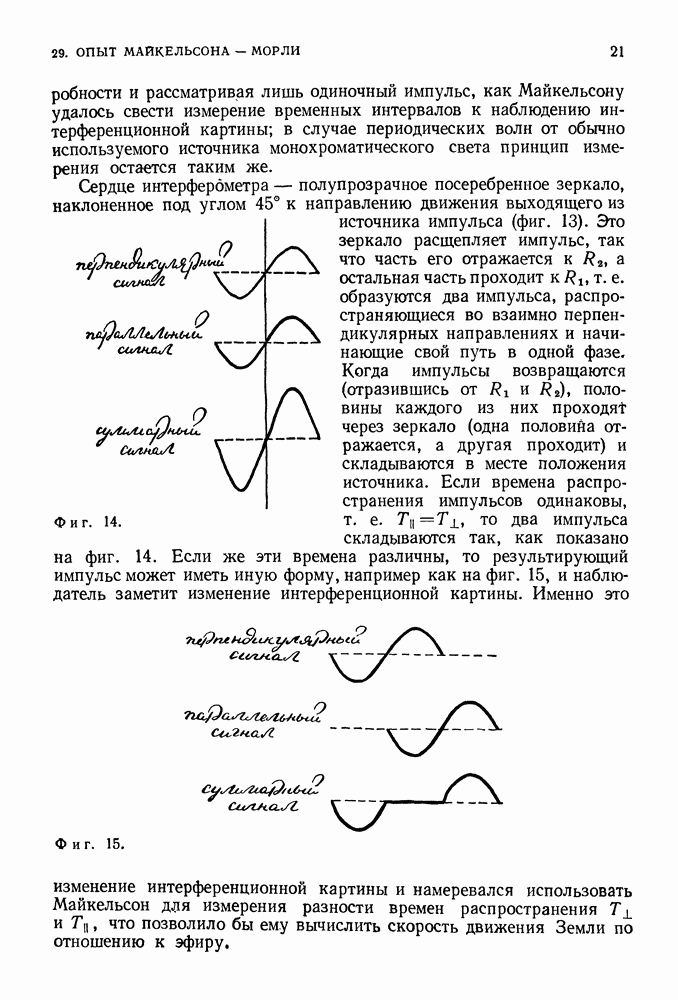
диаграмма Фейнмана для процесса, когда начальные и конечные импульсы и энергия электрона равны 
В отсутствие взаимодействия электрона с электромагнитным полем он обозначается непрерывной прямой линией. Если же электрон взаимодействует с полем, то он излучает и поглощает фотон, как показано на фиг. 270, Здесь изображена другая фейнмановская диаграмма, соответствующая входу и выходу, электрона с импульсом и энергией  . В промежутке между входом и выходом электрон излучает и поглощает фотон.
. В промежутке между входом и выходом электрон излучает и поглощает фотон.

Фиг. 269.

Фиг. 270.
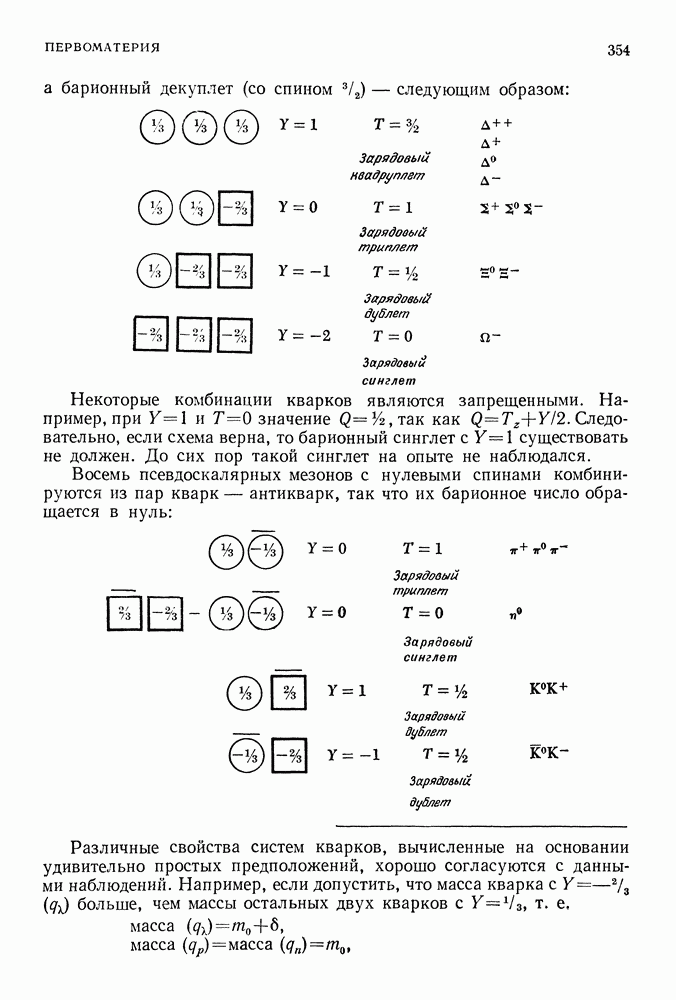
Если необходимо определить амплитуду вероятности события, состоящего в том, что электрон с заданными энергией и импульсом остается электроном с теми же энергией и импульсом, то эту амплитуду можно представить в виде суммы всех процессов такого рода; подобных процессов бесчисленное множество. На фиг. 271 изображены различные диаграммы Фейнмана для электрона, у которого начальные и конечные значения импульса и энергии одинаковы и равны 

Фиг. 271.
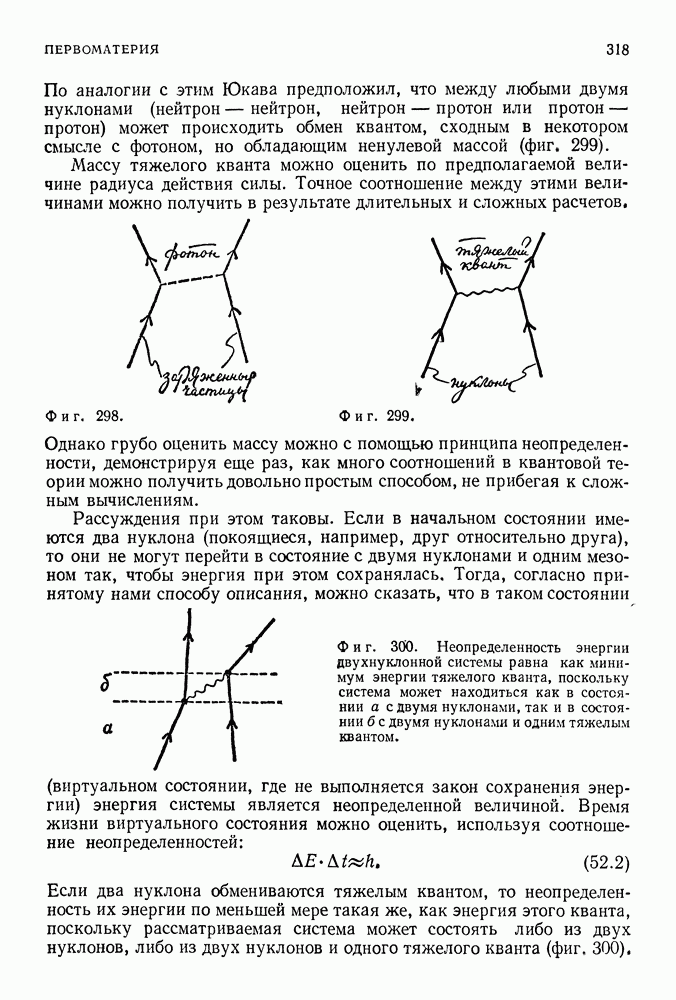
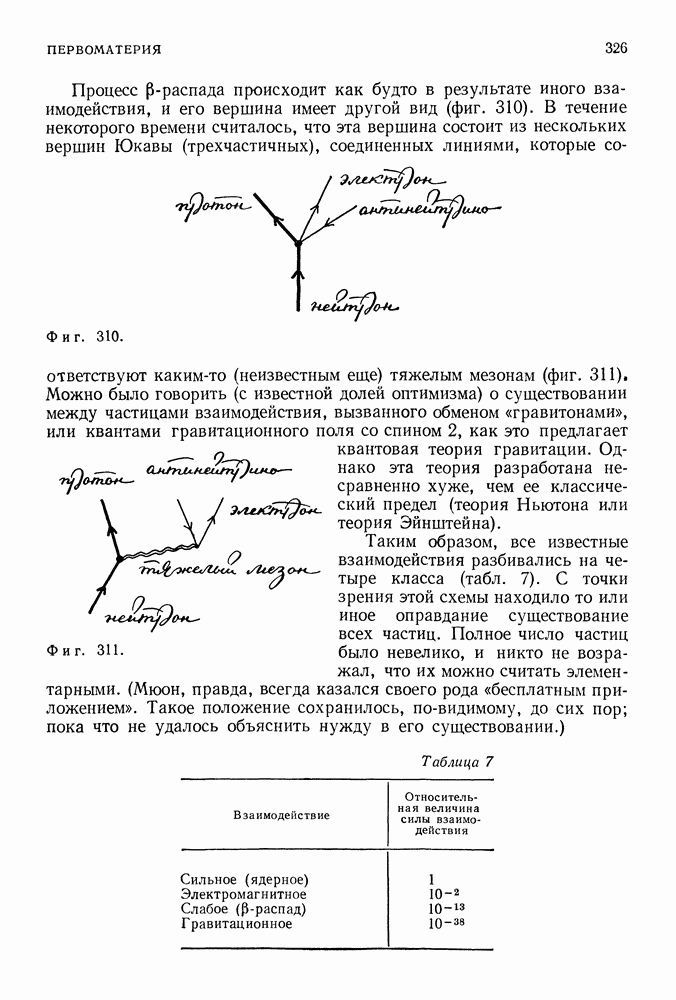
Можно думать, что движение электрона, который не испытывает действия внешних сил, должно обладать некоторыми свойствами инерциального движения, и это действительно так даже в квантовой теории поля, Однако при своем движении по инерции электрон может излучить и поглотить один, два или любое другое число фотонов. Такая возможность сама по себе не порождала бы никаких дополнительных проблем (так как вероятность события, состоящего в том, что электрон после излучения и поглощения фотонов станет обладать другими энергией и импульсом, равна нулю), если бы вклады от каждого из этих процессов не обращались в бесконечность. Бесконечно большие результаты получаются и при расчетах многих других процессов (некоторые из них будут упомянуты позже).
Бесконечно большие и потому лишенные смысла значения, полученные в результате расчетов, вызвали полное замешательство среди
физиков того времени. С одной, стороны, расчеты процессов наинизшего порядка, скажем обмена одним фотоном между двумя электронами, приводили к конечным результатам, которые прекрасно согласовывались с данными наблюдений, С другой же стороны, расчеты процессов более высокого порядка, которые в принципе должны были давать меньшие вклады в полную амплитуду вероятности, приводили к расходящимся результатам. (Последние равны бесконечно большим величинам, умноженным на  в какой-то степени.) Физики тех лет, как правило, принимали во внимание только результаты расчетов для процессов наинизшего порядка, которые совпадали с данными измерений, и отбрасывали то, что относилось к процессам более высокого порядка, так как было непонятно, что с ними делать. Этот прием — оставлять только то, что имеет конечную величину и какой-то смысл, и отбрасывать бесконечно большие величины — был доведен до такой степени «совершенства», что один из физиков (Роберт Сербер) иронически заметил: если число обращается в бесконечность, это не означает, что им можно пренебречь. Квантовая теория поля находилась в таком плачевном состоянии вплоть до окончания второй мировой войны, когда Фейнману, Швингеру, Томонаге и Дайсону удалось, используя идеи, предложенные Крамерсом и развитые Бете, успешно отделить конечные от бесконечных величин, появляющихся в теории.
в какой-то степени.) Физики тех лет, как правило, принимали во внимание только результаты расчетов для процессов наинизшего порядка, которые совпадали с данными измерений, и отбрасывали то, что относилось к процессам более высокого порядка, так как было непонятно, что с ними делать. Этот прием — оставлять только то, что имеет конечную величину и какой-то смысл, и отбрасывать бесконечно большие величины — был доведен до такой степени «совершенства», что один из физиков (Роберт Сербер) иронически заметил: если число обращается в бесконечность, это не означает, что им можно пренебречь. Квантовая теория поля находилась в таком плачевном состоянии вплоть до окончания второй мировой войны, когда Фейнману, Швингеру, Томонаге и Дайсону удалось, используя идеи, предложенные Крамерсом и развитые Бете, успешно отделить конечные от бесконечных величин, появляющихся в теории.
Рассмотрим, например, собственную энергию электрона, т. е. ту дополнительную энергию, которая обусловлена его взаимодействием с фотонами. Это взаимодействие описывается приведенными ранее диаграммами для случая движения электрона в пустом пространстве. При расчетах получаются бесконечно большие значения энергии. Но этому не следует придавать излишне большого значения, поскольку при помощи формальных технических приемов окончательные результаты делаются конечными. Однако взаимодействие электрона с фотонным полем приводит к; появлению дополнительной энергии электрона, а поскольку энергия эквивалентна массе, это означает появление дополнительной массы у электрона. Поэтому если вначале полагают, что масса электрона равна  то после учета описанных выше процессов эта масса
то после учета описанных выше процессов эта масса  увеличивается на некоторую величину
увеличивается на некоторую величину  т. Тогда полная масса электрона
т. Тогда полная масса электрона

В эксперименте же наблюдают именно «полную» массу  Начальная же масса
Начальная же масса  является ненаблюдаемой величиной: нельзя наблюдать движение электрона по инерции в отсутствие электромагнитного поля, так как электрон заряжен и всегда взаимодействует
является ненаблюдаемой величиной: нельзя наблюдать движение электрона по инерции в отсутствие электромагнитного поля, так как электрон заряжен и всегда взаимодействует
с собственным электромагнитным полем. Суть теории перенормировок состоит в утверждении, что бесконечной, а следовательно, лишенной смысла является величина  которая сама по себе не наблюдается. Наблюдается лишь сумма
которая сама по себе не наблюдается. Наблюдается лишь сумма  которая и является измеряемой массой электрона. На основании этого полагают, что
которая и является измеряемой массой электрона. На основании этого полагают, что  (ненаблюдаемая «голая» масса) тоже равна бесконечно большой величине, причем такой, что
(ненаблюдаемая «голая» масса) тоже равна бесконечно большой величине, причем такой, что

Аналогичным образом полагают, что другие процессы, приводящие к бесконечным результатам, исправляют исходный заряд электрона таким образом, что наблюдаемый заряд

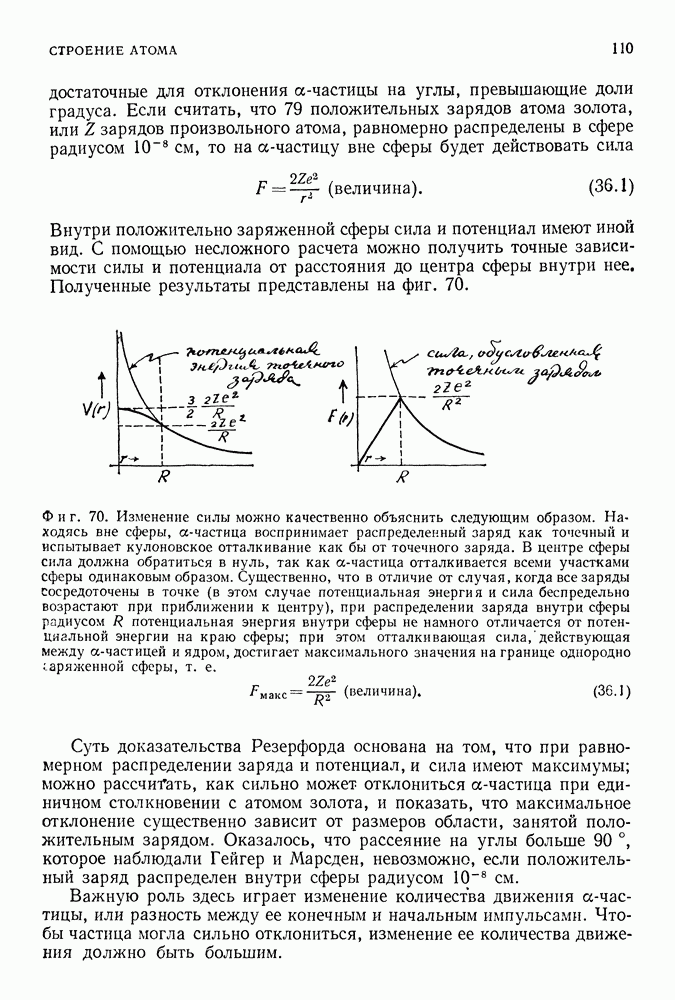
И снова наблюдаемой величиной считается лишь полный заряд е.
Вся идея перенормировок содержится в следующей теореме: все расходящиеся части различных графов связаны с изменением заряда и массы электрона. Если при расчетах любого сколь угодно сложного процесса заменить  на
на  на
на  то результаты окажутся конечными. Так стали возможными расчеты вкладов от любых процессов произвольного порядка (любых диаграмм) с помощью четко сформулированного метода: достаточно только исправить заряд и массу электрона так, чтобы эти величины стали равны наблюдаемым значениям.
то результаты окажутся конечными. Так стали возможными расчеты вкладов от любых процессов произвольного порядка (любых диаграмм) с помощью четко сформулированного метода: достаточно только исправить заряд и массу электрона так, чтобы эти величины стали равны наблюдаемым значениям.

Фиг. 272.

Фиг. 273.
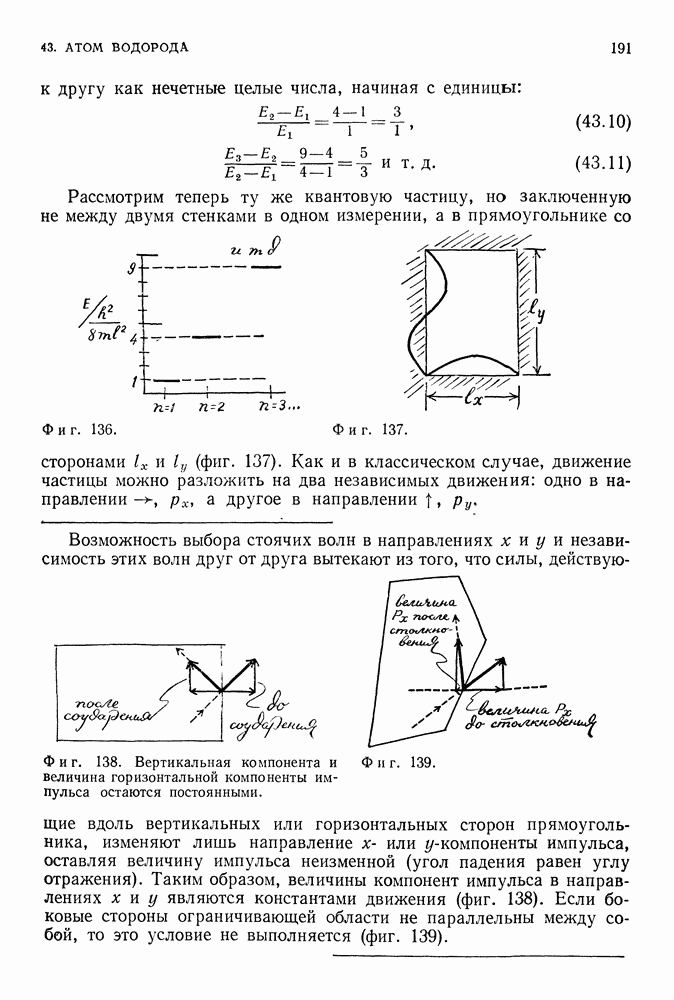
Используя этот замечательный метод, удалось определить чрезвычайно малые радиационные поправки к таким, например, величинам, как магнитный момент электрона. В случае магнитного момента электрона основной вклад в эффект дает диаграмма, изображенная на фиг. 272. Она описывает процесс, состоящий в том, что электрон излучает в точке 0 фотон, взаимодействует с внешним полем в точке У, а затем в точке 2 поглощает испущенный ранее фотон. Процесс наинизшего порядка, когда не учитываются радиационные поправки, представлен на фиг. 273, где электрон взаимодействует лишь с внешним магнитным полем в точке 1. Чтобы вычислить теперь вклад первого графа (фиг. 272), вносящего свою лепту в полную амплитуду электрона, взаимодействующего с электромагнитным полем, следует правильно
учестьг) собственную энергию электрона, которая определяется диаграммой, изображенной на фиг. 274. Если это сделать, то после сложнейших вычислений можно получить (впервые эти вычисления провел Швингер; они являются, по-видимому, самыми длинными и сложными расчетами, которые когда-либо проводил человек) исправленную величину магнитного момента электрона, которая известна под названием аномального магнитного момента.

Фиг. 274.

Фиг. 275
Современное теоретическое значение аномального момента (отнесенное к значению обычного момента  ) равно
) равно

в то время как измеренное значение

Таким образом, вычисленное и экспериментальное значения согласуются с точностью до одной миллионной.

Фиг. 276.
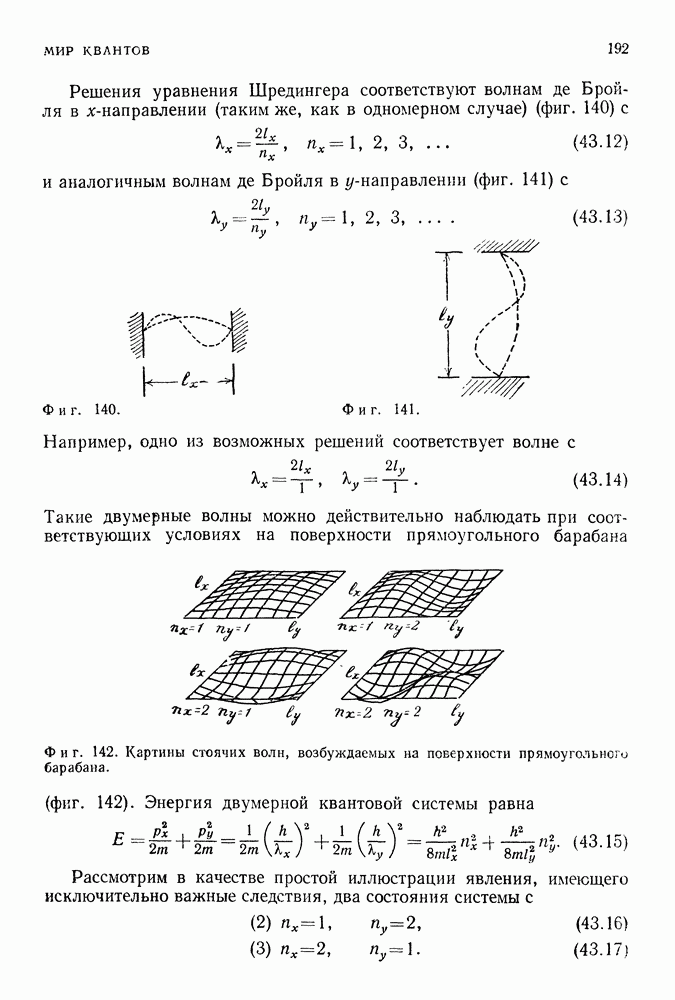
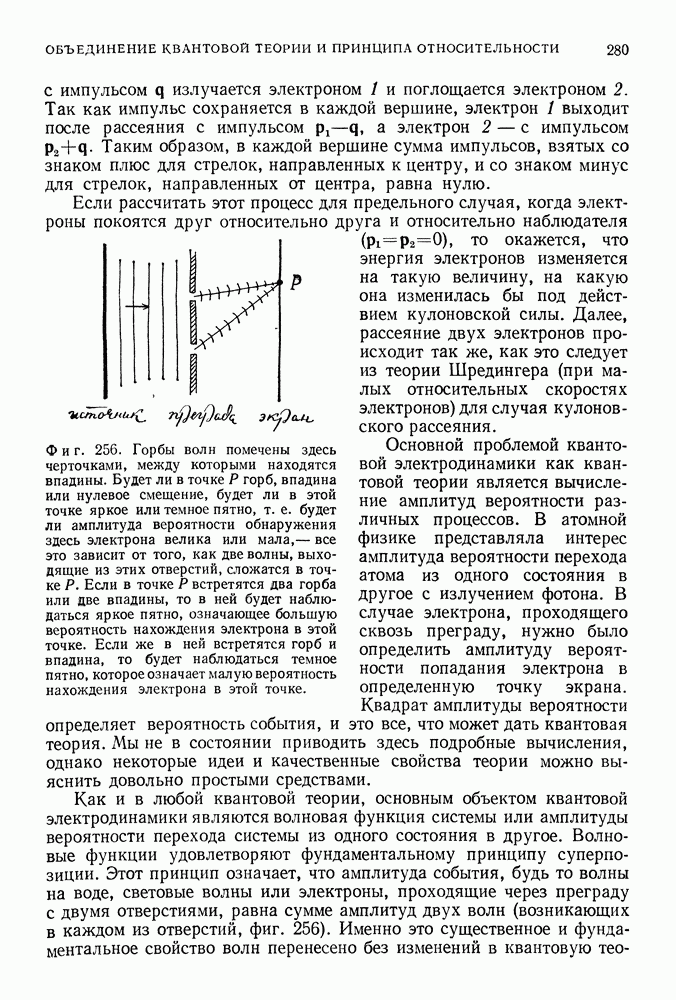
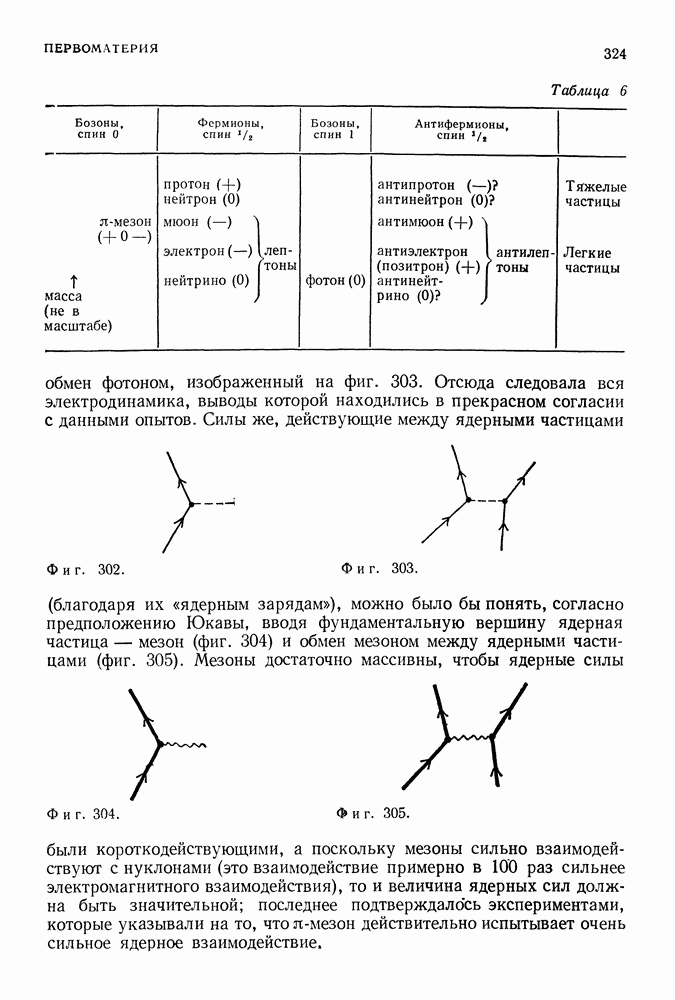
Аналогичным способом можно определить поправки и к самому закону Кулона. В квантовой теории поля этот закон вытекает из рассмотрения процесса, изображенного на фиг. 275 и состоящего в том, что две заряженные частицы обмениваются одним фотоном. Однако в такой процесс вносит вклад и диаграмма, изображенная на фиг. 276. Излученный фотон, прежде чем он достигает точки  рождает электрон-позитронную пару в точке 3, аннигилирующую с образованием фотона в точке 4, который затем поглощается второй частицей. Возможность образования электрон-позитронных пар приводит к своего рода поляризации вакуума (подобно тому, как в присутствии внешних зарядов положительные и отрицательные заряды диэлектрика расходятся
рождает электрон-позитронную пару в точке 3, аннигилирующую с образованием фотона в точке 4, который затем поглощается второй частицей. Возможность образования электрон-позитронных пар приводит к своего рода поляризации вакуума (подобно тому, как в присутствии внешних зарядов положительные и отрицательные заряды диэлектрика расходятся
в разные стороны, в результате чего диэлектрик поляризуется), которая искажает поля, вызвавшие поляризацию Так были получены поправки к закону Кулона, которые были подтверждены измерениями чрезвычайно слабого расщепления уровней атома водорода.
Согласно релятивистской теории Дирака, уровни  водородного атома должны обладать одинаковыми энергиями.
водородного атома должны обладать одинаковыми энергиями.

Фиг. 277.

Фиг. 278.
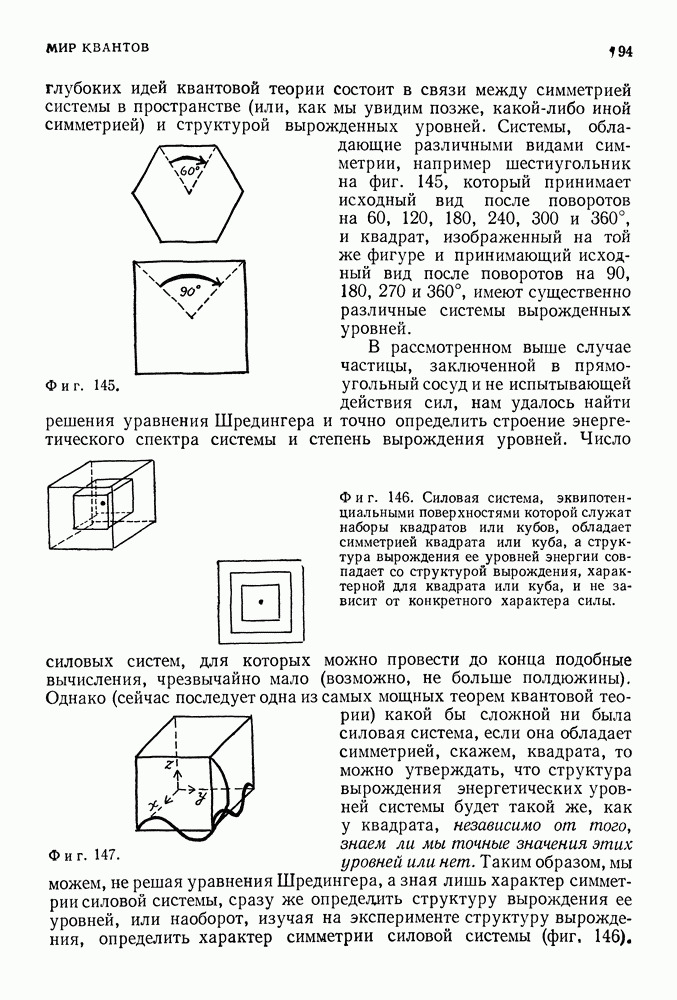
Однако вскоре после окончания второй мировой войны У. Лэмб,используя оборудование, появившееся в связи с развитием радиолокационной техники, обнаружил, что энергии этих уровней различаются на  эВ (фиг. 277). Это расщепление уровней, получившее название лэмбовского сдвига, пытались объяснить радиационными поправками, и именно это послужило толчком для разработки новых методов вычислений и теории перенормировок в квантовой электродинамике,
эВ (фиг. 277). Это расщепление уровней, получившее название лэмбовского сдвига, пытались объяснить радиационными поправками, и именно это послужило толчком для разработки новых методов вычислений и теории перенормировок в квантовой электродинамике,

Фиг. 279.

Фиг. 280.
Основной вклад в лэмбовский сдвиг дают поправки к величине магнитного момента электрона (фиг. 278) и поляризация вакуума (фиг. 279) Удобно сравнивать теоретическое и экспериментальное значения частоты излучения (частота в 109 Гц отвечает энергии  эВ), соответствующей переходу между уровнями
эВ), соответствующей переходу между уровнями  (фиг, 280),
(фиг, 280),
Сравнение теории и эксперимента дает [1]:

Вероятно, существуют фундаментальные проблемы, связанные с согласованностью квантовой электродинамики (теории взаимодействия квантовых электронов с фотонами максвелловского поля), Однако сейчас можно сказать, что эта теория в том виде, как она была развита (включая и методы вычислений), дала результаты, совпадающие с измерениями поразительно точно. В настоящее время вряд ли кто-нибудь усомнится в том, что различные ее соотношения, использованные, например, при вычислении магнитного момента электрона, сколько-нибудь серьезно изменятся в будущем, даже если теория будет пересмотрена, В этом смысле квантовая электродинамика является самой современной физической теорией, которая, как мы полагаем, внутренне вполне согласована.
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
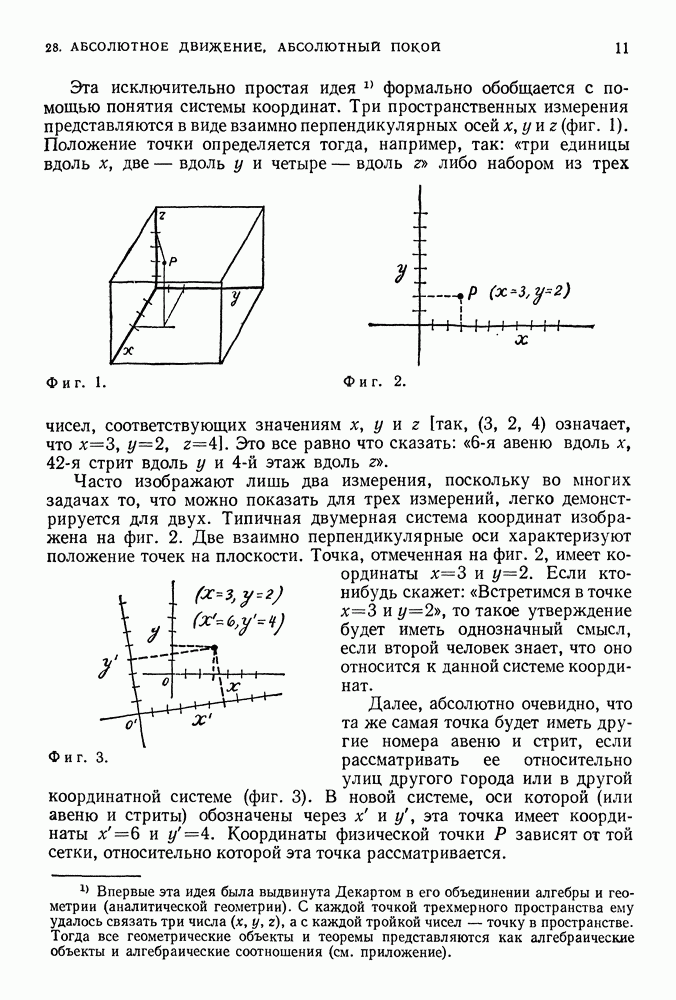
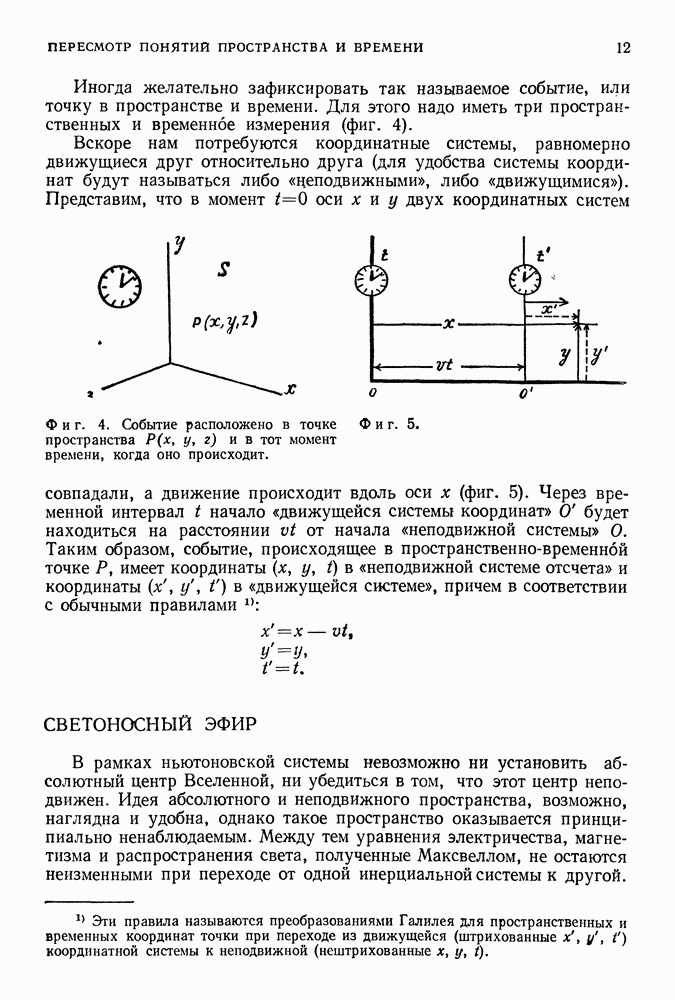
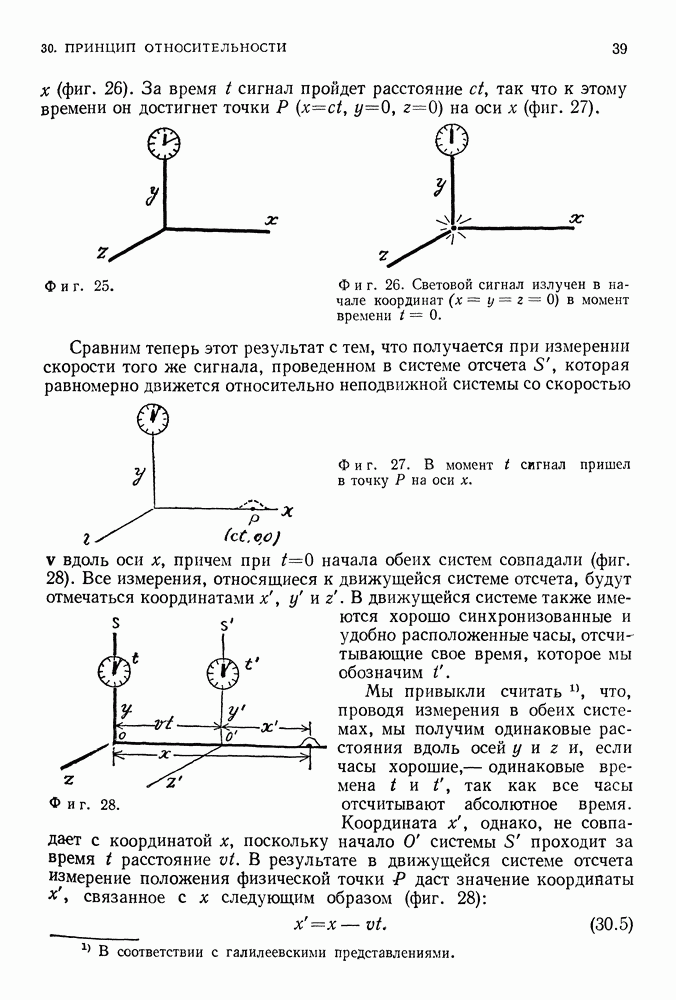
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
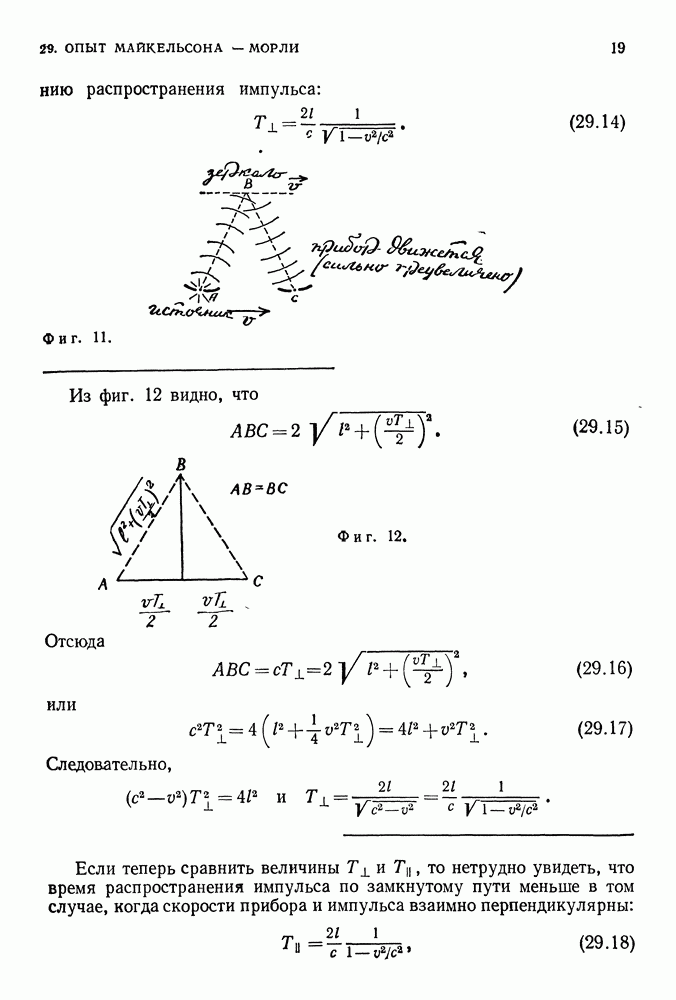
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
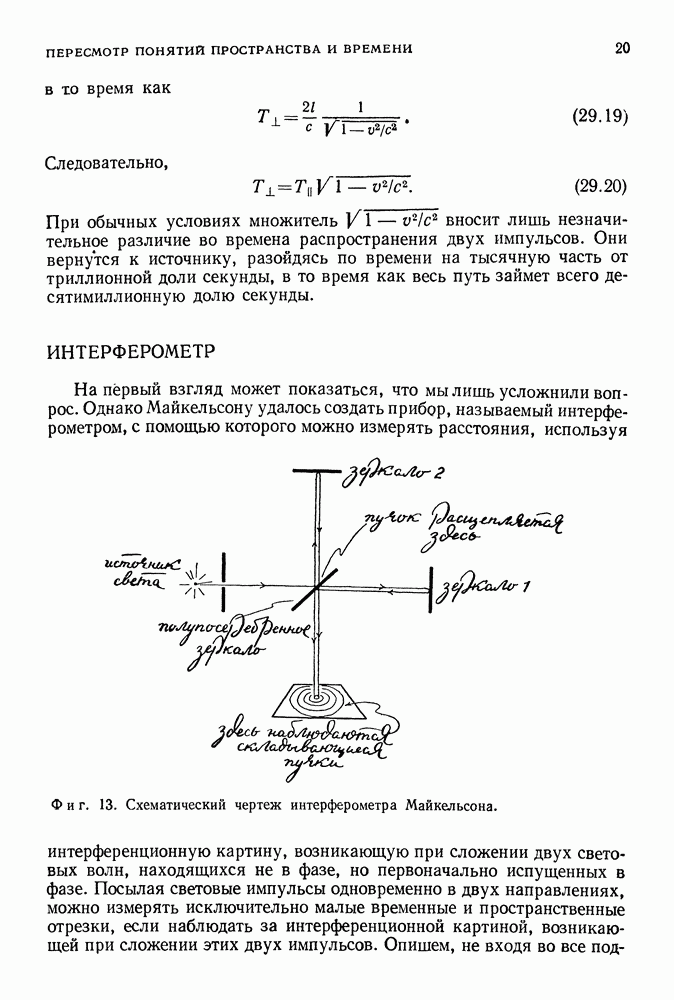
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
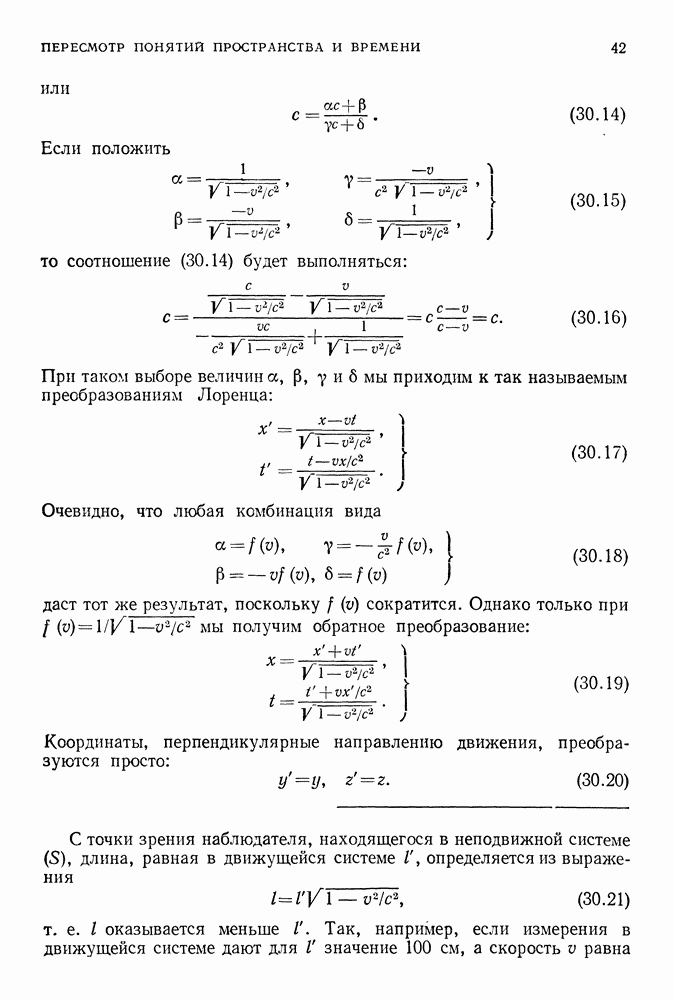
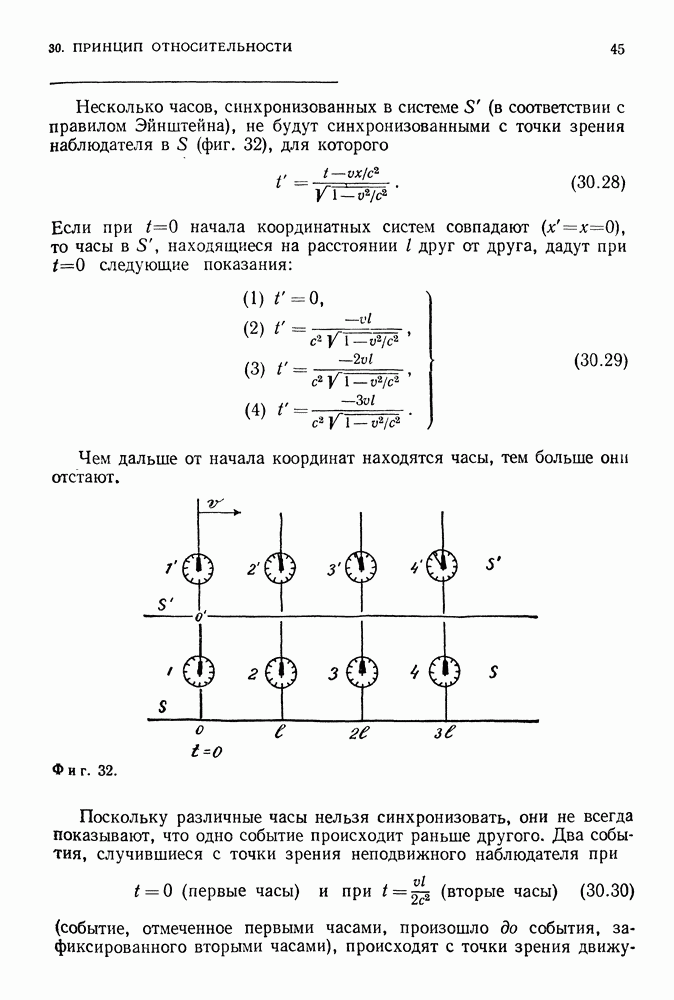
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
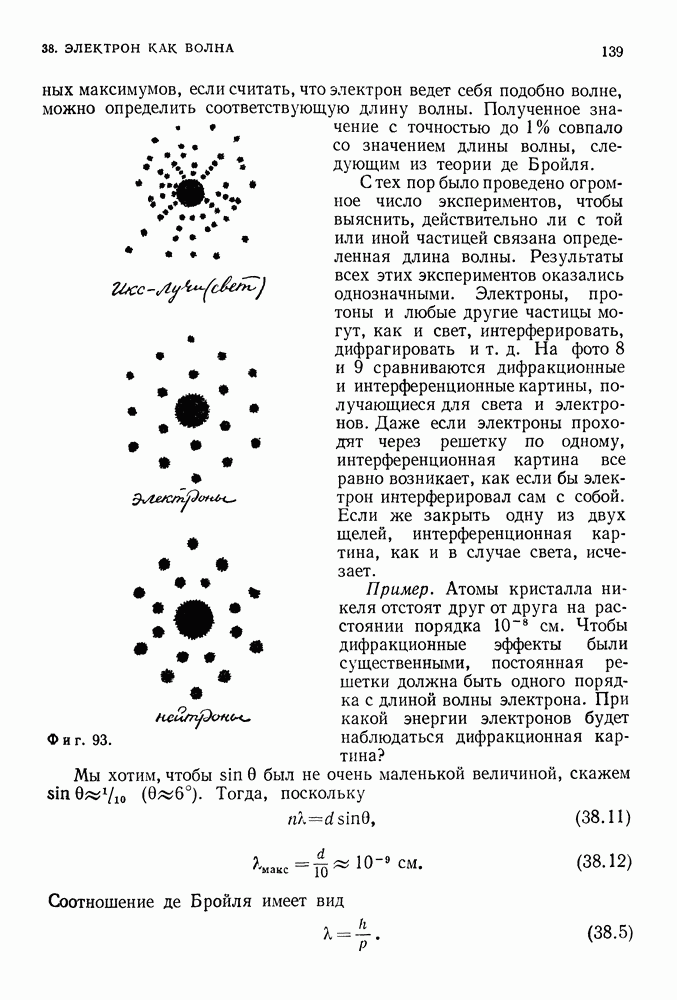
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
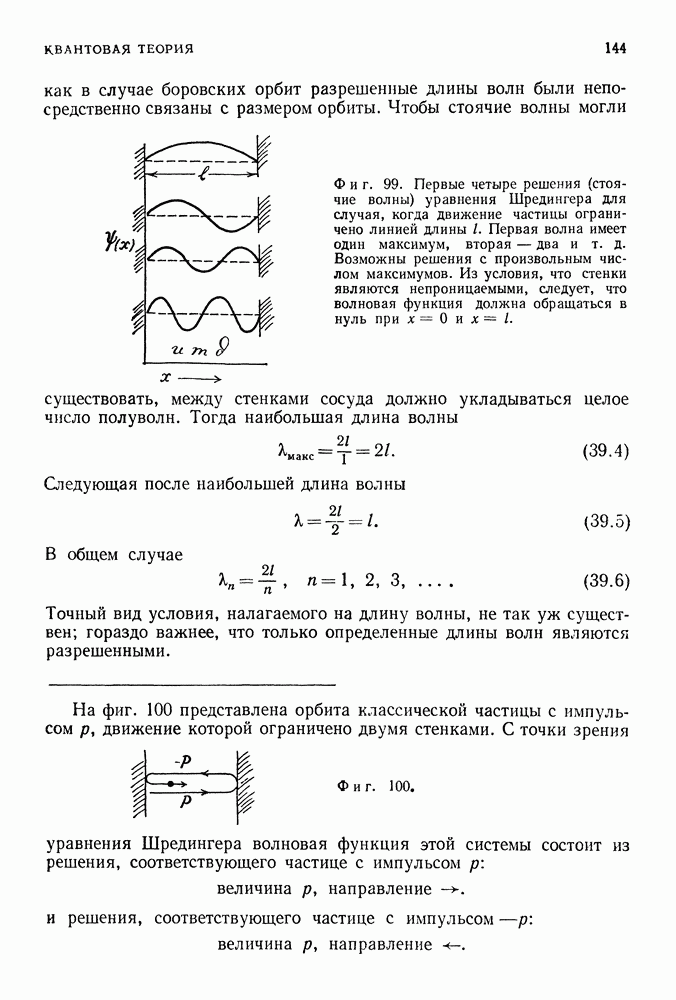
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
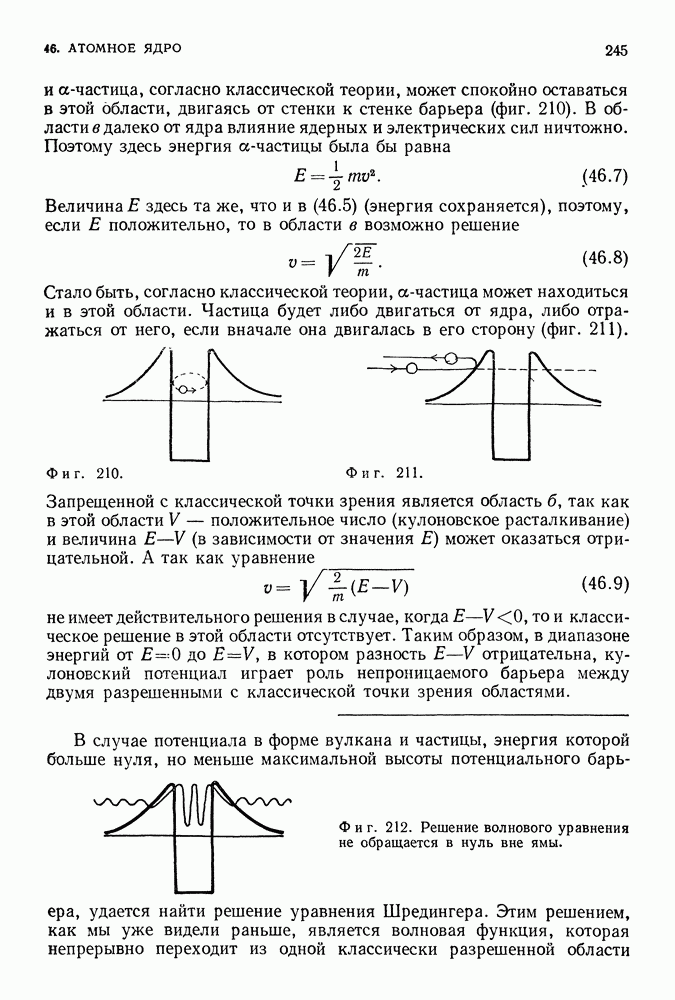
- СВОБОДНЫЕ РЕШЕНИЯ
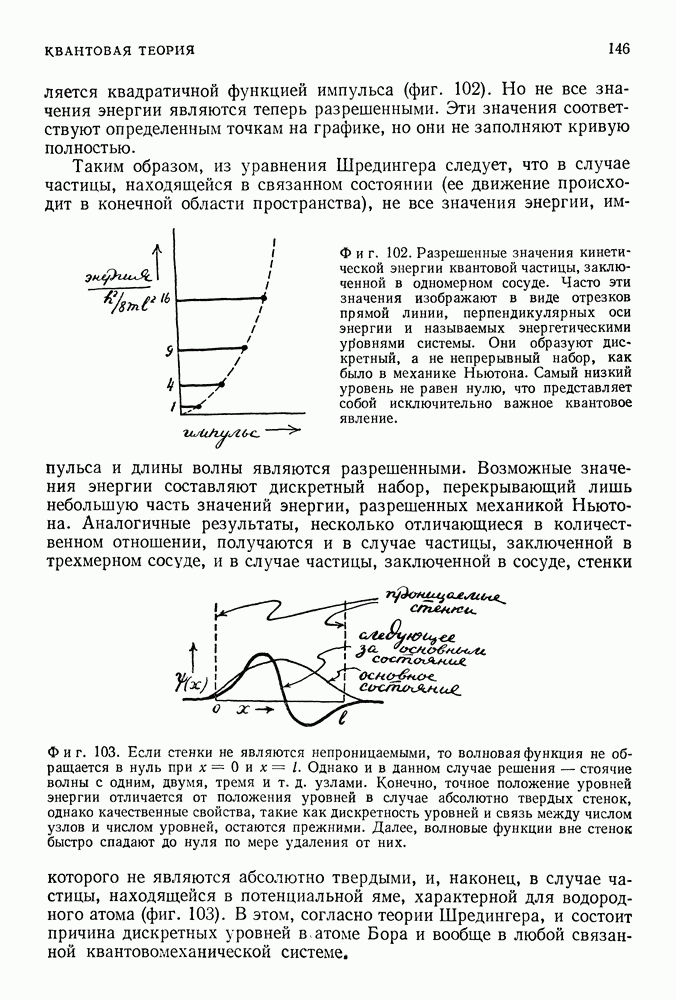
- СВЯЗАННЫЕ РЕШЕНИЯ
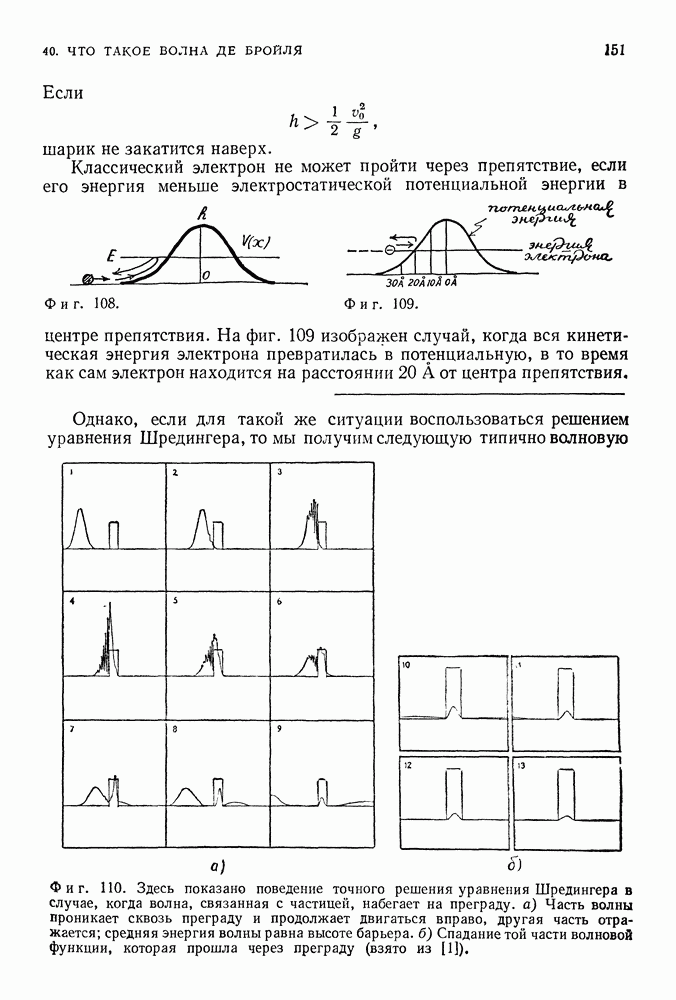
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
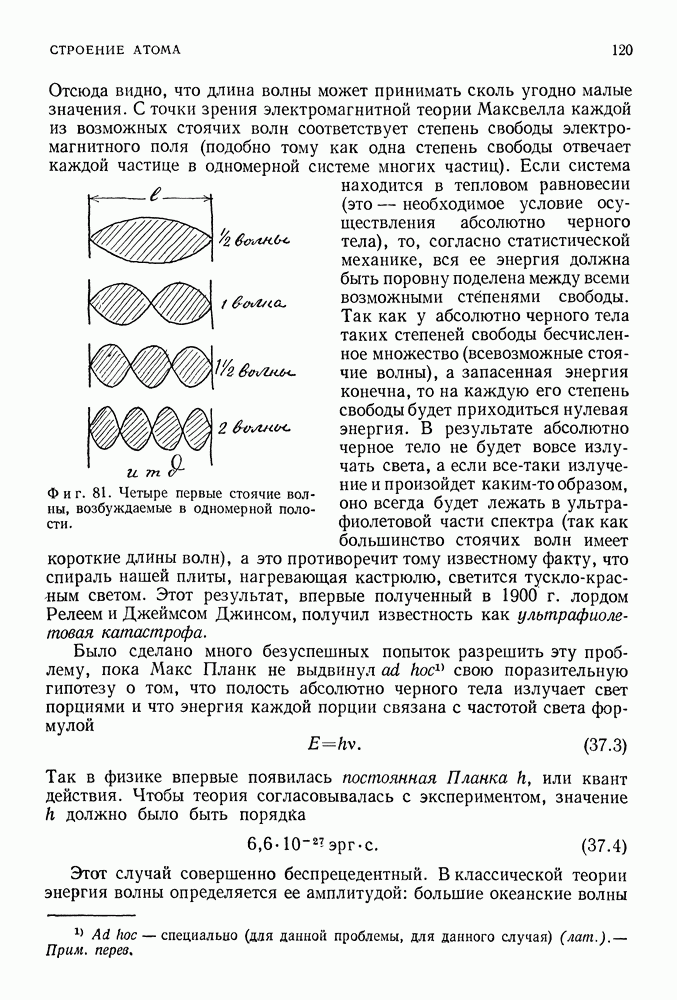
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
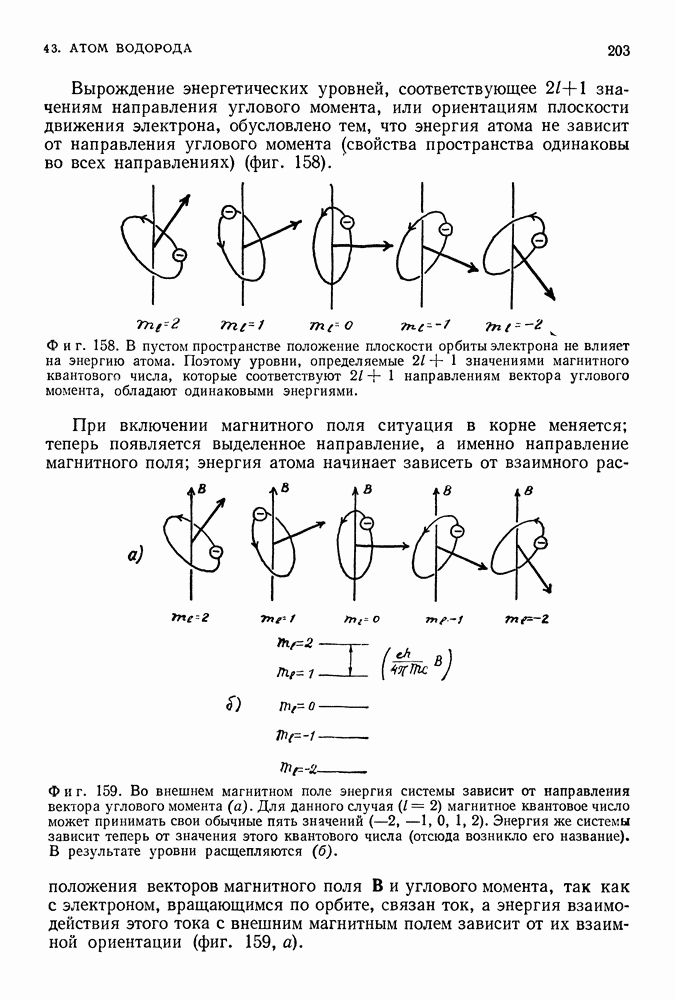
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
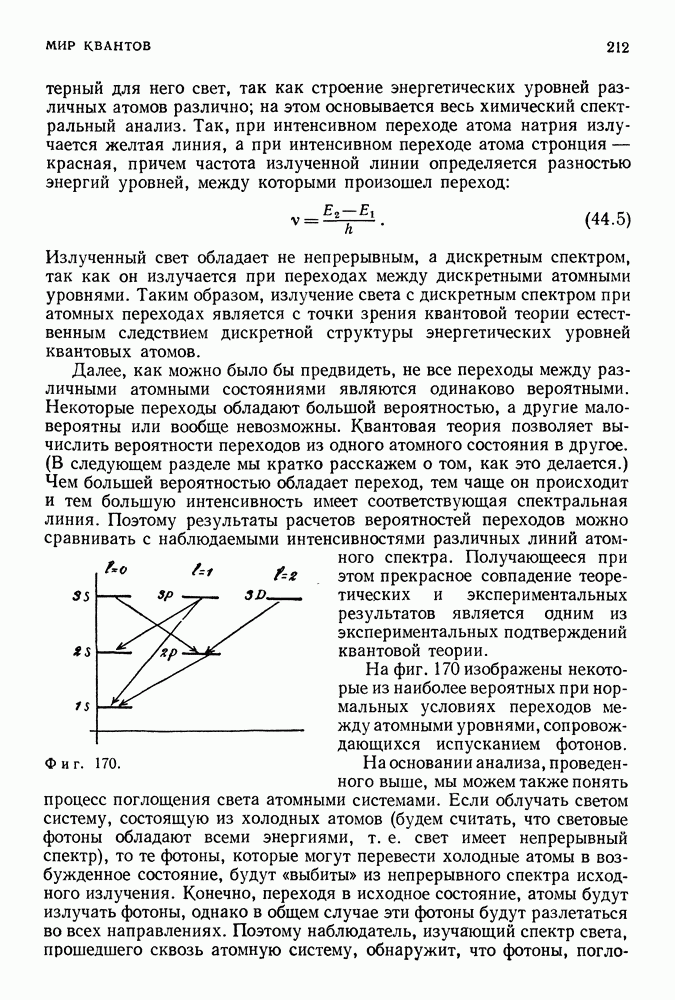
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
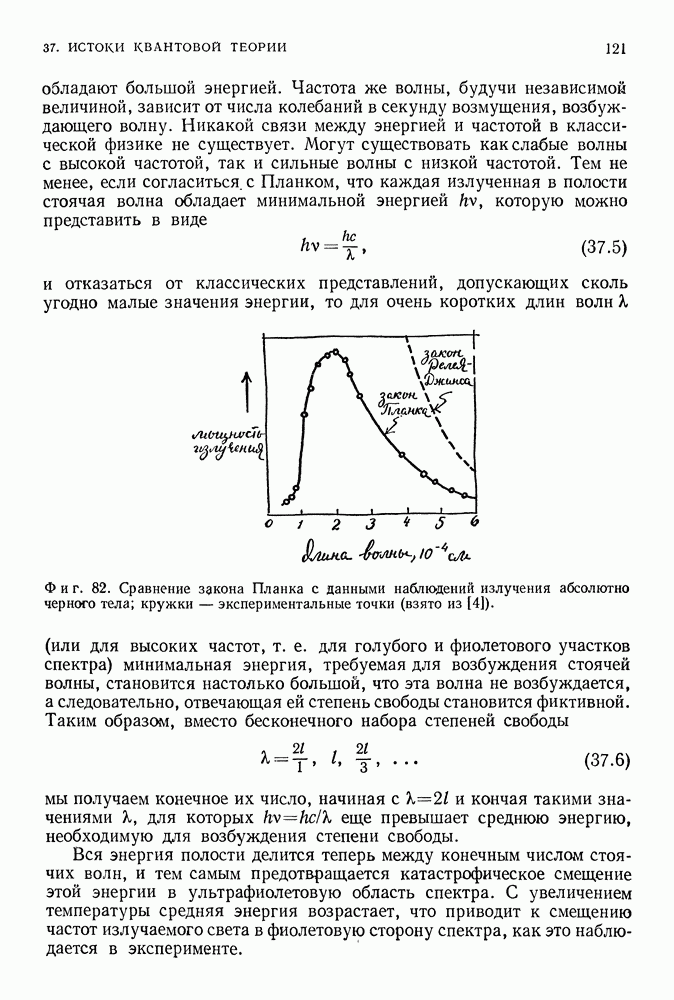
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
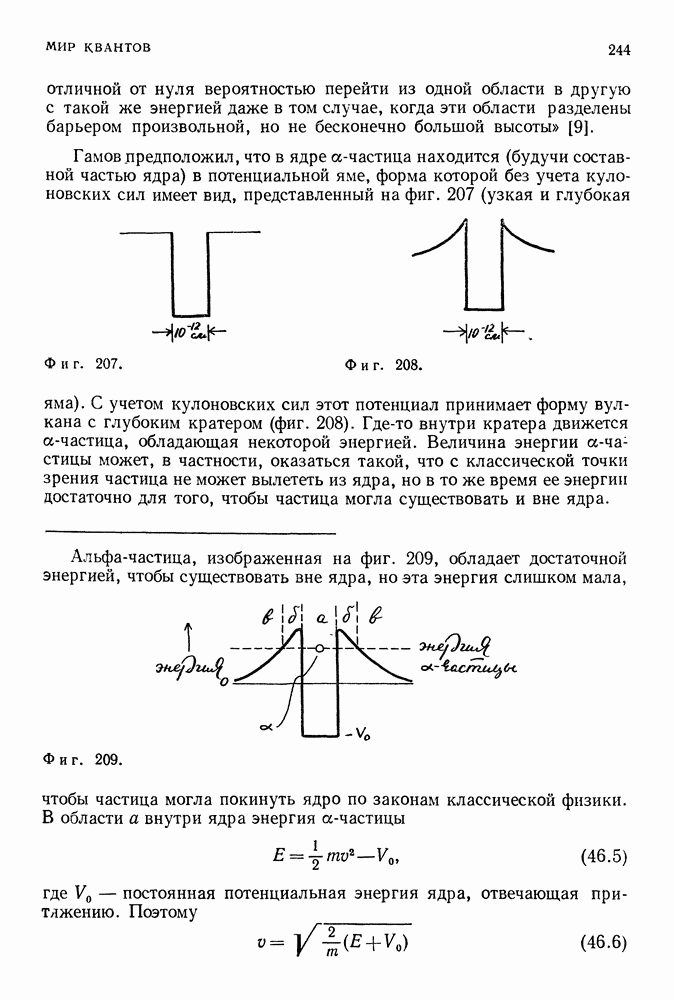
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
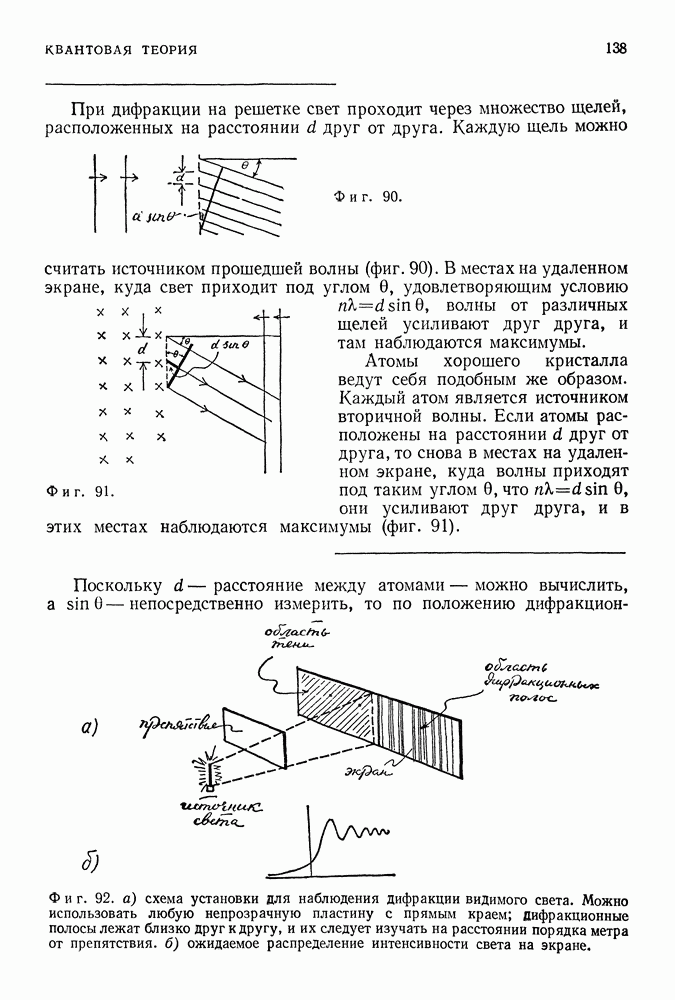
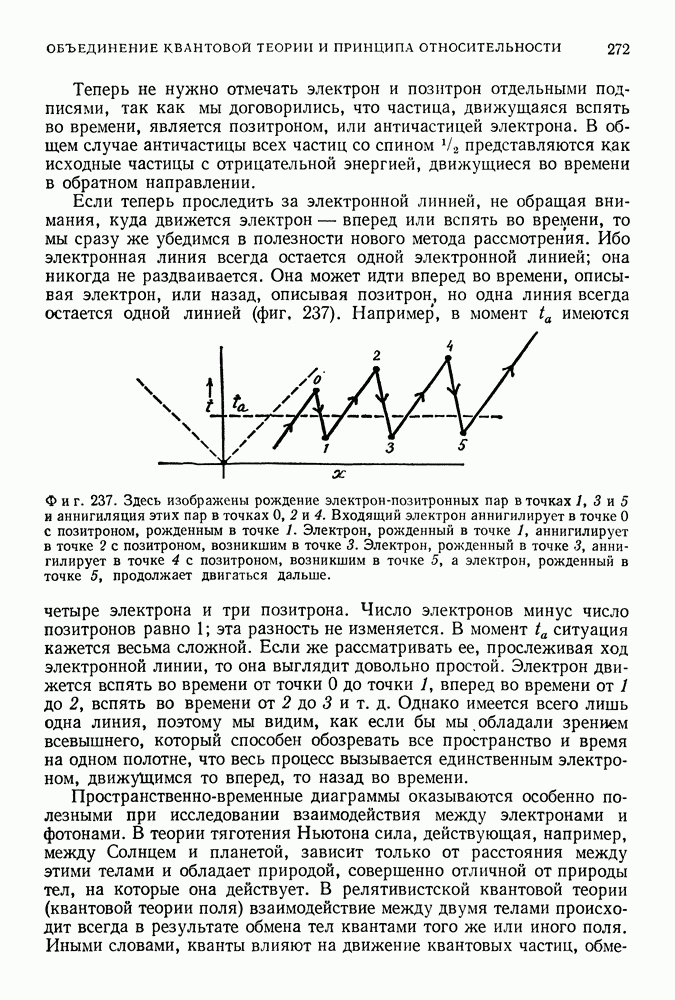
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
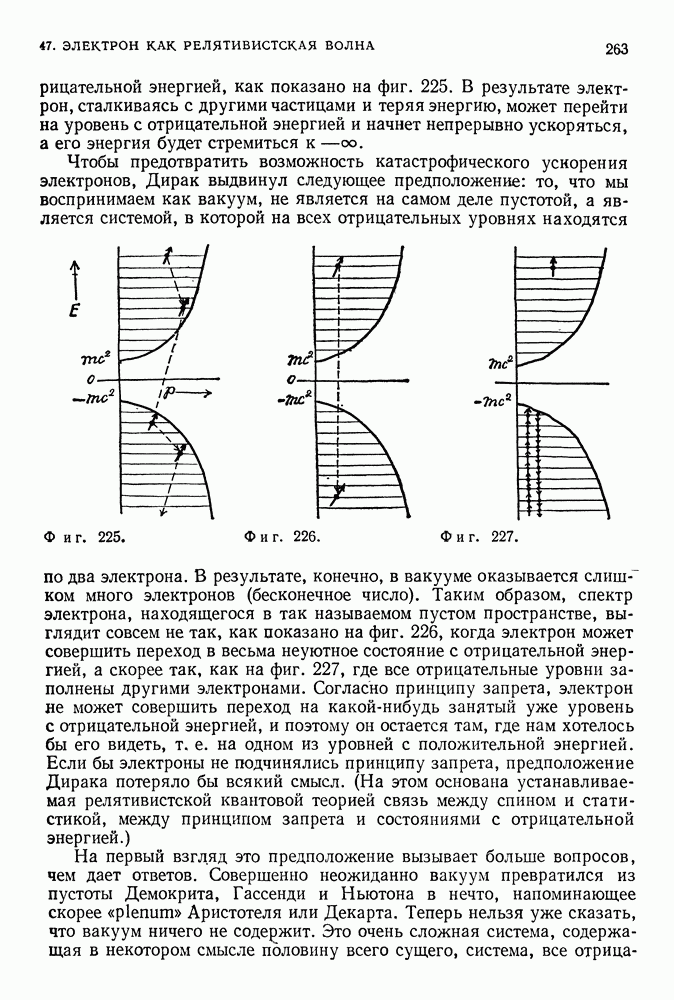
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
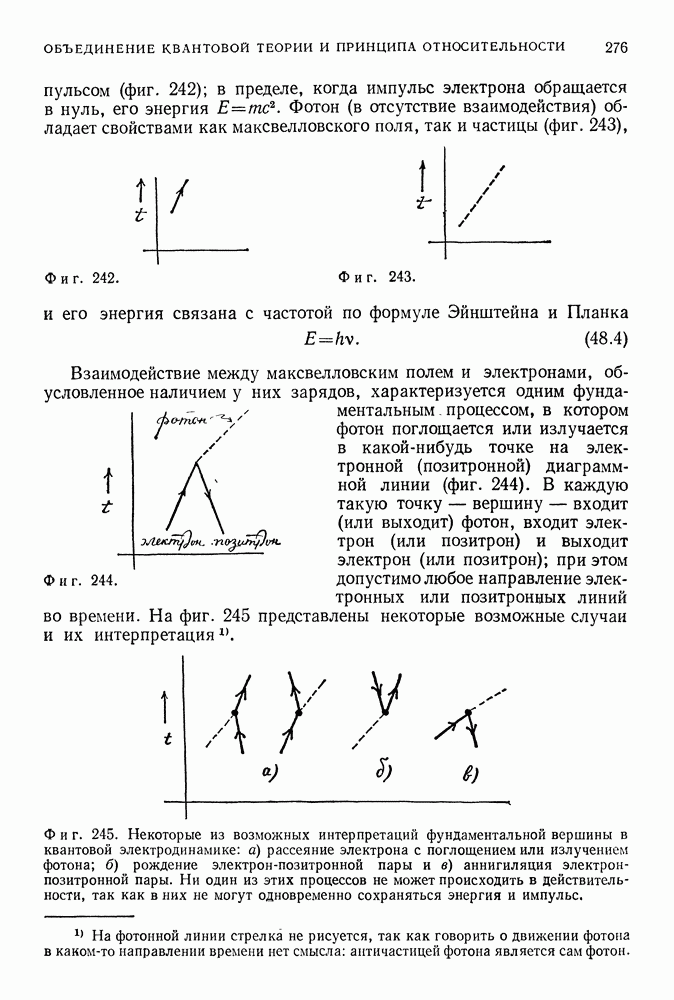
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
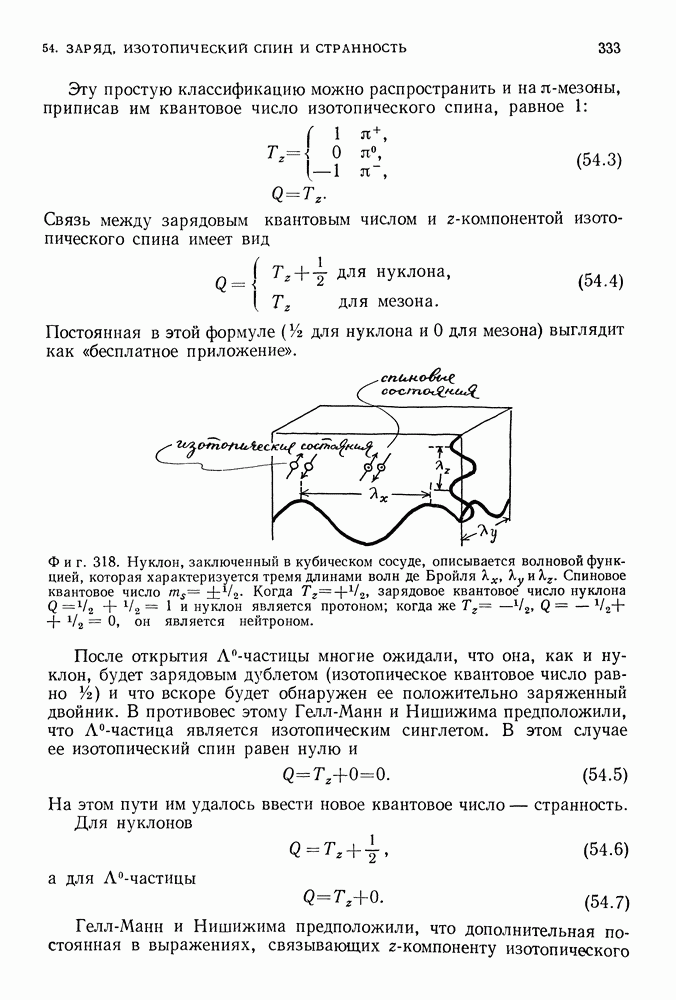
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА