| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
СВОБОДНЫЕ РЕШЕНИЯ
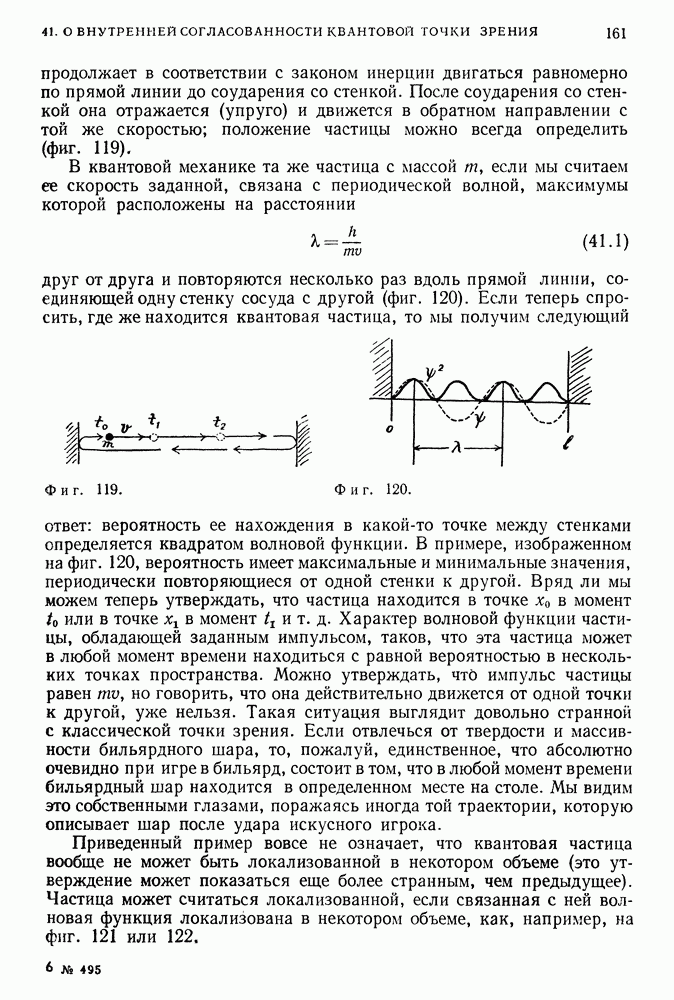
Для свободной частицы (частицы, на которую не действуют силы) из уравнения Шредингера следуют результаты, предложенные ранее де Бройлем. Решение возможно при любых положительных значениях энергии; в нерелятивистской теории энергия и импульс связаны между Собой формулой

Длина волны де Бройля, соответствующая волне с импульсом 

В отсутствие внешних сил импульс не изменяется; волна сохраняет свою форму и в этом смысле обладает свойством инерции.
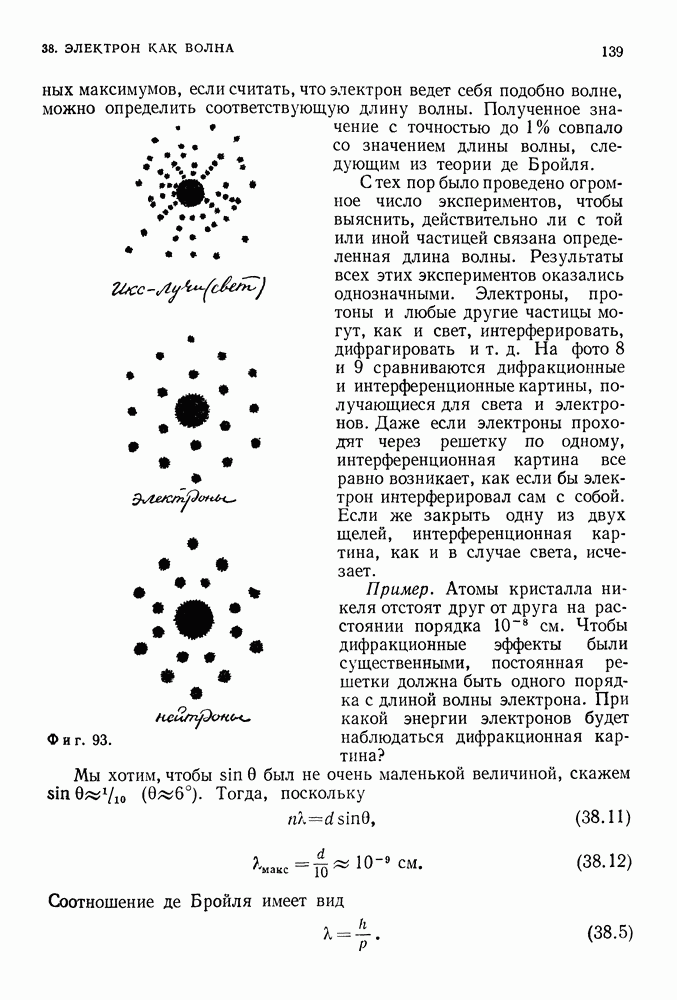
На границе раздела двух сред или при прохождении около препятствия эти волны проявляют  этически те же свойства, что и изученные нами ранее волны — возмущения на поверхности воды, волны в пружине или световые волны. Например, волна Шредингера отражается от непроницаемой преграды или частично отражается и частично проникает при попадании на проницаемую преграду (фиг. 95). От твердой, зеркалоподобной границы волна отражается таким образом, что ее угол падения равняется углу отражения. Если граница проницаема, то существуют падающая, отраженная и преломленная волны, которые подчиняются правилам, рассмотренным в гл. 17,
этически те же свойства, что и изученные нами ранее волны — возмущения на поверхности воды, волны в пружине или световые волны. Например, волна Шредингера отражается от непроницаемой преграды или частично отражается и частично проникает при попадании на проницаемую преграду (фиг. 95). От твердой, зеркалоподобной границы волна отражается таким образом, что ее угол падения равняется углу отражения. Если граница проницаема, то существуют падающая, отраженная и преломленная волны, которые подчиняются правилам, рассмотренным в гл. 17,

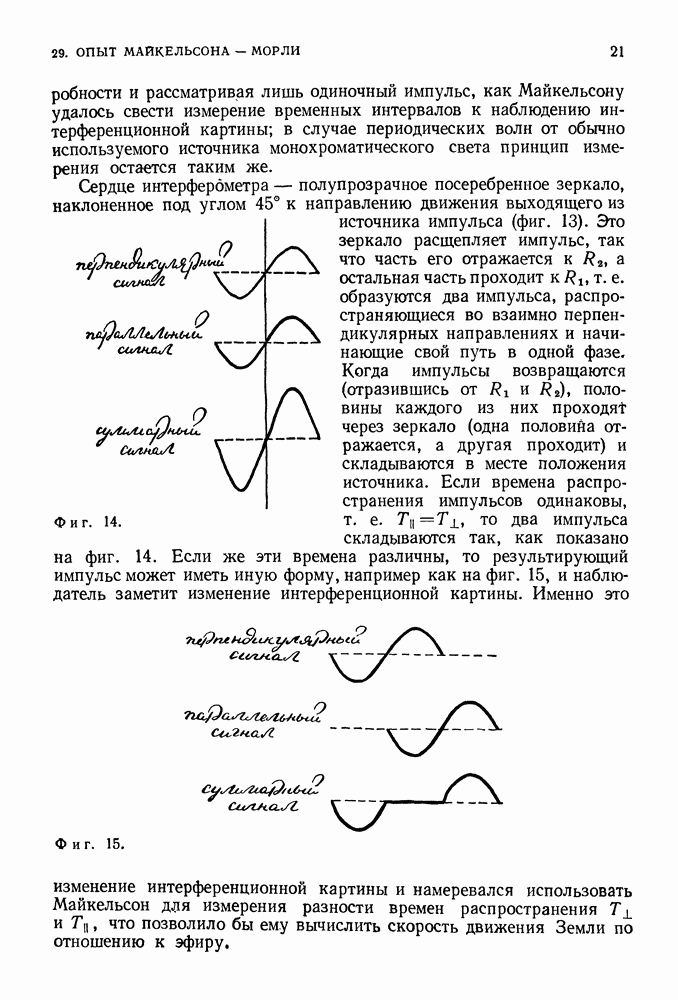
Фиг. 96.
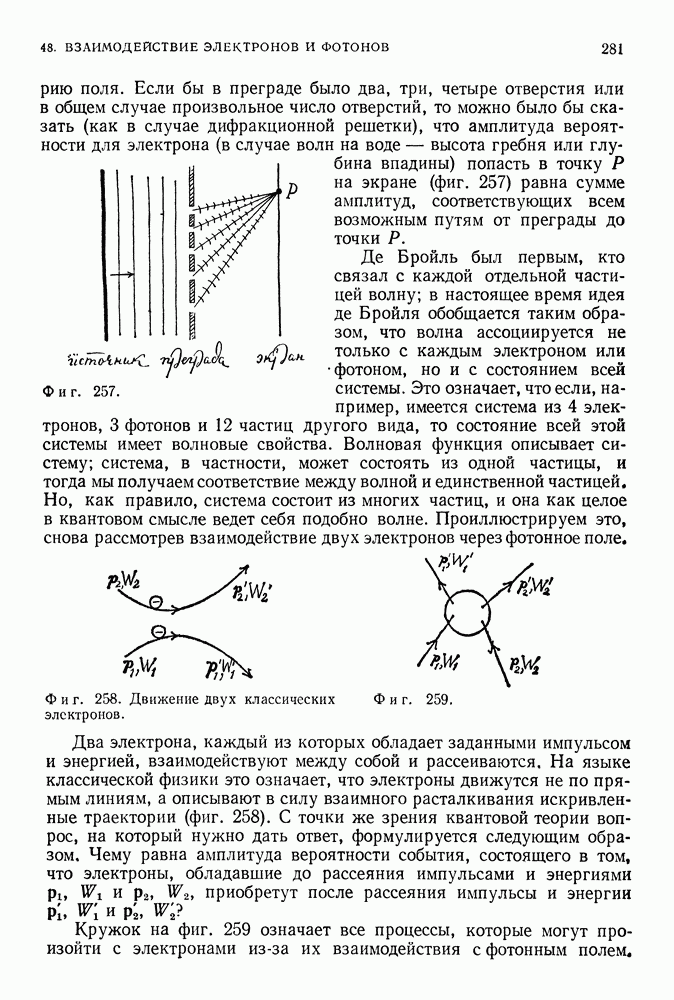
Изучая фотографии, демонстрирующие свойства световых волн или волн на воде, мы можем получить некоторое представление и о свойствах волны Шредингера. Эта волна, имеющая длину Я, проходя через отверстие шириной  в непрозрачном экране (фиг. 96), дифрагирует (как и световая волна или волна на воде), причем угловое положение первого максимума определяется из соотношения
в непрозрачном экране (фиг. 96), дифрагирует (как и световая волна или волна на воде), причем угловое положение первого максимума определяется из соотношения  Если эта волна проходит через экран с двумя отверстиями, то образуется дифракционная картина, показанная нами ранее,
Если эта волна проходит через экран с двумя отверстиями, то образуется дифракционная картина, показанная нами ранее,
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
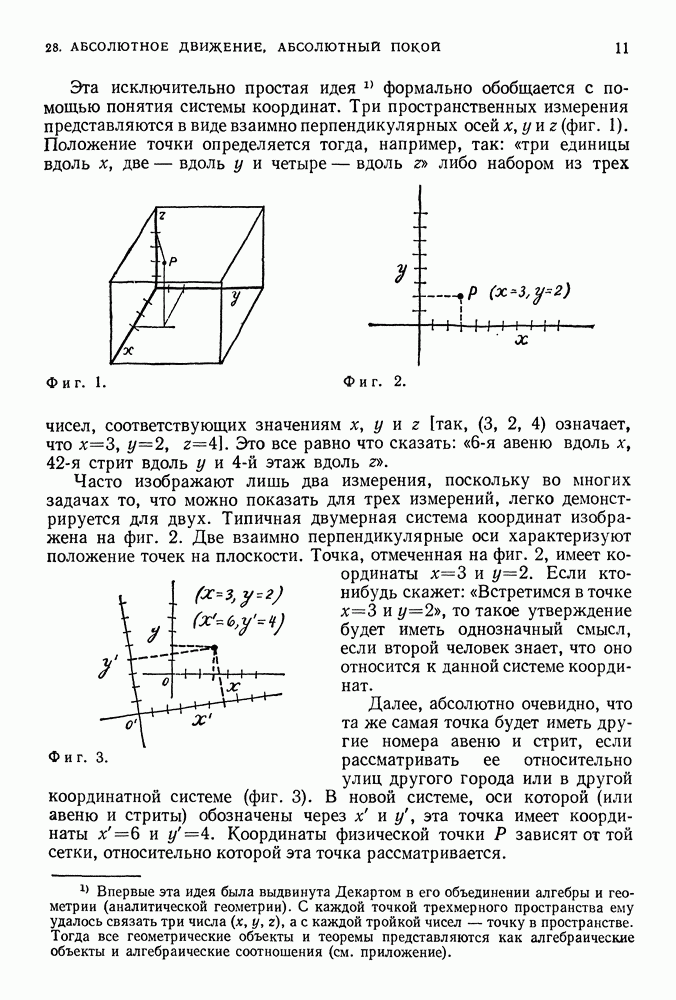
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
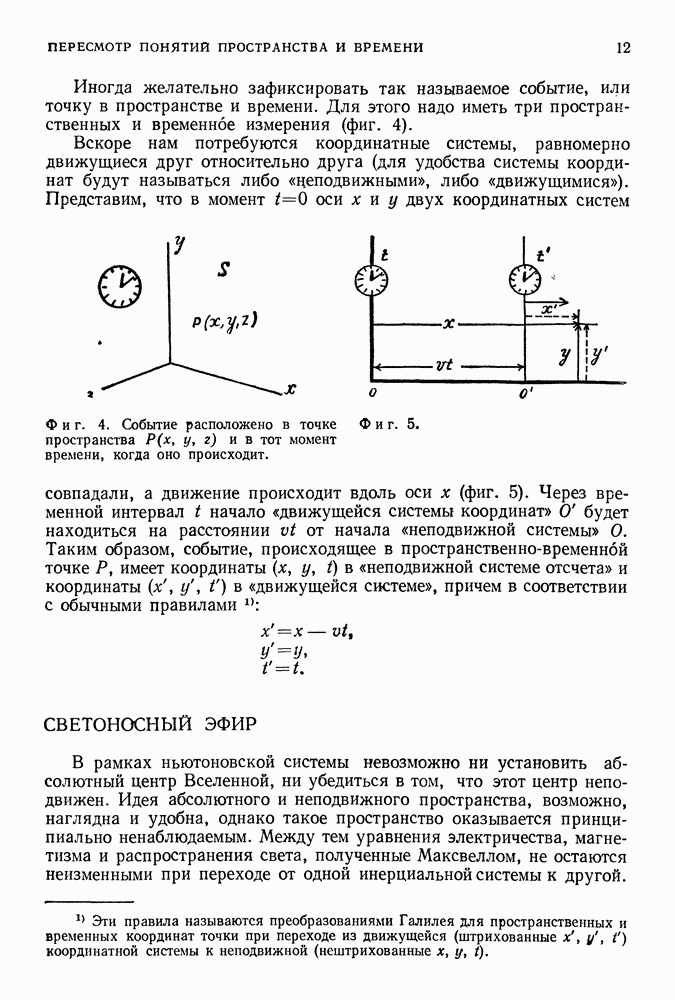
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
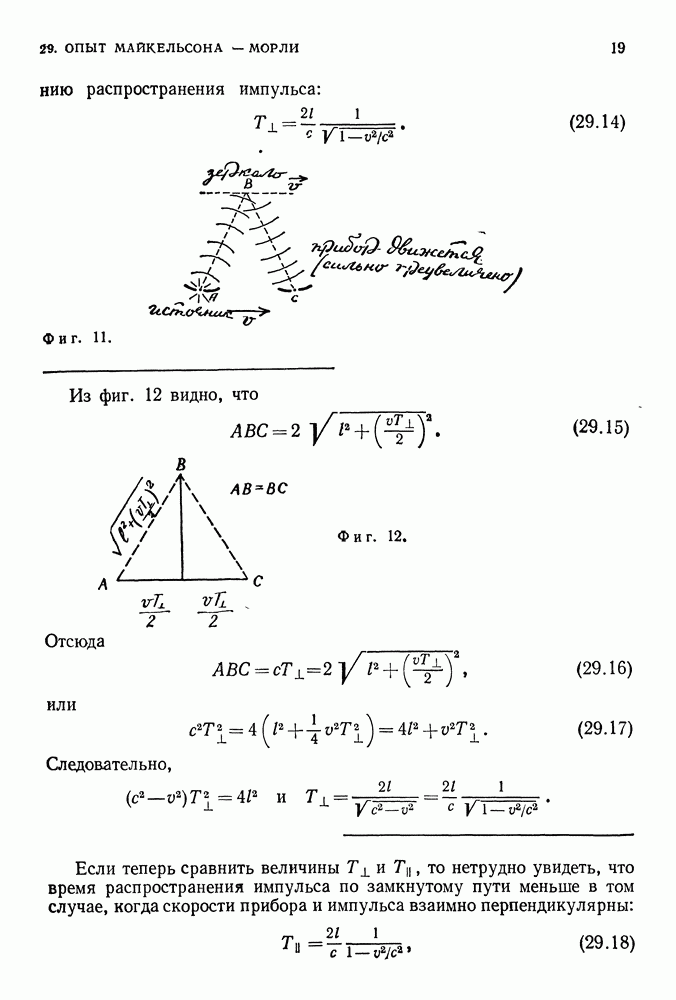
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
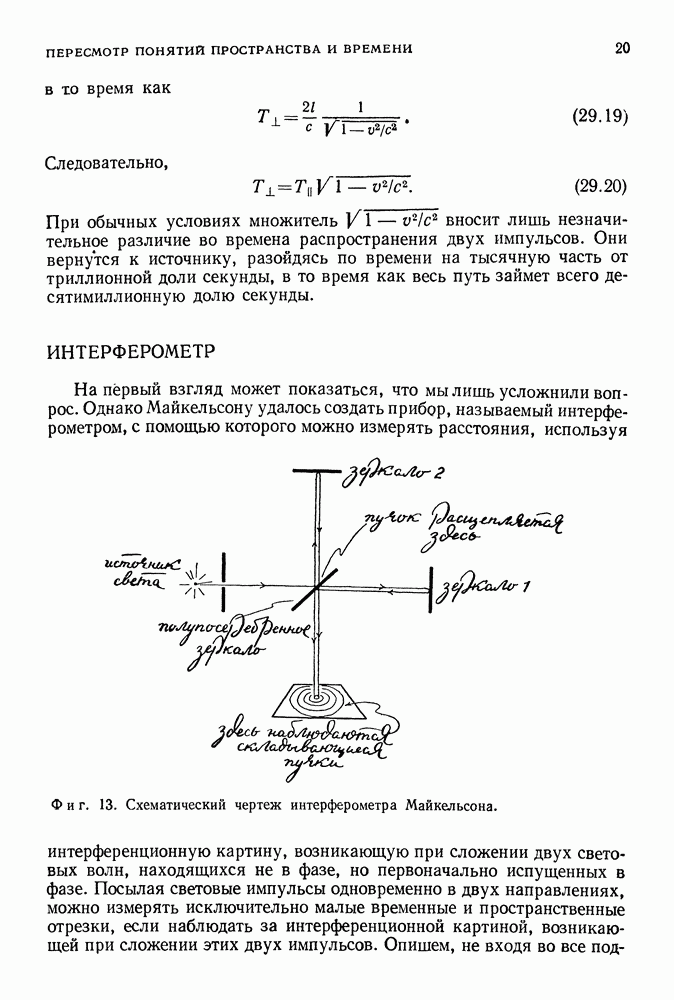
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
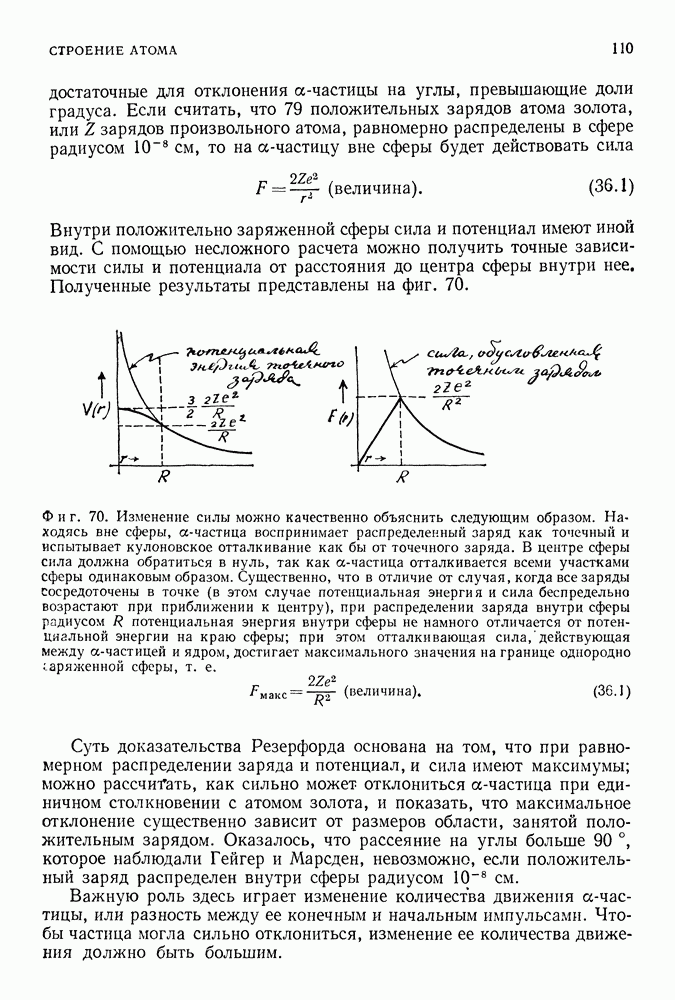
- 36. АТОМ РЕЗЕРФОРДА
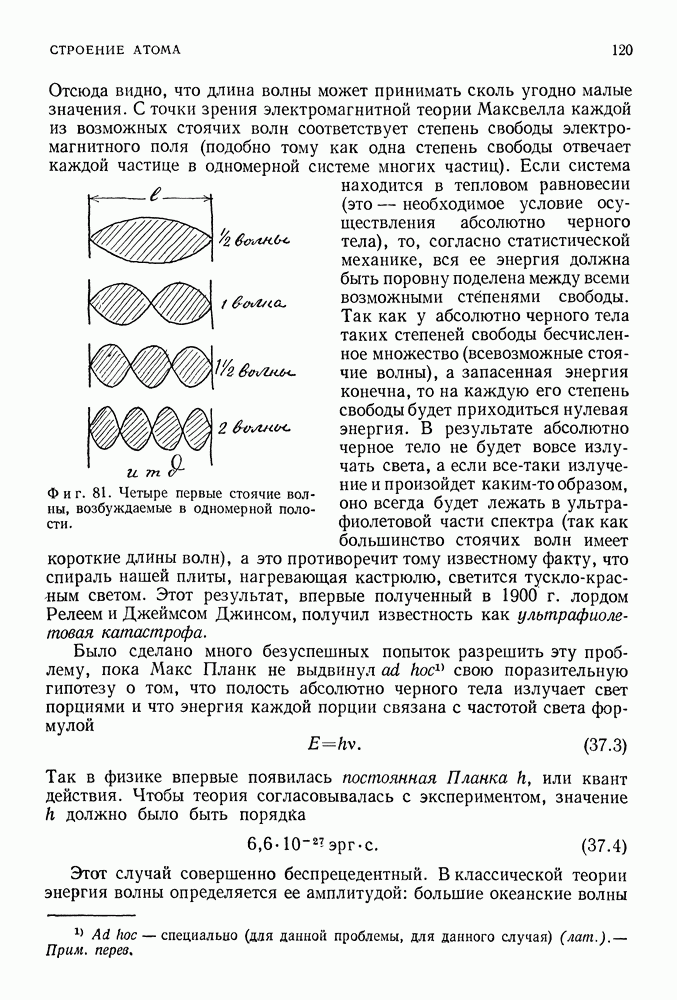
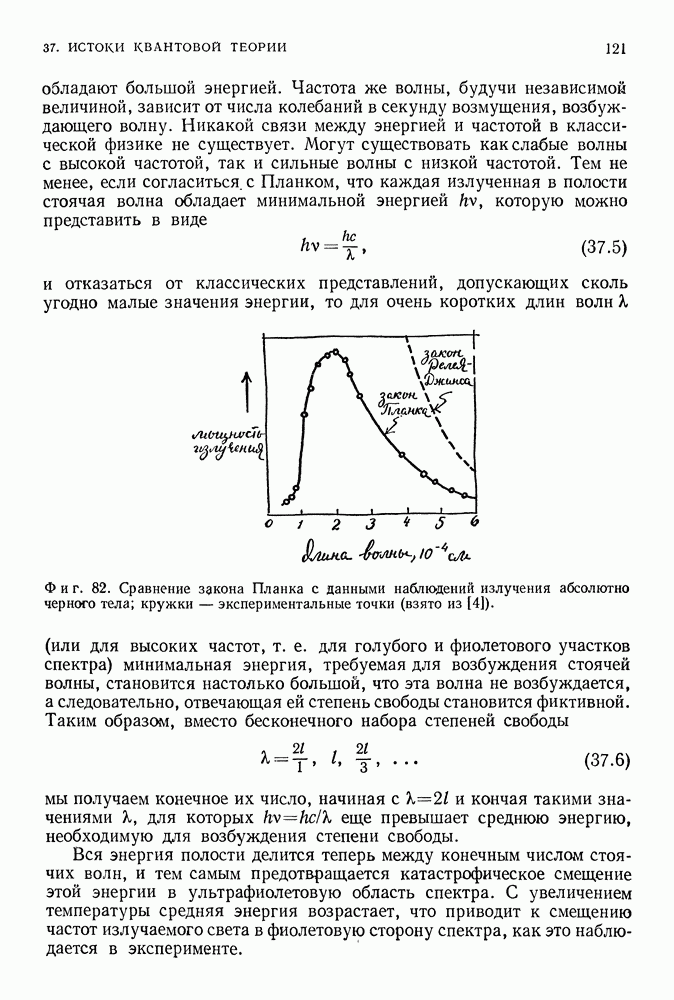
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
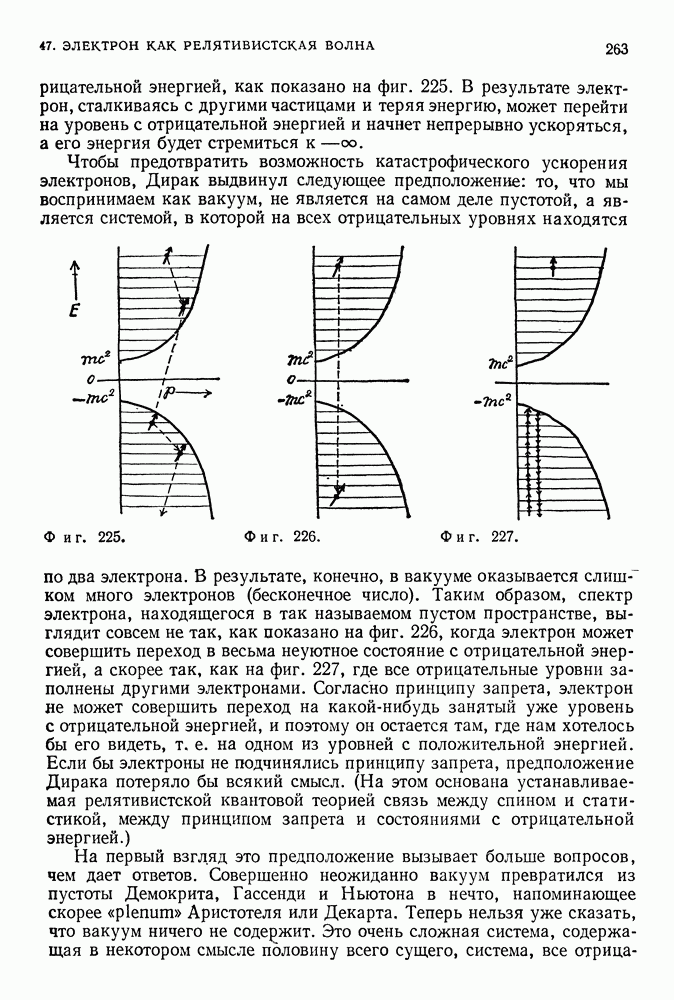
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
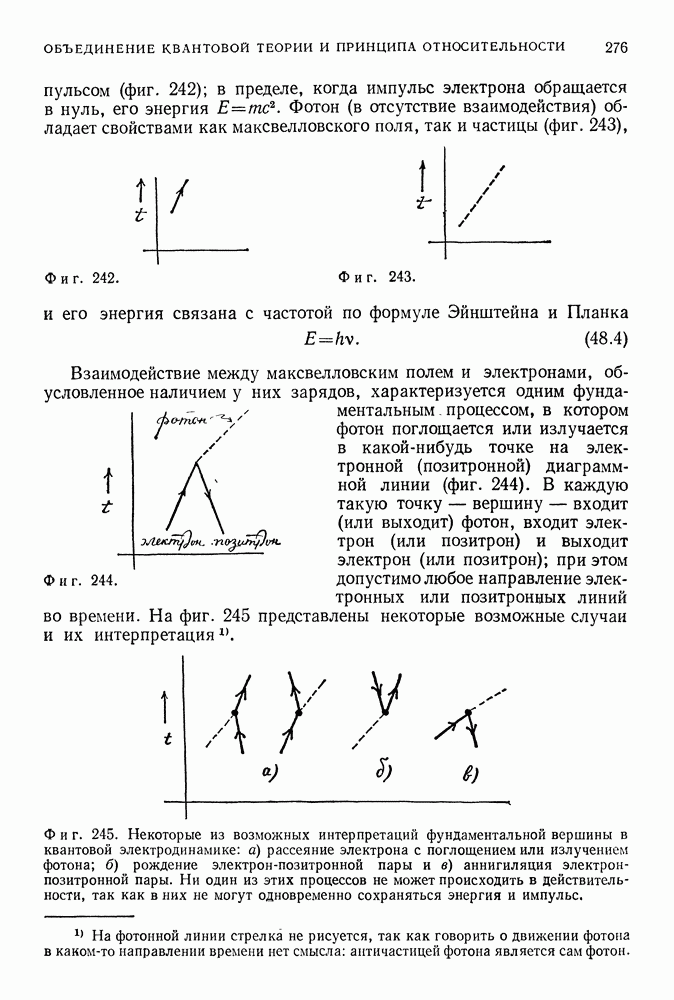
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
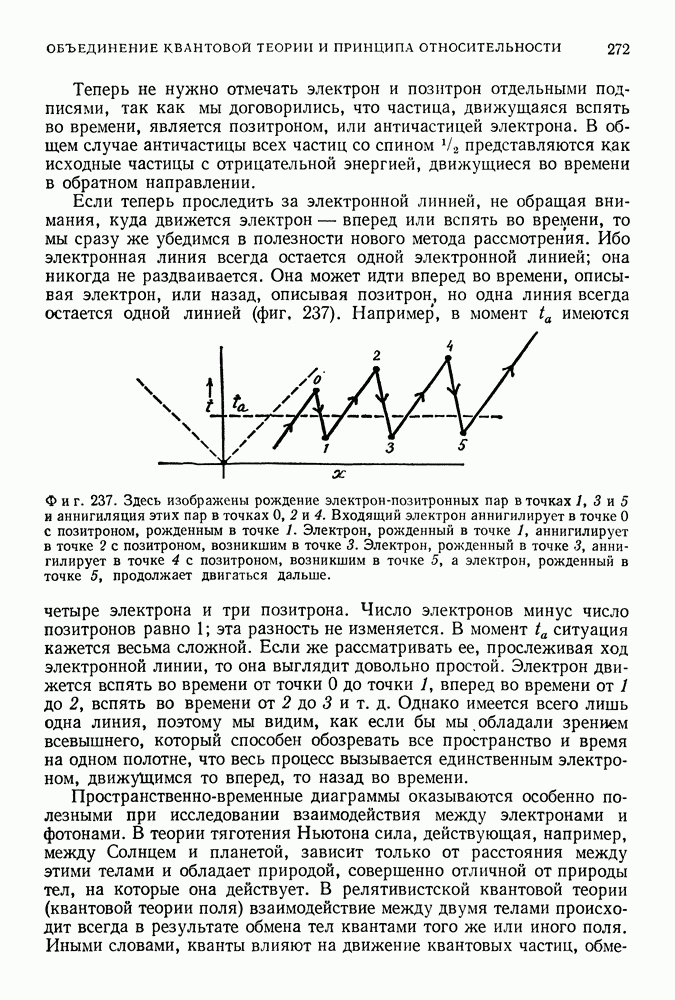
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
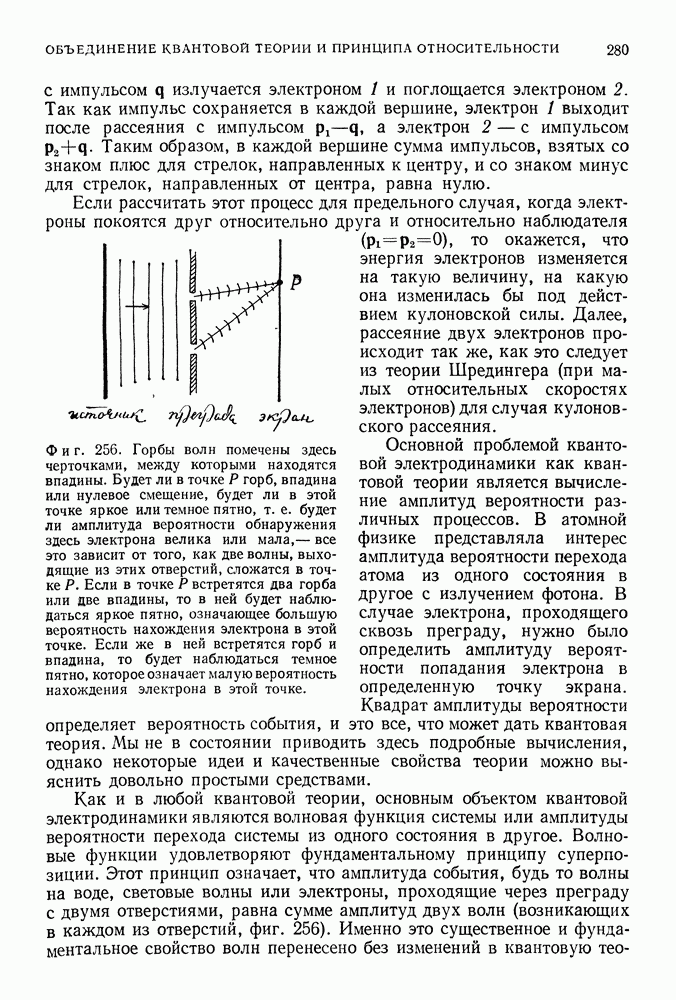
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА