| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Принцип запрета определенным образом связан с симметрией волновой функции системы многих частиц относительно перестановки тождественных частиц.
Волновая функция квантовой системы из 2, 3,..., N частиц (для простоты мы не учитываем сейчас их спины) является в общем случае функцией N координат  . Координата первой частицы
. Координата первой частицы  второй
второй  Тогда
Тогда

есть волновая функция системы из  частиц. При заданных значениях
частиц. При заданных значениях  волновая функция определяет некоторое число. Квадрат этого числа
волновая функция определяет некоторое число. Квадрат этого числа

интерпретируется как вероятность того, что частица 1 находится в точке  частица 2 — в точке
частица 2 — в точке 

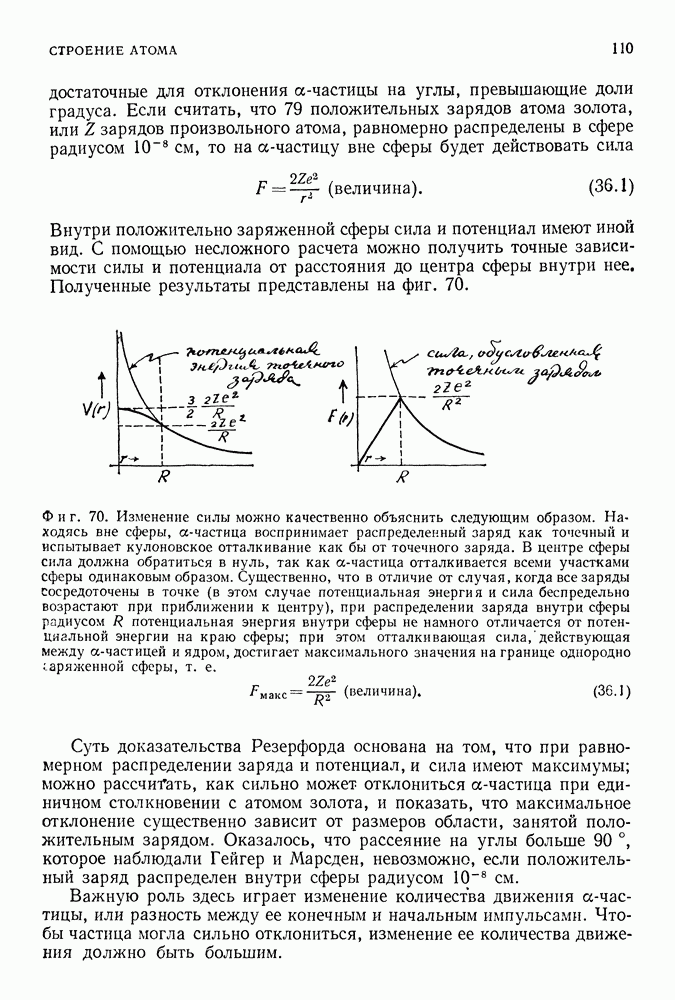
Фиг. 178,
Волновая функция системы многих частиц удовлетворяет главному свойству суперпозиции: сумма двух волновых решений тоже является решением при тех же условиях. Таким образом, вся система из  частиц обладает основными свойствами волны — свойством интерференции и т. п. Все это налагает серьезные ограничения на вид волновой функции системы, состоящей из большого числа тождественных частиц. Об этих ограничениях рассказывается ниже.
частиц обладает основными свойствами волны — свойством интерференции и т. п. Все это налагает серьезные ограничения на вид волновой функции системы, состоящей из большого числа тождественных частиц. Об этих ограничениях рассказывается ниже.
Рассмотрим систему квантовых частиц (скажем, состоящую из двух электронов, как на фиг. 179); пусть электрон 1 находится в  электрон 2 - в
электрон 2 - в  , их спины направлены в одну сторону, а волновая функция системы имеет вид
, их спины направлены в одну сторону, а волновая функция системы имеет вид


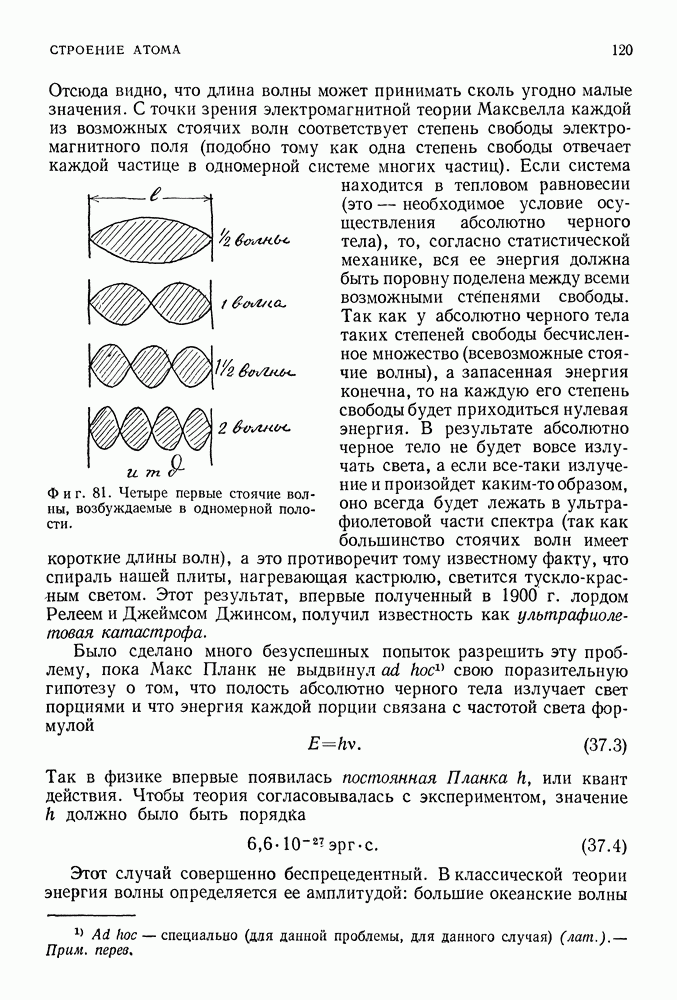
Фиг. 179.

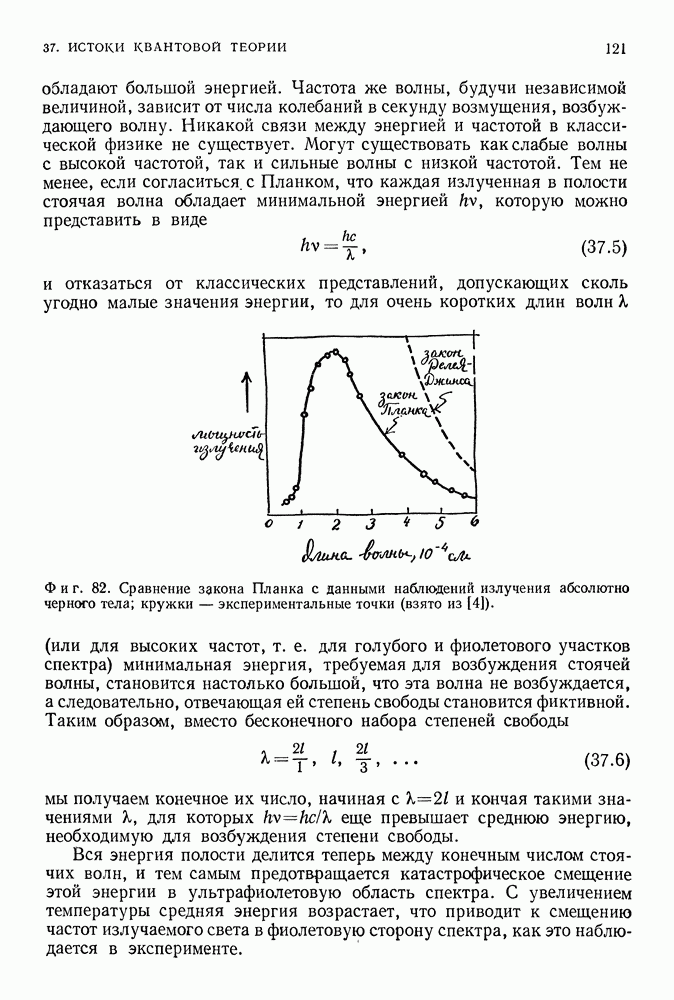
Фиг. 180.
Представим теперь, что электроны поменялись местами: электрон 1 перешел в  а электрон 2— в
а электрон 2— в  (фиг. 180).
(фиг. 180).
Если частицы различны или если они обе — электроны, но отличающиеся один от другого (скажем, электрон 1 несколько старше электрона 2), то в таком случае имеет какой-то смысл утверждение, что система на фиг. 180 отличается от системы на фиг. 179. Если же
обе частицы тождественны во всех отношениях, то тогда становится непонятным, чем эти системы различаются между собой. С точки зрения классической теории, различить их можно, если пометить одну частицу цифрой У, другую цифрой 2, а затем следить за движением этих частиц (фиг. 181). В квантовой же теории нет никакого смысла различать между собой две тождественные частицы, так как теперь мы не в состоянии проследить за их движением.

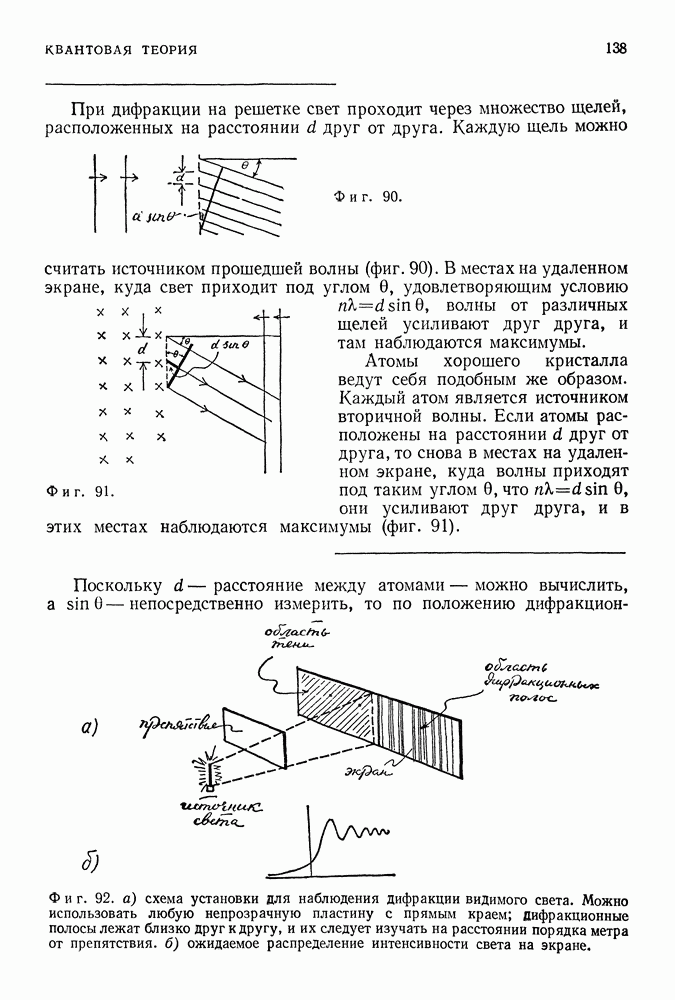
Фиг. 181.
Если частицы перемещаются, то через некоторое время они перепутываются; если позднее мы обнаруживаем частицу, то мы никаким способом не сможем узнать, какую из двух частиц мы обнаружили (фиг. 182).
Это ограничение (если мы согласились с ним) можно выразить в виде условия, накладываемого на волновую функцию системы из двух частиц. Величина  есть вероятность нахождения частицы 1 в точке
есть вероятность нахождения частицы 1 в точке  и частицы 2 в точке
и частицы 2 в точке  со спинами, направленными вверх.
со спинами, направленными вверх.

Фиг. 182. Электрон 1 и электрон 2 сближаются  сталкиваются
сталкиваются  и рассеиваются
и рассеиваются  Спрашивается, где на фигуре в) находятся электрон 1 и электрон 2?
Спрашивается, где на фигуре в) находятся электрон 1 и электрон 2?
Величина  есть вероятность нахождения частицы 1 в точке
есть вероятность нахождения частицы 1 в точке  и частицы 2 в точке
и частицы 2 в точке  со спинами, снова направленными вверх. Если обе частицы неразличимы между собой, то на основании вышеприведенных рассуждений можно написать, что
со спинами, снова направленными вверх. Если обе частицы неразличимы между собой, то на основании вышеприведенных рассуждений можно написать, что

т. е. вероятность реализации первой ситуации (частица 1 в  и частица 2 в
и частица 2 в  равна вероятности реализации второй ситуации (частица
равна вероятности реализации второй ситуации (частица  частица 2 в
частица 2 в  Поскольку частицы абсолютно одинаковы, эти две ситуации физически неразличимы. Из выражения (45.1) можно сразу же получить
Поскольку частицы абсолютно одинаковы, эти две ситуации физически неразличимы. Из выражения (45.1) можно сразу же получить

или

В первом случае говорят, что волновая функция симметрична относительно перестановки двух частиц; в результате мы получаем так называемую статистику Бозе. Во втором же случае говорят, что волновая функция антисимметрична относительно перестановки двух частиц, а соответствующая статистика называется статистикой Ферми.
Тогда принцип запрета выражается в виде так называемого свойства антисимметрии волновой функции:

которое означает, что волновая функция в состоянии а (электрон 1 в  и электрон 2 в
и электрон 2 в  равна минус волновой функции в состоянии
равна минус волновой функции в состоянии  (электрон 1 в
(электрон 1 в  и электрон 2 в
и электрон 2 в  ). Если оба электрона находились бы в одном и том же месте,
). Если оба электрона находились бы в одном и том же месте,

то волновая функция

в силу антисимметричности была бы равна самой себе со знаком минус:

Из всех чисел этому уравнению удовлетворяет только одно — нуль. Таким образом, волновая функция двухэлектронной системы, которая подчиняется принципу запрета, равна нулю в том случае, когда координаты двух электронов совпадают; если спины электронов не направлены в разные стороны, два электрона не могут находиться слишком близко друг от друга.
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
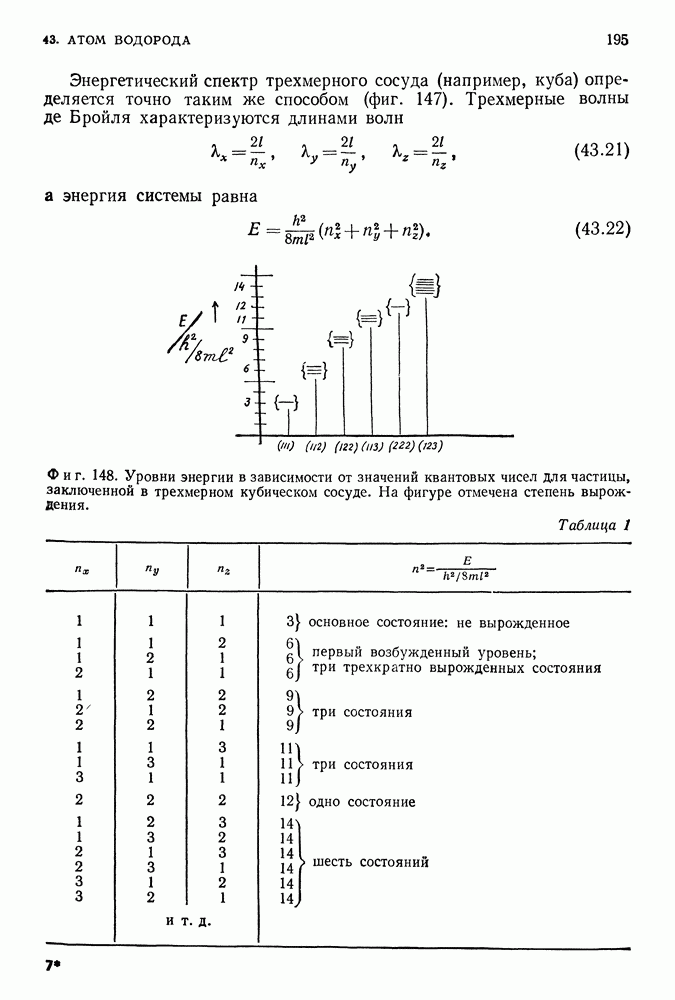
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
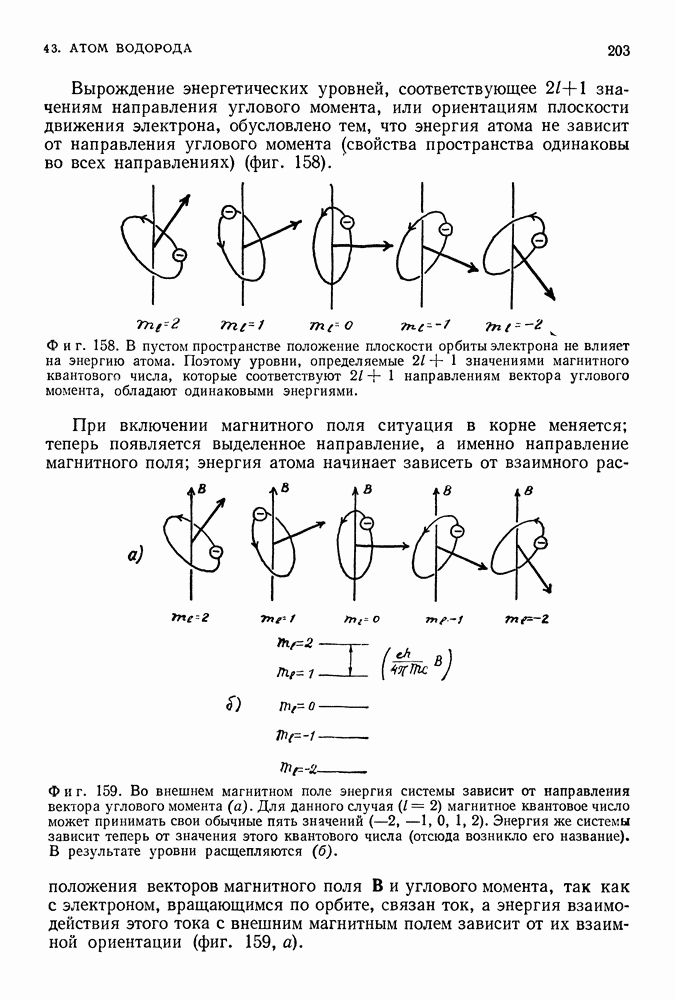
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
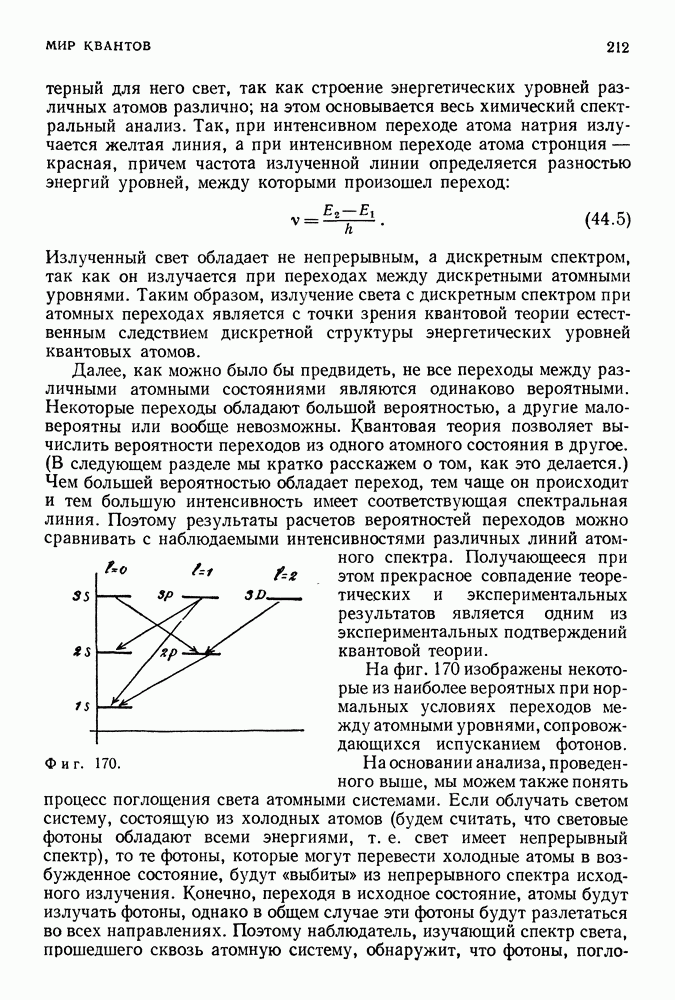
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
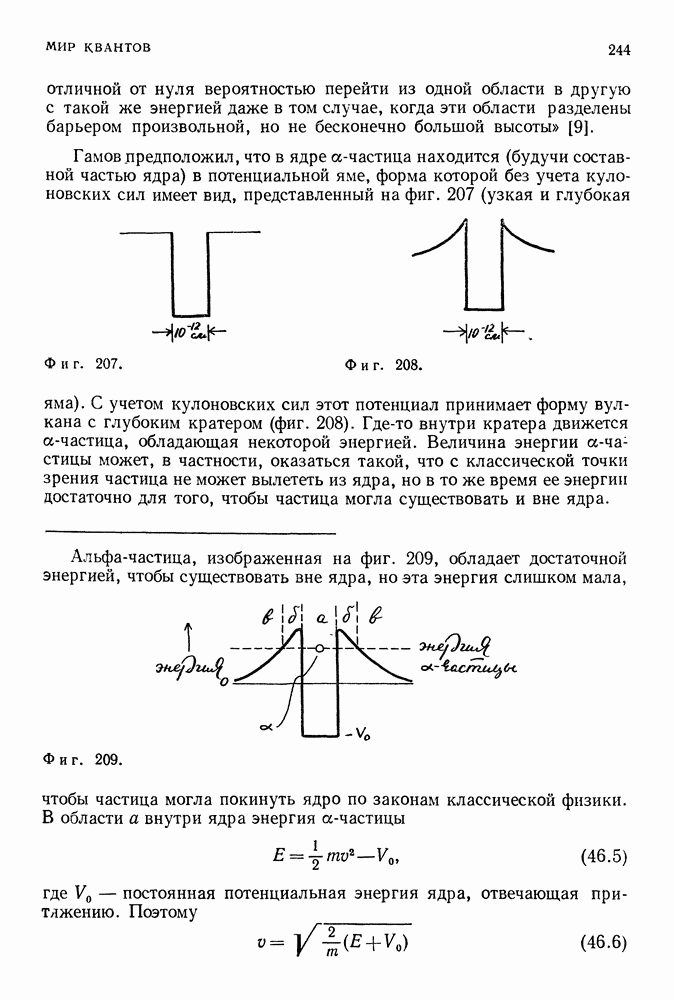
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА