| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
В то время, когда построение атома было уже завершено, работа над созданием модели ядра была еще в самом разгаре. Возможно, если бы ядро представляло собой один заряд  с массой
с массой  , никаких дополнительных проблем и не возникло бы. Однако в этом случае пришлось бы ввести множество различных и не связанных между собой понятий. Поэтому в целях экономии и на основании опытных данных (превращение одного ядра в другое, излучение ядрами протонов, нейтронов, а-частиц, электронов и у-лучей) следовало признать, что ядра состоят из более простых объектов, которые каким-то образом удерживаются
, никаких дополнительных проблем и не возникло бы. Однако в этом случае пришлось бы ввести множество различных и не связанных между собой понятий. Поэтому в целях экономии и на основании опытных данных (превращение одного ядра в другое, излучение ядрами протонов, нейтронов, а-частиц, электронов и у-лучей) следовало признать, что ядра состоят из более простых объектов, которые каким-то образом удерживаются
вместе и могут после соответствующей перегруппировки образовать другое ядро.
Несложный расчет показывает, что для того, чтобы ядра могли считаться состоящими из нейтронов и протонов, удерживающихся вместе под действием приложенных между ними сил, следует ввести новый вид сил. С помощью классических сил — гравитационной или электромагнитной — невозможно разумным образом объяснить устойчивость ядерного вещества. Кулоновская сила расталкивания, действующая между положительно заряженными протонами, равна

а гравитационная сила притяжения дается формулой

где  — масса протона, так что их отношение составляет
— масса протона, так что их отношение составляет

Малость этой величины (зависящей для ядерных частиц от их массы и заряда) является причиной того, что гравитационные силы считаются в ядрах несущественными по сравнению с электрическими.
На этом основании приходится допустить, что между ядерными частицами (протонами и нейтронами) действует какая-то иная притягивающая сила, превышающая расталкивающее влияние электромагнитных сил, причем эта сила должна быть настолько большой, чтобы устойчивые ядра могли существовать вопреки электромагнитному расталкиванию между положительными зарядами; об устойчивости ядер говорит хотя бы то, что только к концу девятнадцатого века удалось наблюдать превращение одного ядра в другое.

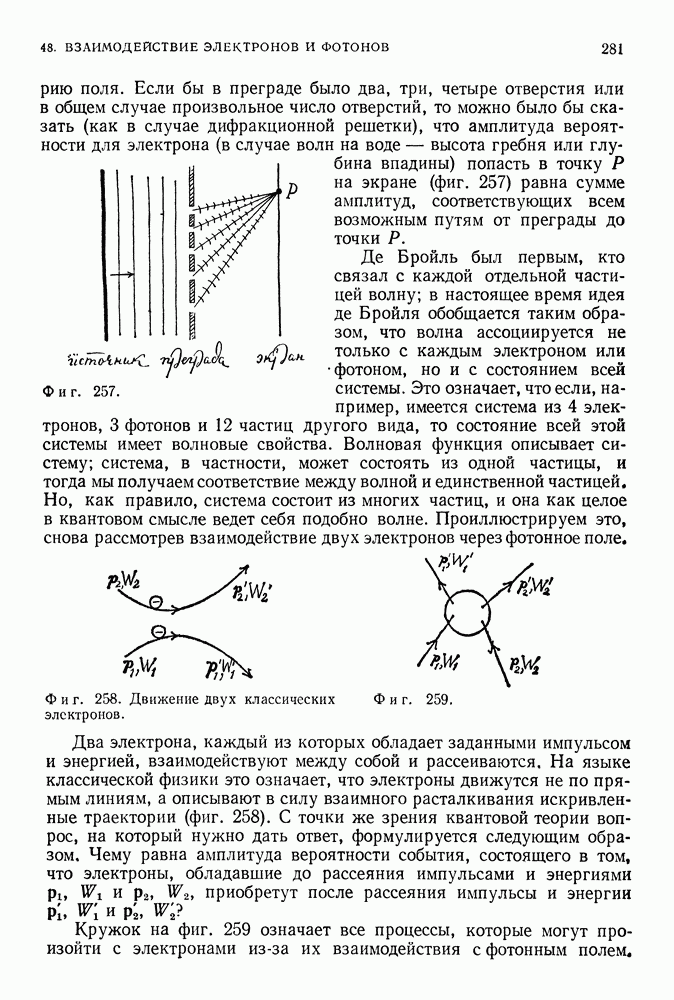
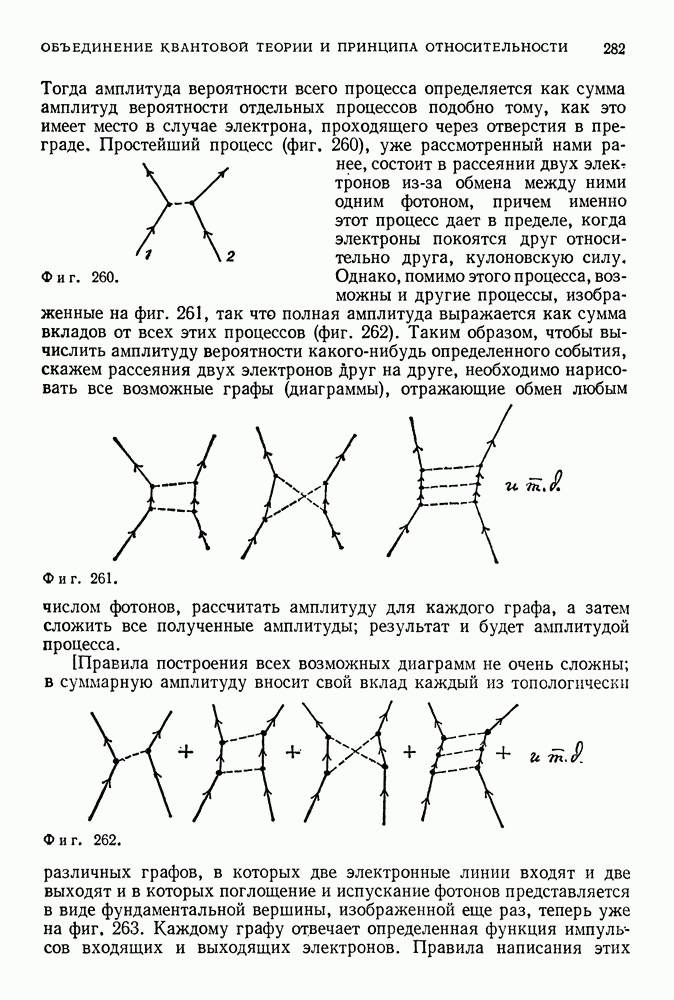
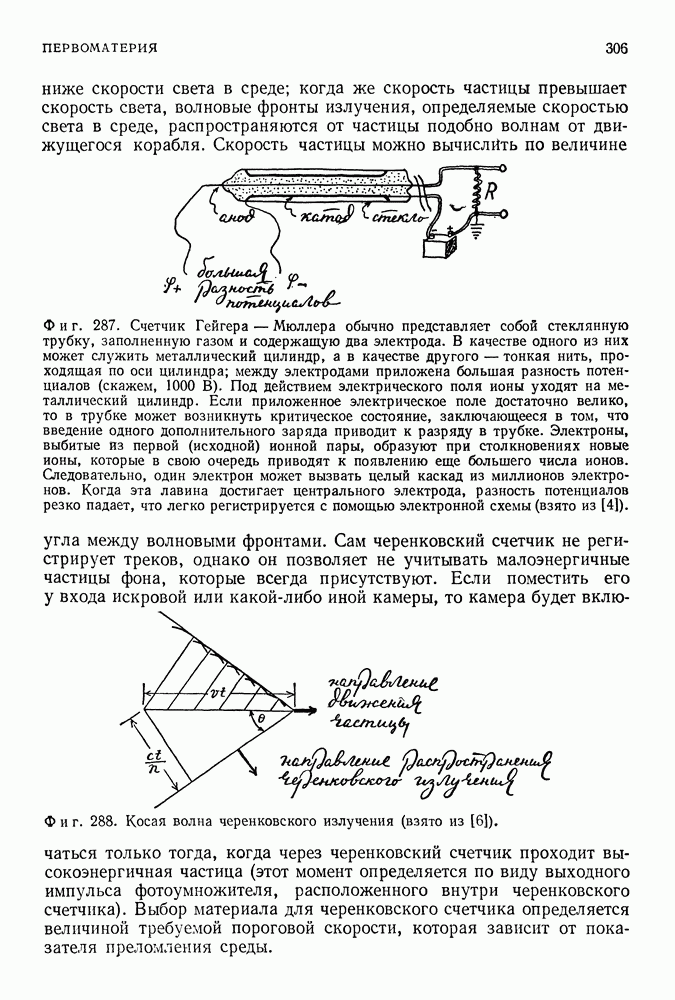
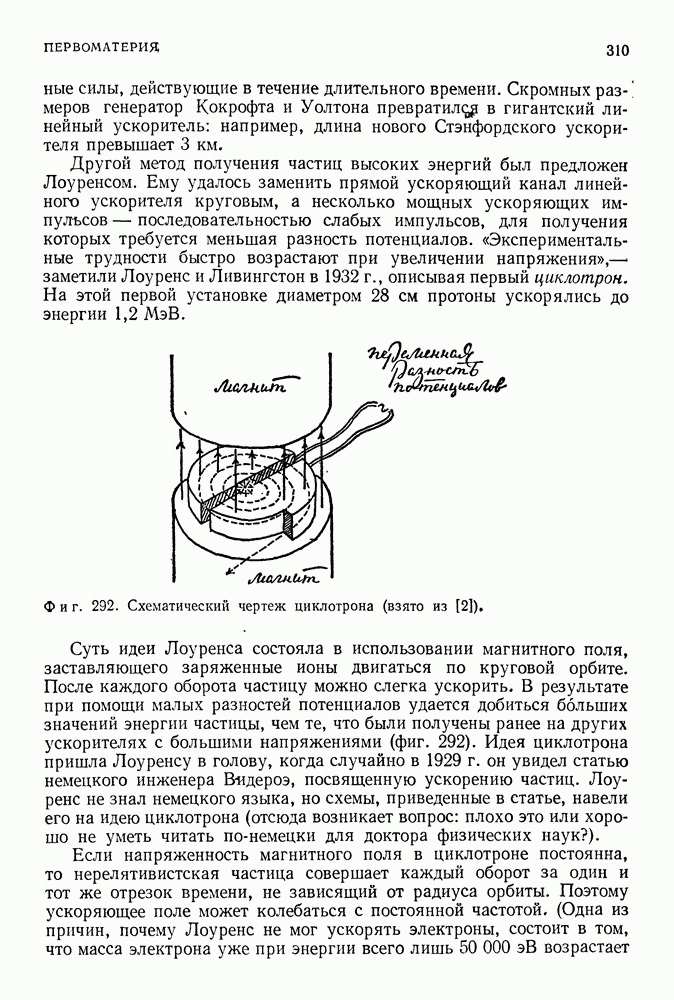
Фиг. 199.
Величину характерной энергии взаимодействия нуклонов легко оценить, используя тот факт, что ядерные силы притяжения должны превышать электромагнитные силы расталкивания, действующие между положительными зарядами. Так, в ядро, содержащее 50 положительных зарядов, удается ввести еще один протон (в результате получится ядро с  если на преодоление электрических сил затрачивается энергия порядка 10 МэВ. Действительно, электрическая энергия протона, находящегося внутри такого ядра, близка к 10 МэВ (фиг. 199):
если на преодоление электрических сил затрачивается энергия порядка 10 МэВ. Действительно, электрическая энергия протона, находящегося внутри такого ядра, близка к 10 МэВ (фиг. 199):

Из этих оценок видно, что характерная энергия ядерных частиц и ядерных процессов исчисляется миллионами электронвольт, а не десятками электронвольт, как это было в случае атомных процессов. (Электроны в атоме находятся примерно на расстоянии  см от ядра, протоны же в ядре находятся на расстоянии порядка
см от ядра, протоны же в ядре находятся на расстоянии порядка  см друг от друга. В результате соответствующие кулоновские силы различаются между собой множителем 108.)
см друг от друга. В результате соответствующие кулоновские силы различаются между собой множителем 108.)
Эти оценки совпадают с наблюдаемыми значениями энергии, получающимися при простых ядерных экспериментах. Энергия атомных переходов имеет порядок электронвольт. Энергия же продуктов ядерных превращений —  и у-лучей — обычно порядка миллиона электронвольт. Характерная энергия ядерных процессов настолько велика по обычным масштабам, что с ее помощью можно измерить соответствующий дефект массы:
и у-лучей — обычно порядка миллиона электронвольт. Характерная энергия ядерных процессов настолько велика по обычным масштабам, что с ее помощью можно измерить соответствующий дефект массы:

В 1905 г. Эйнштейн, говоря о своем соотношении между энергией и массой, предлагал:
«Не исключена возможность того, что теорию удастся проверить для веществ, энергия которых меняется в большой степени (например, для солей радия)» [8].
Сравнение масс и кинетических энергий исходных и конечных ядер, участвующих в ядерных процессах, дает, вероятно, наиболее точное и убедительное подтверждение справедливости формулы Эйнштейна.
Измеренные массы протонов и нейтронов можно сравнить с массой ядра, содержащего эти частицы. Получающуюся разность масс (дефект массы) можно сопоставить с измеренными значениями энергии, высвобождающейся при слиянии протонов и нейтронов или затраченной при расщеплении ядра. В качестве примера рассмотрим дейтрон — ядро изотопа водорода, содержащее один протон и один нейтрон. Проведем расчет, напоминающий бухгалтерский баланс:

Величина 2,225 МэВ есть энергия, которая выделяется при слиянии протона и нейтрона с образованием дейтрона или требуется для разделения дейтрона на протон и нейтрон. Этот вывод можно проверить, измеряя энергию фотона, расщепляющего дейтрон (фиг. 200).
В общем случае энергия связи ядра (энергия основного состояния ядерной системы при условии, что энергия нуклонов, на которые оно расщеплено, полагается равной нулю) определяется либо по измеренному значению энергии, необходимой для ресщепления ядра на составляющие его частицы (протоны и нейтроны), либо по разности масс ядерной системы и отдельных протонов и нейтронов, из которых состоит эта система.

Фиг. 200. Если дейтрон вначале покоился, то минимальная энергия фотона, способного вызвать этот процесс, равна энергии связи дейтрона (небольшим изменением положения центра масс мы пренебрегаем); масса фотона  масса дейтрона
масса дейтрона  масса протона
масса протона  масса нейтрона. Измеренная величина минимальной энергии равна 2,226 0,003 МэВ.
масса нейтрона. Измеренная величина минимальной энергии равна 2,226 0,003 МэВ.
Энергия и разность масс (дефект массы) связаны между собой с помощью соотношения Эйнштейна (как было в случае дейтрона),
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
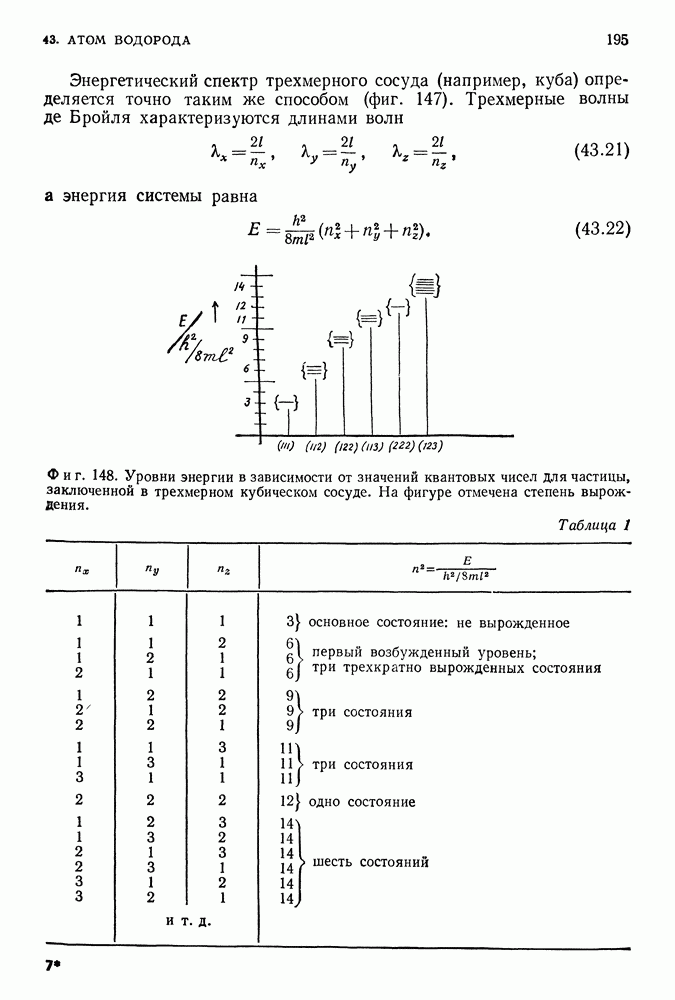
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
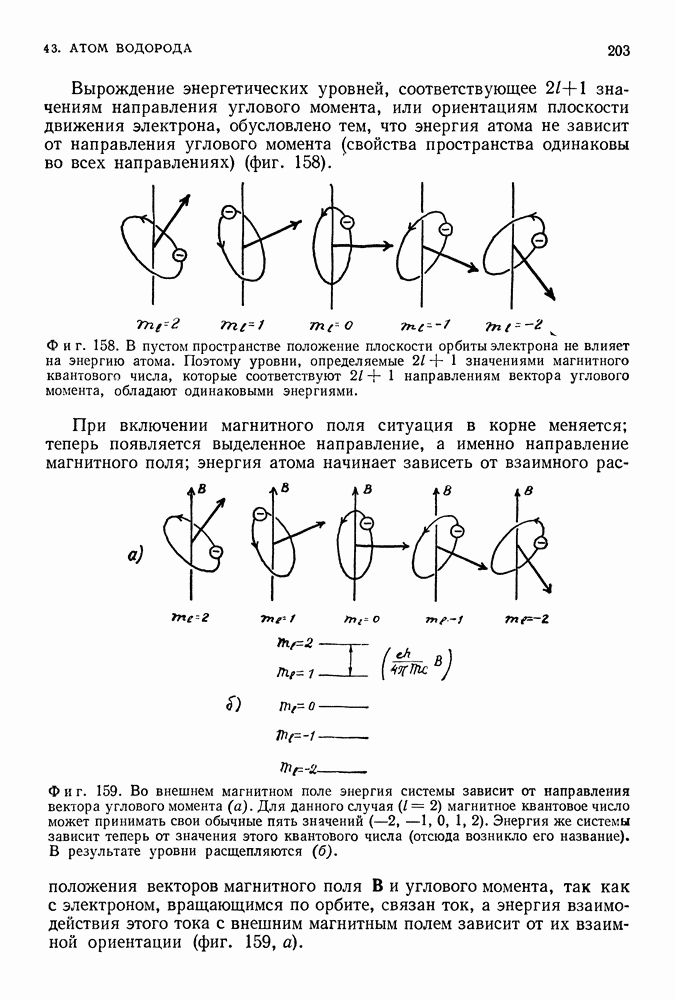
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
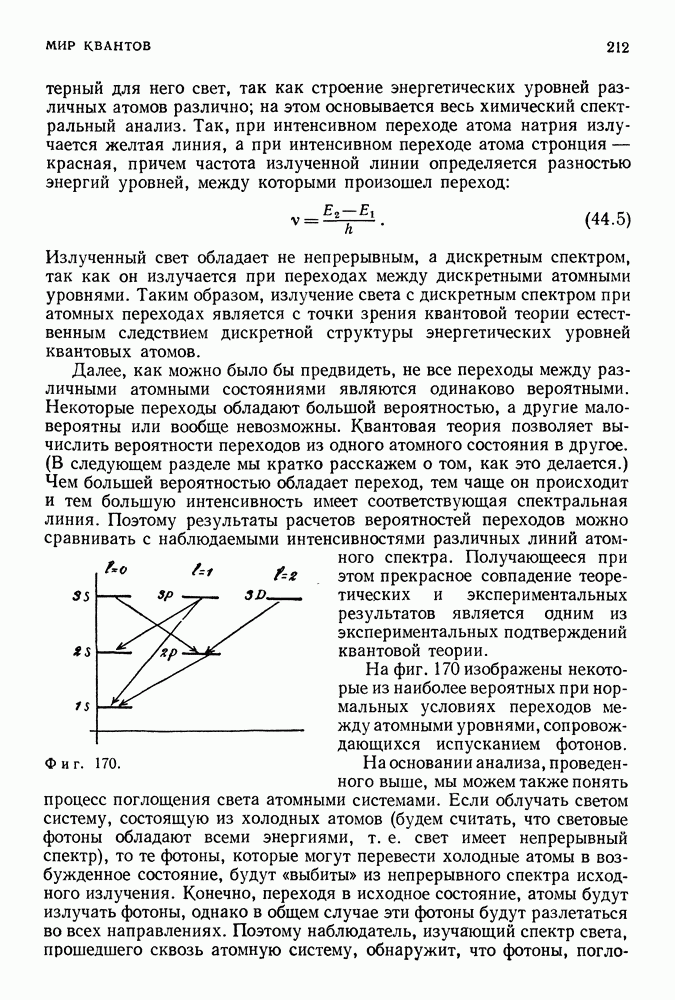
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
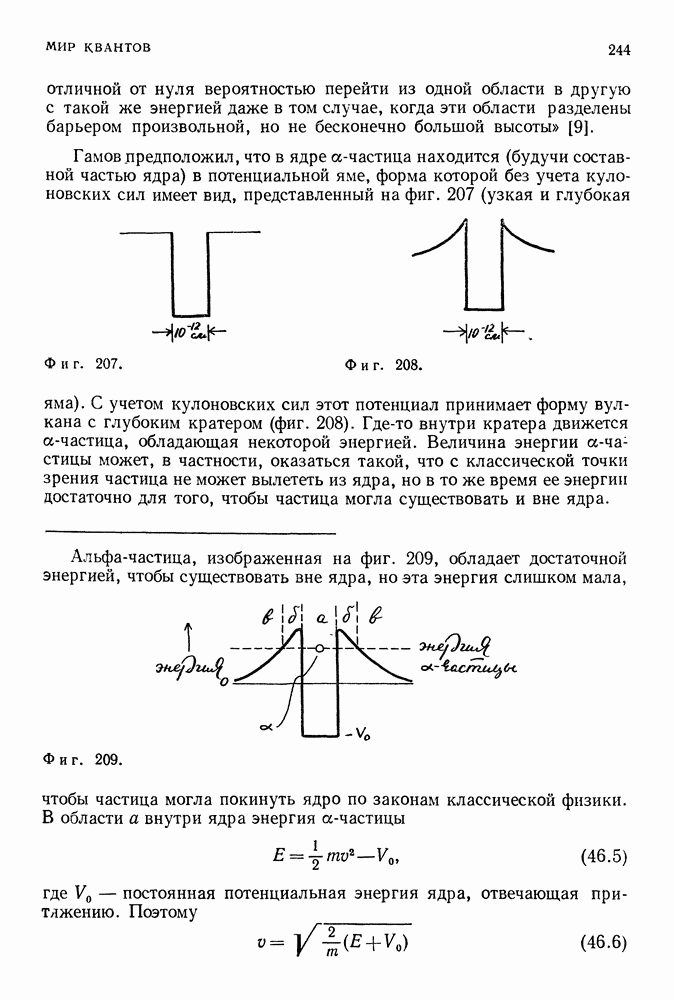
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
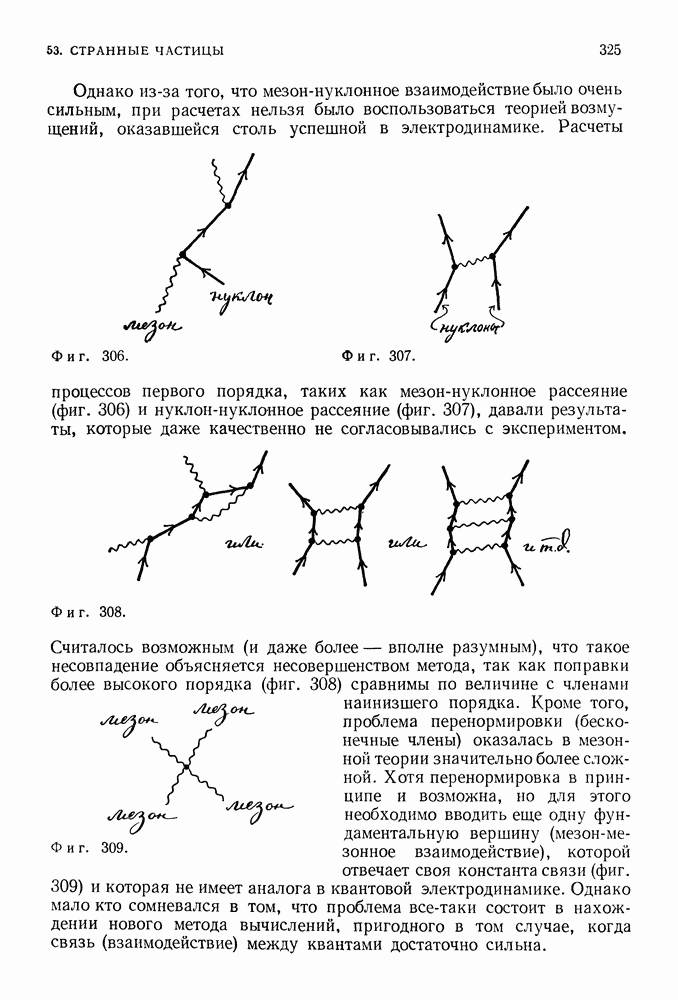
- 53. СТРАННЫЕ ЧАСТИЦЫ
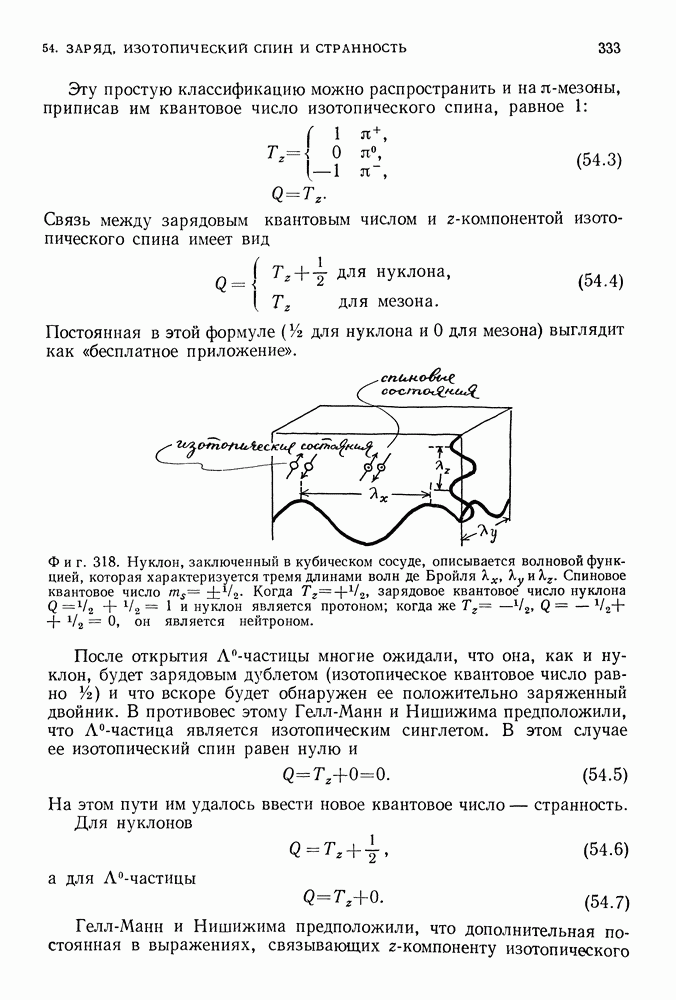
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
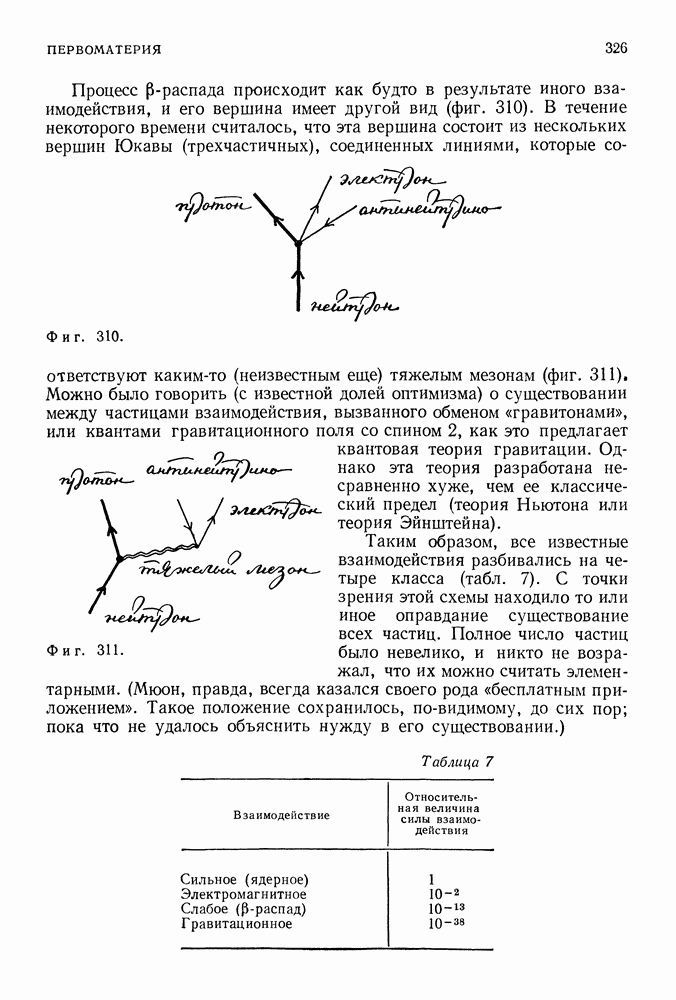
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА