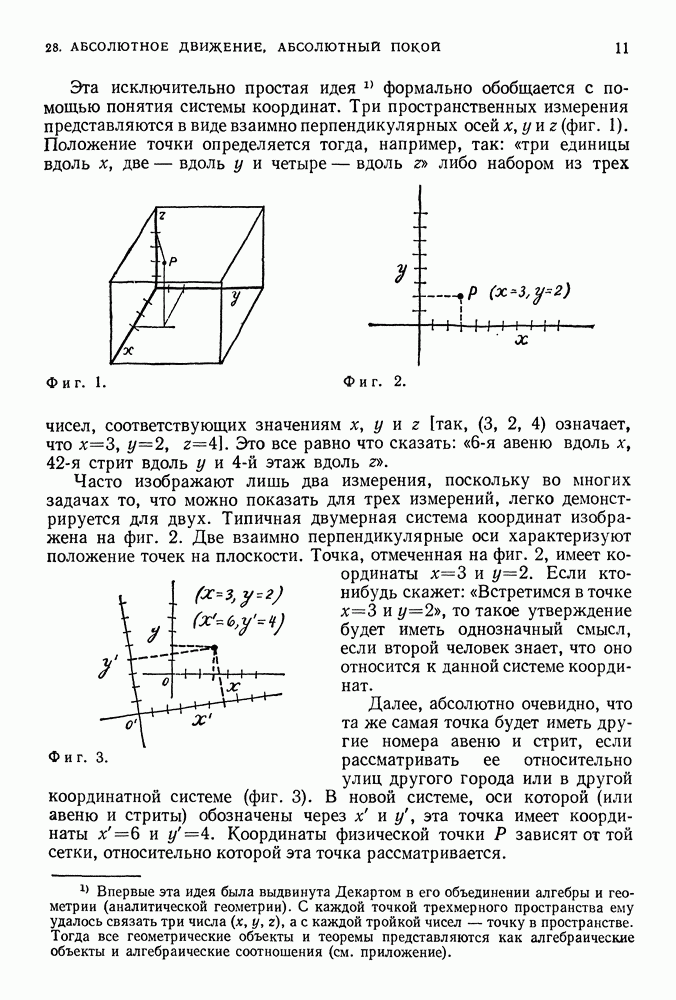
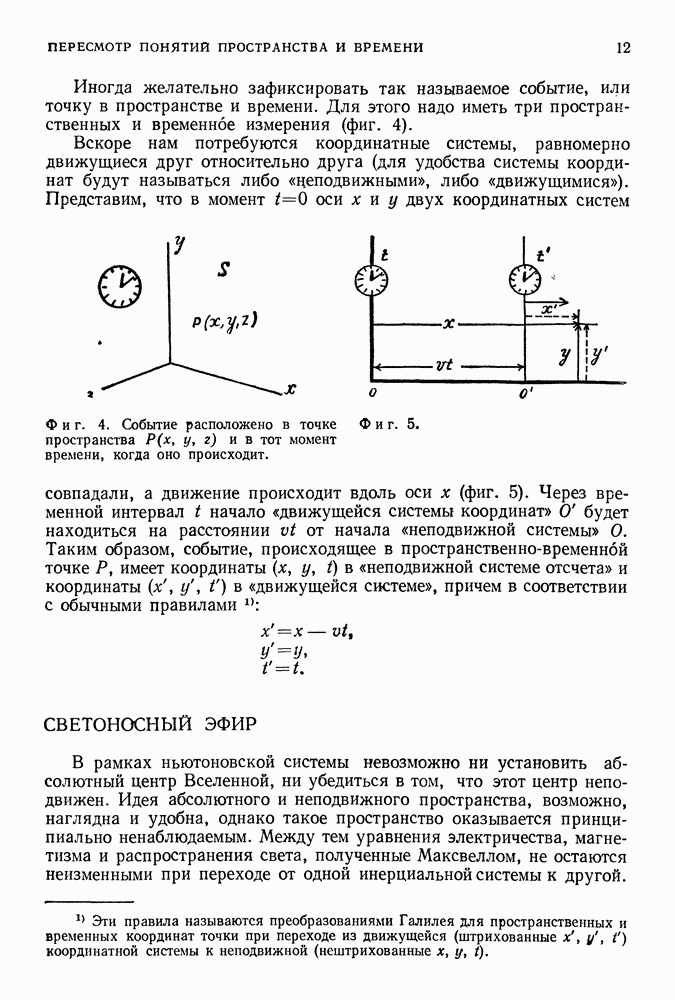
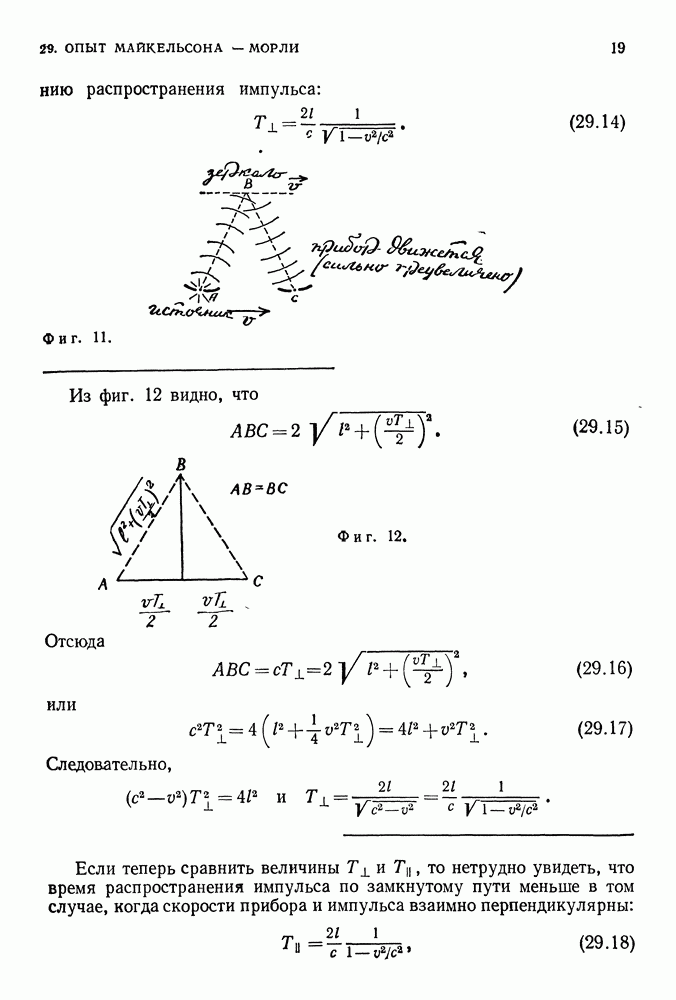
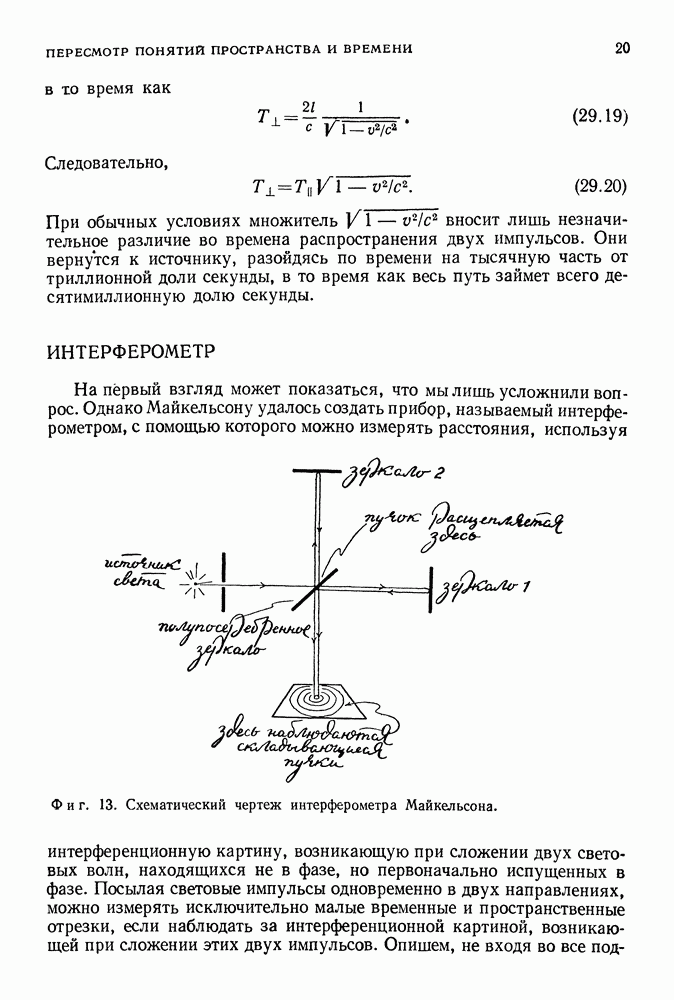
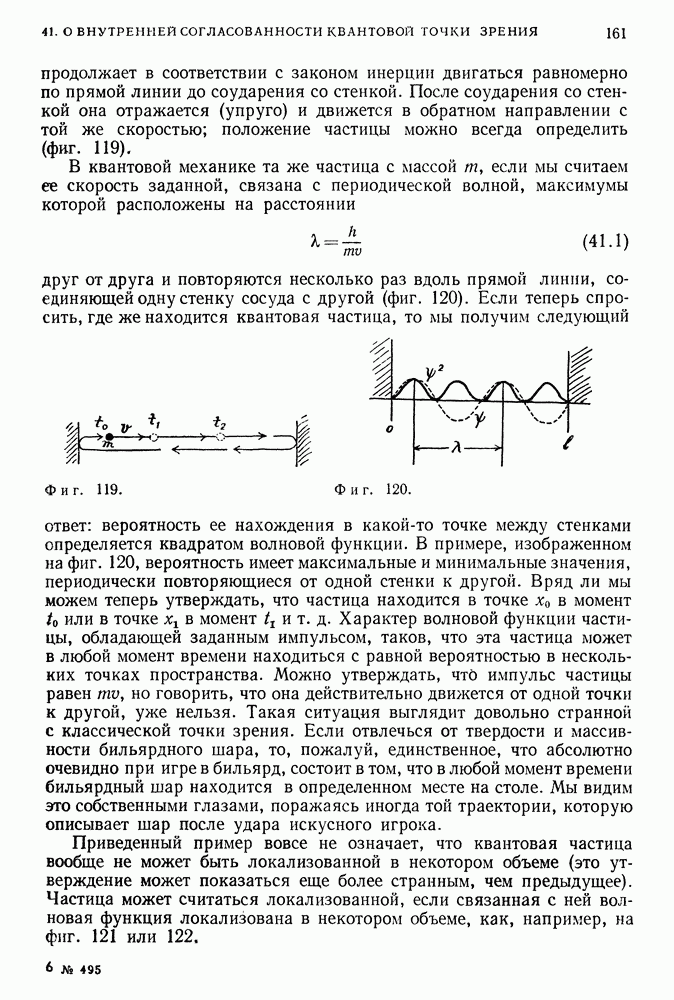
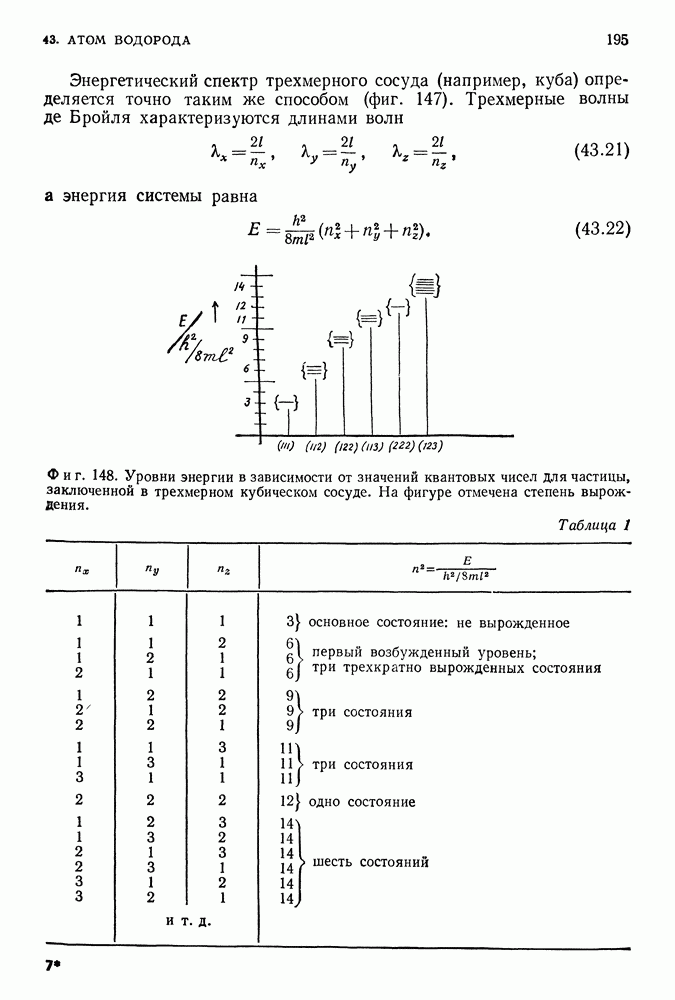
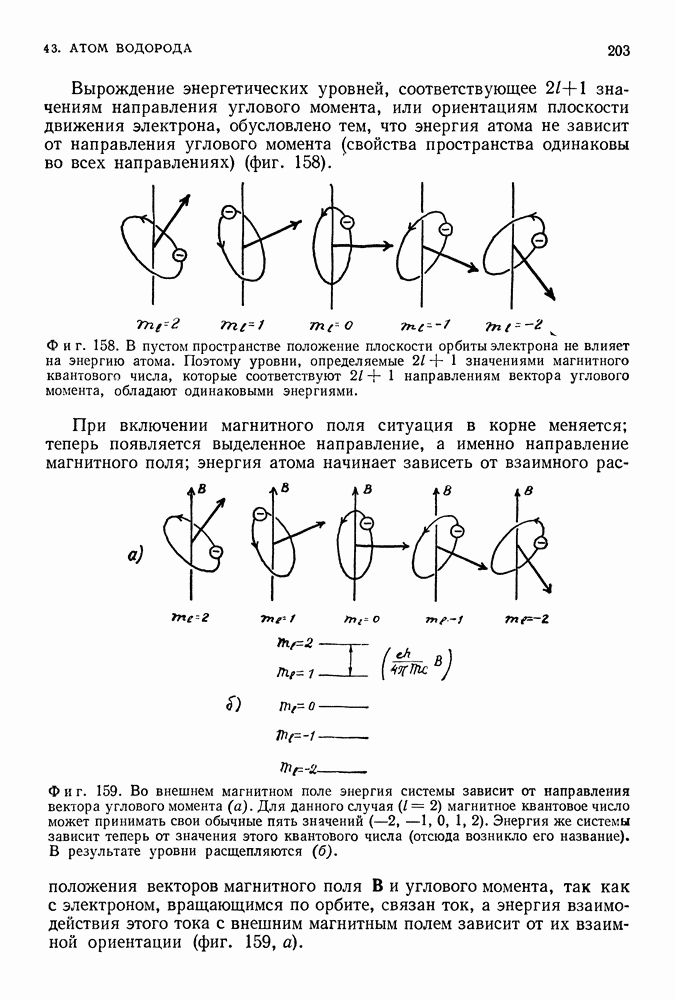
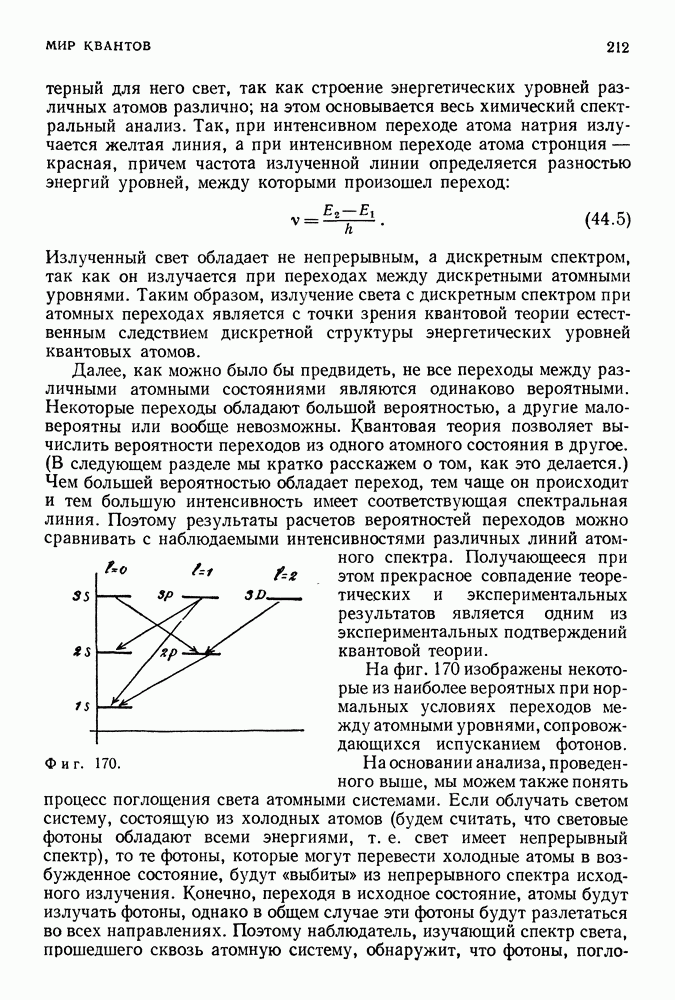
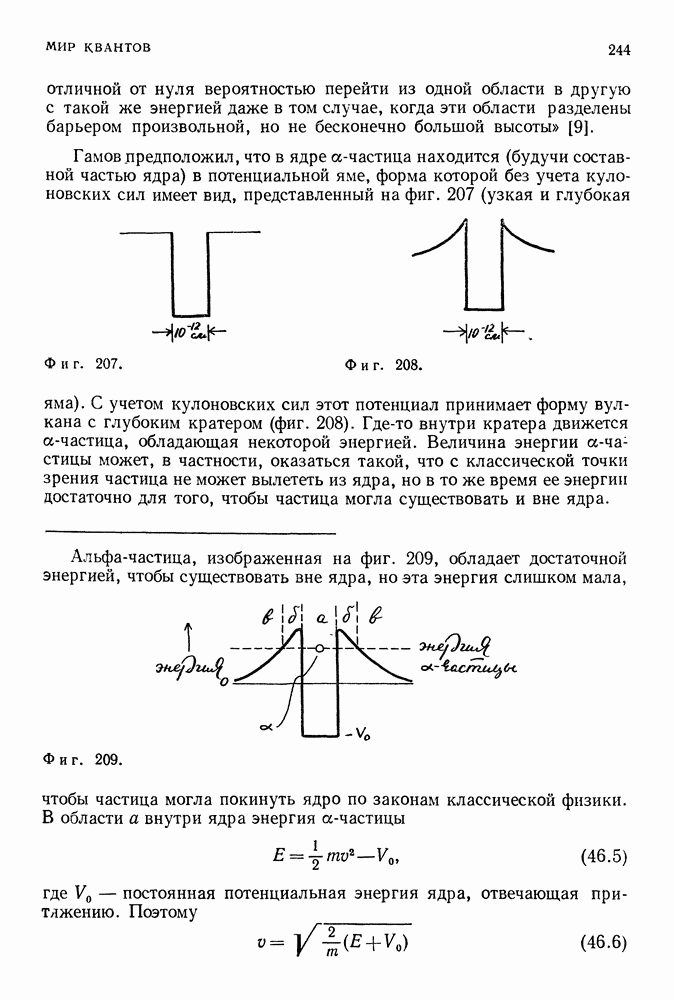
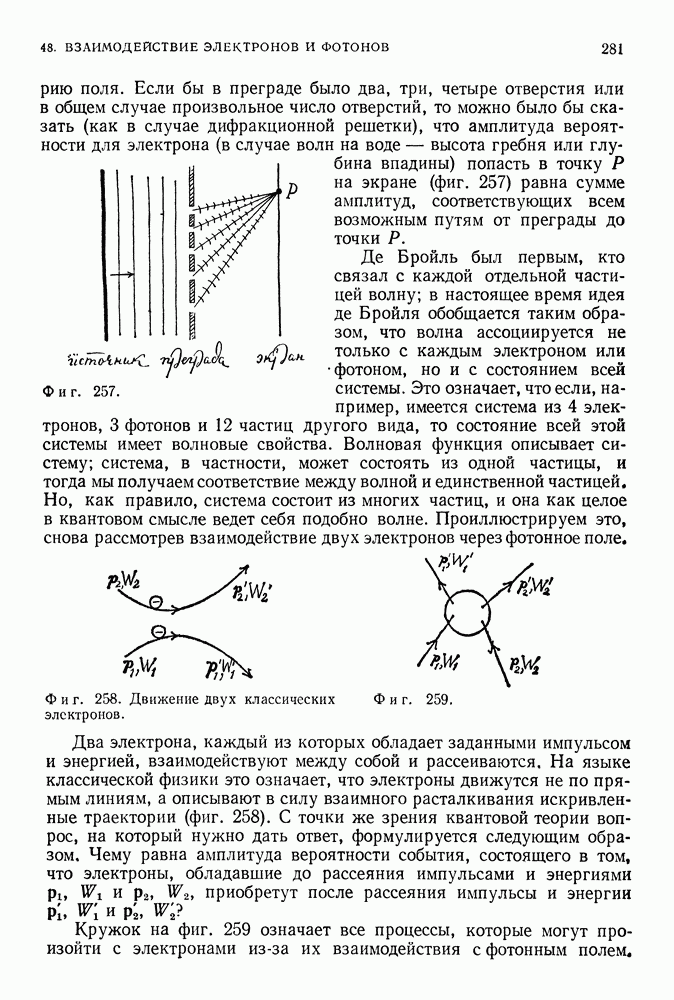
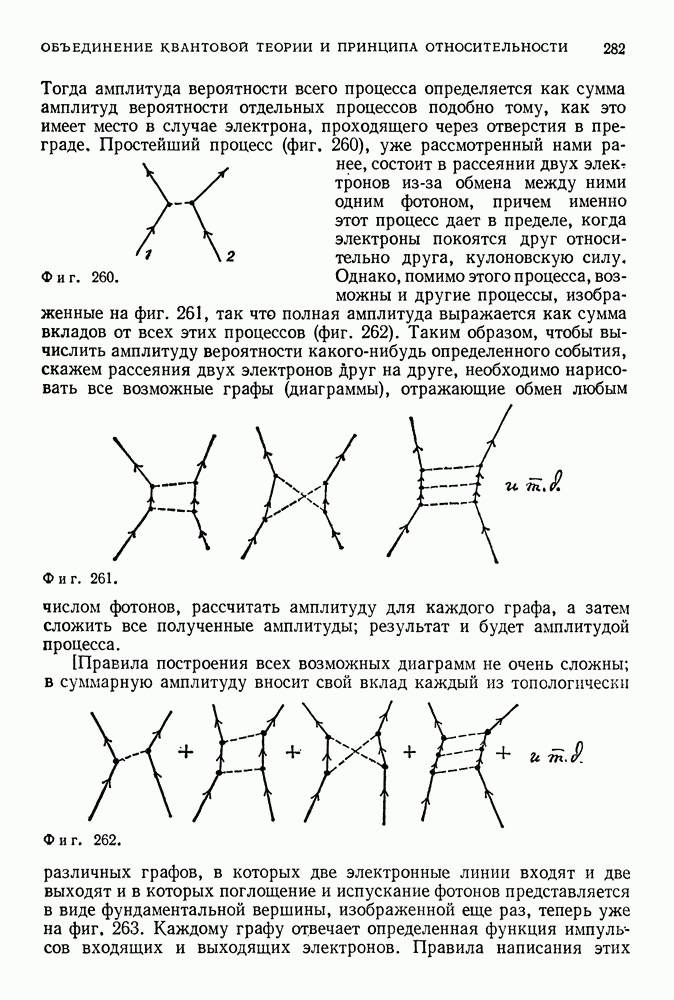
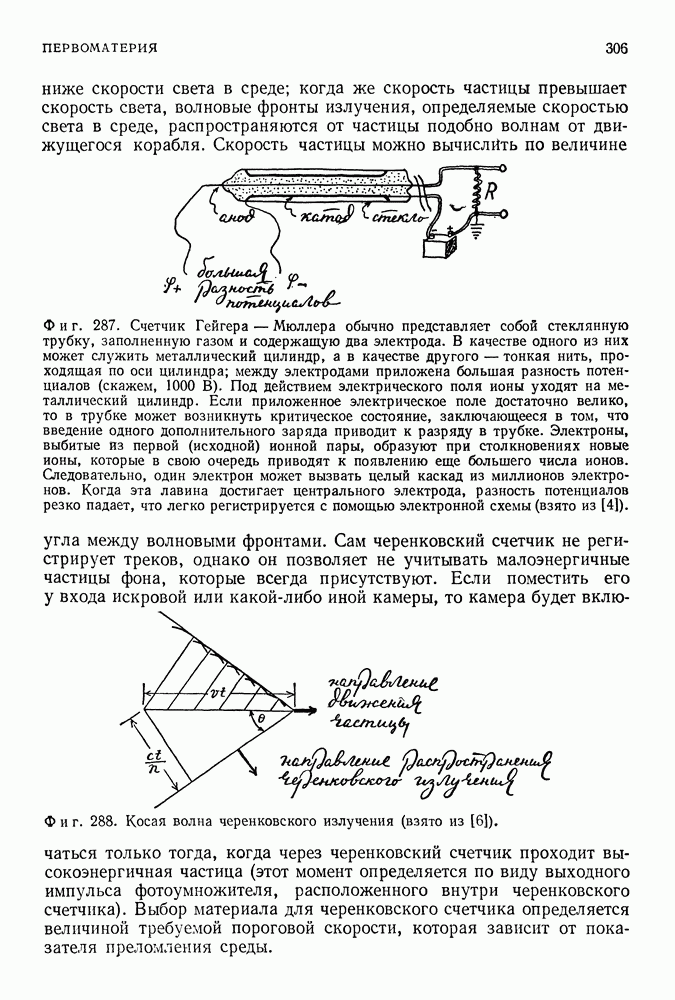
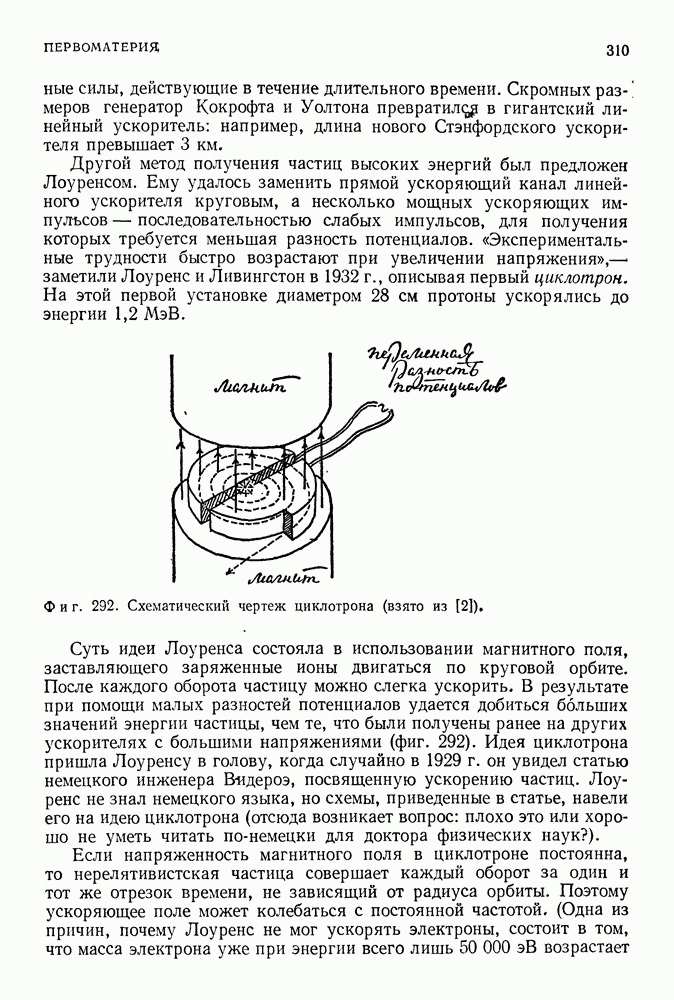
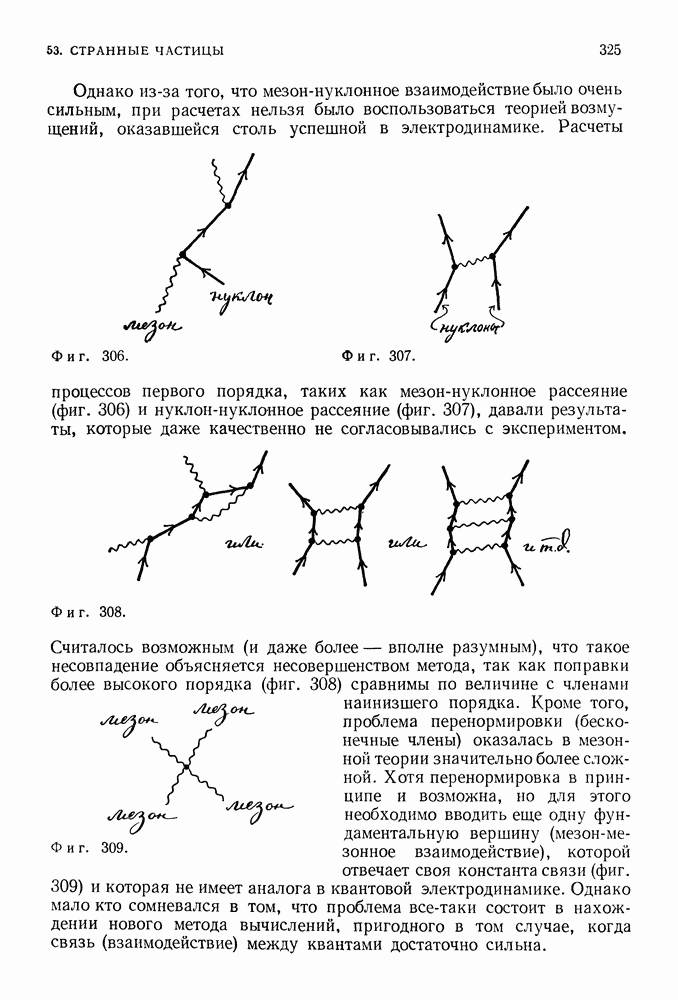
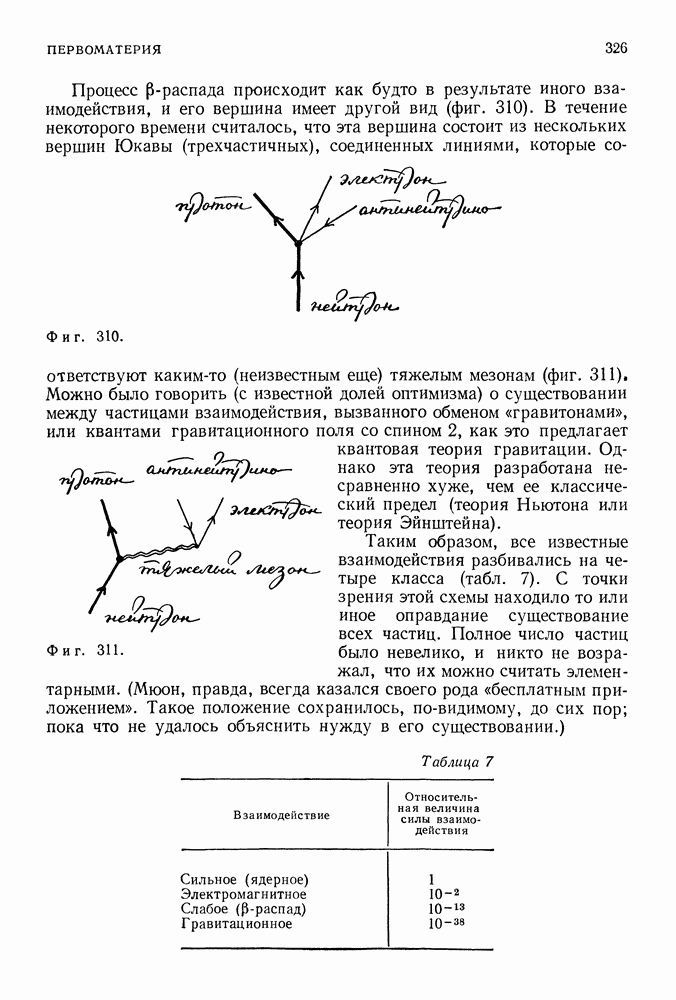
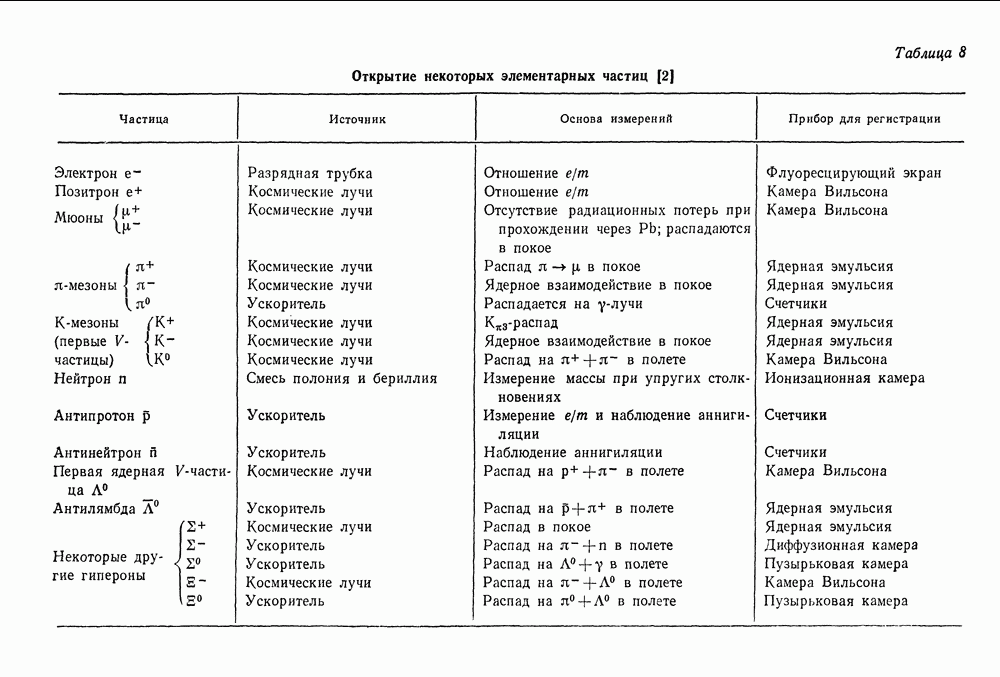
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
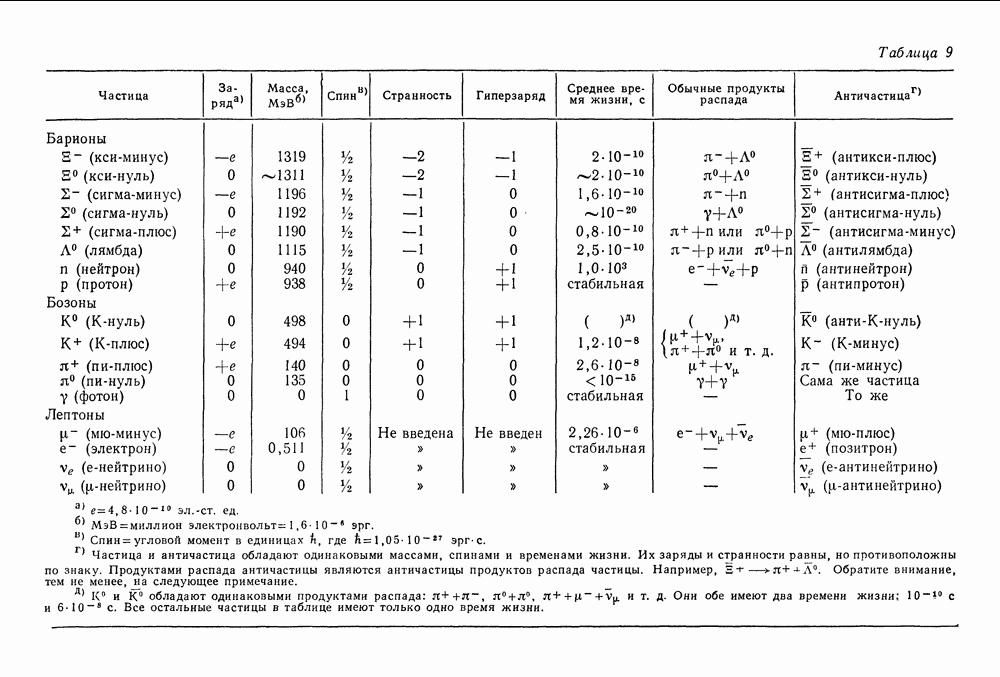
ВОДОРОДНЫЙ АТОМ БОРА
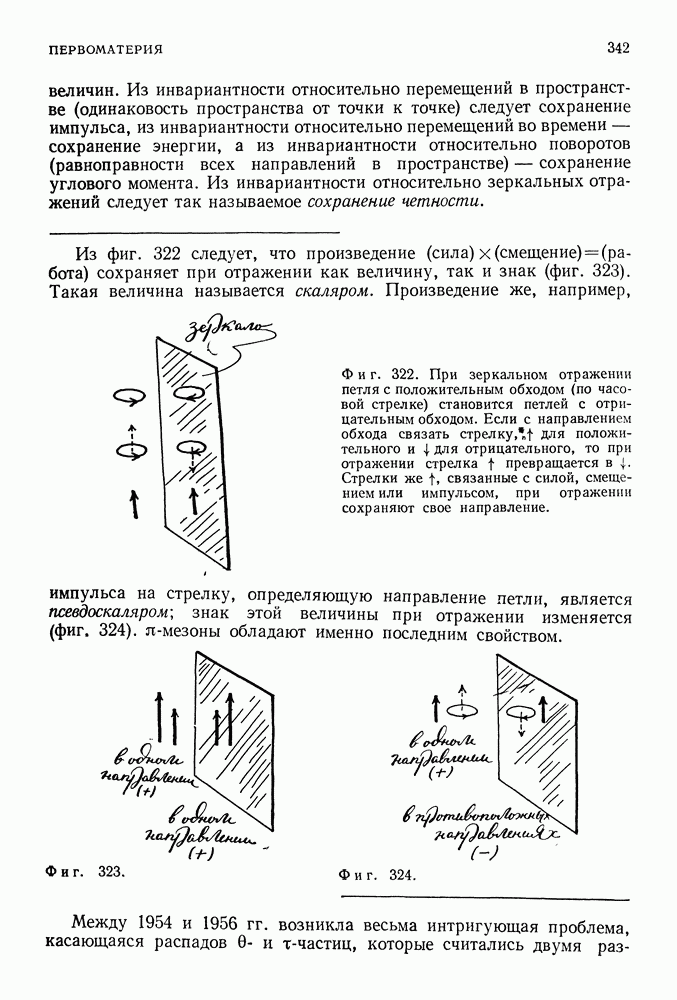
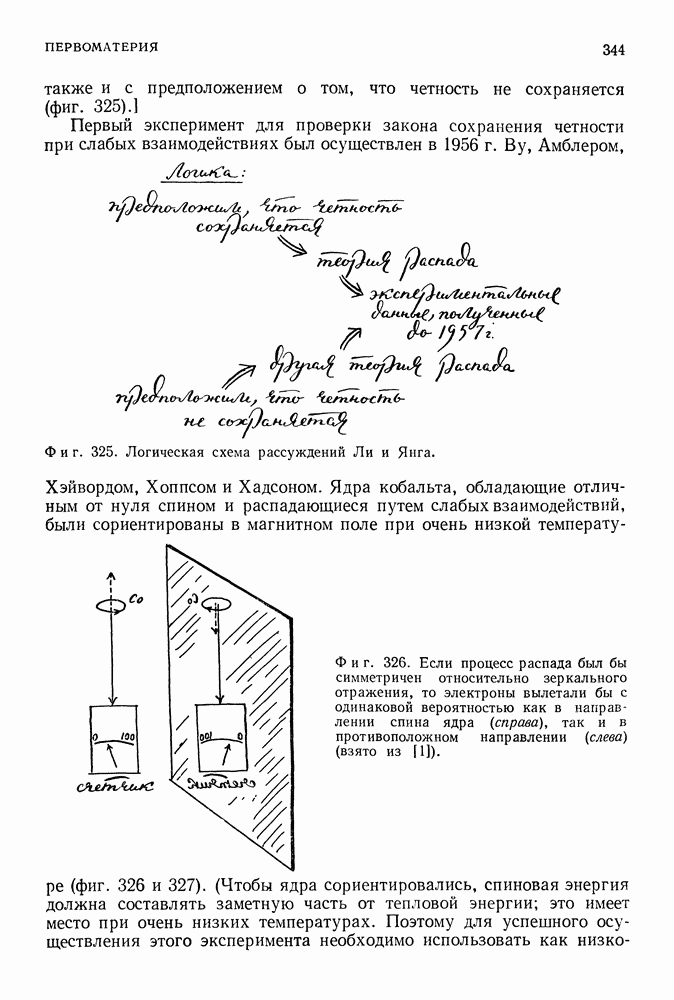
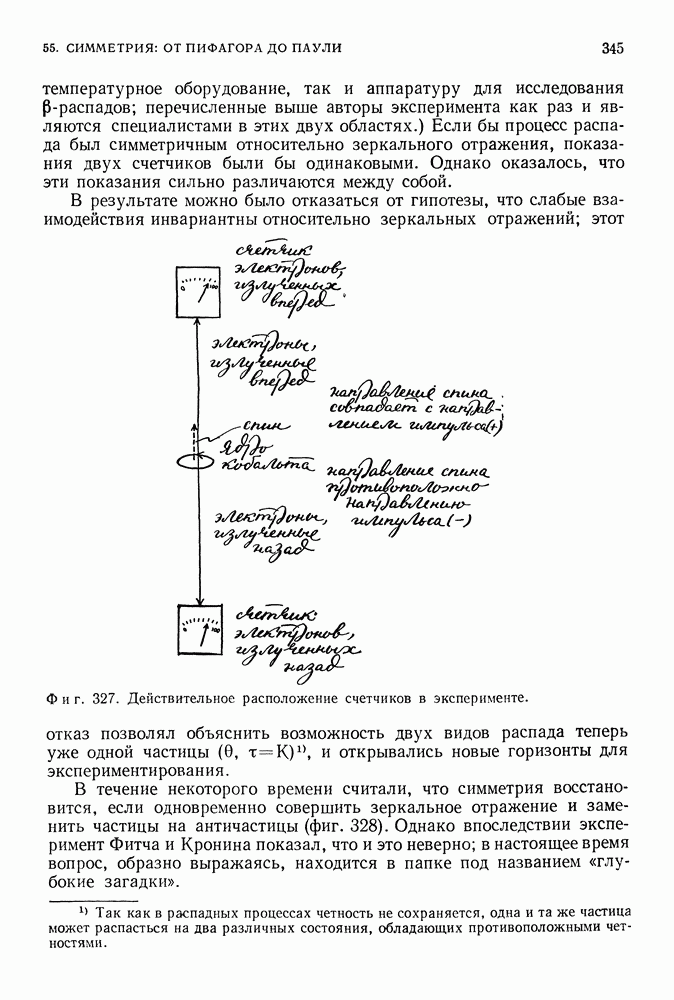
Как все изменилось за двадцать лет! В 1890 г. считалось, что физическая картина мира полностью завершена старыми мастерами. Казалось, что каждая ее линия столь успешно объясняет все разнообразие явлений природы, что нанесение окончательных мазков кистью является просто делом времени и терпения. Но к 1911 г. ситуация резко изменилась. Оказались абсолютно непонятными и странными следующие явления: дискретный характер испускания и поглощения электромагнитного излучения, устойчивость атома Резерфорда, связь между энергией и частотой света и, наконец, квант действия Планка, открытие которых было подготовлено всём развитием классической физики. Наступило время великих йеремен, время новых захватывающих приключений, новых возможностей, время ломки старых представлений и создания на их месте новых.
В 1913 г. Бор предложил свою модель атома. Это был атом Резерфорда с положительным зарядом в центре, сконцентрированным в очень малом объеме, с электронами, вращающимися по круговым орбитам вокруг ядра в соответствии со вторым законом Ньютона и притягивающимися к нему согласно закону Кулона. Ускорение электрона (как и любого другого тела, движущегося равномерно по окружности)

направлено к центру окружности.
Сила, действующая между электроном и ядром, является притягивающей, направлена от электрона к ядру и для водорода, ядро которого содержит один элементарный заряд, равна по величине

На основании второго закона Ньютона

или

т. е. удвоенная кинетическая энергия равна потенциальной энергии
Полная энергия электрона на орбите (кинетическая плюс потенциальная)

или с учетом (37.12),

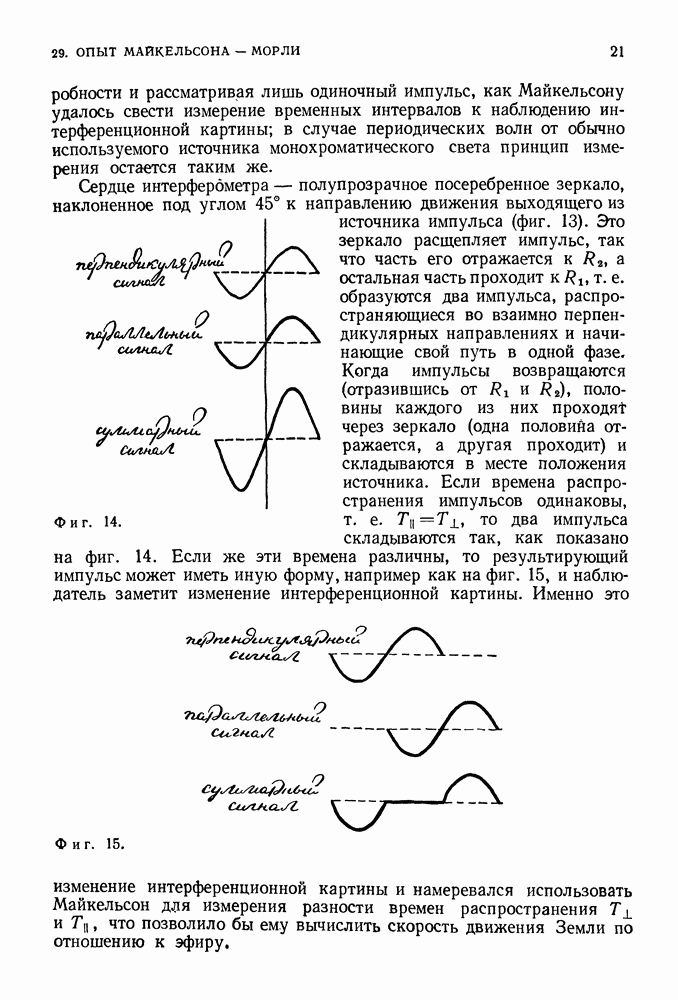
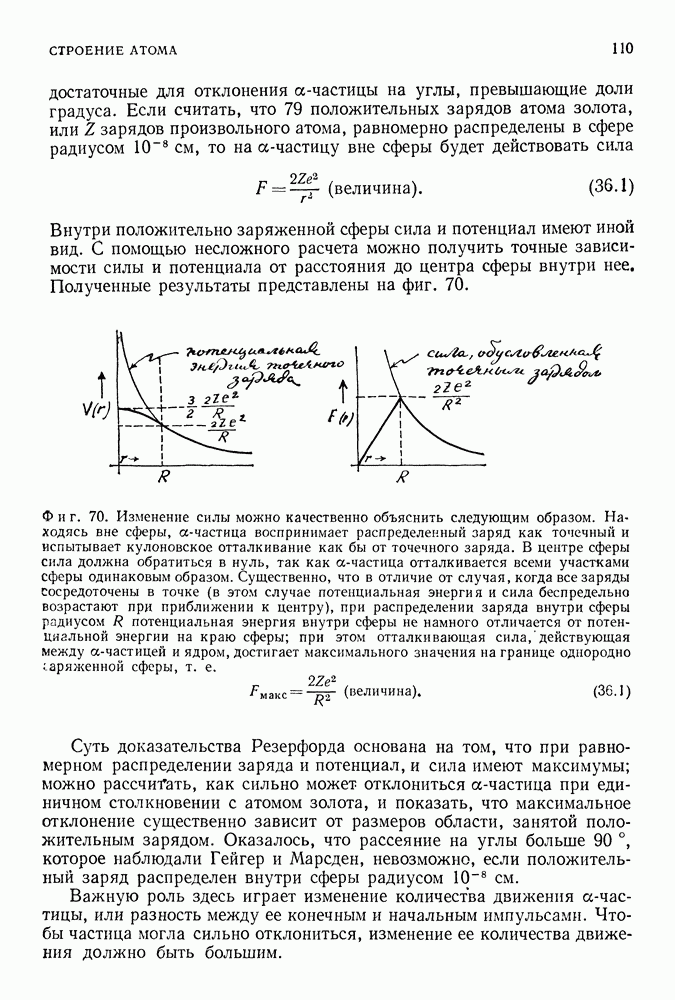
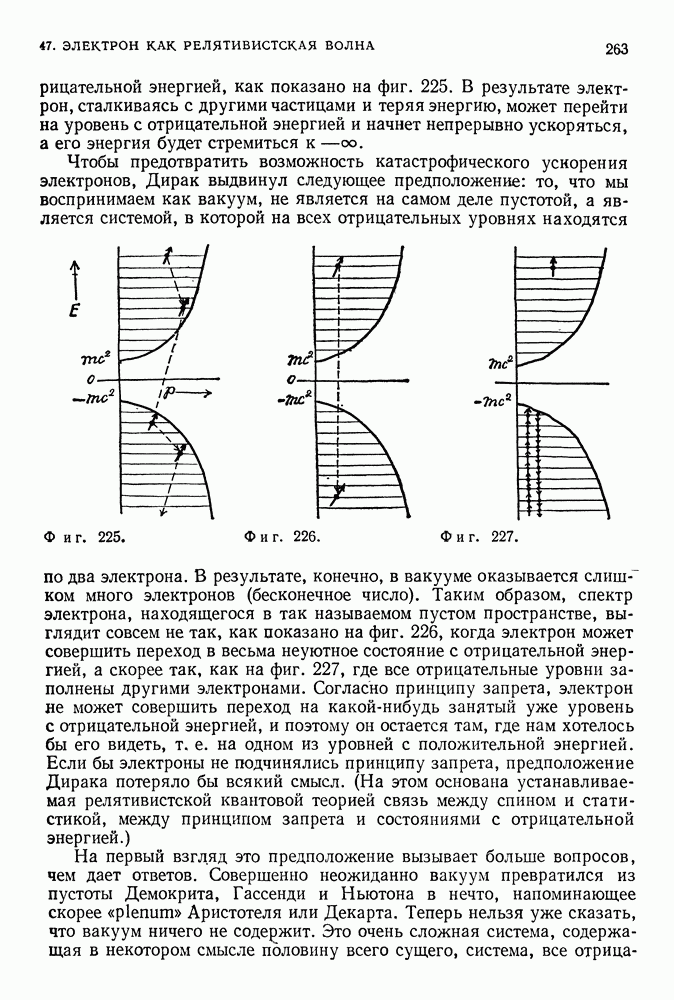
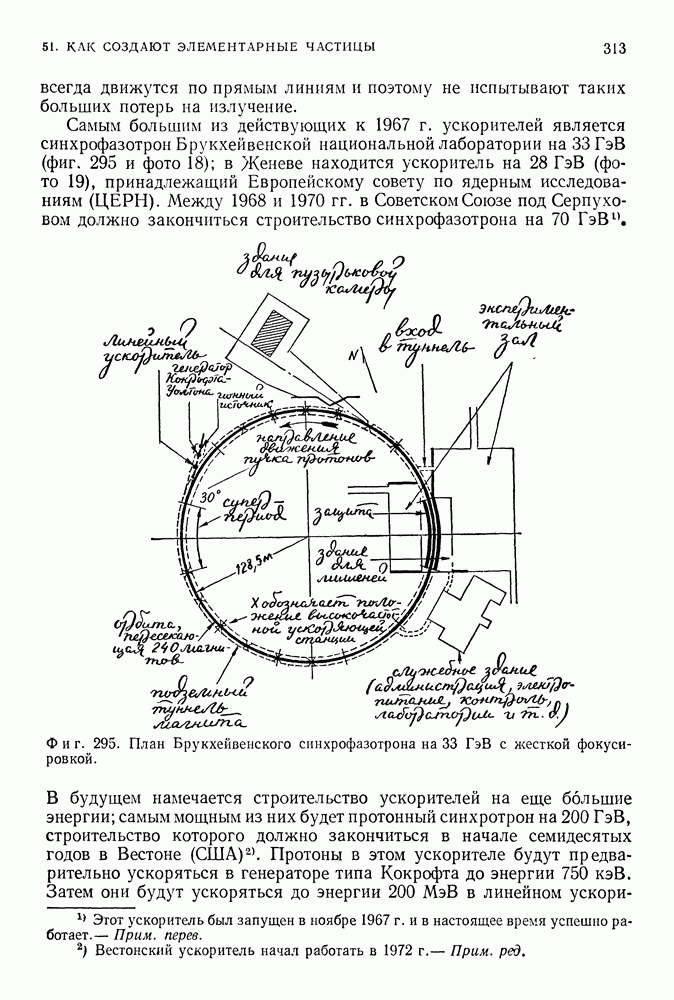
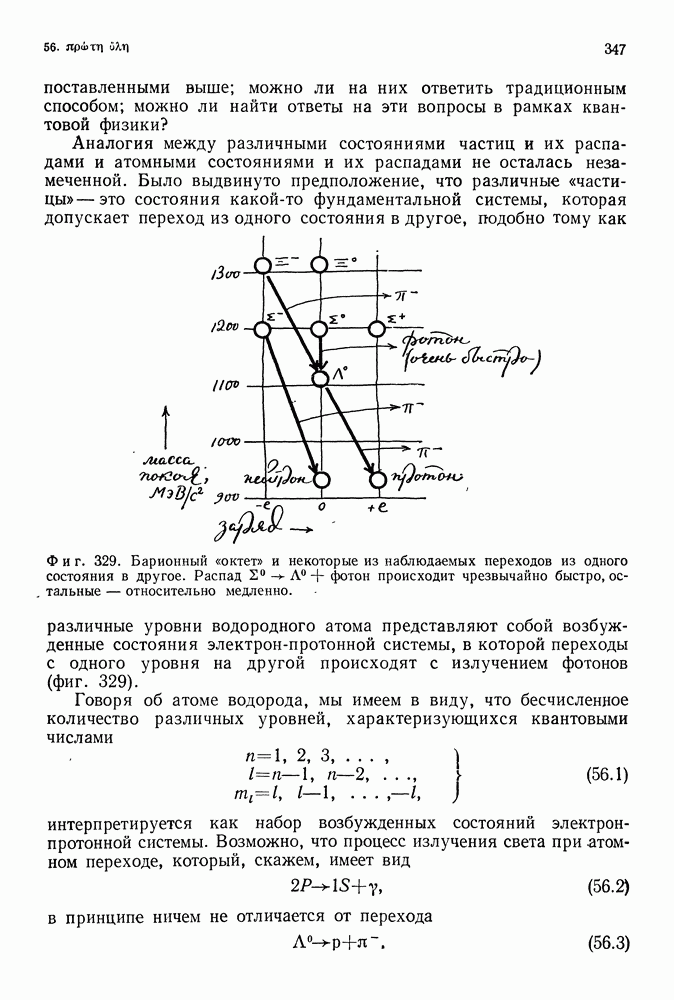
(фиг. 85).
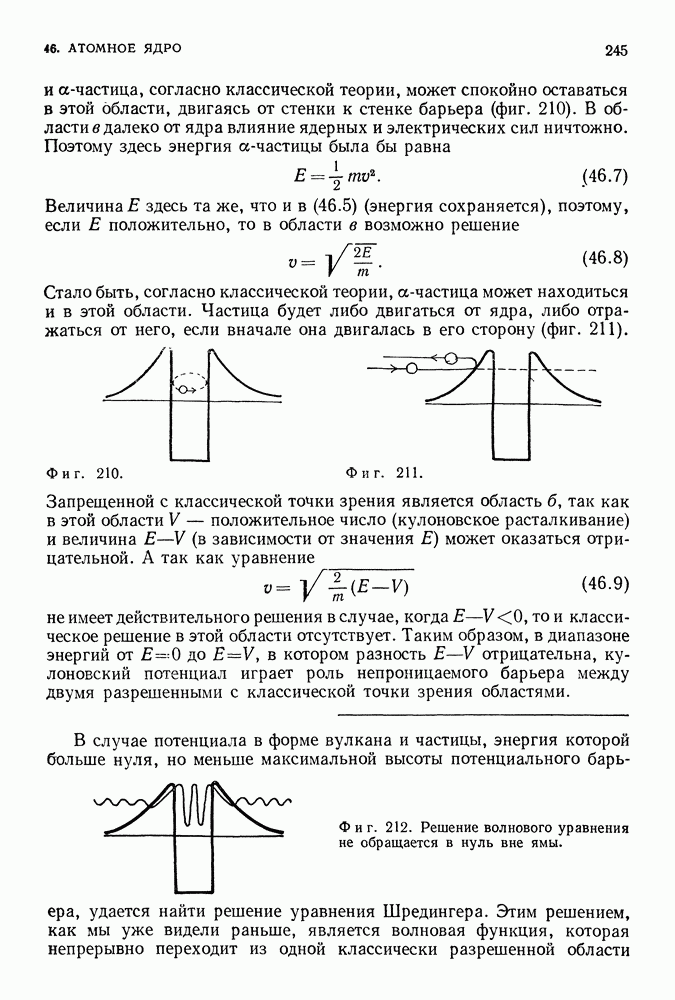
Таким образом, полная энергия равна по величине половине потенциальной энергии. Это справедливо как для электрона, вращающегося вокруг положительно заряженного ядра, так и для планеты, движущейся вокруг Солнца. Мы предположили, что электрон вращается по круговой орбите, что он подчиняется второму закону Ньютона и что он притягивается к положительно заряженному центру в соответствии с законом Кулона. Любая круговая орбита является разрешенной для электрона, и нас пока не интересует вопрос об его излучении. До сих пор все наши предположения были чисто классическими. Но нам и не удалось пока преодолеть ни одной трудности.

Фиг. 85.
В этом месте Бор вводит свою знаменитую гипотезу: из всех возможных орбит, заявляет он, являются разрешенными только те, для которых выполняется квантовое условие, связанное с соотношением Эйнштейна и Планка. Квантовое условие Бора ограничивает возможные значения углового момента электрона, способного двигаться по различным орбитам. Для круговой орбиты величина углового момента электрона (равного, согласно определению из гл. 14, произведению импульса на длину плеча) дается выражением

Бор выдвинул предположение, что только те орбиты, для которых угловой момент удовлетворяет условию

т. е. равен по величине целому числу  — произвольное целое число) постоянных Планка, деленному на
— произвольное целое число) постоянных Планка, деленному на  являются разрешенными Как мы увидим, квантовое условие позволяет электронам вращаться только по некоторым из возможных круговых орбит. Однако, согласно теории Максвелла, электрон должен излучать энергию и на этих
являются разрешенными Как мы увидим, квантовое условие позволяет электронам вращаться только по некоторым из возможных круговых орбит. Однако, согласно теории Максвелла, электрон должен излучать энергию и на этих
орбитах. Эту трудность Бор разрешил (если можно так выразиться) декретным способом. Он постулировал, что электрон вопреки теории Максвелла, вопреки опытам Герца, вопреки всему, во что верили до этого времени, не излучает электромагнитную энергию, когда он находится на стационарной орбите, т. е. орбите, разрешенной квантовым условием. Когда же в таком случае он излучает энергию? Ответ на этот вопрос содержался в третьем постулате Бора. Бор предположил, что электрон излучает электромагнитную волну только тогда, когда он переходит с одной разрешенной орбиты на другую. Точное же значение излученной при этом энергии определяется соотношением Эйнштейна — Планка:

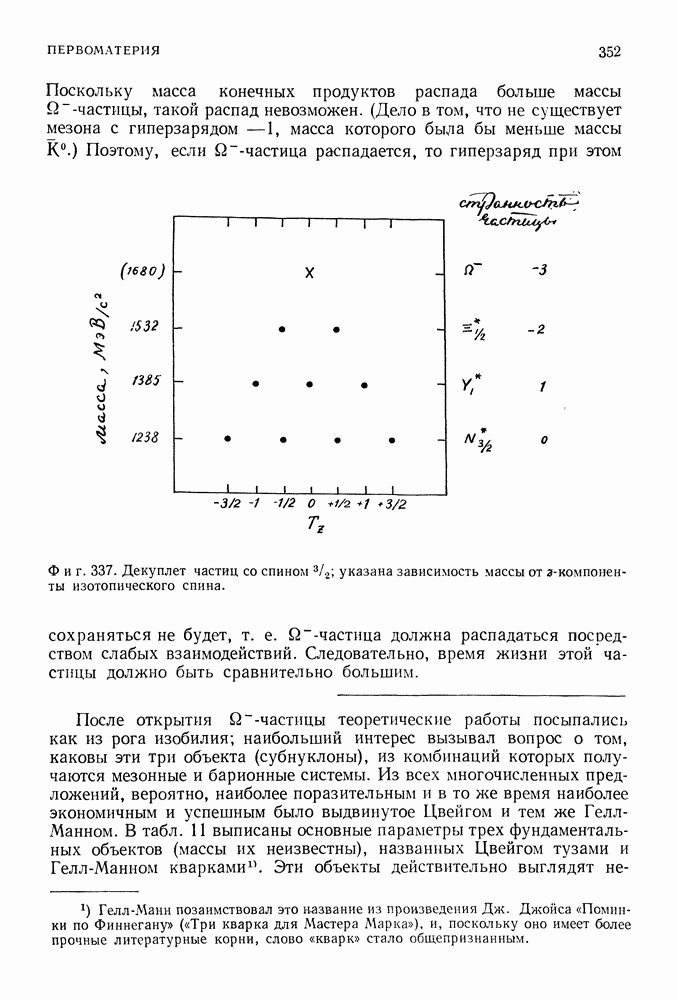
Таким образом, энергия излученного света равна разности энергий двух орбит, между которыми перескочил электрон (фиг. 86).

Фиг. 86.
Каждое из этих предположений — условие квантования, отсутствие излучения при нахождении электрона на одной из стационарных орбит и излучение света при переходе с одной орбиты на другую — противоречит классической теории. Однако ведь надо же было каким-то образом постулировать устойчивость атома. Излучение же порциями, очевидно, согласовывалось с тем, что ранее обнаружили Эйнштейн и Планк. Да и условие квантования несильно отличалось от первоначального условия Планка. Проследим же за этой смесью классических и неклассических постулатов, изучив модель атома, предложенную Бором.
Условие квантования (37.16) дает связь между скоростью электрона и радиусом разрешенной орбиты. Второй закон Ньютона и закон Кулона тоже связывают скорость электрона и радиус орбиты [см. (37.12)]. Если скомбинировать эти два условия — классическое и квантовое, — то мы получим строго определенные радиусы разрешенных орбит:

Из классического условия мы имеем

а из квантового —

Разделив последнее выражение на  получим
получим

Возведем теперь обе его части в квадрат:

а затем разделим на 

Таким образом, мы получили два выражения для  Так как две величины, равные одной и той же величине, равны между собой, имеем
Так как две величины, равные одной и той же величине, равны между собой, имеем

Умножая это выражение на  и деля на
и деля на  получаем (37.18):
получаем (37.18):

Мы пишем у величины  индекс
индекс  чтобы подчеркнуть зависимость
чтобы подчеркнуть зависимость  от
от 
Наименьшему из возможных радиусов, называемому боровским радиусом, соответствует значение 

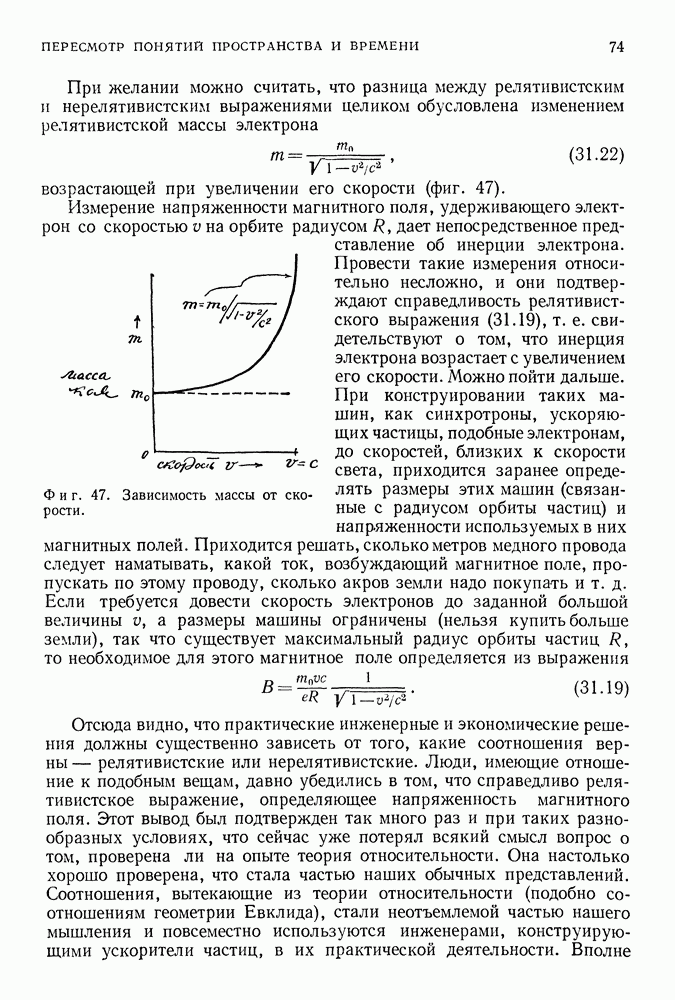
Его величину можно вычислить, подставив сюда значение постоянной Планка (уже известное тогда), а также значения массы и заряда электрона. В результате получим

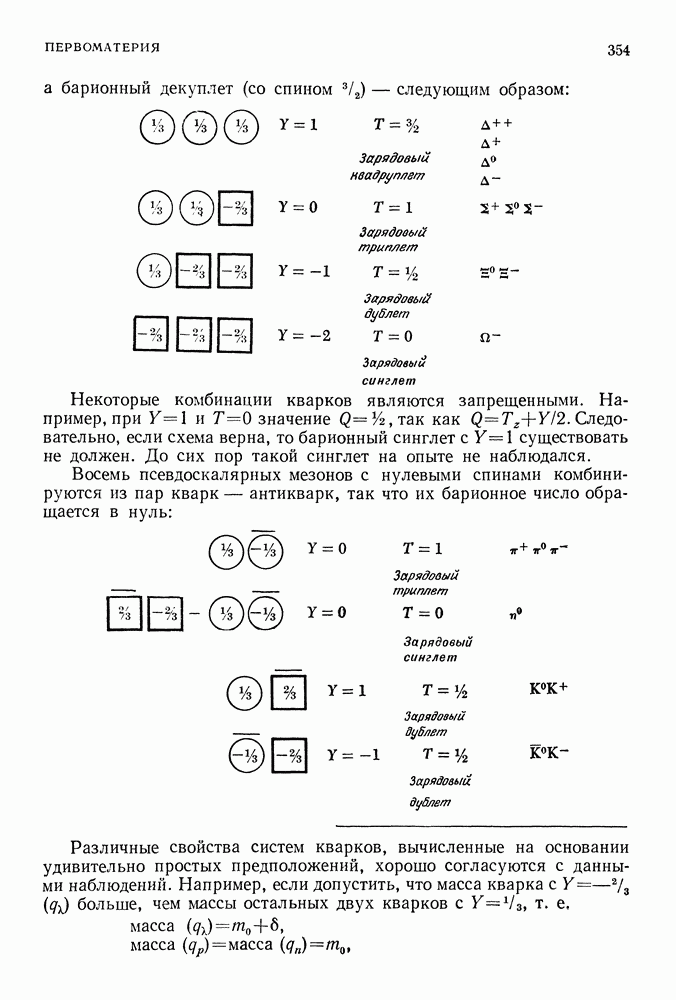
Когда электрон находится на этой орбите (фиг. 87), атом обладает наименьшей полной энергией (или наибольшей отрицательной энергией); в этом случае говорят, что электрон находится в основном состоянии, и дальнейшие переходы между уровнями невозможны.

Фиг. 87,
В соответствии с постулатом Бора атом в этом состоянии не излучает и, стало быть, он устойчив. Далее, все водородные атомы, излучая, постепенно
переходят в это основное состояние и в результате становятся абсолютно одинаковыми.
Уровни энергии, соответствующие различным боровским орбитам, могут быть вычислены следующим образом. С помощью чисто классических рассуждений мы показали, что энергия на произвольной круговой орбите

Отсюда, используя значения радиусов разрешенных боровских орбит, получаем разрешенные уровни энергии

Когда электрон находится на наинизшей боровской орбите (атом в основном состоянии), энергия атома равна

И наконец согласно третьему условию Бора, при переходе с одного уровня энергии на другой

Когда Бор подставил сюда известные в то время значения постоянных  и
и  он получил для коэффициента значение
он получил для коэффициента значение

Этот же коэффициент, вычисленный из частот наблюдаемых спектральных линий серии Бальмера, равнялся

Бор заключил, что
«Соответствие между теоретическим и наблюдаемым значениями лежит в пределах ошибок измерений постоянных, входящих в теоретическую формулу» [9].
Поскольку и  являются целыми числами (
являются целыми числами ( при переходах с одного атомного уровня на другой излученный атомом свет обладает различными дискретными частотами. Положив
при переходах с одного атомного уровня на другой излученный атомом свет обладает различными дискретными частотами. Положив  и
и  -любому целому числу, превышающему 2, мы получаем выражение, сходное с формулой Бальмера, но записанное не через
-любому целому числу, превышающему 2, мы получаем выражение, сходное с формулой Бальмера, но записанное не через
длину волны, а через частоту. Чтобы провести сравнение, выразим частоту через длину волны по формуле

Тогда из выражения (37.31) получим

в то время как формула Бальмера имеет вид

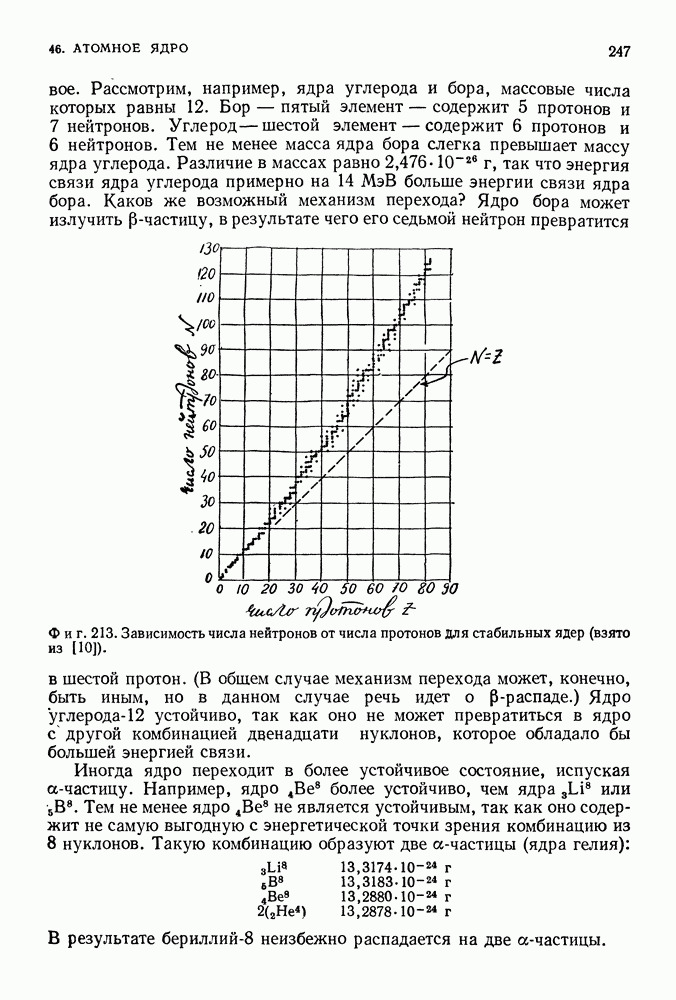
Используя современные значения для постоянных, найдем, что  см. Бальмеровская же константа
см. Бальмеровская же константа  см.
см.
Модель Бора предсказывала существование и других спектральных линий. Формула Бальмера описывает серию, соответствующую переходам электрона с различных уровней на уровень  Естественно ожидать, что существуют серии, соответствующие переходам электрона на уровень
Естественно ожидать, что существуют серии, соответствующие переходам электрона на уровень  уровень
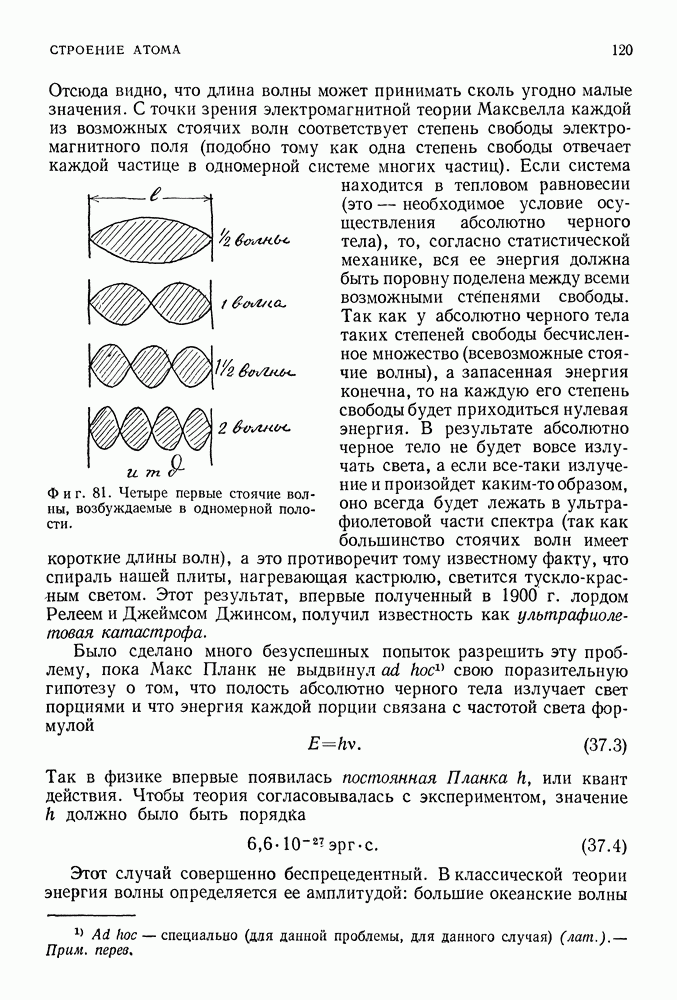
уровень  Эти серии были обнаружены в ходе спектроскопических исследований и известны теперь как серии Лаймана, Пашена, Брекетта и др. (фиг. 88).
Эти серии были обнаружены в ходе спектроскопических исследований и известны теперь как серии Лаймана, Пашена, Брекетта и др. (фиг. 88).

Фиг. 88. Переходы между уровнями водородного атома Бора, приводящие к излучению различных серий.
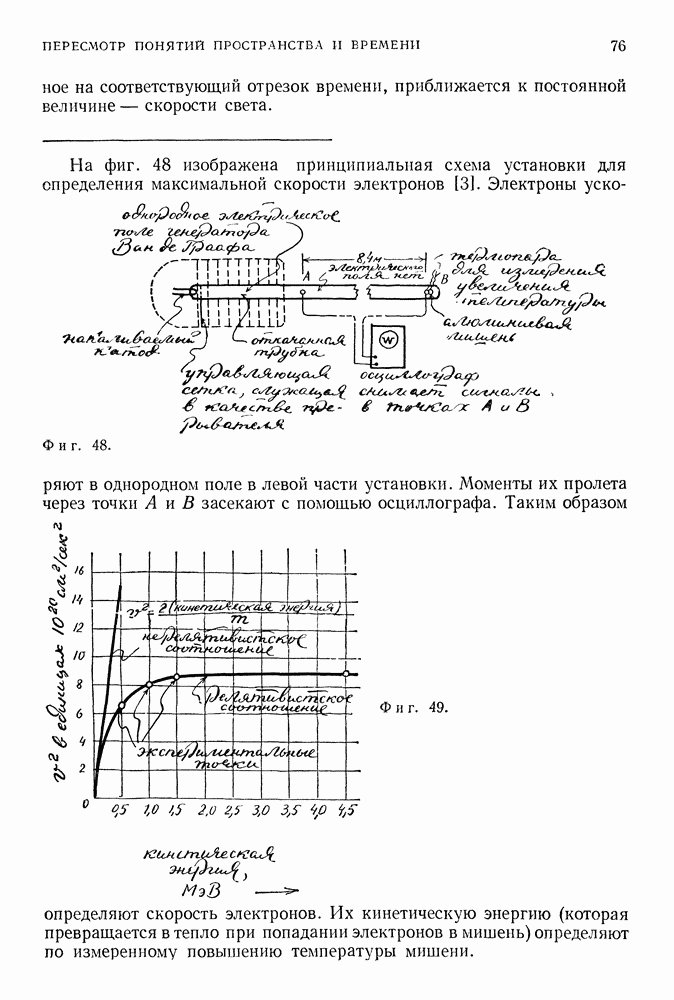
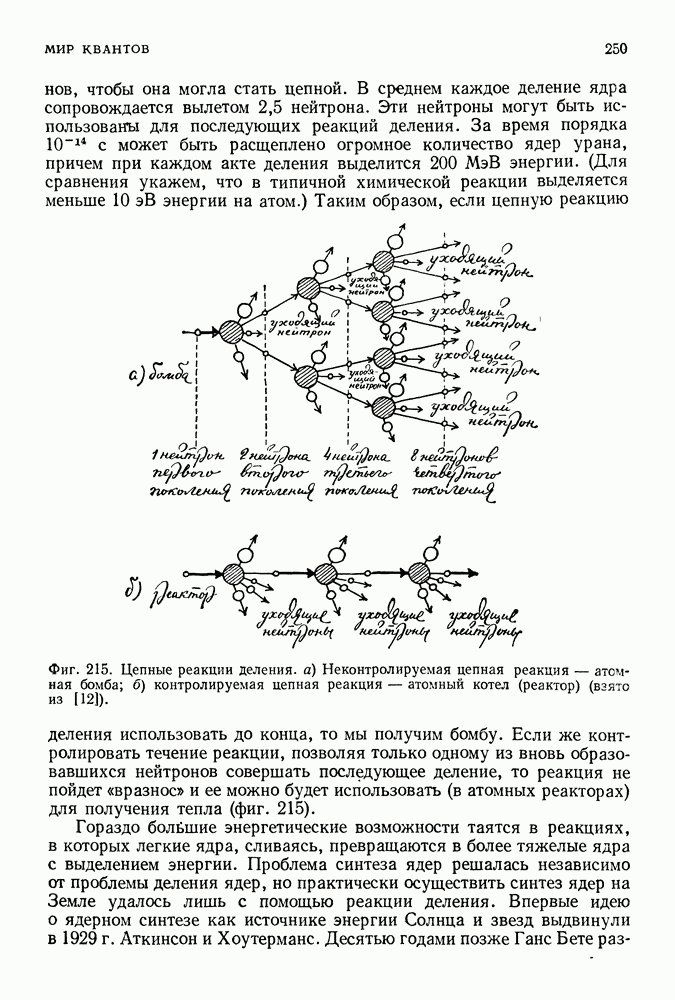
Свою теорию Бор пытался согласовать с теорией Максвелла следующим образом. Электроны, согласно Бору, излучают энергию только при переходах с одной орбиты на другую. Если рассматривать все более и более удаленные орбиты и предполагать, что основная часть переходов происходит между уровнями, номера которых отличаются на единицу, то частота излучения будет стремиться к классической частоте электрона, вращающегося на данной орбите. Таким образом, для удаленных орбит (т. е. тех орбит, для которых все больше справедливы макроскопические условия) излучение, найденное с помощью теории Бора, приближается к излучению, получающемуся из теории Максвелла.
При переходах между боровскими орбитами частота излучения равна

Если

Последнее приближенное равенство справедливо, когда  много больше единицы, т. е. для удаленных орбит. Таким образом, частота света, излученного при таком переходе, приблизительно равна
много больше единицы, т. е. для удаленных орбит. Таким образом, частота света, излученного при таком переходе, приблизительно равна

Но чему равна частота обращения электрона по орбите? Она определяется как число его оборотов за секунду, т. е.

Это выражение можно преобразовать с помощью квантового условия

Отсюда

поэтому

Но

следовательно,

Полученная частота есть частота электромагнитного излучения электрона, обращающегося вокруг ядра, в «классической» модели атома. Мы видим, что она совпадает с частотой перехода с уровня  на уровень
на уровень  для больших
для больших  в боровской модели атома [см. (37.38)].
в боровской модели атома [см. (37.38)].
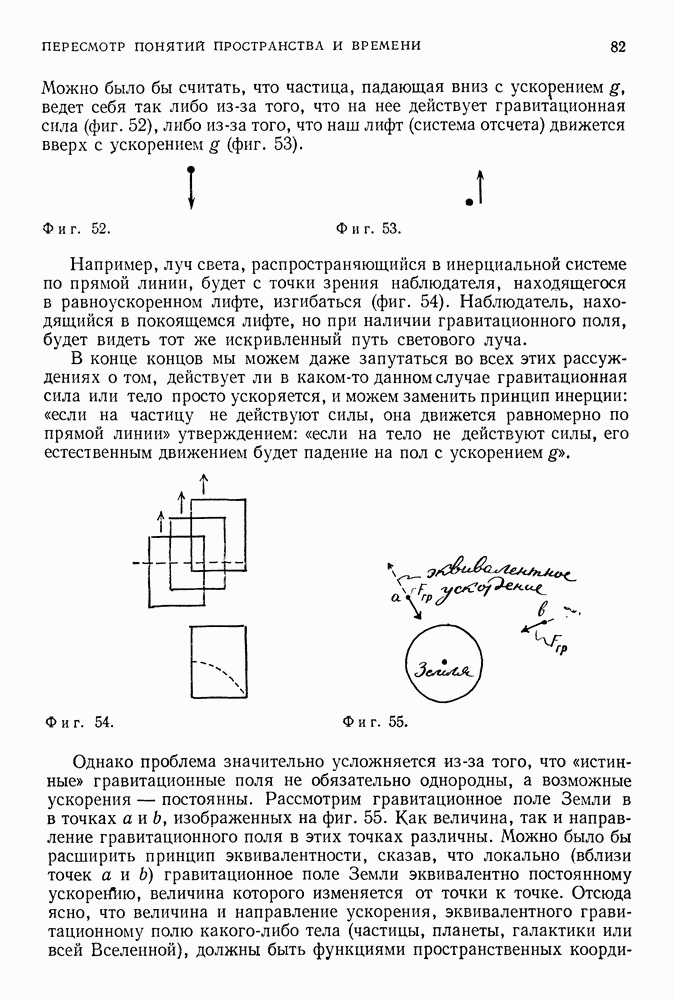
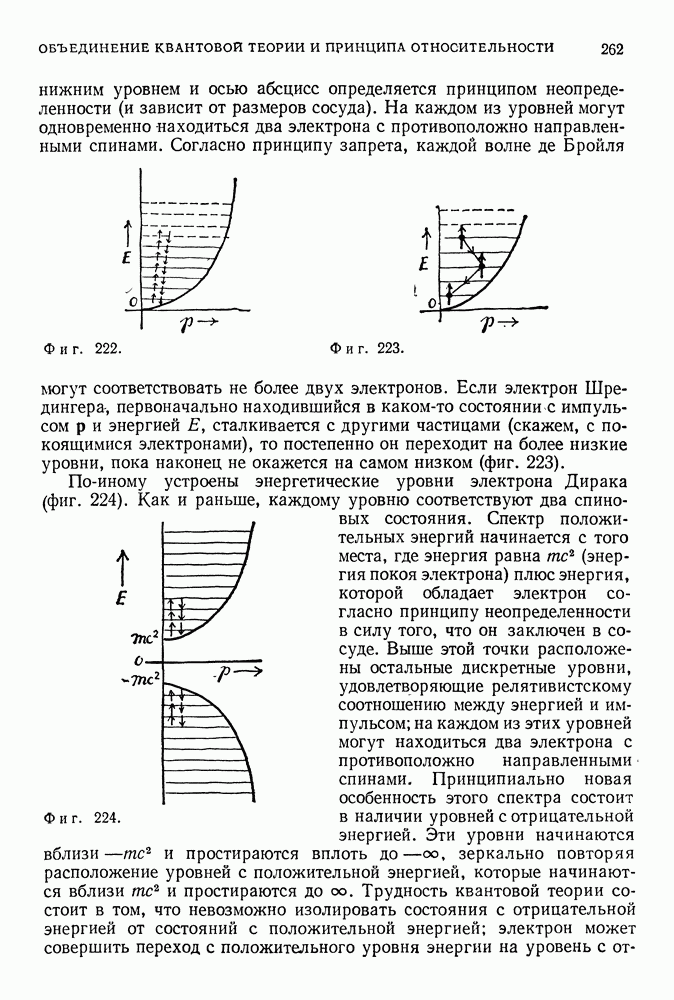
Теория Бора оказалась чрезвычайно успешной. Ему удалось создать устойчивую модель атома резерфордовского типа, использовав идею Эйнштейна и Планка, и получить серии дискретных спектральных
линий, характерные для водородного атома и согласующиеся с серией Бальмера и другими сериями, которые либо были уже обнаружены, либо были открыты позднее. (Серия линий, обнаруженная в спектре гелия — так называемая серия Пикеринга, — была отождествлена с серией, соответствующей переходам боровского типа в ионизованном атоме гелия. Поскольку ионизованный атом гелия состоит из ядра с двумя положительными зарядами и одного электрона, анализ этого атома совпадает с анализом атома водорода, если в последнем заменить значение заряда ядра  на
на  2е.) С помощью дополнительных предположений Бору удалось, по крайней мере качественно, объяснить некоторые свойства (химические) периодической таблицы элементов. Это было большим достижением, однако теория Бора не была полной. В некотором смысле можно сказать, что она вызвала больше вопросов, чем дала ответов. Электрон мог вращаться только на разрешенных орбитах. На этих орбитах он в противовес теории Максвелла не излучал энергии; энергия же излучалась лишь при переходах с одной орбиты на другую. Где же находился электрон в процессе перехода? Существовал ли он вообще между разрешенными орбитами? Существовал ли он в обычном смысле, когда находился на разрешенных орбитах? Кто мог ответить на все эти вопросы?
2е.) С помощью дополнительных предположений Бору удалось, по крайней мере качественно, объяснить некоторые свойства (химические) периодической таблицы элементов. Это было большим достижением, однако теория Бора не была полной. В некотором смысле можно сказать, что она вызвала больше вопросов, чем дала ответов. Электрон мог вращаться только на разрешенных орбитах. На этих орбитах он в противовес теории Максвелла не излучал энергии; энергия же излучалась лишь при переходах с одной орбиты на другую. Где же находился электрон в процессе перехода? Существовал ли он вообще между разрешенными орбитами? Существовал ли он в обычном смысле, когда находился на разрешенных орбитах? Кто мог ответить на все эти вопросы?
После 1913 г. предпринималось много попыток понять то, что сделал Бор. Хотя теория Бора успешно объясняла свойства атома водорода, она не смогла дать количественного описания атомов других элементов. В течение многих лет Бор пытался создать теорию атома гелия. И хотя ему удалось показать некоторую связь своей теории с классической, его комбинация классических, неоклассических и неклассических принципов, впервые успешно объяснившая свойства атома водорода, оставалась такой же загадкой, какой она была, когда Бор начал свои исследования.
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
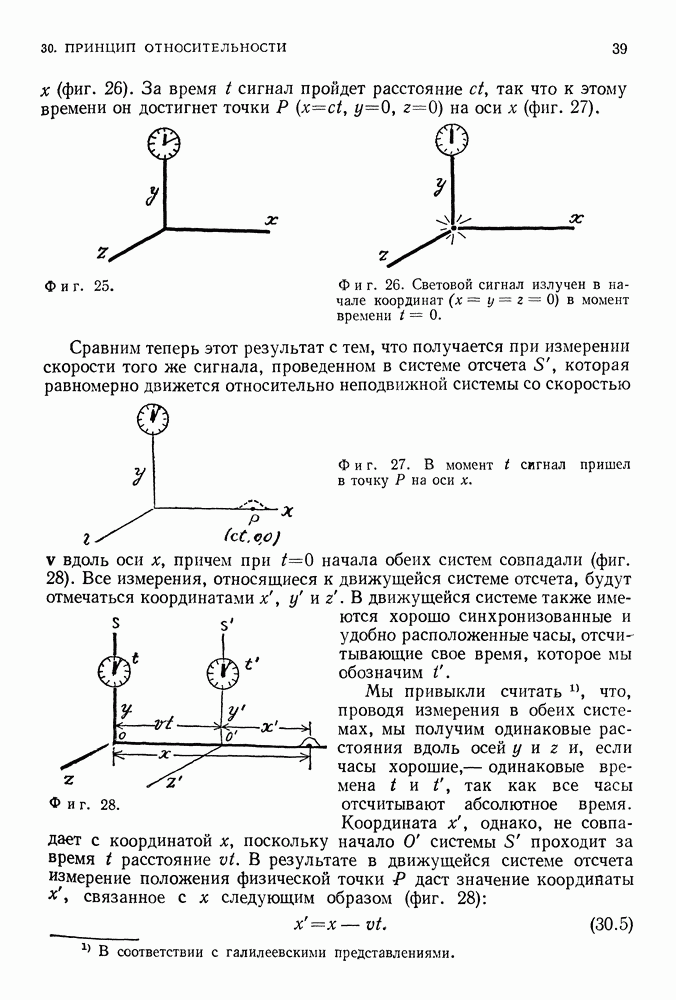
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
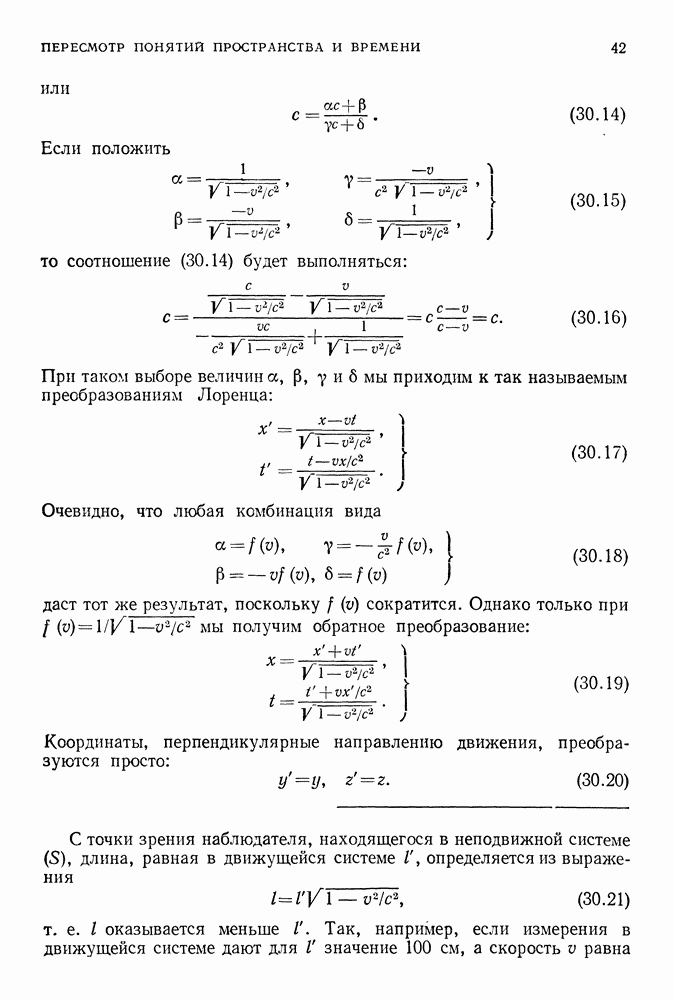
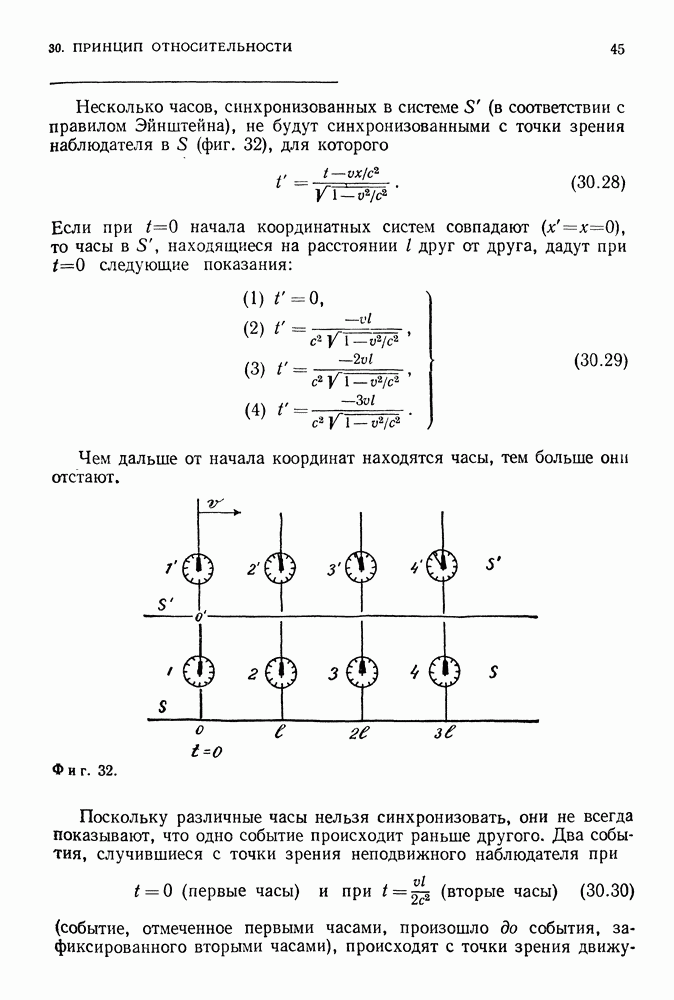
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
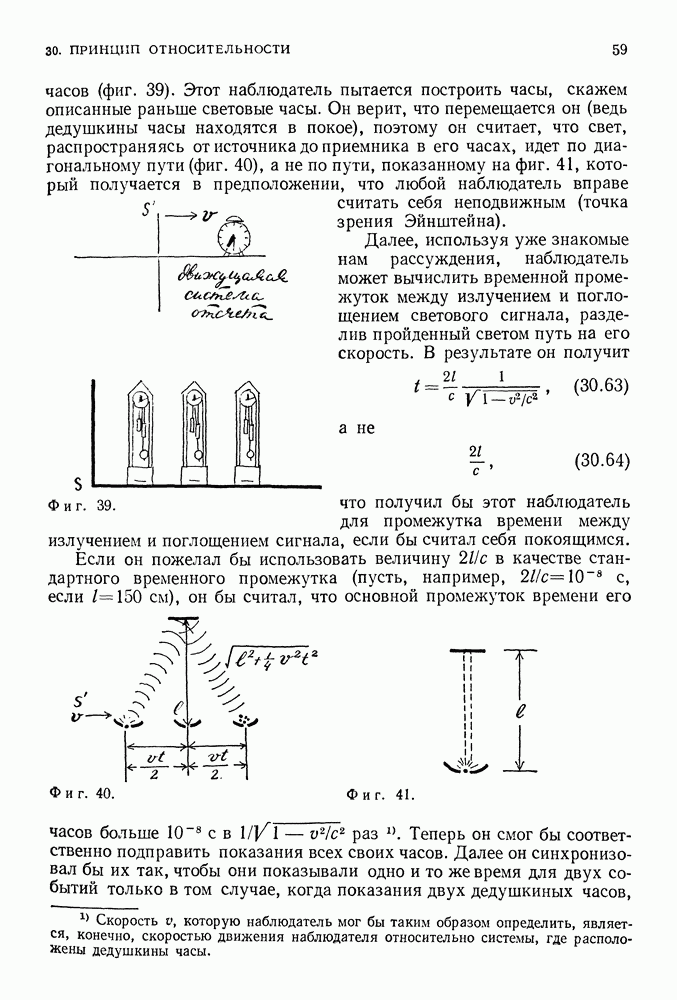
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
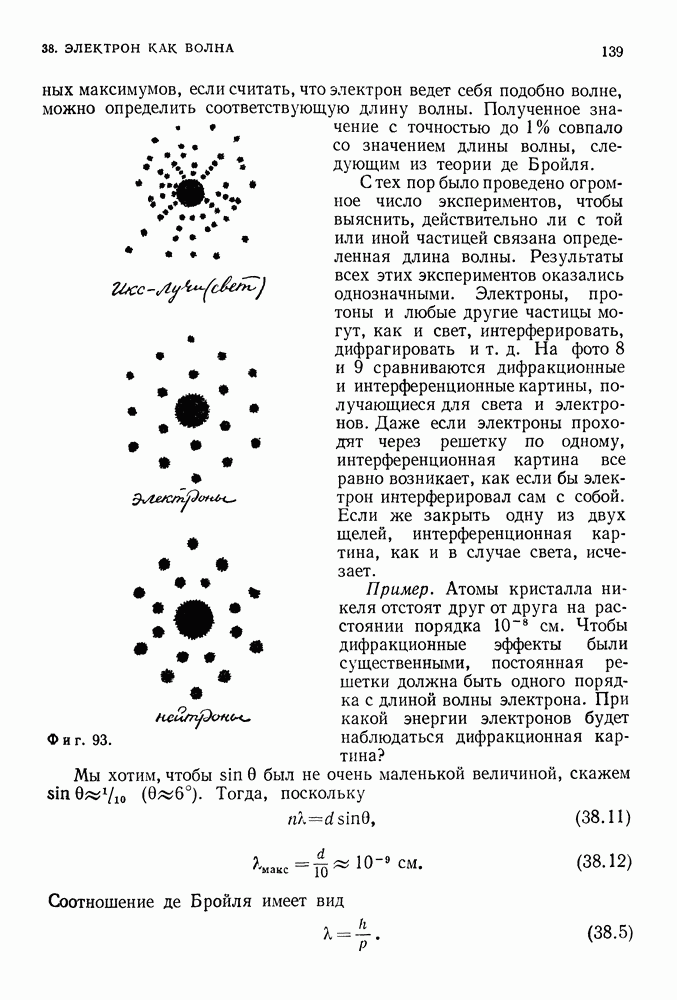
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
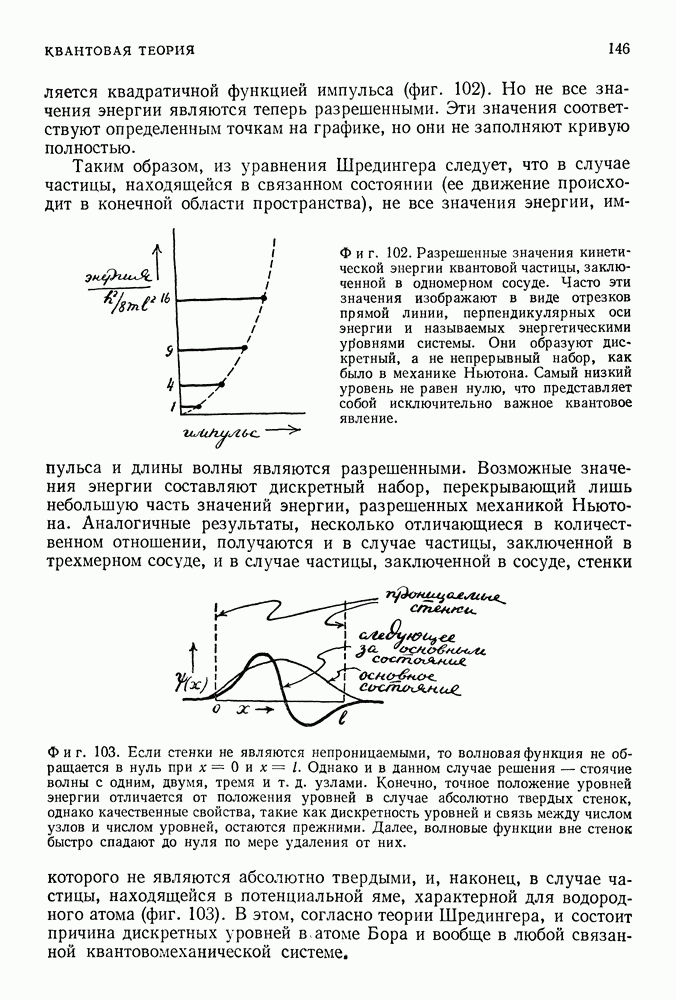
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
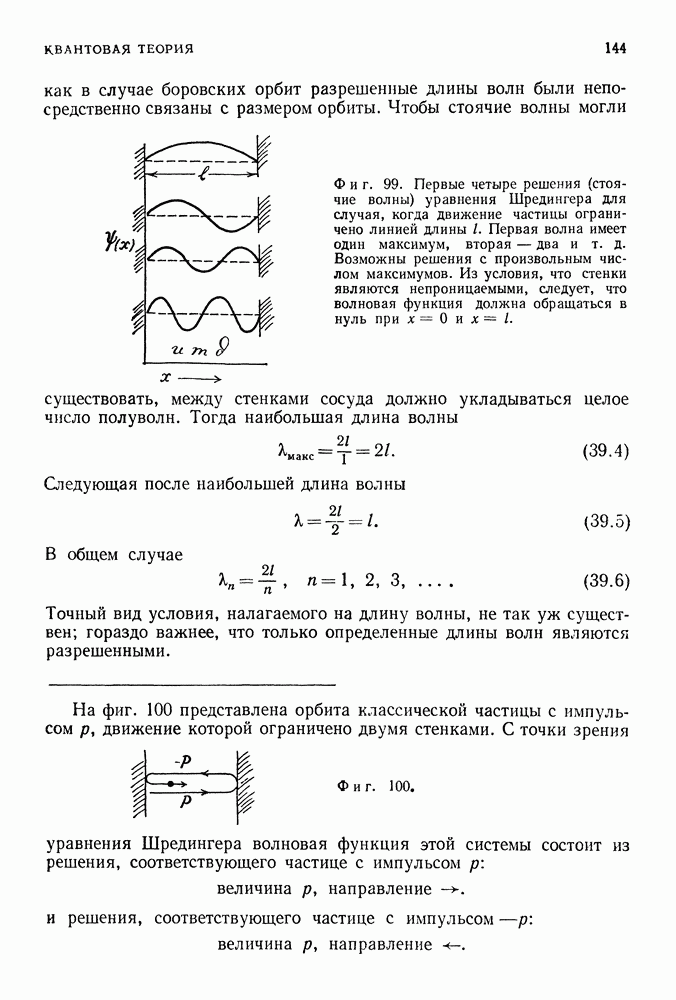
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
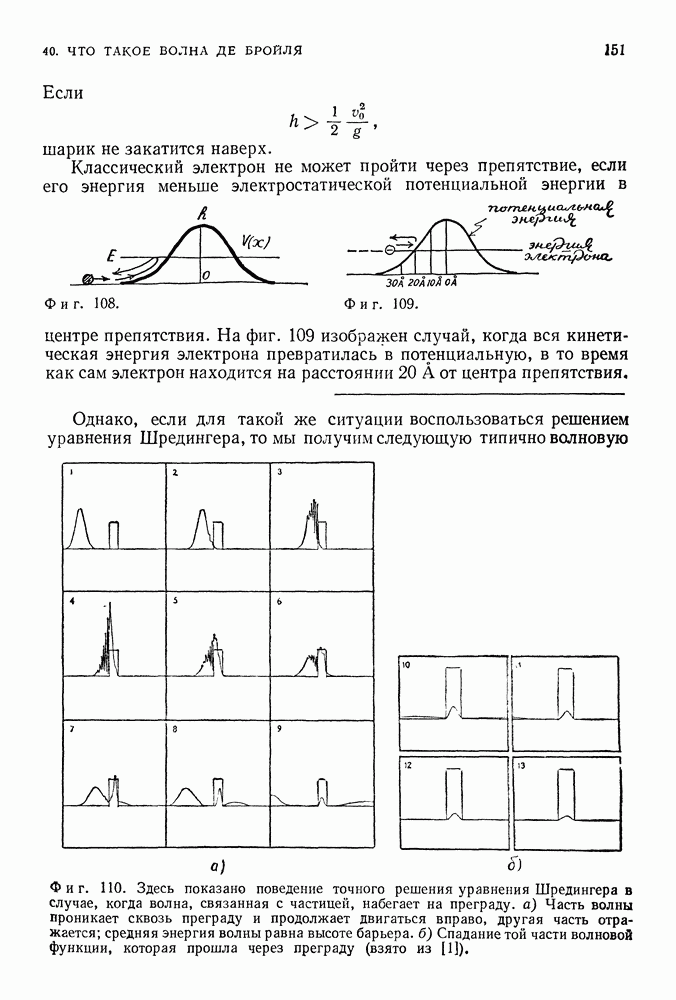
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
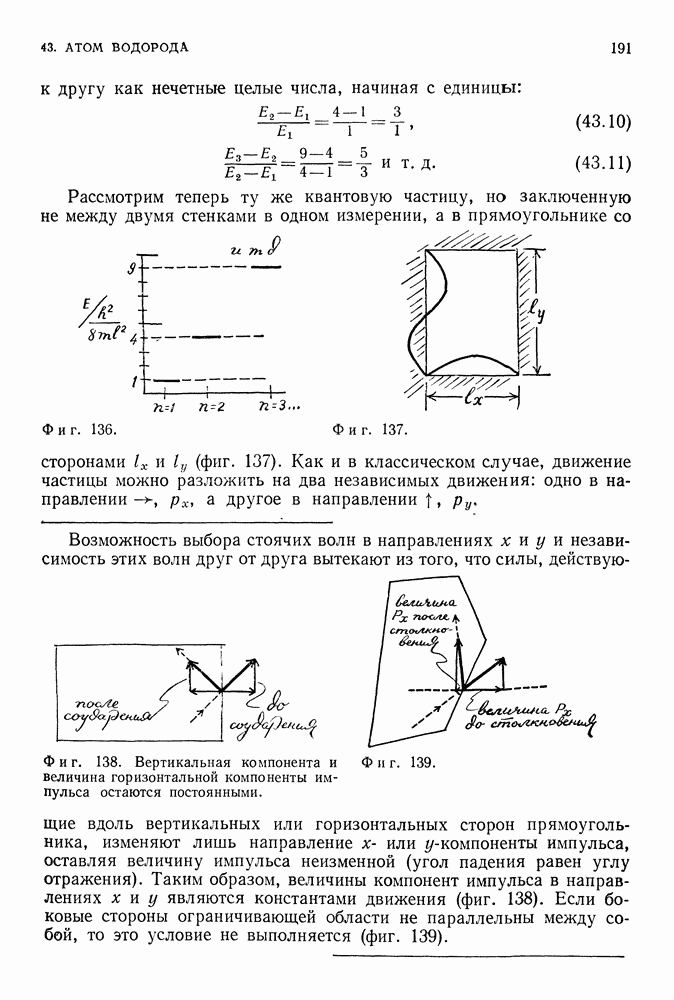
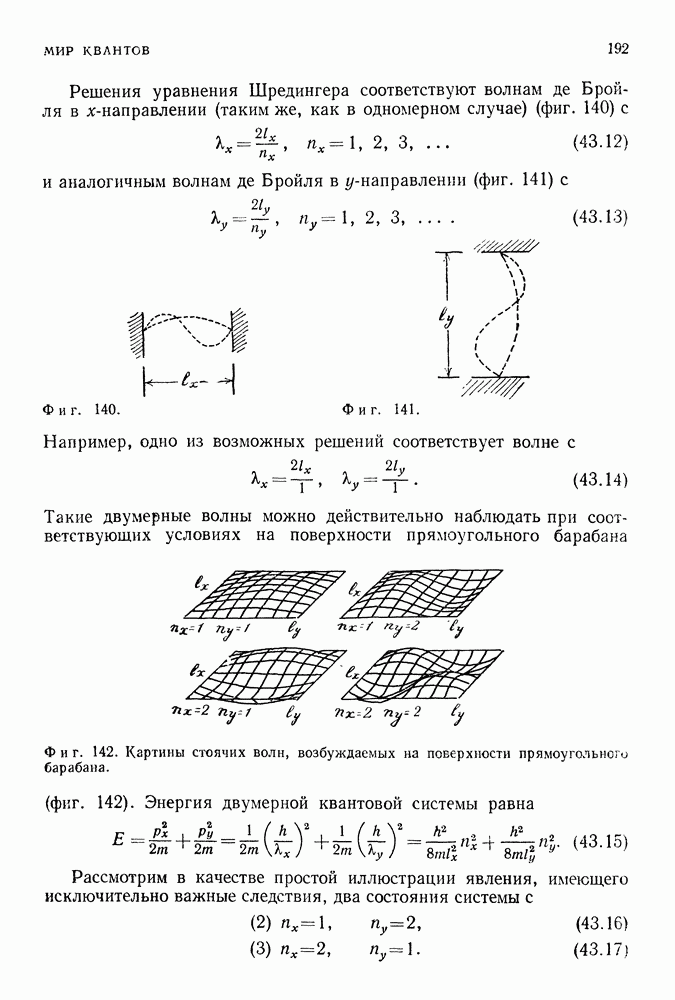
- 43. АТОМ ВОДОРОДА
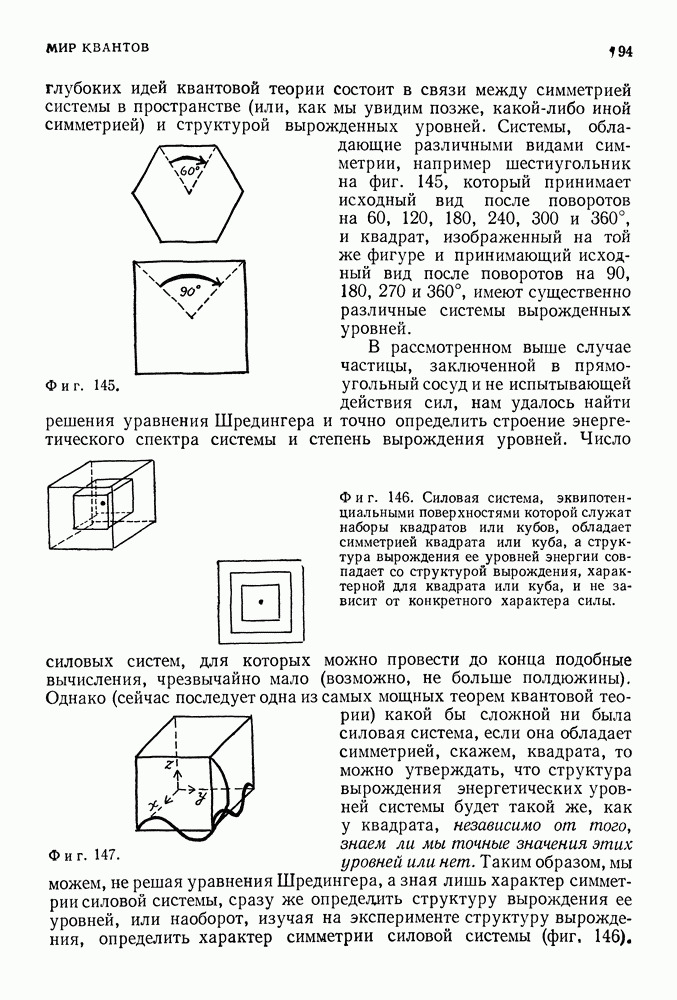
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
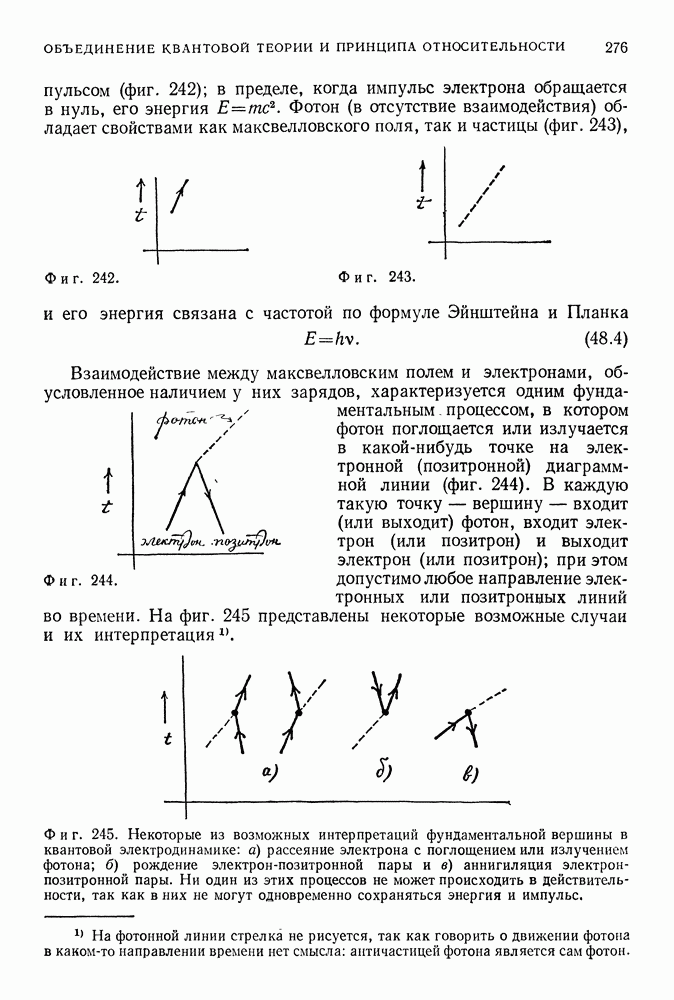
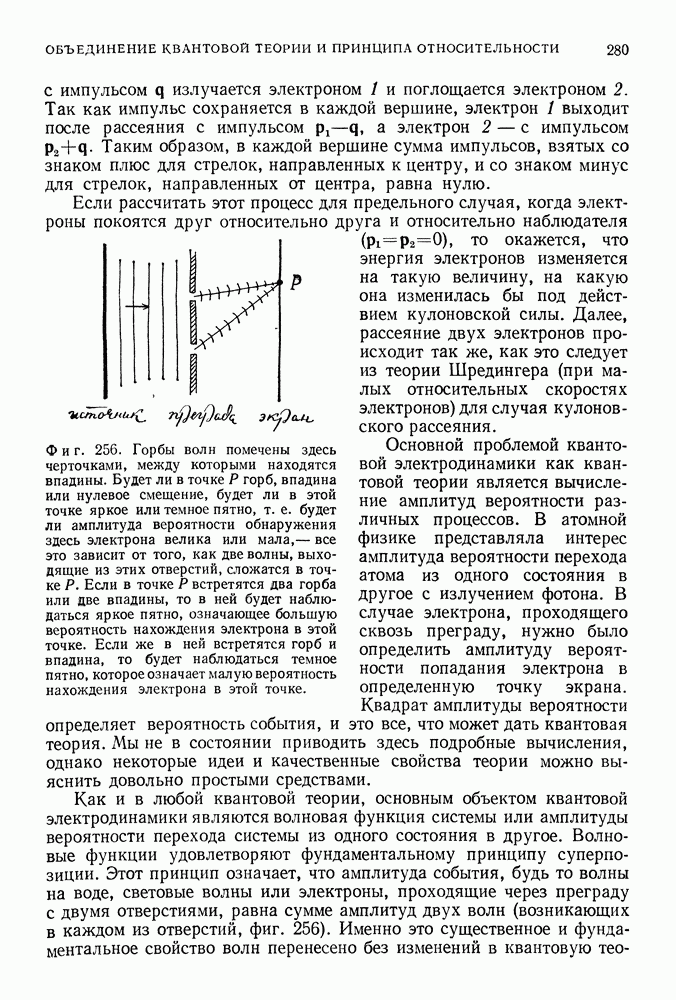
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
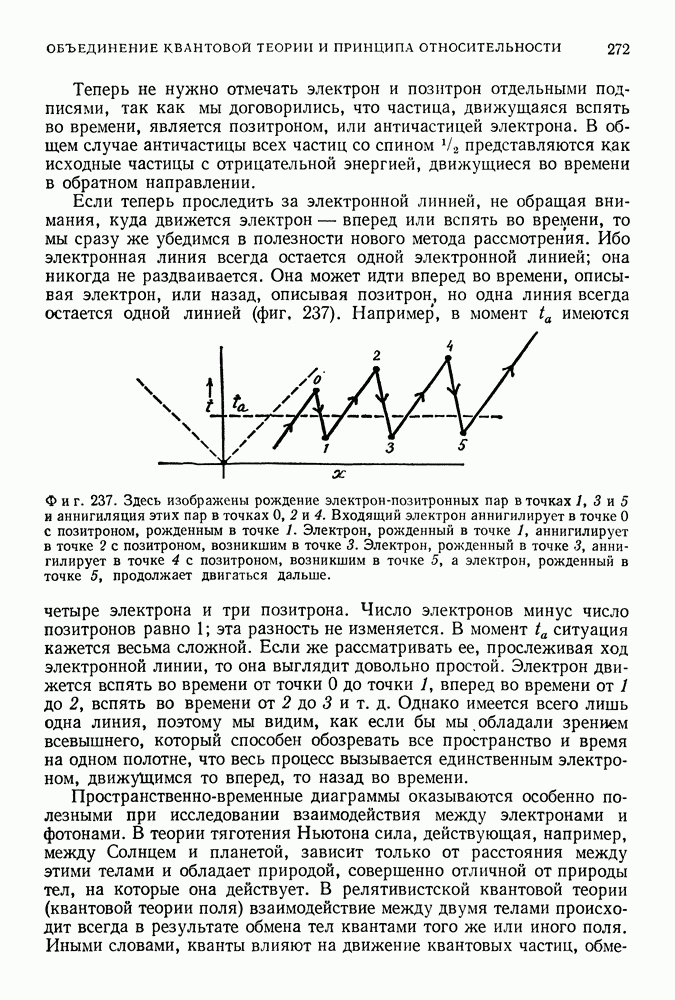
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА